������Ȃ����͂����ɏ����Ă�458
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
�����A�������P������낤����
�O�X��
������Ȃ����͂����ɏ����Ă�457
https://rio2016.5ch.net/test/read.cgi/math/1577457155/
(�g�p�ςł�: 478) �u�喃�Ŗׂ����v���Z���Q�l�ߕ�
���\�[�X���Ƀj���[�X�摜���聖
http://www3.nhk.or.jp/lnews/osaka/20200209/2000025148.html
��NHK���[�J���j���[�X�͌��L����������̂������̂Ō䒍�ӂ�
�ޗnj����̍��Z�ɒʂ��j�q���k�Q�l���喃������ŏ������Ă����^���Ōx�@�ɑߕ߂���܂����B
����̐��k���u�喃���͔|���Ă�����ׂ���v�Ɛe�ɘb�����̂����������ŁA
���k�̓v�����^�[��d���Ȃǂ��������Ă����Ƃ������Ƃł��B
�喃����@�ᔽ�̋^���őߕ߂��ꂽ�͓̂ޗnj����̕ʂ̍��Z�ɒʂ���������ޗǎs�̂P�U�̒j�q���k�Q�l�ł��B
�x�@�ɂ��܂��ƁA�W���[���A����̐��k�����e�Ɂu�喃���͔|���Ă�����ׂ���v�Ƙb���Đe�q���ɂȂ�A
�삯�����x�@�������k���������Ă����v�����^�[��d���A������Ȃǂ��������Ƃ������Ƃł��B
����ɁA���̐��k���u�O�̓��ɗF�l�ɑ喃��������ċz�����v�Ƙb�������߁A
�x�@���F�l�̉Ƃׂ��Ƃ���A���Ȃ��Ƃ��T�O�����̊����喃��
�喃���̎�Ƃ݂�����̂����������Ƃ������Ƃł��B
�Q�l�̓p�C�v�Ȃǂ̋z������������Ă��āA��������u�z�����߂ɑ喃�������Ă������ƂɊԈႢ����܂���v
�Ɨe�^��F�߂Ă���Ƃ������Ƃł��B
�x�@�͑喃�̓���o�H�Ȃǂɂ��ďڂ������ׂ邱�Ƃɂ��Ă��܂��B �~��̔\�y���ŁA���O�Y�́u�����v�������B
�@(����)
�������u�ԁv������A�u�ԁv�̔������Ƃ����l�Ȃ��̂͂Ȃ��B
�@�@�@�@���яG�Y�u�����v(1942) a[n+2]=(D*a[n]+E)/(A*a[n+1]+B*a[n]+C)
���̌^�̐���̉������͂ǂ�����ł����H �s��̖��Ȃ̂ł����A�s����A���������������@���킩��܂���
�Ȃ�(x-6)^2�ł�����ƍs�����̂悤�ɂȂ�̂ł��傤���H
https://i.imgur.com/4imuYt7.jpg ���̖����Ȃ����̂悤�ɍs��������ɕϊ��ł��Ă���̂ł����H
�����Ő\����Ȃ��̂ł������߂ɋ����Ă���������Ə�����܂�😭
https://i.imgur.com/vE9BVGg.jpg ���݂܂��Ԃ��Ȃ��ăe���p���Ă��̂ł�����ڂ͂ł��܂���
��������ڂ���͂�킩��܂���
�T���X�̌����ɑ������F�|�����āA�g�ݗ��ď��@�ł��̂悤�ȘA���������悤�Ƃ����̂ł��������ł���
�r���̌v�Z���Ȃ��ꂷ���ĂĂ킩��܂���c >>5
�s�ɂ͑��d���`�������邩��
�Ⴆ��
|a*x1 a*x2 a*x3|
|b*y1 b*y2 b*y3| =
|c*z1 c*z2 c*z3|
|x1 x2 x3|
|b*y1 b*y2 b*y3| * a =
|c*z1 c*z2 c*z3|
|x1 x2 x3|
|y1 y2 y3| * a * b =
|c*z1 c*z2 c*z3|
|x1 x2 x3|
|y1 y2 y3| * a * b * c =
|z1 z2 z3|
�����藧��
�ڂ����͋��ȏ���ǂ�� 1�s�ڂ�3�s�ڂ��炻�ꂼ��x-6���o���Ă邾���ł�
����������(3,2)�����̃}�C�i�X�������ĂȂ������肵�ĂȂ��H ���A�����������d���`����������Ȃ������̂�
�s�̌v�Z��������
�E��{�ό`
�E���d���`��
�E�]���q�W�J
��3�͍Œ���o����ׂ�
�Ƃ������A��̓I�ȍs�̌v�Z�͑S�Ă���3��g�ݍ��킹�邾���ŏI��� ����p�����Ɂ@�S�@�S�@�X�@�R
�̐����Ǝl�����Z�L�������g�p����
�������P�O�ɓ����鎮������Ă��������B�B�B���肢���܂��B ������
�@
�@�@�S*�S*�X*�R �~ + - ��
�����ŁA�ł����B �����͕�����Ȃ����������X���ł��B
���肢���Ƃ�����X���ł�������Ȃ����ɓ����Ă��炦��X���ł�����܂���B �M���V������24��ނ̕������𑫂����킹����100�ɂȂ�̂��ĕs�v�c�Ȃ�ł����A
�ǂ������d�g�݂�������������܂����H���R�ł��傤���B
�~�����Ǝ��R�ΐ��̒�̘a�͒��z���ɂȂ邩�ؖ����Ă��������B
e + pi = ��
e * pi = ��
�܋�1�~�ł��B �m����1/p��`���Đ����I�Ȓ�`����܂����H >>20
�m����1/p�̒�`�Ƃ͉��ł����H >>16-17
���肪�Ƃ��������܂��B
�ǂ����u�Ƃn�v�ł����B�B�B(���@
���̖�肶��Ȃ����������B�B�B�H
�ł����B�B�B
���������v���܂����B�B�B >>23
(1) y=-2(x-pi/4)
(2) ��[0,pi/4] (-2(x-pi/4) - cos(2x)) dx = (pi^2-8)/16 >>8
>>9>>10
���肪�Ƃ��������܂�😭 �݂��ɑf��a,b��p����an+b�ƕ\���铙������͏��Ȃ��Ƃ���f�����܂ނ��Ƃ��A�Z�p�����藝��p�����ɏؖ�����ɂ͂ǂ�������悢�̂ł��傤���H >>27
b=1�̏ꍇ�͉~�����������g���e�N�j�b�N�Ŋ��Ə����I�Ɏ������͂��B
�����̏ꍇ�̓Z���o�[�O�̊m��1950�N���炢���������ɏؖ����Ă�炵�����Ǒ����ƂĂ�����B
���_�����肷�邵���Ȃ��ł��傤�B >>28
���肪�Ƃ��������܂��I
�T���Ă݂܂��B
�������̏ꍇ�͂ǂ��Ȃ�̂��H�ƍl���Ă����̂ł����A�ƂĂ���ɏI���Ȃ������ł��ˁc
��������̏ꍇ�����ł������ł���悤�撣���Ă݂܂��B c,d:1���傫������
an+b=cd
cd��b (mod a)
cd��an (mod b)
x,y:����
b+ax=an+by=an+b
x=n, y=1 ���݂܂���A������_
an^2+bn+c�̌`�ŏ��������Ȑ��W���������ŁA���ׂĂ�n�ɂ��č������ƂȂ�悤�Ȃ��̂́A���ׂċ����ɂȂ����(��Fn^2+n+4)�ȊO�ɑ��݂���̂ł��傤���H an+b=cd
a��a1 (mod c)
a��a2 (mod d)
b��b1 (mod c)
b��b2 (mod d)
a1n+b1��0 (mod c)
a2n+b2��0 (mod d)
a1n+b1=cx
a2n+b2=dy
(a1-a2)n+b1-b2=cx-dy >>23
(1)y=cos2��
y'=-2sin2��
x=��/4�̂Ƃ��A
y'=-2sin(��/2)=-2
y=-2(x-��/4)
��y=-2x+��/2
x=��/2�̂Ƃ��A
y=-2(��/2-��/4)=-��/2
-2��-��/2��-1������O���t��`���ƑÓ����Ǝv���B
(2)��[x=0����/4](-2x+��/2-cos2x)dx
=[x=0����/4][-x^2+(��/2)x-sin2x/2]
=-��^2/16+��^2/8-1/2
=��^2/16-1/2 >>35
�������ł��肢�������܂��B >>36
a=1���Ƒ��݂��Ȃ��ȁB
������ʂł����� xy���ʏ��(0,0)���n�_�Ƃ��āA�e�_(0,1),(1,1),(1,2),(2,2),(2,3)...�����̏��ɐ����Ō���ŏo����K�i��̐܂��L���l����B
���Ȃ킿L�́An=0,1,2,...�ɑ���
{ (x,y) | x=n, n��y��n+1 }
{ (x,y) | n��x��n+1, y=n+1 }
�̘a�W���ł���B
L�ƒ���y=(1+a)x���͂ފe�̈�ɂ��āA�����̖ʐς̑��a��a�ŕ\���B
������a�͐��̒萔�ł���B ���̍P�����̊ȒP�ȉ��߉\�ł����H
2*((sin(x))^4+(sin(y))^4+(sin(x+y))^4)+4*(sin(x)*sin(y)*sin(x+y))^2-((sin(x))^2+(sin(y))^2+(sin(x+y))^2)^2=0 >>34 ������������܂����B���肪�Ƃ��������܂� c�������̒萔�Ƃ��A
a[1]=c
a[n+1]=a[n]/(2-a[n])^2
�ɂ���܂鐔��{a[n]}������B
�i1�jlim[n����] a[n]=1�@�ƂȂ�c�͈̔͂����߂�B
�i2�j����{b[n]}�����{c[n]}���ȉ��̂悤�ɒ�߂�B
b[n]={a[1]+a[2]+...+a[n]}/n
c[n]={b[n]b[n+1]...b[2n-1]}^(1/n)
���̂Ƃ��i1�j�ŋ��߂��͈͂�c�ɑ��āA�Ɍ�lim[n����] c[n]�����߂�B >>41
�ǂ��c�Ƃ��Ă�a[n]->1�ɂ͂Ȃ�Ȃ��Ȃ��H ��6��傫�����ɕ��ׂ�ƁA���̒l�i�͏���800�~�������Ȃ�B
6�S���̍��v��21000�~�B
��ԑ傫����̒l�i�́H �O>>34
>>46
�������������x�~�Ƃ���ƁA
x+x-800+x-1600+x-2400
+x-3200+x-4000=21000
6x-15�800=21000
x=3500+5�400
x=5500(�~) >>47
��[0,6] (x-800n) dn =21000 >>39
���p�� x, y, ��-x-y �̎O�p�`���l����B
�ӂ̒����� a, b, c �O�ډ~�̔��a��R �Ƃ���B
�����藝���
�@sin(x) = a/2R,
�@sin(y) = b/2R,
�@sin(��-x-y) = c/2R,
2{sin(x)^4 + sin(y)^4 + sin(��-x+y)^4} - {sin(x)^2 + sin(y)^2 + sin(��-x-y)^2}^2
�@= {2(a^4 + b^4 + c^4 - (aa+bb+cc)^2}/(2R)^4
�@= - (a+b+c)(a+b-c)(a-b+c)(-a+b+c)/(2R)^4
�@= - (S/RR)^2,�@�@�@(�w�����̌���)
2sin(x)sin(y)sin(��-x-y) = 2abc/(2R)^3 = S/RR,�@�@(S=abc/4R) �u���O���t�ɏ����̂͒����˂��B�v�ƕ�������
���̂悤�ȍ����Ȏ����ő��҂����͔̂n�����Ă���
���[����Ȃ� ���[�}���\�L�Ŗ��O���ɏ����Ƃ��̍��̃C�J���^�l�Ԃ̔�����
�E�u�����x��Ȃ��Ă����B�v�ƌ���
�E�uKouji�@Takaki�͂��Ȃ��B�v�ƌ���
�E�u���Ȃ����Ƃɂ��܂����B�v�ƉƂ̒�����Ӗ��s���ȉ������������Ă���
���_�Ƃ��āA���[�}���\�L��ς������͂Ȃ��B >>41
(1)
a[n]��1 (n����)����a[n]��1�Ɖ��肷��ƁA�\���傫��n>N�ɑ���0<|a[n]-1|<1/2�����藧��
������|a[n+1]-1|=|(a[n]-1)(a[n]+4)|/(2-a[n])^2>2|a[n]-1|�����疵������
����������a[n]��1�Ɏ������邽�߂̕K�v�\�������́A����k��1�ɂ�����a[k]=1�ɂȂ邱�Ƃł���
c�͈̔͂͏W��A[1]��A[2]��A[3]��...�ɑ����邱��
������A[1]={1}, A[2]={4}, A[n+1]={(1+4x+��(1+8x))/(2x)|x��A[n]}��{(1+4x-��(1+8x))/(2x)|x��A[n]}
(2)
c��A[k]�̂Ƃ�
a[n]=1 (n��k)
���X=��[i=1,k-1](a[i]-1)�Ƃ����
b[n]=1+X/n (n��k)
�Ƌ��܂�
log(b[n]b[n+1]...b[2n-1])=��[i=0,n-1]log(b[n+i])
=��[i=0,n-1]log(1+X/(n+i))
����[i=0,n-1]X/(n+i)
��X log2 (n����)
���
log(c[n])��(1/n)X log2��0 (n����)
c[n]��1 (n����) ���ɓʂŁA��ɐ��Ȋ�f�ɂ���
f(x)f(y)��{f(��xy)}^2�����������
������Ăǂ��Ȃ�܂����H g(t) = log(f(e^t))�@�����ɓ� ���R��w2019�̖��őQ����
x[n+2]=(1+x[n+1])/x[n]
�ŗ^��������̂ɂ��Ă̏o�肪�����ł����A�������5�̐���ɂȂ�܂��B
����Ȃ�łȂ�ł����H
�Ȃ�ʘ_�ł��������^�C�v�̎�������̗��_���Ȃ����ł����H x[1] = a,
x[2] = b,
x[3] = (1+b)/a,
x[4] = (1+a+b)/(ab),
x[5] = (1+a)/b,
x[6] = a,
x[7] = b,
�ȉ������I
n��4 �ɑ���
�@y[n] = (y[n-1] + y[n-2] + 1)/ y[n-3],
�ɂ���Ē�߂��鐔��͎���8�����B
�H�R �m�{P.�t�����N�� �����u [���S�U��] ���w�I�����s�b�N�v���{�]�_�� (1991)
�@p.7-8 >>57
�@g '(t) = (e^t)f '(e^t)/f(e^t) = u f '(u)/f(u),
���P������������
�@{u f '(u)/f(u)} ' > 0,
����ˁH >>60
���肪�Ƃ��������܂�
f(x)=axx+bx+c�Aa,b,c�͐��̏ꍇ��logf(e^x)�����ɓʂɂȂ�̂łȂ@������̂��ȂƎv������ł��������ł����� f(u) ���}�N���[�����W�J����
�@f(u) = �� c_k�Eu^k,�@�@�@�@�@(c_k��0)
�Ƃ���B
�@u f '(u) = �� k c_k�Eu^k,
�@u {u f '(u)} ' = �� kk c_k�Eu^k,
�R�[�V�[�ɂ��
�@f(u)�Eu {u f '(u)} ' �� {u f '(u)}^2,
���@{u f '(u)/f(u)} ' �� 0,
���@g(t) = log{f(e^t)}�@�͉��ɓʁB�@�@>>56 �قށ[�I�S�����W���Ȃ�K�����ɓʂȂ�ł���
���肪�Ƃ��������܂� >>59
�ւ��A����Ȃ̂������ł��ˁB
�ł����ɐ��I���̖{����Ȃ�ł���Ȍ��ۂ��N����̂��̔w�i�Ƃ��̉���Ƃ��͂Ȃ��ł���ˁH >>58
�w�����ƒ����U�x�@�����o��
�ɂ��̕ӂ������������e���������܂��B https://i.imgur.com/fGSqEzP.jpg
������Ƃ������p�ŋl�܂�̖{���ɉ������ł��B >>67
3^x=X�Ƃ��u����
(i) X+1/X=t
t^2=X^2+1/X^2 + 2
(ii) X^2+1/X^2=t^2-2
(t^2-2)t=(X^2+1/X^2)(X+1/X)=X^3+1/X^3+X+1/X=X^3+1/X^3+t
(iii) X^3+1/X^3=(t^2-3)t
���Ƃ͑�����Đ��������(1)�̓�����������
�ȍ~�O�����̖�� >>67
[3]�@�� f(x) = 27^x�{27^(-x) - 5(9^x�{9^(-x)) + 3(3^x�{3^(-x)) -10 �ɂ��āA�ȉ��̖₢�ɓ�����B
�@(1) t = 3^x + 3^(-x) �Ƃ����Ƃ��Af(x) ��t�ŕ\�킹�B
�@(2) t�̂Ƃ肤��l�͈̔͂����߂�B
�@(3) f(x)�̍ŏ��l�ƁA���̂Ƃ���x�̒l�����߂�B
------------------------------------------------------------------------
(1)�@�@
>>69 ���
�@f(x) = (t^3 -3t) -5(tt-2) +3t -10 = t^3 -5tt,
(2)
�@t = 2 + {3^(x/2) - 3^(-x/2)}^2 �� 2,
(3)
�@f(x) + 500/27 = (t+5/3)(t-10/3)^2 �� 0,
�@f(x) �� f(10/3) = -500/27. >>65 ����q�إ���
[1]�@c_n = c_{n-1},
[2]�@c_n = k - c_{n-1},�@c_n = kk/c_{n-1},�@c_n = k c_{n-1}/(c_{n-1} - k),
[3]�@c_n = kk/(k - c_{n-1}),�@c_n = k(c_{n-1} - k)/c_{n-1}),
[5]�@c_n = (c_{n-1} +1) /c_{n-2},�@�@�@(���C�l�X) (���R��2019)
[6]�@c_n = k c_{n-1}/c_{n-2},
[8]�@c_n = (c_{n-1} +c_{n-2} +1) /c_{n-3},�@�@�@(�g�b�h)
k�F�萔 >>66
���肪�Ƃ��������܂��B
���̖{�ǂނƂ��̕s�v�c�Ȏ��������Q�������{�R�{�R��ꂽ�肵�܂��H >>72
�Ⴆ�A
x[n+1]={x[n]-tan^2(��/N)}/{x[n]+1}
�Ƃ���ƁA����N(������N>2)�@�̐����邱�Ɠ����L����Ă��܂��B
����ɂ́A���������� du/dt=-b(1+u^2)�@���W���Ă�悤�ł��B
���ʂɔ����������Ƃ��ĉ������߂�ƁA u =-tan(b(t-t0))�@�ŁA�����I�ȉ��������܂����A
u[n+1]-u[n]=-��b(1+u[n+1]u[n])
�̂悤�ȍ��������s���A������u��������ƁAx[n+1]={x[n]-c^2}/{x[n]+1}
�ƂȂ邪�Ac=tan(��/N)�̎��A���������݂���Ƃ́@���Ƃł��B
>>71 ���Љ�ꂽ���̈ȊO�ŁA�������Ȃ��̂Ƃ���
x[n]=|x[n-1]|-x[n-2]�@�@�@�G����9
x[n+3]=(a0+a1(x[n+1]+x[n+2])+x[n]*x[n+1])/(x[n]-x[n+2])�@�@�G����12
x[n+4]=x[n]*x[n+3]/(x[n]*x[n+2]-x[n+1])�@�@�G����12
�����Љ��Ă��܂��B
>> ���̖{�ǂނƂ��̕s�v�c�Ȏ��������Q�������{�R�{�R��ꂽ�肵�܂��H
�ǂ��ł��傤�H�@���̖{�́A�u�����������̂��A���̂悤�ɂ��ĒT���āA
���̂悤�Ȃ��̂������܂����B�v�Ƃ����X�^���X�ŏ�����Ă��܂��B �g�����v�̃n�[�g�̃J�[�h13������A������3�����o���Ƃ��A����3���̃J�[�h�̘a��13�̔{���ɂȂ�悤�ȑg�ݍ��킹�͉��ʂ肠�邩�H
��낵�����肢���܂��B 074 �P�R�Q�l�ڂ̑f������ 2020/02/12 23:58:03
�g�����v�̃n�[�g�̃J�[�h13������A������3�����o���Ƃ��A����3���̃J�[�h�̘a��13�̔{���ɂȂ�悤�ȑg�ݍ��킹�͉��ʂ肠�邩�H
�ȉ��A�Ǝ��╔��
�ł�1�̗�Ƃ��āA���o�����i2,8,9�j�ɑ��āA�i1,1,1�j�������Ă����A12��܂ő����ďo�Ă����i�j�̑g����̌Z��̂悤�ɍl���Ă���̂ł����A���́i�j�̑g�̍��v��13C3�ɂȂ�̂������ł��܂���
���̗ǂ�����낵�����肢���܂� ���̐��i2.8.9�j����n�܂�i3.9.10�j�`�i1.7.8�j��13�ʂ肠��A���̂ǂ̐����Ƃ����Ȃ����̐��̎�����������Ȃ��ł�
�{���ɂ�낵�����肢���܂� >>73
�Ȃ�قǁB
�����n��ł�����ł�����Ƃ����킯�ł͂Ȃ���ł��ˁB
���Ət�x�݂ɓ���̂œ��肵�Ă݂܂��B
���肪�Ƃ��������܂����B >>286
�Ƃ�����茳�X13C3=286���ꂠ��g�ݍ��킹��13����22�g�݂ɕ��ނ����ł���B
����
123,234,345,456,�d,jqk,qk1,k12
����
124,235,346,457,�d,jq1,qk2,k13
�d�d
�Ŋe�ނɈ���a��13�̔{���ɂȂ���̂�����B
���ނ̒��ɂ�qk1�A���ނ̒��ɂ�346�A�d >>78
���肪�Ƃ��������܂��B
����22�g�ɕ��ނ������ɂǂ��������Ɍ��̐�
�i1.2.3�j��i1.2.4�j���������̂���������Ȃ��ł��B
22�g���Ă��Ƃ͗Ⴆ�i4.8.12�j�Ƃ��͌��̐��ɂȂ蓾��̂ł��傤���H ���22�g���Ď��́A�Ƃ����̂͌��̐��Ƃ��ĂƂ��g�ݍ��킹�������Ă�����Ă����Ӗ��ł� >>88
���̑g�݂��܂��ŏ��Ɍ��߂�̂͐��w�I�ɂ͊��S��\�n��I�ԂƂ�����Ƃň�ʂɂ͂ƂĂ������Ƃł��B
����Ȃ炢���鎫���������ň�ԎႢ���̂��\���Ƃ��đI�ԂȂǂƂ������@�����܂��B
�Ⴆ��48q�Ȃ�R�����܂ޗނ�
48q,59k,6t1,7j2,8q3,
9,k4,t15,j26,q37,k48,
159,26t,37j
��13�Ŏ������ɕ��ׂĈ�ԎႢ�̂�159�Ȃ̂ŃR�����\���Ƃ���Ηǂ��Ƃ킩��܂��B
�ǂꂪ��\���ɂȂ邩�͑�\���̑I�ѕ��̃��[���Ɉ˂�܂��B
�����������ōŌ�Ƃ������[���ɂ��Ă����������������������ǃA���t�@�x�b�g�̏�����
48q123569tjk
�̏����Ƃ����48q����\���Ƃ��đI��܂��B >>81
���肪�Ƃ��������܂�
3�̃J�[�h�̍��ɑ��đ召�W�����߂���ōŏ���1�̎��i1.�`�j���l�����Ƃ��Ă��A36�ʂ�͂��肻���Ȃ̂ŁA���Ƃ�����A���̒��̂������͔���Ă���Ƃ������ł��傤���H >>82
���肪�Ƃ��������܂��A�ł��B���݂܂���B >>62
�����ł��ˁB
���Ȃ��_�u��Ȃ���\����I�ԃ��[����������͈̂�ʂɂƂĂ�����̂őg�̐������̂悤�ȑ�\���̐��𐔂��Ē��ׂ�̂͂ƂĂ�������ɂȂ邱�Ƃ������ł��ˁB
������22�ɂ�������36�͑��������̂ł��̃��[�����Ƒ啪����Ă�Ǝv���܂��B
�����o���Ċm���߂Ă݂�Ƃ����Ǝv���܂��B �Ⴆ�Α�\���̃��[���Ƃ���
(i,jk)����\��(i<j<k)
��
�EI=1�A
�Ej-i��k-j, j-i<13+i-k (��������O�̌��Ԃ̂���j-i����ԏ������Ȃ�悤�ɂ���B�����Ƃ���k-j��j-i���ŏ��ɂ���B
�Ƃ������[���ōs���܂��B
������
2j-1��k��14-j
�Ɛ�������ej�ɑ��ēK������k��16-3j�B
���ꂪ���A��2�ȏ�Ȃ̂�j�͈̔͂�2�`5�B
���ꂼ��k��10,7,4,1����̂Ōv22�ł��B
������c[13,3]��13=286��13=22�̕����y���ɗD��Ă��܂��� 2����
f(x)=ax^2+bx+c
g(x)=cx^2+bx+a
���l����B
�����w-1��x��1�ɂ�����|g(x)|��1�x�����悤�Ɏ���a,b,c��ω�������Ƃ��A-1��x��1�ɂ�����|f(x)|�̍ŏ��l�̍ő�l�����߂�B >>73
�^�����
�@{1-i�tan(��/N)}/{x[n+1] -i�tan(��/N)} - {1+tan(��/N)}/{x[n] -i�tan(��/N)} = 1,
cos(��/N) ���|����
�@��^(-1/2)/{x[n+1] -i�tan(��/N)} - ��^(1/2)/{x[n] -i�tan(��/N)} = cos(��/N),
������
�@��_N = exp(2��i/N) = {1+i/tan(��/N)}/{1-i�tan(��/N)},
�ł���B(1��N�捪)
������
�@y[n] = ��^(-n)/{x[n] - i�tan(��/N)}
�Ƃ�����
�@y[n+1] - y[n] = cos(��/N)��^(-n-1/2),
�@y[n+N] - y[n] = cos(��/N)��^(-n-1/2)��[k=0,N-1] ��^(-k) = 0,
y[n] �͎���N�����B
x[n] ������N�����B �����𥥥�orz.
�^�����
�@{1-i�tan(��/N)}/{x[n+1] -i�tan(��/N)} - {1+���tan(��/N)}/{x[n] -i�tan(��/N)} = 1,
������
�@��_N = exp(2��i/N) = {1+i�Etan(��/N)}/{1-i�tan(��/N)},
�ł���B(1��N�捪) �������� f(f(x))=x ����������
f(x)=(ax+b)/(cx+d) ( �s��A=[a b][c d] , A=A^2 )�@�ȊO�ʼn�������܂����H
��ʉ����������� >>89�@wolframalpha�ɕ������炱��ȗႪ�Ԃ��Ă����B��ʉ��́H������
f(x) = 1/2 (sqrt(c_1^2 + c_2 - 4 x^2) + c_1 x)
f(x) = (c - x^3)^(1/3) ����f(x)=f^(-1)(x)�@������y=x�őΏ̂Ȃ�Ȃ�ł������̂��� �z�����W�[�̏ؖ��ŕ�����Ȃ��Ƃ��낪����̂ŋ����Ă�������
X��n�������l�́AK�����̕W���Ƃ���
(1) H_i(X,X-K)=0�@(i��n)
(2) a��H_n(X,X-K)��0�ł��邱�ƂƁA��ʑ����U������鏀���^j_x:H(X,X-K)��H(X,X-x)�ɂ���
�C�ӂ�x��K��j_x(a)=0�������藧���Ƃ����l
�Ƃ����藝�̏ؖ��ł���
�܂�K���R���p�N�g�ł���ꍇ�����������ƂŁA��ʂ̕W��K�ɂ��Ă�
�ua��H_i(X,X-K)�ɑ��āA����J�W��U��X�����݂��āAU�̕�̓R���p�N�g�ł���
a������b��H_i(U,U-L)�@(L=U��K)�̎��R�ȏ����^�̑��ɂȂ�v
���Ƃ���ؖ����Ă���̂ł������̃J�b�R���͂Ȃ����藧�̂ł��傤��
(�o�T�͒����z�����W�[�㐔��p125�ł�) >>91
f: X�~X -> X�~X; (x,y) |--> (y,x)
f(f(t))=t
��: {T,F} -> {T,F}; T |--> F, F |--> T
��(��(x))=x
t: R^(2�~2) -> R^(2�~2); [[a,b],[c,d]] |--> [[a,c],[b,d]]
t(t(A))=A
... >>92
�܂�C(X,X�_K)��i���̃T�C�N����X�̒P�̕��̃��Ł݃���X�_K�̃T�C�N���ƂȂ���̂ł��B
������U�Ƃ��Ă̓��ɏo�Ă���P�̂̍����̃R���p�N�g�ߖT(�̓���)���Ƃ�܂��B
����Ǝ��R�Ƀ���U�̒P�̕��̂ł����݃���U��(X�_K)=U�_K�̃T�C�N���ɂȂ�܂��B >>94
���肪�Ƃ��������܂�
���ɏo�Ă���P�̂̍����ɂ��ăR���p�N�g�ߖT�����邱�Ƃ͂ǂ̂悤�Ɍ�����̂ł��傤�� ���ʏ�Ɉ�ӂ̒���2�̐����`ABCD�Ɠ_P������AP��PA+PB+PC+PD=r�ƂȂ�悤�ɕ��ʂ��B
�i1�jr�̍ŏ��l�����߂�B
�i2�jr�̒l�ɂ��AP�������Ăł���O�Ղ��Ȑ��ƂȂ邱�Ƃ�����B���̂悤��r�͈̔͂����߂�B
�i3�j�ȉ��̏ꍇ�ɁAP�������Ăł���Ȑ��Ɛ����`�̏d�S�Ƃ̋��������߂�B
(i) r=6�A(ii) r=32 >>95
���������P�̕��̂Ƃ͒P��D����̘A���ʑ��̌`�����`�����ŒP��D�̓R���p�N�g��ԂȂ̂ł��̑����R���p�N�g�A���̗L���������R���p�N�g�ł��B ���萔b,c�́Ab^2-4c<0�����B
2��������x^2+bx+c=0��2������,���Ƃ���Bp,q��0�łȂ����萔�Ƃ��A����{a[n]}���A
a[1]=���Aa[2]=��
a[n+1]=pa[n]+qa[n-1]
�ɂ���߂�B
�i1�j����{a[n]}�����������悤��(p,q)��1�g��߂�B
�i2�j�i1�j�ŋ��߂�1�g�ȊO�ɂ�{a[n]}�����������悤��(p,q)�����݂���Ȃ�A������S�Č��肹��B �O>>48
>>96
(1)r=��2+��2+��2+��2
=4��2
(3)(i)�d�S����̋�����x�Ƃ���ƁA
4�̂���2�͂��킹�Đ����`�̑Ίp��������2��2
���Ƃ�2�̓s�^�S���X�̒藝��肠�킹�āA
2��{x^2+(��2)^2}
4���킹�āA
2��2+2��(x^2+2)=6
��2+��(x^2+2)=3
��(x^2+2)=3-��2
x^2+2=11-6��2
x^2=9-2��18
x=��6-��3 >>97
���肪�Ƃ��������܂��B
�P�̕��̂̑��S��V���R���p�N�g�Ȃ̂ŁAV�̊e�_��(���l�̂̍��W�ł݂�)�J���ŕ����Ă�����
�R���p�N�g�����炻�̂����̗L���Ŕ핢�ł��邽�߁A�����̘a��U�Ƃ����U�̕�͕��̗L���a�Ȃ̂ŃR���p�N�g
�Ƃ��������ō\���ł��܂����A���ӂł��B >>90 ������ƁA
�@f(x) ��x �����Ȃ� g^(-1)(f(g(x))) ����
�̊�K�X >>98
����N�����ɂ́A
���������� tt-pt-q �̍���1�̌��nN�捪�ɂȂ�悢�B
�@(p, q) = (2cos(2m��/N), -1)
�@�������A1��m<N,�@gcd(m,N)=1,�@4m��N,3N ��ӂ̒���n�̐����`S���An^2�̈�ӂ̒���1�̐����`�̃^�C���ŕ�������Ă���B�}�X�ڂ̈�ԍ���̃^�C���ɂ́A1���L����Ă���B
��������ȉ��̂悤��S�ɐ������L�����Ă����B
�E1�̉E�̃^�C����2���L������
�E2�̉��̃^�C����3���L�����A3�̍��̃^�C����4���L������
�E����ŁAS�̍��ォ��2�~2�̐����`�ɐ��������܂����B����ɁA4�̉E�̃^�C����5���L�����A5�̉E�̃^�C����6���L�����A�c�A�ŏI�I��2�̉E�̃^�C����9���L������A3�~3�̐����`����������B
�E�ȉ��A9�̉E��10���c�ƌJ��Ԃ��AS�Ɏ֍s��ɐ������L������B
�y���z
k=0,1,2,...,n�Ƃ���B
����nCk�͂ǂ̏ꏊ�̃^�C���ɋL����邩�B �܂̒���n���̃J�[�h������A���ꂼ���1,2,...,n�̐���1��������Ă���B
���܁A�܂̒����疳��ׂ�1���̃J�[�h�����o���A������Ă��鐔�����Ȃ��Ŕj������B
�c��n-1���̃J�[�h���������܂���A2���̃J�[�h���Ɏ��o���A���ꂼ��ɏ����ꂽ���𗼕��Ƃ��L�^���A�܂ɖ߂����Ƃ��J��Ԃ��s���B
�j�������J�[�h�����ł���܂łɁA
�i1�j���̑���ω���s�����ƂɂȂ邩�i��:�K�v�ȑ���̉̊��Ғl�����߂�j�B
�i2�j���̑���ɂ��L�^���ꂽ���̑��v�̊��Ғl�����߂�B �s����
x^2+y^2 < (x^2+y^2+z^2)/3 < 2z
����x��y��z�Ȃ鎩�R����S�ċ��߂�B >>105
x^2+y^2 < (x^2+y^2+z^2)/3 < 2z
(x^2+y^2+z^2)/3 < 2z
=> 6z-z^2=z(6-z)>0 ��� 1<=z<=5
x^2+y^2 < (x^2+y^2+z^2)/3
=> (z^2)/2 > x^2+y^2
�� min((z^2)/2, 6z-z^2) > x^2+y^2
z=1,2,3,4,5�̂Ƃ����ӂ�
1/2,2,9/2,8,5
�i�ʓ|�Ȃ̂Łj0�͎��R���łȂ��Ƃ���
z=3 => (x,y)=(1,1)
z=4 => (x,y)=(1,1),(1,2)
z=5 => (x,y)=(1,1)
(x,y,z)=(1,1,3),(1,1,4),(1,1,5),(1,2,4) 3������Ԃ̕Ȗ�
C:x^2n+y^2n+z^2n=1�in��2�ȏ�̎��R���̒萔�j
�Ƌ��L�_�������ʂ̂����AC�ƕ��ʂ̋��L�_�S�̂��Ȃ��Ȑ��Ɉ͂܂�镔���̖ʐς��ő�Ƃ�����̂��Ƃ���B
�y���z
���ʃ����F�X�����Ƃ��A����C�̋��L�_�S�̂��Ȃ��Ȑ��̎�����L(��)�Ƃ���B
L(��)���ő�ƂȂ�̂́A�����ƈ�v����Ƃ����ǂ����肹��B xy���ʏ�̕�����y=x^2���G�ɕ`���ƒn�����ɐڂ���ȉ~�ɂȂ���Ęb�����邯��
�o�Ȑ� x^2-y^2=1���G�ɕ`���Ǝ��_�ƃL�����o�X�̊W�ɂ���đȉ~�A�o�Ȑ��A�������̂ǂ�ɂ��Ȃ�̂ł����H (2n,n)��(2n,n-1)�̍ő����1�ł��邽�߂́An�ɂ��Ă̕K�v�\�����������߂�B (2n,n)|n�A(2n,n-1)|n-1�A
��((2n,n),(2n,n-1)) | (n,n-1) n��2�ȏ�̎��R���̒萔�Ƃ���B
n����f_n(x)��
f_n(x)=(x-1)(x-2)...(x-n)
�ɂ��āA�ȉ��̖�ɓ�����B
�i1�j�ek=1,2,...,n-1�ɑ��Af_n(x)��k<x<k+1�͈̔͂ŋɒl���Ƃ邱�Ƃ������B
�i2�jn�͋����Ƃ���B
�i1�j�ŏq�ׂ�n-1�̋ɒl�̒��ŁA���̐�Βl���ł����������̂�a[n]�Ƃ����B
a[n]�͂ǂ̋�Ԃɂ��邩�A�K���Ȑ���j��p����j<x<j+1�̂悤�ɏq�ׂ�B
�i3�j�i2�j�ɂ����āA�Ɍ�lim[n����] a[n]�����߂�B ����L�Ɠ_P���^����ꂽ�Ƃ���P��ʂ鐂���ƕ��s�����K�����ō�}�͉\���H (a-e)(b-f)=(c-e)(d-f)�Ȃ�n�ȉ��̔����̑g(a,b,c,d,e,f)�͂������邩�B >>112
�@(2n,n) = n
�@(2n,n-1) = (2,n-1)�@�@(n:��̂Ƃ�2, n�F�����̂Ƃ�1)
�@n>1
>>114
(1)
f(x) ��R�Ŕ����\�ł���B
f(k) = f(k+1) = 0,
�����̒藝(*)�ɂ��A
�@k<��<k+1,�@f '(��)=0 �Ȃ�̂�����B
�@f ' ��n-1��������������A�e��Ԃɂ��傤��1����B
(2)�@f(n+1-x) = f(x)�@���
�@x = (n+1)/2 �ŋɒl�B
�@n/2 < x < (n/2)+1,
�@a[n] = f((n+1)/2) = (-1)^(n/2) {(n-1)!!}^2 /(2^n)
(3)�@���U����B
*) ���F�u��͊T�_�v������O�ŁA��g���X (1961)
�@p.47�@��Q�� �����@, ��18.�������̐����@�藝19. (�⑫)
>>114
(2)
�@f(x+1)/f(x) = x/(x-n),
�@x<n/2 �̂Ƃ��@|f(x+1)| < |f(x)|,
�@x>n/2 �̂Ƃ��@|f(x+1)| > |f(x)|,
����� f(x)=a[n] �ƂȂ�x��
�@n/2 < x < (n/2) +1 >>110
�~�� x^2 = y^2 + z^2 ��z=1 �Ő�Ƒo�Ȑ� x^2-y^2=1 �ɂȂ�B
�镽��(�L�����o�X)�̌X���ƕ���̌X���̊W�őȉ~�A�o�Ȑ��A�������̂ǂ�ɂ��Ȃ�B f(x)=(x-1)(x-2)...(x-n)-x^k
���ɒl�������Ȃ��悤��2�ȏ�̎��R��n�Ɣ���k�̑g(n,k)�͑��݂��Ȃ����Ƃ������B �O�p�`ABC�̓��ډ~�ƊO�ډ~������~�ɂ��Ă̔��]�Ō݂��Ɉڂ肠���Ă���Ƃ�
���̉~�̒��S�Ɣ��a�����߂Ă������� >>120
�@(n,k)=(2,2) �̂Ƃ��@f(x) = -3x+2�@(�P������)
�@n�F����, k�F�, k>n �̂Ƃ����P�������B>>121 a,b�𐳂̐��Ƃ����Ƃ��A��f(x)=1/(x^a(x^b+1)) ��[0,��)�܂ł̍L�`�ϕ�����������悤��a,b�̕K�v�\�����������߂�B
�������肢�܂��B �p.�P�C�Q�C�S�C�W�A�E�E�E�A�Q�O���@�Ƃ�������P����I�Ƃ��A���̍ō������P�ƂȂ�u�m���v�͂����قǂ��H
�����̏W���ōl���Ȃ��Ă����܂��܂���
����L���Ƃ��Ă������Ƃ��Ă����܂��܂��� ���������ŗǂ��Ȃ� 1/9
2�i���Ȃ�m��1���� >>126
�u�[�@���
�������m����0.30102�c >>126
���߂�Ȃ����B>>127����͈��C�͂Ȃ���ł��B���X�̏o��҂���Ȃ�ł��B
������荞�ݒ���...���Z�������̂ł�����A�ڂ����̓K���A�X���ł���Ă܂��B�B�B
�u�u�[�v���ɕ����Ȃ��ŁI
�@�@�@�@�@�撣���ĉ������I 1,2,...,n�̐��������ꂽ�J�[�h��1�����A���vn���̃J�[�h������B
A�N�͂���n���̒�����1��I�сA����ɏ����ꂽ��N���L������B
B�N�͈ȉ��̎菇�ŁAN����肷��B
�@B�N��1,2,...,n�̒�����D���Ȑ���1�I�сAA�N�ɓ`����B
�AA�N�͂��̐���N�ȏゾ�����ꍇ�A�u�ȏ�v�Ɠ�����BN�����������ꍇ�A�u�����v�Ɠ�����B
�@���̇@�ƇA���s�����Ƃ��u����v�ƌĂԁB
�B������J��Ԃ��B
�y���z
B�N��N����肷��܂łɁAB�N�͉�����s���K�v�����邩�A���̊��Ғl��E(N)�Ƃ����B
E(N)�����߁A�܂�j=1,2,...,N�̂Ȃ���E(j)�͂����̈قȂ�l���Ƃ邩�q�ׂ�B���ׂĂ�j�ɑ�E(j)�������l�����ꍇ�́A�قȂ�l��1�Ƃ���B >>125
�x���t�H�[�h�@������Ȃ��́H ����
(a+b)/(c+d)=cd/ab
�������R��a,b,c,d�ŁA(a+b)/(c+d)��
cd/ab���Ƃ��Ɋ����ł�����̂��l����B
�i1�j���̂悤��(a,b,c,d)�͖����ɑ��݂��邩�q�ׂ�B
�i2�j�i1�j�ɂ����āA�����ɑ��݂���ꍇ��(a,b,c,d)��a��100�������̂�1���߂�B
�܂��L���g�������݂��Ȃ��ꍇ�́A���ׂċ��߂�B �_O�𒆐S�Ƃ��锼�ar�̉~C������B
C�̎���̓_P�ɂ�����ڐ���L�AL���2�_A,B����OAB�����O�p�`�ɂȂ�悤�ɂƂ�B
B����OA�ɐ��������낵�A���̐�����C�Ƃ̌�_�̂���B�ɋ߂�����T�Ƃ���B
��AT/OT�����߂�B >>133
T���~�Ƃ̌�_�ł��낤�ƂȂ��낤�ƁA
B����OA�ɉ��낵��������̓_�Ȃ�AAT��OT�ł���i�� >>124
�@0 < a < 1 < a+b,
���̂Ƃ�
��[0,��] f(x)dx = ��[0,1] f(x)dx + ��[1,��] f(x)dx
�@< ��[0,1] 1/x^a dx + ��[1,��] 1/x^(a+b) dx
�@= 1/(1-a) + 1/(a+b-1),
a��1 �̂Ƃ�
�@x^b + 1 �� 2�@�@�@(0<x<1)
��[0,1] f(x)dx >��[0,1] 1/(2x^a) dx = ��
a+b��1 �̂Ƃ�
�@x^b + 1 �� 2x^b�@�@�@(x>1)
��[1,��] f(x)dx >��[1,��] 1/{(x^a)(2x^b)} dx = �� ����������@������̂�
1100101
��i�@���\�i�@�@
�E����
1+4+32+64=101
������
�P���Q�{���ĂP����
�O���Q�{
1, 3, 6, 12, 25, 50, 101 �O>>99
>>133
AT/OT=1
��T���~C��ɂ��낤�ƂȂ��낤�Ɛ��O�p�`��1�̒��_��������������Εӂɉ��낵�������́A�������邵�A���̓r���̂ǂ̓_�Ƃ��Ƃ�2���_������ł�����2�̕ӂ̒����͓���������B
>>135�����B ���ʂP�U�ƐԋʂS������B�������P�O�̔��Ɋe�X�Q������ׂɕ��z����Ƃ��A
�ԋʂQ���������������傤�ǂP�ł���m�������߂�B
�ʂ̓���ꏊ�ɂ��āA�l�����Ȃ��ėǂ��A�Ƃ����C���[�W���킫�܂���
�ŏ��̔��ɐԋʓ����Ƃ����ꍇ�ɂ�1/19�~16/17�~6�ƂȂ�A���ꂪ10C1�~9C2������̂ł͂Ȃ��ł��傤���i�m����1���Ă��܂��܂����c�j
�ǂȂ�����낵�����肢���܂� �ԋ�4�����ɓ��ꂢ���Ƃ���
p(1��2���������A3��4���ʔ�)
=1/9�~6/7
�� ���߂�m����
1/9�~6/7�~6�B 10�~9�~8�~4/C[20,4]=192/323 -2��x+y��2�c�@
-2��y+z��2�c�A
-2��z+x��2�c�B
���̎�x�̒l������߂�Ƃ�������
3��������2�Ŋ�����
-3��x+y+z��3
-2��-(y+z)��2������
-5��x��5
����͊ԈႢ��
�@+�B���-4��2x+y+z��4�A
-4-(y+z)��2x��4-(y+z)
�A�Ƃ��킹��2�Ŋ���-3��x��3
�����炾�Ɛ������������o�܂�
�����������ɒH�蒅�����[�g�ƊԈႢ�̃��[�g�͂ǂ��Ⴄ�̂ł��傤�H
�܂����������[�g��x�̒l�悪������������Ƃ����ۏ͂ǂ����炫�Ă���̂ł����H >>142
���������Ƃ��͖�蕶�̏�ׂĂ��g��Ȃ��Ƃ����Ȃ�
�����̕��@�́A�s�����@�A�B��������3�S�Ďg���Ă�
���ď��߂̕��@�́A�s�����A�͎g���Ă�B�܂���3�̂���1�͎g���Ă�
�����Ŋ̐S�Ȃ̂��A�u�s�����@�A�B�𑫂���2�Ŋ��������́c�C�v�Ɏc��2�̕s�����@�B�̏�܂܂�Ă��邩�ǂ�����
���_���猾���Ɗ܂܂�Ă��Ȃ�
�l���Ă݂Ăق������A���g���ׂ�2�̏��@�B��
-2��x+y��2�@�c�@
-2��z+x��2�@�c�B
�����A���̇@�B�Ɛ�̓��e�ō�����s����
-3��x+y+z��3�c�C
�͑Γ����낤���H
�Γ�����Ȃ��A������瑼������낤�Ǝ��s���낵�Ă݂�����A���̂������Ȃ��Ɖ��ƂȂ��C�Â����낤
�Ƃ������ƂŁA�����Ȃ��������_�Ƃ��Ă�
�u�@�A�B�����킹�č�����s�����C�̏��́A�@�P�Ƃ̏��ƇB�P�Ƃ̏������킹���������Ȃ��v
�u������C���@�B�̑���Ɏg���ƁA�s�\���ȉ��o��v 0��x+y��a�c�@
0��x-y��b�c�A
�O���t�����Ă݂���
0��x��(a+b)/2�@�Ƃ͂Ȃ�Ȃ����Ƃ͌�����ˁB�B
�������������Ƃ��l���Ă݂���킩�肻�� >>140,141
���肪�Ƃ��������܂�
������96/323�ł�
��A�l�̋^��ɓ����Ē�����Ɗ������ł� >>136
���肪�Ƃ��������܂��B
a,b�𐳂̐��Ƃ����Ƃ��A��f(x)=1/(x^a(x^b+1)) �̃��v���X�ϊ��̎������W�����߂�B
���肢���܂��B >>145
20�̏ꏊ��4�̐ԋʂ����邩��A�����C[20,4]
2�͓��锠��I�Ԃ̂�10�ʂ�A1���̔����I�Ԃ̂�9�~8�ʂ�
1���̔��ɂ�4�ʂ�̓���������� �O>>138
>>139
���P�Q�R�S�T�U�V�W�X10
���@�B�D�F�H�J�L�N�P�R
�A�C�E�G�I�K�M�O�Q�S
�@�A�B�c�c�Ɣԍ����ɋʂ����Ă����ƁA �@�����̊m��=4/20A�A�����̊m��=3/19
�����̊m��=16/18
�C�����̊m��=15/17 7 �D����=��14/1�D 1 �c�c
�J�J�J�J�J�����̊m��=2�m/1��0=1/1
������ƕ������������������A���ׂĊ|�����킹��ƁA4845����1
��1/4845 >>145
p(1�ڂ�2�ڂ�����)=1/19
p(2�ڂ�3�ڂ��ٔ� | 1�ڂ�2�ڂ�����)=16/17
�� ���߂�m����1/19 �~ 16/17 �~ 6�B >>147 ����
20�̏ꏊ��4�̐ԋʂ����邩��A�����C[20,4]
2�͓��锠��I�Ԃ̂�10�ʂ�A1���̔����I�Ԃ̂�9�~8��2�ʂ�
1���̔��ɂ�4�ʂ�̓����������
9�~8��2�~4/C[20,4]=96/323 �F������肪�Ƃ��������܂�
1/19�~16/17�~6���ƁA���̈ʒu���l������ĂȂ��ł���ˁB�Ⴆ�Δ���1�ڂ���2�F���Ƃ��āA���̎���1/19�~16/17�~6�ɂȂ��Ĕ���2�ڂɓ��鎞��1/19�~16/17�~6�ɂȂ��āA�S����1/19�~16/17�~ 6�~10C1�~9C2�ɂȂ�Ǝv���̂ł����A�Ȃ�����͍l�����Ȃ��ėǂ��̂ł����H >>151
1/19�~16/17�~6���Ă͉̂����Ӗ�����v�Z�Ȃ́H
������������@�͋ʂ�����ꏊ��20�������ׂĖ���ׂɋʂ����i��1�j�A2���ɋ�����Ƃ��Ɉ�̋�肾��2�Ƃ��Ԃł���i��2�j�m���Ɠ����ƍl���A
��1��20C4�ʂ�
��2�͐ԋʂ��������I�ԑI�ѕ���10C3�ʂ�ł��̂���2�������I�ԑI�ѕ���3C1�ʂ��1����2�̋��͐Ԃ��ǂ���ɂ���̂��ł��ꂼ��2�ʂ肠��̂�10C3�~3C1�~2^2 >>153
�ԋ�A�ɑ��Đԋ�B��A�Ɠ������ɓ���m����1/19�A�c��̐ԋʈ�ɑ��āA���ʂƓ����ɂȂ�m��16/17�A�ǂ̓�̐ԋʂ��ꏏ�ɂȂ邩�̑g������4C2�ł��B >>151
���̈ʒu���l���悤���l���܂���2�ڂ̋���1�ڂƓ����m����1/19�B
���̈ʒu���ĉ��H �܂̒���n�̋�ʂł��鋅������B
�ŏ��ɑ܂���m�̋������o������A�����̋���܂̒��ɖ߂��B
���ɑ܂���k�̋������o�����Ƃ��A���̒��ɍŏ��Ɏ��o���ꂽ�������傤��c�܂܂��m����n,m,k,c�ŕ\���B >>153
�ԋ�C�͂ǂ��ɂ�����������́H >>153
�悤�₭�킩����
�ȗ������ɏ�����20/20�~1/19�~18/18�~16/17�~4C2���Ă��Ƃ�
���̌v�Z�Ŕ�����ʂ��Ă邶��Ȃ���
10C1�~9C2��������K�v���o�Ă���̂�
��1�ɐԋ�A������i2/20�j�A��1�ɐԋ�B������i1/19�j�A��2�ɐԋ�C������i2/18�j�A��3�ɐԋ�D������i2/17�j�ƍl�����ꍇ����
���̏ꍇ�A��1�A2�A3�ɂǂ̐ԋʂ�����̂���4C2�~2C1�~1C1�ʂ肠�邩��
����2/20*1/19*2/18*2/17*4C2*2C1*1C1*10C1*9C2�ƂȂ�v�Z�����96/323�ɂȂ� >>154 157
�e�ɉ��Ă��������A���肪�Ƃ��������܂��B
���̈ʒu�i�ǂ̔��ɐԋʂ�2���邩�j����ʂ��邱�Ǝ��̂��i���Z���X�������Ƃ悤�₭�C�Â��܂����B
���A�l�ŗ������邱�Ƃ��o���܂����B
�܂��A���₵�ɂ���Ǝv���܂����A���̎��͂܂���낵�����肢���܂��B �O>>148�����B
�ԍ��U�炸�ɂ���Ă݂�B
��������������������
��������������������
��
����2�̑I�ѕ���4�b2�ʂ�B
���Ɠ������ɓ��遛�̑I�ѕ���16�b2�ʂ�B
����1�́��͂��Ȃ炸���Ɠ������ɓ���B
(4�b1)(16�b2)=4�16�15/2
=480
480/4845=160/1615
=32/323
���������̐�����Ȃ��B >>123
(n,k) = (2,3) �̂Ƃ�
�@f(x) = (x-1)(x-2) - x^3,
�@f'(x) = -3 +2x -3x^2 = -(8/3) - 3(1/2 -x)^2 �� -8/3,
(n,k) = (2,5) �̂Ƃ�
�@f(x) = (x-1)(x-2) - x^5,
�@f '(x) = -3 +2x -5x^4 = -(35/16) -(1/2)x^2 -2(1/2 -x)^2 -5(xx -1/4)^2 �� -35/16, �s�̌v�Z��������Ȃ��̂ŋ����Ă�������
���fn���s��(z_i,j)�ɑ���
z_i,j=a_i,j+b_i,j��-1�Ƃ����ȉ��̌`��2�����s���i,j=1,�c,n�܂ŕ��ׂ���2n���s����l����
[a_i,j�@�@b_i,j ]
[-b_i,j�@a_i,j ]
���̍s��̍s�͌��̕��f�s��̍s�̐�Βl��2��ɓ��������Ƃ��ؖ�����Ƃ������ł� >>101
����(z_i_j)�̑�i�s��k�{���j�s�ɑ����ƑΉ�����2n���̍s��ł͑�2i-1�s��k�{���2j-1�s�ɁA��2i�s��k�{���2j�s�ɑ������ɂȂ�B
�ǂ���̍s��̍s���ω����Ȃ��B
���̕ό`�����Ō��̍s���Ίp���ł��邩��Ίp�s��̏ꍇ�ɂ������߂������B >>162
���A���̕ό`�{���l�̕ό`�̗�o�[�W�����őΊp���ł���ł����B ���I=[0,1]��̘A����f:I��R�̑S�̂�C[0,1]�Ƃ��AC[0,1]��̋�����
d(f,g):=max{|f(t)-g(t)||0��t��1}
�ɂ���Ē�߂�BC[0,1]�̕����W��X��
X={f_k|f_k(t)=kt, k��R}
�Ƃ����Ƃ�
d(X)=inf[f��X]d(f,1)
�̒l�����߂�(������1�͒萔��1(t)=1)
������d(X)=1�ƂȂ��Ă܂�
k��1�̂Ƃ�d(f_k,1)=�u|kt-1|�̍ő�l�v=k-1������Ak��R�ɂ��ĉ������Ƃ��d(X)=0�ɂȂ�̂ł́H�Ǝv���̂ł����A����͉����Ⴄ�̂ł��傤���H >>164
d(f_k,1)
=max{|f_k(0)-1|,|f_k(1)-1|}
=max{|0-1|,|k-1|}
�ł��B ���L�̎��̐ϕ����̓������@�ǂȂ����킩��܂��B
{ cos(X) + sin(X) } * { cos(X) }^0.8 >>165
���[�������A�ő�l����������k-1����Ȃ��Ȃ���
k=3/2�̂Ƃ�max|kt-1|��k-1=1/2�ł͂Ȃ�t=0�̂Ƃ���1���낤�c�c�A�z�Ȃ��Ƃ��Ă���
���肪�Ƃ��������܂� ax+by=1 ���ʂ�ɉ��߂��邱�ƂŒP�ʉ~�̋ɁA�ɐ��ɂ���
�ɓ_(a,b) �̋ɐ���̓_��(a,b)��ʂ钼���ɂȂ邱�Ƃ������ɂȂ�̂��B�B ���N�̓�֍��Z�̖��炵���ł����A�O�p��Ȃ��łǂ��������ǂ��ł��傤���B���������������B
AB=6,BC=10,CA=8�́�ABC�̊O�ډ~��K�Ƃ���B
��BC�Ɋւ���B�Ɣ��Α��ɂ���K�̌ʏ�ɓ_P���Ƃ�APA+PB+PC���ő�ƂȂ�悤�ɂ���B
�i1�jK�̔��a�����߂�B
�i2�jPA+PB+PC�̍ő�l�����߂�B
�i3�jPA+PB+PC���ő�ɂ���P��Q�Ƃ���BQ�̈ʒu�����߂�B
�i4�jQ���璼��AB�ɐ��������낵�A������Q�̌�_��H�Ƃ���BCH�̒��������߂�B �@�u�ɐ���̓_�̋ɐ��́v�ɒ���
���߂Ƃ�(a,b) ��(x,y)�̓��ς̐������ǂ���ɂ��낷���Ƃ����Ӗ�
���̓Ȑ����`���Ɛ��`�㐔�̒m���ŃV���v���ɉ��߂ł���̂��ȁH >>123
�@n=2, k�F�, k��3 �̂Ƃ�
�@f '(x) = -3 +2x -k�x^(k-1) �� -3 +2x < -1,�@(x<1)
�@�@�@= -5/2 - 2(1/2 -x)^2 - {k�x^(k-3) - 2}x^2 < -5/2,�@(|x|>1)
��� f(x) �͒P�������B >>169
�i1�j��ABC�͒��p�O�p�`������A���a���T
�i2�j�ő�ɂȂ�̂�ABPC�̖ʐς��ő�ɂȂ�Ƃ�������17��2
�i3�j�i2�j�̗��R�ɂ��BC�̕��s�����~K�Ɛڂ���_�B
�i4�j��蕶���Ӗ��s���B >>169
�i4�j������AB�̉����Ƃ̌�_��H�Ƃ���Ƃ����Ӗ��Ȃ�A��113 >��BC�Ɋւ���B�Ɣ��Α��ɂ���K�̌�
���Ăǂ��̂��Ƃ��H A�Ɣ��Α��̌�A���
�ӂƎv�������ǎO�_����̘a�����̋Ȑ����ĂȂ�H �����肪�Ƃ��������܂��B
���̒��ŋL���������e�������Ă��āA��L��������ϐ\����܂���ł����B >>166
�� sin(X)�{cos(X)}^0.8 dX = -(1/1.8){cos(X)}^1.8
{cos(X)}^2 = Y�@�Ƃ�����
��{cos(X)}^1.8 dX = (-1/2)�� Y^0.4 (1-Y)^(-0.5) dY
�@= -(1/2)�a(1.4, 0.5 | Y)
�@= -(1/2)�a(1.4, 0.5 | {cos(X)}^2)
�s���S�x�[�^�� >>162
���肪�Ƃ��������܂�
�Ίp�����l����悩������ł��� >>172
> �ő�ɂȂ�̂�ABPC�̖ʐς��ő�ɂȂ�Ƃ�
�����炷�܂Ȃ�
������Ăǂ����Ă����������ł��H >>180
>>169�̖��̓������������Ă�����҂͔[���ł��Ȃ����낤����A
�ꉞ�������Ă����Ɓ|
�i1�j�͐����ȗ��B
�i2�j���̖��́i3�j����ԓ���B�l���l�����̂́|
PA�̍ő�l��PA�����a�̂Ƃ��ŁA���̂Ƃ�PA��BC������
PA�{PB�{PC��BC�{BP�{CP
�܂�BC�{BP�{CP���ő�̂Ƃ����l����悭�A
BC�͈�肾����BP�{CP���ő�̂Ƃ����l����悢�B
BP�{CP���ő�ɂȂ�̂͂ǂ̎����͓�̍l����������B
�@�@�����������قǖʐς͑傫���B���ʐς��ő�̂Ƃ����l����悢�B
�A�@�������ρ����敽�ς��ABP��CP�̂Ƃ���BP�{CP�͍ő�B
�䂦��BP��CP��5��2�@AP�͕��ׂ��̒藝���7��2
�i3�j�́i2�j�̐����̒ʂ�B
�i4�j�~���p�̒藝�ɂ���BCQ����BAQ��45��
�䂦��AH��7�@���Ƃ́�AHC�ɎO�����̒藝��K�p���ā�113 >>169
�����������肠��Ƃ��Ȃ肵��ǂ����Ǘ���
��BCD=90���ABD=AC�ƂȂ�E��BC�Ɋւ�A�Ɣ��Α��ɂƂ�B
E����BD���DE=BC�ƂƂ�B
��DEF=90���AEF=AB�ƂȂ�F��BC�Ɋւ���A�Ɣ��Α��ɂƂ�B
S��D����FR�ɉ��낵�������̑��Ƃ���B
���_P�ɑ��A������CP��D,F���牺�낵�������̑���Q,R�Ƃ���B
���̎���ACP�̊O�ډ~�̔��a=��DFS�̊O�ډ~�̔��a�Ɓ�ACP=��DFS�ɂ��AP=DS=QR�B
�撣���PQ=PB�A(�R����P�̈ʒu�ɂ��2�P�[�X�����Ă߂�ǂ�)
�ȏ�ɂ��PA+PB+PC=BR�ŋ��߂�ő�l��F=R�ƂȂ�Ƃ���P������BF��̎��B >>181
> PA�{PB�{PC��BC�{BP�{CP
����͂��̒ʂ�ł�����
> �܂�BC�{BP�{CP���ő�̂Ƃ����l����悭�A
> BC�͈�肾����BP�{CP���ő�̂Ƃ����l����悢�B
������Ă����ł��傤���H
BP+CP�����̍ő�l����x�������Ƃ���PA��BP+CP�����̍ő�l�����Ƃ���PA����x���đ傫���Ȃ邱�Ƃ����蓾�Ȃ��ƌ����Ă���̂ł��傤�� >>183
�������̂悤�Ȃ��Ƃ��N����Ȃ�A
PA�{PB�{PC��BC�{BP�{CP
�ƂȂ��Ă��܂��B ��������AP+BP+CP���ő�ɂȂ�P��BP+CP���ő�ɂȂ�P�̓Y���Ă邩�ƁB >>169
�g���~�[�̒藝�g���Čv�Z�����
�ő�l��2*sqrt(145)
PA=120/sqrt(145),PB=90/sqrt(145),PA=80/sqrt(145) �̂Ƃ� �Ȃ�قǁB
A���܂ތ�BC���D��BD:CD=AB+BC:AC+BC�ƂƂ�̂��B �g���~�[�̒藝�͉��@�藝�Ɠ�����Ȃ��̂�����`�[�g������
�����̕��@�͂킩���
PA=x,PB=y,PC=z
10x=6z+8y
y^2+z^2=10^2 ...�i���j
L=x+y+z=(9y+8z)/5 ���i���j�~�Ɛڂ���Ƃ��ɍő� >>184
����A�����Ȃ�Ƃ͌���Ȃ��Ǝv������
�l�͓K�������ǗႦ��PB+PC�̍ő傪10�ł��̂Ƃ���PA��5�i�܂肱�̂Ƃ���PA+PB+PC=15�j�Ȃ��ǁA
PB+PC��9�̎���PA��7�ɂȂ蓾��Ȃ�PA+PB+PC=16�ƂȂ�PB+PC���ő�̎������傫���Ȃ蓾��
���̂悤�Ȃ��Ƃ��N���Ȃ����Ƃ������Ă���̂��ǂ������Ă��Ƃł� >>190
�ł��܂��g���~�[���炢�܂ł͏����ƌ����Ă�����Ȃ��H >>190
BC�{BP�{CP�̍ő�l��L�Ƃ��A���̂Ƃ���BP�{CP�̒l�����Ƃ���B
����BP�{CP������肘�����������AAP��BC��肘�ȏ�傫����A
PA�{PB�{PC��BC�{BP�{CP�ƂȂ��Ă��܂��B
AP��BC���傫���Ȃ邱�Ƃ͂��肦�Ȃ��B
�܂�AP��BC��肘�ȏ�傫���Ȃ邱�Ƃ͂��肦�Ȃ��B ���ꂩ��ꎞ�Ԃقǒ��f���邪�A
>>169�̖��͍��Z�����̖�肾����A
>>186�̂悤�ȕ��G�ȓ����ɂ͂Ȃ�Ȃ��͂��ł���B >>193
��r�̎d�������������ł���
���Ȃ���PA�{PB�{PC��BC�{BP�{CP����BP�{CP���ő�̂Ƃ�PA�{PB�{PC���ő�ɂȂ�ƌ����Ă��܂�
����P�ŋL�q����ƍ�������̂�BP�{CP���ő�ɂȂ�_P��P'�Ƃ��܂�
���Ȃ��̐��ł�PA�{PB�{PC�̍ő�l��P'A�{P'B�{P'C�Ƃ������ƂɂȂ�܂�
������P''���l�����Ƃ�P''B+P''C��P'B�{P'C��菬�����Ȃ�܂�
P'B�{P'C-(P''B+P''C)=x>0�Ƃ����Ƃ�P''A-P'A>x�ƂȂ邱�Ƃ����蓾�Ȃ��ƌ����Ă��Ȃ��̂ł͂Ȃ����Ƃ������Ƃł� �O>>159
>>169
(1)K�̔��a=5
(2)PA+PB+PC=10+8+6=24
(3)Q(1.4,-4.8)
(4)C(5,0)
H(-5.4,0.3)
CH=��(10.4^2+0.3^2)
=��(108.16+0.09)
=��108.25
=10.404326�c�c
��肪��������������H
����Ȕ��[�Ȓ����o���ĈӖ�����́H ���������Ƃ����ɐ������o�Ă�̂ɂ�������Ă������ȃ��X���Ă��鑊�ς�炸�̌|����2�l�B >>195���N���b�N�������A�y�[�W�͌���Ȃ������B
������l�̓������Ԉ���Ă���̂�������Ȃ����A
>>196�ɓ����Ă����Ɓ|
������������Ζʐς͑傫�����ʐς��ő�Ȃ�PA�{PB�{PC���ő�A
�Ƃ������R�ɂ���Ėl�̉�Q�̈ʒu���������ƍl����B
�Ȃ��Ȃ�l�p�`ABPC�̖ʐς́�ABP�{��APC�ŁA
����͎����Ƃ���AP��2���BP��CP���܂�ł��邩��ł���B
AB��AC�͈�肾����A����AP��2���BP��CP���܂�ł��钷����
�ł������Ƃ����ʐς��ő�ɂȂ�B
����������Ύl�p�`ABPC�̖ʐς��ő�̂Ƃ��AAP�{BP�{CP���ő�ɂȂ�B >>199
���̍l��������BC�a�Ƃ��遢ABC���l�����Ƃ�A���ǂ��ɂ����Ă�PB+PC���ő�ƂȂ�Ƃ�PA+PB+PC���ő�ɂȂ邱�ƂɂȂ�i���̂Ƃ�PB+PC=10��2=14.1421356�c�c���j
A��B�ɂ������߂��Ƃ���ɂƂ��PA+PB+PC��15��2=21.213�c�c�ɂǂ�ǂ�߂Â��̂�22�ȉ��ɏo����
�������A���̂Ƃ�P��PB=8�APC=6�̈ʒu�ɂƂ��PB+PC=14�Ł���菬������PA+PB+PC��22���傫��
�܂�APB+PC���ő�ɂȂ�Ƃ�PA+PB+PC���ő�ɂȂ�Ƃ����̂͊ԈႢ >>139
10*(choose(18,2)-9)/choose(20,4)=1440/4845=288/969 >>201
�����ɂȂ��ĂȂ�����
=96/323 >>169
�̊��o�̓����̂܂Ƃ߁B
AB=c�ABC=a�ACA=b�Ƃ����Č�BC��A���܂ޑ���BD:CD=AB+BC:AC+BC����D���Ƃ�B
AB+BC=kBD�AAC+BC=kCD�Ȃ�k���Ƃ��
(AP+BP+CP)BC
=AB�ECP+ AC�EBP+ BC�EBP+ BC�ECP (��g���~�[)
=(AC+BC)�EBP+ (AB+ BC)�ECP
=kCD�EBP+kBD�ECP
=kBC�EDP (��g���~�[)
�ɂ��AP+BP+CP���ő�ƂȂ�̂�DP�����a�ƂȂ�Ƃ��ł���B
���Ȃ킿BP:CP=CD:BD=AC+BC:AB+BC�ƂȂ�Ƃ��ł���B
�{��ł�BP:CP=9:8�ƂȂ�Ƃ��ł���B �O>>197
�V���N�������̎藿���B �ڋ��҂͉B�ꂽ�Ƃ��납��A�}�C�N�ł������̂������Ȃ��̂��H
�ӂ�����ȁI���X�����J�X���I
�w�����X�s�[�J�[�ł����H�ǂ��Ɏd�|�����̂ł��傤���H
�c�ɂ̈ꌬ�Ɖ����ƁA�Ȃ�ł�������ł��ˁH
�������������Ă���킯�ł͂Ȃ��̂ɁA�u������I�v�Ƃ͂����Ȃ���̌����ł��傤���H
���߂āA�����Ă���A���̑����@���Ă��� a,b,c�����䐔����Ȃ��Ƃ�1/(a+x),1/(b+x),1/(c+x)����������ƂȂ�x�����߁A
���̌��ʂ�}�`�I�ɐ������� �Ȃ�قǁA>>186�̓������������ƕ������B
BP=x�ACP=y�Ƃ�����AP+BP+CP��9x/5+8y/5�ŁAx^2+y^2=100
����𖢒�搔�@���g���čő�l�����߂��̂��낤�B
����������搔�@��m��Ȃ����w�����ǂ�����ĂƂ��̂��B
�����(2)�͂���ʼn����Ă�(4)���ǂ�����ĉ����̂��B
>>205�̕��@�ł��A(4)���ǂ�����ĉ����̂��B
���������Ė��̍쐬�҂��Ԉ���Ă���̂ł͂Ȃ��̂��H AB=c, BC=a, CA=b �Ƃ����B�g���~�[���
�@L = AP+BP+CP = (b+a)/a�BP + (c+a)/a�CP,
(b+a)^2 + (c+a)^2 - L^2
�@= (b+a)^2 + (c+a)^2 - {(b+a)/a�BP + (c+a)/a�CP}^2
�@= kk(a^2 -BP^2 -CP^2) + {(c+a)/a�BP - (b+a)/a�CP}^2
�@�� 0,
L �� ��{(b+a)^2 + (c+a)^2} = ak,
�����Ɂ@k = (1/a)��{(b+a)^2 + (c+a)^2},
������ AP = ak, BP = (b+a)/k, CP = (c+a)/k �̂Ƃ��B ������������A�g���b�L�[�Ȗ����Q�[���G�����ł�����������݂����Ȃ́H >>209
0 = 1/(a+x) - 2/(b+x) + 1/(c+x)
�@= {(2b-a-c)(x-b) + 2(bb-ac)}/{(a+x)(b+x)(c+x)}
�@= (2b-a-c)(x-b)/{(a+x)(b+x)(c+x)},�@�@(�� bb=ac)
2b-a-c��0 ���@x=b >>169��(4)�͂��Ԃ�A
Q����BC�ɉ��낵�������̑���H�Ƃ���A�Ƃ����Ӗ����낤�B
���ꂾ�Ɠ�����128/29�ł���B >>214
���O�̉̓S�~�A�����ƑS�R���Ⴄ��B���ʂȎ��Ԃ���ꂳ��
���̊F�l�̉͑���̕��j��OK
��֍��Z�̖����m�[�q���g�ɂ��Đݖ�i3�j�i4�j��lj����Ă݂����A�g���~�[�̒藝���č��Z�̏펯����Ȃ������悩�A�ӊO�ɓ��������
�i1�j�͈Ղ������邪���Z�����������o�����߂Ɏc���Ă����� >>215
�قڃg���~�[�O��̏o����Ăǂ����H >>211 �����Ͽ
�@AP = ak - (b+a)/k - (c+a)/k, �O>>206
17��2=24.0416306�c�c��24
�킸���ɒ����B
�ǂ�ȂƂ����B
�ǂ�ȂƂ����B
P(x,y),A(-1.4,4.8),B(-5,0),C(5,0)�Ƃ���PA=��{(x+1.4)^2+(4.8-y)^2},PB=��{(x+5)^2+y^2},PC=��(5-x)^2+y^2},PA+PB+PC=��(25+2.8x+1.4^2-9.6y+4.8^2)+��(25+10x+25)+��(25-10x+25)=��(25+2.8x+1.96-9.6y+16�1.44)+��(50+10x)+��(50-10x)
=��(25+2.8x+1.96-9.6y+16+6.4+0.64)+��(50+10x)+��(50-10x)
=��(50+2.8x-9.6y)+��(50+10x)+��(50-10x)
=��{50+2.8x-9.6��(25-x^2}+��(50+10x)+��(50-10x)
{50+2.8x-9.6(25-x^2)^(1/2)}^(1/2)+(50+10x)^(1/2)+(50-10x)^(1/2)�������=0�Ƃ����x�̒l�́A >>215
���O�͐l�ԂƂ��ăS�~�i�� n��2�ȏ�̎��R���A���a�͈͂�k:1,2,�c,n-1�ŁA[]�̓K�E�X�L���Ƃ��āA
��[k^2/n]��(n-1)(n-2)/3�@�͐������܂����H
�܂��Ai�����R���Ƃ���n=10^(2i)+1�̌`�ł���킳���Ƃ���ɓ����͐������܂����H >>221
����͂ǂ����玝���Ă������Ȃ�H
����H
���藧��������Ȃ��ƂȂ��v����́H >>222
�Â��m�[�g�߂Ăďo�Ă�������Ȃ̂łȂ����藧�Ǝv�����̂��͂����v���o���܂��An��30�܂ł̐����ƁA1000000�ȉ��̐����烉���_���őI�Q�O��n�ł͐������m�F�����悤�ł��B�����Ă����������p�b�Ǝv�����Ȃ������̂ŕ����܂����B >>223
�ł͐��藧���ĂȂ��\��������̂ˁB >>223 �����ł��B����킵���Ă��݂܂���B
���m�[�g�������Ƃ���A���������͈ꕔ�̑f���Ƃ����̔C�ӂ̍�����(�������e�w���͍ő�1)�Ɍ�����Ɛ������Ă����悤�ł��B
�Ⴆ��n=2,5,13,17,29,37,41...��An=17*29,2*13*37,5*13*17*29*41...�Ȃǂł͓����������܂����An=31,(5^3)*(17^2)�Ȃǂł͓����������܂���ł����B
�����ؖ������Ⴊ�킩�����狳���Ă����Ƃ��ꂵ���ł��B >>221 �̎咣��
��[k=1 to n-1]Mod(k^2,n) �� n(n-1)/2
�Ɠ����ł��ˁB
�A������ n-1 �̕�����������ƁA������ n �ɂ���]�̕��ς� n/2 �ȉ����@�Ƃ������̂ł��B
��ʂɁA������]�̘a�@���@�������]�̘a�@�ł����A
������]�̘a�@���@�������]�̘a�@�ƂȂ�A
��[k=1 to n-1]Mod(k^2,n) = n(n-1)/2
�ƂȂ�܂��B����͋��炭�A�Ώ̓I�܂�A�up��������]�̎��An-p��������]�v�̎����Ǝv���܂��B a,b,c��萔����a��0�Ƃ��A��f(x)�Ag(x)��
�@f(x)=ax+b�A�@g(x)=1/(x+c)
�ɂ���Ē�߂܂��B����f(g(x))=g(f(x))��x�ɂ��Ă̍P�����ƂȂ�悤��a,b,c�̑g(a,b,c)�����ׂċ��߂Ȃ����B
���肢���܂��B n���f��p�̏ꍇ�� p=4k+1 �܂��� p=2 �ł��ˁB
�k��P��[�@���l
�@((-1)/p) = (-1)^((p-1)/2)
�@�@�@= 1�@�@(p=4k+1)
�@�@�@= -1�@�@(p=4k-1) >>227�@�ɕt�������܂��B
n=25 �̕�����]�́A1,4,6,9,11,14,16,19,21,24�@�őΏ̓I�ɂȂ�܂����A
10�����Ȃ��̂ŁA�����͐������܂���B
n�������̎��́An/2 �A��̎��́A(n-1)/2 �@�Ƃ����������t�������܂��B �Ȑ�C:y=|sin(n��x)|�i0��x��1�j�Ƃ���B
C��y��x�ɑ����镔���̑S�̂̒����̑��a��L_1�A���l��y��x�ɑ����镔���̑S�̂̒����̑��a��L_2�Ƃ���B
lim[n����] L_1/L_2�����߂�B >>230
p=7�̂Ƃ��͕�����]��
1,2,4
�őΏ̓I�ł͂Ȃ���B
�O���Ɋ���Ă�B
�O���ɂ�鎖�͂����Ă��㔼�ɂ�鎖�͂Ȃ����������Ȃ��Ƃ����Ȃ��B >>232
>>227�ŏ�����
>> ��ʂɁA������]�̘a�@���@�������]�̘a�@�ł����A
�ɑ���w�E�ł��傤���H
������]�̌��������ȉ��Ȃ̂ŁA���R�Ə�̕s���������藧���낤��
�v���ď����Ă��܂��܂������A�s�����̐��ۂ͈ȉ��̘_���ɂ͖��W�ŁA
���u������]�̘a�@���@�������]�̘a�v�̖����t�Ƃ��Ďg���Ă��܂��܂����B
�]���āA>>227�̎��̕������C�����܂��B
�~�F��ʂɁA������]�̘a�@���@�������]�̘a�@�ł����A
�~�F������]�̘a�@���@�������]�̘a�@�ƂȂ�A
���F�����A������]�̘a�@���@�������]�̘a�@����������Ȃ�A >>233
������]�̑S�̘̂a�ƕ������]�̘a�͈�v���܂����H
n7�̎�
������]�̘a��1+2+4=7
�������]�̘a��3+5+6=14
�ł��B �͂��B���̒ʂ�ł��B
n=7�ł́A��[k^2/n]��(n-1)(n-2)/3 �̎��́A
����=[1/7]+[4/7]+[9/7]+[16/7]+[25/7]+[36/7]=0+0+1+2+3+5=11
�E��=6*5/3=10
�Ȃ̂ŁA�s�����̕����������܂��B
���������̏����ɂ��čl�@���Ă���A227�㔼�����̑ΏۊO�̎���Ȃ̂ŁA
�Ȃ��An=7�����グ���Ă��邩�^��ŁA�ɋ����Ă��܂��B ����H
��݂܂����������ȁH
������]�̘a�����ϔ��]�̘a
���咣���Ă�悤�ɓǂ݊ԈႦ�܂����B
�����܂���B ���Ȃ݂Ɍ㔼��i=3�Ƃ��ł��_���ł��B
10^6+1��11�Ŋ����Ă����mod4��3�Ȃ̂Ń_���ł��B ���A�����������B
11�ł͊����Ȃ����ǁA�v�Z�@�ł������_���ł����B �܂������ł����B
�ł��Ԉ���Ă�
print $ sum [mod (n^2) 1000001 | n<-[0..1000000]]
500000500000
i=3�ł͐������Ă܂��ˁB
������10^(2i)+1�̑f���q���S��mod4��1�Ȃ�Đ�������̂��Ȃ��H �������Ap��3(mod4)�����q�ɂȂ鎖�͂Ȃ��̂��B
multiplicity��1�ȉ����ǂ������������Ȃ̂��B
�݂��Ă���B �A�����܂�
����ōŌ�ɂ���B
10^202+1�̓_������Ȃ��H
10^202+1
=100^101+1
=(1+100)(1-100+10000-�d(-100)^100)
��
(1-100+10000-�d(-100)^100
��1+1+�d+1 (mod 101)
������10^202+1��101^2�Ŋ������K�X ���镡�f���� f(z) = ��[k=0,��] (z^k / k!) �Ɩ��������Œ�`���܂��B
�܂�w�����ł����A�܂����̎�������m�炸�A��O�p��(sin, cos)���m��Ȃ����̂Ƃ��܂��B
���������̎��������͊��m�Ƃ��܂��B
f(z) �� ���鏃�����̎����������ł��鎖�������Ă��������B
�o�T�͓��ɂ���܂���A������������܂���B >>209
> a,b,c�����䐔����Ȃ��Ƃ�1/(a+x),1/(b+x),1/(c+x)����������ƂȂ�x�����߁A
> ���̌��ʂ�}�`�I�ɐ�������
���ab�̉~�ɑ��Ĕ��]�ňڂ肠����_�Ɖ~�̒��a�̗��[�͒��a������Ȃ��i���a�_��j >>242
�܂���`������
exp(x+y) = exp(x) exp(y)
exp(r+i��) = exp(r)(cos�� + i sin��)�Fcos��, sin�Ƃ͒P�ɋ����Œ�`���ꂽ��
���ؖ�����
���f�����|����
exp(2r) = exp((r+i��)+(r-i��)) = exp(r)(cos�� + i sin��)exp(r)(cos�� - i sin��)
= exp(r)^2 |cos�� + i sin��|^2�@�� |exp(i��)| = 1
�Ƃ�����Ƃ���� exp(i��)�� 1 + i�� �����璆�Ԓl�̒藝��exp(i��)�� 1 ��n�捪�ɂł���
���Ȃ킿 exp(i��)�̓Ƃ̎����� ���aa�̉~A�ƒ��ab�̉~B�����aa+b�̉~C�ɓ��ڂ��Ă���Ƃ�
A��B�ɊO�ڂ�C�ɓ��ڂ���~�̔��a��a,b�ŕ\��
���W����Čv�Z���Ă݂�������������̂��ώG�ɂȂ肷���Čv�Z�ł��܂���B
���Ԃ�L�����Ȃ̂łǂ����ɉ������Ă�Ǝv���ł����������Ă���������Ȃ��̂�
���肢���܂��B >>245�@�����Y��@�~A�Ɖ~B�͊O�ڂ��Ă܂� >>244 ���肪�Ƃ��������܂�
|exp(i��)| = 1 �����܂ł͗����ł��B ������...
> �Ƃ�����Ƃ���� exp(i��)�� 1 + i�� �����璆�Ԓl�̒藝��exp(i��)�� 1 ��n�捪�ɂł���
>���Ȃ킿 exp(i��)�̓Ƃ̎�����
���̘_���W�J�͌������̂ł͂Ȃ��ł��傤���H
���Ԓl�̒藝�łԂ��������Ăق����l�̐��������������ł��B
1 ��n�捪�� exp(i��)�� �\���鎖 (���͂Ȃ�炩�̎���) �� exp(i��)�̎����������m�łȂ��ƌ����Ȃ����Ǝv���܂��B �A���t�@�E���{|�w�p�f���Q
�i���n�E���n�E�H�w�E��w�j
ttp://x0000.net/ >>245-246
A��B�ɊO�ڂ�C�ɓ��ڂ���~��D�Aa,b�a�ł͂Ȃ����a�AD�̔��a��r
A,B,C,D�̒��S�̍��W�����ꂼ�� (-b,0), (a,0), (0,0), (x,y) �Ƃ��A
D�̒��S��A,B,C�̒��S�Ƃ̋������l��ƁA
[1] (x+b)^2 + y^2 = (a+r)^2,
[2] (x-a)^2 + y^2 = (b+r)^2,
[3] x^2 + y^2 = (a+b-r)^2.
x,y������������a([1]-[3])+b([2]-[3])�����ƁAr�̈ꎟ���ɂȂ�
r = ab(a+b)/(aa+ab+bb)�B |exp(i��)| = 1 ������
{exp(i��) | ����R} �̋O�Ղ͂P��ʂ�L�E�ȋȐ��B
�����`�Ȃǂ̖����ɒ����Ȑ������m��Ȃ������� >>242
�@f(z+w) = ��[k=0,��] (z+w)^k /k!
�@�@�@= ��[k=0,��] ��[m+n=k] (z^m /m!)(w^n /n!)�@�@(2������)
�@�@�@= (��[m=0,��] z^m /m!)(��[n=0,��] w^n /n!)
�@�@�@= f(z) f(w)�@�@���� �w������
����
�@f(iy) = cos(y) + i�sin(y)
�Ƃ����B
�@cos(y) = Re{f(iy)} = ��[k=0,��] (-1)^k y^(2k)/(2k)!
�@sin(y) = Im{f(iy)} = ��[k=0,��] (-1)^k y^(2k+1) /(2k+1)!
�w������
�@f(iny) = f(iy)^n,
�� �h�E���@�����̌���
�@cos(ny) + i�sin(ny) = {cos(y)+i�sin(y)}^n,
�ƂȂ�A�������Ƌ������ɕ������ n�{�p���� ���o��B
�@f(iy)f(-iy) = f(0) = 1,
���
�@cos(y)^2 + sin(y)^2 = 1, ���� cos(y), sin(y) �̗�_���������B
cos(0) = 1,
cos(2) = ��[k=0,��] (-1)^k (4^k)/(2k)!
�@= 1 -4/(2!) + 16/(4!) - 64/(6!) + ���
�@= 1 -2 +2/3 -4/45 + ����
�@< 0
0<y<2 �� cos(y) �̗�_ p/2 ������B
�@cos(p/2) = 0,
�@sin(p) = 2sin(p/2)cos(p/2) = 0,
0<y<4 �� sin(y) �̗�_p������B i�����ɓ����������̒����̒l���������ƃ[���Ȃ̂Œ萔
�ω��ʂ�����ɔ�������ƒ萔
�ɂȂ鎖���킩��̂�
i�����ւ̈ړ��͉~�����葬�x�ʼn�葱���鎖�͂킩��
�̂ŁA�ؖ��͂ł���
������͎O�p���̎������������X�^���_�[�h�Ȃ����ƌ��Ǔ����Ȃ̂Ŗʔ��݂͂͂Ȃ���������Ȃ�
�G���K���g�Ȏ��ό`�Ȃ�_�@�͂ǂ����ɂ���̂��낤�� cos(p) = 2cos(p/2)^2 -1 = -1,
f(i(p/n))^n = f(ip) = cos(p) + i�sin(p) = -1,
f(i2p) = (-1)^2 = 1, �w����������
�@f(z+2pi) = f(z)f(2pi) = f(z),
��`(�}�N���[�����W�J)����
�@{sin(y)} ' = cos(y),
�@{cos(y)} ' = -sin(y),
���o��B
>>254
�@cos(y)^2 + sin(y)^2 = f(iy)f(-iy) = f(0) = 1,
����L�E�ł��邱�Ƃ͕�����܂������ �f���ɍl�����
�Ecos(2)<0���`���玦���B
�Ecos(0)=1�Ƃ��킹��cos(c)=0�����ŏ��̎��������݂���B
�E0<x<c��cos(x)>0�ɂ��sin(x)�͒P������A�����sin(0)=0�ɂ��sin(c)>0�B
�Esin^2+cos^2=1�ɂ��sin(c)=1�B
�Eexp(ic)=i�B
�Eexp(A+B)=exp(A)exp(B)�d(✳︎)�������Ă�����exp(4ci)=1�A�Ă�(✳︎)�ɂ��exp(x)�͎���4ci�����B
�Ƃ�����Ȃ��H >>250
> [3] x^2 + y^2 = (a+b-r)^2.
���̎��͒��S (a-b,0) ������ȉ��̂悤�ɏC�����ĉ�����
{(x + b)^2 + y^2 = (a + r)^2, (x - a)^2 + y^2 = (b + r)^2, (x - a + b)^2 + y^2 = (a + b - r)^2}
r = (a + b)^3/(2 (a^2 + 4 a b + b^2))�@�ɂȂ�悤�ł��B���肪�Ƃ��������܂��� >>253 ����...���Ԓl�̒藝�������Ŏg����ł��ˁB����������Ă܂����B
cos(0) = +1
cos(2) = 1 - 2^2/2! + 2^4/4! - 2^6/6! + 2^8/8! - ...
< 1 - 2^2/2! + 2^4/4! - 2^6/6! +2^8/8! * (1 + 0 + 2^4/8^4 + 0 + 2^8/8^8...)
< 1 - 2^2/2! + 2^4/4! - 2^6/6! +2^8/8! * 2
= -43/105 < 0
�� ����p��(0,2) �ɂ��� cos(p) = 0, sin(p) = �}1 (������m��K�v�͂Ȃ�)
exp(ip)^4 = ( 0 �} i )^4 = 1 �܂�4�捪������ꂽ�̂�
exp(i(x+4p)) = exp(ix) * exp(i4p) = exp(ix) * exp(ip)^4 = exp(ix)
exp(ix) �̎����� 4p (�����͂��̉����̈�) �ł���B�Ƃ肠���������܂ł�OK�ł��B
���݂̂Ȃ�������肪�Ƃ��������܂����B����l����Q�l�ɂȂ�܂��B �@-1��������].
�@((-1)/n) = 1.
�@x^2��-1�@(mod n)�@����������.
�@������]�̕��z���Ώ̓I.
�@�@�@��
�@k=1,2,����,n-1 �ɂ����� mod(k^2,n) �̕��ς� n/2.
�@��[k=1,n-1] mod(k^2,n) = n(n-1)/2. >>259
����f�J���g�̉~�藝���Ă̂Ō��Z���Ă݂�ƍ���Ȃ�����Ԉ���Ă���̂�������܂��� �O�p���̉��@�藝�A���a��1�o�ł���Ȃ�
�P����0�ȊO�ŃT�C����0�ɂȂ�_�̒l���Ԃ����߂ΎO�p���̎������͂ł�
�܂�����������̌`����o�邵�A�O�p���̎������̘b���� >>261
�����A�ꎞ�����̉\�����v���܂������A�@>>230�@���������������B
�u-1��������]�v�����ł́A�s�\���Ȏ�������܂��B
�������A�K�v�����ł��邱�Ƃ́A�ԈႢ�Ȃ��Ǝv���܂��B
���ɂ��A50,125,169,250,289���A���̗�O�ɓ��Ă͂܂�̂ŁA
2^r*p^s�@�������Ar=0,1�Ap�͑f���As=2,3,4,...
�^�����O����Ώ\���Ȃ̂�������܂���B
���A����ƁA230�̓��e���C�����܂��B
�un�������̎��́An/2 �v�Ə����܂������An�������̎��́An/2��������]�Łi��n��4�̔{���ł͂Ȃ��j�A
n/2����������ŁA������]�A�������]�̌������ꂼ��An/2-1 ���@�łȂ���Ȃ�܂���B >>259�@�ŏ��Ɠ�Ԗڂ̎��̉E�ӂ� a �� b�@���t�ɂ����{�P���܂��Ă��@
���ʓI��>>250�ƈ�v����
solve {(x + b)^2 + y^2 = (b + r)^2, (x - a)^2 + y^2 = (a + r)^2, (x - a + b)^2 + y^2 = (a + b - r)^2}
r = (a b (a + b))/(a^2 + a b + b^2) >>264�@�ɕ⑫
n=p^2�ƕ\�����Ƃ��A
��[k=1,n-1] mod(k^2,n) = n(n-1)/2
�̍��ӂɂ����āAk=a*p�̍��́Amod((a*p)^2,p^2)=0�@�ƂȂ�A
�ƂĂ��A���� n/2 ���ێ����邱�Ƃ͂ł��Ȃ��Ȃ邽�߁A���O����Ȃ���Ȃ�Ȃ��@�Ƃ������Ƃł��ˁB n���������̂Ƃ��� n�Ƒf�Ȍ����W�߂��W�� {k|gcd(k,n)=1�A������} = (Z/nZ)^ �ōl��������ǂ��ł��傤�ˁB
���������
-1��������]�@(mod n)
�@�@��
(Z/nZ)^ �ɂ����� mod(k^2,n) �̕��ς� n/2.
��[k��(Z/nZ)^] mod(k^2,n) = n��(n)/2.�@
��(n)�̓I�C���[��totient���ł��B �@-1 ��������]�@(mod n)
�@n=��p�@�Ȃ�@((-1)/n) = ��((-1)/p),
�k����[�@���l
�@((-1)/p) = 1�@�@(p=4k+1 �܂��� p=2)
�@�@�@�@= -1�@�@(p=4k+3)
n�� 4k+3�^�̑f��p��S���ł����܂ނ��A�Ō��܂�B
�@������0�@���@+1�@���@����
�@��@���@-1�@���@�s����
�ł��傤������ �`���[�g�̃`�F�o�̒藝�̋t�̏ؖ��̏���"�pBAC�܂��͂��̑Β��p�̓����ɂ���"�Ƃ����L�q�������ł����A"���̑Β��p�̓����ɂ���"�̈Ӗ���������Ȃ��ł��B
��낵�����肢���܂��B ���w2�N���ł��B�����(3)�͂Ȃ�ł����Ȃ��Ȃ�ł��傤���B�����炩�ɒ������Ⴄ����H������Ȃ��̂ŋ����ĉ������B
https://i.imgur.com/9Kk35Id.jpg >>270
�����ɏ�����Ă��������������B�̈ʒu�����肳��Ă��炸�ӎO�p�`�ł��邱�Ƃ����蓾�邪�����łȂ����Ƃ����蓾�邩��
���̐}�̌����ڂ̖��ł͂Ȃ��� >>270
���w�Z�Ő}�`�������悤�ɂȂ�����
https://blogimg.goo.ne.jp/user_image/5c/98/c565f994fd990e4943020e3f714950a8.jpg
�����2�Ԃ̂悤�Ȗ��Ō��������őI��ł悩�������ǁA���w�̐}�`�̃��x���ł͌����ڂ͊W�������_���I�ɖ��m�ȍ������Ȃ���������Ƃ݂͂Ȃ��Ȃ��Ƃ����Öق̃��[��������
�����Ă݂���̂��Ƃ��w�Z�ł͖������Ă���Ă��Ȃ������C�͂��� ���X270�ł��B
�l���ĉ������������肪�Ƃ��������܂��B��K�A���x��͎g��Ȃ����Ȃ̂ŁA�Ȃ�ł����Ȃ����ĂȂ��Ă�̂��ؖ��o���Ȃ��č����Ă���ł����B
�����A�w�Z�Ŏ���ɍs���Ă��܂��B�ؗj����w�N���e�X�g�Ȃ̂Ŋ撣��܂��B���肪�Ƃ��������܂����I�I �O>>219
P(x,y),A(-1.4,4.8),B(-5,0),C(5,0)�Ƃ���ƁA
x^2+y^2=25
PA=��{(x+1.4)^2+(4.8-y)^2}
=��(25+2.8x+4�1.96+16�1.44-9.6y)
=��(2.8x-9.6y+41+0.64+0.064+7.84)
=��(2.8x-9.6y+48.84+0.704)
=��(2.8x-9.6y+49.544)
PB=��{(x+5)^2+y^2}
=��(25+10x+25)
=��(50+10x)
PC=��{(5-x)^2+y^2}
=��(50-10x)
PA+PB+PC=��(2.8x-9.6y+49.544)+��(50+10x)+��(50-10x)
={2.8x+9.6(25-x^2)^(1/2)+49.544}^(1/2)+(50+10x)^(1/2)+(50-10x)^(1/2)
������=0�Ƃ���ƁA
(1/2){2.8x+9.6(25-x^2)^(1/2)+49.544}^(-1/2){2.8+4.8(25-x^2)^(-1/2)}+(1/2)(50+10x)^(-1/2)+(1/2)(50-10x)^(-1/2)=0
{2.8x+9.6(25-x^2)^(1/2)+49.544}^(-1/2){2.8+4.8(25-x^2)^(-1/2)}+(50+10x)^(-1/2)+(50-10x)^(-1/2)=0
{2.8x+9.6(25-x^2)^(1/2)+49.544}^(1/2){2.8+4.8(25-x^2)^(-1/2)}+{2.8x+9.6(25-x^2)^(1/2)+49.544}(50+10x)^(-1/2)+{2.8x+9.6(25-x^2)^(1/2)+49.544}(50-10x)^(-1/2)=0
x�̒l�́A1.4��肿�����Ȃ肻���ȗ\�������܂��B >>270
��BCD��30���Ə�����Ă��Ȃ�����B >>270
�����A��肪�u���̐}�`�͓ӎO�p�`���H�v
�Ɩ��ꂽ���̂�������A�\�ȉ͎��̎O�B
A:�u�͂��v���u�ӎO�p�`�ƌ�����v
B:�u�������v���u�ӎO�p�`�ƌ����Ȃ��v
C:�u�s���v���u�ӎO�p�`���ǂ�������Ȃ��v
���̖��́A�u�ӎO�p�`���H�v�Ɩ���Ă���̂ł͂Ȃ��A
�u�ӎO�p�`�ƌ����邩�H�v�Ɩ���Ă���B
�܂�A�u�����̎����A.�Ɖ��邩�H�v�Ɩ���Ă���̂ŁA
�uNo�v���u�����Ȃ��v�ƂȂ�B 270�ł��B�ӎO�p�`���Əؖ����鎖���ł��Ȃ��B�Ƃ����Ӗ��̖�肾�����Ƃ������ł��ˁB�����Ɨ����o���Ă܂���ł����B���肪�Ƃ��������܂��I �`���[�g�̃`�F�o�̒藝�̋t�̏ؖ��̏���
�O�p�`ABC������A��AB�A��AC�̕ӏ�܂��͂��̉�������ɓ_Q�A�_R�����鎞�A�_P�͕�BC��ɂ���B
��BR�ƕ�BQ�̌�_O��"�pBAC�܂��͂��̑Β��p�̓����ɂ���"�Ƃ����L�q�������ł����A"���̑Β��p�̓����ɂ���"�̈Ӗ���������Ȃ��ł��B
��낵�����肢���܂��B >>273
>�l���ĉ������������肪�Ƃ��������܂��B��K�A���x��͎g��Ȃ����Ȃ̂ŁA�Ȃ�ł����Ȃ����ĂȂ��Ă�̂��ؖ��o���Ȃ��č����Ă���ł����B
>�����A�w�Z�Ŏ���ɍs���Ă��܂��B�ؗj����w�N���e�X�g�Ȃ̂Ŋ撣��܂��B���肪�Ƃ��������܂����I�I
�Ȃ�ق�
�}�̏����Ԃ肩��A�ӎO�p�`�Ɍ����Ȃ��悤�ɂ́A������Ă���̂ŁA�����ڂł́u�����Ȃ��v�͕�����
���͗��R�t�������ǁA>>275-276����
��BCD��30���Ƃ��āA�ӎO�p�`�ɂ��邱�Ƃ��\����
��BCD��30���Ƃ��āA�ӎO�p�`�ɂ��Ȃ����Ƃ��\��
�܂�A���_B�̈ʒu���A�ӎO�p�`�ɂȂ�Ȃ��悤�Ɏ�邱�Ƃ��\������Ƃ����̂��A���̗��R���낤��
���݂ɁA�������Ƃ͒��_D�ɂ��Ă������āA�O�p�`ACD�ɂ��Ă��ӎO�p�`�Ƃ͌����Ȃ� >>278
>�`���[�g�̃`�F�o�̒藝�̋t�̏ؖ��̏���
>�O�p�`ABC������A��AB�A��AC�̕ӏ�܂��͂��̉�������ɓ_Q�A�_R�����鎞�A�_P�͕�BC��ɂ���B
>��BR�ƕ�BQ�̌�_O��"�pBAC�܂��͂��̑Β��p�̓����ɂ���"�Ƃ����L�q�������ł����A"���̑Β��p�̓����ɂ���"�̈Ӗ���������Ȃ��ł��B
���L�� Yahoo�m�b�� �u�`�F�o�̒藝�œ��p�̑Β��p�Ɍ�_������Ƃ��v�ɐ}�������
�܂��A�ʏ�́A�u�`�F�o�̒藝�̑�1�̏ꍇ�F�O�p�`ABC�̓����̓_O��3�{�̒����������v�A�u�`�F�o�̒藝�̑�2�̏ꍇ�F�O�p�`ABC�̊O���̓_O��3�{�̒����������v��2�݂�������
"���̑Β��p�̓����ɂ���"�́A��3�̏ꍇ�ɂȂ邾�낤
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1237275857
�`�F�o�̒藝�œ��p�̑Β��p�Ɍ�_������Ƃ� Yahoo�m�b��
gag********����2010/2/26
https://ja.wikipedia.org/wiki/%E3%83%81%E3%82%A7%E3%83%90%E3%81%AE%E5%AE%9A%E7%90%86
�`�F�o�̒藝
https://upload.wikimedia.org/wikipedia/commons/thumb/c/c7/Ceva%27s_theorem_1.svg/220px-Ceva%27s_theorem_1.svg.png
�`�F�o�̒藝�̑�1�̏ꍇ�F�O�p�`ABC�̓����̓_O��3�{�̒����������
https://upload.wikimedia.org/wikipedia/commons/thumb/e/e7/Ceva%27s_theorem_2.svg/250px-Ceva%27s_theorem_2.svg.png
�`�F�o�̒藝�̑�2�̏ꍇ�F�O�p�`ABC�̊O���̓_O��3�{�̒���������� �m��
A�`�[��6�l : B�`�[��6�l���[�X�Q�[����16��������B
1��15�_
2��12�_
3��10�_
4��9�_
5��8�_
6��7�_
7��6�_
8��5�_
9��4�_
10��3�_
11��2�_
12��1�_
�̔z�_�̏ꍇ�A�e�`�[���̍��v�_��656:656�̈��������ɂȂ�m���������Ă��������B >>280
���肪�Ƃ��������܂��I������܂����I�I >>281
����͌v�Z�@�}�^�[�̂�B >>283
�v�Z�@�}�^�[�H
���݂܂���A�f���a���̂ł悭�킩��܂���B >>284
�v����Ɋw���ȍ~�ŏK�����w�̌����g���đ��Ă炭�ɂȂ�킯�ł��Ȃ��̂Ōv�Z�@�ɂ�点������������B
���w�܂Ƃ��ɕ���������o����肶��Ȃ��B
����ȉ���Ȃ������͎̂��Ԃ̖��ʁB
���������ق��������B >>285
�{���ɖ��m�ł��݂܂���B���w�͓��ӂł͂Ȃ����A�m�荇���ɂ��m���ɋ����l�����Ȃ��̂ł��̌f���𗊂�ɂ��Ă��܂��B
�v�Z�͂�����ł���̂ŁA�����������ł������Ē��������ł��B �������炵��������������̂��H
�P���ɁA�S���̏ꍇ�𐔂��グ�邵���Ȃ���
656�_���ɂȂ�g�ݍ��킹�̐��𐔂��グ��
�S�̂̑g�ݍ��킹�̐��Ŋ���A�����Ȃ��悤�Ɍ����邪
�v�����
�܂����̃��[�X�ŋN����g�ݍ��킹��12C6��924�ʂ�
������
�����16�������S����924��16��ʂ�N���肤��
���̉��S���ʂ肩�̂����ł��傤�Ǔ_���������ɂȂ��Ă�P�[�X�����ʂ肠�邩�����Ĕ䗦���v�Z����Ίm���͏o��
������
�܂����ۂɂ͂��������ʂ��O�サ�Ă������_���ɂȂ�P�[�X�͂��邩�����������Ɛ�����̂͏��Ȃ��Ȃ��āA�����ʂ肩���S���ʂ肩�ōςނ�������Ȃ����� �O>>274
>>245
���߂�~�̔��a��x�Ƃ����ƁAA��B�ɊO�ڂ�C�ɓ��ڂ���~�̒��S��D�Ƃ��āA��DBA����с�DBC�ɂ����ė]���藝���A
cos��DBA={(b/2+x)^2+(a/2+b/2)^2-(a/2+x)^2}/2(b/2+x)(a/2+b/2)
cos��DBC={(b/2+x)^2+(a/2)^2-(a/2+x)^2}/2(b/2+x)(a/2)
cos��DBA=cos��DBC���A
{(b/2+x)^2+(a/2+b/2)^2-(a/2+x)^2}a
={(b/2+x)^2+(a/2)^2-(a/2+x)^2}(a+b)
{(b+2x)^2+(a+b)^2-(a+2x)^2}a
={(b+2x)^2+a^2-(a+2x)^2}(a+b)
(b^2+4bx+4x^2+a^2+2ab+b^2-a^2-4ax-4x^2)a
=(b^2+4bx+4x^2+a^2-a^2-4ax-4x^2)(a+b)
ab^2+4abx+4ax^2+2a^2b+ab^2-4a^2x-4ax^2
=ab^2+4abx+4ax^2-4a^2x-4ax^2+b^3+4b^2x+4bx^2-4abx-4bx^2
2a^2b+ab^2
=b^3+4b^2x-4abx
2a^2+ab
=b^2+4bx-4ax
4(a-b)x=b^2-ab-2a^2
x=(b^2-ab-2a^2)/4(a-b) >>281
C[12,6]=924�ʂ�́u���ʕ����v���A��_=41�Ƃ̍��ŕ��ނ��A����0�`20�ɂȂ�̂́A���ꂼ�ꎟ
48,47,47,44,43,39,37,32,30,25,22,18,15,11,10,6,5,3,2,1,1
f=48+47(x+1/x)+47(x^2+1/x^2)+44(x^3+1/x^3)+43(x^4+1/x^4)+39(x^5+1/x^5)+37(x^6+1/x^6)+
32(x^7+1/x^7)+30(x^8+1/x^8)+25(x^9+1/x^9)+22(x^10+1/x^10)+18(x^11+1/x^11)+15(x^12+1/x^12)+
11(x^13+1/x^13)+10(x^14+1/x^14)+6(x^15+1/x^15)+5(x^16+1/x^16)+3(x^17+1/x^17)+2(x^18+1/x^18)+
(x^19+1/x^19)+(x^20+1/x^20)
�Ƃ��āAf^16 �̒萔����924^16�@�Ŋ��������̂�����
3861707060011302197274473352442662107544339496/924^16
=0.0136781633711920174806098975... �O>>288
�������ς��B��������B >>264
�u-1��������] (mod n)�v������An��4q+3�^�̊�f����4���܂݂܂���ˁB
�܂��A�������qp^2������n�����O���ꂻ���B�@�@>>230 >>266
�@n=p^2 (p=4q+1) �ƕ\�킳���Ƃ���
�@��[k=1,n-1] mod(k^2,n) = n��(n)/2 = np(p-1)/2 < n(n-1)/2,
�@�̍��ӂɂ����āAk=a*p �̍��� k^2��0 �ƂȂ�B
�@�����x�L�̏ꍇ���A�����̒��� k^2��0 �ƂȂ�k����������̂œ��l�B
�� n�� {2,5,13,17,29,37,41,����} �̗v�f�����X1��܂ށB�@�@>>225
>>268 �͓P�܂��B�B�B >>289
���肪�Ƃ��������܂��I�I
�����đS�R�����Ⴂ�������炷�݂܂���A
1/10000�̊m���ƌ����Ă��܂��Ă��ǂ��̂ł��傤���B �`���a�̒P�˂Ƃa���`�̒P�˂��Ȃ��Ȃ�t�ʑ����Ȃ�
�t�ʑ����Ȃ��Ȃ�S�P�˂͂Ȃ�
�`���a�̒P�˂Ƃa���`�̒P�˂��Ȃ��Ȃ�S�P�˂͂Ȃ�
�S�P�˂�����Ȃ�`���a�̒P�˂Ƃa���`�̒P�˂����� �O>>290
>>245
���߂�~�̔��a��x�Ƃ����ƁAA��B�ɊO�ڂ�C�ɓ��ڂ���~�̒��S��D�Ƃ��āA��DBA����с�DBC�ɂ����ė]���藝���A
cos��DBA=[(b/2+x)^2+{(a+b)/2}^2-(a/2+x)^2]/{2(b/2+x)(a+b)/2}
={(b+2x)^2+(a+b)^2-(a+2x)^2}/2(b+2x)(a+b)
cos��DBC=[(b/2+x)^2+(a/2)^2-{(a+b)/2-x}^2]/2(b/2+x)(a/2)
={(b+2x)^2+a^2-(a+b-2x)^2}/2(b+2x)a
cos��DBA=cos��DBC���A
(b^2+4bx+4x^2+a^2+2ab+b^2-a^2-4ax-4x^2)a=(b^2+4bx+4x^2+a^2-a^2-b^2-4x^2-2ab+2ax+2bx)(a+b)
(2b^2+4bx+2ab-4ax)a=(4bx-2ab+2ax+2bx)(a+b)
(2b^2+4bx+2ab-4ax)a=(4bx-2ab+2ax+2bx)a+(4bx-2ab+2ax+2bx)b
2ab^2+4abx+2a^2b-4a^2=4abx-2a^2b+2a^2x+2abx+4b^2x-2ab^2+2abx+2b^2x
2ab^2+2a^2b-4a^2+2a^2b+2ab^2=2a^2x+2abx+4b^2x+2abx+2b^2x
x=(2ab^2+2a^2b-4a^2+2a^2b+2ab^2)/(2a^2+2ab+4b^2+2ab+2b^2)
=(4ab^2+4a^2b-4a^2)/(2a^2+4ab+6b^2)
=(2ab^2+2a^2b-2a^2)/(a^2+2ab+3b^2)
=2a(b^2+ab-a)/(a^2+2ab+3b^2)
���܂������������ȁB
�菑������x=2ab/3(a+b)
�g�тŌ��Z����ƕς�����B �O>>294�����B
>>245
���߂�~�̔��a��x�Ƃ����ƁAA��B�ɊO�ڂ�C�ɓ��ڂ���~�̒��S��D�Ƃ��āA��DBA����с�DBC�ɂ����ė]���藝���A
cos��DBA=[(b/2+x)^2+{(a+b)/2}^2-(a/2+x)^2]/{2(b/2+x)(a+b)/2}
={(b+2x)^2+(a+b)^2-(a+2x)^2}/2(b+2x)(a+b)
cos��DBC=[(b/2+x)^2+(a/2)^2-{(a+b)/2-x}^2]/2(b/2+x)(a/2)
={(b+2x)^2+a^2-(a+b-2x)^2}/2(b+2x)a
cos��DBA=cos��DBC���A
(b^2+4bx+4x^2+a^2+2ab+b^2-a^2-4ax-4x^2)a=(b^2+4bx+4x^2+a^2-a^2-b^2-4x^2-2ab+2ax+2bx)(a+b)
(2b^2+4bx+2ab-4ax)a=(4bx-2ab+2ax+2bx)(a+b)
(2b^2+4bx+2ab-4ax)a=(4bx-2ab+2ax+2bx)a+(4bx-2ab+2ax+2bx)b
2ab^2+4abx+2a^2b-4a^2x=4abx-2a^2b+2a^2x+2abx+4b^2x-2ab^2+2abx+2b^2x
2ab^2+2a^2b+2a^2b+2ab^2=2a^2x+4a^2x+2abx+4b^2x+2abx+2b^2x
x=(2ab^2+4a^2b+2ab^2)/(2a^2+4a^2+2ab+4b^2+2ab+2b^2)
=(4ab^2+4a^2b)/(6a^2+4ab+6b^2)
=(2ab^2+2a^2b)/(3a^2+2ab+3b^2)
=2ab(a+b)/(3a^2+2ab+3b^2) >>292
�����A�u1/100�̊m���ƌ����Ă��܂��Ă��ǂ��̂ł��傤���B �v
�Ɛq�˂�ꂽ�Ȃ�A���ۂ�1/73�ʂ̊m���Ȃ̂ŁA���\�p�[�Z���g�̌덷�͂��邯�ǁA
�����Ȃ����Ƃ��Ȃ��ƕԎ����邩������܂���B���A
0.013678�@�Ɓ@0.0001�@�ł́A136�{�Ⴂ�܂��B�_���ł���B �S�P��
(A B C)(A B)(�b)�������͑Ή�
�S��
(A B C)(AB C)AB��A��B���Ή�
(A B)��AB
���̎�������S�˂͑S�P�˂ɕϊ��ł���Ƃ����邩�H >>281
�V�~�����[�V�����v���O������100�������Ĉ��������̕p�x���o���Ă݂��B
x=c(1:10,12,15)
sim <- function() sum(replicate(16, sum(x[sample(12,6)])))==656
k=1e6
mean(replicate(k,sim()))
> mean(replicate(k,sim()))
[1] 0.013522 >>296
���݂܂���A�P���Ȋ��Ⴂ���Ă܂����B
�������肪�Ƃ��������܂��B >>299
�����S�R�����ł��Ȃ��ł����ǁA���ʂ܂ŏo���Ē����Ă��肪�Ƃ��������܂��B
���̋��͂��Ē����������������肪�Ƃ��������܂����I�I�������g�ł����܂藝���ł��Ă��Ȃ���Ⴂ�Ȏ���ł��݂܂���ł����B �i1�j��>3�������B
�i2�j(1+1/n)^n��W�J���邱�Ƃɂ��Ae<3<�������B 5���~�̏��iA��6���~�̏��iB������B
A��B�����킹��200���~�ɂȂ�悤�ɂ������B
�������AA��B�͍��킹��320�w��������̂Ƃ���B
���̎�A��B�͂��ꂼ�ꉽ���w������悢���B
�m�b�����݂����������B
��낵�����肢�\���グ�܂��B �O>>295
>>303
�ܖ��~�̏��i�ɕS���\���B�Z���~�̏��i�ɎO�\���B�����قǂ��B
�ܖ��~�̏��i���O�\�l�ƘZ���~�̏��i���܌ɂȂ�܂���B���킹�ĎO�\��B
��T���v�������Ďl�\�Ƃ���B���l�̏]�҂��Q�点��B�����قǂ��B
�O�S��\�ɂ����Ȃ�܂���B
�t�ɘZ���~�̏��i�ɋ�\���A�ܖ��~�̏��i�ɕS�\���B�����قǂ��B
�Z���~�̏��i���\�܌ƌܖ��~�̏��i����\��B���킹�ĎO�\���ɂȂ�܂���B
����ȁB�Z���~�̏��i���܌ƌܖ��~�̏��i����\���ɂ��Ă͂����قǂ��B
�O�\���ƕS�O�\�ܖ��ŕS�Z�\�ܖ��~�ɂȂ�܂���B
���Ƃ̎O�\�ܖ��͐l����ɓ��Ă�悢�ł͂Ȃ����B����Ƃ��ۂ��ۂɓ���邩�B
�͂����͂��͂��c�c�B
�͂����͂��͂��c�c�B n�������̂Ƃ���
�@n=2m (m�͊�A�������q�������Ȃ�)
�ƕ\�킹��B�@�@�@>>291
���̂Ƃ�
�@��[k=1,n-1] mod(k^2,n) = 2��(������]) - (n/2),
�܂�
�@��(������]) + ��(���]) = 1+2+����+(n-1) = n(n-1)/2,
�Em=4q+1 �̏ꍇ
�@��(������]) - ��(���]) = m,
�@��(������]) = mm,
�@��[k=1,n-1] mod(k^2,n) = n(n-1)/2,�@�@(����)
�Em=4q+3 �̏ꍇ
�@��(������]) - ��(���]) = -m,
�@��(������]) = m(m-1),
�@��[k=1,n-1] mod(k^2,n) = n(n-3)/2,�@�@(�s����) ����Ȃɘb����Ȃ킯�Ȃ��B
issqare n = (==n) $ (^2) $ truncate $ sqrt n
ss n = (2*) $ sum [mod (k^2) n | k<-[1..n]]
rec n =(n, ss n, n*(n-1))
main = do
mapM_ print $ take 30 $ map rec [
(1,0,0)
(2,2,2)
(3,4,6)
(4,4,12)
(5,20,20)
(6,26,30)
(7,28,42)
(8,24,56)
(9,48,72)
(10,90,90)
(11,88,110)
(12,76,132)
(13,156,156)
(14,154,182)
(15,140,210)
(16,112,240)
(17,272,272)
(18,258,306)
(19,304,342)
(20,260,380)
(21,364,420)
(22,418,462)
(23,368,506)
(24,296,552)
(25,500,600)
(26,650,650)
(27,576,702)
(28,588,756)
(29,812,812)
(30,730,870) ����͊ȒP��������
>>302
(1)�@�� (�~�̎���)/(���a) �Ƃ���B
�P�ʉ~�ɓ��ڂ��鐳�W�p�`���l���A���_��
�@(1,0)�@(1/��2,1/��2)�@(0,1)�@����
�Ƃ���B��ӂ̒�����L�Ƃ����
�@�� > 4L = 4��{(1/2)+(1-1/��2)^2} = 4��(2-��2) > 4/��(��3) = 3.0393
*)�@2-��2 > 1/��3 = 0.57735
�P�ʉ~�ɓ��ڂ��鐳12�p�`���l���A���_��
�@(1,0)�@((��3)/2,1/2)�@(1/2,(��3)/2)�@(0,1)�@����
�Ƃ���B��ӂ̒�����L�Ƃ����
�@�� > 6L = 6��{(1/2)^2 + (1-(1/2)��3)^2} = 6��(2-��3) > 6��{(��7)/10} = 3.0862
*)�@2-��3 > (1/10)��7 = 0.264575
(2)
�@(1+1/n)^n = ��[k=0,n] �b[n,k] (1/n)^k
�@= ��[k=0,n] {n(n-1)����(n-k+1)/(n^k)} (1/k!)
�@< ��[k=0,n] 1/k!
�@< ��[k=0,��] 1/k!
�@< 1 + 1 + (1/2)��[k=2,��] 1/3^(k-2)
�@= 2.75
�@n���� �Ƃ���B (1)�͐�6�p�`�� 3 �ɂȂ��� ��12�p�`(��6�p�`�̊e�ӂɉ���������) ���Ƃ�����m���ɑ傫������
���Ă̂���_������ >>310
���\��p�`���炢��Ȃ���K�X�B �����Ǝv�����ǁ@>>314 �̈ӌ����Ă݂悤�B
>>309
�@4 - (��2 + 1/��3)^2 = (5-2��6)/3 = (��25 - ��24)/3 > 0,
�@4 - {��3 + (��7)/10}^2 = (9.3 - 2��21)/5 > (��86 -��84)/5 > 0, M���������l�̂Ƃ���
A_p={q��M : p��q��piecewise�����Ȑ��Ō��ׂ�}
�Ƃ������Ƃ�A_p�͊J�W���ł��邱�Ƃ������Ă������� >>245�̓�����>>295�ł͂Ȃ��̂����H >>313
�C�ӂ� x (�� A_p) �ɑ��ċǏ����W�n(U,��)�Ƃ����Ɋ܂܂��J��S[x] (���S:��(x)) ���l����.
V[x] := ��^{-1}(S[x]) �Ƃ���. ����� M��̊J�W���ł���.
�C�ӂ� y (�� V[x]) �ɑ��� ��(x)�ƃ�(y)�����ԃp�����[�^���� line(t) �� S[x] �Ɋ܂܂�,
p����x �Ɏ���Ȑ��� ��^{-1}(line(t)) �ڂ������� y �� A_p .
����� V[x] �� A_p �ł���, A_p = ��{x �� A_p} V[x] �͊J�W���ł���. ���ʂɖ�������
�ꎞ�Ɨ��ȗȒP�ɖ������邾�� ���d��͎g�������ƂȂ��̂ł����A
���̖��Ӗ���������܂���B
�ڂ���������肢���܂��B
https://imgur.com/tdh3DkC >>318
�����̃w�b�^�N�\�Ȗ��wwwww
���芴�����Ȃ�wwwwww print $ exp $ (/3) $ log $ 3
1.4422495703074085
print $ (!!100) $ iterate (sqrt.sqrt.(*3)) 1
1.4422495703074083 >>318
��̓d��v�Z��
�Q���� a[n+1] = a[n]^{1/4} * 3 ���\���ċA�v�Z�ɑ�������.
�����l�����l�ł���Ώ�ɓ����l �� �Ɏ������邱�Ƃ�,
�O���t y=x^{1/4}*3 �� y=x �̊T�`���疾�炩�ł���.
���̎� �� = ��^{1/4} * 3 �����藧��.
����� �� = 3^{4/3} ��������.
���l�ɑQ���� a[n+1] = a[n]^{1/8} * 3 �̏ꍇ��
�� = ��^{1/8} * 3 �����藧��
�� �� = 3^{8/7} = 3^{1/7} * 3
�܂�
�u�� �L�[�� 3 ���Ă��� 3�|����v ���J��Ԃ�
�K�v�Ȍ����܂ł̒l�ω��������Ȃ����� 3�Ŋ���.
����� 3^{1/7} (�̋ߎ��l) ��. >>321
log_3(a[n]) = b[n]�@�Ƃ����B
�@a[n+1] = a[n]^(1/4) * 3�@�̂Ƃ�
�@b[n+1] = (1/4) b[n] + 1,
�@b[n+1] - 4/3 = (1/4) (b[n] - 4/3)
�@�@�@�@�@�@= (1/4^n) (b[1] - 4/3)
�@a[n+1] = �� * (a[1] /��)^(1/4^n)�@���@��=3^(4/3)
�@a[n+1] = a[n]^(1/8) * 3�@�̂Ƃ�
�@b[n+1] = (1/8) b[n] + 1,
�@b[n+1] - 8/7 = (1/8) (b[n] - 8/7)
�@�@�@�@�@�@= (1/8^n) (b[1] - 8/7)
�@a[n+1] = �� * (a[1] /��)^(1/8^n)�@���@��=3^(8/7)
x=�� �ł� y=x^(1/m) �̌X�� <1�A�z���I
x=0 �ł� y=x^(1/m) �̌X�� >1�A�����I a,b,c,d�͎����Ƃ���B
ax+b>c
bx^2+cx+a>0
cx^3+ax+b>0
�����ׂĖ���������x�̏W���ƁAd<x��������x�̏W������v���Ă���B
�i1�ja,b,c�̕��������ꂼ�꒲�ׂ�B+,0,-�̂����ꂩ2�ȏ����肤��ꍇ�́u�s��v�Əq�ׂ�B
�i2�jd�͂ǂ̂悤�Ȓl�����q�ׂ�B >>321
���e�ɂ��肪�Ƃ��������܂��B
�ŋ߂͐��w�\�t�g����g���Ă����̂ŁA
������͂����Ƃ��A����܂ł̒l���ۑ�����A
����ɓ��͂���ƁA���̒l�ɑ��鉉�Z�ɂȂ�
���Ƃ�Y��Ă��܂����B
�ӂ��̓d��ł������ł��ˁB
�� = 3^{4/3}�@�� �@�m�F���܂����B �W�� X ��ɉ��@+�ƌĂ����Z���`���A�Ȃ�����+�́A
1. ����������
2. ����������
3. ���@�P�ʌ�0�����݂���
4. X�̂��ꂼ��̗v�fx�ɑ��āA���̉��@�t��-x�����݂���
�������̂Ƃ��܂��B
�܂��AX�̂��ꂼ��̗v�fx�ɑ��āA���̎��R��n�{���A
�@nx=x+�c+x�@�in��x�̘a�j
�ƒ�`���܂��B
�ȏ�̐ݒ�̂��ƁAX�̗v�fx�Ǝ��R��n�����ꂼ��C�ӂɑI�Ƃ��A
ny=x
����X�̗v�fy�̑��݂�ۏł��܂����H
�ł���ꍇ�ɂ́A�X�P�b�`�ł��悢�̂ŁA�ؖ��������Ē�����K���ł��B >>325
�W�� X �Ƃ��Đ����̏W�����ɂƂ�����H >>326
���肪�Ƃ��������܂��B
������₷������ł��ˁB
�ƂĂ�������܂����B N��1���傫�������̂Ƃ��A���f���╡�f���ʂ��g�킸��
cos(1�~2��/N)+cos(2�~2��/N)+�E�E�E+cos(N�~2��/N) = 0
���ؖ�����B
N�������̎��͒P�ʉ~��N�������Ă݂�ΑΏ̐����炷���ؖ��ł��܂��B
N����̎�������ĔY��ł��܂��B
���肢���܂��B
�w�I�ɉ����̂��A�O�p���̌�������g���ĉ����̂��A���w�I�A�[�@�́uN�v������ɂ��邩�����������E�E�E�E�B
���f���ʂ��g���Ώؖ��͊ȒP�ł��B
exp[i(1�~2��/N)]�Aexp[i(2�~2��/N)]�A. . . exp[i(N�~2��/N)]
��N��������
x^N-1=0
�̉��Ȃ̂ʼn��ƌW���̊W����
exp[i(1�~2��/N)]+exp[i(2�~2��/N)]+�E�E�E+ exp[i(N�~2��/N)]=0
�ƂȂ�܂��B����̎�����
cos(1�~2��/N)+cos(2�~2��/N)+�E�E�E+cos(N�~2��/N) = 0
�ł��B ���f���ʂȂg��Ȃ��Ă��ȒP�ł�������
N��2 ��� sin(��/N) >0,
�Ϙa����
�@2sin(��/N)�Ecos(2k��/N) = sin((2k+1)��/N) - sin((2k-1)��/N),
�� k=1,2,����N �ł����B >>329
�s��: M :={(cos(2��/N), -sin(2��/N)),( +sin(2��/N), +cos(2��/N))} �ƒu����
M^k = {(cos(k2��/N), -sin(k2��/N)),( +sin(k2��/N), +cos(k2��/N))} (�A�[�@�Ŏ�����)
S := M + M^2 + ... + M^N �ƒu����...
MS = M^2 + M^2 + ... + M^{N+1}
(M-1)S = M^{N+1} - M = M - M = 0
det(M-1) = (c-1)^2 + s^2 = 2 (1-c) = 4 sin(��/N)^2 ��� S = 0
S��[1,1]������� cos(1�~2��/N)+cos(2�~2��/N)+�E�E�E+cos(N�~2��/N) = 0 ��. ���ʃ���ɖʐ�1�́�ABC������B
����ɓ_P���Ƃ�A
m����PAB+��PBC+��PCA��n�c(F)
�ƂȂ�悤�ɂ������B
������3�_X,Y,Z���꒼����ɂ���Ƃ��A��XYZ=0�Ƃ���B
�i1�jm,n�͎��R���Ƃ���B(F)�𐬂藧������P�����݂���悤��n�̍ŏ��l�����߂�B
�i2�jm�́i1�j�ŋ��߂�n�ɓ������Ƃ���B(F)�����悤��P�������Ƃ��AP����������̈�̖ʐς�m,n�ŕ\���B �Ȃɂ��ǂ���������Ă�̂�1�~�����킩���B ���N�̓���̃p�N���݂����Ȗ�肪����ł�� ���ʃ���ɖʐ�1�́�ABC���Œ肳��Ă���B
�ȉ��A��XYZ�̖ʐς�S�̂Ƃ���XYZ=S�Ə����B�܂�3�_X,Y,Z���꒼����ɂ���Ƃ��A��XYZ=0�Ƃ���B
�i1�j����̔C�ӂ̓_P�ɑ�
m����PAB+��PBC+��PCA
�𐬗����������m�̒��ŁA�ő�̂��̂�M�Ƃ���B
M�����߂�B
�i2�jN��M���傫�����R���̒萔�Ƃ���B�����
M����PAB+��PBC+��PCA��N
�����悤��P�������Ƃ��AP����������̈�̖ʐς�N�ŕ\���B �@�@�@
�y���w�z�@���N�̓���̓������ȒP�������@��������Ȃ��l���Ă���́c�c�H
http://hayabusa9.5ch.net/test/read.cgi/news/1582861742/
�@�@�@�@ g��n�������s��Aj��n�������s��Ƃ���
t(g)jg=j�Ȃ�g�̑S�̂͌Q�ł����H >>339
���Aj�͌Œ肳��Ă܂��A��s��ł� >>329
cos(1�~2��/N)+cos(2�~2��/N)+�E�E�E+cos(N�~2��/N)
=2sin((N+1)��/N)sin��/2sin(��/N)
=0 cos(1�~2��/N)+cos(2�~2��/N)+�E�E�E+cos(N�~2��/N)
=2sin((N+1)��/N)sin��/sin(��/N)
=0 cos(1�~2��/N)+cos(2�~2��/N)+�E�E�E+cos(N�~2��/N)
=sin((N+1)��/N)sin��/sin(��/N)
=0 �R���i�����̊m���Ƃ����Ғl�Ƃ��^�ʖڂɍl�����l���Ă���H >>245
���]�~�̕��@�ŋ��߂Ă݂��B
(�L���ɂ��Ă͐} https://imgur.com/dMxFIRN ���Q��)
r/R = OP/OQ�@{�����}�`}
�@= (a+b)^2 /OQ^2�@{���]�~}
2R = (a+b)^2/a - (a+b) = (a+b)(1+b/a)-(a+b) = (a+b)(b/a)
OQ^2 = OT*OS�@{���ׂ��̒藝}
�@= OT*( OT - 2R*cos(t) )�@= OT^2 - 2R*OT*cos(t)
�@= ((a+b)^2/a)^2 + (n*2R)^2 - 2R*(a+b)^2/a
�@= (a+b)^2 ((1+b/a)^2 - (1+b/a)(b/a)) + n^2* (a+b)^2(b/a)^2
�@= (a+b)^2 ( 1+b/a + n^2*(b/a)^2 )
�����
r = (1/2) (a+b)(b/a) / ( 1+b/a + n^2*(b/a)^2 ) = (1/2) ab (a+b) / ( a^2 + ab + n^2*b^2 )
(���łȂ̂� n�����ډ~�̔��a�����߂�) >>331
>>329�ł�
���肪�Ƃ��������܂��B���ӂ��܂� >>344
cos((N+1)��/N)sin��/sin(��/N) �o��シ���ɉ��o�ďI������b�ɂ��܂ŔS�����Ă�́H >>349
����͉�@����ɏo�Ă邾���ł͂Ȃ����ɂ���
���I�}�G�ɂ͋����Ă���
�u�I������v�Ǝv���Ă�Ⴂ���� >>339
�Ȃ��gg'�����̎����藧�����邩�ǂ����m���߂�́H
�����Ƃ����̂�g^-1g'������ g �� g' �����̏W���̗v�f�Ȃ��
�@t{g^(-1) g'} = t(g') t{g^(-1)},
���
�@t{g^(-1) g'} j {g^(-1) g'}
�@= t(g') [ t{g^(-1)} j g^(-1)] g'
�@= t(g') j g'
�@= j.
���@g^(-1) g' ���v�f�B
n���P�ʍs����v�f�B(�P�ʌ��ƂȂ�)
�s��j�ƍ����ȍs��̑S�̂͌Q���Ȃ��B �� �s��j�̍����ϊ��̑S�̂͌Q���Ȃ��B
�ɒ��� >>331
�Ϙa�������
�@cos(k��) = {sin((k+1/2)��) - sin((k-1/2)��)}/{2sin(��/2)},
�����
�@cos�� + cos(2��) + ���� + cos(N��)
�@= {sin((N+1/2)��) - sin(��/2)}/{2sin(��/2)}
�@= cos((N+1)��/2)�sin(N��/2)/sin(��/2), x�𐳂̎��萔�Ƃ���B
a[1]=x
a[n+1]=x^a[n]
�ɂ�萔��{a[n]}���`����B
lim[n����] a[n] ����������Ƃ��Ax����肤��l�͈̔͂����߂�B >>315
�Ȃ�ق�
���͉���������ʂ��������������ɂȂ��ĂȂ��������ł���
���肪�Ƃ��������܂� >>345
R��SEIR MODEL
dS(t)/dt = mu*(N-S) - b*S(t)*I(t)/N - nu*S(t)
dE(t)/dt = b*S(t)I(t)/N - (mu+sig)*E(t)
dI(t)/dt = sig*E(t) - (mu+g)*I(t)
dR(t)/dt = g*I(t) - mu*R + nu*S(t)
mu:���R���S�� b:������(S->I)
nu:���N�`���L����(S->R) sig:���Ǘ�(E->I),g:��(I->R)
�Ńv���O������g��ŃN���[�Y�D�ɕ����߂Ă������Ƃ��̎����\�z���������ƗV��ł݂��B
Javascrpt�ł̃O���t�\������y�[�W���������B
http://www.public.asu.edu/~hnesse/classes/seir.html
���ǁA������������킩��Ȃ�������p�I�ł͂Ȃ������B >>351
t(gg')j(gg')=t(g')t(g)jgg'=t(g')jg'=j
t(g)jg=j�̍��E����t��������t(g^-1)jg^-1=j
�Q�ɂȂ肻���Ȃ�ł���������Ƃ���Ŗ{���ɗǂ��̂�������Ȃ������̂ŕ����܂��� �����@�����������Z�ɂ��ĕ��Ă���
�P�ʌ��Ƌt�������邱�Ƃ���������
�y�Ȃ̂�
�����@���������Z�ɂ���g^-1g'�ƒ�`�������Z�ɂ��ĕ��Ă��邱�Ƃ���������
���R�ɒP�ʌ��Ƌt���̑��݂������� >>358
>�Q�ɂȂ肻���Ȃ�ł���
���łȂ�Ȃ������m��Ȃ��Ǝv���̂��m��Ȃ� >>355
�@(1/e)^e �� x �� e^(1/e),
�ߎ��l�@0.065988035 �� x �� 1.44466786
�Q�l��
���Z�~�����u���w�̖��v��(1)�W, ���{�]�_�� (1977)�@��112
���Z�~�����u���w�̖��v��(2)�W, ���{�]�_�� (1978)�@�t�^1 (�W�����Y)
K.Knopp: "Theorie und Anwendung der unendlichen Reihen" (��5�łȂ� p.110) a>0��萔�Ƃ��Ax>0��
x^a=log(a)x [a���Ƃ���ΐ�]
�̉��̌������߂�Ƃ�������
e^(1/e)�����̂�����ɋ��E�������Ă��̑O���3��1�ƕς��炵���̂ł���
�F�X�����Ă݂���ł�����̓I�ɉ����菇���S�R�킩��܂���
�����m�̕����肢���i�X >>362��
a^x=log(a)x [a���Ƃ���ΐ�]
�������ł��B
�����܂���ł����B���ӂ�xy���ʂɃv���b�g�����y=x�ɑ��Ώ̂ł� >>357
�����A���������w��w
�����������Ăق������̂ł���ˁ` e^(1/e)=1.44466786101
���ꂾ����v�Z�ԈႢ�������ԈႢ��� �����͕����Ă���̂ł�����@���킩��Ȃ��Ƃ������Ƃł�
>>364�������̂ł��������݂̂ł���
��̓I�ȉ�@�������m�̕����炵���炨�肢�������܂� >>368
���肪�Ƃ��������܂��I�I�I������Ȃ�
���ɂ������̂ł��ˁc�����Ƃ��Ă���܂��� https://rio2016.5ch.net/test/read.cgi/math/1543158054/143
������2�s�ڂ̂Ƃ��ł��傢�v�Z�~�X�B a = e^{-1/e} �Ƃ��ׂ��������B AB=4�ABC=6�ACA=5�́�ABC�̊O�ډ~��K�Ƃ���B
�܂�K��ɓ_D������ABD��K�̒��a�ł���B
�_A���܂܂Ȃ�����K�̌ʂ̏��BE=5�ƂȂ�_E���Ƃ�AE����BD�ɐ��������낵����_��H�Ƃ���B
AH�̒��������߂�B >>363
0 < a < e^(-e) �@�̂Ƃ��R��
e^(-e) �� a < 1�@�̂Ƃ��P�@{a=e^(-e) �̂Ƃ� (1/e,1/e)}
a = 1�@�@�@�@�@�̂Ƃ��H�@�@log_a ���`�ł��Ȃ��B
1 < a < e^(1/e)�@�̂Ƃ��Q��
a = e^(1/e)�@�@�@�̂Ƃ��P�@(e,e)
e^(1/e) < a�@�@�@�̂Ƃ��O��
(����)�@�����X���S�S�X�� 143 �� 170
�@e^(1/e)�@���@e^(-e) >>371
a:=BC=6, b:=CA=5, c:=AB=4
AH^2 = c*c + BH^2 - 2*c*BH* cos��ABH {�]���藝}
cos��ABH = cos��ABD = c/BD = c/b*(b/BD)=c/b*sin��B {�����藝}
BH = BE*cos��EBH = b*sin��BDE = b*sin��B
cos��B = (a*a+c*c-b*b)/(2*a*b) {�]���藝}
�����
AH = sqrt(c*c + (b*b -2*c*c)*(sin��B)^2 )
= sqrt( c*c + (b*b -2*c*c)*( 1- ((a*a+c*c-b*b)/(2*a*c))^2 ) )
= 3/16* sqrt(319) = 3.348857... >>371�̏����I�ؖ�
�g���~�[�̒藝�ɂ��O�ډ~�̒��a��16/��7
���Ƃ͏����v�Z���邾���B
������>>373�ɓ����B BD sin��B = BD sin��BDE = BE = 5
�� BD = 5 / sin��B = 5 / ��{1 - ( aa+cc - bb )^2/( 2ac )^2} = 16 / ��7
�O�ډ~�̒��a�� >>374 �Ɠ����ɂȂ�܂����B
�g���~�[�̒藝 ���g�����ߕ����C�ɂȂ�܂��B�N�������Ă��������B ���̓g���~�[�m��Ȃ����w�����ǂ�����ĉ����̂��m�肽���� �O>>314
>>371
�]���藝���A
cosA=(4^2+5^2-6^2)/2�4�5
=25/40
=5/8
sinA=��(64-25)/8
=��39/8
2R=BD=BC/sinA
=6�8/��39
=48/��39
��BEH�䁢BDE���A
BE:BH=BD:BE
BH=BE^2/BD
=25��39/48
A����BD�ւ̐���AF=AB(AD/BD)
=4�4��(35/13)/(48/��39)
��AD=��(BD^2-AB^2)
=��(48^2/39-16)
=��(12^2�4^2-39�16)/��39
=4��(144-39)/��39
=4��35/��13
AF=��105/4
BF=��(4^2-105/16)
=��151/4
FH=BH-BF
=BE(BE/BD)-BF
=5(5��39/48)-��151/4
=(25��39-12��151)/48
AH=��(AF^2+FH^2)
=��{105/16+(25��39-12��151)^2/48^2}
=2.56809247�c�c
�ʂ̎O�p�`�̑����ł���āAAH=2.87469999�c�c�̉\��������B
�}���琳�����̂͂��̓�̂ǂ��������ƁB �O>>378�����B
>>371
�]���藝���A
cosA=(4^2+5^2-6^2)/2�4�5
=5/40
=1/8
sinA=��(64-1)/8
=3��7/8
2R=BC/sinA=BD
=6�8/3��7
=16/��7
��BEH�䁢BDE���A
BE:BH=BD:BE
BH=BE^2/BD
=25��7/16
A����BD�ւ̐����̑���F�Ƃ���ƁA
BF=AB^2/BD
=16��7/16
=��7
FH=BH-BF
=25��7/16-��7
=9��7/16
AF=��(AB^2-BF^2)
=��16-7
=��9
=3
AH=��(AF^2+FH^2)
=��(9+81�7/256)
=��9(256+63)/16
=3��319/16
=3.34885708�c�c >>363
y=a^x=log[a]x
x=log[a]y=a^y a,b�������̒萔�Ƃ��A
f(x)=x^2+ax+b
g(x)=4x(1-x)
�ƒ�߂�B�܂�n=1,2,...�ɑ�g_{n}(x)��
g_{n}(x)=g(g_{n-1}(x)), g_{0}(x)=x
�ɂ���`����B
���̂Ƃ��ȉ�����f(x)��S�ċ��߂�B
�w0<t<1/2�ł������t�����݂��A���ׂĂ�n�ɑ���
f(g{n}(t)) = g{n}(t)
�ƂȂ�B�x �X���Ⴂ��������܂��A��ʓI�ȍl�����������Ă��������Ȃ��ł��傤���H
https://i.imgur.com/fKR9UzG.png
�}�̂悤�Ȍ�Ղ̖ڏ�ɋ��ꂽ�}�̂悤�ȊX�H������B
��������E��֍ŒZ�o�H�Ō������l�ƁA�E�ォ�獶���֍ŒZ�o�H�Ō������l������ŏo��m���͂����炩�H
�������A��l�Ƃ������ɏo�����ē������x�ŕ������̂Ƃ��A�����R�[�X�͍ŒZ�R�[�X�̒����烉���_���ɑI�Ԃ��̂Ƃ���
���͍ŒZ�����őΊp�ɒ����܂ł̑S�o�H�̐���20�ʂ�A����ɐi�މ\���͂��ꂼ��1/20�Ȃ̂ŁA1/20�~1/20��1/400
�ƍl���܂����B
�������A������1/64�ŁA
�����ǂނƂ��ꂼ�ꂪ3��Ԑi�ۂɍ����ʂ�m���͂��ꂼ��1/8�Ȃ̂ŁA1/8�~1/8��1/64�ƂȂ��Ă��܂����B
�u�����R�[�X�͈��Ԑi�ނ��ƂɍŒZ�R�[�X�̒����烉���_���ɑI�Ԃ��̂Ƃ���v
�ł�����ꂼ��̍���ʉߊm����(1/2)^3=1/8�ŊԈႢ�Ȃ��Ƃ͎v���̂ł����A
�u�����R�[�X�͍ŒZ�R�[�X�̒����烉���_���ɑI�Ԃ��̂Ƃ���v
�Ƃ������͂�ǂ�20�R�[�X���烉���_���ɑI�Ԃƍl���Ă��܂�
���ꂼ��̍���ʉߊm����1/20�ƍl���܂����B
������Ɠ����c�O�Ȃ̂ŕ��͖��������̂��̂�����Ȃ̂ł����A
���ʂ̐l�͂��̕��͂�ǂ݂��ꂼ��̍���ʉߊm����1/8�Ƃ����ɂ킩��̂ł��傤���H >>382
�u�����_���v�̉��߂���ӂłȂ���Ζ�蕶�ɕs��������
�t�ɁA�ł��̗��R�L����1/400�Ə������Ȃ����͐����Ƃ��ׂ� �O>>379
��������E��ɍs���l�������ʂ�m���́A
�ŏ��̕���ō��E1/2���̊m���ō���I�сA
���̕���ō��E1/2���̊m���ō���I�сA
3��ڂ̕���ō��E1/2���̊m���ō���I�Ƃ�������A
(1/2)(1/2)(1/2)=1/8
�E�ォ�獶���ɍs���l�������ʂ�m���́A
�ŏ��̕���ō��E1/2���̊m���ʼnE��I�сA
���̕���ō��E1/2���̊m���ʼnE��I�сA
3��ڂ̕���ō��E1/2���̊m���ʼnE��I�Ƃ�������A
(1/2)(1/2)(1/2)=1/8
��������E��ɍs���l�ƉE�ォ�獶���ɍs���l���o�����m���́A
(1/8)(1/8)=1/64
=0.015625
1.5625��
�����ɉ��������Ă��قƂ�Lj����Ȃ����B
�o�����̊m����1-1/e
63�������Ă����̂ɁB >>379
�@�����ł��B
�@(���N���߂Ă���ˁH) �O>>384
>>385�����ĂĂ悩�����B
���[�Ȑ��l������Ⴄ�̂��Ǝv�����B
���̑O��a��b�ŕ\���������̂�������Ă邾��H
�Y��Ȍ`�����A������Ⴄ���Č���Ȃ�����Ȃ����B �O>>386
>>379�����B����()���������B
��(16-7) >>376
AE=6������ABD=a�Ƃ����āA�l�p�`ABED�Ƀg���~�[�̒藝��K�p����悢�B 1����7�܂ł̐�����1�������ꂽ�J�[�h������B�����̃J�[�h��
1�A2�A3�A4�A5�A6�A7
�̏��ɕ���ł���B
���̎��A���ׂẴJ�[�h���ŏ��̈ʒu�ƈႤ���ѕ��͉��ʂ肠�邩�H
���̖��킩�����������Ⴂ�܂����H >>388 ���肪�Ƃ�
6x = 5��(xx - 4^2) + 4��(xx - 5^2)
6x - 5��(xx - 16) = 4��(xx - 25)
36xx + 25 (xx - 16) -60x ��(xx - 16) = 16(xx - 25)
45x = 60��(xx - 16) ...
7xx = 16^2
�� x = 16/��7
���͑㐔�v�Z��i�߂Ă���������̂��D���Ȃ�ł����A
���̏ꍇ�͂������Ɛ��l����Čv�Z�����ق����y�ł��ˁB
x = a / sinA = a / ��{ 1- (cosA)^2} = a / ��{ 1 - (bb+cc - aa)^2 / (2bc)^2 }
�@= 2abc / ��{ ((b+c)^2 - aa)( aa - (b-c)^2 ) }
�@= 2abc / ��{ 2((ab)^2 + (bc)^2 + (ca)^2) - a^4 - b^4 - c^4 ) {�Ώ̎�!!}
�����܂ŗ��Ă��琔�l��������̂͋�s�ł��B >>391
���肪�Ƃ��������܂��B
�ł����A���̓��ł͂�����̃T�C�g�����Ă���@���v�����܂���ł����c �p���h�b�N�X�H�H�H
���L���ł����A
https://imgur.com/a/0765i7e
�Ɍ��l�����Ƃ����
(��2)^x��x �Ƃ�����̂ŁA���ӂ̑ΐ����Ƃ��ĕό`�����
logx^(1/x)��log2^(1/2) �ƂȂ���
x=2 �����ɂȂ��Ă��邱�Ƃ͕�����܂��B
�Ƃ��낪�A(��2)^x��x�@�̉����O���t��
�l�����
y��(��2)^x�@�E�E�@�@�@�Ɓ@y=x �E�E�A�@�̌�_�̂����W������
���邪�Ax=2�ɂ�����@�̔����W���͂P��菬�����̂�
���̓_�ł͐ڂ��Ă��Ȃ��B�܂������Ă���B
�@�͂����傫���Ɣ����W�����P���傫���Ȃ��Ă����̂ŁA
�����P�ӏ������Ƃ��낪����͂��B���̂Ƃ��̂����Ɍ��l�Ƃ�������
�ɂȂ�A�Ɍ��l���Q���邱�ƂɂȂ��Ă��������B
����͂ǂ����ԈႢ�ł����B >>395
logx^(1/x)��log2^(1/2)�ł�����2���邩��u�Ƃ��낪�v�Ƙ_����̂͂Ȃ��������悤�Ɏv��
���̓_�͕ʂɂ��āA�u(��2)^x��x�Ƃ����Ă���������悢�v���Ă̂͋Ɍ�����������Ƃ킩���Ă���ꍇ�Ȃ�Ȃ����H �⑫���܂��B
��logx^(1/x)��log2^(1/2)�ł�����2���邩��u�Ƃ��낪�v�Ƙ_����̂͂Ȃ��������悤�Ɏv��
���̂܂܂̌`�ł͉����Q�ł��邱�Ƃ͕����邪�A�Q���邱�Ƃ�������܂���B
�Ƃ��낪�Alogx^(1/x)��log2^(1/2)���O���t�ōl����ƁA�Ɍ��l�͂P�ł���͂��Ȃ̂�
�Q�̉������邱�Ƃ��͂����肷��B
�Ƃ����Ӗ��ł��B
�����̓_�͕ʂɂ��āA�u(��2)^x��x�Ƃ����Ă���������悢�v���Ă̂͋Ɍ�����������Ƃ킩���Ă���ꍇ�Ȃ�Ȃ����H
�m���ɂ��̖��͋Ɍ��l�����݂���Ƃ��ĉ����̂͘_���I�ł͂Ȃ��ł����A
���ɕ��@�͂���܂����H�@
�u�Ɍ��l������Ƃ���A���ꂪ�Q�ł��邱�Ƃ��ؖ�����v�̂���ō��ꂽ���̉\���͂Ȃ��ł����ˁB �Ɍ��l�����݂���Ƃ������肪�U�����牽���N���Ă��s�v�c����Ȃ�
�Ɍ��͖����傶��Ȃ��́H >>395
> �����P�ӏ������Ƃ��낪����͂��B���̂Ƃ��̂����Ɍ��l�Ƃ�������
���� >>398
�Ɍ��l���Q�ł��邱�Ƃ��ؖ�����
�Ƃ������Ȃ�ł��B ���肪�U�̂��̂��瓱�o���ꂽ����͕s��ł���
���ꂪ���������w�E�_���w�ł��� >>395
> �����P�ӏ������Ƃ��낪����͂��B���̂Ƃ��̂����Ɍ��l�Ƃ�������
����
�u�Q��ڂɌ����Ƃ���̂��̒l�͋Ɍ��l�ł͂Ȃ��v�Ƃ������Ƃł��ˁB
����͂ǂ�����Ď��������̂ł��傤���H >>394
1, 2, �c, n �̊��S����̐��� A_n �Ƃ���B
A_7 �����߂�悢�B
���� *, *, *, *, *, *, * ���ȉ��̂悤�ɕ\�킷���Ƃɂ���B
1, 2, 3, 4, 5, 6, 7 �������牽�Ԗڂ���\���C���f�b�N�X
*, *, *, *, *, *, *
1, i, *, *, *, *, *
i, *, *, *, *, *, *
�Ƃ����^�C�v�̊��S����̐��� B_7 �Ƃ���B
1, i, j, *, *, *, *
i, j, *, *, *, *, *
�Ƃ����^�C�v�̊��S����̐��� B_6 �Ƃ���B
1, i, j, k, *, *, *
i, j, k, *, *, *, *
�Ƃ����^�C�v�̊��S����̐��� B_5 �Ƃ���B
1, i, j, k, l, *, *
i, j, k, l, *, *, *
�Ƃ����^�C�v�̊��S����̐��� B_4 �Ƃ���B
1, i, j, k, l, m, *
i, j, k, l, m, *, *
�Ƃ����^�C�v�̊��S����̐��� B_3 �Ƃ���B
1, i, j, k, l, m, n
i, j, k, l, m, n, *
�Ƃ����^�C�v�̊��S����̐��� B_2 �Ƃ���B >>394
1, 2, *, *, *, *, *
2, *, *, *, *, *, *
�Ƃ����^�C�v�̊��S����̐��͒�`�ɂ�� B_7 �ł���B
1, 2, *, *, *, *, *
2, *, *, *, *, *, *
�Ƃ����^�C�v�̊��S����̐��͒�`�ɂ�� B_7 �ł���B
1, 3, *, *, *, *, *
3, *, *, *, *, *, *
�Ƃ����^�C�v�̊��S����̐��͒�`�ɂ�� B_7 �ł���B
1, 4, *, *, *, *, *
4, *, *, *, *, *, *
�Ƃ����^�C�v�̊��S����̐��͒�`�ɂ�� B_7 �ł���B
1, 5, *, *, *, *, *
5, *, *, *, *, *, *
�Ƃ����^�C�v�̊��S����̐��͒�`�ɂ�� B_7 �ł���B
1, 6, *, *, *, *, *
6, *, *, *, *, *, *
�Ƃ����^�C�v�̊��S����̐��͒�`�ɂ�� B_7 �ł���B
1, 7, *, *, *, *, *
7, *, *, *, *, *, *
�Ƃ����^�C�v�̊��S����̐��͒�`�ɂ�� B_7 �ł���B
�� A_7 = 6 * B_7
1, i, *, *, *, *, *
i, 1, *, *, *, *, *
�Ƃ����^�C�v�̊��S����̐��� A_5 �ł���B
1, i, *, *, *, *, *
i, j, *, *, *, *, *
�Ƃ����^�C�v�̊��S����̐��͒�`�ɂ�� B_6 �ł���B
�� B_7 = A_5 + 5*B_6 �ȉ����l�ɂ��āA
B_6 = A_4 + 4*B_5
B_5 = A_3 + 3*B_4
B_4 = A_2 + 2*B_3
B_3 = A_1 + 1*B_2
B_2 = 1
�ƂȂ�B
�܂Ƃ߂�ƁA
A_7 = 6 * B_7
B_7 = A_5 + 5*B_6
B_6 = A_4 + 4*B_5
B_5 = A_3 + 3*B_4
B_4 = A_2 + 2*B_3
B_3 = A_1 + 1*B_2
B_2 = 1
���l�ɍl���āA
A_5 = 4*B_5
A_4 = 3*B_4
A_3 = 2*B_3
A_2 = 1*B_2
�ł���B
�������ƁA
A_7 = 6 * B_7
B_7 = 4*B_5 + 5*B_6
B_6 = 3*B_4 + 4*B_5
B_5 = 2*B_3 + 3*B_4
B_4 = 1*B_2 + 2*B_3
B_3 = 0 + 1*B_2
B_2 = 1
�ƂȂ�B
��
B_3 = 1
B_4 = 1 + 2*1 = 3
B_5 = 2 + 9 = 11
B_6 = 9 + 44 = 53
B_7 = 44 + 265 = 309
A_7 = 6 * 309 = 1854 A_n �� n ����ʂ̏ꍇ�ɋ��߂���@�́A�u������v�ׂĂ��������B
�m���A����a�v����̐��w�ǖ{�V���[�Y�Ɋ��S����i����j�ɂ��ďڂ������������܂����B �܂�A=A+1����
����͐��w�ł͂Ȃ�
�R���s���[�^���͎���
������˂��Y���Ő��w�E�_���w���q���� >>400
2�̂킯�Ȃ�����C�^�Y�����ł��� >>394
https://ideone.com/3uGXix
Python�Ń`�F�b�N���܂������ǂ���炠���Ă����悤�ł��B ���܂Ȃ�
�������Ⴂ���Ă����悤�ŋɌ���2�̂悤�� >>400
�Q����: a[1] = ��2, a[n+1] = ��2^a[n] (n��1) �Œ�`����鐔�� a[n] ���l����.
a[1] = ��2 < 2
a[n] < 2 �Ɖ��肷���
�@a[n+1] = ��2^a[n] < ��2^2 = 2
�@(x < 2) �ɂ����� x < ��2^x �Ȃ̂� a[n] < ��2^a[n] = a[n+1]
�A�[�@��� a[n] �� ��ɗL�E(< 2)�ȒP����������ł���. ����ċɌ��l a (��2) ������.
�Q�������ӂ̋Ɍ������� a = ��2^a
���� 2�� (a=2, a=4) �̂������� a ��2 �����̂�
a=2 �݂̂ł���B
�����
lim ��2^(((...(��2^(��2^��2))...))) = 2
�܂��O���t���疾�炩�����H�ƂȂ肪���ł����A�����ł�������킯�ł��B >>412
���肪�Ƃ��������܂����B
���������w�̃v���ł��ˁB >>395
�@f(x) = (��2)^x�@�@���� �@
�͉��ɓʂ�����Ax=2 �ł̐ڐ����㑤�ɂ���B
�@y > 2 + f '(2)(x-2),
�@0 < 2 - a[n+1]
�@�@< f '(2)(2-a[n])
�@�@< ����
�@�@< {f '(2)}^n�(2-a[1]),
f '(2) = log(2) = 0.693147 < 1�@��������� (�z���I) �m�C�}���������̂��̂悤�Ȓ�`�Ȃ̂��A�N���킩�����������Ⴂ�܂����H >>413
�w��1�N���x������@���Z�����H >>413
>>412�̂悤�ɒ莮�����ď����l�ɂ���Ăǂ��̕s���_�ɋz������邩���ς�邱�Ƃ��ώ@����̂͑�w���N�x���̂悭���鉉�K���̈�� >>414
2 - a[n+1] < f '(2)(2-a[n])
����͂Ȃ�ŁH
���̎��� 2 + f '(2)(a[n] - 2) < a[n + 1]
�ƂȂ邪
x=2�ɂ�����f(x)�̐ڐ���y = x�Ȃ�
a[n] < a[n + 1] < 2���
a[n + 1]��x���W��y���W�Ƃ݂Ȃ��Đ��藧���ǁA��������Ȃ����� �ȊO��a[n+1]=f(a[n])�^�̑Q���������������ł��Ȃ��l�����ȁB f(a[n+1]) = f(a[n])=(��2)^(a[n])�� >>418
> x=2 �ɂ�����f(x)�̐ڐ��� y=x �Ȃ�
�@x=2 �ɂ����� y=f(x) �̐ڐ��� y = f(2) + f '(2)(x-2) �ł��B
>>395 ��
�@f(x) = (��2)^x�@�@���� �@
�Ƃ������̂�
�@f(2) = 2,
�@f '(2) = log(2) = 0.693147���
�ł�
>�@x=2 �ɂ�����@�̔����W���͂P��菬�����̂ł��̓_�ł͐ڂ��Ă��Ȃ��B
>�@�܂������Ă���B
�ł��B
�@y=f(x) �͉��ɓʂ�����A
�@f(x) �� f(2) + f '(2)(x-2) = 2 + f'(2)(x-2),
���āA�{��ɖ߂���
�@a[n+1] = f(a[n]) > 2 + f '(2)(a[n]-2),
���@2 - a[n+1] < f '(2)�(2-a[n]) < ���� ���ꌩ��Ⴗ���킩���
a(n+1)=(��2)^a(n)�Ƃ���
a(0)��2�Ȃ�a(��)=2
2<a(0)��4�Ȃ�a(��)=4
https://i.imgur.com/PG4Kxwx.jpg ���������������u�O���t�������ĊK�i���y=x�ɔ��˂�����悤�Ȍ`�œ_���v���b�g���Ă����Ύ������킩�肻���v�Ȃ����
��ʂɂǂ������ΊȌ��Ɏ�����낤���H �@a[0]<4�@�̂Ƃ��@a[n]��2,
�@a[0]=4�@�̂Ƃ��@a[n]=4,
�@a[0]>4�@�̂Ƃ��@a[n]����
�ł����B xy���ʏ��2��2�����̃O���t
y=x^2
y=f(x)
������A����2�͒������Ă���B
���̂Ƃ��Af(x)�͂ǂ̂悤�Ȍ`��2���������l����B
�i1�j���̂悤��f(x)�ŁA2���̌W���̐�Βl��1�ł�����̂����݂��邱�Ƃ������B
�i2�j�����̒萔a,b,c��p���A���̂悤��f(x)�����ׂċ��߂�B �@f(x) = ax^2 +bx +c �@(a��0)
�Ƃ����B
�@f(x) - x^2 = (a-1)x^2 +bx +c,
�@{(x^2) '�f '(x) +1}/2 = x(2ax+b) + 1/2 = 2ax^2 +bx +1/2,
����炪���ʍ���2���A�܂��Ⴗ�邱�Ƃ���
�Ea=-1, b:�C��, c=1/2.
�Ea��0, b=0, c=(a-1)/4a.
���Ȃ� �����������܂߂��
�Ea��0, b=0, c=(1-a)/(-4a).
�ł��ˁB >>405
�Ԏ����x��Ă��݂܂���I
�悭������܂����I
�{���ɂ��肪�Ƃ��������܂��I �R���i�����̏ꍇ
���ҁA�������Ă��邪�a������l�ւ̊����͂Ȃ��A
�������Ă��邪�a��Ȃ������͂���A�a��A�d�a���̂T��Ԃ�����܂��i�������ɂ�邪�j
���̊����A���m���ׂ郂�f���͂���܂���
�����̓�����Ԃ�����A������ԂŘA���ɉe������ �x���g�����E�`�F�r�V�F�t�̒藝�ŁA�ȉ���URL�ɓ����Ă���������ƍK���ł��B���݂܂���B
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11220784871 >>432
���������o�ւɂȂ��Ă�̂ɍr�炵�Ă�ˁ[��N�Y�A���˂� >>431
>>357 �� SEIRH model
S: ����
E: �������Ă��邪�a������l�ւ̊����͂Ȃ�
I1: �������Ă��邪�a��Ȃ������͂���
I2: �a��
H: �d�a��
��: ���R���S��
b: ������(S->I)
��: ���N�`���L����(S->R)
��: ���Ǘ�(E->I),
g: ��(I->R) >>431
���{��������ɌJ��Ԃ��@ �P�`�Q�T�Ԃ��R��Ƃ������Ƃ̎Z�o�����́@���Ȃ낤�ȁH
100�l�̏W�c�i�N���X�^�[�j�łP���ɓ`�d����m����2���A�����҂͂P�l�Ƃ���
ReedFrost���f���ō�}����ƁA�R��͂P�`�Q�T�ԂƂ����}�ɂ͂Ȃ邯��
�Ċ����������Ă����肷�邵���f���̑O���Ă͂܂�̂��͋^�╄�����ȁB
https://i.imgur.com/DoQ64FM.jpg
100�l�̏W�c�i�N���X�^�[�j�Ŋ����҂͂P�l�Ƃ��ĂP���ɉ��ׂP�O��E�l�ƐڐG���A
�P�l�P����̊����m�����P���A��������30���A������5���Ƃ���
SEIR���f���Ōv�Z����ƁA�����̃s�[�N��110���߂łƂĂ��P�`�Q�T�Ԃ��R��Ƃ͌����Ȃ��B
> SEIR2(contact_rate=10,transmission_probability=0.01
+ ,infectious_period=30,latent_period=5,mu=0,
+ nu=0, s=99,e=0,i=1,r=0,timepoints = seq(0,365,by=0.5),axes=TRUE)
Ro = 3 peak time I = 109.5 peak time E = 89
�O���t�ɂ����
https://i.imgur.com/EiG2HzI.jpg
# Parameters
contact_rate = 10, # number of contacts per day
transmission_probability = 0.01, # transmission probability
beta = contact_rate * transmission_probability, # tranmission rate
infectious_period = 20, # infectious period
gamma = 1 / infectious_period, # Prob[infected -> recovered]
latent_period = 5, # latent perior
sigma = 1/latent_period, # The rate at which an exposed person becomes infective
mu = 0, # The natural mortality rate
nu = 0 , # vaccination moves people from susceptible to resistant directly, without becoming exposed or infected.
Ro = beta/gamma, # Ro - Reproductive number.
# Initial values for sub-populations.
s = 99, # susceptible hosts
e = 0, # exposed hosts
i = 1, # infectious hosts
r = 0, # recovered hosts
# Compute total population.
N = s + i + r + e,
# Output timepoints.
timepoints = seq (0, 365, by=0.5), >>435
> >>431
> ���{��������ɌJ��Ԃ��@ �P�`�Q�T�Ԃ��R��Ƃ������Ƃ̎Z�o�����́@���Ȃ낤�ȁH
�L�҉�����߂����_�ŁA���ׂĂ̔��ǎ҂͕⑫����Ă��āA
����2�T�Ԉȓ��őS�Ă̊����҂͖���݂ɏo��A�ɈႢ�Ȃ��Ƃ���
�f�l�̑f�p�Ȋ��ҁB 2�ȏ�̎��R��k�̑f�����S�̂���Ȃ�W����S_k�Ak+1�̑f�����S�̂���Ȃ�W����T_k�Ƃ���B
�ȉ��̖���(P)���l����B
(P):�wS_n�̗v�fa��T_n�̗v�fb�ŁA|a-b|=1�ƂȂ���̂����݂���B�x
(P)���^�ł���Ƃ�a[n]=1�A�U�ł���Ƃ�a[n]=-1�Ƃ���Ƃ��A
��[n=2,3,...,2020] a[n]
�̕����肹��B >>431
���g�J-���H���e���������@���ȁB
�ʍ��E�����Ȋw�u�������Ǝ��R�v�T�C�G���X�� (1993)
�@�́@p.146-150
���Z�~�����u���w�E����100�̕������v���{�]�_�� (1989)
�@�́@p.218-219 ����� p.222-224
���Z�~�����u���w100�̖��v���{�]�_�� (1984)
�@�́@p.202-204
���w�Z�~�i�[(�A��)�u���Ԍn�̐������ۊw�v���{�]�_�� (1982/5�`1984/6)
G.F.�K�E�[�F�u���������v�v���� (1981)�@�g�c�q�� ��@204p.
R.���[�[���F�u�����w�ɂ�����_�C�i�~�J���V�X�e���̗��_�v(������͂Ƃ��̎���6) �Y�Ɛ}�� (1974,1988)
�@�@�R�����Ƃق���@�@339p.
�R�����ƁF�u����^���ۂ̐��w�v(��b���w�V���[�Y11) ���q���X (1972,2005)
�@�@�@172p.�@3520�~ >>436
100�l�̏W�c�i�N���X�^�[�j�łP���ɓ`�d����m����2���A�����҂͂P�l�Ƃ���
ReedFrost���f���ō�}����ƁA�R��͂P�`�Q�T�ԂƂ����}�ɂ͂Ȃ邯��
�Ċ����������Ă����肷�邵���f���̑O���Ă͂܂�̂��͋^�╄�����ȁB
://i.imgur.com/DoQ64FM.jpg ���L�̖��ł����A
https://imgur.com/a/3pV0ffV
��������@OA(i)��OA(j)�Ɉڂ�AOA(j)��OA(i)�Ɉڂ�̂�
O�ƒ��_��ʂ钼���Ɋւ���Ώ̈ړ��ł���ƒf�肵�ĉ���
�Ă������ł����H �ȑO���̃X���ŁA���L�̐���ɂ���
lim[n����] a[n]=2
�ł��邱�Ƃ����������������܂����B
a[n+1]=(��2)^a[n]
a[1]=��2
�Ƃ����
a[3]={(��2)^(��2)}^(��2)=2
�ƂȂ�܂��B
a[n]�͒P����������Ɍ�����̂ł����Aa[3]=a[��]=2�Ȃ̂łǂ����Ō������Ă���̂ł��傤���H
�ΐ����Ƃ��Ă��O���t�������������Ă��܂��Ba[n]�̑��������ɂ��ċ����ĉ������B >>442
>a[3]={(��2)^(��2)}^(��2)=2
>�ƂȂ�܂��B
�Ȃ�܂��� �w���ł͑����Z��|���Z�ƈ���Č����@���͐��藧���܂���
���ʂł�����ʒu��ς���ƌ��ʂ��ς��ƌ������Ƃł� �E�C���X�����Q�O�ʑ̂̌`�����Ă���̂��������Ă����͉̂������R�Ȃ낤���H >>442
���ʂ�t�����Ɏw��������q�ɂȂ��Ă���Ƃ��͎w���ɏ�������Ă�ق�����v�Z�����
a^a^a^a���v�Z���鏇�����ʂ��g���Ė��������a^{(a^(a^a)} >>446
���i�̎�ނ����Ȃ��Ă��ނ���ł́H >>440
���钸�_��O��ʂ钼���Ɋւ���Ώ̈ړ��A�ƂȂ邱�Ƃ��������Ȃ̂ł́H >>449
>���钸�_��O��ʂ钼���Ɋւ���Ώ̈ړ��A�ƂȂ邱�Ƃ��������Ȃ̂ł́H
OA(i)��OA(j)�Ɉڂ�AOA(j)��OA(i)�Ɉڂ邩�璸�_��O��ʂ钼����
�ւ���Ώ̈ړ����ƒf�肵�Ă����ł���ˁB
�������Ɂi�P�j�������Ƃ������Ƃ�OK�ł����B
����Ƃ��i�P�j���ؖ�������ɑΏ̈ړ����Ƃ������Ƃ�������
�Ƃ������Ƃł����H �摜��URL���Čf���܂����AIE�ł͕\������Ȃ��悤�ł��B
https://imgur.com/a/3pV0ffV �Ώ̈ړ��ł��邱�Ƃ��g�킸��(1), (2) �������Ƃ������Ƃł�
(2)����������i�Ƃ������r������j�A����ϑΏ̈ړ��L���ȁ`�� >>452
���肪�Ƃ��������܂����B
�����̐��E�ł͂��ꂵ���Ȃ��ȂƎv���Ă��A
���ꂾ�ƌ��߂��Ȃ��ŁA���_�����œW�J
����킯�ł��ˁB n��6�̔{���Ƃ���
1��t<u<v����t+u+v��n�ƂȂ鐮��t,u,v�̑g�����͉��ʂ肠�邩
��낵�����肢���܂� >>454
#{ u+v+w=n } = (n+2)(n+1)/2
#{ u+v+w=n ,u=v} = n/2+1
#{ u+v+w=n ,u=v=w} = n/3+1
��#{orbits} = ((n+2)(n+1)/2 + 3(n/2+1) + 2(n/3+1))/6 ���A�Ԉ�����B
������Ȃ���<���B
�Ȃ�
{t+u+v=n, u��v, v��w, w��u} = (n+1)(n+2)/3 - 3(n/2+1) + 3(n/3+1) - (n/3+1)
��{orbits} = ((n+1)(n+2)/3 - 3(n/2+1) + 3(n/3+1) - (n/3+1))/6 �����܂��A�ȉ���2�_�Ԃ̃��[�v�Ɋւ��鎿��̓����Ɖ�������肢�������܂��B
���z�̋��x�v�Z�Ŕ��ɍ����Ă܂��B
https://okwave.jp/qa/q9719865.html
�N�����̂��������肢���܂��B >>456
���肪�Ƃ��������܂�
���݂܂���B��������肢���Ă���낵���ł��傤���H
��낵�����肢���܂� >>458
U={ t+u+v=n }
A={ t+u+v=n ,t=u}
B={ t+u+v=n ,u=v}
C={ t+u+v=n ,v=t}
�Ƃ�����
#U = (n+2)(n+1)/2
#A = #B = #C = n/2+1
#A��B = #B��C = #C��A = #A��B��C= n/3+1
�����������ɂ��
{t+u+v=n, u��v, v��w, w��u} = (n+1)(n+2)/3 - 3(n/2+1) + 3(n/3+1) - (n/3+1)
������
#{orbits} = ((n+1)(n+2)/3 - 3(n/2+1) + 3(n/3+1) - (n/3+1))/6�B >>459
#U = (n - 1) * (n - 2) / 2
�ł͂Ȃ��ł��傤���H #A = #B = #C = n / 2
�ł͂Ȃ��ł��傤���H #A��B = #B��C = #C��A = #A��B��C= n / 3
�ł͂Ȃ��ł��傤���H >>454
t + u + v = n
�ƂȂ�悤�� 0 �ȏ�̐����̑g (t, u, v) �̌����܂����߂�B
���F
k �� 0 �ȏ�̐����Ƃ���B
x + y = k
�ƂȂ�悤�� 0 �ȏ�̐����̑g (x, y) �́A k + 1 ����B
�ؖ��F
�S�Ẳ�����ׂ�ƁA (0, k), (1, k - 1), �c, (k, 0) ������A���͑S���� k + 1 ����B
t = 0 �̂Ƃ��A u + v = n - t = n + 0 = n �ƂȂ�悤�� 0 �ȏ�̐����̑g (u, v) �̐��́A
�����A n + 1 ����B
t = 1 �̂Ƃ��A u + v = n - t = n - 1 �ƂȂ�悤�� 0 �ȏ�̐����̑g (u, v) �̐��́A
�����A n ����B
t = 2 �̂Ƃ��A u + v = n - t = n - 2 �ƂȂ�悤�� 0 �ȏ�̐����̑g (u, v) �̐��́A
�����A n - 1 ����B
�c
t = n �̂Ƃ��A u + v = n - t = n - n = 0 �ƂȂ�悤�� 0 �ȏ�̐����̑g (u, v) �̐��́A
�����A 1 ����B
��
t + u + v = n
�ƂȂ�悤�� 0 �ȏ�̐����̑g (t, u, v) �̌��́A (n + 1) + (n) + (n - 1) + �c + 1 = (n + 1) * (n + 2) / 2 �ł���B ���ɁA
t + u + v = n
�ƂȂ�悤�� 1 �ȏ�̐����̑g (t, u, v) �̌������߂�B
���̌��́A
(t + 1) + (u + 1) + (v + 1) = n
�ƂȂ�悤�� 0 �ȏ�̐����̑g (t, u, v) �̌��ɓ������B
t + u + v = n - 3
�ƂȂ�悤�� 0 �ȏ�̐����̑g (t, u, v) �̌��́A
>>463
���A
(n - 2) * (n - 1) / 2 �ł���B U := {(t, u, v) | t + u + v = n, t, u, v �� {1, 2, 3, �c}}
A := {(t, u, v) | t + u + v = n, t = u, t, u, v �� {1, 2, 3, �c}}
B := {(t, u, v) | t + u + v = n, u = v, t, u, v �� {1, 2, 3, �c}}
C := {(t, u, v) | t + u + v = n, v = t, t, u, v �� {1, 2, 3, �c}}
�Ƃ����B �F������肪�Ƃ��������܂��B
������1/12n^2�|1/2n�{1�ɂȂ�܂� >>464
���A
#U = (n - 2) * (n - 1) / 2 �ł���B ���ɁA
2*t + v = n
�ƂȂ�悤�� 1 �ȏ�̐����̑g (t, v) �̌������߂�B
�S�Ẳ�����ׂ�ƁA (t, v) = (1, n - 2), �c, (n/2 - 1, 2) ������A���͑S���� n/2 - 1 ����B
��
#A = n/2 - 1
�ł���B ���l�ɂ��āA
#B = n/2 - 1
#C = n/2 - 1
�ł���B A �� B = B �� C = C �� A
=
A �� B �� C
=
{(t, u, v) | t + u + v = n, t = u = v, t, u, v �� {1, 2, 3, �c}}
=
{(t, t, t) | 3*t = n, t �� {1, 2, 3, �c}}
�ł���B 3*t = n
�ƂȂ�悤�� t �̌��� 1 �ł��邩��A
#(A �� B) = #(B �� C) = #(C �� A)
=
#(A �� B �� C)
=
1
�ł���B b,c�͎����̒萔�Ƃ���B2�̕�����
C:y=x^2
D:x=(y-b)^2+c
�����قȂ�3�_P,Q,R�Ō�����Ă���AC��D�͓_P�Őڂ��Ă���B
�_P��y���W������2�_��y���W�����������A�_Q��x���W���_R��x���W��菬�����Ƃ��A�ȉ��̖₢�ɓ�����B
�i1�j�_P��x���W�͓_Q��y���W���傫���A���A�_R��x���W��菬�������Ƃ������B
�i2�j�̈�E��F���ȉ��̂悤�ɒ�߂�B
E:�u������C�̌�QP�ƁA������D�̌�QP�Ƃň͂܂�镔���v
F:�u������C�̌�QR�ƁA������D�̌�QR�Ƃň͂܂�镔���v
���̂Ƃ��AE,F�̖ʐς����ꂼ��b,c�ŕ\���B
�i3�j�i2�j�ŋ��߂�E,F�̖ʐςɂ��āA���̑召���r����B ������ɂ��A
#(A �� B �� C)
=
#A + #B + #C
- #(A �� B) - #(B �� C) - #(C �� A)
+ #(A �� B �� C)
=
3*(n/2 - 1)
- 3*1
+ 1
=
(3/2)*n - 5
�ł���B
#U - #(A �� B �� C) = (n - 2) * (n - 1) / 2 - ((3/2)*n - 5) #U - #(A �� B �� C)
=
(n - 2) * (n - 1) / 2 - ((3/2)*n - 5)
=
(1/2) * (n^2 - 6*n + 12) #U - #(A �� B �� C)
�́A
t + u + v = n
�ƂȂ�悤�Ȍ݂��ɈقȂ� 1 �ȏ�̐����̑g�̌��ł���B
t + u + v = n ���� t < u < v
�ƂȂ�悤�� 1 �ȏ�̐����̑g�̌��́A���� 1/3! �ł���B
��(1/12) * (n^2 - 6*n + 12)
�ł���B �����
����ɔ����ł���Ă��B
���R���Ȃ�n��n-3�ˁB >>466
((n+2)*(n +1)/2 - 3*(n/2 - 2) - 3*n - 1 )/6
= (1/12*n^2-1/2*n+1)
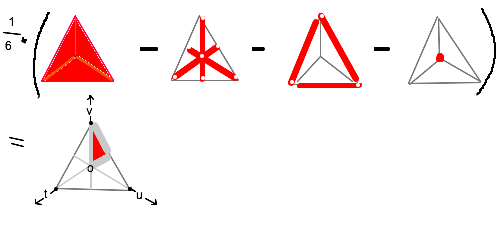 >>475
>>475
���肪�Ƃ��������܂��B
���A�����ɓw�߂Ă��܂��B >>476
>>477
���肪�Ƃ��������܂��B
���A�����ɓw�߂Ă��܂��B �ɂ�
1/6�~�on-1C2�|(n/3�|1)�~3�|(n/6�|1)�~3�|1�p
�Ə����Ă���̂ł����A
���̎��͊e���������Ӗ����Ă���̂������Ă��炦�Ȃ��ł��傤���H n-1C2
����́A
a + b + c = n ���� 1 �� a < b
�ƂȂ�悤�ȉ��̐��ł��B
(n/3�|1)�~3
����́A
a + a + b = n ���� 1 �� a < b
a + b + a = n ���� 1 �� a < b
b + a + a = n ���� 1 �� a < b
�ƂȂ�悤�ȉ��̐��ł��B
(n/6�|1)�~3
����́A
a + b + b = n ���� 1 �� a < b
b + a + b = n ���� 1 �� a < b
b + b + a = n ���� 1 �� a < b
�ƂȂ�悤�ȉ��̐��ł��B �������܂��F
n-1C2
����́A
a + b + c = n ���� 1 �� a, b, c
�ƂȂ�悤�ȉ��̐��ł��B
(n/3�|1)�~3
����́A
a + a + b = n ���� 1 �� a < b
a + b + a = n ���� 1 �� a < b
b + a + a = n ���� 1 �� a < b
�ƂȂ�悤�ȉ��̐��ł��B
(n/6�|1)�~3
����́A
a + b + b = n ���� 1 �� a < b
b + a + b = n ���� 1 �� a < b
b + b + a = n ���� 1 �� a < b
�ƂȂ�悤�ȉ��̐��ł��B 1
����́A
a + a + a = n ���� 1 �� a
�ƂȂ�悤�ȉ��̐��ł��B �T�C�R����10��U��Ƃ��A1��1��ȏォ��2��2��ȏ�ł�m�������Ă������� ���m����60%�A������m����40%�̃Q�[�����J��Ԃ��s���B
�v��10���A�܂��͗v��10�������_�ŃQ�[�����I������B
�v��10���Ƃɂ��Q�[�����I������m�������߂�B n = 18 �̏ꍇ���l���܂��B
binomial(n - 1, 2) �͈ȉ��̉��ɑΉ����܂��B
{1, 1, 16} = {t, u, v}
{1, 2, 15} = {t, u, v}
{1, 3, 14} = {t, u, v}
{1, 4, 13} = {t, u, v}
{1, 5, 12} = {t, u, v}
{1, 6, 11} = {t, u, v}
{1, 7, 10} = {t, u, v}
{1, 8, 9} = {t, u, v}
{2, 2, 14} = {t, u, v}
{2, 3, 13} = {t, u, v}
{2, 4, 12} = {t, u, v}
{2, 5, 11} = {t, u, v}
{2, 6, 10} = {t, u, v}
{2, 7, 9} = {t, u, v}
{2, 8, 8} = {t, u, v}
{3, 3, 12} = {t, u, v}
{3, 4, 11} = {t, u, v}
{3, 5, 10} = {t, u, v}
{3, 6, 9} = {t, u, v}
{3, 7, 8} = {t, u, v}
{4, 4, 10} = {t, u, v}
{4, 5, 9} = {t, u, v}
{4, 6, 8} = {t, u, v}
{4, 7, 7} = {t, u, v}
{5, 5, 8} = {t, u, v}
{5, 6, 7} = {t, u, v}
{6, 6, 6} = {t, u, v}
(n/3 - 1)�~3 �͈ȉ��̉��ɑΉ����܂��B
{1, 1, 16} = {t, u, v}
{2, 2, 14} = {t, u, v}
{3, 3, 12} = {t, u, v}
{4, 4, 10} = {t, u, v}
{5, 5, 8} = {t, u, v}
(n/6 - 1)�~3 �͈ȉ��̉��ɑΉ����܂��B
{2, 8, 8} = {t, u, v}
{4, 7, 7} = {t, u, v}
1 �͈ȉ��̉��ɑΉ����܂��B
{6, 6, 6} = {t, u, v} >>480
�̉ł́A��������g��Ȃ��ōς݂܂��ˁB �W�B�G���W�B�G���A�������Ⴀ��܂���B >>485
�ŒZ�� 10�� (10�� or 10��) �A�Œ��� 19�� (����9��, ����10�� or ����10��, ����9�� ) �̃Q�[���ł���.
n��ڂŏ��p�^�[�������� n-1 ��ڂ܂ł̓��ŗv 9�� �����̕��т𐔂��グ��悢.
p = 0.6 , q = 1-p = 0.4 �Ƃ���.
�m��: P = C{9,9} p^10 q^0 + C{10,9} p^10 q^1 + ... + C{18,9} p^10 q^9
�@�@= p^10/9! * ��{k=0, 9} (k+9)! /k! q^k
�@�� 0.8139
( ���Ԃ��v�Z���₷���`�ɂ͂Ȃ�Ȃ��Ǝv�� ) ����w�͎����̌��ʂ̕��͂��������̂ł���
����A���ϓ_���Ⴗ����(or ��������)�������ʂ̃f�[�^���������ꍇ�A
��W�c�̊w�͂��Ⴗ����(or ��������)�̂�
����Ƃ���肪�������(or �Ղ�������)�̂�
�ǂ��炪��Ȍ����Ȃ̂��A���ʂ�����@�͂���܂����H >>490
10�{���ł�90%�����Ȃ���ł��ˁA�ӊO�Ə������ċ����܂����B
���̖��A�W���̏�肢�v�Z�e�N�j�b�N�ʼn�����̂��ƔY��ł��܂������A�R���s���[�^�I�ȗ͋Z�̌v�Z�ɗ��炴��Ȃ��̂ł��ˁB
�[�������Ă��������Ă��肪�Ƃ��������܂��B >>484
> N=6^10
> A0=5^10
> B0=5^10
> B1=10*5^9
> A0B0=4^10
> A0B1=10*4^9
> 1-(A0+B0+B1-(A0B0+A0B1))/N
[1] 0.41467302314603127 "�T�C�R����10��U��Ƃ��A1��1��ȏォ��2��2��ȏ�ł�m��"
rm(list=ls())
options(digits=22)
# ��(1��1��ȏ�@�ȁ@2��2��ȏ�ł�) == 1���O��@�Ɂ@(�Q��0�� �� 2���P��j
N=6^10 # ���ׂĂ̏���
A0=5^10 # 1��0��̏ꍇ
B0=5^10 # 2���O��̏ꍇ
B1=10*5^9 # 2���P��̏ꍇ
A0B0=4^10 # 1��0��̏ꍇ��2���O��̏ꍇ
A0B1=10*4^9 # 1��0��̏ꍇ��2��1��̏ꍇ
1-(A0+B0+B1-(A0B0+A0B1))/N
N - (A0+B0+B1-(A0B0+A0B1))
N
25073692/60466176
6268423/15116544
# �V���~�ׂ��ɐ����グ��
library(gtools)
pm=permutations(6,10,rep=T)
f <- function(x){
sum(x==1)>0 & sum(x==2)>1
}
r=sum(apply(pm,1,f))�@# 25073692
sim <- function(){
f(sample(6,10,rep=TRUE))
}
mean(replicate(1e6,sim()))
�P�O�O����̃V�~�����[�V�����ł̊���
> mean(replicate(1e6,sim()))
[1] 0.41464000000000001 >>484
����A: 1��1��ȏ�ł�
����B: 2��2��ȏ�ł�
�m��: P = P (A �� B) = 1 - P(��(A �� B )) = 1 - P(��A �� ��B)
= 1 - P(��A) - P(��B) + P(��A �� ��B)
= 1 - P{1��0��} - P{2��0��܂���1��} + P{"1��0��" ���� "2��0��܂���1��"}
= 1 - (5/6)^10 - ( (5/6)^10 + 10*(1/6)*(5/6)^9 ) + ( (4/6)^10 + 10*(1/6)*(4/6)^9 )
�� 0.414673 >>486
�{���ɒ��J�ɉ��Ă��������Ă��肪�Ƃ��������܂��B
���A�l�łقڕ��������̂ł����A1/6�͂��ׂĂ̐����ɂ��čl���Ă��邩��A���̒���6�̔{���ɊY��������̂��Ď��ŁA1/6�~�ɂȂ��Ă���Ƃ������ő��v�ł��傤���H >>491
�Ȃ�ŗL��Ǝv����
���̃f�[�^���K�v >>485
100����̃V�~�����[�V����
> sim=function() sum(rbinom(19,1,0.6))>=10
> mean(replicate(1e6,sim()))
[1] 0.813875
> >>491
�K���Ƀf�[�^������Ĕ�����@���l���Ă݂��B
�ߋ��ₘ���P�O�O�₠���Ă��̐��𗦂͕��ϒl�V���̃�(7,3)�̃x�[�^���z�ɏ]���Ƃ���B
������P�O�△��ׂɒ��o���Ă��̔z���a�Ƃ���B
����W�c�ł�a�̐��𗦂̔z���y�Ƃ���B
��
> x
[1] 0.786 0.737 0.370 0.688 0.678 0.617 0.873 0.803 0.770 0.451 0.628 0.681 0.785 0.610
[15] 0.936 0.568 0.774 0.851 0.735 0.846 0.809 0.795 0.914 0.539 0.674 0.859 0.444 0.623
[29] 0.747 0.527 0.530 0.543 0.571 0.598 0.710 0.749 0.760 0.804 0.734 0.873 0.455 0.858
[43] 0.763 0.773 0.552 0.714 0.656 0.705 0.707 0.416 0.736 0.380 0.592 0.679 0.663 0.632
[57] 0.778 0.753 0.845 0.852 0.647 0.619 0.691 0.521 0.776 0.958 0.502 0.806 0.803 0.497
[71] 0.746 0.868 0.669 0.723 0.699 0.631 0.759 0.580 0.736 0.641 0.481 0.622 0.752 0.469
[85] 0.505 0.600 0.658 0.795 0.792 0.376 0.738 0.846 0.806 0.655 0.740 0.755 0.837 0.707
[99] 0.816 0.913
> a
[1] 0.623 0.641 0.795 0.770 0.678 0.804 0.568 0.688 0.600 0.376
> y
[1] 0.689 0.775 0.684 0.739 0.833 0.804 0.774 0.760 0.720 0.797
x �� a �ł����肵��
> t.test(a,x)
Welch Two Sample t-test
data: a and x
t = -0.89507, df = 11.082, p-value = 0.3898
�L�Ӎ��Ȃ��Aa�͖�肪�������(or �Ղ�������)�Ƃ������Ƃ͂Ȃ��B
�� �� a �ł����肵��
> t.test(a,y)
Welch Two Sample t-test
data: a and y
t = -2.3877, df = 11.637, p-value = 0.03487
a �� y �Ƃ̕��ϒl�ɂ͗L�Ӎ�(�댯��0.059)������B
���̏W�c�̊w�͂��Ⴗ����(or ��������)�ɊY������B
���A�Б�����Ȃ� p-value = 0.01743 >>490
�����\�������
3104812540377/3814697265625 >>492
��������ω������āA�P�O�{���ŏ����ƂȂ�m�����O���t�ɂ��Ă݂܂����B
https://i.imgur.com/TbKX5Jo.jpg
10�{���m����90%�ɂȂ�̂͏�������0.6420744�̂Ƃ��Z�o����܂����B >>491�ɕ⑫���܂��B��肽�����Ƃ́A
���ϓ_���Ⴂ�e�X�g�̃f�[�^�������������Ƃ��A
A�@���k�͕��ʂȂ̂ɋ��t�������������o���Ă���̂��A
B�@���t�͕��ʂ̖�������Ă���̂ɐ��k���o�J������̂��A
A�������������A����Ƃ�B�������������A
���邢��A��B�̊�^�̊�����7�F3�Ȃ̂�2�F8�Ȃ̂��A
�e�X�g�̓_�̃f�[�^����A�����ɂ��ĉ��炩�̏������Ƃ������o���Ȃ����Ȃ��Ɓc
>>497
����ς薳���ł����ˁc
�O�҂ƌ�҂ł͂��Ƃ��Ε��z�̌`�ɈႢ���o����Ƃ����܂��H
>>499
>�ߋ��ₘ���P�O�O�₠���Ă��̐��𗦂͕��ϒl�V���̃�(7,3)�̃x�[�^���z�ɏ]���Ƃ���B
�x�[�^���z�ɂ��Ă��܂�m�����Ȃ��̂ł����A
�u���Q�̐��𗦂�����7���v�Ƃ�������m�ł���A
y�̃f�[�^�̕��ς�7�����Ă���̂Ŏ��O�ɗ\�z������
t����ɂ���Ă�����m�M�ł��܂����A
���܂͂��́u���Q�̐��𗦂�����7���v�Ƃ�������m�Ȃ̂ł��B >>454
1��t<u<v,�@t+u+v=n,
���� (t,u,v) �� q(n) �Ƃ��肠��A�Ƃ���B
t>1 �̏ꍇ��
�@(t-1,u-1,v-1) �� 1�� t-1 < u-1 < v-1 �����A�a�� n-3 �ƂȂ�B
�@q(n-3) �ɓ������B
t=1 �̏ꍇ��
�@(u-1,v-1) �� 1�� u-1 < v-1 �����A�a�� n-3 �ƂȂ�B
�@[(n-4)/2] = [n/2] -2 �Ƃ��肠��B
�����������ƑQ����
�@q(n) = q(n-3) + [n/2] - 2,
�����l�@q(6) = 1,
n ��3�̔{���̂Ƃ���
�@q(n) = (nn/12) - (n/2) + 1 - (1/4)mod(n,2),
��ʂɂ�
�@q(n) = (nn/12) - (n/2) + 1 - (1/4)mod(n,2) - (1/3)d(n),
������
�@mod(n,2) = n - 2[n/2],
�@d(n) = 0�@(n��3�̔{��),�@�@= 1�@(���̑�) >>502
�N��A-B���Ⴂ�l�ł��錴����A���Ⴂ�̂�B�������̂����肳���悤�Ƃ��Ă����
���̎����̌��ʂ����Ŕ��肷��͖̂���
>>499�̂悤�ȉߋ��̃f�[�^�������Ă�
����̎������̓�Փx���ߋ��Ɣ�r����ɂ�
�ߋ��̖������҂ɍ���̎�����������K�v������
>>499
�ł͂��������ݒ�i�ߋ���̒����獡��̎������𒊏o�j�ƂȂ��Ă��邪
>���ϓ_���Ⴂ�e�X�g�̃f�[�^�������������Ƃ��A
>A�@���k�͕��ʂȂ̂ɋ��t�������������o���Ă���̂��A
>B�@���t�͕��ʂ̖�������Ă���̂ɐ��k���o�J������̂��A
>A�������������A����Ƃ�B�������������A
>���邢��A��B�̊�^�̊�����7�F3�Ȃ̂�2�F8�Ȃ̂��A
>�e�X�g�̓_�̃f�[�^����A�����ɂ��ĉ��炩�̏������Ƃ������o���Ȃ����Ȃ��Ɓc
�ł͂���Ȑݒ�ɂ͂Ȃ��Ă��Ȃ�
X������Y�������ʂ�
A������B�������ʂ�
��̂ǂ���r����HX�ɂ�B�����邢��A�ɂ�Y�������Ȃ��Ă͔�r���悤���Ȃ�����H >>502
�N��A-B���Ⴂ�l�ł��錴����A���Ⴂ�̂�B�������̂����肳���悤�Ƃ��Ă����
���̎����̌��ʂ����Ŕ��肷��͖̂���
>>499�̂悤�ȉߋ��̃f�[�^�������Ă�
����̎������̓�Փx���ߋ��Ɣ�r����ɂ�
�ߋ��̖������҂ɍ���̎�����������K�v������
>>499
�ł͂��������ݒ�i�ߋ���̒����獡��̎������𒊏o�j�ƂȂ��Ă��邪
>���ϓ_���Ⴂ�e�X�g�̃f�[�^�������������Ƃ��A
>A�@���k�͕��ʂȂ̂ɋ��t�������������o���Ă���̂��A
>B�@���t�͕��ʂ̖�������Ă���̂ɐ��k���o�J������̂��A
>A�������������A����Ƃ�B�������������A
>���邢��A��B�̊�^�̊�����7�F3�Ȃ̂�2�F8�Ȃ̂��A
>�e�X�g�̓_�̃f�[�^����A�����ɂ��ĉ��炩�̏������Ƃ������o���Ȃ����Ȃ��Ɓc
�ł͂���Ȑݒ�ɂ͂Ȃ��Ă��Ȃ�
X������Y�������ʂ�
A������B�������ʂ�
��̂ǂ���r����HX�ɂ�B�����邢��A�ɂ�Y�������Ȃ��Ă͔�r���悤���Ȃ�����H >>502
>�O�҂ƌ�҂ł͂��Ƃ��Ε��z�̌`�ɈႢ���o����Ƃ����܂��H
�����������k�W�c���ǂ̂悤�Ȑ��藧���Ȃ̂��̉���������Ȃ疳��
���ʂ̕��zC�̌`���������悤�Ȑ��k�W�c�̐��藧���i���z�jA��������ł��t�Z�ł��邩�� >>496
1/6�~�on-1C2�|(n/3�|1)�~3�|(n/6�|1)�~3�|1�p�Ƃ�������
n-1C2�|(n/3�|1)�~3�|(n/6�|1)�~3�|1 �̕����ɂ��čl���܂��B
����́A n = 18 �̏ꍇ�A t + u + v = 18 �݂̌��ɈقȂ�1�ȏ��3�̐�������Ȃ���̌���\���Ă��܂��B
(t, u, v) = (1, 2, 15) �Ƃ��������������Ƃ��܂��B
����ƁA���Â鎮�ɁA�ȉ���6�̉��������邱�Ƃ��ł��܂��B
6 = 3! �� (1, 2, 15) �̏���̐��ł��B
(t, u, v) = (1, 2, 15)
(t, u, v) = (2, 15, 1)
(t, u, v) = (15, 1, 2)
(t, u, v) = (15, 2, 1)
(t, u, v) = (2, 1, 15)
(t, u, v) = (1, 15, 2) n-1C2�|(n/3�|1)�~3�|(n/6�|1)�~3�|1 �̉��͈ȉ���114�̉������ׂăJ�E���g���Ă��܂��B
�ł��̂ŁA t < u < v �Ƃ������̌������߂�ɂ́A 3! = 6 �Ŋ���K�v������܂��B
(1, 2, 15)
(2, 15, 1)
(15, 1, 2)
(15, 2, 1)
(2, 1, 15)
(1, 15, 2)
-----------------------------
(1, 3, 14)
(3, 14, 1)
(14, 1, 3)
(14, 3, 1)
(3, 1, 14)
(1, 14, 3)
-----------------------------
(1, 4, 13)
(4, 13, 1)
(13, 1, 4)
(13, 4, 1)
(4, 1, 13)
(1, 13, 4)
-----------------------------
(1, 5, 12)
(5, 12, 1)
(12, 1, 5)
(12, 5, 1)
(5, 1, 12)
(1, 12, 5)
-----------------------------
(1, 6, 11)
(6, 11, 1)
(11, 1, 6)
(11, 6, 1)
(6, 1, 11)
(1, 11, 6)
-----------------------------
(1, 7, 10)
(7, 10, 1)
(10, 1, 7)
(10, 7, 1)
(7, 1, 10)
(1, 10, 7)
-----------------------------
(1, 8, 9)
(8, 9, 1)
(9, 1, 8)
(9, 8, 1)
(8, 1, 9)
(1, 9, 8)
----------------------------- (2, 3, 13)
(3, 13, 2)
(13, 2, 3)
(13, 3, 2)
(3, 2, 13)
(2, 13, 3)
-----------------------------
(2, 4, 12)
(4, 12, 2)
(12, 2, 4)
(12, 4, 2)
(4, 2, 12)
(2, 12, 4)
-----------------------------
(2, 5, 11)
(5, 11, 2)
(11, 2, 5)
(11, 5, 2)
(5, 2, 11)
(2, 11, 5)
-----------------------------
(2, 6, 10)
(6, 10, 2)
(10, 2, 6)
(10, 6, 2)
(6, 2, 10)
(2, 10, 6)
-----------------------------
(2, 7, 9)
(7, 9, 2)
(9, 2, 7)
(9, 7, 2)
(7, 2, 9)
(2, 9, 7)
-----------------------------
(3, 4, 11)
(4, 11, 3)
(11, 3, 4)
(11, 4, 3)
(4, 3, 11)
(3, 11, 4)
-----------------------------
(3, 5, 10)
(5, 10, 3)
(10, 3, 5)
(10, 5, 3)
(5, 3, 10)
(3, 10, 5)
----------------------------- (3, 6, 9)
(6, 9, 3)
(9, 3, 6)
(9, 6, 3)
(6, 3, 9)
(3, 9, 6)
-----------------------------
(3, 7, 8)
(7, 8, 3)
(8, 3, 7)
(8, 7, 3)
(7, 3, 8)
(3, 8, 7)
-----------------------------
(4, 5, 9)
(5, 9, 4)
(9, 4, 5)
(9, 5, 4)
(5, 4, 9)
(4, 9, 5)
-----------------------------
(4, 6, 8)
(6, 8, 4)
(8, 4, 6)
(8, 6, 4)
(6, 4, 8)
(4, 8, 6)
-----------------------------
(5, 6, 7)
(6, 7, 5)
(7, 5, 6)
(7, 6, 5)
(6, 5, 7)
(5, 7, 6)
----------------------------- >>505
>>>499�̂悤�ȉߋ��̃f�[�^�������Ă�
���̏ꍇ
�ߋ��̎����W���ʼnߋ��₪�W���ł���ƍl����
�Ƃ������Ƃ���O��
�N���X���Ď������>>499�̂悤�ɔ�r�͉\ >>502
�x�[�^���z��I�̂͒�`�悪0�`1�����痐���������y�Ƃ��������̗��R�B���K���z����-���`+���Ȃ̂Ő��𗦂����ɂȂ�����1�����肷�邩��B >>510
���x�������f�����������Ă��܂��A�\�������܂���B
���J�ɉ��Ē����܂��āA���肪�Ƃ��������܂��B
�p�������Ȃ���A����Ɨ����ł��܂����B
6�̔{���ł��邱�Ƃɂ���āAt��u��v�ł���ꍇ������A4�̔{���Ƃ���������t��u��v�ɂ͂Ȃ蓾�Ȃ��킯�ł��ˁB
�����āA���߂����̂��At<u<v�̎��ł��邩��A�Ō��3�I��6�Ŋ���K�v������Ƃ������ł��ˁB
�{���ɐF�X�Ǝw�����ĉ�����A���肪�Ƃ��������܂��B >>503
���肪�Ƃ��������܂��B
���A�����ɓw�߂Ă��܂��B ���̖������肢���܂��B�ȒP�����Ȃ̂ł����_P�̍��W���o���Ȃ��ō����Ă��܂��B
b,c�͎����̒萔�Ƃ���B2�̕�����
C:y=x^2
D:x=(y-b)^2+c
�����قȂ�3�_P,Q,R�Ō�����Ă���AC��D�͓_P�Őڂ��Ă���B
�_P��y���W������2�_��y���W�����������A�_Q��x���W���_R��x���W��菬�����Ƃ��A�ȉ��̖₢�ɓ�����B
�i1�j�_P��x���W�͓_Q��x���W���傫���A���A�_R��x���W��菬�������Ƃ������B
�i2�j�̈�E��F���ȉ��̂悤�ɒ�߂�B
E:�u������C�̌�QP�ƁA������D�̌�QP�Ƃň͂܂�镔���v
F:�u������C�̌�QR�ƁA������D�̌�QR�Ƃň͂܂�镔���v
���̂Ƃ��AE,F�̖ʐς����ꂼ��b�܂���c�ŕ\���B
�i3�j�i2�j�ŋ��߂�E,F�̖ʐςɂ��āA���̑召���r����B >>515
>�i1�j�_P��x���W�͓_Q��x���W���傫���A���A�_R��x���W��菬�������Ƃ������B
�}���玩��
>�i2�j�̈�E��F���ȉ��̂悤�ɒ�߂�B
>E:�u������C�̌�QP�ƁA������D�̌�QP�Ƃň͂܂�镔���v
>F:�u������C�̌�QR�ƁA������D�̌�QR�Ƃň͂܂�镔���v
>���̂Ƃ��AE,F�̖ʐς����ꂼ��b�܂���c�ŕ\���B
�ʓ|������
>�i3�j�i2�j�ŋ��߂�E,F�̖ʐςɂ��āA���̑召���r����B
�������͊g��k����1�����Ȃ�����
�ړ������Ă�����EF���t�]����Ƃ��낪1�J����������͎̂�������
�ʓ|������ �Ȃ߂����ጩ�o���̂���M�Ղ�
�܂����N�O�̎��_�Ńh�N�^�[�����ԈႢ�Ȃ��{�l�ł͂Ȃ�����
�Ƃ肠�����E�ӂ��v�Z���Ă݂���H >>518
�\�L��: e{i}[k] �� �P�ʃx�N�g�� e_i �� k������\��.
e{i}[k] = ��{i,k} �� Ae{j} = e{��(j)} ���
a[i,j] = ��[k,m] ��{i,k} a[k,m] ��{m,j} = e{i}^t A e{j} = e{i}^t e{��(j)} = ��{ i, ��(j) }
�摜�̕��͂悭���ĂȂ�. ������͉����Ȃ��Ǝv��. x>0�Œ�`����A���̎����l���Ƃ��f(x)�ŁAf(x)-[f(x)]���P�������ł�����̂��l����B
�i1�j���̂悤��f(x)�̗��1������B
�i2�j����w���ׂĂ�x�ɑ�0<f(x)< 1�x�̐^�U���q�ׂ�B >>520
�N���l�b�J�[�̒�`�𗝉����Ă��Ȃ��ł� >>520
(�A�����炵�܂�)
��_ij�ɂ�����ij��A�̍s�y�ї��\���Ă����ł͂Ȃ��A���Ȃ킿�N���l�b�J�[�̉��t�������͕\�������v�f�̍s����ї�ړI�ɕ\���Ă���Ƃ͌���Ȃ��Ƃ������Ƃł�낵���ł����H (�ǂ����Ă��P�ʍs��̗v�f�̃N���l�b�J�[�ȍ~�o�Ă��Ă��Ȃ��������߁A�N���l�b�J�[�̉��t���������ǂ����Ă��\�������s��̗v�f�̍s�y�ї��\���L�����ȂƉ��߂��Ă���܂����B) �O>>387
>>515
(1)�}��`���ƁA
P,Q����2�ی��AR����1�ی��ɂ��邱�Ƃ��킩��B
������C:y=x^2
�̒��_��(0,0),����y���B
������D:x=(y-b)^2+c
�̒��_��(b,c),����x=b�B
�����2�̕������͂Ƃ��ɓ��ł��̌W����1������A�����ȗ��ł������ɑ����ȕ������ŁAC�����v����90����]����(c,b)�ړ��������D�ɂȂ�B
��ӂ��_P��y���W������2�_��y���W�����������A�_Q��x���W���_R��x���W��菬��������A
�_P��x���W�͓_Q��x���W���傫���A���A�_R��x���W��菬�����ʒu�ɂ���B�i2�jx����y���ɕ��s��4�̒����ň͂܂ꂽ�����`���������1:2�ɕ�����悤�ɍ�}����ƁA
Q(-q,q^2)(q��0)�Ƃ��āA
E�̖ʐ�=SE(b,c)
=q^3/3-(q+c)b+(1/3)(-q-c)(q^2-b)+(1/3)bc
=q^3/3-bq-bc-q^3/3-cq^2/3+bq/3+bc/3+bc/3
=-2bq/3-bc/3-cq^2/3
F�̖ʐ�=SF(b,c)
=(c^2-b)(-2c)(4/3)-(1/3)(c^2-q^2)(-c+q)-{(-2c^3/3-4q^3/3-2c(c^2-q^2)}
�܂�F���������덷����B
�i3�jSE(b,c)��SF(b,c) >>525
����͎����ŏ������m�[�g�ł͂Ȃ��̂�. �ȒP�Ȏ����킴�킴������ɂ��������Ă���悤�Ɍ����܂���.
���F�B(?)�̃m�[�g��蕁�ʂɋ��ȏ��ǂ��������ł���.
�N���l�b�J�[�� ��
��̓Y���������������̂� 1 ����ȊO�� 0 �ƂȂ� 2�ϐ����Ǝv���悭��,
�P�ʍs��̐����\���Ɂu���v�g����Ƃ��������̎��ł�.
��:
f[2] = 0*f[1] �@�@�@+ 1*f[2] �@�@+ 0*f[3]
�@�@= ��[2, 1]*f[1]+ ��[2, 2]*f[2] + ��[2, 3]*f[3]
�@�@ = ��[k=1...3] ��[2, k] f[k] �N���l�b�J�[�̃f���^�͂�����2�l�̓�ϐ����ł�
f(i,j)
��1(i��j�̂Ƃ�)
��0(i��j�̂Ƃ�)
�Ƃ������ł�
�����Ă鎖�́u���̒u���s��A��i�s��j�Ԗڂ̐���a_ij�̓�_i��(j)�ɓ������v
�Ƃ��������ł� �O>>527�����B
�~�����ȕ�����
�@���@���@��
�������ȕ����� >>503
U := {(t,u,v) | t+u+v=n, 1��t,u,v}
#U = C[n-1,2] = (n-1)(n-2)/2,
#{(t,u,v) | t+u+v=n, 1��t=u<v} = [(n-1)/3],
#{(t,u,v) | t+u+v=n, 1��t<u=v} = [(n-1)/2] - [n/3],
#{(t,u,v) | t+u+v=n, 1��t=u=v} = [n/3] - [(n-1)/3] = 1 - d(n),
�ӁX������
#A = #B = #C = [(n-1)/2],
�܂��@A��B = B��C = C��A = A��B��C,
�@#(A��B��C) = 1 - d(n),�@�@(3|n �̂Ƃ�1, ����ȊO��0)
#(A�tB�tC)
�@= #A + #B + #C - #(A��B) - #(B��C) - #(C��A) + #(A��B��C)
�@= 3[(n-1)/2] - 2{1-d(n)}
�@= 3n/2 -5 + (3/2)mod(n,2) + 2d(n),�@�@�@�@�@���� (*)
q(n) = (#U - #(A�tB�tC))/6
�@= (nn/2 -3n +6 - (3/2)mod(n,2) - 2d(n))/6
�@= (nn/12) - (n/2) + 1 - (1/4)mod(n,2) - (1/3)d(n),
*)�@[(n-1)/2] = (n + mod(n,2))/2 -1, >>521
(1)�@f(x) = 1/(x+1)^a + [(x+1)^a],�@�@a>0
(2)�@�U >>521
(1)�@f(x) = exp(-ax) + [ exp(ax) ],
�@�@a >0,
(2)�@�U �O>>530
>>527�����B
q��0�Ƃ���Q(-q,q^2) �����̓Y���̐ϋ�Ԃ̐ψʑ��̃C���[�W���悭�킩��Ȃ��̂ŋ����Ă�������
�Ⴆ�Ύ����S��R�̉Z�̒���R^���ɂ��ċ��I=[0,1]�̖����̒���I^���Ƃ���������Ԃ��l�����
���̓����Ƃ����̂͋�W���ɂȂ�Ƃ����̂͐������ł��傤���H
�ψʑ��̊J��Ƃ͗L���̓Y���ɂ��ĊJ�W���ŁA�c��̖����̓Y���ɂ��Ă͑S��ԂɈ�v������̂Ƃ������ƂȂ̂�
I^���Ɋ܂܂��悤�ȊJ�W���͋�W���݂̂ł���E�E�E�Ƃ����悤�ɍl�����̂ł��� >>535
������ԂȂ̂�I^���Ɋ܂܂��J�W�����l����̂͂Ȃ��H ����������I^�������l���Ă�킯����Ȃ��̂� �����ł��AR^���ł̓������l���Ă���̂ŕ����W��I^���ƌ������ق����ǂ������ł��傤�� R^���ɂ�����I^���̓����͋�Ő������� ���Ƃ���
I^����(x_n)
�ɑ���
lim(x_1,�c,x_n,-1,-1,�c)=(x_n) >>540
���肪�Ƃ��������܂�
�_��̎����Ƃ̊W�ɂ��Ă͂܂��悭�m��Ȃ��ł����A
���̗�������������(x_n)�̔C�ӂ̋ߖT��R^���_I^���̓_���܂܂�邱�Ƃ������܂���
�Ȃ�قǂł� >>357
SEIR���f���ŗL�a�����P���ɌŒ肵�āA�W�c�̃T�C�Y��ω������ăV�~�����[�V�������Ă݂����ǃs�[�N�͕ς��Ȃ��ȁB
���̃��f���ł͏W��K�͂̑召�ɂ͉e������Ȃ��Ƃ������ƂɂȂ�ȁB
https://i.imgur.com/343K91V.png
�L�a����ω������ė��s�̕ϑJ���O���t�ɂ���ƁA
https://i.imgur.com/SZ15LKT.png
https://i.imgur.com/gnJVFnd.png
�L�a�����S�O�����炢�Ɉ����グ��ƃI�����s�b�N�̂Ƃ��ɂ͗��s���������Ă��邱�ƂɂȂ邗�������� ���䑏���@�W��̎Q���l���Ɗ����g��m���̕\�����J���Ă���̂���
�ǂ������A���S���Y���Ōv�Z����̂��m���Ă������������Ⴂ�܂����H
https://i.imgur.com/f3Tes5g.jpg >543(����)
���Ȃ��Ƃ���l�̊����҂���ɎQ�����Ă���m�����o���Ă��邾������Ȃ����ȁH
p=�L�a��, n=��Q���l����
1-(1-p)^n >>544
�L�a��1/100000��100�l�̏W��Ȃ炻���Ɋ����҂��܂܂��m����
> n=100
> (q=1-(1-p)^n)
[1] 0.0009995052
������
���ꂪ1000�����ōs��ꂽ�Ƃ����
> 1-(1-q)^1000
[1] 0.6321224
�U���ȏ�̊m���łǂ����Ŋ����g�債�Ă��邱�ƂɂȂ�Ȃ��B �O>>534
>>515�ϕ������畉���B
P(p,p^2),Q(q,q^2),R(-c,c^2)�ɕύX����B
�̈��A,B,C,G,H,I,J�c�c�ƃA���t�@�x�b�g��U��A�����`�̖ʐρA����т���1/3,2/3�̖ʐς𑫂���������B ��w���w���ʃe�X�g����30�N�x���s��������5��(v)�͖��Ƃ��Đ������ĂȂ���
����N���w�E���ĂȂ��̂��H
�别��Ȃ� ���Q�������ɓ������ď����QR���Œ��Ƃ���������t���čl�������Ă���
PQR���ŏ��^�����Ă��đΏ̐���������������Ă����̖{�����ς��Ȃ��Ƃ������Ƃ͒ʏ�̏ؖ����Ȃ狖����邪
���̖��͏ؖ����ł͂Ȃ��I������I�Ԗ�肾����
�ؖ�����������ł��̏ؖ��ɉ������������点���Ă��邱�ƂɂȂ�
�܂�
���w�̖��ƌ����ׂ��ł͖���
�u�x�����v���鈫�� ���P��Lie�㐔�̗L����������\����Cartan �̒藝��Weyl�̒藝�ł���Ӗ����肳��Ă�Ǝv���܂����A���������\���̕��ނ��Ăǂ̂��炢�킩���Ă����ł��傤���B
�ł����Affine Lie�㐔��ʎq�Q�Ɋւ��Ă��\���̕��ނ��ǂ̂��炢���ׂ��Ă���̂��m�肽���ł��B
�ڂ�������낵�����肢���܂��B n�����R���̒萔�Ƃ���B
0��x��n�ł������x�ɑ���(n+1)����f(x)=x(x-1)(x-2)...(x-n)���l����B
�s����cos(2��f(x))��0������Ԃ̒����̑��a��L(n)�Ƃ���Ƃ��Alim[n����] L(n)/n�����߂�B �O>>546
>>515(2)�����`����������(1or2)/3�~�cx���~��y���ŗ�������ƁA
E=(2/3)(q-c)(q^2-b)+(q-c)(b-p^2)+(1/3)(p-q)(q^2-p^2)-(1/3)(p-c)(b-p^2)
F=(2/3)(-2c)c^2-(1/3)(-2c)(c^2-b)+(1/3)(p-c)(c^2-p^2)-E-(1/3)(p-c)(b-p^2)
F�͈��������Ă��瑫���đ����������Ԃ�����������BE�������Ă邩��E�������A
F=(2/3)(-2c)c^2-(1/3)(-2c)(c^2-b)+(1/3)(p-c)(c^2-p^2)-{(2/3)(q-c)(q^2-b)+(q-c)(b-p^2)+(1/3)(p-q)(q^2-p^2)-(1/3)(p-c)(b-p^2)}-(1/3)(p-c)(b-p^2)
=-4c^3/3+2c^3/3-2bc/3+p(c^2-p^2)/3-c(c^2-p^2)/3-(2/3)(q-c)(q^2-b)-(q-c)(b-p^2)-(1/3)(p-q)(q^2-p^2)+(1/3)(p-c)(b-p^2)-(1/3)(p-c)(b-p^2)
������C,D���y����������4��������x^4-2bx^2-x+b^2+c=0�̉��ƌW���̊W���A
q=c-2p
p^2+2pq-2pc-qc=-2b
p^2q-2pqc-p^2c=1
-p^2qc=b^2+c
2���ڂ�ό`���A
p^2+q(2p-c)-2pc+2b=0
p^2-q^2-2pc+2b=0
p^2-q^2=2pc-2b
p-q=p-(c-2p)=3p-c
q-c=c-2p-c=-2p
q^2-b=(c-2p)^2-b=c^2-4pc+4p^2-b
�����������A
E=(2/3)(-2p)(c^2-4pc+4p^2-b)+(-2p)(b-p^2)+(1/3)(3p-c)(2b-2pc)-(1/3)(p-c)(b-p^2)
=(-4p/3)(c^2-4pc+4p^2-b)-2pb+2p^3+2p(b-pc)-(2c/3)(b-pc)-pb/3+bc/3+p^3/3-cp^2/3
=-4pc^2/3+16p^2c/3-16p^3/3+4pb/3-2pb+2p^3+2pb-2p^2c-2bc/3+2pc^2/3-pb/3+bc/3+p^3/3-cp^2/3
=-4pc^2/3+16p^2c/3-16p^3/3+4pb/3-2pb+2p^3+2pb-2p^2c-2bc/3+2pc^2/3-pb/3+bc/3+p^3/3-cp^2/3
(E��F���v�Z�r���ł��݂܂���) >>521
(1)
�@f(x) = 1/(1+ax)^b + [ (1+ax)^b ],�@�@a>0, b>0
�@f(x) = exp(-xx/(2��)) + [ exp(xx/(2��)) ],�@�@��>0
�@f(x) = 1/cosh(ax) + [ cosh(ax) ],�@�@a>0
�@f(x) = 1/��(ax+2) + [ ��(ax+2) ],�@�@a>0
�����J�[�������܂�m��Ȃ����̂ť��^^ �O>>551
>>515(2)�O��
x����y���ɕ��s��4�̒����ň͂܂ꂽ�����`��1:2�ɕ��������������}���A
P(p,p^2)(p��0),Q(q,q^2)(q��0)�Ƃ��āA
�����`����������(1or2or3)/3�~�c(x������)�~��(y������)�ŗ�������ƁA
E=(2/3)(q-c)(q^2-b)+(q-c)(b-p^2)+(1/3)(p-q)(q^2-p^2)-(1/3)(p-c)(b-p^2)
F=(2/3)(-2c)c^2-(1/3)(-2c)(c^2-b)+(1/3)(p-c)(c^2-p^2)-E-(1/3)(p-c)(b-p^2)
F�͈��������Ă��瑫���đ����������Ԃ�����������BE�������Ă邩��E�������A
F=(2/3)(-2c)c^2-(1/3)(-2c)(c^2-b)+(1/3)(p-c)(c^2-p^2)
-{(2/3)(q-c)(q^2-b)+(q-c)(b-p^2)+(1/3)(p-q)(q^2-p^2)-(1/3)(p-c)(b-p^2)}
-(1/3)(p-c)(b-p^2)
=-4c^3/3+2c^3/3-2bc/3+p(c^2-p^2)/3-c(c^2-p^2)/3
-(2/3)(q-c)(q^2-b)-(q-c)(b-p^2)-(1/3)(p-q)(q^2-p^2)+(1/3)(p-c)(b-p^2)
-(1/3)(p-c)(b-p^2)
=-4c^3/3+2c^3/3-2bc/3+p(c^2-p^2)/3-c(c^2-p^2)/3-(2/3)(-2p)(q^2-b)-(-2p)(b-p^2)-(1/3)(3p-c)(2b-pc)
=-4c^3/3+2c^3/3-2bc/3+p(c^2-p^2)/3-c(c^2-p^2)/3+(4p/3)(b-2pc+b^2)+2p(b-p^2)-(p-c/3)(2b-pc)
=-4c^3/3+2c^3/3-2bc/3+c^2p/3-p^3/3-c^3/3+p^2c/3+4pb/3-8pc/3+4pb^2/3+2pb-2p^3-2pb+p^2c+2bc/3-pc^2/3
=-4c^3/3+c^3/3-7p^3/3+4p^2c/3+4pb/3-8pc/3+4pb^2/3
=-c^3-7p^3/3+4p^2c/3+4pb/3-8pc/3+4pb^2/3
(2)�㔼�ɂÂ��B �O>>553
>>515
(2)�㔼
������C,D���y����������4��������x^4-2bx^2-x+b^2+c=0�̉��ƌW���̊W���A
2p+q-c=0�����@
p^2+2pq-2pc-qc=-2b�����A
-(p^2q-2pqc-p^2c)=-1�����B
-p^2qc=b^2+c�����C
�A���p^2+q(2p-c)-2pc+2b=0
�@���2p-c=-q
�����p^2-q^2-2pc+2b=0
p^2-q^2=2pc-2b
p-q=p-(c-2p)=3p-c
q-c=c-2p-c=-2p
q^2-b=q^2-p^2+p^2-b=2b-2pc+p^2-b=b-2pc+p^2
�����������A
E=(2/3)(-2p)(c^2-4pc+4p^2-b)+(-2p)(b-p^2)+(1/3)(3p-c)(2b-2pc)-(1/3)(p-c)(b-p^2)
=(-4p/3)(c^2-4pc+4p^2-b)-2pb+2p^3+2p(b-pc)-(2c/3)(b-pc)-pb/3+bc/3+p^3/3-cp^2/3
=-4pc^2/3+16p^2c/3-16p^3/3+4pb/3-2pb+2p^3+2pb-2p^2c-2bc/3+2pc^2/3-pb/3+bc/3+p^3/3-cp^2/3
=-4pc^2/3+16p^2c/3-10p^3/3+pb-2p^2c-2bc/3+2pc^2/3+bc/3+p^3/3-p^2c/3
=-2pc^2/3+3p^2c-3p^3+pb-bc/3
�B�c+�C���A
-2pqc^2-p^2c^2=b^2+c+1
-2p(c-2p)c^2-p^2c^2=b^2+c+1
-2pc+4p^2c^2-p^2c^2=b^2+c+1
3p^2c^2-2pc-b^2-c-1=0
�d����������A
c^2+3(b^2+c+1)=0
p=c�}��{c^2+3(b^2+c+1)}/3c^2
=1/3c
��E=-2pc^2/3+3p^2c-3p^3+pb-bc/3
=-2(1/3c)c^2/3+3(1/3c)^2c-3(1/3c)^3+(1/3c)b-bc/3
=-2c^3/9+1/3c-1/9c^3+b/3c-bc/3
F=-c^3-7(1/3c)^3/3+4(1/3c)^2c/3+4(1/3c)b/3-8(1/3c)c/3+4(1/3c)b^2/3
=-c^3+4/27c+4b^2/9c+4b/9c-8/9-7/81c^3 �O>>553-554���ʒ����B
p=[c�}��{c^2+3(b^2+c+1)}]/3c^2
=1/3c >>515
D�̒��_(c,b)��b���Œ肵���܂�c��(������)�������B
C��D���_P(x.y)�Őڂ��������
�@(xx-b)^2 -x +c = 0,
�@4x(xx-b) -1 = 0,
b<3/4 �̂Ƃ��� ���̎���������
�@x(P) = (1/2){[1-��(1-B^3)]^(1/3) + [1+��(1-B^3)]^(1/3)},
�@y(P) = x(P)^2
�@�@�@ = (1/4){[1-��(1-B^3)]^(2/3) + [1+��(1-B^3)]^(2/3) +2B},
�������@B =4b/3.
b<3/4 �̂Ƃ� (B<1)�@1�����Őڂ���B
b=3/4 �̂Ƃ� (B=1)�@2�����Őڂ���B
�@ c = -3/4�@ P(x,y) = (-1/2,1/4) (�ϋȓ_?)
�@ c = 15/16�@P(x,y) = (1,1)
b>3/4 �̂Ƃ� (B>1)�@3�����Őڂ���B �s�p�O�p�`�́u�s�p�v���ėp��͓���Ŏg���u������s���v���Ƃ����Ӗ��ł́u�s�p�I�v���C���[�W�����
����͂ނ���݊p�O�p�`�̕��ɂȂ��Ă��܂����猙�Ȋ��������� �O>>555�����̖ړI�Y��Ă��B����ɓ�����B
>>515
p=1/3c������A
�_P(p,p^2)=(1/3c,1/9c^2) �O>>558
>>515
�_P�̍��W�́A
P(1/3c,1/9c^2)
(1)
�_P��x���W��p=1/3c
�_Q��x���W��q=c-2p
p-q=3p-c=1/c-c��0
�������C��������D�ɓ_P�œ��ڂ���ɂ�c��-1������B
���_Q��x���W�͓_P��x���W��菬�����B
�_R��x���W��-c��1/3c
���_R��x���W�͓_P��x���W���傫���B (n,k)�͓W����nCk�Ƃ������B
k=1,2,...,p�ɑ��āA((p,k),k)��(p,k)�̍ő����1�ƂȂ�悤�ȑf��p��1���߂�B ����
((p,1),1)=p=(p,1)�����Ȃ��B �O>>559�C�����B
E=(2/3)(q-c)(q^2-b)+(q-c)b+q^3/3-b^3/3-��
�܂��킸����(p,p^2),(0,b^2+c),(0,0)�����ԗ̈惿����������Ȃ��B �O>>564
P(p,p^2),O(0,0),D��x�ؕ�(0,b^2+c)�����ԗ̈惿���܂������ǁA
E=-10b/9c+20/27c-4/27c^3+c^3/3-2c/3-b^3/3-��
F=-4c^3/3-bc/3+7c/9+b/c-20/27c+4/27c^3+b^3/3+��
F-E=-4c^3/3-bc/3+7c/9+b/c-20/27c+4/27c^3+b^3/3+��-(-10b/9c+20/27c-4/27c^3+c^3/3-2c/3-b^3/3-��)
=-4c^3/3-bc/3+7c/9+b/c-20/27c+4/27c^3+b^3/3+��+10b/9c-20/27c+4/27c^3-c^3/3+2c/3+b^3/3+��
=-4c^3/3-bc/3+7c/9+19b/9c-20/27c+8/27c^3+2b^3/3-20/27c-c^3/3+2c/3+2��
=-5c^3/3-bc/3+13c/9+19b/9c-40/27c+8/27c^3+2b^3/3+2��
=-5c^3/3-bc/3+13c/9+19b/9c-40/27c+8/27c^3+2b^3/3+2�� �O>>565
>>515�_P(1/3c,1/9c^2)
�_Q(c-2/3c,c^2-4/3+4/9c^2)
�_R(-c,c^2)
E=-10b/9c+20/27c-4/27c^3+c^3/3-2c/3-b^3/3-��
F=-4c^3/3-bc/3+7c/9+b/c-20/27c+4/27c^3+b^3/3+����=bc/3-(-c^3)/3+(-2c)(2c^2-2b)/6-(2c^2/3-F)+E
F+����E���o��B
E-����F���o��B
(2)
F+��=-4c^3/3-bc/3+7c/9+b/c-20/27c+4/27c^3+b^3/3+��+bc/3-(-c^3)/3+(-2c)(2c^2-2b)/6-(2c^2/3-F)+E
E=4c^3/3+bc/3-7c/9-b/c+20/27c-4/27c^3-b^3/3-bc/3-c^3/3+2c^3/3-2bc/3+2c^2/3
��E=5c^3/3+2c^2/3-7c/9-b/c+20/27c-4/27c^3-b^3/3-2bc/3
E-��=-10b/9c+20/27c-4/27c^3+c^3/3-2c/3-b^3/3-��-{bc/3-(-c^3)/3+(-2c)(2c^2-2b)/6-(2c^2/3-F)+E}
F=10b/9c-20/27c+4/27c^3-c^3/3+2c/3-b^3/3+{bc/3-(-c^3)/3+(-2c)(2c^2-2b)/6-(2c^2/3)}
=10b/9c-20/27c+4/27c^3-c^3/3+2c/3-b^3/3+bc/3+c^3/3-2c^3/3+2bc/3-2c^2/3
��F=-2c^3/3-2c^2/3+2c/3+10b/9c-20/27c+4/27c^3-b^3/3+bc
(3)F-E=-2c^3/3-2c^2/3+2c/3+10b/9c-20/27c+4/27c^3-b^3/3+bc-(5c^3/3+2c^2/3-7c/9-b/c+20/27c-4/27c^3-b^3/3-2bc/3)
=-7c^3/3-4c^2/3+13c/9+19b/9c-40/27c+8/27c^3+5bc/3
c��0�����A����E��F�������͓̂���B����Đ}�Ő�������B
������D�͕�����C�Ɠ����ȗ��ŁA��]�����Ē��_�����킹���y=x^2�̃O���t�ƈ�v�����邱�Ƃ��ł��A
F��E���d�˂�ƁA
E��R(-c,c^2)����(0,b)�Ɉ������������ƕ�����C�ň͂܂ꂽ�̈�G�̒��ł҂����������C�ɉ����悤�Ɏ��܂邪�A���̗̈�G��F�̒��ł҂����������C�ɉ����悤�Ɏ��܂�B
��E��G��F >>566
(1)�͐��S�܂��̕W�����A����ł��ꂪ(2)�̂悤�Ȍ`���œ���ł��肻���B���x���͓����̂Ė�B >>566
����3�i�K���炢�ɕ����đ��X�̒i�K�œK�Ƀp�����[�^��I�ׂΌv�Z�ʂ͂���Ȃɑ����Ȃ��B
�Ō�͑ȉ~�̋ɍ��W�\����m���Ă���Ɗy 566���ĊO�S�A�d�S�A���S�̊W��m���Ă�Ɗy�ɂȂ�܂����H >>571
�Ƃ肠�����O�S��d�S�͖��W
�����ƃG���K���g�ȉ�@���Ƃǂ��Ȃ̂��͒m��Ȃ�
(1) �܂�BC���Œ肵������ ���S�̋O�Ղ��ǂ�Ȍ`���m�F����.
�z�u����]������BC�𐂒��ɂƂ�� �����̈��x���ɕ��s�ɂƂ��̂Ōv�Z�͊y
(2) BC��̈�_P���Œ肵�ăO���O�����Ă݂�� �O��(1) �� �O��(�̈�) �������.
OP�𐅕��ɂƂ��āA�O��(1)��"���S" �̋O�Ղ�����Ƃ悢.
(3) �̈�(2)�ɓ_(b,0) �� ����悤��P�ɂ��āA ���̋��E���� (�ȉ���) �ȉ~�̐����m���Ă�ɍ��W�\������܂ł��Ȃ������B ���ꕪ��������炵���炨�肢���܂�
>>549 �O>>568
rie�Ȃ̂�riko�Ȃ̂�oniroku�Ȃ̂��B ���}�k�W�����̎�v�Z�ƃR���s���[�^�̌v�Z�ǂ��炪�����H >>574
�̂��̕���������������Ƃ�������x�����������X����
��w�@���x���̎��₾���炱���œI����͓̂����Ȃ��낤��
��y�̉@�����w�������ɕ���������������Ȃ����H
���̎�����w����������ۑ�Ƃ��ďo���ꂽ�Ƃ��i4������C�m�ɓ���w���ւ̋�������̉ۑ���ۂ��Ƒz�����Ă�j�A
����ł����y�̉@�������Ȃ��Ƃ��A�Ȃ���傤���Ȃ����c
�w���[�㐔�Ɨʎq�Q�x�i�J��r�V�j�͓ǂ��Ƃ�����H
M1�̎��ɓǂ��A�ǂ݂₷���{��������
���̋��ȏ��̌㔼�ɁA�A�t�B���i�Ƃ�����Mac-Moody�j���[�㐔�Ƃ��ʎq�Q���ڂ��Ă�����
�N�̎���̓����܂ōڂ��Ă����ǂ����͊o���Ă��Ȃ� ���R�Ɛ��w���w�т����̂ł����ǂ�ȕ��삪�������߂ł����H
��w���w�͂܂�Ȃ����T�{���Ă����̂łقƂ�Ǎ��Z�~�܂�ł��B
�Ă������H�w�n�̑�w���w���Ėʔ�����ł����H ����a,b,c��
�i�A�ja>0,b>0,c>0
�i�C�j(1/a)+(1/b)+(1/c)=1/abc
�����B
A=��(1+a^2)+1-a
B=��(1+b^2)+1-b
C=��(1+c^2)+1-c
�Ƃ����Ƃ��A�ȉ��̒l��a,b,c�ɂ��Ȃ��萔�ɂȂ邱�Ƃ������A���̒l�����߂�B
AB+BC+CA-2(A+B+C-1) x^2-2y^2-xy+3y-1��������������Ƃ������̓r�������킩��܂���B
�Ƃ������A
������
(x-2y+1)(x+y-1)�ɂȂ�̂͊��ł킩�����̂ł����A
�r�����ŁA
x^2-yx+(2y-1)(y-1)
�̎��ɁA-yx���ǂ��ɏ������̂��Ƃ����d�g�݂��킩��܂��A�Ȃ������ȒP�ɂ����ɑg�ݍ��ނ��Ƃ��o����̂��悭�킩��܂���B
��悪����Ȃ�܂������A-yx�͓��ł͂���܂����A�l���Â炢�ł��B
���ݍӂ��ċ����ĉ�����܂��ł��傤���A
���肢���܂��B >>582
(x+a)(x+b)=x^2+(a+b)c+ab >>583
���肪�Ƃ��������܂��B
�����������ݍӂ��ċ����Ă��������Ȃ��ł��傤�� �O>>575
>>582
x^2-2y^2-xy+3y-1��������������ƁAx^2���̌W����1�Œ萔����-1������A
(x+ay+1)(x+by-1)�Ƃ����`�ɂȂ�Ǝv���B
a��b�����ł킩��̂͂������ȁB���NJm���ɓ��Ă�Ȃ�v�Z����ق��������B
�W�J����ƁA
-2y^2=aby^2�����@
-xy=axy+bxy�����A
3y=-ay+by�����B
�@���y=0�̂Ƃ�x=�}1
y��0�̂Ƃ��@�̕ӁX��y^2�Ŋ���ƁA
ab=-2�����C
�A���xy=0�̂Ƃ�x=0�܂���y=0
xy��0�̂Ƃ��A�̕ӁX��xy�Ŋ���ƁA
a+b=-1�����D
�B���y=0�̂Ƃ�x=�}1
y��0�̂Ƃ��B�̕ӁX��y�Ŋ���ƁA
-a+b=3�����E
�D-�E���a-(-a)=-1-3
2a=-4
a=-2
�C�ɑ�������(-2)b=-2
b=1
��(x-2y+1)(x+y-1)
�r�����A
x^2-yx+(2y-1)(y-1)
�Ƃ����ό`�͎v�����Ȃ������By^2���ƒ萔���ň�������������Č����Ă�̂��ȁH
-yx�����������ǂ����͂킩��܂���B����A-yx���邶��Ȃ����B
���ӂ�-yx�������āA����x��0,y��0�Ȃ�A�ӁX��-yz�Ŋ��邱�Ƃ�-yz���������Ƃ͂ł���Ǝv���B
�ӁX������邩����Ȃ�����0����Ȃ���0���̈Ⴂ�ŁA���ł��ꎟ���ł�yz�ł��A0����Ȃ���Ί����͂��B >>579 , >>581
����ǂ�����Ď����̂��N�������Ă�������.
x+y+z=��, tan(x) + tan(y) + tan(z) = tan(x)tan(y)tan(z)
a = cot(x), A = ... =1/sin(x) + 1 - cot(x), B= . . .
����ōs���̂��ȂƗ\�z�͗��Ă����̂̃X�}�[�g�Ȏ��ό`���v�������т܂���. >>580
typo�ł����A�����ǂ��� �O>>589
>>579(�O��)
(�C)���bc+ca+ab=1�����@
AB+BC+CA-2(A+B+C-1)
={��(1+a^2)+1-a}{��(1+b^2)+1-b}+{��(1+b^2)+1-b}{��(1+c^2)+1-c}+{��(1+c^2)+1-c}{��(1+a^2)+1-a}-2[{��(1+a^2)+1-a}+{��(1+b^2)+1-b}+{��(1+c^2)+1-c}-1]
={��(1+a^2)+1-a}{��(1+b^2)+1-b}+{��(1+b^2)+1-b}{��(1+c^2)+1-c}+{��(1+c^2)+1-c}{��(1+a^2)+1-a}-2{��(1+a^2)+1-a+��(1+b^2)+1-b+��(1+c^2)+1-c-1}
={��(1+a^2)+(1-a)}{��(1+b^2)+(1-b)}
+{��(1+b^2)+(1-b)}{��(1+c^2)+(1-c)}
+{��(1+c^2)+(1-c)}{��(1+a^2)+(1-a)}
-2{��(1+a^2)+��(1+b^2)+��(1+c^2)+2-a-b-c}
=��(1+a^2)(1+b^2)+(1-a)��(1+b^2)+(1-b)��(1+a^2)+(1-a)(1-b)
+��(1+b^2)(1+c^2)+(1-b)��(1+c^2)+(1-c)��(1+b^2)+(1-b)(1-c)
+��(1+c^2)(1+a^2)+(1-c)��(1+a^2)+(1-a)��(1+c^2)+(1-c)(1-a)
-2{��(1+a^2)+��(1+b^2)+��(1+c^2)+2-a-b-c}
=��(1+a^2)(1+b^2)+(1-a)��(1+b^2)+(1-b)��(1+a^2)+1-a-b+ab
+��(1+b^2)(1+c^2)+(1-b)��(1+c^2)+(1-c)��(1+b^2)+1-b-c+bc
+��(1+c^2)(1+a^2)+(1-c)��(1+a^2)+(1-a)��(1+c^2)+1-c-a+ca
-2{��(1+a^2)+��(1+b^2)+��(1+c^2)+2-a-b-c}
=��(1+a^2)(1+b^2)+(1-a)��(1+b^2)+(1-b)��(1+a^2)
+��(1+b^2)(1+c^2)+(1-b)��(1+c^2)+(1-c)��(1+b^2)
+��(1+c^2)(1+a^2)+(1-c)��(1+a^2)+(1-a)��(1+c^2)
-2{��(1+a^2)+��(1+b^2)+��(1+c^2)+2-a-b-c}
+3-2(a+b+c)+bc+ca+ab �O>>588(�O��)
�O�X>>579(�㔼�����)
�@��������ƁA
=��(1+a^2)(1+b^2)+(1-a)��(1+b^2)+(1-b)��(1+a^2)
+��(1+b^2)(1+c^2)+(1-b)��(1+c^2)+(1-c)��(1+b^2)
+��(1+c^2)(1+a^2)+(1-c)��(1+a^2)+(1-a)��(1+c^2)
-2{��(1+a^2)+��(1+b^2)+��(1+c^2)+2-a-b-c}
+3-2(a+b+c)+1
=��(1+a^2)(1+b^2)+(1-a)��(1+b^2)+(1-b)��(1+a^2)
+��(1+b^2)(1+c^2)+(1-b)��(1+c^2)+(1-c)��(1+b^2)
+��(1+c^2)(1+a^2)+(1-c)��(1+a^2)+(1-a)��(1+c^2)
-2{��(1+a^2)+��(1+b^2)+��(1+c^2)+2-a-b-c}
+4-2(a+b+c)
=��(1+a^2)(1+b^2)+(1-a)��(1+b^2)+(1-b)��(1+a^2)
+��(1+b^2)(1+c^2)+(1-b)��(1+c^2)+(1-c)��(1+b^2)
+��(1+c^2)(1+a^2)+(1-c)��(1+a^2)+(1-a)��(1+c^2)
-2{��(1+a^2)+��(1+b^2)+��(1+c^2)}
=��(1+a^2)(1+b^2)+��(1+b^2)-a��(1+b^2)+��(1+a^2)-b��(1+a^2)
+��(1+b^2)(1+c^2)+��(1+c^2)-b��(1+c^2)+��(1+b^2)-c��(1+b^2)
+��(1+c^2)(1+a^2)+��(1+a^2)-c��(1+a^2)+��(1+c^2)-a��(1+c^2)
-2{��(1+a^2)+��(1+b^2)+��(1+c^2)}
=��(1+a^2)(1+b^2)-a��(1+b^2)-b��(1+a^2)
+��(1+b^2)(1+c^2)-b��(1+c^2)-c��(1+b^2)
+��(1+c^2)(1+a^2)-c��(1+a^2)-a��(1+c^2)
�����ԏ������ȁB >>582
2y-1��-(-2y+1)���Ǝv���Ă݂�� >>586
>x+y+z=��, tan(x) + tan(y) + tan(z) = tan(x)tan(y)tan(z)
tan(x+y+z)=0
(tan x+tan y+tan z-tan x tan y tan z)/(1-tan x tan y-tan y tan z-tan z tan x)=0
tan x+tan y+tan z-tan x tan y tan z=0 �E�ƌP���̑I�l�����Œ��w���x�̍���Ɛ��w���o���ł����A���w�������ς蕪����܂���B
�ǂȂ��������Ă�������m(_ _)m
https://i.imgur.com/yAdk2f8.jpg >>592
����͂������ɕ����Ă��������Ƃ��������悤���Ȃ�
�������ɖ�茩�Ď��͂ʼn�@��҂ݏo����͓̂V�˂��� >>586
�@a = cot(x),�@b = cot(y),�@c = cot(z),
�Ƃ�����
�@1/a + 1/b + 1/c - 1/abc = tan(x)+tan(y)+tan(z) - tan(x)tan(y)tan(z)
�@= sin(x+y+z)/{cos(x)cos(y)cos(z)},
�@A-1 = tan(x/2),�@B-1 = tan(y/2),�@C-1 = tan(z/2),
���
(�^��) = (A-1)(B-1) + (B-1)(C-1) + (C-1)(A-1) - 1
�@= tan(x/2)tan(y/2) + tan(y/2)tan(z/2) + tan(z/2)tan(x/2) - 1
�@= -cos((x+y+z)/2)/{cos(x/2)cos(y/2)cos(z/2)}
�@= -(1/a +1/b +1/c -1/abc)�cos(x)cos(y)cos(z)/{2sin((x+y+z)/2)cos(x/2)cos(y/2)cos(z/2)}
�ł���^^
---------------------------------------------------------
���@�����̗���
e^{i(x+y+z)} = e^(ix)�e^(iy)�e^(iz)
�@= {cos(x)+i�sin(x)}{cos(y)+i�sin(y)}{cos(z)+i�sin(z)}
�@= cos(x)cos(y)cos(z){1+i�tan(x)}{1+i�tan(y){1+i�tan(z)},
��������
cos(x+y+z) = cos(x)cos(y)cos(z) - sin(x)sin(y)cos(z) - cos(x)sin(y)sin(z) - sin(x)cos(y)sin(z)
�@= cos(x)cos(y)cos(z){1 - tan(x)tan(y) - tan(y)tan(z) - tan(z)tan(x)},
��������
sin(x+y+z) = sin(x)cos(y)cos(z) + cos(x)sin(y)cos(z) + cos(x)cos(y)sin(z) - sin(x)sin(y)sin(z)
�@= cos(x)cos(y)cos(z){tan(x) + tan(y) + tan(z) - tan(x)tan(y)tan(z)}, tan�̉��@����g����
tan(x+y+z) = (tx + ty + tz - txtytz) / (1 - txty - tytz - tztx)
[����1] x+y+z = �@���@tanx + tany + tanz = tanx tany tanz
[����2] x+y+z = ��/2�@���@tanx tany + tany tanz + tanz tanx = 1
a = cot(x) (0<x<��/2), b= ... �ƒu����. {�� ����1}
A = 1 + 1/sin(x) - cot(x) = 1 + X,
X := (1-cos(x))/sin(x) = 2 sin(x/2)^2 / sin(x) = sin(x/2)/cos(x/2) = tan(x/2)
(2-A)(2-B)(2-C) + ABC = {2(AB+BC+CA) - 4(A+B+C-1)} + 4
(2-A)(2-B)(2-C) + ABC = (1-X)(1-Y)(1-Z) + (1+X)(1+Y)(1+Z)
= 2 + 2(XY+YZ+ZX) = 2 + 2*1 = 4 {�� ����2}
�� (AB+BC+CA) - 2(A+B+C-1) = {(2-A)(2-B)(2-C) + ABC}/2 -2 = 2 - 2 = 0
�ł���. �w�I�Ӗ��Ȃǂ�����Ȃ狳���ė~����. >>591, >>594 ���肪�Ƃ��������܂� �ʉ� (�ŏ����炱��ł悩����)
(AB+BC+CA) - 2(A+B+C-1)
= (1+X)(1+Y)+(1+Y)(1+Z)+(1+Z)(1+X) - 2(3+X+Y+Z -1)
= 3 +2(X+Y+Z) + XY+YZ+ZX - 4 - 2(X+Y+Z)
= -1 + XY+YZ+ZX = 0 {�����2} �ǂ����Ă�������Ȃ���肪�������̂Ŏ���ł��B�����w��2�N�ł��B
l����̎��A��₀¹ dˡ/dxˡ (x²-1)ˡ dx ������`�ŕ\���B
��`�g�����W�����h���������ɂ��W�J������r���ɏo�Ă����̂ł����s�Ԃ��Ȃ���Ă����̂ŕ�����܂���ł����B
��낵�����肢���܂�m(_ _)m >>585
���肪�Ƃ��������܂�
�Ȃ�ƂȂ��ł����A�킩�����悤�ȋC�����܂��B
�����܂�̌`�������ł��ˁB >>599
�����܂�̌`���Ă����Ȃ�x^2+(a+b)x+ab=(x+a)(x+b)���������Ă�Ή����邾�� >>601
������˂����畷���Ă�
�������l�Ⴂ��w�̂����� >>601
���ȏ��̕��ɂ́ul����̏ꍇ�A
Aₗ=(2l+1)��₀¹Pₗ(x)dx [������Pₗ(x)��l���̃��W�����h��������]
�v
��
�uRodrigues�̌����𗘗p����ƁA�ϕ����v�Z�ł���
Aₗ=(-1/2)⁽ˡ⁻¹⁾ᐟ² ((2l+1)(l-2)!!)/(2((l+1)/2)!)
��������B�v
�Ə����Ă���܂����B
���ȏ��̓W���N�\���d���C������3��(�a���4��)�ŁA����p.140�̂Ƃ���ł��B >>603
�Ƃ肠����Pn(x)��(1-2xt+t^2)^(-1/2)��t^n�̌W���炵������
��[0,1] (1-2xt+t^2)^(-1/2) dx ���v�Z���Ă����n���̌W������������Ȃ��H
�ϕ��͊ȒP�����An�����̌W���͈�ʉ��藝�ŏo����݂��������B >>603
m:=2k + 1 {l �� 1 �ƌ������ɂ����̂� m �ɂ���}
d^{m-1}/dx^{m-1} (x²-1)^m �ɂ���
(x²-1)...(x²-1) �e���̔�����
�u0�K����1�K���������ɂ���ꍇ�v or�u 3�K�ȏ�̍�������ꍇ�v �͏�����̂�
2�K�������݂̂���Ȃ�p�^�[�����l����悢.
2�K�����̃y�A�����O��: (m-2)!!
�@1��ڂ̔����ƃy�A�ƂȂ������ m-2 �ʂ�, �܂��y�A��g��ł��Ȃ����̔����Ƃ̃y�A�� m-4 �ʂ�, ... }
m������ 2�K������ (k ��) ��(�����t��)�I�ѕ�: m!/(m-k)!
��[0,1] d^m/dx^m (x²-1)^m dx
= [ d^{m-1}/dx^{m-1} (x²-1)^m ]{x=0,1} + 0
= [ m!/(m-k)!* (m-2)!! * (x²-1)^{k+1} (2)^k ] {x=0,1}
= m!/(m-k)!* (m-2)!! * (-1)^k * 2^k
= m!*(m-2)!/((k+1)!*(k-1)!) * 2 * (-1)^k
��͍D���Ȃ悤�ɐ������Ă���
(m-2)!! = (m-2)(m-4)... 1 = (m-2)(m-3)(m-4)... 1 / {(m-3)(m-4)...2} = (m-2)!/(2k-2)!!
(2k-2)!! = 2^(k-1) * (k-1)! >>604
���肪�Ƃ��������܂��A������g������@�������Ă݂܂�
>>605
����Ȃ����������ł��ˁc�c���肪�Ƃ��������܂����I >>602������厸�s���Ăĉ��z������
�܂����ʂɓǂ�r�����Ȃ��Ɍ��_����������Ă邩����Ď����
���Ⴀ���_����������ɏ����Ă��Ă͕̂��ʂ̂���肾���Ă��Ƃɂ͋C�Â����� >>598
(�^��) = ��[0,1] P_L(x) dx
= [ {1/(2^L�L!)}(d/dx)^(L-1)�(xx-1)^L ](x=0,1)
L�͊�Ƃ���B
x=1 �̂Ƃ�
�@L��(xx-1)���q�̂����A���Ȃ��Ƃ��P�͔�����Ƃ�邩��A�O
x=0 �̂Ƃ�
�@(xx-1)^L �̒��� x^(L-1) �̌W���͂Q�������ɂ��
�@�@(-1)^((L+1)/2) �b(L, (L-1)/2)
�@�@= (-1)^((L+1)/2) L! /{((L+1)/2)! ((L-1)/2)!}
�@�@= -(-2)^((L-1)/2) L! (L-2)!! /{((L+1)/2)! (L-1)!}
�@(2^L�L!) �Ŋ�����
�@�@= -(-1/2)^((L-1)/2) (L-2)!! /{2 ((L+1)/2)! (L-1)!}
�@(L-1) ���������� (L-1)! �{�ɂȂ�B
�@x=0 �͉����� -1 �{����B
�@�@(-1/2)^((L-1)/2) (L-2)!! /{2 ((L+1)/2)!} >>598
2�N�ł���Ȃ��Ƃ��́H
����� >>608
�Ȃ�قǁA������f���ɓW�J������Y��ɉ�������ł��ˁc�c���������v�Z�͂�b���܂��A���肪�Ƃ��������܂����I
>>609
�w���̕��ł͂Ȃ��̂ł����A�t�x�ݒ��Ɍv�Z�͂�������̂����������̂ŁA�w�L�т��ĕ����Ă��܂�(��)
�݂Ȃ��J�ɂ��肪�Ƃ��������܂����B �R���������͂ǂ��Ȃ�̂��Ďv�������������L=0�̂Ƃ���������0�ɂȂ�̂ˁB
���X�ʔ����B �����Ȋw��b�\���u���Ȋw�ҏ܁v�̎�ܒʒm���Ă����邩�킩��܂����H�H x^x+y^y��z^z �ix��y��z�j
���������R��x,y,z�͑��݂��܂����H >>613
���݂��Ȃ�
z��3�ȏ�Ƃ��Ă悭�Az>y>x�Ƃ��Ă悢
�����
z^z=(z^y)*(z^(z-y))>(z^y)*3>z^y+z^y>y^y+x^y>y^y+x^x �{���ɉe�����Ȃ�����
(z^y)*(z^(z-y))��(z^y)*3
������ �{���ɉe�����Ȃ�����
(z^y)*(z^(z-y))��(z^y)*3
������ �T�Z�������̂ł����A�����ĉ������B
�R��������w���ƃR���i�E�C���X���z�����ނ��Ƃ����҂���܂����H ����ȂƂ���Ƀt���N�^����
ABACABADABACABAEABACABADABACABA
edcba�@�@�@�@�@�@edcba
�@�@�@1 a�@ 10000 e
�@�@ 10 b�@ 10001 a
�@�@ 11 a�@ 10010 b
�@�@100 c�@ 10011 a
�@�@101 a�@ 10100 c
�@�@110 b�@ 10101 a
�@�@111 a�@ 10110 b
�@ 1000 d�@ 10111 a
�@ 1001 a�@ 11000 c
�@ 1010 b�@ 11001 a
�@ 1011 a�@ 11010 b
�@ 1100 c�@ 11011 a
�@ 1101 a�@ 11100 c
�@ 1110 b�@ 11101 a
�@ 1111 a�@ 11110 b
�@�@�@�@�@ �@11111 a �C�ӂ�n�̐����̒�����m�̐��������o�����@�ŁA���o���������̘a��m�̔{���ɂȂ�悤�Ȃ��̂����݂���Ƃ����B
���̂悤��n�Ƃ��ėL�蓾����̂̒��ōŏ��̂��̂�m�̎��ŕ\���B
���Ƃ���m=3�Ȃ狁�߂�l��5�B m(m+n)-n^2=1
�������̐����̑g(m,n)���l����B
���̂悤��(m,n)�͖����ɑ��݂��邱�Ƃ������B m(m+n)-n^2=1�c(*)
�������̐����̑g(m,n)���l����B
�i1�j���̂悤��(m,n)�͖����ɑ��݂��邱�Ƃ������B
�i2�j(*)�������ׂĂ�n�ɂ킽���āA�ȉ��̘a�i�����a�j���v�Z����B
��1/(n^2+1) >>619�@���낢��ȗႪ�����Ă������BABACABA pattern���Ė��O�܂ł��Ă���
�n�m�C�̓��̓�������������
https://en.wikipedia.org/wiki/ABACABA_pattern >>620
m�Ŋ������Ƃ��̗]��(��])���l����B
�C�ӂ�n�̐�����
�E{0,1,����,m-1} �̂ǂꂩ�� m �ȏ�܂�
�E{0,1,����,m-1} �����ׂĊ܂�
�̂����ꂩ�����Ȃ�Ή\�B
�@n = (m-1)^2 +1�@�Ȃ�Ή\�B
(�����n�̏���B�ŏ���n�͂����Ə������̂���) �� m����̂Ƃ��B
--------------------------
m�������̂Ƃ���
�C�ӂ�n�̐�����
�E{0,1,����,m-1} �̂ǂꂩ�� m �ȏ�܂�
�����Ȃ�Ή\�B
�@n = m(m-1) +1 >>624
(1)
�t�B�{�i�b�`�����g����
�@(m, n) = (F_{2k-1}, F_{2k})�@�@�@(k�F���R��)
�Ƃ�����
�@m(m+n) - nn = F_{2k-1}F_{2k+1} - F_{2k}^2
�@= (-1)^{2k-2}
�@= 1,
�ƂȂ�A��ӂ����B���ꂪ���ׂĂƎv����B
*)�@�t�B�{�i�b�`�� F_k �ɂ���
�@F_{k+1}�F_{k+3} - (F_{k+2})^2
�@= (F_{k+1})^2 - F_k�F_{k+2}
�@= ����
�@= (-1)^k�{F_1�F_3 - (F_2)^2}
�@= (-1)^k.
(2)
�@1/(nn+1) = {m(m+n)-nn}/{m(m+n)}
�@= n/(m+n) - (n-m)/m
�@= F_{2k}/F_{2k+1} - F_{2k-2}/F_{2k-1},
���
�@��[k=1,K] 1/(nn+1) = F_{2K}/F_{2K+1}
�@�� 1/�� = (��5 -1)/2. >>628
Fibonacci�Ƃ͓������������Ⴄ�B >>629
�@�Ӗ��s������
��̓I�ɏ�����
�@k=1 �̂Ƃ��@(m,n) = (1,1)
�@k=2 �̂Ƃ��@(m,n) = (2,3)
�@k=3 �̂Ƃ��@(m,n) = (5,8)
�@k=4 �̂Ƃ��@(m,n) = (13,21)
�@�@���� >>626
�����ŏ��͋��ŕ����Ă��̍l�@�����Ă��̂ł���������m�ł����ɔj�]�����̂ł��̃X���ɓ����܂���
>>621�����������ۂ��ł� >>631
fibonacci����̓�����������
x^2-x-1�B
(2m+n)^2-5n^2=4�̓�����������
x^2-5=0�B �ԈႦ���B
x^2-5y^2=4
������
(1+��5)^n=x+y��5
���B�݂��Ă���B 1�̃T�C�R����N���A�o��N�̖ڂ̐ς�
An�Ƃ���B���̎�An��6�̔{���ɂȂ�m����n��p���ĕ\���B 1-p(all 1,3,5)-p(all 1,2,4,5)+p(all 1,5) >>636
���Ȃ��Ƃ����2�̔{�������Ȃ��Ƃ����3�̔{���ł��邱�ƂƁA���Ȃ��Ƃ����6�̔{���ł��鎖���ǂ�����ď�������Ηǂ��̂����l�ɐ����ł�����A�����ł��Ă��܂���B
���݂܂���B�����Ē�����ƗL��ł��B >>635
���@���@1�`�Q�O�ŃV�~�����[�V�������Ă݂��B
sim <- function(n,k=1e5){ # n:�T�C�R����U��� k:�V�~�����[�V������
sub <- function(n){
prod(sample(6,n,replace=TRUE))%%6==0 # n��̖ڂ̐ς�6�ŏ��Z������]��0���H
}
mean(replicate(k,sub(n))) # 0�ƂȂ銄����Ԃ�
}
p=sapply(1:20,function(n) sim(n))
data.frame(p)
p
1 0.16560
2 0.41369
3 0.61413
4 0.75417
5 0.84134
6 0.89669
7 0.93356
8 0.95765
9 0.97254
10 0.98093
11 0.98873
12 0.99175
13 0.99458
14 0.99611
15 0.99737
16 0.99849
17 0.99899
18 0.99924
19 0.99963
20 0.99978 �������Ȃ�܂������m�����V���~���[�V�������Ă����Z�ȊO�Ɏg���Ȃ��� >>638
1 : 1/6
2 : 5/12
3 : 133/216
4 : 325/432
5 : 6541/7776
6 : 4655/5184
7 : 261493/279936
8 : 535925/559872
9 : 9796381/10077696 �u�C�ӂ�3�ȏ�̊n�ɂ��āAn-1�̐���n,��2n,��3n,...,��(n-1)n�̂����A���������������ł�����̂̌��Ɗ�ł�����̂̌��͓������v
���藧���Ă���ۂ���ł����Ǐؖ����Ă���܂����H >>635
1-(4^n+3^n-2^n)/6^n ���@���|�@�����������������i���j�o
�@�@���������������i�������j
�@�@���������D���������i���j
�@�@�����P�|�i�S�O���{�R�O���|�Q�O���j�^�U�O��
�@�@���Q�����������������D�������������i���j�m�Q�n
�@�@�������������i���Q�C�T�C�����������i���Q�j�j
�p
�����R�O
�������i���@�����@�P�F���j�o
�@�@�������i���C�V�F�V�C���i���j�C�V\���V�j
�p
1 : 1/6
2 : 5/12
3 : 133/216
4 : 325/432
5 : 6541/7776
6 : 4655/5184
7 : 261493/279936
8 : 535925/559872
9 : 9796381/10077696
10 : 19786525/20155392
11 : 358427653/362797056
12 : 239941975/241864704
13 : 12991999021/13060694016
14 : 26030320685/26121388032
15 : 469096926613/470184984576
16 : 938923986325/940369969152
17 : 16909350566461/16926659444736
18 : 3758920371605/3761479876608
19 : 609083700366373/609359740010496
20 : 1218351814233125/1218719480020992
21 : 21932542135610701/21936950640377856
22 : 43868026759785805/43873901280755712
23 : 789659760174634933/789730223053602816
24 : 526455508992460775/526486815369068544
25 : 28429161282767803741/28430288029929701376
26 : 56859074012717372765/56860576059859402752
27 : 1023472347053496500293/1023490369077469249536
28 : 2046956711331417849925/2046980738154938499072
29 : 36845364987782900777581/36845653286788892983296
30 : 24563640732593188077775/24563768857859261988864 �����\�� �����\�� �V�~���l
1 1/6 0.1666666667 0.16695
2 5/12 0.4166666667 0.41535
3 133/216 0.6157407407 0.61633
4 325/432 0.7523148148 0.75147
5 6541/7776 0.8411779835 0.84065
6 4655/5184 0.8979552469 0.89742
7 261493/279936 0.9341170839 0.93430
8 535925/559872 0.9572277235 0.95693
9 9796381/10077696 0.9720853854 0.97253
10 19786525/20155392 0.9816988427 0.98123
11 358427653/362797056 0.9879563438 0.98787
12 239941975/241864704 0.9920503944 0.99250
13 12991999021/13060694016 0.9947403258 0.99509
14 26030320685/26121388032 0.9965136865 0.99644
15 469096926613/470184984576 0.9976858939 0.99761
16 938923986325/940369969152 0.9984623256 0.99840
17 16909350566461/16926659444736 0.9989774191 0.99890
18 3758920371605/3761479876608 0.9993195484 0.99937
19 609083700366373/609359740010496 0.9995470005 0.99943
20 1218351814233125/1218719480020992 0.9996983180 0.99976
> >>635
����: (���3) �� 6 = ((2��4��6)��3) �� 6
�@�@= (2��3) �� (4��3) �� (3��6) �� 6
�@�@= (2��3) �� (4��3) �� 6
{�ȗ��L�@�͓K���ɐ������Ă�������}
P1 := P(��), �@P2 := P(���ȁ�), ...
Q1 := P(�ʁ�), �@Q2 := P(�ʁ��ȁʁ�), ...
Qk = ((6-k)/6)^n
P1 = 1 - Q1
P2 = 1 - 2*Q1 + Q2
P3 = 1 - 3*Q1 + 3*Q2 - Q3
P4 = 1 - 4*Q1 + 6*Q2 - 4*Q3 + Q4
�m��: P((2��3) �� (4��3) �� 6) = (P2 + P2 + P1) - (P3 + P3 + P3) + P4
�@�@= P1 + 2*P2 - 3*P3 + P4�@= 1 - Q2 - Q3 + Q4
�@�@= 1 - (4/6)^n - (3/6)^n + (2/6)^n
�܂����ʂ�����H�v�̗]�n����ł�����{�ɒ����ȕ��@���̂�܂���. >>636�637 >>642
3|An�@�́@not (all 1,2,4,5)
�@p(3|An) = 1 - p(all 1,2,4,5) = 1 - Q2 = 1 - (4/6)^n,
2|An�@�́@not (all 1,3,5)
�@p(2|An) = 1 - p(all 1,3,5) = 1 - Q3 = 1 - (3/6)^n,
(3|An or 2|An)�@�́@not (all 1,5)
�@p(3|An or 2|An) = 1 - p(all 1,5) = 1 - Q4 = 1 - (2/6)^n,
�m���Fp(6|An) = p(3|An and 2|An)
�@�@= p(3|An) + p(2|An) - p(3|An or 2|An)
�@�@= 1 - Q2 - Q3 + Q4
�@�@= 1 - (4/6)^n - (3/6)^n + (2/6)^n.
�܂����ʂ�����H�v�̗]�n����ł����A��{�ɒ����ȕ��@���̂�܂����B �{���ɉ����H�v�ł��ĂȂ���������u��{�ɒ����v�Ə����������Ȃ̂�
�������悤�Ɏ~�߂��̂ł��傤���ˁB�f���ɕ|����ł���... >>577
���X���肪�Ƃ��������܂��B���Ԏ��x��Ă��݂܂���B
���͍��A�ׂ̕��삭�炢�Ń|�X�h�N�����Ă��܂��B
���̍ɂȂ�ƒp���������ĕ����ɕ����Ȃ����₪�����Ă��܂��܂��āA
�Ȃ��Ȃ��{�ׂĂ��ڂ��Ă��Ȃ��̂ō����Ă��܂����B
�����炭�܂Ƃ܂��������͂Ȃ��A�U�����Ă���_���ׂȂ��Ƃ����Ȃ��\��������̂�
���x�ڂ������ȕ��ɕ����Ă݂܂� >>641
�����[�A�m���ɐ��藧���Ă���ۂ��I
�ؖ��͂킩��Ȃ����A�ʔ����� �ʔ������ǎ���̃t�����ďo�肵�Ă���̂��E�U���B
�l�Ԑ��^���B Excel�ŏ������������������A
>>641
�̖�����A���̂悤�ɏ��������Ă������������ȁH
�i���̖����q=2�ɑ����j
�u2�ȏ�̐���q��1�Œ肷��B
m��C�ӂ�1�ȏ�̐����Ƃ���Bn=qm+1�Ƃ����An-1�̐���n,��2n,��3n,...,��(n-1)n�̂����A����������q�Ŋ�������̂̌���m�ł���v >>651�����`�B����������������Ă݂܂��������藧���Ă����ł��B�������Ŗl���l���Ă݂܂��B >>650
x,y�͐��̎����Ƃ���B
x^x-2(x^y)(y^x)+y^y��0�������B >>653
�U
2^2-2*2^2*2^2+2^2=-24<0 >>650
�Ƃ������̒萔�Ƃ���B
�i1�jr�ɂ��Ă̕�����cos(��+r)=sin(r��)�͂����̐��̎������������B
�i2�j���l�ɁA
-sin(��+r)=rcos(r��)-r/2�͂����̐��̎������������B >>651
��������
�ؖ��Ɏ��|�����Ă݂܂� >>653 >>655
�����������̃��x���Ⴂ�̎����ŋC�Â��Ȃ��́H >>651 ������������ƕς��Ă����ƈ�ʉ����āA
n�𐳂̋����A[]�͏����Ƃ��āA
�u����a(k)=[��{k(n+1)}] �@1��k��n�A
����b_i(k)��a(k) (mod i) i|n,0��b_i(k)��i�A
N{k:b_i(k)=j}��b_i(k)=j�ƂȂ�k�̌���\���ƁA
N{k:b_i(k)=j}+N{k:b_i(k)=i-j}=2n/i�����藧�B�v
�ł����������ł��ˁB>>641��i=2�̏ꍇ�A>>651��j=0�̏ꍇ�B
>>641���l���Ă܂������A���[i^2/(n+1),(i+1)^2/(n+1))��[(n-i)^2/(n+1),(n-i+1)^2/(n+1))�Ɋ܂܂�鐮���̐�����ɂQ�ł��邱�Ƃ��K���ɕ����������ĕs�����������Ƃ킩��̂ŁA�����炭�����܂����B >>657
���w���Z���x�A30���A��ڈ��Ƃ��Ă���܂��B >>658�A������
��ʉ�������n�̋����W�Ȃ��Ȃ邩������܂���ˁi�{���ɐ��藧���Ă���j >>641
���ۂɃ`�F�b�N���Ă݂��Ƃ���An=46341�ȉ��ł́A�������Ă���Ɗm�F�ł������ǁA
n=46343�ȏ�ł́A�s�������ۂ��B
�in=46343�̎��A���23169�ŁA������23173�j
�E�덷�̉\�����^�������ǁA�P�ƂŔ������Ă���̂ł͂Ȃ��An=46343�ȏ�ŘA�����ĕs����
�E[sqrt(i*n)]��[i*n/sqrt(i*n)]����v���邩�̃`�F�b�N���ʉ�
�ǂȂ����A�����肢���܂��B >>661
46343^2 > 2^31 ������I�[�o�[�t���[�̉\���́H
���{�������ł���Ă�́H 46341^2 < 2^31 < 46343^2
���ꂩ�@���炵�܂����B >>653
(1,1)�_�Ƃ���u���Ȑ��̊O�� (�����Ɖ���) �̗̈�Ő��藧�B
�@{(x,y) | 0<x<0.932806�@or�@0<xy<1�@or�@0<y<0.932806}�@���܂ށB
�@
���E���͓_
�@(1, 1.66038753819)
�@(0.932806, 1.220063)
�@(1, 1)
�@(1.220063, 0.932806)
�@(1.66038753819, 1)
��ʂ�B ���w����3����2������
��3��(6)�̉��s���ł�
https://i.imgur.com/MxjdNDW.jpg 0.5�~2+2.5�~7+4.5�~13+6.5�~9+8.5�~6+10.5+1=197
197��38=5.2�����Ǝv���̂ł��� >>661
�|���Ȃ��Ă����̂ŔώG�ł����ꉞ�ؖ��������Ă����܂��B
�un�͋���,k��{1,2,...,n}�Ƃ���B
1<��(n+1),��(n-1)(n+1)<n<��{n(n+1)}<n+1���A���[0,1)��[n,n+1)�ɂ́�{k(n+1)}����܂܂��.
i,j��{1,2,...,n-1}�Ƃ���B
(i+1)^2-i^2=2i+1<2(n+1)�����[i,i+1)�Ɋ܂܂��悤�ȁ�{k(n+1)}�͍��X�Q�B
[i,i+1)�Ɂ�{k(n+1)}���Q�܂܂��
��i<��{j(n+1)},��{(j+1)(n+1)}<i+1
��i^2<(n+1)j,(n+1)(j+1)<(i+1)^2
��(n-i)^2>(n+1)(n+1-2i)+(n+1)(j+1)>(n+1)(n-2i+j)
(n-i+1)^2<(n+1)(n+1-2i)+(n+1)j=(n+1)(n-2i+j+1)
�́�{(n-2i+j)(n+1)}<n-i,n-i+1<��{(n+1)(n-2i+j+1)}
��[n-i,n-i+1)�Ɂ�{k(n+1)}��0�܂܂��
[i,i+1)�Ɂ�{k(n+1)}��0�܂܂��
��{j(n+1)}<i,i+1<��{(j+1)(n+1)}
��j(n+1)<i^2,(i+1)^2<(j+1)(n+1)
��(n-i)^2<(n+1)^2-2(n+1)(i+1)+(n+1)(j+1)=(n+1)(n-2i+j)
(n-i+1)^2>(n+1)^2-2(n+1)i+j(n+1)=(n+1)(n-2i+j+1)
�ˁ�{(n+1)(n-2i+j)}<n-i,n-i+1<��{(n+1)(n-2i+j+1)}
��[n-i,n-i+1)�Ɂ�{k(n+1)}��2�܂܂��
[i,i+1)��1�܂܂��
��{(j-1)(n+1)}<i����{j(n+1)}<i+1<��{(j+1)(n+1)}
��(j-1)(n+1)<i^2��j(n+1)<(i+1)^2<(j+1)(n+1)
�ˁ�{(n+1)(n-2i+j-1)}<n-i<��{(n+1)(n-2i+j)}<n-i+1����{(n+1)(n-2i+j+1)}
��[n-i,n-i+1)�Ɂ�{k(n+1)}���P�܂܂��
�����,i��n/2,�Ȃ��[i,i+1)��[n-i,n-i+1)�ɂ́�{k(n+1)}���Q�܂܂�A
i=n/2�Ȃ��[i,i+1)�ɂ́�{k(n+1)}���P�܂܂��B
n��0,2(mod 4)�ŏꍇ�������čl����ƁA��ӂ̐������킩��B�v
��̏ؖ��������Ă���Ύ����悤�ȉ�@�ł����炭N{k:a(k)=pd�}i}+N{k:a(k)=n-pd∓i}=2(��������)�������āA>>658�̈�ʉ������������Ȃ̂ł����A�Ԉ���Ă����猳���q���Ȃ��ł��ˁB >>661
����A�������Ȃ������ǁB
> sim <- function(m){
+ n=2*m+1
+ i=1:(n-1)
+ a=sqrt(i*n)
+ b=floor(a)
+ cat(sum(b%%2==0),sum(b%%2==1),'\n') # �����̐��A��̐�
+ sum(b%%2==0)==sum(b%%2==1) # mean(floor(a)%%2==0)==0.5�ł�����
+ }
> sim((46343-1)/2) # n=2*23171+1=46343
23171 23171
[1] TRUE
> sim(46343)
46343 46343
[1] TRUE x,y�͐��̎����Ƃ���B
x^(2x) - 2(x^y)(y^x) + y^(2y) �� 0,
(����)
log �͒P������������
�@(x-y){log(x)-log(y)} �� 0
�@(x/y)^(x-y) �� 1,
�@(x^x)(y^y) �� (x^y)(y^x),
�����
(����) �� x^(2x) -2(x^x)(y^y) + y^(2y)
�@= (x^x - y^y)^2
�@�� 0, 10�����Q�{�P�܂ł͐������邱�Ƃ��m�F�B
> sim <- function(m,print=FALSE){
+ n=2*m+1
+ i=1:(n-1)
+ a=sqrt(i*n)
+ b=floor(a)
+ if(print) cat(sum(b%%2==0),sum(b%%2==1),'\n') # �����̐��A��̐�
+ mean(floor(a)%%2==0)==0.5 # sum(b%%2==0)==sum(b%%2==1) �Ɠ���
+ }
> sim=Vectorize(sim)
> flg=sim(1)
> i=1
> k=1e5
> while(flg & i < k){
+ i=i+1
+ flg=sim(i)
+ }
> i
[1] 1e+05 >>666
>0.5�~2+2.5�~7+4.5�~13+6.5�~9+8.5�~6+10.5+1=197
0.5�Ƃ�2.5�Ƃ����ĂȂɁH�Ō�{1�Ƃ́H (1�2+3�7+5�13+7�9+9�6+11)/38=217/38=5.71�c�c��5.7(��)
�i(-_-)�a�@�@�a>>665
�i���܁�ށ@ ��a������
��`(_)_)��~�@�a������
�_���҃ҁ�_������_�_�_
�_�_�_�_��(_ _))`�܂�`
�_�_�_�_�_�_�_`�Ҥ�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_`�O>>589 ���Z�p�`ABCDEF�̕�AB��ɓ_G���Ƃ�A�܂����Z�p�`�̓����ɓ_H����CGH�����O�p�`�ƂȂ�悤�ɂƂ�B
���̂Ƃ��AG�̂Ƃ���ɂ�炸�AH�͂��钼����ɂ��邱�Ƃ������B >>672
���肪�Ƃ��A�������܂���
>>671
0�ȏ�2����������0�ȏ�1�ȉ��ǂl����l����̂�0.5���~2�l�ƍl���܂���
+1�́~1�̊ԈႦ�ł� >>674
�Ƃ肠�����U���͂Ƃ������Ƃ���
��In
=��[0,��]sin^2(nt)/(t^2+��^2)dt
=1/2��[0,��](1-cos(2nt)/(t^2+��^2)dt
��1/2��[0,��]1/(t^2+��^2)dt
=1/8
���ȁB >>673
���f���ʏ�ōl����B
O=0, A=1, B=e^(i��/3), C=e^(i2��/3) = B - 1, ... , E= -B, ...
G = A + AB*t = 1 + (e^(i��/3)-1)*t = 1 + C*t �@ ( t �� [0,1] )
�ƒu����
H = G + GC * e^(i��/3) = (1 + e^(i2��/3)*t) + (e^(i2��/3) - 1 - e^(i2��/3)*t) * e^(i��/3)
= (e^(i2��/3) + 1)*t - e^(i��/3)
= B*(t - 1) = t*O + (1-t)*E
�� H��OE������ɂ̂�B >>651�����������̂ł�
>>658
b_i(k)�̒�`���悭�킩��Ȃ��ł��c�B
a(k)�́�̐��������ł���ˁBb_i(k)��a(k)��i�Ŋ������]��H
���Ƃ����0��b_i(k)��i-1��1��b_i(k)��i�̂ǂ��炩�̂悤�ȋC�������ł���
j=0�̂Ƃ���b_i(k)=0��b_i(k)=i�𗼕��l�����ł����H
���ƁA>>651�ł�n�͋����ł���ł�OK�ł���A�Ƃ����\�z�ł��B >>667
�㔼�Atypo��c�_�̏d��������̂ŁA�������J�߂ɂ܂Ƃ߂�Ƃ����Ȃ邩�ȁH
(���1)�@(���ɂ� <�A���A>�A�� �̂����ǂꂩ1������)
i �� ��{j(n+1)}
��i^2 �� (n+1)j
��(n-i+1)^2=(n+1-i)^2=(n+1)(n+1-2i)+i^2 �� (n+1)(n+1-2i)+(n+1)j=(n+1)(n-2i+j+1)
��(n-i+1)^2 �� (n+1)(n-2i+j+1)
��n-i+1 �� ��(n-2i+j+1)(n+1)
(���2) ���1��i��i+1�Ƃ�j��j-1��j+1����ꂽ���̂��܂߂�ƁA����4���킩��
i �� ��{(j-1)(n+1)}��n-i+1 �� ��(n-2i+j)(n+1)
i �� ��{j(n+1)}��n-i+1 �� ��(n-2i+j+1)(n+1)
i+1 �� ��{j(n+1)}��n-i �� ��(n-2i+j-1)(n+1)
i+1 �� ��{(j+1)(n+1)}��n-i �� ��(n-2i+j)(n+1)
���̕��2��4���g���ƁA����3�̂��Ƃ�������
[i,i+1)�Ɂ�{k(n+1)}�̌`��2�܂܂��
�̂���j�����݂�, i����{j(n+1)},��{(j+1)(n+1)}<i+1
�̂���j�����݂�, ��{(n-2i+j)(n+1)}<n-i,n-i+1����{(n+1)(n-2i+j+1)}
��[n-i,n-i+1)�Ɂ�{k(n+1)}�̌`��0�܂܂��
[i,i+1)�Ɂ�{k(n+1)}�̌`��1�̂݊܂܂��
�̂���j�����݂�, ��{(j-1)(n+1)}<i����{j(n+1)}<i+1����{(j+1)(n+1)}
�̂���j�����݂�, ��(n-2i+j-1)(n+1)<n-i����(n-2i+j)(n+1)<n-i+1����(n-2i+j+1)(n+1)
��[n-i,n-i+1)�Ɂ�{k(n+1)}�̌`��1�܂܂��
[i,i+1)�Ɂ�{k(n+1)}�̌`��0�܂܂��
�̂���j(0��n��������Ȃ�)�����݂�, ��{j(n+1)}<i,i+1����{(j+1)(n+1)}
�̂���j(0��n��������Ȃ�)�����݂�, n-i����{(n-2i+j)(n+1)},��{(n+1)(n-2i+j+1)}<n-i+1
��[n-i,n-i+1)�Ɂ�{k(n+1)}�̌`��2�܂܂�� >>674
n�𐳂̐����Ƃ��A
�@I_n = ��[0,n��] n (sin x)^2 /{x^2 + (n��)^2} dx
�Ƃ���B
(i) k�𐳂̐����Ƃ���Ƃ��A�s����
�@�@��[(k-1)��,k��] (sin x)^2 /{x^2 + (n��)^2} dx �� 1/{2��[(k-1)^2 + n^2]},
�����藧���Ƃ������B
(ii) lim[n����] I_n�@�����߂�B >>678�ւ̎��ȃ��X�B
����j=0�̂Ƃ��͏����ub_i(k)=i�v�͒P�Ɂub_i(k)=0�v�Ɠ��������ƍl����A�̂�������A
>>658�͂����Ă����ł��B
>>667�̍Ō�̒i���ɂ��āB
����A�O�i�܂ł̘_�@�Ŋ��ɁA����������n/2����̃G���A��
����������n/2��菬�̃G���A�ł́A[i,i+1)��[n-i,n-i+1)�ɕK������������2�܂܂��Ƃ���"�Ώ̐�"�͎�����Ă��邩��A
����G���A�ł̗]�肪j�Ȃ�A��菬�G���A�ł̗]���-j�Ȃ킯�ŁA
�S�̂��g�[�^���ōl���Ęa���Ƃ��2�{�J�E���g���邱�ƂɂȂ�킯�ŁA�u�قځv�ؖ��I����Ă܂��H
�������AExcel���߂Ă邾���ł͂���"2�Ώ̐�"�͋C�t���Ȃ������ȁc
�����Ă݂�Ίm���ɂ����Ȃ̂ł����A������ >>677
���肪�Ƃ��������܂�
���ʐ}�`�Łu���꒼����́�OGE=180���v���g�������A���f�����ʂ̕��������₷���̂ł��傤�� >>674 (i)
���Ԃ�
�@1/{2��(k^2 + n^2)} < ��[(k-1)��,k��] (sin x)^2 /{x^2 + (n��)^2} dx < 1/{2��[(k-1)^2 + n^2]},
���낤�ˁB >>682 �e�����₷���Ǝv�����@�ʼn��������Ǝv���܂��B
�t�Ɏ���
> ���ʐ}�`�Łu���꒼����́�OGE=180���v���g��
������̕��@��������Ȃ��̂ŋ����ė~�����ł��B
( ��OGE=180�� �͕ʂ̉����̏����ԈႢ���Ǝv���܂��� ) >>675
�������Ăǂ�����
�����0.5*2��������
���w����n����肾�� a�𐳂̒萔�Ƃ���Bn=1,2,...�ɑ��Ċ�f_n(x)���A
f_1(x)=ax(x-1)
f_n+1(x)=f(f_n(x))
�ɂ�菇����߂Ă����B
�i1�j0<��<1����0<f_1(��)<1�ƂȂ�悤�ȃ��͈̔͂�a�ŕ\���B
�i2�j0<��<1�Ƃ���B���ׂĂ̎��R��k�ɑ���0<f_k(��)<1�ƂȂ�悤�ȃ��͈̔͂�a�ŕ\���B
�i3�j�i2�j�ɂ����ă�����肤��l�͈̔͂�s<��<t�ƕ\���Ƃ��A�Ɍ��llim[a����](t-s)�����߂�B >>683
���q�� x=(k-1/2)�� �Ɋւ��č��E�Ώ́A�𗘗p�����
�@��[(k-1)��,k��] (sin x)^2 /{x^2 + (n��)^2} dx = 1/{2��[(k-1/2)^2 + c + n^2]},
������ 0 < c < 1/4, >>665
[3]
�@���̓x�����z�\�́A�Ԃ����炳��̃N���X��
���k38�l��1�w���ɓǂ{�̍�����
�Ă܂Ƃ߂����̂ł��B�@����ɂ��āA���̖�
���ɓ����Ȃ����B�������A���Γx���͏�����
3�ʂ��l�̌ܓ����āA������2�ʂ܂ŕ\�킵��
���܂��B�@�@�@�@�@�@�@�@�@�@(���v�Z�\)
(5)�@x,y�ɂ��Ă͂܂鐔�����ꂼ�ꋁ�߂Ȃ����B
(6)�@1�w���ɓǂ{�̍����̕��ς͉����ł�
�@���B�����͏�����2�ʂ��l�̌ܓ����āA����
�@��1�ʂ܂ŋ��߂Ȃ����B
�@�@�@�@�@�ǂ{�̍���
�@�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�@�K��(��)�@�@�@�@�x��(�l)�@���Γx��
�@�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�@0�ȏ� �`�@2�����@�@2�@�@�@�@�@0.05
�@2�@�@�`�@4�@�@�@�@7�@�@�@�@�@0.18�@�@
�@4�@�@�`�@6�@�@�@�@13�@�@�@�@�@x
�@6�@�@�`�@8�@�@�@�@9�@�@�@�@�@0.24
�@8�@�@�`�@10�@�@�@�@6�@�@�@�@�@y
�@10 �@�`�@12�@�@�@�@1�@�@�@�@�@0.03
�@�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�@�@�� �v�@�@�@�@�@38�@�@�@�@�@1.00 �������@�@�@�@�@�@�@178 �` 216�@(��)
1�l������̕��ύ����@�@4.68421 �` 5.68421�@(��/�l)
�����@�@�@�@�@�@�@�@�@4.7 �` 5.7�@(��/�l) ������n�̕��z�͓��z
�@P_n = C[38, n-178] / 2^38,�@�@�@(178��n��216)
�Ƃ��邪�A�X�̂��ߐ��K���z N(197, ��^2) �ŋߎ����Ă��悢�B
��^2 = n/4 = 19/2. 1�b�Ԃ�30��Ɏ擾�ł��鐔��
1539538600�A3079077200�A4618615800......
1�b�Ԃ�60��擾�ł���z��
769769300�A1539538600�A2309307900......
���̐��l�����������Ă��邩������܂����H ���̏�������1���傫��r�����݂��邱�Ƃ������Ă�������:
n��C�ӂ̐��̐����Ƃ���Ƃ�
1<n<p<r�n
�ł���悤�ȔC�ӂ̑f��p�ɑ���
��[k=0��n] {C(n, k)}^4 ��p�̔{��
���������� >>688
����������2�����Ƃ�1�̂���
0�`1�̊K���l��0.5
���l��
2�`3�̊K���l��2.5
����ȕ��ɂȂ邩�琳����������>>666 ������1�ʂ܂ŏo���Ӗ�����Ȃ�
�L���������ۂ��������Ⴄ���ǂ����ł͂Ȃ��킯����H
���_�����Ȃ����������ǂȂ�����Ƌ^�� >>692
���a�Ȃ�r=2�Ŏ��x�������ǎl��a��r=2����n=3�ł��łɐ������Ȃ����Ȃ��B
����͎�����H
�z���g�ɐ��������H >>694
>������1�ʂ܂ŏo���Ӗ�����Ȃ�
�Ȃ�ŁH
���Ⴀ0�ȏ�2�����̐l��3�l�����畽�ς́H ����Ȋ����Ȃ��Ƃ�����Ă�킯��
���v�����{���ɂ����Ă����̖�肾�� 1��x1��<x2��<........xk��n�̓��l�ό`��
1��x1<x2-1<........xk-(k-1)��n-(k-1)�ƂȂ闝�R���S��������܂���B�\����Ȃ��̂ł����A���������肢���܂��B(x1��<x2��x2-x1��2��\���Ă��܂�) 698�ł�
���݂܂���B���ȉ������܂����B
���Ⴂ�����Ă��܂����B���p���������B���݂܂���B �������킩��ɂ������l�L���p�X �u�Q�v�u�v�u�́v�����݂̎��_����K�ȗp��ɕς��邢���A�C�f�A����Ă��ꂽ���Ƃ��Ă���܂����H
���̎O���ďd�v�x�̂��ɖ��O�Ɠ��e�����܂�ɂ�������Ă܂���ˁH >>701
�l���łȂ����
�ǂ��ł��ǂ� �h�C�c�ꂾ�̉p�ꂾ�̃t�����X�ꂾ�̂ŕς��Ă���Ȃ��ƈӖ��Ȃ������ ����A���Ƃ��A�u�R�v�u�́v�u���v�Ƃ��ǂ��H AB=b,AD=d�̒����`ABCD�̕�AB��ɓ_E�A��AD��ɓ_F�����R�ɂƂ�B
�܂������`�̓����ɓ_G���Ƃ�A��GEF�����p�O�p�`�ƂȂ�悤�ɂ���B
���̂悤��E,F,G�̂Ƃ���͐F�X���邪�A�����̉\�ȂƂ���̑S�Ă��l�����Ƃ��A�_G����������̈�̖ʐς����߂�B >>693-697
�Ђ���u������������Ⴀ�����߂���v >>687
�@�� = x - (k-1/2)��,�@�@|��| < ��/2,
�Ƃ����B
�@( 1/{[(k-1/2)�� + ��]^2 + (n��)^2} + 1/{[(k-1/2)�� - ��]^2 + (n��)^2} )/2
�@�� (1/[(k-1/2)^2���^2 + (n��)^2]) {�P- ��/[(k-1/2)^2���^2 + (n��)^2]�E��^2},
�@��(n,k) = [n^2 - 3(k-1/2)^2]/[(k-1/2)^2 + n^2],
�@��[-��/2,��/2] (cos��)^2�{�P- ��/[(k-1/2)^2���^2 + (n��)^2]�E��^2} d��
�@�@= (��/2) {�P- (��^2 -6)/(12�[(k-1/2)^2���^2 + (n��)^2])���}
�@�@= (��/2) {�P- c/[(k-1/2)^2 + n^2]},
�@c(n,k) = (��^2 -6)/(12��^2)�E��(n,k) = 0.03267274 ��(n,k)
���Ȃ菬�����B ����
��[-��/2,��/2] (cos��)^2 d��
�@= [ (�� - sin��cos��)/2 ](��=-��/2,��/2)
�@= ��/2,
��[-��/2,��/2] (�ƥcos��)^2 d��
�@= [ (��^3)/6 + (2��^2 -3)sin(2��)/8 + ��cos(2��)/4 ](��=-��/2,��/2)
�@= (��/2)�(��^2 -6)/12, >>688
[3]
�@���̓x�����z�\�́A����������� ����̃N���X��
���k38�l��1�w���ɓǂ{�̍�����
�Ă܂Ƃ߂����̂ł��B�@����ɂ��āA���̖�
���ɥ��� >>692
�@a(n) = ��[k=0��n] {C(n,k)}^4
n��12 �ł�
1�@�@�@�@�@�@ 2�@�@2,
2�@�@�@�@�@�@18�@�@2�3�3,
3�@�@�@�@�@ 164�@�@2�2�41,
4�@�@�@�@�@1810�@�@2�5�181,
5�@�@�@�@ 21252�@�@2�2�3�7�11�23,
6�@�@�@�@263844�@�@2�2�3�3.�3�7�349,
7�@�@�@ 3395016�@�@2�2�2�3�3�61�773,
8�@�@�@44916498�@�@2�3�3�3�11�75617,
9�@�@ 607041380�@�@2�2�5�11�31�89009,
10�@�@8345319268�@�@2�2�11�13�67�71�3067,
11�@116335834056�@�@2�2�2�3�3�13�499�249079,
12 1640651321764�@�@2�2�7�7�13�643897693,
�E{(1+x)(1+y)(1+z)(1+w)}^n �̑Ίp�� {(xyzw)^k �`�̍�} �̌W���a
�E{(1+x)(1+y)(1+z)[1+1/(xyz)]}^n �̒萔��
http://oeis.org/A005260 >>695
r�͐�������Ȃ��Ă��������ˁH
r = 1+�Á@�Ƃ����� >>712
�ł����ʂɏo��~�X�ȋC������B >>705
>>706�̉҂͗��R�������Ă��Ȃ����A
G��EF�a�Ƃ���~����ɂ���ƍl����ƁA
E��A����B�܂œ����AF��A�ɌŒ肳��Ă���ƍl����ƁA
G��AB�a�Ƃ��锼�~�����B
����E��B�ɌŒ肳��Ă���Ƃ��AF��A����D�܂œ����ƁA
G��BD�a�Ƃ���~�ɓ��ڂ��钷���`ABCD����A
AB�a�Ƃ��锼�~���������������B
����G�͒����`ABCD���̑S�̈���B 1/(1-x+x^2)��1/(1-x-2x^2)��x�ׂ̂������ɓW�J���Ax^n�̌W�������ꂼ��p[n],q[n]�Ƃ����B
�i1�j�C�ӂ�n�ɑ���p[3n]��n�ɂ��Ȃ��萔�ł��邱�Ƃ������A���̒l�����߂�B
�i2�j3q[n]-p[3n]��n�ŕ\���B >�i1�j�C�ӂ�n�ɑ���p[3n]��n�ɂ��Ȃ��萔�ł��邱�Ƃ������A���̒l�����߂�B
p[3] = -1, p[6] = +1 �萔�ɂȂ�܂����ˁH �����ʂ��ԈႦ�Ă܂��H ��A���͂łłĂ���Ŗސ���͓��v�w�̋��ȏ��ɂ̂��Ă���Ŗސ���Ƃ͕ʕ��ł����H
���v�w�̖{�ɂ̂��Ă���Ŗސ���́A�m�����z�▧�x���̃p�����[�^�[�t���ꂽ�����l���A�^�̕��z����Ɨ��ɓ���ꂽ�m���ϐ���p���āA�ޓx�����ő剻���ăp�����[�^�[�𐄒肷����̂��Ǝv���܂��B
�������A�Ⴆ�ΐ��`��A���ƁA�ex�ɑ�y�̒l�����K���z�ɏ]���Ă���Ƃ��Ă��A���ꂼ�ꕽ�ς��Ⴄ�̂œ��ꕪ�z����Ɨ��ɓ����Ă��܂���B >>715-716
���Ԃ͂����Ă邯�ǁA�un�ɂ��Ȃ��萔�v���ē��{�ꂪ�Ԉ���Ă�B
1�߂̗L�����́A����f���͈̔͂�(x-a)(x-b)�ƈ������������
a��b��1��6�捪�ƂȂ�B
������1/(x-a)��1/(x-b)�ׂ̂������W�J���l���A2�ׂ̂������W�J�̐�
�ł��邱�Ƃ���x^3�Ax^6�Ax^9�̌W�������߂Ă݂�B
2�߂̗L������3�{��������������B
2�̗L�����ׂ̂������W�J���l���A2�ׂ̂������W�J�̘a����3q[n]���o���B >>718
�i1�j���v�Z���܂������m����(-1)^n�ɂȂ���n�Ɉˑ����Ȃ��Ƃ͌����܂���ˁB���肪�Ƃ��������܂��B
�i2�j�̌v�Z�A�i�������j�~�i�������j����n���̌W�����ǂ��o���������j�������Ȃ��ł��B����������肢���܂��B
�ǂ���琔�w����1���̌v�Z���炵���ł��B >>719
3/(1-x-2xx) = 3/((1-2x)(1+x)) = 2/(1-2x) + 1/(1+x)
�@= 2/(1-(2x)) + 1/(1+(-x)) = 2* (1 + (2x) + (2x)^2 + ... ) + (1 + (-x) + (-x)^2 + ... )
�@= ...
>>718 �́u�������������v���q���g�ł��� �Ƃ����� p[3n] �������悤�ɂ��� (-1)^n �o������ƈႤ�̂ł����H > 2�ׂ̂������W�J�̐� �ł��邱�Ƃ���x^3�Ax^6�Ax^9�̌W�������߂Ă݂�B
�ς����߂���j�ł��ł���̂ł���... ���Čv�Z����悤��...
�������������Ȃ�
1-x+xx = (1+xxx )/(1+x) = (e^{+��i/3} - x) (e^{-��i/3} - x) ���
1/(1-x+xx) = (1/(2i*sin(��/3)))*( e^{+��i/3}/(1-e^{+��i/3}x) - e^{-��i/3}/(1 - e^{-��i/3}x) )
x^{3n} �̌W��
(1/(2i*sin(��/3)))* e^{+��i/3}* (-1)^n - e^{-��i/3}*(-1)^n = (-1)^n 1/(1-x+x^2) = (1+x)/(1+x^3) = (1+x)(1-x^3+x^6-x^9+�c) = 1+x-x^3-x^4+x^6+x^7-x^9-x^10+�c >>690
��������
n = �� �} �� = 197 �} ��(19/2) =�@193.92 �` 200.08
�Ƃ���ƁA�����@5.1 �` 5.3 >>711
a(n) �������Ȃ��ŏ��̑f��p (>n) �� b(n) �Ƃ����
n�@�@b(n)�@�@b(n)/n
--------------------------
1�@�@3�@�@�@3.0000
2�@�@5�@�@�@2.5000
3�@�@5�@�@�@1.6667
4�@�@7�@�@�@1.7500
5�@�@13�@�@�@2.6000
6�@�@11�@�@�@1.8333
7�@�@11�@�@�@1.5714
8�@�@13�@�@�@1.6250
9�@�@13�@�@�@1.4444
10�@�@17�@�@�@1.7000
11�@�@17�@�@�@1.54545
12�@�@17�@�@�@1.4167
r < 1.4167�@�@(���) >>719 >>722
>718�ł��B�ׂ������W�J�̐ςł��̂͂���Ȋ����ł�
�܂��A 1/(1-x+x^2)=1/{(x-a)(x-b)} �ƈ������������
a=(1+i��3)/2=e^(2��i/6), b=(1-i��3)/2=e^(-2��i/6) �ł���
������ a^3=-1 �� 1/b=a �ɒ��ӂ��Ă���
1/(x-a)=1/(-a) * 1/{1-(x/a)}
=1/(-a)*{1+(x/a)+1+(x/a)^2+1+(x/a)^3+�c}
���l��
1/(x-b)=1/(-b) * 1/{1-(x/b)}
=1/(-b)*{1+(x/b)+1+(x/b)^2+1+(x/b)^3+�c}
=1/(-b)*{1+(x/b)+1+(x/b)^2+1+(x/b)^3+�c}
=(-a)*(1+ax+1+(ax)^2+1+(ax)^3+�c)
����ƁA
1/(x-a) * 1/(x-b)
��x^(3n)�̍��́A
(x/a)^(3n)*1+(x/a)^(3n-1)*ax+(x/a)^(3n-2)*(ax)^2+ �c +(x/a)^2*(ax)^(3n-2)+(x/a)*(ax)^(3n-1)+(ax)^(3n)
����Ă��̌W����
(1/a)^(3n)+(1/a)^(3n-2)+(1/a)^(3n-4)+ �c +a^(3n-4)+a^(3n-2)+a^(3n)
=(1/a)^(3n)*{1+a^2+a^4+ �c +a^(6n-4)+a^(6n-2)+a^(6n)}
=(1/a)^(3n)*{1-(a^2)^(3n+1)}/(1-a^2)
=1/(-1)^n *{1-a^(6n)*a^2}/(1-a^2)
=(-1)^n
���镪��ł͂���Ȃׂ������W�J�̐ς������̂ł����A
�ł��A���̖��ł�>723�̕����G���K���g�ł��� >>727
�������Atypo�c
�O���̌v�Z�́A��������
1/(x-a)=1/(-a) * 1/{1-(x/a)}
=1/(-a)*{1+(x/a)+(x/a)^2+(x/a)^3+�c}
���l��
1/(x-b)=1/(-b) * 1/{1-(x/b)}
=1/(-b)*{1+(x/b)+(x/b)^2+(x/b)^3+�c}
=1/(-b)*{1+(x/b)+(x/b)^2+(x/b)^3+�c}
=(-a)*(1+ax+(ax)^2+(ax)^3+�c)
�ł���orz �w��O�҈��p�I�x�A�Ȃ߂�̂����������ɂ����n���e���r �����䂷���Ăǂ��̂����̂ƕ������Ă��Ă��邪�A���͌����_�ʼn��̗��v�����Ă��Ȃ���
���̖������������������̂ɁA�ꂩ���ȏ����排����̓I�ɂȂ�Ȃ���Ȃ�Ȃ��̂��H
���̗��v�ɂ��Ȃ�Ȃ��������J��Ԃ��l�Ԃ����邱�Ƃɑ��Ă͊��S�ɗ���s�\�ł���B
���Ǝґ������Ƃ������Ƃ��������Ă��Ă��邪�A������̐��͏�Ɏq����
�{�C�X�`�F���W���[���g���ĕK�����Ƃ��������悤���Ȃ��B
������̌����点�͎l�Z�������������̃h�c�ɂŌJ��Ԃ���Ă���킯����
���ꂪ�����܂ł����u����Ă���̂��s�v�c�Ȃ��Ƃ��B (x+y)^2(x-y)^2(x^2+y^2)^2
�̓�����
x^8-2x^4y^4+y^8
�ɂȂ��ł����A�����
x^16-2x^4y^4+y^16
�ł͂Ȃ��ł��傤���H
�r������
(x+y)^2(x-y)^2(x^2+y^2)^2
= {(x+y)(x-y)(x^2+y^2)}^2
= {(x^2-y^2)(x^2+y^2)}^2
= �i��^4-y^4)^2
�ɂȂ��čŌ����W�J�����
(x^4-y^4)(x^4-y^4)
��
x^16-2x^4y^4+y^16
���Ǝv���̂ł����E�E�E
�Ԉ���Ă܂����H ���w�̖��ő��݂͏ؖ�����Ă��邪�������Ă��Ȃ����̂��ĂȂ���܂����H >>732
�ł������ȉ������܂���
�w���@�����Ԉ���Ă����悤�ł�
x^4 * x^4 = x^8
�ł��� >>733
���������Ă���ő�̑f�������傫���f���Ƃ� >>735
�Ȃ�قǁB�B����̈Ӑ}�͋�̗�͉���Ȃ����Ǒ��݂��邱�Ƃ����͏ؖ�����Ă�����̂͂���̂��ȁH
���Ă������Ƃł����B �[�[�^���̔��ȗ�_�̎����̉����Ƃ��������� ���Ƃ͎����S�̂̏����Â��ł����Đ������Ȃ����̂Ƃ� >>738
������Ă����N������̓I�Ȑ�����@��Ꭶ���鎖���Ă��肦���ł����ˁH >>733
�A���S���Y���n�͂��������̑�����Ȃ��́H
�����̒藝�ɂ��ƌv�Z�ʂ̉�����nlogn�����\���@�͕s���A�݂����� >>740
V=L�����ł�����ď����Ă���⃓ >>742
���ΓI�ɖ������Ƃ��������ĂȂ���
�w�\���\�ł���Əؖ��ł���x���ƂƁw���ۂɍ\���ł���x���Ƃ͈Ⴄ�ł��� >>743
�H
> ZFC+V=L �ł͂������̘_������ R�i���ۂɂ͔C�ӂ̏W���j���t���邱�Ƃ��]���B >>744
���̌����������Ăł�������n�ł͂��������_�����̑��݂��ؖ��ł���Ƃ��������ł���
���������_�����̑��݂��A��������O�̌����n�i�P�Ȃ�ZFC�Ƃ��j�ƓƗ��ȏꍇ�������ƍl�����悤�� �k���鐔�l�ɂ���
�e���ڂ��l�̌ܓ����č��v�����l��
���v�l���l�̌ܓ����č��v�����l��
��v���Ȃ��m����
1-( (6/(�~�k))^(1/2) )
�ŋ��܂邻���Ȃ�ł��B
���P�@���̎��̓������������ĉ������B
�Ȃ��~�������E�E�E�H
���Q�@
���N�A�����ɂ���������p���AA,B,C,D,E�̂T�l�Ŏx�������ƂɂȂ��Ă܂��B
��p�͖��N�ς��̂ł����A
�T�l�̎x�����䗦�́Aa%�Ab%�Ac%�Ad%�Ae%�@�ia>b>c>d>e>0�j
�Ŗ��N���ł��B
�i�Ⴆ��32.3%�A24.1%�A21.6%�A16.8%�A5.2%�j
�P�~�����͎l�̌ܓ����܂����A��v���Ȃ���������A�ō��z�i�}�P�~�j�����܂��B
�܂�AA��N�N�Ԃ̒����z�̍��v�̊��Ғl�͖�O�~�ł��i�����炭�j�B
�Q�O�N�o�����Ƃ��AA�̒����z�̍��v���{�P�O�~�ɂȂ�m���͂�����ł����H
N�N�o�����Ƃ��AA�̒����z�̍��v��M�~�ɂȂ�m���͂�����ł����H >>745
�������̘_����
��������ۂɂ����������̂���̓I�ɍ����Ă��Ƃ���Ȃ��́H >>746
L�����Ő��K���z���o�Ă���W���ȁH
�m�����x����1/��(2��)�Ƃ����̂��������悤�� >>745
>���̌����������Ăł�������n�ł͂��������_�����̑��݂��ؖ��ł���Ƃ��������ł���
�����ZFC�łł���ł���
��̓I�ł͖����� 1���̍d�݂�n���A�\���o������1�A�����o������0�����蓖�Ă邱�Ƃœ����鐔�̗��x1,x2,�cxn�Ƃ���B�������s�ɂ��A�V���ɓ����鐔�̗��y1,y2�cyn�Ƃ��鎞�A
x1y1+x2y2�c�cxnyn�������ɂȂ�m����Pn�ƒu���ƁA2���藝�ɂ��A
2Pn=(3/4+1/4)^n+(3/4-1/4)^n�ƂȂ�B
�Ɖɏ����Ă���̂ł����A2Pn=(3/4+1/4)^n+(3/4-1/4)^n���ǂ�����o�Ă����̂��킩��Ȃ��ł��B
��낵�����肢���܂��B f:R-{0}->R �ɑ�, lim[x->0](f(x)+f(2x))=a (�L���m��l)�̂Ƃ�, lim[x->0]f(x)=a/2
������Đ������H f(x) = a/2 + sin{�Υlog(x)/log(2)}
f(x) = a/2 + cos{�Υlog(x)/log(2)} >>751
f(x) = 1 �@x��(1/2,1]
f(x) = 0 �@x��(1/2^2,1/2]
f(x) = 1 �@x��(1/2^3,1/2^2]
.. . .
f(x) = 1 x��(1/2^{2k+1}, 1/2^{2k} ]
f(x) = 0 x��(1/2^{2k+2}, 1/2^{2k+1}]
(�}�C�i�X�������l�ɒ�`)
lim[x->0](f(x)+f(2x))=1 (�L���m��)
lim[x->0] f(x) (�s�m��) >>750
x1y1+x2y2�c�cxnyn������(=2m) �ɂȂ�p�^�[����
(x,y)=(1,1)�̃y�A�� 2m�A���̃y�A(n-2m ��)�� (0,0)(0,1)(1,0) �̂ǂꂩ�̑g�ݍ��킹
Pn = ��[0��2m��n] C{n,2m} 3^(n-2m) /(2^n * 2^n)
�@= ��[0��k��n] C{n,k} 3^(n-k) (1 + (-1)^k)/2 /4^n
�藝���
2 Pn = (3+1)^n /4^n + (3-1)^n /4^n
�@= (3/4 + 1/4)^n + (3/4 - 1/4)^n >>753
�@f(x) = [ 1 + sin(�Υlog(x)/log(2)) ]
�ł����邩�B
����ɂ��Ă� 27.66�b�Ő��������ꂽ�Ƃ́A�����ł�����B >>749
�w����\���x�Ɓw�������`����_�����̑��݁x�͈��Ȃ��H��������
>�������AZFC ��A��ʘA���̉������������̌n ZFC+GCH �ɂ����ẮAR ��̐������`����_�����͑��݂��Ȃ�[1]�B
�Ƃ��邯�lj��������ɁH >>746
L�̎�������l���z�Œ��o���ĂQ�`�T�O�ŃV�~�����[�V�������Ă݂��B
https://i.imgur.com/ppslW60.png
L���傫���Ȃ��1-( (6/(�~�k))^(1/2) )�Ɉ�v����悤�ł��B
�����͌��҂ɂ��C���B
rm(list=ls())
f45 <- function(a) { # �l�̌ܓ�
x=a-floor(a)�@# floor(a):a���Ȃ������K�E�X�L��[x]�Ɠ���,x:����������x�ɓ����
floor(a)+ (x>=0.5) # x��0.5�ȏ�Ȃ�P�������łȂ��Ȃ�O��������
}
f45(1.5) ; f45(2.5)
round(1.5) ; round(2.5)
sim <- function(n=3,k=1e4){
sub <- function(n){
x=runif(n) # ��l���z����(����)���̔z�� round�Ȃ�runif(n,0,2)
y=numeric(n) # y�F�l�̌ܓ��ł̐���������z��
for(i in 1:n) y[i]=f45(x[i]) # ���̊e�������l�̌ܓ�����y�ɓ����
f45(sum(x))!=sum(y) # x�̑��a�̎l�̌ܓ�����y�̑��a���قȂ��TRUE��Ԃ�
}
r=mean(replicate(k,sub(n))) # k�̃V�~�����[�V�����ł�TRUE�̕p�x��Ԃ�
p=1-( sqrt(6/(pi*n)) ) # ���_�l�H
return(c(r,p))
}
L=2:50
plot(L,sapply(L,function(x) 1-( sqrt(6/(pi*x)))),bty='l',type='l')
re=t(sapply(L,function(x) sim(x)))
plot(re,bty='l',pch=19,asp=1,xlab='�����l',ylab='���_�l',type='l')
abline(a=0,b=1,lty=3) >>746
���ꂿ����ƑO�ɖʔ������X���ɂłĂ������Ȃ��́H
��������ĂȂ����������H >>746
�����_������: x[i] {�Ȃ�炩�͈̔͂̈�l���z}
�����_����: ��[i] �� [-0.5,0.5) {��l���z}
A = ��[i=1,L] round(x[i]+��[i]) = ��[i=1,L] x[i]
B = round( ��[i=1,L](x[i]+��[i]) ) = A + round(��[i=1,L]��[i])
A=B�@�́@-0.5 < ��[1]+��[2]+...+��[L] < 0.5
s := ��[1]+��[2]+...+��[L]
���S�Ɍ��藝��� L����̎��A
�m�����z: f(s) �� 1/��(2�Ѓ�) * exp(- s^2/(2�Ѓ�) )
�W����: �� �� (��L)* ��1, ( ��1 := ��{ ��[��=-0.5,+0.5] ��^2 d�� } = 1/��12 )
1-P = ��[s=-0.5,+0.5] f(s) ds �� 1/��(2�Ѓ�) = ��(6/(��L)) ����
> �����_������: x[i] {�Ȃ�炩�͈̔͂̈�l���z}
������̓����_���ł���K�v�͂Ȃ����� >>752-753
���肪�Ƃ��������܂�
���͂����Ŕ��Ⴊ�ł��āA�A���Ȃ琳�����悤�ȃ_���Ȃ悤�ȁH�Ǝv���Ă����̂ł���
�S�R�_���ł��� >>746
�l�̌ܓ��O�̎x������5.5,4.5,3.5,2.5,1.5�Ƃ����A��-2�~�ɂȂ�Ȃ����ȁH >>754
���肪�Ƃ��������܂��B
= ��[0��k��n] C{n,k} 3^(n-k) (1 + (-1)^k)/2 /4^n��
(1 + (-1)^k)/2�͂ǂ�����ďo�Ă����̂ł��傤���H
���݂܂���B��낵�����肢���܂��B k����̎��� 0 �A�����̎��� 1 �ƂȂ�̂�
����ŋ������̂ݎ��o�����a (���̎�) �Ɠ����ɂȂ�܂��B >>762
�l�̌ܓ��O�̎x���z�����������l�ɂȂ邱�Ƃ͖����Ǝv���܂����E�E�E
���̂����H a,b�݂͌��ɑf�Ȏ��R���Ƃ���B
�i1�ja+bi���Ɍ`���̌`�ŕ\���Bi�͋����P�ʂł���B
�i2�j�C�ӂ̎��R��n�ɑ��āA(a+bi)^n�͎����łȂ����Ƃ������B >>762
���̐����x�Ƃ���
x��x/�x�̔�Ŕz������Γ�����B ��`
�E�Q�̖�����s1,s2��R^N���A���鍀�����̍����S�Ĉ�v����Ƃ��u���l�v
�E������s��R^N�́u����ԍ��vd�Ƃ́A������̓��l�ނ̑�\����
�@��v�ӏ��̐擪�ƂȂ鍀�̉ӏ��̔ԍ�
���ăQ�[�����͂��߂悤
�o��҂͖������100��p�ӂ���
�������҂ɂ͗�̔ԍ��i�P�`100�j��������
�҂͗�̔ԍ����P�����I��
�o��҂͎c���99����҂Ɏ���
�҂�99��̌���ԍ��̍ő�lD��m��
�o��҂́A�҂��I�P��́A
D+1�Ԗڂ̍��������҂Ɏ���
�҂�D+1�Ԗڂ̍������̏��
�I��̑�\����m��
�܂�������ĂȂ��I���D�Ԗڂ̍���
��\���̍��ƈ�v����@�҂̏���
��\���̍��ƈ���Ă���Ώo��҂̏���
���ĉ҂����m���́H
�i�o�W�@���w�Z�~�i�[2015�N11�����@�u�����薳���ځv�j >>768�̑���
�����ŁA����ǎ҂��ȉ��̂悤�Ȕ������s����
https://rio2016.5ch.net/test/read.cgi/math/1576852086/550
�i�v�|�j
�u������m����0��
�@������̓��l�W�͔F�߂�
�@���l�ނ̑�\���̑��݂��F�߂�
�@����������ԍ�d�̑��݂͔F�߂Ȃ��I
�@����ԍ������݂��Ȃ���Q�[���͐������Ȃ��v
��L�̔����͐������H
��`�i�Čf�j
�E�Q�̖�����s1,s2��R^N���A���鍀�����̍����S�Ĉ�v����Ƃ��u���l�v
�E������s��R^N�́u����ԍ��vd�Ƃ́A������̓��l�ނ̑�\����
�@��v�ӏ��̐擪�ƂȂ鍀�̉ӏ��̔ԍ�
��L���l�ނ̑�\���́A���l�ނ̂ǂ̗v�f�Ƃ����l
���������āA����ԍ��͎��R���ƂȂ炴��Ȃ��������H >>768
���l�łȂ��ƌ���ԍ����݂��Ȃ�����
���ɂȂ��ĂȂ����ǁH �y�i2�j������z
a,b�݂͌��ɑf�Ȏ��R���Ƃ���B
�i1�ja+bi���Ɍ`���̌`�ŕ\���Bi�͋����P�ʂł���B
�i2�j�C�ӂ̑f��p�ɑ��āA(a+bi)^p�͎����łȂ����Ƃ������B ����H
���Z���w�͍��Z���w�X���ɏ����� ���w�f���Q ttp://x0000.net
(�A���t�@�E���{|�w�p�f���Q) >>769
>���l�ނ̑�\���̑��݂��F�߂�
�Ȃ��H >>768
�Ȃɂ���H���w�̖��ɂȂ��ĂȂ����H
�S�e�S�e�������͂������Ă邯�nj��lj҂͍ŏ��Ɉ������I������
���ƑI���̂ǂ������Ƃ��A�V������������Ă邯�ǂ��̂��ƑI�ђ����������ł��Ȃ��Ȃ�Ӗ��Ȃ����B
������������100��̎�����̕��z���^���ĂȂ��̂Ɋm�����ւ���������Ȃ��ł���H >>770
�����l�łȂ��ƌ���ԍ����݂��Ȃ�
�����Ȃ閳��������铯�l�ނ̗v�f�ł�����
���R�A�����̏������铯�l�ނ̑�\���Ɠ��l�ł�
���̏ꍇ�A���l�W�̒�`�Ƃ��āA��\���Ƃ̈�v�ӏ������݂��܂�
���ꂪ������̌���ԍ��Ƃ������Ƃł��@
���������Ă����Ȃ閳����ɂ����݂��܂�
���c����A���ɂȂ��ĂȂ����ǁH
>>768�̖��́u�҂����m���́H�v�ł� >>775
>>���l�ނ̑�\���̑��݂��F�߂�
>�Ȃ��H
�I�������ɂ���Ċe���l�ނ����\�����I�o�ł���
�Ƃ����̂����L���̐����ł� >>776
�����lj҂͍ŏ��Ɉ������I������
����
�����̂��ƑI�ђ����������ł��Ȃ�
��U���߂���I�тȂ����͂ł��܂����
���Ȃ�Ӗ��Ȃ�
�Ƃ͂����܂���@�����Q�[���𑼂̐l�ɂ���Ă��炤���Ƃ͉\�ł�
�l�ɂ���đI�ԗ�͈قȂ�܂�����
��������������100��̎�����̕��z���^���ĂȂ��̂Ɋm�����ւ���������Ȃ�
���͂ǂ̐l�ɂ���Ă��炤�ꍇ�ɂ��A����100��͕ς��܂���
100��̎�����͂ǂ�Ȃ��̂������Ă��Ă����܂��܂���
���̏ꍇ�A���z�́u�҂��ǂ̗��I�Ԃ��v�����ŁA
����͑S���̃����_���i��l���z�j�ł�
���ꂾ���œ��������܂�܂� >>779
�������݂킩���B
�m���ƌ����Ă邭���ɑ��x��Ԃ�
�S���̃����_��
�Ƃ����o�ĂȂ����B
���ꂾ���œ��������Ƃ܂�܂����Ă����Ȃ瓚���m���Ă��ł���H
�����킩���́H >>780
���x��Ԃ͂Q�O�o�P�C�Q�C�E�E�E�C�P�O�O�p�ł���
>>768�̋L���ɂ͂�������͏����Ă���܂�
���ۂɐq�˂����₢��>>769�̂ق��ł����A
���Ƃ̖���m��Ȃ��Ɨ����ł��Ȃ��̂�
>>768�̖₢�����킹�ď������Ă��������܂���
�����������̂͊ȒP�ł����A
>>768�̖�ɂ��Ă�
�����A���l����������
(�q���g�j
�҂��I����̌���ԍ������Ƃ����Ƃ�
�҂����̂́A����D�������Ȃ�W�ɂȂ��Ă���Ƃ����H >>781
��@>>768�̋L��
���@>>768�̋L�����́u�o�W�v >>781
2^100
�ē��l�Ɋm���炵��2����100�H
100�̖�������Ȃ��́H
��̒���100�̂�H
�����Ă鐔����0��1�H
���w�̖��Ƃ��Đ������邽�߂̏����ĂȂ�������B
������
p(�I��̌���ԍ�<d)�~1
+p(�I��̌���ԍ�>d)�~0
+p(�I��̌���ԍ�=d)
�~p(�I��̌���ԍ���d�Ԗ�=�I��̑�����ނ̑�\����d�Ԗ�|�I��̌���ԍ�=d)
�ƕ�������ɂ��Ă���̑I����̕��z���킩��Ȃ��Ɠ����o��n�Y���Ȃ��B >>777
>�����Ȃ閳��������铯�l�ނ̗v�f�ł�����
>���R�A�����̏������铯�l�ނ̑�\���Ɠ��l�ł�
�܂�
��\�����I��Ă��Ă���ɂ��Ă̌���ԍ��Ƃ������ƁH
����͂܂�
���Ă̐��玩�R���ւ̎ʑ���1�^�����Ă�����Ă��ƂˁH
�I���Ȃ�ŗL�邩������Ȃ�����
�҂����������Ȃ��������ł���H
�m����Ԃ��^�����ĂȂ����ƂɂȂ邩��
����ς���Ƃ͌����Ȃ��Ǝv�� >>784
���A�����B>>784�̌㔼�̓_�����B
(�I��̌���ԍ�<d)�Ƃ������ۂ����Ƃ͌���Ȃ���B
����̕��z��������Ȃ���Βl�������炩�ȑO�ɉ����ǂ������킩���̂��B ���z�ȑO��"������̑S��"�Ȃ�ē��R�����W��������ǂ�ȏW�������ɂȂ�̂�����܂��^���Ȃ��Ɩ��ɂȂ�Ȃ���B
����ł͂ǂ��Ȃ��Ă�́H >>781
>���x��Ԃ͂Q�O�o�P�C�Q�C�E�E�E�C�P�O�O�p�ł���
�Ⴄ�ᖳ������
�I������100��
���̂ǂꂩ����l�ɑI��
����͂�������
����100�̂ǂꂪ�����������镨��
�\�ߌ��܂��Ă��Ă�����͒m�炳��Ă��Ȃ�����
�m�����z�ɂ͐���Ȃ�
�����Ȃ��ᖳ���H >>783
����
[Q(tan(��/2p):Q]��[Q(cos(2��/p)]=��(p/2)
�f����n�ɂ���Ȃ�B
�Z���X�Ȃ��Ȃ��B >>784
2^100�́A100�̗L���W���ׂ̂��W��
��100�̖�������Ȃ��́H
�������̂͌Œ肵�Ă܂�
�܂�A���z���l����K�v�͂���܂��� >>778
�͂��B
�I�������̉��肪�ǂ��ɂ�������ĂȂ������̂������܂����B >>785
���I���Ȃ�ŗL�邩������Ȃ�����
���҂����������Ȃ��������ł���H
���͑I��100�����Ȃ���̂ł����Ă�
�҂��I�ꍇ������u�͂���̗�v�̌����قڌ��܂��Ă��܂�
���������āA100��ǂ�1���I�Ԋm����1/100�Ȃ�
�҂����m�����قڌ��܂�܂� >>788
��100�̂ǂꂪ�����������镨��
���\�ߌ��܂��Ă��Ă�����͒m�炳��Ă��Ȃ�����
���m�����z�ɂ͐���Ȃ�
>>792�ɂ������܂������A���͕������̌���
���܂��Ă��܂��̂Ŋm���͌��܂�܂�
���łɂ����A�m��m��Ȃ��A��
�m�����z���ǂ����Ƃ͖��W�ł��� >>788
>����100�̂ǂꂪ�����������镨��
>�\�ߌ��܂��Ă��Ă�����͒m�炳��Ă��Ȃ�����
>�m�����z�ɂ͐���Ȃ�
>�����Ȃ��ᖳ���H
�u�҂͗�̔ԍ����P�����I�ԁv�Ń����_���ɑI�ׂΈ�l���z�ɂȂ�B
�܂�
�������͂�������1����A100��̂����ꂩ�������_���ɑI���A���������Ђ��m����1/100�ȉ��B >>786-787
100��̐���͌Œ肵�܂��@���������ĕ��z���l����K�v�͂���܂���
�����ԏ�ł̊��̉������A���͍l����K�v������܂��� >>794
���������͂�������1����
�C�t���܂�����
�����Ȃ�ł��@100���I�ꍇ
�P�D����ԍ����ő�l�ƂȂ��1�����݂��遨�P���u�������v
�Q�D����ԍ����ő�l�ƂȂ��2��ȏ㑶�݂��遨�u�������v�Ȃ�
�ƂȂ�܂�
�i�P�̏ꍇ����ԍ����ő�l�̗��I�ԂƂ���D�A
�@�Q�̏ꍇ�ǂ̗��I��ł��@������D�j
�P�̏ꍇ�A�҂����m����99/100
�Q�̏ꍇ�A�҂����m���͂P
�ł��� >>796
�A�z�����ȁH
���ɂȂ��Ă�̂�>>784�ł����Ȃ�I��̌���ԍ������傤��d�A�܂�c��99��̌���ԍ������܂��ܑI��̌���ԍ��ƈ�v����ꍇ�ɂ͖�蕶����͂ǂ����̂����ɂȂ邩�m�肵�Ȃ��ł���H
�܂�҂������ɂȂ锠��99���Ȃ̂�100���Ȃ̂��킩��Ȃ��ł��傤���H >>797
���I��̌���ԍ������傤��d�A
���܂�c��99��̌���ԍ������܂��ܑI��̌���ԍ���
����v����ꍇ�ɂ́E�E�E
>>796�ŏ������ʂ�A������Ȃ��̂�
�ǂ̗��I��ł��҂������܂�
���҂������ɂȂ锠��99���Ȃ̂�100���Ȃ̂��킩��Ȃ�
99�̏ꍇ�������100�̏ꍇ������@�Ƃ������Ƃ�4649 >>784�̎��ł���
p(�I��̌���ԍ�<=D)�~1
+p(�I��̌���ԍ�>D)�~0
�ł悢�ł��� >>799����D�����݂����Ɍ������
�ȉ��̂悤�ɏ����̂�������
p(�I��̌���ԍ�<=����99��̌���ԍ��̍ő�l)�~1
+p(�I��̌���ԍ�>����99��̌���ԍ��̍ő�l)�~0 >>798
�ł��傤�H
��������>>768�̖���
�܂̒���99�̓����肭����1�̓����肭�����n�Y�������̂ǂ����v100�������Ă܂��B��������Ђ��m���́H
�Ɠ����ɂȂ���H
�����o��킯�Ȃ��B >>802
P(����)��99/100���Ⴞ�߂Ȃ�H >>801
>>769�ɂ��ăR�����g���肢���܂�
>>802
�Q�̏ꍇ�����邱�Ƃ��q�ׂ����
���ꂼ��̊m����������ł���
>>803
�ꍇ�������Ă����������ق��������ł��� �҂��I���̏��������m�������߂�F�i�قɂ���j
�݂����ȏo��Ȃ�܂��킩�邯�ǂȂ� >>805
���{�I�ɂ�
�u�P�O�O�{�̐������邠�݂������ŊO�ꂪ�P�̏ꍇ
�@������m�������߂�v
�Ƃ����̂Ɠ������Ǝv���܂����@���ł����H
��L�̖���
�u���݂������S�̂̋�Ԃɂ�����X�̂��݂��������I���m���v
�Ȃ�čl���Ȃ��ł��傤�H �{���I�ɓ����ɂ��Ă����������V���v���ɏ��������Ęb��
�S�̋�Ԃ̒��ŌX�̂��݂��������I���m�������āA
�{���͍l���˂Ȃ�Ȃ����Ƃ��ȗ����Ă邾���̘b�Ȃ��� >>793
�\�ߌ��܂��Ă����ł���H
�Ȃ炻��Ȃ��V���Ă�����
�P�`�P�O�O�Ƀ�pi=1�̊m�����z���l����
�ł悭�Ȃ��H �ǂ��l���Ă������肭����99�ɂȂ�Ƃ��A100�ɂȂ�Ƃ����V���v���Ȍ������肻���ɂȂ����ǁB
�����Ȃ�Ȃ�H >>806
>�u�P�O�O�{�̐������邠�݂������ŊO�ꂪ�P�̏ꍇ
>�@������m�������߂�v
>�Ƃ����̂Ɠ������Ǝv���܂����@���ł����H
���Ⴀ
p1===p100=1/100�Ƃ������ƂˁH
����ŁH k��1��k��n�̎��R���Ƃ���B
n��������f(x)�ɑ��āAg(x)={(1+x)^k}g(x)���l����B
g(x)�������W���������Ȃ�Af(x)�������W���������ł��邱�Ƃ��ؖ�����B >>768
������x�m�F���Ă݂��
�܂����̖�蕶�ł̓_��
�������Ăɂ��ē��l�ނ�ݒ肵��\�������߂Ă����i��\�������߂���̂͑I���������j
100�̖�������̂��ꂼ��ɂ��ē��l�ނ̑�\���Ƃ̈Ⴂ�̂���Ō�̍��ԍ������߂���i����ԍ��̒�`�j
100�̖�������̂����P��ׂɑI��
�c����99�̌���ԍ��̍ő�l�����I����ԍ�����������Ώ���
�傫����Ώ����������܂�Ȃ��H�i���X�j
������Đ���W�Ȃ���
100�̒��ōő��I�Ԃ��ǂ������Ă��Ƃ���Ȃ��H
�\�ߍő�̐��l�͌��߂��Ă��邩��
�����ׂɑI�Ԃ��ǂ�����1/100���Ă��Ƃ�
�����܂ł͌��ǐ���W�Ȃ������H >>807
���{���͍l���˂Ȃ�Ȃ����Ƃ��ȗ����Ă邾��
����͖��ɑ��鍪�{�I�Ȍ��������� >>769
>�u������m����0��
>�@������̓��l�W�͔F�߂�
>�@���l�ނ̑�\���̑��݂��F�߂�
>�@����������ԍ�d�̑��݂͔F�߂Ȃ��I
>�@����ԍ������݂��Ȃ���Q�[���͐������Ȃ��v
����ԍ��͒�`�ł���Ǝv����
����Ǎŏ��̖�蕶�ł�
���ɑ��錈��ԍ��ł��邩��������Ă��Ȃ�����
���̓_���n�b�L�������Ȃ��Ə�L�̂悤�Ɍ����l�i�����������v����>>770�j�����Ă����������Ȃ��̂ł́H
������ɂ���
�Ȃ���肭�ǂ����ƌ����ĉ��Ɋ��������̖�肾�Ǝv���� >>812
���܂����̖�蕶�ł̓_��
���Ȃ��̏C�����C�C���_�����Ƃ�����E�E�E�_���ł���
�_�����̂P
���c����99�̌���ԍ��̍ő�l�����I����ԍ�����������Ώ���
�u�i�ő�l�j��菬�����v�ł͂Ȃ��u�i�ő�l�j�ȉ��v�ł���
�_�����̂Q
���傫����Ώ����������܂�Ȃ��H
�傫����Ε����A�ł����ł���
�i�K�^�ɂ���v����ꍇ�͂��邪�A�����͊m���O�Ƃ��邱�Ƃ��ł��邩��j
��L�̃_���o���������Ă������������
��������Đ���W�Ȃ���
��100�̒��ōő��I�Ԃ��ǂ������Ă��Ƃ���Ȃ��H
�����A���̒ʂ�ł���
���\�ߍő�̐��l�͌��߂��Ă��邩��
�������ׂɑI�Ԃ��ǂ�����1/100���Ă��Ƃ�
�����A���̒ʂ�ł���
�������܂ł͌��ǐ���W�Ȃ������H
�����A���̒ʂ�ł���
�܂������ł��d�v���Ǝv���Ă���ł����H >>814
������ԍ��͒�`�ł���Ǝv����
�����ł��傤
�ł��Ȃ��Ƃ����l�́A���l�ނ�������Ă��ł��傤
������Ǎŏ��̖�蕶�ł�
�����ɑ��錈��ԍ��ł��邩��������Ă��Ȃ�
�������Ă��Ȃ��̂ł͂Ȃ��A
�����𗝉��ł��Ă��Ȃ��̂ł��傤
�����ł���܂œǂޕK�v������܂���
�����̓_���n�b�L�������Ȃ���
����L�̂悤�Ɍ����l�����Ă����������Ȃ��̂ł́H
�u����ԍ����L���łȂ��v�Ƃ����咣��
����ԍ��̐����������ł��Ȃ��Ƃ����̂Ƃ�
���{�I�ɈقȂ�A�Ǝv���܂��� >>814
���Ȃ���肭�ǂ����ƌ����ĉ��Ɋ�������
���w���̒�`�̋L�q�͂������������������̂ł����ǂ�
�ʑ��̒�`�Ȃ�Ă��̍ł�����̂ł���
�Ȃ�ŁA����Ȓ�`���Ă�̂����ǂ����ł͕�����Ȃ�
�����ʼn䖝�ł����ɋߓ���T�����Ƃ���l�͐��w�ɂ͌����܂����
�Ȃʂ̂��Ƃ�������ق��������Ƃ������܂��� >>812
>�傫����Ώ����������܂�Ȃ��H�i���X�j
����ԍ����O������1�O�Ȃ��\���ƈقȂ��Ă��邱�Ƃ͊m�肾���畉��
1�ȏ�O�Ȃ��\���ƈقȂ邩�ǂ�����1/10���ȁH
1�O�ł��邩�ǂ����͕�����Ȃ��������ς�m���͌����Ȃ��̂ł́H
1�O���ǂ������Ă���ԍ������߂Ă����Ď��R���S�̂̒��ł��̐��l��1�O���ǂ��������猈��ԍ��̎��R���S�̂ɂ����镪�z���^�����Ȃ��Ɖ��������Ȃ��悤�� >>815
����������
���m�Ȗ��ɂ��Ă���o�����Ă��Ă� >>816
>������Ǎŏ��̖�蕶�ł�
>�����ɑ��錈��ԍ��ł��邩��������Ă��Ȃ�
>
>�������Ă��Ȃ��̂ł͂Ȃ��A
>�����𗝉��ł��Ă��Ȃ��̂ł��傤
>�����ł���܂œǂޕK�v������܂���
�u�x�������������
�������� 1.
������������C�Z��������.�����ꂼ��ɁC��������������.
�ǂ�Ȏ��������邩�͂܂��������R�C�Ⴆ��n�Ԗڂ̔���e^�����Ă��悢���C���ׂĂ̔��Ƀ����Ă��悢.
�������ł���߂����č\��Ȃ�.�����Ĕ����݂ȕ���.
���x�͂��Ȃ��̔Ԃł���.�В[���甠���J���Ă䂫���̎�����`���Ă悢���C��̔��͊J�����ɕ����܂c���˂Ȃ�ʂƂ��悤.
�ǂ̔�������܂c�����͂��Ȃ������߂���.
�����̃��[���͂�����. �����������̒��̎������s�^���ƌ������Ă���C���Ȃ��̏���. �����Ȃ��Ε���.
���헪�͂���ł��傤��? �Q�D
�@�������̂�낤�Ƃ��邱�Ƃ�Q�̃R�[�V�[��̏W���l�W�ŗޕʂ���R���\�������肩��(�̖`��)�Ɏ��Ă���.
�A�������Ƃ��т������l�W���g��.
������̏W�� R^N���l����.
s = (s1�Cs2�Cs3 �C�E�E�E)�Cs'=(s'1�C s'2�C s'3�C�E�E�E )��R^N�́C����ԍ������̂����ۂ���v�����n0�Fn >= n0 �� sn�� s'n �Ƃ����ls �` s'�ƒ�`���悤(����R�[�V�[�ׂ̂������).
�O�̂��ߐ��ڗ����`�F�b�N����ƁCs��s'��1962�Ԗڂ�����v���Cs'��s"��2015�Ԗڂ�����v����Ȃ�Cs��s"��2015�Ԗڂ�����v����.
�`�� R^N ��ޕʂ��邪�C�e�ނ����\��I�сC��\�n��܂ɒ~���Ă���.
�I�ɂ͏��ˉe R^N�� R^N/�`�̐ؒf��I���ƂɂȂ�.
�C�ӂ̎�����S �ɑ��C�܂����������������Ă����Ɠ��l��(�����t�@�C�p�[��)��\r= r(s)�����傤�Lj���o�����.
s��r�Ƃ���������悸���ƈ�v����ԍ���s�̌���ԍ��ƌĂсCd = d(s)�ƋL��.
�܂�sd�Csd+1�Csd+2,�E�E�E��m���s�̗ނ̑�\r �͌��߂���.
�X�ɁC���炩�̎���ɂ��d���m�炳��Ă��Ȃ��Ă��C����D>=d �ɂ���sD+1�C sD+2�CsD+3�C�E�E�E
���m�炳�ꂽ�Ƃ���Ȃ�C���ꂾ���̏��Ŋ��� r = r(s)�͎��o���C ����������d= d(s)�����܂�C
����sd(����sd�Csd+1�C�E�E�E�CsD ��������)�����߂��邱�Ƃɒ��ӂ��悤.
(�⑫)
sD+1�C sD+2�CsD+3�C�E�E�E�F������D+1�Ȃǂ͉��t�Y���� �R�D
���ɖ߂�C��������100��ɕ��ׂ�.
���̒��g�͎������ɒm�炳��Ă��Ȃ����C �Ƃɂ�����l��̔������C��2��̔�������100 ��̔�������100�{�̎�����S^1,S^2�C�E�E�E�CS^lOO�𐬂�(���ɏ悹���͎̂w���ł͂Ȃ��Y��).
�����̗�͂��̂��̌���ԍ�������.
���āC 1�`100 �̂����ꂩ�������_���ɑI��.
�Ⴆ��k���I�ꂽ�Ƃ���.
s^k�̌���ԍ������̗�̌���ԍ��ǂ�����傫���m����1/100�ɉ߂��Ȃ�.
�@��1��`��(k-1) ��C��(k+1)��`��100��̔���S���J����.
��k��̔������͂܂������܂܂ɂ��Ă���.
�J�������ɓ��������������āC��\�̑܂�������C S^1�`S^(k-l),S^(k+l)�`S100�̌���ԍ��̂����̍ő�lD����������.
�@���悢���k�� ��(D+1) �Ԗڂ����̔��������J����FS^k(D+l)�C S^k(D+2)�CS^k(D+3)�C�E�E�E.����
�@D >= d(S^k)
�����肵�悤.���̉��肪�������m����99/100�C�����ĉ��肪�����������C��̒��ӂɂ����S^k(d)�����߂���̂ł�����.
�����炢����ƁC����̂��ƁC s^k(D+1)�Cs^k(D+2)�Cs^k(D+3)�C�E�E�E�����đ�\r��r(s~k) �����o����̂�
��r ��D�Ԗڂ̎���r(D)�����āC �u��k���D�Ԗڂ̔��ɓ�����������S^k(D)��r(D)�Ɠq����C�߂ł����m��99/100�ŏ��Ă�.
�m��1-�� �ŏ��Ă邱�Ƃ����炩�ł��낤.
(�⑫)
S^k(D+l)�C S^k(D+2)�CS^k(D+3)�C�E�E�E�F������^k�͏�t���Y�����A(D+l)�Ȃǂ͉��t�Y���� >>819-820
�d�v�ł��邱�Ƃ�������
�����łȂ����Ƃ͋������Ȃ�
�u�x�Ƃ͖��W
���R�̂��Ƃł����ǂ� 4.
�uR^N/�` �̑�\�n��I�ӏ��őI���������g���Ă���.
���̌���R^N ��R^N/�` �̐ؒf�͔���ɂȂ�.
�����͗L���ȃ��B�^���̃��x�[�O����W���̗�(Q/Z���u�����L�����v�ŗޕʂ�����\�n�C 1905�N)�ɂ�������ł���.�v
�u�t�ɔ���ȏW������������ɂ͑I���������v��(�\�����F�C�C 1970�N)����C���̐헪�͂ӂ����ǂ��납�W���I�Ƃ��������邩������Ȃ�.
�������C�I�����������W�����o�R�������炨����C �ƕЕt����̂́C�ʔ����Ȃ��悤�Ɏv��.
���㐔�w�̌`�����ł͊m���͑��x�_�ɂ���ĉ��߂����䂦�C���x�_�͊m���̊�b�C �Ɛ��w�҂͐M��������.
�����C���x�_�I���߂��J�m�j�J���C �Ƃ����؋��͂Ȃ��̂����C���������`�����Ȃ킿��b�C �Ƃ����̂����v���낤.
�m���͐��w���z���čL���鐶�����Ȃ̂ł���(���w�Ɏ����Ȃ炳�ꂽ�������ł��䂵�₷�������).�v 5.
�u����������Ɩʔ����̂́C�Ɨ����Ɋւ��锽�Ȃ��Ǝv��.
�m���̒��S�I�Ώۂ́C�Ɨ��Ȋm���ϐ��̖�����
X1�CX2�CX3�C�c�ł���.
�������������������ɂ́C
(1)�����ڈ����C
(2)�L���̋Ɍ��Ƃ��ĊԐڂɈ����C
��̕��j���\�ł���.
�m���ϐ��̖������́C�C�ӂ̗L�����������Ɨ��̂Ƃ��C�Ɨ��C�ƒ�`����邩��C(2)�̈�����.
(�Ɨ��Ƃ͌���Ȃ��ɂ�����R�����S���t�̊g���藝�Ȃǂ��L���������.)
�������C�f�p�ɁC�������ڈ����Ȃ��̂�?
������Ƃ���Ǝ������̐헪�͓ڍ����Ă��܂�.
n�Ԗڂ̔���Xn�̃����_���Ȓl�������āC���锠�̒��g�Ă悤�Ƃ������āC
���̔���X �Ƒ���X1�CX2�CX3�C�E�E�E���܂�܂閳�����Ƃ��ēƗ��Ȃ�C
���Ă������Ȃ��ł͂Ȃ����|�|���̔�������͈���炦�Ȃ��̂�����.
���헪�Ȃ��锤�Ȃ��C�Ɗ������������̒��ς́C���ӎ���(1)�ɍ������Ă����C�Ƃ�����.
�ӂ����Ȑ헪�́C�m���ϐ��̖������̓Ɨ����̔����������̂�����C �Ƃ����Ă��悢.�v
�h���������C���Ă��锤��������̂��C�Ɗ������邾�낤.
�������������������Ă���̂ł͂Ȃ����C�Ƌ^���ǎ҂����낤.����ǂݒ����Ă�����������.
�����͂ق�Ƃ��ɏ�L�̂Ƃ���.�����̎������^�����C��������Ă�����������ŁC��������Ă�C�Ƃ����̂�.
�Ƃ��낪�Ƃ��낪--�{�L���̖ړI�́C�m��99%�ŏ��Ă����Ȑ헪�������邱�Ƃɂ���.
���̖���Peter Winkler���Ƃ̒��̂ݘb���Ă玨�ɂ���.���͌��^�����[�}�j�A�����肩��d���ꂽ�炵��.�h
�ȏ� >>768�̕��͂��������̂́A���̋L���̂܂܂ł�
�f���ł͒�������Ǝv�����̂���ꂾ���A
�����̊m���ϐ��Ƃ������Ƃ������e����
�\�Ȍ��������ق��������Ǝv�������Ƃ����� n�����R���Ƃ���B
�܂̒���n�̐���2�̔���������B�ȉ��̎��s���J��Ԃ��s���B
�y���s�z
1)�܂̒����疳��ׂɓ�����2�̋������o���A
�u�Ƃ��ɔ����̏ꍇ�A�w�����x�Ƃ���v
�u����1�Ɛ�1�̏ꍇ�A�w�����x�Ƃ���v
�u�Ƃ��ɐ��̏ꍇ�A�w�������x�Ƃ���v
2)�w�����x�܂��́w�����x�̏ꍇ�A���s���I������B�w�������x�̏ꍇ�A����1�s���s���B
���̎��s���I������܂łɍs�������s�̉̊��ҒlE(n)��n�ŕ\���A�܂����s���w�����x�ŏI����������t���m����n�ŕ\���B >>813
���{�I�ɂ̓\���Ɠ���������>>806�ɏ����Ă���Ǝv������ >>827
�o�������o���Ȃ��̂�
�S���_�� >>824
>�d�v�ł��邱�Ƃ�������
>�����łȂ����Ƃ͋������Ȃ�
�N�S�������ł��Ă��Ȃ���
�����ł��Ă��Ėڂ�w���Ă��邩����
�S���_�� >>832
�A���^�̖]�݂́J���m�Ȗ��J��>>821�ȍ~�ɂ����Ƃ�����
�ԂԂ����ĂȂ��ʼn����Ă݂���H �Ⴆ��1,2,3,...�Ƃ����������铯�l�ނ̑�\���͉��ɂȂ�́H ���Ⴀ1,2,3,...�̌���ԍ���1�ł���
���l�ɐ���a_1,a_2,a_3,...�������铯�l�ނ̑�\����a_1,a_2,a_3,...�����炱�������ԍ���1
�܂�C�ӂ̎�����̌���ԍ���1�Ƃ������Ƃł���
���肪�Ƃ��������܂� >>838
1,2,3,...�̓��l�ނ̑�\���� 1.2,3,...�ɂ����Ȃ�
2,1,3,...�̌���ԍ���3���� ����������������ƌ�����Ă�
����ԍ��Ȍ�͑S����v���Ă�Ǝv���Ă�����>>768
>��`
>�E�Q�̖�����s1,s2��R^N���A���鍀�����̍����S�Ĉ�v����Ƃ��u���l�v
>�E������s��R^N�́u����ԍ��vd�Ƃ́A������̓��l�ނ̑�\����
>�@��v�ӏ��̐擪�ƂȂ鍀�̉ӏ��̔ԍ�
����
1,2,3,...���\���ɂ����ꍇ
1,1,3,...�̌���ԍ���1����
��`���̕s������
������ >>801�̒��̐l�X�Ƃ͊ւ��Ȃ��������������B >>841
��̐l�͖��炩�ɓ�����������
�K���A�X�����^�c����폜���ꂽ�̂����R
---
https://rio2016.5ch.net/test/read.cgi/math/1576852086/581
�P�D���ԓI�ɂ͌����ς݂ł��B���̏؋��ɁA���̃X���ɎQ�������O�҂Ȃ�
�i�����A�����Ԉ���Ă���ƂȂ�����A����Ȃ��̂ł͂Ȃ��j
�Q�D�h�Ղ�͏I������h�I�� ���K���A�X���̃X����̏���
�R�D�����ŏ\���A���كT���̃o�J���������v���m�点�Ă��܂���A
�@�@���̃X���ł˂��i�O�O >>840
������ԍ��Ȍ�͑S����v���Ă�Ǝv���Ă�����
�ǂݕ����e�G����ˁH
�u�Q�̖�����s1,s2��R^N���E�E�E��v����Ƃ��v
�Ə����Ă��邵 �R���i�̌��ŋ^��Ɏv�����̂�����
����ׂɂP�O�O�O�l�𒊏o����PCR�������s������P�O�l���z���ł������B
PCR�����̊��x�O�D�V�A���ٓx�O�D�X�Ƃ��ėL�a���̊��Ғl�ƂX�T���M����Ԃ́H
�L�a���̎��O�m�����z����l���z�Ɖ��肵�Č����z����̗L�a�����x�[�^���z�ŏo���B
���̗L�a���Ɗ��x�E���ٓx������z���I�������v�Z�B
���̗z���I�������g���ėL�a�����t�Z�Ƃ����A���S���Y���Ōv�Z������
> sim()
mean mode lower upper
0.010969194 0.009870096 0.005034295 0.017532847
���̃A���S���Y�����Ă����Ă�H >>843
����͓��l�̒�`
����ԍ��̒�`�ɂ͂Ȃ� >>845
���g���čl���Ă�H
�E���l�W����`�ł���A���l�ނ����݂���
�E���l�ނ��炻�̑�\�����I�ׂ�@�i���l�ނ������̏ꍇ�A�I���������K�v�j
�E�ǂ̖�������K�����铯�l�ނɑ�����
�E�ǂ̖�����������铯�l�ނ̑�\���Ƃ͓��R���l�ł���
�E���l�W�̒�`����A�K����v����J�n�ӏ������݂���
�@��������������̌���ԍ�
�ق�A���l�̒�`�őS�����܂� >>768�̖�����̓��l�W�ƌ���ԍ��������ł������ւ̎���
>>769�́u����ǎҁv�H��
https://rio2016.5ch.net/test/read.cgi/math/1576852086/552
�i�v�|�j
�E�������̗L����̏ꍇ�A����ԍ��͊m���P�ł�
�E�����炍�����̋Ɍ����Ƃ�ƁA����ԍ��͊m���P�Ł�
���̍l�������Đ������H �傫��n�̔��������Ă����ɑ傫��a,b,c�̂��̂����ԂȂ����߂�Ƃ��āA���̍��v��s�ɂȂ�a,b,c�̑g�ݍ��킹�̋��ߕ��͂ǂ̂悤�ɂȂ�̂ł��傤�� ���̓��{��ʼn��������l�ɓ`���̂��낤���H >>846
>�E���l�W�̒�`����A�K����v����J�n�ӏ������݂���
>�@��������������̌���ԍ�
��v����͍̂ŏ��̍�����v���Ă����̂�
��������悸���ƈ�v���Ă��邻�̐擪�Ƃ�����`�ɂ��Ȃ��ƃ_���_��
�N�����ǂ߂ĂȂ��˂� >>768
>��`
>�E�Q�̖�����s1,s2��R^N���A���鍀�����̍����S�Ĉ�v����Ƃ��u���l�v
>�E������s��R^N�́u����ԍ��vd�Ƃ́A������̓��l�ނ̑�\����
>�@��v�ӏ��̐擪�ƂȂ鍀�̉ӏ��̔ԍ�
���l�ނ̑�\���u�Ɓv�́u��v�ӏ��v�Ƃ����̂ł̓_��������
���ꂾ�Ə�������v���Ă��炭��v���Ȃ��Ă���Ƃ��납���͂����ƈ�v���Ă�Ƃ��̌���ԍ���1�Ƃ������ƂɂȂ邩���
��`�������ɂ��Ȃ��Ă͂����Ȃ��Ƃ����ӎ��������Ȃ��̂͐��w�I�ł͖����� >>847
��
�������킹�����������邩�猾��Ȃ� >>851
����������悸���ƈ�v���Ă��邻�̐擪�Ƃ�����`�ɂ��Ȃ���
�ǂݎ�ꂽ�Ȃ�OK
>>852
����`�������ɂ��Ȃ��Ă͂����Ȃ�
�ǂݎ�ꂽ�Ȃ�\��
>>853
���������킹������������
�Ȃ�قǁE�E�EID:BUSW/Nah��
�������̋Ɍ����Ƃ�ƁA����ԍ��͊m���P�Ł�
�ɑS�ʎ^���A�� ID:BUSW/Nah���ւ̖₢
Q.����n�ȉ���10�i������9/10������n
�@����l�H��
�@�u�����炎�����̋Ɍ��ŗL��������9/10���������v
�@����z���g�H �^�X���b�h�̎��̑���H�w������
�G�i�H�j�����嗝�w�����Ǝv������œ{�苶��
https://rio2016.5ch.net/test/read.cgi/math/1576852086/589-590
�悢�q�݂̂�Ȃ͂���ȑ�l�ɂȂ�����_������ ������[n=1,2,...]1/(n^2+a)���v�Z���邱�Ƃɂ��A(e^��-e^(-��))/(e^��+e^(-��))���������ł��邱�Ƃ��ؖ�����B >>854
�u�x�������蕶
�������قƂ�LjӖ��Ȃ����̂�
���炽�߂悤�Ƃ��Ȃ��̂�NG
�}���Ń_������ >>764
�ԓ��x���Ȃ��Ă��܂��A�\�������܂���B
���肪�Ƃ��������܂��B ���w�f���Q ttp://x0000.net
(�A���t�@�E���{|�w�p�f���Q) >>844(���ȃ��X)
��T�ɋC�������̂œP�܂�m(_ _)m >>862
>>853
�N�̎v�f�͊��ɔj�Y���Ă���ċC���t���Ȃ��݂���
�z���g�ɉ���Ȃ��l�ԂȂ̂��ȁH >>857
��[n=1,2,����] 1/(nn+a)
�@= (1/2)��[n��Z] 1/(nn+a) - 1/(2a)
�@= �Υcoth(��a)/(2��a) - 1/(2a),
�@�����W�����@�������H
a=1 �̂Ƃ�
�@��[n=1,2,����] 1/(nn+1) = (��/2)coth(��) - 1/2, �m�������X�̐��`�������M�̕X�̕��`������Ԃł���Ƃ����ؖ��ŁA��������M�̓_��xn�̋Ɍ���M�̕�ɑ�����Ƃ����b���o�Ă����̂ł����A���R�����Ă������� �����������ƕ����Ă��݂܂���A�������܂��� n���̍d�݂��ɓ����āA�\�̏o�����̂���苎��A�d�݂��c���Ă���A����1���������ɓ����ĕ\�̏o�����̂���苎�邱�Ƃɂ���
���̎��A�S����苎��m�������߂�B
�ł́A1��ڂɕ\���o�����̂�������Ƃ��āA(1-1/4)^n�Ɠ������o���Ă���̂ł����A���ʂɍl���ĉ��������ƁA�S���ۂ��قȂ�Ǝv���̂ł����A�Ȃ����̉��������\�Ȃ̂ł��傤���H >>867
�S�ẴR�C����2���邤����1��ł��\���o��ΑS�Ď�苎�邱�ƂɂȂ邩��
�S���ۂ��قȂ��Ă��\��Ȃ�
2���Ƃ�3���Ƃ��ŗ����̂����őS���ۏ����o���Ă݂�Ε����邩���m��Ȃ� >>https://rio2016.5ch.net/test/read.cgi/math/1511604229/999
�~����ȃf�^�����Ȃ���
�Z���S�ɐ��������w��̖��������̏ؖ��_�� >>868 �����o���Ă݂��̂ł����A�C�}�C�`�������肱�Ȃ��ł��c >>870
�����o�������̑S�Ăɂ����Ȃ�m������������Ō���ׂĂ݂Ă͂ǂ����낤�� >>871
n=10�̂Ƃ��ő�������Ōv�Z���Ă݂�
> rm(list=ls())
> n=10
> dec2nw <- function(num, N, digit = n){
+ r=num%%N
+ q=num%/%N
+ while(q > 0 | digit > 1){
+ r=append(q%%N,r)
+ q=q%/%N
+ digit=digit-1
+ }
+ return(r)
+ }
> d=t(sapply(0:(2^n-1),function(num) dec2nw(num,2,n))) # 10���̃R�C���̗��\�̏���i�O����菜���\�Ƃ���j
> head(d) ; tail(d)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 0 0 0 0 0 0 0 0 0 0
[2,] 0 0 0 0 0 0 0 0 0 1
[3,] 0 0 0 0 0 0 0 0 1 0
[4,] 0 0 0 0 0 0 0 0 1 1
[5,] 0 0 0 0 0 0 0 1 0 0
[6,] 0 0 0 0 0 0 0 1 0 1
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1019,] 1 1 1 1 1 1 1 0 1 0
[1020,] 1 1 1 1 1 1 1 0 1 1
[1021,] 1 1 1 1 1 1 1 1 0 0
[1022,] 1 1 1 1 1 1 1 1 0 1
[1023,] 1 1 1 1 1 1 1 1 1 0
[1024,] 1 1 1 1 1 1 1 1 1 1
> d1=apply(d,1,sum) #�@�e�s���Ƃ̍��v�������ł�����
> sum((1/2)^d1)/2^n�@ # �e�s���ƂɁ@(1/2) ^ ���̖������v�Z���č��Z����@
[1] 0.056314
> (1-1/4)^n
[1] 0.056314
���v�����B n=20�ł�100����̃V�~�����[�V����
> # simulation
> sim <- function(n){
+ (flip1=sample(0:1,n,rep=T)) # 0:1����d����������n�I�z���flip1�Ƃ���
+ (flip2=sample(0:1,sum(flip1),rep=T))�@# 0:1����flip1�̑��a�I�z���flip2�Ƃ���
+ sum(flip2)==0 # flip2�̑��a���O���ۂ���Ԃ�
+ }
> mean(replicate(1e7,sim(20))) # 100���s���đS����苎�����������v�Z
[1] 0.0031899
> (1-1/4)^20
[1] 0.0031712
�܂��A�ߎ������B >>867
1���̍d�݂���菜����Ȃ��m���́A�����Ƒ����Ƃ�������1/4
���̗]���ہi1���̍d�݂���菜����鎖�ہj�̊m����3/4
�ǂ̍d�݂̗��\���ł邩�͓Ɨ����ۂ�����A(3/4)^n�ł�����Ȃ��́H ��������
(1/1^2)+(1/2^3)+(1/3^4)+...
�����߂�B >>828
�V�~�����[�V�����v���O�����̗��K�@�������͌��҂ɂ��C��
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
En 1.0000 1.1991 1.4378 1.6744 1.9163 2.1544 2.3992 2.6329 2.9352 3.1542 3.4106
Pn 0.3405 0.1997 0.1483 0.1148 0.0917 0.0775 0.0700 0.0608 0.0516 0.0458 0.0416
[,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22]
En 3.6105 3.8742 4.1257 4.3780 4.6665 4.7706 5.0866 5.4512 5.6246 5.8261 6.1474
Pn 0.0375 0.0381 0.0383 0.0308 0.0295 0.0296 0.0269 0.0223 0.0227 0.0221 0.0239
[,23] [,24] [,25] [,26] [,27] [,28] [,29] [,30]
En 6.5768 6.5863 6.8209 7.0221 7.3743 7.652 7.8525 8.1056
Pn 0.0217 0.0204 0.0189 0.0202 0.0183 0.017 0.0166 0.0161
fn <- function(n){
B=c(rep(1,n),0,0) # 1:�� 0:����
flg=3 # draw�������l
i=0 # ���s�̉J�E���^�[
while(flg==3){ # draw�Ȃ�J��Ԃ��@1:win 2:lose 3:draw
i=i+1
flg=(1:3)[sum(sample(B,2))+1] # (1:3)[sum(c(0,0))+1] : win
}
c(i=i,flg=flg)
}
sim <- function(n){
k=1e4
re=t(replicate(k,fn(n)))
c(mean(re[,'i']),mean(re[,'flg']==1)) # �Ə�����Ԃ�
}
n=1:30
re=sapply(n,sim)
En=re[1,]
plot(n,En,bty='l',pch=19)
Pn=re[2,]
plot(n,Pn,bty='l',pch=19)
rownames(re)=c('En','Pn')
re ����{a[k]}��
a[k]={nCk*(-1)^(k+1)}/k
�Ƃ����B
�K�v�ł����
lim[n����]{(1+1/2+...+1/n)-ln(n)}=0.5772...��p���Ĉȉ��̖₢�ɓ�����B
�i1�jlim[n����] {1/ln(n)}*��[k=1,...,n]a[k]=1
�������B
�i2�j���̋Ɍ��ׂ�B
lim[n����] {1/ln(n)}*��[k=1,...,n]❲��[j=1,...,k](a[j]/j)❳ >>828
E(n) = (n+2)*(n+1)/(4*n+2)
> E(1:30)
[1] 1.0000 1.2000 1.4286 1.6667 1.9091 2.1538 2.4000 2.6471 2.8947 3.1429 3.3913
[12] 3.6400 3.8889 4.1379 4.3871 4.6364 4.8857 5.1351 5.3846 5.6341 5.8837 6.1333
[23] 6.3830 6.6327 6.8824 7.1321 7.3818 7.6316 7.8814 8.1311
>876�̃V�~�����[�V�����Ƌߎ����Ă���
pw=choose(2,2)/choose(n+2,2) # Pr[win]
pl=2*n/choose(n+2,2) # Pr[lose]
p=pw+pl
q=1-p # Pr[draw]
# 1*p + 2*q*p + 3*q^2*p + 4*q^3*p + i*q^(i-1)*p
# ��[i=1,i=m] i*q^(i-1)*p
# p*��i*q^(i-1)
# p*��d(q^i)/dq
# p*d(��q^i)/dq
# p*d((1-q^m)/(1-q))
# m���� q^m��0
# p*d/dq(1/(1 - q)) = p/(1 - q)^2 = 1/p >>828
2�j�@ 1/(n+1)�@���ȁH
�V�~�����[�V�������������̂ǂ��炩���ԈႢ���� >>828
n�������̏ꍇ
P[win] = (n+2)/2 * 2!n!/ (n+2)! = 1/(n+1) {n+2���V���b�t�����ċE�ɔ���}
E[n; win] = ( 1 + 2 + ... + (n+2)/2 ) * 2!n!/ (n+2)! = ...
E[n; lose] = (1*2n + 2*2(n-2) + .... + n/2*2*2 ) * 2!n!/ (n+2)!�@{n+2���V���b�t�����ċE�ɍ���or�����A���̌���ɔ�}
�@= ...
n����̏ꍇ�����l
(�֗��Ȍ���)
1*N + 2*(N-1) + ... +(N-1)*2 + N*1
1*(N+1-1) + 2*(N+1-2) + ... +(N-1)*(N+1-(N-1)) + N*(N+1-N)
= (1+2+...+N)(N+1) - (1^2 + 2^2 + ... + N^2)
= N(N+1)(N+1)/2 - N(N+1)(2N+1)/6 = N(N+1)(N+2)/6 >>828
k��ڂɂ������ɂȂ�m����pk�Ƃ����
k+1��ڂ̎n�܂鎞�_�ł͐�n-2k�ɂȂ��Ă���̂�
n-2k<2�Ȃ�p(k+1)=0
n-2k��2�Ȃ�p(k+1)=pk�E(n-2kC2)/(n-2k+2C2)=pk�E(n-2k)(n-2k-1)/(n-2k+2)(n-2k+1)
n-2k=0,1������ł�
p(k+1)=pk�E(n-2kC2)/(n-2k+2C2)=pk�E(n-2k)(n-2k-1)/(n-2k+2)(n-2k+1)
�Ƃ��Ă悢�̂�
���̑Q������0�ɂȂ�܂łƍl�����
k+1��n/2��p(k+1)=p1�E(n-2k)(n-2k-1)/n(n-1)=(n-2k)(n-2k-1)/(n+2)(n+1)
k+1>n/2��p(k+1)=0
k+1��ڂɏI������m����pk-p(k+1)�Ȃ̂Ŏ��s�̊��Ғl��
��(k+1)(pk-p(k+1))=��pk-���[��ʓ| �w�p�̋���f���Q - �A���t�@�E���{
ttp://x0000.net
���w �����w ���w �����w �V���w �n���n�w
IT �d�q �H�w ����w ���� ���� �Ȃ� >>881
�����s�������̂��H
�������s�Ǝv���ĉ��悤�Ƃ��Ă����B >>884
�����Ȃ�ȒP�����ł��傤����>>880�͔��ʼn����Ă� 2^2^2^2^2^2
��
https://ja.wolframalpha.com/input/?i=2%5E2%5E2%5E2%5E2%5E2
�ɂ����āA
�Ō�̐���:
...7437428736
�ł���Ƃ������A���̍����́H >>880
�ǂ��ł��������Ƃ����A
1*N + 2*(N-1) + ... +(N-1)*2 + N*1 = N(N+1)(N+2)/6
�̕ʏؖ��B
�E�ӂ� C(n+2,3) �ł��邪�A��������̂悤�ɍl����B
1,2,3,4,�c,n+2 ��n+2�̐�����3�I�ԑI�ѕ��ɂ��Ă�
�I��3�̐������A�^�A�E�ƌĂԂ��Ƃɂ���ƁA
�^�ɑI�Ԑ��ŏꍇ�����ł���B
�^��2�ƂȂ�I�ѕ��́A��1�ʂ�*�En�ʂ�B
�^��3�ƂȂ�I�ѕ��́A��2�ʂ�*�E(n-1)�ʂ�B
�^��4�ƂȂ�I�ѕ��́A��3�ʂ�*�E(n-2)�ʂ�B
�c
�^��n+1�ƂȂ�I�ѕ��́A��n�ʂ�*�E1�ʂ�B ��t��l@HayatoChiba
�������i�H�j���w�̎�����������̂ł����A�������̂��߉摜�Y�t�ł��������������B�ʔ����b�肾�Ǝv���̂ł����A���������m�̕����܂��ł��傤���B�i������Ɖ��������ǁA�ł������Ă��������E�E�E�j
https://pbs.twimg.com/media/ETybe_oUMAAfIhq.jpg
https://twitter.com/HayatoChiba/status/1242039227069550592
https://twitter.com/5chan_nel (5ch newer account) �ӂ̒������S�Đ����̑��p�`�ɂ����āA���Ȃ��Ƃ�2�ȏ�̓��p[���W�A��]�͖������ł��邱�Ƃ�����. >>886
����1: �I�C���[�ӊ�
�@��(5^10) = 5^9 (5-1) = 5^9*2^2
����2: ���[�N���b�h�ݏ��@
�@1745224 *2^10 - 183 *5^10 = 1 �@{�v�Z���@�͏ȗ�}
2^{2^{2^{2^{2^{2 }...} �� 0�@(mod 2^10)�@ {��2�̈��q�̑����͖��炩...}
2^{2^{2^{2^{2^{2 }...}
�� 2^{ 2^{ 1024*64 } (mod 5^9*2^2) }} �@(mod 5^10) {��t�F���}�[�̏��藝}
�� 2^{ 406736 } �@(mod 5^10) �@{��}
�� (1-5)^203368 �@(mod 5^10)
�� 1 + (-5)*C{203368,1} + 5^2* C{203368,2} +... +(-5)^9 *C{203368,9}�@(mod 5^10)
�� 5788111�@(mod 5^10)
�����l��]�藝���
2^2^2^2^2^2 �� 0*(-183*5^10) + 5788111*(1745224*2^10)�@(mod 2^10*5^10)
�� (57*10^5 + 88111)* (17*10^5*45224)* 1024 (mod 10^10)
�� ((57*45224 + 88111*17)*10^5 +88111*45224 )*1024 (mod 10^10)
�� 421427437428736 (mod 10^10)
�� 7437428736 (mod 10^10)
�� 2^2^2^2^2^2 = ..... 7437428736
�� �����͑��{���v�Z�\�Ȑ����\�t�g�ɔC�����B
�펯�I�Ȍ����ōς܂������Ȃ�㔼�Ɠ��l�� (1-5)^{ 1024*32 } (mod 5^9) etc. ���v�Z������悢�B >>888
�]�ڂ��ł�
��t��l@HayatoChiba �搶��
https://www.nippyo.co.jp/shop/magazines/latest/4.html
���w�Z�~�i�[ �@2020�N4����
�����w�Ƃ̌������������c�c��t��l�@8
https://ja.wikipedia.org/wiki/%E5%8D%83%E8%91%89%E9%80%B8%E4%BA%BA
��t ��l�i���� �͂�ƁA1982�N1��18�� - �j�͓��{�̐��w�ҁA���k��w�ޗ��Ȋw��������������[1]�B
����
�������v���Ďs���܂�B�����������P�����w�Z���o�āA2005�N���s��w�H�w�������H�w�ȑ��ƁB2009�N���s��w���w�����Ȑ����H�w��U���m�ے��C���B���͗͊w�n���_�A�����������A����є���`�����������B
��w3�̎��Ɂw����Ȃ�킩��H�w���Ŋw�Ԑ��w�x���o�ł���[2]�B
�܂��C�m�ے��݊w���Ɂw�x�N�g����͂���̊w���� �x���o�ł����B�i�������̂͊w���S�̎����Ƃ����j
2013�N����B��w�}�X�E�t�H�A�E�C���_�X�g���������y����[3]�B
2015�N�ɑ��{�\�z�i���{���f���j�̏ؖ�������[4]�B
2019�N�x����B��w��ސE�����k��w�ޗ��Ȋw�����������̋���[5]�B >>890
�����ς蕪������肪�Ƃ��B
log���g�����@���l�b�g��ōڂ��Ă������Ⴄ���@������ȁB >>891
https://en.wikipedia.org/wiki/Walsh_function
Walsh function From Wikipedia
https://mathworld.wolfram.com/WalshFunction.html
Walsh Function -- from Wolfram MathWorld
https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%80%E3%83%9E%E3%83%BC%E3%83%AB%E5%A4%89%E6%8F%9B
�A�_�}�[���ϊ��i�E�H���V��?�A�_�}�[���ϊ���A�_�}�[��?���[�f�}�b�w��?�E�H���V���ϊ��A�E�H���V���ϊ��A�E�H���V��?�t�[���G�ϊ��Ƃ��Ă��m���Ă���j�̓t�[���G�ϊ��̈�ʉ���1�ł���B
���̕ϊ��̓t�����X�̐��w�҃W���b�N�E�A�_�}�[���A�h�C�c�̐��w�҃n���X�E���[�f�}�b�w���A�A�����J�̐��w�҃W���Z�t�EL�E�E�H���V���i�p��Łj�ɂ��Ȃ�Ŗ�������Ă���B https://sites.google.com/site/allamsnumbers/home/the-beginning-of-the-beyonds/hyperoperational-numbers
It turns out that the leading digits of this number can be computed,
by taking the log10(2) accurate to at least 19735 decimal places,
and multiplying it by the decimal expansion of 2^^5.
Below are the first and last 40 digits of 2^^6.
2120038728808211984885164691662274630835...............8862693010305614986891826277507437428736
���������ǂ�ł��������ǂ��B >>887
�X�ɂǂ��ł��������Ƃ����A
�@1�N + 2�(N-1) + ���� + (N-1)�2 + N�1
��
�@{1 + 2x + 3x^2 + ���� + k�x^(k-1) + ���� }^2
�@= (1 + x + x^2 + x^3 + ���� + x^k + ���� )^4
�@= 1/(1-x)^4
�@= ��[k=0,��] �b[k+3, 3] x^k,
�ɂ����� x^(N-1) �̌W���ɓ������B
���@�b[N+2, 3] = N(N+1)(N+2)/6.
�Ȃ��@1/(1-x)^a = ��[k=0,��] �b[k+a-1, a-1] x^k, >>875
��[k=1,��] 1/(k^k)�@=�@1.291286
��[k=1,��] 1/(k^(k+1))�@=�@1.138390
��[k=1,��] 1/(k^(k+2))�@=�@1.066873
��[k=1,��] 1/(k^(k+3))�@=�@1.032685
(����)
��[k=1,��] 1/(k^(k+a))�@>�@1 + 1/(2^(2+a)) geogebra�łT�_��ʂ�Ȑ���`�����Ƃ���
�T�_���猈�܂�œ_��Q�ߐ��̍�}���@�͂ǂ��������̂ł��傤���H ����{a[k]}��
a[k] = {nCk*(-1)^(k+1)}/k
�Ƃ����B
�K�v�ł����
lim[n����] {(1+1/2+...+1/n)-ln(n)} = 0.5772... ��p���Ĉȉ��̖₢�ɓ�����B
�i1�jlim[n����] {1/ln(n)}*��[k=1,...,n]a[k] = 1
�������B
�i2�j���̋Ɍ��ׂ�B
lim[n����] {1/ln(n)}*��[k=1,...,n]❲��[j=1,...,k](a[j]/j)❳ >>898
�E�Ȑ��̒��S
�E�~�ƓȐ���4��_
����}�ł���̂ŁAX��, Y�� ��������.
�o�Ȑ�: (aY)^2 - (bX)^2 = 1 �� a, b �𐔎��ŋ��߂Ă��܂��悢
�@https://imgur.com/nUiPUqs
�ȉ~: ��}�I�����[�ŊȒP�ɋ��܂遫
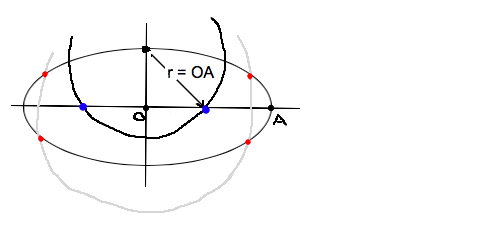 >>899
>>899
��[k=1..n]a[k] = ��[k=1..n] C{n,k} (-1)^{k+1}/k
= ��[k=1..n] ��[x=0,1]dx C{n,k} (-x)^{k-1}
=lim[�Á���] ��[x=��,1]dx ( x^{-1} - x^{-1}(1-x)^n )
=lim[�Á���] ��[x=��,1]dx x^{-1} - ��[x=0,1-��]dx (1-x)^{-1} x^{n} )
=lim[�Á���] -log(��) - ��[k=n+1..��](1-��)^k/k
=lim[�Á���] -log(��) - ��[k=1..��](1-��)^k/k + ��[k=1..n](�`)
=lim[�Á���] -log(��) + log(1-(1-��)) + ��[k=1..n](�`)
= ��[k=1..n] 1/k
= {��[k=1..n] 1/k - ln(n)} + ln(n)
lim[n����]��[k=1..n]a[k]/ln(n) = 0.5772.../�� + 1 = 1 lim[�Á���] ����Ȃ��� lim[�Á�0] >>899 ��(2)
��[k=1..n]��[j=1..k] a[j]/j = ��[j=1..n]��[k=j..n] a[j]/j = ��[j=1..n] (n-j+1) a[j]/j
= (n+1)��[j=1..n]a[j]/j�@-�@��[j=1..n]a[j]
��[j=1..n]a[j]/j
= ��[j=1..n] C{n,j} ��[x=0,1]dx ��[y=0,1]dy (-xy)^{j-1}
= ��[x=0,1]dx ��[y=0,1]dy {1 - (1-xy)^n }/{1 - (1-xy)}
= ��[x=0,1]dx ��[y=0,1]dy 1 + (1-xy) + ... + (1-xy)^{n-1}
= ��[x=0,1]dx 1 + (1-x/2) + ... + (1-(1-x)^n)/nx
= ��[x=��,1]dx ��[k=1,n] 1/xk - x^{-1}(1-x)^k/k
= ��[k=1,n] { 1/k * (-ln(��)) - ��[x=0,1-��]dx (1-x)^{-1} x^k/k }
= ��[k=1,n] { 1/k * (-ln(��)) - {��{[m=1,��] - ��[m=1,k]} (1-��)^m/mk }
= ��[k=1,n]��[m=1,k] 1/mk
= { ��[k=1,n]��[m=1,n] 1/mk + ��[k=1,n] 1/kk }/2
= { (��+ln(n)+��)^2 + ��^2/6 + �� }/2�@�@�y ��=0.5772..., ���� 0, ���� 0 (n����) �z
�� lim[n����] { ��[k=1..n]��[j=1..k] a[j]/j }/ { n*ln(n)^2 } = 1/2
����͏���ɕς������Ă������ ���̃X���A���x�������Ȃ��Ă����� �Ɍ����삪�G�Ɍ����Ȃ����Ȃ��̂ŏ������������Ă��� (���ۂ͓����e)
0 < �� < 1 �Ƃ���.
��[k=1..��] (1-��)^k/k = -ln(1-(1-��)) = -ln(��) �E�E�E(1)
N �� n < N, (1-��)^N/�� < �� �ƂȂ�悤�ɂƂ�.
��[k=n+1..N] (1-��)^k/k = ��[x=0,1-��]dx ��[k=n+1..N] x^{k-1}
= ��[x=0,1-��]dx (x^n�@-�@x^N)/(1-x)
= ��[x=��,1]dx (1-x)^n/x�@-�@��(N)
= -ln(��) + ��[k=1..n] C{n,k} (-1)^{k} (1-��^k)/k�@-�@��(N) �E�E�E(2)
N�̏������ 0 < ��(N) < ��
(1)-(2) ���
��[k=1..n] (1-��)^k/k = ��[k=1..n] C{n,k} (-1)^{k+1} (1-��^k)/k + ��(N)
�� �� +0 �̋Ɍ����Ƃ���
��[k=1..n] 1/k = ��[k=1..n] C{n,k} (-1)^{k+1} 1/k
��. �ςȂƂ����������̂Œ���
0 < �� < 1 �Ƃ���.
��[N] := ��[x=0,1-��]dx x^N/(1-x)
��[N] := ��[k=N+1,��](1-��)^k/k
N �� n < N, (1-��)^N/�� < ��, ��[N] < �� �ƂȂ�悤�\���傫���Ƃ�. (�ÂɈˑ�)
������� 0 < ��[N] < �� �ł���.
��[k=1..��] (1-��)^k/k = -ln(1-(1-��)) = -ln(��) �E�E�E(1)
��[k=n+1..N] (1-��)^k/k = ��[x=0,1-��]dx ��[k=n+1..N] x^{k-1}
= ��[x=0,1-��]dx (x^n - x^N)/(1-x)�@=�@��[x=��,1]dx (1-x)^n/x�@- ��[N]
= -ln(��) + ��[k=1..n] C{n,k} (-1)^{k} (1-��^k)/k�@- ��[N] �E�E�E(2)
(1)-(2) ���
��[k=1..n] (1-��)^k/k�@+ ��[N] = ��[k=1..n] C{n,k} (-1)^{k+1} (1-��^k)/k�@ + ��[N]
�� �� +0 �̋Ɍ����Ƃ���
��[k=1..n] 1/k = ��[k=1..n] C{n,k} (-1)^{k+1} 1/k
��. ����������Ɗ撣���Ă݂�.
��[k=1,n] C{n,k}(-1)^{k+1}/k
= ��[k=1,n] ��[x=0,1]dx C{n,k} (-x)^{k-1}
= ��[k=1,n] ��[x=0,1]dx C{n,k} (x-1)^{k-1}
= ��[x=0,1]dx { (1+(x-1))^n - 1 } / (x-1)
= ��[x=0,1]dx (x^n - 1) / (x-1)
= ��[x=0,1]dx ��[k=0,n-1] x^k
= ��[k=1,n] 1/k
��[j=1..n]a[j]/j
= ��[j=1..n] C{n,j} ��[x=0,1]dx ��[y=0,1]dy (-xy)^{j-1}
= ��[x=0,1]dx ��[y=0,1]dy {1 - (1-xy)^n }/{1 - (1-xy)}
= ��[x=0,1]dx ��[k=0,n-1] ��[y=0,1]dy (1-xy)^k
= ��[x=0,1]dx ��[k=1,n] (1-(1-x)^k) / kx
= ��[x=0,1]dx ��[k=1,n] (1-x^k) / k(1-x)
= ��[k=1,n] 1/k ��[x=0,1]dx ��[m=0,k-1] x^m
= ��[k=1,n] 1/k ��[m=1,k] 1/m
= ��[k=1,n]��[m=1,k] 1/km
�Â��log�W�J���g���Ȃ�ăA���G�l�[����... �Ǝ����ł��v���Ă����̂ŃX�b�L������. ���V���v����...
f(x) := (-1)*��[k=1..n] C{n,k}(-x)^k / k
f�f(x) = ��[k=1..n] C{n,k}(-x)^{k-1}
�@= (1 - (1-x)^n)/x = (1-(1-x)^n)/(1-(1-x)) = ��[k=0..n-1] (1-x)^k
��[k=1,n] C{n,k}(-1)^{k+1}/k
�@= f(1) - f(0) = ��[x=0,1]dx f�f(x) = ��[k=1..n] 1/k
��2�����̕����ł��̂͋p���Ėʓ|��������Ȃ�. ����قǂł��Ȃ�����.
g(x,y) := (-1)*��[k=1..n] C{n,k}(-xy)^k /kk
��[x]��[y]g(x,y) = ��[k=1..n] C{n,k}(-xy)^{k-1}
�@= (1- (1-xy)^n) / xy�@= (1- (1-xy)^n) / (1- (1-xy))
�@= ��[k=0..n-1] (1-xy)^k
��[x]g(x,y) = ��dy ... = ��[k=1..n] (1-(1-xy)^k) / kx�@{�� ��[x]g(x,0)=0}
�@= ��[k=1..n] y(1-(1-xy)^k) / k(1-(1-xy))
�@= ��[k=1..n] ��[m=0..k-1] y(1-xy)^m / k
g(x,y) = ��dx ... = ��[k=1..n] ��[m=1..k] { 1- (1-xy)^m }/mk�@{�� g(0,y)=0}
�� ��[k=1..n] C{n,k}(-1)^{k+1} /kk
�@= g(1,1) = ��[k=1..n] ��[m=1..k] 1/mk �@��[k=1..n] a[k] = 1 + 1/2 + 1/3 + ����� + 1/n = H[n],
�Ƃ����B
�@��[j=1..k] a[j]/j = ��[j=1..k] {C(n,j) (-1)^(j-1)} /jj
�@= ��[j=1..k] (1/j) ��[m=1..j] 1/j
�@= ��[j=1..k] H[j]/j
�@= (1/2)H[k]^2 + (1/2)��[j=1,k] 1/jj,
�܂ŏo���B
�@��[k=1..n] ��[j=1..k] a[j]/j
�@= {(n+1)/2}{H[n]^2 - ��[k=1,n] 1/kk} - H[n],
���ȁH
H[n] �` log(n) + ���@�@�@�y�� = 0.5772...�z �������̕��j�ɉ����Ĉ�ʉ����Ă݂�.
f{0} := f(x_1,...,x_m) := -��[k=1..n] C{n,k}(-x_1***x_m)^{k} /k^m
f{m} := ��[x_1]...��[x_m] f = { 1-(1-x_1***x_m)^n } / { 1-(1-x_1***x_m) }
�@= ��[k_1=0..n-1] (1 -x_1***x_m)^k_1
f{m-1} = �� dx_1 f{m} = ��[k_1=1..n] { 1 - (1 -x_1***x_m)^k_1 }/{ x_2***x_m) }
�@= ��[k_1=1..n] x_1 { 1 - (1-x_1***x_m)^k_1 }/{ 1 - (1-x_1***x_m) }
�@= ��[k_1=1..n] (x_1/k_1) ��[k_2=0..k_1-1] (1-x_1*...*x_m)^k_2
f{m-2} = �� dx_2 f{m-1}
�@= ��[k_1=1..n](x_1/k_1) ��[k_2=1..k_1] (x_2/k_2){ 1 - (1-x_1***x_m)^k_2 }/{ 1 - (1-x_1***x_m) }
�@= ��[k_1=1..n](x_1/k_1) ��[k_2=1..k_1] (x_2/k_2) ��[k_3=0..k_2-1] (1-x_1*...*x_m)^k_3
. . . ...
f{1} = ��[1��k_{m-1} ��...��k_1�� n] (x_1***x_{m-1})/ (k_1***k_{m-1}) ��[k_m=0..k_{m-1}-1] (1-x_1*...*x_m)^k_m
f = f{0} = �� dx_m f[1] = ��[1��k_m��...��k_2��k_1��n] { 1-(1-x_1*...*x_m)^k_m } /(k_1***k_m)
�� ��[k=1..n] C{n,k}(-1)^{k+1} /k^m = ��[1 �� k_1 �� k_2 ��...�� k_m �� n] 1/(k_1*k_2**k_m)
�Ȃ��Ȃ��ʔ�����������ꂽ. ���̎�����
�@lim[n����] { ��[k=1..n] C{n,k}(-1)^{k+1} /k^m } / ln(n)^m = 1/m!
��������. >>910 ����
�@��[j=1..n] a[j]/j = ��[k=1..n] {C(n,k) (-1)^(k-1)} /kk
�@= ��[k=1..n] (1/k) ��[m=1..k] 1/m
�@= ��[k=1..n] H[k] /k
�@= (1/2)H[n]^2 + (1/2)��[k=1,n] 1/kk,
�͏o���B�@������ k<n �ɑ���
�@��[j=1..k] a[j]/j
���o���̂�����@(�� a[j] �͉A��n�Ɉˑ�����)�@(2) �Ɏg�������ɂȂ��B�B�B
�ނ���
�@��[k=1..n] ��[j=1..k] a[j] /j
�@= ��[k=1..n] (n+1-k) a[k] /k
�@= ��[k=1..n] (n+1-k) {C[n,k] (-1)^(k-1)}/kk
�@= {(n+1)/2}{H[n]^2 - ��[k=1,n] 1/kk} - H[n],
�Ƃ�������������� �����̃X���b�h�̐����͋L���̈Ӗ�����킩���
�͂��߃A���S���Y�������Đ��w�͂��߂��l���܂����H >>913 �܂��ԈႦ���B
�@��[k=1..n] ��[j=1..k] a[j] /j
�@= ��[k=1..n] (n+1-k) a[k] /k
�@= ��[k=1..n] (n+1-k) {C[n,k] (-1)^(k-1)}/kk
�@= {(n+1)/2}{H[n]^2 �{ ��[k=1,n] 1/kk} - H[n],
�@�@�@�@�@�@�@�@�@�@�� >>908-909
�@�P�ϐ��ł��ł������B�B�B
f(x) := ��[k=1..n] a[k] x^k
�@= (-1)��[k=1..n] C[n,k]/k�E(-x)^k
�@= ��[k=1..n] (1-(1-x)^k)/k,
f(1) = ��[k=1..n] a[k]
�@= ��[k=1..n] 1/k = H[n],
g(x) := ��[k=1..n] a[k]/k�Ex^k
�@= -��[k=1..n] C[n,k]/kk�E(-x)^k
�@= ��[k=1..n] (1-(1-x)^k)/k�(��[m��k] 1/m),
g(1) = ��[k=1..n] a[k]/k
�@= ��[k=1..n] ��[m=k..n] 1/mk
�@= (1/2){H[n]^2 + ��[k=1,n] 1/kk},
�������
��[k=1..n] (n+1 - k) a[k]/k�Ex^k = (n+1)g(x) - f(x),
x��1 �Ƃ���
��[k=1..n] (n+1 - k) a[k]/k
�@= (n+1)g(1) - f(1)
�@= ((n+1)/2){H[n]^2 �{ ��[k=1,n] 1/kk} - H[n], 1�ϐ��ł���Ă݂�.
f[m](x) := ��[k=1..n] C{n,k}(-1)^{k+1} x^k/k^m
h[m](x) := ��[1��k_m��...��k_1��n] (1-(1-x)^{k_m}) / (k_1*k_2*...*k_m)
�Ef[1](x) = h[1](x) �͏ؖ��ς�.
�Ef[q](x) = h[q](x) �����肷��.
�Ef[q+1](x) = ��[t=0,x]dt f[q](t) / t = ��[t=0,x]dt h[q](t) / t
�@= ��[1��k_q��..��k_1��n] 1/(k_1*k_2*..*k_q)
�@ �@* ��[t=0,x]dt (1-(1-t)^{k_q})/(1-(1-t))
�@= ��[1��k_q��..��k_1��n] 1/(k_1*k_2*..*k_q)
�@�@ * ��[k=0..k_q-1] ��[t=0,x]dt (1-t)^k
�@= ��[1��k_q��..��k_1��n] 1/(k_1*k_2*..*k_q)
�@�@ * ��[k=1..k_q] (1-(1-x)^k)/k
�@= h[q+1](x)
�A�[�@�ɂ�� h[m](x)=f[m](x) (m=1..��)
����[k=1..n] C{n,k}(-1)^{k+1}/k^m = f[m](0) = h[m](0)
�@ = ��[1��k_1��..��k_m��n] 1/(k_1*k_2*..*k_m)
�������p�Ⴊ����̂Ȃ�m�肽���ł�. ����A_0A_1��ɂ���_A_2�𒆐S�Ƃ����_�Ώ̂�A_0��A_1���ړ������_�̂���A_2�ɋ߂�����A_3�Ƃ���B
����A_3�ƈ�ԋ߂������ɂ����_A_2 �� A_0 or A_1��A_3�𒆐S�ɓ_�Ώ̂ňړ������Ƃ�A_3�Ƌ߂�����A_4�Ƃ���B
���l�ɓ_�Ώ̂ňړ������_A_m�Ɉ�ԋ߂��Q�_��A_m�𒆐S�Ƃ��ĂP�W�O�x��]�������_�̂���A_m�ɋ߂�����A_(m+1)
�Ƃ���BA_0A_1�FA_0A_2��1�Fp �̂Ƃ� A_0A_1�FA_0A_m ��m�����̂Ƃ��ǂ��Ȃ邩�H >>918 �璷�������̂Œ���
�u���l�ɓ_�Ώ̂ňړ������_A_m�Ɉ�ԋ߂��_��A_m�𒆐S�Ƃ��ĂP�W�O�x��]�������_��A_(m+1)�Ƃ���v ��n�p�`T���^�����Ă���B
T�Ƒ�����n�p�`�ŁA����n�̒��_�����ׂ�T�̎���ɂ���A����T�Ƃ͈قȂ���̂����݂��邱�Ƃ������B >>918�@�䂪�L�������ƍŋߐړ_����_�ɂȂ��Ă��܂��̂�
A_0A_1�FA_0A_2��1�Fp �@(p�͖������j�@ 50��̔n���Ȃ�����������ȃX�����������Ƃ�
�ȑO���畷�������Ǝv���Ă������A�����ł����H
������57�ł��A�Ȃ�49�B�̍�8��
�����̗��e���̍�8��.�Ȃ̗��e���̍�8�ł��B
2�`3���ƒ��������Ȃ����A����͂��Ȃ背�A���Ǝv�����m�����ƁA�ǂ̂��炢�ł��傤���H
������������ >>923
�����\�N��̒j�����Ƃ̐l���s���~�b�h�̕��z����
����ׂɑI���ō̍����W�ɂȂ�m��p���v�Z����p^3�Ōv�Z�B
�����K������������Z�ɂȂ�̂�
�N���2-3�̊m���Ƃ̔�Ř_���������������낤�ˁB ��������͖���ׂɑI�Ԃ킯����Ȃ����m���ł��Ȃ��悤�ȋC������ �O>>672
>>923
�N�̍�8�͐��܂�N�ł�����7�`9���܂ł�8���Ƃ݂Ȃ��A���x�̈���Ⴂ��12�����ő�Ƃ����Ƃ��A4�g�̕v�w�̂���1�g��8���ɂȂ�B���ꂪ3�g�̕v�w�ł����Ȃ�m���́A
(1/4)^3=1/64
��100/64=1.5625(��)
8�����̂�25�����炢������A�m���I�ɒႭ�Ȃ��B����Ɉ�`�I�Ɏ��Ă���Ƃ��l������B �O>>926
���͐\�N���܂�A�����ƕ�Ƒc��͈�N���܂�A�����̑c��͖��N���܂�ŏ\���N���O��94�ŖS���Ȃ�܂����B
����̑c���͖�99�ʼn��N���O�ɖS���Ȃ�܂����B
�c��͂��̉��N���O�ɖS���Ȃ�܂������A�c����艽���N���ň�����͗���ĂȂ������͂��B
�����̑c���͕���3���炢�̂Ƃ�66�ŖS���Ȃ��������Ȃ̂ŁA1880�N��1881�N�̐��܂�ŁA�����̑c���1905�N���܂ꂾ�Ǝv���܂��B
����̑c���1923�N���܂�ŁA����̑c����1916�N��1917�N�̐��܂ꂾ�Ǝv���܂��B
48�̎����̑����̊��Ғl�͉����B ����z=0��̒P�ʉ~���~�Ƃ��A������h(>1)�̒��~�����l����B
�i�P�j����z=x+a�����~���Ƌ��L�_�����悤�A����a�������Ba�̎�蓾��l�͈̔͂����߂�B
�i�Q�j�i�P�j�ŋ��߂�a�͈̔͂̍ŏ��l��m�A�ő�l��M�Ƃ���B
[m,M]���������1����ׂɂƂ�A�����r�Ƃ����B
����z=x+r�ɂ��~���̐ؒf�ʂ̖ʐ�S(r)���Έȏ�(2/��3)�Έȉ��ƂȂ�m�����A�����_�ȉ�1���܂ŋ��߂�B
�����_��2���ȉ��͐�̂Ă�B >>926
�Ȃ��8����4�g��1�g�Ȃ́H
����Ȃɑ�����Ȃ�
1�`3�����炢�͑����ĔN�����������A�ȋC�����邪
����ȊȒP�Ȍv�Z�ł͂Ȃ��Ǝv����
�Ⴆ�Ή������Ȃ�45�����Ǝ����̗��e���Ȃ̗��e��45���Ȃ�Č����I�ɂ͂��肦��Ǝv������ >>928
(1)
���~���� -1��x��1 �� 0��z��h �͈̔͂Ɋ܂܂�邩��
�@-1 �� z-x �� h+1
�� a�̎�蓾��l�� -1��a�� h+1 �Ɍ���B
�t�ɁA
-1��a��0 �̂Ƃ��� (1,0,a+1) ���A
0��a��h �̂Ƃ��� (0,0,a) ���A
h��a��h+1 �̂Ƃ��� (-1,0,a-1) �����L�_�Ɏ��B
�ȏ���Aa�̎�蓾��l�͈̔͂� -1 �� a �� h+1. �O>>927
>>926
���N�Ⴂ���N�ƌ��邩1�Ⴂ�ƌ��邩�ňႤ���犱�x�̈��肪12�N�Ƃ��đO��܂߂�3�N�������N�Ƃ݂Ȃ���̈��1/4�Ƃ����Ӗ��ł����B
���v������ƕv��7�Έȏ�N����Ă����̂�11���Ȃ�ŁA8�ΔN���10�����炢����Ȃ����ƁB a,b���L������
�@a+��(a^2+4b) = 2+2��2
�����Aa=2, b=1 �ƌ����܂����B �ڂ����͂��C���Ȃ�����a=m/n,b=p/q�ł���ĕ��ꕥ���Ĉꎟ�Ɨ����ł�����Ⴄ�H >>932
a+��(a^2+4b) = 2+2��2
��
��(a^2+4b) = 2+2��2 -a
��
a^2+4b = (2+2��2 -a)^2
��
b = (3+2��2) - (1+��2) a
������ a, b ���L�����Ȃ� ��2 ����ł��������� a=2 �ł���K�v������,
���̎� b=2 �ł���.�@�܂葼�̗L�����y�A�ł͂��蓾�Ȃ�����������. ���̎� b=1 �ł���.�@�܂葼�̗L�����y�A�ł͂��蓾�Ȃ�����������. Q�F�L�����S��
�Ƃ���
���̂Ƃ�
��a,b��Q�G�@a+��(a^2+4b) = 2+2��2�@���݂�
��a,b��Q��O��Ƃ���
a�F=2
b�F=1
�Ƃ����悢
�ƌ����� ����Ă���̂́A
�@��a,b��Q { a+��(a^2+4b) = 2+2��2�@�� (a=1 �� b=2) }
����Ɠ����Ș_����
�@��a,b��Q { (a��1 �� b��2) �� a+��(a^2+4b) �� 2+2��2 }
��
�@��[ ��a,b��Q { (a��1 �� b��2) �� a+��(a^2+4b) = 2+2��2 } ]
�Ȃł�OK �܂��Ƃ�Ȃ����
�ʁ́@���l�@�@�Z
�́@���l�@�ʁ@�@����͖��W �������S�̖���̕s���ݐ�����
�͈�ʂɖ����W�����猳��I�ю�邱�Ƃ͂ł��Ȃ��̂�
��a,b��Q�C�@a=1, b=2�@
�Ə������Ƃ͂ł��Ȃ�
�K��
��a,b��Q�G�@a=1�Cb=2
�ł��� ���ꂾ����
�̂�́u���ׂĂ̌��ɑ��āv
�Ƃ�������͑S���Ԉ���Ă���
�{���̂Ă� �ȒP�ł����̂ʼn������������ė~�����ł��B
https://i.imgur.com/b6U7pOL.jpg �O>>931
>>942
x�̕��тɂ���2�̓��������̕ӂ�y�Ƃ����ƁA
�O��(2,6,2y)�ƎO��(x,3x,8)�̎O�p�`������������A
2:x=2y:8=y:4
��xy=8�����@
�Ε�8�̍����Ȓ��p�O�p�`��1�ƎΕ�3x�̒��p�O�p�`�ɂ����ăs�^�S���X�̒藝���A
8^2-y^2=(3x)^2-(x+y)^2
64=9x^2-x^2-2xy
�@�������A
64=8x^2-16
8=x^2-2
x^2=10
x=��10
�}����x��3���炢�����炠���Ă�͂��B >>942
�~�ɓ��ڂ���O�p�`�̈�ӂ����̉~�̒��a�Ȃ�A���̕ӂɑΌ�����p�����p�ł��邱�Ƃ𗘗p����B
x^2+(3x)^2��(2�~5)^2 ����� x����10
http://i.imgur.com/TUmodHy.png >>942
�}����A�~�̒��a 10 �����߂āA�~�ɓ��ڂ���3�ӂ̒��� 6�A8�A10(���a) �̒��p�O�p�`�̕ӂ̒���8�����߂�B
2�ӂ̒�����8�ɓ������ӎO�p�`�̒�ӂ̒����� 2y y��0 �Ƃ���B
�}����A�Β��p���݊p�݂̌��ɑ����ȎO�p�`�ɂ��āA8�Fx��2y�F(10-8)��y�F1 �� xy��8�B
�}����A�~�ɓ��ڂ���~���p���������݂��ɑ����ȎO�p�`�̐����ƎO�����̒藝���A
��( (��(8^2-y^2))^2 + (x+y)^2 )�Fx��6�F2��3�F1
�� 3x����( (��(8^2-y^2))^2 + (x+y)^2 )�B
�� 9x^2��8^2-y^2 + (x+y)^2��64 + x^2 + 2xy
�� 4x^2��32+xy��32+8��40 �� x^2��10 �� x����10 (�� x��0)�B ��̒��_A����Ε�BC�ɉ����������� AH
�O�ډ~�̒��S�� O
AO�̉������Ɖ~���̌�_�� D
AO�̉������ƕ�BC�̌�_�� X
�Ƃ���B
AOD�͒��a������
�@��ACD=90��,�@�@AD = 10,
�O�����̒藝��
�@AC = ��(AD^2 - CD^2) = ��(10^2 - 6^2) = 8,
��ӂ�胢ACX�͓ӎO�p�`
�@AX = AC = 8,
�@DX = AD - AX = 10 - 8 = 2,
��ACX �� ��BDX ���
�@BD = (AC/AX)BX = (AC/AX)x,�@
��CDX �� ��ABX ���
�@AB = (CD/DX)BX = (CD/DX)x,
AOD�͒��a������ ��ABD = 90�,
�ĂюO�����̒藝��
�@AD^2 = AB^2 + BD^2 = {(CD/DX)^2 + (AC/AX)^2}x^2 = �E�E�E�E
�ȉ� >>945 �̂Ƃ��� �e�_�̖��̂�>>947����ɍ��킹��
��ACD�����p�O�p�`�ł��邱�Ƃ���AC=8
��AXC���ӎO�p�`��AB=8
C����AD�ɐ������~�낵����F�Ƃ���
��AFC�́�ACD�Ƒ����ł���̂�AF�ACF�����܂�AFX�����܂�̂ł�������O������CX=(8��10)/5
��XCD�䁢XAB�ł���̂�x=��10
>>945����̂ق������ꂢ���ȁc�c >>946�͒��a��ʂ�Ȃ��Ă��A�ӎO�p�`��3�ӂ̒�����������ΓK�p�o���邱�Ƃ����邩��A����Ӗ��ŗL�͂ȋ��ߕ��ɂȂ��Ă���B ����A�~�ɓ��ڂ���O�p�`��3�ӂ̒����A�ӎO�p�`�̓�����2�ӂ̒�����������A>>846��2�s�ڈȍ~�̂悤�ȉ�@�͓K�p�o���邱�Ƃ�����B
���̍ہA���a�]�X�͊W�Ȃ��B >>945
3x ���ǂ�����N���ďo�Ă���̂��m�肽���ł�.
���p�O�p�`�̑������� x : 1 = 10 : x �@�� x^2 = 10
��( 10^2 - x^2 ) = ��90 = 3x
x�̌��ʂ�m������� "���R" �����Ă������Ƃ͈Ⴄ�̂ł��傤���H >>952
947�̌����Ƃ���́�CDX�䁢ABX ��� CD:DX=AB:BX
AB=CD�BX/DX=6�x/2=3x >>953
�����ł����B���肪�Ƃ��B ��CDX�䁢ABX�݂����ȑ������l�I�ɒ��X�i�̑����j�ƌĂ�ł�̂������������낤�� �����Ƃ��āA�������`
�̌����Ă邱�Ƃ��悭�킩��Ȃ��ł��B��A�ł��傤���H
https://i.imgur.com/inNmDpU.jpg N����1��2000���l�̂����A�j�������l�ł��邩�𐄒肷��B
����N��������X�l�𒊏o���A�M�����99%�덷�}1%�Ō��肵�����BX�͂����ȏ�łȂ���Ȃ�Ȃ����B >>956
�C�ӂ̕������������P�ʃx�N�g����e���Ƃ���ƁA�C�ӂ̕�����������������d���ł���x�N�g����d��e���ƂȂ�
�����a���Ƃ��悤���Ă��Ƃ��Ǝv�� �ʒu�x�N�g�� x �̐�����傪��]������ǂ�����Ă邩���Ęb��
�˂��̊G��`���͍̂ڂ�����̂͏��w�҂ɂ͍����̌��ł��傤��... ��]�̃C���[�W������Ă�B
��]�^���̉~���x�N�g���̍����ɒu���̂��Ȃ��Ȃ��A�����w�^�Ȃ�H�Ǝv���Ă��܂��B
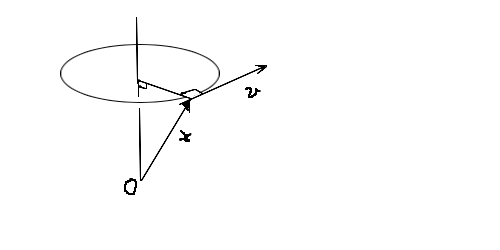 >>957
>>957
N=1.2���Ƃ��A�j����Np�l�ł���Ƃ���
�����_����X�l�I�Ƃ�n�l���j���ł���m���́AP(n)=C[Np,n]C[N(1-p),X-n]/C[N,X]
�����z������A���Ғl��Xp�A���U��(N-X)/(N-1)Xp(1-p)�����A
N���ł���p��1/2�ɋ߂��̂ŁA���Ғl��X/2�A���U��X/4�Ƃ��āA���K���z�ɏ]���Ƃ݂Ȃ�
�����(n-X/2)/��(X/4)�͕W�����K���z�ɏ]���A�����99%�M����Ԃ́}2.58
n=X/2(1�}1/100)�̂Ƃ��A�}X/200=�}2.58��(X/4)�AX=(2.58*200)^2/4��66000���x�K�v ����͂����b�ɂȂ�܂����B�}�`�ł܂����ɂ��������̂ŋ����Ă���������Ɗ������ł��B
�O���AB=AC�����Ȃ̂ł����A������̂�����A�A
https://i.imgur.com/azKedaY.jpg >>957
�j����ɂ���ĈႤ��Ȃ����ȁH
�ߎ��l�����߂���A����Ȋ����ɂȂ�������
�j���� sample_size
1 0.30 32465
2 0.31 33065
3 0.32 33634
4 0.33 34172
5 0.34 34679
6 0.35 35155
7 0.36 35600
8 0.37 36015
9 0.38 36399
10 0.39 36752
11 0.40 37075
12 0.41 37367
13 0.42 37629
14 0.43 37859
15 0.44 38059
16 0.45 38228
17 0.46 38366
18 0.47 38474
19 0.48 38550
20 0.49 38597
21 0.50 38612 >>965
�M�����95���Ōv�Z���Ă����B
99%�̐��l�͂�����B
> d
�j�q���� sample_size
1 0.025 6680
2 0.050 12805
3 0.075 18613
4 0.100 24087
5 0.125 29225
6 0.150 34035
7 0.175 38514
8 0.200 42660
9 0.225 46475
10 0.250 49959
11 0.275 53110
12 0.300 55930
13 0.325 58418
14 0.350 60574
15 0.375 62398
16 0.400 63891
17 0.425 65052
18 0.450 65882
19 0.475 66379
20 0.500 66545 >>967
�O���t�ɂ����炱��ȃO���t�ɂȂ����B���������ȁH
https://i.imgur.com/ZRiF30q.png >>968
��W�c�̒j�q�̊�����p�AX�l�I�Ƃ��̒j�q�̐l����n�Ƃ���ƁA
n�̕��U��Xp(1-p)�����A�����p=1/2�Œu���������ɂ��̂܂ܗp����Ȃ�A
(n-X/2)/��(Xp(1-p))���W�����K���z�ɏ]���ƌ��āA�����99%�M����Ԃ́}2.58������A
n=X/2(1�}1/100)�̂Ƃ��A�}X/2/100=�}2.58��(Xp(1-p))�AX^2=(200*2.58)^2Xp(1-p)�A
X=266200p(1-p)�A�ƍl����Γ��ɂȂ� >>968
y=265395.864*x*(1-x)�Ƃ������������ȁB
https://bellcurve.jp/statistics/course/9122.html
�ŐM����ԕ�=0.01�ɂȂ邎�̒l�����߂������B
99%�M����ԂȂ̂�1.96�łȂ�2.56�� >>969
���X���肪�Ƃ��������܂��B
���������d�˂Ă݂܂����B
https://i.imgur.com/axElxnp.png �����傫�����琳�K���z�ŋߎ��Ƃ��������ŁA���{�̐l�����͕K�v�Ȃ��̂������[���B >>964
����CD��Ɂ�FBD��20���ƂȂ�悤�ɓ_F���Ƃ�
BC��BF��EF��DF�ƂȂ邱�Ƃ�������x�����Ƃ��\ >>955
"Butterfly Problem" �Ɏg���邩���c
���Z�~�����u���w�̖��v
�@��(1)�W ���{�]�_�� (1977) ��63
�@��(2)�W ���{�]�_�� (1978) �t�^-2 (���� ��)
�@���w�Z�~�i�[ 1971�N8�����̋L�� >>964
��A = ��
��ABD = (1/3)��CBD = (60-��)/2,
��BCE = 30+��,
��DCE = 30�
�Ƃ���B
CD��ɓ_F����ABF=60߂ɂȂ�悤�ɂƂ�B
��BFC = ��C�@���@BC = BF,
��BCE = ��BEC�@���@BC = BE,
�� BE = BF�@�Ɓ@��EBF = 60߁@���@��BEF�͐��O�p�`�B
��FBD = 30�+��/2 = ��FDB�@���@ DF = BF
DF=EF�@���@��DEF = ��EDF
= 60�+��/2,�@�@(�� ��DFE = 60�- ��)
�� x = ��EDF - ��BDC = 30�
���Z�~�����u���w�̖��v��(2)�W�A���{�]�_�� (1978)
�@��21
�u�����O���[���v�u�t�����N�����̑��v�Ɖ]���炵����� �����O���[�̖��
E. M. Langley: The Math. Gazette�i1922/10�j����сi1923/5) >>957
���Ԃ���(�}��)�A�ێR����(�O�A���}��)�A�l�c����(�Q)
����� �O>>966
>>964
x=30���̂Ƃ��A
BD��EC�̌�_��P�Ƃ��āA
��AED�䁢BEP
����p(20��,50��,110��)���������B
��AED:��BEP=t:1�Ƃ����ƁA
BC=1,
CD�Ԃ�F���Ƃ��āA
BF=EF=DF=1
��ABC�䁢BCF���A
CF=1/(t+1)
��ӂ��AB=AC
AD=t-1/(t+1)
��ABD���ӎO�p�`������A
AP:AD=1:t���A
PD=t-1/(t+1)-(1/t){t-1/(t+1)}
=t-1/(t+1)-{1-1/t(t+1)}
=t-1/(t+1)-1+1/t(t+1)
={t^2(t+1)-t-t(t+1)+1}/t(t+1)
=(t^3-2t+1)/t(t+1)
=(t^2+t-1)(t-1)/t(t+1)
��PFD���ӎO�p�`������A
PF=PD=(t^2+t-1)(t-1)/t(t+1)
BP=(1/t)AD
=1-1/t(t+1)=1-{sin20��/(sin80��-20��)}(sin20��/sin80��)
=0.820779646�c�c
��0.82
��PBC�ɂ����Đ����藝���A
BP=sin50��/sin70��
=0.815207469�c�c
��0.82
��x=30���͂��Ȃ肠���Ă�B �ŋ߂̘b��ɍ��킹�Ă����������ɂ��Ă��݂��B
���{�l1��2680���l����R���i�����Ґ�����������X�l�𒊏o����PCR�������āA�M�����99%�덷�}1%�Ō��肵�����B
PCR�����͊��x0.6�C���ٓx0.9�Ƃ���B
���l�𒊏o����Ώ\���Ƃ����邩�H (�C���j
�ŋ߂̘b��ɍ��킹�Ă����������ɂ��Ă��݂��B
���{�l1��2680���l����R���i�����Ґ�����������X�l�𒊏o����PCR�������āA�����Ґ�(�������z���Ґ�)��M�����99%�덷�}1%�Ō��肵�����B
PCR�����͊��x0.6�C���ٓx0.9�Ƃ���B
���l�𒊏o����Ώ\���Ƃ����邩�H ���L�̎��̐Ԑ����̈Ӗ����킩��܂���B�iIE�ł͌���Ȃ��݂����ł��j
�s�̋L���̒��g u+wv �͋�̓I�ɂǂ��������ɂȂ�̂ł����H
wv�Ƃ����̂͂S�~�S�̍s��Ȃ�ł����H
�E�ӂ��Q�̕��s�l�ӌ`�̖ʐς̘a�ł��邱�Ƃ͕�����܂��B
https://imgur.com/a/kz9qXIX >>983
u+w��v����ׂč����s�Ȃ�łȂ����H >>928
(2)
m=-1, M=h+1,
�@z-x = r,
�@(z+x-r)/��2 = u�@�Ƃ�����
�@x = u/��2,
�@z = u/��2 + r,
���~���̎����f�ʂ�
�@uu/2 + yy �� 1,�@�@(�ȉ~)
�@-(��2)r �� u �� (��2)(h-r),
�ƂȂ�B
-1 �� r �� min{h-1,1}�@�̂Ƃ�
�@S(r) = (��2){arccos(-r) + r��(1-rr)},
Max{h-1,1} �� r �� h+1�@�̂Ƃ�
�@S(r) = (��2){arccos(r-h) - (r-h)��[1-(r-h)^2]},
min{h-1,1} �� r �� Max{h-1,1}�@�̂Ƃ�
�@S(r) = (��2)��,�@�@(h��2)
�@S(r) = (��2){arccos(-r) + r��(1-rr) + arccos(r-h) -(r-h)��[1-(r-h)^2] -��},
�@�@(h��2) >>982
���肪�Ƃ��������܂����B >>928
>>986
h < 1.1844 �̂Ƃ��� S(r) < �� �Ŋm����0�B
h > 1.1844 �̂Ƃ� S(h/2) �� ��,
h �� 1.3314982535855 �̂Ƃ�
�@0.3314982535855 �� r �� h - 0.3314982535855�@�́@S(r) �� ��,
h �� 1.4104 �̂Ƃ� S(h/2) �� 2��/��3,
h �� 1.521924793186316 �̂Ƃ�
�@0.521924793186316 �� r �� h - 0.521924793186316�@�́@S(r) �� 2��/��3,
�ςȖ��B�B�B�B >>981
>�M�����99%�덷�}1%��
�H >>981
>PCR�����͊��x0.6�C���ٓx0.9�Ƃ���B
������M�l����N�l���Ɗ�����p=M/(M+N)
����z���������o��̂�
0.6M+0.1N�Ȃ̂ŗz��������q=(0.6M+0.1N)/(M+N)=0.1+0.5p
���̎����g���ĕW�{�̗z�����������犴��������Ԑ��肷��́H >>989
99%�M����ԕ���1%�ȉ��ɂ��� �M�����99%���Ĕn������˂��� �M�����99%���Ĕn������ȁB
�ӂ��A99���M����ԂƌĂԂ���B >>989
���̕�������������ɂ����ȁB
���{�l1��2595���l����R���i����������������X�l�𒊏o����PCR�������āA
������(�������z����)�̐M�����99%����1%�ȓ��Ō��肵�����B
PCR�����͊��x0.6�C���ٓx0.9�Ƃ���B
���l�𒊏o����Ώ\���Ƃ����邩�H r�𐳂̎����萔�Ƃ���B2�̔��~��
C:x^2+y^2=1(y��0)
D:(x-r-1)^2+y^2=r^2(y��0)
������B
C,D�̊O���ɂ���~�ŁA���S��y���W�����ł���A�܂�C,D�̌ʁi�[�_�͏����j�ɂ��O�ڂ��Ȃ��瓮���~��K�Ƃ���B
�i1�jK�̒��S��(1,3)�̂Ƃ��AK��C,D�̂�����ɂ��ڂ���悤��r�̒l�����߂�B
�i2�jK�̒��S��(a,b)�ł���AK��C,D�̂�����ɂ��ڂ���Ƃ���B���̂Ƃ��Aa,b�͂�����ʂ�ɒ�܂邱�Ƃ������B
�i3�jK�������Ƃ��AC,D,K�̂�����ɂ��O�ڂ���~�̒��S���`���̈�����߂�B >>994
>>990�ł����́H
��1%�ȓ��Ƃ�p�}1%�ł����H >>998
>>969��p��0.6p+(1-p)(1-0.9)�ɒu�������čő�l�����߂邾�� ���̃X���b�h�͂P�O�O�O���܂����B
�V�����X���b�h�𗧂ĂĂ��������B
life time: 52�� 10���� 13�� 48�b 5�����˂�̉^�c�̓v���~�A������̊F���܂Ɏx�����Ă��܂��B
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�s�v���~�A������̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
��300�~���瓽���ł��w�����������܂��B
�� �v���~�A������o�^�͂����� ��
https://premium.5ch.net/
�� �Q�l���O�C���͂����� ��
https://login.5ch.net/login.php ���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B


