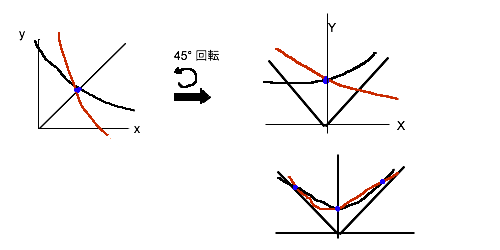
1解から3解への境界. その時、y = a^x は y=x の 交点P にて 傾き -1 となる.
直線 y = x の線対称よりも x = 0 の線対称 が分かりやすいので,
y = a^x のグラフを 45度回転する.
-qX + qY = a^(q X + q Y) (q=1/√2と置いた)
条件より (0,Y) にて dY/dX = 0 となるので、
(1) +qY = a^(q Y) (←式に(0,Y)を代入)
(2) -q = a^(q Y) log(a) q (←式を微分してから(0,Y)とdY/dX=0 を代入)
(1)(2)式より -q = +qY log(a) q つまり qY = -1/log(a) が分かり, これを(1)に代入すると
-1/log(a) = a^(-1/log(a)) = e^(-1) ∴ a = e^(1/e)
よって 0< a < e^(1/e) では 交点P で dY/dX < 0 つまり dy/dx < -1 となる. その結果3解を持つ.