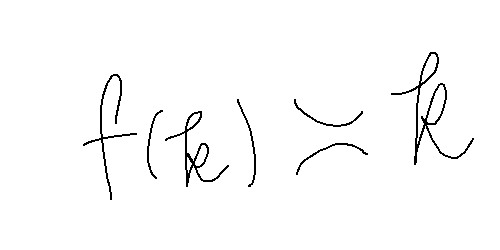������Ȃ����͂����ɏ����Ă�449
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
�����A�������P������낤����
�O�X��
������Ȃ����͂����ɏ����Ă�448
https://rio2016.5ch.net/test/read.cgi/math/1540218853/ >>5
�ꉞ�m�F�ł��������҂ł����H >>5
�����O�X����>>974�Ɠ���l���Ȃ�A�Ȃ����߂Ƃ����Ďv����ł����H >>9
>>4�̏�̃����N�̓N�b�L�[�������߂�ꂽ���猩�ĂȂ��B
�͂Ăȃ_�C�A���[�̕��͖��肪Zorn�̕��ɂȂ��ĂȂ��B
�u�C�ӂ̍��i�S���������W���j����E�����悤�ȏ����W���͋ɑ匳�����D�v
��
�������́A
�u�S�Ă̑S���������W������E�����������W���̑S�Ă̌��͋ɑ匳�Ɋ܂܂��B�v >>4�̂����Ŏ����ŏؖ���Z�߂Ă݂܂�����
�����̏ؖ��̋ؓ��Ŏ������Z�߂Ă������̂������ʂ��قڔ����ɂȂ�܂���
�����ł��� >>7
���ׂ��Ƃ���>>4�̂͂Ăȃu���O�̎��M�҂�
http://surgery.matrix.jp/diaries.html
���s����w���w�������{�`������
�݂����ł��� ���w�ƌĂׂ�قǂ̂��̂ł��Ȃ��ł������₵�Ă����ł����H
�m���̖��Ȃ̂ł��� a�Ab�Ac�̎O�̐����������_����10��I��ł�������Ăꂩ�H
���̎��̗��_�l�́H
���Ə�L��10��J��Ԃ������̗��_�l�́H >>16
�������ւ��ł����܂���
a�Ab�Ac�̒����烉���_���Ő�������I��܂�
���̐����Ă鎖��10��J��Ԃ�����
���Ă邱�Ƃ��ł��܂����H
���̎��̎������鐔�l�́H >>17
a��b��c���Ă�ƌ����Ӗ��H
1/3�̊m���ŕ\���ł�R�C���ŕ\���o��̊��Ғl�����߂���Ă��ƁH >>17
�K���ɐ������Ă݂�
a, b, c �ŋ�ʂ����J�[�h�������āA���ɗႦ�� 1����N �܂łǂꂩ�̐����������Ă���.
����1���������_���őI��āA���Ȃ��͂��̗��̐����Ă�.
�^��_1. �J�[�h���̐����� �d������Ȃ̂��H�Ȃ��Ȃ̂��H
�^��_2. �J�[�h���̐����� ���������Ȃ��Ȃ̂��H ���̏ꍇ, �O��Ă������͈̔͂��i����.
�^��_3. ���������Ȃ��Ƃ��� �O�ꂽ�J�[�h���̐����͒����̂��H ���̏ꍇ, ���ɓ����J�[�h��������K�����Ă�.
�^��_4. ���Ȃ��ɃJ�[�h�̋�ʂ͂��̂��H �O�Ɠ����J�[�h�����Ă�, ���ꂪ����ł���̂�?
�^��_5. ���m�̏��𗘗p���ď�����ڎw���C�͂���̂��H ����Ƃ������_���ɓ���������̂��H
�����������Ă邩���������̂�
���������������Ă���Ȃ��ƒN���������Ȃ�. (X,O)���ʑ���ԁBA��X�Ƃ��܂�
A�ɂ�����J�W��V��V=A��U�AU��O�@�ƊȒP�ɕ\���܂����A
A�ɂ�����W��B�͊ȒP�ɕ\���܂����H B=A��F�AF��X�̕W���Ə����܂��� logaMN=logaM+logaN�ł����ǁA
-logaMN�̎��͂ǂ��Ȃ��ł����H
-logaM-logaN�ɂȂ��ł����H �Ȃ��������₫��
�Ȃ��A��̎���-1���|��������������� ���肪�Ƃ��������܂�
����������ł��� �����̏o���̈������n���Z���ł��� log�ȑO�̖��Ƃ���
x=a+b �Ȃ�� -x=-a-b
�����̂͂Ȃ� ���́u�������v�Ƃ����͔̂�����Ǝv�����A������Ƃ��ǂ���
����͂����ƍ��Z���̒i�K�ŗ��n�����n���˂��� m,n�����R���Ƃ���B�s����
log_2[13] < m+(p/n)�c(*)
�ɂ��Ĉȉ��̖₢�ɓ�����B
�i1�jp��n��菬�������̎����Ƃ���B���̂Ƃ�m�����߂�B�����݂̂ł悢�B
�i2�jp=1�̂Ƃ��A�s����(*)�̌덷���ŏ��ɂ���n�����߂�B
�����Ō덷�Ƃ́A(*)�̉E�ӂ��獶�ӂ��������l�̐�Βl�ł���B
�i3�j�i2�j�ɂ����āAp=5�̏ꍇ�͂ǂ����B >>17
10/3�Ɏ�������l�q���V�~�����[�V�������Ă݂��B
https://i.imgur.com/0l6ynoB.png ��������������������������
��������������������������
��������������������������
��������������������������
��������������������������
��������������������������
��������������������������
��������������������������
��������������������������
��������������������������
��������������������������
��������������������������
�������������������������� >>31
���肪�Ƃ�
���̎���8��ȏ㓖�Ă��m�����Ăǂꂭ�炢����H >>31
���肪�Ƃ�
���̎���8��ȏ㓖�Ă��m�����Ăǂꂭ�炢����H >>31
10/3�Ɏ������Ă��H����H �y���J���F�i57�j�����z�@�l�������N�Q�O���l������قǔ픘���ĉ��������A����ɂV�O�܂œ����ĉ���
http://rosie.5ch.net/test/read.cgi/liveplus/1543371270/l50 >>29
(1)
�@m=3.
(2)
13^10 = 137858491849 > 137438953472 = 2^37,
���
log_2[13] > 37/10 = 3.70 ���ʂ̗̈� y^2-x^2 < 1 ���� x^2-y^2 > 1 ���� x > 0 ��D�Ƃ���B
D�Ɋ܂܂��i�q�_�ŁA����y=x��ɂȂ����̂̌����L�����ǂ������q�ׁA�L���ł���Ȃ炻�̌������߂�i1�����݂��Ȃ��ꍇ��0�Ƃ���j�B >>33
(1�{10+45)/3�O10��56/59049 �����Ȃ̂��H
(1+10*2+45*2^2)/3^10��201/59049 ������Əꍇ�̐�
0��@�@1024�ʂ�
1�@�@�@5120
2�@�@�@11520
3�@�@�@15360
4�@�@�@13440
5�@�@�@8064
6�@�@�@3360
7�@�@�@960
8�@�@�@180
9�@�@�@20
10�@�@�@1 �~C1�AC2�����̂悤�ɒ�߂�
C1: x^2+y^2=4
C2:(x-2)^2+y^2=1
���̎��AC1�AC2�ɊO�ڂ���~C�̒��S�����߂�
���ꂪ�����܂���
���S�̍��W��pq�Ƃ����ā�p^2+q^2 -1 = ��(p-2)^2+q^2 �������ƁA3(p-1)^2-q^2=3/4�@�ƂȂ�܂����A
���̂������_����2�ȏ㗣��AC2�̒��S����1�ȏ㗣�ꂽ����̓_�݂̂����������܂���ˁA�A
��������ǂ����������̂������Ă�������>< �����I�Ȏ���Ȃ�ł����A�}�̂悤�ȁA���̐^��ׂ�����݂����ȋL�����Ăǂ������Ӗ��ł����H
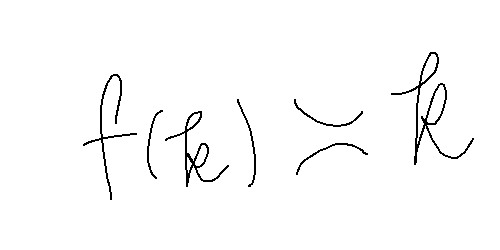 >>44
>>44
�������ꂾ���H����3�H >>46
�����͂��ꂾ���ł�
�_�̋O�Ղ����߂���Ȃ̂œ����͖����ɂ���܂� �uA �ł��� �� B �ł���v���ؖ�����̂ɁA��uB �łȂ� �� A �łȂ��v���ؖ�����Ƃ����ؖ��@������܂��B
����Ɣw���@�ł̏ؖ��͓������Ƃł���Ƃ���{�i���F�v���w���U���w�x�j�ɏ����Ă���܂��B
�ł����A�A�}�]���̃��r���[�ŁA����a�v����̖{�Ɂ��̓��e�������Ă�����������͊Ԉ���Ă���Ƃ������̂�����܂����B
���F�v����ƃA�}�]���̃��r���A�[�̂ǂ��炪�������̂ł��傤���H >>34
> sum(dbinom(8:10,size=10,prob=1/3))
[1] 0.003403953
> p=1/3
> choose(10,8)*p^8*(1-p)^2 + choose(10,9)*p^9*(1-p)^1 + choose(10,10)*p^10*(1-p)^0
[1] 0.003403953 >>49
�V���傫���m��������
> pbinom(7,size=10,prob=1/3,lower.tail = FALSE)
[1] 0.003403953 >>42
>>43
���肪�Ƃ�
���ۂ��ƈӊO�Ɠ�������
�^�����������H ���̖���(A)���U�ł��邱�Ƃ������B
�܂�����(B)�̐^�U�肹��B
�ǂ̂悤��2����f(x)�ɂ��Ă��A
(A)
f(0),f(1),f(2018)
�̂�����̒l�������ł���Ȃ�A
���ׂĂ̐���n�ɑ���f(n)�͐���
(B)
f(0),f(1),f(2018),f(2019)
�̂�����̒l�������ł���Ȃ�A
���ׂĂ̐���n�ɑ���f(n)�͐��� >>44 >>47
C1�CC2�̌�_�� (x, y) = (7/4, (1/4)��15) ������
�u�o�Ȑ�
�@3(x-1)^2 - y^2 = 3/4
�̂��� x>7/4 �̕����v
����ˁH
�֑������ǁAC�̒��S��(p,q)�A���a�����Ƃ����
C�F�@(x-p)^2 + (y-q)^2 = r^2,
�@(p, q) = ((2r+7)/4, �}(1/4)��{3(2r+1)(2r+5)} )�@�@r>0 >>44
>���̂������_����2�ȏ㗣��AC2�̒��S����1�ȏ㗣�ꂽ����̓_�݂̂����������܂���ˁA�A
�����������B >>48
���f�����_�Ńu�C�u�C���킵�Ă����̐l�̉�҂Ƃ� >>54
�Ȃ������̓_��荶�Ȃ�����S�Ă����ƕ������ł����H �܂��Ȃ����̓_��荶�Ȃ��ɂǂꂩ�̏��������Ȃ��ƕ�����̂ł��傤���H >>61
3/2��x��7/4 �̂Ƃ�
�@(p,q) �� (C1��C2)
�@�~C1�CC2�̓���������ڂ���B
�@0 �� r �� 1/2,
�@C �� (C1��C2)
x�� 1/2 �̂Ƃ�
�@�~C1�CC2�̊O��������ڂ���B
�@C �� (C1 U C2)
�@-r �� 5/2 >>62
����}�������Ă݂�����Ȃ̂��낤�Ƃ������Ƃɂ͂Ȃ�̂��낤���A
�܂��ɂ��̂��Ƃ𐔎��Ŏ����ĖႢ�����Ǝv���Ă���̂��@>>61�B ���F�v���w���U���w�x�̑�2�́u�O���t�ƃ}�b�`���O�v�̃E�H�[�~���O�A�b�v�N�C�Y��
5 �~ 5 �̖��@�w�̗��������
�Ƃ�����肪����܂��B
���҂ɂ��ƃE�H�[�~���O�A�b�v�N�C�Y�́A�u�����l����Ε�������v�������ł��B�u����قǍ���ł͂Ȃ��v�Ƃ�
�����Ă��܂��B
���̗\���m�����Ȃ��l�� 5 �~ 5 �̖��@�w�̗�����̂́A����ȂɊȒP�Ȃ��Ƃł��傤���H >>63
�����ł��ˁB
�����Ŏ����Ăق����ł��B
�͔͉ł͋��ʌ���7/4���E�Ȃ疞�����B�ȊO��؏����ĂȂ���
����S�R��������Ȃ��Ȃ��H�Ƃ����v��Ȃ�������ł��� >>64
> ���F�v���w���U���w�x�̑�2�́u�O���t�ƃ}�b�`���O�v�̃E�H�[�~���O�A�b�v�N�C�Y��
>
> 5 �~ 5 �̖��@�w�̗��������
>
> �Ƃ�����肪����܂��B
>
> ���҂ɂ��ƃE�H�[�~���O�A�b�v�N�C�Y�́A�u�����l����Ε�������v�������ł��B�u����قǍ���ł͂Ȃ��v�Ƃ�
> �����Ă��܂��B
>
> ���̗\���m�����Ȃ��l�� 5 �~ 5 �̖��@�w�̗�����̂́A����ȂɊȒP�Ȃ��Ƃł��傤���H
5�~5�̓��e�����w�Q�g�ݍ��킹�邾��������ȒP�B
0 1 2 3 4 0 1 2 3 4
2 3 4 0 1 3 4 0 1 2
4 0 1 2 3 1 2 3 4 0
1 2 3 4 0 4 0 1 2 3
3 4 0 1 2 2 3 4 0 1
����5�i����5�̈ʁA�E��1�̈ʂƂ݂�Ηǂ��B �Ƃ肠�����L�������ă����g�킸�ɏ����o���Ă݂�����Ǝv���� >>67
2S-S������Ă݂���ꂢ�ɏ������H >>68
����223�Ɗ��Ⴂ�������� >>66
���̗\���m�����Ȃ��l�� 5 �~ 5 �̖��@�w�̗�����̂́A����ȂɊȒP�Ȃ��Ƃł��傤���H >>67
S(r):=Sum[r^k,{k,0,n}]
��r�Ŕ�������ƁA
dS(r)/dr=Sum[k r^(k-1),{k,0,n}]
������r=1/2�ɂ��čŌ��2^(n-1)�������������Ȃ��́H ���̊�͌������Ȃ��Ƃ����Ȃ���A�O�����排������A�����Ă������X�����l�ԒB
�K�L�̐��₨������̐��A���̐�������B�{�C�X�`�F���W���[���g���Ă���̂�������Ȃ����B
�u�V�c�É���n���ɂ��₪���āB�v
���̏��H�삩������Ȃ����A�����O�����B���������ł������B���f���B���������ɂ���B
�ǂꂾ���A�l�Z�����O����A����������ē����Ă����A���傪���������ʂƌ������čs���Ă݂���Ă�B
���X���������Ȃ�A�`���s������B AB=2,AC=3�ł��遢ABC�̊O�ډ~�̒��S��O�A���ډ~�̒��S��I�Ƃ���Ƃ��AOI�̍ő�l�����߂�B ���ꂩ��A�悭�O����u�����v�ƕ������Ă���B���܂ō��v3�x�B
�Ӗ��s���߂��āA�������������̂�������Ȃ��B
�͂����茾���Ē��������邩��A���߂̂��悤�̂Ȃ����߂�����ȁB >>70
�悭������ۂ��Ă��肶��Ȃ������킗������ 20�l(5��)�Ŗ���������B1,2,3,4�ʂ����m���͂��ꂼ��25%�Ɖ��肷��B
���ꂼ��̑��14��s���āA���Ȃ��Ƃ�1�l��4�ʂ���x�����Ȃ��m���͂����炩�B �ʑ����(S,O1)�A(S,O2)�ɑ���
(S,O1)���R���p�N�g�A(S,O2)���n�E�X�h���t��O2��O1�̂Ƃ�O1=O2�ƂȂ邱�Ƃ������ĉ����� >>78
�ǂ��ł���������14����Ĕ��[����
���Ԃ�Ԉ���Ă�Ǝv�����ǁA�P���ɍl�����
{1�|(3/4)^14)}*20 >>80
�C�ӂ� o1 �� O1 �� x �� o1 ���Ƃ�.
���̂Ƃ��C�ӂ� y �� S - o1 �ɑ��� O2�ŕ������\
�܂� S - o1 ���`��Ƃ���2��: ua, ub �����݂���
�@x �� ua(y) �� O2, �@ y �� ub(y) �� O2, �@ua(y) �� ub(y) = ø (�� O2�n�E�X�h���t)
S �� O1�J�W����: { o1, ub(y �� S - o1) } �Ŕ핢����,
����L�������W����: { o1 , ub(y_1), ..., ub(y_N) } �ł��핢�\�ł���. (�� O1�R���p�N�g)
o2 := ��{k=1..N} ua(y_k) �ƒu����
�@o2 �� O2, �@o2��(S - o1) �� o2�� (��{k=1..N} ub(y_k)) = ø
�� x �� o2 �� O1
�܂� x �� O2���_�ł���̂� o1 �� O2
����� O1 �� O2 �������ꂽ.
�O��� O2 �� O1 �� ���킹�� O1=O2 �ł���. >>81
4�l1��4�킾�ƁA(3/4)^4*4�@���Ǝv��������
�m����1���邩��Ԉ���Ă�͖̂������� ��) �� x �� o2 �� O1
��) �� x �� o2 �� o1 �e�B�[�c�F�̊g���藝�ŋA�[�I�ɊJ�W��������ؖ��@��ǂ�ł���A
�ǂ��������ɊJ�W���������Ă�̂���������Ղ��ؖ��������Ă�̂ǂ����ɂȂ��H ����~C�̎���ɑ��قȂ�6�_A,B,C,D,E,F���AA���炱�̏��ɔ����v���ɂȂ�悤�ɂƂ�B
��ACE�Ɓ�BDF�̋��ʕ����̑��p�`��K�Ƃ���B
K�̊e���_�����ׂē���~����ɂ���Ƃ��A6�_A,B,C,D,E,F�̔z�u�͂ǂ̂悤�ȏ����������B
�K�v�\���Ȍ`�ŏq�ׂ�B �܂̒���4�̋ʂ������Ă���A�e�X�̋ʂɂ�1����4�܂ł̐�����1��������Ă���B�܂��܂̊O�ɂ������4��ނ̋ʂ��\���Ȑ��p�ӂ���Ă���B
���̂Ƃ��A�ȉ��̑�����J��Ԃ��s���B
�u�܂̒�����ʂ�1���o�����Ƃ��́A���̋ʂ̔ԍ���k�Ƃ���B
(A)k��3�ł���Ƃ��A�܂̊O����k�ȏ�4�ȉ��̔ԍ��������ꂽ�ʂ�1�I�ԁB���������̒��łǂ̋ʂ��I��邩�͓��l�Ɋm���炵���B�I�ꂽ�ʂ�lj����A���o�����ʂ�܂ɖ߂��B
(B)k=4�̂Ƃ��A�܂̊O����1�ȏ�4�ȉ��̔ԍ��������ꂽ�ʂ���I�сA�ȉ�(A)�Ɠ��l�̑�����s���B�v
��F���̑�����J��Ԃ��s�����Ƃ��An��ڂ̑���ő܂̒�������o���ʂɏ����ꂽ���̊��ҒlE(n)�����n�����Ƃ����Ƃ���E(n)�̋Ɍ��l�����߂�B 86��87����ؓ�ł͂����܂���B
86�͎���������ƌ����Ă���̂ł͂Ȃ��ł��傤���B
87�͋Ɍ������Ȃ�ȒP���Ǝv���܂��B >>74
��
��A��C���Ȃ�ׂ������āAB��I���Ȃ�ׂ���������ƁA��ABC���ő���ɂЂ炢�āA�~I�͍ŏ��A�~O�͍ő�ƂȂ�AOI�͍ő�ƂȂ邪�A�����ɑ傫���ł���B �ǂ����Ă��͔͉ǂ���̐ϕ��ɂȂ�Ȃ��̂ł����A
�ό`�̂ǂ����Ԉ���Ă���̂������Ă��������B�i�̃}���ň͂�ł���Ƃ��낪��܂���j
https://i.imgur.com/Ye1AehM.jpg
https://i.imgur.com/dAfmUwY.jpg >>90
�Z�L�u���r�u���̂Ƃ��������ɐϕ����Ȃ��ƃ_���Ȃ�H >>87
sim <- function(n){
x=1:4
k=0
while(k<n){
y=sample(x,1)
x=append(x,ifelse(y==4,sample(1:4,1),sample(y:4,1)))
k=k+1
}
return(mean(x))
}
�P�O�O�O��̃V�~�����[�V�������P�O�O����������
> re=replicate(100,sim(1000))
> summary(re)
Min. 1st Qu. Median Mean 3rd Qu. Max.
2.843 2.914 2.940 2.939 2.960 3.059
���Ғl�͂R�Ɏ�������݂����B
��͉��͒B�l�ɂ��C�� >>83�@
4�l(1��)4��̏ꍇ�́A���X����̐l���Ɗm��
0�l�@6/64
1�@�@36/64
2�@�@21/64
3�@�@1/64 >>87
�����l��
((1+2+3+4)/4+(2+3+4)/3+(3+4)/2+(1+2+3+4)/4)/4
2.875
���ȁH >>78
> dbinom(0,5,dbinom(0,14,1/4))
[1] 0.914029 >>96
����A����������
> 5*dbinom(0,14,1/4)
[1] 0.08908974 ��K�q��_���̃��f���Ƃ��Č����I�W���_������Ǝv���Ă���̂ł����A�����I�W���_�͈�K�q��_����p���č��ꂽ���̂ł͂Ȃ���ł����H
���������I�W���_����K�q��_���̏�ɂ���ꂽ�Ȃ�A�ؖ��͓����T�O�ɂȂ��Ċ��S���Ȃǂ͎����ɂȂ�Ǝv���^��Ɏv���܂����B
�������萔���_���w�������ΊȒP�ɉ���������x�̊��Ⴂ���Ƃ͎v���̂ł����A�����Ă��������Ȃ��ł��傤���B >>98
���O������
> ���������I�W���_����K�q��_���̏�ɂ���ꂽ�Ȃ�A�ؖ��͓����T�O�ɂȂ��Ċ��S���Ȃǂ͎����ɂȂ�Ǝv���^��Ɏv���܂����B
�Ǝv�����͉̂��̂ł����H >>99
���_�K���Ƙ_���I����������������A�Ǝv���Ă����̂ł����A�����l����ƌ����I�W���_�̂ق��������������̂ł���͂��������Ȃ�܂��ˁB
��`����������m�F���Ă݂܂��B >>98
�L�[���[�h�́u���^�v�ł�
���^�𗝉��ł���A������ւ�͂������肵�܂� ���낢��v�Z���Ă��Ĉȉ��̗\�z�𗧂Ă��̂ł����������ł��傤���H
�u0��a_0��a_1��1�ɑ��Az^2+a_1�{a_0=0 �̍��̐�Βl�� 1 �ȉ��D�v
wolfram�ł�������������Ă��Ȃ��Ȃ����Ⴊ������Ȃ��̂Ő������C������̂ł����ؖ����ł��܂���D
�����Ĉ�ʂɁA
�u0��a_0��a_1���E�E�E��a_{n-1}��1�ɑ��Az^n+a_{n-1}�{�E�E�E�{a_0=0 �̍��̐�Βl�� 1 �ȉ��D�v
�����藧���܂����ˁH
��낵������������肢���܂��B >>102
���݂܂���C�E�����ȉ��̒ʂ�������܂��D
�u0��a_0��a_1��1�ɑ��Az^2+a_1z�{a_0=0 �̍��̐�Βl�� 1 �ȉ��D�v
�u0��a_0��a_1���E�E�E��a_{n-1}��1�ɑ��Az^n+a_{n-1}z^{n-1}�{�E�E�E�{a_0=0 �̍��̐�Βl�� 1 �ȉ��D�v >>102
��낵������Ă��Ƃ͂��������Ȃ��Ă��������
�o�[�J >>103
�ŏ��� n=2 �����Ȃ�ؖ��͊ȒP
�� �����Ƃ��� 1/�� = r*exp(i��) �ƒu��
1 + a1 * r*exp(i��) + a0 * r^2*exp(i2��) = 0 �ƂȂ�̂� r^2 a0 = 1 (�}���Q��)
����� |��| = 1/r = ��a0 < 1 �ł���B
 >>102-103
>>102-103
����Ȃ̂�����܂����B n=2 �̂Ƃ�
�@a2 z + a1 + a0 /z = 0
�̋�����
�@a2 y - a0 y / |z|^2 = 0,
y��0 ���
�@|��| = ��(a0/a2), ��ʂ�n�̂Ƃ���a_[n-1]��1�̉��肪����Ȃ獪�ƌW���̊W���疾�炩�ł͂Ȃ��́H �����炵����ł����N�������m���Ă܂����H
��l�������w�G���ɏo�肳��Č듚��80�������������炵���ł�
https://i.imgur.com/4uyRsv7.jpg x?0.0130925
x?0.277987
x?0.941488 log_0.01(x) = 0.01^x
x �� 0.0130925
x �� 0.277987
x �� 0.941488 >>117
�������������͉̂���3�ɂȂ�̂͂ǂ̂悤��a�̎��������@�ł��B
�����̂Ƃ�͈͂̐��l���̂͒m���Ă��܂� ���c�����̖{�ɂ悭�f�ڂ���Ă��肾��� >>119
���̈��c�Ƃ������l�͓������������Ȃ���ł����H ���n�̑�w�������ԈႦ���炵����
���O�͈̔͂ʼn�����炵���� >>120
���ώG�炵������w�ł��Ƃ��Ă��o�Ȃ����x���������
��@�̑I�ѕ��ɂ͋C�����Ă˂Ƃ������P�̏��b�ň��c���悭�g���Ă�
���������ƂȂ������̓I�ȉ�@�͉����V���l >>121-122
�����Ȃ�ł����B���肪�Ƃ��������܂��B
�u�}��`���ē����Ăˁv�Ƃ��ԈႦ������C���X�ł��ˁB f(x)=a^x-logax�Ƃ����āAf�f(0)=0�ƂȂ邘�̉����Q�������ċɒn��f(x)�̕���������ւ���Ă�����ˁH >>112
�Ђ�[�A�ق�Ƃ��Ba���������Ɖ����R����B
�Ȃ�ƂȂ�a���傫���Ƃ��̃O���t���x����Ă��ˁB
y=x�Ƃ̌�_��(logax)�f <(a^x)�f �ɂȂ�R���ȁH
�Ƃ������ƂŁAa<1/e ?
�Ȃe�L�g�[�� >>124
���킟�A��L���炯
f(x)=a^x-logax�Ƃ����āAf�f(0)=0�ƂȂ邘�̉����Q��������f(x)�̋ɒl�ŕ���������ւ���Ă��������ˁH ���W�����h���̒藝���g�����Ȃ�
���:100!�̖���0�̐������߂Ȃ����@��:������0�̐��́u10�ʼn����邩�A���Ȃ킿2�Ŋ������5�Ŋ�����̏��Ȃ��ق��ł���v
�u�v�̕������킩��Ȃ��B
1����100�̂������̂���10�ł��������邩���Ă�����100��10��10����H
100��5��20����Ȃ���ȁH
�����ĂĎ����̍l�����Y���Ă邱�ƂɋC�Â������u�v�̂Ƃ���������Ƃ������Đ������Ă���B 1�A2�A3�A4�A5���|�����킷��120��0�ň���܂��ˁH
������1-5�̒���10�Ŋ���鐔�͂Ȃ�
2�Ŋ���鐔��5�Ŋ���鐔���|�����̂�10�Ŋ����悤�ɂȂ����̂ł�
����Ȃ��ł� >>124,126
�������ˁBf(0)=-���@�Af(1)=a ������A0��1�̊ԂɕK��
���������āAx=a^x �͂��̈�B
�ł����āAf�f(x)= ln(a)a^x -1/(x ln(a)) ������Af�f(0)=��, f(1)>0
�[���ƂŁAx=a^x�̉���x0�Ƃ���ƁAf�f(x0)<0�Ȃ�A
0<x<x0 �� x0<x<1�̗���ԂɕK����������B���Ă��ƂŁA
f�f(x0)=ln(a)a^x0-1/(x0ln(a)) <0 ���Ă̂��A�����R�ȏ゠��
���߂̏������ȁBa^x0=x0����f�f(x0)=0 �ƂȂ�̂�ln(a)=-1/x0
��a=1/e^e =0.0659�c�@�̎��Ȃ̂ŁAa������悩���������
������łȂ��H�i�ȂA�����̃��W�b�N���������悤��.. ) >>129
�����ƁAf�f(1)>1/ln(a){a(ln(a)^2 -1}������Aln(a)^2>a ����f�f(1)<0
���ˁB���Ă��Af�f(0)��f�f(1)���W�Ȃ��ˁB������Ƃ��폜�ŁB
�X�}���B ���������B
�Q�����������ǂQ���S�R�킩�����ww
�Q�[���ɓ������
https://orekou.net/i/mrpj >>127
Haskell�搶�ɐ����Ă��炢�܂����B
Prelude> length $ filter (=='0') (reverse (show(product[1..100])))
30 �P�O�O�O�O�I����
Prelude> length $ filter (=='0') (reverse (show(product[1..10000])))
5803
�������ł��B �P�O����������Ă���܂����B
Prelude> length $ filter (=='0') (reverse (show(product[1..100000])))
68620 >>127
5��1�肫���̂�5,10,15,20,30,35,40,45,55,60,65,70,80,85,90,95��16��
5��2�肫���̂�25,50,75,100��4��
100�I��5�Ŋ��肫���́A���߂�1��~16�{2��~4��24��
>>132
�����ȊO�������ĂȂ������H >>125
a<1/e����Ȃ��āAa<1/e^e �Ə��������肾�����B�X�}�\�B >>112
a �̒l�ɂ��ꍇ�������ʓ|���������܂��ˁA���̖��B ������ł��邱�Ƃ��ؖ��ł���A
0 < a < e^(-e)
�������ł��邱�Ƃ��ؖ��ł����Ǝv���܂��B ������ł��邱�Ƃ͐}���疾�炩�ł����B �ŏ��̋Ɍ�������$\omega$���̂��̂��W���Ƃ��Ċ܂ނ悤�Ȏ����͍̂\���o���܂����H
�悭
$0 = \emptyset, 1 = \{0\}, 2 = \{0,1\}, ...$
�Ŏ��R�����߂Ă��܂����C���̍\��������Ă�����L�����̂̍\���i�K�ŏ��W�����������
�����̂̍\���i�K�ŃR�[�V�[��̏W����������肵�Ă����̂�
�ǂ������0,1,2,...�����Ǝ����̂̒��̎��R���Ƃ��Ⴄ�C�����܂��D
������$0 = \emptyset, 1 = \{0\}, 2 = \{0,1\}$�Ƃ����ȂƂ���ɏ�����Ă���̂�
$\omega$���W���Ɏ��悤�Ȏ����̂��\���\���Ƃ������Ƃ�O��ɂ��Ă���̂��Ƃ��v����̂ł��D
����Ƃ������Ƃ낤���W�Ȃ�$\omega$�͂��̂܂܂̌`�ŕۑ�����Ď����̂̈ꕔ�ƂȂ�̂ł����H >>141
����ł�����H
�Ƃ肠�����R�[�V�[��̓��l�ނƂ��Ƃ��ĕ��ʂɎ����̍\�����Ƃ��āA���R�������ăւ����Ęa�Ɛς��Ē�`��������������B >>113
1������3���ւ̋��E. ���̎��Ay = a^x �� y=x �� ��_P �ɂ� �X�� -1 �ƂȂ�.
���� y = x �̐��Ώ̂��� x = 0 �̐��Ώ� ��������₷���̂�,
y =�@a^x �̃O���t�� 45�x��]����.
-qX + qY = a^(q X + q Y)�@(q=1/��2�ƒu����)
������� (0,Y) �ɂ� dY/dX = 0 �ƂȂ�̂ŁA
(1)�@+qY = a^(q Y) (������(0,Y)����)
(2)�@-q = a^(q Y) log(a) q (���������������(0,Y)��dY/dX=0 ����)
(1)(2)����� -q = +qY log(a) q �܂� qY = -1/log(a) ��������, �����(1)�ɑ�������
-1/log(a) = a^(-1/log(a)) = e^(-1)�@�� a = e^(1/e)
����� 0< a < e^(1/e) �ł� ��_P �� dY/dX < 0 �܂� dy/dx < -1 �ƂȂ�. ���̌���3��������.
 >>142
>>142
���肪�Ƃ��������܂��D
�������ɂ܂�������R���\�����āCR���玩�R��N�������̂ƃւ̍���R'�����C
R��R'�ɂ͓s���ǂ��S�P�˂����܂��ˁD
R'��̎Z�@�͑S�P�˂ŗv�f��R�Ɉڂ���R��̎Z�@�Œ�`�ł������ł��ˁD �ԈႦ��
�� a = e^(-e) ������. 0<x��a(a�͐��̎���)��������x�̑S�̂���Ȃ�W����U�Ƃ���B
���̏��������悤��a�̒l���߂�B
�uU�̂ǂ�2�̗v�f�̐ς��Ƃ��Ă��A����͐����ɂȂ�Ȃ��v >>146
����
�u���قȂ�2�́v��lj� >>146
a �� 1 �Ȃ���������B
0 < x1 < x2 �� a �� 1 �� 0 < x1 * x2 < 1 * 1 = 1 �Ȃ̂ŁB
1 < a �Ȃ���������Ȃ��B
x1= 2/(1+a), x2= (1+a)/2 ������
0 < x1 < 1 < x2 < a�@�� x1*x2 = 1 �Ȃ̂ŁB >>135
���w�E�̒ʂ�A�����ȊO�������Ă��܂����B
�ȉ��ɒ���
Prelude> length $ takeWhile (=='0') $ reverse(show(product[1..100]))
24
Prelude> length $ takeWhile (=='0') $ reverse(show(product[1..100]))
24
Prelude> length $ takeWhile (=='0') $ reverse(show(product[1..1000]))
249
Prelude> length $ takeWhile (=='0') $ reverse(show(product[1..10000]))
2499 �P�O���I�ł͖����ɂO��
Prelude> length $ takeWhile (=='0') $ reverse(show(product[1..100000]))
24999 >>135
t0fn <- function(n){ # terminal 0 of factorial n ( n=10, 10!=3628800 => 2
m=floor(log(n)/log(5))
ans=0
for(i in 1:m) ans=ans+n%/%(5^i)
ans
}
t0fn=Vectorize(t0fn)
t0fn(10^(1:12))
�P�O�I����P���I�܂Ŗ����̂O�̐�
> t0fn(10^(1:12))
[1] 2 24 249 2499 24999
[6] 249998 2499999 24999999 249999998 2499999997
[11] 24999999997 249999999997 >> 127
�l�����Ƃ��Ă�
100! = 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 ... 99 100
����Ɋ܂܂�� ���q2 �̌���m�肽��.
[100/2]=50 (2�̔{���̐�) ���ꂾ���ł� 4=2^2 �̔{����1�J�E���g��������Ȃ��̂�...
[100/2^2]=25 (4�̔{���̐�) �𑫂��B ���ꂾ���ł� 8=2^3 �̔{����2�J�E���g��������Ȃ��̂�...
[100/2^3]=12 (8�̔{���̐�) �𑫂��B (�ȉ����l)
...
[100/2^7]= 0
100! �Ɋ܂܂�� ���q5 �̌���m�肽��.
[100/5] = 20 (5�̔{���̐�) ���ꂾ���ł� 5=5^2 �̔{����1�J�E���g��������Ȃ��̂�...
[100/5^2] = 4
[100/5^3] = 0
�a���r����܂ł��Ȃ� ���q5 �̌� 24 �̕������Ȃ�.
100! �� 10^24 �Ŋ����āA10^25 �ł͊����Ȃ�. �܂薖���� 0 �� 24 ���ł���. >>143 �� ����3����Əؖ������C�ł�����ł���
3 ��葽���͂Ȃ�Ȃ��̂͂ǂ�����Ď������炢���ł��傤���H
���Ώ̐����� 0 < x < 1 �ł͉��������̂͊m���ł��B
y = a^x �� y=x �Ƃ̌�_(��, ��) �ɂ�
�X��: log(a) �� < -1 �Ȃ� �� < x < 1 �͈̔͂� y = log_a(x) �Ƃ̌�_������ (�� �Ⴆ�Β��Ԓl�̒藝�Ƃ��H)
"��_������" �Ƃ͂������̂� 2�ȏ�Ȃ��Ƃ͌���Ȃ��킯�ł���... ���Z���w�ł͂Ȃ���������ǁA�����ė~����
�ʏ�̑��x��70%�̑����Ńv���C���������ҏW���Ă���̂����ǁA
�����ʏ�̑����ɕҏW������
�����������ɂ���Ζ{���̃Q�[�����x�Ɠ�������ɂȂ邾�낤���H
50%�ŗV�Ȃ�P����200%�ɕҏW��������̂͂킩����c n��2�ȏ�̎��R���Ƃ��A3�ӂ̒�����n,n+1,n+2�ł���O�p�`T_n���l����B
T_n�̖ʐς�S_n�Ƃ���Ƃ��AS_n�̐�������a_n��n�ŕ\���B
������a_n��n�̑������ƍ����݂̂ŕ\���A�K�E�X�L����floor���Ȃǂ͎g�p���ʂ��ƁB >>154
�ʏ푬�x * 70/100 = �v���C���x�@�̗��ӂ� 100/70 ��������
�ʏ푬�x = �v���C���x * 100/70 = ���摬�x * 1.428... �� ���摬�x * 143/100
�Ȃ̂� 143 % �ɕҏW����Ηǂ��ł��B
%, �p�[�Z���g, parcent , �S�����Ƃ������܂��ˁB
����͊�� 100 (cent) �Ƃ������̕��ʂ�\���܂��B 3x+y+x(dy/dx)=0
�����������̏����I��肾����
���̉���a��C�Ӓ萔�Ƃ���
3x^2+2xy=a
�܂���
3x+2y=a
�ǂ������������H >>153
f(x)=a^x - loga(x)
���l����Af(x)=0 �̉����R���z���Ȃ����Ƃ͂����炩����B
f�f(x)=ln(a) a^(x) - 1/(x ln(a)) ���Af�f(x)=0 �̉��ia^x ��1/(xln(a)^2)�̌�_�j
�͂��������Q�����Ȃ��i�ؖ��͏ȗ����܂��j�B
���������āAf(x)=0�̉��͂��������R�B�Ȃ�ƂȂ�A���Ɖ��̊ԂŕK��
f�f(x)=0�ƂȂ�̂ŁA�����S�ȏ゠��Af�f(x)=0�̉����R�ȏ゠�邱��
�ɂȂ邩��B >>157
3x+2y=a �����ł��邽�߂ɂ�a=0�łȂ�����Ȃ�ǁA
�����3x^2+2xy=a �Ɋ܂܂�Ă��ˁB >>158
�����o���܂����B���肪�Ƃ��������܂��B >>157
�ϕ��̌v�Z�ԈႦ�Ă�
�����͂�������
3x^2+2xy=a n!�Ŗ�����0��777����n�����߂�B �ȉ��̖�3�̉�������܂���B��2�̌��ʂ�p����Ə����Ă���܂����A��2�� A �͐����ł��B����A��3�̉��� x �͎����ł��B
��2�̌��ʂ��g���Ȃ��̂ł͂Ȃ��ł��傤���H
��2.
S ����łȂ������̏W���Ƃ���B���鐮�� A �����݂��āA���ׂĂ� n �� S �ɑ� A �� n�i���邢�́A���ׂĂ� n �� S �ɑ��� A �� n�j�����藧�Ȃ�A S �͍ŏ����i���邢�͍ő匳�j�������Ƃ��ؖ�����B
��3.
R �̃A���L���f�X���ƑO��2��p���āA�C�ӂ̎��� x �ɑ��� m �� x < m + 1 �������� m �����݂��邱�Ƃ������B
��2.�̉F
���ׂĂ� n �� S �ɑ��� A �� n �Ƃ���B���̂Ƃ����� n - A�in �� S�j�̏W���� N �̋�łȂ������W���ł��邩��A N �̐��ɂ���čŏ��� k_0 �������A n_0 = A + k_0 �� S �̍ŏ����ł���B
��3.�̉F
�A���L���f�X���ɂ���� n_1 < x < n_2 �ƂȂ鐮�� n_1, n_2 ������B������ n > x �������� n �̍ŏ����� m + 1 �Ƃ���悢�B >>162
�Ȃ��B
�@5^5 = 3125,
3125�I�̑f���������Ɋ܂܂�����5�̐���
�@5^4 + 5^3 + 5^2 + 5^1 +1 = 781,
���@3125�I�̖����ɂ� 0 �� 781���ԁB
3125 �̑f���������Ɋ܂܂�����5�̉�5�B
3124�I�̑f���������Ɋ܂܂�����5�̐��� 776��
���@3124�I�̖����� 0 �� 776�����Ȃ��B
*�@n�I �͈���2�� [n/2] ��ȏ�܂݁A�\�������B >>164
������⊴���c�邪�����Ă݂�B
�u��3.�̉v�̌㔼�u n > x �������� n �̂��ׂāv�� S �Ƃ��Ė� 2 ��K�p�B
S ����łȂ��̂� n_2 ���܂ނ���B f(x,y)=0(x���������̂Ƃ�),0(x���L������y�͖������̂Ƃ�),1/q(x,y���L������y=p/q(����)�̂Ƃ�)
�ƒ�߂�Ƃ�f�̓��[�}���ϕ��Ł��[I�~I]f(x,y)dxdy=0�ƂȂ邱�Ƃ������ĉ����� >>165
���̒ʂ�ł��B
>151�̌v�Z���ŎZ�o�����
3121�I����3130�I�̖����̂O�̐��͈ȉ��̒ʂ�ł��B
> t0fn(3121:3130)
[1] 776 776 776 776 781 781 781 781 781 782
1000�ȉ����ł͌�������͈̂ȉ��̒ʂ�B777�����h���������̂Ŗ��ɂ��Ă݂܂����B
> which(is.na(x))
[1] 5 11 17 23 29 30 36 42 48 54 60 61 67 73 79 85 91 92
[19] 98 104 110 116 122 123 129 135 141 147 153 154 155 161 167 173 179 185
[37] 186 192 198 204 210 216 217 223 229 235 241 247 248 254 260 266 272 278
[55] 279 285 291 297 303 309 310 311 317 323 329 335 341 342 348 354 360 366
[73] 372 373 379 385 391 397 403 404 410 416 422 428 434 435 441 447 453 459
[91] 465 466 467 473 479 485 491 497 498 504 510 516 522 528 529 535 541 547
[109] 553 559 560 566 572 578 584 590 591 597 603 609 615 621 622 623 629 635
[127] 641 647 653 654 660 666 672 678 684 685 691 697 703 709 715 716 722 728
[145] 734 740 746 747 753 759 765 771 777 778 779 780 786 792 798 804 810 811
[163] 817 823 829 835 841 842 848 854 860 866 872 873 879 885 891 897 903 904
[181] 910 916 922 928 934 935 936 942 948 954 960 966 967 973 979 985 991 997
[199] 998 (�֑�)
y = f(x)�@�̃O���t�̋ȗ���
�@�� = |f "(x)|/[1 + f '(x)^2]^{3/2},
y = a^x �̋ȗ���
�@�� = (log(a)^2 a^x)/[1 + log(a)^2 a^{2x}]^{3/2} �� (2/��27)log(1/a)
�@�ȗ����ő�ɂȂ�_x1�� a^{x1} = 1/[��2�Elog(1/a)] �̂Ƃ�
y = log(x)/log(a) �̋ȗ���
�@�� = log(a)^2�x/[1 + log(a)^2�x^2] ^{3/2} �� (2/��27)log(1/a),
�@�ȗ����ő�ɂȂ�_�� x2 = 1/[��2�Elog(1/a)] �̂Ƃ��B
�@a^{x2} = e^{-1/��2} = 0.49306869
0 < a < e^{-(1/��2)e^{1/��2}} = 0.23833123�c �̂Ƃ���
�@a^{x1} < a^{x2}
�@x1 > x2,
������A�Č��������蓾��B�i���ۂ� 0 < a < e^{-e} = 0.065988036�c�̂Ƃ�)
e^{-(1/��2)e^{1/��2}} = 0.23833123�c < a < 1 �̂Ƃ���
�@a^{x1} > a_{x2}
�@x1 < x2,
������A�Č����͖����낤�B >>112
���c������̖{�ɉ͍ڂ��Ă��i���吔�w��1�_�ł������Ƃ���@�F���n�ҁj
���R�̔����łƂĂ������v�Z�����Ȃ��Ƃ킩��Ȃ��̂œr���͏ȗ����܂���
0��a �� e^(1/e) �̂Ƃ��R��
e^(1/e)��a ��1�̂Ƃ��P��
78���̉���Ғ�63����
�u���炩��1�v�ƊԈႦ��
�듚�̒��ɂ͑�w����������
�Ƃ̂��� 0<x��2�ɑ��A
f(x)=(1+1/x)^(sinx)
�ƒ�߂�B
�i1�jlim[x��0] f(x)�@�����߂�B
�i2�jy=f(x)�̃O���t��`���B
�i3�jf(x)�̍ő�lM�����߁A ���̕s������������n�����߂�B
��������=3.14...,e=2.71...�ł��邱�Ƃ͊��m�Ƃ��ėǂ��B
n/10��f(e)<(n+1)/10 >>171
�i3�j���ƂĂ�����Ăł��܂��� z"��z�̋��f����\�����̂Ƃ���B
�ȉ��̕��f��z�ɂ��Ă̘A���������������B
���������A���͕��f���̒萔�Ƃ���B
z^2-��zz"-��z"=0
|z-����|=1 http://rsc.hatenablog.com/entry/2018/11/12/180034
�`�`�d�̂T�l�����̂悤�ɔ������Ă���
�`�u�a�̓E�\�����v
�a�u�b�̓E�\���ł͂Ȃ��v
�b�u�c�D�d�͂ǂ�����E�\�����v
�c�u�d�̓E�\�����v
�d�u���̓E�\���ł͂Ȃ��v
�T�l�̂����A���l�����E�\�����Ă���B���̂Ƃ��m���ɂ����邱�Ƃ͂ǂꂩ�B
�I����
�P�A�`�̓E�\���ł���
�Q�A�a�̓E�\���ł���
�R�A�b�̓E�\���ł͂Ȃ�
�S�A�c�̓E�\���ł���
�T�A�d�̓E�\���ł͂Ȃ�
������ē�����H
��������Ō����悤�Ƃ�����A�Y���Ȃ��ɂȂ��Ă��܂����B
dat=gtools::permutations(2,5,c(T,F),F,T)
colnames(dat)=LETTERS[1:5]
dat=as.data.frame(dat)
attach(dat)
dat[A&!B,] ; dat[!A&B,]
dat[B&C,] ; dat[!B&!C,]
dat[C&!D,] ; dat[!C&D,]
dat[C&!E,] ; dat[!C&E,]
dat[D&!E,] ; dat[!D&E,]
dat[A&!B&C&!D&!E&E,]
dat[!A&B&C&!D&!E&E,] >>170
a=0.01��Wolfram�搶�ɕ����Ă݂��B
https://www.wolframalpha.com/input/?i=solve+0.01%5Ex%3Dlog(x)%2Flog(0.01)+for+x
�R�����Ԃ��Ă��B >>177
�̐S�̂Ƃ����J�b�g����Ă��
�O���t�Ȃ�Amac��grapher�g���ƕ֗�����B
https://imgur.com/a/u7NaLk8 X,Y���ʑ���ԁAf:X��Y��A���ʑ�
B��Y�Ƃ���
X,Y�̕��p�f��cx,cy�Ƃ���킷
���̎��Af^{-1}(cy(B)) �� cx( f^{-1}(B) ) �ł��邪�A�� �͐��藧���܂����H
���藧���߂̏����͉��ł����H ����
X,Y���ʑ���ԁAf:X��Y��A���ʑ�
B��Y�Ƃ���
X,Y�̕��p�f��cx,cy�Ƃ���킷
���̎��Acx( f^{-1}(B) ) �� f^{-1}(cy(B)) �ł��邪�A�� �͐��藧���܂����H
���藧���߂̏����͉��ł����H �����ɂ��Ă̗��_�Ȃ��ł́A�ؖ��ł��Ȃ����R���A�����A�L�����ɂ��Ă̐������Ă���܂����H C�̔������������Ƃ����D�̔����Ɩ�������
�̂�C�̓E�\���ł���B���E�\�� >>183
C���R���Ȃ�
D��E���R���łȂ����ƂɂȂ�
D�̔�������E�͉R���A
�����C���R�����瓱���ꂽE�͉R���łȂ����ƂƖ������Ȃ��H >>180
>���̎��Acx( f^{-1}(B) ) �� f^{-1}(cy(B)) �ł��邪�A�� �͐��藧���܂����H
�����W�����X�����U�ʑ��AY�������ʑ��Ȃ�
cx( f^{-1}(B) ) = B
f^{-1}(cy(B)) = Y
�Ȃ̂łȂ肽���Ȃ��B >>182
�t�B�{�i�b�`����̈�ʍ������߂� >>184
> >>183
> C���R���Ȃ�
> D��E���R���łȂ����ƂɂȂ�
> D�̔�������E�͉R���A
> �����C���R�����瓱���ꂽE�͉R���łȂ����ƂƖ������Ȃ��H
C���R�����猾���邱�Ƃ�D�܂���E���R���Ȃ̂Ŗ������ĂȂ��B
�v�[���㐔���
a=1-b, b=c=(1-d)(1-e), d=1-e, e=e
�̉������߂���B
���l�ό`����
a=1-b, b=c=e(1-e)=0, d=1-e, e=e
�����
a=1, b=c=0, d=1-e
���K�v�\�������B >>186
�Ȃ�قǂˁB
���w�E���肪�Ƃ��������܂��B >>182
�Ɍ��g���čl���邱�Ƃ��������Ȃ� dat=gtools::permutations(2,5,c(T,F),F,T)
colnames(dat)=LETTERS[1:5]
dat=as.data.frame(dat)
attach(dat)
dat[A&!B,] ; dat[!A&B,] # a=1-b
dat[B&C,] ; dat[!B&!C,] # b=c
dat[C&!(D&E),] ; dat[!C&(D&E),] # c =(1-d)(1-e)
dat[D&!E] ; dat[!D&E] # d=1-e
dat[A&!B&C&!(D&E),]
dat[A&!B&C&(!D|!E),]
> dat[A&!B&C&!(D&E),]
A B C D E
10 TRUE FALSE TRUE TRUE FALSE
11 TRUE FALSE TRUE FALSE TRUE
12 TRUE FALSE TRUE FALSE FALSE
> dat[A&!B&C&(!D|!E),]
A B C D E
10 TRUE FALSE TRUE TRUE FALSE
11 TRUE FALSE TRUE FALSE TRUE
12 TRUE FALSE TRUE FALSE FALSE
�ƌ��ʂ������܂����B
���肪�Ƃ��������܂����B >>174
����N�����肢���܂�
���F�͓������Ȃ̂�z�����ƃ��ŕ\����͂��Ȃ̂ł��� >>174
�̓z���g�ɖ�肠���Ă�̂��^��Ȃ�ȁB
������������Ȃ����B >>180
> ���藧���߂̏����͉��ł����H
�uf ���J�ʑ��ł��鎖�������v���Ɨ\�z�B
���ꂪ�\���������Ǝ����̂͊ȒP�����ǁA�K�v�����ł��鎖�̏ؖ������J�����B 10������10 = 10�����i10����10)�@=�@10����(10^10^10^10^10^10^10^10^10^10)
�E�E�E�E�E�E����ł����Ă�H �k����l
n��2�ȏ�̎��R���Ƃ��A3�ӂ̒����� n�Cn+1�Cn+2 �ł���O�p�` T_n ���l����B
T_n �̖ʐς� S_n �Ƃ���Ƃ��A(4/��3)S_n �̐������� b_n ��n�̐��������ŕ\�킹�B >>197
�u������Ȃ���� �v�Ɩ��������������Ă݂��I ���Ă͈̂Ⴄ��Ȃ���...
�w�����̌������
(4/��3)S_n = ��( (n+1)(n+1)(n-1)(n+3) )
= (n+1) ��( (n-1)(n+3) )
= (n+1)^2 ��( (n-1)(n+3)/(n+1)^2 )
= (n+1)^2 ��( 1 - 4/(n+1)^2 )
= (n+1)^2 ( 1 - 2/(n+1)^2 - 2�� /(n+1)^4) ) (�� �e�C���[�W�J �� ��(0,1) )
= (n+1)^2 - 2 - 2�� /(n+1)^2
= (n+1)^2 - 3 + 0.???
b_n = (n+1)^2 - 3 = n^2 + 2n -2 >>198
>>155 �����Ȃ������܂��B >>193
������Ȃ��ƌ������Ƃ͊ȒP�Ȗ��ł����H >>199
������ "�̂�" �ŕ\���Ȃ����͂����킩��.
a_n �͑������ŕ\����Ɖ��肷���
a_n + ��_n = (��3)/4 ( n^2 + 2n -2 + ��_n ). (��_n, ��_ n �� (0,1))
���ӂ� n^2 �Ŋ����� n �� �� ���Aa_n = (��3)/4 ( n^2 + ? + ? )
(��3)/4 n^2 �������Ă��� n �Ŋ����� n �� �� ���A a_n = (��3)/4 ( n^2 + 2n + ? )
a_3 = 3 ��� a_n = (��3)/4 ( n^2 + 2n -15+12/��3 )
����������� a_4 =9, ... �����Ȃ�.
>������a_n��n�̑������ƍ����݂̂ŕ\��
�����g���Ƃǂ��ɂ��Ȃ�̂��H �܂Ƃ��ȉ������Ă���̂Ȃ狳���Ăق���. https://www.dropbox.com/s/iamd69ifr92qpke/�������ƘA����DD16-06-09.pdf
�̒藝11(Tietze�̊g���藝����1)�̏ؖ���������܂���B
���w�I�A�[�@�ɂ��W����(F_d)���`���Ă��鏊�Ȃ̂ł����A
F_{k/(2^n)} �� F_{(k+1)/2^n} �̢�Ԃɂ��飕W�� F_{(2k+1)/(2^(n+1))} ������Ē�`���Ă���̂ł����A
�A�[�I�Ȓ�`�����邽�߂ɂ́A�c�_�͂����ŏI���ׂ��ł͂Ȃ��A
F_{k/(2^n)}�@�Ɓ@F_{(2k+1)/(2^(n+1))}�@�Ȃ�тɁA
F_{(2k+1)/(2^(n+1))}�@�Ɓ@F_{(k+1)/2^n}�@���Ȍ�̋A�[�I��`���p�������邽�߂̏������m�F���ׂ��ł���͂��ł��B
���̊m�F���ׂ�������������܂���B
��낵�����肢���܂��B >>204
���ڂ��������ƁA���10�����p���ā@F_{(2k+1)/(2^(n+1))}�@������Ă���̂ł����A
���̂��߂ɂ́A
L_{(2k+1)/2^(n+1)}�@���@A �� Int( F_{(k+1)/2^n} )�@�c��
�����藧���Ă��Ȃ�������Ȃ��킯�ł��B
���R����͖������ɂ͐��藧���Ȃ��킯�ł���܂�����A�A�[�I��`��n+1�X�e�b�v�ɍs����O�ɣ�An�X�e�b�v�̎��_��
(F_{k/2^n}) �c���ɁAF_{(k+1)/2^n}�c �ɂ���(L_{(k+1)/2^n}�Ɋւ���)���炩�̏��������藧���Ă��Ȃ���Ȃ�Ȃ��킯�ł�
���̉��炩�̏�����������܂���B
��قǂ́A
int_A L_{(k+1)/2^n)}�@���@A �� Int( F_{(k+1)/2^n} )
(int_A �͕������A�ɂ�����J�j��p�f)
�Ȃ̂��Ȃ��`�Ǝv���Č������̂ł����A�ǂ����c�_����肭���Ɍq���炸�����Ă��܂����B
��낵�����肢���܂��B >>205
������ƌ����ԈႦ�܂����B�������܂��B
int_A L_{(k+1)/2^n)}�@���@A �� Int( F_{(k+1)/2^n} )
�����肷��Ɓ��͋A������܂��B
����������g���āAF_{(2k+1)/(2^(n+1))}���`���鏊�܂ł͋c�_��i�߂邱�Ƃ��o���܂��B
�������An+2�X�e�b�v�ڂւƋc�_��i�߂邽�߂̏����̊m�F���ǂ�����悢��������܂���B ���Ȃ�L���Ȗ��炵������������������Ė�����
������ւ����������Ƃ����ӌ������̖��̃X���ł͑吨�炵�������̓����ɑS���[���ł��Ȃ�
�ƌ����킯�Ő������Ƃ��̗����������ĉ������B
2�̕����̖��ƌĂ��
�����ɂ����̓�����������2����D
��̕����ɂ͑����̔{�̂����������Ă���
�i��������ς���ƁC��̕����ɂ͑����̔����̂����������Ă���j�D
�A���C����������Ă��邩�͕�����Ȃ��D
���Ȃ��́C2�̕����̂����C�ǂ��炩���I�сC�Ȃ��̂��������炦��D
���Ȃ����C��I�Ƃ���10,000�~�������Ă����D
�����ŁC�u���Ȃ����]�ނȂ�C������̕����Ƒւ��Ă��ǂ��ł���v�ƌ�����D
���āC���́u�ւ���ق��������C�ւ��Ȃ��ق��������v���D >>208
�Ȃ��[���ł��Ȃ����ƌ����Ƒւ��������ǂ��Ƃ���Ɩ��炩�ɖ������錻�ۂ��������邩�炾�B
��̕������J����1���~�������Ă����ꍇ������̕��̕����ɂ�2���~��5��~�������Ă������
������ւ����ꍇ�̊��Ғl��(20000+5000)��2=12500�~������ς��������ǂ��Ƃ����ӌ����吨������
�P�D�������������̗������������Ȃ�ŏ��ɊJ���������ɂ���������Ă��Ă�������ւ����������Ƃ������ɂȂ�B
�Q�D�܂�ŏ��ɑI�������J���Ă��̋��z�����ĂȂ��ꍇ�ł��A���₻�������I�������J���Ȃ��ł�������ւ����������Ƃ������ɂȂ�B
�R�D���Ƃ���Ƃ���A�����B������A����͍ŏ��ɑI������I��B����͍ŏ���A����ƕʂ̕�����I�Ԑl���Ƃ����
B����͍ŏ��ɑI��A����ƈႤ���������Ȃ���"A����Ɠ��������ɑւ����ꍇ"
A�����B����͍ŏI�I�ɓ���������I���ɂȂ�
��������ɕ�����ւ����������Ƃ������Ȃ�ŏI�I�ɂ͓���������I��ł���̂�
"������ւ���B����"�̂ق���A�������ɓ�������ƌ������炩�ɊԈ�������_�ɂȂ�B
>>209
�ŏI�I�ɑI�����ɓ����Ă�����z�̊��Ғl��1���~����ł���Γ��Ƃ��܂��B >>210
��B����͍ŏ���A����ƕʂ̕�����I�Ԑl���Ƃ���
���̉�����������_�ła�̑I���͖���ׂł͂Ȃ�
�a������ׂɑI��������ꍇ�Ɣ�ׂĊ��Ғl���قȂ��Ă����Ȃ� �����ɓ������z�̊m�����z���^�����ĂȂ��Ɗ��Ғl�͂����Ȃ����� >>211
���ɂQ�̕�������ʂ���ׂɂP�͐ԐF�ł�����͐F�Ƃ���BA�����B���I�ԑO�͓��R
�Ԃ̕������̕��������Ғl�͓�������ˁH
�Ƃ��낪A���Ԃ̕�����I��B���̕�����I�u�ԂɐԂƐ̕����̒���
���z�̊��Ғl���قȂ�l�ɂȂ���Ď��H �ݒ肪�����ɑ����Ă��Ȃ����琶����p���h�b�N�X�Ȃ�łȂ��̂��Ȃ�
�����ɂ�1���~�����������ł������̂����������ł������̂��͊m���Ō��܂���̂ł͂Ȃ��̂ł́H
�m���Ō��܂���̂ł͂Ȃ��̂Ŋ��Ғl�̌v�Z���o���Ȃ� >>214
���肪�Ƃ��B
A����̎��_��������Ȃ�B����̎��_���猩�Ă�������ւ��������ǂ��Ȃ�
���݂��Ɍ�������Ɨ�������������Ƃ����������Ȍ��_�ɂȂ�Ƃ������������Ėڂ���ł����B
�����̌��_�Ƃ��ĕ�������������������(���Ғl����)�ƌ����̂͊��S�ɊԈႢ���Ɗm�M���܂����B
�������E�E�E���̌�̐�����ǂݑ����Ē����ɏ��o���Ă��܂���͗����ǂ݂��Ă��܂��܂����B�ށA��߂��邗
���P���ŊȒP�Ȗ��̗������������̂ɂ���ȓ���������w(�����܂Ŏ������x�����猩��)
���K�v�Ȃ�đz�������Ȃ������ł��B
����>>214����Љ�̂��̃y�[�W�̐����ł�������ւ��������ǂ����ǂ����Ƃ������_�͏����Ė����̂ł���
�m�F�Ȃ̂ł�������214����̏Љ���y�[�W�̐R�w�@��w�o�ϊw������
���Y �אl����͍ŏI�I�ɕ����͑ւ��������ǂ��ƌ����Ă��ł��傤���H
����Ƃ��ւ��Ă��ւ��Ȃ��Ă������ƌ����Ă�̂ł��傤���H
���������͑ւ��������ǂ��A�ւ��Ȃ������ǂ��A���邢�͑ւ��Ă��ւ��Ȃ��Ă�����
�̂R�̂ǂꂩ�ɂ����Ȃ�Ȃ��Ǝv�����ǂ��̂ǂ���Ӗ����錾�t��>>214����Љ��
pdf�t�@�C���ɂ͌�������܂���ł����B >>214
���nj��_�Ƃ��Ă�
�E�����ǂ����͂��L�`���Ɗm���_�̋c�_�ł��ɂ̓Ƃ̕��z�����߂Ă��Ȃ��Ɠ����͏o�Ȃ��B
�E�����ȃƂ̕��z�ŕς������������ۂ�����Ă݂�Ɠ��ɂȂ�ꍇ�����ɂȂ�ꍇ�������Ĉ�T�ɂ͌����Ȃ��B
�E�v�Z���邽�߂̌����Ƃ��͏����Ă��邩��F�X�����Ă݂ĂˁB
���Ǝv���B
�܂�����Ⴛ�����Ƃ������_�Ȃ��ǂ��������ς��k���ɒ��ׂĂ݂�Ƃ����̂�����Ȃ��ƁB >>171
����́i3�j�����肢���܂� Prelude> let e = exp 1 in exp $ (sin e) * (log $ 1+1/e)
1.137328442017264 >>217
>���nj��_�Ƃ��Ă�
���̌��_�Ƃ�>>217����̌��_�H����Ƃ����Y �אl����̌��_�H
>���ɂȂ�ꍇ�������Ĉ�T�ɂ͌����Ȃ��B
�ŏ��ɑI�����̒��̋��z���ւ����ꍇ�̕����̊��Ғl�����ɂȂ�ꍇ������Ȃ�
�ŏ��ɑI�����ɋ��z������������Ă������ł����H�P�ł����̂ŋ����ĉ������B >>149-150
�ԈႢ�����܂߂Ď�����������B�B�B
�v���O�����ŏo�Ă���肾���ǁA���w�ł����X�ł���B
���W�����h���̒藝�̗�肻�̂��̂��B
�v���O���~���O�ʼn����z�̐��w�͎����Ă�B >>220
�킽���̌v�Z�͂ł�pdf�̓��e��S���͒ǂ��Ȃ�����
�\�\
pdf p6
�����������ŁC�����ƌ����I�Ȏ��O���z�Ƃ��Ďw�����z�c����уK���}���z�c���l���Ă݂悤�D
�c
���Ȃ킿�������������邱�Ƃ��L���ƂȂ���������߂�ƁC(12)���̎w�����z�ɂ��Ă�
x <4 log 2/��
�ƂȂ�C(13)���̃K���}���z�ɂ��Ă�
x <2(r + 1) log 2/��
�ƂȂ邱�Ƃ��������D
�\�\
�������ȁB >>222�����>>217����Ɠ���l���H
���������Ȃ�>>220�ł�������ɑ���������̂ł�����x������������邯��
>>217��>���nj��_�Ƃ��Ă�
���̌��_�Ƃ�>>217����̌��_�H����Ƃ����Y �אl����̌��_�H >>223
����ł��B
���_�Ƃ���PDF�Ƃ��Ă܂Ƃ߂Ă���킯�ł͂Ȃ��̂Ŏ���PDF��ǂ��_�ł��ˁB >>224
���肪�Ƃ��B
>>217��
>�E�����ȃƂ̕��z�ŕς������������ۂ�����Ă݂�Ɠ��ɂȂ�ꍇ�����ɂȂ�ꍇ�������Ĉ�T�ɂ͌����Ȃ��B
�����>>217����̈ӌ����ȁH����Ƃ����Y�אl����̈ӌ��H ����a�v���w��͓���1�x��ǂ�ł��܂��B
�_���I�ɂ������ȕ������ǂ���甭�����܂����B
f �� Z ����̎ʑ��Ƃ���B
S ������W���Ƃ��A
f(n) �� S �ł���悤�� n �� N �����Ȃ��Ƃ�1�͑��݂���Ƃ���B
T := {n �� N | f(n) �� S} �Ƃ���B
T �� N �̕����W��������A�ŏ��� min �s �����݂���B
m = min T �Ƃ���B
-----------------------------------------------------------------
�ȏ�̏ŁA����a�v����́A
m-1 �� T �Ɋ܂܂�Ȃ�
�ƌ��_���Ă���c�_������܂��B >>212
���ӁB
����ɕK���P���~������Ƃ������[������Ȃ�����ˁB
���̃��[���Ȃ���Ғl�P�Q�T�O�O�~�ł����B >>218
> f <- function(x) (1+1/x)^sin(x)
> f(0)
[1] 1
> curve(f(x),0,2*pi)
> M=optimise(f,c(0,2*pi),maximum=TRUE)$obj
> fe=f(exp(1))
> 10*fe
[1] 11.37328
n=11 >>225
>>�E�����ȃƂ̕��z�ŕς������������ۂ�����Ă݂�Ɠ��ɂȂ�ꍇ�����ɂȂ�ꍇ�������Ĉ�T�ɂ͌����Ȃ��B
>
>�����>>217����̈ӌ����ȁH����Ƃ����Y�אl����̈ӌ��H
���̈ӌ��ł���B
pdf�ŃƂɉ����Č��������ق����ǂ���ƈ����Ⴊ�ڂ��Ă�̂ň�T�ɂ͂����Ȃ��Ƃ܂Ƃ߂܂����B
����ȓ˔��q���Ȃ��܂Ƃߕ��ł͂Ȃ��Ǝv���܂��B X���ʑ���ԂƂ��܂��B
A��X�̕����W���Ƃ��܂�
int��X�ɂ�����J�j��p�f�A
int_A ��A�ɂ�����J�j��p�f�Ƃ��܂�
���̎�D��X�̕����W���Ƃ������A
int_A( A��D ) = A��int(D) �͐��藧���܂����H ���@��A�ɂ�����J�W���̐������琬�藧���܂���
���́��ł��B >>231
X = R�~R�AA=D=R�~{0}�Ƃ����Ƃ�
Int_A(A��D) = int_A A = A
A �� int (D) = A �� ∅ = ∅
�Ȃ̂Ő��藧���Ȃ��ł��B >>174 >>192
���̎�����
z = u + ����,�@|u| = 1,
�Ƃ�����B�܂��@����" = A�C����" = B �Ƃ����B
�������̎��ɓ�����
0 = z^2 -��zz" -��z"
= u^2 + 2����u + (����)^2 - {A��"u + ������u" + (1+AB)��} - (��u" + B��")
= u^2 + (2���� -A��")u + (����)^2 -(1+AB)�� - B��" - (����+1)��u",
������ u" = 1/u ������
0 = u^3 + (2���� -A��")u^2 + {(����)^2 - (1+AB)�� -B��"}u - (����+1)��,
���F��3���������ł����ǁc >>233
����Ƌ��b��
0 = 1 + (2��"��" -A��)u + {(��"��")^2 - (1+AB)��" -B��}u^2 - (��"��"+1)��"u^3,
�ƘA������Ǝ����������邩�ȁH https://www.youtube.com/watch?v=Zys26fr6qPI
���̖��Ȃ�ł����A����̕����ʐς��������߂�a,b�����߂Ă��܂���
���͂ł͂ł��Ȃ������̂�a,b�̏o�����������Ă��������Ȃ��ł��傤��
f'(x)��1��-2�����ČX�����C�R�[�����邱�Ƃ��������v�������т܂���ł��� >>236
�ڐ���y =px+q�Ƃ���Ƃ�
x^4 + ax^3 + bx^2 - (px+q) = (x-1)^2(x+2)^2
�ʼnE�ӂ�x^4+2x^3-3x^2-4x+4������
a=2�Ab=-3�Ap=4�Aq=-4�B >>237
���肪�Ƃ��������܂����I �d�ϕ����|x-y|/(1+x+y)^�� dxdy (x,y��0 0������1)���Ăǂ����������ł����H X���ʑ���ԂƂ���
A,B��X�̕W���Ƃ���B
f:A��[0,1]��A���ʑ��Ƃ���B
s��[0,1]�Ƃ���B
���A
�@A��B={a��A|f(a)��s}
�����肷��B
���̎��A
�@{a��A|f(a)<s}��A��int(B)
�͐��藧���H
�������Aint��X�ɂ�����J�j��p�f�ł���B
��낵�����肢���܂��B ���̖��
http://rsc.hatenablog.com/entry/2018/11/12/180034
��
�����҂͉R�����Ȃ���
�R���͉R�������Ƃ����Ȃ����Ƃ�����
�ƃt�@�W�[�ȉR���ɂ����瓚�����邾�낤���H
�`�`�d�̂T�l�����̂悤�ɔ������Ă���
�`�u�a�̓E�\�����v
�a�u�b�̓E�\���ł͂Ȃ��v
�b�u�c�D�d�͂ǂ�����E�\�����v
�c�u�d�̓E�\�����v
�d�u���̓E�\���ł͂Ȃ��v
�T�l�̂����A�R���͒N���H >>242
���Ȃ��Ƃ�A,C�������҂�BDE���R���Ƃ�����������A
BC�������҂�ADE���R���Ƃ�����������̂ŁA������
���邯�ǁA��ӂɂ͌��܂�Ȃ��B >>242
�������邩�H�Ȃ�R���͕K���R�����̏ꍇ�̉�
(A,B,C,D,E) = (1,0,0,1,0), (1,0,0,0,1)
�͉������炠��B
��ʉ���
A�ˁ�B
B��C
C�ˁ�D�ȁ�E
D�ˁ�E
E��E
���Ȃ킿�u�[���㐔�ŕ�����
AB=0
B(1-C)=0
C(D+E+DE)=0
DE=0
E(1-E)=0
�������B
C=0�̂Ƃ���B=0�ADE=0�B
C=1�̂Ƃ���D=E=0�AAB=0�B
�ƂȂ邩��
(A,B,C,D,E) = (0,0,0,0,0), (0,0,0,0,1), (0,0,0,1,0), (1,0,0,0,0), (1,0,0,0,1), (1,0,0,1,0), (0,0,1,0,0), (0,1,1,0,0), (1,0,1,0,0) �B >>242
solver�ł̓���
testimonies = [
(¥x->x!!1 == False),
(¥x->x!!2 == True),
(¥x->(x!!3==False) && (x!!4)),
(¥x->x!!4 == False),
(¥x->x!!4 == True)
]
isCompatible ts theCase = and $ zipWith (||) (map not theCase) (map (¥x -> x theCase) ts)
cases = (!! (length testimonies)) $ iterate (¥x-> [a:b|a<-[True,False],b<-x]) [[]]
main = mapM_ print [theCase | theCase<-cases, isCompatible testimonies theCase]
*Main> main
[True,False,True,False,True]
[True,False,False,True,False]
[True,False,False,False,True]
[True,False,False,False,False]
[False,True,True,False,True]
[False,False,True,False,True]
[False,False,False,True,False]
[False,False,False,False,True]
[False,False,False,False,False] >>242>>245
����
testimonies = [
(¥x->x!!1 == False),
(¥x->x!!2 == True),
(¥x->(x!!3==False) && (x!!4==False)),
(¥x->x!!4 == False),
(¥x->x!!4 == True)
]
isCompatible ts theCase = and $ zipWith (||) (map not theCase) (map (¥x -> x theCase) ts)
cases = (!! (length testimonies)) $ iterate (¥x-> [a:b|a<-[True,False],b<-x]) [[]]
main = mapM_ print [theCase | theCase<-cases, isCompatible testimonies theCase]
*Main> main
[True,False,True,False,False]
[True,False,False,True,False]
[True,False,False,False,True]
[True,False,False,False,False]
[False,True,True,False,False]
[False,False,True,False,False]
[False,False,False,True,False]
[False,False,False,False,True]
[False,False,False,False,False] >>241
�K���������藧���Ȃ��B
X��R �Ƃ��āAX �ɂ� R �̒ʏ�̈ʑ������Ĉʑ���ԂƂ���B
A��[0,1], B��[0,1/2] �ƒu���ƁAA,B��X�̕W���ł���B
f�FA��[0,1] �� f(x)��x �ƒ�`����ƁAf�͘A���ł���B
s��1/2 �Ƃ���ƁA{a��A|f(a)��s}��[0,1/2]��B��A��B �ł���B�������A
{a��A|f(a)��s}��[0,1/2), A��int(B)��(0,1/2)
�ł��邩��A{a��A|f(a)��s}��A��int(B) �͐��藧���Ȃ��B >>247
���肪�Ƃ��������܂�
���͂���ؖ��ł��̕������T���Ă����̂�
���Ⴊ����ƕ��������̂ŕʃ��[�g����l���邱�Ƃɂ��܂� >>239 >>240
��� |x-y|/(1+x+y)^�� dxdy�@(x,y��0, 3����)
= 2 ��� Y / (1+X)^�� dX dY�@(0�� X:=(x+y) <+�� ,0�� Y:=(y-x) ��X)
= �� X^2 / (1+X)^�� dX (0�� X <+��)
= �� X^{3-1}/(1+X)^{3+(��-3)} dX
= B(3, a-3) = ��(3)��(a-3)/��(a) = 2 / ((a-1)(a-2)(a-3)) wolfram �̌v�Z�ƍ���ˁ[�ȁA���������ȁ[�Ǝv������
���R�r�A���̃t�@�N�^�[��Y��Ă���
X := x + y
Y := -x + y
|��(X,Y)/��(x,y)| = 2
��� |x-y|/(1+x+y)^�� dxdy�@(x,y��0, 3����)
= 2 ��� Y / (1+X)^�� dX dY / 2�@(0�� X:=(x+y) <+�� ,0�� Y:=(y-x) ��X)
= ... = 1/( (��-1)(��-2)(��-3) )
wolfram�ŏd�ϕ��ł���̂͏��߂Ēm����.
integral_0^infinity integral_0^infinity |x-y|/(1+x+y)^5 dx dy
= 1/24 (��=5 �̏ꍇ). �� �̋L���̂܂܂ł̓_��������. >>249�@�⑫
�����ϕ�2��̂��Ɛϕ�1��
(1/2)��XX/(1+X)^a dX
= -(1/2(a-1)) XX/(1+X)^(a-1) +(1/(a-1))��X/(1+X)^(a-1) dX
= -(1/2(a-1)) XX/(1+X)^(a-1) -(1/(a-1)(a-2)) X/(1+X)^(a-2) +(1/(a-1)(a-2))��1/(1+X)^(a-2) dX
= -(1/2(a-1)) XX/(1+X)^(a-1) -(1/(a-1)(a-2)) X/(1+X)^(a-2) -(1/(a-1)(a-2)(a-3))1/(1+X)^(a-3) +c ����2�N
���`���w
(2)��������܂���
������肢���܂�
https://i.imgur.com/lX8taCC.jpg x = (-8/17) * a + (-15/17) * b', where b' = (-1, 4, 17)^T
y = c - x >>244
���X���肪�Ƃ��������܂��B
�u�[���㐔�̓h�E�����K���̖@�����炢���������ł��Ă��Ȃ��̂�
C�ˁ�D�ȁ�E�@�́@C(D+E)=0�łȂ���C(D+E+DE)=0�ƂȂ�̂��킩��Ȃ��Đ�ɐi�߂Ȃ��Ă���܂��B >>254
X��Y �� ��(X �� ��Y) ������ X(1-Y) = 0�B
�Ȃ̂� C�ˁ�D�ȁ�E �� C(1-(1-D)(1-E)) = 0�A���Ȃ킿 C(D+E+DE)=0�B >>252
b' := b - (<a, b> / |a|^2) * a �Ƃ����ƁA
<a, b'>
=
<a, b> - (<a, b> / |a|^2) * <a, a>
=
<a, b> - (<a, b> / |a|^2) * |a|^2
=
<a, b> - <a, b>
=
0. >>246
�����i���ɂ́j�����Haskell�R�[�h���肪�Ƃ��������܂��B
�j�S������
isCompatible ts theCase = and $ zipWith (||) (map not theCase) (map (\x -> x theCase) ts)
�������ł��Ȃ��ł��܂��B
�������������K���ł��B c' = c - (<a, c> / |a|^2) * a - (<b', c> / |b'|^2) * b' �Ƃ����ƁA
<a, c'>
=
<a, c> - (<a, c> / |a|^2) * <a, a> - (<b', c> / |b'|^2) * <a, b'>
=
<a, c> - (<a, c> / |a|^2) * |a|^2 - (<b', c> / |b'|^2) * 0
=
<a, c> - <a, c> - 0
=
0. >>252
<b', c'>
=
<b', c> - (<a, c> / |a|^2) * <b', a> - (<b', c> / |b'|^2) * <b', b'>
=
<b', c> - (<a, c> / |a|^2) * 0 - (<b', c> / |b'|^2) * |b'|^2
=
<b', c> - 0 - <b', c>
=
0. >>252
x * a + y * b = [(<a, b> / |a|^2) * y + x] a + y * b'.
x * a + y * b' = [x - (<a, b> / |a|^2) * y] * a + y * b.
������A
a, b �����镔����Ԃ� a, b' �����镔����Ԃ͓������B >>252
<x * a + y * b', c'>
=
x * <a, c'> + y * <b', c'>
=
x * 0 + y * 0
=
0 + 0
=
0. >>252
c' �� W �̔C�ӂ̌��ƒ�������B
c' = c - (<a, c> / |a|^2) * a - (<b', c> / |b'|^2) * b'
������A
c = (<a, c> / |a|^2) * a + (<b', c> / |b'|^2) * b' + c'.
(<a, c> / |a|^2) * a + (<b', c> / |b'|^2) * b' �� W.
c' �� W^��
������A
c �́A W �̌��� W^�� �̌��̘a. >>257
Fazzy version �Ȃ�\�� theCase �ɑ���
theCase �ɂ����� X �͉R���ł��邩�AX�̏،���theCase���K������B
�����ׂĂ̏ؐlX�ɂ��Đ������邱�Ƃ������B
theCase �� theCase!!i �� i �Ԗڂ̏ؐl�������Ȃ�True, �R���Ȃ�False���Ƃ�List�B
map not theCase �͂��� True �� False ���Ђ�����Ԃ������́B
(map (¥x -> x theCase) ts) �� (map (¥x -> x theCase) ts)!!i �� i �Ԗڂ̏ؐl�̏،���theCase���������Ȃ��Ƃ���True�A��������Ƃ�False�ɂȂ�List�B
�e�ؐl�ɂ������Ă����ꂩ�� True �ɂȂ邱�Ƃ����������炻��� zipWith (||) �Ř_���a���Ƃ��Ă����� and �ł��ׂ� True �ƂȂ��Ă��邩���m�F���Ă��܂��B
�܂��A�z���g�͂���ȋZ�g���ׂ��ł͂Ȃ���ł����ǂˁB
�ǐ������邵�B
���Ȃ݂�
(||) = (�ؐl���R�� �� �،���theCase���������Ȃ�)
�̂�����
(==) = (�ؐl���R���Ȃ�،���theCase�Ɩ����A�ؐl�������Ȃ�،���theCase�ƓK��)
����������ΉR������ɉR��Version��solver�ɂȂ�܂��B x := (<a, c> / |a|^2) * a + (<b', c> / |b'|^2) * b',
y := c'
�Ƃ���悢�B >>255
�f�������X���肪�Ƃ��������܂����B
����Ŏ��ɐi�߂܂��B >>263
������肪�Ƃ��������܂����B
���S�҂ɂ͓�ǃR�[�h�ł����B >>255
A���R���Ȃ�
�^�������Ƃ���A�ˁ�B����AB=0������
�R�����Ă���Ƃ���AB=1�ł�?
�R���͐^�����R�����̂łǂ��������ɂȂ�̂��낤���A�Ƃ����̂����̋^��ł��B >>267
X�̏،���Y�ł���Ƃ��܂��B
�ʓ|�Ȃ̂�X�������҂Ƃ��������X�Ƃ��܂��B
�u�����҂͕K�����������Ƃ������A�R���͐^�����R�������v
�Ƃ����������ł� X��Y �Ƃ�������ɖ������Ȃ����f�� M ��T�����ł��B
X�AY �̃��f��M�ł̐^���l��x y�Ƃ���Ƃ�X��Y�̐^���l��1-x(1-y) (=X���������̂�Y���ԈႢ�Ƃ������Ƃ͂Ȃ�)�ł��B
���ꂪ 1 �ɂȂ�Ƃ��Ȃ̂� 1-x(1-y) = 1�A���Ȃ킿 x(1-y) = 0 ����������Ƃ��� M �� X �̏،��ɓK����������ł��B
A�̏،�����B�ł���̂Ń��f�� M �ł�A,B�̐^���l�� a,b �Ƃ���� a(1-(1-b)) = 0�A���Ȃ킿 ab=0 �����f�� M �� A �̏،����瓾��������ɖ������Ȃ������ł��B
���ې^���l�����Ă͂߂Ă݂��
a b ab=0 M�͓K��
�\�\�\�\�\�\�\�\�\�\
0 0 �@���@ �@���@�@M�ɂ����� A ���R���Ȃ̂� b �̒l�ɂ�炸 M �� A �̏،����瓾��������ɖ������Ȃ��B(A�̏،��͍l���ɂ���Ȃ��Ă悢�B)
0 1 ���@�@ ���@�@M�ɂ����� A ���R���Ȃ̂� b �̒l�ɂ�炸 M �� A �̏،����瓾��������ɖ������Ȃ��B(A�̏،��͍l���ɂ���Ȃ��Ă悢�B)
1 0 ���@�@ ���@�@M�ɂ����� A �͐������̂�A�̏،��͊��Ă��Ȃ���Ȃ�Ȃ����AB���R���Ȃ̂�A�̏،��Ɩ������Ȃ��B
1 1�@ ✕�@�@ ✕�@�@ M�ɂ����� A �͐������̂�A�̏،��͊��Ă��Ȃ���Ȃ�Ȃ����AB�������҂Ȃ̂�A�̏،��Ɩ�������B
�ƂȂ���ab=0��A�̏،����瓾���������M���������邩�ۂ��Ɠ��l�ł��邱�Ƃ��m���߂��܂��B >>268
���J�ȉ�����肪�Ƃ��������܂����B
�R���͕K���R�����Ȃ�A�̏،���A=1-B�Ƃ������ɂȂ�̂ł��ˁB >>229
�l�̈ӌ��ɂ��ĕ����̂��ςł��������킩�����狳���ĉ������B
���Y�אl�����pdf�ŃƂɉ����Č��������ق����ǂ���ƈ����Ⴊ�ڂ��Ă��
�Ƃ̎��ł������̌��������爫���ꍇ�Ƃ͍ŏ��ɕ����J�����������牽�~���o���ꍇ���Ə����Ă���̂ł��傤���H >>270
�Ƃ肠����pdf�ɂ���
�ŏ��̕����̒��g��x�~�Ƃ��ăƂ�����1/�ɂ̎w�����z�ɏ]���ꍇ�ɂ�
x �� 4log2/��
�̏ꍇ�A���� r/�ɁC���U r/��2 �̂̃K���}���z�ɏ]���ꍇ�ɂ�
x ��2(r+1)log2/��
�̏ꍇ�ɂ͌��������ꍇ�̂ق������Ғl������炵���ł��B
�Ȃ����������ꍇ�̊��Ғl��3x/2�ɂȂ�Ȃ����̗��R��p3�E�J�����̐^�����肩��������n�܂��Ă���͗l�B
�������̂������1mm���ǂ܂����_�������ĂȂ��̂ł������炸�B >>263
>>268
�������Ƃ��v���Œ��J�ȉ�����肪�Ƃ��������܂����B
������Q�l��R�ɈڐA���Ă݂܂����B
# dat : all possible combinations
n=5 ;arg=list()
for(i in 1:n) arg[[i]]=0:1
dat=do.call(expand.grid,arg) # expand.grid(0:1,0:1,...)
dat=as.matrix(dat)
colnames(dat)=LETTERS[1:n]
# A=>!B, B=>C, C=>!D&!E, D=>!E, E=>E
is.compati<-function(i,x){ # i:index of honest, x: possible combination
switch(i, # 1..n
x['B']==0, # testified by A (=LETTERS[1])
x['C']==1, # testified by B (=LETTERS[2])
x['D']==0 & x['E']==0, # ...
x['E']==0,
x['E']==1)
}
check=function(x){
re=NULL
honest=which(x==1) # index of honest
for(i in honest){
re=append(re,is.compati(i,x))
}
all(re)
}
dat[apply(dat,1,check),]
�������ʂ������܂����B
> dat[apply(dat,1,check),]
A B C D E
[1,] 0 0 0 0 0
[2,] 1 0 0 0 0
[3,] 0 0 1 0 0
[4,] 1 0 1 0 0
[5,] 0 1 1 0 0
[6,] 0 0 0 1 0
[7,] 1 0 0 1 0
[8,] 0 0 0 0 1
[9,] 1 0 0 0 1
���肪�Ƃ��������܂����B �킽�������X�g�B
�ςȏ��Z�g���ēǂ݂ɂ��������B
������ƒ����Ȃ邯�Ljȉ��̕����悩�����B
���w�`�b�N�����B
(==>) x y = not x || y
axions = [
(¥x-> x!!0 ==> (x!!1 == False)),
(¥x-> x!!1 ==> (x!!2 == True)),
(¥x-> x!!2 ==> ((x!!3 == False) && (x!!4 == False))),
(¥x-> x!!3 ==> (x!!4 == False)),
(¥x-> x!!4 ==> (x!!4 == True))
]
isCompatible axions model = and $ [ axion model | axion<-axions ]
models = (!! 5) $ iterate (¥x-> [a:b|a<-[True,False],b<-x]) [[]]
main = mapM_ print [ model | model<-models, isCompatible axions model]
*Main> main
[True,False,True,False,False]
[True,False,False,True,False]
[True,False,False,False,True]
[True,False,False,False,False]
[False,True,True,False,False]
[False,False,True,False,False]
[False,False,False,True,False]
[False,False,False,False,True]
[False,False,False,False,False] >>271
���肪�Ƃ��������܂��B
>>271����̎��������Ă�킯����Ȃ��̂œ{��Ȃ��ŕ����Ă��炢�����̂ł�����
���X�̖���2�̕����������Ă���2�ɂ͂����������Ă�Ƃ����b�Ȃ̂�
�����������Ȃ������ǂ��ꍇ������Ƃ����Ȃ炻�̂��̏ꍇ�̓�����
2�~�Ƃ�1���~�Ƃ������̐����Ŗ�����Ίm���ɊԈႢ�ł��B
���̂Ȃ�l���s�ɍs����4log2/�ɉ~���ɓ���ĉ������ƌ����Ăࢉ������Ă��ł����H���{��Řb���ĉ��������
�����Ă��܂��͂��ł��B
�ŏI�I�ȓ������P�̐����ɂȂ錻���̖��������ׂ̕��@�Ƃ��ēr���Ő������g������L�����g�����肷��͕̂��ʂł���
�����ɂ܂ŋL���␔�����������炻��͊��S�ɊԈႢ�ŗL�鎖�͐��w�̋��Ȏ��ł��킩��܂��B
�������>>271����ɂ��ĉ����������Ă�킯����Ȃ��̂Ō�����Ȃ��ł��������B
�����c�O�Ȃ�����Y�אl����͍ŏ��͂��炵���l�����������Ă���̂ɓr�����畕���̖��ƊW�Ȃ�
�ʂ̐��w�̖��ɂ���ւ��Ă��܂��Ă��̎����ō���������ɂ��Đ������Ă��邾����
�ŏ��̕����̖��ɂ��Ă͓����������ĂȂ��̂�����������Ȃ̂������Ė����悤�ł��ˁB
�����N���������ɂ��Đ����o���Ȃ������͎̂c�O�ł��������������Ƃ肪�o�����͖̂ʔ��������ł��B 1���~���������_�ŁA�p�ӂ��ꂽ������5��~��1���~�A���邢��1���~��2���~�̂ǂ��炩�ł���Ƃ킩�邯��
�ǂ���ł���̂��͊m���Ō��܂邱�ƂȂ̂��낤���H >>275
���̓_�ɂ��Ă�pdf�ł͌��y����Ă܂���B
�Ƃ肠���������̂����𐮐��ɂ��Đ����l�����Ƃ�Ȃ����z�ɂ��Ă��܂��ƂƂƂ���9999�~�����Ă����_�Ŏc��̕�����19998�~�����Ă邱�Ƃ��m�肵�Ă��܂�����A�Ȃɂ���肪���p�ɓ���Ȃ��Ă��܂��̂ŘA�����z�̏ꍇ����ɍl���邱�Ƃɂ��Ă邻���ł��B
�m���ɏ��Ȃ��Ƃ��u��ڂ̕������������Ƃ�10000�~�ł���Ƃ��A�����Е��̕����ɓ����Ă邨���̏����t�����Ғl��15000�~�Ȃ̂��H�v��������̂ɂ͂���ŏ\���ɂ������܂��B
���ɂ͂��́h�ȒP�ȃP�[�X�ł̌��h�ł��ڂ܂��܂�����ww �l�ʑ�PABC�ɑ��A3��PA,PB,PC�ƌ���镽�ʂŁA���̎l�ʑ̂�̐ς̓�����2�̕����ɕ���������̂��l����i���ʂ͕ӂ̗��[�_�Ƃ͌����Ȃ����̂Ƃ���j�B
����ɁA���̂悤�ȕ��ʂ�P���牺�낵�������̒�����p�AA���牺�낵�������̒�����a�Ƃ���B(p,a)��1�Œ肵�ė^����A����ɑΉ����镽�ʂ͂���1�ł��邱�Ƃ������B P(0,0,0) A(4,0,0) B(0,4,0) C(0,0,4)
X(3,0,0) Y(0,32/9,0) Z(0,0,3) �� ����XYZ
U(3,0,0) V(0,3,0) W(0,0,32/9) �� ����UVW >>276
����A�����ƍ���Ȃ���Ȃ������Ă��Ƃɂ͎��ۂɕ�����2�����p�ӂ���Ă��炸����ȕ��z�͑��݂��Ȃ�
���̖��ł��̕��z�����݂��邱�Ƃ����肷�邱�Ƃ��Ó��Ȃ̂��ǂ����H
���̖��́A
�i��҂�5��~��1���~�̓����Ă��镕����p�ӂ��A�u�ǂ��炩���ǂ��炩��2�{�̋��z�������Ă��܂��v�Ƃ�������
����҂��Е���I�ђ��g���������茩���Ƃ���1���~�ł�����
�i��҂͑ւ��Ă������ł���ƌ���
����҂͑ւ����������ƍl����ׂ����ǂ���
�Ɠ����ƍl����ׂ��Ȃ�Ȃ����낤��
���̂Ƃ��A����҂��p�ӂ��ꂽ������5��~��1���~�ł�������1���~��2���~�ł����������m���ōl���邱�Ƃ͐������̂�
���ۂɎ������J��Ԃ��Ɓi�����̎����Ȃ̂ŏ��5��~��1���~�����p�ӂ���Ă��Ȃ��j�A
�����ɎQ����������҂̔�����1���~������킯�����ւ�����100���������邱�ƂɂȂ�
�m���ōl�����ꍇ�Ɩ�������̂͊m���ōl���邱�Ƃ��ԈႢ�ł��邩��ł͂Ȃ��̂� >>242
���i�R����fuzzy�R���ɑΉ��B
# dat : all possible combinations
n=5 ;arg=list()
for(i in 1:n) arg[[i]]=0:1
dat=do.call(expand.grid,arg) # expand.grid(0:1,0:1,...)
dat=as.matrix(dat)
colnames(dat)=LETTERS[1:n]
# A=>!B, B=>C, C=>!D&!E, D=>!E, E=>E
is.compati.H<-function(i,x){ # i:index of honest, x: possible combination
switch(i, # 1..n
x['B']==0, # testified by A (=LETTERS[1])
x['C']==1, # testified by B (=LETTERS[2])
x['D']==0 & x['E']==0, # ...
x['E']==0,
x['E']==1)
}
is.compati.L <- function(i,x){# is compatible for liars?
# i:index of liars, x: possible combination
switch(i, # 1..n
!(x['B']==0), # testified by A (=LETTERS[1])
!(x['C']==1), # testified by B (=LETTERS[2])
!(x['D']==0 & x['E']==0), # ...
!(x['E']==0),
!(x['E']==1))
}
check=function(x,Strict){
re=NULL
honest=which(x==1) # index of honest
for(i in honest){
re=append(re,is.compati.H(i,x))
}
if(Strict){
liar=which(x==0) # index of liar
for(i in liar){
re=append(re,is.compati.L(i,x))
}
}
all(re)
}
dat[apply(dat,1,function(x) check(x,Strict=TRUE)),]
dat[apply(dat,1,function(x) check(x,Strict=FALSE)),]
> dat[apply(dat,1,function(x) check(x,Strict=TRUE)),]
A B C D E
[1,] 1 0 0 1 0
[2,] 1 0 0 0 1
> dat[apply(dat,1,function(x) check(x,Strict=FALSE)),]
A B C D E
[1,] 0 0 0 0 0
[2,] 1 0 0 0 0
[3,] 0 0 1 0 0
[4,] 1 0 1 0 0
[5,] 0 1 1 0 0
[6,] 0 0 0 1 0
[7,] 1 0 0 1 0
[8,] 0 0 0 0 1
[9,] 1 0 0 0 1 >>277
> ���ʂ͂���1��
�����Ƃ͌���Ȃ��ł���
 �R���͕K���R����
�R���͕K���R����
A�uB�͉R���ł͂Ȃ��v
B�uC�͉R�����v
B�uA�͉R������C�������Ă���v
�����҂ƉR���̉\���̑g�ݍ��킹�́H
�P�F������ 0:�R��
A B C
[1,] 1 0 1
[2,] 0 0 1
[3,] 1 1 0
[4,] 1 0 0
[5,] 0 0 0
�ł����Ă܂��H >>282
�듚���ȁA�l������(._.) >>282
���ꂵ���c��Ȃ�����
> dat[apply(dat,1,function(x) check(x,Strict=TRUE)),]
A B C
1 1 0
�R���͕K���R���̐������Ƃ��āA�R���͋C�܂���ɂ��Ă�
> dat[apply(dat,1,function(x) check(x,Strict=FALSE)),]
A B C
1 1 0
�Ɠ������ʁB
�v���O�����Ɏ��M���Ȃ��̂ŁA�����ł̌������肢���܂��B �Ō��B�̔����͂��̂悤�ɐݒ�
C���uA��...�v�ƌ����������҂���������ꂸB���⑫�����A
B�uA�͉R������C�������Ă���v ����ł悳�����ȋC��
���i�R��
> dat[apply(dat,1,function(x) check(x,Strict=TRUE)),]
A B C
1 1 0
�t�@�W�[�R��
> dat[apply(dat,1,function(x) check(x,Strict=FALSE)),]
A B C
[1,] 0 0 1
[2,] 1 1 0
[3,] 0 0 0 �������(���O��)
A=1�� 1 ? ? , A=0 �� 0 ? ?
B=1�� ? 1 ? , B=0 �� ? 0 ?
�lj�����: A�uB�͉R���ł͂Ȃ��v
A=1�� 1 1 ? , A=0 �� 0 0 ?
�lj�����: B�uC�͉R�����v
B=1�� ? 1 0 , B=0 �� ? 0 1
�lj�����: B�uA�͉R������C�������Ă���v(A�̏�Ԃɂ���C�����y�������͐^)
B=1�� 1 1 0 , B=0 �� 1 0 1
A,B�̏�ԂŏՓ˂��Ȃ��g�ݍ��킹�� 1 1 0 �̂� >>216
��A����̎��_��������Ȃ�B����̎��_���猩�Ă�������ւ��������ǂ��Ȃ�
�����݂��Ɍ�������Ɨ�������������Ƃ����������Ȍ��_�ɂȂ�Ƃ������������Ėڂ���ł����B
�������̌��_�Ƃ��ĕ�������������������(���Ғl����)�ƌ����̂͊��S�ɊԈႢ���Ɗm�M���܂����B
�S�Ă͊m�����z�ɂ��̂ł́H
��l�Ƃ����������ق����L���ɂȂ�����ʂɋN������B
���Ғl���{���ǂ����ƁA���ۂɓ������邩�ǂ����Ƃ͕ʖ��B
���z�y�A�� ( �P�� 2 )�A ( 2 �� 4 )�A ( 4 �� 8 ) �� 3 �p�^�[�����Ƃ���B
�����O�̃p�^�[���͂ǂ�������m�� 1/3 �ŋN����B
��l�̕����̋��z�� 2 �ő���̋��z�� 4 �̏ꍇ�A2 �̐l�� 1 �� 4 �m���Ŋ��҂�
4 �̐l�� 2 �� 8 �m���Ŋ��҂���̂ŁA�ǂ���̐l���������������L���ɂȂ�B k�̎O���9��@�Ƃ���0�܂��́|1�܂���1�ƍ����ł���
k�̎O���0�A�}1�imod9�j
������Ƃ�����Ă����ǂǂ������ߒ��ł����Ȃ�́H >>287
���X���肪�Ƃ��������܂��B
�R���͏�ɉR�������i�R���̂Ƃ���
> dat[apply(dat,1,function(x) check(x,Strict=TRUE)),]
A B C
1 1 0
�Ō��_����v���Ĉ��S�B >289
k = 3n + r�@(m=-1, 0, 1)
k^3 = r^3 + 3 r^2 (3n) + 3 r (3n)^2 + (3n)^3
�� r^3 (mod 9) >>284
���i�R���̂Ƃ��̎O�Ԗڂ̏����̈������ǂ����Ǝv���B
B���R���Ȃ�uC���uA�͉R���v�ƌ������v���ے肳������
�uC���z���g�Ɍ������̂́uA�͐����ҁv�v
�Ƃ����\����
�uC��A�������҂Ƃ��R���Ƃ��Ȃ�Ƃ������ĂȂ��v
�Ƃ����\��������Ǝv���B
�̂�
(�R��, �R��, ������)
���c��Ǝv���B
�܂�R�Ԃ߂̏�����
B �� ( C �� �� A)
�ł͂Ȃ���
B �� ( C �� ��A )
�ɂȂ�Ǝv���B
�܂肱������Fuzzy�R���̏ꍇ�Ɠ��������ɂȂ�Ǝv���B >>292
A��腖��剤�ł��A�ƌ������\�������邯��
�����͉R���ƌ������̔ے�͐����҂ƌ������ƍl����悤�ɖ��ݒ肵������B
C���uA��...�v�ƌ����������҂���������ꂸ�A�ɂ����̂�
�uC���uA�͉R���v�ƌ������v�̔ے��
�uC���uB�͉R���v�ƌ������v�Ƃ��̉\����r�����邽�߁B >>279
�����̂Ƃ��A����҂��p�ӂ��ꂽ������5��~��1���~�ł�������
��1���~��2���~�ł����������m���ōl���邱�Ƃ͐������̂�
���ʂɐ������Ǝv�����ǁB
�P�ɂ��ꂪ1/2������Ȃ��ĕs��������A���Ғl�v�Z���ł��Ȃ��Ƃ��������̘b���ƁB �����ꓹ������܂�
�ǂ��炩���V���s���łǂ��炩���n���s���ł�
���ꂼ��̕����ꓹ�ɂ����ԂɁA
YES�i�͂��j/NO�i�������j�œ������鎿���
��x�������邱�Ƃ��ł��܂�
��Ԃ͂����{���̂��Ƃ������V�g���A
�����E�\�����������̂ǂ��炩�Ȃ̂ł����A
�ǂ���Ȃ̂��͌����������܂���
�ǂ�Ȏ��������ΓV���s���̓���m�邱�Ƃ��ł��܂��� ���ꂪ���R���ŕ��q��1�ł���悤�ȗL������P�ʕ����ƌĂԁB
�ȉ��̂悤�ɒ�`�����P�ʕ�������Ȃ鐔��a[n]�ɂ��āAa[12]�����߂�B
�Ea[1]=1/2
�En>2�̂Ƃ��Aa[n]��
�ua[1]+...+a[n]��1�����ƂȂ�悤�ȒP�ʕ����ōő�̂��́v >>295
���������炪�V���ւ̓����ƕ������Ƃ���
�͂��@�Ɠ����܂����H �f��u���r�����X �����̖��{�v('86 �ē�:�W���E�w���\��) ��
���̘_���p�Y�����������V�[��������.
��l���T�� (�W�F�j�t�@�[�E�R�l���[) �� >>297 �Ɠ����悤�Ȑ������������o����.
...���A�����������Ă����ɗ��Ƃ����ɗ��Ƃ����.
�Ȃ��? �����������̂ɁI �� ����(�f���B�b�h�E�{�E�C)�̓C�W����������. >>294
�������������Ő\����Ȃ����A>>279���������Ă邱�ƂƖ{���I�ɓ�������Ȃ����ƁB
���łɒN�������g����ꂽ���_�Ō��肵�Ă�̂Łi�m�����z�Ō����A�������T��~��
�Q���~����1.0��0�ɂȂ��Ă�j���Ғl���]�X����̂͒m��ʂ����Ńi���Z���X�Ƃ��H
������Ɩ���ς��āA����Ȃ�ǂ����낤�B
5��~���蕕���ƂP���~���蕕���̃y�A�ƁA�P���~���蕕���ƂQ���~���蕕���̃y�A��
��g���p�ӂ���Ă���B
���Ȃ��ɂ́A���ꂼ��̃y�A�ŕ����̒��g�̋��z���{�Ⴄ���Ƃ������m�炳��Ă���B
�����ŁA�܂��A�ǂ��炩�̃y�A��I���ꂽ�B����ɁA���̃y�A�̈���̕���������
�P���~�������Ă����B���Ȃ킿�A��������̕����ɂ͂T��~���A�Q���~��1/2�̊m���œ���
�Ă��邱�ƂɂȂ�B�����ŁA�����y�A���ŕ������������Ă��ǂ��Ƃ���ꂽ��A��������
���ł��낤���H �F�����Ԉ���Ă���\����Ȃ����ǁA�����̃p���h�b�N�X�́A
�u���g�������Ă��Ȃ���Ԃœ��l�̋c�_������ƁA�ǂ������ɂ����ꍇ���ς����ق������Ғl���������ƂɂȂ�s�����ł���v
�Ƃ������������C������
������pdf�̎w�E�́A���̋c�_��
(*)�u�S�Ă�x�ɑ��A�����̒��g��(x,2x)�ƂȂ�m����(x,x/2)�ƂȂ�m���͓������v
�Ƃ������Ƃ��ÂɎg���Ă��邯�ǁA������ĕ��z�̎�������ŕς�����Ⴄ���瓖��O����Ȃ���˂��Ă���
���w�ɂ�����m���̖����āA��蕶�Ŗ��L���Ă��Ȃ������͎��R�ɓ��m�����ƌ��߂Čv�Z������
�T�C�R���̏o�ڂƂ��܂��狅�����o���Ƃ�
�����̖��ł�(*)�͎��R�ɍl����Ɛ��������Ƃ��Ɖ��肵�����Ȃ邯�ǁA���͌����Ɍv�Z����Ƃ���Ȃ��Ƃ͂Ȃ����Ă����̂����炭�肾�ƍl���Ă�
���ꂽ�����͋��̑g�ݍ��킹�������ɍl�����邹���ŘA�����z�������o���K�v���o�Ă��邩��
��ʓI�ɖ��������ޖ��Œ��ςɗ���Ɗ�Ȃ�
>>279�ł́A���߂���g�ݍ��킹�����߂��Ă���m���v�Z�����Ӗ��ɂȂ�Ǝ咣���Ă邯�ǁA����͂��܂�Ӗ��̂Ȃ��b����
�T�C�R���̏o�ڂ����m�����ƐM���Ė��������Ă���l�ɑ�
�u�T�C�R���ɍH�w�I���u���g�ݍ��܂�Ă���1�̖ڂ����o�Ȃ��Ƃ����炻�̌v�Z�͌�肶��Ȃ��̂��v
�Ɠ˂�����ł��銴��
���w�̖��Ƃ��Ď��g�ޏꍇ�́A���̕ӂ͈�l�ȕ��z���Ɖ��肵�Đ��l�v�Z�����݂�̂��ړI������ >>299
���̐ݒ�ŁA�������������ăV�~�����[�V�������Ă݂��B
x=list(c(0.5,1),c(1,2)) #�@�����̃y�A
sim <- function(){
y=x[[rbinom(1,1,0.5)+1]] #�y�A��I��
z=y[rbinom(1,1,0.5)+1] # �I�y�A����P�����I��
c(y=y,z=z) #c(�I�y�A�̊z,�I�����̊z)
}
re=t(replicate(100000,sim())) # 10����̌J��Ԃ����ʂ�ۑ�
idx1=which(re[,'z']==1)�@# �I�������P���~�̏ꍇ�̃y�A�𒊏o
chg=apply(re[idx1,-3],1,function(x) x[which(x!=1)]) # �������ē�������z
> mean(chg) # ���̕��ϒl
[1] 1.248531
(2+0.5)/2�ɑ��� �E��g�̋��z�y�A�ϑz��
�����͓�Ȃ̂ŋ��z�͓�����Ȃ��B
��g�̋��z�y�A���l���邽�߂ɂ͎O�̋��z���K�v�ɂȂ邩��
��g�̋��z�y�A���l����̂͊ԈႢ���B
�E�ϐ��̌�p��
���Ғl�v�Z���̒��� x/2 �̕��� x �͑傫�����̋��z��\��
2x �̕��� x �͏��������̋��z��\���Ă���̂ňقȂ�l��\���Ă���B
����� x ���g���Ċ��Ғl�v�Z������������Ƃ��p���h�b�N�X�̌������B
�E�m���̍��o��
�I�����̋��z����肵���ꍇ
�������������Ĕ{�ɂȂ�m���Ɣ�������m�����������Ƃ͌���Ȃ��B >>300
>�u�T�C�R���ɍH�w�I���u���g�ݍ��܂�Ă���1�̖ڂ����o�Ȃ��Ƃ����炻�̌v�Z�͌�肶��Ȃ��̂��v
�����̖��͂܂��ɂ��������Ȃ�Ȃ��́H���Ęb���ƁB
������I�Ԑl�����肷��m�����z�Ǝ��ԂƂ���������Ă���Ƃ����B ��w���ł��B�g���������������̕ό`��������Ȃ������Ă��܂��B
https://i.imgur.com/DVNKVoK.jpg >>305
�����Ȃ�ł��B�X����������Ē�����ƍK���ł��B >>304
|sinx|��|x|
�͂����H
�i�O���t������Ȃ炷��������j
�����x-y/2�̎��ɓK�p���Ă��� >>302�@����
�E�m���̍��o��
���z�y�A (A, 2A) �� A ���m�� 1/2 �Ŏ����̕����ɓ����Ă���B
2A ���m�� 1/2 �Ŏ����̕����ɓ����Ă���B
�����玩���̕����̋��z�� X �Ƃ����
������̕����� X/2 �������Ă���m����2X �������Ă���m�����A �ǂ���� 1/2 ���B >>301
�������A���̐ݒ�ł́A���������ق������ɂȂ�Ɗ��҂ł��܂���ˁB
�������A1���~���܂܂Ȃ��y�A�i���Ƃ��A3���~��6���~�Ƃ��j�ƁA5000�~��1���~�̃y�A
�œ������s������A1���~���o�Č�������Ί��Ғl�i�ƌ����Ă����̂��ȁH�j��5000�~��
�̂ő��ɂȂ�܂��B
�܂��A1���~���܂܂Ȃ��y�A�ƁA1���~��2���~�̃y�A�ł���A��������Ί��Ғl��2���~
�œ����܂��B
�܂�A1���~���o������Ƃ����āA������5000�~��2���~���Ƃ����m���͕K������1/2
�ł͂Ȃ��A���ꂼ��1��0��0��1�̉\�������肤��B�܂�A�팱�҂̒m�蓾�����
����ł́A���Ғl�����ł������������߂��Ȃ��Ƃ������Ƃ��悭�킩��Ǝv���܂��B >>303
�������z��I�����邱�Ƃ̓T�C�R�����̂悤�ȏł��\������A�Ӗ����Ȃ��b�ƕ\������
�������Ŋ̂Ȃ̂́A�Âɉ��肵�Ă���
�u����(*)��"���R��"�����ł���v
�����͐������Ȃ��Ƃ������Ƃ��ƍl���Ă���
���̎w�E�ƁA�ɒ[�ȗ���l���邱�Ƃ��ł���Ƃ����w�E�̊Ԃɂ͑傫�Ȋu���肪����
����܂��������ŁA�������z�̗�������Ă���Ȃ當��͑S���Ȃ��ł� ������ƕ����̖���>>214��pdf�ǂ�ōl���Ă݂����Ƃ܂Ƃ߂Ă݂�B
�����X�ɂȂ�܂��B
�\����Ȃ��B
�܂����������������ق����K�����ł��̊��Ғl�͌���1.25�{�ɂȂ�ؖ�
pdf�Ɠ������Ƃ����Ȃ����̕����ɓ����Ă���z��\���m���ϐ��Ƃ���B
�ŏ��̕�����x�~�̊m����1/2P(��=x)+1/2P(��=x/2)�B
�ŏ��̕�����x�~���A������̕�����2x�~�����Ă�m����1/2P(��=x)�A
�ŏ��̕�����x�~���A������̕�����x/2�~�����Ă�m����1/2P(��=x/2)�B
����čŏ��̕�����x�~�̂Ƃ��́A������̕�����2x�~�����Ă�����t���m��P(������|��=x)=1/2P(��=x)/(1/2P(��=x)+1/2P(��=x/2))�A
����čŏ��̕�����x�~�̂Ƃ��́A������̕�����x/2�~�����Ă�����t���m��P(������|��=x)=1/2P(��=x/2)/(1/2P(��=x)+1/2P(��=x/2))�B
����Č������������ɓ����Ă��邨���̊��Ғl��
E=1/2P(��=x)/(1/2P(��=x)+1/2P(��=x/2)) 2x + 1/2P(��=x/2)/(1/2P(��=x)+1/2P(��=x/2)) x/2
=(2P(��=x)/(P(��=x)+P(��=x/2)) + 1/2P(��=x/2)/(P(x = ��)+P(��=x/2)))x
�����ň�l���z�����肵�Ă邩��p=P(��=x)=P(��=x/2)�ł���B
����������
E=(2 p/(p+p) +1/2 p/(p+p))x = 5/4x
�ƂȂ�B
�Ŗ��ɂȂ�̂͂���
�u�����ň�l���z�����肵�Ă邩��p=P(��=x)=P(��=x/2)�ł���B�v�̕����B
�Ȃ��Ȃ玖��(��=a)�͈قȂ�a�̒l�ɂ��đS�Ĕr���ł���A�����̊m�����h�S���������h�Ȃ�Ă��肦�Ȃ��B
���Ǐ�̏ؖ��͂����������肦�Ȃ����z�����肵�Ȃ��Ɛ��������Ȃ��B
�����܂Ő��w�I�Ȋm������Ғl�̋c�_������Ȃ�h���肦�Ȃ�����h�̘b�͖������Ă���������pdf�ł͂��������ꍇ�̘b���h�ϕ��s�\�ȕ��z (improper distribution)�h�Ƃ��Đ�̂ĂȂ��ŋc�_���悤�Ƃ��Ă�B
���������̕����͉ʂ����Ĉ�ʓI�ȕ��@�Ƃ�����̂��w�����x���̊m���_�����m��Ȃ��킽���ɂ͂킩��Ȃ������B
�Ƃɂ������ɂ���́h���Ғl1.25�{���h�𐳓�������ɂ͊w�����x���̕��ʂ̊m���_�̔��e�ł͖������ۂ��C������Ƃ����̂����̎��̈ӌ��B
�ȏ�ł��B�X�������X�}�\�B >>311
��������傶��Ȃ��̂�improper distribution�͏���������
����ŃO�O�����Ƃ���A�L���łȂ����x���m�����x�Ƃ��Ĉ����i�H�j�݂����Șb������炵���B�B
(https://www.encyclopediaofmath.org/index.php/Degenerate_distribution
��Comments) >>312
�����Ȃ�ł��ˁB
���������̂����܂��g���h���ׂĂ� a�ɂ�������P(��=a)�����l�h�ł��̌��ʂƂ��āh���Ғl����������1.25�{�ɂȂ�h���ă��f���������ł����˂��H
�����ƌ��������͈͂ł͂����܂ő�l�C�Ȃ��{�C�ŕ������c�_���Ă�L���͌�����Ȃ������B
�L�����݂������������Ă�l�����邩������܂���ˁB
�܂��������Ă�>>214��pdf����S���͗����o���ĂȂ����ɂ͔L�ɏ��������ł�����w �����t���m���̈Ӗ����킩���Ă���Z���ł��킩����ł����
�^����ꂽ���ɂ���Ċm���͕ϓ����邵���Ғl���ς��
�����t���m���Ƃ��x�C�Y�m���͂��������b�Ȃ�ł��� �������Ƃ���B
�C�ӂ̎��R��n�ɑ���
(��+1)^n - (��-t)^n
���L�����ƂȂ邽�߂̎���t���������ׂ��K�v������t=1�ł��邱�Ƃ������B
�܂����̏������K�v�\�������ł��邩�肹��B ���N�̋ߑ�̐��w�R���e�X�g�̖��Ɋւ�����̂Ȃ̂ł����C
�A�h�o�C�X�����������D
���̂悤�Ȗ��ł��F
n��3�ȏ�̎��R���C�萔a���ba�b���P���݂��������Ƃ���D
�@�@z^n�{az^(n�|1)�{az�{1��0
���̕������̉��͂��ׂĕ��f���ʏ�̉~�bz�b���P��ɂ��邱�Ƃ������D
�ȉ��̂悤�ɍl���܂����D
z��w^2�Ƃ����Dw��0����
�@�@w^(2n�j�{aw^(2n�|2)�{aw^2�{1��0
�@�@w^n�{aw^(n�|2)�{aw^(2�|n)�{w^(�|n)��0
����̉������ׂĕ��f���ʏ�̉~�bz�b���P��ɂ��邱�Ƃ����������D
f(��)��cosn�Ɓ{acos(n�|2)�Ɓ@(0���Ɓ���)���l����ƁC
f(k��/n)��(�|1)^k�{acos((n�|2)��/n)
k����̂Ƃ����̒l���Ƃ�C�����̂Ƃ����̒l���Ƃ�D
k��1�C2�C�c�Cn�́C��ԁi(k�|1)��/n�Ck��/n)�j�ŕ�����ς���̂ŁC
�e��Ԃ�1����f(��)��0���݂������̂��Ƃ邱�Ƃ��ł���D
��_1�C��_2�C�c�C��_n�@�i0����_1����_2���c����_n���j
�Ƃ���ƁCw��cos��_k�{��sin��_k�ɂ��āC
�@�@w^n�{aw^(n�|2)�{aw^(2�|n)�{w^(�|n)��2f(��_k�j��0�D
�����ŁC��_k�Ƃ��̕��f�����Ȃ��̂́C���ׂĈقȂ��Ă��āC�S����2n�D
�@�@w^(2n�j�{aw^(2n�|2)�{aw^2�{1��0
���̕������̉����ׂĂɂȂ��Ă��āC
���ׂĕ��f���ʏ�̉~�bz�b���P��ɂ���D�@����
�������ł��傤���H �C�����͂킩�邪�����ňӌ����炤�̂͂ǂ����ƁB >>315
(��+1)^1 - (��-t)^1 = 1+ t ���L�����ł��邱�Ƃ��K�v�B
(��+1)^2 - (��-t)^2 = 2�� + 2��t +1 - t^2 ���L�����ł��邱�Ƃ��K�v�B
�� t=-1���K�v�B
�t�ɂ��̂Ƃ�(��+1)^n - (��-t)^n=0�͗L�����B >>317
f(z) = z^n + ax^{n-1} + az + 1 = Q(z) + P(z),
�@P(z) = az + 1,
�@Q(z) = z^n + az^{n-1},
�Ƃ����B
���� |a| <1 ����@|z| <1�@�ˁ@ P(z) �� 0,
�܂��A|z|=1 ��ł́@|P(z)| = |a+1| = |Q(z)|,
�藝 2.1�@�@|z| <1�@�ˁ@|P(z)| > |Q(z)|�@�ˁ@f(z) �� 0.
������ |Q(z)/P(z)| �Ɂu�ő�l�̌����v��K�p����B�i���͔��������c�j
�i*�@Ahlfors �� p.134 ���Q�Ɓj
�Ƃ���ŁAf(z) �͎��ȑ�������������
�@z^n f(1/z) = f(z)
�@f(1/��) = 0�@�@�́@�@f(��) = 0,
�P�ʉ~�̓����ɂ��� f(z) �̍��ƒP�ʉ~�̊O���ɂ��� f(z) �̍����P�P�ɑΉ�����B
����� �藝 2.1 ����Af(z) �͒P�ʉ~�̓����ɂ��O���ɂ����������Ȃ��B
�܂�@f(z) �̍��͂��ׂĒP�ʉ~����ɂ���B
�m�O�F KU-RIMS�u���^ (2009/Oct)
http://repository.kulib.kyoto-u.ac.jp/dspace/bitstream/2433/141059/1/1665-03.pdf >>317
�kEnestrom-�|�J�̒藝�l
http://suseum.jp/gq/question/2869�@�i�A���h�����_���j >>295
���������瓚�����邾�낤���H
���͂Ȃ��悤�Ɏv����B
�����ɐl�Ԃ̖�Ԃ�������ăE�\���{���ɂ��C�܂���ɓ�����B
��Ԃ͂��݂��̑����͒m���Ă���B
YES�i�͂��j/NO�i�������j�œ������鎿�������ł����邱�Ƃ��ł���B
�ǂ�Ȏ��������ΓV���s���̓���m�邱�Ƃ��ł��邩�H >>309
�P���~�����鎖�O�m�������m�łȂ��Ƃ����ӌ��Ȃ瓯�ӂł��B >>300
�T�C�R���͌����ɂ��ق�1/6���ŏo��悤�ɂȂ��Ă����1/6�Ɖ��肷�邱�ƂɈӖ��͂��邾�낤
�����̖��̏ꍇ�͌����ɂ͊m�肵�Ă��邩��T�C�R���Ɠ����ɍl����ׂ��ƌ����̂��k�قȂ̂ł͂Ȃ��̂���
�m�肵�Ă��鎖���ɑ��ĕ�������������ƂŊm���Ō��܂邱�Ƃł��邩�悤�ɍ��o������i��҂ɃC���`�L������ƍl����ׂ��Ȃ̂ł͂Ȃ������Ă��Ƃ���Ȃ����� �����ɂ��̒���҂ɂȂ����ꍇ�u�i��҂͎��͒��g��m���Ă��Ă����炪�ǂ������������̂����m���Ă���B�����č�������I�l�ɂ����ւ��Ă������ł���ƌ����Ă���v�ƍl���đւ��Ȃ��ƍl���邩���m��Ȃ�
���s���œ����̖������Ȃ̂ł͂Ȃ����낤�� ���������m���ōl���悤�Ƃ����l�����͍��\�ɑ����\�������������m��Ȃ��Ǝv���Ă���
�����Ȉӌ������Ă��ꂼ��ɂȂ�قǂƎv���Ă��܂������������ >>322
����
�R�l�ɓ������₵�đ������Ō��߂�����ȁB �m���ōl���悤�Ƃ��邱�Ǝ��̂��ԈႢ�Ȃ�Ȃ���
�P�ɁA�{�z�ɂȂ�m���Ɣ��z�ɂȂ�m����1/2���ƍ��o���Ă邾���̂���
�u�m�肵�Ă鎖���ɑ��ā`�v�Ȃ�Ă̂�
�g�����v������e�B�E�z�[�����ł�����������A���o�͂����ł͂Ȃ� >>327
�u�O�l�̒��ɂ��܂���ȓz�͂��邩�H �v
������:YES, �R��:NO, ���܂���:YES or NO
YES��1�l �� �����҂����� YES �Ɠ�����.
�@ �����҂� �u�V���s���͂����炩�H�v�ƕ����Ηǂ��B
YES��2�l �� �R�������� NO �Ɠ�����.
�@ �R���� �u�n���s���͂����炩�H�v�ƕ����Ηǂ��B ���w�ň�ԓ��������Đ��_�w�H >>329
���X���肪�Ƃ��������܂��B
�������Ŕ��f�ł���Ƃ������Ƃł���ˁB
�����������ݒ�̕����������ȁH
�����ҁA�i�K���R�����j�R���A�C�܂����3�l������B
�����̑����͒m���Ă��邪�A���҂̑����͒N���m��Ȃ��B
�R�����m�肷�邽�߂�YES�ANO�œ������鎿��i�����j�͉����H �m�����z�̈��
(1,2)�~1�g�@�@(2,4)�~6�g�@�@(4,8)�~3�g�@�@(8,16)�~1�g
�������Ғl
1��2�@�@2��3.57�@�@4��4�@�@8��7�@�@16���W
�E���Ғl���v�Z����Ƃ��Ɏg���m���� 1/2 �Ƃ͌���Ȃ��B
�E�������������������L�����A�������Ă��ς��Ȃ����A���邢�͌������Ȃ������L�����́A�I�����̋��z�ɂ���ĈقȂ�B
�E�ǂ���̕�����I��ł��������������������悢���Ƃ�����B
�E���z�̋��z�y�A�̕p�x�����z�̋��z�y�A�̕p�x�� 2�{�̂Ƃ��́A�������������Ă����Ȃ��Ă��L�����ɕς��͂Ȃ��B �u���Ȃ��̑����� "���܂���" ���H �v
������:NO, �R��:YES, ���܂���:YES or NO
NO��1�l �� �����҂�����NO �Ɠ�����.
�@ �����҂� �u�V���s���͂����炩�H�v�ƕ����Ηǂ��B
NO��2�l �� �R�������� YES �Ɠ�����.
�@ �R���� �u�n���s���͂����炩�H�v�ƕ����Ηǂ��B
��͂�ŏ��̖�肪�G��Ȃ̂�
��������Đݒ��t��������قǂ܂�Ȃ��Ȃ�悤�Ɏv���B >>331
������Ԃ̘b�ł���Ȃ��̂�...
NO��1�l �� �����҂�����NO �Ɠ�����.
�@ �����҂� �u�R���͂������H�v�Ǝw�����ĕ����Ηǂ��B
NO��2�l �� �R�������� YES �Ɠ�����.
�@ ������ �R�� >>332
���ۂ̊m�����z���ǂ����Ȃ�Ă킩��܂�����
���������b���������Ȃ�A�������͖��s�����Ƃ���̂���ԑÓ��ł�
�ł�����A��ԒP����1/2�Ƃ����ł�
��ϊm���̖��Ȃ�ł���A���������Ă̂� >>333
���ݒ�́A
�����̑����͒m���Ă��邪�A���҂̑����͒N���m��Ȃ��B >>335
������Ȃ�����1/2�ɂ����Ȃ���
���1/2�ɂ���Ɩ�����������Ƃ����b�ł��傤 >>337
�����Ȃ�Ăǂ��ɂ����ł����H
�m���͎�ϓI�Ɍ��߂�����A���Ғl����ϓI�����Ă����̂��Ƃł� >>307
�Ȃ�قǗ����ł��I�������������Ӓv���܂��I >>338
�I�����̋��z�����Ƃ��� 1 �~�������Ƃ��܂��B
��������̕����̋��z�� 1/2 �~�ł���m���ƂQ �~�ł���m�����Ƃ��� 1/2 �ł��邽�߂ɂ́A
2�g�̋��z�y�A�A(1/2 �~, 1 �~) �A(1 �~, 2 �~) �̊m�����������Ȃ���Ȃ�܂���B
�����ŁA�I�����̋��z�� 1/2 �~ ��������A2 �~�������肵�����Ƃ��l����ƁA
�����_�@�ŁA(1/2^2) �~, 1/2 �~) �� (1/2 �~, 1 �~) �̊m�����������A
(1 �~, 2 �~) �� (2 �~, 2^2 �~) �̊m�������������Ƃ��킩��܂��B
������J��Ԃ��ƁA((2^m �~, 2^(m+1) �~) �̌`�̋��z�y�A�̊m�������ׂē��������ƂɂȂ�A
�����̘a��������ɂȂ��Ă��܂��A�m���̐��w�I��`�ɔ����鎖�ԂɂȂ�܂��B >>336
NO��1�l �� �����҂�����NO �Ɠ�����.
�@ YES�Ɠ�����2�l�Ɂu���Ȃ��̑����� "���܂���" ���H �v
�@��₢������B�������h��Ȃ���� "�R��"
���̖��͂܂�Ȃ��B
�L����Ŋm�肷�邱�Ƃ����ꂽ����͑��݂��Ȃ��B >>340
�Ӗ��s���ł�
������2�����Ȃ��̂ɂȂ������ʂ�l�����ł����H >>324
�����Ɠǂ�ł�������
>>300�ɂ��������ʂ��ʓI�ɕ������̃p���h�b�N�X�ƌĂ��̂�
�u���g�������Ă��Ȃ���Ԃœ��l�̋c�_������ƁA�ǂ������ɂ����ꍇ���ς����ق������Ғl���������ƂɂȂ�s�����ł���v
�Ƃ����_���Ǝv���܂�(������炷�݂܂���)
���g������ꍇ�ɘb�����肵�Ă��܂��Ă��܂���
���w�I�ɂ��̖����l����Ȃ�A�����̒��g�͂Ƃ���A�����z��p���Č��肳��Ă���ƍl����̂����R����
�����Ē����I��(*)���������Ă������ƍl���Čv�Z����Ə�̃p���h�b�N�X�Ɋׂ�킯�ł����A���̕����w�E���Ă���ʂ肱�̏����͖�������Ȃ��Ƃ����̂����̖��̊�
pdf�ł�improper distribution���l���邱�ƂŐ����������Ă��܂����A�ǂ���ɂ��敪�z�̎����ɂ���Ċ��Ғl�͕ς���Ă��܂��悤�ł�
�ŏ�����5��~��1���~�����p�ӂ��Ă��Ȃ�������`�Ƃ����̂́A�ɒ[�ȕ��z���ɏo���Đ��w�I�v�l��������Ă��邾���ł���A��͂�1�̖ڂ����o�Ȃ��T�C�R����z�肵�Ă���̂Ɠ��l�̏��Ǝv���܂� �ς��Ȃ��ꍇ�̊��Ғl��
1/2*x(���������������I��)+1/2*(����͈Ⴄ������I��)*(1/2*x+1/2*2x)=5x/4
�ς��Ȃ��ꍇ��5x/4,�ς����ꍇ��5x/4�����s�����Ȃ�ł����H ����Ȑݒ�Ȃ�ǂ��ł��H
�P���~�̕����ƂQ���~�̕����̃y�A����ꂽ�傫�ȕ�����疇�A
�T��~�̕����ƂP���~�̕����̃y�A����ꂽ�傫�ȕ�����疇�p�ӂ��A
�悭���������������ő傫�ȕ������P���I�сA�y�A�̒��̂P�����J������P���~�ł������B
�y�A�̂�������ɑւ��錠�����s�g�����������������H 2�ϐ�x(t)�Ay(t)�̘A�������������('��t�ł̔����Aa�Ab�͒萔)
x'=x-ay+(x^2+y^2)(by-x)
y'=ax+y-(x^2+y^2)(bx+y)
�ɑ��āAr=��(x^2+y^2)�A��=��-(b/2)log(x^2+y^2)�Ɨ^��������r'�A��'�����ꂼ��r�Aa�Ab��p���ĕ\���B(r�A�Ƃ�xy�̋ɍ��W�ϊ����̃p�����[�^)
�r���v�Z���܂߂Ă��肢���܂� >>346
�����邩�������邩�͔��X
���x�ł��`�������W�o����̂Ȃ�1���~�������Ƃ��͑ւ����������i�����܂ł��Ȃ���2���~�������Ƃ��͑ւ��Ȃ��������A5��~�������Ƃ��͑ւ����������j
1���o���Ȃ��Ƃ��Ɋ��Ғl�ōl���邱�Ƃ��Ó��Ȃ̂��ǂ����͓N�w >>347
x�f=x-ay+(x^2+y^2)(by-x) = r (c-as)+r^3 (bs-c)
y�f=ax+y-(x^2+y^2)(bx+y) = r (ac+s)-r^3 (bc+s)
�� = �� - (b/2)log(x^2+y^2) = �� - b log(r)
r�f = (x/r) x�f + (y/r) y�f
�@= c ( r (c-as)+r^3 (bs-c) ) + s (r (ac+s)-r^3 (bc+s))
�@= r - r^3
x tan�� = y �@�ˁ@ x�f tan�� + x �Ɓf/cos��^2 = y�f
�Ɓf = (y�f c - x�f s) /r = ( (ac+s)-r^2 (bc+s) )c - ( (c-as)+r^2 (bs-c) )s
�@= a - b r^2
�Ӂf =�Ɓf - b r�f /r
�@= a - b r^2 - b (r - r^3)/r
�@= a - b
�v�Z�~�X���邩������ǁA����ŕ��j�͕�����ł��傤. >>341
��͂�A�C�܂���̂�炬�Ɉˑ����Ȃ��ƉR���͓���ł��Ȃ��ˁB >>349
������܂����A�����܂� ��������_�ʼnE�ƍ��ɓ���������Ă���A�Е��݂̂����ɒʂ���B
���傤�nj����_�ɂ�3n�l�̐l�����āA���̂���n�l�͖{���̂��Ƃ����������An�l�̓E�\�����������An�l�͖{�����E�\�����m���Ō����B
�ނ�3n�l�ɓ���������A���ꂼ�������邱�Ƃ��ł���B
�m���ɑ��ɂ��ǂ蒅���鎿�������B >>352
>297�̎�������ē��𑽐����ō̗p��������B ���^��p�f�ɂ���
�A���̗L�E
��
�A���˗L�E
�̕��̎��������킩��Ȃ��ł� �{���̂��Ƃ�������Ȃ��l�ƉR��������Ȃ��l�̓�������v���Ă��ꂪ�����ȏ�ɂȂ邩�瑽�����Ő����������킩��̂͂悢�Ƃ��āA
>>297�̎���������Ƃ��{�����R�����m���Ō������Đl�����͂ǂ������邱�ƂɂȂ�낤���H >>355
�����Ɍ����C�܂���l�ԂɂƂ��Ă�YES��No�œ������鎿�₶��Ȃ���ˁB >>346
�ʂɐ�g������Ȃ��Ă��P�g�ł��������Ƃł���B�ǂ����̑g�ݍ��킹��
�������͓��m���ł�����������B1���~�ł�Ύ��ւ����ق����������
���҂ł��܂��B
�����A���g��m�炸�ɁA1���~���낤���A5��~���낤���A�����łĂ��Ă�����
����Ƃ����헪���Ƃ����ꍇ�A���Ғl�͂�͂�12500�~�Ȃ�ł���ˁB
�ŁA�����o�Ă��Ă��������Ȃ��Ƃ��헪���Ƃ����Ƃ��Ă���͂�12500�~
�ŕς���̂ł��B���������āA���g��m�炸�ɐ헪�𗧂Ă�̂ł���A
�Ƃ肩���悤���A�Ƃ肩���܂����A�ǂ����ł��������ƂɂȂ�܂��B
����A���g��5��~��1���~��2���~���Ƃ킩���Ă���A���R�헪�͏o��
�������z����ŕς��܂���ˁB5��~�Ȃ�Ƃ肩���A2���~�Ȃ炻�̂܂܁A
���Ă͎̂����ł����A1���~�Ȃ��͂���Ғl��1���~������̂Ŏ�ւ�
��Ƃ������ƂŁB
���O�m����m���Ă邩�m��Ȃ����Ő헪���ς���Ă��܂��͓̂�����O��
�����Γ�����O�Ȃ�ł����ǁB >>348
������J��Ԃ�����ł���ƍl����A���Ғl�ɂ��Ӗ����o�܂���ˁB
��疜�~�����āA200���~��1/1000�̊m���œ����邭�������ǂ���
�Ƃ���1�����̔��łɎQ������̂͂�������Ғl�������Ă��ł��܂��ǂ� >>358
�������A���g��m�炸�ɁA1���~���낤���A5��~���낤���A�����łĂ��Ă�
����������Ƃ����헪���Ƃ����ꍇ�A���Ғl�͂�͂�12500�~�Ȃ�ł���ˁB
(5��+1��+1��+2��)/4��11250�~�@����Ȃ��́H >>355
�C�܂���ɂ��鎿���Yes�Ɠ����邩�ƕ����Ă�Yes�Ƃ�No�Ƃ��������Ȃ�����I���Ȃ甒�[���ȁB�������ł����Ƃ�������B
�����Yes/No�œ������鎿��ɂ���Ȃ�
�w�u�E�����ɒʂ��铹���������Yes�Ɠ����邩�v��Yes�Ɠ����邩�x��YES�Ɠ����邩�H
�Ȃ�C�܂����Yes/No�œ������鎿���OK?
�����ƃG���K���g�Ȏ��₪���肻���B ����������Ȃ��H�m���_�ɂ͂����鐔�w�Ȃŕ�����m���_�ȊO�ɂ��m���Ɏ�ϊm���Ȃ�Ă��̂�����炵�����B
�܂����ꂪ�Ȃ�Ȃ̂��悤����ǁA����Ɋ�Â�����1.25�{�ɂȂ��ł���H���Ғl�B
���w�̊m���_�̘b����Ȃ����Ă����炱���ł���悤�Șb�ł��Ȃ��ł���H �p�@������̊��Ғl�́H(�����O�̉��{�H)
�`�P�@�m�����z(�S���܂��͈ꕔ)�Ɋւ���������������Ȃ���Ί��Ғl�͋��߂��Ȃ�
�`�Q�@���鉼�������A���Ғl�͂��̉���ɉ���������l�ɂȂ�
�D�݂̖��ŁA�ǂ������������̂��H >>363
�ǂ�������������Ƃ������Ă���
A2�̂��鉼��Ƃ����̂����z�̑I���̂��Ƃ��w���Ă���Ȃ�A�S����������
�u�I�����̒��g�Ɋւ�炸�A���������ق�����Ɋ��Ғl�������Ȃ�v�Ƃ����p���h�b�N�X�ɑ���Ƃ��Ă�
�u���҂���鐫���w�C�ӂ�x�ɑ�����(x,2x)�ƂȂ�m����(x,x/2)�ƂȂ�m���͓������x������(���ʂ̈Ӗ��ł�)���z�͑��݂��Ȃ��v
�����K���Ă���Ǝv��
�����A1�A2���������咣 >>288
>��l�̕����̋��z�� 2 �ő���̋��z�� 4 �̏ꍇ�A2 �̐l�� 1 �� 4 �m���Ŋ��҂�
>4 �̐l�� 2 �� 8 �m���Ŋ��҂���̂ŁA�ǂ���̐l���������������L���ɂȂ�B
�������͂��̐����͊Ԉ���Ă���Ǝv���܂��B
2�̐l�͓����܂���4�̐l�͑����܂�����ǂ���̐l�������邱�Ƃɂ͂Ȃ�܂���B
������2�̐l�̗��ꂩ��l�����1��4�����m���H�Ŋ��ҏo��������
4�̐l�̗��ꂩ��l���Ă�2���o��m����8���o�铯�m���Ŋ��҂ł�������
�ǂ�������������������̂悤��"������"(�������d�v)���ǎ��ۂ͓�����Ȃ�����s�v�c�Ȃ�ł��B
>���Ғl���{���ǂ����ƁA���ۂɓ������邩�ǂ����Ƃ͕ʖ��B
�ʖ��ł͂���܂������W�ł͂���܂���B
�Ⴆ��1��U��̂�300�~������T�C�R�������肻�̑���o���ځ~100�~��
���炦��Q�[��������Ƃ���Ɗ��Ғl��350�~�ł��B
���̃T�C�R����1��U��Ə��ꍇ��������ꍇ������ł��傤��100�l��1��U���
����100�l�̎������̍��v�͖w�ǂ̏ꍇ�T�C�R����U��O���������Ă���͂��ł��B
���Ғl�Ƃ͂������������̂��̂ł��B >>365�̑���
�Ȃ̂ł����>>288����Ƃ��ċ������p�^�[���ɓK�������čl����Ȃ�
���z�y�A�� ( �P�� 2 )�A ( 2 �� 4 )�A ( 4 �� 8 ) �� 3 �p�^�[���̕���������Ƃ���B
��������ꂼ��e1000���v6000�ʂ̕��������S���̕����ɘA�Ԃ����܂��B
1�̓����������͂P�`1000��2��������������1001�`2000��
4��������������3001�`4000�ƌ������ɂ����đS���Ɍ������������ǂ������܂��B
�����߂��傤�͌��������������A�܂���Ғl����������������������O���{�ɂȂ�悤�Ɍ�����̂�
�S�����������������ƌ����܂��B�����ŕ����ɘA�Ԃ�2�������Ă���l��1002�̐l�ƌ�����(����̓y�A�Ȃ̂Ō���ł�)���l�ɕ����̘A��1005�̐l�͘A��5�̐l�ƌ������܂��B
������6000�l�S���������������������ʁA�������l������Α������l�����܂����S����
�ŏ��ɕ������J���Ď�ɓ��ꂽ���z�̍��v�͌����O�ƕς��܂���B
���������������ꍇ�̊��Ғl���{���Ɍ�������O����1.25�{�������Ȃ�3000���������J��Ԃ���
�S�����z�������Ȃ��̂͌����I�ɂقƂ�ǂ��肦�܂���B���z�͌���1.25�{�ɋ߂Â��͂�������ł��B
���Ғl�Ƃ͂������������̂��̂��Ƃ͑O�ɏ������Ƃ���ł��B
���̎����畕������������ƌ����O�������Ғl��1.25�{�ɂȂ�Ƃ����̂͊ԈႢ���Ǝv���܂��B
���̎����玄�͌��̖��ɖ߂��2�̕����̂����̈���J����1���~�������ꍇ
������̕�����2���~��5000�~�Ȃ͍̂ŏ������`����Ă���̂Ŋm���ł���
��L�̗��R������Ғl��12500�~����Ȃ���10000�~�Ȃ̂ł���2�̎����ɐ���������ɂ�
�c��̕�����2���~�������Ă���m����5��~�����Ă���m���̔��������Ȃ��Ƃ���p�^�[����������܂���B
�����������[���o������������܂ŒN����������Ȃ��̂ŁE�E�E ���̎�������8�̐l�͊m���ɑ������ >>363
���͓����邩�O���̓�Ɉ�����瓖����m����1/2�ł���A�𐳂����Ǝv�����ǂ����̘b���Ǝv���B >>366
�{���͖����ɂ���g�ݍ��킹���l�����Ȃ��Ƃ����Ȃ��̂ɁA����ɗL���̃p�^�[���ɂ��Ă邩�炨�����Ȃ��Ƃ��N���Ă���
�L���̘b�Ɩ����̘b�ɂ͑傫�Ȋu���肪���邩��A�����z��z�肵�Ȃ���
���x�������Ă邯�ǁA�������ł̈Öق̉����
�u�C�ӂ�x�ɑ�����(x,2x)�ƂȂ�m����(x,x/2)�ƂȂ�m���͓������v
���̏��Ƃ��ꂪ��������Ă��Ȃ��͕̂�����H ����
�K���A�����z�ɂ��Ȃ��Ƃ����Ȃ��킯�ł͂Ȃ��A���U���z�ɏ]���Ƃ��Ă�����
���������̏ꍇ���L���݂̂̃p�^�[���ōl����͈̂Ӗ����Ȃ� >>366
�S����6000��
1��1000�ʁA2��2000�ʁA4��2000�ʁA8��1000��
1�̐l�̌����O���v�l�@�@1*1000��1000
2�̐l�̌����O���v�l�@�@2*2000��4000
4�̐l�̌����O���v�l�@�@4*2000��8000
8�̐l�̌����O���v�l�@�@8*1000��8000
���v�́A21000
1�̐l�̌����㍇�v�l�@�@2*1000��2000�@
2�̐l�̌����㍇�v�l�@�@1*1000+4*1000��5000
4�̐l�̌����㍇�v�l�@�@2*1000+8*1000��10000
8�̐l�̌����O���v�l�@�@4*1000��4000
���v�́A21000�@�@�@�@�@
1�̐l�@�@1000�@���@2000
2�̐l�@�@4000�@���@5000
4�̐l�@�@8000�@���@10000
8�̐l�@�@8000�@���@4000 >>369
�����͗L�������Ȃ��̂ɂȂ������̃p�^�[���������ł����H >>346
����������Ƃ�����ʉ����Ă݂܂���H
�P���~�̕����ƂQ���~�̕����̃y�A����ꂽ�傫�ȕ����� H ���A
�T��~�̕����ƂP���~�̕����̃y�A����ꂽ�傫�ȕ����� L ���p�ӂ��A
�悭���������������ő傫�ȕ������P���I�сA�y�A�̒��̂P�����J������P���~�ł������B
�y�A�̂�������ɑւ��錠�����s�g�������̊��Ғl���AH,L��p���ĕ\���H �{���������ł��Ȃ��ƗႦ�b�������Ȃ� >>372
�����̖��ł͂Ȃ��������f�����l���Ă��邩��
���������m���_�Ƃ����̂͐������f�����\�����āA���̏�Ő��w�����悤�Ƃ����w��ł�
(1�~,2�~)�̏ꍇ��(1���~,2���~)�̏ꍇ��(1���~,2���~)�̏ꍇ���z�肷��Ƃ����̂͊m���Ɍ����I�ł͂Ȃ����ǁA���w�̖��Ƃ��đ�����Ȃ�z�肷�ׂ�
���̂悤�ȍl�����ɔے�I�ȍl�������͎̂��R�ł�
�����A�������̃p���h�b�N�X�͐��w�̖��Ƃ��čl�����Ƃ��ɐ�������̂Ȃ̂ŁA������������Ȃ炻�������������͋N���Ă��܂���
���̏�̋�̓I�Ȑݒ莟��Ƃ���������O�̓��������邾�� >>375
�ł�������2�����Ȃ��ł���H >>376
�������f���Ƃ��ẮA2���̕����̒��g�͒P�Ɋm���ϐ�(�����̉���)�ɉ߂��Ȃ�
�����āA�����ɂ���\�����l������Ƃ����̂́A�������f���̌��t�ŏ����Ίm���ϐ��̒l���R^2(���U�ł��Ȃ�Z^2)�ɂ���Ƃ��������̘b
�����̐��͒l��̎����ɑΉ����Ă��邾���ŁA�m���ϐ��̎�肤��l�̌��̗L�����Ƃ͉���W����܂��� �������łɌ��_�͏o�Ă�Ǝv�����ǂ�
�܂�Ȃ���肾����Ƃ������A���̐ݒ肪�ȒP�Ȋ��Ɍ��_��������₱��������A���_�𗝉��ł��ĂȂ��l�������Ǝ��₵�����Ă銴�� >>369
>�{���͖����ɂ���g�ݍ��킹���l�����Ȃ��Ƃ����Ȃ��̂ɁA����ɗL���̃p�^�[���ɂ��Ă邩�炨�����Ȃ��Ƃ��N���Ă���
�A�����z�ƌ������t���g���Ă���l�͊F���X�̗L���̖��̒��Ŗ����̖��ɂ���ւ���
���邩�炨�����Ȑ����ɂȂ��Ȃ����Ǝv���B
�����͂Q�œ����Ă���̂͂��������琮���̋��z�ł��B�����čŏ��ɊJ���ďo�Ă������z��1���~
������c��̕����ɓ����Ă���̂�5��~��2���~�A�S�ėL���̐����ł���H
�����Ă���ɍŏI�I�Ȑ�����������
�P.��������������
�Q.�������Ȃ�������
�R.�������Ă����Ȃ��Ă�����
�̂ǂꂩ�Ƃ����P���Ȃ��̂Ő����œ������o�Ă鎞�_�ł���͓����Ƃ��Ă͊ԈႢ�ł��B
�������̏�L�P.�|�R.�̓�����I�����Ƃ��Đ������o�Ă��Ă��ǂ��ł������̏ꍇ�ł�
���͌����Ɏ��s���鎖���o������Ȃ̂����瓖�R�L���̖�肾�Ǝv���܂��B
�����̖��Ȃ炻��͎��s�s�\�ł��傤�H
�����ɂ���������l�͖����̖����̕�����p�ӂ��Ă��ł��Ȃ��������̂������ɓ���Ă��ł�����܂��� >>380
���̓_�ɂ��Ă�>>370�Œ��������ʂ�A�A���ł���K�v�͂Ȃ�
�{���ɉ��x�������Ă���ǁA���g�����Ȃ��o�[�W�������܂߂Ă̕������
���̏ꍇ�A���z������Ƃ����̂͏����t���m�������߂Ă�Ɖ��߂����
�����ɂ��Ă͑��Ɏw�E���Ă�l���������ǁA������ɂ��邩�ɂ���ĈقȂ邩��
���w�̖��ɒu��������Ƃ��͊��Ғl�̑召�ɒu�������邱�Ƃ��������A�p���h�b�N�X�͊��Ғl�v�Z�̍ۂɐ�������̂�������Ғl�ɂ��Ęb�����Ă�́A������H
���ꂩ��A�����̖��Ɛ������f���Ƃ͐藣���Ȃ��ƃ_���ł�
>>375��>>377��ǂ�ł������� �����ɗǂ��������v�����܂����I
�����Ɋm�����z�Ƃ������t���g���܂�������������؎g���܂���B
�L���̖�肾���炱�������o���܂����B
�������Ă݂�ƃ����e�B�z�[�����Ǝ��Ă��Č��t�Ɣ��z�̖��ł����B
�����ł����̂͊��������Lj���Ă���p���������̂Ŗ��������Ă݂܂��B
�Ƃ肠���������ŏ�����>>366��
>�c��̕�����2���~�������Ă���m����5��~�����Ă���m���̔��������Ȃ��Ƃ���p�^�[����������܂���B
����͊ԈႢ�ł����B A���������J�����Ƃ���10000�~�������Ă����B
B����A����Ɂu������ς��邱�Ƃ��ł���B1�ɂ�1�~���A����1�ɂ�99999�~�������Ă���B�v�Ǝ����������B
������ς���ׂ����B >>375
�����̏�̋�̓I�Ȑݒ莟��Ƃ���������O�̓��������邾��
���̓�����O�̓��������[�����Ă���Ȃ�����
(1,2)�A(2,4)�A(4,8)�A��3�g6�ʂ̐ݒ�ł̌�������Ғl
1��2�A2��2.5�A4��5�A8��4 ���X�����ĂȂ����ǂ������ł��u�[���ł��Ȃ��I�v���Ė\��܂�����낤�Ȃ� ���𐳂��������ʂ������̘_���I���{��͂��Ȃ��̂������̌����B >>360
���A�����ł����ˁB���݂܂���B
�������悤�����܂����A�ǂ����������11250�~�ɂȂ�Ƃ����̂����X�ł��B �������͂ɂȂ�܂����A>>380��ǂݒ����ċC���������Ƃ������Ă����܂�
���͂����ԑO�ɓ\���Ă���pdf��O���ɒu���Ă��邩��A�p���h�b�N�X�̉������ړI���ƍl���Ă������ǁA�悭�ǂݒ����Ɠ˂��������Ă���l�́u������ς���ׂ����ۂ��v�Ƃ����_�������C�ɂ��Ă���悤������A�������ꗂ��������̂�������Ȃ�
�������̃p���h�b�N�X��
�u������I�Ƃ��A���̕����̒��g�Ɉ˂炸��������̒��g�̊��Ғl��1.25�{�ɂȂ�v
�Ƃ�������
�{���͂Q�Ƃ��Γ��Ȃ̂ɂ���������˂��Ęb
����͌����̖��𗣂�ĕ������𐔊w�̖��Ɖ��߂��Ă���A���̂悤�Ȑ����������z�̑��݂𐔊w�I�ɔے肷�邱�Ƃ�����������
����A���̐l���C�ɂ��Ă���Ǝv����ς���ׂ����ۂ��Ƃ������͎��̐��������ōςނƎv����
�u�����̒��g��(x,2x)��(2x,x)�̂����ꂩ�Ȃ̂ŁA��������������Ƃ��A���Ƃ���x��I��ł����ꍇ��x�~���A2x��I��ł����ꍇ��x�~�̑�������A�����ɂ��lj��œ�������z�̊��Ғl��0�v
�������A����͏�̃p���h�b�N�X�̉����ɂ͉����q�����Ă��Ȃ�
�Ȃ��Ȃ�A��̃p���h�b�N�X�́A����̕����̋��z��m���Ă��鎞�ɂ�������̋��z�̊��Ғl���v�Z����A�Ƃ��������t���m�������b
���̐����ł͂�������̕����̋��z�̊��Ғl�v�Z��������Ă��邾���ŁA�ǂ������������̂��͎w�E�ł��Ă��Ȃ�
���������Ӗ��Ŏ��͂����Ɗm�����z��p�����������f�����g��Ȃ���Ȃ�Ȃ��Ə����Ă��܂��� ���X>>210��
�u�Ȃ�Ŋ��Ғl12500�ȂH�[��������I�v
����n�܂��āA�Ƃ��낪�����ł͌`���t�]����
�u�Ȃ��12500����Ȃ��I�[��������I�v
�ɂȂ�Ƃ����B
���X���͂ǂ��Ȃ�H >������I�Ƃ��A���̕����̒��g�Ɉ˂炸��������̒��g�̊��Ғl��1.25�{�ɂȂ�
������A���Ғl���v�Z���邽�߂ɕK�v�Ȋm�����z���s���Ȃ̂ł����Ȃ�Ƃ͌���Ȃ����Ă����ł���B
�����ɂȂ�m����0�Ȃ�A���Ғl��2�{�����A2�{�ɂȂ�m����0�Ȃ���Ғl�͔����B�ǂ�������m��
�Ȃ���Ғl��1.25�{�B >>390
���̐����������o���l���������ǂ�����S�R�Ⴂ�܂�
����͔���Ƃ��ĕ������z����Ă邾��
���ꂾ���ł́A���������悤�ȕ��z�����݂���̂����Ȃ��̂����������Ă��Ȃ��܂܂ł�
�����������͂������������������z�����݂��Ȃ����Ƃ𐔊w�I�Ɏ������Ƃł�
���̏ؖ���pdf�ɂ�����܂����A�����̃X���ł����J�ɏ����Ă�l�����܂����� �p��ł�wiki���ڂ����B
ttps://en.wikipedia.org/wiki/Two_envelopes_problem
Second mathematical variant �̂Ƃ���ɁA
�m�����z��ݒ肵���o�[�W�����������Ă���B ���Ɉ�ڂ̕�������o����z�����m�̐�x��2x�̓�ʂ肵�����肦���A�����
�̏o��m�������ꂼ��0.5���Ƃ���A��ڂ̕�������o����z�̊��Ғl��1.5x
�ɂȂ�B����A��ڂ̕�������x���o��m����0.5�A2x���o��m���� 0.5 �Ȃ̂ŁA
��ڂ̕�������o����z�̊��Ғl�� 0.5*2x + 0.5*x =1.5x �œ����ɂȂ�B
�܂�A�������悤�����܂������Ғl�͓����ɂȂ�B
����Ax �̋�̓I�Ȑ��l���������Ă���A��ڂ̕������J�������_�ł��������
�l���m�肵�Ă��܂��̂ŁA�������ׂ����ǂ����͈�ڂ̕����̒��g����ƂȂ�B ���炵�܂����D317�@�ł��D
>>320�@����
>>321�@����
�����[�����i�A�h�o�C�X�j�����肪�Ƃ��������܂��D
�����̍l�������Ƃ��������̂����C�ɂȂ�Ƃ���Ȃ̂�
�������C�Â��̂��Ƃ�����܂����炨�肢���܂��D
�ʂ̏��ł��A�h�o�C�X�����߂����Ǝv���܂��D (x,y,z)=(sin��,cos��,tan(��-��/3))
����������L�����ƂȂ�Ƃ��A(x,y,z)�Ƃ��čl������g�����ׂċ��߂�B
�Ƃ����߂�K�v�͂Ȃ��B 6�ӂ̒�����8,9,10,11,12,13�ł���l�ʑ̂̑̐ς�L����p�Ǝ��R��n��p����p��n�ƕ\���Ƃ��An�����߂�B >>391
>���������悤�ȕ��z�����݂���̂����Ȃ��̂����������Ă��Ȃ��܂܂ł�
�ǂ��������@�ł���A2�ʂ̕����̒��g���m�肵�����_�ŁA������J����A������
�ǂ��Ȃ邩�͊m�肵�Ă���̂ŁA�������������{���̊m�����z��1,0��0,1�Ȃ̂��ȁB
0.5��0.5�Ƃ������Ƃ͂��肦�Ȃ��H >>399
�P���~���I���m����
�P����I�Ƃ��ɑ����ɂQ��������m�����܂��ĂȂ��܂܂̋c�_����Ȃ��̂��Ȃ��B 2�ʂ̕������m�肷��ۂ�5��~��1���~�̑g�ɂȂ邩�A1���~��2���~�̑g�ɂȂ邩�͓��m���Ƃ���
�͍���B�ŁA�ǂ��炩��2�ʂ��I�ꂽ���Ƃ̊m���Ƃ��ẮA�O�҂̏ꍇ�A1�ʖڂ�1���~�Ȃ�
2�ʖڂ�5��~���o��m����1�Ȃ̂Ŋ��Ғl�i���Ă̂��ς����j��5��~�A��҂̏ꍇ����2�ʖڂ�
2���~���o��m����1�Ȃ̂Ŋ��Ғl��2���~�B�������A�ǂ���̑g���킹���I�ꂽ�̂��Ƃ����m��
�܂ōl�����Ċ��Ғl���Ƃ�A���ꂼ��1/2�Ȃ̂ŁA12500�~�B
����ɁA1�ʖڂ�5000�~��2���~�ł���\���܂Ŋ܂߂Ċ��Ғl���Ƃ�A1�ʖڂŏo����z��
���Ғl��11250�~�B���R�A2�ʖڂŏo����z�̊��Ғl��11250�~�ƂȂ�̂ŁA�����o�Ă�����
�����������Ƃ������Ƃɂ͂Ȃ�Ȃ��B�����܂ł�2�ʂ̕�����I�Ԋm�����ǂ�������m���ɂȂ�
�Ƃ�������1���~���o���ꍇ�Ɍ����ẮA2�ʖڂɊ��҂����ق������ɂȂ�Ƃ��������B >>401
1���~���I���m���͂ǂ��ݒ�H >>402
�{�z�ɂ��邩���z�ɂ��邩�͌ܕ��ܕ��Ƃ���Ƃ���
1���~���I���m����2���~���I���m��*0.5��5��~���I���m��*0.5���܂ނ��ƂɂȂ��ˁH (1,2)�A(2,4)�A(4,8)
�J���O���Ғl�@3.5��3.5(1�{)
�J������Ғl�@1��2(2�{)�@2��2.5(1.25�{)�@4���T(1.25�{)�@8��4(0.5�{)
�ő�z�ȊO�͌�������Γ��ɂȂ�(���Ғl��1�{)
�ő�z�̏�����Ȃ����Ƃǂ��Ȃ邩�H
�T���N�g�y�e���X�u���O�̃p���h�N�X�Ɏ��Ă�Ǝv���� >>404
�T���N�g�y�e���X�u���O�̃p���h�b�N�X�̏ꍇ�͈ꉞ�m���_�̃��f���Ƃ��Ă͐������Ă邯�ǁA�ł������I�Ȋ��o�Ƃ͂���Ă��ˁH�������B
�ł����̕����̃p���h�b�N�X�� �h���ׂĂ̏ꍇ�Ŋ��Ғl1.25�{�h �͂�����������Ȋm���̃��f�������Ȃ��B
���̍��͂ł����B �Q�[���̎�Î҂� ���z{x,2x} ��2���������m���� P(x) �Ƃ��悤.
P(5000) = P(10000) = 1/2, P(��)=0 �����肵�Ă����̂��H
����Ȃ̐ݖ�ɖ����ȏ�A�i���ɂ킩��Ȃ��B
�m���̐����� �� P(x) = 1 �Ȃ̂͊m��.
[�I���������̂܂��헪]�ł̊��Ғl
E1 = �� x*P(x) *(1/2) + 2x * P(x) *(1/2) = 3/2 �� x*P(x)
[�I��������������헪]�ł̊��Ғl
E2 = �� 2x*P(x) *(1/2) + x * P(x) *(1/2) = 3/2 �� x*P(x)
�����ς��킯�Ȃ����.
�ł����X�ƃJ�L�R�������Ă���Ă̂́A�������ĂȂ��l�����Ȃ肢��낤. ���đI�������J������ ���z Q ���m�F�ł���. �����Ȃ�m����
A = P(Q) * (1/2) + P(Q/2) * (1/2)
���ꂪ�ȍ~�̏����t���m���̕���ƂȂ�.
A���̂͌v�Z�ł��Ȃ��Ă��\��Ȃ��A�ŏI�I�ɂ͊m���� P(Q) : P(Q/2) �������K�v�ɂȂ�.
�������邵�Ȃ��ɊW�Ȃ� ���z Q �̎����͊m�肵������A���� E1 �� E2 �͖Y��Ă���.
[���̂܂��헪]�ł̊��Ғl
E3 = ( Q * P(Q) * (1/2) + Q * P(Q/2) * (1/2) )/A = Q
����Ⴛ����. �ł��������v�Z�ł���̂͗ǂ���.
[��������헪]�ł̊��Ғl
E4 = ( 2Q * P(Q) * (1/2) + Q/2 * P(Q/2) * (1/2) )/A (��ʂɂ� E4 �� E3 �ł���)
2�����������m����ɂ���đ��v�͕ς��.
P(Q) : P(Q/2) = 1 : 1 ���Ƃ�����AE4 = 2Q*(1/2) + Q/2 *(1/2) = 5Q/4 (+Q/4 �̓��ł���)
���v�̕���_�ɂ���
2Q * p + Q/2 * (1-p) = Q �� p = 1/3
�܂� P(Q) : P(Q/2) = 1 : 2 �ł���.
���Ƃ��� P(Q) : P(Q/2) = 1 : 3 �Ȃ�����헪�� (���Ғl�I�ɂ�)���ł���.
������āA����ȉ��X�Ƌc�_���d�˂�悤�ȓ��e����Ȃ�����. �ߋ��X���̂��̂�\���Ă���
�����
�P�@�Q�̕���������A���ɂ��ꂼ�ꂨ���������Ă���B�����Ă�����z�̔�͂P�F�Q�Ƃ���B
�Q�@�����_���Ɉ����I�ԁB�i�܂�A���z�������ق���I�Ԃ��A�Ⴂ�ق���I�Ԃ��A���ꂼ��̊m����1/2�ł���Ƃ���B�j
�R�@�I�����̒��������10000�~�������B
�S�@���̂Ƃ������̑܂ɓ����Ă�����z��5000�~��20000�~�ł���B
�T�@���ꂼ��̊m����1/2�ł���B
�U�@����đ����̑܂̋��z�̊��Ғl��12500�~�ƂȂ�A�I�����̋��z��1.25�{�B
�V�@���߂ɑI���z�������Ȃ�ꍇ�ɂ����Ă��A�����̕�����2�{�A1/2�{�ł���m���͂��ꂼ��1/2�ł���B
�W�@���߂ɑI�����̋��z�������Ȃ�ꍇ�ɂ����Ă�������I�ׂ�1.25�{�ɂȂ�B
P�@����ĕ����̋��z�����Ȃ��Ă��A�������������̊��Ғl�͑I�����̋��z��1.25�{�ɂȂ�B�{���H
Q�@��l������̕����A�ʂ̈�l�������̕����I�B�ނ�͒��g�������Ɍ݂��Ɍ������邱�Ƃɂ���Ċ��Ғl��1.25�{�ɂȂ�B�{���H
R�@���g�������ɁA����ς肱�����ɂ���B����ς肱�����ɂ���B�ƌ������邾���Ŋ��Ғl��1.25�{�A1.25�{�Ƒ�����B�{���H
����
A�@�T�̊m���ɂ͍������Ȃ��B�T�͏����t���m���ł����ĂQ�̊m���Ƃ͕ʕ��ł���A
�@�u���߂ɂǂ̂悤�Ȋm�����z�ł�������ꂽ�̂��H�v�Ɉˑ�����B
�@���ꂪ�^�����Ă��Ȃ��̂Łu���ꂼ��̊m���͕�����Ȃ��v�������B
B�@���̗���ɏ]�������͂Ȃ����T���������Ɖ��肵�Ęb��i�߂悤�B
�@�܂�A�P�ɂ����ĂT���������Ȃ�悤�Ȋm�����z�ł�������ꂽ���̂Ƃ��悤
�@(���ۂ��̂悤�Ȋm�����z�͑��݂���)�B�@���̏ꍇ�ɂ͂U�͐������B
C�@�������Ȃ���A�V�𐳂����Ƃ��邱�Ƃ͕s�\�ł���B
�@�܂�A�V���������Ȃ�悤�Ȋm�����z�͑��݂��Ȃ��B
�@����āA�W�ȍ~�͌��������̉��ł̍l�@�ł��薳�Ӗ��ł���B
D�@�������A�W����������悤�ȕ����ւ̂����̓�����̊m�����z�͑��݂���B
�@���Ȃ݂ɁA���̊m�����z�̊J���O�̊��Ғl�͂ǂ���̕�����������ɔ��U���Ă���B >>408
����ς蕪�����ĂȂ��B
�N�����̑傫���l�Ɉ�������ꂽ�낤�ȁB(���������m���߂�C�͂Ȃ�) �����܂��Ԃ������Ă܂��܂Ƃ܂��ĂȂ��ł����r���܂�
>>388
>����͌����̖��𗣂�ĕ������𐔊w�̖��Ɖ��߂��Ă���A���̂悤�Ȑ����������z�̑��݂𐔊w�I�ɔے肷�邱�Ƃ�����������
���̍s�ƍŌ��1�s�ȊO�͑S�ē��ӂ��܂��B
����2�s���ے肷��ƌ����킯����Ȃ��悭�킩��Ȃ��Ƃ��������ł��B
>>382�ŗǂ��������v�������ƌ������̂ł������͂܂���肭�����ł��Ȃ��̂�
>>288�������p�^�[���̏ꍇ���������Ŗ������ɂȂ��邩�ƍl���Ă݂܂����B
1.�ŏ��ɏo��������1���������������̊��Ғl��2��+1�̗��v�����҂ł���
2.�ŏ��ɏo��������2���������������̊��Ғl��2.5��+0.5�̗��v�����ҏo����
3.�ŏ��ɏo��������4���������������̊��Ғl��5��+1�̗��v�����ҏo����
4.�ŏ��ɏo��������8���������������̊��Ғl��4��-4�̑������ҁH�o����
���̓�2�D��3.��1.��4��2�{�̃p�^�[��(1�2�̏ꍇ��2���o���ꍇ��2��4�̏ꍇ��2���o���ꍇ)���L��̂�2�{�����1-4�̏ꍇ�̗��v�̊��Ғl�̍��v��1+0.5�~2+1�~2+(-4)=0
�ƂȂ���Ғl��1.25�{�ŗL��悤�Ɍ�����̂͊ԈႢ�Ŏ��ۂ�1�{���Ɣ���
���Ғl��1.25�{�ɂȂ�ꍇ�͊m���ɑ��݂���A�����̏ꍇ����������̂�
�ŏ��ɑI��������o�����z�������ɓ����ꂽ���z�̓��̍ő�l�ł��ŏ��l�ł��Ȃ�
���̔{�z����є��z�����̕����ɓ����Ă���\��������ꍇ(288����̃p�^�[������2��4)�݂̂��ƌ��������Ǝv���B
�����Ă��̔{�z�܂��͔��z�̐��������݂��Ȃ��z���ŏ��̕�������o���Ă��܂����ꍇ
�͗Ⴆ�ő�̐��l�̏ꍇ�͂��̔��z�����Ғl�܂�0.5�ɂȂ�ŏ��̐��l�̏ꍇ�͊��Ғl��2�ɂȂ�B
���̖��͍ŏ��̕�������o�����z�̐��i�ɂ���Ďc��̕����̊��Ғl���ϓ�����_�����킹��_�Ȃ�Ȃ����Ǝv���B ����
�����Ă��̍ŏ��̕�������o�����z�̐��i(�{�z�┼�z���c��̕����ɑ��݂��Ȃ�)
����I�ԑ��͒m�鎖�͏o���Ȃ��������ɂ�������ꂽ���̐l�ɂ͔����Ă���B
�����ɂ�������ꂽ���̐l���炷��ƕ����̊��Ғl�͑S�R�s�v�c�ł͖���1�{�Ɍ�����
�܂�����Ƃ��Ă��̌����̕�����1�2�4�8�������Ă���Ƃ���Ɠ��R�P�̔�����0.5��
���݂��Ȃ���8�̔{��16�����݂��Ȃ��B
����͓Ƃ茾�����Ǎŏ��̖��Ƃ͕ʂ̘b�ɂȂ邯��1�2�4�8��1��2��4��8����
5��1���2���4����1250�2500�5��1���̂R�̃p�^�[��������Ƃ��ĕ�����
��������ꂽ�l�ɂ���1���~�����̔{�z�܂��͔��z�������̒��ɑ��݂��邩�ǂ�����
�����đ��݂���Ɠ���������Ғl��1.25�{�Ŋm�肷�邯�Ǒ��݂��Ȃ��Ɠ�����ꂽ����Ғl�̓}�C�i�X�{�ƂȂ�E�E�E����1���̔{�Ɣ��z�����݂��邩�ǂ����Ŋ��Ғl�͕ς��E�E�E
�܂��������炭�l���Ă݂܂� ���J���Ł@�@���Ғl�s�ϐ��@�@���@�@���M����
�J���Ł@�@�@���Ғl�s�����@�@���@�@����Ǝv��
�@�@�@�@�@�@���Ғl1.25�{���@���@�@�^�`����
�@�@�@�@�@�@���Ғl�s�ϐ��@�@�~�@�@�����ā~�ɂ��Ă݂�
�@�@�@�@�@�@ ���o�H�ˑ����iPath dependence�j
�u������ɂ����āA�l��g�D���Ƃ錈�f�́A
�i�ߋ��̏ƌ��݂̏͌��i�K�ł͑S�����W�ł������Ƃ��Ă��j
�ߋ��̂ɂ��̐l��g�D���I���������f�ɂ���Đ������v
�Ƃ������_�ł� >>402
1/2�ł���B5000�~��2���~��1/4�B��������Ғl��11250�~�B
>>403
�i5000�~�A1���~�j�Ɓi1���~�A2���~�j�̓�g����ǂ��炩��I�сA
����ɂ��ꂼ�ꂩ��1���~��I�Ԃ̂�����A1���~���I���m����
0.5*0.5+0.5*0.5=0.5 >>404
�ő�z�������Ƃ͂ł��Ȃ��ł���ˁB
�������A���̍ő�z�ő������邩�炱���A�����O��̊��Ғl���������Ȃ��āA
�����̒��g�ɂ�炸���������ق������Ƃ����p���h�b�N�X���������Ȃ��B >>415
���̂悤�ɂ���ő�z�͑��݂��Ȃ��Ȃ�̂ł�
�E��[n=1~��]a_n=1�ƂȂ鐳����{a_n}���P�I�ьŒ�
�E0�`1��Ԃŗ���x��������
�E�����g�̋��z�̑g�ݍ��킹��(k,2k)�Ƃ�������2�ʂ�p�ӂ���
�A���Ak��
��[n=1~k-1]a_n �� x < ��[n=1~k]a_n
�������R��
�E�Q���҂�2���̕�����������I��
����Ȃ�ő�z�͂�����ł����₹��
���Ȃ݂�(k,2k)���I���m����a_k�ƂȂ�
���܂�a_k��I������ƁA�����t���̊��Ғl����Ɍ��̕����̋��z������悤�ɂ��ł���
�����Ŏ��s�s�\�Ƃ��C�ɂ���Ȃ�A�����̑���ɓ��_���Ⴆ��Ƃ����ł�����
���邢�͒��ۓI�Ȑ��w�̖�肾�Ǝv���Ă����Ζ��Ȃ� >>416
���ꂾ�Ə��Ȃ����̕����̋��z�Ƃ�k�ƂȂ�m��������x�̉E�A�����z����F(t) = P(x < t)�Ƃ����
�@P(�Ɓ�k) = P(x < ��[n=1~k]a_n) = F(x < t)
�ɂ��
�@P(��=k) = F(��[n=1~k]a_n) - F(��[n=1~k-1]a_n)
�ƂȂ�܂��B
x�̕��z��[0,1]��Ԃ̈�l���z�Ȃ�F(t) = t (0��t��1) �Ȃ̂�
�@P(��=k) = ��[n=1~k]a_n - ��[n=1~k-1]a_n = a_k
�ƂȂ�܂��B
��Ƃ��� a_k = (1/2)^k�Ax����l���z�Ȃ�
�@P(��=k) = (1/2)^k
�ł��B
���� P(��=k) �͈��l�ɂ͂Ȃ�܂���B
������܂��ł��B
�EP(��=k)�����
�E��[k] P(��=k) = 1
�̂Q����������͂��Ȃ���ł���B >>417
�w�E���Y���Ă���Ǝv���܂�
P(��=k)���萔�ł���K�v�͂���܂���
�����Ŗ��Ȃ̂�E(Y|X=k)��k�̑召�ł�
(X�͑I�����̒��g�AY�͂�������̕����̒��g)
a_k��K�ɐݒ肷���
��k E(Y|X=k) > k
�Ƃł��܂�(=1.25k�͂�������ł�)
�Ⴆ��
a_k=(1/2)*(2/3)^k
�̏ꍇ�Ɍv�Z���Ă݂Ă�������
���Ƃ��Ƃ�>>404�́u�S�Ă̕����ɑ����������Ƃ��̊��Ғl������荂�����邱�Ƃ͂ł��邩�v�Ƃ����^��ւ̒�Ăł�
���1.25�{�ɂȂ�Ƃ͈ꌾ�������Ă��܂��� >>418
�S�Ă̕����ɑ����������Ƃ��̊��Ғl������荂�����邱�Ƃ͂ł��邩�v
��������������No�ł���H
����������Îґ��̗p�ӂ���Ƃ̕��z��L^1=���Ғl�v�Z�\�Ƃ͌���܂��AE(��)����������Ƃ���
��Ɍ����ł���ɕێ��ł�
�@E(�l�����z) = 3/2 E(��)
�ł��B
���Ȃ݂ɂ��̖����Q�[�����_�Ƃ���
�@
�E��Îґ��̐헪��E(��)�����ł���Ƃ�p�ӂ���B
�E�Q���ґ��̐헪�͍ŏ��ɊJ���������̋��z�ɉ����ĕێ�����������I������B
�Ƃ���ƁA�����Q���ґ�����Îґ��̐헪��m�蓾���ꍇ�ɂ͌��������ꍇ�ƕێ������ꍇ�̊��Ғl���v�Z������̂ŁA���̍�������I�ׂΊ��Ғl��3/2E(��)���傫���ł��܂��B
�������t�ɎQ���ґ�����������邱�Ƃ��ł��Ȃ��ꍇ�A�Q���ґ��� �g��Ɍ����헪�h�A�g��ɕێ��헪�h �ȊO�̐헪���Ƃ�ƁA��Îґ��͐�̂Q�̐헪�̏ꍇ��茋�ʂ������Ȃ�Ƃ�I�ׂ܂��B
�܂�A���̏ꍇ�̎Q���ґ��̃~�j�}�b�N�X�헪�� �g��Ɍ����헪�h�A�܂��� �g��ɕێ��헪�h �ł��̏ꍇ�̊��Ғl�͂Ƃ��� 3/2 E(��) �ł��B >>419
�����܂���B�����B
�Q���ґ��̃~�j�}�b�N�X�헪��[0,��]��
r �`s �� log[2]r/s �� Z
�œ��l�ނ������߂Ċe���l��C���Ƃ�r[C]��[0,��]���߂āAx���ŏ��̕����̋��z�Ƃ���
x��C�Ax<C[r]�Ȃ�����Ax��C[r]�Ȃ�ێ�
�ł��B(���ׂĂ�r[C]��0�Ȃ��ɕێ��헪�A���ׂĂ�r[C]�����Ȃ��Ɍ����헪�B)
���̏ꍇ��Îґ����ǂ�ȃƂ������Ă��Ă����Ғl��3/2E(��)�ȏ�ɂȂ�܂��B
�t�ɂ����ꂩ��C�ɑ�����r��
�Ex=2r �Ȃ�����Ax=r �Ȃ�ێ�
�ƂȂ���̂�����Ύ�Îґ��͏��{r,2r}��p�ӂ���ΎQ���҂̊l��������z�͏��r�ƂȂ�A3/2E(��) = 3/2 r ��菬�����Ȃ��Ă��܂��܂��B >>398
4�ʑ�ABCP��6�ӂ̓���
�@(AB)^2 = x�C(CP)^2 = X,
�@(BC)^2 = y�C(AP)^2 = Y,
�@(CA)^2 = z�C(BP)^2 = Z,
�Ƃ���Ɓ@�̐�V �̓���
V^2 = (1/288)| 0, x, y, z, 1 |
�@�@�@�@�@�@�@ | x, 0, X, Y, 1 |
�@�@�@�@�@�@�@ | y, X, 0, Z, 1 |
�@�@�@�@�@�@�@ | z, Y, Z, 0, 1 |
�@�@�@�@�@�@�@ | 1, 1, 1, 1, 0 |
�@= (1/12)^2 {xX(-x+y+z-X+Y+Z) + yY(x-y+z+X-Y+Z) + zZ(x+y-z+X+Y-Z) -xyz -xYZ -XyZ -XYz},
(Euler�̌����ASommerville �̌���) ����ł�
�֓��B�̢�W���ƈʑ���@BP6.2.10�@�ł��B
�I�������ɂ��a �� ��_i X_i �����݂���B
�Ƃ��ċc�_��i�߂Ă��܂��B
�������A�P�ɐϏW������̌�����邾���ŗǂ��̂ł���A�P�ɢ
�@�@�ϏW����_i X_i����ł��鎞�͒藝�͖��炩�ɂȂ藧�̂�
�@�@�ϏW����_i X_i�͋�ł͂Ȃ��Ɖ��肵�ďؖ�����悢�B
��Ƃ����_�@�ɂ���ďؖ����o�����Ȃ���ł����H
���������ł���A���̒藝��AC���g�킸���ďؖ��o������Ď��ɂ͂Ȃ�܂��ˁH �ȂQ�Ă�Ԃɑ��̕����烌�X�����ĂĎ֑���������܂��A�A�A�A
>>416
���̗�͒P�� (1,2),(2,4),�c(2^(n-1),2^n)�Ƃ������g�̕����̑g��n->���ŗp�ӂ����
�Ɠ����b�ł���ˁB����ł́u�ő�z�ƂȂ镕����I�Ԃ��Ƃ��ł��Ȃ��v�킯�ł��B
���� >>415�Łu�ő�z�������Ƃ��ł��Ȃ��v�ƌ����Ă�̂͂��������Ӗ��ł��B
�����I�ɂ͕s�\�Ȑݒ�ł���ˁB
�ŁA���������悤��n->�����\���Ƃ��āA�����̑g���J�����̊��Ғl�����U���Ȃ�
�悤�ɏd�ݕt���m���őI��ł��A�m���ɏ�Ɍ��������������ɂȂ�Ƃ����p��
�h�b�N�X�����藧�������ȋC�����܂��B�d�݂̕t�����ɂ���Ắi���Ƃ��� 1/4^n��
����Ɗ��Ғl��0.8�{�ɂȂ�j�A��������Ə�ɑ�������p�^�[�������܂��ˁB
�������An�ɏ����^����A�p���h�b�N�X�͂������ɉ������܂����B >>419
�Q�[�����_�̘b��͎��̎�|�ƈႤ�̂łǂ��ł������ł�
��ł������܂�����
��k E(Y|X=k) > k
�Ƃ��邱�Ƃ͉\�ł���H
E(��)���������邩������Ȃ��Ƃ������Ă܂����A���̏��������������悤�ȏꍇ�͂������������܂���
�J��Ԃ��ɂȂ�܂����A���͂�����������Ώ�̐��������悤�ɂł���Ƃ������Ƃ������Ă��邾���ł� >>423
�����Ŏ��s�s�\�Ȃ̂͂����ł���
�����ȗ�����p�ӂ��邱�Ƃ͖����ł���
�ׂ������Ƃ������A�L���ȏꍇ�ł������ɖ���ׂɂ��邱�Ƃ͌�����s�\�Ȃ̂ŁA���s�\�����C�ɂ���Ӗ��͂Ȃ��Ǝv���Ă��܂���
���Ƃ��ƁA�m������Ғl�̌v�Z�͖��𐔊w�̌��t�ɒu�������ď��߂ĈӖ��������̂Ȃ̂�
���w�I�ɂ͋Ɍ����Ƃ�ȂǂƎv�킸�Ƃ��ł��Ȃ��ł����ˁH
Z��a_k�ɉ��������U���x������悢�Ǝv���Ă����̂ł���
�����m���_�͋�肾����A�Ԉ�������Ƃ������Ă��炷�݂܂��� m�An�����R���Ƃ���B
x�ɂ��Ă̕�����
x^m(1-x^n)=1
�����̗L�����������悤��(m,n)�̑g�����ׂċ��߂�B
�Ȃ������ɑ��݂���ꍇ�͂����̑g�̋K�����ɂ��ďq�ׁA���݂��Ȃ��ꍇ�́u�Ȃ��v�ƋL�����̗��R���Ȍ��ɏ����B >>423
�����X�����A�����I�ɕs�\�Ȑݒ�Ƃ͂ǂ��������Ƃ��H
�z�ʒʂ�Ɂu�����̕����v��p�ӂ���K�v�͂Ȃ��ł���H
���Ƃ��A(2^n,2^{n�{1}) (n��0) �̕����� (1/3)(2/3)^n �̊m����
�o������Ƃ��A��������Ώ�ɓ�������(�͂�)�B
�������E�� (2^n,2^{n�{1}) (n��0) �̕����� (1/2)(2/3)^{n�{1} �̊m����
�p�ӂ��邽�߂ɂ́A�\�� 2/3 �̊m���ŏo��R�C����1���p�ӂ��āA
���q����ɂ͌����Ȃ��悤�ɂ��̃R�C���𗠂��o��܂ʼn��x�����������āA
�����o�����_�ŁA���̂Ƃ��܂łɏo���\�̍��v��n�Ƃ��āA2�̃����p����
�G���s�c��2^n��2^{n�{1}�������āA����2�̃����p�������z2^n, 2^{n�{1}��
�����Ɍ����ĂāA�������̒��ɓ���āA��������q����ɓn�������B
�܂�A���̐ݒ�����������邽�߂ɗp�ӂ��ׂ�������1�������ł悭�āA
�厖�Ȃ̂͊m�� (1/3)(2/3)^n ���������邱�Ƃł���A
���̊m������������ɂ̓R�C���g�X���邾���ł����B
�S�ėL���̎菇�Ō������E�Ŏ����\�B >>427
>�z�ʒʂ�Ɂu�����̕����v��p�ӂ���K�v�͂Ȃ��ł���H
���������ꂽ��ł́An������Ȃ��傫���P�[�X�ł̓R�C�����������X��
�����Ȃ���Ȃ炸�A�����I�ɂ͂ǂ����ɏ�����ł��Ă��܂��܂���ˁB
�Ƃ͂����An���\���傫������܂��ԈႢ�Ȃ����������ق������ɂȂ�͂�
�Ȃ̂͊m���B�ł��A���Ғl�Ƃ��Ă͍ő�z�����邱�Ƃœ����ɂȂ��Ă��܂���
�ł���ˁB
�����ƃV���v���ɁA���I�Ȃ��̂��l����������ƁBn�̕����Ɉ����
100n�~�̓����肭���������ĂāA���Ƃ͋���ہB���̕����������_���Ɉ����
100�~�����đI��Ŕ����Ƃ������l����Ύ����悤�Ȃ��̂��ƁB�n�Y���đ�
����m����(n-1)/n�Ȃ̂ŁAn->���ł͐�ɑ�����͂��Ȃ�ł����ǁA���Ғl��
100�~�̂܂܁B �q�����܂���������A�ȉ��̐����ɔ[�����Ă��܂���
���܂��ŏ��ɂP���~�Q�b�g�B
�����ɁA�T��~����������R�{�̂P���T��~�ɂ���`�����X�ɒ���ł���B
�����킷�ׂ����H
���`�����X�̑傫���ɂ�肯��B�i�m��1/3�ȏ�Ȃ畽�ϓI�ɓ��j >>418
>a_k=(1/2)*(2/3)^k
���ꂾ�ƍŏ��ɃQ�b�g�ł�����z�̊��Ғl���������Ȃ��̂ł́H
���Ғl�̓�a_k(3/2)2^k�ł�����Aa_k��(1/2)^k��菬�����Ȃ��Ƃ��߂ł���ˁB
��������ƁA2^k���o�����ɁA������ւ����牽�{�ɂȂ�Ɗ��҂���邩�Ƃ�����
{a_k*(1/2)+a_(k+1)*2}/{a_k+a_(k+1)}
�ł�����Aa_k��k�ɂ��Ȃ��萔���Ɠ��R5/4�ŁA�ւ���Ɠ��B
a_k��r^k ���Ƃ���Ɓ@(1+4r)/2(1+r)�ɂȂ�̂ŁAr=1/2 ��1�ɂȂ�Ar��������
�������Ȃ�ƕ�����ւ���Ƒ������邱�ƂɂȂ�B >>429
x�����̗L�����ł���Ƃ���A0<x<1�̂͂��Ȃ̂ŁA
x=b/a �ib<a��a,b�͌��������Ȃ��j
�Ƃ����Ď��ό`����悢�̂ł́H �łȂ���(1-x^n)�����ɂȂ����Ⴄ�ł���B >>428
�����������ꂽ��ł́An������Ȃ��傫���P�[�X�ł̓R�C�����������X��
�������Ȃ���Ȃ炸�A�����I�ɂ͂ǂ����ɏ�����ł��Ă��܂��܂���ˁB
���@A�N��B�N���W�����P��������B�������A�ǂ��炩��1������܂�
�W�����P����������Ƃ���B���̂Ƃ��AA�N��1������m�������߂�B
���̖��̉́u1/2�v�����A���Ȃ���
�u�i���ɂ������ɂȂ�p�^�[���ł͏��������Ȃ�����A1/2�ɂȂ�Ȃ��v
�Ƃ�
�u�������E�ł͂ǂ����ɏ�����ł��Ă��܂��A1/2�ɂȂ�Ȃ��v
�Ƃ��������肩�ˁH dy/dx=c�̍��ӂ�dy����dx�ƍl����dy=cdx�Ƃ���̂͌��Nj������́H >>426
m�An�����R���A x�𐳂̗L�����Ƃ���.
0 < x < 1 �Ȃ�� 0 < x^m(1-x^n) < 1
1 �� x �Ȃ�� x^m(1-x^n) �� 0
����� x^m(1-x^n) = 1 �����̗L�����������悤��(m,n)�̑g�͑��݂��Ȃ�. >>431
(1/2)*(2/3)^k�̗�͎������������܊ԈႦ�Ă��܂����A���݂܂���
(k,2k)�ƂȂ�m����(1/2)*(2/3)^k�Ƃ��Ă��܂������A��������
(2^k,2^(k+1))�ƂȂ�m����(1/2)*(2/3)^k�A���̑��̑g�ݍ��킹�̎���0
�Ƃ������z���o������ł���
���Ғl�����U���錏�ɂ��Ă͂��łɐG�ꂽ�ʂ�
���͍ŏ������т��ď����t���Ғl�̘b�����Ă邾���ł� >>436
�����A�̈Ӗ������ɂ��
1�ϐ��̏ꍇ�͂��̂����ŕϐ��ϊ������߂Ă��ԈႤ���Ƃ͂Ȃ����A�p���ɏ����Ȃ��Ȃ���͂Ȃ����A���w�I�Ȑ������͕��ʂ͂���Ȃ��Ǝv�� >>435
���ہA�������E�ł͌�����1/2�ɂ͂Ȃ�Ȃ��ł��傤�ˁB
��l���W�����P���𑱂��邱�Ƃ��ł���̏����N��Ƃ���ƁA
�Ō�܂ň��������ŏI���\��������̂�1/2���(1/3)^N����
�������Ȃ�͂��B >>436
�����`���̘b�Ȃ瑽�l�̂̌`�ɂ��Ƃ���
�Ƃ肠����R^n�Ȃ�|�A���J���̕�肩�炨�� >>317
z�̕��f������Z�Ƃ���B �^���� a��R ���A
(Z^{n-1} + Z) (z^n + 1) = -a (Z^{n-1} + Z) (z^{n-1} + z) = (Z^n + 1) (z^{n-1} +z),
0 = (Z^{n-1} + Z) (z^n + 1) - (Z^n + 1) (z^{n-1} + z)
�@= [(zZ)^{n-1} - 1] (z-Z) + (zZ-1) [z^{n-1) - Z^{n-1}]
�@= (zZ-1) (z-Z)��[k=0,n-2] ((zZ)^k - (1/2)z^k Z^{n-2-k} - (1/2)z^{n-2-k} Z^k)
�@= (zZ-1) (z-Z)��[k=0,n-2] (1/2) (z^k - z^{n-2-k}) (Z^k - Z^{n-2-k})
�@= (1/2) (|z|^2 -1) (z-Z)��[k=0,n-2] | z^k - z^{n-2-k} |^2
��[k=0,n-2] | z^k - z^{n-2-k} |^2 = 0 �̂Ƃ�
�@|z|^2 -1 = 0 �����藧�B
z-Z=0�Cz��R �̂Ƃ�
�@(z^n + 1)^2 - (z^{n-1} + z)^2 = (zz-1) [z^{2n-2} - 1]
�@= (zz-1)^2 [z^{2n-4} + z^{2n-6} + �c�c + zz + 1]
�@�� 0,
�@���������� zz-1 = 0 �̂Ƃ��B����ȊO�̏ꍇ��
�@| z^n + 1 | > | z^{n-1} + 1 | > | az^{n-1} + az |
���s�����B >>431
>��������(2^k,2^(k+1))�ƂȂ�m����(1/2)*(2/3)^k
�����]���ŏ���ɂ����ǂݕς��Ă����̂ŁA�����͂܂�������肠��܂���B ����>>438�͎����Ŕ[���s���܂łق��Ƃ��Ă�����Ȃ��H
�����Ȃ�ɔ[���s���܂ōl��������ł���H
�킯�̂킩���r���o�ߕ��Ă���^�C�v�ł��Ȃ����������B �����͓�����Ȃ��̂ɖ������]�X�����Ă�悤�ȃ��x���̒Ⴂ�l�͖����ł����ł���[ �����͓�����Ȃ��Ă��A�o�Ă�����z�̉\���͖����ɂ��邩��ˁB
���z�̉\����L���Ɍ����Ă��܂��A�p���h�b�N�X�͐����Ȃ��B �����P�̗�����āA�C�ӂ̒l�Ő��藧�͂����A�Ƃ����v�l�p�^�[���́A
��|�l�ɒʂ���Ƃ��낪���� >>445
���Ȃ��͂������肽�������ł����Ɠǂ�łȂ��悤�ł���
���͈�т���
�u(�l�����̊��Ғl�͔��U���Ă邯��)�����t���Ғl����Ɍ����傫���Ȃ镪�z�v
���\���ł���ƌ����Ă邾��
���X��>>404�̋^��ɑ���b��
����ɑ����̂��I�O��ȃc�b�R�~������Ă�
�u(>>417)��Ɋ��Ғl1.25�{�͖����v
�c���͑傫���ł���Ə����������ŁA1.25�{�ɂł���Ƃ͈ꌾ�������ĂȂ�
�u(>>431)�ŏ��ɃQ�b�g�ł�����z�̊��Ғl���������Ȃ��̂ł́H�v�A���̑��v�Z
�c>>424�Ŏ������łɏ��������Ƃ�������̓I�Ȍv�Z��lj����ČJ��Ԃ��Ă邾��
���߂���悭�m���Ă��鐳���������������Ă邾���ł�
��{�I�Șb�Ȃ̂Œ��ׂ�Γ������e�͂�����ł��o�Ă��܂���
�ǂ����Ă������Ԉ���Ă��邱�Ƃɂ������悤�ł����A>>431��>>424�Ɠ����ȓ��e���܂�ł���̂ŁA���ꂾ�Ƃ��̐l���Ԉ���Ă邱�ƂɂȂ�܂��� >>446
�����̖����̗L�����ƁA��肤��l�̉\���̗L��������������ɂ��Ă邾��
�����̖��ł͂Ȃ����w��̃��f���ōl����Ȃ������ł��\�ł�
�����̖����͊m���ϐ����l������Ԃ̎����ɑΉ����Ă邾��
�m���ϐ��̑��̗L�����Ƃ͉���W����܂��� m�An�����R���Ƃ���B
x�ɂ��Ă̕�����
x^m(1+x^n)=3
�����̗L�����������悤��(m,n)�̑g�����݂��邩�ǂ������肵�A���̗��R���q�ׂ�B >>441
�Ȃ��������E���ƃW�����P���̉ɏ��������̂ł����H
�l�Ԃɂ͎���������̂ŁA��������܂ł̃W�����P����
���̓I�ɕs�\�A�݂����Șb�ł����H
���̉F���̎��Ԃ͂ǂ����L���ł���A���������
�F�����̂��̂����ł��邩����������A�݂����Șb�ł����H
�W�����P���̊m�����l����Ƃ��́u�������E�v�ɁA
�ǂ����Ă���ȃi���Z���X�Ȋϓ_���������ނ̂ł����H
���Ȃ����g���Ă���u�������E�ł͕s�\�v�Ƃ����ᔻ�̎d���́A
����ȃi���Z���X�Ȋϓ_����̔ᔻ�Ȃ̂ł����H
��������A���Ȃ��̌����Ă��邱�Ƃ͓I�O��ŁA>>425�̎w�E���I�m�ł��ˁ�
�������ȗ�����p�ӂ��邱�Ƃ͖����ł���
���ׂ������Ƃ������A�L���ȏꍇ�ł������ɖ���ׂɂ��邱�Ƃ͌�����s�\�Ȃ̂ŁA���s�\�����C�ɂ���Ӗ��͂Ȃ��Ǝv���Ă��܂���
�����Ƃ��ƁA�m������Ғl�̌v�Z�͖��𐔊w�̌��t�ɒu�������ď��߂ĈӖ��������̂Ȃ̂� ���₪�킩��ɂ���������������܂���B
�v�����
��ʑ���Ԃ̗�(X_i)�ɂ��āA�eX_i���A���ł���Ȃ�A�����̒��σ�_i X_i �͘A���ł���
�͑I���������g�킸���ďؖ��o���邩
�Ƃ�������ł� >>449
�������t���Ғl����Ɍ����傫���Ȃ镪�z
�m���ɂ����������z���l���邱�Ƃ͂ł��܂����A�����ɂ͍�蓾�Ȃ��ł���ˁB
������z�e���̃p���h�b�N�X��z�N�����܂��ˁB���������z�e�����l���邱�Ƃ�
�ł��邯�ǁA�����ɂ͍��Ȃ��B
�Ȃ�p���h�b�N�X�������ɂ͋N����Ȃ��B�̐S�ȓ_�͂����Ȃ�Ȃ��ł����H ����������Ȃ��H
�K���������������ق��̏����t�����Ғl�̕����傫���Ȃ镪�z����A������Ă���[�������܂ŒT���Ă�������炢�������B >>452
�������E�ł̏펯�Ɛ����I���_�Ƃ̘������p���h�b�N�X�ƌĂԂ̂ł���A
��͂茻�����E�Ŏ����\�ȃ��f�����ǂ������l����ׂ��Ȃ̂ł́H
���������ȗ�����p�ӂ��邱�Ƃ͖����ł���
�����ȗ����Ƃ������t�̈Ӗ����B���������̂Ń��X���܂���ł������A���Ƃ�
�����_�����������ɕۏ��ꂽ�Ƃ��Ă��A���ۂ̌v�Z�ł͗����l�����߂�L��
�����ɏ��������̂ŁA��͂�����\�ȏ���z�������Ō��܂��Ă��܂��܂��ˁB
������ɂ���A���Ȃ��̋c�_����{�I�ɊԈ���Ă���Ƃ͎v���܂���i�Ƃ���
���̌��_���Ԉ���Ă�\���͔F�߂܂������j�B
���Ғl����������悤�ȃP�[�X�ł́A�����t�����Ғl�Ƃ��Ă͌�����������
���Ғl���������Ȃ�̂ŁA�����I�ȃp���h�b�N�X�͎c��܂��ˁB�ǂ���������
�̂����͂������C�ɂȂ�܂��B ���w�̖ʐϔ�̖��
AF:EF�����߂�
BE:EC��3:2�Ȃ̂Ł�BEF:��CEF��3:2
��BCF��5�Ƃ���AFC��X�Ƃ���
AD:BD��1:3�Ȃ̂�X:5��1:3�AX��5/3
��AFC��5/3�Ł�CEF��2�Ȃ̂�5/3:2��5:6
����AE:EF��5:6
�ȏ�͂킩��܂��B�ł�AD:BD����n�߂�Ƃ��������Ȃ�܂��B
AD:BD��1:3�Ȃ̂Ł�ADF:��BDF��1:3
��ABF��4�Ƃ���AFC��X�Ƃ���
BE:EC��3:2�Ȃ̂�X:4��2:3�AX��8/3
��AFC��8/3�Ł�CEF��2�Ȃ̂�8/3:2��4:3
AF:EF��4:3�ɂȂ��Ă��܂��܂�
�ǂ����Ԉ���Ă�̂������ĉ�����
https://i.imgur.com/wrGpQDc.jpg >>458
���̂Ƃ���ł́u��CEF��2�v���Ă��������ǂ�����o�Ă����́H >>459
���������Ă݂�Εςł���
�����l���Ă݂܂� ��͉����܂���
�ł������ԈႢ�Ȃ�ǂ�����Ă��܂�����
�ʐϔ���ăR�c�Ƃ�����܂��H
�⏕����������������Ȃ����Ⴂ���Ȃ���肾�Ƃ����Ⴒ���Ⴕ�ď��X�킩��Ȃ��Ȃ�
�����������Ċ���邵���Ȃ��̂��� >>451
�������݂����Ƃ��� x = a/b (a, b �݂͌��ɑf�Ȏ��R��) �ƒu��.
x^m (1 + x^n ) = 3 ���
a^m ( b^n + a^n ) = 3 b^{n+m}
a, b �݂͌��ɑf�Ȃ̂� a=3, m=1 �ł���.
( b^n + 3^n ) = b^{n+1}
( 1 + (3/b)^n ) = b
���ӂ����R���ƂȂ肦��̂� b=1 �܂��� b=3 �̎��ł���.
�������������� n �͑��݂��Ȃ�.
����ĉ��͑��݂��Ȃ�. ������ƒ���
a^m ( b^n + a^n ) = 3 b^{n+m}
a, b �݂͌��ɑf�Ȃ̂� ( a=1 ) �܂��� (a=3, m=1 ) �ł���.
�Ea=1 �̏ꍇ
b^n + 1 = 3 b^{n+m}
(1/b)^m + (1/b)^{n+m} = 3
1/b �� 1 ��蓙���������͂��肦�Ȃ�.
�Ea=3, m=1 �̏ꍇ (�ȉ���) >>455
���ɋ�̓I�ɗ^���Ă��ł���������
>>454�̕������z�̑��ݎ��͔̂F�߂Ă��܂�
���Ȃ������b�ɂ��Ă���Ă܂����
�������肽��������������܂��� >>454>>457
�ʂɎ��̓p���h�b�N�X�������ɋN����Ȃ�Ĉ�x�������ĂȂ�
>>404�̋^������āA����������@���������(��������ł͎��s�s�\�Ȏv�l����)
�����Ε������Ă��炦���ł�����
���Ȃ�������ɖϑz���Ď��̎咣��P���Ȃ��āA�ˋ�̎��ɔ��_���ЂƂ�x�ɓ����Ă邾��
���̉��߂������Ă����܂��ƁA���̕��z�̑��݂��������Ƃ�
�u(�l�����̊��Ғl�����U����Ȃǂ�)���������ޏł́A���Ғl�Ƃ����w�W��(���Ȃ��Ƃ����̂܂g���̂ł�)���ĂɂȂ�Ȃ��v
�Ƃ������Ƃ��ƍl���܂�
���ꂩ��A���s�\���s�\���������邾���ł͍��{�I�ȉ����ɂ͂Ȃ��Ă��Ȃ��Ǝv���Ă��܂�
(����͂����܂Ōl�̊��z�ł�)
��ڂ̗��R�Ƃ��ẮA�v�l�������邢�͐������f���Ƃ��Ă͍l�����邩��ł���
��ڂ́A���������w�ǑS�Ă̐������f���͌����ƈ�v���Ȃ��ƍl���Ă��邩��ł�
���ׂ�ꂽ������������I�Ԋm���͂ӂ�1/2�Ƃ��Čv�Z���܂����A�����ɂ͈�v���Ȃ��ł��傤
N�̂��̂���P�I�ԏꍇ�����l�ł�
���̔z�u�̎d����Ɩ��̋�A�I�Ԑl�̊��o���ɍ��E�������̂ł�
�ǂ���̕�����I�Ԋm�������l�Ɋm���炵���Ƃ��Ă���̂́A�m���_�𑖂点�邽�߂�
���z�������ɒu�������Ă���ɂ����܂���
�����̖��𐔗����f���ɒu�������Đ������悤�Ƃ������݂͐��w�I���Ǝv���܂����A�������f����
�����̖��ɒu��������(���̂Ɍ��肷��)�K�v�͂Ȃ��ƍl���Ă��܂�
�J��Ԃ��܂����A�����͌l�I�Ȋ��z�ł�
���s�s�\�����炱��ȃ��f���Ŋ��Ғl�v�Z������Ӗ��͂Ȃ��Ƃ����l���������߂܂����A���v�������͂���܂���
�Â� ��L�̍l���ɂ��A���s�\���ɋ������Ȃ������̂ŃX���[���Ă��̂ł����A�C�ɂȂ��Ă������Ƃ��Ă����܂�
>>431�����݂�ƁA�l�����̊��Ғl�����U���邩����s�s�\�Ɣ��f���Ă���悤�ł����A����͉��̂ł����H
�����̃Q�[���ł͕����̒��g�͏�ɗL���ł���A���Ғl�̎������͒��ڊW�����悤�Ɏv���܂�
���z�I�ȗ������u���Ȃ��Ǝ��s�s�\�Ȃ̂łǂ����݂����s�͂ł��܂���
���Ȃ݂ɁA�p���h�b�N�X�̉����̂������̈�Ƃ��Ă͏�ɗL�E�Ȍ��p�����g���Ƃ������@������悤�ł���
�R�C���g�X�̃p���h�b�N�X�Ɠ��l�ł���
���p���̑I���͜��ӓI�Ȃ̂ŁA�ǂ�قǂ̈Ӗ�������̂��͔����ł���
�����炭�R�C���g�X�̗�Ɠ��l�ɍl��������ŗl�X�ȉ����̕��@�����蓾��̂ł��傤 �p���h�b�N�X���������Ȃ����ƂȂ�ē��R�̋��ʔF�����Ǝv���Č��y���ĂȂ������̂ł����A���ꂪ�s���������̂�������Ȃ��ł���
���̓_�͊��Ⴂ�����Ă����Ƃ����炷�݂܂���ł��� >>422
���������ʂ�ŁA���̒��ϏW������ł��邩�Ȃ����ɉ����ďꍇ��������
�ؖ�����Ηǂ��̂ł�����A�w��W�����ʑ���ԂƂ��ĔF�߂�x�Ƃ�������ł���A
�I�������͕K�v����܂���B
(X, O) ���ʑ���Ԃł��邽�߂̏����ɁAX ����W���ł��邱�Ƃ�v�����闧�ꂾ�ƁA
���̐ϏW������łȂ����Ƃ��ؖ����邽�߂ɁA�I���������K�v�ł��B �� : X ����W���ł��邱�Ƃ�v�����闧��
�� : X ����W���łȂ����Ƃ�v�����闧�� 2008�N�@12808���l�@�{ 5���@��
2009�N�@12803���l�@�| 5���@��
2010�N�@12806���l�@�{ 3���@��
2011�N�@12780���l�@�|26���@������ ������������
2012�N�@12752���l�@�|28���@������ ������������
2013�N�@12730���l�@�|22���@������ ��������
2014�N�@12709���l�@�|21���@������ ��������
https://blog.goo.ne.jp/jpnx05/e/a618afaa0113f2a33fbc495f48a2b8c4
�ږ�����̖{���̖{���́A�������̂������ɂ��l���������B���āA
�u�������̂ł͔�Q���Ȃ������v�Ɛ��������邽�߂̓��v�I���������m�ۂ������̂��Ǝ��͍l���Ă���B
���C�A�}�u���Oentry-376.html >>464
�ւ��H�ŏ��̕����̋��z��A,���Ƃ̕���B�Ƃ���(�p���Wikipedia�̐ݒ�)
�C�ӂ� k �ɑ���
E(B | A = k) > k
���������镪�z�������H
�Ƃ������Ƃ�
E(B | A=k) > E(A | A=k)
���C�ӂ� k �ɂ��Đ��藧�B
�Ƃ������Ƃ�
E(B) > E(A)
�ȂB���̕��z���ƁB�Ȃ�قǁB >>471
���łɏ������ʂ肻�̏��������������ꍇ��E(��)�����U���Ă��܂��܂�
(��=���Ȃ����̋��z)
���RE(A),E(B)�����U���Ă��܂�����A���̂Q�̑召��r�͈Ӗ�������܂���
�����t���Ғl�͗L���l�Ȃ̂Ōv�Z�ł��܂���
���ꂭ�炢�̂���Wikipedia�ɂ������Ă���Ǝv���܂��� ����ł����H�Ƃ��k^1 �łȂ��Ă������Ȃ�ǂ��������R�ɁB a��1�łȂ������Ƃ��A
f(x)=1�ix���L�����̂Ƃ��j
f(x)=a�ix���������̂Ƃ��j
�Ɗ�f(x)���߂�B
a���ǂ̂悤�ɒ�߂Ă��Af(x)�͂�����Ƃ���s�A���ł��邱�Ƃ������B >>473
���ݓK���ɓ˂�����ł邾���ł���
Wikipedia���p���Ƃ��Ȃ���낭�ɓǂ�łȂ����A���łɉ��x�������ς݂̂��Ƃ��܂��˂�����ł�����
���Ғl�͔��U������ĉ��x�������Ă�̂ɁA���ō��X�uL^1�łȂ��Ă����Ȃ�v�Ƃ��g���`���J���Ȃ��Ə����Ă�́H�H >>475
���܂�A�ǂ�łȂ������B
�ӂ�܂��B
�������ɂ��ĂȂ����Ă�̂͌������ǂĂ�����������Ȃ��悤�ȕa�I�ȗ�͍l���Ă܂���Ƃ����Ă�Ǝv�����B
���̗���ǂ�łȂ����Ǒ��x�_�̓����ł����܂��Ă��Ȃ�a�I�Ƃ�������͂Ȃ���B
�m����l^1���̐���������Α��݂��Ă��s�v�c�͂Ȃ��Ǝv���B >>468
�ł����
���肪�Ƃ��������܂� >>478
���������߂�����������܂���ˁA�ӂ��Ă����܂�
Wikipedia�̋L���͒����̂œǂދC�ɂȂ�Ȃ��Ǝv���܂����A�����ƓǂނƋ�̗���\�����āA�v�Z���ڂ��������Ă���܂���
���x�_�̌��t������ď�����Ă͂��܂����A��������ɐ������͉\�ł�
(���ʂɑI���x����������U�I�Ȋm����Ԃ���R�ւ̉ϕ��ł͂Ȃ������ƂȂ�͂��ł�) �g�̏�ɍ���Ȃ�������Ƃ���낤�Ƃ��邩��A�{������ǂ�ǂ������Ă��ł���
������2�����Ȃ���ł� >>480
���������B�����炱���B
l^1�łȂ��Ă����Ȃ�����͔C�ӂ� x �ɑ���
E( B | A = x)
=P(��=x)/(P(��=x) + P(��=x/2)) �~ 2x �@�@ �@(A�̕����� x �~�̂Ƃ��� B �̕����� 2x)
+ P(��=x/2)/(P(��=x) + P(��=x/2)) �~ x/2 (A�̕����� x �~�̂Ƃ��� B �̕����� x/2)
> x
�� 2P(��=x) + 1/2 P(��=x/2) > P(��=x) + P(��=x/2)
�� P(��=x) > 1/2 P(��=x/2)
����������Ƃ��B
������
P(��=2^n) = (1/3)(2/3)^n (n=0,1,2,3,�c) =0 (otherwise)
�Ƃł�����Ώ����͊m���ɖ������ˁB
�������x��2�{�ɂȂ邲�ƂɊm���̂ق���1/2�{���傫���Ȃ邱�Ƃ������Ȃ̂ŕK�R�I��l^1�ɂ͓���Ȃ����ǁB >>466
���l�����̊��Ғl�����U���邩����s�s�\�Ɣ��f���Ă���悤�ł����A����͉��̂ł����H
���͂���Ȃ��ƌ����Ă܂���B
���s�s�\�Ȃ͖̂����傪���ނ���ł����āA���Ғl�����U���邩��Ƃ����킯�ł͂���܂���B
���Ғl���������Ă��A�����s�\�Ȑݒ�ł���͓̂������ƁB
���Ғl���������Ȃ��ƍ���̂́A�������Ȃ��ꍇ�Ƃ����ꍇ�̊��Ғl����r�ł��Ȃ�����Ƃ���
�����̘b�ł��B >>465
�����Ȃ�������ɖϑz���Ď��̎咣��P���Ȃ��āA�ˋ�̎��ɔ��_���ЂƂ�x�ɓ����Ă邾��
����Ȃ��Ƃ������o���͖ѓ��Ȃ���ł����A�A�A�A�B
���̐l������Ă�P���c�b�R�~�ƍ������Ă�����̂ł́H�@���͈�т���415�𖼏���Ă܂��B
����������Ώ���z���Ȃ����邱�Ƃ�>>423�ŏ������悤�Ɂi�ǂ݂������Ă݂�Ƃ���
�ЂƂs���Ăł������j>>415�����������_�ł��łɗ����ς݂ł��B
�Ƃ������ƂŁA�Ƃ��ɂ��Ȃ��Ƒ傫�Ȉӌ��̑���͂Ȃ��Ǝv���Ă܂��̂ŁA�������炸�B 2a^2+2a+1���������ƂȂ鎩�R��a�̂���k�Ԗڂɏ��������̂�a_k�Ƃ����B
a_(n+2)=6a_(n+1)-a_n+2�����藧���Ƃ��ؖ����� ��g�̘A��������
��
2x+y=-1
ax+3y=2
��
2x-3y=b
4x+5y=-2
�ɂ����āA���̉���x��y�����ւ���Ƃ��̉��ɂȂ��Ă���B���̎�a��b�̒l�����߂�
�Ƃ�����肪����̂ł��� >>485
(2a_n+1,��(2a_n^2+2a_n+1))��pell������
x^2 - 2y^2 = 1
�̉��B
������Ƃ���
x= ((1+��2)^m + (1-��2)^m)/2, y=�c
x ����ƂȂ�̂�m�������̂Ƃ��B
�����
2a_n + 1 = ((3+��8)^n + (3-��8)^2)/2�B
�����b_n = 2a_n +1�͑Q����
b_(n+2) = 6 b_(n+1) - b_n
���݂����B�ȉ�ry >>483
�����t���Ғl�����邾���Ȃ��E(��)�̎������͊W�Ȃ��ł��傤
�l�����̊��Ғl�����U���Ă���P�[�X�ł������t���Ғl�͌v�Z�\�ł���A�������f���̏�ł�"�p���h�b�N�X"�������Ă��܂�
>>482�̕����ڍׂȌv�Z��������Ă���̂œǂ�ł݂Ă͂ǂ��ł��傤��
���łɌ��y�����ʂ�A�l�X�ȍl�����ɂ��������邱�Ƃ͉\�Ƃ���Ă�����̂ł���
>>423�₻�̑��̃��X��ǂތ���A�ǂ����l�����̊��Ғl���������Ȃ��Ɛ������f���Ƃ��Đ������Ȃ��Ƃ����v�����݂�����悤�ɂ݂��܂�
�m���ϐ��̒�`�ɉϕ��͊܂߂Ȃ��Ă��悢�͂��ł�
E(��)�����U����ꍇ�Ǝ�������ꍇ���₽��Ƌ�ʂ��Ă܂����
>>454�ɂ����āA�O�҂͎��s�s�\������p���h�b�N�X�͐����Ă��Ȃ��Ƃ��Ă���
�܂�>>457�ł́A��҂̏ꍇ"�̂�"�����I�ȃp���h�b�N�X���c��Əq�ׂĂ���
(���₠�Ȃ�����ɗp���Ă����Œ�z���ݒ肳��Ă���ł͔������Ȃ��̂ł������悭�Ӗ����������Ă��Ȃ��̂ł���)
���̕ӂ肩��A�����������ɍl���Ă���̂��낤�Ɛ��@�����̂ł����Ⴂ�܂�����
�܂��܂��Ӗ���������Ȃ��Ȃ�܂��� >>484
�m���ɁA���̐l�̂悭������Ȃ��w�E����������ɂ��Ă���܂���
���Ȃ��̃��X�Ō����A>>454���ɂ�����u�����Ŏ��s�ł��Ȃ�����`�v�_�ł���
���͎n�߂��璊�ۓI�Ȑ������f���ōl��������Ə����Ă���̂ɁA
����Ɍ����̖��Ɣ]���ϊ����ĉ��x�����l�̔��_���Ă���܂� >>485 >>487
����
(2a_n+1,��(2a_n^2+2a_n+1))��pell������
x^2 - 2y^2 = -1
�̉��B
������Ƃ���
x= ((1+��2)(3+��8)^m + (1-��2)(3-��8)^m)/2, y=�c
�����
2a_n + 1 = (1+��2)(3+��8)^n + (1-��2)(3-��8)^n)/2�B
�ȉ����l�B >>486
��)
2x+y=-1
ax+3y=2
��)
2x-3y=b
4x+5y=-2
���j��x,y�����ւ���
��)
2y-3x=b
4y+5x=-2
�ɂ���
��)�� 2x+y=-1��
��)�� 4y+5x=-2��
�A����������������������Ȃ��́H >>491
�镪�ɂ����܂���A���肪�Ƃ��������܂���
�����Ȃ�ł����ǁA����̗�����������Ȃ���
���肪�Ƃ��������܂����B >>488
���ǂ����l�����̊��Ғl���������Ȃ��Ɛ������f���Ƃ��Đ������Ȃ�
����Ȃ��Ǝv���Ă����܂��A�����Ă����܂���B���Ȃ��̏���Ȏv�����݂ł��B
�����܂ł���������܂ނ���u�����ɂ͍�蓾�Ȃ��v�ݒ肾�Ƃ������Ƃł��B
�l�����̊��Ғl�����ɍS��̂͐������f���Ƃ��Đ������邩�ǂ����ł͂Ȃ��A����������
�������邵�Ȃ��ɂ�����炸���Ғl�͓����Ȃ̂ɁA�����t���m���Ŋ��Ғl���݂�ƌ�����
���ق����������邩��A�u�����I�p���h�b�N�X�v�Ƃ��Đ�������Ƃ������ƂȂ�ł����B >>494
�����ł��B
�������t���m���Ŋ��Ғl���݂�ƌ��������ق����������邩��
�ł͂Ȃ��A�l�����Ғl����������ꍇ�́u���������ق�����������v�ł����ˁB ��w���w�̎���ł�
�������(X,d)�AU��X�ɑ��āAU�̒��a��diam(U) := sup{d(x,y)|x,y��U}
�ƒ�`���Ă���{�͗ǂ��������܂��B
�ł��A�������U=�ӂ̃P�[�X���Ăǂ��Ȃ��ł����H
diam(��)=0�@�ɂ�������ł����H
�ł��Asup�̒�`���l������ sup��=-���@�̕����܂��������肫�܂� ���ʂ̓ӂ͋�����Ԃł͂Ȃ��Ƃ���Ǝv���܂� >>485
(a+1)^2+a^2=m^2������s�^�S���X���̐������g���Ηe�� >>494
>>495
�s���ǂ������Ă��܂����A�u����悤�Ɍ�����v�Ə�������ł���
����͎v�����݂ł͂Ȃ����Ȃ��̃��X�̂����������玩�R�ɐ��@���ꂽ���Ƃł�
�������Ƃ��J��Ԃ��Ă邾���ł���
���Ȃ������Ă���ł��낤���Ⴂ���w�E���Ă����܂�
�܂��A���Ғl�����U����ꍇ�ł������̃p���h�b�N�X�͔������Ă��܂�
�{���͗D��̂Ȃ��͂��̓̕����Ȃ̂ɁA�I�r�[��A<B�ɂȂ��Ă��܂�
�l�����z���������Ă��Ȃ��Ă��A2���̕����ɗD�Ȃ����Ƃ͐������Ă���͂��ł�
���ɁA���Ғl����������ꍇ�͏�ɑ�������p���h�b�N�X����������Ə����Ă��܂���
����͂ǂ������ł����H
(2^k,2^(k+1))�̊m����^������@�ł́A(1,2)��1���������Ƃ��͌����ɂ�蓾������̂ŁA��ɑ����邱�Ƃɂ͂Ȃ�܂���
�������A���̒l�������ȂǕ����̒��g�̑g�ݍ��킹�̎�����ς����邱�Ƃ͂ł��܂�
�A���A��ɑ��������(-1)�{�����邱�Ƃŏ�ɓ�������ɂł���̂ŁA�����͖{���I�ɓ����ł�
�Ȃ���ɑ�����������l������Ə����Ă���̂��͖{���ɑS���Ӗ���������܂���
�܂��A�O�҂̏ꍇ���u�����ɋN���蓾�Ȃ�����v�ƈ�R���A��҂̏ꍇ�́u�p���h�b�N�X������v�Ƃ��Ă��܂���
�����u�����Ŏ��s�s�\�����炱�̃p���h�b�N�X�͍l����Ӗ����Ȃ��v�Ƃ�������Ȃ�A�l�����z�̎����ɊW�Ȃ���Ɏ��s�s�\������A���������l����Ӗ��͂Ȃ��ł��傤
���邢�́A�l�����z�����U���Ă���Ǝv�l�����ł����s�ł��Ȃ��ƍl���Ă���̂�������܂��A�����̊l�����z�͗L���l�Ȃ̂őS���W����܂���
�����Ƃ����A���Ɋl�����z�����ƂȂ�ꍇ���܂܂�Ă����Ƃ��Ă��AR��{�}��}�ɒl���Ƃ�Ǝv����͂���Ȃ���܂�܂�
�����̂����ǂꂩ�P�͓��Ă͂܂�ƐM���Ă���̂ł��� >>496
�ӂ���W���ɑ��Ă͂��܂��`���Ȃ��Ǝv���܂�
�����Ē�߂�Ȃ�-����0�ł��傤��
diam�̏I���R�Ƃ݂Ȃ���[0,��)�Ƃ݂Ȃ����̈Ⴂ���x�ł��傤
���Ȃ݂ɋ�W���̋L��∅�̓ӂƎ��Ă��܂����ʂ̋L���ł�
�m���Ă��œ��͂��ʓ|����������g����������������܂��O�̂��� �W���ƒ萔����0�ł͂Ȃ����W��ԓ��̕��ʂ̎������A�����\�����������d��A���ɂȂ�悤�ɂ��̕��ʏ�ɂȂ��_���܂�4�_�����߂�B ���R���S�̂̂Ȃ��W��N����N�ւ̎ʑ��S�̂̏W��Map(N,N)��
����g �� ��n f(n) �� g(n)
�ŏ���������B
M := { m �� Map(N,N) | m�͋��`�P������ }
�Ƃ��ĕ��������W���ƍl����B
M�͐���W���ł����H >>503
���ᑶ�݂��܂���
�p�����܂� (p-q)^3=p+q�����f��p,q�����߂�B
���R��k,l,m,n��k!+l!+m!=2^n�����Ƃ��A(k,l,m,n)�����߂�B
����Ȃ̂ł����S�R�킩��܂���ł����B���������肢���܂��B >>506
1���
p-q=n�Ƃ���(n�͎��R��)
p+q=n^3,p-q=n���
p=n(n^2+1)/2
n��3�̂Ƃ��An>2,1+n^2>2���E�ӂ͑f���ƂȂ�Ȃ�
n=1�̂Ƃ�
(p,q)=(1,0) (�f���łȂ��̂ŕs�K)
n=2�̂Ƃ�
(p,q)=(5,3)
����āA���������̂�(p,q)=(5,3)�̂Ƃ��̂�
2���
k��l��m�Ƃ��Ă悢
l!�y��m!��k!�̔{���ƂȂ�̂ŁA���ӂ�k!�̔{��
����A�E�ӂ͑f�����Ƃ���2���������Ȃ��̂ŁAk!��2�̃x�L��ŏ����Ȃ���Ȃ�Ȃ�
�����k=1�܂���k=2
�Ek=1
�E�ӂ͋����Ȃ̂ō��ӂ�����
l!������(��l��2)�̎��Al��m����m!�������Ȃ̂ō��ӂ͊�ƂȂ��Ă��܂�
�����l=1�łȂ���Ȃ�Ȃ�
���̂Ƃ�
m! = 2^n - 2 = 2(2^(n-1)-1)
n=1�̂Ƃ��E�ӂ�0�ƂȂ�A�������m�͑��݂��Ȃ�
n>1�̂Ƃ��A2^(n-1)-1�͊�Ȃ̂ŁA�E�ӂ̑f�����������l�����Ƃ��A2��1���������Ȃ�
m!�����̂悤�ɂȂ�̂�m=2,3�̂Ƃ��̂�
m=2�̂Ƃ�n=2,m=3�̂Ƃ�n=3
�Ek=2
����2�Ŋ�����
1+(l!/2)+(m!/2)=2^(n-1)
��قǂƓ��l�̍l�@�ɂ��Al!/2�͊�łȂ���Ȃ�Ȃ��̂�l=2�܂���l=3
l=2�̂Ƃ�
m! = 2^n - 4 = 4(2^(n-2)-1)
n=1,2�̂Ƃ��������m�͑��݂��Ȃ�
n>2�̂Ƃ��A2^(n-2)-1�͊�Ȃ̂ŁA�E�ӂ̑f�����������l�����Ƃ��A2��2���������Ȃ�
�������Am!�����̂悤�ɂȂ�m�͑��݂��Ȃ�
l=3�̂Ƃ�
m! = 2^n - 8 = 8(2^(n-3)-1)
n=1,2,3�̂Ƃ��������m�͑��݂��Ȃ�
n>3�̂Ƃ��A2^(n-3)-1�͊�Ȃ̂ŁA�E�ӂ̑f�����������l�����Ƃ��A2��3���������Ȃ�
m!�����̂悤�ɂȂ�̂�m=4,5�̂Ƃ�
m=4�̂Ƃ�n=5
m=5�̂Ƃ�n=7
�ȏ�����������g��
(k,l,m,n)=(1,1,2,2),(1,1,3,3),(2,3,4,5),(2,3,5,7)
�y�т�����k,l,m�Ɋւ�����ёւ� >>508
�ƂĂ����J�ȉ�����肪�Ƃ��������܂����B ����ł��B
z�f���Ƃ��āAz��0�̂Ƃ�|z|/z�̋Ɍ����Ăǂ��Ȃ�܂����H >>510
wolfram�搶��limit dies not exist.�̓�
https://www.wolframalpha.com/input/?i=limit(x-%3E0,y-%3E0,abs(x%2Biy)%2F(x%2Biy)) >>499
>�u����悤�Ɍ�����v�Ə�������ł���
������A���������Ă��܂��̂͂��Ȃ��̊Ԉ�����v�����݂��炾�Ƃ������Ƃł��B
�{�l�������ς�ے肵�Ă��邱�Ƃ��A�u���R�ɐ��@���ꂽ�v�ȂǂƐ���������悤
�Ȃ����t�͂������Ȃ��̂��Ǝv���܂���B
���Ƃɑ������͂����ς�炸��ǂƂ������A�v���Ⴂ�ɂ�邲�w�E����ł��B
�������̌J��Ԃ��ɂȂ�̂ł��Ԏ����܂��A��ÂɂȂ��đf���ɓǂݕԂ���
�������������������������\�͂����������ƐM���Ă���܂��B >>502
�N������킩�����������Ⴂ�܂���ł��傤���c >>514
�����������̈Ӗ����킩��܂���B
�O�O���Ă��炵���̏o�Ă��Ȃ����B >>513
���Ȃ��̕\���ł͂����l���Ă���悤�Ɏ��ɂ͌�����A�ƌ����Ă����ł�
����͎��������������Ƃ������Ƃł���A���Ȃ��͂����l���Ă���ƒf�肵�Ă���̂ł͂���܂���
���Ȃ��̍l���ƈႤ�Ƃ��Ă��A�\���ɖ�肪����ȏ�A���������邱�Ƃ����Ă�����܂�
>>499�̑�����ǂ߂ǂ����Ă��̂悤�ɐ��@�����̂���������ł��傤����A���_�������Ȃ炻����̓��e�ɋ�̓I�ɓ�������@���ł����H
��̓I�Ȍ��y������Č�ǁE�v���Ⴂ�ɂ��w�E�Ə����Ă��܂����A��̓I�ɂǂ�����ǂȂ̂ł����H
>>494-495��ǂތ���A
�u���Ғl����������ꍇ��2���̕����͓��������A���U����ꍇ�͂����ł͂Ȃ��v
�u���U����ꍇ�͖�������܂ނ��ߌ����Ŏ��s�ł��Ȃ�����p���h�b�N�X�͐����Ă��Ȃ��v
�u��������ꍇ�͏�ɓ�������͂���Ȃ����A��ɑ�����������邱�Ƃ��ł���̂ŁA�p���h�b�N�X��������v
�Ƃ��Ȃ��͍l���Ă���Ƃ����ǂݎ��܂���
���̉���ɏ]���Ă��ꂼ��ɔ��_�����Ă��܂�
�u�v�����Ȃ̂��A�������������w�I�ȋL�q�Ɍ�肪����̂��A��̓I�Ɏw�E���Ē�����Ƃ��肪�����ł� >>514
������
�d��A���̈Ӗ���m��Ȃ��ł�
���W��ԂƂ����̂�3������Ԃ̂��ƁH >>510
�Ɍ`�� z = r exp(i��) �ŏ����A|z|/z = exp(-i��)
�Ȃ̂� z �� 0 �ւ̋߂Â����ɂ������͕ς��B
�Ίp�� ������l �� �Ɏ�������悤�ɋ߂Â��� exp(-i��) �Ɏ������邵
�Ƃ��������Ȃ��悤�ɋ߂Â��Ύ������Ȃ��B f(n,a,x)=x^n+ax
I[k]=�� [k to k+1] f(n,a,x) dx
�ɑ��Ĉȉ��̓���(*)���l����B
I[k-1]=I[k]=I[k+1] ... (*)
����(*)�𐬗����������k�����݂���悤�ɁA���R��n�Ǝ���a���߂����B
���̂悤��n,a�͑��݂��邩�B
���݂���ꍇ�A���̂悤��n,a�̗��1������B�܂��C�ӂ�n�ɑ��āA����a���Ƃ�A����(*)����k�����݂���悤�ɂł��邩���ׂ̂�B
���݂��Ȃ��ꍇ�A���̗��R���q�ׂ�B >>515
>�\���ɖ�肪����ȏ�
������A���ꂪ���Ȃ��̎�ϓI���f�ȂƂ������Ƃ��܂������ĔF�����ׂ��ł��傤�B
����𐢂̒��ł́u�v�����݁v�Ƃ����̂ł��B
����͂���Ƃ��āA>>499�̒��i�ɂ��Ă͂܂����������Ă��Ȃ��̂��������ʂ�ŁA
>>513�̌�i�ŏq�ׂ����Ƃɂ��ẮA���l�т��ēP�����܂��B���݂܂���ł����B
��ÂɂȂ�Ȃ��Ƃ����Ȃ��͎̂��̂ق��ł����ˁB
�l�����z�̊��Ғl����������P�[�X�ł́A�������������������邪�A�����z�����ꍇ��
�͂����Ȃ�Ȃ��Ƃ������Ƃ��������Ă���܂����B���������āA���̏ꍇ���l���ɂ����
���Ғl�v�Z���������A�����t�����Ғl�ƁA���������������ꍇ�̊��Ғl�͈�v����̂�
���Ғl�̃p���h�b�N�X�Ȃǐ����܂���ˁB�������Ɍ��������ق�����������Ƃ������Ƃ�
���R����܂���B���w�E�Ɋ��ӂł��B
���u���Ғl����������ꍇ��2���̕����͓��������A���U����ꍇ�͂����ł͂Ȃ��v
����͂��̒ʂ�B���U����ꍇ�ɂ��Ă͏�Ɍ��������ق������ɂȂ��Ă��܂��̂œ���
�ł͂Ȃ��Ǝv���Ă��܂��B
���u���U����ꍇ�͖�������܂ނ��ߌ����Ŏ��s�ł��Ȃ�����p���h�b�N�X�͐����Ă��Ȃ��v
�����Ɏ��s�ł��Ȃ��Ƃ����_�Ńp���h�b�N�X�Ƃ͌ĂׂȂ��Ƃ�������ł��B����������A
���̉���̉��ł͘_���I�ɂȂ�̖������Ȃ��B
���u��������ꍇ�͏�ɓ�������͂���Ȃ����A��ɑ�����������邱�Ƃ��ł���̂ŁA�p���h�b�N�X��������v
����ɂ��ẮA��ŏq�ׂ��ʂ�A���̊ԈႢ�ŁA��ɑ�������͂���Ȃ��̂ŁA����
�t�����Ғl�̊��Ғl���Ƃ�A�ǂ���̕����ɂ������Ȃ��̂ŁA�L���̕��z�̏ꍇ�Ɠ����ŁA
�Q���̕����͊��Ғl�I�ɂ͓����ɂȂ�B
�L���̏ꍇ�������ł����A���Ғl�I�ɂ͓����ł����Ă��A��������������������i���邢��
��������j�m�������|�I�ɍ����Ƃ����͂���������܂����A�������A������
������������m�������|�I�ɍ����̂Ɠ����ŁA����������ăp���h�b�N�X�Ƃ͌����Ȃ��B �V�����b�h��Ђ� �吨�̍s�������ɕ���ł���B�H�꒷���V�����b�h���ׂ��ꖇ�̎�����������ނ͂����5���̒f�Ђɔj���Ԃ̍s���ɓn���B �Ȍ� n �Ԃ̎Ј����f�Ђ���������A�ނ͂��̒����� n ���̒f�Ђ�I��ł������e�X5���̒f�Ђɔj���Ă��� n +1�Ԃ̍s���ɓn���B2006�������̒f�Ђ����2006���ȏ�̒f�Ђ����ɍH���ɓn���͉̂��Ԃ̍H�����B
�ׂ������J�ɋ����ĉ����� 1����1999��2�悵�����̂̒��ŏ\�̈ʂ���ł�����͉̂����邩�B >>523
> sum((1:1999)^2%/%10%%2)
[1] 400 >>518
���肪�Ƃ��������܂����B
Wolfram�̂Q�s�߂�
���������Ӗ��������̂��Ɣ[���B
(limit does not exist)
(value may depend on x, y path in complex space) >>522
n�l�߂�5*n����n+1�l�߂ɓn���B >>520
��������A���ꂪ���Ȃ��̎�ϓI���f�ȂƂ������Ƃ��܂������ĔF�����ׂ��ł��傤�B
����𐢂̒��ł́u�v�����݁v�Ƃ����̂ł��B
�Ƃ���܂����A���Ȃ������̌���F�߂܂�����ˁH
���̎��_�ŕ\���ɖ�肪�������̂͂��Ȃ����F�߂鎖�����Ǝv���̂ł���������
�������瓱�������Ȃ��̊��Ⴂ�͎����ł͂Ȃ������悤�ł����A������ɂ��Ă͏��߂��玄�̎�ς��Ɩ��L���Ă���܂�
�����U����ꍇ�ɂ��Ă͏�Ɍ��������ق������ɂȂ��Ă��܂��̂œ���
�ł͂Ȃ��Ǝv���Ă��܂��B
�����I��ł���͂����ł����A�I�ԑO�ɂ͗D�Ȃ��͂����Ƃ��łɏ����Ă���܂�
�����Ɠǂ�ł܂��H
�������Ɏ��s�ł��Ȃ��Ƃ����_�Ńp���h�b�N�X�Ƃ͌ĂׂȂ��Ƃ�������ł��B
���̊��ɂ͑ԓx�������͂������獬����������
>>494�ł�(���Ⴂ�ɂ����̂ł͂���܂�����)���Ғl����������Ő����I�p���h�b�N�X��������ƈ�x�͏����Ă��܂������
(���łɓP�����Ƃ͏��m���Ă��܂����A���Ȃ��̎v�l��H�ɂ��čl���邽�߁A�����Ă����ł͂��̂悤�Ȑ������f���̑��݂����肵�Ă����܂�)
�����ŋN����Ȃ����疳���Ƃ�������Ȃ�A���Ғl���������Ă��悤�ƌ����Ŏ��s�ł��Ȃ��̂����珉�߂���p���h�b�N�X�ł͂Ȃ��͂��ł�
����ŁA�������f���ɂ�����p���h�b�N�X��F�߂Ă���Ȃ�A��̂悤�ɍl���邱�Ƃɂ��A���Ғl�����U����ł��p���h�b�N�X�������Ă��܂�
�Â� �u�����t���Ғl�����ĂɂȂ�Ȃ����Ƃ�����v�Ƃ������_�Ȃ番����̂ł����A�����t���Ғl�ɂ�鉿�l���f�͍m��
(�̕����͓����łȂ��A�Ƃ͂����菑���Ă���)���������ŁA���̌��ʓ������s�����Ȃ��Ƃɑ���
�u�����I�ȃp���h�b�N�X���v(���Ғl�����̃P�[�X)
�u���s�s�\������p���h�b�N�X�ł͂Ȃ��v(���Ғl���U�̃P�[�X)
�ƁA�قȂ闧��ɂȂ��Ă��܂�
�Ƃ��Ɍ�҂ɂ��ẮA�������f����̌v�Z��e�F���Ă����Ȃ���A�������ꍇ�͐��w�I�v�l���������Ƃ������܂�ɗ��\�Ȍ��_���ƍl���܂�
���L���̏ꍇ�������ł����A�`�`
����͒P�ɁA���Ғl�����f��Ƃ��ēK���Ȃ��ꍇ������Ƃ������Ƃ̏؍��ɉ߂��܂���
�܂��A�L���̏ꍇ�A�����⎞�Ԑ�������������A����Ӗ��ł͑Ó��Ȋ�ł��邱�Ƃɕς��͂���܂���
�T���N�g�y�e���u���N�̃p���h�b�N�X��A��ʉ������������ɂ�����p���h�b�N�X�͑S�����̈Ⴄ���̂ł�
�ǂ���炻�̕ӂ�������ł��Ă��Ȃ��悤�ł���
�Ȃɂ����̑傫�Ȏv���Ⴂ������A���Ȃ����������\��������ƍl���Ă��܂������A�ǂ���炻��͂Ȃ������ł�
����w�E���Ă������Ƃ����X�ɂȂ��ĔF�߂����ƂŁA���̃��X���낭�ɓǂ�ł��Ȃ�����(�������͗����ł��Ă��Ȃ�����)
���Ƃ��悭������܂���
���ɂ����x�w�E���Ă��X���[����Ă�����̂���������܂����A�����炭�����������ƂȂ̂ł��傤 >>528
�����炭����܂ł̒f�Ђ��ꏏ�ɓn���Ă�������A4n���������Ă����̂ł́H >>523
���R���͂��ׂ�
10n+m�@n�͔����Am��0~9�̐���
�̌`�ŏ�����
(10n+m)^2��10*2nm+m^2 (mod 100)
2nm�͋����Ȃ̂ŁA(10n+m)^2�̏\�̈ʂ̋���m^2�̂���ƈ�v
0^2~9^2���v�Z����ƁA���̂悤�ɂȂ�m��m=4,6�݂̂ƕ�����
����āA��̈ʂ�4,6�ł��鐮���̐��𐔂���悭�A
2*200=400(��) >>522
�j��Ȃ������̂����ɓn���ݒ�H >>524
��@z=b+ic�Ƃł������Ď��ɑ�����Ď���=0�A����=0�̊W���狁�߂�
��������3b^2=c^2�����܂�͂�����������̎��ɑ�����ĂR�������Q���܂���
�i��Βl�ɒ��Ӂj�Е��͒P�������A�����Е��͋ɒl�̂����������a�͈̔͂�
���̌����ς�� >>524
�ꖇ��
z^3=3|z|+a
�E�ӂ͎������A���ӂ�����
�����
z=r*e^i�Ɓ@��=0,2��/3,4��/3 r��(���Ƃ͌���Ȃ�)����
�Ƃ�����
���̂Ƃ�
r^3=3r+a
���Ƃ�r�̉��̌���a�ŕ��ނ���W���I�Ȗ��
(r=0�����ɂ��Ƃ���z�̉��̌�������̂Œ���)
��
�v�Z������
x^2y^2-x^2-y^2=0 (x>0,y>0)
�ƂȂ������ǁA�}���g��Ȃ��Ɛ�������ς�����ȗ�
�v�Z�~�X���Ă邩������Ȃ��� >>524
z^3 = |z| + a �͎���������
z = |z| exp�� �Ƃ����An �𐮐��Ƃ���
|z|^3 = |z| + a ���� 3�� = 2n��
�܂��� -|z|^3 = |z| + a ���� 3�� = (2n+1)�� >>524
����
z^3 = 3|z| + a �͎���������
z = |z| exp�� �Ƃ����An �𐮐��Ƃ���
|z|^3 = 3|z| + a ���� 3�� = 2n��
�܂��� -|z|^3 = 3|z| + a ���� 3�� = (2n+1)�� >>539
>>537�̂悤�ɂ��ďꍇ����������������y�Ǝv��� >>535
a[0]=5
a[1]=a[0]-1 + 1*5
a[2]=a[1]-2 + 2*5
a[3]=a[2]-3 + 3*5
...
a[n]=a[n-1]-n+5*n
=a[n-1]+4*n
a[n+1]=a[n] + 4(n+1)
a[n] =a[n-1]+4*n
a[n+1]-a[n]=a[n]-a[n-1]+4
��̍����Ƃ���b[n]=a[n+1]-a[n]�Ƃ�����
b[n]=b[n-1]+4�œ�������
�ȉ��� >>541
a[n]��n�Ԗڂ̎Ј������̎Ј��ɓn������ >>541
b[0]=a[1]-a[0]=9-5=4
b[1]=a[2]-a[1]=17-9=4*2
b[2]=a[3]-a[2]=29-17=4*3
...
b[i]=4*(i+1)
b[i] = a[i+1]-a[i]
b[i-1] = a[i] -a[i-1]
b[i-2] = a[i-1] -a[i-2]
....
b[1] = a[2] -a[1]
�[i=1,n] b[i]=a[n+1]-a[1]
=
�[i=1,n] 4*(i+1) = 4*n(n+1)/2 + 4*n
a[n+1]=4*n(n+1)/2 + 4*n+a[1]
a[n]= 4(n-1)n/2 + 4*(n-1) + a[1]
=2*n^2 +2*n + 5
2*n^2 +2*n + 5 > 2006�ƂȂ�ŏ���n�����߂�
1��������n��
2*n^2 +2*n + 5 < 2006���m�F�B
32�Ԗڂ� 1989�������2117����n�� �v���O�����̕��������Ċy�B
���ɂ��Ă݂��d��݂����Ȃ��B
> a=NULL
> a[1]=9
> f= function(N){
+ if(N==1) return(a[N])
+ for(n in 2:N){
+ a[n] =a[n-1]+4*n}
+ return(a[N])
+ }
> f=Vectorize(f)
> f(1:50)
[1] 9 17 29 45 65 89 117 149 185 225 269 317 369 425 485
[16] 549 617 689 765 845 929 1017 1109 1205 1305 1409 1517 1629 1745 1865
[31] 1989 2117 2249 2385 2525 2669 2817 2969 3125 3285 3449 3617 3789 3965 4145
[46] 4329 4517 4709 4905 5105 C[x,y]⊕C[x,y]��C[x,y]��C[x,y]���Q�Ƃ݂��Ƃ��A
�����^C[x,y]⊕C[x,y]��C[x,y]�̌`�͂ǂ��܂Ō���ł��܂����H >>545
C[x,y]=R�Ƃ�����R�̂Q��(a,b)�ɂ����
(x,y)��ax+by
�̌`�����Ă�����̑S�́B >>546
���肪�Ƃ��������܂�
�ǂ̂悤�Ɏ�����ł��傤���H �߂^�̋L���Ƃ���
Hom(R,M)=M �@(f �� f(1))
Hom(M,L)�~Hom(N,L)��Hom(M⊕N,L)�@((f,g) �� ((m.n) �� f(m) + g(n)))
�����^��^���邱�Ƃ��m�F����
Hom(R⊕R,R) �� Hom(R,R) �~ Hom(R,R) �� R �~ R
�̓��^�ʼnE�ӂ�(a,b)�����ӂ̂ǂ��䂤�ʑ��ɑΉ��t�����邩�m�F����B >>519
I[k] = (1/(n+1))[(k+1)^{n+1} - k^{n+1}] + a(k + 1/2),
I[k] - I[k-1] = (1/(n+1))[(k+1)^{n+1} + (k-1)^{n+1} -2 k^{n+1}] + a,
n����̂Ƃ��͋���䂦�A
I[-1/2] - I[-3/2] = I[1/2] - I[-1/2]
a�����܂����A������0�ɂł���B
���@I[-3/2] = I[-1/2] = I[1/2],
(��)
�@n=3�Ca=-5/4 �̂Ƃ�,
�@�@I[k] - I[k-1] = 3(kk -1/4),
�@n=5�Ca=-91/48 �̂Ƃ�,
�@�@I[k] - I[k-1] = 5(kk -1/4)(kk +5/4), >>523
�\�̈ʂ̐��͉�2���Ō��܂�B���20�Ƃ���B
1�@�c�@04, 46, 54, 96
3�@�c�@06, 44, 56, 94
5�@�c�@16, 34, 66, 84
7�@�c�@24, 26, 74, 76
9�@�c�@14, 36, 64, 86 >>519
�@I[k] - I[k-1] = (1/(n+1))[(k+1)^{n+1} + (k-1)^{n+1} -2 k^{n+1}] + a
�@�@= (2/(n+1))(j=1,[(n+1)/2]) C(n+1,2j) k^{n+1-2j} + a
n�������̂Ƃ��Ak�ɂ��ĒP�������B
a���ǂ�����Ă�������0�ɂ͂Ȃ�Ȃ��B �����������m����3�o�Ă���s����������Ăǂ�����ĉ�����ł���?
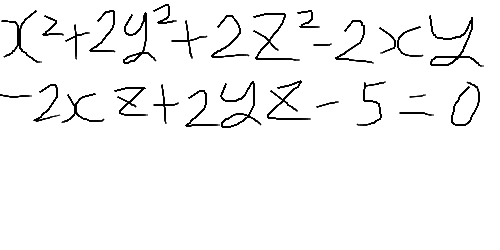 0����n�܂�A�����_����+1��������-1���鑀���(�m��1/2��)�A60��s���B
0����n�܂�A�����_����+1��������-1���鑀���(�m��1/2��)�A60��s���B
��x����Βl��16�ȏ�ɂȂ�Ȃ��m�������߂�B
�܂��A�ŒZ16��ڂ�16�ȏ�ɂȂ�B�܂��A16�ȏ�ɂȂ����ꍇ���̌���l���Ȃ��Ă��m���ɉe���͂Ȃ��B
�܂��A��Βl16�̓_�ɒ����ꍇ�K������͋����ł���B
���ǂ��Ȃ��Ă��܂��̂ŁA��Βl��16�ɂȂ鐔�l��A�ƌ����B
���j�́A16�ȏ�ɂȂ�m���ׂĂ����悤�ɂ���B
�܂��A16��ڂ�A�ɂ��ǂ蒅���m���B
��U+�̕��ɍi�荞�݁A��Βl���Ώ̓I�Ȃ̂œ�{����Ηǂ��B
�����16��ڂł��ǂ蒅���m����1/2^16
-�̕����l����ƁA16���A�ɂ��ǂ蒅���\����1/2^15
���̒��q��18��ځA20���...�Ƃ���ׂčs���A60��ڂ܂Œ��ׂĂ�����x�̖@������������B
���������16�ȏ�ɂ��ǂ蒅���\���̓�(�P30_k=8)1/2^(2k-1)�Ɨ\�z�ł���
����������Ɗȗ������āA1/(2^13)��(�P23_k=1)1/4^k
���䐔��̘a�̌������g����
{1/(2^13)}�~(1-1/4^23)/3=(1-1/4^23)/(3�~2^13)
=(4^23-1)/(3�~2^59)��16�ȏ�ɂȂ�m��
1���炱�����������A
16�ȏ�ɂȂ�Ȃ��m��=(3�~2^59-4^23+1)/3^2^59
������v�Z�@�ɑł�����99%���炢�ɂȂ����̂ł��������Ă܂����H
https://i.imgur.com/ZXk3DYm.jpg ���Z�Ȃ��Lindelof
�̏ؖ��ł����A�������AC�g���Ă܂����H �ǂ��ł��ǂ����Ƃł���
http://www.kurims.kyoto-u.ac.jp/~motizuki/students-japanese.html
��
���n�@�q�I
���Đl�̊�ʐ^�����ł�
���̐l�͐��]���������ł����H
��(��)��
http://physmathseminar.web.fc2.com/discourse/2016/spring/kyoto-sp_abst/resume_yuji.pdf
��
����������x�������ēǂ߂���x�ɂ͏ؖ���t���Ă���Ǝv��
�ƌ����Ă����Ȃ���
���Z�Ȃ�� Lindelof �ł���.�̏ؖ���
��C�ӂ̊J�핢���^����ꂽ�J��̕����핢�ɂ��ו�����邱�Ƃ��玩���ł���.��Ȃ�ꌾ�ōς܂��Ă��܂��B
���̕��̖��O���O�O��ƏG�˂ł��邱�Ƃ����������܂���
���̏o����l�Ɍ���ꂪ���ł����A������������ł��Ă��邱�ƂȂ���F�o���ē��R���룂Ƃ����l���������Č����܂��B
�ʂ̕����������ؖ��ł�
http://www2.itc.kansai-u.ac.jp/~afujioka/2017/st3/171204st3.pdf
�ŁA10�s�|���ďؖ����Ă��܂��B
���͂����������J�ȋL�q��������̕����D�������Ă܂��ˁB >>555
�v�Z�@�ŊT�Z�l�����ق����Ȃ�
Prelude> let next x = zipWith (+) (take (length x) $ 0:x) ((tail x) ++ [0])
Prelude> let xs = iterate next $ (take 15 $ repeat 0) ++ [1] ++ (take 15 $ repeat 0)
Prelude> let n = 60 in (/(2^n)) $ fromInteger $ sum $ (!!n) xs
0.9207659703106129
�ɂȂ����B
�����Ȃ�
Prelude> import Data.Ratio
Prelude Data.Ratio> let n = 60 in (%2^n) $ sum $ xs !! n
69202887261377303 % 72057594037927936
�̂悤�ł��B �l�C�s�A����0,1�̍��W��ʂ�͓̂�����O�����ǂȂ��X����1�Ȃ�ł����H
limh��0a^h-1/h���Čv�Z�ł��܂�����(���� �l�C�s�A����0,1�̍��W��ʂ�͓̂�����O�����ǂȂ��X����1�Ȃ�ł����H
limh��0a^h-1/h���Čv�Z�ł��܂�����(���� >>558
�����P�����s����0.92�Ă��܂����B
��̎��ɂ��Ăł����A�Ⴆ�Ύ���18��ڂł��ǂ蒅���m���́u18��ڂɂ��ǂ蒅���̂�17��+��-�̕��ɍs���A�������͋t�̕��֍s�����v�ƍl���āA
���̏ꍇ18��v���������ɍs��(1/2)^18���̗p���܂����B
������+��-�����l����̂œ�{����1/2^17�ł��B
������J��Ԃ��čs���܂����B
2��ȏ�t�̕����֍s���Ȃ�܂�20��ڂƂ��Ɋ܂܂�邾���Ȃ̂ŁB
�������v�������܂����B
���̏ꍇ�́A17���+��1���-�ł��̂ŁA���ꂾ�����܂��l���܂��B
�Ⴆ�A1��ڂ�-�A�c���17���+�ƂȂ�m���́A1/2^18�ł��B
���ꂪ�A����ڂ�-���o�邩�H�Ƃ����p�^�[�����A1�`16��ڂ܂ł�16�ʂ肠�邽�߁A
18��17��+,1��-�ƂȂ�̂�16�~1/2^18�ł��B���l��-��17��A+��1��̏ꍇ��16�~1/2^18�Ȃ̂ŁA18��ڂŏI������m����1/2^13�ł��B
18��ڂ̊m���͂���ŋ��ߏI������̂ł����A20��ځA22��ڂȂǂ͂��������ꍇ�̐��������ɂ����Ȃ�̂ŁA����Ƃ���ł��B -����ڂ�-���o�邩�ł��������(18��̗�Ō�����16)�̓R���r�l�[�V�����ŏo�������H
-�ł���������Ƌ����ƃR���r�l�[�V�����Ȃ̂ł�����������藝�������ĊȒP�ɂł���̂��H
-�ł������ƂɑI�ԑO�̌����ς�����Ⴄ���疳�����H
-�������R���r�l�[�V���������Ƃ��Ă�1-(16�ȏ�ɂȂ�m��)������99%�ȏ�Ȃ͕̂ς��Ȃ��H
...
-�[k��-7��7]((60,30+k)-2�~(60,14+k))
��2^60�Ŋ���Əo�Ă���H
((a,b)�͓W��)
�ȂǂƎv�f���Ă��܂� >>559
e^x�̔����̓��o����������Ώo�Ă��邪�A�Ђ�߂��̂͌��\������Ȃ�
lim[h��0](a^h-1)/h
=lim[h��0](a^h-1)/log_a(a^h)
=lim[h��0](a^h-1)/log_a(a^h-1+1)
=lim[h��0]1/log_a((a^h-1+1)^(1/(a^h-1)))
a^h-1=t�ƒu���ƁA
=lim[t��0]1/log_a((t+1)^(1/t))
log���͘A��������lim���Ƃ鏇�������ւ��邱�Ƃ��ł��A
=1/log_a(lim[t��0]((t+1)^(1/t)))
e=lim[t��0](t+1)^(1/t)������A
=1/log_a(e)=ln(a)
a=e�Ȃ��lim[h��0](a^h-1)/h=1�ɂȂ� >>564
��ԍŌ�̎��ŗǂ��낤. ���������藝�ł���.
�32����2k�������o�H��Ƣ0����2k�������r���Ő�Βl��16������̂̓�, -16�����16��ʂ�o�H�����Έ�ɑΉ������邱�Ƃ��\�ł���. ���̏ꍇ�����l�ł���, 2�{��, 0����2k�������o�H�̑����������.
�}���Q�Ƃ���:
https://i.imgur.com/CJDZmgr.jpg >>553
(x-y)^2+(y+z)^2+(z-x)^2=5+x^2
�ƕό`���Ă���l�����H >>555
���z�ŗ������������ăV�~�����[�V�������P�O�O������ĕp�x��������
> mean(replicate(1e6,all(abs(cumsum(0.5-rbinom(60,1,0.5))*2)<16)))
[1] 0.920739
�ɂȂ�܂����B >>566
�n�߂ĂԂ������_�Ő܂�Ԃ���
�32��2k��Ƣ���Ȃ��Ƃ�1��16��ʂ�0��2k�
�-32��2k��Ƣ���Ȃ��Ƃ�1��-16��ʂ�0��2k�
���Ή����ꂿ�Ⴄ�̂�
����Ȃ��Ƃ�1��Â�16,-16��ʂ�o�H��̓_�u���J�E���g���ꂿ����Ă܂�
�16��-16��2k��̏ꍇ�Ƣ-16��16��2k��̏ꍇ�����Â�����������A���l�ɢ64��2k��Ƣ-64��2k��ɑΉ�������
2�~(60,k-2)�������Ηǂ������ł��傤���H >>570
#include <iostream>
using namespace std;
int main() {
// your code goes here
double pattern[31][61];
for(int j=0;j<61;j++){
for(int i=0;j<31;j++){
pattern[j][i]=0;
}
}
pattern[15][0]=1;
for(int j=1;j<61;j++){
pattern[30][j]=pattern[29][j-1];
pattern[0][j]=pattern[1][j-1];
for(int i=1;i<30;i++){
pattern[i][j]=pattern[i-1][j-1]+pattern[i+1][j-1];
}
}
double dprob=0;
for(int k=0;k<31;k++){
dprob+=pattern[k][60];
printf("%f ¥n", pattern[k][60]);
}
// 2^60�Ŋ��邪�v�Z�߂�ǂ��̂Ŏ蔲���B
dprob/=1024;
dprob/=1024;
dprob/=1024;
dprob/=1024;
dprob/=1024;
dprob/=1024;
printf("prob=%f ¥n", dprob);
return 0;
}
�R���s���[�^�ɉ�������Ȃ�p�X�J���̎O�p�`�����p����肪����܂�
ideone�ɓ\��t�����s������92%�ƂȂ�܂��� ��Βl��16������Ȃ��悤�Ɂ`���Ă�́A>>566�ŏЉ��Ă��鋾���������J��Ԃ��g���ł������ł�
��{�I�ɂ�>>571�̍l�����ł悢�Ǝv���܂�
��ʂ�n�ɑ��ẮA�����[+16��-16��+16]��������肷��̂ŁA���X�Ƒ����������K�v�ƂȂ�܂���
(2n+1)��̈ړ���2^(2n+1)�ʂ肠��܂����A���̂��������������̂�
2*((2n+1,n)+(2n+1,n-1)+...+(2n+1,n-7)-(2n+1,n-8)-(2n+1,n-9)-...-(2n+1,n-23)+(2n+1,n-24)+...)
�ƂȂ�܂�
(�n��8�͑����Z�A���̎���16�͈����Z�A�ȍ~��16���Ƃɕ�������ւ�)
�����2^(2n+1)�Ŋ���Ίm�����o�܂�
60��̏ꍇ��61��̂Ƃ��Ɗm���͓����Ȃ̂�
2^(-60)*((61,30)+...+((61,23)-(61,22)-...-(61,7)+(61,6)+...+(61,0))
�ƂȂ�Ǝv���܂� 16������Ȃ��悤�ɁA�ł͂Ȃ��A16�ȏ�ƂȂ�Ȃ��悤�ɁA�ł���
�����ԈႦ�܂���
���̌v�Z�͂����Ɛ������ݒ�̕��ōl���Ă��Ă���܂� >>548
�Ȃ�ق�
�ƂĂ�������₷�������ł�
���肪�Ƃ��������܂��I�I >>573
(�z���ǂ��Е������̎��͏ꍇ�������Ȃ��Ă��ǂ��̂ł����B)
�����ɋz���ǂ�����Ƃ����܂ŏꍇ�������������Ă��܂��Ƃ����̂͒m��Ȃ������̂ŗǂ��o���ɂȂ�܂����B >>556
�ǂ��ł��ǂ����Ƃł����A
* �l�ɂ���Ė����x�����͈قȂ�̂ŁA����ł͖��������Ȃ��������邾�낤�B
���̏ꍇ�ɂ� [2] �� [4] �� [6] �� [8] �� [10] ���Q�Ƃ��Ă��������B
�����āB
--------------------------------------
����2.1�@�@(p.8)
�@(1)�@���Z�@�ˁ@Lindelof
�@(2)�@���Z�@�ˁ@���@�ˁ@countable chain condition (c.c.c.) >>553
�@(x-y-z)^2 + y^2 + z^2 = 5,
�ƕό`���Ă���l�����H
�@{x-y-z, y, z} = {0, �}1, �}2} >>578
���̂Ƃ���ł��ˁB
Prelude> [(x,y,z)| y<-[0..3],z<-[0..3],w<-[0..3],let x=w+y+z, w^2+y^2+z^2==5]
[(3,0,1),(3,0,2),(3,1,0),(3,1,2),(3,2,0),(3,2,1)] >>572
������đ�������ł̕p�x�v�Z�ł����H >>579
���̐�����Y��Ă��B
Prelude> [(x,y,z)| y<-[-3..3],z<-[-3..3],w<-[-3..3],let x=w+y+z, w^2+y^2+z^2==5]
[(-3,-2,-1),(-3,-2,0),(-1,-2,0),(-1,-2,1),(-3,-1,-2),(-3,-1,0),(1,-1,0),(1,-1,2),(-3,0,-2),(-1,0,-2),(-3,0,-1),(1,0,-1),(-1,0,1),(3,0,1),(1,0,2),(3,0,2),(-1,1,-2),(-1,1,0),(3,1,0),(3,1,2),(1,2,-1),(1,2,0),(3,2,0),(3,2,1)] >>570
���������G�ɂ��Ă݂�B
# 0����n�܂�A�����_����+1,0,-1���鑀���(�m��1/6,1/3,1/2��)�A60��s���B
# ��x����Βl��16�ȏ�ɂȂ�Ȃ��m�������߂�B
x=c(1,0,-1)
p=c(1/6,1/3,1/2)
n=60
m=16
�Ƃ����ăV�~�����[�V����
> mean(replicate(1e6,all(abs(cumsum(sample(x,n,rep=TRUE,prob=p)))<16)))
[1] 0.186135 ����ق�Ƃ��Ɍv�Z�����Ă܂����H�i���i�̍Č����̂ق��ł��j
https://i.imgur.com/0e6p5My.png
��i�͂킩�����̂ł����A
�����I�ɐM�����Ȃ�������ł����E�E�E �����ƍ����ˁH
> sn=0.98
> sp=0.98
> plr=sn/(1-sp)
> p=0.05
> o=p/(1-p)
> po=o*plr^2
> po/(1+po)
[1] 0.9921488 ���Z�̖��ł��B�����܂���B���w���ӂȕ����肢���܂��Bhttps://i.imgur.com/nW7sYV8.jpg �L�a�����Ƃ���
> sn=0.98�@# ���x
> sp=0.98 # ���ٓx
> plr=sn/(1-sp) # �z���ޓx��
> p=0.05 # 5%
> o=p/(1-p) # ���̃I�b�Y
> po=o*plr^2 #�Q��z���ł̃I�b�Y
> po/(1+po) #�@�m���ɖ߂�
[1] 0.9921488 �L�a�����Ƃ���
> sn=0.98�@# ���x
> sp=0.98 # ���ٓx
> plr=sn/(1-sp) # �z���ޓx��
> p=0.05 # 5%�@�L�a��
> o=p/(1-p) # ���̃I�b�Y
> po=o*plr^2 #�Q��z���ł̃I�b�Y
> po/(1+po) #�@�m���ɖ߂�
[1] 0.9921488 >>583
�����ɏo�Ă��鐔�������Ōv�Z�����
�z��248�̂���49��������A199�����Ȃ�
�Q��ڂ̌����̐��𗦂��P��ڂƂ͓Ɨ���98���Ȃ�
������ŗz����48.02
���Ȃ��ŗz���� 3.98
�������48.02/(48.02+3.98)��0.923 >>589
������98%���z���ɂȂ�̂ł�����
�z���̂���98%��������Ȃ���B >>589
����͂Q���ėz���ł��������҂ɐ�߂���̊������o���Ă��邾���ŁA���̊��҂̊��̊m���ł͂Ȃ���B >>590-591
�z���̂���98%�����ȂǂƂ͌����Ă��Ȃ���
�����ŋ��܂�92.3���Ƃ����̂́A�Q���ėz���ł������Q�ɐ�߂���̊����Ȃ̂�����A���̕��͂͐������̂ł͂Ȃ��̂��H >>592
�K�v�ȏ��͂��̊��҂����ł���m������B ���ł����Ă��P���z���ɂȂ�Ȃ������m����
�Q��Ƃ��A���ɂȂ����m�����܂܂�ĂȂ���ˁH >>583
���łȂ��l�̕����f�R�����̂ŋU�z����2�������o�Ȃ��Ƃ��Ă�1��̌������ƋU�z���Əo�Ă��܂��l�̐��͂��Ȃ�̐��ɂȂ��Ă��܂�
�������A2��A���U�z���ƂȂ�ƈ�C�ɂ��̐�������̂�2��A���ŗz���ƂȂ����l�͂��̂قƂ�ǂ��{���Ɋ��Ƃ������ƂɂȂ�
��i�Ɠ����悤�ɋ�̓I�Ȑl�����v�Z���Ă݂�킩��₷���Ǝv���� �L�a��0.05
���x�i�^�z����)=0.98
���ٓx(1-�U�z����)=0.98
> 10000*0.05*0.98*0.98/(10000*0.05*0.98*0.98 + 10000**(1-0.05)*(1-0.98)*(1-0.98))
[1] 0.9947717 �X�}���A�L�a���T������Ȃ��ĂO�D�T���������B
> (10000*0.005*0.98*0.98)/(10000*0.005*0.98*0.98 + 10000**(1-0.005)*(1-0.98)*(1-0.98))
[1] 0.9263123 >>585
X(x, y, z) �Ƃ��� OX��OA�Ƃ̊p�x��45�x�ȉ��ɂȂ�悤�ɓ��ς���v�Z�����
��(x^2 + y^2 + z^2) �� y + z
�܂��A�~���̒�ʂ�\���� y + z = 1 �ɑ��Č��_���ɂ��邩��
��(x^2 + y^2 + z^2) �� y + z �� 1
�f�ʂ͕������ƒ����Ɉ͂܂ꂽ�̈�ɂȂ�̂ŁA�ʐς͊ȒP�Ɍv�Z�ł���B >>597
�r����*���������������� >>599
���w�E���肪�Ƃ�
> (10000*0.005*0.98*0.98)/(10000*0.005*0.98*0.98 + 10000*(1-0.005)*(1-0.98)*(1-0.98))
[1] 0.9234615
>�ł����B > (10000*0.005*0.98*0.98)/(10000*0.005*0.98*0.98 + 10000*(1-0.005)*(1-0.98)*(1-0.98))
[1] 0.9234615
> sn=0.98
> sp=0.98
> plr=sn/(1-sp)
> p=0.005
> o=p/(1-p)
> po=o*plr^2
> po/(1+po)
[1] 0.9234615
�����̋L�q�ʂ�̐��l���ȁB �ł�����A���ۂ̌����ł͂ǂ��Ȃ낤��
���łȂ��̂�1��ڂ̌����ŗz���Əo���l���������������������Ƃ��ɗz���Əo�闦����2���Ȃ낤���H
���łȂ��̂ɂ��̌������ƌ���ėz���Əo�Ă��܂��l�͍Č����ł�����ς�z���Əo�闦�͂����ƍ�����Ȃ��낤��
�Č����͓��������ł͂Ȃ��ʂ̎�@�ɂ�錟�����Ȃ��ƈӖ��Ȃ���H ������a�C�́A�זE���̃G�l���M�[�H��E�~�g�R���h���A��
�ʂ�����Ă��Ȃ����Ƃ�����
�Ñ�̎��R���ɂ̓K���̗v���ɂȂ���̂͑��݂����A
�K���͊�������H���E���C�t�X�^�C���̕ω���������
�h�l�דI�����h�Ȃ̂ł�
���K���Ȃǂɑ��Ď�p�������Ȃ�ꂽ�Ƃ����L�q�������̂�
17���I�ɓ����Ă���ŁA200�N�O�ɂ悤�₭�A�T�^�I�ȃK����
��w�����ŏ��߂ĕ���邱�ƂɂȂ�܂�
�K���͌���l�̐ꔄ����
�K���̗B��̃G�l���M�[���̓u�h�E���ł���
���K�����̂���H�i�≖���ɋC���g���O��
�u�h�E���̌��ɂȂ�Y�������ⓜ���̐ێ���~�߂�ׂ��ł���
�Y�������ⓜ������Ԃ̔��K���������ł���
���S�̂̃~�C�����������ʁA�K����������������́A
�v�g���}�C�I�X������i�a�b�S�O�O�`�Q�O�O�N�j�Ƀ_�t���I�A�V�X�ɏZ��ł���
�g��ʐl�h�̒����K����Ⴞ���ł���
��ᇑg�D�̓����̓~�C�������Ă�
�ۑ�����邱�Ƃ������I�����ɂ��ؖ�����Ă��܂�
�ނ���K���g�D�́A����g�D�����ǍD�ɕۑ�����邱�Ƃ���A
�Ñ�ɂ͂قƂ�ǃK�������݂��Ȃ������ƍl�����܂�
�J�C�������قƉ��B�̔����قɈ��u����Ă���~�C���ɂ��Ă�
���ː��w�I�����������Ȃ��܂������A
��͂�K���̍��Ղ͔�������܂���ł��� >>598
�Ȃ�45�x�ȉ��Ȃ̂ł����H���ʏゾ�Ə��45�x���Ǝv���܂����B >>604
�����ɂ�������������ł͂Ȃ��̂ł����H >>585
�@xyz��Ԃ�3�_ �n(0,0,0), �`(0,1/2,1/2), �a(0,1,0) ������B
���~���b�͂n�_�Ƃ��A�`���ʂ̉~�̒��S�ɂ����A�܂������n�a������1�Ƃ���B
(1) �_ (x,y,z) ���b�̑��� (���_�n�ƒ�ʂ̉~�����܂�) �ɂ��邽�߂̕K�v�\�����������߂�B
(2) �b�̕\�ʂ���ѓ�����z���ɐ����ȕ��ʂŐ����f�ʐς̍ő�l�����߂�B >>603
�U�z���ɂȂ錴�����덷�ȊO�ɂ��������������Ȃ���
�U�z�����Č�����邾�낤�ˁB
�~�ł̐����w�I�U�z���Ƃ��悭�m���Ă���B >>585 >>607
(1)�@
�@��AOX �͏��45��
cos(��AOX) = cos(��/4) = 1/��2,
�@(y+z) = 2(��OA�E��OX)
�@= 2�|OA|�|OX|�cos(��AOX)
�@= 2���(1/2)���(xx+yy+zz)�1/��2
�@= ��(xx+yy+zz),
���@2yz = xx,�@�@(�� y,z�͓�����)
����
�@0 �� y+z �� 1�@�@(�� y��0, z��0)
(2)
�@z���Œ肷��ƁA
�@(1/2z)xx �� y �� 1-z,�@�@�@(�������� �� �������Ɉ͂܂ꂽ����)
�@S(z) = (4/3)��(2z)�(1-z)^{3/2} �� ��(3/8),
��@(3/8) - S(z)^2 = (3/8) - (4/3)^2�(2z)�(1-z)^3 = (2/9)�(1/4 -z)^2�{2 + (5-4z)^2} �� 0,
z=1/4 �ōő�l ��(3/8) ���̘A����������-1<x<1�A-1<y<1�͈̔͂ɉ������Ƃ��A����a,b�̖������ׂ��������q�ׂ�B
a(1-b)x-by=1
ax+b(1-a)y=1 �F�l���肪�Ƃ��������܂��I
>>603
>>608
��������Ȃ��̂��Ƃ��C�ɂȂ�Ȃ�ƂȂ�������₵�Ă��̂��Ǝv���܂��B
�����ł�2��̌����̌��ʂ��Ɨ��ŁA�L�a���݂̂��ɏ]�����̂��ђ��I���N���Ă�Ƃ͂ƂĂ������܂����ˁB >>562
��>>556����ł͂Ȃ���ł���AC�g��Ȃ��ؖ������ĉ������B >>609
GM-AM ���
�@(3z)(1-z)(1-z)(1-z) = (3/4)^4 - (3/16)(1/4 -z)^2�{2 + (5-4z)^2} �� (3/4)^4,
���������� z=1/4 �̂Ƃ��B xy���ʂɒ���2�̐���PQ������B�[�_P��y���̐��̕����ɂ���A�[�_P����o�Ē[�_Q��ʂ锼�����́A���~(x-1)^2+y^2=1,y>0�ɓ_(1+cos��,sin��)(0<��<��)�Őڂ���BP��y���̐��̕��������܂Ȃ������Ƃ��AQ���`���O�Ղ�C�Ƃ���BC���͂ޕ����̖ʐς����߂�B
��낵�����肢���܂��B >>610
a=0 �̂Ƃ��@���Ȃ��B
(a-1)(b-1) +1 = 0 �̂Ƃ��@���Ȃ��B
a[(a-1)(b-1) +1] �� 0 �̂Ƃ��������B
�@x = (2-a)/{a[(a-1)(b-1) +1]},
�@y = -1/[(a-1)(b-1) +1],
-1<x<1 ���
�@0 < aa[(a-1)(b-1) +1]^2 - (2-a)^2 = {a(a-1)(b-1) +2}(a-1)(ab-a+2),
�@
-1<y<1 ���
�@�@(a-1)(b-1)[(a-1)(b-1) +2] >0,
�@�@a,b<1�@�܂��́@a,b>1�@�܂��́@(a-1)(b-1)<-2
0<a<1, b<1, b<(a-2)/a,
a<0, b<1, b<(a-2)(a+1)/(a(a-1)),
a<0, b>(a-2)/2, (a-1)(b-1)<-2,
0<a<1, b>(a-2)(a+1)/(a(a-1)), (a-1)(b-1)<-2,
a>1, b<(a-3)/(a-1), (a-1)(b-1)<-2,
a>1, b>1,
�̂����ꂩ�������ƁB >>614
�Ȑ����ƂŔ}��ϐ��\�������
x=2sin��
y=-2cos��+(1+cos��)/sin��
�v�Z����ƁA��=��/6�ƃ�=5��/6�œ����_(1,2)��ʂ邱�Ƃ�������
����ă�=��/6~5��/6�ň͂܂�镔���̖ʐς����߂邱�ƂɂȂ�
���Ƃ�
��[��/6,��/2](y(��)-y(��-��))(dx/d��)d��
���v�Z���邾��
���Ǝv�� >>519
�@n����̂Ƃ�
�@�@a = - ((3/2)^{n+1} - (1/2)^{n+1}) /(n+1), k=-1/2�@>>549
�@n�������̂Ƃ�
�@�@I[x] - I[x-1] = [(x+1)^{n+1} + (x-1)^{n+1} -2x^{n+1}] / (n+1),
�@����� x �Ŕ��������
�@�@(x+1)^n + (x-1)^n - 2x^n > 0�@�@�@(���@y=x^n �͉��ɓ�)
�@�䂦�A�P�������B�����͍��X�P�B
�@a, k �Ȃ��B�@�@>>551 >>612
��ʂ�R���Ƃ���
R + R����R�ւ�R�����^f�́A
(a,b) = a(1,0) + b(0,1)
�Ƃ����邱�Ƃ���A
f(1,0)�ƁAf(0,1)
�̑��Ō��肳���̂ŁA
�����^�S�̂�R+R�ɓ��^
�ǂ��Ɏg���Ă�H >>618
����H���X�Ԃ���Ă�H
>>562��>>556
>���Z�Ȃ��Lindelof
>
>�̏ؖ��ł����A�������AC�g���Ă܂����H
�܂�
���̈ʑ����Z�ȊJ������v�ˁu�C�ӂ̊J�핢���Z�����핢�����v
�̏ؖ���AC������Ȃ��̃��X����Ȃ���ł����H >>614
OQ = {(2sin�� -1) / tan(��/2) } * ( sin(��/2) , cos(��/2) ) + ( 1 , 2 )
�ƂȂ邩�� �� = ��/2 �Ƃł������ċɍ��W�̂��� �� = ��/12 �` (5/12)�� �� ��(1/2){ }^2 d�����v�Z�B ������Ԃɂ͂��̊�������(��ӂ�)���݂���
�Ƃ�������̏ؖ���AC���g�킸���Ă��ؖ��o����̂ł����H >>616���肪�Ƃ��������܂��B���Ȃ݂�2���[�g3-3�ł����Ă܂����H >>621
����������ԂƂ��Ă���ˁH
�R�[�V�[��̓��l�ނ̂Ȃ���ԂƂ��Ĉ�ӂɒ�܂��ˁH >>623
�����牴��>>621�̏ؖ���AC���g�����ǂ������ĕ����Ă�
���݂��邩�ǂ����͕����ĂȂ���
�l�̘b�𗝉����� ��̓I�ɍ\������̂͏ؖ��ɂȂ�Ȃ��Ƃł��H
����Ƃ��A�܂���(���݂�����)��Ӑ��������̂ɑI���������K�v���ǂ����ŔY��ł�̂��� >>614
���_����PQ�i�܂���PQ�̉����j�։��낵�������̑���R�Ƃ�����
R�̋O�Ղ�cardioid
OQ=(2sin��, (1+cos��)/sin�� - 2cos��)
�ł����Ă�Ǝv�� >>614
�Ƃ͈̔͂�Arctan(4/3)����<��
�������ϕ��͈͂ł͂Ȃ� >>628�ʐς̓�����2��3 -3�ł����Ă܂����ˁH >>629
Wolfram�搶
https://www.wolframalpha.com/input/?i=plot+x%3Dsin(t),+y%3D((1%2Bcos(t))%2Fsin(t)+-+2*cos(t)),+from+pi%2F6+to+5*pi%2F6
https://www.wolframalpha.com/input/?i=integrate(2*cos(t)*((1%2Bcos(t))%2Fsin(t)+-+2*cos(t)),t,5*pi%2F6,pi%2F6) >>614
PQ=2�Ƃ�������������̂�
�Ȑ��ɂ͂Ȃ�Ȃ��Ǝv���B
��=��/6�̂Ƃ�PQ�͂�����ɂȂ邩�l���Ă݁B >>615
���肪�Ƃ��������܂��B���̌`����2�����̉�]�s��Əc�x�N�g��(x,y)��A�z�����̂ł����A�s�����������͂�͂�Ȃ������ł��� �]���q�s���������Ό��ʂ����悭�Ȃ� U(n)=�oX��C^(n�~n)|X*+X=0�p
Herm(n)= �oY��C(n�~n)|Y*=Y�p
��n^2�������x�N�g����Ԃł��邱�Ƃ̏ؖ������ꂼ�ꋳ���Ă��������B
X��n�~n���f�����s��AX*��X�̃G���~�[�g�����ł��B(Y�����l�ł�) >>631
���Ȍ����͂��Ă邩��A����ň͂܂�Ă镔�������߂���Ė��Ȃ�Ȃ��́H >>634
���ꂼ��̍s��ɂ����鐬�����ǂ̂悤�ɂȂ��Ă��邩���l���������Ȃ����ȁB >>614
�ڐ��̌X���� -(1/tan��) ������
�@y = y(P) - (1/tan��)x,
PQ=2 ������
Q (x,y) = (2sin��, y(P) - 2cos��)
�ڐG��������
�@y(P) = (1+cos��)/sin�� = 1/tan(��/2),
(x,y) = (2sin��, y(P) - 2cos��)
�@= (2sin��, (1+cos��)/sin�� -2cos��)�@�@>>627
C�� �� = ��/6, 5��/6 �Ŏ��Ȍ������Ă���B�@>>635
���ߓ_ (1,2) �� (2,1) �̊Ԃ���������B
��/6<��<��/2 �̂Ƃ��i�����j
�@y1 = 2/x - 2(1-1/x)��(1-xx/4)
��/2���Ɓ�5��/6 �̂Ƃ��i�㑤�j
�@y2 = 2/x + 2(1-1/x)��(1-xx/4)
���̍���
�@y2 - y1 = 4(1-1/x)��(1-xx/4)
�����
S = ��[1,2] (y2-y1) dx
�@= ��[1,2] 4(1-1/x)��(1-xx/4) dx
�@= [ 2(x-2)��(1-xx/4) +4log(1+��(1-xx/4)) -4log(x/2) +4arcsin(x/2) ](x=1,2)
�@= ��3 - 4log(2+��3) + 4��/3�@
�@= 0.653009424656001443644 >>630�@��
Q (x, y)
x = 2sin��,
y = (1+cos��)/sin�� -2cos��,
dx = 2cos��d��
���
S = -�� y dx
�@= -��[��/6, 5��/6] {(1+cos��)/sin�� - 2cos��} (2cos��)d��
�@= [ -2cos��(1-sin��) - 4log|sin(��/2)| +2�� ]
�@= ��3 - 4log((��3+1)/(��3 -1)) + 4��/3
�@= 0.653009424656001443644 �ȉ��̏���������ABC�����݂���Ȃ�Η�������A���݂��Ȃ��Ȃ���̂��Ƃ��ؖ�����B
�EBC��3��������_��B�ɋ߂�������P,Q�Ƃ���ƁAAB,AP,AQ,AC�͂��̏��ɓ���������Ȃ� �y�A�m�̌����݂Ďv��������0�����݂�����Ăǂ���������? >>557
�ǂ��ł��ǂ����Ƃł����A�������猩�����s���Ă�̂��ȁH
�v�킸�u����ɂ���v�Ɖ]���Ă��܂����B >>639
���_A����Ε�BC�ɉ���������AH�̒�����h�Ƃ���B
BC��̓_X�ɂ��āA
�@AX^2 = AH^2 + HX^2 = hh + xx,
x ��H����X�܂ł̋����B
�@AX = ��(hh+xx)
��x�ɂ��ĉ��ɓʂŁA�X����x�Ƌ��ɒP���ɑ�������B
��BC��ɓ��Ԋu��4�_�Ƃ����Ƃ��AA����̋����̍��͂��ׂĈقȂ邩��
����������Ȃ��Ȃ��B a_1 = 1
a_2 = 2
a_(n+2) = 2a_(n+1) + a_n (n=1,2,...)
�Ő����̗�{a_n}���߂�B�C�ӂ̊�f��p�ɂ��āAa_p��p�Ŋ������]������߂�B
���̖��������Ă��������B����Ď�������o�܂���B >>643
a_(2m+1) = ��[k=0�`m]C(2m+1,2k+1)2^k
p����f���Ȃ�� 0��i��p �Ȃ鐮��i�ɂ��ēW�� C(p,i)��0 (mod p) �ƂȂ�̂�
a_p �� 2^{(p-1)/2} (mod p)
�����
a_p �� 1 (mod p) (p �� �}1 (mod 8) �̂Ƃ�)
a_p �� -1 (mod p) (p �� �}3 (mod 8) �̂Ƃ�) �㐔�ɂ����颊�ꣂ͔Z�x�̈�Ӑ������藧���܂����A
�ʑ���Ԃɂ����颊�ꣂ͔Z�x�̈�Ӑ��͗v������Ă��Ȃ�(�H)�݂����ł���
�ǂ����Ă���ȈႢ���N�����ł����H ������g(x)�͘A�����ł���Ƃ����̂��ǂ�����o�Ă������킩��܂���B
�܂����̋��ȏ��̐����̂悤�ȗ����ł�����ł����H
�l�b�g�ł͕����ň����Ă͂Ȃ�Ȃ��Ƃ������Ă���܂�
�������̔����\��dy/dx�̕\�L�𗝉��ł��Ȃ��ƐF�X�����ł��Ȃ��悤�Ȃ̂ō����Ă܂�
https://i.imgur.com/510ki6x.jpg >>646
�㐔�ɂ�������͋�ԑS�̂����邱�Ƃƈꎟ�Ɨ��ł��邱�Ƃ������B
�ʑ���Ԃɂ�������͐������邱�Ƃ����v�����Ȃ�����A�Z�x�ɂ��Ă͈�ӂłȂ��Ȃ�B
�Ⴆ�A�ʏ�̘a�A�X�J���[�{����`���ꂽ�x�N�g�����R^2�ɂ���
{(1,0),(0,1)} ��R^2������B���Ɋ��ƂȂ�B
{(1,0),(0,1),(2,0)} �͊��ł͂Ȃ���R^2������B
�����ƌ��������Ă�(��Z�ł��悢)R^2������B
�ʑ����X�ɂ��Ă����l�B
B��P(X) (P(X)��X�̙p�W��)��X�̊��Ƃ����Ƃ��AB��X�̊J�W���������Ă�(����Z�ł�����)��͂���ƂȂ�B �V�O���C�h���ƌĂ�Ă�����ɂ��Ԃ�p�^�[�������鎖�͉������̂ł����A�������ʉ��ł��܂���B���̃T�C�g�ł����₵���̂ł����A�悭������Ȃ������̂ŁA�����Ă��������B
�̂ăA�J��twitter�Ŏ��₵����
https://twitter.com/tate_go
goo����Ŏ��₵����
https://oshiete.goo.ne.jp/qa/10866096.html
https://twitter.com/5chan_nel (5ch newer account) X�ʑ���ԂƂ��܂�
x��X �Ƃ��A V(x):={U��X�bU��x����_�Ƃ��Ċ܂�}
���̂Ƃ��C�ӂ̃Ӂ�S��V(x) �ɑ���S�̂��Ƃ𢂘�̋ߖT�n��ƌ����Ă����̂ł����H >>653
��U: nbd of x ��V��S V��U
�����Ȃ��ƃ_���ł��B >>654�ߖT�n�̒�`���C�}�C�`����ӂ�Ȃ̂ł����A
�X�̕����W��A���A���ł���Ƃ́`�`��Ƃ�����`�͂����Ă�
�x��X��X�̕����W���nV�Ƃɂ������āAV��x�̋ߖT�n�ł���Ƃ́`�`��Ƃ�����`���Ē��X�������܂�����
��`���n�b�L���Ɗm�F�������̂ł��� >>654
�����"��{"�ߖT�n�̒�`�ɂ��Ă̗v���ł��B
���������Ă�̂͒P�Ȃ颋ߖT�n��ɂ��Ă̒�`�ł��B
�P�Ȃ颋ߖT�n��̕��̒�`�ł�"�S"�ߖT�n�̒�`(x����_�Ƃ��Ċ܂ޏW���S�Ă̏W��)�͂����Ă��A"�S"�ł͂Ȃ����ʂ̋ߖT�n�̒�`�͌������܂��� >>653�ɂ�����V(x)��������S�ߖT�n�ł����
�ł��Ӂ�S��V(x)�Ȃ�S�ɑ��Ģ�ߖT�n�ł��飂Ƃ������t���p�����鎞������܂��B
������AS�ɂ͂ǂ������������v�������̂��Ƃ����̂�����ł��B >>658
����Ȃ̂�
�ߖT�n�Ȃ킯�Ȃ����B
��o�Ȃ��Ⴂ���Ȃ�{(-1,1)}��0�̋ߖT�n�ɂȂ��Ă��܂��B
���R�ߖT�n�Ƃ�������ɂ�>>654�̂悤�Ȑ������Ȃ��ƁB
�P�Ɂu�ߖT���P�͊܂ޏW���v���ߖT�ƌĂԂ킯�Ȃ����B
wiki�ɂ�
�e�ߖT V �ɑ��ċߖT��̌� B �� V �Ɋ܂܂����̂��Ƃ�邱��
�����������B >>659
������o�Ȃ��Ⴂ���Ȃ�{(-1,1)}��0�̋ߖT�n�ɂȂ��Ă��܂��B
�������Ȃ��O
�����Ⴂ���Ƃ�˂O >>659
���O�����̎���𗝉����ĂȂ����Ƃ���������
���O�݂����ȃA�z�͂��܂��Ƃ�
��X�������ɉ̘J�͊|��������� >>659�����݂����ȓ��{�����ɗ����o����A�z�͎v���o�������ł��C���C�����Ă����
������S�~��]
���O�͐��w�ȑO�̔]�݂��Ȃ� ���h��u�ڋq���{���ɕK�v���������́v���A�i���O�Q�[����
https://headlines.yahoo.co.jp/hl?a=20180513-00000005-it_nlab-life
�Q���}2018���E�t�ł̘b���uLiqueur the GAME (���L���[���E�U�E�Q�[��)�v
http://www.comonox.com/entry/boardgames/open/Liqueur-the-GAME
�u�Ɛl�͗x��v���v���C���āu�T��v�ƂȂ��āu�Ɛl�v���Ŕj���]������h�o�h�o�ɒ���
https://gigazine.net/news/20170921-hanninha-odoru-sugorokuya/
�אl�̉��l�ρA�������Ă܂����H�w���Ȃ���m��Ȃ����Ȃ��̗אl�x�V�т܂���
http://www.unjyou.com/entry/2017/12/14/220000
�u�X�R���v�̓J�[�h�Q�[���ɋ�������ȏ��S�҂̓���p�ɍœK�A�T�C�R����U����
�J�[�h���W�߂ǂ�ǂ��̊X�W�����ď�����ڎw��
http://news.livedoor.com/article/detail/10962802/
��x���i��n���j�̂悤�ȃJ�[�h�Q�[���uReCURRRing�i���J�[�����O�j�v
http://www.tk-game-diary.net/recurrring/recurrring.html
���킢���Ђ��𑝂₵�đ��₵�đ��₵�܂���I �g��l�p�h�J�[�h�Q�[���w�V�F�t�B�x
http://www.moguragames.com/entry/shephy/
���@�����\����w���z���x��V�т܂���
http://www.unjyou.com/entry/2017/09/02/200000
���z�ʉ݂�V�тȂ���w�ׂ�{�[�h�Q�[���uTHE���z�ʉ݁v
https://www.makuake.com/project/the-kasotsuka/ a[1]=��/16�Aa[n+1]=(1/16)a[n]�Ƃ���Ƃ��A�ȉ��̋Ɍ������߂�B
lim[n����] ��[k=1 to n] sin{a[n]} ����������������܂���B
�ʑ����X�ɂ�����x���Ƃ̋ߖT�n�͂���1���������Ax�̊�{�ߖT�n�͖����Ɏ���Ƃ������Ƃł����� �J�ߖT�n�@�͕K�������@�ߖT�n�̌��������킯�ł͂Ȃ��ł���ˁH
�Ƃ������Ƃ͊J�ߖT�n�ƋߖT�n�͕ʊT�O�Ƃ������Ƃł����H
�Ⴆ�A���[�N���b�h��Ԃōl�����
U = { (-e,e) | e���̎���}�@�Ƃ���ƁA�����0�̊J�ߖT�n�ł����A
����͋ߖT�n�̌����̓���1��
�@�@A��0�̋ߖT�ł���AA��B�Ȃ��B��0�̋ߖT�ł���
�����܂���B
B�Ƃ���(-e,e)��N�@(N�͎��R���S�̂̏W��)�@�Ƃ������ >>666
a[n] = ��/(16^n)�@�͓��䐔��B
sin ���}�N���[�����W�J����Ɠ��䋉���ɂȂ�B
��/[1!(16^1 -1)] - (��^3)/[3!(16^3 -1)] + (��^5)/[5!(16^5 -1)] - (��^7)/[7!(16^7 -1)] + �c
= ��/15 - (��^3)/(3!�4095) + (��^5)/(5!�1048575) - (��^7)/(7!�268435455) + �c
= 0.2081799833135020539 >>668
�ʑ����X�Ƃ��̒���1�_a���Œ肷��ƁA�_a��(�S)�ߖT�n�͈�ӂɒ�܂��Ă���
(�u�_a�̋ߖT�S�̂̏W���v����`�Ȃ̂�)
�J�ߖT�n�͊J�ߖT���W�߂����̂ł���A�ߖT�ƊJ�ߖT�͈قȂ���̂Ȃ̂œ��R�Ȃ���ߖT�n�Ƃ͕ʂ̊T�O
�w�E�̒ʂ�A��ʂɊJ�ߖT�n�͋ߖT�n�ƈ�v���Ȃ�
�������A��{�ߖT�n�ɂ͂Ȃ��Ă��� >>670
���肪�Ƃ��������܂�
�X�b�L�����܂���
�ꉞ�m�F�ł����A�(�S)�ߖT�n��Ƃ����\�L�̓e�L�X�g�ł��悭�������܂����A
����͢�ߖT�n�����ǁA�ߖT�S�����W�߂Ă邩��S�ߖT�n�Ƃ������������o���邾���ł����āA�P�ɋߖT�n�Ƃ����ǂ�ł��������ł��飂Ƃ����Ӗ��ł����H ��{�ߖT�n�͖����Ɏ���B
�Ⴆ��R^2�Ƀ��[�N���b�h��������ꂽ���̂ƃ}���n�b�^����������ꂽ���̂͂��ꂼ��قȂ�J������`�����B
����_x������āA���̓_�𒆐S�Ƃ����J���̑S�̂�x�̊�{�ߖT�n�Ȃ̂ŁA2��ނ̊�{�ߖT�n����܂������ƂɂȂ�B
���Ȃ݂ɂǂ���̋������Ƃ��Ă��U�������ʑ��͓����B
�X�Ɍ�����1≤p<���ɑ���(R^2���)p-�m�����Ƃ������̂���܂��āA���̃m��������U������鋗���ɂ��J�����l���邱�Ƃ��o����B
�����͊�{�ߖT�n�͂����Ƃ�������ˁB
>>671
�S�ߖT�n���Č��t�����߂ĕ��������番����Ȃ��B
�����Ȃ�u�_x�̋ߖT�S�̂̏W��N(x)�v���ĕ��ʏ������ǁA�ߖT�n�́u�n�v�Ƃ������t�ɑS���W�߂Ă�����ĈӖ�����������̂ł́B >>671
�S�ߖT�n���Č��t�����߂ĕ��������番�����B
�����Ȃ�u�_x�̋ߖT�S�̂̏W��N(x)�v���ĕ��ʏ������ǁA�ߖT�n�́u�n�v�Ƃ������t�ɑS���W�߂Ă�����ĈӖ�����������̂ł́B 12^2 = 144 ........................ 21^2 = 441
13^2 = 169 ........................ 31^2 = 961
�̐��ł����Ȃ�̂͑��ɂ���H >>672�A673
���肪�Ƃ��������܂� >>634
n=1�Ƃ��Ă݂�B
x*+x=0
��x���������Ƃ������ƁA�܂�
x=iy (y�͎����j
������A���Ƃ���i������B
n����ʂł������悤�ɍl����Ƃł���B >>674
3����900�@<-> 009 ���܂߂��
Prelude> [(x,y)|x<-[0..9],y<-[0..9],let z=(10*x+y)^2, z<1000,let a=z `div` 100,let b=z `mod` 100 `div` 10, let c=z `mod` 10,100*c+10*b+a==(10*y+x)^2]
[(0,0),(0,1),(0,2),(0,3),(1,0),(1,1),(1,2),(1,3),(2,0),(2,1),(2,2),(3,0),(3,1)] ���ꐔ����O���܂܂Ȃ��ĂR���ɂȂ�Ȃ�
[(x,y)|x<-[1..9],y<-[1..9],let z=(10*x+y)^2,x<y,let a=z `div` 100,let b=z `mod` 100 `div` 10, let c=z `mod` 10,100*c+10*b+a==(10*y+x)^2]
[(1,2),(1,3)] �Q�悪�S���ɂȂ鐔���ŊY������̂͂Ȃ��݂������ȁB
Prelude> [(x,y)|x<-[0..9],y<-[0..9],x<y,let z=(10*x+y)^2,let a=z `div` 100, let a1=a `div`10,let a2=a `mod` 10,
let b=z `mod` 100 `div` 10, let c=z `mod` 10,1000*c+100*b+a2*10+a1==(10*y+x)^2]
[] �����������Z���͏������ނ̂�߂Č� >>680
�C�ӂ̕��f���W����2����f(x)�ɑ��āAg(x)=sin(f(x))���������łȂ����Ƃ��ؖ�����B
������f(x)��2���̌W����1�Ƃ���B ���،����Љ�Ă� sin�̖����ϕ\���̏����I�ؖ�
https://twitter.com/genkuroki/status/1074570815901814785
https://pbs.twimg.com/media/DumkdV6U8AAeCXy.jpg
���̏ؖ��ɂ��ċ����Ă��������B
�I�Ղ� m���� �̋Ɍ����Ƃ�ۂ�
�u�e���̋Ɍ��v���Ƃ��Ă��� �u�����̋Ɍ��v���Ƃ��Ă��܂��B
���̐������������I�Ɏ����ɂ͂ǂ������炢���̂ł��傤���H
�Ⴆ�� a_1 = a_2 = ... = a_m = 2^{1/m} �ɑ���
lim[m����] { ��[k=1, m] a_k } = lim[m����] 2 = 2
��[k=1, ��] { lim[m����] a_k } = ��[k=1, ��] 1 = 1 �� 2
�݂����ɁA��ʂ̖����ςł͂��̂悤�Ɉ�����Ƃ͌���܂���B
https://twitter.com/5chan_nel (5ch newer account) >>682
�̓������j�̏ؖ��ɒ��킵�����Ƃ���B
����������͈̂�v�̒藝�g�������̂�|s| << 1�Ƃ��Ă悢�B
f_n(t) = log (1-sin^2(��s/~)/sin^2(��[t]/~)) (t��m+1)
. 0 (t��m+1)
�Ƃł������Ă�����f_n(t)�̈�l�ϕ����������Ă����B
����Ɛϕ��ƋɌ����삪�����\��
lim[m����] �� [1,��] f_m(t) dt = �� [1,��] lim[m����] f_m(t) dt
���炢����B >>682
���Y���v�̉�͓���I�̖����ς̐߂ɓ��l�̕��j�Ŏ�����肪�ڂ��Ă܂��� ����(3)��(4)�𗊂ށc
�l�p�̋߂���ł��c
https://i.imgur.com/s3aiLVM.jpg >>685
��AOC=150�����g����AC^2�͋��܂�
�ʐς�1/2AB•AC•sin��BAC���v�Z >>685
�ΐ����Ƃ�����ɂȂ��āATannery �̒藝�̎g����`�ɂȂ�B
���Ȃ݂�Tannery �̒藝�͋Ɍ��̏����̒m���ŏؖ��ł���B �������ł������`�㐔���ދ��ł��B
�Ӗ��̂킩��Ȃ��v�Z�����X�Ƃ���������̂���啪��Ȃ͉̂��̂ł��� ������L���̒��ɕ����߂邱�Ƃ͉\�ł����H
���ƁA�����ƑS�͎̂��͓������̂ł��傤���H >>689
���݈Ӌ`��������Ȃ����R�͎��g�̕��s���ɂ����̂ƍl����ׂ�
���`�㐔�ł����A�l�X�ȕ���Ŏ��R�ɏo�Ă���ΏۂȂ̂Ő��w�̒��ł͂ƂĂ����
�㐔�ł��ł���͂ł��ǂ��ł��o�Ă���
����炩�璊�ۓI�Ɏ��o���ꂽ�T�O��v�Z����`�㐔�Ƃ��Ċw�Ԓi�K�ł͑ދ��Ɋ�����͎̂d���Ȃ��Ǝv�� >>686
�ǂ������肪�Ƃ��������܂��B
�������A
����AOC=150��
�͂ǂ�����ĕ������ł��傤���H ������Ύq�œ���̏o�ڈȏ���o���Ƃ����v�Z��������Ȃ��̂ŋ����Ē��������c�c
�Ⴆ��6��6���Ύq�őS��6�ɂ���m�����o�����Ǝv����
1/6 x 1/6 x 1/6 x 1/6 x 1/6 x 1/6��1/46656�ɂȂ�Ǝv���̂�����
���ꂪ���Ɏ��ۂɂ�����Ύq���݂��Ȃ�����������
3�ʃ_�C�X��̓��A���3�̖ڂƈ���g2�̖ڈȏ�h
5�ʃ_�C�X�l�̓��A�O��5�̖ڂƈ���g4�̖ڈȏ�h
�����������ɂǂ��������Ɍv�Z��������������Ē��������c�c �NjL�B
���Ȃ݂ɍ��m�肽���̂͏�ɒ����Ύq�̏o�ڂ�
3�ʃ_�C�X��̓��A���3�̖ڂƈ���g2�̖ڈȏ�h
5�ʃ_�C�X�l�̓��A�O��5�̖ڂƈ���g4�̖ڈȏ�h
����Z���Ύq�̍��v�����m���ł��c�c �����AsinBAC=1/��2������BAC=45���Ȃ̂��A�A
����ƕ���������A���肪�Ƃ� >>694
���ꂼ��̖ڂ�1/3�A1/5�ŏo����̂Ƃ���
3�ʂ�3*3��9�ʂ�̂���(3,3)�A(3,2)�A(2,3)������3/9=1/3
5�ʂ�25�ʂ�̂���5�ʂ肾����1/5
�|�����킹��1/15�Ȃ�łȂ����H >>694
2*(1/3*2/3) * 4*(1/5)^3*2/5 a��R^2�ɂ����錴�_���Œ肵����]�Ab�����_��ʂ钼���ɂ�鋾�f�Ƃ���ƁA�����I��a��b���Ǝv���̂ł����A�ǂ̂悤�ɏؖ��ł���ł��傤���B >>698
(2*(1/3*2/3) -(1/3)^2) * (4*(1/5)^3*2/5 - (1/5)^4) >>696���ԈႦ�Ă���
5�ʂ�625�ʂ�̂���5�ʂ肾���� >>700
(1/5)^4��3�{����K�v�������H ���ǁA�ꍇ�̐��𐔂��������ԈႢ�ɂ����ȁB
> gr3=as.matrix(expand.grid(1:3,1:3))
> f3 <- function(x){
+ any(x==3) & all(x>=2)
+ }
> gr3[apply(gr,1,f3),]
Var1 Var2
[1,] 3 2
[2,] 2 3
[3,] 3 3
>
> gr5=as.matrix(expand.grid(1:5,1:5,1:5,1:5))
> f5 <- function(x){
+ all(x>=4) & sum(x==5)>=3
+ }
> gr5[apply(gr5,1,f5),]
Var1 Var2 Var3 Var4
[1,] 5 5 5 4
[2,] 5 5 4 5
[3,] 5 4 5 5
[4,] 4 5 5 5
[5,] 5 5 5 5 >>690
����������L���̒��ɕ����߂邱�Ƃ͉\�ł����H
�ց�x����[ x��{x}���� ]
�L���L����ɂ���ĕ\���ꂽ�\��(�_����)�̒��ɢ�����̗v�f�����W���ւ����݂��飂Ƃ����Ӗ������߂��Ă��܂� �����F
�Ӂ��ցȁց�x����[ x��{x}���� ] ����
��[ �Ӂ��� �� ��x���� x��{x}���� ] >>705
�m���ɍs�ŋ�ʂł��܂���
���肪�Ƃ��������܂� >>683 >>684 >>688
���肪�Ƃ��������܂��B�����ł��܂����B
(k��m) q[m,k] := ( sin(��s/(2m+1))/sin(��k/(2m+1)) )^2 �� (s/(2k/��))^2 = (��/2)^2 * 1/k^2 �� (��/2)^2 =: ��
(m<k) q[m,k] := 0 �� ��/k^2 �� ��
|a[m,k]| := |log(1-q)| �� q/(1-q) �� (��/k^2)/(1-��) = (��/(1-��)) /k^2 =: M[k]
�� ��[k=1,��]a[m,k],�@�� ��[k=1,��]a[��,k]�@(�� ��[k=1,��]1/k^2 = ��^2/6)
�̓� ��N ��m
|��[m]| := | ��[k=1,��]a[��,k] - ��[k=1,��]a[m,k] |
�� ��[k=N+1,��]M[k] + ��[k=N+1,��]M[k] + ��[k=1,N] | a[��,k]-a[m,k] |
< ��/3 + ��/3 + ��/3 = ��
�� lim[m����]��[m] = 0�@(Tannery �̒藝)
��[k=1,��](1-q[��,k]^2) = exp{ ��[k=1,��]a[��,k] }
= exp{ ��[k=1,��]a[��,k] - ��[k=1,��]a[m,k] } exp{ ��[k=1,��]a[m,k] }
= exp{��[m]} exp{��[k=1,��]a[m,k]}
= exp{��[m]} ��[k=1,��]( 1-q[m,k]^2 )
= lim[m����] ��[k=1,��]( 1-q[m,k]^2 ) = lim[m����] ��[k=1, m]( 1-q[m,k]^2 ) �ŏ��̕ӂ�ł�����Ɣ��C�����K�v�Ȃ̂ɋC�Â��܂������A
�w�E�͕s�v�ł��B�Ȗ��Ȃ̂ŁB ���̓������ؖ����ĉ���������܂���
f_i(i��1,�c,n)�͕��[a,b]��Œ�`���ꂽ���A�����ł�
https://i.imgur.com/sADw8Sg.jpg >>712
���f(x)g(y)dxdy=(��f(x)dx)(��g(x)dx)
���J��Ԃ��g���āA�E�ӂ�det��W�J�������ɏo�Ă���e����ϕ��̐ςɃo����
�E�ӂ͕ϐ��̃��x���t�����Ă镪�A�����������xn!��o�Ă���͂� ���f���ʏ�̌��_�łȂ�2�_A(��),B(��)��ʂ钼���Ɍ��_���琂�������낵�A�����2�����̌�_��C(��)�Ƃ���B
���̂Ƃ���=�����ƂȂ邽�߂̕K�v�\�������́A�u��,�����i�@�@�@�@�j�̏�ɂ��邱�Ƃł���v�B
�ɂ��Ă͂܂�K���Ȑ}�`�����߂�B >>714
���_�𒆐S�Ƃ���P�ʉ~����H >>714>>715
�����������ɑ��ă��ƑΏ̂Ƃ����������v�邩 >>714
D(2��) �Ƃ���� AO = AD �Ȃ̂� |��| = |�� - 2��|
�� = ���� �Ȃ� |��| = |�� - 2����|
�� �� 0 ������ 1 = |1 - 2��|
���Ȃ킿 |�� - 1/2| = 1/2
���l�� |�� - 1/2| = 1/2
E(1/2) �𒆐S�Ƃ��锼�a 1/2 �̉~����ɂ���
�i������ O(0) �������j ���ϋ�Ԃɂ������́A"�����̋��"�̕��"���z"�o���邱�Ƃ̏ؖ��ɂ�AC���g���Ă��܂����H
X=��_i X_i �ϋ�ԂƂ��܂�
A_i �� X_i�@���W���Ƃ��܂�
���̎��A cl(��_i A_i) = ��_i cl_i(A_i) �����藧���܂��B----��
�������Acl��X�ɂ������Acl_i ��X_i�ɂ������ł��B
���̏ؖ��ɑI������(AC)�͎g���Ă��܂����H �������������A�ǂ����
�@�@cl(��_i A_i) �� ��_i cl_i(A_i)
�̏ؖ��ɉ�����AC���g���Ă���悤�Ɏv���܂����A�������ł��傤���H >>721
�t�� �Ȃ�ŕK�v���Ƃ������́H
�W���_�̌���ZF�� ��������ɂ��ĂȂ��ł����ˁH >>721
���߂�A���傢�ƏC��
��܊W���t�ɂ݂���
cl(��_i A_i) �� ��_i cl_i(A_i) �@�͑I�������͕K�v
cl(��_i A_i) �� ��_i cl_i(A_i) �@�͑I�������͕s�v �ߋ��ɉƒ닳�t�̐搶�ɏo���ꂽ���A3�N�ԓ������o��
�N��������������
�uX���ǂ̂悤�ȂƂ��ɁA��X���������ɂȂ邩�����B�v >>726
����͂킩�邯�ǁA�ؖ��͓���Ȃ��ł����H p��8�Ŋ�����1�]��f���Ƃ����
p=A^2+B^2, p=C^2+2*D^2
(A,C�͊�AB,D�͋���)�Ə����܂����A���̂Ƃ�
B��0 (mod 8) �� C�߁}1 (mod 8)
�ł�
�����͂����x^4��2 (mod p)������������������2�̕��@�ŏ���������ǁA���̎��_�͂���܂����H >>726
��`���̂��̂�g�ݍ��킹�������̂悤�ȓ����ȁB >>727
�ȒP����
�u��X���L�����ł������P�v�����߂�uP�����Ȃ����́v�����̓����ɂȂ�
�Ⴆ��Y=��X�Ƃ����āAY�͗L����������X=Y^2�͗L�����̎���
�}�W�ł��ꂾ���@��������Ȃ� �L�����̎���͗v�������ŕ\���ĕ�����/�������ŕ\���鐔
���̌`�ɂȂ�Ȃ����͑S�ā�X�������� >>732
�����ŕ�����/�������ŕ\���鐔�u�̂݁v���L�����ɂȂ�ؖ��Ȃ�Ăł���̂��H
�����͎v���t���� ��{���v�w�̉��K���ł��B
A,B2�l��2�̃T�C�R�����g���Ĉȉ��̓q�����s���B
2�̃T�C�R���𓊂��Ėڂ̘a��x�Ƃ���Ƃ��Ax�������̎���A��B��x������100�~�d�݂����炢�A�A����̎���A��B��x������100�~�d�݂�^����B���̎�A�����炤(���̏ꍇ�͎x�������z)�̕��U�����߂�B
����Ȃ�ł����ǁA���U���������Ă�5,000�ɂȂ��Ă��܂���ł����A��548,333�ɂȂ��Ă܂��B
�������������ĖႢ�����ł��A���肢���܂��B >>734
���Ғl��0�Ȃ̂ŁA���̕��ς��v�Z����悢
�܂��߂Ɍv�Z���Ďl�̌ܓ�������̒l�ɂȂ�܂� >>733
���������������c�c�c
���ꂪ�����ł��Ȃ��̂͂��Ȃ��̐ӔC�Ŏ��̐ӔC�ł͂Ȃ�
�ō��ɒ��J�ɉ������ȁH
�@����̎���X�̕������AY=��X�͗L���������������̂ǂ��炩�ł���B
�A�]���āA
(a)�uY���������ƂȂ�X�̏����v
(b)�uY���L�����ƂȂ�X�̏����v
���̂ǂ��炩�������߂�Ζ��͉�����B
(b)�ׂ邱�Ƃɂ���B
������X=Y^2�͏�ɐ��藧���AX��Y�͈�Έ�Ή����邱�Ƃ͎����ł���B
�܂�Y���L�����ł���ꍇ�AX�͗L�����̎���ƂȂ�B
�t�������ł��邩�炱��ŕK�v�\���������������ɂ킩��B
�܂�AY���L������X���L�����̎����X��������/�������ŏ�����
���Ȃ��̎���͂��ꂷ�痝���ł��ĂȂ��Ƃ������ƂŘ_����ɒl���Ȃ��B (��)���� X �ɂ��Ă̖���
P: ��X �͗L�����ł���
Q: X �͕����L�����ł���
�܂����ꂪ���l�ł��鎖���m���߂�B
{P �� Q}�@��X = a/b (����) �@�� �@X = a^2/b^2 (����) �ł���B
{Q �� P}�@X = a^2/b^2 (����)�@���@ ��X = a/b (����) �ł���B
����� P ↔ Q (���l) �ł���Anot Q ↔ not P ��������B
�܂�A
X �͕����L�����ł͂Ȃ��@↔�@ ��X �͖������ł���(�L�����ł͂Ȃ�)
��Ȃ̎�������/�����炩w���Ė��قǁA
{P��Q}���������� {Q �� P} ���������C�ɂȂ��Ă��肷��̂Œ��ӂ��K�v�B
>>736 �Əd���������e���������A�܂������Ă��܂����̂�... 29�N�x�Z���^�[1A�ǎ�����ł�
�ua����������1+a^2=b^2�Ȃ�Ab�͖������v
���̖��肪�ǂ����U�炵���̂ł����A���Ⴊ�v�����܂���B
�����ǂ���͂���܂����H �ua����������1+a^2=b^2�Ȃ�Ab�͖������v
����F a=��3 �̂Ƃ� b=2
1+ (��3)^2 = 2^2 >>739
�����{�������肪�Ƃ��������܂�
��������������b�ɗL���������Ă݂Ď���k�������x���������̂ł��傤�� �L�����Ƃ��������������̂͂܂��͐������玎�����̂ł�
b=1,2...�Ǝ����Ă�������������܂��� >>741
���w1A�̋��ȏ��Ɂ�n���������ɂȂ�n�̗Ⴊ�o�Ă���낤�ˁB
n�ɏ���1,2,3,4,5,6,7,8,�E�E�E�����čs���A>>740����� 3 ��>>739�� 8 ����������A�Ƃ���
���w�͎������I�̐��_��������������B >>742
>>743
���肪�Ƃ��������܂�
�{���Ɏ����͑�ł��ˁB�g�ɂ��݂܂���
�e���p�炸�Ɏ����ł���悤�ɐS�����܂� >>736
>>737
����Ɨ����ł��܂���
���肪�Ƃ��������܂��� �����_�E�L���̃��[�W�I�[�ƃX���[���I�[�̈Ⴂ�������Ă��������B
�����Ȃ��Řb���Ă�������Ƃ��肪�����ł��B >>734
��`�ɏ]���Čv�Z
gr=expand.grid(1:6,1:6)
w=apply(gr,1,sum)
ev=100*w[w%%2==0]
od=-100*w[w%%2==1]
p=rep(1/36,18)
m=sum(p*ev+p*od) #���Ғl=0
sum(p*(ev-m)^2+p*(od-m)^2) #���Ғl����̓��[�����g=���U
> sum(p*(ev-m)^2+p*(od-m)^2)
[1] 548333.3
�ǂ������v�Z�����āA5000���ł�H >>747
> �����̎�
200 400 600 400 600 800 400 600 800 600 800 1000 600 800 1000 800 1000 1200
> ��̎�
-300 -500 -700 -300 -500 -700 -500 -700 -900 -500 -700 -900
-700 -900 -1100 -700 -900 -1100
>
�e�X�̊m��1/36�Ōv�Z���邾���B
X�̕��U��X �̂Q��̕��ρ@�[�iX�̕��ρj�̂Q��
�ł��v�Z�ł���i�������Ƃ����ǁj >>746
O(x)�͍��Xx�̍������܂܂�Ȃ�
o(x)��x^2�ȏ�̍����܂܂�� >>743
�v���O�����ɎZ�o�����Ă݂��B�R���܂ŁB
> n=999
> is.whole <- function(x) floor(x)==x
> ans=NULL
> for (i in 1:n){
+ j=sqrt(i)
+ k=sqrt(i+1)
+ if(!is.whole(j) & is.whole(k)){
+ ans=rbind(ans,c(i,k))
+ }
+ }
> ans
[,1] [,2]
[1,] 3 2
[2,] 8 3
[3,] 15 4
[4,] 24 5
[5,] 35 6
[6,] 48 7
[7,] 63 8
[8,] 80 9
[9,] 99 10
[10,] 120 11
[11,] 143 12
[12,] 168 13
[13,] 195 14
[14,] 224 15
[15,] 255 16
[16,] 288 17
[17,] 323 18
[18,] 360 19
[19,] 399 20
[20,] 440 21
[21,] 483 22
[22,] 528 23
[23,] 575 24
[24,] 624 25
[25,] 675 26
[26,] 728 27
[27,] 783 28
[28,] 840 29
[29,] 899 30
[30,] 960 31
> (a+bi)^n�������ƂȂ�悤�Ȏ��R��n�����݂��邽�߂ɁA���R��a,b���������ׂ��������q�ׂ�B
������i�͋����P�ʂł���B F(x)������������Ă���_���L���Ƃ����������uF(x)���������v�ƌĂԂƂ��A���͐��藧���H
�uF(x),G(x)���������Ȃ��, 1)F(x)+G(x), 2)F(x)G(x), 3)F(G(x)), 4)exp(F(x)), 5)log(F(x)) �́������v �������f������`���������� >>751
n=1�̂Ƃ� a��ℕ ���� b=0
����� n>2 �̂Ƃ� a��ℕ���������������Ȃ邩�l����Ηǂ�(b=0 �͂���ȏ�������������ł��Ȃ�)���Aa��ℕ �Ȃ�C�ӂ�n �ɂ��� (a+bi)^n=a^n �͎����ɂȂ�B
�䂦�ɔC�ӂ� n �ɑ��Ă� a��ℕ ���� b=0 lim(n����)�@��(k=1��n) (1/n)*f(k/n) =�@��(0��1)�@f(x)dx�@����敪���ς̌����ł���ˁH
�@
A�@=�@lim(n����)�@1/n * ��(k=1��n) 1/k
��������߂����Ƃ��āA
���̏ꍇf(k/n)=1/k�ƂȂ�Ȃ��Ƃ����Ȃ��ł�����f(x)=1/nx�ł����
�����ɂ��Ă͂߂ā�(0��1) 1/nx dx�@���ꔭ�U���܂���ˁH
A�͖��炩�Ɏ������܂���ˁH(���Ƃ���n��2�̃x�L�ɂȂ�Ƃ����l���ďォ��}�������������)
������Ăǂ������킯�Ȃ�ł��傤�H
�ǂ�������Ԃ��Ƌ敪���ς̌����͎g���Ȃ���ł����H
���ł��g����킯�ł͂Ȃ��ɂ�������炸�A�L�q�̂Ȃ��ŏؖ��Ȃ��ŗp���ėǂ����ƂɂȂ��Ă���ĕs�v�c�Ȃ�ł��� f�F[0,1]��R �����[�}���ϕ��\�Ȃ�敪���ς̌������g����
����ʉ�����Ȃ烋�x�[�O�̎����藝���˂�
���Ȃ݂ɁAf(x)=1/nx ���� n �ɂ��ˑ����Ă邩�� f_n(x)=1/nx �ȂǂƏ����Ȃ�����߂ł��傤
�ł����ꂾ�� ��(k=1��n) (1/n)*f_n(k/n) �ɂȂ����Ⴄ����敪���ς̌`�ɂł��ĂȂ�
n�Ɉˑ����Ȃ���f(x)���g���� ��(k=1��n) (1/n)*f(k/n) �Ƃ����`�ɂł��Ȃ���敪���ςƂ͌ĂȂ������
�����āA�敪���ς̌`�ɂł��ĂȂ��Ƃ������Ƃ́A
�敪���ς��g���邩�ǂ����Ƃ����b�܂œ��B�ł��ĂȂ��Ƃ������Ƃł���A
�u���敪���ς��g����̂��H�v�Ƃ����^��_�Ƙb�����ݍ����ĂȂ�
�S�̓I�ɂ߂��Ⴍ���� �Ɍ��̎���������ɕς��Ă邾���Ȃ̂�
�W�Ȃ��Ƃ��ŕ�������Ă�悤���� R��̃��[�N���b�h�����Ɠ��l�ȋ�����ԂŊ���������ԂłȂ����̂��� >>751
�������� a, b, n �����݂����Ƃ���ƁAIm{ (a + b i)^n } = 0 �ł���
a , b �݂͌��ɑa�Ƃ���. �K�v�Ȃ��Ŏ��R���{����悢.
�k1�l a=b=1 �Ȃ� n=4 �� (1+1 i )^4 = 4 �ƂȂ�̂Ŗ��Ȃ�.
�k2�l a, b �ǂ��炩�� 1 �ł͂Ȃ��ꍇ
�k2.1�ln��� n = 2m+1 �̏ꍇ
n a^{n-1} b + .... + (-1)^m b^{n} = 0
a | b^n �ƂȂ��Ă��܂��̂� ����͂��肦�Ȃ�.
�k2.2�l�����n�͋��� n = 2m
���̂Ƃ� (a + b i)^m �͏������܂��͎����ł���.
�k2.2.1�l(a + b i)^m ���������̏ꍇ
Re{ (a + b i)^m } = 0 ��� m�͊�ł���. ( a | b^m �͕s�� )
m = 2m�f + 1 �Ƃ�����
(a + b i)^m = (-a i + b)^{2m�f + 1} * (-1)^m�f * i
������ Im{ (-a i + b)^{2m�f + 1} } = 0 �͂��肦�Ȃ�. ( b | a^{m} �͕s�� )
�k2.2.2�l ����� (a + b i)^m �͎����ł���.
�A�[�I�� n = 2*2*2*...*2 �A������ (a + b i)^2 �͎����ł���B
���A����͕s�\�ł��� (a=b=1 �ł͂Ȃ��̂�)
�ȏ���A���R��a,b���������ׂ������� a=b �݂̂ł���B
(���R���͂O���܂܂Ȃ��Ƃ���������Ƃ�܂���) > a | b^n �ƂȂ��Ă��܂��̂� ����͂��肦�Ȃ�.
a=1, b��1 �Ƃ��̏ꍇ�������Ƃ��Ă��̂ŏ�̏ؖ��͖Y��Ă���. >>759
����d_1�Ƌ���d_2�����l�̂���萔C,c>0�����݂���
cd_1(x,y)��d_2(x,y)��Cd_1(x,y) ��x,y��R �ƂȂ�
�Ƃ������ƂȂ� d�����[�N���b�h�m�����Ɠ��l�ȋ����Ƃ���
{x_n}_(n��N)��R��d�����̈Ӗ��ł̃R�[�V�[��Ƃ����
|x_n-x_m|��Cd(x_n,x_m)��0 (n,m����)
���{x_n}�̓��[�N���b�h�m�����̈Ӗ��ł��R�[�V�[��
(R,���[�N���b�h�m����)�̊���������{x_n}�͂���x��R�Ƀ��[�N���b�h�m�����̈Ӗ��Ŏ�������
����������d(x_n,x)��C|x_n-x|��0 (n����)
����{x_n}��d�����̈Ӗ��ł�x�Ɏ�������
����������(R,d)�͊���������� >>761>>762
n>2�̂Ƃ��́AIm{ (a + b i)^n }��W�J�������̂��悭���߂�An�̋��Ɉ˂炸
a|b^k (i.e. a=1)
b|a^(n-1) (i.e. b=1)
����������
(k��n�̋��ɂ���ĈقȂ�) ��(2��3) logx*(x^2+1)/(x^2-1)^2 dx
����ǂ��������ϕ����߂���ł��傤���H
���Z�ŏo���`�������W���Ȃ̂ł����A�S�����������܂���
(log2)/6+(log3)/8�@�������炵���̂ł����A���o�ߒ����K���o���ƌ����܂���
�ǂȂ������������������Ȃ��ł��傤���E�E�E >>765
(-x/(x^2-1))'=(x^2+1)/(x^2-1)^2
���g���ĕ����ϕ�����ǂ��� >>767
�������������������I�I�I�X�b�L�������܂����I���X�b�L��
�����ŕ����Đ����ł�����
�ł����ꎩ�͂Ŏv�����̂��Ȃ薳�������ł��˂� ��(logx)^(-1/2) dx
���������肢���܂� >>768
(x�̑�����)*log(x)�̐ϕ��ł܂����������͕̂����ϕ����Ǝv��
����͕���ɓ�悪���邨�A�Ŕ�r�I�y�ɕ����ϕ��ł���
>>769
�������ł͖���
���ʂ����m�肽���Ȃ�wolfram�����g�������Ǝv�� >>765
1/2*log(x)* { 1/(1-x)^2 + 1/(1+x)^2}
��@log(x) * (1/(1-x))'dx = log(x)/(1-x) - ��(1/x)*(1/(1-x))dx
��(1/x)*(1/(1-x))dx = �� 1/x -1/(1-x) dx = log(x) - log(1-x)
�ƕό`���Ă����Ε����ϕ��łł���͂��B >>765
���������Ȃ悤�ɂ������邯��...
�� dx logx*(x^2+1)/(x^2-1)^2
= �� d{logx} x* logx * (x^2+1)/(x^2-1)^2
= �� dy y/2 * cosh(y)/(sinh(y))^2 �@{ y = logx }
= [ y/2 * ( -1/sinh(y) ) ] - �� dy 1/2 *( -1/sinh(y) )
= [ logx * ( -x/(xx-1) ) ] + �� dx 1/(xx - 1)
= [ logx * ( -x/(xx-1) ) ] + (1/2) [ log(x-1) + log(x-1) ]
= ...
{-x/(xx-1) }�f = ... ���g���������A�Ȃ�Ă̂͌�m�b����Ȃ��̂��ȁB
���ɂ͎v������ł���B = [ logx * ( -x/(xx-1) ) ] + (1/2) [ log(x-1) + log(x-1) ]
������
= [ logx * ( -x/(xx-1) ) ] + (1/2) [ log(x-1) - log(x+1) ]
�ɒ��� >>772
���������
(ax+b/(x^2-1))'
���v�Z����a,b�����߂Ă��
�L�����Ɏ������߂���y���Ǝv���Ď������炤�܂��v�Z�ł������Ċ���
�œK�Ȃ������ǂ����͍D�݂ɂ��Ǝv�����ǁA���̂������̂͑S���V����I����Ȃ��� a�������Ƃ���B
xy���ʂ̌��_��(1,a)�����ԋȐ��S�̂���Ȃ�W����S_a�Ƃ���B
�ȉ��́i�����j�����悤��a���Ƃ邱�Ƃ��ł��邩�B�@
�i�����j
�uS_a�̗v�f�ɁA���́i����A�j�����Ȑ�C�����݂���B
�i����A�j0��x��1�͈̔͂�x��ׂɑI�сA����ɑΉ�����C��̓_(x,y)���Ƃ�B���̂Ƃ��Ay���L�����ƂȂ�m��p��p>t�ƂȂ鐳�̎���t���Ƃ��B�v >>775
(0,0),(1/3,1),(2/3,1),(1,a)�����ɒ����Ō��܂�����Ƃ�Aa�Ɉ˂炸p=1/3�ɂȂ�̂ł́H
�ǂ������Ⴂ���Ă��炷�܂� >>751
( >>761 �̒��� �� ���� )
�k2.*.*�l�̉ӏ��� a �� 2, b�� 2 �ɕύX
�k3�la=1, b �� 2 �̏ꍇ
�k3.1�ln����̏ꍇ
(1+bi)^{n} = ( n b - C{n,3} b^3 + .... �} b^{n} ) i + ... = 0i + ...
n= b n�f �ł��� ���� �ub �͊�v�ł���.
(1+bi)^{2n} = ( 2n b - C{2n,3} b^3 + .... �} b^{2n-1} ) i + ... = 0i + ...
������
C{2n, 2k-1} = (2n)! / (2n-2k+1)!(2k-1)! = 2n/(2n-2k+1) * (2n-1)!/(2n-2k)!(2k-1)!
= 2*n/(2n-2k+1) * C{2n-1, 2k-1}
�擪��2�� �����(2n-2k+1) �ŏ�����鎖�͂Ȃ��̂� C{2n, 2k-1} �͏�ɋ���
����ɂ�� b^{2n-1} �������ƂȂ��Ă��܂��s�����ł���B
�k3.2�l n �� ���� 2m �����̏ꍇ
(1+bi)^{m} �͏����� �܂��� �����ł���B
�k3.2.1�l(1+bi)^{m} ���������̏ꍇ
(1+bi)^{m} = ( 1 - C{m,2} b^2 + .... + ...* b^{...} ) + ... * i = 0 + ... * i
b | 1 �ƂȂ�s���� ( b �� 1 �Ȃ̂�)
�k3.2.2�l (1+bi)^{m} �������̏ꍇ
�A�[�I�ɉ]�X�k2.2.2�l�Ɠ��l �� �s����
�k4�la��2, b=1
(a+i)^{n} ���������Ƃ�����
��� (1 - a i)^{2n} = (i + a)^{2n}/ i^{2n} = (a+i)^{2n}*(-1)^n �͎���
���Ƃ́A b < 2 �ɂȂ��������� �k3�l�Ɠ��� �� �s����
���������V���v���ɂł��邾�낤���A����� a = b ���������ƌ��_�����B >>777
��: (1+bi)^{2n} = ( 2n b - C{2n,3} b^3 + .... �} b^{2n-1} ) i + ... = 0i + ...
��: (1+bi)^{2n} = ( 2n b - C{2n,3} b^3 + .... �}2n b^{2n-1} ) i + ... = 0i + ...
...
?: ����ɂ�� b^{2n-1} �������ƂȂ��Ă��܂��s�����ł���B
�����͂����������... ���͒��߂��B �`���s���́�������n���ɂ��₪���ĂƂ���������t���鐺���������Ă��܂�
���́��������N�ł��邩��������܂���B�`���s���̎��X�Ȍ����点�Ƃ�������掂ɂ͔��f���ł܂� >>751
a,b�͐������Ƃ���B(a�{ib)^n��a_n�{ib_n, a_n,b_n��R (n��1) �ƒu���ƁA
a_1��a, b_1��b, a_{n�{1}��aa_n�|bb_n, b_{n�{1}��ba_n�{ab_n (n��1)
�ł���B���w�I�A�[�@�ɂ��An��1 �̂Ƃ�
a_n �� (2a)^{n�|1}a (mod a^2�{b^2), b_n �� (2a)^{n�|1}b (mod a^2�{b^2)
��������B ���1�@a,b�݂͌��ɑf�Ȑ������ŁA����n��1�ɑ���(a�{bi)^n�͎����Ƃ���B
���̂Ƃ��Aa��b��1�����藧�B
�ؖ��@a^2�{b^2��2 �Ɖ��肷��Ba^2�{b^2����f����f�����Ƃ��Ď����Ȃ��Ȃ�A
a^2�{b^2��2^m, m��2�ƕ\����̂ŁAa^2�{b^2��0 (mod 4) �ƂȂ邪�A
���ꂪ���藧�ɂ�a,b�Ƃ��ɋ����łȂ���Ȃ炸�Aa,b���݂��ɑf�ł��邱�Ƃɖ�������B
����āAa^2�{b^2�͊�f����f�����Ƃ��Ď��B���̂悤�Ȋ�f����1�I���p�Ƃ���B
����n��1�ɑ���(a�{bi)^n�͎���������A���̂Ƃ�(a�{bi)^{2n}�������ł���B
����āA����n��2�ɑ���(a�{bi)^n�͎����ł���B����n�ɑ���b_n��0�ł���A
����� b_n��0 (mod a^2�{b^2) �ł���A����� (2a)^{n�|1}b��0 (mod a^2�{b^2) �ł���A
����� (2a)^{n�|1}b��0 (mod p) �ł���B����āAp�b(2a)^{n�|1}b �Ȃ̂ŁA
p�b2�܂���p�ba�܂���p�bb�ł���Bp�͊�f��������Ap�ba�܂���p�bb�ł���B
p�ba�̂Ƃ��́Ap�b(a^2�{b^2)�ɂ��p�bb�ƂȂ�̂ŁA
a,b���݂��ɑf�ł��邱�Ƃɖ�������Bp�bb�̂Ƃ������l�ɖ�������B
����āAa^2�{b^2��2�łȂ���Ȃ�Ȃ��B����āAa��b��1�ƂȂ�B �藝1�@a,b�͐������ŁA����n��1�ɑ���(a�{bi)^n�͎����Ƃ���B
���̂Ƃ��Aa��b�����藧�B
�ؖ��@gcd(a,b)��d �Ƃ���Aa��da', b��db', gcd(a',b')��1 �ƕ\���āA
����n��1�ɑ���(a'�{b'i)^n�͎����ł���B����āA���1�ɂ��a'��b'��1�ł���B
����āAa��b�ł���B
�藝2�@������a,b�ɂ��āA(a+bi)^n�������ƂȂ�悤��n��1�����݂��邽�߂�
�K�v�\�������́Aa��b�����藧���Ƃł���B
�ؖ��@(a+bi)^n�������ƂȂ�悤��n��1�����݂���Ȃ�A�藝1�ɂ��A
a��b�ł���B�t�ɁAa��b�Ȃ�An��4�̂Ƃ�(a+bi)^n�͎����ł���B n��3�ȏ�̐����̂Ƃ�tan(��/n)���L�����ƂȂ�̂�n=4�̂Ƃ��Ɍ���B
���� tan(��/3)�͖������ł���B
n �� 5 ��tan(��/n)���L�����Ƃ���B
n ����̑f���q p �����Ă� tan(��/p)���L�����ł���B
������tan(��/p)�͔{�p�������������
0 = c[p,1] - c[p,2]x^2 + c[p,3]x^2 - �c �} x^(p-1)
�̉��ł��邩��A�L�����ł���Ƃ����tan(��/p) = 1,p�̂����ꂩ�����Ȃ��B
������ x=1 �̂Ƃ��͉E�Ӂ߁}1 (mod p)�ł���A x=p �̂Ƃ��͉E�Ӂ�p (mod p^2)�ł��邩��0�ɂȂ�Ȃ��B
�ȏ�ɂ��n�͂Q�ׂ��łȂ��Ƃ����Ȃ������肩��n��8�̔{���ł��邪�A���̂Ƃ�tan(��/8)���L�����ƂȂ薵������B
�ȏ�ɂ��tan(��/n)���L�����ƂȂ�̂�n=4�̂Ƃ��݂̂ł���B
(�ʉ�)
Q(cos(2��/n))��Q(tan(��/n))�̍��X�Q���̊g��ł���AQ(cis(2��/n))��Q(cos(2��/n))�㍂�X2���̊g��ł���B
�����tan(��/n)���L�����̂Ƃ�[Q(cis(2��/n)):Q]��4�ł���B
������[Q(cis(2��/n)):Q]=��(n) (Euler�fs totient) �ł��邩��
n = 1,2,4,8,3,6,12,5 �Ɍ����邪�A�������݂����̂� n=4 �݂̂ł���B �ʉ����
Q(cos(2��/n))��Q(tan(��/n))�Ɋ܂܂�AQ(cis(2��/n))��Q(cos(2��/n))�㍂�X2���̊g��ł���B
�����tan(��/n)���L�����̂Ƃ�[Q(cis(2��/n)):Q]��2�ł���B
������[Q(cis(2��/n)):Q]=��(n) (Euler�fs totient) �ł��邩��
n = 1,2,4,3 �Ɍ����邪�A�������݂����̂� n=4 �݂̂ł���B a_1, a_2, �c, a_n ��S�����W�� S �̌��Ƃ���B
b_1, b_2, �c, b_n �� S �̌��Ƃ���B
c_1, c_2, �c, c_n �� S �̌��Ƃ���B
{1, 2, �c, n} �̒u�� ��, �� �ňȉ��������̂����݂���Ƃ���B
�e i �� {1, 2, �c, n} �ɑ��āA
a_i = b_��(i)
a_i = c_��(i)
���̂Ƃ��A
b_1 �� b_2 �� �c �� b_n
c_1 �� c_2 �� �c �� c_n
�Ȃ�A
���ׂĂ� i �ɑ��āA
b_i = c_i
�����藧���Ƃ��ؖ�����B >>786
�قƂ�Ǔ�����O�����
������Əؖ������������Ȃ�A�[�@�g������ ����Ȃ�ł����Ƃ������͎��̐������(?)��
(3��3)/4-5/2<0�Ə�������ؖ��K�v�Ƒ傫���~�Ə�����܂����B����ɂ́u��2,��3�Ȃǂ̋ߎ��l��p���Ȃ��ŋc�_���邱�Ɓv�Ə����Ă���܂������A���̏ꍇ1.7<��3<1.8�Ə����Ă����߂Ȃ̂ł��傤���H >>788
�ڍ����ē�悷���������� 2.89��3��3.24���炻����ɓ����͉̂��������Ȃ��Ǝv����B
�ƂŊo���Ă����ߎ��l�g�����Ⴞ�߂���Ă��Ƃ���Ȃ� >>788
> 1.7<��3<1.8�Ə����Ă����߂Ȃ̂ł��傤���H
�����_������
�Ȃ�1.7<��3<1.8�ƌ�����̂��������Ȃ��� �Ȃ�قlj������܂����B�悭���W�Ȃ̂ł͉�����������e���2�Ȃǂ̋ߎ��l���g���Ă����̂Ŏ����Ȋ����Ŏg���Ă����̂��Ǝv���Ă��܂����B�C�����Ă������Ǝv���܂��B >>788
1.7<��3<1.8
�������Ă����ŏ\���ł��傤
���̖��Ȃ�A��3<1.8�����ŏ\���ł����B
��3�̋ߎ��l�����߂邱�Ƃ����ɂȂ�悤�Ȗ��Ȃ�Ƃ�����
�����������ł��Ȃ������ł�
�u��3=1.73... �Ȃ̂Łv�̋c�_�͐��w�I�ɕs�K�Ƃ�������Ȃ̂ł��傤 >>791
(1.7)^2<(��3)^2<(1.8)^2��y=��x�͒P��������������Ə��������H >>788
���Ƃ���o�c�͈�a������Ȃ��B�ꌾ�����Ƃ��Ȃ̂łƂ������Ƃ��Ώ\������B��3��2�ɕς��Ă����藧���炢�̂��̂Ȃ̂� >>795
���̕]�������̃��C���łȂ��Ƃ��Ă�
(3��3)/4-5/2
<3•2/4-5/2 (���3<2)
=-1<0
���炢�͏����ׂ����� ��3��2��薾�炩�䂦
�܂��}�b�N�X�ł�����ł����ł��� ���Z���w�̉Łu���炩�v��u�����v���g���͔̂���������x�^�[�ł���
�����������ĂȂ��̂Ɠ��������A��Ȃ�������v���ɂȂ�₷��
��̂悤�ɏ��������ł�����Ɛ����ł������킴�킴�g���K�v���Ȃ� ��3<2���g���Ȃ��Ƃ����ɂ��������ł��� ���낢�날�肪�Ƃ��������܂����B���̖�莩�͓̂���͂Ȃ���ł����A�v�Z���₽��Ƒ����ďł��Ă��ĂQ�悷��������Ƃ��Y��Ă܂����B�{�Ԃł͋C�����܂��B a,b�����R���Ax=(��51+a)/b�Ƃ���B
x��0<x<1�����A�����_�ȉ���1�ʂ̐�����0�łȂ��A��2�ʂ̐�����0�ł���悤��a,b��1�g�^����B >>802
0.1��x<0.11�ƂȂ�a,b����g�^����悢�B
0.1��(��51+a)/b<0.11
10b��100(��51+a)<11b
7.1<��51<7.2���i�v�Z���j�Aa=1,b=80�����B >>772
����� (xx-1)^2 = (x+1)^2�(x-1)^2 ��1�����q�����i2�����q�Ȃ��j������
���������ɕ������
�@1/(x+1)^m�A�@1/(x-1)^n
�̌`�̍��̘a�ɂȂ�A�ϕ��ł���͂��B �������g�|���W�[�I�ɓ������ǂ��ŕ��ނ����牽��ނ��炢���邩���ׂ�
����ȂЂƂ��Ă��Ȃ��̂ł��傤���H �~����ɐԋ�6�Ɣ���6�Ԋu�ɕ��ׂ�B���̕��ו��̑��������߂�B
��]���Ĉ�v������ו��͓���Ƃ��Ĉ����B ����1��
m,n�͎��R���Ƃ���B
�~����ɐԋ�m�Ɣ���n�Ԋu�ɕ��ׂ���ו��̑�����f(m,n)�Ƃ���Ƃ��A�ȉ��ɓ�����B
�i1�jm'>m�Ȃ��f(m',n)>f(m,n)�ł��邱�Ƃ��������B
�i2�j2�ȏ�̐���n���Œ肷��Bn��菬��������p���Ƃ�A�Ɍ�
lim[m����] f(m+1,p)/f(m,n)
���l����B���̋Ɍ����L���̒l�Ɏ�������悤��p��S�ċ��߂�B ���a1�̉~����ɐ��܊p�`ABCDE�����ڂ��Ă���B
���̐��܊p�`�̑Ίp��AC,CE,EB,BD,DA�����сA���`S�����i�]����A,C,E,B,D,A�̏��ł��̐��`����M�����ł���j�B
S��AC�̎���Ɉ��]�����Ăł��闧�̂̑̐ς�V�Ƃ���Ƃ��A�s����n��V<n+1��������n�����߂�B S = {a_1, a_2, �c, a_n}
�C�ӂ� 1 �� i < j �� n �ɑ��āA
a_i �� a_j
�����藧�Ƃ���B
���̂Ƃ��A
#S = n
�ł��邱�Ƃ��ؖ�����B #S��n�͎����i��ʂɌ��ɏd�������閈��#S�͌���j
������T={1,2,�c,n}����S�ւ̒P�˂����݂���̂�
n=#T��#S
�����#S=n >>809
#{a_1} = 1 �͖��炩
#{a_1,..., a_k} = k (k < n) �����肷���
�O�������� {a_1,..., a_k} �� {a_[k+1]} = ø �Ȃ̂�
#{a_1,..., a_k, a_[k+1]} = #( {a_1,..., a_k}��{a_[k+1]} )
= #{a_1,..., a_k} + #{a_[k+1]} = k + 1
�A�[�@�ɂ�� #{a_1,..., a_n} = n �ł���B >>810
>>811
���肪�Ƃ��������܂����B x �� a (mod 4)
x �� b (mod 6)
�ɐ����� x �����݂��邽�߂̕K�v�\�������́A
a �� b (mod 2)
�ł��邱�Ƃ������B �y���n�z����100�l�̗��𓐎B���������R���F�{��y����(42)�˓Ɛg�E��B��@���E���͐��w
https://leia.5ch.net/test/read.cgi/poverty/1545445074/ >>813
{�K�v�����̏ؖ�}
X = a + 4m = b + 6n (n,m �͓K���Ȑ���) ���
a = b + 2 (3n - 2m) �� b (mod 2)
{�\�������̏ؖ�}
a �� b (mod 2) �܂� a = b + 2k (k�͓K���Ȑ���)�Ȃ�
case k �� 0 (mod 3):
�@X = a = b + 2k
case k �� 1 (mod 3):
�@X = a -8 = b + 2k -8
case k �� 2 (mod 3):
�@X = a -4 = b + 2k -4
����(�̈��)��^����B >>815
���肪�Ƃ��������܂����B ���̓������S�����ɂȂ�悤�ɒ萔b�̒l�����߂�
bx^2-4bx+(8b^2-4b+1) m,n�͎��R���Ƃ���B
�~����ɐԋ�m�Ɣ���n�Ԋu�ɕ��ׂ���ו��̑�����f(m,n)�Ƃ���Ƃ��A�ȉ��ɓ�����B
�i1�jm'>m�Ȃ��f(m',n)>f(m,n)�ł��邱�Ƃ��������B
�i2�j2�ȏ�̐���n���Œ肷��Bn��菬��������p���Ƃ�A�Ɍ�
lim[m����] f(m+1,p)/f(m,n)
���l����B���̋Ɍ����L���̒l�Ɏ�������悤��p��S�ċ��߂�B �p���ŕ��Ă���悤�ȑ㐔�n�ɖ��O�͂���܂����H >>819
x^x�̃O���t�����ċߎ��ł�������H >>819
e < 30/11 = 2.72727�c�@���
e^e < (30/11)^{30/11},
�Ƃ����
2�(16^11)�(11/30)^30
= (8^15)�(121/900)^15
= (242/225)^15
= (1 + 17/225)^15
= 1 + 17/15 + �c�@�@�@(2���W�J����)
> 2,
���@(30/11)^30 < 16^11,
���@(30/11)^{30/11} < 16, >>823
�� e < 30/11 = 2.72727�c
���ĕs�����͉��������ɏo�Ă����ł����ˁH >>819
e < 49/18 = 2.7222222�@����
e^e < (49/18)^{49/18},
�Ƃ����
(7/6)^13 = 96889010407 / 13060694016 = 7.418366 < 8,
���@(7/6)^98 < 8^{98/13} < 8^{23/3}
���@(49/18)^49 = 2^49�(7/6)^98 < 8^{49/3}�8^{23/3} = 8^24 = 16^18,
���@(49/18)^{49/18} < 16, >>825
�� e < 49/18 = 2.7222222
���ĕs�����͉��������ɏo�Ă����ł����ˁH >>824
�@�c���V�ɋ����Ă��炢�܂����B
e > 299/110 = 2.718182
�i����͉~�������������c�j >>827
����ł͕s�������t����������A�ǂ����݂����Ӗ��B >>824 >>826
(1 + 1/n)^{n + 1/2} �͒P�������Ȃ̂�
e < (1 + 1/n)^{n + 1/2},
e^2 < (1+1/5)^11 = (6/5)^11 < (30/11)^2,
e^2 < (1+1/8)^17 = (9/8)^17 < (49/18)^2, >>824 >>826
e = ��[k=0,��]�@1/k!
�@= 1/0! + 1/1! + 1/2! + ��[k=3,��]�@1/k!
�@< 1/0! + 1/1! + 1/2! + ��[k=3,��]�@1/(3!�E4^{k-3})�@�@�@(���䋉��)
�@= 5/2 + (1/3!)/(1-1/4)
�@= 49/18
�@< 30/11, >>831
�������̂ق������R���ˁB wikipedia�̃e�g���[�V�����̍��ڌ��Ă���
���������
n��, ne �������ɂȂ�悤�Ȑ��̐��� n �͑��݂��邩�B���� 4�� �͐�����
�i�@��^(��^(��^��))���������j
���ď����Ă�������ł���
����Ȃ��Ȃ�킯���������Ƃ����v���Ȃ���ł���
�Ȃ�Łu���Ɂv�Ƃ������Ă����ł����ˁH >>806
����������Ɛ�����ƂP�R�ʂ肩�ȁH >>834
�R����P�O�܂ł𐔂��������
> bracelet(3:10)
[1] 4 6 8 13 18 30 46 78
�ɂȂ����B >>833 ����Ȃ̂�����ƌv�Z���Ă݂�Ε����邶���B
pi
= 3.1415926535897932384626433832795028842
pi^pi
= 36.462159607207911770990826022692123666
�ق�A�����ɂȂ�킯�Ȃ������w
pi^pi^pi
= 1340164183006357435.2974491296401314151
��H
? pi^pi^pi^pi
= 9.080222455390617769723931713284287746 E666262452970848503
����.... ���ڌv�Z�Ŋm���߂�̖�������B >>833
���Ȃ�Łu���Ɂv�Ƃ������Ă����ł����ˁH
n=3�܂ł͐����ɂȂ�Ȃ����Ƃ��������Ă邩�炶��Ȃ��ł��傤���B �u�p�C�m�p�C�m�p�C�v�܂ł͏����_�ȉ��܂Ōv�Z�ł���킯�ł��ˁB
����A�M�b�`�����`�����ƌĂ�ł͂ǂ��ł��傤���@���e�g���[�V���� �������A4^^�@��������������т�����V����(^^) 22*��*��*��*��=2143.00000275 >>840
�����琮���ɋ߂��Ă��A�̐�����̐����{�͐����ɂ͂Ȃ蓾�Ȃ��ł���B
>>838
�M�b�`�����`�����͌����ɂ����̂ŃM�b�`�����ł������ȁB
3^^���u��3�M�b�`�����v�ƌĂԂƂ��B ���w�̏ؖ��͐��l�����Ƃ͕ʕ�
���l�����͗\�z�����ł��Ȃ�
���̏ؖ��ɂ͐V�����_�@�̔������K�v�� ��Q���P�O�i�����W�J�����Ƃ��ɂP��������o�Ă��邩�H���Ă����P�O�O���^�Ǝv����悤�Ȗ���ł���
�����Əؖ�����ĂȂ� >>839,841
���߂�A�L�@���Ԉ���Ă��B
�~ 4^^��
�� ��^^4 >>841
https://ja.wikipedia.org/wiki/�قƂ�ǐ���
���̃��}�k�W�����̌v�Z�̔w�i�ɂ͒J�R�u���\�z�i���W�����[���藝�j������A�u�Ȃ蓾�Ȃ��v�Ǝv���̂̓��}�G�����@�J������B �͒��z���Ȃ̂͂킩���Ă邩�琮����̐����{�������ɂȂ�Ȃ��͎̂����Ȃ̂ł́B �ȉ����ؖ�����B
�L���� f(x) / g(x) �́A g(x) ��
g(x) = g_1(x) * g_2(x) * �c * g_l(x)
�ƌ݂��ɋ��ʈ��q�������Ȃ��悤�Ɉ�����������ƁA
f(x) / g(x) = h(x) + h_1(x) / g_1(x) + h_2(x) / g_2(x)�c + h_l(x) / g_l(x)
deg h_j < deg g_j
�ƁA�������ƗL�����̘a�ɕ����ł���B >>847
�Ɋ֘A���܂����A��쌒�����w�㐔����x�Ɉȉ��̋L�q������܂��B
�u����� g_j(x) �͊���ȑ������̃x�L��ɂȂ��Ă���̂Łv�Ə����Ă���܂����A���̗��R�͉��ł����H
�L���� f(x) / g(x) �́A g(x) ��
g(x) = g_1(x) * g_2(x) * �c * g_l(x)
�ƌ݂��ɋ��ʈ��q�������Ȃ��悤�Ɉ�����������ƁA
f(x) / g(x) = h(x) + h_1(x) / g_1(x) + h_2(x) / g_2(x)�c + h_l(x) / g_l(x)
deg h_j < deg g_j
�ƁA�������ƗL�����̘a�ɕ����ł���B
����� g_j(x) �͊���ȑ������̃x�L��ɂȂ��Ă���̂ŁA p_j(x) / q_j(x) �� K[x] �̊���ȑ����� p(x) ���g����
q(x) / (p(x))^m, deg q < m * deg p
�̌`�����Ă��邱�Ƃ�������B g(x) = (x^2 + 1) * (x + 1) * (x + 2),
g(x) �́A
g_1(x) = (x^2 + 1) * (x + 1)
g_2(x) = (x + 2)
�ƌ݂��ɋ��ʈ��q�������Ȃ��悤�Ɉ�����������܂����A
g_1(x) �͊���ȑ������ׂ̂���ł͂���܂���B g(x) = (x^2 + 1) * (x + 1) * (x + 2),
g(x) �́A
g(x) = g_1(x) * g_2(x),
g_1(x) = (x^2 + 1) * (x + 1)
g_2(x) = (x + 2)
�ƌ݂��ɋ��ʈ��q�������Ȃ��悤�Ɉ�����������܂����A
g_1(x) �͊���ȑ������ׂ̂���ł͂���܂���B >>650
�W���V�O���C�h�� f(x)=1/(1+exp(-x)) ��
f'(x)=f(x)(1-f(x)) �����藧����Af��n�K������f[n]�Ƃ������� f[n+1]=f[n](1-f[n]), f[0]=1/(1+exp(x))
�̈�ʍ������߂�悢�Ǝv�����낤���A���̑Q�����̓��W�X�e�B�b�N�ʑ��̂ЂƂł����Ĉ�ʍ��͋��߂��Ȃ����Ƃ��m���Ă���B �������������ł���Ɖ������ꂵ���̂ł��傤���H �ϕ��̌v�Z�ɗ��p����ȊO�ʼn�������܂����H �ȉ��̉摜�̐Ԑ����������ӏ��ł����A�Ȃ�7���ł͂Ȃ�8���̑������Ȃ̂ł��傤���H
https://imgur.com/ocZqzMK.jpg n�͎��R��
1����2n�܂ł̎��R�����珬�������̂��珇�Ɋ�A�����A��A�����ƂȂ�悤�Ɏ��R����2k�Ƃ��Ă䂭
���̑g�ݍ��킹�̐��́H >>845
���u�Ȃ蓾�Ȃ��v�Ǝv���̂̓��}�G�����@�J������B
�n���͂��O�����[�̂��@>>846�������Ɏw�E���Ă���Ă�Ƃ���B ��W�c���z�� F �Ƃ���Ƃ��A��W�c���璊�o���ꂽ�i����ׁj�W�{ (random sample) �Ƃ͕��z F �ɏ]���Ɨ������z�m���ϐ��� x1, x2, ... �̂��Ƃł���B
��Wikiprdia�̕W�{(���v�w)�Ƃ����y�[�W�ɏ�����Ă���̂ł����A�m�����zF�Ɗm���ϐ�x_i�͂��ꂼ��ǂ�����ǂ��ւ̎ʑ��ł����H ���i���w�Z�R�N���j�ɕ�����܂������A�������킩��Ȃ��A���肢���܂��B
4�l���痈���N���̂����ԍ��̐����ł��B���̐����Ɂu�~�v�u�{�v�u�|�v�u���v
�L���̂ǂꂩ�����Ď�������܂��B
�i �j���g�킸�A�S�̐����̏��Ԃ͓���ւ��Ȃ����̂Ƃ���B
�u�~�v�������g���ē������Q�Ԗڂɑ傫�Ȃ��̂͂ǂ�ł��傤�H
A����F�R�S�P�W�O
B����F�P�R�U�Q�S
C����F�Q�S�T�R�P
D����F�R�T�P�V ����
�u�~�v�������g���ē������Q�Ԗڂɑ傫�Ȑ����ɂȂ���̂͂ǂ̔N���ł����H ���i���w�Z�R�N���j�ɕ�����܂������A�������킩��Ȃ��A���肢���܂��B
4�l���痈���N���̂����ԍ��̐����ł��B���̐����̊ԂɁu�~�v�u�{�v�u�|�v�u���v
�L���̂ǂꂩ�����Ď�������܂��B
�i �j���g�킸�A�S�̐����̏��Ԃ͓���ւ��Ȃ����̂Ƃ���B
�u�~�v�������g���ē������Q�Ԗڂɑ傫�Ȑ����ɂȂ���̂͂ǂ̔N���ł����H
A����F�R�S�P�W�O
B����F�P�R�U�Q�S
C����F�Q�S�T�R�P
D����F�R�T�P�V >>854
(a+c+e)x^7 + (3a+b+d+e+f)x^6 + (5a+4b+f+g)x^5 + (3a+9b-2c-3e+h)x^4 + (-a+12b-2d-e-3f-g)x^3 + (-5a+11b-f-2g-h)x^2 + (-4a+6b+c+2e+2g-2h)x + (-2a+2b+d+2f+2h)
= 2x^7 + 8x^6 + 13x^5 + 20x^4 + 15x^3 + 16x^2 + 7x + 10,
�̌W��������������
a+c+e = 2,
3a+b+d+e+f = 8,
5a+4b+f+g = 13,
3a+9b-2c-3e+h = 20,
-a+12b-2d-e-3f-g = 15,
-5a+11b-f-2g-h = 16,
-4a+6b+c+2e+2g-2h = 7,
-2a+2b+d+2f+2h = 10,
�����������
a = 181/225,
b = 91/45,
c = 41/25,
d = 78/25,
e = -4/9,
f = 8/9,
g = 0,
h = 4/3,
�ƂȂ����B >>854
�����ʼn���
a=1, b=2, c=1, d=3, e=0, f=0, g=0, h=1,
�ƂȂ�悤�Ɍ��̌W���������
a+c+e = 2,
3a+b+d+e+f = 8,
5a+4b+f+g = 13,
3a+9b-2c-3e+h = 20,
-a+12b-2d-e-3f-g = �P�V,
-5a+11b-f-2g-h = 16,
-4a+6b+c+2e+2g-2h = 7,
-2a+2b+d+2f+2h = �V,
�ƂȂ����B
x^6 �̌W�����T�Ȃ̂͒P�Ȃ��A���H�@�������Ђǂ����ȏ����B >>860
>�S�̐����̏��Ԃ͓���ւ��Ȃ�
4�̐������āA�Ȃ�̂��ƁH5���̐���4���̐������邯�ǁH >>860
����͖��̏��������Ȃ����Ăǂ��l������悢���킩��Ȃ�
�Ⴆ�A�R�T�P�V�̏ꍇ�A�L�������邱�Ƃ��ł���ӏ���3�B
����āA�u�~�v�������g���A�Œ�1�����ɂ͋L����������̂Ƃ��āA
3�~517��1551
35�~17��595
351�~7��2457
3�~5�~17��255
3�~51�~7��1071
35�~1�~7��245
3�~5�~1�~7��105
��7�ʂ�̕��@������B
A����F�R�S�~�P�~�W�O��2720
B����F�P�R�~�U�Q�S��3264
C����F�Q�S�~�T�R�~�P��1272
D����F�R�T�~�P�V��595
�̂悤�ɂ����ꍇ��A����2�Ԗ�
�Ꭶ�͏ȗ����邪�A��������ς���AB�����C�����D�����2�Ԗڂɂł���B
����ē����́uA���� �܂��� B���� �܂��� C���� �܂��� D����v�ƂȂ邪�A
����͑z����ł͂Ȃ��낤
���ɏ���������Ύ����Ăق����B >>840
��^2 = 10 - 13/(10^2)
��^3 = 31 + 1/(31*5),
��^6 = (31^2) + 374/(31^2),
���Ė{���ɖ������Ȃ́H - 171,172
�~�����ɂ��Č�荇���� - 240 >>857
���x�_�̌��t�ł����Ίm���ϐ��͊m����Ԃ��瑪�x��Ԃւ̉���
���z�͊m���ϐ������܂鑜���x >>866
���肪�Ƃ��������܂�
�Ⴆ�A���{�l�S�̂��W�c�Ƃ��A10�l��I��Őg�����Ƃ����m���ϐ���X_1, ... ,X_10'�Ƃ���ƁAX_i�͓��{�l�S�̂���R�ւ̎ʑ��ŁA����1�l�͐g����l�ɂƂ�A���̐l��0���Ƃ�ƂȂ�̂ł��傤���H p(x) �� n �����W���������Ƃ���B
�� �������Ƃ��A p(��) = 0 �Ƃ���B
�� �̋��f���� �� �Ƃ���ƁA p(��) = 0 �ł���B
p(x) �� (x - ��) * (x - ��) �͎��W����2���������ł���B
p(x) �� (x - ��) * (x - ��) �Ŋ��������͎��W���������ƂȂ�B
�Ƌ��ȏ��ɏ����Ă���̂ł����A�up(x) �� (x - ��) * (x - ��) �Ŋ��������͎��W���������ƂȂ�v�Ƃ����̂�
�����ɂ����A�ȉ��̂悤�ɏؖ����Ȃ���Ȃ�܂��H
C[x] ��ŁA
p(x) = (x - ��) * (x - ��) * q1(x)
�ƈ�ӓI�ɏ�����B
R[x] ��ŁA
p(x) = (x - ��) * (x - ��) * q2(x) + r(x)
deg r < deg q2
�ƈ�ӓI�ɏ�����B
R[x] �̌� p(x) = (x - ��) * (x - ��) * q2(x) + r(x) �� C[x] �̌��ł�����B
C[x] �ł̊���Z�̈�Ӑ��ɂ��A r(x) = 0 �łȂ���Ȃ�Ȃ��B
����āA
p(x) = (x - ��) * (x - ��) * q2(x)
q2(x) �� R[x] �̌��ł��邩��A�咣�����藧�B p(x) �� n �����W���������Ƃ���B
�� �������Ƃ��A p(��) = 0 �Ƃ���B
�� �̋��f���� �� �Ƃ���ƁA p(��) = 0 �ł���B
(x - ��) * (x - ��) �͎��W����2���������ł���B
p(x) �� (x - ��) * (x - ��) �Ŋ��������͎��W���������ƂȂ�B
�Ƌ��ȏ��ɏ����Ă���̂ł����A�up(x) �� (x - ��) * (x - ��) �Ŋ��������͎��W���������ƂȂ�v�Ƃ����̂�
�����ɂ����A�ȉ��̂悤�ɏؖ����Ȃ���Ȃ�܂��H
C[x] ��ŁA
p(x) = (x - ��) * (x - ��) * q1(x)
�ƈ�ӓI�ɏ�����B
R[x] ��ŁA
p(x) = (x - ��) * (x - ��) * q2(x) + r(x)
deg r < deg q2
�ƈ�ӓI�ɏ�����B
R[x] �̌� p(x) = (x - ��) * (x - ��) * q2(x) + r(x) �� C[x] �̌��ł�����B
C[x] �ł̊���Z�̈�Ӑ��ɂ��A r(x) = 0 �łȂ���Ȃ�Ȃ��B
����āA
p(x) = (x - ��) * (x - ��) * q2(x)
q2(x) �� R[x] �̌��ł��邩��A�咣�����藧�B >>863
�S�l�̐����̈Ӗ��ł���B 1�܂���-1���Ƃ�n�̐���a_1,a_2,...,a_n������B
���������Ă����̘a
S_n = ��[i=1 to n] a_i
��-n����n�܂ł̂����ꂩ�̐����l���Ƃ�B
�i1�j-n≤k≤n���݂�������k��^����B����S_n=k���������鐮���̑g{a_1,...,a_n}�����݂���Ƃ�T_[n,k]=1�A���݂��Ȃ��Ƃ�T_[n,k]=0�Ƃ���B
�C�ӂ�n�ɑ��āAT_[n,k]=0�ƂȂ�g{a_1,...,a_n}�����݂��邱�Ƃ������B
�i2�jN[n] = ��[k=-n to n] T_[n,k] �ɑ��A���̋Ɍ������߂�B
lim[n����] N[n]/(2n+1) >>871
���ɂȂ��ĂȂ����B
T�̒�`����a�͑�������Ă�̂ɁA�㔼�Łh�`�ƂȂ�a�����݂��鎖�������h���ĂȂ��˂�H
���傤���Ȃ����v�Z�ɗ͓����O�ɂ��������Ɋ�{�I�ȂƂ��납���x��蒼��������������B�}�W�ŁB >>872
��蕶�G�X�p�[���ď��������Ă���܂��H �G�X�p�[������Ƃ肠����n�̋��ŏꍇ�킯����悳���� Theorem:
Every infinite subset of a countable set A is countable.
The theorem show that, roughly speaking, countable sets represent the "smallest" infinity: No uncountable set
can be a subset of a countable set.
�u�Z�W�� A �̖��������W���͂��ׂĉZ�ł���v�Ƃ����藝�ɂ��A
�Z�W�����ŏ��̖����ł���Ƃ�����Ƃ������Ƃ������Ă���܂��B
�Ȃ��A�u�Z�W�� A �̖��������W���͂��ׂĉZ�ł���v�Ƃ������Ƃ���Z�W�����ŏ��̖����ł����
������̂ł��傤���H >>875
����\�藝����Z�����ȉ��̔Z�x�͂��ׂāA�Z�����W���̂��镔���W���̔Z�x�ł��邩��B >>877
[2]
k��n�͎��R���� 1��k��n �����Ă���B
���̂Ƃ� 2k�̐��̐�������Ȃ�� (a_1, a_2, ����, a_{2k}) �Ŏ��� (i), (ii) ���Ƃ��ɖ��������̂̌����An��k��p���ĕ\�킹�B
(i)�@1 �� a_1 < a_2 < ���� < a_{2k} �� 2n
(ii)�@a_i - i (i=1,2,����,2k) �͋����B
�u���R���v�Ɓu���̐����v�͓�������ˁH >>875
�ŏ��̖����Z�x�͔C�ӂ̖����Z�x�ȉ��ł���
�C�ӂ̖����W���̕����W���ɂ͍ŏ��̖����Z�x�̂��̂�����
�Z�W���̕����W���ɂ͍ŏ��̖����Z�x�̂��̂�����
�Z�W���̖��������W���͉Z�ł��邩��ŏ��̖����Z�x�͉Z�ł��� ����\�藝�͔C�ӂ̔Z�x�̑召��r���\�ɂ��邪
�u�ŏ��v�͒�`���̂ɔ�r�\���܂�ł���̂Ő���\�藝�͕K�v�Ȃ� >>879-880
�����Ȃ�ł����H
����\�藝���Ȃ��Ă��C�ӂ̖����W���͔Z�x�ŏ��̖����W�������݂���ؖ��ł����ł����H ����
�C�ӂ̖����W���͔Z�x�ŏ��̖��������W�����������������ł����H >>877 �� >>855 �Ɠ������ł��ˁB
> ... n��k��p���ĕ\�킹�B
F(n,k) �ł����\�����ɂ����
���炩�� F(n, n) = 1 �ł���
�Q����: F(n,k) = F(n-1, k) + ��[m=k-1, n-1] F(m, k-1) �����B
�A���S���Y���̓s���� F(m, 0) = 1 (m��0), F(n,m) = 0 (n< m) �Ƃ��Ă����B
�����܂ł͎�������������邾�낤�B
F(n,1) = ��[m=1, n] (F(m,1)-F(m-1,1)) = ��[m=1, n] m = n(n+1)/2 = C{n+1, 2}
F(n,2) = ��[m1=2, n] (F(m1,2)-F(m1-1,2))
= ��[m1=2, n] ��[m2=1, m1-1] F(m2, 1)
= ��[m1=2, n] ��[m2=1, m1-1] ��[m3=1, m2] m3
= ��[m1=1, n-1] ��[m2=1, m1] ��[m3=1, m2] ��[m4=1, m3] 1
= ��[n-1 �� m1 �� m2 �� m3 �� m4 �� 1] 1
= C{(n-1)+4-1, 4} = C{n+2, 4}
����Ĉ�ʂ�
F(n,k) = ��[n-k+1 �� m1 �� m2 �� ... �� m{2k} �� 1] 1 = C{(n-k+1)+2k-1, 2k} = C{n+k, 2k}
�Ȃ̂ł͂Ȃ����H�Ɨ\�z���� (���ۂ� F(n,3) �܂Ō��Ďv������)
k�����Ő������Ɖ��肷���
F(n,k) = ��[m1=k, n] ( F(m1, k) - F(m1-1,k) )
= ��[m1=k, n] ��[m2=k-1, m1-1] F(m2, k-1)
= ��[m1=1, n-k+1] ��[m2=k-1, m1+k-2] F(m2, k-1)
= ��[m1=1, n-k+1] ��[m2=1, m1] F(m2+k-2, k-1)
= ��[m1�f=1, n-k+1] ��[m2�f=1, m1�f] ��[m2�f �� m1 �� m2 �� ... �� m{2k-2} �� 1] 1 (��������)
= ��[n-k+1 �� m1�f �� m2�f �� m1 �� m2 �� ... �� m{2k-1} �� 1] 1
= ��[n-k+1 �� m1 �� m2 �� m3 �� ... �� m{2k} �� 1] 1�@
= C{(n-k+1)+2k-1, 2k} = C{n+k, 2k}
�A�[�@�ɂ��\�z�̐��������m�F�ł����B
�����Ԃ�ƊȒP�Ȏ��ɂȂ���...
�Ȃ�炩�̉��߂ɂ��h�����ŋ��܂�̂�������Ȃ��B 2k�̐��̊�ő��a��2n�ȉ��̑g��
������2k��0�ȏ�̋����ő��a��2n-2k�ȉ��̑g��
������2k��0�ȏ�̐����ő��a��n-k�ȉ��̑g��
������2k+1��0�ȏ�̐����ő��a��n-k�̑g��
���ȁH >>883
a_{0}=0,a_{2k+1}=2n+1 �Ƃ��āAb_{m}=a_{m} - a_{m-1}�@,(m=1,2,3,...,2k,2k+1)�@���Ƃ�Ab_{m}�͂��ׂĐ��̊
c[m]=(b_{m}-1)/2�@�ƕϐ��ϊ�����Ac�͔����Ł@��[m=1,2k+1]c[m]=n-k�@�����������B���̉��̐���
H[2k+1,n-k]=C[2k+1+n-k-1,n-k]=C[n+k,n-k]=C[n+k,2k]�@�ŋ��܂�B >>885 �Ȃ�قǕ��������B�N�������ȁB
>>884 �� >>885 �Ɠ����Ȃ̂�������Ӗ���������Ȃ������B ���Z���w�̒��ł̓`���[�g���ɂ��ڂ��Ă���ƃ��W���[�Ȍ����������� https://imgur.com/myArDNG.jpg
���ς���㎮�ł��邱�Ƃ̏ؖ��ł����A�ꍇ�����ɂ��ĉ��̐������Ȃ��̂ňӖ��s���ł��B
����͂ǂ�ȏꍇ���������Ă����ł����H
���ɕ�����ɂ����ł��B >>890
��������ɁAi �� j ��ł��A������ k �� l ���ǂ��ʒu���邩���������Ă݂�B
���R�ȏꍇ�����ł��邱�Ƃ�����͂��B >>890
�܂��Ai��j�͌Œ肳��Ă��āAk��l��k<l������Ď��R�ɓ������Ă��邱�Ƃ��ӎ�
�ek,l�̑g�ɑ���x_��(k)-x_��(l)���ǂ��Ȃ邩���݂Ă���
����ƁA��(k)�̒l�́uk=i�v�̏ꍇ�Ɓuk=j�v�̏ꍇ�Ɓuk��i,j�v�̏ꍇ��3�ʂ�ŕ�����K�v������
��(l)�����l
����āA���ꂼ��3�ʂ肸����̂ŁA������g�ݍ��킹�����̂̂������ۂɉ\�Ȏ���6�ʂ�ɕ�����K�v������
�E�uk��i,j�v�ul��i,j�v(�摜�P��)
�E�uk=i�v�ul��i,j�v(�摜�Q��)
�E�uk=j�v�ul��i,j�v(�摜�T��)
�E�uk��i,j�v�ul=i�v(�摜�ł͔����Ă�)
�E�uk��i,j�v�ul=j�v(�摜�S��)
�E�uk=i�v�ul=j�v(�摜�R��)
(�uk=j�v�ul=i�v�Ȃǂ͑召�W����s��)
���Ƃ́A�v�Z���ʂ�S�āu(��������)-(�傫����)�v�̌`�ɑ����邱�ƂŁA���������]�������̂��������邩�𐔂��Ă���
�摜�Ŕ����Ă���ꍇ�����͑召�W���ω����Ă��Ȃ��̂ŏؖ��ɉe���͂Ȃ�
���Ȃ݂ɁA�ЂƂ��ėאڌ݊�((i,i+1)�̌`�̌݊�)�Ɍ����Ď����Ώ\���ł���A���̏ꍇ�͕��������]����̂�x_i-x_(i+1)�����Ȃ̂ł����Əؖ��͊ȒP�ł� ���ς̉���Ȃ�Đ��`�㐔�̖{�ɏ����Ă��邾��B
�����Ȗ{��ǂ�ł�悤�����A
�܂�����ȂƂ���𗝉��ł��ĂȂ������Ƃ͍����������B
�s�������ł��ĂȂ������Ƃ͂ȁB �W���_�ɂ����đ��ݗʉ��L���̎g�������悭�킩��܂���B
�������������̂́A�摜�̏ؖ����ɂ��Ăł��B
�X�^�[�g�̖��肩��A�ؖ��������S�[���̖���ւƁA�_���I�ɓ��l�Ȏ��ό`���J��Ԃ��Ă���̂ł����A
�摜��GAP�̂Ƃ���ŁA���ݗʉ��L���̏����̎d�����悭�킩��܂���B
����낵�����肢���܂��B
https://i.imgur.com/YuQC9Ii.jpg >>894
��ʂ�
A={f(x)|x��B}�͘_�����ŏ����Ƃǂ̂悤�ɂȂ�ł��傤���A�l���Ă݂�Ƃ�����������Ȃ��ł���
���͕��ʂ̘_�����ł͂Ȃ��A���ʂ̊T�O����������B����Ă���̂ŁA���ʂ̘_�����ɏ���������Ƌ@�B�I�ȏ������ł���悤�ɂȂ�͂��ł� >>894
f(A) = { f(x) | x �� A } (���p�\�L)
= { y �� Y | ��(x �� X) x�� A �� y =f(x) } (�����\�L)
��(x �� X) x�� A �� y =f(x)
��
��(x �� X) x�� A �� x �� f^-1({y}) )
��
��(x �� X) x�� (A �� f^-1({y})) )
��
A �� f^-1({y}) �� ø ������A�����肪�Ƃ��������܂��B
>>895
���ǂ�ł���{�ł͂��̕ӂ�̘b�������s���Ă������̂ŁA����ǁA�����I�W���_�̖{�������ǂ�ł݂悤�Ǝv���܂��B
>>896
�����Ax��y�Ƃ������ɂ��Ă̋c�_�͂����܂�
|�p�̒��Ŋ������Ă���ׂ��ł����āA
���������Ӗ��ŁA�ŏ��̎��_�ŁA�܂��ʉ��L��(�����ł́�)���g���āAx�Ƃ����������g���܂��琔�w�I�Ώە��Ƃ��Ĉ����h�Ɛ錾���Ȃ���Ȃ�Ȃ��A�Ƃ������Ƃł��傤���B(�v���O���~���O�ł����ϐ��̐錾�̂悤�Ȃ��́H)
���̏�ŁAx��A�Ƃ�������ɂ���āAx�ɈӖ��t�������Ă����c 2�s�ڂ̐����\�L�����t�Ƃ��ĉ��߂���ƁA
�u�ʑ�f�ɂ����Y�̂��錳y�ɔ����A����A�̌��ł�����悤�ȕ�(X�̌�)�����݂���A�Ƃ������Ƃ��^�ł���悤��y��S�ĕ��ׂ�v
�Ƃ��������ł��傤���B
������悤�ȕ�����Ȃ��悤�Ȋ��o�Ȃ̂ŁA�Ƃɂ������ɂ��A�}���ق֍s���Č����I�W���_�̖{���J���Ă݂悤�Ǝv���܂��B �ʑ��Ɗ��̈Ⴂ�������Ă��������B �\�̏o��m����p(1/2≤p<1)�̃R�C����k���A�\�̏o��m����q(0<q≤1/2)�̃R�C����n-k������B
�����n���̃R�C���𓊂���Ƃ��A�\���o�閇���̊��Ғl�����߂�B
������k��0�܂���n�ł����Ă��悢�B >>900
�@kp + (n-k)q�@
(��)�@�ق̒��ŃR�C�����m�����͂ł����t�������Ƃ�
�@�@�˂��ꂽ�R�C�����m�����ݍ����ă_���S�ɂȂ�u�A���J�[���ʁv�Ƃ�
�@�@��������c >>890
�@�݊���=(i,j) (������ i<j) �ɂ�� x_k - x_L �̕ω��̎d���ׂ�B
�Ek��i,j�@L��i,j �̂Ƃ�
�@#{i,j,k,L} = 4,
�@(x_k-x_L)�@�͌��̂܂�
�Ek=i ���� L=j �̂Ƃ�
�@#{i,j,k,L} = 2,
�@x_i - x_j�@���@- (x_i - x_j)
�@k=j ���� L=i �͂��肦�Ȃ��B
�E�c���Ă���̂� k, L �̈�������� i�܂���j �̏ꍇ�B
�@#{i,j,k,L} = 3,
(1) k<i�@L=i,j �̂Ƃ�
�@(x_k-x_i)(x_k-x_j)�@���@���̂܂�
(2) k=i,j�@j<L �̂Ƃ�
�@(x_i-x_L)(x_j-x_L)�@���@���̂܂�
(3) i=k<L<j�@�܂��́@i<k<L=j�@�̂Ƃ�
�@(x_i-x_m)(x_m-x_j)�@���@���̂܂�
�@�����Ɂ@m=i,����,j
�ȏォ��@���@���@-��
�ǂ����Ă��ʓ|�ȏꍇ�����ɂȂ��Ă��܂�....orz�B�@�@>>893 >>893
������ς���㎮�ł��邱�Ƃ͊ȒP�ɕ�����܂��B >>890
1 �� k < l < i, i < k < l, l �� j, j < k < l �� n
���̏ꍇ�������Ӗ��s���ł��B
k < l < i
k < i < l < j
k < i < j < l
i < k < l < j
i < k < j < l
j < k < l
�Ə����Ă���Ε�����̂ł����B >>890
���ƁA
x_��(k) - x_��(i) = x_k - x_j (k < i)
�������Ă��܂��H
���Ȃ݂ɁA���̖{�̒��҂͏�쌒������ł��B >>890
1 �� k < l < i, i < k < l, l �� j, j < k < l �� n
�� l �� j ���Ă���ł����H
��������A
1�@�� k < l �� n, k �� i, k �� j, l �� i, l �� j
�Ɗy�ł��܂���ˁB
��쌒������͓ǎ҂̓ǂ݂₷���Ȃǟ|���C�ɂ��Ă��܂����ˁB >>892
>>902
���肪�Ƃ��������܂����B
��͂��쌒������̏ꍇ�����̏������͕�����ɂ����ł���ˁB >>885
���̂Ƃ���ł��ˁB
�ŏ��� a_i = i (i=1,2,����,2k) �Ƃ����ƁA2n-2k �̗]�肪����B
�����2��P�ʂƂ��� a_1 �` a_{2k}, a_{2k+1} �� 2k+1�ɕ��z����Ba_{2k+1} �̓_�~�[�ϐ��B
�ea_m �̏�Ɂu2�v�� c[m] �悹�܂��B�i���̂Ƃ� a_m�`a_{2k+1} �� 2c[m] �������₷�B)
�[m=1, 2k+1] c[m] = n-k,
2k+1 �̒����� n-k ��I�ԏd���g�����́@H[2k+1, n-k]
(n-k) + 2k ���� 2k ���́u�d��v��I�Ԃ����́@C[n+k, 2k] �J���_�m�̌����ɂ��Ď���ł��B
3����������3���� ��, ��, �� �Ƃ��܂��B
��, ��, �� ��\�킷3�̎�������܂��B
���ۂɁA {��, ��, ��} = {1�Ԗڂ̎��ŕ\����鐔, 2�Ԗڂ̎��ŕ\����鐔, 3�Ԗڂ̎��ŕ\����鐔}
�ɂȂ��Ă��邱�Ƃ͊m�F����K�v������Ǝv���܂����A��쌒������́w�㐔����x�ł͊m�F���Ă��܂���B
�܂����ł���ˁH �J���_�m�̌����ɂ��Ď���ł��B
3����������3���� ��, ��, �� �Ƃ��܂��B
3���������̉���\�킷3�̎�������܂��B
����3�̎����ׂĂ�3���������̉��ł��邱�Ƃ͕�����܂��B
����� {��, ��, ��} = {1�Ԗڂ̎��ŕ\����鐔, 2�Ԗڂ̎��ŕ\����鐔, 3�Ԗڂ̎��ŕ\����鐔}
�ɂȂ��Ă��邱�Ƃ��m�F����K�v������Ǝv���܂�
��쌒������́w�㐔����x�ł͊m�F���Ă��܂���B
�܂����ł���ˁH �ϐ�a_1,...,a_n�͂��ꂼ��-1�܂���1�̒l���Ƃ�A�C�ӂ�i,j�ɑ���a_i��a_j�͓Ɨ��ȕϐ��ł���B
�ea_i�̒l�ɂ��A�����̘aa_1+...+a_n��-n����n�܂ł̂����ꂩ�̐����l���Ƃ�B
�i1�j�aa_1+...+a_n�̒l��n-1�Ƃ͂Ȃ�Ȃ��B���̂悤��a_1,...,a_n�̗��1������B
�i2�j�i1�j�̂悤�ɁAa_1,...,a_n���ǂ̂悤�ȑg�ݍ��킹��-1�܂���1�̒l���Ƃ��Ă��A�aa_1+...+a_n�Ƃ��ĕ\���ł��Ȃ�������-n�ȏ�n�ȉ��̂��̂����݂���B
���̂悤�Ȑ����̌���N[n]�Ƃ����Ƃ��A�ȉ��̋Ɍ������߂�B
lim[n����] N[n]/(2n+1) ����a�v���w�㐔�ւ̏o���x�ł́A
a^3 + b^3 + c^3 - 3*a*b*c = (a + b + c)*(a + b*�� + c*��^2)*(a + b*��^2 + c*��)
�Ƃ��������g���ē����Ă��܂��B���̓������ł́A
{��, ��, ��} = {1�Ԗڂ̎��ŕ\����鐔, 2�Ԗڂ̎��ŕ\����鐔, 3�Ԗڂ̎��ŕ\����鐔}
�͎����ł��B ��쌒������̋c�_�̎d���ł́A
{��, ��, ��} = {1�Ԗڂ̎��ŕ\����鐔, 2�Ԗڂ̎��ŕ\����鐔, 3�Ԗڂ̎��ŕ\����鐔}
�͎����ł͂���܂���B �Z���Ԃł����A��쌒������́u�s�e���[���h�v�Ɋ���Ă��珼��a�v����́u�e���[���h�v�ɍs����
����a�v����̐������@���ɐ��m�ō��ؒ��J����������܂��ˁB ���ꂾ������{���_�����_���������Ă�����e�m�q���N���[�� ��쌒������́w�㐔����x�������Ă���l�̓J���_�m�̌����̂Ƃ�������Ă݂Ă��������B
��쌒������̋c�_�̎d���ł́A
{��, ��, ��} = {1�Ԗڂ̎��ŕ\����鐔, 2�Ԗڂ̎��ŕ\����鐔, 3�Ԗڂ̎��ŕ\����鐔}
�͎����ł͂���܂���B ��쌒������̋c�_�͈ȉ��̂悤�Ȋ����ł��F
x^3 - p*x - q = 0
�����������B
(u + v)^3 - p*(u + v) - q = 0 �c (A)
�����A u, v ��������悢�B
�W�J���āA
u^3 + v^3 + (3*u*v - p)*(u + v) - q = 0
u^3 + v^3 = q
3*u*v = p
�ƂȂ�悤�� u, v �� (A) �������炻�̂悤�� u, v ��������悢�B u^3 + v^3 = q
3*u*v = p
��
(u^3 - v^3)^2 = (u^3 + v^3)^2 - 4*u^3*v^3 = q^2 - (4/27)*p^3
��
u^3 - v^3 = �}sqrt(q^2 - (4/27)*p^3)
u^3 = (1/2)*(q + sqrt(q^2 - (4/27)*p^3)
v^3 = (1/2)*(q - sqrt(q^2 - (4/27)*p^3)
or
u^3 = (1/2)*(q - sqrt(q^2 - (4/27)*p^3)
v^3 = (1/2)*(q + sqrt(q^2 - (4/27)*p^3)
u, v �̑Ώ̐�����A
u^3 = (1/2)*(q + sqrt(q^2 - (4/27)*p^3)
�Ɖ��肵�Ă���ʐ�������Ȃ��B u = ((1/2)*(q + sqrt(q^2 - (4/27)*p^3))^(1/3)
or
u = ��*((1/2)*(q + sqrt(q^2 - (4/27)*p^3))^(1/3)
or
u = ��^2*((1/2)*(q + sqrt(q^2 - (4/27)*p^3))^(1/3)
u*v = p/3
�����藧�悤�ɒ��K�����킹��ƁA
u = ((1/2)*(q + sqrt(q^2 - (4/27)*p^3))^(1/3)
�ɑ��ẮA
v = (p/3)*((1/2)*(q + sqrt(q^2 - (4/27)*p^3))^(-1/3)
�ƂȂ�B
u = ��*((1/2)*(q + sqrt(q^2 - (4/27)*p^3))^(1/3)
�ɑ��ẮA
v = ��^2*(p/3)*((1/2)*(q + sqrt(q^2 - (4/27)*p^3))^(-1/3)
�ƂȂ�B
u = ��^2*((1/2)*(q + sqrt(q^2 - (4/27)*p^3))^(1/3)
�ɑ��ẮA
v = ��*(p/3)*((1/2)*(q + sqrt(q^2 - (4/27)*p^3))^(-1/3)
�ƂȂ�B 👀
Rock54: Caution(BBR-MD5:1341adc37120578f18dba9451e6c8c3b) D = 4*p^3 - 27*q^2
�Ƃ����ƁA
x^3 - p*x - q = 0
�̉��́A
((1/2)*(q + sqrt(-D/27)))^(1/3) + (p/3)*((1/2)*(q + sqrt(-D/27)))^(-1/3),
��*((1/2)*(q + sqrt(-D/27)))^(1/3) + ��^2*(p/3)*((1/2)*(q + sqrt(-D/27)))^(-1/3),
��^2*((1/2)*(q + sqrt(-D/27)))^(1/3) + ��*(p/3)*((1/2)*(q + sqrt(-D/27)))^(-1/3)
�ł���B ���łɁA����a�v����̉�@�������܂��B
x^3 + 3*p*x + q = 0 �c (B)
�Ɖ��������B
A^3 + B^3 = -q
A*B = -p
���� A, B ���������Ƃ���B
(B)�́A
x^3 + (-A)^3 + (-B)^3 - 3*x*(-A)*(-B) = 0 �c (C)
�Ə�����B
���� a^3 + b^3 + c^3 - 3*a*b*c = (a + b + c)*(a + b*�� + c*��^2)*(a + b*��^2 + c*��)
�� a = X, b = -A, c = -B �Ƃ��đ������ƈȉ��̓�����������B
x^3 + (-A)^3 + (-B)^3 - 3*x*(-A)*(-B) = (x - A - B)*(X - A*�� - B*��^2)*(X - A*��^2 - B*��)
(C)�́A
(x - A - B)*(X - A*�� - B*��^2)*(X - A*��^2 - B*��) = 0
�Ə�����B
����āA(B)�̉��̏W���́A
{A + B, A*�� + B*��^2, A*��^2 + B*��}
�ł���B A^3 + B^3 = -q
A*B = -p
���� A, B �����߂����B
A^3 + B^3 = -q
A*B = -p
��
A^3 + B^3 = -q
A^3*B^3 = -p^3
������A
A^3, B^3 �́A
t^2 + q*t - p^3 = 0
�̉��ł���B
A^3 = (-q + sqrt(q^2 + 4*p^3))/2
B^3 = (-q - sqrt(q^2 + 4*p^3))/2
�́A
A^3 + B^3 = -q
A^3*B^3 = -p^3
�����B
A = ((-q + sqrt(q^2 + 4*p^3))/2)^(1/3)
B = ((-q - sqrt(q^2 + 4*p^3))/2)^(1/3)
A*B = -p
�����藧�悤�ɁA���K�����킹��A
A^3 + B^3 = -q
A*B = -p
�̉� A, B ��������B 👀
Rock54: Caution(BBR-MD5:1341adc37120578f18dba9451e6c8c3b) ��w�Ɛ��w�̊W�̐���p�Ƃ����ɂ߂Ă݂����Ȃ��B���p�Ƒ����������Ȃ��������B �d�@���@��@���@���@�w�p�̖ړI�Ō�������B���͂��ڂ낾�������ǁB ln(2) = 0.69314718056
ln(3) = 1.09861228867
ln(5) = 1.60943791243
ln(7) = 1.94591014906
��2 = exp(1/2 * ln(2)) = 1.41421356237
��3 = exp(1/2 * ln(3)) = 1.73205080757
��5 = exp(1/2 * ln(5)) = 2.2360679775
��7 = exp(1/2 * ln(7)) = 2.64575131106 ����v�Z�@�������āA2�̗L������10���̓��͂ɑ��āA1�b�ʼn����揜�̂ǂꂩ��L������10���Ōv�Z�o����Ƃ��܂��B�����v�Z�@��2���̑召��r��1�b�ŏo���邱�Ƃɂ��܂��B
���̌v�Z�@�����ׂāA�z���Ōq���A
���� x(-100<x<100,�L������10��) �ɑ��w�����̌v�Z�le^x��L������10�����x�ŏo�͂�����悤�ɂ������ł��B
�v�Z�@�Ԃ̔z����ʂ鎞�Ԃ�-1���|���鎞�Ԃ͖����ł��܂��B
�L������10���ŁA�v�Z���Ԃ��ŒZ�ɂ���ɂ͂ǂ������z�u�������̂ł��傤���H
�Ȃ��A�v�Z�@�̌��͂�����ł��ǂ��ł������������ŏ��Ȍ����]�܂����ł��B
���Ȃ݂�e^100=2.68*10^43�ł��B
�L�������ƌ��������������Ȃ��悤�ɂ��肢���܂��B
�܂��A���όv�Z���Ԃ������Ȃ�Ή��ł��ǂ��ł��B
|x|<10�Ō��\�����Ax=100�t�߂ł͒x���Ȃ��Ă��\��Ȃ��A�Ƃ��������ł��B
�����e�͊��m�Ƃ��āAx�͑S���܂���B
�����l���Ă���͎̂w��������2�i�����APade�ߎ���2�i�ƃ}�N���[�����W�J�Ȃǂł��B exp(2 * ln(1.41421356237)) = 1.99999999999
exp(2 * ln(1.73205080757)) = 3
exp(2 * ln(2.2360679775 )) = 5
exp(2 * ln(2.64575131106)) = 6.99999999998 >>934
�\�i��x�͏�������8or 9���̐��ł��B
�Ō��e^x�o�͂͌덷�̗ݐύl���ėL������8���ł��ǂ��ł��B ��쌒�����w�㐔����x��ǂ�ł��܂��B
�uC �̕����� K �ɑ��āA C �̌� ��1, ��2, �c, ��m ���^����ꂽ�Ƃ��A K �� ��1, ��2, �c, ��m ���܂� C ��
�ŏ��̕����̂� K(��1, ��2, �c, ��m) �ƋL���A�� K �� ��1, ��2, �c, ��m ��Y�����Ăł����̂Ƃ����B�v
���̌�ŁA
�uK(��1, ��2, �c, ��m) = {g(��1, ��2, �c, ��m)/f(��1, ��2, �c, ��m) | f, g �� K[x1, x2, �c, xm], f(��1, ��2, �c, ��m) �� 0}�v
�����藧��
�Ə�����Ă��܂��B
������ď��������������Ȃ��ł����H
K �� ��1, ��2, �c, ��m ���܂� C �̕����̂̒��ɍŏ��̂��̂����݂��邩�ǂ����H
�Ƃ����̂��܂����ɂȂ�܂���ˁB
�ŁA�����ɁA�ŏ��̑̂͑��݂��邱�Ƃ�������܂��B
����́A
{g(��1, ��2, �c, ��m)/f(��1, ��2, �c, ��m) | f, g �� K[x1, x2, �c, xm], f(��1, ��2, �c, ��m) �� 0}
�ł��B
���̍ŏ��̑̂� K(��1, ��2, �c, ��m) �ƋL���A�� K �� ��1, ��2, �c, ��m ��Y�����Ăł����̂Ƃ����B
�Ƃ������ꂪ���������ꂾ�Ǝv���܂��B ���邢�́A
�uC �̕����� K �ɑ��āA C �̌� ��1, ��2, �c, ��m ���^����ꂽ�Ƃ��A K �� ��1, ��2, �c, ��m ���܂� C ��
�����̂̋��ʕ����͑̂ɂȂ�B����� K �� ��1, ��2, �c, ��m ���܂� C �̍ŏ��̑̂ł��� K(��1, ��2, �c, ��m)
�ƋL���A�� K �� ��1, ��2, �c, ��m ��Y�����Ăł����̂Ƃ����B�v
�Ə����ׂ��ł���ˁB ��쌒������̖{�݂͂�Ȃ���ȕ��ɃX���[�X�ɓǂ�ł������Ƃ��ł��܂���B
�����Ɉ���������Ƃ��낪�o�Ă��܂��B
����Ӗ��P���ɂȂ�܂��ˁB ���W�F���h
�ی��m
�㓇������@���{����q
����ŃO�O��łĂ��邪�A
�ی��m�����琸�_�ی������@��m���Ă���A
�����x�@���A�L���}�Ƒn���w��Y���̎E�l�H�쎸�s�̂��ƂƁA
�C���L�e�b�N�����̔ƍ߂ɂ��Ă̘b�����A
�g�����C���L�e�b�N�ɂ�����̂�����A
���̎E�l�H�쎸�s����
�����x�@�A�L���}��
�n���w��Y���A
������
�X�L���w�b�h�̔��ԂɃz�N��������o�J�A
���킹���ĎO���̓��{���x�@�ɐN�������e�����X�g��
�f�v�����悤�Ǝ���ɉ����������l�ɓ{������f�v�����s����
�����鋥���`�� >>892
�݊���=(i,j) (������ i<j)�́A�אڌ݊������𑱂������̂Ɠ����ł��ˁB
(i,i+1)�@(i+1,i+2)�@�����@(j-2,j-1)�@(j-1,j)�@�@
(j-i)���Ɂ@x_i ��j�ԖڂɁ@x_j��(j-1)�Ԗڂɗ���B
j-i>1 �̂Ƃ��͍X��
(j-2,j-1)�@(j-3,j-2)�@�����@(i+1,i+2)�@(i,i+1)
(j-i-1)����x_j �� x_i�ɗ���B
���킹�� 2(j-i)-1 ��̗אڌ݊�������
�@���@���@-��
�������ɊȒP�ł��B >>934
���̏ꍇ�̋ߎ����́A�w�����̂悭�m��ꂽ����:
e^x=1+x+x^2/2!+x^3/3!+�c
�₻��Pade�ߎ����g������tanh�̘A����:
(e^(2x)-1)/(e^(2x)+1)=x/(1+x^2/(3+x^2/(5+x^2/(7+x^2/(9+�c)))))
��ʕ����Ȃ��ł��̂܂܌v�Z��������͂邩�ɑ����Ȃ�܂��B
���̘A������6���őł����e^(-2)����e^(2)�܂ł�10���̐��x�Ōv�Z�ł��܂��B
�i����������Z�̋��ȕ��ʂ̌v�Z�@�ł͂��̕��@�͎g���܂���j
��ԏk���̊�{�͉��@�藝e^(x+y)=e^x*e^y�𗘗p���āA
x���炠�鐔(����or log2,log10�̐����{)�������ċߎ���ɕ������@�ł��B
x��1/2�{���ċߎ����2�悷����@�Ȃǂ͐��x��������̂ŗv���ӂł��B
��ԕ����E�k�����@��libc�Ȃǂ̋�̓I�ȃR�[�h����������������₷���Ǝv���܂��B
��^�v�Z�@�ȂǂɎ�������Ă���ɒ[�ȗ�ł́A
�ׂ�����Ԃɕ������ꂽ�Ⴂ����(2����3��)�̋ߎ������ʂ�(���S���琔��)
�����Ă��āAx�̃r�b�g�p�^�[������ߎ����̔ԍ�(�����l)������o���Q�Ƃ���Ƃ���
���@���Ƃ��Ă��܂��B���̕��@���ƃ������̋�������̍��������ł��܂��B >>943
���[�A�����W�J�g�����ł���
exp�v�Z���Ă���V�O���C�h���g�����Atanh���������̕����j���[�����l�b�g���[�N�Ɏg�������ȋC�����Ă��܂���
��������ʏ���͎����ł������삪����ł���
�덷�ݐύl���������q�ɎQ�Ƃ���͕̂s�������ł���...
���肪�Ƃ��������܂��I >>751
x=a+bi�ƒu���ƁAx^n��ℝ�ƂȂ�悢�̂�
��r��ℝ ; x^n=r
�����
a=r^(1/n) cos(2��/n), b=r^(1/n) sin(2��/n)
�Ƃ�����悢�Ǝv���܂� �ϐ�a_1,...,a_n�͂��ꂼ��-1�܂���1�̒l���Ƃ�A�C�ӂ�i,j�ɑ���a_i��a_j�͓Ɨ��ȕϐ��ł���B
�ea_i�̒l�ɂ��A�����̘aa_1+...+a_n��-n����n�܂ł̂����ꂩ�̐����l���Ƃ�B
�i1�j�aa_1+...+a_n�̒l��n-1�Ƃ͂Ȃ�Ȃ��B���̂悤��a_1,...,a_n�̗��1������B
�i2�j�i1�j�̂悤�ɁAa_1,...,a_n���ǂ̂悤�ȑg�ݍ��킹��-1�܂���1�̒l���Ƃ��Ă��A�aa_1+...+a_n�Ƃ��ĕ\���ł��Ȃ�������-n�ȏ�n�ȉ��̂��̂����݂���B
���̂悤�Ȑ����̌���N[n]�Ƃ����Ƃ��A�ȉ��̋Ɍ������߂�B
lim[n����] N[n]/(2n+1) �C�ӂ̎l�p�`��2�̈قȂ�Ίp�������̎l�p�`�̓����Ō���邱�Ƃ����� �@CONVEX�W������Ȃ��Ă��A���ɂ͂���̂����B�@�A�i���� >>948
�ʎl�p�`�Ȃ炻���ł����A���l�p�`�i�V�`�H�j�ł͐��藧�����K�X https://imgur.com/KQJUMlP.jpg
���6.21�Ɂum' �� n �Ƒf�ł���v�Ə����Ă���܂����A���炩�Ɍ��ł��B
���̕��6.21�̏ؖ��͉����������Ƃ��Ă���̂ł��傤���H �������[
���炩�Ɍ���Ă�̂��[
�c�c�ŁA����́H�H�H m' �� d �Ƒf�ł���
�ɒ������̕����̈Ӗ��͒ʂ�܂��ˁB ���̏ؖ��̍ŏ��̕����ŁA
d �� n �̔C�ӂ̖Ƃ���ƁA 1 �̌��n d �捪�͂��ׂ� {1, ��, ��^2, �c, ��^(n-1)} �Ɋ܂܂�邱�Ƃ������Ă��܂��B
1 �̌��n d �捪�� 1 �̌��n d' �捪�́A d �� d' �̂Ƃ����炩�ɈقȂ�܂��B
�ȏ���A
��_{d �� n �̖�} {1 �̌��n d �捪} �� {1, ��, ��^2, �c, ��^(n-1)}
�ł���A
��_{d �� n �̖�} {1 �̌��n d �捪}
�݂͌��ɋ��ʕ����̂Ȃ��a�W��
�ł��B
{1, ��, ��^2, �c, ��^(n-1)}�@�� ��_{d �� n �̖�} {1 �̌��n d �捪}
���m���߂Ă���̂��㔼�����ł��ˁB >>951
�͏�쌒�����w�㐔����x�ł����A�ؖ��Ɍ�肪�����ɁA������ɂ����ł��ˁB
�Ȃ��A
>>955
�̂悤�ɏ����Ȃ��̂ł��傤���H �����Ő������������Ĉ�ؐ����Ȃ��̓��Ăɋ߂��ł���ˁB
0�_�ł��ˁB �����̒��Ō��_���o�Ă�Ȃ���L���ɏ��� �������Ȃ��Ɛ����Ă����Ȃ��� �����_�ł̎����̊w�͂����ϓI�Ȑ��w�Ȃ̊w�����̃��x���ɗy���ɓ��B���ĂȂ������킩���Ă邾�낤���A���X�͂��̗��R�������Ă͂���낤���ǁA�������X��S�����ւ���ɂ͒x������낤�B
����Ӗ��J�������Ă��������e�T������̂𐔊w�̊y���݂Ƃ���̂�������ł͂Ȃ��납�H
�N�ɖ��f������ł��Ȃ����B �����܂���A������ďؖ������Ă܂����H
��蕶�́u���s�̎���x=0��������-1��x��1�Ő��藧���Ƃ������v�Ƃ������̂ł�
�����[x=0�����đΐ�������Ă�̂͂��̂��߂ł��B
�����C�����������ƌ�����
�@���̕��͂̎���x=0�Œ�`�ł��Ȃ��̂ɂ����ό`���ē���ꂽf(0)=0���g���Ă���
�if(x)�̘A�����͔������\�Ȏ��_�ł����Ă邩�炱��͋C�ɂ��Ȃ��Ă悢�̂ł��傤���H�j
�Af`(x)��0<x<1�Ő��Af(0)=0�A���ꂾ����f(x)��0<x<1�Ő��ƌ�����̂��H
�i������f(x)�������\�ł��鎞�_�Ŏ����Ƃ��Ă悢�̂ł��傤���H�j
�ǂ̂悤�ȕ���t�������܂Ƃ��ȏؖ��ɂȂ�ł��傤���H
��낵�����肢���܂�m(_ _)m
https://i.imgur.com/sHKqXYk.jpg
https://i.imgur.com/3P1SUQP.jpg >>962
�L�q���ꂽ�ؖ��ɑ傫�Ȗ��͂Ȃ��B
�C�ɂȂ镔���́A�Ⴆ�A�ȉ��̂悤�ȋL�q�Ƃ���悢�B
x��0 �̏ꍇ�����l�Ȃ̂ŁA�ȉ��͈ꉞ�@0��x��1�̉��ł̋L�q�Ƃ���B
�����ׂ��s�����͌`�̏�ł́@�u0��x��1�@�̂Ƃ��@(1/x)f(x)��(1/x)g(x)�v �ƂȂ��Ă���B
����́@0��x��1 �̂��ƂŁ@f(x)��g(x)�@�Ɠ��l�䂦�A0��x��1�̂��ƂŁ@f(x)��g(x)�@�������Ώ\���B
����@f(x)�Ag(x) �͂��̎��̌`����@-1��x��1 �Œ�`���ꂽ�����\�Ȋ��Ƃ݂Ȃ����Ƃ��ł��@���Ɂ@f(0)=g(0)=0�@�䂦
0��x��1 �̉��Ł@f(x)��g(x) ���������Ƃ��ł���@���Ɂ@0��x��1�@�̂Ƃ��ł��@f(x)��g(x)�@�����藧���Ă��邱�Ƃ����������ƂɂȂ�B
����āA�ȉ��́@0��x��1 �̉��Ł@f(x)��g(x)�@�������ؖ��ł���B
�̂悤�ɏ����悢 >>963
�����Ax=0�̎���f(x)��g(x)�͐������܂����B �@ �̏������̖��ɂ����Ȃ��B���w�ł͂Ȃ�����̖��B
�̈�ԍŏ��ł����Ȃ� f�F(�|1,1)��R ��
f(x)��log(x�{1)�|(x�|1)log(1�|x) �ƒ�`���Ă��܂��A
f(0)�������ɒ�`����Ă���̂�f(0)���g����B�܂��Af�̑����ׂ�
�u0��x��1�ɂ�����f(x)��0�v
�������A�����ό`���邱�Ƃ�0��x��1�̏ꍇ�ɂ����錳�X�̎���������B
�܂�A��`�悪�L���Ƃ��납��o�����ċ����Ƃ���Ɍ��肵�Ă����悤�ȏ��Ԃ�
�������Ή��̖����N���Ȃ��Ƃ������ƁB
�A �����ɂ͏ؖ����K�v�B
��ʂɁAF�F(0,1)��R �����`�P���������� lim[t��0]F(t)��0 �Ȃ�A
0��x��1�̂Ƃ� F(x)��0 �ł���B
�Ȃ��Ȃ�A0��x��1��C�ӂɎ��Ƃ��A0��t��x/2 �͈̔͂�
F(t)��F(x/2) �Ȃ̂ŁA���̎��� lim[t��0] ������ 0��F(x/2) �ł���A
�܂� F(x/2)��F(x) �ł��邩��A0��F(x) �ƂȂ�B0��x��1�͔C�ӂ���������A
0��x��1�̂Ƃ� F(x)��0 �ł���B >>964
�K���ɏC�����ēǂ�ł��������B >>966
�܂��ɂ��̕���������ӏ��ł��̂Łc�c
>>965
���肪�Ƃ��������܂��B�Ȃ�ƂȂ����������C�����܂�m(_ _)m >>968
���Ȃ�w���������璆�����̎���劽�}���ȁB
�������v�\�t�gR�����E�������o���Ȃ����ǁB >>967
> >>966
> �܂��ɂ��̕���������ӏ��ł��̂Łc�c
���������āA
f(0)=g(0)=0 �Ə����Ă��邱�Ƃ��g���Ăǂ��C�������炢���̂����킩��Ȃ��̂��E�E�E >>970
�\����Ȃ��ł����A
�u0��x��1 �̉��Ł@f(x)��g(x) ���������Ƃ��ł���@���Ɂ@0��x��1�@�̂Ƃ��ł��@f(x)��g(x)�@�����藧���Ă��邱�Ƃ����������ƂɂȂ�B
����āA�ȉ��́@0��x��1 �̉��Ł@f(x)��g(x)�@�������ؖ��ł���B�v
�������炱���܂őS�ĊԈ���Ă���̂ɂȂ��܂��ォ��ڐ��Ń��X���ė����̂���������܂���B
���ۂ̂��Ȃ��̃X�L�����ǂ̂悤�Ȃ��̂ł���A���̂ł����ȉ��̗����������ĂȂ��̂ɉ��Ă����Ƃ������ł����
���Ă��������ۂ́A���╶���悭�ǂ܂ꂽ�ق����ǂ����Ǝv���܂��B https://news.yahoo.co.jp/byline/kosakunoboru/20181228-00109363/
�����̏����E�A�Q�O�P�W�N��U��Ԃ�\�\�������m�ƃA�}������
�Í�o | ��㏤�Ƒ�w�A�~���[�Y�����g�Y�ƌ�������C������ Yahoo 12/28(��) 14:45
(����)
�@�Q�O�P�W�N�̏����E�͌����̈�N�������B�Ȃ�Ƃ����Ă���Ԃ̏o�����͂P�Q�����ɗ����펵�ԏ������t���Z�b�g�Ō������A�L���͐l�V�����i�R�P�j���a���A�H���P����i�i�S�W�j���Q�V�N�Ԃ�ɖ����ƂȂ������Ƃ��낤�B
���N���ĂɎO���B���̉\��
�@�Ăɂ͂W�̃^�C�g�����W�l�̊��m�ŕ����������������A�H�ɖL�����V�i�Q�W�j���a���������ƂŁA���㉽�l���̊��m�Ƀ^�C�g�����W�܂闬��Ɍ������Ă���B
�@��̓I�Ɏ����ƖL���i���ʁE�����j�͍����V�F���l�i�R�O�j�ւ̒��팠�𑈂��`�����ʐ�łU���O�s�ƒP�Ǝ�ʁA���N���Ăɂ͎O���̉\��������B
�@�N��������n�܂������̒���҂ɂȂ����L���������`�����ʐ�łT���P�s�ƉH����i�Ɠ����ŖL����ǂ��Ă���A�������O���̓����J���Ă���B
�@�n�Ӗ������i�R�S�j��������̒���҂ɂȂ��Ă���̂łP�N���J���Ԃ�̕������i�Q�O�P�V�N�P�Q�����߂͗����E�����j�̉\���\�����B 2�̓_�����Ԑ��̒��ŁA�ł������̒Z�����̂͐����ł��邱�Ƃ������Ă��������B �܂����O���B�O�X���ł��������₵�Ă�����A�n���B �����������̖��ł����A��������͂���܂����H
g = g(��) , h = h(��)��R���C1�����Ƃ��ĂQ�K�̏����������
d^2w/dt^2 + g(w)(dw/dt) + h(w) = 0
���l����B���萔�� > 0 , �� > 0�����݂�
��g , h�͎��̏��������Ɖ��肷��B
g(��) �� �� , h(0) = 0 , h'(��) �� �� (�� �� R)
�Ƃ���B���̂Ƃ��A�C�ӂ�a,b��R�ɑ���w(0) = a , w'(0) = b�ƂȂ�悤�ȉ�w(t)��t �� 0�ő��݂��邱�Ƃ������B�܂�lim[t����]w(t) = 0�������B
�q���g�FH(��) = ��[0����]h(��)d�łƂ���
(d/dt){(1/2)(dw/dt)^2 + H(w(t))} = (dw/dt)((d^2w/dt^2) + h(w(t))) �Q�̓_�����Ԑ܂���̒��ŁA�ł������̒Z�����̂͐����ł��邱�Ƃ������Ă��������B
�@�@�@�@�@�@�@�P�P�P
�Ȃ�u�E�Ȃ��ǥ��� >>977
�Ȑ��̒���>=�܂���̒����Œ�`����邩��u�E����ˁH >>978
�Ɓ[�Ƃ낶���H
�u�V�������c�̒v�������B ��ABC�́u�O���v���I��܂�� A-P1-�c-Pn-B �̒����̉����� AC+CB�B
����� AB ��蒷���B
��ABC�́u�O���v���I��Ȑ������l���H
���������Ȃ�u�E���� �����Ɏ����ăn�^�ƋC���t�����B
�Ȑ��́u�����v����`����Ă��Ȃ����Ƃɥ��� >>981
2�_���q���Ȑ��̒����́A2�_���q���܂���̒����̏���Œ�`����邩��A2�_���q�������͐܂���Ȃ̂ŁA���̒����͂��ׂĂ̋Ȑ��̒����ȉ��B
�����_����^����ꂽ���̂ł͂Ȃ��A�����l�Ԃ���`������B >>982
���Ă��A���̈�A�̗���͑O�X���ł��W�J����Ă���Ȃ��B
�������̌J��Ԃ��B �ŒZ�͒����ł͂Ȃ��đ��n������� X^2 + x + 3xy 2y^2 + 3y - 2
�������� >>986
x^2 + x + 3xy+ 2y^2 + 3y - 2
=x^2+2xy+y^2+x+xy+y^2+3y-2
=(x+y)^2+y(y+x)+(x+y)+2y-2
=(x+y)^2+(y+1)(x+y)+2(y-1)
=(x+y+2)(x+y+y-1)
=(x+y+2)(x+2y-1)
�Ɖ����Ă݂͂����Ax�����[�W�w��������3xy2y^2�ɂȂ��Ă���̂ňႤ��������Ȃ� >>987
2y^2��y^2����ƕ������邱�Ƃ��v������̂͂������Ǝv��
�Ȃ�ŁA�����x+y��y�ɂ킯�悤�Ǝv�������������o���Ȃ����� (1)x^2,xy,y^2�����邩��Ƃ肠������������
(2)�Œ��(���̏ꍇ��x,y�̂ǂ���ł���)�̕ϐ��Ɋւ��ĉ����Ă݂�
(3)����������̌���&�����藝
(4)���Ă����ۂ��ň����藝 ����͊Ԉ���Ă���Ǝv���܂����A�ǂ��������Ȃ��̂������ĉ������B
https://i.imgur.com/lIDrO9m.jpg �����\�Ȋ�f�� f(0)=0 ���� f '(0)=�� �ł��鎞
lim[�Ɓ�0] f(1-cos(2��))/(��^2) �͂����炩�B
(����)
x = 1 - cos(2��)�@�Ƃ����B
lim[�Ɓ�0] x = lim[�Ɓ�0] {1-cos(2��)} = 0,
f(1-cos(2��))/(��^2) = {f(x)-f(0)}/x * (1-cos(2��))/(��^2),
lim[x��0] {f(x)-f(0)}/x = f'(0) = ��,
lim[�Ɓ�0] {1-cos(2��)}/(��^2) = lim[�Ɓ�0] 2sin(2��)/(2��) = 2,�@�i�����s�^���j
�� lim[�Ɓ�0] f(1-cos(2��))/(��^2) = 2��,
�R�����g
g(��) = f(1-cos(2��)) �� ��^2 �̊��ł��邱�Ƃ��ӎ����A0�~�� (�s��`)�ƂȂ镪�����͉�����܂��傤�B �kWolstenholme�̒藝�l
�f�� p �ɑ���
p��5�@�ˁ@1 + 2^(-1) + 3^(-1) + �c�c + (p-1)^(-1) �� 0�@�@(mod pp)
p��5�@�ˁ@1 + 2^(-2) + 3^(-2) + �c�c + (p-1)^(-2) �� 0�@�@(mod p)
p��7�@�ˁ@1 + 2^(-3) + 3^(-3) + �c�c + (p-1)^(-3) �� 0�@�@(mod pp)
p��7�@�ˁ@1 + 2^(-4) + 3^(-4) + �c�c + (p-1)^(-4) �� 0�@�@(mod p)
p��7�@�ˁ@1 + 2^(-5) + 3^(-5) + �c�c + (p-1)^(-5) �� 0�@�@(mod p)
p��7�@�ˁ@1 + 2^(-7) + 3^(-7) + �c�c + (p-1)^(-7) �� 0�@�@(mod p^3) ?
[�S�S�V.990] �kFaulhaber�̒藝�l
�Em ����̂Ƃ�
�@S_m (n) = ��_[k=1,...,n] k^m = {1/(m+1)} P_m(n(n+1))
�@P_m �� (m+1)/2 ���̃��j�b�N�������B
�Em �������̂Ƃ�
�@S_m (n) = ��_[k=1,...,n] k^m = {1/(m+1)}(n+1/2) P_m(n(n+1))
�@P_m �� m/2 ���̃��j�b�N�������B
[�S�S�V.991] ���R��p��1���߁A�ȉ��̐���a[n]���l����B
a[1]=p
a[n+1]=a[n]-��(a[n])
���߂�a[n]=0�ƂȂ�n��p�ŕ\���B >>993
>[�S�S�V.990]
���ꉽ�H ���}����
�@n �` e^(e/4)���p �Ă�ł���@���̂ǂ�������
�����S���@�����݂����`♫
[�S�S�V.1000]�@�@�� �S�S�V�X���̃��X [1000] �@�@�@�@�@ �ȁQ��
�@�@�@�@�@�i �L�D�M �j �@�{�N�������b�ɂȂ�܂����B
�@�@�@�@ /�@�@�@�@ �R
�@�@�@�@ ���A__X__,�mJ
�@ �@ �@ /�L�܁܁R
�@�@�@�@���� �@ �@�܂� �@���N���悢���N��
�@�@�@�� �i�@�@�@�j ��
�@�@�@�@�@ V�PV ���̃X���b�h�͂P�O�O�O���܂����B
�V�����X���b�h�𗧂ĂĂ��������B
life time: 35�� 13���� 48�� 17�b 5�����˂�̉^�c�̓v���~�A������̊F���܂Ɏx�����Ă��܂��B
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�s�v���~�A������̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
��300�~���瓽���ł��w�����������܂��B
�� �v���~�A������o�^�͂����� ��
https://premium.5ch.net/
�� �Q�l���O�C���͂����� ��
https://login.5ch.net/login.php ���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B