分からない問題はここに書いてね458

**１３２人目の素数さん** · 2020/02/10(月) 00:06:16.90

さあ、今日も１日がんばろう★☆

前スレ
分からない問題はここに書いてね457
https://rio2016.5ch.net/test/read.cgi/math/1577457155/

(使用済です: 478)

**１３２人目の素数さん** · 2020/03/21(土) 18:30:36.61

どう考えても当たりくじが99個になるとき、100個になるときがシンプルな言い回しありそうにないけど。
答えなんなん？

**１３２人目の素数さん** · 2020/03/21(土) 18:32:21.73

>>806
>「１００本の線があるあみだくじで外れが１つの場合
>　あたる確率を求めよ」
>というのと同じだと思いますが如何ですか？
じゃあ
p1===p100=1/100ということね？
そんで？

**１３２人目の素数さん** · 2020/03/21(土) 18:34:06.24

kを1≦k≦nの自然数とする。
n次多項式f(x)に対して、g(x)={(1+x)^k}g(x)を考える。
g(x)が整数係数多項式ならば、f(x)も整数係数多項式であることを証明せよ。

**１３２人目の素数さん** · 2020/03/21(土) 18:49:21.96

>>768
もう一度確認してみると
まずこの問題文ではダメ
無限数列総てについて同値類を設定し代表元を決めておく（代表限を決められるのは選択公理より）
100個の無限数列のそれぞれについて同値類の代表元との違いのある最後の項番号が決められる（決定番号の定義）
100個の無限数列のうち１つを無作為に選び
残った99個の決定番号の最大値よりも選んだ決定番号が小さければ勝ち
大きければ勝ち負け決まらない？（半々）
これって数列関係なくて
100個の中で最大を選ぶかどうかってことじゃない？
予め最大の数値は決められているから
それを無作為に選ぶかどうかの1/100ってことか
ここまでは結局数列関係ないじゃん？

**１３２人目の素数さん** · 2020/03/21(土) 18:52:29.68

>>807
＞本当は考えねばならないことを省略してるだけ

それは問題に対する根本的な誤解があるね

**１３２人目の素数さん** · 2020/03/21(土) 18:55:10.38

>>769
>「当たる確率は0だ
>　無限列の同値関係は認める
>　同値類の代表元の存在も認める
>　しかし決定番号dの存在は認めない！
>　決定番号が存在しなければゲームは成立しない」
決定番号は定義できると思うよ
けれど最初の問題文では
何に対する決定番号であるかを説明していないから
その点をハッキリさせないと上記のように言う人（自分もそう思った>>770）が居てもおかしくないのでは？
いずれにせよ
なんだか回りくどいこと言って煙に巻くだけの問題だと思った

**１３２人目の素数さん** · 2020/03/21(土) 18:58:44.21

>>812
＞まずこの問題文ではダメ
あなたの修正もイイかダメかといわれれば・・・ダメですね

ダメその１
＞残った99個の決定番号の最大値よりも選んだ決定番号が小さければ勝ち

「（最大値）より小さい」ではなく「（最大値）以下」ですね

ダメその２
＞大きければ勝ち負け決まらない？

大きければ負け、でいいですよ
（幸運にも一致する場合はあるが、そこは確率０とすることができるから）

上記のダメ出しをさせていただいた上で

＞これって数列関係なくて
＞100個の中で最大を選ぶかどうかってことじゃない？

ええ、その通りですよ

＞予め最大の数値は決められているから
＞それを無作為に選ぶかどうかの1/100ってことか

ええ、その通りですよ

＞ここまでは結局数列関係ないじゃん？

ええ、その通りですよ

まさか数列が最も重要だと思ってたんですか？

**１３２人目の素数さん** · 2020/03/21(土) 19:04:04.15

>>814
＞決定番号は定義できると思うよ

そうでしょう
できないという人は、同値類を誤解してるんでしょう

＞けれど最初の問題文では
＞何に対する決定番号であるかを説明していない

説明していないのではなく、
説明を理解できていないのでしょう
理解できるまで読む必要がありますよ

＞その点をハッキリさせないと
＞上記のように言う人が居てもおかしくないのでは？

「決定番号が有限でない」という主張は
決定番号の説明が理解できないというのとは
根本的に異なる、と思いますよ

**１３２人目の素数さん** · 2020/03/21(土) 19:07:00.65

>>814
＞なんだか回りくどいこと言って煙に巻くだけ

数学書の定義の記述はだいたいそういうものですけどね
位相の定義なんてその最たるものですね
なんで、こんな定義してるのか一回読んだだけでは分からない
そこで我慢できずに近道を探そうとする人は数学には向きませんね
なんか別のことをやったほうがいいとおもいますよ

**１３２人目の素数さん** · 2020/03/21(土) 19:08:05.83

>>812
>大きければ勝ち負け決まらない？（半々）
決定番号より前だけど1つ前なら代表元と異なっていることは確定だから負け
1つ以上前なら代表元と異なるかどうかは1/10かな？
1つ前であるかどうかは分からないんだからやっぱり確率は言えないのでは？
1つ前かどうかってある番号を決めておいて自然数全体の中でその数値の1つ前かどうかだから決定番号の自然数全体における分布が与えられないと何も言えないような

**１３２人目の素数さん** · 2020/03/21(土) 19:08:55.38

>>815
もういいや
正確な問題にしてから出直してきてね

**１３２人目の素数さん** · 2020/03/21(土) 19:09:47.60

>>816
>＞けれど最初の問題文では
>＞何に対する決定番号であるかを説明していない
>
>説明していないのではなく、
>説明を理解できていないのでしょう
>理解できるまで読む必要がありますよ
忖度せよっていう問題ね
酷すぎｗ

**１３２人目の素数さん** · 2020/03/21(土) 19:18:55.68

1.
箱がたくさん，可算無限個ある.箱それぞれに，私が実数を入れる.
どんな実数を入れるかはまったく自由，例えばn番目の箱にe^πを入れてもよいし，すべての箱にπを入れてもよい.
もちろんでたらめだって構わない.そして箱をみな閉じる.
今度はあなたの番である.片端から箱を開けてゆき中の実数を覗いてよいが，一つの箱は開けずに閉じたまま残さねばならぬとしよう.
どの箱を閉じたまま残すかはあなたが決めうる.
勝負のルールはこうだ. もし閉じた箱の中の実数をピタリと言い当てたら，あなたの勝ち. さもなくば負け.
勝つ戦略はあるでしょうか?

**１３２人目の素数さん** · 2020/03/21(土) 19:19:23.31

２．
　私たちのやろうとすることはQのコーシー列の集合を同値関係で類別してRを構成するやりかた(の冒頭)に似ている.
但しもっときびしい同値関係を使う.
実数列の集合 R^Nを考える.
s = (s1，s2，s3 ，・・・)，s'=(s'1， s'2， s'3，・・・ )∈R^Nは，ある番号から先のしっぽが一致する∃n0：n >= n0 → sn＝ s'n とき同値s ～ s'と定義しよう(いわばコーシーのべったり版).
念のため推移律をチェックすると，sとs'が1962番目から先一致し，s'とs"が2015番目から先一致するなら，sとs"は2015番目から先一致する.
～は R^N を類別するが，各類から代表を選び，代表系を袋に蓄えておく.
幾何的には商射影 R^N→ R^N/～の切断を選んだことになる.
任意の実数列S に対し，袋をごそごそさぐってそいつと同値な(同じファイパーの)代表r= r(s)をちょうど一つ取り出せる訳だ.
sとrとがそこから先ずっと一致する番号をsの決定番号と呼び，d = d(s)と記す.
つまりsd，sd+1，sd+2,・・・を知ればsの類の代表r は決められる.
更に，何らかの事情によりdが知らされていなくても，あるD>=d についてsD+1， sD+2，sD+3，・・・
が知らされたとするならば，それだけの情報で既に r = r(s)は取り出せ，したがってd= d(s)も決まり，
結局sd(実はsd，sd+1，・・・，sD ごっそり)が決められることに注意しよう.
(補足)
sD+1， sD+2，sD+3，・・・：ここでD+1などは下付添え字

**１３２人目の素数さん** · 2020/03/21(土) 19:20:29.15

３．
問題に戻り，閉じた箱を100列に並べる.
箱の中身は私たちに知らされていないが，とにかく第l列の箱たち，第2列の箱たち第100 列の箱たちは100本の実数列S^1,S^2，・・・，S^lOOを成す(肩に乗せたのは指数ではなく添字).
これらの列はおのおの決定番号をもつ.
さて， 1～100 のいずれかをランダムに選ぶ.
例えばkが選ばれたとせよ.
s^kの決定番号が他の列の決定番号どれよりも大きい確率は1/100に過ぎない.
　第1列～第(k-1) 列，第(k+1)列～第100列の箱を全部開ける.
第k列の箱たちはまだ閉じたままにしておく.
開けた箱に入った実数を見て，代表の袋をさぐり， S^1～S^(k-l),S^(k+l)～S100の決定番号のうちの最大値Dを書き下す.
　いよいよ第k列の(D+1) 番目から先の箱だけを開ける：S^k(D+l)， S^k(D+2)，S^k(D+3)，・・・.いま
　D >= d(S^k)
を仮定しよう.この仮定が正しい確率は99/100，そして仮定が正しいばあい，上の注意によってS^k(d)が決められるのであった.
おさらいすると，仮定のもと， s^k(D+1)，s^k(D+2)，s^k(D+3)，・・・を見て代表r＝r(s~k) が取り出せるので
列r のD番目の実数r(D)を見て，「第k列のD番目の箱に入った実数はS^k(D)＝r(D)と賭ければ，めでたく確率99/100で勝てる.
確率1-ε で勝てることも明らかであろう.
(補足)
S^k(D+l)， S^k(D+2)，S^k(D+3)，・・・：ここで^kは上付き添え字、(D+l)などは下付添え字

**１３２人目の素数さん** · 2020/03/21(土) 19:21:11.62

>>819-820
重要であることを強調し
そうでないことは強調しない

忖度とは無関係

当然のことですけどね

**１３２人目の素数さん** · 2020/03/21(土) 19:22:41.17

4.
「R^N/～の代表系を選んだ箇所で選択公理を使っている.
その結果R^N →R^N/～の切断は非可測になる.
ここは有名なヴィタリのルベーグ非可測集合の例(Q/Zを「差が有理数」で類別した代表系， 1905年)にそっくりである.」

「逆に非可測な集合をこさえるには選択公理が要る(ソロヴェイ， 1970年)から，この戦略はふしぎどころか標準的とさえいえるかもしれない.
しかし，選択公理や非可測集合を経由したからお手つき，と片付けるのは，面白くないように思う.
現代数学の形式内では確率は測度論によって解釈されるゆえ，測度論は確率の基礎，と数学者は信じがちだ.
だが，測度論的解釈がカノニカル，という証拠はないのだし，そもそも形式すなわち基礎，というのも早計だろう.
確率は数学を越えて広がる生き物なのである(数学に飼いならされた部分が最も御しやすいけれど).」

**１３２人目の素数さん** · 2020/03/21(土) 19:22:57.30

5.
「もうちょっと面白いのは，独立性に関する反省だと思う.
確率の中心的対象は，独立な確率変数の無限族
X1，X2，X3，…である.
いったい無限を扱うには，
(1)無限を直接扱う，
(2)有限の極限として間接に扱う，
二つの方針が可能である.
確率変数の無限族は，任意の有限部分族が独立のとき，独立，と定義されるから，(2)の扱いだ.
(独立とは限らない状況におけるコルモゴロフの拡張定理なども有限性を介する.)
しかし，素朴に，無限族を直接扱えないのか?
扱えるとすると私たちの戦略は頓挫してしまう.
n番目の箱にXnのランダムな値を入れられて，ある箱の中身を当てようとしたって，
その箱のX と他のX1，X2，X3，・・・がまるまる無限族として独立なら，
当てられっこないではないか－－他の箱から情報は一切もらえないのだから.
勝つ戦略なんかある筈ない，と感じた私たちの直観は，無意識に(1)に根ざしていた，といえる.
ふしぎな戦略は，確率変数の無限族の独立性の微妙さをものがたる，といってもよい.」

”ばかばかしい，当てられる筈があるものか，と感じられるだろう.
何か条件が抜け落ちているのではないか，と疑う読者もあろう.問題を読み直していただきたい.
条件はほんとうに上記のとおり.無限個の実数が与えられ，一個を除いてそれらを見た上で，除いた一個を当てよ，というのだ.
ところがところが--本記事の目的は，確率99%で勝てそうな戦略を供することにある.
この問題はPeter Winkler氏との茶のみ話がてら耳にした.氏は原型をルーマニアあたりから仕入れたらしい.”

以上

**１３２人目の素数さん** · 2020/03/21(土) 19:30:59.41

>>768の文章を書いたのは、元の記事のままでは
掲示板では長すぎると思ったのが第一だが、
無限個の確率変数とか可測性とかいう脇道を
可能な限り削ったほうがいいと思ったこともある

**１３２人目の素数さん** · 2020/03/21(土) 20:27:13.34

nを自然数とする。
袋の中にn個の青球と2個の白球がある。以下の試行を繰り返し行う。

【試行】
1)袋の中から無作為に同時に2個の球を取り出し、
「ともに白球の場合、『勝ち』とする」
「白球1つと青球1つの場合、『負け』とする」
「ともに青球の場合、『あいこ』とさる」
2)『勝ち』または『負け』の場合、試行を終了する。『あいこ』の場合、もう1回試行を行う。

この試行が終了するまでに行った試行の回数の期待値E(n)をnで表し、また試行が『勝ち』で終了する条件付き確率をnで表せ。

**１３２人目の素数さん** · 2020/03/21(土) 20:51:21.68

1)4/3
2)1/3

**１３２人目の素数さん** · 2020/03/21(土) 21:05:54.33

why?
＞円の中心を定規のみで作図することは出来ない
https://twitter.com/potetoichiro/status/1130475152938897408
https://twitter.com/5chan_nel (5ch newer account)

**１３２人目の素数さん** · 2020/03/21(土) 21:29:56.56

>>813
根本的にはソレと同じだって>>806に書いてあると思うんだけど

**１３２人目の素数さん** · 2020/03/21(土) 21:45:25.70

>>827
出直しも出来ないのな
全くダメ

**１３２人目の素数さん** · 2020/03/21(土) 21:46:37.72

>>824
>重要であることを強調し
>そうでないことは強調しない
君全く理解できていないか
理解できていて目を背けているかだね
全くダメ

**１３２人目の素数さん** · 2020/03/21(土) 22:02:15.94

>>832
アンタの望みの゛正確な問題゛は>>821以降にあげといたよ
ぶつぶつ言ってないで解いてみたら？

**１３２人目の素数さん** · 2020/03/21(土) 22:42:37.09

>>834
頑張ってね～

**１３２人目の素数さん** · 2020/03/22(日) 00:59:46.69

例えば1,2,3,...という数列が属する同値類の代表元は何になるの？

**１３２人目の素数さん** · 2020/03/22(日) 01:34:19.90

>>836
1.2,3,...でいいよ

**１３２人目の素数さん** · 2020/03/22(日) 01:49:36.75

じゃあ1,2,3,...の決定番号は1ですね
同様に数列a_1,a_2,a_3,...が属する同値類の代表元はa_1,a_2,a_3,...だからこれも決定番号は1
つまり任意の実数列の決定番号は1ということですね
ありがとうございます

**１３２人目の素数さん** · 2020/03/22(日) 02:22:03.52

>>838
1,2,3,...の同値類の代表限を 1.2,3,...にするんなら
2,1,3,...の決定番号は3だよ

**１３２人目の素数さん** · 2020/03/22(日) 02:25:32.63

ああそうかちょっと誤解してた
決定番号以後は全部一致してると思ってたけど>>768
>定義
>・２つの無限列s1,s2∈R^Nが、ある項から先の項が全て一致するとき「同値」
>・無限列s∈R^Nの「決定番号」dとは、無限列の同値類の代表元の
>　一致箇所の先頭となる項の箇所の番号
だと
1,2,3,...を代表元にした場合
1,1,3,...の決定番号は1だな
定義自体不味いね
酷すぎ

**１３２人目の素数さん** · 2020/03/22(日) 02:37:19.34

>>801の中の人々とは関わらない方がいいかも。

**１３２人目の素数さん** · 2020/03/22(日) 06:35:46.07

>>841
主の人は明らかに頭がおかしい
ガロアスレが運営から削除されたのも当然

---
https://rio2016.5ch.net/test/read.cgi/math/1576852086/581
１．世間的には決着済みです。その証拠に、このスレに参加する第三者なし
（多分、私が間違っているとなったら、こんなものではない）
２．”祭りは終わった”！ｗ私ガロアスレのスレ主の勝利
３．ここで十分、あほサルのバカさ加減を思い知らせてやりますよ、
　　このスレでねｗ（＾＾

**１３２人目の素数さん** · 2020/03/22(日) 06:38:59.28

>>840
＞決定番号以後は全部一致してると思ってたけど
読み方が粗雑じゃね？
「２つの無限列s1,s2∈R^Nが・・・一致するとき」
と書いてあるし

**１３２人目の素数さん** · 2020/03/22(日) 07:50:24.15

コロナの件で疑問に思ったのだけど

無作為に１０００人を抽出してPCR検査を行ったら１０人が陽性であった。
PCR検査の感度０．７、特異度０．９として有病率の期待値と９５％信頼区間は？

有病率の事前確率分布を一様分布と仮定して検査陽性後の有病率をベータ分布で出す。
その有病率と感度・特異度をから陽性的中率を計算。
その陽性的中率を使って有病率を逆算というアルゴリズムで計算したら

> sim()
mean mode lower upper
0.010969194 0.009870096 0.005034295 0.017532847

このアルゴリズムってあってる？

**１３２人目の素数さん** · 2020/03/22(日) 08:34:49.54

>>843
それは同値の定義
決定番号の定義にはない

**１３２人目の素数さん** · 2020/03/22(日) 08:44:12.08

>>845
頭使って考えてる？

・同値関係が定義できれば、同値類が存在する
・同値類からその代表元が選べる　（同値類が無限個の場合、選択公理が必要）
・どの無限列も必ずある同値類に属する
・どの無限列も属する同値類の代表元とは当然同値である
・同値関係の定義から、必ず列が一致する開始箇所が存在する
　→そこが無限列の決定番号

ほら、同値の定義で全部決まる

**１３２人目の素数さん** · 2020/03/22(日) 08:55:42.55

>>768の無限列の同値関係と決定番号が理解できた方への質問

>>769の「ある読者」曰く
https://rio2016.5ch.net/test/read.cgi/math/1576852086/552
（要旨）
・長さｍの有限列の場合、決定番号は確率１でｍ
・だからｍ→∞の極限をとると、決定番号は確率１で∞

この考え方って正しい？

**１３２人目の素数さん** · 2020/03/22(日) 09:06:18.42

大きさnの箱があってそこに大きさa,b,cのものを隙間なく埋めるとして、その合計がs個になるa,b,cの組み合わせの求め方はどのようになるのでしょうか

**１３２人目の素数さん** · 2020/03/22(日) 09:16:09.13

一般解なんて出せるものなのか？

**１３２人目の素数さん** · 2020/03/22(日) 09:17:51.68

この日本語で何かが他人に伝わるのだろうか？

**１３２人目の素数さん** · 2020/03/22(日) 10:02:57.97

>>846
>・同値関係の定義から、必ず列が一致する開始箇所が存在する
>　→そこが無限列の決定番号
一致するのは最初の項も一致していいのよ
そこから先ずっと一致しているその先頭という定義にしないとダメダメ
君こそ読めてないねｗ

**１３２人目の素数さん** · 2020/03/22(日) 10:06:56.46

>>768
>定義
>・２つの無限列s1,s2∈R^Nが、ある項から先の項が全て一致するとき「同値」
>・無限列s∈R^Nの「決定番号」dとは、無限列の同値類の代表元の
>　一致箇所の先頭となる項の箇所の番号
同値類の代表元「と」の「一致箇所」というのではダメだって
それだと初項が一致してしばらく一致しなくてあるところから先はずっと一致してるときの決定番号は1ということになるからね
定義を厳密にしなくてはいけないという意識を持たないのは数学的では無いね

**１３２人目の素数さん** · 2020/03/22(日) 10:08:24.33

>>847
ぷ
何を言わせたいか分かるから言わない

**１３２人目の素数さん** · 2020/03/22(日) 11:43:08.52

>>851
＞そこから先ずっと一致しているその先頭という定義にしないと
読み取れたならOK

>>852
＞定義を厳密にしなくてはいけない
読み取れたなら十分

>>853
＞何を言わせたいか分かる
なるほど・・・ID:BUSW/Nah氏
ｍ→∞の極限をとると、決定番号は確率１で∞
に全面賛同、と

**１３２人目の素数さん** · 2020/03/22(日) 11:47:03.77

ID:BUSW/Nah氏への問い

Q.長さn以下の10進小数の9/10が長さn
　ある人曰く
　「だからｎ→∞の極限で有限小数の9/10が長さ∞」
　これホント？

**１３２人目の素数さん** · 2020/03/22(日) 11:51:06.17

某スレッドの自称大阪大工学部卒氏
敵（？）が東大理学部卒と思い込んで怒り狂う
https://rio2016.5ch.net/test/read.cgi/math/1576852086/589-590

よい子のみんなはこんな大人になっちゃダメだよ

**１３２人目の素数さん** · 2020/03/22(日) 12:03:59.16

級数Σ[n=1,2,...]1/(n^2+a)を計算することにより、(e^π-e^(-π))/(e^π+e^(-π))が無理数であることを証明せよ。

**１３２人目の素数さん** · 2020/03/22(日) 13:26:37.77

>>854
忖度させる問題文
しかもほとんど意味ないものを
あらためようとしないのはNG
マルでダメだな

**１３２人目の素数さん** · 2020/03/22(日) 13:44:59.90

>>764
返答遅くなってしまい、申し訳ございません。
回答ありがとうございます。

**１３２人目の素数さん** · 2020/03/22(日) 13:55:41.25

数学掲示板群 ttp://x0000.net
(アルファ・ラボ|学術掲示板群)

**１３２人目の素数さん** · 2020/03/22(日) 14:02:38.08

>>844(自己レス)
誤謬に気がついたので撤回しますm(_ _)m

**１３２人目の素数さん** · 2020/03/22(日) 14:04:27.32

>>858
>>855に答えましょうね

**１３２人目の素数さん** · 2020/03/22(日) 19:48:33.60

>>862
>>853
君の思惑は既に破産してるって気が付かないみたい
ホントに下らない人間なのかな？

**１３２人目の素数さん** · 2020/03/22(日) 20:16:50.88

>>857
Σ[n=1,2,････] 1/(nn+a)
　= (1/2)Σ[n∈Z] 1/(nn+a) - 1/(2a)
　= π･coth(π√a)/(2√a) - 1/(2a),
　ランジュヴァン函数？

a=1 のとき
　Σ[n=1,2,････] 1/(nn+1) = (π/2)coth(π) - 1/2,

**１３２人目の素数さん** · 2020/03/22(日) 20:29:34.41

ノルム空間Xの線形部分空間Mの閉包がXの閉線形部分空間であるという証明で、収束するMの点列xnの極限がMの閉包に属するという話が出てきたのですが、理由教えてください

**１３２人目の素数さん** · 2020/03/22(日) 20:33:46.31

おかしいこと聞いてすみません、解決しました

**１３２人目の素数さん** · 2020/03/22(日) 21:07:30.74

n枚の硬貨を同時に投げて、表の出たものを取り去り、硬貨が残っていれば、もう1回だけそれらを同時に投げて表の出たものを取り去ることにする
この時、全部取り去る確率を求めよ。

解答では、1回目に表が出たものも投げるとして、(1-1/4)^nと答えを出しているのですが、普通に考えて解いた時と、全事象も異なると思うのですが、なぜこの解き方が可能なのでしょうか？

**１３２人目の素数さん** · 2020/03/22(日) 21:27:03.19

>>867
全てのコインが2回投げるうちに1回でも表が出れば全て取り去ることになるから
全事象が異なっても構わない
2枚とか3枚とかで両方のやり方で全事象書き出してみれば分かるかも知れない

**１３２人目の素数さん** · 2020/03/22(日) 21:54:57.20

>>https://rio2016.5ch.net/test/read.cgi/math/1511604229/999
×あんなデタラメなもの
〇完全に正しい数学上の未解決問題の証明論文

**１３２人目の素数さん** · 2020/03/22(日) 22:13:02.85

>>868 書き出してみたのですが、イマイチしっくりこないです…

**１３２人目の素数さん** · 2020/03/22(日) 22:19:41.32

>>870
書き出したもの全てにそうなる確率を書き込んで見比べてみてはどうだろうか

**１３２人目の素数さん** · 2020/03/22(日) 23:00:24.46

>>871
n=10のときで総当たりで計算してみた

> rm(list=ls())
> n=10
> dec2nw <- function(num, N, digit = n){
+ r=num%%N
+ q=num%/%N
+ while(q > 0 | digit > 1){
+ r=append(q%%N,r)
+ q=q%/%N
+ digit=digit-1
+ }
+ return(r)
+ }
> d=t(sapply(0:(2^n-1),function(num) dec2nw(num,2,n))) # 10枚のコインの裏表の順列（０を取り除く表とする）
> head(d) ; tail(d)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 0 0 0 0 0 0 0 0 0 0
[2,] 0 0 0 0 0 0 0 0 0 1
[3,] 0 0 0 0 0 0 0 0 1 0
[4,] 0 0 0 0 0 0 0 0 1 1
[5,] 0 0 0 0 0 0 0 1 0 0
[6,] 0 0 0 0 0 0 0 1 0 1
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1019,] 1 1 1 1 1 1 1 0 1 0
[1020,] 1 1 1 1 1 1 1 0 1 1
[1021,] 1 1 1 1 1 1 1 1 0 0
[1022,] 1 1 1 1 1 1 1 1 0 1
[1023,] 1 1 1 1 1 1 1 1 1 0
[1024,] 1 1 1 1 1 1 1 1 1 1
> d1=apply(d,1,sum) #　各行ごとの合計＝裏がでた枚数
> sum((1/2)^d1)/2^n　 # 各行ごとに　(1/2) ^ 裏の枚数を計算して合算する　
[1] 0.056314
> (1-1/4)^n
[1] 0.056314

合致した。

**１３２人目の素数さん** · 2020/03/22(日) 23:20:34.47

n=20での100万回のシミュレーション

> # simulation
> sim <- function(n){
+ (flip1=sample(0:1,n,rep=T)) # 0:1から重複を許してn個選んだ配列をflip1とする
+ (flip2=sample(0:1,sum(flip1),rep=T))　# 0:1からflip1の総和個選んだ配列をflip2とする
+ sum(flip2)==0 # flip2の総和が０か否かを返す
+ }
> mean(replicate(1e7,sim(20))) # 100万回試行して全部取り去った割合を計算
[1] 0.0031899
> (1-1/4)^20
[1] 0.0031712

まあ、近似した。

**１３２人目の素数さん** · 2020/03/22(日) 23:24:01.87

>>867
1枚の硬貨が取り除かれない確率は、裏裏と続くときだから1/4
その余事象（1枚の硬貨が取り除かれる事象）の確率は3/4
どの硬貨の裏表がでるかは独立事象だから、(3/4)^nでいいんじゃないの？

**１３２人目の素数さん** · 2020/03/22(日) 23:36:46.27

無限級数
(1/1^2)+(1/2^3)+(1/3^4)+...
を求めよ。

**１３２人目の素数さん** · 2020/03/22(日) 23:54:02.20

>>828
シミュレーションプログラムの練習　数理解は賢者にお任せ

[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
En 1.0000 1.1991 1.4378 1.6744 1.9163 2.1544 2.3992 2.6329 2.9352 3.1542 3.4106
Pn 0.3405 0.1997 0.1483 0.1148 0.0917 0.0775 0.0700 0.0608 0.0516 0.0458 0.0416
[,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22]
En 3.6105 3.8742 4.1257 4.3780 4.6665 4.7706 5.0866 5.4512 5.6246 5.8261 6.1474
Pn 0.0375 0.0381 0.0383 0.0308 0.0295 0.0296 0.0269 0.0223 0.0227 0.0221 0.0239
[,23] [,24] [,25] [,26] [,27] [,28] [,29] [,30]
En 6.5768 6.5863 6.8209 7.0221 7.3743 7.652 7.8525 8.1056
Pn 0.0217 0.0204 0.0189 0.0202 0.0183 0.017 0.0166 0.0161

fn <- function(n){
B=c(rep(1,n),0,0) # 1:青玉 0:白玉
flg=3 # drawを初期値
i=0 # 試行の回数カウンター
while(flg==3){ # drawなら繰り返す　1:win 2:lose 3:draw
i=i+1
flg=(1:3)[sum(sample(B,2))+1] # (1:3)[sum(c(0,0))+1] : win
}
c(i=i,flg=flg)
}
sim <- function(n){
k=1e4
re=t(replicate(k,fn(n)))
c(mean(re[,'i']),mean(re[,'flg']==1)) # 回数と勝率を返す
}
n=1:30
re=sapply(n,sim)
En=re[1,]
plot(n,En,bty='l',pch=19)
Pn=re[2,]
plot(n,Pn,bty='l',pch=19)
rownames(re)=c('En','Pn')
re

**１３２人目の素数さん** · 2020/03/23(月) 00:22:10.10

数列{a[k]}を
a[k]={nCk*(-1)^(k+1)}/k
とおく。
必要であれば
lim[n→∞]{(1+1/2+...+1/n)-ln(n)}=0.5772...を用いて以下の問いに答えよ。

（1）lim[n→∞] {1/ln(n)}*Σ[k=1,...,n]a[k]=1
を示せ。

（2）次の極限を調べよ。
lim[n→∞] {1/ln(n)}*Σ[k=1,...,n]❲Σ[j=1,...,k](a[j]/j)❳

**１３２人目の素数さん** · 2020/03/23(月) 04:05:11.11

>>828
E(n) = (n+2)*(n+1)/(4*n+2)

> E(1:30)
[1] 1.0000 1.2000 1.4286 1.6667 1.9091 2.1538 2.4000 2.6471 2.8947 3.1429 3.3913
[12] 3.6400 3.8889 4.1379 4.3871 4.6364 4.8857 5.1351 5.3846 5.6341 5.8837 6.1333
[23] 6.3830 6.6327 6.8824 7.1321 7.3818 7.6316 7.8814 8.1311

>876のシミュレーションと近似している

pw=choose(2,2)/choose(n+2,2) # Pr[win]
pl=2*n/choose(n+2,2) # Pr[lose]
p=pw+pl
q=1-p # Pr[draw]
# 1*p + 2*q*p + 3*q^2*p + 4*q^3*p + i*q^(i-1)*p
# Σ[i=1,i=m] i*q^(i-1)*p
# p*Σi*q^(i-1)
# p*Σd(q^i)/dq
# p*d(Σq^i)/dq
# p*d((1-q^m)/(1-q))
# m→∞ q^m→0
# p*d/dq(1/(1 - q)) = p/(1 - q)^2 = 1/p

**１３２人目の素数さん** · 2020/03/23(月) 05:09:19.45

>>828
2）　 1/(n+1)　かな？
シミュレーションかこっちのどちらかが間違いだな

**１３２人目の素数さん** · 2020/03/23(月) 11:47:06.63

>>828
nが偶数の場合
P[win] = (n+2)/2 * 2!n!/ (n+2)! = 1/(n+1) {n+2個をシャッフルして偶境界に白白}
E[n; win] = ( 1 + 2 + ... + (n+2)/2 ) * 2!n!/ (n+2)! = ...
E[n; lose] = (1*2n + 2*2(n-2) + .... + n/2*2*2 ) * 2!n!/ (n+2)!　{n+2個をシャッフルして偶境界に黒白or白黒、その後方に白}
　= ...
nが奇数の場合も同様

(便利な公式)
1*N + 2*(N-1) + ... +(N-1)*2 + N*1
1*(N+1-1) + 2*(N+1-2) + ... +(N-1)*(N+1-(N-1)) + N*(N+1-N)
= (1+2+...+N)(N+1) - (1^2 + 2^2 + ... + N^2)
= N(N+1)(N+1)/2 - N(N+1)(2N+1)/6 = N(N+1)(N+2)/6

**１３２人目の素数さん** · 2020/03/23(月) 12:56:08.97

>>828
非復元試行だね？

**１３２人目の素数さん** · 2020/03/23(月) 13:39:57.58

>>828
k回目にあいこになる確率をpkとすると
k+1回目の始まる時点では青石がn-2k個になっているので
n-2k<2ならp(k+1)=0
n-2k≧2ならp(k+1)=pk・(n-2kC2)/(n-2k+2C2)=pk・(n-2k)(n-2k-1)/(n-2k+2)(n-2k+1)
n-2k=0,1いずれでも
p(k+1)=pk・(n-2kC2)/(n-2k+2C2)=pk・(n-2k)(n-2k-1)/(n-2k+2)(n-2k+1)
としてよいので
この漸化式で0になるまでと考えると
k+1≦n/2でp(k+1)=p1・(n-2k)(n-2k-1)/n(n-1)=(n-2k)(n-2k-1)/(n+2)(n+1)
k+1>n/2でp(k+1)=0
k+1回目に終了する確率はpk-p(k+1)なので試行回数の期待値は
Σ(k+1)(pk-p(k+1))=Σpk-うーん面倒

**１３２人目の素数さん** · 2020/03/23(月) 14:28:40.31

学術の巨大掲示板群 - アルファ・ラボ
ttp://x0000.net

数学物理学化学生物学天文学地理地学
IT 電子工学言語学国語方言など

**１３２人目の素数さん** · 2020/03/23(月) 15:20:20.77

>>881
非復元試行だったのか？
復元試行と思って解答しようとしていた。

**１３２人目の素数さん** · 2020/03/23(月) 15:29:26.68

>>884
復元なら簡単すぎでしょうから>>880は非復元で解いてる

**１３２人目の素数さん** · 2020/03/23(月) 16:59:20.79

2^2^2^2^2^2
は
https://ja.wolframalpha.com/input/?i=2%5E2%5E2%5E2%5E2%5E2
において、
最後の数桁:
...7437428736
であるというが、その根拠は？

**１３２人目の素数さん** · 2020/03/23(月) 19:49:00.11

>>880
どうでもいいことだが、
1*N + 2*(N-1) + ... +(N-1)*2 + N*1 = N(N+1)(N+2)/6
の別証明。

右辺は C(n+2,3) であるが、これを次のように考える。
1,2,3,4,…,n+2 のn+2個の数から3つ選ぶ選び方については
選んだ3つの数を左、真ん中、右と呼ぶことにすると、
真ん中に選ぶ数で場合分けできる。
真ん中が2となる選び方は、左1通り*右n通り。
真ん中が3となる選び方は、左2通り*右(n-1)通り。
真ん中が4となる選び方は、左3通り*右(n-2)通り。
…
真ん中がn+1となる選び方は、左n通り*右1通り。

**１３２人目の素数さん** · 2020/03/23(月) 19:51:38.16

千葉逸人@HayatoChiba

珍しく（？）数学の質問をしたいのですが、文字数のため画像添付でお許しください。面白い話題だと思うのですが、何かご存知の方いますでしょうか。（ちょっと悔しいけど、でも教えてください・・・）
https://pbs.twimg.com/media/ETybe_oUMAAfIhq.jpg

https://twitter.com/HayatoChiba/status/1242039227069550592
https://twitter.com/5chan_nel (5ch newer account)

**１３２人目の素数さん** · 2020/03/23(月) 20:11:02.23

辺の長さが全て整数の多角形において、少なくとも2つ以上の内角[ラジアン]は無理数であることを示せ.

**１３２人目の素数さん** · 2020/03/23(月) 20:48:10.79

>>886
準備1: オイラーφ関数
　φ(5^10) = 5^9 (5-1) = 5^9*2^2

準備2: ユークリッド互除法
　1745224 *2^10 - 183 *5^10 = 1 　{計算方法は省略}

2^{2^{2^{2^{2^{2 }...} ≡ 0　(mod 2^10)　 {∵2の因子の多さは明らか...}

2^{2^{2^{2^{2^{2 }...}
≡ 2^{ 2^{ 1024*64 } (mod 5^9*2^2) }} 　(mod 5^10) {∵フェルマーの小定理}
≡ 2^{ 406736 } 　(mod 5^10) 　{※}
≡ (1-5)^203368 　(mod 5^10)
≡ 1 + (-5)*C{203368,1} + 5^2* C{203368,2} +... +(-5)^9 *C{203368,9}　(mod 5^10)
≡ 5788111　(mod 5^10)

中国人剰余定理より
2^2^2^2^2^2 ≡ 0*(-183*5^10) + 5788111*(1745224*2^10)　(mod 2^10*5^10)
≡ (57*10^5 + 88111)* (17*10^5*45224)* 1024 (mod 10^10)
≡ ((57*45224 + 88111*17)*10^5 +88111*45224 )*1024 (mod 10^10)
≡ 421427437428736 (mod 10^10)
≡ 7437428736 (mod 10^10)

∴ 2^2^2^2^2^2 = ..... 7437428736

※ ここは多倍長計算可能な数式ソフトに任せた。
常識的な桁数で済ませたいなら後半と同様に (1-5)^{ 1024*32 } (mod 5^9) etc. を計算したらよい。

**１３２人目の素数さん** · 2020/03/23(月) 21:20:30.94

>>888
転載おつです
千葉逸人@HayatoChiba 先生か

https://www.nippyo.co.jp/shop/magazines/latest/4.html
数学セミナー　2020年4月号
＊数学との向き合いかた……千葉逸人　8

https://ja.wikipedia.org/wiki/%E5%8D%83%E8%91%89%E9%80%B8%E4%BA%BA
千葉逸人（ちばはやと、1982年1月18日 - ）は日本の数学者、東北大学材料科学高等研究所教授[1]。

略歴
福岡県久留米市生まれ。福岡県立明善高等学校を経て、2005年京都大学工学部物理工学科卒業。2009年京都大学情報学研究科数理工学専攻博士課程修了。専門は力学系理論、微分方程式、および非線形函数方程式。

大学3回生の時に『これならわかる工学部で学ぶ数学』を出版した[2]。

また修士課程在学中に『ベクトル解析からの幾何学入門』を出版した。（書いたのは学部４回生の時だという）

2013年より九州大学マス・フォア・インダストリ研究所准教授[3]。

2015年に蔵本予想（蔵本モデル）の証明をした[4]。

2019年度より九州大学を退職し東北大学材料科学高等研究所の教授[5]。

**886** · 2020/03/23(月) 21:24:18.67

>>890
さっぱり分からんが回答ありがとう。
logを使う方法がネット上で載っていたが違う方法もあるんだな。

**１３２人目の素数さん** · 2020/03/23(月) 21:31:34.88

>>891
https://en.wikipedia.org/wiki/Walsh_function
Walsh function From Wikipedia

https://mathworld.wolfram.com/WalshFunction.html
Walsh Function -- from Wolfram MathWorld

https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%80%E3%83%9E%E3%83%BC%E3%83%AB%E5%A4%89%E6%8F%9B
アダマール変換（ウォルシュ?アダマール変換やアダマール?ラーデマッヘル?ウォルシュ変換、ウォルシュ変換、ウォルシュ?フーリエ変換としても知られている）はフーリエ変換の一般化の1つである。

この変換はフランスの数学者ジャック・アダマール、ドイツの数学者ハンス・ラーデマッヘル、アメリカの数学者ジョセフ・L・ウォルシュ（英語版）にちなんで命名されている。

**886** · 2020/03/23(月) 21:45:32.24

https://sites.google.com/site/allamsnumbers/home/the-beginning-of-the-beyonds/hyperoperational-numbers
It turns out that the leading digits of this number can be computed,
by taking the log10(2) accurate to at least 19735 decimal places,
and multiplying it by the decimal expansion of 2^^5.
Below are the first and last 40 digits of 2^^6.

2120038728808211984885164691662274630835...............8862693010305614986891826277507437428736

こっちも読んでも分からんけれども。

**１３２人目の素数さん** · 2020/03/24(火) 00:41:48.96

>>887
更にどうでもいいことだが、
　1･N + 2･(N-1) + ････ + (N-1)･2 + N･1
は
　{1 + 2x + 3x^2 + ････ + k･x^(k-1) + ････ }^2
　= (1 + x + x^2 + x^3 + ････ + x^k + ････ )^4
　= 1/(1-x)^4
　= Σ[k=0,∞] Ｃ[k+3, 3] x^k,
における x^(N-1) の係数に等しい。
∴　Ｃ[N+2, 3] = N(N+1)(N+2)/6.

なお　1/(1-x)^a = Σ[k=0,∞] Ｃ[k+a-1, a-1] x^k,

**１３２人目の素数さん** · 2020/03/24(火) 01:10:08.53

↑　一般化された二項展開公式

**１３２人目の素数さん** · 2020/03/24(火) 01:44:42.10

>>875

Σ[k=1,∞] 1/(k^k)　=　1.291286
Σ[k=1,∞] 1/(k^(k+1))　=　1.138390
Σ[k=1,∞] 1/(k^(k+2))　=　1.066873
Σ[k=1,∞] 1/(k^(k+3))　=　1.032685

(下限)
Σ[k=1,∞] 1/(k^(k+a))　>　1 + 1/(2^(2+a))

**１３２人目の素数さん** · 2020/03/24(火) 14:18:31.14

geogebraで５点を通る二次曲線を描いたときに
５点から決まる焦点や漸近線の作図方法はどうやればいいのでしょうか？

**１３２人目の素数さん** · 2020/03/24(火) 15:06:33.54

数列{a[k]}を
a[k] = {nCk*(-1)^(k+1)}/k
とおく。
必要であれば
lim[n→∞] {(1+1/2+...+1/n)-ln(n)} = 0.5772... を用いて以下の問いに答えよ。

（1）lim[n→∞] {1/ln(n)}*Σ[k=1,...,n]a[k] = 1
を示せ。

（2）次の極限を調べよ。
lim[n→∞] {1/ln(n)}*Σ[k=1,...,n]❲Σ[j=1,...,k](a[j]/j)❳

**１３２人目の素数さん** · 2020/03/24(火) 20:13:20.63

>>898
・二次曲線の中心
・円と二次曲線の4交点
が作図できるので、X軸, Y軸が得られる.
双曲線: (aY)^2 - (bX)^2 = 1 の a, b を数式で求めてしまえばよい
　https://imgur.com/nUiPUqs
楕円: 作図オンリーで簡単に求まる↓

**１３２人目の素数さん** · 2020/03/25(水) 00:53:30.65

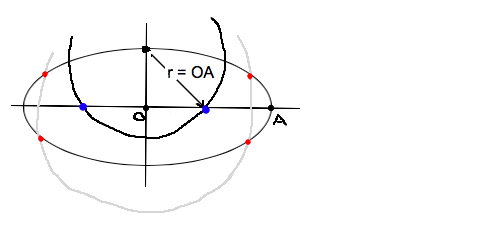>>899
Σ[k=1..n]a[k] = Σ[k=1..n] C{n,k} (-1)^{k+1}/k
= Σ[k=1..n] ∫[x=0,1]dx C{n,k} (-x)^{k-1}
=lim[ε→∞] ∫[x=ε,1]dx ( x^{-1} - x^{-1}(1-x)^n )
=lim[ε→∞] ∫[x=ε,1]dx x^{-1} - ∫[x=0,1-ε]dx (1-x)^{-1} x^{n} )
=lim[ε→∞] -log(ε) - Σ[k=n+1..∞](1-ε)^k/k
=lim[ε→∞] -log(ε) - Σ[k=1..∞](1-ε)^k/k + Σ[k=1..n](～)
=lim[ε→∞] -log(ε) + log(1-(1-ε)) + Σ[k=1..n](～)
= Σ[k=1..n] 1/k
= {Σ[k=1..n] 1/k - ln(n)} + ln(n)

lim[n→∞]Σ[k=1..n]a[k]/ln(n) = 0.5772.../∞ + 1 = 1

**１３２人目の素数さん** · 2020/03/25(水) 00:54:49.21

lim[ε→∞] じゃなくて lim[ε→0]

**１３２人目の素数さん** · 2020/03/25(水) 14:39:45.07

>>899 問(2)
Σ[k=1..n]Σ[j=1..k] a[j]/j = Σ[j=1..n]Σ[k=j..n] a[j]/j = Σ[j=1..n] (n-j+1) a[j]/j
= (n+1)Σ[j=1..n]a[j]/j　-　Σ[j=1..n]a[j]

Σ[j=1..n]a[j]/j
= Σ[j=1..n] C{n,j} ∫[x=0,1]dx ∫[y=0,1]dy (-xy)^{j-1}
= ∫[x=0,1]dx ∫[y=0,1]dy {1 - (1-xy)^n }/{1 - (1-xy)}
= ∫[x=0,1]dx ∫[y=0,1]dy 1 + (1-xy) + ... + (1-xy)^{n-1}
= ∫[x=0,1]dx 1 + (1-x/2) + ... + (1-(1-x)^n)/nx
= ∫[x=ε,1]dx Σ[k=1,n] 1/xk - x^{-1}(1-x)^k/k
= Σ[k=1,n] { 1/k * (-ln(ε)) - ∫[x=0,1-ε]dx (1-x)^{-1} x^k/k }
= Σ[k=1,n] { 1/k * (-ln(ε)) - {Σ{[m=1,∞] - Σ[m=1,k]} (1-ε)^m/mk }
= Σ[k=1,n]Σ[m=1,k] 1/mk
= { Σ[k=1,n]Σ[m=1,n] 1/mk + Σ[k=1,n] 1/kk }/2
= { (γ+ln(n)+α)^2 + π^2/6 + β }/2　　【 γ=0.5772..., α→ 0, β→ 0 (n→∞) 】

∴ lim[n→∞] { Σ[k=1..n]Σ[j=1..k] a[j]/j }/ { n*ln(n)^2 } = 1/2
分母は勝手に変えさせてもらった

**１３２人目の素数さん** · 2020/03/25(水) 15:33:24.20

このスレ、レベル高くなってきたね

**901** · 2020/03/26(木) 10:34:43.57

極限操作が雑に見えなくもないので少し書き直しておく (実際は同内容)

0 < ε < 1 とする.
Σ[k=1..∞] (1-ε)^k/k = -ln(1-(1-ε)) = -ln(ε) ・・・(1)

N を n < N, (1-ε)^N/ε < ε となるようにとる.
Σ[k=n+1..N] (1-ε)^k/k = ∫[x=0,1-ε]dx Σ[k=n+1..N] x^{k-1}
= ∫[x=0,1-ε]dx (x^n　-　x^N)/(1-x)
= ∫[x=ε,1]dx (1-x)^n/x　-　α(N)
= -ln(ε) + Σ[k=1..n] C{n,k} (-1)^{k} (1-ε^k)/k　-　α(N) ・・・(2)
Nの条件より 0 < α(N) < ε

(1)-(2) より
Σ[k=1..n] (1-ε)^k/k = Σ[k=1..n] C{n,k} (-1)^{k+1} (1-ε^k)/k + α(N)
ε → +0 の極限をとって
Σ[k=1..n] 1/k = Σ[k=1..n] C{n,k} (-1)^{k+1} 1/k
を得る.

**１３２人目の素数さん** · 2020/03/26(木) 11:46:58.26

変なとこがあったので訂正

0 < ε < 1 とする.
α[N] := ∫[x=0,1-ε]dx x^N/(1-x)
β[N] := Σ[k=N+1,∞](1-ε)^k/k
N を n < N, (1-ε)^N/ε < ε, β[N] < ε となるよう十分大きくとる. (εに依存)
条件より 0 < α[N] < ε である.

Σ[k=1..∞] (1-ε)^k/k = -ln(1-(1-ε)) = -ln(ε) ・・・(1)

Σ[k=n+1..N] (1-ε)^k/k = ∫[x=0,1-ε]dx Σ[k=n+1..N] x^{k-1}
= ∫[x=0,1-ε]dx (x^n - x^N)/(1-x)　=　∫[x=ε,1]dx (1-x)^n/x　- α[N]
= -ln(ε) + Σ[k=1..n] C{n,k} (-1)^{k} (1-ε^k)/k　- α[N] ・・・(2)

(1)-(2) より
Σ[k=1..n] (1-ε)^k/k　+ β[N] = Σ[k=1..n] C{n,k} (-1)^{k+1} (1-ε^k)/k　 + α[N]

ε → +0 の極限をとって
Σ[k=1..n] 1/k = Σ[k=1..n] C{n,k} (-1)^{k+1} 1/k
を得る.

**１３２人目の素数さん** · 2020/03/26(木) 15:42:53.55

もうちょっと頑張ってみた.

Σ[k=1,n] C{n,k}(-1)^{k+1}/k
= Σ[k=1,n] ∫[x=0,1]dx C{n,k} (-x)^{k-1}
= Σ[k=1,n] ∫[x=0,1]dx C{n,k} (x-1)^{k-1}
= ∫[x=0,1]dx { (1+(x-1))^n - 1 } / (x-1)
= ∫[x=0,1]dx (x^n - 1) / (x-1)
= ∫[x=0,1]dx Σ[k=0,n-1] x^k
= Σ[k=1,n] 1/k

Σ[j=1..n]a[j]/j
= Σ[j=1..n] C{n,j} ∫[x=0,1]dx ∫[y=0,1]dy (-xy)^{j-1}
= ∫[x=0,1]dx ∫[y=0,1]dy {1 - (1-xy)^n }/{1 - (1-xy)}
= ∫[x=0,1]dx Σ[k=0,n-1] ∫[y=0,1]dy (1-xy)^k
= ∫[x=0,1]dx Σ[k=1,n] (1-(1-x)^k) / kx
= ∫[x=0,1]dx Σ[k=1,n] (1-x^k) / k(1-x)
= Σ[k=1,n] 1/k ∫[x=0,1]dx Σ[m=0,k-1] x^m
= Σ[k=1,n] 1/k Σ[m=1,k] 1/m
= Σ[k=1,n]Σ[m=1,k] 1/km

εやらlog展開を使うなんてアリエネーだろ... と自分でも思っていたのでスッキリした.

**１３２人目の素数さん** · 2020/03/26(木) 18:19:07.01

よりシンプルに...

f(x) := (-1)*Σ[k=1..n] C{n,k}(-x)^k / k
f’(x) = Σ[k=1..n] C{n,k}(-x)^{k-1}
　= (1 - (1-x)^n)/x = (1-(1-x)^n)/(1-(1-x)) = Σ[k=0..n-1] (1-x)^k

Σ[k=1,n] C{n,k}(-1)^{k+1}/k
　= f(1) - f(0) = ∫[x=0,1]dx f’(x) = Σ[k=1..n] 1/k

問2をこの方向でやるのは却って面倒かもしれない.

**１３２人目の素数さん** · 2020/03/26(木) 19:42:03.72

それほどでもなかった.
g(x,y) := (-1)*Σ[k=1..n] C{n,k}(-xy)^k /kk
∂[x]∂[y]g(x,y) = Σ[k=1..n] C{n,k}(-xy)^{k-1}
　= (1- (1-xy)^n) / xy　= (1- (1-xy)^n) / (1- (1-xy))
　= Σ[k=0..n-1] (1-xy)^k
∂[x]g(x,y) = ∫dy ... = Σ[k=1..n] (1-(1-xy)^k) / kx　{∵ ∂[x]g(x,0)=0}
　= Σ[k=1..n] y(1-(1-xy)^k) / k(1-(1-xy))
　= Σ[k=1..n] Σ[m=0..k-1] y(1-xy)^m / k
g(x,y) = ∫dx ... = Σ[k=1..n] Σ[m=1..k] { 1- (1-xy)^m }/mk　{∵ g(0,y)=0}

∴ Σ[k=1..n] C{n,k}(-1)^{k+1} /kk
　= g(1,1) = Σ[k=1..n] Σ[m=1..k] 1/mk