������Ȃ����͂����ɏ����Ă�462
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
�����A�������P������낤����
�O�X��
������Ȃ����͂����ɏ����Ă�461
https://rio2016.5ch.net/test/read.cgi/math/1594131967/
(�g�p�ςł�: 478) >�O�X��999
�������ĂȂ���������A�ݒ肪�����Ȃ�A
�O�X��1000�̒ʂ�A���̑̊��͍��o�ł���\��������
�����͋��炭�u��������̕��v���Ⴄ���炾�Ǝv����
���̏ꍇ�A�Ή���Ƃ��Ă͈ȉ��̂悤�Ȃ��Ƃ��l������
A ���ɂ����錩������̕��𑪒肵�A����� a �Ƃ���B
B ���ɂ����錩������̕��𑪒肵�A����� b �Ƃ���B
(1) b = a �ƂȂ�悤�ɁA���̐ݒ�����邩�A
�@�܂��̓��j�^�[�Ƃ̕����I�ȋ���������B
(2) a : b = 300 : x �ƂȂ�悤�ɑ��x x ��ݒ肷��B �m�����z���ł�
�@���鍑�̑哝�̑I�� A, B �� 2 �l������₵���D�I���\�z�����邽�߂ɁC�L���҂��疳��� �ɒ����Ώۂ�I�яo���CA, B �ǂ���̌��҂��x�����邩�A���P�[�g�����������Ƃ���
����� �ɑI�� 300 �l�� 180 �l���CA ���x������Ɖ����D
���̂Ƃ��C�ȉ��̖₢�ɓ�����
2-1. �W�{�䗦�i�W�{���ρj x �̒l���ȉ��̒�����I������
(1) 0.2, (2) 0.3, (3) 0.4, (4) 0.5, (5) 0.6
2-2. A �̎x���� p �� 97% �ߎ��M����Ԃ����߂�
(1) [0.5445628,0.6554372], (2) [0.5386231,0.6613769], (3) [0.5271397,0.6728603],
(4) [0.5010192,0.6989808], (5) [0.4916005,0.7083995]
�P��߂�0.6�ƕ�����܂�
�Q��߂��킩��܂��� ���邢�́A�u�]���v�ƕ��̔䂪�Ⴄ���Ƃ����o�̌�����������Ȃ���
A ���ł͍��� 53cm �̓��A���� 25cm ������A�]���� 28cm
���̔䂪���̊��ł������ɂȂ�悤�ɕ�������Ηǂ���������Ȃ�
�Ⴆ�� B ���ł͍��� 39cm ������A���� x cm �Ƃ���Ɨ]���� 39-x cm
���̔䂪�����ɂȂ�悤�ɂ��邽�߂ɂ́A
25 : 28 = x : (39-x) �������� x = 975/53 ≈ 18.396 cm ���ĂƂ���
�v���C���₷�����ǂ����͂킩��� �O�X�� �W�J�}��ɕ`���ꂽ�~���~���ʼn]�X�̌�
�W�J�}�̉~�ʊp: ���f
�~���p(���ƕ���̊p): �� �Ƃ����
�E( r*cos��, r*sin�� ) �� ( r*sin��*cos(2��/���f), r*sin��*sin(2��/���f), r*cos�� )
�E���f = 2�� sin�� �@{�� ��`�ł̃��f ���~���ł̈���ɑ���}
�����2������3�����Ή���
( x, y ) �� ��(x*x+y*y) * ( sin��*cos(atan2(y, x) /sin��), r*sin��*sin(atan2(y, x) /sin��), cos�� )
�ƂȂ�B���Ƃ͉~��\���p�����[�^�Ȑ����ƍ�������悢�B
��. https://imgur.com/a/LPeEo2Z
�W�J�}�̊O�ɏo���~�͌Еt�����ꂽ�����W�J�}�ɕ`����Ă�ƌ��Ȃ��Ηǂ��B
sin�� = 1/n �̂Ƃ��ɂ� n ���̓W�J�}�őS�ی������ƂɂȂ�B
���_�����1���[�v�� �~���ł� n ���[�v�ƂȂ�B �O�X��952
��PNA��2�ӂ�5,�Εӂ�3��3�̓ӎO�p�`�ŁA�������ӂ̕Е��͒��_��M�ŁA
��NMP�ɂ����ė]���藝���A
NM=��o(5/2)^2+5^2-2(5/2)5cos72���p
NX=1+NM
=5.85021392731�c�c n�����R���Ƃ��āA�ȉ��̃X�^�[�����O�̌���
ln(n!) �� {n+(1/2)}*ln(n)-n+(1/2)*ln(2��)
���m���Ă���A�E�ӂ͍��ӂ̗ǂ��ߎ��ƂȂ��Ă���B
�ł͏㎮�𐳂̎���x�ɂ��čl�����Ƃ��A�E�ӂ͍��ӂ̗ǂ��ߎ��ƂȂ邩�B
���Ȃ킿{x+(1/2)}*ln(x)-x+(1/2)*ln(2��)��ln{��(x)}�̗ǂ��ߎ��ƂȂ��Ă��邩�B �O>>6�O�X����5.44409�c�c�Ƃ�����Ə������Ȃ����̂́A�~���̓������V���[�g�J�b�g�������炾�Ǝv���B����ŁA���I�@�W�J�}�̐�`�̏�Œ��������čő�l�o�������ȁA�ƁB �����`Z:ABCD�̒��_A��ɋ�X���A���_C��ɋ�Y���u����Ă���B
����S�N��T�N���ȉ��̂悤�ȃQ�[�����s���B
�wS�N��T�N�̓T�C�R����U��A�ȉ��̒ʂ�ɋ�����iS�N�̏ꍇ�͋�X�AT�N�̏ꍇ�͋�Y�j�B
�E�o���ڂ�3�̔{���Ȃ������Ȃ�
�E�o���ڂ�3�Ŋ����1�]�鐔�̏ꍇ�AZ�̔����v���Ō����ׂ̒��_�ɋ����
�E�o���ڂ�3�Ŋ����2�]��a�̏ꍇ�AZ�̎��v���Ō����ׂ̒��_�ɋ����
�܂�S�N���T�C�R����U��A��X�����i��U�j�B
������T�N���T�C�R����U��A��Y�����i��U�j�B
�Ȍ�S�N�AT�N�A�c�ƌ��݂ɃT�C�R����U��A������Ă����B
����̋�u���ꂽ���_�Ɏ����̋���B�����ꍇ�A�����Ƃ���B�x
(1)���̃Q�[���͌�U���K���ł��邱�Ƃ��ؖ�����B
(2)���̃Q�[���Ɉȉ��̂悤�ȃ��[����������B
�wT�N��������傤��n���������_��T�N���������Ă��Ȃ��ꍇ�AS�N�̏����Ƃ���x
S�N����������m����p�Ƃ���Ƃ��A|p-(1/2)|���ŏ��ɂ���n�����߂�B >>7
�X�^�[�����O�̌����̓�(x)�̑Q�ߓW�J�ł�����
�����瓖�Rn�����łȂ�����x�̑傫���Ƃ���ł̋ߎ����^���Ă� >>11
���̐}��
y��x^2�Ƃ����̂́i���̐ϕ��͈͂ł́jx=��y
x+y��2�Ƃ����̂�x=2-y �L���̈Ӗ��Ŏ���ł��B�W�� R �Ƃ��̌� x ���������Ƃ��AR �̉E��� n �C�E���� + ��
����ꍇ�A�ǂ������Ӗ��ɂȂ�̂ł��傤���H
https://dotup.org/uploda/dotup.org2219260.png >>13
R�̉E���n��R��n�̒��ϏW���BR^n={(x1,x2,x3,�cxn)|x1��R,x2��R,x3��R,�c,xn��R}
R�̉E���Ɂ{�͐��̎����S�̂̏W���BR_+={x��R|x>0}
>>13�͂��������킹�����̂�����A�܂�R_+��n�̒��ϏW���B{(x1,x2,x3,�cxn)��R^n|x1>0,x2>0,x3>0,�c,xn>0}
���������ׂĐ��̎����ł���悤��n�������W�̑S�̂Ǝv���悢�B���Ƃ���R�̉E���2�A�E���Ɂ{�Ȃ�������1�ی���\���B >>14
�����A�L���������܂��B
����ω摜�ł����������Ƙb�������ł��ˁB �������́A���@https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q10105842365
�ł����A�@���̕��@�ł͉��Ⴂ�܂��B
30���オ34.7���Ȃ�A34.7 = 21 + Ce^-30k �Ƃ��� C�����̎��_�ł͊m��ł��Ȃ����l�Ƃ��܂��B
�ꎞ�Ԍ�ɂ�����x�v���Ƃ���܂����A����͌ߌ�12��30�����Ǝv���܂��̂ŁA�������Ă���90����
�Ǝv���܂����B�@����Ȃ�
90���オ34.1���Ȃ�A34.1 = 21 + Ce^-90k�@�Ƃ��A�����e^-kt = m�Ƃ����
13.7 = Cm�A13.1 = Cm^3�A�@�ƂȂ�@m^2 = 13.1 / 13.7 �ƂȂ�܂��B
�������� m = 0.977854794�A�@����� 0.6 = C(m – m^3) �ɑ������ƁAC = 14 �ƂȂ�܂��B
�����34.7 = 21 + 14e^-kt����At = 0�̎����S���ɂ͑̉��� 35���ł���A���S���Ԃ́A
�������A�ߌ�11��30�����30���O�́A�ߌ�11�����Ǝv���܂����A��肪�����
�w�E���ĉ������B
�Ȃ�Yahoo�́A���S�����l�̕��ϕ��M��36���Ƃ���Ȃǂ͗����ł��܂���B >>5
�~���̏�ɉ��������������Ă݂��B���_�̊p�x�͂R�O�x�~�Q
https://i.imgur.com/c13YyLZ.png ����{�́u2���O���t�̍ő�}�b�`���O�ƍŏ��핢�̑傫���͓������B�v�Ƃ����藝�̏ؖ��ɏ璷�ȕ���������̂ł͂Ȃ����Ǝv���Ă���̂ł����A���̒藝�ɂ��Ēm���Ă���l�͂��܂����H >>18
����������}�����ĉ~���W�J�}(���ʂ̒������P�A���_�̊p�x���Q���j�̏�̓_A(p,q�j���ǂ��Ɉړ����邩���v�Z�����B
https://i.imgur.com/qOojo9N.png
�ǂ�����Č��������̂��H >>16
���x: T=T(t),�@����: u=21.0 {�萔}
��p�@��: dT/dt = ��*(u - T)
dT/(T-u) = -�� * dt
�� T(t)-u = C*exp(-��t) = C*��^{-t},�@ ��:=exp(��)
{���S������ ��_: t=0 �Ƃ���}
T(0)-u = 36.9 -21.0 = 15.9�@{���l�̕��ϕ��M: 36.89�� (���O�O����)}
T(x)-u = 34.7 -21.0 = 13.7
T(x+1)-u = 34.1 -21.0 = 13.1
��
(1)�@C = 15.9
(2)�@C*��^{-x} = 13.7
(3)�@C*��^{-x-1} = 13.1
(2)��(3) ��� �� = 13.7/13.1
(2)��� logC - x*log�� = log(13.7)
x = ( logC - log(13.7) ) /log��
�@= ( log(15.9) - log(13.7) )/( log(13.7) - log(13.1) )
�@= 3.325...
�@�� 3����20��
������S������
�@11��30�� - 3����20�� = 8��10�� �Ɛ���ł���B
(�ڂ�����̂�Yahoo�̉͒ǂ��ĂȂ�) >>17, >>21
�Ɉ�ʓI�ȕ��ϕ��M���o�ė���̂́A���ł������X�b�L�����܂���
���w�E���肪�Ƃ��������܂��B >>22
���Ƃ��ɉ��x�������̂��킩��Ȃ����炻���͐������邵���Ȃ����낤 C_0 - C_0' = C_1 - C_1' ���� C_1' �� C_0'�ł���悤�ȗL���W��C_0, C_0', C_1, C_1'�̗�Ȃ�Ė{���ɂ���܂����H ��(1-tan^2(t))�̐ϕ��̉������������Ă��������B
�����0�����/4�̒�ϕ���(��2-1)�ɂȂ�炵���̂ł����A
�����F���(a^2-x^2)dx=1/2(x��(a^2-x^2)+a^2�Earcsin(x/a))�̌����Ōv�Z�����Ƃ���Ⴄ���ʂɂȂ��č��f���Ă��܂��B C_0 �� C_0', C_1 �� C_1', C_0 - C_0' = C_1 - C_1'�ł���悤�ȗL���W��C_0, C_0', C_1, C_1'�̗�Ȃ�Ė{���ɂ���܂����H �O�X���D950,958
O (0, 0, 0)
A (3, 0, 0)
B (-3, 0, 0)
M (3/2, 0, 2)
N (-3/2, 3(��3)/2, 0)
P (0, 0, 4)
�Ƃ����B
���ƕ���̂Ȃ��p�����Ƃ����
�@sin�� = 3/5,�@cos�� = 4/5,
�W�J�}E�ɂ�����ɍ��W�� (r,��) �̓_X��
�~����S��ł̓f�J���g���W��
X ((3/5)r�cos((5/3)��), (3/5)r�sin((5/3)��), 4-(4/5)r)
�~����S�̑S�ȗ� K=0 ������
�@(dL)_s = (dL)_e,
�@1 = L_s = L_e �� MX_e = ��(25/4 -5r�cos�� + rr)
���̏����� NX ���ő�ɂ���B �A�����݂܂���A
��(x/(x^2-x+1)^2)dx�̉������������Ē����Ȃ��ł��傤���B
0����1�܂ł̒�ϕ���1/27(9+2��3)�ɂȂ邻���ł��B >>31
�Ȃ����݂��Ȃ��Ǝv���̂��䂷���� �ȒP�����ň��������Ƃ����v����� >>27
�@tan(t) = x,
�@t = arctan(x),
�Ƃ�������
�@dt = dx/(1+xx),
����B
��2 arcsin( (��2)sin(t) ) - arctan( sin(t)/��cos(2t) )
���̎��� a=1/��2�@�Ƃ����B
��{cos(t)^2 - aa} /cos(t) dt
�@= arcsin( sin(t)/��(1-aa) ) - a�arctan(a�tan(t)/��(1-aa)),
�@|a|<1
�X����F�c�쥈ꏼ: �u���w����I�v, ��g�S��221 (1956)
�@p.204�@���ق� >>31
�����Ēނ��Ă݂�
>>26�̗�i�{���ɂ���܂��j
C_0 := {1, 2}, C_0' := {2}, C_1 := {1, 2, 3}, C_1' := {2, 3}
>>28�̗�i�{���ɂ���܂��j
���� ��W�����l����Ζ��炩�Ȃ��ǁA�u�x���Ĕ��i�H�j�ȗ�����p�ӂ��܂��� >>27
��[t=0,��/4] dt ��(1-tan²(t))
�@= ��d{tan(t)} cos²(t) ��(1-tan²(t))
�@= ��[x=0,1]dx ��(1-x²) /(1+x²)�@�@{ x=tan(t) }
�@= ��[t=0,��/2] dt cos²(t) / (1+sin²(t))�@�@{ x=sin(t) }
�@= ��[t=0,��/2] dt (1-sin²(t)) / (1+sin²(t))
�@= -��/2 + ��[t=0,��/2] dt 2/(1+sin²(t))
�@= -��/2 + 1/2 * ��[t=0,2��] dt 1/(1+sin²(t))
�@= -��/2 + 1/2 * ��2�@�@{��1}
�@= ��/2 * (��2 - 1)�@{ ���l�ϕ��ł��`�F�b�N�� }
��1
��[t=0,2��] dt 1/(1+sin²(t))
�@= -i*��[t=0,2��] d{e^{it}} e^{-it}/(1+sin²(t))
�@= 4i*��dz�@z/((z²-��)(z²-��)) �@�@{ z=exp(it) ��2 }
�@=-8��* ((+�ヿ)/(2(+�ヿ)(��-��)) + (-�ヿ)/(2(-�ヿ)(��-��)) { �����藝 }
�@= ��2
��2
(1/z)/ ( 1 - (zz -2 + 1/zz )/4 )
�@= -4z/(z⁴ - 6z² + 1)
�@= -4z/((z²-��)(z²-��))�@{ ��=(3-��8), ��=(3+��8), |��|<1, 1<|��| } >>34
���肪�Ƃ��������܂�
x-1/2 = y �Ƃ������f��������Ē����܂��ł��傤�� �����̌v�Z����Wolfram��搶�ɕ����u�X�e�b�v���Ƃ̉���v�Ńq���g�����炦���� >>36
���肪�Ƃ��������܂��B������܂����B
�����ɓ���邽�߂�x�̎����ƌW�����Ȃ��Ƃ����Ȃ�������ł��ˁB >>39
���m�F�ł��܂����B
�ڂ����ߒ����L�q���Ă��������A���肪�Ƃ��������܂��B >>41 Wolfram �͂����܂Ŗ��\�ł͂Ȃ��B
"��[t=0,��/4] dt ��(1-tan²(t))" �Ŋۓ��������
��ϕ� ... = 1/2 (sqrt(2) - 1) �� ≈ 0.65065
�@�� "���̃N�G���ɂ́u�X�e�b�v���̉���v�͂���܂���B"
�Əo��B (����������Ƃ��Ă����ۋ����Ɩ`���������������Ȃ�)
�l��\�����Ă�������ȊԂ�u���� ���� ��lj��ŏo���Ă���̂ŁA
���l�v�Z�̒l�� �����e�[�u��������ׂ� 1/2 (sqrt(2) - 1) �� ���E���Ă��Ă��Ȃ����ȁB ���W���ʏ�̓_�ŁC�����W�������ł���悤�ȓ_���i�q�_�Ƃ����܂��D������ y=x2 �͖����̊i�q�_��ʂ�܂��D����ɑ��ĕ����� y=x2+��2
�͊i�q�_��ʂ�܂���D
���1�@k=1,2,3,4
�ɑ��āC���傤�� k
�̊i�q�_��ʂ�������������Ă��������D(�������̎��͍��W���ɕ��s�Ƃ͌���܂���D)
���2�@���傤�� 5 �̊i�q�_��ʂ������������ł��傤���D >>45
��[t=0,��/4] dt ��(1-tan²(t))
�ɂ��Č����A�s��ϕ������݂���ł���
https://www.wolframalpha.com/input/?i=%E2%88%AB+%E2%88%9A%281-tan%C2%B2%28t%29%29+dt
���ۋ����Ɩ`���������������Ȃ��̂Ńq���g�Ə��������A
�`�������ł������͐����ł���
��̗�ł����A�� ��(1 - u^2)/(u^2 + 1) du �܂ł͖��ۋ��ł�������̂ŁA���̕s��ϕ����킩��悭�āA
��搶�ɂ������Ȃ�炵��
https://www.wolframalpha.com/input/?i=%E2%88%AB+%E2%88%9A%281+-+u%5E2%29%2F%28u%5E2+%2B+1%29+du
����̃X�e�b�v���Ƃ̉����`���Ɓi���� >>36
�̉��̕��̎��َ͐҂̎ʂ��ԈႢ�ł��������B
����ł��l�т𥥥� (AA��)
(����)
�� ��{cos(t)^2 -aa} /cos(t) dt
�@= arcsin( sin(t)/��(1-aa) ) - a�arcsin( a�tan(t)/��(1-aa) ),
�@= arcsin( sin(t)/��(1-aa) ) - a�arctan( a�sin(t)/��{cos(t)^2 -aa} ),
�@|a|<1
>>39
��1
�@��1/{1+sin(t)^2} dt = (1/��2) arctan((��2)t), ��1
�@��1/{1+sin(t)^2} dt = (1/��2) arctan((��2)tan(t)),
�ł����B �K�E�X���Ɋւ���
f(x) =��y �O�����z (1�|t�O2)e�O(�|t�O2)dt (x ��R).
���̂Ƃ�
(1) lim�yx��+���zf(x), lim�yx���|���zf(x) �����߂�.
(2) y = f(x)�̋ɒl�ƕϋȓ_�����߂�
f(x)=��[0,x] (1-t^2)e^(-t^2) dt
=��[0,x] e^(-t^2) dt - ��[0��x] (t^2)e^(-t^2) dt
=��[0,x] e^(-t^2) dt - ��[0��x] (-t/2)(-2t)e^(-t^2) dt
=��[0,x] e^(-t^2) dt + ��[0��x] (t/2)(-2t)e^(-t^2) dt�Ƃ���
�Ƃ���܂ł͂킩��܂��� ���ɐi�߂܂���
��y�O�����ze�O�|x�O2dx =���/ 2�Ƃ����̂������݂����ł��� >>46
���3
�@�������̎������W���ɕ��s�ȂƂ���
�@k��2�@�܂��́@k=��
�Ɍ��邱�Ƃ������B (����)
������
�@�@f(x) = axx + bx + c
�����قȂ�3�̊i�q�_ (x_i, f(x_i)) ��ʂ�Ƃ���B
���O�����W���̕�Ԍ������A�W�� a, b, c �͗L�����B
n�a �� n�b �������ƂȂ�悤�Ȑ���n�������点��
�@f(x�+n) = f(x�) + (n�a)(2x�+n) + (n�b) �������B
���@�i�q�_�@(x�+n, f(x�+n)) ���Ƃ���B
���@k = ���@�@�@�@�@�@�@�@�@�@�@�@�@�@(�I)
���1 �� ���2 �̉������ 8��8��8��8��8�b�炵����� >>30
x - 1/2 = y
�Ƃ����ƁA��ϕ�����
�@(y+1/2)/(yy+3/4)^2 = y/(yy+3/4)^2 + (1/2)/(yy +3/4)^2
�@= y/(yy+3/4)^2 - (1/3)(yy-3/4)/(yy+3/4)^2 + (1/3)/(yy+3/4),
�ϕ�����
�@-(1/2)/(yy+3/4) + (1/3)y/(yy+3/4) + (2/��27)arctan(2y/��3)
�@= (y/3 -1/2)/(yy+3/4) + (2/��27)arctan(2y/��3)
�@= (1/3)(x-2)/(xx-x+1) + (2/��27)arctan((2x-1)/��3),
0�`1 �̒�ϕ��� (9+2��3)/27 = 0.7364��� �ɂȂ�B >>47
Wolfram��搶�̃q���g�ɏ]���Ē�ϕ� I := ��[0,��/4] ��(1-tan^2(t)) dt ���v�Z����Ƃ���Ȋ�����
�܂� u = tan(t) �ƒu�������
I = ��[0,1] ��(1 - u^2)/(u^2 + 1) du
���� u = sin(s) �ƒu�������
I = ��[0,��/2] cos^2(s)/(sin^2(s) + 1) ds
= ��[0,��/2] (1/cos^2(s))/((tan^2(s)/cos^2(s)) + (1/cos^4(s))) ds
= ��[0,��/2] (1/cos^2(s))/(1 + 3tan^2(s) + 2tan^4(s)) ds
�Ō�� x = tan(s) �ƒu�������
I = ��[0,��] 1/(1 + 3x^2 + 2x^4) dx
= ��[0,��] 1/((1 + 2x^2)(1 + x^2)) dx
= ��[0,��] 2/(1 + 2x^2) dx - ��[0,��] 1/(1 + x^2) dx
= (��2 - 1) ��/2
���R�Ȍv�Z���ǂ����͒m��� >>29
r = PX = 3.055475
�� = -0.302010
�̂Ƃ��ő��
X ( 1.605907,�@-0.884314,�@1.555620)
N (-3/2, (3��3)/2, 0)
NX = 4.918699
���ȁH >>53
�@���ʁ��O����
���������Ȃ炢����ł�����B�@�������O�Q
�����P�@y���@Sqrt[2]�@���O�Q�@�@�o�O�C�O�p�̂�
�����Q�@����
�����R�@�B�B�B
k���S�@�B�B�B
�����T�@�����Ȃ���H�@�B�B�B
�Ƃ�����肾��H >>6
�O�X���� >>973 >>974 �܂ł͐��������ǁA
>>975 �Ȍ�͉������Ȃ��B
���p ��NPM = ��NPA = arccos(0.46) = 62.61289�� >>56
�@MX_e = 1
�@MX_c = 0.99533947�@�@�@(���Ȗʂ�����)
>>57
�@������܂ő҂� >>50
�����ϕ��ɂ��
�@f(x) = (x/2) e^(-xx) + (1/2)��[0��x] e^(-tt) dt,
�@f �f(x) = (1-xx) e^(-xx),
�@f "(x) = 2x(xx-2) e^(-xx),
�Ƃ����̂��g���݂����ł���� p��0<p<1�̎����Ƃ��āA�\�̏o��m����p�A���̏o��m����1-p�̃R�C��������B
���̃R�C����n�������ɓ����A�\���o�������𐔂���B��������vk��J��Ԃ��Am��ڂ̌J��Ԃ��ɂ����ĕ\���o��������a[m | k,n]�Ə����B
�Ⴆ��3���̃R�C����2���A�e��ŕ\�̏o�����������ꂼ��3��,0���ł������Ȃ�Aa[1 | 2,3]=3�Aa[2 | 2,3]=0�ł���B
�i1�jS[n,k] = ��[m=1,k] a[m | k,n]�Ƃ���B
lim[k����] (S[n,k]/nkp)�����߂�B
�i2�jn=6m�Ƃ���B2m��(S[n,k]/nkp)��4m�ƂȂ�m��p[m]�ɂ��āA�Ɍ�lim[m����] p[m]�����߂�B >>5
����݂܂����B�f���炵���I�L�O�ɓ����ۑ����܂����B
�����GeoGebra�ō쐬�ł���ˁH >>61
�i�P�j���v���O�����g��Ő��肳���Ă݂��B
> sim <- function(n,p,k=1e5) sum(rbinom(1:k,n,p))/(n*k*p)
> f=Vectorize(sim)
> n=2:20
> p=seq(0,1,0.1)
> z=outer(n,p,f)
> quantile(z,na.rm=T)
0% 25% 50% 75% 100%
0.9949167 0.9996160 1.0000000 1.0005092 1.0129500
�ǂ����P�����̂悤���ȁB >>39 (���ȃ��X)
��1 ���������V���v���ɂł����B
�� [t=0,2��] dt 1/ (1+sin²(t))
= 2 �� [t=0,��] dt 2/(2 + 1-cos(2t) ) = 2 �� [t=0,492��] dt 1/(3-cos(t))
= -2i �� dz 1/( 3z - (z² + 1)/2 ) = 4i �� dz 1/(z² -6z +1)
= 4i �� dz 1/((z-��)(z-��))�@{ ��=(3-��8), ��=(3+��8) }
= -8�� * 1/(��-��)
= -8�� * 1/(-2��8) = ��2
�������s��ϕ�( >>49 )��m���Ă�Ȃ瑦���v�Z�ł���B
>>62 �͂�GeoGebra�ł��B
�����^���ƈ���Ď��R�ɃO���O������������͖ʓ|����Ǝv���Ă���A
�O�X�� >>991 �̂悤�ȉ�ʃL���v�`���Ȃ�ȒP���ƋC�t���܂����B >>61
���݂܂���A�i2�j���Ԉ���Ă��܂����B
�i2�jn=6N�Ƃ���B2N��(S[n,k]/kp)��4N�ƂȂ�m��p[n]�ɂ��āA�Ɍ�lim[n����] p[n]�����߂�B >>54
y/(yy+3/4)^2 + (1/2)/(yy +3/4)^2
= y/(yy+3/4)^2 - (1/3)(yy-3/4)/(yy+3/4)^2 + (1/3)/(yy+3/4)
���݂܂���A�����̌v�Z�����܂������܂���B �ȉ��̖��𐔊w�I�����s�b�N�ɏo�肵���琳�𗦂ǂꂭ�炢�ɂȂ�܂����ˁH
V��L���W���Ƃ���BL��V�̕����W�����Ƃ���BL�͉��Z��, ���Ɋւ����Ă���Ƃ���B
A��C��B �� A=C or B=C�����藧�Ƃ��AA<B�Ə������Ƃɂ���B
P:={S | S = A-B ���� A, B��L���� B < A}�Ƃ����B
���̂Ƃ��ȉ��̖��肪���藧���Ƃ��ؖ�����B
A_0 = �� L < A_1 < �c < A_{l-1} < �� L = A_l�Ƃ���ƁAP = {A_l - A_{l-1}, A_{l-1}-A_{l-2}, �c, A_{1}-A_{0}}�����藧�B >>67
���݂܂���A�m�F�ł��܂����B
���肪�Ƃ������܂��B >>68
�e�����X�E�^�I�ł��������ȁH �R�C���̖���
���s�̑S�̂����z�ɂȂ邱�Ƃ���������
�v�Z�Ȃ��ŏo������ �O>>8
5.8502�c�c���ő傾�낤�H ��[-1��1] 1/x^2dx
�����߂�ہA���̂悤�ɋc�_���ē���ꂽ�l-2�͐������Ȃ��B���̋c�_�̂ǂ�������Ă��邩������B
�c�_:f(x)=1/x^2�Ƃ����ƁAF(x)=-1/x��f(x)�̌��n���ł��邩��A���̒藝��p���āA
(�藝)f����ԁmb,a�n�Œ�`���ꂽ�A���Ȋ��AF��f�̌��n���Ƃ���Ƃ��A
��[b��a] f(x)dx F(a)-F(b)
�����藧�B
����āA
F(1)-F(-1)=-2�Ɠ����ꂽ�B >>74�̖��N�������Ă��������I
f(x)�����̒l���Ƃ�Ȃ��̂ɂǂ����Ă���Ȃ��Ƃ��N�����ł����H f����ԁm-1,1�n�ŘA���Ȃ�Ⴄ��� >>76
�m���ɁI
���肪�Ƃ��������܂����I >>68
����G���K���g�Ɏ����ɂ͂ǂ�����ȁH
�ޮ�������ް�̍\���藝���Ɏ����Ɩʓ|�����Ljȉ��̂悤���ďo����
�܂���̏W����P�A���̏W����P'�Ƃ��Ă�����P'��P�͖��炩
P��P'������
B<A�ɑ��āA�������������
A_0=A'_0<A'_1<�c<B<A<�c<A'_k=A_l
�ƂȂ鍽������(�L��������)
C<D,C'<D'�Ƃ���
C��C',C��D',D��C',D��D'��2�~2�ɔz�u�����Ƃ�
�����������g�͓�����=��������<�̊W�ɂ���
<�̏ꍇ�A���̍��W���͈�v���邱�Ƃ�������
(�P�Ȃ�W���̌v�Z�����ǁA�������ʓ|)
�����(A_i)��(A'_j)��2�����I�ɔz�u���邱�Ƃ�
���W��A-B��A_i�����̂ǂ����̍��W���Ɉ�v���邱�Ƃ��킩��P��P'�������� �y����i�H�j�z
V := {1, 2}
L := {{1}, V}
P = {∅, {2}}
A_0 := �� L = {1}
A_1 := �� L = V
{A_{1}-A_{0}} = {{2}} ∌ ∅ �����ĂȂ�����A<B�̒�`��A��B�͉��肳��Ă�͂� >>79-80
�ԈႦ�܂����B
V��L���W���Ƃ���BL��V�̕����W�����Ƃ���BL�͉��Z��, ���Ɋւ����Ă���Ƃ���B
A��B�̐^�����W���ŁAA��C��B �� A=C or B=C�����藧�Ƃ��AA<B�Ə������Ƃɂ���B
P:={S | S = A-B ���� A, B��L���� B < A}�Ƃ����B
���̂Ƃ��ȉ��̖��肪���藧���Ƃ��ؖ�����B
A_0 = �� L < A_1 < �c < A_{l-1} < �� L = A_l�Ƃ���ƁAP = {A_l - A_{l-1}, A_{l-1}-A_{l-2}, �c, A_{1}-A_{0}}�����藧�B �y����i�H�j�z
V := {1, 2}
L := {∅, {1}, {2}, V}
P = {{1}, {2}, V}
A_0 := �� L = ∅
A_1 := {1}
A_2 := �� L = V
A_{2}-A_{1} = {2}
A_{1}-A_{0} = {1} >>82
����A V �� P �ɑ����Ȃ����� >>81
V�Ƃ�L�Ƃ��L������������ �y����i�H�j�z
V := {1, 2}
L := {∅, V}
P = {V}
A_0 := �� L = ∅
A_1 := {1}
A_2 := �� L = V
A_{2}-A_{1} = {2}
A_{1}-A_{0} = {1} >>85
����A���̏ꍇ P = ∅ ���H
�������ǂ��ōl����̂��킩���� >>56
r = PX = 3.055475
�� = -0.302010473
�̂Ƃ��ő��
X ( 1.60590483,�@-0.88430965,�@1.55562000)
N ( -3/2, (3��3)/2, 0)
NX = 4.9187000017 >>81
>A��B�̐^�����W���ŁAA��C��B �� A=C or B=C�����藧�Ƃ��AA<B�Ə������Ƃɂ���B
>P:={S | S = A-B ���� A, B��L���� B < A}�Ƃ����B
C��L�H�H >>78
�����ȗ����ł���
A-B�̊e�v�f��A_i��̂ǂ����Œlj������
�����lj������^�C�~���O�̈Ⴄx,y��A-B���������Ƃ����
A_i��x��y�̂ǂ��炩�������܂ނ��̂����݂���
�����B��B��(A��A_i)��A�ƂȂ薵������̂�
A-B�̑S�v�f�͂���A_i����A_(i+1)�̒i�K�ň�Ăɒlj������
���̂Ƃ�A-B�ȊO�̗v�f��A_i�ɒlj����ꂽ�Ƃ����
��̋c�_��A'_k�ɓK�p���邱�ƂŖ������킩��̂ŁA
A_(i+1)-A_i��A-B�Ɉ�v���� >>79-80
��������Ȃ��Ƃ��낪����܂����B
V��L���W���Ƃ���BL��V�̕����W�����Ƃ���BL�͉��Z��, ���Ɋւ����Ă���Ƃ���B
A, B��L�̗v�f�Ƃ���BA��B�̐^�����W���ŁAC��L����A��C��B �� A=C or B=C�����藧�Ƃ��AA<B�Ə������Ƃɂ���B
P:={S | S = A-B ���� A, B��L���� B < A}�Ƃ����B
���̂Ƃ��ȉ��̖��肪���藧���Ƃ��ؖ�����B
A_0 = �� L < A_1 < �c < A_{l-1} < �� L = A_l�Ƃ���ƁAP = {A_l - A_{l-1}, A_{l-1}-A_{l-2}, �c, A_{1}-A_{0}}�����藧�B �~�����ʂ̓W�J�}�̐�`��ɐ���L���Ђ��B
�W�J�}����~����g�ݗ��āA�W�J�}���L�ł���������C�Ƃ���B
(1)L����`�̔��a�̈ꕔ�łȂ��ꍇ�AC�͐����i���Ȃ킿�����}�`�j�łȂ����Ƃ������B
(2)L����`�̔��a�̈ꕔ�łȂ��ꍇ�AC��1�̕��ʏ�ɏ��i���Ȃ킿���ʐ}�`�j���Ƃ͂��邩�B >>91
(1)
L���W�J�}�̐�`�̒��S��ʂ�Ƃ�
C�͐܂���ł���̂ŁA�����ł͂Ȃ��������}�`�ł͂���B
L����`�̒��n�̈ꕔ�ł͂Ȃ��Ƃ�
�w���@�Ŏ����BC�������ł���Ɖ��肷��B
L����`�̔��a�̈ꕔ�łȂ�����C�͉~���̕���̈ꕔ�ł͂Ȃ��B
����������C�̂��ꂼ��̒[�_��ʂ�悤�ȈقȂ�2�{�̕�������݂���B
�قȂ����͒��_�Ō����̂ŁA����2�{�̕�����܂ޕ��ʃ���1�ɒ�܂�B
����C�̒[�_���Ƃ��ɕ��ʃ���ɂ��邩�����C�S�̂����ʃ���Ɋ܂܂��B
�܂�C�͉~�����ʏ�̐}�`�ł����邩��AC�͉~�����ʂƕ��ʃ��̋��ʕ����Ɋ܂܂��B
�������~�����ʂƕ��ʃ��̋��ʕ�����2�{�̕���ł��邩��A����ɐ���C���܂܂�邱�Ƃ�C������̈ꕔ�ł͂Ȃ����Ƃɖ�������B
�ȂI�n���t�V�т��Ă���݂����ł������肱�Ȃ����ǁA�����Ȃ��Ƃ������ƌ����Ă���̂����炱��Ȃ��̂��B�X�}�[�g�ł͂Ȃ����o�͂���B >>90
�ׂ����ؖ��������Ă���
P={S | S = A-B ���� A, B��L���� B < A}
P'={A_l - A_(l-1), A_(l-1)-A_(l-2), �c, A_1-A_0}
�Ƃ����Ă���
P=P'����������
P'��P�͖��炩�Ȃ̂ňȉ��AP��P'������
A-B��P���Ƃ�
�咣1
x��A-B(����)�ɑ��ā�! i(0��i��l-1) s.t. x��A_(i+1)-A_i
�� x��B(��L)�̗v�f�ł͂Ȃ��̂�A_0=��L�̗v�f�ł͂Ȃ�
�����x��A��A_l=A_0+��(A_(i+1)-A_i)(���a)�Ȃ̂�
�ǂ�����i��x��A_(i+1)-A_i�ł���
�咣2
A-B�̊e�v�f�ɑ��ď��i�͓����l�ł���
���Ȃ킿��! i s.t. A-B��A_(i+1)-A_i�ƂȂ�
�� �����قȂ�x,x'��A-B��
x��A_(j+1)-A_j�Ax'��A_(j'+1)-A_j' (j<j')�ł������Ƃ���
���̂Ƃ�B��(A��A_(j+1))(��L)��x���܂�x'���܂܂Ȃ�����
B⊊B��(A��A_(j+1))⊊A�ƂȂ邪����͉���B<A�ɔ�����
�咣3
A-B=A_(i+1)-A_i�ł���
�� B<A�𗼑��ɉ������邱�Ƃő����
(A_0=)A'_0<A'_1<�c<B(=A'_s)<A(=A'_(s+1))<�c<A'_k(=A_l)
�邪��Ɠ����c�_�ɂ����
��! j s.t. A_(i+1)-A_i��A'_(j+1)-A'_j
������A-B(��A_(i+1)-A_i)�ł���������j=s�ł���
A_(i+1)-A_i��A'_(s+1)-A'_s=A-B�ƂȂ�
�����A-B��P'�ƂȂ�P��P'�������� >>91
(2)�������ĂȂ������ȁB�����́u����v
�W�J�}�̐�`�̒��S�p��180�����傫���Ƃ��AL����`�̒��a�̈ꕔ�ƂȂ�悤�ɂƂ�Ε��ʐ}�`�i���_�Ő܂��܂���j�ɂȂ�B �i���a�̈ꕔ���Ĕ��a�̈ꕔ����Ȃ��́H�j >>95
���S��ʂ�悤�Ȑ������Ƃ�Δ��a�̈ꕔ�ł͂Ȃ������a�̈ꕔ�ł͂���B r=4sin��(��/8 ���Ɓ��@��/4)�ň͂܂ꂽ�}�`�̖ʐ� >>94
���肪�Ƃ��������܂��B
�i1�j�͎����Ȃ̂ɘ_�̎d���������炸�A�i2�j�Ɏ����Ắu��������낤���ǗႪ�������Ȃ��v��Ԃł����B
�ؖ��ƍ\����������Ă����������肪�Ƃ��������܂����B ��������ł�����
������
�u���i����S�Ċ܂ޕ��ʂŐؒf�j�������~���Ȑ��i�̈ꕔ�j�͉~���̓W�J�}��Œ����ɂȂ邩�H�v
���Ė�肾�Ǝv���Ă�
�����Ȃ��Ǝv������ >>98
(2)�͐����̉��������S��ʂ���̈ȊO�̋Ȑ���T���Ă����Ȃ��́H >>99
�W�J�}�̒��S��ʂ�����ȊO��
�~���������璼���ɂȂ�Ȑ��͂��邩�H
�Ƃ�����肩�Ǝv�����B ���ꂩ��̒[�������������邩�ȁH
�~���p�i����Ǝ��̂Ȃ��p�j�����̉~�����ʂ̓W�J�}�_�����_�ɂ����ɑΏ̂ɒu���B
���A�~����ʂ̉~�̓W�J�͍l���Ȃ��B
�~�����ʓW�J�}��̓_A�̍��W��(p,q)�Ƃ���ƓW�J�}���~���������Ƃ���A�̎O�������W��p,q,�Ƃŕ\�킹�B >>102
�~����ɑ��݂����钼���i�����j�͕���ȊO�ɂȂ�����T���Ă����ʂȋC�����Ă����B >>91
(2)
�W�J�}�̐�`�ɑ����`�̐�̉~�ʂ͉~�����������ʂƕ��s�ȉ~�ɂȂ邩�瓯�ꕽ�ʂɂ���ˁB >>102
����͒���
�~���p�i����Ǝ��̂Ȃ��p�j�����̉~�����ʂ̓W�J�}�_�����_�ɂ����ɑΏ̂ɒu���B
���A�~����ʂ̉~�̓W�J�͍l���Ȃ��B
�~�����ʓW�J�}��̓_A�̍��W��(p,q)�Ƃ���ƓW�J�}���~���������Ƃ���A�̎O�������W��p,q,���ŕ\�킹�B >>106
���w�E�ʂ�B���̔��肪�������̂ˁB �i�Ȃ�ł��̐l��������낤�c�H�j >>99-101
��蕶���u��`�̓����ɐ���L�v�ł͂Ȃ��u��`��ɐ���L�v�Ƃ��Ă��邵�A�킴�킴���a�ł͂Ȃ����a�̈ꕔ�Ƃ��Ă��邩��
�~�X���[�h������Ӑ}�̂Ђ�������肾�Ǝv���B
����ɂ��Ă�(1)�́u�����i���Ȃ킿�����}�`�j�v�̏����������炵�����ǂˁB
�����łȂ����Ƃ͎����邯�ǒ����}�`�łȂ����Ƃ͎����Ȃ�����B >>87
�̎��ӂœ_X (x,y,z) �������Ƃ��� NX �̂悤��
r = PX�F�@3.055400�@�@�@3.055450�@�@�@3.055475�@�@�@3.055500�@�@�@3.055550
�ӁF�@�@-0.302032543�@-0.302017830�@-0.302010473�@-0.302003116�@-0.301988400
x�F�@�@1.605832887�@1.605880851 �@1.605904833�@1.605928816�@1.605976783
y�F�@�@-0.884347011�@-0.884322105�@-0.884309650�@-0.884297194�@-0.884272277
z�F �@�@1.55568�@�@�@1.55564�@�@�@1.55562�@�@�@1.55560�@�@�@1.55556
NX�|4.9187�F�@-3.2E-10�@�@15.0E-10�@�@17.3E-10�@�@15.1E-10�@�@-2.8E-10 >>97
�Ƃ͈̔͂� �����Ɓ����@�Ƃ���B
(r,��) ���ɍ��W�Ƃ���ƁA�^���͉~
�@xx + (y-2)^2 = 4
��\�킷�B
���߂�ʐ�S�́A
(���S�p2���̋|�`�̖ʐ�) = 4�� - 2sin(2��) = �� - 2,
����
(���S�p2���̋|�`�̖ʐ�) = 4�� - 2sin(2��) = ��/2 - ��2,
�����������̂�����
S = ��/2 - 2 + ��2 = 0.98501
���邢�́A�ϕ����g����
(1/2)��rr d��
�@= 4��2(sin��)^2 d��
�@= 4��{1 - cos(2��)} d��
�@= 4�� - 2sin(2��),
����� �����Ɓ��� �Őϕ�����
S = 4(��-��) - 2sin(2��) + 2sin(2��)
�@= ��/2 - 2 + ��2
�@= 0.98501 a�͐��̎��萔�Ƃ���B
xy���ʏ�ɓ_A(0,a)�ƋȐ�C:y=sin(x)������B
A��ʂ�X����-1/4�ł��钼���́AC�Ɖ��̋��L�_�������Ba�̒l�ɂ��ꍇ���������ċ��߂�B �ɕ�����r=1+cos(��)�ɂ��\�����xy���ʏ�̋Ȑ�C���Ax���̎���Ɉ��]�����Ăł��闧�̂�K�Ƃ���B
����x=a��K��2�̕����ɕ�������Ƃ��A�������ꂽ���ꂼ��̗��̂̑̐ς��������Ȃ�悤�Ȏ���a�����߂�B >>29
r = PX = 2.58456488
�� = 0.394546670
�̂Ƃ��ŏ���
X ( 1.227371115,�@0.947813995,�@1.932348096)
N ( -3/2, (3/2)��3, 0)
NX = 3.72771883923586 >>109
���ɉƂ������W�J�}��̐�����
�~���ɑg�ݗ��Ă���ǂ�ȕ������ŕ\����̂��낤���Ǝv�����B >>113
�p�X�J����嗋��������H >>105
�v�Z�����ݓ����Ă��āA�����Ă��邩�ǂ������M���Ȃ��B
x=sqrt(p^2+q^2)*sin(��)*sin(atan(p/q)/sin(��))
y=sqrt(p^2+q^2)/(tan(��)*sqrt(1+tan(��)^-2))
z=sqrt(p^2+q^2)*sin(��)*(1-cos(atan(p/q)/sin(��))) >>113
���l�ϕ��ŋ��߂���
> uniroot(function(x) vol(x)-V/2,c(0,2))
$root
[1] 0.7901378
�Ƃ����l�ɂȂ����B
�������͌��҂ɔC�����B �T�C�N���C�h�̒�ϕ��ɂ��Ă̎���
x=a(�Ɓ|sin��), y=a(1�|cos��)�ł���T�C�N���C�h�Ȑ��̒����̌v�Z��
t=0����t=2�ł͂Ȃ��Ct=k����t=2��+k �܂ł̂��̂Ƃ�����,
�Ȑ��̒������ς�炸 8a �ƂȂ闝�R���������B
�T�C�N���C�h�̐}������Ɖ��ƂȂ��������ς��Ȃ����Ƃ͗����ł��邯���, ������v�Z���ŕ\�����@���悭������Ȃ��̂ŋ����ė~�����ł��B
�ꍇ������������̂��� >>112
�_A(0,a) ��ʂ�X����-1/4�ł��钼��
�@y = a - x/4,�@�@��
C:�@y = sin(x),
�̋��L�_�̌���
�@y = f(x) = sin(x) + x/4,
�@y = a,
�̋��L�_�̌��ł���B
x��0 �ł� f(x)��0<a �Ȃ̂ŁAx>0 �ōl����Ώ\���B
x = 4.459708725 + 2n�@(n��0) �ŋɏ�
�@b = f(4.459708725) = 0.146681344
�@f(4.459708725 + 2n��) = b + n��/2,
x = 1.823476582 + 2n�@(n��0) �ŋɑ�
�@c = f(1.823476582) = 1.424114982
�@f(1.823476582 + 2n��) = c + n��/2,
�����
0<a<b �܂��� c+n��/2<a<b+(n+1)��/2 �̂Ƃ��@�����@1��
a=b+n��/2 �܂��� a=c+n��/2 �̂Ƃ��@�@�����@2��
b+n��/2 < a < c+n��/2 �̂Ƃ��@�@�����@3�B >>119
���������
L(0,k) = L(2��,2��+k)
����� L(k,2��) ��������
L(0,2��) = L(k,2��+k)
�����ɁA
L(b,c) = ��(b,c) ��{(dx/d��)^2 + (dy/d��)^2} d��
�@= 4a��(b,c) (1/2)sin(��/2) d��
�@= 4a [ -cos(��/2) ](b,c)
�@= 4a{cos(b/2) - cos(c/2)}, >>113
�S�̐� V= lim{ �� �� y² ��x }
�@= ��[��=0,��]d�� �� (r*sin��)² * -d(r*cos��)/d��
�@= �� ��[��=0,��]d�� (1+c)² s² (s + 2cs)
�@= �� ��[��=0,��]d�� (1+c)²(1+2c)(1-c²) s
�@= �� ��[c=-1,+1]dc (1+2c+c²)(1+2c)(1-c²)
�@= �� ��[c=-1,+1]dc (1+5c²)(1-c²)�@{����̋��}
�@= �� ��[c=-1,+1]dc (1+4c²-5c⁴)
�@= �� (2+8/3-10/5) = 8��/3
[��=0,��]�ő̐ϔ����ɂȂ�Ƃ��� ��=cos�� �ƒu��
4/3 = ��[c=��,+1]dc (1+2c+c²)(1+2c)(1-c²)
�@= ��⁶/3 +��⁵ +��⁴/2 -4��³/3 -2��² -�� +5/2
��⁶/3 +��⁵ +��⁴/2 -4��³/3 -2��² -�� +7/6 = 0 �� [0,1] �͈͂ʼn���
���l�v�Z��: �� = 0.51987146393... �@{ ���Ԃ���(������, ������? )�͏o���Ȃ� }
a = r*cos�� = (1+��)�� = 0.79013780294... >>118
�J�[�W�I�C�h�̑̐ς�8/3�Ȃ̂�
a��
31/12 - (1/2 (x + x^2 - (2 x^3)/3 + 1/6 (1 + 4 x)^(3/2))) = 4/3 �@, 0<x<2
�̉��܂ł͏o�������A���ꂪ�����Ȃ��̂�
Wolfram�ɂ��肢����
x��0.79013780294837779465���B f(x)=sin(x^100)��x=0�𒆐S�Ƀe�C���[�W�J����
������sinx�̃e�C���[�W�J�����m�Ƃ��ėp���Ă悢
�悤����ɍ������̃e�C���[�W�J���Ăǂ����������ł����H �Ȃ�ق�
F(x+t)=��F^(n)(x)t^n/n!
���g����2�ʂ��
h(x+t)=��F^(n)(x)t^n/n!
f(g(x+t))=f(��g^(k)(x)t^k/k!)=f(g(x)+T)=��f^(i)(g(x))T^i/i!
(T=��[k=1�`��]g^(k)(x)t^k/k!�Ƃ�����)
(T^i/i!=����(g^(k)(x)/k!)^(q_k)/(q_k)!�~t^(��k(q_k))(�����W�J))
�ƌv�Z���ė�����t^n�̌W��������ׂ銴����
���Rsin(x^100)���v�Z����̂ɂ͕K�v�Ȃ����ǂ� >>125
�͂��`���肪�Ƃ��������܂� >>126
�����ł���
�_���Ƃ��Ēm���Ă����A���ۂ̌v�Z�̓T�C�g�̍ŏ��̋L�q�ʂ�œ���Ȃ� >>118
���̐l�Ƃ̌��ʂ���v�����̂Ō��ʂɎ��M�����Ă܂����B
https://i.imgur.com/6nHgxU3.png
�`����a��0.5�`1.5�̊Ԃł��낤�Ǝv����
�����e�J�����ŏo�����O���t
https://i.imgur.com/zQzcoPJ.png
�V�~�����[�V�����ƈ�v����ƋC���������B ������{a[n]}��n������a[n]��0�ł���B
���̂Ƃ�lim[n����] (n^p)*a[n]��0�łȂ��萔�Ɏ�������悤�ȗL����p�́A���݂��Ă����X1�ł��邱�Ƃ��ؖ�����B >>131
�L����p,q�ɂ��� lim[n����] (n^p)*a[n]=s��0 , lim[n����] (n^q)*a[n]=t��0�Ƃ���B
lim[n����] {(n^p)*a[n]}/{(n^q)*a[n]}=s/t �ł��邩�� lim[n����] n^(p-q)=s/t
���������� p=q ���� s=t �ł���B 1/(2+cosx)�̌��n���́H
�P���Ȃ̂ɂ��낢�����Ăł��Ȃ�����wolfram�搶�ɕ������炦�����������o���Ă�����ł����ǁA�Ȃ�Ƃ��ȒP�ɉ������@�Ȃ���ł����ˁc >>133
dx/(2+cosx)
=2dt/(3+t^2)
=(2/��3)arctan(t/��3)
=(2/��3)arctan((1/��3)tan(x/2)) >>135
����ς�u���͕K�{�ɂȂ銴���ł����� 0�`9�������ꂽ�J�[�h�����Ƀ����_���ɕ���ł���
�������牽�����J�[�h���A�c�����J�[�h�̊Ԃɏ�肭�}�����邱�Ƃ�0�`9��9�`0�̏��ɕ��ג������Ƃ��l����
�Ⴆ��2,8,9,6,5,3,4,1,0,7�̏�ԂȂ�2,9,4,7��4�����A
�c����8,6,5,3,1,0�̊Ԃɓ�����9,8,7,6,5,4,3,2,1,0�ɏo����
�ǂ�ȕ��тł�8���ȏ㔲���K�v���Ȃ����Ƃ͂����킩��
7�������K�v��������т͑��݂��邩�H f(x) =��y �O�����z (1−t�O2)e�O(−t�O2)dt (x ��R).
���̂Ƃ�
(1) lim�yx��+���zf(x), lim�yx��−���zf(x) �����߂�.
(2) y = f(x)�̋ɒl�ƕϋȓ_�����߂�
E[n] = ��[0��+��] (t^n)e^(-t^2) dt �ƒu���āA�����ϕ�
E[n] = [ { t^(n+1)/(n+1) }e^(-t^2) ]_(0��+��) - ��[0��+��] { t^(n+1)/(n+1) }e^(-t^2)�E(-2t) dt
= { 0 - 0 } + { 2/(n+1) }��[0��+��] t^(n+2) e^(-t^2) dt
= { 2/(n+1) } E[n+2].
����āA
E[2] = (1/2) E[0] = ���/4,
lim[x��+��] f(x) = E[0] - E[2] = ���/4,
lim[x��-��] f(x) = ��[0��-��] (1 - t^2)e^(-t^2) dt = ��[0��+��] (1 - u^2)e^(-u^2) (-du)�@�G t = -u
= - ��[0��+��] (1 - u^2)e^(-u^2) du = ���/4.
���̂悤�Ȃ����ł�����ꍇ�����̂����}�P�A�}��Q�̂Ƃ��͂ǂ������
���߂܂��� 2^n + 3^m = (n-m)!
�������R���̑g(n,m)�͑��݂��邩�B
������n>m�Ƃ���B >>139
>>140 �̒ʂ�
2^n+3^m�͊�Ȃ̂�(�����Ɗ�̉��Z�Ȃ̂œ��R)�An-m��2�ȏ�̂Ƃ����炩�ɖ������Ȃ�(�K��ɕK��2���܂ނ���)
n-m=1�̂Ƃ�2^n+3^m��1�ɂȂ�(n,m)�͑��݂����������Ȃ�
����đ��݂��Ȃ� >>137
�ǂ�����4���̑g�͕K�����Ă��邩
���A3���Ȃ�o���邯��... >>123
�J�[�W�I�C�h�̑S�̐ς������e�J�����ł���Ă݂��B
> IO <- function(N=1e7){
+ x=runif(N,-0.25,2)
+ y=runif(N,-1.3,1.3)
+ z=runif(N,-1.3,1.3)
+ v=diff(range(x))*diff(range(y))*diff(range(z))
+ v*mean(
+ (x>=0 & z^2+y^2 < 1/2*( sqrt(4*x + 1) + 2*x + 1 - 2*x^2))
+ |
+ (x<0 & (z^2+y^2 < 1/2*( sqrt(4*x + 1) + 2*x + 1 - 2*x^2)) &
+ (z^2+y^2 > 1/2*(-sqrt(4*x + 1) + 2*x + 1 - 2*x^2)))
+ )
+ }
> IO() ; 8/3*pi
[1] 8.375686
[1] 8.37758
N=1000�}���R�ł�������A���Ƌߎ����Ă���B b,c�͎����̒萔�Ƃ���B
������C:y=x^2+bx+c��x���Ƒ��قȂ�2�_P,Q�Ō����B
�܂�C��y���Ƃ̌�_��R�A3�_P,Q,R��ʂ�~��K�Ƃ���B
���̂Ƃ��AK��b,c�ɂ��Ȃ���_��ʂ邱�Ƃ������B c = 0 �̏ꍇ���l������Ă��Ȃ��͖̂��Ƃ��Ă������� �Ă�b,c���萔�Ȃ�P,Q,R�͒�_��K�͒�~��� >>147
R �� P, Q �ƈقȂ�Ƃ͏����Ă��Ȃ������
�i���Z���X�Ȏ�����̏L�������� �Q�̉�����,���Ƃ����
(��,0)(��,0)(0,����)��3�_��ʂ�~�ł���
���̉~�̕����������߂��
x(x-(��+��))+y(y-(����+1))+����=0
�ł���
���̉~�͕K���_(0,1)��ʂ� y=(x-p)(x-q)
(x-p)(x-q)+y^2=ky
pq+(pq)^2=kpq
k=pq+1
(x-p)(x-q)+y^2=(pq+1)y
-(x-q)=qy
-(x-p)=py
(x,y)=(0,1) �Ă��A�}�`�I�ɕ����邩
S=(0,1)�Ƃ����OPS��ORQ�������ɂȂ邩��
OPQR�͌����������p��180�x�ł��蓯�~��ɂ��� >>136
�K�{�ł��Ȃ������
1/(2+cos(x)) = (2-cos(x))/(4-cos(x)^2)
�@= 2/(3cos(x)^2 + 4sin(x)^2) - cos(x)/(3+sin(x)^2)
�@= 2/{1+(4/3)tan(x)^2}/(3cos(x)^2) - cos(x)/(3+sin(x)^2)
���
��1/(2+cos(x)) dx = (1/��3)arctan((2/��3)tan(x))
�@- (1/��3)arctan((1/��3)sin(x)),
�@= (2/��3)arctan((1/��3)tan(x/2),�@�@�@>>135 >>150
������b,c�͒萔���ď����Ă���̂ɁAb�Ac�ɂ�炸���Ă̂�����������������
�킩���́H ��1/(2+cos(x)) dx
�@= (1/��3) arctan((2/��3)tan(x)) - (1/��3) arctan((1/��3)sin(x))
�@= (1/��3) arctan((��3)sin(x)/(1+2cos(x)))
�@= (2/��3) arctan((1/��3)tan(x/2), >>156
��w�����̖�蕶�Ȃ�Ă��������Ȃ���X�� �S���S���̑�C�S��́A�ꔭ�K���̑�C���ɕC�G����B
������ؖ����Ă��������B >>145
��ӂ�� y=x²+bx+c = (x-��)(x-��) �@( ��,����R, ������ ) �Ƃ��Ă悢�B
{ b,c�����R�ɓ�����̂͏d��������2��������͈͂łƂ��������낤 }
�~���S��x���W�͎����Ȃ̂�
�@�~K:�@(x - (��+��)/2)² + (y - y₀)² = r²�@(���m��: y₀, r )
3�_�ʉߏ������
�E((��-��)/2)² + y₀² = r²
�E((��+��)/2)² + (���� - y₀)² = r²
������ y₀ = (���� + 1)/2, r²=(��²+��² +��²��² +1)/4
2�ϐ�������: f(��,��) := (x - (��+��)/2)² + (y - y₀)² - r² �@{x,y�͒萔}
�@= (x - (��+��)/2)² + (y-���� + ����-y₀)² - r²
�@= x² -(��+��)x + (y-����)² + (y-����)(���� - 1) + 0
�@= x²+y²-y -x (��+��) +(1-y) ����
f(��,��) ���P���I��0�ƂȂ�̂�
(x,y) = (0,1) �̎��݂̂ł���B
�܂� �~K �͏�� �_ (0,1) ��ʂ�B���̂悤�ȓ_�͑��ɂȂ��B ��肶��Ȃ���ł�����
���f�����s��@O(n,C)
��
���j�^���s��@U(n)
���ĉ����Ⴄ��ł����H (1/��2) * {{1, i}, {i, 1}}�̓��j�^���s��ł��邪�A���f�����s��ł͂Ȃ��B >>165
��������邩���Ȃ������Ęb�ł����� �����s��T��
�@T T^t = E�@�@�@(t �͓]�u)
���j�^���[�s��U��
�@U U�� = E�@�@�@�@(�� �͕��f���b&�]�u)
�������s��@O(n,R) �� U(n)
[ ��2, i ]
[ -i, ��2 ]
�͒����s���A���j�^���[�ł͂Ȃ��B >>137
https://mathtrain.jp/szekeres ���
�@Erdos-Szekeres�̒藝�Fa,b �𐳂̐����Ƃ���B�e�������قȂ钷�� ab+1 �̐�����Ƃ��C�ȉ��̓�̂������Ȃ��Ƃ���͕K�����݂���B
�@1�F���� a+1 �̕�����ŁC�P�������Ȃ���
�@2�F���� b+1 �̕�����ŁC�P�������Ȃ���
a=b=3 �Ƃ��邱�ƂŁA�e�������قȂ钷��10�̐���ɂ͒���4�̒P�������܂��͒P�������ȕ������݂��邱�Ƃ�������
����āA7�������K�v��������т͑��݂��Ȃ� >>169
���w�Ȃ̕��ł����H
�ǂ����Ă��������T�C�g�ɍs���������̂������Ă��������B >>169
���肪�Ƃ��������܂��I
�m���Ɍ������@���C�ɂȂ�܂� >>170
�u����������v�ŃO�O���� BC=a,CA=b,AB=c�́�ABC�̓����ɁA2�̉~C��D���ȉ��̂悤�ɒu���B
C��D�̖ʐς����߂�B
�EC�͕�AB,BC�ɐڂ���
�ED�͕�BC,CA�ɐڂ���
�EC��D�͊O�ڂ���
�EC�̖ʐς�D�̖ʐς̘a�́A�\��C��D�̔z�u�̒��ōŏ��ƂȂ� �����܂ł͂ł������ǁA
https://i.imgur.com/yZAuaWn.png
a,b,c�����l�ŗ^�����Ă��Ȃ�����A���Ƃ͂ǂ��������邩���ȁB ���w�͉�́E�E�㐔��3����ɕ��ނ����ƕ����܂����A
�W���_�͂ǂ̕���ɂȂ�̂ł��傤���H https://youtube.com/watch?v=fK_JGVti5y8
��L����̐��w�̐��E�n�}�Ŋe����ɂ��Đ������Ă� >>179�̐������݂����
���`�㐔���㐔
�����ϕ������
�͓�����O������A�w�̑��ɏW���E�ʑ�������Ƃ������Ƃ�
�w�̕���ƍl���Ă�����ł����� ����Ō�܂ł݂Ă���W���_�͊�b�_���Č����Ă܂���
���݂܂��� ������Ȃ��̂ŋ����Ă������������ł��I
0�ł͖����������A���ɑ��Ċ�1/((x-��)(x-��))���ׂ������ɓW�J����B�܂��A����ꂽ�ׂ������̎������a�����߂�B
���˂������܂��I >>182
(1/(x-��))(1/(x-��)) >>184
�R�[�V�[�ώ��Ƃ������Ƃ��낤
�킩��Ȃ������� �u�\�ʂɌ����ЂƂĂ���g�[���X�v�ƈʑ����^�Ȑ}�`���ĂȂ�ł����H �ǂ�ȓ��������߂Ă邩�����Ă͌����邪������������ɂ���Ȃ��ĂȂ���ww >>182
�����������������āA1/(1-x) = 1 + x + x^2 + ... ���g��
>>188
�_A�̒���OC�Ɋւ��đΏ̂ȓ_��A'�Ƃ���ƁA
��OBA'���O�p�`�A��BAA'�߁�BAC�A��CAA'���O�p�`���킩�� �X���`�������炷�܂�
In=��(0��1) x^n/(1+x) dx �Ƃ�����
In=-In-1 +1/n �ƂȂ邱�Ƃ��������Ė�肪�����Ȃ�
�F�X�����ϕ����Ă݂����ǂ��܂�In�ŕ\���Ȃ����ǂǂ���������̂ł��傤 x^n/(1+x) = x^(n-1) - x^(n-1)/(1+x) >>190
Wolfram��搶�ɂ��ƁA�������̊���Z������Ɨǂ��炵��
1/(x+1)
x/(x+1) = 1 - 1/(x+1)
x^2/(x+1) = x - 1 + 1/(x+1)
�c �r�����M���Ă��܂���
In=-In-1 +1/n
�̂������ɂ�������ǂ������Ă��炢������ >>192
���߂�ǂ��������Ƃ����܂����킩���c
����͂��Ȃ��Đ\����Ȃ� ��(0��1)(|log(x)|^(3/2))/��x
���̐ϕ��̉����������Ă��������B�L�`�ϕ��ł��B >>195
�A�[�@�ň�ʍ����ؖ�����Ηǂ� >>196
x = e^(-2t)�@�Ƃ�����
��(0��1)(|log(x)|^(3/2))/��x dx
= 2��(0����) (2t)^(3/2) e^(-t) dt
= 4(��2)��(0����) t^(3/2) e^(-t) dt
= 4(��2)��(5/2)
= 4(��2)(3/2)(1/2)��(1/2)
= 3(��2)(���)
= 3��(2��)
= 7.519884824 >>182
�@1/(��-x) = (1/��){1 + (x/��) + (x/��)^2 + (x/��)^3 + ���� },
�@1/(��-x) = (1/��){1 + (x/��) + (x/��)^2 + (x/��)^3 + ���� },
���
�@(1/����){1 + (1/�� + 1/��)x + (1/��^2 +1/(����) +1/��^2)x^2
�@�@�@�@+(1/��^3 + 1/(������) + 1/(������) + 1/��^3)x^3 + ����}
�@= (1/����)��[k=0,��] (��[i+j=k] 1/(��^i���^j)) x^k, �E������ �̂Ƃ�
�@��[k=0,��] (1/��^{k+1} - 1/��^{k+1})/(��-��)�Ex^k,
�E��=���̂Ƃ�
�@(1/��^2)��[k=0,��] (k+1)(x/��)^k, >>182
���ƃ����ɂ�����A�������a�͋߂����܂ł̋����B
�@�������a = min{|��|, |��|} ��ABC�̊O���Ɂ�PBC���A��ABC�䁢PCB�ƂȂ�悤�ɍ��B
BC=1,AB=b,AC=c�̂Ƃ��A��i��ABC�̖ʐ�:AP^2�j�����߂�B p:=AP�AS:=��ABC�As=(a+b+c)/2
S=��s(s-a)(s-b)(s-c)
|p|^2=a^2+b^2+(a^2+b^2-c^2) >>188 �� ��͊I�ɉ������Ƃ��ċC�Â�����ł����A
�@ c = cos(20��)
�@16*c^4 -8*c^3 -12*c^2 + 4*c + 1 = 0
�����藧�݂����ł��B���̊W���ǂ��������ؖ��ł��܂����H
4�{�p�����Ƃ��S�R�Ⴄ�� cos(80��) �ɂȂ���������ĉ����ȒP�ɂȂ�Ȃ���... ��ӂ̒�����2��3�ł��鐳�O�p�`T�̊O�S��O�Ƃ���B
�܂��AO�𒆐S�Ƃ��锼�ar�̉~���ŁAT�̎��܂��͓����Ɋ܂܂����̂̒�����L(r)�Ƃ���B
0<r<3�͈̔͂�L(r)�������\�ł��邩�ׂ�B >>188
��OBC���ӎO�p�`����Ȃ���
20����16���A80����82���ɂ���ƎO�p���Ȃ��ł͉��������ɂȂ��ȁB ���S�����𗝑z�Ƃ���
�P�O���b�g���̗e��Ɂ@�P���b�g���^���ԁ@����Ă��������Ɂ@�P���b�g���^���ԁ@�r�o����Ă���
�e��̔Z�x���T�O���̂Ƃ����Ԃ��Ƃ̔Z�x���ڂ�ϕ��Ŏ����Ȃ������Č�����肪�킩��܂��� >>210
�ǂ���̉t�̂������ł���
����ĉ����Z�x�͏��0�ł��邩��
�ϕ���p���ĕ\����
��[0,T] (t-t)exp(-t) dt
�ƂȂ� >>209
�����������l�Ȃ牽�炩�̕��@�͂��邩���m��Ȃ����ǂ�
�����O���[�̖��Ƃ��Ǝ��Ă� ���������̖������ł���Ⴂ�Ȃ炷�܂B
��`abcd�ɂ�����
ad//bc,�@ab=4,�@ad=5,�@bc=11
�ł���Aa��ʂ�abcd�̖ʐς��ɂ��钼��������bc�Ƃ̌�_��e�Ƃ���B���̂Ƃ��Abe�̒��������Ƃ߂�B
https://f.easyuploader.app/eu-prd/upload/20200810112911_724b614e41774b753258.png >>213
(11+5)/2=8
AB=4�͕K�v�̖������� >>208
0<r<1 �� L(r)=2��r , L'(r)=2��
1<r<2 �� L(r)={2��-6arccos(1/r)}r , L'(r)=2��-6arccos(1/r)-6r/{r(��r^2-1)}
2<r<3 �� L(r)=0 , L'(r)=0
r=1 , r=2 �ł͔����\�łȂ��B >>213
������h�ABE��x�Ƃ�����
(5+11)*h/2 = x*h/2 * 2
(8-x)h = 0
h>0���x = 8
���w�������Ƃ��ɂ��肻�� https://imgur.com/Gs95gDh.jpg
��̃J�b�g�Z�b�g�̓�̒�`�������ł��邱�Ƃ̏ؖ��������ĉ������B e_1, �c, e_n���J�b�g�Z�b�g�Ƃ���Be_1�ȊO�̂��ׂẴJ�b�g�Z�b�g�̕ӂ���������B�J�b�g�Z�b�g�̒�`���珜����̃O���t���A���ł���B
e_1 = (v_1, v_2)�Ƃ���Bv_1����e_1�𗘗p���邱�ƂȂ����B�\�ȓ_�̏W����V_1�Ƃ���Bv_2����e_1�𗘗p���邱�ƂȂ����B�\�ȓ_�̏W����V_2�Ƃ���B
V_1��V_2�����ԕӑS�̂̏W����{e_1, �c, e_n}�Ɉ�v����B
�݂����Ȋ����ŏؖ���������̂��Ɛ������܂��B >>216
�����S�R���Ⴂ�Ō����Ⴂ�̎�����Ă���
���肪�Ƃ��X�b�L������ >>214
�O�p�`�̍��������Ƃ��Ėʐς̌����ɂ��ꂽ��AB�̒����͌v�Z�ɖ��W�ƋC�Â����ǁA
AB=4�̑���Ɂ�DCE=120���Ƃ�������Ă�����A�������肻��ɋC������Ă��܂��Ȃ��B >>211
�������������ɐi�߂Ȃ���
����t�̂Ƃ�
w(t):�n�}
s(t):�n��
c(t):�Z�x
�Ƃ����
w(0)=5
s(0)=5
c(0)=s(0)/(w(0)+s(0))
c(t)=s(t)/(w(t)+s(t))
w(t+dt)=w(t)+dt
s(t+dt)=s(t)-c(t)*(w(t)+s(t))*dt e_1 = {v_1, v_2}, e_2 = {v_3, v_4}, �c, e_i = {v_{2*i-1}, v_{2*i}}, �c, e_n = {v_{2*n-1}, v_{2*n}}���O���tG = (V, E)�̃J�b�g�Z�b�g�Ƃ���B
e_1�ȊO�̂��ׂẴJ�b�g�Z�b�g�̕ӂ�G���珜�������O���t��G'�Ƃ���B�J�b�g�Z�b�g�̒�`����G'���A���ł���B
G'���v_1����e_1�𗘗p���邱�ƂȂ����B�\�ȓ_�̏W����V_1�Ƃ���BG'���v_2����e_1�𗘗p���邱�ƂȂ����B�\�ȓ_�̏W����V_2�Ƃ���B
V_1 �� V_2 �� ��W�����Ɖ��肷��Bv �� V_1 �� V_2�ƂȂ�_v�����݂���Bv_1����e_1�𗘗p���邱�ƂȂ�v�ɓ��B�\�ł���A
v_2����e_1�𗘗p���邱�ƂȂ�v�ɓ��B�\�ł���B��v_1����e_1�𗘗p���邱�ƂȂ�v_2�ɓ��B�\�ł���B���̂��Ƃ���AG'����
�����e_1���������Ă��O���t�͘A���ł��邪�A�����e_1, �c, e_n���J�b�g�Z�b�g�ł���Ƃ������ƂƖ�������B
����āAV_1 �� V_2 = ��W���ł���B
���ɁAe_1, �c, e_n�͂��ׂ�V_1�̓_��V_2�̓_�����ԕӂł��邱�Ƃ��m�F����B
e_1�͂�������ł���Be_i�i2 �� i �� n�j��V_j�ij = 1 or j = 2�j��2�_�����ԕӂł���Ɖ��肷��B
G'����e_1���������Ae_i��t���������O���t��G''�Ƃ���B�J�b�g�Z�b�g�̒�`����G''�͘A���ł���B
�_v_1�Ɠ_v_2������G''��̃p�XP�����݂���B���̃p�X��e_i���܂܂Ȃ���Ȃ�Ȃ��B����e_i���܂܂Ȃ��Ƃ���ƁA
G'���e_1���܂܂Ȃ�v_1����v_2�ւ̃p�X�����݂��邱�ƂɂȂ��Ă��܂��AV_1 �� V_2 = ��W���ł���Ƃ�����Ŏ��������ʂƖ������Ă��܂��B
�Ƃ��낪�Ae_i�̒[�_��V_j�̓_�ł��邩��A�ǂ���̒[�_��G'���v_j����e_1�𗘗p�����ɓ��B�\�ł���B����āAe_i�̒[�_������e_1�𗘗p���Ȃ�G'��̃p�X�����݂���B
P�Ɋ܂܂��e_i���폜������ɂ��̃p�X�𗘗p����ƁAv_1��v_2������e_1�𗘗p���Ȃ�G'��̃p�X�������邪����́AV_1 �� V_2 = ��W���Ƃ�����Ŏ��������ʂƖ�������B
����āAe_i�i2 �� i �� n�j��V_j�ij = 1 or j = 2�j��2�_�����ԕӂł͂Ȃ��B�����e_1, �c, e_n�͂��ׂ�V_1�̓_��V_2�̓_�����ԕӂł��邱�Ƃ��m�F�ł����B V_1��V_2�̓_������G�̕ӂ�e_1, �c, e_n�ȊO�ɂ͂Ȃ����Ƃ����Ɏ����B���ɁAV_1��V_2�̓_�����Ԃ悤��e_1, �c, e_n�ȊO��G�̕�e = {w_1, w_2}�iw_1��V_1, w_2��V_2�j�����݂����Ƃ���B
G'����e_1�����������O���t��G'''�Ƃ���BG'''�̓J�b�g�Z�b�g�̒�`�����A���ł���Bu, v��G'''�̔C�ӂ�2�_�Ƃ���B
u��V_1, v��V_1�̏ꍇ�Av_1����u�ւ�G'''��̃p�X�����v_1����v�ւ�G'''��̃p�X�����݂��邩��Au����v�ւ�G'''��̃p�X�����݂���B
u��V_2, v��V_2�̏ꍇ�A��̓��l�ɂ��āAu����v�ւ�G'''��̃p�X�����݂���B
u��V_1, v��V_2�̏ꍇ�Av_1����u�ւ�G'''��̃p�X�����v_2����v�ւ�G'''��̃p�X�����݂���B
w_1��V_1, w_2��V_2������v_1����w_1�ւ�G'''��̃p�X�����v_2����w_2�ւ�G'''��̃p�X�����݂���B
�䂦�ɁAu����v�ւ�G'''��̃p�X�����݂���B
�䂦�ɁAG'''�͘A���ł��邪�A����͖����ł���B
�䂦�ɁAV_1��V_2�̓_�����ԕӂ̏W���́AG�̃J�b�g�Z�b�g�Ƃ��傤�Lj�v����B (V_1, V_1��V_1������G�̕ӂ̏W��)�͂������A���ł���B(V_2, V_2��V_2������G�̕ӂ̏W��)�͂������A���ł���B �t�͖��炩������A��̒�`�͓����ł���B �O>>72
>>173
�w�����̌������s=(a+b+c)/2
��ABC=��s(s-a)(s-b)(s-c)
�܂�C,D���Ȃ�ׂ��������Ȃ�悤��C=D=��r^2=E�Ȃ锼�ar�̓��ډ~E������1�`����B
��ABC=(a-2r)(r/2)+(b-2r)(r/2)+(c-2r)(r/2)+r^2��3+3�~2r�~r
=(a+b+c)r/2+(3+��3)r^2
�w�����̌�������s�������ā�ABC=(1/2)^2��(a+b+c)(b+c-a)(c+a-b)(a+b-c)
=(1/2)^2�o2(a+b+c)r+4(3+��3)r^2�p
������4(3+��3)r^2+2(a+b+c)r-��(a+b+c)(b+c-a)(c+a-b)(a+b-c)=0�������ƁA
r=�o-(a+b+c)+��(a+b+c)^2+4(3+��3)��(a+b+c)(b+c-a)(c+a-b)(a+b-c)�p/4(3+��3)
�ŏ��lC=D=��r^2=��(2-��3)�o(a+b+c)^2+2(3+��3)��(a+b+c)(b+c-a)(c+a-b)(a+b-c)-(a+b+c)��(a+b+c)^2+4(3+��3)��(a+b+c)(b+c-a)(c+a-b)(a+b-c)�p/48 E={(x,y);0��x, 0��y, 1��xy��2, -2��y-x^2��2}�Ƃ���Ƃ�
���_E (1/x)+2(x/y) dxdy �̒l�����߂Ă�������
�ϐ��ϊ����ȁH�Ǝv�����̂ł����Ȃ��Ȃ���肭������
���ۂɐϕ��͈͂����߂悤�ɂ�3�����������o�Ă��Ēl���Y��ɋ��܂�Ȃ�����ł�
����������肢���܂� >>226
���O�p�`�Ȃ�A�ŏ��lC=D�ƂȂ邯�ǁA����ȊO���ƈႤ��Ȃ��H >>207 ���ȉ����B
�������̈���������3�{�p�����ł����܂����B
c = cos20��
16*c^4 -8*c^3 -12*c^2 + 4*c + 1
�@= (8*c^3 - 6*c - 1)(2*c - 1)
�@= ( 2*(4*x^3 - 3*x) - 1 )(2*c - 1)
�@= ( 2 cos60�� - 1 )(2*c - 1)
�@= ( 2 * 1/2 - 1 )(2*c - 1) = 0
���ł� >>188 �̉�͊I�ȉ�@
OC = 2 * OB * cos40��
OA = OB
�]���藝���
AC^2 = OA^2 + OC^2 - 2 OA*OC * cos20��
�@= OB^2 * ( 1 + 4*(cos40��)^2 -4*cos40��cos20�� )
�@= OB^2 * ( 1 + 4*(2*c^2-1)^2 -4*(2*c^2-1)*c )
�@= OB^2 * ( 16*c^4 - 8*c^3 - 16*c^2 + 4*c + 5 )
�@= OB^2 * ( 16*c^4-8*c^3-12*c^2+4*c+1 + 4*(1-c^2) )
�@= OB^2 * ( 4*(1-c^2) ) = OB^2 * 4 * (sin20��)^2
(c = cos20��)
�����藝���
sin��OCA / OA = sin20�� / AC
�@sin��OCA = sin20�� / 2sin20�� = 1/2
�@�� ��OCA = 30��
x = ��ACB = ��OCB - ��OCA = 40�� - 30�� = 10�� �����Ȃ�ƃv���O�����ō�}���Čv�Z�������������Ǝv���B
X�̊p�x�́H�i���̂ł͂Ȃ��ĕ��ʐ}�j
https://i.imgur.com/yNDUuDU.png ���K���z�\�݂̂������킩��܂���
�@�����w�̊w���̑̏d X �����K���z N (70,2�O2) �ɏ]���Ƃ��C�̏d�� 75 kg �ȉ��ł���m�������ߕ����킩��܂��� > pnorm(75,m=70,sd=2,lower.tail=TRUE)
[1] 0.9937903
> # ����0�A�W����0�̐��K���z�ɕW��������Ȃ�A(75-����)/�W���� =2.5
> (75-70)/2
[1] 2.5
> pnorm(2.5,m=0,sd=1,lower.tail=TRUE)
[1] 0.9937903
> >>188
��OAB���ɁA��ABD�����O�p�`�ɂȂ�悤��D��݂���ƁA
��DAO�߁�DBO�߁�ABC�ł��邱�Ƃ���A�����܂��Ax=10�������܂� 4 ��@�Ƃ��� 3 �ɍ����ȑf����
1 �ɍ����Ȃ��̂����������ˁH ��(z)���W�����K���z�̕��z��������킷�Ƃ�
��(1.27) �A ��(�|2.17) �̏ꍇ�͒l���ǂ����Ƃ߂܂���
�܂���(z)=0 .99224 �Ƃ����ꍇ�͂��͂����ɂȂ�܂��� >>233
�������ӂ�����̂ł���?
����͕̂W�����K���z�ł� >>235
�Z�p�����̑f���藝�ɂ��Γ������炢 >>237
���͓����B
�\�t�g�E�F�A���Ɠ����ŕW�������Čv�Z���Ă����B
���K���z�\�ł݂�Ȃ玩���ŕW�����B �O>>226
>>228
C��D���������Ȃ����肿�����Ȃ����肷����A
C=D���ŏ��ł�������Ȃ����B
��ABC���ǂ�ȎO�p�`���͐��w�I�Ɍ����Ă킩��Ȃ��B >>236
> # �ӂ͗ݐϕ��z��(��(z)�͊m�����x����-������z�܂Őϕ������l)=pnorm(z)
> �� <- function(z) integrate(function(x) 1/sqrt(2*pi)*exp(-x^2/2),-Inf,z)$value
> ��(1.27) ; pnorm(1.27)
[1] 0.8979577
[1] 0.8979577
> ��(-2.17) ; pnorm(-2.17)
[1] 0.01500342
[1] 0.01500342
> # �ӂ̋t����qnorm
> qnorm(0.99224)
[1] 2.420012 �W�����K���z�̏㑤 1.7% �_�͂��̒��łǂ�ł���
(1) 0.017, (2) 0.102, (3) 0.983, (4) 1.27, (�T)2.12 ���̃f�[�^��
7.5, 5.5, 4, 7, 8.5, 5, 9, 9.5
�f�[�^�͐��K���z�ɏ]���Ƃ���D���̂Ƃ��C�ȉ��̖₢�ɓ�����
1. �W�{���� x �̒l���ȉ��̒�����I������
(1) 1.870829, (2) 2, (3) 3.5, (4) 4, (5) 7
2. �i�s�j�W�{���U s2 �̒l���ȉ��̒�����I������
(1) 1.870829, (2) 2, (3) 3.5, (4) 4, (5) 7
3. �i�s�j�W�{�W���� s �̒l���ȉ��̒�����I������
(1) 1.870829, (2) 2, (3) 3.5, (4) 4, (5) 7
4. ���R�x 7 �̃e�B�[���z�̗��� 0.1 �_ t7 (0.1) �̒l���ȉ��̒�����I������
(1) 1.8595, (2) 1.8946, (3) 2.3060, (4) 2.3646, (5) 3.4995
5. �ꕽ�� µ �� 90% �M����Ԃ����ȉ��̒�����I������
(1) [5.685135,8.314865], (2) [5.660315,8.339685], (3) [5.369412,8.630588],
�P�A�Q�A�R�͂V�A�S�A�Q�ɂȂ�܂����������Ȃ������̂Ŏ��M�Ȃ��ł� >>235
>>238
�`�F�r�V�F�t�̕���Ă̂�����炵���� ����H��Ő��Y����鐸�����i�� 25 ����ג��o���Ē����𑪂�����C���ϒl x �� x = 30 (mm) �ł������D�ߋ��̐����f�[�^�̒~�ςɂ��, ���i�̒����͕W������ 4 mm�̐��K���z�� �]�����Ƃ��������Ă���D
���o���ꂽ 25 �̐��i�ɑ��āC�ȉ��̖₢�ɓ�����
1. �ꕽ�� µ �� 95% �M����Ԃ����Ƃ߂�
2. �ꕽ�� µ �� 95% �M����Ԃ̋�Ԃ̕������Ƃ߂�
3. ��Ԃ̕��� 2.0=2�~1.0 �ȉ��Ƃ������D���Ȃ��Ƃ����̕W�{���K�v�� >>246
> 30+qnorm(.975)*4/sqrt(25)
[1] 31.56797
> 30-qnorm(.975)*4/sqrt(25)
[1] 28.43203
> 2*qnorm(.975)*4/sqrt(25)
[1] 3.135942
> # 2*qnorm(.975)*4/sqrt(n)<2
> # n >
> (qnorm(.975)*4)^2
[1] 61.46334 >>243
> qnorm(1-1.7/100)
[1] 2.120072 >>234
��OBC���ӎO�p�`�ɂȂ�悤�ɖ�肪�ݒ肳��Ă��邩��\�ȋZ���ȁB ���K���z����-�����灇�܂ł��邩��
����ɏ]�����Č����I�ł͂Ȃ��ˁB >>245
�ց[�m��Ȃ�����
�������]�Ȃق��ɕ�̂� >�����̐��w�҂̓w�͂��o�āARubinstein��Sarnak�ɂ���ă�(x;3,2)>��(x;3,1)��99.9%��x�ɑ��Đ��藧���Ƃ�1994�N�ɏؖ�����Ă��܂��B
>100%�łȂ����Ƃ͐^�ɋ����ׂ����Ƃł����āA�s�����̌������t�]����悤�Ȑ���x�������ɑ��݂��邱�Ƃ܂Ŏ�����Ă���̂ł��I�I�I
integers�u���O 2���琔����i�Ԗڂ̑f����p[i]�Ƃ��A2=p[1]����p[n]�܂ł̐�p[1]p[2]...p[n]=P[n]�ƒ�߂�B
�܂����R��k���^����ꂽ�Ƃ��A
e[k] = |f(k)/P[k] - 1|
�ƒ�߂�B
������f(k)�͂��鎩�R��m��p����f(k)=m^2�ƕ\����鎩�R���ł���A���Ae[k]���ŏ��Ƃ�����̂ł���B
���̂Ƃ��A�ȉ��̖��肪�^�ł��邱�Ƃ��ؖ�����B
�@
�wN���\���傫���Ƃ��A
��[k=1,...,N] e[k] < ��[k=N,...,2N-1] e[k]
�����藧�B�x >>188 , >>230
�ϐ�: �� = ��B/2,�@ �� = ��CAD �ł� ��ʉ�@( ��͊I��... )
AB = 1�@ (�p�x�̓X�P�[���s�ςȂ̂�)
��A = 90�� - ��/2 + ��
��C = 180�� - ��A - ��B = 90�� - 3��/2 - ��
BC = cos(2��)+sin(2��)cot(��C) = cos(2��)+sin(2��)tan(3��/2 +��)
CD = ��{ 1+BC^2 - 2*BC*cos(��) }
x = ��C - arcsin( sin(��)/CD )
�v���O������ (�D�݂̌���ɓǂݑւ��Ă�������)
calcX(a, b) = {
my(BC,CD,C,x);
a *= Pi/180;
b *= Pi/180;
C = Pi/2 - 3*a/2 - b;
BC = cos(2*a) + sin(2*a)/tan(C);
CD = sqrt( 1+BC^2 - 2*BC*cos(a) );
x = C - asin( sin(a)/CD );
return( x*180/Pi );
}
calcX(20, 20)
�� 9.9999999999999999999999999999999999999
calcX(18, 18)
�� 10.268038134266935017594064993971120014
�L���̂悢�g�ݍ��킹�́A�����Ƃ���Ȋ���
��,�@��,�@x
12, 18, 12
20, 20, 10
20, 30, 10
12, 42, 12
�ǂ�������I�ɉ�����̂�������Ȃ��B
 >>254
>>254
��͂�A�������ƂȂ�g�ݍ��킹�͂Q�O���̂Ƃ���������܂���ˁB >>254
���X���肪�Ƃ��������܂��B
���f���ʂɍ�}���ĕΊp�̍��Ōv�Z����a=b=18���ł̒l��
> (Arg(D-C)-Arg(A-C))*180/pi
[1] 10.268038134266938
�Ǝ����̃v���O�����̌��ʂƂ���v���܂����B r=4(1+cos��)�@(��/2���Ɓ�3/2��)�@���̋Ȑ��̒��������߂�@�ǂ�����ĉ���������ł���... >>258
�ɍ��W�̌ʒ��̌����g���������
���ꂪ�����ł���̂Ȃ�A�ɍ��W���璼�����W�ɒ���
r(1+cos��)��cos�Ƃ��������x���W�ɁAsin�Ƃ��������y���W�ɂȂ�
�����Œ������W�̌ʒ��̌����g������
�����g�������Ȃ̂ɉ��łł��Ȃ��H
���傷����w >>259
�����Ȃ��Ǝv���B
�C�ӂ̊�t���K�v�����B >>258
�����e�J�����@�ł���Ă݂���P�ɂȂ������ǂ����Ă�H
> # Monte Carlo
> N=1e7
> x=runif(N,-1,0)
> y=runif(N,-4,4)
> r=sqrt(x^2+y^2)
> theta=atan(y/x)
> s=diff(range(x))*diff(range(y))
> s*mean(r<4*(1+cos(theta)))/diff(range(y))
[1] 1 >>261
�ϕ�������A 16 (2-��2)�������ȁB ���݂܂�
����W�c�̐g���̕��ς�170cm,���U��64�ŁA���K���z�ɏ]���B
(a) ���̏W�c�̒����疳��ׂ�1�l���o�������A���̐l�̐g����182cm
�ȏ�ł���m���͂������B�����_�ȉ���4�ʂ܂œ�����B
(b) ���̏W�c�ɂ͐g����168cm �ȏ� 182cm�ȉ��̐l�͖�%���邩�B����
�_��1�ʂ܂œ����Ȃ����B
(C) �V���n�̂����蕨�͐g�������ȏ�łȂ��Ə��Ȃ��B���̏W�c��
98%�ȏオ����Ƃ��A�g�������͉�cm���B�����_�ȉ��͐�グ��
������B z�~��64)+170
(1) z��(180-170)/��64 �̖ʐς�ǂ�
(2) z��(168-170)/��64 �� z �� (182-170)/��64 �̖ʐς�ǂ�
(3) z��(x - 170)/��64 �̖ʐς�0.02�ƂȂ� x �����߂� >>258
(ds/d��)^2 = r^2 + (dr/d��)^2
�@= 16{(1+cos��)^2 +(sin��)^2}
�@= 32(1+cos��)
�@= 64{cos(��/2)}^2,
|ds/d��| = ��{r^2 + (dr/d��)^2}
�@= 8|cos(��/2)|,
L = ��[��/2, 3��/2] |ds/d��| d��
�@= 8��[��/2, 3��/2] |cos(��/2)| d��
�@= 16��[��/2, ��] cos(��/2) d��
�@= 16 [ 2sin(��/2) ](��/2, ��)
�@= 16(2-��2)�@�@�@�@>>262
�@= 9.372583�@�@�@�@>>263 >>264
R���g����Ȃ�
(a)pnorm(182,170,8,lower=FALSE)
(b)pnorm(182,170,8)-pnorm(168,170,8)
(c)qnorm(0.98,170,8,lower=FALSE) >>268
���������A������𗧂���g����悤�ɂȂ�Ƃ������B
>18�݂����ȗV�тɂ��g���Ċy�����B
�������x�ɓ���邯�ǁB �h����ۓ������Ă���悤�ȋC����������A�����ď����\�������Ƀ��X�����B 87 71
85 70 55
83 68 54 41
81 66 53 40 29
79 64 51 39 28 19
77 62 49 38 27 18 11
75 60 47 36 26 17 10 5
73 58 45 34 25 16�@9 4 1
�K��������������`(^_^)� >>210
10���Ԍ�̔Z�x����
50*(0.9^10)%�ł����̂��ȁH >>272 ��
n��1�`44�܂ŕω�������2n�|1�̏o�͂�
4�_�Ƃ��Ă��̎����1�����Ȑ���
���͂�ł��������̂��v���X��������
0 0
0 1 0
0 1 1 0
0 1 2 1 0
0 1 2 2 1 0
0 1 2 3 2 1 0
0 1 2 3 3 2 1 0
0 1 2 3 4 3 2 1 0
���̂悤�Ȑ����\��������
�m���Ă���l�͂��܂����H 2. ���� A �Ǝ��� B���N����m����P(A) = 0.6, P(B) = 0.7 �ł���B����
�t�m�� Pa(B) = 0.8�ł���Ƃ����BPb(A) �����߂�B
���� A �Ǝ��� B���N����m���� P(A) = 0.8, P(B) = 0.7 �ł���BP(A��B) = 0.94���킩���Ă���B���̂Ƃ����� A �Ǝ���B���Ɨ��ł��邩
�ۂ���������Ȃ����B
���������Ē�������K���ł� �O>>240
>>213
��abe=��`aecd������A
ad+ec=be���Ȃ킿5+3=8
be+ec=8+3=11
��be=8 �O>>240
>>213
��abe=��`aecd������A
ad+ec=be���Ȃ킿5+3=8
be+ec=8+3=11
��be=8 ����z�Ɋ܂܂��S���ܗL�� (%) �ׂ��Ƃ���C���̃f�[�^��
7.5, 5.5, 4, 7, 8.5, 5, 9, 9.5
�S���ܗL���͐��K���z�ɏ]���Ƃ���D���̂Ƃ��C�ȉ��̖₢�ɓ�����
1. �W�{���� x �̒l���ȉ��̒�����I������
(1) 1.870829, (2) 2, (3) 3.5, (4) 4, (5) 7
2. �i�s�j�W�{���U s2 �̒l���ȉ��̒�����I������
(1) 1.870829, (2) 2, (3) 3.5, (4) 4, (5) 7
3. �i�s�j�W�{�W���� s �̒l���ȉ��̒�����I������
(1) 1.870829, (2) 2, (3) 3.5, (4) 4, (5) 7
4. ���R�x 7 �̃e�B�[���z�̗��� 0.1 �_ t7 (0.1) �̒l���ȉ��̒�����I������
(1) 1.8595, (2) 1.8946, (3) 2.3060, (4) 2.3646, (5) 3.4995
5. �ꕽ�� µ �� 90% �M����Ԃ����ȉ��̒�����I������
(1) [5.685135,8.314865], (2) [5.660315,8.339685], (3) [5.369412,8.630588],
(4) [5.327975,8.672025], (5) [4.52548,9.47452]
�P�Ԃ�3.5
�Q�Ԃ�4
�R�Ԃ�2�ɂȂ�܂���
�S�Ԉȍ~���킩��Ȃ��ł� �o�������łł��܂���B
n�Ԗڂ̑f����2^n��菬�������Ƃ��ؖ�����B >>280
�x���g����=�`�F�r�V�F�t�̒藝���g����
p_n��2^n�Ȃ��
2^n<p��2^(n+1)�Ȃ�f��p��1�͑��݂���̂�
p_(n+1)��2^(n+1)���킩��
�A�[�@�Ŏ��������ƂɂȂ� >>274
����:
a(n) = {
i = ceil( (-3 + sqrt(8*n+9))/2 ) ; \\ row
j = n - (i-1)*(i+2)/2; \\ column
return( -1 + min( i- (2<j)*(j-2) , j ) )
}
a(1)�`a(65)
0, 0,
0, 1, 0,
0, 1, 1, 0,
0, 1, 2, 1, 0,
0, 1, 2, 2, 1, 0,
0, 1, 2, 3, 2, 1, 0,
0, 1, 2, 3, 3, 2, 1, 0,
0, 1, 2, 3, 4, 3, 2, 1, 0,
0, 1, 2, 3, 4, 4, 3, 2, 1, 0,
0, 1, 2, 3, 4, 5, 4, 3, 2, 1, 0,
(i<j �̎��ɉ��s) �v���O�����R�[�h����Ȃ���
wolfram ���͉\�Ȑ����������� >>281
�ؖ���^���Ă����������肪�Ƃ��������܂��B
�ؖ����鎖���������ɂ��������Ȃ��̂ŁA���Z���w���x�̒m���Ŏ�����ƒ����I�ɍl�����̂ł����A�����ł��Ȃ��̂ł��傤���B 17 11
15 10 5
13 8 4 1
Table[2n-1+C(0,(21mod n)-1),{n,1,9}]
n�����������̎��͂����
n���傫���Ȃ�Ɣj�]���� >>279
R�g����
x=c(7.5, 5.5, 4, 7, 8.5, 5, 9, 9.5)
mean(x)
var(x)
sd(x)
qt(1-0.1/2,df=7)
t.test(x,conf.level = 0.9)
�ŏI���B >>282
���ꂽ����ɈڐA���đ������o�͂��Ă݂܂����B
0 0
0 1 0
0 1 1 0
0 1 2 1 0
0 1 2 2 1 0
0 1 2 3 2 1 0
0 1 2 3 3 2 1 0
0 1 2 3 4 3 2 1 0
0 1 2 3 4 4 3 2 1 0
0 1 2 3 4 5 4 3 2 1 0
0 1 2 3 4 5 5 4 3 2 1 0
0 1 2 3 4 5 6 5 4 3 2 1 0
0 1 2 3 4 5 6 6 5 4 3 2 1 0
0 1 2 3 4 5 6 7 6 5 4 3 2 1 0
0 1 2 3 4 5 6 7 7 6 5 4 3 2 1 0
0 1 2 3 4 5 6 7 8 7 6 5 4 3 2 1 0
0 1 2 3 4 5 6 7 8 8 7 6 5 4 3 2 1 0
0 1 2 3 4 5 6 7 8 9 8 7 6 5 4 3 2 1 0
0 1 2 3 4 5 6 7 8 9 9 8 7 6 5 4 3 2 1 0
0 1 2 3 4 5 6 7 8 9 10 9 8 7 6 5 4 3 2 1 0
�����Ă��邩�ȁH >>284
�f���Ɋւ��邱�Ƃ͎��������ł�������Ƃ������Ǝv��
����Ɋւ��Ă͉�����肢�ʂ̕��@�Ŏ����邩������Ȃ����ǂ� >>282 �͑��a��95
>>287 �͑��a��715 �Ȃ炠���Ă��� ���a���o�͂����
(4n^3-6n^2-4n-3(-1)^n+3)/48�@ >>289
>287�̑��a
> sum(unlist(d))
[1] 715 f(x) = 1+a*sin(x)+b*cos(x)�ɑ��A
g(x) = ��[0,x] (x-t)f(t) dt
�Ƃ����B
���̂Ƃ��C�ӂ̎���x,y�ɂ���
g(x+y)+g(x-y) �� 2g(x)
�����藧�悤�Ȏ���a,b�����������������߂�B >>292
�v�͏�ɉ��ɓʂ��Ă��Ƃ�����P���I�� g''(x)��0 �ƂȂ�悤�ɂ��������ˁH >>113
����݂Ă���Ȗ����v�������B
�J�[�W�I�C�hr=1+cos��
https://upload.wikimedia.org/wikipedia/commons/thumb/3/35/Cardioid.PNG/200px-Cardioid.PNG
�ň͂܂ꂽ�ʂ������̎���ɉ�]�����Ăł��闧�̂̑̐ς�V�Ƃ���B����x=a�����ɉ�]�����Ăł��闧�̂̑̐ς�V/2�ł���悤��a�̒l�͂����炩�H �̐ϖ��͒P���Ȍv�Z���ɂ����Ȃ�Ȃ����
���J�Ɏ��ό`���Ă� �O�삩��uWolfram�搶�ɗ�������w�v�ƃP�`��t�����ďI���B
�̐ϔ������������͐��l�v�Z�ɋA�����邵���Ȃ���Ő��w�I�Ȗʔ��݂͔����B �ϕ����͐ϕ��\�������Ȃ�A���S���Y��������Ă邩��A�قƂ�ǂ̃P�[�X�Ŏ�v�Z�ł��Ӗ��͂���܂�Ȃ��ƌ����Ȃ������
�ϕ���explicit�ɂł��邩�ǂ����s���ł���P�[�X�͂��Ȃ菭�Ȃ��Ȃ��Ă��Ă�
�܂��f�l���K���ɍ�������Ȃ��Z���ł��ł��邩�Aexplicit�ɂ͌v�Z�s�\�̂ǂ������ɂ����Ȃ�Ȃ� �O>>277
>>294�����R�������̑I��������Đ������̂͂킩��B
�̑I����R�����̂͐̑I�肪�Ȃɂ��\����f�����낤���H >>294
V���v�Z�i���l�ϕ��j
> (vb - vg)*2
[1] 24.90338 >>299
�yR����z���v��̓t���[�\�t�g�q ��6�́yGNU R�z [���f�]�ڋ֎~](c)2ch.net
https://rio2016.5ch.net/test/read.cgi/math/1501755792/ n�����R���̒萔�Ƃ���B
xy���ʂɂ����āA�ɕ�����r=1+(2^n)*cos�Ƃŕ\�����Ȑ���C�Ƃ���B
C��̊i�q�_�̌���n�ŕ\���B ���̕��ʂ̒��w�������₵�Ă����v�ł����H 3axy-2ax���J�b�R�Ŋ���Ƃ�
ax(3y-2)��a(3y-2)x�͂ǂ������������̂ł����H
���ƃJ�b�R�̊O�ɏo���������̓J�b�R�̑O��ǂ���ɕt����̂����܂肪�����ł��傤���H ���ɂ����ɋC�����Ă��܂����� >>306
�ǂ������������B�D�݂̖��B >>282 �̉��Z�q����菜����
�����ɕϊ����Ă���`(^_^)� >>311
���ꂭ�炢�����ł��邾��...�Ǝv�������ꉞ�����Ƃ��B
sqrt(x) = ��x
ceil(x) = ⌈ x ⌉�@�@( ceiling function, �V��� )
min(x, y) = if (x �� y) then x else y
(x<y) = if (x < y) then 1 else 0 �Ō�̂� �u�[���l�ł��� False, True �� 0, 1 ����ʂ��Ȃ�����ɓ��L�̋L�@
�����łȂ�����������B ��10cm�̐��܊p�`�̒��S�_���璸�_�܂ł̒����͉�cm��mm�ł����H a n i = div (n-(abs $ n-2*i)) 2
main = do
mapM_ print $ take 10 $ [[a n i|i<-[0..n]] | n<-[0..]]
[0]
[0,0]
[0,1,0]
[0,1,1,0]
[0,1,2,1,0]
[0,1,2,2,1,0]
[0,1,2,3,2,1,0]
[0,1,2,3,3,2,1,0]
[0,1,2,3,4,3,2,1,0]
[0,1,2,3,4,4,3,2,1,0] >>312
wolfram �ŏo�͉\�Ȑ������Ƃ����Ӗ� >>316
����͐����p�`�ł���
���܊p�`��
�Ԑ�1�{�̒����ł��B
https://i.imgur.com/vjXzMrI.jpg >>316
���܊p�`�������B
���f���ʂɍ�}���Čv��
p=ngon(5)
o=mean(p[1:5]);pt(o)
seg(o,p[1]);seg(p[2],p[4])
10*abs(o-p[1])/abs(p[2]-p[4])
[1] 5.257311
��T�����Q�Umm sqrt��ceiling��wolfram�ŏo�͂ł���
column�͖��� >>322
���a�P�̉~�ɓ��ڂ���T�p�`�̑Ίp���̒����͂Qsin�i�Q��/�T�j
�Ίp���̒������P�O�Ȃ�A���a��
> 10 / ( 2*sin(2*pi/5))
[1] 5.257311 >>323 row �� column �� �����̃R�����g������ ����O�p�`�̓��SI�A�T�SI�e�Ƃ���
����II�f�̒��_������II�e�ƎO�p�`�̊O�ډ~�Ƃ̌�_�ɂȂ�͉̂��̂ł����H >>312
��sqrt��ceil��wolfram�`���ɂł���
Table[n-(ceil((-3+sqrt(8*n+9))/2)-1)*(ceil((-3+sqrt(8*n+9))/2)+2)/2,{n,1,40}]
���̔��蕔����wolfram���͌`���ɕό`���Ă���`(^_^)�
return(-1+min(i-(2<j)*(j-2),j)) >>327
���̃L����AA����������ό`�������w >>326
���S�@�T�S�@�O�ډ~�@��google�搶�ɂ��肢�������ԏ�ɒm�b�܂̉��o�Ă����B (x-y)e^(-x^2-y^2)�̋ɒl���ċ��߂��܂����H
��xf=��yf=0��(x,y)�����܂������Ȃ������̂ł��� �ϕ�����̂�������͂���̂ɔ�������̂���������Ȃ��̂͂Ȃ��H �ǂȂ���
>>9�̓����������ĉ����� >>9
�f���ɓǂ��U�K���ł͂Ȃ�����A(1)���ؖ��ł��邽�߂ɂ͑����Ђ˂��ꂽ�����ꒃ�ȃ��[�����߂��K�v�ƂȂ�B
�Ⴆ��
���܂�S�N���T�C�R����U��A��X�����i��U�j�B
��������T�N���T�C�R����U��A��Y�����i��U�j�B
�̕����ɂ��āA�T�C�R�����g����h�U��Ə����Ă��Ȃ��̂�3�̔{�����o�Ă��܂�����A���ʼn���ł��U��Ȃ����Ɖ��߂����
��U�͐�ɏ������Ȃ��A��U�������Ƃ͂���A�i�v�ɏ����҂�����Ȃ����Ƃ�����̂ł��̏�Ԃ���U�K���ƕ\���ł��Ȃ����Ȃ��B
���̉��߂���(2)��p=(1/2)^n�ƂȂ�̂�n=1�̂Ƃ���|p-(1/2)|=0���ŏ��ł���B >>309
���肪�Ƃ��������܂��I
�ċx�ݖ����Ƀe�X�g����������ŕs���ł�����
����C�����ė��܂����I >>330
�����̌����\�̓J�X�����đ� �O>>277
>>314
���߂钷����xcm�Ƃ��A
���܊p�`�̈�ӂ̒�����ycm�Ƃ����ƁA
�Ίp����10cm�ŁA�ق��̑Ίp���ɂ����10:y:10�ɕ�������A����3�̃p�[�c10+y+10�̂���10+y����ӂ̒����Ɠ������B
���̑Ίp���ƈ�̕ӂ����s������B
10(10+y)/(10+y+10)=y
100+10y=20y+y^2
y^2+10y-100=0
y=5��5-5
�ȉ��Č����B
y^2-5^2=�ox-��(x^2-5^2)�p^2
125-50��5+25-25=x^2-2x��(x^2-25)+x^2-25
125-50��5=2x^2-2x��(x^2-25)-25
x^2-x��(x^2-25)-75+25��2=0 t�������Ƃ��Af(t)=sin(t)+cos(t)+��2�Ƃ���B
�i1�jf(t)��0 �������B
�i2�jxy���ʂɂ����āA�ɕ�����f(r)=sin��cos�Ƃɂ���܂�Ȑ���C�Ƃ���BC���_A(a,b)�������Ƃ��Ag(a)=(a+1)(b+1)���ő�ɂ���A�̈ʒu�����߂�B
(3)g(a)���ő�ɂ���a��p�Ƃ����Ƃ��A��ϕ���[0,p] e^(-x^2) dx�͗L�������B Table[Floor[Abs[n-(Floor[(Floor[Sqrt[2n+1]]+1)^2/2]-1/2-Floor[(Floor[Sqrt[2n+1]]+1)/2])]],{n,1,100}]
{0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 2, 1, 0, 0, 1, 2, 2, 1, 0, 0, 1, 2, 3, 2,
1, 0, 0, 1, 2, 3, 3, 2, 1, 0, 0, 1, 2, 3, 4, 3, 2, 1, 0, 0, 1, 2, 3, 4, 4,
3, 2, 1, 0, 0, 1, 2, 3, 4, 5, 4, 3, 2, 1, 0, 0, 1, 2, 3, 4, 5, 5, 4, 3, 2,
1, 0, 0, 1, 2, 3, 4, 5, 6, 5, 4, 3, 2, 1, 0, 0, 1, 2, 3, 4, 5, 6, 6, 5, 4} yz=2wx
zx=2wy
xy=2wz
x^2+y^2+z^2=1
w,x,y,z�̎������́H �O>>338
>>314
���߂钷����xcm�Ƃ��A
���܊p�`�̈�ӂ̒�����ycm�Ƃ����ƁA
�Ίp����10cm�ŁA�ق��̑Ίp���ɂ����10:y:10�ɕ�������A����3�̃p�[�c10+y+10�̂���10+y����ӂ̒����Ɠ������B
���̑Ίp���ƈ�̕ӂ����s������B
10(10+y)/(10+y+10)=y
100+10y=20y+y^2
y^2+10y-100=0
y=5��5-5
���ɐ��܊p�`�̒��S�ƒ��_���Ε�x�Ƃ��钼�p�O�p�`�ɂ����ăs�^�S���X�̒藝���A
(5��5-5)^2/4=x^2-(10-x)^2
150-50��5=4(20x-100)
75-25��5=40x-200
40x=275-25��5
8x=55-5��5
x=(55-5��5)/8
=5.47745751406�c�c
����5cm5mm >>541
x=0�̂Ƃ�y=0 or z=0
(x,y)=(0,0)�Ȃ�(z,w)=(�}1,0)
xyz��0�̂Ƃ�w��0
x,y,z,w�̂������ł�����̂͋����ł���
(x,y,z,w), (-x,-y,-z,-w),
(-x,-y,z,w), (-x,y,-z,w), (-x,y,z,-w),
(x,y,-z,-w), (x,-y,z,-w), (x,-y,-z,w),
�̂����ꂩ�͑S�Đ�
�����x,y,z,w>0�̏ꍇ���l����Ηǂ�
xy/z=zx/y=yz/x���x^2=y^2=z^2
�� x=y=z=2w=1/��3
�ȉ�ry >>340
�����͂��߂̏C�����K�v
87 71
85 70 55
83 68 54 41
81 66 53 40 29
79 64 51 39 28 19
77 62 49 38 27 18 11
75 60 47 36 26 17 10 5
73 58 45 34 25 16�@9 4 1
�ɂ���(^_^)� xy���ʏ�ɁA��ӂ̒�����2��3�́�ABC�Ɠ��_P������B
t��t>2��3�̎����Ƃ���B
�i1�j���_P��PB+PC=t�����Ȃ��畽�ʏ���BP�̕`���O�Ղƕ�AB����_�����Ƃ��́At�̎�肤��l�̏�������߂�B
�ȉ��At�́i1�j�̏�����Ȃ��Ƃ���B
�i2�j�i1�j�ɂ����āAP�̕`���O�Ղƕ�AB�̌�_��T�Ƃ���BBT��t�ŕ\���B
�i3�j�i1�j�ɂ����āAP�̕`���O�Տ��A����ł��߂��_��S�Ƃ���BAS��t�ŕ\���B
�i4�j�_P�͈ȉ��̏��������B
�EPA+PB+PC=r, r>0
�EP�̕`���O�Ղ́�ABC�̓����ɂ���
r�̎�肤��l�͈̔͂����߂�B >>343
> ���ɐ��܊p�`�̒��S�ƒ��_���Ε�x�Ƃ��钼�p�O�p�`�ɂ����ăs�^�S���X�̒藝���A
> (5��5-5)^2/4=x^2-(10-x)^2
10-x���ĉ��H >>314
���܊p�`��
�O�ډ~�̔��a��1�ӂ̒����̔�͂��Ȃ��₱����
�Ίp����1�ӂ̒����̔�͂����鉩����
��������O�O��ƌ����邩�炻������O�ډ~�̔��a�ƑΊp���̔�����߂Čv�Z�����ق�������
�C�i�͂����Ɏv�����݂œK���₱�Ƃ�����ĊԈႦ�邩��M�p������_������ n��1�ȏ�̐����Ƃ���B
(n^2+1)(5n^2+9)�͕������łȂ����Ƃ������B >>331
��f/��x = {1-2x(x-y)}e^(-xx-yy)
��f/��y = {-1-2y(x-y)}e^(-xx-yy)
������0�Ƃ�����
�@x+y = 0,
�@(x,y) = (1/2,-1/2)�@(-1/2,1/2)
���邢�� ����45����
�@u = (x+y)/��2,
�@v = (x-y)/��2,
�Ƃ�����
�@f = (��2)e^(-uu)�Ev�e^(-vv) = g(u)�Eh(v),
�@g '(u) = -2(��2)u e^(-uu),
�@h'(v) = (1-2vv)e^(-vv),
�@(u,v) = (0,�}1/��2)
���@(x,y) = (1/2,-1/2)�@(-1/2,1/2) >>346
����A����Ƃ̘a�ƌ������Ƃ�
Table[{n,89-2 Floor[(-1+Sqrt[1+8n])/2]+(n-(Floor[(-1+Sqrt[1+8n])/2]+1)(Floor[(-1+Sqrt[1+8n])/2])/2)^2-17(n-(Floor[(-1+Sqrt[1+8n])/2]+1)(Floor[(-1+Sqrt[1+8n])/2])/2)},{n,1,44}] >>345
(w,x,y,z) = (0,�}1,0,0)�@(0,0,�}1,0)�@(0,0,0,�}1)�@�c�@6
�@�@�@�@(�}1/(2��3), �}1/��3, �}1/��3, �}1/��3)�@�c�@8�@{(2w)xyz = 1/9}
�v 14�Ƃ��� >>347
(1)2��3<t<4��3
(2)BT=x�Ƃ���B��BCT�ŗ]���藝
(t-x)^2=(2��3)^2+x^2-4(��3)xcos60��
x=(t^2-12)/(2t-2��3)
(3)AS=3-��{(t^2/4)-3} I=[-a,a]�Ƃ���f,f'��I��A���ł���Ƃ�
��_[-a,a]xf(x)dx = (2/3)a^3 f'(b)
�ƂȂ�b��I�����݂��邱�Ƃ������ĉ����� >>350
a[n] = (n^2 + 1)
b[n] = (5n^2 + 9)
�ƒu���B a[n]b[n] ���������łȂ����Ƃ������悢�B
a[n] �� b[n] �̍ő���� gcd(a[n], b[n]) ���l����B
-5a[n] + b[n] = 4
���A gcd(a[n], b[n]) �� 4 �̖ł���B
a[n] �� 4 �Ŋ����邱�Ƃ͂Ȃ��̂ŁA gcd(a[n], b[n]) �� 1 �� 2 �̂����ꂩ�ł���B
���������� a[n] �� b[n] �̋��ׂ�A
n �������̂Ƃ��A gcd(a[n], b[n]) = 1
n ����̂Ƃ��A gcd(a[n], b[n]) = 2
�ƂȂ邱�Ƃ��킩��B
�ȉ��A a[n]b[n] ���������łȂ����Ƃ� n �̋��ɕ����Ď����B
�y n �������̂Ƃ��z gcd(a[n], b[n]) = 1 ���A
���� a[n]b[n] ���������Ȃ�A a[n] ����� b[n] ���������ł���B
�������A n > 0 �̂Ƃ� n^2 < a[n] < (n+1)^2 ��� a[n] �͕������ł͂Ȃ��̂Ŗ�������B
�y n ����̂Ƃ��z gcd(a[n], b[n]) = 2 ���A
���� a[n]b[n] ���������Ȃ�A a[n]/2 ����� b[n]/2 ���������ł���B
������ n = 2k - 1 �ƒu���ƁA b[n] = 20k^2 - 20k + 14 ���
b[n]/2 = 10k^2 - 10k + 7
�ƂȂ�B
����� b[n]/2 �� 5 �Ŋ������]��� 2 �ƂȂ邪�A�������� 5 �Ŋ������]��� 2 �ɂ͂Ȃ�Ȃ��̂Ŗ�������B ����H��Ő��Y����鐸�����i�� 25 ����ג��o���Ē����𑪂�����C���ϒl x �� x = 30 (mm) �ł������D�ߋ��̐����f�[�^�̒~�ςɂ��, ���i�̒����͕W������ 4 mm�̐��K���z�� �]�����Ƃ��������Ă���D
��Ԃ̕��� 2.0=2�~1.0 �ȉ��Ƃ������D���Ȃ��Ƃ����̕W�{���K�v��
61.46334 �Ƃ����l���o���Ƃ�������61���Ƃ��܂����ˁH
62�Ƃ��܂���ˁH n^2+1=N�Ƃ�����
N(5N+4)���������łȂ����Ƃ������Ηǂ�
N�͕������ł͂Ȃ��A�����q��5N+4�̑f���q�ɂ��Ȃ�K�v�����邩�炻���2�݂̂ł���
�Ƃ��낪N=2k^2�Ƃ����đ�������5k^2+2���������ł��邱�ƂɂȂ薵�� �O>>343�����B
>>314
���߂钷����xcm�Ƃ��A
���܊p�`�̈�ӂ̒�����ycm�Ƃ����ƁA
�Ίp����10cm�ŁA�ق��̑Ίp���ɂ����10:y:10�ɕ�������A����3�̃p�[�c10+y+10�̂���10+y����ӂ̒����Ɠ������B
���̑Ίp���ƈ�̕ӂ����s������B
10(10+y)/(10+y+10)=y
100+10y=20y+y^2
y^2+10y-100=0
y=5��5-5
���ɐ��܊p�`�̒��S�ƒ��_���Ε�x�Ƃ��钼�p�O�p�`�ɂ����ăs�^�S���X�̒藝���A
x+��[x^2-�o(5��5-5)/2�p^2]=��[10^2-�o(5��5-5)/2�p^2]
���Ƃ͌v�Z�B
5.2���炢���ȁH �O>>359
x+��[x^2-�o(5��5-5)/2�p^2]=��[10^2-�o(5��5-5)/2�p^2]
x^2+2x��[x^2-�o(5��5-5)/2�p^2]+x^2-�o(5��5-5)/2�p^2=[10^2-�o(5��5-5)/2�p^2]
2x^2+2x��[x^2-�o(5��5-5)/2�p^2]-75/2+25��5/2=[10^2-�o(5��5-5)/2�p^2] �O>>359
x+��[x^2-�o(5��5-5)/2�p^2]=��[10^2-�o(5��5-5)/2�p^2]
x^2+2x��[x^2-�o(5��5-5)/2�p^2]+x^2-�o(5��5-5)/2�p^2=[10^2-�o(5��5-5)/2�p^2]
2x^2+2x��[x^2-�o(5��5-5)/2�p^2]-75/2+25��5/2=[10^2-�o(5��5-5)/2�p^2] �Ō�̃C�R�[�����Ӗ��s�������ċ}�ɂǂ������H���Ċ����ł�
�ǂ�Ȍv�Z�H
https://i.imgur.com/uSaMAhz.jpg �Ƃ肠����e^(ix)=cosx+isinx���g���Ă݂悤�� >>362
e^(i��)=-1�Ōv�Z���邾���ł�
n����̂Ƃ���e�̂Ƃ��S��1�ɂȂ���-2�Ƒł�����
n�������̂Ƃ���e�̂Ƃ��S��-1�ɂȂ���-2�ƍ��킹��-4���o�Ă��� >>364
�����m��܂���ł���
������I�C���[�̌����Ȃ�ł��ˁc
���肪�Ƃ��������܂��� >>365 e^(i��)+ 1 = 0�̓I�C���[�̓������Ă����L���ȓ����Ȃ�ł���B �l�͂܂��A�l�ނ̎��Ǝv���Ă���^^ i�������P�ʂƂ���B����{a[n]}��
a[1]=1,a[2]=i
a[n+2]=a[n+1]+a[n]
�����B
�܂�����{b[n]}��
b[n]=a[n+1]/a[n]
�Œ�߂�B
���f���ʏ�ŁAb[x]���\���_��P[x]�Ƃ���Bj,k,l�𑊈قȂ鎩�R���Ƃ��A3�_P[j],P[k],P[l]���O�p�`�ƂȂ�ꍇ���l����B
���̖ʐ�S[j,k,l]�ɂ��Ĉȉ��̖�ɓ�����B
�i1�j��P[j]P[k]P[l]�̕ӂ̒�����a,b,c(a��b��c)�Ƃ���Ƃ��Aab/S[j,k,l]�����߂�B
�i2�jS[j,k,l]�̎�肤��l�͈̔͂����߂�B ��sin(x^k)dx[0����]�͎������邩���U���邩�l�@����B�Ȃ�k�͎����萔�B ��[0,��] sin(x^k) dx = sign(k) ��[0,��] sin(y) (1/k)y^(1/k-1) dy
|k|>1�@�̂Ƃ������@��(1+1/k) sin(��/2|k|),
|k|��1�@�̂Ƃ����U >>355
���ϒl�̒藝���
f(x) - f(-x) = 2x f '(��)�@�@(-x<��<x)
��[-a,a] xf(x) dx = ��[0,a] x{f(x) - f(-x)} dx
�@= ��[0,a] 2xx f '(��) dx�@�@(-x<��<x)
�@= ��[0,a] 2xx dx f '(b)
�@= (2/3)a^3 f '(b). >>368
��ӂ��
�@a[n] = F[n-2] + F[n-1]��,
�@| a[n] |^2 = F[2n-3],
�@b[n] = a[n+1]/a[n]
�@= (F[n-1] + F[n]��) / (F[n-2] + F[n-1]��)
�@= {F[n-1](F[n-2]+F[n]) - (-1)^n���} / | a[n] |^2, >>357
61�͕K�v�����Ǐ\������Ȃ�����62���ȁB �O>>360-361
�o(5��5-5)/2)^2+(9.51056516295)^2�p/2=50
�ǂ��������Ƃ�H >>349
�v���O�����ō�}���Čv�����Č����Ă݂܂����B
> DOPs(5,T) # �܊p�`��1�ӂƑΊp���̒���(�O�ډ~�̔��a=1)
$side
[1] 1.175570504584946
$diagonal
[1] 1.902113032590307
> DOPs(5)$diagonal/DOPs(5)$side # �Ίp��/�Ӓ�
[1] 1.618033988749895
> (1+sqrt(5))/2 # ������
[1] 1.618033988749895 >>376
# �Ίp��/�Ӓ�
> (2*sin(2*pi/5))�@/�@(2*sin(pi/5))
[1] 1.618033988749895
> (1+sqrt(5))/2 # ������
[1] 1.618033988749895 >>352
�o�͂��S�R����Ȃ�
��͂��Փx���Ⴄ >>345
-1,0,1��81�ʂ��T����������A
w x y z
0 0 0 -1
0 0 -1 0
0 -1 0 0
0 1 0 0
0 0 1 0
0 0 0 1
6�ʂ肪�Ђ����������B Table[{n,41-2 Floor[(-1+Sqrt[1+8n])/2]+(n-(Floor[(-1+Sqrt[1+8n])/2]+1)(Floor[(-1+Sqrt[1+8n])/2])/2)^2-17(n-(Floor[(-1+Sqrt[1+8n])/2]+1)(Floor[(-1+Sqrt[1+8n])/2])/2)},{n,1,20}]
n��ω��������
�܂������Ή��ł��Ȃ� >>371
�� �̒l�͓��R x �Ɉˑ�����킯�ł����A���̂�����͂ǂ�����ď������Ă����ł��傤���H
�� = ��(x) >>314
���������̂͒��J�ɐ}�������ĕ��s�����Ώ̐������Ă����Ή�����B
�����O�p�`��� x/1 = 1/(x-1)
xx -x -1 = 0 �� x = ( 1 + ��5 )/2 �@ {������}
sin(��/2) = (1/2) / x = ... = ( -1 + ��5)/ 4
cos(��/2) = ��(1- sin(��/2)^2 ) = ... = ��(10 + 2��5) /4
x/2 = r * cos(��/2)
�� r / x = 1/2cos(��/2) = ... = ��{(5 - ��5)/ 10} = 0.5257..
����� 10cm * r/x �� 5cm 3mm
�E�}�� ���Z?�p�� GeoGebra�ŕ`�����B �}���t���ĂȂ�����
 ���W��ɍ�}���Ē��_�̍��W���v�Z�ŏo���ǂ̑Ίp���̒������v�Z�ł���B
���W��ɍ�}���Ē��_�̍��W���v�Z�ŏo���ǂ̑Ίp���̒������v�Z�ł���B
�ł����n�I�����ėp�̂�����@�B
��v�Z���Ƒ�ς�����x�A�v���O������g�߂Ή��p�`�ɂȂ��Ă��g����B
��F�O�ډ~�̔��a��1�̐�17�p�`�̈�ӂ̒����ƑΊp���̒�����S�ċ��߂�B ��n�p�`�� ��ʉ�����Ƃ����Ȃ�
���a: r = 1
�ő啝: w=|e^{i2��/n *⌊n/2⌋} - 1| �@{���f���W�ŕ`����}
r/w = 1/��( {1-cos(2��⌊n/2⌋/n)}^2 + sin(2��⌊n/2⌋/n)^2 ) = 1/��( 2 -2cos(2��⌊n/2⌋/n) )
�@n������ �� r/w�@= 1/��( 2 -2cos(��) ) = 1/2
�@n��� �� r/w�@= 1/��( 2 -2cos(�� - ��/n) ) = 1/��( 2 +2cos(��/n) ) = 1/2cos(��/2n) >>378
0 0 0 1 2 ...
�݂����Ȑ�������ł�����̂��A���x������Ă���̂ŁA���ꂪ�ړI���Ǝv���A�����\�����鎮�� >>340 �ŏ�����
����ƁA>>346 �ŏC�����K�v�Ǝw�E����A87 71 85 70 55.... �������ړI�ŁA�ɂ����ƌ���ꂽ�B
�����ŁA>>352 �Łu�C���v�ɓ����镔����\�������B
�{���́A���킹�����ɂ������������AWolfram���u��������v���Ƃ��������Ǝv�����A�������Ă���Ȃ���������A
������݂̂��������B���߂ď����B
Table[Floor[Abs[n-(Floor[(Floor[Sqrt[2n+1]]+1)^2/2]-1/2-Floor[(Floor[Sqrt[2n+1]]+1)/2])]],{n,1,44}]
{0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 2, 1, 0, 0, 1, 2, 2, 1, 0, 0, 1, 2, 3, 2, 1, 0, 0, 1, 2, 3, 3, 2, 1, 0, 0, 1, 2, 3, 4, 3, 2, 1, 0}
��
Table[89-2 Floor[(-1+Sqrt[1+8n])/2]+(n-(Floor[(-1+Sqrt[1+8n])/2]+1)(Floor[(-1+Sqrt[1+8n])/2])/2)^2-17(n-(Floor[(-1+Sqrt[1+8n])/2]+1)(Floor[(-1+Sqrt[1+8n])/2])/2),{n,1,44}]
{87, 71, 85, 69, 55, 83, 67, 53, 41, 81, 65, 51, 39, 29, 79, 63, 49, 37, 27, 19, 77, 61, 47, 35, 25, 17, 11, 75, 59, 45, 33, 23, 15, 9, 5, 73, 57, 43, 31, 21, 13, 7, 3, 1}
�̘a
��Փx�́A����Ȃɍ����Ȃ��B�ʓ|�����������B
87 71 85 70 ...�ɓ����鐔�����A���i�ڂ̉���ڂ̐������A�����Ă��ꂪ�扽���ɓ����邩�����߁A�����g�ݍ��킹�āA
��̂悤�ɕ������ꂽ����\�������o�������B
�Ⴆ�A��ԍ��̐����́A1,3,6,10,...�ƎO�p���ɓ����鍀�����������Ă��邪�A���̂悤�Ȃ��̂ɒ��ڂ��āA�t�Z����悢�B i�������P�ʂƂ���B����{a[n]}��
a[1]=1,a[2]=i
a[n+2]=a[n+1]+a[n]
�����B
�܂�����{b[n]}��
b[n]=a[n+1]/a[n]
�Œ�߂�B
���f���ʏ�ŁA���f��b[x]���\���_��P[x]�Ƃ���B
�i1�jj,k�𑊈قȂ鎩�R���Ƃ���Bj,k��ω�������Ƃ��A����P[j]P[k]�̒����ɂ͍ő�l�����݂��邱�Ƃ������A���̒l�����߂�B
�i2�jj<k�Ƃ���B�i1�j�̍ő�l��^���鎩�R���̑g(j,k)��S�Č��肹��B (1) ������ y^2 = x + ��(x+1) �̐����� (x, y) ��S�ċ��߂�B
(2) (1)�̈�ʉ��Ƃ��āA������
y^2 = x + ��(x+n)
���l����B
�C�ӂ̐��� n �ɑ��A���Ȃ��Ƃ���͐����� (x, y) �����݂��邱�Ƃ������B
�܂��A������ (x, y) �������ɑ��݂���悤�Ȑ��� n �͑��݂��邩�H >>389
����n<0�̂Ƃ��̓_�������
>>388
�Ƃ肠����(1)����
��(x+1)�������Ȃ̂�x=m^2-1(m��Z)�Ə�����
y=|m|-k(k��Z)�Ƃ����đ�������
|m|=(k^2+1)/(2k+1)��N�A2k+1>0��
4|m|-2k+1=5/(2k+1)��Z���
k=0,2�̉\�������Ȃ�
���̂Ƃ��A���ꂼ��(x,y)=(0,1),(0,-1)�ł���őS�� (2)�̌㔼
��(x+n)�������Ȃ̂�x=m^2-n(m��Z)�Ə�����
y=|m|-k(k��Z)�Ƃ����đ�������
|m|=(k^2+n)/(2k+1)��Z��
4|m|-2k+1=(4n+1)/(2k+1)��Z���
2k+1��4n+1�̖łȂ���Ȃ炸
k�͗L���̉\�������Ȃ�
�����(x,y)���L���̉\�������Ȃ� (2)�̑O��
n��0�̂Ƃ�(x,y)=(n^2-n,�}n)
n��-1�̂Ƃ�(x,y)=(n^2+n+1,�}n)
�����Ƃ��Ď��� >>387
b1=i , b[n+1]=1+1/b[n]
(1)
n��2�̂Ƃ���� -��/4��arg(1/b[n])����/4 ���� |1/b[n]|��1 �����藧�B
���̐�`�̈����2�_�Ԃ̋����́�2������ł���̂ŁA3�ȏ�̔C�ӂ�j,k�ɑ���|1/b[j-1]-1/b[k-1]|����2
������ P[j]P[k]=|b[j]-b[k]|=|1/b[j-1]-1/b[k-1]| �ł��邩�� P[1]P[2]=��5 ���ő�ł���B
(2) (j,k)=(1,2) >>390-392
���肪�Ƃ��������܂�
��͂������ E[n] : y^2 = x + ��(x+n) �̐������͗L���Ȃ�ł���
���� n �ɑ��A>>392�̐�����
> n��0�̂Ƃ�(x,y)=(n^2-n,�}n)
> n��-1�̂Ƃ�(x,y)=(n^2+n+1,�}n)
������� E[n] �́u�����ȉ��v�ƌĂсA
�������̐����������Ȃ�u���ȉ������v�ƌĂԂ��Ƃɂ��܂�
�Ⴆ�A>>388��(1)���A E[1] �͔��ȉ��������Ȃ����Ƃ��킩��܂�
����A E[2] �͔��ȉ� (x, y) = (-1, 0) �������܂�
�����Ŏ��̖����o���܂�
���� n �ɑ��A������
E[n] : y^2 = x + ��(x+n)
�����ȉ� (x, y) �����悤�� n ��S�Č��肹��B
�܂��A�����\�Ȃ�����̉���S�ċ��߂�B >>351
��̋c�_��x+y=0�Ƃ�������2�ʂ�̉����o��ߒ����킩��Ȃ��ł��c >>394
�����y����(x+n)�������ł��邱�Ƃ���
��ʂ�n=f(x,y)=(y^2-x)^2-x�̌`�̂Ƃ�(x,y)�����ł���
�Ƃ���������O�̘b�ɂȂ�̂ł́H
�������ƒ�`�����l�ȊO�̐����g(x,y)�ɑ���f�̑��͔���������n�ƂȂ� >>393
���肪�Ƃ��������܂�
n=1,2,3...�ł��ׂĂ�P[n]������~����ɂ��邱�Ƃ��ł����̂ŁA�܂��~�̒��a�����߂āA����P[i]P[j]�����a�̒����Ɠ������Ȃ�i,j��T�����Ƃ��܂���
�����ōs���l�܂����̂ł����Ai=1,j=2�������Ƃ������ƂŁA�ǂݕԂ��Ă�����x���������Ă݂܂� >>396
�m���ɂ����ł���
���̌��������ōl����ƁA����
n=f(x,y)=(y^2-x)^2-x
���i y �̕����̈Ⴂ�������āj 2 �ʂ�ȏ�� (x, y) �ŕ\���� n �͂ǂ̂悤�Ȑ����H
�Ƃ������ƂɂȂ�܂�
�Ⴆ�A
1 = f(0, �}1)
2 = f(2, �}2) = f(-1, 0)
�������������łȂ����������ƁA
������ E[11] �� (x, y) = (-2, �}1), (5, �}3), (110, �}11) �����ɂ��̂ŁA
11 = f(-2, �}1) = f(5, �}3) = f(110, �}11)
�Ƃ��� 3 �ʂ�̕\���������Ƃ��킩��܂�
���̂悤�Ȕ��ȕ\�������� n �͂ǂ̂悤�Ȑ����H�Ƃ������Ƃ��m�肽���ł� >>398
�ǂ���炱�̌��������͕s���S�Ȃ悤�ł�
(x, y) = (5, �}1) �� E[11] �̉��ł͂���܂��A
11 = f(5, �}1)
�Ə�����̂�
�������������������Ă��܂����悤�ł� >>399
y^2-x��0�Ƃ�������������
>>398
���̏ؖ��ɖ߂��
|m|=(k^2+n)/(2k+1)��Z
4|m|-2k+1=(4n+1)/(2k+1)��Z
�ŁA�������Ƃ�2k+1=�}1�̂Ƃ�������
���������̂�4n+1��(�}�f��)�̌`�̂Ƃ��A�ƌ������� >>400
����
���������̂�4n+1���������̂Ƃ��A�� f(x,y)=(x-1)^2+(y-1)^2��
����x^3+y^3-3xy=0�̂��Ƃōŏ��l�����݂��邱�Ƃ������Ă�������߂�Ƃ������Ȃ̂ł���
����搔�@���g���͕̂�����̂ł����ŏ��l�̑��݂��ǂ��������炢���̂�������܂���
�������L�E�W���Ȃ瑶�݂���݂����Ȋ����ł����H���������������L�E�W���Ȃ̂����킩�炸�c
�ǂȂ������肢���܂� ���炩���ߍŏ��l���Ƃ邱�Ƃ��킩���ĂȂ��Ƃ��A����搔�@�ōŏ��l�̌����o���Čォ�牏�t���w�b�Z�s����m�F�����k >>400-401
> y^2-x��0�Ƃ�������������
�Ȃ�ق�
��������ƁA���� n, x, y �ɑ��A
(x, y) �� E[n] �̉� �� n = f(x, y) ���� y^2 �� x
�ƂȂ�܂���
���ȉ������ꍇ�����A���ȉ��������Ȃ��ꍇ�̂ق����ʔ�����������܂���
��̓��l����A���� y �� 0 �̏ꍇ�Ɍ����
E[n] �͔��ȉ��������Ȃ� �� n = f(x, y) ���� y^2 �� x �ƂȂ� (x, y) �͈�g�����Ȃ�
�ƂȂ�܂�
>���������̂�4n+1���������̂Ƃ��A��
�Ȃ�قǁI |4n+1| ���������Ȃ�A
4n+1 = pq, |p| > 1, |q| > 1 ���� p+q-2 �� 0
�ƂȂ�悤�� p, q ��I�сA 2k+1 = p �ɂ���Đ��� k ���߂�ƁA
|m| = (p+q-2)/4 �� 0 �ł���A���̂Ƃ�
y = (q-p)/4 �� �}n
�ł���̂ŁA����ɂ���Ĕ��ȉ��������܂���
�t�ɁA |4n+1| ���f���Ȃ�A |2k+1| = 1, |4n+1| ��� k = 0, -1, 2n, -(2n+1)
�Ɍ�����̂ŁA>>391�̎����玩���ȉ��Ɍ����邱�Ƃ��킩��܂���
�ȏ���A���� n, x, y ����� y �� 0 �ɂ����āA
E[n] �͔��ȉ��������Ȃ� �� n = f(x, y) ���� y^2 �� x �ƂȂ� (x, y) �͈�g�����Ȃ�
�� |4n+1| ���f��
�����藧�B
�܂��A |4n+1| ���������̂Ƃ��A
���ȉ��� |4n+1| �̑f���������ɂ���Ē�܂邱�Ƃ��킩��B
�i n < 0 �̂Ƃ��͕����̐����ɒ��ӂ��K�v�j ���Z�͈͂ł̋Ɍ��̓��Ƃ̂��Ƃł����A���������̍��̖����E�ʒu�Ɋւ�炸1�Ɏ�������Ƃ������_�������ł����ɂ��܂��B
����t=n�ł̍��̖����͌v�Z�ł����A�]���̎d����������܂���B
��낵�����肢���܂��B
�y���z
���ʂ������Ȑ��O�p�`�̔Ō��ԂȂ��~���l�߂��Ă���B�ǂ̔����F�ł���B
����t=1�ɂ����āA1�̔������h��B
���̌�A�e����t=2,3,...�ɂ����āA���̎����ɑ��݂��鍕���ƕӂ����L���锒�������ׂč����h��B����t=n�ɂ����鍕���̖�����a[n]�Ƃ����B
���āA����t=1�ɂ����āA���ʏ�̔C�ӂ�k��(k��2)�̔������h��A��L�Ɠ��l�̑���Ŕ�h���Ă������Ƃ��l����B
t=1�ł̔̓h����i�ʒu�j�ɂ���āAk�������ł�����t=n�ɂ����鍕���̖����͕ω�����B���̍ŏ��l��m[n,k]�A���̍ő�l��M[n,k]�Ƃ���B
���̂Ƃ��ȉ��̋Ɍ����������1�Ɏ������邱�Ƃ��ؖ�����B
lim[n����] m[n,k]/a[n]
lim[n����] M[n,k]/a[n] >>395
e^(-xx-yy) > 0 ������
�@1 - 2x(x-y) = 0,�@�@�c (1)
�@-1 -2y(x-y) = 0,�@�@�c (2)
(1)*y - (2)*x ���
�@y + x = 0,�@�@�@�c (3)
����� (1) �ɓ����
�@1 -2x�2x = 0,
�@x = �}1/2,
(3)��(2)�ɓ����
�@-1 -2y(-2y) = -1 + (2y)^2 = 0,
�@y = ��1/2,
���̂��� (3) �����g������
f(-1/2,1/2) = -e^(-1/2) = -1/��e = -0.60653�@(�ŏ�)
f(1/2,-1/2) = e^(-1/2) = 1/��e = 0.60653�@�@(�ő�)
��2�����B �Ȃ��A�ő�l�E�ŏ��l�����ł悯���
�@f(x,y)^2 = e^(-2uu) (2vv)/e^(2vv) �� 1/e,
�@e^(-2uu) �� 1,�@�@�@�@(������ u=0)
�@e^(2vv) �� e(2vv),�@�@(������ 2vv=1) >>405
�Ƃ肠���� a[n] = 1 + 3n(n-1)/2 ���ȁH
1 �� m[n,k]/a[n] �� M[n,k]/a[n]
������A lim[n����] M[n,k]/a[n] = 1 �������Ώ\�����Ƃ������Ƃ͂킩��
���ϓI�ɂ́A�ǂ�ȏ��������ł����Ă� n ���\���傫���Ȃ��
�����͑S���q�����Ă��܂����� a[n] �� M[n, k] �͑卷�Ȃ��Ȃ�
���Ă��ƂȂ낤�� >>408
����A�Ⴄ���ȁH
>���ʂ������Ȑ��O�p�`�̔Ō��ԂȂ��~���l�߂��Ă���B
>�����ƕӂ����L���锒�������ׂč����h��B
�Ə����Ă��邩��A�C�[���V���^�C�������݂����ɕ~���l�߂��Ă���Ƒz�肵�����ǁA
���������ӂ��ɕ~���l�߂��Ă���\���������
https://upload.wikimedia.org/wikipedia/ja/thumb/7/7d/Shikitume02.gif/180px-Shikitume02.gif
���̏ꍇ�͂ǂ�����ēh���Ă�����
�������̏ꍇ�͉��ɂ����h���Ă͂����Ȃ����[���Ȃ�A
�c�� k �u���Ζ��炩�� M[n, k] = ka[n] ����
�����ł��ӂ��G��Ă�����h���Ă������[���Ȃ̂��� �O>>375
>>314
����������m�Ƃ�������������ƂɂȂ�Ȃ��B
�Ίp������ӂɑ��ĉ�����ł��邱�Ƃ͖��m�Ƃ��ĉ����Ȃ��ƂȂ�ɂ��Ȃ�Ȃ����낤���B
����ȓ��ĕs����������ȁB >>405
��������
�����z�u���Œ肵���ǂ�ȂQ�̖ʐϔ���Ɍ��I�ɂ͈�v���邾�낤���ǁA�en�����ōő�l���Ƃ��Ă��Ĕ�ׂĂ��܂�����Ɍ��͕ς���Ă���
���ɍŏ��z�u�ƍő�z�u�̔��k�ɂȂ��Ĉ�v���Ȃ� ��莩�̂����������悤�ł��݂܂���B���̌��ƂȂ��������܂��B������1997�̑�1��ł��B
���̒ʂ�ɕ��͂ŕ\���ł������肪�A��͂��ł����B
���O�p�`�ł̕~���l�߂͂ŕ\������̂�����Ǝv���܂����B
http://server-test.net/math/php.php?name=tokyo&;v1=1&v2=1997&v3=2&v4=1&y=1997&n=7 >>412
���������A�b���S�R�Ⴄ���
����Ȃ�\���傫��N���Ƃ��
�ǂ��k�̏����z�u���P��z�u��N�X�e�b�v��̏�Ԃɕ����Ă�
�����a_n<b_n<a_(n+N)
a_n=1+3n(n+1)/2������
a_n/b_n��1�����ݓ����̒藝����킩�� >>412
>>405�Ƃ͑S���ʂ̖��Ń����^ ����
n^k+1=2^n
����1�ȏ�̐���(n,k)�����ׂċ��߂�B �O>>410
>>314
���߂钷����xcm�Ƃ��A
���܊p�`�̈�ӂ̒�����ycm�Ƃ����ƁA
�Ίp����10cm�ŁA�ق��̑Ίp���ɂ����10:y:10�ɕ�������A����3�̃p�[�c10+y+10�̂���10+y����ӂ̒����Ɠ������B
���̑Ίp���ƈ�̕ӂ����s������B
10(10+y)/(10+y+10)=y
100+10y=20y+y^2
y^2+10y-100=0
y=5��5-5
���ɐ��܊p�`�̒��S�ƒ��_���Ε�x�Ƃ��钼�p�O�p�`�ɂ����ăs�^�S���X�̒藝���A
x+��[x^2-�o(5��5-5)/2�p^2]=��[10^2-�o(5��5-5)/2�p^2]
x^2+2x��[x^2-�o(5��5-5)/2�p^2]+x^2-�o(5��5-5)/2�p^2=10^2-�o(5��5-5)/2�p^2
2x^2+2x ��[x^2-�o(5��5-5)/2�p^2]=100
x^2+x ��[x^2-�o(5��5-5)/2�p^2]=50
x^2[x^2-�o(5��5-5)/2�p^2]=(50-x^2)^2
100x^2-�o(5��5-5)/2�p^2]x^2=2500
�o40-(��5-1)^2�px^2=1000
(34+2��5)x^2=1000
(17+��5)x^2=500
(289-5)x^2=500(17-��5)
71x^2=125(17-��5)
71x^2=5^2(105-5��5)
x=5��o5(17-��5)/71�p
=5.09831717999�c�c
5.1���Ȃ��ˁB�Ó��Ȓl���B >>415
n^k ��������� n �͊�B
k��2 �̂Ƃ� {����}��2 (mod 4)
n��2 �̂Ƃ� {�E��}��0 (mod 4)
���������� k=1 �܂��� n=1
n=1�̂Ƃ��C�ӂ�k�ɂ��Đ��藧�B
k=1 ���� n��2 �̂Ƃ�
2^n=(1+1)^n=��[r=0~n]nCr>n+1 �ł��邩�琬�藧���Ȃ��B >>418
�v��������ԈႦ�Ă��܂��ˁB�Y��Ă��������B s_p := n (if p = 0)
s_p := ��_{k=1}^{n-1} k^p (if p �� 1)
s_p��n�̑������ɂȂ邱�Ƃ��Ď����ł����H��������Ȃ��ł����H
���Ȃ݂Ɏ�����p+1���ɂȂ�܂��B �����ł���悤�Ȃ�������Ȃ��悤�ȋC������̂Ŏ��₵�܂����B
5�b��s_p��n�̑��������ۂ������Ȃ��Ƃ����Ȃ��Ƃ����n�̑������ɂȂ�Ɠ����܂��B p = 2�̏ꍇ�ł����A
1^2 + 2^2 + �c + (n - 1)^2��n�̑��������ǂ����Ƃ������ƂɂȂ�܂��B �������A�����(1/2)*(n-1)*n�Ȃ̂ő������i2���j�ł��B >>403
����搔�@���g���ɂ͏����������łȂ�������Ȃ��݂����ł������ꂪ�����ł��邩�͂ǂ���������ǂ��̂ł��傤�� >>420
�t�@�E���n�[�o�[�̌��� �s�p�O�p�`��ABC�ɓ��ڂ���3�̈قȂ鐳���`�ƁA���̓����̈�D1,D2,D3���l����B
�����Ł�ABC�ɐ����`S�����ڂ���Ƃ́AS�̈�ӂ���ABC�̂����ꂩ��ӂɊ܂܂�A���̕ӏ�ɂȂ�2���_���c��̓�ӏ�ɂ��邱�Ƃ��w���B
D1��D2��D3�͋�łȂ����Ƃ������B >>427
�Ⴆ���W���ʏ�� A(-1,0),B(100,0),C(0,100)�Ƃ����
BC�̈ꕔ��ӂƂ��鐳���`�͐��S���܂܂Ȃ��B �l�Ԃ͒m�荇���̎��ɂ�鐸�_�I���h�Ŏ������k�ށB
���ڂ̒m�荇���̂��Ƃ�1���m�荇���ƌĂԁB�܂��u�m�荇���̒m�荇���v��2���m�荇���A�u�m�荇���̒m�荇���̒m�荇���v��3���m�荇���A�c�Ƃ��A�C�ӂ�2�l�͕K��6���ȓ��̒m�荇���ł���B
��ʂ�n���m�荇���̑��肪���Ƃ��A�l�Ԃ͎�����[{32/2^(n-1)}-1]���ԏk�ށB
�n�N�炪�����Ƃœ��{�����̎����̑��a���ǂ�قnj������邩���肵�����B >>387
�v���O�����g���100�܂ł̎��R���ł���Ă݂��B
a <- function(n){
x=complex(n)
x[1]=1
x[2]=1i
if(n<3) return(x[n])
for(i in 1:(n-2)){
x[i+2]=x[i+1]+x[i]
}
return(x[n])
}
b <- function(n) a(n+1)/a(n)
P <- function(j,k) abs(b(j)-b(k))
P=Vectorize(P)
N=100
j=k=1:N
z=outer(j,k,P)
max(z) ; sqrt(5)
idx=which(z==sqrt(5))
for(i in idx){
print(c(i%%N,i%/%N+1))
}
�ő�l�́�5
> max(z) ; sqrt(5)
[1] 2.2360679774997898
[1] 2.2360679774997898
�����^����l��
> for(i in idx){
+ print(c(i%%N,i%/%N+1))
+ }
[1] 2 1
[1] 1 2 >>426
���S���܂ނ����łȂ��B
��AB��̓_E�A��BC��̓_F,G�A��CA��̓_H�_�Ƃ�����ڐ����`EFGH�����S���܂ނ��Ƃ������B��AB,��AC�̈ꕔ����ӂƂ�����ڐ����`�ɂ��Ă����l�B
�_H�𒆐S�Ƃ��锼�aGH�̉~��O�Ƃ���B����BE�͉~O�ƌ���邩���EBH����GBH�B�䂦�Ɂ�GBH��(1/2)��ABC�ł��邩��A��B�̓����͐���GH�ƌ����B
���l�Ɂ�C�̓����͐���EF�ƌ����B���������ē��S�͐����`EFGH�̓����ɂ���B �O>>417
>>429
�����ɓn�N�炳��̃T�C���F��������܂��B
�n�N�炳�S���Ȃ�������Ƃ����Ď����̂悤�Ȉꕺ���̎������k�ނȂ�Ă����ꑽ���ł��B >>402
���̖��A��͉����ċ��߂����ł��傤���H
����������搔�@�ł���Ă݂悤�ƁA���炭�����R�l�Ă݂�����
�ȒP�Ȍ`���ɂ͎����Ă��������ɂ���܂���B
Wolfram�����l�������o���܂���B
Minimize[ {(x-1)^2+(y-1)^2, x^3+y^3 -3x y == 0}, {x,y} ]
�� ... ����������
u'(t)=f(u(t))
�̈�ʉ����Ăǂ����߂������ł����H ��sin(x^k)dx[0����]�͎������邩���U���邩�B�Ȃ�k�͎����萔�B
����ɂ��ďڂ��������Ă��炢�����ł� >>438
���̒l��ς��ăv���O�����Ŏ������Ă݂�����
> # ��sin(x^k)dx[0��sin(x^k)dx[0����]
> f <- function(k) integrate(function(x)sin(x^k),0,Inf)
> f(1)
Error in integrate(function(x) sin(x^k), 0, Inf) :
roundoff error is detected in the extrapolation table
> f(runif(1,1,10))
Error in integrate(function(x) sin(x^k), 0, Inf) :
maximum number of subdivisions reached
> f(runif(1,0,1))
Error in integrate(function(x) sin(x^k), 0, Inf) :
roundoff error is detected in the extrapolation table
> f(runif(1,-1,0))
Error in integrate(function(x) sin(x^k), 0, Inf) :
the integral is probably divergent
> f(runif(1,-10,-1))
Error in integrate(function(x) sin(x^k), 0, Inf) :
the integral is probably divergent
�����͂��Ȃ��݂����B >>439
�Ȃ������ł��ˏ� ����ǂ�����Đ��w�I�ɏؖ����������ł����ˁc >>417
10 / ( 2sin(2��/5) )��5.257311 �t���l���ϕ���m���Ă���� k �̒l�ɂ���Ď���������������Ȃ������肷�邱�Ƃ͖��炩
|x| > 1 �Ȃ��������
|x| �� 1 �Ȃ�������Ȃ�
�Ɨ\�z >>442
����
|k| > 1 �Ȃ��������
|k| �� 1 �Ȃ�������Ȃ� >>443
�t���l���ϕ����ǂ����p�����炢����ł����ˁc���������Ƃ��Ɍq�����Ă��銴���ł���?? �t���l���ϕ���sin(x^2)dx[0����]�̎������������̂��Ăǂ�����ł����H�H �O>>417�ʉ��B
>>314
5/sin(2��/5)=5.25731112119�c�c >>445
���C�v�j�b�c�̌����ɋA�������������Ȃ��H >>448
�������A�A�ǂ�Ȋ����łȂ���̂ł����H�H�X������Ώڂ����m�肽���ł� �����������ł����Ȃ�c^k=t�ƒu�����邾����� �s�p�O�p�`��ABC�̓����ɓ_P������A
��PAB,��PBC,��PCA�̒l�͂��ꂼ�ꕪ�����Ă���B
���̏����݂̂ŁA�_P�̈ʒu������1�ӏ��ɓ���ł��邩�B >>451
���肷��ɂ͊p�x�͂Q�킩�������Ȃ����ȁH �������������ĔC�ӂ̌`�̉s�p�O�p�`�������
��PAB��45��,��PBC��30���ɂȂ�P���v���O�����ŒT�������Ă݂��B
https://i.imgur.com/eNZGjq9.png >>454
���s�{���s�s�̒n���B����邪�L���B >>443
�@�����ł�!!
�@��(1+1/k) sin(��/(2|k|))�@�@�@(|k|>1)
>>444-445
�@k=2
�@��(3/2) sin(��/4) = (1/2)��(1/2) (1/��2) = ��(��/8) >>402
�f�J���g�̗t���ł����邩�B�^������
1 = x^3 + y^3 + 1^3 - 3xy
�@= (x+y+1)(xx+yy-xy-x-y+1),
f(x,y) = (x-1)^2 + (y-1)^2
�@= {2(xx+yy-xy-x-y+1) + (x+y-2)^2}/3
�@= {2/(x+y+1) + (x+y-2)^2}/3
�@= {2/(s+1) + (s-2)^2}/3�@�@�@(s=x+y)
�@= (s^3 -3ss +6)/{3(s+1)},
df/ds = {2(s^3 -3s -3)}/{3(s+1)^2} = 0�@���
�@s = ��^(2/3) + ��^(-2/3) = 2.1038034�@�ōŏ�
�@{x,y} = {��^(2/3), ��^(-2/3)},�@�@t = xy = 1,
�@f(x,y) �� 2 - ��^(5/3) + ��^(-5/3) = 0.21838195
�@�� = (1+��5)/2 = 1.618034 0 = x^3 + y^3 - 3xy
�@= (x+y)(xx-xy+yy) - 3xy
�@= s(ss-3t) - 3t,
���
�@t = (s^3)/{3(s+1)}, �s�p�O�p�`��ABC�̓����ɓ_P���^�����Ă���A��APB=x��,��BPC=y��,��CPA=z���ł���B
��ABC�̓����̓_Q�ŁA��AQB,��BQC,��CQA�̂������x���܂���y���܂���z���ɓ��������̂��l����B
�ȉ��̏ꍇ�ɁAQ��P�Ƃ͈قȂ�_�ɂƂ邱�Ƃ͂ł��邩�B
�i1�jx>y��z
�i2�jx��y>z
�i3�jx>y>z >>459
���ׂĂł���B�Ⴆ�AA(-1,-1),B(2,0),C(0,2),P(1,0),Q(0,1) �ȂǁB �������ŋ߂Ƃ��ɁA�����������蓊���X���Ɗ��Ⴂ���Ă��Ȃ����Ǝv�����Ƃ������Ă���C������B
�ꉞ�A�����ŕ����Ă��邩��ɂ͕�����Ȃ����Ȃ̂��낤�Ɖ��߂��ĉ����Ă��邯��ǂ��B
������𓊉����������ǓK�ȃX����������Ȃ��Ƃ������ƂȂ�A�f���ɂ������������̂ɁB
����Ƃ��Ȃ�炩�̈Ӑ}���������m�M�ƂȂ̂��낤���B ���M���Ȃ����炱���Ŋm�F���Ă��Ȃ���
�����ƍ����ꍇ�͓����̗p�ӂ��Ȃ������Ŗʔ������ɂȂ邩�m�F���Ă邱�Ƃ����肻�� >>462
��������邽�߂ɓK�ȃX�������ɂ���̂ɂ킴�킴�����ł����Ă̂����܂����킩��Ȃ��ĂˁB >>460
��ʂ̉s�p�O�p�`�ɂ��Ă͂ǂ��ł��� ����ł���������Ȃ��̂œ������܂�
���R�� n �ɑ��A��ϐ������� f[n](x) ���ȉ��̂悤�ɍċA�I�ɒ�߂�B
f[0](x) = x
f[n](x) = (f[n-1](x))^2 - n
�e n �ɑ��A f[n](x) �̎������̂����ő�̂��̂� a[n] �Ƃ���B
��`��薾�炩�� a[n] �͎����̑㐔�I�����ł���B
(1) n > 1 �̂Ƃ��A a[n] �͖��������H
(2) lim[n����] a[n] �͑��݂��邩�H
�@���݂���Ȃ�A����͖��������H���z�����H
(3) g[n](x) ∊ Z[x] �� a[n] �̍ŏ��������Ƃ���B
�@ g[n](x) = f[n](x) �ƂȂ� n �͂ǂ̂悤�Ȑ����H�����łȂ� n �͂ǂ̂悤�Ȑ����H
�@�܂��A���̂悤�� n ����сA�����łȂ� n �͂��ꂼ�ꖳ���ɑ��݂��邩�H ��ʼn����ʔ������ȌX���͏o���̂��ˁH
���ꂪ�Ȃ��ዻ���Ȃ��� >>467
�ȉ��ɗ\�z�������Ă����܂���
�y�\�z(>>466)�z
(1) a[n] �� n > 1 �ŏ�ɖ�����
(2) lim[n����] a[n] �͑��݂��A���炭���z��
(3) n > 1 ��square-free�����̂Ƃ��Ɍ��� g[n](x) = f[n](x)
�@���������Ăǂ���������ɑ��݂��� ���ʂ�a[n]=��(1+��(2+�c��n)�c)�ɂȂ��Ȃ��̂��H
��������͂��邯�ǎ����l�̑㐔�I�L�q�͖������炵��
https://mathworld.wolfram.com/NestedRadicalConstant.html >>469
����ς肻���Ȃ��ł����ˁH
���͂��̐������ɂ����������\�����悤�Ƃ��čl�����̂� f[n](x) �ł�
���������Ă��̐��͍��X 2^n ���̑㐔�I�����ł��邱�Ƃ��킩��܂�
�����A���̐��� f[n](x) �̍��̒��ōő�ɂȂ邩�ǂ������킩��܂��� f[n](x)�̍��̈�ʎ����}��(1�}��(2�c�}��n)�c)�ɂȂ��Ȃ����� >>457
>df/ds = {2(s^3 -3s -3)}/{3(s+1)^2} = 0�@���
>�@s = ��^(2/3) + ��^(-2/3) ...
�����ŃT�N���Ɖ������܂�̂́A���Ń��B�G�g�̉�@���g���Ă܂����H
����Ƃ���������g���������p�^�[��������̂ł��傤���H
���B�G�g�̉�@ (�Q�l: �O�X�� >>432)
s^3 -3s -3 = 0 �̎��������߂�
a = ... = 2
�� = ... = arccos( 3/2 ) / 3 { �Ƃ͋����ƂȂ� }
... �� e^(+3��*I) = ��{ (3+��5)/2 }
s= a*cos(��) = 2*cos(1/3 * ln((3+��(5))/2) * I )�@{����2���͕��f���ƂȂ�}
�@= 2*cosh( 2/3 * ln( ��{(6+2��5)/ 4} ) )
�@= 2*cosh( 2/3 * ln( (1+��5)/ 2 ) )
�@= e^{+2/3 * ln��} + e^{-2/3 * ln��}
�@= ��^(2/3) + ��^(-2/3) ����
�� ... �� e^(+3��*I) = ��{ (3+��5)/2 }
�� ... �� e^(+3��*I) = (3+��5)/2 >>472
��������
�����đS��+��I������ꍇ����ԑ傫��
-��I�����ēr���ŕ��f���ɂȂ邱�Ƃ����邪��Βl�͏��+��I���������̂̕��������Ă邩����v���� �Ă���x���f���ɂȂ镄���I���������炻�̐�����ɂ͋A���ė��Ȃ����Ƃ������邩 �����Ȃ̂���
�����̑I���� f[5](x) �ł�����ɕ��G����
https://www.wolframalpha.com/input/?i=0+%3D+%28%28%28%28%28x%5E2+-1%29%5E2+-2%29%5E2+-3%29%5E2+-4%29%5E2+-5%29
�Ƃ���ŁA f[n](x) �̓W�J���i�̌W���j�͖����I�ɏ�����̂���
���Ƃ��Β萔�� f[n](0) �����ł��킩��Ȃ����낤�� >>473
���̏ꍇ�͎����P�Ȃ̂�
�J���_�m�ʼn����܂��B n��������f(x)��
f(1)f(2)...f(n)=f(n+1)
�ł�����̂�S�ċ��߂����̂ł���������܂���B
1�ȏ�n�ȉ��̂��鐮��m�ɑ�f(m)=0�A����f(n+1)=0�ł���ΐ�������͕̂�����܂��� >>479
n = 2 �̎��_�Ŏ��R�x�������Ė������� >>479
��ʂɂ̓j���[�g���̕�Ԍ����g���ďo����͂�
f(1)�`f(n)���܂��C�ӂɗ^���āA�Ō��(n+1,f(1)f(2)�cf(n))��ʂ�悤�ɐݒ肷�� �j���[�g�����Ă����O�����W����
��̓I�ɂ�
f(x)=��[i=1,n](x-i)f(i)/n!+��[j=1,n]��[i��j](x-i)f(j)/(j-i) �@f(x) = n+1-x + (x-1)(x-2)����(x-n),
�̂Ƃ�
�@f(1)=n,�@f(2)=n-1,�@����,�@(n-1)=2,�@f(n)=1,�@f(n+1) = n! 1��m��n
�@f(x) = (n+1-x)^m + (n!)^(m-1)�(x-1)(x-2)����(x-n),
�ł������� >>482
�Ⴆ��
n=2�̂Ƃ�
f(1)=a�Af(2)=b�Af(3)=ab�Ƃ���
f(x)=(x-1)(x-2)ab/2+(x-2)(x-3)a/2-(x-1)(x-3)b
n=3�̂Ƃ�
f(1)=a�Af(2)=b�Af(3)=c�Af(4)=abc�Ƃ���
f(x)=(x-1)(x-2)(x-3)abc/6-(x-2)(x-3)(x-4)a/6+(x-1)(x-3)(x-4)b/2-(x-1)(x-2)(x-4)c/2
���̂悤�ɂ��Ĉ�ʂ̏ꍇ�����܂� >>482
����� f(x) = (9/4)x^2 ���ďE���Ă����H >>486
��̗��n=2�̂Ƃ���a��b��9/4��9��������Əo��
(x-1)(x-2)81/8+(x-2)(x-3)9/8-(x-1)(x-3)9=9/4x^2 >>481
�@g(x) ��n���ȉ��̑�����
�@f(x) = g(x) + {g(1)g(2)����g(n) - g(n+1)}(x-1)(x-2)����(x-n)/n!
���ȁH >>487
���A ��[i��j] �� i �� 1 ���� n+1 �܂ł��̂�
�Ȃ�قǁA�������� >>488
�Ȃ�قǁA���̋L�q�ł��s����� �摜�̔����������̈�ʉ��̋��ߕ��������Ă������������ł�
�@�����߂��̂ł������Z���x���̐��w���炠��ӂ�Ȃ��ߑS�R������܂���
��낵�����肢���܂�
https://i.imgur.com/zWFat3W.jpg �}���̔����ϕ��w��f(x) - f(0) �` g(x) - g(0)�Ȃ��f(x)�`g(x)�Ə����Ă���܂����A�Ȃ��ł��傤���H
��(x)�`��(x)�͗����Ƃ���������lim_{x->+0}��(x)/��(x)=1���Ӗ�����L���ł��B �}���̖{�����Ă���l��p.85�̈�ԏ�ɏ����Ă���̂ŎQ�Ƃ��Ă��������B >>493
f(x)-f(0)�`g(x)-g(0)
�̎���f()-f(0)��g(x)-g(0)��������������f(0)=g(0)=0�ɂȂ邩�炩�ȁH f(x)-f(0)->0������Ƃ�����f(0)=0�͌����Ȃ��Ǝv���܂��B �}���̖{�ł����A��(x)=(1/x)*log(x)+1/x^2+o(1/x^2)�̂Ƃ�o(��(x)^2)=o(1/x^2)�ł���Ə����Ă���܂����A����͂Ȃ��ł����H(p.96��ԏ�̂�����j >>496
���A���炵�܂����A�����ł���
���nj�����̂�
f(x)-f(0)�`g(x)-g(0) �d�@
����
(0)=g(0)=0�d�A
�Ȃ��
fx)�`g(x)�d�B
�ł��ć@�ˇB�͂�������܂����
(�����f(x)=1+x, g(x)=x �Ȃ�)
�z���g�ɇ@�ˇB�Ɠǂ߂�Ȃ�M����̗ނ��ł͂Ȃ����� �}���̖{�ł����A��(x)=(1/x)*log(x)+1/x^2+o(1/x^2) �ix->���j�̂Ƃ�o(��(x)^2)=o(1/x^2)�ix->���j�ł���Ə����Ă���܂����A����͂Ȃ��ł����H(p.96��ԏ�̂�����j >>499
���藧���Ȃ��Ǝv��
f(x) = (��(x)^2)/(log(x)) �Ƃ���� f(x) = o(��(x)^2) �����A
x^2 f(x) = x^2 ��(x)^2 /(log(x)) = O(log(x)) �� �� >>498
���肪�Ƃ��������܂��B
>>500
���肪�Ƃ��������܂��B
�����_�E�̋L���W�̘b�͂��܂葼�̖{�ɂ��ڂ��Ă��Ȃ����e�ł��̂ŁA���J�ɏ����Ă������Ƃ�����ǂ������̂ł����A���ɎG�Ȃ�ł��B
���Ȃ݂ɁA>>499�͓r���̌v�Z�ŏo�Ă����ł����A�ŏI�I�Ȍ��ʁi�ȉ��ɏ����܂��j�͊Ԉ���Ă��Ȃ��ł��傤���H(pp.95-96)
(1+x)^(1/x) = 1 + (1/x)*log(x) + (1/(2*x^2))*(log(x))^2 + 1/x^2 + o(1/x^2) (x->��) ���Y���v�̉�͓���1��p.117���1(iv)���܂���>>501�̖��ł����B
�����́A 1 + (1/x)*log(x) + (1/(2*x^2))*(log(x))^2 + o(|log(x)|^2/x^2) �ł����B �ǂ��炪�����Ă���̂��A���邢�͗��������Ă���̂��A���邢�͗����Ԉ���Ă���̂��H�ǂȂ����킩�����������Ⴂ�܂����H (1+x)^h = x^h�E(1+1/x)^h
�}�N���[������
�@x^h = e^{h log(x)} = ��[k=0,��] (1/k!){h log(x)}^k,
��ʓ�����
�@(1+1/x)^h = 1 + h/x + h(h-1)/(2x^2) + ����,
������ h��1/x �Ƃ����B
>>499
�@��(x)^2 = O({log(x)/x}^2) = o(1/x^2)�@(x����)
>>501 �͐������B
>>502 �� x^(1/x) �Ǝv����B (1+x)^(1/x)
=exp( (1/x)log(1+x) )
= 1 + (1/x)log(1+x)
. + (1/2)( (1/x)log(1+x) )^2
. +o( (1/x)log(1+x) )^2
��
(1/x)log(1+x)=(1/x)log(x)+1/x^2+o(1/x^2)
����������ł����� >>499
�������Ȃ��Ǝv��
>>501 >>502
������������ >>492
(1) (x^2-y^2) y' = 2xy
��F/��x = -2xy q(x,y), ��F/��y = (x^2-y^2) q(x,y)
�ƂȂ�� F(x,y) �����߂Ă݂�B
��̔����������� dF = (��F/��x) dx + (��F/��y) dy = 0 �Ɠ���(��)�ł���B(q(x,y)�͐ϕ����q)
�݁�F/��x��y = �݁�F/��y��x �����K�v (�A�������Ƃ��ϕ��\�����Ƃ�) ������̂ŁA
-2xq -2xy ��q/��y = 2xq + (x^2-y^2) ��q/��x
(x^2-y^2)��q/��x + 2xy ��q/��y = -4xq {�ꌩ�ȒP�ɂȂ�C�����Ȃ���...}
q = 1/y^2 �����������B
����� ��F/��x= -2x/y,�@ ��F/��y= x^2/y^2 - 1
�� F(x,y) = -x^2/y - y = 2R {�ϕ��萔}
x^2 + (y - R)^2 = R^2�@�܂�A�����͉~�ł���B
�z���́@y = R �} ��{R^2 -x^2}�@ (-|R| �� x �� +|R|)
�X���������ɂȂ�_ (x=�}|R|) �͋Ɍ��_�Ƃ��ċ��e����邾�낤�B
�ϕ����q���l������� y = 0 (�萔��)���܂����ł���B����͉~���̋Ɍ��ł�����B
(��������������͕̂��������L�Ӗ��Ȕ͈͂̂�) >>492
(2) y' +2y = a*cos(2x)
A��萔�Ƃ����
(Ae^{�}i2x})�f + 2*Ae^{�}i2x} = (2�}2i)Ae^{�}i2x}
����ē�����
y = a/2 * ( e^{+i2x}/(2+2i) + e^{-i2x}/(2-2i) )
�@= a/2 * Re{ e^{+i2x}/(1+i) }
�@= a/4 * Re{ (1-i)e^{+i2x} }
�@= a/4 * ( cos(2x) + sin(2x) )
�Ď���ʉ��ƍ��킹��
y = C * e^{-2x} + a/4 * ( cos(2x) + sin(2x) )
����ʉ��ł���B >>492
(3) y'+y/x = x^m y^m
�����Wolfram�ŃJ���j���O
�@DSolve[ y'[x]+y[x]/x == x^m y[x]^m, y[x],x ]
�@... {{y[x]��(x^(1 + m)/2 - 1/2 m x^(1 + m) + x^(-1 + m) C[1])^(1/(1 - m))}}
�悭������� ��^(1/(1 - m)) ���̂Ȃ̂��낤�B (����Ȃ̎v�����킯���Ȃ�...��)
f(x) = y^{1-m} �ƒu����
f' = (1-m) f/y * y' = (1-m)�@f * (x^m /f - 1/x )
�� f' -(m-1)f/x -(1-m)x^m = 0
f' -p(x) f - q(x) = 0 �^�C�v�̕������� ((2)�ł��g����p�^�[��) ...
f(x) = e^{+��dx p} ��dx( q e^{-��dx p} )�@�@{p=(m-1)/x, q=(1-m)x^m}
= x^{m-1} ��dx ( (1-m)x^m *�@x^{1-m} )
= (1-m) x^{m-1} ( 1/2 * (x^2�@- C^2) )�@�@{�ϕ��萔�͌�m�b�Ő�����}
�����
y = { (m-1)/2 * x^{m-1} ( C^2 - x^2 ) }^{1/(1-m)}�@�@( -|C| �� x �� |C| )
(�������Wolfram���Ɠ����ł���)
���莝���̖{���悭������A����̓x���k�C�̕������̃p�^�[�����������B
�@���Ԃ������邯�ǖY��Ă��B >>492
(1)�͓����`�i���ӂ� x^2 �Ŋ���j
(2)�͐��`
(3)�̓x���k�[�C�` >>492
�@�@(xx-yy)(dy/dx) = 2xy,
�@x = r cos��,�@y = r sin��,
�Ƃ����ƁA�^����
�@(dy/dx) = tan(2��),
���Ȃ킿
�@(���aOP�� P�ł̐ڐ��̂Ȃ��p) = �� = (���aOP�� x���̂Ȃ��p),
x�����_O�ł̐ړ_���Ƃ���ƁA
2�_O, P�ɂ�������p�������������ƂɂȂ�B
�~���p�̒藝�̋t�ɂ��AP�̋O�Ղ� O ��ʂ�~���B
�����`�Ȃ̂Ł@u = y/x�@�Ƃ����B
�@x(du/dx) + u = (dy/dx) = 2xy/(xx-yy) = 2u/(1-uu),
���
�@(1/x)dx = {(1-uu)/u(1+uu)}du = {1/u - 2u/(1+uu)}du,
�@x = 2R u/(1+uu) = 2R xy/(xx-yy),�@{2R:�ϕ��萔}
�@x^2 + (y-R)^2 = R^2, >>492
�B�@(dy/dx) + y/x = x^m y^m,�@�@(m��2�ȏ�̒萔)
�@(1/x)(xy) ' = (xy)^m,
xy=v�@�Ƃ�����
�@(1/x)v ' = v^m,
�@v^(-m) v' = x,
�ϕ�����
�@-{1/(m-1)}v^(1-m) = -(CC-xx)/2,
�@y = v/x = (1/x){(m-1)(CC-xx)/2}^{1/(1-m)}, >>511
> x = 2R u/(1+uu) = 2R xy/(xx-yy),�@{2R:�ϕ��萔}
> x^2 + (y-R)^2 = R^2,
�Ⴍ��
��͑o�Ȑ�
���͉~ >>509
(3)�̉��͂��s���m�Ȃ̂ŏ�������
m: ���� �� y = + { (m-1)/2 * x^{m-1} ( C - x^2 ) }^{1/(1-m)}�@�@
��`��: C>0 �� { x<-C, 0<x<+C }, �@C��0 �� { x<0 },
m: � �� y = �} { (m-1)/2 * x^{m-1} ( C - x^2 ) }^{1/(1-m)}�@�@
��`��: C��0 �� { |x|<C },�@ C��0 �� �����Ȃ�
�Ƃɂ��� �������͐��� y^(1-m) �� �` �ɂȂ�Ηǂ��B >>514 (�Ē���)
m: ���� ��
�@y = + { +(m-1)/2 * x^{m-1} ( C - x^2 ) }^{1/(1-m)}�@�@
�@��`��: C >0 �� { x<-C, 0<x<+C }, �@C��0 �� { x<0 }
�@y = - { -(m-1)/2 * x^{m-1} ( C - x^2 ) }^{1/(1-m)}�@�@
�@��`��: C >0 �� { -C<x<0, +C< x}, �@C��0 �� { x��0 }
y�����̗̈�ɉ��͖����H�ƋC�t���ׂ��������B >>500
O(log(x)) ���Əؖ��ɂȂ��ĂȂ���
x^2 f(x) = log(x) + o(1) �� ��
������ >>386
wolfram���͉\�ɒZ�k����
Table[2n-1+C(0,n-2)+3C(1,(10mod n)-2)+5C(1,n-11)+3C(0,C(0,C(3,n-16)))+11C(0,n-22)+C(0,C(0,C(6,n-29))),{n,1,44}] �킩��Ȃ�����
�킩��Ȃ��܂܂ɂ��Ă������Ƃɂ����
�l�X�͍K���ɂȂ� >>513
��Ƃ���B
�@x = 2R u/(1+uu) = 2R xy/(xx�{yy),
�ł����B >>499
>>499
�}���̂��قڏ����ʂ��܂����B�N����ǂ��Ă��������B
f(x) = (1 + x)^(1/x)
log(f(x)) = (1/x)*log(1 + x) = (1/x)*log(x) + (1/x)*log(1 + 1/x) = (1/x)*log(x) + (1/x)*(1/x + o(1/x))
= (1/x)*log(x) + 1/x^2 + o(1/x^2) (x->��)
f(x) = exp((1/x)*log(x) + 1/x^2 + o(1/x^2))
log(f(x))�̊e����x->���̂Ƃ����ׂĖ�����������e�C���[��������
f(x) = 1 + ((1/x)*log(x) + 1/x^2 + o(1/x^2)) + (1/2)*((1/x)*log(x) + 1/x^2 + o(1/x^2))^2 + o(1/x^2) �� ���ꂪ�Ȃ����藧�̂�������Ȃ��B
= 1 + (1/x)*log(x) + (1/(2*x^2))*(log(x))^2 + 1/x^2 + o(1/x^2)) (x->��) >>520
���������Q�ߓW�J�͉������ꂵ���Ă���ȕ��ɓW�J���Ă����ł����H
x���傫������f(x)��1 + (1/x)*log(x) + (1/(2*x^2))*(log(x))^2 + 1/x^2�̒l���߂��Ƃ������Ƃ������Ċ������Ƃ������Ƃł����H
�ł��ǂꂭ�炢x���傫���Ƃ��ɁA�덷�͂ǂꂭ�炢�Ƃ��������͓����܂���Ӗ�����̂��ȁH���Ďv���܂����B >>521
�܂������Ă鎖�ɂ��������Ӗ����������Ȃ����ʔ������Ȃ��Ƃ����Ȃ疳�����ēǂ܂Ȃ��Ă�������ł͂Ȃ��H
����
f(x) = 1 + ((1/x)*log(x) + 1/x^2 + o(1/x^2)) + (1/2)*((1/x)*log(x) + 1/x^2 + o(1/x^2))^2 + o(1/x^2)
���Ȃ킿
f(x) = 1 + ((1/x)*log(x) + 1/x^2 + p(x)) + (1/2)*((1/x)*log(x) + 1/x^2 + q(x))^2 + r(x)
for some
p(x), q(x), r(x)
such that
lim p(x)x^2 = lim q(x)x^2 = lim r(x)x^2 = 0
���炢�͎����Ŏ����Ȃ��Ƃ��̐扽�����ĂĂ��s���l�܂�� �m���Ɍ����Ă݂�I�[�_�[�v�Z�̐��������������Ƃ��Ă���ܖ���������
exp���炢�s�V�̂������Ȃ���v���낤�Ƃ���Ă��܂����������Ǔ��ɕ����Ƃ� ���藧���Ȃ���Ȃ��́H
�덷���t���̃e�C���[�W�J
exp(h) = 1 + h + h^2/2 + o(h^2) as (h��0)
�ɂ�����
h = (1/x)*log(x) + 1/x^2 + o(1/x^2) as (x����)
�ƒu�����悤�Ɍ����邯��
h^2 �ɂ� (log(x))^2 / x^2 �̍����܂܂�邩�� x^2 ���|�����甭�U����͂�
o(h^2) = o((log(x))^2 / x^2) as (x����)
���Ǝv����
�Ⴆ��
log(x)/x^2 = o((log(x))^2 / x^2) as (x����)
�����A log(x)/x^2 = o(1/x^2) as (x����) �ł͂Ȃ� >>507ID:SfLQkZLB�����>>511ID:U7f6nYy/���J�ɉ�����肪�Ƃ��������܂�
���Ƃł�������������Ă��������܂�
>>510
���肪�Ƃ��������܂�
���ȏ��ƃm�[�g�ʼn�@���m�F���Ă݂܂� >>524
������o(h^k)��o(h ^k)/h^k��0(h��0)�̈Ӗ�����Ȃ��́H
o�̂Ƃ��ɓ����Ă�̂�(logx)^3/x^3
>>520�̎��ł�(logx)^2/x^2�̍���o�̊O�ɂ��邩����Ȃ������Ɍ����� �܂������_�E��o�Ƃ�O��
exp(x)=1+x+x^2/2+O(x^3)
�����ۂ�
exp(x)=1+x+x^2/2+p(x)
for some p(x)
such that
|p(x)/x^3| is bdd.
�Ə��������Ă݂Ă݂鎖�������Ȃ��Ɗ����g�ɂ��Ȃ�
���������킩���Ă����������o���ɗ��ł����ꂽ�n�͂͐g�ɂ��Ȃ������
���w���悤�ȓz�͂��������n���͂����̂ł��������C���Őg�ɂ��Ă���͂��y�������� >>526
>>522�Ɠ����悤�ɏ����A
g(h) = o(h^2) as (h��0) �̒�`�� lim[h��0] g(h)/h^2 = 0 �ł���H
h^2 = (log(x))^2 / x^2 + o(1) as (x����)
������덷���� (log(x))^2 / x^2 ���c���Ă��܂��Ǝv��
> o�̂Ƃ��ɓ����Ă�̂�(logx)^3/x^3
3��͂ǂ�����o�Ă����H
O �i�r�b�O�I�[�j����Ȃ��� o �i�X���[���I�[�j�̘b�ł́H >>628
exp(t)=1+t+t^2/2+O(t^3)
��
t=(1/x)log(x) + 1/x^2 + o(1/x^2)
���g����h�ł���Ȃ�킩��
�g����h�ł��Ȃ��Ȃ�
exp(t)=1+t+t^2/2+p(t)
t= (1/x)log(x) + 1/x^2 + q(x)
�ƃL�`����p(x), q(x)�ƒ萔
|p(x)|<M|t^3|
�Ƃ����Ă݂ăz���g�ɑ�����Ă݂�킩�� >>528
exp(h)=1+h+h^2/2+o(h^2)�Ə����Ă邯��
���ۂ�o�̒��ɓ����Ă�̂�h^3�ȍ~�̍������� ������
|p(t)|<M|t^3|
�ˁB
��������
|p((1/x)log(x)+1/x^2+q(x))|
<M |((1/x)log(x)+1/x^2+q(x))^3|
�ƂȂ�
�R���������Ӗ����邩 >>529
>exp(t)=1+t+t^2/2+O(t^3)
�����A���������g���̂�
����Ȃ�m���ɍ��X
O((log(x))^3 / x^3) ������ x^2 O((log(x))^3 / x^3) = o(1) as (x����)
���� >>499
�Ӗ��s����
�@o(��(x)^2) = o(1/x^2)�@�@�@(x����)
�������̌����H
>>516
�@x^2 f(x) = O(log(x))�@�́A���イ�Ԃ�傫��x�ɂ���
�@m < | x^2 f(x)/log(x) | < M�@�@�@(0<m<M<��)
�̈Ӗ��Ƃ���A�ؖ��ɂȂ��Ă�B
>>520
log(x+1) = log(x) + log(1 + 1/x)
�@= log(x) + 1/x - 1/(2x^2) + 1/(3x^3) - ���,�@�@�@�@ (�}�N���[����)
log(f(x)) = (1/x)log(x+1)
�@= (1/x){log(x) + 1/x - 1/(2x^2) + 1/(3x^3) - ���� }
f(x) = exp[(1/x){log(x) + 1/x - 1/(2x^2) + 1/(3x^3) - ���� }]
�@= 1 + (1/x){log(x) + 1/x - 1/(2x^2) + 1/(3x^3) - ���� }
�@�@+ {1/(2x^2)}{log(x) + 1/x - 1/(2x^2) + ���� }^2
�@�@+ {1/(6x^3)}{log(x) + 1/x - ���� }^3
�@�@+ {1/(24x^4)}{log(x) + ���� }^4
�@�@+ �����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(�}�N���[����)
�ƂȂ�B
1/x^2 �̍��܂Ŏc�� 1/x^3, 1/x^4, ���� �̊|���������������
�@1 + {log(x) + 0}/x + {(log(x))^2 /2 + 0�log(x) + 1}/x^2, ���ǁA�y�A�m�̏�]�����g���Ə�肭�����Ȃ����A
���O�����W���̏�]�����g���Ώ�肭�������Ęb���� 41000
14100
01410
00141
00014
�̂悤�ɁA�Ίp������4�A����ɗׂ荇��������1�A����0��n�~n�̑Ώƍs��̋t�s���n���g���ĕ\���A�Ƃ����̂��킩��܂���B wolfram��搶��n=6�܂ŋ����Ă�������琄��ł���
���X�ʔ��� >>536
���̑Ώ̍s���A�Ƃ���
�����őQ����
f(0)=0, f(1)=1, f(n+2)+4f(n+1)+f(n)=0
���l����ƁA����͓�������=-2+��3���g����
f(n)=(��^n-��^(-n))/2��3�Ɖ�����
n���s��B������f(x)�ƊK�i����(x)���g����
Bij= ��(i-j)f(i-j)-f(i)f(n+1-j)/f(n+1)
�ƒ�߂�Ƃ��ꂪA�̋t�s��ɂȂ��Ă���
����
�P����f(n+1)f(i-j)=f(i)f(n+1-j)-f(n+1-i)f(j)����B��
Bij=��(j-i)f(j-i)-f(j)f(n+1-i)/f(n+1)
�Ƃ�������(�Ώ̍s��ł���)���A���̂Q�ʂ�̕\�����g�����Ƃ�A�̋t�s��ł��邱�Ƃ��ȉ��̂悤�Ɋm���߂���
f(n)���Q�����������Ƃɂ��
�c�x�N�g��{f(i)}_i��A�̑�n�s�ȊO�̉��x�N�g��������
�c�x�N�g��{��(i-j)f(i-j)}_i��A�̑�j�s�Ƒ�n�s�ȊO�̉��x�N�g��������
�c�x�N�g��{f(n+1-i)}_i��A�̑�1�s�ȊO�̉��x�N�g��������
�c�x�N�g��{��(j-i)f(j-i)}_i��A�̑�j�s�Ƒ�1�s�ȊO�̉��x�N�g�������ƒ������Ă���
����ď��2�ʂ��B�̕\������c�x�N�g��{Bij}_i��A�̑�j�s�ȊO�̉��x�N�g������{Aik}_k(i��j)�ƒ������Ă���
�����đ�j��̉��x�N�g��{Ajk}_k�Ƃ̓��ς�1�~(-��(j+1-j)f(j+1-j))=-f(1)=1�ƂȂ�
�����AB=E���Ӗ����Ă���
���[��A�����Ƃ����\���Əؖ������邩��
�܂����ۂɍs��������Ă݂�Ώ�̏ؖ��ł���Ă邱�Ƃ͂ƂĂ��P���Ȍv�Z >>540
����
�� �����đ�j��̉��x�N�g��{Ajk}_k�Ƃ̓��ς�1�~(-��(j+1-j)f(j+1-j))=-f(1)=1�ƂȂ�
�� �����đ�j�s�̉��x�N�g��{Ajk}_k�Ƃ̓��ς�1�~��(j+1-j)f(j+1-j)=f(1)=1�ƂȂ� �Ȃ��ΐ����̃e�C���[�W�J��log(1+x) = x - (1/2)*x^2 + �c��log�̈�����1+x��n�����`�̊���W�J���Ă���̂ł��傤���H
log(x) = ��_{1}^{x} 1/t dt�ƁA�ϕ��͈͂̉��[��1�Ȃ̂Ŋm���ɁAx��1����v���X�}�C�i�X�ǂꂭ�炢���ōl����͎̂��R���Ƃ͎v���܂����Ȃs�v�c�ł��B
log(1+x)�ƈ�����1+x�ɂ���ƃe�C���[�W�J���V���v���ɂȂ�[�����R�͂���܂����H ���a�̈قȂ�����Ȃ���̉~A,B������B
A,B�ɐڂ���~C�̒��S�̋O�Ղ͂ǂ̂悤�ȋȐ����H >>520
�݂Ȃ��肪�Ƃ��������܂����B
�����Ȃ�̉����܂����B
f(x) = exp((1/x)*log(x) + 1/x^2 + o(1/x^2))
log(f(x))�̊e����x->���̂Ƃ����ׂĖ�����������e�C���[��������
f(x) = 1 + ((1/x)*log(x) + 1/x^2 + o(1/x^2)) + (1/2)*((1/x)*log(x) + 1/x^2 + o(1/x^2))^2 + (1/6)*((1/x)*log(x) + 1/x^2 + o(1/x^2))^3 + o(((1/x)*log(x) + 1/x^2 + o(1/x^2))^3)
o(((1/x)*log(x) + 1/x^2 + o(1/x^2))^3) = o(1/x^2)�ł���B
�ؖ��F
p(x) = o(((1/x)*log(x) + 1/x^2 + o(1/x^2))^3)�Ƃ���B
p(x) / (1/x^2) = [p(x) / ((1/x)*log(x) + 1/x^2 + o(1/x^2))^3]*[((1/x)*log(x) + 1/x^2 + o(1/x^2))^3 / (1/x^2)]
p(x) / ((1/x)*log(x) + 1/x^2 + o(1/x^2))^3 -> 0 (x->��)�͉��肩�琬�藧�B
((1/x)*log(x) + 1/x^2 + o(1/x^2))^3 / (1/x^2) = (log(x))^3/x + (log(x))^2/x^2 + log(x)/x^3 + 1/x^4 + o(1/x^2)
(log(x))^3/x, (log(x))^2/x^2, log(x)/x^3, 1/x^4�͂��ׂĖ������ł��邩��
((1/x)*log(x) + 1/x^2 + o(1/x^2))^3 / (1/x^2) -> 0 (x->��)�����藧�B
��p(x) = o(1/x^2)�ł���B
��f(x) = 1 + ((1/x)*log(x) + 1/x^2 + o(1/x^2)) + (1/2)*((1/x)*log(x) + 1/x^2 + o(1/x^2))^2 + o(1/x^2) >>542
����̓e�C���[�W�J�ł͂Ȃ��}�N���[�����W�J���B
log��x=0�Œ�`����Ȃ�����x=1�Ńe�C���[�W�J����͎̂��R�Șb�ŁA������}�N���[�����W�J�Ŏ������悤�Ƃ����log(1+x)�Ƃ���͓̂��R�̂��ƁB >>546
x=2�Ńe�C���[�W�J���Ȃ��̂͂Ȃ��ł����H �����鐳�̐��őI�ԂȂ�1�����ꂢ���Ƃ͎v���́H
�ǂꂩ�ЂƂŒ肵�����͕��s�ړ�����������������A�킴�킴�����Ȃ�悤�Ȓl���g���K�v���Ȃ� >>548
�Ȃ�x=1��I�Ԃ��Y��ɂȂ�̂ł��傤���H���̗��R���m�肽���ł��B x = 0 �ɂ����� n �K�̔����W�������ꂢ�ɂȂ邩�炭�炢�̗��R����Ȃ��� >>550
log(x) = ��_{1}^{x} 1/t dt�̐ϕ��͈͂̉��[��1�ł��邱�ƂƉ����W������܂����H >>551
����܂�W�Ȃ�
�����Č����Ȃ�A log(1) = 0 �ƂȂ邭�炢
���ۂ� log(a+x) �� n �K�������v�Z���Ă݂������� >>540
����n���Ώ̍s��̍s�� f(n) �Ƃ�����
�@f(0) = 1,�@f(1) = x,�@f(2) = xx-1,
(1�s�ځAn�s�ځA1��ځAn��ڂ̂ǂꂩ��)�W�J����ƁA�Q������
�@f(n+2) - x f(n+1) + f(n) = 0,
����A����`�F�r�V�F�t������ ��
�@U_0(x/2) = 1,�@U_1(x/2) = x,�@U_2(x/2) = xx-1,
�܂��A�a�ό���
�@sin((n+3)��) - 2cos�ƥsin((n+2)��) + sin((n+1)��) = 0,
����
�@U_{n+2}(x/2) - x U_{n+1}(x) + U_n(x/2) = 0,
����������ׂ��
�@f(n) = U_n(x/2),
�ƂȂ邱�Ƃ͖��炩�B (����)
�܂��A�a�ό���
�@sin��((n+3)��) - 2cos���ƥsin��((n+2)��) + sin��((n+1)��) = 0,
�`�F�r�V�F�t���������̂��̂͗����Ɏg����̂ŁB�B�B (����)
x=4 ������
f(n) = U_n(x/2)
�@= U_n(2)
�@= sinh((n+1)��)/(sinh ��)
�@= {(2+��3)^{n+1} - (2-��3)^{n+1}) / (2��3),
������
�@cosh �� = 2,�@sinh �� = ��3, �O���ԑQ�����������̂ɂȂ������܂ł����
����ɖ��͍s�ł͂Ȃ��t�s������߂邱�� >>543
�~A,B�̊O������ڂ���~C�̒��S�́A���������̉~���̎}�ɂ���
�~A,B�����Đڂ���~C�̒��S�́A�傫�����̉~���̎}�ɂ���B >>543
�Ƃ��ɊO�ڂ���~�ƂƂ��ɓ��ڂ���~�ň�̑o�Ȑ��i�œ_�Ԃ̋��������a�̍��j
����ɊO�ڂ��A�����ɓ��ڂ���~�ł�����̑o�Ȑ��i�œ_�Ԃ̋��������a�̘a�j
�ŁA�v2��4�{�̑o�Ȑ� �J�b�R�̒��͊��Ⴂ��B�Y��Ă���B a,b��a>b>0�̎����Ƃ���B
���_��O�Ƃ���xy���ʏ�̑ȉ~C:(x^2/a^2)+(y^2/b^2)=1�̏œ_�̂����Ax���W�����ł�����̂�F�Ƃ���B
C�̎����2�_P,Q����POQ=��(0<��<��)�ł���悤�ɓ����Ƃ��A��PFQ=�ƂƂȂ�P,Q�̍��W��a,b,�Ƃŕ\���B ���`�x�[�V�������S��������Ȃ� >>543
�����Ȃ����Ă͈̂���̉~����������̉~�̓����ɂ���ꍇ���Ă̂�����B
���̏ꍇ�͂Q�~�̒��S���œ_�Ƃ���ȉ~�B�Q�~�̕Е��̔��a�����ɂ���ƒ����ɂȂ�A�����Е��̔��a���[���ɂ���Ɠ_�ɂȂ�
���̏ꍇ�͕������ɂȂ�B�i�[���ɂ��Ȃ��Ă��������j >>560
���S��: e = ��(1-b^2/a^2) �ƒu����
O=(0,0), F=(e*a,0) ��2�_��ʂ�~ :
�@(x - e*a/2)^2 + (y - ��{ r^2 -(e*a/2)^2 })^2 = r^2
�� �ȉ~C �Ƃ̌�_ P, Q {r�̊�} �����߂�B
�����藝��� 2r sin�� = |PQ|�A������t�Z���� r = .. {�Ƃ̊�}
����� P=(.. , ..),�@ Q=(.. , ..)�@{�Ƃ̊�}
��B
�V���v���Ȏ��ɂȂ�C�z���������Ȃ����ǁA���������Ď�����H
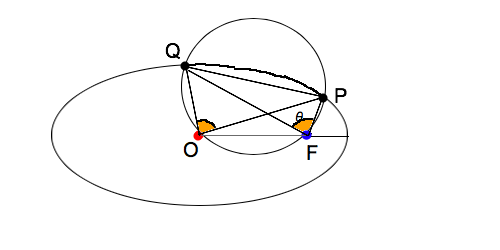 >>557 >>558
>>557 >>558
�~A�̒��S�� A(d/2,0) ���a�� r_a
�~B�̒��S�� B(-d/2,0) ���a�� r_b
�~C�̒��S�� P(x,y) ���a�� R
�@r_a + r_b < d = AB
�Ƃ���B
�EC��A,B�̊O������ڂ���Ƃ�
�@R = AP - r_a = BP - r_b,
�@x = (rb-ra)��{1/4 - yy/[dd-(rb-ra)^2]},
�EC��A,B������Ƃ�
�@R = AP + r_a = BP + r_b,
�@x = (ra-rb)��{1/4 - yy/[dd-(ra-rb)^2]},
�EC��A�̊O������ڂ��AB������Ƃ�
�@R = AP - r_a = BP + r_b,
�@x = -(ra+rb)��{1/4 - yy/[dd-(ra+rb)^2]},
�EC��A�����AB�̊O������ڂ���Ƃ�
�@R = AP + r_a = BP - r_b,
�@x = (ra�{rb)��{1/4 - yy/[dd-(ra+rb)^2]}. ���� �Ͽ.
�@x = (rb-ra)��{1/4 �{ yy/[dd-(rb-ra)^2]},
�@x = (ra-rb)��{1/4 �{ yy/[dd-(ra-rb)^2]},
�@x = -(ra+rb)��{1/4 �{ yy/[dd-(ra+rb)^2]},
�@x = (ra+rb)��{1/4 �{ yy/[dd-(ra+rb)^2]}. >>562
�~A�̒��S�� A(d/2,0) ���a�� r_a
�~B�̒��S�� B(-d/2,0) ���a�� r_b
�~C�̒��S�� P(x,y) ���a�� R
�@d + r_a < r_b�@�@�i�~A���~B�ɓ�����)
�Ƃ���B
�EC��A�̊O������ڂ��AB�ɓ��ڂ���Ƃ�
�@R = AP - r_a = r_b - BP,
�@x = �}(ra+rb)��{1/4 �| yy/[(ra+rb)^2 -dd]},
�EC��A�����AB�ɓ��ڂ���Ƃ�
�@R = AP + r_a = r_b - BP,
�@x = �}(ra-rb)��{1/4 �| yy/[(rb-ra)^2 -dd]} a^a - (a+b)^(a-b) = a - b
�������̐���a,b��S�ċ��߂�B >>567
(a, b) = (1, 1), (2, 1) �݂̂��Ǝv����
�����̖��Ƃ��������s�����̖�肾�낤��
a �� 2 �̂Ƃ��́A�K�v���� b �� a ��葍������ŏ�̉��Ɍ����邱�Ƃ��킩��
a > 2 �Ȃ�A�ؖ��͂킩��Ȃ����A�s����
a^a - (a+b)^(a-b) > a - b
����������͂�
�O���t�������Ζ��炩�Ɏv���邪�A��肢�ؖ����v�����Ȃ�
�Ƃ���������������肩�H f(x)=x³-x²-x-1, g(x)=x²-x-1 �Ƃ���
(1) x�̕����� f(x)=0 �͂����ЂƂ̎��������������A����� 1<��<2 �ł��邱�Ƃ�����
(2) x�̕����� g(x)=0 �̐��̉������Ƃ��āA���ƃ��̑召���r����
(3)��²�ƃ�³�̑召���r����
(3)�̈�ʂɑz�肳����@�̓��̋�̓I�Ȓl�����߂Ă���A���̒l����������������
��³=�����²=��(��+1)=��²+��=(��+1)+��=2��+1
�ɑ�����A1<��²<4 �Ɣ�r������̂ł�
�������A�����ƑN�₩�ȉ�@�����肻���ȋC�����܂��B�����v�������l����������Ă��������B >>569
��r���đ召�W���킩��Ηǂ��́H
����Ȃ�(2)���� 1 < �� < �� ���킩�邩��A
��^2 < ��^2 < ��^3
�Ƃ��邾�����Ǝv������
�t�ɂ��́u��ʂɑz�肳����@�v�͉����������̂��킩��Ȃ� >>570
�v�Z�~�X����
�Y��Ă������� xyz��Ԃ̌��_O�_�A�~C:x^2+y^2=r^2(z=H)���~�Ƃ��钼�~��V������AV��0��z��h(0<h<H)�̕����͐��Ŗ�������Ă���B
����C���1�_����AC�̐ڐ������Ɏ���m�̎��_���ˏo����ƁA���_�͉~���̓����ʂɉ����ĉ��~���n�߂��B
V�Ǝ��_�̊Ԃɖ��C�͂Ȃ����̂Ƃ��āA�ȉ��̖�ɓ�����B
�i1�j���_���~���̑��ʏ�h<z<H���Ă���Ƃ��̑���|v|�����߂�B
�i2�j���_�������ɓ���������A�~���̓����ʂɒ���t�����܂܌��_�܂ʼn��~���邱�Ƃ͉\���B >>569
�� �̋�̓I�Ȓl���g���̂����Ȃ�A
g(3/2) < 0 ��� �� > 3/2 ������A
��^3 = 2��+1 > 4 > ��^2
�Ƃ����� >>569
������v������
g(4) = 11 �𗘗p���āA
g(��^3) = 7��+4 > 11 = g(4) ���
��^3 > 4 > ��^2 >>567-568
���̐��������a��b
a-b=0�̂Ƃ�a^a=1���(a,b)=(1,1)�ƂȂ�
a-b=1�̂Ƃ�a^a=2a���(a,b)=(2,1)�ƂȂ�
�ȉ��Aa-b��2(�����I��a��3)�̂Ƃ����l����
a=3�̂Ƃ�(a,b)=(3,1)�͕s�K�Ȃ̂�a��4�ƂȂ�
����f(x)=(1+x)^(1/x-1)�͑ΐ��������v�Z���邱�Ƃ�
(0<x<1)�ŒP������(f(0)=e,f(1)=1)���킩��̂�
1<(1+b/a)^(a/b-1)<e�ƂȂ��Ă���
������g����
a^a-(a+b)^(a-b)
=a^(a-b)(a^b-((1+b/a)^(a/b-1))^b)
>a^2(a^b-e^b)
��4a(4^b-e^b)
>4a>a-b
�ƂȂ�A(����)>(�E��)�������Ȃ����Ƃ��킩�� >>573
�����_�͉~���̓����ʂɉ����ĉ��~���n�߂��B
�̗��R���s���łǂ����悤���Ȃ��B�ڐ������Ɏˏo������~���𗣂�Ė�����̕����ɔ��ł����͂����낤�B
��蕶�̐ݒ�ɂ͋L�q����Ă��Ȃ����m�̗͂��������莿�_�̓����ɂȂ�炩�̐�����Ƃ����v���Ȃ��B
��V�Ǝ��_�̊Ԃɖ��C�͂Ȃ����̂Ƃ���
�����ĂȂ��͂̏��Ȃ���Ȃ�����A�����Ă���͂͂��ׂċL�q���Ă���B������Ă��Ȃ������͏���ɑz�肵�Ȃ���B��������Ȃ�����B
�����Đ��w�̖��Ƃ��Ă͕s�����炯�œ����悤���Ȃ��B (1)
�@�� = {1 + (19-3��33)^(1/3) + (19+3��33)^(1/3)}/3
�@= 1.839287 < 2,
(2)
�@�� = (1+��5)/2 = 1.618034�@(������)
�@�� > ��
(3)
�@��^3 = ��(��+1)
�@�@= (1/�� +1)(��+1)
�@�@> (1+1)^2�@�@�@(�R�[�V�[)
�@�@> ��^2, >>569
����Ȃ���������
��^2 = �� + 1
�̗��ӂ� 3 �悷��ƁA
��^6 = ��^3 + 3��^2 + 3�� + 1
= ��^3 + 3��(��+1) + 1
= 4��^3 + 1
�ƂȂ�̂ŁA h(x) = x^2 - 4x - 1 �Ƃ���ƁA ��^3 �͕����� h(x) = 0 �̉��ƂȂ�B
h(x) = x(x-4) - 1 ��薾�炩�� h(0) < 0 ���� h(4) < 0 �ł���̂ŁA
������ h(x) = 0 �� 2 �̈قȂ�������������A�����͂��ꂼ�� x < 0, x > 4 �͈̔͂ɂ���B
�� > 0 ��� ��^3 > 0 �ł��邩��A���������� ��^3 > 4
�䂦�� ��^3 > 4 > ��^2 >>569
f(3^(1/2))<0,f(4^(1/2))=f(2)>0 �� 3 < ��^2 < 4
g(4^(1/3))<0,g(5^(1/3))>0 �� 4 < ��^3 < 5 >>569
(1)
f '(x) = 3xx -2x -1 =(x-1)(3x+1)
�@f(-1/3) = -22/27 < 0,�@(�ɑ�)
�@f(1) = -2 < 0,�@�@(�ɏ�)
�@f(5/3) = -22/27 < 0,
�@f(2) = 1 > 0,
���
�@5/3 < �� < 2,
(2)
�@g(1) = -1 < 0,
�@g(5/3) = 1/9 > 0,
���
�@1 < �� < 5/3,
f(x) = x�g(x) - 1,
(��-��)(��+��-1) = g(��) - g(��) = {f(��)+1}/�� - g(��) = 1/�� > 0,
���@��>�� a,b��a>b>0�̎����̒萔�Ƃ���B
xy���ʂ̑ȉ~C:(x/a)^2+(y/b)^2=1�̎���ɂȂ��_�ŁA�ȉ��̏����������̑S�̂���Ȃ�W��S���l����B
�w���̓_��ʂ�AC�ƒ������钼�������傤��4�{���݂���i������������C����������Ƃ́A������C�̌�_�ɂ����āA������C�̐ڐ����������邱�Ƃ��w���j�x
S���\��xy���ʏ�̗̈�����߂�B >>560
��=0 �̎��� P(=Q) �̍��W�����͉�͉�������ꂽ�̂ł����ɋL���B
���S��: e=Sqrt[1-(b/a)^2] �Ƃ���
b < a �� 2b ��
�@x = a*(3 - (Sqrt[3]*Sqrt[-1 + 9*e^2 + 4*e^4 - (1 + 4*e^2)^(3/2) + Sqrt[2]*Sqrt[1 + 26*e^4 +176*e^6 + 32*e^8 + (1 + 4*e^2)^(3/2) - 6*e^2*(1 + 4*e^2)^(3/2) - 16*e^4*(1 +4*e^2)^(3/2)]])/e)/(6*e)
�@y = b*Sqrt[ 1- (x/a)^2 ]
a �� 2b ��
�@x = a*(3 + (Sqrt[3]*Sqrt[-1 + 9*e^2 + 4*e^4 - (1 + 4*e^2)^(3/2) - Sqrt[2]*Sqrt[1 + 26*e^4 +176*e^6 + 32*e^8 + (1 + 4*e^2)^(3/2) - 6*e^2*(1 + 4*e^2)^(3/2) - 16*e^4*(1 +4*e^2)^(3/2)]])/e)/(6*e)
�@y = b*Sqrt[ 1- (x/a)^2 ]
�ڐG�~�̒��S�_: H
|h| = a*( Sqrt[1-12e^2 + Sqrt[1+4e^2]^3] )/(Sqrt[8] Sqrt[1-e^2])
�@b < a �� 2b�@�ˁ@H=(e*a, +|h|)
�@a �� 2b�@�ˁ@H=(e*a, -|h|)
https://imgur.com/a/RaAJa4r
GeoGebra�ŕ`���Ă݂��B������� P�_�̈ʒu���߂� Intersect�@�\�͎g���Ă��Ȃ��B >>584
���o�̕��j
�E�ȉ~: (x/a)^2 + (y/b)^2 = 1
�E�ڐG�~: (x-e*a/2)^2 + (y-h)^2 = (e*a/2)^2+h^2
(1) �ȉ~�Ɖ~�̘A�������� x�ɂ��Ă�4���������������A���̔��ʎ�����Ah^2 =... ��B
(2) h^2=...��������4�������� {LHS}�@�Ɓ@ �d�������4�������� (x-��)^2 (x^2 + ��x + ��) {RHS}
�@���̌W���W���� x = �� ���B LHS��3������������悤�ɃY�����ƊȒP�ɂȂ�B
�@�\�����̕����I���ɖ����ӏ���2����A�����̓O���t�����Ĕ����I�ɋ��߂��B���̘A�������l����Ζ��͂Ȃ��͂��B
�ꍇ�����̋��E�_
�E(x/a)^2 + (y/b)^2 = 1
�E(x-e*a/2)^2 + y^2 = (e*a/2)^2
�@�� (1-(b/a)^2) x^2 - e*a*x + b^2 = 0
���ʎ���� a=2b
h�̕\����� 1-12e^2 + Sqrt[1+4e^2]^3 = 0 �ƂȂ�B��������t�Z���Ă����߂���B
���E�ł� P���W��
�@ (x,y) = a * ( 1/Sqrt[3], 1/Sqrt[6] )
�ƃV���v���ɂȂ�B D = {z �� C | |z - 1| < cos��, |Arg(1 - z)| < ��}�Ƃ���Bz �� D �� |z| < 1���ؖ�����B f(x)=lim[n����] (x-a_1)(x-a_2)(x-a_3)....(x-a_n)�@�@�ia_i�͎����j
���L�E�ł��邽�߂̐���{a_i}�̕K�v�\�������͂ǂ��Ȃ�̂ł��傤���H >>587
�L���� i �������� |x - a_i| �� 1 ����� >>588
�����
��[n=1,��] (1 + 1/n^2) �͎�������炵�� >>586
��ӂɂ��
�@z��D�@��
�@(1-x) = |1-z| cos(Arg(1-z)) > |1-z| cos�� > |1-z|^2,�@���� (*)
�܂�
�@|1-z|^2 = (1-x)^2 + y^2,
������
�@|z|^2 + |1-z|^2 = x^2 + (1-x)^2 + 2y^2
�@�@= 1 - 2(1-x) + 2|1-z|^2
�@�@< 1,�@�@(�� *) �����
��[n=1,��] (1 + xx/(n��)^2) = sinh(x)/x�@�ƂȂ�炵���B
(�I�C���̖�����ϕ\��) >>590
�O�p�s��������
�@|z|^2 + |1-z|^2 < 1 �� |z| + |1-z|, |z|^2 + |1-z|^2 = 2|1/2 - z|^2 + 1/2,
���
|z|^2 + |1-z|^2 < 1�@�@�́@�@|1/2 - z| < 1/2, ���̒�����2�́�ABC�ɂ����āABC=2a�Ƃ����B
�i1�j����a�̒l���ω�����Ƃ��A���̎�肤��l�͈̔͂�s�����ŕ\���B
�i2�j��ABC�̓��p��A�̓�����BC�Ƃ̌�_��D�Ƃ��AA��ʂ�AD�ƒ������钼����l�Ƃ���B�܂�B��[�_�Ƃ��锼����BA�́AA�Ɋւ���B�Ɣ��Α��ɓ_E���Ƃ�B���̂Ƃ�����l����EAC��2�������邱�Ƃ������B >>587
�ȒP�ȏ����ɏ����͖̂����Ȃ�Ȃ�����
�L�E����͗L�E����Ƃ��������Ȃ��̂Ɠ����ŁA�����Č����Ȃ琔��
P[n] := ��[k=1,n] (x-a_k)
���L�E�Ƃ������Ƃ����A����͂����̌��������ł����Ȃ�
�����Ȃ�R�[�V�[�̏��������邯�ǁA�L�E�������Ƃǂ��ɂ�
�Ⴆ�A a_{2k} = x + 1/2, a_{2k+1} = x + 2 �Ƃ���ƁA
P[n] �͗L�E�����������Ȃ�
����A a_k = x - (1 + 1/k) �Ƃ���ƁA a_k �� x-1 (k����) �����A
lim[n����] P[n] = ��[n=1,��] (1 + 1/n) = �� >>586
D����Ȃ�ok
D�����Ȃ�0<cos�����-��/2<��<��/2
z��1�𒆐S�Ƃ��锼�acos���̉~���ɂ���
�����S1����݂��Ίp�Ƃ̓�-��<��<��+��
���̗̈��0,1,cos��e^(�}i��)�_�Ƃ���H�`
�̓����ɂ���(��=��/2-���Ƃ�����)
����ė̈�͒P�ʉ~���ɑ��݂��� �O>>447
>>594
(1)2-2a��2a
2��4a
a��1/2
�܂�2a��0
�����0��a��1/2
(2)�pBAC+�pEAC=180��
�ӁX��2�Ŋ���ƊpBAC/2+�pEAC/2=90��
�pCAD+�pEAC��C���̔���=90��
���Ȃ킿�pCAD����钼���ƊpEAC����钼���͂������ɒ�������B
�������ꂽ�B f(x)���L�E�ɂȂ�x�͈̔͂����Ȃ��߂�a_i�̏���
����ɂ��̂悤��x����_�łȂ��ꍇ�̏���
�Ƃ��Ȃ�l���Ă��ʔ���������
x�͈̔͂���_�łȂ��ꍇ�Af(x)�͂��͈̔͂̂قƂ�ǂ̓_��0�ɂȂ肻�������ǁA�ǂ����낤 xy���ʂ�xy���ʏ��n�{�̈قȂ钼���ŕ������Ăł���̈�̐����l����B�Ȃ������Ō����̈�ɂ́A�̈�E�J�̈�̂�������܂܂��B
�i1�j���̂悤�ɂ��Ăł���̈�̐��̍ő�l��n�ŕ\���B
�i2�j���̂悤�ɂ��Ăł���̈�̐��́An+1����i1�j�ŋ��߂��ő�l�܂ŕ����ʂ肠��B����͉��ʂ�ł��邩�An�ŕ\���B (1) (n^2+n+2)/2
(2) (n^2-n+2)/2 >>598
>x�͈̔͂���_�łȂ��ꍇ�Af(x)�͂��͈̔͂̂قƂ�ǂ̓_��0�ɂȂ肻��
a_n �� x �Ɉˑ����Ȃ�����ŁA f(x) ����������Ȃ炻�����낤��
�����ς� 0 �łȂ��l�Ɏ�������Ȃ獀�̐���� 1 �Ɏ������Ȃ���Ȃ�Ȃ�����A
x-a_n �� 1 (n����) �Ȃ�A�C�ӂ̎��� �� �ɑ��āAx+��-a_n �� ��+1 (n����)
�ƂȂ�̂ŁA f(x) ���������� �� 0 �Ȃ� �� = 0 �łȂ���Ȃ�Ȃ� �قȂ��_0, ..., ��_n�ɑ���n + 1�����s��
(��_i^j)_i,j
�̍s�� >>601
��������������Ȃ炻��
>>602
��[i=0,n]��_i ��[i<j](��_i-��_j) >>586 �� ���ǥ���
D = {z �� C | |z - 1| < cos��, |Arg(1 - z)| < ��}�Ƃ���B
z �� D�@�ˁ@|z-1/2| < 1/2 ���ؖ�����B >>604
>>596�̕H�`��01�a�Ƃ���~�ɓ��ڂ��Ă邩��
�̈�͂��̉~�̓������Ȃ킿|z-1/2|<1/2�ɂ��� >>599 (2)
n�{�̒������A���s���ɂ���ĕ��ނ���B
�e�ނɊ܂܂�钼���̖{���� m_i (i=1,�c,k) �Ƃ���B
�@m_1 + m_2 + ���� + m_k = n,
���̂Ƃ��ł���̈�̑�����
�@1 + n(n+1)/2 - ��[i=1,k] m_i(m_1 - 1)/2,
�Ƃ���ŁA
n���������̎��R���̘a�ŕ\�킷���@�̐��͕����� p(n)
(2) �̓��� �� p(n)
n��11 �ł� p(n) �� (nn-n+2)/2 �Ȃ̂�
�@p(n) �Ƃ���ȉ��̂͂����� n+1
�� 1/i
i=3
��낵�����肢���܂��B���Ԉ���Ă����̂ŁB �e�����������ׂď����B�Ƃ������ł� ���Ȃ̂���
�u�����Ƃ�v�Ɠ����x������� 1/3+1/4....+
�̍Ō�͂ǂ����������ł��傤���H
n�܂ł�������
...+1/(n+2)
���Ǝv���̂ł����An+1�܂łȂ̂�
1/3+1/4...+1/(n+2)+1(n+3)
�ƂȂ�̂ł��傤�� >>610
n+1
�� 1/i
i=3
���̋L���́A1/i��i��3����n+1�܂ő�����č��v����Ƃ����Ӗ��ł��B
�Ȃ̂ŁA1/3 + 1/4 + �c + 1/(n+1)
�������ł��B 1/i��i��n+1����������1/(n+1)����
n+1
��
i=3
���Ă̂́Ai=3����n�܂�(n+1)���̘a���ĈӖ�����Ȃ���
i=3����n�܂���i=n+1�܂ł̘a���ĈӖ��� �����A�����[�h�o���ĂȂ����� 0189 �P�R�Q�l�ڂ̑f������ 2020/08/22 12:05:05
n+1
�� 1/i
i=3
�e�����������ׂď����A�Ƃ������B
���Ȃ������̂ł��肢���܂�
ID:QJgAg0uf
0190 �P�R�Q�l�ڂ̑f������ 2020/08/22 12:36:01
�}���`
ID:TylVx0O5 �T�C�R��6�U���Ėڂ̍��v��26����m�����}���R�t�s�����ƃ`�F�r�V�F�t�s�������g���ĕ]������
�}���R�t�s������21/26�ȉ����Ǝv���̂ł����A�`�F�r�V�F�t�s�������킩��܂���
��낵�����肢���܂� �Ȃ�قǁA��{�����@���Ă��܂����B���肪�Ƃ��������܂� �O>>597
>>616
1+1+6+6+6+6=24�����Ȃ��B
�o�ڂ̐��̍��v��36
6��Ƃ�6���o��m����1/6^6=1/46656
�o�ڂ̐��̍��v��35
1��5���o�Ă��Ƃ�6�̊m����5������ڂɏo�邩6�ʂ肠�邩��(1/6^6)�~6=1/7776
�o�ڂ̐��̍��v��34
5��2��o�Ă��Ƃ�6�̊m����5������ڂƉ���ڂɏo�邩15�ʂ肠�邩��(1/6^6)�~15=15/46656=5/15552
1��4���o�Ă��Ƃ�6�̊m����4������ڂɏo�邩6�ʂ肠�邩��(1/6^6)�~6=1/7776
���킹��5/15552+1/7776=7/15552
�o�ڂ̐��̍��v��33
���c�c a^b+b^c=c^a
�������R���͖����ɑ��݂��邩�H
�Ƃ�����肪�����ł��܂���B�t�F���}�[�\�z�����Ďv�����܂����B
���̂P�Ƃ���(a,b,c)=(1,1,2)�͕�����܂����B
x<y�ł͖w�ǂ̏ꍇy^x<x^y�Ȃ̂ŁA����𗘗p���āA�����ꕔ�̗�O������min(a,b,c)=c�ł��邱�Ƃ�������c�̒l���i�荞�ނƂ���������l�����̂ł����A���̗͂ł͍i�荞�݂����܂��ł��܂���ł����B
���������������܂��ƍK���ł��B��낵�����肢���܂��B >>616
�P�O�O�O����V�~�����[�V������������
> # �T�C�R��6�U���Ėڂ̍��v��26����m��
> sim <- function() sum(sample(6,6,replace = TRUE)) > 26
> mean(replicate(1e7,sim()))
[1] 0.0963488 �O>>618���B
>>616
�o�ڂ̐��̍��v��33
3��5�ł��Ƃ�6�̊m����5�̏o���ɂ����20�ʂ肠�邩��(1/6^6)�~20=5/11664
4��5��1�ł��Ƃ�6�̊m����(1/6^6)�~30=5/7776
1��3�ł��Ƃ�6�̊m����(1/6^6)�~6=1/7776
���킹���5/11664+5/7776+1/7776=1/11664+1/1296
=(1+9)/11664
=10/11664
=5/5832
�o�ڂ̐��̍��v��32
4��5�ł��Ƃ�6�̊m����5��2��ł��Ƃ�6�̊m���Ɠ�����(1/6^6)�~15=5/15552
1��4��5��2��ł��Ƃ�6�̊m���́A
1��ڂ�4���o��5������ڂƉ���ڂɏo�邩10�ʂ肠����4������ڂɏo�邩6�ʂ肠�邩��10�~6=60�ʂ肠����(1/6^6)�~60=10/6^5=10/7776=5/3888
4��2��ł��Ƃ�6�̊m����5��2��ł��Ƃ�6�̊m���Ɠ�����(1/6^6)�~15=5/15552
3��5��1�ł��Ƃ�6�̊m����4��5��1�ł��Ƃ�6�̊m���Ɠ�����(1/6^6)�~30=5/7776
1��2�ł��Ƃ�6�̊m����(1/6^6)�~6=1/7776
���킹���5/15552+5/3888+5/15552+5/7776+1/7776=(5+20+5+10+2)/15552
=42/15552
=21/7776
=7/2592
�o�ڂ̐��̍��v��31
5��5��1��6�̊m����6/6^6=1/6^5=1/7776
1��4��3��5�ł��Ƃ�6�̊m����1��4��5��2��ł��Ƃ�6�̊m���Ɠ�����5/3888
2��4��1��5�ł��Ƃ�6�̊m����������5/3888
3��4��1�ł��Ƃ�6�̊m���͉�����o�Ă��Ă�̂Ɠ�����5/7776
2��5��1�ł��Ƃ�6�̊m����5/7776
1��1�ł��Ƃ�6�̊m����1/7776
���킹���1/7776+5/3888+5/3888+5/7776+5/7776+1/7776=12/7776+10/3888
=(3+5)/1944
=1/243
�o�ڂ̐��̍��v��30
�o�ڂ̐��̍��v��29
�o�ڂ̐��̍��v��28
�o�ڂ̐��̍��v��27
���ׂđ����Əo�ڂ̐��̍��v��26����m���́A �O>>621�Â��B
>>616
�o�ڂ̐��̍��v��30
1+5+6+6+6+6=30�m��5/7776
2+4+6+6+6+6=30�m��5/7776
3+3+6+6+6+6=30�m��5/15552
2+5+5+6+6+6=30�m��5/3888
3+4+5+6+6+6=30�m��(1/6^6)�~6�~5�~4=5/1944
4+4+4+6+6+6=30�m��5/11664
3+5+5+5+6+6=30�m��5/3888
4+4+5+5+6+6=30�m��(1/6^6)�~
4+5+5+5+5+6=30�m��5/15552
5+5+5+5+5+5=30�m��1/46656
�o�ڂ̐��̍��v��29
�o�ڂ̐��̍��v��28
�o�ڂ̐��̍��v��27 >>620
�ǂ���PC�ɗ���Ȃ� 6^6 (= 46656) �ʂ�̑��`�F�b�N�����炦�����ȁB
> �P�O�O�O����V�~�����[�V����
��������Ă����� 0.096�܂ł��������ĂȂ����ă}�k�P�ɂ��قǂ�����B >>622
�C�i���Ăǂ��̌��c���������H >>606
��)�@n���������Ƃ�
n,�@(nn-n+2)/2,�@p(n),�@q(n)=#M,�@M
------------------------------------------------
1,�@1,�@1,�@1,�@{2}
2,�@2,�@2,�@2,�@{3,4}
3,�@4,�@3,�@3,�@{4,6,7}
4,�@7,�@5,�@5,�@{5,8,9,10,11}
5,�@11,�@7,�@7,�@{6,10,12,13,14,15,16}
6,�@16,�@11,�@9,�@{7,12,15,�P�U,18,�P�X,20,21,22}
7,�@22,�@15,�@13,�@{8,14,18,19,20,22,�Q�R,24,25,�Q�U,27,28,29}
8,�@29,�@22,�@18,�@{9,16,21,22,24,25,26,27,28,29,�R�O,�R�P,32,�R�R,�R�S,35,36,37}
9,�@37,�@30,�@21,�@{10,18,24,25,28,�R�O,31,33,�R�S,35,�R�U,�R�V,38,�R�X,�S�O,41,�S�Q,�S�R,44,45,46}
10,�@46,�@42,�@27,�@{11,20,27,28, ����, 56}
---------------------------------------------
{q(n)} = {1,2,3,5,7,9,13,18,21,27,����}
http://oeis.org/A069999
M�̍ŏ����� n+1, �ő匳�� (nn+n+2)/2 ���� ���Ԃ�d��������B
�@�Ƃ��ɗސ�k���������Ƃ���ł͌��Ԃ������B
�@(n)�@���@n+1
�@(n-1,1)�@���@2n,
�@(n-2,2)�@���@3n-3,
�@(n-2,1,1)�@���@3n-2,
�@
�@(2,1,���,1)�@���@(nn+n)/2,
�@(1,1,����,1)�@���@(nn+n+2)/2, >>623
�N����p�x�����Ȃ��̂��V�~�����[�V�������邩�炻��Ȃ��̂���B >>616
�o�ڂ̍��v,�@�m��
------------------------------
36,�@1/6^6,�@�@>618
35,�@6/6^6,�@�@>618
34,�@21/6^6,�@�@>618
33,�@56/6^6,�@�@>621
32,�@126/6^6,�@�@>621
31,�@252/6^6,�@�@>621(*)
30,�@456/6^6,�@�@>622(**)
29,�@756/6^6,
28,�@1161^6^6,
27,�@1666/6^6,
--------------------------------
�v,�@(1666+1161+756+456+252+126+56+21+6+1)/6^6
�@= 4501/6^6 = 0.09647205
(*)�@(355666)�@�������Ă܂��B
(**)�@(455556)�@�̊m���������ł��B ���鐻�i�̎����ɂ��āA���̗ݐϕ��z���͈ȉ��̒ʂ�^�����Ă���B
F(x)=��exp(-��x) (0��x)
(1)�m�����x��f(x)�����߂�B
(2)���Ғl�A�����l�A���l���ʐ������ꂼ�ꋁ�߂�B >>623
111111�`666666���O����U�O�U�|�P���U�i���ŕ\������
�e���̘a���Q�U�|�U���傫���Ȃ�悤�Ƀv���O�������đ������肵�Ă݂��B
dec2n <- function(num, N, digit = 6){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r)
}
pm=sapply(0:(6^6-1),function(x) dec2n(x,6))
f<-function(x) sum(x) > 26-6
s=sum(apply(pm,2,f))
S=ncol(pm)
cat(s,'/',S,'\n')
s/S
> cat(s,'/',S,'\n')
4501 / 46656
> s/S
[1] 0.09647205 >>628
(1) pdf = -��^2exp(-��x) >>630
���������ȁA
-e^x (1 + x) ��^2 �\�t�g�ɔ������Ă��������A>630�ł����݂������ȁB
> D(expression(��*exp(-��*x)),'x')
-(�� * (exp(-�� * x) * ��)) >>628
���̕��z���P�����傶��Ȃ���� >>633
����Ŋ��Ғl��-1�Ȃ����̂� >>627
���𐔂���̂��v���O�����ɂ����Ă݂��B
table(x)
x
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
1 6 21 56 126 252 456 756 1161 1666 2247 2856 3431 3906 4221 4332
22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
4221 3906 3431 2856 2247 1666 1161 756 456 252 126 56 21 6 1 >>634
E(1)���܂�����0 wwww >>635
���̕��z���ĉ����z�ɂȂ�H
���K���z�ŋߎ��ł���̂͂킩�邯�ǁB >>633
�P���������������� >>628
�����܂���ԈႦ�܂���
F(x)=1-exp(-��x)
�ƂȂ�܂��B�X�������肢���܂��B �O>>622
>>626
�o�ڂ̍��v31�͘R�ꂪ���邩�ȁA�Ƃ͎v�����B
30�́A4,4,5,5,6,6���킩��Ȃ��Ȃ����B
26������1����A����Ȃ��낤�B �W��X��������̗v�f��������Ȃ�Ƃ����̂𐳊m�Ɍ����ƁA�ux��X�ƂȂ�悤��x�����݂���Bx��y��y��X�łȂ��v�Ƃ������Ƃł����H
|X| = 1�̒�`�́AX����{x��Z_{+} | x < 1 + 1}�ւ̑S�P�˂����݂���Ƃ������Ƃ��Ǝv���܂��B
1��{x��Z_{+} | x < 1 + 1}�ł���Ax��Z_{+}����1 < x < 1 + 1�ƂȂ�x�͑��݂��Ȃ����߁Ax��1�ˁux��{x��Z_{+} | x < 1 + 1}�łȂ��v�����藧���܂��B
{x��Z_{+} | x < 1 + 1}����X�ւ̑S�P�˂����݂��邽�߁A1��x��X�ƂȂ�x�����݂��܂��Bx��y����y��X�ƂȂ�悤��y�����݂���Ɖ��肷��ƁA
n��y�ƂȂ�悤��n��{x��Z_{+} | x < 1 + 1}�����݂��邱�ƂɂȂ�܂��Bn = 1�łȂ���Ȃ�܂���B����́����ʑ��ł��邱�Ƃɔ����܂��B
����āA�ux��y��y��X�łȂ��v�����藧���܂��B >>639
��`�ɏ]���Čv�Z���邾��
�������āA�m�����x���@ exp(-�� * x) * ��
�m�����x��*x���`��Őϕ����Ċ��Ғl 1/��
�ݐϖ��x���̋t���������
�����l�Flog2/��
���l���ʐ�:log(4/3)/�� 10�̃T�C�R����U���Ėڂ̍��v�Ă�q��������Ƃ������ɂ�����̂��ł��L�����B���̊m���͂����炩�B
�ڂ̍��v�̊��Ғl��35�Ƃ����̂͂킩�邯�ǁA���ꂪ�ŕp�l���Ƃ����̂͂ǂ����Ίm�F�ł��邾�낤�H >>643
���z�����E�Ώ̂Ȃ���Ғl�i���ϒl�j�ƍŕp�l�͈�v����Ƃ����邩�H�Ƃ������ɂȂ�̂��Ȃ��H >>643
�P�O�ɃT�C�R���𓊂��Ėڂ̍��v��35�ɂȂ�m���̃V�~�����[�V������
> sim <- function(n=35) sum(sample(6,10,rep=T))==n
> mean(replicate(1e7,sim()))
[1] 0.0726302
�������̓C�i��搶���{���̌v�Z�͂Ő����Ă����Ǝv���B >>644
���z��������Ȃ�Ώ̂ł����ϒl���ŕp�l�Ƃ͌���Ȃ��ȁB p(35) = 4395456/(6^10) = 0.0726928
p(n) �� p(��)�e^{-(n-��)^2 /(2��^2)},
��=35,�@��^2 =31.09 ���l����v�����ȁB
data.frame(sum=10:60,pips=pips[10:60])
sum pips
1 10 1
2 11 10
3 12 55
4 13 220
5 14 715
6 15 2002
7 16 4995
8 17 11340
9 18 23760
10 19 46420
11 20 85228
12 21 147940
13 22 243925
14 23 383470
15 24 576565
16 25 831204
17 26 1151370
18 27 1535040
19 28 1972630
20 29 2446300
21 30 2930455
22 31 3393610
23 32 3801535
24 33 4121260
25 34 4325310
26 35 4395456 >>647
��^2 =31.09�͂ǂ������v�Z�łłĂ���̂ł��傤���H
�ʂ̕���10*(1+2+3+4+5+6)/6=35�Ƃ킩��܂����B ������̋A�[�@�g���Ζ��x���̈���������邯�ǂ�
����ƕ��ςł̑Ώ̐��Ŏ�����
�ꔭ�ؖ��Ȃ����̂� Coefficient[(x+x^2+x^3+x^4+x^5+x^6)^10,x^35]
=4395456 >>650
�T�C��n��U���č��v��m�ɂȂ�m���� p(n,m) �Ƃ���ƁA
p(1,m) = if m �� {1,2,3,4,5,6} then 1/6 else 0 �Ƃ��āA
p(n+1,m) = (1/6) ��[k=1..6] p(n,m-k) �Ȃ���A
p(n+1,m+1) = p(n+1,m) + (1/6)(p(n,m) - p(n,m-6))
�܂� p(n,m) �� p(n,m-6) �Ƃ̑召�W�����̂܂� p(n+1,m+1) �� p(n+1,m) �Ƃ̑召�W�ɂȂ�
���̂��Ƃ𗘗p������A���w�I�A�[�@�� n �������̂Ƃ� m = 7n/2 �� p(n,m) ���ő�ɂȂ邱�Ƃ�������̂ł� �Ώ̐����g�����Ƃ��K�v����
p(n,m)=p(n,7n-m) a^b+b^c=c^a
����1�ȏ�̐���a,b,c�̑g(a,b,c)��S�ċ��߂�B ��(sinx/x)^2dx (0����)
��(lnx/x^2+1)^2dx (0����) >>637
��l���z
�@p(n) = 1/6�@�@�@(1��n��6)
�@�@�@= 0�@�@�@�@(n<1, n>6)
6�������ݍ����́B
�@P(n) = C(n-1,5) = (n-1)(n-2)(n-3)(n-4)(n-5)/5!,�@�@�@(6��n��11)
�@P(n) = 2771 - (18929/12)n + (2847/8)n^2 - (949/24)n^3 + (17/8)n^4 - (1/24)n^5,
�@�@�@(11��n��16)
�@P(n) = -90049 + (177851/6)n - (46017/12)n^2 + (2893/12)n^3 - (29/4)n^4 + (1/12)n^5
�@�@�@(16��n��21)
�@P(n) = 582931 - (787943/6)n + (46191/4)n^2 - (5917/12)n^3 + (41/4)n^4 - (1/12)n^5
�@�@�@(21��n��26)
�@P(n) = -1198394 + (2393525/12)n - (104043/8)n^2 + (10021/24)n^3 - (53/8)n^4 + (1/24)n^5,
�@�@�@(26��n��31)
�@P(n) = C(41-n,5) = (41-n)(40-n)(39-n)(38-n)(37-n)/5!,�@�@�@(31��n��36)
�@P(n) = 0,�@�@�@(n<6, n>36) >>655
(��) �͕����ϕ�����
��(sin(x)/x)^2 dx = -(sin(x)^2)/x + ��sin(2x)/x dx
�@�@�@�@�@�@= -(sin(x)^2)/x + Si(2x),
������
��[0,��] (sin(x)/x)^2 dx = Si(��) - Si(0) = ��/2,
���邢��
�@��[0,��] {cos(ax) - cos(bx)}/x^2 = (��/2)(b-a),
���g���B
���F�u��͊T�_�v������O�ŁA��g���X (1961)
�@��5�� ���K��� (4),�@p.264
(��) �͔��U���������� >>656
���肪�Ƃ��������܂����B
�ꍇ�������琏���ƕ��G�Ȏ��ɂȂ邱�Ƃ����͗����ł��܂����B >>651
wolfram�ł͂Ȃ���Mathematica�̃R�}���h�ł��傤���H �O>>640
>>643
�o�ڂ̍��v��10�ɂȂ�m����60�ɂȂ�m���́A
1/6^10
�o�ڂ̍��v��11�ɂȂ�m����2��10�ʂ�ŁA
59�ɂȂ�m����5��10�ʂ��10/6^10=5/3�~6^9
�o�ڂ̍��v��12�Ɂc�c
�o�ڂ̍��v��35�ɂȂ�m����1���ɂ������Ȃ���Ȃ����H >>659
���X�́Amathematica�̊����Ǝv���܂����A�Z����Awolframalpha�@�ł����������߂��Ă���܂��B
�����A�������Ԃ��Ă���܂����B
Table[{k,Coefficient[(x+x^2+x^3+x^4+x^5+x^6)^10,x^k]},{k,10,60}]
https://www.wolframalpha.com/input/?i=Table%5B%7Bk%2CCoefficient%5B%28x%2Bx%5E2%2Bx%5E3%2Bx%5E4%2Bx%5E5%2Bx%5E6%29%5E10%2Cx%5Ek%5D%7D%2C%7Bk%2C10%2C60%7D%5D&;lang=ja �����e��
����̓R�s�[�p���̋K�i�ŁA�������̕ӂ��ɂ���ƁA���Ƃ̒����`�ƁA���ĂƉ��̔䂪���������`��������Ƃ���������������Ă�����肾�B
��BC�Ɛ܂��BE���d�Ȃ邱�Ƃ���AAB�FBC�����߂�B
�܂��A���̃R�s�[�p�������̂ւ�Ŕ����ɂ����Ƃ��A���Ƃ̒����`�Əc�Ɖ��̔䂪�����ɂȂ邱�Ƃ��A���𗧂ĂĊm���߂�B
�R�s�[�p���̉摜https://dotup.org/uploda/dotup.org2237290.png.html
���̂킩��₷���摜https://dotup.org/uploda/dotup.org2237293.png.html
�킩��ɂ����Ǝv������낵�����˂������܂�
���ƁA���̉���������낵�� �����w�S���Ƃ����Ă����قǂł��Ȃ���
�����Ă��߂�� ����
������O�ɖ����������Ƃ���͖̂��������ɒ��ނ��Ă��Ƃ������
��l�ɂ͖����ȍs�� ���肪�Ƃ�
������Ƌ��ȏ��������Ă��čl���Ă݂�� >>661
���肪�Ƃ��������܂��B
���s���Ă݂܂������v�Z�̑����ɂт����肵�܂����B >>664
x:1=1:x/2 (x>0)��������������Ȃ��́H ���[�N�̖��Ȃ̂ł������܂������������s���Ƃ��܂���c
��낵�����肢�������܂��B
���̊��ɍő�l�A�ŏ��l�������������߂�B
y=(x^2-2x)^2+4(x^2-2x)+�T �@u = (x^2 -2x) +1,
�Ƃ�����
�@u = (x-1)^2 �� 0,
y = (u-1)^2 + 4(u-1) +5
�@= uu + 2u +2�@�@(u��0 �ŒP������)
�@�� 2,�@���� �ŏ��l (@ u=0, x=1)
x���}���@�̂Ƃ��@y����
�@�ő�l�Ȃ��B �O>>622
>>671
y=(x^2-2x)^2+4(x^2-2x)+5
y'=2(x^2-2x)(2x-2)+4(2x-2)
=4(x-1)(x^2-2x+2)
x^2-2x+2=(x-1)^2+1��0������A
y'=0�ƂȂ�̂�x=1�̂݁B
x���}���̂Ƃ�y��+��
x=1�̂Ƃ�x^2-2x=1-2=-1
�ŏ��ly=(-1)^2+4(-1)+5=1-4+5=2
�������Ȃ��H >>672
���肪�Ƃ��������܂�
u = (x^2 -2x) +1�Ƃ����Ƃ�
+1�̕������Ăǂ�����ł������ł��傤�� >>673
���肪�Ƃ��������܂�
�P�s�ڂɂ������T�������ĂQ�s�ڂ̂�'=�̌�̂Q���łĂ����̂�
�^����W�J����(�Qx-2)�Ő��������Ƃ������Ƃł��傤��
�A�z�߂��Ă��݂܂���c ����{�ɁA��f : N -> N��
f(0) = 1
f(1) = 1
f(n) = f(n-1) + f(n-2) (n �� 2)
�ƒ�`����Ƃ����̂͂��������Ə����Ă���܂��B���̗��R�́A���ꂩ���`���悤�Ƃ�����f : N -> N���g����f�̒l���`���悤�Ƃ��Ă���Ƃ������̂ł��B
���̂����A��f : N -> N��
f(0) = 1
f(1) = 1
f(n) = f(n-1) + f(n-2) (n �� 2)
�������̂����݂��邱�Ƃ��ؖ����Ă��܂��B
�Ȃ����������悤�ȕ�����Ȃ��悤�ȋC������̂ł����A��ɏ��������Ƃ͐������̂ł��傤���H 1�ȏ�22�ȉ��̎��R���̏W����S�Ƃ���
S�̕����W��T�ŁA���̏����������̂��l����
[����] T�ɑ�����C�ӂ�2�̗v�f�̍���4�ł�7�ł��Ȃ�
T�̗v�f���̍ő�l�͂����炩
1 5 9 13 17 21
2 6 10 14 18 22
3 7 11 15 19
4 8 12 16 20 >>676
���̒��x�Ȃ�ǂ����ł�
�����ƕ��G���ƌ�҂̂��悢���Ƃ��邩���� �O�҂́u�����������̂悤��f�����݂��邩�ǂ����킩��Ȃ�����A���݂��邱�Ƃ������K�v������v�Ȃ�[���ł��邵���ی�҂����̗���Ȃ��ǁA���̕����ł͂�����ƍ���������
f(n)�̒l���`����̂Ɏg���Ă�̂�f���̂���(�S�Ă�n�ɂ��Ēlf(n)�̒�܂����Ώ�)�ł͂Ȃ��A����n�܂ł̒lf(n-1),f(n-2)�����g���Ă��炸�A�z��`�ɂ͊Y�����Ȃ� >>676
���̂悤�ȏꍇ�́u�c�ƒ�`����v�́u�c�������̂���ӓI�ɑ��݂��邩��A������c�ƒ�`����v�Ƃ����Ӗ�����
��ӓI�ɑ��݂���̂����炩�ȏꍇ�ɂ悭(���ӎ��ɁH)�g�� >>671
�܂��A y �� x^4 �̌W�������� 4 ����������A�ő�l�����݂��Ȃ����Ƃ͂����ɂ킩��
���l�ɍŏ��l�����݂��邱�Ƃ��킩��
���ɁA y �̃O���t�̌`�ׂ邽�߂� y �̓��� dy/dx ���v�Z����
u(x) = x^2 - 2x
�ƒu���ƁA y = f(u) �Ə����邩��A�������̔������g���� dy/dx �̌v�Z���y�ɂȂ�
���ۂɌv�Z����ƁAx �ɂ��Ă� 2 �������� dy/du = 0 �� x �ɂ��Ď������������Ȃ��̂ŁA
�S�Ă̎��� x �ɑ��� dy/du > 0 �ƂȂ邱�Ƃ��킩��
���������� du/dx �̕����ɂ���ăO���t�̌`�����܂�A y �̍ŏ��l�͋ɏ��l�ł����邱�Ƃ��킩�� >>676
�ċA�I��`�̘b����
�m���Ɍ����Ɍ������̂悤�Ȋ� f �����݂��邱�Ƃ͖��炩�ł͂Ȃ�����A
�ؖ����K�v���낤��
���̏ꍇ�͐��w�I�A�[�@�� f(n) �̒l����ӂɒ�܂邱�Ƃ������Ώ\�����Ǝv������ 0 1 4 9 20 40 78 147 ��
���́H >>683
n = 1, 2, 3, �c �ɑ��A
a[n] = b[n] + A(n-1)(n-2)(n-3)(n-4)(n-5)(n-6)(n-7)(n-8)
�i A �͔C�ӂ̕��f���j
b[n] = 0, 1, 4, 9, 20, 40, 78, 147, B, B, �c
�i B �͔C�ӂ̕��f���j
�Ƃ����Ƃ��� a[9] �����Ȃ��ł��ˁB�����͉����܂���ł����B
�Ⴆ�A����̂͏��w���Ƃ��āA���̐���́����ɂ��镶�͑�͍��܂��ł��傤���H
�X���Ⴂ�Ȃ�\����܂���B >>685
�ɂ���
a[n+4]=2a[n+3]+a[n+2]-2a[n+1]-a[n] �O>>673
>>675
y=(x^2-2x)^2+4(x^2-2x)+5
y'=2(x^2-2x)(2x-2)+4(2x-2)
�Ȃ�5���������̂�������������萔���͏����邾�낤�B5����Ȃ���3�ł�7�ł�-1/2�ł�������͂��B�Ȃ�ł��Bx�Ɗ|�������Ăւ�ŕω��̊����ɉe�����Ȃ��ł�Ȃ��H�@�m��ǁB
x^2-2x���̂��̂��������2x-2���|���Ă����������Ǝv���B�Ȃ�ł��H�@�Ȃ�ł��͒m��ƂȂ����ǁB
�Ȃ�2���o�Ă�������2�����������ł�Ȃ��H
2x�����������2���B >>671
���������Ĕ�����m��Ȃ��܂��͎g���Ȃ��̂�
����Ȃ� u = x^2 - 2x �ƒu���� y �� u �ɂ��ĕ����������āA
����� u �� x �ɂ��ĕ�����������Ηǂ���� >>682
>���̏ꍇ�͐��w�I�A�[�@�� f(n) �̒l����ӂɒ�܂邱�Ƃ������Ώ\�����Ǝv������
���̏ꍇ�͋A�[�I��`������ؖ�����܂ł������� >>686
�Ⴆ����Ȃ̂͂ǂ����낤
0 �Ԗڂ̐� = 0
1 �Ԗڂ̐� = 1
2 �Ԗڂ̐� = 4
�Ƃ��āA
3 �Ԗڂ̐� = 3�~((1 �Ԗڂ̐�)��1 + (2 �Ԗڂ̐�)��2)
4 �Ԗڂ̐� = 4�~((2 �Ԗڂ̐�)��2 + (3 �Ԗڂ̐�)��3)
5 �Ԗڂ̐� = 5�~((3 �Ԗڂ̐�)��3 + (4 �Ԗڂ̐�)��4)
�c
�Ƃ���Ƃ��A 8 �Ԗڂ̐������߂�B >>690
���ꂾ��>>676�������Ă���{�̃X�^���X�ɍ���Ȃ��ł���
�u�A�[�I��`��薾�炩�v���g����Ȃ�>>676�݂����Ȃ��Ƃ͏����Ȃ��͂� >>692
�ǂ������̖{�ł���Ă邱�Ƃ��đ債�����Ƃ��ᖳ��
�A�[�I���������A�[�I�Ɍ��߂���
���x���낤��
�����Ɩ{���I�ɕK�v�ȏ�ʂ͂��낤��
�t�B�{�i�b�`����̒�`���x�ł͈ނ������邾�� >>693
�������ɂ���ȃg�[�g���W�[���������w�̖{�͂Ȃ��Ǝv����
�t�B�{�i�b�`����̒�`�͓����������ŁA���̌�Ɉ�ʂɋA�[�I��`��well-defined�ł��邱�Ƃ������Ƃ��A
�t��well-defined�łȂ���`�̗�������Ƃ��A�����������ꂶ��Ȃ��́H
>>676�̖{�����̖{�ŁA�ǂ�ȗ���ŏ����Ă������̂��킩��Ȃ��Ƃ킩��Ȃ��� x''+2x=tcost�̉������߂Ă��i�K��
(1/(D^2+1))te^(it)�̌v�Z���킩��Ȃ��ł� >>695
�w���B�T�C�h�̉��Z�q�@�H
(1/(D+a))f(x) = e^(-ax) �� f(x)e^(ax) dx
��
D^2 + 1 = (D+i)(D-i)
���g����������Ȃ��́H >>689
�����P�Ȃ̂ł܂������͏K���ĂȂ���ł�
���݂܂���c
���������̕��@�ł���Ă݂܂��I
���肪�Ƃ��������܂� >>696
���݂܂���BD^2+1����Ȃ���D^2+2�ł���
��2���o�Ă��Ă悭�킩��Ȃ��Ȃ��Ă��܂��܂��� >>698
�قƂ�Ǔ�������
D^2 + 2 = (D+i��2)(D-i��2) >>699
�ł��܂����B���肪�Ƃ��������܂��� D = d/dt,
{1/(D+i��2)} t e^(it) = (��2 -1)(-it + ��2 -1)e^(it),
{1/(D-i��2)} t e^(it) = (��2 +1)(it + ��2 +1)e^(it),
{1/(D+i��2)} t e^(-it) = (��2 +1)(-it + ��2 +1)e^(-it),
{1/(D-i��2)} t e^(-it) = (��2 -1)(it + ��2 -1)e^(-it),
{1/(DD+2)} t e^(it) = (t-2i) e^(it),
{1/(DD+2)} t e^(-it) = (t+2i) e^(-it),
{1/(DD+2)} t cos(t) = t cos(t) + 2 sin(t),
���ꂪ�����U�������B
����Ǝ��R�U���i�ŗL�U���j�𑫂���
�@y(t) = t cos(t) + 2 sin(t) + c1 cos(t��2) + c2 sin(t��2), >>691
�킩��₷���ł��B
�����C���[�W�Ƃ��Ă͂����ƕ��͓I�ɂ������̂ŁA�Q�l�ɍH�v���Ă݂܂��B
���肪�Ƃ��������܂����B >>674
������������ƍl���₷���Ȃ邩�炾�낤�ˁB ������
(x^5+x^4+x^3)+(x^4+x^3)+x^3+6(1+x+x^2)+(x+x^2)+x^2=0
�������B >>677
10���ő傾��
��̓I��1,3,6,9,11,12,14,17,20,22��10���Ƃ��
�ȉ��A11�͂Ƃ�Ȃ����Ƃ��ؖ�����
����11�Ƃꂽ�Ƃ���ƁA1�`11��12�`22�̂ǂ��炩��6�ȏオ�܂܂��
11�̘A������������Z/11Z�ōl����Ə�����n�������Ă���Ƃ���n�}4�������Ă��Ȃ����ƂƂȂ�
������Z/11Z��0,4,8,�c,32,36,40�ƌ����`�ŏ������Ƃ�
���̒�����6�ȏ�I�ڂ��Ƃ���ƕK���ׂ�����������I�ԕK�v������A�������� >>705
�� 11�Ƃ�Ȃ����Ƃ��ؖ�����
�� 11�ȏ�Ƃ�Ȃ����Ƃ��ؖ����� >>705
�⑫
11��4�݂͌��ɑf�Ȃ̂�Z/11Z�ɂ�����0,4,8,�c,36,40�͑S�Ă̌������傤��1�x����\����
�~�`�ɕ��ׂāA40��0(=44)���ׂ����ƍl���� �O>>688
>>704
(x^5+x^4+x^3)+(x^4+x^3)+x^3+6(1+x+x^2)+(x+x^2)+x^2=x^3(x^2+x+1)+x^2(x^2+x+1)+x(x^2+x+1)+(x^2+x+1)=(x^2+x+1)(x^3+x^2+x+1)=0
x^2+x+1=(x+1/2)^2+3/4��0
x^3+x^2+x+1=0
(x+1)(x^2-x+1)=0
x^2-x+1=(x-1/2)^2+3/4��0
��x=-1 >>704
x=-2,(1�}i��11)/2,(-1�}i��3)/2 0 = x^5 +2x^4 +3x^3 +8x^2 +7x +6
�@= (x+2)(xx-x+3)(xx+x+1),
xx+x+1 = (x+1/2)^2 + 3/4 �� 3/4,
�܂ō����Ă�B
����
xx-x+3 = (x-1/2)^2 + 11/4 �� 11/4,
����
x=-2 >>643
n�̃T�C�R����U�����Ƃ��̖ڂ̍��v�ŁA�o��m�����ő�̂��̂�
�@p(7n/2) �� ��{6/(35*��*n)}
http://oeis.org/A018901
http://oeis.org/A063419�@�@�@(n�F����) >>649
10�̃T�C�R���𓊂���Ƃ���
�@�� = (7/2)n = 35,
�@p(��) = 4395456/(6^n) = 0.0726928
�@p(m) = p(��){1 - 0.0160823�(m-��)^2 + 1.2415E-4�(m-��)^4
�@�@�@- 6.1676E-7�(m-��)^6 + 2.05E-9�(m-��)^8 - ����}
�@��^2 = 1/(2�0.0160823) = 31.09
(���)
�T�C�R��1�̏ꍇ�̕��U�� 35/12,
�T�C�R��n�̏ꍇ�̕��z�́A�����n�����ݍ����̂�����
�@���U�� (35/12)n,
���������K���z����O��Ă���̂�
�s�[�N�ȗ����猈�߂� ��^2 �Ƃ͈�v���Ȃ��B���܂̏ꍇ��
�@��^2 �� (35/12)n + 1.923 >>704
���̕��������������������Ƃ͖��炩�ł͂Ȃ��Ǝv�����ǁA�ǂ�����Č�����낤
�K���ɑ�����Ă������� x = -2 �� 0 �ɂȂ�H����͂�����Ɩ���������C������
(x^5+x^4+x^3)+(x^4+x^3)+x^3+6(1+x+x^2)+(x+x^2)+x^2
= x^3(1+x+x^2) + x^2(1+x+x^2) + x(1+x+x^2) + 6(1+x+x^2)
= (x^3 + x^2 + x + 6)(1+x+x^2)
�܂łȂ�C���t���邾�낤��
���� g(x) = x^3 + x^2 + x + 6 �̈������������A������ǂ���邩
g(x) = 0 �͐����W���� 3 ���������� x^3 �̌W���� 1 �����琮���������݂���Ɖ��肵�āA
�萔�� 6 �̖���i�荞�߂܂������邯��
���R�ȒP�ɉ�������Ă����Ȃ̂���
�Ⴆ�������̒萔���� 6 ����Ȃ��� 8 �Ƃ���������ȒP�ɉ�����C�����Ȃ�
�ǂ��������藝���g���ΊȒP�ɉ�������Ȃ���Ċ����H >>712
iid�̘a�̕��z�����璆�S�Ɍ��藝�Ő��K���z�ŋߎ��ł���킯����Ȃ��̂��H A�����ȃl�[�^�[��(1)(2)���݂����Ƃ��܂�
(1) A�̙p�덪���(0)
(2) �C�ӂ̋ɑ�C�f�A��m�ɑ��āA�Ǐ���A_m�͗L����
���̂Ƃ�A�͗L���ł���
���R�ȏ����^A��A_m�ŒP�˂ɂȂ���̂�����ƌ������Ƃ������ǁAA = Z/6Z�Ƃ��Ŋ��ɂ��߂������� �ݐϕ��z��
F(x)=4x(1-x) (0��x��1)
�Ƃ���B
�i1�j�m�����x��f(x)�����߂�B
�i2�j���f�B�A���A���[�h�A�~�[�������������ɕ��ׂ�B
�i3�j�L���������g�����߂�B 1+1/2+...=-1/12
���ؖ�����B >>717
�ݐϕ��z�����ĒP�������Ȃ͂��ł́H >>705
11�̎��͍��Ȃ��悤��
Table[2n-b-a+{(n+a)mod4}+4C(0,n-8+a),{a,0,1},{b,0,2},{n,1,10}] >>720
�R�����S���t�̋�����Ԋm���ōl���Ă������� >>716
radA = p1�dpn�Ƃ���A����A_pi��kernel��radA�ɂȂ�C������
A/radA���L���Ȃ�radA^i/radA^(i+1)���S���L�����Q�ɂȂ邩�炻��ł������K�X >>722
���R�₯�lj�����H
�O�O�����o���� �O>>708
>>717(2)��聃���䁃������ �ݐϕ��z����
F(x)=��(x^2+1) (0<x��a)
�ŗ^�����Ă���B
�i1�j����a�̒l�����߁A�܂��m�����x��f(x)�����߂�B
�i2�jE(a) = ��[0��a] xf(x) dx�����߂�B
�i3�jV(a) = ��[0��a] f(x){E(a)-x}^2 dx�����߂�B
�i4�j��[0��a] ��{E(x)V(x)} dx�ƕW�����Ƃ̊W�ɂ��Ę_����B �ݐϕ��z���� 1 �ȉ����Ēm���̂��H >>712
n=8�̃T�C�R���𓊂���Ƃ���
�@�� = (7/2)n = 28,
�@p(��) = 135954/(6^n) = 0.0809435
�@p(m) = p(��){1 - 0.0197967�(m-��)^2 + 1.8862E-4�(m-��)^4
�@�@�@- 12.736E-7�(m-��)^6 + 7.43E-9�(m-��)^8 - ����}
�@��^2 = 1/(2�0.0197967) = 25.2567
n=12�̃T�C�R���𓊂���Ƃ���
�@�� = (7/2)n = 42,
�@p(��) = 144840476/(6^n) = 0.0665388
�@p(m) = p(��){1 - 0.0135455�(m-��)^2 + 0.8858E-4�(m-��)^4
�@�@�@- 3.7175E-7�(m-��)^6 + 1.025E-9�(m-��)^8 - ����}
�@��^2 = 1/(2�0.0135455) = 36.9127 >>705
{1,2,����,22} �����}�ɂ悤�ɕ��ׂ�B
01 - 05 - 09 - 13 - 17 - 21
�@�@ �b �b �b �b
04 - 08 - 12 - 16 - 20
�b �b �b
03 - 07 - 11 - 15 - 19
�b �b �b �b
02 - 06 - 10 - 14 - 18 - 22
�b �b �b �b
01 - 05 - 09 - 13 - 17 - 21
����͎��� (7,4�j�����B��������11�ׂɂ���B
�ׂ荇�����̂��i��,���j�ƂȂ�悤�ɍʐF���邱�Ƃ͂ł��Ȃ�
���̂悤��11���ɕ����邱�Ƃ͂ł��Ȃ��B
�Ȃ��A��L�̂悤�ȕ��������ł���Y�����f��
�u���ݒY�����f�v�Ƃ����炵���B �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@01 - 05 - 09 - 13 - 17 - 21
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �b�@ �b�@ �b�@ �b
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@04 - 08 - 12 - 16 - 20
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�b �@�b �@�b
�@�@�@�@�@�@�@�@�@�@03 - 07 - 11 - 15 - 19
�@�@�@�@�@�@�@�@�@�@�b�@ �b�@ �b�@ �b
�@�@�@�@�@02 - 06 - 10 - 14 - 18 - 22
�@�@�@�@�@�b �@�b �@�b �@�b
01 - 05 - 09 - 13 - 17 - 21 �P�E�ɍs���Ɓ{�S
�P���ɍs���Ɓ{�V
a_{i,j} = 7i + 4j = a_{i-4,j+7} = a_{i+4,j-7} >>728
n=8�̃T�C�R���𓊂���Ƃ���
�@�� = (7/2)n = 28,
�@p(��) = 135954/(6^n) = 0.0809435
�@p(m) = p(��){1 - 0.0197967�(m-��)^2 + 1.8862E-4�(m-��)^4...
��
0.0197967��1.8862E-4�͂ǂ�����o�������Ȃ̂ł��傤���H �L���̏�̓�����`�Q�̈ʐ����āA����ł��܂����H gl(n,q)�̈ʐ�(q^n-1)(q^n-q)�d(q^n-q^(n-1))��q-1�Ŋ������ >>734
�������1���Ɨ��ȃx�N�g���𐔂��Ă�̂�
���ǂ��� �ݐϕ��z����
F(x)={��(x^2+x)}/2 (0��x��a)
�ŗ^�����Ă���B
�i1�jF(x)=1�ƂȂ鐳�̎���a�̒l�����߁A�܂��m�����x��f(x)�����߂�B
�i2�jE(a) = ��[0��a] xf(x) dx�����߂�B
�i3�jV(a) = ��[0��a] f(x){E(a)-x}^2 dx�����߂�B
�i4�j��[0��a] ��{E(x)V(x)} dx�ƕW�����Ƃ̊W�ɂ��Ę_����B 01 02
03 04 05
06 07 08 09
10 11 12 13 14
15 16 17 18 19 20
21 22 23 24 25 26 27
28 29 30 31 32 33 34 35
36 37 38 39 40 41 42 43 44
44 36
43 35 28
42 34 27 21
41 33 26 20 15
40 32 25 19 14 10
39 31 24 18 13 09 06
38 30 23 17 12 08 05 03
37 29 22 16 11 07 04 02 01
��̐�������̐���ɕϊ�����
�A���S���Y���������Ă���(^_^)� https://ja.wolframalpha.com/input/?i=%E4%BA%8C%E9%A0%85%E4%BF%A1%E9%A0%BC%E5%8C%BA%E9%96%93+n%3D300%2C+p%5E%3D0.6&;assumption=%22FSelect%22+-%3E+%7B%7B%22BinomialInterval%22%7D%7D&assumption=%7B%22F%22%2C+%22BinomialInterval%22%2C+%22c%22%7D+-%3E%220.97%22 n��3�Ƃ���B�c2*n�}�X�A��2*n�}�X�̃`�F�X�Ղ��甒�A���̃}�X�ڂ��P����������������`�F�X�ՂŁA
�h�~�m�v�ŕ~���l�߂��Ȃ����̂����݂��邩�B�܂��A���A��2�������������ǂ����B
���̖��ł����A2���O���t�̊��S�}�b�`���O�̖��ƍl���Ă����ł��傤���H >>737
Mathematica�ł́A
In[21]:= Table[{k,p=Floor[(1/2)(Sqrt[8k+1]-1)],q=k+1-p(p+1)/2,(9-q)(10-q)/2+9-p},{k,1,44}]
�ŁA���̂悤�ȏo�͂��܂��B��̎O�p�`�ŁAp�͉��s�ڂ��Aq�͉���ڂ���\���A����ɑΉ�����l�ɕϊ����鎮���A(9-q)(10-q)/2+9-p�ł��B
Out[21]= {{1, 1, 1, 44}, {2, 1, 2, 36}, {3, 2, 1, 43}, {4, 2, 2, 35}, {5, 2, 3, 28}, {6, 3, 1, 42}, {7, 3, 2, 34}, {8, 3, 3, 27}, {9, 3, 4, 21},
> {10, 4, 1, 41}, {11, 4, 2, 33}, {12, 4, 3, 26}, {13, 4, 4, 20}, {14, 4, 5, 15}, {15, 5, 1, 40}, {16, 5, 2, 32}, {17, 5, 3, 25}, {18, 5, 4, 19},
> {19, 5, 5, 14}, {20, 5, 6, 10}, {21, 6, 1, 39}, {22, 6, 2, 31}, {23, 6, 3, 24}, {24, 6, 4, 18}, {25, 6, 5, 13}, {26, 6, 6, 9}, {27, 6, 7, 6},
> {28, 7, 1, 38}, {29, 7, 2, 30}, {30, 7, 3, 23}, {31, 7, 4, 17}, {32, 7, 5, 12}, {33, 7, 6, 8}, {34, 7, 7, 5}, {35, 7, 8, 3}, {36, 8, 1, 37},
> {37, 8, 2, 29}, {38, 8, 3, 22}, {39, 8, 4, 16}, {40, 8, 5, 11}, {41, 8, 6, 7}, {42, 8, 7, 4}, {43, 8, 8, 2}, {44, 8, 9, 1}} >>739
���̂悤�Ɂ��Ɓ��̂Ƃ�������Ɩ��炩�Ƀh�~�m�v�ŕ~���l�߂��܂���B
������ƁA�u���A���P���̂Ƃ��͑��݂��Ȃ����A2���̂Ƃ��͑��݂���B�������A���̗�͏ȗ��B�v�ƂȂ��Ă��܂����B
�ȒP�ȗႪ����̂ɏȗ����Ă���̂��Ȃ��Ȃ̂�������܂���B
���̂悤�Ȏ����ȗ�ȊO�ɁA���A��2������������ꍇ�ɁA�h�~�m�v���~���l�߂��Ȃ���͂���܂����H
�^����ꂽ2���O���t�����S�}�b�`���O�������ǂ������v�Z����v���O����������āA���ׂĂ݂܂������A
n = 3, 4, 5�̂Ƃ��ɂ͎����Ȕ��������ȊO�̔��������������ꍇ�A���ׂĕ~���l�߉\�ł����B
�����An���傫���Ȃ��Ă��A���A��2��������邾���Ȃ̂ŁA�����I�ɍl���ď͕ς��Ȃ��Ǝv���܂����A�ǂ��ł��傤���H
������������
������������
������������
������������
������������
������������ >>741
������Ȃ�\�����ł���H >>742
�́A��ɏ������悤�ɁA�u���A���P���̂Ƃ��͑��݂��Ȃ����A2���̂Ƃ��͑��݂���B�������A���̗�͏ȗ��B�v�ł��B
���X���E�E���o�[�X�����i�H�R�m�{�s�[�^�[�E�t�����N���|�āj�w����g�����_�x�Ƃ����{�ɍڂ��Ă�����ł��B >>742
�����ɖ����ł���Ȃ̎����Ō������Ȃ��悤�Ȃ�{����ǂގ��i�Ȃ�
�ʂ̃m���Ȃ̂���
�܂��������ꂽ���炢����Ȃ��́H >>744
���肪�Ƃ��������܂��B�ȂC�����������ł����A�C�ɂ�����ɐi�����Ǝv���܂��B ���ʂ�n�̉~��`���ƁA���ʂ͂������̗̈�ɕ��������B�g���E�ʂ����L���ėׂ荇���h�̈悪�����F�ɂȂ�Ȃ��悤�ɁA���ʑS�̂�2�F
�ŐF�����ł���B
�ؖ��F
n = 1�̂Ƃ��A���̊O���𔒁A���������œh��B
�g�~�̌���n�̂Ƃ��������F�������\�ł���h�Ɖ��肷��B�~�̌���n+1�̂Ƃ����l����B���܁An�̉~�ŗ̈悪��������Ă���ꍇ��
�z�肵�悤�B�A�[�@�̉�����A����͐������F�����ł���B���ɁAn+1�Ԗڂ̉~�������āA���̉~�̊O���̗̈�̐F�͂��̂܂܂ɂ��āA������
�̈�����܂܂œh���Ă������F�Ɣ��̐F�ɂ���B���̐F�����̎d���͐������F������^���邱�ƈȉ��Ŋm�F���悤�B
��q�̐F�����̎d���́An+1�Ԗڂ̉~�ȊO��n�̉~�̌ʂ��������E�Ƃ���̈�ɂ��Ă͉���ɂ�萳�����B�Ȃ��Ȃ�A�ʂ̗����̗̈��
�F�́A���̗̈悪n+1�Ԗڂ̉~�̓����ɂ���Η����Ƃ��ς��A�܂����̗̈悪�O���ɂ���Η����Ƃ��ς��Ȃ�����ł���B�܂��An+1�Ԗڂ�
�~�̌ʂ��̈�̋��E�ɂȂ�Ƃ��́A���̑O��1�������̈悪�ʂ�`�������2�ɕ�������A���̂����̓����͐F��ς��A�O���͕s�ς�����ł���B
����ŏؖ��͊��������B
�ȉ��̕����̓��{�ꂪ������܂���B��̉������������̂ł��傤���H
�u��q�̐F�����̎d���́An+1�Ԗڂ̉~�ȊO��n�̉~�̌ʂ��������E�Ƃ���̈�ɂ��Ă͉���ɂ�萳�����B�Ȃ��Ȃ�A�ʂ̗����̗̈��
�F�́A���̗̈悪n+1�Ԗڂ̉~�̓����ɂ���Η����Ƃ��ς��A�܂����̗̈悪�O���ɂ���Η����Ƃ��ς��Ȃ�����ł���B�܂��An+1�Ԗڂ�
�~�̌ʂ��̈�̋��E�ɂȂ�Ƃ��́A���̑O��1�������̈悪�ʂ�`�������2�ɕ�������A���̂����̓����͐F��ς��A�O���͕s�ς�����ł���B�v >>747
������܂����B�ȉ��̂悤�Ɏ����Ō��t��₢�܂����B
�u��q�̐F�����̎d���́An+1�Ԗڂ̉~�ȊO��n�̉~�̌ʂ��������E�Ƃ���̈�ɂ��Ă͉���ɂ�萳�����B�Ȃ��Ȃ�A�ʂ̗����̗̈��
�F�́A���̗����̗̈悪n+1�Ԗڂ̉~�̓����ɂ���Η����Ƃ��ς��A�܂����̗����̗̈悪�O���ɂ���Η����Ƃ��ς��Ȃ�����ł���B�܂��An+1�Ԗڂ�
�~�̌ʂ��̈�̋��E�ɂȂ�Ƃ��́A���̑O��1�������̈悪�ʂ�`�������2�ɕ�������A���̂����̓����͐F��ς��A�O���͕s�ς�����ł���B�v �������������̂��悭�킩��₾�ȁB�u�������������̂��H�v�ƕ�����Ă��A�����Ă���ʂ�̂��Ƃ����������̂��낤�Ƃ����B �g�����_�̓V�˃��o�[�X�i���w�I�����s�b�N3������_���j�̖{���������Ėʔ�����肪����܂����B
����������������
����������������
����������������
����������������
����������������
����������������
����������������
����������������
2^n �~ 2^n�̃`�F�X�Ղ���1�̃}�X�ڂ�����菜���������`�F�X�Ղ͈ȉ���L���v�ŕ~���l�߂��邱�Ƃ��ؖ�����B
��
���� �W���[�R�t�X�L�[�ϊ��̋t�ϊ�������Ă݂悤�Ǝv���āA
�h�E���A�u���̒藝�Ōv�Z�ł��Ȃ����ȂƎ��݂��̂ł����A
�W���[�R�t�X�L�[�ϊ��ŎZ�o�������W�ɓK�p���Ă����̍��W�ɖ߂�܂���ł����B
�W���[�R�t�X�L�[�ϊ��̋t�ϊ��ɂ��ďڂ����������Ă�E�F�u�ȂǁA
���炩�̃A�h�o�C�X���������烌�X���������B >>751
�ʔ������ɂ��Ă̘b���������̂Ȃ�X���Ⴂ�ł��B
�ʔ�����肨�����ā`�� 32���
https://rio2016.5ch.net/test/read.cgi/math/1586230333/l50 �W��S�͑��قȂ�(2^n+1)�̎��R��a[1],...,a[2^n]��v�f�Ƃ��A���l�ɏW��T�����قȂ�(2^n+1)�̎��R��b[1],...,b[2^n]��v�f�Ƃ���B
�܂�a[1]=b[1]=2�ł���B
������̏W���ɂ��Ă��A���ׂĂ̗v�f�̘a��2�̗ݏ�̌`�ŕ\����B
�W��S,T���炻�ꂼ��C�ӂ�1�̗v�f��I�ь������Ă��A�������S�y��T�̂��ׂĂ̗v�f�̘a��2�̗ݏ�̌`�ł���B
�W��S,T�Ƃ��čl��������̂����ׂČ��肹��B 2^n�ɒ������Ƃ��Ă�
S = T = {2} �����Ȃ����Ƃ��ȒP�ɏؖ��ł���� �}�Z�}�e�B�J���g���ăN���h�j�}�`�̂RD�̐U���̐}�`�̃V�~�����[�V���������悤�Ƃ��Ă��āA����ɂ��Ę_�����������߂ɁA���Z���x���Ɋȗ������ꂽ���ŃV�~�����[�V�������ł��Ȃ�������Ă��܂��B�搶�ɂ�Sin[m��x]Sin[n��y]Cos[t]�Ƃ��������g���ƌ���ꂽ�̂ł����A�ǂ��ׂĂ��ǂ����Ă��̎��������ꂽ�̂����킩��܂���E�E�B���������̖����ǂꂭ�炢���������ł��Ă��邩���킩��Ȃ��Ƃ���ł����A���ꂩ�Ȃ�Ƃ������Ă��������Ȃ��ł��傤���E�E�E�B AB=a,AC=4a,��BAC=60���́�ABC�ɂ����āA��BAC�̓�����BC�Ƃ̌�_��D�AAC�̒��_��M�AC���璼��AB�ɉ��낵�������̑���H�Ƃ���B
�ʐϔ䁢DMH:��ABC��a�ŕ\���B ��[k=0,n] 3^k�@��2�̗ݏ�ƂȂ�悤��1�ȏ�̐���n��S�ċ��߂�B
������1�ȏ�̐���a�ɑ�a^0=1�Ƃ���B >>761
���t�[�m�b�܂ł�������Ă���̂ŗL����肩�Ǝv������ꋴ��w�Ɏ����悤�ȓ�����肪�������悤�ł��B
����ɂ��Ă��悭�����Ă����܂����� n^2 + 1�̑��قȂ鐮������Ȃ鐔��ɂ́A����n+1�̑����������邩�A���邢�͒���n+1�̌����������邱�Ƃ��ؖ�����B
�ؖ��F
s : a_1, a_2, �c, a_{n^2+1}�𑊈قȂ鐮������Ȃ��Ƃ���Bs�͒���n+1�̑�����������܂܂Ȃ��Ƃ��悤�B�����ŁA�ea_k(k = 1, �c, n^2+1)��
���x��l_k�����̋K���ɂ���Ă���F�el_k��a_k����n�܂�s�̍Œ�����������̒����Ƃ���B���̂Ƃ��A���郉�x��l_j�����݂��āAs��n+1���ȏオ
���̃��x��l_j�������Ƃ����̑��������킩��B���x��l_j������s��n+1���ȏ�́A�����������^����B
�u���̂Ƃ��A���郉�x��l_j�����݂��āAs��n+1���ȏオ���̃��x��l_j�������Ƃ����̑��������킩��B�v���Ȃ�����������̂�������܂���B >>763
���X���E�E���o�[�X�����i�H�R�m�{�s�[�^�[�E�t�����N���|�āj�w����g�����_�x�Ƃ����{�ɍڂ��Ă�����ł��B �O>>725
>>759
��DMH:��ABCp=1:10 �O>>725
>>759
��DMH:��ABCp=1:10 �O>>725
>>759
���l���E�X�̒藝�A�`�F�o�̒藝�A�s�^�S���X�̒藝��聢AHC���̕ӂ̔���m�肵�AD����HM�Ɉ���������DN��x�Ƃ����ƁA
A���N�_�Ƀ��l���E�X�̒藝���A
(AB/BH)�o2a��3/(2a��3-2a/��3)�p(a/��3+x)/(a��3-x)=1
x=a��3/5
��ABC=a^2��3
��DMH=ax/2=a^2��3/10
����DMH:��ABC=1:10 >>763
����n+1�̑����͂Ȃ��Ɖ��肵������S�Ă�l_k��n�ȉ��̂͂�
(l_k��{a_1,a_2,�c,a_(n^2+1)}����{1,2,�c,n}�ւ̎ʑ��ƂȂ�)
�܂�n^2+1�̂��̂�n�ȉ��̐������蓖�ĂĂ�������A
���̑������ɂ���Ăǂ�����n+1���������b�����蓖�Ă��Ă��܂� >>768
���肪�Ƃ��������܂����B >>759
��}���ăv���O�����Ɍv�Z�����Ă݂��B
https://i.imgur.com/yFv7F0m.png
sim <- function(a=1){
plot(NULL,xlim=c(0,5*a),ylim=c(0,2*a),asp=1,ann=F,axes=F)
A=0i ; pt(A,'A')
C=4*a+0i ; pt(C,'C')
B=a*cos(pi/3)+1i*a*sin(pi/3) ; pt(B,'B')
seg(A,B) ; seg(B,C) ; seg(C,A)
d=cos(pi/6)+1i*sin(pi/6)
D=intsect(B,C,A,d)
pt(D,'D')
seg(A,D,lty=3)
M=1/2*(A+C) ; pt(M,'M')
# y-0=tan(pi/3+pi/2)*(x-4*a)
y0=-4*a*tan(pi/3+pi/2)
H=intsect(A,B,C,y0*1i)
pt(H,'H')
seg(B,H,lty=3)
seg(C,H,lty=3)
# ��DMH:��ABC
seg(D,M,col=2)
seg(M,H,col=2)
seg(D,H,col=2)
Tri <- function(a,b,c){
s=(a+b+c)/2
S=sqrt(s*(s-a)*(s-b)*(s-c))
return(S)
}
DMH=Tri(abs(D-H),abs(H-M),abs(M-D))
ABC=Tri(abs(A-B),abs(B-C),abs(C-A))
DMH/ABC
}
���s����
> sim(runif(1))
[1] 0.2 ��T�����V���ɍڂ��Ă����m���̖�肪�ǂ����Ă��[���ł��Ȃ����lj�����Ă����l���肢�I
�y���z
�����ɍs������������́A����Ă�������10�E���ĉƂɎ����A��܂����B���̂����A��Ŏ����������H�ׂ镪��1�����c���A9�����q�ɏo���܂����B���q�ɏo��������1�����c��܂����B
���̌エ������́A�אl�ɁA�c���������������������邱�Ƃ���܂����B
���������̂�����ŁA����������w�삩�痬��Ă�������1�ɓ����Y�������Ă����炵���x�Ƃ����b���܂����B
���q�ɏo�������ɂ́A�����Y�͓����Ă��܂���ł����B����Ƃ������Y�������������~����2�l�ł����A�ǂ��炩1�͂��ׂɂ������������Ȃ���Ȃ�܂���B
���āA�ǂ���̓����c�������ł��傤�H�܂��A�c�������ɓ����Y�������Ă���m���͉�%�ł��傤�H
�y�V���L�ڂ̓����z
10�̓���1��9�ɕ��������A���ꂼ��̃O���[�v�ɓ����Y�������Ă���m����10%��90%�ƂȂ�܂��B���q�ɏo����9�̂���8�ɂ͓����Y�͓����Ă��Ȃ������̂ŁA�c���1�ɓ����Ă���m����90���B����āA���q�ɏo���Ďc���������c���ׂ��ł��B
�q�������Y�̗L���œ���I�킯����Ȃ�������50������Ȃ��ȁH�Ǝv�����ǂǂ��H �����e�B�z�[���̈����_�������ۂ��ȁB
���q�������g�Q���������Œ��g���`�F�b�N�ł����ƍl����ΐV���̓����ł����Ǝv���B 8�͊��ɐ蕪�����̂ɓ����Y�������ĂȂ������Ƃ������Ƃł��傤
�Ȃ̂�90% �q�������Y�̓����ĂȂ�����I�킯�ł͂Ȃ�����1/2����
9�l�̋q��9�̓���n���āA8�Ԗڂ̋q�܂ł��H�ׁA9�Ԗڂ̋q���܂��H�ׂĂȂ��ƍl���āA������10�Ԗڂ̋q���Ǝv������
9�Ԗڂ�10�ԖڂɈႢ�͂Ȃ�
�����e�B�z�[���I�ɂ���ɂ͋q�ɓ����\�͂������ē����Y�̓����Ă铍�͑I�Ȃ��A�Ƃ����悤�Ȑݒ肪�K�v �O>>767
>>771
��10�̂���1�ɓ����Y�������Ă��邩�炻�̓��ɓ����Y�������Ă���m����(1/10)�~100%=10%
���q�ɏo���Ďc�����������q�ɏo���Ȃ������������̓��ɓ����Y�������Ă���m����10%
���ǂ�����c���Ă������B
���̓��ɓ����Y�������Ă���m����10%
���͘f�킳��Ȃ��B ���̎�̂�͂ǂ̂悤�ɂ��ăn�Y�����Ɣ��������̂������Ȃ̂ɂ����𗝉����Ă��Ȃ�����L�����������Ă��Ƃ��� >>777
2�Ɉ������50%����Ȃ��̂��H �O>>777
>>779
����Ă����������k������ԏE������10%�ɂȂ�Ǝv��👵🍑
��ɗ����Ă��܂�����10%�����B
���ꂳ�����Ă����b��100%�ق�ƂȂ�10%�̊m���łǂ̓��������Y�������Ă���\��������B
���ꂳ�������b�̐M�ߐ��ɂ���Ă�10%�����B
���q�ɏo���Ďc�����瓍�������Y�ɂȂ�Ȃ�A���ꂳ������k���������ł��q�ɓ���U�镑���Ǝv���B >>771
�q�͖���ׂɓ���I�Ɖ��肵�ăV�~�����[�V�������Ă݂��B
m=c(rep(0,9),1) # ��10�� 1�������Y����̂���
sim <- function(){
i=sample(10,1)
a=m[i]�@# a:�����B�p�Ɏc������
j=sample(9,1)
b=m[-i][j] # b:�q���c������
c=m[-i][-j] # c:�q���H�ׂ���8��
c(a,b,c)
}
momo=t(replicate(1e6,sim()))
fa <- function(x){ # �q���H�ׂ���c�ɓ����Y�����Ȃ���
sum(x[3:10]==0) & x[1]==1 # ���A�����B�p�Ɏc������a�ɓ����Y�������TRUE��Ԃ�
}
fb <- function(x){ # �q���H�ׂ���c�ɓ����Y�����Ȃ���
sum(x[3:10]==0) & x[2]==1 # ���A�q���c������b�ɓ����Y�������TRUE��Ԃ�
}
mean(apply(momo,1,fa)) # �����B�p�̓��ɓ����Y
mean(apply(momo,1,fb)) # �q�̎c�������ɓ����Y
> mean(apply(momo,1,fa))
[1] 0.100156
> mean(apply(momo,1,fb))
[1] 0.099983
���R�Ȃ���A�ǂ���̊m���������Ƃ����V�~�����[�V�������ʂɂȂ����B 1/n! * ��[t=2n, ��] dt t^n e^(-t) �� 0 ( n�� �� )
���������������B
�ȒP�����Ɏv�����̂ł����ǂ������炢����������Ȃ��Ȃ�܂����B
https://imgur.com/a/Kyf8LdB
�Ɠ_�@�ɂ��X�^�[�����O�����̓��o�ߒ��Ō��ꂽ�̂ŁA
�ł���X�^�[�����O�������g��Ȃ����[�g�ł��肢���܂��B
 ���R�Ȃ���A��������
���R�Ȃ���A��������
> u
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 0 0 0 0 0 0 0 0 0 1
[2,] 0 0 0 0 0 0 0 0 1 0
[3,] 0 0 0 0 0 0 0 1 0 0
[4,] 0 0 0 0 0 0 1 0 0 0
[5,] 0 0 0 0 0 1 0 0 0 0
[6,] 0 0 0 0 1 0 0 0 0 0
[7,] 0 0 0 1 0 0 0 0 0 0
[8,] 0 0 1 0 0 0 0 0 0 0
[9,] 0 1 0 0 0 0 0 0 0 0
[10,] 1 0 0 0 0 0 0 0 0 0
> mean(apply(u,1,fa))
[1] 0.1
> mean(apply(u,1,fb))
[1] 0.1
�łǂ���̓���I��ł������B �����Y�̖��A�݂�Ȃ��肪�Ƃ��I
�ς��Ȃ����Ĉӌ��������Ĉ��S���܂����B�X�b�L���ł��I
���Ȃ݂ɖ��͉������Ȃ�����m�F�ł��Ȃ����Ǒ������̋L���̒��ɂ���͂�
https://mainichi.jp/articles/20200816/ddv/010/070/019000c >>782
�����A n > 0 �̂Ƃ��A�s����
��[k=0,n] (2n)^k/k! < (1/n)*��[k=0,2n] (2n)^k/k! < e^(2n)/n
����������Ǝv�����ǁA�ؖ����킩��Ȃ� >>782
(1/n!)��[t=2n,��] (t^n) e^(-t)dt
�@= e^(-2n) ��[k=0,n] (2n)^k / k!
�@�` ��(2/��n) (2/e)^n,
�X�^�[�����O���g�킸�Ɏ����̂�
�ȒP�Ƃ͎v���Ȃ������� >>782
�Q�l�܂łɁA�ʂ̖{����T�������p����ƁA
log(n) �� ��[n-1/2,n+1/2] log(x)dx ���p����A
�@log((n-1)!) = (n-1/2)log(n) -n +1 -��,
�]����
�@��(n) = (n-1)!
�@�@�@= n^(n-1/2) e^(-n+1-��)
�@�@�@= a n^(n-1/2) e^{-n+��(n)},�@�@�@(1)
�@lim(n����) ��(n) = 0.�@�@�@�@�@�@�@�@(2)
�萔a��Wallis�̌���(253��,(9))
�@��� = lim(n����) (n!)^2�2^(2n) / ((2n)!���n),
����ȒP�ɋ��߂���B
���Ȃ킿 (1) ����������, (2) ��p����A
�@��� = lim(n����) ���� = a/��2.
�̂�
�@a = ��(2��).
����� (1) ����, n���|����
�@n! �` ��(2��) n^(n+1/2) e^(-n).
���ꂪ Stirling �̌����ł���B
�@Stirling�̌����͊ȒP�ɓ���ꂽ���A����
���ؒ厡�F�u��͊T�_�v������O��, ��g���X (1961)
�@��T�́@��͔����@��69�D p.258-259 >>785
�@��[k=1,2n] (2n)^k / k!
�@= ��[k=1,n] {(2n)^k / k! + (2n)^{k+n} / (k+n)!}
�@= ��[k=1,n] {(2n)^k / k!} {1 + (2n)^n / [(k+1)(k+2)����(k+n)]}
�@�� ��[k=1,n] {(2n)^k / k!} {1 + (n-1)}�@�@�@�@(��*)
�@= n ��[k=1,n] (2n)^k / k!,
���ȁH
(*)
�@(2n)^n /(k+1)(k+2)����(k+n) �� (2n)^n / [(n+1)(n+2)����(2n)]
�@= (2n)^{n-1} / [(n+1)(n+2)����(2n-1)]
�@> (2n)^{n-1} / (3n/2)^{n-1}�@�@�@�@�@(GM-AM)
�@= (4/3)^{n-1}
�@> n-1,�@�@�@�@(n��8) >>771
�@�ߏ��̃X�[�p�[���R�����B�j�łP������
��������ׂɂ�������������ˁH ����a,b,c��1��a��2,1��b��2,1��c��2���B
p,q,r��p=bc/(a+b),q=ca/(b+c),r=ab/(c+a)�ƒ�߁Axyz��Ԃ̓_(p,q,r)�������Ăł��闧��K���l����B
�i1�jr�̎�肤��l�͈̔͂����߂�B
�i2�j����t���i1�j�͈͓̔��̒l�Ƃ���BK��z=t�Ő�������̊T�`��}������B
�i3�jK�̑̐ς����߂�B >>785, >>788 ���ꕪ����Ղ��ł��ˁI ���肪�Ƃ��������܂��B
�X�^�[�����O�g��Ȃ���...�Ƃ͌��������̂�
>>786
e^(-2n) ��[k=0,n] (2n)^k / k! �` ��(2/��n) (2/e)^n
�ǂ�������炱�̎������o�ł���̂������Ăق����ł��B ���X���E�E���o�[�X�����i�H�R�m�{�s�[�^�[�E�t�����N���|�āj�w����g�����_�x�Ƃ����{�Ɉȉ��̒藝�������Ă���܂��B
�Ȃ��A�un�ȊO��n�̖v�Ə����Ă���̂ł��傤���H
n = 7�̂Ƃ�7�ȊO��7�̖őf���ł�����̂͑��݂��܂���
��(7) = 6 = 7 * (1 - 1/7)
�ƒ藝��K�p�ł��܂��B
��(n)��n�ȉ��̎��R����n�Ƒf�ł�����̂̌��Ƃ���B
n�ȊO��n�̖őf���ł�����̂�p_1, �c, p_k�Ƃ���B���̂Ƃ�
��(n) = n * (1 - 1/p_1) * �c * (1 - 1/p_k)
�����藧�B t��2n �ł�
�@e^{t/2n} �� (e/2n)t,
�@t^n �� (2n/e)^n�Ee^{t/2},
t >>2t �ł� ����������
��[t=2n,��] (t^n) e^{-t} dt
�@�� (2n/e)^n ��[t=2n,��] e^{-t/2} dt
�@= (2n/e)^n [ 2e^{-t/2} ](t=2n,��)
�@= (2n/e)^n�E2e^{-n}
�@= 2(n/e)^n�E(2/e)^n
�@�` 2{n!/��(2��n)} (2/e)^n,�@(�X�^�[�����O) >>792
�������ɈӖ����Ȃ��悤�Ɏv����
n���f���łȂ��Ƃ��́un�ȊO��n�̖őf���ł�����́v�Ɓun�̖őf���ł�����́v�͓������ƂɂȂ邵�A
n���f���̂Ƃ��́A�un�̖őf���ł�����́v��n�����Ȃ̂ł��̌v�Z����n(1-1/n)=n-1�ƂȂ�A�un�ȉ��̎��R����n�Ƒf�ł�����̂̌��v�ƈ�v���� ��
e^x �� e�x�@(����������x=1)�@���g�����B
t> >2n �ł͏���������덷�����āc >>794
���肪�Ƃ��������܂����B��ҋy�і|�Ď҂̏H�R�m����̃~�X���Ɛ������܂��B >>793
�����ł͏����H�ȋߎ��ł������A
��[2n,2n+M] dt t^n e^{-t}
= ��[0,M]dt (t+2n)^n e^{-t-2n}
= e^{-2n} (2n)^n ��[0,M]dt (1+t/2n)^n e^{-t}
�� e^{-2n} (2n)^n ��[0,M]dt e^{+t/2} e^{-t} (t�� M << n)
= e^{-2n} (2n)^n ��[0,M]dt e^{-t/2}
= ... (M����)
�Ȃ�قǔ[�����܂����B���肪�Ƃ��������܂��B >>790
�i1�j
a,b,c�͓Ɨ��ɓ������Ƃɗ��ӂ���B
ab/(c+a)=b[1-{c/(c+a)}]
=f(b|a,c)
c���Œ肵��c/(c+a)=g(a|c)��a�̊��ƌ���B������g(x|y)��x���ϐ��Ay��萔�Ƃ݂Ȃ����\�L�ł���B
c>0���g(a|c)�͒P�������B�����c�̒l�Ɋւ�炸�A
Max{g(a|c)}=g(1|c),min{g(a|c)}=f(2|c)
����c�̌Œ���O���Ag(a|c)��c�̊�g(c|a)�Ƃ݂�Ba���Œ肵�����g(c|a)�̑����ׂ�B
g(c|a)=c/(c+a)=(c+a-a)/(c+a)=1-a/(c+a)
a>0���Ag(c|a)�͒P�������B
�����g(a|c)��c�Ɋւ��ĒP����������a�Ɋւ��ĒP�������ŁA
Max{g(a|c)}=g(1|2),min{g(a|c)}=g(2|1)
����������1/3��g(a|c)��2/3�ł��邩��A
b/3��f(b|a,c)��2b/3
min{f(b|a,c)}=f(1|1,2)=1/3
Max{f(b|a,c)}=f(2|2,1)=4/3
�ȏ���A1/3��ab/(c+a)��4/3 >>790
�i2�j
1/3��t��4/3�Ȃ�t��1�Œ肷��B
t=ab/(c+a)���Ab=t(c+a)/a
�����
p=bc/(a+b)=tc(c+a)/[t(c+a)+a^2]
q=ca/(b+c)=(c*a^2)/[t(c+a)+ca]
����������2�ϐ�a,c���ǂ������Ηǂ���������܂���B�Œ肳�ꂽt�̒l�ɂ����a,c�͈̔͂��ς���Ă���̂ŏꍇ�������K�v���Ǝv���܂����A�ǂ�������ǂ��ł��傤���B >>787
��͊T�_��ǂݍ���ł����ł����H >>787
lim(n����) ���� = a/��2.
����͂Ȃ��ł����H >>801
���܂���ɏ����Ă�����ł��ˁB �O>>780
>>790(1)
a=b=1,c=2�̂Ƃ�r=ab/(c+b)=1/(2+1)=1/3
a=��2,b=2,c=1�̂Ƃ�r=ab/(c+a)=2��2/(1+��2)=2��2(��2-1)=4-2��2
��1/3��r��4-2��2
1/3��r��4-2��2 >>790(1)�����B
a=b=1,c=2�̂Ƃ�r=ab/(c+b)=1/(2+1)=1/3
a=b=2,c=1�̂Ƃ�r=ab/(c+a)=4/(1+2)=4/3
��1/3��r��4/3 >>787
��͊T�_�̃�_n���������邱�Ƃ̏ؖ����킩��₷�������ł��B �O>>804
>>790(2)
z���W��ab/(c+a)=t�̂Ƃ��A
x���W��bc/(a+b)=ab(b-t)/(a+b)t
y���W��ca/(b+c)=(b-t)a^2/(ab-at+bt)
1/3��t��4/3������A
ab(3b-1)/(a+b)��x��ab(3b-4)/4(a+b)
(3b-1)a^2/(3ab-a+b)��y��(3b-4)a^2/(3ab-4a+4b) >>797
�֑�������
�}�N���[�����W�J
log(1+x) = ��[0,x] 1/(1+y) dy = x - (1/2)x^2 + (1/3)x^3 - ����,
�Ł@x = e^{t'/2n} -1�@�Ƃ�����
t'/2n = [e^{t'/2n} -1] - (1/2)[e^{t'/2n} -1]^2 + ����,
2n+t' = 2n (e^{t'/2n} - (1/2)[e^{t'/2n} -1]^2 + ����),
(2n+t')^n
�@�� (2n)^n (e^{t'/2} - (n/2)[e^{(n+1)t'/2n} - 2e^{t'/2} + e^{(n-1)t'/2n}] ),
(2n+t')^n e^{-t'}
�@�� (2n)^n (e^{-t'/2} - (n/2)[e^{-(n-1)t'/2n} - 2e^{-t'/2} + e^{-(n+1)t'/2n}] ),
��[2n,��] (t^n) e^{-t} dt
�@= e^{-2n}��[0,��] (2n+t')^n e^{-t'} dt'
�@�� e^{-2n} (2n)^n {2 - n[n/(n-1) -2 +n/(n+1)]}
�@= (2/e)^n (n/e)^n {2 - 2n/(nn-1)}
�@�� (2/e)^n n! ��(2/��n) {1 - n/(nn-1)}, >>800
�@�͂��B
>>801
�@�����Ⴎ����Ȏ��Ȃ̂ŗ����܂����B >>799
�ǂȂ�����������肢���܂��B
��`�悪���G�ɕς��Q�ϐ��̏���������Ďv�����܂���B�Ώ̐�����肭�g���Ȃ����Ƃ��v���܂������A�v�����܂���c �i����́j�������ɂ��Ď���ł��B
o(a_n)�Ə��������Ao(*)�͊��̋L�����C���[�W������悤�Ɏv���܂��B
�����M�F���w��͓���x�ɂ́Ao(a_n)�Ƃ����L���̃C���[�W��o�~a_n�ł���Ə����Ă���܂��B
�ǂ������C���[�W����̂����ʂł��傤���H o(a_n)�����̋L�����C���[�W������Ƃ����̂�������܂��ƁA����a_n��a_n���������̖������ł��鐔��̏W����Ή��������o(a_n)�Ƃ���
�C���[�W�ł��B
����A�|���Z�̃C���[�W��������܂��ƁAb_n = o(a_n)�Ƃ����̂�b_n = o �~ a_n�io�͖������ł���A���鐔��j�ƍl����Ƃ����C���[�W�ł��B >>782
����ʔ�����
�����N�����Ă�̂������Ȃ�ɐ������Ă݂���
�|�A�\�����z�̒��S�Ɍ��藝=�X�^�[�����O�̌���
���Ă��Ƃ���������
�R���r�l�[�V�������邢�͎w�����̐����̂�������
�|�A�\�����ze^(-��)��^k/k!�͍Đ����������Ă���(�����n���Ăѓ����z�ɂȂ�)����
���S�Ɍ��藝�ɂ����N�����n�̃|�A�\�����z
e^(-N)N^k/k! (����N�A����N)
��N���傫���Ȃ��Ă����Ɠ����ϓ����̐��K���z
1/��(2��N)e^(-(k-N)^2/2N) (����N�A����N)
�ɋ߂Â��Ă���
k=N���������
�X�^�[�����O�̌���N!�`��(2��N)N^N/e^N
��������
�܂�������N�ł��邱�Ƃ���N���傫���Ȃ����Ƃ�
���S(=����)N����}N/2(����N�ɔ�ׂĔ��ɑ傫��)�͈̔͂ɂقƂ�ǂ̊m���������Ă���
�t�Ɍ�����k=1�`N/2�Ƃ�������ɓ���m���̓[���ɂȂ��Ă���
����͂܂���e^(-N)��[k=1,N/2] N^k/k!��0(N����)���Ӗ����Ă��� ���l��
I_n = (1/n!)��[2n,��] (t^n)e^{-t} dt,
J_n = (1/n!)(2n/ee)^n *2(1-n/(nn-1)),�@>>807
K_n = (1/n!)(2n/ee)^n *2,�@�@�@�@�@�@>>793
n, I_n, J_n, K_n
-------------------------------------------------
4, 0.0996324005, 0.0839700231, 0.114504577
8, 0.02198725355, 0.02093050770, 0.02397494519,
16, 0.001391667287, 0.001371653306, 0.001463479469,
32, 7.4429824464E-6, 7.4125663716E-6, 7.6519227025E-6,
64, 2.90400556165E-10, 2.9007904985E-10, 2.9468462147E-10,
128, 6.1223407676E-19, 6.12056673216E-19, 6.1687631358E-19, >>782
�K���}���z�ƃ|�A�\�����z�̑o�ΐ�
��[t=0,t'] t^s'e^(-t)/s'! + ��[s=0,s'] t'^se^(-t')/s! =1
�Ƃ��v�����
���̎��A�������s�v�c�� ���������Ȃ̂� >>782 �̎��̏ؖ������Ă݂܂����B
https://imgur.com/a/Hi8iXiB
https://imgur.com/a/Kyf8LdB
�ƍ��킹�āA�X�^�[�����O�����̏ؖ����������܂����B
�̂��l�������� ����Ȃ̏ؖ��Ƃ͌�����I
�Ɠ{��ꂻ���ł����A�Ɠ_�@�͎�y��������݂����Ȃ��̂ł�����ˁB >>814
����A�x�C�Y���_�ɂ����鋤�z�Ƃ����̂��W���Ă������� >>788
�@e^{2n} > ��[k=1,2n] (2n)^k / k!
�@= ����
�@> ��[k=1,n] {(2n)^k / k!} (1 + (4/3)^{n-1})
�@> (4/3)^{n-1} ��[k=0,n] (2n)^k / k!,
������
�@e^{-2n} ��[k=0,n] (2n)^k / k! < (3/4)^{n-1} = 0.75^n (4/3),
�����
�@(����) �� (2/e)^n ��(2/��n) = 0.73576^n ��(2/��n)
��菭���傫���B >>811
�ǂ������������Ƃ���Ȃ��́H
���������`�ɖ߂����
b_n = o(a_n) �̒�`�� b_n/a_n �� 0 �ł���H
������ ��_n := b_n/a_n �Ƃ���� ��_n �� 0 ���� b_n = (��_n)*(a_n) >>811
�����Č����Ȃ�
>a_n���������̖�����
�Ƃ����\���̓C�}�C�`����
b_n = o(a_n) �ł� b_n �� 0 �Ƃ͌���Ȃ������
�Ⴆ�A a_n := n^2 �̂Ƃ��A
b_n := n �Ƃ���� b_n = o(a_n) as (n����) ���� b_n �� �� (n����) >>790
����́i2�j���ǂȂ������肢���܂�
�����Ԃ��l���܂����������܂���ł���
�i1�j��1/3��r��4/3�ł� �O>>806
>>790(2)
ab(4b-3)/4(a+b)��x��ab(3b-1)/(a+b)
a^2(3b-4)/(3ab-4a+4b)��y��a^2(3b-1)/(3ab-a+b)
(a+b)+x=ab(b-t)
y(ab-at+bt)=a^2(b-t)
a(a+b)+ax=by(ab-at+bt)
a(a+b)+ax-ab^2y=-by(a-b)t
t=�oab^2y-ax-a(a+b)�p/by(a-b)
�����܂ł͂ł����B
�̈�̌`���킩��Ȃ��B �O>>821
>>790(3)K=3ab^3(8ab-1)/4(3ab-a+b)(3ab-4a+4b)(a+b) >>814
�}�N���[�����W�J
�@e^{t'} = ��[s=0,��] (t'^s) /(s!),
����
�@e^{-t'} ��[s=0,��] (t'^s) /(s!) = 1,�@�@�@(�|���\�����z)
�@e^{-t'} ��[s=0,s'] (t'^s) /(s!) = 1 - e^{-t'} ��[s=s'+1,��] (t'^s) /(s!)
�@= 1 - ��[t=0,t'] (t^s') e^{-t} dt / (s'!), >>797
����ĉ��ǁB
e = lim(N����) (1+1/N)^{N +1/2},
���@(1+t'/2n)^{2n/t' +1/2} �� e,
(1+t'/2n)^n �� (1+t'/2n)^{-t'/4} e^{-t'/2}
�@�� (1 - t't'/8n) e^{-t'/2},
��[0,��] (1 +t'/2n)^n e^{-t'} dt'
�@�� ��[0,��] (1 - t't'/8n) e^{-t'/2} dt'
�@= [ -{2 - (8+4t'+t't')/4n} e^{-t'/2} ](0����)
�@= 2(1 - 1/n),�@�@�@�@�@(>>807 ���Q��) �ȉ��̖��̉��킩��܂���B�X�y���i�[�̕��𗘗p���Ă���̂ł����A������Ȃ��Ƃ��낪����܂��B
�X�y���i�[�̕�肨��шȉ��̖��̉��A�b�v���[�h����Έꏏ�ɍl���Ă��������܂����H
���X���E�E���o�[�X���w���� �g�����_�x�����o�� (1985)
�i�H�R �m�{�s�[�^�[�E�t�����N���|��)�@136p�D2090�~
http://www.kyoritsu-pub.co.jp/bookdetail/9784320013407
�����A�����肾�Ǝv���܂��Ba��c�����Ԑ��������b��d�����Ԑ����͒����`�̑Ίp���ɂȂ�܂��F
�����`�̔�����A����4���_a, b, c, d�ɓB���ł��Ă���Ba��c��+�̓B�Ab��d��-�̓B�ł���B�����āA�ǂ�3�{�̓B���꒼����ɕ��Ȃ��悤�ɂ����Ă�
+��-�̓B�����{�ł��ł����݁A�B�ȊO�ňӐ}���������邱�Ƃ��Ȃ��悤�ɓB�̊Ԃ����Ō��сA��������ȏ�͌��������ɂ͌��ׂȂ��Ƃ���܂Ō��ԁi����
�Ƃ��A�����`�̓����̗̈�͂��ׂĎO�p�`�ł��邱�Ƃɒ��ӂ���j�B���̂Ƃ��A+�ǂ��������Ԏ�������ʂ���a����c�܂œ��B�ł��邩�A�܂���-�ǂ���������
��������ʂ���b����d�܂œ��B�ł���B >>824 (����)
(1+t'/2n)^n �� (1+t'/2n)^{-t'/4} e^{t'/2}
�@�� (1 - t't'/8n) e^{t'/2},
����� e^{-t'} ���|����B >>825
�ȉ���{��+�B�����ԕӂ�+�ӁA��{�́|�B�����ԕӂ��|�ӂƌĂ�
+�B��+�ӂň͂�ꂽ�̈�̓����͑S��+�B��+�ӂƂ��Ă悢
�|�ɂ��Ă����l�ɉ��肷��
+�B��+�ӂ���Ȃ�O���t��+�O���t�ƌĂ�
�|�ɂ��Ă����l�Ɂ|�O���t�ƌĂ�
��>0���\���������Ƃ�
�v���X�O���t�̃ËߖT�������Ē����`�����f����鎞��+�ӂ�H����a��c������邩��+�O���t�̃ËߖT�������Ă��c�����̈�͘A���ł���
������b����d�Ɏ���p�X��+�O���t�̃ËߖT��b,d�ȊO�͓B��ʂ�Ȃ����̂ɂƂ�
���̃p�X���ʉ߂���O�p�`�̒��_�́|�B�͍��X��ł���
�����Ŋe�O�p�`�ɓ��镔���Əo�镔�����~�߂��܂܃p�X�����炵�āA�S�ăO���t��Ł|�O���t�̃ËߖT��ʂ�Ȃ��悤�ɂł���
���̎�����ꂽ�O���t�́|�ӂ�ʂ�Ȃ��p�X�Ȃ̂ł���ɕό`���ăv���X�ӂ����ʂ�Ȃ��悤�ɂł��� >>827
�㔼�C��
+�Ɓ|�t�ɂȂ���
> ���̃p�X���ʉ߂���O�p�`�̒��_��+�B�͍��X��ł���
> �����Ŋe�O�p�`�ɓ��镔���Əo�镔�����~�߂��܂܃p�X�����炵�āA�S�ăO���t���+�O���t�̃ËߖT��ʂ�Ȃ��悤�ɂł���
> ���̎�����ꂽ�O���t��+�ӂ�ʂ�Ȃ��p�X�Ȃ̂ł���ɕό`���ā|�ӂ����ʂ�Ȃ��悤�ɂł��� �O>>822
>>825
ac��bd�̌�_��e�Ƃ���ƁA
��cde�̓�����+�̓B��ł��Ƃ�a����c��2�{�̎��ōs����B
-�̓B��łĂ�b����d��2�{�̎��ōs����B
���Ȃ炸����+��-���łK�v�͂Ȃ��A
����a��c�����ׂ�1�{�̎��ōs���邵�A
b��d�����ׂ�-�ǂ���1�{�̎��Ō��Ԃ��Ƃ��ł���B
�������ꂽ�B �ǂȂ���>>790�́i2�j�����肢���܂� >>807
�X�Ɏ֑���������
(1+t'/2n)^n = {1 - (1/8n)t'^2 + (1/24n^2)t'^3 + {(n-2)/(128n^3)}t'^4 - {(5n-6)/(960n^4)}t'^5 - ����} e^{t'/2},
���g����
��[0,��] (1+t'/2n)^n e^{-t'} dt'
�@= ��[0,��] {1 - (1/8n)t'^2 + (1/24n^2)t'^3 + �����p e^{-t'/2} dt'
�@= 2(1 - 1/n + 5/n^2 - 41/n^3 + ����), >>831
r=4/3�̂Ƃ��f�ʂ�1�_
1��r<4/3�̂Ƃ��f�ʂ�3�p�`
2/3<r<1�̂Ƃ��f�ʂ�5�p�`
r=2/3�̂Ƃ��f�ʂ�4�p�`
1/2<r<2/3�̂Ƃ��f�ʂ�5�p�`
1/3<r��1/2�̂Ƃ��f�ʂ�3�p�`
r=1/3�̂Ƃ��f�ʂ�1�_ �i�[�������āj����͑����ɂȂ�Ȃ��H >>807
�w������ɓW�J����Ȃ�i���v���X�W�J�H�j
�@x = e^{t'/2n} -1�@�Ƃ�����
1 + t'/2n
�@= {1 - (1/2)x^2 + (1/2+1/3)x^3 -(1/2+1/3+1/4)x^4 + ����} e^{-t'/2n},
(1 ⊹ t'/2n)^n
�@= {1 - (1/2!)nx^2 + (5/3!)nx^3 + (1/4!)n(3n-29)x^4 - (2/5!)n(25n-102)x^5 - (5/6!)n(n-1)(3n-134)x^6 + (7/7!)n(n-1)(75n-1262)x^7 + ����} e^{-t'/2},
��[0,��] x^k e^{-t'/2} dt'
�@= ��[0,��] (e^{t'/2n} -1)^k e^{-t'/2} dt'
�@= 2/C(n-1,k)
�@= 2(k!)/{(n-1)����(n-k)},
��[0,��] (1 + t'/2n)^n e^{-t'} dt'
�@= 2(1 - n/{(n-1)(n-2)} + 5n/{(n-1)(n-2)(n-3)} + n(3n-29)/{(n-1)����(n-4)} - 2n(25n-102)/{(n-1)�c(n-5)} - 5n(3n-134)/{(n-2)�c(n-6)} + 7n(75n-1262)/{(n-2)����(n-7)} + ����)
�@= 2(1 -1/n +5/n^2 -41/n^3 +364/n^4 - ����) (����)
1 + t'/2n
�@= {1 - (1/2)x^2 + (5/6)x^3 -(13/12)x^4 +(77/60)x^5 -(29/20)x^6 -(223/140)x^7 +(481/280)x^8 - ����} e^{-t'/2n},
(1 ⊹ t'/2n)^n
�@= {1 - (1/2!)nx^2 + (1/3!)5nx^3 + (1/4!)n(3n-29)x^4 - (1/5!)n(50n-204)x^5 - (1/6!)n(15nn-685n+1714)x^6 + (1/7!)n(525nn-9359n+16862)x^7 + ����} e^{-t'/2},
2(1 -1/n +5/n^2 -41/n^3 +469/n^4 - ����), >>832
�}�N���[�����W�J�̕���
(1+t'/2n)^n
�@= {1 - (1/8n)t'^2 + {1/(24n^2)}t'^3 + {(n-2)/(128n^3)}t'^4
- {(5n-6)/(960n^4)}t'^5 - (3nn-26n+24)/(9216n^5)}t'^6
+ {(35nn-154n+120)/(107520n^6)}t'^7 + ����} e^{t'/2},
��[0,��] (1+t'/2n)^n e^{-t'} dt'
= 2(1 -1/n +5/n^2 -41/n^3 +469/n^4 - ����), f(x + y) = f(x) * f(y)
f(1) = 10
��������g(x) = 10^x�ȊO�ɁA�����ɑ��݂��邱�Ƃ������B >>638
R��Q�x�N�g����ԂƂ��Ă̊��(vi)_i��card(R)��v0=1�̂悤�ɂƂ�
���R��n�ɑ�Q���`�ʑ�gn:R��R��gn(v0)=v0,gn(vi)=n(i>0)�ƂƂ�
fn(x)=10^gn(x)
�͑S�ď������� 1230
�w�R���E�h��{�C�R�b�g���s�ψ���@gakkon_boycott 9��1��
#�g�U��]
#�݂�ȂŊw�R���E�h����{�C�R�b�g���悤
�G���u��w�ւ̐��w�v�̎���Ŗ����J�Â���Ă���w�̓R���e�X�g(�w�R��)�Əh��́A�Y�킪�G�ō̓_�~�X�������A���������肢���Ă������Ă��炦�Ȃ������ȃR���e�X�g�ł��B(����7�����̏h��ł��̔�Q�ɑ����܂����B)���̂悤�ȃR���e�X�g�ɎQ������͎̂��ԂƓw�̖͂��ʂł���A�Q�����鉿�l�͂���܂���B�����Ŏ��́A����ȏ�̔�Q�҂��o���Ȃ��悤�ɂ��邽�߁A�܂��A�o�ŎЂɔ��ȂƉ��P�𑣂����߂ɁA�w�R���E�h��̃{�C�R�b�g���Ăъ|���邱�Ƃɂ��܂����B�����ł������̕������̊����ɂ��^�������A���̃c�C�[�g���g�U���Ē�����K���ł��B
https://twitter.com/gakkon_boycott/status/1300459618326388737
https://twitter.com/5chan_nel (5ch newer account) �N�������Ă�������(�L�G�ցG`)
�P�ꊷ���Í��ňÍ�������Ă��镶����XXY������B���̂Ƃ��A�ŕp�o�����̐��肪���s����m�������߂Ȃ����B
�������A�����͉p��̃A���t�@�x�b�g3����x, y, z�����ŏ�����Ă���B���A�e�A���t�@�x�b�g�̏o������m���́A�傫�������珇��0.5, 0.3, 0.2�ł���B >>841
x0.5y0.3z0.2��
xxy�̊m����75/1000
x0.5y0.2z0.3��50/1000
���l�ɑ��̂�45/1000, 18/1000, 20/1000, 12/1000
�����̓�x0.5�Ȃ̂�(75+50)/(75+50+45+18+20+12)=125/230=25/46 >>844
�����͓K��������K���ɓK�ɂ��Ă� �O>>829
>>833�ꍇ�������B
���q�ɗ��邩�A����ɗ��邩�A�����ɗ��邩�B
���q�A���ꂪ1���傫�����A���������B
r=ab/(c+a)=1/3�ƂȂ�̂�(a,b,c)=(1,1,2)�̂Ƃ��B
1/3��r��1/2
r=ab/(c+a)=1/2�ƂȂ�̂�(a,b,c)=(2,1,2)�̂Ƃ��B
1/2��r��5/9=0.555�c�c
r=ab/(c+a)=5/9�ƂȂ�̂�(a,b,c)=(5/3,1,4/3)
5/9��r��1/��3
1/��3=0.5773502�c�c
r=ab/(c+a)=1/��3�ƂȂ�̂�(a,b,c)=(��3,2��3/3,��3)�̂Ƃ��B
1/��3��r��3/5=0.6
2/3=0.666�c�c
r=ab/(c+a)=2/3�ƂȂ�̂�(a,b,c)=(1,2,2)�̂Ƃ��B
(a,b,c)=(7/5,10/7,8/5)�̂Ƃ���r=2/3
2/3��r��1/��2
r=ab/(c+a)=1/��2�ƂȂ�̂�(a,b,c)=(��2,��2,��2)
������ł����߂邶��Ȃ����B
�ꍇ�����ȂӖ�����̂��H xyz��Ԃ̓_(x,y,z)�͈ȉ������Ȃ��瓮���B
x=ca/(a+b)
y=a+b
z=ab/(b+c)
������a,b,c�͈ȉ����������ł���B
�Ea,b,c�͓Ɨ��ł���A1��a��2�A1��b��2�A1��c��2�͈̔͂�ω�����B
�_(x,y,z)�������ďo���闧�̂̑̐ς����߂�B ���ʏ�ł͑��݂��Ȃ��s�K�ؖ��Ƃ��ꂽ���
AB = 8, BC = 12, ��B = 60��, ��C = 40�� �̂Ƃ��A
�O�p�`ABC�ɊO�ڂ��Ă���~�̔��a�����߂�B
http://suseum.jp/gq/question/3187
�������肵����ǂ����낤�H
���ʏ��
AB = 8, BC = 12, ��B = 60��, ��C = 40�� �Ƃ����O�p�`ABC�����݂���Ȃ炻�̋��̔��a�Ɓ�A�y��CA�̒��������߂�
�Ƃ������Ȃ瓚�����邾�낤���H >>848
atan((��3)/2)= 40.893394649131��
�ŋ��ʏ�Ȃ�p�x�ł��Ȃ邩�疳����� �O>>846
>>847
y�����c�ɂƂ邹�������₷���ł��ˁB �����������琔����n�Ԗڂ̑f����P[n]�Ə����B
�i1�j�f��p�ŁAP[p]+p���f���ƂȂ���̂����ׂċ��߂�B
�i2�j�f��q�ŁAP[q]+q!���f���ƂȂ���͖̂����ɑ��݂��邱�Ƃ������B https://i.imgur.com/CXXqApj.png
��̑g�����_�̌����̏ؖ����Ӗ��s���ł��B�ؖ��̍ŏ���2�������ɂ悭������܂���B �ŏ���2���ł����A�ȉ��̂悤�ł���Ε�����̂ł����B�B�B
{1, �c, u+v+1}����u+v-m+1�̐��������o���āA�����Ɉ��ɕ��ׂ�B
���̂Ƃ��A������u+1�Ԗڂ̐�����u+k+1(0��k��m)�Ə�����B >>852
���X���E�E���o�[�X�����i�H�R�m�{�s�[�^�[�E�t�����N���|�āj�w����g�����_�x�Ƃ����{�ɍڂ��Ă�������ł��B
�����炭�H�R�m���啝�Ɍ�����|�Ă��Ăقڈ�l�ŏ����Ă���Ɛ������܂��B >>853
�������̂����藧���Ƃ́A�ȉ�����ȒP�ɕ�����܂��B
{1, �c, u+v+1}����u+v-m+1�̐��������o���āA�����Ɉ��ɕ��ׂ�B
���̂Ƃ��A������u+1�Ԗڂ̐�����u+k+1(0��k��m)�Ə�����B arcsin(x/sin(x))^log(sin(e^x))���������B x���������Ƃ����
�@|x/sin(x)| > 1,�@�@(x��n��)
arcsin(x/sin(x)) �͋����B �O>>850
>>848
��A=180��-60��-40��=80��
A����BC�ɐ���AH�����낷�Ƃ��̒�����4��3
BH=4,HC=8
�s�^�S���X�̒藝���AC=��o(4��3)^2+8^2�p
=��(48+64)
=��112
=4��7 �m����
�O�ӂ�8:12:4��7�̂Ƃ��O�ډ~���a��(4/3)��21
���ꐔ���̕��т��Y�킾���ǂ�
�������̏ꍇ�A�p�x�����ꂢ����Ȃ��Ȃ� >>859
���ʎO�p�`�̓��p�̘a����180�����B �@i�������P�ʂƂ���B
�@�݂��ɑf�Ȏ��R���̑g(m,k)���^�����Ă���B
�@���R��n�ɑ��A���f����[n]����[n]={(m+ki)/|m+ki|}^n�ɂ���`����B
�i1�j
�@�C�ӂ̑f��p�ɑ��A��[p]�͎����łȂ����Ƃ��ؖ�����B
�@�ȉ��A���R��s,t,u�ɑ��ă�[s],��[t],��[u]�����f�����ʏ�̎O�p�`��3���_���Ȃ��Ƃ��A���̖ʐς�S(s,t,u)�ƕ\���B
�i2�j
�@���قȂ�3�̑f���̑g(p_1,p_2,p_3)��I�сA���f�����ʏ��3�_��[p_1],��[p_2],��[p_3]�_�Ƃ���O�p�`�����B
�@���̂Ƃ��A�g(p_1,p_2,p_3)���ǂ̂悤�ɑI��ł��A����Ƃ͈قȂ�A���قȂ�3�̑f���̑g(p_4,p_5,p_6)�ŁA
�@�@S(p_4,p_5,p_6) > S(p_1,p_2,p_3)
�ƂȂ���̂����݂��邱�Ƃ������B
�@�������g(A,B,C)�Ƒg(D,E,F)���قȂ�Ƃ́A{A,B,C}��{D,E,F}�ł��邱�Ƃ��w���B
�i3�j
�@S(x,y,z)�ɂ͏�������݂��邱�Ƃ������B�܂����̏�������߂�B �O>>859
>>848
8/4��7=0.75592894601�c�c
cos40��=0.76604444311�c�c
�킸������4��7��AC�Ƃ��Ē����̂Œo�܂���K�v������B
���Ȃ킿��ABC�����̂̕\�ʂɂ���悢�B
�ʁ�AC=4��7�ɑ��钆�S�p��2��,
���̂̔��a��r�Ƃ���ƁA
sin��=4/rcos40��=4��/(2��7�~cos40��)
2��/sin��=(cos 40��)��7
r=2��7/��
��ӂɌ��܂肻���Ȃ��B >>864
4�͑f���ł͂Ȃ��ł���
�f����̎��������l������ł� >>865
�R���͓K���ɍ������H
��������́H >>848
r��3.27225
CA��3.17659
��A��210.168��
http://imgur.com/5JtUk3J.gif f_n(x)=x^2-nx+1�Ƃ���B
�i1�j������f_4(x)=0��2������,��(��>��)�Ƃ����B��^2020�̈�̈ʂ̐��������߂�B
�i2�j������f_3(x)=0��2������,��(��>��)�Ƃ����B��^2020�̈�̈ʂ̐��������߂�B �O>>863
>>867A�ւ�����ł���B
����͂������B >>868
a(t)=��^t+��^t�Ƃ�����
a(t)=na(t-1)-a(t-2), a(0)=2, a(1)=n
a(n) �̖@10�ł̗ނ͑����Ƃ�����10�Ń��[�v
��^n��1�̈ʁ�a(t)-1(mod10) >>869
�m���ɉ��̎l�p�`�ɂ݂��� >>867
�͍삠�肪�Ƃ��������܂��B
����ƃC���[�W���킫�܂����B >>868
�@f_n(x) = xx -nx +1 = (x-n/2)^2 - (nn-4)/4,
�@2���@{n�}��(nn-4)}/2
�@f_n(0) = 1,
�@f_n(1) = 2-n < 0,
�@f_n(n) = 1,
���@0 < ��(��) < 1 < ��(��) �g�ݍ��킹�̖��ŋ����ĉ������B
�@�`�I�̖��O�̂�����������܂��B
��̔��ɂ͍Œ�P�ȏ�`�X�P�ȉ��̐���������܂��B
���̂Ƃ��A�P�O�̍��v���K���P�O�O�ɂȂ�����Ƃ�����̑g�ݍ��킹��
���߂���@�͂���ł��傤���B
��
�@�@�@�@�p�^�[����
�@�@�@�@�@��
���̖��O�@A�@�@�@�a�@�@�@�@�b�@�@�@�@�w
�@�@�@�@�X�P�@�@�X�O�@�@�@�Q�O�@�@�@ �c
�@�A�@�@�@�P�@�@�@�Q�@�@�@�P�O�@�@�@ �c
�@�B�@�@�@�P�@�@�@�P�@�@�@�@�Q�@�@�@ �c
�@�C�@�@�@�P�@�@�@�P�@�@�@�@�T�@�@�@ �c
�@�D�@�@�@�P�@�@�@�P�@�@�@�P�R�@�@�@ �c
�@�E�@�@�@�P�@�@�@�P�@�@�@�Q�Q�@�@�@ �c
�@�F�@�@�@�P�@�@�@�P�@�@�@�@�V�@�@�@ �c
�@�G�@�@�@�P�@�@�@�P�@�@�@�@�W�@�@�@ �c
�@�H�@�@�@�P�@�@�@�P�@�@�@�P�S�@�@�@ �c
�@�I�@�@�@�P�@�@�@�P�@�@�@�@�S�@�@�@ �c
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
���v�@�P�O�O�@�P�O�O�@�@�P�O�O�@�@�P�O�O�@�@���v�͕K���P�O�O
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�Œ�͕K���P
����̎��₪����܂�����A����������ł�OK�ł��B
�ŏI�I�ȉ��p�^�[�����邪�v�Z�ŋ��߂���Ηǂ��ł����A
���ۂɂ̓v���O�����őS�p�^�[�����Ă݂����̂ŁA���̕��@��
�킩��Ί������ł��B
�����A��낵�����˂������܂��B >>874
�d���g�ݍ��킹
H[10,90]=C[99,90]=1731030945644 >>874
Binomial(100-1, 10-1) = 1731030945644 >>876
�Ȃ�Binomial(n + k - 1, k - 1)�̂��Ƃ��d���g�����Ƃ�����ł����H ���ʂ̑g�����Ƃ͉��̊W���Ȃ��ł���ˁH�d���g�����Ə����Ɖ������ʂ̑g�����̗ގ����̂悤�ɍ��o���܂����B >>879
1���ʂ̓��������O�t���̔���10�p�ӂ��āA���̔��ɂ���90�̋ʂ�����̂Ɠ������Ƃ�����A
10�̔�����d����������90��I�ԑI�ѕ��Ɠ���
�Ȃ̂ŏd���g���� >>880
�Ȃ�قǁA������܂����B���肪�Ƃ��������܂��B >874��Wolfram�ɐ����Ă��炨����
�@Coefficient[Sum[x^k, {k, 1, 90}]^10, x^100]
�Ɠ��ꂽ���ǃG���[���Ԃ��Ă����B
����9�̎��͌v�Z���Ă��ꂽ���A
Coefficient[Sum[x^k, {k, 1, 90}]^9, x^100]
171200862675 >>867
���������̂͂ǂ��Ȃ낤
AB��BC�����������Ă邵���Ȃ�L�r�V�C
�ǂ��������p�Ȃ낤���ċ^�������
http://imgur.com/0lUpfxL.gif >>874
�v���O�����������Ă݂��B
f <- function(Box,Sum){ # Box:���̐�,Sum�F�����������̍��v�̒l
# �d���������Ă����炒��I�ԑg�ݍ��킹�����
H <- function(n, r, v=1:n) {
if (r == 0)
NULL
else if (r == 1)
matrix(v, n, 1)
else if (n == 1)
matrix(v, 1, r)
else rbind(cbind(v[1], H(n, r - 1, v)), H(n - 1, r, v[-1]))
}
h=H(Box,Sum-Box) # Box�̒�����d����������Sum-Box��I��
nh=nrow(h) # ���̑g�ݍ��킹��
re=matrix(rep(NA,Box*nh),nrow=nh,ncol=Box) # �������m��
a=numeric(Box)
for(i in 1:nh){�@# �e�X�̑I�ѕ�i�ɑ���
for(j in 1:Box) a[j]=sum(j==h[i,]) # �ǂ̔������I�����ꂽ����
re[i,] =a # re��i�s�ɓ����
}
return(re+1) # 1����n�܂镪��
}
���R���v�X�̏ꍇ
> f(Box=3,Sum=9)
[,1] [,2] [,3]
[1,] 7 1 1
[2,] 6 2 1
[3,] 6 1 2
[4,] 5 3 1
[5,] 5 2 2
[6,] 5 1 3
[7,] 4 4 1
[8,] 4 3 2
[9,] 4 2 3
[10,] 4 1 4
[11,] 3 5 1
[12,] 3 4 2
[13,] 3 3 3
[14,] 3 2 4
[15,] 3 1 5
[16,] 2 6 1
[17,] 2 5 2
[18,] 2 4 3
[19,] 2 3 4
[20,] 2 2 5
[21,] 2 1 6
[22,] 1 7 1
[23,] 1 6 2
[24,] 1 5 3
[25,] 1 4 4
[26,] 1 3 5
[27,] 1 2 6
[28,] 1 1 7 >>883
���������̊܂߂Ęa�̓Έȉ��ɂ͂Ȃ�� >>848
�@O (0, 0, 0)
�@A (r cos(8/r), r sin(8/r)cos(B), r sin(8/r)sin(B))
�@B (r, 0, 0)
�@C (r cos(12/r), r sin(12/r), 0)
�@��B = 60��
�Ƃ����B
��C �͕���OAC�ƕ���OBC�̓�ʊp�B
����OAC�̖@�����F�N�g�� ��OA�~��OC ��
�@xy-���ʐ����� rr sin(8/r) sin(B),
�@z�����́@rr [sin(12/r)cos(8/r) - cos(12/r)�sin(8/r)cos(B)],
����A����OBC��xy-���ʂŁA�@�����F�N�g���� (0,0,1)
����炪��C���Ȃ����Ƃ���A��OA�~��OC �̐�����
�@sin(8/r) sin(B)�F[sin(12/r)cos(8/r) - cos(12/r)�sin(8/r)cos(B)]
�@= sin(C)�Fcos(C),
�@= �}sin(40��)�Fcos(40��),
�@CA = r arccos[cos(12/r)cos(8/r) + sin(12/r)�sin(8/r)cos(B)],
C = +40�� ����
�@r = 3.27225023635408
�@CA = 3.�S176589202447
C = -40�� ����
�@r = 2.08421016388903
�@CA = 4.0289210164475 �i�O���t���_�́j�O���t�����^�łȂ����Ƃ�������ʓI�ȕ��@���Ă���܂����H >>887
����݂Ԃ����炢�W���ˁH ���f���ʏ�̓_P(z)��P��ʂ��~C������Ƃ��AP��C��̕ʂ̓_�Ɉڂ�����ϊ�f���l���܂��B
�ϊ�f���{�����Ƃ����ŕ\���܂��B
P��P_1��P_2��...�ƁAP��P���ڂ����_��f���{��������Ƃ��A�C�ӂ�P_i��C��ɂ����āA�ǂ�P_i���S�ĈقȂ�悤��f�͈�ʂɂǂ̂悤�Ȍ`�����Ă��邩���������������B �O>>869
>>886
AC=4.0��3.4��2�o���́A�������ˁB
�ȉ~���ɂ��邵���Ȃ��Ǝv�Ƃ����B �W�V�S�ł��B
�݂Ȃ���A�R�����g�E���肪�Ƃ��������܂����B
�Ȃ�قǁA�d���g�ݍ��킹�Ƃ����̂ł��ˁB
Web�ł����ׂĂ݂ė�����[�߂邱�Ƃ��ł��܂����B
���肪�Ƃ��������܂��B
>> 884 �l
�v���O�������肪�Ƃ��������܂��B
������Ƃ���ȃv���O������������A�A�܂����ł��B
�g���Ă���ȂǂŒ��ׂ܂������AR����Ȃ�ł傤���B
https://cran.ism.ac.jp/�@����W��windows�ł��_�E�����[�h����
�C���X�g���Ă݂܂������A��������Ɏ��炸....
������낵����A������@�ȂNj����Ă���������K���ł��B
�F�l�A���߂܂��Ă��肪�Ƃ��������܂����B��(_ _)m >>889
C�̔C�ӉZ�����W���̔C�ӏ����t����P_i�Ƃ�
P_i��P_(i+1)�Ɉڂ��A����ȊO�̓_�͔C�ӂ̕ϊ� >>889
���������ƗႦ��
z₀ : �~C�̒��S�_�A�� : �C�ӂ̖������Ƃ���
�@f(z) = z₀ + e^{i2��} (z - z₀)
���̃^�C�v�̉�������̂��͕������B
�����܂߂���ʉ��ƂȂ�� >>892 �݂����ɂȂ�B >>891
�����R�ł��B
�����Ŏ��s�ł��܂��B
https://www.tutorialspoint.com/execute_r_online.php
���{��̃R�����g�̂܂܂ł����s�ł��܂����B
��3�A���v��9�ł�������Ă܂��B
��10�A���v��100�̓������s���Ŏ��s�ł��Ȃ��Ǝv���܂��B
�d���g�ݍ��킹�̗ɍċA�����g���Ă���̂Ńl�X�g���[�����ăG���[�ɂȂ�Ǝv���܂��B �����Ƃ�0���Ɓ���/4���Ƃ��A�ɍ��W�n�ɂ����ă�|sin(8��)|��r���Ƃŕ\�����̈�̖ʐς����߂�B �ȉ��̏����������R��m��S�Č��肹��B
�y�����z
0��n��m�����S�Ă̐���n�ɂ��āA�W��(m,n)�͊�ƂȂ�B ��ʉ�����
�p�X�J���̎O�p�`�ʼn����̑S�Ă�p�̔{���łȂ��i��m=ap^k-1(1��a��p-1)�i�ڂ���
���̂悤��m��p�i�\���ōō����ȊO��p-1�̕��Ԑ��ŁA�a��m�ɂȂ�ǂ̂悤��2�̐�n,(m-n)�ɕ����Ă����̑����Z�ŌJ��オ�肪�������Ȃ����ɂƂ��ē����t������
�������������ƓW���̊W�͑O�X���ł��o��
https://rio2016.5ch.net/test/read.cgi/math/1594131967/460 >>895
S = (1/2)���^2 d�� - (1/2)��{�� sin(8��)}^2 d��
�@= (1/2)���^2 cos(8��)^2 d��
�@= (1/4)���^2 {1+cos(16��)} d��
�@= (1/4)���^2 d�� + (1/4)���^2�cos(16��) d��
�@= [ (1/12)��^3 + ��^2�sin(16��)/(64��) ] - ��ƥsin(16��)/(32��) d��
�@= [ (1/12)��^3 + ��^2�sin(16��)/(64��) + �ƥcos(16��)/(512��^2) ]
�@�@- ��cos(16��)/(512��^2) d��
�@= [ (1/12)��^3 + ��^2�sin(16��)/(64��) + �ƥcos(16��)/(512��^2)
�@�@- sin(16��)/(8192��^3) ](��=0,��/4)
�@= (��^3)/768 + �Υsin(4��^2)/1024 + cos(4��^2)/(2048��) - sin(4��^2)/(8192��^3)
�@= 0.04333824242 �@i�������P�ʂƂ���B
�@�݂��ɑf�Ȏ��R���̑g(m,k)���^�����Ă���B
�@���R��n�ɑ��A���f����[n]����[n]={(m+ki)/|m+ki|}^n�ɂ���`����B
�i1�j
�@�C�ӂ̑f��p�ɑ��A��[p]�͎����łȂ����Ƃ��ؖ�����B
�@�ȉ��A�f��p_i,p_j,p_k�ɑ��ă�[p_i],��[p_j],��[p_k]�����f�����ʏ�̎O�p�`��3���_���Ȃ��Ƃ��A���̖ʐς�S(p_i,p_j,p_k)�ƕ\���B
�i2�j
�@���قȂ�3�̑f���̑g(p_1,p_2,p_3)��I�сA���f�����ʏ��3�_��[p_1],��[p_2],��[p_3]�_�Ƃ���O�p�`�����B
�@���̂Ƃ��A�g(p_1,p_2,p_3)���ǂ̂悤�ɑI��ł��A����Ƃ͈قȂ�A���قȂ�3�̑f���̑g(p_4,p_5,p_6)�ŁA
�@�@S(p_4,p_5,p_6) > S(p_1,p_2,p_3)
�ƂȂ���̂����݂��邱�Ƃ������B
�@�������g(A,B,C)�Ƒg(D,E,F)���قȂ�Ƃ́A{A,B,C}��{D,E,F}�ł��邱�Ƃ��w���B
�i3�j
�@S(p_i,p_j,p_k)�ɂ͏�������݂��A���̏���l��(3��3)/4�ł��邱�Ƃ������B 8.33%�̊m���̂��̂�17�Ă�����1����30000�R�C���K�v�ȏꍇ�A�R�C�������K�v�����Ɠ����������Ă�������m(_ _)m >>902
�K��17����Ƃ������ƂȂ疳���ɕK�v
������̊��Ғl��17�����̂�17��0.0833=204.08�c�c�Ȃ̂�205��ȏゾ����615���R�C���K�v
�������A205�I�����ꍇ18��ȏ㓖�I����ꍇ����������16��ȉ��������I���Ȃ��ꍇ������ >>902
>>903�̒���
�K��17����Ƃ������ƂȂ疳���ɕK�v
������̊��Ғl��17�����̂�17��0.0833��2=102.04�c�c�Ȃ̂�103��ȏゾ����309���R�C���K�v >>902
(17/0.083)*30000=6144578 >>902
���̓��z
�����ł͐����m����0.083�ł��鎖�ۂ�17������܂ł̎��s�̐��̕��z
p=0.083
s=17 # ������
s*(1-p)/p # ���������ɂȂ�܂ł̎��s���̊��Ғl�@���̓��z�̊��Ғl�̌���
s*(1-p)/p + s = s/p # �������Ǝ��s���̍��v
s/p*30000 = 6144578 >>905
0.0833�������̂ŁA17������܂łɕK�v�ȃR�C���̊��Ғl��
p=0.0833
s=17 # ������
s*(1-p)/p # ���������ɂȂ�܂ł̎��s���̊��Ғl
s*(1-p)/p + s # = s/p �������Ǝ��s���̍��v
s/p
s/p*30000 # 6122449 �P�O����V�~�����[�V�������ĕ��ϒl�i���Ғl�̋ߎ��l�j���o���Ă݂�
sim <- function(p=0.0833,s=17){
Su=0 # ������
i=0 # ���s��
while(Su<17){
Su=Su+rbinom(1,1,p)
i=i+1
}
return(i)
}
mean(replicate(1e5,sim()))*30000
> mean(replicate(1e5,sim()))*30000
[1] 6117982 �����[�I�F���肪�Ƃ��������܂����I 17���ɓ��B����̂�n��ڂ̒��I�ł���m����
�@q_n = C(n-1,17-1)�p^17�(1-p)^(n-17)�@(n��17)
�@�@�@= 0�@�@�@(n<17)
��[n=17,��] q_n = 1,
E[n] = ��[n=17,��] n�q_n = 17/p = 204.08163265
��[n=17,199] q_n = 0.4935182680
��[n=17,200] q_n = 0.5020417085
��[n=17,204] q_n = 0.5357946506
��[n=17,205] q_n = 0.5441305558
median �` 199.76
200�I����Ƃ��ā@600���R�C���K�v �藝4.4.2�̏ؖ����́u�܂�A�ǂ̕ӂ�1�x�����g����B�v�̌����Ă��邱�Ƃ�������܂���B
��������肢���܂��B
�藝4.4.1
�̂ǂ�2�_�����傤��1�{�̓��ŘA�����Ă���B
�藝4.4.2
�ǂ�Ȉʐ�n�̖�n-1�{�̕ӂ����B
�ؖ��F
�d�b�̃l�b�g���[�N���ɂƂ��ďؖ����悤�B���钬�Ŏ������N����A���̒��Ƀ��b�Z�[�W��d�b�ő��낤�Ƃ����Ƃ���B
�܂��A���̒��̐l�͒��ډ�����Ȃ����Ă��钬�œd�b����B�d�b�������͒��ڂȂ����Ă��钬�֓d�b����B
�d�b�������́A���ڂȂ����Ă��钬�ł܂��d�b���Ă��Ȃ����֓d�b����B�c�A�O���t�͘A���Ȃ̂Ń��b�Z�[�W��
�ǂ̒��ւ��`���B�藝4.4.1���A�ǂ̒��������̂��������Ƃ�1�ʂ�̓��Ō���Ă���B�܂�A�ǂ̕ӂ�1�x����
�g����B���������āA�d�b�͕̉ӂ̖{����1��1�ɑΉ�����B�d�b�������Ȃ��Ƃ��Ɏ�����m���Ă��钬�͂��̒�1��
�����ŁA1��d�b���邽�тɎ�����m�钬���P��������B���������āA�_�i���j�̌��͕Ӂi��M�j�̖{���������傤
�ǂP�����B >>901
����z���g�ɓ��������Ă�́H
�����Ȃ������肩�ǂ����킩��Ȃ��ƍl����C�ɂȂ�� >>911
���Ȃ݂ɁA�p��ŏo�ł���Ă��铯���҂�ɂ��{�̊Y���ӏ��ɂ͈ȉ��̂悤�ɏ�����Ă��܂��F
Theorem 8.2.3 Every tree on n nodes has n - 1 edges.
8.2.2 Let G be a tree, which we consider as the network of roads in a medieval
country, with castles as nodes. The king lives at node r. On a certain day, the
lord of each castle sets out to visit the king. Argue carefully that soon after they
have left their castles, there will be exactly one lord on each edge. Give a proof
of Theorem 8.2.3 based on this.
8.2.2. Any edge has only one lord, since if there were two, they would
have to start from different ends, and they would have then two ways to
get to the king: either continuing as they started, or waiting for the other
and walking together. Similarly, an edge with no lord would have to lead
to two different ways of walking. >>911
�͏H�R�m�E�s�[�^�[�E�t�����N���ɂ��n���K���[�ꂩ��̖|��ł��B >>911
���[�g�m�[�hR����e�m�[�h�i�Ⴆ��A�Ƃ���j�ւ̈�ӓI�ȓ�R���c��B��A��B��A����Έ�ɑΉ�����Ƃ������Ƃ��������Ƃ��Ă���悤�ɂ��������Ȃ���v���܂����A
���������Ă���̂����m�ɂ͕�����܂���B >>910
�X�^�[�����O�̌�����
log(q_n) = log(C(n-1,16)) + 17�log(p) + (n-17)�log(1-p)
�@= log(1-p)�n + 16�log(n) + 17�log(p/(1-p)) - log(16!) - 136/n - 748/nn - ����
�@= log(1-p)�n + 16�log(n) - 71.4435 - 136/n - 748/nn - 18496/(3n^3) - ����
n�Ŕ��������
�@(d/dn){log(q_n)} = log(1-p) + 16/n + 136/nn +1496/n^3 + 18496/n^4 + ����
�@n = 192.576�@�ōő�(�s�[�N)�ƂȂ�B�@q_n = 0.00863234 >>913
���R�A�ǂ̏�������_�͐������ł��B
�i2�j������ĕ�����܂���
�i3�j�͐��O�p�`�Ɍ���Ȃ��߂�����\������Ηǂ��̂Łi2�j����������Γ���͂Ȃ��Ǝv���܂�
�i1�j�͑f����Ȃ̂ʼn��Ƃ��Ȃ肻���ł� R���T�̔C�ӂ̃m�[�h�Ƃ���B
R����R������n-1�̊e�m�[�h�ւ͈�ӓI�ȓ������݂���B
A��R�Ƃ͈قȂ�C�ӂ̃m�[�h�Ƃ���B
R���c��A''��A'��A�Ƃ�����ӓI�ȓ������݂���BA�ɕ�A'-A��Ή�������ʑ��� : V(T) - {R} �� E(T)���l����B
�ӂ͒P�˂ł���B�Ȃ��Ȃ�A���ɁA��(A) = ��(B)�ƂȂ�悤�ȈقȂ�2�_A, B�����݂����Ƃ���ƁA
B = A'�łȂ���Ȃ�Ȃ����A��R���c��A''��A'��A��R���c��A''��A'��R����A' = B�ւ̈�ӓI�ȓ���
���邩���(B) = ��(A') = A''-A' �� A'-A = ��(B)�ƂȂ��Ė������������邩��ł���B
�ӂ͑S�˂ł���B���ɁA��(A) = A'-A�ƂȂ�悤�ȃm�[�hA��V(T) - {R}�����݂��Ȃ��悤�ȕ�A'-A�����݂����Ƃ���B
R����A'�AR����A�ւ̈�ӓI�ȓ������ꂼ�ꑶ�݂���B�����̓��ɂ͕�A'-A�͊܂܂�Ă��Ȃ����Ƃ͖��炩�ł���B
R����A'�ւ̓��A��A'-A�AA����R�ւ̓����l����Ζ��炩�Ȃ悤�ɁAT�ɕH�����݂��邱�ƂɂȂ��Ă��܂����A�����
�����ł���B���ӂ͑S�˂ł���B�ȏ���An-1 = #(V(T) - {R}) = #E(T)�ł���B >>918
����A�����牽�������Č��_�͐������ƌ����Ă�́H >>911�͑���>>919�̂悤�Ȃ��Ƃ����������̂��낤�Ɛ������܂������A�ǂȂ���>>911�̕��͂���ǂł�������܂����H >>916
�ǂ�node�ɂ��̎�̏邪����i������̎�ł͂Ȃ����̏邪����j
���鎞��ĂɁA�����������ɗ̎�B�����̏��ڎw���ė����n�߂�u�Ԃ��l����B
�����n�߂��u�ԁA�̎�B���i�މ��̏�Ɍ��������̏�ɂ���̎�̐l���̓L�b�`����l�ł���
�܂��̎傪���Ȃ����͑��݂��Ȃ��B
�����瓹�̐��Ɖ��ȊO�̗̎�̐��͈�v����B
��x�����g����A�Ƃ����̂͂��������Ӗ��B >>902
���p���
�����m��8.33%�̃x���k�[�C���s��17��������̂ɕK�v�Ȏ��s�̂X�T���M����Ԃ͉��牽�H > # ���ʐ��ł̂b�h
> qnbinom(0.025,17,0.0833)+17 ; qnbinom(0.975,17,0.0833)+17
[1] 123
[1] 307
> # Highest Probability Density Interval�ł̂b�h
> HDInterval::hdi(qnbinom,size=17,prob=0.0833)+17
lower upper
115 297
attr(,"credMass")
[1] 0.95 >>924
�P�O����̃V�~�����[�V�������ʂƏƍ�
> sim <- function(p=0.0833,s=17){
+ Su=0 # ������
+ i=0 # ���s��
+ while(Su<17){
+ Su=Su+rbinom(1,1,p)
+ i=i+1
+ }
+ return(i)
+ }
> re=replicate(1e5,sim())
> quantile(re,c(0.025,0.975))
2.5% 97.5%
122 308
> HDInterval::hdi(re)
lower upper
115 297
attr(,"credMass")
[1] 0.95 >>901
�N�������܂��H
�����Ƃɏo���ꂽ���ł��� >>901
(1)
p=2�̂Ƃ�
�@��[2] = {(m+ki)/|m+ki|}^2 = {(mm-kk)+(2mk)i}/|m+ki|^2,
�@��ӂ�� (m,k)�͎��R�������� mk��1,
�@��[2] �͎����łȂ��B
p����̂Ƃ�
�@Re{ (m+ki)^p } = m��[j=0,(p-1)/2] C(p,2j) m^(p-1-2j) (-kk)^j
�� m�̔{���B
��� ��ӂ�� (m,k) �݂͌��ɑf������
�@|m+ki|^{2p} = (mm+kk)^p �� k^{2p} �� 0�@(mod m)
���@|m+ki|^p ��m�̔{���ł͂Ȃ��B
����������
�@��[p] = {(m+ki)/|m+ki|}^p �� �}1. >>923
n = 122.025 �܂ł�17��B������m���� 2.5%
n = 306.839 �܂�17�B�̊m���� 2.5%
���@���߂��Ԃ�
�@122.025 < n < 306.839
(�Q�l)
�@�@18/p = 216.086
�������ρ@214.432
E[n] = 17/p = 204.816�@�@(p=0.0833)
���W�A���@199.76
���敽�ρ@193.499
�@�@16/p = 192.077
��[n=17,121] q_n = 0.02322393181
��[n=17,122] q_n = 0.02495533764
��[n=17,123] q_n = 0.02678209166
��[n=17,306] q_n = 0.97420660647
��[n=17,307] q_n = 0.97514963127
��[n=17,308] q_n = 0.97606163314 >>930
���A�_����
�Ԉ���Ă�
�\�z�Ƃ��Ă̓��C���̈�l���z�藝�̑f����
�������A0<a<b<1�Ƃ���Ƃ�
lim #{ p �� x | p/�� - [p/��] �� (a,b)}/(x/log(x)) = b-a
�������������ȋC�͂������
����ɂ�
��[p��x] exp(2��i/�� p)/p = o(x/log(x))
��������Ώ\��
�������������Ǝv�����̂�
��[p��x] exp(2��i/�� log(p))/p = o(x/log(x))
������ ����
��[p��x] exp(2��i/�� p) = o(x/log(x))
��������Ώ\��
�������������Ǝv�����̂�
��[p��x] exp(2��i/�� log(p)) = o(x/log(x))
�܂��v����ɑΐ��Ă�s=1+2��i/���̂Ƃ��낾����log(p)�Ƃ����������q������ ���A�C���A�����̂��ȁH
����ulog(p)�́gmod���h�̗ށv����l�ɕ��z���邩��ǂ݂̂������ɂ��邩�炢���̂� �s��A���ȉ��Œ�߂�B
[a b]
[c d]
a^2+c^2=1,b^2+d^2=1
���̍s��A�Ɨ�x�N�g��v=(x,y)^T�ɂ��A��������Av=0��|x|��1����|y|��1�̎����������Ƃ��A���R��n�ɑ���A^n��n�ŕ\���B
�i���L���w^T�x�ōs�x�N�g��(a,b)�̓]�u��\���j v�̏������䂾��
���(x,y)=(0,0)�����Ɏ����A����������čl���Ă����̒萔�{�����������ɐ�Βl��1�ȉ��ɏo����̂ł� ���l���E�X�̒藝�ƃ`�F�o�̒藝�͓��l�ȑo�Β藝�Ƃ݂Ȃ��Ȃ��̂ł����H �����Ő��w�V�܂łȂ��̂̓������������܂�
������1�N�łǂꂭ�炢�̐��w��g�ɂ��邱�Ƃ��\�ł���
�y����8���ԁA����3���Ԃ�\�肵�Ă��܂�
�������ϕ��A���`�㐔�A�����������A���f���_�A�m�����v�A���l���Ă��܂� �����p���̈��e������ǂꂾ���������邩�Ō��܂�
���w���̑f����������Ίy���Ȃ��ǂ� >>937
����Ȗ��ʂȎ��₷��O�ɕ�������H
����Ȃ��߂�H �O���tG�ɂ�2�̈قȂ�H�����݂��Ă��āA���̂ǂ���̕H����a���܂ނƂ���B
�܂�����̕H�͕�b���܂ނ������̕H�͕�b���܂܂Ȃ��Ƃ���B
���̂Ƃ��A�O���tG�����b�����������O���tG'�ɂ͕H�����݂��邱�Ƃ��ؖ�����B >>940
�ԈႦ�܂����B�������܂��B
�O���tG�ɂ�2�̈قȂ�H�����݂��Ă��āA���̂ǂ���̕H����a���܂ނƂ���B
�܂�����̕H�͕�b���܂ނ������̕H�͕�b���܂܂Ȃ��Ƃ���B
���̂Ƃ��A�O���tG�����a�����������O���tG'�ɂ͕H�����݂��邱�Ƃ��ؖ�����B >>941
G����b�̓��������O���t��G"�Ƃ���Mayer-Vietoris��
0��H1(pt��pt)��H1(G")+H1(b)��H1G)
. ��H0(pt��pt)��H0(G")+H0(b)��H0(G)
�����1(G)=��1((G")+1��G"�͏��Ȃ��Ƃ��ЂƂ̕H���������1(G")��1
�� ��1(G)��2
���l�ɂ��ă�1(G)=��1(G')+1�ł��邩���1(G')��1 >>939
����
�������C�ɏ��܂������H
���̃��X�͎��Ԃ̖��ʂł���ˁi�j
���@�̎���̓_���ł����� >>937
��w�̍u�`�́A1�P�ʂ�����45���Ԃ̊w�K���ڈ��ł���B���O��������Ȃ����B�Ȃ̂ő��1.5�T�Ԃ�1�P�ʂ̕��ʁB
��w�̃J���L���������Q�l�ɁA�P�ʐ����A�������ϕ�4�A���`�㐔4�A����������2�A���f���_2�A�m�����v2�Ƃ���ƁA14�P�ʂȂ̂�21�T�ԁB
���K���l����Ƃ����Ǝ��Ԃ����邵�A�T�N�T�N���ł���ΒZ�k�o����B >>933
Cayley-Hamilton �̒藝���
�@AA - (a+d)A + |A|E = O,�@
�����Ɂ@|A| = ad - bc,
���@n��1 �̂Ƃ�
�@A^n = t_n A - t_{n-1}|A|E,
������
�@t_0 = 0
�@t_1 = 1,
�@t_2 = a+d,
�@����
�Q����
�@t_{n+1} = (a+d)t_n - |A|t_{n-1}, >>939
���̈��e��������ȏ�
���̓��͗ǂ��Ȃ� �ʐ�5�̊��S�O���tK_5�����ʓI�ȃO���t�ł͂Ȃ����Ƃ̏ؖ��ł����A�ȉ��̂悤�ɍl���܂����B
�͔͉ƈႤ�̂ł����A�ǂ������������Ƃ���͂���܂����H
K_5�����ʂɕӂ��������邱�ƂȂ��`�����Ɖ��肷��B
n = 5, e = 10�ł��邩��A�I�C���[�̌������̈�̐�f = e - 5 + 2 = 7�ł���B
����A��ԊO���̗̈���������̗̈�͎O�p�`�̂͂��ł��邩��ABinomial(5, 3) = 10��3�p�`�̈�̂����A���Ȃ��Ƃ�9��
��ԊO���̗̈�ł͂Ȃ��Bf = 7 < 9�����炱��͖����ł���B >>945
�@���������������Ƃ�����
�@t_n = (��^n - ��^n)/(��-��),
�@����� ���ƃ��̑Ώ̑�����������A
�@��{�Ώ̎� ��+��=a+d,�@����=|A| �̑������B �u�ʐ�v�̕��ʃO���t�͍ő剽�{�̕ӂ������Ƃ��ł��邩�H�v�Ƃ������̓����Ɉȉ��̂悤�ȋL�q������܂��B
�uG�ʐ���ۂ͈͂ł́A����ȏ�ӂ������邱�Ƃ��ł��Ȃ��O���t�Ƃ���B���̂Ƃ��AG�̂ǂ̗̈���R�ӂ����ň͂܂�Ă���v
G�̈�ԊO���̗̈���R�ӂň͂܂�Ă��邱�Ƃ͂ǂ�����ĕ�����̂ł��傤���H >>917
�s�[�N�t�߂ł�
�@�� = 192.57637716855732
�@�� = 45.975784
�@q_max = 0.008632336568
log(q_n) = log(q_max) - (n-��)^2 /(2��^2) + 8.583E-7�(n-��)^3 - 4E-9�(n-��)^4 + �c
>>928
�@122.025 = �� - 1.75204��
�@306.839 = �� + 2.48528��
���Ȃ��Ώ̂ł���B�ΐ����K���z�ɋ߂��̂����B �s�[�N�ʒu�@�@n=192.576�@>>917�@�@��
95%CI�̉����E����̑��敽�ρ@n=193.499�@>>928
���߂����Ƃ���A�ΐ����K���z�ɋ߂��Ɛ��������B
�@��_g = log(��) = 5.2604928395496
�@��_g = 0.2387405
�@q_max = 0.008632336568
log(q_n) = log(q_max) - {log(n/��)}^2 /{2(��_g)^2}
�@ - 2.64254{log(n/��)}^3 - 0.697889{log(n/��)}^4
�@ - 0.139578{log(n/��)}^5 - �c
95%CI�̉����E�����
�@log(122.025) = ��_g - 1.91114��_g,
�@log(306.839) = ��_g + 1.95120��_g,
����͐��K���z�̏ꍇ (�ʁ}1.960��) �ɋ߂��B
�ΐ����K���z�����肵���Ƃ��� 95% CI ��
�@��_g - 1.960��_g = log(120.611)
�@��_g + 1.960��_g = log(307.481) >>947
�O���t�̎�����3�̃T�C�N�����O�p�`�̗̈�����Ƃ͌���Ȃ�
ex K5�����ӏ������O���t�͋��ʃO���t�ł��邪�A����3�̃T�C�N����7���邪�A���ʃO���t�̎O�p�`�̈��6�����ł��Ȃ� n������ԂɌ��_O��u���An�̃x�N�g��
��OA_1=(1,0,0,...,0,0)
��OA_2=(0,1,0,...,0,0)
...
��OA_n=(0,0,0,...,0,1)
�ɂ���Ē����钼�����W�n(x_1,x_2,...,x_n)���l���܂��B�i���w�I�ɐ������Ȃ��\���ł����܂���j
���̂Ƃ����_����̃��[�N���b�h���������傤��r(r>0)�ł���_�̏W����
(x_1)^2+(x_2)^2+...+(x_n)^2=r^2�c(�A)
�ŕ\�����S�̂��Ǝv���̂ł����A
�@(�A)�Ő������ł��傤��
�A(�A)�͂Ȃ�ƕ\����������ł��傤���B���ȖʁA�����́A��������������܂���
�B(�A)��r��n-1�̊p�ŋɍ��W�\�����邱�Ƃ͉\�ł��傤��
��낵�����肢���܂� �ɍ��W��
x_1 = r cos��_1, x_2 = r sin��_1 cos��_2, x_3 = r sin��_1 sin��_2 cos��_3, �c
x_(n-1) = r sin��_1 sin��_2 �c sin��_(n-2) cos��_(n-1)
x_n = r sin��_1 sin��_2 �c sin��_(n-2) sin��_(n-1)
�Ƃ���Ⴂ���̂� �ɍ��W�̉���F
�܂� x_1 ���W�Ǝc��� n-1 ���������ʂ��l���� x_1 ���W�ƃx�N�g���̊p����_1�Ƃ����
x_1 ������ r cos��_1 �� n-1 ���������� r sin��_1
���l�� x_2 ���W�Ǝc��� n-2 �������l���āc�@�ƌ��������Ɋp�Ƃ��`���čs�� �ŋ߂ǂ��̃X���Ń�(x;4,1)�ƃ�(x;4,3) (4�Ŋ�����1�]��x�ȉ��̑f���̐���3�̂���)�ő��呬�x�ɍ���������Ęb���łĂ��L�������ł����ǂǂ��ł��������H ����܂蒴�͎g��Ȃ��Ȃ�
n�������l�̂Ƃ�
n�������ʂƂ�
n���������̂Ƃ� ����x�ɂ��Ă̊�f_[k](x)���A
f_[1](x) = x^2+x
f_[n+1](x)=log{f_[n](e^x)}
�ƋA�[�I�ɒ�`����B
���̂Ƃ��Ɍ� lim[n��+��] f_[n](0) ����� lim[n��+��] f_[n](1) �����߂�B f_1(x) = x^3 - 3x
f_(n+1)(x) = {f_n(x)}^3 - 3{f_n(x)}
�Ƃ���B
n��3�ȏ�̐����Ƃ���Ƃ��Ax�̕�����f_n(x)=0�̎������̌���n�ŕ\���B >>963
�����̌��� a[n] �Ƃ���B
y=x^3 - 3x �� y=x �̃O���t��`����
�L����̌J��Ԃ��ʑ���0�ɂȂ肤��_�� -2 < x < +2 ���� x���}1 �͈̔͂ɑ��݂��Ă��āA
���͈̔͂ɂ���1�_�̋t���� �d��������3�_�ƂȂ鎖��������B
����� 0�_�̋t���� n ��J��Ԃ����߂��...
a[n] = 1 * 3 * ... * 3 = 3^n �ƂȂ�B ����Ȃ̃O���t��`���Ε����������H
��������ȏ��I�Ȍ������Ŏ����͖̂ʓ|��������Ȃ��B >>965
����̓������ł�����Ƃ��ꂽ���ł�
�U���́i1�j�i2�j�������āA���́i3�j���������ɂ�����A�ǂ���������������������܂���ł���
���肪�Ƃ��������܂���
�_�q���撣���Ă݂܂� >>966
�U���́i1�j�i2�j �͂ǂ��Ȃ��Ă�̂������Ă���B >>963
f_(n+1)(x) = f_1(f_n(x))
������A f_n(x) �̐����� f_1(x) �̐����ɂ���Č��܂�
x > 2 �Ȃ� f_1(x) > 2 �ł���A x < -2 �Ȃ� f_1(x) < -2
�܂��A x �� -2 �� 2 �Ɠ����Ƃ��A f_1(x) �̒l�� -2 �� 2 �� -2 �� 2 �Ɠ�������A
�A�[�I��
f_n(x) �̒l���P���� -2 �� 2 �ƂȂ� x �͈̔͂ɂ����āA f_(n+1)(x) �̒l�� -2 �� 2 �� -2 �� 2 �Ɠ���
���Ƃ��킩��
2 �� -2 �̂Ƃ������l
����āA f_n(x) �̒l���P���ɕϓ����� x �͈̔͂ɂ����āA f_(n+1)(x) �� 3 �� 0 �ɂȂ�
���̂悤�Ȕ͈͂� f_n(x) �ɑ��āA�A�[�I�ɁA 3^n ���邱�Ƃ��킩�� >>968
���̑�4��i1�j�i2�j�ł�
�P�Ȃ�����̖��ŁA�i3�j���A�[�@�ʼn����Ƃ����U�����Ǝv���܂�
���������邱�ƂɋC�����Ȃ��ƋA�[�@���@�\���Ȃ��Ӓn���Ȗ��ŁA����ł���Ƒ吔�Ō������Ƃ�����܂�
http://www.riruraru.com/cfv21/math/tum04f.htm >>970
�Ȃ�قǂ��肪�Ƃ��B �Ă���̕��� 3^n �܂Œ��Ă�Ƃ��Â₩�������Ȃ�....
��������͖ʓ|�L���l���������Ǝv���B�����u������v�ɂȂ�킯���B
�o�葤�� >>964 �������ƒ��J�ɏ������炢�̋C�������Ǝv���B
����܂�ڂ����Ȃ����Ǔ��吔�w�� "���" �āA����Ȃ���Ȃ��ł���B ���܂�A��悭����ƊȌ��ł���ȕςȉł��Ȃ������B ����T�C�g���Q���҂Ƀ|�C���g��z��Ƃ��܂��B
�|�C���g�̓����_���ȗʂ������_���ȃ^�C�~���O�Ōf�ڂ���A�擾�͑������̏����ł��B
�Q���҂̓y�[�W�����t���b�V�����Čf�ڂ���Ă���|�C���g���N���b�N���Ċl�����܂��B
�T�C�g�Ǘ��҂̓g���t�B�b�N�ʂ����������Ȃ��̂ŁA�Q���҂��ꂼ���
�L���b�V����݂��A60�b���ɏ����X�V���܂��B
�L���b�V���̍X�V��60�b���Ȃ̂͑S�Q���҂ɋ��ʂł����A�o���o���̃^�C�~���O��
�X�V����܂��B�i�܂肠��Q���҂̃L���b�V���ł͌f�ڂ���Ă���|�C���g��
�ʂ̎Q���҂̃L���b�V���ł͖��f�ڂƂ������Ƃ�����j
�Q���҂�60�b�Ԃ�2�����t���b�V�����邱�Ƃ�������Ă��܂��B
�|�C���g�̔z�z�͉i�v�ɑ������̂Ƃ��܂��B
���̎��Q���҂ɂƂ��Ă����Ƃ����Ғl�������Ȃ�헪�������Ă��������B �NjL
�Q���҂̓|�C���g�f�ڂ̃^�C�~���O���A�����̃L���b�V�����X�V�����^�C�~���O��������Ȃ����̂Ƃ��܂��B >>673
�v�̓L���b�V���N���A�̃^�C�~���O���ǂꂾ�������悭���肷�邩�H�ł����H
�ŏ��̃t�F�[�Y�ł�1/2���Ԋu�Ń��t���b�V������B
�Ⴆ��n,n+1/2���̃^�C�~���O
����ƍŏ��̃y�[�W�X�V�̂Ƃ��Ɏ����̃L���b�V���N���A�̃^�C�~���O��[n,n+1/2]�Ȃ̂�[n+1/2,n+1]�Ȃ̂����킩��
�O�҂̏ꍇ
���x��n��n+1/4�ŃL���b�V���N���A����
�����n,n+1/4]�Ȃ̂�[n+1/4,n+1/2]�Ȃ̂����킩��
��ʂ�k��ڂ̃y�[�W�X�V�̂Ƃ���[n+a,n+a+1/2^k]�ɍi���邩�玟�̃t�F�[�Y�ł�n+a,n+a+1/2^(k+1)�Ń��t���b�V������
�ׂ����`���[�j���O�ł���ɗǂ��ł��邩������Ȃ����Ǒ�R�����x�X�g�Ȉɗ\�� �N�������Ă��������B
�ϕ��̖��ŁA
0���灇�܂Őϕ���
e^�i-st�jtdt
�Ȃ̂ł����A��
1�^s^2
�ł��B�ǂȂ��������Ă��������܂��A�A�A�B >>976
��fg' = fg - ��f'g ��p����
���̏ꍇ f�ɂ�����̂�t, g�ɂ�����̂�e^(-st) 0 < m < n �ł���悤��
�萔 m,n ������Ƃ���
���̏W�� A ������Ƃ��āAn �̔C�ӂ�
�قȂ���� x1,x2,...,xn �ɂ��āA
���Ȃ��Ƃ� m �̓��� A(xk) = yk ���^�ƂȂ�悤�ɁAn �g�̐��� y1,y2,...,yn ���v�Z�ł��邾�낤���H�@ xyz��Ԃɔ��a1�̉~��2020�z�u����Ă���A�ǂ�2�̉~�����傤��2�_�Ō�����Ă���B
�����2020�̉~�̈ʒu�W���q�ׂ�B ���ꂾ���ňʒu�W���܂��
��̉~�������������炵�Ȃ���R�s�[����悤�ɔz�u����Ώ�����������A��_���Œ肵�Ă��̏[���߂��ߖT�Ɏc��2019�̓_����肳������Έʒu�W�͎��R����H
����Ƃ����S�ʒu�̋����̏���ׂ�Ƃ�������肩�� ���S�ʒu�̋������čő�l��������Ȃ����H >>980�ŏI����Ă��
�₢�ł�3������Ԃ�2�����}�`�̉~��z�u���Ă��邱�Ƃɒ��ӂ���
���ׂẲ~�͓��ꕽ�ʂ܂���
�i���a���~�Ɠ��������傫���j���ꋅ�ʏ�ɂ���
�Ƃ���悢 �~�̒��S�̕��z�̏�����
�C�ӂ�2�_�̋��������̉~�̒��a
�Ȃ̂ŁA���z��1�_�𒆐S�Ƃ���~�Ƃ͌��炸
���[���[�̎O�p�`�̂悤�Ȓ蕝�}�`�ł��悢
�����͊܂܂Ȃ��̂ŁA�ő�l�͂Ȃ� ����2������2�_�Ƃ��Ă���2�_�ʂ�悤�ɃN���N���̂������ >>973
�L���b�V���͕��ʁA���[�U���g���u���E�U��A�v���Ɏ����������
�T�[�o���S���[�U���̃L���b�V����ێ�����͔̂��I�����c
���̒ʂ�̏����ŁA����1�����Ƃ̃y�[�W�̍X�V�����ʂł���Ȃ�
�헪�͂����ނ�>>975��OK
�A�N�Z�X1����2��̏���������0�b�Ƀ��Z�b�g�ƌ��܂��Ă���Ȃ�
�����T���őO�����m�肷��A�Ō�̌��ʂƎ����1��ڂ̌��ʂ�60�b������
��r�\�ƂȂ�̂ŁA����͑O����3�����A�㔼��2�����Ƃł���
��������2�̗ݏ���傫���ł��A1�A2�A5�A13�A�c��
�t�B�{�i�b�`����1����ɂ����l�ɂȂ�
�����̃^�C�~���O�́A������ �Ӂ�1.618�c ��p����
2������ �ӁF1�A3������ �ӁF�ӁF1 �Ƃ���œK���ł��� >>985�̑���
>>974�ōX�V�����͔��ʕs�Ƃ��邪�A�����I�ɂ�
�u�z�z���v�́u�z�z����Ă��܂���v
�̉�ʂ̈Ⴂ�������I�ɂ݂�Əo������̂ŗ��p�ł���
���̏ꍇ�́A�f���I��2���T�����s���̂�>>975�����̂܂g����
��������āA��ʂ̍X�V��헪�Ɏg��Ȃ��Ƃ����
1��2��̃A�N�Z�X�������_���Ɋ���U��̂��őP
�L���b�V���������_���ł͂Ȃ��A�ŏ��̃A�N�Z�X����60�b�ł����
���[�U��60�b���ƂɃA�N�Z�X����̂��őP
�������̏����̃|�C���g�T�C�g�Ƃ�����
�K�b�`�����[���̃��[�\���������i���z�z�Ղ�Ƃ����������� >>984
�قȂ�2�_�Ƃ͏����ĂȂ��̂ŁA�m���ɂ��������ł��ˁ[ �O>>890
>>979
�w偂͒w偂̑��ɕ߂܂����R�K�l���V��C�ӂ�2�_���Œ肵�ăN���N���N���N�������ʼnăR�K�l���V��g�����Ƃ�Ȃ��X�g���X�ɂ���点��B �O>>988�����B
>>979
�w偂͒w偂̑��ɕ߂܂����R�K�l���V��C�ӂ�2�_���Œ肵�ăN���N���N���N�������ʼnĐg�����Ƃ�Ȃ��X�g���X�ɂ�肠�邢�͓ł𒍓����Ď�点��B �u�O���tG��2-���q�����\�ł��邽�߂̕K�v�\�������́A����n��1�ɑ��āAG��2*n-�����ł��邱�Ƃł���B�v�ƃ��o�[�X��̖{�ɏ����Ă���̂ł����A
G���A���łȂ��Ɛ��藧���Ȃ��Ǝv���܂����������ł��傤���H >>2���q�����\�Ƃ́H
�O�O���Ă��o�Ă��Ȃ����ǁH
�O���t���_�݂����ȃ}�C�i�[�Șb�ӂ肽���Ȃ�O�N���Ă��o�Ă��Ȃ��悤�ȒP��͍ڂ���ƃ_������ (1)�@���ꕽ�ʏ�ɂ���A
�@�@�ǂ�2�̉~�̒��S�̋���d�� 0<d<2,�@�@�@>>980
(2)�@���ꋅ�ʏ�ɂ���A(���aR��1)
�@�@�ǂ�2�̉~�̒��S�����̒��S���猩���p�Ƃ��@�@�@>>982
�@�@�@0 < R sin(��/2) < 1,
(3)�@z�����2�_ (0,0,c)�@(0,0,-c) ��ʂ�悤�ɉB0<c��1.
�@�@�@{x cos�� + y sin�� �} ��(1-cc)}^2 + zz = 1,�@�@>>984
�@�@�@y/x = tan��, >>979
���܂̂Ƃ���
(1)�@���ꕽ�ʏ�ɂ���A
�@�@�ǂ�2�̉~�̒��S�ԋ���d�� 0<d<2,�@�@�@>>980
(2)�@���ꋅ�ʏ�ɂ��� (���aR��1)
�@�@�ǂ�2�̉~�̒��S�����̒��S���猩���p�Ƃ��@�@>>982
�@�@�@0 < R sin(��/2) < 1,
(3)�@z�����2�_ (0,0,c)�@(0,0,-c) ��ʂ�A0<c��1.
�@�@�@{x cos�� + y sin�� �} ��(1-cc))}^2 + zz = 1,�@�@>>984
�@�@�@- x sin�� + y cos�� = 0,�@0����<2�� �ʐ�1�̈̕�D�̎���܂��͓����̓_P(x,y)�ɑ��ē_Q(x+y,xy)���l���܂��B
P�������Ƃ��AQ�̑��ݗ̈�̖ʐς�D�̉��{���牽�{�̊Ԃɂ���ł��傤���B
��낵�����肢���܂��B >>995
x+y=u
x-y=v
�Ƃ�����
x+y=u
xy=(u^2-v^2/4
uv���ʏ�̖ʐ�2�̐}�`���ϊ�
w=(u^2-v)^2/4
�ɂ����uw���ʏ�̗̈�Ƃ��Ĉڂ����ꍇ�̖ʐς̒l��ƍl����悢
�� 0�`�� >>996
x+y��xy���L���̒l�ɂȂ�̂ŁA�Ă�����L���̒萔a,b��a�{�`b�{�ƕ\����Ǝv���Ă��܂����B
xy���ʂ̒P�ʉ~�����̂悤�ɕϊ����Ėʐς����߂������肩��A��ʉ����l���܂����B
�������Ⴆ�u���̕ϊ��Ŗʐ�k�{�ɂȂ錳�̗̈�S�̂͂ǂ̂悤�ȏW�����v�ł��A�v�f�̃p�^�[���������ɂ����Č��肵����Ȃ������Ă��傤��
���肪�Ƃ��������܂��� k��1 �̗�ł���
�����` (�ʐςP)
�@(x,y) = (k,0)�@(k+1,0)�@(k,1)�@(k+1,1)
�͎l�p�` (�ʐς�)
�@(x+y, xy) = (k,0)�@(k+1,0)�@(k+1,k)�@(k+2,k+1)
�Ɉڂ�̂ŁA����͖����悤�ł��B
�����͗L�邩���H k=1/6 �̗�ł���
a��0 �Ƃ���
�����` (�ʐςP)
�@(x,y) = (a,a)�@(a+1,a)�@(a,a+1)�@(a+1,a+1)
�͕������Ƃ��̐ڐ��̌��� (�ʐ� 1/6)
�@a(u-a) �� v �� (u/2)^2,�@�@(2a��u��2a+1)
�@(a+1)(u-a-1) �� v �� (u/2)^2,�@�@(2a+1��u��2a+2)
�Ɉڂ�B
�@(u, v) = (x+y, xy)�@�Ƃ����B k>0 �̗�ł���
b>a��2k �Ƃ���
�ߒ����` (�ʐςP)
�@(a-2k, a+2k)�@(a+2k, a-2k)�@(b-2k, b+2k)�@(b+2k, b-2k)
�@�������@k = 1/{8(b-a)},
��2�{�̕������̊� (�ʐς�)
�@v = (u/2)^2,
�@v = (u/2)^2 - (2k)^2,
�@2a��u��2b,
�Ɉڂ�B
b-a �� �� �̂Ƃ� k �� 0
�������������B
>>996 �������B ���̃X���b�h�͂P�O�O�O���܂����B
�V�����X���b�h�𗧂ĂĂ��������B
life time: 40�� 13���� 20�� 49�b 5�����˂�̉^�c�̓v���~�A������̊F���܂Ɏx�����Ă��܂��B
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�s�v���~�A������̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
��300�~���瓽���ł��w�����������܂��B
�� �v���~�A������o�^�͂����� ��
https://premium.5ch.net/
�� �Q�l���O�C���͂����� ��
https://login.5ch.net/login.php ���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B



