������Ȃ����͂����ɏ����Ă�458
���X����950���Ă��܂��B1000����Ə������݂��ł��Ȃ��Ȃ�܂��B
�����A�������P������낤����
�O�X��
������Ȃ����͂����ɏ����Ă�457
https://rio2016.5ch.net/test/read.cgi/math/1577457155/
(�g�p�ςł�: 478) >>846
>�E���l�W�̒�`����A�K����v����J�n�ӏ������݂���
>�@��������������̌���ԍ�
��v����͍̂ŏ��̍�����v���Ă����̂�
��������悸���ƈ�v���Ă��邻�̐擪�Ƃ�����`�ɂ��Ȃ��ƃ_���_��
�N�����ǂ߂ĂȂ��˂� >>768
>��`
>�E�Q�̖�����s1,s2��R^N���A���鍀�����̍����S�Ĉ�v����Ƃ��u���l�v
>�E������s��R^N�́u����ԍ��vd�Ƃ́A������̓��l�ނ̑�\����
>�@��v�ӏ��̐擪�ƂȂ鍀�̉ӏ��̔ԍ�
���l�ނ̑�\���u�Ɓv�́u��v�ӏ��v�Ƃ����̂ł̓_��������
���ꂾ�Ə�������v���Ă��炭��v���Ȃ��Ă���Ƃ��납���͂����ƈ�v���Ă�Ƃ��̌���ԍ���1�Ƃ������ƂɂȂ邩���
��`�������ɂ��Ȃ��Ă͂����Ȃ��Ƃ����ӎ��������Ȃ��̂͐��w�I�ł͖����� >>847
��
�������킹�����������邩�猾��Ȃ� >>851
����������悸���ƈ�v���Ă��邻�̐擪�Ƃ�����`�ɂ��Ȃ���
�ǂݎ�ꂽ�Ȃ�OK
>>852
����`�������ɂ��Ȃ��Ă͂����Ȃ�
�ǂݎ�ꂽ�Ȃ�\��
>>853
���������킹������������
�Ȃ�قǁE�E�EID:BUSW/Nah��
�������̋Ɍ����Ƃ�ƁA����ԍ��͊m���P�Ł�
�ɑS�ʎ^���A�� ID:BUSW/Nah���ւ̖₢
Q.����n�ȉ���10�i������9/10������n
�@����l�H��
�@�u�����炎�����̋Ɍ��ŗL��������9/10���������v
�@����z���g�H �^�X���b�h�̎��̑���H�w������
�G�i�H�j�����嗝�w�����Ǝv������œ{�苶��
https://rio2016.5ch.net/test/read.cgi/math/1576852086/589-590
�悢�q�݂̂�Ȃ͂���ȑ�l�ɂȂ�����_������ ������[n=1,2,...]1/(n^2+a)���v�Z���邱�Ƃɂ��A(e^��-e^(-��))/(e^��+e^(-��))���������ł��邱�Ƃ��ؖ�����B >>854
�u�x�������蕶
�������قƂ�LjӖ��Ȃ����̂�
���炽�߂悤�Ƃ��Ȃ��̂�NG
�}���Ń_������ >>764
�ԓ��x���Ȃ��Ă��܂��A�\�������܂���B
���肪�Ƃ��������܂��B ���w�f���Q ttp://x0000.net
(�A���t�@�E���{|�w�p�f���Q) >>844(���ȃ��X)
��T�ɋC�������̂œP�܂�m(_ _)m >>862
>>853
�N�̎v�f�͊��ɔj�Y���Ă���ċC���t���Ȃ��݂���
�z���g�ɉ���Ȃ��l�ԂȂ̂��ȁH >>857
��[n=1,2,����] 1/(nn+a)
�@= (1/2)��[n��Z] 1/(nn+a) - 1/(2a)
�@= �Υcoth(��a)/(2��a) - 1/(2a),
�@�����W�����@�������H
a=1 �̂Ƃ�
�@��[n=1,2,����] 1/(nn+1) = (��/2)coth(��) - 1/2, �m�������X�̐��`�������M�̕X�̕��`������Ԃł���Ƃ����ؖ��ŁA��������M�̓_��xn�̋Ɍ���M�̕�ɑ�����Ƃ����b���o�Ă����̂ł����A���R�����Ă������� �����������ƕ����Ă��݂܂���A�������܂��� n���̍d�݂��ɓ����āA�\�̏o�����̂���苎��A�d�݂��c���Ă���A����1���������ɓ����ĕ\�̏o�����̂���苎�邱�Ƃɂ���
���̎��A�S����苎��m�������߂�B
�ł́A1��ڂɕ\���o�����̂�������Ƃ��āA(1-1/4)^n�Ɠ������o���Ă���̂ł����A���ʂɍl���ĉ��������ƁA�S���ۂ��قȂ�Ǝv���̂ł����A�Ȃ����̉��������\�Ȃ̂ł��傤���H >>867
�S�ẴR�C����2���邤����1��ł��\���o��ΑS�Ď�苎�邱�ƂɂȂ邩��
�S���ۂ��قȂ��Ă��\��Ȃ�
2���Ƃ�3���Ƃ��ŗ����̂����őS���ۏ����o���Ă݂�Ε����邩���m��Ȃ� >>https://rio2016.5ch.net/test/read.cgi/math/1511604229/999
�~����ȃf�^�����Ȃ���
�Z���S�ɐ��������w��̖��������̏ؖ��_�� >>868 �����o���Ă݂��̂ł����A�C�}�C�`�������肱�Ȃ��ł��c >>870
�����o�������̑S�Ăɂ����Ȃ�m������������Ō���ׂĂ݂Ă͂ǂ����낤�� >>871
n=10�̂Ƃ��ő�������Ōv�Z���Ă݂�
> rm(list=ls())
> n=10
> dec2nw <- function(num, N, digit = n){
+ r=num%%N
+ q=num%/%N
+ while(q > 0 | digit > 1){
+ r=append(q%%N,r)
+ q=q%/%N
+ digit=digit-1
+ }
+ return(r)
+ }
> d=t(sapply(0:(2^n-1),function(num) dec2nw(num,2,n))) # 10���̃R�C���̗��\�̏���i�O����菜���\�Ƃ���j
> head(d) ; tail(d)
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1,] 0 0 0 0 0 0 0 0 0 0
[2,] 0 0 0 0 0 0 0 0 0 1
[3,] 0 0 0 0 0 0 0 0 1 0
[4,] 0 0 0 0 0 0 0 0 1 1
[5,] 0 0 0 0 0 0 0 1 0 0
[6,] 0 0 0 0 0 0 0 1 0 1
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
[1019,] 1 1 1 1 1 1 1 0 1 0
[1020,] 1 1 1 1 1 1 1 0 1 1
[1021,] 1 1 1 1 1 1 1 1 0 0
[1022,] 1 1 1 1 1 1 1 1 0 1
[1023,] 1 1 1 1 1 1 1 1 1 0
[1024,] 1 1 1 1 1 1 1 1 1 1
> d1=apply(d,1,sum) #�@�e�s���Ƃ̍��v�������ł�����
> sum((1/2)^d1)/2^n�@ # �e�s���ƂɁ@(1/2) ^ ���̖������v�Z���č��Z����@
[1] 0.056314
> (1-1/4)^n
[1] 0.056314
���v�����B n=20�ł�100����̃V�~�����[�V����
> # simulation
> sim <- function(n){
+ (flip1=sample(0:1,n,rep=T)) # 0:1����d����������n�I�z���flip1�Ƃ���
+ (flip2=sample(0:1,sum(flip1),rep=T))�@# 0:1����flip1�̑��a�I�z���flip2�Ƃ���
+ sum(flip2)==0 # flip2�̑��a���O���ۂ���Ԃ�
+ }
> mean(replicate(1e7,sim(20))) # 100���s���đS����苎�����������v�Z
[1] 0.0031899
> (1-1/4)^20
[1] 0.0031712
�܂��A�ߎ������B >>867
1���̍d�݂���菜����Ȃ��m���́A�����Ƒ����Ƃ�������1/4
���̗]���ہi1���̍d�݂���菜����鎖�ہj�̊m����3/4
�ǂ̍d�݂̗��\���ł邩�͓Ɨ����ۂ�����A(3/4)^n�ł�����Ȃ��́H ��������
(1/1^2)+(1/2^3)+(1/3^4)+...
�����߂�B >>828
�V�~�����[�V�����v���O�����̗��K�@�������͌��҂ɂ��C��
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
En 1.0000 1.1991 1.4378 1.6744 1.9163 2.1544 2.3992 2.6329 2.9352 3.1542 3.4106
Pn 0.3405 0.1997 0.1483 0.1148 0.0917 0.0775 0.0700 0.0608 0.0516 0.0458 0.0416
[,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20] [,21] [,22]
En 3.6105 3.8742 4.1257 4.3780 4.6665 4.7706 5.0866 5.4512 5.6246 5.8261 6.1474
Pn 0.0375 0.0381 0.0383 0.0308 0.0295 0.0296 0.0269 0.0223 0.0227 0.0221 0.0239
[,23] [,24] [,25] [,26] [,27] [,28] [,29] [,30]
En 6.5768 6.5863 6.8209 7.0221 7.3743 7.652 7.8525 8.1056
Pn 0.0217 0.0204 0.0189 0.0202 0.0183 0.017 0.0166 0.0161
fn <- function(n){
B=c(rep(1,n),0,0) # 1:�� 0:����
flg=3 # draw�������l
i=0 # ���s�̉J�E���^�[
while(flg==3){ # draw�Ȃ�J��Ԃ��@1:win 2:lose 3:draw
i=i+1
flg=(1:3)[sum(sample(B,2))+1] # (1:3)[sum(c(0,0))+1] : win
}
c(i=i,flg=flg)
}
sim <- function(n){
k=1e4
re=t(replicate(k,fn(n)))
c(mean(re[,'i']),mean(re[,'flg']==1)) # �Ə�����Ԃ�
}
n=1:30
re=sapply(n,sim)
En=re[1,]
plot(n,En,bty='l',pch=19)
Pn=re[2,]
plot(n,Pn,bty='l',pch=19)
rownames(re)=c('En','Pn')
re ����{a[k]}��
a[k]={nCk*(-1)^(k+1)}/k
�Ƃ����B
�K�v�ł����
lim[n����]{(1+1/2+...+1/n)-ln(n)}=0.5772...��p���Ĉȉ��̖₢�ɓ�����B
�i1�jlim[n����] {1/ln(n)}*��[k=1,...,n]a[k]=1
�������B
�i2�j���̋Ɍ��ׂ�B
lim[n����] {1/ln(n)}*��[k=1,...,n]❲��[j=1,...,k](a[j]/j)❳ >>828
E(n) = (n+2)*(n+1)/(4*n+2)
> E(1:30)
[1] 1.0000 1.2000 1.4286 1.6667 1.9091 2.1538 2.4000 2.6471 2.8947 3.1429 3.3913
[12] 3.6400 3.8889 4.1379 4.3871 4.6364 4.8857 5.1351 5.3846 5.6341 5.8837 6.1333
[23] 6.3830 6.6327 6.8824 7.1321 7.3818 7.6316 7.8814 8.1311
>876�̃V�~�����[�V�����Ƌߎ����Ă���
pw=choose(2,2)/choose(n+2,2) # Pr[win]
pl=2*n/choose(n+2,2) # Pr[lose]
p=pw+pl
q=1-p # Pr[draw]
# 1*p + 2*q*p + 3*q^2*p + 4*q^3*p + i*q^(i-1)*p
# ��[i=1,i=m] i*q^(i-1)*p
# p*��i*q^(i-1)
# p*��d(q^i)/dq
# p*d(��q^i)/dq
# p*d((1-q^m)/(1-q))
# m���� q^m��0
# p*d/dq(1/(1 - q)) = p/(1 - q)^2 = 1/p >>828
2�j�@ 1/(n+1)�@���ȁH
�V�~�����[�V�������������̂ǂ��炩���ԈႢ���� >>828
n�������̏ꍇ
P[win] = (n+2)/2 * 2!n!/ (n+2)! = 1/(n+1) {n+2���V���b�t�����ċE�ɔ���}
E[n; win] = ( 1 + 2 + ... + (n+2)/2 ) * 2!n!/ (n+2)! = ...
E[n; lose] = (1*2n + 2*2(n-2) + .... + n/2*2*2 ) * 2!n!/ (n+2)!�@{n+2���V���b�t�����ċE�ɍ���or�����A���̌���ɔ�}
�@= ...
n����̏ꍇ�����l
(�֗��Ȍ���)
1*N + 2*(N-1) + ... +(N-1)*2 + N*1
1*(N+1-1) + 2*(N+1-2) + ... +(N-1)*(N+1-(N-1)) + N*(N+1-N)
= (1+2+...+N)(N+1) - (1^2 + 2^2 + ... + N^2)
= N(N+1)(N+1)/2 - N(N+1)(2N+1)/6 = N(N+1)(N+2)/6 >>828
k��ڂɂ������ɂȂ�m����pk�Ƃ����
k+1��ڂ̎n�܂鎞�_�ł͐�n-2k�ɂȂ��Ă���̂�
n-2k<2�Ȃ�p(k+1)=0
n-2k��2�Ȃ�p(k+1)=pk�E(n-2kC2)/(n-2k+2C2)=pk�E(n-2k)(n-2k-1)/(n-2k+2)(n-2k+1)
n-2k=0,1������ł�
p(k+1)=pk�E(n-2kC2)/(n-2k+2C2)=pk�E(n-2k)(n-2k-1)/(n-2k+2)(n-2k+1)
�Ƃ��Ă悢�̂�
���̑Q������0�ɂȂ�܂łƍl�����
k+1��n/2��p(k+1)=p1�E(n-2k)(n-2k-1)/n(n-1)=(n-2k)(n-2k-1)/(n+2)(n+1)
k+1>n/2��p(k+1)=0
k+1��ڂɏI������m����pk-p(k+1)�Ȃ̂Ŏ��s�̊��Ғl��
��(k+1)(pk-p(k+1))=��pk-���[��ʓ| �w�p�̋���f���Q - �A���t�@�E���{
ttp://x0000.net
���w �����w ���w �����w �V���w �n���n�w
IT �d�q �H�w ����w ���� ���� �Ȃ� >>881
�����s�������̂��H
�������s�Ǝv���ĉ��悤�Ƃ��Ă����B >>884
�����Ȃ�ȒP�����ł��傤����>>880�͔��ʼn����Ă� 2^2^2^2^2^2
��
https://ja.wolframalpha.com/input/?i=2%5E2%5E2%5E2%5E2%5E2
�ɂ����āA
�Ō�̐���:
...7437428736
�ł���Ƃ������A���̍����́H >>880
�ǂ��ł��������Ƃ����A
1*N + 2*(N-1) + ... +(N-1)*2 + N*1 = N(N+1)(N+2)/6
�̕ʏؖ��B
�E�ӂ� C(n+2,3) �ł��邪�A��������̂悤�ɍl����B
1,2,3,4,�c,n+2 ��n+2�̐�����3�I�ԑI�ѕ��ɂ��Ă�
�I��3�̐������A�^�A�E�ƌĂԂ��Ƃɂ���ƁA
�^�ɑI�Ԑ��ŏꍇ�����ł���B
�^��2�ƂȂ�I�ѕ��́A��1�ʂ�*�En�ʂ�B
�^��3�ƂȂ�I�ѕ��́A��2�ʂ�*�E(n-1)�ʂ�B
�^��4�ƂȂ�I�ѕ��́A��3�ʂ�*�E(n-2)�ʂ�B
�c
�^��n+1�ƂȂ�I�ѕ��́A��n�ʂ�*�E1�ʂ�B ��t��l@HayatoChiba
�������i�H�j���w�̎�����������̂ł����A�������̂��߉摜�Y�t�ł��������������B�ʔ����b�肾�Ǝv���̂ł����A���������m�̕����܂��ł��傤���B�i������Ɖ��������ǁA�ł������Ă��������E�E�E�j
https://pbs.twimg.com/media/ETybe_oUMAAfIhq.jpg
https://twitter.com/HayatoChiba/status/1242039227069550592
https://twitter.com/5chan_nel (5ch newer account) �ӂ̒������S�Đ����̑��p�`�ɂ����āA���Ȃ��Ƃ�2�ȏ�̓��p[���W�A��]�͖������ł��邱�Ƃ�����. >>886
����1: �I�C���[�ӊ�
�@��(5^10) = 5^9 (5-1) = 5^9*2^2
����2: ���[�N���b�h�ݏ��@
�@1745224 *2^10 - 183 *5^10 = 1 �@{�v�Z���@�͏ȗ�}
2^{2^{2^{2^{2^{2 }...} �� 0�@(mod 2^10)�@ {��2�̈��q�̑����͖��炩...}
2^{2^{2^{2^{2^{2 }...}
�� 2^{ 2^{ 1024*64 } (mod 5^9*2^2) }} �@(mod 5^10) {��t�F���}�[�̏��藝}
�� 2^{ 406736 } �@(mod 5^10) �@{��}
�� (1-5)^203368 �@(mod 5^10)
�� 1 + (-5)*C{203368,1} + 5^2* C{203368,2} +... +(-5)^9 *C{203368,9}�@(mod 5^10)
�� 5788111�@(mod 5^10)
�����l��]�藝���
2^2^2^2^2^2 �� 0*(-183*5^10) + 5788111*(1745224*2^10)�@(mod 2^10*5^10)
�� (57*10^5 + 88111)* (17*10^5*45224)* 1024 (mod 10^10)
�� ((57*45224 + 88111*17)*10^5 +88111*45224 )*1024 (mod 10^10)
�� 421427437428736 (mod 10^10)
�� 7437428736 (mod 10^10)
�� 2^2^2^2^2^2 = ..... 7437428736
�� �����͑��{���v�Z�\�Ȑ����\�t�g�ɔC�����B
�펯�I�Ȍ����ōς܂������Ȃ�㔼�Ɠ��l�� (1-5)^{ 1024*32 } (mod 5^9) etc. ���v�Z������悢�B >>888
�]�ڂ��ł�
��t��l@HayatoChiba �搶��
https://www.nippyo.co.jp/shop/magazines/latest/4.html
���w�Z�~�i�[ �@2020�N4����
�����w�Ƃ̌������������c�c��t��l�@8
https://ja.wikipedia.org/wiki/%E5%8D%83%E8%91%89%E9%80%B8%E4%BA%BA
��t ��l�i���� �͂�ƁA1982�N1��18�� - �j�͓��{�̐��w�ҁA���k��w�ޗ��Ȋw��������������[1]�B
����
�������v���Ďs���܂�B�����������P�����w�Z���o�āA2005�N���s��w�H�w�������H�w�ȑ��ƁB2009�N���s��w���w�����Ȑ����H�w��U���m�ے��C���B���͗͊w�n���_�A�����������A����є���`�����������B
��w3�̎��Ɂw����Ȃ�킩��H�w���Ŋw�Ԑ��w�x���o�ł���[2]�B
�܂��C�m�ے��݊w���Ɂw�x�N�g����͂���̊w���� �x���o�ł����B�i�������̂͊w���S�̎����Ƃ����j
2013�N����B��w�}�X�E�t�H�A�E�C���_�X�g���������y����[3]�B
2015�N�ɑ��{�\�z�i���{���f���j�̏ؖ�������[4]�B
2019�N�x����B��w��ސE�����k��w�ޗ��Ȋw�����������̋���[5]�B >>890
�����ς蕪������肪�Ƃ��B
log���g�����@���l�b�g��ōڂ��Ă������Ⴄ���@������ȁB >>891
https://en.wikipedia.org/wiki/Walsh_function
Walsh function From Wikipedia
https://mathworld.wolfram.com/WalshFunction.html
Walsh Function -- from Wolfram MathWorld
https://ja.wikipedia.org/wiki/%E3%82%A2%E3%83%80%E3%83%9E%E3%83%BC%E3%83%AB%E5%A4%89%E6%8F%9B
�A�_�}�[���ϊ��i�E�H���V��?�A�_�}�[���ϊ���A�_�}�[��?���[�f�}�b�w��?�E�H���V���ϊ��A�E�H���V���ϊ��A�E�H���V��?�t�[���G�ϊ��Ƃ��Ă��m���Ă���j�̓t�[���G�ϊ��̈�ʉ���1�ł���B
���̕ϊ��̓t�����X�̐��w�҃W���b�N�E�A�_�}�[���A�h�C�c�̐��w�҃n���X�E���[�f�}�b�w���A�A�����J�̐��w�҃W���Z�t�EL�E�E�H���V���i�p��Łj�ɂ��Ȃ�Ŗ�������Ă���B https://sites.google.com/site/allamsnumbers/home/the-beginning-of-the-beyonds/hyperoperational-numbers
It turns out that the leading digits of this number can be computed,
by taking the log10(2) accurate to at least 19735 decimal places,
and multiplying it by the decimal expansion of 2^^5.
Below are the first and last 40 digits of 2^^6.
2120038728808211984885164691662274630835...............8862693010305614986891826277507437428736
���������ǂ�ł��������ǂ��B >>887
�X�ɂǂ��ł��������Ƃ����A
�@1�N + 2�(N-1) + ���� + (N-1)�2 + N�1
��
�@{1 + 2x + 3x^2 + ���� + k�x^(k-1) + ���� }^2
�@= (1 + x + x^2 + x^3 + ���� + x^k + ���� )^4
�@= 1/(1-x)^4
�@= ��[k=0,��] �b[k+3, 3] x^k,
�ɂ����� x^(N-1) �̌W���ɓ������B
���@�b[N+2, 3] = N(N+1)(N+2)/6.
�Ȃ��@1/(1-x)^a = ��[k=0,��] �b[k+a-1, a-1] x^k, >>875
��[k=1,��] 1/(k^k)�@=�@1.291286
��[k=1,��] 1/(k^(k+1))�@=�@1.138390
��[k=1,��] 1/(k^(k+2))�@=�@1.066873
��[k=1,��] 1/(k^(k+3))�@=�@1.032685
(����)
��[k=1,��] 1/(k^(k+a))�@>�@1 + 1/(2^(2+a)) geogebra�łT�_��ʂ�Ȑ���`�����Ƃ���
�T�_���猈�܂�œ_��Q�ߐ��̍�}���@�͂ǂ��������̂ł��傤���H ����{a[k]}��
a[k] = {nCk*(-1)^(k+1)}/k
�Ƃ����B
�K�v�ł����
lim[n����] {(1+1/2+...+1/n)-ln(n)} = 0.5772... ��p���Ĉȉ��̖₢�ɓ�����B
�i1�jlim[n����] {1/ln(n)}*��[k=1,...,n]a[k] = 1
�������B
�i2�j���̋Ɍ��ׂ�B
lim[n����] {1/ln(n)}*��[k=1,...,n]❲��[j=1,...,k](a[j]/j)❳ >>898
�E�Ȑ��̒��S
�E�~�ƓȐ���4��_
����}�ł���̂ŁAX��, Y�� ��������.
�o�Ȑ�: (aY)^2 - (bX)^2 = 1 �� a, b �𐔎��ŋ��߂Ă��܂��悢
�@https://imgur.com/nUiPUqs
�ȉ~: ��}�I�����[�ŊȒP�ɋ��܂遫
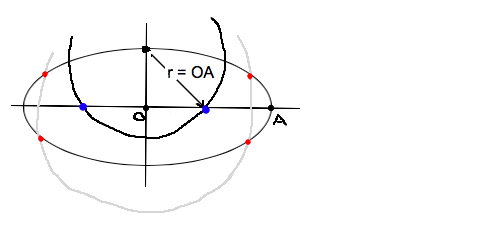 >>899
>>899
��[k=1..n]a[k] = ��[k=1..n] C{n,k} (-1)^{k+1}/k
= ��[k=1..n] ��[x=0,1]dx C{n,k} (-x)^{k-1}
=lim[�Á���] ��[x=��,1]dx ( x^{-1} - x^{-1}(1-x)^n )
=lim[�Á���] ��[x=��,1]dx x^{-1} - ��[x=0,1-��]dx (1-x)^{-1} x^{n} )
=lim[�Á���] -log(��) - ��[k=n+1..��](1-��)^k/k
=lim[�Á���] -log(��) - ��[k=1..��](1-��)^k/k + ��[k=1..n](�`)
=lim[�Á���] -log(��) + log(1-(1-��)) + ��[k=1..n](�`)
= ��[k=1..n] 1/k
= {��[k=1..n] 1/k - ln(n)} + ln(n)
lim[n����]��[k=1..n]a[k]/ln(n) = 0.5772.../�� + 1 = 1 lim[�Á���] ����Ȃ��� lim[�Á�0] >>899 ��(2)
��[k=1..n]��[j=1..k] a[j]/j = ��[j=1..n]��[k=j..n] a[j]/j = ��[j=1..n] (n-j+1) a[j]/j
= (n+1)��[j=1..n]a[j]/j�@-�@��[j=1..n]a[j]
��[j=1..n]a[j]/j
= ��[j=1..n] C{n,j} ��[x=0,1]dx ��[y=0,1]dy (-xy)^{j-1}
= ��[x=0,1]dx ��[y=0,1]dy {1 - (1-xy)^n }/{1 - (1-xy)}
= ��[x=0,1]dx ��[y=0,1]dy 1 + (1-xy) + ... + (1-xy)^{n-1}
= ��[x=0,1]dx 1 + (1-x/2) + ... + (1-(1-x)^n)/nx
= ��[x=��,1]dx ��[k=1,n] 1/xk - x^{-1}(1-x)^k/k
= ��[k=1,n] { 1/k * (-ln(��)) - ��[x=0,1-��]dx (1-x)^{-1} x^k/k }
= ��[k=1,n] { 1/k * (-ln(��)) - {��{[m=1,��] - ��[m=1,k]} (1-��)^m/mk }
= ��[k=1,n]��[m=1,k] 1/mk
= { ��[k=1,n]��[m=1,n] 1/mk + ��[k=1,n] 1/kk }/2
= { (��+ln(n)+��)^2 + ��^2/6 + �� }/2�@�@�y ��=0.5772..., ���� 0, ���� 0 (n����) �z
�� lim[n����] { ��[k=1..n]��[j=1..k] a[j]/j }/ { n*ln(n)^2 } = 1/2
����͏���ɕς������Ă������ ���̃X���A���x�������Ȃ��Ă����� �Ɍ����삪�G�Ɍ����Ȃ����Ȃ��̂ŏ������������Ă��� (���ۂ͓����e)
0 < �� < 1 �Ƃ���.
��[k=1..��] (1-��)^k/k = -ln(1-(1-��)) = -ln(��) �E�E�E(1)
N �� n < N, (1-��)^N/�� < �� �ƂȂ�悤�ɂƂ�.
��[k=n+1..N] (1-��)^k/k = ��[x=0,1-��]dx ��[k=n+1..N] x^{k-1}
= ��[x=0,1-��]dx (x^n�@-�@x^N)/(1-x)
= ��[x=��,1]dx (1-x)^n/x�@-�@��(N)
= -ln(��) + ��[k=1..n] C{n,k} (-1)^{k} (1-��^k)/k�@-�@��(N) �E�E�E(2)
N�̏������ 0 < ��(N) < ��
(1)-(2) ���
��[k=1..n] (1-��)^k/k = ��[k=1..n] C{n,k} (-1)^{k+1} (1-��^k)/k + ��(N)
�� �� +0 �̋Ɍ����Ƃ���
��[k=1..n] 1/k = ��[k=1..n] C{n,k} (-1)^{k+1} 1/k
��. �ςȂƂ����������̂Œ���
0 < �� < 1 �Ƃ���.
��[N] := ��[x=0,1-��]dx x^N/(1-x)
��[N] := ��[k=N+1,��](1-��)^k/k
N �� n < N, (1-��)^N/�� < ��, ��[N] < �� �ƂȂ�悤�\���傫���Ƃ�. (�ÂɈˑ�)
������� 0 < ��[N] < �� �ł���.
��[k=1..��] (1-��)^k/k = -ln(1-(1-��)) = -ln(��) �E�E�E(1)
��[k=n+1..N] (1-��)^k/k = ��[x=0,1-��]dx ��[k=n+1..N] x^{k-1}
= ��[x=0,1-��]dx (x^n - x^N)/(1-x)�@=�@��[x=��,1]dx (1-x)^n/x�@- ��[N]
= -ln(��) + ��[k=1..n] C{n,k} (-1)^{k} (1-��^k)/k�@- ��[N] �E�E�E(2)
(1)-(2) ���
��[k=1..n] (1-��)^k/k�@+ ��[N] = ��[k=1..n] C{n,k} (-1)^{k+1} (1-��^k)/k�@ + ��[N]
�� �� +0 �̋Ɍ����Ƃ���
��[k=1..n] 1/k = ��[k=1..n] C{n,k} (-1)^{k+1} 1/k
��. ����������Ɗ撣���Ă݂�.
��[k=1,n] C{n,k}(-1)^{k+1}/k
= ��[k=1,n] ��[x=0,1]dx C{n,k} (-x)^{k-1}
= ��[k=1,n] ��[x=0,1]dx C{n,k} (x-1)^{k-1}
= ��[x=0,1]dx { (1+(x-1))^n - 1 } / (x-1)
= ��[x=0,1]dx (x^n - 1) / (x-1)
= ��[x=0,1]dx ��[k=0,n-1] x^k
= ��[k=1,n] 1/k
��[j=1..n]a[j]/j
= ��[j=1..n] C{n,j} ��[x=0,1]dx ��[y=0,1]dy (-xy)^{j-1}
= ��[x=0,1]dx ��[y=0,1]dy {1 - (1-xy)^n }/{1 - (1-xy)}
= ��[x=0,1]dx ��[k=0,n-1] ��[y=0,1]dy (1-xy)^k
= ��[x=0,1]dx ��[k=1,n] (1-(1-x)^k) / kx
= ��[x=0,1]dx ��[k=1,n] (1-x^k) / k(1-x)
= ��[k=1,n] 1/k ��[x=0,1]dx ��[m=0,k-1] x^m
= ��[k=1,n] 1/k ��[m=1,k] 1/m
= ��[k=1,n]��[m=1,k] 1/km
�Â��log�W�J���g���Ȃ�ăA���G�l�[����... �Ǝ����ł��v���Ă����̂ŃX�b�L������. ���V���v����...
f(x) := (-1)*��[k=1..n] C{n,k}(-x)^k / k
f�f(x) = ��[k=1..n] C{n,k}(-x)^{k-1}
�@= (1 - (1-x)^n)/x = (1-(1-x)^n)/(1-(1-x)) = ��[k=0..n-1] (1-x)^k
��[k=1,n] C{n,k}(-1)^{k+1}/k
�@= f(1) - f(0) = ��[x=0,1]dx f�f(x) = ��[k=1..n] 1/k
��2�����̕����ł��̂͋p���Ėʓ|��������Ȃ�. ����قǂł��Ȃ�����.
g(x,y) := (-1)*��[k=1..n] C{n,k}(-xy)^k /kk
��[x]��[y]g(x,y) = ��[k=1..n] C{n,k}(-xy)^{k-1}
�@= (1- (1-xy)^n) / xy�@= (1- (1-xy)^n) / (1- (1-xy))
�@= ��[k=0..n-1] (1-xy)^k
��[x]g(x,y) = ��dy ... = ��[k=1..n] (1-(1-xy)^k) / kx�@{�� ��[x]g(x,0)=0}
�@= ��[k=1..n] y(1-(1-xy)^k) / k(1-(1-xy))
�@= ��[k=1..n] ��[m=0..k-1] y(1-xy)^m / k
g(x,y) = ��dx ... = ��[k=1..n] ��[m=1..k] { 1- (1-xy)^m }/mk�@{�� g(0,y)=0}
�� ��[k=1..n] C{n,k}(-1)^{k+1} /kk
�@= g(1,1) = ��[k=1..n] ��[m=1..k] 1/mk �@��[k=1..n] a[k] = 1 + 1/2 + 1/3 + ����� + 1/n = H[n],
�Ƃ����B
�@��[j=1..k] a[j]/j = ��[j=1..k] {C(n,j) (-1)^(j-1)} /jj
�@= ��[j=1..k] (1/j) ��[m=1..j] 1/j
�@= ��[j=1..k] H[j]/j
�@= (1/2)H[k]^2 + (1/2)��[j=1,k] 1/jj,
�܂ŏo���B
�@��[k=1..n] ��[j=1..k] a[j]/j
�@= {(n+1)/2}{H[n]^2 - ��[k=1,n] 1/kk} - H[n],
���ȁH
H[n] �` log(n) + ���@�@�@�y�� = 0.5772...�z �������̕��j�ɉ����Ĉ�ʉ����Ă݂�.
f{0} := f(x_1,...,x_m) := -��[k=1..n] C{n,k}(-x_1***x_m)^{k} /k^m
f{m} := ��[x_1]...��[x_m] f = { 1-(1-x_1***x_m)^n } / { 1-(1-x_1***x_m) }
�@= ��[k_1=0..n-1] (1 -x_1***x_m)^k_1
f{m-1} = �� dx_1 f{m} = ��[k_1=1..n] { 1 - (1 -x_1***x_m)^k_1 }/{ x_2***x_m) }
�@= ��[k_1=1..n] x_1 { 1 - (1-x_1***x_m)^k_1 }/{ 1 - (1-x_1***x_m) }
�@= ��[k_1=1..n] (x_1/k_1) ��[k_2=0..k_1-1] (1-x_1*...*x_m)^k_2
f{m-2} = �� dx_2 f{m-1}
�@= ��[k_1=1..n](x_1/k_1) ��[k_2=1..k_1] (x_2/k_2){ 1 - (1-x_1***x_m)^k_2 }/{ 1 - (1-x_1***x_m) }
�@= ��[k_1=1..n](x_1/k_1) ��[k_2=1..k_1] (x_2/k_2) ��[k_3=0..k_2-1] (1-x_1*...*x_m)^k_3
. . . ...
f{1} = ��[1��k_{m-1} ��...��k_1�� n] (x_1***x_{m-1})/ (k_1***k_{m-1}) ��[k_m=0..k_{m-1}-1] (1-x_1*...*x_m)^k_m
f = f{0} = �� dx_m f[1] = ��[1��k_m��...��k_2��k_1��n] { 1-(1-x_1*...*x_m)^k_m } /(k_1***k_m)
�� ��[k=1..n] C{n,k}(-1)^{k+1} /k^m = ��[1 �� k_1 �� k_2 ��...�� k_m �� n] 1/(k_1*k_2**k_m)
�Ȃ��Ȃ��ʔ�����������ꂽ. ���̎�����
�@lim[n����] { ��[k=1..n] C{n,k}(-1)^{k+1} /k^m } / ln(n)^m = 1/m!
��������. >>910 ����
�@��[j=1..n] a[j]/j = ��[k=1..n] {C(n,k) (-1)^(k-1)} /kk
�@= ��[k=1..n] (1/k) ��[m=1..k] 1/m
�@= ��[k=1..n] H[k] /k
�@= (1/2)H[n]^2 + (1/2)��[k=1,n] 1/kk,
�͏o���B�@������ k<n �ɑ���
�@��[j=1..k] a[j]/j
���o���̂�����@(�� a[j] �͉A��n�Ɉˑ�����)�@(2) �Ɏg�������ɂȂ��B�B�B
�ނ���
�@��[k=1..n] ��[j=1..k] a[j] /j
�@= ��[k=1..n] (n+1-k) a[k] /k
�@= ��[k=1..n] (n+1-k) {C[n,k] (-1)^(k-1)}/kk
�@= {(n+1)/2}{H[n]^2 - ��[k=1,n] 1/kk} - H[n],
�Ƃ�������������� �����̃X���b�h�̐����͋L���̈Ӗ�����킩���
�͂��߃A���S���Y�������Đ��w�͂��߂��l���܂����H >>913 �܂��ԈႦ���B
�@��[k=1..n] ��[j=1..k] a[j] /j
�@= ��[k=1..n] (n+1-k) a[k] /k
�@= ��[k=1..n] (n+1-k) {C[n,k] (-1)^(k-1)}/kk
�@= {(n+1)/2}{H[n]^2 �{ ��[k=1,n] 1/kk} - H[n],
�@�@�@�@�@�@�@�@�@�@�� >>908-909
�@�P�ϐ��ł��ł������B�B�B
f(x) := ��[k=1..n] a[k] x^k
�@= (-1)��[k=1..n] C[n,k]/k�E(-x)^k
�@= ��[k=1..n] (1-(1-x)^k)/k,
f(1) = ��[k=1..n] a[k]
�@= ��[k=1..n] 1/k = H[n],
g(x) := ��[k=1..n] a[k]/k�Ex^k
�@= -��[k=1..n] C[n,k]/kk�E(-x)^k
�@= ��[k=1..n] (1-(1-x)^k)/k�(��[m��k] 1/m),
g(1) = ��[k=1..n] a[k]/k
�@= ��[k=1..n] ��[m=k..n] 1/mk
�@= (1/2){H[n]^2 + ��[k=1,n] 1/kk},
�������
��[k=1..n] (n+1 - k) a[k]/k�Ex^k = (n+1)g(x) - f(x),
x��1 �Ƃ���
��[k=1..n] (n+1 - k) a[k]/k
�@= (n+1)g(1) - f(1)
�@= ((n+1)/2){H[n]^2 �{ ��[k=1,n] 1/kk} - H[n], 1�ϐ��ł���Ă݂�.
f[m](x) := ��[k=1..n] C{n,k}(-1)^{k+1} x^k/k^m
h[m](x) := ��[1��k_m��...��k_1��n] (1-(1-x)^{k_m}) / (k_1*k_2*...*k_m)
�Ef[1](x) = h[1](x) �͏ؖ��ς�.
�Ef[q](x) = h[q](x) �����肷��.
�Ef[q+1](x) = ��[t=0,x]dt f[q](t) / t = ��[t=0,x]dt h[q](t) / t
�@= ��[1��k_q��..��k_1��n] 1/(k_1*k_2*..*k_q)
�@ �@* ��[t=0,x]dt (1-(1-t)^{k_q})/(1-(1-t))
�@= ��[1��k_q��..��k_1��n] 1/(k_1*k_2*..*k_q)
�@�@ * ��[k=0..k_q-1] ��[t=0,x]dt (1-t)^k
�@= ��[1��k_q��..��k_1��n] 1/(k_1*k_2*..*k_q)
�@�@ * ��[k=1..k_q] (1-(1-x)^k)/k
�@= h[q+1](x)
�A�[�@�ɂ�� h[m](x)=f[m](x) (m=1..��)
����[k=1..n] C{n,k}(-1)^{k+1}/k^m = f[m](0) = h[m](0)
�@ = ��[1��k_1��..��k_m��n] 1/(k_1*k_2*..*k_m)
�������p�Ⴊ����̂Ȃ�m�肽���ł�. ����A_0A_1��ɂ���_A_2�𒆐S�Ƃ����_�Ώ̂�A_0��A_1���ړ������_�̂���A_2�ɋ߂�����A_3�Ƃ���B
����A_3�ƈ�ԋ߂������ɂ����_A_2 �� A_0 or A_1��A_3�𒆐S�ɓ_�Ώ̂ňړ������Ƃ�A_3�Ƌ߂�����A_4�Ƃ���B
���l�ɓ_�Ώ̂ňړ������_A_m�Ɉ�ԋ߂��Q�_��A_m�𒆐S�Ƃ��ĂP�W�O�x��]�������_�̂���A_m�ɋ߂�����A_(m+1)
�Ƃ���BA_0A_1�FA_0A_2��1�Fp �̂Ƃ� A_0A_1�FA_0A_m ��m�����̂Ƃ��ǂ��Ȃ邩�H >>918 �璷�������̂Œ���
�u���l�ɓ_�Ώ̂ňړ������_A_m�Ɉ�ԋ߂��_��A_m�𒆐S�Ƃ��ĂP�W�O�x��]�������_��A_(m+1)�Ƃ���v ��n�p�`T���^�����Ă���B
T�Ƒ�����n�p�`�ŁA����n�̒��_�����ׂ�T�̎���ɂ���A����T�Ƃ͈قȂ���̂����݂��邱�Ƃ������B >>918�@�䂪�L�������ƍŋߐړ_����_�ɂȂ��Ă��܂��̂�
A_0A_1�FA_0A_2��1�Fp �@(p�͖������j�@ 50��̔n���Ȃ�����������ȃX�����������Ƃ�
�ȑO���畷�������Ǝv���Ă������A�����ł����H
������57�ł��A�Ȃ�49�B�̍�8��
�����̗��e���̍�8��.�Ȃ̗��e���̍�8�ł��B
2�`3���ƒ��������Ȃ����A����͂��Ȃ背�A���Ǝv�����m�����ƁA�ǂ̂��炢�ł��傤���H
������������ >>923
�����\�N��̒j�����Ƃ̐l���s���~�b�h�̕��z����
����ׂɑI���ō̍����W�ɂȂ�m��p���v�Z����p^3�Ōv�Z�B
�����K������������Z�ɂȂ�̂�
�N���2-3�̊m���Ƃ̔�Ř_���������������낤�ˁB ��������͖���ׂɑI�Ԃ킯����Ȃ����m���ł��Ȃ��悤�ȋC������ �O>>672
>>923
�N�̍�8�͐��܂�N�ł�����7�`9���܂ł�8���Ƃ݂Ȃ��A���x�̈���Ⴂ��12�����ő�Ƃ����Ƃ��A4�g�̕v�w�̂���1�g��8���ɂȂ�B���ꂪ3�g�̕v�w�ł����Ȃ�m���́A
(1/4)^3=1/64
��100/64=1.5625(��)
8�����̂�25�����炢������A�m���I�ɒႭ�Ȃ��B����Ɉ�`�I�Ɏ��Ă���Ƃ��l������B �O>>926
���͐\�N���܂�A�����ƕ�Ƒc��͈�N���܂�A�����̑c��͖��N���܂�ŏ\���N���O��94�ŖS���Ȃ�܂����B
����̑c���͖�99�ʼn��N���O�ɖS���Ȃ�܂����B
�c��͂��̉��N���O�ɖS���Ȃ�܂������A�c����艽���N���ň�����͗���ĂȂ������͂��B
�����̑c���͕���3���炢�̂Ƃ�66�ŖS���Ȃ��������Ȃ̂ŁA1880�N��1881�N�̐��܂�ŁA�����̑c���1905�N���܂ꂾ�Ǝv���܂��B
����̑c���1923�N���܂�ŁA����̑c����1916�N��1917�N�̐��܂ꂾ�Ǝv���܂��B
48�̎����̑����̊��Ғl�͉����B ����z=0��̒P�ʉ~���~�Ƃ��A������h(>1)�̒��~�����l����B
�i�P�j����z=x+a�����~���Ƌ��L�_�����悤�A����a�������Ba�̎�蓾��l�͈̔͂����߂�B
�i�Q�j�i�P�j�ŋ��߂�a�͈̔͂̍ŏ��l��m�A�ő�l��M�Ƃ���B
[m,M]���������1����ׂɂƂ�A�����r�Ƃ����B
����z=x+r�ɂ��~���̐ؒf�ʂ̖ʐ�S(r)���Έȏ�(2/��3)�Έȉ��ƂȂ�m�����A�����_�ȉ�1���܂ŋ��߂�B
�����_��2���ȉ��͐�̂Ă�B >>926
�Ȃ��8����4�g��1�g�Ȃ́H
����Ȃɑ�����Ȃ�
1�`3�����炢�͑����ĔN�����������A�ȋC�����邪
����ȊȒP�Ȍv�Z�ł͂Ȃ��Ǝv����
�Ⴆ�Ή������Ȃ�45�����Ǝ����̗��e���Ȃ̗��e��45���Ȃ�Č����I�ɂ͂��肦��Ǝv������ >>928
(1)
���~���� -1��x��1 �� 0��z��h �͈̔͂Ɋ܂܂�邩��
�@-1 �� z-x �� h+1
�� a�̎�蓾��l�� -1��a�� h+1 �Ɍ���B
�t�ɁA
-1��a��0 �̂Ƃ��� (1,0,a+1) ���A
0��a��h �̂Ƃ��� (0,0,a) ���A
h��a��h+1 �̂Ƃ��� (-1,0,a-1) �����L�_�Ɏ��B
�ȏ���Aa�̎�蓾��l�͈̔͂� -1 �� a �� h+1. �O>>927
>>926
���N�Ⴂ���N�ƌ��邩1�Ⴂ�ƌ��邩�ňႤ���犱�x�̈��肪12�N�Ƃ��đO��܂߂�3�N�������N�Ƃ݂Ȃ���̈��1/4�Ƃ����Ӗ��ł����B
���v������ƕv��7�Έȏ�N����Ă����̂�11���Ȃ�ŁA8�ΔN���10�����炢����Ȃ����ƁB a,b���L������
�@a+��(a^2+4b) = 2+2��2
�����Aa=2, b=1 �ƌ����܂����B �ڂ����͂��C���Ȃ�����a=m/n,b=p/q�ł���ĕ��ꕥ���Ĉꎟ�Ɨ����ł�����Ⴄ�H >>932
a+��(a^2+4b) = 2+2��2
��
��(a^2+4b) = 2+2��2 -a
��
a^2+4b = (2+2��2 -a)^2
��
b = (3+2��2) - (1+��2) a
������ a, b ���L�����Ȃ� ��2 ����ł��������� a=2 �ł���K�v������,
���̎� b=2 �ł���.�@�܂葼�̗L�����y�A�ł͂��蓾�Ȃ�����������. ���̎� b=1 �ł���.�@�܂葼�̗L�����y�A�ł͂��蓾�Ȃ�����������. Q�F�L�����S��
�Ƃ���
���̂Ƃ�
��a,b��Q�G�@a+��(a^2+4b) = 2+2��2�@���݂�
��a,b��Q��O��Ƃ���
a�F=2
b�F=1
�Ƃ����悢
�ƌ����� ����Ă���̂́A
�@��a,b��Q { a+��(a^2+4b) = 2+2��2�@�� (a=1 �� b=2) }
����Ɠ����Ș_����
�@��a,b��Q { (a��1 �� b��2) �� a+��(a^2+4b) �� 2+2��2 }
��
�@��[ ��a,b��Q { (a��1 �� b��2) �� a+��(a^2+4b) = 2+2��2 } ]
�Ȃł�OK �܂��Ƃ�Ȃ����
�ʁ́@���l�@�@�Z
�́@���l�@�ʁ@�@����͖��W �������S�̖���̕s���ݐ�����
�͈�ʂɖ����W�����猳��I�ю�邱�Ƃ͂ł��Ȃ��̂�
��a,b��Q�C�@a=1, b=2�@
�Ə������Ƃ͂ł��Ȃ�
�K��
��a,b��Q�G�@a=1�Cb=2
�ł��� ���ꂾ����
�̂�́u���ׂĂ̌��ɑ��āv
�Ƃ�������͑S���Ԉ���Ă���
�{���̂Ă� �ȒP�ł����̂ʼn������������ė~�����ł��B
https://i.imgur.com/b6U7pOL.jpg �O>>931
>>942
x�̕��тɂ���2�̓��������̕ӂ�y�Ƃ����ƁA
�O��(2,6,2y)�ƎO��(x,3x,8)�̎O�p�`������������A
2:x=2y:8=y:4
��xy=8�����@
�Ε�8�̍����Ȓ��p�O�p�`��1�ƎΕ�3x�̒��p�O�p�`�ɂ����ăs�^�S���X�̒藝���A
8^2-y^2=(3x)^2-(x+y)^2
64=9x^2-x^2-2xy
�@�������A
64=8x^2-16
8=x^2-2
x^2=10
x=��10
�}����x��3���炢�����炠���Ă�͂��B >>942
�~�ɓ��ڂ���O�p�`�̈�ӂ����̉~�̒��a�Ȃ�A���̕ӂɑΌ�����p�����p�ł��邱�Ƃ𗘗p����B
x^2+(3x)^2��(2�~5)^2 ����� x����10
http://i.imgur.com/TUmodHy.png >>942
�}����A�~�̒��a 10 �����߂āA�~�ɓ��ڂ���3�ӂ̒��� 6�A8�A10(���a) �̒��p�O�p�`�̕ӂ̒���8�����߂�B
2�ӂ̒�����8�ɓ������ӎO�p�`�̒�ӂ̒����� 2y y��0 �Ƃ���B
�}����A�Β��p���݊p�݂̌��ɑ����ȎO�p�`�ɂ��āA8�Fx��2y�F(10-8)��y�F1 �� xy��8�B
�}����A�~�ɓ��ڂ���~���p���������݂��ɑ����ȎO�p�`�̐����ƎO�����̒藝���A
��( (��(8^2-y^2))^2 + (x+y)^2 )�Fx��6�F2��3�F1
�� 3x����( (��(8^2-y^2))^2 + (x+y)^2 )�B
�� 9x^2��8^2-y^2 + (x+y)^2��64 + x^2 + 2xy
�� 4x^2��32+xy��32+8��40 �� x^2��10 �� x����10 (�� x��0)�B ��̒��_A����Ε�BC�ɉ����������� AH
�O�ډ~�̒��S�� O
AO�̉������Ɖ~���̌�_�� D
AO�̉������ƕ�BC�̌�_�� X
�Ƃ���B
AOD�͒��a������
�@��ACD=90��,�@�@AD = 10,
�O�����̒藝��
�@AC = ��(AD^2 - CD^2) = ��(10^2 - 6^2) = 8,
��ӂ�胢ACX�͓ӎO�p�`
�@AX = AC = 8,
�@DX = AD - AX = 10 - 8 = 2,
��ACX �� ��BDX ���
�@BD = (AC/AX)BX = (AC/AX)x,�@
��CDX �� ��ABX ���
�@AB = (CD/DX)BX = (CD/DX)x,
AOD�͒��a������ ��ABD = 90�,
�ĂюO�����̒藝��
�@AD^2 = AB^2 + BD^2 = {(CD/DX)^2 + (AC/AX)^2}x^2 = �E�E�E�E
�ȉ� >>945 �̂Ƃ��� �e�_�̖��̂�>>947����ɍ��킹��
��ACD�����p�O�p�`�ł��邱�Ƃ���AC=8
��AXC���ӎO�p�`��AB=8
C����AD�ɐ������~�낵����F�Ƃ���
��AFC�́�ACD�Ƒ����ł���̂�AF�ACF�����܂�AFX�����܂�̂ł�������O������CX=(8��10)/5
��XCD�䁢XAB�ł���̂�x=��10
>>945����̂ق������ꂢ���ȁc�c >>946�͒��a��ʂ�Ȃ��Ă��A�ӎO�p�`��3�ӂ̒�����������ΓK�p�o���邱�Ƃ����邩��A����Ӗ��ŗL�͂ȋ��ߕ��ɂȂ��Ă���B ����A�~�ɓ��ڂ���O�p�`��3�ӂ̒����A�ӎO�p�`�̓�����2�ӂ̒�����������A>>846��2�s�ڈȍ~�̂悤�ȉ�@�͓K�p�o���邱�Ƃ�����B
���̍ہA���a�]�X�͊W�Ȃ��B ���X����950���Ă��܂��B1000����Ə������݂��ł��Ȃ��Ȃ�܂��B
