�ʔ�����肨�����ā`�� 31���
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
�ʔ�����肨�����ā`�� 30���
https://rio2016.5ch.net/test/read.cgi/math/1572866819/997
997 ���O�F�P�R�Q�l�ڂ̑f������[sage] ���e���F2020/01/27(��) 19:28:57.79 ID:VuOY61Uq
���Ƃ���͖{���ɋ����{�ӂ�����, �Ⴆ��
�eXi���W��{-1, 1-��2, ��2}��̗��U��l���z�Ƃ������ɓ����咣�����藧��, �Ƃ����̂͋���������
�����܂ŗ��U�I������, ��ݍ��݂��閈�ɒ��������肪�ǂ�ǂ�"��"�ɂȂ��Ă�������c
�̂��v�]�ɂ������āA����Ă݂��B�����������ɂȂ���ہB
https://i.imgur.com/LXkHRpW.jpg
�F�ʂɂ͈Ӗ��Ȃ��A�P�ɉ����V��ł݂������B
v=c(-1, 1-sqrt(2), sqrt(2)) # �w��̐��l
a=(max(v)-min(v))/2 # a �͂��̕��̔����ɂ���
qn <- function(n,k=1000){ # ���̗��������ł̎�����1000��J��Ԃ�
f=function() abs(sum(sample(v,n,replace=TRUE)))<a �@�@# v����d������邵��n���o���A���a�̐�Βl��a��菬�������TRUE��Ԃ�����
mean(replicate(k,f())) # f��1000��J��Ԃ�TRUE�̕p�x��Ԃ�
}
n=1:1000 #�@����ω�������qn�����s���ăO���t�ɂ���
y=sapply(n,function(n) sqrt(n)*qn(n)) # n��1~1000��sqrt(n)*qn�����s
plot(n,y,pch=19,bty='n',col=sample(colours())) >>2
���肪�����c�\�z��肩�Ȃ���ɂȂ��ĂĈӊO��
�v�������@�ׂȏ����Ȃ̂��A���́c �O�X���̃v�[���̖��B
�ŒZ10�b����Ȃ��́H
�v�[���T�C�h��5�b�A���p�ɋȂ����Č�����������i�s�����ɑ���60���̕����ɔ�т��߂A���傤��10�b�őΊp���ɒB����B
���p�O�p�`�̕ӂ̔䂪1:2:��3�ɂȂ邩��A�v�[���T�C�h����Ίp���܂ŁA�v�[���T�C�h�̎c��̂��傤��2�{�̋������j�����ƂɂȂ�B
�����ł͑����������ɂȂ邩�玞�Ԃ̓v�[���T�C�h��[�܂ōs���̂Ɠ����B�܂�5�b�B�v�[���T�C�h�̂ǂ������т���ł��Ίp���܂�5�b�B
5�b+5�b=10�b
�ǂ��ł����H
���ꂪ�����ł͂Ȃ����B V={(x_1,..,x_n)��[-1/2,1/2)^n | x_1+..+x_n >= 1/2}�̑̐ς����1/2-c/��n�̃I�[�_�[���Č����͉̂��������
n�����P�̂̑̐ς�1/n!�炵���������̑����ɑ��Č������Ă��悳���������� ���̊�Ȋ����͋@�B�w�K�Ō����Ƃ���̋��ʏW�����ۂƓ����������� �܂����������_�l���V�~�����[�V�����������Ă邩�炻��Ȃ���Ǝv�����A���ڑ̐�(�̃I�[�_�[)�v�Z���Ă݂邩�����Ȃ��̂ł́H >>7
����Č����̂͂ǂ����Ɍ�����������Ă����ނ��̕�����Ȃ��āAn���������̂��Ă����̂����ς����C�r�c���Ȃ��Ƃ��������̕�����
��������������Ɗp�̂�����̑̐ς��ǂ�ǂ����Ă����Ē��S�ɋ߂��������y�V�����R�ɂȂ���Č����̂��ʔ��� >>4
���ᎆ�����Ă��Ȃ����B
10cm�~10cm�̐����`�������B
���������S�̔��a10cm�̉~�������B
1cm�E�ɃY���Ĕ��a9.5cm�̉~�������B
1cm�E�ɃY���Ĕ��a9cm�̉~�������B
�d
1cm�E�ɃY���Ĕ��a5cm�̉~�������B
1cm��Y���Ĕ��a4.5cm�̉~�������B
1cm��Y���Ĕ��a4cm�̉~�������B
�d
1cm��Y���Ĕ��a0.5cm�̉~�������B
�R�������10�b�œ��B�ł���̈�B �O>>4
10�b�œ��B���Ȃ��G���A�����݂���B
�ŏ��ɊĎ���������R�[�i�[���甼�a10m�̐�`�͈̔͂͋~����B
���������̉�����60�̕����ɑΊp���Ɍ������Ă�10�b�̎��_�ł͑Ίp���܂œ��B���Ȃ��B
�ŏ��ɊĎ����������n�_�̔��Α��̃R�[�i�[��30�����O���������Ƃ��̐^�̑Ίp���t�߂�30���̃G���A�Ŕ��a10m�̐�`�̊O��10�b�ł͓��B���Ȃ��B
10�b��t�b��ɑΊp������j���Ď����ƁA
���������̉�����i�s�����ɑ���60���Ŕ�т��݁A�Ίp���ɑ��āA
180��-60��-45��=75���̊p�x�ʼnj���ł����Ď������A�����ɓ��B����n�_��������_���݂���B
15����75���̒��p�O�p�`�ɂ����ăs�^�S���X�̒藝���A���������̉�����60���̊p�x�Ŕ�т��ނƂ��̓��B���ԂƁA�Ίp������j���Ď����̓��B���Ԃŗ������A
5+5-��{(10��2-10-t)^2-t^2}(2/��3)(1/2)+��{(10��2-10-t)^2-t^2}(1/��3)+t=10+t >>5-8
�����������ƂȂ�ƕ\�ʂ����Ȃ����B
�i�]�j���E�֑̂Ƃ��R�z�����W�[�����Ř_������P�[�X���������珕���邯�ǁB >>11
�ւ��[�����z�������Ȃ���
�܂�[0,1]^n�̕\�ʕt�߂̐�߂�̐ς̊������ǂ�ǂ���͕̂����邯��
���w�Ȃ��Ɖ��̎��Ƃł��낤�� >>11
����A�z���g���B
���E�����Ȃ��ˁB
(�@��ͥ)�V�� �ւ��`�ւ��`�ւ��` >>9
�C�i���ɑ����č�}�̗��K�ɂP�O�b�œ��B�ł���͈͂̐}�������Ă݂܂����B
��ɏ�ɍs���Ă���E�ɍs���̂��t�������܂����B
https://i.imgur.com/92wYLCv.jpg �O>>10
>>14�ɂ���!!
���������������ň͂�ŁA�^��ӂɍŒx���B�_�̈���ΐ����B ���̐}��4�{�̒����������яオ���Ă�̂�ǂݎ��Ȃ��̂��C�i�̌��E���ȁB >>15
���������Ȃ̂ŕb�����w�肵�ĕ`��ł���悤�Ƀv���O�������Ă݂܂����B
�W�b�A�X�b�A�P�O�b�A�P�P�b�œ��B�ł���͈͂�`���Ă݂܂����B
�������P�O����P�P�b�̊Ԃɂ��邱�Ƃ��ǂݎ��܂��B
https://i.imgur.com/e9mep6G.jpg >>10
���ᎆ�ɍ�}������
�P�O�b�ȓ��ɓ��B�ł��Ȃ��̈悪���̕����Ɣ����B
�����ŋ^��B
���̔��̕����̖ʐς͂������H
�i������ɂ������͂����Ă���܂���̂ň������炸�j
https://i.imgur.com/mfbtwlU.jpg �O>>15
����(10+t)�b��t�����߂���Ă��ƂȂ�B ���������Ăĉ������Ƃ����0=0�ɂȂ邩��݂�ȕ��u���č�}�ɐ����o���Ă�B
�ł��������傢��}����Əo��Ǝv���B �݂�Ȃ��ĒN�H
�Ƃ��������̖��ŏ��̃��X��>>17�̐}�̎l�p�`���ׂ�鎞�����߂Ă邶���B
���̖��ł��鎞���܂łɓ��B�ł��Ȃ��̈悪�l�p�`���Z�p�`�ɂȂ鎖�ɋC�Â��ĂȂ��̂͌N���܂ދɁX�ꕔ�����ő��̏Z�l�݂͂�Ȃ킩���Ă��B
�������̋ɁX�ꕔ�̂ЂƂ��A�z�قLjӖ��Ȃ����X���Ă邩��킩���ĂȂ��l�Ԃ���������悤�Ɍ����邾���B
�����炭���̖��܂��ł��ĂȂ��̂�2�A3�l�������Ȃ��B >>13
>���E�����Ȃ���
����ǂ�����Ċm���߂��� �O>>20
�Ď����̂��锽�R�[�i�[�ƍŒx���B�_�Ɖ��̌��������̔�т��ݒn�_�����ԎO�p�`�ɂ����āA�����藝���t�̓��𗧂Ă���������At�̒l���o�����Ƃ���t��i���������Ă��ԁB ���������ɒP��n���������̂̌���(e/2)�̔炪��߂�̐ς̊����l����
(1^n-(1-e)^n)/1^n=1-(1-e)^n -> 1 (n->��)
�ŗǂ��悤�ȋC�����Ă��� �O>>23
�}��`����t�̒l��11�b��Ȃ��ǁA
�v�Z���ʂ͍��̂Ƃ���A
10+t=13.81376309�c�c(�b)
�������傢���Ȃ��B
�ԈႦ�����Ȃ��B >>22
���ψʑ��̒�`�B
�C�ӂ�x��I^���̓_�Ƃ��̊J�ߖT�̊�U=��(ai,bi) (xi��(ai,bi), �L����������ai=-���Abi=��)���Ƃ�Ƃ�U�͕K��I^���łȂ��_���܂ށB
�܂���_�Ȃ��B I^�����āi�ˉe�j�Ɍ���
������Ɖߌ��ł� >>29
������>>11�͖������ς̈Ӗ��ł���H
�����B �O>>27
t/(10��2-10-t)=sin15��
t=(10��2-10-t)sin15��
=(10��2-10)sin15��-tsin15��
(1+sin15��)t=10(��2-1)sin15��
t=10(��2-1)sin15��/(1+sin15��)
=0.851642332�c�c
10+t=10.851642332�c�c(�b)
60���������Ƃ�����т��݊p��������Ă��Ƃ��B �O>>31
t/(10��2-10-t)=sin13��
t=(10��2-10-t)sin13��
=(10��2-10)sin13��-tsin13��
(1+sin13��)t=10(��2-1)sin13��
t=10(��2-1)sin13��/(1+sin13��)
=0.712964721�c�c
10+t=10.712964721�c�c(�b)
������o�T�������������B >>28
�ʑ��͗ǂ��m��Ȃ����ǁAx���S�̔��a�������������Ƃ��x�̊J�ߖT��I^���Ɋ܂܂��悤�ɏo����Ǝv������ >>33
���̂�����J�ߖT�ƌĂȂ��̂��͑������w�ȈȊO�ł͋����ĂȂ��B
���������x�Ƃ������x�A�ǂ��ł������Ƃ����ǂ��ł������b�Ȃ̂ŋC�ɂ��Ȃ��Ă����B
�������悤�Ǝv���Ƃ܂��܂��撣��Ȃ��ƃ_���ŁA���������w�ȈȊO�̐l�Ԃɂ͖��ɗ����Ȃ��B >>34
������Ԃ��Ƌ��̓����͊J�W�����炢�̔F���Ȃ��ǁA���������̎������J�W������Ȃ��Ȃ銴���Ȃ̂��ȁH
�o������L�[���[�h�Ƃ������q���g�Ƃ������ė~����
���Ȃ݂�>>28�łȂ��L����������ai=-���Abi=�����Ă����������t���̂����m�肽�� >>35
�Ƃ肠�������ϋ�Ԃ̒�`��
https://ja.m.wikipedia.org/wiki/%E7%A9%8D%E4%BD%8D%E7%9B%B8
�ʼn��̂���������`�ɂȂ邩�Ƃ�����
https://ja.m.wikipedia.org/wiki/%E5%B0%84%E5%BD%B1%E6%A5%B5%E9%99%90
������������Xi�̒��ϋ��X��
�@��i���������o���ʑ�X��Xi���A���ɂȂ�Ȃ��ƍ���B
���̂��߂ɂ͂�����x��������J�W�����Ȃ��ƃ_���B
�A�����̋�Ԃւ̘A���ʑ��̑g��fi:Y��Xi���^����ꂽ��A������i�����Ƃ���悤�ȘA���ʑ�f:Y��X�����Ȃ��ƍ���B
���̂��߂ɂ͂��܂�X�ɊJ�W�������肷���Ă�����B
�̗����̗v�������̂�wiki�ɂ����`�B
�L����������ai=-���Abi=���łȂ��ƃ_���Ƃ������[�����Ȃ��ƊJ�W���������߂��ćA�����Ȃ��Ȃ��Ă��܂��B >>32
�Ď����̓v�[���̐���������B >>36
�Ƃ肠�����ϋ�Ԃ̕��Ր����J�ߖT�ɗL����������ai=-���Abi=���Ƃ���������v�����Ă�
�䂦�ɂǂ��x�̊J�ߖT���Ƃ��Ă�I^������͂ݏo�Ă��܂����Ă�������Ȃ̂���
>�L����������ai=-���Abi=���łȂ��ƃ_���Ƃ������[�����Ȃ��ƊJ�W���������߂��ćA�����Ȃ��Ȃ��Ă��܂��B
����ؖ�����̓���������C�ɂȂ�
�Ƃ肠�����ψʑ����ˉe�Ɍ��̓���ȃP�[�X�����Ă̂͗�������������͐ψʑ��̕��Ր������C�ɂ��Ă����܂�l���Ȃ��Ă��ǂ����Ƃ��ۂ��� �O>>32
>>37
10�b�ʼn���ɂ͂Ȃ���B >>38
�ؖ��͂���Ȃɓ���킯�ł͂Ȃ���B
���w�Ȃ̊w������⑲�Ɛ��Ȃ�r�����ɂ��傤�ǂ������炢�B >>40
��������ė�������
https://www.rs.tus.ac.jp/a25594/2018-2019_General_Topology.pdf
�ʑ��̐����̎��ɗL���̋��ʕ������Ƃ鑀��ƁA�ˉep_i:X->X_i�̋t������i�����ȊOX_j�S�̂ɂȂ���ĂƂ��낪�L���̓Y�����������ċ�ԑS��(-��,��)���Ă��������̗R���������̂�
�ˉe��A���ɂ���Ŏ�̈ʑ������悤�Ƃ���Ǝ��R�ƊJ�ߖT�̑�i��������i��ԑS�̂��Ă��܂��قǂł����Ȃ���Ă͖̂ʔ�����
��܂��ȗ���������Ă���Ă��肪�Ƃ� �O>>39`�a____�a ; ; ;
�^�a__`�a�P�P�a; ; ; ;
�a���� �a �� �a ; ; ;
�i(-_-)�a�@�@�a;_;_;_;
�i`�`���a�@ ��a������
��`(_)_)��~�@�a������
�_���҃ҁ�___�a��_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_`�Ȃ��10�b�オ�킩��̂ɓ��B���Ԃ��o�Ȃ��B�ʔ����B �O�X����
�uV_n={(x_1,..,x_n)��[-1/2,1/2)^n | -1/2��x_1+..+x_n<1/2} �̑̐ς�
|V_n|=(1/��)��[-��,��](sinx/x)^(n+1)dx �ł��邱�Ƃ������B�v
�Ƃ������̓�Փx�͂ǂꂭ�炢�ʼnp�^�[���͂������炢����̂��낤���H >>33
>>28,30�ɏ����Ă�����߂��Ɩ��� >>34
>���̂�����J�ߖT�ƌĂȂ��̂��͑������w�ȈȊO�ł͋����ĂȂ��B
�J�ߖT�ł��C�C��
�ʑ����Ⴄ���� >>35
���W�ւ̎ˉe�Ɋւ����ʑ������̂����ʂ�����
�ʂ̈ʑ��ł��C�C >>45
>>33��x���S�̊J����I^���Ɏ��܂�悤�Ȃ��̂�x�̊J�ߖT�Ƃ��Ď���̂ł͂ƌ����Ă邪
>>34�͐ϋ�Ԃ̕��Ր������悤�Ȉʑ��������>>34�̊J���͊J�ߖT�ɂ͂Ȃ�Ȃ��ƌ����Ă�̂ł� >>47
�~>>34�̊J��
��>>33�̊J�� ���������匳��>>11���C�ɂȂ���ǁB
�R�z�����W�[�g���Ƃ������Ă邯�ljk����Ȃ��̂��ȁH �O>>42
10�b77�ł͓��B�ł��Ȃ���10�b85�œ��B�ł���G���A�œM�ꂽ�l�͊Ď����ɂ���Ă͋~���邯�NJĎ����ɂ���Ă͋~���Ȃ��^���ɂ�����Ă��Ƃ��B �^�a��`�a�P�P�a�O>>42
�a����`�a �� �a[��d��
�i(-_-)�a�@�@�a______
�i����~�a�@ ��a������
��`(_)_)�@�@ �a������
�_���҃ҁ�___�a��_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_`�Ίp�����j�����A���������v�[���T�C�h��i��Ői�s�����ɑ���60���̕����ɔ�т��ނƑ����B10+t(�b)�ŊĎ������M��Ă�l�������Ă�Ƃ��ɓ��B����Ƃ��āA
�˂�������܂�5�b�i��Œ��p�ɋȂ�����5�b����10�b�܂ł̂������ɐi�s�����ɑ���60���̕����ɔ�т��ʂ̊Ď������A10+t(�b)�œM��Ă�l�������Ă�Ƃ��ɓ��B���邱�Ƃ��\�B �O>>51
�Ίp����ɊĎ�������x(m)�̈ʒu�œM�ꂽ�l�̂Ƃ��Ɏ�O�̉�����i�s�����ɑ���60���ɔ�т�ł��A���������̉�����i�s�����ɑ���60���̕����ɔ�т���ł������ɓ��B����Ƃ���ƁA
(x/��2-x/��6)(1/2)+(x/��2)(2/��3)=5+{10-(10-x/��2)(1+1/��3)}(1/2)+(10-x/��2)(2/��3)
�ӁX2��6�|���āA
(3+��3)x=10��6+��6(x/��2-10/��3-x/��6)+40��2-4x
(3+��3-��3+1+4)x=10��6-10��2+40��2
8x=(10��6+30��2)
x=5(��6+3��2)/4
=8.36516304�c�c
��5�b�i��Œ��p�ɋȂ�����5�b����10�b�܂ł̂�������60���̕����ɔ�т��ނƂ����B �O>>52
���������̉�����Ƃ̊p�x�Ŕ�т��Ď������j�����Ԃ́A
(10-x/��2)�b�B
�˂�������p�ɋȂ����Ĕ�т��ނ܂ł̎��Ԃ́A
{10-(10-x/��2)(1+1/cos��)}(1/2)
=5-(5-x/2��2)(1+1/cos��)
=-5/cos��+x/2cos�Ɓ�2+x/2��2(�b)
�����ƍŏ��̃R�[�i�[�܂ł�5�b�𑫂��Ƌ~�o���Ԃ́A
(1/sin��)(10-x/��2)-(1/2cos��)(10-x/��2)+(1/2)(10+x/��2)
��������ƁA
-1/sin�Ɓ�2+1/2cos�Ɓ�2+1/2��2=0
-2/sin��+1/cos��+1=0
-2cos��+sin��+sin��cos��=0
(2-sin��)cos��=sin��
cos��=sin��/(2-sin��)
sin^2��+{sin��/(2-sin��)}^2=1
sin^2��(2-sin��)^2+sin^2��=(2-sin��)^2
4sin^2��-4sin^3��+sin^4��+sin^2��=4-4sin^2��+sin^4��
4sin^3��-9sin^2��+4=0
sin^3��-(3sin��/2)^2+1=0
sin^3��+1=(3sin��/2)^2
3sin��/2-��(sin^3��+1)=0�ɂȂ�Ƃ�T���ƁA
��=57.465773447629���̂Ƃ��A
(3/2)(sin57.465773447629��)-��((sin57.465773447629��)^3+1)=0�ƂȂ�ɑ�l��^����B
���������̉�����57.465773447629���̕����ɔ�т��ނƍő��ŋ~�o�ł���B
�~�o���Ԃ́A
(1/sin57.465773447629��)(10-x/��2)-(1/2cos57.465773447629��)(10-x/��2)+(1/2)(10+x/��2)
=(1/sin57.465773447629��-1/2cos57.465773447629��)(10-x/��2)+(1/2)(10+x/��2)
=2.56432763+5+x(1/2��2-0.256432763/��2)
=7.56432763+0.172228045x
10��x��10��2
�~�o���Ԃ�9�b��B���܂�ɂ���������Ď����B >>18
�~�̋��ʐڐ��̕�����
��
��_�̍��W
��
�O�p�`�ɕ��������ӂ̒���
��
�w�����̌���
�͌v�Z�����G�߂��ĉ��ɂ͖������ȁB t=10�̎��_�ʼn��w���̒�����(20,0)��ʂ�X��1/��3�̒����Ƃ킩��ΊȒP�B
���W�ݒ肵�Ȃ��Ă������̒��_����x���ɐ������낵�Ē��p�ӎO�p�`�Ƒ�`�ɕ�����Α����ȎO�p�`�o�܂���(1:1:��2�̂��1:2:��3�̂�����o�Ă��Ȃ�)�̂ł���𗘗p����Β��w���ł�������B
���Ȃ݂Ɏl�p�`���ׂ�鎞�_�̎Z�o����肭�⏕�������Β��w���ł��ł���B
������ʐڐ���1m/�b�ł��ꂼ��X����3��1/��3��ۂ��Ȃ��畽�s�ړ����Ă��鎖���킩��O���ǁB �O>>54
>>57
��=60���̂Ƃ��A
����=0���A
3sin60��/2-��{sin^3(60��)+1}=0.0147020699�c�c
��0
�����w���̌X����1/��3��菭���������Ƃ킩�����By�ؕЂ��ǂ����낤�B��`����20�����Ă�B���w���ɂ͖������Ǝv���B >>58
���g���čl���ĂȂ�����킩���̂���B
>>14�̐}��x����ɒ��S������~��`����Ƃ��ǂ�ǂ��Ă�������ǂ��Ŕ��a0�ɂȂ邩�킩��ˁH���̓_��ʂ���x^2+y^2=100�ɐڂ��钼���͂��݂ɂ͂���グ�H >>58
���_�X�^�[�g�E��S�[���ɍ̂�Ή~�O�i���_���S, �E���̊p���S, �E��̊p���S�j���������ʼn������
�ӂ̔�1:2:��3�̒��p�O�p�`�ƈꎟ���������钆�w���Ȃ������ �O>>58
��=57.465773447629��
���������̉������т��ފp�x��57.465773447629���Ƃ������Ƃ́A
�Ď������ŏ��ɂ���R�[�i�[�̑Ίp�R�[�i�[����A�j���o�H�Ɉ������������A���������̉��ƂȂ��p�́A
90��-57.46773447629��=32.53226552371��
�Ίp���ƂȂ��p�́A
45��-32.53226552371��=12.46773447629��
�Ď�����10�b�߂��Ă���~�o�n�_�ɒB����܂łɉj��������t(�b)�܂��͋���t(m)�́A
(10��2-10-t)sin12.465773447629��=t
(10��2-10)sin12.465773447629��=t+tsin12.465773447629��
t=(10��2-10)sin12.465773447629��/(1+sin12.465773447629��)
=0.735371693
���B����10+t=10.735371693(�b) ���57.�d���ɂ�������Ă����i���ɓ����͏o�Ȃ��˂��B �O>>61
>>62�Ȃ��͉�����B�������ċɒl�����߂Ȃ��l�ɂ͂킩��Ȃ��B
>>54�ŋ~�o���Ԃ��������=0�̂Ƃ���=57.465773447629��
��т��ފp�x�A��т��ޒn�_�A�j�������A�~�o���ԁA���ׂċ��܂�B
60���͓�����������������B����ŋ߂��l�͏o��B���ۂɑ����̂�61���Ȃ̂�59���Ȃ̂��A�Ď����̂Ƃ����̔��f���v�Z�ŋ��߂邱�Ƃɐ��w�̈Ӗ�������Ǝv���B
57����58���͂���ł����B57.465773447629����������҂��������킢��������������B >>63
���̔����v�Z�����������Ɖ��̎v���H
>>14�̐}�̒����̍Ő�[�A�܂蒼���Ɛڂ��Ă���e�~�Ƃ��̒��S�̃v�[���T�C�h�Ƃ̂Ȃ��p�͉��x���ˁH
�Ȃ�Ő}�ɒ��������ꂽ�炻�̒����̕����������߂Ă݂悤�Ǝv���́H
�����������]�X�����ȑO�̕����܂�������_���_���Ȃ�B �O>>63
>>64
60����30����45���œ����������̂͂����Ǝv���B�ł����ǂ̓Ƃň�ʎ��𗧂ĂȂ��ᐳ�m�Ȓl���o�Ȃ��Ǝv���B
60����肿����Ƒ����^�C�~���O�Ŕ�т��ނƁA���̋������Z���Ȃ��ĉj�������͒����Ȃ�B���ǑS�̂Ƃ��ċ����͏��������Z���Ȃ邵�A���p�ɔ�т��ނ̂͂�����30���̕����ɔ�т��ނƂ��Ɠ������Ǝv��������A����Ȃ班�����߂ɔ�т��ނƑ����Ǝv�����B
���߂��������Ǝv���B
����=0�ŋɒl�����߂�ł����Ǝv���B
������ƗE�C������Δ����ł���B����Ȃɓ���Ȃ������B �C�iwolfram�搶�̍̓_�B
(0,0) ����(1,1)�܂ł����鏊�v���ԁB
���x�ōŏ����ˁH >>57
���X���肪�Ƃ��������܂��B
�b�����w�肵�ĕ`��ł���悤�Ƀv���O��������������ł�
���Ԃ��̎��̋ʐς��Z�o����v���O��������낤�Ǝv���Ă������Ǖ��G�����Ē��߂܂����B >>65
wolfram�搶�ɔ��������肢����
https://www.wolframalpha.com/input/?i=%28%28a-b+cot%28x%29%29%2F2%2Bb%2Fsin%28x%29%29%27&;lang=ja
d/dx(1/2 (a - b cot(x)) + b/sin(x)) = 1/2 b csc(x) (csc(x) - 2 cot(x))
csc(x)=1/sin(x)
cot(x)=cos(x)/sin(x)
�܂肭�����
= 1/2 b csc(x) 2/sin(x)(1/2- cos(x))
�ł���B
�C�i�N��B1/2-cos(x)�͂ǂ��ŕ������ς�邩�ˁH
57.�d�̂Ƃ��납�ˁH �O>>65
>>69�����͓������A����悭���āB
�j����l�≏�̋߂��ɂ���l�͋~�o���Ȃ��Ă����B
�܂��ł��M��Ă�l�͎��������ɂ���Ƃ킩���ĂȂ�����M��Ă�킯�����A������Ђ��ς肠���邱�Ƃ͕K�v�B
�������Ղɔ�т��ނƊĎ������M��邱�ƂɂȂ肩�˂Ȃ��B�����������Ƃ��͒��ӂ��Ȃ��ƁB
�����܂�����10�b�ł����Ǝv���B ��̍l������킩��ł���H
��w�����̖��ōŏ��l���Ƃ�p�x��60���݂����Ȃ�����"�L���p"�ɂȂ��Ă邩�ǂ����͂Ƃ������Ƃ��āA�����Ȃ��Ƃ����Ȃ��ŏ��l���g�͌v�Z�@�g��Ȃ��Ɠ����łȂ��悤�Ȓ��r���[�Ȓl�Ȃ킯�Ȃ����H �O>>70
>>71
�����̖�肩�ǂ����͒m��Ȃ��B
�ő����b�����߂悤�Ɣ������ĕ��q=0�ŋɒl�����߂��炽�܂��o���B
���̒l�ɒ[�����o���̂ňႤ�Ƃ������Ă�Ƃ������Ă��m��Ȃ��B �����́u�\�ʁv�l�^�������������߂Ɋ撣���Ă�悤�ɂ��猩����ȁB���̃R�e�B >>72
�����o�ĂȂ��B
�����Č����ΊԈ�����������o�������B
���͂�i���ɃC�i�̃��X���琳�����o�鎖�͂Ȃ��̂��낤���H �O>>72
>>75���̂Ƃ��͂킩���Ċm�M�������ď����Ă邯�ǁA���Ԃ��o�ƂȂ�̂��Ƃ��������ς�킩��Ȃ��B
�Ƃɂ��������v�l�ɂ��ǂ蒅���܂łɎ��Ԃ������邩�炿����Ƒ҂��Ăق����B
�ق�Ƃɉ����������̂��Ǝv�����炢�v�Z�ԈႢ�����Ă�\�������邵�A�t�ɂǂ����ԈႦ���܂܌v�Z�͂����Ă�\��������B �O>>77
y=-(1/��3)(x+10)+10
y=(x+10/��2)��3+10/��2
�̌�_��x���W�́A
-(1/��3)(x+10)+10=(x+10/��2)��3+10/��2
x=-5/2+5��3/2-15��2/4-5��6/4
y���W�́A
y=-(1/��3)(-5/2+5��3/2-15��2/4-5��6/4+10)+10
=15/2-5��3/2+5��6/4+5��2/4
���̌�_��ʂ�A�X�����A
(��3-1)/(��3+1)�̒����ƁAy=-x�̌�_��y���W��Y�Ƃ����B �O>>78
-x={-(��3-1)/(��3+1)}(-x-5/2+5��3/2-15��2/4-5��6/4)+15/2-5��3/2+5��6/4+5��2/4
Y={-(��3-1)/(��3+1)}(Y-5/2+5��3/2-15��2/4-5��6/4)+15/2-5��3/2+5��6/4+5��2/4
(��3+1)Y=-(��3-1)(-5/2+5��3/2-15��2/4-5��6/4)+(��3+1)(15/2-5��3/2+5��6/4+5��2/4)
2Y��3=-(4-2��3)(-5/2+5��3/2-15��2/4-5��6/4)+2(15/2-5��3/2+5��6/4+5��2/4)
Y=(-2/��3+1)(-5/2+5��3/2-15��2/4-5��6/4)+15/2��3-5/2+5��2/4+5��2/4��3
=-2/��3(-5/2+5��3/2-15��2/4-5��6/4)-5/2+5��3/2-15��2/4-5��6/4+15/2��3-5/2+5��2/4+5��2/4��3
=5/��3-5+15��2/2��3+5��2/2-5/2+5��3/2-15��2/4-5��6/4+15/2��3-5/2+5��2/4+5��2/4��3
=25��3/6-10+50��6/12
�~�o����=5+{Y+(10-Y)��3}/2
=5+{25��3/6-10+50��6/12+(10-25��3/6+10-50��6/12)��3}/2
=5+(25��3/6-10+50��6/12+20��3-25/2-50��2/4)/2
=5+(145��3/6+50��6/12-45/2-50��2/4)/2
=5+145��3/12+25��6/12-45/4-25��2/4
=145��3/12+25��6/12-25/4-25��2/4
=10.9432161�c�c(�b) 4�������E�̖��
��ӂ̒�����10m�̗����̂̃v�[���̈�̊p�ɊĎ�����u��.���̊Ď����͐����͕b��1m��,�v�[ ���̉���͕b�� 2m �ňړ�������̂Ƃ���.���̊Ď������v�[���̂ǂ��ւł����B������ɂ́C�ŒZ�ʼn��b �K�v���v�Z����. >>81
�v���O������g��ł���Ă݂��B
�Ď����̍��W��(0,0,0)�Ƃ���ƁA
> opt[1]
$par
[1] 7.691099 7.691099 7.691099
�ւ̓��B���ł����Ԃ�������A
> opt[2]
$value
[1] 13.26518
�b�ƂłĂ����B
��͐����̒B�l�̉�͉��ƈ�v���邩��҂܂̂݁B >>82
���̓_�ɓ�������ŒZ���[�g��
(1.41135,0,0) (0,1.41135,0) (0,0,1.41135)�̂����ꂩ���琅���ɓ���Ƃ������ʂɂȂ����B
�����I�ɂ͕Δ������ĉ����̂��ȁH ���_�l�Ƃ܂��܂�����Ă�ȁB
�܂��������̎����Ă����100%���M������킯�ł͂Ȃ����ǁB >>83
���ꂨ�������Ȃ��H
���̓����n�_(1.41135,0,0)���璼��y=x,z=0�ɉ��낵�������̑������������Ε����������j���������Z���Ȃ�Ȃ��H >>85
�v�[���T�C�h���炵�������ł��Ȃ��Ƃ����O��Ȃ��́H�@�v�[���̕ǂ̂ǂ̓_����ł������ł���Ƃ������ƂȂ牴�͑S���ʕ����v�Z���Ă��邱�ƂɂȂ�B
# O (O���琅�v)
# O-X(X���ォ�琅�v)
# O-X-Y(X��S�����s����Y���ォ�琅�v)
# O-X-Y-Z(X,Y��S�����s����Z���ォ�琅�v)
�Ƃ������ɂ��Ď��Ԃ��v���������ǁB �܂�A����5m�����Ă�����5m�������_����ڕW�ɂނ��ē������\�Ƃ����ݒ�ł����H >>87-88
�������ݒ��4�����Ȃ���v�[���T�C�h�͗����̂̕\�ʂł���H
�\�ʂǂ�����ł������\�ł��B >>88
�����̂̕ӂ��炵�������ł��Ȃ����̂Ƃ��ăv���O������g�̂ł�蒼���܂��B >>89
�v���O��������蒼���Ă݂��B
> opt$objective
[1] 8.327796
�b��
> opt$maximum*e
[1] 5.293786 5.293786 5.293786
�����W
�Ƃ������ʂɂȂ����B ����������W�́@(1.965991, 8.621582, 10)�ƂȂ����B �����Ⴄ�B
���̂Ƃ��Ɠ����œ����n�_����̉j���o�H�Ɠ��������ʂ̂Ȃ��p��60���ł��鎖���K�v������60���ɂȂ��Ă܂���B �����Ⴄ�B
���̂Ƃ��Ɠ����œ����n�_����̉j���o�H�Ɠ��������ʂ̂Ȃ��p��60���ł��鎖���K�v������60���ɂȂ��Ă܂���B �O>>80
>>54�̑O���ƁA
>>61�ōŏ��l�����Ă��ˁH ���Ȃ݂ɃE�\���Ǝv���Ȃ�2007 ���H�� AO�����Ō������Ă݂�Ƃ����B
�R�ق�5+10/��3�o�Ă��邩��B
���ꂾ�����Ԃ����Ă܂��_���Ȃ���������ł��傤�B �O>>96
10.7735�b���10.735�b�̂ق��������B ���Ⴀ�悩���������B
���߂łƂ��B
���Ⴀ�l�b�g���ɓ]�����Ă�͑S���Ԉ���Ă�ˁB
�����[�����B�C�i�B
���Ԃɓ]�����Ă�̏���s�����ˁB �O>>97
>>98�킸��5+10/��3-10.735371693=0.0381309989(�b)�������������ǁA���ĂĂ悩�����B�~���Ȃ������~����^�C�����Ǝv���B >>93
���肪�Ƃ��������܂��B
�����P�O�̕��ʁi�ǁj�����������ꍇ�ɂ͂����O�̕ǂ�ʂ郋�[�g�Ƃ����O�̕ǂ�ʂ郋�[�g�̓������̂��������Ă��܂����B
�������C�����Ă݂���A
> opt$objective # �ŒZ�ł��K�v�ȕb��
[1] 11.74535
�ł����Ԃ�������ʒu��
> (Scrit=opt$maximum*e) # �Œx�_�̍��WScritical = �Ίp���㋗���~�����P�ʃx�N�g��
[1] 7.466237 7.466237 7.466237
��������_�͂̂����ꂩ
(6.541114, 6.541114,10)
(10, 6.541114,6.541114)
(6.541114,10, 6.541114)
�Ƃ����������ɂȂ�܂����B
�܂��A�ʂ̃o�O�����邩������܂���B ��͉������߂悤�Ƃ��܂������A���ꂢ�ɏo�������Ȃ��̂ŁA�Ō��NSolve���g���܂����B���ʂ͎��ł��B
(x,x,0)�A���邢�́A(10,y,y)�ŁA�����ɐi�����āA(p,p,p)�@���������Ƃ��ɗv���鎞�� t�@���ő�K�v���ԁB�������A
x= 4.4181491667177352242257646161...
y= 6.5411105380457743031791097544...
p= 7.4662212132535098497019158523...
t=11.7453528906822212444517842198... >>101
�����p�x
> asin(h/r)*180/pi # ���_�l=60��
[1] 62.69019
�ɂȂ�������A���l���ł̌덷�Ȃ̂��A�v���O�����̃o�N�̉\�����\���ɂ���ȁB �œK���̃A���S���Y����Nelder-Mead�@�ɕς��Čv�Z�������Ă݂��B
> opt$objective # �ŒZ�ł��K�v�ȕb��
[1] 11.69816
> (Scrit=opt$maximum*e) # �Œx�_�̍��WScritical = �Ίp���㋗���~�����P�ʃx�N�g��
[1] 7.43622 7.43622 7.43622
> sim(opt$maximum,print=T) # �Œx�_�ɍő��œ��B����o�H��\��
Z10 Y10 X10 : 11.69816
> (Jz=c(jmpz$par,Lz)) # �����_�̖�z=10�ł̍��W
[1] 6.074329 6.855617 10.000000
���̎��̓����p�x��
> asin(h/r)*180/pi # ���_�l=60��
[1] 59.99515
���_�l�Ƌߎ������I
��́A�o��҂̉�͉��ƈ�v���Ă��邩���y���݁B >>102
���̐��l���Ɠ����p�x���҂�����U�O�x�ɂȂ�܂����B
> x= 4.4181491667177352242257646161
> p= 7.4662212132535098497019158523
> Scrit=c(p,p,p)
> h=p
> J=c(x,x,0)
> r=dit(Scrit,J,1)
> asin(h/r)*180/pi
[1] 60 >>97
��3�̏����\�����痧���̃v�[���̕��Ɉڂ��������Ȃ��́H
���ꂢ�Ȏ��ł̉��͍���Ƃ������Ƃ�����A�v�Z�����v�[���ȏ�Ɋy���߂�Ǝv�����ǁB >>105
>> > (Jz=c(jmpz$par,Lz)) # �����_�̖�z=10�ł̍��W
>> [1] 6.074329 6.855617 10.000000
����A����ȂƂ���ŁA�Ώ̐��̔j�ꂪ�A�D�D�D
�����܂����B�蔲�����ׂ��ł͂���܂���ł����B
>>102�@�͎�艺���܂��B ��L��
105 �ł͂Ȃ��A>>104�̊ԈႢ�ł��B >>107
�Ώ̐����炢����
Z=10�̕��ʂł̓����_��
�i6.074329 ,6.855617, 10)
�i6.855617, 6.074329 ,10)
�̓�����邱�ƂɂȂ�A
�ǂ�����o�R���Ă�
���v���Ԃ͓����ɂȂ�܂����i�܂��A���R�Ƃł��傤���ǁj
> f(jmpz$par[1],jmpz$par[2])
[1] 11.698156288555285
> f(jmpz$par[2],jmpz$par[1])
[1] 11.698156288555285
> ���_�l��
11.69815627019646153787418090069489267584187319472412254855
�ł��B ���Ȃ݂ɕ�������4���������Ȃ̂Ŏ�v�Z�œ����o���̂͑�ςł����Awolfram�搶�ɂ��肢����Γ�d�܂ł̍����ŏo��悤�ł��B
���������̂͊ȒP�ł��B
�ނ������̂́A�������𗧎������ŁA���̏ꍇ�Ȃ瓖����O�ŋ����Ă��炦�鎖���O�����ł͂����܂œ�����O�Ɏv���Ȃ����B
�{��ł͏��v���ԍő�ɂȂ�_��x=y=z��ɂ��鎖�������̂�������B
���̂Ƃ��뎝���Ă��@�͂��܂�������Ȃ��B �O>>99�����B
�O�X>>97
�O�X�̑O>>94
>>54�����p�x=57.465773447629���̂Ƃ����ő��Ƃ킩��A
>>61�~�o����=10�b735371693 >>111
���v���Ԃ̎���Δ������ċɒl���o���̂ł͂Ȃ��́H >>114
���v���Ԃ̂Ȃ����͍ő�l��^����_�ŕΔ����s�\�ł��B
���R�͓��̏ꍇ�Ɠ������A���̒�`��min�����邩��B
���炩�ɖ����ł���o�H�������čŒZ�o�H�ɂȂ��₪�U����A���v����=min{f1,f2,�d,f6}�̌`�ɂȂ�B
�e�X��fi�͕Δ����\�ł����A���߂�_�͂������fi�̋ɒl�ɂ��Ȃ��Ă͂��܂���B
x=y=z�ɐ������Ă��_���B
�莝���̉̕��j�Ƃ��Ă�
�E�܂��U�ɍi��B
�Ex=y=z�ɍi��B
�E������ɂȂ�B
�Emin{f1,f2}�̍ő�l�́H
�ł��B
�U�ɍi��̂͂߂�ǂ����������B
x=y=z�ɍi��Ƃ��낪�莝���̉��͂��܂��Y��łȂ��B
�ȉ��͊ȒP�B ���A�E�\�������B
�E�U�ɍi��B
�E�����Q�ɍi��B
�Ex=y=z�ɍi��
�ł����B
����Ă鎖�͓��H��̂Ɠ����B >>114
�X��f��wolfram�g���ĕΔ������悤�Ǝv���Ă������ǖ��ʂȂȁB
�m���Ɏ����̃v���O�����R�[�h�ł�min���g���Ă���B >>112
�b��͗����̂Ɉڂ��Ă����B �O>>112
>>113�����B
���ꂾ�Ǝv���I
�����p�x�ƂƊĎ������ŏ��ɂ���n�_����Ίp����ɂ���~�o�ꏊ�܂ł̋���x�Ƃ���2�̕ϐ�������B
x���ꎟ������������̂�������Ȃ��B >>81
�P�����̂���p��q��r�Ƃ�
�o�Ha: (0,0,0) -> (x,y,0) -> (p,q,r)
�o�Hb: (0,0,0) -> (0,y,z) -> (p,q,r)
�o�Hc: (0,0,0) -> (x,0,z) -> (p,q,r)
�Ƃ���Ƃ��A�o�Ha�̏��v����
t=��(x^2+y^2)/2+��((p-x)^2+(q-y)^2+r^2)
�̋ɏ��l(��t/��x=0,��t/��y=0)���v�Z�����
t=(��(p^2+q^2)+��3 r)/2,
(x/p=y/q=1-r/(��3 ��(p^2+q^2))�̂Ƃ�)
�ŁA����͌o�Ha�`c�ōł��������B
���̏��v���Ԃ�p=q=r�̂Ƃ��ő�ƂȂ�
t=((��2+��3)/2)p ----(1)
�o�Hd: (0,0,0) -> (10,y,z) -> (p,q,r)
�o�He: (0,0,0) -> (x,10,z) -> (p,q,r)
�o�Hf: (0,0,0) -> (x,y,10) -> (p,q,r)
�Ƃ���Ƃ��A�o�Ha�̏��v����
t=��((10+y)^2+z^2)/2 + ��((10-p)^2+(q-y)^2+(r-z)^2), (y<z�̂Ƃ�)
t=��(y^2+(10+z)^2)/2 + ��((10-p)^2+(q-y)^2+(r-z)^2), (y��z�̂Ƃ�)
�̋ɏ��l(��t/��x=0,��t/��y=0)���v�Z�����
t=(��3 (10-p)+��(q^2+(10+r)^2))/2,
((q-y)/y=(r-z)/(10+z)=(10-p)/(-(10-p)+��3 ��((10+q)^2+r^2))�̂Ƃ�)
�ŁA����͌o�Hd�`f�ōł��������B
���̏��v���Ԃ�p=q=r�̂Ƃ��ő�ƂȂ�
t=(��3 (10-p)+��(p^2+(10+p)^2))/2 ----(2)
(1)(2)��A��������
��(p^2+(10+p)^2)=(��2+2��3)p-10��3
�����������
p=(5/6)(15-4��6+��(249-96��6))
�̂Ƃ�
t=(5/12)(3+��6)(5��3-4��2+��(83-32��6))
=11.69815627... >>119
(1)(2)��A�������Ă̈Ӗ��������ɂ͗����ł��Ȃ������̂ŃO���t�ɂ��Ă݂܂����B
https://i.imgur.com/GG3h127.jpg wolfram��
local minimum sqrt(x^2+y^2)/2+sqrt((p-x)^2+(q-y)^2+r^2) where 0<x<10 and 0<y<10
local minimum sqrt((10+y)^2+z^2)/2 + sqrt((10-p)^2+(q-y)^2+(r-z)^2) where 0<y<10 and 0<z<10 and y<z
local minimum sqrt(y^2+(10+z)^2)/2 + sqrt((10-p)^2+(q-y)^2+(r-z)^2) where 0<y<10 and 0<z<10 and y>=z
����͂������ǁA�ǂ����肭�����Ȃ������B ���v���Ԃ�p=q=r�̂Ƃ��ő�@�Ƃ����̂����ɂ͖��炩�łȂ��̂�
���W�����ꂽ�珊�v���Ԃ��v�Z�����sim2������ăR���s���[�^�ɍő�l��T�������Ă݂��B
�T�����n�߂鏉���l�ɂ���Ď������Ȃ����Ƃ�����̂ŏ����l�𗐐����������Ď���������\������悤�ɐݒ�B
> while(opt$convergence!=0){ #�@�����l�𗐐����������Ď�������܂ŌJ��Ԃ�
+ opt=optim(par=sample(0:10,3),sim2,control = list(fnscale=-1),method='N')
+ }
> opt
$par
[1] 7.436222 7.436221 7.436221
$value
[1] 11.69816
$counts
function gradient
308 NA
$convergence
[1] 0
$message
NULL
�R���s���[�^�ł̒T���l�ł͎���������p=q=r�ɂȂ����B >>122
>���v���Ԃ�p=q=r�̂Ƃ��ő�@�Ƃ����̂����ɂ͖��炩�łȂ��̂�
p���Œ肳����q,r��p��q��r�͈̔͂œ��������Ƃ��l����B
���̂Ƃ��A���v���Ԃ�q�܂���r�̒P�������������疾�炩�B >>123
�����̂łȂ��Ē����̂̂Ƃ������v���ԍő�̓_��
���_�ƍʼn��̒��_�����Ԑ���ɂ���̂��ȁH ���l��ς���
�I�����s�b�N�T�C�Y�E�v�[��50m�~25m�̐��̓������v�[���̈�̊p�ɊĎ�����u���B
���[2.5m�Ƃ���B
���̊Ď����͐��E�L�^�ňړ�������̂Ƃ���B
���j100m���R�` 46�b91�Ő������ړ�
����100m9�b58�Ńv�[�����͂ޖʂ��v�ړ�
���̊Ď������v�[���̂ǂ��ւł����B������ɂ́C�ŒZ�ʼn��b�K�v���v�Z����B
������Ă݂����ǁA�ʼn��̒��_����Ԏ��Ԃ�������Ƃ������ʂɂȂ����̂Ŗʔ��݂��Ȃ������B
�����A���v���ԍő�_�͂��̒��_�ƌ��_�����Ԑ���ɂ���Ƃ����O��ł̃v���O�����Ȃ̂Ō��ʂɂ͎��M���Ȃ��B �������ċɒl��^����p�x�Ƌ������Ǝv����B
�^�a__`�a�P�P�a;;;;;;
�a���� �a �� �a;;;;;;
�i(-_-)�a�@�@�a;;;;;;
�i���܁܁@�@��a������
��`(_)_)��~�@�a������
�_���҃ҁ�___�a��_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_`�O>>118�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_ >>125
> ���[2.5m�Ƃ���B
���̏��H
����͂Ƃ������A�Ίp�܂ł̎��Ԃ́A
75*0.0958=7.185
�ŁA�Ⴆ�v�[���̒��S�܂ł�
(25-12.5tan(asin(9.58/46.91)))*0.0958+12.5cos(asin(9.58/46.91))*0.4691��7.88
����Ȃ��́H
> ���v���ԍő�_�͂��̒��_�ƌ��_�����Ԑ���ɂ���Ƃ����O��
����ȍ����͂Ȃ��A�Ƃ������ԈႢ���낤
�ς��ƍl������̂��A�Ίp��2�������オ�l���t�����A������̗p����ɂ����������� ����̑��x��v�A�����̑��x��w�Ƃ��Am=w/��(v^2-w^2)�Ƃ���B
�v�[����0<x<a�A0<y<b�Ƃ���B
��y=0�����������t�b��ɓ��B�ł���̈��mx+y��mvt�A
��x=0�����������t�b��ɓ��B�ł���̈��my+x��mvt�A
��y=b�����������t�b��ɓ��B�ł���̈��-y+mx��-b+mvt�A
��x=a�����������t�b��ɓ��B�ł���̈��-x+my��-a+mvt
�ł���B
������
mx+y=mvt�d�@�Amy+x=mvt�d�A�A
-y+mx=-b+mvt�d�B�A-x+my��-a+mvt�d�C
�ɂ�����
�@�B�C��A�����ē�����t��t1�A
�A�C�B��A�����ē�����t��t2�Ƃ���Γ��B�����̍ő�l��min{t1,t2}�ł���B �O>>126
>>54�C���B
���������̉�����Ƃ̊p�x�Ŕ�т��Ď������j�����Ԃ́A
(10-x/��2)/sin��(�b)
�\�L�~�X���������B�v�Z���Ԉ���ĂȂ���������ǁB >>127
z�������邩�琅�[�͕K�v�B >>123
�o�H a ��t ��q�ŕΔ��������
(q - y)/��((p - x)^2 + (q - y)^2 + r^2)
�������ƌ�����낤���H >>131
����������Ȃ��āAt�̋ɏ��l�̂ق�
t=(��(p^2+q^2)+��3 r)/2,
����͖��炩��q�܂���r�̑����� >>127
���̂��ƕ��G�ɂȂ�̂ŕ��ʂōl����
���Q�O���c�P�O���̃v�[���ŗ��㑬�x���b�Q���A�������x���b�P���łP�T�D�T�b�œ��B�ł���͈͂�`�悵�Ă݂܂����B
https://i.imgur.com/xZrdUpX.jpg
���w�E�̒ʂ�A�Ίp����ɏ��v���B���ԍő�_������Ƃ����̂͊ԈႢ�ł���Ɗm�F�ł��܂����B >>133
�����܂���A�v���O�����Ƀo�O�������̂œP�܂��Bm(__)m �C�Â����o�O���C�����Ē����`�v�[���ŕ`�悵�܂����B
�Ίp���ƑΊp���������킹�ĕ`�悵�܂����B
���Q�O���c�R�O���̃v�[���ŗ��㑬�x���b�Q���A�������x���b�P���łQ�U�b�œ��B�ł���͈�
https://i.imgur.com/vfPdQff.jpg
���R�O���c�Q�O���̃v�[���ŗ��㑬�x���b�Q���A�������x���b�P���łQ�U�b�œ��B�ł���͈�
https://i.imgur.com/WS21BMz.jpg
>127�̒����ʂ�A�Ίp�̂Q��������ɏ��v���ԍŒ��_���ʒu����悤�ł��B >>132
���X���肪�Ƃ��������܂��B
���@�̂Ȃ̂�p��q��r�Ƃ������肪�������Ƃ������ƂƗ������܂����B >81�̖��𗧕��̂��璼���̂Ɋg�����čl���Ă݂��B
�I�����s�b�N�T�C�Y�E�v�[��50m�~25m�Ő��[2.5m�̐��̓����������̃v�[���̈�̊p�ɊĎ�����u���B
���̊Ď����͐��E�L�^�Œ����̖̂ʏ�␅�����ړ�������̂Ƃ���B
���j100m���R�` 46�b91�Ő������ړ�
����100m9�b58�Ńv�[�����͂ޖʂ��v�ړ�
���̊Ď������v�[���̂ǂ��ւł����B������ɂ́C�ŒZ�ʼn��b�K�v���v�Z����B
�����̂łȂ��Ē����̂̂Ƃ��ɂ́A���v���ԍő�̓_�͌��_�ƍʼn��̒��_�����Ԑ���ɂ͂Ȃ��A�Ƃ������Ƃ������Ă����������̂Ńv���O������g�ݒ������B
���v���ԍő�_�̍��W
par
[1] 49.980916 24.788643 2.288643
���v����
$value
[1] 5.552414
�Ƃ������l���łĂ����B �T�������l�ݒ�ɂ��A���ʂ��������
�����h�ӌ�(�H�j��
> opt
$par
[1] 49.06521 23.86881 1.36881
$value
[1] 5.855706
$counts
function gradient
256 NA
$convergence
[1] 0
$message
NULL
�ɂȂ����B
�m���ɁA���̕������B���Ԃ������B >>128
�B�C�̌�_�����_(a,b)�ɂ���p�̓�����l�Ȃ̂�t1�ł̇@�B�C�̌�_��t2�ł̇A�B�C�̌�_��l��B
�悭�悭�l������t1=t2�������B >>139
�E�\�������B
a,b�̑召��t1,t2�̑召�͈�v����ł����B �O>>129���(�O�X��760)
���������̉�����Ƃ̊p�x�Ŕ�т��Ď������j�����Ԃ́A
(10-x/��2)/sin��(�b)
�˂�������p�ɋȂ����Ĕ�т��ނ܂ł̎��Ԃ́A
{10-(10-x/��2)(1+1/cos��)}(1/2)
=5-(5-x/2��2)(1+1/cos��)
=-5/cos��+x/2cos�Ɓ�2+x/2��2(�b)
�����ƍŏ��̃R�[�i�[�܂ł�5�b�𑫂��Ƌ~�o���Ԃ́A
(1/sin��)(10-x/��2)-(1/2cos��)(10-x/��2)+(1/2)(10+x/��2)
��������ƁA
-1/sin�Ɓ�2+1/2cos�Ɓ�2+1/2��2=0
-2/sin��+1/cos��+1=0
-2cos��+sin��+sin��cos��=0
(2-sin��)cos��=sin��
cos��=sin��/(2-sin��)
sin^2��+{sin��/(2-sin��)}^2=1
sin^2��(2-sin��)^2+sin^2��=(2-sin��)^2
4sin^2��-4sin^3��+sin^4��+sin^2��=4-4sin^2��+sin^4��
4sin^3��-9sin^2��+4=0
sin^3��-(3sin��/2)^2+1=0
sin^3��+1=(3sin��/2)^2
3sin��/2-��(sin^3��+1)=0�ɂȂ�Ƃ�T���ƁA
��=57.465773447629���̂Ƃ��A
(3/2)(sin57.465773447629��)-��((sin57.465773447629��)^3+1)=0�ƂȂ�ɏ��l��^����B
���Ȃ킿���������̉�����57.465773447629���̕����ɔ�т��ނƍő��ŋ~�o�ł���B
�Ď������ŏ��ɂ���R�[�i�[�̑Ίp�R�[�i�[����A�j���o�H�Ɉ������������A���������̉��ƂȂ��p�́A
90��-57.46773447629��=32.53226552371��
�Ίp���ƂȂ��p�́A
45��-32.53226552371��=12.46773447629��
�Ď�����10�b�߂��Ă���~�o�n�_�ɒB����܂łɉj��������t(�b)�܂��͋���t(m)�́A
(10��2-10-t)sin12.465773447629��=t
(10��2-10)sin12.465773447629��=t+tsin12.465773447629��
t=(10��2-10)sin12.465773447629��/(1+sin12.465773447629��)
=0.735371693
���B����10+t=10.735371693(�b) x�Ŕ������Ă��ꂪ0�ɂȂ�ƒT���Ăǁ[�����H
�����̈Ӗ����܂�ŕ������ĂȂ��B
���LjӖ����킩�炸���������o�����炢���Ǝv���Ă邩�����O�i���Ȃ��B �O>>141���(�O�X��760)�čl�@�B
�~�o����ʼn����n�_�͊Ď������ŏ��ɂ���ʒu����Ίp����x(m)�ɂ���ƌ��āA���������̉�����Ƃ̊p�x�Ŕ�т��Ď������j�����Ԃ́A
(10-x/��2)/sin��(�b)
�˂�������p�ɋȂ����Ĕ�т��ނ܂ł̎��Ԃ́A
{10-(10-x/��2)(1+1/cos��)}(1/2)
=5-(5-x/2��2)(1+1/cos��)
=-5/cos��+x/2cos�Ɓ�2+x/2��2(�b)
�����ƍŏ��̃R�[�i�[�܂ł�5�b�𑫂��Ƌ~�o���Ԃ́A
(1/sin��)(10-x/��2)-(1/2cos��)(10-x/��2)+(1/2)(10+x/��2)
x�Ŕ������A
-1/sin�Ɓ�2+1/2cos�Ɓ�2+1/2��2=0�Ƃ���ƁA
-2/sin��+1/cos��+1=0
-2cos��+sin��+sin��cos��=0
(2-sin��)cos��=sin��
cos��=sin��/(2-sin��)
sin^2��+{sin��/(2-sin��)}^2=1
sin^2��(2-sin��)^2+sin^2��=(2-sin��)^2
4sin^2��-4sin^3��+sin^4��+sin^2��=4-4sin^2��+sin^4��
4sin^3��-9sin^2��+4=0
sin^3��-(3sin��/2)^2+1=0
sin^3��+1=(3sin��/2)^2
3sin��/2-��(sin^3��+1)=0�ɂȂ�Ƃ�T���ƁA
��=57.465773447629���̂Ƃ��A
(3/2)(sin57.465773447629��)-��{(sin57.465773447629��)^3+1}=0�ƂȂ�ɏ��l��^����B
���Ȃ킿���������̉�����57.465773447629���̕����ɔ�т��ނƍő��ŋ~�o�ł���B
�Ď������ŏ��ɂ���R�[�i�[�̑Ίp�R�[�i�[����A�j���o�H�Ɉ������������A���������̉��ƂȂ��p�́A
90��-57.46773447629��=32.53226552371��
�Ίp���ƂȂ��p�́A
45��-32.53226552371��=12.46773447629��
�Ď�����10�b�߂��Ă���~�o�n�_�ɒB����܂łɉj��������t(�b)�܂��͋���t(m)�́A
(10��2-10-t)sin12.465773447629��=t
(10��2-10)sin12.465773447629��=t+tsin12.465773447629��
t=(10��2-10)sin12.465773447629��/(1+sin12.465773447629��)
=0.735371693
���B����10+t=10.735371693(�b) >>143
���O�̃��X�ǂ�ł邩�H
x�Ŕ������Ă��ꂪ0�ɂȂ�Ƃ��닁�߂Ăǁ[�����H
����ʼn��ŏ��v���Ԃ��ŏ��ɂȂ�Ƃ�������́H
�����Ƃ����̂������H
����ʼn��̍ŏ��l�����܂�̂��Ƃ���������O�̗������������ĂȂ����瓚�����Ȃ���B
���x�����������H
x�Ŕ��������B
��0�Ƃ��ăƂɂ��ĉ������B
����H�Ȃ�ŃR���œ�������������H�Ǝ����ɖ₢�����Ă݂Ȃ��́H �O>>143
>>144�O�X��760��������A�Ȃ�œ������݂��邩���������Ƃ͖���ĂȂ��B
�����ŒZ�ƂȂ鎞�Ԃ��v�Z����Ƃ���B
������v�Z�����B����Ȃ��BAO�������ĂȂH�@�Ǝv���Ē��ׂ���A�_���݂����������B�����͂�������Ȃ�����������Ȃ����Ǝv�Č������v�Z����p�������߂��Ă��Ȃ����Ǝv���B
�Ȃ��x�Ŕ������ē������݂��邩�m�肽���C�����邵�A�ׂɒm�肽���Ȃ��C������B
�����p�x��60���̂Ƃ����v�Z�����B60���̂Ƃ��͌v�Z���₷�����ǍŒZ�łƂ������Ƃł͊p�x���Â��Ǝv�����B >>145
�Ȃ�œ����������ł��Ƃ܂邩�����Ƃ����ĂȂ����珑���Ȃ��Ă����A�������ĂȂ��Ă������Ďv���Ă邩�炢�܂Ōo���Ă��f�L�t��悤�ɂ����Ȃ�Ȃ���B
�v�Č������ĂȂ�Ŕ��������瓚�����킩��Ƃ������͎v�Ă����́H
���ĂȂ���ˁH
�ȁ[��ɂ��l���ĂȂ���ˁH
�Ȃ�ƂȂ��ŏ��l���߂鎞�͔����B
�ł��ƂŔ����Ȃ�Ăł��Ȃ��B
��[��x�Ŕ������Ă݂悤�I
�����ł����B
60�����ۂ����I
�����Ƃ݂�Ȃ̓�����萳�m�ȃn�Y���I
�J�b�R�����I�I���I
�d�d
���������͎̂v�ĂƂ͂����B >>81�ł��B>>119����̉��قڗp�ӂ��Ă��ł��B
�ЂƂ����R�����g�B
���Ƃ��Όo�Ha: (0,0,0) -> (x,y,0) -> (p,q,r)�ɂ�����(x,y,0)�ɂ��Ă̋ɏ��l�̏o�����Ȃ̂ł����A
����͋�����d(A,P)��P�ɂ��Ă̑S������
d d(A,P)=e(A,P) dP (e(A,P)��AP�x�N�g���Ɠ��������̒P�ʃx�N�g���A�ȉ������j
�ɂȂ邱�Ƃ�p����ƈӖ����͂����肵�܂��B
���̎��̏��v����T��(p,q,r)��A�Ƃ����ė���̑��x��v�A�����̑��x��w�Ƃ���
T = d(O,P)/v + d(A,P)/w
�Ȃ̂�
dT = (e(O,P)/v + e(A,P)/w)dP
�ƂȂ�܂��B
���ꂪ�C�ӂ�z=�O����dP�ɂ���0�ɂȂ�̂�e(OP)/v + e(A,P)/w��xy���ʂ̖@���x�N�g���ƕ��s�ɂȂ�Ƃ��ŁA
���Ȃ킿e(OP)/v + e(A,P)/w��xy���ʂւ̎ˉe��0�ɂȂ�Ƃ��ł��B
�����Axy���畽�ʂւ��낵�������̑�H��OP�̊O���_�ł���A
����e(A,P)��xy���ʂ֎ˉe�������̂̒�����w/v=1/2�ƂȂ�Ƃ��A���Ȃ킿��APH��60���ƂȂ�Ƃ��ł��B
����Ă��̏ꍇP��H����O�̕�����PH/��3�����ړ������_�Ȃ̂�
f1(p,q,r)=(��(p^2+q^2)-r/��3)/2 + 2r/��3/1 = ��(p^2+q^2)/2 + ��3/2r
���o�Ha�̋ɏ��l�ł��B
�o�Hb,c�͕�������ւ��邾���A�o�Hd�ɂ��Ă͓��l�ɍl����
f4(p,q,r)=��((10+q)^2+r^2)/2 + ��3/2(10-p)
�ƂȂ�܂��B �O>>145
>>146������������B
���ꂵ���Ȃ��B
60���̂Ƃ����l����̂͂���ł�����B���ǂ��̂܂ܓ�����60���̂Ƃ��Ƃ���͍̂��Z���܂ŁB
��l�͍��������������B
60���̂Ƃ�����Ȃ��A�Ǝv���ăƂƒu�����킯�ŁA�ꂵ��Ŕ������邽�߂ɒu������Ȃ��B
���m��x�̕�������������ċɒl��^����p�x�Ƃ��o������60���ɂȂ��肿����Ǝ�O�œ��������炢���Ƃ킩�����B���Ȃ��B >>148
������Ɗm�F�����ė~�����B
> ���m��x�̕�������������ċɒl��^����p�x�Ƃ��o������60���ɂȂ��肿����Ǝ�O�œ��������炢���Ƃ킩�����B���Ȃ��B
�R���͖{�C�ŏ����Ă�̂��A����Ƃ��R�R�ň������������烌�X�o�ɕ����邩��Ԉ���Ă�̏��m�łނ肭�艟���ʂ��Ă�낤�ƍl���Ă�̂��ǂ����H
����������x�Ŕ������Ă������Ɩ{�C�Ŏv���Ă��H
x�Ŕ������悤���ƂŔ������悤���D���ȕ��Ŕ������Ă����Ɩ{�C�Ŏv���Ă�́H �O>>148
>>149�ǂ�����ĉ������H�@�Ǝv���ĉ����Ȃ������牽�x����Ă������Ȃ��āA�v�Z�ԈႢ���Ȃ��Ǝv���Ă�����߂������B
�v�Z�ԈႢ����Ȃ�x�Ŕ������ċɏ��l��^����p�x�Ƃ��o�����Ƃ킩�����B
��x�͂�낤�Ƃ���x�ƃƂ̗����Ŕ�������Ƃǂ��Ȃ邩�A�܂��ƂŔ�������Ƃǂ��Ȃ邩�A���Ђ���Ă݂Ăق����B
x�Ŕ������ċɏ��l��^����p�x�Ƃ��o���ċ~�o���Ԃ��o�����̂͂܂����������Ǝv���B���̂Ƃ��됳�������ǂ�����ׂ���̂��Ȃ��B�Ȃ����݂�ȎO�����������Ƃ������Đ������Ă��܂��āA���l���ɂ��銴���B�����p�x��=60���̂Ƃ���葬�����Ƃ͒��ׂ��B >>150
������x�Ŕ������Ă������������͂łȂ��Ɖ��x���w�E���Ă邶���H
�����p��60���łȂ��o�H�͍ŏ��ɂ͂Ȃ蓾�܂���B
�����{�C�ŏo�Ă铚��5+10/��3��菬�����������o���ƌ�������Ȃ���o�̓����̍ŏ����B���Ԃ��ő�ɂȂ�_
(5(1+1/��3),5(1+1/��3))
=(7.886751345948, 7.886751345948)
��
5+10/��3 = 10.773502691896
����ɓ��B�ł���o�H�����Ȃ��ƃ_���B
�킩��H�����H
�v�����x=x.xxx�d�̒n�_�������������10.77350�d��葁�����B�ł���Ƃ���x.xxx�d����ł�����������B
�܂�����Ă����Ȃ����ȁB >>148
�тԂ�̂��Ƃ͂тԂ�ł��A�Ƃ������ؒ厡��z���o������B 7.886751345948/sin(57.465773447629deg)+7.886751345948(1-1/tan(57.465773447629deg))/2
=
10.7826518083
(10-7.886751345948)/sin(57.465773447629deg)+(10-(10-7.886751345948)(1+1/tan(57.465773447629deg)))/2+5
=
10.7759541902
������̌o�H�ł� 10.773502691896�b���O�ɓ��B�ł��Ȃ��B �O>>150
>>61���B����10+t=10.735371693(�b)
��10.7735�c�c
�����p�x��(��)�A���B����10+t(�b)�A���Ƃ̈́����B
>>151�����n�_�́A
�������肩��̋����A
10-(10-x/��2)(1+cos��/sin��)�ɁA
��=57.465773447629���ƁA
x��������Ƃ킩��B
x�͓��B���ԁA
5+{10-(10-x/��2)(1+cos��/sin��)}(1/2)+(10-x/��2)(1/sin��)=10.735371693�Ƀ�=57.465773447629���������A
5+5-(5-x/2��2)(1+cos57.465773447629��/sin57.465773447629��)+(10-x/��2)(1/sin57.465773447629��)=10.735371693
=5+x/2��2+(x/2��2)(0.637910393)-5(0.637910393)+(10-x/��2)(1/sin57.465773447629��)=10.735371693
���߂�x��������Ɠ����n�_���킩��͂��B ���������Ă鎖�S���������ĂȂ��B
�^���̃o�J�ȂȁB wolfram�Ɂ�t/��x=0, ��t/��y=0�������Ă��炨����
x/(2 Sqrt[x^2 + y^2]) + (-p + x)/Sqrt[r^2 + (-p + x)^2 + (-q + y)^2]=0
y/(2 Sqrt[x^2 + y^2]) + (-q + y)/Sqrt[r^2 + (-p + x)^2 + (-q + y)^2]=0
����͂����
r = -(1.73205 sqrt(p^2 + q^2) (p - x))/p, y = (q x)/p�ƕԂ��Ă���x,y�ɂ��ĉ����Ă��炦�Ȃ������B xy���ʂɂ����āAx����̐��̕����̂݁A���x v�A���̑��̗̈�͑��x 1�@�ňړ��ł�����̂Ƃ���B
���_�ɂ���l�����A�ڕW�n�_(cos��,sin��)�@�ɓ��B���ׂ��A�ړ�����B
���̎��A���Z���ԂŖڕW�n�_�ɓ��B����ɂ́A���̐헪���ƃ��A�ǂ��炪�L�������l����B
�헪���F���n�_����A���ږڕW�n�_�̕����֑��x 1 �ňړ�����B
�헪���Fx���ɉ����đ��x v �ňړ�����B
�� �𐳂̏����ȗʂƂ���B�헪�����邢�̓�����Ĉړ����J�n���A�Â̎��Ԃ����������̂��ꂼ��̓��B�n�_��A,B�Ƃ����
A(��cos��,��sin��)�AB(v��,0)
�ڕW�n�_�܂ł̋����́A���ꂼ��A1-�ÁA��((v��-cos��)^2+sin^2��)�@�ƂȂ邪�A���āA�ǂ��炪���������H
��悵�����̓��m�̍����Ƃ��Ĕ�ׂĂ݂�ƁA
(1-��)^2-((v��-cos��)^2+sin^2��) = 1-2��+��^2 -v^2��^2+2v��cos��-1 = ��(2v cos��-2)+(1-v^2)��^2
�Â͏����Ȑ��̗ʂƂ��Ă���̂ŁA�̍�������ƁAcos�Ɓ�1/v�@�Ł@
1-�Á���((v��-cos��)^2+sin^2��) �ƂȂ�B
�܂�A�ړI�n�Ƃ̕����̂��ꂪ�Ƃ�����̂́Av �{�̑��x�ňړ��ł���Ƃ��A�@cos�Ɓ�1/v�@��
�������Ȃ�A���̃R�[�X�͒��ږړI�n�Ɍ��������L���ł���@�Ƃ���B
���̌��_�́A�Ƃ�v�݂̂��֗^���A���̎����ɂ��K�p�B �Ɠ����ɁA���̗ނ��̖��ɑ��A���̐헪���ő��ł��邱�Ƃ������B
���ݒn����ڕW�n�_�ւ̃x�N�g���A���邢�́A���̕����ւ̒P�ʃx�N�g���������A
�I���\�Ȃ������̑��x�x�N�g���������^����ꂽ��A
���ρ@�����E�����@���ő�ɂȂ鑬�x�x�N�g�������@�ɉ����R�[�X�����ő��R�[�X�ł���B
���̐헪�ɏ]���āA�l�����v�[���̖����l����Ȃ�A�����͕K�v�Ȃ��Ȃ�B
�i���̐헪�̔w�i�́A�����̍l�������̂��̂ł��邪�A���_�݂̂𗘗p����Ȃ�A�����͕s�g�p�j
�ړI�n���A(p,q,r) �������A�Ώ̐�����@p��q��r�@�Ƃ��čl����B
���̕����ւ̒P�ʃx�N�g����(p/D,q/D,r/D)�@�A���AD=��(p^2+q^2+r^2)
���ڂ��̕����������ꍇ�A���x�x�N�g����(p/D,q/D,r/D)�Ȃ̂ŁA���ς́A1
����i�ޏꍇ�́A�O�̕��ʂ̓��ǂꂩ�Bp��q��r�@�Ƃ��������ł́A����z=0�@��ɁA�œK�R�[�X�����݂��A
����́A(2p/d,2q/d,0)�@�A���Ad=��(p^2+q^2)
���� t �܂ŁA�ړ������Ƃ��A(2pt/d,2qt/d,0)�Ɉړ����Ă���̂ŁA�ړI�n�ւ̃x�N�g���́@(p-2pt/d,q-2qt/d,r)
���x�x�N�g����(2p/d,2q/d,0)�ł���A���̎��A���̗��҂̊p�x����/3���Ƃ����������������ƁA
t=(1/2)d�}((��3)/6)r�@��������B�}�C�i�X�̕��������Đ�������ƁA�c��̋�����((2��3)/3)r�ŁA
�g�[�^���@(1/2)d-((��3)/6)r+((2��3)/3)r=(1/2){��(p^2+q^2)+(��3)r}�@�̎��Ԃ������� �ȏ�́A���������́u���v�𗘗p���Ȃ��ꍇ�̍ő��R�[�X�ɂ��Ă̋c�_�B
���������̉��𗘗p����ꍇ�́A�܂��́A����x=10�։��낵�����̑��̍��W�A(10,q,r)�������R�[�X���l����B
�����̂̕\�ʂ����ړ��ł��Ȃ��̂ŁA�W�J�}��ōl���邱�ƂɂȂ邪�A���p������2�ӂ�10+r��q�ł��钼�p�O�p�`��
�Εӏ�ɂ�����R�[�X��H��Ȃ���A���������̕��ʂɓ��B�����Ƃ��ɁA(p,q,r)��ڎw�����ƂɂȂ�B
����́A�����ɍL����v�[���A�������A�O�̕���x=0�Ay=0�Az=0�ゾ���́A
���x2�ŕ�����Ƃ��������ŁA(10+r,q,10-p)��ڕW�ɂ���̂Ɠ������ɂȂ�B
�����l����ƁA��قǂ̌��ʂ����̂܂g���āA���̃R�[�X���Ƃ����ꍇ�̃g�[�^�����Ԃ́A
(1/2){��((10+r)^2+q^2)+(��3)(10-p)}
�ł����Ԃ�������n�_�̍��W�ɂ́A(1/2){��(p^2+q^2)+(��3)r}=(1/2){��((10+r)^2+q^2)+(��3)(10-p)}
�Ƃ��������������B�ʓ|�ɂȂ��Ă����̂ŁA�ׂ������Ƃ͏ȗ����邪�A��̎��ŁAp=q=r�Ƃ���
�������������ƁAp=q=r=(5/6)(15-4��6+��(249-96��6))
�i����́A>>119����̌��ʂƈ�v�j
�Ō�[�ǂ������A�ȏ�́A�������g��Ȃ����@�ł���B �O>>154�v�Z�̂Â��B
5+x/2��2+(x/2��2)(0.637910393)-5(0.637910393)+(10-x/��2)(1/sin57.465773447629��)=10.735371693
x=(5-3.189557196+11.8614066-10.735371693)/(0.838728105-0.353553391-0.225535382)
=11.309854(m)�����~�o�n�_�܂ł̒�������
�������肩������n�_�܂ł̋����́A
10-(10-x/��2)(1+cos��/sin��)=10-(10-11.309854/��2)(1+0.637910393)
=6.71971502(m) (7.886751345948,7.886751345948)��10.773502691896�b�ȓ��ɓ��B�ł���n�_��T���ƌ�����7.886751345948�̑S���o�Ă��Ȃ����𗧂Ă�̂͂ǂ��������̍\�����Ă�́H >>158
p��q��r�@�Ƃ��������ł́A����z=0�@��ɁA�œK�R�[�X�����݂��A
�܂ł͗����ł���̂ł����A
��������_�̍��W��
�@(2p/d,2q/d,0)�@�A���Ad=��(p^2+q^2)
���œK�Ƃ͂ǂ����ĕ�����̂ł��傤���H �O>>160
>>161
�~�o�n�_�܂ʼn����ق��̉�����̋����́A
11.309854/��2=7.99727446(m)
�}��`����8m���炢���Ȃ��Ǝv���Ă����炢���l���Ǝv�����B
7.88�c�c���Ɠ����p�x�������n�_���ς��Ǝv���B
7.88�c�c���ǂ�����ďo���l������ˁB
x�ƃƂ𗼕��Ƃ��������邩�A�ƂŔ������āA
x/��2=7.88�c�c���Ă��ƂȂ�A���邢�͂��肤�邩���B��邢�l����Ȃ��B >>143
�܂�����������}�W���ɂ����ނ�
>�����ƍŏ��̃R�[�i�[�܂ł�5�b�𑫂��Ƌ~�o���Ԃ́A
(1/sin��)(10-x/��2)-(1/2cos��)(10-x/��2)+(1/2)(10+x/��2)
x�Ŕ������A
-1/sin�Ɓ�2+1/2cos�Ɓ�2+1/2��2=0�Ƃ���ƁA
x�Ŕ������Ă��ꂪ0�ɂȂ�ƂƂ͂܂蓞�B�n�_(x,x)���ǂ��ɂ��낤�Ɠ��B���Ԃ����ł���悤�ȃƂ�T���Ă��鎖�ɂȂ�B
����Ȓn�_�͑��݂��Ȃ�������wolfram��搶�ɃO���t�����Ă�����Ă�����ȃƂ͑��݂��ĂȂ��B
https://www.wolframalpha.com/input/?i=-1%2Fsin%28x%29%2Bcos%28x%29%2B1%2F2%3D0&;lang=ja
�ɂ�������炸�ǂ����炩�R������
��=57.46773447629
�Ȃ��̐��l���o���B
�����Ă��̓�̐��l�����ɂ������B���Ԃ̍ő�l���o���āA���ꂪ���o�̐��l��菬����������o�̒l�͊Ԉ���Ă�Ƒ������Ă�B
�����Ă���������o�̍ő�n�_
(7.886751345948, 7.886751345948)
�Ɋ��o�̍ŏ��l10.773502691896��葁�����B�ł���o�H�����Ă݂�Ƃ����ƁA����7.886751345948���S���o�Ă��Ȃ����𗧎�����10.773502691896��菬�����ƌ����ē��ӊ�B
�o�J���̎����̌����Ⴄ�B >>162
>> ��������_�̍��W��
>> �@(2p/d,2q/d,0)�@�A���Ad=��(p^2+q^2)
>> ���œK�Ƃ͂ǂ����ĕ�����̂ł��傤���H
�Ȃ�قǁA����킵�������������Ă��܂����悤�ł��B�\����܂���B
(2p/d,2q/d,0)�@�Ƃ����̂́A�����n�_�ł͂Ȃ��A���x�x�N�g���ł��B
���_����A���̕����ɁA����0�@����@�����@t�@�܂ňړ�����ƁA
(2pt/d,2qt/d,0)
�ɓ���܂��B���̒n�_����A�ړI�n���݂�ƁA(p-2pt/d,q-2qt/d,r)�Ƃ��������ɂ���܂��B
���̂܂܁A���̑��x���ێ������܂܁A�i�����������A�헪�������烿�ɐ�ւ��������悢���A
���̔���ɗp����̂��A
�ucos�Ɓ�1/v�v
�Ƃ������ł��B
���̎����s�����ɂȂ鎞�������߂邽�߂́A��������
((p-2pt/d,q-2qt/d,r),(2p/d,2q/d,0))�@=(1/2)*|(p-2pt/d,q-2qt/d,r)|*|(2p/d,2q/d,0)|
�ł��B�i���ӂ͓��ς̎��ł���A�E�ӂ́A�x�N�g���̑傫���̐ς�cos(��/3)�ō\������Ă��܂��B�j
�����ŋ��܂����������A(2pt/d,2qt/d,0)�@�ɑ������ƁA�����n�_���킩��܂��B >>143�ŋ~�o�܂łɍł���������
> ���B����10+t=10.735371693(�b)
��������A�ƌ����Ă���_�̍��W�͂ǂ��Ȃ�H
�܂��A�ǂ����낤��
> ��=57.465773447629���̂Ƃ��A
�̊p�x�ōs�����Z���Ԃ̃R�[�X�͂���킯���� �O>>163
>>166�~�o�n�_�܂ʼn����ق��̉�����̋����́A
11.309854/��2=7.99727446(m)
�~�o�n�_�����W�ł����ƁA�ŏ��ɊĎ���������n�_�����_(0,0)�A�������������y�����Ƃ�A
-x�̕����ɒ��p�ɋȂ�����y������6.71971502m�̒n�_����A
��=57.7465773447629���̕����ɓ������āA���_���o�Ă���A10.735371693�b��ɁA
(x,y)=(-7.99727446,7.99727446)�ɓ��B����B >>167
> ��=57.7465773447629���̕����ɓ������āA���_���o�Ă���A10.735371693�b��ɁA
> (x,y)=(-7.99727446,7.99727446)�ɓ��B����B
���Ⴀ����(7.99727446, 7.99727446)�̒n�_��60���Ō����ޓ_
(10, 6.841000330368)
����������ĉ��b�����邩�����ƌv�Z���Ă݂����ˁH
���̐��l��10.735371693���傫�����ˁH
��������������O�̊m���߂�������Ȃ�����_���_���Ȃ�B >>167
���W
> (x,y)=(-7.99727446,7.99727446)�ɓ��B����B
�܂ł̍ŒZ���Ԃ�
(10+7.99727446-(10-7.99727446)cot(��/3))/2+(10-7.99727446)/sin(��/3)/1��7.3305
�ɂȂ�A�A
(10+7.99727446-(10-7.99727446)cot(��))/2+(10-7.99727446)/sin(��)/1
��=57.7465773447629��
��
> 10.735371693�b
���Z���� �O>>167
>>168��T�ی��ɂ͐����Ȃ��Ƃ����ݒ�ł��B
�ő��ɂȂ�p�x��T������łق��̊p�x��60����90����45�����炢�B
�����n�_�����߂Ă���p�x�����߂���Ȃ��A�������Ċp�x�����܂��Ă�������n�_���v�Z�����B >>170
���������Ă܂��������Ă邩�����ł��ĂȂ��́H
�ǂ��܂œ������́H
�݂�Ȃ�60���œ������ő��ł��闝�R�����ꂾ�����ς��i��ς������ȕ��@�Ŏ����Ă���ˁH
���̂ǂ��Ƃ��ė����ł��Ȃ������Ƃ��Ă��A�����Ď�����60���ȊO�̊p�ł�葁���o�H���݂����Ƃ��Ă��A�Œ���܂��������������n�_�ɍő��ł�������@�����̊p�x�Ȃ̂��m���߂Ă݂�ƌ����Ă��B
�Ȃ�ł���ȊȒP�Ȃ��Ƃ��킩���H
����肻��Ȏ��܂������Ŏv�����Ȃ��́H
�N�̂��̃A�|���X���ǂ��X���̗��ꗐ���Ă邩��킩���́H
���̃A�|���X���܂ő������H
�����o����B �O>>170
��茩�čŏ��Ɏv�������̂�������60���������B
���Ɛ����ő�����2:1������B
���̒����͐������Ǝv���Ă����ǁA�������ă�=57.465773447629���Əo�āA���B���Ԃ��v�Z�����B�܂����̒i�K�Ŕ��M���^�B
�ނ���60���̂Ƃ��v�Z������10�b735�邮�炢�����͂��Ǝv���Čv�Z������A
10�b9�c�c���ďo�āA����!?�@���Ăт����肵���B
��=57.465773447629���̂ق�����=60���̂Ƃ����R���}2�b���������B
���͌��ʂ�����Ă�i�K�B >>165
������肪�Ƃ��������܂����B
�Ō�̕�������Wolfram�ɉ����Ă��������
�l�ԋZ�ł͈��������ɂȂ����ɂȂ�܂����B
Solve[{p - 2 p (x/d), q - 2 q (x/d), r} . {2 (p/d), 2 (q/d), 0} == Norm[{p - 2 p (x/d), q - 2 q (x/d), r}] (Norm[{2 (p/d), 2 (q/d), 0}]/2), x, MaxExtraConditions -> Automatic]
x = (d^3 p^2 (q/d)^2 + d^3 p^2 (p/d)^2 + d^3 q^2 (p/d)^2 + d^3 q^2 (q/d)^2 - sqrt(-d^6 p^2 (r)^2 (q/d)^4 - 2 d^6 p^2 (r)^2 (p/d)^2 (q/d)^2 +
d^6 (-p^2) (r)^2 (p/d)^4 - d^6 q^2 (r)^2 (p/d)^4 - 2 d^6 q^2 (r)^2 (p/d)^2 (q/d)^2 - d^6 q^2 (r)^2 (q/d)^4 + 4 d^4 p^4 (r)^2 (q/d)^2 + 4 d^4 p^4 (r)^2 (p/d)^2 + 8 d^4 p^2 q^2 (r)^2 (p/d)^2 + 8 d^4 p^2 q^2 (r)^2 (q/d)^2 + 4 d^4 q^4 (r)^2 (p/d)^2 + 4 d^4 q^4 (r)^2 (q/d)^2) - 4 d p^4 -
8 d p^2 q^2 - 4 d q^4)/(2 (d^2 p^2 (q/d)^2 + d^2 p^2 (p/d)^2 + d^2 q^2 (p/d)^2 + d^2 q^2 (q/d)^2 - 4 p^4 - 8 p^2 q^2 - 4 q^4))
x = (d^3 p^2 (q/d)^2 + d^3 p^2 (p/d)^2 - d^3 q^2 (p/d)^2 + d^3 q^2 (q/d)^2 + sqrt(-d^6 p^2 (r)^2 (q/d)^4 - 2 d^6 p^2 (r)^2 (p/d)^2 (q/d)^2 +
d^6 (-p^2) (r)^2 (p/d)^4 - d^6 q^2 (r)^2 (p/d)^4 - 2 d^6 q^2 (r)^2 (p/d)^2 (q/d)^2 - d^6 q^2 (r)^2 (q/d)^4 + 4 d^4 p^4 (r)^2 (q/d)^2 + 4 d^4 p^4 (r)^2 (p/d)^2 + 8 d^4 p^2 q^2 (r)^2 (p/d)^2 + 8 d^4 p^2 q^2 (r)^2 (q/d)^2 + 4 d^4 q^4 (r)^2 (p/d)^2 + 4 d^4 q^4 (r)^2 (q/d)^2) - 4 d p^4 -
8 d p^2 q^2 - 4 d q^4)/(2 (d^2 p^2 (q/d)^2 + d^2 p^2 (p/d)^2 + d^2 q^2 (p/d)^2 + d^2 q^2 (q/d)^2 - 4 p^4 - 8 p^2 q^2 - 4 q^4)) >>174
�Ȃ� FullSimplify ���Ȃ��H
X=�̍ŏ��̎���%�Ƃ����
FullSimplify[%, d > 0 && p > 0 && q > 0 && r > 0]
1/6 d (3 + (Sqrt[3] r)/Sqrt[p^2 + q^2]) >>174
165�ł��B����͎������܂߂ẴR�����g�ɂȂ�܂����A���̕������́A��ŊȒP�Ɍv�Z�ł��܂��B
���������������B >>175
���肪�Ƃ��������܂��B
���̋@�\���͂��߂Ēm��܂����B >>174
�u���������������v�Ə����܂������A���ۂɂ��������܂��B
���̐헪����̗v���A��̃x�N�g���AP-Vt �� V �̂Ȃ��p�x����/3�ł���Ƃ�����������
(P - V t).V=(1/2)*|(P -V t)|*|V|
�Ə����܂��B�s���I�h�̓x�N�g���̓��ρA��Βl�L���̓m������\���L���Ƃ��Ă܂��B
�@>>165�ł́A����������\���ŁA����\���Ă������߁A���ꂵ���Ȃ�܂������A�ŏ����炱�������悩�����ł��ˁB
|V|=2�AP.V=p*(2p/d)+q*(2q/d)+r*0=2d�AP.P=p^2+q^2+r^2=d^2+r^2 �ɒ��ӂ��ĕό`�����
P.V-t*V.V = |P -V t|
2d-4t = ��(P.P-2t*P.V+4t^2)
16t^2-16td+4d^2=d^2+r^2-4td+4t^2
12t^2-12td+3d^2-r^2=0
t=(1/12){6d�}��(36d^2-12(3d^2-r^2))}=(1/12){6d�}(2��3)r}
�ƁA������ɁA�ȒP�� t �����߂邱�Ƃ��ł��܂��B �����ʏ�ɖ����ɑ����A1�I�[���̒�R�ō��ꂽ�����`�̊i�q�ɂ����āA
�i�C�g�̓���(�j�n���)�̈ʒu�ɂ���2�̃m�[�h�Ԃ̒�R��
4/��-1/2 �I�[���ł��邱�Ƃ������B
�iGoogle���Ў��� - ��Փx�������邽�߂Ɉꕔ�ȒP���j >>179
�R���͓d�C��R�̒m���Ȃ��Ă�������́H
Google�̎��������炻���͒m��Ȃ��Ă����肵��Ȃ̂��ȁH
�Ƃ肠�����O�O�����璷���ɔ�Ⴕ�Ēf�ʐςɔ���Ⴗ��Ƃ����̂���������Ȃ��B
https://kenkou888.com/category21/dousen_teikou.html ����H
�i�q�_�Ɗi�q�_�����Ԃ悤��1���̒�R���q�����Ă�Ƃ����Ӗ��H
���������āH >>181
�����ł��B
>>179
�̕⑫�ł����A1�I�[���̓������i�q�̗אڃm�[�h�Ԃ̒�R��
�Ώ̐��̈Ӗ���m���Ă���Β��w���ŏo���܂��B
����ʓI�ɂ́A�C�ӂ̓�̃m�[�h�Ԃ̒�R��
�L�����{�L�����~1/�ł���킳��邱�Ƃ������Ă��������B >>180
�O��ƂȂ镨���m���́A���w�����x���̃I�[���̖@���ƃL���q�z�b�t�̖@���݂̂ł��B �܂�ij�ɂ�����d�ʂ�e[i,j]�Ƃ���(0,0)����-1A�A(2,1)��+1A�������Ă�Ƃ���
e[i+1,j]+e[i-1,j]+e[i,j+1]+e[i,j-1]-4e[i,j]
=��i0��j0-��i2��j1
�̂Ƃ���e[2,1]-e[0,0]���ȁH
�����藝�̍��肪����B >>178
�ǂ������肪�Ƃ��������܂����B
d=��(p^2+q^2)�̏��Ȃ���wolfram�ɓ��͂����̂ŕ��G�ȓ��ŕ\�����ꂽ�̂��Ɨ������܂����B >>184
�q���g
���[�����W�J�ɂ����
E(z,w)=��[i,j:����] e(i,j) z^i w^j �O>>173���ꂩ�����p�x60���̌��ߑł�����Ȃ��āA�������Ă݂����Đl���Ȃ����Ȃ��B >>187
�O�X����
https://rio2016.5ch.net/test/read.cgi/math/1572866819/807
���Δ����ŋɒl���o���Ă���B
�v���O�����ł̐��l���ƍ��v�����B
�����̂̕��̌v�Z�ɂ�������B
�I�����s�b�v�[���̒����̂̕����v�Z�̂�����������Ǝv���B >>188
�O�X����807���������҂����A�ɒl�͓�o�����A807�ł͍̗p�����������Ă��܂����B
�������e��824�ɋL���Ă���̂ŁA807������ꍇ�́A824���Z�b�g�Ō��ė~�����B >>187
�Δ����ȊO�͑S�����ߑł��Ǝv���Ă鎞�_�ł������̃X���Ń��X�ł��郌�x���ɓ��B���ĂȂ��B > ���ꂩ�����p�x60���̌��ߑł�����Ȃ��āA�������Ă݂����Đl���Ȃ����Ȃ��B
�C�i�ȊO��60���Ƃ����p�x���g���Ă���l�́A�v���t�������Ŏg���Ă���킯�łȂ��A
�����܂ł��Ȃ��v�Z������A�X�l���̖@�����̒藝��p����60�x�o���Ă������� �^�N�V�[�����̉���
# ���l�n��
# ���^���i���^)
F1=740 # ����^�� Fair
D1=2000 # ����苗�� initial Distance
C1=90�@ # ���Z�^�� Charge by distance
B1=288 # ���Z���� charge By distancce
# �V�^��
F2=500
D2=1200
C2=100
B2=264
https://travel.watch.impress.co.jp/img/trw/docs/1224/505/02_o.jpg
�����ƐV���^������э��z���O���t�ɂ��Ă݂��B
�^�����藦��8.88���ƋL�ڂ���Ă���̂����ǂ�����Čv�Z����낤�H >>187
���ɂP�O�������ďc�ɕ�����ς��ăv�[���T�C�h����Ƃ̊p�x�ō��W(p,q�j�Ɍ������Ĕ�э��ގ��̏��v���Ԃ�
10/2+((p-10)/tan(��)+q)/2+sqrt((10-p)^2+((10-p)/tan(��))^2)
�p�x�����߂���c�����̑��s���������܂��Ă��܂��B
���������������
D[5 + (q + (-10 + p) Cot[��])/2 + Sqrt[(10 - p)^2 + (10 - p)^2 Cot[��]^2], ��]�@��Wolfram�搶�ɂ��肢�����
������((10 - p) Csc[��]^2)/2 - ((10 - p)^2 Cot[��] Csc[��]^2)/Sqrt[(10 - p)^2 + (10 - p)^2 Cot[��]^2]
��ł�����
solve ((10 - p) Csc[��]^2)/2 - ((10 - p)^2 Cot[��] Csc[��]^2)/Sqrt[(10 - p)^2 + (10 - p)^2 Cot[��]^2]==0 for ��
�������O�ɂȂ�Ƃ����߂Ă��炤��
�� = ��/3�@�� = -��/3
�}�C�i�X���ƃv�[���ɔ�э��߂Ȃ�����A�� = ��/3
�ړI�̍��W�Ɋւ��Ȃ��U�O���ƎZ�o����܂����B >>192
8.88%�����������̂Ȃ�A�Ⴆ�A
100m���p�A200m���p�A...�A6600m���p�A6700m���p
�̗����̍��v���A�V���Ŕ�r����ƁA8.8�ʂ̃A�b�v�ɂȂ�B
1200m�ȉ����ƁA�V�^����240�~����
1800m�ʂ���A�t�]���A���̌�A���킶�퍷���傫���Ȃ�A
4200m�ʂ���A240�~�ʍ����Ȃ�B
100m����4200m�ʂ��܂�ׂ�Ȃ����p����l�������Ƃ���ƁA���̉���ɂ��A
���p�z�̑����͂قƂ�ǖ����Ƃ������߂��\�B
�������傫���Ȃ�A�l�グ�̌��ʂ��ǂ�ǂ�傫���Ȃ�B
�ŏI�I�ɂ́A1m�ӂ�̉��Z�^���̔�@90/288�@�F�@100/264�@=�@33:40
�Ȃ̂ŁA21.212121...%�̏㏸�ɋ߂Â��B
���ꂪ�A6.7km�ӂ�ł́A8.8%���Ƃ��������B
�܂�A8.88�ʂɂȂ�悤�A�ŏ�����100m�ƍő勗����6.7km�ӓI�ɑI�����B
�����̐����ɂ͐����͂͑S�������B
���炭�A�����ʗ��p�����̃f�[�^�Ɋ�Â��āA�V���̗�����r�����̂��낤�B
���̏������A8.88%���̐��l�͏o���Ȃ��Ǝv����B >>179
�ł��������B
�܂�(0,0)�ȊO�őQ����
4e(i,j)=e(i+1,j) + e(i-1,j) + e(i,j+1) + e(i,j-1)
�������T���B
e(i,j)=��[|x|,|y|<��] (1-cos((x+y)i)cos((x-y)j))/(1-cosxcosy)dxdy
�����̏��������B
�܂�|i|,|j|������0�ɍs���B
�����œ_i,j�ɓd�ׂ�e[i,j]-e[2-i,1-j]�ƂȂ�B(�������͈�ӁA�m�[�`�F�b�N)
e[0,0]=0, e[2,1]=32��-4��^2
�ł��邩��d�ʍ���64��-8��^2�B
e[1,0]=4��^2�����猴�_����אڂ���4�_�Ɍv16��^2�̓d���������B
����ċ��߂��R�l��(32��-4��^2)/16��^2=4/��-1/2�ł���B
�܂�e[i,i]��
e[i,i]=��(1-cosix))/(1-cos(x)cos(y))dxdy
�ł��邪�Ay�ɂ��Đ�ɐϕ������
e[i,i]=��(1-cosix))/|sin(x)|dx
�ƂȂ�A���̒l�̗̓L�����{�ɂȂ�B
�R���ƑQ�����ɂ��e[i,j]�̓ƃ�^2�̗L���W���̐��`�����ł���B��
e[i,i]�̌v�Z���S���v�����Ȃ������B
e[i,j]�̕�����č���̂��ȁH >>194
���X���肪�Ƃ��������܂��B
�����ƐV���^���ƍ��z�̃O���t�̃A�b�v���[�h��Y��Ă���܂����B
https://i.imgur.com/bElGqRG.jpg
�^����ꂽ�f�[�^��������͕��ϒl�グ���͎Z�o�ł��Ȃ��v���Ă����̂��m�F�ł��܂����B
���鋗���܂ł̏�q���������Ɖ��肵���Ƃ��̕��ς̒l�グ�����O���t�ɂ����
https://i.imgur.com/2PkwY3n.jpg
> which.min((crs-0.0888)^2)
[1] 6869
> pir(6869)
[1] 0.08882413
6�D9�L�����炢�̕��ς�8.9���̒l�グ���ɂȂ�܂����B
�v�Z�����ЂƂ͂��������������g�����̂ł��傤�B �O>>187
>>193
�p�x�����߂���j�����������܂�B�ƂŔ������邩�A�Ƃ�x�̗����Ŕ������邩���ĂƂ��ł����B >>197
https://i.imgur.com/reg8DOz.jpg
O����o������A���o�Ċp�x�Ƃœ�������S(p,q)�ɉj���Ƃ���
AJ�̒�����x�Ƃ����
tan(��)=(10-p)/(q-x)������
x=q-(10-p)/tan(��)
�ƂȂ�A
���v���Ԃ̌v�Z����x�͏����ł���
�@10/2+((p-10)/tan(��)+q)/2+sqrt((10-p)^2+((10-p)/tan(��))^2)
�ƂȂ�B
���̋ɒl��^����Ƃ�p,q�ɂ��Ȃ��̂�>193�ɏ������ʂ�B >>197
>�p�x�����߂���j�����������܂�B
�Ⴄ�A�p�x�����߂��瑖�鋗�����j�����������܂� ���鋗���@10+((p-10)/tan(��)+q)
�j�������@sqrt((10-p)^2+((10-p)/tan(��))^2) >>179�̉��̈�Ӑ��̏ؖ����ł��Ȃ��Ȃ��B
�̂���G���K���g�ȉ����ނ��Ȃ�
4a[ij]=a[i+1j]+a[i-1j]+a[ij+1]+a[ij-1]
���݂����L�E�ȗ�͒萔�Ɍ��鎖������
�̌`�ŏo�肳���2ch�ɂ��炢�G���K���g�ȉ��オ���Đ��Z�~�ɍڂ������Ă������������������ǁA����ǂ�ȏؖ��ł��������H
�N���o���Ă܂��H >>195
�����ł��B�悭�������T���܂����ˁB
���̓������(i',j')���炵�ĕ�����ς��ďd�ˍ��킹�Đ��K������A
2�_(i',j')--(0,0)�Ԃ�1A�̓d���𗬂������̓d�ʂ̎����o�܂��B
�z�肵�Ă����́A2�_(2,1)--(0,0)�Ԃ�1A�̓d���𗬂������̓d�ʂ̎�
e[i+1,j]+e[i-1,j]+e[i,j+1]+e[i,j-1]-4e[i,j]=��i0��j0-��i2��j1
��exp(��-1 (ix+jy))��������i,j�Řa������
(exp(-��-1 x)+exp(��-1 x)+exp(-��-1 y)+exp(��-1 y)-4)E(x,y)=1-exp(��-1 (2x+y))
(������ E(x,y)=��[i,j:����] e[i,j] exp(��-1 (ix+jy)) �ƒu��)
���
E(x,y)=(1-exp(��-1 (2x+y)))/(2cosx+2cosy-4)
������t�[���G�����̌���(�����藝)
e[i,j]=(1/(2��)^2)��[0,2��]��[0,2��]E(x,y)exp(-��-1 (ix+jy))dxdy
��p���ċt�ϊ�����ƁA(2,1)--(0,0) �Ԃ̓d�ʂ�
e[2,1]-e[0,0]=(1/(2��)^2)��[0,2��]��[0,2��](exp(-��-1 (2x+y))-1)(1-exp(��-1 (2x+y)))/(2cosx+2cosy-4) dxdy
=(1/(2��)^2)��[0,2��]��[0,2��] (1-cos(2x+y))/(2-cosx-cosy) dxdy
=4/��-1/2
��ʂ�(0,0)--(i,j)�Ԃ̒�R�l��
(1/(2��)^2)��[0,2��]��[0,2��] (1-cos(ix+jy))/(2-cosx-cosy) dxdy
=(1/(8��^2))��[0,2��]��[0,2��] (1-cos(i(x+y)+j(x-y)))/(1-cosxcosy) dxdy
=(1/(8��^2))��[0,2��]��[0,2��] (1-cos((i+j)x)cos((i-j)y))/(1-cosxcosy) dxdy
=(1/(2��))��[0,��] (1-cos((i+j)x)((1-|sinx|)/cosx)^|i-j|)/|sinx| dx
(0,0)--(i,i)�Ԃ̒�R�l��
(1/(2��))��[0,��] (1-cos((i+j)x))/|sinx| dx
=(2/��)(1+1/3+1/5+1/7+...+1/(|2i|-1)) >>200
���̉���
f(x,y)=��e[kl]exp(ikx+ily)
����������Ɖ��肵��(�d�����̗L����������͎�������)�݂����ׂ����������Ō����܂����B
���������Ⴆ�Ή̓R���������ł����n�Y�Ȃ�ł����A�����̎������Ƃ��������łȂ��̂ŃR���݂̂����Ȃ̂������ĂȂ��ċC���������B
�܂����Ў����ł͂����܂ŋ��߂��Ȃ��낯�ǁB
>>201�̃G���K���g�ȉ��ނ̂�͊m���^���������łȂ��ĕs�������������ȁH
�������������瓙���̗L�E�Ȕ����̑��݂��K�v���ŏo�Ă��Ė������Ƃ������ꂾ�����悤�ȁB
�������Ă��o�Ă��Ȃ��Ȃ��H >>202
�⑫
�����(���_��8��^2�̓d���𒍓�������)
��[0,2��]��[0,2��] (1-cos((i+j)x)cos((i-j)y))/(1-cosxcosy) dxdy
=4��[0,��] (1-cos((i+j)x)((1-|sinx|)/cosx)^|i-j|)/|sinx| dx
��|i|=|j|�� 4��[n=1,|i|] 1/(2n-1) �ɂȂ��� |i|=|j|�����Ŕ��U���܂��B
����A2�_��(0,0)--(2,1)�ŕ�����ς��ďd�ˍ��킹����((0,0)--(2,1)�Ԃ�8��^2�̓d���𗬂�����)
��[0,2��]��[0,2��](cos((i+j)x)cos((i-j)y)-cos((i+j-3)x)cos((i-j-1)y))/(1-cosxcosy)dxdy
=4��[0,��](cos((i+j)x)((1-|sinx|)/cosx)^|i-j|-cos((i+j-3)x)((1-|sinx|)/cosx)^|i-j-1|)/|sinx|dx
�̓��[�}���E���x�[�O�̕����|i|,|j|������0�Ɏ������܂��B
���Ȃ݂ɁA3�����̖����i�q�ł͂��̂悤�Ȕ��U�͋N����܂���B �u�����̃N���[�Y�D�ł�
�D���̊��C�����ʂ炵������13����ɔ��ǂ����z������Ƃ��̋߂��̕����̂�̓v���X��14���u�����Ȃ��Ƃ����Ȃ�
���ꂪ���̑D���̏Ƃ����B
����Ȗ����l���Ă݂��i���͎����ł��܂������Ă܂���j�B
�v�Z�ɂ͒lj��̐ݒ肪���邩������܂���B
���ׂ̂ǂ��炩������������14�������A�ǂ̕�����1���Ŋ�������m��p��1%
�����̔z�u�͒����`�i�܂�n�܂���I�����Ȃ��j�B
���ǂ��邩�A�u�����Ԃ��I���Ή��D�ł���B�S������P�̌��Ƃ��ċq�Ə斱�������킹���l��n��3000�l�B
�N���[�Y�D����S�����D�ł�������̊��Ғl�́H >>190
�������o�Ă���듚��A������|�l���ǂ��[�������邩�Ƃ����Q�[�����Ǝv���ĉ��͊y����ł�B �����̔z�u�͒����`�i�܂�n�܂���I�����Ȃ��j�B
�ǂ̕����ɂ����ׂ�����ƌ����Ӗ��B
�����`�ɈӖ��Ȃ��A�~�`�z�u�ł������B ���� 4a[i,j] = a[i,j+1]+a[i,j-1]+a[i+1,j]+a[i-1,j] =: 4(��a)[i,j] ���S�Ă�(i,j)�Ő��藧�Ȃ�A
�̈�[-n,n]^2�ɑ�����i�q�_(i,j)�S�̂ɂ�����a[i,j]�̍ő�l�A�ŏ��l�́A
�ǂ�����Ӂ�([-n,n]^2)��łƂ�Ȃ���Ȃ�Ȃ�����A��Ӑ��͂��ꂪ���ɂȂ����肷��̂��Ȃ�
�I�ɂ̓��E���B���̒藝�Ɏ��Ă邩��A���̏ؖ��Ɠ�����@���g������͂��Ȃ����낤�� ����1�_�݂̂Ŕ����\�ł���A���̎��鏊�Ŕ����\�łȂ��悤�Ȋ��̗��������B f(x)=x^2 (x: rational)
. =0 (otherwise) �O>>197
�ƂŔ�������̂ƃƂ�x�̗����Ŕ�������̂Ƃǂ������Ó����l���Ă݂����B >>205
�ƂĂ���͓I�ɂ͉����������Ȃ��̂ŃV�~�����[�V�����Ōv�Z���Ă݂��B
�P�O����̃V�~�����[�V�����ŕ��ϒl
> mean(RE)
[1] 57.942
�ƌv�Z���ꂽ�B >>205
�P���ŐV����3�l�Ƃ������ƂȂ̂Ŋ����m����0.1���ɂ��ăV�~�����[�V����������B
> k=1e4
> RE=replicate(k,sim())
> mean(RE)
[1] 30.8222
�S�������D�ł���̂͂P������Ƃ����\�z�ɂȂ����B >>208
���ꂾ�ȁB
�i�q�_�̏W��Sn={(k,l) | |k|+|l|��n}���l����Ƃ��C�ӂ�x��Sn�ɑ��ā�Sn��̊�w(y)��w(y)��[0,1]��w(y)=1�Ae(x)=��w(y)e(y)�������̂����݂���B
����max{|e(x)| ; x��Sn}= max{|e(y)| ; y����Sn}�B
�ؖ���n�ɂ��Ă̋A�[�@�B >>205
�V�~�����[�V�����őS�����D�܂ł̓�����1���̊����m���̊W���O���t�ɂ��Ă݂��B
https://i.imgur.com/u1hsEa4.png
����傫������ƃV�~�����[�V�������I���Ȃ��B
p=0.9999�Ƃ������1���őS�����D�Əu���ɏI��邯�ǁB �O>>211
���߂̍��W�̂Ƃ������A�����̒u�����܂Ől�̐������قȂ��@�������Ă����Ǝv���B
4sin^4��+4sin^3��+5sin^2��-4=0
�V���N�������̒藝�ɂ��Ɓ�60���݂����Ȍ���I�Ȏ����݂������B ���鏬�w�Z�̂���N���X�ł́A�o�X�ʼn����ɍs�����ƂɂȂ����B
�o�X�̍��Ȃ͎��O�Ɍ��܂��Ă������A�ŏ��Ƀo�X�ɏ���������������̍��Ȃ�Y��āA�C�ӂ̍��Ȃɍ����Ă��܂����B
���̎����́A��l���o�X�ɏ�荞�݁A�����̍��Ȃ��Ă�����̍��ȂɁA�����łȂ���Ă���C�ӂ̍��Ȃɍ������B
���̂Ƃ��A�Ō�̎����������̍��Ȃɍ����m���́A�N���X�̎������ɂ�����炸���ł��邱�Ƃ��ؖ�����B >>218
�V�~�����[�V�������Ă݂���A0.5�O��̒l���Ԃ��Ă����B
seat.n <- function(n){ # n: ���k�̐l��
s=1:n # �c����Ȕԍ�
s1=sample(s,1) # �ŏ��̐��k�P�̍���Ȕԍ�s1
s=s[-s1] # s1���c����Ȃ��珜��
for(i in 2:(n-1)){ # ���k�Q���琶�kn-1�܂�
if(i %in% s){ # ���ki�̍���i���c���Ă����
s=s[-which(s==i)] # ���̍��Ȃ�s���珜��
}else{
ls=length(s) # �c����Ȑ� length of s
si=sample(ls,1) # 1:ls�̒�����1�I��si�Ƃ���
s=s[-si] # si�Ԗڂ̍��Ȃ�����
}
}
s==n # ���k���̐Ȕԍ��͂����̐^�U��Ԃ�
}
sim <- function(n,k=1e4){
mean(replicate(k,seat.n(n)))
} n���R����T�O�܂łɕω������čŌ�̎����������̍��Ȃɍ����p�x�������ăO���t�ɂ��Ă݂��B
https://i.imgur.com/Ad8GyDJ.png >>217
>�l�̐������قȂ��@�������Ă���
�����āA��������Γ�����v����B >>218
p(�Ō�̐��k���������Ȃɂ����|�ŏ��̐��k���������Ȃɂ����)=1
p(�Ō�̐��k���������Ȃɂ����|�ŏ��̍Ō�̐��k�̐Ȃɂ����)=0
p(�Ō�̐��k���������Ȃɂ����|�ŏ��̐��k���ŏ��ƍŌ�̐��k�̐ȈȊO�̐Ȃɂ����)=1/2 (�� ���k�̐������Ȃ��ꍇ�ɊҌ������)
�� p(�Ō�̐��k���������Ȃɂ����)=1/2�B ���w�I�A�[�@���g����Ȃ��̂��H >>179�̖��͎����I�ɂ͔[���ł����̂�����>>201�ŏ������G���K���g�ȏؖ����v���o���Ȃ��ă��J���B
�l�b�g�Ō�������ƁA��͂肠��̂͂���͂�
���́��C���^�[�l�b�g��̓������̏ؖ��B
�N���m��܂��H
http://www.cc.miyazaki-u.ac.jp/math/tmp/mzs/home.html
�Ƃ����̂��L���ȉJ�{���ł���A���N�����I�ؖ��͌��Ăł������B���Ƃ��Ƃ͈ꏼ�M�ɂ��p��{�̖��ł��������A�J�{�������I��@�̑��݂𐔃Z�~�́u�G���K���g�ȉ�@�����ށv�ɏo�肵���̂ł���B�ŋ߂ł�
�O�D���Ƃ��Ƃ̉p��{�̒��҂ɂ��ʑ���Ԃ̒[�_���_���g���ؖ�
�P�D���É���w�̎R�c���ɂ��ؖ�
�Q�D�C���^�[�l�b�g��̓������̏ؖ�
�R�D�i�L�E�ȏꍇ�̂ݒʗp����j����͓I�ؖ�
�����݂��邱�Ƃ��m���Ă���B �O>>217
x��+�ɂƂ����̂͂����B
������x�l���Ă݂�B >>224
���̃����N��ɈӖ�������̂��ˁH 51.56095029371006087��
�O>>225
���܂����܂�Ȃ��ȁB >>218
m�l���c���Ă��Ă���Ƃ��A���̂������l���̐������Ȃ��c���Ă��邩�ƍl����ƁA
m-1�l�̐������Ȃ��c���Ă��邩�Am�l�S�Ă̐������Ȃ��c���Ă��邩�ǂ��炩�B
�Ȃ����̂悤�Ȃ��Ƃ������邩�H
m�l�A�c���Ă����ԂŁA����l���w�����āA�����̐Ȃɍ��낤�ƁA�����̐Ȃ�����ł��낤�ꏊ�Ɍ������A
���̐��k�������Ă���̂������Ƃ���B���ł́A�S�Ă̐��k���C��ݒ�Ȃ̂�������Ȃ����A���̐l���w��
���܂��܋��C�ŁA�u���̔ԍ��D������B�����͉��̐Ȃ��B�ǂ����s���B�v�ƒǂ��o�����Ƃ���B
���̒ǂ��o���ꂽ�l���́A�w���������Ė{���̐Ȃɍ��肽�������x�ƐS�̒��Ŕ��_���A�{���̎����̐Ȃ�
�������A����������������ꂽ�̂Ɠ����䎌�u���̔ԍ��D������B�����͉��̐Ȃ��B�ǂ����s���B�v�������āA
�J���𐰂炵���B���ꂪ�J��Ԃ����Ƃǂ��Ȃ邩�H
�ŏ��Ƀo�X�ɏ��A�K���ɍ������l���A�Ȍケ����`�Ə̂����A�`�������ǂ��o�����B
���̒ǂ��o����Ƃ̊ԁA��Ȃɂ́A�S���ω��͖������A�`�ȊO�A�S�Đ������Ȃɍ����Ă���B
�������`�́A�c�����Ȃ̒�����A�K���ȐȂ������č������Ƃ���B
���āA�����ŁA�`���������ȁB������A�����œo�ꂵ���l���w���A���ʂ�C��ݒ�ɂ��āA
�����̐Ȃ����̐l���ɐ苒����Ă��Ďd���Ȃ��K���ɑI�Ȃɒu�������Ă݂悤�B
�����Ⴄ���H�����ς��Ȃ��B
���ł́A�o�X�ɍŏ��ɏ�荞�l�����A�����̐Ȃ������ꂽ�ԍ��D���������ƂɂȂ��Ă��邪�A
�c��Am�l���c���Ă����Ԃŏ�荞�l�����A�ԍ��D�����Ă����̂Ɠ����B
�Ō�ɓo�ꂵ���l���ɐ������Ȃ��c����Ă���m���́A�Ōォ���Ԗڂ̐l�����A�ԍ��D�����Ă��āA
���A�c��̐Ȃ���A�Ԉ�����Ȃ�I�m���ɓ������B�܂�A�P�^�Q�ł���B ���A�Ԉ�����B
�~�F�Ō�ɓo�ꂵ���l���ɐ������Ȃ��c����Ă���m���́A�Ōォ���Ԗڂ̐l�����A�ԍ��D�����Ă��āA
�~�F���A�c��̐Ȃ���A�Ԉ�����Ȃ�I�m���ɓ������B�܂�A�P�^�Q�ł���B
���F�Ō�ɓo�ꂵ���l���ɐ������Ȃ��c����Ă���m���́A�Ōォ���Ԗڂ̐l�����A�ԍ��D�����Ă��āA
���F���A�c��̐Ȃ���A�������Ȃ�I�m���ɓ������Ƃ��Čv�Z�ł���B�܂�A�P�^�Q�ł���B >>223
>>222 �̉J�ɏ�����
�l����n�l�̂Ƃ��̍Ō�̐l�������̐Ȃɍ���m����p[n]�Ƃ��ċA�[�@��p����
n=2�̂Ƃ����炩��p[2]=1/2
n>2�̂Ƃ�p[n-1]=...=p[2]=1/2�Ɖ��肷���
1�l�ڂ������̐Ȃɍ���m�� = 1�l�ڂ��Ō�̐l�̐Ȃɍ���m�� = 1/n, 1�l�ڂ�2����n-1�l�ڂ̐Ȃɍ���m�� = (n-2)/n
�E1�l�ڂ������̐Ȃɍ���Ƃ��̍Ō�̐l�������̐Ȃɍ�������t�m�� = 1
�E1�l�ڂ��Ō�̐l�̐Ȃɍ���Ƃ��̍Ō�̐l�������̐Ȃɍ�������t�m�� = 0
�E1�l�ڂ�k�l��(2��k��n-1)�̐Ȃɍ���Ƃ��̍Ō�̐l�������̐Ȃɍ�������t�m�� = p[n-k+1] = 1/2
�]����
p[n]=(1/n)*1+(1/n)*0+((n-2)/n)*1/2=1/2 >>222
>(�� ���k�̐������Ȃ��ꍇ�ɊҌ������)
���̏ꍇ
2�l�ځ`�Ō�̒u���ꂽ��1�l�ځ`�Ō�̏ꍇ�ƈقȂ��Ă��邯�NjA�[�@�g������ĂȂ�ŁH >>231
1�l�ڂ�2�l�ڂ̐Ȃɍ������ꍇ�A2�l�ڂ͖���������Ă��Ȃ��̂Ɠ����ɂȂ邩�� >>232
1�l�ڂ̐l�͎����̐Ȃɍ���\�������邯���
���̏ꍇ��2�l�ڂ̐l�͂��̉\�����Ȃ��ł���H ����������1�l�ڂ̐Ȃɍ���\��������ƌ������Ƃ�
�킩���� >1�l�ڂ̐l�͎����̐Ȃɍ���\�������邯���
���̏ꍇ�͍Ō�̐Ȃ܂Ŗ��Ȃ����������܂�A�����t���m����1�ɂȂ�(������͂R�̏ꍇ���������Ă���) �O>>227�v�Z�Ɏ��M�Ȃ��B�ɒl�^����Ƃɗ��R�Ȃ��B
�~�o����f(��)=5+{x-(10-x)cos��/sin��}(1/2)+(10-x)/sin��
=5+x/2-(5-x/2)cos��/sin��+10/sin��-x/sin��
=5+x/2-5cos��/sin��+xcos��/2sin��+(10-x)/sin��
f'(��)={5sin^2��-(-5cos^2��}/sin^2��+(-xsin��2sin��-xcos��2cos��)/4sin^2��+(10-x)cos��/sin^2��
=5/sin^2��-1/sin^2��+10cos��/sin^2��-xcos��/sin^2��
=4/sin^2��+(10-x)cos��/sin^2��
f'(��)�̕��q=0���A
2+5cos��-xcos��=0
xcos��=2+5cos��
x=2/cos��+5
�Ȃǂ��͂���˃�=60���Ɖ��肷��ƁA
x=2/(1/2)+5=4+5=9
f(60��)=5+{9-(10-9)cos60��/sin60��}(1/2)+(10-9)/sin60��
=5+(9-1/��3)(1/2)+��3/2
=5+9/2-1/2��3+��3/2
=19/2+1/��3
=(57+2��3)/6
=10.0773503�c�c >>236
�S�z����ȁB
���@���̒ʂ�Ԉ���Ă�B >>235
����������2�l�ځ`�œ����łȂ��Ƃ����Ȃ���
��2�l�ڂɂ�1�l�ڂ̐Ȃɍ���\����������
���̏ꍇ��1�l�ڂ������̐Ȃɍ���ꍇ�Ɠ��l�̓W�J�ɂȂ���Ă킯
���̂���łȂ������́H >>224
��������Ȋ����̗���Ŏ������Ƃ͂ł�����
(��a)[i,j] := (a[i+1,j]+a[i-1,j]+a[i,j+1]+a[i,j-1])/4
�ƒ�߂�ƁA(��^(2n))a ��W�J�������̌W���� ( (cosx+cosy)/2 )^(2n) ��W�J�������̌W���Ɠ��ꎋ���邱�Ƃ��ł��A
���� e^(i(2px+2qy)) �̌W�� c[p,q] �͎������F
c[p,q]=0 when |p|+|q|>n,
c[p,q]=c[p,-q]=c[-p,q],
|p|��|p'| ���� |q|��|q'| �Ȃ�� c[p,q]��c[p',q'].
������ (��^(2n)a)[0,0] - (��^(2n)a)[2,0] �̊e�W���̐�Βl�̘a��
=2��_(p,q��Z, p��0) |c[p,q]-c[p+1,q]|
=2��_(q��Z) c[0,q]
=:S_n��0 (as n����)
�ł��邩��A�z��a[i,j]�� ��a=a ���C�ӂ�(i,j)�ɂ��� |a[i,j]|��M �����Ȃ�A
|a[0,0]-a[2,0]|��MS_n (for��n) ��� a[0,0]=a[2,0].
���l�ɂ��� a[i,j]=a[i,j+2]=a[i+2,j] �������邩��A���Ƃ͗e�ՁB >>240
����A�c�O�Ȃ���J�{�̖��ʼn���ł���̂͐��l�����A��̗L�E���͉���ł��Ȃ��̂ł��B ���Ȃ݂ɂ��̌��ʂ́A�Ⴆ�Ό��_�ȊO������ ��a=a �����悤�ȗL�E�z��a�����߂鎞�ɂ��g����B
���̏ꍇ�A���̂悤��a�̋�̗�̈��>>195�ŋ������Ă���̂�a'�Ƃ������Ƃɂ���ƁA
�������Ɍ��_�ȊO������ ��a=a �����悤�ȗL�E�z�� a'' �� a' �Ƃ͕ʂɑ��݂���Ȃ�A
�萔c��K�ɒ�߂�� a~:=a''-ca' ���S�Ă̊i�q�_�� ��a~=a~ �����L�E�z��ɂȂ邽�߁Aa~�͒萔�B
���Ȃ킿�Aa'' �� a' �ƒ萔�̐��`�����łȂ���Ȃ�Ȃ��B
���l�ɂ��āA����n�_ p_i (1��i��n) ���������i�q�_�S�̂� ��a=a �����悤�ȗL�E�z�� a ��
a[X] = c_0 + ��_(i=1,n) c_i�a'[X-p_i] (c_i�͎���)
�ƕ\���邱�Ƃ��킩��B �O>>236
>>218
���k����x�Ƃ���ƁA
1/2����Ȃ����ȁB���ŁB >>241 �܂����A�����Ƃ��Ă����܂Ȃ� >>244
���������A���Ȃ��Ƃ��L�E�P�[�X�ɂ��Ă͒萔�������Ȃ��Ƃ����b�͉J�{�̖��͂Ƃ�����>>179�̖��ɂ͎g����B
���̂Ȃ�I���͕�������Ȃɏڂ����Ȃ����玩�M�Ȃ����Ǘ��Ɍn�ɂ����Ċe�_�̓d�ʂ͐��d�ɂ��Ⴍ���d�ɂ��͍����̂͂قڎ����ƌ����ėǂ������B
�ނ��떳�����œd�ʂ�0�̕�������ۂǂ��₵���B
���������>>179�̖������ɂ̓L���q�z�b�t�̖@���ƃI�[���̖@���ȊO�ɂ��̕ӂ̒m������������Ⴂ���ȁB >>239
��蒚�J�ɐ�������ƁA�N�������ĂȂ�����
�ꍇ1: 1�l�ڂ�1�l��(����)�̐Ȃɍ���ꍇ (�S���������Ȃɍ����)
�ꍇ2: 1�l�ڂ�2�l�ڂ̐Ȃɍ���ꍇ (2�l�ڂ������_���ɑI�Ȃ���Ȃ�Ȃ�)
�ꍇ3: 1�l�ڂ�3�l�ڂ̐Ȃɍ���ꍇ (2�l�ڂ͐������Ȃɍ���āA3�l�ڂ������_���ɑI�Ȃ���Ȃ�Ȃ�)
...
�ꍇn-1: 1�l�ڂ�n-1�l�ڂ̐Ȃɍ���ꍇ (2�l�ڂ���n-2�l�ڂ͐������Ȃɍ���āAn-1�l�ڂ������_���ɑI�Ȃ���Ȃ�Ȃ�)
�ꍇn: 1�l�ڂ�n�l��(�Ō�̐l)�̐Ȃɍ���ꍇ (n�l�ڂ͐������Ȃɍ���Ȃ�)
�̏ꍇ�������l���܂��B���̏ꍇ�̊m���͂��ׂē�����
P(�ꍇ1)=P(�ꍇ2)=...=P(�ꍇn-1)=P(�ꍇn)=1/n
�ł���A�Ō�̐l�����������t���m����
P(n�l�ڂ�n�l�ڂ̐Ȃɍ���|�ꍇ1)=1
P(n�l�ڂ�n�l�ڂ̐Ȃɍ���|�ꍇ2)=p[n-1] (��2�l�ڂ������_���ɍ�����Ȃ�1�l��,3�l��,...n�l�ڂ�n-1�ȁ�n-1�l�̏ɊҌ�)
P(n�l�ڂ�n�l�ڂ̐Ȃɍ���|�ꍇ3)=p[n-2] (��3�l�ڂ������_���ɍ�����Ȃ�1�l��,4�l��,...n�l�ڂ�n-2�ȁ�n-2�l�̏ɊҌ�)
...
P(n�l�ڂ�n�l�ڂ̐Ȃɍ���|�ꍇn-1)=p[2] (��n-1�l�ڂ������_���ɍ�����Ȃ�1�l��,n�l�ڂ�2�ȁ�2�l�̏ɊҌ�)
P(n�l�ڂ�n�l�ڂ̐Ȃɍ���|�ꍇn)=0
�ƂȂ�܂��B������p[n]���v�Z�����
p[n]=P(n�l�ڂ�n�l�ڂ̐Ȃɍ���)
=��[k=1,n]P(n�l�ڂ�n�l�ڂ̐Ȃɍ���|�ꍇk)P(�ꍇk)
=(1/n)+��[k=2,n-1]p[n-k+1](1/n)
=(1/n)+(n-2)(1/2)(1/n) (��A�[�@�̉���p[n-1]=p[n-2]=...=p[2]=1/2���)
=1/2 >>247
1�l�ڂ�k�l��(k>1)�̐Ȃɍ���ꍇ
2�l�ڂ���k-1�l�ڂ܂ł͎����̐Ȃɍ��邩��
k�l�ڂ�1�l�ڂƓ��l�̏ɂȂ�̂ŋA�[�@�̉��肪�g����
������������k�l�ڂ�1�l�ڂƓ��l�̏Ƃ�
k�l�ڂ�1�l�ڂ̐Ȃɍ�����Ƃ͊F�����̐Ȃɍ��邱�ƂɂȂ�Ƃ������Ƃ�
k�l�ڂ�����ׂ��������Ȃɂ�1�l�ڂ������Ă��邩�獡����Ȃ��烉���_���ɐȂ�I�Ԃ����Ȃ��Ƃ������Ƃ�
1�l�ڂ������̐Ȃɍ�����Ƃ͊F�����̐Ȃɍ��邱�ƂɂȂ�Ƃ������Ƃƍ�����Ȃ̒����烉���_���ɐȂ�I�Ԃ����Ȃ��Ƃ������ƂƓ����Ƃ������� �^�a__`�a�P�P�a�c�~�
�a���� �a �� �a^o^��
�i�@(`)�a�@�@�a��c_)
�i���܁܁@�@��a������
��`(_)_)��~�@�a������
�_���҃ҁ�___�a��_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_`��_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�O>>243�Δ����Ƃ���������O�Ɍ������������Ǘv��1��2��3�̎O�p��K���Ă�Ώ��w�Z��w�N�ʼn�������Ă��Ƃ�����ȁB >>218
�A�[�@�g��Ȃ��Ă��ȒP�ɉ�����Ǝv���B
�Ō�̐l�̐Ȃ�L�A�ŏ��̐l�̐Ȃ�F�Ƃ���B�Ō�̐l��L�ɍ���Ώ����Ƃ��悤�B
�Ō�̐l�̏��������́uL���F����ɍ�����v���ƂŁA�s�k�����́uF���L����ɍ�����v���ƁB
�ŏ��̐l���܂߂��e���Ȃɂ����āAF��L�������m���̒��I��������i�ŏ��̐l�⎩���̐Ȃ������Ă���l�̏ꍇ��F��L�����m���ō����邵�A�����̐Ȃ��Ă���l�̏ꍇF��L��������m����0�j�B
����āA���������Ɣs�k�����������Ȃ̂œ�����1/2�B �e�l�̍���Ȃ����������������Ȃ����Ƃ����l�@�قڂقږ����ʼn�����̐����������� >>228
�̉���
> m-1�l�̐������Ȃ��c���Ă��邩�Am�l�S�Ă̐������Ȃ��c���Ă��邩�ǂ��炩�B
�ɂ����āAm-1�l�̐������Ȃ��c���Ă���Ƃ������l�����ĂȂ��悤�Ɏv���̂���...
m�l�S�Ă̐������Ȃ��c���Ă���ꍇ�́AA���������Ȃɍ����Ă����ꍇ�Œǂ��o���K�v�͂Ȃ���
���̂Ƃ�X�͔ԍ��D�������Ă����Ԃɑ�������
�������Ⴂ�������炷�܂� >>218
�����̐���n�l�Ƃ���
�~�����a1����an�܂�n�̓_���Ƃ�A
�����������������a1�_�Ɋ܂ޓ��ڑ��p�`�������_���ɍ��
�i�������X��A�P�p�`�ƂQ�p�`���F�߂�j
���̑��p�`��an�_�Ɋ܂܂Ȃ��m���Ɠ��� >>250
����ȉ���������Ȃ�ǂ�Ȃɐ�肪�L���ȃQ�[���ł������̏���1/2�ɂȂ��Ă��܂��̂ł́H
�Ⴆ����̂ł��ŏ��̐l���r���ŐȂ��Ȃ������l���T�C�R���U����6���o�����͐����̐ȁA���Ȃ킿�ŏ��̐l�͎����̐ȁA����ȍ~�̐l�͏��L�҂��Ԉ�����Ȃɒ��Ȃ��Ă��Ԃ�Ă�Ȃɍ���A����ȊO�̏ꍇ�̂ݎ��R�ɂ���郋�[���ɂ���Ίm����1/2�łȂ��Ȃ��B >>253
�{���ɂ��̂ӂ��̊Ԃɕۑ��ʑ�����H
��蕶�̕��͕����1�`n�܂łȂ�ł��o�Ă��邯�Ǔ��ڑ��p�`�̕��͕���ɓ�p�������Ȃ����ǁH >>255
�P���ɑ��p�`�̐��𐔂���
an���܂�k�p�`��an���܂܂Ȃ�k-1�p�`�̐����������̂�
�S�̂Ƃ��Ĕ������ɂȂ���čl�������_������ �O>>249�O��x/��2�ɂ��Ă�x���W��x�ɂ��ĉ����Ȃ������B
�ŏ��ɊĎ��l������ʒu����~�o�n�_(x,x)�܂ł̋�����x��2(m)
����[�܂�5�b�A���p�ɋȂ���A
{x-(10-x)/��3}(m)�̒n�_�܂ŁA
{x-(10-x)/��3}(1/2)�b�ōs���A�i�s�����ɑ���60���̕����ɔ�т���ʼnj���A�Ίp������j���ł����Ď��l�Ɠ����ɃA�^�b�N�����B
(_(`.)���S(�Ko�K)�m�c(`e'!�c
~~~ ~~~ ~~~ ~~~ ~~~ ~~~ ~~~
�~�o���Ԃŗ�������ƁA
x��2=5+{x-(10-x)(1/��3)}(1/2)+(10-x)(2/��3)
x��2=5+x/2-10/2��3+x/2��3+20/��3-2x/��3
x(��2-1/2-1+4)=5-10/2��3+20/��3
x=(30+10��3)/(3+2��6-��3)
=7.67326988�c�c
x��2=10.8516423�c�c(�b)
�O�ɂ��̒l�o���čő�����Ȃ��ƂȂ��������Ȃ����B >256
�����H
�Ⴆ��6�l���Ƃ���
325461
�Ƃ����m����
1/6x1x1/4x1x1/2
�ł���͍Ō�̐l�������̐Ȃɍ���Ȃ��ꍇ�ɃJ�E���g�����y���B
���̂悤�Ȏ��ۂ�S���������킹��1/2�ɂȂ鎖������������Ƃ��������B
�R����3��5��6��3�ƌ���Ŏl�p�`�ƑΉ������Ă��������NJm���͘Z�p�`���牽�_���D���ɑI��1/64�Ƃ̓Y����B >>256
���܂����
an���܂�k�p�`���ł���ꍇ��an���܂܂Ȃ�(n+1-k)�p�`���ł���ꍇ���Ή����Ă���� >>256���A�ł����̑��p�`�_�@�͂��܂�����1/2�����ł���ˁB
�f���炵���B �O>>257
>>237
�ǂ����Ō��o�������鐔�l���Ǝv������A>>31�ł��łɂ����Ă���Ȃ��́H >>252
�ŏ���2�s�́A��Ȃ̒��ɂ���������̐Ȃ����A�߂����Ȃ��Ƃ������Ƃ��������������B
�u�Ȃ����̂悤�Ȃ��Ƃ������邩�H �v�Ə����A�������̓_�̐����ɓ��ĂĂ���B
�����āA���̐����̉����Ƃ��āA
�u�����̔ԍ��D�������̂��A1�Ԗڂ̐l���A�i��납�琔���ājm�Ԗڂ̐l���A��ʂł��Ȃ��v
�_���w�E���Am=2�̎����g���ΊȒP�Ɋm���̌v�Z���ł���̂ŁA������g���ē��������߂Ă���B
���A�um-1�l�̐������Ȃ��c���Ă���v�ꍇ�Ɓum�l�S�Ă̐������Ȃ��c���Ă���v�ꍇ
�ɕ����A���ꂼ��ɂ��āA�������������킯�ł͂Ȃ��B
m�l���c���Ă����ԂŁA�um-1�l�̐������Ȃ��c���Ă���v�m���Ɓum�l�S�Ă̐������Ȃ��c���Ă���v
�m�������߁A���w�I�A�[�@��p���āA���������߂���@�����邪�A>>218�ł́A���̎�i��p���Ă��Ȃ��B
>> m�l�S�Ă̐������Ȃ��c���Ă���ꍇ�́AA���������Ȃɍ����Ă����ꍇ�Œǂ��o���K�v�͂Ȃ���
>> ���̂Ƃ�X�͔ԍ��D�������Ă����Ԃɑ�������
����́AX���o�ꂷ��܂��̂��ꂩ���A�����̐Ȃ��苒����Ă���̂����āA�K���ȐȂɍ������B�������A
���̐Ȃ����܂��܂`�̐Ȃł����āA����ȍ~�ɏ�Ԃ���l�����ւ̈��e�������̎��_�Œf�����Ă���ɂ�����B
�������A��ԍŏ��ɏ�Ԃ����`���g���A�K���ɍ��������Ȃ����܂��܁A�{���̂`�̐Ȃł��邱�Ƃ�
�u�܂܂�v�͂�����̂́A�u�`���`�̐Ȃɍ���v�ɂ͊��S�Ή��͂��Ȃ��B
�J��Ԃ����A�u�`���b�A�b���f�A�f���`�v�̂悤�ɉ��������ꍇ�ł���A����ɂ́A�u�`���`�v���܂܂��B ���218�ւ̈��p�́A>>228�ւ̈��p�̊ԈႢ >>254
> ����ȉ���������Ȃ�ǂ�Ȃɐ�肪�L���ȃQ�[���ł������̏���1/2�ɂȂ��Ă��܂��̂ł́H
> �Ⴆ����̂ł��ŏ��̐l���r���ŐȂ��Ȃ������l���T�C�R���U����6���o�����͐����̐ȁA���Ȃ킿�ŏ��̐l�͎����̐ȁA����ȍ~�̐l�͏��L�҂��Ԉ�����Ȃɒ��Ȃ��Ă��Ԃ�Ă�Ȃɍ���A����ȊO�̏ꍇ�̂ݎ��R�ɂ���郋�[���ɂ���Ίm����1/2�łȂ��Ȃ��B
���̃��[����
> �ŏ��̐l���܂߂��e���Ȃɂ����āAF��L�������m���̒��I��������
�ɂ͓�����Ȃ�����H
> �m����1/2�łȂ��Ȃ��B
�ɂȂ��Ă����̖��Ȃ����낤
>>250�͋A�[�@�̈��ȂႶ��Ȃ����Ƃ͎v���� >>264
���̒��I�_�@�Ŗ{���ɐ������m���v�Z�ł���̂��T���ł͂Ȃ������ɏ����o�������̂������Ă��������B >>254�̘_�@���Ԉ���Ă�����Č����Ă��邾������
�Ƃ������A���̒��x�̘_�@(>>250)�������������炢�����Ŋm�F�����
> �ŏ��̐l���܂߂��e���Ȃɂ����āAF��L�������m���̒��I��������
���^�����m�F���邾������ >>266
���Ȃ���>>250�̌����Ă鎖���킩���ł����H
�킽���ɂ�F��L���Ȃ����ɂ��Q�[��������1/2���Č����Ă�悤�ɂ��������܂���B
�����헪�Ƃ��Q�[���Ƃ��������t�g�����������ŏؖ����ł��ĂȂ���Ȃ����Ƌ^���Ă܂��B ���A�헪�Ƃ��͎g���ĂȂ��̂��B
�����Ƃ������Ă邩��Q�[�����_���C����Ă�̂��Ǝv�����B >>262
���肪�Ƃ��A�����ł����B >>218
���̖��́A���̖��ƑΉ����\�B
�J�[�h����������A���ꂼ��ɁA�P���炎�܂ł̐�����������Ă���B
�����̃J�[�h��܂ɓ����B
�v���C���[�́A�P���炎�̒�����A�����ԍ��ƁA�����ԍ������߁A
�����ԍ��A�܂��́A�����ԍ���������Ă���J�[�h���o��܂ŁA�܂̒�����J�[�h��I�ё�����B
�����ԍ��������ďI������m���́H�@ �@ �@�� �@ �@ ���R1/2�ƍl�����܂��B
���o���ꂽ��������A�K���ɑI��č����Ă��܂������Ȕԍ��ɑΉ������܂��B
�i���O���A���łɐ苒����Ă������A���R�͖��Ȃ��j
�擪�̐l�̖{���̍��Ȕԍ����Ɉ������A�Ō�̐l�̍��Ȕԍ����Ɉ��������A
�擪�̐l�̖{���̍��Ȕԍ��������ĉ����A�����r���ŏI�����邩�A
�Ō�̐l�̍��Ȕԍ��������āA�����A���ɍŌ�̐l���������ނ������肳��A
���Ō����Ƃ���́A�Ō�̐l���������Ȃɍ���邩�A����Ȃ����ɑΉ��\�ł��B
�A�C�f�A�̂قƂ�ǂ́@>>250���w�E���ꂽ���̂ŁA�Ή����킩��₷���Ȃ�悤���X�A�����W���Ă܂��B ���{�ō��w��̒�ӎ������ł�
�P�N�F�i�����s�P�O�l
�Q�N�F�i�����s�P�U�l
�R�N�F�i�����s�R�S�l
�S�N�F�i�����s�X�l
�T�N�F�i�����s�P�O�l
�U�N�F���Ǝ��s�Q�U�l
��w�N��120�`130�l�O��B
�����w�N�œ�N����Ƒފw
https://mao.5ch.net/test/read.cgi/doctor/1516439331/1
�ł���Ƃ����B
1�N���w��z 12,145,000�~ 2�N���ȍ~�w��i�N�ԁj�@7,030,000�~
1�w�N��125�l�Ƃ��ď�L�f�[�^����Z�o�����m���i��A1�N����10/125�̊m���ŗ��N�j��p����
���Ƃł���m���Ƒ��Ɛ��̍݊w�N���̊��Ғl�����߂�B
�܂��A�ފw�ɂȂ�m���Ƒފw�҂̍݊w�N���̊��Ғl�����߂�B >>254
���̏ꍇ�ŏ��̐l�̒��Ȃɂ�����F��L�����m���̒��I���Ă��Ȃ��̂œ��R���ʂ͕ς���Ă���Ǝv���܂��� ���鏬�w�Z�̂���N���X�ł́A�o�X�ʼn����ɍs�����ƂɂȂ����B
�o�X�̍��Ȃ͎��O�Ɍ��܂��Ă������A�ŏ��Ƀo�X�ɏ���������������̍��Ȃ�Y��āA�C�ӂ̍��Ȃɍ����Ă��܂����B
���̎����́A��l���o�X�ɏ�荞�݁A�����̍��Ȃ��Ă�����̍��ȂɁA�����łȂ���Ă���C�ӂ̍��Ȃɍ������B
�N���X�̐l����n�Ƃ��Ď����̐Ȃɍ���鐶�k���̊��Ғl��e[n]�Ƃ���Ƃ�lim e[n]/log(n)�����߂�B
����B
�ł��Ȃ������B >>273
����
lim(n-e(n))/log(n)
�ł��B �O>>261
>>271���Ƃł���m���́A
8(4/23)+12.8(20/99)+(3400/99)(4/13)+(180/13)(5/14)+(125/7)(10/23)+(1300/23)
=83.7751427�c�c(��)
�݊w�N���̊��Ғl�́A
6(16/83.7751427�c�c)+7{(83.7751427-16)/83.7751427}
=6.80901256(�N)
�ފw�ɂȂ�m���́A
100-83.7751427�c�c
=16.2248572�c�c(��)
�ފw�҂̍݊w�N���̊��Ғl�́A
1(10/125)(16/115)+2(10/125)(34/115)+3(/)+4(/)+5(/)+6(/)+7(/)���������B >>275
�������E�̌v�Z���ɂ������ɂ��ւ�炸���X���肪�Ƃ��������܂��B
�ʓ|�Ȍv�Z���듚�����̂Ƃ̂�����������C�͂ɂ͂����S���܂��B�����ł͂���܂���B
�ŁA�����̒ʂ�A�p�ӂ������Ƃ͈Ⴂ�܂��B
������ł����A�V�~�����[�V�����l�ƍ��v�������_�l���o���܂����B�ꍇ�������ʓ|�Ȃ̂ŏꍇ�������v���O�����ɂ����܂����B
�V�~�����[�V�����͎w��̊m���ŗ������������Čv�Z�����܂����B
�قڈ�v����l�ł����B >>276
�⑫
�V�~�����[�V�����ł̌��ʂ͈ȉ��̒ʂ�
> mean(RE[,2]==7) # ���Ɗm��
[1] 0.85482
> mean(RE[RE[,2]==7,1]) # ���Ƃ܂ł̍݊w�N��
[1] 6.712606
> mean(tu(RE[RE[,2]==7,1])) # ���Ƃ܂ł̊w��
[1] 52304621
> mean(RE[,3]==2) # �ފw�m��
[1] 0.14518
> mean(RE[RE[,3]==2,1]) # �ފw�܂ł̍݊w�N��
[1] 4.99139
> mean(tu(RE[RE[,3]==2,1])) # �ފw�܂ł̊w��
[1] 40204472
q=1-p # ���N�m��,p=�i���m��
(P=prod(1-q^2)) # ���Ƃł���m�� ��{1 - (2�N�A�����N�m��)}
(Q=1-P) # �ފw�ƂȂ�m��
�̌��ʂƋߎ����Ă��܂��B >>273
�N���X�̎����ɂ�1����n�܂ł̔ԍ����A���Ȃɂ�0����n-1�܂ł̔ԍ������Ă��āA
���Ȃɍ��鑀��͔ԍ����傫�����ɍs�����̂Ƃ���B
�����ō��Ȃɍ��鑀��Ƃ́A�����̔ԍ��Ɉ�v����Ȃ��Ă�������ɁA
�ĂȂ����Ȃ̂ǂ����Ƀ����_���ɍ��铮��������B
���̎��A�����̔ԍ������ȂƈႤ�悤�Ȏ����̐l���̊��Ғl��e'[n]�Ƃ����B
n-e��e'�̌v�Z�ŗB��قȂ�_�́A���Ȕԍ�0��n�̈Ⴂ�ɂ�萶������̂̂݁B
���̈Ⴂ���e������̂́A�ŏ��ɔԍ�n�̎�����0�̍��Ȃɍ���ꍇ�݂̂ł��邩��A
n-e[n]=e'[n]-1/n.
�ŏ��Ɏ���n������m(<n)�ɍ������ꍇ�A���Ƀ����_������������͎̂���m���������ł��邪�A
���̎��_�Ŏc��̎�����1����m�A�c��̍��Ȃ�0����m-1�ł��邩��A
�����m�l�̎�����m�̍��Ȃōs�����s�ƈ�v�B
�i������n=0�̎��̎��s��"�������Ȃ�"���Ƃƒ�߂�B�܂�e'[0]=0. �j
�䂦�ɁA���̂悤�ȑQ���������Ă���B
e'[n]=1+(1/n)��_(m=0,n-1)e'[m]
������
ne'[n]-n = (n-1)e'[n-1]-(n-1) + e'[n-1]
����
e'[n] = ��_(m=1,n) 1/m
��������A���߂�Ɍ��l��1�ƌv�Z�ł���B >>278
�����ł��B
�z���>>222�ƈꏏ�B
�Ōォ��k�Ԗڂ̐��k���������Ȃɍ��ꂽ�Ƃ�0�A�����łȂ��Ƃ�1���Ƃ�ϐ���Xk�Ƃ���B
k:1�`n-1�̂Ƃ�
p(�Ōォ��k�Ԗڂ̐��k���������Ȃɂ����|�ŏ��̐��k���ŏ��̐��k�̐Ȃ��܂��͍Ōォ��k�Ԗڂ̐ȁ`�Ō�̐Ȃɍ���)
= (�ŏ��̐��k���Ōォ��k�Ԗڂ̐ȈȊO�ɍ���|�ŏ��̐��k���ŏ��̐��k�̐Ȃ��܂��͍Ōォ��k�Ԗڂ̐ȁ`�Ō�̐Ȃɍ���)
=k/(k+1)�B
p(�Ōォ��k�Ԗڂ̐��k���������Ȃɂ����|�ŏ��̐��k��2�Ԗڂ̐Ȃ���Ōォ��k-1�Ԗڂ̐Ȃɍ���)=k/(k+1)
(�� ���k�̐������Ȃ��ꍇ�ɊҌ������)�B
�� p(�Ōォ��k�Ԗڂ̐��k���������Ȃɂ����)=k/(k+1)�B
��E(Xk)=1/(k+1)
���炩��E(Xn)=(n-1)/n
��n-e(n)=��[k:1�`n-1]1/(k+1)+(n-1)/n�`log(n)�B �I���W�i���ł��������͂���܂���B�����C�ɂȂ����̂œ��e���܂�
�����̔z�� a[i,j] (i,j∊Z) ���S�Ă̊i�q�_(i,j)�� 4a[i,j]=a[i+1,j]+a[i-1,j]+a[i,j+1]+a[i,j-1] �������Aa�a�z��ƌĂԂ��Ƃɂ���B
��������������0�̉����͂����炩�F
���a�z��a���C�ӂ̊i�q�_X�ɂ��� |a[X]|��|X|^�� �����Ȃ��a�͒萔�ł���B�������A|X|�͓_X�̌��_����̋�����\���B ���Ƃł���m���@�F�@4750970704397512 / 5551115123125783�@= 0.85585879575891107187420816324627437826646454687092053
�ފw�̊m���@�@�@�F�@800144418728271 / 5551115123125783 = 0.144141204241088928125791836753725621733535453129079468759 �P�ʉ~���2n�̓_A1,B1,�d,An,Bn����l�Ɨ��ɑI�щ~�Ղ�n�̐�������A1B1,�d,AnBn�ŕ�������Ƃ��A�ł��鏬�̈�̌��̊��Ғl�����߂�B >>280
�Ƃ肠�������̂Ƃ��낱�̃X���ł�>>240����̏ؖ������オ���ĂȂ��B
���̕��j�ł����Ȃ������������
��(c(p+2,q)-c(p,q)|(|p|+|q|}^����0 (n����)�d�d(��)
�����藧�Ȃ炻�̃���>>280�̏������݂������肵�Ȃ����ȁH
�܂�>>240�����S�ɗ����ł��Ă͂��Ȃ�����킩��Ȃ����ǁB
����(��)�����̎�����0�����Ȃ��Ȃ獡��Ƃ��������P�ł��錩���݂��郌�X�͏オ���ĂȂ��ȁB �O>>275
>>283
n=1�̂Ƃ�2(��)
n=2�̂Ƃ��A
3(1/2)+4(1/2)=3.5(��)
n=3�̂Ƃ��A
4(1/8)+5(1/8)+6(1/4)+7(1/2)=(9+12+28)/8
=6.125(��)
n=4�̂Ƃ��ő�11�A�ŏ�5��
5(1/64)+6(1/64)+7(1/32)+8(1/16)+9(1/8)+10(1/4)+11(1/2)
=(5+6+14+32+72+160+352)/64
=10.015625(��)
n=5�̂Ƃ��ő�16�A�ŏ�6��
=(6+7+16+36+80+176+384+640+192+1280+512+2560+1280)/1024
=(7149+8192)/1024
=15341/1024
=14.9814453�c�c
n=6�̂Ƃ��A�ŏ�7�A�ő�22
7(1/2)^15+8(1/2)^15+9(1/2)^14+10(1/2)^13+11(1/2)^12+12(1/2)^11+13(1/2)^10+14(1/2)^9+15(1/2)^8+16(1/2)^7+17(1/2)^6+18(1/2)^5+�c�c+22(1/2)
n�{�̒����ŕ��������̈�̌��̊��Ғl�́A
(n+1)(1/2)^{n(n-1)/2}+(n+2)(1/2)^{n(n-1)/2}+(n+3(1/2)^{n(n-1)/2-1}+�c�c+{n(n+1)/2+1}(1/2)
�u���b�N�������̂悤�ɊȒP�ɂȂ�̂��Alim[n��+��]�ɔ���̂��A�ʕ����B ���x�v�����ǎv�l�ߒ������X����̉��H
�Z�Z�ƂȂ�c�c�����Ⴄ���B�݂����Ȃ̒N�����߂ĂȂ������w�̎����ł���Ȃ��Ə������H
�����ƃI�t���C���œ����ɒH�蒅���Ă��炻���Z�߂ď����� >>285
n=1�̂Ƃ������͐����ł��B >>284
(��)�͎g�������ł���
���ۂɂ� ��|c[p+2,q]-c[p,q]|=2��c[0,q] �̒l�͐ϕ����g����
C(1+o(1))/��n (as n����, �������萔C��absolute) �ƂȂ邱�Ƃ��v�Z�ł���̂ŁA
|��(a[0,0]-a[2,0])|
����|c[p+2,q]-c[p,q]|(|p|+|q|)^��
��C(1+o(1)) � n^(�� - 1/2) (��|p|+|q|>n �̎��ɌW����0�ƂȂ邽�߁A|p|+|q|��n �͈̔͂Řa���Ƃ�Ηǂ�)
�Ƃ����]���������܂��B
a[0,0]��a[2,0]�̍��ȊO�ɂ����l�̂��Ƃ�������̂ŁA���� ��<1/2 �͏����������Ƃ�������Ǝv���܂��B
���Ȃ݂Ɉ���� a[i,j]:=i (��(i,j)��Z^2) �Ƃ����Ⴉ��A����1�͏��������Ȃ����Ƃ��킩��܂� �O>>285���H�@>>283n=2�̂Ƃ��Ⴄ�́H�@�Ȃ�ŁH�@�N���X����m���ƃN���X���Ȃ��m����1/2������Ȃ��̂����H
�^�a__`�a�P�P�a�c�~��a
�a���� �a �� �a^o^�� `
�i�@(`)�a�@�@�a��c_)�_
�i���܁܁@�@��a�_____/
��`(_)_)��~�@�a��a__�a
�_���҃ҁ�___�a��_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_`��_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_ >>200
�q���g�B
�z���g�͐ϕ��ŋ��߂���Ǘ��Z�B
�܂�4�_�I�ԁB
��łǂ��A1B1A2B2�Ɗ���U�邩���߂�B �_O���S�̔��a1�̉~�̓����ɓ_O�ƈقȂ�_A�����B
������OA���OA�EOB=1�Ȃ�_B�����B
�~����ɓ_P,Q���A����PQ�Ɋւ��ē_O,A,B���������ɗ���悤�ɔC�ӂɎ��B����3�_�͂����������PQ��ɖ����B
����PQ�Ɋւ���A�Ɛ��Ώ̂ȓ_��D�Ƃ���B
��PBD�䁢OBQ�������B >>283
�l�_A1,B1,A2,B2�̕Ίp�����������ɕ��ׂ��1122,2211,1221,2112,1212,2121�̘Z�ʂ�
���̂����A��̎l�͐������݂��Ɍ����Ȃ��ꍇ�ł���A��̓�͌����ꍇ�ł���
�܂�A�����_���Ɍ��߂���̐����������m����1/3
n�{�̐����ɂ��~����������Ă���Ƃ��A�V���Ɉ�{�̐�����������Ƃ���
���̂Ƃ��V���������������̐����ƌ����Ȃ���A���������̈�͈������
�����̐�����{�ƌ����Ȃ�̈�͓�����A�����̐�����{�ƌ����Ȃ�̈�͎O������
�܂�A�V���������������̐����ƌ�������{��+1�̗̈悪�V���ɑ�����
�V�����������������Ƃ��A�����̐���n�{�̂��������{���̊��Ғl��n/3������A
�̈�̐��̑����̊��Ғl��n/3+1�ƂȂ�A
n�{�̐����ŕ������ꂽ�Ƃ��̗̈�̐��̊��Ғl��I(n)�ƒu���ƁAI(n+1)=I(n)+n/3+1�Ə�����
I(n)-I(1)=(n(n-1)/2)/3+(n-1)�AI(1)=2�͎����Ȃ̂ŁAI(n)=n(n-1)/6+n+1 >>292
PQ�̐���������������O�����_�ƂȂ镡�f���W��ݒ肷��B
A�̎����Ώ̓_��C�Ƃ���B
ABCDPQ�̕��f���W��abcdpq�Ƃ���B
PD��PQ�A�����ő����đΏ̈ړ������QC�Ɉڂ邩��d-p=q-c�ł���B
�܂�A���P�ʉ~�Ɋւ��锽�]��C�͂��̎������]������c=1/b�ł���B
P,Q�͒P�ʉ~�ォ�����Ώ̂�����pq=1�ł���B
�ȏ�ɂ��
(d-p)/(b-p)
=(q-c)/(b-p)
=(1/p-1/b)/(b-p)
=1/(pb)
=(q-0)/(b-0)
�ł��邩�灢BDP�Ɓ�BQO�͑����ł���B >>291
�ϕ��ł���Ă݂�
A1,B1,A2,B2�̕Ίp��0,X,Y,Z�Ƃ��āAA1���Œ肵�A��̎O���m���ϐ��ƍl����
���ꂼ��Ɨ���0����2�̊Ԃ̒l������l���z�ɏ]���̂ŁA�m�����x����1/(2��)^3�ƂȂ�
Y��Z������0��X�̊Ԃ̒l�����m���́A
��[0,2��]��[0,x]��[0,x]dydzdx/(2��)^3=��[0,2��]{x^2/(2��)^3}dx=1/3
Y��0��T�̊ԁAZ��T��2�̊Ԃ̒l�����m���́A
��[0,2��]��[0,t]��[t,2��]dydzdx/(2��)^3=��[0,2��]{x(2��-x)/(2��)^3}dx=1/6
������������Ȃ��m��=Y��Z������0��X�̊Ԃ܂��͋���X��2�̊Ԃł���m��=1/3+1/3=2/3
������������m��=Y��0��T�̊Ԃ�Z��T��2�̊Ԃ܂��͂��̋t�ƂȂ�m��=1/6+1/6=1/3 >>296
�����A�f���炵���I
�����Ŏ��w������݂�1/6�������o�Ă���̂��ւ��Ǝv���܂����B �O>>290
>>283
n=1�̂Ƃ�2
n=2�̂Ƃ�3(2/3)+4(1/3)=3.33�c�c
n=3�̂Ƃ�4(2/3)^2+5�3(2/3)(1/3)+6(1/3)(2/3)+7(1/3)^2
=(4+10+12+7)/9
=3.66�c�c
�}��n��n+1�ɔ�炾����킩��Ȃ����낤�B�r���������Ƃ���Ăق����B
n=4�̂Ƃ�5(2/3)^3+6(2/3)^2(1/3)+7(2/3)(1/3)^2+8(/)+9(/)+10(1/3)^2(2/3)+11(1/3)^3��`o`�� �Ƃ肠����n=3�̂Ƃ�n=2�Ɠ����悤�ɂ���Ă݂�����B
6�_�K���ɑI�ԁB
�������O�_����_�Ō����悤�ȓ���ȃP�[�X�͊m��0�Ȃ̂Ŗ�������B
�����v����123456�Ƃ���2�g���킯��B
12,34,56
12,35,46,
�d
�ʼn��ʂ�ł��邩�H
���̈悪4�ɂȂ�͉̂��ʂ肩�H
���̈悪5�ɂȂ�͉̂��ʂ肩�H
���̈悪6�ɂȂ�͉̂��ʂ肩�H
���̈悪7�ɂȂ�͉̂��ʂ肩�H
���Ғl�́H >>298
m�{�̐����Ɍ������������ƁA����m�{�ŕ�������Ă���m+1�̗̈�̏��ʂ邱�ƂɂȂ�
�܂�m+1�̗̈��邱�ƂɂȂ�̂ŁA�̈�̐��͔{������Am+1�̗̈悪�V���ɑ����邱�ƂɂȂ� �O>>298
>>301
2�{�̒����ƌ������钼���������Ɨ̈悪3�����邱�Ƃ͂킩���Ă�B
�܂�m=2�̂Ƃ��Ӗ����ʂ���B
���nj������Ȃ��Ƃ��̊m���𑫂��Ȃ�����B
n=3�̂Ƃ��̈悪4�ɂȂ�̂͌������Ȃ��Ƃ��B
n=2�̂Ƃ��̍l�@���炵�Č�������Ƃ���1/3�Ō������Ȃ��Ƃ���2/3����Ȃ��̂��H
4(2/3)^2+5�3(2/3)(1/3)+6(1/3)^2+7(1/3)^3
=(16+30+18+7)/27
=71/27
���̌v�Z�A
2/3+2/9+1/9+1/27��1�ɂȂ�Ƃ�����Ȃ��ƈӖ��Ȃ���B A1B1��A2B2����������m����1/3�A
A2B2��A3B3����������m����1/3�A
A3B3��A1B1����������m����1/3�A
��������_���R�ł���m���͂��̂R�������Ă��_���B
�����ċ��߂���̂̓R����̎��ۂ��Ɨ��̎��B
�Ɨ��ł͂Ȃ��̂Ń_���ł��B ���a�z��ɂ��čl���Ă����ǁA�ǂ������������������C������c
>>195 ��e�̍\�����Ė{���ɍ����Ă�H
�ȉ��̗v�̂ŁA���_�ȊO�̑S�Ă̊i�q�_�Œ��a�I�ȗL�E�z��͒萔�������݂��Ȃ����Ƃ����������Ȃ��ǁc
�z��a�� a[0,0]=1 ���� a[X]��0 (��X��Z^2) �����A���_�ȊO�Œ��a�I�ȗL�E�z��Ƃ���B
a�̉��� inf_(X��Z^2) a[X] ��0�Ƃ��Ă悢�Ba[X]=0 �����i�q�_X�͑��݂ł��Ȃ����Ƃɒ��ӁB
�z��̗� b_n ��
b_n[0,0] = 1 (n��0)
b_0[p,q] = 0 ( (p,q)�͌��_�ȊO�̊i�q�_)
b_(n+1)[p,q] = b_n[p+1,q] + b_n[p-1,q] + b_n[p,q+1] + b_n[p,q-1] ( (p,q)�͌��_�ȊO, n��0)
�ɂ���߂�ƁA�A�[�I��
b_n[p,q]��b_(n+1)[p,q]��1 (p,q�͑S�Ă̐���, n��0)
�������邽�ߋɌ� b[p,q]=lim_(n����) b_n[p,q] �����݂��A
�z�� b �����_�ȊO�Œ��a�I�ł��邱�Ƃ��킩��B�܂��A�en�ɂ���
b_n[p,q]=b_n[-p,q]=b_n[p,-q]=b_n[q,p]
0��p ���� 0��q �Ȃ�� b_n[p,q]��b_n[p+1,q]
1��p��q �Ȃ�� b_n[p,q]��b_n[p-1,q+1]
b_n[p,q]��a[p,q]
�����藧���Ƃ��A�[�I�Ɏ����邽�߁An�����Ƃ��邱�Ƃ�b�ɂ��Ă����l�̂��Ƃ�������B
�z��a�̉�����0���S�Ă̊i�q�_X�ɂ���a[X]>0�ł��邱�Ƃ���A
�i�q�_�̗� X_n=(p_n,q_n) �ł�����
lim a[X_n]=0, lim(|p_n|+|q_n|)=0
�������̂����݁B������A�i�q�_(p,q)�� max(|p|,|q|)��|p_n|+|q_n| �����Ȃ��
b[p,q] �� b[|p_n|+|q_n|] �� b[p_n,q_n] �� a[p_n,q_n]
�ł��邩��A�i�q�_X�ɂ���|X|�����Ȃ��b[X]��0�����藧�B
��U�����܂ŁB >>304
�����B�z��̗�b_n�̑Q�����ɂ���
��
b_(n+1)[p,q] = b_n[p+1,q] + b_n[p-1,q] + b_n[p,q+1] + b_n[p,q-1]
��
b_(n+1)[p,q] = (b_n[p+1,q] + b_n[p-1,q] + b_n[p,q+1] + b_n[p,q-1])/4 >>304
���x���\����Ȃ��A�����P�����B
�i�q�_��X_n�ɂ���
��
lim a[X_n]=0, lim(|p_n|+|q_n|)=0
��
lim a[X_n]=0, lim(|p_n|+|q_n|)=�� >>304
�������e�͌��_��
4e[0,0]=e[1,0]+e[-1,0]+e[0,1]+e[0,-1]
�����Ă܂����B
4e[i,j]=e[i+1,j]+e[-i-1,j]+e[i,j+1]+e[i,j-1]
�̓L���q�z�b�t�̖@��
(e[i+1,j]-e[i,j]}+(e[-i-1,j] -e[i,j]}+(e[i,j+1]-e[i,j]}+(e[i,j-1] -e[i,j]}=0
��ό`�������̂ł����A���_�͓d�ɂ����Ăēd�����z���o���Ă�̂ł��̓������������Ă��܂���B
>>195��e�͏�ɗL�E�Ȃ̂ł����S�Ă̓_�ŏ�̓�������������Ȃ�J�{�̒藝�ɂ��萔�ɂȂ��Ă��܂��܂��B >>283
(n+2)(n+3)/6 ����
���o�ߒ��͂��ꂩ��l����w �O>>302�����Ȃ�n�Ƃ�m�Ƃ��ň�ʍ��o���ĉ��������z�͋U�҂��ȎҁB1��2�ʃN���A���č�3�ʁB
n=3�̂Ƃ��ŏ���4�ōő傪7�A
4(2/3)(3/4)(1/4)+5(2/3)(4/6)+6(1/3)(4/6)+7(1/3)(2/6)
=4(1/8)+5(4/9)+6(2/9)+7(7/24)
=1/2+32/9+49/24
=(36+256+147)/72
=439/72
=6.0972�c�c
������ƃ}�V�ɂȂ����B >>308
��_�̉\�Ȑ��� n(n-1)/2 �ł���
1��i<j��n�Ƃ���AiBi��AjBj����������m���͊e�X1/3�Ȃ̂�����A
��_�̐��̊��Ғl�� n(n-1)/6
�̈�̐��̊��Ғl�� (n+1)+n(n-1)/6 = (n+2)(n+3)/6 �����ƁA283��>>293�Ŋ��ɉ�����Ă�����
�܂������Ă�̂��Ǝv����w >>292
�����I�ؖ�
AB�a�Ƃ��鏬�~��`���A�o��̓�̎O�p�`�Ƒ�����
��̎O�p�`�����~�̒��ɍ�}�ł���B
��~�Ə��~�̌�_��E�AF�AEF��AB�̌�_��G�A
DB�Ə��~�AQB�Ə��~�̌�_�����ꂼ��H�AI�A
IG�̉����Ə��~�̌�_��J�AJH��PB�̌�_��K�Ƃ���ƁA
��KHB�䁢GIB�ŁA���̓�̎O�p�`�͏o��̓�̎O�p�`�Ƒ����ł���B
��H����I�ł��邱�Ƃ͂����ɕ�����B
���Ƃ́�KBH����GBI�ł��邱�Ƃ������悢���A
���ꂪ�ӊO�Ɠ���A���̂Ƃ��떢�����B >>307
e�����_�Œ��a�I�łȂ����Ƃ͂킩���Ă���̂ł����A���͂����ł͂Ȃ��āA>>304�̒ʂ�
�w���_�ȊO�́x�S�Ă̊i�q�_�Œ��a�I�ȗL�E�z��͒萔�������݂��Ȃ�
�Ƃ������Ƃ������Ă��܂��A�Ƃ������ƂȂ̂ł�
����304�̑�������
c=4b[0,0]-b[1,0]-b[-1,0]-b[0,1]-b[0,-1] �Ƃ����ƁA����n��2�ɂ���
cn = ��_(m=1,n) c
= ��_(m=1,n) ��_(|p|,|q|<m) 4b[p,q] - b[p+1,q] - b[p-1,q] - b[p,q+1] - b[p,q-1]
= ��_(m=1,n) ��_(|p|<m) - b[m,p] - b[-m,p] - b[p,m] - b[p,-m] + b[m-1,p] + b[1-m,p] + b[p,m-1] + b[p,1-m]
= 4b[0,0] + ( ��_(p=1,n) 2b[p,p] + 2b[p,-p] + 2b[-p,p] + 2b[-p,-p] ) - ( ��_(|p|<n) b[n,p] + b[-n,p] + b[p,n] + b[p,-n] )
= o(n) (as n����)
��薵���B���������āAa �͒萔�łȂ���Ȃ�Ȃ��B >>313
e��0�ȏ�̒l���Ƃ�܂����L�E�ł͂���܂����B
>>204�Ŏ�����Ă��܂��B >>314
���玸�炵�܂����c >>195�������Ă܂���ł��� �O>>309
>>311�����������B
n=3����B
�����B
3�̂Ƃ�5�A
4�̂Ƃ�7�A
6�̂Ƃ�12�ł��B 4e(i+1,j)+ e(i-1,j)+ e(i,j+1)+ e(i,j-1)
=
��[�`] (1-cos((x+y)(i+1))cos((x-y)j))/(1-cosxcosy)dxdy
+��[�`] (1-cos((x+y)(i-1))cos((x-y)j))/(1-cosxcosy)dxdy
+��[�`] (1-cos((x+y)i)cos((x-y)(j+1)))/(1-cosxcosy)dxdy
+��[�`] (1-cos((x+y)i)cos((x-y)(j-1)))/(1-cosxcosy)dxdy
-4 ��[�`] (1-cos((x+y)i)cos((x-y)j))/(1-cosxcosy)dxdy
=
��[�`] (2-2cos(x+y)cos((x+y)i)cos((x-y)j))/(�`)dxdy
+��[�`] (2-2cos(x-y)cos((x+y)i)cos((x-y)j))/(�`)dxdy
-4 ��[�`] (1-cos((x+y)i)cos((x-y)j))/(1-cosxcosy)dxdy
=
��[�`] 4(1-cos(x)cos(y)cos((x+y)i)cos((x-y)j))/(�`)dxdy
-��[�`] 4(1-cos((x+y)i)cos((x-y)j))/(1-cosxcosy)dxdy
=
��[�`] 4cos((x+y)i)cos((x-y)j))dxdy
=
��[i0]��[j0]16��^2
�ɂȂ�n�Y�B ��������� >>242 �̍Ō�̎咣����������K�v�����肻����
��
����n�_ p_i (1��i��n) ���������i�q�_�S�̂� ��a=a �����悤�ȗL�E�z�� a ��
a[X] = c_0 + ��_(i=1,n) c_i�a'[X-p_i] (c_i�͎���)
�ƕ\����B
��
����n�_ p_i (1��i��n) ���������i�q�_�S�̂� ��a=a �����z�� a �ł����āA
�C�ӂ̒萔 ��>0 �ɂ��� |a[X]|=O(|X|^��) �����悤�Ȃ��̂́A
a[X] = c_0 + ��_(i=1,n) c_i�a'[X-p_i] (c_i�͎���)
�Ɍ�����B >>292
���ꍡ�N�̓卂�Z�̓�����肶��� >>312�̑���
HB��EI�������ł��邱�Ƃ��������Ƃ��ł���Ώؖ������B
�Ȃ��Ȃ�A���̏ꍇ�A��BHA�͒��p������HA��EI�͕��s�B
����Ɓ�AHI��HIE�͍��p�����瓙�����B
����Ɓ�ABI����AHI����HIE����EBH
��H�Ɓ�I�͓���~���p�œ��������Ƃ����łɎ�����Ă��邩��A�ؖ������B
������HB��EI�������ł��邱�Ƃ��������Ƃ�����B
�卂�Z�̓������Ȃ�A�����ƊȒP�ȉ�@������ɈႢ�Ȃ��i�� n,k�͎��R����k��n�Ƃ���B
���̊J����2k�̔��ʂ�2n-2k�̍��ʂɂЂ���ʂ��ėւ����B
���̂Ƃ��K����2�ӏ��łЂ������n����2�g�ɕ����A
�ǂ���̑g������k�A����n-k����Ȃ�悤�ɂł��邱�Ƃ������B
(�^��w���n�ߋ��� - ���w���̒m���ʼn�����) >>321
�㔼���̐Ԃ̌��ɂ��čl����B
�ʈ�����v���ɉ��Ƃ��㔼���̂����̐��͂��܂܂��A������邩�����̂����ꂩ�B
�������Ƃ��㔼���Ɖ�����������ւ��̂łǂ����̎��_�Ńs�b�^�������ɂȂ�B >>322
�����ˁA�����B
�v�͗��U�Œ��Ԓl�̒藝(����)�B >>280
�ł����B�����1�B
�S��Œ��a�I�Ȕz��a���A���� ��<1 �ɂ��� a[X]=O(|X|^��) �����Ă���Ɖ���B
((��^n)a)[0,0] �ɂ����� a[-n+p+q,p-q] �̌W��c_n[p,q]��
((1+x)(1+y)/4)^n �ɂ����� (x^p)(y^q) �̌W���ƈ�v�B�܂�
c_n[p,q] = 4^(-n)�C(n,p)�C(n,q).�@�i�������啶����C�͓W���j
����āA (��^(2n+1)a)([1,0]+[-1,0]-[0,1]-[0,-1]) �̌W���̐�Βl�̑��a��
��_(p,q�͐���) 4^(-n)�|C(2n+1,p)-C(2n+1,p-1)|�|C(2n+1,q)-C(2n+1,q-1)|
=4C(2n+1,n)^2
=K/n�(1+o(1)). �i������K�͂���萔�j
�ł��邩��A
|a[1,0]+a[-1,0]-a[0,1]-a[0,-1]|
��K(1+o(1))�2^���n^(��-1)��0 (as n����)
��� a[1,0]+a[-1,0]=a[0,1]+a[0,-1].
����� ��a=a ��� a[1,0]+a[-1,0]=2a[0,0].
���l�ɂ��āA�C�ӂ�j���Œ肵������ a[i,j] ����������Ȃ����Ƃ��킩�邪�A|a[X]|=o(|X|) ��� a[i,j] ��i�Ɉˑ����Ȃ��B
���l�ɂ���j�Ɉˑ����Ȃ����Ƃ��킩�邽�߁Aa�͒萔�B ���̃X���œx�X��������^�p�Y���{����̏o��B
2�l�̏C�s�m�����ꂼ���̎R��o��B
2�l�Ƃ������C���̘[�̒n�_����o�����n�߁A�S�[���̎R���̊C���������ł���B
�e�X�̑m�͎R���܂ł̈�{���̎R���݂̂��ړ�����B
�ǂ���̓����r���̒n�_�ł̓X�^�[�g�n�_���C���������A�S�[���n�_���C���͒Ⴂ�B
���̎�2�l�̑m�̓o�������܂����߂��Ă�����̎��_�ł�2�l�̊C�������S�Ɉ�v����l�ɂ��ēo�������邱�Ƃ͉\�ł��낤���H
2�l�̑m�ɋ������s���͎R����i�ނ��߂邩�����~�܂邩�݂̂ł���B
���̖��̌���̐ݒ�͂��ꂾ���œ��R�Öق̗����Ƃ��ăX�^�[�g�n�_����̓��̂�ƊC����^��������A���ł��鎖�͉���ł��܂��B
����͂�����ł����A(����Ⴛ���ł��傤)�A�p�Y���{�̖͔͉͂ł���ŁA���ɂ͂��̉͂��̘A�����ɂȂɂ��敪�I�Ɋ��炩�݂����ȉ��肪�Ȃ��Ɛ������ĂȂ��悤�Ɏv���܂��B
�ǂȂ����A�������̉���̌��ł̍m��I�ȉ��܂��ł��傤���H �O>>316
>>322-323�ԋʂǂ�����o�Ă�����H�@���ʂƍ��ʂ��B �����Ɛ��w�I�ɏ�����
�A����f,g:[0,1]��[0,1]������A
f^(-1)(0)=g^(-1)(0)={0}�A
f^(-1)(1)=g^(-1)(1)={1}�A
�ł��鎞�A�A����p,q:[0,1]��[0,1]�ł�����
p(0)=q(0)=0, p(1)=q(1)=1, f(p(t))=g(q(t)) ��t
�������̂��Ƃ�邩�H
�ł��B
f,g�̘A�����ɂ�����x�������肪����ΊȒP�Ȃ�ł����ǁB >>328
f(x)=2x (0��x<1/4)
f(x)=1/2 (1/4��x<3/4)
f(x)=2x-1 (1/4��x��1)
g(x)=1/2+|x-1/2|sin((��/4)/(x-1/2))
�̏ꍇ�͓o�R�܍��ڕt�߂�p(t)���s�A���ɂȂ�Ǝv���� >>330
���̒��x�̊��Ȃ�{�ɍڂ��Ă�̍m��I�����̂܂ܒʗp���܂��B >>328
�������������ē��̂肪�����\�ł��_���݂����B
f(x)=1/2-(1/2)e^(4+1/(x-1/4)) (x<1/4)
f(x)=1/2 (1/4��x��3/4)
f(x)=1/2+(1/2)e^(4-1/(x-3/4)) (3/4<x��1)
g(x)=1/2+8(x-1/2)^4 sin((��/4)/(x-1/2))
�̂Ƃ�
f^(-1)(g(x))�͕s�A���ŁAf(x)�̓��̐l�͖����̋���������Ȃ��Ƃ����Ȃ� >>332
�Ƃ肠�������̂�̗L���������肷��Α��v�ł��B
���������ɂ߂�f,g�����ɗL�E�ϓ��Ȃ���v�ł��B
���͗L�E�ϓ������Ȃ��Ƃ��A>>328��p,q�Ƃ��ėL�E�ϓ������Ȃ��A�����܂Ŋ܂߂đ��݂����Ȃ�������͎����ĂȂ��̂ł��B
>>332�̗�ł��{�̏ؖ��ōm��I�ɉ�������Ă��܂��܂��B ���Ȃ݂�f���L�E�ϓ��A�����̂Ƃ�
f1(x)=f��[0,x]�ɂ�����S�ϓ��A
f2(x)=f1(x)-f2(x)
�Ƃ�����
f(x)=(f1(c)+x)-(f2(x)+x)
�Ɠ�̋��`�P������A�����̍��ƂȂ�܂��B
g���L�E�ϓ��A���Ȃ�g�������悤�ȕ����������Ă��܂��̂Ŗ{�̏ؖ����ʗp���Ă��܂��܂��B ���A�|�R�|�R�Ԉ���Ă邯�ǓK���ɃG�X�p�[���Ă��������B >>331
��H�m��I�H�ے�I����Ȃ��āH
328�̏��������A����p,q�����݂��Ȃ��̂͊ԈႢ�Ȃ��̂ł́H >>336
���オ���Ă�P�[�X���炢�ł�p,q�͑��݂��邵�܂��B
p,q�͘A���ł��肳������ΗL�E�ϓ����͗v������܂���B ���A���オ���Ă�P�[�X���炢�Ȃ�p,q���L�E�ϓ��Ɏ��܂��B >>338
>�A����p,q:[0,1]��[0,1]�ł�����
>p(0)=q(0)=0, p(1)=q(1)=1, f(p(t))=g(q(t)) ��t
>�������̂��Ƃ�邩�H
�̖₢�ɑ���
>>332�̗�ł��{�̏ؖ��ōm��I�ɉ�������Ă��܂��܂��B
�͖�������悤�Ɏv����̂���
>>332�̗��p,q�A��������f(p(t))=g(q(t))�Ɖ��肷���
���Ԓl�̒藝���q(th)=1/2�ƂȂ�th��[0,1]�����݂��A
t_0=0�ƒu����q(t_i)=1/2-1/(4i+2)�ƂȂ�t_i��[t_(i-1),th] (i=1,2...)�����݂���
������
p(t_i)=f^(-1)(g(q(t_i)))<1/4 (i:even)
p(t_i)=f^(-1)(g(q(t_i)))>3/4 (i:odd)
�����t_i�͒P���L�E�����������p(t)��lim t_i�ŕs�A���ƂȂ薵��
����������Ă���Ύw�E���Ăق��� >>339
����H
�����ł��ˁH
>>332�͔���Ȃ��Ă܂��ˁH
�L�E�ϓ�����Ȃ��̂��ȁH �_�����B�����ɂ͂킩��Ȃ��B
�������̃��x�������܂��B>>328��
�A����f,g:[0,1]��[0,1]������A
f^(-1)(0)=g^(-1)(0)={0}�A
f^(-1)(1)=g^(-1)(1)={1}�A
�ł��鎞�A�A����p,q:[0,1]��[0,1]�ł�����
p(0)=q(0)=0, p(1)=q(1)=1, f(p(t))=g(q(t)) ��t
�������̂��Ƃ�邩�H
������f,g�͋敪�I�ɐ��`(pl)�Ƃ���B
�R���ōm��I�ɉ������܂��B
�L�E�ϓ��ł͖����Ȃ̂��ȁH >>341
�⑫�B
PL�̋敪�͗L���܂łł��B >>340
�N�������Ƃ����{���R�Ȃ�Ȃ��H >>341
>������f,g�͋敪�I�ɐ��`(pl)�Ƃ���B
�߂�����x�������������� >>343
�{�ł͐ݒ�Ȃ��Ȃ�ł���B
�����A���Ƃ����B
�������ɂ���͖������낤�ƁB
���w�I�Ȗʔ����͌������܂����Ƃ肠����pl�͂���v�A�ǂ��܂œ˂����߂�̂��͓�B pl������������߂�Ƃ��Ă��w�敪�I�ɍL�`�P���x�����肪���E����Ȃ����ȁc
���̒l��������㉺���邱�Ƃ������Ă��܂��ƁA�ǂ����Ă�>>330�݂����ȗႪ���Ă��܂��Ǝv���B
�t�Ɋ��l�̏㉺���L����ł���A���Ȃ��ł������i�ؖ��͑����ʓ|���������ǁj �܂�pl�܂ł��ȁH
�ςɍL���Ă�general nonsense�����B �҂āA�t�Ɂw�ǂ̋�Ԃɂ����Ă��萔�ł͂Ȃ��x�Ƃ��������ł������邩�H
�P�ɐ��藧�����������珑���Ă݂������ŁA�m���߂���ł͂Ȃ����� ���������ꖜ�~�̕n�R�l���A�������̗F�B����Ɋ|������������������
��ǂ��ƂɈꖜ�~���|����2n+1�ԏ����ŁA�ǂ��炩�����n+1���������_�ŏI���Ƃ���
�������A�n�R�l�����͓r���ň�Ԃł������z�������_�ŏ��������������s�s�\�ƂȂ�
���͂͌݊p�ŁA���������͂Ȃ����̂Ƃ���
�n�R�l��������m���́H >>345
>�{�ł͐ݒ�Ȃ��Ȃ�ł���B
�{���R
���邢�͌N�������ǂݗ��Ƃ� >>350
�n�R�l�����������r���ō~���̂͂Ȃ��H
�K���ǂ��炩��n+1�����邩�A�n�R�l�������z�����܂ő�������H >>350
�n�R�l�̊l���܋���X�Ƃ���B
�ŏ��ɕn�R�l��i�����鎖�ۂ�Ai�Ƃ���
E(X|Ai)=i�ł��鎖��n��i�ɂ��Ă̋A�[�@�Ŏ����B
n=1�ł͖��炩�B
�܂�i=n�ł����炩�B
n<N�Ő������Ƃ���n=N�Ƃ�i>I�Ő������Ƃ���i=I�Ƃ���B
���̂Ƃ�
E(X|Ai)=
1/2 E(X|Ai �� i+1���͕n�R�l����)
+ 1/2 E(X|Ai �� i+1���͕n�R�l����)
�ł���B
�E�ӑ�1���͋A�[�@�̉���ɂ��(i+1)/2�ł���B
��2����n��1���Ȃ��ꍇ�̕n�R�l��i-1�A�������Ɠ����ɂȂ�̂ł�͂�A�[�@�̉��肩��(i-1)/2�ł���B
����Ď咣�͎����ꂽ�B
����i=0�̏ꍇ�ɂ��n�R�l�̊l���܋��̊��Ғl��0�B�� �O>>327�Ӂ`��`�Ɂ`���`�ڂ��`���`�� ���`���`���`��`����`�ā`�� ���`�Ɓ`���`�ԁ`�̂ȁ`���`�� �́`���`���`���`�����`��`��
/�Q/�l�l_/�Q/�Q�l�l�Q
/_�i�Q)_)/�Q/�i_^�Q)_
/_�i_(�Q)/�Q/�i_^�Q)_
/_�i(`o')/�Q/�io^) )_
/_�i_��_)��_/�i_��_)��
/��ރ҄�-��ށ�ރ҄�-���_/�Q�����c�c_/�Q�����c�c_/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q>>292���l���E�X�̒藝�ōl���Ă�����>>312��A��H���d�Ȃ��ĕ`���Ȃ���ˁB����ȓ����Ƃ�点�邩�H �l�����z���Ă������Q������������z�ˁB
��̓I�ɏ����Ă݂�킩��B
�ȉ�A��n�R�l�AB���������Ƃ���A��w��l����w/l�ŕ\���B
���̎���A�̊l�����zx�Ɗm��p�ł����Ƃ�x(p)�ł���킷�B
n=0�̂Ƃ�
1/0��1(1/2)�A0/1��-1(1/2)
�� ���Ғl0
n=1�̂Ƃ�
2/0��2(1/4)�A2/1��1(1/8)�A1/2��-1(1/8)�A0/1��-1(1/2)
�����Ғl0
n=2�̂Ƃ�
3/0��3(1/8)�A3/2��2(1/4)�A3/1��1(2/32)�A
2/3��-1(2/32)�A1/2��-1(1/8)�A0/1��-1(1/2)
�����Ғl0 ���A��蕶��
�n�R�l��������m����
���B
���Ғl���߂��Ȃ��̂ˁB >>353
�r���ō~���̂͂Ȃ�
>>354
���Ғl�͂��������ʂ�
���Ғl��0�Ȃ̂ɁA�n�R�l�͕����Ă��������ꖜ�ōςݏ��Ă���ȏオ������̂́A
������m���͏����������������̃��^�[�����傫�����������Ă��邩�炾
���̓��ɂȂ�P�[�X���N����m���͂����炩�H�����͕����������� �a�l�l�a�O>>355
�i_(�Q)>>292���Z������
�i(-.-)�̂� ����
�i����)ނ� (^o^))�܁S,
�i�܁�)�@�H �҃�`�҃�~
~~~~~~~~~~~~~~~
���l���E�X�Ƃ��B >>359�Ƃ����
(2^(2n)-C[2n+1,n])/2^(2n+1)
���ȁH
�J�^�������v�Z����̂Ɠ����e�N�B ���A�Ⴄ�B
C[2n+1,n]/2^(2n+1) �C�����悭���Ғl0�ɂȂ��Ă����������Ǝv�������Ǔ�����O�Ȃ̂��d�d >>362
�����I�I�I
���̂悤�ɖ������ς���
�n�R�l���r���ŕ����z���Ă��؋����đ����A�ǂ��炩�����n+1�����Ă�2n+1�Ԃ܂ő�����
���̂Ƃ��ɁA�n�R�l���r���ŕ����z�����ƂȂ������z���ŏI���ꍇ���l����
���s�����͂܂������ς��Ȃ��̂ŏ�L�̊m�������߂����
�r���ň�x�͕����z���Ă��珟���z���ŏI���ꍇ�A�r���ɏ��߂ĕ����z�����������K������
���̍�������œ�Ԉȏ�̏����z�������邱�Ƃɂ��Ō�͏����z���ƂȂ�
���̂Ƃ��������̍�������̐��̏��s���t�ł���ΎO�Ԉȏ�̕����z���ŏI���
�t�ɁA�O�Ԉȏ�̕����z���ŏI���ꍇ�A�r���ɏ��߂ĕ����z���ƂȂ����������K������A
���̌�ɓ�Ԉȏ�̕����z�������邱�ƂŎO�Ԉȏ�̕����z���ŏI���̂ŁA
���̏��s���t�Ȃ�A�r���̕����z�������Ԉȏ��Ԃ��A�Ō㏟���z���ŏI��邱�ƂɂȂ�
�]���āA�r���ŕ����z���Ă��珟���z���ŏI���ꍇ�ƎO�Ԉȏ�̕����z���ŏI���ꍇ�́A
��Έ�ɑΉ����A���̊m���͓�����
��ӂ̊m��=�r���ŕ����z�����ƂȂ������z���ŏI���m��
=�����z���ŏI���m��-�r���ŕ����z���Ă��珟���z���ŏI���m��
=�����z���ŏI���m��-�O�Ԉȏ�̕����z���ŏI���m��
=�����z���ŏI���m��-(�����z���ŏI���m��-��Ԃ̕����z���ŏI���m��)
=1/2-(1/2-n������m��)=n������m��=C[2n+1,n]/2^(2n+1) �O>>360
>>292
OA=t�Ƃ���ƁA
OA�OB=1���OB=1/t
AB=OB-OA=1/t-t n ���P�`�V���l�ׂ��Ƀv���O�����ɐ��������ĕp�x���o���Ă݂��B
> data.frame(n,p)
n p
1 1 0.3750000
2 2 0.3125000
3 3 0.2734375
4 4 0.2460938
5 5 0.2255859
6 6 0.2094727
7 7 0.1963806 C[2n+1,n]/2^(2n+1)
�ɑ������ƁA
> choose(2*n+1,n)/(2^(2*n+1))
[1] 0.3750000 0.3125000 0.2734375 0.2460938 0.2255859 0.2094727 0.1963806
���l�B�v���O�����ł̃J�E���g�R��͂Ȃ������B >>312�ɏ��������Ƃ͊ԈႢ�������̂Œ������Ă����B
PB�ADB�AQB�Ə��~�Ƃ̌�_��E�AF�AG�A
G����QO�ɕ��s�Ɉ��������s���ƁAAB�A���~�Ƃ̌�_��H�AI
IF��PB�Ƃ̌�_��J�Ƃ���ƁA��JFB�䁢HGB�ŁA
���̓�̎O�p�`�͏o��̎O�p�`�Ƃ������B
�A����OQB�䁢HGB�����͖��炩�����A
���̑��̑����́A���̂Ƃ���A�����Ȃ��B
�����������珬�~�ȂǗ��p���Ȃ��Ă�������̂�������Ȃ��B �O>>365���~�Ȃ�@����
((-_-)���v���@(^_^))
[�P]c) ������BU��U�
�P�P]/�____�����m (��)
____/�_/,,(`.`))�܁SU
�P�P�_/�c`-`Ѓ�`�҃�|
�P�P|�__U,~�܁R___/ |
���@| �a�P~U~U~�P�a |
____| �a ���@���@�a |/
_____`�a_________�a�^ ����J�W�m�Ɏ��̂悤�ȃJ�[�h�Q�[��������
n���̃J�[�h������A�e�͗��Ɍ݂��ɈقȂ鐔���������݁A�悭���ďd�˂ĕ�����
�v���[���[�͈ꖇ���J�[�h���߂���A�D���ȂƂ���Ŏ~�߂�
�܂��A�r���Ŏ~�߂��ɍŌ�̈ꖇ���߂������ꍇ�͂����Ŏ~�߂�
�~�߂��Ƃ��̃J�[�h���e���������ő�̐��ł���Ƃ��A�v���[���[�̏����ƂȂ�
�v���[���[�͎��̂悤�ȍ��Ŏ~�߂�ӏ������߂邱�Ƃɂ���
m���ڂ܂ł͎~�߂Ȃ�
m+1���ڂ���́A����܂łɌ����ő�̐����Ă�����~�߂āA�����łȂ���Ύ~�߂Ȃ�
���̕��@���g�����Ƃ��A�����͂����炩�H
n���傫���Ƃ��A��L�����̍ő�͂����炩�H >>349 ���C�ɂȂ��Ė������Ȃ����琳���ɓ��e�i���ꂽ���ǁj
��������ł͖������B
�������������聫��
�A���� f,g:[0,1]��[0,1] �� f^-1({0})=g^-1({0})={0}, f^-1({1})=g^-1({1})={1}, �����A
�ǂ̋�� [a,b] (0��a<b��1) �ɂ����Ă��萔�łȂ��B
���̎��A�A���� p,q:[0,1]��[0,1] �ł����āAp(0)=q(0)=0, p(1)=q(1)=1 ����
f(p(t))=g(q(t)) (��t��[0,1]) �������̂͑��݂��邩�B
���������܂Ŗ�聪��
[0,1]^2 �̕����W��S�� S = { (x,y)��[0,1]^2 : f(x)=g(y) } �Ƃ����ƁA
��_(0,0)��(1,1)��S�̓����A�������ɑ����邱�Ƃ͏ؖ��ł���B
���̖��́A���̓�_�������w�ʏ�x�A�������ɑ����邩�ǂ����A�ƌ�����������B ������Ȃ̂��A���Ȃ̂ʼn����ς݂̂��̂��P��
�A���� f:R��R �͔�Z�̓_�ŋɑ�l���Ƃ蓾�邩�B >>372
���܂����A�����ł͊� f ���_ x_0 �ŋɑ�l���Ƃ�Ƃ́A
x_0 �̂���J�ߖT U �����݂���
x��U ���� x��x_0 �Ȃ�� f(x)<f(x_0)
�������ƂƂ��܂��B >>372
�s�\�B
�ɑ�l���Ƃ�x=a�̏W����S�Ƃ���B
S�̌�a�ɑ��J�W��Ua��f(a)��Ua�ɂ�����max�ƂȂ�悤�ɂƂ�ƈقȂ�a,b�ɑ���Ua��Ub��disjoint�B
�����Ua����L����qa��I�ׂ�q��S����Q�ւ̒P�˂�^����B ���A���Ⴂ>>374�͖�����������orz �t���ȁB
R�͉��Ȃ̂ʼnZ�ߖT�nC���Ƃ��B
C'={U��C|f��C�ŋ��`�̍ő���Ƃ�B}
m:C'��{�ɑ�_}��m(U)=(�ő�l���Ƃ�_)
�Œ�߂�����{�ɑ�_}�ւ̑S�˂�^����B >>370
�����ƍl����(n-m+1)/n m��k��n-1�ɑ���
p(�v���[���[����|k+1���ڂ��ő�)
=p(1�`k���ڂ܂ł̍ő傪1�`m���ڂɂ���)
=m/k
������
pm:=
p(�v���[���[����)
=1/n��[m��k��n-1] m/k
�����
p(m+1)-pm
= 1/n(��[m+1��k��n-1] 1/k -1)�B
�� p(m+1)-pm>0�� ��[m+1��k��n-1] 1/k > 1
������
��[m+1��k��n-1] 1/k
=��[m+1,n] 1/[x] dx
> ��[m+1,n] 1/[x] dx
=log n/(m+1)�A
��[m+1��k��n-1] 1/k
=��[m+1,n] 1/[x] dx
<��[m+1,n] 1/(x-1) dx
=log (n-1)/m
��log(n-1)/m < log n/m�ɂ��pm���ő�ƂȂ�̂�m=[n/e]�̂Ƃ��B �O>>369
>>370
�܂�m/n�̊m����m���ڂ܂łɍő傪�o�Ă邩���ɕ�����B
���m���̍ő�l��1-m/n
����m+1���ڂ���n���ڂ܂ł�m-n���������r���ō��܂Ō����ő�����Ă��܂��A�c��̖����ōő傪�o��\�����c�����܂܃Q�[�����I��点�Ă��܂����ƁB
m+k���ڂō��܂Ō����ő傪�o���Ƃ���ƁA
(m+k)/n
�܂������킩��Ȃ��B
���m��k/(n-m)
(n-m-k)/(n-m)�͕�����B
�g�[�^���ŕ�����m���́A
m/n+(n-m-k)/(n-m)
{m(n-m)+n(n-m-k)}/n(n-m)
=(n^2-m^2-nk)/n(n-m)
�g�[�^���ŏ��m���́A
k/n
����炪������1������A
(n^2-m^2-nk)/n(n-m)+k/n=1
n^2-m^2-nk+k(n-m)=n(n-m)-m^2-mk=-mn
k=n-m
�����m��=(n-m)/n
=1-m/n
�����炱��͍ő�l�����āB
(n-m)/n��菬�����B
���܂Ō����ő�l�Ȃ炻���Ō�����Č����Ă��珟�m����1-m/n���m���ɏ������B
(n-m)/n���|��������̂��H
����(1-m/n)^2 �O>>380
>>370
���m����1-m/n��n�����イ�Ԃ�傫���Ƃ�1�ɋ߂Â��A�܂����Ȃ�100�����B p(�v���[���[����)=1/n��[m��k��n-1] m/k
���Ĕ�O�������ꂢ�Ȏ��ɂ͂Ȃ�Ȃ��̂��B �O>>381
>>379���Ƃ��ΐe�������X�[�g��A,2�`Q,K�̃J�[�h��1���������Ă���A
13/e=4.�c�c������A
5���ڈȍ~�ɍő�l���o��₢�Ȃ⏟���ɏo���ق������m�����������Ă��ƁH >>384
���̖��̐ݒ�͂����܂Ŏq���e�̐���I�ԕ��z�ɂ��Ēm��悤���Ȃ��Ƃ����ݒ�B
�������e��1�`13�̐��������I�Ȃ��Ƃ��������Ȃ�K���o�ăX�g�b�v�����Ȃ��̂̓o�J�B
���������̎�̏��͂Ȃ��A�P�ɏo�����̑召������Ȃ��Ƃ����ݒ�B
�����Đe�̐��̑I�ѕ��̕��z�����ɗ^�����ĂȂ��̂Ŗ{���s�\�B
�Ⴆ�ΐe����ɒP�������ɂȂ�悤�ɐ���I�Ԃ̂Ȃ�q�����Ă�̂�m=n-1���������A��ɒP�������ɑI�ԂȂ�m=0�����q�͏��ĂȂ��B
����������Ȏ��͑������w�ȑ��łȂ��Ƃ킩��Ȃ����낤����A���̕ӂ̓G�X�p�[���Ȃ��Ƃ����Ȃ��B
>>379�̉͐e�̐��̑I�ѕ��̕��z��n!�ʂ肠��召�̕��z�����l�Ɋm���炵���Ƃ��������lj������ꍇ�̉B
�Ⴆ�ΐe��n���̃J�[�h�̐���iid�őI�ꍇ�Ȃǂł͒ʗp����B �O>>384����A����͕ς����B�W���b�N��N�C�[����5���ڂɏo�āA�܂��L���O���o�ĂȂ��̂ɔ�т����畉������Ȃ����B
m��1�ɂ���n���ő�ɂ��ĂȂ�ׂ������҂X�^���X���Ƃ�ɂ��Ă��A�̐S�̃L���O�����Ȃ���Ӗ����Ȃ��B >>379
�����I�f���炵���I
>>378
>>380-381
�c�O�Ȃ���s�����I
>>385
�����_�������������邽�߁u�悭���ďd�˂ĕ�����v�Ƃ����������Ă�����
����ɂ��n!�ʂ肠�鏇�ʂ̃p�^�[���͓��l�Ɋm���炵���ƌ�����Ǝv�� �O>>386
>>379��log{(n-1)/m}��log{n/(m+1)}���ǂ����������Ȃ́H >>388
�K���}���̔��������ĕ����`�ŏ����闘�_������ɂ���A�m���ɂ���������̂����R������ǂ�
�w�����⑽�����A���Ƃ����̐ς݂����ɁA�����a�������`�ŏ���������ĈĊO���Ȃ�����Ȃ� >>388
����A�����ڂ͊ȒP��
p(�v���[���[����)=(m/n)(��(n)-��(m))
���̋Ɍ��̓f�B�K���}���̑Q�ߌ�����(n)=log(n)+O(1/n)���
=(m/n)(log(n/m)+O(1/n)+O(1/m))
=-xlog(x)+O(1/n), x=m/n >>279�ł��B
�c�O�Ȃ���v�Z�ԈႢ���������B
��[1/m+�d1/(n-1)>1�����ő��m�܂ł͂����Ă邯�ǂ��̕������������Ȃ��Ă�B
m�̂��悢�ߎ��l�Ƃ���
m=[(n-1/2)/e+1/2]
�͏o���邯�ǁA>>279���̓}�V�Ȃ����ł���ł������B
(�v�Z�@�g���Ă݂��100����1������Ă�)
>>370�͊��S�ɐ��m�ɓ����������Ƃ���Ί��o�̃f�B�K���}���Ƃ����̋t���Ƃ��g��Ȃ��Ɩ�����������Ȃ��B >>292�̖��ɂ��čl���Ă��Ďv���t���������ЂƂB
���S���n�Ƃ��锼�a�P�̉~������A���a��ɔC�ӂ̓_�`������B
�n�`�̉�����ɂn�`�E�n�a���P�ƂȂ�_�a����}����B ���ł�����A�������B
�����̖��ɂ͕ʉ�������B����������B
https://www.youtube.com/watch?v=ejtPSxoUlRo
�A���A�R�����g���ɂ���ʉ��͋֎~�B
�R�����g���̕ʉ��Ƃ͈Ⴄ�ʉ���������B >>393
���������̂��~�ɂ�锽�]�Ƃ����B
�����̃C���n�̃C�B ���]�B�����Ȃ̂ŏ������ׂ����A>>393�̖��Ƃ͊W�Ȃ��i��
�܁A�����̘A���͏����̖��Ȃǃo�J�ɂ��ē����Ȃ����낤�Ǝv���Ă����i�� ���ׂĂ킩��Ȃ��̂��B
�n�����Ȃ��B �������ɐ����ɐ������Č�_�ł̐ڐ��������A�������Ƃ̌�_���Ƃ邾������ ���ƘA�������݂ŁA�O�X�����������Œu������ɂ���Ă����i�����҂������́j���o�肵�Ă���������
�ȑO�̂��̂Ɠ��l�A�������ł���
�������� f:R^2��{1,2,�c,n} �����݂���悤�Ȑ��̐���n�̂����A�ŏ��̂��̂����߂�F
�A���� p:[0,1]��R^2 �ɂ��āA����p��f�̍���������Ȃ��p������ł���B >>396
����a�̐����̋t��1/a����}����Ƃ������Ȃ�
�����L�[���[�h��"��} �t��"�ʼn���������o�Ă���
�l�����Z�ƕ������͍�}�\�Ƃ����̂���}�̊�b�m�� >>399
a:(0,1)�~(0,1)��(0,1)���i�\�������݂ɕ҂ݍ��ޘA�����Ƃ���B
�����b(x,y)=((atan(x)+2)/4,(atan(y)+2)/4)�Ƃ���B
g:(0,1)��{1,2}��Q��(0,1)�̓������Ƃ���B
f=gab�ƒ�߂�B
p:(0,1)��R^2���萔�łȂ��A�����Ƃ����abp���萔�łȂ��A�����ł���B
���̎��C�ӂ̑��قȂ�L�����̊Ԃɂ͖����������݂��鎖�Ƒ��قȂ閳�����̊Ԃɂ͗L���������݂��鎖����gabp�͒萔�łȂ��B
�����fp���萔�łȂ��B
����ċ��߂�ŏ��l��2�B ���A���܂����B
a�͘A������Ȃ���B>>403�͓P�܂��B >>393�̖��́A�~�ɂ�锽�]�Ƃ��A����ȓ�����ł͂Ȃ��i��
�P�ɕ��ׂ��̒藝�̉��p���ł���i��
����ɏ����̃C���n�̃C�Ƃ������A
���]�Ȃ�ď������ł��K�������Ƃ͂Ȃ��i��
������u�����̃C���n�̃C�v�Ə����Ă���Ƃ���ɁA
���O��̋��h�S������Ă���i��
�������>>402�̂悤�ɍl���ĉ����Ă��������A�����ƊȒP�ȕ��@������B
�n����n�`�ɐ����Ȓ��a�������A�~�Ƃ̌�_���o�A�p�Ƃ��A
�o�`�̉����Ɖ~�Ƃ̌�_���q�Ƃ��A
�p�q�̉����Ƃn�`�̉����Ƃ̌�_���a�Ƃ���ƁA�a�����߂�_�ł���B ���h�S�����Ȃ�����������Ă�́H
����Ȃ��n�̐l�ԂŒm���l�Ԃ��Ȃ��펯��肾���Ă����Ă�H
����������A�z�قǂłĂ����낪�H
����ȏ펯���ł��m��Ȃ��ŏo���̂͂��傤���Ȃ��B
���ׂĂ݂ĕp�o�A�펯��肾�Ƃ킩��Ȃ��̂��A�z���ƌ����Ă�B
�l�̏��������͗�������\�͂Ȃ��ˁH
����������ԍŏ��ɂłĂ�>>294�̏ؖ��ɂ��łĂ�����H
�ǂ�łȂ��́H
�ǂ�ł��킩��Ȃ��́H >>399
�������ł����Ƃ����̂͏o��҂����������ĂȂ��Ƃ����Ӗ��H �ʂɏ����I�Ȗ��������I�ƒm��Ȃ��ŏo�肷��̂͂������ǂ�
������w�E����Ė�̂킩��Ȃ��L����������݂̂͂��Ƃ��Ȃ� ��̂킩��Ȃ��L���������Ă���̂͂��O��̕����i��
�l�͋��h�S�̂��߂�0.99999�c�c���P�Ɛ����Ă���̂ł͂Ȃ����A
��������>>405�̂悤�ȓ������o�ė���Ƃ��v���Ȃ����A
>>294�͏����I�ؖ��ł͂Ȃ��̂ł���B
>>394�̖��ɂ��Ă��A���O��́A�����������Ă��Ă��A�����Ȃ����낤�A
�Ɩl�͍ŏ�����v���Ă����i��
�Ȃ��Ȃ�A>>393-394�̂悤�Ȗ��͂��O��̃v���C�h�������邩�炾�B
�Ƃ����킯�ŁA���O��́A�l�̂��Ƃ͖������āA���w�̘r��ׂɗ�߂悢�B
�������A���O�炪�ǂ�ȂɗD�G�ł��낤�ƁA0.99999�c�c���P���ƌ������r�[�ɁA
���Ԃ̑����Ȑl�X����́A���O��͏���i��
https://www.youtube.com/watch?v=47zjeq13NwY
�����ł���҂͂T��4.99999�c�c�Ƃ����ԈႢ�C�ŔƂ��Ă��邪�A
���O��͂��̍�҂Ɠ����x���Ȃ̂ł���B >>407
����킵���Đ\����Ȃ��A���������Ӗ��ł�
���ɒN����������^���Ă��Ȃ����ǂ����܂ł͒��ׂ��ĂȂ��ł� >>409
�����������炱���ɂ͏����Ȃ�B
�����̊w�͂����̃X���ł̓n�i�N�\���x���Ȃ̂��Ȃ�ł킩���̂��˂��H
�咆�̓������x���ł܂��l�ꔪ�ꂵ�Ă郌�x���ŁB /�Q/�l�l_/�Q/�Q�l�l�Q
/_�i�Q)_)/�Q/�i_^�Q)_
/_�i_(�Q)/�Q/�i_^�Q)_
/_�ie^) )/�Q/�io^) )_
/_�i�ҁQ)��_/�i_��_)��
/��ރ҄�-��ށ�ރ҄�-���_/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q�����c�c_/�Q�����c�c_/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q����`�����ς���́`��
�悵����Ă����A����������I �O>>389�Ƃ����̂낶����ł��`�� ���m����log�͂˂���B�̂��ꂽ������Ɂ`�� �m����log�o�Ă������킩��˂���Ȃ��B�������܂͂������`�� �E��邩�B �a�l�l�m����log����
�i_(�Q)�ǂ�����
�i(-.-)�Ӗ��ȂH
�i����)�
�i�܁�)
~~~~~~~~~~~~~~~
log{n/(m+1)}�������Ȃ̂��H >>411
�ł�>>292�̖��̏����I�ȏؖ��������Ă���i��
�ǂ��������Ȃ����낤���i��
���ŏ����I�Ȗ��𓊍e���邾���ŁA
����Ȃɒ@����}����Ȃ���Ȃ�Ȃ��̂��i��
�r�炵�����Ă���킯�ł͂Ȃ��̂ɁA�r�炵�������i�� >>414
������n�������������B
�Ȃ�ŏ����I�ؖ�����������Ȃ����킩���ĂȂ�����H
���������Ă���蕶�̏�����������z�u���s��Ȃ̂ł߂���߂��Ꮡ���ɂ�����B
����>>294�ŏؖ��オ���Ă���j�������I�ɏĂ������Ƃ���BPD=��BOQ�������̂��C���ɂȂ�B
���j�Ƃ���>>294��C���Ƃ���BP��CQ�̌�_��E�Ƃ���BEOQ������~����ɂ��鎖�𗘗p����肪���邯�ǁA���̂Ƃ�BPE�̈ʒu�z�u��BECQ�̉~����̔z�u�ɂ���ā�BPD�A��BEQ�A��BOQ�̈ʒu�W�������ɕς��B
���̎O�p�����ׂē�������������Εߊp�����Ȃ��Ƃ����Ȃ��Ƃ����o�Ă���B
�����炭����ł͐}���^�����ĂĈʒu�z�u���ׂ������肵�Ă�낤�B
���Ȃ����̒��̏���Ȉ�̈ʒu�z�u���ߑł����ďؖ����Ă邯�ǂ���Ȃ̏ؖ��Ƃ��Ēʗp���Ȃ���B
����������Ȏ����Ȃ��Ă����f���W�Ƃ�ΑS���̃P�[�X�Ђ�����߂Ĉꌂ�ŏؖ��ł���̂ɂȂ�ł���ȈӖ��Ȃ�������́H
��������OA�EOB=1�Ƃ������������u�Ԃɔ��]�w�����f���W�g���Ă݂悤�Ǝv�����z���o�Ă��Ȃ����_�ł����i�Ȃ�B
��������łĂ���B
���ɂ��̃X���̘b��ɂ��Ă����邾���̎��͂͂Ȃ��B
�X�������B >>415
>���ɂ��̃X���̘b��ɂ��Ă����邾���̎��͂͂Ȃ��B
����Ȃ��ƍŏ����番�����Ă���(��
���������̃X���̓X���^�C���炵�ē����o���X���ł͂Ȃ�����A
�����̖����o���Ă������͂��Ȃ̂��B
������X�������Ȃǂƒ@�����؍����͂Ȃ��B
�����>>292�̖��͓卂�Z�̓�����肾�Ƃ�������A
���f���Ȃǎg���ďؖ�������ł͂Ȃ��A
�����ʼn�����͂��̖��Ȃ̂ł���B
����ȏ㏑���ƍr�炵���Ǝv���邩������Ȃ�����A�����Ŏ~�߂�B
���O����l�ɑ���}�Ƃ��U���͂����Ŏ~�߂�悤�ɁB
��������肽����ǂ�ǂ������(�� �a�l�l�a�O>>413
�i_(�Q)>>292��>>370��
�i(-.-)�[�������ł�
�i����)ނ�(^o^))�܁S,
�i�܁�)�����҃�`�҃�~
~~~~~~~~~~~~~~~~~~~~~~
�ł͂Ȃ��Ȃ��B>>292�͑����B������������������܂��킩���B>>370�͊m���B���ׂĂ̏ꍇ���̂��̏ꍇ�̐��B���ׂĂ̏ꍇ�������ł��̏ꍇ�������Ȃ̂��܂��킩���B >>416
���������܂Œ��J�ɐ������Ă܂��������Ă�̂��킩���̂��B
�ǂ��܂ŃA�z�Ȃ�H �Z���ɋA����Č����̂Ȃ�A����������Ȃ��� (a-e)(b-f)=(c-e)(d-f)�Ȃ�n�ȉ��̔����̑g(a,b,c,d,e,f)�͂������邩�B
�����X���̖��
�S�R�킩��� >>420
����͑������Ȃ������ĂȂ��z���K���ɕ������ׂ������̖�肾�Ǝv���B
���̃X���͂킩�����Ȃ牽�����Ă������Ƃ����Ɠ��ȃ��W�b�N�ł��̎�̖�肪�悭�オ���Ă邩�璍�ӂ��Ȃ��ƁB >>421
����������
�ꉞ�撣���ĉ������Ƃ������ǖ̌��Ƃ����̕ӂ���ʉ����Ȃ��Ⴂ���Ȃ����Ă����ǂɂԂ���������
�v���O�����g���OEIS�ɂԂ�����ł������o�Ă��Ȃ��������Q�[ >>420�O>>418
(a-e)(b-f)=(c-e)(d-f)
4�3=6�2
a=6,e=2,b=4,f=1,c=8,d=3
n=8�̂Ƃ��A6�2=4�3�����肤�邩��A
a=8,e=2,b=3,f=1,c=6,d=4
a=8,e=1,b=4,f=2,c=3,d=6�̂Ƃ�8�1=2�4�Ő��藧�B
���������A
n�ȉ��̐��Ł�n�ʂ肠��Ƃ���_�ȗ\�z�������ǁB >>422
���H����Ȏ肪����́H����OEIS���Č����ł����H ���̐���̖@�����́H
�Ȃ�ĕ����ꂽ�Ƃ��͌����@�\���d�� >>399
�������n��2�̏ꍇ�ł���������H >>427
����An���傫���قNJȒP�ł���H
n=3�̂Ƃ���f�͂����ł���B
n=2�̂Ƃ���f������̂��H�����B
�ŏ��l��3 or 2�B R^2�̓_��pathconnected component��1�_�ɂȂ�悤�Ȃ����̕����W���ɕ������邩��
R^1�Ȃ�L�����Ɩ������ŃC�C����
A={(x,y) | x, y��Q} B=R^2-A
�ł悭�Ȃ��H
�A�[�_����y=e��B������
4�ɕ�����
A=Q^2 B=Q�~I C=I�~Q D=I�~I�iI=R-Q�j
�Ȃ炢���ł���
p1,p2:R^2��R
�ɂȂ����炢������
������n=2,3�Ń_���Ƃ������Ƃ͂ǂ������Ηǂ��̂��H >>428
>n=3�̂Ƃ���f�͂����ł���
�ǂ����H �^��w�����ߋ����
������10�{�A��k��3n+1�{�̓��H����Ղ̖ڏ�ɑ�������������B
���̒��̓��H�͍œ�[�ɂ��铌���ɑ��铹�H��삩�珇�ɓ���0�������瓌��9�����A��k�ɑ��铹�H�𐼂��珇�ɓ�k0���������k3n�����ƌĂԁB
3�̔{��3k�ɑ���k3k�����A����0�A3�A6�A9�����͑�ʂ�A���̑��͐������H�ƌĂ��B
�e�����_�ɂ͈ȉ��̂悤�ȋK������߂��Ă���B
�E�������H�Ƒ�ʂ�̌����_�ɂ����ẮA�������H����i������ꍇ�ɂ͍��܂��đ�ʂ�ɍ������鎖�݂̂����o�������i�A�E�܂͂ł��Ȃ��B��ʂ肩��i������ꍇ�ɂ͍��܂��Đ������H�ɂ͂��邩�A���̂܂ܒ��i���鎖�͂ł��邪�E�܂͋֎~�ł���B
�E��ʂ�A�������H�ǂ����̌����_�ł͉E���܁A���i���ׂĉ\�ł���B
���̒��̓쐼�[��X�A�k���[��Y�Ƃ���Ƃ���X����Y�K���ɏ]���ŒZ�o�H�̐������߂�B
�����n=7�̏ꍇ�ł��B >>430
�L�����~�L������1,
�L�����~�������A�������~�L������2�A
�������~��������3�ɂ���B
�R���ł�����͂��B ���A���߂��B
���ꂾ�Ƃ�����2�ɂȂ邩�̂�����������A
�L�����~�L������1,
�L�����~��������2�A
�������~�L������3�A
�������~��������4�ɂ���B
�R���͐������B
�Ȃ̂ōŏ��l��2��3��4�B >>428
���[�������������Ȃ̂��H
2�̎��̓_�����ƌ�����
3�Ƃ�4�Ƃ��ǂ��Ȃ�̂��A���ĕ������ɂȂ邩�ȂƎv�������� >>433
���A�m���ɂ���ŏI��肾��
�T���N�X >>424
n=1,2,�c�c�̎��̓������Ԃ�����łȂo�Ă����烉�b�L�[ �O>>423
>>431
1�{�B
X���瓌��0���𓌂ցB��kn+1���Ƃ̌����_�����܂��k�ցBY�ɒ����o�H�B �O>>437�����B
>>431
1�{�B
X���瓌��0���𓌂ցB��k3n+1���Ƃ̌����_�����܂��k�ցBY�ɒ����o�H�B �O>>438�����B��ʂ�E�܂ł����B
>>431
X���瓌��0���𓌂ցB��k��n[n=1��3n+1]���Ƃ̌����_�����܂��k�ցB�K�X�E�܂���Y�ɒ����o�H�B
��(3n+1)^2�ʂ� �O>>439�����B�������H���|���Ă��B
>>431
(n+1)^2�ʂ� �O>>440�����B
>>431
11(n+1)�ʂ� >>431
����́A�ǂ�����ăV�~�����[�V�������邩�Ȃ��B
�Ƃ肠�����A�����V�̂Ƃ��œ��H����}
https://i.imgur.com/fJDSrQo.jpg �삩���ʂ�ɓ��鐶�����H�͑S���J�b�g�i�ŒZ�Ői�߂Ȃ�����j
��ʂ肩�瓌�ɓ��鐶�����H���S���J�b�g�i�ŒZ�Ői�߂Ȃ�����j
���Ƃ͎��R�ɍl����
��ʂ�ň͂܂ꂽ���łȂ�
1+4C2=7�ʂ�
�����
���[�̑�ʂ�͂P
����ȊO�̓�k�̑�ʂ肪6
�����̑�ʂ�͂P
�ōl������ǂ��̂ł͂Ȃ����� ��ʂ�̒��i���܉E�܂ŕς�邩��>>446���ƍl���ɂ���
�����璼�i��1�ʂ�
�����獶�܂�6�ʂ�
�����璼�i��1�ʂ�
������E�܂�1�ʂ�
����ōl�����
���邢�͑�ʂ�̌����_�ɉ�������鏈�ƉE�ɏo��Ƃ���̘H�����ōl���邩 >>448
>���邢�͑�ʂ�̌����_�ɉ�������鏈�ƉE�ɏo��Ƃ���̘H�����ōl���邩
�����₷����k�t�]�����Ă݂���
�@�P�@�P�@�P�@�P�@�P�@�P�@�P
�P�@�U�@�U�@�U�@�U�@�U�@�U�@�U
�@�P�@�V 13 19 25 31 37
�P 12 48 84 19*6+6-120
�@�P 13 61 61+84=145
����Ȋ����� �u����肵�Ȃ��v�Ƃ��������̉��A�����A����сA��k��0���A3���ň͂܂��
3�~3�̋����̂����ꂩ�̐������H���g�p����ꍇ�A
(1,0)��(2,0)����i�����A(3,1)���A(3,2)����o��ꍇ�����Ȃ��A���v5�ʂ肠��B
�܂�A�������H���m�̌����_�A(3p+s,3q+t)�@(s,t=1,2)�𗘗p����ꍇ�A
�K���A��ʂ蓯�m�̌����_(3p,3q)��(3p+3,3q+3)�𗘗p���Ă���B
��ӂ̏����ɏ]���A�ʂ�����ʂ蓯�m�̌����_�݂̂��v���b�g���A���ԂƁA
�g���ɕω��h�A�g��ɕω��h�A�g�߂ɕω��h�̎O�ʂ�ɕ��ނł���B
�g�߂ɕω��h�̉�k�Ƃ���ƁA�g���ɕω��h�́An-k��A�g��ɕω��h��3-k��ƂȂ�B
�߂ɕω��̏ꍇ�A�������H�̒ʂ���ŁA5�ʂ肠��̂ŁA
��[k=0,3] 5^k*((n-k)+(3-k)+k)!/{(n-k)!*(3-k)!*k!}�@�Ōv�Z�ł��邱�Ƃ�����B
�����@36n^3-54n^2+36n+1 >>450
����
���Ȃ݂ɓ�����3m+1�{�A��k��3n+1�̂Ƃ���
��[0��i��m]C[m,i]C[n,i]6^i
(������j<k�̂Ƃ�C[j<k]=0�Ƃ���)
�ɂȂ�܂��B
>>450����̏ؖ��悭�ǂ߂ł��܂��B
���Ȃ݂ɒ����Ƃ����̂��g����
3F2(-m,-n,1;6)
�Ƃ��\������܂��B
https://www.wolframalpha.com/input/?i=Hypergeometric2F1%28-3%2C-x%2C1%2C6%29&;lang=ja �Ȃ�قǁB�Ƃ������Ƃ́A
��[k=0,m] C[m,k]*C[n,k]*(x+1)^k = ��[k=0,m] C[n+m-k,m-k]*C[n,k]*x^k
�������������ł����A�ؖ��͂ǂ����낤�D�D�D�B ���R��n�ɑ���m=C[n+1,2]�ϐ��̑�����Pn(x[12],�d,x[n-1,n])�Ŏ��̏����������̂����݂��鎖�������B
n�������[�N���b�h��Ԃ̓_p0,�dpn�ɑ��A���̓ʕ��K�Am�̐��̎���a[12],�d,a[n-1n]��d(pi,pj)����ׂ����̂Ƃ���Ƃ�
vol(K)^2=Pn(a[12],�d,a[n-1n])
����������B(�������̃w�����̌���)
�܂����̎��������藧���������B
�����̑g��a[12],�d,a[n-1n]���C�ӂ�{1,�d,n}��k���W��S�ƓY����S�ɓ���C[k2]��a[ij]��I�ԂƂ�
Pk(a[ij])>0
����������Ƃ�n�������[�N���b�h��Ԃ̓_p0,�dpn��a[12],�d,a[n-1n]��d(pi,pj)����ׂ����̂ƈ�v����悤�Ȃ��̂��Ƃ��B(�������̎O�p�s����)
��
p1(x)=x
P2(x,y,z)=(1/16)(x+y+z)(-x+y+z)(x-y+z)(x+y-z)
��n��2�ł͐������Ă��܂��B >>399
n=3�̎��́Af(x,y)�̒l��
1 (x��y���L�����̎�)
2 (x��y�̕Е�������������)
3 (x��y�̗���������)
�Ƃ���Ηǂ��Bfp�̒l��1��3�Œ萔�̏ꍇ�͖��炩��p���萔�B
fp�̒l�����2�ł��鎞�Ap���萔�łȂ��Ɖ���B����ƁA�C�ӂ̗L����q�ɂ���
C(q):=p^(-1)({q}�~R) �� C'(q):=p^(-1)(R�~{q}) �����[0,1]�̕W���ɂȂ�B����������
[0,1]=��_(q:�L����) C(q)��C'(q)
�͕��[0,1]�́A�Z�����̔��a�ȕW���ɂ�ȕ�����^���邪�A
���̂悤�ȕ����͕s�\�ł��邽�ߖ����B >>454
>�͕��[0,1]�́A�Z�����̔��a�ȕW���ɂ�ȕ�����^���邪�A
[0,1]=[0,1]���� >>452
(1+xz)^n = ��[i=0,n]C[n,i]x^i z^i
(1+z)^m = ��[j=0,m]C[m,j]z^j
(1-z)^(-n-1) = ��[j=0,��]C[n+j,j]z^j
���
(1+xz)^n (1+z)^m��z^m�̌W�� = ��[k=0,m] C[m,m-k]C[n,k] x^k
(1+xz)^n (1-z)^(-n-1)��z^m�̌W�� = ��[k=0,m] C[n+m-k,m-k]C[n,k] x^k
������
f(z) = (1+z+xz)^n (1+z)^m/z^(m+1)
g(z) = (1+xz)^n (1-z)^(-n-1)/z^(m+1)
��z=0�ɂ����闯�������������Ƃ������悢�B
�����z=t/(1-t)�ƒu����f(z)dz=g(t)dt��薾�炩 >>455
�Ⴆ�� C(q)=[0,1] �̏ꍇ�Ap�̑�ꐬ�������q�A�������ɖ��������Ƃ���ǁA
���̏ꍇ�͑�����萔�łȂ���Ȃ�Ȃ�����A����p���萔���ł��邱�Ƃ��킩��B
C'(q)�̏ꍇ�����l�B >>455
�̔���͏����Ă邩��������[0,1]�����X�Z�����̔��Ȕ��a�ɂȂ蓾�Ȃ��͐������̂��ȁH
������ؖ����������B >>412
�C�i�����
��������(��)��������ł����H �p.�P�C�Q�C�S�C�W�A�E�E�E�A�Q�O���Ƃ�������P����I�Ƃ��A���̍ō������P�ƂȂ�m���͂����قǂ��H
(���߂��疳���̏W���ōl���Ȃ��Ă��n�j�ł�
����L���Ƃ��Ă������Ƃ��Ă����܂��܂���) log[10]2�A
���ȍō��ʂ�3�̊m���H��log[10](3/2) >>460
jlog2(10)��i<jlog2(10)+1��������i��j�ɑ��ĕK��1���݂���̂�
2^n��m���̐��Ƃ����{1,2,4...,2^n}�ɂ�m�̍ō�����1�ƂȂ鐔�����݂���
���̊m����m/(n+1)=ceil(nlog10(2)+1)/(n+1) ������ceil(x)��x�ȏ�̍ŏ��̐��� >>462 ����
m/(n+1)=floor(nlog10(2)+1)/(n+1) ������floor(x)��x�ȉ��̍ő�̐��� >>458
�W�����Ɩ������Ɓu���㐔�w�̌n���E�E�E�v�X���ł���Ă� /�Q/�Q/�l�l_/�Q/�Q/�Q
/�Q/_�i�Q^_)/�Q/�Q/�Q
/�Q/_�i�Q�Q)/�Q/�Q/�Q
/�Q/_�i (^o)/�Q/�Q/�Q
/�Q/_�i�Q��-��_/�Q/�Q
/�Q/_��ބ��ҁ��/�Q/�Q/�Q/__/__/__/__/__/�Q/�Q/�Q/�Q/�Q/���̂ǂ낾�炯�̂��Ɂ`��������`�� ���������Ȃ��`�́`�킟�`��@���߂�A>>423�̑O>>417�������B
�O>>442�ł�`�ł��� ������ł��Ȃ��� �ڂ���������Ȃ��`���`�ǁ`�� ��� >>458
�������ɏȗ��������Ă��܂����A�\����Ȃ�
>>454 �̕⑫
���[0,1]���A�Z�����̋�łȂ��W���ɂ��
[0,1]=��_(n=0,1,�c)C'_n (������ 0��C_0, 1��C_1, n��m�Ȃ��C_n��C_m=�� �Ƃ���)
�ƕ��������Ɖ���B
�����ŁA����{a_n}, {b_n}�����̂悤�ɒ�߂�B
�܂��A���[0,1]�ɂ�����C_0��C_1�̕�W���́A�A���ȕ����W����^����J���(a_1,b_1)���P�Ƃ�B
�܂�Aa_1,b_1��C_0��C_1 �ł��邱�Ƃɒ��ӁB
(i)n����̎��Aa_(n+1)=a_n �Ƃ���B�܂��A(a_n,b_n)��C_m ����łȂ��悤�ȍŏ���m���Ƃ�A
b_(n+1) = min((a_n,b_n)��C_m) �ƒ�߂�B
�i�J���(a_n,b_n)�̗��[�͂ǂ�������� C_m' (m'<m) �̌��ł��邽�߁A
(a_n,b_n)��C_m = [a_n,b_n]��C_m. �����min�����݁B�j
(ii)n�������̎��Ab_(n+1)=b_n �Ƃ���B�܂��A(a_n,b_n)��C_m ����łȂ��悤�ȍŏ���m���Ƃ�A
b_(n+1) = max((a_n,b_n)��C_m) �ƒ�߂�B
�ȏ�̂悤�ɒ�߂�����{a_n}, {b_n}�� a_n<a_(n+2)<b_(n+2)<b_n �������߁A�ǂ����n�����Ŏ����B
�������A�Ⴆ��a_n�̋Ɍ�A�͑S�Ă�n��1�ɂ��� A��(a_n,b_n) �������߁A
�ǂ� C_n (n��1) �ɂ������Ȃ��B����Ė����B >>466 �ŕςȂƂ���� C'_n ���o�Ă��Ă邯�ǁA����͕��ʂ� C_n �Ƃ��ď������Ă��������c
�]�k�ł͂��邯�ǁA>>399 �̖��ɂ�����R^2��S��R^m�Œu�������Ăł�������l����A
���l�̕��@�ŁA���߂�n�̍ŏ��l��2�ȏ�(m+1)�ȉ��̐����ł��邱�Ƃ��킩��B
��̓I�ɂ́A�� f:R^m��{1,2,�c,m+1}��
f(X)=1+(X�̐����̂����L�����ł�����̂̌�)
�ƒ�߂�A>>454 �Ɠ��l�̕��@��(fp���萔�Ȃ��p���萔)��������͂��B >>463
��͌��݃K���A�X���Ő�^�W�J���ł��B���Q�l�������B >>456
�䉺�����肪�Ƃ��������܂��B
�����A�ڂ��_��Ԃł��������Ƃ��t�H���[�ł��܂����B
��d�A�O�d�ɋ����܂����B�N�₩�Ȏ�@�ɋ���������ł��B
>>�����z=t/(1-t)�ƒu����
���炭�Az=t/(1+t)�@�̃~�X�������̂ł͂Ȃ����Ǝv���܂��B
���̕��ׂ̈ɁA�L���Ă����܂��B ���̐���a,b���݂��ɑf�Ƃ���B
�������x,y��������n=ax+by�Ə����鎞n�͗ǂ������ł���ƒ�`����B
���̐����ł����ėǂ������łȂ����̂̌���a,b�ŕ\���B �O>>465
>>470
���̐�����ax+by�Ə����Ȃ����̂́A1,2
��2�� �܂��͒萔�ƕϐ��̈Ⴂ�𗝉��ł���悤�ɂ��悤 >>470
>���̐����ł����ėǂ������łȂ����̂̌���a,b�ŕ\���B
(a,b)>1�̎��͖�����
(a,b)=1�̎��͖ʓ|������ n���ǂ��Ȃ������A����n+a,n+b�̂ǂ�����ǂ������ł��鎞�A
n+a=bm, n+b=ak ��� a(k+1)=b(m+1).
������k=bk'-1�ł��邩��
n=a(bk'-1)-b.
n�̗ǂ��Ȃ������ n��ab-a-b �ł��邩��Ak'=1.
�ȏォ��A�C�ӂ̗ǂ��Ȃ����� n<N:=ab-a-b �ɂ��āAn+a,n+b�̏��Ȃ��Ƃ�����͗ǂ��Ȃ������B
���������āA0��n��N ��������n�ɂ��āAn���ǂ��Ȃ������Ȃ��N-n�͗ǂ������ł��邱�Ƃ�������B
�܂��AN=N-0���ǂ��Ȃ������ł��邱�ƂƁA
(N-n���ǂ��Ȃ������Ȃ��N-(n+a)��N-(n+b)���ǂ��Ȃ������ł���)���Ƃ���A
0��n��N ��������n�ɂ��āAn���ǂ������Ȃ��N-n�͗ǂ��Ȃ������ł��邱�Ƃ�������B
�ȏ�̋c�_����A����n��[0,N]�ɂ��āAn��N-n�̕Е��������ǂ��Ȃ������ł��邱�Ƃ��킩��B
�䂦�ɁA���߂����(1+N)/2=(a-1)(b-1)/2. >>399 �̗ޑ�ƌ����邩���m��Ȃ����A��������o��҂ɂ͖�����
�����S�̂���Ȃ�W����R�Ƃ����BR�̔C�ӂ̕����W��A�ɂ��āA���̎咣�͐��藧���F
A�̕�W����A�̏��Ȃ��Ƃ�����́AR�̔�Z�ȕ����W�����܂ށB �����S�̂���Ȃ�W���ȂǂƂ������̂͑��݂��Ȃ����A
�����͔�Z�ł͂Ȃ��i�� >>476
R={�L����}��{������}�ł悭�Ȃ��H
{������}���W��F���܂ނƂ����U=R�_F��{�L����}���܂ފJ�W����{�L����}��dense������U=R�B
��{������}���܂ޕW���͋�W���̂݁B >>478
�̓_�����B�݂��Ă���orz >>478
�ꉞ�������Ă����ƁA�Ⴆ�Ζ������̕����W����
{x��[0,1] : x���Q�i�W�J�������A�����_�ȉ���(2n)�ʂ�n���������̎�1�A����ȊO�̎�0}
���ƒ�߂����̓J���g�[���W���Ɠ����ɂȂ�܂� >>480
�J���g�[���W�����ĕW���������H >>481
https://en.m.wikipedia.org/wiki/Perfect_set
��Example��A�J���g�[���W���̋L���́w���j�I���Ӂx�ɂ���ʂ�A�W���B >>454
�������x,y,�̗������������̎���
����ȊO�̏ꍇ�ŕ����Ă���Ă������悤��p���萔�͌����Ȃ��́H �܂��J���g�[���W�����č\���I�ɕW���̋��ʕ������� R���f���œ��_�̂Ȃ�2�̘A���Z�x�̕����W���ɕ������ė~���� (1/4845)(4�b2)(16�b1)(4�b1)
=6�16�4/4845
=2�64/1615
=128/1615
=0.07952569659�c�c
�O>>148
����7.952569659�� >>485
���̏ꍇ�Ap:[0,1]��R^2��Ⴆ�� p(t)=(0,t) �ƒ�߂�����p(t)�������� R^2-{������}^2 �ɑ����邱�ƂɂȂ�� �������W����R��̕W���̉Z�a�ł͏����Ȃ����Ƃ��ؖ����� >>492
R\Q=��_(n��1) C_n �ƉZ�̕W���ɕ����ł����Ɖ���B
0�ȏ�1�ȉ��̑S�Ă̗L������ {q_n}_(n��1) �Ɣԍ��Â�����ƁA
��_(n��1) ((C_n��[0,1])��{q_n}) = [0,1]
�ɂ��A�Z�̕W���ɂ����[0,1]�̔��ȕ������^�����Ă��܂��A>>466�Ɩ����B >>493
�Ȃ�قǑf���炵��
�z����̓x�[���̃J�e�S���[�藝���g�����̂ł��� >>495
R\Q=U_{n��N} C_n�ƉZ�a�ŏ������Ƃ���
Q= {q_n}_{n��N}�Ƃ����
R=U_{n��N} (C_n �� {q_n})�ƂȂ�
������R�͊���������Ԃ��
�x�[���̃J�e�S���[�藝�u��łȂ�����������Ԃ͓��_�������Ȃ��W���̉Z�a�ɂ͂Ȃ�Ȃ��v
����A����C_n�͓��_������C_n��R\Q�̕����W���̂��ߖ��� >>476 �͂ǂ����ے�I�ɉ�������Ă�݂������cBernstein�W��������ɂȂ��Ă���
https://en.m.wikipedia.org/wiki/Bernstein_set
Bernstein�W���̑��ݐ��ɂ��ẮA����pdf�̒藝3.7�Ŏ�����Ă���
https://yamyamtopo.files.wordpress.com/2017/07/ukeru_gene_topo.pdf
�����đ���������@�ŁA>>399�̓�����2�ł��邱�Ƃ��킩��B
�|�C���g�́A�i��Z�ȁj�W���S�̂���Ȃ�W���̔Z�x���AR^2�Ɠ����A���̔Z�x�ł���A�Ƃ������ƁB >>497
���̃|�C���g����>>399�̓�����2�ɂȂ鎖��������kwsk �A���Ɨ��U�ꂵ���I
ttp://x0000.net/topic.aspx?id=3709-0
R* := R �� { e }
(0 �� e �� dx)
a + e = a = a – e (a �� R)
ne = e (n �� Z)
���p��F
Vista��win7�̃t�@�C���̕\�����@��ݒ肷�郁�j���[�����̗�ł��B �F�X�������̂�>>399�̓�����2�ł��邱�Ƃ������܂��B
���Ȃ݂�R^2����R^n�ɕς��Ă����l�ŁA������2�ł��邱�Ƃ������܂��B
R^2�͉Z�ȊJ������̂ŁAR^2�̊J�W���̌��͘A���̔Z�x�B
����āAR^2�̕W���S�̂���Ȃ�W���̔Z�x���������A���̔Z�x�ł���
�䂦�ɁA�萔�łȂ��A���ʑ� f:[0,1]��R^2 �̑��S�̂���Ȃ�W��P�́A
P�̊e�����W���ł��邽�߁A�������A���̔Z�x�����B
������A�A���̔Z�x�����ŏ��̊�����Ƃ����ƁAP���烶�ւ̑S�P�˃ւ����݁B
�����A�[�@�ɂ��AR^2�̓_�� {a_p}_(p��P), {b_p}_(p��P) �ł����āA
�C�ӂ�p��P�ɂ��� a_p��b_p ����
a_p, b_p �� p�_��_(p'��P, ��(p')<��(p)){a_p',b_p'}
�������̂����݁B
�i�C�ӂ�p��P�ɂ���p�͘A���̔Z�x�������ƂƁA
p'��P �ł����� ��(p')<��(p) �������̂̌��͘A���̔Z�x�����ł��邱�Ƃɒ��ӁB�j
B={b_p:p��P} �Ƃ����A�C�ӂ�p��P�ɂ���
b_p��p��B, a_p��p��(R�_B)
�����̂ŁA�����p���Ċ� f:R^2��{1,2} ��
f(X)=1 (X��B�̎�), 2 (����ȊO)
�ƒ�߂�Ηǂ��B >>500
B��R�_B��>>488�̗�ɂȂ邩�� >>501
B��R�_B���A�ǂ̌ʂƂ����ʕ����������Ȃ���Ȃ�Ȃ����Ƃ��l����ƁA�Ȃ�Ǝv��
�ł��A���̂悤�ȗ�ł���Α��ɂ�
Q��C (Q�͗L�����AC�̓J���g�[���W��) �Ƃ��̕�W���݂����ȕ����͂ł����� >>500
�܂��āB�悭�킩��Ȃ��B
b_p���\������Ƃ���ɂ�f���o�Ă��邯�ǃR���͉�X�����Ȃ��Ƃ����Ȃ���f:R^2��{0,1}��f�Ƃ͕ʕ�����ˁH
�ڕW�Ƃ��Ă閽���
��f:R^2��{0,1} ��p:[0,1]��R^2 �d�d
������f�̍\����p��depend���Ă͂����Ȃ��͂������Ǒ��v�H >>502
>Q��C (Q�͗L�����AC�̓J���g�[���W��) �Ƃ��̕�W��
�ȁ[��ق�
���肪�Ƃ� >>503
>������f�̍\����p��depend���Ă͂����Ȃ��͂������Ǒ��v�H
�܂�B������Ă������炆������Ă邩����v >>505
B����鎞��P���o�Ă��āA����P��f���痈�Ă邯�ǁAf��[0,1]����R^2�ւ̘A�����ōD���Ȃ��̂Ƃ��Ă���́H >>506
�[�������Ȃ��Ȃ�P���`���Ă���Ƃ���̂��͂��ɂł����O�ς��Ă݂���H >>507����g�͂ǂ�Ȋ����g���Ă�������ł����H �킩�����B
�A���ʑ��̑��Ƃ��ē�����W���̑S�̂�P���B
�Ȃ�z�� �Ȃ�z���A�����ł����I
�f���炵���I ��ׂ��Af���ӏ��Ŏg�����܂���
�K�v�ł����>>500�͈ȉ��̂悤�ɒ������ēǂ�ł�������
��
�䂦�ɁA�萔�łȂ��A���ʑ� f:[0,1]��R^2 �̑��S�̂���Ȃ�W��P�́A
��
�䂦�ɁA���[0,1]����R^2�ւ̒萔�łȂ��A���ʑ��̑��S�̂���Ȃ�W��P�́A ���10[m]�̐����`ABCD�̃v�[��������
�_D�ł͐����N���o���Ă���A�_D����r[m]���ꂽ�ꏊ�ł�(r/10)[m/s]�܂ł̃X�s�[�h�ł����j���Ȃ�
�_A���琳���`�̒��S�܂ʼnj���̂Ɋ|����ŒZ���Ԃ����߂� >>512
> �_D�ł͐����N���o���Ă���A�_D����r[m]���ꂽ�ꏊ�ł�(r/10)[m/s]�܂ł̃X�s�[�h�ł����j���Ȃ�
�R���͂��̒n�_�ł͂ǂ����̌����������Ă��Ă�r/10�H
D�Ɍ������Ă��悤�����܂����H >>513
�Ƃ肠������蕶�̒ʂ�ǂ̌����ł�r/10
�������Ɍ����ɂ���ăX�s�[�h�ς��Ɠ���Ȃ�
����ȗN���o�����������ɑ��݂��邩�ǂ����͒m��� >>514
�Ȃ�قǁB
���Ⴀ���n�����߂�݂����Ȃ���Ȃ̂��ȁH >>513
���Ӗ��ȕ��͑肾���
����Ȗ��o�肵��������E�� >>515
���n���Ƃ������f�ʐύŏ�������
>>516
�܂����Ⴀ�N���o������Ȃ��ďꏊ�ɂ���Đ�����d�����Ⴄ���Ă��Ƃɂ��Ă��� �O>>490
>>512
�����x��-a�Ƃ��āA
A����ABCD�̒��S�Ɍ������Čʂ�`���悤��t�b�ԉj���ƁA
���x�ɂ��āA
1-at=1/��2
at=1-1/��2�����@
�����ɂ��āA
1�t-(1/2)at^2=2�Υ5(1/4)t-at^2/2=5��/2
2t-at^2=5��
�@��������ƁA
2t-(1-1/��2)t=5��
(1+1/��2)t=5��
t=5��/(1+1/��2)
=5��2/(��2+1)
=5��2(��2-1)
=��(10-5��2)
=9.20151185�c�c(�b) >>517
�f�ʐρH
���S��E�AA����E�ւ�path��p(t)(0<t<1)�Ƃ��ď��v���Ԃ�
T=��[0,1] 10/r |x'(t)|dt
������v�ʂ�
ds^2=(dx^2+dy^2)/r^2
�̂Ƃ��̑��n�������߂�ɂȂ�̂ł́H >>520
���炵�܂���
f(x)=1/||x||�̃O���t��Ő��ϕ������Ă邩��f�ʐς��ŏ�������Ƃ����l���ł�
�������ɂ���Ȃ瑪�n�����ł��� >>512
D�����_�Ƃ��ċɍ��W(rcos��,rsin��)�����
�Ȑ���=f(r), 5��/4=f(10��2)=f(5��2)����j���Ƃ��̎��Ԃ�
T(f)=��[5��/4,10��2]��((cos��-rsin��d��/dr)^2+(sin��+rcos��d��/dr)^2)/(r/10)dr
=10��[5��/4,10��2]��(1/r^2+(f'(��))^2)dr
���̍ŏ��l��f'(��)=0�̂Ƃ���
minT(f)=10��[5��/4,10��2](1/r)dr
=10log2 >>522
�s�����ł�
f�f=0�̏ꍇ�A���E���������܂��� ���܂�AC��D���ԈႦ���A522�͎����� >>512
�ɍ��W�̋Ȑ�r=f(��), 10=f(-��/2), 5��2=f(-��/4)����j�����Ԃ�
T(f)=10��[-��/2,-��/4]��(1+(f'(��)/f(��))^2)d��
��T(f)=0�ɑ���I�C���[���O�����W���̕�������
-(f'/f)^2/(f��(1+(f'/f)^2))-(d/d��)((f'/f)/(f��(1+(f'/f)^2)))=0
���������
(f'^2-f''f)(f^2+f'^2)^(-3/2)=0
���̉���f(��)=a e^(b��)�ŋ��E���������킹���
f(��)=10e^((-��-��/2)(2log2)/��)
���̂Ƃ�
T(f)=10��[-��/2,-��/4]��(1+(2log2/��)^2)/d��
=(5/2)��(��^2+4(log2)^2) �O>>518
8�b��̂��感���B
�j���o�H�͕��������H �O>>526
5/{4log(��5+2)}+5��5/2
=7.58390826(�b) >>525
�f���炵��
�����ł�
>>527
�s���� �O>>527
>>512
�����x��-a�Ƃ��āA
A����ABCD�̒��S�Ɍ������ĕ�������`���悤��t�b�ԉj���ƁA
���x�ɂ��āA
1-at=1/��2
at=1-1/��2�����@
�����ɂ��āA
1�t-(1/2)at^2=1.4789�5
2t-at^2=14.789
�@��������ƁA
2t-(1-1/��2)t=14.789
(1+1/��2)t=14.789
t=14.789/(1+1/��2)
=14.789��2/(��2+1)
=14.789��2(��2-1)
=14.789(2-��2)
=8.66319563�c�c(�b) __����__/__/__/__/__/
_((`.`)_/__/__/__/__/
_(����~`�`���_/����_/
�a�P�P�ҁa�P�P(`)�@)/
�a�_�^�a�a�_�^,U�܁R/
__/__/__/__/_(�Q�Q�Q)
__/__/�Q/�Q/�Q/_UU__/__/__/__/__/__/__/__/__/__/�����c�c�B�O>>529
__/__/__/__/__/__/__/
__/__/__/__/__��_/__/
__/_��~_/__�������̤/
�a�P�P�a�a( (-(`)�@)/
�a�_�^�a�a(`��,U�܁R/
__/__/__/_��_(______)
__/�Q/�Q/�Q�҃�_UU__/__/__/__/__/__/__/__/__/__/>>531�D������B�����Ă�B����Đ��̑傫���������ł��邶��Ȃ����B >>525
����̒��_D���ɂƂ���ɍ��W�ł��ˁB
�@DP = f(��) = 5�e^{-(2log2)��/��} = 5�2^(-2��/��),
�@T(f) = (5/2)��{��^2 + (2log2)^2} = 8.584657992882624266 (�b)
�o�H�͑ΐ��点��B >>529
t�b��̑��x�ƈʒu��
�@v = 1 - at,
�@AP = t - (a/2)tt,
�Ƃ���B
AD=10(m), ��PAD = 45߁@�䂦
���]���藝���
(DP/10)^2 = 1 - (��2)(AP/10) + (AP/10)^2
�@�� 1 - (��2)(AP/10)
�@= 1 - (��2){t -(a/2)tt}/10,
�܂�
�@v^2 = (1-at)^2,
��� (v �� DP/10) �������߂�
�@a = 1/(10��2),
�Ƃ���ƁA���B���Ԃ�
�@t� - (a/2)t�^2 = 5��2 = 1/(2a),
���
�@t� = 1/a = 10��2 = 14.1421356�@(�b)
�ƂȂ�A�~�܂��Ă��܂�����orz ;;;;;;;;�l;;;;;;;;;;
;;;;;;�i�Q�j;;;;;;;;
;;;;;�i�Q�Q);;;;;;;;
;;;;;�i�Q(`);;;;;;;;
;;;;;�i�Q_����;;;;;;
;;��=��ބ��ҁ��;;;;;
�����������݁c�c�B������ɐ����`�̒��S�ɋ߂Â��悤�ɉj�����ق��������ȁB�O>>532�W�I�ɑ��ł���ΉE���ŁA�����ł��������ǂ��イ�Ԃ�߂Â��Ă��璆�S�ɐ肱�ށB�N���ɂ�錸�����ŏ����ɂƂǂ߂�ׂ����B �O>>535
>>512
�����x��-a�Ƃ��āA
A����ABCD�̒��S�Ɍ������Ă܂�����������t�b�ԉj���ƁA���x�ɂ��āA
1-at=1/��2
at=1-1/��2�����@
�����ɂ��āA
1�t-(1/2)at^2=5��2
2t-at^2=14.1421356
�@��������ƁA
2t-(1-1/��2)t=14.1421356
(1+1/��2)t=14.1421356
t=14.1421356/(1+1/��2)
=20/(��2+1)
=20(��2-1)
=20�0.41421356�c�c
=8.28427123�c�c(�b)
����H�@�܂������j�����ق��������̂��B ������1�̐��O�p�`ABC�̕ӂ�P�ʒ�����1�I�[���̓����Ō��сA
��AB,BC,CA�ɒ��_E,F,G�����AEF,FG,GE�ɑ��Ă����������Ō��ԁB
����ɕ�BC�����L����O�p�`EBF�ƎO�p�`GFC�ɑ������l�ɂ��ĕӂ̒��_����蓱���Ō��ԁB
���̑�����ɌJ��Ԃ����Ƃ��AAB�Ԃ�BC�Ԃ̒�R�l�����߂�B A����AD�𒆐S�Ƃ��锼�a10m�̉~���ɉ�����30ߐi�ށBv=1 (m/s)
�@20��/12 = 5.235988 (�b)
��������Ίp���̌�_�Ɍ������� y�������ɒ��i����B
�@�_(5,y) �ł̑��x�� v �� DP/10 = (1/10)��(25+yy)
�@T = ��[5,5��3] (1/v)dy
�@�� ��[5,5��3] (10/DP)dy
�@= ��[5, 5��3] 10/��(25+yy) dy
�@= [ 10 arcsinh(y/5) ](5, 5��3)
�@= 10 (1.3169579-0.8813736)
�@= 4.355843 (�b)
��������v���ā@9.591831 (�b) �C�i�Ƃ������v�Z�@�ɂԂ�����ŏo�Ă���������]���Ń��X���Ė���ԈႤ�Ӗ��킩���N�\�R�e���҂��� >>536
�@v = 1-at,
�@AP = t -(a/2)t^2,
���
�@v^2 - (DP/10)^2
�@= (1-at)^2 - {1 -(��2)(AP/10) +(AP/10)^2}
�@= AP(10��2 -200a -AP) /100,
�E������ a = 1/(10��2) �Ȃ�
�@v^2 - (DP/10)^2 = -(AP/10)^2 �� 0,
v �� DP/10 �ő�ӂ����B
�E�Ƃ��낪
�@1-at�= 1/��2,
�@t� -(a/2)t�^2 = 5��2,
�ƒu����
�@a = 1/(20��2),
�@v^2 - (DP/10)^2 = AP(5��2 -AP)/100 �� 0,
�@v �� DP/10,
�ƂȂ�A��ӂ����Ȃ��B F:R��R��C^2���ňȉ��̏��������Ƃ���
�E����萔0<c,C������Ac��F�f�f(x)��C (x��R)
�Ex^2��F(x) (x��R)
���̂Ƃ��Amin{��_0^1 F(u�f(x)) dx | u �� C^1((0,1)) }�����݂��邱�Ƃ�����. >>543
���炵�܂����C�����܂�
�C�ӂ�a,b��R�ɑ���
min{��_0^1 F(u�f(x)) dx | u �� C^1((0,1)) ,u(0)=a, u(1)=b}�����݂��邱�Ƃ�����.
�ł� �O>>536
>>538
EA�Ԃ̒�R�l��1/2[��]�̂͂������AE�ŎO�c���ɕ��Ă��邩��A
������R�͕���ŁA
(1/2)^3/(1/2+1/2+1/2)
=(1/8)/(3/2)
=1/12
�ɂȂ�B
BE�̒��_����E�܂ł̊Ԃ̒�R�l��1/4[��]�̂͂������ABE�̒��_�ŎO�c���ɕ��Ă��邩��A
������R�͕���ŁA
(1/4)^3/(1/4+1/4+1/4)
=(1/64)/(3/4)
=1/48
�ɂȂ�B
B��BE�̒��_�̒��_����B��BE�̒��_�܂ł̊Ԃ̒�R�l��1/8[��]�̂͂������AB��BE�̒��_�̒��_�ŎO�c���ɕ��Ă��邩��A
������R�͕���ŁA
(1/8)^3/(1/8+1/8+1/8)
=(1/512)/(3/8)
=1/192
AB�Ԃ̒�R�l�́A
1/12+1/48+1/192+1/768+1/3072+�c�c)
=(1/3)(1/4+1/16+1/64+1/256+1/1024+�c�c)
=(1/3){1/(1-1/4)}
=4/9[��]
BC�Ԃ̒�R�l�́A
CA�Ԃ̒�R�l��AB�Ԃ̒�R�l�Ɠ���4/9[��]������A
���肷��ƁA1/9[��] �O>>545
>>512
A���珉��1[m/�b]�A�����x-a[m/�b^2]�ŗ�����`���悤�ɂk[m]���������Ȃ���t[�b]�j���A�I��1/��2[m/�b]�Ő����`�̒��S�ɓ��B�����Ƃ���ƁA
���x�ɂ���1-at=1/��2
at=1-1/��2
�����ɂ���t-(1/2)at^2=�k
t{1-(1/2)(1-1/��2)}=�k
t(1-1/2+1/2��2)=�k
t(1/2+1/2��2)=�k
t(2��2+1)/2��2=�k
t=�k�2��2/(2��2+1)
=�k�2��2(2��2-1)/7
=�k(8-2��2)/7
���������ΐ������Ƃ������k���A
�k=5�(��2)^e�Ȃ�A
t=5�(��2)^e�(8-2��2)/7
=9.4762526�c�c(�b)
�����j���������[�B
�Z���������炩�ȁB A����Ίp���̌�_�܂Œ��i����B
A�t�߂ł͉����xa��傫�� {a=1/(10��2)} ���˂Ȃ�A
���̂܂܂����ɂ���ƁA�㔼�Œx���Ȃ�߂���B �@�@>>534
�������x�����ς��Œ��i�����
v = DP/10
�@= ��{�P - (��2)AP/10 + (AP/10)^2}
�@= (1/��2)��{�P + (1 - AP/5��2)^2},
T = ��[0,5��2] (1/v) dAP
�@= 10 ��[0,1] 1/��(1+uu) du�@�@{�� u = 1 - AP/(5��2)}
�@= 10 [ arcsinh(u) ](u=0,1)
�@= 10 arcsinh(1)
�@= 10 log(1+��2)
�@= 8.81373587�@(�b)
2.7%���炢�x�����B�B�B A(0,-10)
B(10,-10)
C(10,0)
D(0,0)
�Ƃ��A������ y = bxx -10 �ɉ����Đi�ށB
�Ίp���̌�_(5,-5)��ʂ邩�� b=1/5.
v = DP/10
�@= ��{(x/10)^2 + (1-bxx/10)^2}
�@= ��{1 - ((20b-1)/100)x^2 + (bb/100)x^4},
ds = ��{1+(2bx)^2} dx,
T = ��[0,5] (1/v) ds
�@= ��[0,5] ��{1+(2bx)^2} (10/DP) dx
�@= ��[0,5] ��{1+(2bx)^2}/��{1 -((20b-1)/100)x^2 +(bb/100)x^4} dx
�@= 8.6463092�@(�b)
0.72%�قǒx���B�B�B >>550
3���� y = cx^3 -10 �ɉ����Đi�ށB
�Ίp���̌�_(5,-5)��ʂ邩�� c=1/25.
v = DP/10
�@= ��{(x/10)^2 + [1 - (c/10)x^3]^2},
ds = ��{1 + (3cxx)^2} dx,
T = ��[0,5] (1/v) ds
�@= ��[0,5] ��{1+(3cxx)^2} (10/DP) dx
�@= ��[0,5] ��{1+(3cxx)^2}/��{(x/10)^2 + [1-(c/10)x^3]^2} dx
�@= 8.78206166�@(�b)
2.3%���炢�x���B����肵�߂��H �O>>548
���10[m]�̃v�[����A����1/4���g���ė�����ɉj���ׂ��E�R�葫����⋭���R��A���ɐ��Ȃ������Ŕ��a�Ɠ����s�b�`�オ�闆���̒����̂Ԃ����Ԃ�������ƍl���āA
�s�^�S���X�̒藝���A
(5/2)��((2��(1/2))^2+(1/2)^2)
(5/2)��((2��(1/2))^2+(1/2)^2)
=7.95283141�c�c(�b)
�ő�!! �O>>552
�����x��-a�Ƃ��āA
A����ABCD�̒��S�Ɍ������ė�����`���悤��t�b�Ԃ�7.952813141[m]�j���ƁA
���x�ɂ��āA
1-at=1/��2
at=1-1/��2�����@
�����ɂ��āA
1�t-(1/2)at^2=7.952813141
2t-at^2=15.905626282�c�c
�@��������ƁA
2t-(1-1/��2)t=15.905626282�c�c
(1+1/��2)t=15.905626282�c�c
t=15.905626282(2-��2)
=9.31730016�c�c(�b)
�������đ����Ȃ��B n���� y = d x^3 -10 �ɉ����Đi�ށB
�Ίp���̌�_(5,-5)��ʂ邩�� d=1/5^(n-1).
v = DP/10
�@= ��{(x/10)^2 + [1 - (d/10)x^n]^2},
ds = ��{1 + [nd�x^(n-1)]^2} dx,
T(n) = ��[0,5] (1/v) ds
�@= ��[0,5] ��{1+[nd x^(n-1)]^2} (10/DP) dx
�@n�@�@�@T(n)
�@----------------------------------------------------
�@1�@�@8.8137358702�@�@+2.67%�@>>549
�@2�@�@8.6463092000�@�@+0.718�@>>550
�@3�@�@8.7820616603�@�@+2.30%�@>>551
�@4�@�@8.9261905925�@�@+3.98%
�@5�@�@9.0515773221�@�@+5.44%
�@6�@�@9.1577166076�@�@+6.675
�@----------------------------------------------------
�����@8.5846579929�@�@�@>>525 >>533
�ߎ��� (n��2)
�@8.584658{1 +0.0182(n-1.62) -0.0007(n-1.62)^2} >>512�͂���>>525�œ����o�Ă��Ȃ��́H ��{��^2+(2log2)^2}
�����������A2��r=�Ƃ���Ɣ��ar=1/2
�s�b�`��2log2
�����ǂ��������Ƃ�H
�O>>553�s�^�S���X�̒藝���A�����̒����́A
��{��^2+(2log2)^2}
�N���̉e�������������ɒ��S�Ɍ������ĉE������Ȃ��璆�S�Ɏ���o�H���ő��Ȃ̂͂킩��B�Ȃ�Ńs�b�`��2log2�ƈ�ӂɌ��܂�̂��B ����
�@n���� y = d�x^�� -10�@�ł����B
n���� �̂Ƃ��͒��p�ɋ߂Â��B
���F�@A(0,-10) �� (5,-10)
�@DP = ��(100+xx),
�@��[0,5] (10/DP)dx = 10��[0,5] 1/��(100+xx) dx
�@�@= 10 [ arcsinh(x/10) ](x=0,5)
�@�@= 10 arcsinh(1/2)
�@�@= 10 log�Ӂ@�@�@�@{��=(1+��5)/2=1.618034}
�@�@= 4.8121182506�@(�b)
�c�F(5,-10) �� X(5,-5)
�@DP = ��(25+yy),
�@��[5,10] (10/DY) dy = 10��[5,10] 1/��(25+yy) dy
�@�@= 10 [ arcsinh(y/5) ](y=5,10)
�@�@= 10 {arcsinh(2) - arcsinh(1)}
�@�@= 10 {log(2+��5) - log(1+��2)}
�@�@= 10 (1.443635475 - 0.88137358702)
�@�@= 5.6226188816�@(�b)
��������v����
�@T(��) = 10 log{(2+��5)(��2 -1)��} = 10.4347371322�@(�b) �~��̐Ȃɍ�����@���l����B
4�l�Ȃ̏ꍇ�A���ɒ��Ȃ��Ă���4�l��1,2,3,4�Ə����ꂽ�����������āA�����v����1,2,3,4�ƕ��Ԃ悤�ɍ��蒼�����Ƃɂ���B1�̐Ȃ��Œ肳��Ă���Ƃ������Ƃ͂Ȃ��B
����ƁA�ǂ̂悤�ɂ������������Ƃ��Ă����X2�l�̈ړ��ōςނ��Ƃ��ȒP�ȍl�@�ŕ�����B
�ł͈�ʂ�n�Ȃ����Ē��ȍς�n�l��1,2,�c,n�Ə����ꂽ�������������A�ړ����Ȃ���Ȃ�Ȃ��l�͍��X���l���낤���H �O>>556
>>558
4�l������2�l�ړ��B
5�l������3�l�ړ��B
n�l������A
���Xn-2�l�ړ�����Δ����v���ɔԍ����ɕ��ׂ�Ǝv���B >>558
n�l���w���v���Ɂx1,2,�c,n�̔ԍ����������ꍇ�A
�������ɍςސl���́An�������̎�2�l�A��̎�1�l�ƂȂ�B
�܂��A�ǂ̂悤�ɂ����������Ă�1�l�͓������ɍςނ��Ƃ���A
n����̎��̓�����n-1�l�ł��邱�Ƃ��킩��B
n�������Ƃ��AZ/nZ��̔C�ӂ̑S�P��f���Ƃ�B
g(x):=f(x)-x ��Z/nZ��̑S�P�˂�^���Ă���Ɖ��肷���
��_(x��Z/nZ) g(x) = ��_(x��Z/nZ) f(x) = ��_(x��Z/nZ) x = n/2 + nZ
�ƂȂ邪�A�����
��g(x) = - ��x + ��f(x)
�Ɩ����B�䂦��g�͑S�P�˂łȂ��B
���������āAf(x)-f(y)=x-y �����قȂ� x,y��Z/nZ �����݁B
�ȏ�̍l�@����An�l���ǂ̂悤�ɂ����������Ă��A2�l�͓������ɍςށB
����āAn�������̎��̓�����n-2�l�B �ȑO�A���������̃X���ɁA
�~�ɓ��ڂ��鑽�p�`���O�p�`�ɕ��������Ƃ��A
�ǂ̂悤�ɕ������Ă��A
�����̎O�p�`�̓��ډ~���a�̘a�͈��ł���A
�Ƃ�����肪���������A�l�p�`�̏ꍇ�̏ؖ����������B
�~�ɓ��ڂ���l�p�`���A�E�ォ�獶����ABCD�Ƃ��A
�e�ӂ�A���獶����a�Ab�Ac�Ad�Ƃ���B
�~�̒��SO����a�Ab�Ac�Ad�ɉ��낵��������e�Af�Ag�Ah�Ƃ��A
�Ίp��AC�ABD�ɉ��낵��������i�Aj�Ƃ���B
�܂��~�̒��SO�́�ABC�A��BCD�̊O�ɂ���Ƃ���B
�܂��O�ډ~���a��R�A
��ABC�A��ACD�̓��ډ~���a��r1�Ar2
��BCD�A��ABD�̓��ډ~���a��r3�Ar4�Ƃ���B
����ƃJ���m�[�̒藝�ɂ��A
e+f-i=R+r1�Ag+h+i=R+r2 ��e+f+g+h=2R+r1+r2
f+g-j=R+r3�Ah+e+j=R+r4 ��e+f+g+h=2R+r3+r4
�� r1+r2=r3+r4 �ւ��A����Ȗ��O�����Ă�̂��B >>557
�ȉ~ y = -��(100-kxx) �ɉ����Đi�ށB
�Ίp���̌�_X(5,-5) ��ʂ邩�� k=3,
�@v = DP/10
�@�@= (1/10)��{100-(k-1)xx},�@
�@dy/dx = kx/��(100-kxx),
�@ds = ��{(100+k(k-1)xx)/(100-kxx)} dx,
T = ��(1/v) ds
�@= 10��[0,5] (1/DP)(ds/dx)dx
�@= 10��[0,5] ��{(100+k(k-1)xx)/((100-kxx)(100-(k-1)xx))} dx
�@= 8.6698357840
0.992%�قǒx���B
�ߎ���
�@T(n) = 10.434737 - 4.8644/n^0.6 + 3.2450/n^1.2 ���̎��� n=1.61693 �̕ӂ�ŋɏ��l 8.61175 �ƂȂ�B(0.315%�x��)
���̕ӂ��Ȑ� y = 5(x/5)^n -10 �ɉ����Đi�ޏꍇ�̌��E���ȁ` https://matome.naver.jp/odai/2142193955410363201
Naver �܂Ƃ�
�������낭�A�f�G�ŁA�l����������A��w������� 519gug���� 2015�N01��23��
�ł��Z���������@�i���s��w�ҁj
tan�P���͗L�������B
2006�N�@���s��w�@����@���n�@��6��
���L���Ȗ��ł��B2006�N�x����̓������ł��B�قƂ�ǂ̎��������Ȃ������Ƃ̉\��������ł��B
�o�T
http://mathtrain.jp/tan1 >>567
>�قƂ�ǂ̎��������Ȃ�����
�Ȃ�ŁH���@�藝�͗L��������� ���s�̌����l�Ȃ�݂�ȉ������������ǂ� >>567
tan�P�����L�����ł���Ȃ��tan30�����L�����Ŗ��� 4D�G���W����������B
��]����4D�̒������̂̃T���v�����t���Ă���B
�摜�ƃ\�[�X�R�[�h�́F
ttp://x0000.net/topic.aspx?id=3677-0 ���������m���̊��p���ł���l�͏��Ȃ����Ď��ł��傤 ���̗L���� x,y,z �� xyz=1 �����A���R�� a,b,c ��
a=12x(y+1),b=12y(z+1),c=12z(x+1)
�̊W������B
�@a+b+c�@�̒l�� 100�ƍł��߂����́@����сA1000 �ƍł��߂����́A����сA10000 �ƍł��߂����̂�������B 1=144/(ab)+144/(bc)+144/(ca)+3456/(abc)
�ȉ�ry (tan(x))^2���L�����ƂȂ�x�����肹��B ����
(tan(��/n))^2���L�����ƂȂ鎩�R��n�����肹��B >>570
tan(30�) ���L�����łȂ����Ƃ������ɂ�
�@sin(30�) = s �Ƃ����B
�@1 = sin(90�) = 3s -4s^3,
�@(s+1)(2s-1)^2 = 0,
�@s��-1 ������ s=1/2,
�@tan(30�) = s/��(1-ss) = 1/��3,
1/��3 ���L�����łȂ����Ƃ������悢�B
�@1/��3 ���L�����������Ɖ��肷���
�@1/��3 = p/q�@�@�@(p,q�͎��R��)
�@q^2 = 3p^2,
�����ŗ��ӂ�f�������������
�@���ӂ�3�̎w���͋���(�܂���0)�A�E�ӂ�3�̎w���͊
�ƂȂ��� UFD �ɔ�����B�@(����) >>575
�@{ sign(q)�arctan(��|q|) + n�� | q��Q, n��Z }
���� �a��1/2�ɕۂ��Ȃ���G�W�v�g�����̍������{�ɑ��₷
1/2=1/3+1/6=1/4+1/10+1/12+1/15=1/5+1/14+1/20+1/21+1/24+1/28+1/35+1/40=
1/6+1/18+1/30+1/30+1/33+1/36+1/44+1/45+1/60+1/65+1/63+1/70+1/77+1/84+1/88+1/104=
1/7+1/22+1/39+1/42+1/42+1/52+1/55+1/60+1/66+1/70+1/85+1/90+1/99+1/112+1/117+1/119+
1/126+1/126+1/130+1/133+1/144+1/152+1/154+1/165+1/168+1/170+1/198+1/204+1/209+1/228+1/234+1/273=1/2 �L����r�ɑ��āAr������������̕��q�ƕ���̐ς�h(r)�Ƃ����B
�������x�ɂ��� tan(x)^2=p/q (p,q>0 �݂͌��ɑf�Ȑ���) �����藧���Ă���Ɖ��肷��ƁAtan(2x)^2=4pq/(p-q)^2.
(i)p,q�̂����Е���0�łȂ������̎��A�����Е��͊�ł��邩�� p-q �͊�B
�䂦�ɁA4pq �� (p-q)^2 �݂͌��ɑf�ł��邩��
h(tan(2x)^2) = 4pq(p-q)^2 > h(tan(x)^2).
(ii)p,q�̗�������ł��肩���Ȃ��Ƃ������5�ȏ�̎��A4pq �� (p-q)^2 �̍ő����4.
���������āAh(tan(2x)^2)=(1/4)pq(p-q)^2.
���� h(tan(x)^2)��h(tan(2x)^2) �����藧���Ă���Ȃ�A|p-q|=2 ��� tan(2x)^2=pq.
(p��5 �܂��� q��5) ���� |p-q|=2 ���Ap��q�̂ǂ����3�ȏ�ł��邩��A|1-pq|>2.
�䂦�ɁAh(tan(4x)^2) = (1/4)pq(1-pq)^2 > pq = h(tan(x)^2).
�ȏ�̋c�_����Atan(x)^2=p/q��(i)��(ii)�̂ǂ��炩�̏����ɓ��Ă͂܂�Ȃ�A
���� {tan(2^n�x)}_(n��1) �͎����I�ɂȂ�Ȃ��B
����Ax���̗L�����{�̎��͂��̐��K�������I�ɂȂ�̂ŁA
x/��tan(x)^2�̗������L�����ɂȂ�̂� tan(x)^2=0,1/3,1,3 �̎��̂݁B
����� x/��-n = 0, �}1/6, �}1/4, �}1/3 �̏ꍇ�ɑ����B >>580
�����ł��B
���X�ʔ����őf���炵���B
�z��̉�
(tan(m��/n))^2 ���L������m,n���Ⴂ�ɑf�Ȃ�Q(tan(��/n))��Q��2���g��Ȃ̂ł��̂悤��n�����肷��悢�B
cos(2��/n)��Q(tan(��/n)�A[Q(cos(��/2):Q]=��(n)/2 (n��3) �Ȃ̂Ń�(n)��4���K�v�B
�����n=1,2,3,4,5,6,8,10,12���K�v�B
�ȉ�ry
�ł����B (tan(2��/n))^k���L�����ƂȂ鎩�R��n,k�����肹��B �O>>559
>>582
n=8�̂Ƃ��A
tan45��=1
��k���q�ɑ���1^k���q �O>>583�����B�L�����̋L���͂p�ł����B
>>582
n=8�̂Ƃ��A
tan45��=1
��k���q�ɑ���1^k���p �O>>584�����B���R���̋L���͂m�ł����B
>>582
n=8�̂Ƃ��A
tan45��=1
��k���m�ɑ��āA
�^��=1^k=1���m
��n=8�̂Ƃ��Ak�͔C�ӂ̎��R���B
n��8�̂Ƃ��Ak=0
�����Ƃ��肻���Ȋ���������B >>582�̊m�F�B
����Ȃ̊��ł�������tan(2��/n)=1�A�܂���k��2�̂Ƃ��Ɍ�����̂͂킩��܂��B
��ӂ͂�����ؖ����Ȃ����ł��B
���Ȃ킿
(tan(2��/n)^k���L�����ƂȂ�̂�tan(2��/n)=1�A�܂���(tan(2��/n)^2���L�����̏ꍇ�Ɍ��鎖�� �� �� ����B
�ł��B K:=Q(tan(2��/n))��Q(e^(2��i/n)) ��� K/Q �̓A�[�x���g��ł��邩��A
tan(2��/n)^k=p/q �ɂ����� k=2 �Ƃł��Ȃ���Ȃ�Ȃ��B
���Ƃ�>>580�Ɠ����c�Ƃ����͔̂���߂����낤�� �O>>585
1+tan^2��=1/cos�Ƃ��A
tan^2��=1/cos��-1
tan��=��(1/cos��-1)
��=2��/n�Ƃ��āA
tan(2��/n)=��{1/cos(2��/n)-1}
tan^k(2��/n)={1/cos(2��/n)-1}^(k/2)
n=1�̂Ƃ��A
tan^k(2��)={1/cos2��-1}^(k/2)
0=0^(k/2)
k�͔C�ӂ̎��R���B
n=2�̂Ƃ��A
tan^k��={1/cos��-1}^(k/2)
1^k=(-2)^(k/2)
k=0�ƂȂ莩�R���ł͂Ȃ��B
n=8�̂Ƃ��A
tan^k��/4={1/cos(��/4)-1}^(k/2)
1=(��2-1)^(k/2)
k=0�ƂȂ莩�R���ł͂Ȃ��B
��n=1,k�͔C�ӂ̎��R���B
���������Ă��Ƃ��Ă��A�ǂ����ʔ������͂킩��Ȃ��B >>587
�܂����ꂪ�قڑz����ł��B
�������������ɔ�т����B
����t�ɂ����Ă��鎩�R��k�ɂ�����t^k���L�����A����Q(t)��Q��̃A�[�x���g��̂Ƃ�t^2���L�����ł��鎖�������B
�ł��B �����`�̈�ӂ̐����������K�݂̂ō�}���� >>590
A(0,0),B(1,0),C(1,1),D(0,1)��4���_�Ƃ���B
E(a,0) (0<a<1/2) ��K���ɂƂ�B
����AC������BD=F(1/2,1/2)��S
����DE������AC=G��S
����BG������AD=H(0,a)��S
����AH������BC=I(1,1-a)��S
����EI������CD=J(1+a,1)��S
����FJ������AB=(-a,0)��S
����EF������CD=(1-a,1)��S
���̎���AEJC�Ɓ�KACL�̂��ꂼ��̑Ίp���̌�_�����ׂΗǂ��B ���Ⴀ�܂����e�҂ɂ͖����������Lj��
�C�ӂ̕��f���W�������� F��C[x] �ɂ��āA������ f,g,h��C[x] �͑��݂��邩�F
F(x) = f(x)^3 + xg(x)^3 + (x^2)h(x)^3 /�a__�a�@���@�a |߁��B
|�����a�@ �@��a ���� �
( (`e)�@ [�P]�a(`)�@)�
(�P,`����P�P]�a(_��_)~
(_(__����__���a����~ ~
~ ~~(___()~~~ (`)__)~ ~ ~~~ ~~~ ~~~ ~~~ ~~~~�@~~~ ~~~ ~ ~ ~�@~ ~~ ~~~ ~~~ ~~~�@>>590�����`�̑Ίp���̌�_�͐����������ʂ�B�O>>588���Ƃ�����_�A����������̓_���K�v�B��K�ɃV���[�y�����Œ肵�ăR���p�X�݂����ɉ���ǂ����ȁB >>591
����AH������BC�� ����FH������BC
����FJ������AB=(-a,0)��S �� K(-a,0)
����EF������CD=(1-a,1)��S �� L(1-a,1)
�Ƃ������Ƃ��ȁH
���s�l�ӌ`�����Ďh�������ł���
�Ȃ�قǐ����ł�
�z�肵�Ă�����@�̓`�F�o���g�����̂ł��� >>595
�����ł����u��K�v�Ƃ͈ȉ��̔\�͂��������Ȃ����ۓI�ȓ���ł�
�E�^����ꂽ��_�����Ԑ���������
�E��������������
�܂��A�_�Ƃ́u���Ɛ��̌�_�v�A�u�����̒[�_�v�̂��Ƃ��w���܂� >>599
���̗v�̂őΕӂɂ����_������Ă��������ׂ悢 ���[�N���b�h���ʏ�ɎO�_(-1,0),(0,0),(1,0)��������}����Ă����Ԃ���A
�C�ӂ̗L����r�ɂ��ē_(r,0)����}�ł��邱�Ƃ������B >>602
���1
A1,A2,A3�����꒼����ɂ��̏��ɓ��Ԋu�ɕ��ԂƂ��A���̒�����̓_A4��A1,A2,A3,A4�����Ԋu�ɕ��Ԃ悤�ɂł���B
��)P���O�ɂƂ����PA2���Q��C�ӂɂƂ�B
PA1��QA3�̌�_��B1�APA3��QA1�̌�_��B3�Ƃ����B1B3//A1A3�ƂȂ�B
�����菇��Q�����ւ��čs������ɐ���PB1���C1�Ɛ���PB3���C3���Ƃ���B1B3//C1C3�Ƃł���B
C1C3��PA2�̌�_��C2�Ƃ����C2B3��A1A3�̌�_�����߂�A4�ł���B��
���2
A1A2�Ɛ���PA1���B1��PB2���B2�ɂ�����B1B2�����s��A1���鎞A1��A2�̒��_���Ƃ��B
��)A1B2��A2B1�̌�_��Q�Ƃ��鎞�APQ��A1A2�̌�_�����߂钆�_�ł���B��
���3
n��1�ƕ��1�̐ݒ�̌���A1A2��1:2^(n+1)-2�ɓ�������_X��2:2^(n+1)-3�ɓ�������_Y���Ƃ��B
��)P���O�S�ɔC�ӂɂƂ�B
���1�ɂ��A1A2��2^n:2^n-1�ɊO������_Q���Ƃ��B
R�����PA1��ɔC�ӂɂƂ�QR��PA2�̌�_��S�Ƃ���B
A1S��A2R�̌�_��T�Ƃ�PT��A1A2�̌�_��U�Ƃ����U��A1A2��2^n:2^n-1�ɓ�������_�ł���B
���2�ɂ�蒆�_����鑀������x�����肩������X��Y��������B��
�藝
���1�̐ݒ�̌��ɔC�ӂ�1�����̐��̗L����t�ɑ�A1:A2��t:1-t�ɓ�������_���Ƃ��B
��)t=a/b�ƂȂ鎩�R�����Ƃ�B
���2�ɂ��b����̎����߂��Ώ\���ł���B
���R��n��2^n-1��b�̔{���ł���悤�ɂƂ��B
���̎�2^n-1=bc�Ƃ�����a/b=ac/(2^n-1)�ł��邩����1,���3�ɂ��\�ł���B�� >>604
�킠�������A������
�z�肵�Ă��������
�Ey=0 �ȊO��y���ɕ��s�Ȓ���L����}�\�B
�E�S�Ă̐���n�ɂ��ē_(n,0)�͍�}�\�B
�E�䂦�ɁA����L��ɁA�C�ӂɒ��������_�����}�\�B
�E�C�ӂ̐���n,a>0,b>0�ɂ��āA��_(n,0),(n+1,0)��a:b�ɓ�������_����}�\�B
�Ō�̂́A�Ⴆ�Β���L�� y=��2 �ŕ\����A�Ȃ����S�Ă̓_ (e+��m,��2) (m��Z) ����}�ł����Ƃ��āA
��_(n,0),(e,��2)�����Ԓ����Ɠ�_(n+1,0),(e+��(a+b),��2)�����Ԓ����̌�_��P�Ƃ����A
��_P,(e+��a,��2)�����Ԓ�����y=0�̌�_�����߂�_�ɂȂ�B �ȒP��������Ȃ�����
�g�~�ɓ��ڂ���O�p�`�Ŗʐύő�̂��̂͐��O�p�`�ł��鎖�h
�������ŏؖ��ł��܂���
�܂�������l�̓T�N�b�Ɖ�����̂��낤 �O>>595
>>590���A�킩�����I
�����`��܂莆�݂����ɂ҂����蔼���ɐ܂�����B
�ŁA���̐܂�ڂɉ����Ē�K�Ő��������B >>606
��ABC = (1/2)AB�CH
�����Ł@CH�́A���_C�ƒ���AB�̋����B
2���_ A,B ���Œ肵�A���SO�����AB�ɐ��������낷�B
�����Ɖ~���̌�_��X1,X2�Ƃ���B
��AB���AX1, X2 �ň������ڐ����A���aX1-X2 �ɐ���������݂��ɕ��s�B
�~���́A����2�{�̐ڐ��̊Ԃɂ���B
C�����̉~������Ƃ��A ��ABC���ő�ɂȂ�̂� CH ���ő�̂Ƃ��B
���Ȃ킿 C���A2�̐ړ_X�̂��� ��AXB ���s�p�̕��ł���Ƃ��B
���̂Ƃ� AC=BC
A,B,C�����ւ��Ă����l������A���O�p�`�B >>606
��abc�͉~����̑��قȂ�O�_��������O�p�`�ŁA�����̂����Ŗʐύő�ł���Ƃ���
���܁A��abc�����O�p�`�ł͂Ȃ��Ɖ��肵�Aab��bc�̒������قȂ�Ƃ���
�����ac�̐����������~���b�̂��鑤�ɓ_d������A��adc>��abc�Ŗ��� >>590
�����`S���̍�}�ł��\�ł����B
>>591 �̂��ƁA�Ίp��BD�ɕ��s�Ȑ���EH�����܂��B�����ꂪ�~�\
�@����EH �� ����AC�@=�@M(a/2,a/2)
�@����EF �� ����BM�@=�@N(3a/{2(1+a)}, a/{2(1+a)})
�@����AN �� ����BC�@=�@P(1,1/3)
�@����AN:�@y = x/3,
���Ƃ͊ȒP�ł��ˁB
ABCD�������`�̂Ƃ����S�������B >>609
�@ab��bc ���� ��adc > ��abc ���o���̂͂ǂ�����ł��H >>607
�u��K�v�Ƃ�>>597�ɂ���\�͂����L���܂���
���������āu�܂�ڂɉ����Đ��������v�Ƃ����\�͂͂���܂��� >>602�@�֘A
��_���^����ꂽ�Ƃ��ɒ��_�������ō�}�͂ł��Ȃ�
�ؖ����Ăǂ�����ł����H >>613
2�_�����Ȃ�������ł��邱�Ƃ͂���2�_��ʂ钼�����������Ƃ���
���ƓK���Ɉ����������͂���2�_�Ƃ͑S���Ɨ������猋�_�ɉ����𗧂��Ȃ� >>613
��K�������g����ł́A�^����ꂽ��_�̒��_����}�ł��邱�Ƃ́A
�^����ꂽ��_��ʂ钼���ƕ��s�Ȓ�������}�ł��邱�ƂƓ��l�ɂȂ肻����
�������A�w���S�ɓƗ��ł���x���ƂƂ����ǂ��莮���ł��邩���킩���ȁc
>>602�ł�����悤�ɁA���Ԋu�ɗ^����ꂽ�O�_�Ƃ͑S���Ɨ��ɂƂ����_����A
�ʂ̂������̓_����}�ł��Ă��܂������ >>615
>�������A�w���S�ɓƗ��ł���x���ƂƂ����ǂ��莮���ł��邩���킩���ȁc
>>>602�ł�����悤�ɁA���Ԋu�ɗ^����ꂽ�O�_�Ƃ͑S���Ɨ��ɂƂ����_����A
>�ʂ̂������̓_����}�ł��Ă��܂������
�R���p�X�������2����������������Ƃ������Ƃ��d�v
��K�����ł͉����o���Ȃ� n�_�^�����Ă���Ƃ��ɒ�K�ŏo���邱�Ƃ�
����n�_����2�_����Ē���������
���̌�_���܂߂ē_�̌���
n(n-1)/2(n(n-1)/2-1)/2=(n+1)n(n-1)(n-2)/8
�ɑ��₷���Ƃ���
������J��Ԃ��ē_��������ł����₹�邪
���ꂾ�� �Ƃ͌������Ԋu�ȎO�_���^����ꂽ��A602�̒ʂ�Ɏ��ہw�������ł����x�킯������Ȃ��c
��K�������g������}�ɉ����ł��ĉ����ł��Ȃ��̂��A�Ƃ����₢�ɐ��m�ɓ����悤�Ƃ�����A
����͒��X�����łȂ����ȋC������ �Q�_��m:n�ɓ���(�O��)����_��^������m:n�ɊO��(����)����_�͒�����ō�}�ł���
���ǒ��_�͖������_�ɂȂ�B�B �悭�m��ǂ��������ĕ��s�������̓Ɨ������Ă�H �Ƃ������܂��A�����I�ɋ�����Ă����ł͂Ȃ�����ł���A
�w�_��K���ɂƂ�x�Ƃ��������莮������K�v��������
����������͂����炭�A��l�s���S���Q�[���̕������g���ł���Ǝv��
�X�I�ɓ�l�̖��O���w��}�ҁx�Ɓw�_�x�Ɩ��Â��Ă����B
��}�҂́A>>597�ɋL����Ă��鑀������Ă���Ԃ͂����Ǝ����̎�ԁB
�������A��}�҂����钼����ɓ_��K���ɂƂ肽���Ǝv�������́A�܂����̒����̊J�����W������w�肵�A
���̊J�����W���̂����ǂ��ɓ_���Ƃ邩��_�����߂�A�Ƃ���������o�Ȃ���Ȃ�Ȃ��B
�X�ɁA��}�҂͊J�����W���̂����_���ǂ��ɓ_���Ƃ����̂��́A�m�邱�Ƃ��ł��Ȃ��B
�i�������w����͍�}���n�߂Ă��牽�ԖڂɂƂ����_�ł���x���̂悤�ɁA
�K���ɂƂ����_�ɔԍ��t�������āA���Ƌ�ʂ��邱�Ƃ͉\�B�j
���ʏ�ɓK���ɓ_���Ƃ肽���������l�B
���Ȃ킿��ɍ�}�҂��J�W�����w�肵�A���̒�����_����}�����_�����߂�A�Ƃ���������o��B
��}�҂́A�J�W���̒��Ő_���ǂ��ɓ_���Ƃ�������m�邱�Ƃ͂ł��Ȃ��B�ԍ��t���͉\�B
�ŏI�I�ɍ�}�������_����}�ł����}�҂̏����B�����Ȃ��ΐ_�̏����B
��}�҂ɕK���@�����鎞�A���̓_�́w��}�\�ł���x�ƌ����B >>619
�܂�n:m�̊Ԋu�ɂ���O�_����A(n-m):m�̊Ԋu�ɂ���O�_����}���邱�Ƃ��\�Ƃ�����
n:m��������Ȃ�A�ݏ��@�g���ŏI�I��1:1�ɂ��ǂ蒅������A
���ʓI�ɂ��̒�����ɂ���S�Ă̗L���i�I�ȁj�_����}�ł��� >>611
ac�ɐ����Ȍ��̂���d��ʂ���̂͒��a�ōŒ��Ȃ̂Œ��ac�ɑ��鍂����b������������ /�a;;�a�����n�a |;;;;;
|����|((-_-)��a ����;;
(�@(`)(��/c) �a(`)�@);
(�P�P)�u�P�P]�a(_��_)~
(_(__����__���a����~ ~
~ ~~(___()~~~ (`)__)~ ~ ~~~ ~~~ ~~~ ~~~ ~~~~�@~~~ ~~~ ~ ~ ~�@~ ~~ ~~~ ~~~ ~~~>>590�����`�̑Ίp���̌�_�͕ӂ̐����������ʂ�B�O>>607���Ƃ�����_�B��ӂ��̂���������̈�_����ʼn����̒��_�܂Œ�K�Œ����������B
���̒������������Ƃ��ӂƌ�_���ł���B���̌�_���璸�_�Ɍ������ĐV���Ȓ����������������B���̒������������Ƃ��Ίp���ƌ�_���ł���B���̌�_�ɐ�ɂƂ�����ӂ̉�����̈�_���甼�����������ƁA���̔������͂ӂ����ѐ����`�̕ӂƌ����
(>>599�`�F�o�̒藝��萳���`�̕ӂ����)�A���̌�_�ƑΊp���̌�_��ʂ钼���������A������������K�����ň�����B >>613 ��菭�������ア��Ƃ���
�w������}����Ă��Ȃ���Ԃ̕��ʂ���A��K�������g���ĕ��s������}���邱�Ƃ͉\���x
�Ƃ������̂���������B
�ア�Ƃ����̂́A����613���\�Ȃ�����炪�\�ł��邱�Ƃ�������A�Ƃ����Ӗ��B
�����������̕��@�͂����ς�킩���c �O>>624
>>625
��ʂɒ�K�͕��s�Ȓ��������̕���ۂ悤�ɍ���Ă���B
�����s��2�������������Ƃ͉\�B ���s���ƒ��_�̒�̂ݍ�}�\���̓`�F�o�̒藝��蓯�l�ł́H
�����̍�}�͂ǂ��� ���ʏ�ɒ����������^�����Ă���Ƃ��āA��K�����Ő�����}����͖̂������낤��
�ŏ��ɗ^�����Ă�̂�x�������ł���A>>621�̈Ӗ��ō�}�\�Ȑ}�`�́A
����J�W���ɑ�����C�ӂ̎���a�ɂ��āA�ϊ� f(x,y)=(x+ay,y) �ŕs�ςłȂ���Ȃ�Ȃ� >>608>>609
���������I
�������̋c�_����ΊԈ���Ă͂Ȃ�
����Ŏ�����̂́u���O�p�`�ȊO�͍ő�l��^���Ȃ��v�Ƃ�������ł�����
�u���O�p�`�ōő�l�����v�Ƃ������͒��ڌ����Ȃ�
����́u�K������O�p�`���ő�l��^����v�Ƃ��������F�߂Ȃ���Ȃ�Ȃ��Ƃ�������
�܂�������m���߂�̂���w���w�̔��e�ł͊ȒP�Ȃ̂ŁA���ꍞ�݂ł����������������A�������Ⴀ��
�ł��ꉞ���������ł��������[���Ęb
���l�^�͋�������̖�肾���ȂŁA�u���O�p�`�ȊO�̎O�p�`�͕s�K�����������ł͕s�����ɂȂ�v�Ƃ����b��������
�͔͉͉�͓I�ɉ����Ă�����
������ƍH�v����Έꉞ�����ʼn�����ȁA�Ǝv�����̂� >>629
�ꉞ�ł����B
�ӎO�p�`�Ɍ��肵�Ă����̂͊��o�̒ʂ�B
���O�p�`ABC�̊O�ډ~�����Ƃ���B
BC�Ɋւ���A�ƑΏ̂ł���_��D�A
CA�Ɋւ���B�ƑΏ̂ł���_��E�A
AB�Ɋւ���C�ƑΏ̂ł���_��F�Ƃ���B
B�AC���璼��EF�ɉ��낵�������̑���G,H�Ƃ���B
AD�ɐ����Ȍ�PQ�ɑ��ā�APQ����ABC�A������PQ��BC����v����Ƃ��������Ηǂ��B
����PQ��DB�ADC�̌�_��RS�Ƃ����APQ����ARS�œ���������BC=PQ�̂Ƃ������灢ARS����ABC�������Ηǂ��B
R,S���璼��EF�ɉ��낵�������̑���T,U�Ƃ���B
��BCGH=2��ABC�A��RSTU=2��ARS�����灠RSTU����BCGH�������Ηǂ��B
�ȉ�EF�����Ɂ�3�{���ċc�_����B(��3�{�����_���`���Ă����悢���߂�ǂ����������Ȃ̂Ŏ��)
RS��BC���D�ɋ߂����ɂ��鎞�́�RSTU����BCGH�̊O���ɂ͂ݏo���Ă镔���͓��Ɉ�������ł镔���Ɣ�r���ē������Œ����̒Z�������`�ɂȂ��Ă���̂ł��̏ꍇ�͂悢�B
���Α���RS������Ă��鎞�����l�ł���B >>606
�{��ł� ��ABC �̖ʐς�
�@f(C, B-A)
�Ƃ������Ƃ��\�ł��ˁB(���ł��Ȃ����̂悤�ł���)
>>609 ����
��C���Œ肵�� ��A, ��B ��ς����Ƃ��A
�ʐς́A�ӎO�p�`(B-A=0)�̂Ƃ��ɍő�ł���B
�@Max[x] f(C,x) = f(C,0)
���� ��C ��ς����Ƃ��A
�ʐς́AB=C (=��/3) �̂Ƃ��ɍő�ł���B(���O�p�`)
�@Max[C] f(C,0) = f(��/3,0)
�������A�ő�l��
�@Max[C,x] f(C,x) = f(��/3,0)
�܂�u���O�p�`�ōő�l���Ƃ�v�Ƃ������������܂��B(�L�b�p��)
���͂̒��������Ƃ��A���܂��p�����[�^�t���ł��Ȃ����ɂ� >>629 �̂悤�ɂȂ�܂�������
>>623 �����l���ƥ��� >>630
��RSTU����BCGH�������Ηǂ��B
�����ȍ~�������ȒP�ɂł���ȁB
��DEF�̂�����RSTU�̊O���̕����������̕������傫�����Ƃ������Ηǂ��B
RS��BC���D�ɋ߂����ɂ��鎞�́�ERT�A��FSU�����ꂼ��RT�ASU�Ł�RSTU�̑��ɐ܂�Ԃ��Ďl�p�`���Ƃ��A�����Ȃ��Ŏc�镔���͂��傤�ǁ�DRS�ƍ����ȎO�p�`������悢�B
RS��BC���D�ɉ������ɂ��鎞�́�DRS����RSTU�̑��ɐ܂�Ԃ��Ďl�p�`���Ƃ��A�����Ȃ��Ŏc�镔���́�ERT�A��FSU�ɍ����ȎO�p�`������킹�����̂�����悢�B�� >>631
�⑫���܂��B
�@C����/3�@�ˁ@f(C,0) < f(��/3,0)
(����)
�@f(C,|A-B|) �� |A-B| �ɂ��ĒP�������Ȃ̂�
�@f(C,0) = f((��-C)/2, (3/2)|C-��/3|)
�@< f((��-C)/2, (1/2)|C-��/3|)
�@= f(��/3, |C-��/3|)
�@< f(��/3, 0)
�@= (���O�p�`�̖ʐ�). >>633
> �@f(C,0) = f((��-C)/2, (3/2)|C-��/3|)
�R���͉��́H ���p�� (��-C)/2, (��-C)/2, C �̓ӎO�p�`������B >>635
f�͊O�ډ~�̔��a�Œ肳��Ă��ł���ˁH
��Ɋ����ē\�蒼���Ǝv����ł����O�ډ~�̔��a�ς�����Ⴄ�̂ł́H ���A����A�\��Ȃ����Ȃ��Ă������̂��B
���p����蒼�������ˁB
�Ȃ�z���B >>633
����̕��@�͒��X�����ȁB
���̕��@�œ��ډ~�̖ʐύő�Ƃ�3�ӂ̒����̘a�ő�Ƃ������O�p�`�̂Ƃ��Ƃ��������I�Ɏ�����ˁB >>631 >>633 �́A���p�ŕ\�킹��
�@{A, B, C}
�@{(��-C)/2, (��-C)/2, C}
�@{(��-C)/2, ��/6 + C/2, ��/3}
�@{��/3, ��/3, ��/3}
�̏��ɖʐς��g�傷��Ƃ������Ƃł����A
���̌v�Z�������͍��Z���w�͈͓̔��ł��傤�B
���̑��ɂ��A
�@�O�ډ~�̔��a�����̎O�p�`�̏W���͂ǂ�ȏW�����H
�@�Ȃ����܂��p�����[�^�\���ł���̂��H
�Ƃ�������������܂����A������͑�w���w�̖��ł��傤�B >>633
���g���ď����I�Ɏ����Ă݂�܂Ƃ߁B
���a1�̉~�ɓ��ڂ���O�p�`ABC���Ƃ�A
A��B��C�Ƃ��Ă悢�B
�D��BC���DEF����BCD=��/3�A��CBE=��/3�A��BCF=��CBF�ƂȂ�悤�ɂƂ�B
E��������F�̂����ꂩ����CF��ɂ������X�Ƃ���B
���̎�
��ABC����XBC�d(✳︎)
�ł����XBC����XCB�̂����ꂩ�̓�/3�ł���B
�O�҂̂Ƃ�Y,Z�����ꂼ��C,B�A��҂̂Ƃ���Y,Z�����ꂼ��B,C�Ƃ����
��ABC����XYZ
�ł����Z=��/3
�ł���B
W����WXY=��/3
�Ƃ����
��XYZ��XYW�d(✳︎)
�ł��聢XYW�͐��O�p�`�ł���B��
�ؖ���(✳︎)�̂Ƃ���͖ʐς̂����ɓ��ډ~�̔��a��O�ӂ̘a�ɂ��Ă������I�Ɏ�����̂œ��ډ~�A�O�ӂ̘a�ő�������ł��邵�A�ʐς����̌n�Ŏ������Ƃ��ł��Ē��X�C���������B ���̐���n�̔C�ӂ̖�d<n�ɑ��A���鐳�̐���m��������md+1<n��n�ƌ݂��ɑf�ɂȂ�Ƃ����B
n�̕K�v�\�����������߂�B �E�D��BC���
�@��BCF = ��CBF = (��-��A)/2�@( >��/3),
�ƂȂ�悤�� �_F ���Ƃ�B
�@��ABC < ��CBF,
�@��BFC = ��A < ��/3,
�E���CF��� ��EBF = ��/3 �ƂȂ�悤�� �_E ���Ƃ�B
�@��BEF = ��BCF = (��-��A)/2 > ��/3,
���Ȃ킿
�@��CBF > ��EBF > (��-��BEF)/2,
���@��CBF < ��EBF,
�E�D��EF��� ��DEF = ��DFE = ��/3�@�ƂȂ�悤�� �_D ���Ƃ�B
�@��DEF �͐��O�p�`
�@��EBF < ��DEF,
�ȏ�ɂ��
�@��ABC < ��DEF, >>641
n��2(mod 4)�Ƃ���Ƃ�d=n/2�ɑ���dm+1<n����m��1�����Ȃ����A���̂Ƃ�dm+1��n��������������͖�������Ȃ��B
m��1,3(mod4)�Ƃ���Ƃ��C�ӂ�d|n (d<n)�ɑ���d|n/p�ƂȂ�f���qp>2���Ƃ�邪�A���̂Ƃ�n��n/p+1�̋��ʑf���q��p�������蓾���Ap�����ʑf���q�Ȃ�2n/p+1��n�͋��ʑf���q�����������݂��ɑf�ł���A
m��0 (mod 4)�Ƃ���Ƃ��C�ӂ�d|n (d<n)�ɑ���d|n/p�ƂȂ�f���qp�ɂ�����p>2�ł���ΐ�Ɠ����悤�ɂ���m��I�ׂ�B
p=2�̂Ƃ���(n,n/2+1)=1�ł悢�B
�ȏ�ɂ��^����ꂽ������n��0,1,3(mod4)�Ɠ��l�ł���B �O>>626
>>292�������卂�B
OA�EOB=1���������Ȃ��B
���Ƃ͒���PQ�Ő����������AD���ǂ��g�����B
��PBD�䁢OBQ���������߂ɁAO�ɂ���Q�Ɠ_�Ώ̂�Q'�����A��PBA�䁢OBQ'����������ǂ����B
OA�EOB=1�Ɓ�PBA�䁢OBQ'
�ǂ��Ȃ��邩�B
������PD:OQ=PA:1
���邩��ɑ����Ȃ��ǁA�����������킩��Ȃ��B
2�ӂ̔�Ƃ��̊Ԃ̊p���������A���ȁH
OB=1/OA=OQ/OA=OQ/PD=1/PD
�ڌ��藝���ȁH
�l�����H�@�܂��o�Ȃ��H
���������ǂ���ɂ��ؖ�����Ă��Ȃ����H �O>>644
���ʐ}�`�ɕ��f���Ȃ���킯�Ȃ��B
����������3�B
3�g�̕ӂ̔䂪�������B
2�g�̕ӂ̔�Ƃ��̊Ԃ̊p���������B
2�p���������B
����3�̏�����T���Ă݂����Ȃ������Ƃ��Ă��T�����z�A�T�����Ƃ����z�����i�ɂ��ׂ����Ǝv���B >>292
������OAB�������Ƃ��镡�f���ʏ�ōl����B
O(0)
A(a)�@�@0<a<1,
B(1/a)
P(e^(ip))
Q(e^(iq))
�@0 < p < q < 2��,�@0 < q-p < ��,�@
D(e^(ip) + e^(iq) - a�e^i(p+q))
�Ƃ�����
PD = e^(i(p+q)){e^(-ip) -a} = e^(i(p+q))AP~,
QD = e^(i(p+q)){e^(-iq) -a} = e^(i(p+q))AQ~,
|PD| = |AP|
|QD| = |AQ|
�� D�͒���PQ�Ɋւ���A�Ɛ��Ώ̂ł���B
OQ/OB = a�e^(iq) = PD/PB,
�䂦�������낤�ȁB�B�B �O>>645
���������玗���悤�Ȗ�肪�����āA���f���ʼn����Ă������B
���f�����g��Ȃ����������݂��Ȃ��Ƃ����Ȃ��B
��BPA�䁢BOQ'
����BDA�䁢BQQ'
��������A
��BDP�䁢BQO P��AD�̒��_�AO��QQ'�̒��_������A
��BPA�䁢BOQ'
�܂��́�BDA�䁢BQQ'
��������A
��BDP�䁢BQO �O>>648�Ⴄ���B
AP=DP�͌�����B
AD��PQ
OA=t(0��t��1)�Ƃ����ƁA
OB=1/t
AD��PQ�̌�_��R�ABR��OD�̌�_��S�Ƃ���ƁA���l���E�X�̒藝���A
(OB/BA)(AR/RD)(DS/SO)=1
{(1/t)(1/t-t)}(1/1)(DS/SO)=1
DS/SO=(1/t-t)/(1/t)=1-t^2
�킩���B >>292
����l�ɏ����ɂ��������Ă�������̂ł����ɓ\��܂�
������EACB�����a�_��ł���,�~O���A�|���j�E�X�̉~�ł��邱�Ƃɒ��ӂ����
��APC=��CPB=:z
��A,D��PQ�Ɋւ��Đ��Ώ̂Ȃ̂�
DP:PB=PA:PB=AC:CB=EO:OB(EACB�����a�_���O��EC�̒��_������)
=OQ:OB·····�@
(�⑫ OA=a,OB=1/a�Ƃ����)
��OQB=x,��OBQ=y�Ƃ����
��BOQ=180-x-y
�~���p�̒藝,�^���X�̒藝�Ȃǂ���
��EPC=��ECQ=90��-��QEO=90��-(180����EOQ)/2
=(x+y)/2
��APC=��CPB=,���Ώ̂����DPQ=��QPA���
��DPB=2��QPC=180��-2��EPQ=180��-x-y=��QOB·····�A
�@�A���
2�Ӕ��p��������
��PBD�䁢OBQ∎
https://i.imgur.com/NwrNyyo.jpg
https://i.imgur.com/cOvLchw.jpg >>650
> ��BOQ=180-x-y
> �~���p�̒藝,�^���X�̒藝�Ȃǂ���
���̕ӂ肪��蕶�Ŗ�������ĂȂ��_�̔z�u�ł߂��Ⴍ����ꍇ�킯���Ȃ��ƃ_���Ŏ����ؖ��ɂȂ�Ȃ��B �O>>649
>>651
PQ��������AB���܂����悤��Q���Ƃ�����̂��B
�Ȃ�قǁAO,A,B�Ɠ������͈ӊO�ɍL���ˁB
P���Ԃ�č����Ă��B >>651
������ؖ������l�ɋ�������uPQ�Ɋւ���OAB�͓�����������ꍇ������
��}�̂悤�ȏꍇ��PQ���Ђ�����Ԃ������݂̂̂��Ǝv���܂��v�Ƃ̂��� >>653
����Ȃ킯�Ȃ����B
��������OA�EOB=1��OA��OB�ǂ����������Ƃ�����AB��PQ�̈ʒu�̔z�u�Ƃ��Ŋp�x�̌v�Z�Ƃ��S���e������B
�~���p�̔z�u�ɂȂ����艏�ɓ��ڂ���l�p�`�̑Ίp�̈ʒu�ɂ�����B
���ꂼ��ɑ��đS���ǂ����Ƃǂ������o���̂��A�����̂��A�Ƃ��A���S�Ɉ�v������ߊp�̊W�ɂȂ�����B
OA���������AOB���������Ɏn�܂��ďؖ�������Ȃ��z�u�̏ꍇ�킯��3�炢�K�v�ŁA�e�X�ɂ���2�ʂ肩3�ʂ�̏ꍇ�킯���K�v��10�ʂ�����B
OB<OA�̎��͈ꉞ�S���ׂ������ǁA�c��̃P�[�X�S���ׂ����Ƃ��Ă��ƂĂ������C�ɂ͂Ȃ�Ȃ����낤�����߂��B
�}�����ɗ^�����ĂĔz�u�����܂��ĂȂ��Ə����̏ؖ��͂����Ȃ鎖���������Ȃ��B
�������}���Ȃ��Ă�������ƌ��t�Ŋm�肵�Ă��������>>292�͖����B
�����A�p�x�̑����������o��ؖ��͂��̓_�̕���ł鏇�Ԃ̕s�萫�����鎞�͕K�������Ȃ�B >>654
A�͉~O�̓���������OA<OB�Ƃ̂��Ƃł� >>655
�����Ȃ�H
�ł����ꂾ�����Ⴗ�܂Ȃ��B
>>292�̕��͂����ł͊m�肵�Ȃ��_�̔z�u�����`�����`���o�Ă���B
����Ȏ��Ȃ��Ƃ����Ȃ�>>650 �̏ؖ���"�Ȃǂ���"�Ȃ�Ă��܂������Ȃ��őS�������Ă݂Ă�B
���ꂪ�z���g��>>653�Ō����悤�Ɂ@��2�ʂ�ōςނ̂��ǂ��������Ă݂Ă�B �O>>652�����B
>>650
PQ��������BA���܂����悤��Q���Ƃ�����̂��B
�Ȃ�قǁAO,A,B�ɑ��ē������͈ӊO�ɍL���ˁB
P���Ԃ�č����Ă��B �O>>657
>>650
��EPC=��ECQ����Ȃ��Ȃ��B
��EPC=90��������A�ڂ��ԈႢ�����������������d�Ȃ������B
OA=t�Ƃ�����OB=1/t�͓����������B
��APC=��CPB�́A�������Ɍ��邩��ɂ����Ȃ��ǁA����������́H
�ǂ��������Ƃ��낤�B
AC=1-t
CB=1/t-1=(1-t)/t
�������Ɂ�ACP=��CPB�Ɍ�������ǁB���������̖��̊̂��B >>650�̉�ǂ��z�B
�A�|���j�E�X�̉~�⒲�a�_��̒m�����Ȃ��Ɖ����Ȃ��B
���ɒm���������Ă��A
>EACB�����a�_��ł���,�~O���A�|���j�E�X�̉~�ł���
>AC:CB=EO:OB(EACB�����a�_���O��EC�̒��_������)
������������͓̂���B
�㔼�̐����͔ώG�����A�v����Ɂ�DPB=2��QPC=��QOB
x�Ay���̑��̐����͕s�v�B
��莩�g�ɂ͉��̕s�����Ȃ��B �O>>658
>>659
AC:CB=1-t:1/t-1
=1-t:(1-t)/t
=1:1/t
=t:1
EO:OB=1:1/t
=t:1
��������AC:CB=EO:OB�����ǁAAC:CB=EO:OB���m�肽���Ƃ����K�v�����ǂ��Ȃ��ďo�Ă������B
�����炭2�g�̕ӂ̔䂪���������Ƃ������������炾�Ɛ��@����B
����������ƂłȂ��肻���B �O>>660
>>292���B
>>650�𗝉������B
������OA�Ɖ~���̌�_��C,
������BA�Ɖ~���̌�_��E�Ƃ���B
OA=t�Ƃ����ƁA
OB=1/t
AC=1-t
CB=1/t-1=(1-t)/t
��QOB=��QOC�͌�QC�ɑ��钆�S�p������A
�~���p��QPC��2�{�B
��QOB=2��QPC�����@
����PQ�͐���DA�̐�������������A
��DPQ=��QPA
��OPA�䁢OBP(������t:1,��������2�g�Ƃ��̊Ԃ̊p������������)������A
���ꒆ�S�p�p�Ƃ����ӎO�p�`��OPC���͂��ނƁA
��APB��PC�ɂ�������A
��APC=��CPB
4�̊p�𑫂�����DPB�ƁA����2�𑫂�����QPA�ŁA
��DPB=2��QPC�����A
�@�A����DPB=��QOB
��OBQ�ɂ����āA
OQ:OB=OE:OB=1:1/t=t:1�����B
��PBD�ɂ����āA
PD:PB=PA:PB=t:1�����C
�B�C���PD:OQ=PB:OB
2�g�̕ӂ̔�Ƃ��̊Ԃ̊p������������A
��PBD�䁢OBQ �̏�̊������ł����Ď��ȑ����ł�����̂������ɑ��݂��邱�Ƃ������B
�������An��������f��F_2[x]�����ȑ����ł���Ƃ́Af(x)=f(1/x)x^n �������Ƃ������B >>663
q>4���p�Ƃ��Ďʑ�f:Fq�_{0}��Fq��f(x)=x+1/x�Œ�߂�B
S=im(f)�_{0}�̊e��y�ɂ���f(x)=y����Fq�_{0,1}�̌�x��2�����݂��邩��
2#S=q-2
�ł���A#S=q/2-1<q-3�ł��邩��S�ɂ�F4�u�������Ȃ�b��Fq���Ƃ��B
b��F2��̍ŏ���������P(y)�Ƃ���B
Q(x)=P(x+1/x)x^n (n=degP)�Ƃ����B
�㐔�̃��̌�a��f(x)=b�̉��Ƃ����a��Q(x)�̍��ł���B
������[Fq(a):F2]��q�܂���2q�ł��邩��d=[F2(a):F2]��2q,q,2,1�̂����ꂩ�ł���B
d=q�ƂȂ�͕̂�����F(x)=b��Fq�ɉ��������ł���A�����b�̎����ɔ�����B
d=1,2�ƂȂ�Ƃ�F2(b)��F2(a)�ŏ���F4��ƂȂ��͂�b�̎����ɔ�����B
�����F2(a):F2]=2q�ƂȂ�Q(x)��a�̍ŏ��������ł������ł���B
�����Q(x)�̍���P(x)�̍����ɑ��ĕ�����x+1/x=���̉����Ƃ�Ƃ��̑S�̂����玩�ȑ����ł���B�� >>664
����q=2^e�Ƃ���e�͑f���ɂƂ�ł����B
[Fq:F3]=e�ňȊO����ɉ����ăG�X�p�[���Ȃ������܂��B >>664
���ۂɍ\�������̂��c������
�z�肵�Ă��̂́AF2��n���������S�̂̏W����S_n�Ƃ����āAS_n�̌��̌���
(1/n)��_(d|n)��(n/d)2^d
�ɂȂ邱�ƁA���ꂪ������n�ɂ��Ċ�ɂȂ邱�ƁA
����𗘗p����S_n��̑� ��(f)(x)=f(1/x)x^n ���Œ�_�������Ƃ������A�Ƃ��������ł��� �O>>661
>>662(1)(2)(3)�̗U���t�����������B
�ǂ�Ȃ������A���������v�����ǁB �[���Ŋ�������A�J���ǂ���ق� >>631 >>639
�@�O�ӂ̒���a,b,c�̘A�����́A
�@2�ϐ��̘A�����̍����ŕ\�킹�܂��B(�A�[�m���h,1958)
�@���@�q���x���g�u���w�̏����̖��v13��
�@�����������\�Ƃ͌����Ȃ��̂Ŏg���邩�ǂ�������
>>652 >>653
�@0 < p,q < 2��
����
�@0 < |p-q| < ��
�ł��B �cn�A��n�̃}�X�ڂ̂��ꂼ��� 1,2,3,...,n �̐��������Ă����B���̃}�X�ڂ̉��̕��т��s�Ƃ����A�c�̕��т��Ƃ����B�ǂ̍s�ɂ��A�ǂ̗�ɂ��A2�̑Ίp����ɂ�����������1������Ȃ�������͉��ʂ肠�邩���߂�B(2020���啶�n�@��)
���̖����ĕ��ʂɉ�����̂��� �������Ƀ��Ƃ��g���܂���Ȃ��Ɩ�������ˁH �O>>667
>>670
���[�r�b�N�L���[�u�̔��̖ʂɖ����̍��łP,�Q,�R�̂����ꂩ�̐������������ނƂ���ƁA
�R�[�i�[�L���[�u�̔��̖ʂɍ��łP�Ə������Ƃ��A
����ƂƂȂ肠���G�b�W�L���[�u�̔��̖�2���邤����1�ɂQ�Ə����������1�͂R�B
��R�[�i�[�L���[�u�̔��̖ʂɂR��2�����炾�߂�����B
����ŏc�ɂP,�Q,�R�A���ɂP,�R,�Q�ƕ��Ƃ��āA
���̖ʂ̃Z���^�[�L���[�u�͕K�R�I�ɂP�ƂȂ�A
����̑Ίp���͂R,�P,�Q�Ȃ����͂Q,�P,�R�ƕ��ׂ���̂ɑ��A
��������̑Ίp�����P,�P,�P�ƂȂ�A��ӂ����Ȃ��B
��3��2�ł�4�ł�n�ł��s�\�ł���B >>670
n=1�`5�ɂ���1,0,0,48,480
��ʎ������H ���̋���̖���n=4�ʼn\�ł����ƒl�͋��߂��� �Ίp���̗v�f���l���Ȃ���Όv�Z���₷���Ȃ����肷�邾�낤���H
1,2,12,576,�c >>676
�v���O�����̃o�O���C��������An=4��48�ʂ�ƃJ�E���g���ꂽ�B >>679
�v���O�����ɗ�����ƁA
> matrix(B[,counter[1]],n)
[,1] [,2] [,3] [,4]
[1,] 1 2 3 4
[2,] 3 4 1 2
[3,] 4 3 2 1
[4,] 2 1 4 3
> matrix(B[,counter[2]],n)
[,1] [,2] [,3] [,4]
[1,] 1 2 3 4
[2,] 4 3 2 1
[3,] 2 1 4 3
[4,] 3 4 1 2
����n�܂���
> matrix(B[,counter[48]],n)
[,1] [,2] [,3] [,4]
[1,] 4 3 2 1
[2,] 2 1 4 3
[3,] 1 2 3 4
[4,] 3 4 1 2
�ŏI���B �O>>673���ȁB
n=2,3�̂Ƃ���0�ʂ肾���ǁA
n=1�̂Ƃ����P��1�ʂ�Ƃ�����A
n=4�̂Ƃ��Ίp���̓N���X���āA�Ȃ�Ȋ����������B
�c�ɂP,�Q,�R,�S�A
���ɂP,�Q,�S,�R�Ƃ���Ή\�B
�Ίp���͎߉�����A
�S,�P,�Q,�R�������́A
�S,�Q,�P,�R��2�ʂ�B
�ŏ���4�ʂ�B
�c�̕��т�6�ʂ��24�ʂ�B
����2�ʂ��48�ʂ�B
n=1,2,3,�c�c�ɑ���ʂ�̐���_n�́A
��_n=1,0,0,48,�c�c
=n^2(��_n-1)
�c�Ɖ���n�ʂ肸���₵����K�R�I�Ɏ߂������邩�ȁH
��_5�͂���Ȃɑ����Ȃ����B �O>>682
��_5=480�Ȃ�A
��_n=n^2(n-1)��_n-1
�������H
480=5�5�4�48 �O>>683
���܂��|���邩���邩���ĕӁX�����Ɛ擪�ƐK���A
��_n�Ƃ�_4=48��ӂ��c���Ȃ����H
��_n=(n^3��_n-1)-(n^2��_n-1)
��_n-1={(n-1)^3��_n-2}-{{(n-1)^2��_n-2}
��_n-2={(n-2)^3��_n-3}-{{(n-2)^2��_n-3}
�c�c �Ίp���̏������܂܂Ȃ����̂́A���e�����i�ƌĂ��炵��
https://ja.m.wikipedia.org/wiki/%E3%83%A9%E3%83%86%E3%83%B3%E6%96%B9%E6%A0%BC
���e�����i�̑����ɂ��Ă̖����I�Ȍ����́A�����炭�������ĂȂ�����
https://oeis.org/A002860
�Ίp���̏������܂ނ��̂� diagonal latin square �Ƃ��Ă�Ă�݂��������ǁA
������̕����܂��܂���������Ă��Ȃ������� >>680
�Ίp���������O���ƂT�V�U�ʂ�
> matrix(B[,counter[1]],n)
[,1] [,2] [,3] [,4]
[1,] 1 2 3 4
[2,] 2 1 4 3
[3,] 3 4 1 2
[4,] 4 3 2 1
> matrix(B[,counter[2]],n)
[,1] [,2] [,3] [,4]
[1,] 1 2 3 4
[2,] 2 1 4 3
[3,] 3 4 2 1
[4,] 4 3 1 2
�Ŏn�܂���
> matrix(B[,counter[m-1]],n)
[,1] [,2] [,3] [,4]
[1,] 4 3 2 1
[2,] 3 4 1 2
[3,] 2 1 3 4
[4,] 1 2 4 3
> matrix(B[,counter[m]],n)
[,1] [,2] [,3] [,4]
[1,] 4 3 2 1
[2,] 3 4 1 2
[3,] 2 1 4 3
[4,] 1 2 3 4
�ŏI��� �V���~�ׂ����ƃ������s���ɂȂ����B
�P����V�~�����[�V�������Ă悤�₭�A1�݂������B
[,1] [,2] [,3] [,4] [,5]
[1,] 2 5 4 3 1
[2,] 4 3 1 2 5
[3,] 1 2 5 4 3
[4,] 5 4 3 1 2
[5,] 3 1 2 5 4 n=5 �őΊp�����l����ꍇ
����������
����������
����������
����������
����������
��̍��l�p�̂ǂ��ɂ����������͓���Ȃ��B
����Ď��̂悤�ɌŒ肵�ėǂ��i�d���x120�j
����������
���@���A��
�����B����
���C���D��
����������
�l�̍��l�p�̂����ǂ�����ɓ�������������Ɖ��肷��ƁA
������3x3�̐����`�ɁA�������̐������R���邱�ƂɂȂ邪�A
���̐��������邱�Ƃ��\�Ȏc��ꏊ��5x5�����`�̎l���������蓾���A�����B
���Ȃ킿�l�̍��l�p�ɓ��鐔���͑S�ĈقȂ邽�߁A���̂悤�ɌŒ肵�ėǂ��i�d���x2�j
����������
���@�D�A��
���A�B�C��
���C�@�D��
����������
���l�p�̂ǂ������߂Ă����̍��l�p���S�Č��܂邱�Ƃ��킩��B���l�p�����l�B
�䂦�ɏd���x��2*2=4.
�ȏォ��120*2*4=960�ʂ�ɂȂ�c�͂��Ȃ���>>675�͂ǂ�����Čv�Z�����H >>687
�������������1 2 3 4 5 ���e�X�Ⴆ��5 4 2 1 3�@�ɒu��������Ƃ�����A120����ȁB
��
[,1] [,2] [,3] [,4] [,5]
[1,] 4 5 3 1 2
[2,] 3 1 2 4 5
[3,] 2 4 5 3 1
[4,] 5 3 1 2 4
[5,] 1 2 4 5 3
[,1] [,2] [,3] [,4] [,5]
[1,] 5 2 3 4 1
[2,] 3 4 1 5 2
[3,] 1 5 2 3 4
[4,] 2 3 4 1 5
[5,] 4 1 5 2 3
[,1] [,2] [,3] [,4] [,5]
[1,] 2 4 1 3 5
[2,] 1 3 5 2 4
[3,] 5 2 4 1 3
[4,] 4 1 3 5 2
[5,] 3 5 2 4 1
�ȂǂȂ� �T�C�R����1���o��܂ŐU���āA�U�����Ă�M�����u��������B����ڂɂ�����̂��x�X�g���H >>691
�P�O����V�~�����[�V�������ĕp�x���O���t��
https://i.imgur.com/DYbNCto.jpg
sim <- function(){
dice=0
i=0
while(dice!=1){
i=i+1
dice=sample(6,1)
}
return(i)
}
k=1e5
re=replicate(k,sim())
tbl=table(re) ; tbl
which.max(tbl)
plot(tbl/k,bty='l') >>691
n+1��ڂɎn�߂�1���o��m����1/6(5/6)^n�Ō�����������1�x�X�g �O>>683
>>691
�o��܂ň������x�X�g������Ȃ�A
1/6+(5/6)(1/6)+(5/6)(5/6)(1/6)+(5/6)(5/6)(5/6)(1/6)=0.517746917�c�c
5��������̂�4��ځB
��4��ڂ��x�X�g�B �O>>696
�P���P�Ԃ�0.166�c�c
����S�Ԃ�125/1296=0.09645�c�c
��~�q����9,645�~���炦��̂��Ǝv�����B
n��ڂ�5^(n-1)/6^n
�����������B �O>>698
�T�C�R���U����n��ڂ܂ł�1���o��m���́A
�[n=1��n]5^(k-1)/6^k
�ł����H
��l��1�l����܂��镶�w�V�l�܂ɉ��傷��Ƃ��A����ڂɎ�܂�����(5������)�ł��܂����H >>699
�v���O�����g�߂Ήł邯�ǁA�����Ƃ��ŏo���������@�͂���̂��낤���H �O>>699
>>700
100��ڂ܂ł�1�����܂��Ȃ��m���́A
(99/100)^100
100��ڂ܂łɎ�܂���m���́A
1-(99/100)^100=0.633967659�c�c
69��ڂ܂łɎ�܂���m���́A
1-(99/100)^69=0.50016297�c�c
���߉���70��ڂ܂łɎ�܂���m���́A
1-(99/100)^69=0.50516134�c�c
���Ƃ������������I ^69�Ƃ��ǂ�����Čv�Z����̂�
�܂��o���Ȃ����͂Ȃ��� �O>>701
693��ڂ܂łɎ�܂���m���́A
1-(999/1000)^693=0.500099765�c�c
�N��7��B
100�N�v��Ȃ��B99�N�Ŏ�܂���B �ΐ��\���^�����Ă���Ε����邾�� �����ŏo�肵�����ʼn����Ƃ����V�����|�� �O>>703
>>701�����B
���߉���70��ڂ܂łɎ�܂���m���́A
1-(99/100)^70=0.50516134�c�c �ޑ�
1���v���o��܂ŃT�C�R����U���āA�U�����Ă�M�����u��������B
����ڂɓq����̂��x�X�g���H >>710
����
n��ڂɓq���ē�����m���� (n-1)(5/6)^(n-2)*(1/6)^2 �ŁA
���ꂪ�ő�ɂȂ�̂�n=6,7�̎��B E��R^N��̃{�����W���AA��N�~N�s��AL��N�������x�[�O���x�Ƃ��� ���̂Ƃ�
L(A(E))=|detA|L(E)
���������邱�Ƃ��ؖ����� >>711
10����V�~�����[�V�������Ă݂��B
https://i.imgur.com/Mv1Rkfa.jpg
"1���vm(=2)��o��܂ŃT�C�R����U���āA�U�����Ă�M�����u��������B
����ڂɓq����̂��x�X�g���H"
sim <- function(m=2){
pip1=0 # �P�̖ڂ̏o����
i=0 # �T�C�R����U������
while(pip1 < m){
i=i+1
pip1 = pip1 + (sample(6,1)==1)
}
return(i)
}
k=1e5
re=replicate(k,sim())
tbl=table(re) ; tbl
which.max(tbl)
plot(tbl/k,bty='l') >>711
100��ڂ܂ł��v�Z���Ă݂��B
> sapply(1:100,bg)
[1] 1 6 12 18 24 30 36 42 48 54 60 66 72 78 84 90 96 102 108 114
[21] 120 126 132 138 144 150 156 162 168 174 180 186 192 198 204 210 216 222 228 234
[41] 240 246 252 258 264 270 276 282 288 294 300 306 312 318 324 330 336 342 348 354
[61] 360 366 372 378 384 390 396 402 408 414 420 426 432 438 444 450 456 462 468 474
[81] 480 486 492 498 504 510 516 522 528 534 540 546 552 558 564 570 576 582 588 594
bg <- function(x,print=FALSE){ # big gambling
f <- function(n,m=x,p=1/6) choose(n-1,m-1)*p^(m-1)*(1-p)^(n-m)*p
nn=1:(10*x)
y=optimize(function(n) f(n),nn,maximum=TRUE)$maximum
if(print){
plot(nn,sapply(nn,f),bty='l',pch=19)
yy=c(floor(y),ceiling(y))
cat(c(f(yy[1]),f(yy[2])),'\n')
}
return(floor(y))
}
sapply(1:100,bg) �O>>706
>>707
6��ڂ�2��ڂ̓����肪�o��m���́A
1��ڂ̓����肪����ڂɏo�邩���A4��̂͂���ɑ�5�ʂ肠�邩��A
5(5/6)^4(1/6)^2=5^5/6^6
=0.0669795953�c�c
7��ڂ�2��ڂ̓����肪�o��m���́A
1��ڂ̓����肪����ڂɏo�邩���A5��̂͂���ɑ�6�ʂ肠�邩��A
6(5/6)^5(1/6)^2=5^5/6^6
=0.0669795953�c�c
6��ڂ�7��ڂ͖�6.69795953���̊m����2��ڂ̓����肪�o�邪�A���ꂾ���Ńx�X�g���ǂ����͂킩�炸�A�O��ׂ�K�v������B
8��ڂ�2��ڂ̓����肪�o��m���́A
1��ڂ̓����肪����ڂɏo�邩���A6��̂͂���ɑ�7�ʂ肠�邩��A
7(5/6)^6(1/6)^2=7�5^6/6^8
=0.065119051�c�c
5��ڂ�2��ڂ̓����肪�o��m���́A
1��ڂ̓����肪����ڂɏo�邩���A3��̂͂���ɑ�4�ʂ肠�邩��A
4(5/6)^3(1/6)^2=4�5^3/6^5
=125/1944
=0.0643004115�c�c
9��ڂ�2��ڂ̓����肪�o��m���́A
1��ڂ̓����肪����ڂɏo�邩���A7��̂͂���ɑ�8�ʂ肠�邩��A
8(5/6)^7(1/6)^2=8�5^7/6^9
=5^7/6^6�3^3
=0.0620181438�c�c
��5��ځA8��ځA9��ڕӂ�͂������6�����Ă��đ卷�Ȃ����ǁA6��ڂ�7��ڂɓq����̂��x�^�[�B >>715
�ŏ��̂P�������Γ�������ɂ݂���ȁB 1���v1000��o��܂ŃT�C�R����U���āA�U�����Ă�M�����u��������B
����ڂɓq����̂��x�X�g���H
6*1000-6 = 5994 �� 5995��ɓq����̂��x�X�g�ۂ��ȁB
�����A�v�Z���l�̃C�i���������Ă����Ǝv���� �m��p�Ő������鎎�s�ŁAn��ڂ̎��s��m������m����P(n)�ƒu����
P(n)=C[n-1,m-1]p^m(1-p)^(n-m)������A
P(n+1)=C[n,m-1]p^m(1-p)^(n+1-m)=n/(n+1-m)(1-p)P(n)
1��P(n+1)/P(n)�̂Ƃ��A1��n/(n+1-m)(1-p)�An+1-m��n-np�An��(m-1)/p=999/(1/6)=6000-6
�Ȃ̂�5994�܂���5995���x�X�g >>707
�`���[�g�ɂP���O��̃o�[�W�������������A�ŋ߉����� �T�C�R����S�Ă̖ڂ��Œ�1��o��܂ŐU�葱����B�U��̊��Ғl�����߂�B 6(1/6+2/6+3/6+4/6+5/6+6/6) �P����̃V�~�����[�V����
> sim <- function(){
+ flag=FALSE
+ i=0
+ pips=NULL
+ while(flag==FALSE){
+ i=i+1
+ pips=c(pips,sample(6,1))
+ flag=all(1:6 %in% pips)
+ }
+ i
+ }
> k=1e4
> mean(replicate(k,sim()))
[1] 14.7221
> =6/6+6/5+6/4+6/3+6/2+6/1
=14.7 100�����>
k=1e6
> mean(replicate(k,sim()))
[1] 14.70651 �ŏ���1���ł�܂ł̉̊��Ғl
=6/6
1�ڂ��o�Ă��玟���o��܂ł̉̊��Ғl
=6/5
2�ڂ��o�Ă��玟���o��܂ł̉̊��Ғl
=6/4
�ȉ����l
�̊��Ғl�Ȃ̂ŁA�P���ɏ�L�̘a�����߂�悢 �����m��p�̎��s���J��Ԃ��Ƃ��A�ŏ��ɐ�������܂ł̎��s�̊��Ғl�� 1/p
������g���Čv�Z���� >>730
���z�Ƃ����O�����Ă����悤�ȁB >>731
�����ł��B�t�@�[�X�g�T�N�Z�X���z(Fs���z)�Ƃ������܂��B �������܂��B
��������܂łɎ��s�����̕��z
=���z
��������܂ł̉̕��z
=�t�@�[�X�g�T�N�Z�X���z
�ł����B �N�[�|���R���N�^�[���̈�ʉ�
�T�C�R���ӂ���1,2,3���o�鎖��A�A4,5���o�鎖��B�A6���o�鎖��C�Ƃ���B
ABC���S�ď��Ȃ��Ƃ����N����܂ł̕��ς́H >>735
1����̃V�~�����[�V��������
> A=1:3
> B=4:5
> C=6
>
> sim <- function(){
+ flag=FALSE
+ i=0
+ pips=NULL
+ while(flag==FALSE){
+ i=i+1
+ pips=c(pips,sample(6,1))
+ flag=any(A %in% pips) & any(B %in% pips) & any(C %in% pips)
+ }
+ i
+ }
> k=1e4
> mean(replicate(k,sim()))
[1] 7.2577
> 10����
> k=1e5
> mean(replicate(k,sim()))
[1] 7.30537 ���
���ꂪABC�\�z�Ƃ������ ����\���Ƃ���
0508 �P�R�Q�l�ڂ̑f������ 2018/06/30 02:42:25
>>505
������ʉ����āA
�J�[�hA,B,C,D�̔r�o�m����a,b,c,d�Ƃ���B�ia,b,c,d��0, a+b+c+d��1)
�J�[�hA��1���o��܂ň����Ƃ��̕��ϖ�����M(A)�Ƃ���ƁA
����ŃJ�[�hA���o���ꍇ�̖����� 1,�o�Ȃ������ꍇ�̕��ϖ����� 1+M(A) �ƂȂ�B
����� M(A) = a + (1-a)(1+M(A))
����������� M(A)=1/a�A���l�� M(B)=1/b, M(C)=1/c, M(D)=1/d
�J�[�hA,B�����ꂼ��1���ȏ�o��܂ň����Ƃ��̕��ϖ�����M(A,B)�Ƃ���ƁA
����ŃJ�[�hA���o���ꍇ�̕��ϖ����� 1+M(B)
����ŃJ�[�hB���o���ꍇ�̕��ϖ����� 1+M(A)
�ǂ�����o�Ȃ������ꍇ�̕��ϖ����� 1+M(A,B) �ƂȂ�B
M(A,B) = a(1+M(B)) + b(1+M(A)) + (1-(a+b))(1+M(A,B))
�����������M(A,B) = (1 + aM(B) + bM(A)) / (a+b) = (1 + a/b + b/a) / (a+b)
�������� M(A,B) = (1 + ((a+b)/b - 1) + ((a+b)/a - 1)) / (a+b) = ((a+b)/b + (a+b)/a - 1)) / (a+b) = 1/a + 1/b - 1/(a+b)
���l�̌v�Z�ŁA
�J�[�hA,B,C�����ꂼ��1���ȏ�o��܂ň����Ƃ��̕��ϖ�����M(A,B,C)�Ƃ���ƁA
M(A,B,C) = 1/a + 1/b + 1/c - 1/(a+b) - 1/(b+c) - 1/(c+a) + 1/(a+b+c)
�J�[�hA,B,C,D�����ꂼ��1���ȏ�o��܂ň����Ƃ��̕��ϖ�����M(A,B,C,D)�Ƃ���ƁA
M(A,B,C,D) = 1/a + 1/b + 1/c + 1/d - 1/(a+b) - 1/(a+c) - 1/(b+c) - 1/(a+d) - 1/(b+d) - 1/(c+d)
�@�@�@�@�@ + 1/(a+b+c) + 1/(d+a+b) + 1/(c+d+a) + 1/(b+c+d) - 1/(a+b+c+d) ��B >>740
�����A�o����������B a=3/6, b=2/6, c=1/6 �Ƃ���
E=1/a+1/b+1/c-1/(b+c)-1/(c+a)-1/(a+b)+1/(a+b+c)
=2+3+6-1.5-2.0-1.2+1.0
=7.3
�ق�Ƃ��B�V�~�����[�V�����ƈ�v�����B P(n)=(3/6)*((3/6)^(n-1)-(1/6)^(n-1)-(2/6)^(n-1))+(1/6)*((5/6)^(n-1)-(2/6)^(n-1)-(3/6)^(n-1))+(2/6)*((4/6)^(n-1)-(1/6)^(n-1)-(2/6)^(n-1))
E=��[k=3,��]kP(k)=1399/180=7.772222... >>737
100����V�~�����[�V�������ʁ@7.3�ۂ��ˁB
> k=1e6
> mean(replicate(k,sim()))
[1] 7.300615 >>743�@����
P(n)=(3/6)*((3/6)^(n-1)-(1/6)^(n-1)-(2/6)^(n-1))+(1/6)*((5/6)^(n-1)-(2/6)^(n-1)-(3/6)^(n-1))+(2/6)*((4/6)^(n-1)-(1/6)^(n-1)-(3/6)^(n-1))
E=��[k=3,��]kP(k)=73/10 >>746
����>>745�����Ȃ�ł��� p n=(3/6)*((3/6)^(n-1)-(1/6)^(n-1)-(2/6)^(n-1))+(1/6)*((5/6)^(n-1)-(2/6)^(n-1)-(3/6)^(n-1))+(2/6)*((4/6)^(n-1)-(1/6)^(n-1)-(3/6)^(n-1))
main = do
print $ sum [p n| n<-[3..10000]]
-------
0.9999999999999996 ���A���炵�܂����B
�R�[�h�Ԉ���Ă��B
�����ł����B
p n=(3/6)*((3/6)^(n-1)-(1/6)^(n-1)-(2/6)^(n-1))+(1/6)*((5/6)^(n-1)-(2/6)^(n-1)-(3/6)^(n-1))+(2/6)*((4/6)^(n-1)-(1/6)^(n-1)-(3/6)^(n-1))
main = do
print $ sum [(fromInteger n)*(p n)| n<-[3..10000]]
------------
7.300000000000009 >>735
��w�����ł͂��̎�̏o��͌�@�x
�Ȃ��Ȃ�I���Ȃ����Ƃ����s�Ƃ��Ă͂����Ȃ����� >>751
�R�R�������x������Ȃ��ł���H
�ނ���������x�����ᖞ�����Ȃ��l�̕��������̂ł́H �������x��
�܂̒��ɐԋ�7�A����6�A����5�����Ă���B
�ʂ�������o���Ă����ԋʂ�S�Ď��o�������_�ŏI���Ƃ���B
���o�������ʂ̌��̊��Ғl�́H
���Ғl���͈͊O�ɂȂ����̂œ����ł͎g���Ȃ����ǁB >>754
�P�O����V�~�����[�V����
balls=rep(1:3,7:5) # �ʂ̔z�� 1:�� 2:�� 3:��
picked=NULL # ���o���ꂽ�ʂ̔z��
flag=FALSE # �ԋʂ��S�����o���ꂽ����flag
sim <- function(){
while(flag==FALSE){
i=sample(length(balls),1) # �z��balls��index����P�I���
picked=c(picked,balls[i]) # ����index�����̋ʂ�picked�ɂ����
balls=balls[-i]�@�@�@�@�@ # balls�̔z�珜��
flag=sum(picked==1)==7�@�@# �ԋʂ��S�����o���ꂽ��
}
sum(picked==2) # ���o���ꂽ���ʂ̐���Ԃ�
}
k=1e5
mean(replicate(k,sim()))
> mean(replicate(k,sim()))
[1] 5.24854 >>755
���ʂ̌��̕��z���O���t�ɂ��Ă݂��B
https://i.imgur.com/sd8l1wQ.jpg
> summary(re)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 5.00 6.00 5.25 6.00 6.00
�T�D�Q�T�����݂������Ȃ��B
��͉��͌��҂ɂ��C���B �k���l
0<p��1 �Ƃ���B
�m��p�Ŏ���A���N����悤�Ȏ��s���J�Ԃ��s�Ȃ��B
���߂Ď���A���N����܂łɎ��s������n�̊��Ғl�� 1/p.
(����)
�@E{n} = p {1 + 2(1-p) + 3(1-p)^2 + 4(1-p)^3 + ���� }
�@= {1 - (1-p)} {1 + 2(1-p) + 3(1-p)^2 + 4(1-p)^3 + ���� }
�@= 1 + (1-p) + (1-p)^2 + (1-p)^3 + ����
�@= 1/p. Xi��X��i�̂Ƃ�1�A�����łȂ��Ƃ�0�ƒ�߂�q=1-p�Ƃ����
E(X)
=��E(Xi)
=��q^(i-1)
=1/(1-q)
=1/p �Ō�̐ԋʂ��o���̂�n��ڂƂ���B(7��n��18)
�E(n-1)��ڂ܂łɎ��o������/���ʂ�n-7�ŁA�@�b[11,n-7] �Ƃ���B�@(*)
�E���o��n�����܂����Ƃ��āA���Ԃ����ւ�����@��
�@1�`(n-1)��ځ@�@(n-1)! �Ƃ���
�@n��ځ@�@�@�@�@�@7 �Ƃ���
�@(n+1)�`18��ځ@�@(18-n)! �Ƃ���@�k���ۂ͎�o���Ȃ�������l
���������|�����
�@��[n=7,18] 7�(n-1)!�(18-n)!��b[11,n-7]
�@= 11!��[n=7,18] 7(n-1)(n-2)����(n-6)
�@= 11!��[n=7,18] {n(n-1)����(n-6) - (n-1)����(n-6)(n-7)}
�@= 11!(18!/11!)
�@= 18!�@�@�@�@�@�@(�����R)
���ɁAn��ڂ܂ł̔��ʂ̐�w �̊��Ғl�����߂�B
w���|���Ă����� (*)�̏��� 6�b[10,n-8] �ƂȂ�B
�@��[n=7,18] 6�7�(n-1)!�(18-n)!��b[10,n-8]
�@= (6�7/8)10!��[n=8,18] 8(n-1)(n-2)����(n-7)
�@= (6�7/8)10!��[n=8,18] {n(n-1)����(n-7) - (n-1)����(n-7)(n-8)}
�@= (6�7/8)10!(18!/10!)
�@= (6�7/8)18!
���@E{w} = 6�7/8 = 5.25
*)
�@7��n��12�@�̂Ƃ��@��[w=0,n-7] �b[6,w] �b[5,n-7-w] ����
�@13��n��18�@�̂Ƃ��@��[w=n-12,6] �b[6,w] �b[5,n-7-w] ���� (n-1)��ڂ܂ł̔��ʂ̐�w�̕��z�́@�@�@�@�@>>756
�@P_w = (7!/13!)(w+1)(w+2)(w+3)(w+4)(w+5)(w+6),
�@��[w=0,6] P_w = (7!/13!)��[w=0,6] (w+1)(w+2)����(w+6)
�@= (6!/13!)��[w=0,6] {(w+1)����(w+6)(w+7) - w(w+1)����(w+6)}
�@= (6!/13!)(13!/6!)
�@= 1.
E{w} = ��[w=1,6] w�P_w = (7!/13!)��[w=0,6] w(w+1)(w+2)����(w+6)
�@= (7!/13!)��[w=1,6] (1/8){w����(w+6)(w+7) - (w-1)w����(w+6)}
�@= (7!/13!)(1/8)(13!/5!)
�@= (7�6/8)
�@= 5.25 >>760
�����I
�z����o���Ă��������ǎ��͂��鎖�ɋC�Â��Ɛ��s�ŏI���܂��B
�ǂ����悤�H
��܂ő҂��Ă݂܂��ˁB ���ʂ̌�w�̕��z
�@0�@�@�@1�@�@�@2�@�@�@ 3�@�@�@ 4�@�@�@�@5�@�@�@�@6��
1/1716,�@7/1716,�@28/1716,�@84/1716,�@210/1716,�@462/1716,�@924/1716
�@0.06%�@�@0.41%�@�@1.63%�@�@ 4.90%�@�@ 12.24%�@�@ 26.92%�@�@ 53.84% ���ʂ͖���
�ԋ�7����ׂĂ����A���̑O��ƊԂ�8�����ɔ���6�������_���ɓ���Ă����i�d������j
�ԋʂ̌��ɔ��ʂ��������邩���l����Ƃ��A����1�ɂ����Ғl1/8�ƂȂ�̂�6�Ȃ�6/8=3/4
�]���Ă���ȊO�̂Ƃ���ɂ��锒�ʂ̌��̊��Ғl��6-3/4=5.25 �ԋʂ̌��ȊO�ɂ������邩���l����Ƃ�����1�ɂ����Ғl7/8�Ȃ̂�6�Ȃ�6*7/8=5.25�ł悩������ >>754
P(k)=��[k=0,6]��[j=0,5]C[7,6]C[6,k]C[5,j]/(C[18,6+k+j](12-k-j))
E=kP(k)=21/4 >>766
�������Ƀ_�����B
�����猴���I�ɂ̓R���v�Z������ł�����ė����������Ă��A���̌v�Z���Œ�ڂŒǂ�����̂������Ȃ��Ɛ����Ƃ͔F�肳��Ȃ��B �ŏ���_�������̌��іڂ͉���ނ���̂��B ���ʂ͖�������B(13�ōl����)
(�Ō�̐ԋʂ��o��O��) ���ʂ̐���w�Ƃ���ƁA
�Ō��(6-w)�����ʁA���̒��O���ԋʁA���͕s�₾����
�@P_w = (6/13)(5/12)����((w+1)/(w+8))�E(7/(w+7))
�@�@= (7!/13!)(w+1)(w+2)(w+3)(w+4)(w+5)(w+6),
���Ƃ� >>760 �� >>767
����́A�悭������Ȃ���wolfram�Ōv�Z���Ă݂����v����
���R��v����Ƃ͎v���Ȃ����H >>767
P(k)�̒l(k=0�`6)��>>762�ƈ�v���� �Ȃ�ق�
���n��ōl���Ă����Ɣ��z���L����ɂ������A���ׂčl����Ƃ킩��₷���ȁB
�Q�l�ɂȂ� >>767
C[7,6]C[6,k]C[5,j]/C[18,6+k+j]
�����̕������A��6�A��k�A��j�̌v6+k+j��ʂ����o�����Ƃ��̊m��
���q�ƕ���́A�ʂɔԍ���t�����ꍇ�̏ꍇ�̐��ɂȂ��Ă���
�Ō��1/(12-k-j)�ŐԂ����o���m�����|���� >>770
����A�R�����v�Z�ł���Γ������o��Ȃ�Ď����Ă邾���Ȃ���x���̖��Ȃ�ł��ē�����O�B
���x���ʼn����Ƃ����Ӗ��Ȃ炻�̒��œ�\�����x�Ŗ����Ȃ����ۂɂł���Ƃ����Ƃ���܂ł���Č����Ă݂ď��߂Đ����B
�v�Z�@�Ȃ�ł���ł́A���x�����Ă�悤�Ȃ�Ȃ�Ƃ��������x���̖��Ɩ��ł��ďo�肳��Ă����A�ʗp���Ȃ��B �O>>716
>>754
6(7/8)=5.25 >>774
���̖��͓������ŏo�肳���Ƃ͎v��Ȃ� ���̃X���͎ŗL���ȉ̂ݐ����Ƃ�����ł͂Ȃ��낤 _____�� ���___
�_�@(-_-))�@ /|
�_�_�ҁ܃Ҥ /|
�P�P�P�P|��/|
________��P|
�����K�������w2�N���Ȃ�������ȁB
�O>>775�����̊p�x�����C�W�����m��Ȃ��A�܂��Ă�Î~�����ȂǁB ����������ǂ��Ȃ�H
�܂̒��ɐԋ�7�A����6�A����5�����Ă���B
�ʂ�������o���Ă����ԋʂ��S���o�������_�ŏI���Ƃ���B���o�������ʂ̌��̊��Ғl�́H >>780
P(k)=��[j=0,5]4C[7,3]C[6,k]C[5,j]/(C[18,3+k+j](15-k-j)
E=��[k=0,4]kP(k)=881/429 �����̖��������W��A�ł����āA�ǂ݂̌��ɈقȂ� a,b��A ���Ƃ��Ă�
|a-b| ���������ɂȂ�Ȃ����̂͑��݂��邩�B >>754
7/8 * 6=21/4
>>780
4/8 * 6=3 �܂̒��ɐԋ�7�A����6�A����5�����Ă���B
�ʂ�������o���Ă����ԋʂ�S�Ď��o�������_�ŏI���Ƃ���B
���o�������ʂ̌�����c�������ʂ̌����������l�̊��Ғl�́H
���o�������ʂ̌�����c�������ʂ̌����������l�̊��Ғl�́H
���o�������ʂ̌��Ǝc�������ʂ̌����|�����l�̊��Ғl�́H
���o�������ʂ̌��Ǝc�������ʂ̌����|�����l�̊��Ғl�́H >>784
���s���j�b�g�������Ƃ��閳���W���Ƃ������ >>766 ����
P(k)=��[j=0,5]C[7,6]C[6,k]C[5,j]/(C[18,6+k+j](12-k-j))
E=��[k=0,6]kP(k)=21/4 >>786
E1=��[k=0,6](k-(5-j))P(k)=37/8
E2=��[k=0,6](k-(6-k))P(k)=9/2
E3=��[k=0,6](k(5-j))P(k)=35/12
E4=��[k=0,6](k(6-k))P(k)=35/12 >>786
�ŏ��̂Q�͐��`���ł�����B
3�Ԗڂ͓Ɨ����B
�ÎZ�ŋꂵ���͍̂Ōゾ�����ȁB
���ʂЂƂɒ��ڂ��Ď��o�����m����p=7/8�B
����Ď��o������X�̕��z��p=7/8, n=6�̓��z�B
X^2�̊��Ғl��
E(X^2) = �� C[6,k)(1/8)^(6-k) (7/8)^k k^2=93/32�B
https://www.wolframalpha.com/input/?i=sum+binomial%286%2Cx%29+%281%2F8%29%5E%286-x%29%287%2F8%29%5Ex+x%5E2+from+0+to+6&;lang=ja >>787
�c�O�B|111-11|=100 �͕������ɂȂ�܂� >>793
�������A���ꂪ�������� >>784
A = {1, c, c^2, c^3, ����| c>2}
�@c^n - c^m = (c^m) {c^(n-m) - 1},
�@c^(n-m) > 1, �@�@�@(n>m)
�J�^�����\�z�i�~�n�C���X�N�̒藝) �ɂ��
�@c^(n-m) - d^2 = 1�@�ƂȂ� d >1 �͑��݂��Ȃ��B
���@c^(n-m) - 1 �͕������łȂ��B
c^m �� c^(n-m) -1 �݂͌��ɑf������ | c^n - c^m | �͕������łȂ��B
A = {2, 8, 32, 128, 512, ����} �����l�H >>789
�V�~�����[�V�����ŋߎ����Ă݂܂����B
> balls=rep(1:3,7:5) # �ʂ̔z�� 1:�� 2:�� 3:��
> picked=NULL # ���o���ꂽ�ʂ̔z��
> flag=FALSE # �ԋʂ��S�����o���ꂽ����flag
> sim <- function(){
+ while(flag==FALSE){
+ i=sample(length(balls),1) # �z��balls��index����P�I���
+ picked=c(picked,balls[i]) # ����index�����̋ʂ�picked�ɂ����
+ balls=balls[-i]�@�@�@�@�@ # balls�̔z�珜��
+ flag=sum(picked==1)==7�@�@# �ԋʂ��S�����o���ꂽ��
+ }
+ # ���o�������ʂ̌�
+ a0=sum(picked==2)
+ # ���o�������ʂ̌�����c�������ʂ̌����������l
+ a1=sum(picked==2)-sum(balls==3)
+ # ���o�������ʂ̌�����c�������ʂ̌����������l
+ a2=sum(picked==2)-sum(balls==2)
+ # ���o�������ʂ̌��Ǝc�������ʂ̌����|�����l
+ a3=sum(picked==2)*sum(balls==3)
+ # ���o�������ʂ̌��Ǝc�������ʂ̌����|�����l
+ a4=sum(picked==2)*sum(balls==2)
+ return(c(a0,a1,a2,a3,a4))
+ }
> k=1e6
> re=replicate(k,sim())
> apply(re[2:5,],1,mean)
[1] 4.627792 4.500442 2.904962 2.916039
> c(37/8,9/2,35/12,35/12)
[1] 4.625000 4.500000 2.916667 2.916667 >>790,792
�T���N�X
���Ғl�̐��`���Ɨ����̖��Ƃ��Ă��傤�Ǘǂ�������
2�����z�̕��U��npq�Ƃ������Ƃ��g���Ō������قǓ���͂Ȃ�
V(X)=E(X^2)-E(X)^2=6(7/8)(1/8)=21/32
E(X^2)=21/32+(21/4)^2=903/32
E(X(6-X))=6E(X)-E(X^2)=63/2-903/32=105/32 >>784
a1=1
a2=min{x>a1 | x-a1��n^2}=3
a3=min{x>a2 | x-a1, x-a2��n^2}=6
�c
a[n+1]=min{x>an | x-a1,,,x-an��n^2} >>798
���z�̕��U�d�d����Ȃ̂�����������w
�Y�p�̔ޕ�ww >>797
��2��V�~�����[�V�����Ɛ����Ⴄ��
���́H
37/8, 9/2, 105/32, 105/32
��z�� >>801
���܂����B
����i�����o����鎖�ۂ͓Ɨ��łȂ��B
���o����鎖�ۂ̓�������Xi�Ƃ���
E(Xi)=E(Xi^2)=7/8
i��j�̂Ƃ�E(XiXj)=7/8�~8/9=7/9
�Ȃ̂œƗ��ł͂Ȃ��B
�����X=��Xi�Ƃ����
E(X)=6�~7/8=21/4
E(X^2)=6�~7/8+30�~7/9=343/12
E(X(6-X))=6E(X)-E(X^2)=63/2-343/12=35/12
�ł����B
�݂��Ă���orz�B >>802
���[
2�����z����Ȃ����Ă��Ƃ�
�����s������߂�ǂ��� �������Ɨ��ł͂Ȃ��Ȃ�
�����ʓ|�������������� �V�~�����[�V�����łȂ��Đ����グ�Ōv�Z���Ă݂���>>789���������� >>780
���͖������āA�Ԕ��v13�ő�������Ōv�Z���Ă݂��B
TEnr <- function(n,r,zero=0,one=1){ # n(=5),r(=3)���w�肵�� 0 0 1 1 1����1 1 1 0 0�܂ł̏���s������
f=function(x){
re=rep(zero,n) # �e��q
re[x]=one # �w���index��one����
re
}
t(combn(n,r,f)) # one������g�ݍ��킹�ɏ�L��f�����s���ē]�u
}
TE=TEnr(13,7,0,1) # 0:�� 1:�ԁ@13�̕��т̍s�� 1111111000000 ���� 0000001111111�܂�13C7(=1716)��
(x=TE[1000,]) # 1000�s�ڂ̃G���g��
f <- function(x){ # 0 1 1 1 0 1 0 1 0 1 1 0 0 -> 2 ��(1)��4�ɒB���܂ł�0�̐���Ԃ�
i4=which(cumsum(x)==4)[1] # �ݐϘa���ŏ��ɂS�ɂȂ���index��i4�Ƃ���
sum(x[1:i4]==0)�@�@�@�@�@ # i4�܂ł̔�(0)�̌���Ԃ�
}
re=apply(TE,1,f)
sum(re)
length(re)
mean(re)
> sum(re)
[1] 5148
> length(re)
[1] 1716
> mean(re)
[1] 3
���͂R >>806
���P�ƂȂ�2�����z�Ɠ�����
�����Ȃǂł����`�Ȃ�2�����z�Ōv�Z���Ă��������l�ɂȂ邩��
�P�ɓ�����������̂���
�������l�@�̌��ʂ��ǂ���������Ȃ��̂�
����>>786�̑�1�C2��͈��₾��
��3�C4�₾���Ȃ�2�����z�Ōv�Z����Ɛ����������ɂȂ�Ȃ����炱��͗ǖ� >>808
����A���Ғl�̐��`���͕ʂɓƗ����͕K�v�Ȃ��̂Ŗ��Ȃ���B
���z�̌����͎g���Ȃ����ǗႦ�Α���Ȃ獕��i������鎖�ۂ̓�������Bi�A����j������鎖�ۂ̓�������Wj�Ƃ���Έ��ڂ̋��߂���Ғl��
E(��Wj-(5-��Bi))=��E(Wj)-5+��E(Xi)=6�~7/8-5+5�~7/8=37/8�B
�R���͓Ɨ�������Ȃ��B n����r��I��œ����鏇��̑�����P(n, r)�Ƃ���. �C�ӂ�r>1�ɑ���, P(n, r)�͕������łȂ����Ƃ�����. >>809
>����A���Ғl�̐��`���͕ʂɓƗ����͕K�v�Ȃ��̂Ŗ��Ȃ���B
����͕������Ă�
�����炱��2�����z�ʼn����Ă��܂��Ă��ԈႢ��������Ȃ��̂�������ăR�g���� >>812
>����͕������Ă�
���Ƃ��Ɣ��|���Ɣ��|���ɂ����͓̂Ɨ����ɊW���Ȃ����Ƃ�F�����Ă��邩�ǂ��������Ƃ�������������i���ƍ����Ɨ��Ǝv���Ă��j
�Ɨ����`
��Ɨ����`
�Ɨ�����`
��Ɨ�����`
��4��ɂł��ď�肭�s�����Ǝv���Ă�
������ A,A,A,B,B,C,D,E,F,G��10��������ׂ�Ƃ��A�ǂ����œ����������ׂ荇���m�������߂�i���k��E���j >>814
��������Ōv�Z
# A,A,A,B,B,C,D,E,F,G��10��������ׂ�Ƃ��A�ǂ����œ����������ׂ荇���m�������߂�i���k��E���j
library(gtools)
v=rep(1:7,c(3,2,rep(1,5)))
pm=try(permutations(10,10,v,set=F))
tail(pm)
f <- function(x){
n=length(x)
flg=FALSE
for(i in 1:(n-1)){
if(x[i]==x[i+1]){
flg=TRUE
break
}
}
return(flg)
}
(x=pm[10000,])
re=sum(apply(pm,1,f))
library(gmp)
N=nrow(pm)
as.bigq(re/N)
re/N
Big Rational ('bigq') :
[1] 1388609885105903/2251799813685248
> re/N
[1] 0.6166667 ������������x������Ȃ��悤�ȏꍇ�̐����l����B
���̂��߂�CDEFG��S��X�Œu�������A�wA��B�͈�x������Ȃ��x�悤�ȏꍇ�̐����l����B
�i�܂�X�����ׂ͗荇���Ă��ǂ��j
A��B�����ɒ��ڂ������̕��т�
(1)AAABB�ł��鎞�A�Œ�ł� AXAXABXB �Ƃ����X�y�[�X�̋����K�v�B
����A��B�ŋ��ꂽ�U�̋�ԂɎc��̓��X�����邩��A���߂�ꍇ�̐��� 7C2=21.
(2)AABAB�ł��鎞�A�Œ�ł� AXABAB �Ƃ����X�y�[�X�̋����K�v�B
�U�̋�ԂɎc��̎l��X�����邩��A���߂�ꍇ�̐��� 9C4=126.
�c
�ȏ�̂悤�Ɍv�Z��i�߂�ƁA���߂�ꍇ�̐��̍��v��
2*7C2 + 3*8C3 + 4*9C4 + 10C5 = 966
A,B,X�̕��ו��̑����� 10C5 * 5C2 = 2520 �ł��邩��A���߂�m����
966/2520 = 23/60.
�䂦�Ɍ��X�̖�̓����� 1-23/60=0.6166666�c ���a1�̋��ʏ��4�_����l�Ɨ��ɑI�ԂƂ��A����4�_�̓ʕ�̑̐ς̊��Ғl�����߂�B �^�a__`�a�P�P�a ����K
�a���� �a �� �a�@�@ߡ
�i(-_-)�a�@�@�a______
�i���܁�ށ@ ��a������
��`(_)_)��~�@�a������
�_���҃ҁ�___�a_ _))�܂¤�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_`>>817�O>>779
�ʕ�̊��Ғl=(4��/3)1^3=4��/3=4.1887902�c�c �Ă͂��B�O>>818�ŏ������l�S�C�Ƃ悤�ǂȂ��B
�ʕ�͐��l�ʑ̂Ȃ̂��A4�_���ލŏ��̋��Ȃ̂��B >>820
�l�ʑ̂łP�O�O����V�~�����[�V�������ĕ��ϒl�������Ă݂��B
vertices <- function(r=1){
a=runif(2,-pi,pi) # �p�x��,������l���z�őI����
theta=a[1]
phi=a[2]
x=r*sin(theta)*cos(phi)
y=r*sin(theta)*sin(phi)
z=r*cos(theta)
c(x,y,z) # �������W��Ԃ�
}
sim <- function(r=1){
vectors=replicate(4,vertices(r)) # �S�_�̒������W
abs(det(vectors[,2:4]-vectors[,1]))/6 # �l�ʑ̂̑̐�
}
k=1e6
re=replicate(k,sim())
mean(re)
> mean(re)
[1] 0.1069067 ���̏ꍇ�i�ŏ������ۂ��͍l�������j�̂P�O����V�~�����[�V�����̕��ϒl
library(nleqslv)
Abs <- function(x) sqrt(sum(x^2))
sphere <- function(CR){ # CR:Center,Radius
C=CR[1:3]
R=CR[4]
v4=replicate(4,vertices())
c(
Abs(v4[,1]-C),Abs(v4[,2]-C),Abs(v4[,3]-C),Abs(v4[,4]-C)
)-R
}
sphere(1:4/10) # example
sim2 <- function(){
r=nleqslv(1:4/10,sphere)$fvec[4] # �����l 1:4/10 c(0.1,0.2,0.3,0.4)
4/3*pi*r^3
}
sim2()
k=1e5
re=replicate(k,sim2())
mean(re)
> mean(re)
[1] 1.8112 >>821
��# �p�x��,������l���z�őI����
�o�x�ܓx����l���z�ɂ�����ɂɕ��z����Ȃ������H >>824
�O���t�ɂ��Ă݂܂����B
���w�E�ǂ���A�肪�ł܂����B
https://i.imgur.com/Ix5UvMR.png >>824
�����`���ŗ���x,y�������ā@r^2-(x^2+y^2)�����ɂȂ�̂͏��O���āA�k�����Ɠ씼����1/2�����z���ė������������Ă݂��B
https://i.imgur.com/bC0gBW7.png
�������̕�����l���z���ۂ��ȁB >>827
�����10����V�~�����[�V�������āA�ʕ�͋��i�ŏ����̍l���Ȃ��j�Ƃ��Ă݂��
k=1e5
re=replicate(k,sim3())
mean(re)
> mean(re)
[1] 1.800846
�Ƃ����l���łĂ����B >>827
���߂ł���
xyz�ŊO�ƌ��_�͐��Ă���ȊO�͐��K���͂ǂ����Ȃ�
����ł��_�������m��� �ƃӂŖʑf���x�ɍ��킹�ė����ɂ�����ǂ��Ǝv��
dS=cos��d��d�ӂȂ̂ŃƂƂ����l�����m����cos�Ƃɂ���
�܂�z�Ƃ̒����`�ŗ�������������z>cos�Ƃ͏��O���ăƂ����
dV=dxdydz=rdrdS������
xyz�ŋ��̊O�����O���Đ��K�����Ă��{���͓������� dV=drdS
r�͗]�v�������������Ƃ���Ƃ���͕����낤 >>830
������������Ă݂܂����B
vertex <- function(r=1){ #�ܓx�ӎ���̑т̖ʐςɉ����Ĉ�l���z
theta=runif(1,-pi,pi) # �o�x��
p=sqrt(runif(1)) # ���z�m��p����l���z�ɂ���
phi=asin(2*p-1) # �m����p�ɂȂ�ܓx��
x=r*cos(phi)*cos(theta) # �ȍ��W���璼�����W��
y=r*cos(phi)*sin(theta)
z=r*sin(phi)
c(x,y,z)
}
vtx=replicate(5000,vertex())
x=vtx[1,]
y=vtx[2,]
z=vtx[3,]
rgl::plot3d(x,y,z, col="slateblue")
https://i.imgur.com/27K33kB.png >>832
�����4�_����������4�_��ʂ鋅�̔��a��A�����������v�Z�@�ɉ�������
�̐ς�10����̕��ς��Ƃ��
> k=1e5
> hull=replicate(k,sim())
> mean(hull)
[1] 1.160583
�Ƃ������ʂɂȂ����B
���܂�A���M���Ȃ��B
��͉��͌��҂ɂ��C���B ���a�P�̋��ɓ��ڂ��鐳�l�ʑ̂̑̐ς� 8/(9��3) = 0.5132..
>>817�̉��͂����菬�����i�͂��j >>834
vertex <- function(r=1){ #�ܓx�ӎ���̑т̖ʐςɉ����Ĉ�l���z
theta=runif(1,-pi,pi) # �o�x��
p=sqrt(runif(1)) # ���z�m��p����l���z�ɂ���
phi=asin(2*p-1) # �m����p�ɂȂ�ܓx��
x=r*cos(phi)*cos(theta) # �ɍ��W���璼���W��
y=r*cos(phi)*sin(theta)
z=r*sin(phi)
c(x,y,z)
}
�ŁA���̕\�ʂ���S�_�����o����
# �l�ʑ̂̑̐�
sim <- function(r=1,print=F){
v4=replicate(4,vertex()) # �S�_�̒������W
if(print) print(v4)
abs(det(v4[,2:4]-v4[,1]))/6 # �l�ʑ̂̑̐�
}
�łP�O����V�~�����[�V����������
k=1e5
tetra=replicate(k,sim())
mean(tetra)
summary(tetra)
����Ȍ���
> summary(tetra)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0000006 0.0242839 0.0645573 0.0928661 0.1361202 0.5035962
�ő�l��8/(9��3) = 0.5132..�ȉ��ɂȂ��Ă��� �������̕���x,y,z�Ƃ��Ɉ�l���z�ɂȂ��Ă���B
vertex <- function(r=1){
x=runif(1,-1,1) # x ~ ��l���z[-1,1]
phi=runif(1,-pi,pi)�@# �� ~ ��l���z[-��,��]
y=sqrt(1-x^2)*cos(phi) # ��(1-x^2)*cos(��)
z=sqrt(1-x^2)*sin(phi) # ��(1-x^2)*sin(��)
r*c(x,y,z)
}
https://i.imgur.com/xX0mTim.png
https://i.imgur.com/H7hs9w8.png
����ł���Ă݂�ƁA�l�ʑ̂̏ꍇ
> mean(tetra)
[1] 0.1201118
> summary(tetra)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0000003 0.0372266 0.0922805 0.1201118 0.1794858 0.5104545 >>836
>x,y,z�Ƃ��Ɉ�l���z
�ł̓_������
���ʏ�Ɉ�l�ɕ��z����̂Ȃ�
x���W�́�(1-x^2)�̊m�����x�ƂȂ� ���[������
st�����`��s��t�ƈ�l�����_���ɓ_��
���_���S�̉~�̊O�ɂ���Ί���
�����ɂ������s���W����邱�Ƃ�
�m�����x��(1-s^2)�̕��z�Ń����_���Ɏ���
�����xyz�����ꂼ�����Ă�����
���[�_�����Ɨ��Ɏ�����狅�ʏ�ɗ��Ȃ���
���Ⴀ�����x�������yz��cos��sin�ƂŃƂ���l�����_���Ɏ��Ηǂ��� y,z�́�(1-x^2)cos��,��(1-x^2)sin�Ƃ� >>837
���[�ԈႢ��>>836�Ő�������X�}�� <V> = 1/6 = 0.16667 ��������@>>834 �̗v������������� �^�C�x���g�ŏЉ�ꂽ���̓��l�ȉ���
������������ւ̊� f:Z��R �ł����āA�C�ӂ̐��� x,y,z �ɂ���
�y x^2 + 4y^2 = z^2 �Ȃ�� f(x) + 4f(y) = f(z) �z
�������̂�S�ċ��߂� �_�_�_�_�_`������_�_�_
�_�_�_�_��(_ _))`�܂�`
�_�_�_�_�_�_�_`�Ҥ�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_`���_�_�Ƃ����O�p����4�W�܂����l�ʑ̂̑̐ς́A
V=(4/3)Sh
h=1/3(�担�̔��a=1)
S=(��3/4)a^2�Ƃ���ƁA
��ʂ̒��S�����ӂ܂ł̋����̓s�^�S���X�̒藝���A
��{1^2-(1/3)^2}=2��2/3
���O�p�`�̍����́�2
a=��2(2/��3)
=2��2/��3
S=(��3/4)(2��2/��3)^2
=(��3/4)(8/3)
=2��3/3
�O>>820
V=(4/3)(2��3/3)(1/3)
=8��3/27
=0.513200239�c�c
�����܂ł͂킩�����B
1�_�ڂ��C�ӂŁA2�_�ڂ����܂��Ƃ�m���͌�A3�_�ڂ����܂��Ƃ�m������A4�_�ڂ����܂��Ƃ�m����1/2
2�_�ڂ�3�_�ڂ�1��1/2�̂���������Ȃ��Ƃ��߂��Ǝv������A
3�_�ڂ����܂��Ƃ�m����2/3��2�_�ڂ����܂��Ƃ�m����3/4�Ȃ�A
���ׂĂ��܂��Ƃ�m����1/4
V/4=2��3/27
=0.12830006�c�c >>836
�����͂����ς�킩��Ȃ����AWikipedia�ɂ��ΐ��K���z�ɏ]���R�ϐ����狅�ʂ̈�l���z���W������炵���B
x1,x2,x3�`Norm(0,1) �� r=��(x1^2+x2^2+x3^2)�Ƃ���
(x1/r,x2/r,x3/r)���P�ʋ��ʂ̈�l���z�ɂȂ�Ƃ����B
https://ja.wikipedia.org/wiki/%E8%B6%85%E7%90%83%E9%9D%A2
Marsaglia(1972)
https://projecteuclid.org/download/pdf_1/euclid.aoms/1177692644
�������Ă݂��B
�}�������>836�Ɠ������Ax,y,z����l���z���āA���ʂ̈�l���z���Ă���悤�ɂ݂���B
vertex <- function(){ # xi ~ Norm(0,1) , xi/��(��xi^2)
v=rnorm(3,0,1) # ���K���zN(0,1)����R����Ȃ�x�N�g�� v
v/sqrt(sum(v^2)) # v �̒����Ŋ���
}
vtx=replicate(5000,vertex())
par(mfrow=c(3,1))
x=vtx[1,] ; hist(x,col='pink')
y=vtx[2,] ; hist(y,col='orange')
z=vtx[3,] ; hist(z,col='darkgreen')
rgl::plot3d(x,y,z, col='slateblue')
par(mfrow=c(1,1))
# �l�ʑ̂̑̐�
sim <- function(r=1,print=F){
v4=replicate(4,vertex()) # �S�_�̒������W
if(print) print(v4)
abs(det(v4[,2:4]-v4[,1]))/6 # �l�ʑ̂̑̐�
}
k=1e5
tetra=replicate(k,sim()) # k��̃V�~�����[�V����
mean(tetra)
summary(tetra)
BEST::plotPost(tetra)
���Ғl�����z���قړ����B
> mean(tetra)
[1] 0.119512
> summary(tetra)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0000001 0.0368084 0.0918738 0.1195120 0.1789221 0.5093198
�l�ʑ̂̑̐ς̕��z�����l�ł���ȕ��z�B
https://i.imgur.com/yjsaR3Q.png >>844
>�����͂����ς�킩��Ȃ����AWikipedia�ɂ��ΐ��K���z�ɏ]���R�ϐ����狅�ʂ̈�l���z���W������炵���B
�Ɨ��Ɏ�����Ƃ��̊m�����x��e^-(x^2+y^2+z^2)�݂�����r�݂̂̊��ɔ�Ⴗ�邩�炾��
�ł�>>836�ł����Ǝv����
���̋ߎ��ɂ���݂����Ȃ̂��C�ɂ���Ȃ�
>>829�ł����̊O�����O������̍l�����͂���Wikipedia�̂Ɠ������� �R���������W�����ʂ̈�l���z���邱�Ƃ́A�}�����ăC���[�W����ق��ɁA�ǂ�������猟�ł���̂��낤�H
���ʏ�̔C�ӂ̈��ʐςɊ܂܂�鐔�����ł���̂��m�F������@���v�����Ȃ��B
���������f�[�^����l���z���ǂ����͊m�F�ł��邾�낤��
x y z
[1,] 0.4090696 -0.06240392 0.9103669
[2,] -0.1452435 -0.97420684 0.1727002
[3,] -0.1082045 0.53218504 0.8396850
.....
.....
x y z
[4998,] 0.6609463 -0.096259265 -0.7442340
[4999,] 0.5669702 0.758929767 -0.3202661
[5000,] 0.8944673 -0.008481795 -0.4470530 >>846
���ƂƂ��ƃӂŕ������ē_�̐��𐔂��ĖʐςŊ�������H
�\���ׂ�������������Ă�����
�T���v���_���\���������������
�吔�̖@����
���҂����l�ɂ��������W�܂��Ă���͂����� >>847
���X���肪�Ƃ��������܂��B
x,y,z �� �Ɍ`���ɂ��ć��Ɓ@���ӂ͈̔͂ɂ��鐔����l���ǂ����݂�����ȁB �������W����ɍ��W�̃ƃӂ��o���āA������O���t�ɂ��Ă݂܂����B
https://i.imgur.com/swLs0hO.png
���[���a�Ɍ����܂��B
�O���b�h������Ă����Ɋ܂܂��_�𐔂��Ă��̕��z���݂�����̂��ȁH
�ǂ̒��x�̂���Ȃ�A��l���z�Ƃ݂Ȃ���̂��ƍl����Ƃӂ肾���ɖ߂�C������B �ӂ̒������S�ėL�����̑��p�`�ɂ����āA���Ȃ��Ƃ�2�ȏ�̓��p[rad]�͖������ł��邱�Ƃ�����. >>848
���ƃ��ӂ̈͂ޖʐς�cos�� ���ƃ��ӂ���
�Ƃ���k�Ń��Ƃ̕��̒����̒l��
�_�̌�������Ŋ���Ȃ��ƈ��ɂȂ�Ȃ�
���ƃ��ӂ����Ȃ�cos�ƂŊ���Ηǂ� >>819
�@0.1196797201367540���� >>849
>�ǂ̒��x�̂���Ȃ�A��l���z�Ƃ݂Ȃ���̂��ƍl����Ƃӂ肾���ɖ߂�C������B
����=��/n
����=2��/m
�܂苅�ʂ�nm�̗̈�ɕ��������ꍇ�im,n�Œ�j
��l���z�Ȃ�T���v��N�_�ł��̗̈���ɂ���̂�N��cos��/2mn���낤����
�����グ��M�_�Ȃ烰(M-N��cos��/2mn)^2/mn��N�����Ŏ����0�ɋ߂Â��i�吔�̖@���j���Ƃ�����Ƃ��H >>849
>���[���a�Ɍ����܂��B
�������ƂƂ����
�c������cos�Ƃ��|���ē_���v���b�g����Ηǂ�
�����0���Ӂ�cos�Ƃ̗̈���ɋψ�Ɍ�������OK >>849
�������>821�Ƌt�̂��Ƃ�����Ă��邾���̂悤�ȋC������ȁB
��l���z���鋅�ʏ�̓_���Ɍ`���ŕ\�������Ƃ��Ɉܓx�E�o�x����l���z�͂��Ȃ��낤�ȁB >>854
�����𗝉��ł��Ȃ��܂܂ɃO���t�������
plot(��,��*cos(��),bty='n',pch='.',xlab='��(�k�ɓ_����̃��W�A��)' ,,ylab='�Ӂi�o�x)*cos(�Ɓj')
https://i.imgur.com/R8TFUG3.png
����������Ȃ��̂Œf�O�B >>856
�Ƃ�k�ɓ_����̂ɂ���Ȃ�
sin�Ɗ|���� >>855
�ɂɋ߂����������Ƌ����Ȃ邩���
���ʂ̕\�ʐς͉~���̑��ʐςƓ���ł���Ƃ���
2000�N�O����m���Ă��錴�����炷���
xyz�ɗ��Ƃ�����ł����ꂼ��̍��W��ň�l���z�ɂȂ�
�����>>836��
https://i.imgur.com/xX0mTim.png >>850
�����f�}���̒藝���L����q��0�ɑ��� e^(iq) �����z���ł��邱�Ƃ���]�� >>857
�Ƃƃӂ̒�`�͉��}�ɏ���
http://physics.thick.jp/Physical_Mathematics/Section3/figures/fig27.png
rm(list=ls())
vertex <- function(r=1){
x=runif(1,-1,1) # x ~ ��l���z[-1,1]
phi=runif(1,-pi,pi)�@# �� ~ ��l���z[-��,��]
y=sqrt(1-x^2)*cos(phi) # ��(1-x^2)*cos(��)
z=sqrt(1-x^2)*sin(phi) # ��(1-x^2)*sin(��)
r*c(x,y,z)
}
# �������W���ɍ��W��
c2p <- function(xyz){ # (x,y,z) -> (��,��) Cartesian 2 Polar
x=xyz[1];y=xyz[2];z=xyz[3]
r=sqrt(x^2+y^2+z^2) # =1�ɂȂ�x,y,z�̑g����
theta=acos(z/sqrt(x^2+y^2+z^2)) # = acos(z) [0,��]�̒l
phi=ifelse(y>0,acos(x/sqrt(x^2+y^2)), # y>0�Ȃ�� < ��
2*pi-acos(x/sqrt(x^2+y^2)))# y<0�Ȃ�� > ��
c(theta,phi)
}
n=1e5
vtx=replicate(n,vertex()) # n�̓_�����
vtx=replicate(n,vertex()) # n�̓_�����
v=t(vtx) # �]�u����n�s�R��(x,y,z)��
head(v,3) ; tail(v,3)
vp=apply(v,1,c2p) # �e�s����x,y,z -> ��,�ӂɕϊ�
tp=t(vp) # theta ��, phai �� �]�u����n�s2��(��,��)��
fn <- function(x){ # 0<=�� & ��<=sin(��)��������Ԃ�
��=x[1]
��=x[2]
0<=�� & ��<=sin(��)
}
tp1=tp[apply(tp,1,fn),] # fn��TRUE�ɂȂ��,�ӂ𒊏o����
��=tp1[,1]
��=tp1[,2]
plot(��,��*sin(��),bty='n',pch='.', xlab='��(�k�ɓ_����̃��W�A��)',ylab='�Ӂi�o�x)*sin(��)')
# �O���t��
https://i.imgur.com/dtO0oRW.png
�����g���`�o���ꂽ�����̂悤�ȁH >>852
>844�̃V�~�����[�V�������ʂɑ������錋�ʂł��ˁB
�v�Z�@�͂����ς�v�����Ȃ����ǂ� >>860
>�����g���`�o���ꂽ�����̂悤�ȁH
�_�̖��x�������g�̉��łǂ��ł����Ɍ�����ł���
�����狅�ʏ�ň�l���z�����Ă��Ƃ���
����Ɍ������̂��߂�
�_�̖��x����肩�ǂ��������肷��ɂ�
�\���ׂ�����������
��l���z�Ȃ�1�̋����ɂ���͂��̓_�̌��̕��ς��v�Z���Ă�����
����Ǝ����l�Ƃ̍���2���̕��ρi���U�j�łł����Ȃ����Ȃ� >>860
>�����g���`�o���ꂽ�����̂悤�ȁH
����H
�����g��0�`�̕����ƈႤ��
��ɓʂȂ̂ɗ��[�߂��ɕϋȓ_������
�Ȃ�ŁH �C�ӂ̎����ɓ��B�ł���悤�Ȋ��d��͑��݂��邩�H
���d��́A���͂͐����ŗL���̊��������Ă���v�Z���x�͖�����ł���Ƃ���B ���ʂɈ�l���z�炵���_��5000���������āA
�e�X�̓_�ŃƂ�5���̋����ʂɂ��̓_�ȊO�ɂǂꂾ���̓_���܂܂�邩���Z�o�����Ă݂��B
https://upload.wikimedia.org/wikipedia/commons/thumb/2/2f/Spherical_cap_diagram.tiff/lossless-page1-597px-Spherical_cap_diagram.tiff.png
�����l9 ����9.56 �W����3.14�Ƃ����l�ɂȂ����B
> summary(dots) ; sd(dots)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.000 7.000 9.000 9.556 12.000 23.000
[1] 3.148086
�q�X�g�O��������
https://i.imgur.com/4XaXArc.png
# ���ʈ�l���z c(x,y,z)
vertex <- function(r=1){
x=runif(1,-1,1) # x ~ ��l���z[-1,1]
phi=runif(1,-pi,pi)�@# �� ~ ��l���z[-��,��]
y=sqrt(1-x^2)*cos(phi) # ��(1-x^2)*cos(��)
z=sqrt(1-x^2)*sin(phi) # ��(1-x^2)*sin(��)
r*c(x,y,z)
}
n=5000
vtx=t(replicate(n,vertex())) # n�̓_x,y,z������
rgl::plot3d(vtx[,1],vtx[,2],vtx[,3], col="slateblue")
Theta=(pi/180)*5
onCap <-function(x,y,theta){
acos(x %*% y) < theta # �x�N�g���̓��ς̋t�]����theta�����Ȃ狅����ɂ���
}
hmonCap<- function(j){
count=0
for(i in (1:n)[-j]){
count = count + onCap(vtx[j,],vtx[i,],Theta)
}
return(count)
}
dots=sapply(1:n,hmonCap)
summary(dots) ; sd(dots)
hist(dots) ; table(dots)
BEST::plotPost(dots) �ɂɕ��z����@
# �p�x��,������l���z�őI����
����
> summary(dots) ; sd(dots)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.0 6.0 10.0 18.7 17.0 139.0
[1] 26.50699
�W�������傫���̂ň�l�Ƃ͌ĂׂȂ��B
�q�X�g�O������`����https://i.imgur.com/Y8mFUop.png >>863
���ʏ�̖ʐς����ɂ��ăO���b�h��`���Ă��̒��̓_�𐔂���v���O�����͂ł������ɂȂ��̂Œf�O���āA
��L�̂悤�ɎU�z�����_�̎���ɉ��̓_������̂��𐔂���̂ɕς��܂����B
�F�X�Ə������肪�Ƃ��������܂����B >827��
�����`���ŗ���x,y�������ā@r^2-(x^2+y^2)�����ɂȂ�̂͏��O����
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.00 9.00 13.00 12.58 16.00 33.00
[1] 5.694825
�W����5.69�ƑO��҂̊ԂɂȂ����B�@�܂��A�����ƍ��v���������B >>869
�P�ʋ��̕\�ʐς�4�B���̋��ʂŐ�A�i�ؒf�ʂ������j�\�ʐς�3�ƃɕ����邽�߂ɂ́A
���ʂƋ��̒��S�̋����͂����炩�H�@������
y=��(1-x)^2�A��=��[a,1]2��y��(1-(dy/dx)^2)dx�@�������āAa=1/2
���ƕ��ʂ̋�����1/2�Ȃ�A�ؒf�ʂ̔��a��(��3)/2
���̂��Ƃ���A���ʏ����l�ɕ��z�����_������A������A�ԓ��ʏ�ɓ��e����ƁA
���a(��3)/2�̉~���ɔ����̓_������A���̊O���̃h�[�i�c�^�̕����ɔ����̓_���Ȃ���Ȃ�Ȃ��B
>>827�@�̕��@�ł́A���a(��2)/2�̉~�̓��O�œ���邽�߁A���ʏ����l�ɕ��z�����_�Ƃ͂Ȃ�Ȃ��Ǝv����B
�ł͂ǂ�����悢���Ƃ����ƁA[-1,1]�̈�l����x,y,z�������A
x^2+y^2+z^2��1������j���A1�ȉ��Ȃ�AX=x/r�AY=y/r�AZ=z/r�Ar=��(x^2+y^2+z^2)
�Ƃ����̂��A�V���v�����Ǝv����B >>830
>xyz�ŋ��̊O�����O���Đ��K�����Ă��{���͓�������
�����
�X�}���Ӑ}�`����ĂȂ����������m��� >>871
��s�̒��ɁA��J�����Ђǂ��ԈႢ���Ă܂����B�������܂��B
�~�Fy=��(1-x)^2�A��=��[a,1]2��y��(1-(dy/dx)^2)dx�@�������āAa=1/2
���Fy=��(1-x^2)�A��=��[a,1]2��y��(1+(dy/dx)^2)dx�@�������āAa=1/2 >>871
[-1,1]�̈�l����x,y,z�������A
x^2+y^2+z^2��1������j���A1�ȉ��Ȃ�AX=x/r�AY=y/r�AZ=z/r�Ar=��(x^2+y^2+z^2)
�ł���Ă݂܂����B
>866�Ƃقړ������ςƕW�����ɂȂ�܂����B
�@ Min. 1st Qu. Median Mean 3rd Qu. Max.
1.000 7.000 9.000 9.585 12.000 24.000
[1] 3.193939 ���ʂ��A��̕��ʁAx=a��x=a+h�ŃJ�b�g�����Ƃ��̑я�̋Ȗʂ̖ʐς́A
�J�b�g����ʒu�ɂ�炸�A��h�ɂ݈̂ˑ����܂��B
>>866�͂��̐����𗘗p�������@�Ȃ̂ŁA���ʈ�l���z�����鐳�������@���Ǝv���܂��B
����A>>827�̕��@�́A�������Ȃ��Ƃ����w�E�ł��B ��a�̖��ł��B
�y300�l��ΏۂɁu��̃e�[�}�p�[�Np��q�ɍs�������Ƃ����邩�v�Ƃ����A���P�[�g�������Ȃ����Ƃ���Ap�ɍs�������Ƃ�����l��147�l�Aq�ɍs�������Ƃ�����l��86�l�A�ǂ���ɂ��s�������Ƃ̂Ȃ��l��131�l�ł������B
�@�i�P�j�����ɍs�������Ƃ̂���l�̐������߂�B
�@�i�Q�j�ǂ��炩����ɂ����s�������Ƃ̂���l�̐������߂�B�z�@�Ƃ������ł��B���������Ă��Ȃ��Ȃ��������o���܂���ł����B ���̖�菑�����ԈႦ�Ă��܂��܂����B���炵�܂����B ���ł͂Ȃ��ăX���ł��B���S�҂̂��ߗp�ꂪ�����Ⴒ����ɂȂ��Ă��܂��܂����B���x�����炵�܂����B >>876
(1)147+86-(300-131)=64
(2)147-64=83 86-64=22����83+22=105
���������ł��Ȃ����R����B >>875
�ܓx�Ń�+���Ƃł��Ƒт̖ʐς̓��Ƃ����Ȃ��ăƂ̒l�ɂ��ˑ����܂��ˁB �O>>843
>>817
�ʔ������ƌ�������ɂ͂��̂��炢�̂��Ƃ͋N����Ȃ��ƂˁB
���a1�̋��ɓ��ڂ��鐳�l�ʑ̂̈�ӂ�a�Ƃ��āA
���̑̐ς�a^3��2/12
4�̒��_��ׂɂƂ����Ƃ��A�ʕ�̑̐�V�͂��傤�Lj�ӂ�1�̐��l�ʑ̂̑̐ςɂȂ�Ƃ��B
a=1�̂Ƃ�V=��2/12
=0.11785113�c�c �_�_�_�_�_�_�_�_�_�_�_
�_�_�_`�����/��_�_�_�_
�_�_��(_ _ )`�܂¤�_�_
�_�_�_�_�_`�Ҥ�_�_�_�_
�_�_�_�_�_�_�_�_�_�_�_
�_�_�_�_�_�_�_�_�_�_�_
�_�_�_`�O>>881�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_>>817 (1/2)^3=1/8=0.125 �_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_�_ �O>>885
�攼�a1�̋��\�ʂ�A,B���Ƃ�Ƃ�AB��0�`2�̒l��ׂɂƂ邪�A���̂������������Ƃ������Ƃ��Ƃ蓾��l��AB=��2
���l��AC=��2,BC=��2
�����Ƃ��Ƃ蓾�遢ABC�̖ʐς́A
��ABC=(��3/4)(��2)^2
=��3/2
��ABC�̏d�S��G�Ƃ��āA
�l�ʑ�ABCD�́�ABC���ʂƂ������_D�̍���DG��0���܂߂��낢��Ȓl��ׂɂƂ邪�A�����Ƃ��Ƃ蓾��l�́A���̒��S��O�Ƃ���OG�Ɠ������B
�܂�l�ʑ�ABCD�̑̐ς̂����Ƃ��Ƃ蓾��l�́A3�̗Ő��̂��̂��̂�������������1�̎O�p���̑̐ςƓ������B �O>>886�����B
>>817
�l�ʑ�ABCD=(1/3)(1/2)�1
=1/6
=0.166�c�c
��>>886 888���Ɓ[�@�@(�p�`�X����?)
>>887
�@OA,OB,OC�����������OABC�̑̐ς� 1/6
�@>>841 �ƈ�v��� (�������͂Ȃ��낤��) �a���� �a �� �a������
�i(-_-)�a�@�@�a��>>888
�i���܁�ށ@ ��a������
��`(_)_)��~�@�a������
�_���҃ҁ�_������_�_�_
�_�_�_�_��(_ _ )`�܂��
�_�_�_�_�_�_�_`�Ҥ�_�_�_�_�_�_�_�_�_�_`���\�ʂɂ����Ƃ��Ƃ蓾��2�_�ځA3�_�ڂ����ɂƂ�ƔC�ӂ�2�_�͋��̒��S�ɑ��Ē��p�ɂȂ�B
�O>>887���Ƃ�4�_�ڂ��ǂ��Ƃ邩�B3�_�Ō��܂镽�ʂƕ��s�ȁA���̂�����C�ӂ̉~�Ղ̒��ŁA�����Ƃ��Ƃ蓾��~�Ղ͋��̒��S��ʂ��B���̉~�ՂƋ��\�ʂ̋��L���ł���~�����4�_�ڂ�����Ƃ��̎l�ʑ̂̑̐ς́A�Ő������p�ȎO�p���Ɠ��̐ρB
�Ő��̒����͋��̔��a=1������O�p���̑̐�(1/3)Sh�́A
(1/3)(1/2)�1=1/6
=0.166�c�c
�����Ă�Ǝv�����ǁB >>817
���l�ϕ��ɂ���
In[1]:= S[t1_,t2_,p_] := Simplify[Norm[Cross[{Cos[t1]Cos[+p],Cos[t1]Sin[+p],Sin[
t1]}-{0,0,-1},{Cos[t2]Cos[-p],Cos[t2]Sin[-p],Sin[t2]}-{0,0,-1}]]/2]
In[2]:= d[t1_,t2_,p_] := Simplify[Det[{{Cos[t1]Cos[+p],Cos[t1]Sin[+p],Sin[t1]},{
Cos[t2]Cos[-p],Cos[t2]Sin[-p],Sin[t2]},{0,0,-1}}]/(2 S[t1,t2,p])]
h[d_] := Simplify[(Integrate[Cos[t3](d-Sin[t3]),{t3,-Pi/2,ArcSin[d]}]+Integrate[Cos[t3](Sin[t3]-d),{t3,ArcSin[d],Pi/2}])/Integrate[Cos[t3],{t3,-Pi/2,Pi/2}]]
In[3]:= h[d_] := Simplify[(Integrate[Cos[t3](d-Sin[t3]),{t3,-Pi/2,ArcSin[d]}]+In
tegrate[Cos[t3](Sin[t3]-d),{t3,ArcSin[d],Pi/2}])/Integrate[Cos[t3],{t3,-Pi/2,Pi/
2}]]
In[4]:= NIntegrate[Cos[t1]Cos[t2]h[d[t1,t2,p]]S[t1,t2,p]/3,{p,0,Pi/2},{t1,-Pi/2,
Pi/2},{t2,-Pi/2,Pi/2}]/Integrate[Cos[t1]Cos[t2],{p,0,Pi/2},{t1,-Pi/2,Pi/2},{t2,-
Pi/2,Pi/2}]
Out[4]= 0.11968 �O>>889
>>881������O�ʂ��l�̌ܓ�����ƁA
V=0.12 >>891
������1�ʂ��l�̌ܓ�����ƁAV=0 >>890 �̎������Đ��x���グ�Ă݂�
In[1]:= NIntegrate[Cos[t1]Cos[t2]
(2(Sin[2p]Cos[t1]Cos[t2])^2+(Cos[p](-Cos[t1]+Cos[t2]+Sin[t1-t2]))^2+(Sin[p](Cos[t1]+Cos[t2]+Sin[t1+t2]))^2)
/(24Pi Sqrt[(Sin[2p]Cos[t1]Cos[t2])^2+(Cos[p](-Cos[t1]+Cos[t2]+Sin[t1-t2]))^2+(Sin[p](Cos[t1]+Cos[t2]+Sin[t1+t2]))^2])
,{p,0,Pi/2},{t1,-Pi/2,Pi/2},{t2,-Pi/2,Pi/2}, WorkingPrecision->12, PrecisionGoal -> 11]
Out[1]= 0.119679720136 ������ăp�\�R���Ȃ��ł͉����܂����ˁH
�y�x�R���ŋ��`���z�V�^�R���i�E�C���XPCR���������@54�l�@�z��0�l
https://asahi.5ch.net/test/read.cgi/newsplus/1584811696/
����W�c����54�l��ׂɑI���PCR����������z��0�ł������Ƃ���
PCR�����̊��x0.7�@���ٓx0.9�Ƃ��Ă��̏W�c�̗L�a���̊��Ғl��95%�M����Ԃ����߂�B >>893
���l�I�ɂ��������Ȃ��́H R�̕W�����C�u�����͒��ۑ㐔�v�Z�Ȃ�����W�����C�u���������Ȃ琔�l�ϕ������ł��Ȃ�����ȁB >>895
�O�v�Z�����l�����
�m�����x���^�����邩��
���Ƃ͑̐ς̌v�Z���ĕ��Ϗo������������
���͏����Ă��v�Z���ł��������Ȃ� ���a1�̔��~�̓����ɕȐ���`��
���̂Ƃ�(�Ȑ����͂��̈�̖ʐ�)/(�Ȑ��̒���)�̍ő�l�����߂� �O>>891
>>898
�Ȑ��ň͂܂ꂽ�̈悪�ȉ~�̂Ƃ��A
�Z��1,����1/��2
�ʐσ�(1/2)(1/��2)
=��/2��2
����2��(1/2)��(1/��2)
=���2
�ʐ�/����=1/2��2����2
=0.297301779�c�c
匂ʼnz�~���銴�����B >>899
�s����
����Ȃ甼�~���̂���
��/(2(��+2))=0.3055...
�̕����傫�� �O>>899
>>900���~�͒����������Ă��B�s�K���ɁB >>901
������ł����~�ɋ߂Â��邩��䂪0.3055...�ɋ߂��Ȑ����`����
�����>>899�͍ő�l�ł͂Ȃ�
�ł��������Ɗm����sup�͂����Ă�max���������ƂɂȂ��Ă��܂��̂�>>898�͉��肵�܂� ���݂܂���
�u���a1�̔��~�̕����W���Ƃ��ĕȐ���`��
���̂Ƃ�(�Ȑ����͂��̈�̖ʐ�)/(�Ȑ��̒���)�̍ő�l�����߂�v
�������A�����Ō������~��{(x,y)��R^2 | x^2+y^2��1 ,y��0}�̂��Ƃł� l = (sin��/(1+sin��))(��+��/2) + (sin��'/(1+sin��'))(��'+��/2) + cos��/(1+sin��) + cos��'/(1+sin��') + (��-��-��')
S = (��/2)(sin��/(1+sin��))^2 + (��'/2)(sin��'/(1+sin��'))^2 + (1/2)sin��cos��/(1+sin��)^2 + (1/2)sin��'cos��'/(1+sin��')^2 + (��-��-��')/2
maximize S/l where ��,��'��0, ��+��'����
 >>896
>>896
���X���肪�Ƃ��������܂��B
���������A���S���Y���ɂȂ�̂��Ƌ��l���Ă��܂��B
���O���z��I������i��. �L�a���͍��X10%�Ƃ���(0.0.1]�̈�l���z�Ƃ���)�A
�z���m���͐^�z���m���ƋU�z���m���̘a�A
�z�����͂��̊m���œ��z�A >>897
��̓I�ɂ͋��ʏ��2�ϐ��̍��W�nst��������
st���ʏ�̗̈�D�Ƌ��ʂ�(x,y,z)=f(s,t)�őΉ����Ă���Ƃ�
���ʏ�̈�l���z��^����st2�ϐ��̖��x��g(s,t)�����݂�
dS/4��=g(s,t)dsdt
�ƂȂ�
�撣���f,g�͋�̓I�Ȏ��ŗ^���邱�Ƃ͏o����
���ʏ��4�_��p1=f(s1,t1)�E�E�Ep4=f(s4,t4)�ŕ\����
�����4�_�_�Ƃ���4�ʑ̂̑̐ς�\����V(p1,p2,p3,p4)��
���Ƃ����ŕ\���͂��邩��
�����V(f(s1,t1),�E�E�E,f(s4,t4))g(s1,t1)�E�E�Eg(s4,t4)ds1dt1�E�E�Eds4dt4
���v�Z������ǂ����� �O>>901
>>902
y���������(0,0)�ɒ��S�����킹�����a1,���S�p45���̐�`��1�Ε��ׁA����𗼃T�C�h���狲�ނ悤�ɔ��a1/2,���S�p45���̐�`����ׁA���̍��E�[�ɔ��a1/4,���S�p45���̐�`���ʂ����炩�ɂÂ��悤�ɂ������ĕ��ׁA
(0,1),(�}1/��2,1/��2),(�}1/2�}1/2��2,1/2��2),(�}3/4��2�}1/4,1/4��2),(0,0)��8�_�����炩�ɂÂ��悤�Ɍ��ԁB
�_(0,0)�����މ~�ʂ̒��S��(0,t),���S�p���ƂƂ����ƁA
�����藝���A
sin��=(3/2��2+1/2)/2t
�s�^�S���X�̒藝���A
(3/4��2+1/4)^2+(t-1/4��2)^2=t^2
t=(3��2+3)/4
sin��=(4-��2)/6
=0.430964406�c�c
��=25.52877935�c�c
�ʐςƎ������Ƃ���4�ɕ����ċ��߂�B
������傫�Ȑ�`��2���킹�Ėʐσ�/4,����������/2
2�Ԗڂ̐�`��2���킹�Ėʐσ�/16,����������/4
3�Ԗڂ̐�`��2���킹�Ėʐσ�/64,����������/8
�T�̕��̂悤��y���ɐ��Ώ̂Ȏc��̖ʐς�s�Ƃ����ƁA
�ʐ�/����=(��/4+��/16+��/64+s)/{��/2+��/4+��/8+2��t(��/2��)}
=(21��/64+s)/(7��/8+t��)
=(21��/64+s)/{7��/8+(1+��2)(3/4)��}
=(21��/8+8s)/{7��+6(1+��2)��}
=(21��+64s)/{56��+48(1+��2)��}
s�͐�`��������O�p�`��3������2�{�ŏo��B
�Ƃ�x���̂܂ܑ�����Ă悢���͋C�ɂȂ�B >>903
S�̎��� (��/2) �̏��� (��+��/2)/2�A�@(��'/2) �̏��� (��'+��/2)/2�@�ł́H
Steiner�ɏK���đΏ̐������肵�܂����B
�@l(��) = 2(��+��/2){sin��/(1+sin��)} + 2cos��/(1+sin��) + �� -2��,
�@S(��) = (��+��/2){sin��/(1+sin��)}^2 + sin��cos��/(1+sin��)^2 + ��/2 -��.
�ƂŔ�������
(d/d��)(S/l) = {2 - (��+��/2)cos��/(1+sin��)}{�Υcos(2��) -sin(2��) -2��}
�@�@�^{4(1+sin��)(��/2 -�� +�Υsin�� +cos��)^2},
������
�@2 - (��+��/2)cos��/(1+sin��) >0,�@�@(0<��<��)
������
�@�Υcos(2��) - sin(2��) -2�� = 0,
�@�� = 0.4827200003884401212939116114621300267
���̂Ƃ��ő�l
�@(S/l)max. = 0.31702857011315030244270875179918713
����́A���~�̒l ��/(2(��+2)) = 0.3055077351758286 �@�@>>900
���傫���B (�⑫)
�@�ơ = 27.65781870881107747733891798287807�
(S/l)max. = (���~�̔��a) = sin�ơ/(1+sin�ơ)
�@= 0.31702857011315030244270875179918713
(���_�`���S�̋���) = 1/(1+sin�ơ)
�@= 0.68297142988684969755729124820081287 >>905
�܂�1�_�͌Œ肵�čl���ėǂ���
2�_�ڂ�1�_�ڂ�ʂ��~�ōl����
���̏�ň�l���z�Ŏ��Ηǂ�(1����)
3�_�ڂ͔������ň�l�Ɏ�邩��(2����)
4�_�ڂ͋���ň�l��(2����)
�ϕ���5�ϐ��ł悢���� (����)
�@l(�ơ) = 1.48625008894369638043092594627639431
�@S(�ơ) = 4.68806356604781887658254751068492774
�@S/l = 0.31702857011315030244270875179918713
�܂��A��=30�� �̂Ƃ�
�@(���~�̔��a)�@1/3,
�@(���_�`���S�̋���)�@2/3,
�@l(30��) = 2(3��3 +5��)/9 = 1.472358208
�@S(30��) = (3��3 +11��)/27 = 4.645359042
�@S/l = (3��3 +11��)/{6(3��3 +5��)} = 0.31695251
�� = 0 �ł�
�@l(0) = ��+2 = 5.141593
�@S(0) = ��/2 = 1.570796
�@S/l = 0.305507735 >>907
�f���炵��
���l�Ƃ��Ă�0.317028570...�Ő����ł����A
�Ȃ����̌`���ƍő�ɂȂ�̂��ؖ����~�����Ƃ���ł�
�q���g�������ƁA����p�����[�^�t����p�f�̌ŗL�l�����C���[���ɂ�苁�߂āA�Ɍ�������(�ʐ�)/(����)�ɂȂ邱�Ƃ𗘗p���܂� >>911
�Ȑ����͂ސ}�`��
�E�ʏW���Ƃ��ėǂ�
�E����Ă镔���������Ƃ��ėǂ��i�܂�Ȑ��͔����\�j
�E���~�̋��E�ɐڂ��Ă��Ȃ������́A���Ȃ��Ƃ��Ǐ��I�ɋȗ����������Ƃ��ėǂ�
���Ƃ���>>903�̌`�����肵�Ă����͂� >>910
�Q�l
-------------------------------------------------------------
�Ɓ@�@r(��)�@�@�@�@�@l(��)�@�@�@�@�@�@�@S(��)�@�@�@�@�@�@S/l
-------------------------------------------------------------
0���@0.000000000�@�@��+2�@�@�@�@�@�@�@��/2�@�@�@�@�@�@�@0.30550773518
15���@0.205604647�@�@4.906228243054�@�@1.544232748162�@�@0.31474947183
30���@0.333333333�@�@2(5��+3��3)/9 �@�@(11��+3��3)/27�@�@0.31695250990
45���@��2 -1 �@�@�@�@4.351158878394�@�@1.361230101991�@�@0.31284311606
60���@2��3 -3�@�@�@�@4.013126310452�@�@1.211844939375�@�@0.30197029588
75���@0.491333810�@�@3.616783365011�@�@1.021692472380�@�@0.28248649954
90���@0.500000000�@�@�@�@�@�@�@�@�@�@��/4�@�@�@�@�@�@�@0.25000000000
------------------------------------------------------------- >>912
�ʂȂ̂ƁA�ȗ����Ǐ����͂����Ǝv���̂ł����A�����\�Ȃ̂͂ǂ����Ăł��傤�� >>914
����Ă镔���̊O�p���ƂƂ��āA����ȕ��Ƀ�/2�̌X���̒����Ő�������l��S�̕ω����l����ƁA
�钷��x�ɑ���l�̌����� 2x(1-cos(��/2)) (as x��+0)�ŋߎ��ł���̂ɑ��A
S�̌����� (x^2*sin��)/2 (as x��+0) �ŋߎ��ł���B
����āAx>0���\����������߂�A���傫�� S/l �������ł���B
���ƖY��Ă�����
�E�ő�� S/l ��^����Ȑ������݂���
�������K�v����ȁc�債�����ƂȂ�����������
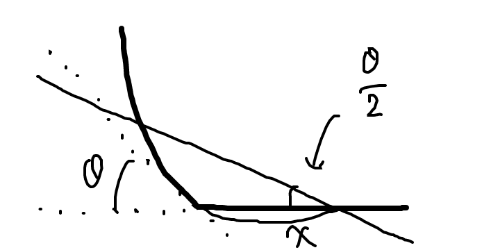 �O>>906
�O>>906
�s�^�S���X�̒藝���A
(3/4��2+1/4)^2+(t-1/4��2)^2=t^2
t=(3��2+3)/4
=3(1+��2)/4
=1.81066017�c�c
t^2=9(3+2��2)/16
sin��=(4-��2)/6
=0.430964406�c�c
��=25.52877935�c�c
�ʐςƎ������Ƃ���4�ɕ����ċ��߂�B
������傫�Ȑ�`��2���킹�Ėʐσ�/4,����������/2
2�Ԗڂ̐�`��2���킹�Ėʐσ�/16,����������/4
3�Ԗڂ̐�`��2���킹�Ėʐσ�/64,����������/8
�T�̕��̂悤��y���ɐ��Ώ̂Ȏc��̖ʐς͓��r��`,�݊p�O�p�`,���������~����Ȃ�B
�ʐ�=��/4+��/16+��/64+��t^2��/360��
+(1/4��2+1/4)(1/4��2)�2
+(1/2��2+1/4)(1/4��2)
-t(3/4��2+1/4)
����=��/2+��/4+��/8+2��t(��/360��)
=7��/8+{3(1+��2)��/2}(��/360��) >>915
���[�Ȃ�ق�...
�������Ɋp����������A�܂�
x��(S/l)(4(1-cos(��/2))/sin�Ƃ��\�������������悢�䂪�o��̂�
���肪�Ƃ��������܂���
Max�̑��݂ł����A���������Ȑ��̏W������̓I�Ɍ����ĂȂ�������ł����A���v�V�b�c�Ȑ��̏W���Ƃ�������炭���݂͌����܂� �O>>916
�ʐ�=��/2
����=2��/2+2=��+2
�Ƃ���ƁA�Ȑ��͂�����ł����~�ɋ߂Â������Ȃ����H
�ʐ�/����=��/(2��+4)
=3.05507735�c�c �O>>918�������Ȑ��̂����B
���a1�̔��~�̃R�[�i�[2�����ar�̉~�ʂʼn~���J�b�g����Ƃ��A
���~�̃J�b�g�����~�ʕ����ɑ��钆�S�p���ƂƂ���ƁA
(1-r)sin��=r
sin��=(1+sin��)r
r=sin��/(1+sin��)
1-r=1/(1+sin��)
r^2=sin^2��/(1+sin��)^2
�ʐ�=��/2-��+(1-r)rcos��+��r^2(��+2��)/2��
=��/2-��+(1-r)rcos��+r^2(��/2+��)
=��/2-��+sin��cos��/(1+sin��)^2+(��/2+��)sin^2��/(1+sin��)^2
����=��-2��+2(1-r)cos��+2��r(��+2��)/2��
=��-2��+2(1-r)cos��+r(��+2��)
=��-2��+2cos��/(1+sin��)+(��+2��)sin��/(1+sin��)
�ʐ�/����={��/2-��+sin��cos��/(1+sin��)^2+(��/2+��)sin^2��/(1+sin��)^2}/{��-2��+2cos��/(1+sin��)+(��+2��)sin��/(1+sin��)}
={(��/2-��)(1+sin��)^2+sin��cos��+(��/2+��)sin^2��}/{(��-2��)(1+sin��)^2+2cos��(1+sin��)+(��+2��)sin��(1+sin��)}
�ƂŔ������A���q=0�Ƃ���ƁA
��=27.6578187�c�c�� >>919
���������ǂ���>>907�ʼno�Ă܂� >>921
���m���łĂ�������X�ƌ듚��A������̂��|���������悤�Ȃ� .��,,
�c`e)�܁`��
�܁`��
�ǃ�)
`�c�L
�ҁL�O>>919�ʉ���T���Ă�B �P�ʐ����`��ʐ�0.21�����̎O�p�`5�ŕ������� �����`�͖ʐς̓���������̎O�p�`�ł͕����o���Ȃ����Ƃ��ؖ����� >>924
�����`�����W [0,1]�~[0,1] �ɂ����B
�A�h�z�b�N������
�����3�_ A(0,1), B(0.4,0), C(1,0.59) ���l�����
����AB���ʐ�0.2�̎O�p�`���o���B
����AC���ʐ�0.205�̎O�p�`���o���B
����BC���ʐ�0.177�̎O�p�`���o���B
�c�����O�p�`ABC�͖ʐς�0.418������AA����BC�̒��_�����������Ƃ����ʐ�0.209���ɓ�������B ���Ȃ݂�
�u�����`��5�̎O�p�`�ŕ��������Ƃ��A��ԑ傫�ȎO�p�`�̖ʐς̉����v
�ɂ��Ă͎��͓�����m��܂���
�����炭>>926�^�C�v���ŏ����Ǝv�����Ǐؖ��o���܂��� n(=10)�l�̒����疳��ׂ�m(=2)�l�I�炻�̒��ɏ��Ȃ��Ƃ���l�̊����҂������B
�S�̂ʼn��l�̊����҂����邩�̊��Ғl�����߂�B
5.345794�l�ł����Ă�H �O>>923
>>929�Ⴄ�Ǝv���B
���Ȃ��Ƃ�1�l�Ƃ������Ƃ́A2�l��1�l��2�l���������Ă���B
2�l��1.5�l���������Ă��邩��A10�l���ƁA
1.5(10/2)=7.5
��7�l��8�l������������B >>924
�����3�_ A(0, 1)�@B(��2 -1, 0)�@C(1, 2-��2)�@���l�����
4�̇��������ɂȂ�@(��2 -1)/2 = 0.20710678 > 1/5
�c�������p2���ӎO�p�`�� (��2-1)^2 = 0.171572875
��ԏ������O�p�`�̖ʐς͈̔͂� 0.1682�`0.18 �ł����� 6.5�̌v�Z��
x=0:n # �����Ґ�:x, ����:n-x
pmf=1- choose(n-x,m)/choose(n,m) # �����҂�x�l�̂Ƃ���m�l���N�����������Ă���m���@���@1 - (���l�S�����̊m��)
pdf=pmf/sum(pmf) # �m�����x��������
(E=sum(x*pdf)) # ���Ғl���v�Z >>932
2�l�̊������̊��Ғl1.5�ɌŒ�ł͂Ȃ��đS�̂̊������Ɉˑ������Ȃ��́H
# p:�����m��
p1=2*p*(1-p) # ��l���������m��
p2=p^2 # ��l�Ƃ������m��
(1*p1+2*p2)/(p1+p2) # �����l���̊��Ғl
1.5�ɂȂ�̂�p=2/3�̂Ƃ��B >>931
�c�{�̒��ɍ����x�Ɣ����10-x�����Ă���m����Q(x)�Ƃ��A
����x�̉���2����č���n�ł���m���́AP(n)=C[x,n]C[10-x,2-n]/C[10,2]
P(1)=C[x,1]C[10-x,1]/C[10,2]=x(10-x)/45�AP(2)=C[x,2]C[10-x,0]/C[10,2]=x(x-1)/90
������AP(n=1,2������=x)=P(1)+P(2)=x(19-x)/90
P(n=1,2������=x)=Q(x)P(n=1,2������=x)=Q(x)x(19-x)/90
P(����=x��n=1,2)=P(n=1,2������=x)/�[k=1,10]P(n=1,2������=k)
=Q(x)x(19-x)/90/�[k=1,10]{Q(k)k(19-k)/90}�A�����ŁAQ���萔�Ȃ�A
P(����=x��n=1,2)=x(19-x)/�[k=1,10]{k(19-k)}=x(19-x)/660
x�̊��Ғl=�[k=1,10]x*x(19-x)/660={19*10*11*21/6-(10*11/2)^2}/660=13/2 �ʔ�����茩���Ă��܂����A���������ȒP�����ǂ��B
n����������ԏ��n�̓_P_1,P_2,�c,P_n���A���ꂼ��̍��W��
P_1:(1,0,0,�c,0)
P_2:(0,2,0,�c,0)
P_3:(0,0,3,�c,0)
�c
P_n:(0,0,0,�c,n)
�ƂȂ�悤�Ɏ��B
P_1�`P_n��n�̓_�ō����(n-1)������Ԃƌ��_O�̋�����d(n)�Ƃ����Ƃ�
lim[n����] d(n) �����߂�B
https://twitter.com/StandeeCock/status/1242443303880028161?s=19
https://twitter.com/5chan_nel (5ch newer account) (n-1)������� (�����ʂƂ��) ��
�@x_1 + (1/2)x_2 + ���� + (1/n)x_n = 1,
�ŕ\�킳���B
���̒����ʏ�̓_X (x_1, x_2, ����, x_n) �ƌ��_O (0,0,����,0) �̋���|OX|��2���
�@|OX|^2 = ��[k=1,n] (x_k)2
�@�@�� {��[k=1,n] (1/k)x_k}^2 / {��[j=1,n] 1/jj}�@�@(�� �R�[�V�[)
�@�@= 1 / {��[j=1,n] 1/jj}
�@�@= d(n)^2,
d(n) = {��[j=1,n] 1/jj}^(-1/2)
�@�@�� {��[j=1,��] 1/jj}^(-1/2)�@�@(n����)
�@�@= {��(2)}^(-1/2)
�@�@= (��6)/��
�@�@= 0.7796968
�ʔ����I (n-1)������� (���ȉ~�ʂƂ��) ��
�@(x_1)^2 + {(1/2)x_2}^2 + ���� + {(1/n)x_n}^2 = 1,
�ŕ\�킳���B
���̒��ȉ~�ʏ�̓_X (x_1, x_2, ����, x_n) �ƌ��_O (0,0,����,0) �̋���|OX|��2���
�@|OX|^2 = ��[k=1,n] (x_k)2
�@�@�� ��[k=1,n] {(1/k)(x_k)}^2
�@�@= 1
�@�@= d(n),
lim[n����] d(n) = 1.
�ʔ����I >>392
�R�����Ă��܂��\����܂���ł���
���� p(m+1)-pm>0�� ��[m+1��k��n-1] 1/k > 1
��[m+1��k��n-1] 1/k<log((n-1)/m)���A(n-1)/m<e�̂Ƃ��A�E��<1���p(m+1)<pm�Ȃ̂ŁA
(n-1)/e<m�̂����ŏ��łȂ�m�͕s�K������[n/e]+1���傫��m�͕s�K
��[m��k��n-1] 1/k>log(n/m)���An/m>e�̂Ƃ��A�E��>1���p(m-1)<pm�Ȃ̂ŁA
n/e>m�̂����ő�łȂ�m�͕s�K������[n/e]��菬����m�͕s�K
�i�܂��Ap([n/e]+2)<p([n/e]+1)�����烰[[n/e]+2��k��n-1] 1/k<1�ŁA
��[[n/e]+1��k��n-1] 1/k<1+1/([n/e]+1)<2�j
��[[n/e]+1��k��n-1] 1/k��1�����̂Ƃ�m=[n/e]�ŁA1�ȏ�̂Ƃ�m=[n/e]+1�ōő傾����A
m=[n/e]+[��[[n/e]+1��k��n-1] 1/k]�̂Ƃ��ő�
���̂Ƃ�m/nlog(n/m)<pm<m/nlog(n/m)+1/n������Apm��1/e >>936
���X���肪�Ƃ��������܂��B
�������Ō��߂鎖���ł͂Ȃ����Ǔ������_�̐l�����Ăق��Ƃ��܂����B �i��j
����̓����̃R���i�z���҂�87�l��������63�l�z���ł������Ƃ����B
�����̊��x0.6�@���ٓx0.9�Ɖ��肵�āA87�l���Ɋ����҂͉��l�Ɛ��肳��邩�H �L���o�N���q100�l���疳��ׂ�5�l���猟�̂��̎悵�Ă��̌��̂��������a���ăR���i���������Ƃ���z���ł������B
100�l�̃L���o�N���q�̗z�����̊��Ғl�����߂� >>929
�x�C�Y�I�ɍl�����
n�l����m�l�I�班�Ȃ��Ƃ���l�̊����҂������Ƃ���B
Ax: x�l�̊����҂�����(x=0~n)�Ƃ�������
B:�Œ��l�̊����z������Ƃ�������
Pr[Ax|B]=Pr[B|Ax]Pr[Ax]/Pr[B]
Pr[Ax]:���O�m��
Pr[B|Ax]:�ޓx
Pr[B]:���Ӗޓx(�K�i���萔)
���߂������ҒlE��
��(x*Pr[Ax|B])/��Pr[Ax|B] = ��(x*Pr[B|Ax]Pr[Ax])/��(Pr[B|Ax]Pr[Ax])
Pr[Ax]��x�ɂ�����炸�萔�ł����
E=��(x*Pr[B|Ax])/��(Pr[B|Ax])
���O�m�����z����l���z�Ɖ��肵�Ă̌v�Z�Ƃ������Ƃ��ȁB �����̖��������ʼn���
�y�z���{���w�I�����s�b�N�\�I 23
�y����z���{���w�I�����s�b�N�\�I �Q�O�O�X�N ��S
https://www.youtube.com/playlist?list=PLvkSrMcoOqr14JV0W3n7rMKvKMoYsOTdl >>946
����ȑf�l����A�ǂ����K���A�X���̃X����ł��B
�ʔ�������ˁi�O�O�G (1) s²+s=n^4-n² ��������s, n�͑��݂��邩�B�L���g����Ȃ炷�ׂċ��߂�
(2) 5^c+s²+s=n^4-n² ��������c, s, n �͑��݂��邩�B�L���g����Ȃ炷�ׂċ��߂� (1)
�@0 = s(s+1) - nn(nn-1) = (s+nn)(s+1-nn),
���@s = -nn �܂��� s = nn-1.�@�@(�����ɂ���) (2)�@s(s+1) �� nn(nn-1) �����������疵���B b(x) �͊���ŁAa�������Ƃ���
b(x)= ��[0, x] b(u) du + ��[a, x+a] b(u) du
�����B
(1) b(a), b(2a) �����߁A
(2) a_n=��[0, na] b(u) du �Ƃ���Ba_1= ��[0, a] b(u) du =1 �Ƃ���a_n��n��p���ĕ\���B �O>>932
>>948(1)
(s,n)=(3,2),(3,-2),
(0,1),(0,-1),
(-1,1),(-1,-1),
(8,3),(8,-3),
(-9,3),(-9,-3) >>951
b(x) = F(x) + F(x+a) - F(a),
�����Ɂ@F(x) = ��[0,x] b(u)du�@�͋���B
b(x+a) = - b(-x-a)
�@= - F(-x-a) - F(-x) + F(a)
�@= - F(x) - F(x+a) + F(a)
�@= - b(x),
����� b(x) �͎���2a�����B �䂦��
b(x) = ��[0,x] b(u)du + ��[0,x] b(u+a)du
�@= ��[0,x] b(u)du - ��[0,x] b(u)du
�@= 0, ���a2�̉~���Ɍ����̂Ȃ��P�ʐ����`��8�l�ߍ��ނɂ͂ǂ�������悢�� >>955
x���̏�ɁA�l�p�����ɎO���ׁA���̏�ɓ��l�ɎO�悹�A���̏�ɓ�𒆉��ɕ��ׂ�
�E���̊p��(3/2,0)�A���i�̉E��̊p��(3/2,2)�A�ŏ�i�̉E��̊p��(1,3)�����A
�ǂ��(0,��7/2)����̋�����2���Ȃ��̂ł����𒆐S�ɉ~���������� �O>>952
>>955
�~�̒��S�����_(0,0)�Ƃ��āA
(-1,1-��3),(-1,-��3),(0,-��3),(0,1-��3)�_�Ƃ���P�ʐ����`�A
(0,1-��3),(0,-��3),(1,-��3),(1,1-��3)�_�Ƃ���P�ʐ����`�A
(-1/2,2-��3),(-1/2,1-��3),(1/2,1-��3),(1/2,2-��3)�_�Ƃ���P�ʐ����`�A
(-1/2,��15/2),(-1/2,��15/2-1),(1/2,��15/2-1),(1/2,��15/2)�_�Ƃ���P�ʐ����`��4��`���A
���Ƃ�4�͂��ꂼ��4�̏ی��ɐ����`�̒��S��u���Ay���ɑ���2���Ώ̂ɂȂ�悤�ɒu���B
x���ɐ��������Ȃ���45�����炢�Ő�ɒu����4�̒P�ʐ����`�ɂ��肬��ڂ��邩�ڂ��Ȃ������炢�ŒT��Ƃ悢�B >>955
https://imgur.com/3vsxb6D
���S�Ɏ�T��ŋl�ߍ���ł݂܂���. ( Geogebra �ō�} )
�`������̃{���P�ŐڐG���Ă�悤�Ɍ�����ӏ������ۂ͗���Ă��܂�. >>956
�~�̒��S��(0,0)�Ƃ����
�@(�}3/2, -(��7)/2) �� (�}3/2, 2 -(��7)/2) �̂Ȃ������`�ɂU��
�@(�}1, ��3) �� (�}1, ��3 -1) �̂Ȃ������`�ɂQ��
�ł��ˁB
*�@2 - (��7)/2 = 0.677124344
�@��3 - 1 = 0.7320508 �O>>957
�c��4�̂���2���3�ی��Ƒ�4�ی��Ɏ�45���œ���悤�Ƃ���ƁA
�_(1/2,��15/2-1)�ƒ���y=x-1/2+1-��3+1/2��2�̋����́A
|4��2-��30-2��6+1|/4=0.929837703�c�c��1
�\�z�ʂ�c���2���1�ی��Ƒ�2�ی��ɓ���邱�Ƃ��ł��Ȃ��B
�܂��3�ی��Ƒ�4�ی��ɓ���悤�Ƃ���2�̒P�ʐ����`���ŏ��ɒu����2�̒P�ʐ����`��1�̒��_(-1,1-��3)�����(1,1-��3)�ӂ��ڂ����܂܂��̓_���x�_�ɉ~�ʑ��ɌX���āA�c��2�̒P�ʐ����`������悤�ɂ���B
�ő���X����Ɠ_(1/2,��15/2-1)�Ƒ�4�ی��ŌX�����P�ʐ����`�̍ł��߂��ӂ̋�����1����͂��B
�_(1,1-��3)�����5/2�̋����ɂ���P�ʐ����`��2�̒��_�����܂莟�您�`���������B ��ӂ̒���3�̐����`���A���a1�̉~5�Ŕ핢���邱�Ƃ͉\�� �ォ�� ��3 =1.7320508 �̕�����1�~��3�̒����`�ɎO��������B
������ (��7)/2 = 1.3322875 �̕����� 3/2 �~ (��7)/2 �̒����`�ɓ�����B
�e�����`�́A�Ίp���̒�����2������A���a1�̉~�Ŕ핢���邱�Ƃ��\�B �k���l���aR�̉~��ɁA���a1�̉~���������݂�
�ɏd�Ȃ镔���������悤�ɒu�������̂ł����A�ő剽��
�܂Œu����ł��傤���B
�ER=2 �̏ꍇ�B
���Z�~�����u���w�̖��@��(3)�W�v���{�]�_�� (1988)
��104
(���{MO�ł��g��ꂽ�炵���B) �召2�̉~��p�ӂ����猋�ʂ͂ǂ��Ȃ邩�� �O>>960���j�ύX�B�ŏ���4�͓����B�X��45���͕ς��Ȃ��B
>>955
5�ځ`8�ڂ̒P�ʐ����`���1�ی��`��4�ی��ɐU�蕪���Ay���ɑ���2��Ώ̂ɁA���ӂ�y=x�܂���y=-x�ƕ��s�ɂȂ�悤�ɒu���ƁA5�ڂ̒P�ʐ����`�̒��_�̍��W�́A
(2-��15/4-��3/2,1/2+��15/4-��3/2),
(2+��2/2-��15/4-��3/2,1/2-��2/2+��15/4-��3/2),
(2+��2-��15/4-��3/2,1/2+��15/4-��3/2),
(2+��2/2-��15/4-��3/2,1/2+��2/2-��15/4-��3/2)
6��,7�ڂ͑�2�ی�,��3�ی��ɒu���Ƃ���8�ڂ̒P�ʐ����`��5�ڂ̒P�ʐ����`�Ƃ҂����肭�������܂�y�������Ɋ�ƁA
y=x-3/2-��2+��15/2��x=1/2�̌�_�́A
(1/2,-1-��2+��15/2)
�Ίp�̒��_�́A
(1/2+��2,-1-��2+��15/2)
x^2+y^2=(1/2+��2)^2+(-1-��2+��15/2)^2
=1/4+2+��2+15/4+3+2��2-��15(1+��2)
=9+3��2-��15-��30
=3.89243177�c�c��4
�����a2�̉~�ɒP�ʐ����`��8����B �O>>967
�ŏ��ɕ`����y��������ʼn~�ʂƐڂ���2�̒P�ʐ����`�̑�3�ی��̂��@,��4�ی��̂��A,���ɕ`�������_���܂ނ̂��B,y����+�����ʼn~�ʂ�2�����Őڂ���̂��C�Ƃ���ƁA�B�ƇG���ڂ��Ȃ��\��������B
�܂�5�ڂ�8�ڂ�ڂ����܂܂��ׂ点�E��]�A6�ڂ�7�ڂ�ڂ����܂܍���]���A�~���ɔ[�߂�B
���Â��Ĕ����V�������B �O>>968
>>955
�~�̒��S��(0,0)�Ƃ��A
(-1,1-��3),(-1,-��3),(0,-��3),(0,1-��3)�_�Ƃ���P�ʐ����`�@�A
(0,1-��3),(0,-��3),(1,-��3),(1,1-��3)�_�Ƃ���P�ʐ����`�A�A
(-1/2,2-��3),(-1/2,1-��3),(1/2,1-��3),(1/2,2-��3)�_�Ƃ���P�ʐ����`�B�A
(-1/2,��15/2),(-1/2,��15/2-1),(1/2,��15/2-1),(1/2,��15/2)�_�Ƃ���P�ʐ����`�C��`���A
5�ڂ̒P�ʐ����`�D���1�ی��ɁA
6�ڂ̒P�ʐ����`�E���2�ی��ɁA
�D�ƇE��y���ɑ��Đ��Ώ̂ƂȂ�悤�ɒu���A
7�ڂ̒P�ʐ����`�F���3�ی��ɁA
8�ڂ̒P�ʐ����`�G���4�ی��ɁA
�F�ƇG��y���ɑ��Đ��Ώ̂ƂȂ�悤�ɒu���A
�D�ƇG��1�̕ӂ��҂����肭�����A
�G�̒��_��1���~�Ɛڂ���悤�ɂ��A
�E�ƇF��1�̕ӂ��҂����肭�����A
�F�̒��_��1���~�Ɛڂ���悤�ɂ���B
�����@�͎����ꂽ�B
��ӂɂ͂Ȃ����A�D�`�G�̒��_�̍��W�����߂邱�Ƃ��ł���B ���܁A����l���R���i�Ɋ������Ă���An�̃R���i�E�C���X�������Ă���
�R���i�͈ꎞ�Ԃ��Ƃɑ������A�m��p��a�����A1-p��b����Ƃ���(0<p<1�Aa��b�͎��R��)
�܂��A�R���i��S�ȉ��ɂȂ�ΐ����m��AT�ȏ�ɂȂ�Ύ��S�m��Ƃ���
�����m���͈̔͂́H
T�𐳂̖�����ɔ�����Ƃ��̐����m���͈̔͂́H �O>>969�ʉ��B
>>955
�@�A�B�͂��̂܂܁A�C�����_�̂ق��ɊB�ɂ������A�D�ƇG����чE�ƇF�����ꂼ��c�ɕ��ׇB�C�����݂��ނ悤�҂��������B
�E�C�D
�F�B�G��6��y���ɑ��č��E���Ώ̂Ȃ̂ŁA
�D�̉E��̍��W(3/2,3-��3)���~���ɂ���ΒP�ʐ����`8�͂��ׂĉ~���ɂ���B
(3/2)^2+(3-��3)^2=9/4+9-6��3+3
=57/4-6��3
=14.25-6�1.7320508�c�c
=14.25-10.3923048�c�c
=3.85�c�c��4
���ςɂ܂܂ꂽ�B ���a2�̉~���Ɍ����̂Ȃ��P�ʐ����`��8��
�i2/3)�~��3 �̒����`���P�l�ߍ��ނɂ͂ǂ�������悢�� >>954
�萔�����Ċ������Ȃ��� >>972
����Ȋ����̋l�߂����Ŕ��a1.9991425�c���炢
http://imgur.com/IiCbKrV.png �����ł��I
(��3�j+ (��15)/2 - 3 = 0.66854248
��(8��7 - 7�j- 2 = 1.763776094
�܂ł͂��������ł��B �[�ĂŌ����@9.1547/4�� = 0.72851
�i�P�ʐ����`8�� 2/�� = 0.63662 ������) �O>>971
>>972
�@�A�B�܂œ����B
�C��y���ؕ�2�̈ʒu��ӂ̎��ɒ��_���Ђ������đ҂����B
�D�E�F�G���1,2,3,4�ی��ɔz�u���Б��Ɋ�ƁA�D�܂��͇E���~���ɂ����邽�߂������ɉ�����A�D�ƇE�����_�ŇC�̂ƂȂ肠��2�ӂƐڂ���`�ɂȂ�B
���Ƃ����ŇD�ƇG�̏c�̖ʂ����킹�ĉ���2/3,�c�Ɂ�3�̕ӂ�����悤�ɂ���ƁA
�E��̒��_(11/3-��3,1/2)�̍��W����A
(11/3-��3)^2+(1/2)^2=3.99273852�c�c��4
�Ȃ�Ƃ��~���ɓ���B
�C�̍���ӂ܂��͉E���ӂ��X����p�x�́A
30���`45���ʼn~�����[�̉\��������B
���Ƃ����l�I�ɂނ�ł��E�[�̒����`�ɂ킸���ɗ]�T���������B�C�͇D�ƇE�̂������ɞ���ɉ������߂�\��������B ���a2�̉~���Ɍ����̂Ȃ� ��(5/8)�~��(3/2) �̒����`���P0�l�ߍ��ނɂ͂ǂ�������悢�� >>978
a^2+((3/2)b)^2��(2a)^2+b^2��2^2
��������a����(5/8),b����(3/2)���ČW�����Ƃ������Ƃ� �O>>977
>978
�����ɉ�����1��2��3�d�˂�Ə�ʂ́A
3��(5/8)-��[2^2-{(1/2)��(5/8)}^2]=0.411159852�c�c
�c��4�~��菬���ȏ�̃G���A�ɁA
���}�[�N�̂悤��2�̒����`���\�̎��ɒu���A���̏��2�����ɒu�����A
�܂��͗r�ّ̈̎��̂悤�ɉ������̒����`���㉺�ɗ����Ēu���A���̂������ɍ��E����n�̎��ɞ���ɂ����ށB x���̏�ɒ����`��Q�����ĎO���ׂ�
���̏�ɒ����ɐQ�����ē���ׂ�
���i�̉E��̊p��(���ӂ̒����~3/2,�Z�ӂ̒���)
��i�̉E��̊p��(���ӂ̒���,�Z�ӂ̒����~2)
�ǂ�������_����̋�����4�Ȃ̂Ō��_���S�̔��~�Ɍ܌͂܂� �����ł��I
�[�ĂŌ����@9.68246 / 4�� = 0.770505
���a2�̉~���Ɍ����̂Ȃ� (2/��13)�~(8/��13) �̒����`��8�l�ߍ��ނɂ͂ǂ�������悢�� �����`��Q�����ĘZ�i�d�˂����̂����A���T�C�h�̒����Ɉ�Â������Ă����t����
�d�˂������`�̊p�܂ł̋���=(���Ӂ�2)^2+(�Z�Ӂ~3)^2=2^2
���ɂ��������`�̊p�܂ł̋���=(���Ӂ�2+�Z��)^2+(�Z��)^2=2^2 >>983����
�~�@���ɂ��������`�̊p�܂ł̋���=(���Ӂ�2+�Z��)^2+(�Z��)^2=2^2
���@���ɂ��������`�̊p�܂ł̋���=(���Ӂ�2+�Z��)^2+(���Ӂ�2)^2=2^2 �܂��ԈႦ����������Ȃ��ċ���^2������ �قڐ����ł��I
�[�ĂŌ����@9.846154 / 4�� = 0.783532
�������ג����������܂肪�����i?) �������܂萔�w���Ċ����ł��Ȃ�����
������̌ߑO���ɐႪ�~��n�߂��B
����Ԃ����߂҂�����ɓ����o���A
1���Ԃ�2�}�C���̏�����������A
�����1���Ԃ�1�}�C���̏�������������B���ĐႪ�~��n�߂������́H
�������A���̓��Ⴊ�~��n�߂�܂ł̐ϐ��0�A��͈��̑����ō~��ς���A����Ԃ��P�ʎ��Ԃ�����ɏ��������̑̐ς͏�Ɉ��Ƃ���B
��L�̂悤��Snow plow problem�̔h���Ƃ���
����ł�2���Ԍ�̉����x��1���Ԍ�̔����ɂȂ�ꍇ�A�Ⴊ�~��n�߂������𐔒l�I�ɋ��߂�ꍇ�ɂ���ƕ֗��Ȑ��\�͂Ȃɂ��H���R�t���ŁB
�d�쓙�͎g��Ȃ����̂Ƃ��� >>986
�@��(8/17) �~ 3��(8/17) �̒����`��7�l�ߍ��ނƏ[�Ă�
�@9.882353 / 4�� = 0.7864
�ƂȂ�A�����`�̓��ډ~�̏[�Ă� (��/4=0.7854) ����B
�Ƃ��ɈӖ��͂Ȃ������� ���߂��c���ԑO�ɐႪ�~��n�߂��Ƃ���B
�ς�������̍����� t+c �ɔ�Ⴕ�A
����Ԃ̑���v(t)�� t+c �ɔ���Ⴗ��B
�@v(t�j= k/(t+c),
���߂���t���܂łɏ���Ԃ��i������
�@��[0,t�nv(t')dt' = ��[0,t] k/(t'+c�jdt'
�@= k�log{(t+c)/c}
��ӂɂ��A
�@k�log{(c+1)/c�p= 2�}�C��
�@k�log{(c+2)/c�p=�i2+1)�}�C��
�@�@
�� 3log{(c+1)/c�p= 2log{(c+2)/c},
���ic+1)^3 = c(c+2)^2,
�� c =�i��5 -1)/2 = 0.618034�i���ԁj= 37.082�i��)
�����x�� -k/(t+c)^2 ������
�@1/(c+2)^2 = 1/{2(c+1)^2},
�@0 = 2(c+1)^2 - (c+2)^2 = cc -2,
�@c = ��2,
�J�͖�X���߂��Ɂ@��ւƕς�邾�낤
Silent night,�@Holy night
���@�������\�B ���ԓ����菜��ʂ�J�A���_t�̂Ƃ��̐�̍�����H(t)=(t+a)/h�Ƃ��A����Ԃ̈ʒu��x(t)
����Ԃ͒Z������dt��dx�i�݁A���̊ԏ����̐�dxH(t)�����Ⴗ�邩��AdtJ=dxH(t)
x(t)=��dx=��dtJ/H(t)=Jh��dt/(t+a)�Ax(t)-x(0)=Jhln((t+a)/a)������A
x(1)-x(0)=Jhln((1+a)/a)=2�Ax(2)-x(0)=Jhln((2+a)/a)=3�A3ln((1+a)/a)=2ln((2+a)/a)
((1+a)/a)^3=((2+a)/a)^2�Aa^2+a-1=0���Aa�̓t�B�{�i�b�`��(��5-1)/2
��͐��߂���(��5-1)/2���ԑO�ɍ~��n�߂�
dx(t)/dt=Jh/(t+a)�Addx(t)/dtdt=-Jh/(t+a)^2������A-Jh/(2+a)^2=(-Jh/(1+a)^2))*1/2�ƒu���ƁA
(2+a)^2=2(1+a)^2�Aa^2-2=0�A�Ȃ̂Ł�2���ԑO
�������\���K�v �O>>980
>>955
�~�̒��S��(0,0)�Ƃ��A
(-1,1-��3),(-1,-��3),(0,-��3),(0,1-��3)�_�Ƃ���P�ʐ����`�@�A
(0,1-��3),(0,-��3),(1,-��3),(1,1-��3)�_�Ƃ���P�ʐ����`�A�A
(-1/2,2-��3),(-1/2,1-��3),(1/2,1-��3),(1/2,2-��3)�_�Ƃ���P�ʐ����`�B�A
(0,2),(-��2/2,2-��2/2),(0,2-��2),(��2/2,2-��2/2)�_�Ƃ���P�ʐ����`�C��`���A
5�ڂ̒P�ʐ����`�D���1�ی��ɁA
6�ڂ̒P�ʐ����`�E���2�ی��ɁA
�D�ƇE��y���ɑ��Đ��Ώ̂ƂȂ�悤�ɒu���A
7�ڂ̒P�ʐ����`�F�̒��S���3�ی��ɁA
8�ڂ̒P�ʐ����`�G�̒��S���4�ی��ɁA
�F�ƇG��y���ɑ��Đ��Ώ̂ƂȂ�悤�ɒu���A
�D�E�F�G�����ꂼ��1�̒��_�ʼn~�Ɠ��ڂ���悤�ɒu���Ȃ��ł��傤���H�@����2��3��3�Ɛςݏd�˂Đ�������ȊO�̒u�������Ȃ��Ƃ����炿���Ƃ��ʔ�����肶��Ȃ��ł��B �O>>991
>>955�\�z�B
�@�A��y���ɑ��Đ��Ώ̂Ƀn�̎��^�ɒu���A�@�̉E���ӂ̌X����4/3�A�A�̍����ӂ̌X����-4/3�Ƃ�y����Őڂ���悤�ɂ���B
�B�͌��_�t�߂ɒ��S��u���������A�C��y���ɑ���45����]�������_��(0,2)��(0,2-��2)�ɒu���B
�D�`�G�̒��S���1�`4�ی��ɒu���A
�D�G�͇A�Ɠ����X���ɂ��A�E�F�͇@�Ɠ����X���ɂ���ƁA
�@,�A,�C�`�G�����ꂼ��1���̒��_�ʼn~�ɓ��ڂ���悤�ɒu�����Ƃ����肬��ł��Ȃ����Ǝv���B �O>>992
>>955�ʉ��B
�@�A��y���ɑ��Đ��Ώ̂ɒu���A�A�̍���ӂ̌X����3/4,�����ӂ̌X����-4/3�ɂ���B
�B�̒��S�����_�ɔz�u��x��,y���ɐ������A�C��y���ɑ���45����]�A���_��(0,2),(0,2-��2)�ɔz�u����B
�D�̍���ӂƉE���ӂ̐ؕЂ̍���7/5�B
�A�D�G�̍���ӂ̌X����3/4,
�@�E�F�̉E��ӂ̌X����-3/4�ɂ��킹�A
�D���߂������ς��グ�ćG�̍��[��x���W��1/2���傫���A���E�[�̍��W��2��a���A
x^2+y^2��4�͈̔͂ɂ�������B
�D�̍��[�̒��_���C�̉E���ӂ��킸���ɉ��ɂƂ�ɂ́A
y=x+2-��2��0.4�������A
y=0.4+2-��2=0.985786438�c�c
(0.4,0.98)�Ƃ���Ɗm���ɇC�ƇD�͗���Ă��āA
�D�̏�[�̍��W�́A
(0.4+0.8,0.98+0.6)=(1.2,1.58)
1.2^2+1.58^2=3.9364��4
�D�̉E�[�̍��W�́A
(1.2+0.6,1.58-0.8)=(1.8,0.78)
1.8^2+0.78^2=3.8484��4
�D�̉��[�̍��W�́A
(0.4+0.6,0.98-0.8)=(1,0.18)
�D�̉E���ӂ���чG�̍���ӂ̕������́A
y=3(x-1)/4+0.18
�G�̍��[�̍��W��(0.56,-0.15)�Ƃ���ƁA
�G�̉E�[�̍��W�́A
(0.56+0.8+0.6,-0.15-0.8+0.6)
=(1.96,-0.35)
1.96^2+(-0.35)^2=3.9641��4
�G�̍����ӂ���чA�̉E��ӂ̕������́A
y=-4(x-0.56)/3-0.15
�A�̍��[��y���ɐڂ���Ƃ�������A�A�̏�[��x���W0.8�������A
�A�̏�[�̍��W��(0.8,-0.47)
�A�̍��[�̍��W��(0,-1.07)
�A�̉��[�̍��W��(0.6,-1.87)
0.6^2+(-1.87)^2=3.8569��4
�A�̉E�[�̍��W��(1.4,-1.27)
1.4^2+(-1.27)^2=3.5729��4
���P�ʐ����`8��^��1�ȊO�����ׂĐ������邱�ƂȂ����a2�̉~���ɔ[�߂邱�Ƃ��ł���B [0,1]��̖�����x�ɑ��āA
x�̘A�����W�J��[a_0;a_1,a_2,...]�Ƃ���.
p_n(x):= [a_0;a_1,a_2,...,a_n]�Ƃ����Ƃ��A
�Ɍ�lim(n����) (x-p_n(x))^(1/n)�����߂�. �O>>993�����B�D�̍���ӂƉE���ӂ̐ؕЂ̍���5/4�B
>>955
�P�ʐ����`�@�A�̒��_��(0,-1.07),(�}0.6,-1.87),(�}1.4,-1.27),(�}0.8,-0.47)
�P�ʐ����`�B�̒��_��(-0.5,0.5),(-0.5,-0.5),(0.5,-0.5),(0.5,0.5)
�P�ʐ����`�C�̒��_��(0,2),(-��2/2,2-��2/2),(0,2-��2),(��2/2,2-��2/2)
�P�ʐ����`�D�E�̒��_��(�}0.4,0.98),(�}1,0.18),(�}1.8,0.78),(�}1.2,1.58)
�P�ʐ����`�F�G�̒��_��(�}0.56,-0.15),(�}1.16,0.95),(�}1.96,-0.35),(�}1.36,0.45)�ɂ���B �����̖��������ʼn���
�a�Z�y���w����1�� �ߋ���z
https://www.youtube.com/watch?v=QSoet6pQ3Nc >>996
���~�̒��a��D
���~�̒��a��d
�������̒����� 2L
�Ƃ���B
���̑����ɂ�� D�FL=L�Fd
�������̒��� L = ��(Dd)�@�c (1)
D�������ς����Ƃ��A
�E���~�̖ʐς́i��D/2)�� �ς��B
�E���F�����̖ʐς́i2L - ��D/2)�� �����ς��B
���F�����̖ʐς��ő�ƂȂ�Ƃ�
�@2L - ��D/2 = 0�@�c�@(2)
(1)(2)����L��������
�@d = D(��/4)^2, >>987�̂܂˂����Ă݂�
��̍~����͈��ł͂Ȃ�����ɐ����A�~��~��ňȍ~�͗n���o�����̂ƕύX����
�~��n�߂Ă���t���Ԍ�̎��_�ł̐�̐ς��鑬�x��cos(��t/3)�Ƃ���(0<t<4)
���ߑO�ɐႪ�~��n�߂Đ��߂��珜��Ԃ��ғ�������
�Ⴊ�~��n�߂Ĉꎞ�Ԕ���̎��_�ň�}�C���̏��Ⴊ�ł���
����ɂ��̌�30���ň�}�C���̏��Ⴊ�ł���
�Ⴊ�~��n�߂����Ԃ�m��ɂ͂ǂ�ȕ\���K�v�� =1000+1000-1000*1000/1000 ���̃X���b�h�͂P�O�O�O���܂����B
�V�����X���b�h�𗧂ĂĂ��������B
life time: 71�� 5���� 26�� 30�b 5�����˂�̉^�c�̓v���~�A������̊F���܂Ɏx�����Ă��܂��B
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�s�v���~�A������̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
��300�~���瓽���ł��w�����������܂��B
�� �v���~�A������o�^�͂����� ��
https://premium.5ch.net/
�� �Q�l���O�C���͂����� ��
https://login.5ch.net/login.php ���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B



