�ʔ�����肨�����ā`�� 29���
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
�@�@�@���@�@ .���@�@�@���@�@�@��.�@�@�@�H�@ �@ ���@�@�@���@ �@ �@�@�@ ___ �@ i
�@�@�@�́@�@ �ށ@�@�@�� �@�@ �́@�@�@�ׁ@�@�@�ށ@�@�@�ށ@�@�@�@�@�@| ___ / | �R�@��
�@�@�@�X�@�@ �́@�@�@��@�@�@��.�@�@�@���@�@�@�Ɂ@�@�@��.�@ �@�@ �@ �.|�@!�@��/
�@�@�@���@�@ ��.�@�@�@���@�@�@���@�@�@ �G�@�@�@�́@�@�@�݁@�@�@�@�@�L�@|__! _�^�@�@��
�@�@�@�Ɂ@�@ ��@�@�@���@�@�@�� �@�@�@�T �@�@ �� �@�@ ��
�@�@�@���@�@ ���@�@�@��.�@�@�@�� �@�@ .�́@�@�@���@�@�@���@�@�@�@�@�@�����]���]�@��
�@ �@ �߁@ �@�@�@�@�@�@�@��@�@�@�@ �@�@�@ ���@�@�@��.�@ �@ �@ �@ ����__.|__
�@�@�@�ā@�@ ��.�@�@�@�� �@�@ �@�@�@�@�@ �@�@.���@�@�@�� �@�@�@�@�@ �����@.!�@�@ ��
�@�@�@���@�@.�H �@�@ .���@�@�@�ԁ@�@�@�@�@ �@�@�́@�@�@���@�@�@�@�@�@ ' .���@.!
�@�@�@�� �@�@ �ׁ@�@�@��. �@�@ ���@ �@ �@ �@�@�@ ��
�@�@�@ �@�@�@ �� �@�@ �߁@�@�@��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@��@�@�@�@�@�@�@�@�@�@�@ ��<
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ,'�L�@,,.�R
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@....,,,,___i''�L �E�@��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@! ���]-�@�@ �@!
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ޤ�R�@�@�@�@ �
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�J'' '�-�"�L �O�X��997(1)
AP=BP=��2���AB=2��2
ABCD�̎�����2��2�~4=8��2 �O>>5�C���B
AB�̏��AB��ł͂Ȃ��Ɖ��߂��܂����B
(1)6��2 �Čf(�O�X��996)
��R�̕������B��ɂ͌����Ă���A�S�Ă̕�͈�{�̒����R�ɒʂ���Ĉ꒼���ɕ���ł���B
�܂��A���n��ނ���A�e��ނ̕�̌��͗l�X�ł��邪�S�ċ����ł��邱�Ƃ͕������Ă���B
�R�����ؒf���������̉�ɕ����邱�ƂŁA�R�������O�����ƂȂ�2�l�̐l�Ԃŕ���邱�Ƃ��l����B
���̂Ƃ��A��̌�����тɊւ�炸�An��ؒf���邱�Ƃŏ�ɋϓ��ɕ�����邱�Ƃ������B
�ÓT�N�C�Y�Ə����܂������Atopological proof�����݂��邱�Ƃ��m���Ă��܂�
�����̂���l������q���g��A�C�f�A�������Ă����܂� >>5
�����`ABCD�͈��2�Ə����Ă���� ��s�ł������ł��\���Ƃ�
997 �P�R�Q�l�ڂ̑f������ sage 2019/01/25(��) 02:50:08.43 ID:PhzqWDq+
����ʔ���
2�̊Ԋu�̐����`�����_��ABCD�Ƃ�����B
��AB�̏�ɓ_P�����A��AP=BP=��2�Ƃ�����B
1)���̎��AP���܂߂�5�p�`APBCD�̎������͂������ȁH
2)�_P��(1)�̎�����ς��Ȃ��悤�ɓ_B�_D�̉�������ƂȂ�悤�ɓ_P��������B
���̌��ʎl�p�`APCD�ƂȂ�����B
���̎��̓_DP�Ԃ̒����͂������ȁH
3)�_P��(2)�̏�Ԃɂ��鎞�A�_P1�Ƃ��A(1)�̎���������ʂ悤�ɓ_P�����܂��_BD�̒�����ɓ��������̓_��P2�Ƃ�����B
�_P1���_P2���������Ԃ͂����H
�Ȃ��A�����������Ԃ�1�ɂ�1sec�Ƃ����B
4)���������_P�̋O�����O���t�ɕ`���B
�_P1��(0,0)��ʂ�悤�ɏ�ɓʂŏ�������B
����(x,y)=(2,0)�𒆐S�Ƃ�(0,0)��ʂ锼�~��������������B
�O���Ɖ~�ň͂܂�Ă鏊�̖ʐς͂�������
�H 1)5�p�`�̎�����
���2��3�ӂ�
AP=PB=��2�ɂ��
6+2��2 >>7
����31��������_���Ȃ�ƍl������������ >>9 >>12
2)
�@BP = p��2 �Ƃ�����
�@AP^2 = (1+p)^2 + p^2,
�Ƃ���ŁA 1) ���
�@AP = CP = (6+2��2 -2 -2)/2 = 1+��2,
�������
�@p = {��(5+4��2) -1}/2 = 1.132241882312
�@DP = DB + BP = (2+p)��2 = 4.42965895059852 �ł�>>7��topological proof�̃q���g�������Ă����܂�
�ȒP�̂���n=2�Ƃ��Ă����܂�
(������őz�肵�Ă���ؖ����@�ł���Έ�ʂ�n�ɑ��Ă����̂܂ܓK�p�ł��܂�)
�ȉ��̕����g���܂�
���
f:S^2��R^2��A���ʑ��Ƃ���Ƃ�
f(x)=f(-x)
�ƂȂ�x��S^2�����݂���
���̏ؖ��͈Ղ����ł�(�m��Ȃ��ꍇ�͍l���Ă݂Ă�������)
�^����ꂽ��̗�Ɉˑ�����A���ʑ�f:S^2��R^2�����܂����ƁA��肩�璼���Ɍ��̖��肪������܂�
�ǂ̂悤��f��I�ׂ悢���l���Ă݂Ă������� >>13
�ڂ������肢���܂�
�����I�ȏؖ����@�͂���̂�������܂��A�c�����Ă���܂��� >>9
�킩����
(2)
P����AB����ǂꂭ�炢����Ă邩
AP:PB:BA=��2:��2:2�ɂ�萂�����낷�ƍ�����1:1:��2������1
�_�̐����ړ����Ă��O���͕ς��Ȃ�����B�̐^���B�̐^����P��P' ��u��
PP'�Ԃ͕ӂ��痣��Ă鋗���ɂ��^�́�2/2
DB�̒����͈��2�ɂ��2��2
������DP�̋�����
2��2 + ��2/2 = 5��2 / 2����Ȃ����ȁH >>9 >>12
2)
�@BP1 = p��2 �Ƃ�����
�@AP1^2 = (2+p)^2 + p^2 = 2 + 2(1+p)^2,
�Ƃ���ŁA 1) ���
�@AP1 = CP1 = (6+2��2 -2 -2)/2 = 1+��2,
�������
�@p = ��(1/2 + ��2) - 1 = 0.38355107
�@DP1 = DO + OP1 = ��2 + (1+p)��2 = ��2 + ��(1+2��2) = 3.37085025
3)
�@AP1 = CP1 = 1+��2 = a,
�@OP1 = (1+p)��2 = 1.95663668743 = b,
�Ƃ�����
�@A(-��2, 0)�@B(0, ��2)�@C(��2, 0)�@D(0, -��2)
�@P1(0, b)�@P2(0, -b)�@Q1(a, 0)�@Q2(-a, 0)
P�̋O�Ղ͑ȉ~
�@(x/a)^2 + (y/b)^2 = 1, �����_�N�c�͂��߂���S���Ⴄ�Ǝv���]
�_P�͑ȉ~�ɂ͂Ȃ�Ȃ��B
2�_2�ӌŒ�̏ꍇ���s�ړ������H
�ȉ~�̏ꍇ�͏œ_�Œ�̏ꍇ������
�����o��ҍ��Z�����Ǝv������3C�܂ł̌v�Z���Ǝv���� >>17
���_�̐����ړ����Ă��O���͕ς��Ȃ�����
���̐}�̍��E�̊O�����������Ƃ������ƁH
https://i.imgur.com/LTdqUAP.jpg >>20
���������������Ɖ��͎v����
����6+2��2��
�ł��Ⴄ���ۂ��� >>19
2)
�@BP1 = p��2 �Ƃ�����
�@AP1 + BP1 = ��{(2+p)^2 + p^2} + p��2 = ��{2 + 2(1+p)^2} + p��2,
�Ƃ���ŁA 1) ���
�@AP1 + BP1 = 2��2,
�������
�@p = 1/3
�@DP1 = DB + BP1 = 2��2 + (1/3)��2 = (7/3)��2,
3)
�@AP + BP = 2��2,
����ˁB >>9�@�C����
> ��AB�̏�ɓ_P�����A��AP=BP=��2�Ƃ�����B
��ABCD�̊O���ɓ_P�����AAP = BP = ��2 �Ƃ����j�_�B
> 2)�_P��(1)�̎�����ς��Ȃ��悤�ɓ_B�_D�̉�������ƂȂ�悤�ɓ_P��������B
> ���̌��ʎl�p�`APCD�ƂȂ�����B
2) �_P��(1)�̎�����ς��Ȃ��悤�ɁA����BD�̉�������ɓ_P�������j�_�B
���̌��ʌ܊p�` APBCD �ƂȂ����j�_�B
> 3)�_P��(2)�̏�Ԃɂ��鎞�A�_P1�Ƃ��A(1)�̎���������ʂ悤�ɓ_P�����܂��_BD�̒�����ɓ��������̓_��P2�Ƃ�����B
3) (2)�̏�Ԃɂ���_P�̈ʒu�� P1�Ƃ��A(1)�̎���������ʂ悤�ɓ_P�����A����BD�ƍĉ���_��P2�Ƃ����j�_�B ��
3)
�@AP + BP = 2��2,
���
�@(xx/2) + (y-1)^2 = 1,
����͑ȉ~�A�����B
����BD�@y=x�@�Ƃ̌�_��
�@P_1 (4/3, 4/3)�@
�@P_2 (0, 0)
�A�����B ��
(3)
�� �� (��2)cos�ӁC�@�@�� �� 1+sin��
�Ƃ��������B
ds = ��{(dx)^2 + (dy)^2},
s =��[-��/2, arcsin(1/3)] ��{1+(sin��)^2} d��
=��[-1, 1/3] ��{(1+tt)/(1-tt)} dt
= 2.256224416017548793463688895981454170195765856203120990202091790152911696637111818875640341701872164
�����B >>15
�_�����B�T�b�p���������B
�����������Ȃ������܂��B
�ǂ����������l���ĂȂ��݂��������B �O>>6�uAB�̏�v�Ƃ��������������������B�ǂ����܂��ɁA�ǂ̂悤��ABCD��`��������AB�̏�͈قȂ�ꍇ������B
�����`ABCD�̊O���A���Ȃ킿��AB�ɂ��Đ����`ABCD�̂Ȃ�����P���Ă��Ƃ��Ɖ��߂����B
(2)P��B�ɑ���AB������a�ACB������b�̒n�_�ɓ������Ƃ���ƁA
A��P��C�̒�����2��2+2�̂ܕς��Ȃ�����A
AP=PC=(2��2+2)/2
=��2+1
DP=2��2+BP
�s�^�S���X�̒藝���A
AP^2=(1+��2)^2=(2+a)^2+b^2
a^2+4a+4+b^2=3+2��2
a^2+4a+4+a^2=3+2��2
2a^2+4a+1-2��2=0
a=-2+��{4-(2-4��2)}/2
=-1+{��(2+4��2)}/2
BP^2=a^2+b^2=2a^2
BP=a��2
DP=2��2+BP
=2��2+a��2
=2��2+��(1+2��2)-��2
=��2+��(1+2��2) ��蕶�Ɍ�L�������ē�Փx�グ��̂�� >>15
���������̃����h�C�Ȃ猳�l�^�ǂ�����E���Ă����������Ă��炦�܂���ł��傤���H >>34
���ɖ����l���Ă���l�����邩������Ȃ��Ǝv���҂��Ă��܂����A���݂܂���
�Љ�悤�Ƃ��Ă����ؖ��̏o�T�͂�����̘_���ł�
https://m.tau.ac.il/~nogaa/PDFS/Publications/The%20Borsuk-Ulam%20Theorem%20and%20bisection%20of%20necklaces.pdf
(��2-3)
�ȉ��An=2�̏ꍇ�ɂ��ĊȒP�ɉ���������Ă����܂�
>>15�ŗ^��������Borsuk–Ulam�̒藝�ƌĂ�Ă���L���Ȓ藝(�̓���ȏꍇ)�ł�
S^2,R^2��S^n,R^n�ɒu�����������̂��{���̎咣�ł�
�ؖ��͑㐔�g�|���W�[�̋��ȏ���������Ɨǂ��ł��傤
�p���wikipedia�ɂ��ڂ��Ă���悤�ł�
���X�̖��͗��U�I�Ȑݒ�ł��邽�߁A����K�p����ׂɂ́A�܂�����A���I�Ȑݒ�ɒu��������K�v������܂�
��̓I�ɂ�
�R�����[0,1]=I
��Η��I�݂̌��ɑf��2�̕����W���ւ̕���I=V_1��V_2
(��̑�����N�Ƃ���Ƃ��A��P�̐�߂��Ԃ̒�����1/N�ƍl���āA��̎�ނɂ���ĕ����B
pdf�ł�coloring�ƕ\��)
�R�̐ؒf�c�cI�݂̌��ɑf�ȋ�Ԃւ̕���I=U_1��U_2��U_3
�܂��AS^2�̌��ɑ��uI�̕����y��2�l�ւ̕��z�v��Ή������܂�
��̓I�ɂ́A(x,y,z)��S^2�ɑ�
�����c�cU_1=[0,x^2],U_2=(x^2,x^2+y^2],U_3=(x^2+y^2,1]
���z�c�cA=��_{i|(x,y,z)�̑�i��������} U_i��B=��_{i|(x,y,z)�̑�i��������} U_i
�ƒ�߂܂�
�Ō�ɁAf=(f_1,f_2):S^2��R^2��
f_i(x,y,z)=��(A��V_i)
(A�Ɋ܂܂����i�̕��"��")
(�ɂ̓��x�[�O���x)
�ƒ�߂܂�
f���A���ł��邱�Ƃ͖��炩�ł��傤
�Ō�ɁA����f�ɑ�����K�p����A���̎咣��������܂�
(�Ȃ�����Ŏ�����邩�͂悭�l����ƕ�����Ǝv���܂�)
pdf�ł́A��2�Ō��̖����g�������A���I�Ȗ����`���A��3�ł���������Ă��܂� >>35
�Ȃ�قǁI���炵���I
���� Borsuk–Ulam �g�������̖��͎���ł����H >>35
�Ƃ���������_�����܂�܂��̖��Ȃ̂��B >>36-37
����قǐ��I�łȂ����ƂĂ��ʔ����ؖ����Ǝv�����̂ŁA�����ŏЉ�悤�Ǝv���܂���
�C���g���ɂ��ƁA���̘_�����ȑO�Ƀg�|���W�[�ƋA�[�@��p�����ؖ����Ȃ���Ă��܂����A����ɔ�ׂĂ��ȒP�ȕʏؖ���^�����`�̂悤�ł�
�܂��A�㔼�ł͍������ւ̈�ʉ����l���Ă��܂� >>38
�ʔ����ؖ��ł��ˁB
Borusk-Ulam�̏ؖ����ʔ��������ł��B
wikipedia�ɂ�RP(n)�̃R�z�����W�[�̘b�g���ĂĂ�����Ɠ���������ǂ��̕ӂ̕����Ă�l�ɂ͏펯�Ȃ낤�Ȃ��ƁB
�ł����̖��l���Ă�r���Ŏ��R�ɃR�z�����W�[�̎���������ꂽ�̂łȂ�Ƃ������ł��܂����B
�������ɂȂ�܂����B >>39
��ʂ�n�ɑ��Ď����ɂ�(�R)�z�����W�[�̗��_���K�v�Ȃ̂ŏ����m�����K�v�ł���
n=2�̏ꍇ�͎��͊�{�Q���g�������Ŏ����܂�
�܂��Awikipedia�̏ؖ������߂Č����̂ł����AHurewicz�̒藝�y��RP^n�̃R�z�����W�[�̊\�����g���Ă���A�������ɗv�������m���������ł��ˁA���炵�܂���
Hatcher��Algebraic Topology�Ƃ������ȏ��ł���A���������ȒP�ȏؖ����ڂ��Ă��܂�
(n=2��Thm1.10,��ʂ�n��Prop2B.6•Cor2B.7)
������̋��ȏ��͒��҂������Ō��J���Ă���̂ŋ���������ǂ���
http://pi.math.cornell.edu/~hatcher/AT/AT.pdf
���ƁA���܂葼�̐l�������������Ă��Ȃ��b��ɂ��Ă������X���Ă��܂����݂܂���
�ז��ł�����T���܂� >>40
>http://pi.math.cornell.edu/~hatcher/AT/AT.pdf
���肪�Ƃ��������܂��B�ǂ�ł݂܂��B
�����ł��ˁB
p251
�\�\
one can use the same argument with Z2 coefficients to deduce that H
H^*(RP(n); Z2) ≈ Z2[��]/(��^(n+1) with |��| = 1
�\�\
���Ԍ����Ċ撣���Ă݂܂��B �O>>30 �K �B ߡ �K���
�a���� �K�B �K�B�� �K
�i(-_-)�߁��K�B� � ��
�i����)~ �����ݸ݁c�c
��P�P�P�P].-))�܁S��K
��/_UU�_���҃�`�҃ҁB
(3)�͑ȉ~�Ȃ̂��B ���@�I�����_�Ƃ������O�}�`�Ƃ����݂̘b�Ȃ́H �O�X��>>854�̖{�l�ɂ�����
���x�͍��Z���w�ʼn����Ăق����Ƃ�����Ȃ���ł�낵�����肢���܂�
n�����R���Ƃ���B����{a_n}�y��a_0�� a_0 = 1 , a_n = a_n-1 +3-(-1)^n �ƁA�܂�����{p_n}���A�f���������������珇�ɕ��ׂ�����ƒ�߂�B
(1) a_n �̈�ʍ���1�̎��ŕ\���B
(2) b_n = a_n / p_n �ƒ�߂�Bb_1 * b_2 * b_3 * ... * b_n-1 * b_n ���Ƃ肤��ő�l�ƁA���̎���n�̒l��S�ċ��߂�B >>44
(1) a_n = 3n + {3 - (-1)^n}/2, >>45
(1)�����ł�
����Ƃ�(2)�������Ă݂Ă������� >>48
�ł� �b���ɕ����Ă����܂��傤�B �W���[�J�[���������g�����v�T�Q���̒�����P����
�J�[�h���o���A�\�����Ȃ��Ŕ��̒��ɂ��܂���
�����āA�c��̃J�[�h���悭���Ă���
�R�������o�����Ƃ���A�R���Ƃ��_�C���ł�����
���̂Ƃ��A���̒��̃J�[�h���_�C���ł���m���͂����炩
�R�D����_�C�����P�Q�������܂ł͕ς�炸�P�^�S�ŁA
�P�R���ڂ��������Ƃ��ɏ��߂ĂO�ɂȂ�
�����̐���n�ɑ���
{1-n(n-1)(n-2)(n-3)(n-4)(n-5)(n-6)(n-7)(n-8)(n-9)(n-10)(n-11)(n-12)/13!}/4
�o�͂�0��n��13�͈̔͂�
�P�^�S
�P�^�S
�P�^�S
�P�^�S
�P�^�S
�P�^�S
�P�^�S
�P�^�S
�P�^�S
�P�^�S
�P�^�S
�P�^�S
�P�^�S
�O �T�^�肾�Ǝv���܂����l�̂������L���C�ȉ����肻���Ȃ̂ł��肢���܂�
n(��1)������Ԃɂ����āA����n-1������ԏ�ɑ��݂��Ȃ�n+1�̓_������B����n������Ԃ�n+1�̓_���瓙�����ȓ_�����܂邱�Ƃ������B >>54
��Ԃӂ��̐����Q���������ʎg����������Ă���@�H
P0�`Pn�ƕ��ׂ�P(i-1)Pi�̐����Q���������ʂ�Ai�Ƃ���B
Ai�̖@���x�N�g����vi�Ƃ���Ai�̕�������vi�E(OP�x�N�g��)=ci�Ƃ����B
v0�`vn�������Ԃ̎�����n�����Ȃ炷�ׂĂ�vi�ƒ�������w���Ƃ��B
���̂Ƃ�w�E(OP(i-1)�x�N�g��)=w�E(OPi�x�N�g��)�����ׂĂ�i�ɂ��Č����邩��A���̒l��d�Ƃ���A���ׂĂ�Pi�͕���w�E(OP�x�N�g��)=d�Ɋ܂܂�邩�疵���B
����ĘA��������vi�E(OP�x�N�g��)=ci�͉������B >>54
�����A�m��܂���ł����c�I
�l�̂�������Y��ł���
���肪�Ƃ��������܂� �擪�ԗ����珇��
1����n�܂ł̔ԍ�������n���Ґ��̗�Ԃ�����
������n��2�ȏ�Ƃ���
�e�ԗ���ԐF�A�F�A���F�̂����ꂩ1�F�œh��Ƃ��A
�ׂ荇�����ԗ��̏��Ȃ��Ƃ�������ԐF�ƂȂ�悤��
�F�̓h����͉��ʂ肩
3 5 11 21 43 85 171 341 683 1365 2731 5461 10923 21845 43691
(2^(n+2)-(-1)^n)/3 384=8!!�@
53760=2(10!!)+12!!
8755200=8(12!!)+13(14!!)
1805690880=15(14!!)+12(16!!)+9(18!!)
471092428800=10(16!!)+15(18!!)+16(20!!)+5(22!!)
153043438141440=4(18!!)+2(20!!)+3(26!!)
60836834554675200=(20!!)+17(22!!)+15(24!!)+16(26!!)+12(28!!)+(30!!)
�K�����������Ă���`(�E�ցE)�m �\�[�X��
N�g�̃J�b�v��(���킹��2N�l)������ׂɉ����ɕ���
�ǂ̃J�b�v���ɂ��Ă��ގ��Ɣޏ����ׂ荇��Ȃ�
�m�������߂�
a(n)=a(n-1)+a(n-2)/((2n-1)(2n-3)),a(1)=0,a(2)=1/3
�̈�ʍ������߂̏��� �g�����v�̑�������
2�`10�܂ł̐������`���ꂽ�J�[�h���e�X�[�g��1�����ƁA
�W���[�J�[�̃J�[�h��24������
�S�Ă������Ė���ׂɐ蒼����12���̃J�[�h��ׂɈ������Ƃ�
����12���̃J�[�h�̂����W���[�J�[�ȊO�ɂ�������Ⴄ������
������Ă���m���͂����炩
Sum[choose(24,k)*choose(9,12-k)*4^(12-k), {k, 3, 12}]/(choose(60,12))
�o�́@7371811052/66636135475 �g�����v����ƈ��{����Ƀm�[�x���܂��I �W���[�J�[���������g�����v�T�Q���̒�����P����
�J�[�h���o���A�\�����Ȃ��Ŕ��̒��ɂ��܂���
�����āA�c��̃J�[�h���悭���Ă���
�R�������o�����Ƃ���A�R���Ƃ��_�C���ł�����
���̂Ƃ��A���̒��̃J�[�h���_�C���ł���m���͂����炩
�ŏ��ɔ��ɂ��܂��������P�^�S��
�������珙�X�Ɋm���������Ă䂫�A
�R�D����R���_�C�����o�������P�O�^�S�X
�R�D����P�R���_�C�����o���Ƃ��ɂO�ɂȂ�
��������ŕ\�����Ƃ��ł���
���̐���a��萔�A�R�D����n���̃_�C�����o��Ƃ���
�m0��a��124�n�C�m0��n��13�n�͈̔͂Ő����������
P(D)=((n-13)(a-4n-125))/(a(n-52)-7n^2+92n+6500)
P(D)=((n-13)(a+4n+1))/(a(n-52)+7n^2-216n-52) ��Q�Җ��\�鏑�p�C�Y������̃S�L�u���E�Q�\���\���鏑�_���}��c����`�N�\�܂݂�̕ė����E����
�S�L�u���c����`�̎q���͊�`�ė��m��L�`�K�C��`�q���ł��� ��a(n)=a(n-1)+a(n-2)/((2n-1)(2n-3)),a(1)=0,a(2)=1/3 �̈�ʍ�
a(n)=Hypergeometric1F1[-n;-2n;-2] ����̊�����ɍ�������
P1st
(6n^3+20n^2-n-27)(n-1)/24�@�i��j�c�c�@
(6n^4+14n^3-21n^2-26n+24)/24�@�i�����j�c�c�A
Q1st
(6n^2+10n-3)(n+1)(n-1)/24�@�i��j�c�c�B
(6n^2-2n-5)(n+2)n/24�@�i�����j�c�c�C
��m1 0 1 0 1 0 1 0 1 0 1 0 1 0�n�̂ݏo�͂������
((-1)^(n+1)+1)/2�@�c�c�D
�����m0 1 0 1 0 1 0 1 0 1 0 1 0 1�n�̂ݏo�͂������
((-1)^n+1)/2�@�c�c�E
�@x�D+�Ax�E
((6n^3+20n^2-n-27)(n-1)/24)(((-1)^(n+1)+1)/2)+((6n^4+14n^3-21n^2-26n+24)/24)(((-1)^n+1)/2)
P1st =�o12n^4+28n^3-42n^2-52n-3(-1)^n+51�p/48
�Bx�D+�Cx�E
((6n^2+10n-3)(n+1)(n-1)/24)(((-1)^(n+1)+1)/2)+((6n^2-2n-5)(n+2)n/24)(((-1)^n+1)/2)
Q1st =�o12n^4+20n^3-18n^2-20n-3(-1)^n+3�p/48 >>66
�قق�
���������g���ƃV���v���ɏ������ł��ˁ[ ����̍����^�����i�N���}�[�j
1�e1[a; b; z] = 1 + ��[k=1, ��] {a(a+1)����(a+k-1)/b(b+1)����(b+k-1)} z^k /k!
1�e1[-n; -2n; z] = {n!/(2n)!} ��[k=0, n] {(2n-k)!/(n-k)!k!} z^k, 4�ʂ��ΐF��2�ʂ��ԐF�̃T�C�R��������Ƃ���
���̃T�C�R����20��U���āA�ΐF(G)�ƐԐF(R)�̂ǂ��炪
�o�������L�^����
����3�̑I��������P��I�ԂƂ���
�������Ȃ����I�I������20�̋L�^�̂ǂ�����
��v�����25�h�����炦��
1.RGRRR
2.GRGRRR
3.GRRRRR
�I����1�͑I����2�ɓ����Ă���A�܂��A
���̑I���������Z���ɂ��S��炸�A
�팱�҂�65%�͑I����2��I��
25�h���̓q�����b�̏ゾ���̌`�̒����ł��A
���ʂɌ����ȍ��͌����Ȃ����� �X��27 #795 �̈�ʉ����g���C
�cM�}�X�A��N�}�X�̃t�B�[���h{(x,y)|x��{1,�c,N},y��{1,�c,M}}�̑��قȂ�2�}�X�ɕ��u���A
�c�D�挟��((1,1)���c��(1,N)��(2,1)���c)��P��
���D�挟��((1,1)���c��(M,1)��(1,2)���c)��Q�Ƃ�
��ɂ����ꂩ�̕���������ق��������Ƃ���Q�[��
��̒u�����p�^�[���̐�=MN(MN-1)/2�ɑ��āA
P,Q���ꂼ��̏��p�^�[���̐���P(M,N),Q(M,N)�Ƃ���
�ƌ����Ă��A�����Ȃ��ʉ��͓���̂ŁA�܂��͕Е��̃p�����[�^���Œ肵�Ă������v�Z���Ă݂�
n��0 (mod 2) �̂Ƃ� P(2,n) = Q(n,2) = (3nn-4n�@)/4, Q(2,n) = P(n,2) = (5nn-10n+4)/4
n��1 (mod 2) �̂Ƃ� P(2,n) = Q(n,2) = (3nn-4n+1)/4, Q(2,n) = P(n,2) = (5nn-10n+5)/4
n��0 (mod 6) �̂Ƃ� P(3,n) = Q(n,3) = (12nn-10n�@)/6, Q(3,n) = P(n,3) = (15nn-22n+ 6)/6
n��1 (mod 6) �̂Ƃ� P(3,n) = Q(n,3) = (12nn-13n+1)/6, Q(3,n) = P(n,3) = (15nn-25n+10)/6
n��2 (mod 6) �̂Ƃ� P(3,n) = Q(n,3) = (12nn-10n+2)/6, Q(3,n) = P(n,3) = (15nn-22n+ 8)/6
n��3 (mod 6) �̂Ƃ� P(3,n) = Q(n,3) = (12nn-13n-3)/6, Q(3,n) = P(n,3) = (15nn-25n+ 6)/6
n��4 (mod 6) �̂Ƃ� P(3,n) = Q(n,3) = (12nn-10n+4)/6, Q(3,n) = P(n,3) = (15nn-22n+10)/6
n��5 (mod 6) �̂Ƃ� P(3,n) = Q(n,3) = (12nn-13n-1)/6, Q(3,n) = P(n,3) = (15nn-25n+ 8)/6
�������Ă݂�Ƃ��ꂼ������������肻���B
���̋C�ɂȂ�Α������Ǝw�����̑g�ݍ��킹�ŏ�����̂�������Ȃ��B q��2�ȏ�̐����An��1�ȏ�̐����Ƃ���B
1�̙p����=e^(2��i/q)���g���āA
f_q(n)=(q-1)/2+��{k=1�`(q-1)}((��^k)^n * (��^k - 1)/(2 - ��^k - ��^(-k)))
�ŕ\������ f_q(n) �͂ǂ̂悤�Ȓl���Ƃ邩�H (3!!/3+0)/3!!=1/3
(5!!/3+0)/5!!=1/3
(7!!/3+1)/7!!=12/35
(9!!/3+14)/9!!=47/135
(11!!/3+190)/11!!=731/2079
(13!!/3+2799)/13!!=1772/5005
(15!!/3+45640)/15!!=20609/57915
(17!!/3+823724)/17!!=1119109/3132675
(19!!/3+16372071)/19!!=511144/1426425
(21!!/3+356123690)/21!!=75988111/211527855
����������������������������������������
1 14 190 2799 45640 823724 16372071 356123690
1
14
190
2799
45640
823724
16372071
356123690
a(n)=((2n-1)!!/3+��)/(2n-1)!!����
���������������Ă���`(�E�ցE)�m >>74
����ȑ������͑��݂��܂���
���������X���Ⴂ�ł����A���̃X���ł����������A�����Ă���r�炵�̂悤�Ȃ̂ŃX���[�����ł��� >>75
�������������݂��Ȃ��ؖ������Ă���`(�E�ցE)�m https://www.gaiki-seijouki.jp/column1/368/
�L�`�K�C�j�z���U�������v�ł����d���L�^����M�����Ȃ��s�����ƃj�z���U�����ł��� >>71 �͎������ŏ����Ƃ����Ȃ�
P(2,n) = Q(n,2) = (3/4)n^2-n+(1/2)-(1/2)(-1)^n
Q(2,n) = P(n,2) = (5/4)n^2-(5/2)n+(9/2)-(1/2)(-1)^n
P(3,n) = Q(n,3) = 2n^2-(23/12)n+(1/12)+(1/4)(n+1)(-1)^n-(1/3)cos(2��n/3)+(��3/9)sin(2��n/3)
Q(3,n) = P(n,3) = (5/2)n^2-(47/12)n+(4/3)+(1/4)n(-1)^n-(1/3)cos(2��n/3)+(��3/9)sin(2��n/3) >>73
����́@2 -��^k -��^(-k) = - (��^k -1)^2 /(��^k),
k �� q-k ��g�ɂ��Čv�Z�����
f_q(n) = (q-1)/2 -(1/2)��[k=1,q-1] {��^(kn)(��^k -1) + ��^(-kn)(��^(-k) -1)}(��^k) /(��^k -1)^2
�@= (q-1)/2 - (1/2)��[k=1,q-1] {��^(k(n+1))(��^k -1) - ��^(-kn)(��^k -1)} /(��^k -1)^2
�@= (q-1)/2 - (1/2)��[k=1,q-1] {��^(k(n+1)) - ��^(-kn)} /(��^k -1)
�@= (q-1)/2 - (1/2)��[k=1,q-1] ��[j=-n,n] ��^(kj)
�Ƃ���ŁA
��[k=1,q-1] (��^m)^k
�@�@�@=�@q-1�@�@�@(��^m=1) (m��q�̔{���܂���0)
�@�@�@= -1�@�@�@�@(��^m��1)
-n ���� n �܂ł̐����̂����Aq�̔{���� (0���܂߂�) 2[n/q]+1 ������
f_q(n) = n - q[n/q]�@= (n��q�Ŋ������]��) �y�������I�������B�E���܂Ƃ������点�ƍߎ҂̎����ƏZ�������J�z
�@����E�疾�i�����s������˂U�|�Q�R�|�P�U�j
���������B�E�����点���܂Ƃ��ƍߎ҂̃��[�_�[�I���݁^�ƍߑg�D�̈���ŗl�X�Ȕƍߍs�ׂɎ����߂Ă���
�@��w���ŏX���قǂ̊w���R���v���b�N�X�̉�^���ϑԂŐH�����D�Ƃł���^�X���ŕs�C���Ȋ���������I�ł���
�A�F���ρi�����s������˂U�|�Q�R�|�Q�P�n�C�c�j���[�˂Q�O�Q�j
���F���ŏX�������Ă���X�����؉F���ρ^��w���Ől�Ԑ����X�������łȂ�����̐l���ł�����x�Ə��ƃZ�b�N�X�����邱�Ƃ��ł��Ȃ��قǗe�p���X���ł���
�B�F�썂�u�i�����s������˂U�|�Q�R�|�Q�P�n�C�c�j���[�˂P�O�R�j
���F�썂�u��youtube�̎���������ɒZ���Ԃɉ��S���玞�ɂ͉�����Ƒ��₵���荂�]���E��]���̐�������l�ł��������₵���茸�炵����Ȃǂ�
�@youtube�̐���ȉ^�c���������M�����Ȃ킹��悤�ȔƍߓI�Ɩ��W�Q�s�ׂ��s���Ă��܂�
���F�썂�u�͌��݁A�����ی��s���Ɏ��Ă���ƍߎ҂ł��^�ǂ�ǂ�x�@������ɒʕ�E�������Ă���Ă�������
�y�ʕ��z
�������敟���������i�������ہj
���P�Q�S�|�W�T�T�T
�����s�����旧�T�|�P�R�|�P
���O�R�|�R�U�X�T�|�P�P�P�P
�C�����i�����s������˂U�|�Q�R�|�P�X�j
����w��E���V���F�����k�k�@������w��E���V���E�����k�k�͍��w���ƌn������I�ɑ������Ă��遙��
�@�����k�k�̓R���v���b�N�X�̉�łƂɂ�����Ӓn�������^�X���Ȍ`���Ō����点���y����ł���܂��Ɉ����̂悤�ȘV�k�ł���
�D���Y�E���c�i�����s������˂U�|�Q�U�|�U�j
���ƍߎ�d�҈���E�疾�̎q���^�����t�炦���Ɍ����Ȃ�ɂȂ��Ă�������̃t���^�e�q���ꑰ������Ē�\
�E�����i�����s������˂U�|�Q�R�|�Q�R�j
��������͕v�w�̖�̉c�T�b����H�����ٔ��v���C�̍Œ��ɍ����e���ɂǂ������ɕ���Ď���i�߂��ĎE���ꂻ���ɂȂ������Ƃ�����
�F���؋`���i�����s������˂U�|�Q�R�|�Q�O�j �����j���ɂȂ�ƕ����X�ɍs���Ă��� ��n=3�̂Ƃ��A10/49�ƂȂ����125��ލ쐬
Table[((n-13)(a-4n-125))/(a(n-52)-7n^2+92n+6500),{a,0,124},{n,3,3}]
��n=0�̂Ƃ��͂��ׂ�1/4
Table[((n-13)(a-4n-125))/(a(n-52)-7n^2+92n+6500),{a,0,124},{n,0,0}]
��n=13�̂Ƃ��͂��ׂ�0
Table[((n-13)(a-4n-125))/(a(n-52)-7n^2+92n+6500),{a,0,124},{n,13,13}]
318 ���O�F�P�R�Q�l�ڂ̑f������[sage] ���e���F2019/03/07(��) 18:00:45.97 ID:TVoNUVmm
�����ʑ吔�̐��E�ł�10/49���o�͂���
Table[((n-13)(a-4n-125))/(a(n-52)-7n^2+92n+6500),{a,10^68,10^68+150},{n,3,3}] �w����5����܂�
3���炤�ƑS���ʼn��ɂȂ�܂����x
2
8���낪�{�P
�ꕔ���L�҂��ς�邾����5�̂܂܂���ˁH
�N������Ⴄ�������ĂȂ�
�l�Y�~���N�b�L�[��3���炤�̂�������Ȃ�
�������������������̂������� 20�܂ł̎��R�����d����������10���ɕ���a[1], a[2], a[3], ...a[10]�Ab[1], b[2], b[3], ...b[10]�Ƃ���B������
S = ��(k=1��10)a[k]b[k] = a[1]b[1]+a[2]b[2]+a[3]b[3]+�c�c+a[10]b[10]
�Ƃ���B�F�X�ȕ������ɂ���S���l�����Ƃ��AS�̍ő�l�ƍŏ��l�A�y�т��̎��̕������͂ǂ̂悤�Ȃ��̂�
����Ɉ�ʂ�2n�̐�(n�͎��R��)��n����2�g�ɕ����āA
a[1]�Aa[2]�Aa[3]�A�c�c ����� b[1]�Ab[2]�Ab[3]�A�c�c
�Ƃ�
S = ��(k=1��n)a[k]b[k] = a[1]b[1]+a[2]b[2]+a[3]b[3]+�c�ca[n]b[n]
�Ƃ���B�F�X�ȕ������ɂ���S���l�����Ƃ��AS�̍ő�l�ƍŏ��l�A�y�т��̎��̕������͂ǂ̂悤�Ȃ��̂� >>85
(19,20)�̃y�A���Ȃ���ő�ł͂Ȃ��B
�� (a,19),(b,20)�̑g�ݍ��킹�̎�
19�E20 + a�Eb - 19�Ea - 20�Eb = (20 - a)(19-b) > 0
�ȉ����l�ɂ��čő�l��
1�E2 + 3�E4 + �d + 19�E20 = 1430
(1,20)�̃y�A���Ȃ���ŏ��ł͂Ȃ��B
�� (a,1),(b,20)�̑g�ݍ��킹�̎�
1�Ea + 20�Eb - a�Eb - 1�E20 = (20 - a)(b - 1) > 0
�ȉ����l�ɂ��čŏ��l��
1�E20 + 2�E19 + �d + 10�E11 = 770 >>86
�����ł�
�������莦���̂͂��ʓ|���Ǝv���܂���������Ȃ��ƂȂ������ł����� ���̐}��, ��FJG�͐��O�p�`, �l�p�`FBCE�͐����`�ł���. ��KJG�̑傫�������߂�.
https://i.imgur.com/h43Hkcg.jpg >>88
K����BC�ɐ����������Č�_��P�Ƃ���
JB=(1/��3)BF
BP=PK=(1/(1+��3))BF
BP/JB=PK/JB=((��3)/(1+��3))
tan��KJG=PK/(JB+BP)
=((��3)/((1+��3)+(��3)))
=(6-��3)/11
��KJG��21.2��
���ꂢ�Ȓl�ɂ͂Ȃ��� �o��K�C�W���K���ɊG�`���ďo���Ă���Ȃ��瓖����O �����͏o��X�������玩����o���͖̂����B
����̂̓`�F�b�N���Â������ˁB
�v�Z�@�g����Ȃ猟�Z���Ă���ɂ���悩�����̂ɁB ���܂茩�Ȃ��A�A�v���[�`�@���v�������̂ŁA���e
(1)�@��[k=1,n]cot^2(k��/(2n+1)) = n(2n-1)/3�@������
(2)�@����g���āAn(2n-1)/(2n+1)^2 < (3/��^2)��[k=1,n]1/k^2 < 2n(n+1)/(2n+1)^2�@������ ����������
����������
����������
����������
��������������
��������������
��������������
��������������
��������������
�������������� > sapply(1:20,function(k) treasure0(4,5,k))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
�Z���L�� 9 84 463 1776 5076 11249 19797 28057 32243 30095 22749
�����L�� 9 83 453 1753 5075 11353 20057 28400 32528 30250 22803
���� 2 23 224 1316 5353 16158 37666 69513 103189 124411 122408
[,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20]
�Z���L�� 13820 6656 2486 695 137 17 1 0 0
�����L�� 13831 6657 2486 695 137 17 1 0 0
���� 98319 64207 33788 14114 4571 1106 188 20 1
�S�~�T�̏ꍇ
��F�P�@����
��F�Q�`�T�@�Z���L��
��F�U�`�P�R�@�����L��
��F�P�S�`�Q�O�@����
(17!/(18-k)!)/(k-1)!+(15!/(16-k)!)/(k-1)!+(13!/(14-k)!)/(k-1)!+(11!/(12-k)!)/(k-1)!+(10!/(11-k)!)/(k-1)!+(8!/(9-k)!)/(k-1)!+(5!/(6-k)!)/(k-1)!+(4!/(5-k)!)/(k-1)!,k=5 >>95
(2)�𗘗p�������(2)=��^2/6��������H 8��83�ɕ���K�v
Table[(17!/(18-k)!)/(k-1)!+(15!/(16-k)!)/(k-1)!+(13!/(14-k)!)/(k-1)!+(11!/(12-k)!)/(k-1)!+(10!/(11-k)!)/(k-1)!+(8!/(9-k)!)/(k-1)!+(5!/(6-k)!)/(k-1)!+(4!/(5-k)!)/(k-1)!,{k,1,20}] �m���̂̓��H��̓����ł������ȁB���N���������ȁH >>98
�ł���
>>100
(1)�̓��o�͍���Ǝv�����ǁA�������ɂȂ��Ă����Ƃ́D�D�Dorz >>101
����(1)�̕s�������������ɂȂ��Ă���Ȃ���B
���H��̂̓`�F�r�V�F�t�̑������g����
��(sin k��/2n)^(-2)
�����߂�������B1990�N�������B�������H�v����ƃ�(2)���v�Z�ł���B
�Ȃ��������N���\��Ȃ����� �g������茤���@90���H��h �Ō�������Əo�Ă���B
���Ȃ݂ɂقړ������e��PDF��_��̐搶������Ă��L��������B ���ꂻ��B��������撣��ƃ�(2)���v�Z�ł���B >>95
���̃�(2)�̉�@�̏o�T��1953�N�̃��V�A��̘_��
http://mi.mathnet.ru/eng/umn8256
�ŁAwikipedia�ɂ���1960�N��ɂ͍L���m����悤�ɂȂ��������ł��B ���������Z���w�̕����ɍڂ��ĂȂ������H >>106
��g�̌����W���ς�ς�߂����Ăā@�����[�������������܂����@>>95�@��(1)�ł��B
�ǂ�����Ď����̂��l���Ă���ƁA�o�[�[�����Ɏg���邱�ƂɋC�Â��܂����B
�����̐l�ɂ��A�ʔ����Ǝv���Ă���������Ǝv���A�����ɓ��e���܂������A
�L���m���Ă����@�������悤�ł��ˁB�Ǖ��ł����B
��肪�Ƃ��������܂��B Table[(17!/(18-k)!)/(k-1)!+(15!/(16-k)!)/(k-1)!+(13!/(14-k)!)/(k-1)!+(12!/(13-k)!)/(k-1)!+(8!/(9-k)!)/(k-1)!+(7!/(8-k)!)/(k-1)!+(6!/(7-k)!)/(k-1)!+(3!/(4-k)!)/(k-1)!+(2!/(3-k)!)/(k-1)!,{k,1,20}]
�����L��
���S��v��>>97 Table[(17!/(18-k)!)/(k-1)!+(15!/(16-k)!)/(k-1)!+(13!/(14-k)!)/(k-1)!+(11!/(12-k)!)/(k-1)!+(10!/(11-k)!)/(k-1)!+(8!/(9-k)!)/(k-1)!+(5!/(6-k)!)/(k-1)!+(4!/(5-k)!)/(k-1)!+(1!/(2-k)!)/(k-1)!,{k,1,20}]
�Z���L����
{9, 84, 463, 1776, 5076, 11249, 19797, 28057, 32243, 30095,
9 84 463 1776 5076 11249 19797 28057 32243 30095
22749, 13820, 6656, 2486, 695, 137, 17, 1, 0, 0}
22749 13820 6656 2486 695 137 17 1 0 0
���S��v>>97
�����>>99 > sapply(1:12,function(k) treasure0(3,4,k))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
�Z���L�� 5 26 73 133 167 148 91 37 9 1 0 0
�����L�� 5 27 76 140 176 153 92 37 9 1 0 0
���� 2 13 71 222 449 623 609 421 202 64 12 1
��������
��������
��������
Table[(9!/(10-k)!)/(k-1)!+(7!/(8-k)!)/(k-1)!+(6!/(7-k)!)/(k-1)!+(3!/(4-k)!)/(k-1)!+(2!/(3-k)!)/(k-1)!,{k,1,12}]
�����L����
Table[(9!/(10-k)!)/(k-1)!+(7!/(8-k)!)/(k-1)!+(5!/(6-k)!)/(k-1)!+(4!/(5-k)!)/(k-1)!+(1!/(2-k)!)/(k-1)!,{k,1,12}]
�Z���L����
���S12�}�X���S��v
Table[(12!/(12-k)!)/k!-(2((9!/(10-k)!)/(k-1)!+(7!/(8-k)!)/(k-1)!)+(6!/(7-k)!)/(k-1)!+(5!/(6-k)!)/(k-1)!+(4!/(5-k)!)/(k-1)!+(3!/(4-k)!)/(k-1)!+(2!/(3-k)!)/(k-1)!+(1!/(2-k)!)/(k-1)!),{k,1,12}]
������ �}�`�̖�肾�����炱��Ȃ̂͂ǂ���
Q. xy���ʏ�� x^2+y^2=1+|x|y ��}������ �@|x|^2 - |x|y + yy = 1,
�͍��E�Ώ�
����45߉�
�@(x+y)/��2 = u,�@(x-y)/��2 = v,
�Ƃ����B
x��0 �̂Ƃ�
�@1 = xx -xy +yy = (1/2)uu + (3/2)vv,
x��0 �̂Ƃ�
�@1 = xx +xy +yy = (3/2)uu + (1/2)vv,
�ȉ~��2�������ē\�荇�킹�����́B�n�[�g�`�H ��������1�������Ă݂�B
���R�����͂Ȃ����A�������ӌ����o���玩���̉��o�����Ǝv���B
���Ȃ��͐V�����̃C�j�V����(�A���t�@�x�b�g1����)�Ă�q���ɎQ�����邱�ƂɂȂ����B
���̏����̂Ƃ��A���Ȃ��͂ǂ̂悤�ɓq�����s�����H
�E�V�����̃C�j�V�����Ă�Ί|������3�{���A�O���Ί|�����͉�������B
�E�����̃C�j�V�����ɓq���邱�Ƃ��\�ŁA�����̓q�����͈قȂ��Ă��悢�B
�E���̎��̌��������\����鎞�ɂ����l�ȓq�����J�Â���邱�Ƃ��\�z�����B �v�X�ɓ��e�B�i�l�I�Ɂj�������Ȃ̂Œ���
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
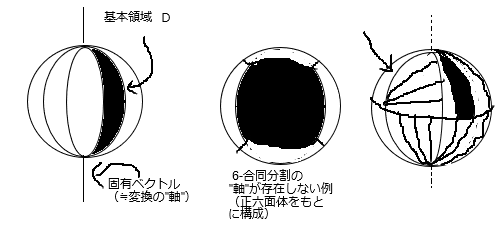
���̎咣�͐��藧���F����S^2�i��R^3�j��
�ES^2 = ��_(n=1�`5) f_n(D)
(������ D �� S^2 �̃��x�[�O���ȕ����W���Af_i �͒��s�Q�̌��ŕ\�����P���ϊ�)
�En��m �̎� f_n(D)��f_m(D) �́i�������l�̂Ƃ��Ă�S^2�́j��W��
�����悤�ɍ����ȂT�̃p�[�c f_n(D) (n=1,�c,5) ��"����"���鎞�A
f_n��(f_m)^(-1) (n��m)
�ƕ\�����S�Ă̍����ϊ��ɋ��ʂ�����ŗL�x�N�g�������݂���B
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
�T�����łȂ��A�Ⴆ��4,6,8,12,20�ł���ΐ����ʑ̂𗘗p���Ď����łȂ����������������A
�����H�v�����60��S�Ă̂W�̔{�����\�B
�i���������������ł���Ƃ́A��̂悤�ȏݒ�ŋ��ʂ�����ŗL�x�N�g�����u���݂���v���Ƃ������B
�܂��̎咣�́u���ʂ�5-���������͑S�Ď����ł���v�ƌ�����������j >>119 �̕⑫
�܂�Ƃ���A���ʂ̒��Łu��{�̈�v�Ȃ���̂��߂�
����ƍ����Ȑ}�`�����������ʂɃ����Ȃ��_�u���Ȃ��\�荇�킹��̂����������B
n���ǂ�Ȑ��̐����ł����̐}�݂����ɂ�����܂�����n-�����������ł�����ǁA
����͂ǂ̗̈悩��ʂ̂ǂ̗̈�Ɉڂ��ɂ����鋤�ʂ̒�����"��"�ɂ��ē������Ηǂ����Ƃ���A
�����͂���قǖʔ��݂̂Ȃ����������Ƃ��āu�����v�Ȃ��̂ƒ�߂��B
�^��6-���������͋��ʂ�"��"�ɂ�������̂����݂��Ȃ����ߔ��B
�E�͔���32-���������B�_�������ɂȂ肻�������ǁA
���Ŏ�����������̕����̂����ŋ��ʂ̎��ƂȂ�Ȃ��B���̂W�̔{�������l�B
�i�������ɂႮ�ɂ�ł��܂�B�}�E�X�ŊG�`���̂ނ����c�j
 >>120
>>120
�A���łȂ��Ƃ��\��Ȃ��B�ł����x�[�O���ȏW���ł���Ή��ł��n�j
�i���x�[�O�����́A�ǂ����Ă������郌�x���̂���₾�Ԃ���W���ł��܂�����悤�ɁA�Ƃ����Ӑ}�j > sapply(1:20,function(k) treasure0(4,5,k))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
�Z���L�� 9 84 463 1776 5076 11249 19797 28057 32243 30095 22749
�����L�� 9 83 453 1753 5075 11353 20057 28400 32528 30250 22803
���� 2 23 224 1316 5353 16158 37666 69513 103189 124411 122408
[,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20]
�Z���L�� 13820 6656 2486 695 137 17 1 0 0
�����L�� 13831 6657 2486 695 137 17 1 0 0
���� 98319 64207 33788 14114 4571 1106 188 20 1
4�~5�̏ꍇ
��F1�@����
��F2�`5�@�Z���L��
��F6�`13�@�����L��
��F14�`20�@����
����������
����������
����������
����������
�Z���L����
Table[choose(17,k-1)+choose(15,k-1)+choose(13,k-1)+choose(11,k-1)+choose(10,k-1)+choose(8,k-1)+choose(5,k-1)+choose(4,k-1)+choose(1,k-1),{k,1,20}]
�����L����
Table[choose(17,k-1)+choose(15,k-1)+choose(13,k-1)+choose(12,k-1)+choose(8,k-1)+choose(7,k-1)+choose(6,k-1)+choose(3,k-1)+choose(2,k-1),{k,1,20}]
������
Table[choose(19,k-1)+choose(17,k-2)+choose(15,k-2)+choose(13,k-2)+choose(8,k-2)+choose(1,k),{k,1,20}] >>119 ���m��I�ɉ��������̂ŕB�q���g�������ƁA��͂萳20�ʑ̂𗘗p������̂ł����B
���Ȃ݂ɑS�Ă̋�����R�ł��\�B�V�ȏ�̊�͂܂��ړr�������Ă��Ȃ��̂ł悯���������c �A������B
>>124 ���̏ꍇ�m��I�ɂƂ����̂́A�咣�̔��Ⴊ���������Ƃ������Ƃł�
�i�����łȂ�5-������������������ȂƊ��҂��Ȃ��璲�ׂĂ������̂ł��c�j ������5�̏ꍇ��(�A����D�ɂ��)�������݂͂���
2n�̏ꍇ�́A����n�������炳��ɐԓ��ɂ�镪�����l���������� (1)���̏������� �L���� s,t ��������
�E0 �� t �� 1/��2
�E61/80 �� s
�Es^2 = 2t^2-2t+1
(2)���̏������� �ʑ��p�` ��������B
�E���ׂĂ̒��_�́A�P�ʉ~�̎���܂��͓����ɂ���A�����W�͗L����
�E���ׂĂ̕Ӓ��́A�L����
�E������ 31/5 �ȏ� >>126
�����A�A���Ȃ̌������̂��@������
2n�̏ꍇ�A�������̐}�̂��Ƃ������Ă�̂Ȃ�c�O�B����͂ǂ��ϊ����Ă����͕s�ς����������Ȃ���
�i���ʂ̌ŗL�x�N�g�����������ŗǂ�����A�ŗL�l�܂ňꏏ����Ȃ��Ă��ǂ��B�Ⴆ�A
�@����A�ւ̕ϊ��ł͎��͌ŗL�l1�̌ŗL�x�N�g���A�@����B�ւ̕ϊ��ł͎��͌ŗL�l-1�̌ŗL�x�N�g���ƂȂ�j
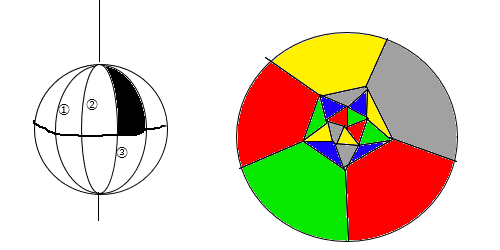
�ꉞ����5-���������̂ЂƂ̗���E�}�ɋ����Ă����܂��B
�킩��ɂ����ł�������\�ʑ̂𗧑̎ˉe�ŕ��ʂɗ��Ƃ����݂����ȃm���ŕ`���Ă܂��B
�O�~�̉~���͖{���͈�_��\���A�e�����F�̗̈�S�̂���̃p�[�c�ɂȂ��Ă܂��B
�{���Ȑ��ŕ`�����ׂ��Ƃ��������܂����A�ӂ����L���Ă�A�_�������L���Ă铙�̈ʒu�W�͕ۂ��Ă�̂�
��������{���̌`���z�����Ă������������orz
 >>128
>>128
�A���B�̕ϊ����A�Q�̗̈�̋��L����1�_�̕����Ɏ����Ƃ��ĉ�]������A�Ƃ���悢�̂ł́H >>129
���ۂ���͌ŗL�x�N�g���̂P�Ȃ��ǁA�G�ɕ`����Ă钼�����ŗL�x�N�g���ł��邱�Ƃɕς��͂Ȃ����
����ŁA�����̒�`���u�`�`���ʂ�����ŗL�x�N�g�������݂���v������A���̌ŗL�x�N�g���̑��݂Ɋւ�炸����͎����ɂȂ��
"��"�ƕ\������Ɗe�ϊ��ň�����Ȃ��悤�Ɏv���邯�ǁi����͂�����̌��t�I�т��ǂ��Ȃ������Ǝv���A���܂Ȃ��j
���̐}�̏ꍇ�A���y���Ă������������x�����Ƃ�A�A����B�ւ̕ϊ��� f(x,y,z)=(x,-y,-z) �ƕ\���邩��
(1,0,0) �̑��� (0,cos��,sin��) �Ƃ���������"��"�������Ƃ��킩��i�����Đ}�̒����̕��������̒��Ɋ܂܂��j >>130
�������⌳�̒�`�͌ŗL�x�N�g�������L���Ȃ����Ęb�ł�����
�l���Ă邤���Ɏ��O���Ă܂����A���h >>127 (1)
�^����
�@s^2 = t^2 + (1-t)^2
�s�^�S���X��������A���R�� a, b �ɂ��
�@s�@= (aa+bb)/N,
�@t�@= (aa-bb)/N,
�@1-t = 2ab/N,
�ƕ\�킹��B
�@N = aa+2ab-bb,
s �� 61/80 ���
�@0.41421356 = ��2 -1 < a/b < (61-��1042)/19 = 1.51157764�@�܂��́@4.90947499 = (61+��1042)/19 < a/b,
0 �� t < 1/��2 ���
�@1 �� a/b < {1+��(4-2��2)}/(��2 -1) = 5.02733952
�������
�@1 �� a/b < (61-��1042)/19 = 1.51157764
�Ȃ�Ώ\���B
��) a=b, s=1, t=0, >>132
�@�����Ͽ
s �� 61/80 ���
�@0.41421356 = ��2 - 1 < a/b < (19+��4082)/61 = 1.35886117
0 �� t < 1/��2 ���
�@1 �� a/b < 1 + ��2 + ��(4+2��2) = 5.02733949
�����̋��ʕ�����
�@1 �� a/b < (19+��4082)/61 = 1.35886117 >>127 �̏o��҂ł��B
�܂��ŏ��� (1) �̑������@�u0 �� t �� 1/��2�v ���u1/2 �� t �� 1/��2 �v�ɕύX�����Ă��������B
����́A(2)�ɂ�����A�u�ʑ��p�`�v���u���p�`�v�Ƃ��Ă��܂��悤�ȏd��ȃ~�X�ł����B�\����܂���B
�ɂ�������炸�A132����ɂ́A�u1/2 �� t �� 1/��2 �v�ƕύX���ꂽ�Ƃ��Ă��A�Ή��\�ȂقǁA
���J�ɉ����Ă��������A���ӂ������܂��B
s,t�̕\����A4.90947499=(61+��1042)/19 < a/b�@< {1+��(4-2��2)}/(��2 -1)=5.02733952
�Ȃǂ���A�\���߂�����e�ł��B
a:b=5:1���̗p����ƁA���R�ƁA(s,t)=(13/17,12/17)�@�������܂�����B
���łɂ��C�Â����Ƃ͎v���܂����A���̖��쐬�̂��������́A�L���ȓ������u��>3.05���ؖ�����v�ł��B
61/80�Ƃ��������́A�������玝���Ă������̂ł��B >>127
���傤���˂����� (2) ������������
�@A (1, 0)
�@B (1 - 8nn/(nn+1)^2, 4n(nn-1)/(nn+1)^2)
�@C (c, c)
�Ƃ����B
�������@c = {21(n^4-6nn+1) + 80n(nn-1)}/{41(nn+1)^2} < 1/��2,
n��6 �̂Ƃ���16�p�`�i�� 1/8�j�ƂȂ�B
AB �� ��2n�F�c(nn-1) �̒��p���̎Εӂ䂦
�@AB = 4n/(nn+1),
BC �� ��20�F�c21 �̒��p���̎Εӂ䂦
�@BC = (29/41){1 - 4n(nn+2n-1)/(nn+1)^2},
����L = 8 (AB+BC),
�EL �� 31/5 �ȏ�ƂȂ�̂� n=7,8,9 �̏ꍇ�B
n=6,�@L = 8 (0.64864865 + 0.12451674) = 6.185323095
n=7,�@L = 8 (0.56000000 + 0.21615610) = 6.20924878
n=8,�@L = 8 (0.49230769 + 0.28409872) = 6.21125126
n=9,�@L = 8 (0.43902439 + 0.33619651) = 6.20176724
n=10, L = 8 (0.39603960 + 0.37726813) = 6.18646187 �����l�ł����B���̖��͐������ƂƂ炦�ĕ��������O�����Ƃ����ɉ������Ƃ���ƃh�c�{�ɂ͂܂�Ǝv���܂��B
����̊p�x�����A�s�^�S���X�O�p�`�����炩���ߒT���o���A�ړI�̑��p�`�̈�ӂɍ����悤��
�k�����A���W�ɓ��Ă͂߂Ă����Ό������܂��B�ȉ��A�p�ӂ��Ă������ł��B
11sin(��/11)=3.099...�A12sin(��/12)=3.105�Ȃ̂ŁA�ӂ̐���12�ȏ�łȂ����6.2���Ȃ����Ƃ�����܂��B
�����ŁA���ی����ɁAA(a,a)�AB(b,c)�AC(c,b)�@���l���A�c��͑Ώ̃R�s�[���Ăł�������12�p�`���l���܂��B
���x�A���v��15�x�X�����Ƃ��A�����̂���ʒu�_�Ƃ���l�Ȕz�u�̎d���ł��B
���̏ꍇ�A�K�v�Ƃ���s�^�S���X�O�p�`�́A�Εӂ̊p�x��60�x�̂��̂ł��B1:��3:2�̔�̎O�p�`�ł����A
����ɋ߂����̂Ƃ��āA120:209:241�@���̗p���邱�ƂƂ��܂��BA(a,a)���A��̂悤�Ȕz�u�̐��\��p�`��
�꒸�_���Ƃ�����A��ӂ̒�����(��3-1)a�ƂȂ�܂��B��3-1=0.7320...�ɋ߂��l�Ƃ���11/15=0.7333...���̗p����ƁA
b=a+(11a/15)*(120/241)=329a/241�A�@c=a-(11a/15)*(209/241)=1316a/3615
���̏ꍇ�S���́A8*(11a/15+1316a/3615)=31736a/3615�@�ŁA(��2)a�Ŋ����6.207673�ƂȂ�A
12�p�`��p�����̂ł����A���肬�薞���ł������Ȃ��Ƃ�����܂��B
a�Ƃ��āA241*3615/Floor[241*3615*sqrt(2)+1]=58081/82139�@���g����
A(58081/82139,58081/82139)�AB(79289/82139,317156/1232085)�AC(317156/1232085,79289/82139)
�ق��ɂ��A�O��ނ̃s�^�S���X�O�p�`��p���āA
X0=(1,0)�AX1=X0+(3/7)*(-9/41,40/41)�AX2=X1+(9/20)*(-204/325,253/325)�AX3=X2+(18/37)*(-1161/1289,560/1289)
�Œ�܂�14�p�`�Ȃǂ�����܂��B >>135 ����ĕς��Ă݂��B
�@A (1,0)
�@B (1 - 8nn/(nn+1)^2, 4n(nn-1)/(nn+1)^2)
�@C' (c', c')
�Ƃ����B
������ c' = (4/7){1 + n(n-3)(3n+1)/(nn+1)^2},
n��6 �̂Ƃ���16�p�`�i�� 1/8)�ƂȂ�B
c' < 1/��2 = 0.70710678 ��� n��8.
AB�� ��2n�F�c(nn-1) �̒��p���̎Εӂ䂦
�@AB = 4n/(nn+1),
BC'�� ��3�F�c4 �̒��p���̎Εӂ䂦
�@BC' = (5/7){1 - 4n(nn+2n-1)/(nn+1)^2},
����L = 8 (AB+BC),
�EL �� 31/5 �ȏ�ƂȂ�̂� n=8,9,10,11 �̏ꍇ�B
n=7, L = 8 (0.56000000 + 0.21828571) = 6.22628571, c' = 0.71222857�@(���i)
n=8,�@L = 8 (0.49230769 + 0.28689772) = 6.23364328, c' = 0.70667794
n=9, L = 8 (0.43902439 + 0.33950880) = 6.22826549, c' = 0.69992352
n=10, L = 8 (0.39603960 + 0.38098506) = 6.21619729, c' = 0.69298528
n=11, L = 8 (0.36065574 + 0.41444312) = 6.20079088, c' = 0.68629785
n=12, L = 8 (0.33103448 + 0.44195685) = 6.18393070, c' = 0.68003397 >>136
�Ȃ�قǁB
(1,0) (0,1) ��ʂ��Ȃ���� 12�p�`�ʼn\�ł�����ȁB
(1,0) (b,c) (c,b) (0,1) ��12�p�`�́A�����̕Ӓ��� |b-c|��2 �Ȃ̂ő��A�E�g�ł�����B
�܂�
�@A (1,0)
�@B (1 - 8nn/(nn+1)^2, 4n(nn-1)/(nn+1)^2)
�@D (4m(mm-1)/(mm+1)^2, 1 - 8mm/(mm+1)^2)
�@E (0,1)
��12�p�`��
�@BD = {(mn-m-n-1)^2 - 2(m+n)^2}/[(mm+1)(nn+1)]�E��2
�ŃA�E�g�ł�����B >>136
BA = AC = 638891/1232085 = 0.51854458
B~B = CC~ = 2�(317156/1232085) = 0.51482812
L = 4 (BA+AC+CC~) = 7648376/1232085 = 6.20766911
�m���ɉ\�ł�����B >>137
���钸�_����A�L��������(x���W�ψʁAy���W�ψʁA�������ׂĂ��L����)�����_��T�������Ȃ�A
�ȒP�ł��B�ǂ�Ȃ��̂ł������̂ŁA�s�^�S���X�O�p�`�������Ă�������̂ł��B�������k�ڂ�
�L�����{�ł�������Ύ��R�ł��B����Ύ��R�[���� >>136 �ŋL������͗����Ƃ����̕��j�ɂ����̂ł��B
�������A(t,t)�^�̒��_����������ɗL�������������Ȃ���Ȃ�Ȃ��ƂȂ�A��ςł��B
�������ɂ̂ݓ������܂����A����ΌŒ�[���ł��B���͂��̕��j�͖ʓ|�������Ǝv���A�[���炠����߂�
���܂������A>>137�@���ł́A������s���Ă��܂��B�悭������ꂽ�ƁA���V���Ă܂��B
���ۂɃv���b�g���Ă݂܂������A���̕ω��ɂ���āA���_�̕��z�����\�ω����܂��ˁB
�ʏ��������Ȃ����̂�A�P�ʉ~�̊O�ɏo����̂�����܂������A���͈͓̔���n�ɑ��A
���������܂��B
n�͐����Ɍ���܂���B�L������ok�ł��ˁB���炵�����Ǝv���܂��B >>127
���̎�|�ɓY������Ȃ����������Ljꉞ�B���R�� n �ɑ���
a = 4n^4+8n^3-4n-1 = (2n^2-1)(2n^2+4n+1),
b = 8n^3+12n^2+4n = 4n(n+1)(2n+1),
c = 4n^4+8n^3+8n^2+4n+1 = (2n^2+2n+1)^2,
d = 8n^3+12n^2+8n+2 = 2(2n+1)(2n^2+2n+1)
�ƒ�߂� ��=(a+bi)/c �Ƃ����A|��|=1, |1-��|=d/c �ƗL�����ɂȂ��Ă���邩��A
���܂����Ǝ��R�� m ���߂ĕ��f���ʏ�̓_�W�� {a^n}_(n=-m,�c,m) �����Ɍ��ׂΎ����ȊO�̏�����S�Ė������B
�_�W�������Ɍ���Łi��^m �� ��^(-m) ������Łj�ʑ��p�`���ł��邽�߂� m ���������ׂ������͂Ƃ����ƁA
��^1 ���� ��^m �܂ł��S�ď㔼���ʂɂ��邱�Ƃ̂݁B�i���̂��� m �̑傫���͂������� ��n/2 ���x�ɐ��������j
n ���\���傫���Ƃ���ꂾ���ӂ��~�ɋ߂Â�����A������ 31/5(<��) ����悤�� n ���Ƃ邱�Ƃ͉\�B
�c�����Ď��ۂɂƂ��Ή����Ȃ��ǁA�v�Z���ώG�ɂȂ邽�ߌv�Z�@�ɗ��邵���Ȃ��̂���_�B�ꉞ���_�����ȏ�̒ʂ� > n�͐����Ɍ���܂���B�L������ok�ł��ˁB
�����ł��������B������`�g�C������
>>135
�E�ʏ����@(nn-1)/2n > 1+��2�@����
�@n > 1+��2 + ��{2(2+��2)} = 5.02733949
�Ec = (21/41){1 + (8/21)n(2n-5)(5n+2)/(nn+1)^2} < 1/��2�@����
�@n > {881 + (29��2)[29+��(2�29�29+881��2)]}/(17�47) = 5.36862925
�EL �� 31/5 �ȏ�ƂȂ�̂�
�@6.45963968 < n < 9.13156611
>>137
�E�ʏ����@(nn-1)/2n > 1+��2�@����
�@n > 1+��2 + ��{2(2+��2)} = 5.02733949
�Ec' = (4/7){1 + n(n-3)(3n+1)/(nn+1)^2} < 1/��2�@����
�@n > {31 + (5��2)[5+��(50+31��2)]}/17 = 7.93257298
�EL �� 31/5 �ȏ�ƂȂ�̂�
�@6.10446338 < n < 11.04823360
�����̋��ʕ�����
�@7.93257298 < n < 11.04823360
�ł����邩�B >>141
c+a = 2{2n(n+1)}^2,
c-a = 2{(n+1)^2 - n^2}^2,
c = {(n+1)^2 + n^2}^2
cc - aa = bb,
b = 2{2n(n+1)}{(n+1)^2 + n^2},
dd - (c-a)^2 = bb,
d = 2{(n+1)^2 - n^2}{(n+1)^2 + n^2} = 2{(n+1)^4 - n^4} >>141
�� = arcsin(b/c),
�Ƃ�����
m = [ ��/�� ]
L = 2m(d/c) + 2sin(m��),
n=3
�@a=527, b=336, c=25^2, d=14�25, ��=0.56758821841666, m=5,
�@sin(5��) = 28515500892816/(c^5) = 0.29900669864185�@�� Q
�@L = 2�5�(14/25) + 2sin(5��) = 6.1980133972837
n=4
�@a=1519, b=720, c=41^2, d=18�41, ��=0.44262888469558, m=7,
�@sin(7��) = 1637671530080839800240/(c^7) = 0.043177033944429�@�� Q
�@L = 2�7�(18/41) + 2sin(7��) = 6.2326955313035
�EL �� 31/5 �ȏ�@�����@n��4
n=17
�@a=373319, b=42840, c=613^2, d=70�613, ��=0.1142546313550, m=27,
�@sin(27��) = 0.056687202872879�@�� Q
�@L = 2�27�(70/613) + 2sin(27��) = 6.2797691855174
n=18
�@a=466487, b=50616, c=685^2, d=74�685, ��=0.10808179674906, m=29,
�@sin(29��) = 0.00722048512511925�@�� Q
�@L = 2�29�(74/685) + 2sin(29��) = 6.2801344009072
�@
�EL �� 6.28 �ȏ�@�����@n��18 >>144
�ǂ������肪�Ƃ��Bn=3 �̎��_�ł���10�P�^�����Ă��̂ˁc
������ n=4 �ƈӊO�Ƒ����^�C�~���O�ŏ�������������Ă����� ��~�̒��SO�̔������~�ƕ��s�ȕ��ʃ��ő̐ς������ɂȂ�悤�ɐؒf����
����ɁA��~�ƃ��̒����ɂ����̕��ʂƕ��s�ȕ��ʃ��Ŕ�����ؒf����
���ɂ��f�ʂ̒��S��O'�A����̓_��P�Ƃ���Ƃ��A
��OPO'�����߂� �O>>42
>>146
���a1�̔������~���獂���ւ܂ő����W�߂��Ƃ��A�̐ς���(�̐�4��/3)��1/4�Ƃ���ƁA
��/3=��0�`��(1-t^2)dt
1/3=[t-t^3/3]0�`��
1/3=��-��^3/3
��^3-3��+1=0�\�\�@
��=sin��OPO'
�@���������ƁA
3��^2-3=0
y=f(��)=��^3-3��+1�̃O���t�̌`���A
��=-1�̂Ƃ��ɑ�A
��=1�̂Ƃ��ɏ��l-1���Ƃ�B
�@�̒l��0�ƂȂ�ւ́A
0���ց�1�̂������0���̂Ƃ��B
��OPO'��18�� �O>>147�����B
{sin(20��)}^3-3sin(20��)+1=0.0139483266��0
20�����킸���ɑ傫�����A�����l�ł�20���������Ƃ��߂��B ��[0,a](1-x^2)dx = 1/2�E2��/3���
a-a^3/3 = 1/3 �B
�� (2b) - (2b)^3/3 = 1/3�B
�� 3b - 4b^3 = 1/2�B
�� 3(sin��) - 4(sin��)^3 = 1/2�B
�� sin3�� = sin(��/6)�B
�� ��=��/18�B >>148
�s����
>>149
�����ł� >>149-150���H�@10���͂�������B����Ȃ�������̉~�Ղ�������1/3�ɂȂ�́H�@�O>>148�������Ȃ��H�@10����1/3���B
�P]/�_�Q�Q�Q�Q�Q�Q�Q
�Q/�_/ �@�@,,������/|
�P�_/ �@�@�c`o`Ђ�))|
�P|�_�Q�Q�QU,~�܁S� |_
�n| �a�P�P�P�PU~~U / /
�Q| �a ���@�� �a |/ /
_�@`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P ����18�ƍ���2�̌v20�̋ʂ��܂ɓ����Ă���B
�u����ׂɑ܂���ʂ�1���o�����̋ʂ͖߂��Ȃ��v�Ƃ������Ƃ��J��Ԃ��B
���߂č��ʂ��o��܂łɔ��ʂ��o�����Ƃ��āA�ł��m���̍����̂�0, 6, 9, 18�̂������瓚����B ���Ԃ�t�x�݂̏h����ۓ��������낤�B���x���I�ɂ��[�������B >>152����1�H�ׂĖ߂��Ȃ��m����18/20=9/10�B����2�H�ׂĖ߂��Ȃ��m����(9/10)(17/19)=63/190�B����3�H�ׂī���߂��Ȃ��m����(63/190)(16/18)=28/95�B����4�H�ׂ�̰��߂��Ȃ��m����(28/95)(15/17)=84/323�B
����5�H�ׂı�!! (84/323)(14/16)=72/323�B����6�\�\(72/323)(13/15)=312/1615�B9���ȁH �O>>151
�P]/�__�Q�Q�Q�Q�Q�Q
�Q/�_/�@�@�@�����@/|
�P�_/�@�@�@((`-`)/ |
�P|�_�Q�Q�Q,U��U�| |__
�n| �a�P�P�P~U~U | / /
�Q| �a ���@�� �a |/ /
_�@`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P V(��) = ��[0�`2sin��] (1-xx) dx
�@= (2��/3) [(3/2)x - (1/2)x^3](x=0,2sin��)
�@= (2��/3) {3sin�� - 4(sin��)^3}
�@= V(��/6) sin(3��),
�ʔ����B �悭����L���b�`�R�s�[�u2�l��1�l������ɂȂ�v
���́A����ɂ͐����̃J���N��������̂�
���ۂɂ́A���{�l��50�܂łɜ��m���́A���v��ł́A�Ȃ��2��
60�ł�7���ȉ��ɉ߂��Ȃ�
80�ł�37���ȉ�
90��100�܂Ő�����l���ׂĂ����킹�āA�悤�₭�u2�l��1�l�v�ƂȂ�
�i���������Z���^�[�������Z���^�[�u�ŐV���v�v���j >>157
��������
���ʑO�܂łɃK���ɂ�����m���A�Ƃ������t�ʂ�̓�����O�̒�`���� http://ganjoho.jp/reg_stat/
�@���@���v�@���@���v�@���@�ŐV���v �Ȃ�Ŏ���������Ȃ̂ɓ����Ⴄ��H�@�v�Z�ԈႦ�����ȁH�@10�����ȁH�@�O>>155
�P]/�_�Q�Q�Q�Q�Q�Q�Q
�Q/�_/ �@�@,,������/|
�P�_/ �@�@�c`_`Ђ�))|
�P|�_�Q�Q�QU,~�܁R' |_
�n| �a�P�P�P�PU~U~ / /
�Q| �a ���@�� �a |/ /
_�@`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P �O>>160
��~�ƃ��̒����ɂ����̕��ʂƕ��s�ȕ��ʃ�
����������B
��~�ƕ��ʃ��ɕ��s�ȕ��ʃ��Ƃ����Ӗ��ł͂Ȃ��̂��H�@�����͓_���A�_�ɕ��s���Ă̂͂��������ȁB >>155
�s�����ł�
20���Ď��o�������A�����o��^�C�~���O��C(20,2)=190�ʂ肠��܂�
�����͑S�ē��l�Ɋm���炵���ł�
�������߂ɍ����o��̂�19�ʂ�B6���o�č����o��̂�13�ʂ�B���l�ɑI��������10�ʂ�A1�ʂ�B
�����0���ł��m���������ƌ��_����܂� �O>>161
���ʃ��͒�~�ƕ��ʃ��̂��傤�ǒ����ɂ���Ƃ��āA
��0�`2sin��OPO'(1-t^2)dt=(4��/3)(1/2)(1/2)
=��/3
[t-t^3]0�`2sin��OPO'=1/3
2sin��OPO'-8(sin��OPO')^3/3=1/3
6sin��OPO'-8(sin��OPO')^3=1�\�\�@
��̉ŁA�����ʃ��Ő����Ƃ��́�OPO'����ɂ����OP'O"�͂قƂ��20������������A
��OPO'=10���Ɨ\�z�����B �ɇ@�����A�A
s(in10��)��8(sin10��O^3=1
�����ꂽ�B
(���������̉\������) �O>>163�C���B
���ʃ��͒�~�ƕ��ʃ��̂��傤�ǒ����ɂ���Ƃ��āA
��0�`2sin��OPO'(1-t^2)dt=(4��/3)(1/2)(1/2)
=��/3
[t-t^3]0�`2sin��OPO'=1/3
2sin��OPO'-8(sin��OPO')^3/3=1/3
6sin��OPO'-8(sin��OPO')^3=1�\�\�@
��̉ŁA�����ʃ��Ő����Ƃ��́�OPO'����ɂ����OP'O"�͂قƂ��20������������A
��OPO'=10���Ɨ\�z�����B�@�ɑ�����A
6(sin10��)-8(sin10��)^3
=6(0.173648178)-8(0.173648178)^3
=6(0.173648178)-8(0.00523613325)
=1
�������ꂽ�B >>164
sin10����0.173648178
�͂����܂ŋߎ��l�ł����Đ^�̒l�łȂ����߂���͐��w�I�ȏؖ��ł��Ȃ�ł�����܂���
���Ȃ킿������Ă܂��� �O>>164
>>165
���������ȁA
6(sin10��)-8(sin10��)^3�̒l���҂�����=1�ƂȂ�����B��1����Ȃ��B�ߎ�����Ȃ��B�M���Ăق����B�т����肵�����A�������낢�Ǝv���B���A�Ȃ�ł����Ȃ邩�͂܂����ꂩ��l�������Ƃ���B
20�����Ɣ����ɒl���Y����̂ɁA10�����ƂȂ����҂����肾�����B >>166
�ߎ��l�ł͂Ȃ��҂�����1�ɂȂ邱�Ƃ͂��ł�>>149�Ŏ�����Ă܂�
�����������Ƃ����������̂ł͂Ȃ���>>164���S�����w�̏ؖ��ɂȂ��Ă��Ȃ��Ƃ������Ƃ��������������ł� >>167
3�{�p�ȑO�ɃC�i�Ƃ������z�́u�ؖ��v�Ƃ����T�O��m��Ȃ��낤�� ���S��O�ɂ��锼�����A���̒�ʂƕ��s�ȕ��ʃ��Őؒf�����Ƃ���A
�����̑̐ς������� sin(3��) �{�ɂȂ����B
����ɁA��ʂƕ��ʃ����瓙�����ȕ��ʃ����Ƃ�B
�@���Ɣ����Ƃ̌��~��C�Ƃ��AC��̈�_��P�Ƃ���Ƃ��A
�@OP�ƒ�ʂ̂Ȃ��p�����߂�B �O>>166
>>171
���ʃ��̒��S��O'�Ƃ��A�����𐅕��ʂŐ���(��ʁ`���ʃ��`���ʃ��܂�)�������߂�(����0�`2sin��OPO'�Őϕ�����)�ƁA
��0�`2sin��OPO'(1-t^2)dt=(4��/3)(1/2)(1/2)=��/3
[t-t^3/3]0�`2sin��OPO'=1/3
2sin��OPO'-(8/3)(sin��OPO')^3=1/3
6sin��OPO'-8(sin��OPO')^3=1
�O�⓯�l�A��OPO'=10�K
���ʃ��Ɣ����̒�~�����s�������ӂ̊p�́�OPO'�̍��p�ŁA10�� �O>>172
>>171���B
(4��/3)(1/2)(sin3��)=��/3
2sin3��=��
sin3��=��/3
3��=30��
��=10��
����ӂ̊p�̓� �O>>173�����B
(4��/3)(1/2)(sin3��)=��/3
2sin3��=��/3
sin3��=��/6
3��=30��
��=10��
����ӂ̊p�̓� 10���̋ߎ��l������10���d��Ōv�Z������1�ɂȂ邩������Ȃ�����
10���̋ߎ��l������50���d��Ōv�Z������1�ɂ͂Ȃ���� ��y�̓d��͔����ł���B�O>>174�V�i�R���Ŏ�܂��ĉf�扻����̂��y���݂ɂ��Ă���B
�P�P]/�_�Q�Q�Q_����
�Q�Q/�_/�@,,��(___))
�P�P�_/�@�c`-`Ђ���|~
�P�P|�____U,~�܁R/ |__
���@| �a�P�P~U~U~| / /
�Q�Q| �a�@���@�a |/ /
_____`�a�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P������Δ݂����B�������߂Ȃ����ǁB�����Ƃ������낢�����o���Ăق����B �Ƃ肠�����m�M�ɂȂ������������B
��ɓ���ł͂Ȃ��B 6sin10��-8(sin10��)^3=1
���ꂩ���̕s�v�c��R�����Ă���Ȃ����B�Ȃ�ł҂�����10���ȂB�ł���ΐ}�ɕ`���āB�]�ł킩��悤�Ȑ}���B
�O>>176�����������B�J�~���Ă������Ȃ��炢�C���������Ă��Ă�B
�P�P]/�_�Q�Q�Q_����
�Q�Q/�_/�@,,��(___))
�P�P�_/�@�c~-~Ђ� /|
�P�P|�____U,~�܁R/ |
���@| �a�P�P~U~U~| /
�Q�Q| �a�@���@�a |/
_____`�a�Q�Q�Q�a�^
�P�P�P�P�P�a�P/
���@�@���@�a /
�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P �i������
�[���H��
�q�g���h�L�S�L�u���l�g�E������Q�҂����H���Ď��E���� >>179�ʔ������@����
�o���Ă桑O>>178(^o^))
[�P]�@ �ݸ݁c�c�@U��U�
�P�P]/�____�����m (��)
�Q�Q/�_/,,(`.`))�܁SU/
�P�P�_/�c`-`Ѓ�`�҃�/
�P�P|�__U,~�܁R___�^|
���@| �a�P~U~U~�P�a |
�Q�Q| �a ���@���@�a |/
_____`�a_________�a�^
�P�P�P�P�P�P�P�P�P >>178
���ނ���R�e���ĂĂ��� ����l��̈قȂ�2�_A,B�͐���AB���Ȃ��Ă���B����AB���O��������B���������̏����ō�}���邱��:
����̂����ƃR���p�X����
����̂����͒������������߂���
��R���p�X��1��̂ݎg�� >>183�Ȃ�ŃR�e������
�v��́H �O>>182(^o^))
[�P]�@ �ݸ݁c�c�@U��U�
�P�P]/�____�����m (��)
�Q�Q/�_/,,(`.`))�܁SU/
�P�P�_/�c`-`Ѓ�`�҃�/
�P�P|�__U,~�܁R___�^|
���@| �a�P~U~U~�P�a |
�Q�Q| �a ���@���@�a |/
_____`�a_________�a�^
�P�P�P�P�P�P�P�P�P�N�W������������̓R�e���O����B>>184
�R���p�X��������x�ǂ��Ŏg�����BAB��̎O�����n�_���Ƃ���ȂȂ��Ǝv�����ǂ����B�Ă��Ƃ�AB�ɑ��鐂��������ɐj��u�������B���������̓R���p�X���Ȃ��Ă�������B
���̂�����AB�ɑ����߂ɒu���A�Б���A���Ƃ��钼�����A�����Б���B���Ƃ��钼�����Ɉ����B������t�̎߂œ��l�ɍs����AB��Ίp���Ƃ����Ђ��`���`����B���̂�����̑Ίp����AB�̐����������B
���Ė���AB�̐���������̂ǂ��ɃR���p�X�̐j��u��������Ȃ��BAB�̎O�����n�_�̂ǂ��炩����ɃR���p�X�̉��M��u���ȂȂ��B
�R���p�X�̒�����AB�Ƃ����AB�̒��_����R���p�X�̐j��u���ʒu�܂ł̒����́A�O�����̒藝���A
��{AB^2-(AB/6)^2}=(��35)AB/6
����͕`���Ȃ������B
�R���p�X�̒�����(1/2)AB�Ƃ����AB�̒��_����R���p�X�̐j��u���ʒu�܂ł̒����͓��l�ɁA
��{(AB/2)^2-(AB/6)^2}=(2��2)AB/6
=(��2)AB/3
����͕`����\��������B������������B �ڕ��ʂ������Ȃ���̂������R���p�X�������� �摜�r�炵�������悭���ځ[����@�͂Ȃ����ˁH >>187�ڕ��ʂ͂�[��](Y)
�߂���B�O>>185(~e~( )
[�P]�@ �ݸ݁c�c U��~�
�P�P]/�___�����m (���j
�Q�Q/�_/,(`.`))�܁SU /
�P�P�_/�c`-���`�҃� /
�P�P|�__U,~�܁R___�^|
���@| �a�P~U~U~�P�a |
�Q�Q| �a ���@���@�a |/
_____`�a_________�a�^
�P�P�P�P�P�P�P�P�P�摜���\��Ȃ��Ă��ꂾ���ǁA����[��]�݂����Ȋ����ŁA���̂�����AB�ɑ��߂ɒu���A�Ō�ɃR���p�X�ŎO�����ł���Ǝv���B >>187
�{���w��łł����Ȃ��H >>178
-8x^3+6x-1=0�̉���sin10���ɂȂ闝�R���l������Ă��ƁH ���̋���ے��Ȃ�D�G�ȍ��Z���ł��ł��������� ����_�w���ɓ��w�ł���w�͂�����ł���B >>184
����AB��ɂȂ��P�_Z���Ƃ�B
�R���p�X��Z�𒆐S�Ƃ�����AB�ƌ����傫���̉~��C���g���B
����AB��C�̌�_��D, E�Ƃ���B
���̂����Œ���DZ���g���A�~��C�Ƃ̌�_��D~�Ƃ���B
���̂����Œ���EZ���g���A�~��C�Ƃ̌�_��E~�Ƃ���B
���̂����Œ���D~E~���g���B����͒���AB�ƕ��s�ł���B
AB�AD~E~�̕��s��������1�{�g������������
DED~E~ �������`�ł��邱�Ƃ��g�����B
���̂����Œ����`�̊e�ӂ�2�����ł���A2����AB�AD~E~���瓙�����̒������g����B �����`DED~E~�̈�ӂ�3��������B�������A���̏����ō�}���邱�ƁF
����̂�������
����̂����͐������������߂����i�����`�̒������j �P]/�__�Q�Q�Q�Q�Q>>190
�Q/�_/�@�@�����@/|����
�P�_/�@�@((`-`)/ |����
�P|�_�Q�Q,U��U�| |__��
�n| �a�P�P~U~U | / /��
�Q| �a�@���@�a |/ /��
_�@`�a�Q�Q�Q�a�^_/�ȁB
�P�P�P�P�P�P�P�P�a�@/
���@ ���@ ���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�Px����sin�ɂȂ�Ƃ�10���ɂȂ�Ƃ��v���O>>188�ɁA0��x��1�͈̔͂�0���ɂ��邠��l�Ɍ��܂��Ă��܂��B�m�肽���̂͒l����Ȃ��B
sin10����10���̂ق��B
�Ȃ��҂�����10���Ȃ̂��B
��������ɂ͎����Ȃ�̓������o����������ǂ����ł������B�J�^!! >>192
�����ƕW���I�ȃ��x���̖��ł���
3�{�p�̌����g���������� >>196
��1������_�w�����ʼn����Ȃ��Ƃ̂��܂���m������B >>194
>>194
�Ίp��DD~�CEE~�̌�_�� Z(0,0) �Ƃ���B
�ӂ̒������@DE = D~E~ = 2p,�@�@DE~ = D~E = 2q�@�Ƃ���B
D (-p,-q)�@E (p,-q)�@D~(p,q)�@E~(-p,q)
��DE��ɓ_S (-ps,-q)�@��D~E~��ɓ_T (-pt,q)�@��C�ӂƂ�B(0<s<t<1 �Ƃ���)
SZ�̉����ƕ�D~E~�̌�_��S~(ps,q)
TZ�̉����ƕ�DE�̌�_��T~ (pt,-q)
S~T~ // ST
����ST�ƑΊp��DD~�̌�_��U (-(s+t)p/(2-s+t), -(s+t)q/(2-s+t))
����ST�ƑΊp��DD~�̌�_��V (-(s+t)p/(2+s-t), (s+t)q/(2+s-t))
����S~T~ �ƑΊp��DD~�CEE~�̌�_�� U~�CV~
UV~�̉����ƕ�DE~�CED~�̌�_�� W (-p,-qs)�CX~(p,-qt)
VU~�̉����ƕ�DE~�CED~�̌�_�� X (-p,qt)�CW~(p,qs)
����������
�@SW~ // S~W // TX // T~X~ // DD~ �@(�X�� q/p)
�@SW // S~W~ // TX~ // T~X // EE~�@(�X�� -q/p)
5�{�g�̕��s����2����ꂽ�B �����I�ɁA��K�ƃR���p�X�ɂ���}�ŕ`���o����u2���̌�_�v�i���͒����ł��~�ʂł��j�́A���ׂĒ�K�݂̂ŕ`����Ƃ����藝�����邩��A
���ɂ̓R���p�X0��ɂł���͂��Ȃ� >>198 (����)
SW�CT~X�ƑΊp��DD~�̌�_��F�CG�Ƃ���B
FT~��GS�̌�_��H�CFX��GW�̌�_��I�Ƃ���B
DH�̉�����ED~�̌�_�� J (p, -q/3)�@�@EJ = (2q)/3
DI�̉�����D~E~�̌�_�� K (-p/3, q)�@�@E~K = (2p)/3
�ƂȂ�B
�Ȃ��A�e�ӂ�3�������ꂽ�̂ŁA����AB�̕��s���͖����ɉg����B
(��)�@�A�t�B���ł́A�c���ɐL�k���čl���Ă��悢�B
���Ƃ��ΐ����`(p=q)�ɂ��čl����ƁA���Ίp���̌X�p��45���ƂȂ�B
��ӂɑ��闼�Ίp���̌X�p�����������Ƃ��d�v�B >>199
���Ԃ�A�ł��Ȃ��Ǝv����B�i�L����ł́j n���L�����̂Ƃ��A����AB��1/n�̒����̐��������邱�Ƃ���������
�R���p�X���g����2��ɂ���ƁA����܂���������Ċy�����Ȃ�� >����_�w���ɓ��w
�N�ɂ��ł��Ȃ� >>190���̎��Ȃ�
x=cos80��=1.73648178�ł����藧�B��������Ȃ��āA������̐ς������ɂȂ�悤�ɐ����ɐ������������ɍ��������Ő����ɐ�Ƃ�����A�̓���ŁA���̂���������́�OPO'���A�Ȃ��҂�����10���ɂȂ�̂��A���̕s�v�c�������Ă܂��B
�P]/�_�Q�Q�Q�Q�O>>195
�Q/�_/�@�����@�@/|
�P�_/�@((`-`)��/ |
�P|�_�Q_U,~�܁S� |__
�n| �a�P�P~U~~U| / /|
�Q| �a�@���@�a |/ / |
_�@`�a�Q�Q�Q�a�^_/�@|
�P�P�P�P�P�P�P�P�a�@/
���@ ���@ ���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P ������C�U�[�r�[���̔@
`_')������҂�����10��
�P]/�__�_________�Ő�
�Q/�_/ ���_.~�� /|�点
�P�_/�@((`-�_��/ |���
�P|�_�Q_U,~�܁_| |__��
�n| �a�P�P~U~~U�_/ /|
�Q| �a�@���@�a |/�_ |
___`�a�Q�Q�Q�a�^_/ �_
�P�P�P�P�P�P�P�P�a�@/`
���@ ���@ ���@�@�a /��
�Q�Q�Q�Q�Q�Q�Q�Q�a/��
�P�P�P�P�P�P�P�P�P���������B�O>>204�Ă������A�҂�����10�����ȁH�\�\�������ē��������Ƃ����ʔ��������B >>204�����Bcos10��=0.173648178�O>>205
����@�@�@
`_')����߯�@
�P]/�__�_________
�Q/�_/ ���_.~�� /|
�P�_/�@(`e'�_��/ |
�P|�_�Q_U,~�܁_| |__
�n| �a�P�P~U~~U�_/ /|
�Q| �a�@���@�a |/�_ |
___`�a�Q�Q�Q�a�^_/ �_
�P�P�P�P�P�P�P�P�a�@/*
���@ ���@ ���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P >>200
D (0,0)�@S (2a,0)�@T~ (2b,0)�@X (0,2mb)�@W (0,2ma)
�Ƃ����
�Ίp��DD~�F�@y = mx�@�@�@(m=q/p)
SW�F�@y = m(2a-x)
T~X�F�@y = m(2b-x)
SW��DD~�̌�_�@F (a,ma)
T~X��DD~�̌�_�@G (b,mb)
FT~�F�@y = {ma/(2b-a)}(2b-x),
GS�F�@y = {mb/(2a-b)}(2a-x),
�����̌�_�@H (3ab/(a+b),mab/(a+b))
DH�F�@y = (m/3)x, �������C^1����f(x)�ɂ���lim(x����)f(x)�͎�������Ƃ����Ƃ��A�ȉ��̖�ɓ�����
(1)f'���P�������̏ꍇ�Alim(x����)f'(x)=0�ƂȂ邱�Ƃ��ؖ�����
(2)f���P�������ł���
lim(x����)f'(x)��0�Ƃ͂Ȃ�Ȃ���������� >>184
����l��ɓ_B�𒆐S�Ƃ��ē_A��ʂ�~C����}����B�~C�ƒ���l�̌�_��A�łȂ�����A'�Ƃ���B
����l��ɂȂ��_P���~C�̓����ɂƂ�A����OP��̓_Q��C�ӂɂƂ�B
AP��A'Q�̌�_��R�AA'P��AQ�̌�_��R'�ARR'��PB�̌�_��S�Ƃ����B
RB��SA�̌�_��T�APT��l�̌�_��U�����AU�͐���AB�̒��_�ɂȂ�B
����RR'�Ɖ~C�̂Q�̌�_�����ꂼ��V,W�Ƃ����B
����VB�Ɖ~C�̌�_��V�łȂ�����V'�A����WB�Ɖ~C�̌�_��W�łȂ�����W'�Ƃ����A
����VW�A����l�A����V'W'�͑S�ĕ��s�ł���A���̏��œ��Ԋu�ł���B
����V'W'�ォ��C�ӂɓ_O���Ƃ�AOA��VW�̌�_��D�AOU��VW�̌�_��E�AOB��VW�̌�_��F�Ƃ����B
�_O�����_�Ƃ��ē�_A,B�̈ʒu�x�N�g�������ꂼ��(1,0),(1,1)�ƂȂ�悤�ɍ��W�n���߂�ƁA
���� O(0,0), A(1,0), B(1,1), A'(1,2), D(2,0), E(2,1), F(2,2) ������}����Ă��邱�ƂɂȂ�̂ŁA
���Ƃ͗Ⴆ��AE��A'F�̌�_G(3,2)�AAD��A'E�̌�_H(3,0)�AGH��BE�̌�_I(3,1)���̂悤�ɍ�}������A
OG��AB�̌�_(1,2/3)�AOH��AB�̌�_(1,1/3)�Ƃ������߂��_��������B >>209 ����
�P�i���Q�s��
��F����OP��̓_Q��C�ӂɂƂ�B
���F����BP��ɓ_Q��C�ӂɂƂ�B
�R�i���T�s��
��FOH��AB�̌�_(1,1/3)
���FOI��AB�̌�_(1,1/3) >>208
(1)
������ f '(a) >0 �ƂȂ�a�����݂����Ȃ��
�@x��a�@�ˁ@f '(x) �� f '(a) = b,
�@f(x) �� f(a) + b(x-a)�@���@���@(x����)
�ƂȂ��Ė�������B
���@f '(x) �� 0
���@�P�������ŏ�ɗL�E�������������B
�@lim[x����] f '(x) = L �� 0,
L < 0 �Ȃ�A��=(-L)/2 �ɑ��� ���� N ��������
�@x > N�@�ˁ@|f '(x) -L| < �� = (-L)/2,
�@�@f(x) < f(N) +(-L)/2�E(x-N)�@���@-���@�@(x����)
�ƂȂ��Ė�������B
�� L=0
(2)
���Ƃ���
�@f '(x) = sin(nnx)�@�@�@�@( 2n�� < x < (2n+1/nn)�� )
�@�@�@�@ = 0�@�@�@�@(���̑�)
�@f(x) �� 2��(2) = ��/3�@�@(x����)
�E�L���ȗ�
�@f '(x) = x/{1+ x^6�sin(x)^2},
���F�u��͊T�_�v������O�ŁA��g���X(1961)�@p.141
�@��3�� �ϕ��@�@���K���(3)-(9) f(x)=1-x^2+x^4-x^8+x^16-x^32+�c+(-1)^n�Ex^(2^n)+�c
�Ƃ���Ƃ�f(x)��[0,1)�ŘA������
�Б��Ɍ�lim(x��1-)f(x)�͑��݂��Ȃ����Ƃ������B >>214
�@x �` 1 - (��2)(1/4)^n �̕ӂ�ŋɑ� �` 0.5027
�@x �` 1 - (1/��2)(1/4)^n �̕ӂ�ŋɏ� �` 0.4973
�@x �` 1 - (1/2)^n �̕ӂ�ł� �� 1/2
�ł����˂� >>213
n��0 �̂Ƃ� (-1)^n�Ex^(2^n)��x^(2^0)��x^1�Ȃ̂ŁA
f(x)=1-x^2+x^4-x^8+x^16-x^32+�c+(-1)^n�Ex^(2^n)+�c
�ł͂Ȃ�
f(x)= x -x^2+x^4-x^8+x^16-x^32+�c+(-1)^n�Ex^(2^n)+�c
����ˁH >>213
a��lim(x��1-)f(x)��R �����݂���Ƃ���B
f(x)����[n��0�`��]x^{4^n}(1�|x^{4^n}) �Ȃ̂ŁA0��x��1��m��1��C�ӂɎ��Ƃ��A
f(x^{1/4^m})
����[n��0�`��]x^{4^{n�|m}}(1�|x^{4^{n�|m}})
����[n���|m�`��]x^{4^n}(1�|x^{4^n})
�ƂȂ�Bm���{���Ƃ���ƁAx^{1/4^m}��1 �Ȃ̂ŁA
a����[n���|���`��]x^{4^n}(1�|x^{4^n})
�ƂȂ�B���ꂪ�C�ӂ�0��x��1�Ō����邱�ƂɂȂ�B �������Ax��1/2, 1/3 �̂Ƃ��� ��[n���|���`��]x^{4^n}(1�|x^{4^n}) �̒l��
���l�v�Z����ƁA�����l�ɂ͂Ȃ�Ȃ����Ƃ��\�z�����B
�����ɈႤ�l�ɂȂ邱�Ƃ������ɂ́A�K���ȗL�����܂ł͌����Ɍv�Z���A
�c��̏�]���͎G�ɏ㉺����]�����邾���ł悢�B
���̋����͎����̃X�s�[�h���ɂ߂đ����̂ŁA����ł����Ƃ��Ȃ�B
�������A��v�Z�ł͒ǂ����Ȃ����ʂł͂��� (�Oo�O) >>213
���̖��͉ߋ��X��26
http://rio2016.5ch.net/test/read.cgi/math/1518967270/
��318�ł��o�肵�܂����������҂����Ȃ��̂ōďo��ł� >>220
��F318
���F381
�A�����܂� >>220-221
>>217-218�ʼn͏I����Ă�͂������ǁH
�ǂ����Ԉ���Ă��H >>222
>�����ɈႤ�l�ɂȂ邱�Ƃ������ɂ́A�K���ȗL�����܂ł͌����Ɍv�Z���A
>�c��̏�]���͎G�ɏ㉺����]�����邾���ł悢�B
���ꂪ�������悢���A�����ĂȂ��̂ŕs�����B >>223
�{���I�ł͂Ȃ��ˁB
a����[n���|���`��]x^{4^n}(1�|x^{4^n})�@(0��x��1)
�����������_�Ŗ{���I�Ȗ����͊��ɏo�Ă���B���Ƃ͂����̐��l�v�Z�B
�l�Ԃ̎�ł��I���悤�ȏ�肢�]���̎d�������邩������Ȃ����A
���w�ł�����܂����A����͖{���ł͂Ȃ��B ���������������Ƃ����ƁA�{���I�ł͂Ȃ��Ƃ���ɂ��������
�u�s�����v�Ƃ������o���̂̓o�J�o�J�����Ƃ������ƁB ���ꂪ�����I�[�_�[�v�Z��������A�]���̎d���܂ŏd�v�ȈӖ��������A
�����ł� x��1/2, 1/3 �ɂ����� ��[n���|���`��]x^{4^n}(1�|x^{4^n}) �̒l��
��r���邾���Ȃ̂ŁA�����̐��l�v�Z�ł���A�]���̒��g�����Ă��N�������Ȃ��B
�ꉞ�A�G�ȕ]���ɂ��v�Z��������Ă����Ă�邪�A����Ȃ̌��Ăǂ��������H
0��x��1��n��Z�ɑ��� 0��x^{4^n}(1�|x^{4^n})��x^{4^n}�|x^{4^{n�{1}} �Ȃ̂ŁA
m��M ��������m,M�ɑ���
0����[n��m�`M�|1]x^{4^n}(1�|x^{4^n})��x^{4^m}�|x^{4^M}.
�����
0����[n��m�`��]x^{4^n}(1�|x^{4^n})��x^{4^m},
0����[n���|���`M�|1]x^{4^n}(1�|x^{4^n})��1�|x^{4^M},
0����[n���|���`��]x^{4^n}(1�|x^{4^n})��1.
���ɁA0��x��1�̂Ƃ� g(x)�F����[n���|���`��]x^{4^n}(1�|x^{4^n}) �͎�������
0��g(x)��1�ł���B ���ɁAM��m ��������M,m�ɑ���
g(x)����[n��M�`m�|1]x^{4^n}(1�|x^{4^n}),
g(x)��(��[n���|���`M�|1]�{��[n��M�`m�|1]�{��[n��m�`��])x^{4^n}(1�|x^{4^n})
��1�|x^{4^M}�{��[n��M�`m�|1]x^{4^n}(1�|x^{4^n})�{x^{4^m}
�ł��邩��A
g(1/3)����[n��M�`m�|1](1/3)^{4^n}(1�|(1/3)^{4^n}),
g(1/2)��1�|(1/2)^{4^M}�{��[n��M�`m�|1](1/2)^{4^n}(1�|(1/2)^{4^n})�{(1/2)^{4^m}.
�ƂȂ�B����M���|4, m��2�Ƃ���
g(1/3)����[n���|4�`1](1/3)^{4^n}(1�|(1/3)^{4^n})���F��,
g(1/2)��1�|(1/2)^{4^{�|4}}�{��[n���|4�`1](1/2)^{4^n}(1�|(1/2)^{4^n})�{(1/2)^{4^2}���F��
�ƂȂ�B��,���Ƃ��ɗL�����̌v�Z�ł����Ȃ����A�l�Ԃ̎�Ōv�Z����͖̂���������̂ŁA
wolfram alpha �Ő��l�v�Z����B����ƁA
����0.499849960745428543744377819829608038347726011327545975385
����0.499054407972774107790531301512118479363010992347234146756
�ƂȂ�̂ŁAg(1/2)����������g(1/3)�Ƃ������ƂɂȂ�B�܂�g(1/3)��g(1/2)�ł���Bqed >>224 - 226
����ȂɔM���Ȃ�Ȃ��ŁB
�Ⴆ�AF(x)=��(0,��) sin(xt)/t dt ��x>0�Œ萔���ɂȂ�̂ŁA
a����[n���|���`��]x^{4^n}(1�|x^{4^n})
���萔���ł͂Ȃ��ۏ͂Ȃ��ƌ������������B
���̖��̏o�T����
G.H.Hardy "On Certain Oscillating Series", Quar. J. Math. 38 (1907)
�ŃG���K���g�ȉ��萸���ȉ͌�������Ώo�Ă��܂��B >>218 �̎��_�ł́u�`���Ƃ��\�z�����v�Ƃ���������ĂȂ����������
�������������ʂł���Ɗm���߂Ă����̂Ȃ�u�`���Ƃ��v�Z�ɂ��m���߂���v�Ƃ��̕����悩�������� >>209����ꂽ�Ƃ����}���Ă݂��B�r����U��A'�̊O���ɂȂ����B����ȏ�͍�}�ł��Ȃ��B
[�P]�O>>206
�P�P]/�______________
�Q�Q/�_/,,���@�@�@�@ )
�P�P�_/�c-_-Ё@�@�@ /|
�P�P|�__U,~�܁R___�^||
���@| �a�P~U~U~�P�a ||
�Q�Q| �a ���@���@�a |/
_____`�a_________�a�^ ____/�_/! ��OP�ザ���
�P�P�_/�c-_-Ђ�OB���!
�P�P|�__U,~�܁R___�^||
���@| �a�P~U~U~�P�a ||
�Q�Q| �a ���@���@�a |/
_____`�a_________�a�^
�O>>230�������܂����B ��OA=(1,0)�̂Ƃ��A
|��OB|��|��OA|������ŁAO��C�ӂɂƂ�ƁB
��OB��(1,1)
x����y���������ɂƂ��Ă�O��C�ӂɂƂ�Ɩ����B�����Ȃ��B
|��OB|��1 ,�~
�P�P�_/�c-_-� �O>231/|
�P�P|�__U,~�܁R___�^||
���@| �a�P~U~U~�P�a ||
�Q�Q| �a ���@���@�a |/
_____`�a_________�a�^ �O>>232�O�X>>231
��OA=(1,0),��OB=(1,1)�Ƃ���ƁA
|��OA|=1,|��OB|=��2
O�̂Ƃ肤��O�Ղ͉~C�̓_A�ɂ�����ڐ��ɂ��ĉ~C�̂Ȃ����ɕ`���A
l��Ώ̎��Ƃ����Ȑ��B
O��V'W'��ɂ���Ƃ���ƁAO�͔C��(��)�ł͂Ȃ������܂��͓���(��)�̂���_�ɂȂ�B
��AOB���Ax����y���̂Ȃ��p�̔����ɂȂ�Ή\�B
OU//VW�������_E���Ȃ��B
�Ă��Ƃ�O��V'W'��ɂ͂Ȃ����Ă��Ƃ��B
�V'W'�ォ��O���Ƃ�Ƃ͂ǂ��Ƃ�H�@�Ȑ��̂ǂ��ł��������Ă��ƁH
(���𒆁c�c)
OB=OA��2����O�̋O�Ղ�`���Ȃ��ƔC�ӂ�O���Ƃ�Ȃ��B �O>>233
O�AU�AT�AE�AP�̏��Ɉ꒼���ɕ��ԁA�ł����Ă�H
�܂�C�ӂ�P�ɑ��āA
V'W'��ɂ���O�͈�ӂɌ��܂�H�@�C�ӂ̂���Ȃ��AOA=1�AOB=��2�����A��������O���Ă��ƁH
����Ȃ�(1,2/3)��(1,1/3)���������Ɍ��܂�BAB���O�����ł���B
���˂ɂ܂܂ꂽ�B >>209 �̎O�i����s�ڂ͏������t���炸��������
���F�_O�����_�Ƃ��ā`�`�`(1,0),(1,1)�ƂȂ�悤�ɍ��W�n���߂�ƁA
�V�F���̕��ʂ�_O�����_�Ƃ��ā`�`�`(1,0),(1,1)�ƂȂ�悤�ȃx�N�g����Ԃƌ��Ȃ��ƁA
�̕����������� >>226 >>227
�@g(x^4) = g(x),
�@log| log(x) |�@������ log(4) �����c
��
�@g(1/2) = g(1/16) = 0.4972522664711 < ��
�@g(1/3) = 0.50127862853167 > ��
�@g(1/4) = g(1/��2) = 0.502747733528894 g(1/2) = g(1/16) = 0.4972522664 7110579821 9691998556 5993689265 0429538854 9508079518
g(1/3) = g(1/81) = 0.5012786285 3167081181 3508586478 6965549098 0669739652 4161337761
g(1/4) = g(1/��2) = 0.5027477335 2889420178 0308001443 4006310734 9570461145 0491920482 >>236
�@g(x^4) = 1- g(x^2) = g(x),
���������ȁB 10�l�����Ȃ���5�����Ɋ��蓖�Ă�
�A���A�e�����̒����3�l�Ƃ���
���蓖�ĕ��͉��ʂ肠�邩 �ő剟�����݇B�B�A�@�@�O>>234�����ł��Ȃ��B�A�A�A�@
��l�����Ƃ������Ȃ�A�A�A�A�A
�P�P]/�_____________
�Q�Q/�_/ .���@�@�@�@)
�P�P�_/�c~-~Ђ��@�@/|
�P�P|�__U,~�܁R�_�^||
���@| �a�P�P~U~U�a ||_
�Q�Q| �a ���@�� �a |/
_____`�a________�a�^ /
�P�P�P�P�P�P�P�P�P�P�a
���@ ���@ ���@ ���@ �a
____________________�a
�P�P�P�P�P�P�P�P�P�P�P ���鍑�̎��Y���͌Y�����Ŗ���1��R�C���𓊂���B
������n���A�����ĕ\���o��Ƃ��̓��̂����ɌY�����s�����B
�ŏ��ɃR�C���𓊂�������1���ڂƂ���
�Y�����s�����܂ł̓����̊��Ғl��n��p���ĕ\���i�v�Z�ߒ����K�v�j�B E = (1/2)(1+E) + (1/4)(2+E) + (1/8)(3+E) + �d + (1/2^n)(n+E) + (1/2^n)n >>243
�����ł��B
���Ȃ݂�E�ʼn����� E=-2+2�E2^n ���ꌋ�ǃG�v�V�����E�f���^�_�@�ɂ�����f���^�̍\��������Ă�ɉ߂���
�Ӗ����Ȃ�
����������������I�ɋA�[�ʼn������Ă�
����Ȃ̐��w����Ȃ� �N�����̐��w�Ƃ����̂͑S�˂����肳��Ă��钆��
�S�˂��ؖ����Ă���ƌ����Ă���ɉ߂��Ȃ�
���肵�����̂��ؖ����Ă��܂��Ƃ����̂�
�㐔�w�ɂ����鏉���I�ȃ~�X����
��蒼���Ă���
�ނ�������ȃN�C�Y www.businessinsider.jp post-168357
���{�����l�g�E���q�g���h�L�S�L�u����Ƃ��Ԃ��E�� ���̒��Ɂu����́����Q�v����ꍇ�̗ʎq���v�̖��
�E�P�[�X�P�@�u�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����v�@���̉E�Ł������ϑ������m�͗��R���̂P
�E�P�[�X�Q�@�u�����@�@�@�@�@�@�@�@�@�@�@�@�@�@�v�@���̍��Ł������ϑ������m���͂R���̂P
�E�P�[�X�R�@�u���@�@�@�@�@�@�@�@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���͂R���̂P
�ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m���͂Q���̂P����
�ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ����ꂽ�ꍇ�@
�@�E�c�����������̉E�̊ϑ����u�Ŋϑ������m���͂����炩�H
�@�E�c�����������̍��̊ϑ����u�Ŋϑ������m���͂����炩�H
���̖��͓������o���̂͊ȒP������
�������o�����
���ł����Ȃ�́H�ƔY�ޖ�肾 >>249
�n�� 1����2��
��t 3����4��
��� 6����9����12������������6����9���Ȃ���ɂ����Ă킩����Ă��Ƃɂ͂Ȃ�Ȃ��B�܂�12�����B
�܂�n���t��1��3�����B
(����)�n��1����t3�����(����)12�� >>251
�����̒��Ɂu����́����Q�v����ꍇ�̗ʎq���v�̖��
���E�P�[�X�P�@�u�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����v�@���̉E���Ł������ϑ������m�͗��R���̂P
���E�P�[�X�Q�@�u�����@�@�@�@�@�@�@�@�@�@�@�@�@�@�v�@���̍����Ł������ϑ������m���͂R���̂P
���E�P�[�X�R�@�u���@�@�@�@�@�@�@�@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���͂R���̂P
���ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m���͂Q���̂P����
���ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ����ꂽ�ꍇ�@
���@�E�c�����������̉E�̊ϑ����u�Ŋϑ������m���͂����炩�H
���@�E�c�����������̍��̊ϑ����u�Ŋϑ������m���͂����炩�H
����
���Ɏc�����P�́������́u�E�v�̊ϑ����u�Ŋϑ������m���͂R���̂Q
�i�Q���̂P�@�~�@�H���R���̂P�@�@�H���R���̂Q�j
���Ɏc�����P�́������́u���v�̊ϑ����u�Ŋϑ������m���͂R���̂P
�i�P�@�|�@�R���̂Q�@���@�R���̂P�j
�����͊ȒP�ɋ��߂�ꂽ��
�o����������Ȏ��ɂȂ��Ă��� �P�j���̒��ɋ�ʂ̂����Ɓ����L�����ꍇ�̊m��
�@�P�[�X�P�@�u�@�����@�@�@�@�@�@�v�@���̍����Ł������ϑ������m���S���̂P
�@�P�[�X�Q�@�u�@�@�@�@�@�@�@�����v�@���̉E���Ł������ϑ������m���S���̂P
�@�P�[�X�R�@�u���@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���S���̂P
�@�P�[�X�S�@�u���@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���S���̂P
�Q�j���̒��ɋ�ʂ̂��Ȃ��������L�����ꍇ�̊m��
�@
�@�P�[�X�P�u�����@�@�@�@�@�@�@�@�v�@���̍����Ł������ϑ������m���R���̂P
�@�P�[�X�Q�u�@�@�@�@�@�@�@�@�����v�@���̉E���Ł������ϑ������m���R���̂P
�@�P�[�X�R�u���@�@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���R���̂P
���
�@��ʂ̂��Ȃ�������
�@�o���@�A���p���o���p�@�Ɓ@�o���@�A���p���o���p�@�̂ǂ���̋K���ɏ]���̂��H
���j
���̖��͖ʔ����Ɗ�������̂��H
����Ƃ��[���Ȏ��ԂƊ�������̂��H
�����ł͗ʎq����Ƃ��Đ[���Ȏ��ԂƂ����F��������
���w�ł͂ǂ�ȔF���Ȃ̂����������� �P�j���̒��ɋ�ʂ̂����Ɓ����L�����ꍇ�̊m��
�@�P�[�X�P�@�u�����@�@�@�@�@�@�v�@���̍����Ł������ϑ������m���S���̂P
�@�P�[�X�Q�@�u�@�@�@�@�@�@�@�����v�@���̉E���Ł������ϑ������m���S���̂P
�@�P�[�X�R�@�u���@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���S���̂P
�@�P�[�X�S�@�u���@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���S���̂P
�Q�j���̒��ɋ�ʂ̂��Ȃ��������L�����ꍇ�̊m��
�@
�@�P�[�X�P�u�����@�@�@�@�@�@�@�@�v�@���̍����Ł������ϑ������m���R���̂P
�@�P�[�X�Q�u�@�@�@�@�@�@�@�@�����v�@���̉E���Ł������ϑ������m���R���̂P
�@�P�[�X�R�u���@�@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���R���̂P
���
�P�j�́u�S�̃P�[�X�v������
�Q�j�́u�R�̃P�[�X�v�����邪
�u�S�̃P�[�X�v���R�u�̃P�[�X�v�Ɍ��炷�Ƃ��Ɂ@�o���@�A���p���o���p�@���g�p���邩�H
���j
���̖��̉͊ȒP�����s�v�c�Ȋ��������Ă��� ���̒��Ɂu����́����Q�v����ꍇ�̗ʎq���v�̖��
�E�P�[�X�P�@�u�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����v�@���̉E�Ł������ϑ������m�͗��R���̂P
�E�P�[�X�Q�@�u�����@�@�@�@�@�@�@�@�@�@�@�@�@�@�v�@���̍��Ł������ϑ������m���͂R���̂P
�E�P�[�X�R�@�u���@�@�@�@�@�@�@�@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���͂R���̂P
���P�@�P�[�X�P�̏ꍇ
�@���j�@�ŏ��Ɂ������́u�E�v�̊ϑ����u�Ŋϑ������m���́H
�@���j�@���Ɏc�����P�́������́u�E�v�̊ϑ����u�Ŋϑ������m���́H
���Q�@�P�[�X�Q�̏ꍇ
�@���j�@�ŏ��Ɂ������́u���v�̊ϑ����u�Ŋϑ������m���́H
�@���j�@���Ɏc�����P�́������́u���v�̊ϑ����u�Ŋϑ������m���́H
���R�@�P�[�X�R�̏ꍇ
�@
�@���P�j�@�ŏ��Ɂ������́u�E�v�̊ϑ����u�Ŋϑ������m���́H
�@���P�j�@���Ɏc�����P�́������́u���v�̊ϑ����u�Ŋϑ������m���́H
�@���Q�j�@�ŏ��Ɂ������́u���v�̊ϑ����u�Ŋϑ������m���́H
�@���Q�j�@���Ɏc�����P�́������́u�E�v�̊ϑ����u�Ŋϑ������m���́H
�@
�@ ���ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m���͂Q���̂P����
���ꂪ�ԈႢ�Ő�������3����2 >>258
�����ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m���͂Q���̂P����
�����ꂪ�ԈႢ�Ő�������3����2
���ꂾ��
�ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m���͂R���̂Q
�ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m���͂R���̂P
�ɂȂ�ς�
�ŏ���
�E�Ŋϑ�����邩���Ŋϑ�����邩
�ܕ��ܕ��� >>25�W
�����ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m���͂Q���̂P����
�����ꂪ�ԈႢ�Ő�������3����2
�ԈႦ���̂Œ���
���ꂾ��
�ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m���͂R���̂Q
�ŏ��ɔ��̍��̊ϑ����u�Ł����ϑ������m���͂R���̂P
�ɂȂ�ς�
�ŏ���
�E�Ŋϑ�����邩���Ŋϑ�����邩
�ܕ��ܕ���
�ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m���͂Q���̂P
�ŏ��ɔ��̍��̊ϑ����u�Ł����ϑ������m���͂Q���̂P
�������� �P�[�X1�ƃP�[�X3�͉E���Ɂ������݂���̂ŁA�ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m����3����2
�P�[�X2�ƃP�[�X3�͍����Ɂ������݂���̂ŁA�ŏ��ɔ��̍��̊ϑ����u�Ł����ϑ������m����3����2
���������āu�ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m���v��
�u�ŏ��ɔ��̍��̊ϑ����u�Ł����ϑ������m���v�𑫂�����100%�ɂȂ�Ǝv���Ă�H >>261
�����������āu�ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m���v��
���u�ŏ��ɔ��̍��̊ϑ����u�Ł����ϑ������m���v�𑫂�����100%�ɂȂ�Ǝv���Ă�H
�ŏ��ɉE�Ŋϑ������m���͂T�O���@�{�ŏ��ɍ��Ŋϑ������m���͂T�O�����P�O�O�� >>261
�����������āu�ŏ��ɔ��̉E�̊ϑ����u�Ł����ϑ������m���v��
���u�ŏ��ɔ��̍��̊ϑ����u�Ł����ϑ������m���v�𑫂�����100%�ɂȂ�Ǝv���Ă�H
�ŏ��ɉE�Ŋϑ�����邩���Ŋϑ�����邩�̂Q������
���E���Ώ̂����炻�ꂼ��̊m���͂T�O����
�E�Ŋϑ������m���ƍ��Ŋϑ������m���𑫂��P�O�O���ɂȂ�
�P�O�O���ȊO�ɂȂ邱�Ƃ͂��肦�Ȃ�
���Ƃ����E�Ŋϑ������m�����W�O���Ȃ�
�c��̂Q�O�����Ăǂ�ȏ�ԂȂH
�i�z�����o���Ȃ��j ���ŏ��ɉE�Ŋϑ�����邩���Ŋϑ�����邩�̂Q������
�P�[�X1�ƃP�[�X3�͂��������A�P�[�X2�͈Ⴄ�B�P�[�X2�̏ꍇ�͍��E�Ɂ�������̂�����A�E����ł��A������ł��ϑ������B
�u�ŏ��ɉE�Ŋϑ������m���v�̔r�����ۂ́u�ŏ��ɍ��Ŋϑ������m���v�ł͂Ȃ��A�u�ŏ��ɉE�Ŋϑ�����Ȃ��m���v��
�ŏ��ɉE�Ŋϑ������m����66.66������@�{�@�ŏ��ɉE�Ŋϑ�����Ȃ��m����33.33��������P�O�O����������
�����O��������A�Ō��wikipedia�́u�����e�B�z�[�����v�Ƃ��� ttp://www.juen.ac.jp/gp/yousei/exercise/iwasaki/exercise08.pdf
��ǂ�Ŋ��z�������� �u�ϑ������Ƃ���1���ۖڂ��E�Ɗϑ������m���v�ƁA
�u�E���ϑ������Ƃ��Ɏ��ۂ��ϑ������m���v���������ĂȂ��H
�O�҂�1���ۖڂ��E�Ŋϑ�����邩���Ŋϑ�����邩�͔r���A�Ώ̂ŁA�m����1/2
>>251�̈Ӑ}�͂���������Ȃ��H
>>255�̊e�P�[�X�����l�Ɋm���炵���Ƃ������肪�Ó����͒m��� >>257
�����P�@�P�[�X�P�̏ꍇ
�@�����j�@�ŏ��Ɂ������́u�E�v�̊ϑ����u�Ŋϑ������m���́H
�@�����j�@���Ɏc�����P�́������́u�E�v�̊ϑ����u�Ŋϑ������m���́H
�����Q�@�P�[�X�Q�̏ꍇ
�@�����j�@�ŏ��Ɂ������́u���v�̊ϑ����u�Ŋϑ������m���́H
�@�����j�@���Ɏc�����P�́������́u���v�̊ϑ����u�Ŋϑ������m���́H
�P�[�X�P�ƃP�[�X�Q�͑Ώ̂Ȃ̂�
���P�Ɩ��Q�͓̉�����
�ŏ��Ɂ����ϑ������ꍇ�@���E�ō��������̂�
�ŏ��ɉE�Ł����ϑ������\���͂P�^�Q
�ŏ��ɍ��Ł����ϑ������\���͂P�^�Q
���P�@���j�@�����@�\���͂P�^�Q
���Q�@���j�@�����@�\���͂P�^�Q �����P�@�P�[�X�P�̏ꍇ
�@�����j�@�ŏ��Ɂ������́u�E�v�̊ϑ����u�Ŋϑ������m���́H
�@�����j�@���Ɏc�����P�́������́u�E�v�̊ϑ����u�Ŋϑ������m���́H
�����Q�@�P�[�X�Q�̏ꍇ
�@�����j�@�ŏ��Ɂ������́u���v�̊ϑ����u�Ŋϑ������m���́H
�@�����j�@���Ɏc�����P�́������́u���v�̊ϑ����u�Ŋϑ������m���́H
�ŏ��E�Ł����ϑ������\���~���Ɂ����E�Ŋϑ������\�����������E�Ŋϑ������\��
�ŏ����Ł����ϑ������\���~���Ɂ������Ŋϑ������\�������������Ŋϑ������\��
�P�^�Q �@�~�@�H�@���@�P�^�R�@
�H�@���@�P�^�R�@�@�~�@�Q�^�P�@���@�Q�^�R�@
���P�@���j�̓����@�@�Q�^�R
���Q�@���j�̓����@�@�Q�^�R >>265
���u�ϑ������Ƃ���1���ۖڂ��E�Ɗϑ������m���v�ƁA
���u�E���ϑ������Ƃ��Ɏ��ۂ��ϑ������m���v���������ĂȂ��H
�d�q���ϑ�����ꍇ��
���̓������X�N���[���ɂȂ��Ă���
�d�q��������Ό���
�ŏ��ɔ��̉E���̃X�N���[���ɋP�_���ł����
�ŏ��ɓd�q�͔��̉E�Ŋϑ����ꂽ
�ŏ��ɔ��̍����̃X�N���[���ɋP�_���ł����
�ŏ��ɓd�q�͔��̍��Ŋϑ����ꂽ
���E�͏����ɍ��������̂�
�ŏ��ɉE�Ŋϑ������\�����ŏ��ɍ��Ŋϑ������\����
�ǂ�����������P�^�Q �����Ȃ��B�O>>252����͖������ˁB�����Ȃ����ǁB��l�����ŐQ�邩�B
�P�P]/�_____________
�Q�Q/�_/ .���@�@�@�@)
�P�P�_/�c~-~Ђ��@�@/|
�P�P|�__U,~�܁R�_�^||
���@| �a�P�P~U~U�a ||_
�Q�Q| �a ���@�� �a |/
_____`�a________�a�^ /
�P�P�P�P�P�P�P�P�P�P�a
���@ ���@ ���@ ���@ �a
____________________�a
�P�P�P�P�P�P�P�P�P�P�P >>265
���P�j���̒��ɋ�ʂ̂����Ɓ����L�����ꍇ�̊m��
�@���P�[�X�P�@�u�����@�@�@�@�@�@�v�@���̍����Ł������ϑ������m���S���̂P
�@���P�[�X�Q�@�u�@�@�@�@�@�@�@�����v�@���̉E���Ł������ϑ������m���S���̂P
�@���P�[�X�R�@�u���@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���S���̂P
�@���P�[�X�S�@�u���@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���S���̂P
���Q�j���̒��ɋ�ʂ̂��Ȃ��������L�����ꍇ�̊m��
�@ ���@�P�[�X�P�u�����@�@�@�@�@�@�@�@�v�@���̍����Ł������ϑ������m���R���̂P
�@���@�P�[�X�Q�u�@�@�@�@�@�@�@�@�����v�@���̉E���Ł������ϑ������m���R���̂P
�@���@�P�[�X�R�u���@�@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���R���̂P
�ʏ�̕����̐�������
�@�P�[�X�P�@�u�����@�@�@�@�@�@�v�@
�@�P�[�X�Q�@�u�@�@�@�@�@�@�@�����v�@
�@�P�[�X�R�@�u���@�@�@�@�@�@�@���v�@
�@�P�[�X�S�@�u���@�@�@�@�@�@�@���v�@
����
�@�P�[�X�P�@�u�����@�@�@�@�@�@�@�v�@
�@�P�[�X�Q�@�u�@�@�@�@�@�@�@�����v�@
�@�P�[�X�R�@�u���@�@�@�@�@�@�@���v�@
�@�P�[�X�S�@�u���@�@�@�@�@�@�@���v�@
�����
�P�[�X�R�ƃP�[�X�S�͓����
�u����Ȃ�P�v�Ƃ������ƂłP�̃P�[�X�ɂ���
�����n�̐l�͐��w�͒P�Ȃ铹��Ȃ̂ŕʂɋC�ɂ͂��Ȃ�����
�P�[�X�̏ꍇ�́u����Ȃ�P�v��
���̏ꍇ�́u����ȁ����Q����v�Ƃ��Ă�
�悤����ɕ����̐����ł�
�P�[�X�̏ꍇ�́@�o���@�A�@���p���o���p�@��
���̏ꍇ�́@�@�@�@�o���@�A�@���p���o���p�@�Ƃ��Ă�
����͐��w�n�̐l����݂�ǂ�Ȏ��Ȃ̂�
������������ �����A���E�����Ɋϑ��J�n���čŏ���1�ڂ́����ϑ������B
���炭���āA2�ڂ́����ϑ��������Ă��ƂˁB
�ŏ��ɉE���̂݊ϑ����Č����邩�ǂ����B�Ǝv���Ă�
����̌����Ă邱�Ƃ����������Ǝv������A����������������������Ȃ��ƍl����d�v��
��������ŏ���1�ڂ͍��E�Ōܕ��ܕ����B
������2�ڂ�3����2�̊m���œ������Ŋϑ������B
�ʂɂ��������Ƃ���͂Ȃ��ˁB
�m���ɂ��Ēm�����Ȃ��l��2�ڂ��ܕ��ܕ��ƍl���邾�낤���ǁA
���ꂪ�܂��� ttp://www.juen.ac.jp/gp/yousei/exercise/iwasaki/exercise08.pdf �ʼn������Ă��� �́ANHK��2355�̔ԑg�ŁA�Љ�ꂽ�Z��(���w)�g���b�N�ŁA�}�W�b�N�i���o�[9�Ƃ�����肪�A�C�ɂȂ��Ă܂��B
�^�C�g�������o���ĂȂ��A�l�b�g�Œ��ׂĂ��A��蕶�����͂���܂���ł����B�N���m���Ă���l�͋����Ă��������B���̂Ƃ��́A�ʔ��������L��������܂����B >>270
�܂��A��������
> �@�P�[�X�P�@�u�@�����@�@�@�@�@�@�v�@���̍����Ł������ϑ������m���S���̂P
> �@�P�[�X�Q�@�u�@�@�@�@�@�@�@�����v�@���̉E���Ł������ϑ������m���S���̂P
> �@�P�[�X�R�@�u���@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���S���̂P
> �@�P�[�X�S�@�u���@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���S���̂P
�̊e���ہA
> �@�P�[�X�P�u�����@�@�@�@�@�@�@�@�v�@���̍����Ł������ϑ������m���R���̂P
> �@�P�[�X�Q�u�@�@�@�@�@�@�@�@�����v�@���̉E���Ł������ϑ������m���R���̂P
> �@�P�[�X�R�u���@�@�@�@�@�@�@�@���v�@���̍��E�Ł������ϑ������m���R���̂P
�̊e���ۂ����l�Ɋm���炵���Ƃ͂Ȃ�Ȃ����낤
���ꂼ��̃P�[�X1�A2�����m���A�O�҂̃P�[�X3�A4�����m���ɂȂ�̂́A�Ώ̂Ɖ��肷��ł����Ƃ��āA
�O�҂�1�A2��3�A4
��҂�1�A2��3
�̊m�����ǂ��Ȃ邩�͉��莟��
��҂̃P�[�X��3�ʂ肵���Ȃ�����ƌ����āA�������Ɋe�m����1/3�ɂ͂Ȃ�Ȃ�
> �悤����ɕ����̐����ł�
> �P�[�X�̏ꍇ�́@�o���@�A�@���p���o���p�@��
> ���̏ꍇ�́@�@�@�@�o���@�A�@���p���o���p�@�Ƃ��Ă�
�u�P�[�X�̏ꍇ�v�A�u���̏ꍇ�v�₱�̎��������Ӗ�����̂���������Ȃ����A
���l�Ɋm���炵���Ɖ��肷�邩����ŁA1/3�ł�1/4�ł�����ȊO�ɂł��Ȃ�Ƃ��������Ȃ���Ȃ��� >>273
�����ꂼ��̃P�[�X1�A2�����m���A�O�҂̃P�[�X3�A4�����m���ɂȂ�̂́A�Ώ̂Ɖ��肷��ł����Ƃ��āA
���O�҂�1�A2��3�A4
����҂�1�A2��3
���̊m�����ǂ��Ȃ邩�͉��莟��
����҂̃P�[�X��3�ʂ肵���Ȃ�����ƌ����āA�������Ɋe�m����1/3�ɂ͂Ȃ�Ȃ�
�����̏ꍇ�͐��������ǂ����͊ϑ����ʂɖ������Ȃ����ǂ����Ȃ̂�
�P�[�X�̌����R�ł��ꂼ��̊m�����ЂƂ����P�^�R�ƌ����Ă�
���ꂪ�ϑ����ʂƖ������ĂȂ��̂Ŗ�莋�͂��Ȃ� >>271
����������ŏ���1�ڂ͍��E�Ōܕ��ܕ����B
��������2�ڂ�3����2�̊m���œ������Ŋϑ������B
���ʂɂ��������Ƃ���͂Ȃ���
�������̂������傫��
�u���̉E�[�̃X�N���[���v�Ɓu���̍��[�̃X�N���[���v�̋������P���N�������Ƃ���
�ŏ��Ɂu���̉E�[�̃X�N���[���v�Ł����ϑ����ꂽ�ꍇ
�u���̍��[�̃X�N���[���v�Ł����ϑ������m���͂P�^�R�ƂȂ�
�E�[�̃X�N���[���ƍ��[�̃X�N���[���̋����͂P���N�Ȃ�
�����Ői��ł��P�N������
�Ƃ��낪�E�[�̃X�N���[���Ł����ϑ����ꂽ�r�[��
���Ԃ����������[�̃X�N���[���Ł����ϑ������m���͂P�^�R�ɂȂ� >>273
> �悤����ɕ����̐����ł�
> �P�[�X�̏ꍇ�́@�o���@�A�@���p���o���p�@��
> ���̏ꍇ�́@�@�@�@�o���@�A�@���p���o���p�@�Ƃ��Ă�
�����I�W���_�̑̌����Ł@�o���@�A���p���o���p�@�Ƃ�
�u����Ȃ�P�v�Ƃ��Ă�
�u����ȁ����Q��������v�Ƃ����ꍇ�́@�o���@�A���p���o���p�ƂȂ�
�P�[�X�������S��R�b�v�ɕς��Ă��o���@�A�@���p���o���p�@�͕��Ղ���
�P�[�X�����ɕς���Ɓ@�o���@�A�@���p���o���p�ƂȂ��Ă��܂�
�u�@�o���@�A�@���p���o���p�v��@�u�o���@�A�@���p���o���p�v��
���̐����Ɉˑ����Ă�Ƃ������ƂɂȂ�
�i���̐����Ɉˑ�����@���͕����@���j �}���`�����Ǝ����ǂދC���ǂ�ǂ�Ȃ��Ȃ���
�����X�����܂����Ŏ��n��ǂ��ēǂނ̂��ʓ|������ >>271
����������ŏ���1�ڂ͍��E�Ōܕ��ܕ����B
��������2�ڂ�3����2�̊m���œ������Ŋϑ������B
���ʂɂ��������Ƃ���͂Ȃ���
�����w�҂͂����s�v�c�Ȍ��ۂƌ��Ă�
�ŏ��́������E�ǂ��炩�Ŋϑ�������
�c�������̊ϑ��m�����ω�����
���̉E�[�̃X�N���[����
���̍��[�̃X�N���[���̋������P���N�̏ꍇ��
�������ŏ���`���Ă��P�N�����邵
���������ď���`���鎖�͕����@���Ƃ��ĕs�\
�Ƃ��낪���̉E�[�̃X�N���[���ōŏ��Ɂ����ϑ�������
�u���Ɂu���S�́v��
�c�����������̉E���Ŋϑ������\���͂Q�^�R�ɂȂ�
���̍����Ŋϑ������\���͂P�^�R�ƂȂ�
�傫���͂P���N�����锠�S�̂ŏu����
�c�������̊ϑ��m�����ω�����̂�
�����x���z�����Ȃ��Ƃ��������@���Ɛ��������Ƃ�Ȃ�
�ƕ����w�҂͍l���Ă��� >>278
�������������b�������������̂�
����͒P�Ɂu�ʎq�͊w�͔�Ǐ��I�ł���v���Ă����̘b���Ǝv��
�A�C���V���^�C�����ʎq�͊w�ɉ��^�I�����������̂P�ł���A�ÓT�͊w�I�ɍl����Εs���������ǁA���ł͖����Ƃ��ł͂Ȃ��ʎq�͊w�̐����̂P�Ƃ��ė�������Ă� 1�ȏ�22�ȉ��̎��R���̏W����S�Ƃ���
S�̕����W��T�ŁA���̏����������̂��l����
[����] T�ɑ�����C�ӂ�2�̗v�f�̍���4�ł�7�ł��Ȃ�
T�̗v�f���̍ő�l�͂����炩
1 5 9 13 17 21
2 6 10 14 18 22
3 7 11 15 19
4 8 12 16 20
Table[2n-b-a+{(n+a)mod4}+4C(0,n-8+a),{a,0,1},{b,0,2},{n,1,10}]
{3, 6, 9, 8, 11, 14, 17, 20, 19, 22}
{2, 5, 8, 7, 10, 13, 16, 19, 18, 21}
{1, 4, 7, 6, 9, 12, 15, 18, 17, 20}
{3, 6, 5, 8, 11, 14, 17, 16, 19, 22}
{2, 5, 4, 7, 10, 13, 16, 15, 18, 21}
{1, 4, 3, 6, 9, 12, 15, 14, 17, 20} >>249
��������́u�������܂�Ȃ̂��H�v���Ă�̂ɁA
�Ȃ��ς��a��瓚���ĂH >>279�u�ʎq�͊w�͔�Ǐ��I�ł���v
�����S�̏ꍇ�͈ʒu�͓_�ŕ\���������
�����S�͈ʒu���_�ŕ\�������Ǐ��I�ȑ��݂Ƃ������ƂɂȂ�
�ϑ��O�̓d�q�̈ʒu�͓_�ł͕\���ł���
���̒��S�̂Ŋϑ������m�������邾���Ȃ̂�
�ʒu���Ǐ��I�ȓ_�ŕ\���ł��Ȃ��Ƃ������ƂŔ�Ǐ��I���݂ƌĂ��
�Q�̃����S�͈ʒu���قȂ�̂�
�����S���g�������玗�Ă��Ă��ʒu�ŋ�ʂ���
�Q�̓d�q�̏ꍇ�͔�Ǐ��I���݂Ȃ̂�
�ʒu���܂߂đS����ʂł��Ȃ��Ƃ�����ԂɂȂ�
����ȓd�q���Q���݂���Ƃ�����Ԃ��\�ɂȂ� >>283
����͊m�����߂̘b�ł����āA(��)�Ǐ����Ƃ͕ʂ̘b�ł� >>284����͊m�����߂̘b�ł����āA(��)�Ǐ����Ƃ͕ʂ̘b�ł�
�ϑ������O�̓d�q��
�_�ŕ\�������悤�Ȉʒu�ɂ͑��݂��Ȃ�
���Ƃ��Δ��̒��̉E���̃X�N���[���œd�q���ϑ����ꂽ�ꍇ
�d�q�͋P�_�Ƃ��Ċϑ�����邯��
�ϑ����O�ɓd�q�͋P�_���ӂ̂ǂ����̓_�ɑ��݂��Ă��킯�ł͂Ȃ� ��������ʎq���v�������ɂ��̃X���̓��e�Ō���Ă�A�z�͂܂����������Ă�����
����������� �������������͉��̉��X��������Ă����b����Ȃ�
�A�z������Ă��邾���Ŗʔ����̂�������Ȃ����Ă��� ����ȂƂ���ɏ������ޓz���������Ƃł��H
�������Ȃ炱�̃X������I�T���o���Ę_���ł������Ăǂ��� Table[{1-n(n-1)(n-2)(n-3)(n-4)(n-5)(n-6)(n-7)(n-8)(n-9)(n-10)(n-11)(n-12)/13!}/4,{n,0,13}]
Table[(1-C(0,n-13))/4,{n,0,13}]
����Z���ł��� ��������
�����ƒ�x���̖ʔ��������݂�Ȃł킢�킢���������� >>290
��x���̖ʔ�����肪�~�������H
�ƒ닳�t�̃g���C���V�������w��n������B�u�������̓��[�g�ƃA�L�����̓��[�g�ƃΈȊO�v
nagata�����w�C@kamere112
����AYouTube�ɂ��閳�����Ɠ����1�V�[�������ǁA�L�����Ɩ������̐����K�o�K�o����ˁH
https://i.imgur.com/WR0wZ6G.png
nagata�����w�C
�g���C���Ȃ̖�������ł��ˁB�������܂œ��X��cm�Ƃ������Ă�m������ȃK�o�K�o�Ȏ��Ƃ�����̂͗��ɁA�A
���c���`@tomo3141592653
�����������������Ɛ�������g���C�̍u�t�A�s�^�S���X�h�̎c�}�Ȃ̂ł́B
�w���p�[�|@merazoma25252
�ŋߘb��ɂȂ��Ă�g���C�̗L�����Ɩ������̓�������Ă���}�ɍĐ��~�܂��ē���폜���ꂽ
https://i.imgur.com/SylD7RP.jpg
���[�ρ[������@superZ_th
��ł��ł��Ȃ����߁A�L�����ł���B
https://i.imgur.com/nfsp27p.jpg
�\�[�X
https://twitter.com/kamere112/status/1117796154408783872
https://twitter.com/5chan_nel (5ch newer account) C: ���f���S��
R: �����S��
Q: �L�����S��
Z: �����S��
N: ���R���S��
�g�p��. 1 �� N �� Z �� Q �� R �� C. �O>>269
>>88
K����BC�ɐ���KP�������B
tan��KJG=KP/JP�\�\�@
KP=BP=BG{BP/(GP+BP)}
=(1/��3){��3/(��3+1)}
=1/(1+��3)
=(��3-1)/(��3+1)(��3-1)
=(��3-1)/2�\�\�A
JP=1/��3+1/(��3+1)
=(��3+1+��3)/��3(��3+1)
=(1+2��3)(��3-1)/��3(��3+1)(��3-1)
=(5-��3)/2��3
=(5��3-3)/6�\�\�B
�@�ɇA�B�������A
tan��KJG=��3(��3-1)/(5-��3)
=��3(��3-1)(5+��3)/(5-��3)(5+��3)
=(3-��3)(5+��3)/22
=(15-3-2��3)/22
=(6-��3)/11
��0387995381
=tan21.2060231��
����KJG=21.2060231�� >>88�O>>293�����B
K����BC�ɐ���KP�������B
tan��KJG=KP/JP�\�\�@
KP=BP=BG{BP/(GP+BP)}
=(1/��3){��3/(��3+1)}
=1/(1+��3)
=(��3-1)/(��3+1)(��3-1)
=(��3-1)/2�\�\�A
JP=1/��3+1/(��3+1)
=(��3+1+��3)/��3(��3+1)
=(1+2��3)(��3-1)/��3(��3+1)(��3-1)
=(5-��3)/2��3
=(5��3-3)/6�\�\�B
�@�ɇA�B�������A
tan��KJG=��3(��3-1)/(5-��3)
=��3(��3-1)(5+��3)/(5-��3)(5+��3)
=(3-��3)(5+��3)/22
=(15-3-2��3)/22
=(6-��3)/11
��0.387995381
=tan21.2060231��
����KJG=21.2060231�� �Ȃ�ƁB
�O�p��g����悤�ɂȂ����B n�l�|���̒�����������
�����ɁA2�l�g�̃J�b�v���������ƃ����_����
�ʒu�ɍ����Ă���
�A���A�e�J�b�v���ׂ͗荇���č���A1�l��1�l���̈֎q���L���A
��x�������瓮���Ȃ����̂Ƃ���
�����A������3,4�l�ڂ̂Ƃ���ɃJ�b�v��������A6,7�l�ڂ�
�Ƃ���ɂ��J�b�v��������ƁA5�l�ڂ̂Ƃ���͎g���Ȃ��܂܂�
�Ȃ邱�ƂɂȂ�
���̂悤�Ɋe�J�b�v���̓����_���Ȉʒu���L���Ȃ���A
����Ȃ��Ȃ�܂ŃJ�b�v���͍����Ă���
���̂Ƃ��A�Ō�ɍ��E�����܂��ċ�Ȃ̂܂�
�g��ꂸ�c��֎q�̐��͂����ɂȂ�Ɗ��҂���邩�A
n�ŕ\�� �O>>294
>>296
�O�Ȃ���J�b�v��������Ăق��̃J�b�v��������Ȃ��B�Ȃ����Ȃ�����������ɂ���čŏ��̋�Ȃ�1��0�ɂȂ�B�����6���ނ��l����B
n=6K,6K+1,6K+2,6K+3,6K+4,6K+5�̂Ƃ��A
��Ȃ̐��́A
0�`2K,1�`2K+1,0�`2K,1�`2K+1,0�`2K,1�`K+1
���Ғl�́A
K,K+1,K,K+1,K,K+1
n�ŕ\���ƁA[P]��P���Ȃ��ő�̐����Ƃ��āA
n�������̂Ƃ�[n/6]
n����̂Ƃ��A[n/6+1] �O>>297
1��n��15�ŋ�Ȃ̊��Ғl�𐔎����狁�߁A���ۂ̋�Ȃ̐��Ɣ�ׂ�ƁA�قƂ�ǂ����Ă�Bn=4�̂Ƃ���n=10�̂Ƃ��͓��ʂȂ̂��ȁB
n=1�̂Ƃ��A
[1/6+1]=[7/6]=1�c�c1 ��
n=2�̂Ƃ��A
[2/6]=[1/3]=0�c�c0 ��
n=3�̂Ƃ��A
[3/6+1]=[3/2]=1�c�c1 ��
n=4�̂Ƃ��A
[4/6]=[2/3]=O�c�c0or2
���Ғl��1 �~
n=5�̂Ƃ��A
[5/6+1]=[11/6]=1�c�c1 ��
n=6�̂Ƃ��A
[1]=1�c�c0or2
���Ғl��1 ��
n=7�̂Ƃ��A
[7/6+1]=[13/6]=2�c�c1or2or3
���Ғl��2 ��
n=8�̂Ƃ��A
[8/6]=[4/3]=1�c�c0or2
���Ғl��1 ��
n=9�̂Ƃ��A
[9/6+1]=[3/2+1]=[5/2]=2�c�c1or3
���Ғl��2 ��
n=10�̂Ƃ��A
[10/6]=[5/3]=1�c�c0or2or4
���Ғl��2 �~
n=11�̂Ƃ��A
[11/6+1]=[17/6]=2�c�c1or3
���Ғl��2 ��
n=12�̂Ƃ��A
[12/6]=2�c�c0or2or4
���Ғl��2 ��
n=13�̂Ƃ��A
[13/6+1][19/6]=3�c�c1or3or5
���Ғl��3 ��
n=14�̂Ƃ��A
[14/6]=[7/3]=2�c�c0or2or4
���Ғl��2 ��
n=15�̂Ƃ��A
[15/6+1]=[5/2+1]=3�c�c1or3or5
���Ғl��3 �� �O>>299�����B
n=6K+4�̂Ƃ��͋�Ȃ�1������݂������BK�͐��̐����Ƃ��āB
��Ȃ̐��̊��Ғl�́A
n�������ŁA����6K+4�łȂ��Ƃ��A[n/6]
n����܂��́A������6K+4�̂Ƃ��A[n/6+1] �O>>300
4,10,16,22,28,34,40,46,52�c�c
16��52�������Ă݂�ȋ����B�B�����ȁB .com/toshio_tamogami/status/1110356301664514048
�R���A���p�u�q�g���h�L�����S�~�ƍߎҎ��E����q�g���h�L�E�����s�� >>299
���ɂ��̓����͂ǂ���
�Ⴆ�An=4�̏ꍇ�́A��Ȃ̐���0,2�ƂȂ�m�������̓������Ƃ��Ă���̂�
�Q�l
����������������
https://rio2016.5ch.net/test/read.cgi/math/1549700978/279
������Ȃ����͂����ɏ����Ă�478
https://rio2016.5ch.net/test/read.cgi/math/1511604229/401 >>303�̃����N�挩�Ă݂�킩��B
�Œ���Q�����Ɠ������̘b���킩���ĂȂ��Ɩ����B
���g�����\���Ȃ�A�[�@�ł����邩������Ȃ����ǁB �ϕ��̂�������Ƃ����m��������� n�Ȃ̂Ƃ��̊��Ғl��S(n)�Ƃ���B
S(0)=0�AS(1)=1�ł���B
1�g�ڂ̃J�b�v��������ƁA�A��������Ȃ͍��E2�ɕ��f�����B
����A�����ɃJ�b�v���������Ă��E���ɉe����^���Ȃ��B�E���������ɉe����^���Ȃ��B
�����̘A��������Ȃ̐���0�`n-2���������m���Ō����B�E��������
�Ȃ̂ŁAS(n)=(S(0)+S(1)+���+S(n-2))*2/(n-1)�����藧��
���Ƃ͂킩��� >>60
�Q�����F�@a(n) = a(n-1) + a(n-2)/((2n-1)(2n-3)),
�@a(1) = 0, a(2) = 1/3, a(3) = 1/3, a(4) = 12/35, a(5) = 47/135,�@����
a(n) = 1F1(-n,-2n,-2)�@�@���@1/e�@�@(n����)�@�@>>66-69
b(n) = (2n-1)!!a(n)�@
�͎��R����ŁAOEIS�ɂ���B
�Q�����F�@b(n) = (2n-1)b(n-1) + b(n-2),
�@b(1) = 0, b(2) = 1, b(3) = 5, b(4) = 36, b(5) = 329, ����
b(n) �� Number of loop-less linear chord diagrams with n chords.
�w���^����F�@exp{��(1-2x) -1}/��(1-2x) = ��[k=0,��) {b(k)/k!}x^k
http://oeis.org/A278990
�����t���o�[�W����
�@(-1)^n b(n) = Y_n(-1)
�@Y_n ��n���̃x�b�Z����
http://oeis.org/A000806 ������������������������������������
���������������������������������������������� ����A����k�l�|���̈֎q�ł�x�l���An-k-2�l�|���ł�y�l���A
�Ǘ������X�y�[�X����Ɗ��҂����Ƃ���Ak�l�|���̈֎q��
n-k-2�l�|���̈֎q�����������x+y�l���̌Ǘ��X�y�[�X��
�o����Ɗ��҂����
�ȏ���A�ŏ��̃J�b�v����k+1,k+2�ڂ��L�����Ȃ�A
�Ǘ����Ďc��X�y�[�X��a_k + a_n-k-2�l���Ɗ��҂����
�e�ʒu�ɍ���m���͂܂����������_���ł��邩��A
���̎��ۂ�1/(n-1)�̊m���ł�����
�̂ɁAa_n��a_0,a_1, �E �E �Ea_n-2��p���Ď��̂悤�ɕ\����
a_n=(1/(n-1))sum[a_k + a_n-k-2,{k,0,n-2}]
�@�@=(2/(n-1))sum[a_k,{k,0,n-2}]
���̎������Ȍ��ɂ���
���ӂ�n-1�{�������ɂ��āAn��n+2��������������
n+1����������������
(n-1)a_n=2sum[a_k + a_n-k-2,{k,0,n-2}]
(n+1)a_n+2 - na_n+1=2sum[a_k,{k,0,n}]-2sum[a_k,{k,0,n-1}]=2a_n
��(n+1)a_n+2=na_n+1 + 2a_n >>306
������O���ԑQ�����ɕό`����wolfram �˂����߂Γ����������� ��a_n�̕]��
a_n=Sum[(-2)^k(n-k)/k!,{k,0,n-1}]
�@�@=(n)Sum[(-2)^k/k!,{k,0,n-1}]-Sum[(-2)^k/(k-1)!,{k,1,n-1}]
��n�����̋Ɍ����l����
a_n��(n)Sum[(-2)^k/k!,{k,0,��}]+(2)Sum[(-2)^(k-1)/(k-1)!,{k,1,��}]
�@�@=n/e^2 + 2/e^2=(n)e^(-2) + (2)e^(-2)��(n)e^(-2)
�]���āAn���\���傫�����Aa_n�����Ǘ������֎q�̐���
�S�̂�e^(-2)�Ƃ��������ɂȂ�ƍl������ >>306
�Q�����F�@(n+1) S(n+2) = n S(n+1) + 2 S(n),
�@S(1) = 1, S(2) = 0, S(3) = 1, S(4) = 2/3, S(5) = 1, S(6) = 16/15, S(7) = 11/9,
����F�@x�exp(-2x)/(1-x)^2 = ��[k=0,��]�@S(k) x^k,
s(n) = (n-1)! S(n)�@�͎��R����ŁAOEIS �ɂ���B
�Q�����F�@s(n+2) = n{s(n+1) + 2s(n)},
�@s(1) = 1, s(2) = 0, s(3) = 2, s(4) = 4, s(5) = 24, s(6) = 128, s(7) = 880,
http://oeis.org/A087981 lim (x��1�Ay��1)�@x(1-y^n)-y(1-x^n)+y^n-x^n/(1-x)(1-y)(x-y)
n��1���傫�����R�� ���q��
�@| 1,�@1,�@1 |
�|| x,�@y,�@z |
�@|x^n,y^n,z^n|
�����
�@| 1,�@1,�@1 |
�|| x,�@y,�@z | = -(x-y)(y-z)(z-x) = -��,
�@|x^2,y^2,z^2|
����� Vandermonde �s�A�܂荷�ρB�i�{��ł� z=1�j
(�^��) = ��[i��0, j��0, k��0, i+j+k=n-2] x^i y^j z^k
{�E�ӂ̍���} = {n-2 ��3�̔����̘a�ɕ���������@}
�@= {n���狫�E2��I�ԕ��@}
�@= C[n, 2]
�@= n(n-1)/2. ���q������� x,y,z �̌�㎮������
�@(�^��) = (x,y,z ��(n-2)���̑Ώ̎�) = P_n(x+y+z, xy+yz+zx, xyz)
P_2 = 1,�@P_3 = x+y+z,�@P_4 = (x+y+z)^2 - (xy+yz+zx),
P_5= (x+y+z)^3 -2(x+y+z)(xy+yz+zx) +xyz,
P_n= (x+y+z)P_{n-1} - �i����+����+�����jP_{n-2} + (xyz)P_{n-3},
[�����X���S�V�W.450-452]�@�Ɠ��������ǥ��� �����A���Ȃ݂Ɉ��������ɂ���z�肵�Ă� ���w�y���K�����l60�͂���� ������������������������
������������������������
������������������������
������������������������
������������������������
������������������������
������������������������
������������������������
������������������������
������������������������ [�P]�ȂȂ��̂��A��
�P�P]_������衑O>>301
�P�P��/�___________
_____/�_/�@�@�@�@�@)
_____�_/.,���@�@�@/|
_____�P�c-_-Ё@�@/ |
�P�P|�__U,~�܁R�^| |_
���@| �a�P~U~U�a | / )
____| �a�@���@�a |/ /|
_____`�a______�a�^_/ |
�P�P�P�P�P�P�P�P�P�a (1)
�@���R��n�Ɛ��̎���a�ɑ��@P_n = a^n + 1/a^n�@�Ƃ����B���̂Ƃ��Q����
�@�@P_{n+1} = (a + 1/a) P_n - P_{n-1},
�������B
(2)
�@x^2 + 1/x^2 = 7�@�̂Ƃ��@x^3 + 1/x^3 ����� x^5 + 1/x^5 �̒l�����߂�B�������Ax>0 �Ƃ���B
�����X���S�V�W-438 >>323
(1)
P_{n+1} = a^(n+1)+1/a^(n+1) = (a + 1/a)(a^n+1/a^n)- (a^(n-1)+1/a^(n-1)) = (a + 1/a) P_n - P_{n-1},
(2)
�@x^2 + 1/x^2 = 7�@���A(x+1/x)^2-2 = 7�Ax+1/x = ��5�A����ď�Q��������AP_{n} = x^n+1/x^n�@�Ƃ��āAP_{3} = 6��5�AP_{5} = 17��5 �O>>322
>>323(2)�͎O���Ƃ�441�ʼn��������B���ό`����x+1/x������āB
�P�P/�___________
___/�_/�@�@�@�@�@)
___�_/ .,���@�@ /|
___�@ �c-_-Ё@ / |___
�P|�__(�`��)��^| /�@ )
__| �a�P~UU~�a |/�@ /|
___`�a______�a�^___/|
�P�P�a�@�@�@�a�P�P�a ���w���bot
//twitter.com/mathhappylife/
//twitter.com/bot_mathematica/ (��)
//twitter.com/HimaginaryMp/
//twitter.com/math_TomoK/
�������bot
//twitter.com/seisu_bot/
//twitter.com/handmade_math/ (2)
�������ϕ�������bot
//twitter.com/Int_cal/
�g�������bot
//twitter.com/Cprbot/
�m�����bot
//twitter.com/kaku_ritu_bot/
���Z���w���bot
//twitter.com/7k_x/
//twitter.com/basicmath_TomoK/ (���Z���w��{���)
//twitter.com/kisaragikikyo1/�@(�{�C)
//twitter.com/mathbot77/�@�@(���w���)
//twitter.com/integerbot77/ (�������)
//twitter.com/integralbot77/�@(�ϕ����)
//twitter.com/probabilitybot/�@(�m�����)
https://twitter.com/5chan_nel (5ch newer account) �k���l
�����p�`�ɂ͂���ɓ��ڂ��鐳���`�����݂��邱�Ƃ������B
���w���u����
//twitter.com/HimaginaryMp/status/1121732161030119424
https://twitter.com/5chan_nel (5ch newer account) >>327���1�̐��O�p�`�̒��ɂ͈�Ӂ�3/4�̓��ڂ��鐳���`�����݂��邵�A���1�̐����`�̒��ɂ͈�Ӂ�2/2����1�܂ł̔C�ӂ̎����̐����`�����݂���B
�O>>325���1�̐��܊p�`�̒��ɂ�������Ɣ͈͂ɕ��̂���ӂ��������`�����݂���B�Ă��Ƃʼn��X�Ƒ��݂���B
]/�________________
/�_/ �����@ �����@/|
�_/ (�@(`) ((`-`)/ |
|�__(����)~,U��U�| |__
| �a�P�҃ҁP~U~U | / /
| �a�@���@���@�a |/ /
_`�a__________�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
__________________�a/
�P�P�P�P�P�P�P�P�P�P >>327
�����p�`�̕�AB�𑽊p�`�̎��𐳂̌����ɉ���������̏��ɕ��Ԃ悤�ɂƂ�B
AB�̒��_M���瓮�_P,Q��P�͐��̕�����Q�͕��̕����ɍŌ�P,Q��AB�̑Β��_�A�܂���AB�̑Εӂ̒��_�łԂ���܂Ŏ����ړ�������B
�����`PQRS�����̏��ɕ��̌����ɂƂ�B
�ŏ�R�͐����p�`�̓����ɂ��邪�Ō�͊O���ɂ���̂łǂ����Ŏ���ɂ̂�Ƃ�������B
���̂Ƃ��̐����`PQRS�͂��ׂĂ̒��_�������p�`�̎���ɂ̂�B �E��3�p�`
�@A(1/��3, 0)�@B(x1, 1/2),�@C(x1, -1/2)
�@x1 = -1/(2��3) = -0.288675135
�@x2 = 11/(2��3) -3 = 0.175426480
��BC��Ɂ@P(x1, L/2)�@Q(x1, -L/2)
���̕ӏ�Ɂ@�@R(x2, -L/2)�@S(x2, L/2)
L = x2 - x1 = 2��3 -3 = 0.464101615
��PQRS �͈�ӂ�L�̐����`�B
�E4�̔{���̂Ƃ��͖��炩�B
�E��5�p�`
�@A(1,0)�@B((-1+��5)/4, ��{(5+��5)/8})�@C(-(1+��5)/4, ��{(5-��5)/8})
�@D(-(1+��5)/4, -��{(5-��5)/8})�@E((-1+��5)/4, -��{(5+��5)/8})
�@P(x1, L/2) Q(x1, -L/2) R(x2, -L/2) S(x2, L/2)
������
�@x1 = {3��5 - ��(10(5+��5)) -1}/4 = -0.699576038
�@x2 = {2��(10(5-��5)) -��(10(5+��5)) +5��5 -11}/4 = 0.5471135116
�@L = x2 - x1 = (5+��5)/(2+��{2(5+��5)}) = {��(10(5-��5)) - (5-��5)}/2 = 1.246689549
��PQRS �͈�ӂ�L�̐����`
�E�����p�`
�@45� ������2�{�̒����������An�p�`�Ƃ̌�_��
�@P(-L/2, L/2)�@Q(-L/2, -L/2)�@R(L/2, -L/2)�@S(L/2, L/2)
�Ƃ����B��PQRS �͈�ӂ�L�̐����`
�E��6�p�`�̂Ƃ�
�@A(1, 0)�@B(1/2, (��3)/2)�@C(-1/2, (��3)/2)�@D(-1, 0)�@E(-1/2, -(��3)/2)�@F(1/2, -(��3)/2)
�@L = 3-��3 = 1.2679491924 ���p�`�̒��_�̍��W��
�@A(1,0)�@B(cos(2��/n), sin(2��/n))�@C(cos(4��/n), sin(4��/n))�@����
�Ƃ��Ώ㉺�Ώ̂ł���B
�@���� y=a �Ƒ��p�`�̋��ʕ����̒����̔����� h(a) �Ƃ����B
�@�㉺�Ώ̂�����@h(-a) = h(a),
�@�ʑ��p�`������Aa=0 �ōő�ƂȂ�A|a| �ɂ��ĒP�������ł���B
�@x=h(y)�@�Ɓ@x=�}y (45ߐ�) �͓_ (L/2, �}L/2) �Ō�������B
�@���� y=�}L/2 �Ƒ��p�`�̋��ʕ����̒�����L�ƂȂ�B
�@�� ��ӂ�L�̐����`�ɐڂ���B �Ȃ��B�O>>328���p�`�́��������[�x�b�h�ŃC�`���C�`�����悤���B
]/�______________
/�_/ �����@ ���� �_
�_/ (�@(`) ((`-`)/|
|�__(����)~,U��U�||___
| �a�P�҃ҁP~U~U ||�@/
| �a�@���@���@�a |/ /
_`�a__________�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
__________________�a/
�P�P�P�P�P�P�P�P�P�P �P���œ�����B
�ԋʂS�A���ʂQ�A���ʂQ�̌v�W�̋ʂ����ɓ����Ă���B����ׂɂP���o���ē����F�̋ʂ����o�����ʂƋ��ɔ��ɂ����B���������J��Ԃ����Ƃ��A���̂Ȃ��ɂ͂��{�W�̋ʂ����邪�A���ʂ̌��̊��Ғl�́H >>333
�����������Ⴄ�Ƒ��̐l�ʔ����Ȃ��Ȃ邩�珑���Ȃ��ˁB �O>>332
>>333
n/4+8
8����Ή����ʂ�2���҂ł��邩�獇�v10��Ȃ�B
������B >>335
n=1�̂Ƃ�33/4 = 8.75�ł����B�Ȃ�قǁB �܂�������
>>335
n=1�̂Ƃ�8.25�ˁB
�\���͂Q���R�A�ł����Ғl��8.25�B �O>>335
����A�m���͖���ς�邩����Ғl���ς�邩������Ȃ��ȁB
�܂�o��ʂ͂ǂ�ǂ�o��B�����ʂ��o�₷���ʂ�����B���������o�đ����Ă���Ɖ����ʂ͂ǂ�ǂ�o�ɂ����Ȃ�B
��ς��ȁA�����ʁB
n/4��菬�����ȁB
���������肷��낤���H�@���B����L���ȁB
��n+1=(1/4)��n
���������B
������������������B �O>>338
n/4+2�ł����́H
�Ȃɂ��ʔ����́H
�����ʂ��o��m�����˂�1/4�Ȃ́H �ǂ����ā@�O�@�Ȃ�Č�ɒu����B >>339
��Ȃ킯�Ȃ��B
����͐��U�@�ʼn������Ƃ���Ƒ�ς����ǁA���܂���������Ƃ�����Ɖ����Ėʔ����Ƃ������B
���U�@�ʼn����Ȃ��l�ɖʔ����͂킩��܂���B �k���l
(1)�@x>0 �ɂ�����@x^x �̍ŏ��l�����߂�B
(2)�@x>0 �̂Ƃ� x^x > 1 - (2/e)��x�@�������B
(3)�@lim[x��+0]�@x^x�@�����߂�B
[�����X���S�T�Q�D588,591,605] >߁܁܁�~�c�`���U�@���
>߁܁�~�c�` �@�O>>339
>߁܁�~�c�`�@�킩�����
|�@�@ __________
|�@���� ���� �@/�_
|�i(-_-)-_-)) / �
|�i`��u~U��U�/�^|
| �a�҃�~UU~�a�@|
| �a ���@�� �a�@|
�ځa�Q�Q�Q�Q�a�^|
�P�P�P�P�P�P�a�@|
���@���@���@�a�@|
�Q�Q�Q�Q�Q�Q�a�^|
�P�P�P�P�P�P�a�@|
���@���@���@�a�@|
�Q�Q�Q�Q�Q�Q�a�^|
�P�P�P�P�P�P�a�@|
���@���@���@�a�@|
�Q�Q�Q�Q�Q�Q�a�^|
�P�P�P�P�P�P�a�@|
���@���@��,�c�~�|
�Q�Q�Q�Q�Q��`,`;,'
�Q�Q�Q�Q�Q_U��U�;,
/�Q/�Q/�Q/;_~U U~_;
/�Q/�Q/�Q/�Q��_/�Q
/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Ȃ肷�܂��h�~�̂��߂ɑO>>������悤�ɂȂ����B�C�O�̗��w���m���玿�₳�ꂽ�B����͌N���������̂����āB �O>>343�傫���^��͍�����B���������͂Ȃ��Ďq�ǂ������͐��B�s���N��I�����W�Ȃ�ĂȂ���!!�@�����������B
����I����������2�̏ꍇ�̐��́A
2�~6/8
������3�̏ꍇ�̐��́A
3�~2/8
2��ڏI����������2�̏ꍇ�̐��́A
2�~6/8�~7/9
������3�̏ꍇ�̐��́A
3�~(6/8�~2/9+2/8�~7/9)
������4�̏ꍇ�̐��́A
4�~(2/8�~2/9)
3��ڏI����������2�̏ꍇ�̐��́A
2�~6/8�~7/9�~8/10
������3�̏ꍇ�̐��́A
3�~(6/8�~7/9�~2/10+6/8�~2/9�~8/10+2/8�~7/9�~8/10)
������4�̏ꍇ�̐��́A
4�~(2/8�~2/9�~8/10+2/8�~7/9�~2/10+6/8�~2/9�~2/10)
������5�̏ꍇ�̐��́A
5�~2/8�~2/9�~2/10
4��ڏI����������2�̏ꍇ�̐��́A
2�~6/8�~7/9�~8/10�~9/11
������3�̏ꍇ�̐��́A
3�~(6/8�~7/9�~8/10�~2/11+6/8�~7/9�~2/10�~9/11+6/8�~2/9�~8/10�~9/11+2/8�~7/9�~8/10�~9/11)
������4�̏ꍇ�̐��́A
4�~(2/8�~2/9�~8/10�~2/10+2/8�~7/9�~2/10�~9/11+6/8�~2/9�~2/10�~9/11+2/8+7/9�~8/10�~9/11+7/9�~8/10�~9/11)
������5�̏ꍇ�̐��́A
5�~(2/8�~2/9�~2/10�~9/11+2/8�~2/9�~9/10�~2/11+2/8�~7/9�~2/10�~2/11+6/8�~2/9�~2/10�~2/11)
������6�̏ꍇ�̐��́A
6�~2/8�~2/9�~2/10�~2/11
(����)
n��ڏI����������2�̏ꍇ�̐��́An�̕������|���邩��A
2�~6/8�~7/9�~8/10�~9/11�~�c�c�~(n+5)/(n+7)
=2�~6�~7/(n+6)(n+7)
=84/(n+6)(n+7)
������3�̏ꍇ�̐��́A
3�~{6/8�~7/9�~8/10�~9/11�~�c�c�~(n+4)/(n+6)�~2/(n+7)+6/8�~7/9�~8/10�~9/11�~�c�c�~2/(n+6)+(n+5)/(n+7)+�c�c+2/8�~7/9�~8/10�~�c�c�~(n+4)/(n+6)�~(n+5)/(n+7)}
������4�̏ꍇ�̐��́A�c�c
������n+2�̏ꍇ�̐��́A
(n+2)�~2/8�~2/9�~2/10�~�c�c2/(n+7)
=(n+2)2^n�7!/(n+7)!
(�ȉ��A�C�ӂ̍l������) �O>>344����I��������2�̏ꍇ�A
2�~6/8=3/2
����3�̏ꍇ�̐��A
3�~2/8=3/4
���Ғl��3/2+3/4=9/4
=2.25
2��ڏI��������2�̏ꍇ�A
2�~6/8�~7/9=7/6
����3�̏ꍇ�A
3�~(6/8�~2/9+2/8�~6/9)=3�24/72
=1
����4�̏ꍇ�A
4�~(2/8�~3/9)=1/3
���Ғl��7/6+1+1/3=(7+6+2)/6
=5/2
=2.5
3��ڏI��������2�̏ꍇ�A
2�~6/8�~7/9�~8/10=2�6�7/8�9�10
=7/60
����3�̏ꍇ�A
3�~(6/8�~7/9�~2/10
+6/8�~2/9�~8/10
+2/8�~7/9�~8/10)
=3�2�(6�7+6�8+7�8)/8�9�10
=146/120
=73/60
����4�̏ꍇ�A
4�~(2/8�~3/9�~8/10
+2/8�~7/9�~3/10
+6/8�~2/9�~3/10)
=4�2�3(6+7+8)/8�9�10
=21/30
=7/10
����5�̏ꍇ�A
5�~2/8�~3/9�~4/10=1/2�3
=1/6
���Ғl��7/60+73/60+7/10+1/6=(80+42+10)/60
=132/60
=22/10
=2.2
(�Â��c�c) �O>>345(�Â�)4��ڏI��������2�̏ꍇ�A
2�~6/8�~7/9�~8/10�~9/11 =2�6�7/10�11
=42/55
����3�̏ꍇ�̐��A
3�~(6/8�~7/9�~8/10�~2/11
+6/8�~7/9�~2/10�~8/11
+6/8�~2/9�~7/10�~8/11
+2/8�~6/9�~7/10�~8/11)
=3�2�3(6�7�8)/8�9�10�11
=18�6�7/9�110
=84/110
=42/55
����4�̏ꍇ�̐��A
4�~(2/8�~3/9�~6/10�~7/11
+2/8�~6/9�~3/10�~7/11
+2/8�~6/9�~7/10�~3/11
+6/8�~2/9�~3/10�~7/11
+6/8�~2/9�~7/10�~3/11
+6/8�~7/9�~2/10�~3/11)
=4(2�3�6�7+2�6�3�7
+2�6�7�3+6�2�7�3
+6�7�2�3)/8�9�10�11
=4�5(2�3�6�7)/8�9�110
=3�3�7/9�11
=7/11
����5�̏ꍇ�̐��A
5�~(2/8�~3/9�~4/10�~9/11
+2/8�~3/9�~6/10�~4/11
+2/8�~7/9�~3/10�~4/11
+6/8�~3/9�~4/10�~5/11)
=5(2�3�4�9+2�3�6�4
+2�7�3�4+6�3�4�5)/8�9�10�11
=6(36+24+28+60)/72�2�11
=148/12�2�11
=74/132
=37/66
����6�̏ꍇ�̐��A
6�~2/8�~3/9�~4/10�~5/11
=6�3�4�5/8�9�5�11
=1/11
���Ғl��42/55+42/55+7/11+37/66+1/11
=84/55+80/110+37/66
=(504+240+185)/330
=929/330
=423/190
=2.8151515�c�c
���Ғl��e�ɋ߂Â��̂��H
n��ڏI��������2�̏ꍇ�A
2�~6/8�~7/9�~�c�c�~(n+5)/(n+7)
=2�~6�~7/(n+6)(n+7)
=84/(n+6)(n+7)
����3�̏ꍇ�A
3�~{(6/8)(7/9)(8/10)(9/11)��c�c�(n+4)/(n+6)�~2/(n+7)
+(6/8)(7/9)(8/10)(9/11)��c�c�2/(n+6)+(n+5)/(n+7)+�c�c
+(2/8)(7/9)(8/10)��c�c�(n+4)/(n+6)�~(n+5)/(n+7)}
=6�4(6+7+8)/{8�9�10���(n+5)(n+6)(n+7)}
=7/{10�11�12����(n+5)(n+6)(n+7)}
����4�̏ꍇ�A�c�c(�d��C���I�@��)
n�����̂Ƃ��A
���Ȃ킿�ԋ�4�A����2�A����2����1�Ƃ��ē���F��2�߂������n�������Ƃ��̉��ʂ̌��̊��Ғl��e�Ɨ\�z����B >>342
(1)�@x�log(x) �̍ŏ��l�����߂�悢�B
�@{x�log(x)} ' = 1 + log(x) = 0,
���� x=1/e
�@x�log(x) �� -1/e,
�@x^x �� e^(-1/e) = 0.6922���� >>342
(1)
x��1/e �ł� x��1/e �ł� ��[x, 1/e] {log(u)�|log(1/e)�pdu �� 0,
���@x�log(x�j= -1/e + ��[x, 1/e] {log(u)�|log(1/e)�pdu �� -1/e,
���@x^x �� exp(-1/e) = 0.6922���� �@���ŏo�����Ȗ��
���[�N���b�h��ԏ�̋�łȂ��W���S�̂̏W��C�ɑ���
�[����d��
d(E,F):=inf{|x-y| | x��E,y��F} (E,F��C) (| |�̓��[�N���b�h�m����)
�Ƃ��Ē�߂�
���̂Ƃ��ȉ��̖�ɓ�����
(1)E,F��C����E���R���p�N�g�̂Ƃ��A|x-y|=d(E,F)�ƂȂ�x��E,y��F�����݂��邱�Ƃ��ؖ�����
(2) |x-y|=d(E,F)�ƂȂ�x��E,y��F�����݂��Ȃ��悤��E,F��C�̗�������� >>349
�ʔ������Ƃ������͗ǖ�̗ނ����� (1)���Ȃ���(2)�͈ӊO�Ɏv�����ɂ��������H �������w�ɂ̓S�~�����c���Ă��Ȃ��̂��H >>351
����Ȃ��Ƃ͂Ȃ��ł�
(2)�����ł����ʂɗU�������ʼn�����Ǝv���܂� ���������A�����ȃ��x���̏o�肪�����Ă��B
����ɏ�����͂Ȃ����ǁA�w�����Ƃ������킷��Ȃ琔�I���̖��Ƃ���������ۂǗL�Ӌ`�Ȗ��ɂ݂���B ����Ȃ��Ƃ͂Ȃ��ł��B
>>342 (2)�������ƕ��ʂɗU�������ł͉����Ȃ��Ǝv���܂��B >>351�̃��X��>>349�Ɠ���l�����Ɗ��Ⴂ����
�v�����ɂ����Ƃ������t�Ƀ��b�Ƃ����Z�l�����w���ł��킩��Ƌ������Ă��܂���Ɉ����Ȃ��Ȃ��Ă��܂����} �������Ȃ��ǂˁB
�܂��ɐ��w�Ȃŕ�����I�[�\�h�b�N�X�Ȗ��B
�ł����������Ƃ��ł͂��̎�̃I�[�\�h�b�N�X�Ȗ��͕]�����������Ă��܂��B
�����鐔�I���I�Ȃ�̕����]�������Ȃ�X��������B �}�W���X���ďW���ƈʑ��̍u�`�ʼn��K���ɏo�邩�Ȃ��Ē��x�̖��ł���
�Ȃ��Ă��Ƃ܂ł͎v��Ȃ����ǖʔ������ł͂Ȃ��Ǝv��
���ꂪ�ǖ₾�Ƃ����������悭������Ȃ� 2�����ȏ�͂����ɂ킩��i�Ǝv���j���ǁA1�����͂�����ƍl���� ����Ȃ��Ƃ͂Ȃ��ł��B
(2)�������ƗU�������ł͉����Ȃ��Ǝv���܂��B
�L�������̃��[�N���b�h��Ԃł́A�R���p�N�g�@�́@�L�E�W���B
�L�E�W���Ȃ̂ɃR���p�N�g�łȂ��Ƃ���ƁA���������ł��ˁB (2)��E,F�̗L�E�����Ďw�肳��ĂȂ��Ȃ��H�ꎟ���̏ꍇ
E=Z_+ (���̐����S��)
F={n+2^(-n)| n��Z_+}
�Ƃ���Ώ����������������ł����l�ɒ�߂�������� �u���X�g����w�̐��w��Andrew Booker�����A
33��3�̗������̍��v�ŕ\�����ƁA���Ȃ킿
33��x^3�{y^3�{z^3�Ƃ����������̉������߂邱�Ƃɐ�������
(8866128975287528)^3+(-8778405442862239)^3+(-2736111468807040)^3=33
https://fabcross.jp/news/2019/20190507_33.html x = 8866128975287528 = 2^3�E7�E467�E378289�E896201,
y = -8778405442862239 (prime),
z = -2736111468807040 = -2^7�E5�E89917�E47545783,
x + y = 87723532425289 (prime),
x + z = 6130017506480488 = 2^3�E31�E24717812526131,
y + z = -11514516911669279 = -5009413�E2298576083,
x = 101(x+y) + w, y = -100(x+y) - w,
w = 6052200333339 = 3�E73019�E27628427,
�����X���S�T�Q-831,840,841 https:/twitter.com/SOhbWq37LsuZ0pp/status/1121810596486193152
��Q�҃j�z���U���q�g���h�L���E��
https://twitter.com/5chan_nel (5ch newer account) x^3 + y^3 + z^3 = (x+y+z)^3 - 3(x+y)(y+z)(z+x),
x + y + z = -2648387936381751 = -(3^3)�E43�E547�E4170249653, >>348
�@log �͒P������������ ��[1/e, x] {log(u)�|log(1/e)�pdu �� 0, k�����R���Ƃ��An=2^k�Ƃ����B
�f���̂����A�S�Ă̌��̐����𑫂���n�ɂȂ���̑S�̂���Ȃ�W����S_n�Ƃ���B
k=1,2,...�ɂ��āAS_n�������W���ƂȂ�k�����Ȃ��Ƃ�1���݂��邱�Ƃ������B >>364 �̗ޑ�
(1) x + y + z = 33,
(2) x^2 + y^2 + z^2 = 33, (2��)
(4) x^4 + y^4 + z^4 = 33,
(5) x^5 + y^5 = 33,
�������R�� x, y, z �����߂�B
�����X���S�T�Q-840,890 1�ȏ�22�ȉ��̎��R���̏W����S�Ƃ���
S�̕����W��T�ŁA���̏����������̂��l����
[����] T�ɑ�����C�ӂ�2�̗v�f�̍���4�ł�7�ł��Ȃ�
T�̗v�f���̍ő�l�͂����炩
1 5 9 13 17 21
2 6 10 14 18 22
3 7 11 15 19
4 8 12 16 20
Table[2n-b-a+{(n+a)mod4}+4C(0,n-8+a),{a,0,1},{b,0,2},{n,1,10}]
{3, 6, 9, 8, 11, 14, 17, 20, 19, 22}
{2, 5, 8, 7, 10, 13, 16, 19, 18, 21}
{1, 4, 7, 6, 9, 12, 15, 18, 17, 20}
{3, 6, 5, 8, 11, 14, 17, 16, 19, 22}
{2, 5, 4, 7, 10, 13, 16, 15, 18, 21}
{1, 4, 3, 6, 9, 12, 15, 14, 17, 20} (2)
x^x = (��x)^(2x)
�@= {(��x)^(��x)}^(2��x)
�@�� exp(-1/e)^(2��x)�@�@�@�@�@>>348
�@= exp{-(2/e)��x}
�@�� 1 -(2/e)��x, >>372
(��x)^(��x)��e^(1/e)���ǂ�����Ďv�������������ĉ����� log(x) �͒P������������Ax��1/e �ł� x��1/e �ł�
�@��[1/e, x] {log(u) - log(1/e)�pdu �� 0,
���@x�log(x�j= -1/e + ��[1/e, x] {log(u) - log(1/e)�pdu �� -1/e,
���@x^x �� exp(-1/e) = 0.6922���� ����
��
������L���^�̃^�C����
��������������
��������������
��������������
��������������
��������������
��������������
��������������
���̍����������������S�̂ɁA�R��Ȃ��d���Ȃ��n�~�o�����ɕ~���l�߂邱�Ƃ͉\�� ��������������
��������������
��������������
��������������
��������������
��������������
�������������� ���ׂ���
��������Ȃ��}�X���邾��
2 �ԑg�̓r���ł����A�t�B�T�C�g�ւ̓]�ڂ͋֎~�ł� (ܯ��� 2bc1-wkih) 2019/05/20(��) 01:16:34.88 ID:MpRKv/HW0
@
�܌��Ղ̐��w�Ȃ̓W����100�}�X�ϕ����Ȃ�ǂ�
http://pbs.twimg.com/media/D66Jye6UcAEjpRy.jpg
https://twitter.com/Optie_f/status/1129992066912493568
https://twitter.com/5chan_nel (5ch newer account) >>375
�s�\�B
�`�a�`�a�`���`
�b�c�b�c�b�c�b
�`�a�`�a�`�a�`
���c�b�c���c�b
�`�a�`�a�`�a�`
�b�c�b�c�b�c�b
�`�a�`���`�a�`
�k���̃^�C��(15��)�͂a�b�c�A�`�b�c�A�`�a�c�A�`�a�b�̂����ꂩ�ɒu����Ȃ���Ȃ�Ȃ��B
�a�b�c�A�`�b�c�A�`�a�c�A�`�a�b���ꂼ��̖�����a,b,c,d(���Ra,b,c,d��0)�Ƃ���ƁA
�Ֆʂ̍\�����`�~16�A�a�~10�A�b�~10�A�c�~9�ł��邽�߁A
b+c+d��16
a+c+d��10
a+b+d��10
a+b+c��9
�����������a��-1,b=c=5,d=6�ƂȂ�B
�a�b�c�̖��������ƂȂ邽�߁A�����������͂Ȃ��B ��������������
��������������
��������������
��������������
��������������
��������������
��������������
�ł����� >>378
�����ƊȒP�ɁF
�ǂ̂k���^�C����378�̐}�̂`�̗̈���Q�ȏ��߂邱�Ƃ͂ł��Ȃ��̂ŁA15���̂k���^�C�����ǂ̂悤�ɒu���Ă�16�ӏ��̂`�̗̈�߂邱�Ƃ��ł��Ȃ� >>380
�����@���ꂪ�z�肵�Ă������ł��� >>375���̎��ゾ���āA������������������Ǝv�����Ƃ��납��Ђ�����Ԃ��B���ꂪ�V�˂��Ă��B�O>>346
�P]/�___________
__/�_/ ,,������/|
�P�_/ �c`-`Ђ�))|__
�P|�___U,~�܁S' |�@�_
�n| �a�P�P`U~U�@/�@�@)
�Q| �a�@���@�a /�@�@/|
_�@`�a______�a/____/ |
�P�P�P�P�P�P�P�P�P�a /
__________________�a/
�P�P�P�P�P�P�P�P�P�P �lA�ƐlB�����܂��B
�lA�ƐlB��10km����Ă��āA�lA�͐lB�Ɍ�������0.8m/s,�lB�͐lA�Ɍ�������1m/s�œ����܂��B
���x�ω��͂Ȃ��Ƃ����Ƃ��A�lA�ƐlB������Ⴄ�̂͊J�n���牽����? �O>>382
>>384
48x+60x=10000
���f�B �O>>386
>>384
x=10000/108
=2500/27
=833.33�c�c/9
=92.5925925925�c�c(��)
92����͂܂��������ĂȂ��B
93����͂����������āA�u�����I�v�Ƃ��A�u�悧�I�v�Ƃ��A�u�v���Ԃ��ˁv���C���Ă��H�@�Ƃ��A�u�����ˁv������A����Ȃł��Ȃ���A�Ƃ������Ă�B >>384
���x�ω��͂Ȃ��Ȃ�@92.59����ɐ��ʏՓ˂���
�u���܂��ǂ����Ă�H�v�u���܂����i�[�v�Ƃ������Ă�B >>390
> �u���܂����i�[�v�Ƃ������Ă�B
�����������c �k���l
�~K��ɑ��قȂ�3�_A,B,C������B��ABC�̓��S��I�Ƃ���B
(1) ��AIB - (1/2)��C �����߂�B
(2) �_C���~K����Ƃ��AI�̋O��L�����߂�B
(3) ��AB�̒��_�iC�̔��Α��j��M�Ƃ���B��AIM=��IAM,�@��BIM=��IBM �������B
(4) L�̒��S�����߂�B >>392
�ʔ������ǂ��̐ݖ₾��(2)����Ȃ��ˁH ���̒i�K�ł�L�͂܂��m�肵�܂����^^
�i�C���j
(2) I�̋O�Ղ� A,B ��[�_�Ƃ���~�ʂƂȂ邱�Ƃ������B���̉~��L�Ƃ���B >>394
����A�Ƃ䂤��(3)��Ɏ������Ⴆ�Ύ����I��(2)��(4)����C�Ɏ������Ⴄ��ł́H
�܂��������ǁB ���Z�̂Ƃ��ɓǂQ�l���ɁA�o���̈����o��҂̗U���ɏ]���K�v�͂Ȃ��A�د�I �Ƃ������Ă��̂��������ȁB
���҂͖Y�ꂽ���A�����l�C�̂����������C�ɂȂ��Ă�\���Z�u�t�������悤�ȁB >>392
I�͓��S�䂦��IAB=��IAC=���A��IBC=��IBA=���A��ICA=��ICB=��(��+��+��=��/2)�Ƃ�����B
������CI��K�̌�_��M�f�ƒu���B
��ACM�f=��BCM�f=�����M�f��C���܂܂Ȃ���AB�̒��_�H�ɓ������B
��BAM=��(��~���p�̒藝)�ɂ���MAC=2��+���ł��邩���AMC=��-(2��+��)-��=2���ł���A��AMI=��+���A��AIM=��-(2��+��+��)=��+���ɂ��A��MAI��M�p�Ƃ���ӎO�p�`�ł���B
�����MA=MI�ł���B
�ȏ�ɂ��I�͒��SM�A���aMA�̉~L��̓_��K�̓����ɂ���B
�t��L�ォ��K�̓�����I���Ƃ�A������MI��K�̌�_��C�ƒu����I�́�ABC�̓��S�Ɉ�v����B
�ȏ�ɂ��I�̋O�Ղ�L���K�̓����ɂ��镔���̑S�̂ł���B uxOtXfl_GF8
�������������������u�[�������S�L�u���p�N���Y�ƃj�z���U���q�g���h�L�������E��
�y�l�S�~�p�N�����j�z���U���q�g���h�L�����Ė��[���o�ɋs�E���� /h2K5mcWSn0c
���ʂ��ł����グ��l�g�E���L���I�^��Q�҃��C�v�������{�l�j�z���U����p�������{�݂Ɏ̂ĂĎE�� >>397
�����ł��B
�@��AIM = ��IAC + ��ICA = ��+��
�@��IAM = ��IAB + ��BAM = ��IAB + ��BCM = ��+��
����@MA=MI �ł��ˁB
�@�i��AMI = ��AMC = ��ABC = 2�� �͂Ƃ肠�����g���܂���j �O>>388
>>402(1)
�r�f������
����������
����������
����������
�������� �O>>403
>>402(2)m�An���Ƃ��Ɋ�̂Ƃ��B >>402(5)
�@Somos-4�� �Ƃ��]���炵���B
http://oeis.org/A006720 >>402
���T(1)
(a)�@�w���@�ɂ��B
a_(k+2) �� a_(k+3) ���݂��ɑf�łȂ������Ɖ��肷��B
���ʂ̑f������p�Ƃ���B
�Q�����ɂ�� {a_(k+1)}^2 = a_(k+3)�a_(k-1) - a_(k+2)�a_k�@��p�̔{���B
a_(k+1) ��p�̔{���B(*)
���l�ɂ��ā@a_(k+3), a_(k+2), ����, a_3 �͂��ׂ�p�̔{���B
����͑�ӂƖ����B
�� a_(k+2) �� a_(k+3) �݂͌��ɑf�B
a_(j-1) �� a_j �����l�B�i2��j��k+3)
a_(k+1) �� a_(k+3) ���݂��ɑf�łȂ������Ɖ��肷��B
���ʂ̑f������p�Ƃ���B
�Q�����ɂ�� a_(k+2)�a_k = a_(k+3)�a(k-1) - {a_(k+1)}^2�@��p�̔{���B
a_(k+2) �܂��� a_k ��p�̔{���B�i*)
����͏�L�Ɩ����B
�� a_(k+1) �� a_(k+3) �݂͌��ɑf�B
a_k �� a_(k+3) ���݂��ɑf�łȂ������Ɖ��肷��B
���ʂ̑f������p�Ƃ���B
�Q�����ɂ�� {a_(k+1)}^2 = a_(k+3)�a(k-1) - a_(k+2)�a_k�@��p�̔{���B
a_(k+1) ��p�̔{���B�i*)
����͏�L�Ɩ����B
�� a_k �� a_(k+3) �݂͌��ɑf�B
*)�@a_1, a_2, ����, a_(k+3) �͂��ׂĐ����Ƃ�������B >>402
���T(1)
(b)�@
a_(k+i) = A_i�@�Ɨ��L����B
A_4 = a_(k+4) = N,
A_1�A_3 + (A_2)^2 = A_0�N,
A_1�A_5 = (A_3)^2 + A_2�N,
A_1�A_2�A_6 = A_1(A_3�A_5 + NN) = A_3(A_1�A_5) + A_1�NN = (A_3)^3 + A_2�A_3�N + A_1�NN,
(A_1)^2�A_3�A_7 = (A_1)^2�{(A_5)^2 + A_6�N} = (A_1�A_5)^2 + (A_1)^2�A_6�N,
(c)
�@(A_1)^3�(A_2)^2�A_3 M
�@= (A_1)^3�(A_2)^2�A_3 {A_5�A_7 + (A_6)^2}
�@= (A2)^2�(A1�A5){(A1)^2�A3�A7} + A1�A3 (A1�A2�A6)^2
�@= (A2)^2�(A1�A5){(A1�A5)^2 + (A1)^2�A6�N} + A1�A3 (A1�A2�A6)^2
�@= (A2)^2�{(A3)^2 + A2�N}{[(A3)^2 + A2�N]^2 + (A1)^2�A6�N} + A1�A3 {(A3)^3 + A2�A3�N + A1�NN}^2
�@= (A3)^6�{A3�A1 + (A2)^2}
�@�@+ {(A1)^2�A2�A6 + 2A1�(A3)^3 +3(A2)^2�(A3)^2}A2�(A3)^2 N
�@�@+ {(A1)^2�(A2)^3�A6 + 3(A2)^4�(A3)^2 +2(A1)^2�(A3)^4 + A1�(A2)^2�(A3)^3} NN
�@�@+ {2(A1)^2�(A3)^2 + (A2)^4} A2 N^3
�@�@+ (A1)^3�A3 N^4
�@�� (A_3)^6�{A_3�A_1 + (A_2)^2}
�@= A_0�(A_3)^6 N
�@�� 0�@�@�@�@�@�@�@�@�@�@(mod N)
�Ƃ���ŁA(a) ��� �@A_1�A_2�A_3 �� N=A4 �݂͌��ɑf�B
M �� N �̔{���B
A_8 = a_(k+8) = M/N �͐����B ����
http://shochandas.xsrv.jp/divisor/somos.htm
���w�Z�~�i�[ 1993�N3����, ���{�]�_��, �u�G�����v
�ꏼ �M �u�������T���|���낢��Ȋ��|�v �X�k�o�Łi1998) p.84-87
�@�@187p�D2268�~ >>390
�u�����͕ω����Ȃ��Ƃ��āv
���x�^�[���� >>392
�k�ޑ�l
�~K��ɑ��قȂ�3�_A,B,C������B��ABC�̏d�S��G�A���S��H�A�O�S��O�Ƃ���B
(1) ��OH = 3��OG �������B�@�@�@(Euler)
(2) �_C���~K����Ƃ��AG�̋O�Ղ̒��SM�����߂�B
(3) �_C���~K����Ƃ��AH�̋O�Ղ̒��SN�����߂�B
(4) ��ON = 3��OM�@�������B
��OG = (��OA + ��OB + ��OC)/3,
��OH = ��OA + ��OB + ��OC,
�炵�����ǥ��� 5�~6�̏ꍇ
��F1�@����
��F2�`8�@�Z���L��
��F9�`21�@�����L��
��F22�`30�@����
������������
������������
������������
������������
������������
�Z���L����
Table[sum[C(2n-1+C(0,n-2 mod7)+3C(0,n-4)+C(1,n-7),k-1),{n,1,14}],{k,1,30}]
�����L����
Table[sum[C(2n-1+C(0,30mod n)-C(0,n-2)-2C(0,n-5)-C(1,n-8),k-1),{n,1,14}],{k,1,30}]
������
Table[sum[C(2n-1-3C(1,n-9),k-2),{n,9,14}],{k,1,30}]+Table[C(29,k-1)+C(1,k),{k,1,30}]
5 * 6 [2] : 203 , 197 , 35
5 * 6 [3] : 1801 , 1727 , 532
5 * 6 [4] : 11418 , 11008 , 4979
5 * 6 [5] : 55469 , 54036 , 33001
5 * 6 [6] : 215265 , 211894 , 166616
5 * 6 [7] : 685784 , 680768 , 669248
5 * 6 [8] : 1827737 , 1825076 , 2200112
5 * 6 [9] : 4130886 , 4139080 , 6037184
5 * 6 [10] : 7995426 , 8023257 , 14026332
5 * 6 [11] : 13346984 , 13395944 , 27884372
5 * 6 [12] : 19312228 , 19372871 , 47808126
5 * 6 [13] : 24301031 , 24358063 , 71100756
5 * 6 [14] : 26642430 , 26684251 , 92095994
5 * 6 [15] : 25463979 , 25488051 , 104165490 �������𓊂�����ꂽ���̂��H �����H �l�g�E�����Ă���ς�2�����G�����D���Ȃ̂�
�Ђ��� �w�ꂢ��x�c
�����[�������Ԃ₭
���̏u�ԃn�b�Ƃ���
���̐����[���������[�}���[�[�^�����𖾂����̂��H
�����v�����̂�
�ꂢ���끨�[���_
�큨�[�[�^���ɂ����镪���̘a
�܂����A���̐����[�������c�@�������������H
�����������o��
�ڂ�������Ɨߘa�Ə����ꂽ�F��������
���[�����̎p�͖�������
�قǂȂ��A���[�����̓��[�}���\�z���������Ă��炸
�P�Ȃ�V�����̔��\��������Ƃ�m����
���߂́u�ꂢ��v�ɐS�����~�܂肻���ɂȂ������^�ł��� �L�`�K�C�l�g�E���r�炵�ɗ���Ȏ��˂� 7�~8�̏ꍇ
��F1�@����
��F2�`16�@�Z���L��
��F17�`43�@�����L��
��F44�`56�@����
����������������
����������������
����������������
����������������
����������������
����������������
����������������
�Z���L����
Table[sum[C(2n-1+C(0,n-2 mod18)+3C(0,n-4)+3C(1,n-7)+7C(0,n-11)+C(1,n-16)+C(1,n-18),k-1),{n,1,27}],{k,1,56}]
�����L����
Table[sum[C(2n-1+C(0,n-1 mod14)+C(0,n-3 mod18)+3C(1,n-5)+3C(1,n-9)-19C(0,n-14)-C(1,n-17)-C(1,n-19),k-1),{n,1,27}],{k,1,56}]
������
Table[sum[C(2n-1-3C(1,n-20)-3C(1,n-18)-8C(1,n-16),k-2),{n,16,27}],{k,1,56}]+Table[C(55,k-1)+C(1,k),{k,1,56}] 7 * 8 [2] : 751 , 722 , 67
7 * 8 [3] : 13213 , 12546 , 1961
7 * 8 [4] : 169815 , 161494 , 35981
7 * 8 [5] : 1708176 , 1634573 , 477067
7 * 8 [6] : 14026034 , 13521709 , 4920693
7 * 8 [7] : 96716833 , 93921622 , 41278945
7 * 8 [8] : 571625198 , 558773693 , 290095184
7 * 8 [9] : 2940723248 , 2890925540 , 1744319612
7 * 8 [10] : 13327198939 , 13162957237 , 9116895304
7 * 8 [11] : 53717709609 , 53254225291 , 41930280380
7 * 8 [12] : 194070976396 , 192951568390 , 171360762514
7 * 8 [13] : 632475500322 , 630177011156 , 627260220922
7 * 8 [14] : 1869295969469 , 1865362789969 , 2070073204362
7 * 8 [15] : 5032748390589 , 5027434867987 , 6193066240064
7 * 8 [16] : 12389874719763 , 12385213035831 , 16873864084671
7 * 8 [17] : 27980641402960 , 27981556314178 , 42035336024662
7 * 8 [18] : 58125229289763 , 58139877526913 , 96062882957224
7 * 8 [19] : 111326498505381 , 111364943071921 , 201964537970498
7 * 8 [20] : 196977669970830 , 197048666795639 , 391587225396961
7 * 8 [21] : 322510102010304 , 322617018858127 , 701638985697449
7 * 8 [22] : 489306306855569 , 489444206271532 , 1163831929136799
7 * 8 [23] : 688690248074025 , 688846020744196 , 1789759515397979
7 * 8 [24] : 900050700996225 , 900206640621300 , 2554774361679750
7 * 8 [25] : 1092975958236546 , 1093115221856691 , 3388349400127275
7 * 8 [26] : 1233862233565383 , 1233973593552186 , 4178612556991503
7 * 8 [27] : 1295273249461927 , 1295353120172050 , 4794316279376103
7 * 8 [28] : 1264553645519991 , 1264605044607097 , 5119531910633352 >>402
���S (1)
�@AB = 1,
�@��BAO = �Ɓ@�Ƃ�����
�@A(cos��,0)�@B(0,sin��)
����
�@|x|^(2/3) + |y|^(2/3) = 1,
�A�X�e���C�h > sapply(1:12,function(k) treasure0(3,4,k))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
�Z���L�� 5 26 73 133 167 148 91 37 9 1 0 0
�����L�� 5 27 76 140 176 153 92 37 9 1 0 0
���� 2 13 71 222 449 623 609 421 202 64 12 1
��������
��������
��������
�Z���L����
Table[sum[C(2n-1+C(0,n-2),k-1),{n,1,5}],{k,1,12}]
�����L����
Table[sum[C(2n-1+C(0,3mod n),k-1),{n,1,5}],{k,1,12}]
������
Table[C(11,k-1)+C(9,k-2)+C(7,k-2)+C(1,k),{k,1,12}] �~������11�i�@�Ōv�Z���Ă����R���s���[�^�[��
1857�����̂Ƃ���ňٕς����m���A���̕�������ʂɕ\�����n�߂�
���̕\����0��1�݂̂����o�ꂹ���A������̋�Ԃ��Ƃɂɐ܂�Ԃ���A
0��1�ɂ���Ă���}�`�������яオ�����c
0000000011111100000000
0000011110000111100000
0001110000000000111000
0011000000000000001100
0110000000000000000110
1000000000000000000001
1000000000000000000001
0110000000000000000110
0011000000000000001100
0001110000000000111000
0000011110000111100000
0000000011111100000000 ��
�J�[���Z�[�K�����w�R���^�N�g�x�̗���
�i�f��łł͖��������Łj ��
p�i�@�Ȃ�o��m�� (1/p)^(12*22)
p=11 ���� 8.4658�~10^274 ���1��
�ł��o�₷�� p=2 �̏ꍇ�ł��@2.964�~10^79 ���1��
10�i�@�� 0.8923�~10^79 ��
10^20 �����炢�ł͏o�������Ȃ�����
���݂͖� 3.14�~10^13 ���iGoogle�j���炢���H ���炢��������
��Die Kasteleyn-Fisher-Temperley-Formel fur die Anzahl der Domino ...
http://oops.uni-oldenburg.de/1773/1/Bachelorarbeit%20von%20Ina%20Lammers.pdf ��
��
��
�R���^�N�g�E�����Y�@�ł��ˁB �ŏ��������Ɩ������̏ؖ�
�������ɑ��Af(��)=0�����L�����W��������f�����݂��������̓��ŏ������ōō������̌W����1�ƂȂ���̂��ŏ��������ƌĂԁB
⑴��=2,��2 �̍ŏ������������߂�B
⑵�������̍ŏ���������f�Ƃ���B�L�����W��������g��g(��)=0�����Ȃ�Ag��f�Ŋ����鎖�������B
⑶���������Ƃ��Af(��)=0�Ƃ���B
���̎�f������ōō������̌W����1�Ȃ��f�̓��̍ŏ��������ƂȂ鎖�������B
⑶p:�f���Ƃ��An��2�Ƃ���B
x^n-p������ł��鎖��p����
1+p^(1/n)+p^(2/n)+�c+p^((n-1)/n)�͖������ł��鎖�������B (1)
�@�� = 2,�@�@�@�@f(x) = x-2,
�@�� = ��2,�@�@�@f(x) = xx-2,
(2)
�@g(x) = f(x)Q(x) + R(x),�@�@�@deg(R) < deg(f)
�Ƃ���B��ӂ��
�@R(��) = g(��) = 0,
������ R(x)��0 �Ƃ����f(x)�̍ŏ����ɔ�����B
���@R(x) = 0,
�@g(x) = f(x)Q(x),
(3)
�@(2)���Af(x) �̓��̍ŏ��������̒萔�{�B >>402
���Q
(1)
�@t = 2/(5^m)�@�Ƃ���B�܂��� t = 3/(5^m) �Ƃ���B
�@������ m�͏\���傫�����A 5^(m-1) > 1/�� �Ƃ���B
(2)
�@t = ��[n=1,��] t_n / 5^n�@�Ƃ���B
�@t_n �� 3�@�ˁ@a_n = 0
�@t_n = 3�@�ˁ@a_n = 1
�ɂ�� a �� �b_2 ���߂�@a+t �� �b_2 �����`�̓y�n���d���4��������Ƃ��A�o���邾���d��̒�����Z������ɂ͂ǂ�������悢���H
�������d��͒��������łȂ��Ȑ��ł��悢���A�������Ă��悢 >>430
�̘_�̋��ȏ��őS�������C�����邪
(4)
f(x):=x^n-p,
t:=p^(1/n) ����͖ܘ_������,
��:=1+t+t^2+�c+t^(n-1) ����͐��̎����ł���0�łȂ�(���Ƃŋt���g���̂ňꉞ��)
f(x)=(x-t)*[x^(n-1)+tx^(n-2)+t^2x^(n-3)+�c+t^(n-1)]
f(1)=1-p=(1-t)��
������ -(1-p)/��+1=t
���������L�����Ȃ�t�͗L�����ɂȂ薵������
����ă��͖������ł��� �� �����l�������L�̖����������Ă��炢����.
�n�[��-�o�i�b�n�̒藝�ƑI�������̓��l���ɂ���
�C�ӂ̐��^���X�ɑ��Ď����łȂ�(���Ȃ킿{X}�ł͂Ȃ�)���^��Ԃ̑�
{X_��}_(�Ɂ���)
�����݂���
X��(��_(�Ɂ���))X_��
�ƂȂ邩�H
�オ���藧�Ƃ��b-���^�ʑ����X_�ɂ̕������A_�ɂ��`��Ƃ�����^�Ċ�f_�ɂɂ���
f_�Ɂ�p_�� on A_��
�ƂȂ�Z�~�m����p_��:X_�Ɂ�[0, ��)�����݂���Ƃ�(��_(�Ɂ���))f_�ɂ̊g��f:X���b�����݂���
f��(��_(�Ɂ���))p_�� on X
�ƂȂ邩�H
���̏ꍇ����I���������]�����H �O>>404
>>433
�����`�̈�ӂ̒���x������d���p�ӂ��A�c���ɏ\�����悤�ɗ��Ă�B�d��łł���4�̓y�n�̖ʐς͂�������A
(x/2)^2=x^2/4
�����}�[�N�̒����ɂ��鉡�_���˂������Ȃ��}�`����45����]�����d����l�������A
(���+��2-2/���)x��2x
�����2x����B�s�v�c�ȕs�v�c�ȃ��[�g�p�C�B �O>>436
>>433
�~�ʂ̋ȗ���������B
�ӂ�90�����ˁA�Ίp����60�����˂�ۂ��A���S�������`�̕ӂ̉�����ɂ���A����������4�̉~�ʂ�`���B
�����`�̑Ίp���̒����t�߂̂��イ�Ԃ�Z�������Ńr�L�j�̂悤��4�̉~�ʂ�2����Y���ɂ������Č��ԂƁA2x�������d�肪�\��������Ȃ��B 0<a<1/2 �Ƃ���B�����`��
�@A(a, a)�@B(a, 0)�@C(0, 0)�@D(0, a)
�Ƃ���B
�@AB = a,
�@��AOB = 15�
�@1/sin(15�) = ��2 + ��6,
�@1/tan(15�) = 2 + ��3,
�~�̒��S�@O(-(1+��3)a, 0)
���a R = a/sin(15�) = (��2 +��6)a,
�@RR = 4(2+��3)aa,
��OAB = (1/4)RRsin(30�) = RR/8 = (2+��3)aa/2,
(0,0)���܂ރp�[�c�̖ʐς�
�@S = (��/12 - 1/4)RR = (��/3 - 1)(2+��3)aa,
���ꂪ 1/4 �ɓ���������
�@a = 0.461041286651148
���E�̒�����
�@L = 4(��R/12) + (1-2a)��2 = {(��/3)(��2 + ��6) - 2��2}a + ��2 = 1.9755928847815
�@(2-L)/2 = 0.01220355760925 �O>>437
�����`�̒��_����ӂ��O(�܂��͉�)��t�������������_�𒆐S�Ƃ��āA
���ar�̉~�ʂ̒��S�p30���̐�`������t�A����r/2�̒��p�O�p�`�������A�����`�̖ʐς�1/8������A�����`�̈�ӂ�1�Ƃ��āA
(4��r^3/3)(30/360)-(r/2)(t/2)=1/8
��r^3/9-rt/4=1/8
8��r^3-18rt=9
��t=4��r^2/9-1/2r�\�\�@
�r�L�j�̐ڍ���=2(1/2-r/2)��2
4�̉~�ʂ̒���=2��r(30/360)�4
=2��r/3
�d��̒���=2��r/3+2(1/2-r/2)��2
=2��r/3+(1-r)��2�\�\�A
����_�p60���̒��_�Ƃ���O��(r�2r�r��3/2)�̒��p�O�p�`�ɂ����āA
t+r/2=r��3/2
t=(��3-1)r/2
�@���A
4��r^2/9-1/2r=(��3-1)r/2
8��r-9=9(��3-1)
r=9��3/8��
�A���A
�d��̒���=2��r/3+(1-r)��2
=2�Υ9��3/8�Υ3+(1-9��3/8��)��2
=3��3/4+(1-9��3/8��)��2 �O>>440
�d��̍ŒZ�̒���=1.83609277�c�c �O>>441�����B
>>433
�����`�̈�ӂ̒�����1�Ƃ���ƁA
��r^2(30/360)-(1/2)t(r/2)=1/8
2��r^2-4tr=3
t=��r/2-3/4r�\�\��
��`���̉s�p30����60���̒��p�O�p�`�ɂ��āA
r/2+t=r��3/2
t=r(��3-1)/2�\�\��
�������A
��r/2-3/4r=r(��3-1)/2
��r^2/2-3/4=r^2(��3-1)/22(��+1-��3)r^2=3
r=��{3/2(��+1-��3)}
���ɑ�����A
t=(��3-1)��{3/8(��+1-��3)}
��(�ǂ�����悢���̓���)�͂܂��A�����`�̒��_����ӂ̉�����́A
(��3-1)��{3/8(��+1-��3)}�̈ʒu�ɃR���p�X�̐j(�܂��̓��W���[�̂O�ڐ�)���h���A
���a��{3/2(��+1-��3)}�̔����~��ӂ���Ίp���܂ŕ`�����Ƃł���B
���l�̐}�`�𐳕��`�̓��꒸�_����90������������ɂ��傤�ǃR���p�X�܂��̓��W���[���������ƃN���X����悤�ɔ����~��`���B
�Ίp�̒��_�����������ɓ��l�̔����~��`����4�̉~�ʂ��`����B
���Ƃ͑Ίp����Ɏd��̕���_��2�ł���悤�ɒZ�����ڂł������Ȃ��悢�B �O>>442���l�̒����B
(�d��̒���)=��{2/3(��+1-��3)}+��2-��{6/(��+1-��3)}-��{3(��+1-��3)/8}
=0.93988125�c�c �O>>443
��{3/2(��+1-��3)}
=�Υ0.93988125�c�c
��2=1.41421356�c�c
-��(6/��+1-��3)=-1.57800505�c�c
-��{3(��+1-��3)/8}=-0.9505673�c�c
1.9���炢�̋����̒����̐��l���A�Ȃ��Ȃ��o��r��t�͂����Ă�͂��B >>439�@����
�@S = (��/12 - 1/4)RR + aa = {(��/3 - 1)(2+��3) + 1}aa, �O>>444�܂Ƃ߁B
>>433
�����`�̓y�n��1�w�N�^�[���Ƃ��āA�ǂ�������������l����B
����܂ł̌v�Z���ʁA
r=��{3/2(��+1-��3)}
=0.789002525�c�c
t=(��3-1)r/2
=0.288794968�c�c
���ӂ܂���ƁA
100(r-t)=50.0207556�c�c
100m����y�n�̔����n�_�̂킸��2�p�悩��d������Ă͂��߁A�����O�ɃJ�[�u�����Ă������ƂɂȂ�B
�d��̌`�͐����`��45����]�����H�`�̂悤�Ɍ���Ƌ����}�[�N�̒����̉��_(�����`�ł����ƑΊp���̒����t��)���˂��o�Ă��Ȃ��`�ɂȂ�B
�~�ʕ�����4�̔����~��2���`�����ƂɂȂ邪�A����2��30���d�Ȃ��Ă���B
�ǂ�����������B
�@28m88�p�����`�̓y�n�̋��������牏�ɉ����ĉ�������Y��łB
�A���̒n�_����78m90�p�̈ʒu�ɂ��鉏��̒n�_���N�_�ɔ����~��`���B
�B�s���������Ίp����̒n�_��2���镪��_�̂�����1������ڈ�����Ă����B
�C�@�A�B�̗���œ��l�̔����~������3�`���B
�D�����`�̓y�n�̑Ίp����̒����t�߂�2�̕���_���d��Ō��ׁB
����_�̋������C�ɂȂ邪��������Ȃ�ňȏ�Ƃ��܂��B >>439
>>445
���l�͐����ł�
�ŏ����̏ؖ������肢���܂� �O>>446
�d��̒����́A
2��{3/2(��+1-��3)}/3+��2{1-��3/2(��+1-��3)}
=1.95087851�c�c
1�w�N�^�[���̓y�n�Ȃ�A195m8�p8�o���x�̎d�肪�v��B4�ɕ������y�n�̂�����2�͂ق��̂��ׂĂ̓y�n�ƂƂȂ肠�����A�c���2�͂������ɂƂȂ肠��Ȃ���ŁA4�l�̂��������Ƃ�����邢����2�l�ɂ���2��^�����炢���B �O>>448�l�@�B
�d��̒����̓������́A
��������29m84�p
�Ȑ�����41m31�p2�o�~4
=165m24�p8�o
���킹�āA
29.84+41.312�~4
=29.84+165.2408
=195.088
195m8�p8�o �O>>449
>>450�悩�����ł��ˁB
�f����e���r�ɂ����݂����ɕ����␔�����c���ł��B ��r^2(30/360)-(1/2)t(r/2)=1/8
2��r^2-6tr=3
t=(��r/3-3)/6r�\�\��
��`���̉s�p30����60���̒��p�O�p�`�ɂ��āA
r/2+t=r��3/2
t=r(��3-1)/2�\�\��
�������A
��r/3-1/2r=r(��3-1)/2
2��r^2-3=3r^2(��3-1)
(2��+3-3��3)r^2=3
r=��{3/(2��+3-3��3)}
���ɑ�����A
t={(��3-1)/2}��{3/(2��+3-3��3)} 3�������(R^3)���~��(S^1)�̔��a�Ŗ��ߐs�����ɂ͂ǂ�������悢���H
�������C�~���̔��a�͂��ꂼ��قȂ��Ă悢 �Z�������̎��ԈÏ������ł��ĂȂ����B �O>>452�v�Z���B
�O�X>>451�����B
r=��{3/(2��+3-3��3)}
=0.85675483�c�c
t=��r/3+1/2r
={(��3-1)/2}��{(3/(2��+3-3��3)}
=0.313594032�c�c
2��r/3+��2-[2(��2/2)��{3/(2��+3-3��3)}]
=1.99696238�c�c
(����)�ǂ������炢�����̓���(���@)�͂��łɎ������B
(�����������߂�Ƃ͖���Ă��Ȃ����A����͎���I�ȍl�@�ł�)
1�w�N�^�[���̐����`�̓y�n��4��������ŒZ�̊Ԏd��̒����́A
199m69�p6.238�o �O>>459
���2���c�����܂܍ŒZ�̊Ԏd��̒�����\���Ă݂�B
�Ԏd��̑�����=2��r(30/360)�4+��2-��2(r/2)
=2��r/3+��2-(��2/2)r
r=��{3/(2��+3-3��3)}��������ƁA
�Ԏd��̑�����
=��2+{(4��-3��2)/6}��{3/(2��+3-3��3)} >>455
�قڑ��x�_�̍\������B
������āB �O>>460
>>439�́A�Ȃ��2m46�p�����点�Ă�́H >>461
���x�[�O���x�̂��ƂȂ���W�����l�p�`�Ŗ��ߐs��������Ǝv������S^1�ł����l�ɏo����́H >>463
�d�ϕ��Ɨݎ��ϕ��B
�K�`���Ɣ����ϕ��B���[�v��Ԃ̎w���藝������ˁE�E�E�B >>463
�I���͏o�T�H�m���Ă邩�珑���Ȃ����ǂł����B
>>461���������玝���Ă����̂��͒m��Ȃ����ǁB �ԈႦ���B
�o��҂�>>455�ˁB
���̖{�͖��̏o�T���ڂ��Ă���ǒ��҂͂����w�̃R���s���[�^�T�C�G���X�̋����ɋ����Ă�������Ƃ���B �l�I�ɂ̓����_���E�H�[�N�̍ċA����|���A�̍ċA���藝�ɒ��������b�ċC�������Ȃ��B
�����B�̊m���ʐς��Ӗ�����ʂ��ĂȂf�G���H�B �O>>462
�Ԏd��̑�����
=���S�p15���̓�\�l���~�~4
+����_�̋���
=2��r(15/360)�~4+L
=��r/3+L
(��2-L)/2=rcos75����2
��2-L=2rcos(45��+30��)��2
=2r(cos45��cos30��-sin45��sin30��)��2
=r{(��2)(��3)/2-��2(1/2)}��2
=r(��3-1)
L=��2-r(��3-1)
�Ԏd��̑�����
=��r/3+��2-r(��3-1)
=(��/3+1-��3)r+��2 �O>>469����Ƃł����B
>>433
�y�n�̋���������A���ɉ����Ď�O��t�������ꂽ�Ƃ��ɍY��ł��A���̒n�_�𒆐S�ɔ��ar�\���[�g���̓�\�l���~���܂������O�Ɍ�����y�n�̉��̐^��ӂ���y�n�̑Ίp���܂ŕ`���B
��~�ʂ͉�����90���ŏo�āA�Ίp���ɑ���60���œ��˂��ĎO�c���̕����120�����ɂ���Ȃ�B
�ŁA�s���������n�_�͑Ίp�����2���镪��_�̂�����1������A�ڈ������B
�������𗧂āAt��r�����߂�B��\�l���~�͒��S�p15���̐�`�Œ��S���y�n�̋���������t���[�g���͂ݏo���ĂāA�Ίp���ɑ���45��-15��=30��(90��-60��=30���Ƃ�������)�͂ݏo���Ă��ŁA���t�A����rcos75���̎O�p�`���\�l���~��������Ɛ����`�̓y�n��1/8�ɂȂ�B
��r^2(15/360)-(1/2)t(rcos75��)=1/8
��r^2-12trcos75��=3
��r^2-12tr(cos45���cos30��-sin45���sin30��)=3
��r^2-12tr(��2/2)(��3/2)-(��2/2)(1/2)=3
��r^2-3tr(��6-��2)=3�\�\�@
��\�l���~�̒��̉s�p15����75���̒��p�O�p�`�ɂ��āA
rsin75��=rcos75��+t
r(sin45��cos30��+cos45��sin30��)
=r(cos45��cos30��-sin45��sin30��)+t
r{(��2/2)(��3/2)+(��2/2)(1/2)}
=r{(��2/2)(��3/2)-(��2/2)(1/2)}+t
r(��6+��2)=r(��6-��2)+4t
r��2=2t
t=r/��2
�@�ɑ������ƁA
��r^2-3(r/��2)r(��6-��2)=3
��r^2-3r^2(��3-1)=3
(��+3-3��3)r^2=3
r=��{3/(��+3-3��3)}�\�\�A
�Ԏd��̑�����
=���S�p15���̓�\�l���~�~4+����_�̋���
=2��r(15/360)�~4+��2-2(rcos75����2)
=��r/3+��2-2r{(��6-��2)/4}��2
=��2+(��/3+1-��3)r
�A��������ƁA
�Ԏd��̑�����
=��2+��(��/3+1-��3)
=1.97559288�c�c
�Ίp���̋t�̋������̑���������l�̉~�ʂ̊Ԏd���2���āA�����`�̓y�n�̑Ίp����ɂ���2�̕���_���Ԏd��Ō��ׂ��ׂĂ̊Ԏd�肪�Ȃ��芮������B �O>>470�����B
���1(�P�ʂȂ�)�ŏ�������ŁA�`����t�\���[�g���̏\���[�g���͂Ȃ��ŁB >>470
�ŏ��ł��邱�Ƃ̏ؖ������Ă������� >>439
���@����
�@sin(��-��) = sin��cos�� - cos��sin��,
�@tan(��-��) = (tan�� - tan��)/(1 + tan��tan��),
15� = 60�-45� = 45�-30߁@���,
�@sin(15�) = (��3 -1)/(2��2) = 1/(��2 + ��6),
�@tan(15�) = 2 - ��3 = 1/(2 + ��3), m�͎��R���A��m * (2mCm)/(4^m) ��m�����̋Ɍ��l�́H
�Ƃ�����������Ă����畛���I�ɏo�����A�ȒP�Ȃ炷�݂܂���A >>474
(2m)C(m)��(2m)!/((m!)^2)
m! �` (��(2��m))((m/e)^m)
(2m)! �` (��(4��m))((2m/e)^m)
�����ɓK�p���Đ���
�Ɍ��l�� 1/��(��)
�ō����Ă�H ���B�搶����̖��ł��B
�O����P�̊Ԃ�
�P�@�L�����͉�����ł������B
�Q�@�������͉�����ł������B
�R�@���z���͉�����ł������B
�S�@�����͉�����ł������B
�T�@�L�����Ɩ������ƒ��z���́A�ǂꂪ��ԑ����ł������B C: ���f���S��
R: �����S��
Q: �L�����S��
Z: �����S��
N: ���R���S��
�g�p��. 1 �� N �� Z �� Q �� R �� C. ���B�搶����̖��ł��B
�O����P�̊Ԃ�
�P�@�L�����͉�����ł������B
�Q�@�������͉�����ł������B
�R�@���z���͉�����ł������B
�S�@�����͉�����ł������B
�T�@�L�����Ɩ������ƒ��z���́A�ǂꂪ��ԑ����ł������B ���������Ƃ��Ȃ��̂ŁA�킩��܂���B �O>>471�{�����B
1�2�4 �����B
3 e�Ƃ��Ƃ�i�Ƃ����������Ǝv�����ǁA�������炵���B
5�������������B
e^����^e
�����ς����傤�͂ς��������傤��肨�������B ���z���{�����������z���H
���z���{���������������H �ł͏�������ς��܂��B
�O����P�̊Ԃ�
�P�@�L�����͉�����ł������B
�Q�@�������͉�����ł������B
�R�@�����͉�����ł������B
�S�@�L�����Ɩ������ł́A�ǂ��炪�����ł������B >>484
������
�ł͏�������ςւ܂��B
���ȁB ��������B�搶����̏o��ł��B
���̂����A�������̂͂ǂ�ł����B
�P�@1/2+1/4�{1/8�{�c�c�͂P�ɂȂ�B
�Q�@0.99999�c�c�͂P�ł���B
�R�@0.99999�c�c��0.9�{0.09�{0.009�{�c�c�Ɠ����ł͂Ȃ��B
�S�@0.99999�c�c�͍ŏ�����9������������ł���B
�T�@�L����������Ȃ鐔��̋Ɍ��l�����������ł���B
�U�@�L����������Ȃ鐔��̋Ɍ��l�����������ł���B
�V�@�����������̂��Ɍ��l�ł���B
�W�@�����������̂��Ɍ��l�ł���B
�X�@���������͎����ł���B
10�@���������͕K���Ɍ��l�����B
11�@�����������݂���B
12�@���R�����́��ɂ͂Ȃ�Ȃ����A�����̂͑��݂���B
13�@�����͘A����������B
14�@���͓_�̏W���ł���B
15�@��������Ŏ����������_�̏W���͐��ɂȂ�B
16�@��������ɔ�Z�̎��������݂���B
17�@�����W�������݂���B
18�@�Z�����W���͏W���ł͂Ȃ��B
19 ���R���̖����������̖����̕��������B
20�@�L�E�ȒP������͎�������i�Ɍ��l�����j�B
21�@�̐ςQ�̐������̂����݂���؋��͂Ȃ��B �ȉ~�ʂ��`�_�͂������邩�H
�`�_...��ȗ�����v���Ă���_ >>491
�������ȉ~�ʂ�a,b,c���݂��ɈقȂ鐳�̎����Ƃ���
x^2/a^2+y^2/b^2+z^2/c^2=1
����(x,y,z)�̏W���ł��� > sapply(1:20,function(k) treasure0(4,5,k))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
�Z���L�� 9 84 463 1776 5076 11249 19797 28057 32243 30095 22749
�����L�� 9 83 453 1753 5075 11353 20057 28400 32528 30250 22803
���� 2 23 224 1316 5353 16158 37666 69513 103189 124411 122408
[,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20]
�Z���L�� 13820 6656 2486 695 137 17 1 0 0
�����L�� 13831 6657 2486 695 137 17 1 0 0
���� 98319 64207 33788 14114 4571 1106 188 20 1
4�~5�̏ꍇ
��F1�@����
��F2�`5�@�Z���L��
��F6�`13�@�����L��
��F14�`20�@����
����������
����������
����������
����������
�Z���L����
Table[sum[C(2n-1+C(0,(21mod n)-1),k-1),{n,1,9}],{k,1,20}]
�����L����
Table[sum[C(2n-1+C(0,6mod n)-C(0,C(3,n-2)-1),k-1),{n,1,9}],{k,1,20}]
������
Table[C(19,k-1)+C(17,k-2)+C(15,k-2)+C(13,k-2)+C(8,k-2)+C(1,k),{k,1,20}] >>47
�P���~�����́u�e���K�v�Ɖ]���Č덷�̓����B�B�B
tera = 10^12 1�K = 0.01 �~
1�e�� �K = 10^12 �K = 10^10 �~ = 0.01 ���~ �͂��߂ď������ނ̂ł����A�����͐��w�̋^�����������ł������Ƃ���ł����H�f������͂��߂ĂŗD�����������Ă�������m(__)m >>496
���ꂷ������f�ł��Ȃ��n���͏����� ���(߄D߁�߄t�)��߯ �X�C�[�X�C�[�A�X�[�_���������A�X���X���X�C�X�C�̈ꐇ�[�[ ���ꂳ��Ƃ��k����̂�������Ă��܂���
�ǂ��炩��l����ɗ����܂���
�ǂ��炪�������ł��傤�H >>491 >>492
�`�_�͂S����B0<a<b<c �Ƃ����
�@(�}a���{(bb-aa)/(cc-aa)}, 0, �}c���{(cc-bb)/(cc-aa)} )
�`�_�ł̐ڕ��ʂƕ��s�Ȗʂ�
�@��(bb-aa)�(x/a) + ��(cc-bb)�(z/c) = (���),
�����őȉ~�ʂ��ƁA�f�ʂ͉~�ɂȂ�B �����I�@�O>>480����`��`�̂����Ƃ�`�������`���`�ȁ`��@���Ƃ��Ƃ҂�����Ƃ҂�������@���Ƃ��ҁ`������@�킩���Ȃ��B�������Ȃ�����B�ǂ����������Ȃ��H
�P]/�_______________
�Q/�_/ �@�@�@�����@/|
�P�_/�@�@�@ ((-_-)/ |
�P|�________(����)~ |_
�n| �a�P�P�P�P�҃� / /
�Q| �a ���@�� �a |/ /
_�@`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P ���L���P���Q�����X�^�[
�����X�^�[�Ƃ́A���悻8.08�~10^53�C���m�ɂ�
2^46�E3^20�E5^9�E7^6�E11^2�E13^3�E17�E19�E23�E29�E31�E41�E47�E59�E71=
808017424794512875886459904961710757005754368000000000��
������Ȃ鋐��ȌQ�ł���
���Ȃ݂ɃA�{�K�h���萔�͂��悻6.02 �~10^23�ł���
�����X�^�[�͖L���ȍ\�����������[�������Ώۂł��� lim[n����]��[1,n+1] | sin��x / x |dx / logn�����߂� k��x��k+1�@�ˁ@1/(k+1) �� 1/x �� 1/k,
�䂦
I/(k+1) < ��[k,k+1] |sin(��x)|/x dx < I/k,
������
I = ��[k,k+1] |sin(��x)| dx = ��[0,1] sin(��x) dx = [ -cos(��x)/�� ](x=0,1) = 2/��,
(���q) > I��[k=1,n] 1/(k+1) > I��[2,n+2] (1/x) dx = I {log(n+2) - log(2)},
(���q) < I��[k=1,n] 1/k < I{1 + ��[1,n] (1/x) dx } = I {1 + log(n)},
���@lim[n����] (���q)/log(n) = I = 2/��, >>433
�O���t���_�̊ϓ_�����܂��ɍi���Ǝv�� n���̋��݂�����(n��2). ���̋��݂̒���1�������d���̈Ⴄ���̂��������Ă��邪, ����͑��̂��̂ƌ����������Ȃ�.
�V����3��g���Ă�, �d���̈Ⴄ���݂����o���Ȃ��Ƃ���. ���̂Ƃ�n�̍ŏ��l�����߂�. �O>>507
>>514
n=4
�����3��ʂ�Ƃ��Ȃ炸����d�����Ⴄ�B �O>>515�⑫�B
������3��Ƃ������d���̂Ƃ��́A3��ʂ�ɍڂ����������������I�@�Ƃ킩��B �Ⴄ��
13�͏d�����y�����܂œ��肷��ꍇ�̍ŏ��l������ 13�����Əd�����y�����ʂ���K�v��������ΕK������o����
14�����Əd�����y�����ʂ���K�v�͂Ȃ��Ă��K������o����Ƃ͌���Ȃ�
�ŏ��l��14�� n���̑��ɖ{���Ƃ킩���Ă�����݂�1�������n�̍ŏ��l��15�ɂȂ�̂����̖��̖ʔ����Ƃ��� >>514
n=2 �͂ǂ���Ƃ��u���Əd�����Ⴄ�v����u1�������������Ă���v�ɔ����A���s������
�i���ɖ�蒆�ɖ{���E�U���Ƃ������t�Â��������Ă���A�U�����{�����d�����y�������킩��Ȃ����n=2�̂Ƃ�����ł��Ȃ��̂�2�������ƂȂ�j
������n��3�ł�� Table[Quotient[1/2+sqrt(2n),1],{n,1,36}]
{1, 2, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 5, 6, 6, 6, 6, 6, 6,
7, 7, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 8, 8, 8} �O>>517
n=4�̂Ƃ��͓���ł���B���Ⴀn=5���ˁB
n=5�̂Ƃ�����ł��Ȃ��\��������B
5���̂���3����ʂ�A�ʂ�3����ʂ낤�Ƃ��Ă����Ȃ炸�ꖇ�͓����R�C���ɂȂ�B���̓��̑��ʂ������l�Ȃ炻�̓��Ƃ��ʂ����ꖇ���������Ƃ킩�邪�A�Ⴄ�l�Ȃ�4���̂�����1�����d���̈Ⴄ�R�C�����B
4���̂���3����ʂ�O��ڂ̑��ʂőO���̑��ʂ̂����ǂ���̉�ɂ����������킩��B
�ǂ���̉�ɂ����������킩���Ă��A�\���̂���̂����ǂ��炪�d���̈Ⴄ�R�C�����͂킩��Ȃ��B
��n=5 �܂����łɏオ���Ă��鐳������www >>511
���łɏオ���Ă��邪�A�`���g�������ǥ����
1/x �͉��ɓʂ�����
�@2/(k+1/2) < 1/x + 1/(2k+1-x),
�䂦
�@I/(k+1/2) < ��[k,k+1] |sin(��x)|/x dx < I/k,
(���q) > I��[k=1,n] 1/(k+1/2) > I��[3/2,n+3/2] (1/x) dx = I {log(n+3/2) - log(3/2)},
(���q) < I��[k=1,n] 1/k < I{1 + ��[3/2,n+1/2] (1/x) dx = I {1 + log(n+1/2) - log(3/2)}, 0315
�ӂ�L@Fu_L12345654321
�w�R��1�����������܂����I
�ƂĂ��������ł��I
����������://pbs.twimg.com/media/D-IuUuqVUAALnAB.jpg
����������://twitter.com/Fu_L12345654321/status/1144528199654633477
https://twitter.com/5chan_nel (5ch newer account) >>521
�u���̋��݂̒���1�������d���̈Ⴄ���̂��������Ă��邪,�v�Ƃ�����������An���̋��݂̂Ȃ��Ɂu�d���̈Ⴄ���́v��1�������Ȃ��Ɠǂݎ���
�u�d���̈Ⴄ���́v���u���݂͕��ʂ��̏d��, �Ƃ����̂����܂��Ă����ł���Ɣ�ׂďd��or�y�����́v�Ƃ����Ӗ��Ŏg���Ă���Ɖ��߂ł���
���̉��߂�n=2�ɂ��čl����ƁA�V�������g���铹��Ȃ��Ƃ��������ł́A�ǂ��炪�u�d���̈Ⴄ���́v�����ʂł��Ȃ����ƂɂȂ� ���̋��݂̏d���̖����āA�������ȕ������Ă����H >>529
�o��҂�>>528�ŁA������n��2���Ǝ咣���Ă���̂ł́H n=2�������Ȃ�m���ɂ��̒ʂ�ňꌾ���Ȃ���www >>97>>123>>493
4�~5�̏ꍇ
��F1�@����
��F2�`4�@�Z���L��
��F5�`13�@�����L��
��F14�`20�@����
�{���~�X ���w�̖����Č������i�]�i�]���� 8�~9�̏ꍇ
��F1�@����
��F2�`22�@�Z���L��
��F23�`57�@�����L��
��F58�`72�@����
������������������
������������������
������������������
������������������
������������������
������������������
������������������
������������������
�Z���L����
Table[sum[C(2n-1+C(0,n-2)+3C(1,(10mod n)-2)+7C(0,n-11)+C(1,n-12)+9C(0,n-16)+C(0,C(0,C(5,n-22))),k-1),{n,1,35}],{k,1,12}]
�����L����
Table[sum[C(2n-1+C(1,(n+1)-C(floor((1+sqrt(8(n+1)))/2),2))-C(0,n-5)-3(C(0,n-9)+C(1,n-13))-7C(0,n-20)-C(0,C(0,C(4,n-23))),k-1),{n,1,35}],{k,1,16}]
������
Table[sum[C(2n-1-3C(0,C(0,C(4,n-24)))-8C(0,C(0,C(3,n-20)))-7C(0,n-20),k-2),{n,20,35}],{k,1,72}]+Table[C(71,k-1)+C(1,k),{k,1,72}] �O>>523�O���������ɗʂ�Ȃ��̂��I
���Ⴀ�������B
n=5�̂Ƃ��A
2�����ʂ��ē����ˎc���1�����Ⴄ
2�����ʂ��ĈႤ��4���̂����̂ǂꂩ���Ⴄ
���ځA
4���̂���2����ʂ��ē����ˎc��2���̂����ǂ��������Ⴄ
4���̂���2����ʂ��ĈႤ��2���̂����ǂ��������Ⴄ
�O��ځA
�ǂ��������Ⴄ�Ƃ킩����2���ȊO�̋���1������V����Œނ肠�킹�A�Е����ǂ��������Ⴄ�Ƃ킩����1���ƐT�d�ɓ���ւ��A
�ނ肠�����˂ǂ��������Ⴄ�Ƃ킩����2���̂����̎c���1�����Ⴄ�Ƃ킩��
�ނ肠��Ȃ������˂��̓���ւ������݂��Ⴄ�Ƃ킩��
�������ꂽ�B �O>>535
>>514
n=5�̂Ƃ��A
4���̋��݂�2�����ʂ��Ēނ肠�����ˎc���1�����Ⴄ����
4���̋��݂�2�����ʂ��Ēނ肠��Ȃ�������2�����̂����ǂ������ɏd���̈Ⴄ���݂�����
2��ځA2�����̂����ǂ�������1�����ŗʂ��Ēނ肠�����˗ʂ��Ă��Ȃ�2���̂����ǂ��������d���̈Ⴄ����
3��ځA�ق���3���͂��ׂē����d��������ł��̂�����1��������ɍڂ��A2��ڂŗʂ��ĂȂ�����2���̋��݂̂���1����V���̂�������ɍڂ��ނ肠�����ˍڂ��ĂȂ����݂��d���̈Ⴄ����
2��ڂŗʂ��ĂȂ�����2���̋��݂̂���1����V���̂�������ɍڂ��ނ肠��Ȃ������ˍڂ������݂��d���̈Ⴄ����
����ł����B
��n=6�Ɨ\�z���� �O>>536
>>514
n=6�̂Ƃ��A
���ځA2�����ʂ��Ēނ肠�����ˎc��2���̂����ǂ��������Ⴄ�d���̋���
���ځA�����d���̋���4���̂���1����V���̈���ɍڂ��A�c��2���̂����ǂ�������V���̂�������ɍڂ��ނ肠�����ˍڂ��ĂȂ����݂��d���̈Ⴄ����
�c��2���̂����ǂ�������V���̂�������ɍڂ��ނ肠��Ȃˍڂ������݂��d���̈Ⴄ����
���ځA2�����ʂ��Ēނ肠��Ȃ�4���̂����̂ǂꂩ���d���̈Ⴄ����
���ځA2�����̂����ǂ�������1�����V���ɍڂ��A�ނ肠�����ˍڂ��ĂȂ�2���̂����̂ǂ��������d���̈Ⴄ����
�O��ځA�����d����4���̋��݂̂����ǂꂩ��V���̕Е��ɍڂ��A�d���̈Ⴄ���݂��܂�2���̂����̂ǂ���������������ɍڂ��ނ肠�����ˍڂ��ĂȂ����݂��d���̈Ⴄ����
�d���̈Ⴄ���݂��܂�2���̂����̂ǂ���������������ɍڂ��ނ肠��Ȃˍڂ������݂��d���̈Ⴄ����
����ł����B
n=7�Ɨ\�z����B �O>>537
>>514
n=7�̂Ƃ�2�����ʂ��Ēނ肠�����ˎc��3���̂����̂ǂꂩ���d���̈Ⴄ����
3��ڂ܂łɓ���ł����B
n=8�̂Ƃ������l�ɓ���ł������B
n=9�̂Ƃ��A���ځA2�����ʂ��Ēނ肠�����ˎc��5���̂����̂ǂꂩ���d���̈Ⴄ����
������5���̋��݂̂���2�����ʂ��Ēނ肠��ȂƂ��O��ڂ܂ł������Ă��ŁA���v�l���邱�ƂɂȂ�B
��n=9 �O>>538
>>514
��������H
n=9�̂Ƃ��A
2�����ʂ��Ă�3�����ʂ��Ă��O��ڂ܂łɓ���ł��Ȃ��B >>539
������n=2 (�ʂ̉��߂ł�n=14)
�ł��Ȃ��ȊO�͑S���F�߂Ă����... �O>>539
>>541
n=2��n��3�̑�ӂ����Ȃ����ߕs�K�B �O>>542
���>>514
>>541
n=14�Ƃ��������ƂȂ��Ă�l�́An=9�`13�̂Ƃ��A���Ȃ��Ƃ���A����n�ŎO��ڂ܂łɓ���ł�����Ď������́H �������̖�艽���������Ƃ��ƌ������L����肾����Ȃ��B �O>>543���>>514
>>538�Ő���n=9���������Ǝv�������ǁAn=5�̏ꍇ��O��ɂ��Ă���ł��������܂Ƃ߂܂��B
����ɂ���Ȃ�Ȃ�����n=8�̂Ƃ��O��ڂ܂łɓ���ł��邱�Ƃ�������Ȃ��B
n=9�̂Ƃ��A
���ځA2�����ʂ��Ēނ肠�����ˎc��5���̂����̂ǂꂩ���d���̈Ⴄ����
���ځA5���̋��݂̂���4���̋��݂�2�����ʂ��Ēނ肠�����ˎc���1�����Ⴄ����
���ځA5���̋��݂̂���4���̋��݂�2�����ʂ��Ēނ肠��Ȃ�2�����̂����ǂ������ɏd���̈Ⴄ���݂�����
�O��ځA2�����̂����ǂ�������1�����ŗʂ��Ēނ肠�����˗ʂ��ĂȂ�2���̋��݂̂����ǂ��������d���̈Ⴄ����
�O��ځA2�����̂����ǂ�������1�����ŗʂ��Ēނ肠��Ȃ˗ʂ���2���̋��݂̂����ǂ��������d���̈Ⴄ����
�l��ځA�ق���3���͂��ׂē����d��������ł��̂�����1��������ɍڂ��A�O��ڂŗʂ��ĂȂ�����2���̋��݂̂���1����V���̂�������ɍڂ��ނ肠�����ˍڂ��ĂȂ����݂��d���̈Ⴄ����
�O��ڂŗʂ��ĂȂ�����2���̋��݂̂���1����V���̂�������ɍڂ��ނ肠��Ȃˍڂ������݂��d���̈Ⴄ����
�l��ڂœ���ł������O��ڂ܂łɓ���ł��ȂB
����3�����ʂ��Ă݂�B�i�Â��j �O>>546�Â��B
���>>514
n=9�ŁA
���ځA3�����ʂ��Ēނ肠�����ˎc��3���̂����̂ǂꂩ���d���̈Ⴄ����
���ځA3���̋��݂̂���2���̋��݂�1�����ʂ��Ēނ肠�����˗ʂ�Ȃ�1�����d���̈Ⴄ����
���ځA3���̋��݂̂���2���̋��݂�1�����ʂ��Ēނ肠��Ȃ�2���̋��݂̂����ǂ�����1�����d���̈Ⴄ����
�O��ځA2���̋��݂̂����ǂ�����1����Е��̓V���ɍڂ��A��������ɂق���7���̂�����1�����ڂ��ނ肠������2���̋��݂̂����ڂ��Ȃق��̋��݂��d���̈Ⴄ����
�O��ځA2���̋��݂̂����ǂ�����1����Е��̓V���ɍڂ��A��������ɂق���7���̂�����1�����ڂ��ނ肠��Ȃ�2���̋��݂̂����ڂ����ق��̋��݂��d���̈Ⴄ����
���ځA3�����ʂ��Ēނ肠��Ȃ˂���6���̋��݂̒��ɈႤ���݂�������ځA3������2�����ɂ�����ނ肠�����ˊO����2���̂����ǂ��������d���̈Ⴄ����
�O��ڂœ���ł���B
���ځA3������2�����ɂ��Ă��ނ肠��Ȃ�2�������v4���̂����̂ǂꂩ���d���̈Ⴄ����
�O��ځA2������1�����ɂ�����ނ肠�����ˊO����2���̂����ǂ��������d���̈Ⴄ����
�O��ڂ܂łɓ���ł��Ȃ����l��ڂœ���ł���B
n=8�̂Ƃ��A�i����n=8�ł�����������ł����͎̂l��ځj
n=7���܂��������B 13���ł̓�����@
13����4,4,5�ɕ�����B���ꂼ��AA�O���[�v�AB�O���[�v�AC�O���[�v�Ɩ���
A�O���[�v4��������ɁAB�O���[�v4���𑼕��ɍڂ���B
[1]�ނ荇�����ꍇ
�@C�O���[�v5���̒��ɋU�������邱�Ƃ������B
�@C�O���[�v��3���ƁA2���ɂ킯�A���ꂼ��C1��C2�Ɩ���
�@�{��3��(A�O���[�v�AB�O���[�v�̍��v10�͂�������{��)��C1�O���[�v�̎O�����ڂ���B
�@�ނ荇���AC2�̂ǂ��炩���U���BC2�̈ꖇ�ƁA�{���ꖇ���ڂ���悢�B�ȉ���
�@�ނ荇��Ȃ���AC1�̃O���[�v3���̒��ɋU�������邱�ƂƁA�U���̌y�d�������B�ȉ���
[2]A�O���[�v�������������ꍇ
�@A�O���[�v���Ɂu�d���U���v�����邩�AB�O���[�v���Ɂu�y���U���v�����邩�̂����ꂩ�B
�@C�O���[�v�T���ƁAA�O���[�v�̂R����B�O���[�v���̂Q�����ׂ�
�@�ނ荇���AA�̎c�������̂��AB�̎c��2���̒��ɋU��������B���̏ꍇ�AB�̎c���V���̗����ɍڂ���悢
�@��������������AA�O���[�v�̂R���̒��ɁA���������オ���B�O���[�v���̂Q���ɋU�̂�������B�ȉ����B
[2]B�O���[�v�������������ꍇ
�@[�Q]�Ɠ��l�Ȃ̂ŏȗ� �O>>547�������悤�Ǝv�������A����ς蓯���������B
>>514
n=9�̂Ƃ��A
���ځA
3�����ʂ��Ēނ肠�����˗ʂ�Ȃ�3���̂����̂ǂꂩ���d���̈Ⴄ����
3�����ʂ��Ēނ肠��Ȃ˗ʂ���6���̂����̂ǂꂩ���d���̈Ⴄ����
���ځA
6���̂�����2������ʂ��Ēނ肠�����˗ʂ�Ȃ�2���̂����̂ǂ��������d���̈Ⴄ����
6���̂�����2������ʂ��Ēނ肠��Ȃ˗ʂ���4���̂����̂ǂꂩ���d���̈Ⴄ����
�O��ځA2���̂����ǂ������Ȃ����ł��邪�A4���̂����̂ǂꂩ�Ȃ����ł��Ȃ��B
n=7�An=8�̂Ƃ��́A2�����ʂ��ĎO��ڂœ���ł��邪�An=9�̂Ƃ��́A3�����ʂ��Ă�����3���������d���Ȃ�ǂ�3���������d���̋��݂��܂ނ�����ł��Ȃ��B
n=9�̂Ƃ��A2�����ʂ��Ĉ��ڂ������œ��ڕʂ�2�����ŗʂ��ĈႤ�Ƃ��Ă��A�O��ڂ���4���̂�����2����ʂ��ē����Ȃ�A���������2���̂����ǂ��������Ⴄ�d�����Ƃ킩���Ă͂��Ă��A�ǂ������Ⴄ�d���̋��݂�����肷��v�ʂ͎l��ځB
��n=9 9���̓�����@
9�̋��݂�ABCDEFGHI�Ƃ���
1 �E�ɋ���ABCD�A����EFGH�Ŕ�ׂ�
2a 1���ނ荇��Ȃ��Ƃ�
�E��ABE�A����CDF�Ŕ�ׂ�
3a 2a���ނ荇�킸�E�̌X�����A1�̉E�̌X���Ɠ����Ƃ�
�E��A�A����B�Ŕ�ׂ�
�ނ荇��Ȃ����1�̉E�̌X���Ɠ������A�ނ荇����E���d�����Ⴄ
3b 2a���ނ荇�킸�E�̌X�����A1�̍��̌X���Ɠ����Ƃ�
�E��C�A����D�Ŕ�ׂ�
�ނ荇��Ȃ����1�̉E�̌X���Ɠ������A�ނ荇����F���d�����Ⴄ
3c 2a���ނ荇���Ƃ�
�E��A�A����G�Ŕ�ׂ�
�ނ荇��Ȃ����G�A�ނ荇����H���d�����Ⴄ
2b 1���ނ荇���Ƃ�
I���d�����Ⴄ �O>>549
>>514
n=9�̂Ƃ��͓���ł��Ȃ��B
�������ɓ���ł���Ƃ��Ă��A
n=10�̂Ƃ��A
���ځA4�����ʂ��ē����ˎc��2���̂����̂ǂ��������d���̈Ⴄ����
�����ڂœ���
���ځA4�����ʂ��ĈႤ��8���̂����̂ǂꂩ���d���̈Ⴄ����
�����ځA2�����ʂ��ē����ˎc��4���̂����̂ǂꂩ���d���̈Ⴄ����
���ځA2�����ʂ��ĈႤ�˂���4���̂����̂ǂꂩ���d���̈Ⴄ����
�O��ځA4���̂���2����ʂ��ē����ˎc��2���̂����̂ǂ��������d���̈Ⴄ����
�O��ځA4���̂���2����ʂ��ĈႤ�˂���2���̂����̂ǂ��������d���̈Ⴄ����
�l��ځA�d���̈Ⴄ���݂��܂�2���̂�����1����Е��̓V���ɍڂ��A�ق��̏d��������6���̂�����1���������Е��̓V���ɍڂ��ނ肠������2���̂����ڂ��Ȃ�1�����d���̈Ⴄ����
�d���̈Ⴄ���݂��܂�2���̂���1����Е��̓V���ɍڂ��A�ق��̏d��������6���̂���1���������Е��̓V���ɍڂ��ނ肠��Ȃ�2���̂����ڂ���1�����d���̈Ⴄ����
�O��ڂ܂łɓ���ł��Ȃ��B
��n=9�܂���n=10 n=9��10�̂Ƃ���1��ڂ�3�����悹�������������
���Ƃ�n=12�Ƃ�13�̂Ƃ��̂������l��������킩�� 10���̓�����@
10�̋��݂�ABCDEFGHIJ�Ƃ���
1. �E�ɋ���ABCD�A����EFGH�Ŕ�ׂ�
2a. 1. ���ނ荇��Ȃ��Ƃ�
�@�E��ABE�A����CDF�Ŕ�ׂ�
3a. 2a. ���ނ荇�킸�E�̌X�����A1. �̉E�̌X���Ɠ����Ƃ�
�@�E��A�A����B�Ŕ�ׂ�
�@�ނ荇��Ȃ����A�AB�̓�1. �̉E�̌X���Ɠ������A�ނ荇����E���d�����Ⴄ
3b. 2a. ���ނ荇�킸�E�̌X�����A1. �̍��̌X���Ɠ����Ƃ�
�@�E��C�A����D�Ŕ�ׂ�
�@�ނ荇��Ȃ����C�AD�̓�1. �̉E�̌X���Ɠ������A�ނ荇����F���d�����Ⴄ
3c. 2a. ���ނ荇���Ƃ�
�@�E��A�A����G�Ŕ�ׂ�
�@�ނ荇��Ȃ����G�A�ނ荇����H���d�����Ⴄ
2b. 1. ���ނ荇���Ƃ�
�@�E��A�A����I�Ŕ�ׂ�
�@�ނ荇��Ȃ����I�A�ނ荇����J���d�����Ⴄ
�O����>>550�ƑS������
�Ƃ������A������
> �O��ڂ܂łɓ���ł��Ȃ��B
> ��n=9�܂���n=10
�Ə������Ƃ���ŁA�u>>551�ɂ͓���ł��܂���ł����v�A�Ƃ����咣�ł����Ȃ��A
n=9�A10�œ��肷����@���Ȃ����Ƃ̏ؖ��ɂ͑S���Ȃ�Ȃ�����
���ۓ����Ƃ������Ⴊ�o���� �O>>551
���>>514
n=9�̂Ƃ��A
9���̋��݂�4�����ʂ�̂͂���ĂȂ������B
4�����ʂ��ēV�����ނ肠�����˗ʂ�Ȃ��݂��d���̈Ⴄ����
4�����ʂ��ēV�����ނ肠��Ȃ˗ʂ���8���̋��݂̂����̂ǂꂩ���d���̈Ⴄ����
�ǂ�����4���ɏd���̈Ⴄ���݂��܂܂�Ă邩�͂܂��킩��Ȃ��͂����B
�܂�8���̋��݂�ʂ��ĈႤ�d���̋��݂��݂���Ƃ����v�ʂ�����B
n=8�̂Ƃ��́A�ő��O��ڂ��B�܂�n=9�̂Ƃ��͎l��ڂ̌v�ʂ��K�v�ɂȂ�B
>>550�̖���
��Ӂu�d���̈Ⴄ���̂��������Ă��邪, ����͑��̂��̂ƌ����������Ȃ��v
�ɏ]���Ȃ�AA��Е��̓V���ɍڂ�B�������Е��̓V���ɍڂ��邱�Ƃ͂ł��邪�A�����������Ȃ�A�AB�A2�̋��݂����E�ɒu�������邱�Ƃ͂ł��Ȃ��B
�{�������������Ȃ��͂��̋��݂ɂ��イ�Ԃ�y���C���N�̃}�W�b�N�ŃA���t�@�x�b�g����������������Ȃ����A���[���ᔽ�Ŏ��i�ƌ��킴������Ȃ��B
A��B���ނ肠������E���Ⴄ�d���̋���
�͂킩��B
A��B���ނ肠��Ȃ�A�܂���B���Ⴄ�d���̋���
�ƌ����邪�A
A��B���ނ肠��Ȃˈ��ڂ̓V���̉E�̌X���Ɠ����ق����d���̈Ⴄ����
�͂ǂ����B
A��B���v�ʑO�Ɍ������Ă�悤�ȋC�����邵�A�����Ă�悤�ȋC������B
C��D������ق��ł͂Ȃ�A��B������ق��ɏd���̈Ⴄ���݂��܂܂�Ă��A������A��B��V���ɍڂ����Ƃ���̌v�ʂƓ����X���ɂȂ�ق����d���̈Ⴄ���݂��A�ƁB nCk��nk�������R���g(n,k)�����߂� n=9�̎��̉��̈��
LLLRRRSSS
LLRSSLRRS
LRLLRSRSS >>550,553�͑傫���ԈႦ�Ă�
> 3a 2a���ނ荇�킸�E�̌X�����A1�̉E�̌X���Ɠ����Ƃ�
> �E��A�A����B�Ŕ�ׂ�
> �ނ荇��Ȃ����1�̉E�̌X���Ɠ������A�ނ荇����E���d�����Ⴄ
> 3b 2a���ނ荇�킸�E�̌X�����A1�̍��̌X���Ɠ����Ƃ�
> �E��C�A����D�Ŕ�ׂ�
> �ނ荇��Ȃ����1�̉E�̌X���Ɠ������A�ނ荇����F���d�����Ⴄ
10���̂������ԈႢ�ŁA�������͂���
9���̓�����@
9�̋��݂�ABCDEFGHI�Ƃ���
1. �E�ɋ���ABCD�A����EFGH�Ŕ�ׂ�
2a. 1. ���ނ荇��Ȃ��Ƃ�
�@�E��ABE�A����CDF�Ŕ�ׂ�
3a. 2a. ���ނ荇�킸�E�̌X�����A1. �̉E�̌X���Ɠ����Ƃ�
�@�E��A�A����B�Ŕ�ׂ�
�@�ނ荇��Ȃ����A�AB�̓�1. �̉E�̌X���Ɠ������A�ނ荇����F���d�����Ⴄ
3b. 2a. ���ނ荇�킸�E�̌X�����A1. �̍��̌X���Ɠ����Ƃ�
�@�E��C�A����D�Ŕ�ׂ�
�@�ނ荇��Ȃ����C�AD�̓�1. �̉E�̌X���Ɠ������A�ނ荇����E���d�����Ⴄ
3c. 2a. ���ނ荇���Ƃ�
�@�E��A�A����G�Ŕ�ׂ�
�@�ނ荇��Ȃ����G�A�ނ荇����H���d�����Ⴄ
2b. 1. ���ނ荇���Ƃ�
�@I���d�����Ⴄ > �{�������������Ȃ��͂��̋��݂ɂ��イ�Ԃ�y���C���N�̃}�W�b�N�ŃA���t�@�x�b�g����������������Ȃ����A���[���ᔽ�Ŏ��i�ƌ��킴������Ȃ��B
�u���ꏊ�ŊǗ�����������A�g����Ȃ�tⳂ��g���Ă��������낤
���݂���ʂł��Ȃ����Ƃ́A�Ǘ��ł��Ȃ����Ƃ̗��R�ɂ͂Ȃ�Ȃ�
> A��B���ނ肠������E���Ⴄ�d���̋���
���������ʂ�>>557��3a. ��AB���ނ荇���AF���Ⴄ�d���̋��݂ɂȂ�
����̓I�ɂ́A1. ��ABCD�����ɌX���Ă����F���y�����݁AEFGH�����ɌX���Ă����F���d�����݂ɂȂ�
�Ȃ��Ȃ�A
2a. �ŌX���Ă���̂�ABCDEF�̂ǂꂩ
3a. �Œނ荇���Ă���̂�AB�ł͂Ȃ�
CDE��1. ��2a. �ŏ���Ă���M�̌X�����t�ł���CDE�ł͂Ȃ�
> A��B���ނ肠��Ȃˈ��ڂ̓V���̉E�̌X���Ɠ����ق����d���̈Ⴄ����
������݂��A2���ď���Ă���M�̌X�����قȂ�A���̋��݂͏d�����قȂ���݂ł͂Ȃ� �O��ڂ̒�����4���c���Ă���Γ���ł��Ȃ��̂�
����n�̍ŏ��l�͂P�U >>559
����Ȃ�14����15���̂Ƃ�����o���邱�Ƃ������Ă݂� �������Ȃ���
n���̋��݂�����(n��3).
���̋��݂̒���1�������d���̌y�����̂��������Ă��邪,
����͑��̂��̂ƌ����������Ȃ�.
�V����3��g���Ă�, �d���̌y�����݂����o���Ȃ��Ƃ���.
���̂Ƃ�n�̍ŏ��l�����߂�. ��14���̎�
7�����ڂ��Čy���ق��ɋU��������
�y��7���̂���1�����c����3�����ڂ���
�ނ荇���Ύc����1�����U��
�ނ荇��Ȃ��Ƃ��͌y��3���̓�
1�����ڂ��Ēނ荇���Ύc�����ꖇ���U��
�ނ荇��Ȃ���Όy���ق����U�� >>561
>>514�Ƃ͑S���ʂ̖��Ȃ���ǁH
���̖��Ȃ�15�ǂ��납�����Ƒ������Ōy�����݂����ł��� ���̂���ł��P�U�ȏ�͓���ł��Ȃ�
�P�T���������� �ǂ���̖����A����ł��閇���̉����������������A
����ł���ő喇�����傫�����œ���ł��Ȃ����Ƃ��ؖ���������d�v�Ȃ��ǂ�
����ɂ��Ă�>>561�͂܂�����Ȃ� �ŏ���9�����V���ɏ悹������A��������ΌX���Ă��ނ荇���Ă�27������1/3��9���ɂȂ� ���R���Œ�`���ꂽ��f_t�����̗l�ɒ�߂�:
f_t(n)=��[k=0,n] C(n, 5k+t)
��, t=0,1,2,3,4�̎����X�ɏA����, f_t(n)��, 1�̋���5�捪��1����p���ĕ\��.
�A��a<b�Ȃ�2���R��a,b�ɑ�C(a,b)=0�Ƃ���. �O>>554���A�������Ԃ����������B
���>>561
n=9�̂Ƃ��A
���ځA9���̋��݂̂���3������V���ɍڂ��ނ肠�����ˍڂ��Ȃ�3���̋��݂̂����̂ǂꂩ���y������
���ځA9���̋��݂̂�����3������V���ɍڂ��ނ肠��Ȃˏオ�����ق���3���̋��݂̂����̂ǂꂩ���y������
���ځA3���̋��݂̂����̂ǂꂩ�Ƃǂꂩ��V���ɍڂ��ނ肠�����ˍڂ��Ȃ��݂��y������
3���̋��݂̂����ǂꂩ�Ƃǂꂩ��V���ɍڂ��ނ肠��Ȃˏオ�����ق��̋��݂��y������
n=9�̂Ƃ��͓��ڂ܂łɓ���ł���B
��n=27 �c��3����1��Œ����ł��邩��3��Œ����ł���
�ő��n��
���R^3=�Q�V >>570
�@k_max = [ (n-t)/p ],�@�@�@�@�@(t=0,1,�c,p-1)
��`����
�@(1+��^s)^n = ��[t=0,p-1] f_t(n) ��^(st),�@�@�@�@(s=0,1,�c,p-1)
����1 �͂P��p�捪������
�@��[s=0,p-1] ��^s = 0,
�@(1/p)��[s=0,p-1] ��^{s(t-t')} = ��_{t,t'}
������g����
�@f_t(n) = (1/p)��(s=0,p-1) ��^(-st) (1+��^s)^n,
�{��ł� p=5. �������Ȃ���
n���̋��݂�����(n��3).
���̋��݂̒���1�������d���̌y�����̂��������Ă��邪,
����͑��̂��̂ƌ����������Ȃ�.
�V����3��g���Ă�, �d���̌y�����݂����o���Ȃ��Ƃ���.
���̂Ƃ�n�̍ŏ��l�����߂�.
�c��3����1��Œ����ł��邩��3��Œ����ł���
�ő��n��3^3=27
�d���̌y�����݂����o���Ȃ�n�̍ŏ��l��28.
�d���̂��y���̂�����ł��Ȃ����݂�
1���������Ă���ꍇ�͓��肷��̂Ɍy�����݂̂�
2�{�̓�Փx�ɂȂ�Ǝv����̂�
����o���Ȃ�n�̍ŏ��l��14.�i���[�_�X�|�l���X�j >>514
1��ڂɉE��5��ABCDE�A����5��FGHEJ�Ŕ�ׂ�ƂĉE�ɌX�����ꍇ�A
ABCDE�̂ǂꂩ���d�����݂��AFGHIJ�̂ǂꂩ���y�����݂��̂��߁A�ǂꂪ�d�����Ⴄ���݂���10�ʂ�̏ꍇ������
�V��1��̔�r�ł́A�E�ɌX���A���ɌX���A�ނ荇����3�ʂ�̏������ꂸ�A
�c��2��̔�r�ł�3�O2=9�ʂ�̏�������Ȃ��ׁA�ŏ���5�����ł�3��œ���ł��Ȃ�
�ŏ���4������r���ČX�����ꍇ�́A>>557�̒ʂ��r����8���̒�����c��2��œ���ł���
�ŏ���4������r���Ēނ荇�����ꍇ�́A8���̐���ȋ��݂��g���ĉ����̕s���̋��݂���c��2��̔�r�œ���ł��邩�̘b�ɂȂ�
�V���ɕs���̋��݂�4���Ɖ������̐��������݂��ڂ��Ĕ�r���ČX�����ꍇ�A���10�ʂ�ɂȂ������Ɠ��l�A4�ʂ�̏ꍇ���l�����A�c��1��̔�r�ł͓���ł��Ȃ�
�����1��ڂɒނ荇�����ꍇ�A2��ڂ̔�r�ł�3���܂ŕs���̋��݂��ڂ�����i�E�ɕs��3���A���ɐ���3�����j
2��ڂ�3���ڂ��Ēނ荇�����ꍇ�A�V���ɕs���̋���2�����ڂ���ƁA1��̔�r�ł͂ǂ��炪�d�����قȂ���݂�����ł��Ȃ�
�����1��ځA2��ڂŒނ荇�����ꍇ�́A1�������s���̋��݂��ڂ�����
���̎��Ō�܂ōڂ��Ȃ����݂�1���܂łȂ����ł��邩��A3��̔�r�œ���ł��閇���͑����Ă��A
8+3+1+1=13��
13���̓�����@�͑���>>548���邩�����ł��Ȃ�n�̍ŏ��l��14
�������A�s�������邩�� �@>>548�ɃR�����g�����������܂����̂ŁA��ɃR�e�n��������^�[�Q�b�g�ɁA���X�⑫�ƁA�R�����g���B
>>577�@>>�c��2��̔�r�ł�3�O2=9�ʂ�̏�������Ȃ��ׁA�ŏ���5�����ł�3��œ���ł��Ȃ�
�y�@10�ʂ�̉\�����c�����B�@�V���́A�ނ荇���A�E�ɉ�����A���ɉ�����̎O�ʂ�̌��ʂ������o����B�@�z
�y�@�悹�����ǂ̂悤�ɍH�v���悤�Ƃ��A�V�����̎g�p�ł́A�����錋�ʂ́A�O�ʂ�̓��=9�ʂ肵�����蓾�Ȃ��̂ŁA�@�z
�y�@10�ʂ肷�ׂĂ����ɂ߂邱�ƂȂǕs�\�Ƃ������́B�@�z
���̖��ł͏��ɂ��̂悤�Ȏ��_���d�v�B
>>548�ł͎����悤�ȃP�[�X���r���Ŕ������Ă��܂��B
�ŏ��̓V���g�p�Œނ荇�����ꍇ�A�c��܌̃R�C������y�d�s���̕s���̃R�C�������������Ȃ���Ȃ�Ȃ��Ȃ��Ă��܂��B
�u��Ɠ��l�A10�ʂ�̉\�����A���̓V���g�p�Ō��ɂ߂���ƂȂ��Ă���̂ł́H�v
�Ƃ����^�₪�������邩������܂��A�D�D�D���͈Ⴄ�̂ł��B
>>548�́A�uA���d���AA���y���A...�AD���y���AE���s���v�ƁAE�̃R�C���ɂ��ẮA�y�d�ʂ��Ă��Ȃ����߁A9�ʂ�
�ōς�ł���̂ł��BE�͍Ō�܂ŁA�V���ɏ悹��ꂸ�ɁA�u���܂����s���ȃR�C�����v�ƌ��_����Ă���̂ł��B
���̂悤�Ȃ��Ƃ��\�Ȃ̂͂���������B�]���Čy�d�s���R�C����V�� k ��g�p�Ō��ɂ߂���̂́A
(3^k+1)/2��������ƌ������ƂɂȂ�܂��B
����A�V���O��Ȃ�A14�Ȃ̂ł́H�@�����ł��B�������A���̎������Ă͂܂�̂́A�{���̃R�C�����\���p�ӂ���Ă��邱�Ƃ������ł��B
�����玝���Ă����{���̃R�C���X���ƁA�^�[�Q�b�g�P�S���̒�����I�X���̃R�C�����r�B
���̌��ʁA�X���̃R�C���̒�����y�d�����ς݂̋U�R�C����T���A���A�T���̃R�C������y�d�s���̋U�R�C����T�����ɕω����܂��B
���ꂪ�����\�Ȃ̂́A����������������K�v�͖����ł��傤�B�L�[�͕ʘg�ŗp�ӂ���Ă���{���̃R�C���̂��L�邩�������ł��B �V���Ȃ���ŁA������������B
�����̕��͌��\�y���߂�Ǝv���܂��B
�܂��܂��L�����Ǝv���̂ŁA�u�T���v�Ό�����Ǝv���܂����A�l���邱�Ƃ������u�ʔ����v�̂��Ǝv���̂ŁA
�������̕��A���邢�́A�T���ē��������������́A���̕ӂ��z������������Ǝv���܂��B
�T�̏d���̈قȂ�u�d��v������܂��B�����V�����g���ďd�����ɕ��ׂ����Ǝv���܂��B
���āA�m���ɕ��בւ���ɂ́A�V���͍Œች��g�p����K�v������ł��傤���H
��̓I�Ȏ菇���v�������ׂȂ���l������́u�W��H�v�A���_����l������́u�V��I�v�Ɠ�����̂ł͂Ȃ���
�Ǝv���܂����A���Ăǂ��ł��傤�H
�Ƌ�̓I�Ȏ菇�A���������l�����������B
���Ȃ݂ɁA�S�̏d��Ȃ�A�g�[�i�����g�����ŁA��ԏd���̂��R��œ��肵�A���Ɉ��핉�����m���ׂ�
��Ԍy��������肵�A�c���������ׂĂQ�ʁA�R�ʂ����A�̂悤�ɁA�T��ʼn\�ł��B ������ƁA�������܂��B
�O�F�m���ɕ��בւ���ɂ́A�V���͍Œች��g�p����K�v������ł��傤���H
��F�Œች��̓V���g�p�ŁA�m���ɕ��בւ�����ł��傤�B �O>>571
���>>580
���ځA5�̏d��̂���1����V���ɍڂ��A�d���d��H(heavy)�ƌy���d��L(light)����肷��ƁA
H��L
���ځA���l�ɏd���d���H2�ƌy���d���L2����肷��ƁA
H2��L2
�O��ځ`�Z��ځA����1�̏d��A(another)��H�AH2�AL�AL2�̂ǂꂩ�ƓV���ɂ����AA�̏d��̏d������T��̂ɍő�4����A
H��A�AH2��A�AL��A�AL2��A
����ځAH��H2��V���ɍڂ��A
H��H2
����ځAL��L2��V���ɍڂ��A
L2��L
�d��̏d�����͓���ł��A
H��H2��L2��L��A
�ő�8��̌v�ʂ��K�v�B
�O��ځ`�Z��ڂŁA
���Ƃ���A��L�Ȃ�A
����ڂ̌v�ʂ͕s�v�ŁA
���v7��̌v�ʂł悢�B
���ő�8��̌v�ʂ��K�v�ŁA���Ȃ��Ƃ�7��̌v�ʂ��K�v�B �O>>581���_�̒��O��������B
���>>580
���ځA5�̏d��̂���1����V���ɍڂ��A�d���d��H(heavy)�ƌy���d��L(light)����肷��ƁA
H��L
���ځA���l�ɏd���d���H2�ƌy���d���L2����肷��ƁA
H2��L2
�O��ځ`�Z��ځA����1�̏d��A(another)��H�AH2�AL�AL2�̂ǂꂩ�ƓV���ɂ����AA�̏d��̏d������T��̂ɍő�4����A
H��A�AH2��A�AL��A�AL2��A
����ځAH��H2��V���ɍڂ��A
H��H2
����ځAL��L2��V���ɍڂ��A
L2��L
�d��̏d�����͓���ł��A
H��H2��L2��L��A
�ő�8��̌v�ʂ��K�v�B
�O��ځ`�Z��ڂŁA
���Ƃ���A��L�Ȃ�A
����ڂ̌v�ʂ͕s�v�ŁA
H��H2��L2��A��L
���v7��̌v�ʂł悢�B
���ő�8��̌v�ʂ��K�v�ŁA���Ȃ��Ƃ�7��̌v�ʂ��K�v�B ����菇���ɏ]���ă\�[�g����ƁA�u�^���悯��S���ǁA������P�O��K�v�v�Ƃ������Ƃ����邩������܂���B
�܂��ʂ̎菇���ɏ]���ă\�[�g����ƁA�u�^���悯��T���ǁA������X��K�v�v
�D�D�D
���Ƃ��������������邩������܂���B
���ł́A�u�m���ɕ��בւ���v���Ƃ������ɂ��Ă܂��B
�^�������Ă��A���ꂱ��̉̎g�p����������A�\�[�g��K�������ł���A�Ƃ����A���̍ŏ��̉ƁA�菇���̒��g��₤�Ă��܂��B
�]���āA�����́u����菇���v�̂���͂P�O��A�u�ʂ̎菇���v�͂X��Ƃ������ƂɂȂ�܂��B
�����͂������s�����̒l�ł��B
>>581�A>>582
�W��ƌ������Ƃł����A�����ł͂���܂���B
�w���_����l������́u�V��I�v�x�Ə��������R���l���Ă݂Ă��������B
�ʂ̎��_�Œ��߂Ă݂Ă��������B �wn���̋��݂�����(n��2).
���̋��݂̒���1�������d���̈Ⴄ���̂��������Ă��邪,
����͑��̂��̂ƌ����������Ȃ�.
�V����3��g���Ă�, �d���̈Ⴄ���݂����o���Ȃ��Ƃ���.
���̂Ƃ�n�̍ŏ��l�����߂�x
���d���̈Ⴄ���݂����o����ő�l��13
�V����1���Âȏ�ڂ��Ēނ荇�����̋��݂�
�����ȋ��݂ł��邱�Ƃ��m�肷��
�ŏ���4���Âڂ��Ēނ荇������8���͐������m��
�c��5���̒��Ƀj�Z���݂�����
�X������8���̒��Ƀj�Z���݂�����
�j�Z���܂�5���̓��A3���Ɛ����ȋ���3�����ׂ�
�ނ荇���Ύc��2���̓���1������m�肵�Ă���
�����ȋ��݂Ɣ�ׂ�ǂ̋��݂��j�Z�����m�肷��
�ނ荇��Ȃ���A�w�d�����y�������m�肵�Ă���3���x��
�Ȃ�̂Ŏ��̈��Ŋm�肷��
4���Âv8�����X���A�ǂ��炩��
�d�����y�����̋��݂�����
���̏ꍇ�A�݂���4������1���Â��G�N�X�`�F���W����
�����ɏ��m��ς݂̐����ȋ��݂�Б���3��������
4�����v��
�ނ荇���ΐ����ȋ���3���̑���Ɏ�菜����
3���̋��݂��w�d�����y�������m�肵�Ă���3���x�ƂȂ�̂�
���̈��Ŋm�肷��
�X�����t�ɂȂ����Ƃ��̓G�N�X�`�F���W�������݂��j�Z
���̓�̋��݂̂����ǂ��炩�𐳎��ȋ��݂Ɣ�ׂ��
��m��
�X���ω����Ȃ���G�N�X�`�F���W���Ȃ�����3���̋��݂�
�w�d�����y�������m�肵�Ă���3���x�ƂȂ�
�����̎��A�j�Z���݂��d�����y�������������肳���
����14�����Ƃ����1��̒������K�v�ɂȂ�
�ȏ�ɂ��A
�d���̈Ⴄ���݂����o���Ȃ�n�̍ŏ��l��14. ����ł͋���14�����Əo���Ȃ����Ƃ������Ă���ƌ����Ȃ���Ȃ�����
�S�R�ʂ̕��@�ʼn\�����m��Ȃ�
�ʂ̕��@�ł��낤�Əo���Ȃ����Ƃ������K�v�����邯�ǂ��Ȃ�ʓ|������
14���ȏゾ�Əo���Ȃ����Ƃ������̂͏d�����y�����܂œ��肷�邱�Ƃ����߂��Ă�����̕��������ƊȒP����
�i13���ł��o���Ȃ����ǂ���������̂͂�����Ƃ����ʓ|�j ���ؑΏۂ̂P�S�������Ȃ���A�V���ɍڂ��閇���ɂ��A���̂悤�ȕ��������܂��B
�V�F�V�F�O�@���@�d�d�d�d�d�d�d�@�y�y�y�y�y�y�y�@�@�i14�ʂ�j
�U�F�U�F�Q�@���@�d�d�d�d�d�d�@�y�y�y�y�y�y�@�{�{�@(12�ʂ�)�^�@�{�{�{�{�{�{�{�{�{�{�{�{�@�s�s�@�i4�܂���3�ʂ�j
�T�F�T�F�S�@���@�d�d�d�d�d�@�y�y�y�y�y�@�{�{�{�{�@(10�ʂ�)�^�@�{�{�{�{�{�{�{�{�{�{�@�s�s�s�s�@�i8�܂���7�ʂ�j
�S�F�S�F�U�@���@�d�d�d�d�@�y�y�y�y�@�{�{�{�{�{�{�@(8�ʂ�)�^�@�{�{�{�{�{�{�{�{�@�s�s�s�s�s�s�@�i12�܂���11�ʂ�j
������̎����낤�Ƃ��A�K���A9�ʂ�ȉ��ɕ���悤�Ȏ菇�͑��݂��܂���B
�������A�{���̃R�C�����ꖇ�ł��L��A�\�ł��B�i�O��͊ȕւ̂��߂X�����g���܂������A�P���ł�ok�j
�{���P���ƃ^�[�Q�b�g�̂S�������킹���T���ƁA�^�[�Q�b�g�T�����ׂ�ƁA
[�{]�d�d�d�d�@�y�y�y�y�y�@�{�{�{�{�{�@(9�ʂ�)�@�^�@[�{]�{�{�{�{�{�{�{�{�{�@�s�s�s�s�s�@(10�܂���9�ʂ�)�@�@
�i�y�Əd���t�ɂ����������邪�A�{���I�ȍ��͂Ȃ��̂ŏȗ��j
�̂悤�ɕ��܂��B�ǂ���ɂȂ낤�Ƃ�9�ʂ�ł��B�X�����ꍇ�̎��̎��
�d�d�d�y�y�y�@�Ɓ@[�{]�{�{�{�{�{�@
�d�y��������������^�オ��A�O�̏d�^�y�̂����ꂩ�A�ނ荇���A���V���ɍڂ��Ă��Ȃ��A�d�y�y�̂ǂꂩ���U���ł��B
�܂�A�P�S���ł̉ۂ́A�ʘg�Ŗ{���̃R�C�����p�ӂ���Ă��邩�ǂ����Ɉ˂�܂��B
�s�F�d���U���A�y���U���A�{���A������̉\����������
�d�F�d���U�����{���ł��邱�Ƃ��m�肵�Ă�����
�y�F�y���U�����{���ł��邱�Ƃ��m�肵�Ă�����
�{�F�{���Ɗm�肵�Ă����� �O>>582
>>585
n=14�̂Ƃ��A
���ځA5������V���ɍڂ��A�ނ肠������A�ڂ��Ȃ�4���̒��ɏd���̈Ⴄ���݂�����B
���ځA�c��4���̂���1������V���ɍڂ��A�ނ肠������A�ڂ��Ȃ�2���̂����̂ǂ��������d���̈Ⴄ���݂��Ƃ킩��B
�O��ځA�ڂ��Ȃ�2���̂�����1����V���ɍڂ��A�ڂ��Ȃ�2���ȊO�̋��݂�1����������̓V���ɍڂ��A�ނ肠������A
�ڂ��Ȃ�2���̂����A�O��ڂ��ڂ��Ȃق��̋��݂��d���̈Ⴄ���݂��Ɠ���ł���B
�O��ځA�ڂ��Ȃ�2���̂�����1����V���ɍڂ��A�ڂ��Ȃ�2���ȊO�̋��݂�1����������̓V���ɍڂ��A�ނ肠��Ȃ�A
�ڂ��Ȃ�2���̂����A�O��ڂ͍ڂ����ق��̋��݂��d���̈Ⴄ���݂��Ɠ���ł���B
���ځA5������V���ɍڂ��A�ނ肠��Ȃ�A�ڂ���10���̒��ɏd���̈Ⴄ���݂�����B
���ځA�Е���5���̂���2������V���ɍڂ��A�ނ肠������A�O����1�����d���̈Ⴄ���݂��Ɠ���ł���B
���ځA�Е���5���̂���2������V���ɍڂ��A�ނ肠��Ȃ�A�ڂ���4���̒��ɏd���̈Ⴄ���݂�����B
�O��ځA4���̂���1������V���ɍڂ��A�ނ肠������A�ڂ��Ȃ�2���̂����̂ǂ��������d���̈Ⴄ���݂����A�ǂ���������ł��Ȃ��B�\�\�@
�O��ځA4���̂���1������V���ɍڂ��A�ނ肠��Ȃ�A�ڂ���2���̂����̂ǂ��������d���̈Ⴄ���݂��Ɠ���ł���B
�@�̂悤�ɎO��ڂ܂łɂ��Ȃ炸����ł���Ƃ͂�����Ȃ��B
��n��14
�in=13�����������ǁj >>588
���ꂾ�Ɠ����Ƃ��Ă̓o�c����
> ���ځA5������V���ɍڂ��A�ނ肠������A�ڂ��Ȃ�4���̒��ɏd���̈Ⴄ���݂�����B
> ���ځA�c��4���̂���1������V���ɍڂ��A�ނ肠������A�ڂ��Ȃ�2���̂����̂ǂ��������d���̈Ⴄ���݂��Ƃ킩��B
�c
> �O��ځA4���̂���1������V���ɍڂ��A�ނ肠������A�ڂ��Ȃ�2���̂����̂ǂ��������d���̈Ⴄ���݂����A�ǂ���������ł��Ȃ��B�\�\�@
> �O��ځA4���̂���1������V���ɍڂ��A�ނ肠��Ȃ�A�ڂ���2���̂����̂ǂ��������d���̈Ⴄ���݂��Ɠ���ł���B
�̕��@�ł�3��œ���ł��Ȃ��A�Ƃ������Ƃ������������ŁA
3��œ���ł��鑼�̕��@������\����ے�ł����A
> ��n��14
�ƌ��_�t�����Ȃ�
����
> �@�̂悤�ɎO��ڂ܂łɂ��Ȃ炸����ł���Ƃ͂�����Ȃ��B
���̖��ł́A�u�O��ڂ܂łɂ��Ȃ炸����ł���Ƃ͂�����Ȃ��v�Ƃ������Ƃ��u�O��ڂœ���ł��Ȃ��v�ƌ����Ă��邩��� �O>>588
>>585
n=13�̂Ƃ��A
���ځA5������V���ɍڂ��A�ނ肠������A�ڂ��Ȃ�3���̒��ɏd���̈Ⴄ���݂�����B
���ځA�c��3���̂���1������V���ɍڂ��A�ނ肠������A�ڂ��Ȃ�1�����d���̈Ⴄ���݂��Ƃ킩��B
���ځA�c��3���̂���1������V���ɍڂ��A�ނ肠��Ȃ�A�ڂ���2���̂����̂ǂ��������d���̈Ⴄ���݂��Ƃ킩��B
�O��ځA�ڂ����Е����ڂ��Ȃ�1���̋��݂ƌ������A�ނ肠������A���ڍڂ��ĎO��ڍڂ��Ȃ�1�����d���̈Ⴄ���݂��Ɠ���ł���B
���ځA5������V���ɍڂ��A�ނ肠��Ȃ�A�ڂ���10���̒��ɏd���̈Ⴄ���݂�����B
���ځA�Е���5���̂�����2������V���ɍڂ��A�ނ肠������A�ڂ��Ȃ�1�������������5���̌v6���̒��Ɉ�����d���̋��݂�����B
�O��ځA6���̂�����2������V���ɍڂ��A�ނ肠������A�ڂ��Ȃ�2���̂�����1�����d���̈Ⴄ���݂��Ƃ킩�邪�ǂ������d���̈Ⴄ���݂��͓���ł��Ȃ��B�\�\�@
���ځA5���̂����̕Е��̂�����2������V���ɍڂ��A�ނ肠��Ȃ�A�ڂ���4���̒��ɏd���̈Ⴄ���݂�����B
�O��ځA4���̂�����1������V���ɍڂ��A�ނ肠������A�ڂ��Ȃ�2���̂����̂ǂ��������d���̈Ⴄ���݂����A�ǂ������d���̈Ⴄ���݂��͓���ł��Ȃ��B�\�\�A
�O��ځA4���̂�����1������V���ɍڂ��A�ނ肠��Ȃ�A�ڂ���2���̂����̂ǂ��������d���̈Ⴄ���݂����A�ǂ������d���̈Ⴄ���݂��͓���ł��Ȃ��B�\�\�B
�@�A�B���A�v�ʂ̌��ʂ�����ɂ���Ă͓���ł��Ȃ����Ƃ�����B >>590
�����炟�A
����ł��Ȃ����Ƃ�����菇������������āA���̈Ӗ����Ȃ�����
�Ӗ�������̂́A
�K������ł���菇����ł��������A
�K������ł���菇���u������݂��Ȃ��v���Ƃ��������A
�̂ǂ��炩
���łɁA
1��ڂ�5�����V���ɏ悹���3��ł͓���ł��Ȃ��Ȃ邱�Ƃ́A��ŏ�����Ă���� �N�Ƃ͌���Ȃ����ǁA��������
�u��̗��l�̕]���ȂǁA�����ł��V���Ȑi�����o�����炻��͖ڊo�܂������ʂł���v�ł��邩�̂悤�ȕ����ŁA
�����ɏo�肳���S�Ă̖��A������قƂ�ǂ��������͂����肵�Ă�悤�Ȃ��̂ɑ��ĉ�l�@�𐂂ꗬ����������Ă̂́A
���܂�ɂ���̖�����肷���Ƃ������A�����܂ŗ������邽�߂̒m���͔�����ĂĂ��g�����Ȃ������Ȃ������Ȃ̂��͂킩���
���x���z������r�炵�ɂȂ���Ă��Ƃ͗������Ăق���
������Ȃ�܂������A�����܂ő����Ă�̂�����Ƃǂ������̃��x���̂��Ƃ������ł��ĂȂ��݂�������
�����Ɠ�����ŝ��˂邩�A���ƂȂ����m�f����̂������Ȃ����ċC�͂��邯�ǁc �݂�ȗD�����ˁB�͂������
�u�C�i�Ƃ������R�e�n���͉����������Ă��Ȃ��o�J�^���ł���v
�ƌ��������̂ɁB �����o�����̖@���Ȃ�ŁA���ƂȂ������N��Mathpower�̐��w�̌����p�ɗp�ӂ��Ă���肩����
��i�@�\�L�������ɂP��������悤�Ȕ����̂��Ƃ��I�f�B�A�X�ƌĂԁB
��������ϐ��������� f �����݂��邱�Ƃ������F
�C�ӂ̐��̐��� n �ɂ��āAkn ���I�f�B�A�X�ɂȂ�悤�� f(n) �ȉ��̐��̐��� k �����݂���B >>595
f(n) = 9n �����������B
��) n �͊�Ƃ��Ă悢�B
n �܂��� 3n �̂����ꂩ�̖�������01�ƂȂ�B
���̐���m�Ƃ��Am�Ɠ��������Ő擪���Ɩ������̂�1�ő��̌���0�ł��鎩�R����l�Ƃ����lm�̓I�f�B�A�X�ł���B
�����k = lm/n ��9n�ȉ��̐����ł���B >>596
����߂�����V���v���c�v���������c
�����ł� �R�e�t���Ă���Ă����NG��������B�ז��Ȃ����Ŗ��Q
�ނ���R�e�̂Ȃ��o��K�C�W������ ���d���̈Ⴄ���݂����o����ő�l��13 �O>>590���>>514>>585
n=9�̂Ƃ�>>544>>549�ǂ����Ă�����ł��Ȃ��B
n=8�̂Ƃ��A
���ځA3������V���ɍڂ��A�ނ肠������A�c��2���̂����̂ǂ������̋��݂��d���̈Ⴄ���݂��Ƃ킩��B
���ځA�c��2���̂����� 1����Е��̓V���ɍڂ��A��������̓V���Ɏc��1���ȊO�̋��݂��ڂ��A�ނ肠������A�c��2���̂����̂���1�����d���̈Ⴄ���݂��Ɠ���ł���B
���ځA3������V���ɍڂ��A�ނ肠��Ȃ�A�ڂ���6���̒��ɏd���̈Ⴄ���݂�����B
���ځA6���̂�����2����Е��̓V���ɍڂ��A��������̓V����6���̂����̕ʂ�2�����ڂ��A�ނ肠������A�ڂ��Ȃ�2���̒��ɏd���̈Ⴄ���݂�����B
���ځA6���̂�����2����Е��̓V���ɍڂ��A��������̓V����6���̂����̕ʂ�2�����ڂ��A�ނ肠��Ȃ�A�ڂ���4���̒��ɏd���̈Ⴄ���݂�����B
�O��ځA�ڂ��Ȃ�2���̂�����1����Е��̓V���ɍڂ��A��������̓V���ɍڂ��Ȃ�2���̂����̂���1���ȊO�̋��݂��ڂ��A�ނ肠������A�ڂ��Ȃ�2���̂����̂���1�����d���̈Ⴄ���݂��Ɠ���ł���B
�O��ځA�ڂ��Ȃ�2���̂�����1����Е��̓V���ɍڂ��A��������̓V���ɍڂ��Ȃ�2���̂����̂���1���ȊO�̋��݂��ڂ��A�ނ肠��Ȃ�A���ڂōڂ��Ȃ�2���̂����̎O��ڂōڂ���1�����d���̈Ⴄ���݂��Ɠ���ł���B
n=7�̂Ƃ��A>>538
n=6�̂Ƃ��A>>537
n=5�̂Ƃ��A>>536 �O>>600�㔼�B
n=4�̂Ƃ��A(�Â�)
���ځA4���̂�����1����Е��̓V���ɍڂ��A4���̂����̕ʂ�1������������̓V���ɍڂ��A�ނ肠������A�ڂ��Ȃ�2���̂����̂ǂ��������d���̈Ⴄ���݂��Ƃ킩��B
���ځA4���̂�����1����Е��̓V���ɍڂ��A4���̂����̕ʂ�1������������̓V���ɍڂ��A�ނ肠��Ȃ�A�ڂ���2���̂����̂ǂ��������d���̈Ⴄ���݂��Ƃ킩��B
���ځA�ڂ��Ȃ�2�����ڂ���2�����ǂ�����2���ɂ���2���̂�����1����Е��̓V���ɍڂ��A��������̓V����2���̂�����1���ȊO�̋��݂��ڂ��A�ނ肠������A2���̂����̍ڂ��Ȃق���1�����d���̈Ⴄ���݂��Ɠ���ł���B
���ځA�ڂ��Ȃ�2�����ڂ���2�����ǂ�����2���ɂ���2���̂�����1����Е��̓V���ɍڂ��A��������̓V����2���̂�����1���ȊO�̋��݂��ڂ��A�ނ肠��Ȃ�A2���̂����̍ڂ���1�����d���̈Ⴄ���݂��Ɠ���ł���B
n=3�̂Ƃ��A
���ځA3���̂�����1����Е��̓V���ɍڂ��A��������̓V���ɕʂ�1�����ڂ��A�ނ肠������A�ڂ��Ȃ�1�����d���̈Ⴄ���݂��Ɠ���ł���B
���ځA3���̂�����1����Е��̓V���ɍڂ��A��������̓V���ɕʂ�1�����ڂ��A�ނ肠��Ȃ�A�ڂ���2���̂����̂ǂ��������d���̈Ⴄ���݂��Ƃ킩��B
���ځA2���̂�����1����Е��̓V���ɍڂ��A��������̓V���ɍڂ��Ȃ�1�����ڂ��A�ނ肠������A2���̂����̈��ڂɍڂ��A���ڂ͍ڂ��Ȃق���1�����d���̈Ⴄ���݂��Ɠ���ł���B
���ځA2���̂�����1����Е��̓V���ɍڂ��A��������̓V���ɍڂ��Ȃ�1�����ڂ��A�ނ肠��Ȃ�A2���̂����̈��ڂɍڂ��A���ڂ��ڂ������݂��d���̈Ⴄ���݂��Ɠ���ł���B
n=2�̂Ƃ��́A2�̏d���̈Ⴄ���݂����邾���łǂ����̋��݂��d���̈Ⴄ���݂��͓���ł��Ȃ��B
�ȏ�ɂ��An��3�Ƃ���Ȃ�An�̍ŏ��l�́An=9 1��Œ����\�ȍő吔��3
2��Œ����\�ȍő吔��8
3��Œ����\�ȍő吔��13
4��Œ����\�ȍő吔��21
0, 3, 8, 13, 21, 34, 47, 64, 84, 105, ... ���Ȃ��Ƃ�(3^n-1)/2�ʼn\�ł�����͌�����������ȁB
���ꂪ�ő�̏ؖ��͒m��Ȃ����ǁB >>600
> n=9�̂Ƃ�>>544>>549�ǂ����Ă�����ł��Ȃ��B
> �ȏ�ɂ��An��3�Ƃ���Ȃ�An�̍ŏ��l�́An=9
���Ȃ�������o���Ȃ���������Ƃ����āAn=9�ł͓��肷�邱�Ƃ��s�\���Ƃ͌����Ȃ�
> ���ځA3������V���ɍڂ��A�ނ肠������A�c��2���̂����̂ǂ������̋��݂��d���̈Ⴄ���݂��Ƃ킩��B
1��ڂ�3�����悹���9���ȏ����肷�邱�Ƃ͏o���Ȃ��Ȃ�
�����1�����A2���������� >>602
��H���łR����U�����肷��͖̂����ł́H
�Q���ׂČX�������ɁA�ǂ��炪�U���Ȃ̂������ʂł��Ȃ�����c
>>603 �̒ʂ� 1, 4, 13, 40, �c (3^n-1)/2 ������������
�ؖ��̓r���܂ł͂����炭����Ȋ���
����N�̒������Ɉ��ł��X������A
�ŏI�I�ɓ�����u�ǂ̂����肪�U�����v�Ƃ������ƍ��킹��
�u�U�����{���Ɣ�ׂďd�����y�����v�܂ł킩�邩��A
�U�����{�����d�����y������m��K�v�������U�����������邽����̏ꍇ�A���Ȃ킿
�un��S�Ă̔�r�ŌX���Ȃ��v
�ꍇ�ƍ��킹��An��̔�r�ŏ��Ȃ��Ƃ� (N-1)*2+1 ��̏ꍇ����ʂł���K�v������B
�]���� (N-1)*2+1 �� 3^n ��� N��(3^n+1)/2.
���Ƃ́A�ŏ��ɉ�����r�����Ƃ��Ă��A�X�����ꍇ�ɋ�ʂ��ׂ��ꍇ�̐��������ɂȂ邽�߁A
���̗]�肪�����Ă��܂����Ƃ��瓙�����������邱�Ƃ͂Ȃ��A�݂����� >>604
> 1��ڂ�3�����悹���9���ȏ����肷�邱�Ƃ͏o���Ȃ��Ȃ�
> �����1�����A2����������
1��ڂ�3�����悹��Ɠ���ł��Ȃ��Ȃ�̂�12���ȏ�ŁA
11���܂ł͓��肷�邱�Ƃ͂ł�����
>>600��8���������ĂȂ�9�����o���Ȃ��̂��킩��Ȃ� n,m�𐳂̐����Ƃ���Ƃ��A
��=2^(1/n)+3^(1/m)
�Ƃ����B�����W���̑�����f(x)�ŁAf(��)=0�������̂����݂��邱�Ƃ������B
�\�ł���A���Z���x���܂ł̐��w�ł��肢�������܂��B ��n��̒����Ŕ�������ő�l
Table[2(n^2-n)+1,{n,3,20}]
{13, 25, 41, 61, 85, 113, 145, 181, 221, 265, 313, 365, 421, 481, 545, 613, 685, 761}
��n��̒����Ŕ������Ȃ��ŏ��l
Table[2(n^2-n+1),{n,3,20}]
{14, 26, 42, 62, 86, 114, 146, 182, 222, 266, 314, 366, 422, 482, 546, 614, 686, 762} �O>>601���>>514>>585
>>600�A���J�[�����B
n=9�̂Ƃ��A
>>554���ځA4�����\�\
>>549���ځA3�����\�\
���ځA2�����\�\
�ȏ�ɂ��A�ǂ����Ă�����ł��Ȃ��B
n=8�̂Ƃ��A�i�ȉ������j n=9�̎��\�ł�����@�オ���Ă܂����ȁB >>605
4���40���������͕s�\ >>600�̖�����1�����₷������n=9��������̂ɉ���>>549�Ŏv�l��~����̂��H
4�����̉�����ɂ��� �O>>609
>>610
��ӁA>>514�u����i���݁j�͑��̂��̂ƌ����������Ȃ��v�ɑf���ɂ��������ĉ��ׂ����B��ӂɔ����铚�Ă�F�߂�킯�ɂ͂����Ȃ��B
�}�W�b�N�͎g���Ă܂���A�tⳂ͎g���܂��A�u���ꏊ�����߂܂����A�V���ɍڂ���Ƃ��͕tⳂ��O���܂����A�Ƃ������Y����F�߂�킯�ɂ͂����Ȃ��B >>607
f(x) �̍������̌W���� (x^n - 2)^m + (x^m - 3)^n - x^(mn) �Ɏ��Ă邯�ǁA�Ⴄ�����....������ >>613
�����������Ȃ��Ȃ�ǂ�����Ă����ʕs�\���� �O>>613
>>616�����������Ȃ����݂��������邽�߂̓V������Ȃ��̂��B������߂Ȃ��łق����B ���������Č����������Ȃ�������ڈȍ~�̑���łP��ڂɂǂ�Ƃǂ���ڂ������킩��Ȃ��Ȃ���ĈӖ��ɂƂ�Ƃ��H�H�H
����ȃ��[���Ȃ�n=3�ł��łɕs�\�����wwwww >>611
40������4��œ���͉\�B��_�I�ɂ́A(3^4-1)/2=40�@������\�ƍl�����邵�A���ۂɁA���Ɏ����悤�ȕ��@�ʼn\�B
�Ȍ�A���̋L�����g�����Ƃɂ���B
�s�F�d����������Ȃ����A�y����������Ȃ����A��������������Ȃ��R�C��
�d�F�d����������Ȃ����A��������������Ȃ��R�C��
�y�F�y����������Ȃ����A��������������Ȃ��R�C��
���F�������R�C��
���ڂɁA13�����ڂ���悢�B����ƁA�u�d13�y13��14�v�܂��́A�u�s14��26�v�ɕ������B
�u�d13�y13��14�v��[�d9�y5]��[��10�d4]�ɂ��Ĕ�r����悢�B����ƁA�u�d9��31�v���u�y5�d4��31�v���u�y8��32�v�ɕ������B
�i����́A�V���̌��ʂ��A�u�����d���v�A�u�E���d���v�A�u�ނ荇���v�ɑΉ��B�j
�u�s14��26�v�́A[��1�s4]��[�s5]�ɂ��Ĕ�r����悢�B����ƁA�u�d4�y5��31�v���u�d5�y4��31�v���u�s5��35�v�ɕ������B
�u�d4�y5��31�v�́A[�d2�y2]��[�d1�y1��2]�ɂ��Ĕ�r����悢�B����ƁA�u�d2�y1��37�v���u�y2�d1��37�v���u�d1�y2��37�v�ɕ������B�Ȍ㗪�B
�u�s5��35�v�́A[��3]��[�s3]�ɂ��Ĕ�r����悢�B����ƁA�u�y3��37�v���u�d3��37�v���u�s2��38�v�ɕ������B�Ȍ㗪
���Ȃ݂ɁA�������R�C�����ʘg�ňꖇ�L���41���A�܂�u�s41��1�v����S��ʼn\�B
[��1�s13]��[�s14]�Ŕ�r����A�u�d13�y14��15�v���u�y13�d14��15�v���u�s14��28�v�ɕ�����܂��B�Ȍ㗪�B >>619
���ڂɁA13�����ڂ��Ă��ǂ���̃O���[�v�ɏd�����y������
���݂�����̂��̔���͂ł��Ȃ�
�w�j�Z���ǂ��炩�ɂ���x�Ƃ������
�d�����y�����̊m�蔻��ɂ́A�������K�v�ɂȂ� �����ƍ��{�I��
�u�s14��26�v�ɕ����ꂽ�Ƃ���
�c��3��ŕs14�͓���ł��Ȃ��Ǝ����ŏ����Ă��� >>620,621
> �c��3��ŕs14�͓���ł��Ȃ��Ǝ����ŏ����Ă���
>>578
> ���ڂɁA13�����ڂ��Ă��ǂ���̃O���[�v�ɏd�����y������
> ���݂�����̂��̔���͂ł��Ȃ�
2��ځF�u�d+�y26���v�̎�
�u�d�{�y9���v�A�u�d�{�y9���v�����E�̏d�̐����m�A�y�̐����m�������Ŕ�r��
�X����1��ڂƌX��������9��(1��ځA2��ڂƂ��ɏd�����A�܂��͂Ƃ��Ɍy����)�A�ނ荇���Ύc���9���ɍi���A
�u�d�{�y9���v�A�u�d�{�y9���v�A�u�d�{�y9���v�ɕ���
3��ځF�u�d+�y9���v�̎�
�u�d�{�y3���v�A�u�d�{�y3���v�����E�̏d�̐����m�A�y�̐����m�������Ŕ�r��
�u�d�{�y3���v�A�u�d�{�y3���v�A�u�d�{�y3���v�ɕ���
4��ځF���l�ŏI�� >>619
3��ڂ̒�����
�u�d2�y1��37�v���u�y2�d1��37�v���u�d1�y2��37�v�̏����Ƃ���
��������c��1����ŁA��̓I�ǂ�����ăj�Z�肷��̂���(�L��֥`)�H >>620�@>>621
�X�����ꍇ�ɂ́A�u�d13�y13��14�v�ɂȂ�B26�ʂ�̂����ꂩ�ł��邩����肷��悢�����B3^3=27�ȉ��Ȃ̂ŁA�\�B
�ނ荇�����ꍇ�ɂ́A�u�s14��26�v�ƂȂ�B
14�̓�{��28�ŁA3^3=27���āA�s�\�ł͂Ȃ����Ǝv���邩������Ȃ��B
>>�c��3��ŕs14�͓���ł��Ȃ��Ǝ����ŏ����Ă���
�Ƃ̏������݂����邪�A���͂���܂ŁA��т��āu�s14�v�����Ȃ�A�s�\�����A
�ʘg�Ő������R�C�����L��A�\���Ə����Ă���B
�u�ʘg�v�Ƃ����̂́A����A�u����v�Ɍ����������ƌ�����B
���ڈȍ~�́A����p�Ő������R�C�����������A���ꂪ���p�ł��邩��B
�ړI�́A14���̃R�C���̒�����A�s���Ȉꖇ����肵�A���ꂪ�y���̂��d���̂����ɂ߂鎖�ł͂Ȃ��B
�����P�ɕs���Ȉꖇ����肷��悢�B�V���ɍڂ��Ē������A�U�������ɂ߂�ꍇ�A�K���y�d�̏���
�t������Ă��܂��B�]���āA14���̒�����ꖇ��3��̓V���g�p�ł͕s�\�ł͂Ȃ����Ǝv���邩��
����Ȃ��B���A����͐������Ȃ��B
14������1�������̏����A13���̃R�C���̒�����A�d���U������肷�邩�A�y���U������肷�邩
���ׂĂ��{���Ɗm�F����悢�B��������A26�ʂ�ɁA���ׂĖ{���Ƃ�����ʂ�������A
27�ʂ�ɗ��������A��_�I���27�ɔ[�߂邱�Ƃ��ł���B
�ŏ��Ɏ�菜���ꂽ�R�C���́A��x���V���ɍڂ��瓾�邱�ƂȂ��A�u���܂��͋U���v��������������D�D�D��������Ȃ��B >>623
> �u�d2�y1��37�v���u�y2�d1��37�v���u�d1�y2��37�v�̏����Ƃ���
> ��������c��1����ŁA��̓I�ǂ�����ăj�Z�肷��̂���(�L��֥`)�H
�����܂ł��Ă���H
�u�d1�A�d1�v�܂��́u�y1�A�y1�v�Ŕ�r
�X���A�u�d1�A�d1�v�Ȃ�d�����A�u�y1�A�y1�v�y�����A�ނ荇���Ύc�� >>623
>>�u�d2�y1��37�v���u�y2�d1��37�v���u�d1�y2��37�v�̏����Ƃ���
������̏ꍇ���A�V���̕Е���[��2]�A������[�d1�y1]�@�ƍڂ���悢�B �������A>>625����̕��@�ł�ok >>622
�w2��ځF�u�d+�y36���v�̎�
�u�d9�{�y9���v�A�u�d9�{�y9���v�����E�̏d�̐����m�A
�y�̐����m�������Ŕ�r�x�ɕύX�����Ƃ���
�����s�\�ɂȂ�̂͂Ȃ�����(�L��֥`)�H ��ʂɃR�C���̖���m��3�ȏ�(3^n-1)/2�ȉ��̏ꍇ�A�[�@���g���Ĉȉ��̂悤��n�sm��̍s���݂��鎖��������B
�S�Ă̗v�f��LRS�B
�ǂ�m��������Ȃ�n�̍s���܂܂��L��R���������B
x,y���قȂ镔����Ƃ�z��y��L��R�����ւ�����Ƃ���Ƃ��Ax�Ay�Az�͑S�đ��قȂ�B
�����m���̃R�C���̏ꍇ�An��ʼn\�Ǝ�����B
������m=(3^n-1)/2�̏ꍇ�ɂ͑S��S����Ȃ����܂ނ̂ŁA�U�R�C���̏d���A�y���͔���ł��Ȃ��P�[�X���܂ށB
���ꂪ�ŗǂł��鎖��������Ɗ撣��Ώo�����B
�U�R�C���̏d���y������肵�����ꍇ�ɂ͏�̕]��-1���ő喇���ɂȂ�B >>628
> �w2��ځF�u�d+�y36���v�̎�
> �u�d9�{�y9���v�A�u�d9�{�y9���v�����E�̏d�̐����m�A
> �y�̐����m�������Ŕ�r�x�ɕύX�����Ƃ���
> �����s�\�ɂȂ�̂͂Ȃ�����(�L��֥`)�H
�O�̂��߁A>>622��
> �u�d�{�y9���v
�͏d�ƌy�̍��v������9���ł����āA
> �u�d9�A�y9�v
�ł͂Ȃ������
�u�d+�y36���v�̎��A �u�d9�{�y9���v�A�u�d9�{�y9���v�����E�̏d�̐����m�A�y�̐����m�������A���܂�0�Ŕ�r�Ŕ�r����ƁA
�ނ荇���ꍇ�̎��ې���0�ʂ�A
�E�ɌX���ꍇ�̎��ې��́A�E�̏d9�ʂ�A���̌n9�ʂ�A���v18�ʂ�ŁA�c����̔�r�œ��������3�O2=9�ł͓���ł��Ȃ�
���ɌX���ꍇ�����l >>628
�V�����g���ƁA��ʂɁA���ɌX���A�E�ɌX���A�ނ荇���̂����ꂩ�̌��ʂ܂��B
���݁A�\���� z �ʂ�L�����Ƃ��āA����ڂ��������āA�V�����g�������ʁA
���ɌX�����ꍇ�F�\�� z1 �ʂ�
�E�ɌX�����ꍇ�F�\�� z2 �ʂ�
�ނ荇�����ꍇ�F�\�� z3 �ʂ�
�ƂȂ�Ƃ��܂��B���R�A z = z1 + z2 + z3 �ł��B
�\���� z �ʂ肠��Ƃ��A�V�����@m = {log[3](z)} ��g�p���āA�U�������ł��܂��B�@�G{x}�͐�グ���Ƃ���
�u����ڂ����v�ɂ���āAz�@���Az1�Az2�Az3�A�̂����ꂩ�ɕ��܂����A���̎��A
m-1 �� {log[3](z1)}
m-1 �� {log[3](z2)}
m-1 �� {log[3](z3)}
�̂��ׂĖ������悤�ȍڂ����łȂ��ƁA���̍ڂ����́u���s�v�ł��B���ɓ�����O�̂��Ƃł��B���A
>>�����s�\�ɂȂ�̂͂Ȃ�����(�L��֥`)�H
�ɑ��ẮA���̂悤�ȉ����ł��܂���B �G�N�X�`�F���W�������݃O���[�v��
�c�蒲����2��c���Ă���Ȃ�5���܂Ŕ���\��
�Ƃ������́A>>619[�d9�y5]��[��10�d4]��
[�d9�y5]��[��9�d5]�̃G�N�X�`�F���W����ɒu�������邱�Ƃ��ł���
�䂦�ɁA28�����G�N�X�`�F���W�Ŕ���\�ƂȂ�
�u�d14�y14��14�v�̍��v42���̒�����j�Z���m��ł��� >>632
> �u�d14�y14��14�v�̍��v42���̒�����j�Z���m��ł���
�o���Ȃ�
�\���̂��鎖�ې��͏d14+�y14=28�ʂ�
3��̔�r�œ�������ʂ�3�O3=27�ʂ�ł͓���ł��Ȃ� �ʔ����Ȃ�����A���A�����~�߂� �P���ɏ��ʂ�����14�����s�\�������̂͂���Ɠ���B
�Ⴆ�ΐ�z�����m���Ƃ����R�C�����ꖇ�����14���ł��\�B
���̂��ꂪ�\�ɂȂ邩�Ƃ�����13���̌y�d��26�ʂ�ɉ����Ĉ�x���X���Ȃ��Ƃ����ꍇ�Ɉ�x���ڂ��ĂȂ��R�C�����j�Z���m�Ƃ����y�d���m��o���Ȃ���ʂ��lj��ł���̂�
14���ł��U�R�C�������ł���\���͎c���Ă���A���ې�z�����m�R�C�����ꖇ������̂悤�ȑ��肪�\�ł��鎖��������B
�܂��z�����m�R�C�����Ȃ��ꍇ�ɂ�14���ł��P���ɏ��ʂ����ł͕s�\�ƌ����鎖�͏o�����A�����͈�H�v�K�v�B >>635
14���̏ꍇ�ɂ��ā@>>587�@�ł́A�{���̃R�C�����ʘg�ŗp�ӂ���Ă���ꍇ�ƁA����Ă��Ȃ��ꍇ�ɕ����A
�O�҂͉\�A��҂͕s�\�ł��邱�Ƃ��A��̓I�Ȏ菇��Y���āA�����Ă���܂��B�������������B >>636
�Ȃ�قǁB�����͂����N���A���Ă��ł��ˁB
���Ȃ݂Ɏ��̌�������H�v��
�P��ڍڂ��Ȃ��R�C���̖����͍��X5���B
���̂Ȃ��6���ȏ�c���Ēނ荇���ƁA�c��\����12�ʂ�B
��x���ڂ��Ȃ��R�C���͍��X�ꖇ�ł��ꂪ�d���U�R�C���ƌy���U�R�C���̏ꍇ���܂Ƃ߂Ă�11�ʂ�c���Ă��܂��B
�P��ڂɏ悹��R�C���̖����͍��X8���B
���̂Ȃ��10���ȏ�悹�ČX���Ɖ\����10�ʂ�c��B
�܁A���ʂɂ��Ă̋c�_�����傢���������������ł����B
���l�ɂ���n��̏ꍇ�A(3^n+1)/2���͕s�\�������܂��B �O>>617���>>514
>>618
n=3�̂Ƃ��A
>>601�ɂ��A
����ł���B >>638
�C�i�̉��߂Ȃ�>>601���A�E�g�ł���H
�����������Ȃ�����A�P��ڒނ荇��Ȃ�������A�悹���ǂ��������U�R�C�������ǁA�V�����牺�낵���u�Ԃ����ǂ���悹������킩��Ȃ��Ȃ�Ȃ�A�P��ڂ̏��͂�2��ڂɎg���Ȃ��B
�����܂ōڂ����̗������z�����m�ł�����R���N�����������U�R�C�������ł��Ȃ�����m���ɋU�R�C������肷����@�Ȃ��ł���H
����ČN�̉��߂Ȃ�n=3���ŏ��l�ł��������B ��c��Ȃ��Ȃ�3����ď����ɂ܂�ňӖ����Ȃ��Ȃ���
���������������Ɖ����ڂ��悤�ƒނ荇��Ȃ������瓖�R����o���Ȃ�
�S�̂������1���������c���đ��������悹�Ēނ荇�����ꍇ�����c����1�����U���Ƃ킩�邪
���R�ɗ��邱�ƂɂȂ�̂ōŏ���3���ł���ꍇ�ł���m���ɉ���œ���o����Ƃ����͑��݂��Ȃ�
�ŏ��������ł��낤�ƍŏ��l�Ȃ� �O>>638���>>514
>>639
����>>600-601�̓Z�b�g�ł��B
�v�ʂ������ʂ͂������ɋ��݂�V�����牺�낵�Ă��L���Ɏc��܂��B�����܂ł��O��ڂ܂Ōv�ʂ������ʂǂ����Ă�����ł��Ȃ�n�̍ŏ��l�͂������Ƃ������ƁB
n=3�̂Ƃ��͓���ł��邩����ɂ͂Ȃ�Ȃ��B
�V���ɍڂ���O�̋��݂������A���AB���AE���ƈ�����Č�������̂́A�{���v�ʂ��Ȃ���Ό����ڂ͓���ł���͂��̋��݂�I��œV���ɍڂ���Ƃ�����ӂɂ�����Ȃ��s�ׁB����ɑ��A���[���ᔽ���Ǝw�E�����B �O>>741
>>600�̒���(�Čf��)�B
�~>>544����>>554 ���łɏオ���Ă����ɂ��ẮA����͌������̂��Ȃ��R�C�����������Ă邩��_���Ƃ����A�����̉ł͋L���Ɏc�邩��OK�Ƃ����B
�Ȃɂ���wwww �O>>642
>>643
���݂������ƓV���ɍڂ��A�ނ肠�������ނ肠��Ȃ����̌��ʂŌ������Ă��������B
���݂�A��B���Ȃ���ł��B������1�����d���̈Ⴄ���݂������ł��B �����������Ȃ��̂ɋL���Ǝ������ǂ�����đΉ��t���ł���̂��낤 �A�z����ˁH
9���R�C������������K�X�����A�Ƃ�B�Ƃ����O�t���Ă邾�������H
�z���b�g�ɂ킩��Ȃ��́H �V���ɏ悹���r�[�ɋ�ʂ����悤�ɂȂ�̂�
�a�V���� /�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/
�͂����ă~�X�����邩 �wn���̋��݂�����(n��2).
���̋��݂̒���1�������d���̈Ⴄ���̂��������Ă��邪,
����͑��̂��̂ƌ����������Ȃ�.
�V����4��g���Ă�, �d���̈Ⴄ���݂����o���Ȃ��Ƃ���.
���̂Ƃ�n�̍ŏ��l�����߂�x
���d���̈Ⴄ���݂����o����ő�l��40
�V����1���Âȏ�ڂ��Ēނ荇�����̋��݂�
�����ȋ��݂ł��邱�Ƃ��m�肷��
�ŏ���13���Âڂ��Ēނ荇������26���͐������m��
�c��14���̒��Ƀj�Z���݂�����
�X������26���̒��Ƀj�Z���݂�����
�j�Z���܂�14���̓��A9���Ɛ����ȋ���9�����ׂ�
�ނ荇���Ύc��5���̓���3������m�肵�Ă���
�����ȋ��݂Ɣ�ׂ�
�ނ荇���Ύc��2���̓���1������m�肵�Ă���
�����ȋ��݂Ɣ�ׂ�j�Z���m��
3�����ނ荇��Ȃ���w�d�����y�������m�肵�Ă���3���x
�ƂȂ�̂Ŏ��̈��Ŋm�肷��
�j�Z���܂�9���Ɛ����ȋ���9�����ނ荇��Ȃ���A
�w�d�����y�������m�肵�Ă���9���x�ƂȂ�̂�
���̓��Ŋm�肷��
13���Âv26�����X���A�ǂ��炩��
�d�����y�����̋��݂�����
���̏ꍇ�A�݂���13������4���Â��G�N�X�`�F���W����
�����ɏ��m��ς݂̐����ȋ��݂�Б���9��������
13�����v��
�ނ荇���ΐ����ȋ���9���̑���Ɏ�菜����
9���̋��݂��w�d�����y�������m�肵�Ă���9���x�ƂȂ�̂�
���̓��Ŋm�肷��
�X�����t�ɂȂ����Ƃ��̓G�N�X�`�F���W�������݂��j�Z
����4+4���̋��݂ł����1���ẪG�N�X�`�F���W���s��
�����
�w�d�����y�������m�肵�Ă���3���x�Ɓw�d�y�ǂ��炩������2���x
�ƂȂ�̂ŁA���̈��Ŋm�肷��
�X���ω����Ȃ���G�N�X�`�F���W���Ȃ�����9���̋��݂�
�w�d�����y�������m�肵�Ă���9���x�ƂȂ�
�����̎��A�j�Z���݂��d�����y�������������肳���
�i�������A�w�d�y�ǂ��炩������2���x��50���̊m���Ńj�Z�Ƃ���
���̂ݔ���j
����41�����Ƃ����1��̒������K�v�ɂȂ�
�ȏ�ɂ��A
�d���̈Ⴄ���݂����o���Ȃ�n�̍ŏ��l��41. /�Q/�Q/�Q/�Q/�Q/�Q/�Q
/�Q�l�l__/�Q/�l�l_/__
/_(�Q)_)_/�Q(�Q)_)/__
/_( _�Q)_/�Q( _�Q)/__
/_(^)�@)_/�Q(`)�@)/__
/_(�ҁQ)_/__(_��_)/__
��ރ҄���ށ�ރ҄����_/__/_�����c�c�Q/�Q/�����c�c/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�V���ɍڂ����u�ԂɌ������������H�@�Ȃɂ�������B�O>>644�ǂ������̓V���ɍڂ������݂��A�d���̈Ⴄ���݂������Ƃ��́A�V���ɍڂ����u�ԂɌ������������B�肥�������炷���B�����c�c [�d9�y5]��[��10�d4]�Ȃ�Đ����ꖇ�ł��炳�Ȃ��Ă�
[�d9�y4]��[��9�d4]�̋ϓ������̃G�N�X�`�F���W�Ŕ���\�I >>650
����܂肵�������炠���Ă��炢�������Ƃ����Ƃ��ƁA
�E�����u�S�ẴR�C���ɖ��O�����ċ�ʂ��邱�Ƃ��ł��Ȃ��v�Ƃ�������ʼn����Ă���Ȃ�A
����͑��̐l�������Ă�����̏����ƑS���Ⴄ���̂�����A�R��ׂ��������������
�w�i�I�ȁj�o��҂̗���Ƃ��āA�V�������Ƃ��Ē�N����x���ƁB
������A�����ɂƂ��Ė������ł�������Ƃ��̂��Ƃ�������ŁA�ȁB
���ꂪ�ł��Ȃ��悤�ł���A�������J��Ԃ��Ă�s�ׂ�
�u��蕶�ƊW�Ȃ��������l�������Ƃ����X�Ɛ��ꗬ���Ă�v�����̒P�Ȃ�r�炵�ł����Ȃ�����A���₩�ɂ�߂邱�ƁB
�u���炪����ɃR�C������ʂ��Ă��B�������̕�����蕶�𐳂������߂��Ă���炻��ɏ]����v
���Ă͖̂���������ȁA��Ɍ����Ă����ƁB�ǂ�������ʂ��������Ǝv�����̂���������Ɛ���������A
�H���Ⴂ�����L���Ă��荇�킹���悤�Ƃ������ɁA��l�Ŏ����ݒ�̖��̎v�l�ߒ��𐂂ꗬ���Ă�̂͂��̕��Ȃ���ȁB
�E�����V���ɖ��Ƃ��ē��e���鎞�́A���������ӎ��ɂǂ�ȉ�������Ă����̂����悭�l���邱�ƁB
���x�������������o�������݂����ɂȂ�Ȃ��悤�ɁA���̖��ݒ肳������ΒN�ł���ʂ�ɉ��߂ł���悤�ɂ��邱�ƁB
���ɍ���̏ꍇ�A�R�C���̋�ʂɊւ��邠�̔F�������̐l�̂���ƈႤ���Ƃ����炩�ɂȂ��Ă����A���̓_�ō��������܂�Ȃ��悤�ɁB
�E�����N�������̖��ݒ�ɋ����������ď�������ł������̂܂܂�����x���Ƃ�𑱂���悵�B
�����N�����������������Ȃ���A���̐ݒ�̖��͂���܂ŁB���������p�ӂ��Ă����������\�����肷����x�ŏI���B
�E���łɌ����ƁA�o��҂̗�����Ă̂͂���������{�I�ɖ�����������l�����肷�鑼�̐l���A�q���g���o�����蔻�肵���肵�Č���邱�Ƃ���Ƃ�����̂ł����āA
�N�������������ĂȂ��A�܂��Ă⎩�ȉ��������ł��Ă��Ȃ������ݒ�̖����A���̉������ĂȂ��o��҂��v�l�ߒ������x�����x�����ꗬ���A�Ȃ�Ă̂͂�߂邱�ƁB
�E�������݂Ȃ���l����Ƃ��������Ƃ͂�߂āA�����̃��X�������Ȃ肷���Ȃ��悤�ɁA������x�����Ȃ�ɐ������Ă��珑�����ނ��ƁB
�킩��Ȃ����Ȃ� >>641
����K����4���Â悹�č��ɏ悹�����E�ɏ悹�����悹�ĂȂ����݂��Č����Ă�����������
�ʂɏ悹��O�ɖ��O���Ȃ���o���Ȃ��킯����Ȃ��A�ǂ��ɕ��ނ��Ă邾��������
�悹����̋��݂Ȃ��ʂ��Ă�������ł���H
������킩��Ȃ��H �O>>650
>>652�^����ꂽ���������̂��ʔ�����ŁA���肷��C�͂Ȃ��ł��B
n��2��n��3�ɂ��ׂ��Ƃ����w�E�͂����Ƃ��ȉ��肾�Ǝv���܂����B
��ӂ�f���ɎƂ߁An=9�̂Ƃ�����ł��Ȃ����Ƃ����łȂ��An=3�`8�̂Ƃ�����ł��邱�Ƃ����ׂĎ����ׂ��ŁA�����������Ɗȕւɐ����ł��邩������Ȃ����ǁA�L���̏ꍇ�����Ő����m��Ă��Ŋe�X�������ق����������悭�킩��Ǝv���܂����B
>>653�ڂ������Ƃ̋��݂���ʂ��Ă��������ǂ����A��҂ł��鉴�ɂ͂킩��Ȃ��B�o��҂ɐu���Ăق����B
�����V���ɍڂ������Ƃ̋��݂͂���1���̂����Ăقڂ��ׂĂ������d���Ȃ�ŁA���݂����E�ǂ����̎M�ɍڂ������ō�������̂͗��_�I�ɂ͂킩��܂������A�Y�����Ɗ����܂����B
�{������1�̏d���̈Ⴄ���݂��݂�������A���Ƃ̋��݂͌������Ȃ��Ă����͂��B�v�ʂ��Ĉ�ڂŌ���������@�������Ǝv���܂��B > >>652�^����ꂽ���������̂��ʔ�����ŁA���肷��C�͂Ȃ��ł��B
���̔�����
> >>653�ڂ������Ƃ̋��݂���ʂ��Ă��������ǂ����A��҂ł��鉴�ɂ͂킩��Ȃ��B�o��҂ɐu���Ăق����B
> �����V���ɍڂ������Ƃ̋��݂͂���1���̂����Ăقڂ��ׂĂ������d���Ȃ�ŁA���݂����E�ǂ����̎M�ɍڂ������ō�������̂͗��_�I�ɂ͂킩��܂������A�Y�����Ɗ����܂����B
> �{������1�̏d���̈Ⴄ���݂��݂�������A���Ƃ̋��݂͌������Ȃ��Ă����͂��B�v�ʂ��Ĉ�ڂŌ���������@�������Ǝv���܂��B
�����ƍ��킹��A����
�u���͗^����ꂽ����"�����̉��l�ς���߂Ŕ��f��������"�������̂��ʔ������A���̑����̐l�̉��߂ƍ��킹���莩���̉��߂𑼐l���킩��悤���������肷��w�͂����܂���v
���Č����Ă邱�ƂɂȂ邯�ǁA�܂�
�u���͖�蕶�Ƃ͊W�Ȃ��������l�������Ƃ����X�Ɛ��ꗬ���Ă邾���̍r�炵�ł��v
�ƔF�߂Ă���Ă��Ƃł����ˁH�����Ƃ��������Ăǂ����s���Ă��傤������ �V������́A��p�X���𗧂ĂāA�����ōD���Ȃ�������B
���܂ʼn��������܂̃p�Y��������ĂH���(߄D߁�߄t�)��߯ >>624
14������1������菜���A13���̃R�C���̒�����A
�d���U������肷�邩�A�y���U������肷�邩
���ׂĂ��{���Ɗm�F����悢
��������A26�ʂ�ɁA���ׂĖ{���Ƃ�����ʂ�������A
27�ʂ�ɗ��������A��_�I���27�ɔ[�߂邱�Ƃ��ł���
�ŏ��Ɏ�菜���ꂽ�R�C���́A��x���V���ɍڂ��瓾�邱�ƂȂ��A
�u���܂��͋U���v��������������D�D�D��������Ȃ�
��3��ڂ̒����Ŏc��2������Ƃ���
����s�\�ɂȂ�m����50%���� >>657
>>����s�\�ɂȂ�m����50%����
����́A
40���̐^�䔻���100%�����ł��A���A�قƂ�ǂ̏ꍇ�A�U���Ɣ��f���������A�d���U�����y���U�������A
����ł��邪�A�u�c��̌y�d�s���̃R�C���̒�����ꖇ�̋U�R�C���̌��ɂ߂�v�Ƃ������[�g��ʉ�
����ꍇ�Ɍ���A�i�^�䔻��͂�����Ƃł��邪�A�j�U���Ɣ��f���������A�d���U�����y���U�����̔��f�͂ł��Ȃ��B
�Ƃ�����|�̃R�����g�ł�낵���ł��ˁB
�@>>657�̏������݂ł́A���e���n�m���Ă���҂Ȃ�A�u�U���̌y�d����v�ɑ��Ắu����s�\�v
�Ƃ����Ӗ����낤�ƁA�D�ӓI�ɓǂݎ�邱�Ƃ��ł��܂����A��ʓI�ȓǎ҂Ȃ�A�u�^�䔻��v�ɑ��Ă�
�R�����g�Ɠǂ݂��˂Ȃ��Ǝv���̂ŁA�ꌾ�A�������Ă��炢�܂��� �C�����܂��B
�O�F����ꍇ�Ɍ���A�i�^�䔻��͂�����Ƃł��邪�A�j�U���Ɣ��f���������A�d���U�����y���U�����̔��f�͂ł��Ȃ��B
��F����ꍇ�Ɍ���A�i�^�䔻��͂�����Ƃł��邪�A�j�U���Ɣ��f���������A�d���U�����y���U�����̔��f�͂ł��Ȃ������m����50%�ŋN����B >>658
�S���Ⴂ�܂�(�L��֥`)
�u�s14��26�v����>>657�̕��@�Œ��������
40���̐^�䔻���100%�����ł��Ȃ��ꍇ������A
�c��2���̔����1��ōs��Ȃ���Ȃ�Ȃ��Ƃ���
����s�\�ɂȂ�m����50%����̂ł� �Ƃ������Ƃ́A
�u�̌y�d�s���̃R�C������A���̓V���g�p�Ōy�d�s���̋U�R�C�������ɂ߂鎖�͂ł��Ȃ��B�v
�Ƃ����咣�ł��ˁB�����A�����Ȃ�A�̃R�C���ƓV����n���ꂽ�Ȃ�A������������܂���B
�������A�����ł́A40���̃R�C���̒�����A�U���̌�₪�ɍi��ꂽ�Ƃ��������̒��ɂ���܂��B
�{���Ɗm�肵�Ă���R�C����38���L��܂��B
�{���Ɗm�肵�Ă���R�C���ꖇ��V���̕Е��ɍڂ��A�y�d�s���̃R�C���̓��̈ꖇ�������Е��ɍڂ��܂��B
�X���A�V���ɍڂ����y�d�s���������R�C�����U���ł��B�X�����ŁA�d���U�����A�y���U���������f�ł��܂��B
�ނ荇���A�V���ɍڂ����Ȃ����R�C�����U���ł��B�������A���ꂪ�A�d���U�����A�y���U�����͔��f�ł��܂���B
���̕��@�ł��A�ł��Ȃ��ƌ�����̂ł����I�I�I�@
�^�䔻��͂P�O�O���ʼn\�B�������A�قƂ�ǂ̏ꍇ�́A�d���̂��y���̂������f�\�B
�����A�u�y�d�s���v�Ƃ������[�g�����ǂ����ꍇ�́A�^�䔻��͂�����Ƃł��Ă��A50%�̊m���ŁA
�y�d����͂ł��Ȃ��B�Ƃ������_�ɁA���ӂ���܂��ˁB >>661
�w14������1������菜���A13���̃R�C���̒�����A
�d���U������肷�邩�A�y���U������肷�邩
���ׂĂ��{���Ɗm�F����悢�x
���̒����ɐ�����26���̋��݂��g�p���Ȃ���
����s�\�ɂȂ邱�Ƃ����� �u40���̒�����A�y�d�s���̋U�R�C���P�����S��̓V���g�p�œ��肷����v
��
�u14���̒�����A�y�d�s���̋U�R�C���P�����R��̓V���g�p�œ��肷����v
�͈قȂ�܂��B�O�҂͉\�ŁA��҂͕s�\�ł��B
�u�O�҂͉\���v�Ƃ����c�_�ɂ����āA�u��҂͕s�\���v�Ɠ����Ă��Ӗ�������܂���B
���Ȃ����s���Ă��邱�Ƃ́A���ɂ���ł��B
�O�҂̒��ŁA��҂Ɏ����������܂��B�Ȃ̂ɂȂ��u�\�v�ƂȂ�̂��H
����ɐ�����^�����̂��A>>624�̓��e�ł��B
�O�҂̒��Ő������҂Ǝ������A��҂ƈقȂ�̂́A�������R�C���̗L���ł��B
�O�҂̒��Ő������҂Ɏ����ɂ́A�������R�C�������邪�A��҂ɂ͖����B
���̈Ⴂ���A�\�Ȃ̂��s�\�Ȃ̂��Ɍ���I�ȉe����^���܂��B �� ���̃R�C��������A���̒��Ɉꖇ�����y�d�s���̋U�R�C�����܂܂�Ă���B
�V���@k�@��̎g�p�ŋU�R�C�������ɂ߂���@���@�̍ő�l�����߂�B
�������A�ʘg�ŁA�P���̖{���̃R�C���������ꍇ�ƁA����ꍇ�A���ꂼ��ɂ��ē�����B
�Ƃ�����肪�������ꍇ�A�����ꍇ�́A(3^k-1)/2�A����ꍇ�́A(3^k+1)/2�@�������ƂȂ�܂��B
��_�I�ɂ́A�V�� k ��̎g�p�Ƃ����̂́A3^k�@�ʂ肩��̌��̌��ɂ߂��\�Ƃ��܂��B
���ꂪ�ǂ��l���Ă��A����ł��B
�ʘg�ŁA�R�C�����p�ӂ���Ă��Ȃ��ꍇ�̓����A(3^k-1)/2�@�́A�d���̂��A�y���̂��̌��ɂ�
���s���Ă��镪�̓�{���{���ƁA3^k-1�@�ŏ��3^k��������Ă���̂ŁA���Ȃ����A
�ʘg�ŁA�R�C�����p�ӂ���Ă���ꍇ�̓����A(3^k+1)/2�@���{����ƁA3^k+1�@�ŁA3^k�@��
�����Ă��܂��B�u���̂悤�Ȃ��Ƃ͂��蓾�Ȃ��̂ł́v�Ƃ����^��ɑ��������A
>>624�@�̌㔼�ȂǂɋL�������e�ł��B
�l�܂�Ƃ���A�y�d�s���ȃR�C�����@�̎��R�x(?)�́A2n�@�ł͂Ȃ��A2n-1�@���Ƃ������̂ł��B
������肪�A�u�U�R�C������肵�A�y�d�����f����v�Ȃ�A2n�@�ł����A�u�U�R�C������肹��v����
�Ȃ̂ŁA��̃R�C���͏����A���̂����A�`�F�b�N�������ׂẴR�C�����������Ƃ����ꍇ�������āA
(n-1)�~2+1=2n-1�ɂł���Ƃ����b�ł��B �F�ʼn����Ă銴���ق�����ł���
����ʼn����Ӗ��̂��邱�Ƃ��������炻�ꂾ����"�F��"�C�`�o���ɂȂ�邩���
�A���N�\�R�e�Ɠ���Ȃ� �V���r�炵�N�ɂ͍��������̂��� �C�i�����NG���Ă�̂Ŗ{�l�̃��X�͌����Ȃ����ǁA
>>639�͏��� (���)>>514
n��2��n��3�ɕύX�B
(����)
n=3�A4�̂Ƃ��A>>601���A�O��ڂ܂łɓ���ł���B
n=5�An=6�An=7�An=8�̂Ƃ��A>>600���A�O��ڂ܂łɓ���ł���B
n=9�̂Ƃ��A>>554���A�V����4�����ڂ���Ɠ���ł��Ȃ��B
>>549���A�V����3�����ڂ��Ă�2�����ڂ��Ă�����ł��Ȃ��B
�V����1�����ڂ��Ă��O��ڂ܂łɓ���ł���̂�6���܂ŁB���Ǝc��3���̂����̂ǂꂪ�d���̈Ⴄ���݂�����ł��Ȃ����Ƃ�����B
�ȏ�3��n��9�̂��ׂĂ�n�ɂ����Čv�ʂ��āA3��n��8�ł͏d���̈Ⴄ���݂͓���ł��邪�An=9�̂Ƃ��́A�ǂ����Ă�����ł��Ȃ��B
���ǂ����Ă�����ł��Ȃ�n�̍ŏ��l��9�ł���B �W�Ȃ����ǃv���O�����ʼn���������ڂ��Ă�l�����邯�ǂ��܂�ʔ����Ȃ��� ����Ȑl�����H��v�Z�łł���悤�Ȃ��̂��肾�����Ǝv������
���������L�����Ȃ� �I�����^����ꂽm�ɑ��ċ�̓I�ɐ����ǂ��悹���
[log[3](2m)]+1��Ńj�Z���m�������邩�v���O�����g������ȁB
�܂��܂��y���������ȁB ���͖ʔ�������v���O������������ �����ł͖������ł����v�����Ă��܂����̂�
(1)���[�N���b�h���� R^2 �̕����W�� A �ł����Ď��̐����������̂͑��݂��邩�F
��� [0,1] ���� R^2 �ւ̘A���Ȏʑ� f ����l�łȂ��Ȃ�Ax��[0,1] �ł����� f(x)��A �������̂��������Ȃ����̂��Ƃ��.
(2)���ɏW�� A ��
A = { (a,b)��R^2 | a��b���L�����ł��邩�A����{1,a,b}���L�����̏�ꎟ�Ɨ�}
�ƒ�߂��ꍇ�A���� A ��(1)�̐���������. >>676
���Z���w�̔��������ꂨ������ �d�y�ǂ��炩������2����
100������\�ł��� �O>>669�b�ς����ǁA�^�]�Ƌ��̏C�����肾�����ƌ��肾�����邶���A����Ōソ��������ŁA�ǂ�����!?�@���ĂȂ��Ď��ԂƂ��đ�ʎ��_���ĕs���i�s���i�s���i�s���i�c�c����������āA���ԂƓd�Ԓ����������Ă��傤���Ȃ������ȁB
����A������������Ȃ����H�@�l����������ǂځB����͂炩�����B�Z���^�[�����݂����Ȃ̂�������܂����S�ɂ킩�邩����Ȃ��B����Ƃ��p��Ƃ��ł��܂Ɏ��M�Ȃ��̂�����Ƃ����������ǁA�l����ܑ��ɂȂ��Ă邨�����ŋ~���邱�Ƃ��������悤�ȁB
�܂萳�������Ă�͔�r������̂������ẮA���ΓI�Ȃ��̂Ȃ�B �^�]�Ƌ��̃y�[�p�[�e�X�g�ŁA������Ȃ�Ă܂����肦�Ȃ��B >>683�����v������B�l���ɂ͂����Ȏ��G������B���w�̓�₪�����u�ԃC�P�C�P�ǂ�ǂ�����ق�����ăn�[�g�������邱�Ƃ�����A���肦�Ȃ����炢�ɓ�����|���ĂƂ藐����邱�Ƃ������B�O>>682
�P]/�______________���
__/�_/�@�@�@�@�@�@/|ߡ
�P�_/�@�@�@�@�@�@/ |�K
�P|�___________�^| |__
�n| �a�P�P�P�P�a | / /
__| �a ���@�� �a |/ /�
___`�a________�a�^_/�K
�P�P�P�P�P�P�P�P�P�a��
�n�@�@�� �@�@���@ �a /
_____����_________�a/�
�P��(-.-))�� ��~�P�P�B
.�@�@�@�M�ҁ@__ ���
1��2�Ƃ��A2��3�Ƃ���B���̂Ƃ�1+2�͂������H ��e^x = 0!(1)e^x+C
��xe^x = -1!(1-x/1!)e^x+C
��x^2 e^x = 2!(1-x/1!+x^2/2!)e^x+C
�c�c �O>>684
>>685
1+2�͑�ӂ��A2+3
2+3�͑�ӂ��A3+3
���^��=3+3=6 >>687
-��(n+1,-x) * (-x)^{-n-1} * x^{n+1}
���͑�2��s���S�K���}���D >>579�@�ɂ�5�̏d���V�����g���ă\�[�g��������Љ�܂����B
�o��`���͈قȂ��Ă��܂��܂����A�ȒP�Ɍ����ƁA
�u7��ȓ��̓V���g�p�ŁA5�̏d����d�����ɕ��ׂ�菇���l����v�Ƃ������ł��B
�ꌏ�̌듚������܂������A���̑��̉͂���܂���ł����B
�����̕��Ɋy����ł��炢�����A�m���Ă�����̓��e���������Ă������������炾�Ǝv���܂��B
�������A�����\�����Ԃ��������̂ŁA���̂��肢����艺���܂��B >>692
A��E�AB��C���ׂ�B
A��E�AB��C�Ƃ��Ă悢�B
A��B���ׂ�BA��B�Ƃ��Ă悢�B
�����܂łR���A��B��C���m��B
����B��D�A���̌��ʂɉ�����D��A�܂���C���r���ĂQ���A�AB�AC�AD�̏��ʂ��m�肷��B
���̂S�̏��ʂ�P��X��Y��Z�Ƃ���B P���ŏ��͊m��B �����v�̂łQ���E�AX�AY�AZ�̏��ʂ��m��ł���B
��������ɂȂ�ׂ�Q��R��S��T�Ƃ���P���ŏ��͊m�肵�Ă�������ŏI���ʂ� P��Q��R��S��T�B �O>>690
>>692�ꌏ�̌듚�Ƃ͂����A����������܂���Ȃ�A�N�̈�l�����ł͂�����ʂ��B >>693�@����̕��@�Ɠ��e�͓���ł����A�p�ӂ��Ă������u�}��I���@�v�ƁA�ʎ��_����̃R�����g���A�b�v���܂��B
���A���A���A���A���F�܂̏d�肪�Γ��ɑ��݂��Ă�����
�������A�������A���F��̏�Ԃ���A1�Ԗڂ�2�ԖځA3�Ԗڂ�4�Ԗڂ��r���āA�d���������ɖ�����悤�\�L�B[�V�����g�p]
�����������A���@�@�F��̏�Ԃ���A������Ă���d�����r���A���בւ�����ԁB[���g�p]
��
��
���������������@�@�F��̎O�A�����ɁA�Ǘ����Ă�����}���B�ŏ��ɎO�A�̐^�ƁA���ɎO�A���̂ǂ��炩�Ɣ�r���A�l�A������
�� �@(��)�@ �@ �@ �@ �@ ���ʂɂ��A�����̏d�肪�A���̏d��ɂȂ���ꍇ�ƁA���̏d��ɂȂ���ꍇ������B[���g�p]
�� �@(��)
�������������������F��̎l�A�̌���O�A�ɁA�����̏d���}�����ܘA�������B[(�����Ă�)���g�p]
���̂悤�Ȍo�H��H��A����ȓ��Ń\�[�g���\�ł��B�ȉ��A�ʎ��_�ł̉���ɂȂ�܂��B
��_�I���n����l����ƁA5! = 120 < 128 = 2^7 ����A7��ʼn\���낤�ƁA�\�z�ł��A���ۏ�̂悤�ɉ\�ł��B
4�̏d��ŁA�ł��d�����̂��A�g�[�i�����g�`���œ��肷�邱�Ƃɂ��܂��B�i3��V�����g�p���܂��B�j
�g�b�v�ɂȂ������̂�A�AA�Ɉ���ŕ��������̂�B�AA�Ɍ����ŕ��������̂�C�AC�Ɉ���ŕ��������̂�D�Ƃ��A
�Q�����Ă��Ȃ��d���E�Ƃ��܂��B���̒i�K�ŁAA,B,C,D�̊Ԃł̏��Ԃ́AABCD,ACBD,ACDB�̎O�ʂ肪�l�����A
E�́A�e�p�^�[���̂����ꂩ�̈ʒu�ɓ��邽�߁AA�`E�܂ł̏��Ԃōl����ƁA15�ʂ肪�c����Ă��܂��B ����4��ڂ̓V���g�p�ɂȂ�܂����A�����ŁAE��A���ׂ��Ƃ��܂��BE>A�Ȃ�3�ʂ�AE<A�Ȃ�12�ʂ�ɕ��܂����A
����ł́A�c��O��ł͕��בւ����܂���B���l��E��D�̔�r���A3�ʂ��12�ʂ�ɕ��A�s�\�Ȃ̂��킩��܂��B
����ł́AE��B�ł́H�@E>B�ƂȂ�ƁAABCD�ł�2�ʂ�AACBD�ł�3�ʂ�AACDB�ł�4�ʂ�Ȃ̂ŁA���v9�ʂ�B
��͂�A���̔�r�����s�ł��邱�Ƃ��킩��܂��B
�ŁAE��C�݂̂��c����܂��B�@E>C�ƂȂ�ƁAABCD�ł�3�ʂ�AACBD�ł�2�ʂ�AACDB�ł�2�ʂ�Ȃ̂ŁA���v7�ʂ�BE<C�Ȃ�8�ʂ�ƁA
���̔�r�Ȃ�A�c��O��ʼn\�Ȃ��Ƃ��킩��܂��B���̑��AE���g��Ȃ����@���A5�ʂ��10�ʂ�ɕ��铙�A�s�\�Ȏ����킩��܂��B
�܂�A4��ڂ̔�r�́A�i�����ł̃l�[�~���O�ł́jE��C�Ƀ��j�[�N�ɍi���Ă��܂��B���̂悤�ɁA��r��̕����
�������A��r���[�g�����������Ă����A�S�[���ɂ��ǂ蒅���܂��B���̌㑱�̔�r���@�͏ȗ����܂����A�������⑫���Ă������B
�O��ڂ̔�r�́A�Ώ̐�������킩��悤�ɁA�u�g�b�v�v�ł͂Ȃ��A�u�Ōy�ʁv�����߂��r�ł��\�ł��B
���A�����ȊO�̕��@�A�Ⴆ�A�S��I��E��o�ꂳ�������Ȃ邩������܂��A���̂悤�ȕ��@�͑S�Ď��s���邱�Ƃ��A
���̃J�E���g����킩��܂��B
�u�\�[�g�ς݂�2^k-1�̏d��v�ɁA��̏d��������A�V����k��g�p���āA�u�\�[�g�ς�2^k�̏d��v�ɂ���̂́A
��_�I�ɖ��ʂ��Ȃ��A����Β�ł��Bk=2�̏ꍇ����̐}���ŏЉ�����@�ł͑��p���Ă��܂��B
���̒�ɏ]���A�S��ڂɑ����Č܉�ڂ�E���o�ꂷ��̂����R�ł��B�������A�����A�l��ڂ̔�r��E>C�Ȃ�A
EABCD�AAEBCD�AABECD�AEACBD�AAECBD�AEACDB�AAECDB�@�Ƃ���7�ʂ�ɍi���Ă��܂����A
A��E�̔�r�Ƃ�����̑��AB��C�̔�r�Ƃ������@�����݂��Ă��邱�Ƃ�⑫���Ă����܂��B ���ꐎ�̐��������̂Ƃ��̎g�p��[log[2] n!]+1��ɂȂ�H n=2�͗�O�Ƃ��Ĉ����Ƃ��āA�w���w�P�O�O�̖��x�ɂ��ƁA
11�ȉ��ł͐������A13�ł͓��Ă͂܂�Ȃ��B14(13�̌�A�H)�ł̒l�́A33��34���s���Ƃ���B
�Â��{�Ȃ̂ŁA�ǂ����ɍX�V�f�[�^�͗L��Ǝv����B ����A���S���Y���ɂ��K�v�̕\���AKnuth�̖{�Ɍ������B
n=1�`11,20,21�@�ŁA���_�I����={log[2](n!)}�@�Ɉ�v����B�@�G{x}�͐�グ��
n=12�`19,22�`24�@�Ł@���_�I�����@+1 �@
25,26,27�@�Ł@���_�I�����@+2
28�`33�@�Ł@���_�I�����@+3 >>698
�ց[�A�ʔ������I
>>699
kunth�̉��Ė{�ł����H �wThe Art of Computer Programming�xVol.3 Sorting and Searching
�ł� >>687
�����ϕ��ɂ��
��(x^n)(e^x) dx = (x^n)(e^x) - n��(x^{n-1})(e^x) dx
�@= (x^n)(e^x) - n(x^{n-1})(e^x) + n(n-1)��(x^{n-2})(e^x) dx
�@= (x^n)(e^x) - n(x^{n-1})(e^x) + n(n-1)(x^{n-2})(e^x) - n(n-1)(n-2)��(x^{n-3})(e^x) dx
�@= ����
�@= (e^x)��[r=0,n] (-1)^r (n!/(n-r)!)(x^{n-r}).
�E�Q�l��
�X���E�F�c��E�ꏼ �u���w����I�v ��g�S��221 (1956) p.153
�@��IV�� ��1�� ��33 (i) 1022^(1023^1024) + 1024^(1023^1022) �� 1023 �ʼn����邩
��ʉ�����
(n-1)^{n^(n+1)} + (n+1)^{n(n-1)} �� n �ʼn����邩
2���������
(n-1)^{n^(n+1)} = -1 + n^(n+2) - (1/2)n^(n+3){n^(n+1)-1} + ����
(n+1)^{n^(n-1)} = 1 + n^n + (1/2)n^(n+1)}{n^(n-1)-1} + ����
��� n��B
��1023�� >>705
>��ʉ�����
�������An�������Ȃ�0�� >>708
�������An=2 �Ȃ� 1��
1^(2^3) + 3^(2^1) = 1^8 + 3^2 = 1 + 9 = 10, �������B
n�̏�]�� 1+(-1)^n�Ȃ��ǁA
1+1=2=n �̃P�[�X���������Ă���B ��������n^(n+1)�Ŋ����Ȃ��͖̂��炩�Ȃ�H >>711
�����Ȃ��Ƃ��A>>705�̍ŏ��̂Q���������݂�� (1+n^2)n^n
�Ȃ̂ŁAn^(n+1)�ł͊����Ȃ��B
���Ƃ́A�R���ڈȍ~��n^(n+1)�̔{���ɂȂ��Ă邩�ǂ���
�Ȃ��A�m���Ɍ`�����n^(n+1) �������Ƃ��ē����Ă�
���ǁA�����k!�����邩��˂��B�v����� n^(n-1)Ck�~n^k
��n^(n+1)Ck�~n^k ��k>=2 �� n^(n+1)�Ŋ����邩�ǂ����B
k��n^(n-1)�Ƃ�n^(n+1)�Ƃ��f�̏ꍇ�ɂ͖��炩�Ȃ��c�B
�����łȂ��ꍇ�Ak�Ƃ��ꂼ��Ƃ̌���L1,L2�Ƃ��āA
n^(n+k-1)/L1 ��n^(n+k+1)/L2 ��n^(n+1)�Ŋ����邱��
��������������ǂˁB
���������Ӗ��ł�n^n�Ŋ����邩�ǂ����ɂ��Ă�����
���Ƃ������邯�ǁA�オ������Ύ����I��OK�B ����ς�>>705�̎��ό`�����ł�1023��ƌ��_�Â����Ȃ���ˁB
�����ЂƋc�_�K�v�B >n^(n+k-1)/L1 ��n^(n+k+1)/L2 ��n^(n+1)�Ŋ����邩
n����Ȃ���Ak=2�̂Ƃ��ɂ͖��炩���ˁB
n^(k-2)/L1 (2<L1��k)�� n^k/L2 ( 2< L2 ��k)��L1,L2��
�f�����������ă`�F�b�N����Ί���ꂻ���ȋC������B
L1�̑f�����̈��a^s�Ƃ���ƁAa��n�̑f�����ł�����
���Ƃ���n^(k-2)��a^(k-2)�������Ƃ��Ă��i�������An
����Ȃ̂�a��2���傫���f���j
a^s��L1��k ���@a^(k-2)��a^(a^s -2)
a^(k-2)/a^s �� a^{(a^s)-s -2) a��3,s��1���A
a^s -s -2 ��0 �@���������āAa^(k-2)/a^s ��1 �͊���
���B����Ȋ����ōs���������ȁH
�������A�����ƊȒP�Ɏ����Ȃ����̂��B �~�@L1�̑f�����̈��a^s�Ƃ����
���@L1�̑f�����̈��a�Ƃ��Aa^s�������Ƃ���� n���������q���܂܂Ȃ���̂Ƃ��� n��
(����)
C(N,k) = (N/k)��[i=1,k-1] (N-i)/i
a��n�̑f�����Ƃ���B(��f��)
1��i��N-1 �̂Ƃ��@(N-i)/i �̕���E���q�Ɍ����a�͓̉������B
�܂��Ak�̒��Ɍ����a�̉́@< k/(a-1) �� k, �䂦 k-1 �ȉ��B
N=n^(n-1) �̂Ƃ�
�@C(N,k) �� a^(n-k) �̔{���A���������� n^(n-k) �̔{��
N=n^(n+1) �̂Ƃ�
�@C(N,k) �� a^(n+2-k) �̔{���A���������� n^(n+2-k) �̔{���B n = 1023
�@= 32^2 - 1
�@= (32+1)(32-1)
�@= 33�E31
�@= 3�E11�E31 >>716 �⑫
k�̑f���������ɂ�����f��a�̉�
�@=�@[k/a] + [k/a^2] + [k/a^3] + ���� + [k/a^k]
�@�� k/a + k/a^2 + k/a^3 + ���� + k/a^k
�@< k/(a-1), >>716
n���������q���܂�ł�ƑʖڂȂ́H >>714�̂������ƕ������q���낤���������q���낤��
�܂�ł��Ă��An����Ȃ�n��ɂȂ肻�������ǁH a^s | n�@�Ƃ���B(s��1)
C(N,k) = (N/k)��[i=1,k-1] (N-i)/i
�̂����f����a���c��̂� (N/k) �̂Ƃ���B
N=n^(n-1) �ɂ� a �� (n-1)s ��邪�Ak �ɂ� (k-1)�ȉ��B
���@(N/k) �ɂ� (n-1)s - (k+1) ��ȏ�
���@(N/k) n^k �ɂ� (n-1+k)s - (k-1) = ns + (k-1)(s-1) �� ns ��ȏ�
�Ȃ̂� OK �ł���ˁB >>705�̈�ʉ��ɂ��āA�Ƃ肠�����A�v�Z�@���Ă݂��Ƃ���A
3����1023�܂ł̊n�ɂ��āA
(n-1)^{n^(n+1)} + (n+1)^{n(n-1)} �� n^n (mod n^(n+1))
�ł��邱�Ƃ͎����� >>721
�ł���ˁB
>>714�����������������ď��������Ă����܂��B
��ʂɁA
C(N,k)=(N/k)*C(N-1,k-1) �Ȃ̂ŁAk��N�̍ő����L
�Ƃ��āAk=qL�Ƃ����ƁAq��N/L�͑f�Ȃ̂ŁAq��C(N-1,k-1)
�̖łȂ���Ȃ�Ȃ��B ���������āAC(N,k)��N/L��
�{���ł���B�����O��Ƃ��āA>>705�̓W�J�̊e�X��
k�Ԗ�(k��2)�̍��̐�Βl M=(n^k)*C(N,k) ��]������ƁA
M��(n^k)N/L �̔{���ɂȂ�͂��BL��L= (a^s)*(b^t)�c ��
�f�������������Ƃ��AN��n�̗ݏ�ł���A�����̑f����
a,b�c�͂��ׂ�N�̑f�����ł���An�̑f�����ł�����B
�����ŁAn����ł���An^(k-2)��L�Ŋ����邱�Ƃ������B
a��n�̑f�������An^(k-2)��a^(k-2)�������Ƃ��Ď����A
k��L��a^s���a^(k-2)/a^s��a^(a^s-s-2)�B�@a��3, s��1���A
a^s-s-2��0�@�ƂȂ�̂ŁAa^(k-2)/a^s��1 �A�܂�n^(k-2)
��a^s��Ƃ��Ď��B����L�̑f�����ɂ��Ă����l�Ɍ�
����̂ŁAn^(k-2)��L��Ƃ��Ď��B
���������� M ��(n^k)N/L = N*(n^2)*n^(k-2)/L �̔{����
���邱�Ƃ���AM��N*(n^2)�̔{���ł���ƌ�����B
�ȏ���A
N=n^(n-1)�̏ꍇ�AM �� n^(n+1)�̔{��
N=n^(n+1)�̏ꍇ�AM �� n^(n+3)�̔{��
����āA>>705�̓W�J�̂Q�Ԗڈȍ~�̍��͂��ׂ�n^(n+1)
�̔{���ł���B >>722
����J���܂ł��Bwolframalpha�ɂ�点�Ă݂悤�Ƃ�����ł����A
�����ł���n=7�܂ł����E�ł����� >>724
���݂܂���A���ȃ��X�ŏC�����Ƃ��܂��B
>>>705�̓W�J�̊e�X��k�Ԗ�(k��2)�̍��̐�Βl
k=0����n�܂�̂ŁAk�Ԗڂł͂Ȃ��A(k+1)�Ԗڂł��ˁB
���������āA�Ōォ���s�ځA
>����āA>>705�̓W�J�̂Q�Ԗڈȍ~�̍��͂��ׂ�n^(n+1)
�̂Ƃ���́A�u�W�J�̂R�Ԗڈȍ~�̍��v�ɂȂ�܂��B a��3
>>718 �̕]�������ǂ���
�@k��2 �ł� k-2��ȉ�
N=n^(n-1), k��2 �̂Ƃ�
�@C(N,k) �� n^(n+1-k) �̔{���B�@M �� n^(n+1) �̔{���B
N=n^(n+1), k��1 �̂Ƃ�
�@C(N,k) �� n^(n+2-k) �̔{���B�@M �� n^(n+2) �̔{���B�@�@>>716 �t�u���g�����Ɩ��B
���
p ��f���Av��p�i�t�u�Ƃ���B
a,b��p�i�P����a ��b (mod p)�ł���Ƃ���B
���̂Ƃ�
v(a^n - b^n) = v(a-b) + v(n) �藝
n����Ƃ���B
x = (n+1)^{n^(n-1)} + (n-1)^{n^(n+1)}�Ƃ����B
���̂Ƃ�
v(x) = nv(n)
����������B
����
max{e | x �� 0 (mod n^e)} = n
�ł���B
(��)
p��n�̑f���q�Ƃ��A����p�i�t�u�Ƃ���B
���ɂ��
v((n+1)^{n^(n-1)} - 1) = v(n+1 -1) +(n-1)v(n) = nv(n)
v((n-1)^{n^(n+1)} - (-1)) = v(n-1 +1) +(n+1)v(n) = (n+2)v(n)
�ł��邩��咣�͐�������B R�������̂Ƃ��āAg:[0,1]��R�������Ƃ���Ƃ��A
��_0^1 f(x)g(x)dx=0
�ƂȂ�P���I�ɂ�0�ł͂Ȃ��A����f:[0,1]��R�����݂��邱�Ƃ����� >>730
f(t,x)= sin(��(x-t))
I(t)=��f(t,x)g(x)dx
�Ƃ����B
I(t)�͎����藝�ɂ��A���B
I(0) = -I(1) >>731
g�͉����Ƃ͌����Ă܂����ϕ����Ƃ͌����ĂȂ��̂Ŏ����藝���g���Ȃ��Ǝv���܂��� >>730
����{���ɐ��藧�́H
R�̕����W��A�ɑ��Ċ�1_A��
(1_A)(x)=1 (x��A�̎�), (1_A)(x)=0 (����ȊO�̎�)
�ƒ�߂āA0�ȏ�1�ȉ��̑S�Ă̗L�������P�o�����鐔��� {q_n}_(n=1,2,�c) �Ƃ����B
�W��A_m��
A_m = ��_(n=1,2,�c) ( q_n - 1/(logm�2^n) , q_n + 1/(logm�2^n) )
�Ƃ����āA��g~:R��[0,��]��
g~(x) = ��_(m=2,��) (1_(A_m))(x)
�ƁA�����Ċ�g:R��[0,��)��
g(x)=0 (g~(x)=���̎�), g(x)=g~(x) (����ȊO)
�ƒ�߂�B
���̎��A0��1�̊Ԃ̂ǂ̗L����q���Ƃ��Ă��A�C�ӂ̃�>0�ɂ���
��_(q-��,q+��) g(x)
=��_(q-��,q+��) g~(x) (g~�ɂ�遇�̋t���̓��x�[�O��W���ɂȂ邩��)
����_(q-��,q+��) ��_(m=2,��) (1_(q - c/logm , q + c/logm))(x) (c�͂��鐳�̐�)
=��_(m=2,��) 2min(��,c/logm)
=��
�ƂȂ邩��Af���P���I��0�łȂ��A�����ł���A
����0��1�̊Ԃ̗L�����̋ߖT�ŁAf�̐�Βl�����鐳�̐�����ɑ傫�����ƂɂȂ邩��
��_(0,1) |g(x)f(x)|dx = ��
�ƂȂ��Ă��܂� I0 = ��_0^1 g(x) dx
I1 = ��_0^1 x g(x) dx
�Ƃ����B
I0=0 �̂Ƃ� f(x) = 1,
I0��0 �̂Ƃ� f(x) = x - I1/I0, �ߎ��P����K���ɏ����W�J�̐����������č��Ȃ� �O>>694
[���]�����̔����ő�̑Ίp�������Ɉ��]�������ʉߕ����̑̐ς����߂�B
�A���A���̓��M�����[�T�C�Y�̃{�b�N�X�^�C�v(88�o�~55�o�~23�o)�Ƃ���B �C�ӂ̋���a�ɂ��āA����K�ȓ�̑f���������̍���a�ɂȂ邱�Ƃ��ؖ�����B
�����܂����H�i�L-`�j >>737
���Y�C�I
����H
�����͂���́H �v�����̖�肾�낤���A
100�����炢�܂ł̑S�Ă̋����ɂ��Ă��̂悤�ȑf���̑g�����邱�Ƃ����������Ȃ�
���I�̓��ɂȂ�\���͂���B �ȂC�ӂ̒����̓���������Ȃ��f���̑g������Ƃ��^�I���ؖ����ĂȂ����������B
�Ȃ�������Ɏ�����Ă��� ����a�ɕς�����S�[���h�o�b�n�����
�{���ɉ�����̂��H �A������ 2a-1 �̎��R��
(2a)! +2, (2a)! +3, ����, (2a)! +(2a-1), (2a)! +(2a)�@�͂��ׂč������ł���B
(2a)! +1 �� (2a)! +(2a)+1 �����ɑf���ƂȂ�悤�Ȃ������݂��邩�H
(2a)! -(2a), (2a)! -(2a-1), ����, (2a)! -3, (2a)! -2 �ł��悢�B
�u���Z���w�̔���������v(������ł������f�����������݂���)
http://mathtrain.jp/primedesert (�C��)
a! +2, a! +3, ����, a! +(a-1), a! +a�@�� a-1 �͂��ׂč������ł���B
a! +1 �� a! +a+1 �����Ɋ�f���ƂȂ�悤�ȋ���a�����݂��邩�H
a! -a, a! -(a-1), ����, a! -3, a! -2 �ł����l�B a �� 966 �܂ł͑��݂���炵���B
http://www.asahi-net.or.jp/~KC2H-MSM/pbsb/pbsbm006.htm
600����̂͊m���B
������ p��4000�� �܂ŒT�����Ă� ��p �� 4000 �炵���B�@
http://math.a.la9.jp/a2prd.htm
���������́���
�@http://math.a.la9.jp/2prd.htm a+1 ���f���Ȃ�� a!+1 �� a+1 �̔{���ł���B >>736
�k���824�l
3�ł̒����� a,b,c (0<a��b��c, aa+bb+cc=1) �̒����̂��A�̑Ίp�������Ƃ��ĉ�]�������B
���̂Ƃ��ʉ߂��镔���̑̐ς����߂�B
�����X���S�T�S - 824,839,842,846-848,875-876
(�ށF�����H��,1993�N) >>736
�@aa = 23�23/11298 = 0.0468224464507
�@bb = 55�55/11298 = 0.267746503806
�@cc = 88�88/11298 = 0.685431049743
�̑Ίp����u���Ƃ���B
�@�@r(u) = (1/a)��(1-aa)�u�@�@�@�@(0 < u < aa)
�A�`�D�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(aa < u < 1-cc)
�E�@r(u) = (1/c)��(1-cc)�(1-u)�@�@(1-cc < u < 1/2)
�E' r(u) = (1/c)��(1-cc)�u�@�@�@�@(1/2 < u < cc)
�D'�`�A'�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(cc < u < 1-aa)
�@' r(u) = (1/a)��(1-aa)�(1-u)�@�@(1-aa < u <1)
�@���@S(u) = ��r(u)^2,
�@���@V = ��[-1/2,1/2] S(u)du,
V(�@) = V(�@') = ��(a^4)(1-aa)/3 = 0.00218832
V(�E) = V(�E') = ��{(1-cc)/cc}(8c^6 -1)/24 = 0.0946902 �O>>736
�P�ʂ�c�u�ł��肢���܂��B >>747
Legendre's conjecture? >>744
�Ea+1 ���f���̂Ƃ��A�E�B���\���ɂ��
�@�@a! + 1 �� (a+1) �̔{���@�@>>747 >>748
�@�@a! ���������B
�Ea+1 ���������̂Ƃ�
�@�@a! + (a+1) �� (a+1) �̔{��
�@�@a! + (a+2) �͋����B
����� ���݂��Ȃ��B
>>751
�@11298 c�u �� �P�@�@�Ƃ���B >>730
�ʑ���:C([0,1])��R��
��(f)=��_0^1 f(x)g(x)dx
�ƒ�߂�
���̂Ƃ��AKer��={0}�Ƃ���A�ӂ͐��`���P��
����������#A��A�̔Z�x�Ƃ����
#C([0,1])��#R
����͖���
����������Ker�Ӂ�{0}�ƂȂ�A����f�����݂��� >>753�@����
�@112.98 c�u �� �P�@�@�Ƃ���B >>754
�ϕ��łȂ����炠����ł���H �����s��A�������łȂ��Ƃ��A�C�ӂ̐��̐�c�ɑ��āAA+cE�͐����ł��邱�Ƃ������B �P�P]/�_______����_
____/�_/ .,��(___))|
�P�P�_/ �c`-`Ђ��/ |
�P�P|�___U,~�܁S�| |_
���@| �a�P�PU~~U | / )
____| �a�@���@�a |/ /|
_____`�a______�a�m / |
�P�P�P�P�P�P�P�P�P�a |
�n�@�@���@�@ ���@ �a /
__________________�a/
23�~55�~88=111.32(c�u)
�O>>751���邭���]��������300���炢�����̂��ȁH �O>>760
>>751�����B
c�u��c��^3 �O>>761
[���]�g�т��ő�̑Ίp�������Ɉ��]�������ʉߕ����̑̐ς����߂�B
�A���A�g�т̃T�C�Y�́A
112�o�~51�o�~15.1mm�Ƃ���B (1)
S^2������ʂƂ���
f:S^2��S^2���A���ł���Ƃ��A
f(x)=x �ƂȂ� x��S^2�����݂��邱�Ƃ�����
(2)
�O�������x�N�g����Ԃɂ͐ς��A���ƂȂ�悤�ȑ̂̍\���͓���Ȃ����Ƃ��ؖ����� �m���̖��B
�O�̔��̒��ɐ�����������B
����҂���I��ɁA�I��ĂȂ���̔��̂����O�ꔠ���J�������i����O�ꔠ�ł�������_���ŊJ���j
����҂�����ς��鎖���ł����ꍇ�A����ς������������H����Ƃ��m���͕ς��Ȃ����H �����e�B�E�z�[����肾��B>>764
�ς����ق������B�����������m���́A�ς��Ȃ���1/3�A�ς����2/3
���Ə����t���m���ŋ��܂�B >>765�����B���\�L���Ȗ�肾��ˁB
�����͕ς��Ȃ����ǁA�悭�悭�l������m���͕���Ċ����ŁB�s�v�c�Ȗ�肾��B �O>>762
>>764
����҂�����ς��Ȃ��ꍇ�A
�ꔭ�ڂœ��Ă�m���́A
1/3�\�\�@
����҂�����ς���ꍇ�A
�ꔭ�ڂœ��Ă�m���́A
1/3�\�\�A
�ꔭ�ڂ��O���Ĕ���ς��ēڂœ��Ă�m���́A
(2/3)�(1/2)=1/3�\�\�B
�A�B���A
1/3+1/3=2/3�\�\�C
�@�ƇC���r����ƁA
1/3��2/3
������҂�����ς���ꍇ�̂ق�������ς��Ȃ��ꍇ��蓖����m���͍����B �u����1�I�ꍇ�͂���1�������Ȃ瓖�����
����2�I�ꍇ�͂��̂����̂ǂ��炩�ɐ����������Ă���Γ�����ł�
����1�I�т܂����H2�I�т܂����H�v
���Ă������Ɠ������Ƃ����� �����̕��͂������Ŋm���߂Ȃ��^�C�v�̑��M�� >>763
(1)
(x,y,z)��(y,-x,-z)�͕s���_�������Ȃ��̂Ŗ�肪���
deg(f)��-1�����肷���Lefschetz�s���_�藝����]��
(2)
���̂悤�Ȑύ\�������݂���Ɖ���
f:S^2��S^2; x��x^2/|x^2|
�ƒ�߂�
f(x)=f(-x)��肱���
g:RP^2��S^2
��U������
g�͒P�˂ł���A�܂�RP^2���R���p�N�g�ł��邱�Ƃ���Ag�͓����ʑ��ƂȂ�
������RP^2��S^2�͈ʑ����^�ł͂Ȃ��ׂ���͖��� (��)�@"�O��" (����)
���� �� ���� �̃X�J���[�{�̂Ƃ�
�������A�������A���~������ (����q)
�́@����łȂ�
���@������łȂ�
���@UFD�łȂ�
���@��ideal����łȂ�
���@Euclid����łȂ�
���@�̂łȂ� �O>>767
>>769���_���������イ�Ԃ�Ȃ����B���͍��E�e�ԋ߂ŖZ�����B������������ă��X�g�V�[�������������ɂȂ�B����2�y�[�W�����B >>773
�����炢�܂ł����Ă����w���ł���悤�ɂȂ��̂���B
�ʂɐ��w�ł���悤�ɂȂ�Ȃ��Ă��l���ō��邱�Ƃ͂Ȃ����A�����ɑ��Ă����̋C�����œ������Ă�Ȃ牽����Ă����ɂ��ł���悤�ɂȂ��B
���̂�������Ȃ��Ȃ邼�H >>773
�ꔭ�ڂ��O���Ĕ���ς��ēڂœ��Ă�m���́A
(2/3)�(1/2)=1/3�\�\?
���̕ӂ������ĂȂ��B1/2�͂ǂ����痈���́H
���܂��ܓ�������v�����Ƃ��������ŁA�_���W�J��̓o�c�ɂȂ�B �O>>773
>>774��͍��E��180���������˂���A�̂���B
>>775���ς����炠��2�����c���Ă˂�����˂����B�ǂ�����������Ȃ���1/2����˂����B
�ȂɌ����Ă邾�B �O>>776
�����낪�D���ŁA
�O���������܂܁A
��180���ȏイ����ɉăL�X������A
���̐l�ɂ܂����������ł��B
�������w�ŁA
�܂���킷�̂݁B �O����m���Ă�������ς�R�C�c�ǂ����傤���Ȃ��ȁB �O>>777
>>778
________________�
(.-�-)�ȂɌ����Ă��!
_`''~ >>776
��ڂ̔����n�Y���ł��邱�Ƃ�O��ɒu���Ă��ˁH�H�Ȃ������肩�n�Y����������́H�H
�E��ڂ̔����n�Y���̏ꍇ�i2/3�j
�c���̓��n�Y�����J������遁�ς��ē�����m���͂P�B������2/3�~1��2/3�B����B
1/2�Ȃ�ďo�Ă��Ȃ��B �O>>779
>>780�Ȃ�ŁB�ꔭ�ڊO��ēڂ͎c��2�̂����ǂ���������B
�ڂ�S���q�b�g�����鐦���z�͂�������1�����A�ӂ�1/2���B �l�^�Ō����Ă��Ȃ������Ă��炢�̊��Ⴂ >>782
���܂��Ă����l�^����� ������2/3�Ƃ����̂͂ǂ����ŕ����Ă��āA�ڂ̑O�ɂ���1/3,2/3,1/2�Ƃ���K���ɑg�ݍ��킹��2/3�ɂȂ����A�o�������ĂƂ��Ȃ�ł���H �O>>781
>>784���̖��͏��߂Č����B�������Ăĉ������B >>781
���������Ⴂ���Ă�|�C���g��B
����ABC�Ƃ����āAA��I��Ńn�Y���������ꍇ�ˁB
�EB��������̎�
C���J�������BA����B�ɕς����1�̊m���œ�����
�EC��������̎�
B���J�������BA����C�ɕς����1�̊m���œ�����
���̂ӂ�1/2���B�Ƃ����̂������I�ɂ����v���̂�������Ȃ����ǁA���ۂ͌���ĂāB�����Ǝ����Ƙ��������܂�閽��Ƃ��āA���̖��͗L���Ȃ̂�B
������A���̖��ɂ͖��O�܂ł��Ă�B >>785
�_���I�ɍl�����
1/3 + 2/3 �~ 1/2
�ȂǂƂ������͏o�Ȃ��B��������
1/3 �~ 0 + 2/3 �~ 1�B
�Ȃ�CM�Ō����Ă��������͌v�Z�̂��߂ɂ���̂ł͂Ȃ��B
���ꎩ�g�����t�Ȃ̂��B
������ 2/3 �ɂȂ�Ȃ�ł������킯�ł͂Ȃ��B ���������Ă������������邾���̂���������͕̂s�\���� �O>>785
�����������猩�����ƂȂ��ߒ����o���������o���Ă݂ȁB �C�i����A�C�i����A
>>767
������҂�����ς���ꍇ�A
���ꔭ�ڂœ��Ă�m���́A
��1/3�\�\�A
����ς������A�ꔭ�ڂɑI���̔��͊J���Ȃ����Ƃɂ������ǁA
���̇A�̊m�������Z���Ă�̂͂ǂ����ĂȂ́H �����̐��l�����������Ă鎮�ȂǂȂ�̈Ӗ����Ȃ��Ƃ����̂����̂킩���̂��˂��H
�܂������̐��l���킷�̂��ړI�Ő��������肵�Ĉ�l�x�Ɏ���̂��ړI�Ȃ炻��ł��������B >>789
����Ő��w�̉�������o�c����B
�_���I�Ɍ���Ă�������Ă邩��F���w�E���Ă����B
����ȃ��X��������Ă��A��ԉ��������Ă�̂͌N���g����Ȃ����B �O>>789
>>786A����B�ɕς���1�̊m���œ���������Ȃ�AC�ɕς��Ă���0����˂����B
�܂�ڂ�1/2�Ȃ�B
>>790�ꔭ�ڂœ��Ă��ꍇ�ƁA�ꔭ�ڊO��ēڂĂ��ꍇ�𑫂����������B >>793
C�͊J������Ă邩��ς����Ȃ����H�H
�ς�����͓̂�����ł���B��������B �O>>793
>>794������C���J���������A������������B
������Ȃ�I�ׁB
�͂���Ȃ�B���B �܂��������낤�ȁB
�C�i�̐��w�͂����Ƃ����w���x���Ŏ~�܂��Ă�B
�O�p��Ƃ��͂ǂ����̃T�C�g���Ȃ��ēƏK�����݂��������ǁA�_���ƏW���̒P�����o���ĂȂ��Ɗm���͓����o����悤�ɂ͂Ȃ�Ȃ��B
�C�i�̓��W�b�N�{���{��������ȁB ���܂ǂ������e�B�E�z�[���A�������A�����W���Ȃ����^�ŊԈ���Ă��˂鏊��������Ƃ́B
��蕶�Ɍ��͂Ȃ��̂�
���ƍl������̂̓C�i������蕶�𐳊m�ɓǂ�ł��Ȃ������Ƃ������ƁB
�r���ł͕K���O�ꂪ���J������B>>764�ǂ�
��I �O>>795
P�������C���g�ݍ��킹����H�@�����͒m���Ă邳�B�I�}�[�N���K�悳�B
>>764�ʉ��B
�ǂ����A�����Ɍ����ĕς����ق������B����Đe���A����������ɊO��̔����̂ĂĂ�����₵�A������m���͏オ���Ȃ��B
2�{���ȁB
1/3��2�{�B
�ς��Ȃ��ꍇ�A1/3�\�\�@
�ς���ꍇ�A�ς���܂ł�1/3�̊m���œ�����Ƃ�����A
2/3�͊O���I��łāA�ς����瓖���������b�L�[���ĂȂ�B�\�\�A
1/3�͎c��2�����̊o��ŊO��������ɂ������ƂɂȂ�B
�@�A���A
1/3��2/3
�������ꂽ�B �C�i����͔���ς��܂��I�Ɛ錾������ɁA
�ŏ��ɑI����^����ɊJ�����Ⴄ���[�����p���l�炵��
���������l��ԑg�ɌĂ�ł͂����Ȃ��� �ŏ�������Ă����悢�@�\�𐧌����ď�������_����Ԃ̖�肾�낤�Ɛi�����Ă݂� �O>>798
�ǂ������ɂ�������2/3�ɂȂ邱�Ƃ͂킩�����B
���ǂȂɂ��ʔ����H
�������Ėʔ��Ȃ��ȁB
���O����悤�Ȑ������炭�肪����ł��Ȃ��B �O>>802
>>799�ȂA�ԑg���āH
�ȂɂɌĂԂH�@���w�̔ԑg�Ȃ���ōs�����Ă��������܂���B
�o�������Ƃ𐔎��Ԓ��x�̒Z���Ԃœf�������y�[�p�[�����Ƃ͈Ⴄ�A�ʔ������w�Ȃ�ˁB >>802
�������Ɓu�ς���K�v�͂Ȃ��v�Ɗ�����̂����w�I�Z���X�̂���l�ŁB�����ǁA�����ƌ������ɘ�������������Ƃ����̂��A���̖�肪�L���ƂȂ������ȁB
����>>793�̂悤�Ȍ��������l����肷�錻���̂������B
���w�I�ɂ͒�������肾��B ������2ch�̓A�z���肾�ȁi��
�����e�B�E�z�[�����̐����́A
�u�ǂ����I��ł��m����1/2�œ����v�ł���i��
���A���L�̃X���ł��̖���_���Ă��邩��A
����������Ή��L�̃X���ցi��
�A���`���s���A������A�^���҂͂��f��i��
���㐔�w�̓C���`�L���炯
https://rio2016.5ch.net/test/read.cgi/math/1567930973/l50 �ꉞ������ɂ������Ă����ƁA
�N���l���Ă������͂����ł���i��
���J����O�́A
�O�̔��̂ǂꂩ��Ɍi�i�������Ă���̂�����
�ǂ��I��ł�������m����1/3�ł���B
���J������́A
��̔��̂����ǂ��炩��Ɍi�i�������Ă���̂�����
�ǂ����I��ł�������m����1/2�ł���i�� >>805>>806
���̐l�͎���o�ł̃g���f���{���`���܂���Ă���^���̃L�`�K�C�ł�
�Ƃɂ����_���I�E���w�I�Șb���ʂ��܂���
���̃X���Ō��ꂽ�ۂɎז��������ׂɒP�ƃX���ւƒǂ��o�����o�܂�����܂��̂ŁA�����ł̃��X�o���T����悤�肢�܂�
���̃��X�ɑ���������������\��������܂����A��������ȍ~�͔ނɂ͐G��܂���
�ǂ����Ă����_�������l�͓\���Ă���X���ɍs�����Ƃ��I�X�X�����܂� �X�����������l�тɖ��
S^2�̐ڑ����瓾����S^1���̐����W��(�R)�z�����W�[���v�Z���� 1845
��������@dy_dt_dt_dx 8��28��
�w�R��8����S�R�[�X1����1�ʂƂ�܂����I
�}�W�Ŋ������ł��I
������������n�ɕ������撣�肽���Ǝv���܂��I
https://twitter.com/dy_dt_dt_dx
https://twitter.com/5chan_nel (5ch newer account) >>807
>>807
>�Ƃɂ����_���I�E���w�I�Șb���ʂ��܂���
���ꂪ���O��i��
>�P�ƃX���ւƒǂ��o�����o�܂�����܂��̂�
���O�ɒǂ��o���ꂽ�o�܂͂Ȃ����A
���������ǂ��o���ꂽ���Ƃ��Ȃ��i��
���O�̓T�����i�� 100���̕���o���Ƃ��A
���̂����P�������������肭�����Ƃ���B
�A���A���̂���99�����`�̔����Ŕ���o���Ƃ��A
�c��̂P�����a�̔����Ŕ���o���Ƃ���B
�P�@�`�̔����ɕ��������Ă���m���ƁA
�a�̔����ɕ��������Ă���m���́A���ꂼ�ꂢ���炩�B
�Q�@�`�Ƃa�̂ǂ���Ŕ���������������m�����������B
���ꂪ�����ł���Ȃ�A>>805-806���������ƕ���i�� �l�����̃X���Ř_����C�͂Ȃ��̂ł���i��
�����烂���e�B�E�z�[�����ɂ��Ę_��������Ή��L�X����
���㐔�w�̓C���`�L���炯
https://rio2016.5ch.net/test/read.cgi/math/1567930973/l50
���Ȃ݂�>>812�̖��ɂ��Ẳ҂�
���̂Ƃ����l�����ŁA�s�����ł���i�� �N�͕ʂ̃X���Ŏ咣���Ȃ����B�킴�킴���̃X���܂Ŋ���o���K�v���Ȃ��ł��傤�ɁB
�N������ƍr��邩��A�F��ȃX���Ɋ���o���s�ׂ̓X���r�炵�ɑ��Ȃ�Ȃ���B �����e�B�z�[�����̘b����֎~�����������w �O>>803
>>812
�P
100���̕��̂����P���������肭��������A
�`�̔�����99���̂����A
1�(99/100)���������肭��������A
�`�̔����ɕ��������Ă���m���́A
1�(99/100)��99�~100=1(��)�\�\�@
�a�̔�����1���̂����A
1�(1/100)���������肭��������A
�a�̔����ɕ��������Ă���m���́A
1�(1/100)��1�~100=1(��)�\�\�A
�Q
�@�A���A
�`�Ƃa�͓����m���B �C�i���Ɏ���
�@{{}}��{{{}}}�A{}��{{}}�ł��邪�A����{}��{{{}}}���H
�@�R��A�������́A�ہA�œ�����ꂽ�� >>816
�܂����ꂾ�����Ⴂ���N����₷���ʔ��������Ď���w a,b���݂��ɑf�Ȑ����Ƃ���
���̎����R��X�AY��p����
aX�{bY�̌`�ŕ\���Ȃ����R���̌��͂����� ��ӂ��@ab��0
�Eab <0 �Ȃ�@0
aX+bY=1�@���� X,Y��N ������B(�ݏ��@�A������]�藝)
�Ea<0, b<0 �Ȃ� �`N
�@���ׂĂ̎��R���B���Ƃ������Z�x(Cardinality)�H ���̒萔a,b�ɑ���
c[n]=��[0,��/2](a^2 sin^2(x) + b^2 cos^2(x))^(-n)dx
�Ƃ����B
|t|���\���������Ƃ��A��[n=0,♾] c[n]t^n �����߂�B >>824
��[n=0,��] c[n]t^n
= ��[n=0,��]��[0,��/2] (t/(a^2 sin^2(x) + b^2 cos^2(x)))^n dx
�@|t|<min(a^2,b^2)�Ɖ��肵�Đϕ��Ƙa�����ւ���
= ��[0,��/2] 1/(1-t/(a^2 sin^2(x) + b^2 cos^2(x))) dx
= ��/2+��[0,��/2] t/((a^2-t)sin^2(x)+(b^2-t)cos^2(x)) dx
�@��(a^2-t) tan(x) = ��(b^2-t) tan(y) �ƒu��
= ��/2+��[0,��/2] t/��((b^2-t)(a^2-t)) dy
= (��/2)(1 + t/��((b^2-t)(a^2-t))) >>825
�����A�����ˁB�����B i�������P�ʁAa�𐳂̐��Ƃ�
�Ȑ� C�_ -a�Aa�Aa+i��A-a+i�����Ȃ钷���`�̋��E�ɔ����v������t�������̂Ƃ���B
(1) ��[C] e^(-iz^2)/(1 + e^(2(���)z)) dz �����߂�B
(2) a�����̋Ɍ����� ��[-��,��](cos(x^2) + i sin(x^2))dx ���v�Z����B >>817
�P�@�~
�Q�@��
�T�O�_�i�� �@��[n=1,��] �� (t/{aa�sin(x)^2 + bb�cos(x)^2})^n dx
�@= �� t/{aa�sin(x)^2 + bb�cos(x)^2 -t} dx
�@= �� t/{(aa-t)sin(x)^2 + (bb-t)cos(x)^2} dx
�@= t/��{(bb-t)(aa-t)}��dy�@{ �� ��{(aa-t)/(bb-t)}�tan(x) = tan(y)}
�@= t/��{(bb-t)(aa-t)} y
�@= t/��{(bb-t)(aa-t)} arctan(��{(aa-t)/(bb-t)}�tan(x)),
������ ���F0����/2, >>827
���̖��̏o�T��
ttps://kconrad.math.uconn.edu/blurbs/analysis/gaussianintegral.pdf
�ɂ���1940�N��̕����̕����炵�� �O>>817
>>828�ȂɌ����Ă��B
���ׂĂ̏ꍇ���̂��̏ꍇ�̐��ł����Ă邶��Ȃ����B >>831
���̕��̊m���̖��͐�p�X��������̂ŋc�_�͂�����łǂ���
���㐔�w�̓C���`�L���炯
https://rio2016.5ch.net/test/read.cgi/math/1567930973/ >>822
a>0, b>0 �̎�
�Eab+1�ȏ�
�@n-a, n-2a, ����, n-ba (b��)�̂����ꂩ�� b�̔{���B
�@n-b, n-2b, ����, n-ab (a��)�̂����ꂩ�� a�̔{���B
�@�Y���Ȃ��B
�Eab�ȉ�
�@1��X��b-1,�@1��Y��a-1,
�@aX+bY �� a(b-X)+b(a-Y) �̃y�A�̘a�� 2ab.
�@����� <ab, ������ >ab. (=ab �͂Ȃ�)
�� (a-1)(b-1)�̔����� <ab �ł���A�܂��d�����Ȃ��B
�� �Y������̂� ab - (a-1)(b-1)/2 = (a+1)(b+1)/2 -1 �B�@>>823 >>831
�ہi��
�P�̏ؖ����܂������Ӗ��s�����i��
�C�i��A���O�̕ςȏؖ��𗝉��ł��҂̓C�i���i�� �O>>831
>>817�V���v���Ŕ��������̉�@�B�����Ƃ����R�ŁA�킩��Ȃ��l�X���~������method�B���Ƃ��o��҂�̓_�҂ɗ���͂��Ȃ��Ă��A�����Ƃ��ꂩ�ɓ͂��͂��B >>824
��������
�@G(t) = ��[n=1,��] c[n] t^n
�Ƃ����B
�@-{(G^3)/(2tt)}{tt�[1/G(t)^2 - (2/��)^2]} "
�@= G" - (3/G)(G')^2 + (4/t)G' -(G/tt){1 -(2G/��)^2}
�@= 0
���
�@1/G(t)^2 - (2/��)^2 = (t�̈ꎟ��)/tt,
�@G(t) = (��/2) t/��{(bb-t)(aa-t)}, C[n,k]=n!/((n-k)!k!)�Ƃ���Ƃ�
��[n=1,��] (-1)^(n-1)/(n^2 (2n-1) C[2n,n]) = ��^2/6 - 5log^2((1+��5)/2)
�������B ���2�̏���䊐�a������A���̈�ӂ_�����_�܂ő��䊐������������L����Ƃ��A���䊐��̐��T�p�`�̖ʐς����߂�
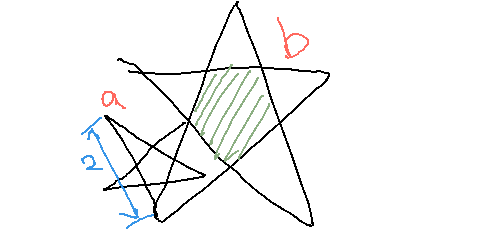 ���`���ɂ���
���`���ɂ���
���_�`��_�̋����� 2,
���܊p�`�̕Ӓ��� 2/��,
�ʐς� 5cot(��/5) /��^2
�@= ��(25+10��5) /��^2
�@= 6.8819096/��^2
�@= 2.62865556
�� = (1+��5)/2 = 1.618034�@�@(������) 0.9999...��1�Ƃ͐���Ȃ��悤�Ȏ�����̃n�E�X�h���t�ʑ���Ԃ��߂�
����������a_n�ɑ��āA�n�E�X�h���t�ʑ����X�ɂ�����lim(n����)a_n=����X�̒�`�́A
�C�ӂ̃��̊J�ߖT�ɑ��āA���鎩�R��N�����݂��āAn��N �Ȃ���̊J�ߖT��a_n���܂܂�� �Ƃ������Ƃł���
�����
0.999...9(9��n��)=a_n�Ƃ��A
0.999...:=lim(n����)a_n�ƒ�`���� >>841
�ʑ�f:R��R��
f(x)=x+1 (x��Z), x(otherwise)
�Ƃ���T���ɂ��ʏ�ʑ��̈����߂��Ƃ����
f(lim[T�ʑ�](1-1/10^n))
=lim[�ʏ�ʑ�]f(1-1/10^n)
=lim[�ʏ�ʑ�](1-1/10^n)
=1
���
lim[T�ʑ�](1-1/10^n))=0 >>842
�f���炵�� �����đ���
>�Ƃ���T���ɂ��ʏ�ʑ��̈����߂��Ƃ����
��
�Ƃ���T��f�ɂ��ʏ�ʑ��̈����߂��Ƃ����
���Ă��Ƃ���ˁH
�ꉞ�p�ӂ��Ă��̂͂���Ȋ���
d(x,y)= |x-y| (x,y��(0,1) �܂��� x,y��(0,1)^c)
,|1-x-y| (x��(0,1) ���� y��(0,1)^c)�܂��� (y��(0,1) ���� x��(0,1)^c)
�Ƃ����d��R��̋����ɂȂ��Ă��̋����ʑ��̏�ł�0.999...=0�ƂȂ� >>831
�ۂƂ��� ���R���肯�� �Ẳʂā@�@�@ �@�c�����I�q (�Îs)
�@�@�@�����V�� (2017/Oct/02)
�۔ۂ� ����� ��̓��̑̉��@�@�@�@�@�@�r�c���q
�۔۔� �S�Ղ̔� ��(���Y)������@�@�@�@������j
�@�@�@��W�w�V�҂��՞فx �[��p���� (2015/Oct)�@2860�~ (0,1)^c (x��0 �� x��1) �͂��̂܂܂�
(0,1) ���t�����ɂ����ł����邩�B d(x,y) = | g(x)-g(y)|
g(x) = x + (2x-1)[ x(x-1)/(xx-x+1) ]
�Ƃ� >>838
f(x)=��[n=1,��] x^(2n)/(n^2 C[2n,n]) �ƒu��
y=f(x)�͔��������� (4-x^2)y''-xy'=��(4-x^2)(��(4-x^2)y')'=4 ���������������
f(x)=2(arcsin(x/2))^2
���̘aS��
S = ��[0,1] -f((��-1)x)/x^2 dx
�@= 2��[0,1] (arcsinh(x/2))^2/x^2 dx
�@�c x=2sinh(t)�ƒu����2���ϕ�
�@= 2��[0,log��]{log(1+e^(-t))-log(1-e^(-t))}dt - 8(log��)^2
�@�c log(1�}x)��W�J���č��ʐϕ�
�@= -2{Li2(1/��)-Li2(-1/��)} + 2{Li2(1)-Li2(-1)} - 8(log��)^2
�����Ƀ�=(1+��5)/2, Li2(x)=��[n=1,��] x^n/n^2
Li2(x)��
�ELi2(1) = ��(2) = ��^2/6
�ELi2(-1) = -(1/2)��(2) = -��^2/12
�ELi2(x)-Li2(1-1/x) = ��^2/6 - log(1-x)log x + (1/2)(log x)^2
����(�Ō�̎���x��1�Ő��藧���ƂƗ��ӂ̔��������������Ƃ���킩��)
���̎���x=1/�ӂ�����������̊W1-��=-1/�ӂ���
Li2(1/��)-Li2(-1/��) = ��^2/6 - (3/2)(log��)^2
�����
S=��^2/6 - 5(log��)^2 �ޑ�: ��[n=1,��] (-1)^(n-1)/(n^3 C[2n,n]) = (2/5)��[n=1,��] 1/n^3 �������B >>849
�A�y���[�̌���
�@��(3) = ��[n=1,��] 1/n^3 = 1.202056903159594284����
�ǂ�����ďo����ł��傤�ˁB
���Z�~�����u���̐��E�v���{�]�_�� (1982) p.147�`
(�֑�)
��(3) = ��[n=1,��] 1/n^3
�@�@= 5/4 - ��[n=2,��] 1/{n^3�(n^2 -1)}
�@�@= 1 + ��[n=1,��] 1/{n^3�(4n^4 +1)}
�@�@= 77/64 + ��[n=2,��] 4/{n^3�(n^2 -1)(9n^4 + 3n^2 +4)}
�@�@�@= 9/8 + ��[n=1,��] 4/{n^3�(9n^8 + 18n^6 + 21n^4 + 4)}
�@4n^4 +1 = (2nn+1)^2 - (2n)^2,
�@9n^8 + 18n^6 + 21n^4 + 4 = (3n^4 +9nn +2)^2 - {6n(nn+1)}^2,
>>850
�@�������B(e = 2.718281828459045���� (�l�C�s�A��) �Ȃ��) >>848
�@xy '= ��[n=1,��] 2/(n�C[2n,n])�Ex^(2n),
�@y " = ��[n=0,��] 2(2n+1)/((n+1)�C[2n+2,n+1])�Ex^(2n)
�@(4-xx) y " = ��[n=1,��] {8(2n+1)/((n+1)�C[2n+2,n+1]) - 2(2n-1)/(n�C[2n,n])}�Ex^(2n)
�@�@= ��[n=1,��] {4/C[2n,n] - 2(2n-1)/(n�C[2n,n])}�Ex^(2n)
�@�@= ��[n=1,��] 2/(n�C[2n,n])�Ex^(2n),
�����
�@(4-xx) y " - xy ' = 0.
�@x = 2sin�Ɓ@�Ƃ�����
�@(d/d��) = ��(4-xx)�(d/dx)
��ӂ��
�@(d/d��)^2 y = 4,
�@y = 2��^2, >>852
�@1/��(4-xx) = ��[n=0,��] 2 C[2n,n] (x/4)^(2n),
�@arcsin(x/2) = ��[n=0,��] 2 C[2n,n]/(2n+1) (x/4)^(2n+1),
2�悷��� C[2n,n] ������ɗ���B >>848 ���
f(ix) = -2{arcsinh(x/2)}^2 = -2{log[(x+��(xx+4))/2]}^2,
��(3) = ��[0,1] (-5)f(ix)/x dx, �@1/��(4+xx) = ��[n=0,��] 2(-1)^n C[2n,n] (x/4)^(2n),
��x�Őϕ�����
�@arcsinh(x/2) = ��[n=0,��] 2(-1)^n C[2n,n]/(2n+1) (x/4)^(2n+1)
�@= log[(x + ��(xx+4))/2] = -log[(��(xx+4) - x)/4], >>849 >>854
��[n=1,��] (-1)^(n-1) x^(2n)/(n^2 C[2n,n]) = 2(arcsinh(x/2))^2
���
S = 4��[0,1] (arcsinh(x/2))^2/x dx
�@�c x=2sinh(t)�ƒu�������ϕ�
�@= -8��[0,log��] t log(e^t - e^(-t)) dt
�@= -8��[0,log��] t {t - ��[n=1,��] e^(-2nt)/n} dt
�@= -(8/3)(log��)^3 - 4(log��)Li2(1/��^2) - 2Li3(1/��^2) + 2Li3(1)
������
Lik(x)=��[n=1,��] x^n/n^k
�ELik(x)+Lik(-x) = 2��[n:even] x^n/n^k
�@= (1/2^(k-1))Lik(x^2)
�ELi3(x)-log(x)Li2(x) + Li3(1-x)-log(1-x)Li2(1-x) + Li3(1-1/x)-log(-1+1/x)Li2(1-1/x)
�@= -(1/3)(log(x))^3+(log(x))^2log(1-x)+Li3(1)
��x=1/�ӂ������W��1-1/��=1/��^2,1-��=-1/�ӂ�p�����
(5/4)Li3(1/��^2)+(5/2)(log��)Li2(1/��^2) = -(5/3)(log��)^3+Li3(1)
�����
S = -(8/3)(log��)^3 - (8/5)(-(5/3)(log��)^3+Li3(1)) + 2Li3(1)
�@= (2/5)��(3) >>851
��(5)=��[n=1,��](-1)^n R(n)/C[2n,n] ���������W���̗L����R(x)���������
��(5)���������ł��邱�Ƃ��ؖ��ł���\�������邪�A���̋�̓I��R�͑��݂��邩�H �������ɖʔ������ł�����B�ȒP�ɉ����������Ȃ����ǁB ���a1�̋��ʏ�Ɏ��̒���1�̕Ȑ���`��
�Ȑ��ň͂܂�鋅�ʏ�̗̈�̖ʐς̍ő�l�����߂� >>859
�����C�����܂�
���ʏ�ł̕Ȑ��ň͂܂��̈�͓�o���邯��
�ʐς͂��̓�̓����������Ƃ��܂� >>859
�Ƃ肠��������1�̏��~�Ő��Ă݂�
���������̖ʐς�2��-��(4��^2-1)
�傫�����̖ʐς�2��+��(4��^2-1)
�����Ă��܂�Ӗ��͂Ȃ����ǂ����̐ς�1 ���������Ă��̎�̖��̉��͕K����ȗ��̋Ȑ��ɂȂ����肷��̂��ȁH �O>>835
>>859-860
�ő�̕Ȗʂ͉~��������A���̕\�ʂ���n��t{0��t��1-��(1-1/4��^2)}�܂Œ��S�Ɍ������Č@��A���̒n�_��ʂ鐅���ȉ~�Ղ̉~����t=0����1-��(1-1/4��^2)�܂ő����W�߂�ƁA
2��{0�`1-��(1-1/4��^2)}��(2t-t^2)dt
=2�\�\(�ϕ����s��)
=2��-��(4��^2-1)
�����������Ƃ��B >>863
���s���Ă���͂�܂����ǁA
���̉~���̕t�߂̒n�ʂ����ɑ��Ăǂꂾ���X���Ă͂邩
�悤�l���͂�����C�i�͂�Ȃ������͂��ǂ��� �����ϕ��ɂ��
I = ���{t(2-t)} dt
�@= (t-1)��{t(2-t)} + ��(1-t)^2 /��{t(2-t)} dt
�@= (t-1)��{t(2-t)} + ��1/��{1-(t-1)^2} dt - I
�@= (t-1)��{t(2-t)} + arcsin(t-1) - I,
��
�@I = (1/2)(t-1)��{t(2-t)} + (1/2)arcsin(t-1), ���a 1/(2��) = 0.1591549431 �̏��~�ŒP�ʋ�����Ă݂�B
���̒��S���珬�~�ɐ��������낵�A���̌�����z���Ƃ����
(�\�ʐ�) = 2��|��z|
�@= 2��{1 - ��[1 - 1/(4��^2)] }
�@= 2�� - ��(4��^2 - 1)
�@= 0.080087887
�܂�
�@arcsin(1/(2��)) = 0.1598346264 ���͋��̕\�ʂ̗̈�D�ɂ���
D�̖ʐ�=3�~(D�ƒ��S�̓ʕ�̑̐�)�����a
���g���ƍ��Z���ł��������肷��B >>861
>>863
>>866
���_���猾���Ή~�Ő����ł��� �ő含�̏ؖ������肢���܂�
�q���g�̓K�E�X�E�{�l�̒藝�ł� >>859-860
�\�ʐ�=2��(2t-t^2)^(3/2)/(3/2)(2-2t)
=2��(2t-t^2)^(3/2)/3(1-t)�\�\�@
�}��`���ƁA
t=1-��(1-1/4��^2)
1-t=��(1-1/4��^2)
=(1-1/4��^2)^(1/2)�\�\�A
t^2=1-2��(1-1/4��^2)+1-1/4��^2
=2-2��(1-1/4��^2)-1/4��^2
2t-t^2=2-2��(1-1/4��^2)-{2-2��(1-1/4��^2)-1/4��^2}
=1/4��^2�\�\�B
�@�ɇA�B��������ƁA
�\�ʐ�=2��(2t-t^2)^(3/2)/3(1-t)
=2��(1/4��^2)^(3/2)/(1-1/4��^2)^(1/2)
=2��(1/4��^2)^(3/2)/(1-1/4��^2)^(1/2)
=2��(1/4��^2)��(1/4��^2)/(1-1/4��^2)^(1/2)
=(1/4��^2)/(1-1/4��^2)^(1/2)
=1/2��(4��^2-1)
=0.0256573341�c�c
�O>>863�����Ă�̂��ȁH �����Ă�B
���ʂ̂������s�ȕ��ʂ̊Ԃɂ��镔����
�@(�\�ʐ�) = 2��r�|��z|
�@��z�F���ʂ̊Ԋu
�@r�F���ʂ̔��a �O>>869
���a1�̋�����f�ʂ̎�����1�̌����������Ƃ�����A����̖ʐς́A
��(1/2��)^2=1/4��
�\�ʐς͂����菭���傫���Ȃ��Ƃ����Ȃ��B
�O>>869
�\�ʐ�=[(2t-t^2)^(3/2)/3(1-t)](t=0�`1-��{1-��(1-1/4��^2)}�\�\�@
t=1-��(1-1/4��^2)
t^2=1-2��(1-4��^2)+1-1/4��^2
=2-2��(1-1/4��^2)-1/4��^2
2t-t^2=2{1-��(1-1/4��^2)}-{2-2��(1-1/4��^2)-1/4��^2}
=2-2��(1-1/4��^2)-{2-2��(1-1/4��^2)-1/4��^2}
=1/4��^2�\�\�A
1-t=��(1-1/4��^2)�\�\�B
�@�ɇA�B��������ƁA
�\�ʐ�=(1/4��^2)^(3/2)/3��(1-1/4��^2)
=(1/4��^2)��(1/4��^2)/3��(1-1/4��^2)
=1/3�8��^3��(1-1/4��^2)
=1/12��^2��(4��^2-1)
(��1/4�ł����Ă�̂��ȁH) �����Ă�B
(�\�ʐ�) = 2��|��z|
= 2��{1 - ��[1 - 1/(4��^2)] }
> 2��{1 - [1 - 1/(8��^2)] }
= 2��/(8��^2)
= 1/(4��)
= 0.079577471546 �O>>871
>>859-860
�\�ʐρ�1/4��=0.0795774715�c�c
�c��݂̂Ԃ��\�ʐς͒f�ʐς��傫���B
0.08���炢�ɂȂ��Ȃ����ȁH�@������������0.08�����邩���B �O>>873
�ǂ������0.08�������H
>>859-860 �O>>875
�~����0����1�܂ő����W�߂�����ł����Ă�Ȃ��́H ������ϕ����ĖʐςɂȂ�
�͕��ʂ܂ł̘b�B
��Ԑ}�`�ł��ɂ͂��ꂾ���ł̓_���B �O>>875
>>876���̂̕\�ʐς��ēy��݂����ɐςݏd�˂ăo�E���N�[�w���@�ł��Ȃ��́H �O>>878�O�X>>876
>>877���Ⴀ�ǂ������0.08������v�Z�������H�@�o�E���N�[�w���@���Ƃ�����v���Ă��B�ǂ���Ŏ������Ƃ��Ӗ��킩���킯���B
>>859-860 >>878
�����ł��������邪�ł��Ȃ����̂�����B
���ʂ̏ꍇ�͕����ł���B
����h�Ő��Ăł���ʂ̒�����l�A���̔��a��R�Ƃ���
��l R/ ��(R^2-h^2) dh
���v�Z����Ώo��B
�� ���ʑS�̂̏ꍇ��l=2��(R^2-h^2)������
��[-R,R]l R/ ��(R^2-h^2) dh
=�� [-R,R] 2��R dh
=4��R^2
����������B
���ʂ� �e������ϕ��f �ł͂łȂ��B
�������q�����������ŋ��ʂ��ĂȂ��Ɩ����B >>879
�C�i���ɂ͂�������������������₷���͂���
���̂̃X�C�J��炪�����܂ܓ��������ŗ�ɂ��邱�Ƃ��l����
����ƁA�X���C�X�������̌����͓����͂��Ȃ̂ɁA�ΐF�̔�̕��͒[�̂ق��قǍL���͂���
���Ă���͉��̂ł��傤�H�@
�����ėΐF�̔�̕��͎��̌��݂̉��{���炢����ł��傤���H �O>>879
����1�̐���̔��a�́A
1/2��
�s�^�S���X�̒藝���A
���a1/2�̉~�̒��S����A���a1�̋��̒��S�܂ł̋����́A
��(1-1/4��^2)
(���������)
�\�ʐς͎����𑫂��W�߂��̂��A
�\�ʐ�=2��{1-��(1-1/4��^2)}
�����͂Ȃ��
���a1/2�̉~�̒��S����A���a1�̋��̒��S�܂ł̋���
��2���|���Ď���1�̓��������̋��̂̕\�ʐς��o��H >>882
> �s�^�S���X�̒藝���A
> ���a1/2�̉~�̒��S����A���a1�̋��̒��S�܂ł̋����́A
> ��(1-1/4��^2)
> (���������)
�ǂ����H
> �\�ʐς͎����𑫂��W�߂��̂��A
> �\�ʐ�=2��{1-��(1-1/4��^2)}
�\�ʐ�=��[��(1-1/4��^2),1] 2��(1-h^2)/��(1-h^2)dh
�ǂ̈ܓx�̓_���܂ނ������Ō��܂����Ⴄ�̂��B
�ӊO�ɃI�����Cw �O>>882
>>883
��(1-h^2)/��(1-h^2)dh
�����2�ƁA��������h�̒n�_�Ő����ɐ������a���A�|�����킹�ďo������������(1-1/4��^2)����1�܂ő����W�߂Ă�Ǝv����ł����A�Ȃ����q�ƕ��ꂪ�����Ȃ�ł��傤�H
(����/����)dh�ɂ��������Ȃ��B
����
�\�ʐ�=2��[��(1-1/4��^2),1]dh
=2��{1-��(1-1/4��^2)}
�ł����ł���ˁH �O>>884�Â��B
2�ƁA��������h�̒n�_�Ő����ɐ������a���A�|�����킹�ďo�����������A
��(1-1/4��^2)����1�܂ő����W�߂�ƁA
�\�ʐ�=2��[��(1-1/4��^2),1]dh
=2��{1-��(1-1/4��^2)}
=2��-��(4��^2-1)
dr����Ȃ���dh���B�����W�߂�����ɂ����������̂�dh�ɂ���B�킩�����B ��>���̑O�ɂ܂��A���R��x�y�z�Ƃ͕ʂ̎��� X�Y�Z��x:y:z=X:Y:Z�����藧�悤�ɉ��肵�āA����X�Y�Z�̏�� Z=X+r �Ƃ����Ă���c�_����̂Ȃ�Ηǂ��B
�����݂܂���B���̕��@�ŁA���܂������ł��邩���A�킩��܂���B
���̕��@�Ő����ł��Ȃ���Ώؖ��ƔF�߂܂���B >>868
�Ȑ��̓����ɋɎ����Ƃ�B
�Ȑ����ɍ��W�ŕ\�킵����(*)��
�@�� = f(��) ��0,
�@f(0) = f(2��),
�Ƃ���B
����L�Ɩʐ�S��
�@L[f] �� ��[0,2��] sin(f(��)) d��,
�@S[f] = ��[0,2��] {1-cos(f(��))} d��,
�ƕ\�킹��B
�������� L[f]=1 �̉��ŔĊ�
�@I[f;��] = S[f] - �ɥ(L[f]-1),
��f�ŕϕ������
�@��I = ��[0,2��] {sin(f(��)) -��cos(f(��))} ��f d��,
�C�ӂ� ��f �ɑ��� I[f;��] ���◯�l�ƂȂ邱�Ƃ���
�@sin(f(��)) -��cos(f(��)) = 0,
�@f(��) = arctan(��) = arcsin(1/(2��)),
*) �����q�_�q�_������A�����L���čL���邱�Ƃ��\�B �O>>885
>>866�͓����͂����Ă�Ǝv�������ǁA�r�����Ԃ��Ƃ�ł��B
���߂�>>885���ꂮ�炢�͏����Ăق��������B�ǂ������0.08�������r�����K�v���Ǝv���B
2��-��(4��^2-1)=0.080087887�c�c��0.08
�C���e�O�����A�ϕ���ԁA�ϕ����̃l�b�g��ł̏������͍ĔF���ł����B
��[�ϕ����](�ϕ���)dh >>888
���肪�Ƃ��������܂�
�Ȑ���xy���ʂɎˉe�����Ƃ��ɉ~�Ɠ����ɂȂ�Ƃ��āA
�ɍ��W��=f(��)�̃Ƃ�xy���ʂɂ�����Ίp���Ǝv���̂ł����ӂ͂Ȃ�̗ʂł��傤�� xy���ʂɎˉe�����Ƃ��̓��a�ł����H ����Ƃ�xz�����̕Ίp�ł��傤��
����Ǝ������s�����ɂȂ��Ă܂������̂܂ܕϕ����Ĉ�����̂ł��傤�� >>890
���Ԃ�O�����ɍ��W�̎����͌��܂��Ă���(x,y,z)=(r sin��cos��,r sin��sin��,r cos��)���Ǝv��
���̂Ƃ�
L = ��[0,2��] ��(sin^2(f(��))+(f'(��))^2) d��
S = ��[0,2��]��[0,f(��)] sin�� d��d��
= ��[0,2��] {1-cos(f(��))} d��
�͍����Ă� �_���N�C�Y
�S��������A�p�[�g�Ƃ��̉Ǝ�A�����ĂV�l�̊w���Ŏ���������B
�w���͍���c�̌�A�A�p�[�g�̑O�Ńg�����v(�W���[�J�[����)����P�������āA�����̃J�[�h�͌����ɂ��݂��̃J�[�h���m�F����B
���̌�A�p�[�g�ɓ���A���������镔�����S����P�I��ň�ĂɈړ�����B
�Ǝ�͑S�Ă̕����̊w���̃J�[�h�̃}�[�N�i�n�[�g�A�X�y�[�h�Ȃǁj���m�F���A�}�[�N���Q��ވȏ㑶�݂��镔�����������ꍇ�A�e�w���ɓ��������ɂ���w���̃J�[�h�����݂��m�F��������ŁA�܂���Ăɕ������ړ�������(���̂Ƃ��ړ����Ȃ��Ă��悢)�B
������A�قȂ�}�[�N�����݂��镔�����Ȃ��Ȃ�܂ŌJ��ւ����B
������ɂ���āA�J�[�h�̔z���ɂ�����炸n��ړ�����Ύ������I����������Ƃ��An�̍ŏ��l�Ƃ��̎��̍����l���Ă��������B����������c��́A����̃}�[�N������ׂ�����A�ڂȂǂō��}�𑗂邱�Ƃ͂��߁B >>892
�Ȃ�ق� ���肪�Ƃ��������܂� �������ɂ��̃p�����[�^(��,��)�Ȃ炻���Ȃ�܂���
�Ȃ̂Ŗ��͕s�����ŕϕ���������̂��ǂ����ł��� >>893
n=0
���
(1) ���O�Ƀ}�[�N���Ƃ�0�`3�����蓖�ĂĂ���
(2) �����ȊO�̐l�̃}�[�N�̑��a��4�Ŋ������]��+1�����ɓ���
(�S���̃}�[�N�̑��a)-(�����̃}�[�N) mod 4 �́A�}�[�N�������l�Ȃ瓯��������A
���ׂĂ̕����Ƀ}�[�N�������l���U�蕪������B >>894
�ǂ䂱�ƁH
�ŏ��l���Ƃ�Ƃ��ŕϕ���0�ɂȂ�Ƃ͌���Ȃ��H
����Ƃ��ŏ��l���Ƃ邱�Ƃ������Ȃ��ƃ_���ƌ������H >>896
���݂܂��� ���ȉ������܂���
�ŏ���
�����Ċ���
L[f] �� ��[0,2��] sin(f(��)) d��
�Ƃ��ĕs�����ŏ��������ă��O�����W���搔�@�ŕϕ����Ă܂����A���̕ϕ�=0�Ƃ��Ƃ̔Ċ��̕ϕ�=0�ň�v���闝�R�͂Ȃ낤���Ǝv�����̂ł���
�ɂ����ł��ő�������߂�̂ł���ʼn�����̔Ċ��ōl����Ώ\���Ȃ�ł��� >>898
�K�E�X �{�l�g�����Ȃ������܂��B �P����X�܂ł̐����������ꂽ�J�[�h���ꖇ���A���v�㖇����BA,B,C�̎O�l�Ő����ăQ�[��������B
�Q�[���̐i�s�҂ł���A�͂܂��A�������ǂ�ȃJ�[�h�̑g�����������ɂǂ�Ȑ錾�����邩�ɂ��ẴA���S���Y�����yB��C�����Ɂz�`������A�㖇�̒����疳��ׂɘZ���������B
���̌�B���c��̒����疳��ׂɓ������AC���c��̈ꖇ�������B�O�l�Ƃ��A�J�[�h�̒��g�͑��l�Ɍ����Ȃ��B
A�͐���������`�����A���S���Y���ɏ]���Đ錾������B
���̂悤�Ȑi�s�ŃQ�[�������鎞�A�S�����������J�[�h�̑g�ݍ��킹���ǂ�ȏꍇ�ł����Ă����̏������S�Ė��������悤�ȃA���S���Y���͑��݂��邩�F
(1)B��C�̃J�[�h���m��ł���
(2)C�́A�����������Ă��Ȃ��ǂ̃J�[�h�ɂ��Ă��AB������������Ă��邩�ǂ����m��ł��Ȃ�
��A�́AB�����ɏ���`������悤�ȓ`�B��i�͎����Ȃ����̂Ƃ���B
���錾�̓��e�̓A���S���Y���݂̂ɂ���Č��܂�̂ł����āA�Ⴆ��
�u�������������J�[�h�̑g�Ɋւ��鎖����錾����v
���̂悤�ȁA�J�[�h�̑g�ɑ��Đ錾����ӂɒ�܂�Ȃ����͕̂s�B >>900
�Ӗ����������B
�Ⴆ�������錾�Őɂ��������������Ȃ��錾�͂ǂ�Ȃ̂�����́H �Ⴆ��
�����̎����Ă�J�[�h�̍��v��9�Ŋ������]���xx�ł���
�݂����Ȃ̂͂���Ȃ�H >>902
�����Ƃ��� 9, 10, 11 �̂����ꂩ���g�����ꍇ�͏���������炵��
8�ȉ��ł�B��C�����ł��Ȃ��ꍇ������
12�ȏ�ł�C��B�����ł���ꍇ������ >>901
�Ⴆ�� >>902 �̃A���S���Y���Ƃ��A���Ƃ́w�����������ĂȂ��ŏ��̃J�[�h�̐����́����ł���x�Ƃ��̓A���S���Y���Ƃ��ċ�������B
�����̏ꍇ�́A�ǂ�����ɂ����������͖������Ȃ��̂�����ǂ��c
>>902 �̏ꍇ�ɂ��čl����ƁA�Ⴆ��C��1���AB��3,5���z��ꂽ�Ƃ���ƁA
C��A�̐錾����AB�̃J�[�h�̑g�ݍ��킹�Ƃ���(2,6),(3,5),(8,9)�̂ǂꂩ�ł��邱�Ƃ��킩��B
����������ł�B��4��7�������Ă��Ȃ����Ƃ�C�ɂ킩���Ă��Ă��܂����߁A���Ƃ��Ă͕s�K�ƂȂ�B ���������A���S���Y���Ƃ��ċ�����Ȃ��̂́A�Ⴆ��
�u�����������Ă��Ȃ��J�[�h�̐������ǂꂩ������v
�݂����Ȃ��́B
�܂肱�̖��ł̃A���S���Y���Ƃ����̂́AA�ɔz����J�[�h�̑g�S�̂̏W���i�L���W���j����A���{��̕�����S�̂̏W���ւ̎ʑ��A�̂悤�ɔF�������Ă�����������ƁB
�������l�悪���{��̕�����łȂ����R���S�̂̏W���Ƃ��ł����Ă��ǂ��B
�wA���ǂ�ȃJ�[�h�̑g�����������ɂǂ�Ȑ錾�����邩�x���AB��C�ɂ��m��ł���Ƃ������Ƃ��́B ���ł킴�킴����ȉ�肭�ǂ����ݒ�ɂ����̂��Ƃ����ƁA�Ⴆ��
�y�P����V�܂ł̃J�[�h��A,B,C�O�l�ɂ��ꂼ��3,3,1�̖����Ń����_���ɔz��A
A��B���w�����̎�D�Ɋւ��鎖���x��錾���邱�Ƃ�A��B�����ɎO�l�̃J�[�h�̓�����m�肳����ɂ͂ǂ�����Ηǂ����z
�Ƃ������ɂ�����
�yA��B���A�����������Ă���J�[�h�̑gxyz�ɂ��āwA�܂���B�̂ǂ��炩��xyz�Ƃ�����D�ł���x�Ɛ錾����Ηǂ��z
�Ƃ����ʉ��A�݂����Ȃ̂�r�����邽�߂Ƃ������ƂɂȂ邩��
�����̎�D��xyz�̎��ɂ���錾���w�����̎�D��pqr�ł���x�Ƃ����\�����܂�ł���Ȃ�A���̐錾�͎�D��pqr���������ɂ���錾�Ɠ����A�Ƃ������Ƃ�S�ۂ��������� >>905
>���{��̕�����S�̂̏W���ւ̎�
���w�ɂȂ�Ȃ������� >>907
�������{��i�Ŏg�������j�̒莮���Ƃ����o�R�������Ȃ���A���̌�ɏ������ʂ�w���R���S�̂̏W���x�ւ̎ʑ��ł��ǂ����A�����S�̂����Ă���
���ۂ̂Ƃ��� >>902 �̃A���S���Y���́A�J�[�h�̘Z���g�S�̂̏W������{0,1,�c,8}�ւ̎ʑ��ɂȂ��Ă��� >>908
�Ȃ������`���Ă����ׂ�
���w�Ȃ�� >>909
�����W���������߂���̒l��Ƃ��Ă̕�����S�̂̍\���͖₤�ĂȂ�����A�����Ԃɍ������莮���Ƃ��������������肾��������
������ƌ��t���炸�ŕs�e�����������m��Ȃ��A���܂� >>910
�ł��܂������������͂킩�����B
�Ȃ��Ȃ��Ƀ��Y�C�B �ł�������
���
X={1,�d,9}�̔C�ӂ̎O��{i,j,k}�ɑ��AX�̎O�������W������Ȃ�W��S�ňȉ��̐����������̂����݂���B
(1) {i,j,k}��S
(2) �C�ӂ�X�̓�x,y�ɑ�{x,y,z}��S�ƂȂ�X�̌�z�����傤�ǂЂƂ��݂���B
(��) L/K��̂̒P��Galois�g��ŃK���A�Q��3���z�g��̓�̒��ςƂȂ���̂ɂƂ�B
L=K(��)�Ƃ��A��1,�d��9�����̋������Ń�i,��j,��k��
[K(��i,��j,��k):K]=3
�����悤�ɓY�������Ă����B
��̓I�ɂ̓K���A�Q�̈ʐ�3�̌��Ђ��Ƃ胿i=���A��j=�Ѓ��A��k=�ЃЃ��Ƃ���Ηǂ��B
S={{x,y,z}| [K(��x,��y,��z):K]=3}
�����߂鐫��������
A��B,C�ɗ^������Ƃ���B,C�ɓn�����O��i,j,k�ɑ��ĕ��̏�������S���Ƃ肱����l�ɓ`����B
B��3���̂���2���������Ă邩��c�����m�肷�邱�Ƃ��ł���B
����C�ɓn��������i�Ƃ���i�ȊO��l�����Ƃ����Ȃ��Ƃ����m���Ƃ���{i,l,m}��S�ƂȂ�̂�C��l���܂܂�Ȃ��ƌ��_�t���鎖�͏o���Ȃ��B
����i���܂�S�̌����K��l���܂ނƂ����i,l�ȊO�̈قȂ�p,q���Ƃ�Ƃ���������{i,p,l},{i,q,l}���Ƃ���S�̌��ƂȂ�����ɔ�����B
�����S��i���܂�l���܂܂Ȃ��������̂�C��l���܂܂��ƌ��_�t���鎖�͏o���Ȃ��B�� >>912
�\�����Ă�W���Ƃ������������Z�������Ă�Ȃ��ǁA
�����m�F���ׂ����Ƃ��c
�e�g{i,j,k}�ɑ��ĕ��̏�������S�̑��݂͌����邯��ǁA
���̂悤��S�͈�����ł͂Ȃ�����A�A���S���Y���Ƃ��ċ�����邽�߂ɂ�
�u�e�g{i,j,k}�ƁA����ɉ�����B,C�ɓ`����W��S�̑Ή��W�v�����炩���ߌ��߂ċ��L����K�v������B
�i�����Ă��̎����ӂ��Ȃ���Ȃ�Ȃ��̂��A
�Ⴆ��������{1,2,3}�ɑ��Đ錾�����S_0���A{1,2,3}�݂̂ɑ��Đ錾�������̂������Ȃ�A
A��S_0��錾�����u�ԁAB�����łȂ�C���S���̓��m��ł��Ă��܂����ƂɂȂ�A�Ƃ������ƁB�j
�܂��A�錾����S���ABC�ɓn������D�̑g�Ƃ��Ă��蓾��\���ꗗ�\�Ƃ��đ������������̂ł���A
S�̔C�ӂ̌�P={p,q,r}�ɂ��āABC�ɓn������D��P�������ꍇ�̐錾��S�ł���K�v������B
�i�������̑gP��P'�Ő錾�����W��S��S'���قȂ������̂ł���Ȃ�A
S�Ƃ����錾�����邱�Ƃ�P'�̉\�����r������Ă��܂��j >>913
�Ȃ�قǁB
S�̑I������̃A���S���Y���Ȃ̂ł�����B,C�ɏ�����Ȃ��悤�ɂ��Ȃ��ƃ_�����Ă��ƂˁB
���Y�C�d�d >>900
��������
�C 123 145 167 189 246 258 279 349 357 368 478 569
�� 124 135 168 179 238 259 267 347 369 456 489 578
�n 125 134 169 178 236 247 289 358 379 459 468 567
�j 126 137 148 159 235 249 278 346 389 457 568 679
�z 127 136 149 158 239 248 256 345 378 467 579 689
�w 128 139 146 157 237 245 269 348 356 479 589 678
�g 129 138 147 156 234 257 268 359 367 458 469 789
A�́A�����̎����Ă��Ȃ�3�����A���̐��\�̂ǂ̍s�ɏ�����Ă��邩��錾����
�EB�́A���̐��\�̐錾���ꂽ�s�Ǝ����̃J�[�h����AC�̃J�[�h���m��ł���
�EC�́A���̐��\�̐錾���ꂽ�s�Ǝ����̃J�[�h����ł́A�����������Ă��Ȃ��ǂ̃J�[�h�ɂ��Ă�B������������Ă��邩�ǂ����m��ł��Ȃ� >>915
�����A�������B
�ǂ�����č�����́H >>915
��)B��2��4�AC��7���������ꍇ
A�͎����̃J�[�h��2��4��7���Ȃ����Ƃ��킩��̂Łu�n�v��錾����(B��C���ǂ̃J�[�h�������Ă��邩�͒m��Ȃ�)
B�́A�n�̍s��2��4���܂ޑg�ݍ��킹��247�����Ȃ��̂ŁAC��7�������Ă��邱�Ƃ����ł���
C�́A�n�̍s��7���܂ޑg�ݍ��킹��178�A247�A379�A567��4�ʂ肠�邽�߁A���ꂾ���̏��ł�7�ȊO�̂ǂ̃J�[�h�ɂ��Ă��A����������Ă��邩�ǂ�������ł��Ȃ� >>916
�܂��ŏ���123����129�����ꂼ��̍s�ɐU�蕪���Ă����āA�s���Ɋ܂܂��ǂ̃y�A�����Ȃ��悤�ɑ��̑g�ݍ��킹��z�u���Ă������炱���Ȃ�������
���ƁA�O��Ƃ��Đ錾�̎�ނ�7�ʂ�B�����葽���Ă����Ȃ��Ă������Ȃ� >>918
�͋Z���I
������܂����w���ȁB >>919
�J�[�h�̖�����9�ȊO�̏ꍇ�H >>915
�吳���A���炵���c�I
{1,2,x}�̊���U�肾������悭�����܂Ŋ���������ꂽ�ˁc
���͎������ŏ��Ɍ��������͗͂킴�ŁA
�N�����Y��ȍ\�������Ă��ꂽ�烉�b�L�[���x�̂��Ƃ͍l���Ă����ǁA��͂����̂��ȁc
�ȉ��͗]�k
�g�ݍ��킹���w�̒��� BIBD (Balanced Incomplete Block Design) �Ƃ��������Ώۂ����邯�ǁA
���̖��́w�X���W���Ɋ܂܂��O�g�S�̂���Ȃ�W���́A����(9,3,1)-�f�U�C���ɂ�镪���x�����߂���ƌ���������ꂽ�肷��
���Ȃ݂ɂ��ꂪ�P����V�܂ł̃J�[�h�̏ꍇ�A(7,3,1)-�f�U�C���͑��݂��邯��ǁi�ŏ��̗L���ˉe���ʁj�A
(7,3,1)-�f�U�C���ɂ�铯���悤�ȕ����͑��݂��Ȃ����Ƃ��킩��i������ꉞ��v�Z�Ŋm���߂���j �]�k����
n��3�ȏ�̐����Ƃ��鎞�A��������(n,3,1)-�f�U�C�������݂��邽�߂̕K�v�\�������� n��1,3 (mod 6) �ł��邱�Ƃ��킩���Ă���
http://mathworld.wolfram.com/SteinerTripleSystem.html
n���W���Ɋ܂܂��O�g�S�̂���Ȃ�W����(n,3,1)-�f�U�C���ɂ�镪�����\��n�́A
n=3�i�����ȕ����j��n=9�i����̖��j���������ɂ͊m���߂��ĂȂ�����ǂ��A���������������Ċ��ɂ���Ă��肷��낤���c >>921
����
>>923
������ƈ�ʉ�����Ă�炵������
�A�h�z�b�N�ł͂Ȃ�����݂Ԃ��ł͂Ȃ�
��̓I�ȋ��ߕ�������Ǝv���� >>924
�u�f�U�C���v�ƌĂ�Ă�����̂Ɓu�����v�ƌĂ�Ă�����̂ł͂���������قȂ邩�ȂƎv��
(n,3,1)-�f�U�C���Ƃ����̂́An�p�`�̕ӂƑΊp���̂��ׂĂ��O�ӌ`�ʼnߕs���Ȃ������s�������Ɠ��^�ŁA
���̕K�v�����́An��3�ȏ�̊����nC2��3�̔{���Ƃ������ƂɂȂ邩��An��1,3 (mod 6)�ł��邱�Ƃ͗����ł��邵�A�\��������͂Ȃ��̂��낤���ǁA
�����ɂ��ẮA(n,3,1)-�f�U�C�������ł��ׂĂ̎O�ӌ`�̃p�^�[�����ߕs���Ȃ������s�������ɂȂ�̂œ�Փx�������āA���̑��݂�\�����@�͈�ؓ�ł͂����Ȃ���Ȃ����ȁB
�ނ���v�Z�@�����̖�肩�ƁB
�g�����l����Ȃ�A�Ƃ肠����n=13�̉��͑��݂���̂��ǂ����H ��ʉ��ɂ��Ă͎���wiki��Steiner triple systems�̌㔼�ŐG����Ă�B
https://en.m.wikipedia.org/wiki/Steiner_system
n=9�ł�up to iso�ňقȂ��������邻���ȁB
��n=15�ł͂ǂ����Ƃ�����肪�m��I�ɉ�����Ă�B
n=13�̏ꍇ���ؗ�ɖ������Ă�͓̂���Ė����Ȃ̂������I�ɖ����Ȃ̂��͓�B >>926
���肪�Ă�
�m���ɁA���������̂��ď��������̕����������Ă����Ȃ����ǂȂ�
������ʓI��6n+1�^�̐����ŕs�\���Ƃ����炻��͂���Ŗʔ������ǁA�����邩�ǂ����c
13C3=286�̌�����Ȃ�W�����A11��26���W���ɕ�������Ƃ�����A�\�ȏꍇ�̐�������
286!/((26!^11)*11!)��4.75*10^279
�ʂ�ɂȂ邩��A�R���s���[�^�[�ŒT������Ƃ�������ƌ����ǂ����@���l���Ȃ��Ƒ�ςȂ��ƂɂȂ肻�� �ʃX���ŏo�Ă����B
�������̂��ǂ����m��Ȃ�
xi ��n �̐��̐��Ƃ���
m(k)=(��(xi�̈قȂ�k�̐�)/c[n,k])^(1/k)
�Ƃ����Ƃ�
m(k)��m(k+1)
�������B
�s�����X���ł͉������Ă�̂��ȁH �k�}�N���[�����̕s�����l
�ł��ˁB���Z���w�̎���X��Part401 - 745 ������ň��p���Ă܂ˁB
�k�j���[�g���̕s�����l
�@P(k-1)P(k+1) �� P(k)^2�@�@�@�@������ P(k) = m(k)^k
����o���̂͂ǂ�����ʂł����A����̏o�����͂��낢��ł��B
�s�����X���̕��͒��ږ@�i�����Ȃ��j�ł����ʓ|�Ȃ̂ł����߂��܂���B
���̉e�������B
Hardy�ALittlewood & Polya: "Inequalities", Cambridge (1934) ��2.22 ����51-55
���Z�~�����F�u���w�̖��v ��(1)�W�A���{�]�_�� (1977)
�@��21 �̉���ł͎������p���Ă��܂��B�������g���܂�����r�I�Z���ł��B
Beckenbach & Bellmann: "Inequalities", Ergebnisse�p��, Springer-Verlag (1961) p.11 �����A�������s�����X���B
�Ƃ����ɘb��ɏ���Ă��̂ˁB
����[�ȁ[�Ƃ͎v�������ǁB �ϑԂǂ��� �����ł�����ˁB�i���_�ߌ��t�j ����ʕs������������Ƃ��܂��g���ƍs����ȁB �ǂ��������Ƃ��ˁH �������܂��I >>934
���̏ؖ��ʔ������nj㔼�����ʂ���Ȃ��̂��ȁH
�����Ă�̂�
���j�b�N���W��n��������P(x)��n-k���̌W����sk�Adk=sk/c[n,k]�Ƃ����B
P(x)=0�̉������ׂ�x<0�ɂ���Ƃ�(dk)^(1/k)�͒P�������B
��P'(x)/n�ɑ��ē��l�̍\����s'k�Ad'k���\��������k<n�ɑ���dk=d'k���������鎖��P'(x)=0�̉������ׂ�x<0�ɂ��鎖�������Ă�B
�ł��������炱�̎��_��k=n-1�Ƃ��Ă����C������B
�����Ă��̏ꍇ��am��gm�ňꌂ�I���̂悤�ȁB k=n �̏ꍇ
�@{d_(n-1)}^(1/(n-1)) �� (d_n)^(1/n),�@�@�@�@�����@(*)
�� am-gm �ňꌂ���낤���ǁAk<n �̏ꍇ�͂��̂܂܂���o�Ȃ��B
>>934 �̃~�\��n�̕������炷���ƁB
�@{d_1,d_2,����,d_(n-1)} ��ς����ɕ������� n-1 �Ɍ��炷�B
������J��Ԃ���
�@{d_1,d_2,����,d_k} ��ς����ɕ������� k �Ɍ��炷�B
����� (*) ��K�p����Ak<n �ɑ��Ă�
�@{d_(k-1)}^(1/(k-1)) �� (d_k)^(1/k),
���o��B �����������������ȁB
�܁A�ǂݕ����������������Ō㔼�Ȃɂ���Ă邩�͂킩�����B
�咣
���j�b�Nn��������p(x)=0�̉������ׂ�x<0�ɂ���A���̌W��n-k���̌W����sk�Ƃ��Adk=sk/c[n,k]�Ƃ����Ƃ��A1��k��n-1�ɂ�����d[k]^(1/k)��d[k+1]^(1/(k+1))�B
����������B
key��q(x)=p'(x)/n�Ƃ����Ƃ�q(x)�����j�b�N��������q(x)=0�̉������ׂ�x<0�ɂ���A���l�̍\����ek���\�������1��k��n-1�ɂ�����dk=ek�܂ŗe�ՁB
�����܂œǂ�ŁA�Ȃ�p(x)�̎����̋A�[�@�ŋA�[�@�̉��肪�g���Ȃ�k=n-1�̎��݂̂����������Ǝv���āA�����͂���Ȃɓ���Ȃ�����Ǝv���Č㔼���łȂ�������A�Ȃ�̎��͂Ȃ��A�㔼�͂��̏ꍇ�J�Ɏ����Ă邾���Ȃ̂ˁB
�I���Ȃ�܂�k=n-1�̎��͋A�[�@�p����amgm�ňꊇ�������Ƃ��āA���̌�A�[�@�ŏ������ȁB
n=2�̃P�[�X�ł͈ꊇ�����ς݂̃P�[�X�����Ȃ��B
n=l�ł�����Ƃ���n=l+1�̂Ƃ��͈ꊇ�����ς݂̃P�[�X�ƋA�[�@�̉��肪�g����P�[�X�����Ȃ��B���Ƃ��B
�܁A��̖��ł����B
���������ł����B >>929
�@���ږ@ (�����Ȃ�) �̊T�������B
n�ɂ��Ă̋A�[�@�ɂ��B
�@(n������k���̊�{�Ώ̎�)/C[n,k] = P(k),
�����x��lj�����
�@(n+1������k���̊�{�Ώ̎�)/C[n+1,k] = Q(k) �Ƃ����B
�X��
�@P(0) = Q(0) = 1,�@P(-1) = Q(-1) = P(n+1) = 0
�Ƃ���B�������
�@(n+1)Q(k) = (n-k+1)P(k) + k�P(k-1)�x,
��������Čv�Z�����
�@(n+1)^2 {Q(k)^2 - Q(k-1)Q(k+1)}
�@= (n-k)(n-k+2){P(k)^2 - P(k-1)P(k+1)}
�@+ (n-k)(k-1){P(k-1)P(k) - P(k-2)P(k+1)}x
�@+ (k+1)(k-1){P(k-1)^2 - P(k-2)P(k)}xx
�@+ {P(k) - P(k-1)x}^2,
�ƂȂ�B(�`���g�ʓ|����������Ƃ͉����g���ĂȂ�)
�A�[�@�̉��肩��
�@P(k-1)/P(k-2) �� P(k)/P(k-1) �� P(k+1)/P(k),
�ƂȂ�̂�
�@Q(k)^2 - Q(k-1)Q(k+1) �� 0,�@�@�@(�I) >>939
P��Q���ׂĂ鎮��P�̂Ƃ���trace���ȂƂ��Ă��ł����H
Q�̂���T�C�h��x(n+1)�̍���P�̑��ɂ͏o�Ă��Ȃ��̂͂��������̂ł́H >>940
sk=symmetricsumof x1�cxn
nCkPk=sk
tk=symmetricsumof xx1�cxn=xsk-1+sk
n+1CkQk=tk=xnCk-1Pk-1+nCkPk
(n+1)/(n-k+1)Qk=xk/(n-k+1)Pk-1+Pk
(n+1)Qk=xkPk-1+(n-k+1)Pk >>941
���Ax��n+1�����ڂˁBi see >>934 >>937 �̎Q�l��
�@�����N�ƁF�u�s�����v�@���w���[ (2012)�@�̒藝1.1.4(McLaurin) �����������ؖ��B
���������Ă�Ǝv�����ǃ_�������B
A��affine��ԁApi�Aqj��A�̓_���ui�Avj���d�݂Ƃ���B
f(p)��A��̍L�`�ʊ���qj��{pi}�̕ʕ�ɑ����d�ݕ��ς��������A���Ȃ킿��uipi=��vjqj�Ƃ���B
���̎���uif(pi)����vjf(qj)����������B
�����
���̐��̑g��xu�ɑ�f((tu))=exp(��tu log xu)�Œ�`���ꂽ�ʊ��ɓK�p������ł����C�������B �ȉ~ x^2/a^2 + y^2 =1 ��x�����S�ɉ�]�����ďo�����ȉ~�̂�D�Ƃ�, ���� y=�}p �ł���D��3�������܂�
3�ɕ������ꂽD�̑̐ς��������Ƃ�, |p|>1/4 �������Ă������� >>945
a=1�Ƃ��Ă悢�B
�����ׂ���
��[-p,p]��(1-y^2)dy=1/3�E4/3��|p|>1/4
�ł���
��[-1/4,1/4](1-y^2)dy<4/9
�ŏ\���B
LHS=47/96=0.489583333333�d
RHS= 0.444444444444�d
�ʁH ����0.1�{0.11�{0.111�{0.1111�{0.11111�{�c�c�Ƃ���B
�������̂Ƃ��A���^���̋Ɍ��l�����߂�B ���̏ؖ��̂ǂ����������������w�E����B
�g��1�{1/2�{1/3�{1/4�{�c�c
�@��1/2�{1/2�{1/4�{1/4�{1/6�{1/6�{1/8�{1/8�{�c�c
�@��1�{1/2�{1/3�{1/4�{1/5�{1/6�{1/7�{1/8�{�c�c���g
�䂦�ɂg���g >>948
���B����ɂ���
���B����̈Ӗ��ł́c�͐��ł͂Ȃ��ł�����A�s�����͐��藧���܂���
�I���ł� >>949�͎��⏭�N(��
���̏��N�͋�̓I�Ȗ��ɂ͓������Ȃ����o�J���N(��
���w�̒m�����o���邾���̏��N�ł���(�� ���B����͋��啶�w���Ř_���͎���o�ł̃g���f���{�ɏ������̂��ƏK���������ł�
������債�����ƂȂ���ł��� �������Ă��̏��N�͉��X�Ɩl�ɔS�����Ă���(��
2ch�ł��L���̔S�����ł���(��
�ŁA���ǁA���ɂ͓����Ȃ�(�� 0.999...=1�ł͂Ȃ�(��)�ƎU�X�����Ă����āA���X���ʂ̐��w�����o���Ă���Ӗ����킩��Ȃ���ł����ǖ{��
���w�I�ȓ����͂������ɏ����܂���
���B���w�I�ɂ�H��H�͖����łȂ��ŏI���ł�
���������������ƂɈ�ѐ����������ė~������ł����� >>953
����͎��⏭�N�ɑ��Č����Ă���B
�l�͂��̃X�����r�炻���Ƃ����Ӑ}�Ȃǂ܂������Ȃ��̂ł���B
���⏭�N�������ł������珑�����܂ł��B ���Ⴀ�����ɖ߂��ċc�_���܂��傤�� >>654
���̃X�����r�炷�ȃo�J
�S���L�`�K�C �ǂ��l���Ă��r�炵�Ă�̂͂��Ȃ��ł����(��)
0.999....��0.999...�����藧�Ǝv���Ă�l����������ł����X���b�h�ł͂���܂����H >>948
an<bn
�ł�
liman=limbn
�ƂȂ����Ƃ����邩��ł��� >>959
1�l�������Ȃ��̂����� (1)�3�ȏ�̔C�ӂ̐���n�ɑ�xⁿ+yⁿ��zⁿ��������̐����̑g(x,y,z)�͑��݂��Ȃ����Ƃ������B
(2)��C�ӂ̐��̐����̑g(x,y,z)�ɑ�xⁿ+yⁿ��zⁿ�����3�ȏ�̐���n�͑��݂��Ȃ����Ƃ������B
(3)�3�ȏ�̔C�ӂ̐���n�ɑ����鐳�̐����̑g(x,y,z)�����݂�xⁿ+yⁿ��zⁿ��łȂ����Ƃ������B
(4)3�ȏ�̔C�ӂ̐���n�ɑ��Axⁿ+yⁿ��zⁿ�������̐����̑g(x,y,z)�͑��݂��Ȃ����Ƃ������B (1)
������������(x,y,z)�����݂����Ƃ���ƁA
���Ȃ��Ƃ�
x^3+y^3=z^3 (a)
����
x^6+y^6=z^6 (b)
(a)^2=(b)���
(x^3+y^3)^2=x^6+y^6
������x^3*y^3=0
�����������x,y�͑��݂��Ȃ��B
(2)
��������n�����݂����Ƃ���ƁA
���Ȃ��Ƃ����鐮��(x,y,z)�ɑ���
x^n+y^n=z^n
����
x^n+y^n=(z+1)^n
�ӁX������
0=(z+1)^n-z^n>0
����͖����B
(3)
�3�ȏ�̂��鐮��n�����݂��C�ӂ̐��̐����̑g(x,y,z)�ɑ�x^n+y^n��z^n�
�������悢�B
n=4�Ƃ���B
�������������ux^4+y^4=z^2�������̐����̑g(x,y,z)�͑��݂��Ȃ��v
���ؖ�����Ώ\�������ǂ߂�ǂ������̂ŁA
https://mathtrain.jp/mugenkouka
�����Ɋۓ����B
(4)
�t�F���}�[�̍ŏI�藝�B�]�����ȉ����B >>945
D:�@(x/a)^2 + y^2 + z^2 = 1,
����y�Ő����f�ʂ�
�@(x/a)^2 + z^2 = 1-p^2�@�@(�ȉ~)
�@S(y) = ��a(1-y^2)
V(p<y<1) = ��[p,1] S(y)dy = ��a��[p,1] (1-y^2)dy
�@= ��a [ y - (1/3)y^3 ](p��1)
�@= (��/3)a(p+2)(p-1)^2
V(-1<y<1) = 4(��/3)a
3�������@(p+2)(p-1)^2 = 4/3,
�����������
p = 2cos(120�- ��/3) = 0.2260737137892083 < 1/4
������ �� = arccos(-1/3) = 109.47߁@(�l�ʑ̊p) ���邢��
V(1/4<y<1) / V(-1<y<1) = (1/4)(1/4 +2)(1/4 -1)^2
�@= (3/4)^4
�@< 1/3�@�@�@(�� *)
�� p < 1/4
*)�@4^4 - 3^5 = 256 - 243 = 13 > 0, >>963 (3) �̗���
�����~���@�ɂ��B
x^4 + y^4 = zz �������R�� (x,y,z) �����݂���Ɖ��肷��B
���̂悤�� (x,y,z) �̑g�ł����ŏ��̂��̂��l����ƁA
(xx,yy,z) �̍ő����1�ƂȂ�B
{���� (xx,yy,z) ������d (d>1)������ (xx/d,yy/d,z/d) ��
���ƂȂ邩��B}
(x,y,z) ��2�͊������Ax�͊�Ƃ��Ă��悢�B
(xx,yy,z) �͍ő����1�ł���u�s�^�S���X���v�Ȃ̂ŁA
�݂��ɑf�Ȏ��R��p,q��p����
�@xx = pp-qq,�@yy = 2pq,�@z = pp+qq,
�ƕ\�킹��B
��P������ (x,q,p) ���ő����1�ł���s�^�S���X����
�Ȃ�̂ŁA���l�Ɏ��R��r,s��p����
�@x = rr-ss,�@q = 2rs,�@p = rr+ss,�@�@����(1)
�ƕ\�킹��B�ȏ�̎�����
�@yy = 2pq = 4prs
p,r,s �̂ǂ�2���݂��ɑf�Ȃ̂ŁA���ꂼ�ꕽ�����ƂȂ�F
�@p = PP,�@r = RR,�@s = SS,
������ (1) �̑�R�������킹��
�@R^4 + S^4 = P^2
�ƂȂ茳�̕������̐V������ (R,S,P) ������ꂽ���A
�@P �� P^4 = pp < pp+qq = z�@���A�����z�̍ŏ����ɖ�������B
�Q���t�H���g�u�������̐������v�ق�, �����}�� ���w�V��5 (1960)
�@�@�@��� �_ (��) ��т��Ă�������������
�n�����H ��тł���������Z������ɂ��e���̂������l�݂����ō��،��ɔᔻ����Ă�
3+4��4+3�͂�����ƂȂ��c���ł�������
�a�̌����@�������藧���Ȃ����w�Ȃ�Đ��w�҂ƕ����w�҂����g��ˁ[���낗
�ǂ�ȃG���W�j�A�ɂ���H�ɂ��v��Ȃ��v�l��
����Ȃ��̂���ɏ��w�Z�������Ă����p���������邾����
https://twitter.com/genkuroki/status/480213429026709505
https://twitter.com/5chan_nel (5ch newer account) �u�q�ǂ����S�l�V��ł��܂����B�����ɂ��炽�Ɏq�ǂ����R�l����Ă�
�܂����B�q�ǂ��͉��l�ɂȂ�܂������H�v
�@�O�̍����^�������ς��ԓI�œ������݂��Ă�����̂�ΏۂƂ��Ă���
�̂ɑ��āC���̑����^�͎��ԓI�\���������Ă���Ƃ����_���͂������
���B�O�̏ꍇ�ɂ́C�������鍀�S�ƂR�͂قڑΓ��ł����āC���@��
�@�@�@4 + 3 = 3 + 4
�̂�����ŕ\�L���Ă��C�Ӗ��セ���Ⴂ�͂Ȃ��������C���̑����̏ꍇ��
�́C������̂S�Ɖ����̂R�Ƃ͂܂����������قȂ��Ă���B�S�͏��߂ɑ�
�݂��Ă��邢��Γy��ł���C�R�͂��Ƃ���������鑝�����ɂ����Ȃ��B
������C�Ӗ��̏ォ��͊m���ɁC
�@�@�@4 + 3 �� 3 + 4
�ł����Č����ɂ͌����@���͐��藧���Ȃ��B���̗��ӂ́s�l�t����������
��̂́C�����̌��ʂƂ��Ăɂ����Ȃ��B
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
��� �_�F�w���̉Ȋw �`���������̊�b�`�x �ނ����[�@���當��7 (1975) >>971
���ʂ��������ꂪ���@����� ����Ƃ���+3��+4���Ⴄ�͓̂�����O
�d�v�Ȃ̂́u���@�v�ł�a+b=b+a�����藧�Ƃ����F���ł�����
�����F�������Ȃ�����͖����l���� ����
����ܐ��w��肷����ƃo�J�ɂȂ�̂��悭�킩�� �O>>897
>>970-971
���炽�ɂ���Ă����q���̐���3�A����Ɍ����炢���q���̐��𑫂��ƁA
3+4=7(�l) ���������@���ƌĂ�ł���̂��Ƃ������t�V�тɂ����Ȃ���
���ʂƂ��ď�ɐ��藧���Ƃ������Č����@���Ƃ��č̗p����Ă���ƍl����̂����ʂȂ�Ȃ����낤��
�Ӗ�����������Ȃ���_�����Ƃ������o�����Ƃɂ͂Ȃ�̈Ӗ����Ȃ� ����1�{1/2�{1/3�{1/4�{1/5�{�c�c�Ƃ���B
�������̂Ƃ��As/n�̋Ɍ��l�����߂�B ���Y�ɂ���Ă��A�������Ԃ�
�]���r���A�Âɉ��肵�Ă����B >>973
����������Ƃ킩���Ă�l���đ�������܂肢�Ȃ��Ǝv����ł����
�@3+4��4+3�̑��삪�Ⴄ����
�A�����̒l������������
�|���Z�Ƃ������Z�������Ƃ����̂́A�@���킩���Ă邩�ǂ����𗧎��̂Ƃ��ɂ����Ǝ����Ȃ����A�Ƃ��������̘b�Ȃ�ł����ǁA�A�ƍ������n�߂邩��킯�킩��Ȃ��Ȃ�킯�ł��� >>980
>�@3+4��4+3�̑��삪�Ⴄ����
3(+4)��(4+)3�̂ǂ���ł��C�C�Ƃ����̂��������Ȃ��Ƃ� 3
+
4
�ł�������
4
+
3
�ł������� 5�ׂ̂���(5^t �@��t�͎��R���j�ɂ���
���ꌅ�ڂ͏��5�it��1�ɂ�����)
���ڂ͏��2�it��2�ɂ����āj
���O���ڂ�1��6��2�ʂ�̐����̌J��Ԃ�(t��3�ɂ����āj
���l���ڂ�3,5,8,0��4�ʂ�̐����̌J��Ԃ�(t��5�ɂ�����)
���܌��ڂ�1,7,9,5,6,2,4,0��8�ʂ�̐����̌J��Ԃ�(t��6�ɂ�����)
���Z���ڂ�3,9,7,8,1,7,5,5,8,4,2,3,6,2,0,0��16�ʂ�̐��̌J��Ԃ�...
���̗l�ɁA5�ׂ̂���̉�t���ڂ�2^(t-2)�ʂ�̐����̌J��Ԃ��ł���ƍl������i��t��2�ɂ����āj
���N��������ؖ��E�����ł���G�����l�͂���������Ȃ��ł��傤���H
Excel�œK���Ɍv�Z���Ă��甭�����Ă��܂��āA�Ȃ�ł��낤���ĂȂ�ݑ����Ă܂�... >> ���ꌅ�ڂ�...
>> ���ڂ�...
>> ���O���ڂ�...
>> ���l���ڂ�...
>> ���܌��ڂ�...
>> ���Z���ڂ�...
�Ƃ��������
���ꌅ��...
����...
���O����...
���l����...
���܌���...
���Z����...
����n�܂鎿�╶�ɁA�K�ɕς���A������Ȃ�����������ƋC�Â��͂��B >>978
log(n)<s<1+log(n)���n������s/n��0 >>978
�R�[�V�[�̕s������
�@s(n)^2 = (1 +1/2 +1/3 + ���� +1/n)^2
�@�@�� (1+1+1+�����+1)(1/1^2 + 1/2^2 �{ 1/3^2 + ����� + 1/n^2)
�@�@< n{1 + 1/(1�2) + 1/(2�3) + ����� }
�@�@= n{1 + (1-1/2) + (1/2-1/3) + ����� }
�@�@= 2n,
�䂦
�@s(n)/n < ��(2/n), �ɂ��ق�>>986
���͕��}�����ǁA�ʔ�����������������Ă��Ƃ��H >>988
log(n)<s<1+log(n)���g����͂� s/��n��0 >>981
�y�A�m�Z�p�I�ɍl�����
3+4=s(s(s(s(3))))
4+3=s(s(s(4)))
�őS�R�Ⴄ��ł����� ���������u�����Z�v�Ƃ����T�O��100%�l�Ԃ̖ϑz�ł����Ď��R�E�ɑ����Z�ȂǑ��݂��Ȃ�
�L�j�ȗ������Ƃ����������Z�̊T�O��������ƒ�`���Đ��������A�u��t�̗����v���y�A�m�Z�p�Ƃ�������
���w���A���w���A���Z���ɑ����Z�␔�w��������̂Ƀy�A�m�Z�p�ȂǕ@�����قǂ��K�v�Ȃ�
�Ƃ�v���A�}�ʂ������A�����p�A�v�����J������
�����̐��E�Ƀy�A�m�Z�p�Ȃ�ĕK�v�ɂȂ�Ȃ�
���w�̏ۉ�̓��ɂ����肷���ē������������Ȃ����̂����w�� >>991
(4+)3�͂�
3�ɂS�𑫂��Ƃ������Ƃ̕ʂ̕\���Ȃ�
��ɏ����˂Ȃ�Ȃ��Ƃ����̂͘���
��ł����ł��߂ł��C�C >>991
���łɂ�����
3=s(s(s(0)))
4=s(s(s(s(0))))
�Ȃ���
3+4=s(s(s(s(s(s(s(0)))))))
4+3=s(s(s(s(s(s(s(0)))))))
�œ����Ƃ����̂������@����
�{���I�ɂ͍������̌����@�����
+4��+3���Ⴄ�Ƃ����̂�
x+4��x+3�Ɗ��i���邢�͑���j�Ƃ��ĈႤ�Ƃ������Ƃ��� >>988
�R�[�V�[�̕s������
�@s(n)^3 �� (1+1+1+�����+1){1 +1/(2��2) +1/(3��3) +���� +1/(n��n)}^2
�@�@�@�@< n ��(3/2)^2,
���� ��(3/2) ����������B
�@��k > {��(k+1/2) + ��(k-1/2)}/2,
���
�@1/(k��k) < 2/{k[��(k+1/2) + ��(k-1/2)]}
�@= 2{��(k+1/2) - ��(k-1/2)}/k
�@< 2{��(k+1/2) - ��(k-1/2)}/��(kk-1/4))
�@= 2{1/��(k-1/2) - 1/��(k+1/2)},
���@��(3/2) = 1 + ��[k=2,��] 1/(k��k)
�@< 1 + 2��(2/3)
�@= 2.63299316
���@s(n) < 1.90677663n^(1/3),
������g����͂�
�@s(n)/��n < 1.90677663/n^(1/6)�@���@0�@(n����)
�Ȃ��A ��(3/2) = ��[k=1,��] 1/k^(3/2) = 2.612375348682����
�@����͓��v�͊w�ɏo�Ă���yo! y=1/x^a �͉��ɓʂ�����
�@1/k^a < ��[k-1/2,k+1/2] 1/(x^a) dx,
a>1 �̂Ƃ�
�@��(a) = 1 + ��[k=2,��] 1/(k^a)
�@< 1 + ��[3/2,��] 1/(x^a) dx
�@1 + (1/(a-1))(2/3)^(a-1)
�@< 1 + 1/(a-1)
�@= a/(a-1). �ȉ��͒P�Ȃ闎�����Ńf�^����
S(��)=log(��)+���́��ł̔����́A1/��
�ぇ�́��ł̔����́A(1/(2�ぇ))
��S/��N = (1/��) �� (1/(2�ぇ)) = 2/�ぇ
��S/��N = 0 >>985
�������̂Ƃ��Alog(n)�����ƂȂ�͂������i��
���͒��a�����ŁA�������̂Ƃ��A������������As/n����/��
����`�F�U�����ς̒藝�ɂ��A���̑悎����1/n������A
�������̂Ƃ��A1/n��0������As/n��0
�܂蓚���́�/����0
���āA�ǂ��炪�������ł������i�� >>998
���s�^���̒藝���g���A
lim[x����]logx/x=lim[x����](logx)�f/(x)�f=lim[x����]1/x=0
s/��n d�ł�
lim[x����]logx/��x=lim[x����](2/��x) =0 ���̃X���b�h�͂P�O�O�O���܂����B
�V�����X���b�h�𗧂ĂĂ��������B
���݂����W�v�i����j
�y�j�̖��z 1
�y�����q�z 0
�y���z 0
�y�_�z 0
�y�P�N�z 0
�y���_�z 0
�y���t�z 0
life time: 284�� 7���� 59�� 18�b 5�����˂�̉^�c�̓v���~�A������̊F���܂Ɏx�����Ă��܂��B
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�s�v���~�A������̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
��300�~���瓽���ł��w�����������܂��B
�� �v���~�A������o�^�͂����� ��
https://premium.5ch.net/
�� �Q�l���O�C���͂����� ��
https://login.5ch.net/login.php ���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B




