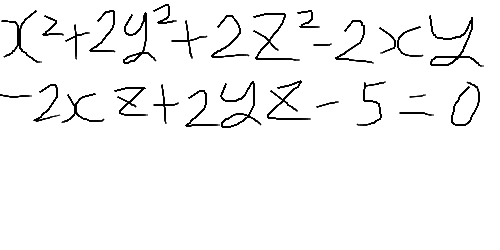分からない問題はここに書いてね449

**１３２人目の素数さん** · 2018/11/26(月) 00:00:54.72

さあ、今日も１日がんばろう★☆

前スレ
分からない問題はここに書いてね448
https://rio2016.5ch.net/test/read.cgi/math/1540218853/

**１３２人目の素数さん** · 2018/12/10(月) 21:19:01.37

>>474
有理数の稠密性

**１３２人目の素数さん** · 2018/12/10(月) 21:19:25.06

２つの封筒問題(two envelopes problem)
https://rio2016.5ch.net/test/read.cgi/math/1544444323/

**１３２人目の素数さん** · 2018/12/10(月) 21:34:24.53

>>475
すまん、読んでなかった。
謝ります。
収束性についてなんか言ってるのは見たけどてっきり収束しないような病的な例は考えてませんといってるんだと思った。
その例も読んでないけど測度論の内部でおさまってるんなら病的というつもりはないよ。
確かにl^1性の制限無ければ存在しても不思議はないと思う。

**>>422です** · 2018/12/10(月) 21:56:01.43

>>468
ですよね
ありがとうございます

**１３２人目の素数さん** · 2018/12/10(月) 23:02:15.17

>>478
私も言い過ぎたかもしれませんね、謝っておきます

Wikipediaの記事は長いので読む気にならないと思いますが、ちゃんと読むと具体例を構成して、計算も詳しく書いてありました
測度論の言葉を避けて書かれてはいますが、もちろんすぐに正当化は可能です
(特別に選んだ測度を備えた離散的な確率空間からRへの可積分ではない可測関数となるはずです)

**１３２人目の素数さん** · 2018/12/10(月) 23:04:58.94

身の丈に合わない難しいことをやろうとするから、本質からどんどん遠ざかってるんですよ

封筒は2つしかないんです

**１３２人目の素数さん** · 2018/12/10(月) 23:36:04.79

>>480
いえいえ。こちらこそ。
l^1でなくていいなら条件は任意の x に対して

E( B | A = x)
=P(θ=x)/(P(θ=x) + P(θ=x/2)) × 2x 　　　(Aの封筒が x 円のときの B の封筒が 2x)
+ P(θ=x/2)/(P(θ=x) + P(θ=x/2)) × x/2 (Aの封筒が x 円のときの B の封筒が x/2)
> x

⇔ 2P(θ=x) + 1/2 P(θ=x/2) > P(θ=x) + P(θ=x/2)

⇔ P(θ=x) > 1/2 P(θ=x/2)

が成立するとき。
だから
P(θ=2^n) = (1/3)(2/3)^n (n=0,1,2,3,…) =0 (otherwise)
とでもすれば条件は確かに満たすね。
もちろんxが2倍になるごとに確率のほうは1/2倍より大きくなることが条件なので必然的にl^1には入らないけど。

**415** · 2018/12/11(火) 00:18:31.07

>>466
＞獲得金の期待値が発散するから実行不可能と判断しているようですが、それは何故ですか？

私はそんなこと言ってません。
実行不能なのは無限大が絡むからであって、期待値が発散するからというわけではありません。
期待値が収束しても、実現不可能な設定であるのは同じかと。

期待値が収束しないと困るのは、交換しない場合とした場合の期待値が比較できないからという
だけの話です。

**415** · 2018/12/11(火) 00:42:47.97

>>465
＞あなたが勝手に妄想して私の主張を捻じ曲げて、架空の私に反論しひとり悦に入ってるだけ

そんなことをした覚えは毛頭ないんですが、、、、。
他の人がいれてる単発ツッコミと混同しておられるのでは？　私は一貫して415を名乗ってます。

無限を導入すれば上限額がなくせることも>>423で書いたように（読みかえしてみるといま
ひとつ不明瞭ですがｗ）>>415を書いた時点ですでに了解済みです。

ということで、とくにあなたと大きな意見の相違はないと思ってますので、あしからず。

**１３２人目の素数さん** · 2018/12/11(火) 00:57:23.44

2a^2+2a+1が平方数となる自然数aのうちk番目に小さいものをa_kとおく。
a_(n+2)=6a_(n+1)-a_n+2が成り立つことを証明せよ

**１３２人目の素数さん** · 2018/12/11(火) 01:47:46.17

二組の連立方程式

あ
2x+y=-1
ax+3y=2

い
2x-3y=b
4x+5y=-2

において、あの解のxとyを入れ替えるといの解になっている。この時aとbの値を求めろ
という問題があるのですが

**１３２人目の素数さん** · 2018/12/11(火) 01:52:37.54

>>485
(2a_n+1,√(2a_n^2+2a_n+1))はpell方程式
x^2 - 2y^2 = 1
の解。
これをといて
x= ((1+√2)^m + (1-√2)^m)/2, y=…
x が奇数となるのはmが偶数のとき。
よって
2a_n + 1 = ((3+√8)^n + (3-√8)^2)/2。
よってb_n = 2a_n +1は漸化式
b_(n+2) = 6 b_(n+1) - b_n
をみたす。以下ry

**１３２人目の素数さん** · 2018/12/11(火) 01:58:15.33

>>483
条件付期待値を見るだけならばE(θ)の収束性は関係ないでしょう
獲得金の期待値が発散しているケースでも条件付期待値は計算可能であり、数理モデルの上では"パラドックス"が生じています
>>482の方が詳細な計算を書かれているので読んでみてはどうでしょうか
すでに言及した通り、様々な考え方により解消することは可能とされているものですが
>>423やその他のレスを読む限り、どうやら獲得金の期待値が収束しないと数理モデルとして成立しないという思い込みがあるようにみえます
確率変数の定義に可積分は含めなくてもよいはずです

E(θ)が発散する場合と収束する場合をやたらと区別してますよね
>>454において、前者は実行不可能だからパラドックスは生じていないとしている
また>>457では、後者の場合"のみ"数理的なパラドックスが残ると述べている
(私やあなたが例に用いていた最低額が設定されている状況では発生しないのでここもよく意味が分かっていないのですが)

この辺りから、そういう風に考えているのだろうと推察したのですが違いましたか
ますます意味が分からなくなりました

**１３２人目の素数さん** · 2018/12/11(火) 02:05:21.19

>>484
確かに、他の人のよく分からない指摘もごっちゃにしておりました
あなたのレスで言えば、>>454等における「現実で実行できないから～」論ですね
私は始めから抽象的な数理モデルで考えればいいと書いているのに、
勝手に現実の問題と脳内変換して何度も同様の反論しております

**１３２人目の素数さん** · 2018/12/11(火) 02:16:22.30

>>485 >>487
訂正
(2a_n+1,√(2a_n^2+2a_n+1))はpell方程式
x^2 - 2y^2 = -1
の解。
これをといて
x= ((1+√2)(3+√8)^m + (1-√2)(3-√8)^m)/2, y=…
よって
2a_n + 1 = (1+√2)(3+√8)^n + (1-√2)(3-√8)^n)/2。
以下同様。

**１３２人目の素数さん** · 2018/12/11(火) 02:18:31.23

>>486

あ)
2x+y=-1
ax+3y=2

い)
2x-3y=b
4x+5y=-2
い）のx,yを入れ替えて

う)
2y-3x=b
4y+5x=-2

にして
あ)の 2x+y=-1と
う)の 4y+5x=-2の
連立方程式を解くだけじゃないの？

**１３２人目の素数さん** · 2018/12/11(火) 02:24:46.17

>>491
夜分にすいません、ありがとうございました
そうなんですけど、それの理屈が分からなくて
ありがとうございました。

**１３２人目の素数さん** · 2018/12/11(火) 03:35:32.51

https://blog.goo.ne.jp/nichikon1/e/da81f66fa7c437e7ca19667c2bf35065
↑これおもろいｗ、コメント読んでみて。

出来たらみんなに広げていってほしいな。

**415** · 2018/12/11(火) 09:20:07.54

>>488
＞どうやら獲得金の期待値が収束しないと数理モデルとして成立しない

そんなこと思ってもいませんし、言ってもいません。あなたの勝手な思い込みです。
あくまでも無限大を含むから「現実には作り得ない」設定だということです。

獲得金の期待値収束に拘るのは数理モデルとして成立するかどうかではなく、そっちだと
交換するしないにかかわらず期待値は同じなのに、条件付き確率で期待値をみると交換し
たほうが得をするから、「数理的パラドックス」として成立するということなんですが。

**415** · 2018/12/11(火) 09:23:39.49

>>494
訂正です。

＞条件付き確率で期待値をみると交換したほうが得をするから

ではなく、獲得期待値が収束する場合は「交換したほうが損をする」でしたね。

**１３２人目の素数さん** · 2018/12/11(火) 14:05:47.37

大学数学の質問です

距離空間(X,d)、U⊆Xに対して、Uの直径をdiam(U) := sup{d(x,y)|x,y∈U}
と定義している本は良く見かけます。
でも、これってU=φのケースってどうなるんですか？
diam(φ)=0　にしたいんですか？
でも、supの定義を考えたら supφ=-∞　の方がまだしっくりきます

**１３２人目の素数さん** · 2018/12/11(火) 14:09:09.81

普通はφは距離空間ではないとすると思います

**１３２人目の素数さん** · 2018/12/11(火) 14:57:25.55

>>485
(a+1)^2+a^2=m^2だからピタゴラス数の性質を使えば容易

**１３２人目の素数さん** · 2018/12/11(火) 15:06:49.56

>>494
>>495
都合良く切り取っていますが、「あるように見える」と書いたんですよ
これは思い込みではなくあなたのレスのおかしさから自然に推察されたことです

同じことを繰り返してるだけですね
あなたがしているであろう勘違いを指摘しておきます

まず、期待値が発散する場合でもある種のパラドックスは発生しています
本来は優劣のないはずの二枚の封筒なのに、選んだ途端にA<Bになってしまう
獲得金額が収束していなくても、2枚の封筒に優劣がないことは成立しているはずです

次に、期待値が収束する場合は常に損をするパラドックスが発生すると書いていますね
これはどういう状況ですか？
(2^k,2^(k+1))の確率を与える方法では、(1,2)で1を引いたときは交換により得をするので、常に損することにはなりません
もちろん、負の値を許すなど封筒の中身の組み合わせの取り方を変えれば作ることはできます
但し、常に損をする状況は(-1)倍をすることで常に得をする状況にできるので、これらは本質的に等価です
なぜ常に損をする状況だけ考えられると書いているのかは本当に全く意味が分かりません

また、前者の場合を「現実に起こり得ないから」と一蹴し、後者の場合は「パラドックスがある」としていますね
もし「現実で実行不可能だからこのパラドックスは考える意味がない」という立場なら、獲得金額の収束に関係なく常に実行不可能だから、そもそも考える意味はないでしょう
あるいは、獲得金額が発散していると思考実験でも実行できないと考えているのかもしれませんが、一回あたりの獲得金額は有限値なので全く関係ありません
もっといえば、仮に獲得金額が∞となる場合が含まれていたとしても、R∪{±∞}に値をとると思えばやはり問題なく定まります

これらのうちどれか１つは当てはまると信じているのですが

**１３２人目の素数さん** · 2018/12/11(火) 15:10:39.77

>>496
ふつう空集合に対してはあまり定義しないと思います
あえて定めるなら-∞か0でしょうね
diamの終域をRとみなすか[0,∞)とみなすかの違い程度でしょう

ちなみに空集合の記号∅はφと似ていますが別の記号です
知ってる上で入力が面倒くさいから使っただけかもしれませんが念のため

**１３２人目の素数さん** · 2018/12/11(火) 15:16:29.30

>>500
成る程

**１３２人目の素数さん** · 2018/12/11(火) 15:45:55.99

係数と定数項が0ではない座標空間内の平面の式を作り、それを表す方程式が重回帰式になるようにその平面上にない点を含む4点を決めよ。

**１３２人目の素数さん** · 2018/12/11(火) 21:15:20.13

自然数全体のなす集合NからNへの写像全体の集合Map(N,N)に
ｆ≦g ⇔ ∀n f(n) ≦ g(n)
で順序を入れる。

M := { m ∈ Map(N,N) | mは狭義単調増加 }
として部分順序集合と考える。

Mは整列集合ですか？

**１３２人目の素数さん** · 2018/12/11(火) 21:16:59.36

>>503
反例存在しますね
却下します

**１３２人目の素数さん** · 2018/12/11(火) 21:25:06.79

>>498
具体的にお教え願いたい

**１３２人目の素数さん** · 2018/12/11(火) 22:27:38.70

(p-q)^3=p+qを満たす素数p,qを求めよ。
自然数k,l,m,nがk!+l!+m!=2^nを満たすとき、(k,l,m,n)を求めよ。
高一なのですが全然わかりませんでした。ご教授お願いします。

**１３２人目の素数さん** · 2018/12/11(火) 23:27:30.68

>>506
http://27.110.35.148/univsrch/ex/data/2015/1n/m01/m1n1514.html

**１３２人目の素数さん** · 2018/12/11(火) 23:32:30.28

>>506
1問目
p-q=nとおく(nは自然数)
p+q=n^3,p-q=nより
p=n(n^2+1)/2
n≧3のとき、n>2,1+n^2>2より右辺は素数とならない
n=1のとき
(p,q)=(1,0) (素数でないので不適)
n=2のとき
(p,q)=(5,3)
よって、条件を満たすのは(p,q)=(5,3)のときのみ

2問目
k≦l≦mとしてよい
l!及びm!はk!の倍数となるので、左辺はk!の倍数
一方、右辺は素因数として2しかもたないので、k!も2のベキ乗で書かなければならない
よってk=1またはk=2

・k=1
右辺は偶数なので左辺も偶数
l!が偶数(⇔l≧2)の時、l≦mからm!も偶数なので左辺は奇数となってしまう
よってl=1でなければならない
このとき
m! = 2^n - 2 = 2(2^(n-1)-1)
n=1のとき右辺は0となり、これを満たすmは存在しない
n>1のとき、2^(n-1)-1は奇数なので、右辺の素因数分解を考えたとき、2を1つしかもたない
m!がそのようになるのはm=2,3のときのみ
m=2のときn=2,m=3のときn=3

・k=2
両辺2で割って
1+(l!/2)+(m!/2)=2^(n-1)
先ほどと同様の考察により、l!/2は奇数でなければならないのでl=2またはl=3

l=2のとき
m! = 2^n - 4 = 4(2^(n-2)-1)
n=1,2のときこれを満たすmは存在しない
n>2のとき、2^(n-2)-1は奇数なので、右辺の素因数分解を考えたとき、2を2つしかもたない
しかし、m!がそのようになるmは存在しない

l=3のとき
m! = 2^n - 8 = 8(2^(n-3)-1)
n=1,2,3のときこれを満たすmは存在しない
n>3のとき、2^(n-3)-1は奇数なので、右辺の素因数分解を考えたとき、2を3つしかもたない
m!がそのようになるのはm=4,5のとき
m=4のときn=5
m=5のときn=7

以上より条件を満たす組は
(k,l,m,n)=(1,1,2,2),(1,1,3,3),(2,3,4,5),(2,3,5,7)
及びこれらのk,l,mに関する並び替え

**１３２人目の素数さん** · 2018/12/11(火) 23:48:35.09

>>508
とても丁寧な解説ありがとうございました。

**１３２人目の素数さん** · 2018/12/11(火) 23:54:35.58

質問です。
zを複素数として、z→0のとき|z|/zの極限ってどうなりますか？

**１３２人目の素数さん** · 2018/12/12(水) 00:02:13.34

ありません

**１３２人目の素数さん** · 2018/12/12(水) 00:28:07.59

>>510
wolfram先生もlimit dies not exist.の答
https://www.wolframalpha.com/input/?i=limit(x-%3E0,y-%3E0,abs(x%2Biy)%2F(x%2Biy))

**415** · 2018/12/12(水) 00:40:57.21

>>499
>「あるように見える」と書いたんですよ
だから、そう見えてしまうのはあなたの間違った思いこみからだということです。
本人がきっぱり否定していることを、「自然に推察された」などと正当化するよう
なお言葉はいかがなものかと思いますよ。

あとに続く文章も相変わらず誤読というか、思い違いによるご指摘ばかりです。
同じ事の繰り返しになるのでお返事しませんが、冷静になって素直に読み返して
いただければご理解いただける能力をお持ちだと信じております。

**１３２人目の素数さん** · 2018/12/12(水) 00:54:31.33

>>502
誰かこれわかる方いらっしゃいませんでしょうか…

**１３２人目の素数さん** · 2018/12/12(水) 01:18:22.36

>>514
そもそも問題の意味がわかりません。
ググってもらしいの出てこないし。

**１３２人目の素数さん** · 2018/12/12(水) 01:19:01.18

>>513
あなたの表現ではそう考えているように私には見える、と言っているんです
これは私がそう感じたということであり、あなたはこう考えていると断定しているのではありません
あなたの考えと違うとしても、表現に問題がある以上、そう感じることを非難されても困ります
>>499の続きを読めばどうしてそのように推察したのかも分かるでしょうから、反論したいならそちらの内容に具体的に答えたら如何ですか？

具体的な言及を避けて誤読・思い違いによる指摘と書いていますが、具体的にどこが誤読なのですか？
>>494-495を読む限り、
「期待値が収束する場合は2枚の封筒は等価だが、発散する場合はそうではない」
「発散する場合は無限大を含むため現実で実行できないからパラドックスは生じていない」
「収束する場合は常に得をする状況はつくれないが、常に損をする状況をつくることができるので、パラドックスが生じる」
とあなたは考えているとしか読み取れません
その仮定に従ってそれぞれに反論をしています
「」が誤りなのか、私が書いた数学的な記述に誤りがあるのか、具体的に指摘して頂けるとありがたいです

**１３２人目の素数さん** · 2018/12/12(水) 01:21:09.56

>>514
同じく
重回帰式の意味を知らないです
座標空間というのは3次元空間のこと？

**１３２人目の素数さん** · 2018/12/12(水) 01:23:16.59

>>510
極形式 z = r exp(iθ) で書けば、|z|/z = exp(-iθ)
なので z の 0 への近づき方により収束は変わる。
偏角θ がある値 α に収束するように近づけば exp(-iα) に収束するし
θが収束しないように近づけば収束しない。

**１３２人目の素数さん** · 2018/12/12(水) 09:43:30.78

f(n,a,x)=x^n+ax
I[k]=∫ [k to k+1] f(n,a,x) dx
に対して以下の等式(*)を考える。
I[k-1]=I[k]=I[k+1] ... (*)

等式(*)を成立させる実数kが存在するように、自然数nと実数aを定めたい。

このようなn,aは存在するか。
存在する場合、そのようなn,aの例を1つ挙げよ。また任意のnに対して、あるaをとれば、等式(*)を満たすkが存在するようにできるかをのべよ。
存在しない場合、その理由を述べよ。

**415** · 2018/12/12(水) 10:07:58.54

>>515
>表現に問題がある以上
だから、これがあなたの主観的判断なんだということをまずもって認識すべきでしょう。
それを世の中では「思いこみ」というのです。

それはそれとして、>>499の中段についてはまったくもってあなたのおっしゃる通りで、
>>513の後段で述べたことについては、お詫びして撤回いたします。すみませんでした。
冷静にならないといけないのは私のほうでしたね。

獲得金額の期待値が収束するケースでは、交換した方が損をするが、下限額を取る場合に
はそうならないということを見逃しておりました。したがって、その場合を考慮にいれて
期待値計算を見直せば、条件付き期待値と、無条件交換した場合の期待値は一致するので
期待値のパラドックスなど生じませんね。無条件に交換したほうが損をするということも
当然ありません。ご指摘に感謝です。

＞「期待値が収束する場合は2枚の封筒は等価だが、発散する場合はそうではない」
これはその通り。発散する場合については常に交換したほうが得になってしまうので等価
ではないと思っています。

＞「発散する場合は無限大を含むため現実で実行できないからパラドックスは生じていない」
現実に実行できないという点でパラドックスとは呼べないという立場です。言い換えれば、
その仮定の下では論理的になんの矛盾もない。

＞「収束する場合は常に得をする状況はつくれないが、常に損をする状況をつくることができるので、パラドックスが生じる」
これについては、上で述べた通り、私の間違いで、常に損をする状況はつくれないので、条件
付き期待値の期待値をとれば、どちらの封筒にも差がないので、有限の分布の場合と同じで、
２枚の封筒は期待値的には等価になる。

有限の場合もそうですが、期待値的には等価であっても、交換した方が得をする（あるいは
損をする）確率が圧倒的に高いという状況はもちろんつくれますが、しかし、宝くじを買った
方が損をする確率が圧倒的に高いのと同じで、これをもってパラドックスとは言えない。

**１３２人目の素数さん** · 2018/12/12(水) 13:37:37.02

シュレッド会社の大勢の行員が一列に並んでいる。工場長がシュレッドすべき一枚の紙を受け取った時彼はそれを5枚の断片に破り一番の行員に渡す。

**１３２人目の素数さん** · 2018/12/12(水) 13:39:34.89

以後 n 番の社員が断片を受け取った時、彼はその中から n 枚の断片を選んでそれらを各々5枚の断片に破ってから n +1番の行員に渡す。2006枚未満の断片を受け取り2006枚以上の断片を次に工員に渡すのは何番の工員か。

細かく丁寧に教えて下さい

**１３２人目の素数さん** · 2018/12/12(水) 13:40:46.40

1から1999を2乗したものの中で十の位が奇数であるものは何個あるか。

**１３２人目の素数さん** · 2018/12/12(水) 13:44:29.48

https://i.imgur.com/4fBrR1t.jpg
と
https://i.imgur.com/AoH4Sgo.jpg
高校数学ですがお願いします

**１３２人目の素数さん** · 2018/12/12(水) 14:53:16.61

>>523

> sum((1:1999)^2%/%10%%2)
[1] 400

**１３２人目の素数さん** · 2018/12/12(水) 15:02:21.11

>>522
> 2006%/%5
[1] 401

**１３２人目の素数さん** · 2018/12/12(水) 15:05:56.89

>>518
ありがとうございました。
Wolframの２行めは
そういう意味だったのかと納得。
(limit does not exist)
(value may depend on x, y path in complex space)

**１３２人目の素数さん** · 2018/12/12(水) 15:08:12.73

>>522
n人めは5*n枚をn+1人めに渡す。

**１３２人目の素数さん** · 2018/12/12(水) 15:44:21.01

>>520
＞だから、これがあなたの主観的判断なんだということをまずもって認識すべきでしょう。
それを世の中では「思いこみ」というのです。
とありますが、あなた自分の誤りを認めましたよね？
その時点で表現に問題があったのはあなたも認める事実だと思うのですが･･････
そこから導いたあなたの勘違いは事実ではなかったようですが、そちらについては初めから私の主観だと明記しております

＞発散する場合については常に交換したほうが得になってしまうので等価
ではないと思っています。
一方を選んでからはそうですが、選ぶ前には優劣がないはずだとすでに書いております
ちゃんと読んでます？

＞現実に実行できないという点でパラドックスとは呼べないという立場です。
その割には態度がちぐはぐだから混乱させられる
>>494では(勘違いによるものではありましたが)期待値が収束する状況で数理的パラドックスが生じると一度は書いていましたよね
(すでに撤回したことは承知していますが、あなたの思考回路について考えるため、あえてここではそのような数理モデルの存在を仮定しておきます)
現実で起こらないから無視という立場なら、期待値が収束していようと現実で実行できないのだから初めからパラドックスではないはずです
一方で、数理モデルにおけるパラドックスを認めているならば、上のように考えることにより、期待値が発散する状況でもパラドックスが生じています

つづく

**１３２人目の素数さん** · 2018/12/12(水) 15:44:38.09

「条件付期待値が当てにならないこともある」という結論なら分かるのですが、条件付期待値による価値判断は肯定
(二枚の封筒は等価でない、とはっきり書いている)したうえで、その結果導かれる不合理なことに対して
「数理的なパラドックスだ」(期待値収束のケース)
「実行不可能だからパラドックスではない」(期待値発散のケース)
と、異なる立場になっています
とくに後者については、数理モデル上の計算を容認しておきながら、困った場合は数学的思考を放棄するというあまりに乱暴な結論だと考えます

＞有限の場合もそうですが、～～
それは単に、期待値が判断基準として適さない場合があるということの証左に過ぎません
また、有限の場合、回数制限や時間制限を取っ払えば、ある意味では妥当な基準であることに変わりはありません
サンクトペテルブルクのパラドックスや、一般化した封筒問題におけるパラドックスは全く質の違うものです
どうやらその辺りも理解できていないようですね

なにか私の大きな思い違いがあり、あなたが正しい可能性もあると考えていましたが、どうやらそれはなさそうです
さんざん指摘していたことを今更になって認めたことで、私のレスをろくに読んでいなかった(もしくは理解できていなかった)
ことがよく分かりました
他にも何度指摘してもスルーされているものがたくさんありますが、おそらくそういうことなのでしょう

**１３２人目の素数さん** · 2018/12/12(水) 15:48:51.89

>>528
おそらくそれまでの断片も一緒に渡していくから、4n枚ずつ増えていくのでは？

**１３２人目の素数さん** · 2018/12/12(水) 15:55:56.41

>>523
自然数はすべて
10n+m　nは非負整数、mは0~9の整数
の形で書ける
(10n+m)^2≡10*2nm+m^2 (mod 100)
2nmは偶数なので、(10n+m)^2の十の位の偶奇はm^2のそれと一致
0^2~9^2を計算すると、そのようになるmはm=4,6のみと分かる
よって、一の位が4,6である整数の数を数えればよく、
2*200=400(個)

**１３２人目の素数さん** · 2018/12/12(水) 15:58:48.13

２つの封筒問題(two envelopes problem)
https://rio2016.5ch.net/test/read.cgi/math/1544444323/

**１３２人目の素数さん** · 2018/12/12(水) 16:47:06.28

>>522
破らなかったのも次に渡す設定？

**１３２人目の素数さん** · 2018/12/12(水) 17:29:40.89

>>534
そうだと思います。

**１３２人目の素数さん** · 2018/12/12(水) 18:19:56.27

>>524
上　z=b+icとでもおいて式に代入して実部=0、虚部=0の関係から求める
虚部から3b^2=c^2が求まるはずだから実部の式に代入して３次式が２つ求まって
（絶対値に注意）片方は単調増加、もう片方は極値のある関数だからaの範囲で
解の個数が変わる

**１３２人目の素数さん** · 2018/12/12(水) 19:21:13.94

>>524
一枚目
z^3=3|z|+a
右辺は実数より、左辺も実数
よって
z=r*e^iθ　θ=0,2π/3,4π/3 rは(正とは限らない)実数
とかける
このとき
r^3=3r+a
あとはrの解の個数をaで分類する標準的な問題
(r=0を解にもつときはzの解の個数が減るので注意)

二枚目
計算したら
x^2y^2-x^2-y^2=0 (x>0,y>0)
となったけど、図を使わないと説明が大変だから省略
計算ミスってるかもしれないし

**１３２人目の素数さん** · 2018/12/12(水) 19:33:47.96

>>524
z^3 = |z| + a は実数だから
z = |z| expθ とおけば、n を整数として
|z|^3 = |z| + a かつ 3θ = 2nπ
または -|z|^3 = |z| + a かつ 3θ = (2n+1)π

**１３２人目の素数さん** · 2018/12/12(水) 19:35:15.93

>>524
訂正
z^3 = 3|z| + a は実数だから
z = |z| expθ とおけば、n を整数として
|z|^3 = 3|z| + a かつ 3θ = 2nπ
または -|z|^3 = 3|z| + a かつ 3θ = (2n+1)π

**１３２人目の素数さん** · 2018/12/12(水) 20:04:09.56

>>539
>>537のようにして場合分けを避けた方が楽と思われ

**１３２人目の素数さん** · 2018/12/12(水) 22:13:01.52

>>535
a[0]=5
a[1]=a[0]-1 + 1*5
a[2]=a[1]-2 + 2*5
a[3]=a[2]-3 + 3*5
...
a[n]=a[n-1]-n+5*n
=a[n-1]+4*n

a[n+1]=a[n] + 4(n+1)
a[n] =a[n-1]+4*n

a[n+1]-a[n]=a[n]-a[n-1]+4
定石の差をとってb[n]=a[n+1]-a[n]とおけば

b[n]=b[n-1]+4で等差数列

以下略

**１３２人目の素数さん** · 2018/12/12(水) 22:15:21.25

>>541
a[n]はn番目の社員が次の社員に渡す枚数

**１３２人目の素数さん** · 2018/12/12(水) 23:04:54.44

>>541
b[0]=a[1]-a[0]=9-5=4
b[1]=a[2]-a[1]=17-9=4*2
b[2]=a[3]-a[2]=29-17=4*3
...
b[i]=4*(i+1)

b[i] = a[i+1]-a[i]
b[i-1] = a[i] -a[i-1]
b[i-2] = a[i-1] -a[i-2]
....
b[1] = a[2] -a[1]

納i=1,n] b[i]=a[n+1]-a[1]
=
納i=1,n] 4*(i+1) = 4*n(n+1)/2 + 4*n

a[n+1]=4*n(n+1)/2 + 4*n+a[1]
a[n]= 4(n-1)n/2 + 4*(n-1) + a[1]
=2*n^2 +2*n + 5

2*n^2 +2*n + 5 > 2006となる最小のnを求めて
1を減じたnで
2*n^2 +2*n + 5 < 2006を確認。

32番目が 1989枚を受け取り2117枚を渡す

**１３２人目の素数さん** · 2018/12/12(水) 23:08:02.64

プログラムの方が早くて楽。
俺にしてみりゃ電卓みたいなもんだ。

> a=NULL
> a[1]=9
> f= function(N){
+ if(N==1) return(a[N])
+ for(n in 2:N){
+ a[n] =a[n-1]+4*n}
+ return(a[N])
+ }
> f=Vectorize(f)
> f(1:50)
[1] 9 17 29 45 65 89 117 149 185 225 269 317 369 425 485
[16] 549 617 689 765 845 929 1017 1109 1205 1305 1409 1517 1629 1745 1865
[31] 1989 2117 2249 2385 2525 2669 2817 2969 3125 3285 3449 3617 3789 3965 4145
[46] 4329 4517 4709 4905 5105

**１３２人目の素数さん** · 2018/12/12(水) 23:58:22.18

C[x,y]⊕C[x,y]とC[x,y]をC[x,y]加群とみたとき、
準同型C[x,y]⊕C[x,y]→C[x,y]の形はどこまで決定できますか？

**１３２人目の素数さん** · 2018/12/13(木) 01:14:42.78

>>545
C[x,y]=RとおいてRの２元(a,b)によって
(x,y)→ax+by
の形をしているもの全体。

**１３２人目の素数さん** · 2018/12/13(木) 01:28:10.70

>>546
ありがとうございます
どのように示せるでしょうか？

**１３２人目の素数さん** · 2018/12/13(木) 01:37:45.82

≡を同型の記号として
Hom(R,M)=M 　(f → f(1))
Hom(M,L)×Hom(N,L)≡Hom(M⊕N,L)　((f,g) → ((m.n) → f(m) + g(n)))
が同型を与えることを確認して

Hom(R⊕R,R) ≡ Hom(R,R) × Hom(R,R) ≡ R × R

の同型で右辺の(a,b)が左辺のどうゆう写像に対応付けられるか確認する。

**１３２人目の素数さん** · 2018/12/13(木) 05:50:08.78

>>519

I[k] = (1/(n+1))[(k+1)^{n+1} - k^{n+1}] + a(k + 1/2),

I[k] - I[k-1] = (1/(n+1))[(k+1)^{n+1} + (k-1)^{n+1} -2 k^{n+1}] + a,

nが奇数のときは偶関数ゆえ、

I[-1/2] - I[-3/2] = I[1/2] - I[-1/2]

aをうまく取れば、同時に0にできる。

∴　I[-3/2] = I[-1/2] = I[1/2],

(例)
　n=3，a=-5/4 のとき,
　　I[k] - I[k-1] = 3(kk -1/4),

　n=5，a=-91/48 のとき,
　　I[k] - I[k-1] = 5(kk -1/4)(kk +5/4),

**１３２人目の素数さん** · 2018/12/13(木) 06:25:12.63

>>523

十の位の数は下2桁で決まる。奇数は20とおり。
1　…　04, 46, 54, 96
3　…　06, 44, 56, 94
5　…　16, 34, 66, 84
7　…　24, 26, 74, 76
9　…　14, 36, 64, 86

**１３２人目の素数さん** · 2018/12/13(木) 07:12:53.60

>>519

　I[k] - I[k-1] = (1/(n+1))[(k+1)^{n+1} + (k-1)^{n+1} -2 k^{n+1}] + a
　　= (2/(n+1))(j=1,[(n+1)/2]) C(n+1,2j) k^{n+1-2j} + a

nが偶数のとき、kについて単調増加。
aをどう取っても同時に0にはならない。

**１３２人目の素数さん** · 2018/12/13(木) 11:55:12.15

https://i.imgur.com/bUTG2sJ.jpg
トコロイドの問題です。

**１３２人目の素数さん** · 2018/12/13(木) 14:36:22.01

こういう未知数が3つ出てくる不定方程式ってどうやって解くんですか?

**１３２人目の素数さん** · 2018/12/13(木) 15:22:27.22

とりあえず一文字消すとか

**１３２人目の素数さん** · 2018/12/13(木) 15:27:31.90

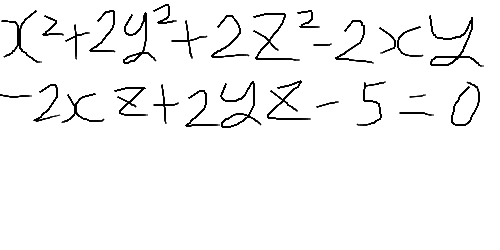0から始まり、ランダムに+1もしくは-1する操作を(確率1/2で)、60回行う。
一度も絶対値が16以上にならない確率を求めよ。

まず、最短16回目で16以上になる。また、16以上になった場合その後を考えなくても確率に影響はない。
また、絶対値16の点に着く場合必ず操作回数は偶数である。
くどくなってしまうので、絶対値が16になる数値をAと言う。
方針は、16以上になる確率を調べていくようにする。
まず、16回目でAにたどり着く確率。
一旦+の方に絞り込み、絶対値より対称的なので二倍すれば良い。
よって16回目でたどり着く確率は1/2^16
-の方も考えると、16回でAにたどり着く可能性は1/2^15
この調子で18回目、20回目...としらべて行き、60回目まで調べてある程度の法則性を見つける。
そうすると16以上にたどり着く可能性はΣ(￣30_k=8)1/2^(2k-1)と予想できる
もうちょっと簡略化して、1/(2^13)Σ(￣23_k=1)1/4^k
等比数列の和の公式を使うと
{1/(2^13)}×(1-1/4^23)/3=(1-1/4^23)/(3×2^13)
=(4^23-1)/(3×2^59)が16以上になる確率
1からこれを引くから、
16以上にならない確率=(3×2^59-4^23+1)/3^2^59
これを計算機に打ち込んだら99%ぐらいになったのですが合ってますか？
https://i.imgur.com/ZXk3DYm.jpg

**１３２人目の素数さん** · 2018/12/13(木) 17:26:50.63

第二可算ならばLindelof

の証明ですが、これってAC使ってますか？

**１３２人目の素数さん** · 2018/12/13(木) 17:49:46.17

どうでも良いことですが

http://www.kurims.kyoto-u.ac.jp/~motizuki/students-japanese.html
の
湯地　智紀
って人の顔写真が女です

この人は性転換した方ですか？

彼(女)は
http://physmathseminar.web.fc2.com/discourse/2016/spring/kyoto-sp_abst/resume_yuji.pdf
で
＞＞ある程度満足して読める程度には証明を付けてあると思う
と言っておきながら
第二可算ならば Lindelof である.の証明を
｢任意の開被覆が与えられた開基の部分被覆により細分されることから自明である.｣なる一言で済ましています。

この方の名前をググると秀才であることがうかがわれますが
勉強の出来る人に見られがちですが、｢自分が理解できていることなんだから皆出来て当然だろ｣という考えが透けて見えます。

別の方が書いた証明では
http://www2.itc.kansai-u.ac.jp/~afujioka/2017/st3/171204st3.pdf
で、10行掛けて証明しています。
私はこういう丁寧な記述をする方の方が好感を持てますね。

**１３２人目の素数さん** · 2018/12/13(木) 18:04:54.98

>>555
計算機で概算値だけほしいなら
Prelude> let next x = zipWith (+) (take (length x) $ 0:x) ((tail x) ++ [0])
Prelude> let xs = iterate next $ (take 15 $ repeat 0) ++ [1] ++ (take 15 $ repeat 0)
Prelude> let n = 60 in (/(2^n)) $ fromInteger $ sum $ (!!n) xs
0.9207659703106129
になった。
分数なら
Prelude> import Data.Ratio
Prelude Data.Ratio> let n = 60 in (%2^n) $ sum $ xs !! n
69202887261377303 % 72057594037927936
のようです。

**１３２人目の素数さん** · 2018/12/13(木) 19:16:32.26

ネイピア数が0,1の座標を通るのは当たり前だけどなぜ傾きが1なんですか？
limh→0a^h-1/hって計算できませんよね(小声

**１３２人目の素数さん** · 2018/12/13(木) 19:16:48.09

ネイピア数が0,1の座標を通るのは当たり前だけどなぜ傾きが1なんですか？
limh→0a^h-1/hって計算できませんよね(小声

**１３２人目の素数さん** · 2018/12/13(木) 19:17:33.32

連投失礼

**１３２人目の素数さん** · 2018/12/13(木) 19:36:01.67

>>556
使いません。

**１３２人目の素数さん** · 2018/12/13(木) 19:39:29.55

>>558
私も単純試行させ0.92を得ていました。

上の式についてですが、例えば私は18回目でたどり着く確率は「18回目にたどり着くのは17回+か-の方に行き、もう一回は逆の方へ行く時」と考えて、
この場合18回思った方向に行く(1/2)^18を採用しました。
そして+と-両方考えるので二倍して1/2^17です。
これを繰り返して行きました。
2回以上逆の方向へ行くならまた20回目とかに含まれるだけなので。

しかし思い直しました。
正の場合は、17回の+と1回の-ですので、これだけをまず考えます。
例えば、1回目に-、残りの17回で+となる確率は、1/2^18です。
これが、何回目に-が出るか？というパターンが、1～16回目までの16通りあるため、
18回中17回+,1回-となるのは16×1/2^18です。同様に-が17回、+が1回の場合も16×1/2^18なので、18回目で終了する確率は1/2^13です。
18回目の確率はこれで求め終えられるのですが、20回目、22回目などはもう少し場合の数が数えにくくなるので、難しいところです。

**１３２人目の素数さん** · 2018/12/13(木) 19:43:42.91

-何回目に-が出るかでかけるもの(18回の例で言えば16)はコンビネーションで出せそう？
-でもそうすると級数とコンビネーションなのでもしかしたら二項定理をつかって簡単にできるのか？
-でも項ごとに選ぶ前の個数が変わっちゃうから無理か？
-しかしコンビネーション足すとしても1-(16以上になる確率)だから99%以上なのは変わらない？
...
-納k＝-7→7]((60,30+k)-2×(60,14+k))
を2^60で割ると出てくる？
((a,b)は二項係数)

などと思惑しています

**１３２人目の素数さん** · 2018/12/13(木) 20:53:59.20

>>559
e^xの微分の導出を検索すれば出てくるが、ひらめくのは結構難しいかなぁ

lim[h→0](a^h-1)/h
=lim[h→0](a^h-1)/log_a(a^h)
=lim[h→0](a^h-1)/log_a(a^h-1+1)
=lim[h→0]1/log_a((a^h-1+1)^(1/(a^h-1)))
a^h-1=tと置くと、
=lim[t→0]1/log_a((t+1)^(1/t))
log関数は連続だからlimをとる順序を入れ替えることができ、
=1/log_a(lim[t→0]((t+1)^(1/t)))
e=lim[t→0](t+1)^(1/t)だから、
=1/log_a(e)=ln(a)
a=eならばlim[h→0](a^h-1)/h=1になる

**１３２人目の素数さん** · 2018/12/13(木) 21:34:39.00

>>564
一番最後の式で良かろう. 所謂鏡像定理である.
｢32から2kへ向かう経路｣と｢0から2kへ向かう途中で絶対値が16を超えるものの内, -16より先に16を通る経路｣を一対一に対応させることが可能である. 負の場合も同様であり, 2倍し, 0から2kへ向かう経路の総数から引く.
図を参照せよ:
https://i.imgur.com/CJDZmgr.jpg

**１３２人目の素数さん** · 2018/12/13(木) 22:35:33.74

>>553
整数解？

**１３２人目の素数さん** · 2018/12/13(木) 22:37:37.83

うーんこの循環論法

**１３２人目の素数さん** · 2018/12/13(木) 22:42:28.84

>>553
(x-y)^2+(y+z)^2+(z-x)^2=5+x^2

と変形してから考えるんじゃ？

**１３２人目の素数さん** · 2018/12/13(木) 23:02:22.86

>>555
二項分布で乱数発生させてシミュレーションを１００万やって頻度をだすと

> mean(replicate(1e6,all(abs(cumsum(0.5-rbinom(60,1,0.5))*2)<16)))
[1] 0.920739

になりました。

**１３２人目の素数さん** · 2018/12/13(木) 23:30:19.30

>>566
始めてぶつかった点で折り返すと
｢32→2k｣と｢少なくとも1回16を通る0→2k｣
｢-32→2k｣と｢少なくとも1回-16を通る0→2k｣
が対応されちゃうので
｢少なくとも1回づつ16,-16を通る経路｣はダブルカウントされちゃってます

｢16→-16→2k｣の場合と｢-16→16→2k｣の場合を一回づつ引けばいいから、同様に｢64→2k｣と｢-64→2k｣に対応させて
2×(60,k-2)を引けば良さそうでしょうか？

**１３２人目の素数さん** · 2018/12/13(木) 23:32:21.43

>>570

#include <iostream>
using namespace std;

int main() {
// your code goes here
double pattern[31][61];

for(int j=0;j<61;j++){
for(int i=0;j<31;j++){
pattern[j][i]=0;
}
}
pattern[15][0]=1;
for(int j=1;j<61;j++){
pattern[30][j]=pattern[29][j-1];
pattern[0][j]=pattern[1][j-1];
for(int i=1;i<30;i++){
pattern[i][j]=pattern[i-1][j-1]+pattern[i+1][j-1];
}
}

double dprob=0;
for(int k=0;k<31;k++){
dprob+=pattern[k][60];
printf("%f ¥n", pattern[k][60]);
}
// 2^60で割るが計算めんどいので手抜き。
dprob/=1024;
dprob/=1024;
dprob/=1024;
dprob/=1024;
dprob/=1024;
dprob/=1024;
printf("prob=%f ¥n", dprob);
return 0;
}

コンピュータに解かせるならパスカルの三角形を応用する手があります
ideoneに貼り付け実行したら92%となりました

**１３２人目の素数さん** · 2018/12/14(金) 00:17:04.36

絶対値が16を上回らないように～ってやつは、>>566で紹介されている鏡像原理を繰り返し使えばできそうです
基本的には>>571の考え方でよいと思います
一般のnに対しては、さらに[+16→-16→+16]が被ったりするので、延々と足し引きが必要となりますね
(2n+1)回の移動は2^(2n+1)通りありますが、そのうち条件を満たすものは
2*((2n+1,n)+(2n+1,n-1)+...+(2n+1,n-7)-(2n+1,n-8)-(2n+1,n-9)-...-(2n+1,n-23)+(2n+1,n-24)+...)
となります
(始め8つは足し算、その次の16個は引き算、以降は16個ごとに符号入れ替え)
これを2^(2n+1)で割れば確率が出ます

60回の場合は61回のときと確率は同じなので
2^(-60)*((61,30)+...+((61,23)-(61,22)-...-(61,7)+(61,6)+...+(61,0))
となると思います

**１３２人目の素数さん** · 2018/12/14(金) 00:33:55.25

16を上回らないように、ではなく、16以上とならないように、ですね
書き間違えました
下の計算はちゃんと正しい設定の方で考えてしております

**１３２人目の素数さん** · 2018/12/14(金) 03:26:07.54

>>548
なるほど
とても分かりやすかったです
ありがとうございます！！