�u�n�b�L���O�v����u���ӂ̂������v�܂ł���L���J�o�[���鋐��f���Q �w�T�����˂�x�ւ悤�����I
�T��
�y�����Ёz���Z���w�̎���X��Part397 [���f�]�ڋ֎~]©2ch.net
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
0002�P�R�Q�l�ڂ̑f������
2016/03/22(��) 12:29:29.23ID:oJvo4lxN0003�P�R�Q�l�ڂ̑f������
2016/03/22(��) 22:07:53.72ID:Xelz7CxE0004�P�R�Q�l�ڂ̑f������
2016/03/28(��) 17:41:10.98ID:ZvlnS/kc0005�P�R�Q�l�ڂ̑f������
2016/04/03(��) 08:50:20.74ID:ygh8RQg70006�P�R�Q�l�ڂ̑f������
2016/06/21(��) 01:04:04.08ID:tvDMtNSO3�����Œʊ��ڕW��8���B�����Ă����?
0007�P�R�Q�l�ڂ̑f������
2016/12/24(�y) 13:37:45.07ID:Gn0blMJ50008�� ��2VB8wsVUoo
2016/12/24(�y) 14:12:16.19ID:kEm4zZD90009�� ��2VB8wsVUoo
2016/12/24(�y) 14:12:33.79ID:kEm4zZD90010�� ��2VB8wsVUoo
2016/12/24(�y) 14:12:48.34ID:kEm4zZD90011�� ��2VB8wsVUoo
2016/12/24(�y) 14:13:04.05ID:kEm4zZD90012�� ��2VB8wsVUoo
2016/12/24(�y) 14:13:21.01ID:kEm4zZD90013�� ��2VB8wsVUoo
2016/12/24(�y) 14:13:36.34ID:kEm4zZD90014�� ��2VB8wsVUoo
2016/12/24(�y) 14:13:51.85ID:kEm4zZD90015�� ��2VB8wsVUoo
2016/12/24(�y) 14:14:08.08ID:kEm4zZD90016�� ��2VB8wsVUoo
2016/12/24(�y) 14:14:23.65ID:kEm4zZD90017�� ��2VB8wsVUoo
2016/12/24(�y) 14:14:42.05ID:kEm4zZD90018�P�R�Q�l�ڂ̑f������
2016/12/24(�y) 21:05:36.50ID:lfAsO9WY0019�� ��2VB8wsVUoo
2016/12/24(�y) 21:14:39.31ID:kEm4zZD90020�P�R�Q�l�ڂ̑f������
2016/12/25(��) 13:12:48.49ID:BZO1HpZq0021�� ��2VB8wsVUoo
2016/12/25(��) 13:18:09.81ID:O010A8Dr0022�P�R�Q�l�ڂ̑f������
2016/12/26(��) 13:09:32.74ID:A4YqIMg70023�P�R�Q�l�ڂ̑f������
2017/10/12(��) 18:28:23.67ID:l3bawjyR������ċ�̓I�ɋ��܂�܂����ˁH
�y���z
���i���j�A���i���j�͎��̓������������Ƃ���
�i��+2�j���i���j+�i��-1�j�O2 ���i���j�����i��-3�j
���̂Ƃ� ���i���j���i��-1�j�O2�Ŋ������]��y�т��i���j���i��+2�j�Ŋ������]������߂�
0024�P�R�Q�l�ڂ̑f������
2017/10/27(��) 09:47:59.13ID:SVplqvSL10�~�ʁA50�~�ʁA100�~�ʁA500�~�ʂ�g�ݍ��킹�č��v3000�~�ɂ���ɂ͉��ʂ�̕��@�����邩�B�i�ޑ���w�j
�Ƃ������ŁA��(�����j�Ȃ�ł����A
{1}10�~�ʂ�50�~�ʂŁA50*n�~(n�͎��R���j�Ƃ���ɂ́A50�~�ʂ�i��(i=0,1,2......,n)�Ƃ���ƁA�A10�~�ʂ�5(n-i)�ƌ�
�܂邩��A(n+1)�ʂ�
{2}10�~�ʁA50�~�ʁA100�~�ʂŁA100:n�~(n�͎��R���j�ɂ���ɂ́A100�~�ʂ�i��(i=0,1,....,n)�Ƃ���ƁA�c���100(n-i),
���Ȃ킿50(2n-2i)�~�B
10�~�ʂ�50�~�ʂ̑g�ݍ��킹��{1}�ɂ��(2n-2i+1)�ʂ�B
�ȉ���
�Ȃ��A10�~�ʂ�50�~�ʂ̑g�ݍ��킹��{1}�ɂ��(2n-2i+1)�ʂ�B�ƂȂ�̂��悭�킩��Ȃ��̂ł����������肦�܂��H
���Ȃ݂ɓ�����2492�ʂ�ł��B
0025�P�R�Q�l�ڂ̑f������
2017/10/27(��) 10:03:32.38ID:SVplqvSL50*n�~��50�~��10�~��n+1�ʂ�ɕ\�����̂ŁA
50(2n-2i)�~��50�~��10�~��2n-2i+1�ʂ�ɕ\�����Ƃ����Ӗ��ł��傤���H
(+1�͑S��10�~�ʂ̏ꍇ)
002625
2017/10/27(��) 10:10:25.75ID:SVplqvSL0027�P�R�Q�l�ڂ̑f������
2017/10/27(��) 10:54:58.28ID:SVplqvSL0028�P�R�Q�l�ڂ̑f������
2017/10/27(��) 12:10:45.30ID:yj6wmWSa������Ȃ����͂����ɏ����Ă�435
http://rio2016.2ch.net/test/read.cgi/math/1507993404/
������ł��肢���܂�
0029�P�R�Q�l�ڂ̑f������
2018/01/30(��) 17:27:05.22ID:UjQ/0HBt��Ƃ��Ă�
m�E-n
�݂����Ȋ���
�������
m�E(-n)
����Ȃ��Ƃ����Ȃ���
0030�P�R�Q�l�ڂ̑f������
2018/01/30(��) 21:31:35.29ID:/cBV7J36�������ƌ���̋���͂Ȃ�����悭�g��
�������菑�����ƌ���̋��ꂪ����
����Ƃ͕ʂɍ��Z���w�͑������������w�������Ă�Ǝv��
���Ă����̂��ԈႢ�Ȃ�
0031�P�R�Q�l�ڂ̑f������
2018/01/31(��) 13:15:31.81ID:8QlaJedN0032�P�R�Q�l�ڂ̑f������
2018/01/31(��) 23:27:23.21ID:b7aN4TTT���́u�w���v�����ŁA�D�܂����Ȃ��Ǝw�����邱�Ƃ�
���̂܂ɂ����w�I�ɐ������Ȃ��ɂ���ւ��̂�
�w�Z���炾�B
0033�P�R�Q�l�ڂ̑f������
2018/02/04(��) 12:55:39.20ID:e/Db4a5+0034�P�R�Q�l�ڂ̑f������
2018/02/04(��) 18:03:48.53ID:ZSC0ZBE6(3/8)x - (1/4)�osin(2x)�p + (1/32)�osin(4x)�p + C�ƂȂ�܂��B
�������������3/8�Ƃ����萔�����c���Ă��܂��̂�
���X��(sinx)^4�Ƃ͕ʕ��Ȃ̂ł͂Ȃ��ł��傤���H
0035�P�R�Q�l�ڂ̑f������
2018/02/04(��) 21:38:08.23ID:e/Db4a5+=3/8-(1/2)(1-2(sin(x))^2)+(1/8)(1-8(sin(x))^2+8(sin(x))^4)
=(sin(x))^4
0036�P�R�Q�l�ڂ̑f������
2018/02/04(��) 22:38:22.40ID:AUGvMeKo�ǂ������肪�Ƃ��������܂����B
0037�P�R�Q�l�ڂ̑f������
2018/02/09(��) 17:54:46.44ID:XyC0rd8D�����b�ɂȂ�܂�
�����Ē��������̂ł����A����(2)�̌��_����
m��0,1,9�̂Ƃ�1��
�Ƃ���܂����A����m��0���܂܂��̂ł���
D<0�AD>0�̏ꍇ���͗������Ă���܂����A���������킩��܂���
��������������
��낵�����肢�������܂�
http://fast-uploader.com/file/7073721608949/
0038�P�R�Q�l�ڂ̑f������
2018/02/09(��) 18:09:12.91ID:XyC0rd8D���K���Ă�[2]�����ڂɓ����ĂȂ�����
m��0�̂Ƃ�x��1/3�Ȃ�킷��Ă�
�����������Đ\�������܂���ł���
�܂��킩��Ȃ��Ƃ��낪�������Ƃ��́A�ǂ�����낵�����݂܂�
0039�P�R�Q�l�ڂ̑f������
2018/02/16(��) 09:24:07.08ID:Dex7qXuX0040DJ�w�p�@
2018/02/16(��) 09:33:10.94ID:yN3n4O8g�N�w���͐i��ł��܂��Ă���B
0041�P�R�Q�l�ڂ̑f������
2018/02/16(��) 14:17:54.26ID:6NSHnPZ40042�P�R�Q�l�ڂ̑f������
2018/02/27(��) 21:20:27.55ID:VcviioR40043�P�R�Q�l�ڂ̑f������
2018/03/15(��) 14:15:52.22ID:bi82FW8e�Ȃɂ����肷�邩�H
����͂ǂ�������Ԃɂ����āA
�����ؖ��������̂��H�Ƃ������Ƃɂ����
�ؖ����悤�Ƃ���l���ݒ肷��A
�Ƃ������Ƃł�낵���ł��傤���H
0044DJ�w�p�@
2018/03/15(��) 15:33:15.89ID:PJTefRNB0045DJ�w�p�@archive gemmar
2018/03/15(��) 15:34:15.75ID:PJTefRNB0046�P�R�Q�l�ڂ̑f������
2018/03/15(��) 22:09:11.18ID:S5Y2guKa0047�P�R�Q�l�ڂ̑f������
2018/03/18(��) 12:29:59.04ID:t9RW70mPa*d - b*c = 0 �Ȃ�Ε������� x = a / c �܂��� b / d �ƂȂ�A2�̉��������Ȃ�����
a*d - b*c �� 0 �ł���B
�Ə����Ă���܂��B
a*d - b*c = 0 �Ȃ�Ε������� x = a / c �܂��� b / d
�ƂȂ�̂͂Ȃ��ł����H
0048�P�R�Q�l�ڂ̑f������
2018/03/18(��) 12:39:13.07ID:t9RW70mP�Q����x_{n+1} = (a*x_{n} + b) / (c*x_{n} + d)���l����B
x_{n}�����Ȃ��x_{n+1}�����ł���Ə����Ă���܂��B����͂Ȃ��ł��傤���H
0049�P�R�Q�l�ڂ̑f������
2018/03/18(��) 12:45:00.04ID:IOSmuSYR�}���`�|�X�g����̂͂Ȃ��ł����H
0050�P�R�Q�l�ڂ̑f������
2018/03/18(��) 13:06:42.97ID:t9RW70mPc��0�܂���d��0�ł���B
c��0�Ȃ��(a*x + b) / (c*x + d) = (a*x + a*d/c) / (c*x + d) = a/c
d��0�Ȃ��(a*x + b) / (c*x + d) = ((b*c/d)*x + b) / (c*x + d) = b/d
�Ƃ������Ƃł��傤���A�قȂ��̉������킯�ł�����Ac��0�ł��B
x = a/c �ƂȂ��ĈقȂ��̉��������Ƃɖ����ŏ\�����Ǝv���܂��B
0051�P�R�Q�l�ڂ̑f������
2018/03/18(��) 13:09:30.08ID:t9RW70mP(a*�� + b) / (c*�� + d) = (a*�� + b) / (c*�� + d)�Ȃ��
(a*d-b*c)*(��-��)=0�A��=���ƂȂ邩�炾�Ǝv���܂��B
0052�P�R�Q�l�ڂ̑f������
2018/03/19(��) 11:32:10.27ID:upbElimKa_1 = a, a_2 = b, a_n = p*a_(n-1) + q*a_(n-2) �in = 3, 4, �c�j
�Œ�܂鐔�� {a_n} �ɂ���
(1) a_n �� ��, ��, a, b, n ��p���ĕ\���B
(2) lim_{n �� ��} a_(n+1) / a_n �����߂�B
0053�P�R�Q�l�ڂ̑f������
2018/03/19(��) 11:38:40.69ID:upbElimK�L���ȎQ�l���ɂ��̖�肪�ڂ��Ă��܂����B
���ۂɓ����ŏo�肳�ꂽ���ł��B
���̎Q�l���̉Ɍ�肪����܂����B
���₷����肾�Ǝv���܂��B
�o��҂̑z�肵�Ă��������̎Q�l���̌�����ł������̂��A
����Ƃ��������ł������̂����C�ɂȂ�܂��B
�o��҂��҂��N�����ɋC�t�����A���̎Q�l���Ɠ�������������
�v������ł��܂����Ƃ����ꍇ�����蓾���Ǝv���܂��B
�ǂ��ł��傤���H
0054�P�R�Q�l�ڂ̑f������
2018/03/19(��) 11:46:13.89ID:upbElimK�����āA��肪�\�ʉ����Ȃ������Ƃ����\�����������Ǝv���܂��B
��w�͓������̖͔͉����J���ׂ��ł͂Ȃ��ł��傤���H
0055�P�R�Q�l�ڂ̑f������
2018/03/19(��) 13:33:34.84ID:NtNVExs20056�P�R�Q�l�ڂ̑f������
2018/03/21(��) 10:27:25.64ID:RsMGXF8A2�̐���̊W�ɂ��Ď���ł��B
�ŗL�l�A�ŗL�x�N�g�����W���Ă���Ƃ����͕̂�����̂ł����A���`�㐔�I�ɂ͂ǂ̂悤��
���������̂ł��傤���H
0057�P�R�Q�l�ڂ̑f������
2018/03/21(��) 10:28:21.03ID:RsMGXF8A0058�P�R�Q�l�ڂ̑f������
2018/03/21(��) 10:31:47.81ID:RsMGXF8A(x1, x2) = a1 * (p1, q1) + b1 * (p2, q2)
�ƕ�������A(an, bn)�����܂�Ƃ��������͕�����܂��B
�ł��A>>56�̂����͂���Ƃ͈Ⴂ�܂��B
0059�P�R�Q�l�ڂ̑f������
2018/03/21(��) 10:43:09.64ID:RsMGXF8A�A���ꎟ�������������łȂ����������߂̏��������߂�Ƃ��ɁA
�u��̎�����p, q����������Ɓv�Ə����Ă���܂����A����͂ǂ��������Ƃł����H
0060�P�R�Q�l�ڂ̑f������
2018/03/21(��) 10:46:20.14ID:1tWK96Z3���̕��@���g���Č��ʂ��ǂ�����ċ��߂邩�Ō�܂Ő����ł���̂�
0061�P�R�Q�l�ڂ̑f������
2018/03/21(��) 10:51:06.34ID:RsMGXF8A(xn, yn) = a1*r^(n-1)*(p1, q1) + b1*r^(n-1)*(p2, q2)���Ǝv���܂��B
0062�P�R�Q�l�ڂ̑f������
2018/03/21(��) 10:51:43.20ID:RsMGXF8A0063�P�R�Q�l�ڂ̑f������
2018/03/21(��) 12:45:48.26ID:RsMGXF8A0064�P�R�Q�l�ڂ̑f������
2018/03/21(��) 12:48:09.53ID:RsMGXF8A���������̌��ʂ𑼂̉ӏ��ň��p���Ă����肵�܂��B
0065�P�R�Q�l�ڂ̑f������
2018/03/21(��) 17:29:34.41ID:RsMGXF8A�����������x�ȎQ�l���͂Ȃ��ł��傤���H
0066�P�R�Q�l�ڂ̑f������
2018/03/21(��) 20:59:16.73ID:RsMGXF8A0067�P�R�Q�l�ڂ̑f������
2018/03/21(��) 21:12:11.30ID:cKPG6Iop�u���Ȃ��ɂł��銄��̕��@�v�@�@��{�o��
0068�P�R�Q�l�ڂ̑f������
2018/03/25(��) 20:59:19.82ID:Opi6c9Sw0069�P�R�Q�l�ڂ̑f������
2018/03/26(��) 01:16:04.78ID:U3K3CgRp0070�P�R�Q�l�ڂ̑f������
2018/03/27(��) 14:36:50.51ID:pYnfAUB20071�P�R�Q�l�ڂ̑f������
2018/03/27(��) 20:40:21.74ID:8V8dlGHE0072�P�R�Q�l�ڂ̑f������
2018/04/04(��) 00:36:29.68ID:75nh5gA/(b�|c)�oa2��|(b +c)a +bc�p
�����܂ł͂킩�������A
�|(a�|b)(b�|c)(c�|a)�������Ȃ̂���
�Ȃ�(a�|b)�̑O�Ɂ|�����̂��{���ɂ킩��Ȃ��B�����Ă��������B
0073�P�R�Q�l�ڂ̑f������
2018/04/04(��) 00:43:36.26ID:oWdSM6/e0074�P�R�Q�l�ڂ̑f������
2018/04/04(��) 00:46:26.81ID:75nh5gA/���A�{���ł��ˁB
�Ȃ�����Ȋ�b�̊�b���킩��Ȃ������̂����ɂ����C���ɂȂ�܂����B�܂��܂����K�ʂ�����܂���ˁB
���肪�Ƃ��������܂����B
0075�P�R�Q�l�ڂ̑f������
2018/04/04(��) 00:49:06.20ID:c4jXYUQpa��b��c��a�@�Ƃ�������ۂ����\�L�̔��������ێ����邽�߁B
���́@�P�Ɂ@(b-c)(a-b)(a-c) �@�Ƃ��Ă����h�Ȑ������B
0076�P�R�Q�l�ڂ̑f������
2018/04/04(��) 01:01:16.31ID:bqj+3tHD0077�P�R�Q�l�ڂ̑f������
2018/04/04(��) 01:03:49.39ID:oWdSM6/e0078�P�R�Q�l�ڂ̑f������
2018/04/04(��) 01:18:00.66ID:t9F2nnfF0079�P�R�Q�l�ڂ̑f������
2018/04/04(��) 06:28:53.99ID:9RHCHEXS���s�Ƃ́A�N�ɂ��Ă̓n�C���x���Ȃ��Ƃ��o��������Ȃ���
�̂���
0080�P�R�Q�l�ڂ̑f������
2018/04/07(�y) 23:18:00.67ID:ORAsWCDw��`�͗������Ă���Ǝv���܂�
�Ⴆ��1+1/2+1/4+�c��2�Ɏ�������͕̂�����܂�
1���̃`���R���ɂ��āA�c��̂��̔����𑫂��āc���Ă���Ă����ƈꖇ�̃`���R���傫���Ȃ�Ȃ��݂�����
����Ȋ����Œ����I�ɂ����Ȃ낤�Ȃ��Ĕ[���ł����ł�����
e�̏ꍇ��1��肿����Ƃ����傫�������ɂ����Ă������疳���ɑ傫���Ȃ��Ă��������Ȋ��������܂�
�����ɂ�����Ƃ��傫���Ȃ��Ă������疳���ɂȂ�C������̂ł�
�Ȃ�łȂ�Ȃ��̂ł����H�H
0081�P�R�Q�l�ڂ̑f������
2018/04/07(�y) 23:28:18.81ID:sST1TAxu����Ɠ����ł���
0082�P�R�Q�l�ڂ̑f������
2018/04/07(�y) 23:32:57.72ID:7vaLagHl�܂��Ŏ��₵�Ă���Ƃ��āA�����̃q���g�����
��_[n=1,,��]�i1/n^k) �́@����1�Ŕ��U�A����1�@�Ŏ���
���l�������
0083�P�R�Q�l�ڂ̑f������
2018/04/07(�y) 23:39:28.17ID:ORAsWCDw�}�W����I�����ĕs�v�c�����I
�����ɑ傫���Ȃ�Ȃ��d�g�݂��C�ɂȂ��
���肪�Ƃ�
�l���Ă݂�
0084�P�R�Q�l�ڂ̑f������
2018/04/07(�y) 23:42:23.66ID:7vaLagHl�����œ����o���Ă邶���
>�Ⴆ��1+1/2+1/4+�c��2�Ɏ�������͕̂�����܂�
0085�P�R�Q�l�ڂ̑f������
2018/04/07(�y) 23:45:13.77ID:ORAsWCDw�����킩��Ȃ���c
�݂�Ȃ݂����ɓ��悭�Ȃ�����ˁI
�ł��{���͓����悤�ȂƂ���ɂ�����Ă��Ƃ��ȁH
���肪�ƁI�V�O�}�̘b�����������l���Ă݂�
0086�� ��2VB8wsVUoo
2018/04/08(��) 06:36:26.67ID:Q7nh09vl0087�� ��2VB8wsVUoo
2018/04/08(��) 06:36:47.84ID:Q7nh09vl0088�� ��2VB8wsVUoo
2018/04/08(��) 06:37:09.83ID:Q7nh09vl0089�� ��2VB8wsVUoo
2018/04/08(��) 06:37:29.79ID:Q7nh09vl0090�� ��2VB8wsVUoo
2018/04/08(��) 06:37:56.94ID:Q7nh09vl0091�� ��2VB8wsVUoo
2018/04/08(��) 06:38:17.36ID:Q7nh09vl0092�� ��2VB8wsVUoo
2018/04/08(��) 06:38:39.60ID:Q7nh09vl0093�� ��2VB8wsVUoo
2018/04/08(��) 06:39:03.44ID:Q7nh09vl0094�� ��2VB8wsVUoo
2018/04/08(��) 06:39:27.89ID:Q7nh09vl0095�� ��2VB8wsVUoo
2018/04/08(��) 06:39:52.76ID:Q7nh09vl0096�P�R�Q�l�ڂ̑f������
2018/04/09(��) 12:57:51.84ID:9elG49/M0097�P�R�Q�l�ڂ̑f������
2018/04/10(��) 23:56:46.78ID:0Wxl59g0���ׂĂ̐���x�ɂ���f(x)=a*x^2+b*x+c�̒l�������ɂȂ邽�߂̕K�v�\�����������߂�
�Ƃ�����Փx5���̖�肪����܂��B
���Aa+b, a-b, c�������ƂȂ��Ă��܂��B�璷�ȉ��Ǝv���̂ł����ǂ��ł����H
�ua, b�̋���v���Ac�������v�Ƃ����̂������̉ł��B
0098�P�R�Q�l�ڂ̑f������
2018/04/10(��) 23:57:27.67ID:0Wxl59g00099�P�R�Q�l�ڂ̑f������
2018/04/10(��) 23:58:15.12ID:0Wxl59g00100�P�R�Q�l�ڂ̑f������
2018/04/11(��) 00:12:16.28ID:isce9Ubya, b�̋���v���Ac������
���̕��������ł���
0101�P�R�Q�l�ڂ̑f������
2018/04/11(��) 05:51:12.06ID:rJ40FMa9a,b,c�������Ƃ͏����ĂȂ����H
0102�P�R�Q�l�ڂ̑f������
2018/04/11(��) 08:27:25.94ID:7O9NLb15a+b, a-b�������@�� a, b������
�ł��B�����āA
a+b, a-b�������@�́@a+b������
�ł��B
0103�P�R�Q�l�ڂ̑f������
2018/04/11(��) 08:46:01.78ID:isce9Uby0104�P�R�Q�l�ڂ̑f������
2018/04/11(��) 08:56:48.08ID:C1xHIuA60105�P�R�Q�l�ڂ̑f������
2018/04/11(��) 09:29:11.98ID:qhVjaT10�ǂ��������Ă����Ă�������
0106�P�R�Q�l�ڂ̑f������
2018/04/11(��) 09:32:36.70ID:C1xHIuA6a+b, a-b�������@�� a, b������
�ɂ��Ẵ��X�ł́H
0107�P�R�Q�l�ڂ̑f������
2018/04/11(��) 09:35:16.08ID:qhVjaT101�������ɂȂ�Ǝv���Ă����Ƃ����v���܂����
0108�P�R�Q�l�ڂ̑f������
2018/04/11(��) 09:37:41.24ID:C1xHIuA6a+b, a-b�������@�� a, b������
���U�ł��邱�Ƃ��������߂���w
0109�P�R�Q�l�ڂ̑f������
2018/04/11(��) 17:11:08.45ID:EeQ2vVvi0110�P�R�Q�l�ڂ̑f������
2018/04/11(��) 17:41:45.61ID:C1an/aHY0111�P�R�Q�l�ڂ̑f������
2018/04/11(��) 18:33:24.28ID:EeQ2vVvi�������s�j�L�I�b�X�I�I�b�X�I
0112�� ��2VB8wsVUoo
2018/04/13(��) 18:19:38.68ID:uddKuSDq0113�� ��2VB8wsVUoo
2018/04/13(��) 18:19:57.48ID:uddKuSDq0114�� ��2VB8wsVUoo
2018/04/13(��) 18:20:18.23ID:uddKuSDq0115�� ��2VB8wsVUoo
2018/04/13(��) 18:20:37.81ID:uddKuSDq0116�� ��2VB8wsVUoo
2018/04/13(��) 18:20:58.69ID:uddKuSDq0117�� ��2VB8wsVUoo
2018/04/13(��) 18:21:17.76ID:uddKuSDq0118�� ��2VB8wsVUoo
2018/04/13(��) 18:21:36.82ID:uddKuSDq0119�� ��2VB8wsVUoo
2018/04/13(��) 18:21:56.99ID:uddKuSDq0120�� ��2VB8wsVUoo
2018/04/13(��) 18:22:17.10ID:uddKuSDq0121�� ��2VB8wsVUoo
2018/04/13(��) 18:22:39.27ID:uddKuSDq0122�P�R�Q�l�ڂ̑f������
2018/04/14(�y) 01:20:19.62ID:jmRykOUA0123�P�R�Q�l�ڂ̑f������
2018/04/14(�y) 09:23:00.10ID:7UzfzUkx���̎���x�ł��̋t���̏���������x/4�ɓ������A�������A0<1/x��3�������̂����ׂċ��߂�B
���ȉ��ł����A�Ō�ɁA0��x/4<1���`�F�b�N���Ă��܂���B����̓`�F�b�N���Ȃ��Ă������̂ł��傤���H
https://imgur.com/wElrEDc.jpg
0124�P�R�Q�l�ڂ̑f������
2018/04/14(�y) 12:51:28.30ID:jmRykOUA0125�P�R�Q�l�ڂ̑f������
2018/04/15(��) 21:48:23.96ID:sZvWvLh2�}�W���X����Ƃ��̖��ɂ��Ă͂��Ȃ��Ă��悢
0126�P�R�Q�l�ڂ̑f������
2018/04/15(��) 21:55:41.34ID:IwCdN2WB�Ȃ��ł����H
0127�P�R�Q�l�ڂ̑f������
2018/04/15(��) 23:22:39.87ID:5igJqGu8x�̉����P�ɍi�����Ƃ���(��(n�{1)-1)/2������1��菬��������B
0128�P�R�Q�l�ڂ̑f������
2018/04/15(��) 23:24:45.74ID:5igJqGu8x�̉����P�ɍi�����Ƃ���(��(n�{1)-n)/2������1��菬��������B
0129�P�R�Q�l�ڂ̑f������
2018/04/15(��) 23:32:54.25ID:64a61H4K0130�P�R�Q�l�ڂ̑f������
2018/04/15(��) 23:45:22.44ID:5igJqGu8��(n^2+1)-n��1/(��(n^2+1)+��n)��1�����炾��
0131�P�R�Q�l�ڂ̑f������
2018/04/15(��) 23:47:19.97ID:64a61H4K�ł��A���̂悤�ȋL�q������ׂ��ł���
0132�P�R�Q�l�ڂ̑f������
2018/04/15(��) 23:47:42.06ID:5igJqGu80133�P�R�Q�l�ڂ̑f������
2018/04/15(��) 23:49:53.56ID:5igJqGu8�ŏI�I�ɋ��߂������\�����������Ă�A�L�q�͂���Ȃ�
0134�P�R�Q�l�ڂ̑f������
2018/04/16(��) 00:02:13.85ID:22oFWnI30135�P�R�Q�l�ڂ̑f������
2018/04/16(��) 01:22:55.08ID:e7Sgewxi0136�P�R�Q�l�ڂ̑f������
2018/04/16(��) 01:41:54.18ID:22oFWnI3�\���Ȃ�L�q�͂���Ȃ��Ƃ������Ƃł����̂ŁA�r�����͂Ȃ��Ă������̂��ȂƎv���������ł�
0137�P�R�Q�l�ڂ̑f������
2018/04/16(��) 02:05:54.88ID:MzSTInWA���͉̉����ĂȂ��B
0138�P�R�Q�l�ڂ̑f������
2018/04/16(��) 02:08:15.76ID:22oFWnI3�r�����͎������킩���Ă����A���������Ă��ۂɂȂ�Ƃ������Ƃł���
0139�P�R�Q�l�ڂ̑f������
2018/04/16(��) 07:23:06.94ID:aYK7ekq/�ŏI�I�ɋ��܂������������ɂȂ��Ă��邩�͊m���߂�K�v������܂���ˁH
�����Q�l���̑��̖��ł͂��̂悤�ȏꍇ�A�������ɂȂ��Ă��邩�m����
�Ă���ꍇ���قƂ�ǂł��B
0140�P�R�Q�l�ڂ̑f������
2018/04/16(��) 12:36:18.29ID:1A38i3Dk0141�P�R�Q�l�ڂ̑f������
2018/04/16(��) 17:34:40.90ID:KAazPsM7A=-B�����藧���Ă���B>0�ł���Ȃ�AA<0�ƌ����Ă����̂ł��傤���B
0142�P�R�Q�l�ڂ̑f������
2018/04/16(��) 18:06:48.35ID:22oFWnI30143�P�R�Q�l�ڂ̑f������
2018/04/16(��) 18:15:17.07ID:KAazPsM70144�P�R�Q�l�ڂ̑f������
2018/04/17(��) 06:09:30.91ID:jecWUWL+�̓r�������肢���܂��B
0145�P�R�Q�l�ڂ̑f������
2018/04/17(��) 06:43:31.24ID:IjkzZCd90146�P�R�Q�l�ڂ̑f������
2018/04/17(��) 08:47:44.77ID:KqjZggHi0147�P�R�Q�l�ڂ̑f������
2018/04/17(��) 12:54:37.42ID:cOZu//pr0148�P�R�Q�l�ڂ̑f������
2018/04/17(��) 14:22:16.78ID:jecWUWL+���ȉ������܂���
0149�� ��2VB8wsVUoo
2018/04/20(��) 05:51:22.42ID:bErUPD6U0150�� ��2VB8wsVUoo
2018/04/20(��) 05:51:43.21ID:bErUPD6U0151�� ��2VB8wsVUoo
2018/04/20(��) 05:52:01.72ID:bErUPD6U0152�� ��2VB8wsVUoo
2018/04/20(��) 05:52:21.91ID:bErUPD6U0153�� ��2VB8wsVUoo
2018/04/20(��) 05:52:40.71ID:bErUPD6U0154�� ��2VB8wsVUoo
2018/04/20(��) 05:52:58.91ID:bErUPD6U0155�� ��2VB8wsVUoo
2018/04/20(��) 05:53:18.79ID:bErUPD6U0156�� ��2VB8wsVUoo
2018/04/20(��) 05:53:38.60ID:bErUPD6U0157�� ��2VB8wsVUoo
2018/04/20(��) 05:53:56.72ID:bErUPD6U0158�� ��2VB8wsVUoo
2018/04/20(��) 05:54:17.91ID:bErUPD6U0159�P�R�Q�l�ڂ̑f������
2018/04/20(��) 13:08:40.11ID:Tvdpa5s30160�� ��2VB8wsVUoo
2018/04/21(�y) 01:42:53.11ID:egA1fDFk0161�� ��2VB8wsVUoo
2018/04/21(�y) 01:43:13.15ID:egA1fDFk0162�� ��2VB8wsVUoo
2018/04/21(�y) 01:43:32.40ID:egA1fDFk0163�� ��2VB8wsVUoo
2018/04/21(�y) 01:43:53.22ID:egA1fDFk0164�� ��2VB8wsVUoo
2018/04/21(�y) 01:44:14.44ID:egA1fDFk0165�� ��2VB8wsVUoo
2018/04/21(�y) 01:44:34.95ID:egA1fDFk0166�� ��2VB8wsVUoo
2018/04/21(�y) 01:44:56.04ID:egA1fDFk0167�� ��2VB8wsVUoo
2018/04/21(�y) 01:45:17.65ID:egA1fDFk0168�� ��2VB8wsVUoo
2018/04/21(�y) 01:45:39.52ID:egA1fDFk0169�� ��2VB8wsVUoo
2018/04/21(�y) 01:46:04.49ID:egA1fDFk0170�P�R�Q�l�ڂ̑f������
2018/04/22(��) 12:57:09.05ID:9hXwjWmh0171�P�R�Q�l�ڂ̑f������
2018/04/23(��) 00:06:49.09ID:N5MmAEGl0172�P�R�Q�l�ڂ̑f������
2018/04/23(��) 00:11:29.45ID:N5MmAEGl�����ł��܂���
0173�P�R�Q�l�ڂ̑f������
2018/04/24(��) 11:00:54.00ID:IPMZQy8dcos��=1/2,�|1
���ł����Ȃ�̂��킩��܂���B��낵�����肢���܂��B
0174�P�R�Q�l�ڂ̑f������
2018/04/24(��) 11:50:05.14ID:p8lCeEr5cos��=x�Ƃ�����
(2x-1)(x+1)=0
�ƂȂ�܂���
0175�P�R�Q�l�ڂ̑f������
2018/04/24(��) 19:45:31.34ID:IPMZQy8d���肪�Ƃ��������܂��B
0176�P�R�Q�l�ڂ̑f������
2018/04/26(��) 12:45:03.47ID:StU6wdOA2���s���� a*x^2 - a*x - 24 < 0 �̉��� -3 < x < b �ł���Ƃ��A
a, b �����߂�B
���F
-3 < x < b
��
(x + 3) * (x - b) < 0
��
x^2 + (3 - b)*x -3*b < 0
�c
�ȂǂƏ����Ă���܂��B
-3 < x < b
��
(x + 3) * (x - b) < 0, -3 < b
��
x^2 + (3 - b)*x -3*b < 0, -3 < b
�Ə����Ȃ��Ă̓_���ł���ˁH
0177�P�R�Q�l�ڂ̑f������
2018/04/26(��) 12:46:18.18ID:StU6wdOA��͂�A���w�̑f�l�������ƁA�����Ȃ��Ă��܂��̂ł��傤���H
0178�P�R�Q�l�ڂ̑f������
2018/04/26(��) 13:40:20.89ID:EnJnxgMy0179�P�R�Q�l�ڂ̑f������
2018/04/26(��) 13:52:51.22ID:9LPr/TnT0180�P�R�Q�l�ڂ̑f������
2018/04/26(��) 14:27:52.70ID:Ar5YutdU�y�A�m�Z�p���܂ޔC�ӂ̖������Ȍ����n�ɑ��A���郂�f��M,N����ј_�����ӂ����݂��āAM|=�ӂ���N|���ӂƂł��邱�Ƃ������A�Ƃ�����肪�킩��܂���
0181�P�R�Q�l�ڂ̑f������
2018/04/27(��) 19:06:47.41ID:DJBs+gIF���Z���͂킩���ł���낵
0182�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 07:35:37.41ID:I9SB8aSA�u�x�������������Ă���Ă������ǁA���t�x������3�H���A�����}�x������3�H���B
���킹���60���͂����ł���v
���̌v�Z�͂ǂ��������݂������ł��傤���B
0183�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 07:43:10.88ID:trnscwsy0184�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 11:52:46.17ID:h/YbeCUK0185�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 17:31:22.67ID:CO/HPhId����x�ɂ��Ă̕s����
�QK-1��x���V�A�@�@-2K-5��x��K+�P
���ɖ�����x�����݂��鎞�AK�����l�͈̔͂́H
�Ƃ������őO���̕s������2K-1���V�Ȃ�x�͑��݂���A�����K��4
�㔼�̕s�����͓��l��-2��K�Ȃ炘�͑��݂���A����ė����������̂�-2��K��4
�Ɖ�������Ԉ���Ă܂����B�ł͑O���̕s��������x���QK-1�Ax���V�Ƃ��������A
�㔼�̕s��������x��-2K-5�Ax��K+1�Ƃ�����������
�QK�|1���V�A�QK-1 ��K+1�A-�QK-5���V�A-�QK-5��K+1��4�������瓚����-2��K��2
�ƂȂ��Ă܂����B���ێ����̉ł͂悭�Ė��̉ł͑ʖڂ�K=�R����ꂽ��
5��x���V�A-11��x���S�ƂȂ莩���̉͊Ԉ���Ă���Ƃ����͕̂��������̂ł���
�Ȃ��P����2�̕s�����̏��������킹�����̂������Ƃ͂Ȃ�Ȃ��̂������ł��܂���B
���������肢���܂��B
0186�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 17:38:43.05ID:NGRVO0jd���ʂ̉��������ǂ����܂ł͌����Ă��Ȃ���ł���
���ꂼ��͉������A�ƌ����Ă邾���ŁA���̉��������ɂȂ邱�Ƃ����邩�ǂ����܂ł͌����Ă܂���
0187�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 18:07:16.07ID:CO/HPhId���肪�Ƃ��������܂��B�����̏o���������ł�
�����ɂ͉��͂��邯�ǂ��ꂪ���ʂƂ͌���Ȃ��d�B
�킩��܂����B�C��t���邱�Ƒ����Ȃ��c�B
0188�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 22:25:12.26ID:4LKHbqol-2 < x < 0 �͈̔͂ɂ���悤�Ȓ萔 a �̂Ƃ肤��l�͈̔͂����߂�B
���̖��ł����A2�̎������Ə����Ă���܂��B
���̕������͈قȂ��̎����������ƍl���Ă����̂ł��傤���H
����Ƃ��d�������ꍇ���l���Ȃ���Ȃ�Ȃ��̂ł��傤���H
0189�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 22:26:50.77ID:NGRVO0jd2�̉����d�Ȃ������̂��d���ł�
0190�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 22:27:30.30ID:weWrnK/L0191�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 22:36:33.66ID:4LKHbqol���ȏ��ɂ����̂悤�ȏd���̏ꍇ���܂ނƂ����u�펯�v�ɂ��Ă͏����Ă���܂���B
0192�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 22:38:59.31ID:weWrnK/L���������̂��C�ɂ���Ȃ玩���̗����錾���Ă��瓚�Ă������悢
���Ɠ������W��Q�l���������Ƃ��
0193�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 22:39:16.72ID:4LKHbqol�������������쐬����o��҂̐_�o��������܂���B�N���ǂ�ł���ʂ�ɂ���
���߂ł��Ȃ��悤�Ȗ�肩�ǂ����Ȃ��邱�Ƃ�S�����Ă��Ȃ��킯�ł��B
0194�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 22:42:45.59ID:+cRGa5/a���������ł��̂悤�ȕ��₪�o����A�����̗����������ʼn���Ηǂ��ł��傤
0195�P�R�Q�l�ڂ̑f������
2018/04/28(�y) 22:49:12.85ID:NGRVO0jd���閳�����Ȍ����n�т̔C�ӂ̃��f���ɑ��Ă���_�����ӂ���ɐ^�ƂȂ�Ȃ�A�т���ӂ�LK�ɂ����ďؖ��\�ƂȂ邱�Ƃ������A�Ƃ�����肪�킩��܂���
0196�P�R�Q�l�ڂ̑f������
2018/04/29(��) 12:15:46.36ID:gKIbFnP+�u
2�������� x^2 + (2 - a)*x + (4 - 2*a) = 0 �� -1 �� x �� 1 �͈̔͂�
���Ȃ��Ƃ�1�̎����������悤�Ȓ萔 a �̒l�͈̔͂����߂�B
�v
�̍ŏ��̂Ƃ���Ɉȉ��̂悤�ɏ�����Ă��܂��F
�u
�傫���́A���� (A)�A(B) �ƕʂ�邪�A (B) �͍X�ɍׂ��������čl����B
(A) -1 < x < 1 �͈̔͂ɁA2�̉������i�d�����l����j�B
(B) -1 �� x �� 1 �͈̔͂�1�̉������ix = �}1 �ȊO�͏d�����l���Ȃ��j�B
�v
2�����������d�������ꍇ��2����������2�̉������Ƃ����u�v��F�߂�A
(A) �͖�肠��܂���B
(B) �����ł��B (B) �ɂ��A x = -1 �܂��� x = 1 �̂Ƃ��ɂ͏d�����l���邱�Ƃ�
�Ȃ�܂����A�d�������ꍇ�A-1 �� x �� 1 �͈̔͂�2�̉��������ƂɂȂ�܂��B
�ł��̂ŁA�u-1 �� x �� 1 �͈̔͂�1�̉������ix = �}1 �ȊO�͏d�����l���Ȃ��j�v�Ƃ���
�͖̂������Ă��܂��B
���̖{�̒��҂́A�`���[�g�������Ғ��ƂȂ��Ă��܂��B
�̃v�����������{�ł��傤���A���x�����Ⴗ���܂��B
0197�P�R�Q�l�ڂ̑f������
2018/04/29(��) 12:17:15.04ID:gbW3SPPi���閳�����Ȍ����n�т̔C�ӂ̃��f���ɑ��Ă���_�����ӂ���ɐ^�ƂȂ�Ȃ�A�т���ӂ�LK�ɂ����ďؖ��\�ƂȂ邱�Ƃ������A�Ƃ�����肪�킩��܂���
0198�P�R�Q�l�ڂ̑f������
2018/04/29(��) 12:19:52.20ID:gKIbFnP+>>196
�̖��̓�Փx�� ���������� �ɂȂ��Ă��܂��B
�ō���Փx�ł��B
�P���őދ��ȁA�܂�Ȃ��ꍇ�����̖��ł����A�ō���Փx�ƕ]�����Ă��܂��B
�������^���܂��B
0199�P�R�Q�l�ڂ̑f������
2018/04/29(��) 12:20:29.96ID:gbW3SPPi���̓��x�����Ⴍ��>>197�̖�肪�킩��܂���ł���
���x�����������Ȃ��Ȃ狳���Ă��������܂����
�킩��Ȃ�����͂��ł�����
0200�P�R�Q�l�ڂ̑f������
2018/04/29(��) 12:24:01.72ID:gbW3SPPi�Ӓn�����Ȃ��ŋ����Ă�������
0201�P�R�Q�l�ڂ̑f������
2018/04/29(��) 12:39:06.56ID:gbW3SPPi0202�P�R�Q�l�ڂ̑f������
2018/04/29(��) 12:57:28.37ID:NUj6OhXR0203�P�R�Q�l�ڂ̑f������
2018/04/29(��) 13:20:48.78ID:gKIbFnP+��͂�A�Q�l���Ƃ����ǂ��܂Ƃ��Ȑ��w�҂������Ȃ��ƃ_���ł��ˁB
0204�P�R�Q�l�ڂ̑f������
2018/04/29(��) 13:21:12.99ID:gbW3SPPi���閳�����Ȍ����n�т̔C�ӂ̃��f���ɑ��Ă���_�����ӂ���ɐ^�ƂȂ�Ȃ�A�т���ӂ�LK�ɂ����ďؖ��\�ƂȂ邱�Ƃ������A�Ƃ�����肪�킩��܂���
����͂��Ȃ��ł��킩��Ȃ���ł��傤���H
0205�P�R�Q�l�ڂ̑f������
2018/04/29(��) 16:10:11.30ID:4zeNF/cM0206�P�R�Q�l�ڂ̑f������
2018/04/30(��) 12:40:57.79ID:GN2GPqGL0207�P�R�Q�l�ڂ̑f������
2018/04/30(��) 16:21:37.78ID:ELXrJoE7P+1���f���Ƃ͌���Ȃ���ˁH
�Ⴆ��2 �~ 3 �~ 5 �~ 7 �~ 11 �~ 13 + 1 = 59 �~ 509��������
�Ȃ̂ɂǂ����Ă���őf���������ɂ��邱�Ƃ�������́H
0208�P�R�Q�l�ڂ̑f������
2018/04/30(��) 16:24:25.27ID:1Sw4S+sv0209�P�R�Q�l�ڂ̑f������
2018/04/30(��) 16:24:32.09ID:9GopzljD0210�P�R�Q�l�ڂ̑f������
2018/04/30(��) 16:25:16.16ID:KGGc0OY6p+1���f���ł͂Ȃ��ꍇ�Ap+1�͑f������������邪�Ap�̒�`��肻�̑f�����͍ő�̑f���ȉ��ɂȂ邱�Ƃ͂��肦�Ȃ�
����āAp+1�̑f�����͍ő�̑f�����傫���Ȃ���Ȃ炸�A����
0211�P�R�Q�l�ڂ̑f������
2018/04/30(��) 16:28:37.19ID:ELXrJoE7�n�������ĂȂ�ł����Ȃ�̂��킩��Ȃ��A�A�A
0212�P�R�Q�l�ڂ̑f������
2018/04/30(��) 16:29:40.45ID:ELXrJoE7�Ȃ�قǁI�킩��܂����I
�݂Ȃ��肪�Ƃ��������܂����I
0213�P�R�Q�l�ڂ̑f������
2018/04/30(��) 22:44:48.47ID:7WMUSr3s��
�ǂ̂悤�ɋ��߂��܂����H
�Ȃ�ƂȂ�e�ɂȂ肻���ł����B
0214�P�R�Q�l�ڂ̑f������
2018/04/30(��) 23:03:10.35ID:w/Kfy5xc(a_1 + �c + a_n) / n �� a
�����藧�̂ŁA
������ e �ł��B
0215�P�R�Q�l�ڂ̑f������
2018/04/30(��) 23:05:11.79ID:w/Kfy5xc(a_1 + �c + a_n) / n �� a
�����藧�̂͒��ϓI�ɖ��炩�ł��B
0216�P�R�Q�l�ڂ̑f������
2018/05/01(��) 00:50:11.95ID:tIjj4serhttp://yaplog.jp/drosselmeyers/archive/115
����J�[�h�Q�[���̈�����i�ׂĂ݂�
https://kdsn.xyz/original_card_print_price/
�m��ɍœK�A���싳�ށI����I���W�i���J�[�h�Q�[���Ő����̕��I
http://yuu73.xsrv.jp/jisaku-kyouzai
�[������n�߂�{�[�h�Q�[������
https://trap.jp/post/450/
�{�[�h�Q�[���͂ǂ����̂��A�����Ȃ�ɍl����
http://roy.hatenablog.com/entry/2014/07/09/124824
�J�t�F���}���@�{�[�h�Q�[���ɃA���T�[���n�}�闝�R
http://style.nikkei.com/article/DGXMZO10921930R21C16A2000000?channel=DF260120166491
�{�[�h�Q�[���̓W���C�x���g�u�Q�[���}�[�P�b�g�v�̐����L�^���炱�ꂩ���
�s��ɕK�v�Ȃ��Ƃ�ϑz���Ă݂��B6�N�Ԃ̗���Ґ����ځi2016�N4�����_���ׁj
https://bodoge.hoobby.net/columns/00001
�{�[�h�Q�[���s�ꂪ�N���E�h�t�@���f�B���O�̏o���ŋ}�����𐋂��s��K�͂��g�咆
http://gigazine.net/news/20150820-board-game-crowdfunding/
�u29�Ί����A2�N�O�ɉ�Ђ����߂��B�{�[�h�Q�[�������n�߂�3700���~��
����グ�����lj��������������Ƃ͂���H�v���낢��
http://labaq.com/archives/51880196.html
���{�{�[�h�Q�[���E�ْ̈[���ɕ����I�{�[�h�Q�[���f�U�C�i�[�Ƃ��Đ����Ă����ɂ́H
https://bodoge.hoobby.net/columns/00013
0217�P�R�Q�l�ڂ̑f������
2018/05/01(��) 09:34:14.08ID:csuz60fU0218�P�R�Q�l�ڂ̑f������
2018/05/01(��) 13:42:34.95ID:1mbxLN1Y���̂Ƃ��Af'(z)�̗��������߂Ȃ����B
0219�P�R�Q�l�ڂ̑f������
2018/05/01(��) 13:46:48.74ID:nsDZ0Bac0220�P�R�Q�l�ڂ̑f������
2018/05/01(��) 15:03:18.84ID:1mbxLN1Y�����B
�����A���̖��H�w���ŏo�肳�ꂽ�������҂�60�l���A2�`3�l�������Ȃ������B
�F�A��̂킩��Ȃ������ό`���肵�Ċ�b�ɖ߂���Ă��Ƃ��o���Ȃ������l���قƂ�ǂ������B
0221�P�R�Q�l�ڂ̑f������
2018/05/01(��) 15:03:50.63ID:1mbxLN1Y�����A���J�[��>>219�ɂ��Ă�����
0222�P�R�Q�l�ڂ̑f������
2018/05/01(��) 15:10:15.69ID:nsDZ0Bac0223�P�R�Q�l�ڂ̑f������
2018/05/01(��) 16:09:29.88ID:1mbxLN1Y���w�������̌v�Z���ƌ��Ă�낤�ˁB���X�̒�`��厖�ɂ��ĂȂ��B
0224�P�R�Q�l�ڂ̑f������
2018/05/01(��) 16:18:36.07ID:nsDZ0Bac0225�P�R�Q�l�ڂ̑f������
2018/05/01(��) 17:05:49.63ID:1mbxLN1Y����
���ԂO�悩���w�킩���Ă��B
�H�w���̂����ɓƊw�ŁA�W��/�ʑ��_�A���x�_�A���ׁ[�O�ϕ��A����́A�m���_�A�m���ߒ��_�A���l�́A�����A���낢����܂����B
���̕ӂ̐��w�Ȃ̑�w�@�����m���ƑM���͂����鎩�M������B
0226�P�R�Q�l�ڂ̑f������
2018/05/01(��) 17:12:46.35ID:1mbxLN1Y>>218�͖{���͂���Ȗ�肾�����B
�w��f(z)�͕��f���S��(z��C)�Ő����Ȋ��Ƃ���B���̂Ƃ��Af'(z)�̗�����0�ƂȂ邱�Ƃ��ؖ����Ȃ����x
0227�P�R�Q�l�ڂ̑f������
2018/05/01(��) 17:44:08.91ID:nsDZ0Bac���閳�����Ȍ����n�т̔C�ӂ̃��f���ɑ��Ă���_�����ӂ���ɐ^�ƂȂ�Ȃ�A�т���ӂ�LK�ɂ����ďؖ��\�ƂȂ邱�Ƃ�����
��낵�����肢���܂�
0228�P�R�Q�l�ڂ̑f������
2018/05/01(��) 18:31:11.14ID:nsDZ0Bac����ς�A�H�w�̐l�͐��w�̊�b����킩��Ȃ����Ă��Ƃł���
0229�P�R�Q�l�ڂ̑f������
2018/05/01(��) 18:59:12.90ID:nsDZ0Bac�����܂����
���̂ł��傤���H
0230�P�R�Q�l�ڂ̑f������
2018/05/01(��) 20:35:53.88ID:nsDZ0Bac���������A���N���N����������肾����폟�Ȃ�ˁE�E�E�B
���܂ɂ́A�����Ȃ������Ȃ����ƔY��ŕ����Ă݂����A���ꂪ���̐؎��ȔY�݁B
0231�P�R�Q�l�ڂ̑f������
2018/05/01(��) 20:39:45.20ID:1mbxLN1Y���Ɗ�b���w�ĂȂɁH
�����n�H������H
0232�P�R�Q�l�ڂ̑f������
2018/05/01(��) 20:51:11.71ID:nsDZ0Bac0233�� ��2VB8wsVUoo
2018/05/01(��) 20:51:41.69ID:o9N8stUi0234�� ��2VB8wsVUoo
2018/05/01(��) 20:52:40.26ID:o9N8stUi0235�� ��2VB8wsVUoo
2018/05/01(��) 20:52:57.03ID:o9N8stUi0236�� ��2VB8wsVUoo
2018/05/01(��) 20:53:14.38ID:o9N8stUi0237�� ��2VB8wsVUoo
2018/05/01(��) 20:53:33.80ID:o9N8stUi0238�� ��2VB8wsVUoo
2018/05/01(��) 20:53:51.52ID:o9N8stUi0239�� ��2VB8wsVUoo
2018/05/01(��) 20:54:10.40ID:o9N8stUi0240�� ��2VB8wsVUoo
2018/05/01(��) 20:54:29.40ID:o9N8stUi0241�� ��2VB8wsVUoo
2018/05/01(��) 20:54:49.13ID:o9N8stUi0242�� ��2VB8wsVUoo
2018/05/01(��) 20:55:08.08ID:o9N8stUi0243�P�R�Q�l�ڂ̑f������
2018/05/01(��) 21:28:53.72ID:1mbxLN1Y>>230�̔������Đl�ԓI�ɂǂ��Ȃ�
�X���Ⴂ�n�߂����������̂����ꂾ���ǁA�������ĉ�����������Ƃ���Ȃ�H
0244�P�R�Q�l�ڂ̑f������
2018/05/01(��) 21:35:34.36ID:1mbxLN1Y�l�ɖ₤�悤�Ȗ����ł͂Ȃ��B
0245�P�R�Q�l�ڂ̑f������
2018/05/01(��) 21:59:09.27ID:nsDZ0Bac���̕ӂ̐��w�Ȃ̑�w�@�����m��������̂ł͂Ȃ�������ł����H
0246�P�R�Q�l�ڂ̑f������
2018/05/01(��) 22:47:48.44ID:fEEfCxMo�����A�Ɗw�Ŋw���̂�����A�S�Ēm���Ă�킯����Ȃ��B
�w��b���w�x�炵����227�͐������͉��̕��삾��H
0247�P�R�Q�l�ڂ̑f������
2018/05/01(��) 22:49:45.70ID:nsDZ0Bac0248�P�R�Q�l�ڂ̑f������
2018/05/01(��) 22:50:34.71ID:fEEfCxMo0249�P�R�Q�l�ڂ̑f������
2018/05/01(��) 22:51:16.88ID:fEEfCxMo0250�P�R�Q�l�ڂ̑f������
2018/05/01(��) 22:51:50.78ID:nsDZ0Bac0251�P�R�Q�l�ڂ̑f������
2018/05/01(��) 22:57:38.36ID:fEEfCxMo���[�Ɓc
>>250��>>225�ɏグ������̑��̖����ǂ��ŏo���������ƁH
0252�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:00:32.80ID:nsDZ0Bac0253�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:08:36.85ID:fEEfCxMo���[�Ɓc������x��������
>>250��>>225�ɏグ������̑��̖����ǂ��ŏo���������ƁH
0254�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:09:59.73ID:fEEfCxMo���ĂȂ�܂���H
0255�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:10:02.55ID:nsDZ0Bac�v�Z�͂ł��邯�ǁA���_�͂킩��܂��[����Ă��Ƃł����
0256�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:11:32.28ID:nsDZ0Bac0257�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:12:05.06ID:fEEfCxMo>>230�̔����͐����Ȑl�ł͂Ȃ���ˁB
0258�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:12:50.99ID:nsDZ0Bac0259�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:13:14.43ID:fEEfCxMo�͒m��Ȃł��ˁB
0260�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:13:47.46ID:nsDZ0Bac0261�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:15:33.84ID:fEEfCxMo0262�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:18:02.64ID:nsDZ0Bac0263�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:18:11.13ID:fEEfCxMo���Ⴀ�X���[���Ă���������
>>222�݂����ɐ���ꂽ��J�`���Ƃ���ł���H
������>>224�ƃ��X����M���̐l�Ԑ����^���܂��ˁB
0264�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:20:21.09ID:fEEfCxMo���������ւ��Ă��ł��傤��
���Ȃ��l���ʼn������Y�I�Ȃ��Ƃ��ĂȂ��ł���ˁH
0265�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:20:58.99ID:nsDZ0Bac���Z���w�̃X���b�h�ł���ȃ��X�𓊍e����̂́A�����m��Ȃ����Z������Ƀ}�E���g�Ƃ낤�Ƃ�������A�ȊO�ɂȂ��ł����
�����������Ƃ���Ă��d���Ȃ��ł���
0266�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:22:20.22ID:fEEfCxMo���}�E���g���悤�Ɓc
���₽���̉ɒׂ��ł��B
0267�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:22:59.77ID:nsDZ0Bac�}�E���g���ɂ��������܂����
0268�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:24:48.61ID:nsDZ0Bac�ȂM���Ȃ��Ă�݂����ł�����
0269�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:25:40.49ID:fEEfCxMo�X���[���Ȃ���������b������������
0270�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:27:03.88ID:nsDZ0Bac0271�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:27:40.78ID:fEEfCxMo0272�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:29:02.66ID:nsDZ0Bac���Ȃ���>>220�Ńo�J�ɂ��Ă���Ȃ���ł����H
0273�P�R�Q�l�ڂ̑f������
2018/05/01(��) 23:46:59.84ID:FZ/wj2xr0274�P�R�Q�l�ڂ̑f������
2018/05/02(��) 00:41:40.58ID:8T2p95Px0275�P�R�Q�l�ڂ̑f������
2018/05/02(��) 12:30:21.98ID:/Aqvw5mB������m���߂鎿��ɓ�����ꂸ��^����
�Ƃ������Ƃł����H
0276�P�R�Q�l�ڂ̑f������
2018/05/02(��) 12:54:02.45ID:M5tu7v3O0277�P�R�Q�l�ڂ̑f������
2018/05/02(��) 13:03:00.75ID:bZrCT+Ax0278�P�R�Q�l�ڂ̑f������
2018/05/02(��) 13:03:47.11ID:M5tu7v3O�Ȃ��B
0279�P�R�Q�l�ڂ̑f������
2018/05/02(��) 13:07:09.88ID:aZ0kijPt����������H
�Ȃ����Ƃ�����́H
0280�� ��2VB8wsVUoo
2018/05/03(��) 13:06:13.04ID:J8oAAFtV0281�� ��2VB8wsVUoo
2018/05/03(��) 13:06:36.85ID:J8oAAFtV0282�� ��2VB8wsVUoo
2018/05/03(��) 13:06:57.38ID:J8oAAFtV0283�� ��2VB8wsVUoo
2018/05/03(��) 13:07:17.85ID:J8oAAFtV0284�� ��2VB8wsVUoo
2018/05/03(��) 13:07:38.91ID:J8oAAFtV0285�� ��2VB8wsVUoo
2018/05/03(��) 13:07:58.49ID:J8oAAFtV0286�� ��2VB8wsVUoo
2018/05/03(��) 13:08:17.66ID:J8oAAFtV0287�� ��2VB8wsVUoo
2018/05/03(��) 13:08:35.23ID:J8oAAFtV0288�� ��2VB8wsVUoo
2018/05/03(��) 13:08:48.31ID:J8oAAFtV0289�� ��2VB8wsVUoo
2018/05/03(��) 13:09:09.27ID:J8oAAFtV0290�P�R�Q�l�ڂ̑f������
2018/05/03(��) 13:30:44.62ID:4YhlTbJU0291�P�R�Q�l�ڂ̑f������
2018/05/04(��) 08:22:45.30ID:13O6Km1R0292�P�R�Q�l�ڂ̑f������
2018/05/04(��) 10:22:53.45ID:AYd+05q9���N�̍u�`���͂Ȃ�ł����H
0293�P�R�Q�l�ڂ̑f������
2018/05/04(��) 13:45:45.69ID:e0Bk9Gb8x^2 + a*x +a*b^2 = 0 �c (A)
x^2 + b*x +b*a^2 = 0 �c (B)
�͋��ʂ̉��������̂Ƃ���B
(1) (A)��(B)�̂ǂ��炩������d�������Ƃ��A���ʂ̉������߂�B
(2) (A)��(B)�̂ǂ�����d���������Ȃ��Ƃ��A���ʂłȂ����̏��Ȃ��Ƃ�����͕��ł��邱�Ƃ������B
�Ђǂ����ł��ˁB
0294�P�R�Q�l�ڂ̑f������
2018/05/04(��) 13:46:19.21ID:e0Bk9Gb8f(x) = x^2 + a*x +a*b^2
g(x) = x^2 + b*x +b*a^2
�Ƃ����B
(A)�͏d���������Ȃ�����A a �� 0 �ł���B
��ʐ������킸�� a < b �Ɖ��肵�Ă悢�B
-b/2 < -a<2 �ł���B
{x �� R | f(x) = 0 �܂��� g(x) = 0} �͕��łȂ���������Ȃ�W���ł���B
��
f(0) �� 0 ���� -b/2 > 0
��
a^2*b �� 0 ���� b < 0
��
b �� 0 ���� b < 0
�ƂȂ邪����͖����ł���B
�����
{x �� R | f(x) = 0 �܂��� g(x) = 0} �͕��ł���������܂ށB
��g(x) = 0 �̏��������̉��́A���ł���B
0295�P�R�Q�l�ڂ̑f������
2018/05/04(��) 13:47:08.16ID:e0Bk9Gb80296�P�R�Q�l�ڂ̑f������
2018/05/04(��) 13:48:38.29ID:e0Bk9Gb8�u(A)�͏d���������Ȃ��v�Ƃł��܂��B
�Ђǂ����ł��ˁB
0297�P�R�Q�l�ڂ̑f������
2018/05/04(��) 13:49:13.06ID:e0Bk9Gb8�u(A)�܂���(B)�͏d���������Ȃ��v�Ƃł��܂��B
�Ђǂ����ł��ˁB
0298�P�R�Q�l�ڂ̑f������
2018/05/04(��) 20:56:59.60ID:Fwo0VEqi����ǂ��̖��H
0299�P�R�Q�l�ڂ̑f������
2018/05/05(�y) 09:47:31.16ID:tEdcrB57a=1
b=2
>>296>>297
a=-1
b=0
0300�P�R�Q�l�ڂ̑f������
2018/05/05(�y) 10:00:42.16ID:kwaxj6Evx^2 + a*x +a*b^2 = 0 �c (A)
x^2 + b*x +b*a^2 = 0 �c (B)
�͉��������̂Ƃ���B
(2) (A)��(B)�̂ǂ�����d���������Ȃ��Ƃ��A���ʂłȂ����̏��Ȃ��Ƃ�����͕��ł��邱�Ƃ������B
0301�P�R�Q�l�ڂ̑f������
2018/05/05(�y) 10:01:47.77ID:kwaxj6Evx^2 + a*x +a*b^2 = 0 �c (A)
x^2 + b*x +b*a^2 = 0 �c (B)
�͉��������̂Ƃ���B
(2) (A)�܂���(B)���d���������Ȃ��A���ʂłȂ����̏��Ȃ��Ƃ�����͕��ł��邱�Ƃ������B
0302�P�R�Q�l�ڂ̑f������
2018/05/05(�y) 10:03:03.97ID:kwaxj6Eva, b ���قȂ�萔�Ƃ��A2��2��������
x^2 + a*x +a*b^2 = 0 �c (A)
x^2 + b*x +b*a^2 = 0 �c (B)
�͉��������̂Ƃ���B
(2) (A)�܂���(B)���d���������Ȃ��Ƃ��A(A)�܂���(B)�͕��̉��������Ƃ������B
0303�P�R�Q�l�ڂ̑f������
2018/05/05(�y) 10:07:14.40ID:kwaxj6Ev(1)��(2)����̖��ɉ������ނƂ����̂����������̌����ł��B
�Z���X���Ȃ��ƌ��킴��܂���B
0304�P�R�Q�l�ڂ̑f������
2018/05/05(�y) 10:19:34.58ID:tEdcrB57>>302�͈�����������ł��邱�Ƃ������Ȃ��Ă������̂Ŗ�肪�Ⴄ
0305�P�R�Q�l�ڂ̑f������
2018/05/05(�y) 17:16:15.66ID:oI3zjkm/��
cosx������y=-sinx�̈Ⴂ��������܂���B
0306�P�R�Q�l�ڂ̑f������
2018/05/05(�y) 17:23:42.00ID:vn0wm8Ig0307�P�R�Q�l�ڂ̑f������
2018/05/06(��) 14:59:23.84ID:9aRha6eI�O�p���Ƃ����͉̂��̍��ꂽ�̂ł��傤���H
���Z�ɓ����Ă����Ȃ藝�R���Ȃ��o�Ă���Sin�Ɓ�a/c����90�x����Ȃ����ă��̈Ӗ���������Ȃ���ł����c
0308�P�R�Q�l�ڂ̑f������
2018/05/06(��) 15:07:17.01ID:FzJFoTTthttp://jbpress.ismedia.jp/articles/-/46369?page=2
����ȋL��������܂���
�V���w�Ƃ��ŕK�v�������݂����ł���
90���ł͂Ȃ��Ƃ����̂́A��3�ɂȂ�Ƃ��̂ق������w�I�ɂ��������������Ă���Ƃ����̂��킩��Ǝv�� �܂�
���Ɛ��w�ɂ���܂藝�R�����߂Ȃ��ق��������ł���
���w�͌��߂�ꂽ���[���ɏ]���Ė��������p�Y���Q�[���ł�
������Ȋw���ʼn��p�ł���ꍇ������܂����A��{�I�ɂ́A���Ȃ��Ƃ����O�I�ɂ͉Ȋw�ł͂Ȃ��̂ŁA�N�w�╶�w�ȂǂƓ������w�Ȃ�ł���
�܂��A���Z�͈͓̔��Ȃ���̏ꍇ�̓O�O��Ώo�Ă���Ǝv���܂�����
0309�� ��2VB8wsVUoo
2018/05/07(��) 12:03:01.26ID:EWP32cBY0310�� ��2VB8wsVUoo
2018/05/07(��) 12:03:20.99ID:EWP32cBY0311�� ��2VB8wsVUoo
2018/05/07(��) 12:03:41.09ID:EWP32cBY0312�� ��2VB8wsVUoo
2018/05/07(��) 12:03:59.43ID:EWP32cBY0313�� ��2VB8wsVUoo
2018/05/07(��) 12:04:20.92ID:EWP32cBY0314�� ��2VB8wsVUoo
2018/05/07(��) 12:04:40.03ID:EWP32cBY0315�� ��2VB8wsVUoo
2018/05/07(��) 12:05:01.90ID:EWP32cBY0316�� ��2VB8wsVUoo
2018/05/07(��) 12:05:24.12ID:EWP32cBY0317�� ��2VB8wsVUoo
2018/05/07(��) 12:05:40.91ID:EWP32cBY0318�� ��2VB8wsVUoo
2018/05/07(��) 12:05:57.23ID:EWP32cBY0319�P�R�Q�l�ڂ̑f������
2018/05/07(��) 12:47:16.71ID:SWI/sRCA0320�� ��2VB8wsVUoo
2018/05/07(��) 16:22:56.87ID:EWP32cBY0321�� ��2VB8wsVUoo
2018/05/07(��) 16:23:15.81ID:EWP32cBY0322�� ��2VB8wsVUoo
2018/05/07(��) 16:23:34.54ID:EWP32cBY0323�� ��2VB8wsVUoo
2018/05/07(��) 16:23:53.96ID:EWP32cBY0324�� ��2VB8wsVUoo
2018/05/07(��) 16:24:12.03ID:EWP32cBY0325�� ��2VB8wsVUoo
2018/05/07(��) 16:24:33.25ID:EWP32cBY0326�� ��2VB8wsVUoo
2018/05/07(��) 16:24:53.34ID:EWP32cBY0327�� ��2VB8wsVUoo
2018/05/07(��) 16:25:12.04ID:EWP32cBY0328�� ��2VB8wsVUoo
2018/05/07(��) 16:25:30.24ID:EWP32cBY0329�� ��2VB8wsVUoo
2018/05/07(��) 16:25:46.64ID:EWP32cBY0330�P�R�Q�l�ڂ̑f������
2018/05/09(��) 13:28:23.33ID:D8i3yt6A0331�P�R�Q�l�ڂ̑f������
2018/05/16(��) 11:15:38.53ID:hpTFF7qj�藝���̂��̂͂킩��܂����w���v�Z���킩�炸���₵�܂���
��낵�����肢���܂�
https://i.imgur.com/y5krm7F.jpg
0332�P�R�Q�l�ڂ̑f������
2018/05/16(��) 11:42:18.18ID:9vjRMy7+(2/x)^(10-k)=2^(10-k)/x^(10-k)=2^(10-k)*x^(k-10)
������Ǝw�����o����ł�����A�Ȃ�܂���
0333�P�R�Q�l�ڂ̑f������
2018/05/17(��) 00:16:40.74ID:ZE4fxdOl0334�P�R�Q�l�ڂ̑f������
2018/05/18(��) 19:30:56.92ID:vmQVU3pI����a, ����r, ����l, ����n �̓��䐔��̘a�� Sn �Ƃ���B
Sn = (a-lr)/(1-r) = (lr-a)/(r-1)
���o���肢���܂��B
0335�P�R�Q�l�ڂ̑f������
2018/05/18(��) 19:39:06.37ID:vmQVU3pISn=a+ar+ar^2+...+l
rSn=ar+ar^2+...+lr
(1-r)Sn=a-lr
Sn=(a-lr)/(1-r)=(lr-a)/(r-1)
0336�P�R�Q�l�ڂ̑f������
2018/05/18(��) 23:37:06.31ID:ubh02zX530�l�̐��k�����̃e�X�g�����Ƃ���A
��A�CB�CC�̐����Ґ��͏���22�l�A18�l�A14�l�ł������B
���̂Ƃ��A���_��5�_�ł�������(AB2��݂̂̐����҂܂���C1��݂̂̐�����)�̐l���̍ő�l��
�����炩�B
���낢�듖�Ă͂߂Ȃ��璲�ׂ�ƁA�Ⴆ��
�@�uAB2��̂ݐ����E�E�E16�l�AC�̂ݐ����E�E�E8�l�AAC2��̂ݐ����E�E�E4�l�A�S����E�E�E2�l�v�̏ꍇ
�����̍ő�l��^����ꍇ(�܂�24�l������)�ɂȂ肻�����ȁA�Ǝv�����̂ł���
�����Ɖ����ɂ͂ǂ̂悤�ɍl����悢�ł��傤���B
���Ԃ�s�����Ɏ������ނ̂ł͂Ȃ����Ǝv���̂ł�������ł��B
��낵�����肢���܂��B
0337�P�R�Q�l�ڂ̑f������
2018/05/19(�y) 22:55:59.30ID:CbhwwpWB�Ⴆ�x�ɒ��ڂ����x�̍��ͣ�ƕ�����āuax��2x�v�̂悤�ɕ����̍�����̂̓_���ł܂Ƃ߂�(a+2)x�Ȃ�OK�ł���ˁB�O�҂��ԈႢ�����ł��܂����B�P�ɖ������̓��ލ������鐮������Ȃ��̂ł����B
0338�P�R�Q�l�ڂ̑f������
2018/05/20(��) 12:52:06.81ID:hV4zR5AA0339�P�R�Q�l�ڂ̑f������
2018/05/21(��) 11:53:35.39ID:O6sAWet2���F
x ��2�������� 25*x^2 - 35*x + 4*k = 0 ���قȂ�2�̉��������A
���ꂼ�� sin(��), cos(��) �ŕ\�킳���Ƃ��A�萔 k �̒l�����߂�B
�F
���ƌW���̊W�ɂ��
sin(��) + cos(��) = 7/5 �c (1)
sin(��) * cos(��) = 4*k/25 �c (2)
(1) �̗��ӂ�2�悷���
[sin(��)]^2 + [cos(��)]^2 + 2*sin(��)*cos(��) = 49/25
�����
1 + 2*sin(��)*cos(��) = 49/25
�䂦��
sin(��)*cos(��) = 12/25
����� (2) ���� 4*k/25 = 12/25
���������� k = 3
0340�P�R�Q�l�ڂ̑f������
2018/05/21(��) 11:54:09.73ID:O6sAWet20�_�ł���ˁA����ȉB
0341�P�R�Q�l�ڂ̑f������
2018/05/21(��) 12:18:22.90ID:O6sAWet2x ��2�������� x^2 - sqrt(2)*x + k = 0 ���قȂ�2�̉��������A
���ꂼ�� sin(��), cos(��) �ŕ\�킳���Ƃ��A�萔 k �̒l�����߂�B
�F
���ƌW���̊W�ɂ��
sin(��) + cos(��) = sqrt(2) �c (1)
sin(��) * cos(��) = k �c (2)
(1) �̗��ӂ�2�悷���
[sin(��)]^2 + [cos(��)]^2 + 2*sin(��)*cos(��) = 2
�����
1 + 2*sin(��)*cos(��) = 2
�䂦��
sin(��)*cos(��) = 1/2
����� (2) ���� k = 1/2
���������� k = 1/2
0342�P�R�Q�l�ڂ̑f������
2018/05/21(��) 12:19:10.37ID:O6sAWet2��肪���̂悤�Ȗ�肾������S�R�_���ȉł���ˁB
0343�P�R�Q�l�ڂ̑f������
2018/05/21(��) 12:26:45.98ID:O6sAWet2x ��2�������� x^2 - 2*x + k = 0 ���قȂ�2�̉��������A
���ꂼ�� sin(��), cos(��) �ŕ\�킳���Ƃ��A�萔 k �̒l�����߂�B
�F
���ƌW���̊W�ɂ��
sin(��) + cos(��) = 2 �c (1)
sin(��) * cos(��) = k �c (2)
(1) �̗��ӂ�2�悷���
[sin(��)]^2 + [cos(��)]^2 + 2*sin(��)*cos(��) = 4
�����
1 + 2*sin(��)*cos(��) = 4
�䂦��
sin(��)*cos(��) = 3/2
����� (2) ���� k = 3/2
���������� k = 3/2
0344�P�R�Q�l�ڂ̑f������
2018/05/21(��) 12:27:02.26ID:O6sAWet2��肪���̂悤�Ȗ�肾������S�R�_���ȉł���ˁB
0345�P�R�Q�l�ڂ̑f������
2018/05/21(��) 12:27:36.47ID:O6sAWet20346�P�R�Q�l�ڂ̑f������
2018/05/21(��) 12:28:44.69ID:O6sAWet2�͉����d���ł��B
>>343
�͉��� sin(��), cos(��) �ŕ\�킳��܂���B
0347�P�R�Q�l�ڂ̑f������
2018/05/21(��) 15:40:20.96ID:bPLA4dePx ��2�������� 25*x^2 - 35*x + 4*k = 0 ���قȂ�2�̉��������A
���ꂼ�� sin(��), cos(��) �ŕ\�킳���
��
k=3
�Ƃ������q�ׂĂ���܂ł�����A��蕶�ŗ^�����Ă���O��̐^�U�͊W�Ȃ�
0348�P�R�Q�l�ڂ̑f������
2018/05/21(��) 17:36:58.59ID:O6sAWet2x ��2�������� x^2 - 2*x + k = 0 ���قȂ�2�̉��������A
���ꂼ�� sin(��), cos(��) �ŕ\�킳���Ƃ��A�萔 k �̒l�����߂�B
������́��̈Ӗ��ł���ˁB
���F
x ��2�������� x^2 - 2*x + k = 0 ���قȂ�2�̉��������A
���ꂼ�� sin(��), cos(��) �ŕ\�킳���B���̂Ƃ��A�萔 k �̒l�����߂�B 👀
Rock54: Caution(BBR-MD5:1341adc37120578f18dba9451e6c8c3b)
0349�P�R�Q�l�ڂ̑f������
2018/05/21(��) 17:53:49.59ID:bPLA4deP�Ⴂ�܂��B
�u�\�����v�ƒf�����Ă���Ƃ��Ȃ�������Ɏv������ł邾���ł��B
���{�����������������Ǝv���܂��B
0350�P�R�Q�l�ڂ̑f������
2018/05/21(��) 17:56:32.31ID:C/5rhAys�����^���̌����w�E�������Ƃ����邪�����Ɖ��Ԃ��Ă�����
0351�P�R�Q�l�ڂ̑f������
2018/05/22(��) 02:13:01.56ID:uEAD/TKEx ��2�������� 25*x^2 - 35*x + 4*k = 0 ���قȂ�2�̉��������A���ꂼ�ꕽ���̘a��1�������Ƃ�k�̒l�����߂Ȃ���
��k=3
�͂�����
0352�P�R�Q�l�ڂ̑f������
2018/05/22(��) 08:33:07.83ID:yXdy01CVx ��2�������� 25*x^2 - 35*x + 4*k = 0 ���قȂ�2�̉��������A
���ꂼ�� sin(��), cos(��) �ŕ\�킳���Ƃ��A�萔 k �̒l�����߂�B
���̖��́A���̈Ӗ��ł���ˁB���炩�ɁB
���F
x ��2�������� 25*x^2 - 35*x + 4*k = 0 ���قȂ�2�̉��������A
���ꂼ�� sin(��), cos(��) �ŕ\�킳���B���̂Ƃ��A�萔 k �̒l�����߂�B 👀
Rock54: Caution(BBR-MD5:1341adc37120578f18dba9451e6c8c3b)
0353�P�R�Q�l�ڂ̑f������
2018/05/22(��) 11:51:48.86ID:yGAQEFRZhttp://imgur.com/IAL4wpv.jpg
0354�P�R�Q�l�ڂ̑f������
2018/05/23(��) 13:12:42.98ID:5Vv/9fhG0�� < A < 180��
�Ƃ��A
a^2 = b^2 + c^2 - 2*b*c*cos(A)
�����藧���Ă���Ƃ���B
���̂Ƃ��A
3�ӂ̒����� a, b, c �� b, c �̋��ފp�� A �ł���悤�ȎO�p�`�͑��݂��邩�H
0355�P�R�Q�l�ڂ̑f������
2018/05/23(��) 14:16:57.03ID:SaS67Pru0356�P�R�Q�l�ڂ̑f������
2018/05/23(��) 14:39:15.20ID:cqx5U6TUb^2+c^2 = a^2+2bc*cosA
(b+c)^2 = a^2+2(1+cosA)bc > a^2�@�i�� 1+cosA > 0�j
(b-c)^2 = a^2-2(1-cosA)bc < a^2�@�i�� 1-cosA > 0�j
�� |b-c| < a < b+c
����āAa,b,c�͎O�p�`�̐��������i�O�p�s�����j�����A
�R�ӂ̒�����a,b,c�̎O�p�`��b,c�̋��ފp���ƂƂ����
�]���藝��� a^2 = b^2+c^2-2bc*cos�� �Ȃ̂ŁC
cos�� = cosA ���Ȃ킿 �� = A �ƂȂ�B
0357�P�R�Q�l�ڂ̑f������
2018/05/23(��) 14:59:45.87ID:5Vv/9fhG���肪�Ƃ��������܂����B
0358�P�R�Q�l�ڂ̑f������
2018/05/25(��) 13:52:40.64ID:0CPlB49F0359�P�R�Q�l�ڂ̑f������
2018/05/25(��) 17:03:52.30ID:OmkR2SiPhttps://mathtrain.jp/sqrtsqrt
0360�P�R�Q�l�ڂ̑f������
2018/05/25(��) 17:53:41.44ID:0CPlB49F�����N��ɂ͏ؖ���������Ă��܂��A�ؖ��͂ǂ����̂ł��傤���H
sqrt(8-2*sqrt(3)) = sqrt(4+sqrt(13)) - sqrt(4-sqrt(13)) = �c
�̂悤�Ȍv�Z�𑱂��čs���āA������2�d�������O����Ƃ������Ƃ͂Ȃ��̂ł��傤���H
sqrt(8-2*sqrt(3))
https://www.wolframalpha.com/input/?i=sqrt(8-2*sqrt(3))
sqrt(4+sqrt(13)) - sqrt(4-sqrt(13))
https://www.wolframalpha.com/input/?i=sqrt(4%2Bsqrt(13))+-+sqrt(4-sqrt(13))
0361�P�R�Q�l�ڂ̑f������
2018/05/27(��) 13:38:12.99ID:mdaxXKvj���̏ꍇ�A�ӂ���p�x�����߂邱�ƂɂȂ�̂� acos(���/�Ε�)�Ōv�Z���邱�ƂɂȂ�Ǝv����ł����A
���/�Ε�=acos�Ƃł͂Ȃ��̂͂ǂ����Ăł����H
0362�P�R�Q�l�ڂ̑f������
2018/05/27(��) 14:18:24.90ID:mdaxXKvj���ȉ������܂���
0363�P�R�Q�l�ڂ̑f������
2018/05/27(��) 19:21:30.17ID:vMpKRBo5cos^2��=7/16�ƂȂ�Ƃ���܂ł͂킩��̂ł���
����������ۂɉE�ӂ��傫�ȃ��[�g�ň͂܂�Ă���Ӗ����킩��܂���
cos^2������cos�������߂邽�߂ɗ��ӂ�cos���Ŋ�����
cos2��=7/16��cos���ɂȂ�Ȃ��̂͂Ȃ��ł����H
https://i.imgur.com/UjEWrrc.jpg
0364�P�R�Q�l�ڂ̑f������
2018/05/27(��) 19:22:58.35ID:a10sXM8ohttps://i.imgur.com/CHtOf1R.jpg
0365�P�R�Q�l�ڂ̑f������
2018/05/27(��) 19:46:37.14ID:iUUbZ73Zhttps://www.youtube.com/watch?v=apxtSqxjw08&;t=13s
�N�Ƃł���������Ă����܂������u���[�_�[�̏����v
https://www.youtube.com/watch?v=3ud3ImlX9GQ
���[�_�[�V�b�v�̒�`�A�}�l�W�����g�Ƃ̈Ⴂ
https://www.youtube.com/watch?v=0bAaoxiFyVc
�`�[�����[�_�[�ɕK�v�Ȃ�������̃X�L��
https://www.youtube.com/watch?v=vMohhH0M0_E
���[�_�[�K���I�o�����i�̋��ʍ��I�I
https://www.youtube.com/watch?v=7N44-wu7_RY
������b����u�T�̏��F�́v�M���W�\�z
https://www.youtube.com/watch?v=0cuevK_9gJ8
�ق߂�Z�p �W�X�e�b�v - �l�ԊW�����܂������J�ߕ��̋Ɉ�
https://www.youtube.com/watch?v=TEzEI2CVPvg
����I���[�_�[�V�b�v���m������B4��ނ̃��[�_�[�V�b�v�X�^�C������ɕ��͂��s��
http://mag.executive.itmedia.co.jp/executive/articles/0907/15/news038.html
0366�P�R�Q�l�ڂ̑f������
2018/05/27(��) 20:04:11.22ID:2ROWd2cH�Q�l���̃~�X����ˁH
0367�P�R�Q�l�ڂ̑f������
2018/05/27(��) 20:48:46.61ID:5VmNsrCG���ۂɂ���Ă݂�Ⴂ�����
0368�P�R�Q�l�ڂ̑f������
2018/05/27(��) 21:31:08.94ID:0eozSXd8k>0
k^2=9
���ď����^����ꂽ��ǂ�����ĉ����H
�ʂ�k=9/k���Ă��Ă��������ǁA��������ǂ�����́H
�`����w
�Ԃ��͂��͂��́I�I�I
0369�P�R�Q�l�ڂ̑f������
2018/05/27(��) 21:41:50.23ID:2ROWd2cHk=9/k���
logk=log(9/k)=log9-logk=2log3-logk
��2logk=2log3
��logk=log3
��k=3
0370�P�R�Q�l�ڂ̑f������
2018/05/27(��) 21:43:33.77ID:bcx6g4Dj0371�P�R�Q�l�ڂ̑f������
2018/05/27(��) 21:48:26.89ID:JlVk5Goyk=9/k���
k^2=9
k=�}3
��������Ă킴�Ɖ���肵�Ēm��������̒m����U��l���Ȃ�Ă������m���Ă܂����H
�o�J�A���Ă�����ł���
0372�P�R�Q�l�ڂ̑f������
2018/05/27(��) 21:52:17.21ID:2ROWd2cHk>0�̏����������Ƃ��Ă܂���
���o�J����
0373�P�R�Q�l�ڂ̑f������
2018/05/27(��) 21:56:02.03ID:JlVk5Goy���閳�����Ȍ����n�т̔C�ӂ̃��f���ɑ��Ă���_�����ӂ���ɐ^�ƂȂ�Ȃ�A�т���ӂ�LK�ɂ����ďؖ��\�ƂȂ邱�Ƃ������A�Ƃ�����肪�킩��܂���
���o�J�Ȃ�ŋ����Ă���������
0374�P�R�Q�l�ڂ̑f������
2018/05/27(��) 22:00:06.97ID:JlVk5Goy�o�J�Ȃ�ő��������ė~������ł�����
0375�P�R�Q�l�ڂ̑f������
2018/05/27(��) 22:11:38.64ID:EdUtsj53�����A��������
0376�P�R�Q�l�ڂ̑f������
2018/05/27(��) 22:20:53.42ID:2ROWd2cH�킩��Ȃ���ł��ˁi�j
0377�P�R�Q�l�ڂ̑f������
2018/05/27(��) 22:23:34.62ID:JlVk5Goy���呲�Ƃ����̂ɍ��͐����ی��������Đ������Ă�����Ė{���ł����H
0378�P�R�Q�l�ڂ̑f������
2018/05/27(��) 22:28:17.88ID:2ROWd2cH�E�{���ɂȂɂ������Ȃ��{���N�����Z��
�E������킩����x�̑�w���w�̓��e���悭���������ɏ����Ă�E���R�]
�E�b��ɂ��Ă���Ȃ��n�����ǓƂ�킷���߂ɓ���������J��Ԃ������̔p�l
�҂̓���
�E�C�P�����̃G���[�g���吶�E����@��
�E���w�����ăo���o�������Ă�r�W�l�X�}��
�E���z�[�Ŏ�
0379�P�R�Q�l�ڂ̑f������
2018/05/27(��) 22:33:21.46ID:JlVk5Goy�ł��A���Ȃ����͖��E�ł�����ˁH
0380�P�R�Q�l�ڂ̑f������
2018/05/27(��) 22:38:11.81ID:Y8hBeKse0381�P�R�Q�l�ڂ̑f������
2018/05/28(��) 11:33:08.42ID:bMm0TG6u0382�P�R�Q�l�ڂ̑f������
2018/05/28(��) 12:57:49.71ID:0x2VP8D2>>371
>>372
���̗���D��
>>363
cos�Ŋ����Ă��Ȃ��āA1/2��i���[�g����̂Ɠ����j���Ă��
0383�P�R�Q�l�ڂ̑f������
2018/05/28(��) 16:36:41.70ID:7DoP0x8Y0384�P�R�Q�l�ڂ̑f������
2018/05/28(��) 16:39:48.22ID:7DoP0x8YAB = 3, BC = 5, CD = 6, DA = 5, ��B = 120���̎l�p�`ABCD
�����̖��͐Ԃ��`���[�g���ɍڂ��Ă�����ł��B
���̗ނ̖��ł́A�ʎl�p�`�Ȃ̂������łȂ��̂��A��肩���
����ł��Ȃ��悤�Ȗ����ȒP�ɍ��܂��B
0385�P�R�Q�l�ڂ̑f������
2018/05/28(��) 16:43:08.43ID:7DoP0x8Y���A���`�F�b�N���Ă݂���A��͂菟��ɓʎl�p�`�ł���Ɖ��肵���}��
�`���Ă��܂��B
���l�p�`���Ɠ��R�A�v�Z���ʂ�����Ă��܂��B
0386�P�R�Q�l�ڂ̑f������
2018/05/28(��) 17:58:23.82ID:9xZHOAUO0387�P�R�Q�l�ڂ̑f������
2018/05/28(��) 19:01:26.79ID:GtBRvjFW0388�P�R�Q�l�ڂ̑f������
2018/05/28(��) 20:08:47.51ID:7DoP0x8Y�A�b�v���[�h����܂ł��Ȃ��A
�u
���̐}�`�̖ʐ� S �����߂�B
AB = 3, BC = 5, CD = 6, DA = 5, ��B = 120���̎l�p�`ABCD
�v
�Ƃ������ł��B
0389�P�R�Q�l�ڂ̑f������
2018/05/28(��) 20:09:17.41ID:7DoP0x8Y�Ǒf�l�������Ă��܂���ˁB
0390�P�R�Q�l�ڂ̑f������
2018/05/28(��) 20:43:39.22ID:9xZHOAUO�����{���Ŋm�F���Ă��Ă��
0391�P�R�Q�l�ڂ̑f������
2018/05/28(��) 21:41:30.10ID:kdVc2zFn���l�p�`�Ȃ�B��240���ɂȂ��Ȃ��ł����H
0392�P�R�Q�l�ڂ̑f������
2018/05/28(��) 22:27:30.73ID:uNj9Yc2L>>389��������Ƃ͋�������
�ǂ��ɂ���B���l�p�`�̓��p�����ď����ĂȂ�����I�Ƃ܂Ō����Ȃ�����A�A�A
0393�P�R�Q�l�ڂ̑f������
2018/05/28(��) 22:51:19.44ID:6hX4sYOa�����͂̏��߂ɒf�菑��������
0394�P�R�Q�l�ڂ̑f������
2018/05/29(��) 02:36:11.06ID:cuIjcuNHhttps://www.youtube.com/watch?v=y3WFObrOIoQ
�z���G������Q&A vol.155�N�Ƃ̂�����
https://www.youtube.com/watch?v=2n1O4oUeIXg
�x�]�M���u���ƂɏA�E�Ȃ�āA�Ƃ����ɃI���R���v�u���̎���A���ł���I���R���v
https://www.youtube.com/watch?v=gSvIk_Bnwlo
�x�]�M���̖������������I�u�܂�Ȃ��d���Ȃ��������߂�I�y�������Ƃ������I�v
https://www.youtube.com/watch?v=4w3XOl5CoU8
�x�]�M���@���߂�ꂽ���[���̏������ːl���I���ŁA���E�ґ�����
https://www.youtube.com/watch?v=CYRo8o2Y_D8
�y�x�]�M���z���T�����[�}���K���I�N�炢�������d�����߂���H���͂����茾���đS�����ʂ��I�I
https://www.youtube.com/watch?v=IgyRIVdvxhk
���ꂩ��͌l�̎���I�q�J���͘b����肢���q�J�L���͕ҏW����肢�B
���ꂩ��̒ʉ݂̖����͂ǂ��Ȃ�̂����b����
https://www.youtube.com/watch?v=4hQngvBCugA
�l��������҂��I���C�u�z�M���オ�{�i�I�ɂ���ė��Ă��̗̈��
����Ɋg�債�Ă����������璘���ɂȂ�l����������
https://www.youtube.com/watch?v=1H0R-kBtUOo
0395�P�R�Q�l�ڂ̑f������
2018/05/29(��) 14:44:18.51ID:vTovl9q8��(1�|X)���́A���[�g�̒����v�Z���A(X�|1)�ɂ��Ă͂Ȃ����߉��ł����H
0396�P�R�Q�l�ڂ̑f������
2018/05/29(��) 17:33:58.91ID:6ltIIHde0397�P�R�Q�l�ڂ̑f������
2018/05/29(��) 18:32:15.85ID:1rjXMf1Q0398�P�R�Q�l�ڂ̑f������
2018/05/29(��) 18:44:09.80ID:5XIe+UrT0399�P�R�Q�l�ڂ̑f������
2018/05/29(��) 20:57:25.49ID:1rjXMf1Q0��X���̈�
0400�P�R�Q�l�ڂ̑f������
2018/05/29(��) 22:21:15.55ID:Gk5xSpOR3/4x�O3y�O3�|1/2x�O3y�O2�{x�O2y�O2
�r�����܂ߋX�������肢���܂��B
0401�C�i ��/7jUdUKiSM
2018/05/29(��) 23:13:06.10ID:2oLTtdTc��B=120��=30��+90���Ƃ��đ�`ABCD��`���ƁA
S=(3+6)AD/2
=(9/2)AD�\�\�@
CD�̒��_��M�Ƃ���ƁA
��BCM�߁�AMD�i�Ε�BC=AM=5�̒��p�O�p�`�j
�ӂ̔�1:2:��3���A
BM=AD=(5��3)/2�\�\�A
�@�A���A
S=(9/2)(5��3)/2
=(45��3)/4
0402�P�R�Q�l�ڂ̑f������
2018/05/29(��) 23:59:42.95ID:Kce5ASMb���ꂼ�S�̖���
0403�P�R�Q�l�ڂ̑f������
2018/05/30(��) 11:28:56.97ID:PMZrRFyz+ 2*a^2*b^2 + 2*a^2*c^2 + 2*a^2*d^2 + 2*b^2*c^2 + 2*b^2*d^2 + 2*c^2*d^2
+ 8*a*b*c*d
���̎���������������B
����͂ǂ��l���Ĉ���������������̂ł��傤���H
0404�P�R�Q�l�ڂ̑f������
2018/05/30(��) 15:06:06.44ID:h7Hdv4Si���@�Q�Fa+b=2x�Aa-b=2y�@���Ȃ킿�Aa=x+y�Ab=x-y�������āA���ό`���Ă݂�
����ł�����Ȃ���Ac=t+s�Ad=t-s�Ȃ�
���@�R�F�Ⴆ�Aa=1,b=2,c=4,d=8�������A��̓I�Ȑ��l�ɒ����A��������
����ł�����Ȃ���Aa=20,b=5,c=1,d=0�Ƃ��Aa=1000,b=100,c=10,d=1�Ƃ��ł�����Ă݂�B
0405�P�R�Q�l�ڂ̑f������
2018/06/01(��) 15:05:50.06ID:hSfqlL340��x��5�͈̔͂ɂ��邱�Ƃ�q�Ƃ���
p��q���\�������ƂȂ�悤��a�̒l�͈̔͂�0<a��5�ƂȂ�Ə����Ă���̂ł���0<a�ɂȂ�̂������ł��܂���
0406�P�R�Q�l�ڂ̑f������
2018/06/01(��) 18:57:43.79ID:95DMKOFA1)�x�N�g��OP���x�N�g��OA�A�x�N�g��OC��p���ĕ\���B
2)�����̒����̔�BQ�FQC�����߂�B
1�͉�������ł���2���킩��܂���
0407�P�R�Q�l�ڂ̑f������
2018/06/01(��) 19:07:52.20ID:BYmcKCiW0408�P�R�Q�l�ڂ̑f������
2018/06/01(��) 21:30:33.48ID:95DMKOFA������������������������B
0409�P�R�Q�l�ڂ̑f������
2018/06/01(��) 21:51:09.35ID:r5pfr3ga0410�P�R�Q�l�ڂ̑f������
2018/06/01(��) 21:58:33.78ID:r5pfr3ga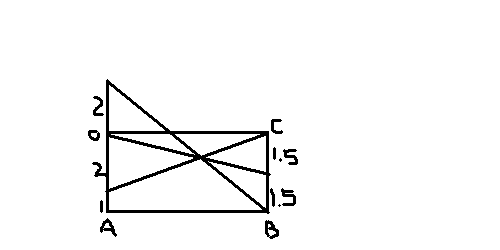
0411�P�R�Q�l�ڂ̑f������
2018/06/01(��) 22:22:18.43ID:BYmcKCiW(1)�̉ߒ��łc�o�F�o�b���S�F�R�����܂邱�ƂƁ��o�n�c�䁢�o�p�b����
0412�P�R�Q�l�ڂ̑f������
2018/06/01(��) 23:33:13.99ID:95DMKOFA���ʏ�ɎO�p�`ABC�Ɠ_P������A����
PA+PB+PC=BC(�S�ăx�N�g��)
�����藧���Ă��鎞�A�_P�͂ǂ̂悤�Ȉʒu�ɂ��邩�B
0413�P�R�Q�l�ڂ̑f������
2018/06/01(��) 23:39:03.78ID:vwGOqrSO0414�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 02:30:17.46ID:G2b8XSzz�����`�AMac��BathScaphe�ł݂Ă���ǐ}���C�����C���\������Ă�I
�ǂ�������炱���Ȃ�́H
0415�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 07:20:50.17ID:lKHAy+cq�N��������������
0416�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 08:18:53.63ID:o6xuXmiU�up��q���\�������v�Ƃ����������͂���܂���
0417�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 10:10:53.41ID:2/RVIMzwhttps://imgur.com/JB7i9Su.jpg
�����̉ł��B
https://imgur.com/xi7tySG.jpg
���̉Ђǂ����܂��H
H ��ʂ�� CD �ƕ��s�Ȓ�����
�� BC �ƌ����_�� F
�� ED �ƌ����_�� G
�Ƃ���B
���l�p�� ABCDE �̐���ł���O�p�` AFG ���l����B
���炩�� AF = AG = FG = 20 �ł���B
����āA�O�p�` AFG �͐��O�p�`�ł���B
���炩�ɁA���̋��̐���͐��O�p�` AFG �ɓ��ڂ��Ă���B
����āA���炩�ɁA���̋��̔��a�́A (10/3)*sqrt(3) �ł���B
0418�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 10:13:09.53ID:XhWTO6Ij0419�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 10:24:23.12ID:lKHAy+cqp���\�������ƂȂ�悤�Ȃł���
0420�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 10:26:01.34ID:2/RVIMzw�O�p�` ABC �͉s�p�O�p�`�Ƃ���B���̂Ƃ��A�e�ʂ��ׂĂ��O�p�` ABC ��
�����l�ʑ̂����݂��邱�Ƃ������B
0421�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 10:26:30.43ID:2/RVIMzw�Ԃ��`���[�g���ɍڂ��Ă��遫�̖��ł����A�������ł��ˁB
�O�p�` ABC �͉s�p�O�p�`�Ƃ���B���̂Ƃ��A�e�ʂ��ׂĂ��O�p�` ABC ��
�����Ȏl�ʑ̂����݂��邱�Ƃ������B
0422�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 10:29:33.08ID:2/RVIMzw0423�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 10:42:41.64ID:XhWTO6Ij���₭��ł����H
0424�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 12:38:21.30ID:lKHAy+cq������������
0425�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 12:44:27.75ID:Oq5/2M0sp��q�̏\���������Ă��Ƃ́up�Ȃ�Ώ��q����������v���Ă��Ƃ���
����ł킩�邾��
0426�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 12:46:44.29ID:Oq5/2M0s0427�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 13:32:41.01ID:lKHAy+cq0428�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 13:49:34.52ID:97/rHTf50429�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 17:45:18.16ID:Qe1TBQQS�ŏ��̖��̋L�q�ŁAa�ɂ��ẮA�Ȃ�Ə����Ă���́H
0430�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 17:51:56.95ID:lKHAy+cq405�ɏ������̂�p��q�ł��邽�߂̏\�������ƂȂ�悤��a�̒l�͈̔͂ł�
0431�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 18:33:26.89ID:o6xuXmiU����a���A�Ƃ�����a���A�Ƃ����̐���a���A�Ƃ������Ă˂������Ă�[����
�n���Ȃ����蕶�����̂܂��������̂�
�up��q���\�������v�݂����ɏ���ɖ�蕶���o�J�̂����ɍ�蒼������{����
���ɂ̓e���[�������ĂȂ�a�ɂ��Ă̏������ڂ��Ă˂����H���ĕ����Ă�
�S�~���B�N�\�n���̎G���̂����ɖ�菟��ɕς���Ȃ��Ă�L�`�K�C���B
0432�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 18:53:15.29ID:K0/bPyHw���閳�����Ȍ����n�т̔C�ӂ̃��f���ɑ��Ă���_�����ӂ���ɐ^�ƂȂ�Ȃ�A�т���ӂ�LK�ɂ����ďؖ��\�ƂȂ邱�Ƃ������A�Ƃ�����肪�킩��܂���
�킩��Ȃ���ł����H
���Ȃ����o�J���Ƃ������Ƃł����H
0433�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 18:59:44.32ID:o6xuXmiU���S���藝���ؖ��\
�͂��_�j
0434�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 18:59:59.54ID:YWXiUpuc0435�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:00:40.69ID:o6xuXmiU���͂킩��܂�����B���Ȃ��͂킩��Ȃ���ł���ˁH
�Ƃ������Ƃ�
���Ȃ����o�J���Ƃ������Ƃł����ł��ˁH������������������
0436�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:02:01.36ID:o6xuXmiU���������A���N���N����������肾����폟�Ȃ�ˁE�E�E�B
���܂ɂ́A�����Ȃ������Ȃ����ƔY��ŕ����Ă݂����A���ꂪ���̐؎��ȔY�݁B
0437�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:03:13.62ID:K0/bPyHw���S���藝�̏ؖ��͂킩���ł����H
���͂킩��܂�����
0438�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:06:38.97ID:o6xuXmiU�m�F�ł����A
���Ȃ��͔n�����Ƃ������Ƃł����ł��ˁH������������������
0439�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:08:06.22ID:K0/bPyHw�������H
���͂킩��܂�����o�J�ł͂Ȃ��ł���
0440�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:09:39.38ID:o6xuXmiU���Ȃ���>>432
0441�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:10:20.24ID:o6xuXmiU���Ȃ���>>432�ł킩��܂�����ď����Ă܂���H
�o�J���Ă��Ƃł����ł��ˁH
0442�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:11:26.79ID:K0/bPyHw���͂킩�邩��o�J�ł͂Ȃ��ł���
0443�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:12:20.81ID:o6xuXmiU���Ȃ���>>432�ł킩��܂�����ď����Ă܂���H
�o�J���Ă��Ƃł����ł��ˁH
0444�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:15:27.22ID:K0/bPyHw���͂킩�邩��o�J�ł͂Ȃ��ł���
0445�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:16:38.21ID:o6xuXmiU�������Ȍ����n�т̔C�ӂ̃��f���ɑ��Ă���_�����ӂ���ɐ^�ƂȂ����
���S���藝�ɂ��т���ӂ�LK�ɂ����ďؖ��\�ƂȂ�܂���
�Ȃ�ł���Ȃ��Ƃ��킩��Ȃ���ł����H�H�H
�o�J���Ă��Ƃł����ł��ˁH
0446�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:17:39.43ID:K0/bPyHw���͂킩�邩��o�J�ł͂Ȃ��ł���
0447�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:18:24.58ID:o6xuXmiU���Ȃ���>>432�ł킩��܂�����ď����Ă܂���H
�o�J���Ă��Ƃł����ł��ˁH
0448�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:19:10.87ID:K0/bPyHw���͂킩�邩��o�J�ł͂Ȃ��ł���
0449�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:20:07.92ID:o6xuXmiU���Ȃ���>>432�ł킩��܂�����ď����Ă܂���H
�o�J���Ă��Ƃł����ł��ˁH
0450�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:22:36.93ID:K0/bPyHw���͂킩�邩��o�J�ł͂Ȃ��ł���
�����������Ȃ����{���ɂ킩���Ă��邩�ǂ����������ł���
���S���藝�Ƃ͂����������ŁA�����p���Ăǂ̂悤�ɏؖ��ł��邩�����Ă݂Ă���܂��H
0451�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:24:38.84ID:o6xuXmiU���Ȃ���>>432�ł킩��܂�����ď����Ă܂���H
�o�J���Ă��Ƃł����ł��ˁH
0452�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:24:57.68ID:K0/bPyHw���͂킩�邩��o�J�ł͂Ȃ��ł���
�����������Ȃ����{���ɂ킩���Ă��邩�ǂ����������ł���
���S���藝�Ƃ͂����������ŁA�����p���Ăǂ̂悤�ɏؖ��ł��邩�����Ă݂Ă���܂��H
0453�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:26:14.91ID:o6xuXmiU���Ȃ���>>432�ł킩��܂�����ď����Ă܂���H
�o�J���Ă��Ƃł����ł��ˁH
0454�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:27:01.77ID:K0/bPyHw���͂킩�邩��o�J�ł͂Ȃ��ł���
�����������Ȃ����{���ɂ킩���Ă��邩�ǂ����������ł���
���S���藝�Ƃ͂����������ŁA�����p���Ăǂ̂悤�ɏؖ��ł��邩�����Ă݂Ă���܂��H
0455�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:28:37.28ID:o6xuXmiU���Ȃ���>>432�ł킩��܂�����ď����Ă܂���H
�o�J���Ă��Ƃł����ł��ˁH
0456�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:28:46.14ID:K0/bPyHw���͂킩�邩��o�J�ł͂Ȃ��ł���
�����������Ȃ����{���ɂ킩���Ă��邩�ǂ����������ł���
���S���藝�Ƃ͂����������ŁA�����p���Ăǂ̂悤�ɏؖ��ł��邩�����Ă݂Ă���܂��H
0457�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 19:29:51.38ID:o6xuXmiU���Ȃ���>>432�ł킩��܂�����ď����Ă܂���H
�o�J���Ă��Ƃł����ł��ˁH
0458�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 20:02:56.56ID:K0/bPyHw�킩��Ȃ��̂ł��傤
0459�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 20:10:15.48ID:o6xuXmiU���Ȃ���>>432�ł킩��܂�����ď����Ă܂���H
�o�J���Ă��Ƃł����ł��ˁH
0460�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 20:24:30.88ID:K0/bPyHw�����������Ȃ����{���ɂ킩���Ă��邩�ǂ����������ł���
���S���藝�Ƃ͂����������ŁA�����p���Ăǂ̂悤�ɏؖ��ł��邩�����Ă݂Ă���܂��H
0461�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 20:31:03.46ID:o6xuXmiU���Ȃ���>>432�ł킩��܂�����ď����Ă܂���H
�o�J���Ă��Ƃł����ł��ˁH
0462�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 20:41:22.56ID:K0/bPyHw0463�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 20:49:27.76ID:o6xuXmiU���Ȃ���>>432�ł킩��܂�����ď����Ă܂���H
�o�J���Ă��Ƃł����ł��ˁH
0464�P�R�Q�l�ڂ̑f������
2018/06/02(�y) 20:56:58.50ID:Qe1TBQQS���ł�>>431���w�E����Ă���ʂ�A��蕶�̖`���ɕ���(�L��)a������\�����ɂ��ď����ĂȂ��̂��낤���A�Ƃ�������ł��B
���W�̉��@0��a��5�@�ƂȂ��Ă���̂ł���A
�ŏ�����u���̐�a�ɂ��āA�ȉ��̖�ɓ�����v�ȂǂȂ��Ă���̂ł͂Ȃ��̂��낤���A�Ƃ�������ł��B�@
�����u����a�ɂ��Ĉȉ��̖�ɓ�����v�ƂȂ��Ă���Ȃ�A���̉͊ԈႢ�ł��B
0465�P�R�Q�l�ڂ̑f������
2018/06/03(��) 23:57:10.33ID:NpAun9Dk0466�P�R�Q�l�ڂ̑f������
2018/06/04(��) 07:15:55.55ID:kvqOk5eD>>463
����l����悧
����Ȓ��x�Ȃ̂��H
�S���_���I�ɑ����ׂ��ĂȂ���
0467�P�R�Q�l�ڂ̑f������
2018/06/04(��) 08:59:50.39ID:6HdYFqxb�y�A�m�Z�p���܂ޔC�ӂ̖������Ȍ����n�ɑ��A���郂�f��M,N����ј_�����ӂ����݂��āAM|=�ӂ���N|���ӂƂł��邱�Ƃ�����
0468�P�R�Q�l�ڂ̑f������
2018/06/04(��) 13:45:47.64ID:qVhRS52G0469�P�R�Q�l�ڂ̑f������
2018/06/06(��) 10:50:34.75ID:I31rhA5H���̂Ƃ��A A �� B �� C �������B
0470�P�R�Q�l�ڂ̑f������
2018/06/06(��) 10:50:53.51ID:I31rhA5Ha = 2*R*sin(A)
b = 2*R*sin(B)
c = 2*R*sin(C)
a, b ,c �ɑ��鉼����A
sin(A) �� sin(B) �� sin(C)
(1)�O�p�` ABC ���݊p�O�p�`�܂��͒��p�O�p�`�̏ꍇ
��B ���O�p�` ABC �̍ő�̊p�ł���Ɖ��肷��ƁA
sin(B) = sin(180�� - A - C) = sin(A + C)
0�� < A < A + C �� 90�� ������A
sin(A) < sin(A + C) = sin(B)
����́A sin(A) �� sin(B) �ɖ�������B
����āA ��B �͎O�p�` ABC �̍ő�̊p�ł͂Ȃ��B
��C ���O�p�` ABC �̍ő�̊p�ł���Ɖ��肷��ƁA
sin(C) = sin(180�� - A - B) = sin(A + B)
0�� < A < A + B �� 90�� ������A
sin(A) < sin(A + B) = sin(C)
����́A sin(A) �� sin(C) �ɖ�������B
����āA ��C �͎O�p�` ABC �̍ő�̊p�ł͂Ȃ��B
�ȏ���A ��A ���O�p�` ABC �̍ő�̊p�ł���B
90�� �� A = 180�� - B - C
B �� B + C �� 90��
C �� B + C �� 90��
sin(B) �� sin(C) ������A
C �� B
�ȏ���A A �� B �� C
(2)�O�p�` ABC ���s�p�O�p�`�̏ꍇ
0�� < A < 90��
0�� < B < 90��
0�� < C < 90��
sin(A) �� sin(B) �� sin(C)
������A
A �� B �� C
0471�P�R�Q�l�ڂ̑f������
2018/06/06(��) 11:19:05.42ID:I31rhA5H1�̎O�p�`�ɂ����āA�傫���ӂɌ����������p�́A�������ӂɌ���������
�p���傫���B����āA a �� b �� c �ł��邩�� A �� B �� C
0472�P�R�Q�l�ڂ̑f������
2018/06/06(��) 11:20:51.74ID:I31rhA5H�p���傫��
�Ƃ��������͏ؖ��Ȃ��Ɏg���Ă������̂ł��傤���H
���Z���w�̖��ɂ����āA�����ؖ��Ȃ��Ɏg���Ă悭�A�����ؖ��Ȃ��Ɏg���Ă͂Ȃ�Ȃ���
�Ƃ������[���͂ǂ����ŕ���������Ă���̂ł��傤���H
���[�����������ɁA�����o�肵�Ă���Ƃ�����A���܂�ɂ��������Șb�ł��B
0473�P�R�Q�l�ڂ̑f������
2018/06/06(��) 11:26:59.91ID:hEC4hMnU�O�i�_�@��p����C�ӂ̐��w�̏ؖ��́A�O�i�_�@��p���Ȃ��ʏؖ��������Ƃ�����
0474�P�R�Q�l�ڂ̑f������
2018/06/06(��) 11:32:01.50ID:kw0zJ0wR�������ƌ��ɂ���Ĉ͂܂ꂽ�O�p�`�̖ʐς��̂��̂ł͂Ȃ��A
���̑O�i�K�ɂ�����u�O�p�`�̖ʐρv�ɂ��Ď���ł��B
���̋L�q�̎O�p�`�̖ʐς̐������A�ǂ̂悤�ɂ��ďo�Ă���̂�
������܂���B
�����i���{���j�^�Q�����C���̒��_�Ƃ����
������y����2�i���̓��j��̂R�_�i���C��2�j�C�i���C��2�j�C�i���C��2�j�̍��O�p�`�̖ʐς́C
�i1�^8�j�i���|���j3�ł���B
0475�P�R�Q�l�ڂ̑f������
2018/06/06(��) 11:33:59.63ID:I31rhA5H0476�P�R�Q�l�ڂ̑f������
2018/06/06(��) 12:15:38.51ID:T0lhZDVF�ϕ�����Ă�Ȃ炢����1/6������
�ϕ���m��Ȃ��Ȃ�}�`�ƕ��������x�N�g���ŏK���ʐό�����
���w���ł��킩���@�����邩�������
0477�P�R�Q�l�ڂ̑f������
2018/06/06(��) 12:53:54.00ID:TUSGQldc0478�P�R�Q�l�ڂ̑f������
2018/06/06(��) 13:02:05.67ID:p1acT6fD��`�̖ʐς�������Ȃ�
��-���̑�`���炁-���Ƃ�-���̑�`������������
0479�P�R�Q�l�ڂ̑f������
2018/06/06(��) 13:22:12.86ID:vvRzGekLhttp://arukinagaraomoukoto.com/?p=199
�u���������͏��������v�@��q�̃C�X�������k��t�ȂNj`�����@�g���R�@
http://mainichi.jp/articles/20160603/ddl/k13/040/209000c
�J�^�[�����肪�Ƃ������{�ɂW�O���~��LNG�S�O�O���g���x��
https://blogs.yahoo.co.jp/xoxdunubxox/19936207.html?__ysp=5Zyw6ZyHIOaUr%2BaPtCDjgqvjgr%2Fjg7zjg6s%3D
�����̃N�E�F�[�g�Ƃ��������e�����I�����{��k�Ђł�400���~���̎x��
http://okutta.blog.jp/archives/1739450.html
�k�Д�Ў҂̎x���́u�{���̃W�n�[�h�v���{�Љ�ɐ����郀�X����8
http://business.nikkeibp.co.jp/article/life/20111110/223777/
�C�X�������k�̕����L���X�g���k���܂Ƃ��Ȍ�
0480�P�R�Q�l�ڂ̑f������
2018/06/06(��) 15:37:16.90ID:Qzhx4Evf⑴�pA�ƁA3�ӂ̒���BC.CA.AB�����߂�B
�Ƃ�������
⑴�@���A sinA/7= sinB/5= sinC/3=�k(�萔)�Ƃ����A�Ɖ���ɏ�����Ă���̂ł����k�Ƃ������R�͂Ȃ��ł����H
0481�P�R�Q�l�ڂ̑f������
2018/06/06(��) 15:49:53.75ID:nXIl+XZ0��������g��L����������B
0482�P�R�Q�l�ڂ̑f������
2018/06/06(��) 17:22:19.92ID:Qzhx4Evf��k�͂�߂Ă�������
0483�P�R�Q�l�ڂ̑f������
2018/06/06(��) 17:28:02.61ID:UiOoA6Gv0484�P�R�Q�l�ڂ̑f������
2018/06/06(��) 17:31:07.97ID:UiOoA6Gv�̂Ƃ����ʂ銴���ł��Ƃ߂�Ȃ���ł��傤���H
0485�P�R�Q�l�ڂ̑f������
2018/06/06(��) 17:35:09.71ID:UiOoA6Gv0486�P�R�Q�l�ڂ̑f������
2018/06/06(��) 22:19:45.07ID:vvRzGekLhttps://www.youtube.com/watch?v=apxtSqxjw08&;t=13s
�N�Ƃł���������Ă����܂������u���[�_�[�̏����v
https://www.youtube.com/watch?v=3ud3ImlX9GQ
���[�_�[�V�b�v�̒�`�A�}�l�W�����g�Ƃ̈Ⴂ
https://www.youtube.com/watch?v=0bAaoxiFyVc
�`�[�����[�_�[�ɕK�v�Ȃ�������̃X�L��
https://www.youtube.com/watch?v=vMohhH0M0_E
���[�_�[�K���I�o�����i�̋��ʍ��I�I
https://www.youtube.com/watch?v=7N44-wu7_RY
������b����u�T�̏��F�́v�M���W�\�z
https://www.youtube.com/watch?v=0cuevK_9gJ8
�ق߂�Z�p �W�X�e�b�v - �l�ԊW�����܂������J�ߕ��̋Ɉ�
https://www.youtube.com/watch?v=TEzEI2CVPvg
����I���[�_�[�V�b�v���m������B4��ނ̃��[�_�[�V�b�v�X�^�C������ɕ��͂��s��
http://mag.executive.itmedia.co.jp/executive/articles/0907/15/news038.html
0487�P�R�Q�l�ڂ̑f������
2018/06/06(��) 23:40:49.57ID:GvvwXYAK0488�P�R�Q�l�ڂ̑f������
2018/06/07(��) 08:48:16.73ID:V855DpbBhttps://imgur.com/yXPOKKN.jpg
�F
https://imgur.com/BosGxXJ.jpg
�O�p�` ACP �̖ʐς��ő�ɂȂ�̂́A���炩�ɁA�_ P �� �� AC �̐^�ɂ���Ƃ��ł��B
���̂Ƃ��A���R�A�O�p�` ACP �͓ӎO�p�`�ɂȂ�܂��B
�Ȃ��A��̉摜��2���ڂ̂悤�ȋc�_�����Ă���̂ł��傤���H
0489�P�R�Q�l�ڂ̑f������
2018/06/07(��) 09:27:08.53ID:2SZqvUPg0490�P�R�Q�l�ڂ̑f������
2018/06/07(��) 09:32:07.72ID:V855DpbBhttps://imgur.com/MUIUdbI.jpg
���̖��Ő��l�p���̍�������肭�ǂ����@�ŋ��߂Ă���̂͂Ȃ��ł��傤���H
��ӂ̒����� 6 �̐����`�̑Ίp���̒����̔����ł�����A�����ɁA 3*sqrt(2)
�ł���ƕ�����͂��ł��B
0491�P�R�Q�l�ڂ̑f������
2018/06/07(��) 09:34:58.85ID:V855DpbB����Ƃ��̖�莩�̂�����肾�Ƃ͌����܂���ˁB
�i�C�j�ő̐ς����߂�Ƃ��ɁA���Ɂi�I�j�͓̉����Ă���̂ŁA
�����I�Ɂi�C�j�Ɓi�I�j�͓������ł��B
0492�P�R�Q�l�ڂ̑f������
2018/06/07(��) 09:36:43.89ID:V855DpbB���̖��̂悤�ɁA�U���`���̖��ŁA���̗U���̈Ӑ}��������Ȃ����Ƃ����̂�
�ǂ��Ȃ�ł��傤���H
0493�P�R�Q�l�ڂ̑f������
2018/06/07(��) 13:35:15.47ID:zMB5aIB80494�P�R�Q�l�ڂ̑f������
2018/06/07(��) 17:24:19.85ID:nEMHR8Pc�ǂȂ��������Ē����܂����H
0495�P�R�Q�l�ڂ̑f������
2018/06/07(��) 17:28:44.57ID:BLDmLkdD0496�P�R�Q�l�ڂ̑f������
2018/06/07(��) 17:33:02.20ID:b8NKkSVn����������x,y,z��k�̎��ŕ\���邩����₷��
0497�P�R�Q�l�ڂ̑f������
2018/06/07(��) 18:33:34.71ID:nEMHR8Pc���₷���Ƃ͋�̓I�Ɂc�t�ɒu���Ȃ��Ɖ����Ȃ��Ƃ������Ƃł����H
���������ڂ������肢���܂��B
0498�P�R�Q�l�ڂ̑f������
2018/06/07(��) 20:10:32.94ID:2SZqvUPg���̊W���g�����ƂŁA�]���藝����cosA�����܂�A�Ƃ����̂����̎d�g�݁B
�@�̒萔��L�ƒu�����ƂŁA�O�ډ~�̔��aR���g����a�Ab�Ac���قڋ@�B�I�Ȍv�Z�ŋ��܂�̂�
��r�I�ȒP�Ȗ��ɂȂ��A�Ƃ������ƂȂ̂ł��傤�B
0499�P�R�Q�l�ڂ̑f������
2018/06/07(��) 22:46:25.05ID:nEMHR8Pc�Ə�����Ă����̂ł����ԈႢ�ł���ˁHx<0�ł���ˁH
0500�P�R�Q�l�ڂ̑f������
2018/06/07(��) 22:50:02.45ID:vhEWfiTa0501�P�R�Q�l�ڂ̑f������
2018/06/07(��) 22:50:45.94ID:2SZqvUPg0502�P�R�Q�l�ڂ̑f������
2018/06/07(��) 23:04:28.26ID:nEMHR8Pc�ǂ����Ăł����H�̑I������<�Ɓ�������ꍇ�ǂ��炪�������̂ł����H
0503�P�R�Q�l�ڂ̑f������
2018/06/07(��) 23:08:38.90ID:vhEWfiTa�������ɁAx��0���Ƃ���ƁAx=0�̂Ƃ��A|x|=-x��x��0�����藧���Ȃ��Ȃ�A�̂Ō��Ԃ��Ƃ��ł��Ȃ��Ȃ�܂�
0504�P�R�Q�l�ڂ̑f������
2018/06/08(��) 16:09:59.17ID:HZ26Mlpp���ȏ��ɍڂ��Ă����Βl�̒�`|a|=a(a��0) -a(a<0)(a�͎���)�Ɩ������Ă��܂��H
0505�P�R�Q�l�ڂ̑f������
2018/06/08(��) 16:30:34.10ID:ABV4bfoi0506�P�R�Q�l�ڂ̑f������
2018/06/08(��) 16:37:26.91ID:HZ26Mlpp0507�P�R�Q�l�ڂ̑f������
2018/06/08(��) 16:43:11.27ID:ABV4bfoi���Œ�`���悤�����Œ�`���悤��>>505�ɂ����2�̒�`�͓����ɂȂ邩��
�v����ɒ�`�́����ǂ����ł��������ǁA|x|=-x �� x��0�͌��ɂȂ�
0508�P�R�Q�l�ڂ̑f������
2018/06/08(��) 16:48:05.63ID:HZ26Mlpp0509�P�R�Q�l�ڂ̑f������
2018/06/08(��) 16:53:05.20ID:39UqleKm���v
0 ��������3�ʂ�ɏꍇ���������ق����N�ɂ͍����Ă邩�������
0510�P�R�Q�l�ڂ̑f������
2018/06/08(��) 16:55:24.33ID:ABV4bfoi������
���{�I�Ɋ��Ⴂ���Ă邩���m��Ȃ�����⑫�����Ă��炤�ƁA���ȏ��̒�`�u|x|=-x (x��0)�v�Ƃ����̂�
�ux��0��������K��|x|=-x�Ƃ������Ɍ��߂邯�ǁA|x|=-x������Ƃ�����x��0�Ƃ͌����ĂȂ��v
���ĉ��߂���Ɨǂ���
0511�P�R�Q�l�ڂ̑f������
2018/06/08(��) 17:07:44.59ID:HZ26Mlpp0512�P�R�Q�l�ڂ̑f������
2018/06/08(��) 18:25:11.15ID:t6Yqw1mG0513�P�R�Q�l�ڂ̑f������
2018/06/09(�y) 03:28:17.51ID:1chaosaV0514�P�R�Q�l�ڂ̑f������
2018/06/09(�y) 11:53:50.02ID:kua1xXAu0515�P�R�Q�l�ڂ̑f������
2018/06/09(�y) 12:23:13.74ID:zOCFbf30u(a)�� a (a��0), �|a (a��0)
�ƒ�`����ƁAu �� R �S�̂Œ�`���ꂽ���ł���B
���ɁAu(x) �� x��0 �Œ�`����Ă���Au(0)��0 �ł���B�܂��A
��x��R [ u(x)���|x �� x��0 ]
�����藧�B
0516�P�R�Q�l�ڂ̑f������
2018/06/09(�y) 12:28:29.54ID:zOCFbf30�� ��x��R [ u(x)���|x �� x��0 ]
�� ��x��R [ u(x)���|x �� x��0 ]
0517�P�R�Q�l�ڂ̑f������
2018/06/09(�y) 15:44:07.28ID:twWCmcXX�摜�����m�F���������B
����P
�n�����b�N���P�O�Okg�̐l������ē�ӏ��ɉ����͂͂ǂ̂��炢�ł��傤���H
�h�ꂽ��W�����v���ď��悤�Ȃ��Ƃ͂Ȃ��Éd�Ƃ��Ă��������B
����Q
�Ԃ牺�������l�����낷�܂��݂͒邵���܂ܒ�~����Ƃ��ꂼ��̊��ԂƎ����Ă���l��
�d���͋ϓ��ł��傤���H
�܂����̏ꍇ���[�v�̊p�x�⋗���i�Œ�ʒu�j�͉d�ɉe������̂ł��傤���H
�p�������Ȃ���̎���ƂȂ�܂����A��������낵�����肢���܂��B
https://i.imgur.com/6bEIkrf.png
0518�P�R�Q�l�ڂ̑f������
2018/06/10(��) 11:28:36.59ID:KscdBwrD���ۂɎg��ꂽ������Ȃ��ł��傤���A�����Ӗ��������ł����H
��́A����Ȃ��̐��w�ł����ł��Ȃ��ł���ˁB
0519�P�R�Q�l�ڂ̑f������
2018/06/10(��) 11:46:45.07ID:+/Y7hAcj0520�P�R�Q�l�ڂ̑f������
2018/06/10(��) 13:25:07.07ID:ZPKOfWe80521�P�R�Q�l�ڂ̑f������
2018/06/10(��) 14:06:15.07ID:TdrkMfYU���w�ł��Ȃ�ł��Ȃ�����
�f�[�^���͂Ɏg������Ƃ������R�ŁA
�ǂꂩ�̉Ȗڂŋ����Ȃ��Ƃ����Ȃ�����
���w�ɑg�ݓ��ꂽ�̂�B
�ꉞ�A���v�w�҂́A���v�w�͊m���_����b�ɂȂ��Ă�Ǝ咣���Ă��邩��ˁB
�܂��A���_���v�Ƃ����̂͐��w����Ȃ�����B
�Ȃ�Ƃ������肢�݂����Ȃ���B
����v�o�J�ǂ����呛�����āA�f�[�^�T�C�G���e�B�X�g��
���s���Ă�����狳���n�߂��B
���ȏȂ͕��n������A���̂����肪�S�������ł��ĂȂ��ˁB
���v���_�Ȃ�Ď���w��B
�Ȃ�̉��l���Ȃ���B
���Z���ɋ�����̑唽���B
0522�P�R�Q�l�ڂ̑f������
2018/06/10(��) 14:08:07.41ID:TdrkMfYU����Ȃ̓��v�̒m���Ƃ͂Ȃ�̊W���Ȃ��B
�l����l���x����Ȃ��B
�l���Ȃ��l���x�����B
0523�P�R�Q�l�ڂ̑f������
2018/06/10(��) 14:11:05.35ID:+/Y7hAcj���l���Ȃ����Ă͈̂Ⴄ�Ǝv���܂���
0524�P�R�Q�l�ڂ̑f������
2018/06/11(��) 07:06:40.61ID:6e6LuSP/0525�P�R�Q�l�ڂ̑f������
2018/06/11(��) 07:14:09.42ID:mzNKee4X�݂�Ȑ��w�Ȃ�ĖY��Ă܂�����
0526�P�R�Q�l�ڂ̑f������
2018/06/11(��) 11:30:54.47ID:seOWQupA�v���Ċw����Α������₤��
0527�P�R�Q�l�ڂ̑f������
2018/06/11(��) 13:16:10.10ID:wEUesvHDlim(1/n)��[k=1�`2n] (n/k)-(1/n)��[k=1�`n] (n/k)
=��[0�`2] dx/x-��[0�`1] dx/x
=��[1�`2] dx/x
=log2
0528�P�R�Q�l�ڂ̑f������
2018/06/11(��) 14:01:59.73ID:oLebGqJN��[0�`2] dx/x �� ��[0�`1] dx/x �͔��U����̂őʖځB
0529�P�R�Q�l�ڂ̑f������
2018/06/12(��) 16:21:58.28ID:loUUDmA40530�P�R�Q�l�ڂ̑f������
2018/06/12(��) 16:34:46.57ID:8uRl0d4z�E���Z�ł́��͐��ł͂Ȃ��u������ł��傫���Ȃ�v�Ƃ������ہE��Ԃ�\���L����
�E�̂���̊���ɏ]��
���̑��������[���ł�������Ŕ[������
0531�P�R�Q�l�ڂ̑f������
2018/06/12(��) 17:34:30.82ID:breZQF25�S�̏W���͊J�W���ŁA�J��Ԃ͊J�W���ŁA�J��Ԃ�(a,b)��{x|a��x��b}�Ƃ����悤�ɏ�����܂�
���̗ސ���(-��,��)��{x|-����x����}�Ə�������ł���
0532�P�R�Q�l�ڂ̑f������
2018/06/13(��) 00:26:26.49ID:ua/Kh8my0533�P�R�Q�l�ڂ̑f������
2018/06/13(��) 11:31:12.54ID:583kargY�ݏ��@���g���悤�ɉ������Ă���̂ł���
�ǂ�ł��悭�킩��܂���
5-�i12-5�~2�j�~2�Ƃ͂ǂ�����ǂ��o�Ă�����ł����H
https://i.imgur.com/jExTg1b.jpg
0534�P�R�Q�l�ڂ̑f������
2018/06/13(��) 12:05:03.64ID:BQsPba/j���߂Čݏ��@���p�ɂ��Đ������Ă����Ƃ���܂Ŗ߂��ēǂ痝���ł��܂���
0535�P�R�Q�l�ڂ̑f������
2018/06/14(��) 09:31:22.82ID:mxBGyFKThttps://seleck.cc/685
https://trello.com/
�{�[�h�̃��j���[ �� Power-Ups����g���\ Slack DropBox�Ȃ�
Trello Chrome�g���@�\�@elegant
ttp://www.kikakulabo.com/service-eft/
trello�̃I�[�v���\�[�X����
�����c�[�� 2
https://www.google.com/intl/ja_jp/sheets/about/
�����c�[�� 3
https://slack.com/intl/ja-jp
https://www.dropbox.com/ja/
https://bitbucket.org/
https://ja.atlassian.com/software/sourcetree
https://www.sketchapp.com/
ttp://photoshopvip.net/103903
ttps://goodpatch.com/blog/sketch-plugins/
Trello Chrome�g���@�\�v���O�C���W
https://chrome.google.com/webstore/search/trello?_category=extensions
Slack�v���O�C���W
https://slack.com/apps
Sketch�v���O�C���W
https://sketchapp.com/extensions/plugins/
https://supernova.studio/
0536�P�R�Q�l�ڂ̑f������
2018/06/14(��) 10:50:32.81ID:L3CJZ/1x(4)�ɂ��Ď���ł��B
�ϗ� x �͊K���l�ł�����A x �̒����l�͌����ɋ��܂�A 160 cm �ł���Ǝv���܂��B
������ƁA�⊮���� 160.75 cm ���Ƃ��Ă��܂��B
���̉͂��������ł���ˁH
0537�P�R�Q�l�ڂ̑f������
2018/06/14(��) 10:53:39.99ID:L2SRJeq0�����l�̒�`���m�F���Ă�������
0538�P�R�Q�l�ڂ̑f������
2018/06/14(��) 11:02:45.81ID:L3CJZ/1x0539�P�R�Q�l�ڂ̑f������
2018/06/14(��) 13:24:40.22ID:AaixVZjg����������
0540�P�R�Q�l�ڂ̑f������
2018/06/14(��) 15:47:41.59ID:L3CJZ/1x���肪�Ƃ��������܂����B
���Ȃ݂ɁA
>>536
�͐Ԃ��`���[�g���ł��B
�I���W�i���̖��Ȃ̂ŁA�{�����o�₷���̂ł͂Ȃ����Ǝv���܂��B
0541�P�R�Q�l�ڂ̑f������
2018/06/14(��) 16:13:21.75ID:9WoIjmAX�ł�50�l�̐g���̒����l���A158�`162�̊K���Ƀf�[�^���ϓ��ɕ��z���Ă���Ɖ��肵�ċ��߂��낤
0542�P�R�Q�l�ڂ̑f������
2018/06/16(�y) 15:13:17.65ID:aX5XKQzC#D = 25
#E = 9
#F = 17
#G = 20
#H = 10
D �� E �� F
E �� G �� H
�Ƃ���B
#(D �� G) �̉\�ȍő吔�����߂�B
0543�P�R�Q�l�ڂ̑f������
2018/06/16(�y) 15:21:41.74ID:aX5XKQzC������Ĉ���ł���ˁH
���̎�̖����Ă�����ł������ꂻ���ł���ˁB
�ł��A�Ȃ�ƂȂ�����Ă���Ή�����悤�ȃ��x���̖��ɂ��Ă���܂��ˁB
��ʓI�ȉ���͂Ȃ������ł��ˁB
���s���낷�邵���Ȃ����ł��ˁB
����ł���ˁH
0544�P�R�Q�l�ڂ̑f������
2018/06/16(�y) 15:32:05.57ID:aX5XKQzC#(D �� G) �� #G = 20
#(D �� G) = 20 �ƂȂ�悤�� D, E, F, G, H, U ���\������悢�B
��
#(E �� F) �� #(E) + #(F) = 9 + 17 = 26
#D = 25
��
max{#D, #E, #F, #G, #H} = #D
�ɒ��ڂ���B
U = D = {1, 2, 3, �c, 25}
�Ƃ���B
#D = 25
D �� U
E = {1, 2, 3, �c, 9}
F = {9, 10, 11, �c, 25}
�Ƃ���B
E �� U
F �� U
#E = 9
#F = 25 - 8 = 17
D = E �� F ������A D �� E �� F
G = {1, 2, 3, �c, 20}
�Ƃ���B
G �� U
#G = 20
E �� G = E
H = {1, 2, 3, �c, 10}
�Ƃ���B
H �� U
#H = 10
E �� H
E �� G = E
������A
E �� G �� H
#(D �� G) = 20
0545�P�R�Q�l�ڂ̑f������
2018/06/16(�y) 15:34:11.10ID:aX5XKQzC0546�P�R�Q�l�ڂ̑f������
2018/06/17(��) 02:47:52.96ID:SQeQUx3E0547�P�R�Q�l�ڂ̑f������
2018/06/17(��) 03:42:19.02ID:Rf37kXEa0548�P�R�Q�l�ڂ̑f������
2018/06/17(��) 10:33:21.99ID:7YwtgFpaIJ�̒��_��P�AJH�̒��_��Q�AHI�̒��_��R�Ƃ���Ƃ�
�O����AP�ABQ�ACR��1�_�Ō����܂����H
0549�P�R�Q�l�ڂ̑f������
2018/06/17(��) 10:50:46.64ID:Mnf6xpK6�E�A�����J�̓C���f�B�A���r�łƓy�n���D�A�z��f�ՂŐ��������L�`�K�C���Ƃł���B
�E���̉��炵�����j�𔖂߂邽�߁A��������Ȃ��싞��s�E�̍߂���{�ɔ킹�A����͐��`�ʂ������E��
�A�����J�����S������������B
�E�������Y�}�Ɩk���N�����Ċ؍��̓A�����J����������S���ł���B
�E�����̎O�����ɔ����Ƒ����������{�ւ̔j��s�ׂ̎菕�������Ă�͕̂�����Ȃ��A�����J�ł���B
�E�k���N�Ƀ~�T�C����ł����Ă�̂̓A�����J�ł���B�����̓��{�̊C�̐N�����㉟�����Ă�̂��A�����J�ł���B
�E���{�ւ̃^�J�������ƌ�H���������݂����؍��������Ƃ��Ƃ�Â₩�����������Ă�̂��A�����J�ł���B
�E���{��łڂ��s�ׂ𗠂ő���Ȃ���A����Ă��ƈ̂����ɕČR��n��u�����{���Ď����Ɨ���
�j�Q���Ă�̂̓A�����J�ł���B
�EGHQ�̐��Ȍ�A�A�����J�͍ݓ����N�l����{�̊Ԑڎx�z�̓���Ƃ��A�l�X�ȏd�v�|�X�g��^�����{�l���������ʑ���
���{�l�̊Ď����s�킹�Ă���B
�E�|�\�E�ɂ����Đl�C���Ȃ��ɂ�������炸�A�ݓ���n�[�t�������͔��l���N�p�����̂̓A�����J�̈��͂����邩��ł���B
�E�A�����J�͖f�Ս����̃h�������֙[�����邱�Ƃ���{�ɋ������B�G���h���X�ɕč��킹�A�����J�o�ςƃh����
�x���邱�Ƃ��������Ă���B
�E�A�����J�ُ͋k�����Ə���ł�������ɏW������{���{�ɍs�킹�A���{�l��n�R���敾�����A���͒ቺ�Ɠ��{�l�팸��
�O��I�ɍs�킹�Ă���B
�E�A�����J�͓��{���{�Ɉږ����ʂɓ���邱�Ƃ𖽗߂��A���{�̕����ƒ������A���{�𓌓�A�W�A�̂悤�ȕn�R����
���t�卑�ɂ��悤�Ƃ��Ă���B
�E�A�����J�͎����������ۋْ��œ��{�������A���{�̖@���ƌ��@�̏�Ɉʒu����TPP��������FTA�����сA���{�̎匠��D��
���{�l��z��ɂ��悤�Ƃ��Ă���B
0550�P�R�Q�l�ڂ̑f������
2018/06/17(��) 13:57:32.16ID:RvJZHTGb0551�P�R�Q�l�ڂ̑f������
2018/06/18(��) 12:53:37.43ID:gqjjEmEJ6�ł�9�ł���������́B
��� �S�̏W��U={1,2,3,�c,100�p�Ƃ���
�W��A={n |n��6�Ŋ�����100�ȉ��̎��R���p
n(A)=16
�W��B={n |n��9�Ŋ�����100�ȉ��̎��R��}
n(B)=11
�Ə����Ă���̂ł����W��A���c�̂Ƃ����n���g�������R�ƏW��B�ɂ�n���g�������R��������Ȃ��ł��B�W��A��n�ƏW��B��n�͈Ⴄ�Ǝv���܂����c
0552�P�R�Q�l�ڂ̑f������
2018/06/18(��) 13:02:33.09ID:eGF8UeY1���Z���H
0553�P�R�Q�l�ڂ̑f������
2018/06/18(��) 13:16:46.67ID:u/FeauBv0554�P�R�Q�l�ڂ̑f������
2018/06/18(��) 13:19:47.26ID:gqjjEmEJ���Z���w�̎���X���Ə����Ă���̂ł����c
0555�P�R�Q�l�ڂ̑f������
2018/06/18(��) 13:22:32.58ID:u/FeauBv>>552�Ɍ������̂ŋC�ɂ��Ȃ��ł�������
n�ł�m�ł�x�ł��Ȃ�ł�������ł��A�����
�W���̒��g��\�����߂ɁA�Ƃ肠���������g���������ŁA�W���̊O�ł͈Ӗ��������܂���
0556�P�R�Q�l�ڂ̑f������
2018/06/18(��) 13:32:11.96ID:gqjjEmEJA��B�œ����������g���Ă��\��Ȃ���Ă܂����H
0557�P�R�Q�l�ڂ̑f������
2018/06/18(��) 13:45:57.86ID:u/FeauBv0558�P�R�Q�l�ڂ̑f������
2018/06/18(��) 13:58:48.01ID:eGF8UeY1�N�������Ă��悢�X���ł��邱�Ƃɕς��͂Ȃ��ˁB
0559�P�R�Q�l�ڂ̑f������
2018/06/18(��) 14:08:27.53ID:gqjjEmEJ���݂܂���
0560�P�R�Q�l�ڂ̑f������
2018/06/19(��) 20:40:08.95ID:OP9HU1ID5�~�d�݁F 3 ��
10�~�d�݁F 2 ��
50�~�d�݁F 2 ��
100�~�d�݁F 3 ��
���̍d�݂̃Z�b�g�������Ă���Ƃ���B
�����̍d�݂��g���Ďx��������z�̂����A���̎x�����Ɏg����d�݂̑g������
��ʂ肵���Ȃ����̂̐������߂�B
0561�P�R�Q�l�ڂ̑f������
2018/06/19(��) 21:50:15.91ID:PSHlXrbV72
0562�P�R�Q�l�ڂ̑f������
2018/06/19(��) 22:01:10.04ID:+Z0hi4Oo0563�P�R�Q�l�ڂ̑f������
2018/06/20(��) 16:47:56.30ID:s02DjmhL5�~�d�݁F 3 ��
10�~�d�݁F 2 ��
50�~�d�݁F 2 ��
100�~�d�݁F 3 ��
���̍d�݂̃Z�b�g�������Ă���Ƃ���B
�����̍d�݂��g���Ďx��������z�̂����A���̎x�����Ɏg����d�݂̑g������
��ʂ肵���Ȃ����̂̐������߂�B
������v�Z���邽�߂̃v���O������������̂ł����A�������������o�܂���B
�ǂ����Ԉ���Ă���̂ł��傤���H
http://codepad.org/KYsvalF1
0564�P�R�Q�l�ڂ̑f������
2018/06/20(��) 16:58:17.67ID:PMkcgvhX0565�P�R�Q�l�ڂ̑f������
2018/06/20(��) 17:00:25.24ID:s02DjmhL���������͐������ł��B
0566�P�R�Q�l�ڂ̑f������
2018/06/20(��) 18:08:17.41ID:+37XW5M80567�P�R�Q�l�ڂ̑f������
2018/06/20(��) 18:11:04.16ID:NGJUAayd>>561�������ł���
0568�P�R�Q�l�ڂ̑f������
2018/06/20(��) 18:11:27.03ID:s02DjmhLfor i in range(1, n + 1):
����print(i)
�����s����ƁA
1
2
3
4
5
6
7
8
9
10
�ƕ\������܂��B
0569�P�R�Q�l�ڂ̑f������
2018/06/20(��) 18:45:28.76ID:+37XW5M8������ĂP����Ȃ���Ȃ��́B
0570�P�R�Q�l�ڂ̑f������
2018/06/20(��) 18:49:07.01ID:+37XW5M80571�P�R�Q�l�ڂ̑f������
2018/06/20(��) 19:04:41.03ID:s02DjmhL�́A�Ԃ��`���[�g���ɍڂ��Ă�����ł��F
https://imgur.com/dKrjuDe.jpg
���̃y�[�W�܂ł̂Ƃ���ň�Ԃ̓�₾�Ǝv���܂��B
�`���[�g���ɍڂ��Ă�������ɕ�����ɂ����ł��B
���{��͂��Ȃ��l�������Ă��邩��ł��B
0572�P�R�Q�l�ڂ̑f������
2018/06/20(��) 19:12:38.35ID:s02DjmhL�����͑��������Ă���Ǝv���܂��B
0573�P�R�Q�l�ڂ̑f������
2018/06/20(��) 19:43:46.60ID:NGJUAayd�S���v�f�����o���Ă݂���킩��܂���
���Ƃ���14�Ȃ�ł����ǁA10+4��5+5+4��2�ʂ肠��܂����
���ꂾ�Ƃ��������g�ݍ��킹����ʂł��Ȃ���ł�
�ǂ����10+4�ƂȂ�܂�����
0574�P�R�Q�l�ڂ̑f������
2018/06/20(��) 20:35:50.61ID:s02DjmhL�Ȃ�قǁA���肪�Ƃ��������܂����B
0575�P�R�Q�l�ڂ̑f������
2018/06/21(��) 11:26:45.95ID:PvtCPiGJ�i1�j�̃v���O�����ł��B
http://codepad.org/l5ebLxIi
0576�P�R�Q�l�ڂ̑f������
2018/06/21(��) 11:29:39.58ID:PvtCPiGJ(2)�̃v���O�����ł��B
http://codepad.org/2L7NBaUQ
0577�P�R�Q�l�ڂ̑f������
2018/06/21(��) 11:30:42.33ID:PvtCPiGJ(3)�̃v���O�����ł��B
http://codepad.org/Qwv8xxB5
0578�P�R�Q�l�ڂ̑f������
2018/06/21(��) 12:22:26.41ID:tIZfHF8q�X���`�������蕶�͓]�ڂ��Ȃ����ǁA�ʔ������X���̔��ʑ̖̂���
���̃v���O�����ŊȌ��ɏ������肷��̂��Ȃ��H
0579�P�R�Q�l�ڂ̑f������
2018/06/21(��) 18:08:31.45ID:PvtCPiGJ(3)�̃`���[�g���̉ł����A������ɂ����ł���ˁH
https://imgur.com/pNrMpjM.jpg
0580�P�R�Q�l�ڂ̑f������
2018/06/21(��) 18:24:38.25ID:PvtCPiGJ�N��
>>571
��(3)�̕�����₷�������肢���܂��B
0581�P�R�Q�l�ڂ̑f������
2018/06/21(��) 18:32:17.40ID:PvtCPiGJ���̉������ł���l�͂��܂����H
�Ӗ��s������Ȃ��ł����H
0582�P�R�Q�l�ڂ̑f������
2018/06/21(��) 18:32:33.42ID:PvtCPiGJ��ǂ��邵���Ȃ��ł���ˁH
0583�P�R�Q�l�ڂ̑f������
2018/06/21(��) 18:46:55.41ID:PvtCPiGJ1, 1, 1, 1, 1
5, 5, 5
10, 10
�i�Q�j41
1, 1, 1, 1, 1, 1
5, 5, 5
10, 10
�i�R�j42
1, 1, 1, 1, 1, 1, 1
5, 5, 5
10, 10
�i�S�j43
1, 1, 1, 1, 1, 1, 1, 1
5, 5, 5
10, 10
�i�T�j4
1, 1, 1, 1
�i�U�j9
1, 1, 1, 1
5
�i�V�j34
1, 1, 1, 1
5, 5
10, 10
�i�W�j39
1, 1, 1, 1
5, 5, 5
10, 10
�i�X�j3
1, 1, 1
�i�P�O�j2
1, 1
�i�P�P�j1
1
�i�P�Q�j0
0584�P�R�Q�l�ڂ̑f������
2018/06/21(��) 18:54:26.59ID:PvtCPiGJ�x������1�~�d�݂�5���܂܂��ꍇ���l����B
�x���� = 1 + 1 + 1 + 1 + 1 + �c
1 + 1 + 1 + 1 + 1 = 5 ������A
���̎x�����ɂ́A���ׂĂ�5�~�d�݂��܂܂�Ȃ���Ȃ�Ȃ��B
����āA
�x���� = 1 + 1 + 1 + 1 + 1 + 5 + 5 + 5 + �c
5 + 5 = 10 ������A
���̎x�����ɂ́A���ׂĂ� 10�~�d�݂��܂܂�Ă��Ȃ���Ȃ�Ȃ��B
����āA
�x���� = 1 + 1 + 1 + 1 + 1 + 5 + 5 + 5 + 10 + 10 = 40
0585�P�R�Q�l�ڂ̑f������
2018/06/21(��) 18:56:49.60ID:PvtCPiGJ�x������1�~�d�݂�6���܂܂��ꍇ���l����B
�x���� = 1 + 1 + 1 + 1 + 1 + 1 + �c
1 + 1 + 1 + 1 + 1 = 5 ������A
���̎x�����ɂ́A���ׂĂ�5�~�d�݂��܂܂�Ȃ���Ȃ�Ȃ��B
����āA
�x���� = 1 + 1 + 1 + 1 + 1 + 1 + 5 + 5 + 5 + �c
5 + 5 = 10 ������A
���̎x�����ɂ́A���ׂĂ� 10�~�d�݂��܂܂�Ă��Ȃ���Ȃ�Ȃ��B
����āA
�x���� = 1 + 1 + 1 + 1 + 1 + 1 + 5 + 5 + 5 + 10 + 10 = 41
0586�P�R�Q�l�ڂ̑f������
2018/06/21(��) 18:57:30.92ID:PvtCPiGJ�x������1�~�d�݂�7���܂܂��ꍇ���l����B
�x���� = 1 + 1 + 1 + 1 + 1 + 1 + 1 + �c
1 + 1 + 1 + 1 + 1 = 5 ������A
���̎x�����ɂ́A���ׂĂ�5�~�d�݂��܂܂�Ȃ���Ȃ�Ȃ��B
����āA
�x���� = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 5 + 5 + 5 + �c
5 + 5 = 10 ������A
���̎x�����ɂ́A���ׂĂ� 10�~�d�݂��܂܂�Ă��Ȃ���Ȃ�Ȃ��B
����āA
�x���� = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 5 + 5 + 5 + 10 + 10 = 42
0587�P�R�Q�l�ڂ̑f������
2018/06/21(��) 18:58:29.49ID:PvtCPiGJ�x������1�~�d�݂�8���܂܂��ꍇ���l����B
�x���� = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + �c
1 + 1 + 1 + 1 + 1 = 5 ������A
���̎x�����ɂ́A���ׂĂ�5�~�d�݂��܂܂�Ȃ���Ȃ�Ȃ��B
����āA
�x���� = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 5 + 5 + 5 + �c
5 + 5 = 10 ������A
���̎x�����ɂ́A���ׂĂ� 10�~�d�݂��܂܂�Ă��Ȃ���Ȃ�Ȃ��B
����āA
�x���� = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 5 + 5 + 5 + 10 + 10 = 43
0588�P�R�Q�l�ڂ̑f������
2018/06/21(��) 19:01:51.18ID:PvtCPiGJ�x������1�~�d�݂�4���܂܂�A5�~�d�݂�1�����܂܂�Ȃ��ꍇ���l����B
�x���� = 1 + 1 + 1 + 1 + �c
10 = 5 + 5 ������A�x�����ɂ́A10�~�d�݂�1�����܂܂�Ȃ��B
����āA
�x���� = 1 + 1 + 1 + 1 = 4
0589�P�R�Q�l�ڂ̑f������
2018/06/21(��) 19:03:04.56ID:PvtCPiGJ�x������1�~�d�݂�4���܂܂�A5�~�d�݂�1���܂܂��ꍇ���l����B
�x���� = 1 + 1 + 1 + 1 + 5 + �c
10 = 5 + 5 ������A�x�����ɂ́A10�~�d�݂�1�����܂܂�Ȃ��B
����āA
�x���� = 1 + 1 + 1 + 1 + 5 = 9
0590�P�R�Q�l�ڂ̑f������
2018/06/21(��) 19:05:06.38ID:PvtCPiGJ�x������1�~�d�݂�4���܂܂�A5�~�d�݂�2���܂܂��ꍇ���l����B
�x���� = 1 + 1 + 1 + 1 + 5 + 5 + �c
5 + 5 = 10 ������A�x�����ɂ́A���ׂĂ�10�~�d�݂��܂܂�Ȃ���Ȃ�Ȃ��B
����āA
�x���� = 1 + 1 + 1 + 1 + 5 + 5 + 10 + 10 = 34
0591�P�R�Q�l�ڂ̑f������
2018/06/21(��) 19:05:46.36ID:PvtCPiGJ�x������1�~�d�݂�4���܂܂�A5�~�d�݂�3���܂܂��ꍇ���l����B
�x���� = 1 + 1 + 1 + 1 + 5 + 5 + 5 + �c
5 + 5 = 10 ������A�x�����ɂ́A���ׂĂ�10�~�d�݂��܂܂�Ȃ���Ȃ�Ȃ��B
����āA
�x���� = 1 + 1 + 1 + 1 + 5 + 5 + 5 + 10 + 10 = 39
0592�P�R�Q�l�ڂ̑f������
2018/06/21(��) 19:10:09.81ID:PvtCPiGJ�x������1�~�d�݂�3���܂܂��ꍇ���l����B
�x���� = 1 + 1 + 1 + �c
5 = 1 + 1 + 1 + 1 + 1 ������A�x�����ɂ́A5�~�d�݂�1�����܂܂�Ȃ��B
10 = 5 + 5 ������A10�~�d�݂�1�����܂܂�Ȃ��B
����āA
�x���� = 1 + 1 + 1 = 3
0593�P�R�Q�l�ڂ̑f������
2018/06/21(��) 19:11:03.06ID:PvtCPiGJ�x������1�~�d�݂�2���܂܂��ꍇ���l����B
�x���� = 1 + 1 + �c
5 = 1 + 1 + 1 + 1 + 1 ������A�x�����ɂ́A5�~�d�݂�1�����܂܂�Ȃ��B
10 = 5 + 5 ������A10�~�d�݂�1�����܂܂�Ȃ��B
����āA
�x���� = 1 + 1 = 2
0594�P�R�Q�l�ڂ̑f������
2018/06/21(��) 19:11:31.54ID:PvtCPiGJ�x������1�~�d�݂�1���܂܂��ꍇ���l����B
�x���� = 1 + �c
5 = 1 + 1 + 1 + 1 + 1 ������A�x�����ɂ́A5�~�d�݂�1�����܂܂�Ȃ��B
10 = 5 + 5 ������A10�~�d�݂�1�����܂܂�Ȃ��B
����āA
�x���� = 1
0595�P�R�Q�l�ڂ̑f������
2018/06/21(��) 19:12:03.92ID:PvtCPiGJ�x������1�~�d�݂�1�����܂܂�Ȃ��ꍇ���l����B
�x���� = �c
5 = 1 + 1 + 1 + 1 + 1 ������A�x�����ɂ́A5�~�d�݂�1�����܂܂�Ȃ��B
10 = 5 + 5 ������A10�~�d�݂�1�����܂܂�Ȃ��B
����āA
�x���� = 0
0596�P�R�Q�l�ڂ̑f������
2018/06/21(��) 19:14:53.28ID:PvtCPiGJ�`���[�g���͉̉��������Ă���̂��悭������܂���B
0597�P�R�Q�l�ڂ̑f������
2018/06/21(��) 19:25:51.48ID:b+hwKMoM(1)
(1+8)*(1+3)*(1+2)*(1+2)*(1+3)-1=9*4*3*3*4-1
(2)
1,5,10�~�d�݂�50,100�~�d�݂ɕ����čl����
(20+15+8+1)*((300+100)/50+1)-1=44*9-1
(3)
0,1,2,3,4,9,34,39,40,41,42,43
0,50,150,250,350,400
12*6-1=71
0598�P�R�Q�l�ڂ̑f������
2018/06/21(��) 19:34:07.23ID:PvtCPiGJ���̉Ŗ��_�����炦��̂ł��傤���H
0599�P�R�Q�l�ڂ̑f������
2018/06/21(��) 19:58:15.08ID:b+hwKMoM(3)�ɂ����ĕ⑫����Ƃ����̂Ȃ�A�Ⴆ�A
�u���ŗ^�����Ă���d�݂̂����A1,5,10�~�d�݂��g����43�~�ȉ��̎x�������s���ہA
���邢�́A50,100�~�d�݂��g����400�~�ȉ��̎x�������s���ہA���̎x�����̏ꍇ�́A
�g���d�݂����j�[�N�ɒ�܂�B�v���炢�ł��傤���B
���ƁA�u���_�����炤�̍����v�ł͂Ȃ��A�u���w�I�ȍl�����v�Ɏ��������ĉ��Ă܂��B
0600�P�R�Q�l�ڂ̑f������
2018/06/22(��) 18:52:19.40ID:D6k3TIiO0601�P�R�Q�l�ڂ̑f������
2018/06/22(��) 20:08:38.14ID:sDkbryo20602�P�R�Q�l�ڂ̑f������
2018/06/23(�y) 00:03:05.04ID:T1taZlhX���̂܂��ڂɁZ��Ɓ~�������B�������A�~��͉��ɂ�
�c�ɂ������ē���邱�Ƃ͂Ȃ��B���̂悤�ȁZ�A�~��̓������
������ a_n �Ƃ���B
���ׂĂ� n �ɂ���
a_(n+2) = c*a_(n+1) + d*a_n
�ƂȂ�悤�Ȓ萔 c�A d �����߂�B
0603�P�R�Q�l�ڂ̑f������
2018/06/23(�y) 00:15:16.12ID:T1taZlhX�ȒP�ł���ˁB
https://imgur.com/qCr3rJB.jpg
�ł��A�Ԃ��`���[�g���̉����ɒ����ł��B
�`���[�g���͖{���ɂ悢�Q�l���Ȃ̂ł��傤���H
0604�P�R�Q�l�ڂ̑f������
2018/06/23(�y) 13:03:50.84ID:hZkdPDzR0605�P�R�Q�l�ڂ̑f������
2018/06/23(�y) 14:24:39.35ID:mZ2523yu�`���[�g�Ƃ����̂�ɂ��Ă���悤�ł����A�S�����ɗ����Ȃ��ł���ˁB
����Ȃ��Ƃ��A�����Ɖ���₷�������ɂ��Ăق����ł��ˁB
�f�l�������Ă���̂Ŗ����ł��傤���B
0606�P�R�Q�l�ڂ̑f������
2018/06/24(��) 13:31:26.73ID:NNnxgqJO0607�P�R�Q�l�ڂ̑f������
2018/06/24(��) 20:13:13.55ID:UKEgL2ds�@ax^2 + bx + c�@�Ƃ������� a(x + Z)^2 + Y�@�̌`�ɕϊ�����B
���̕ϊ��̂����̓��[���ɏ]���Ă�邾���Ȃ̂ł킩��܂��B
�ϊ��������ʁAZ��Y�œ��̃O���t�̒��_���킩��B
�Ȃ�ɂ��l�����A�Ƃ肠�����A�o���܂����B
�ł��A�킩��Ȃ��̂́A���_�Ƃ��ċ��܂�������������Ă���������v���Ȃ��_�ł��B
���Ƃ��A
�@y = x^2 + 6x +8�E�E�E�E�E�E�EA
�����������
�@y = (x + 3)^2 - 1
�ƂȂ�A
�@���_���W��(-3 , -1)
�ƂȂ�܂��B
����x = -3�����Ƃ̎�A��x�ɑ�����Ă݂܂��B
�@y = (-3)^2 + 6*(-3) + 8
�ƂȂ�A
�@y = 9 -18 + 8
�ƂȂ�A
�@y = 19
�ƂȂ�܂��B
�@y = -1
�ɂȂ��ĂȂ���ł����E�E�E�E�ƈӖ����킩��Ȃ��Ȃ��Ă��܂��B
������Ċm�F���邱�Ǝ��̂��ԈႢ�Ȃ�ł��傤���H
0608�P�R�Q�l�ڂ̑f������
2018/06/24(��) 20:15:53.47ID:nUG4kBzA0609�P�R�Q�l�ڂ̑f������
2018/06/24(��) 20:17:19.33ID:UKEgL2ds�����E�E�E�E�E�Borz
�����Ƃ���łT�����Y��ł����E�E�E�B
0610�P�R�Q�l�ڂ̑f������
2018/06/24(��) 20:18:45.94ID:UKEgL2ds���w��]�����ۂ��ĒP���v�Z����ł��Ȃ��Ȃ��B
���肪�Ƃ��������܂����B
0611�P�R�Q�l�ڂ̑f������
2018/06/24(��) 20:18:54.37ID:nUG4kBzA�ǂ��l���Ă��킩��Ȃ����́A������Ȃ��ԈႦ���Ă邱�Ƃ�8�����炢����܂�
0612�P�R�Q�l�ڂ̑f������
2018/06/24(��) 21:00:54.50ID:ajBsNK7D0.9��0.9���|�����0.81
0.9��0.81�𑫂���1.71
0.81��0.9���|�����0.729
1.71��0.729�𑫂���
�Ƃ�����Ƃ��ɑ�����Ƃ��āA������ďo����鐔���͖����ɑ����Ă����̂��^��ɂȂ����̂Ŗ����ɑ����Ă����̂��ǂ���������
������鐔�͖����ɏ������Ȃ��Ă��������������肻���ȋC�����邯�ǁA�ǂ�Ȃɏ��������ł������ɑ�����邩�����͂Ȃ��̂�������Ȃ���
�����ɂ͂��̓������o���鐔�w�I�f�{���Ȃ��̂ł��Ȃ���[��
0613�P�R�Q�l�ڂ̑f������
2018/06/24(��) 21:50:48.40ID:nUG4kBzA�ŏI�I�ɂ�
1/(1-0.9)=10�ɂȂ�܂�
0614�P�R�Q�l�ڂ̑f������
2018/06/25(��) 01:39:41.92ID:x1njTMte�g���N�X
0615�P�R�Q�l�ڂ̑f������
2018/06/29(��) 12:32:34.37ID:c600oslH=
Binomial(n, 0)^2 + Binomial(n, 1)^2 + �c + Binomial(n, n)^2
��g�����_�I�ȈӖ��ɂ����@�ȊO�̕��@�ŏؖ�����B
0616�P�R�Q�l�ڂ̑f������
2018/06/29(��) 12:38:56.17ID:xlnN1di10617�P�R�Q�l�ڂ̑f������
2018/06/29(��) 12:45:56.31ID:c600oslH�Ƃ肠���������Ă݂Ă��������B
0618�P�R�Q�l�ڂ̑f������
2018/06/29(��) 12:52:30.95ID:xlnN1di10619�P�R�Q�l�ڂ̑f������
2018/06/29(��) 13:04:07.33ID:c600oslH�Ƃ肠�����A
Binomial(2*n, n)
=
Binomial(n, 0)^2 + Binomial(n, 1)^2 + �c + Binomial(n, n)^2
������
�Ƃ������ɕύX���܂��B
0620�P�R�Q�l�ڂ̑f������
2018/06/29(��) 13:09:23.22ID:xlnN1di10621�P�R�Q�l�ڂ̑f������
2018/06/29(��) 16:25:54.92ID:q8XMxjx70622�P�R�Q�l�ڂ̑f������
2018/06/29(��) 17:13:54.73ID:c600oslHBinomial(n, 0)^2 + Binomial(n, 1)^2 + �c + Binomial(n, n)^2
=
Binomial(n, 0) * Binomial(n, n) + Binomial(n, 1) * Binomial(n, n-1) + �c + Binomial(n, n) * Binomial(n, 0)
������A���̎�����ؖ��ł��܂��ˁB
���肪�Ƃ��������܂����B
0623�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:05:23.85ID:YiFFCn2e0624�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:18:28.59ID:DUaX6qZt0625�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:23:51.28ID:YiFFCn2e����͂ǂ�ȂƂ���Ȃ̂ł��傤���H
0626�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:25:08.18ID:DUaX6qZt0627�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:26:57.57ID:YiFFCn2e�P�O�i�@�łP+�P=�Q�@�����藧���Ȃ����E���ĉF���̂ǂ����ɑ��݂��܂����H
0628�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:27:50.28ID:DUaX6qZt0629�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:28:53.78ID:YiFFCn2e����͂ǂ�ȂƂ���Ȃ̂ł��傤���H
0630�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:29:20.44ID:DUaX6qZt0631�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:34:44.41ID:YiFFCn2e0632�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:35:50.60ID:DUaX6qZt0633�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:36:29.88ID:YiFFCn2e0634�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:41:15.33ID:DUaX6qZt���w�ɂ����āA�����Ƃ́A�P�Ȃ�L���ł���A�Ӗ����̂��̂Ƃ͕ʂ̑��݂Ȃ̂ł�
1+1=2
���B�͂�����݂āA�Ӗ���z��ł��܂����ǁA�悭�l���Č���ƁA���̎��̉��߂͂�������킯�ł�
���̑��l�ȉ��߂̒��ŁA��X�͂������̋��ʔF���Ƃ��āA��̉��߂����肵�A���̉��߂̌��ňӖ���F������킯�ł�
+�͕��ʂ̑����Z�ŕ����̌������Z�q�ł͂Ȃ����A1�͐��w��1�ł�����2�ł͂Ȃ��ȁ[�A�Ƃ��킩��̂ŁA��������Ɍ��܂��Ă��ꂪ�����������Ƃ킩��킯�ł���
���āA���Ȃ��͂��̉��߂̃u�����Œ肵�Ă��܂��܂���
�Ƃ���ƁA1+1=2�̈Ӗ��͌��肳��Ă��܂��܂�
�Ƃ������ƂŁA���̎��͉F���S�̂Ő��������Ƃ������ƂɂȂ�킯�ł�
����͂Ȃ����A�Ƃ����ƁA���Ȃ������̎��̉��߂̎d���𐧌���������ł�
0635�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:43:43.24ID:DUaX6qZt����͂�ł�
����͂Ȃ�ł����H
��ł����
����ȊO�̓����͂���܂���
����|���Ɩڂ̑O�ɂ����A�ʕ����Ƃ��F�X�ȓ��������ł��܂����ǁA���Ȃ�������ƌ����Ă��ł�����A��Ɍ��܂��Ă��ł���
0636�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 21:47:57.10ID:YiFFCn2e�e�ȉ���Ɋ��ӂ��܂�
���肪�Ƃ��������܂���
0637�P�R�Q�l�ڂ̑f������
2018/07/01(��) 12:19:02.10ID:51GRULJl����ɂ��ׂĂ������F�ł���i1�j�̌��ʂ𑫂������̂�1���������
1�ڂ�3�ڂ��قȂ�m���ɂȂ�Ӗ����킯�킩��܂���
�ǂȂ����A�킩��₷�������Ă�������
https://i.imgur.com/N346eej.jpg
0638�P�R�Q�l�ڂ̑f������
2018/07/01(��) 12:41:58.71ID:AISthe0d0639�P�R�Q�l�ڂ̑f������
2018/07/01(��) 13:25:42.46ID:jtkXm4GI0640�P�R�Q�l�ڂ̑f������
2018/07/01(��) 13:30:03.38ID:CP4JuE851,3���قȂ�F(2�͍l�����Ȃ�)�ɂȂ�m��
=1- [1,3�������F(2�͍l�����Ȃ�)�ɂȂ�m��]
�l�����Ȃ����Ă�3���Ђ��O��2�������̂�����1��3�����̊m���̌v�Z�͖ʓ|
������[1,3�������F]=[�S�������F]+[1,3�͓�������2�����Ⴄ]���̎��̉E�ӂ͌v�Z���₷���̂ł��������g����
0641�P�R�Q�l�ڂ̑f������
2018/07/01(��) 13:48:43.30ID:oT8cQQWo0642�P�R�Q�l�ڂ̑f������
2018/07/01(��) 14:42:04.36ID:dmzfkstN0643�P�R�Q�l�ڂ̑f������
2018/07/01(��) 16:19:17.87ID:SPVeqSAm���肪�Ƃ��������܂�
���w�͂������߂܂�
0644�P�R�Q�l�ڂ̑f������
2018/07/01(��) 20:02:42.62ID:vVlH6QWw0645�P�R�Q�l�ڂ̑f������
2018/07/01(��) 22:37:27.79ID:rVhm/AiM0646�P�R�Q�l�ڂ̑f������
2018/07/02(��) 08:45:42.86ID:LQmZJHvX0647�P�R�Q�l�ڂ̑f������
2018/07/02(��) 11:42:05.57ID:8jXyKZ/t�p��Ȃ�covariance
�L���Ȃ��^2
0648�P�R�Q�l�ڂ̑f������
2018/07/02(��) 11:43:29.50ID:8jXyKZ/t���A���U�ƍ�������
0649�P�R�Q�l�ڂ̑f������
2018/07/02(��) 12:57:27.42ID:4eGNskj/50!��0�͉����Ԃ������߂�Ƃ���
�摜�̂悤�Ȍv�Z�ŋ��߂���킯���킩��܂���
�����o�ł̔��`���[�g�ȏ�ɁA�킩��₷���������Ă����������肢���܂�
https://i.imgur.com/12KMQv6.jpg
0650�P�R�Q�l�ڂ̑f������
2018/07/02(��) 13:36:55.87ID:btxpp3TZ10 = 5*2
15 = 5*3
20 = 5*4
25 = 5*5
30 = 5*6
35 = 5*7
40 = 5*8
45 = 5*9
50 = 5*5*2
��*�� �́���5��10�A ���ɂ�5��2�A10+2=12�B10^12�Ŋ�����B
100!�܂łȂ� 20+4=24�A10�O24�Ŋ�����
200!�܂łȂ� 40+8+1=49�A10~49�Ŋ�����B�Ō��1��125=5^3
0651�P�R�Q�l�ڂ̑f������
2018/07/02(��) 13:52:12.45ID:c7Xltbe02*1, 2*2, �c, 2*25
�� 25 ���݂���B
1 ���� 25 �܂ł̐����̂��� 2 �̔{���́A
2*1, 2*2, �c, 2*12
�� 12 ���݂���B
1 ���� 12 �܂ł̐����̂��� 2 �̔{���́A
2*1, 2*2, �c, 2*6
�� 6 ���݂���B
1 ���� 6 �܂ł̐����̂��� 2 �̔{���́A
2*1, 2*2, 2*3
�� 3 ���݂���B
1 ���� 3 �܂ł̐����̂��� 2 �̔{���́A
2*1
�� 1 ���݂���B
����āA 50! ��f�������������Ƃ��� 2 �̎w���́A 25 + 12 + 6 + 3 + 1 = 47 �ł���B
1 ���� 50 �܂ł̐����̂��� 5 �̔{���́A
5*1, 5*2, �c, 5*10
�� 10 ���݂���B
1 ���� 10 �܂ł̐����̂��� 5 �̔{���́A
5*1, 5*2
�� 2 ���݂���B
����āA 50! ��f�������������Ƃ��� 5 �̎w���́A 10 + 2 = 12 �ł���B
�ȏォ��A 50! �� 10^min{47, 12} = 10^12 �Ŋ����邪�A 10^13 �ł͊����Ȃ��B
����āA������ 0 �� 12 ���ԁB
0652�P�R�Q�l�ڂ̑f������
2018/07/02(��) 19:24:04.84ID:FgoaTNrS�v�����10�̍ޗ��ƂȂ�5��50!�̒��ʼn������邩�H���l����Ηǂ�������ł���
25��50��������ۂɂ�5��2���̎�ł���̂�
5,10,15,20,30,35,40,45,����1���� 8�~1
25,50����2���� 2�~2
8�~1+2�~2��12
�l�͒��ۓI�Ȃ��Ƃ������ł������������̂�
���̂悤�ȍl���������Ȃ��Ɨ������ł��܂���ł���
�������Ă���摜�̎���5�̍̏W�Ƃ����ϓ_���猩������
50��5+50��5^2
�u50��5�ɂ���Ă��ł�5����50�܂ł̊Ԃ�5�̔{������1����5���������Ă�̂�
25��50����͗�O�I�ɂ����Ė�����0��1������10���������邽�߂̑f�ނł���5��2���̏W�ł���̂ň�x1���������ɂ��ւ�炸������x1�������������Ƃ��ł���̂���
�i25��50�����5��2��Ƃ��j�v
�Ƃ������Ƃ𗝉����邱�Ƃ����炭�ł��܂���ł���
�l�͂��������l���������Ȃ��Ƃ��̖�肪�����ł��܂���ł���
��1�ɂ��Ă��̒��ۓI�v�l�͂̕n�����̓��o���ł����H
�Ƃɂ��������Ă��������A���肪�Ƃ��������܂���
0653�P�R�Q�l�ڂ̑f������
2018/07/02(��) 22:03:10.68ID:dcaiJ3+H���w���D���ɂȂ낤�I
0654�P�R�Q�l�ڂ̑f������
2018/07/03(��) 00:58:02.75ID:jd9bwgWc0655�P�R�Q�l�ڂ̑f������
2018/07/03(��) 17:43:24.70ID:XBCU9OSI�����ꍇ�A���̓�����͑S���ʼn��ʂ肠�邩�B
�i�P�j
1�̔��ɂ��ׂẴ{�[��������ꍇ��1�ʂ�B
�i�Q�j
���� A, B, C �ƃ��x�������Ă���ꍇ�ɁA
��̔��������Ƃ�1�����Ȃ�������̐��́A
3^n - 3
�ʂ肠��B
�����烉�x�����͂����݂��ɋ�ʂ����Ȃ��悤�ɂ���ƁA
���x�������Ă����Ƃ��ɂ́A�قȂ������Ƃ��ăJ�E���g
����Ă��� 3! �ʂ�̓������ 1 �ʂ�̓�����Ƃ��ăJ�E���g
�����悤�ɂȂ�B
����āA���x�����͂��������ɁA��̔��������Ƃ�1�����Ȃ�
������̐��́A
(3^n - 3) / 3! = (3^(n-1) - 1) /2
�ʂ肠��B
�i�P�j�Ɓi�Q�j�����v���āA
(3^(n-1) + 1) / 2
�ʂ肠�邱�ƂɂȂ�B
0656�P�R�Q�l�ڂ̑f������
2018/07/03(��) 17:51:59.71ID:XBCU9OSI���̖��́i�P�j�̏ꍇ���������Ȃ���Δ��ɊȒP�Ȗ��ł����A
�Ԃ��`���[�g���ł̓�Փx�� ���������� �ƂȂ��Ă��܂��B
�����āA���̉����ł��F
https://imgur.com/HBvFHJx.jpg
���ʂɏ璷�ȉł���ˁH
�Ȃ��`���[�g���͕W���I�ȎQ�l�����Ƃ���Ă���̂ł��傤���H
0657�P�R�Q�l�ڂ̑f������
2018/07/03(��) 18:53:46.20ID:aIR8/Kt30658�P�R�Q�l�ڂ̑f������
2018/07/03(��) 19:20:01.14ID:4NmD8J1d(3^0+3x1^0+2x0^0)/6=1.
0659�P�R�Q�l�ڂ̑f������
2018/07/03(��) 23:19:14.07ID:Kwy/00A7�͂����m�f�ɓ��ꂽ�ق�����������
0660�P�R�Q�l�ڂ̑f������
2018/07/04(��) 10:32:27.57ID:1w66loLI������6���̍d�݂����o���Ƃ��A���o�����͉��ʂ肠�邩�H
������ނ̍d�݂݂͌��ɋ�ʂł��Ȃ����̂Ƃ���B
0661�P�R�Q�l�ڂ̑f������
2018/07/04(��) 13:50:13.23ID:EkfZO2ui��ʂł��Ȃ�������12C6
0662�P�R�Q�l�ڂ̑f������
2018/07/04(��) 13:54:28.72ID:1w66loLI�u������ނ̍d�݁v�͋�ʂł��܂��A1�~�d�݂�10�~�d�݂͂�������ʂł��܂��B
0663�P�R�Q�l�ڂ̑f������
2018/07/04(��) 14:29:39.19ID:g/Q81fAxmain = print $ length [(a,b,c)|a<-[0..4],b<-[0..2],c<-[0..6],a+b+c==6]
15
0664�P�R�Q�l�ڂ̑f������
2018/07/04(��) 15:18:43.18ID:9455rGrq�\�������ďI���B
�\�����ł͂�����ƁE�E�E�Ǝv���Ȃ�
10�~�d�݂̎��o������3�ʂ�B���̂��ꂼ��ɑ�1�~�d�݂̎��o������5�ʂ�B
�����̎��o�����̂��ꂼ��̑g�ɍ��v������6�ƂȂ�悤��50�~�d�݂̎��o����������̂�
���߂���o�����̑�����3�~5=15=�ʂ�B
0665�P�R�Q�l�ڂ̑f������
2018/07/04(��) 20:27:32.10ID:gJbzVP+7https://i.imgur.com/l02xQZf.jpg
�Ȃɏ����x��1���ƌ��߂��ė��ӂɑ������
2^n�𐬂藧�����Ă��ł����H
�������x��1�̂Ƃ���2^n�ɂȂ���Ă����Ȃ�Ȃ��ł����H
�Q�l���̕ҏW�҂��l�ɉ������������̂��Ӗ����킩��܂���
0666�P�R�Q�l�ڂ̑f������
2018/07/04(��) 21:13:55.60ID:l5c9XbcA����͂ǂ�����ĉ����̂ł����H
0667�P�R�Q�l�ڂ̑f������
2018/07/04(��) 21:15:46.02ID:LehMY3zE�w�Z�Ŕ��킳�ꂽ�Q�l���̐^�������Ȃ���
0668�P�R�Q�l�ڂ̑f������
2018/07/04(��) 21:59:22.42ID:foR26SUl��蕶���悭�ǂ݂܂��傤
0669�P�R�Q�l�ڂ̑f������
2018/07/04(��) 22:24:29.03ID:08SqyJqV>x��1�̂Ƃ���2^n�ɂȂ���Ă���
�悭�������Ă���B
0670�P�R�Q�l�ڂ̑f������
2018/07/04(��) 23:02:53.78ID:pFIIIExfx^3y-xy^3-x^2+y^2+2xy-1
0671�P�R�Q�l�ڂ̑f������
2018/07/04(��) 23:22:59.99ID:foR26SUl0672�P�R�Q�l�ڂ̑f������
2018/07/05(��) 06:13:39.89ID:/HHcHIwq���̉������̂��Ƃł��B
0673�P�R�Q�l�ڂ̑f������
2018/07/05(��) 09:04:29.87ID:cs7OPyk60674�P�R�Q�l�ڂ̑f������
2018/07/05(��) 09:45:16.40ID:D6Qx/qB1����ȊO�̓����̏o�����͂Ȃ��ł����H
0675�P�R�Q�l�ڂ̑f������
2018/07/06(��) 17:36:35.27ID:cq6SBV8mabcd �͈ȉ��̏��������Ȃ���Ȃ�Ȃ��B
���ʂ�̈Ïؔԍ������邩�B
(1)
#{a, b, c, d} = 4 �ł���B
(2)
a - b �� 1 (mod 10) �łȂ��B
b - c �� 1 (mod 10) �łȂ��B
c - d �� 1 (mod 10) �łȂ��B
d - a �� 1 (mod 10) �łȂ��B
b - a �� 1 (mod 10) �łȂ��B
c - b �� 1 (mod 10) �łȂ��B
d - c �� 1 (mod 10) �łȂ��B
a - d �� 1 (mod 10) �łȂ��B
0676�P�R�Q�l�ڂ̑f������
2018/07/06(��) 22:50:12.17ID:cq6SBV8m����H����Ȃɓ���ł����H���̖��H
0677�P�R�Q�l�ڂ̑f������
2018/07/08(��) 07:14:11.96ID:+SQHaCed�藝�̏ؖ���ǂݔ���āA�藝���g���������ƃ��o�C�ł����H
0678�P�R�Q�l�ڂ̑f������
2018/07/10(��) 10:29:34.20ID:2RfxZ1jC5(x-2)+9(y+1)=0���琮���������߂�ۂ�
x-2=9k���ƌ��肳���̂͂Ȃ��ł����H
���ꂼ��2�̍��̘a�ɂ����0����邽�߂ɂ�
�Е������A�����Е������̐��ɂȂ邱�Ƃ͂킩��܂�
���̖��̓�����x-2=9k, y+1=-5k�ł����A�t��
x-2=-9k, y+1=5k
����_���Ȃ낤���A�Ǝv���Čv�Z���ė^���ɑ��������1�ł͂Ȃ�-19�ƑS�R�Ⴄ�l�ɂȂ����̂�
�_���Ȃ��Ƃ͂킩��܂���
�������Ȃ��_���Ȃ̂����킩��܂���
0679�P�R�Q�l�ڂ̑f������
2018/07/10(��) 10:37:15.92ID:ea/ja8gQhttps://i.imgur.com/SD8h7k7.png
�^������
a(x-p)+b(y-q)=0�̌`�܂ŋ��߂�
b>0�̂Ƃ���x=bk+p, b<0�̂Ƃ���x=-bk+p...�Ƃ������Ƃ����o���Ă����
���̎�̖��͉����܂���
�ǂ����Ă��A5(x-2)+9(y+1)=0�Ȃǂ̎��ɂ�����
x-2=9k�ƂȂ�̂��A�D�ɗ����Ȃ��Ƃ������A���o�I�ɁA�������肱�Ȃ��̂ł�
�ǂ������������\�ł����H
0680�P�R�Q�l�ڂ̑f������
2018/07/10(��) 10:44:10.54ID:mVxio/MZ5(2-x)=9(y+1)
5��9�݂͌��ɑf������ 2-x ��9�̔{���ɂȂ邵���Ȃ�
0681�P�R�Q�l�ڂ̑f������
2018/07/10(��) 10:58:20.76ID:mVxio/MZ����
��������_���Ȃ낤���A�Ǝv���Čv�Z���ė^���ɑ��������1�ł͂Ȃ�-19�ƑS�R�Ⴄ�l�ɂȂ����̂�
�����_���Ȃ��Ƃ͂킩��܂���
�����v�Z�~�X���Ă�@���̂������ł����Ȃ�
0682�P�R�Q�l�ڂ̑f������
2018/07/10(��) 12:06:49.16ID:xp4zAh0715�i�̊K�i�����鏸����͉��ʂ肠�邩�B
���̖����ē��I�v��@�ʼn������ł��ˁB
�A���S���Y���I�Ȗ����o�肳����ł��ˁB
0683�P�R�Q�l�ڂ̑f������
2018/07/10(��) 12:21:04.53ID:MDGkixZj0684�P�R�Q�l�ڂ̑f������
2018/07/10(��) 12:24:08.10ID:7O7Q0+gE0685�P�R�Q�l�ڂ̑f������
2018/07/12(��) 12:07:35.15ID:2D5qKHUs�݊p�O�p�`�͂����ł��邩�H
�F
�Ⴆ�A�_ A_1 �� {A_2, �c, A_n, B_1, �c, B_n, C_1, �c, C_n} �� 3*n-1 �̓_�̒�����
2�_��I��ō����݊p�O�p�`�̌��� Binomial(3*n-1, 2) �B���̂悤�ȏW����
�_�̂Ƃ���� 6*n �ʂ肠�邩��A���߂���́A Binomial(3*n-1, 2) * 6 * n �B
���͐Ԃ��`���[�g���ɍڂ��Ă�����Ƃ��̉ł��B
���̉Ŗ��_�����炦��̂ł��傤���H
�������������̂��͕�����̂ł����A�_ A_i, B_i, C_i ���ǂ̂悤�ɔz�u����Ă��邩
�ȂǑS������������܂���B
0686�P�R�Q�l�ڂ̑f������
2018/07/12(��) 13:24:39.07ID:KOhJ2Zj4https://bodoge.hoobby.net/columns/00013
�A�i���O�Q�[���s�ꂪ�u�N���E�h�t�@���f�B���O�v�Ő���オ�郏�P
https://www.sbbit.jp/article/cont1/34394
�t���[�����X�̃f�U�C�i�[����l�ł������Ⴡ�[�J�[�𗧂��グ���`�u�I�C���N�Q�[���Y�v
https://kaigyou.dreamgate.gr.jp/jigyoukeikakusho_sample_kaisetsu/interview/871/
�Q�[���f�U�C�i�[���k�� in ����
http://studio.oinkgms.com/post/167544468047
�C�x���g�N�ƉƂ��g�{�[�h�Q�[���h���J�Â��Ă���9�̗��R�Ƃ�
http://tsunagu-smile.jp/qa/
�Q�[���\�t�g�̗L����Ƃ����߂�3�l�Ń{�[�h�Q�[�����J��
https://shikin-pro.com/news/2730
�����̃I���W�i���{�[�h�Q�[������肽���I �d���ɂ������I
https://hajicolle.smt.docomo.ne.jp/channel06/cat027/det000461.html
�N���E�h�t�@���f�B���O��1000���~�����W�߂��I�@�u7�̏K���{�[�h�Q�[���v��
���������邽�߁A�v���X�����[�X�����p�������R�Ƃ�
http://prtimes.co.jp/works/2353/
�u29�Ί����A2�N�O�ɉ�Ђ����߂��B�{�[�h�Q�[�������n�߂�3700���~��
����グ�����lj��������������Ƃ͂���H�v���낢��
http://labaq.com/archives/51880196.html
�{�[�h�Q�[���s��K�͂܂�킩��I�Q�[���}�[�P�b�g�A�W����A�{�h�Q�J�t�F�܂Ƃ�
http://tsunagu-smile.jp/post-4533/
0687�P�R�Q�l�ڂ̑f������
2018/07/13(��) 15:27:20.18ID:dWai5ihd�~�������O�ڑ��p�`�����ʼn�����������ĉ��Ō�����́H�ʐς���Ȃ��Ɩ�������ˁH
0688�P�R�Q�l�ڂ̑f������
2018/07/13(��) 16:04:07.77ID:3TYwN0uYhttps://i.imgur.com/nFD5zOI.jpg
0689�P�R�Q�l�ڂ̑f������
2018/07/13(��) 16:11:59.42ID:HZRO7Pkq�����ƌ����B
0690�P�R�Q�l�ڂ̑f������
2018/07/13(��) 16:34:08.78ID:U0fRAErR0691�P�R�Q�l�ڂ̑f������
2018/07/14(�y) 05:28:53.09ID:cD5eYwqb0692�P�R�Q�l�ڂ̑f������
2018/07/16(��) 09:18:29.38ID:wABLI2CW���W�A������u�ŋ��߂���@�������Ă�������
0693�P�R�Q�l�ڂ̑f������
2018/07/16(��) 09:55:49.37ID:YEpohRsI0694�P�R�Q�l�ڂ̑f������
2018/07/16(��) 11:01:48.62ID:TK0dZODUlog(1+t)��(t^s)/s
�����������ł�
��t�Ŕ������čŏ��l��]��������@�ł͂ł����̂ł���
���Ɩʓ|�����������̂ł����Ɗy�ȕ��@����܂���
0695�P�R�Q�l�ڂ̑f������
2018/07/17(��) 20:41:32.58ID:MuZI6MUv�ȉ��̖�肪�ڂ��Ă��܂����A�Ђǂ����ł��ˁB
�d���������̂������Ȃ��̂��������Ă���܂���B
�u
�P�� statistics ������B
���̒P�ꂩ��C�ӂ�4����������č���鏇��̐������߂�B
�v
0696�P�R�Q�l�ڂ̑f������
2018/07/17(��) 20:48:21.51ID:BRgc1w3O0697�P�R�Q�l�ڂ̑f������
2018/07/17(��) 20:50:46.58ID:GYOQH8mP������Ă��Ax�ȊO�ɉ���ab�Ƃ�a+b���o�Ă���̂ł��傤���H
0698�P�R�Q�l�ڂ̑f������
2018/07/17(��) 21:05:00.96ID:BRgc1w3O0699�P�R�Q�l�ڂ̑f������
2018/07/17(��) 21:16:41.28ID:MuZI6MUv�d���������Ȃ��C�ӂ�4�����Ȃ̂�
�d�����������C�ӂ�4�����Ȃ̂�
����蕶��ǂ�ł�������܂���B
0700�P�R�Q�l�ڂ̑f������
2018/07/17(��) 21:32:27.60ID:BRgc1w3O0701�P�R�Q�l�ڂ̑f������
2018/07/17(��) 21:48:23.16ID:MuZI6MUv0702�P�R�Q�l�ڂ̑f������
2018/07/17(��) 21:51:08.80ID:BRgc1w3O0703�P�R�Q�l�ڂ̑f������
2018/07/17(��) 22:02:15.97ID:l55P1S3U0704�P�R�Q�l�ڂ̑f������
2018/07/17(��) 22:07:35.37ID:MuZI6MUv�d���������Ȃ��ƁA���܂�Ȃ����ɂȂ��Ă��܂��̂ŁA�����ł��傤�ˁB
0705�P�R�Q�l�ڂ̑f������
2018/07/17(��) 22:07:40.76ID:l55P1S3U0706�P�R�Q�l�ڂ̑f������
2018/07/17(��) 22:13:12.71ID:l55P1S3U0707�P�R�Q�l�ڂ̑f������
2018/07/18(��) 00:43:14.12ID:gHK0w7uV�����A���Ȃ��́u���z���v�ɂ��Ă��A���ꂪ��������Ȃ��̂ł͂Ȃ��ł��傤���B
0708�P�R�Q�l�ڂ̑f������
2018/07/18(��) 13:48:10.23ID:BSC5gXR6�搶�͍����I�ŕ����ɂ����ł�
0709�P�R�Q�l�ڂ̑f������
2018/07/18(��) 14:53:13.82ID:r8Q8PNlT0710�P�R�Q�l�ڂ̑f������
2018/07/18(��) 16:32:23.24ID:RbLGIfX8���̂Ƃ���_[0,1] f(x) dx >0 �͖��炩�Ȋ�K�X���ł���
�ǂ̂悤�Ɏ�����ł������B
0711�P�R�Q�l�ڂ̑f������
2018/07/18(��) 16:50:32.51ID:bnAtVhhu���w�̖��ł���g�������Ȃ����疾�炩�Ə����Ă����_����鎖�͂Ȃ��B
�ł������Ǝ��w�͈͓̔��ŏؖ��ł��邩��ؖ����}�X�^�[���Ă����ɉz�������Ƃ͂Ȃ��B
�܂��ŏo�邱�Ƃ͂Ȃ����ǁB
�����łłȂ�����}�X�^�[���Ȃ��Ă����Ƃ������Ă��͗��n�Ɍ����Ȃ��B
0712�P�R�Q�l�ڂ̑f������
2018/07/18(��) 18:50:34.62ID:Hs6Mh1Ut�ǂ��ؖ������ł����H
�ł��A�����̐l�����ł������_���̕����Ă܂�����
0713�P�R�Q�l�ڂ̑f������
2018/07/18(��) 19:38:53.82ID:8CGmpcvz�����ł���
0714�P�R�Q�l�ڂ̑f������
2018/07/18(��) 22:43:39.58ID:xNa7HBmh�Ƃ肠�������Z�̋��ȏ��ɂ̂��Ă�
f(x)��g(x), a<b�̂Ƃ�
��[a,b]f(x)dx �� ��[a,b]g(x)dx
�͔F�߂邱�Ƃɂ���B�i��������ϒl�̒藝���炾���邯�ǁB�j
���́u����������x��[a,b]�ɂ�����f(x) = g(x)���P���I�ɐ�������Ƃ��v�̃p�[�g�B
��������������Ƃ���
F(t) = ��[a,t]g(x)dx - ��[a,t]f(x)dx
�Ƃ����BF(a) = F(b) = 0�B
����a<c<b��F(c) > 0�Ƃ���ƕ��ϒl�̒藝����c<d<b��F�f(d) = F(b) - F(c) < 0�ƂȂ�d���Ƃ��B
���������̂Ƃ�F�f(d) = g�f(d) - f�f(d) �� 0��薵���B
�����F(c)��0�B
���F�f(t) = g(t) - f(t)��0��F(a)=0���F(c)��0.
�ȏ�ɂ��a<c<b�ɂ�����F(c) = 0�B
�Ƃ���0=F�f(c) = g(c) - f(c)���P���I�ɐ�������B
�����ɂ�łȂ����ǁB��w������������Ƃ����ؖ��K�����B
���������ϕ��̒�`���̕ς���Ă��邵�ˁB
�Ƃ͂������Z���w�͈͓̔��Ȃ�͈͓��Ńx�X�g�������C�������Ȃ��ƌ��Ǘ��n�̍��͈炽�Ȃ��B
0715�P�R�Q�l�ڂ̑f������
2018/07/19(��) 07:41:26.26ID:y4DptdmH0716�P�R�Q�l�ڂ̑f������
2018/07/19(��) 15:49:22.36ID:QxmdrQQV0717�P�R�Q�l�ڂ̑f������
2018/07/19(��) 16:59:46.72ID:7hzs8Xf8�ŏ���������Ȃ������̂�
�킴�킴�O�����̒藝��OP�̋������o����
P����X���ɐ����Ȓ�����X���̌�_R�ɂ���Ăł���
�O�p�`OPR����]���藝���g����cos�������߂�OP�Ɗ|���Z������Ƃ��S�����ʂɂȂ�܂���
�m���ɂ����OPcos��=2�ɂȂ����̂ł���...
�Ȃ�OPcos���͓_P��x���W���̂��̂ɂȂ��ł����H
��������OPcos���Ƃ����̂͂Ȃ�ł����H�H
https://i.imgur.com/VW1FdwM.jpg
0718�P�R�Q�l�ڂ̑f������
2018/07/19(��) 17:18:03.10ID:QxmdrQQV����������������������������������������������������������
0719710
2018/07/19(��) 17:34:53.89ID:itYrVtji�e�Ȑl�����čK���ł����B���肪�Ƃ��������܂��B
���Ȃ�712�͖l����Ȃ��ł��B
0720�P�R�Q�l�ڂ̑f������
2018/07/19(��) 21:16:47.14ID:Aeo+MeIiOP�Ƃ���̂͌��_O�Ɠ_P�̋���
0721�P�R�Q�l�ڂ̑f������
2018/07/20(��) 09:34:57.91ID:apaHx6QQOPcos���͐���OP�̒����ƎO�p��cos���̐ς�\�����ł��邪�A���ꂪ�_P��x���W���̂��̂ɂȂ闝�R�́A�R�T�C���̒�`�ׂčl���悤
0722�P�R�Q�l�ڂ̑f������
2018/07/20(��) 18:19:02.79ID:L7k1kcuUrcos�Ɓ�r�~x/r��x
���肪�Ƃ��������܂���
0723�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 00:41:22.68ID:vto3t2b20724�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 05:46:40.69ID:yrjF7QVv>>403
>>406
>>412
>>474
>>480
>>483
>>517
0725�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 06:38:41.60ID:opVMLW0b>>533
>>536,541
>>602,603
>>612,613,614
>>619,622
>>623-636,646
>>637
0726�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 06:58:08.78ID:opVMLW0b>>649-652
>>655,656
>>660
>>666
>>670
>>678,679
>>682
0727�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 06:58:34.22ID:opVMLW0b>>685
>>687
>>688
>>694
>>695
>>710,714
>>717
0728�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 07:02:57.07ID:sf/YhJ19���n�����Ē萔���̈Ⴂ�������Ĉ�ɒ�܂�̂ł͂Ȃ���ł����H
0729�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 07:34:08.85ID:yKLNXALy����1�ɂȂ邩��
0730�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 09:23:37.52ID:sf/YhJ19-1/(1+x^(1/3))+1=(x^(1/3))/(1+x^(1/3))
�ł���
���肪�ƃi�X
0731�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 09:35:33.37ID:Me1nA4lfWolfram|Alpha�l�H��
(a+b+c-d)(b+c+d-a)(c+d+a-b)(d+a+b-c)
��ʼn����Ȃ����͎����ɏo�Ȃ�or�o�Ă��݂�ȉ����Ȃ��̂ŋC�ɂ��Ȃ��Ă悢
0732�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 09:37:50.86ID:Me1nA4lf(1)
CP:PD=s:(1-s), BP:PE=t:(1-t)�Ƃ�����
OP��=(1-s)OC��+sOD��=(1-s)OC��+s(2/3)OA��=(2s/3)OA��+(1-s)OC��
OP��=(1-t)OB��+tOE��=(1-t)(OA��+OC��)+t(2/5)OC��=(1-t)OA��+(1-3t/5)OC��
OA��,OC���͈ꎟ�Ɨ��ł��邩��
2s/3=1-t, (1-s)=(1-3t/5) �� s=3/7, t=5/7
OP��=(2/7)OA��+(4/7)OC��
(2)
OQ:QP=u:(1-u), BQ:QC=v:(1-v)�Ƃ�����
OQ��=uOP��=u((2/7)OA��+(4/7)OC��)=(2u/7)OA��+(4u/7)OC��
OQ��=(1-v)OB��+vOC��=(1-v)(OA��+OC��)+vOC��=(1-v)OA��+OC��
OA��,OC���͈ꎟ�Ɨ��ł��邩��
2u/7=1-v, 4u/7=1 �� u=7/4, v=1/2
BQ:QC=(1/2):(1/2)=1:1
(2)�ʉ�1
>>410
(2)�ʉ�2
>>411
0733�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 09:38:21.87ID:Me1nA4lfPA��+PB��+PC��=BC��
��OA��-OP��+OB��-OP��+OC��-OP��=OC��-OB��
��OA��+2OB��=3OP��
��OP��=(1/3)OA��+(2/3)OB��
P�͕�AB��2:1�ɓ�������_
O��P�Ƃ����̂�>>413
0734�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 09:39:23.60ID:Me1nA4lf��
�������@�𐳌��藝a/sinA=b/sinB=c/sinC�ƕӁX������
a/7=b/5=c/3(��a:b:c=7:5:3)
���̎�̎��i�A��j��a/7=b/5=c/3=k�Ƃ�����
a=7k,b=5k,c=3k�̂悤��1�ϐ��ŕ\���Ƃ悢
��
�w�����̌������
15��3=��((15/2)k)((1/2)k)((5/2)k)((9/2)k)��15��3=(15��3)(k^2)/4��k=�}2
a,b,c>0���k=2,a=14,b=10,c=6
������u���O�̎O�p�`�v������
A=120��
�������̕ʉ�(>>498�㔼)
�������@��(sinA)/7=(sinB)/5=(sinC)/3=L�Ƃ�����
sinA=7L,sinB=5L,sinC=3L
�����藝���
sinA=a/(2R),sinB=b/(2R),sinC=c/(2R)
�����
a=14RL,b=10RL,c=6RL
�����a,b,c��1�ϐ�L�ŕ\���Ă���
�i���Ȃ݂�k=2RL�Ƃ�����a=7k,b=5k,c=3k�j
���̂܂܈ȍ~�̌v�Z���s���Ă��悢
�������̕ʉ�(>>498�O��)
�]���藝���
(7k)^2=(5k)^2+(3k)^2-2(5k)(3k)cosA��(30k^2)cosA=-15k^2��cosA=-1/2
(sinA)^2=(1-(cosA)^2)���
sinA=�}(��3)/2
0��<A<180�����
sinA=(��2)/3
��ABC=(1/2)bcsinA���
15��3=(1/2)(5k)(3k)(��3)/2��15��3=(15��3)(k^2)/4
�ȉ���
0735�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 09:42:23.08ID:Me1nA4lf������4�s�ڂ�
sinA=(��3)/2
�ɒ���
0736�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 09:42:56.25ID:Me1nA4lf�X����tan(45��+15��)=��3��2
0737�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 09:55:42.28ID:6t36aLAR�@���n�͐w�A���n�͓���@�i�w�u�����h�͒��� ���Z���V��
https://headlines.yahoo.co.jp/hl?a=20180719-00010000-koukousei-soci
0738�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 10:03:47.29ID:Me1nA4lf����̓R�s�y���H
W���f(��₷��,�w��̈���,�u�����h��,�A�E����,�c)���傫���̂��낤
�R�X�p���Ƃł����t���悤��
0739�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 10:36:17.61ID:Me1nA4lf��������160cm�Ȃ͓̂��ӂ��邪�A
>>541�̉����ɏ]���ƁA�Q�l���ɍڂ��Ă�������
(160.75+161)/2=161.875(cm)����Ȃ��́H
0740�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 11:01:49.62ID:Me1nA4lf���ȉ���
[158,162)��16�l��
158+4*0/16
158+4*1/16
158+4*2/16
�c
158+4*15/16
�̂悤�ȕ��z����16�l�̕��ς�159.875(cm)�ɂȂ�̂�
158+4*1/32
158+4*3/32
158+4*5/32
�c
158+4*31/32
�̂悤�ȕ��z����
16�l�̕��ς�160(cm)
50�l�̒����l��(160.625+160.875)/2=160.75(cm)
0741�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 11:02:40.32ID:Me1nA4lf�ŏ���1�𑫂��Ȃ��Ȃ�10-1=9�Ɏ�������i��������0.9*(1/(1-0.9))=9�j
0742�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 11:03:00.51ID:Me1nA4lf�M������
0743�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 23:16:45.06ID:tlFqWklE0744�P�R�Q�l�ڂ̑f������
2018/07/21(�y) 23:26:36.87ID:ZAC5rhyg�����ł� �o���܂��傤
0745�P�R�Q�l�ڂ̑f������
2018/07/22(��) 00:01:06.55ID:yqBEvn5f0746�P�R�Q�l�ڂ̑f������
2018/07/22(��) 00:42:12.50ID:SAIPrBTa0747�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:26:07.04ID:xp4F6Fcj2�{�Ƃ��͂����m���� 22/35 �ł���Ƃ����B�����肭���͉��{���邩�B
���āF
�����肭���̖{���� n �{�Ƃ���ƁA n �͐����ŁA��������
1 �� n �� 13 �c (1)
�͂��ꂭ���̖{���� 15 - n �{�ł���B15�{����2�{�����o���g������
Binomial(15, 2) �ʂ�
���̂����A2�{�Ƃ��͂����ꍇ�́A
Binomial(15-n, 2) �ʂ�
����āA��������
Binomial(15-n, 2) / Binomial(15, 2) = 22/35
����������āA n = 3 or 26
(1) ���� n �̒l�� n = 3
���������āA�����肭���̖{����
3�{
0748�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:29:32.14ID:wgGsbJ+Y��`���瓱��
0749�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:29:45.40ID:Ug1/d9QdC��P��p���Ĉꔭ�ŕ\�����@�͎v���t���Ȃ����A>>664������
0750�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:29:56.25ID:xp4F6Fcj�����̏������Ă킴�킴�����K�v�͂Ȃ��ł���ˁH
26 > 15 ������ n = 26 �͕s�K�B
n = 3 �̂Ƃ��A
Binomial(15-n, 2) �͒�`�����B
����āA n = 3 �͉��B
0751�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:30:19.96ID:Ug1/d9Qd����͂ނ���d�݂�12���Ƃ���ʂ��Ă�H�o�����Ԃ͋�ʂ��ĂȂ���
0752�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:30:43.75ID:Ug1/d9Qd�ȉ��A(a,b,c)�͗�x�N�g��
AB��=(2,2,2)
����AB��̓_H��(x,y,z)=(2,1,0)+k(2,2,2)�ƕ\����
PH��0�AAB��0���
PH��L
��PH���EAB��=0
��(2+2k-1,1+2k-2,0+2k-3)�E(2,2,2)=0
��(2k+1)*2+(2k-1)*2+(2k-3)*2=0
��k=1/2
H(3,2,1)
0753�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:31:06.87ID:Ug1/d9QdW|A�l�H��
(x^2-(xy-1))(y^2+(xy-1))
0754�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:31:30.60ID:Ug1/d9Qdx-2=-9K,y+1=5K�Ƃ������Ƃ���
(x,y)=(-9K+2,5K-1)��5x+9y=-45K+10+45K-9=1
��̗�
�c
K=-2�̂Ƃ�(x,y)=(20,-11)��5x+9y=100-99=1
K=-1�̂Ƃ�(x,y)=(11,-6)��5x+9y=55-54=1
K=0�̂Ƃ�(x,y)=(2,-1)��5x+9y=10-9=1
K=1�̂Ƃ�(x,y)=(-7,4)��5x+9y=-35+36=1
K=2�̂Ƃ�(x,y)=(-16,9)��5x+9y=-80+81=1
�c
�ƁA�����ƌ��̎�5x+9y=1�����Ă��邼
��������K=-k�Ƃ���Ax-2=9k,y+1=-5k�Ƃ������̂Ɠ������ƂɂȂ�
>>679�̂悤��b�̐����ł̏ꍇ�����͕s�v
>>679�̌㔼�����̋^��ɂ��Ă�>>680���Q��
0755�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:31:54.27ID:Ug1/d9Qd[����2007����-1(1)]
3���ԑQ�����𗧂Ă�
n�i�̊K�i�̏������a_n�ʂ�Ƃ����
a_1=1,a_2=2,a_3=3
n��4��
i) �ŏ���1�i�������Ƃ�
�c��n-1�i�̏������a_(n-1)�ʂ�
ii) �ŏ���2�i�������Ƃ�
������莟��1���͕K��1�i����
�c��n-3�i�̏������a_(n-3)�ʂ�
�����a_n=a_(n-1)+a_(n-3)
a_4=a_3+a_1=3+1=4
a_5=a_4+a_2=4+2=6
a_6=a_5+a_3=6+3=9
�c
a_15=a_14+a_12=189+88=277
277�ʂ�
�u1����2�i���邱�Ƃ͘A�����Ȃ��v�Ƃ����������Ȃ����
(a_0=1,)a_1=1,a_(n-2)=2
a_n=a_(n-1)+a_(n-2)
�ł���t�B�{�i�b�`����ɂȂ�
�K�i�̏�����̖��͐`���ɂ��ڂ��Ă��͂�
0756�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:32:12.99ID:Ug1/d9Qd���̈ӌ��͂ƂĂ�������
�O�ڑ��p�`���g���ĕ]������Ƃ��́A�ʐςŔ�r����̂����ēI�ɂ͖���
0757�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:34:47.62ID:xp4F6Fcj�ʐς��낤���������낤���A���w�I�ɂ͌����ł͂Ȃ��c�_�ł���ˁH
�ǂ��炪���ϓI�ɂ�������邩�Ƃ������ɂȂ邩�Ǝv���܂��B
�Ȃ��A�ʐς̂ق�������₷���̂ł��傤���H
0758�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:40:22.37ID:Ug1/d9QdB�̎�����A�̎������傫����͗p�ӂɎv���t����
B�̖ʐς�A�̖ʐς��傫����͎v���t���Ȃ�����
����Ċ��o�I�Ɏ���₷��
0759�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:46:09.23ID:Ug1/d9Qd�]�k�����A�P�ʉ~�ɊO�ڂ��鐳���p�`�̎����Ɩʐς͓������i��������͈Ⴄ���j
�ڍׂ�
http://rio2016.5ch.net/test/read.cgi/math/1518967270/41-42
0760�P�R�Q�l�ڂ̑f������
2018/07/22(��) 11:47:19.20ID:Ug1/d9Qd>>687
�]�k�����A�P�ʉ~�ɊO�ڂ��鐳���p�`�̎����Ɩʐς͓������i��������͈Ⴄ���j
�ڍׂ�
http://rio2016.5ch.net/test/read.cgi/math/1518967270/41-42
0761�P�R�Q�l�ڂ̑f������
2018/07/22(��) 12:05:07.47ID:Ug1/d9Qd-1/((x^a)+1)��1/((x^-a)+1)�̍���1�Ȃ̂́A���̌����ڂ���͋C�t���ɂ������낤
0762�P�R�Q�l�ڂ̑f������
2018/07/22(��) 12:08:38.73ID:Ug1/d9Qdp=log[b](c)�Ƃ����ƁA�ΐ����̒�`���
b^p=c
�Ƃ���ŁA�w�����̐������
b^(ap)=(b^p)^a=c^a
����āA�ΐ����̒�`���
ap=log[b](c^a)
����������
alog[b](c)=log[b](c^a)
����a=-1�̂Ƃ�
-log[b](c)=log[b](1/c)
�ΐ����̏d�v�Ȑ���������A��x��������ËL���ׂ�
0763�P�R�Q�l�ڂ̑f������
2018/07/22(��) 12:12:36.55ID:Or+ghVKchttps://dotup.org/uploda/dotup.org1591191.png
0764�P�R�Q�l�ڂ̑f������
2018/07/22(��) 12:13:45.07ID:xp4F6Fcj������ 3 �����o���Ƃ��A�����ꂽ�J�[�h�̐����̘a�������ɂȂ�m���� 4 / 7 �ł���
�Ƃ����B���� 1 �̃J�[�h�͉������邩�B
���������g�����Ƃ��m���̖����Ă�����ł����܂����A�ʓ|�Ȗ������܂���ˁB
�ł��A�����ʓ|�Ȃ����ł������Ƃ͌����Ȃ��ł���ˁB
0765�P�R�Q�l�ڂ̑f������
2018/07/23(��) 03:49:45.92ID:PvxqG8NK>>474
>>517
>>637
>>688
>>694
>>695
0766�P�R�Q�l�ڂ̑f������
2018/07/23(��) 03:50:16.48ID:PvxqG8NK>>602,603
>>619,622
>>649-652
>>655,656
>>685
>>710,714
>>717
0767�P�R�Q�l�ڂ̑f������
2018/07/23(��) 11:46:15.30ID:UwwnVRxelog10 6^n
nlog10 6
n(log10 2+log10 3)
n(0.3010+0.4771)
9��0.7781n��10
�ƍl����͉̂����œ������ł����H
0768�P�R�Q�l�ڂ̑f������
2018/07/23(��) 15:41:53.26ID:2tkO71O1����
(p,p^2),(q,q^2)��ʂ钼���̎���
y=((q^2-p^2)/(p-q))(x-p)+p^2=(p+q)x-pq.
y=rx^2+sx+t��y=ux+v��x=��,���Ō����Ƃ���B
r��^2+s��+t=u��+v, r��^2+s��+t=u��+v.
��(ux+v-rx^2-sx-t)dx
=-(1/3)rx^3+(1/2)(u-s)x^2+(v-t)x+C
���
��[��,��](ux+v-rx^2-sx-t)dx
=(1/6)[-2r(��^3-��^3)+3(u-s)(��^2-��^2)+6(v-t)(��-��)]
=(1/6)(��-��)[-2r(��^2+����+��^2)+3(u-s)(��+��)+6(v-t)]
=(1/6)(��-��)[-2r(��^2+����+��^2)+3u��+3u��-3s��-3s��+6v-6t]
=(1/6)(��-��)[-2r(��^2+����+��^2)+3(u��+v)+3(u��+v)-3s��-3s��-6t]
=(1/6)(��-��)[-2r(��^2+����+��^2)+3(r��^2+s��+t)+3(r��^2+s��+t)-3s��-3s��-6t]
=(1/6)(��-��)[r��^2+r��^2-2r����]
=(r/6)(��-��)^3.
����͂�����u1/6�����v�ł���B
����̐�Βl�́A�������ƒ����ň͂܂�镔���̖ʐς�\���Ă���B
0769�P�R�Q�l�ڂ̑f������
2018/07/23(��) 15:42:41.37ID:2tkO71O1a<b�Ƃ��Ĉ�ʐ�������Ȃ��B
A(a,a^2),B(b,b^2),C(c,c^2)=((a+b)/2,((a+b)/2)^2)�Ƃ���B
����AB:y=(a+b)x-ab�́AC'((a+b)/2,(a^2+b^2)/2)��ʂ�B
A''(a,0),B''(b,0),C''(c,0)�Ƃ���B
��@1�i�O�p�`�̖ʐ�(>>477)�j
��ACB
=��ACC'+��BC'C
=(1/2)((a^2+b^2)/2-((a+b)/2)^2)(c-a)
+(1/2)((a^2+b^2)/2-((a+b)/2)^2)(b-c)
=(1/2)((a^2+b^2)/2-((a+b)/2)^2)(b-a)
=(1/2)((a^2)/4+(b^2)/4-ab/2)(b-a)
=(1/8)(b-a)^3.
��@2�i��`�̖ʐ�(>>478)�j
��ACB
=��`AA''B''B-��`AA''C''C-��`CC''B''B
=(1/2)(a^2+b^2)(b-a)
-(1/2)(a^2+c^2)(c-a)
-(1/2)(c^2+b^2)(b-c)
=(1/2)((a^2)b-a^3+b^3-(b^2)a-(a^2)c+a^3-c^3+(c^2)a-(c^2)b+c^3-b^3+(b^2)c)
=(1/2)((a^2)b-(b^2)a-(a^2)c+(c^2)a-(c^2)b+(b^2)c)
=(1/2)(b-a)(c-b)(a-c)
=(1/2)(b-a)((a+b)/2-b)(a-(a+b)/2)
=(1/2)(b-a)((a-b)/2)((a-b)/2)
=(1/8)(b-a)^3.
��@3�i�ϕ��j
��ACB
=(����AB�ƕ�����y=x^2�ň͂܂�镔���̖ʐ�)
-(����AC�ƕ�����y=x^2�ň͂܂�镔���̖ʐ�)
-(����CB�ƕ�����y=x^2�ň͂܂�镔���̖ʐ�)
=(1/6)(b-a)^3-(1/6)(c-a)^3-(1/6)(b-c)^3
=(1/6)(b-a)^3-(1/6)((a+b)/2-a)^3-(1/6)(b-(a+b)/2)^3
=(1/6)(b-a)^3-(1/6)((b-a)/2)^3-(1/6)((b-a)/2)^3
=(1/6-1/48-1/48)(b-a)^3
=(1/8)(b-a)^3.
0770�P�R�Q�l�ڂ̑f������
2018/07/23(��) 15:45:03.56ID:2tkO71O1�NjL
��@3��>>476�̕��j�B
0771�P�R�Q�l�ڂ̑f������
2018/07/23(��) 15:46:01.73ID:2tkO71O1ssstttiiac����4�����I��ŕ��ׂ�B
�d���������ꍇ
10*9*8*7=5040(�ʂ�).
�d���������Ȃ��ꍇ
(ssst)(sssi)(sssa)(sssc)
(sstt)(ssti)(ssta)(sstc)(ssii)(ssia)(ssic)(ssac)
(sttt)(stti)(stta)(sttc)(stii)(stia)(stic)(stac)(siia)(siic)(siac)
(ttti)(ttta)(tttc)(ttii)(ttia)(ttic)(ttac)(tiia)(tiic)(tiac)(iiac).
�����
4+4+4+4
+6+12+12+12+6+12+12+12
+4+12+12+12+12+24+24+24+12+12+24
+4+4+4+6+12+12+12+12+12+24+12
=386(�ʂ�).
�ʉ�
�d���������Ȃ��ꍇ
(wwww)�i���ו���1�ʂ�j�@(w)�̑I�ѕ��͖����B
(wwwx)�i���ו���4�ʂ�j�@(w,x)�̑I�ѕ���4+4��8�ʂ�B
(wwxx)�i���ו���6�ʂ�)�@(w,x)�̑I�ѕ���3�ʂ�B
(wwxy)�i���ו���12�ʂ�j�@(w,x,y)�̑I�ѕ���6+6+6��18�ʂ�B
(wxyz)�i���ו���24�ʂ�j�@(w,x,y,z)�̑I�ѕ���5�ʂ�B
�����
1*0+4*8+6*3+12*18+24*5=386(�ʂ�).
0772�P�R�Q�l�ڂ̑f������
2018/07/23(��) 15:46:39.29ID:2tkO71O1��������ĉ�����肾����A���̗��ꂪ�悢�B
0773�P�R�Q�l�ڂ̑f������
2018/07/23(��) 17:30:52.31ID:Drxs2eYe1. f(x)�͔����\
2. 1 < f(x)
3. xf'(x) - f(x)\log{f(x)} < 0
4. 1<a�̂Ƃ��Af(x) < a^x
���̂Ƃ��Alim_{x����}{f(x)}^{1/x} = 1�ƂȂ邱�Ƃ������B
���Z���w�݂̂Ō����ȏؖ����^������B
{f(x)}^{0} = 1������Alim_{x����}{f(x)}^{1/x} = 1�Ƃ���߂Ă���B
���������Ȃ�A�����Ă���B
0774�P�R�Q�l�ڂ̑f������
2018/07/23(��) 17:56:50.21ID:eEF9pg4M1+t>1���log(1+t)>0������log(log(1+t))�Əo����̂𗘗p����B
f(s)=log((t^s)/s)-log(log(1+t))=slogt-logs-log(log(1+t))�Ƃ����B
�����s�Ŕ��������
f'(s)=logt-1/s.
i) 0<t<e��logt<1�̂Ƃ�
0<s��1�͈̔͂�f'(s)<0�ł���f(s)��s=1�ōŏ��l���Ƃ�B
f(1)
=1logt-log1-log(log(1+t))
=logt-log(log(1+t))
=log(t/log(1+t)).
ii) t��e��logt��1�̂Ƃ�
0<s��1�͈̔͂�f(s)��s=1/logt�ŋɏ��l���Ƃ�B
f(1/logt)
=(1/logt)(logt)-log(1/logt)-log(log(1+t))
=1+log(logt)-log(log(1+t))
=1+log((logt)/log(1+t)).
�������0���傫�����Ƃ͊ȒP�Ɏ������Ȃ����H
����āAt>0�̂Ƃ��A0<s��1�͈̔͂�f(s)>0.
���������āAt>0, 0<s��1�̂Ƃ�
log((t^s)/s)-log(log(1+t))>0
��log(log(1+t))<log((t^s)/s)
��log(1+t)<(t^s)/s. ��
0775�P�R�Q�l�ڂ̑f������
2018/07/23(��) 18:06:23.87ID:eEF9pg4M�\���傫��x�ɂ���
f(x)^(1/x)<(a^x)^(1/x)=a
lim[x��+��]a=a���
lim[x��+��](f(x)^(1/x))�͏ォ�牟��������B ��
0776�P�R�Q�l�ڂ̑f������
2018/07/23(��) 18:36:24.65ID:eEF9pg4M��n��-1/2 �� n��1/2.
0��((��3)/2)(��((n^2)-1/4))-1/4
��1/4��((��3)/2)(��((n^2)-1/4))
��(��3)/6����((n^2)-1/4)
��1/12��(n^2)-1/4�@�i�旼�ӂ����j
��0��(n^2)-1/3
��n��-(��3)/3 �� n��(��3)/3.
((��3)/2)(��((n^2)-1/4))-1/4��1
��((��3)/2)(��((n^2)-1/4))��5/4
�́�((n^2)-1/4)��(5��3)/6
��(n^2)-1/4��25/12
��(n^2)-7/3��0
��-(��21)/3��n��(��21)/3.
�ȏ�̋��ʕ�����
-(��21)/3��n��-(��3)/3, (��3)/3��n��(��21)/3.
�ŏ���n�����Ƃ����悤�ȏ���������ƁA�摜�̂悤�ȓ����ɂȂ�B
0777�P�R�Q�l�ڂ̑f������
2018/07/23(��) 18:38:22.50ID:eEF9pg4M>>688
(n^2)-1/4��0
��n��-1/2 �� n��1/2.
0��((��3)/2)(��((n^2)-1/4))-1/4
��1/4��((��3)/2)(��((n^2)-1/4))
��(��3)/6����((n^2)-1/4)
��1/12��(n^2)-1/4�@�i�旼�ӂ����j
��0��(n^2)-1/3
��n��-(��3)/3 �� n��(��3)/3.
((��3)/2)(��((n^2)-1/4))-1/4��1
��((��3)/2)(��((n^2)-1/4))��5/4
�́�((n^2)-1/4)��(5��3)/6
��(n^2)-1/4��25/12�@�i�旼�ӂ����j
��(n^2)-7/3��0
��-(��21)/3��n��(��21)/3.
�ȏ�̋��ʕ�����
-(��21)/3��n��-(��3)/3, (��3)/3��n��(��21)/3.
�ŏ���n�����Ƃ����悤�ȏ���������ƁA�摜�̂悤�ȓ����ɂȂ�B
0778�P�R�Q�l�ڂ̑f������
2018/07/23(��) 19:30:03.34ID:ec/Ku8sn694�̎҂ł�
i) 0<t<e�̂Ƃ�t/log(1+t)>0
ii) t��e�̂Ƃ�(logt)/log(1+t)>1/e
�͖��̌��̕s�����Ƃقړ����ɂ݂��܂������̂��Ƃǂ�����Ƒz�肳��Ă��ł��傤���H
0779�P�R�Q�l�ڂ̑f������
2018/07/23(��) 19:49:22.25ID:eEF9pg4M����ȍ~�����ۂɎ������킯����Ȃ�
1�ϐ��ł��₷���Ȃ����Ǝv�������A����ς�_���H
0780�P�R�Q�l�ڂ̑f������
2018/07/23(��) 22:12:00.67ID:Drxs2eYe1 < f(x)^{n+1} < a�ƂȂ邱�Ƃ͂����킩�邪�A
a>1�Ȃ̂ŁAlim_{x����} 1 = 1 <= lim_{x����} f(x)^{n+1} <= lim_{x����} a = a
�ł��邩��Alim_{x����} f(x)^{n+1}��1����a(a>1)�̊ԂɎ������邩�U���B
����́Aa���ǂꂾ�����������Ă������Ȃ�B
�s���S�ȏؖ��B
0781�P�R�Q�l�ڂ̑f������
2018/07/23(��) 22:28:03.99ID:CO3G9BSd�����X���܃\
3. xf'(x) - f(x)\log{f(x)} < 0
���̎߂��H
��2����
log f(x) / f(x)
�ł����́H
0782�P�R�Q�l�ڂ̑f������
2018/07/24(��) 05:44:44.89ID:931V5y+G�����畨���̎���X���ł�낤
(1)
�����E�����A��������������ꂼ�ꐳ�Ƃ���悤�ɍ��W���Ƃ�B
���[�v�ɂ͂��炭�͂�
�u�n�����b�N���烍�[�v�ɂ͂��炭�́vF_h=(0kgf,-100kgf)
�u���̃t�b�N���烍�[�v�ɂ͂��炭�́vF_l=(a,b)
�u�E�̃t�b�N���烍�[�v�ɂ͂��炭�́vF_r=(c,d)
���[�v�͐Î~���Ă��邩��A�����̘a��0�ł���B
�肠���̎���
0kgf+a+c=0��a=-c
-100kgf+b+d=0
�܂��A��p����p�̖@�����AF_l�Ƌt�����Ɂu���[�v���獶�̃t�b�N�ɂ͂��炭�́v���Ȃ킿���͂���p���Ă��邪�A
���̒��͂̓��[�v�̌����ł��邽�߁AF_l�̓��[�v�Ɣ��̌����ł���B
����āAb/a=2/(-1.8)
���l�ɁAd/c=2/1.8
a=-c���b=d
�肠���̎����Ab=d=50kgf
����āAa=-c=-45kgf
�ȏ���
|F_l|=��(a^2+b^2)=��(-45^2+50^2)kgf=67kgf
|F_r|=��(c^2+d^2)=��(45^2+50^2)kgf=67kgf
�Ȃ��A���[�v�����ɕ����Ă���Ƃ��������͏d�v�����A50cm�Ƃ������l�͎g��Ȃ������B
(2)
�芊�Ԃ͗͂̌�����ς��邾��������A���[�v�̊p�x��l�̈ʒu�Ɋւ�炸100kgf�̗͂ň����Ȃ���Ȃ�Ȃ��B
�u���[�v����1�̊��Ԃɂ͂��炭�́v�́A���[�v��2�̕�����100kgf���ł���i���͂̌����̓��[�v���Ȃ��p��2�������A�傫���͐}�̏ꍇ����100kgf���j�B
�������t�����Ɂu�ǂ��犊�Ԃɂ͂��炭�́v�����݂��Ă肠���Ă��邽�߁A���Ԃ͐Î~���Ă���B
0783�P�R�Q�l�ڂ̑f������
2018/07/24(��) 05:49:29.85ID:931V5y+G0784�P�R�Q�l�ڂ̑f������
2018/07/24(��) 05:50:27.93ID:931V5y+G0785�P�R�Q�l�ڂ̑f������
2018/07/24(��) 12:14:39.96ID:CvQK2L5u�Ȃ�x^3��3x^2�ɂȂ�̂ł����H
0786�P�R�Q�l�ڂ̑f������
2018/07/24(��) 12:34:40.84ID:8sUm3wV90787�P�R�Q�l�ڂ̑f������
2018/07/24(��) 12:34:41.05ID:5mVcetgS�ȉ��̖��̉��Ђǂ����܂��B
xy ���ʏ�� 16 �̓_�̏W�� {(x, y) | x, y �� {0, 1, 2, 3}} ���l����B
���̏W������قȂ�3�_��ׂɑI�Ԏ��s�ɂ����āA����
�u�I��3�_���O�p�`�̒��_�ƂȂ�A���̎O�p�`�̖ʐς� 9/2 �ł���v
�̋N����m�������߂�B
0788�P�R�Q�l�ڂ̑f������
2018/07/24(��) 12:39:27.92ID:5mVcetgS�F
���炩�ɁA
�u�I��3�_���O�p�`�̒��_�ƂȂ�A���̎O�p�`�̖ʐς� 9/2 �ł���v
�ł���ꍇ�A���̎O�p�`�̒��_�̂���2�_�́A
(0, 0), (0, 3), (3, 0), (3, 3)
�̒��̈قȂ�2�_�ł���B
�u�I��3�_���O�p�`�̒��_�ƂȂ�A���̎O�p�`�̖ʐς� 9/2 �ł���v
�ƂȂ�悤��3�_�̑g�����̌��́A������� 8 + 4 = 12 �ƂȂ�B
����āA�����́A 12 / Binomial(16, 3) = 3 / 140 �ł���B
0789�P�R�Q�l�ڂ̑f������
2018/07/24(��) 12:53:41.02ID:5mVcetgS�F
���炩�ɁA
�u�I��3�_���O�p�`�̒��_�ƂȂ�A���̎O�p�`�̖ʐς� 9/2 �ł���v
�ł���ꍇ�A���̎O�p�`�̒��_�̂���2�_�́A
(0, 0), (0, 3)
(0, 3), (3, 3)
(3, 3), (3, 0)
(3, 0), (0, 0)
�̂����ꂩ�ł���B
�u�I��3�_���O�p�`�̒��_�ƂȂ�A���̎O�p�`�̖ʐς� 9/2 �ł���v
�ƂȂ�悤��3�_�̑g�����̌��́A������� 8 + 4 = 12 �ƂȂ�B
����āA�����́A 12 / Binomial(16, 3) = 3 / 140 �ł���B
0790�P�R�Q�l�ڂ̑f������
2018/07/24(��) 16:16:07.79ID:luh87V5E0791�P�R�Q�l�ڂ̑f������
2018/07/24(��) 17:16:45.75ID:m2wnfXQA0792�P�R�Q�l�ڂ̑f������
2018/07/24(��) 20:33:56.64ID:s/nQCRmp0793�P�R�Q�l�ڂ̑f������
2018/07/24(��) 21:28:30.90ID:ljEv4jny�����ł��Ȃ��̂Ȃ�ق��ĂĂ��������ˁB
���̎���ɈӖ��͂���܂����A���Ȃ��̎���ɂ͉��̈Ӗ����Ȃ��̂ŁB
0794�P�R�Q�l�ڂ̑f������
2018/07/24(��) 21:31:31.87ID:wDGdaTKKhttps://i.imgur.com/3EUZzix.jpg
https://i.imgur.com/P539Xvr.jpg
https://i.imgur.com/D26JwjX.jpg
https://i.imgur.com/Ucen9Pt.jpg
https://i.imgur.com/Tu8AaXq.jpg
https://i.imgur.com/3hk0Naq.jpg
https://i.imgur.com/KmXMy9f.jpg
https://i.imgur.com/Ah3eUN5.jpg
https://i.imgur.com/JwsbQgV.jpg
https://i.imgur.com/UIKTjY2.jpg
0795�P�R�Q�l�ڂ̑f������
2018/07/24(��) 21:41:15.28ID:lhpiAqWw���Ȃ��̎��₱�����̈Ӗ�������܂���̂ŏ������܂Ȃ��ł��������ˁB
0796�P�R�Q�l�ڂ̑f������
2018/07/24(��) 21:53:54.15ID:1zUH7+frf(x+a)=f(x)+Aa+o(a)
�Ɛ��`�ߎ����邱�Ƃ��l���܂�
A=[f(x+a)-f(x)-o(a)]/a��f'(x) (a��0)
�ł�����
f(x+a)=f(x)+f'(x)a+o(a)�ƂȂ�A��v�����l�����
df=f'(x)dx�Ə������Ƃ��ł��܂���
0797�P�R�Q�l�ڂ̑f������
2018/07/24(��) 22:59:59.16ID:sNKVyQGy0798�P�R�Q�l�ڂ̑f������
2018/07/25(��) 04:58:24.77ID:EASAIavE(df(x))/(dx)
��lim[h���}0](f(x+h)-f(x))/((x+h)-x)
����́i���݂���j�܂���x�ɂ�����f(x)�̌X��
>>785
(d(x^3))/(dx)
=lim[h���}0]((x+h)^3-x^3)/((x+h)-x)
=lim[h���}0](3hx^2+3h^2x+h^3)/h
=lim[h���}0](3x^2+3hx+h^2)
=3x^2
0799�P�R�Q�l�ڂ̑f������
2018/07/25(��) 05:02:36.17ID:EASAIavE���炩�Ɂ`
�̕����̌����ȏؖ��������Ȃ����Ȃ�
0800�P�R�Q�l�ڂ̑f������
2018/07/25(��) 09:24:43.15ID:4IauL9c20801�P�R�Q�l�ڂ̑f������
2018/07/25(��) 09:32:35.34ID:4IauL9c2���ʂɂR�_�I�ԏꍇ�͂P�Q�ʂ�B
0802�P�R�Q�l�ڂ̑f������
2018/07/25(��) 14:34:43.61ID:RLO81c52�Ȃ�Œ萔��c�̓�����0�ɂȂ��ł����H�H
0803�P�R�Q�l�ڂ̑f������
2018/07/25(��) 14:48:48.76ID:seYwwYj4�̓Á�0 ��0 s.t. ��x |x-a|��|(c-c)/(x-a)-0|���Â�����ł�
0804�P�R�Q�l�ڂ̑f������
2018/07/25(��) 14:49:08.95ID:3a5LJJ99���Ȃ��̎��₱�����̈Ӗ�������܂���̂ŏ������܂Ȃ��ł��������ˁB
0805�P�R�Q�l�ڂ̑f������
2018/07/25(��) 15:18:21.09ID:FxD1zx7b��͓���I��p.139�藝6.10�̏ؖ��ł����A
�u�]���� f^(-1) �� y_0 �ŘA���ł���B�v
�Ƃ���܂����A�Ȃ��A����������̂ł��傤���H
0806�P�R�Q�l�ڂ̑f������
2018/07/25(��) 16:25:39.31ID:NUuuX50l���肪�Ƃ��������܂��I
0807�P�R�Q�l�ڂ̑f������
2018/07/25(��) 16:25:48.75ID:OudMyBSl0808�P�R�Q�l�ڂ̑f������
2018/07/25(��) 16:26:27.44ID:46AWINrh0809�P�R�Q�l�ڂ̑f������
2018/07/25(��) 19:09:07.24ID:nX4cSFpe���ӂ�x�Ŕ��������
2x��1
�ǂ��ł���
0810�P�R�Q�l�ڂ̑f������
2018/07/25(��) 19:27:12.84ID:dv/3c74Y0811�P�R�Q�l�ڂ̑f������
2018/07/25(��) 20:22:44.06ID:PrWHDeJm���ꂨ�������ˁH
x=1/2�����̎��Ő��藧����
0812�P�R�Q�l�ڂ̑f������
2018/07/25(��) 22:29:16.40ID:RsvmddO10813�P�R�Q�l�ڂ̑f������
2018/07/25(��) 22:53:07.91ID:XUnY7vy+0814�P�R�Q�l�ڂ̑f������
2018/07/25(��) 23:42:15.30ID:X8Ci6iz90815�P�R�Q�l�ڂ̑f������
2018/07/26(��) 00:05:46.27ID:xu9Vtb0J0816�P�R�Q�l�ڂ̑f������
2018/07/26(��) 01:10:58.71ID:I53/TiKZ�ǂ��������ƂȂ̂������ĉ�����
https://i.imgur.com/AqeoIz5.jpg
0817�P�R�Q�l�ڂ̑f������
2018/07/26(��) 01:34:57.04ID:xu9Vtb0J|a+b|��|a|+|b|�@�́i�P�j�ŏؖ�����Ă���B
�܂�A�����������ā@�C�ӂ̎���x�Ay�ɂ���|x+y|��|x|+|y| �Ƃ��Ă����̕s�����͐������B
������ x=a+b�Ay=-b �Ƃ����
|a|=|a+b-b|=|x+y|��|x|+|y|=|a+b|+|-b|=|a+b|+|b| �䂦�A�@|a|-|b|��|a+b|
0818�P�R�Q�l�ڂ̑f������
2018/07/26(��) 03:33:00.54ID:QNJwJ78qab=0�̂Ƃ��A|ab|=ab
ab>0�̂Ƃ��A|ab|=ab
�����|ab|��ab
����������(a=0)��(b=0)��(a>0��b>0)��(a<0��b<0)
�͎�������������������
0819�P�R�Q�l�ڂ̑f������
2018/07/26(��) 07:31:53.78ID:g+RkUMtl�������������s�v����
0820�P�R�Q�l�ڂ̑f������
2018/07/26(��) 07:34:11.12ID:QNJwJ78q�摜���悭����
0821�P�R�Q�l�ڂ̑f������
2018/07/26(��) 11:37:54.31ID:4WJyibWY��̎����킩��₷���ȒP�ɉ������@�������Ă�������
1.�@��l����97�O3���v�Z����
2.�@a^3-b^3���g��
3.�@97���i100-3�j�ƒu��������(a-b)^3���g��
4.�@�����Ƃ������@������
0822�P�R�Q�l�ڂ̑f������
2018/07/26(��) 12:49:22.91ID:/r1wDInk����ł͂Ȃ��A�S�����ۂɎ����Ă݂��炢���ł���B����Ă݂�̂���Ԃł��B
0823�P�R�Q�l�ڂ̑f������
2018/07/26(��) 12:52:29.86ID:cjFJlyDD0824�P�R�Q�l�ڂ̑f������
2018/07/26(��) 18:32:52.20ID:HDSqfVy5����Ƃ���̈Ӗ����킩��܂���
���肪�Ƃ��������܂�
0825�P�R�Q�l�ڂ̑f������
2018/07/26(��) 19:02:24.07ID:QNJwJ78q(�^��)
=1-912673/1000000=87327/1000000
���j2
(�^��)
=(1-97/100)(1+97/100+9409/10000)
=(3/100)(29109/10000)
=87327/1000000
���j3
(�^��)
=1-(1000000-3*10000*3+3*100*9-27)/1000000
=1-1+90000/1000000-2700/1000000+27/1000000
=87327/1000000
3���Ȃ�
0826�P�R�Q�l�ڂ̑f������
2018/07/27(��) 00:29:21.02ID:RKzn154Y>821�ł��B���肪�Ƃ��������܂��B
�����������疂�@�̂悤�ȊȒP�ȕ��@������̂����Ɗ��҂����̂ł����A
����ȃ��V�̂����b�͂Ȃ��ł���˂�
3���̌����H�W�J���H���g���Ċ撣��܂��I
����x���Ȃ��Ă����܂���B���肪�Ƃ��������܂����B
0827�P�R�Q�l�ڂ̑f������
2018/07/28(�y) 21:27:57.93ID:SbO4yD9B���������āA�`�����������c���ĂȂ����{�搶���Ď��͎��݂��Ă��Ȃ��ˋ�̐l���Ƃ�����Ȃ��ł��傤���B
0828�P�R�Q�l�ڂ̑f������
2018/07/28(�y) 22:16:40.55ID:FG6cZVOWhttps://www.yutori528.com/wp-content/uploads/2018/03/20171124204322.png
0829�P�R�Q�l�ڂ̑f������
2018/07/31(��) 13:16:30.79ID:1jhvI+DZ0830�P�R�Q�l�ڂ̑f������
2018/08/01(��) 17:39:48.28ID:j6P6fd4Yhttps://i.imgur.com/keVj8Q1.jpg
https://i.imgur.com/4jJol5y.jpg
0831�P�R�Q�l�ڂ̑f������
2018/08/01(��) 21:19:40.37ID:sWT18pDM�o�J�̂����ɔw�L�т������W����ł�������
�`���[�g�ł�����Ƃ��B
0832�P�R�Q�l�ڂ̑f������
2018/08/01(��) 21:40:28.17ID:BfR+NmsS0833�P�R�Q�l�ڂ̑f������
2018/08/01(��) 22:35:24.03ID:eUeIh8BV���̎��ό`�͉쐬�҂̎���ȁB
0834�P�R�Q�l�ڂ̑f������
2018/08/02(��) 04:14:55.23ID:I3jlqf27���肪�Ƃ�
0835�P�R�Q�l�ڂ̑f������
2018/08/02(��) 08:42:03.95ID:yW9eKYC/�Ȃɂ��u���肪�Ƃ��v�Ȃ�
�e���[��>>830�Łu���ό`���Ȃ�ł����Ȃ�̂����킩��܂���v�ď����Ă邾�낤���{�P
����ɑ���>>833�͎��ό`���Ȃ�ł����Ȃ�̂������Ă�̂��H���H�����B
>>833�������Ă�̂́u���ό`���Ȃ�ł����Ȃ�̂��v����Ȃ��u�Ȃ�ł���Ȏ��ό`�����邩�v����[�N�Y���B
�u�Ȃ�ł���Ȏ��ό`�����邩�v�̓e���[���g�����ł�>>830�Łu�����ׂ邽�߁v�Ə����Ă邾�낤���B�n�����B
�Ă߁[�̋^��́u���ό`���Ȃ�ł����Ȃ�̂��v�ɑ��ē�����̂�>>831�́u���������v���낤���{�P���B
��T�ɂ��Ƃ���B�o�J�̃A�z�̃N�\�̃S�~�̖��\�̖𗧂����̂Ђ�������̃K�L���B
0836�P�R�Q�l�ڂ̑f������
2018/08/02(��) 10:45:51.24ID:I3jlqf27�Ȃ��߂�
�������Ȃ��̂ŋ����Ă�������
0837�P�R�Q�l�ڂ̑f������
2018/08/02(��) 10:46:55.93ID:nwaSDmPv���閳�����Ȍ����n�т̔C�ӂ̃��f���ɑ��Ă���_�����ӂ���ɐ^�ƂȂ�Ȃ�A�т���ӂ�LK�ɂ����ďؖ��\�ƂȂ邱�Ƃ�����
�킩��Ȃ���ł����H
0838�P�R�Q�l�ڂ̑f������
2018/08/02(��) 11:35:23.96ID:Aawfc3bg0839�P�R�Q�l�ڂ̑f������
2018/08/02(��) 13:55:55.11ID:NW9iDW38835���̓o�J�̃A�z�́i�ȉ���
0840�P�R�Q�l�ڂ̑f������
2018/08/02(��) 14:07:33.06ID:hrZADakX�ꋉ�G�X�p�[����͒ʂ�Ȃ��������ȁB
0841�P�R�Q�l�ڂ̑f������
2018/08/04(�y) 18:53:22.60ID:VblSSaDK�����̊m���͂��ׂāA
���� A �̋N����ꍇ�̐� / �N���肤�邷�ׂĂ̏ꍇ�̐�
�Ōv�Z�ł��܂��B
�Ȃ��e���s�̊m���̐ςł킴�킴�v�Z����̂ł��傤���H
�������Ƃł���ˁH
0842�P�R�Q�l�ڂ̑f������
2018/08/05(��) 10:51:47.70ID:wBnYHfP8�ǐS�I�ȓX�@������
0843�P�R�Q�l�ڂ̑f������
2018/08/05(��) 12:28:04.85ID:ndB8G4Nk4�~����1.1.2.X���o��m���͂ǂ����߂܂����H
0844�P�R�Q�l�ڂ̑f������
2018/08/06(��) 12:45:18.50ID:ReWxtnxQ0845�P�R�Q�l�ڂ̑f������
2018/08/09(��) 12:49:06.12ID:V5PjC5T1�ǂ������������p��Ȃ�ł��傤���B
�����{�ƒ萔�{�ł͎w�������Ӗ����Ⴄ��ł��傤���B
0846�P�R�Q�l�ڂ̑f������
2018/08/09(��) 13:19:20.69ID:1xDyQzpf0847845
2018/08/09(��) 17:58:58.77ID:V5PjC5T1�Ȃ�قǕ��ʂɈႤ��ł��ˁB
���������������ėL�������܂����B
0848�P�R�Q�l�ڂ̑f������
2018/08/10(��) 06:04:51.26ID:OV0NXniN0849�P�R�Q�l�ڂ̑f������
2018/08/10(��) 06:34:08.13ID:6zx9Xbcp�E�{���ɂȂɂ������Ȃ��{���N�����Z��
�E������킩����x�̑�w���w�̓��e���悭���������ɏ����Ă�E���R�]
�E�b��ɂ��Ă���Ȃ��n�����ǓƂ�킷���߂ɓ���������J��Ԃ������̔p�l
�҂̓���
�E�C�P�����̃G���[�g���吶�E����@��
�E���w�����ăo���o�������Ă�r�W�l�X�}��
�E���z�[�Ŏ�
0850�P�R�Q�l�ڂ̑f������
2018/08/10(��) 06:44:54.26ID:w3widXJH�E����������������G���[�g���Z��
�E�l�b�g���发�Œ��ׂ����āA����������ŏ����Ă�X�[�p�[���]
�E���x�����߂��Ɏ��������w�͉�
�҂̓���
�E�u�T�����̒�ӂe�����吶�E�e������@��
�E���w�ƊW�Ȃ��j�[�g�E���E
�E��ېŁA�N���ؔ[��
0851�P�R�Q�l�ڂ̑f������
2018/08/10(��) 07:06:25.25ID:3b34RinS0852�P�R�Q�l�ڂ̑f������
2018/08/10(��) 13:22:21.83ID:f5zd+h1c0853�P�R�Q�l�ڂ̑f������
2018/08/10(��) 13:38:20.12ID:LTrURKS9���ɑ�l�Ɏ��悭�Ȃ��Ƃ���܂������Z���w�͈̔͊O������g��Ȃ��悤���ǂ��Ƃ����Ӗ��Ȃ̂ł��傤���Ha=b=0�łȂ���Ύg���Ă悢�̂ł��傤���H�ia,b������0�ɂȂ�Ȃ���悢�H�j
0854�P�R�Q�l�ڂ̑f������
2018/08/10(��) 14:58:23.30ID:a2Q09sjV�I�b�N�X�t�H�[�h���w�~�j���T�ł͂���́u�s��̎����v�Ə����Ă���܂��B
2x3�Ƃ����̂��s��̎����������ł��B
�ʂ̖{�ɂ́u�s��̌^�v���Ə�����Ă���܂��B
�E�B�L�y�f�B�A�̉p��łɂ́u�s��̃T�C�Y�v���Ə����Ă���܂��B
�ǂꂪ�{���Ȃ�ł��傤���B
0855�P�R�Q�l�ڂ̑f������
2018/08/10(��) 18:14:37.11ID:pYN6HXOgn�sn��Ȃ�un����(����)�s��v�ƌ������A��ʂ̍s��ɑ��Ď����ȂǂƂ͌���Ȃ�
�^�͒m���
0856�P�R�Q�l�ڂ̑f������
2018/08/10(��) 18:14:54.45ID:pYN6HXOg0857�P�R�Q�l�ڂ̑f������
2018/08/10(��) 18:29:43.49ID:1gynkk5k0858�P�R�Q�l�ڂ̑f������
2018/08/10(��) 18:52:15.24ID:a2Q09sjV�um x n�^�̍s��v�Ȃ�Č����������Ă���{������܂��B
���́u�^�v��type�ł͂Ȃ�size�̖��ł��傤���ˁH�H�H
�I�b�N�X�t�H�[�h���w�~�j���T�ɍڂ��Ă���u�s��̎����v��order of matrix�ł��B
https://www.onlinemathlearning.com/matrices-types.html
https://www.vitutor.com/alg/matrix/matrices_types.html
��ł�types of matrices�Ƃ��čs�s��i�s�x�N�g���H�j�Ƃ���s��i��x�N�g���H�j
�Ƃ��P�ʍs��Ƃ��[���s��Ƃ����������Ă��܂��B
�s��x�̂��Ƃ��Ⴀ��܂���ˁB
https://en.wikipedia.org/wiki/Matrix_(mathematics)#Size
�E�B�L�y�f�B�A�̉p��łł́A�s��x��size�ƌĂ�Ă��܂��ˁB
�����������������B
�um�~n���̍s��v�Ȃ�Č�����������Ă��܂��B
0859�P�R�Q�l�ڂ̑f������
2018/08/10(��) 18:53:08.33ID:a2Q09sjVhttps://www.quora.com/How-do-we-find-the-order-of-a-matrix
0860�P�R�Q�l�ڂ̑f������
2018/08/10(��) 20:13:10.80ID:zWKD+DnF�x�N�g���̕��f���{�Ă̂�2�����ł���C���[�W�ł��Ȃ�
�Ȃ���
0861�P�R�Q�l�ڂ̑f������
2018/08/10(��) 21:47:45.18ID:pYN6HXOg�@�B�I������Ȃ�������ɂ��Ă͂����Ȃ�
Don't think, feel.
0862�P�R�Q�l�ڂ̑f������
2018/08/10(��) 21:48:30.28ID:pYN6HXOg0863�P�R�Q�l�ڂ̑f������
2018/08/10(��) 23:35:05.30ID:BCUTJOxx1xn�s���n���̍s�x�N�g���Amx1�s���m���̗�x�N�g���ƌĂ肷��Ƃ���*��
�̂��Ƃ��Ǝv���Ă��܂����ǁA����͂���Ő������̂ł��傤���B
0864�P�R�Q�l�ڂ̑f������
2018/08/11(�y) 12:51:12.83ID:l6Wvlr0y0865�P�R�Q�l�ڂ̑f������
2018/08/11(�y) 20:57:44.45ID:ptgjDdzlorder���^�Ƃ������Ƃ����̂ł́H
0866�P�R�Q�l�ڂ̑f������
2018/08/12(��) 19:35:54.22ID:GKqHxK+60867�P�R�Q�l�ڂ̑f������
2018/08/20(��) 12:34:52.04ID:tGIOG7QK�\�\�\�\�\�\
��[k=2..n]k
����ō���鐔��̈�ʍ��������Ă�������
0868�P�R�Q�l�ڂ̑f������
2018/08/21(��) 06:39:02.78ID:qu4riARb0869�P�R�Q�l�ڂ̑f������
2018/08/21(��) 12:02:36.14ID:0VsK5pzRy=(x+a/2)^2-a^2/4+b��蒸�_��(-a/2,-a^2/4+b)
i) -a/2<1
ii) 1��-a/2<3
iii) 3��-a/2<5
iv) 5��-a/2
�ŏꍇ����
0870�P�R�Q�l�ڂ̑f������
2018/08/21(��) 13:06:02.74ID:gtFiLDqi�̈�̒[�_�ƒ��_�̂�
x=2�̂Ƃ��ŏ��ƂȂ�
�Ƃ��邩��x=2�͗̈�̒[�_�łȂ� ���ɒ��ڂ���ƒ��_��x���W��2�܂莲��2
(1��x��5)�����玲���牓��x=5�̂Ƃ��ő�l3���Ƃ�B
����Ŏ��Q���Ă�ĘA������a��b���o��
0871�P�R�Q�l�ڂ̑f������
2018/08/22(��) 00:08:22.91ID:88xVGg0S�X�ɔC�ӂ̓_P(px,py)���L��B
�C�ӂ̎l�p�`(ul,ur,dl,dr)���ł̍��WP'(x,y)���Ȃ킿
P = ( ul * x + ur * (1.0 - x ) ) * y + (dl * x + dr * (1.0 - x)) * (1.0 - y))
�ƂȂ�_P'(x,y)�̋��ߕ��͑��݂��܂����H
0872�P�R�Q�l�ڂ̑f������
2018/08/22(��) 19:02:10.37ID:1oShQj7D0873�P�R�Q�l�ڂ̑f������
2018/08/24(��) 21:37:43.25ID:uGgCYAp+�}�`�s��z���̂܂��ɂP��]�����Ăł��闧�̂�z=a�Ő�������̐}�`�̖ʐς��r(a)�ŕ\���Ȃ����B�������A0��a��4�Ƃ���B
���̖��łs(0,0,a)�Ƃ����Đ���BC,AC�Ƃ̌�_�����ꂼ��P,Q�Ƃ����āA��(PT^2-QT^2)�����߂�悢�ƍl���ĉ����܂����B
P(0,2-1/2a,a),Q(1-1/4a,0,a)�Ƃ������Ƃ��ł��v�Z�������ʂ�S(a)����(3/16a^2-3/2a∔3)�ƂȂ�܂����B
������������ƃ�(4-a^2)/5�ƂȂ��Ă��ĈقȂ��Ă��܂��B
�ł͐��ˉe�𗘗p���Ă���Ă���̂ł����A���̂��̂����͊Ԉ���Ă���̂ł��傤���H
�܂��ǂ��Ԉ���Ă���̂������Ē����Ȃ��ł��傤���H
��낵�����肢���܂��B
0874�P�R�Q�l�ڂ̑f������
2018/08/24(��) 21:49:06.79ID:KL8GFrzC������(PT^2-QT^2)�����߂�悢�ƍl���ĉ����܂����B
�����
�������ŏ��ɂȂ�̂͐����̑��ɂ����Ăł���
0875�P�R�Q�l�ڂ̑f������
2018/08/24(��) 21:51:10.05ID:uGgCYAp+�Ȃ�قǁB�ŏ��l���Ԉ���Ă���̂ł��ˁB
������x�悭�l���ĉ����Ȃ����Ă݂܂��B
���肪�Ƃ��������܂����B
0876�P�R�Q�l�ڂ̑f������
2018/08/24(��) 21:52:08.42ID:KL8GFrzC
0877�P�R�Q�l�ڂ̑f������
2018/08/24(��) 21:54:12.95ID:l0zth8fT0878�P�R�Q�l�ڂ̑f������
2018/08/25(�y) 05:37:30.95ID:J8Lq7V50T(0,0,a), P(0,(-1/2)a+2,a), Q((-1/4)a+1,0,a)
TP=(-1/2)a+2, TQ=(1/2)TP, PQ=��(TP^2+TQ^2)=��(TP^2+(1/4)TP^2)=((��5)/2)TP
T����PQ�ɉ��낵�������̑���H�Ƃ����
TP:TH=QP:QT���
TH=TP*QT/QP=TP*(1/2)TP/((��5)/2)TP=((��5)/5)TP
S(a)
=��TP^2-��TH^2
=��(TP^2-(1/5)TP^2)
=��(4/5)TP^2
=��(4/5)((-1/2)a+2)^2
=��(1/5)(-a+4)^2
S(4)=0������a=4�̂Ƃ������藧��
0879�P�R�Q�l�ڂ̑f������
2018/08/25(�y) 05:41:39.01ID:J8Lq7V500880�P�R�Q�l�ڂ̑f������
2018/08/30(��) 22:06:56.80ID:PL7NgMTGk��������̂Ƃ��@(k+0.5)pi - x_k ��0�Ɏ�������Ƃ����܂����B
0881�P�R�Q�l�ڂ̑f������
2018/08/31(��) 21:34:32.93ID:Q8WwdP0g12A+20B+30C��1200
3A��12B��6C��4A
�Ƃ������Ȃ̂ł����A�����A�^�}�łȂ�Ƃ���J����A��35�@B��9�@C��20�Ƃ��������ł����̂ł���
�ǂ̂悤�ɉ����̂����ʂȂ̂ł��傤���B
0882�P�R�Q�l�ڂ̑f������
2018/08/31(��) 23:25:13.50ID:aTwlZgPC0883�P�R�Q�l�ڂ̑f������
2018/09/01(�y) 10:38:48.56ID:McE3RziY�i2�j�́Asint<0����<t<2�ɂȂ�Ȃ����Ƃ��悭�킩��܂���
�l�̓T�C���̒l��0�����Ȃ��O�A��l�ی��͈̔͂�\���Ă���Ƃ������ƈȊO�Ȃɂ��킩��܂���
���̖��͉������������̂ł���
0884�P�R�Q�l�ڂ̑f������
2018/09/01(�y) 10:59:49.33ID:i0tk9zAX���w�Z�̂����720�x��360�x�Ɠ������Ă̂������
����������������肵�Ė߂��Ă����p�x����3�ی���4�ی��ɂ���������� �p�x���̂͑�R�Y������p�x������킯
�Ƃ�0�`2��
t����-��/6�Ƃ�����t�͈̔͂�-��/6�`(2��-��/6)�ɂȂ�
���̊p�x�̒��ő�3��4�ی��ɂ���͈͂������Ă���
���Ă̂�180�x���ƍl���Ă�������
�Ƃ�0�`360�x�ɑ���t��-30�`330�x�� ���̊p�x�̒��ő�3��4�ی��̈ʒu�ɂ���z�l����킯��
���������Ă鎖�͏��w�Z���x������
0885�P�R�Q�l�ڂ̑f������
2018/09/02(��) 18:18:18.67ID:WnW6aDui0886�P�R�Q�l�ڂ̑f������
2018/09/06(��) 18:33:13.20ID:UYIHG+Chhttps://youtu.be/LazHFJDufYA?t=709
�������18:30�b�̂Q��ڂ̗��K��肪������܂���B
�u�قȂ�S�_�`�A�a�A�b�A�c������A�x�N�g���`�a���x�N�g���c�b�̂Ƃ��A
�x�N�g���`�c���x�N�g���a�b�����藧���Ƃ������B�v
����Ɂu�x�N�g�����o�ꂷ��ƕ��s�l�ӌ`���o����v�Ɖ��������܂����B
�Ȃ��A���s�l�ӌ`�Ȃ̂��H�����`�ł̓_���Ȃ̂ł����H
0887�P�R�Q�l�ڂ̑f������
2018/09/06(��) 19:51:58.99ID:nBpbA6t2�`�a�{�a�b���`�b
�`�c�{�c�b���`�b
�`�a���c�b
���̂R�̓������g���ł���
0888�P�R�Q�l�ڂ̑f������
2018/09/06(��) 22:37:05.69ID:8yZteJvi�x�N�g���`�a���x�N�g���c�b�����ǂ�ȂS�_A,B,C,D�ɑ��Ă����藧���Ƃ������Ȃ��Ƃ����Ȃ����琳���`�ł͂���
�����Ƃ����Ε��s�l�ӌ`�ł�����
0889�P�R�Q�l�ڂ̑f������
2018/09/06(��) 23:20:28.34ID:O3aHnyGu�p�x��2�Έȏ�╉�ɂ܂Ŋg��������ʊp���������艟�����Ă��炱�̖����������B
��ʊp���������Ȃ��Ȃ��Ƃ��̖��̉��ËL���Ă����̈Ӗ����Ȃ��B
0890�P�R�Q�l�ڂ̑f������
2018/09/06(��) 23:24:27.58ID:O3aHnyGu��ʂ�AB=BC�ł͂Ȃ�����B
4�_A�AB�AC�AD���ƕ��s�l�ӌ`���Ă��Ƃ��琬�藧���Ȃ��Ȃ�ꍇ�����邪�A
����͈قȂ�4�_�Ȃ̂ŕ��s�l�ӌ`�ƂȂ�B
0891�P�R�Q�l�ڂ̑f������
2018/09/07(��) 06:19:53.96ID:xiAsQi+b�꒼����̏ꍇ�́H
0892�P�R�Q�l�ڂ̑f������
2018/09/09(��) 09:40:51.29ID:GwsSbvc5�A�W�A�l�̘b���Ă�̂�
�u�Ȃ��A�W�A�l�Ȃ́H���{�l����_���Ȃ́H�v���Č����Ă�̂Ɠ����B
���R���{�l���o�Ă��邱�Ƃ����邪�A���{�l����Ȃ��A�W�A�l��
�o�Ă���ꍇ������̂ŁA���{�l�ƌ��肵�Ă͂����Ȃ��Ƃ�������
0893�P�R�Q�l�ڂ̑f������
2018/09/09(��) 13:06:04.00ID:sfEQbxyD0894�P�R�Q�l�ڂ̑f������
2018/09/09(��) 16:09:28.96ID:IZNGwMC3�����������܂��ł��傤���H
(7+7��5)/2
���̕��q�ɂQ������̂�
7/2����7��5/2�����킹�ĕ\�L�������̂Ƃ������߂ō����Ă��܂����H
0895�P�R�Q�l�ڂ̑f������
2018/09/09(��) 16:10:28.25ID:J8hH/OfJ0896894
2018/09/09(��) 17:05:31.55ID:IZNGwMC3�����f���������܂���
0897�P�R�Q�l�ڂ̑f������
2018/09/10(��) 22:44:12.72ID:8MrzCUqj�u�ŏ��lm(a)�����߂�B�v�ɑ��āA
�@�@a���O�̂Ƃ��@�@�@a^2�{4���@�i����a�̂Ƃ��j
�@�@0������1�̂Ƃ��@�@�@�S�@�@�@�i����1�̂Ƃ��j
�@�@1��a�̂Ƃ��@�@�@ a^2�|4���@�i����a+1�̂Ƃ��j
�̂悤�ɓ�������A�����c���s�v�Ƃ������ƂŁA���_����܂����B
��蕶���u�ŏ��l�����߂�B�v�̂Ƃ��́A�����c�������̂ɁA�ǂ����Ăł����H
0898�P�R�Q�l�ڂ̑f������
2018/09/10(��) 22:47:15.83ID:YBWobjUE��蕶��S��������
�\�Ȃ�摜�ŏグ��
0899�P�R�Q�l�ڂ̑f������
2018/09/10(��) 22:58:52.67ID:8MrzCUqj0900�P�R�Q�l�ڂ̑f������
2018/09/10(��) 23:13:40.29ID:J30rr35o�w�u�E�E�E�v�̂悤�ɓ������x�Ƃ����@�u�E�E�E�v�̒��̉������_�̑ΏۂȂ̂�������s���B
>>898���̎w���ɉ����Ăق����B
>>899
��蕶�ɂ���ĈႢ�������ꍇ�����邵�A����ꍇ������A�Ƃ��������悤���Ȃ��B
0901�P�R�Q�l�ڂ̑f������
2018/09/10(��) 23:39:49.67ID:8MrzCUqj�Ƃ������ŁC��
�@a���|2�̂Ƃ��@a^2�{4a�{4�@�i����a+2�̂Ƃ��j
�@0��a��2�̂Ƃ��@�@�@�O�@�@�@�@�ix=0�̂Ƃ��j
�@2��a�̂Ƃ��@�@�@�@a^2�@�@�@�ix=a�̂Ƃ��j
�Ə�������A�u�����c�̂Ƃ��v���s�v�Ƃ������ƂŌ��_����܂����B
m(a)���Ȃ��A�����u�ŏ��l�����߂�B�v�̂Ƃ��́A�ux=�c�̂Ƃ��v�������̂�
�Ⴂ�͉��Ȃ낤�Ƃ������ƂŔY��ł��܂��B
0902�P�R�Q�l�ڂ̑f������
2018/09/10(��) 23:54:59.54ID:koM2hu+M�{�Ԃł͂ǂ���ł��ǂ����Ǝv���܂����A�搶�̌������������ł���A�Ƃ������Ƃ���ł�
m(a)�����߂�A�Ƃ���̂ŁA�����ł�a��m(a)�̊W�����߂��Ă���ƍl�����܂�
a�̒l�����肳���ƁA�u���b�N�{�b�N�X�ɓ����čŏI�I��m(a)�Ƃ����l���o�Ă���A���ꂪ���̈Ӗ��ł���
����̎����a��m(a)�ŁAy�Ƃ�x�̓u���b�N�{�b�N�X�̒��g�ł�
�u���b�N�{�b�N�X�͒��g��m��Ȃ����炢���킯�ŁA�킴�킴�O�ɏo���K�v�͂Ȃ��ł���
�Ⴆ�A�e���r�̓����d�g�݂�m��Ȃ��Ă��e���r�͌���܂�
�e���r�̃X�C�b�`�����x�ɁA��ʂ̉��ɓ����̓d���͊���ȂƂ�������Ă������獢��܂����
����Ȋ����ł�
0903�P�R�Q�l�ڂ̑f������
2018/09/11(��) 00:00:35.30ID:w+UDT0OS�N���������B
x������͈͂̒��ōl����Ƃ��A��f(x)�̂���lm�����̊��̍ŏ��l�ł���Ƃ́A
(1)f(A)=m�ƂȂ�A�����͈̔͂̒��ɑ��݂��A(2)���͈̔͂̒��̂ǂ̒lx�ɑ��Ă�f(x)��m�����藧���Ă���
��2�����������Ƃ��������B
���������āA�ŏ���^����x�i�N�̉L�q�̒��́@x=a+2�̂Ƃ��Ax=0�̂Ƃ��Ax=a�̂Ƃ��j�����邱�Ƃ�
�Ȃ�猸�_�̑Ώۂɂ͂Ȃ�Ȃ��B�ނ���L�q���ĂȂ������_�̑ΏۂƂȂ�B
0904�P�R�Q�l�ڂ̑f������
2018/09/11(��) 00:16:51.22ID:OX5eoiL50905�P�R�Q�l�ڂ̑f������
2018/09/11(��) 00:42:02.65ID:Gyf0GRF8�u�S�Ă̎���x�ɑ��Ē�`�����f(x)�v�̍ŏ��l��ϐ�a�ɑ�����Ƃ��ċ��߂���Č���ꂽ����
�ŏ��l���o������̒���x=a�̎��Ƃ��̏��͗~���������̒i�K�ŏ����Ė����̂͌��_�Ώۂ�����
�ŏI�I�ɓ����Ƃ��Ă܂Ƃ߂鎞��a�̊��Ƃ��ĕ\���Ă���̂�x�ɂ��Ă̏��Ƃ������ĂȂ����Ȃ��ĂȂ�̂͂���
0906�P�R�Q�l�ڂ̑f������
2018/09/11(��) 01:22:41.64ID:Cpfzsf5M�����������t������������g�����Ƃ�������Ă��Ȃ��̂ɓ����̏ꍇ�������Ȃ���Ό��_�Ƃ�����Ă�����
����ɗ����ɋꂵ��
0907�P�R�Q�l�ڂ̑f������
2018/09/11(��) 01:37:04.35ID:5wZvlX50https://twitter.com/mas20285
https://twitter.com/keepmathtop
https://twitter.com/kyuuchan_
https://twitter.com/xPuGPq8Tn9GWCJb
https://i.imgur.com/EuqD4Nf.png
https://i.imgur.com/AcRxZW4.jpg
https://i.imgur.com/4Dk16V9.jpg
https://i.imgur.com/JHemyAu.jpg
https://i.imgur.com/L463soq.jpg
https://i.imgur.com/jpf8lOd.jpg
https://twitter.com/5chan_nel (5ch newer account)
0908�P�R�Q�l�ڂ̑f������
2018/09/11(��) 01:54:17.05ID:w+UDT0OS�ǂ����ĕs�v�Ȃ�ł����A�Ƃ͕����Ă݂����ˁB
���̉ɂ͂ǂ�ȉႪ�l������H
0909�P�R�Q�l�ڂ̑f������
2018/09/11(��) 03:30:15.59ID:we3PZMMX���������ꍇ�������Ԉ���Ă���
0910�P�R�Q�l�ڂ̑f������
2018/09/11(��) 08:12:51.16ID:K5DPyEMQ���̓��ĂŐ����ɂ��Ă��炨���Ƃ����͖̂������B
�����_���炦���̂Ȃ�D�����搶���B0�_�ł����������Ȃ��B
0��a��2�̒��ŁAa��2�̏ꍇ�Ax��2��x��4�B
���Ă̂悤�ɁA����x�͈̔͂�y�̍ŏ��l��0�Ƃ����̂͂��蓾�Ȃ��B
>>909�������Ă��邪�A��������a�̏ꍇ���������������B
���_���ꂽ���R�͂������ȁBx���]�X�͊W�Ȃ��ȁB
0911�P�R�Q�l�ڂ̑f������
2018/09/11(��) 08:24:05.08ID:0BBEL6R1����͒v���I�Ȃ̂�0�_�ł�����܂�
0912�P�R�Q�l�ڂ̑f������
2018/09/11(��) 09:22:50.29ID:QBWN+JGl��͓I�ȉ�@�̗��_�̓C���[�W�ɗ���Ȃ��Ă������Ƃ�����
��̓I�Ȑ}�`�͍l���Ȃ������悢
0913�P�R�Q�l�ڂ̑f������
2018/09/11(��) 09:46:22.28ID:gGtjePr0����x=�c���s�v�����猸�_�����Ɩ{���ɂ������̂ł�����̋��t�͉����킩���ĂȂ�
0914�P�R�Q�l�ڂ̑f������
2018/09/11(��) 18:38:07.19ID:xnwwPEdC����ɂ����̒l�͂���Ȃ��̂Łu�s�v�v��
�ԃy���ŏ�������A
���k������Ɂu�����͕s�v�Ȃ̂ɏ��������灢�ɂȂ����v
�ƈ��ʊW�����Ă��܂���
0915�P�R�Q�l�ڂ̑f������
2018/09/11(��) 19:16:05.91ID:w+UDT0OS�����̏������𐳊m�ɍČ����ĂȂ���Ƃ��Ⴄ�́H
0916�P�R�Q�l�ڂ̑f������
2018/09/11(��) 22:14:24.20ID:9IiE9UPua�̏ꍇ�����͒P���Ƀ^�C�v�~�X�ł��B���݂܂���B
0917�P�R�Q�l�ڂ̑f������
2018/09/13(��) 22:38:56.84ID:svWshe0b���Ⴀ�A�����ʂ�̓��Ă������Č��Ă�B
0918�P�R�Q�l�ڂ̑f������
2018/09/14(��) 00:58:15.42ID:ZGYvSl7o��ӂ�1�̐����ʑ̂ʃ��Ɏˉe�������̂��̐}�`�̖ʐς͈̔͂����߂�Ƃ������Ő}�`�̍ŏ��l���l���Ă��܂��B
�����͂ł���̂ł����A�����ɏؖ�����ƂȂ�Ƃ��܂����j�������Ȃ��č����Ă��܂��B
�����̕��j�ł�
1:�}�`�ɓ��e������̐}�`�̑Ώ̂łȂ��O�_���A���e�����}�`�̒��S��O�Ƃ��ăx�N�g���ŕ\���B
2:�Z�p�`�̎��ɂ͓��e�}�̔����ƂȂ�O�p�`�����邱�Ƃ������B
3:��̎����Œ肵�ĉ�]���������A���ʐς��ŏ��ƂȂ�͎̂���@���Ƃ���ʂ����Ɛ����ɂȂ������ł���B
4:����ɕʂ̎����Œ肵�����ɉ�]���������ɍŏ��ɂȂ�̂͐}�`���Ђ��`�ƂȂ鎞�ł���B
�Ƃ�������Ŏ������Ƃ��Ă���̂ł����A3���������ł��B
0919�P�R�Q�l�ڂ̑f������
2018/09/14(��) 01:34:13.36ID:b4gluaAu��̖ʂ̖ʐς�S�Ƃ���B
��̒��_P�����L����S��A,B,C,D���l����A,B,C,D�������ɓ����鑤�c(A)�Ƃ��Ĉ�ʐ�������Ȃ��B
A,B,C,D�̖@���x�N�g����(1,1,1),(-1,1,1),(1,-1,1),(-1,-1,1)�Ƃ��Ă悢�B
�����̒P�ʕ����x�N�g����(xy,z)�Ƃ���(A)��
x+y+z��0�A-x+y+z��0�Ax-y+z��0�A-x-y+z��0�B
���̂Ƃ��ˉe���̖ʐς�
((x+y+z)S + (-x+y+z)S + (x-y+z)S + (-x-y+z)S)/��3 = (4/��R)Sz�B
���ǎˉe���̖ʐς̎�肤��l�͈̔͂�
x^2+y^2+z^2=1�Ax+y+z��0�A-x+y+z��0�Ax-y+z��0�A-x-y+z��0�c(B)
��x,y,z�������Ƃ���
(4/��R)Sz
�͈̔́B
z���Œ肵���Ƃ�(B)����(x,y)�����݂��������
�~ x^2+y^2 = 1-z^2 �Ɛ����` |x+y| �� z, |x-y| �� z �����L�_������
�Ȃ̂ŃT���b�Ƌ��܂�n�Y�B
0920�P�R�Q�l�ڂ̑f������
2018/09/15(�y) 19:46:33.58ID:3Xu8KOYU(1,0,0)(0,1,0)(0,0,1)(-1,0,0)(0,-1,0)(0,0,-1)
�ƕ���ax+by+cz=0 ������(a^2+b^2+c^2=1)
�ōl������ǂ��ł��傤?
���ꂼ��̓_��
(1-a^2,-ab,-ac) (-ab,1-b^2,-bc) (-ac,-bc,1-c^2)
(a^2-1,ab,ac) (ab,b^2-1,bc) (ac,bc,c^2-1)
�Ɉڂ邩��
���˂����ʐς�|a|+|b|+|c|�ɂȂ�
a��0 b��0 c��0����a^2+b^2+c^2=1�͈̔͂ōl����
(a,b,c)��(1,1,1)�̓��ώ�肤�� �͈͍l������
�ŏ��ɂȂ�̂�
(a,b,c)=(1,0,0),(0,1,0),(0,0,1)
�܂萳���`�ɂȂ鏊�ł��ˁB
�����ʑ̂������猩��ƂЂ��`���ۂ��������Ă���l���������ǐ����`�������
0921�P�R�Q�l�ڂ̑f������
2018/09/15(�y) 21:35:51.91ID:JJPiuzLj����
����̒��_P�����L����S��A,B,C,D���l����A,B,C,D�������ɓ����鑤�c(A)�Ƃ��Ĉ�ʐ�������Ȃ��B
���ꂤ���BA,B,C,D�̑Ζʂ�A�f,B�fC�fD�f�Ƃ��ĉ\���͂������, A,B,C,D�f�������ɓ����鑤�c(C)
���̏ꍇ��
x+y+z��0�A-x+y+z��0�Ax-y+z��0�Ax+y-z��0�Ax^2+y^2+z^2 = 1
�����Ƃ��̎ԉf���̖ʐ� (2x+2y+2z)/��3 S�͈̔́B
-x+y+z = u�Ax-y+z =v�Ax+y-z = w�Ƃ�����
u��0�Av��0�Aw��0�A((v+w)/2)^2 + ((w+u)/2)^2 + ((u+v)/2)^2 = 1�A
�ɂ�����u+v+w�͈̔͂����߂�悢�B
�����u+v+w = t�Ƃ����ĕ�����
u��0�Av��0�Aw��0�A
(u-t/2)^2 + ((v-t)/2)^2 + ((w-t)/2)^2 = 1
��������������t�͈̔́B
�����̍��ӂ�u=v=w=t/3�̂Ƃ��ŏ��lt^2/3�Au,v,w�̂����Q��0�̂Ƃ��ő�lt^2/2�B
����Ď����������̂�
t^2/3 �� 1 �� t^2/2
�̂Ƃ��B�ȉ�ry
0922�P�R�Q�l�ڂ̑f������
2018/09/16(��) 00:15:04.55ID:F93nUP/s��Ŏ��₵�����̂ł��A�x�N�g���\���ʼn������܂����A���肪�Ƃ��������܂�
0923�P�R�Q�l�ڂ̑f������
2018/09/17(��) 11:33:47.97ID:nPpbt7st���Ƃ��ؖ����ĂĂ��C��������
0924�P�R�Q�l�ڂ̑f������
2018/09/17(��) 13:31:53.04ID:XQlAb8nz0925�P�R�Q�l�ڂ̑f������
2018/09/18(��) 01:15:57.10ID:zdl4hmKr0926�P�R�Q�l�ڂ̑f������
2018/09/18(��) 07:25:35.22ID:85JOj1Q30927�P�R�Q�l�ڂ̑f������
2018/09/18(��) 12:39:55.56ID:wiWZ/8HL��́A���S�p�Ƃ̐�`�̖ʐϋ��߂�̂����Ė{���I�ɂ͓�������
0928�P�R�Q�l�ڂ̑f������
2018/09/18(��) 18:11:19.37ID:Km2ZLC/b�����������Ƃ������q�͌��܂��Ă���B
�ϕ���������Ȃ���Ȃ��āA�ȉ��̂ǂꂩ�����ݑ��˂Ă��邱�Ƃ������B
1)�~����(��)�Ƃ͉����B�~����(��)�̒�`�͏��w�Z�ŏK���
2)�����}�`�̑Ή����钷���̔䂪2�{�Ȃ�ʐς͉��{���B�����͒��w�Z���B
3)180�����Ƃ͂ǂ��������Ƃ��B�ʓx�@�͍��Z1�N���̕K�C�������B
����3���X���X���������Ȃ��Ȃ�A��a���̌����͋��炭�ϕ��ł͂Ȃ��B
�ϕ��̗y����O�̏����T�O�ł��������Ă���B
����3�������ɐ����ł���̂Ɉ�a����������Ȃ�A
���̂Ƃ����߂Đϕ��̔����Șb�ɋ^��������Ă���ƌ����邾�낤�B
��x��Âɍl���Č������������B
0929�P�R�Q�l�ڂ̑f������
2018/09/18(��) 18:44:15.41ID:Sav6VD9b�܂��͂�������������������B
https://2ch.vet/re_maguro_poverty_1535964420_a_0
https://ja-jp.facebook.com/masaoki.iwasaki.9
https://twpro.jp/kainoko1
https://www32.atwiki.jp/wslc/pages/21.html
https://twitter.com/mas20285
https://twitter.com/keepmathtop
https://twitter.com/K46_N700_hikari
�����w��1-F�S�C�̊�薏�T�搶�����o�C�B
�����w���ɋ߂�̂�3�N�ځB
�S���Ȗڂ͐��w�B
���q�e�j�X���̌ږ�����Ă���B
�������o�C�Ƃ����ƁA2013�N4������2015�N3���܂ŋ{�O�����ɓ����Ă����炵���A���q���w����sex�������Ƃ��o���āA����ꂽ����B
���ł����t�𑱂��Ă���̂��������s�v�c�Ȋ�������B
���搶���āA�c�C�b�^�[��Facebook������Ă�݂���������A�`���Ă݂ẮH
https://i.imgur.com/QlmRJRA.jpg
https://i.imgur.com/gwhRBYF.jpg
https://i.imgur.com/R4zalpP.jpg
https://i.imgur.com/mz5APEc.jpg
https://i.imgur.com/e5qzzlE.jpg
https://i.imgur.com/GSC0Ksw.jpg
https://i.imgur.com/Nke9iTe.png
https://i.imgur.com/eqZly2J.jpg
����͂Ȃ�Ȃ̂�I
https://twitter.com/5chan_nel (5ch newer account)
0930�P�R�Q�l�ڂ̑f������
2018/09/18(��) 18:52:06.87ID:Km2ZLC/b�̐S�Ȃ̂���Y��Ă����B���܂�ɂ�����������A
�������ɂ킩��Ȃ��Ƃ͎v��Ȃ����O�̂��߁B
4)�ʐςƂ͉����B�����`�̖ʐς́A�Ȃ�(�c�̒���)�~(���̒���)���B
����͏��w�Z2�N�����炢���B���Ȃ��Ƃ��~�������O�ɏK���
����ɑ����ł��Ȃ��Ȃ�d�ǂ�������Ȃ��B
0931�P�R�Q�l�ڂ̑f������
2018/09/18(��) 19:08:37.66ID:l1E2qqLL0932�P�R�Q�l�ڂ̑f������
2018/09/18(��) 22:59:32.52ID:85JOj1Q3�L��S�������ɓ����đ̐ς��o����
������`�Ă߂��͂��߂�1/2��r^2�ĂȂႢ
0933�w�p
2018/09/18(��) 23:07:34.05ID:bdccv7Cm0934�P�R�Q�l�ڂ̑f������
2018/09/18(��) 23:35:50.82ID:l1E2qqLL���̖ʐϑ����ďo�������������
0935�P�R�Q�l�ڂ̑f������
2018/09/18(��) 23:48:29.25ID:u5mdSfin���Z�ɂȂ��Ă��A���ʏ�̔��ar�̉~�̖ʐς���r^2 �̏ؖ��ǂ��납
�܂����̖ʐςƂ͉����ɂ��Ă̒�`���疞���ɗ^�����ĂȂ�����
0936�P�R�Q�l�ڂ̑f������
2018/09/18(��) 23:54:07.47ID:wa/1jcBE0937�P�R�Q�l�ڂ̑f������
2018/09/19(��) 00:01:25.82ID:zvew606s0938�P�R�Q�l�ڂ̑f������
2018/09/19(��) 21:17:09.66ID:XITMvXb+���ar�̉~�̖ʐς́A��r^2�B
���ar�̉~�̎����́A2��r�B
�p�x��rad�̐�`�̌ʒ��́Ar�ƁB
���ꂩ��A�p�x�Ƃ̐�`�̖ʐς́A
��r^2*(r��)/(2��r)��1/2*r^2*�ƂɂȂ�B
�ʓx�@���g��Ȃ��ꍇ�A�~��1������A�p�x��360�����B
��`�̊p�x���Ɓ��Ƃ���A��`�̖ʐς́A��r^2*(�Ɓ�/360��)�ɂȂ�B
��`�̖ʐςȂ�āA�ʓx�@���g��Ȃ���A���w�Z2�N���̂₳������肾�B
0939�P�R�Q�l�ڂ̑f������
2018/09/19(��) 21:47:22.57ID:XITMvXb+�ʐς̍l�����́A���w�Z�ŏK���B
�����`�̖ʐς��A�c�̒����~���̒����ŕ\����邱�Ƃ������ł��Ȃ��Ȃ�A
���̎q�̐��w�͂́A���w�Z�̒�w�N���x���ƌ��킴��Ȃ��B
�������ɂ���͂��������Ȃ��B
�܂��A�Ɍ��Ɋւ��錵���ȏؖ��͂��Ȃ����A
�~�̖ʐς���r^2�ɂȂ邱�Ƃ̐����͒��w�Z�ŏK���B
���ꂪ�����ł��Ă��Ȃ��Ƃ�����A��������Ȃ��肾�B
���x�_���l���Ă����ł͂Ȃ��B�f�p�Ȗʐς̍l�����͂ƂĂ��ȒP���B
���w�Z3,4�N�Ȃ�\�������ł���B
0940�P�R�Q�l�ڂ̑f������
2018/09/19(��) 23:16:36.73ID:bmil4jiq0941�P�R�Q�l�ڂ̑f������
2018/09/19(��) 23:36:49.50ID:JinVsCH6�͔͉������Ă��������܂���ł��傤��
��낵�����肢���܂�
���
���鎑�i�����͍��i����20%�ł���B���̎�����1�x�s���i�ƂȂ����҂͕K��2��ڂ�������̂Ƃ��A2��ڂł����i�ł��Ȃ������҂́A�Ȍ���Ȃ����̂Ƃ���
���̎����̍��i�҂̕��ώ͉���
0942�P�R�Q�l�ڂ̑f������
2018/09/19(��) 23:40:05.64ID:dHok8gN8http://rio2016.2ch.net/test/read.cgi/math/1537106483/
�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 54 [���f�]�ڋ֎~]
http://rio2016.2ch.net/test/read.cgi/math/1483872494/
���������X���b�h�Ȃ�A�e�𖼏��K�v�͂Ȃ��Ǝv���܂���
0943�P�R�Q�l�ڂ̑f������
2018/09/19(��) 23:47:45.62ID:JinVsCH6���������X���������Ƃ������̂ł���
������ŏo�����܂��̂ŁA>>941�̎���͎�艺���܂�
�����������܂���
0944�P�R�Q�l�ڂ̑f������
2018/09/22(�y) 18:04:17.33ID:hHcXowJH����l�Ɂu���w�ǖ{�v�����߂���
�m���ɗǂ������Ȗ{�Ȃ̂ł����ʂ������̂Ŗ����Ă��܂�
0945�P�R�Q�l�ڂ̑f������
2018/09/22(�y) 18:07:32.21ID:E+fu1y5y0946�P�R�Q�l�ڂ̑f������
2018/09/23(��) 12:52:51.38ID:vx+NXTHe�����Ɠǂz�͏��Ȃ�����ߏ��]������Ă��
0947�P�R�Q�l�ڂ̑f������
2018/09/23(��) 12:54:07.61ID:PH84y1u6�����܂ł킩��ɂ���������ςȂ��Ə�����Ă�킯�Ȃ���ł�
0948�P�R�Q�l�ڂ̑f������
2018/09/24(��) 12:59:11.89ID:PvI9iGzA0949�P�R�Q�l�ڂ̑f������
2018/09/24(��) 18:09:34.69ID:20s//uRv0950�P�R�Q�l�ڂ̑f������
2018/09/25(��) 13:38:32.50ID:QyVcw+aD0951 �y4.9m�z
2018/09/25(��) 20:22:34.25ID:831HQZG+��肪���̒��ʼn����郌�x���Ȃ̂��ǂ�
0952fusianasan
2018/09/25(��) 20:23:45.29ID:831HQZG+����挩���
0953�P�R�Q�l�ڂ̑f������
2018/09/25(��) 20:24:20.37ID:831HQZG+0954�P�R�Q�l�ڂ̑f������
2018/10/07(��) 14:36:36.72ID:5DRIK+m3�������w�Z�ŏK���܂������A���铙���������Ă��̎��ɂ���
�u���ӂ�x�Ŕ�������ƁA�A�A�v�Ƃ���������������܂���
���ӂɂQ����������A���ӂ��悵���肷��̂Ɠ����C�y����
�����Ă������̂ŁA������Ƃт����肵�܂���
�������āA�����ƂȂƂĂ����G�Ȃ��̂Ǝv���Ă�����ł����A
�ǂ�ȓ����ɂł��g������̂Ȃ�ł����H
0955�P�R�Q�l�ڂ̑f������
2018/10/07(��) 18:24:42.38ID:WDkQwWME�Ӗ����킩��Ȃ��B
�Ⴆ�Ay=x^2�Ƃ��������������ꍇ�A
���i�A���Ȃ��͂�����ǂ̂悤�ɕ\���Ă�B
���Ȃ݂ɁA���͈ȉ��̂悤�ɏ����Ă���B
y'=2x ���邢�́A(dy/dx)=2x
0956�P�R�Q�l�ڂ̑f������
2018/10/07(��) 20:36:31.07ID:5DRIK+m3���܂��`���Ȃ������̂ŁA��̓I�ɏ����܂��B
�uf(x)��(x-a)^2�Ŋ������Ƃ��̗]����A
a�Af(a)�Af'(a)��p���ĕ\���v
�Ƃ������ŁA
f(x)=(x-a)^2 · Q(x) + px+q
�ȂǂƂ����Ƃ���܂ł͂킩��̂ł����A���̎��̗��ӂ�
��������Ɓc�Ɖ�@�������Ă����̂ŁA������Ƌ^���
�v�����̂ł��B
�܂��K�����ĂŒm��Ȃ�������������Ȃ��ł����A
�������g���̂͊���������Đڐ������߂���A
�������̂��̂̌v�Z��肵���������Ƃ��Ȃ������̂ŁA
�u����ȂƂ���Ŏg���Ă����́H�v
�Ǝv���Ď��₵�܂����B
������A�������o�Ă�����A���ӂ��悵����A���ӂ��[����
��������Ƃ����A������������ł悭�g�����@��
�����悤�ɁA�C�y�Ɏg����̂��ȁH�Ǝv���Ď��₵�܂����B
0957�P�R�Q�l�ڂ̑f������
2018/10/07(��) 20:39:33.46ID:5DRIK+m3���ȃ��X�ł�
�~�u�[���Ŋ�������v
���u�[���łȂ����Ŋ�������v
�ł�
0958�P�R�Q�l�ڂ̑f������
2018/10/07(��) 20:43:23.29ID:I2sIXbF/��f(x+h)-f(x)=g(x+h)-g(x)
��{f(x+h)-f(x)}/h={g(x+h)-g(x)}/h
��lim[h��0]{f(x+h)-f(x)}/h=lim[h��0]{g(x+h)-g(x)}/h
��f'(x)=g'(x)
0959�P�R�Q�l�ڂ̑f������
2018/10/07(��) 20:52:41.02ID:D/OxZX71(2)���w�E���Z����̓N���X�̋��ɂ���悤�Ȗڗ����Ȃ����݂�����
(3)�l�Ƙb���Ƃ��ڂ����킳�Ȃ��A�܂��{�\�{�\�Ə����Ȑ��ł���ׂ�
(4)�͌^�Ȃlj��������W����Ƃ�����ɂȂ��Ă���
(5)�t�@�b�V�����Z���X���_�T���A�܂��t�@�b�V�����W�̒m���ɖR����
(6)�l�Ƙb���Ă�������y���܂��鎖���o���Ȃ�
(7)��ɋ����s�R�A�܂��e���V�������Ⴂ
(8)�����̕����łQ��������Ă鎞����ԗ�������
(9)�l�b�g�ł͋��C�����A���A���ł͎�C�ŃV���{�C
(10)�X���ŃJ�b�v������������ƓG�ӂ�����
(11)�`�r�A���K�l�A�f�u�A�K���A�V�p�A�n�Q�̂����ꂩ�ł���
(12)�l���������ǂ����Ă邩�����ɋC�ɂȂ�
(13)2�����L�����ɗ�����������������Ƃ�����
(14)���e�@�ł͂Ȃ�����or�����Ŕ����
(15)�e�p�ɃR���v���b�N�X�������Ă���
(16)���Â��ŋC�セ���Ȉِ����^�C�v
(17))��l�Ńt�@�~���X�ɍs���ĐH���������Ƃ�����
(18)�ِ��ƗV��A�ِ��̉ƂɗV�тɍs�����o�����Ȃ�
(19)�ʓ|�Ȃ��Ƃ͐e�ɂ���Ă��炤���Ƃ�����
(20)���������ăA�j���▟��A�Q�[���𑲋Ƃł���
0960�P�R�Q�l�ڂ̑f������
2018/10/07(��) 21:01:15.96ID:it7EQ2Eg=���ē������ĈӖ��ł���
�������̂Ȃ��牽���Ă��ς��܂�����
0961�P�R�Q�l�ڂ̑f������
2018/10/07(��) 22:31:08.66ID:WDkQwWME�́A>>958��>>960�ł��Ă��܂��ˁB
�����������Ɠǂ߂Ώ\���ł��傤�B
���A�撣���Ă��������ˁB
0962�P�R�Q�l�ڂ̑f������
2018/10/11(��) 10:57:22.88ID:pH6LMRjy(5),(11),(13),(14),(17),(18)
�����Ă͂܂邯�ǁA����͂ǂ��Ȃ��
���ȑ�w��
0963�P�R�Q�l�ڂ̑f������
2018/10/11(��) 16:10:02.52ID:sFTkpsnw�@�@�@�@�@�@�@�@�@ ,/�@:::::�R�@�@�@ �@,/�@�@::::�R�@�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@,i�@�@�@::::::�R�@�@,/�@�@�@�@::::�R
�@�@�@�@�@�@�@�@ ,i�@�@�@�@�@ """/�@�@�@�@�@�@::::�R
�@�@�@�@�@�@�@�@,i�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@::::�R�@�@�@�@�@�@
�@�@�@�@�@�@�@ ,i�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �@�@::::i
�@�@�@�@�@�@�@i�@�@���@�@�@�@�@�@�@���@�@�@ �@�@�@:::::i�@�@�@�@�@�@�@�@�͂ɂ�`�`�`�`�`�`�`�`���
�@�@�@�@�@�@�@i�@�@�@�@�@�@�@�@�@�@�@�@�@�@�_|�^�@ :::::i
�@�@�@�@�@�@�@i�@�@�@�@�@|�P�P|�@�@�@�@ �@�^|�_�@ ::::i�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�Ji�@�@�@�@�@ �@ �m�@�@ �@�@�@�@�@�@�@ ::::i
�@�@�@�@�@�@�@�@�J���@�@�@�@�@�@�@�@�@�@�@�@�@�@�@::::/�@�@�@�@�@�@�@
�@�@�@�@�@�@�@�@�@/�L�J�J�J�@�@�@�@�@�@�@�@�@ """""�R
�@�@�@�@�@�@�@�@ ,i:::::::�@�@�@�@�@�@�@�@�@�@�@�@�@::::::::::�R�܁R�@�@�@�@
�@�@�@�@�@�@�@�@,i::::::�@�@�@�@.......�@�@�@ �@�@�@�@�@ :::::::::i�R�@�@�R
�@�@�@�@�@�@�@�@i::::�@�@�@�@.�@.�@........�@�@�@ �@�@�@�@::::::::i�m�@ �@i�@�@�@
�@�@�@�@�@�@�@�@i::::�@�@�@�@.�@..�@....�@.....�@�@�@ �@�@::::::::::i �@�@/
�@�@�@�@�@�@�@�@�Ji::::�@�@�@..�@..�@�@....�@.......�@ �@�@:::::::::/__,�m�@�@�@�@�@
�@�@�@�@�@�@�@�@ �J�R:::::�@�@�@�@�@�@�@�@�@ �@�@:::::::::::/
�@�@�@�@�@�@�@�@�@�@�M"�@"�@ "�@�@"�@�@�@""""�@�@�@�@
0964�P�R�Q�l�ڂ̑f����n
2018/10/11(��) 18:52:45.31ID:OYjzbvEh�ȉ��A���₩�痣��邪�A
�������̊���Z�̖��ɔ������g���̂�
��肷�����Ǝv���B
�g�킸�ɍςޕ��@�����邩���B
0965�P�R�Q�l�ڂ̑f������
2018/10/12(��) 09:43:04.88ID:GRxlK+xon=1,2�̂Ƃ������ł��傤���B
0966�P�R�Q�l�ڂ̑f������
2018/10/12(��) 19:46:54.25ID:XClNk0HB0967�P�R�Q�l�ڂ̑f������
2018/10/12(��) 20:47:19.42ID:c72A1ukK���w�̎�����
ax+x��x(a+1)�Ə������猸�_����Ă��܂��̂ł��傤���H
0968�P�R�Q�l�ڂ̑f������
2018/10/12(��) 21:33:52.13ID:72cesl8m0969965
2018/10/12(��) 21:50:07.63ID:GRxlK+xo�����������
�g�����̐� C[n,3] (n=3,4,5,�E�E) �̂Ȃ��ɕ������͂�����ł������ɂ���܂����H
n=3�̂Ƃ���C[3,3]=1 �� n=4�̂Ƃ���C[4,3]=4�����ł��傤���B
0970�P�R�Q�l�ڂ̑f������
2018/10/12(��) 21:55:34.11ID:UbZGNwQq0971�P�R�Q�l�ڂ̑f������
2018/10/13(�y) 01:05:48.36ID:0aqObBBf�E2�̔{����4�̔{����3�̔{��������ł���Ƃ���2�̔{����2�Ŋ����2�ł�3�ł����肫��Ȃ����ɂȂ�
0972�P�R�Q�l�ڂ̑f������
2018/10/13(�y) 01:50:06.41ID:qVm3bbN1C[n,3] = abc/6 ((a,b,c) �͘A������3��)�Ƃ�����b��ac�ƌ݂��ɑf�A(a,c) = 1,2�B
�����2,3�ȊO�̑f���q�̑��d�x��a,b,c�S�ċ����B
2,3�ɂ��Ă̑��d�x����ł�����̂͂��傤�Lj�B
�����
(a.b,c) = (6x^2,y^2,z^2)�A(2x^2,3y^2,z^2)�A(2x^2,y^2,3z^2)�A
�@�@�@�@ (3x^2,2y^2,z^2)�A(x^2,6y^2,z^2)�A(x^2,2y^2,3z^2)�A
�@�@�@�@ (3x^2,y^2,2z^2)�A(x^2,3y^2,2z^2)�A(x^2,y^2,6z^2)
�Ƃ�����B
u^2-2v^2 = 1��(u,v) = (3,1)�Au^2-2v^2 = -1��(u,v) = (1,1)�Au^2-3v^2 = 1��(u,v) = (2,1)�Au^2-3v^2 = -1�̉�
�ɂ��K����̂�(a,b,c) = (2,3,4)�A(1,2,3)�B
0973�P�R�Q�l�ڂ̑f������
2018/10/17(��) 18:27:59.17ID:ppuaXtV2(2a-1)x^2+(b-2)x+(3c+9)=0
���̂Ƃ��Ax�ɂ��Ă̍P�����Ȃ��
2a-1=0, b-2=0, 3c+9=0�ƂȂ邱�Ƃ̗������킩��܂���
������āA�t�ɂ����ƁAx^2��x�̌W���A�����Ē萔���̊e������
0�ȊO�̒l�łȂ��ƁA���v��0
���ꂪ�����I�ɂ������肫�܂���A�{���ɂ����Ȃ�́H�Ǝv���Ă��܂��܂��B
������������A�������Ⴄ�����ix^2��x�Ȃǁj�𑫂����������Ƃ��Ă�
���0�ɂȂ邱�Ƃ͂Ȃ��A�Ƃ������Ƃ��A���̖@���̍����ɂȂ��Ă���̂��Ƃ��l���܂�����
x^2-x=0����x�̉��́Ax(x-1)=0�Ax=1�A���̂悤�ɑ��݂��A�����Ƃ���
�u�����̈Ⴄ�������m�������Ēl��0�ɂȂ邱�Ƃ͂Ȃ��v��ے肷�邱�Ƃ��ł���̂�
�l��2a-1=0, b-(���j��������鍪�������S�Ɏ����Ă��܂��܂���
0974�P�R�Q�l�ڂ̑f������
2018/10/17(��) 19:24:41.13ID:O4XG5fOc�S�Ă�x�ɑ���(2a-1)x^2+(b-2)x+(3c+9)=0���Ă��Ƃ́Ay=(2a-1)x^2+(b-2)x+(3c+9)�̃O���t��x���ɒ���t�����Ă��Ƃł�
y=0�̒��O�ɂȂ�Ȃ��ƃ_���ł���
�W����0�ɂȂ�Ȃ��ƃ_���ł���
0975�P�R�Q�l�ڂ̑f������
2018/10/17(��) 22:43:40.97ID:w43ZlZqkC[50,3] �͂ǂ���������̂ł���
0976�P�R�Q�l�ڂ̑f������
2018/10/18(��) 00:13:27.27ID:AC5Di51ta,b,c�͒萔������ϐ�x���ς����������Ă����ď���ɕς��Ă�������Ȃ��B
������>>974�������悤��x�̒l�Ɋւ�炸���0�ɂȂ���Ă����̂͑S��0�ɂȂ邵�����蓾��̂ł���
0977�P�R�Q�l�ڂ̑f������
2018/10/18(��) 00:46:32.91ID:MxKVVcoK> ����ł�
> (2a-1)x^2+(b-2)x+(3c+9)=0
> ���̂Ƃ��Ax�ɂ��Ă̍P�����Ȃ��
> 2a-1=0, b-2=0, 3c+9=0�ƂȂ邱�Ƃ̗������킩��܂���
�������Ƃ��� 0 �ł���@�Ƃ́A�S�Ă̌W����0�ł��邱�Ƃƒ�`�����B
�]���ā@�������@(2a-1)x^2+(b-2)x+(3c+9)�@���@0�@�ł��邽�߂̕K�v�\��������
2a-1=0, b-2=0, 3c+9=0�@�ƂȂ�B
�Ƃ��낪�A���������@f(x)=(2a-1)x^2+(b-2)x+(3c+9 ���P���I��0�ł���A�Ƃ�
�������Ƃ���0�ł���̂Ƃ͈���āA
��f(x)�̒�`����ϐ�x���ǂ̂悤�Ȓl���Ƃ��Ă����f(x)=0�ƂȂ邱�ƁA�ƒ�`�����B
���i���w�̒��ɂ́A�������Ƃ��Ắ@0�@�ł͂Ȃ����A����𑽍������ƌ����ꍇ�́@0�@�Ƃ����悤�Ȃ��̂�����B
����ɂ���@�P���I�Ɂ@0�@�ł���@�Ƃ́A���Z���x���̏ꍇ��
��`�������̊��Ƃ��ď�Ɂ@0�@�̈Ӗ��Ƃ��Ĉ����̂����̎�|�̂悤�Ȃ̂ŁA
�Ƃ��Ă͗Ⴆ�Ύ��̂悤�Ȃ��̂��l������B
f(0)=0�Ȃ̂Ł@f(0)=3c+9=0�B����āAc=-3
�܂����̂Ƃ��A�@f(1)=0�Ȃ̂Ł@(2a-1)+(b-2)=0�Af(-1)=(2a-1)-(b-2)=0 �A������@2a-1=0�@���@b-2=0
�t�ɁA�@2a-1=0�Ab-2=0�A3c+9=0�@�Ȃ�Ζ��炩�ɂ��ׂĂ�x�̒l�ɑ��ā@f(x)=0�@�ł���B
0978�P�R�Q�l�ڂ̑f������
2018/10/18(��) 00:59:28.70ID:BoJlALsC�����i���w�̒��ɂ́A�������Ƃ��Ắ@0�@�ł͂Ȃ����A����𑽍������ƌ����ꍇ�́@0�@�Ƃ����悤�Ȃ��̂�����B
����܂���
���f�����l����ɂ��Ă��A�������A���Ȃ킿�A���̈��̐��������l����Ȃ�A��v�̒藝��肠�镔����0�Ȃ�S�̂�0�ł�
�������Ƃ͗L�������őł���ł�����A�������a�͖�����A���Ȃ킿���f���S�̂�0�ƂȂ�܂�
0979�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:11:11.10ID:MxKVVcoK�W��2�̑f�̏�ő��������@x^2+x�@���l����ƁA����͏��0���ƂȂ�܂��B�@
0980�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:13:16.71ID:BoJlALsC�E��
0981�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:13:29.75ID:BoJlALsC�E��
0982�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:13:58.44ID:BoJlALsC�E��
0983�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:14:17.55ID:BoJlALsC�E��
0984�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:14:34.92ID:BoJlALsC�E��
0985�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:14:52.56ID:BoJlALsC�E��
0986�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:15:10.20ID:BoJlALsC�E��
0987�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:15:27.98ID:BoJlALsC�E��
0988�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:15:44.45ID:BoJlALsC�E��
0989�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:16:01.16ID:BoJlALsC�E��
0990�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:16:22.12ID:BoJlALsC�E��
0991�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:16:39.77ID:BoJlALsC�E��
0992�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:16:56.43ID:BoJlALsC�E��
0993�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:16:59.70ID:MxKVVcoK0994�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:17:12.48ID:BoJlALsC�E��
0995�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:17:41.99ID:BoJlALsC�E��
0996�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:18:00.91ID:BoJlALsC�E��
0997�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:18:17.47ID:BoJlALsC�E��
0998�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:18:34.17ID:BoJlALsC�E��
0999�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:18:51.45ID:MxKVVcoK1000�P�R�Q�l�ڂ̑f������
2018/10/18(��) 01:18:53.19ID:BoJlALsC�E��
10011001
Over 1000Thread�V�����X���b�h�𗧂ĂĂ��������B
life time: 939�� 13���� 22�� 18�b
10021002
Over 1000Thread�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�s�v���~�A������̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
��300�~���瓽���ł��w�����������܂��B
�� �v���~�A������o�^�͂����� ��
https://premium.5ch.net/
�� �Q�l���O�C���͂����� ��
https://login.5ch.net/login.php
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
�j���[�X
- �~�}���A�ꎞ156�~��@34�N�Ԃ���l���X�V�c ��3 [BFU��]
- �~�}���A�ꎞ156�~��@34�N�Ԃ���l���X�V�c ��2 [BFU��]
- �y����z����A���Z���������ێ��@�lj����グ������ [PARADISE��]
- ���v���}�C�⋴�u��������Ȃ�A�V�Q�v�@�g�~�[�Y��́u4�`5���~�̂Ă��悤�Ȃ���v�����ɕs���� [�l�M���ǂ�]
- �y�����[�j���O���B�z�Q�@���s��і덁���̋c�����E�����A�ݐE�킸���X�R���Ő��ŒZ [�M�ず]
- �yYouTube�z�u�Q�T�Ԃł�����14����Đ��c�v���������g��排����h���_����ŘI�悵���\�z�O�́u���������v [Ailuropoda melanoleuca��]
- NFL 2024 Draft Part 1
- �Ƃ点��
- NFL 2024 Draft Part 2
- LAD @ WSH ��8
- ����z
- �y���zAFC U23�A�W�A�J�b�v �J�^�[��2024 ���{-�J�^�[��
- �P�h���P�T�V�~�I�I�I�I�I�I�I�I�I�I [252835186]
- ������Ƒ҂��āI���܉~���̐i�s�Ɏ��ł��Ȃ��ƁA���{�l������ł��܂����H�����H [882679842]
- �y�ߕ�z���ʂ��Ȃ���A�_�������2 [252711327]
- �G�`���Ȃ����lj����`���������lj����v�����Ȃ�
- ����A���Z���������ێ��B�lj����グ������ [256556981]
- �y�ߕ�z1�ԃJ�b�R�����j�̑̌^�A�K�`�ł킩��Ȃ�����������������BMI24���炢�ł������H [308389511]

