�ʔ�����肨�����ā`�� 29���
�� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�
�W���[�J�[���������g�����v�T�Q���̒�����P����
�J�[�h���o���A�\�����Ȃ��Ŕ��̒��ɂ��܂���
�����āA�c��̃J�[�h���悭���Ă���
�R�������o�����Ƃ���A�R���Ƃ��_�C���ł�����
���̂Ƃ��A���̒��̃J�[�h���_�C���ł���m���͂����炩
�ŏ��ɔ��ɂ��܂��������P�^�S��
�������珙�X�Ɋm���������Ă䂫�A
�R�D����R���_�C�����o�������P�O�^�S�X
�R�D����P�R���_�C�����o���Ƃ��ɂO�ɂȂ�
��������ŕ\�����Ƃ��ł���
���̐���a��萔�A�R�D����n���̃_�C�����o��Ƃ���
�m0��a��124�n�C�m0��n��13�n�͈̔͂Ő����������
P(D)=((n-13)(a-4n-125))/(a(n-52)-7n^2+92n+6500)
P(D)=((n-13)(a+4n+1))/(a(n-52)+7n^2-216n-52) ��Q�Җ��\�鏑�p�C�Y������̃S�L�u���E�Q�\���\���鏑�_���}��c����`�N�\�܂݂�̕ė����E����
�S�L�u���c����`�̎q���͊�`�ė��m��L�`�K�C��`�q���ł��� ��a(n)=a(n-1)+a(n-2)/((2n-1)(2n-3)),a(1)=0,a(2)=1/3 �̈�ʍ�
a(n)=Hypergeometric1F1[-n;-2n;-2] ����̊�����ɍ�������
P1st
(6n^3+20n^2-n-27)(n-1)/24�@�i��j�c�c�@
(6n^4+14n^3-21n^2-26n+24)/24�@�i�����j�c�c�A
Q1st
(6n^2+10n-3)(n+1)(n-1)/24�@�i��j�c�c�B
(6n^2-2n-5)(n+2)n/24�@�i�����j�c�c�C
��m1 0 1 0 1 0 1 0 1 0 1 0 1 0�n�̂ݏo�͂������
((-1)^(n+1)+1)/2�@�c�c�D
�����m0 1 0 1 0 1 0 1 0 1 0 1 0 1�n�̂ݏo�͂������
((-1)^n+1)/2�@�c�c�E
�@x�D+�Ax�E
((6n^3+20n^2-n-27)(n-1)/24)(((-1)^(n+1)+1)/2)+((6n^4+14n^3-21n^2-26n+24)/24)(((-1)^n+1)/2)
P1st =�o12n^4+28n^3-42n^2-52n-3(-1)^n+51�p/48
�Bx�D+�Cx�E
((6n^2+10n-3)(n+1)(n-1)/24)(((-1)^(n+1)+1)/2)+((6n^2-2n-5)(n+2)n/24)(((-1)^n+1)/2)
Q1st =�o12n^4+20n^3-18n^2-20n-3(-1)^n+3�p/48 >>66
�قق�
���������g���ƃV���v���ɏ������ł��ˁ[ ����̍����^�����i�N���}�[�j
1�e1[a; b; z] = 1 + ��[k=1, ��] {a(a+1)����(a+k-1)/b(b+1)����(b+k-1)} z^k /k!
1�e1[-n; -2n; z] = {n!/(2n)!} ��[k=0, n] {(2n-k)!/(n-k)!k!} z^k, 4�ʂ��ΐF��2�ʂ��ԐF�̃T�C�R��������Ƃ���
���̃T�C�R����20��U���āA�ΐF(G)�ƐԐF(R)�̂ǂ��炪
�o�������L�^����
����3�̑I��������P��I�ԂƂ���
�������Ȃ����I�I������20�̋L�^�̂ǂ�����
��v�����25�h�����炦��
1.RGRRR
2.GRGRRR
3.GRRRRR
�I����1�͑I����2�ɓ����Ă���A�܂��A
���̑I���������Z���ɂ��S��炸�A
�팱�҂�65%�͑I����2��I��
25�h���̓q�����b�̏ゾ���̌`�̒����ł��A
���ʂɌ����ȍ��͌����Ȃ����� �X��27 #795 �̈�ʉ����g���C
�cM�}�X�A��N�}�X�̃t�B�[���h{(x,y)|x��{1,�c,N},y��{1,�c,M}}�̑��قȂ�2�}�X�ɕ��u���A
�c�D�挟��((1,1)���c��(1,N)��(2,1)���c)��P��
���D�挟��((1,1)���c��(M,1)��(1,2)���c)��Q�Ƃ�
��ɂ����ꂩ�̕���������ق��������Ƃ���Q�[��
��̒u�����p�^�[���̐�=MN(MN-1)/2�ɑ��āA
P,Q���ꂼ��̏��p�^�[���̐���P(M,N),Q(M,N)�Ƃ���
�ƌ����Ă��A�����Ȃ��ʉ��͓���̂ŁA�܂��͕Е��̃p�����[�^���Œ肵�Ă������v�Z���Ă݂�
n��0 (mod 2) �̂Ƃ� P(2,n) = Q(n,2) = (3nn-4n�@)/4, Q(2,n) = P(n,2) = (5nn-10n+4)/4
n��1 (mod 2) �̂Ƃ� P(2,n) = Q(n,2) = (3nn-4n+1)/4, Q(2,n) = P(n,2) = (5nn-10n+5)/4
n��0 (mod 6) �̂Ƃ� P(3,n) = Q(n,3) = (12nn-10n�@)/6, Q(3,n) = P(n,3) = (15nn-22n+ 6)/6
n��1 (mod 6) �̂Ƃ� P(3,n) = Q(n,3) = (12nn-13n+1)/6, Q(3,n) = P(n,3) = (15nn-25n+10)/6
n��2 (mod 6) �̂Ƃ� P(3,n) = Q(n,3) = (12nn-10n+2)/6, Q(3,n) = P(n,3) = (15nn-22n+ 8)/6
n��3 (mod 6) �̂Ƃ� P(3,n) = Q(n,3) = (12nn-13n-3)/6, Q(3,n) = P(n,3) = (15nn-25n+ 6)/6
n��4 (mod 6) �̂Ƃ� P(3,n) = Q(n,3) = (12nn-10n+4)/6, Q(3,n) = P(n,3) = (15nn-22n+10)/6
n��5 (mod 6) �̂Ƃ� P(3,n) = Q(n,3) = (12nn-13n-1)/6, Q(3,n) = P(n,3) = (15nn-25n+ 8)/6
�������Ă݂�Ƃ��ꂼ������������肻���B
���̋C�ɂȂ�Α������Ǝw�����̑g�ݍ��킹�ŏ�����̂�������Ȃ��B q��2�ȏ�̐����An��1�ȏ�̐����Ƃ���B
1�̙p����=e^(2��i/q)���g���āA
f_q(n)=(q-1)/2+��{k=1�`(q-1)}((��^k)^n * (��^k - 1)/(2 - ��^k - ��^(-k)))
�ŕ\������ f_q(n) �͂ǂ̂悤�Ȓl���Ƃ邩�H (3!!/3+0)/3!!=1/3
(5!!/3+0)/5!!=1/3
(7!!/3+1)/7!!=12/35
(9!!/3+14)/9!!=47/135
(11!!/3+190)/11!!=731/2079
(13!!/3+2799)/13!!=1772/5005
(15!!/3+45640)/15!!=20609/57915
(17!!/3+823724)/17!!=1119109/3132675
(19!!/3+16372071)/19!!=511144/1426425
(21!!/3+356123690)/21!!=75988111/211527855
����������������������������������������
1 14 190 2799 45640 823724 16372071 356123690
1
14
190
2799
45640
823724
16372071
356123690
a(n)=((2n-1)!!/3+��)/(2n-1)!!����
���������������Ă���`(�E�ցE)�m >>74
����ȑ������͑��݂��܂���
���������X���Ⴂ�ł����A���̃X���ł����������A�����Ă���r�炵�̂悤�Ȃ̂ŃX���[�����ł��� >>75
�������������݂��Ȃ��ؖ������Ă���`(�E�ցE)�m https://www.gaiki-seijouki.jp/column1/368/
�L�`�K�C�j�z���U�������v�ł����d���L�^����M�����Ȃ��s�����ƃj�z���U�����ł��� >>71 �͎������ŏ����Ƃ����Ȃ�
P(2,n) = Q(n,2) = (3/4)n^2-n+(1/2)-(1/2)(-1)^n
Q(2,n) = P(n,2) = (5/4)n^2-(5/2)n+(9/2)-(1/2)(-1)^n
P(3,n) = Q(n,3) = 2n^2-(23/12)n+(1/12)+(1/4)(n+1)(-1)^n-(1/3)cos(2��n/3)+(��3/9)sin(2��n/3)
Q(3,n) = P(n,3) = (5/2)n^2-(47/12)n+(4/3)+(1/4)n(-1)^n-(1/3)cos(2��n/3)+(��3/9)sin(2��n/3) >>73
����́@2 -��^k -��^(-k) = - (��^k -1)^2 /(��^k),
k �� q-k ��g�ɂ��Čv�Z�����
f_q(n) = (q-1)/2 -(1/2)��[k=1,q-1] {��^(kn)(��^k -1) + ��^(-kn)(��^(-k) -1)}(��^k) /(��^k -1)^2
�@= (q-1)/2 - (1/2)��[k=1,q-1] {��^(k(n+1))(��^k -1) - ��^(-kn)(��^k -1)} /(��^k -1)^2
�@= (q-1)/2 - (1/2)��[k=1,q-1] {��^(k(n+1)) - ��^(-kn)} /(��^k -1)
�@= (q-1)/2 - (1/2)��[k=1,q-1] ��[j=-n,n] ��^(kj)
�Ƃ���ŁA
��[k=1,q-1] (��^m)^k
�@�@�@=�@q-1�@�@�@(��^m=1) (m��q�̔{���܂���0)
�@�@�@= -1�@�@�@�@(��^m��1)
-n ���� n �܂ł̐����̂����Aq�̔{���� (0���܂߂�) 2[n/q]+1 ������
f_q(n) = n - q[n/q]�@= (n��q�Ŋ������]��) �y�������I�������B�E���܂Ƃ������点�ƍߎ҂̎����ƏZ�������J�z
�@����E�疾�i�����s������˂U�|�Q�R�|�P�U�j
���������B�E�����点���܂Ƃ��ƍߎ҂̃��[�_�[�I���݁^�ƍߑg�D�̈���ŗl�X�Ȕƍߍs�ׂɎ����߂Ă���
�@��w���ŏX���قǂ̊w���R���v���b�N�X�̉�^���ϑԂŐH�����D�Ƃł���^�X���ŕs�C���Ȋ���������I�ł���
�A�F���ρi�����s������˂U�|�Q�R�|�Q�P�n�C�c�j���[�˂Q�O�Q�j
���F���ŏX�������Ă���X�����؉F���ρ^��w���Ől�Ԑ����X�������łȂ�����̐l���ł�����x�Ə��ƃZ�b�N�X�����邱�Ƃ��ł��Ȃ��قǗe�p���X���ł���
�B�F�썂�u�i�����s������˂U�|�Q�R�|�Q�P�n�C�c�j���[�˂P�O�R�j
���F�썂�u��youtube�̎���������ɒZ���Ԃɉ��S���玞�ɂ͉�����Ƒ��₵���荂�]���E��]���̐�������l�ł��������₵���茸�炵����Ȃǂ�
�@youtube�̐���ȉ^�c���������M�����Ȃ킹��悤�ȔƍߓI�Ɩ��W�Q�s�ׂ��s���Ă��܂�
���F�썂�u�͌��݁A�����ی��s���Ɏ��Ă���ƍߎ҂ł��^�ǂ�ǂ�x�@������ɒʕ�E�������Ă���Ă�������
�y�ʕ��z
�������敟���������i�������ہj
���P�Q�S�|�W�T�T�T
�����s�����旧�T�|�P�R�|�P
���O�R�|�R�U�X�T�|�P�P�P�P
�C�����i�����s������˂U�|�Q�R�|�P�X�j
����w��E���V���F�����k�k�@������w��E���V���E�����k�k�͍��w���ƌn������I�ɑ������Ă��遙��
�@�����k�k�̓R���v���b�N�X�̉�łƂɂ�����Ӓn�������^�X���Ȍ`���Ō����点���y����ł���܂��Ɉ����̂悤�ȘV�k�ł���
�D���Y�E���c�i�����s������˂U�|�Q�U�|�U�j
���ƍߎ�d�҈���E�疾�̎q���^�����t�炦���Ɍ����Ȃ�ɂȂ��Ă�������̃t���^�e�q���ꑰ������Ē�\
�E�����i�����s������˂U�|�Q�R�|�Q�R�j
��������͕v�w�̖�̉c�T�b����H�����ٔ��v���C�̍Œ��ɍ����e���ɂǂ������ɕ���Ď���i�߂��ĎE���ꂻ���ɂȂ������Ƃ�����
�F���؋`���i�����s������˂U�|�Q�R�|�Q�O�j �����j���ɂȂ�ƕ����X�ɍs���Ă��� ��n=3�̂Ƃ��A10/49�ƂȂ����125��ލ쐬
Table[((n-13)(a-4n-125))/(a(n-52)-7n^2+92n+6500),{a,0,124},{n,3,3}]
��n=0�̂Ƃ��͂��ׂ�1/4
Table[((n-13)(a-4n-125))/(a(n-52)-7n^2+92n+6500),{a,0,124},{n,0,0}]
��n=13�̂Ƃ��͂��ׂ�0
Table[((n-13)(a-4n-125))/(a(n-52)-7n^2+92n+6500),{a,0,124},{n,13,13}]
318 ���O�F�P�R�Q�l�ڂ̑f������[sage] ���e���F2019/03/07(��) 18:00:45.97 ID:TVoNUVmm
�����ʑ吔�̐��E�ł�10/49���o�͂���
Table[((n-13)(a-4n-125))/(a(n-52)-7n^2+92n+6500),{a,10^68,10^68+150},{n,3,3}] �w����5����܂�
3���炤�ƑS���ʼn��ɂȂ�܂����x
2
8���낪�{�P
�ꕔ���L�҂��ς�邾����5�̂܂܂���ˁH
�N������Ⴄ�������ĂȂ�
�l�Y�~���N�b�L�[��3���炤�̂�������Ȃ�
�������������������̂������� 20�܂ł̎��R�����d����������10���ɕ���a[1], a[2], a[3], ...a[10]�Ab[1], b[2], b[3], ...b[10]�Ƃ���B������
S = ��(k=1��10)a[k]b[k] = a[1]b[1]+a[2]b[2]+a[3]b[3]+�c�c+a[10]b[10]
�Ƃ���B�F�X�ȕ������ɂ���S���l�����Ƃ��AS�̍ő�l�ƍŏ��l�A�y�т��̎��̕������͂ǂ̂悤�Ȃ��̂�
����Ɉ�ʂ�2n�̐�(n�͎��R��)��n����2�g�ɕ����āA
a[1]�Aa[2]�Aa[3]�A�c�c ����� b[1]�Ab[2]�Ab[3]�A�c�c
�Ƃ�
S = ��(k=1��n)a[k]b[k] = a[1]b[1]+a[2]b[2]+a[3]b[3]+�c�ca[n]b[n]
�Ƃ���B�F�X�ȕ������ɂ���S���l�����Ƃ��AS�̍ő�l�ƍŏ��l�A�y�т��̎��̕������͂ǂ̂悤�Ȃ��̂� >>85
(19,20)�̃y�A���Ȃ���ő�ł͂Ȃ��B
�� (a,19),(b,20)�̑g�ݍ��킹�̎�
19�E20 + a�Eb - 19�Ea - 20�Eb = (20 - a)(19-b) > 0
�ȉ����l�ɂ��čő�l��
1�E2 + 3�E4 + �d + 19�E20 = 1430
(1,20)�̃y�A���Ȃ���ŏ��ł͂Ȃ��B
�� (a,1),(b,20)�̑g�ݍ��킹�̎�
1�Ea + 20�Eb - a�Eb - 1�E20 = (20 - a)(b - 1) > 0
�ȉ����l�ɂ��čŏ��l��
1�E20 + 2�E19 + �d + 10�E11 = 770 >>86
�����ł�
�������莦���̂͂��ʓ|���Ǝv���܂���������Ȃ��ƂȂ������ł����� ���̐}��, ��FJG�͐��O�p�`, �l�p�`FBCE�͐����`�ł���. ��KJG�̑傫�������߂�.
https://i.imgur.com/h43Hkcg.jpg >>88
K����BC�ɐ����������Č�_��P�Ƃ���
JB=(1/��3)BF
BP=PK=(1/(1+��3))BF
BP/JB=PK/JB=((��3)/(1+��3))
tan��KJG=PK/(JB+BP)
=((��3)/((1+��3)+(��3)))
=(6-��3)/11
��KJG��21.2��
���ꂢ�Ȓl�ɂ͂Ȃ��� �o��K�C�W���K���ɊG�`���ďo���Ă���Ȃ��瓖����O �����͏o��X�������玩����o���͖̂����B
����̂̓`�F�b�N���Â������ˁB
�v�Z�@�g����Ȃ猟�Z���Ă���ɂ���悩�����̂ɁB ���܂茩�Ȃ��A�A�v���[�`�@���v�������̂ŁA���e
(1)�@��[k=1,n]cot^2(k��/(2n+1)) = n(2n-1)/3�@������
(2)�@����g���āAn(2n-1)/(2n+1)^2 < (3/��^2)��[k=1,n]1/k^2 < 2n(n+1)/(2n+1)^2�@������ ����������
����������
����������
����������
��������������
��������������
��������������
��������������
��������������
�������������� > sapply(1:20,function(k) treasure0(4,5,k))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
�Z���L�� 9 84 463 1776 5076 11249 19797 28057 32243 30095 22749
�����L�� 9 83 453 1753 5075 11353 20057 28400 32528 30250 22803
���� 2 23 224 1316 5353 16158 37666 69513 103189 124411 122408
[,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20]
�Z���L�� 13820 6656 2486 695 137 17 1 0 0
�����L�� 13831 6657 2486 695 137 17 1 0 0
���� 98319 64207 33788 14114 4571 1106 188 20 1
�S�~�T�̏ꍇ
��F�P�@����
��F�Q�`�T�@�Z���L��
��F�U�`�P�R�@�����L��
��F�P�S�`�Q�O�@����
(17!/(18-k)!)/(k-1)!+(15!/(16-k)!)/(k-1)!+(13!/(14-k)!)/(k-1)!+(11!/(12-k)!)/(k-1)!+(10!/(11-k)!)/(k-1)!+(8!/(9-k)!)/(k-1)!+(5!/(6-k)!)/(k-1)!+(4!/(5-k)!)/(k-1)!,k=5 >>95
(2)�𗘗p�������(2)=��^2/6��������H 8��83�ɕ���K�v
Table[(17!/(18-k)!)/(k-1)!+(15!/(16-k)!)/(k-1)!+(13!/(14-k)!)/(k-1)!+(11!/(12-k)!)/(k-1)!+(10!/(11-k)!)/(k-1)!+(8!/(9-k)!)/(k-1)!+(5!/(6-k)!)/(k-1)!+(4!/(5-k)!)/(k-1)!,{k,1,20}] �m���̂̓��H��̓����ł������ȁB���N���������ȁH >>98
�ł���
>>100
(1)�̓��o�͍���Ǝv�����ǁA�������ɂȂ��Ă����Ƃ́D�D�Dorz >>101
����(1)�̕s�������������ɂȂ��Ă���Ȃ���B
���H��̂̓`�F�r�V�F�t�̑������g����
��(sin k��/2n)^(-2)
�����߂�������B1990�N�������B�������H�v����ƃ�(2)���v�Z�ł���B
�Ȃ��������N���\��Ȃ����� �g������茤���@90���H��h �Ō�������Əo�Ă���B
���Ȃ݂ɂقړ������e��PDF��_��̐搶������Ă��L��������B ���ꂻ��B��������撣��ƃ�(2)���v�Z�ł���B >>95
���̃�(2)�̉�@�̏o�T��1953�N�̃��V�A��̘_��
http://mi.mathnet.ru/eng/umn8256
�ŁAwikipedia�ɂ���1960�N��ɂ͍L���m����悤�ɂȂ��������ł��B ���������Z���w�̕����ɍڂ��ĂȂ������H >>106
��g�̌����W���ς�ς�߂����Ăā@�����[�������������܂����@>>95�@��(1)�ł��B
�ǂ�����Ď����̂��l���Ă���ƁA�o�[�[�����Ɏg���邱�ƂɋC�Â��܂����B
�����̐l�ɂ��A�ʔ����Ǝv���Ă���������Ǝv���A�����ɓ��e���܂������A
�L���m���Ă����@�������悤�ł��ˁB�Ǖ��ł����B
��肪�Ƃ��������܂��B Table[(17!/(18-k)!)/(k-1)!+(15!/(16-k)!)/(k-1)!+(13!/(14-k)!)/(k-1)!+(12!/(13-k)!)/(k-1)!+(8!/(9-k)!)/(k-1)!+(7!/(8-k)!)/(k-1)!+(6!/(7-k)!)/(k-1)!+(3!/(4-k)!)/(k-1)!+(2!/(3-k)!)/(k-1)!,{k,1,20}]
�����L��
���S��v��>>97 Table[(17!/(18-k)!)/(k-1)!+(15!/(16-k)!)/(k-1)!+(13!/(14-k)!)/(k-1)!+(11!/(12-k)!)/(k-1)!+(10!/(11-k)!)/(k-1)!+(8!/(9-k)!)/(k-1)!+(5!/(6-k)!)/(k-1)!+(4!/(5-k)!)/(k-1)!+(1!/(2-k)!)/(k-1)!,{k,1,20}]
�Z���L����
{9, 84, 463, 1776, 5076, 11249, 19797, 28057, 32243, 30095,
9 84 463 1776 5076 11249 19797 28057 32243 30095
22749, 13820, 6656, 2486, 695, 137, 17, 1, 0, 0}
22749 13820 6656 2486 695 137 17 1 0 0
���S��v>>97
�����>>99 > sapply(1:12,function(k) treasure0(3,4,k))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11] [,12]
�Z���L�� 5 26 73 133 167 148 91 37 9 1 0 0
�����L�� 5 27 76 140 176 153 92 37 9 1 0 0
���� 2 13 71 222 449 623 609 421 202 64 12 1
��������
��������
��������
Table[(9!/(10-k)!)/(k-1)!+(7!/(8-k)!)/(k-1)!+(6!/(7-k)!)/(k-1)!+(3!/(4-k)!)/(k-1)!+(2!/(3-k)!)/(k-1)!,{k,1,12}]
�����L����
Table[(9!/(10-k)!)/(k-1)!+(7!/(8-k)!)/(k-1)!+(5!/(6-k)!)/(k-1)!+(4!/(5-k)!)/(k-1)!+(1!/(2-k)!)/(k-1)!,{k,1,12}]
�Z���L����
���S12�}�X���S��v
Table[(12!/(12-k)!)/k!-(2((9!/(10-k)!)/(k-1)!+(7!/(8-k)!)/(k-1)!)+(6!/(7-k)!)/(k-1)!+(5!/(6-k)!)/(k-1)!+(4!/(5-k)!)/(k-1)!+(3!/(4-k)!)/(k-1)!+(2!/(3-k)!)/(k-1)!+(1!/(2-k)!)/(k-1)!),{k,1,12}]
������ �}�`�̖�肾�����炱��Ȃ̂͂ǂ���
Q. xy���ʏ�� x^2+y^2=1+|x|y ��}������ �@|x|^2 - |x|y + yy = 1,
�͍��E�Ώ�
����45߉�
�@(x+y)/��2 = u,�@(x-y)/��2 = v,
�Ƃ����B
x��0 �̂Ƃ�
�@1 = xx -xy +yy = (1/2)uu + (3/2)vv,
x��0 �̂Ƃ�
�@1 = xx +xy +yy = (3/2)uu + (1/2)vv,
�ȉ~��2�������ē\�荇�킹�����́B�n�[�g�`�H ��������1�������Ă݂�B
���R�����͂Ȃ����A�������ӌ����o���玩���̉��o�����Ǝv���B
���Ȃ��͐V�����̃C�j�V����(�A���t�@�x�b�g1����)�Ă�q���ɎQ�����邱�ƂɂȂ����B
���̏����̂Ƃ��A���Ȃ��͂ǂ̂悤�ɓq�����s�����H
�E�V�����̃C�j�V�����Ă�Ί|������3�{���A�O���Ί|�����͉�������B
�E�����̃C�j�V�����ɓq���邱�Ƃ��\�ŁA�����̓q�����͈قȂ��Ă��悢�B
�E���̎��̌��������\����鎞�ɂ����l�ȓq�����J�Â���邱�Ƃ��\�z�����B �v�X�ɓ��e�B�i�l�I�Ɂj�������Ȃ̂Œ���
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
���̎咣�͐��藧���F����S^2�i��R^3�j��
�ES^2 = ��_(n=1�`5) f_n(D)
(������ D �� S^2 �̃��x�[�O���ȕ����W���Af_i �͒��s�Q�̌��ŕ\�����P���ϊ�)
�En��m �̎� f_n(D)��f_m(D) �́i�������l�̂Ƃ��Ă�S^2�́j��W��
�����悤�ɍ����ȂT�̃p�[�c f_n(D) (n=1,�c,5) ��"����"���鎞�A
f_n��(f_m)^(-1) (n��m)
�ƕ\�����S�Ă̍����ϊ��ɋ��ʂ�����ŗL�x�N�g�������݂���B
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
�T�����łȂ��A�Ⴆ��4,6,8,12,20�ł���ΐ����ʑ̂𗘗p���Ď����łȂ����������������A
�����H�v�����60��S�Ă̂W�̔{�����\�B
�i���������������ł���Ƃ́A��̂悤�ȏݒ�ŋ��ʂ�����ŗL�x�N�g�����u���݂���v���Ƃ������B
�܂��̎咣�́u���ʂ�5-���������͑S�Ď����ł���v�ƌ�����������j >>119 �̕⑫
�܂�Ƃ���A���ʂ̒��Łu��{�̈�v�Ȃ���̂��߂�
����ƍ����Ȑ}�`�����������ʂɃ����Ȃ��_�u���Ȃ��\�荇�킹��̂����������B
n���ǂ�Ȑ��̐����ł����̐}�݂����ɂ�����܂�����n-�����������ł�����ǁA
����͂ǂ̗̈悩��ʂ̂ǂ̗̈�Ɉڂ��ɂ����鋤�ʂ̒�����"��"�ɂ��ē������Ηǂ����Ƃ���A
�����͂���قǖʔ��݂̂Ȃ����������Ƃ��āu�����v�Ȃ��̂ƒ�߂��B
�^��6-���������͋��ʂ�"��"�ɂ�������̂����݂��Ȃ����ߔ��B
�E�͔���32-���������B�_�������ɂȂ肻�������ǁA
���Ŏ�����������̕����̂����ŋ��ʂ̎��ƂȂ�Ȃ��B���̂W�̔{�������l�B
�i�������ɂႮ�ɂ�ł��܂�B�}�E�X�ŊG�`���̂ނ����c�j
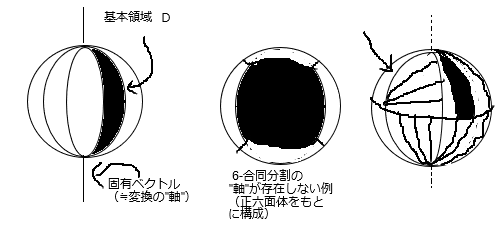 >>120
>>120
�A���łȂ��Ƃ��\��Ȃ��B�ł����x�[�O���ȏW���ł���Ή��ł��n�j
�i���x�[�O�����́A�ǂ����Ă������郌�x���̂���₾�Ԃ���W���ł��܂�����悤�ɁA�Ƃ����Ӑ}�j > sapply(1:20,function(k) treasure0(4,5,k))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
�Z���L�� 9 84 463 1776 5076 11249 19797 28057 32243 30095 22749
�����L�� 9 83 453 1753 5075 11353 20057 28400 32528 30250 22803
���� 2 23 224 1316 5353 16158 37666 69513 103189 124411 122408
[,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20]
�Z���L�� 13820 6656 2486 695 137 17 1 0 0
�����L�� 13831 6657 2486 695 137 17 1 0 0
���� 98319 64207 33788 14114 4571 1106 188 20 1
4�~5�̏ꍇ
��F1�@����
��F2�`5�@�Z���L��
��F6�`13�@�����L��
��F14�`20�@����
����������
����������
����������
����������
�Z���L����
Table[choose(17,k-1)+choose(15,k-1)+choose(13,k-1)+choose(11,k-1)+choose(10,k-1)+choose(8,k-1)+choose(5,k-1)+choose(4,k-1)+choose(1,k-1),{k,1,20}]
�����L����
Table[choose(17,k-1)+choose(15,k-1)+choose(13,k-1)+choose(12,k-1)+choose(8,k-1)+choose(7,k-1)+choose(6,k-1)+choose(3,k-1)+choose(2,k-1),{k,1,20}]
������
Table[choose(19,k-1)+choose(17,k-2)+choose(15,k-2)+choose(13,k-2)+choose(8,k-2)+choose(1,k),{k,1,20}] >>119 ���m��I�ɉ��������̂ŕB�q���g�������ƁA��͂萳20�ʑ̂𗘗p������̂ł����B
���Ȃ݂ɑS�Ă̋�����R�ł��\�B�V�ȏ�̊�͂܂��ړr�������Ă��Ȃ��̂ł悯���������c �A������B
>>124 ���̏ꍇ�m��I�ɂƂ����̂́A�咣�̔��Ⴊ���������Ƃ������Ƃł�
�i�����łȂ�5-������������������ȂƊ��҂��Ȃ��璲�ׂĂ������̂ł��c�j ������5�̏ꍇ��(�A����D�ɂ��)�������݂͂���
2n�̏ꍇ�́A����n�������炳��ɐԓ��ɂ�镪�����l���������� (1)���̏������� �L���� s,t ��������
�E0 �� t �� 1/��2
�E61/80 �� s
�Es^2 = 2t^2-2t+1
(2)���̏������� �ʑ��p�` ��������B
�E���ׂĂ̒��_�́A�P�ʉ~�̎���܂��͓����ɂ���A�����W�͗L����
�E���ׂĂ̕Ӓ��́A�L����
�E������ 31/5 �ȏ� >>126
�����A�A���Ȃ̌������̂��@������
2n�̏ꍇ�A�������̐}�̂��Ƃ������Ă�̂Ȃ�c�O�B����͂ǂ��ϊ����Ă����͕s�ς����������Ȃ���
�i���ʂ̌ŗL�x�N�g�����������ŗǂ�����A�ŗL�l�܂ňꏏ����Ȃ��Ă��ǂ��B�Ⴆ�A
�@����A�ւ̕ϊ��ł͎��͌ŗL�l1�̌ŗL�x�N�g���A�@����B�ւ̕ϊ��ł͎��͌ŗL�l-1�̌ŗL�x�N�g���ƂȂ�j
�ꉞ����5-���������̂ЂƂ̗���E�}�ɋ����Ă����܂��B
�킩��ɂ����ł�������\�ʑ̂𗧑̎ˉe�ŕ��ʂɗ��Ƃ����݂����ȃm���ŕ`���Ă܂��B
�O�~�̉~���͖{���͈�_��\���A�e�����F�̗̈�S�̂���̃p�[�c�ɂȂ��Ă܂��B
�{���Ȑ��ŕ`�����ׂ��Ƃ��������܂����A�ӂ����L���Ă�A�_�������L���Ă铙�̈ʒu�W�͕ۂ��Ă�̂�
��������{���̌`���z�����Ă������������orz
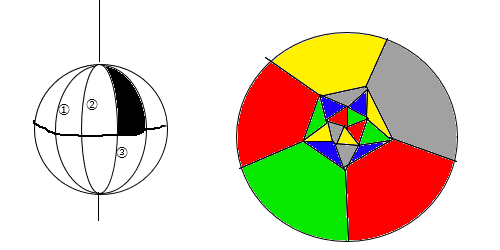 >>128
>>128
�A���B�̕ϊ����A�Q�̗̈�̋��L����1�_�̕����Ɏ����Ƃ��ĉ�]������A�Ƃ���悢�̂ł́H >>129
���ۂ���͌ŗL�x�N�g���̂P�Ȃ��ǁA�G�ɕ`����Ă钼�����ŗL�x�N�g���ł��邱�Ƃɕς��͂Ȃ����
����ŁA�����̒�`���u�`�`���ʂ�����ŗL�x�N�g�������݂���v������A���̌ŗL�x�N�g���̑��݂Ɋւ�炸����͎����ɂȂ��
"��"�ƕ\������Ɗe�ϊ��ň�����Ȃ��悤�Ɏv���邯�ǁi����͂�����̌��t�I�т��ǂ��Ȃ������Ǝv���A���܂Ȃ��j
���̐}�̏ꍇ�A���y���Ă������������x�����Ƃ�A�A����B�ւ̕ϊ��� f(x,y,z)=(x,-y,-z) �ƕ\���邩��
(1,0,0) �̑��� (0,cos��,sin��) �Ƃ���������"��"�������Ƃ��킩��i�����Đ}�̒����̕��������̒��Ɋ܂܂��j >>130
�������⌳�̒�`�͌ŗL�x�N�g�������L���Ȃ����Ęb�ł�����
�l���Ă邤���Ɏ��O���Ă܂����A���h >>127 (1)
�^����
�@s^2 = t^2 + (1-t)^2
�s�^�S���X��������A���R�� a, b �ɂ��
�@s�@= (aa+bb)/N,
�@t�@= (aa-bb)/N,
�@1-t = 2ab/N,
�ƕ\�킹��B
�@N = aa+2ab-bb,
s �� 61/80 ���
�@0.41421356 = ��2 -1 < a/b < (61-��1042)/19 = 1.51157764�@�܂��́@4.90947499 = (61+��1042)/19 < a/b,
0 �� t < 1/��2 ���
�@1 �� a/b < {1+��(4-2��2)}/(��2 -1) = 5.02733952
�������
�@1 �� a/b < (61-��1042)/19 = 1.51157764
�Ȃ�Ώ\���B
��) a=b, s=1, t=0, >>132
�@�����Ͽ
s �� 61/80 ���
�@0.41421356 = ��2 - 1 < a/b < (19+��4082)/61 = 1.35886117
0 �� t < 1/��2 ���
�@1 �� a/b < 1 + ��2 + ��(4+2��2) = 5.02733949
�����̋��ʕ�����
�@1 �� a/b < (19+��4082)/61 = 1.35886117 >>127 �̏o��҂ł��B
�܂��ŏ��� (1) �̑������@�u0 �� t �� 1/��2�v ���u1/2 �� t �� 1/��2 �v�ɕύX�����Ă��������B
����́A(2)�ɂ�����A�u�ʑ��p�`�v���u���p�`�v�Ƃ��Ă��܂��悤�ȏd��ȃ~�X�ł����B�\����܂���B
�ɂ�������炸�A132����ɂ́A�u1/2 �� t �� 1/��2 �v�ƕύX���ꂽ�Ƃ��Ă��A�Ή��\�ȂقǁA
���J�ɉ����Ă��������A���ӂ������܂��B
s,t�̕\����A4.90947499=(61+��1042)/19 < a/b�@< {1+��(4-2��2)}/(��2 -1)=5.02733952
�Ȃǂ���A�\���߂�����e�ł��B
a:b=5:1���̗p����ƁA���R�ƁA(s,t)=(13/17,12/17)�@�������܂�����B
���łɂ��C�Â����Ƃ͎v���܂����A���̖��쐬�̂��������́A�L���ȓ������u��>3.05���ؖ�����v�ł��B
61/80�Ƃ��������́A�������玝���Ă������̂ł��B >>127
���傤���˂����� (2) ������������
�@A (1, 0)
�@B (1 - 8nn/(nn+1)^2, 4n(nn-1)/(nn+1)^2)
�@C (c, c)
�Ƃ����B
�������@c = {21(n^4-6nn+1) + 80n(nn-1)}/{41(nn+1)^2} < 1/��2,
n��6 �̂Ƃ���16�p�`�i�� 1/8�j�ƂȂ�B
AB �� ��2n�F�c(nn-1) �̒��p���̎Εӂ䂦
�@AB = 4n/(nn+1),
BC �� ��20�F�c21 �̒��p���̎Εӂ䂦
�@BC = (29/41){1 - 4n(nn+2n-1)/(nn+1)^2},
����L = 8 (AB+BC),
�EL �� 31/5 �ȏ�ƂȂ�̂� n=7,8,9 �̏ꍇ�B
n=6,�@L = 8 (0.64864865 + 0.12451674) = 6.185323095
n=7,�@L = 8 (0.56000000 + 0.21615610) = 6.20924878
n=8,�@L = 8 (0.49230769 + 0.28409872) = 6.21125126
n=9,�@L = 8 (0.43902439 + 0.33619651) = 6.20176724
n=10, L = 8 (0.39603960 + 0.37726813) = 6.18646187 �����l�ł����B���̖��͐������ƂƂ炦�ĕ��������O�����Ƃ����ɉ������Ƃ���ƃh�c�{�ɂ͂܂�Ǝv���܂��B
����̊p�x�����A�s�^�S���X�O�p�`�����炩���ߒT���o���A�ړI�̑��p�`�̈�ӂɍ����悤��
�k�����A���W�ɓ��Ă͂߂Ă����Ό������܂��B�ȉ��A�p�ӂ��Ă������ł��B
11sin(��/11)=3.099...�A12sin(��/12)=3.105�Ȃ̂ŁA�ӂ̐���12�ȏ�łȂ����6.2���Ȃ����Ƃ�����܂��B
�����ŁA���ی����ɁAA(a,a)�AB(b,c)�AC(c,b)�@���l���A�c��͑Ώ̃R�s�[���Ăł�������12�p�`���l���܂��B
���x�A���v��15�x�X�����Ƃ��A�����̂���ʒu�_�Ƃ���l�Ȕz�u�̎d���ł��B
���̏ꍇ�A�K�v�Ƃ���s�^�S���X�O�p�`�́A�Εӂ̊p�x��60�x�̂��̂ł��B1:��3:2�̔�̎O�p�`�ł����A
����ɋ߂����̂Ƃ��āA120:209:241�@���̗p���邱�ƂƂ��܂��BA(a,a)���A��̂悤�Ȕz�u�̐��\��p�`��
�꒸�_���Ƃ�����A��ӂ̒�����(��3-1)a�ƂȂ�܂��B��3-1=0.7320...�ɋ߂��l�Ƃ���11/15=0.7333...���̗p����ƁA
b=a+(11a/15)*(120/241)=329a/241�A�@c=a-(11a/15)*(209/241)=1316a/3615
���̏ꍇ�S���́A8*(11a/15+1316a/3615)=31736a/3615�@�ŁA(��2)a�Ŋ����6.207673�ƂȂ�A
12�p�`��p�����̂ł����A���肬�薞���ł������Ȃ��Ƃ�����܂��B
a�Ƃ��āA241*3615/Floor[241*3615*sqrt(2)+1]=58081/82139�@���g����
A(58081/82139,58081/82139)�AB(79289/82139,317156/1232085)�AC(317156/1232085,79289/82139)
�ق��ɂ��A�O��ނ̃s�^�S���X�O�p�`��p���āA
X0=(1,0)�AX1=X0+(3/7)*(-9/41,40/41)�AX2=X1+(9/20)*(-204/325,253/325)�AX3=X2+(18/37)*(-1161/1289,560/1289)
�Œ�܂�14�p�`�Ȃǂ�����܂��B >>135 ����ĕς��Ă݂��B
�@A (1,0)
�@B (1 - 8nn/(nn+1)^2, 4n(nn-1)/(nn+1)^2)
�@C' (c', c')
�Ƃ����B
������ c' = (4/7){1 + n(n-3)(3n+1)/(nn+1)^2},
n��6 �̂Ƃ���16�p�`�i�� 1/8)�ƂȂ�B
c' < 1/��2 = 0.70710678 ��� n��8.
AB�� ��2n�F�c(nn-1) �̒��p���̎Εӂ䂦
�@AB = 4n/(nn+1),
BC'�� ��3�F�c4 �̒��p���̎Εӂ䂦
�@BC' = (5/7){1 - 4n(nn+2n-1)/(nn+1)^2},
����L = 8 (AB+BC),
�EL �� 31/5 �ȏ�ƂȂ�̂� n=8,9,10,11 �̏ꍇ�B
n=7, L = 8 (0.56000000 + 0.21828571) = 6.22628571, c' = 0.71222857�@(���i)
n=8,�@L = 8 (0.49230769 + 0.28689772) = 6.23364328, c' = 0.70667794
n=9, L = 8 (0.43902439 + 0.33950880) = 6.22826549, c' = 0.69992352
n=10, L = 8 (0.39603960 + 0.38098506) = 6.21619729, c' = 0.69298528
n=11, L = 8 (0.36065574 + 0.41444312) = 6.20079088, c' = 0.68629785
n=12, L = 8 (0.33103448 + 0.44195685) = 6.18393070, c' = 0.68003397 >>136
�Ȃ�قǁB
(1,0) (0,1) ��ʂ��Ȃ���� 12�p�`�ʼn\�ł�����ȁB
(1,0) (b,c) (c,b) (0,1) ��12�p�`�́A�����̕Ӓ��� |b-c|��2 �Ȃ̂ő��A�E�g�ł�����B
�܂�
�@A (1,0)
�@B (1 - 8nn/(nn+1)^2, 4n(nn-1)/(nn+1)^2)
�@D (4m(mm-1)/(mm+1)^2, 1 - 8mm/(mm+1)^2)
�@E (0,1)
��12�p�`��
�@BD = {(mn-m-n-1)^2 - 2(m+n)^2}/[(mm+1)(nn+1)]�E��2
�ŃA�E�g�ł�����B >>136
BA = AC = 638891/1232085 = 0.51854458
B~B = CC~ = 2�(317156/1232085) = 0.51482812
L = 4 (BA+AC+CC~) = 7648376/1232085 = 6.20766911
�m���ɉ\�ł�����B >>137
���钸�_����A�L��������(x���W�ψʁAy���W�ψʁA�������ׂĂ��L����)�����_��T�������Ȃ�A
�ȒP�ł��B�ǂ�Ȃ��̂ł������̂ŁA�s�^�S���X�O�p�`�������Ă�������̂ł��B�������k�ڂ�
�L�����{�ł�������Ύ��R�ł��B����Ύ��R�[���� >>136 �ŋL������͗����Ƃ����̕��j�ɂ����̂ł��B
�������A(t,t)�^�̒��_����������ɗL�������������Ȃ���Ȃ�Ȃ��ƂȂ�A��ςł��B
�������ɂ̂ݓ������܂����A����ΌŒ�[���ł��B���͂��̕��j�͖ʓ|�������Ǝv���A�[���炠����߂�
���܂������A>>137�@���ł́A������s���Ă��܂��B�悭������ꂽ�ƁA���V���Ă܂��B
���ۂɃv���b�g���Ă݂܂������A���̕ω��ɂ���āA���_�̕��z�����\�ω����܂��ˁB
�ʏ��������Ȃ����̂�A�P�ʉ~�̊O�ɏo����̂�����܂������A���͈͓̔���n�ɑ��A
���������܂��B
n�͐����Ɍ���܂���B�L������ok�ł��ˁB���炵�����Ǝv���܂��B >>127
���̎�|�ɓY������Ȃ����������Ljꉞ�B���R�� n �ɑ���
a = 4n^4+8n^3-4n-1 = (2n^2-1)(2n^2+4n+1),
b = 8n^3+12n^2+4n = 4n(n+1)(2n+1),
c = 4n^4+8n^3+8n^2+4n+1 = (2n^2+2n+1)^2,
d = 8n^3+12n^2+8n+2 = 2(2n+1)(2n^2+2n+1)
�ƒ�߂� ��=(a+bi)/c �Ƃ����A|��|=1, |1-��|=d/c �ƗL�����ɂȂ��Ă���邩��A
���܂����Ǝ��R�� m ���߂ĕ��f���ʏ�̓_�W�� {a^n}_(n=-m,�c,m) �����Ɍ��ׂΎ����ȊO�̏�����S�Ė������B
�_�W�������Ɍ���Łi��^m �� ��^(-m) ������Łj�ʑ��p�`���ł��邽�߂� m ���������ׂ������͂Ƃ����ƁA
��^1 ���� ��^m �܂ł��S�ď㔼���ʂɂ��邱�Ƃ̂݁B�i���̂��� m �̑傫���͂������� ��n/2 ���x�ɐ��������j
n ���\���傫���Ƃ���ꂾ���ӂ��~�ɋ߂Â�����A������ 31/5(<��) ����悤�� n ���Ƃ邱�Ƃ͉\�B
�c�����Ď��ۂɂƂ��Ή����Ȃ��ǁA�v�Z���ώG�ɂȂ邽�ߌv�Z�@�ɗ��邵���Ȃ��̂���_�B�ꉞ���_�����ȏ�̒ʂ� > n�͐����Ɍ���܂���B�L������ok�ł��ˁB
�����ł��������B������`�g�C������
>>135
�E�ʏ����@(nn-1)/2n > 1+��2�@����
�@n > 1+��2 + ��{2(2+��2)} = 5.02733949
�Ec = (21/41){1 + (8/21)n(2n-5)(5n+2)/(nn+1)^2} < 1/��2�@����
�@n > {881 + (29��2)[29+��(2�29�29+881��2)]}/(17�47) = 5.36862925
�EL �� 31/5 �ȏ�ƂȂ�̂�
�@6.45963968 < n < 9.13156611
>>137
�E�ʏ����@(nn-1)/2n > 1+��2�@����
�@n > 1+��2 + ��{2(2+��2)} = 5.02733949
�Ec' = (4/7){1 + n(n-3)(3n+1)/(nn+1)^2} < 1/��2�@����
�@n > {31 + (5��2)[5+��(50+31��2)]}/17 = 7.93257298
�EL �� 31/5 �ȏ�ƂȂ�̂�
�@6.10446338 < n < 11.04823360
�����̋��ʕ�����
�@7.93257298 < n < 11.04823360
�ł����邩�B >>141
c+a = 2{2n(n+1)}^2,
c-a = 2{(n+1)^2 - n^2}^2,
c = {(n+1)^2 + n^2}^2
cc - aa = bb,
b = 2{2n(n+1)}{(n+1)^2 + n^2},
dd - (c-a)^2 = bb,
d = 2{(n+1)^2 - n^2}{(n+1)^2 + n^2} = 2{(n+1)^4 - n^4} >>141
�� = arcsin(b/c),
�Ƃ�����
m = [ ��/�� ]
L = 2m(d/c) + 2sin(m��),
n=3
�@a=527, b=336, c=25^2, d=14�25, ��=0.56758821841666, m=5,
�@sin(5��) = 28515500892816/(c^5) = 0.29900669864185�@�� Q
�@L = 2�5�(14/25) + 2sin(5��) = 6.1980133972837
n=4
�@a=1519, b=720, c=41^2, d=18�41, ��=0.44262888469558, m=7,
�@sin(7��) = 1637671530080839800240/(c^7) = 0.043177033944429�@�� Q
�@L = 2�7�(18/41) + 2sin(7��) = 6.2326955313035
�EL �� 31/5 �ȏ�@�����@n��4
n=17
�@a=373319, b=42840, c=613^2, d=70�613, ��=0.1142546313550, m=27,
�@sin(27��) = 0.056687202872879�@�� Q
�@L = 2�27�(70/613) + 2sin(27��) = 6.2797691855174
n=18
�@a=466487, b=50616, c=685^2, d=74�685, ��=0.10808179674906, m=29,
�@sin(29��) = 0.00722048512511925�@�� Q
�@L = 2�29�(74/685) + 2sin(29��) = 6.2801344009072
�@
�EL �� 6.28 �ȏ�@�����@n��18 >>144
�ǂ������肪�Ƃ��Bn=3 �̎��_�ł���10�P�^�����Ă��̂ˁc
������ n=4 �ƈӊO�Ƒ����^�C�~���O�ŏ�������������Ă����� ��~�̒��SO�̔������~�ƕ��s�ȕ��ʃ��ő̐ς������ɂȂ�悤�ɐؒf����
����ɁA��~�ƃ��̒����ɂ����̕��ʂƕ��s�ȕ��ʃ��Ŕ�����ؒf����
���ɂ��f�ʂ̒��S��O'�A����̓_��P�Ƃ���Ƃ��A
��OPO'�����߂� �O>>42
>>146
���a1�̔������~���獂���ւ܂ő����W�߂��Ƃ��A�̐ς���(�̐�4��/3)��1/4�Ƃ���ƁA
��/3=��0�`��(1-t^2)dt
1/3=[t-t^3/3]0�`��
1/3=��-��^3/3
��^3-3��+1=0�\�\�@
��=sin��OPO'
�@���������ƁA
3��^2-3=0
y=f(��)=��^3-3��+1�̃O���t�̌`���A
��=-1�̂Ƃ��ɑ�A
��=1�̂Ƃ��ɏ��l-1���Ƃ�B
�@�̒l��0�ƂȂ�ւ́A
0���ց�1�̂������0���̂Ƃ��B
��OPO'��18�� �O>>147�����B
{sin(20��)}^3-3sin(20��)+1=0.0139483266��0
20�����킸���ɑ傫�����A�����l�ł�20���������Ƃ��߂��B ��[0,a](1-x^2)dx = 1/2�E2��/3���
a-a^3/3 = 1/3 �B
�� (2b) - (2b)^3/3 = 1/3�B
�� 3b - 4b^3 = 1/2�B
�� 3(sin��) - 4(sin��)^3 = 1/2�B
�� sin3�� = sin(��/6)�B
�� ��=��/18�B >>148
�s����
>>149
�����ł� >>149-150���H�@10���͂�������B����Ȃ�������̉~�Ղ�������1/3�ɂȂ�́H�@�O>>148�������Ȃ��H�@10����1/3���B
�P]/�_�Q�Q�Q�Q�Q�Q�Q
�Q/�_/ �@�@,,������/|
�P�_/ �@�@�c`o`Ђ�))|
�P|�_�Q�Q�QU,~�܁S� |_
�n| �a�P�P�P�PU~~U / /
�Q| �a ���@�� �a |/ /
_�@`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P ����18�ƍ���2�̌v20�̋ʂ��܂ɓ����Ă���B
�u����ׂɑ܂���ʂ�1���o�����̋ʂ͖߂��Ȃ��v�Ƃ������Ƃ��J��Ԃ��B
���߂č��ʂ��o��܂łɔ��ʂ��o�����Ƃ��āA�ł��m���̍����̂�0, 6, 9, 18�̂������瓚����B ���Ԃ�t�x�݂̏h����ۓ��������낤�B���x���I�ɂ��[�������B >>152����1�H�ׂĖ߂��Ȃ��m����18/20=9/10�B����2�H�ׂĖ߂��Ȃ��m����(9/10)(17/19)=63/190�B����3�H�ׂī���߂��Ȃ��m����(63/190)(16/18)=28/95�B����4�H�ׂ�̰��߂��Ȃ��m����(28/95)(15/17)=84/323�B
����5�H�ׂı�!! (84/323)(14/16)=72/323�B����6�\�\(72/323)(13/15)=312/1615�B9���ȁH �O>>151
�P]/�__�Q�Q�Q�Q�Q�Q
�Q/�_/�@�@�@�����@/|
�P�_/�@�@�@((`-`)/ |
�P|�_�Q�Q�Q,U��U�| |__
�n| �a�P�P�P~U~U | / /
�Q| �a ���@�� �a |/ /
_�@`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P V(��) = ��[0�`2sin��] (1-xx) dx
�@= (2��/3) [(3/2)x - (1/2)x^3](x=0,2sin��)
�@= (2��/3) {3sin�� - 4(sin��)^3}
�@= V(��/6) sin(3��),
�ʔ����B �悭����L���b�`�R�s�[�u2�l��1�l������ɂȂ�v
���́A����ɂ͐����̃J���N��������̂�
���ۂɂ́A���{�l��50�܂łɜ��m���́A���v��ł́A�Ȃ��2��
60�ł�7���ȉ��ɉ߂��Ȃ�
80�ł�37���ȉ�
90��100�܂Ő�����l���ׂĂ����킹�āA�悤�₭�u2�l��1�l�v�ƂȂ�
�i���������Z���^�[�������Z���^�[�u�ŐV���v�v���j >>157
��������
���ʑO�܂łɃK���ɂ�����m���A�Ƃ������t�ʂ�̓�����O�̒�`���� http://ganjoho.jp/reg_stat/
�@���@���v�@���@���v�@���@�ŐV���v �Ȃ�Ŏ���������Ȃ̂ɓ����Ⴄ��H�@�v�Z�ԈႦ�����ȁH�@10�����ȁH�@�O>>155
�P]/�_�Q�Q�Q�Q�Q�Q�Q
�Q/�_/ �@�@,,������/|
�P�_/ �@�@�c`_`Ђ�))|
�P|�_�Q�Q�QU,~�܁R' |_
�n| �a�P�P�P�PU~U~ / /
�Q| �a ���@�� �a |/ /
_�@`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P �O>>160
��~�ƃ��̒����ɂ����̕��ʂƕ��s�ȕ��ʃ�
����������B
��~�ƕ��ʃ��ɕ��s�ȕ��ʃ��Ƃ����Ӗ��ł͂Ȃ��̂��H�@�����͓_���A�_�ɕ��s���Ă̂͂��������ȁB >>155
�s�����ł�
20���Ď��o�������A�����o��^�C�~���O��C(20,2)=190�ʂ肠��܂�
�����͑S�ē��l�Ɋm���炵���ł�
�������߂ɍ����o��̂�19�ʂ�B6���o�č����o��̂�13�ʂ�B���l�ɑI��������10�ʂ�A1�ʂ�B
�����0���ł��m���������ƌ��_����܂� �� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�



