くだらねぇ問題はここへ書け

**634 100点満点中100点を超えた** · 2024/02/17(土) 05:23:29.93

>>634は、出題ミスにしてさ
F(1)＝2　∧　F(0)＝0　∧
F(-1)＝-2/3 で滑らかで単調増加の関数F(x)は何かな❓
っていう問題にすり替えるとよろしい💃

お絵かきは、キニシナイでください

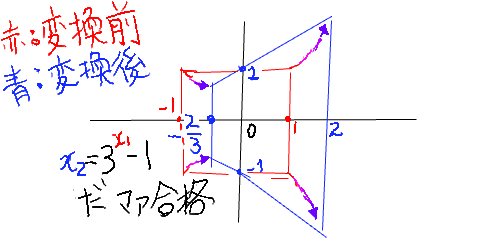
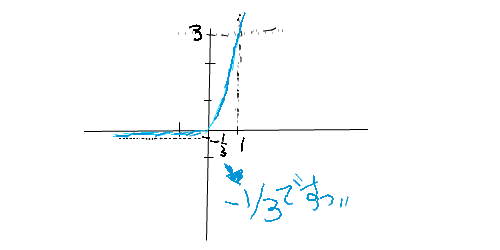
**634 実は自作自演** · 2024/02/17(土) 05:43:07.10

>>637よ、問題をすり替えるなら、以下のお絵かきの如く
F(1)＝3　∧　F(0)＝0　∧
F(-1)＝-1/3 で滑らかで単調増加の関数F(x)は何かな❓
だ。チミにはわかるかな❓　ポクは今はマダ解らん。今は

**１３２人目の素数さん** · 2024/02/17(土) 07:48:06.70

F(x) = 2(4^x - 1)/3,
ぢゃダメか？

**１３２人目の素数さん** · 2024/02/17(土) 08:07:01.54

↑ の補足。
c-1/2, c, c+2 が等比数列だと仮定すれば
　0 = (c-1/2)(c+2) - cc = (3/2)c - 1,
∴　c= 2/3.

**634** · 2024/02/17(土) 09:06:11.98

>>639 ありがとう。モチロン数学板はポクより天才😺

**１３２人目の素数さん** · 2024/02/17(土) 14:33:37.24

すいません、健康についての問題なんですが
たぶん三角関数の積分で求められると思うんですが解説見ても自信なく
計算の解説と回答をお願い致します

血の中にとけた糖質量（血糖値）が食事後2時間かけてサインカーブの様にゆっくりと上がって下がると仮定します（1時間後が頂点になる）
て、2時間あたりの血糖値の積分値が2000mg/dlの場合、血糖値のMax値（1時間後と仮定）は
いくらになるのでしょうか？？

∫（サインx+1）dx？？？
2000=-cosx+xぐらい検索したのですがそこから頂点までわからなくなりました?

**642** · 2024/02/17(土) 16:00:04.51

大事な事、書き忘れました
食事前の血糖値は90mg/dlとします。
食事後90mg/dlから上がって1時間後にmax値になり
2時間後に90mg/dlに戻ります

**１３２人目の素数さん** · 2024/02/17(土) 16:00:43.00

>>635
直角双曲線とすると
　F(x) = 4x/(5-3x),
かなぁ。　　x<5/3 に限れば単調増加。
　漸近線は x=5/3 と y=-4/3.
　焦点 ( (5-2√10)/3, (2√10 -4)/3 ) と
　　　 ( (5+2√10)/3, (-2√10 -4)/3 )

**１３２人目の素数さん** · 2024/02/17(土) 16:06:08.67

球の最密充填計算してあーだこーだしてるんだけど
プログラミングでは球同士が埋もれて重なることがあるんだわ
プログラミングの問題と言えばそうなんだけど
なんだかなぁ、、、
プログラミング板で愚痴るべきか、、、

**１３２人目の素数さん** · 2024/02/17(土) 16:44:45.64

大学以降の数学の知識がないと「2の√2乗が超越数であること」を示すのは困難とききました

では、高校数学の範囲内で「2の√2乗が無理数であることを示すこと」は可能なのでしょうか？

**１３２人目の素数さん** · 2024/02/18(日) 15:51:57.95

>>634
3次式
　F(x) = x(xx+3x+4)/4,
　F '(x) = {3(x+1)^2 + 1}/4 ≧ 1/4.　… 単調増加。

**１３２人目の素数さん** · 2024/02/18(日) 17:26:30.20

↑ の補足
3点を通る2次式は x(5+3x)/4 だけど、
これは x<-1 では単調増加にならない。そこで
　F(x) = x(5+3x)/4 + k･x(x-1)(x+1)/4
　　　= x(k･xx + 3x + 5-k)/4,
とおいてみる。
F(x) が単調増加となる条件は
　F '(x) = 0 が2つの実解をもたないこと。
　F '(x) = (3k･xx + 6x + 5-k)/4,
　D = (3/2)^2 - 12k(5-k) ≦ 0,
　0.69722436 < k < 4.30277564
　k = 1, 2, 3, 4 はこれを満たす。

F(x) = x(xx+3x+4)/4,
F(x) = x(2xx+3x+3)/4,
F(x) = x(3xx+3x+2)/4,
F(x) = x(4xx+3x+2)/4,

**１３２人目の素数さん** · 2024/02/18(日) 19:03:54.87

>>647
>>648
なるほどね

**１３２人目の素数さん** · 2024/02/18(日) 20:48:38.08

ナール。

と主人は引張ったが「ほど」を略して考えている。
　　　　　　夏目漱石「吾輩は猫である」(1905-1906)
　　　　　　　↑ 前の千円札の人

**１３２人目の素数さん** · 2024/02/19(月) 03:40:59.86

＞＞634
　F(x) = (3+5x)/4 - (3/4)k'{(k'+1)/(k'+xx) - 1}

(-1,-1/2) と (1,2) を通る直線 y=(3+5x)/4 は (0,0) を通らない。
そこでローレンツ分布関数を引いて (0,0) も通るようにした。
F(x) は単調増加だから、F '(x)=0 は2実解をもたない。
∴　(557-40√157)/243 ≦ k' ≦ (557+40√157)/243,
　　0.229635541375 < k' < 4.35472659854

**１３２人目の素数さん** · 2024/02/19(月) 12:11:36.41

＞＞634
　F(x) = (3+5x)/4 - (3/4){e^(1-xx) - 1}/(e-1),

(-1,-1/2) と (1,2) を通る直線 y=(3+5x)/4 は (0,0) を通らない。
そこで正規分布関数を引いて (0,0) も通るようにした。
F '(x)=0 は実解をもたないから F(x) は単調増加。

**１３２人目の素数さん** · 2024/02/19(月) 17:14:19.22

球充填問題について書かれた本ってありますか？
どの分野の書籍を探せばいいんだろ
線形代数かな？
何か知ってたら教えて下さい

**prime_132** · 2024/02/19(月) 23:52:04.75

かなり古いけど…

一松信：「パッキングの問題」,
　　数セミ増刊『数学100の問題』, 日本評論社（1984/Sept)
　　p.27-29

一松信：京都大学数理解析研究所講究録, No.676, p.1-4 (1988/Dec)

スローン (町田元･訳)「球の充填問題」,
　『サイエンス』1984年3月号, 日経サイエンス社

J.H.Conway - N.J.A.Sloane "Sphere packings, lattices and groups"
Springer-Verlag (1998)

N.J.A.Sloane, “The sphere-packing problem”.
　Documenta Mathematika 3, p.387–396. (1998)

**１３２人目の素数さん** · 2024/02/20(火) 01:39:10.33

F(x) = {(x+1)^c - 1}/2,
　　　x≧-1 で単調増加。
　　c = log(5)/log(2) = 2.3219280948873623478703194294893901758648313930245806120547563958...

**１３２人目の素数さん** · 2024/02/21(水) 01:59:32.02

三角関数
　F(x) = (5x+3)/4 - (3/8){1+cos(πx)},
　F '(x) = 5/4 + (3π/8)sin(πx)
　　　= 1.25 + 1.1781sin(πx)
　　　≧ 0.0719

**１３２人目の素数さん** · 2024/02/21(水) 14:50:23.94

↑をチョト改良?
　F(x) = (5x+3)/4 - (3/4){(1/√2) + cos(3πx/4)}/(1/√2 + 1),
　F '(x) = 5/4 + (3/4)(3π/4)sin(3πx/4)/(1/√2 + 1)
　　　= 1.25 + 1.03517 sin(3πx/4)
　　　≧ 0.21483

**１３２人目の素数さん** · 2024/02/22(木) 13:50:54.38

4次元立方体をテセラクトというのはわかったのですが
5次元、6次元と増やしていったときそれぞれの立方体の名前は何というのでしょうか？
なんか名前がかっこいいから調べたく思いまして

**１３２人目の素数さん** · 2024/02/22(木) 16:47:10.78

>>644
双曲線なら斜交の方がいい？
　F(x) = (5/4){x + √(xx +(8/15)^2)} - 2/3,

**１３２人目の素数さん** · 2024/02/24(土) 01:15:57.45

大学以降の数学の知識がないと「2の√2乗が超越数であること」を示すのは困難と聞きました

では、高校数学の範囲内で「2の√2乗が無理数であること」を示すのは可能なのでしょうか？

**１３２人目の素数さん** · 2024/02/24(土) 16:31:04.39

[第1段]：2^{√2} が代数的数であるとする
a＝2^{√2} とおく
仮定から、aは実数であって、aは実数の代数的数である
a＝2^{√2} とおいているから log_|a|＝√2×log|2| である
よって a＝2^{√2} から 2^{√2}＝e^{√2×log|2|} が成り立つ
[第2段]：ところで、1＜√2＜3/2 だから 2^{√2}＜2^{3/2} である
また e＞2 から log|2|＜1 であって、4/3＜√2＜3/2 だから
log|2|＜4/3＜√2×log|2|＜3/2×log|2| から e^{√2×log|2|}＞e^{4/3} である
よって、2^{√2}＞e^{4/3} を得る
[第3段]：故に、log_2|e^{4/3}|＜√2 から log_2|e|＜3/4×√2 であって、
e＜2^{3/4×√2} から 1＜3/4×√2×log|2|、即ち e^{(2√2)/3}＜2 である
よって、e＜3 から 3^{(2√2)/3}＜2 であって、3^{2√2}＜8 を得る
[第4段]：しかし、3^{2√2}＞3^2＝9 だから、3^{2√2}＜8 が得られたことは
3^{2√2}＞8 なることに反し、矛盾する
この矛盾は 2^{√2} が超越数ではないとしたことから生じたから、
背理法により 2^{√2} は超越数である

eの近似値や 2＜e＜3 などの大小関係は高校数学の範囲の筈だから、
超越数の定義が分かっていれば 2^{√2} の超越性も
高校数学の範囲で示せる気がしないでもないんだが…

**１３２人目の素数さん** · 2024/02/24(土) 17:37:10.94

>>661
なんでいつも出鱈目書いてるの

**１３２人目の素数さん** · 2024/02/24(土) 18:03:01.67

[第3段]：故に、log_2|e^{4/3}|＜√2 から log_2|e|＜3/4×√2 であって、
e＜2^{3/4×√2} から 1＜3/4×√2×log|2|、即ち e^{(2√2)/3}＜2 である
よって、e^{2√2}＜8 を得る
[第4段]：しかし、e^{√2}＞8^{1/2}＝2√2 だから e^{2√2}＞8 である
故に、e^{2√2}＜8 が得られたことは e^{2√2}＞8 なることに反し、矛盾する
この矛盾は 2^{√2} が超越数ではないとしたことから生じたから、
背理法により 2^{√2} は超越数である

**１３２人目の素数さん** · 2024/02/24(土) 18:04:34.49

>>662
間違えたところは訂正した

**１３２人目の素数さん** · 2024/02/24(土) 18:27:40.03

>>663
>>664
根本的に間違ってるから無意味

どこにも代数的数であることを使ってないから代数的数を超越数に書き換えれば超越数ではない「証明」になるから間違い

**１３２人目の素数さん** · 2024/02/24(土) 18:35:42.79

>>665
>代数的数を超越数に書き換えれば超越数ではない「証明」になる
ゲルフォント・シュナイダーの定理から、そうはならない

**１３２人目の素数さん** · 2024/02/24(土) 18:49:01.45

体Q上 a＝2^√2 のn次の最小多項式を考えても、
その次数が1であることは明らかだから、
結局はaの無理性の証明に帰着する

**１３２人目の素数さん** · 2024/02/24(土) 19:05:34.41

>>666
だから>>661>>663は間違い

**１３２人目の素数さん** · 2024/02/24(土) 19:20:32.42

>>668
ゲルフォント・シュナイダーの定理に従えば、そうはならないという事実がある
2^√2 の無理性の証明を高校数学の範囲で証明してもつまらない
2^√2 を互いに素な整数を使って有理数で表して議論していって矛盾を導く可能性が高い

**１３２人目の素数さん** · 2024/02/24(土) 19:21:14.82

書き換えた「証明」

-------------------------------------------------------------------------------

[第1段]：2^{√2} が超越数であるとする
a＝2^{√2} とおく
仮定から、aは実数であって、aは実数の超越数である
a＝2^{√2} とおいているから log_|a|＝√2×log|2| である
よって a＝2^{√2} から 2^{√2}＝e^{√2×log|2|} が成り立つ
[第2段]：ところで、1＜√2＜3/2 だから 2^{√2}＜2^{3/2} である
また e＞2 から log|2|＜1 であって、4/3＜√2＜3/2 だから
log|2|＜4/3＜√2×log|2|＜3/2×log|2| から e^{√2×log|2|}＞e^{4/3} である
よって、2^{√2}＞e^{4/3} を得る
[第3段]：故に、log_2|e^{4/3}|＜√2 から log_2|e|＜3/4×√2 であって、
e＜2^{3/4×√2} から 1＜3/4×√2×log|2|、即ち e^{(2√2)/3}＜2 である
よって、e^{2√2}＜8 を得る
[第4段]：しかし、e^{√2}＞8^{1/2}＝2√2 だから e^{2√2}＞8 である
故に、e^{2√2}＜8 が得られたことは e^{2√2}＞8 なることに反し、矛盾する
この矛盾は 2^{√2} が代数的数ではないとしたことから生じたから、
背理法により 2^{√2} は代数的数である

**１３２人目の素数さん** · 2024/02/24(土) 22:20:27.85

>>670
「背理法により 2^{√2} は代数的数である」とあるが
2^{√2} はゲルフォント・シュナイダーの定理より超越数であることが判明しているので
その証明は誤っている

**１３２人目の素数さん** · 2024/02/24(土) 22:23:38.33

>>669
高校の数学教師が高校生に対して「2の√2乗が無理数であることを示せ」という証明問題を出すのは
無理なのでしょうか？

**１３２人目の素数さん** · 2024/02/24(土) 23:03:40.47

>>671
だから>>661>>663は間違い

**１３２人目の素数さん** · 2024/02/25(日) 02:18:44.81

>>670
>>673
コピペした証明が間違っている

[第1段]：2^{√2} が代数的数であるとする
a＝2^{√2} とおく
仮定から、aは実数であって、aは実数の代数的数である
a＝2^{√2} とおいているから log|a|＝√2×log|2| である
よって a＝2^{√2} から 2^{√2}＝e^{√2×log|2|} が成り立つ
[第2段]：ところで、1＜√2＜3/2 だから 2^{√2}＜2^{3/2} である
また e＞2 から log|2|＜1 であって、4/3＜√2＜3/2 だから
log|2|＜4/3＜√2×log|2|＜3/2×log|2| から e^{√2×log|2|}＞e^{4/3} である
よって、2^{√2}＞e^{4/3} を得る
[第3段]：故に、log_2|e^{4/3}|＜√2 から log_2|e|＜3/4×√2 であって、
e＜2^{3/4×√2} から 1＜3/4×√2×log|2|、即ち e^{(2√2)/3}＜2 である
よって、e^{2√2}＜8 を得る
[第4段]：しかし、e^{√2}＞8^{1/2}＝2√2 だから e^{2√2}＞8 である
故に、e^{2√2}＜8 が得られたことは e^{2√2}＞8 なることに反し、矛盾する
この矛盾は 2^{√2} を代数的数と仮定したことから生じたから、
背理法により 2^{√2} は超越数である

集合Aを A＝{2^x| xは代数的無理数 } と定義すれば、
Aは区間 [0、+∞) 上のルベーグ測度に関する零集合である
同様に、実数の代数的数全体の集合Bは
区間 (-∞、+∞) 上のルベーグ測度に関する零集合である
2^{√2} を代数的数と仮定すると、同時に2つの零集合A、B上で
議論していって矛盾が得られるようになっているから、正しい

**１３２人目の素数さん** · 2024/02/25(日) 02:44:54.60

>>674
間違い

**１３２人目の素数さん** · 2024/02/25(日) 02:51:55.98

>>675
2^{√2} を代数的数と仮定すると A⊂B が成り立つから、零集合A上で議論して矛盾を得る

**１３２人目の素数さん** · 2024/02/25(日) 03:18:08.69

A⊂B → 2^{√2}∈A∪B
零集合A上 → 零集合 A∪B 上

**１３２人目の素数さん** · 2024/02/25(日) 03:27:26.35

>>672
こういう問題を高校生に出すのは止めた方がいい
多分、出題しても完答できる人は殆どいないと思う
無理性を証明するにしても、乗法的独立の知識は要する

**１３２人目の素数さん** · 2024/02/25(日) 12:31:59.03

連立方程式で質問です
1個１００円のりんごと1個100円の梨を10個1000円分買いました
りんごと梨はいくつ購入されたでしょう

ってなったとき答えって10通りあると思うんですけど式を解くと0ででてきちゃいます
解き方が間違ってるんでしょうか

**１３２人目の素数さん** · 2024/02/25(日) 12:45:36.60

りんごも梨も少なくとも1つは買ってるなら、9通り？

**１３２人目の素数さん** · 2024/02/25(日) 14:35:34.45

梨はナシでもいいが、りんごがないのは無しだ？
それなら 10通り…

**１３２人目の素数さん** · 2024/02/25(日) 14:45:43.90

>>679
それは連立してないからです
100円が意味をなしてないからです

**１３２人目の素数さん** · 2024/02/25(日) 14:58:27.46

>>659
双曲線 (斜交)

漸近線は　y = -2/3　と　y = m･x - 2/3,　(m=5/2).

焦点 ( ±(8/15)√(2√29)･sin(θ/2), -(2/3) 干 (8/15)√(2√29)･cos(θ/2) )
　= ( ±(4/15)√(√29 - 2), -(2/3) 干 (4/15)√(√29 + 2) )
ここに　θ = arctan(m),

**６７２** · 2024/02/27(火) 10:54:20.18

>>678
ありがとうございます

やはり高校数学の範囲を逸脱しているのかあ…

**１３２人目の素数さん** · 2024/02/28(水) 06:56:21.78

>>684
2^{√2} が代数的数であるとする
a＝2^{√2} とおく
aは実数の代数的数である
指数関数 y＝2^x は単調増加で正の値を取るから、
仮定から a＞2 であって、a^2＞4 を得る
また、仮定から a^{√2}＝2^2＝4 であって、(1/a)^{√2}＝1/4 である
a＞1 から指数関数 y＝(1/a)^x は単調減少で正の値を取るから、1/a＞1/4 である
よって、4＞a＞2 であって、2＞a＞√a＞√2 から 4＞a^2＞a＞2 である
故に、a^2＞4 と a^2＜4 が両立し、実数の大小関係に反し矛盾が生じる
この矛盾は実数 2^{√2} を代数的数と仮定したことから、2^{√2} は実数の超越数である
実数の超越数は無理数だから、2^{√2} は無理数である

今更だが、有理数(または実数の代数的数)の稠密性を使えば、こういう証明はある

**１３２人目の素数さん** · 2024/02/28(水) 07:04:49.78

>>685
間違い

**１３２人目の素数さん** · 2024/02/28(水) 07:15:42.22

>>686
実数体R上、実数の代数的数の全体は加減乗除の演算に関して体をなし、
実数の代数的数は有理数と同様に実数体R上稠密である

**１３２人目の素数さん** · 2024/02/28(水) 07:22:01.52

>>686
実数論の有理数の稠密性も分からない人間に間違いって判定されたくない

**１３２人目の素数さん** · 2024/02/28(水) 07:49:43.06

>この矛盾は実数 2^{√2} を代数的数と仮定したことから
>「生じたから」、2^{√2} は実数の超越数である

**１３２人目の素数さん** · 2024/02/28(水) 07:52:16.12

>>684
2^{√2} が代数的数であるとする
a＝2^{√2} とおく
aは実数の代数的数である
指数関数 y＝2^x は単調増加で正の値を取るから、
仮定から a＞2 であって、a^2＞4 を得る
また、仮定から a^{√2}＝2^2＝4 であって、(1/a)^{√2}＝1/4 である
a＞1 から指数関数 y＝(1/a)^x は単調減少で正の値を取るから、1/a＞1/4 である
よって、4＞a＞2 であって、2＞a＞√a＞√2 から 4＞a^2＞a＞2 である
故に、a^2＞4 と a^2＜4 が両立し、実数の大小関係に反し矛盾が生じる
この矛盾は実数 2^{√2} を代数的数と仮定したことから
生じたから、2^{√2} は実数の超越数である
実数の超越数は無理数だから、2^{√2} は無理数である

**１３２人目の素数さん** · 2024/02/28(水) 08:47:58.92

2^{3/2} が代数的数であるとする
a＝2^{3/2} とおく
aは実数の代数的数である
指数関数 y＝2^x は単調増加で正の値を取るから、
仮定から a＞2 であって、a^2＞4 を得る
また、仮定から a^{2/(3/2)}＝2^2＝4 であって、(1/a)^{2/(3/2)}＝1/4 である
a＞1 から指数関数 y＝(1/a)^x は単調減少で正の値を取るから、1/a＞1/4 である
よって、4＞a＞2 であって、2＞a＞√a＞√2 から 4＞a^2＞a＞2 である
故に、a^2＞4 と a^2＜4 が両立し、実数の大小関係に反し矛盾が生じる
この矛盾は実数 2^{3/2} を代数的数と仮定したことから
生じたから、2^{3/2} は実数の超越数である

**１３２人目の素数さん** · 2024/02/28(水) 10:27:53.48

>>691
2^{3/2} が代数的数であることは確定しているから 2^{3/2} にその論法は通用しない
原理的には、実数論では有理数の加減乗除をもとに無理数を定義して有理数体Qを完備化するのと同様に、
実数の代数的数の加減乗除をもとに実数の超越数を定義して実数の代数的数の全体を完備化出来る
その後、実関数について微分積分を展開していくという理論展開も原理的には出来る
その考え方を応用しただけ

**１３２人目の素数さん** · 2024/02/28(水) 10:38:28.88

>>691
注意しておくけど、2^{3/2}＝2√2 は
有理数体Qに √2 を添加した代数拡大体 Q(√2) に属し、
Q(√2) は超越拡大体ではない

**１３２人目の素数さん** · 2024/02/28(水) 10:40:05.03

こいつ前もおんなじ突っ込み受けてたやつやろ
一ミリも成長してない

**１３２人目の素数さん** · 2024/02/28(水) 10:43:09.56

>>692
2^{√2} が代数的数であるなら>>690は使えないから
>>690の前に2^{√2} が代数的数でないことを証明しないと

**１３２人目の素数さん** · 2024/02/28(水) 10:45:05.76

>>694
そういう微分積分の理論展開も原理的には出来るから、本でも読んでよく考えてみな

**１３２人目の素数さん** · 2024/02/28(水) 10:49:14.50

1<r<2のとき2^{r} が代数的数であるとする
a＝2^{r} とおく
aは実数の代数的数である
指数関数 y＝2^x は単調増加で正の値を取るから、
仮定から a＞2 であって、a^2＞4 を得る
また、仮定から a^{2/r}＝2^2＝4 であって、(1/a)^{2/r}＝1/4 である
a＞1 から指数関数 y＝(1/a)^x は単調減少で正の値を取るから、1/a＞1/4 である
よって、4＞a＞2 であって、2＞a＞√a＞√2 から 4＞a^2＞a＞2 である
故に、a^2＞4 と a^2＜4 が両立し、実数の大小関係に反し矛盾が生じる
この矛盾は実数 2^{r} を代数的数と仮定したことから
生じたから、2^{r} は実数の超越数である

**１３２人目の素数さん** · 2024/02/28(水) 10:58:51.29

有理数体Qに実数の超越数eを添加した超越拡大体 Q(e) の加減乗除をもとに
超越数を定義して Q(e) を完備化することは原理的には出来るが、
このときは超越拡大体 Q(e) を完備化する前に実数の超越数eが既に含まれているので、
体 Q(e) を完備化した後微分積分を理論展開して
それを超越性を示すのに応用することは一般には出来ない

**１３２人目の素数さん** · 2024/02/28(水) 11:00:39.05

>>697

>>698でも読んでどうぞ

**１３２人目の素数さん** · 2024/02/28(水) 11:07:41.61

>>698と同様なことは、一般に実数体Rの部分体なる超越拡大体についていえる

**１３２人目の素数さん** · 2024/02/28(水) 12:22:15.14

>>697
という訳で、実数の代数的数の全体をAで表わすことにすれば、
体Aの超越拡大体 A(2^{√2}) についても>>698と同様なことがいえる
だから、>>697の考え方は実数について代数的数か超越数かの判定には適用できない

**１３２人目の素数さん** · 2024/02/28(水) 14:00:54.59

そもそも>>691の言ってる事が理解できてない時点で数学Aすら理解できてない。
数学Aの時点で自分が落ちこぼれてることすら理解できる知能がない。

**１３２人目の素数さん** · 2024/02/28(水) 16:02:47.38

>>702
そもそも、>>690は高校ではなく大学の微分積分に基づいた証明である

**１３２人目の素数さん** · 2024/02/28(水) 16:26:43.49

数学Aで落ちこぼれてる人間が大学の微積の議論できるはずないやろ
そんなレベルの話すら理解できる知能がないんだよ。

**１３２人目の素数さん** · 2024/02/28(水) 16:33:55.99

>>704
高校の微分積分と大学の微分積分が同じだと思ったら大間違い
高校の微分積分では実数論が幾何的直観に基づいていて曖昧だが、
大学の微分積分では幾何的直観に基づかず実数論をする

**１３２人目の素数さん** · 2024/02/28(水) 16:36:51.96

>>704
第一、高校の微分積分ではε-δ論法をしていないだろ

**１３２人目の素数さん** · 2024/02/28(水) 17:07:59.85

まぁ高木といっしょ
自分の事世紀の天才とでも思ってるんやろ
高校数学の時点で落ちこぼれてるゴミ

**１３２人目の素数さん** · 2024/02/28(水) 17:12:39.85

指摘が難しすぎるようなので簡単に
4＞a＞2から2＞aは出ない

**１３２人目の素数さん** · 2024/02/28(水) 17:16:40.16

>>707
高校数学は計算が大半を占めていて論理的に曖昧な部分があるから
大学数学を理解するのに高校数学をしっかり理解する必要はない
高校の実数論は、連結な数直線の幾何的直観に基づいているから曖昧である

**１３２人目の素数さん** · 2024/02/28(水) 17:30:14.99

>>709
間違いの指摘をするなら、回りくどい指摘ではなく
そのように簡単にしてくれた方が分かり易くてありがたい

**１３２人目の素数さん** · 2024/02/28(水) 17:31:33.37

高木ということ一緒
おそらく糖質なんやろ
少なくとも高校の段階から知能の向上が止まってっる
もっと前かもしれないが

**１３２人目の素数さん** · 2024/02/28(水) 17:32:05.91

>>708

>>710は>>708へのレス

**１３２人目の素数さん** · 2024/02/28(水) 17:34:57.36

>>711
くどくど他人のこというなら、>>690のような証明に成功してからいってくれ

**１３２人目の素数さん** · 2024/02/28(水) 17:58:47.43

>>710
背理法で証明するなら仮定を使って矛盾を導かなければできないっていう根本的な指摘だよ

**１３２人目の素数さん** · 2024/02/28(水) 17:59:46.40

>>713
成功してない

**１３２人目の素数さん** · 2024/02/28(水) 18:09:45.25

>>714-715
理解出来ない人間には理解出来ないだろうが、実は>>674の証明は正しい

**１３２人目の素数さん** · 2024/02/28(水) 19:12:29.16

>>716
>>714での指摘通り全部間違った証明だよ

**１３２人目の素数さん** · 2024/02/28(水) 20:36:15.10

【デコホーム】　北海道に　｀中国人専用´　住宅街
https://mao.5ch.net/test/read.cgi/build/1709004231/l50

**１３２人目の素数さん** · 2024/02/28(水) 23:16:32.58

高木そっくりwwwwwww

**１３２人目の素数さん** · 2024/02/29(木) 02:10:14.79

>>717
元々、微分積分の理論を有理数から無理数を定義したときと同様に
実数論から再構成してから微分積分の理論を再展開し、
それを実数の超越性の証明に応用して示す長い証明である
>>716では結果だけを切り取って書いたから間違いに見えるだけ

**１３２人目の素数さん** · 2024/02/29(木) 02:12:10.41

>>716では → >>674では

**１３２人目の素数さん** · 2024/02/29(木) 02:18:07.65

>>717
実数の代数的数の全体がなす体から実数の超越性を定義して
実数論を再展開するときは最小多項式の次数や
ディオファンタス近似などを使う必要があって、
有理数から無理数を定義した実数論とは様相が全く違う

**１３２人目の素数さん** · 2024/02/29(木) 02:49:35.18

>>674では集合 A＝{a^x| xは代数的無理数、aは1より大きい代数的数 } と
実数の代数的数の全体がなす体Bの共通部分 A∩B が空集合であることを示した方が速い

**１３２人目の素数さん** · 2024/02/29(木) 03:02:44.91

実数の代数的数の全体がなす体から実数の超越性を定義して
実数論を再展開して微分積分の理論を再展開しても、
その再展開した微分積分は従来の微分積分と殆ど同じで、
再展開した微分積分には殆ど使い道がなく意味は殆どないだろうから、
>>674では結果だけを切り取って書いた

**１３２人目の素数さん** · 2024/02/29(木) 05:20:02.57

4/3=1.3333333333<0.9802581434=sqrt(2)log(2).

**１３２人目の素数さん** · 2024/02/29(木) 10:42:57.75

[第1段]：集合Aを A＝{a^x| xは代数的無理数、aは1より大きい実数の代数的数 }
と定義する。Bを実数の代数的数の全体がなす体と定義する
集合Aと体Bの共通部分 A∩B について、A∩B≠∅ と仮定する
集合Aと体Bの定義から、或る代数的無理数x、或る a＞1 なる a∈B が存在して、
a^x∈A∩B であって、A∩B⊂B だから a^x∈B である
nを a^x の最小多項式の次数とする
Case1)：n≧2 のとき。このとき、a^x はn次の代数的無理数だから、
リウビルの定理より a^x に対して或る c＞0 なる実数cが存在して、
両方共に任意の整数p、q p≧1 に対して、|a^x－q/p|＞c/(p^n) である
また、無理数 a_x を連分数展開して考えれば、a^x に対して可算無限個の
既約分数 q'/p' p'≧2 が存在して |a^x－q'/p'|＜1/(p')^2 が成り立つ
よって、a^x に対して可算無限個の既約分数 q'/p' p'≧2 が存在して
c/(p')^n＜|a^x－q'/p'|＜1/(p')^2 であって、
c/(p')^{n-2}＜(p')^2|a^x－q'/p'|＜1 即ち (p')^2|a^x－q'/p'|＜1 である
故に、既約分数 q'/p' p'≧2 について分母の p' が p'→+∞ と+∞に発散させて
既約分数 q'/p' p'≧2 を取れば、或る既約分数 q'/p' p'≧2 が取れて
既約分数 q'/p' p'≧2 は (p')^2|a^x－q'/p'|≧1 を満たし矛盾が生じる

**１３２人目の素数さん** · 2024/02/29(木) 10:45:31.62

Case2)：n＝1 のとき。このとき、a^x は正の有理数だから、
a^x に対して両方共に或る互いに素な整数 p、q p≧1 が存在して a^x＝q/p である
また、仮定からxは代数的無理数である。
xの最小多項式の次数をmとすると、m≧2 であってxはm次の代数的無理数である
よって、Case1)の議論におけるnをmで、a^x をxで、それぞれ書き換えて
Case1)と同様な議論を繰り返せば、矛盾を得る
Case1)、Case2)から、起こり得るすべての場合について矛盾が生じる
この矛盾は、A∩B≠∅ と仮定したことから生じたから、背理法により A∩B＝∅ である
[第2段]：よって、AとBの各定義から、Aに属する実数の代数的数は存在しない
故に、Aの定義から、任意の1より大きい実数の代数的数a、
任意の代数的無理数xに対して、a^x は実数の超越数である
[第3段]：故に、任意の正の代数的数a、任意の代数的無理数x
に対して、a^x は実数の超越数である
[第4段]：√2 は代数的無理数なることに注意すれば 2^{√2} は実数であって超越数である

**１３２人目の素数さん** · 2024/02/29(木) 11:28:32.36

**１３２人目の素数さん** · 2024/02/29(木) 18:31:29.67

xは代数的無理数であるというだけで矛盾するってことは
代数的無理数は存在しないってことになるんだが

**１３２人目の素数さん** · 2024/03/01(金) 11:17:35.68

[第1段]：集合Aを A＝{a^x| xは代数的無理数、aは1より大きい実数の代数的数 }
と定義する。Bを実数の代数的数の全体がなす体と定義する
集合Aと体Bの共通部分 A∩B について、A∩B≠∅ と仮定する
集合Aと体Bの定義から、或る代数的無理数x、或る a＞1 なる a∈B が存在して、
a^x∈A∩B であって、A∩B⊂B だから a^x∈B である
nを a^x の最小多項式の次数とする
Case1)：n≧2 のとき。このとき、a^x はn次の代数的無理数だから、
リウビルの定理より a^x に対して或る c＞0 なる実数cが存在して、
両方共に任意の整数p、q p≧1 に対して、|a^x－q/p|＞c/(p^n) である
また、無理数 a_x を連分数展開して考えれば、a^x に対して可算無限個の
既約分数 q'/p' p'≧2 が存在して |a^x－q'/p'|＜1/(p')^2 が成り立つ
よって、a^x に対して可算無限個の既約分数 q'/p' p'≧2 が存在して
c/(p')^n＜|a^x－q'/p'|＜1/(p')^2 であって、
c/(p')^{n-2}＜(p')^2|a^x－q'/p'|＜1 即ち (p')^2|a^x－q'/p'|＜1 である
故に、既約分数 q'/p' p'≧2 について分母の p' が p'→+∞ と+∞に発散させて
既約分数 q'/p' p'≧2 を取れば、或る既約分数 q'/p' p'≧2 が取れて
既約分数 q'/p' p'≧2 は (p')^2|a^x－q'/p'|≧1＞(p')^2|a^x－q'/p'|
を満たし矛盾が生じる
Case2)：n＝1 のとき。このとき、a^x は正の有理数だから、
a^x に対して両方共に或る互いに素な整数 p、q p≧1 が存在して a^x＝q/p である
また仮定から、aは代数的数だから、aの最小多項式の次数をmとすれば、
m≧1 であってaはm次の代数的数である

**１３２人目の素数さん** · 2024/03/01(金) 11:20:33.75

Case2-1)：m≧2 のとき。このとき、aはm次の代数的無理数であって、
Case1)の議論におけるnをmで、a^x をaで、それぞれ書き換えて
Case1)と同様な議論を繰り返せば、矛盾を得る
Case2-2)：m＝1 のとき。このとき、aは1より大きい正の有理数だから
aに対して両方共に或る互いに素な整数 p''、q'' p''≧1 が存在して a＝q''/p'' である
よって、(q''/p'')^x＝q/p であって、q≧1 から (q''/p'')^x・(p/q)＝1 である
しかし、仮定からxは代数的無理数だから、1とxは有理数体Q上1次独立である
また、有理整数環Zは体Q上の単位元1を含む単位的部分環である
故に、環Z上の加群を考えれば、(q''/p'')^x・(p/q)≠1 であって、矛盾が生じる
Case2-1)、Case2-2)から、n＝1 のときにすべての起こり得る場合について矛盾を得る
Case1)、Case2)から、すべての起こり得る場合について矛盾が生じる
この矛盾は、A∩B≠∅ と仮定したことから生じたから、背理法により A∩B＝∅ である
[第2段]：よって、AとBの各定義から、Aに属する実数の代数的数は存在しない
故に、Aの定義から、任意の1より大きい実数の代数的数a、
任意の代数的無理数xに対して、a^x は実数の超越数である
[第3段]：故に、任意の正の代数的数a、任意の1とは異なる代数的無理数x
に対して、a^x は実数の超越数である
[第4段]：a＝2、x＝√2 のとき。√2 は代数的無理数なること
に注意すれば 2^{√2} は実数であって超越数である

**１３２人目の素数さん** · 2024/03/01(金) 11:26:28.28

[第3段]について
任意の正の代数的数a、任意の1とは異なる代数的無理数x
→ 任意の1とは異なる正の代数的数a、任意の代数的無理数x

**１３２人目の素数さん** · 2024/03/01(金) 22:56:52.83

〔問題〕
a,b,c を正の整数とし、1≦a<b<c とする。
　M = 1 + 3^a + 3^b + 3^c
が立方数となるような (a,b,c) の組は無数にあることを示せ。

・高校数学の質問スレ_Part432 - 883

**１３２人目の素数さん** · 2024/03/02(土) 14:00:51.98

有理数と無理数はどちらも無限大に存在するが、仮に有理数と無理数を同数無限大に出尽くしたとしても、更に無理数のほうが多く存在することを証明せよ

**１３２人目の素数さん** · 2024/03/02(土) 21:25:10.60

有理数を小数で表わすと、
有限桁で切れるか又は循環小数となる。
その循環節の間に1桁ずつ数字を挟もう。

たとえば 3,1,4,1,5,9,2,6,5,3,5,8,9,7,9,3,2,…
の第k項、k+L項、k+2L項、…は循環しないので、
それらを挟んでいくと、すべて無理数になる。
(k, L) の取り方は無限にあるから、
1個の有理数が無限個の無理数に対応する。。。

**１３２人目の素数さん** · 2024/03/09(土) 18:28:10.26

>>733
　(a, b, c) = (n+1, 2n+1, 3n)
　M = (1+3^n)^3,

面白スレ43問目　318-319

**１３２人目の素数さん** · 2024/03/20(水) 19:47:12.86

一つの無理数、たとえばπにたいして有理数は3、3.1、3.14、3.141、...って無限にあるけど
有理数も無理数もどちらも無限大でいいんじゃね