分からない問題はここに書いてね448
レス数が900を超えています。1000を超えると表示できなくなるよ。
>>828
6回やればA2回B2回が期待できる。
300×2+100×2=800(点) >>829-830
ありがとうございました。
1回だけ引いた場合の期待値×繰り返す回数って計算でいいんですか?
これってカードが4枚や5枚になったり、点数が変わっても同じですか? >>827
なるほどそのf(x)の係数になっているのか
だとするとf(x)=0の4つの解が異なる2実解と互いに共役な複素数解であることを使えば
もっと簡単に導けるな >>831
毎回同じ条件(箱から1枚引いては戻す)場合はそう。「反復試行」と呼び、「二項分布」に従う。高校数Bでやるはず。教科書にものってんじゃないかな 期待値は高校の指導要領から外れた。
ので高校数学の範囲では期待値求める問題でないし、期待値に関する公式も原則使えない。
どうでもいいですが〜♬ >>834
平均値って期待値じゃないの?
統計でどう教えるんだろ? A・B・C 三枚のカードが入った各々3枚ずつ計9枚入った箱がある。そこから1枚引き、カードは戻さないを6回繰り返す。Aを引いた時は300点、Bは100点、Cは0点もらえる。6回繰り返した時の点数の期待値はいくらか。
A・B・Cそれぞれ1/3の確率で引けるとする。
この方が面白いね。 △ABCで、BC=a、CA=b、∠A=α、∠B=βである。
a<bのとき、以下の不等式が成り立つことを示せ。
(b/a)^2 < (1-cosβ)/(1-cosα) < (β/α)^2
これを平面図形で示せといわれたのですが分かりません。 https://i.imgur.com/jChlpB1.jpg
テスト勉強しているのですが2.(3)が分からないのでどなたかご教示下さい >>839
原点で不連続である。
ε ∈ (0, 1) とする。
δ を任意の正の実数とする。
P = ((δ/2) * cos(δ/2), (δ/2) * sin(δ/2))
とすると、
原点と点 P の距離は、 δ/2 であり、 δ よりも小さい。
|f(P) - f(0)| = |1 - 0| = 1 > ε どのような内積からも導きかれないノルムの例教えてください。証明もお願いします。 >>841
James R. Munkres 著『Analysis on Manifolds』のp.9 Exercise 3に例があります。 >>819 >>827
(a^2 -b)(c^2 -d) = (7/6 -f/2)^2 - (20/27)^2/(7/6 +f/2)
= - (1/3) [(13+2√11)^{1/3} - (13-2√11)^{1/3}]^2
= - 0.2376189664261441
< 0, 空ではないHの部分集合Aに対してconv(A)=AならばAは凸集合である。の証明が分かりません。 conv(A) は Aを含む最小の凸集合である。
conv(A) = A なら A 自体がその凸集合である。
どこに悩む要素があるのか... 電車の広告で見た中学入試問題かなにか。
「11から20までの整数のうち、連続する自然数の和では表せない
ものをすべてあげなさい。」
うまい解き方あるのかな?奇数が連続する2つの自然数の和に
なることはほとんど自明だから、偶数だけチェックすればいいけど。
自作問題:素数が3つ以上の連続する自然数の和では表せないことを示せ。 >>846
有名どこでは
nがa〜bの和なら2n=(b+a)(b-a+1)より2nは2べきでなくnも2べきでない。
逆にnが2べきでないなら2nも2べきでなく2n=xy、x>y、x、yの奇遇がことなるを満たすものがとれてnはa=(x-y+1)/2〜
b=(x+y-1)/2の和になるってのがあるね。 1+2+3+4+5+6=21を眺めて
20,18,14も候補から外れるな >>849
2+3+4+5=14
3+4+5=12 2×20=5×8
(8+5-1)/2=6
(8-5+1)/2=2
20=2+3+4+5+6 リストアップなら10まで考えないとダメだね。
1〜:3 6 10 15 21 28 35 45 55
2〜: 5 9 14 20 27 34 44 54
3〜: 7 12 18 25 32 42 52
4〜: 9 15 22 29 39 49
5〜: 11 18 25 35 45
6〜: 13 20 30 40
7〜: 14 24 34
8〜: 17 27
9〜: 19
出てこないのは1,2,4,8,16。 2個以上の連続した自然数の和Sは、
その個数が奇数の場合、個数をa、真ん中の数をbとしてS=abと表され、
個数が偶数の場合、個数を2b、真ん中の2つの数の和をaとしてS=abと表される。
いずれの場合もaは3以上の奇数。よって、Sは必ず3以上の奇数を約数として持つ。
(すなわち、2以外の素因数を持つ)
逆に、Sが3以上の奇数の約数aを持っていれば、S=abと分解した上で、
そのa,bを用いて上記2通りのアプローチで少なくとも連続した2個以上の
「整数」の和で表すことができる。
そして、それが2個以上の「自然数」の和となる条件を調べると、
2つのアプローチの片方が必ず実現可能であることがわかる。
よって、Sが2個以上の連続した自然数の和で表されるための必要十分条件は
Sが2以外の素因数を持つこと。 ホモロジー群が同型だがホモトピー型が異なる幾何学的実現をもつ単体的複体の例を教えて下さい (X,O)を位相空間
opをこの空間の開核作用素
clをこの空間の閉包作用素
とし、op,clをP(X)からP(X)への写像とみなす。(P(X)はXの巾集合)
この写像の合成についてなりたつ式って何でしたっけ?
op・cl・op = op だったっけ?
op・cl・op・cl = op・cl だったっけ? >>857
上はダメ
反例R\{0}わ。
下は言える。
閉集合 F に対し ici F= i F が言えれば良い。
ci F ⊂ F ゆえ ici F ⊂ i F。
i F ⊂ ci F ゆえ i F ⊂ ici F。 サンクス
じゃあ同様の議論で
cl・op・cl・op = cl・op も言えそうだな F(x)=∫(x→x+1)te^(-|t|)dtについて、xがすべての実数を動くとき、F(x)が最大および最小となるxの値をそれぞれ求めよ。
詳しい解答解説お願いします。 >>860
絶対値外して部分積分
そんなこともできないのかゴミ野郎w >>860
x≦-1 のとき
F(x) = exp(x){(e-1)x +1} < 0,
x≧0 のとき
F(x) = exp(-x-1){(e-1)x +(e-2)} > 0,
-1≦x≦0 のとき
F(x) = ∫[x,0] t・exp(t) dt + ∫[0,x+1] t・exp(-t) dt
= {(1-x)exp(x) - 1} + {1 - (2+x)exp(-x-1)}
= (1-x)exp(x) - (2+x)exp(-x-1),
F(-1/2) = 0,
点(-1/2,0) について対称
F '(x) = (x+1)exp(-|x+1|) - x・exp(-|x|) = 0,
より
x = -e/(e-1) で最小 { F(x) = -(e-1)exp(-e/(e-1)) }
x = 1/(e-1) で最大 { F(x) = (e-1)exp(-e/(e-1)) } 距離空間(X, d)について質問です。
A, B⊂Xについて
δ(A∪B)≦d(A, B)+δ(A)+δ(B)
であることの証明が考えつきません。
どなたかお教えいただければ幸いです。
なお、A, B⊂Xに対して
δ(A)=sup{d(x, y)|x, y∈A}
d(A, B)=inf{d(x, y)|x∈A, y∈B} 距離空間(X, d)について質問です。
A, B⊂Xについて
δ(A∪B)≦d(A, B)+δ(A)+δ(B)
であることの証明が考えつきません。
どなたかお教えいただければ幸いです。
なお、A, B⊂Xに対して
δ(A)=sup{d(x, y)|x, y∈A}
d(A, B)=inf{d(x, y)|x∈A, y∈B} >>847
ひぇー、即答ですね。確かにその通りですね。恐れ入りました。 >>867
a_1∈A, b_1∈B s.t. δ(A∪B) = d(a_1, b_1)
a_0∈A, b_0∈B s.t. d(A, B) = d(a_0, b_0)
となっているとする。
三角不等式より
d(A∪B) = d(a_1, b_1) ≦ d(a_1, a_0) + d(a0, b_1)
≦ d(a_1, a_0) + d(a_0, b_0) + d(b_0, b1)
≦ δ(A) + d(A, B) + δ(B)
(最後の不等号はδの定義より) >>854
これまたお見事ですね。
初等的に導かれて面白い問題ですが、知る人ぞ知る問題なのかな。 >>867
a_1∈A, b_1∈B s.t. δ(A∪B) = d(a_1, b_1)
a_0∈A, b_0∈B s.t. d(A, B) = d(a_0, b_0)
となっているとする。
三角不等式より
d(A∪B) = d(a_1, b_1) ≦ d(a_1, a_0) + d(a_0, b_1)
≦ d(a_1, a_0) + d(a_0, b_0) + d(b_0, b_1)
≦ δ(A) + d(A, B) + δ(B)
(最後の不等号はδの定義より) >>867
A, Bが開集合ならa_i∈A, b_j∈Bとするとまずい。
sup, infなので。 >>872
δ(A∪B)=d(a_1, b_1)
d(A, B)=d(a_0, b_0)
となるa_0, a_1∈A, b_0, b_1∈Bの存在があやふやですよね。
これでは証明になっていないと思います。 >>873
存在があやふやだと?どこまで自分の頭で考えたんだ?
A, Bが開のときは、それらは、 Xに対するA, Bの補集合の元。 問題というか質問なんですが
統計学でt検定ってデータでいうと1変数じゃないですか?
n変数(次元)のデータに対して各クラスに有意差があるないってどういうふうに検定したらいいですか? >>874
つまりA, Bの元でないこともあるってことですよね笑 >>867
d(A,B)の定義より
∀(ε>0) ∃(x'∈A, y'∈B) d(x', y') < d(A,B) + ε
(1)∀(x∈A, y∈B) d(x,y)≦ d(x,x')+d(x',y')+d(y',y) < δ(A)+δ(B)+d(A, B) + ε
δ(A),δ(B)の定義より
(2)∀(x,y ∈A) d(x,y)≦ δ(A) ≦ δ(A)+δ(B)+d(A, B)
(3)∀(x,y ∈B) d(x,y)≦ δ(B) ≦ δ(A)+δ(B)+d(A, B)
(1)-(3)より
(4)∀(x,y ∈A∪B) d(x,y) < δ(A)+δ(B)+d(A, B) + ε
δ(A∪B) の定義より
(5) ∀(ε'>0) ∃(x'',y'' ∈A∪B) δ(A∪B) - ε' < d(x'',y'')
(4),(5)より
∀(ε, ε'>0) δ(A∪B) - ε' < δ(A)+δ(B)+d(A, B) + ε
∴ δ(A∪B) ≦ δ(A)+δ(B)+d(A, B) >>838
(左)
AB = c とおく。
第二余弦定理より
1-cosα = {aa-(b-c)^2} /2bc = (a-b+c)(a+b-c)/2bc,
1-cosβ = {bb-(c-a)^2} /2ac = (b+c-a)(a+b-c)/2ac,
より
aa(1-cosβ) - bb(1-cosα)
= aa{1 - (cc+aa-bb)/2ac} - bb{1 - (bb+cc-aa)/2bc}
= {a(b+c-a) - b(a-b+c)}(a+b-c) /2c
= (b-a)(a+b-c)^2 /2c
> 0, (← b-a>0)
また、
1-cosβ > 1-cosα,
cosβ < cosα,
β > α,
(右)
sin(x) は 0<x<π で上に凸だから
sin(α/2) > (1-α/β)sin(0) + (α/β)sin(β/2) = (α/β)sin(β/2),
(1-cosβ)/(1-cosα) = {sin(β/2)/sin(α/2)}^2 < (β/α)^2, >>877
昨日この質問をした者です。
納得できました。
本当にありがとうございます。 >>838 >>878
0 < (b-a)/2R (← 題意)
= sinβ - sinα (← 正弦定理)
= 2sin((β-α)/2)cos((α+β)/2) (← 和積公式)
ここで 0 < (α+β)/2 < π/2 だから
sin((β-α)/2) > 0,
β > α, >>881
非自明な結び目(e.g. trefoil knot)の管状近傍を用意してS^3からくり抜いたものをMとおく。
∂M上のループlでそのMでのホモロジー類が0であるものをとる。
lとちょうど一個共有点を持つループをmとおく。
整数i(i≠0)を選びホモロジー類がm+|iであるループxを選ぶ。
xの帯状近傍に沿ってD^2×Iの側面∂D^2×Iを貼り付けたものをNとおく。
∂NはS^2なのでここにS^3を貼り付けたものをXとおく。
Xはホモロジー3球面になる。
証明はXの基本群をVan Kampen's theoremで計算する。 a^2+b^2=n
a^3+b^3=m
の時aとbを求めなさい この問題簡単そうでかなり計算が手こずり、ab
の 4次方程式と三次方程式の連立方程式になり、最終的に二次方程式として解けるようなのですが、うまくいきませんどなたかご教授お願いします a=b=n=m
そもそも実数だか整数だかの条件が無い 自然数を添え字とする開集合列(A_{n,m})に対して、
∪_n ∩_m A_(n,m) は開集合となるか?
よろしくお願いします。
(個人的には上手な足し合わせによって開集合になりそうな気がするんだけどな) 何のヒントにもなってない。4数とも実部虚部ともにゼロではない、とかの意味か? clを閉包作用素、
(Un),(Vm)は自然数n,mを添え字とする開集合の列
とする時、
∪_n Un \ ∪_m cl(Vm)
∪_m Vm \ ∪_n cl(Un)
は適切な和の取り方によって同時に開集合と出来ますか? すいませんa,b,をm,nの式で表せだったら大丈夫でしょうか >>885
(1) a^2+b^2= (a+b)^2 - 2ab = n
(2) a^3+b^3 = (a+b)^3 - 3(a+b)ab = m
より ab を消去
(a+b)^3 - 3(a+b)((a+b)^2 - n)/2 = m
∴ (a+b)^3 - 3n(a+b) + 2m = 0
これを (a+b)についての3次方程式として解き, (1) から ab の値を得る.
後は 2次方程式 x^2 - (a+b)x + ab = 0 を解けば (a, b) が求まる. >>885
常套的な方法で、対称式 x=a+b、y=ab とおいてx、y の連立方程式を導き、それから2次方程式を解く、かな?
具体的には
a^2+b^2=n から x^2-2y=n
a^3+b^3=m から x(n-y)=m
この2式から y を消せば x の3次方程式 x^3-3nx+2m=0 が得られるので、それを解けばよい。 ヤンミルズ方程式と質量ギャップ問題ってどうやって解けば良いの? Wolframに入れたかが答が理解できなかった
Solve[{a^2+b^2==n,a^3+b^3==m},{a,b}] >>894 >>895
(a+b)^3 -3n(a+b) +2m = 0,
の根は
a+b = 2(√n)cosθ,
ここに cos(3θ) = -m/{n^(3/2)}
(*) 本問では n^3 - mm = (3aa-2ab+3bb)(ab)^2 > 0, > a+b = 2(√n)cosθ,
> ここに cos(3θ) = -m/{n^(3/2)}
>
a bは複素数らしいけどね。
まぁだからcosθの値域についてますます気にする必要ないんだけど。 >>898
https://i.imgur.com/VUu8EPe.jpg
答えに出てくる
Root[f, i] は方程式fのi次の根、f(x)=0のi番めの解を意味している。
で、& は無名の関数を作る記号で #1 ってのは関数の1番めの引数
(この文中の「#」は#じゃないけど#みたいな記号の意)
つまり Root[2#1^6-3#1^4n-2#1^3m+3#1^2n^2+m^2-n^3 &,1] は
方程式 2x^6 -3x^4n-2x^3m+3x^2n^2+m^2-n^3=0 の1番めの解 >>894 >>895
mm-n^3≧0 のときは
x^3 -3nx +2m = 0,
の根は
a+b = - [m +√(mm-n^3)]^{1/3} - [m - √(mm-n^3)]^{1/3}, すみません。厳密には数学の問題なのか分からないんですが、教えていただけると幸いです。
ある物理量Pに関してp1,p2,p3,・・・が与えられた時、p1でp2,p3,・・・を無次元化することを考える。
単純にp1で除せばいいのかと思いましたが、p1とp2,p3,・・・ではp1だけ符号が異なっているとします。
この場合、無次元化して正の数で表したい場合はどうすればよいのでしょうか?
説明が下手で申し訳ないです。数学なのかも怪しいですが、どなたか教えていただける方がおりましたらどうかよろしくお願いします。 何故それが数学だと思うのか不思議でならんが、単純に絶対値とったらあかんの? 塾で一度だけ担当してくれた先生が
連続ってどういうこと?ときいてきたのでつながっている事と答えたら
それはれん○○??の事だと言っていたのですが
何と言っていたか思い出せないのですが何かそういう言葉はありますか?
連続は近づいていけることだと言っていました 点Oを中心とする半径1の円上に、定点A,Bがある。ABはこの円の直径である。
この円周上を相異なる2つの点P,Qが、PQ=1となるように動く。
(1)PQ⊥ABのとき、PAの長さを求めなさい。ただしPA≦PBとします。
(2)A,P,B,Qをこの順に結んで出来る図形が凸四角形であるとき、その面積の最大値を求めなさい。凸四角形とは、へこんでいない四角形を指します。 ∫sinx cosx dx を部分積分で求めようとしてわけわからなくなってしまいました
どこがおかしいですか?
https://i.imgur.com/r0tQ20D.jpg (1) |PA| = 2 sin(π/12) = 2 √{ (1 - cos(π/6))/2 } = √{ ( 4 - 2√3 )/2 } = (√3 - 1) / √2
(2) Aは円孤AQ上にある. ∠ABP = ∠AOP / 2 , ∠ABQ = ∠AOQ / 2 , ∠AOP + ∠AOQ = π/3
面積[APBQ] = (1/2)*2cos(∠ABP)*2sin(∠ABP) + (1/2)*2cos(∠ABQ)*2sin(∠ABQ)
= sin(∠AOP) + sin(π/3 - ∠AOP) = 2 sin(π/6) cos( ∠AOP - π/6 ) = cos( ∠AOP - π/6 )
(1)と同じ配置 ∠AOP=π/6 にて 最大値 1 となる
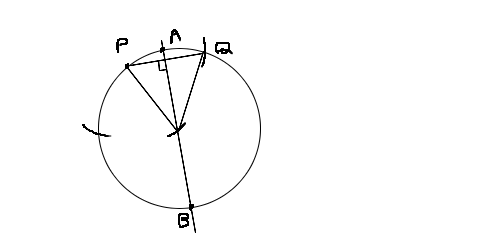 x Aは円孤AQ上にある
x Aは円孤AQ上にある
o Aは円孤PQ上にある >911
不定積分だとしたら定数(例えば C) を追加したほうがいいでしょう。
∫ sin(x)cos(x) dx = -cos(x)^2 /2 + C
∫ sin(x)cos(x) dx = sin(x)^2 /2 + C’
どちらでもよいのです。sin(x)^2 = - cos(x)^2 + 1 ですので、定数の差が 1 だけズレているだけですね。
定積分ならその差は結果に影響しません。 >>914
あーーなるほど!ありがとうございました ∫fdx=Sとおいてしまいたいけど、Sには積分定数分の不定性が残っていて
Sが一意に定まらないからこういう置き方はしちゃダメってことなのね。
これで 0=1 の証明をされたら間違い箇所を訂正するのに苦労しそう。 logを含む関数でCによって式の形が全然違って見えるので前痛い目にあったんですが
完全に忘れてましたwポンコツですね…… logの時とは全然違うかと。
∫sinxcosx dx = S(x) とおくと
S(x) = -cosx cosx - ∫(-cosx)(-sinx)dx
= -(cosx)^2 - S(x)
よって
2S(x) = -(cosx)^2 …(1)
また
S(x) = sinx sinx - ∫(sinx)(cosx)dx
= (sin x)^2 - S(x)
よって
2S(x) = (sinx)^2 …(2)
(2)-(1)より
0 = (sinx)^2 + (cosx)^2 = 1
よって
0=1 が証明された。
さて、どこが間違っているのでしょうか。 >>918
logも関数の形によっては原始関数の表現を結構いじれますよね。同じ話だと思います。 やっぱり本格的に数学を勉強したいなら、プリンストン大学かケンブリッジ大学のトリニティ・カレッジに入るべきなんですかね・・・? 部分空間の次元が無限である線形空間の次元が無限になることの証明と,可換群の定義のうち結合則のみを満たさないような例(の存在)が分かりません。 >部分空間の次元が無限である線形空間の次元が無限になることの証明
無限次元部分空間 S ⊂ X で, 線形空間 X は有限次元 (n次元) と仮定します.
Xの基底を {e_1, e_2, ..., e_n} と置きます.
Sの基底集合から n + 1 個選択して { g_1, ...., g_[n+1] }
それぞれをX基底で展開します. g_j = Σ[i=1,n] a[i , j ] e_i
g_j [k=1...n+1] が一次独立なので、「係数行列 a[i , j] の列は一次独立」です.
しかし a[i,j] は (n,n+1)型の行列なので、それは不可能です。(∵ 例えば左基本変形による掃き出し法)
矛盾が示せたので、Xの次元は無限です. >>909
ありがとうございます
連結で調べてみたのですが集合で使う言葉なのか難しそうですね
高校の微分とか積分で連結って重要ですか? >>925
連結じゃないと中間値の定理が使えないけど高校数学では(多分)区間上の関数しか考えてないから知らなくても問題ないと思います どうして a/b ∻ c/d = ad/bc なの 教えて〜 レス数が900を超えています。1000を超えると表示できなくなるよ。
