������Ȃ����͂����ɏ����Ă�453
���X����950���Ă��܂��B1000����Ə������݂��ł��Ȃ��Ȃ�܂��B
�����A�������P������낤����
�O�X��
������Ȃ����͂����ɏ����Ă�452
http://rio2016.5ch.net/test/read.cgi/math/1555080760/
(�g�p�ςł�: 478) >>835
�@��������Ȃ��Ă������Ȃ�
���s�� AD�ABC �̊Ԋu���P�Ƃ���B
A (cot(48�), 1)
B (0, 0)
C (cot(48�)+cot(54�), 0)
D (cot(30�), 1)
cot(48�) = ��{2 + (5+2��5) -2(��3)��(5+2��5)}
cot(54�) = tan(36�) = ��(5-2��5)
cot(30�) = tan(60�) = ��3,
���
�@cot(30�) - cot(48�) - cot(54�)
= ��{2 + (5-2��5) -2(��3)��(5-2��5)}
= cot(84�)
��BCD = 96�
��ACD = 42� �O>>845���͂ł����B
6��[0�`1]{��[��(t-t^2/4)�`��3/2](1-t-��(1-x^2)dx+��[��3/2�`��3-t��3/2](1-t-x/��3)dx}dt
sin��=��(t-t^2/4),cos��=1-t/2�Ƃ����ƁA�����O�������o���ق��������ȁA�Ǝv���Ă���B �O>>852
���l�ʑ�PABC��z=t�Ő����f�ʂ́A�J�����̒��S�p��2�ƂƂ��āA
3��3(2-t/2)^2-1+3��-3sin2��
0��t��1�̂Ƃ�0���Ɓ���/3
�~���ł���ʂ��Ďc�����K���̑̐ς́A
��3��3(2-t/2)^2-1+3��-3sin2��d��dt[��=0�`��/3][t=0�`1] ���܂ł���Ă�����
30������Ώ\���Ȗ�肾�� ������P(z; 1)=�[n=0,��](1/2 C n)(z - 1)^n
��|z|=1�̎����~����̓_�𒆐S�Ƃ���e�C���[�W�J�����Ăǂ��Ȃ�̂ł��傤�� �O>>853
���l�ʑ�PABC��z=t�Ő����f�ʂ́A�J�����̒��S�p��2�ƂƂ��āA
3��3(2-t/2)^2-1+3��-3sin2��
0��t��1�̂Ƃ�0���Ɓ���/3
�~���ł���ʂ��Ďc�����K���̑̐ς́A
��3��3(2-t/2)^2-1+3��-3sin2��d��dt[��=0�`��/3][t=0�`1]
t=2(1-cos��)
��3��3{2-(1-cos��)}^2-1+3��-3sin2��d��[��=0�`��/3]
��3��3(1+cos��)^2-1+3��-3sin2��d��[��=0�`��/3]
=��3��3(1+2cos��+cos^2��)-1+3��-3sin2��d��[��=0�`��/3]
=��3��3(��+2sin��+��/2+sin2��/4)-1+3��-3sin2��d��[��=0�`��/3]
=3��3{��/3+2sin(��/3)+(��/3)/2+sin2(��/3)/4)-1+3(��/3)-3sin2(��/3)}
=3��3(��/3+��3+��/6+1/2)-1+��-3��3/2
=3��3(��/2+��3+1/2)-1+��-3��3/2
=3��3��/2+9+3��3/2-1+��-3��3/2
=(1+3��3/2)��+8
�v�Z�ԈႦ�����ȁH >>856 �����ƒP���ɍs���܂��傤��....
�~���������Ď�肷���������̑̐�(�O�������Č����Ă�����ȁH) �Ȃ�
������ȕ��j�ŋ��߂��܂�.
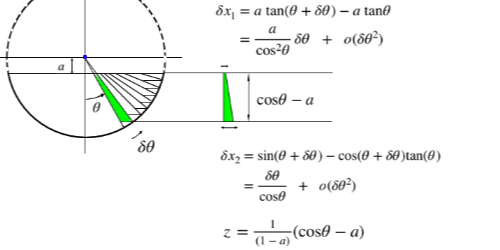
���a1����1�̉~�����ߐؒf�������̂̑̐� V �����߂���.
��ӂ̐ؒf�ʒu�� a , cos(��) = a �Ƃ��� c = cos�� �Ɨ��L����
V(a) = �� [��= -�� �` +��] d�� { (1/2).(a/cc) + (1/3).(1/c - a/cc) } (c-a)^2 . 1/(1-a)
= �� [��= -�� �` +��] d�� (a + 2c)(cc -2ac +aa) /6cc. 1/(1-a)
= �� [��= -�� �` +��] d�� ( 2c -3a +aaa/cc ) /6 . 1/(1-a)
= { 2.sin�� -3a.�� +aaa.tan�� } / {3(1-a)}
= { (2+aa)��(1-aa) - 3a.acos(a) } / {3(1-a)}
����� 0 �� a �� 1 �ł̏ؖ��ł����A-1 �� a < 0 �ł����̂܂ܓ��������g���܂�. (�ؖ��͗���)
�Ⴆ�� V(-1) = ��/2 ���A�������蔼���̐ςɂȂ��Ă�̂͐}�`�̑Ώ̐���������炩.
 >>853
>>853
���ǃz���g�̍ŏI�w�����ĂȂ�Ȃ�H �P]/�_______�O>>856
�Q/�_/�@�@,,���@�@/|
�P�_/�@�@�c-_-Ё@/ |
�P|�______U,��U�/| |__
�n| �a�P�P�PU~~U | / /
�Q| �a ���@�� �a |/ /
___`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P
�Ԃ������Ă������傢�l����B 2��2019���5�Ŋ������]��
�������𗘗p���Ă��肢���܂� 2^2 = 4 �� -1 (mod 5)
2^(2*1009 + 1) = (2^2)^1009 * 2 �� (-1)^1009 * 2 = -2 �� 3 (mod 5) �O>>859
����1�̒P�ʉ~��(�̐σ�)�̒��S�p120���̐ؓ��O�����`�����O�����`��(�̐ς͂킩��)��1/2�Ȃ̂�2/3�Ȃ̂��A���l�ʑ�PABC�̒��ƊO�ł�����ɕ�������̂��B�������琄�肷��B �O>>862����Ɖ������B
���l�ʑ�PABC=1/3�3��3�2
=2��3
���l�ʑ�PABC��z=1����̕���(���l�ʑ�PABC��1/8)���o���A
2��3(7/8)=7��3/4
x^2+y^2��1��0��z��1�̉~��(�̐σ�)�����̐��O�p�����o���A
7��3/4-3��3/4=��3
���߂闧�̂̑̐�=��3-(��-3��3/4)(2/3)
=3��3/2-2��/3
=0.503681109�c�c >>842 >>846
�� - T[n] = (6/��)��[k=n+1 to ��] 1/kk
�@= 2(6/��){1/(2n+1) - 1/[3�(2n+1)^3] + 7/[15�(2n+1)^5] - 31/[21�(2n+1)^7] + ����}
�� - S[n] = 4��[k=n+1 to ��] {(-1)^(k-1)} /(2k-1)
�@= (-1)^n {1/n - 1/(4�n^3) + 5/(16�n^5) - 61/(64�n^7) + ���� }
���`�ށA������ ������I�C���[�}�N���[������1/n�œW�J�ł�����āB >>853 >>856
�@z = t�@�@�@�@(�� ���Ӗ�?)
�@������ (2-t)/2,
�@���̖ʐ� (3��3){(2-t)/2}^2,
�@�J�����̎O�p�`�̖ʐς́@cos��sin�� = (1/4)(2-t)��{t(4-t)},
�@����ȊO�̐�`�̖ʐς́A���S�p�̔����ŁA��/3 - �� = ��/3 - arccos((2-t)/2),
�@���`�R�̖ʐς�
�@�@(3��3){(2-t)/2}^2 - 3cos��sin�� - ��+ 3��
�@= (3��3){(2-t)/2}^2 - (3/4)(2-t)��{t(4-t)} - �� + 3arccos((2-t)/2),
����� 0<t<1 �Őϕ����� 4��3 - 2�� �O>>864
>>865�ɂ��ĉ�����܂��B
���l�ʑ�PABC(�̐�2��3)����A
���l�ʑ�PABC��z=1����̕���(���l�ʑ�PABC��1/8)���o���A
2��3(7/8)=7��3/4
x^2+y^2��1��0��z��1�̉~��(�̐σ�)�����̐��O�p��(3��3/4)���o���A
7��3/4-3��3/4=��3
�����܂ł��Ɛ��l�ʑ̓������i�C�t�Ő�o�����݂����ȏ�ԂȂ킯�ł��B
�������炳��Ƀ������̒��̉ʓ����X�v�[���ł��킰���Ƃ��݂����ɐ�o���Ȃ��ƁB
�͍���1�̉~���ł��B
3��3/4�͍���1�̐��O�p���ł��B
���߂闧�̂̑̐�=��3-(��-3��3/4)(2/3) ��2/3�Ƃ����͎̂O�����`���̓������o��������ł��B
�O�����`�����A���l�ʑ�PABC�̎߂̑��ʂ��A�����ƊO����2:1�ɕ������ł��B
���S�p��120���Ȃ�ŎO�����`�Ƃ��������g�`�ł��B
=3��3/2-2��/3
=0.503681109�c�c
����(2/3)�̔䗦�ɋC�Â��̂Ɏ��Ԃ�������܂����B
xy���ʂ�z=1���ʂ��O�����`���̏��Ɖ���͍����Ȋ��g�`�ł��B���l�ʑ�PABC�̑��ʂŎ߂ɐ����Ƃ��A�������ɂ͈�_�Ɏ������Ă����`�ł����A������ɂ͒����Ɏ������Ă����A���Ȃ킿���[�̓�_�ɁB
�����2:1�̔䗦�ɂȂ邱�Ƃ������ł��܂����B
>>868z=t���ʂŐ��Đϕ�����������d��(���͂�)���@��������Ȃ��Ǝv������ł����A��蒼���I�Ŋw�I�ȁA�������̐�o���̂悤�ȕ��@�ɕύX���܂����B
z=t�Ő�����œ����l���o���Ƃ́A����ς�0.6�c�c�������Ȃ̂��B ��������ł͂Ȃ��ďؖ������ĉ������B
����1:2�ɂȂ�́H �O>>869�ł����g�͎߂ɐ�ق����������āc�c
�Q/�Q/�Q/�Q/�Q/�Q/�Q/
�Q/�Q/�Q/�Q/�Q/�Q/�Q/
�Q/�Q/�Q/�Q/�Q��_/�Q/
�Q/_��~_/�Q�������̤/
�a�P�P�a�a( (-(`)�@)/
�a�_�^�a�a(`��,U�܁R/
�Q/�Q/�Q/_��_(�Q�Q�Q)
�Q/�Q/�Q/�Q�҃�_UU�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/ �ؒf�ʂ��߂�^���ɃX�p�b�Ɛ�ƒf�ʂɉ~�A�ȉ~�������Ėʓ|�B ������Ă݂���>>842�𑶍݂��Ȃ���ˁH
p<1����0�ɂȂ���p��1���ƐU��������B >>869
2:1 ���]�X�Ƃ���̂� ���g�ߐ肪���g���ɂȂ��Ă�Ǝv���� �u��� * ���� * (1/3)�v ���g���܂����H
�������f�ʂ��S�đ����`�� ���_����̋����ɔ�Ⴕ�ăT�C�Y���ς�� (�������̓���) �ꍇ��...
�� [z=0�`h] dz S (z/h)^2 = S.h.(1/3) �̂悤�� 1/3 �t�@�N�^�[������܂��B
����̂͂����ł͂���܂���B �Ⴆ�ΐ������f�ʂ͑����`�ł͂���܂���B
>>857 �œ��o�����ߐؒf�̎��g����
V(1/2) = { (2+1/4)��(1-1/4) - (3/2). acos(1/2) } / {3(1-1/2)} = (3/4).��3 - ��/3
{�l�ʑ� - (1/2).�l�ʑ�} - {�~��} + {�~���ō�肷������}
= (1- 1/8). 2��3 - �� + 3. { (3/4).��3 - ��/3 } = 4��3 - 2��
���ꂪ�����ł��B a, b �������Ƃ��A a < b �Ƃ���B��� [a, b] �� R �ƔZ�x�����������Ƃ��ȉ��̃q���g�𗘗p���Ď����B
�q���g�F A �� (a, b) ���Z�����W���Ƃ���A A �` A �� {a, b} �͔�r�I�ȒP�Ɏ������Ƃ��ł���B���ꂩ�� (a, b) �` [a, b] ���B �uA �` A �� {a, b} �͔�r�I�ȒP�Ɏ������Ƃ��ł���v
�Ə�����Ă��܂����A�����ł͂Ȃ��̂ł��傤���H �E�ӂ͗v�f�������Ă�̂ɔZ�x���������Ȃ��Ă܂���
�����ł͂Ȃ��ł�
{1}��{1,2,3}���炩�ɔZ�x���Ⴂ�܂���
����͂Ȃ��Z�x���������Ȃ�̂ł��傤�� �Z�����W���̒�`�ł����A N �ƔZ�x���������Ƃ��ɁA�Z�����W���ƒ�`���Ă��܂��B ���A�u�����v�Ƃ������������Ă���̂ŁA�����܂ł��Ȃ����Ƃł��ˁB A = {a_0, a_1, a_2, �c }
a_0 �� a
a_1 �� b
a_2 �� a_0
�c
a_k �� a_{k-2}
�c �̈�D_0�̓����ɐ����_a_0���Ƃ�Ca_0�𒆐S�Ƃ����e�C���[�W�J����f_0(z)�Ƃ���D
f_0(z)�̎����~D_1�����S��D_0�Ɋ܂܂�Ă���ꍇ�CD_1�̋��E�̉~����D_0�̋��E�̋Ȑ��ɓ��ڂ��邱�Ƃ������D D_0={|z|<1}�Œ�`���ꂽ��1/(z-2)�̎����~��|z|=2�B >>881
�̈�D_0�� f(z) �������iD_0�ɓ��ٓ_���Ȃ��j�Ƃ��������������Ă܂�B
>>884
�@f(z) = 1/(z-2)
�@D_0 = {z| |z|<1 }
�@a_0 = 0,
�Ƃ����
�@f_0(z) = -1/2 - z/4 - zz/8 - ����
�����~ D_1 = {z| |z|=2 }
���̏ꍇ�́u�����~D_1 �����S�� D_0 �Ɋ܂܂�Ă���v�����܂���B �O>>874
>>871�~���ō�肷�����͎̂O�����`��(���g)��1/3����Ȃ��̂��H
(�~��-���O�p��)(1/3)
=(��-3��3/4)(1/3) �����~�@D_1 = {z| |z-a0|=R }
�������a�@R = {a_0 ���� f(z)�̓��ٓ_�܂ł̋���(�̍ŏ��l)} >>886
��肷�����̂� �ߐ芗�g���R�ł��B (�ΐF)
V(1/2) = (3/4).��3 - ��/3
���ꂪ�ߐ芗�g�P�̑̐ςł��B�����P�Œ��S���� 1/2 �����Y�����Ƃ�����̎ߐ�ł��B
�Ȃ̂ő������ɂ͂R�{���Ă��܂��B+3. { (3/4).��3 - ��/3 }
 �c����V�E��ؓo�u�Y ���w���w�̃��W�b�N�ƏW���_�x��ǂ�ł��܂��B
�c����V�E��ؓo�u�Y ���w���w�̃��W�b�N�ƏW���_�x��ǂ�ł��܂��B
�J���g���E�x�����V���^�C���E�V�����[�_�[�̒藝�̏ؖ��Ɏg�����1.12�ip.57�j�̏ؖ��ł����A
�v���I�Ȍ������܂����B
���̂悤�Ȋ�{�I�Ȗ���̏ؖ��Ō��Ƃ����̂��M�����܂���B
�������A�������������Ƃ��d���郍�W�b�N��W���_�̖{�ɂ����Ăł��B
���̒��҂�͈�̉����l���Ă���̂ł��傤���H >>881
>>885 �̌����悤�� �u�̈�D_0�� f(z) �������v��t���������...
f(z) = (1/2��i) ��_{C} d�� f(��) / (�� - z) ���̌������g���܂��B (�����̏ؖ��̓R�[�V�[�̐ϕ��藝���g��)
�u�����~(���aR)���̈拫�E�ɐڂ��Ă��Ȃ��v�Ȃ�
R< R' �Ȃ�l���Ƃ��āA���S a ���a R' �̎��[�g C �����̓����� D0 �Ɋ܂܂��悤�ɂł��܂��B
|z-a| < R' �ƂȂ�C�ӓ_ z �ɑ��āA
f(z) = (1/2��i) ��{C} d�� f(��) / ( (��-a) - (z-a) )
= (1/2��i) ��{C} d�� f(��) �� (��-a)^{-k-1} (z-a)^{k} �@( |z-a|/|��-a| =|z-a|/R ' < 1 ��苉���͎�������)
= �� g_k /k! (z-a)^k �@( �W�J�W��: g_k = (k!/2��i) ��{C} d�� f(��) (��-a)^{-k-1} �� z �Ɉˑ����܂���)
����͎������a �� R' �ȏ�ł��鎖���Ӗ����܂��B
����āu�����~(���aR)���̈拫�E�ɐڂ��Ă��Ȃ��v�Ƃ����O��͌��ł��B �̈�D_0�Ő����Ȃ�ĉ����Ă��_���Ȃ͖̂��炩�B
�Œ�ł���`�ł���ɑ��(���ۂɂ͂���͍ő�ɂȂ�)��D_0�ɂȂ�Ȃ�����_���B
����_�ł̎������a = ��͓I�ɐڑ��ł��Ȃ��_�ň�ԋ߂��_�܂ł̋���
���g�킹�����낤���ǂ��̂��߂ɂ�D_0�����q�ׂ��悤�ȗ̈�łȂ��Ɛ������Ȃ��B
�܂��������߂���M���M���������邯�ǁA�����
������ f �̉�͐ڑ��\�ȍő�̈悪���炩�ȋȐ��ň͂܂�Ă���ꍇ
�Ƃ����قƂ�NjN����Ȃ��悤�Ȃ��傤���Ȃ��ݒ�ɂȂ��Ă��܂��B
�ꉞ����������̓����N�����͂��邯�ǁB �Ȃ�ق�
�u�����~�� D0�̓����ɂ���v��
�u�����~(���aR)���̈拫�E�ɐڂ��Ă��Ȃ��v
�͓����ł͂Ȃ��ł��ˁB
f(z) = �� g_k /k! (z-a)^k
�� D0 ���z���Ď�������\��������܂�����ˁB �O>>886�����B
>>890
��肷�����͎̂ߐ芗�g���R��(����)�B
(��肷�����ߐ芗�g3��)
=(��-3��3/4)(1/3)
(��肷�����ߐ芗�g�P��)
=(��-3��3/4)(1/3)(1/3)
�����P�Œ��S����1/2�����Y�����Ƃ�����̎ߐ�(����)�B
�������ɂ͂R�{(����)�B
(��-3��3/4)(1/3)(1/3)3
=(��-3��3/4)(1/3)
���߂�̐�
=(2��3)(7/8)-��
+(��-��3/4)(1/3)
=(7/4)��3-��+��/3-��3/12
=(5/3)��3-(2/3)��
�H��(3/2)��3-(2/3)��
��o�������Ȃ��悤���ɐ�o�����ꍇ���傫���Ȃ����B�Ȃ����H > (��肷�����ߐ芗�g�P��)
> =(��-3��3/4)(1/3)(1/3)
> �����P�Œ��S����1/2�����Y�����Ƃ�����̎ߐ�(����)�B
�����...
V(1/2) = (3/4)��3 - ��/3
����ɂ͓��ӂ��Ă���Ȃ��̂ȁB
���Ɠ������j�Őϕ��v�Z���Ƃ͌���ǁA���Ȃ�y�ȕ�����B
�l�b�g�ɓ]�����Ă�������s���ȁH�Ǝv�������́B ���W��ԏ�̊i�q�_���A�u�C�ӂ̗����̂ɂ��Ē��_�̂������Ȃ��Ƃ���͐F���h���Ă���v�悤�ɗL�����̐F�œh��B
���̎����ׂĂ̒��_�������F�œh���Ă���悤�ȗ����̂����݂��邱�Ƃ������B �y�ɉ����Ȃ狁�߂�̈��1/6���c�ɐ���
6��[1/2,1] (2-2t)(��3t- ��(1-t^2))dt
�ł������ǂȁB ����z���g�Ɋy���Ȃ�
1/6�p�[�c�ڐϕ�����Ȃ� >>834 (��) �������������Ɗy�ł́H
�ŏI�v�Z�܂Ń��[�g�Ȃ炪�o�Ă��Ȃ��̂��������B �O>>896���g�̔䗦�͂���ς�2:1����Ȃ������B
���g3�ǂ�ł�3���ׂĂł��A���g�̒��ƊO�̑̐ϔ��n:s�Ƃ���ƁA
n:s=8:��3
�搳�O�p���䂩�琳�O�p���Ɗ��g3�̒�(���g��n/n+s)���������̐ςƁA���O�p���䂩��~���������Ĉ������������g3�̊O(���g��s/n+s)�𑫂����̐ς���v���邩��
n:s���o���B����Ōv�Z����Ƌ��߂�̐ς�0.6�c�c�ɂȂ邩������Ȃ��B �܂��D���D���͂��邪�A���Z�����炢�ɂ�点��Ȃ�arccos���g���̂����Z���ɂ͂��������n�[�h���������B
�v�Z���̂��̂�>>899�͎���
��[1/2,1]t(1-t)dt
��[1/2,1]t��(1-t^2)dt
��[/2,1]��(1-t^2)dt
�̎O�B
��Ԗڂ͊y���A�������悭�݂��1/6�����̔����A��Ԗڂ��u���Ŋy���A�O�Ԗڂ���t=sin �Ƃ̒u����m���ĂȂ��Ƌꂵ�������B
���������x�ȏ�̃��x����ڎw���Ȃ�arccos����݂��o���Ȃ��ƃ_�������ǂˁB
�~���͏c�ɐ�Ƒї̈�ɂȂ��Ċy�ɂȂ�Ƃ����̂͊o��������ꂽ���A��ꊴ�Ƃ��ďc�Ɋ��������U�߂Ă݂�̂͒�݂����Ȃ���Ǝv���Ă��B
���ɂ����𗧂��Ȃ�����www z=t�Ő�̂���ԑf�����Ǝv�����ǂˁB�ςȒu������킯�ł��Ȃ��������ł��ꔭ�ŏo�邵 ���̖��̉�@�����Ă��������Ȃ��ł��傤���H
�����ł�����炨���炭�Ԉ���������ɂȂ��Ă�̂ŁE�E�E
https://imgur.com/eqrfmk0
https://imgur.com/YtAMHeU > t=sin �Ƃ̒u����m���ĂȂ��Ƌꂵ�������B
���̌v�Z���A�Ƃ���������...
�� {t=0,x} ��(1-t^2)dt = �� ��(1-sin��^2)d{sin��} = �� cos��^2 d��
= (1/2). �� {1 + cos2��} d�� = (1/2){ �� + (1/2).sin2�� }
= (1/2){ �� + cos��sin�� } = (1/2){ asin(x) + x��(1-xx) } (���ꂾ���č��Z���ɂ͋�s�ł́H)
�܂����Z�͊y������
(1/2){ asin(x) + x��(1-xx) }�f = (1/2){ 1/��(1-xx) + ��(1-xx) - xx/��(1-xx) } = ��(1-xx)
[t=1/2, 1 ]�Ȃ� �}�`�I�ɒl���o���Ă��܂��܂��傤�B
��[1/2,1]��(1-t^2)dt = (1/2).(��/3) - (1/2).{(1/2).(��3 /2)} = ��/6 - (1/8).��3
 �O>>901
�O>>901
���l�ʑ̂��������g�̗���͂ǂ��Ȃ�H
�ނ����ɂ��B
���l�ʑ�(�̐�2��3)���������g(��-3��3/4)�̒��ƊO�̑̐ϔ䗦n:s���炵�����߂Ȃ��B �~���͏c�ɐ���ĈӊO�ɑS����̃��[������Ȃ���ww
�܂����ɂ������ɗ����Ȃ�����ˁB
���w�̏Z�l�͎��w���Ƃ��ł͋�J���Ȃ����B
�ʐςɋA�����Ēu�����Ȃ��̂��A�������ǂˁB
�������ʐςɋA���ł��Ȃ��Ƃ������邩����ɂ͒u���̕����܂��o����ƌ���ꂽ�ȁB
���͐̂̂��b�����ǁB
����Șb�����肾�Ǝ������Ă�����B >>905
��ϕ��̒u��������acos�ɖ߂��Ȃ���B
�ϕ��͈͂���/6�`��/2�ɕς��Ă��̂܂܂Ԃ����ނ����B �O>>906
���l�ʑ̂̑��ʂ̌��z��2������1:2:��5�̒��p�O�p�`�𑫂����߂��犗�g�𑤖ʂŐ����O�����o��̂��ȁH ��͐ڑ��Ƃ����܂ŕ����Ă��Ĉ�x���g�������ƂȂ����lj��ɖ𗧂́H �O>>910
��(1-t)^2��ϕ�����Ƃǂ��Ȃ�����H
�u���������Ȃ����B �O>>912�����猾�������Ȃ��B�u���Ȃ�点�邩��B1�ǂ��납3�������H �O>>914
z=t�Ő������l�ʑ̂̐����1�̖��̖ʐς��l���Ă邪�A
t=0�̂Ƃ��́A
6(��3/2-��/6)�ŁA
z=t�̂Ƃ����̒��S�̒�����1����2-t�܂�2-t-1=1-t���邯�ǁA�����z=0�̂Ƃ��̐}�`�Ƒ����ł͂Ȃ���ˁB
t=0�̂Ƃ���/6�������P�ʉ~�̒��S�p���At��������Ƃ����Ă�������B
��肪�������Ȃ�ɂ�āA���̉s�����Ȃ��Ȃ��Ė�莩�̂���肶��Ȃ��Ȃ�B�����ł͂Ȃ����̂��Ƃ݂Ȃ��Ă͂��߂��Ǝv�����B �O>>915
>>801
�l�ʑ�PABC=2��3
���̂�����0��z��1�̕����́A
2��3(7/8)=7��3/4
�����̍���1�̒P�ʉ~���������ƁA
7��3/4-��
�������������g�`�́A���l�ʑ̂̑��ʂ��O�̕����́A���ʂ̌��z��2������A
6��[0�`1/2](1/2)u�2udu
=6[0�`1/2]u^2du
=6{(1/2)^3/3}
=6(1/24)
=1/4
����𑫂��ƁA
7��3/4-��+1/4=0.63949626�c�c
�Ō�ɑ����Ƃ���Ń𗍂߂���������ł����B
����Ƃ�0��t����3/2�ŁA
�s�^�S���X�̒藝���A
(x+1/2)^2+t^2=1�ŁA
6��[0�`��3/2]x^2dx(dt/dx)
�Ƃ�����ł��傤���H
x�̈ꎟ�̍����o���ŁA��Ȃ�ł����B >>885 >>888
�u�̈�D_0 �� f(z)�������v���������Ȃ��Ƃ���B
�@D_0 ���� f(z) �̓��ٓ_(��͐ڑ��ł��Ȃ��_) z~ ������B
�@�������aR = min{ |z~-a_0|, a_0 �` ��D_0�̋���}
����������
�@|z~ - a_0| �� a_0�`��D_0 �����傫���ꍇ�� >>881 �͐������邪
�@|z~ - a_0| �� a_0�`��D_0 �����������ꍇ�� >>881 �͕s�����B �O>>917
����4��3-2�������̏ꍇ�A
2��3(7/8)-��+���g�O=4��3-2��
�����g�O=9��3/4-��
(���g�O1��=3��3/4-��/3)
2��3(7/8)-3��3/4-���g��=4��3-2��
�����g��=2��-3��3
(���g��1��=2��/3-��3)
���g(��-3��3/4)�ɑ��銄���́A
���g�O�\�\41.0040324��
���g���\�\58.9959676��
6:4�Ă��Ƃ�3:2
1:1��2:1�̂��������炢���B�Ȃ���q���䗦���B �����`ABCD�iAB<AC�j�́�A��2�������锼������L1�Ƃ���B
L1��ɓ_P���A����PC�ƑΊp��BD�i����BD�j����_�����悤�ɂƂ�B
���̂Ƃ��A�ȉ��������B
�uPC=BD�ƂȂ邽�߂̕K�v�\�������́APC��BD���������邱�Ƃł���B�v �O>>919����1�̒P�ʉ~�����ɂ��钆�S�p120���̊��g�����z��2�̐��l�ʑ̑��ʂŐ��������̑̐ς��A���̊��g��59���ɂ�����Ƃ��Ď�����B
���l�ʑ�PABC(�̐�2��3)����A
���l�ʑ�PABC��z=1����̕���(���l�ʑ�PABC��1/8)���o���A
2��3(7/8)=7��3/4
x^2+y^2��1��0��z��1�̉~��(�̐σ�)�����̐��O�p��(3��3/4)���o���A
7��3/4-3��3/4=��3
����1�̒P�ʉ~�����̊��g��3���o���A
���߂闧�̂̑̐�=��3-(��-3��3/4)(59/100)
=(1+1.77/4)��3-0.59��
=(1.4425)(1.7320508)-(0.59)(3.14159265)
=2.4984892-1.8535396
=0.6449496�c�c
��0.645 �W�� A ��̉��Z���l����B
�Ⴆ�A2�����Z�́A A^2 ���� A �ւ̊��ł��B
�萔�́A A^1 ���� A �ւ̊��Ȃ̂��Ǝv������A A^0 ���� A �ւ̊��ł���Ə����Ă���܂����B
�Ȃ��ł��傤���H >>923
�ǂ��������Ƃł��傤���H
���������A2�����Z��3�����Z�ƍl���邱�Ƃ��ł��܂��ˁB (Q, 0, +, <) �� (Q^+, 1, �~, <) �͓��^���ۂ��H R_0 := ��
R_{n+1} := P(R_n)
�� R_n ���`����B�������AP(A) �͏W�� A �̂��ׂĂ̕����W���̏W����\���B
R_�� := ��_{n �� N} R_n
�Ƃ���B
R_�� �͋A�[�I�ł��邱�Ƃ������B >>929
���̖��̕W���I�ȉ͂ǂ�Ȋ����ł��傤���H
�F
(1)
�� �� {��} = R_1 �� R_��
(2)
���ɁA���w�I�A�[�@�ɂ��A���ׂĂ̎��R�� n �ɑ��āA
R_n �� R_{n+1}
�����藧���Ƃ��ȉ��Ŏ����F
R_0 = �� �� R_1
R_k �� R_{k+1} �Ɖ��肷��B
x �� R_{k+1} �Ƃ���B
x �� R_k �� R_{k+1}
�� x �� R_{k+2}
����āA R_{k+1} �� R_{k+2} �����藧�B
x �� R_�� �Ƃ���B
x �� R_n �ƂȂ� 1 �ȏ�̎��R�� n �����݂���B
{x} �� R_n �ł���B
x �� R_{n-1} �� R_n �ł���B
�� x �� {x} �� R_n
�� x �� {x} �� R_{n+1} �� R_��
�ȏォ��A R_�� �͋A�[�I�ł���B
x �� {x} �� R_{n-1} �O>>921
>>829���킩��Ȃ��B
r���Ȃɂ�\���Ă邩���킩��Ȃ���ł���B
r�Ƃʼn~�ʂ̒�����\���Ƃ�����A
(�~�ʂ̒����~����)(1/2)�Œ��p�O�p�`�̊��Ƃ݂����Ȗʐς��o��̂��ȁH
0��r��1��0���Ɓ���/3�Őϕ�����6�{����̂Ɠ������Ȃ��H >>933 ���܂莩�M�Ȃ����ǎQ�l�܂ł�
�F�� c1, c2, ... , c6 �Ə����Â��ċ�ʂ���
(1) �܂� c1 �őO�ʂ�h��A�w�ʂ̐F�͂T�F�̑I�����\ (�~ 5)
�c��S�F�̒��ň�� �Ⴂ���Ԃ̐F�� ��ʂ�h��
�c��3�ʂ̓h����͂��ꂼ��قȂ�h����ƂȂ� (�~ 3! )
�v: 5 * 3! = 30 �ʂ�
(2) 5�F��6�ʂ�h��̂ŁA����F�ɂ��Ă� 2�ʂŏd���h��ƂȂ� (�~ 5)
�d���F�őS��/�w�ʂ�h��
�c��S�F�̒��ň�� �Ⴂ���Ԃ̐F�� ��ʂ�h��
���ʂ̓h����c��3�F����I������ (�~ 3)
�c��2�ʂ̓h����͉�]�Ώ̂ɂ�蓯�l�ƂȂ�
�v: 5 * 3 = 15 �ʂ�
(3) �h������ɂ�� 3�ʈȏ�ł̏d���F�͂��肦�Ȃ�
4�F��6�ʂ�h��̂ŁA����Q�F���Ă��ꂼ��Q�ʂł̏d���h�肪�������� (�~ C{4,2})
���̓��ŎႢ���Ԃ̐F�� �O/�w�ʂɁA�c��� ��/���ʂɓh��
�c��2�ʂ̓h����͉�]�Ώ̂ɂ�蓯�l�ƂȂ�
�v: C{4,2} = 6 �ʂ� >>932
>>829��
��ʂ̖ʐό`���~����
���ʂŖʐϕ�����Ƒ̐ς��o��Ƃ�����w�̋��{���w���x�����킩��Ȃ��Ɨ����ł��Ȃ��B
��1)
��(1-r^2)rdrd�� ��0��r��1�A-���Ɓ��Őϕ�����Ɣ��a1�̔����̑̐ςƂȂ�A0��r��1/2�A-���Ɓ��Őϕ�����Ƃ��̂�����ʂ̔��a��1/2�̉~���Ɋ܂܂�镔���̑̐ςɂȂ�B
��2)
(1-r)rdrd�� ��0��r��1�A-���Ɓ��Őϕ�����Ɣ��a1�A����1�̉~���̑̐ςƂȂ�B >>935�ǂ������肪�Ƃ��B�ϐ���2�ł������Ȗʐς𑫂��W�߂�����Ǝv������ł����B�O>>932�����ɂ�������Ȃ���肾�Ƃ킩��܂����B �N�ԂQ�O�O���~����̃X�^�[�g�ŔN�R�O���~�̏����Ɣ��N���ƂɂP�O���~�̏����ł͌�҂̕������B
�i���j
�N�R�O���~�̏����̏ꍇ�A���N��̏����z�́A�R�O�����~�B
���N�łP�O���~���̏����̏ꍇ�A����ڂ̏����͂P�O�����~�B�N�ԂQ��̏���������P�N�ł́A�P�O���{�P�O�i���{�P�j���Q�O��+�P�O���~�B
��+�P=�Q���Ȃ̂ŁA���N���Ƃ̏����̂��N�ڂ̏����́A�Q�O�i�Q���|�P�j+�P�O���S�O���\�P�O���~�B
��ҁ\�O�҂͂P�O���|�P�O���~�Ȃ̂ŁA���Ǔ��z�ƂȂ�̂͂P�N�ڂ����ŁA���̌�́A���N�ɂP��̏����̕����A�����͑傫���Ȃ邱�Ƃ�������B
���N���Ƃ�10�������̌v�Z�����������Ǝv���̂ł����A���̌��͍����Ă܂��ł��傤���H
�܂��A���N���Ƃɋ��^���x������Ƃ����O��ł��Ȃ�����O�҂̕����L���ɂȂ�Ǝv���̂ł����ǂ��ł��傤���H
��������낵�����肢�������܂��B �܂����o�I�ɂ͔����ȑ̐ϑ������킹��Ƃ��������ōs���Ȃ��͂Ȃ��B
>>935�̗�2�Ȃ�rdrd�Ƃ���ʐρB
��r�A���Ƃ���r�ƃƂ��ω����������ar+��r�A���S�p���Ƃ̐�^���甼�ar�A���S�p���Ƃ̐�^���ʂ������̂��ʂƂ���ƁA���̒�ʐς�r��r���ƁB
���̒n�_�ł̉~���̑��ʂ܂ł̍�����1-r������A���̒��̑̐ς�(1-r)r��r���ƁB����𑫂����킹��Ɖ~���̑̐ρB
�Ń�r���Ƃ�drd�ƂƓǂݑւ���>>935�͈͓̔��Őϕ�����B
�܂�r�Őϕ������
��[0,1](1-r)rdr = 1/6�B
������ƂŐϕ�����
��[-��,��] 1/6d�� = ��/3
�ƂȂ��ʐρ~������3 �Ɉ�v����B
���̒��x�̗����łقڎ��p��͖��Ȃ��B
���̕��@�Ŏl�p���Ƃ��F�X����Ă݂Ď��یv�Z�̊������킩���Ă��炿���Ƃ������_������Ă݂�̂��A���B a,b,c,x,y,z�͑S�Đ��̎����Ƃ��āAxyz=1�Ƃ���B���̂Ƃ�
(ax^2+bx+c)(ay^2+by+c)(az^2+bz+c) ��(a+b+c)^3�@�@������
��� ���W���ʏ��(0,0),(1,0),(1,1),(0,1)�_�Ƃ��鐳���`S������B
S�̎���܂��͓����ɁA�قȂ�2�_A(a,p),B(b,q)���Œ肳��Ă���B
S�ƍ����Ȑ����`T���AT�̎����A,B���Ƃ��ɏ��悤�ɓ������B
���̂Ƃ��AS��T�̋��ʕ����̖ʐς��ő�ƂȂ�T�̒u�������������B �O>>936
>>938���̂Ƃ���A��/3�ɂȂ�܂����B������Ă��݂����ł��B
��ʂ̒P�ʉ~�̊O��r���Ƃ�(0��r��1)�A�ʔK�̔�𑫂��W�߂�悤�ɁA���߂�̐ς�1/6�����߂��Ǝv���܂����B
r=0�̂Ƃ��A
���a1�̌ʂ̒����̓�/3
�ʔK�̔�̍�����1
�ʔK�̔�̖ʐς́A
(��/3)�1�(1/2)=��/6
r=1�̂Ƃ��A
���a2�̉~�ʂ̒�����0
�ʔK�̔�̍�����0
�ʔK�̔�̖ʐς�0
r�ɑ���A
���a1+r�̌ʂ̒����́A
���S�p��(0���Ɓ���/3)�Ƃ��āA
(1+r)��
�ʔK�̔�̍�����1-r
�ʔK�̔�̖ʐς́A
(1+r)��(1-r)(1/2)
=(1-r^2)��/2
���߂�̐ς́A
6��[r=0�`1][��=0�`��/3]{��(1-r^2)��/2}drd��
=3��(r-r^3/3)��[r=0�`1][��=0�`��/3]
=2��[��=0�`��/3]
�Ƃ͂ǂ���������̂ł��傤���H >>939
�R�[�V�[(3)���g���B
�@
Xi, Yj, Zk �� 0 �̂Ƃ�
(X1 + X2 + ���� + Xn)(Y1 + Y2 + ���� + Yn)(Z1 + Z2 + ���� + Zn) �� (G1 + G2 + ���� + Gn)^3,
�������@Gi = (XiYiZi)^(1/3).
(����1)
(����) - (�E��)
= ��[i��j] (XiYjZj + XjYiZj + XjYjZi - 3GiGjGj)
+ ��[i<j<k] (XiYjZk + XiYkZj + XjYiZk + XjYkZi + XkYiZj + XkYjZi - 6GiGjGk)
�� 0,
(����2)
�R�[�V�[(2)��2��g����
(X1 + X2 + ���� + Xn)(Y1 + Y2 + ���� + Yn)(Z1 + Z2 + ���� + Zn)(G1 + G2 + ���� + Gn)
�� (G1 + G2 + ���� + Gn)^4,
��@(XiYiZiGi)^(1/4) = Gi, >>942
�R�[�V�[=�V�����@���c�s�����̒��ԂȂ̂�...
����Ȃ̂ǂ��Œm��܂����H (����1) �ŁA �����Ȃ� �� 0 �ƕ]���ł��闝�R���m�肽�� ���R���̏W�����S�����W���ł��邱�Ƃ��Ăǂ�����ďؖ������ł����H ���A���w�I�A�[�@�ł��ˁB
���ꂪ�K�v�ł��ˁB �O>>941�C���B
���߂�̐ς́A
6��[r=0�`1][��=0�`��/3]{��(1-r^2)��/2}drd��
=3��(r-r^3/3)[r=0�`1]��[��=0�`��/3]��d��
=2���/3
=2��^2/3
�Ȃ킯�Ȃ��ł���ˁB
r��������ƃƂ͌���B
����Ⴖ��Ȃ����ƁB
�������̎��̒��Ŋ|�����킹�Ă�̂����������悤�ȁB
�O�p�`(1/2)(1+r)rcos�Ƃ����`(1+r)�Ƃ��������f�ʐ�(1/2)(1+r)rcos��-(1+r)�Ƃ�0����1�܂ő����W�߂�ق������������B
6��[r=0�`1][��=0�`��/3]{(1/2)(1+r)rcos��-(1/2)(1+r)��(1+r)}drd��
3��[r=0�`1][��=0�`��/3]{(1+r)rcos��-(1+r)��(1+r)}drd��
�ϐ���2����łȂ��B >>946
���̓��ɂȂ���Ă��Ƃ̓y�A�m������
�u�ŏ��̏������v�Ȃ��`���� >>868 �̑���
���R�̖ʐς�
�@(3��3){(2-t)/2}^2 - 3cos��sin�� - �� + 3��
= (3��3){(2-t)/2}^2 - (3/4)(2-t)��{t(4-t)} -�� + 3arccos((2-t)/2) = S(t)
����� 0�`z �Őϕ�����
��[0, z] S(t) dt = (2��3)[1 - {(2-z)/2}^3] - (1/4){z(4-z)}^(3/2) -��z -3(2-z)arccos((2-z)/2) + 3��{z(4-z)},
������ z=1 �Ƃ����� 4��3 - 2��
�~���̊e�_�̍��� h(r,��) ��ϕ������̐�3v�� V=2��3 ����������l�ƈ�v�B >>829 >>944
��̍s��
�@(XiYjZj + XjYiZj + XjYjZi)/3�@= AM�@(��������)
�@GiGjGj�@=�@GM�@(���敽��)
�@AM �� GM
���̍s�����l�B ���݂܂���A���߂Ă��̖������肢���܂��B
�����`ABCD�iAB<AD�j�̓��p��A��2��������L�Ƃ���B
L��ɓ_P���A����PC�ƑΊp��BD����_�����悤�ɂƂ�B
���̂Ƃ��A�ȉ��������B
�uPC=BD�ƂȂ邽�߂̕K�v�\�������́APC��BD���������邱�Ƃł���B�v ���X����950���Ă��܂��B1000����Ə������݂��ł��Ȃ��Ȃ�܂��B