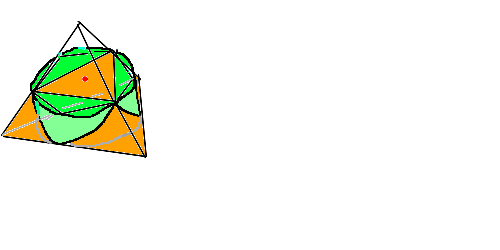������Ȃ����͂����ɏ����Ă�453
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
�����A�������P������낤����
�O�X��
������Ȃ����͂����ɏ����Ă�452
http://rio2016.5ch.net/test/read.cgi/math/1555080760/
(�g�p�ςł�: 478) �\���o��m��p(0<p<1)�̋�ʂ̂��Ȃ�2���̃R�C��������B
�i1�j����2���̃R�C����1����������B�����Ƃ������o��m�������߂�B
�i2�j����2���̃R�C���̕Е��Ƀy����A�Ə����A���������B�Ə����B���̂����ł���2���̃R�C����1����������Ƃ��A�����Ƃ������o��m�������߂�B
�i3�j�R�C����1�����ł͂Ȃ��A2�������ɓ�����ꍇ�A�i1�j�i2�j�̊m���͕ω����邩�B ��������������������������������������
������������������������������������
����������������������������������
��������������������������������
������������������������������
����������������������������
��������������������������
������������������������
����������������������
��������������������
������������������
����������������
��������������
������������
����������
��������
������
����
�� ��
����
������
��������
����������
������������
��������������
����������������
������������������
��������������������
����������������������
������������������������
��������������������������
����������������������������
������������������������������
��������������������������������
����������������������������������
������������������������������������
�������������������������������������� ���Đ��E��̌v�Z���x���ւ������{�̃X�[�p�[�R���s���[�^�[
�u���v���鐫�\������p�@�̐��������Ƃ�3������
�n�܂��Ă��āA14���A��v�ȕ��i�����J����܂���
�u���v�̌�p�@�ƂȂ�V�����X�[�p�[�R���s���[�^�[�̊J���́A
���̃v���W�F�N�g�Ƃ��ė����w�������ƕx�m�ʂ��i�߂Ă��āA
���Ƃ�3������n�[�h�E�F�A�Ȃǂ̐������n�܂��Ă��܂�
14���́A���Z���s���R���s���[�^�[�̓��]�Ƃ�������
�b�o�t���������Z�������u�ƁA�v�Z���x���グ�邽��
�b�o�t���Ȃ��A��p���s���V�X�e���{�[�h��
�Ă�鑕�u1�䂪�s���ŕw�Ɍ��J����܂��� ���܂��Ă��܂����̂ōēx
{1/n:n��N}��{0}���W���ł��邱�Ƃ�������p���ďؖ�����ɂ͂ǂ����������ł����H �k���l
n��2�ȏ�̎��R���Ƃ���B
n�ɑ��āAk<n<2k�������R��k�S�̂���Ȃ�W�� S_n ���l����B
�W���̘a C[n,k] + C[2k,n] ���ŏ��ɂ���悤�� S_n �̗v�f��1�Ƃ�Ak��n�ŕ\���B
[�O�X��.013, 020] �܂ÁAC[n,k] �� C[2k,n] ��k�ɑ��ăv���b�g����B
�Бΐ��ڐ��Ńv���b�g����Ə�ɓʂł���B
C[n,k] �� C[2k,n] �ƂȂ邋�̕ӂ�ōŏ��ɂȂ�ł��낤�Ɨ\�z����B
�X�^�[�����O�̋ߎ������g����
�@0 = log�iC[2k,n]) - log�iC[n,k])
�@�� (2k+1/2)log(2k) + (k+1/2)log(k) + (n-k+1/2)log(n-k) - (2k-n+1/2)log(2k-n) -(2n+1)log(n),
n,k >>1 �̂Ƃ��� k/n = x �Ƃ�����
�@2x�log(2x) + x�log(x) + (1-x)log(1-x) - (2x-1)log(2x-1) = 0,
�@x = 0.63477252011487296
���̂��ƁA�ǂ����邩���� >>6
> ���܂��Ă��܂����̂ōēx
> {1/n:n��N}��{0}���W���ł��邱�Ƃ�������p���ďؖ�����ɂ͂ǂ����������ł����H
S= {1/n:n��N}��{0}�̓_��an��x>0�Ɏ�������Ȃ�x�̋ߖT(x/2,2x)�ɑ�����an�̕�����bn������B
������S�� {1/n:n��N}��{0}�͗L���W���䂦�W���ł��邩��Abn�̋Ɍ��͂܂�S�� {1/n:n��N}��{0}�̌��B
��x = lim bn ��S�B ���P���\-���P��
�@�@ �x�� _ ���x�@�@�@�@�Q
�@�@�i�� ���@��)�@�@�^�^
�@�@���@�@�@�@���@�^�^
�@�@�b�@�@�@�@�@|�^�^
�@�@�b�@�@ �@�@/�^�@�@�@�@
..�@�@|_/�P|_�^ >>7
n���������Ƃ��� k �� k/n
n k k/n
-----------------
9 5 0.556
12 7 0.583
15 9 0.600
18 11 0.611
21 13 0.619
24 15 0.625
27 16 0.593
30 19 0.625
40 25 0.625
50 31 0.620
60 37 0.617
80 50 0.625
100 63 0.630
200 126 0.630
500 317 0.634
���@�@���@�@0.63477252
----------------- �k���l
�@10 - 7/48 < 6��(2) < (��2 + ��3)^2�@�@�������B
�������@��(2) = 1 + 1/4 + 1/9 + ���� = ��[k=1,��] 1/kk �E
��(2) = 1 + 1/4 + 1/9 + ��[k=4,��] 1/kk
�@< 49/36 + ��[k=4,��] 1/(kk-1/4)
�@= 49/36 + ��[k=4,��] {1/(k-1/2) - 1/(k+1/2)}
�@= 5/6 + 19/36 + 2/7
�@= (1/6)(5 + 205/42),
���@6��(2) < 5 + 205/42 < 5 + 44/9 < 5 + 2��6 = (��2 + ��3)^2,
�@6 - (22/9)^2 = 2/81 > 0�@���@��6 > 22/9,
��
��(2) = ��[k=1,��] 1/kk
�@= 2 - ��[k=1,��] {2/(2k-1) -2/(2k+1) -1/kk}
�@= 2 - ��[k=1,��] {4/(4kk-1) - 1/kk}
�@= 2 - ��[k=1,��] 1/{(4kk-1)kk}
�@= 2 - 1/3 - 1/60 - 1/315 - ��[k=4,��] 1/{(4kk-1)kk}
�@> 2 - 89/252 - (1/63)��[k=4,��] 1/kk
�@= 2 - 89/252 - (1/63){��(2) - 49/36},
���@6��(2) > 10 - 7/48 = 9.854167
�k�n�l
�@3.139134 < ��{6��(2)} < ��2 + ��3 = 3.146264 ���
��ʂ̏o���Ȃ��Q���̃R�C����U���āu���v�u���v���o��m����
��ʂ̏o����R�C�����Q��U���āu���v�u���v���o��m����
�������H�@����Ƃ��قȂ邩�H
���j
�E�u�s�ٕʐ��v�Ƃ͑f���q����ʂł��Ȃ�����
�E�u���ȓ��ꐫ�������Ȃ��v�Ƃ͑f���q����ʂł��Ȃ����� 2nCk (���͎��R���Ak��0����2n�̎��R���j
�̂�����ԑ傫������2nCn�ł��邱�Ƃ̓p�X�J���̎O�p�`�����m�Ƃ��Ȃ��ꍇ�ǂ̂悤�ɂ��Ă킩��܂����H a[k] = C[2n,k+1] - C[2n,k]
�@= (2n)!/{(k+1)!(2n-k-1)!} - (2n)!/{k!(2n-k)!}
�@= (2n-2k-1)(2n)!/{(k+1)!(2n-k)!},
���
1 = C[2n,0] < C[2n,1] < ���� < C[2n,n-1] < C[2n,n] > C[2n,n+1] > ���� > C[2n,2n-1] > C[2n,2n] = 1
�p�X�J�������g�������ʓ|�����H >>16
>>17
k+1��k�̍��ׂ��2nCn���ő傾�ƕ�����Ƃ������Ƃł���
���肪�Ƃ��������܂� ��ABC�̕�BC�̒��_��M�Ƃ���ƁA
��A=2��MAC�ƂȂ����B
��B�A��C���Ƃŕ\���B �y�ޑ�z
����������́A�Ƃ��������2���Ԃ�����w�Z�ցA���]�Ԃɏ���ďo�|���A20����Ɏ��]�Ԃ���ꂽ�̂ŁA������������n�߂܂����B
��ꂽ���]�Ԃ̃n���h���̊p�x���Ƃ��g���ĕ\���B >>21
�s���n���h���ɂ����炢���̂ɁB
��=90���Ɛ��肷��B
���]�Ԃœk����(120/20)=6�{�ő����Ίw�Z�����u�Ԃ܂ŏ���B
�s���n���h���Ȃ�\�B
����=90�� �c�c_��_�c
�c�i^o^))
�c����`�S
�i^.^))���j
�҄��ҁSJ
�c�����ҁ��
__��ރC���[�W�t���b�V���\�\��O>>22�J�~���Ă���! 3��100���19�Ŋ��������܂�́H ���� 1,4/3,7/9,10/27,13/81,�c�̑�n���܂ł̘a
��ʍ������߂�܂ł͕������ł����V�O�}�v�Z��������܂��� ��ABC�̕�BC�̒��_��M�Ƃ���ƁA
��B=2��MAC�ƂȂ����B
��A�A��C���Ƃŕ\���B Table[3^(1-n)(3n-2),{n,1,15}]
{1, 4/3, 7/9, 10/27, 13/81, 16/243, 19/729, 22/2187, 25/6561,
28/19683, 31/59049, 34/177147, 37/531441, 40/1594323, 43/4782969} >>28
���炵�܂����A��MAC=�Ƃł��B �u�Ȑ��͂��鐳���`��4���_�����Ɋ܂ށv���Đ��藧���������ȂƎv������ł����Ǎ��Z���w�Ŏ����܂����H
���Ԓl�̒藝�����܂��g������ł����������ǎv�����Ȃ��B�B �u���ʏ�̂R�̊i�q�_������Ő��O�p�`����邱�Ƃ͂ł���̂��H�v
���ϓI�ɁA�ł��Ȃ��悤�Ɏv���̂ł����A�ؖ����ł��܂���B
�������ł��傤���H >>32
���f���ʂ��g����Ȃ�2,3�s >>32
���O�p�`��1���_�����_O�ɂ���Ɛݒ肵�č����x���Ȃ�
�i�q�_A(m,n)��3���_��1�Ƃ��A���f���ʂ̉�]���g����OA��60����]������B
A�̈ړ����B�Ƃ��AB���i�q�_�Ȃ灢OAB�����O�p�`�ƌ�����B
B(x,y)�Ƃ���
x+yi=(cos60��+isin60��)(m+ni)
=[ {(1/2)m-(��3/2)n} + {(��3/2)m+(1/2)n}*i ]
m,n�͐���������(��3/2)m��(��3/2)n��0�ɂȂ�Ȃ���x��y���������ɂȂ��Ă��܂�
����������m=n=0�B����������ł�O��A����v����OAB�͎O�p�`�ɂȂ�Ȃ��B
�����3���_�������Ɋi�q�_�ɂȂ邱�Ƃ͂Ȃ� >>31
�u�����`��3���_���܂ށv�Ȃ�C�ӂ̓_����ł������
���̓_��ׂ̓_�ɕς�����ǂ��� >>34
�D���߂̍̓_�ŁA20�_��5�_���炢�H >>14���
����ʂ̏o���Ȃ��Q���̃R�C����U���āu���v�u���v���o��m����
����ʂ̏o����R�C�����Q��U���āu���v�u���v���o��m����
���������H�@����Ƃ��قȂ邩�H
��ʂ̏o���Ȃ��Q���̃R�C����U����
�ŏ��ɗ����ł�m���͂P�^�Q��
�ŏ��ɕ\���o��m�����P�^�Q��
�u�����o��m���P�^�Q�v�{�u�\���o��m���P�^�Q�v���u�����\���o��m�����P�^�P�u
�����܂ł͕ʂɕs�v�c�Ȃ��Ƃ͉����Ȃ�
���͂��������
�ŏ��ɃR�C���̗������肵�����Ƃ�
�c�����R�C�������ɂȂ�m���͂����炩
���Ă��Ƃ� >>37
��ʂ̏o����Q���̃R�C����U�����ꍇ��
�ŏ��ɂP���̃R�C�������Ɍ��肵�Ă�
�ŏ��ɂP���̃R�C�����\�Ɍ��肵�Ă�
���̃R�C���̊m���͗��ƕ\�����m���łP�^�Q�ƂȂ� ��ʏo���邩�ǂ����͊W�������A�R�C����2������Ƃ��R�C����2����Ƃ������ƂɈӖ������� >>38
�Ƃ��낪��ʂ̏o���Ȃ��Q���̃R�C���̏ꍇ��
�ŏ��ɂP���̃R�C�������Ɍ��肵�����
�u���̃R�C�������ɂȂ�m���v�Ɓu���̃R�C�����\�ɂȂ�m���v���قȂ�
���R�̎�����
�ŏ��ɂP���̃R�C�����\�Ɍ��肵�����
�u���̃R�C�����\�ɂȂ�m���v�Ɓu���̃R�C�������ɂȂ�m���v���قȂ� >>39��ʏo���邩�ǂ����͊W������
���l�����������邩�ǂ�����
�m���ɑ傫�ȉe����^���邪
���j
���l������������ꍇ��
��ʂ��o���Ȃ���Γ���łP��
��ʂ̏o���Ȃ������Q����Ƃ����ꍇ��
���l�����������ĂȂ� ���Ⴀ�A�܂������v���Ă�Ⴂ�������
��ʏo���Ȃ��Ă��ʕ��ł���Ƃ��������͕ς��� ����u�Ώۂ��t�F���~���v�ɏ]���ˑΏۂ���ʂł��Ȃ��v
�����ɔF�߂��Ƃ��āA������Ƃ�����
����u�Ώۂ���ʂł��Ȃ��ˑΏۂ��t�F���~���v�ɏ]���v
�Ƃ͂Ȃ�Ȃ��̂����A����������͂��̓���悭�������� �Ȃ����قǒ�x���Ȋm���̋c�_���W�J����Ă邯�ǁB
������Ȃ�ł�����Ȃ������ȃ~�X���Ă�l�ԕ����w�Ȃɂ���킯�Ȃ��B
�m�������̍��Z������Ȃ��́H >>42��ʏo���Ȃ��Ă��ʕ��ł���Ƃ��������͕ς���
�u��ʂł��Ȃ��v�Ƃ������Ƃ́u���ȓ��ꐫ�������Ȃ��v�Ƃ��\�������
�u���ȓ��ꐫ�v�Ƃ�
�����͎������������ȊO�͎����ȊO��
�����Ƒ�����ʂł�����
�u���ȓ��ꐫ�v�������Ȃ��Ƃ�����Ԃ�
�����Ƒ��Ƃ���ʏo���Ȃ����
�Ƃ������ƂŁu�ʕ��ł���v�Ƃ������Ƃ��������Ȃ���Ԃ��� >>45
���W���Ⴆ�ΏՓ˂��Ȃ������ʂł����Ȃ��́H >>43
�����E�ł�
��ʂ��ł��Ȃ��Ώۂ̓��v���t�F���~���v�Ɩ��Â��� >>46���W���Ⴆ�ΏՓ˂��Ȃ������ʂł����Ȃ��́H
�����́u�s���ʐ��v�Ƃ����̂�
�ʒu���܂߂Ă����镨���ʂ͋�ʂł��Ȃ��Ƃ�����Ԃ���
�Ƃ������Ƃ�
���W�i�ʒu�j���܂߂ċ�ʂ��ł��Ȃ� >>46���W���Ⴆ�ΏՓ˂��Ȃ������ʂł����Ȃ��́H
�����S�̏ꍇ�͍��W(�ʒu�j���قȂ�̂�
��ʂ��o����
�d�q�̏ꍇ�͍��W�i�ʒu�j���܂߂�
�����镨���ʂ���ʂł��Ȃ�
�����Ŋm�����v�������S�Ɠd�q�ňقȂ��Ă��� >>46
�����S�̏ꍇ��
���W�P�ɂ��郊���S�P��
���W�Q�ɂ��郊���S�Q�Ƃ�����ʂ��t������
�����d�q�̏ꍇ�͈ʒu���܂߂đS�Ă̕����ʂŋ�ʂ��t�����Ȃ��̂�
�d�q�P�Ƃ��d�q�Q�Ƃ��̎��ʖ���t���鎖�͕s�\ >>46���W���Ⴆ��
�Q�̓d�q��
�ʒu���܂߂đS�Ă̕����ʂ���ʂł��Ȃ���
�d�q�̎����Ă��镨���I��������ʂł��Ȃ�
�ϑ������m���������I�����̂P����
������Q�̓d�q�̊Ԃŋ�ʂł��Ȃ�
�����S�̏ꍇ�͊ϑ������m����
�����S�P�ƃ����S�Q�ŋ�ʂ����
���ꂼ�ꂪ�Ɨ����Ċϑ������m���������Ă���
�Ƃ��낪�d�q�̏ꍇ��
�ϑ������m���Ƃ��������I�Ȑ�����
�Q�̓d�q�ŋ�ʂł��Ȃ�
�i���s�ٕʐ��j
�悤�����
�d�q�P���ϑ������m���Ƃ�
�d�q�Q���ϑ������m���Ƃ�
�d�q����ʂ��Ċm����_���鎖���ł��Ȃ�
�P�P�̓d�q�̊m�����Ę_���邱�Ƃ��o���Ȃ��̂�
�d�q�Q���ϑ������m���Ƃ���������
�m�����_������ �R�C������Ȃ������̂���
�ϑ��o���邩�ǂ����Ȃ�ĊW�Ȃ��� >>52�R�C������Ȃ������̂���
��ʂł��Ȃ��R�C����
��ʂł���R�C����
���ƕ\�Ƃ��������ʂ̊ϑ��m����
�ʂɖ��͂Ȃ� �悭�u���[�o�b�N�X�̍��Z�������̖ʔ��b�ŏo�Ă���b�����Lj�m�����Ő����������ł��ĂȂ��B >>53
��ʂ̂ł��Ȃ��R�C���̏ꍇ��
�R�C���P�̗��̏o��m���Ƃ�
�R�C���Q�̗��̏o��m���Ƃ�
�Q���̃R�C����
�R�C���P�E�R�C���Q�Ƃ����悤�Ɏ��ʂ��鎖�͂ł��Ȃ�
�悤����ɂQ���̃R�C�����u���E���v�ƂȂ�m��
�Ƃ����悤�ɂQ���̃R�C�������ʂ��Ȃ��\�L���K�v�ɂȂ� >>54�悭�u���[�o�b�N�X�̍��Z�������̖ʔ��b�ŏo�Ă���b�����Lj�m�����Ő����������ł��ĂȂ��B
���w���ł����������n�Ȃ琳�����c�����Ă邪 >>55
��ʂł���R�C���̏ꍇ��
�E�R�C���P�����̂ł�m��
�E�R�C���P���\�̂ł�m��
�E�R�C���Q���\�̏o��m��
�E�R�C���Q�����̏o��m��
�Ƃ����\�L�ɂȂ�
��ʂ̂ł��Ȃ��Q���̃R�C���̏ꍇ�̓R�C���P�E�R�C���Q�Ƃ��̎��ʂ͏o���Ȃ��̂�
�E�Q���̃R�C�����u���E���v�ɂȂ�m��
�E�Q���̃R�C�����u�\�E�\�v�ɂȂ�m��
�E�Q���̃R�C�����u���E�\�v�ɂȂ�m��
�Ƃ����\�L�ɂȂ� �ϑ��o���邩�ǂ����ŋ�ʏo���邩�ǂ����������Ȃ�\���ȊO�̏����ϑ����Ȃ��Ⴂ����������˂���
�������������Ƃ�����Ă���Ƃ����\���̏�����ϑ����Ă��ĂQ���̋�ʂ����Ȃ���Ƒ��̏����ϑ����ĂQ���̋�ʂ̂����������\���̏o���͂ǂ��Ȃ��
�����ɂ���ďo��������Č�����̂��H �A���A���A���A���A���A���A���A���A���A���A��
�A���A���A���A���A���A��
�A���[���F�f���`�I Arrivederci�I ID:vs1gXaD9�͑O�̃X�����炢��r�炵
1����10�`20���X���x�A���g�X�b�J�X�J�̐��w���ǂ����X�𓊍e
���X�͕Ԃ��Ă��邪�����Ɠ������Ƃ��������Ȃ����ߘb�����ݍ���Ȃ�
�����ɂ��j���J�ۏo���̃A�z�ȃ��X�����ē˂����݂����Ȃ�C�����͕����邪�A�}�W�Ŏ��Ԃ̖��ʂ�����X���[���� ID:vs1gXaD9�������Ă��Ă����l�H >>58
��ʂ̏o���Ȃ��R�C����
��ʂɏo���Ȃ��d�q�����Ƃ��Ă�̂���
���̒��̂Q�̓d�q��
���̉E���̊ϑ����u�Ŋϑ�����鎖���R�C���̗����ϑ����ꂽ�Ƃ��Ƃ�
���̍����̊ϑ����u�Ŋϑ�����鎖���R�C���̕\���ϑ����ꂽ�Ƃ��Ƃ��Ă� �O>>23
>>28�����A�]���A�{�p�A���̐������m������C���Ƃŕ\�������B��A���Ƃŕ\����C������B
>>32���イ�Ԃ�Ȑ��̊i�q������K���ȕ��œ��Ԋu�Ɉ����A���O�p�`�̎O�̒��_���i�q�ɍڂ�����ƍl����B ���₪�ł��Ȃ������ǂ�����Ď����܂����H�ł��̉��オ���ĂāA����́u����ł���v�͂Ȃ��Ȃ��B ���w�ȂȂ��Nj����w�@�̉ߋ���N�\������ǂǂ��������������H >>26
��ʍ��@a_k = (3k-2)/3^(k-1),�@�@�@>>29
S_n = ��[k=1,n] a_k = ��[k=1,n] (3k-2)/3^(k-1) = (1/4){15 - (6n+5)/3^(n-1)}, �O>>63�ł���Ƃ��߂���ł���B���邢�͖������ƗL�����̍ő����0�A�𗝗R��3���_���Ɋi�q�ɍڂ��邱�Ƃ͂ł��Ȃ��ƌ�����̂��ǂ��Ȃ̂��B
>>64���Ղ��炟�ՁB >>65
�u�]����R�[�X�Ɛ�啪��́H >>58
���ϑ��o���邩�ǂ����ŋ�ʏo���邩�ǂ����������Ȃ�\���ȊO�̏����ϑ����Ȃ��Ⴂ����������˂���
���̒��ɋ�ʂ̂ł��Ȃ��R�C�����Q������
�i���̉E���ƍ����Ɋϑ����u������j
�P�[�X�P�@�E�E�E�Ɗϑ������m��
�P�[�X�Q�@���E���Ɗϑ������m��
�P�[�X�R�@���E�łP���Âϑ������m��
�P�[�X�P�̏ꍇ�͉E�E�E�Ŋϑ�����邪
�P�@���̎��ɃR�C�������E���Ɗϑ������m���́E�E�E
�Q�@���̎��ɃR�C�����\�E�\�Ɗϑ������m���́E�E�E
�R�@���̎��ɃR�C�������E�\�Ɗϑ�������m���́E�E�E >>57
����ʂ̂ł��Ȃ��Q���̃R�C���̏ꍇ�̓R�C���P�E�R�C���Q�Ƃ��̎��ʂ͏o���Ȃ��̂�
���E�Q���̃R�C�����u���E���v�ɂȂ�m��
���E�Q���̃R�C�����u�\�E�\�v�ɂȂ�m��
���E�Q���̃R�C�����u���E�\�v�ɂȂ�m��
���Ƃ����\�L�ɂȂ�
��ʂ̂ł��Ȃ��Q���̃R�C���������Z�b�g�ƂȂ���
�u���E���v�Ƃ��u�\�E�\�v�Ƃ��u���E�\�v�ɂȂ�m���������Ă���Ƃ������Ƃ�
�X�̃R�C�����Ɨ����āu�\�v�Ƃ��u���v�Ƃ������m���������Ă���킯�ł͂Ȃ�
�悤����ɋ�ʂ̂ł��Ȃ��Q���̃R�C����
�Ɨ����ĂȂ��̂� >>70
��ʂ̂ł��Ȃ��Q���̃R�C�����Ɨ����ĂȂ��Ƃ������Ƃ�
�P���̃R�C���̊ϑ����ʂ��c��̂P���̊ϑ��m���ɉe����^����Ƃ������Ƃ�
�i���ʊW�����j >>71
�Q���̋�ʂ̂ł��Ȃ��R�C����U����
�ŏ��ɂP���̃R�C���̗��\���m�肷���
���̃R�C�������ƕ\�̊ϑ��m�����قȂ��Ă���
�悤����ɍŏ��Ɋϑ����ꂽ�ϑ����ʂ�
���Ɋϑ������m���ɉe����^���Ă��܂�
�i���ʊW������j ���ʏ��AB=AC=1,BC=a(0<a≤1)�̓ӎO�p�`ABC������B
��ABC�̊O�ډ~��K�ABC�̒��_��M�Ƃ���BK�̌ʂ�AM�ɂ�蕪�����A�����_B���܂ޕ��̌ʂɓ_P���Ƃ�A�܂��_Q��MP�Ɋւ��ē_A�̔��Α��ɂƂ�A��MPQ�����O�p�`�ƂȂ�悤�ɂ���B
3�_A,B,Q�����꒼����ɂ���Ƃ��AAP�̒��������߂�B �O>>67
>>73
A(0,0)
M(0,��(1-a^2/4))
B(a/2,��(1-a^2/4))
Q(3a/4,-a��3/4)
P(3a/4,a��3/4)
AP=��(9a^2+3a^2)/4
=(a��12)/4
=(a��3)/2 >>65
���ƁA�������O�����������Ă����ė~����
���͏ڂ������������Ȃ���Α㐔�E�E��͂̂����ꂩ���������Ă����� �Ȑ��̒����̖�肪������܂���B
�͂��݂��������邭�炢�͕�����̂ł����A�ǂ̊��ŋ��߂Όʒ����v�Z�ł��邩�����ĉ������B
�Q�l���ł��B��낵�����肢���܂��B
�k���l
���̎���x�ɑ��Ē�`���ꂽ��f(x)=sin(1/x)���l����B
a�𐳂̎����Ƃ��Axy���ʏ�̋Ȑ�C:y=f(x)��a≤x≤a+1�̕����̒�����L(a)�Ƃ���Ƃ��Alim[n����]L(a)=1�������B >>77
n���� �� a���� ���H
1 �� ��(1 + (f�f)^2) �� 1 + (1/x^2) �ł������� ��͂͊��ƃK�`�œ����肪�o�邱�Ƃ�����܂�
�Ղ������ł����ς����߁A�����L���Ă����܂��傤
��r�I�����₷���㐔�A���Ɋӂ蓦����̂��ǂ��ł����A�����ł����˂����܂��Ǝv���܂�
�u�Ȃ�ʼn�͐�U�H�H�H�v ����͂Ƃ������Ă��������Ă���
>>81�������� ���̂悤�ȃQ�[�����l����
�e�`�[���P�O�l���ĂP�O���̋��݂��D���Ȃ悤�ɕ��z����i��l�O���ȏ�P�O���ȉ��j
�P�O�l���烉���_���Ɉ�l��I��őΐ푊��̃`�[�������݂̖����������`�[���������Ƃ���i������0.5�������j
�\�ȕ��z���@���ׂĂɂ��Ĉ���`�[�������݂��Ė�����̑ΐ킪�����_���ɍs����Ƃ���Ƃ�
�������ő�ɂ���ɂ͋��݂̕��z���ǂ�����̂���ԗǂ����H >>80
�R�[�X�������ė~������������
�܂���[��rims�Ȃ炱��ȏ��Ŏ��₵�Ȃ���
��b�Ȗڂ͏o��X�������邩��ߋ���������܂�����̂���������悤�ɂȂ�
�Ⴆ�Ώd�ϕ��A�s��v�Z�A����⋉���̎������A�����藝�͕p�o
���Ȗڂ�2��I�������A��͂͂����������x�_�E����́E�������������o��
�l�I�ɂ͊���͔͂�r�I�����₷����肪�����Ǝv��
�����̑I���͐�啪���D�݂ɂ��
������������肪2�△���������ׂ̈ɕی��ŃK���A���_������Ă����l�����ɑ���
���������O�̖����������Ƃ��ǂꂭ�炢�]�������̂��͕s��
�p��͒��ȒP�A�p��ŃX�e�[�g�����g�������������ƂȂ��Ă��������K������������Ǝv����
�����̕�����Ȃ���肪����Ƃ��͗F�B�Ƌ��͂��邩�A�@�����W�ŗޑ��T���Ƃ����Ǝv��
��Ղ���Ȃ��ꍇ�́A�����܂ł��Ȃ�����]����w�������ƘA�������悤��
��������ł͐�啪��Ɋւ��鎿��ɉ����āA(��ՂłȂ��ꍇ��)�����ĂȂ����̉����������������邱�Ƃ����邩��A�����{�Ԃʼn����Ȃ��������������Ă����������� y≤2x-3����y≥0����y≤-3x+6���\��xy���ʏ�̗̈��D�Ƃ���B
D����x^2-xy+y���ő�ɂ���_�̍��W�����߂�B ���ȑ�ɓ����ċ���@�Ƀ����_���Ăł����ł����H �N�������̉��ɕ��������Ă���
���Z�n�̖{�ǂ�łĐM�p�n���Ƃ������d�g�݂��o�Ă�������
����l��100���~�̂���10%����������90���~��݂��o���āA����90���~���肽�l�͕ʂ̐l��90���̂���10%����������81����݂��o���āc���Ă̂��J��Ԃ��ƍŏI�I�ɑS�̂Ƃ��čő�900���݂��o����Ƃ̂��ƂȂ��i����͂Ȃ�Ƃ��C���[�W�ł���j�B
90+81+�c
�悭�킩���̂͂�����
���̌v�Z��100����0.1��1000��
1000���|100���i�ŏ���100���j��900��
�Ƃ������ŊȒP�ɏo����炵�����A����100����0.1�̈Ӗ����킩��Ȃ�
100����0.1�Ŋ�����Ă̂�100���̂Ȃ���0.1����������̂����Ă��Ƃł���H
�ɒ[�Ɍ�������1000�����Ăǂ����痈������Ă���
��̐����Ȃ�܂������ł������ a_0 = 100
a_n = 0.9 �~ a_{n-1} (n��1)
�œ��䋉���̘a�in��1�ł̑��a�j���v�Z����� 0.1 �Ŋ���Ƃ�������͈ꉞ�o�Ă���
��>>88�ɏ����Ă�����������R�Ȃ��̂Ȃ̂��ǂ����͂킩��� >>89
�����Ă���Ă��肪���������̐������ƃA�z�ȉ��ɂ͂悭�킩���i�A���_�[�o�[�̈Ӗ����킩���ĂȂ��j
���ׂĂ���m���ɓ��䋉�����Č��t�͏o�Ă���
�ł�������������ӂ��ċ����Ăق��� �ŏ��ɑ݂��z��90����
�ȍ~���� 90% �����X�Ƒ݂��킯�Ȃ̂�
���z = 90 �~ (1/(1-0.9)) = 900 (���~)
���̌v�Z�ɓ��䋉���̘a�̌�����p���� >>58
���������������Ƃ�����Ă���Ƃ����\���̏�����ϑ����Ă��ĂQ���̋�ʂ����Ȃ���Ƒ��̏����ϑ����ĂQ���̋�ʂ̂����������\���̏o���͂ǂ��Ȃ��
�������ɂ���ďo��������Č�����̂��H
��ʂ̂��Ȃ��f���q�Ƃ����ꍇ��
�ʒu���܂߂đS�Ă̕����ʂŋ�ʂ����Ȃ�
�����̕����ʂŋ�ʂ��o����ꍇ��
����͋�ʂ̂ł��Ȃ����Ƃ͂���Ȃ���
�m�����v����ʂ̏o������̂Ƃ��Ĉ����� >>85
���肪�Ƃ��������܂�
���݂܂���B����RIMS�ł� >>58
��ʂ̏o���Ȃ��Q�̕��Ƃ�
���l������������Q�̕��Ƃ������Ƃ�
���C�v�j�b�c�̌����́u����ҕs���ʂ̌����v
������Q�̕��� >>85
�Ƃ���������̐��w�Ȃ̉@����rims�ȊO�ɂ����ł����H
���וs���ł��݂܂��� >>95
���w����(���w�n)��RIMS(������͌n)������
����ɐ��w�����̏ꍇ�͔��m�ے��ɐi�ޑO��̐�[�R�[�X�Ǝ�ɏC�m���ŏA�E�����ՃR�[�X�ɕ������
���w����
https://www.math.kyoto-u.ac.jp/
RIMS
http://www.kurims.kyoto-u.ac.jp/ja/index.html
���w�����ȕ�W�v��
http://www.sci.kyoto-u.ac.jp/ja/_upimg/kce/AfM4Rg/files/application_mc20%281%29.pdf
���������ꂼ�ꏊ�������܂��Ă邩�璍��(��W�v����p14�`18)
�@����������ʁX
�w���������搶�ɂ���Ăǂ�����邩���߂�Ƃ����Ǝv��
��ՃR�[�X�łȂ��ꍇ�͗\�ߘA��������Ă����ׂ�
�@��������Œ��ژb���̂����� >>96
���肪�Ƃ��������܂��B
���w�����ł��ˁB
���ׂĂ݂܂�
����ς�rims�Ɣ�ׂ�Ɠ��w��Փx�͉�����̂ł��傤���H �N������𐔎��ɏo���Ȃ����ȁH
�ȉ��̊�b�l�Ɨv�fA�`D�̑g�ݍ��킹�莮�ɓ��Ă͂߂ē���(Y)���ő�ɂȂ�g�ݍ��킹���o�������B�����������������B
��b�l=30
�W��X 1.0
�v�fA �ŏ��P��1 �ő�l10
�v�fB �ŏ��P��3 �ő�l30
�v�fC �ŏ��P��10 �ő�l70
�v�fD �ŏ��P��-5 �ő�l-50
���莮
Y=��b�l-(1���*X)-(2���*X)-...
����
�@�e�v�f�͍ŏ��P�ʂ̔{���Ŋe��ɕ����\�A�A���e�v���ő�l�ɂ��Ȃ�������Ȃ��B
�A�v�fC,D�������g��ꂽ�i�K�ŌW��X��1.5�ɕω����Ė߂�Ȃ��Ȃ�B
�B���莮��1���,2���,,�Ƒ����ߒ��Ń}�C�i�X�l�ɂȂ��Ă͂����Ȃ����Ō�̉�̂݃}�C�i�X�l�ł��ǂ��B
��1
1��� X=1.0 D=-50
2��� X=1.0 A=1
3��� X=1.5 A=9 B=30 C=70
Y=30-(-50)-(1)-(109*1.5)
=-84.5
��2
1��� X=1.0 C=20 B=9
2��� X=1.5 D=-50
3��� X=1.5 A=10 B=21 C=50
Y=30-(29)-(-50*1.5)-(81*1.5)
=-45.5 >>97
��Ղ͂��Ȃ艺����
��[��RIMS�͑�������قǕς��Ȃ��Ǝv��
������啪���w����������]����҂̑��݂⋳���̋C���ɂ��˂� >>34
�x���Ȃ�܂������A���肪�Ƃ��������܂����B
���f���ʂ܂ōl���Ȃ��Ă��A
�_B��X���W���v�Z����Ɓi�r���͏ȗ��j�A
(m-��3n)/2
�ƂȂ�Am,n�������Ȃ̂ŁA����͖������ł���ˁB
������_B�͊i�q�_�ł͂��肦�Ȃ��B
�E�E�E�ŁA�����ł��ˁB
�Q�l�ɂȂ�܂����B �O>>74
>>100���ꂪ>>67�Ō��������������Ƃł��B >>101
�ł���ƌ��߂���ł���Ⴄ�́H >>100
���₢��Ax���W�����l����̂ł͂��߂ł�
���f���ʂ��g�����͕ʂƂ��Ă��A>>34�ɂ���悤�ɁA���W�̗v�f���Q�Ƃ��l����K�v�͂���܂� >>103
�_��X���W����������������AY���W�����ł���A
���̓_�͊i�q�_�ł͂��蓾�Ȃ��ł���ˁB
������X���W���������ł��邱�Ƃ����������_��Q.E.D.�Ǝv���̂ł����E�E�E >>102����������������~
�P]/�__________�O>>101
__/�_/,,�� ����/|~~~~~
�P�_/�c`_`�___))|__~~~
�P|�__U,~�܁R/�@|�@�_~
�n| �a�P�P`U~U�@/�@�@)
�Q| �a�@���@�a /�@�@/|
___`�a______�a/____/|~
�P�P�P�P�P�P�P�P�P�a~~
~~~~~~~~~~~~~~~~~~~~~~~~ �O>>105
��3�Ԋu�œ��Ԋu�Ɋi�q����������ǂ����H
�c������������Ȃ��Ɗi�q�Ƃ͌ĂȂ��̂��H �i�q���ě�q�Ɏ��Ă�~
�P]/�__________�O>>106
__/�_/_��_ ����/|~~~~~
�P�_/�c~-~Ђ�_))|__~~~
�P|�__U,~�܁R/�@|�@�_~
�n| �a�P�P`U~U�@/�@�@)
�Q| �a�@���@�a /�@�@/|
___`�a______�a/____/|~
�P�P�P�P�P�P�P�P�P�a~~
~~~~~~~~~~~~~~~~~~~~~~~~ >>106
���W���ʏ�̓_�ŁAX���W�AY���W���Ƃ��ɐ����̂��̂��u�i�q�_�v�ƌĂԂ�
�ł͂Ȃ��ł��傤���H >>32
���ʏ�̊i�q�_�����łł������鐳�O�p�`���������Ƃ��āA���s�ړ��A�k�����s�����Ƃɂ��A3���_��
O(0,0),P(a,b),Q(c,d)�@a,b,c,d�͐����ōő����1
�Ƃ����Ă���ʐ��͎����Ȃ��B�Ӓ���������A
a^2+b^2=c^2+d^2=(a-c)^2+(b-d)^2�@���@a^2+b^2=c^2+d^2=2(ac+bd)
�������邪�A�T�d�Ɍ������s���ƁAa,b,c,d���ׂĂ������łȂ��ƁA�������邱�Ƃ��m�F�ł��A
�ő����1�ł���悤�Ȑ������͖������Ƃ�����B
����ɂ��A3���_���i�q�_�ł��鐳�O�p�`�͖����ƌ�����B �ϕ�����������w�ׂ�PDF�͂��邩�ˁH(�L��֥`) >>100
��]�𑨂���͍̂��W���ʂ�蕡�f���ʂ̕����i�i�Ɋy�B�v�Z���ÎZ�ōς�
�s��m���Ă�Ȃ�Ƃ������A����ȃ��x���̎��₷�鎞�_�ł�����Ɓc��
���W���ʂɂ������̂��C�~�t�B���������B >>58
���������������Ƃ�����Ă���Ƃ����\���̏�����ϑ����Ă��ĂQ���̋�ʂ����Ȃ���Ƒ��̏����ϑ����ĂQ���̋�ʂ̂����������\���̏o���͂ǂ��Ȃ��
�d�q�̏ꍇ�͂ǂ�Ȏ������Ă���ʂ��ł��Ȃ�
�悤����Ɂu����̓d�q���Q����v �Ƃ�����ԂȂ�
�u���ȓ��ꐫ�������Ȃ��v�Ƃ������Ƃ�
�����Ƒ��l����ʂ��邱�Ƃ��ł��Ȃ��Ƃ������Ƃ�
�����Ƃ����l�Ƃ��̃��x���鎖����ł��Ȃ���ԂȂ�
�����͉��X�Ƃ����ϑ��m���������Ă���Ƃ�
���l�͉��X�Ƃ����ϑ��m���������Ă���Ƃ��̕\�L���ł��Ȃ���ԂȂ�
�]����
����̂Q�l�͉��X�Ƃ����m���������Ă���Ƃ����\�L�ɂȂ�
�X���Ɨ����Ċϑ��m���������Ă���̂ł͂Ȃ�
��ʂ̏o���Ȃ�����̂Q�l�����X�Ƃ����m���������Ă���Ƃ������ƂɂȂ� >>104
�����Ax���W�����ł̓_���ł�
n=0�̏ꍇ��Y��Ă܂��H >>112
��ʂ̏o���Ȃ��Q�̕��Ƃ�
���l�������W�Ŕ��˗��E�Ώ̗��E���ڗ����ɖ��������̊W��
�u��ʂ̏o���Ȃ��Q�̕��v�Ƃ�
�u����̂��̂��Q����v
�Ƃ�����ԂȂ̂�
����̂`���Q�L�����ꍇ
���R���ƑΉ�������
�`�P�Ƃ��`�Q�Ƃ��̕\�L�͏o���Ȃ��̂�
�Ƃ������Ƃ�
�`�P�����m���Ƃ�
�`�Q�����m���Ƃ����\�L�͏o���Ȃ�
��ʂ̂ł��Ȃ��Q�̂`�����m��
�Ƃ������ƂɂȂ� >>58
���s�ٕʐ��Ƃ�
�u���E���v�Ƃ��u�\�E�\�v�Ƃ��u���E�\�v�Ƃ�����Z�b�g�ƂȂ�
�u���v�Ɓu�\�v�Ƃ����P�ʂɕ�����Ȃ�����
�Q���̃R�C������ʂł���ꍇ��
�R�C���P���u���v�ɂȂ�Ƃ��u�\�v�ɂȂ�Ƃ�
�R�C���Q���u���v�ɂȂ�Ƃ��u�\�v�ɂȂ�Ƃ�
�u���v�Ƣ�\�v���P�i�ɂȂ��Ă�
�Q���̃R�C������ʂł��Ȃ��ꍇ��
�R�C���P�Ƃ��R�C���Q�Ƃ��̂悤�Ɏ��R���ƑΉ����������ʂ͏o���Ȃ�
�悤����ɈقȂ郉�x���Â��͕s�\�Ȃ�
�Ƃ������ƂłQ���̋�ʂł��Ȃ��R�C����
�u���E���v�̊m���͂�����Ƃ�
�u�\�E�\�v�̊m���͂�����Ƃ�
�u���E�\�v�̊m���͂�����Ƃ�
���ƕ\���Z�b�g�ɂȂ��ĕ����ł��Ȃ� >>99
��Ղ�������Ƃ́H
����͕s���ł��݂܂���B ���� ���w �ɕ������̐ϕ�
(1)��(2)�̉�������������܂���
��������肢���܂� >>116
��[�R�[�X�͉@���̍ۂɎw���������w�����Ȃ���Ȃ炸�A10�l�サ���ʂ�Ȃ�
��ՃR�[�X�͓���̎w�������ɂ��킯�ł͂Ȃ��A�l����30�l�ȏ���
��������̓��e���S���Ⴄ(��Ղ̕����y)
����������ŁA��[��RIMS�̓�Փx�͂���قǕς��Ȃ����A��ՃR�[�X�͔�r�I����₷��
���ꂭ�炢�͒��ׂ��炷�������邩�班���͒��ׂ�Ȃ������������� >>120
���肪�Ƃ��������܂�
�����ł��ˁB�������蒲�ׂ�ȕt���܂� >>113
�m���ɂ����ł��ˁB
�����O �܂�`���w����ɂ����āA����ɂ��̂w���W�������̏ꍇ�́A
�a�̂w���W�������ɂȂ�̂ŁA
�a�̂x���W���������ł��邱�Ƃ������Ȃ��ƃ_���ł���ˁB
���ł����E�E�E ���a5�̉~K�̎����AB=1�ƂȂ�2�_A,B���AK�̓����ɓ_C���Ƃ�A��ABC�����O�p�`�ƂȂ�悤�ɂ���B
�܂�K�ɓ��ڂ��AA��1�̒��_�Ƃ��鐳�O�p�`��APQ���l����B�������AP��K�̎���ɂ���A�܂���AP�ƕ�BC�Ƃ���_M�������̂Ƃ���B
��MCQ�̖ʐς����߂�B >>109
�������낻���Ȕ��z���Ƃ������Ƃ͂킩��܂��B
�����A
> a^2+b^2=c^2+d^2=(a-c)^2+(b-d)^2�@���@a^2+b^2=c^2+d^2=2(ac+bd)
> �������邪�A�T�d�Ɍ������s���ƁAa,b,c,d���ׂĂ������łȂ��ƁA�������邱�Ƃ��m�F�ł��A
���킩��܂���B
�ł���A���������ڂ��������Ă��������B >>124
�ǂ����Ă�������Ȃ��Ȃ�A�߂�ǂ��������Nj��ɂ��đS���̏ꍇ��悭�ˁH
���̍�ƒ��ɁA���e�҂̈Ӑ}��������ł���
�߂�ǂ��������đ��l�ɓ�����O�Ɏ����Ŏ���� >>14
����ʂ̏o���Ȃ��Q���̃R�C����U���āu���v�u���v���o��m����
����ʂ̏o����R�C�����Q��U���āu���v�u���v���o��m����
���������H�@����Ƃ��قȂ邩�H
�قȂ�
�Q���̃R�C������ʂ��ꍇ
�@�R�C���P���u���v�̊m���@�@�P�^�Q
�@�R�C���P���u�\�v�̊m���@�@�P�^�Q
�@�R�C���Q���u���v�̊m���@�@�P�^�Q
�@�R�C���Q���u�\�v�̊m���@�@�P�^�Q
�Q���̃R�C������ʂ��Ȃ��ꍇ
�@�R�C���Q�����u���E���v�̊m���@�P�^�R
�@�R�C���Q�����u�\�E�\�v�̊m���@�P�^�R
�@�R�C���Q�����u���E�\�v�̊m���@�P�^�R ��������ȕs�тȘb��߂Ă���B
���̃R�C���̘b�̂̂��Ă�\�[�X�͂��ďI���ł������H >>123�O>>107
A(0,5)
B(3��11/10,49/10)
C((3��11-��3)/20,(99-3��33)/20)
P(5��3/2,5/2)
Q(0,0)�̂Ƃ��́A
����AP�ƒ���BC�̌�_M(x,y)����с�MCQ����ӂɒ�܂�Ǝv���B
����AP��y=-x/��3+5
����BC��y={(3��33-1)/(3��11+��3)}(x-3��11/10)+49/10
y���������āA
-x/��3+5={(3��33-1)/(3��11+��3)}(x-3��11/10)+49/10
-x/��3+1/10={(3��33-1)/(3��11+��3)}(x-3��11/10)
��3-10x={(3��33-1)/(3��11+��3)}(10x��3-3��33)
��3-10x={(3��33-1)(3��11-��3)/(99-3)}(10x��3-3��33)
��3-10x={(100��3-3��11-9��11)/96}(10x��3-3��33)
��3-10x={(100��3-12��11)/96}(10x��3-3��33)
��3-10x={(25��3-3��11)/24}(10x��3-3��33)
24(��3-10x)=(25��3-3��11)(10x��3-3��33)
24��3+3��33(25��3-3��11)=240x+750x-30x��33
240x+750x-30x��33=24��3+225��11-99��3
990x-30x��33=225��11-75��3
(198-6��33)x=45��11-15��3
2(33-��33)x=5(3��11-��3)x=5(3��11-��3)(33+��33)/2(33^2-33)
=5(96��11)/2112
=5�2^5�3��11/2^6�3�11
=5��11/22
y=5-5��33/66
M(5��11/22,(330-5��33)/66)
���\�\ ���
�Q�̋�ʂ̏o���Ȃ��R�C�����ɐU�����ꍇ
�@�ŏ��ɂP���̃R�C�����u���v�ɂȂ�m���͂P�^�Q��
�@�ŏ��ɂP���̃R�C�����u�\�v�ɂȂ�m���͂P�^�Q����
�@�c�����P���̃R�C�����u���v�ɂȂ�m����
�@�ŏ��ɂP���̃R�C�����u���v�ɂȂ����ꍇ�͂����炩�H
�@�c�����P���̃R�C�����u�\�v�ɂȂ�m����
�@�ŏ��ɂP���̃R�C�����u���v�ɂȂ����ꍇ�͂����炩�H
�@�c�����P���̃R�C�����u���v�ɂȂ�m����
�@�ŏ��ɂP���̃R�C�����u�\�v�ɂȂ����ꍇ�͂����炩�H
�@�c�����P���̃R�C�����u�\�v�ɂȂ�m����
�@�ŏ��ɂP���̃R�C�����u�\�v�ɂȂ����ꍇ�͂����炩�H >>123�O>>128
����CM�́A
y={(3��33-1)/(3��11+��3)}(x-3��11/10)+49/10���ȒP�ɂ��āA
(3��33-1)x-(3��11+��3)y+15��11-5��3=0
����CM��Q(0,0)�Ƃ̋����́A
(15��11-5��3)/��{(3��33-1)^2+(3��11+��3)^2}
=(15��11-5��3)/��400
=(15��11-5��3)/20
=(3��11-��3)/4�\�\�@
C((3��11-��3)/20,(99-3��33)/20)�ƁA
M(5��11/22,(330-5��33)/66)�̋����́A
��[{5��11/22-(3��11-��3)/20}^2+{(330-5��33)/66-(99-3��33)/20}^2]
=��[{(25��11-15��11+5��3)/110)^2+{(3300-50��33-99�33+99��33)/660}^2]
=��[{(10��11+5��3)/110)^2+{(33+49��33)/660}^2]
=��{(1100+50��33+75)/110^2+(33�33+66�49��33+49^2�33)/660^2}
=��{(1175+50��33)/12100+(33�33+66�49��33+49^2�33)/36�12100}
=��{(235+10��33)/2420+(33+22�49��33+49^2)/12�1100}
=��{(47+2��33)/484+(2434+22�49��33)/12�1100}
=��{(47+2��33)/484+(1217+11�49��33)/6�1100}
=��{(47+2��33)/484+(1217+539��33)/6600}
=��{(47+2��33)�150+(1217�11+539�11��33)/6600�11}
=��{(47�150+300��33+13387+5929��33)/6600�11}
=��{(7050+300��33+13387+5929��33)/6600�11}
=(1/110)��{(20437+6229��33)/6}�\�\�A
����MCQ=�@��A/2
={(3��11-��3)/880}��{(20437+6229��33)/6} �Q���̋�ʂ̂ł��Ȃ��R�C�����L�����ꍇ
�P���ÃR�C����U�����ꍇ��
�Q���̃R�C�����ɐU�����ꍇ
���E���ƂȂ�m���͈قȂ邩�H >>127�\�[�X��
�u���w�̒��̕����w�v������w�o�ʼn�@��X�p����
�̂Ȃ���
�u�܂����������̈قȂ�m�����v���������Ă�������
�@�����̐��w�҂�Y�܂��Ă���Ȃ̂ł�����
�@���Ƃ������ł͂����Ȃ��Ă���Ƃ��������킯�����Ȃ���
�@���w�I�ɂ��̂Q�𐔊w�_���̂Ȃ��ɋ��������邱�Ƃ��ł��Ȃ����낤��
�@�Ƃ������Ƃ͕����ɋ����������w�҂Ȃ�F�C�ɂ��Ă�v
�Ƃ��� >>132�܂����������̈قȂ�m�����v���������Ă�������
����̌�����
�m�����v�����̐����Ɉˑ����镨���@���̂悤�ɂȂ��Ă邱�ƂȂ̂�
�悤����Ɋm�����v��
���̐����Ɉˑ����Ȃ����ۓI�ȊT�O�ɂȂ����Ȃ��̂� >>132
�R�C���̖�肪����Ȃ炻��ł����B
������������B >>134
ID��NG����Ⴂ������
���X�Ǝ��ȃ��X�����蓯���������݂ɉ��x�����X�������ʓ��e�������Ă���͎̂����ł��������Ȃ��Ƃ������Ă���Ƃ������o������r�炵���Ă��Ƃ��� >>136�����ł��������Ȃ��Ƃ������Ă���Ƃ������o������
�{�[�Y���v�ƃt�F���~���v�Ƃ����Q�̓��v���������Ă�Ƃ����̂�
�����ł͕����@���Ƃ݂Ă���̂ŕʂɖ��͂Ȃ���
���w�̏ꍇ�͊m�����v�����̐��������̂Ƃ���
���ۉ��ł��ĂȂ��Ƃ������ƂŖ��ɂ���Ă�Ƃ����Ă邱�Ƃ�
�u���w�̒��̕����v�ŋL����Ă�Ƃ������Ƃ�`�����̂��� >>131
���Q���̋�ʂ̂ł��Ȃ��R�C�����L�����ꍇ
���P���ÃR�C����U�����ꍇ��
���Q���̃R�C�����ɐU�����ꍇ
�����E���ƂȂ�m���͈قȂ邩�H
�����ԈႦ���̂Œ���
�Q���̋�ʂ̂ł��Ȃ��R�C�����L�����ꍇ
�P���̃R�C�����Q��U�����ꍇ��
�Q���̃R�C�����ɐU�����ꍇ��
�m���͈قȂ邩�H �����������邹�[��(�M�E�ցE�L)
�b������ˁ[��(�M�E�ցE�L) >>138�����B�O>>130
(1/2)^2=1/4 https://i.imgur.com/4f1xXDk.jpg
�ΐ����̖ʐςƃƂ̋��ߕ��������낭������ >>84 �P�O�l�͑�������̂łS�l�Ōv�Z�����m�� �i��������ŕ��Ϗ����v�Z���������j
(1111) 76/128
(0112) 71/128
(0022) 66/128
(0013) 60/128
(0004) 47/128 �O>>142
>>143�Ȃ��Ȃ��G�����ΐ}�`���`���ĂĂ悢�B
�܂�����������`�A2�~2�̎l�����̂��=�Υ2^2/4
�������獶�E�̔����������ƁA�������������ǂЂƂ܂������B
�Υ2^2/4-��/2-��/2
�܂������ĂȂ��t���܂̔��p�������́A2�~2�̐����`���甼���̃�2�������ď㉺�����ɂ������ŁA
(2^2-�Υ1^2)/2
����������āA
�Υ2^2/4-��/2-��/2-(2^2-�Υ1^2)/2
���Ƃ͂���ɂ����������������E���̏c2�̕ӂ�2�̉~�ʂň͂܂ꂽ�����𑫂��B
���̏c���̃w���̂悤�ȕ�����2�̉~�ʂ̐���(�J�[�u)���Ⴄ����A�ʁX�ɕ����ċ��߂���ǂ����B
���a2�̐�`�̐ڐ���90���Ȃ�ŁA���傤�ljE�̃̔��a�ɂȂ�悤�Ɉ�����B����Ńw�����㉺�ɕ��������B
�����`���㉺�ɓ���悤�����������ƁA��`�̃Ƃ����p�A�Β��p�A���S�p�Ƃ������ɓ������p�Ƃ��ď������߂�B
�����ׂ���̕����̐�`�́A
�Υ1^2(��/2��)
�����ׂ����̕����͐��Ώ̂Ȏl�p�`�����`�������������ł��邪�A���̎l�p�`�́A�Β��p�Ƃ����������Ƃ��ɒ��p��L����O�p�`�̕����������ł��邽�ߓ��ψړ��ł��A���2�̐����`�̉������̖ʐς��Ƃ킩��B
1�2-��2^2(��/2��)
���߂锒�J�b�g���p���̖ʐς́A
�Υ2^2/4-��/2-��/2-(2^2-�Υ1^2)/2
+�Υ1^2(��/2��)
+1�2-��2^2(��/2��)
=-(4-��)/2+��/2+2-2��
=-2+��/2+��/2+2-2��
=��/2-3��/2
=(��-3��)/2 >>143
�S�~�݂����Ȑ}��������
�҂������₷���悤�ɏ��������ē_�ɖ��O��U��
���ꂩ��ǂ��܂ł��ΐ������ׂ����Ƃ���܂Ŗ��m�ɂ���
���������瓚���Ă�� >>145
���肪�Ƃ��������܂��I
>>146
�����ւ�\����܂���ł����B
���̃N�\�o�J����l�F�l�̏������}�����̂܂܃A�b�v���Ă��܂��܂����B �O>>145�⑫�B
cos(��/2)=2/��5
sin(��/2)=1/��5
tan(��/2)=1/2
tan(26.5655��)��1/2
��=53.131�c�c >>118
���x�������܂���
�ǂȂ������Ԃ�������A�����ĉ�����Ə�����܂��B >>149
wolframalpha�ɂ���Ă��炦 >>118 >>135 >>149
5.22�@����2�̋Ȑ��ň͂܂ꂽ�����̖ʐς����߂�B
�@�@(1)�@�~ r = 2sin�ƁC�@�~ r = 6sin��
�@�@(2)�@�S���` r = a(1+cos��)�C�@�~ r = 2a cos�Ɓ@(a>0) AB=5,BC=3,��ABC=60���́�ABC�ɂ����āACA=�m�A�n�A�O�ډ~�̔��aR�́m�C�n�ł���B
�܂����BC��Ɂ�BPC�̖ʐς��ő�ƂȂ�悤�ɓ_P���Ƃ�ƁAAP=�m�E�n�ł���B
���̂Ƃ�BP��R�̑召���r�����
BP�m�G�nR
�ł���A���l��BP��CA�̑召���r�����
BP�m�I�nCA
�ł���B
�k���l
�m�A�n�m�C�n�m�E�n�ɓ��Ă͂܂���������߂�B
�܂��m�G�n�m�I�n�ɓ��Ă͂܂邢���ꂩ�̋L�����ȉ�����I������B
�i�I�����j�@<�@=�@> >>152
>>151
���W�ɂ��Ɖ�(1)8��(2)(��a^2)/2�ɂȂ�悤�ł��B ���ȉ������܂����B
r>=0�ɂȂ�͈͂Őϕ�����Ώo���܂��ˁB
�����������܂����B ���_�̋ߖT��C^�����̊�f��R�S�̂Ɋg�����邱�Ƃ́A�uC^�����̊��͑������R���݂ɂ̂���̂ŁA�v
�ȒP�ł���Ə����Ă���{������̂ł����A�ǂ�����Ċg������̂ł��傤���H �_O�𒆐S�Ƃ���~C�̎���ɑ��قȂ�2�_A,B,C������AAB=1�AAC=3�ł���B
�܂�����BO��AC�͌�_D�������AOD=3/2�ł���B
BC�̒��������߂�B��������ACB<90���ł���B >>88�̌������ǂ���ς芄��Z�̈Ӗ����悭�킩��Ȃ�
100����0.1�Ŋ�������1000���ɂȂ���Ăǂ��������ƁH100���̒���0.1��1000��������Ă��������͂킩�����>>88�݂����ȋ�̓I�Șb�ɂȂ�Ɨ����ł��Ȃ� >>156
���̎���̌��t�̒ʂ�Ȃ疳���Ȕ��Ⴊ����B
�Ⴆ��(-��/2,��/2)�Œ�`���ꂽC^������
sin(tan(x))
��[-��/2,��/2]�ɘA���Ɋg�����邱�Ƃ���ł��Ȃ��B ���s�l�ӌ`��ABCD�ɂ����āA��ABC=�Ɓi0<��≤90���j�AAB=3�ABC=4�ł���B
����3���_A,B,C��ʂ�~K�Ɠ_D�̋�����1/2�ł���Ƃ����B�������~S�Ɠ_P�̋����Ƃ́AS�̎����P�ƍł��߂��_��Q�Ƃ����Ƃ���PQ�̒������w���B
sin�Ƃ̒l�����߂�B ���R��a,b,c,d��ad-bc=1�����B
a,b,c,d�̂������Ȃ��Ƃ���g�̎��R���݂͌��ɑf�ł��邩�A�܂��͓��������Ƃ������B ad �� bc �݂͌��ɑf�i1�ȊO�̌��������Ȃ��j
�� (a,b) (a,c) (b,d) (c,d) �͂ǂ���݂��ɑf�B >>153
�@B = 60�
�@cos(B) = 1/2,
���]���藝����
�@CA^2 = AB^2 + BC^2 -2�AB�BC�cos(B) = 19,
�@CA = ��19�@�@�@���� [�A]
�����藝����
�@R = CA/{2sin(B)} = CA/��3 = ��(19/3)�@�@���� [�C],
�@sin(A) = (BC/CA)sin(B) = (3/��19)(��3 /2) = (3��3)/(2��19) = 0.596040
�@cos(A) = 7/(2��19) = 0.802955
�@2sin(A/2) = ��{2 - 2cos(A)} = ��(2 - 7/��19) = 0.627766
�@2sin(B+A/2) = ��(2 + 8/��19) = 1.958399
P�͕�BC����̋������ő�ƂȂ�_�@�ˁ@��BC�̒��_
�@��AOP/2 = (��AOC+��COP)/2 = B + A/2 = 60� + A/2,
�@AP = 2Rsin(B+A/2) = ��(19/3) ��(2 + 8/��19) = ��{(38+8��19)/3}�@�@���� [�E]
�@BP = 2Rsin(A/2) = R��(2 - 7/��19) = 0.627766�R
�@BP �� R�@�@�@�����@[�G]
�@CA = ��19 = R��3,
�@BP �� CA�@�@�����@[�I] >>171
A (3cos��, 3sin��)
B (0, 0)
C (4, 0)
D (4+3cos��, 3sin��)
�Ƃ����B
K�̒��S�� O (2, y) �Ƃ����ƁA
�@y = (3-4cos��)/(2sin��),
K�̔��a��
�@R = ��(25-24cos��) / 2sin��,
K��̓_Q~�ɂ���
�@Q~D = (OQ~ + Q~D) - R �� OD - R,
�@QD = OD - R
�@�@ = ��{25-24cos(3��)} / 2sin�� - R,
�@QD = 1/2 ���
�@�� = 0.0211151976�@�@�@1.46102566
sin�� = 0.0211136286 0.9939812476 �O>>148
>>157 BC=��[4r^2-{(2r-3)^2/(2r+3)^2}]
>>161 sin��=t/r
cos��=��{1-(t/r)^2}
=(3^2+4^2-4t^2)/2�3�4
=(25-4t^2)/24
(25-4t^2)^2/24^2=1-t^2/r^2
(25-4t^2)^2�r^2=24^2(1-t^2)
r^2=24^2(1-t^2)/(25-4t^2)^2
sin��=t/��{24^2(1-t^2)/(25-4t^2)^2}
=t(25-4t^2)/24��(1-t^2)
�s�^�S���X�̒藝���A
(3sin��)^2+(4-3cos��)^2=4t^2
9sin^2��+16-24cos��+9cos^2��=4t^2
9(1-cos^2��)+16-24cos��+9cos^2��=4t^2
25-24cos��=4t^2
t^2=25/4-6cos��
sin��=t(25-4t^2)/24��(1-t^2)
=cos�Ɓ�(25/4-6cos��)/��(1-25/4+6cos��)
=cos�Ɓ�(25-24cos��)/��(24cos��-19)
sin^2��=cos^2��(25-24cos��)/(24cos��-19)
2sin��cos��=(cos^2��-sin^2��)(25-24cos��)/(24cos��-19)
2sin��cos��(24cos��-19)=(1-2sin^2��)(25-24cos��)
48sin��(1-sin^2��)-38sin��cos��=25-50sin^2��-24cos��+48sin^2��cos��
48sin��-48sin^3��-38sin��cos��=25-50sin^2��-24cos��+48sin^2��cos��
���f ���Z���ł�
��(0��1) �yx/��(1+x^2)�z^3 dx
����v�Z����̂ɁA��(1+x^2)�����ƒu�������
d��/dx=x/�����@dx=��/x d��
�ƂȂ��āA��(1����2) (x^3/��^3) * (��/x) d�� �ƂȂ�A�����v�Z�ł��܂����A
�����Ō`����ł���/x���o�Ă���̂��C��������(x=0�ɂȂ�̂�)�̂ł����A
����͓��Ăɂ����Ƃ��ǂ�����������悢�ł��傤���H
���邢�͕��ꂪ�[���ɂȂ�悤�ȏꍇ�͂����������̕ό`�͌��ł��傤���H >>167
�܂����Z�̋��ȏ��Ɍ����Ƃ��čڂ��Ă���̂������g���Ƃǂ����Ă������Ȃ�ˁB
���̋C���������͑�w��N�ŏK�������W���A�������͍L�`�ϕ��g����悤�ɂȂ�Ɖ��������B
�������Ȃ���g��Ȃ��Ă����Z�̋��ȏ��͈͓̔��ł��ł��Ȃ��Ȃ����낤���ǂ���Ȃ̏o��҂͋��߂ĂȂ����낤���B
�̉Ȃ炻��ŋ����Ă��炦�邵�A�����̋C�����������������������Ȃ��w�̋��{�̋��ȏ���ǂ݂�����������Ǝv���B ��������肾�B
x=tan�ƂȂǂƒu�����A�J�n��a��0����ɂ��ォ��a��0�Ƃ��ׂ����낤�B 2x + x2 + x3 + 6x4 = -2
x + 2x2 + x3 + x4 =1
x + x2 + 2x3 + x4 =1
x + x2 + x3 + 2x4 = a
�s��̖��ł��B ���̘A�������������������悤�ɁA�萔a���߂āA�������߂�B
(x1,x2,x3,x4)=c(-4,1,1,1)+(-2,1,1,0) a=0 1�`3�s�ڂ�������
�@4(x + x2 + x3 + 2x4) = -2 +1 +1 = 0
�ƂȂ邩��
�@a = 0,
(x, x2, x3, x4) = ( 2-4t, t, t, t-1)�@�@�@t�͔C�� �O>>166
>>157 BC=��[4r^2-{(2r-3)^2/(2r+3)^2}]
�s�^�S���X�̒藝���A
(2r)^2=1^2+3^2=10
r=��10/2
��BC=��[4�5/2-{(��10-3)^2/(��10+3)^2}]
=��10-(19-6��10)/(19+6��10)
=��10-(19-6��10)^2/(361-300)
=��10-361-360+38�6��10
=228��10-721 >>167
(x dx) ���P�̉�Ǝv���悢�B���܂̏ꍇ�́Ax�́y �z�̒�����o�Ă���B
���邢�́A1 + x^2 = y �Ƃ����� 2x dx = dy ������ 1/x �͏o�Ă��Ȃ��B
��(0��1) {x/��(1+x^2)}^3 dx = ��(1��2) (y-1)/[2y^(3/2)] dy ��w���w�A���v�w�ɂ��Ă̎���ł��B
�\�����v�ʁA�t�B�b�V���[�E�l�C�}���̕���藝�ɂ��āA�ȉ��̗�͐������ł��傤���H
��������`�̐����m���͂��Ƃ���B�����͂R������܂�
�s����B
x_k��k��ڂɎ���������������1�A�������������Ȃ�������0�̒l���Ƃ�B
x��(x_1,x_2,�E�E�E,x_n)�Ƃ���Bn�͎������R��ڂɐ����������̎����ł���B
���v�ʂs(�w)���R��ڂɎ����������������̎����Ƃ���B
���̎��A�s(�w)���\�����v�ʂł��邱�Ƃׂ�B
�o(�w�����b�s(��)�����G��)
��1/{(n�|1)�b2}
��肐�̒l�ɂ��Ȃ��̂ŁA�s(�w)�͏\�����v�ʂƌĂׂ�B
������t�B�b�V���[�E�l�C�}���̕���藝�ł����ׂ�
�o(�w����)
��p^3(1�|p)^(n�|3)
��p^3(1�|p)^(�s(��)�|3)
���Ah(x)��1�Ag(T(x),p)��p^3(1�|p)^(�s(��)�|3)�ƕ����ł���̂ŁA�s(��)�͏\�����v�ʂƌ�����B ����ł�
3�_�����ꂼ��x�Ay�Az����ɂ���O�p�`�ŁA�O�p�`�̎��̒�����1�ƂȂ�O�p�`�S�̂̏W���͂ǂ̂悤�Ȑ}�`�ɂȂ�܂����H
�_�̏d���⋫�E���Ȃǂׂ̍��ȋc�_�͕s�v�ł��B �藝�F
������ a_0 + a_1*x + a_2*x^2 + �c + a_n*x^n + �c �ɑ��āA���̂悤�Ȑ��������� �� ���������܂�B
|x| < �� �ł���C�ӂ� x �ɑ��āA a_0 + a_1*x + a_2*x^2 + �c + a_n*x^n + �c �͐�Ύ�������B
|x| > �� �ł���C�ӂ� x �ɑ��āA a_0 + a_1*x + a_2*x^2 + �c + a_n*x^n + �c �͔��U����B
�n�F
������ a_0 + a_1*x + a_2*x^2 + �c + a_n*x^n + �c �� 0 �łȂ��������a�������߂̕K�v�\�������́A
�K���Ȑ��̒萔 c, M ��I��ŁA���ׂĂ� n �ɂ��� |a_n| �� c*M^n ����������悤�ɂł��邱�Ƃł���B
�Ȃ��A���ꂪ��ԏ�̒藝�̌n�Ȃ̂ł��傤���H n�̖��m�������S�ɋ��߂邽�߂ɂ�n�̓Ɨ���(�����łȂ�)���������K�v�ł���Ƃ�������͐������ł����H
���̖���̖��O�A�ؖ��͂���܂����H
���`�ȏꍇ�Ȃ狳�ȏ��ɍڂ��Ă��܂�������`�ȏꍇ�ł���ɐ��藧���Ă���C�����܂� �O>>176
BO=r=2���炢�H
����BO�Ɓ�ABC�̌�_��B�łȂ��ق���B'�Ƃ���ƁA
��ADB'�䁢BDC
DC=t�Ƃ����ƁA
(r+3)/2(3-t)=t/(r-3/2)
r^2=9/4+3t-t^2
B'C=(r-3/2)/(r+3/2)
BB'=2r
BC^2=4r^2-{(r-3/2)^2/(r+3/2)^2}
={4r^2(r+3/2)^2-(r-3/2)^2}/(r+3/2)^2
={4r^2(r^2+3r+9/4)-(r^2-3r+9/4}/(r+3/2)^2
=(4r^4+12r^3+8r^2+3r-9/4)/(r+3/2)^2 >>178
�Ȃ����ĂȂ�A�藝����ؖ��ł��邩�炾�낤
���������������ar>0������
�˒藝���A0<x<r�ƂȂ�x�ɑ�,�������͐�Ύ������邽��x=1/M(M>1/r)�Ƃ���ƁA
|an|(1/M)^n����|a_k|(1/M)^k<c
�ƂȂ�c>0�����݂���
�˂���c,M>0�����݂��A�C�ӂ�n��N�ɑ�|an|<c*M^n
�����ɑ��A����c,M>0�����݂��A�C�ӂ�n��N�ɑ�|an|<c*M^n
�˔C�ӂ�s(0<s<1)�ɑ��A|an|*(s/M)^n<cs^n
�˃�|ak|*(s/M)^k<��cs^k=c/(1-s)�ƂȂ�A��������x=s/M>0�Ő�Ύ�������
�˒藝���ς��������܂�A0<s/M<1/M����
�ː�������0�łȂ��������a�ς�����
�璷���낤������� >>182
���肪�Ƃ��������܂��B
>>178
�͈ꏼ�M����̖{�ɍڂ��Ă��閽��ł��B
�Ȃ��A������n�Ƃ��Ė{�ɏ������������̂�����ł��B����Ȃɏd�v�Ȗ���ł��傤���H �ꏼ�M����̖{�ɂ́A���ɂ��A�Ӗ��s���Ȍn������܂��F
2�ׂ̂����� f(x), g(x) �̎������a���Ƃ��� �� �ȏ�Ȃ�A
��*f(x) + ��*g(x) �̎������a�� �� �ȏ�ł���B
f(x)*g(x) �̎������a�� �� �ȏ�ł���B
�Ƃ����藝�̌n�Ƃ��āA
f(x) �̎������a�� 1 �ȏ�Ȃ�A f(x) / (1-x) �̎������a�� 1 �ȏ�ł���A
f(x) / (1 - x) = �� s_n * x^n, where s_n = a_0 + �c + a_n
�Ƃ������肪�����Ă���܂��B
�Ȃ��A���̖�����n�Ƃ��ď������̂�����ł��B �����͖{���ɏ��߂��猋�ʂ����܂��Ă邩�H�Ƃ����Q�[�����_�̘b��
���̂悤�ɏؖ����Ă���l�������ł����A�{���ɏؖ��ɂȂ��Ă܂����H
https://twitter.com/cobnutsinterest/status/1131158401474416640
https://twitter.com/5chan_nel (5ch newer account) >>183
���������ďd�v�ƌ��Ȃ����ɂ�邪�A�N�ł��m���Ă�L������ł͂���
�e�L�X�g���Ɍn�������ꍇ�́A�P�ɗL�p�Ȃ��̂ł��邩�A���邢�͂���ȍ~�̂ǂ����ł��̎咣���g���ׂł��邱�Ƃ��قƂ�� > 3*40^(2*82)+1��ȓ��ŏ����͕K���I���B
����A�������̂��H �@�@�@�@�@�@�@��__��
�@�@�@�@�@�@�i�L�́M�@�j
�@�@�@�@�@�@ �i����*�܁�)
�@�@�@�@�@ �@�@/__�m�ցR__ >>197
�L���m�芮�S���Q�[��������őP��������ΐ��K���A���K���A�K�����������̂����ꂩ�ł���̂͊ԈႢ�Ȃ��B >>188
> > 3*40^(2*82)+1��ȓ��ŏ����͕K���I���B
> ����A�������̂��H
�Ֆʂ̏�Ԑ����ォ��l����ƁA1��̏��2*82�ʂ��40��̑g�ݍ��킹������A
3*(2*82)^40+1����Ȃ����Ȃ��H ���邩�ǂ������l����Ȃ��Ƃ����Ȃ�����A3*(2*82*2)^40+1��
�d�v�Ȃ̂́A�ǂꂭ�炢�ŗ}�����邩�ł͂Ȃ��A�L�����ǂ������������獱���Ȃ��Ƃ����� �S�Ă̋ǖʂ�3����邽�玟�͕K�������ɂȂ���Ă��Ƃ�
���ۂɂ͂����Ə��Ȃ��萔�ȓ��Ō���or�����ɂȂ�͂������ǂƂ肠�����L���ł��邱�Ƃ͊ԈႢ�Ȃ���
�����͂ǂ��ł������Ƃ͌����A82���ĂȂ��82�H
��u�����ꏊ�͔Ֆ�81�������2�����̌v83�����Ȃ�H >>181
179�ł�
�A���藝��179�̎咣���S�R�Ȃ����Ă�悤�Ɋ����Ȃ���ł���
����ȓ�������Ă�킯����Ȃ��ł�
�Ⴆ��
���m�萔a�Ab������
a^2+b^2=25
a=3
�Ƃ�����̏������������2�̖��m�萔a��b�͊��S�Ɍ���ł��܂�
���l�Ɏ����̍��܂ł̌o�������疽��
�u���`�E����`�ɂ�����炸�������Ɩ��m���̐�����v����ΑS�Ă̖��m��������ł���v
�����藧�Ǝv���Ă��܂�
���̖���̐^�U��m�肽���ł� >>193
�Ֆ�81�����͐��ƌ��̂ǂ���̋��81*2�ʂ�
�������ƌ��ǂ���̋�䂩��2�ʂ�
���킹��81*2+2=82*2�Ƃ������Ƃ��� ����
z=x^2+y^2
z=0
�̉��́A{(0,0,0)} �����̎����\�ǖʐ���10^68���炢��
�g�����v�T�Q���̏���̐��i52�I�j�△�ʑ吔�i10^68�j�Ɠ������炢
http://www.nara-wu.ac.jp/math/personal/shinoda/legal.pdf >>195
�Ȃ�قǂ��������z�����Ă�̂�
���������A���E���ԁE�j�n�͒u���Ȃ��ʒu������A�����E�ʏ��E���y�ы��̋�͐���Ȃ��A����̓_���ȂǂȂǂ��邩����ۂ͂����Ƃ����Ə��Ȃ��� �A�[�@�̕����͓��ɖ��Ȃ���ł�����
�A�[�@���Ă悭�h�~�m�|���ɗႦ���܂����ǁA>>186�͖l�̊��o���ƃh�~�m���}�����ꂵ�Ă�C��������ł��B
�܂�Ap(k)�̔Ֆʂ�K���Ɖ��肵�Ă��Ap(k�|1)�̔Ֆʂł�p(k)�̔ՖʂɂȂ����w���Ƃ͌���Ȃ�����A
���ꂾ��p(k)�����肵�����Ƃƌq����Ȃ��c�H�����ł���H���č������ł� �����ł����_���̂͋^���ĂȂ���Ő\�����Ƃ��܂� >>194
�u����v�̈Ӗ��́H
���̗Ⴞ��(a,b)=(3,4),(3,-4)���������A���͕����ł������̂��H�L���܂ŋ����H
sin(x)=0�͉��������ɑ��݂��邪�A���̏ꍇ�ł����肳�ꂽ�ƍl����́H
�����ł��ǂ��Ȃ�Ӗ��̂Ȃ��咣�ɂȂ�Ǝv����
�̂ƁA�������Ƃ��ċ������̑I���͉������̂��H >>199
p(k)��k��܂Ŏw�����Ƃ��Ɍ����S�Ă̔Ֆʂ��W�߂��W��
�Ȃ̂ŁAp(k-1)����P�Ֆʂ�I�ԂƂ��A���̔Ֆʂ���������w�����Ƃœ�����S�Ă̔Ֆʂ�p(k)�Ɋ܂܂�Ă���
��������Ȃ��Ǝv���܂� ���c�C�[�g��K���ɓǂ�ł���ŁA�O�̂��ߓǂݕԂ�����P(k)�̒�`�������
>>202�͂��̂܂܂��ƕςȂ̂œK���ɓǂݑւ��Ă������� �͂��A�W���Ƃ��l���܂���
������������Ɓu�����őP�Ȃ�c�v�Ă����������Ӗ�����̂��ȂƁB
p(k)���őP�̔ՖʂłȂ���A����l��k�ȉ��ŁA"�K�s���ɕK���肪���݂��Ă��܂�����"������͂��ł��B
����ł����������̋c�_�̃e�[�}�Ƃ����̂́A�u����p(k)�̔Ֆʂ̒���"�K�s���ɕK���肪���݂��Ă��܂������Ȃ�����܂Ŗ߂���悤�Ȑ}"�����݂��邩�H�v
���Ǝv������ł��������ł͂Ȃ��̂ł����B >>204
���c�C�[�g���Ԃ������ǁu�őP�̔Ֆʁv���čl�����͏o�ĂȂ��Ǝv��
����Ֆʂɂ�����őP��̒�`��
�u�K���ՖʂɂȂ��B���ꂪ�����ꍇ�͕K���������ՖʂɂȂ��B������Ȃ��ꍇ��(�K�s�ՖʂɂȂ�肵���Ȃ��̂�)�ǂ�ł��悢�v
�����āA�őP��̎�ނɂ���ċA�[�I�ɔՖʂ̎�ނ��m�肳���Ă����A�ƍl���Ă���(�c�C�[�g�ł����K����(iii)��p���Ă���)
�Ȃ̂�
�u�K�s�Ֆʂɂ����ĕK����(=�K���ՖʂɈڍs�����)�����݂���v
�Ƃ������Ƃ͋N���蓾�Ȃ�
�������̂悤�Ȏ肪���݂���Ȃ�A���̔Ֆʂ͂��Ƃ��ƕK���ՖʂƔ��ʂ���Ă��邩�� >>199
�ǖ�p(k)������ԂŐ��K���Ɖ��肷��ƁA
����Ԃ�p(k-1)��p(k)���܂߂����K���ɂȂ�ǖʂɂȂ�悤�łĂ�������p(k-1)�͐��K���ɂȂ�
p(k)������ԂŐ��K���Ɖ��肷��ƁA
����Ԃ�p(k-1)�́A
p(k)���܂߂����ׂĂ̎��̋ǖʂ����K���ɂȂ�Ȃ��p(k-1)�͐��K���ɂȂ�A
p(k)�ȊO�̎�Ɉ�������������A���K�s���Ȃ��A���ׂĂ̎��̋ǖʂ����K�������������Ȃ��p(k-1)�͈��������ɂȂ�A
p(k)�ȊO�̎�ɐ��K�s�����肷�ׂĂ̎��̋ǖʂ����K���A���������A���K�s�Ȃ��p(k-1)�͐��K�s�ɂȂ�
���́Ap(k-1)�ɑΉ����鎟�̋ǖʂ̏W��(p(k)���܂ށj�����ׂĐ��K���A���������A���K�s�Ɋ��蓖�Ă��邩������ǁA
�����ŁA�ǖʂ̖������[�v�����݂����A�ǂ�ȋǖʂ��ǂ�Ȏ�ł��L����ŏI�ǂɂȂ�A�Ƃ������Ƃ������Ă���
����ɂ��Ap(k-1)����I�ǂ܂łɌ���邷�ׂĂ̋ǖʂɐ��K���A���������A���K�s�����蓖�Ă邱�Ƃ��ł��āAp(k-1)�����蓖�Ă邱�Ƃ��ł��� >>157
�~K�̎���ɑ��قȂ�R�_A,B,C������Ƃ���B�~K�̔��a�����Ƃ���B
�@O (0, 0)
�@A (r�cos��, r�sin��)
�@B (r�cos��, r�sin��)
�@C (r�cos��, r�sin��)
�@D ((3/2)cos��, (3/2)sin��)
��ӂ��
�@2r�sin((��-��)/2) = AB = 1,
�@2r�sin((��-��)/2) = AC = 3,
�@2r�sin((��-��)/2) = BC,
�܂�
OB:�@y = (tan��)x,
��=0 �Ƃ����
AC:�@y = (r-x)/tan(��/2),
��_D�͂��̗���������B
���@cos(��/2-��) = 1/tan(��/2),
r = 2.06707551803854068
�@{r^6 - 3r^5 + (33/4)r^3 - (117/16)r^2 - (27/8)r + (9/16) = 0 �̐���}
sin(��/2) = 1 / 2r = 0.241887630924318018
cos�� = 0.882980748011641818
sin�� = 0.469409201700181301
�� = 0.48862156358647885663
sin(��/2) = 3 / 2r = 0.725662892772954
tan(��/2) = 1.054665301733036072
1/tan(��/2) = 0.948168104475221164
�� = 1.62399468360912675
BC = 2.222862396800842775 �O>>185
>>157
��ABC�̊O�ډ~�̔��a��r�Ƃ��A����BO�ƊO�ډ~�̌�_�̂���B�łȂ��ق���B'�Ƃ���ƁA
BD=r+3/2
DB'=r-3/2
��ABD�䁢CB'D(��2�p��������)���A
BD=2r����AC=3�ɒ��ӂ���AC��D�ŕ�������ƁA
BD:B'D=AD:CD
(r+3/2):(r-3/2)
=(3/2r)(r+3/2):(3/2r)(r-3/2)
AD=(3/2r)(r+3/2)
=(6r+9)/4r
CD=(3/2r)(r-3/2)
=(6r-9)/4r
�s�^�S���X�̒藝���A
AB'=��(BB'^2-AB^2)
=��(4r^2-1)
��AB'D�䁢BCD(��2�p��������)���A
AB':BC=AD:BD=B'D:CD
{(6r+9)/4r}:(r+3/2)
=(r-3/2):{(6r-9)/4r}
(r+3/2)(r-3/2)={(6r+9)/4r}{(6r-9)/4r}
r^2-9/4=(36r^2-81)/16r^216r^4-36r^2=36r^2-81
16r^4-72r^2+81=0
(4r^2-9)^2=0
4r^2-9=0
r=3/2
(D�AB'�AC����v����̂͂����������ǖ���)
BC=AB'(BD/AD)
=��(4r^2-1)�(r+3/2)4r/(6r+9)
=��(4�9/4-1)�(3/2+3/2)4(3/2){6(3/2)+9}
=��8�3�4(3/2)/(9+9)
=2��2�(18/18)
=2��2 �������O�O������wiki�ɖʔ������Ƃ�������Ă���
> �ȑO�́u����ǖʂɖ߂铯��菇��A��3��v�Ƃ������[���ł��������A����ǖʂɖ߂�菇����������ꍇ�A���̃��[���ł͖����Ɏw����𑱂��邱�Ƃ��\
�菇��2�ʂ�iA��B�Ƃ���j�̏ꍇ�AAB�Ƃ���Ή���o����Ǝv����ABABABABAB�Ƃ���Ă��܂��Ƃ���ς�����ɂȂ�
�����ɂȂ�Ȃ��悤�ɂ���ɂ͂ǂ̂悤�ɂ��Ă����Ηǂ���
�iwiki�̒��߂Ɉ�Ⴊ�ڂ��Ă���j >>206
�l�͂��̍l�������ƁA�ŏI���ʂ��揟�㏟�����ɂȂ邱�Ƃ̂ݎ����Ă���ɂ������A
�͂��߂���ǂꂩ�Ɍ��܂��Ă邱�Ƃ܂͎����ĂȂ��H�i�I�ǂ܂Ōq�����Ă邩�͂킩��Ȃ��j���ă`��������ł������v�����ł���
���邢�͂��������L���m����Q�[�������肵���Ƃ��́A���ʂאs�����đo�����œK�헪��I���ł��邱�Ƃ������Ƃ���̂��i�m���ɒ����I�ɂ͎����ł����j
�Ă�����Q�[�����_�����ă}�b�N�X�~�j�Ƃ��i�b�V���ύt���g��Ȃ��Əؖ��������Ǝv���Ă���ňӊO�ł����B f(x) := �� a_n * x^n �̎������a�� �� > 0 �Ƃ���B
�� a_n * x^n �� N ���܂ł̕����a�� f_N(x) �Ƃ���B
�� �� 0 < �� < �� �ł���悤�Ȏ����Ƃ���B
[-��, ��] �Œ�`���ꂽ�� f(x) - f_N(x) ���l����B
max |f(x) - f_N(x)| �� 0 �iN �� ���j �������B >>209
cube-free binary word �Ƃ��ŃO�O��ΐF�X�o�Ă���� >>161 >>165
�@cos�� = c �Ƃ����B
�@1/2 = QD = OD - R = {��(25 - 24(-3c+4c^3)) - ��(25-24c)} / 2��(1-cc),
�@1- cc �� 0,
���
�@cc - (1/96)c - (1/2) �� (7/32)��5 = 0,
�@c = (1/192) + ��{(1/192)^2 + 1/2 �} (7/32)��5)}
�@�@= 0.9997770825�@�@�@�@0.10955035103
���@sin�� = 0.0211136286�@�@�@�@0.9939812476 >>161���B�O>>208
48sin��-48sin^3��-38sin��cos��=25-50sin^2��-24cos��+48sin^2��cos��
48sin��(1-cos^2��)-38sin��cos��=25-50(1-cos^2��)-24cos��+48(1-cos^2��)cos��
48sin��-48sin�ƥcos^2��-38sin��cos��=25-50+50cos^2��-24cos��+48cos��-48cos^3��
48sin��-48sin�ƥcos^2��-38sin��cos��=-25+50cos^2��+24cos��-48cos^3�� ����ł��B
3���_�����ꂼ��x�Ay�Az����ɂ���O�p�`�Ŏ��̒�����1�̂��̑S�̂̏W���͂ǂ̂悤�ȗ��̂ɂȂ�܂����H
���j�ł��ǂ��̂ŃA�h�o�C�X�~�����ł��B Thurston �̎��o�I�˔\
Thurston �Ƃ���Princeton �̋����ɂȂ��Ă�l��������ǁC
�ނɂ��� RaoulBott �� Michigan ��w�ɋ������C�ނ̓��w�̃e�X�g�Ɋւ��āD
Thurston �����i�����邩�C�����Ȃ����C�F�X�Ƌc�_�ɂȂ����炵���D
����́C�����o���Ă��C�ނ͊G����`���Ă�����Č����D
����S�R�����Ȃ�����{���ɕ������Ă���̂��C�������Ă��Ȃ��̂��C������Ȃ����āD
�ނ͎��o�I�ȓƓ��̍˔\�������Ă��ł��ˁD������C����͂���ŗǂ���ł��D
����� Princeton ��w�̋����ɂ��Ȃ����D���������l�������ł� >>215
2�̕Ӓ������������Ȃ�����2�����A���̂ɂȂ��
1�̕Ӓ���0�`1/2�͈̔�
�Ή����钸�_�͕ӂ̒[�_�̐������ɋ��܂�͈͂Ő���ꂽ�ȉ~���� �N��>>88�ɂ��ċ����Ă���
�v�����100���~0.9=90�� 90���~0.9=81�� 81���~0.9=72.9���c������v�Z�������Ă��ׂĂ𑫂��Ă����ƍŏI�I��1000���ɂȂ�Ƃ̂��Ɓi���̐����͂킩��j
�����������100����0.1�̌v�Z�����œ����o������Ă����������킩���
���w���݂����Ȋ���Z�̊��o�����Ȃ����痝���ł��Ȃ��i100���̕���0.1���������牽�l�ɕ������邩�H�݂����Ȋ��o�����Ȃ��j
���ꂩ�����Ă��� >>218
S-nS�@ �Ō���
���Z���w�̗��n�ŏK��
���̎��ƁA�S�̂Ɍ���0.9������������
�p�ӂ��Ă���A�S�̂������Z����悢
100�{90�{81�{72.9�{�c��S
�@ �@ 90�{81�{72.9�{�c��0.9S
�ォ�牺��������
100��S�|0.9S��0.1S
���߂�S�̒l��
S��100/(1�|0.9)��100/0.1��100�~10
S��1000 >>218
����͂ǂ��H
��������
1-x^n=(1-x)(1+x+x^2+...+x^(n-1))
����
(1-x^n)/(1-x)=1+x+x^2+...+x^(n-1)
|x|<1�An�����̎�
1/(1-x)=1+x+x^2+...+x^n+x^(n+1)+...
> �v�����100���~0.9=90�� 90���~0.9=81�� 81���~0.9=72.9���c������v�Z�������Ă��ׂĂ𑫂��Ă����ƍŏI�I��1000���ɂȂ�Ƃ̂��Ɓi���̐����͂킩��j
����ɓ��Ă͂߂�Ȃ�
1,000,000/(1-0.9)=1,000,000*(1+0.9+0.9^2+...) ��(x^2+y^2)+��(y^2+z^2)+��(z^2+x^2) = 1
z=t(0≤t<1) >>217
���̂ɂȂ�Ȃ����Ăǂ��������Ƃł��傤���H �Ō��The Flawed Proof��g(x)�������I�萔���ƂȂ�Ƃ����藧���Ȃ��͕̂�����̂ł����A���̏��3�y�[�W�ɂ킽���ď����Ă���ؖ������̃|�C���g���N���A�ł��Ă��Ȃ��悤�Ɏv���܂�
�Ƃ����̂�k=(g'(x)+v)h�Ȃ킯�ł����A���ꂪ���������̖��ƂȂ��Ă���g(x+h)-g(x)�Ȃ̂ł����āAg(x)���萔�ƂȂ��Ă��镔���ɂ��Ă͂�͂�h���ǂ����������Ă�k=0�ƂȂ��Ă��܂����߁Ak�ł̏��Z���܂�w�͒�`�ł��Ȃ����ƂɂȂ��Ă��܂�����ł�
����ɂ��Ăǂ��Ȃ̂ł��傤���H���̉p�T�C�g�̏ؖ����������Ă���̂ŗL���Ȏ�@�Ȃ̂ŋ��炭�����Ă���̂ł��傤���A����Ȃ玄�̉����Ⴄ�̂ł��傤��
https://i.imgur.com/nVd2Flj.jpg
https://i.imgur.com/gECuyWH.jpg
https://i.imgur.com/l612nZw.jpg �Ȃ�Ƃ������A�摜���Q�Ƃ���C���S���N���Ȃ��{�� ���ԂȎ�����Ȃ���
��ڂȎ��ł��Ȃ���
�{���ڂ�Ȏ��ł��Ȃ��āA�T�o�Ȏ����ĉ��H �h���A�u���̒藝�̖������Ă��ł���
1 + cos�� + cos2�ƥ���cos n�� ��
cos n/2�� sin n+1/2�� / sin��/2����v����̂ŏؖ������Ə����Ă���܂�
�ǂ�����v���ĂȂ��悤�Ɍ����܂����A���̓�͉��̈�v���Ă���ƌ�����̂ł��傤���H �O>>214
2sin��(24-19cos��-24cos^2��)=-25+24cos��+50cos^2��-48cos^3�� >>219
0.1���Ă����������o�Ă��闝�R�͂��̐����ŗ����ł����C������
�ł��A�z�Șb������100��0.1�Ŋ�����Ă����Ӗ����킩����
�ǂ����Ă�100�̒���0.1�������̂���̂��H���Ă����v�l�����ł��Ȃ��i���̏ꍇ1000�j
�ł�90+81+72.9+�c���đ����Ă�0.1��1000��o�ꂷ��킯����Ȃ��ł���
�c�t�Ȏ���Ő\����Ȃ��� >>226
�����Â炢�A���ʎg��
�Ƃ肠������cosk��sin(��/2)���v�Z���Ă݂��炢���Ǝv���� >>217
�ȉ~�ɂȂ�����������������Ă��炦�Ȃ��ł��傤���H ���ʏ�Ɂ�ABC�Ɠ_P������AP��PA+PB+PC���ŏ��ɂ���_�ł���B
��ABC�̎�����L�Ƃ���Ƃ��AL/2��PA+PB+PC�̑召���r����B ���̖�苳���ĉ�����
1�K�v
2�K�v�ł��\���ł��Ȃ�
3�K�v�\��
���Ǝv����ł��������Ă鎩�M�Ȃ��ł�
https://i.imgur.com/ZwSQ18v.jpg �����Ă�����ˁH
��ӂ́A�Ӓ���2�̗����̂�8���_�B
(1)�́A�e�ʂ��ɍL����6���ʂ̍����B
(2)�́A(0,0,0)��(2,2,2)�ɐڂ��Ȃ�6�ł��ɉ�������6�����̍����B
(3)�́A��ӂƓ����B >>231
��A �� 120� �̂Ƃ��AP=A
�@PA �{ PB + PC = AB + AC,
�@L/2 = (AB+BC+CA)/2 < AB + AC,�@�@(���s����)
��ABC ��120߈ȏ�̒��_�������Ȃ��Ƃ��AP�̓t�F���}�[�_�B
�@PA + PB + PC = x + y + z,
�@��APB = ��BPC = ��CPA = 120� ������
AB = ��(xx+xy+yy) < x + y,
BC = ��(yy+yz+zz) < y + z,
CA = ��(zz+zx+xx) < z + x,
L/2 = (AB+BC+CA)/2 < x+y+z, >>228
���w�����x���̊���Z�̎d�������̂܂܊o���Ă����̂�
����ᕪ������ >>236
�S�̂̐����P������̐���������
�S�̂̐������������P������̐�
����ɂƂ��Ċ���Z�͂��̗����ł����Ȃ�
������܂��ŋ����Ăق���
>>88��100����0.1��1000���i900���j�����߂��܂����Č����Ă������ł��Ȃ�
����Z�̖{�����킩���ĂȂ� �������̔����̏ؖ��ɂ��Ă���Ɏ���Ȃ̂ł���
�����S�̂Ŕ����\�Ȏ���f(x), g(x)���Ƃ���f(g(x))�̔������l����
�Ƃ��ɁA
g(x)���ux���܂ސ��̒���������Ԃŏ�Ɉ��l�ƂȂ�v�悤�Ȃ��Ƃ̂Ȃ��ꍇg(x+h)-g(x)��h���\���������Ƃ��0�ɂȂ邱�Ƃ͂Ȃ����狳�ȏ��Ȃǂɂ悭�ڂ��Ă���Ԉ�����ؖ��ł������
x���܂ސ��̒���������Ԃň��l�ƂȂ�Ƃ��A
���̋�Ԃ̒[��x�łȂ��ꍇ��h���������Ƃ��g(x)�͂˂Ɉ��ŁA�܂������0
�[��x�ł���ꍇ�͗����������l����0
�܂���df(g(x))/dx=f'(g(x))g'(x)
�ƍl�����̂ł����A���̏ؖ�(�H)��g(x)=(x^2)sin(1/x) (g(0)=0�Ƃ���Δ����\)
�̂Ƃ��ɂ����Ă͂܂�̂ł��傤���H
f(g(x))��x=0�ł̔����W�����l����ƁAg(x)�͌��_�t�߂Ŗ�����U������̂łǂ̂悤�Ȍ��_���܂ޏ�������Ԃ��Ƃ��Ă����̋�Ԃ̓�����g(0+h)-g(0)=0�A�܂�g(h)=0�Ȃ�h������킯�ł� �S����x�ɑ��A�ǂ̂悤�Ȑ��̎����Â������Ă��Ă�sup|f(x)-x|<�Â���sup|f'(x)-1|<�Â���������C1�������ʑ��̗�������Ă��������B >>239
�ꎟ���ȊO�łȂ�ׂ���R���肢���܂� >>237
�v�Z����Ƃ����Ȃ�Ƃ����ɉ߂��Ȃ�
�ό`�������Ƃ̐����ɂ͕K�������Ӗ�����������Ƃ͌���Ȃ�
�������̉��̌����Ƃ��v�Z���Ă������炻�̌`�ɂȂ����Ƃ��������悤���Ȃ�����H >>232
���������̂ŕK�v�ł��\���ł��Ȃ��������ɂȂ�̂͂��߂Ă݂� >>232
(2)�͏\����������Ȃ����� >>244
�͂��B�ԈႢ�ł����B
�u�K�v�ł��\���ł��Ȃ��v�������ɂ�
����݂̂Ő������������
�����݂̂Ő���������������ꂼ�ꎦ���Ηǂ�
�����(2)�̏ꍇ
x=y=z=0 �� x=0,y=1,z=2 ������ɂ����� >>237
1��10���������0.1�ɂȂ���
�ʂɂ��̂܂܂̗����ŏ[������
�����ɘf�킳��Ď����̗������g���Ȃ�����������
���M�����Ă����̂� >>241
�m���ɂ���͂킩��
�ł������킩���̂͒P�Ȃ鐮����������
�������̊���Z�̌����i����Ɠ������j��>>88�̋�̗�ɂǂ����Ă͂܂��Ă�̂��������ł��Ȃ�
���̂��߂ɉ��p����������Z�̈Ӗ����m�肽������ �Z���Č��͂Ƃ������A���Z���Č��͂ȁE�E�E >>247
�����������ŋl�܂��Ă���̂�
100����0.1�ŋ��߂������̂Ȃ��
�u0.1�����{������100���ɂȂ邩�v
�����Ȃ���
�u����0.1�{������100���ɂȂ邩�v
�̂ǂ��炩�����Ȃ����낤 ���̃X���ɍ���Ȃ��Ǝv���Ȃ珬���w�X���ɗU������������낤 ��֎����̎Z���̂悤�Ȃ��̂Ȃ�Ƃ������A�����̌v�Z�́A�A�A >>250
���w�ŗc�t�ȓ��e�̘b���Đ\����Ȃ�
�ł��Ō�ɂ�����x�����������Ď��₵����
�����킩���̂͋�s�̐M�p�n���̌v�Z
��s�̐M�p�n�����Ă̂͗a���̈ꕔ���c���Ă���ȊO��݂��o�����Ă����d�g��
�Ⴆ��A��s���a����10%�����c���Ă���ȊO��a��Ђɑ݂��o���Aa��Ђ�b��Ђւ̎x�����ɂ��̋����g���B
��������ƍ��x��b��Ђ����̋���B��s�ɗa����B��s�͂܂����̈ꕔ�i10%�j���c���Ă���ȊO��݂��o���c���Ă̂��J��Ԃ��Ƌ�s�S�̗̂a���͑����Ă������Ă������Ƃ炵��
���ꂪ100���i�ŏ��̗a���j+100���~0.9=90���A90���~0.9=81�� 81���~0.9=72.9�c
0.9���|�������ďo���l�i90+81+72.9+�c+�ŏ���100�j�����ׂđ������킹����1000��
�ŏ��̗a��100���͍ő�900�������đS�̂�1000���ɂȂ�Ƃ̂���
�ł����ȏ��ɂ�����Ȍv�Z�͂���K�v�͂Ȃ��A100����0.1�i�ꕔ�c�������̗��j��1000���ł����Ƃ̂���
�����Ă�������ŏI�I��1000�����Ƃ����̂͂킩�邯�ǁA100����10%�i�݂��Ȃ������ꕔ�j�Ŋ�������S�̗̂a����1000�����ƌ����Ă������ł��Ȃ� >>247
> >>88�̋�̗�ɂǂ����Ă͂܂��Ă�̂�
�����ɂ͓��ɈӖ����������Ă��Ƃ���
�v�Z������100����0.1�ɂȂ����Ƃ��������Ȃ̂ł����ɈӖ������߂悤�Ƃ��邱�Ǝ��̂ɖ���������i���ʂƂ��ďo�Ă������ɏ�ɈӖ�������������킯�ł͂Ȃ��j
�����Č����Ȃ�A����̐�Βl��1�����̏ꍇ��n��傫�����Ă�����ar^n��0�ɋ߂Â��Ă����̂�
���䐔��̘a�ua�i1-r^n�j/�i1-r�j�v�͏������i1-����j�ɋ߂Â��Ă������Ă��Ɓi>>219�ɏ�����Ă��邱�Ƃ����t�ɂ������������ǁj >>253
���w�̂ł��Ȃ��l�̓����Ƃ��ĈӖ����l����Ƃ����̂�����܂���
���ɈӖ��͂Ȃ���ł���
������������������킯�ł�
���̌����̏o�����͋����邱�Ƃ��ł��Ă��A���̎����̂̎��Ӗ���C���[�W�Ƃ��������̂͋����邱�Ƃ��ł��܂���
���Ȃ����g�������̒��Ŕ[������ׂ����̂ł�
�����̑����Z�̓����S�����킹�Ă����C���[�W
�����̑����Z�͕R�̒����𑫂��Ă����C���[�W
�ǂ������{���̃C���[�W���Ȃ�ĈӖ��Ȃ��ł���� �������������̂��l���邩��킩��Ȃ��̂ł͂Ȃ��āA�P�Ɍ�����𐂂�Ă��邾���ł���
�v�́A�ł��Ȃ���������l���邱�ƂɑS�͂��₵�Ă���킯�ł� �Ⴂ�܂���H
�킩��Ȃ��l�͍l�������ł�
�������w���ł���l�͉����l���Ȃ��̂łł���̂ł�
�{���ɐ��w���ł���l�́A������ӂ̉��l���f����̑I���ł���̂ł� 1+2+3+4+�c��1��(-12)�����Č���ꂽ����
�Ȃ�-12�Ŋ���̂��킩��܂��� ���p����������Z�̈Ӗ����āc�B
������������Z���̂��{���͊ȒP�Ɏg�����Ⴂ���Ȃ��Ƃ������c�B�ςƋt�Z�̊W�ł��鎖�̓����Ƃ��ď��w���ɂ킩��₷�������Ă邾���ł����āc
���p�����c�c�c �O>>227
>>161
2sin��(24-19cos��-24cos^2��)=-25+24cos��+50cos^2��-48cos^3��
sin��=��(1-cos^2��)
2��(1-cos^2��)�(24-19cos��-24cos^2��)=-25+24cos��+50cos^2��-48cos^3��
4(1-cos^2��)(24-19cos��-24cos^2��)^2=(-25+24cos��+50cos^2��-48cos^3��)^2
AC=2r�sin��
BD=2r+1/2 >>253
�Ӗ�����l���Ă݂���
���̎d�g�݂̏ꍇ�A�ꕔ�Ƃ����̂�0�����傫��100����菬��������A�����ł�����0���傫��1��菬�����Ƃ������ƂɂȂ�
10���̗�ł�����1/10
1/10���c���̂�9/10��݂�����
�����ōŏ��̗a����100���~��10�{�ł���1000���~��p�ӂ���i����10�{��10�Ƃ����̂�1/10��10 ���j
����1000���~����a������z�������Ă������Ƃ��l���邱�Ƃɂ���
�ŏ���100���~�������R�����1000���~��1/10�ŁA�����������900���~�ƂȂ�
����90���~��900���~��1/10�ŁA�����������810���~
����81���~��810���~��1/10�ŁA�����������72.9���~
�c�c
��Ɏc���1/10�������Ă������ƂɂȂ�A�c��͂ǂ�ǂ�0�~�ɋ߂Â��Ă���
�܂�A�a���̘a�͍ŏ��̗a����10�{�ł���1000���~�ɂǂ�ǂ�߂Â��Ă������ƂɂȂ�
�������ʉ������20��=1/5�Ȃ�5�{�����A30��=1/3.3333�c�c�Ȃ�3.3333�c�c�{����Ηǂ����Ƃ��킩�� 72.9���~�̂Ƃ����729���~�̌��
��ʓI�ɂ��̌v�Z�ŗǂ����Ƃ͂ǂ����Ő���������Ă���Ǝv�����Ȃ� �������䋉���F
a+ar+ar2+⋯a+ar+ar2+⋯
�� −1��r��1 �̂Ƃ��������C
���̒l�� a��(1−r �j�ɂȂ�
a��100���Ar��0.9
100����0.1 p��f���A����Z���1�ϐ���������A=Z[t]�Ƃ���
����n,k��0�Ƃ���p^n-1���̑�������=1+t+�c+t^(p^n-1)��A�AI=(p^k,��)��A�̃C�f�A���Ƃ���
���̂Ƃ�A���QA/I�̒��������߂�A�Ƃ�����肪������܂���
�o�T�͐�]�u�㐔�w2�v��p156�ŁA�����ł�Z���Q�Ƃ���A��(Z/p^kZ)^(p^n-1)�Ɠ��^�Ȃ̂Œ���k(p^n-1)�ƂȂ��Ă��܂���
Z���Q�Ƃ��Ă̒�����A���Q�Ƃ��Ă̒�������v����ۏ͂ǂ��ɂ���̂ł��傤���H
��낵�����肢���܂� �����Ȃ�̂͂Ȃ��ł����H
���o��������������
���Z���ł�
https://i.imgur.com/QI21k9y.png z=re^i��+���Ƃ����Ēu���ϕ�����Ζ��炩 f : [0,1]=I��S^1��R^2
f(x)=(cos2��x,sin2��x)
�̋t�ʑ�f^-1���A���łȂ����Ƃ����������̂ł����A�ǂ̂悤��I�̊J�W��U���Ƃ��Ă���A�t��(f^-1)^-1(U)���J�W���łȂ��ł����H >>268
�P�˂łȂ��̂ŋt�ʑ��͂���܂���� >>268
�t�ʑ�����ď����Ă݂�킩��Ǝv�� >>268
I�ł͂Ȃ�[0,1)�̊ԈႢ�ł���
�_����Ƃ�ΘA���łȂ��͕̂������ł����A�J�W���ł�낤�Ƃ���ƕ�����Ȃ��ł� AB=x,AD=y�ix<y�j�̒����`ABCD�ɂ����āA��DAB������锼������L�Ƃ���B������L��A��[�_�Ƃ��A�����`ABCD�̓�����ʂ���̂Ƃ���B
C����Ίp��BD�ɉ��낵�������̑���H�Ƃ��A����HC��L�Ƃ̌�_��P�Ƃ���B
���̂Ƃ��A�ȉ��̒��������߂�B
�i1�jAH
�i2�jPH �O>>267
>>255
���т͊Ö��������B
�x�m�͎_���������B �� �� (0, ��/2) ��C�ӂɎ��Œ肵���Ƃ��A���f���ʂ̕����W��
{z | arg(1 - z) �� ��} �� {z | |z| < 1} ������ 1 �ɋ߂Â����Ƃ��� f(x) �� f(1)
�ƂȂ�܂����A
�� �� (0, ��/2) ��C�ӂɎ��Œ肵���Ƃ��A���f���ʂ̕����W��
{z | |z| < 1} ������ 1 �ɋ߂Â����Ƃ��� f(x) �� f(1)
�ƂȂ�Ȃ���������Ă��������B 👀
Rock54: Caution(BBR-MD5:1341adc37120578f18dba9451e6c8c3b) f(z) = ��a_n * x^n
�ł��B
�������a�� 1 �Ƃ��܂��B >>278
�������a1�Ȃ�f(1)�Ȃ�Ē�`����Ȃ����B �̐�1�̒�����ABCD-EFGH
�_P,Q��AP:PB=1:1, AQ:QE=1:2���݂���
��GPQ�̏d�S��X
HX�ƕ���ABCD�̌�_��Y�Ƃ���
(1)�l�ʑ�GPQY�����ς���
(2)AB:AD:AE=4:2:3�̂Ƃ��A�}�`R��|HR|/|AQ|=��HR·��HQ�����_R�S�̂̏W���ƒ�߂�
�܂��}�`R������GPQ�ɂ������Ăł���Ȑ���S�Ƃ�Z��HZ���ŏ��ɂȂ�S��̓_�Ƃ���
�l�ʑ�APYZ�̑̐ς����߂� >>280
�r�����M�ɂȂ�����(2)��HR��AQ���x�N�g���ł� >>280
���߂�Ȃ���
AP:PD=1:1�ł��� ����^�������Ɛ��^���������ĉ����Ⴄ�́H >>276 >>278
�@z = 1 - �åexp{i(��/2)cos(1/��)} �ɉ����ĂP�ɋ߂Â��ꍇ���l����B
�@�� = 1/n�� (n�F���R��) �ł́@arg(1-z) = �}��/2�A|z| = |1+i��| > 1�@�䂦�@f(z) �͑��݂��Ȃ��B
���F Stolz�̊p
|1-z| < (2/cos��)(1-|z|),
�A�|�x���̘A�����藝 >>274 >>283
�f�J���g����
�@A(0,0)�@�@B(x,0)�@�@C(x,y)�@�@D(0,y)
�Ƃ����B
������L:�@Y = X�@(X��0)
�Ίp��BD:�@X/x + Y/y = 1,
����HC:�@xX - yY = xx - yy,
�����̑��@H (x^3/(xx+yy), y^3/(xx+yy))
����HC��L�Ƃ̌�_�@P (x+y, x+y)
(1)�@AH = ��{(x^4-xxyy+y^4)/(xx+yy)} �O>>275
�O�X>>260
>>161
�s�^�S���X�̒藝���A
(4-3cos��)^2+(3sin^2��)^2=(2r+1/2)^2�\�\�@
�����藝���A
2t/sin��=2r�\�\�A
�]���藝���A
cos��=3^2+4^2-(2t)^2/2�3�4�\�\�B
�A���t=rsin��
�B�ɑ������ƁA
cos��=25-r^2sin^2��/24
�@������ƁA
16-24cos��+9cos^2��+(3-3cos^2��)^2=4r^2+2r+1/4
16-24cos��+9cos^2��+(3-3cos^2��)^2=4r^2+2r+1/4
16-24cos��+9cos^2��+9-18cos^2��+9cos^4��=4r^2+2r+1/4
25-24cos��-9cos^2��+9cos^4��=4r^2+2r+1/4
100-96cos��-36cos^2��+36cos^4��=16r^2+8r+1
99-96cos��-36cos^2��+36cos^4��=16r^2+8r
16r^2+8r-99+96cos��+36cos^2��-36cos^4��=0
r=[-4+��{4^2-16(-99+96cos��+36cos^2��-36cos^4��)}]/16
={-4+��(16-16+1600-16�96cos��-16�36cos^2��+16�36cos^4��)}/16
={-4+4��(100-96cos��-36cos^2��+36cos^4��)}/16
={-1+��(100-96cos��-36cos^2��+36cos^4��)}/4
r+1/4=��(25-24cos��-9cos^2��+9cos^4��)/2
(2r+1/2)^2=25-24cos��-9cos^2��+9cos^4�� �u�G�X�J���[�^�[�̎g�p�Ɋւ���A���P�[�g���肢�v
�y�{�A���P�[�g�ɂ��āz
���̃A���P�[�g�́A���s����w��w���̎��Ɓu���f�B�J���E�f�[�^�E�T�C�G���X�v�̋���̈�ōs���Ă���A���P�[�g�ł��B
���̃A���P�[�g�̌��ʂ͈�ʂɂ͌��J���܂���B
�܂��A���̃A���P�[�g�ł́A�l���͎��W�v���܂���B
>>285 ��z�� �~�� |z|=1 �̊O�ɏo�Ă��܂��̂Ŏ������܂��B�Ͽ
�@z ���~�� |z - 1/2| = 1/2 �ɉ����ĂP�ɋ߂Â����ꍇ���l���܂��B
�@z = (1/2){1 + e^(i(��-2��))},�@�@
�@arg(1-z) = �� �� ��/2�@�Ƃ����Ƃ��}�Ⴊ����悢�̂ł��ˁB �O>>289
>>274(1)
H��BD��y^3:x^3�ɕ�����B
��AH=��(x^6+y^6)/(x^2+y^2)
(2)PH=��k[{y^2(1-y^2)+x^2(1-x^2)}/{y(1-y^2)-x(1-x^2)}-y^3/(x^2+y^2)]^2+[{y^2(1-y^2)+x^2(1-x^2)}/{y(1-y^2)-x(1-x^2)}-x^3/(x^2+y^2)]^2�l �ꏼ�M���w��͊w�����㊪�i�V�Łj�x��ǂ�ł��܂��B
�ȉ��̒藝7.17�Ɂu�s��ϕ� F_n(x)�v�ȂǂƏ�����Ă��܂����A��ϕ����������ł���ˁB
���ƁA max_{a �� x �� b} | f_n(x) - f(x) | �ȂǂƏ����Ă��܂����A�e n �ɑ��čő�l��
���݂���Ƃ���������Âɂ��Ă���Ƃ������Ƃł��傤���H
�u�n�v�́A�Ȃ��藝7.17�̌n�Ȃ̂ł��傤���H
�藝7.17
����̊e�� f_n(x) ����� f(x) ����� [a, b] �Őϕ��\�ł���A
max_{a �� x �� b} | f_n(x) - f(x) | = ��_n �� 0 �in �� ���j
�Ȃ�A�s��ϕ� F_n(x) = ��_{a}^{x} f_n(t) dt �� F(x) = ��_{a}^{x} f(t) dt �Ɏ�������B
�n
��Ύ�������D���������ϕ��\�������Ƃ��鋉�� ��(x) = �� f_n(x) �ɂ��āA
���ʐϕ� ��_{a}^{b} ��(x) dx = �� ��_{a}^{b} f_n(x) dx ���ł���B �藝7.17����n���ؖ����Ă��������B 2�ʑ̌QDn�̒��S���Ăǂ����߂�����ł����H �O>>291
>>280
A(0,0,0)�Ƃ���ƁA
P(1/2,0,0)
Q(0,1/3,0)
G(1,1,1)
X(1/2,5/9,2/3)
Y(-1/8,0,3/2)
�O��9/8�A1�A3/2�̒����̂���AY-PQG�ȊO�̕������킬���Ƃ��Ă����B
ABCD-EFGH��DA������1/8�ADC������1/2�̂��������̂�A'YC'D-E'ZG'H�Ƃ���ƁA
(������A'YC'D-E'ZG'H)=(9/8)�1�(3/2)
=27/16
�킬���Ƃ������́A
�܊p��G-DHEQP
�l�p��G-C'G'ZY�ȂǑ����B ����������������Ă݂��B�O>>295
~�����@�@�@�@�@ ����
(-.-))�@�@�@�@ (`)�@)
[�P]_)�@�@�@�@�@U��U�
�P�P]/�____�����m(��)
�Q�Q/�_/,,(`.`))���,|
�P�P�_/�c`-`Ѓ�`�҃�|
�P�P|�__U��U�___�^| |
���@| �a~U~U~�P�a | /
�Q�Q| �a �� �� �a |/
_____`�a_______�a�^
�P�P�P�P�P�P�P�P >>295
�}�`�͗����̂ł͂Ȃ������́A����ɕӂ̒������s��Ȃ̂ł��̉�@�͂܂������� �����Ă��������ȁB�@���ː� y=ax2��+bx+c�ɂ��Ē��_���_(1,3)�ŁA�_(-1,1)��ʂ�Ȃ�� a=(�A)�@b=(�C)�@c=(�E) ���_�̍��W����
�@y = a(x-1)^2 + 3,
�_(-1,1) ��ʂ邩��
�@a = -1/2,
�@b = 1,
�@c = 5/2, �O>>297
>>280(1)������!!
�P]/�_�Q�Q�Q�Q�Q�Q�Q
�Q/�_/ �����@�����@/|
�P�_/ ((~-~)((`o')/ |
�P|�__,U��U�(��u~)�@|_
�n| �a~UU~ �P`�҃� / /
�Q| �a ���@�� �a |/ /
___`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P
A(1,0,1)
B(1,1,1)
C(0,1,1)
D(0,0,1)
E(1,0,0)
F(1,1,0)
G(0,1,0)
H(0,0,0)
P(1/2,0,1)
Q(1,0,2/3)
PQ�̒��_M�́A
M(3/4,0,5/6)
X(1/2,1/3,5/9)
Y(9/10,3/5,1)
�恨HY=(9/5)��HX
XY=��{(2/5)^2+(4/15)^2+(4/9)^2}
=2��217/45
PM��GM������A
��PGQ=(1/2)PQ�GM
=PM�GM
=��(11/108)���(119/108)
=��1309/108
�O�p��Y-PGQ=(1/3)��PGQ�XY
=(1/3)(��1309/108)(2��217/45)
=7��5797/7290 >>274 >>283 >>286
(1)
BH/DH = (BH/CH)(CH/DH) = (BC/CD)^2 = (AD/AB)^2 = (y/x)^2,
�� H �� �Ίp��BD�� yy�Fxx �ɓ�������B
�������̑��@H (x{xx/(xx+yy)}, y{yy/(xx+yy)})
AH = {��(x^6 +y^6)} / (xx+yy) = ��{(x^4 -xxyy +y^4)/(xx+yy)},
(2)
�_ (x+y/2, y/2) �𒆐S�Ƃ��� ABCD �� 90߉�
�@A �� A' (x, x+y)
�@B �� C (x, y)
�@C �� C' (x+y, y)
�@D �� D' (x+y, x+y) �� L
�ƂȂ�B
�@����HC �� �Ίp��CD' �� BD�ɐ���������AD' ��HC��ɂ���B
�� P = D'
�@PH = (xx+xy+yy)/��(xx+yy), ��(x) = �� f_n(x) ���ϕ��\�ł��邱�Ƃ͂ǂ�����ē����̂ł��傤���H
�藝7.17
����̊e�� f_n(x) ����� f(x) ����� [a, b] �Őϕ��\�ł���A
max_{a �� x �� b} | f_n(x) - f(x) | = ��_n �� 0 �in �� ���j
�Ȃ�A�s��ϕ� F_n(x) = ��_{a}^{x} f_n(t) dt �� F(x) = ��_{a}^{x} f(t) dt �Ɏ�������B
�n
��Ύ�������D���������ϕ��\�������Ƃ��鋉�� ��(x) = �� f_n(x) �ɂ��āA
���ʐϕ� ��_{a}^{b} ��(x) dx = �� ��_{a}^{b} f_n(x) dx ���ł���B >>303
�͈ꏼ�M����́w��͊w�����㊪�i�V�Łj�x����̈��p�ł��B
�Ⴆ�A����a�v���w��͓����x�ɂ͈ȉ��̒藝������܂��F
��� [a, b] �� f_n �����[�}���ϕ��\�ŁA f �Ɉ�l��������Ȃ�A f �� [a, b] �Ń��[�}���ϕ��\�ŁA
lim ��_{a}^[b} f_n(x) dx = ��_{a}^{b} f(x) dx
�����藧�B
>>303
�Ƃ��낪�A�ꏼ�M����́w��͊w�����㊪�i�V�Łj�x�ɂ́A�藝7.17�̑O�ɁA��l�����̒�`���珑���Ă���܂���B
����ȏł��́u�n�v���ˑR�A����܂��B
�ꏼ�M����͑��v�Ȑl�Ȃ̂ł��傤���H
���ł���V�łɕҏW�������Ƃ��̕ҏW�~�X�ł��傤���H >>303
��max_{a �� x �� b} | f_n(x) - f(x) | = ��_n �� 0 �in �� ���j
���̏����ȂƎv���Ă��ł����� >>306
��l��������Ƃ������Ƃł��ˁB lim(x to ��) x|sin(��/x)|=��lim(x to 0)sinx/x=1��p�����Ɏ����B
�����邩�ȁH�H �@f(x)=2x��(-��,+��)�ŘA���ł��邱�Ƃ��C�v�V�����f���^�_�@�Ŏ����B
�Af(x)=��x��[0,+��)�ŘA���ł��邱�Ƃ��C�v�V�����f���^�_�@�Ŏ����B
��낵�����肢���܂� �i1�j�Ε�BC�̒�����a�ł��钼�p�O�p�`��ABC������B
���̖���(P)��(Q)�͓��l�ł��邱�Ƃ������B
(P)AB+AC���ő�ƂȂ�
(Q)��ABC�̖ʐς��ő�ƂȂ�
�i2�j��ʂ́�PQR�ɂ��āA���̖���(S)��(T)�͓��l�ł��邩�B������p�𐳂̒萔�Ƃ��āAQR=p�Ƃ���B
(S)PQ+PR���ő�ƂȂ�
(T)��PQR�̖ʐς��ő�ƂȂ� �ǂ�����ő�l���Ƃ�Ȃ��P�ɋU�ł��閽��䂦���l�B >>312
���H�U�ł��邱�Ƃ��ؖ����Ă݂�� >>261
�킴�킴���肪�Ƃ�
�Ȃ�ƂȂ��C���[�W�͂ł������ǁc
����ς�Ȃ��S�̗̂a���̊z���o�Ă���̂��͗����ł��Ȃ� >>314
�Ȃ�1000���~�p�ӂ���H���Ă��Ƃ��낤�H
1000���~�p�ӂ���>>261�ɂ��鑀�������Ǝc��͌��薳��0�ɋ߂Â����}�C�i�X�ɂ͂Ȃ�Ȃ�
�]���āA�p�ӂ���̂�800���~�Ƃ��Ȃ瑫��Ȃ��Ȃ邵�A1200���~�Ƃ��Ȃ�]���Ă��܂�
�Ȃ�1000���~�Ȃ̂��ƌ����A1000���~�Ȃ�c�肪���薳��0�ɋ߂Â����}�C�i�X�ɂ͂Ȃ�Ȃ��Ƃ������Ƃ��N���邩��
1000���~���ƂȂ������Ȃ邱�Ƃ��킩�������ƌ����A�����Ȃ�̂͂�����p�ӂ����Ƃ��Ȃ̂����v�Z������1000���~���Ƃ킩��������
�����Ă��̌v�Z�Ƃ͍ŏI�I�Ɂu�ŏ��̗a���z�ł���100���~���c������0.1�Ŋ���v�Ƃ������̂ł���A
���̌v�Z�͈�ʉ����Čv�Z���Ă����Ɓu�ŏ��̗a���z���c�������Ŋ���v�ƈ�ʉ��o���邱�Ƃ��킩�� ���������ł�
�I�C���[�̒萔�͗L�����ł���
>�����������ł������Ƃ���B�C�ӂ̗L���� 1/p p��2�ȏ�̐��� �ɑ���
>|���|1/p|��| lim_{n��+��}( 1�{1/2�{�c�{1/n�|log(n) )�|1/p |
>��lim_{n��+��}( 1�{1/2�{�c�{1/n�|log(n) )�|1/p
>��( 1�{1/2�{�c�{1/p�|log(p) )�|1/p
>��1�{1/2�{�c�{1/(p�|1)�|log(p)
>��0�A
>�]���āA����2�ȏ�̐�����k�����݂��āAp��k �̂Ƃ� |���|1/p|��( 1�{1/2�{�c�{1/p�|log(p) )�|1/p��1/k��1/p�B
>�̂ɁA0��|���|q/p|��1/p^2��|���|1/p| �����悤�Ȋ���L���� q/p p��2 �͖������݂���B
>(�c�ȉ����c)
���������葼�̕�������l���Ă݂͂����A���̕����� ����lim_{n��+��}( 1�{1/2�{�c�{1/n�|log(n) ) �ɓ������Ă����B
�����ɁA��_n��1�{1/2�{�c�{1/n�|log(n) n��2 �͒��z���ŁAn��2 �̂Ƃ� {��_n} �͉��ɗL�E�ȒP��������B
�����㐔�I�������łȂ����Ƃ܂ł͏ؖ��o�������A�f�B�I�t�@���^�X�ߎ��ł̓��̒��z���܂ł͂����Ȃ��B
���̒��z�����f�B�I�t�@���^�X�ߎ��ŏؖ����悤�Ƃ���ƁA�قڎ����I�Ƀ������z���ł��邱�Ƃ������Ĉ�ʓI�ɐ��藧�悤�ȏؖ��ɂȂ�B
��͂�A���͗L�����������B >>316
�o�J�^���B
����ȃR�s�y���肷��ȁB ���̊F�l�AID:RCiqoacY �̃��X�͖������Ă����ł��B smrdifk�ƃA�t�^�[�ł��т������Ƃ��邯�ǍŒႾ������
�H���������Ȃ����A�������s�����B���ꂽ�̌�������b���ď���Ɏv���o���{�肷���ŋ���EX�o�[�T�[�J�[�̕������������Ȃ��̂��ă��x��
�����Ă��Ȃ��̂ɐ����œ|��ďW�����Î��ɓ��@���Ď��ɂ������`�Ƃ������o���Ė��f�|������������l���߂Č��� >>313
QR=p�ƌ��������������ł͔C�ӂ�P�ɑ��Ă��̎���PQ+PR���ő�ɂȂ�ƌ�������͋U�B �}�`�H�̖������₵�����̂ł����ǂ̂悤�ɏ������߂悢�ł��傤���H ���㐔�w�̌n�� �H�w�����G�k �ÓT�K���A���_���ǂ�66
294 �F�P�R�Q�l�ڂ̑f������[sage]�F2019/05/30(��) 18:26:24.67 ID:kbENVFaQ���ꂶ��A�������������Q��B �O>>301
>>161
(2r+1/2)^2=25-24cos��-9cos^2��+9cos^4��
4r^2+2r+1/4=25-24cos��-9cos^2��+9cos^4��
(4r+1)^2=100-96cos��-36cos^2��(1-cos^2��)�\�\�@
�����藝���A
AC/sin��=2r
4r^2�sin^2��=AC^2�\�\�A
�]���藝���A
cos��=(3^2+4^2-AC^2)/2�3�4
=(25-AC^2)/24�\�\�B
�A���B�ɑ�����A
cos��=(25-4r^2�sin^2��)/24
24cos��=25-4r^2�sin^2��
24cos��=25-4r^2�sin^2��
4r^2�sin^2��=25-24cos�� 4r^2�2(5-24cos�ƥ)/
-cost22�@
2r=��(25-24cos��)/sin��
4r=2��(25-24cos��)/sin��
�@�ɑ�����A) [{��(25-24cos��)/sin}}��1)]2=100-96cos��-36cos^2��(1-cos^2��)) {25-24cos��)/sin��}2^+1��(25-24cos��)/sin++�ƃ�100-96cos��-36cos^2��(1-cos^2��)
(���f ) log(1+2+3)=log(1)+log(2)+log(3)
����͂ǂ�����ďؖ������炢���ł��傤���H ���ӂ�exp�i�j�ɓ�����
exp(log(1+2+3)) = exp(log(1)+log(2)+log(3))
1+2+3 = exp(log(1))*exp(log(2))*exp(log(3))
1 + 2 + 3 =1 * 2 * 3
���܂��܈�v���Ă����Ď��ł��� log(2+2)=log(2)+log(2) �����邼 �O>>323
>>116
(1+2��(25-24cos��)/sin��)^2=100-96cos��-36cos^2��(1-cos^2��)
1+4��(25-24cos��)/��(1-cos^2��)+4(25-24cos��)/(1-cos^2��)=100-96cos��-36cos^2��(1-cos^2��)
(1-cos^2��)+4��(25-24cos��)��(1-cos^2��)+4(25-24cos��)=100(1-cos^2��)-96cos��(1-cos^2��)-36cos^2��(1-cos^2��)^2
1-cos^2��+4��{(25-24cos��)(1-cos^2��)}=-100cos^2��+96cos�ƥcos^2��-36cos^2��(1-cos^2��)^2
1-cos^2��+4��(25-24cos��-25cos^2��+24cos^3��)=-100cos^2��+96cos�ƥcos^2��-36cos^2��(1-2cos^2��+cos^4��)
4��(25-24cos��-25cos^2��+24cos^3��)=cos^2��-1-100cos^2��+96cos^3��-36cos^2��+72cos^4��-144cos^6�� 4��(25-24cos��-25cos^2��+24cos^3��)=
�����������ď����Ȃ��B
999cs^2��+96cos^3��-36cos^2��+72cos^4��-144cos^66 ��-1/
-1 n�����R���Ƃ���Ƃ��A�W���̘a�̒l
(2n,k)+(3n,k)
���ő�ɂ��鎩�R��k��n�ŕ\���B �O>>328
>>161
(1+2��(25-24cos��)/sin��)^2=100-96cos��-36cos^2��(1-cos^2��)
1+4��(25-24cos��)/��(1-cos^2��)+4(25-24cos��)/(1-cos^2��)=100-96cos��-36cos^2��(1-cos^2��)
(1-cos^2��)+4��(25-24cos��)��(1-cos^2��)+4(25-24cos��)=100(1-cos^2��)-96cos��(1-cos^2��)-36cos^2��(1-cos^2��)^2
1-cos^2��+4��{(25-24cos��)(1-cos^2��)}=-100cos^2��+96cos�ƥcos^2��-36cos^2��(1-cos^2��)^2
1-cos^2��+4��(25-24cos��-25cos^2��+24cos^3��)=-100cos^2��+96cos�ƥcos^2��-36cos^2��(1-2cos^2��+cos^4��)
4��(25-24cos��-25cos^2��+24cos^3��)=cos^2��-1-100cos^2��+96cos^3��-36cos^2��+72cos^4��-36cos^6��
4��(25-24cos��-25cos^2��+24cos^3��)=-1-135cos^2��+96cos^3��+72cos^4��-36cos^6��
16(25-24cos��-25cos^2��+24cos^3��)=(-1-135cos^2��+96cos^3��+72cos^4��-36cos^6��)^2
400-384cos��-400cos^2��+384cos^3��=1+18225cos^4��+9216cos^6��+5184cos^8��+1296cos^12��+270cos^2��-192cos^3��-144cos^4��+72cos^6��-135�96cos^5��-135�72cos^6��+135�36cos^8��+96�72cos^7��-96�36cos^9��-72�36cos^10��
�ǂ�����ĉ�������!?�@������Ȃ���H
399-384cos��-670cos^2��+576cos^3��-18081cos^4��+12960cos^5��+432cos^6��-6912cos^7��-10044cos^8��+3456cos^9��+2592cos^10��-1296cos^12��=0
cos�Ɓ�0.0601
��sin�Ɓ�0.9399 �������� �@���̕����ĉ����炵���炦�����H >>161��>>213�̐l�́A
~�����O>>330�@�@����
(-.-))cos�Ƃ́@(`)�@)
[�P]_)2�����Ɂ@ U��U�
�P�P]/�____�����m(��)
�Q�Q/�_/,,(`.`))���,|
�P�P�_/�c`-`Ѓ�`�҃�|
�P�P|�__U��U�___�^| |
���@| �a~U~U~�P�a | /
�Q�Q| �a �� �� �a |/
_____`�a_______�a�^
�P�P�P�P�P�P�P�P���Ƃ��Ă�݂����Ȃ��ǁA���������ł���H�@�܂Ƃ��ɂ������cos�Ƃ�12�����ɂȂ��B >>329
�@k>1 �ł́@(3n,k) �ł悭�ߎ��ł��邪�A(2n,k) �̉e������������B
�@3n/2 ���킸���ɏ��������ōŏ��ɂȂ�B
�@k = [3n/2] >>332
�ߋ��₪������̂₪�ǂ������炦�����H >>335
������b�����蒼��
�킩���Ă���Ƃ���͂����I��邩�炻��ȂɎ��Ԃ͊|����Ȃ�
���Ԃ�������Ȃ����ς肻��������Ȃ��ᖳ�����Ă��� >>335
�悭����̂͗F�B�ƈꏏ�ɉ@�����������
���Ƃ͉@�����W������Ή����������������������
�������Ă�Ί�b���͉�����悤�ɂȂ�͂�
���̖��͂������w�̍˔\����������������Ă�������悤�ɂȂ�Ȃ����璍�� >>161 >>165 >>213
24cos�� = (2+3cos��)^2 - (2-3cos��)^2
�@= OD^2 - OA^2
�@= (r + QD)^2 - r^2
�@= (r + 1/2)^2 - r^2�@�@�@�@(QD=1/2)
�@= r + 1/4,
���@4r+1 = 96cos�Ɓ@�@----- (1)
(2),(3) ����
�@r = ��(25-24cos��) / (2sin��),
���ꂩ�� r ��������
�@(24cos��)^2 - (24cos��)/4 -288 �}126��5 = 0,
�@24cos�� = 1/8 + ��{(1/8)^2 +288 �}126��5},
�@�@= 23.994649979937�@�@�@2.6292084248375
cos�� ��������
�@4{1 - [(4r+1)/96]^2}rr = 25 - (4r+1)/4 = 99/4 - r,
�@{r(4r+1)/96}^2 - r(4r+1)/4 + 99/16 = 0,
�@r = -1/8 + ��{(1/8)^2 +288 �}126��5}
�@�@= 23.744649979937�@�@�@2.3792084248375
�~�̒��SO�͑Ίp��BD��ɂ͂Ȃ��Ǝv�����ǥ���
�@BD < 2r + 1/2, ���肢���܂��B
�ԐQ�̂���������ɓ�����Ƃ��C�o���ڂ̍ő�l���T�ɂȂ�m�������߂�D >>337
���w�̍˔\�������z�����w�̉@�s���Ă��������납�H �˔\�ȏ�ɋ������Ȃ��̂ɕ��ꍞ��Ō��������Q�b�g��������悤�ȓz��̕����_�O�Ȃ�ŁB >>343
�s���͎̂��R�����s���ĉ�����́H�Ƃ͂Ȃ�B�ŏ�����A�E����\��Ȃ�s���Ӗ��Ȃ��� >>343
���C���������Ƃ���Α��Ƃ͖��Ȃ��ł���
�ړI�������̃����g���A���������낤�ƁA�����ׂ̗̈L�Ӌ`�Ȃ��̂ł��낤�ƁA�l�̎��R�����s���Ă͂����Ȃ����R�ɂ͂Ȃ�Ȃ�
�ǂ����A�E����Ȃ�Ӗ��Ȃ��A�Ə����Ă�l�����邪�����͎v��Ȃ�
�A�E��ɉe�����Ȃ��Ƃ��Ă��A��肽�������������ĉ@�ɍs���Ȃ炻�̐l�ɂƂ��Ă͂����ƈӖ������� >>346
�Ȃ��A�E�ƕ��̓�ґ���ȂH�����o������̂��낤�B����������玞�Ԃ͌��邪�A�@�ɂ����ďA�E����Ȃ�摗��ł����Ȃ��B
���쓙�ɂ���邪���w�Ȃ甎�m���C�m�̕����A�E���ǂ��ꍇ�������A�����l�����l������C�m�ŏA�E���Ď�Ő��w�ł��ǂ����낤�B
�������l�̎��R�����A�͂Ȃ�����A�J�|�X����ā`�Ƃ������Ƃ���߂Ă�Ȃ�A�E�����߂�B >>347
���ꂱ���l���悾���A���ʂ͐�僌�x���̐��w��Ɗw�Ŋw�Ԃ̂͑������
�܂��Ă⓭���Ȃ���ƂȂ�Ǝ��Ԃ���邱�Ƃ�����
�搶�̂��Ƃŕ���������w���B�Ŏ��R�ɃZ�~�i�[�����ł�����͂������ɗ��_�ƌ�����Ǝv��
���ہA�A�E������肾�������������𑱂���������A�Ƃ������R�ʼn@�ɗ���l�͂������Ă���
���m�ɍs���ׂ��Ƃ͑S���v���ĂȂ��������Ă����Ȃ�
���X�̎��₪�u(�˔\���Ȃ��Ă�)�@�ɍs���Ă����̂��v������A�C�m�܂Ŋw��ł���A�E���邱�Ƃ�z�肵�ď����Ă����� �u�J���g�[���W���ɓ����Ȉʑ���Ԃ��J���g�[����ԂƌĂԁv
���ăE�B�L�y�f�B�A�ɏ����Ă��������ǁA�J���g�[���W�����ďW��������܂��ʑ������ĂȂ���ˁH
�J���g�[���W����̂ǂ̈ʑ��̂��ƂȂ�ł��傤���H ��x�̐ϕ���2/3x��x�ɂȂ�͉̂��̂ł����H ���f���W���L����f(x)��f(f(f(x)))=x�������̂����ׂċ��߂� ���܂ɕ����Ă��邱������������Ēނ�Ȃ́H�ړI���s���Ȃ��B ���ׂ�
�����ݖ�͂قƂ�ǂ�
�����̏o��r�炵�̓��e
��A�҂͂�������ɂ��ĂȂ� ��悷��Ɗ�ɂȂ�����ƁA��悷��Ƌ����ɂȂ��͂ǂ�����ċ��߂�́H �y����z�N�I�J�[�h500�~������������[���D�Ҍ��������Ⴆ��@
https://pbs.twimg.com/media/D8DDhi3VsAAyYKw.jpg�@�@�@�@
�@�@�@�@�@
�@ �X�}�z�ł����ނ����@�@�@�@
�A ����o�^���ς܂���@�@
�B �}�C�y�[�W�ֈړ�����B�@
�C ���҃R�[�h�����҃R�[�h����͂��� [Rirz Tu]�i�X�y�[�X�����j
�@�@�@�@�@
���Ȃ�X�ɃN�I�J�[�h����������[���D�Ҍ��������c������^�_�Ŕ����܂��B�@�@�@�@�@
�@�@�@�@�@�@
�ȒP�ɓ���ł��܂��̂Ő����p�������@�@�@ >>347
���ɏA�E�ƕ��̗����͌�������
���O���w�̕��������Ƃ���H
���w��Ɗw�ŕ�����̂������ɑ�ς��������ĂȂ����� >>354
�@h(z) ���t��1�������ϊ��Ƃ����
�@f(z) ����ӂ����@�́@�@h^(-1)(f(h(z))) ����ӂ���
���ȁH
��
�@f(z) = -1/z �}1,�@1/(1-z), -1/(1+z), ��z, ��~z�@�Ȃ�
�@h(z) = 1/z, 1-z >>161�O>>333
>>165
�_O��y���W���Ȃ�ŁA
(3-4cos��)/2sin��
�ɂȂ��ł����H �O>>363�킩�����킩�����B
OA^2=OB^2�ŏo���B
y=(3-4cos��)/2sin�� ttp://ebsa.ism.ac.jp/ebooks/sp/sites/default/files/ebook/1321/pdf/ch01-05.pdf#search=%27%E9%A0%86%E4%BD%8D%E7%9B%B8%E9%96%A2%E4%BF%82%E6%95%B0%E3%81%AE%E8%A8%BC%E6%98%8E%27
�����́A
�u�W���v���Ȃ������Ȃ�̂�������܂����ĉ������B�Q���ڂ�-1/2����n�܂��Ă����ł��B >>360
����A�A�E����������̔N�Ƃ��͒m����B������x����Ă����瓭����Ő��w�ł��邾��(���������l�͐��̒��ɑ�R����)�B
�Ɗw���āA���̎���l�b�g�ł����Ȑl�ƌq�������炳���A�A�A�l�b�g����Ȃ��Ă��h�c�ɂłȂ���Α�͎̂Љ�l���w�T�[�N���݂����Ȃ̂��������肷��킯�����B ��̃��x���Ɛ��̃��x���i�Ɉ����̂͂����������� �O>>365
1-cos^2��=25-24cos3��
1-cos^2��=25-24(4cos^3��-3cos��)
96cos^3��-cos^2��-72cos��-24=0
(��cos��-��)(��cos^2��-��cos��+��)=0
���������ł���H �u���ɂ���Ă����Ȃ�A�J�|�X����ā`�݂����ɐi��ł��������Ȃ����ǁA����͌�����(��ō˔\���Ȃ��݂����Ȃ��ƌ����Ă�)�����w�͂������v�Ƃ����O��Řb�����Ă����肾��������H
�A�J�|�X����Ă����Ȃ��Ȃ�A�E���Ď�ł��ȊO�ɕ��@���Ȃ��Ǝv���̂����B�e�����������Ƃ��łȂ�����B �Ȃ�ŃA�J�|�X�ڎw�����@�ɍs���Ȃ��ŏA�E���̓���Ȃ�
�A�J�|�X�ɋ��������Ă����̕����������ĉ@�ڎw���z�Ȃ�Ă�����ł������ >>370
�_�_���X�b�Q�[����ĂĐ����������Ă邩������� ��w�����ɂȂ�ȊO�@�ɍs���Ӗ��Ȃ��Ƃ��v���Ă�̂��H
����x��̍l�����
�A�E�̎��т��w���������@���̕����ǂ����B
�I�O��ȓ��������o���ĂȂ��Ƃ��������Ɩ{�C�ŗ����o����Ǝv���Ă���
�܂Ƃ��ȗ��w�̕����Ă��畁�ʂ͗����o���Ȃ����ĕ����邾��B
�l�b�g�ɂȂ�ł�����������Ă�Ǝv���Ȃ� ���͂����Ɛ��w�̕����������ĉ@�ɍs�������̂ɏA�E������ł�����x�Ȃ痼���o���邾��`���Č���ꂽ�琦���C�����B
�A�h�o�C�X����Ă闧��Ƃ��Ă͎���Ȃ̂�������Ȃ����ǁB
�����Q�l�ɂȂ�Ȃ� ���w�̕����������ǐ������̎����ɐ��w�̍˔\������Ƃ͌����Ȃ�����A�˔\�Ȃ��Ă��@�ɍs���Ă������H���ĕ�������ł����āc
�܂��B���������g�ǂ��������̂����܂��ĂȂ�����킩��Ȃ��B
�A�E���ܘ_���������ǁA���w�̕��������Ƃ��������Ă̂����邵�B
�������Ȃ��Ƃ��@���x���̐��w���Ȃ�����͓̂�����Ă̂����͕����� �����ʼn������悤���s���̂ɂȂ�ŏ������ނ�ł��傤�� �@�ɍs�����A�A�E���邩�͊F��ȔY�ނ�����C�����͕������B�����a�C�����ˁB
�����������̒��Ő������Ă���܂����Ȃ����B n,k�͎��R���ŁAn>k�ł���B
����x�̕�����
x^n-kx = x^k-nx
�̎�������S�ċ��߂�B �O>>369
>>161
OB+1/2=OD�ɕӁX2sin�Ƃ��|���A
��(25-24cos��)+sin��=��(25-24cos3��) >>329 >>334
�@��(n+1) = n!�@�ƂȂ�悤�Ȏ��� ��(x) �������ė���B
f(x) = (2n)!/{��(x+1)��(2n-x+1)} + (3n)!/{��(x+1)��(3n-x+1)},
�̋ɑ�� x=k �Ƃ���B
=============================================
n�@�@�@k�@�@�@�@�@f(k)�@�@�@�@�@f(3n/2)
---------------------------------------------
1�@�@1.28453�@�@5.21648�@�@�@�@5.09296 = 16/��
2�@�@2.74024�@�@24.4379�@�@�@�@24
3�@�@4.31935�@�@143.648�@�@�@�@142.79685
4�@�@5.90302�@�@953.290�@�@�@�@952
5�@�@7.45305�@�@6718.72�@�@�@�@6716.93673
6�@�@8.97830�@�@48842.4�@�@�@�@48840
7�@�@10.4902�@�@361454 �@�@�@�@361451.0954
8�@�@11.9957�@�@2705980�@�@�@�@2705976
9�@�@13.4981�@�@2.04249E+7 �@�@20424920.56107
10�@�@14.9992�@�@1.55133E+8 �@�@155133024
12�@�@17.9999�@�@9.07527E+9 �@�@9075269896
14�@�@21.0000�@�@5.38259E+11�@�@538259058480
----------------------------------------------
f '(x) = 0 �̍��� 3n/2 �̋߂��ɂ��邩��A�j���[�g���@
�@k �` 3n/2 - f '(3n/2)/f "(3n/2)
�ŋ��߂邱�Ƃ��\�B
x = 3n/2 �̕ӂ�ł�
(2n)!/{��(x+1)��(2n-x+1)} �` 2^(4n)�(1/3)^(3n/2) ��{4/(3n��)}exp{-[ln(3) - 2/(3n)](x - 3n/2)},
f '(3n/2) �` �|2^(4n)�(1/3)^(3n/2) ��{4/(3n��)}�[ln(3) - 2/(3n)],
(3n)!/{��(x+1)��(3n-x+1)} �` 2^(3n)���{2/(3n��)}exp{-[2(3n-1)/9nn](x - 3n/2)^2},
f "(3n/2) �` �|2^(3n)���{2/(3n��)}�[4(3n-1)/9nn], �a�@�ɍs������A�����ƕa�C�Ȃ�ł��傤�B
���A���e�@�ł����H����͎���B >>369
(cos�� - ��){96(cos��)^2 + (96��-1)cos�� + (96���� -��-72)}
(cos�� - ��){96(cos��)^2 + (96��-1)cos�� + (24/��)}
�� = (1/24){(1/12) + [(1/12)^3 + 1746 - ��62102]^(1/3) + [(1/12)^3 + 1746 + ��62102]^(1/3)}
�@= 1.004643929533
������ ��������悤�ȃƂ͑��݂��Ȃ��B OD=1/2�@���Ӗ��s����� �O>>379�����Ȃ����B
�~K�̒��S(2,y)=(2,(3-4cos��)/2sin��)��O�Ƃ���ƁA
��ABC�̊O�ډ~�̔��a�́A
OB=��{2^2+(3-4cos��)^2/(2sin��)^2
=��{4+(9-24cos��+16cos^2��)/4sin^2��}
=��{16+9-24cos��)/2sin��
=��(25-24cos��)/2sin��
OD=��{(4+3cos��-2)^2+{3sin��-(3-4cos��)/2sin��}^2
=��{(2+3cos��)^2+{3sin��-(3-4cos��)/2sin��}^2
=��{4+12cos��+9cos^2��+9sin^2��-3(3-4cos��)+(9-24cos��+16cos^2��)/4sin^2��}
=��{4+12cos��+12cos��+(9-24cos��+16cos^2��)/4sin^2��}
=��(16sin^2��+24�4sin^2��cos��+9-24cos��+16cos^2��)/2sin��
=��{25+96(1-cos^2��)cos��-24cos��}/2sin��
=��(25+72cos��-96cos^3��)/2sin��
=��{25+24(3cos��-4cos^3��)/2sin��
=��(25-24cos3��)/2sin��
(�O�ډ~�̔��a)+1/2=OD���A
��(25-24cos��)/2sin��+1/2=��(25-24cos3��)/2sin��
�ӁX2sin�Ɗ|���āA
��(25-24cos��)+sin��=��(25-24cos3��)
sin��=��(25-24cos3��)
-��(25-24cos��) >>373
����A�s���Ӗ��Ȃ��Ƃ͌����ĂȂ���B�A�E�͕���ɂ�肯����B
�t�Ɏ���x������Ȃ��Đ��w�������Ȃ�@�s���ȊO�ɕ��@�Ȃ�����킴�킴���₵�Ȃ�����Ǝv���B �t�ɉ@�s���Ă͂����Ȃ����R���ĂȂ�B
�����Ȃ����R�͌o�ϓI������邾�낤���B
�s�����ǂ����͌l�̎��R�����B f(x)=x�O(n-1) logx
f(x)�̑�n������
���C�v�j�b�c�̌������g�����Ǝv�����c ����⏑�����I��>>345(=>>367)��>>384�͓���l�����Ǝv���Ă����LjႤ�̂��H
�����>>373�Ƃ͕ʐl�����A>>345���͂�����Ɓu(�A�J�|�X��炸�ɏA�E����Ȃ�@�ɍs��)�Ӗ��Ȃ��v�Ə����Ă邩�炻���ɑ��郌�X���Ǝv����
���s���͎̂��R�����s���ĉ�����́H�Ƃ͂Ȃ�B�ŏ�����A�E����\��Ȃ�s���Ӗ��Ȃ��� ������Ȃ����Ƃ������A�p�����������炢�����I�Ȏ��₪����܂��B�t�̂̔Z�x�ɂ��Ăł��B
����ō�����������Ă܂��B
�ޗ��̓A���}�I�C���ƃG�^�m�[���B
�I�C�������t�ŁA�G�^�m�[���Ŕ��߂�Ƃ����������ł��B
���Ƃ��͂R�O�p�[�Z���g�̔Z�x�̍�������鎞�́A
�I�C��3ml�ɂ������ăG�^�m�[����10ml�ł����H7ml�ł����H �}�N���Ƃ��������킩��l�����H >>388
���ʂ͎��ʃp�[�Z���g�������d���킩���Ɓc >>391
�������ɁA�ǂ����������d�������ꍇ�͂ǂ��ł��傤���H >>392
30���́����n�t���Ă̂�10�O�����̂���3�O�����������A7�O�������n�}���ĈӖ����� ���w�̘b�ɂȂ邪
�n�t�̑̐ς͗n�}�Ɨn���̑̐ς̘a�ɂȂ�Ȃ����Ƃ�����
�t�̓��m�̍����t�ł����l
�������������d�ʁ��Ɣ�ׂđ̐ρ��͂��܂�g���Ȃ� >>386
f_n(x) = x^(n-1) log(x),
D f_n(x) = x^(n-2){1 + (n-1)log(x)},
����� n-1 ����������
D^n f_n(x) = (n-1) D^(n-1) {x^(n-2) log(x)}
n�ɂ��Ă̋A�[�@��
D^n f_n(x) = (n-1)!/x, �����̐��E�ł̓I�C��3ml���G�^�m�[��7ml�ƍ����Ă��30���ƌĂ�ł��邩���m��Ȃ��ȁA��d���ǂ��ł��邩�Ƃ��o���オ�肪��ml�Ȃ̂��Ƃ��͖�������
���������Ȃ�Ɛ��w�ł������ł����w�ł��Ȃ��̂ō����̐��ƂɊm�F���邵���Ȃ��Ȃ邯�� >>386
�k�ޑ�l
f_n(x) = x^(n-1) log(x),
�̂Ƃ�
D^k f_n(x) = x^(n-1-k) {(n-1)(n-2)����(n-k)log(x) + ��[j=0,k-1] (-1)^(k-1-j) (n-1)(n-2)����(n-j)/[j!(k-j)]}
�������B �O>>383
>>388
(����)�G�^�m�[��7ml�ƃI�C��3ml�ō��������Ƃ���ƁA�����̗ʂ́A
7+3=10(ml)
�I�C���̔Z�x�́A
3/10�~100=30(��)
���G�^�m�[����7ml �F�l
�ǂ������肪�Ƃ��������܂����B�P���ɍl���Ă��Ă悩�����悤�ň��S���܂����B
�^�₪�������܂����B����ł����͐Q�����ƂƂ��ɂ�������Q�ꂻ���ł��B d�O2x/dt�O2+3dx/dt+2x=t�O2+t�̈�ʉ�
�����ăN�������X �܂�����������Ȃ��������߂ăN�������X�B >>401
�������2�����Ł@�@x(t) = tt/2 -t +1,
��������
�@(DD+3D+2)x(t) = (D+1)(D+2)x(t) = 0,
���A������
�@x(t) = C1 e^(-t) + C2 e^(-2t), cos(x)-sin(x)+x=cos(t)-1��x�ɂ��ĉ��������̂ł����ǂ������ R^n�ł͂���_�̋ߖT�ɑ��A����Ɋ܂܂��悤�Ȑ^�ɏ������ߖT���Ƃ�܂����A���̂悤�ȋ�Ԃɖ��O�͂��Ă���̂ł��傤���H >>405
�����ɉ����͓̂����������@�ߎ����Ȃ�o�邾�낤���ǁB
x�������炵��
�@x = X - (3��/4)
�Ƃ����B�^����
�@X + (��2)sin(X) = cos(t) +(3��/4) -1 = (1+��2)Y,
�@(3��/4) -2 �� (�E��) �� 3��/4,
�@0.14785581945 �� X �� 1.0974663127
���ӂ�X�̊���ŁA�}�N���[�����W�J�����
�@Y = a{X/��2 + sin(X)} = X + a{-(1/3!)X^3 +(1/5!)X^5 -(1/7!)X^7 +(1/9!)X^9 - ����},
�������@a = 2-��2 = 0.585786437627
�t�ɉ�����
�@X = Y + (a/6)Y^3 +(aa/12 - a/5!)Y^5 + (a^3/18 -aa/90 +a/7!)Y^7 + (55a^4/1296 -11a^3/864 +41aa/60480^a/9!)Y^9 + ���� sinx��n-1����������
(n-1)(sinx)^(n-2)(cosx)�ɂȂ�̂������Ȃ�ł����ǂ��r�����ƍl�������킩��܂���
������������ m>n
X:m�����̋��E�����l��
N:n�����̑��l��
f:X��N ���炩
y��N��f��f�̋��E�ւ̐���f|��X�̑o���ɑ��Đ����l��f^-1(y)��X�͋��E�̂��銊�炩��m-n�������l�̂ł���B����ɁA���E��(f^-1(y))��f^-1(y)�Ɓ�X�̋��ʕ����Ɉ�v����
���肢���܂��c >>408
(f(g(x)))'��f'(g(x))�Eg'(x)
f(y)��y^(n-1)
g(x)��sin x �s��̎��₵���l�ł�
�F���肪�Ƃ��������܂��� >>407 (����)
a = 2-��2 ������
�@X = Y + {(2-��2)/3!}Y^3 + {(58-39��2)/5!}Y^5 + {(5266-3697��2)/7!}Y^7 + {(956274-675503��2)/9!}Y^9 + ����
������
�@X = x + (3��/4),
�@Y = (��2 -1){cos(t) -1 +(3��/4)}, �O>>398���@�͕ς����炾�߂���B >>412
y = 2{1 - cos(��x)} = ��[k=1,��] (-1)^(k-1) {2/(2k)!} x^k,
�̂Ƃ�
x = {Arccos(1 - y/2)}^2 = ��[n=1,��] {2�(n-1)!(n-1)!/(2n)!} y^n,
y = 2{cosh(��x) �| 1} = ��[k=1,��] {2/(2k)!} x^k,
�̂Ƃ�
x = {2�log[(��(4+y) + ��y)/2] }^2 = ��[n=1,��] (-1)^(n-1) {2�(n-1)!(n-1)!/(2n)!} y^n, >>412
y = (4!/2)[cos(x^{1/4}) + cosh(x^{1/4}) -2] = x + ��[k=2,��] {4!/(4k)!} x^k,
�̂Ƃ�
x = y - (4!/8!)y^2 + (4�23/7)(4!/12!)y^3 - (12�461/7)(4!/16!)y^4 + (32�340591/77)(4!/20!)y^5 - ���� AB=AC�̓ӎO�p�`��ABC�̕�BC�̒��_��D�Ƃ���B
����AD����_P���l����BAP����AB�ɉ��낵�������̑���H�ADP����AC�ɉ��낵�������̑���I�Ƃ���Ƃ��APH+PI�̍ő�l�����߂�B �O>>416
>>420
PH+PI��PA+PD=AD ���Z���w�ł�
(a+b)^3 - 3ab(a+b) + c^3 - 3abc
��
(a+b+c)(a^2+b^2+c^2-ab-bc-ca)
�������ł��邱�Ƃ͓W�J����Ε�����̂ł���
�㎮�������֕ϊ�������@��������Ȃ��ł�
�����Ă������� �܂� (a+b)^3 + c^3 ����������
�킩��ɂ������ a+b = t �Ƃł����� >>422
(a+b)^3 + c^3��- 3ab(a+b) - 3abc��ʁX�ɂ܂Ƃ߂Ă݂�
(a+b)^3 + c^3�́ia+b+c)^3����]�v�Ȃ��̂������Ƃ����`�ɂ���Ƃ��̗]�v�Ȃ��̂��ia+b+c)�������Ɏ����Ƃ��킩��
- 3ab(a+b) - 3abc�͂܂Ƃ߂�ia+b+c)�������Ɏ����Ƃ��킩��
�]���đS�̂�(a+b+c)�ł������Ƃ킩��
���Ƃ͐������邾�� >>422
- 3ab(a+b) - 3abc��a+b+c�������Ɏ����Ƃ͂����ɂ킩�邾�낤
(a+b)^3 + c^3��a+b+c�������Ɏ����Ƃ�x^3+y^3�̈����������o���Ă�������ɂ킩��
�����͂�������Y��Ă����̂ň����藝�ōl�������nj��Ȃ炷���ɋC�Â��悤�Ɋ���Ă����ׂ� >>423
>>425
���肪�Ƃ��������܂� >>422
(a+b)^3 - 3ab(a+b) + c^3 - 3abc = (a+b+c)(a^2+b^2+c^2-ab-bc-ca)
=(a+b+c)((a-b)^2+(b-c)^2+(c-a)^2)/2
=a^3+b^3+c^3-3abc=(a+b+c)(a+��b+��^2c) (a+��^2b+��c)
��^3=1,��^2+��+1=0 >>427
�Ō�̈��������͎O���������̉��̌������̂��́I �����܂���ԈႦ���̂ōČf���܂�
�y���z
AB=AC�̓ӎO�p�`��ABC�̕�BC�̒��_��D�Ƃ���B
����AD����_P���l����BAP����AB�ɉ��낵�������̑���H�Ƃ���Ƃ��APH+PC�̍ő�l�����߂�B >>430
������AB�ɂԂ���Ƃ���
�ŋ߂͎g���Ȃ����t�炵����
���̂Ȃ��l�ɑ��鍷�ʂ��Ƃ��Ȃ�Ƃ�
���t��������ȂƂ���܂ŗ����̂��� 20162�ȏ�̎��R���́A2�̉ߏ萔�̘a�ŕ\����邱�Ƃ����ɏؖ�����Ă���B
�ł́A28123��2�̉ߏ萔�̘a�ŕ\���B �O>>429
>>421
PH+PC��PA+PC��AD+DC
=AD+(1/2)BC >>418
�@X = ��x,�@Y = ��y�@�Ƃ����ƥ���
Y = 2 sin(X/2) = ��[k=0,��] (-1)^k /[(2k+1)!�(4^k)] X^(2k+1),
�̂Ƃ�
X = 2 Arcsin(Y/2) = ��[n=0,��] C(2n,n)/[(2n+1)�16^n] Y^(2n+1),
Y = 2 sinh(X/2) = ��[k=0,��] 1/[(2k+1)!�(4^k)] X^(2k+1),
�̂Ƃ�
X = 2 log[{Y+��(4+YY)}/2] = ��[n=0,��] (-1)^n�C(2n,n)/[(2n+1)�16^n] Y^(2n+1), >>419
X = x^{1/4},�@Y = y^{1/4} �Ƃ����ƥ���
Y^4 = (4!/2)[cos(X) + cosh(X) -2] = X + ��[k=2,��] {4!/(4k)!} X^{4k},
�̂Ƃ�
X = Y - (1/4)(4!/8!)Y^5 + (1175/448)(4!/12!)Y^9 - (18375/128)(4!/16!)Y^13 + (7698965625/315392)(1/20!)^17 - ���� >>432
28123�͊������A��Ƌ����̑g�����B
�����Ō��n�I�ߏ萔���������B�@http://oeis.org/A091191
��̌��n�I�ߏ萔 < 28123�@�@�@�@(36��)
945, 1575, 2205, 3465, 4095, 5355, 5775, 5985, 6435, 6825,
7245, 7425, 8085, 8415, 8925, 9135, �X�T�T�T, 9765, 11655, 12705,
12915, 13545, 14805, 15015, 16695, 18585, 19215, 19635, 21105, 21945,
22365, 22995, 24885, 25935, 26565, �Q�W�O�R�T.
(��̊��S���͖�����)
�����̌��n�I�ߏ萔
12, 18, 20, 30, 42, 56, 66, 70, 78, �W�W,
102, 104, 114, 138, 174, 186, 196, 222, 246, 258,
272, 282, 304, 308, 318, 354, 364, 366, 368, 402,
426, 438, 464, 474, 476, 498, 532, 534, 550, 572,
582, 606, 618, 642, 644, 650, 654,
678, 748, 762, 786, 812, 822, ����
(�����̊��S���� 6, 28, 496, 8128, ����)
�ȏ�ɂ��
28123 = 28035 + 88,
28123 = 9555 + (88*211), >>429
BC = a, AB = AC = b, AP = p �Ƃ�����
AD = ��(bb-aa/4),
DH = (a/2b)��(bb-aa/4),
�_P�͐���AD����B
PH��p�ɔ�Ⴗ�邪�APC = ��{(AD-p)^2 + (a/2)^2} ��p�ɂ��ĉ��ɓʁB
�䂦�� PH+PC��p�ɂ��ĉ��ɓʂŁA�[�_(A�CD)�̂����ꂩ�ōő�l���Ƃ�B
�����
b �� b0 �̂Ƃ��@��
b < b0 �̂Ƃ��@(a/2b)��(bb-aa/4)} + (a/2)
������
b0 = (1/6){1 + (19-3��33)^(1/3) + (19+3��33)^(1/3)}a = 0.9196433776a, ���ʑ���wikipedia�Ɂu�J�ł��ł��Ȃ����ʑ��̗���\������̂͂�������Ȃ��v���ď����Ă���ǎ��ۂǂ�Ȃ̂������ł��傤�� n�����R���Ap��f���Ƃ���Ƃ��A
(n^2+1)(5n^2+9)-2p
���������ƂȂ�(n,p)�̑g�������ɑ��݂��邱�Ƃ������B 1000�ȏ�̔C�ӂ̒��������A�������Ȃ�ׂ�500�ɋ߂��Ȃ����������Ε֗��Ȃ�ŒN�������Ă�������
�������鐔�͐����A�����͐�������Ȃ��Ă����v�ł� >>442
���̎l�̌ܓ��������܂߂ď�肭��������������ł����ǁA�����̓����ᖳ���ł��� >>439
�Ⴆ�Ε��[0,3]=X�̕����W��A��
A={0}��(1,2)
�ƒ�߂�ƁA���ʑ�X��X/A�͊J�ł��ł�����܂���
���Ȃ݂�X/A�̓n�E�X�h���t�łȂ��ʑ���Ԃł� 1. �S�̏W��U��9�ȉ��̎��R���Ƃ�, U �̕����W���� A = {xEU; x �͋��� }, B = {x in U; x<=6}, C = {5,6,7}�Ƃ���B�ȉ��� (1)-(5) �̏W�����A��ɂȂ���ĊO���I�L�@�ŏ�������(��: C = {1, 2,3,4,8,9)
(1) A�o�[, (2) A�� B, (3) AUC, (4) A��B��C, (5) (A��B�o�[�j�o�[��C
6. �ʑ� f : R �� R, x �� x^2+1�Ǝʑ�g: R �� R, x �� COSx �ɂ���,�����ʑ�gof �� fog��
������
7. �ȉ��̒q (1)-(6) �͖��肩�ۂ�������A����Ȃ��,���̐^�U��T�܂��� F �œ�����(T��
�^�AF�͋U��\��)
(1) 10000�͑傫�Ȑ��ł���B
(2) 2.018�͗L�����ł���B
(3) (all x in R)(x^4-2x^2+1 > 0)
(4) (exist x �� R) (x^3 - x^2+ x - 1 = 0)
(5) (all c in R)exist x in R)(x^4-c=0)
(6) (all(x, y) in R)(xy not = 0 �� x^2+y^2 > 0)
8. P.O.R�͖���Ƃ���B�ȉ��̘_���� (1)-(5) �̐^���l��,P��Q��T(�^)�AR��F(�U)�̏ꍇ�ɂ��Čv�Z���AT�܂�F�œ�����B
(1) notP, (2) P��Q (3) QVR,
(4) PV(Q��-R), (5) (PAnotQ) �� R
9. �S�̏W����U = {x in Z ;0<=x<=9}�Ƃ���.U��̖���� p(x), q(x) ��,���ꂼ��, p(r):x^3 - 7x^2 +10x = 0, �����,q(x):x<=4�ƒ�`����B�ȉ��̖� (1)-(4) �ɓ�����.
(1) �^���W�� P = {x in U;p(x)���^}���O���I�L�@�œ�����.
(2) �^���W��Q={x in U;q(x)���^}���O���I�L�@�œ�����.
(3) (p(x)��g(x)�̐^���W����S1�Ƃ���.S1��P��Q�ŕ\���A����ɊO���I�L�@�œ�����B
(4)not(p(x)Vq(x))�̐^���W���� S2 �Ƃ���BS2��P�o�[��Q�o�[�ŕ\���A����ɊO���I�L�@�œ�����B >>411
�@n = 500q + r,�@�@(0��r<500)
�@n/(q+1) < 500 �� n/q,
�ǂ��炪 500 �ɋ߂����H
�@n/(q+1) + n/q - 1000
�@= n(2q+1)/(q(q+1)) - 1000
�@= ((2q+1)r -500q)/(q(q+1)),
�����
0 �� r < 500q/(2q+1)�@�̂Ƃ��@n/q - 500 < 500 - n/(q+1),
500q/(2q+1) �� r < 500�@�̂Ƃ��@n/q - 500 �� 500 - n/(q+1),
����
1000(q-1)q/(2q-1) < n �� 1000q (q+1)/(2q+1) �̂Ƃ�q��������B >>444
���肪�Ƃ��������܂�
����R��(0�܂�)�ƕ��ɕ��������l�ނƂ��ł��ǂ������ł���
�n�E�X�h���t�ɂ��Ă͖��K�������̂ł������ɂȂ�܂��� >>441 >>443
�����ɂ����
�@q = [ (1 + (n/500) + ��(1+(n/500)^2) )/2 ], >>446 >>448
n��5238 �ł�
q=2�@�@666<n��1200
q=3�@�@1200<n��1714
q=4�@�@1714<n��2222
q=5�@�@2222<n��2727
q=6�@�@2727<n��3230
q=7�@�@3230<n��3733
q=8�@�@3733<n��4235
q=9�@�@4235<n��4736
q=10 �@4736<n��5238
(500q-250) �` (500q+250)�@��������� >>440
�ǂȂ������ꓚ�����܂��� �^�U����̖��
��x��R (x<1⇨��y��Q,x<r<1)
������Đ^�ł����Ă��ˁH >>450
>>440
����Ȃ̐��������H
�o�T�́H >>451
�u�w ��x��R (x<1 �� ��r��Q, x<r<1)�x�͐^�B�v�ł����Ă�B
�Ƃ�������ˁB
�^�ł����Ă��B
[1/(1-x)] + 1 = N,�@r = 1 - 1/N �Ƃ����B >>453
���肪�Ƃ��I
���Ƃ������
X={x��R|0��x<5�p Y={y��R|-10<y��100}
���̏W���͑Γ��ł��邩�ǂ����B
�Γ��łȂ��ꍇ�͗��R����B
�S�P�˂ł͂Ȃ��P�˂�����Γ��ł͂Ȃ��Ő����H >>440
m^2 = (n^2+1)(5n^2+9)-2p
�Ƃ���B
(n^2+1)(5n^2+9) �� 1,4 (mod 8)
������
(n^2+1)(5n^2+9) - m^2 �� 0,4,1,3,5,7 (mod 8)
�䂦��p=2���K�v��(n^2+1)(5n^2+9)-4���������ɂȂ���̂������ɂȂ��Ƃ��߂�����n��100000�łЂƂ��Ȃ����ǁH >>455
����H
(n^2+1)(5n^2+9)-4=5(n^2+1)^2�����畽�����ɂȂ�킯�Ȃ��B
������Ȃ��́H >>455
(n^2+1)(5n^2+9)-4 �� 5,8,13 (mod 16)
�䂦�ɍ��ӂ͕������łȂ� X={x��R|0��x<5}
A={a��R|-5<a��0}
B={b��R|-110<b��0}
Y={y��R|-10<y��100}
X��A��x��a=-x�Ɏʂ����ƂőΓ�
A��B��a��b=22a�Ɏʂ����ƂőΓ�
B��Y��b��y=b+100�Ɏʂ����ƂőΓ�
�Γ��͓��l�W������X��Y���Γ� >>455
n = 4q + r (0��r<4)
�Ƃ�����
(nn+1)(5nn+9) = 32{40q^3 + 40rq^2 + (15rr+7)q + 5r(r+1)(r-1)/2 + 6r}q + (rr+1)(5rr+9)
�@�� (rr+1)(5rr+9)�@�@�@(mod 32)
�@�� 9, -4, 17�@�@�@(mod 32)
�@�� 1, 4�@�@�@�@�@�@(mod 8)
mm �� 0, 1, 4�@�@�@(mod 8) >>455
m = 4q + r (0��r<4)
�Ƃ����B
q�������̂Ƃ�
mm = 16qq + 8rq + rr �� rr�@�@(mod 16)
q����̂Ƃ�
mm = 16qq + 8r(q+1) -16 + (4-r)^2 �� (4-r)^2�@�@(mod 16)
�����
mm �� 0,1,4,9�@�@(mod 16) ���̖��I�i�V���X����(2)(3)����
http://imgur.com/a/TqsoVur >>462
(1)A�͎�����2�̒���
B�͊p�x��5��/4 ����3��/2�̖�
c��-1+i�𒆐S�Ƃ��锼�a1�̉~�Ł@�����H >>462
�S�������\���ł����邯��
z=a+bi��
���Ƃ͍��W���ʂ�(a,b)�̋O�ՂƗ̈���l���邾�� >>280>>301���ꂠ���Ă�̂��ȁH�@�O>>433
�P�P]/�_;;;;;;;;;;;;;;
;;;;/�_/;,,�;;;;;;;;;)
�P�P�_/�c-_-�;;;;;;;/;
�P�P|�_;U,~�܁R;;;�^|;
���@| �a�P~U~U~�P�a |;
�Q�Q| �a ���@���@�a |/
;;;;;`�a_________�a�^;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;; >>461
(8�}r)^2 = 64 �}16r +rr �� rr�@�@(mod 16)
���@|r| �� 4 �ōl����
mm �� 0,1,4,9�@�@(mod 16) X��∅:�ʏ�A��
X=A��B
A��B��∅:�ʏ�A��
��A,B:�ʏ�A��
�͐������ł����H ���a1�̉~C�ɓ��ڂ��鐳N�p�`�̖ʐς�S[N]�AC�ɊO�ڂ��鐳N�p�`�̖ʐς�T[N]�Ƃ���B���̂Ƃ��A�ȉ��̎���n�����Ƃ����Ƃ��̋Ɍ������߂�B
�i1�j(T[7(n+1)] -T[7n])/(S[7(n+1)] -S[7n])
�i2�j(T[7(n+1)] -S[7n])/(S[7(n+1)] -T[7n]) >>468
�}�N���[�����W�J��
�@S[N] = (N/2)sin(2��/N) = ��{1 -(1/3!)(2��/N)^2 +(1/5!)(2��/N)^4 -(1/7!)(2��/N)^6 + ���� }
�@T[N] = N tan(��/N) = ��{1 +(1/3)(��/N)^2 +(2/15)(��/N)^4 +(17/315)(��/N)^6 + ���� }
(1)
�@S[M] - S[N] = -(2/3)��(1/MM -1/NN){1 -(1/5)�Υ(1/MM+1/NN) +(2/105)��^4�(1/M^4 +1/(MMNN) +1/N^4) - ���� }
�@T[M] - T[N] =�@(1/3)��(1/MM -1/NN){1 +(2/5)�Υ(1/MM+1/NN) +(17/105)��^4�(1/M^4 +1/(MMNN) +1/N^4) + ���� }
�ӁX�����
�@(T[M]-T[N])/(S[M]-S[N]) = -(1/2){1 +(3/5)��(1/MM+1/NN) +(1/175)��^4(46/M^4 +67/(MMNN) +46/N^4) + ��� }
(M, N)��(��, ��) �̂Ƃ� -1/2 �Ɏ����B
(2)
�@T[M] - S[N] = ��{(��/3)(1/MM +2/NN) + (2/15)��^4�(1/M^4 -1/N^4) + ���� }
�@S[M] - T[N] = ��{-(��/3)(2/MM +1/NN) + (2/15)��^4�(1/M^4 -1/N^4) + ���� }
�ӁX������
�@(T[M]-S[N])/(S[M]-T[N]) ���@-(1/MM +2/NN)/(2/MM +1/NN)�@=�@g(M/N)
�@-2 �� g �� -1/2, >>469
����ł��܂���
���肪�Ƃ��������܂��� >>471
�R�ł���
����������ĉ����� >>467,472
�Ⴆ��
X=(0,4)
A=(0,2)��(3,4)
B=(1,3]
�Ȃ��
X=A��B
A��B=(1,2) >>470
�i2�j�͎������Ȃ���ł����H
���l�v�Z���Ǝ�������悤�Ɍ����܂����� �@M/N �� ��������@g(M/N) ����������B
�{��ł́@M = 7(n+1),�@N = 7n ������
�@M/N = (n+1)/n �� 1�@�@(n����)
�@g(M/N) = g((n+1)/n) �� g(1) = -1�@�@(n����) >>473
���߂�Ȃ���
A,B�͊J�W���Ƃ������肪�����Ă��܂��� >>476
�J�W�����Ɖ��肷��ƁAI�̃R���p�N�g�����玦�����Ƃ��ł��܂��ˁB���肪�Ƃ��������܂����B �uf(x)��g(x)��x=a�Őڂ���Ȃ��f(x)-g(x)=k(x-a)^2�@�Ə�����v���Ƃ̏ؖ������肢���܂�
���܂������ł��܂����̌������g���Ƃ��ɂ�����₷��̂ł� >>479
���炵�܂���>>480��3�����Ə����܂�����
�Е��͓��A�����Е��͈ꎟ���i�����j
�ł� >>478,481
f(x)=k(x-a)^2+l(x-a)+m
g(x)=n(x-a)+o
�Ƃ�����
f,g��x=a�Őڂ���̂ŁA
f(a)=g(a)
f'(a)=g'(a)
���A
m=o
l=n
����āA
f(x)-g(x)=k(x-a)^2 >>478
�@f(x), g(x)�@���������̏ꍇ�����l�ɂ��āA
�@f(a) - g(a) = 0,�@�@�@�@(�� x=a �ň�v����)
�����藝�ɂ��
�@f(x) - g(x) = h(x)�(x-a),
x=a �ł̌X����
�@h(a) = f '(a) - g '(a) = 0,�@�@�@(�� x=a �Őڂ���)
�����藝���
�@h(x) = k(x)�(x-a),
�����
�@f(x) - g(x) = k(x)�(x-a)^2, >>475
r>1 �Ƃ���B
n����̂Ƃ�
�@M = r^n,�@N = r^(n+1),�@�@M/N = 1/r,
n���)�̂Ƃ�
�@M = r^(n+1),�@N = r^n,�@�@M/N = r,
�Ƃ����W�O�U�O�o�H�� (M,N) �� (��,��) �Ƃ����ꍇ
M/N �͐U������B >>485
| f(x) | = | ��_{0}^{x} (x - t) * f''(t) dt | �� ��_{0}^{x} | (x - t) * f''(t) | dt
= ��_{0}^{x} (x - t) * | f''(t) | dt �� ��_{0}^{x} (x - t) * x dt
= (1/2)*x^3 - (1/3)*x^3 = (1/6) * x^3 = x^3 / 3! �ȉ���(A)��(B)���g���܂��B
(A)
| �� f(t) dt | �� �� | f(t) | dt
(B)
f(t) �� g(t) �̂Ƃ��A
�� f(t) dt �� �� g(t) dt �������܂��F
>>485
| f(x) | = | ��_{0}^{x} (x - t) * f''(t) dt | �� ��_{0}^{x} | (x - t) * f''(t) | dt
= ��_{0}^{x} (x - t) * | f''(t) | dt �� ��_{0}^{x} (x - t) * t dt
= (1/2)*x^3 - (1/3)*x^3 = (1/6) * x^3 = x^3 / 3! >>488
���J�ɂ��肪�Ƃ��������܂��B
�����o���܂����B 2n x 2n �̐����`��
1 x 2 �̃h�~�m�Ŗ��߂�ꍇ�̐����l���܂�
���Ƃ��A2x2�̐����`��1x2�̃h�~�m�Ŗ��߂�ꍇ�̐��́A2�ʂ�ł�
4x4�̐����`��1x2�̃h�~�m�Ŗ��߂�ꍇ�̐��́A36�ʂ�ł�
��ʂɁAn=0,1,2,3,,,,�̂Ƃ��A
1, 2, 36, 6728, 12988816, 258584046368,,,
�ƂȂ�A��ʍ��́A
��[j=1 to n]��[j=1 to n]{4cos^2 ��j/(2n+1)+4cos^2 ��k/(2n+1)}
�ƂȂ�悤�Ȃ̂ł����A
�ǂ̂悤�ɂ��̌������������̂ł��傤��? >>490
��ʍ��̎���a[n]�Ƃ�����a[n+1]�Ƃ̊W >>490
wikipedia
https://en.wikipedia.org/wiki/Domino_tiling
�ɂ���
Temperley & Fisher (1961) and Kasteleyn (1961)
�ɂ���ēƗ��ɔ������ꂽ�Ƃ���B
�������_����
Temperley, H. N. V.; Fisher, Michael E. (1961), "Dimer problem in statistical mechanics-an exact result", Philosophical Magazine, 6 (68): 1061–1063, doi:10.1080/14786436108243366
��
Kasteleyn, P. W. (1961), "The statistics of dimers on a lattice. I. The number of dimer arrangements on a quadratic lattice", Physica, 27 (12): 1209–1225, Bibcode:1961Phy....27.1209K, doi:10.1016/0031-8914(61)90063-5.
���Ǝv���B
�������_���ǂނ̂������̂ł́H �e���Ɉ��邪���
m�~n �̒����`�̏ꍇ��
��(j=1�c[m/2]) ��(k=1�c[n/2])�@{4cos(j��/(m+1))^2 + 4cos(k��/(n+1))^2}
�炵���B
2�~n �����`�̏ꍇ��
�@�� = (1+��5)/2 = 1.61803399�@�Ƃ����B�@�@�c ������
�@�� - 1/�� = 1,
��(k=1�c[n/2]) {1 + 4cos(k��/(n+1))^2}
�@= ��(k=1�c[n/2]) {3 + 2cos(2k��/(n+1))}
�@= ��(k=1�c[n/2]) {��^2 + (-1/��)^2 + 2cos(2k��/(n+1))}
�@= ��(k=1�c[n/2]) {�� - (-1/��)exp(2ik/(n+1))} {�� - (-1/��)exp(-2ik��/(n+1))}
�@= ��(k=1�cn) {�� - (-1/��)exp(2ik��/(n+1))}
�@= {��^(n+1) - (-1/��)^(n+1)}/(�� + 1/��)
�@= F_(n+1)�@�@�@�@�@�@�@�@�@�@�@�@�c �t�B�{�i�b�`��
�Q�l����
�E���Z�~�����u���w100�̖��v���{�]�_��(1984) p.90-92
�@http://oeis.org/A004003
�@http://oeis.org/A065072 >>490
����ɏؖ��ڂ��Ă邭�����B
https://inis.iaea.org/collection/NCLCollectionStore/_Public/38/098/38098203.pdf?r=1&;r=1
Section2
A famous result of Kasteleyn [8] and Temperley and Fisher [18] counts the
number of domino tilings of a chessboard (or any other rectangular region).
In this section we explain Kasteleyn's proof.
�������ȁB �E2�~2n �̒����`
�@�����������@tt-t-1,
�@-1/�� = (1-��5)/2,
�@�� = (1+��5)/2,
�@F_(n+1) = {��^(n+1) - (-1/��)^(n+1)}/(�� + 1/��),
�@�������@1/(1-z-zz),
�E3�~2n �̒����`
�@�����������@tt -4t +1,
�@�� = 2-��3,�@�� = 2+��3,
�@P_n = {(1+��3)��^n - (1-��3)��^n}/(��-��)
�@�������@(1-z^3)/(1-4z^3+z^6)
�u�h�~�m�ɂ��^�C������v(���套�)�@36p.
http://www.ms.u-tokyo.ac.jp/~kazushi/proceedings/domino.pdf
�u�����`�̈�̃h�~�m�^�C������ɂ��āv(�w�套��H)�@17p.
http://www.gem.aoyama.ac.jp/~kyo/sotsuken/2010/fujino_sotsuron_2010.pdf >>496
���ϕ���b�̋Ɉ�
�Ƃ������Z�������̎Q�l���ɂ��܂��������ڂ��Ă��� �� exp(-x) * sin(x) dx
=
-exp(-x) * sin(x) + �� exp(-x) * cos(x) dx
=
-exp(-x) * sin(x) - exp(-x) * cos(x) - �� exp(-x) * sin(x) dx
--------------------------------------------------------------------------------
2 * �� exp(-x) * sin(x) dx
=
-exp(-x) * sin(x) - exp(-x) * cos(x)
=
-exp(-x) * (sin(x) + cos(x))
--------------------------------------------------------------------------------
��
�� exp(-x) * sin(x) dx
=
(-1/2) * exp(-x) * (sin(x) + cos(x)) 👀
Rock54: Caution(BBR-MD5:1341adc37120578f18dba9451e6c8c3b) >>499
���肪�Ƃ��������܂��B
�ϕ��͂킩��܂��B
������[k,k+1]�Œ�ϕ������cosxk���c���Ă��܂�(2)�ȍ~�ʼn����Ȃ��Ȃ��Ă��܂��C�����܂��B������������Ȃ��ł��B (-1/2) * exp(-(k + 1) * ��) * (sin((k + 1) * ��) + cos((k + 1) * ��))
-
(-1/2) * exp(-k * ��) * (sin(k * ��) + cos(k * ��))
=
(-1/2) * exp(-(k + 1) * ��) * cos((k + 1) * ��)
-
(-1/2) * exp(-k * ��) * cos(k * ��)
=
(-1/2) * exp(-(k + 1) * ��) * (-1)^(k + 1)
-
(-1/2) * exp(-k * ��) * (-1)^k
=
(1/2) * exp(-(k + 1) * ��) * (-1)^k
+
(1/2) * exp(-k * ��) * (-1)^k
=
(-1)^k * (1/2) * (exp(-(k + 1) * ��) + exp(-k * ��))
��
S_k
=
| (-1)^k * (1/2) * (exp(-(k + 1) * ��) + exp(-k * ��)) |
=
(1/2) * (exp(-(k + 1) * ��) + exp(-k * ��)) >>500
cos(n * ��) = (-1)^n
�ł��B >>501
���肪�Ƃ��������܂��B
�����I�Ȏ���Ő\����܂���Sk�͂Ȃ���Βl�ň͂ނ̂ł��傤���H >>503
�� exp(-x) * sin(x) dx
�̔�ϕ��� exp(-x) * sin(x) �ɂ��čl���܂��B
k �������̂Ƃ��A
k * �� �� x �� (k + 1) * �� �ł��邷�ׂĂ� x �ɑ���
���
exp(-x) * sin(x)�@�� 0
�ł��B
k ����̂Ƃ��A
k * �� �� x �� (k + 1) * �� �ł��邷�ׂĂ� x �ɑ���
���
exp(-x) * sin(x)�@�� 0
�ł��B
���������āA
k �������̂Ƃ��A
S_k = ��_{k * ��}^{(k + 1) * ��} exp(-x) * sin(x) dx
�ł��B
k ����̂Ƃ��A
S_k = (-1) * ��_{k * ��}^{(k + 1) * ��} exp(-x) * sin(x) dx
�ł��B �ł��̂ŁA
S_k = | ��_{k * ��}^{(k + 1) * ��} exp(-x) * sin(x) dx |
�ł��B ��� [0 * ��, 1 * ��] ��� exp(-x) * sin(x) �̃O���t�F
https://www.wolframalpha.com/input/?i=plot+exp(-x)+*+sin(x)+from+x+%3D+0+to+x+%3D+pi
��� [1 * ��, 2 * ��] ��� exp(-x) * sin(x) �̃O���t�F
https://www.wolframalpha.com/input/?i=plot+exp(-x)+*+sin(x)+from+x+%3D+pi+to+x+%3D+2*pi
��� [2 * ��, 3 * ��] ��� exp(-x) * sin(x) �̃O���t�F
https://www.wolframalpha.com/input/?i=plot+exp(-x)+*+sin(x)+from+x+%3D+2*pi+to+x+%3D+3*pi
��� [3 * ��, 4 * ��] ��� exp(-x) * sin(x) �̃O���t�F
https://www.wolframalpha.com/input/?i=plot+exp(-x)+*+sin(x)+from+x+%3D+3*pi+to+x+%3D+4*pi ��ϕ��� exp(-x) * sin(x)
�́@exp(-x)�@�͏�ɐ��ł��B
sin(x) ��
k �������̂Ƃ��A
[k * ��, (k + 1) * ��] ��ŏ�� 0 �ȏ�ł��B
sin(x) ��
k ����̂Ƃ��A
[k * ��, (k + 1) * ��] ��ŏ�� 0 �ȉ��ł��B �摜�Ő\����Ȃ��ł�����낵�����肢���܂�
https://i.imgur.com/WxL3oIq.png �� 3.7
f(x,y) �� {-a��x��a}�~R �� x,y �ɂ��A���ŁA����
���鐳�萔 C, K �� p<1 �ɂ���
�@|f(x,y)| �� (C/|x|^p)(|y|+1),
�@|f(x,y) - f(x,z)| �� (K/|x|^p)|y-z|,
�����悤�Ȋ��Ƃ���B
���̂Ƃ��ϕ�������
�@�@��(x) = c + ��[0,x] f(s,��(s)) ds
�� [-a,a] ��ɘA�������ӂ�����������Ƃ������B r = exp(-��) �� 0.04321�@�Ƃ����B
sin(k��+y) = (-1)^k�sin(y)�@(0<y<��)�@���
�@S_k = r^k ��[0,��] exp(-y) sin(y) dy = S_0�r^k,
���@��[k=0,n] S_k = S_0 ��[k=0,n] r^k
�@= S_0 {1 - r^(n+1)}/(1-r)
�@�� S_0 /(1-r)
�@= 0.5451657�@�@�@(n����)
�����ŁAS_0 = (1+r)/2 = 0.521607
��@1/2 = [ -(1/2)exp(-x){sin(x)+cos(x)} ](x=0,��)
�@= ��[0,��] exp(-x)sin(x)dx
�@= ��[k=0,��] (-1)^k�S_k
�@= S_0 ��[k=0,��] (-r)^k
�@= S_0 /(1+r), �����E�����̊m���ɂ��Ă̎���ł�
���镟���̓��I�܋��Ɠ��I�m�������L�̒ʂ肾�Ƃ��܂�
�P���F�P�O�O�~ �P�T��
�Q���F�T�O�~ �R�O��
�R���F�P�O�~ �T�O��
�S���F�������� �T��
�����������͂R���ŕ������P�Ƃ��ė��p�ł��܂�
���{��
���̏ꍇ�A�������P��������̊��Ғl�͂ǂ��Ȃ�܂����H
�P�`�R�������Ȃ�P���Ȋ���Z�œ����o����̂ł����A�ǂ����Ă��������܂߂��m���̌v�Z���@���킩��܂���
�ǂȂ��������������肢���܂� �̊F�l�ɂ͊ȒP�����邩������܂��A�{���ɐ��w�����Ő\���킯����܂���
���q��ɒʂ��Ă��܂����A�G�X�J���[�^�[���ŕw�ŋ�J�������ɂ����܂ł����̂ŁA���w����퐶���ɉ��p����\�͂��s�����Ă��܂�
�{���ɂ��萔�����������邾���Ȃ̂ł����A�ǂ������͂�݂��Ă��������Ȃ��ł��傤���E�E�Em(__)m ���������ʂɎ����Ă���ꍇ��1��������̊��Ғl���l������Ă��ƂȂ�4����1/3���������錠���Ƃ��Čv�Z����Ⴂ����Ȃ����H
1�����������Ă��Ȃ��Ȃ�4���͂Ȃ��̂Ɠ��� ������1��������̋��K�I���l=������1��������̊��Ғl �Ƃ��Ă悢�Ƃ���B
������1��������̊��Ғl��x�Ƃ���ƁA�����������̋��K�I���l��x/3�~�ƂȂ�B�����
x=100�~0.15+50�~0.3+10�~0.5+(x/3)�~0.05
�����������
x=2100/59��35.59
�ƂȂ�B ���Ғl�̑��݂Ƃ����������͎������Ă��Ƃɂ��Ă�́H E(n)=��[a=0,n]C[n,a]��[b=0,n-a]C[n-a,b]��[c=0,n-a-b]C[n-a-b,c](15/100)^a�~(30/100)^b�~(50/100)^c�~(1000000*a+500000*b+100000*c) ��ABC�́A���̃u���J�[���_�A�O�S�A���S�����꒼����ɂ���Ƃ����B
���̂悤�ȁ�ABC�̌`����q�ׂ�B �ȉ��̏����̂��ƂŁAab+bc+ca�̎�肤��l�͈̔͂����߂�B
�Ea,b,c�͎����ŁA���Ȃ��Ƃ�1��0�ȉ��ł���A���Ȃ��Ƃ�1��0�ȏ�ł���B
�E-2≤a+b+c≤2
�E-1≤a≤1�A-1≤b≤1�A-1≤c≤1 �@�@ �P
�@�@�P�P
�@�@�Q�P
�@�P�Q�P�P
�P�P�P�Q�Q�P
���ɗ���s�͂Ȃ�ł��傤�H �������̔���3���Œ��I���Ă�����ɑ��Ă͔����͂��炦�Ȃ����� �����\���͂킩��܂���
1 1�Ǝn�܂�t�B�{�i�b�`����ɂ��āAarctan(1/F_n)�̖����a�͂ǂ��Ȃ�ł��傤��
n����̂Ƃ������������킹��ƃ�/2�Ȃ͎̂����܂� >>523
(1)�@(-��, ��)
�@{a,b,c} = {n, n, -1} �̂Ƃ� n(n-2) �� ��
�@{a,b,c} = {n, -n, 1} �̂Ƃ� -nn �� -��
(2)�@(-��, 4/3]
ab+bc+ca �� (1/3)(a+b+c)^2 �� 4/3,
�@{a,b,c} = {n, -n, 1} �̂Ƃ� -nn �� -��
(3)�@[-1, 3]
ab+bc+ca �� (1/3)(a+b+c)^2 �� 3,
�@������ a=b=c=�}1 �̂Ƃ��B
ab+bc+ca = -1 + (1/2)(1-a)(1-b)(1-c) + (1/2)(1+a)(1+b)(1+c) �� -1,
�@������ {a,b,c} = {a,-1,1} {-1,b,1} {-1,1,c} �ȂǁB >>522
�@��P = (�Ɂ�A + �ʁ�B + �ˁ�C)/(��+��+��),
�̂Ƃ��_P�̏d�S���W�� (�ɁF�ʁF��) �Ƃ���B
�d�SG�́@�@�P�F�P�F�P
�O�SO�́@�@sin(2A)�Fsin(2B)�Fsin(2C)
���SH�́@�@tan(A)�Ftan(B)�Ftan(C)
�i��OH =��OA +��OB +��OC = 3��OG,�@�@OG�FGH = 1�F2�@�I�C���[��)
���u���J�[���_�́@(ac/b)�F(ba/c)�F(cb/a)
���u���J�[���_�́@(ab/c)�F(bc/a)�F(ca/b) >>525��P�܂�
>>524 312211 >>527
����������s���Ƃ��Ȃ����ɂȂ�݂���
Prelude> let fibs = map head $ iterate(¥[x,y]->[x+y,x]) [0,1]
Prelude> (/pi) $ sum $ zipWith (*) (cycle [1,0]) $ map (atan.recip.fromInteger) $ take 10000 $ drop 1 $ fibs
0.49999999999999983
Prelude> (/pi) $ sum $ zipWith (*) (cycle [1,0]) $ map (atan.recip.fromInteger) $ take 10000 $ drop 2 $ fibs
0.41650938439782204 >>527
a[n]=arctan(1/F[n])
�Ƃ����
a[2n+1]=a[2n]-a[2n+2]
���������邩��A������g���Ɗ�Ɍ��肵���a�͊ȒP�ɕ������
arctan��Fibonacci����g�ݍ��킹�������ɂ��Ē��ׂĂ݂����A���Ȃ��Ƃ���̏ꍇ�Ɠ������j�ł����ɏo���邱�Ƃ͂Ȃ����ۂ� >>523
�S�Ă̏������u���v�̏ꍇ��-1≤ab+bc+ca≤4/3�ł����H a > b �� 0 �������Ƃ���B���� (a_n) �����̂悤�ɋA�[�I�ɒ�`����B
a_9 = a, a_1 = b �Ƃ����B n �� 1 �Ƃ��A a_n �܂Œ�܂��Ă���Ƃ���B
a_n > 0 �̂Ƃ��́A q_n = [a_{n-1} / a_n] �Ƃ����� a_{n+1} = a_{n-1} - q_n * a_n �� 0 �ƒ�߂�B a_n = 0 �̂Ƃ��́A q_n = a_{n + 1} = 0
�Ƃ���B
1. a = ��2, b = 1 �̂Ƃ��A���� (a_n) �����߂�B >>533
������ [-1,1] �ł��B
-1��a��0, -1��b��1, 0��c��1�@�Ƃ��Ă悢�B-2��a+b+c��2 �͎����I�ɐ�������B
ab+bc+ca �� (a+c)b �� |a+c||b| �� 1,
�@������ (a,b,c) = (-1,-1,0)�@(0,1,1) �̂Ƃ�
ab+bc+ca = -1 + (1/2)(1-a)(1-b)(1-c) + (1/2)(1+a)(1+b)(1+c) �� -1,
�@������ (a,b,c) = (-1,b,1) �̂Ƃ� >>534
a_n = (��2 - 1)^(n-1),�@�@(n��2)
q_n = [ 1+��2 ] = 2,�@�@(n��2) z�͕��f���ʏ��|z|��1�̂Ƃ�
|(1+z) e^(-z) -1|��(2e+1) |z|^2������ g(z) = e^(-z) -1 +z = [k=2,��] (-z)^k /k!,
|g(z)| = |��[k=2,��] (-z)^k /k! | �� ��[k=2,��] |z|^2 /k! �� |z|^2 ��[k=2,��] 1/k! = (e-2)|z|^2,
(����) = |(1+z)(1-z+g(z))-1| = | -zz + (1+z)g(z)| �� |z|^2 + |1+z||g(z)| �� |z|^2 + 2(e-2)|z|^2 = (2e-3)|z|^2, >>534
a > b �� 0 �������Ƃ���B���� (a_n) �����̂悤�ɋA�[�I�ɒ�`����B
a_0 = a, a_1 = b �Ƃ����B n �� 1 �Ƃ��A a_n �܂Œ�܂��Ă���Ƃ���B
a_n > 0 �̂Ƃ��́A q_n = [a_{n-1} / a_n] �Ƃ�����
a_{n+1} = a_{n-1} - q_n * a_n �� 0 �ƒ�߂�B a_n = 0 �̂Ƃ��́A q_n = a_{n + 1} = 0
�Ƃ���B
1. a = ��2, b = 1 �̂Ƃ��A���� (a_n) �����߂�B
a_0 = ��2
a_1 = 1
�܂��A n �� 2 �̂Ƃ��A a_n �� 0 ���� a_{n-1} / a_n = ��2 + 1 �ł��邱�Ƃ𐔊w�I�A�[�@�ŏؖ�����B
(1)
a_2 = a_0 - [a_0 / a_1] * a_1 = ��2 - [��2 / 1] * 1 = ��2 - [1.41421356�c] = ��2 - 1 �� 0
�ł���A
a_1 / a_2 = 1 / (��2 - 1) = ��2 + 1
�ł���B
k �� 2 �Ƃ��A
a_k �� 0
�ł���A
a_{k-1} / a_k = ��2 + 1
�ł���Ɖ��肷��B
a_{k+1} = a_{k-1} - [a_{k-1} / a_k] * a_k = a_k * (a_{k-1} / a_k - [a_{k-1} / a_k]) = a_k * (��2 + 1 - [��2 + 1])
= a_k * (��2 + 1 - [1.41421356�c + 1]) = a_k * (��2 + 1 - [2.41421356�c]) = a_k * (��2 + 1 - 2) = a_k * (��2 - 1) �� 0
�ł���A
a_k / a_{k+1} = a_k / (a_{k-1} - [a_{k-1} / a_k] * a_k) = a_k / [a_k * (��2 - 1)] = 1 / (��2 - 1) = ��2 + 1
�ł���B�y�ؖ��I���z >>534
�䂦�ɁA
n �� 2 �̂Ƃ��A q_n = [a_{n-1} / a_n] = [��2 + 1] = [1.41421356�c + 1] = [2.41421356�c] �� 2
�ł���B
����āA (a_n) �� n �� 2 �̂Ƃ��A
a_{n+1} = a_{n-1} - 2 * a_n
�����B
b_n = (��2 - 1)^(n-1) �Ƃ���ƁA
b_1 = 1 = a_1
b_2 = ��2 - 1 = a_2
�ł���A
n �� 2 �̂Ƃ��A
b_{n+1} = (��2 - 1)^n = (��2 - 1)^2 * (��2 - 1)^(n-2) = (3 - 2 * ��2) * (��2 - 1)^(n-2)
= [1 - 2 * (��2 - 1)] * (��2 - 1)^(n-2) = (��2 - 1)^(n-2) - 2 * (��2 - 1)^(n-1) = b_{n-1} - 2 * b_n
�ł��邩��A���w�I�A�[�@�ɂ��A
n �� 2 �̂Ƃ��A
a_n = b_n = (��2 - 1)^(n-1)
�ł���B �ȉ~S��AB�a�i���a�j�ACD��Z�a�i���a�j�Ƃ��A���̎�����K�ł���B
AB�a�Ƃ���~�̎�����L�ACD�a�Ƃ���~�̎�����M�Ƃ���Ƃ��A�ȉ���2�����̑召���r����B
K,(L+M)/2 �C�ӂ̗����̂�S�ĈقȂ�傫���̗����̂ŕ����邱�Ƃ�
�\���ˁH(�L��֥`) �����W��������=0�̕�������z��n�d���Ȃ炻�̋��f����n�d���ɂȂ肻���Ȃ�ł������܂������܂��� ���ݕϐ��Ƃ͂ǂ��������̂������̂ł��傤���B
�ϑ��ϐ��ɊW���鉽�炩�̕ϐ��Ƃ������߂ő��v�ł��傤���B �����W�������� f(x) �ɂ���
�@f(x) = (x-��)^n�g(x)
�Ȃ��
�@f(x) = (x-��~)^n�g(x)~
Im(��)��0 �Ȃ�
�@f(x) = {(x-��)(x-��~)}^n �Eh(x),�@�@�@�@�@h�͎��W��
X,Y�������̂Ƃ�
�@X+iY=0�@�́@X=Y=0�@�́@X-iY=0 >>542
�@�s�\�ł��B
(Luzin�̖���3������)
�E�Q�l����
���Z�~�����u���w�̖��v��Q�W�A���{�]�_�ЁAp.185 (1978)
�@�t�^�|10�@�����̂̂��镪���ɂ��� �ʃX���ł����X������ł���
�r��Ă����������̂ł�����ł����₳���Ē����܂�
�ΐ��������̖��ɂ��ĂŁA����ł�
log_{3}(x)�{log_{3}(x-8)=2��ό`����log_{3}(x(x-8))=2
x(x-8)=3^2
(x�{1)(x-9)=0
�ƂȂ��Ă���̂ł���
log_{3}((x)(x-8))-2log_{3}(3)=0
[log_{3}((x)(x-8))]�^[2log_{3}(3)]=0
(x(x-8))/(3^2)=�O
�ƂȂ�Ȃ��̂ł��傤���H �Ȃ�Ȃ�����
x=0�Ő��藧�킯���Ȃ� �������Ȃ�
log_{3}(x(x-8))-2log_{3}(3)=0
log_{3}(x(x-8))-log_{3}(3^2)=0
log_{3}(�ix(x-8)�j/(3^2))=0
(x(x-8))/(3^2)=1
�ƂȂ��H >>550
�����Ȃ�ق�
�����o���܂������肪�Ƃ��������܂� >>541
AB = 2a,
CD = 2b,
a �� b > 0,
�Ƃ�����
�@K = 4a��[0,��/2] ��{1 -(k�sin��)^2}d�� = 4a E(k), k=��(1-bb/aa),
�@L = 2��a,
�@M = 2��b,
�@K �� ��(a+b) = (L+M)/2. >>552
�k���l
0<k<1 �̂Ƃ�
�@��{1 - (k�sin��)^2} �� (cos��)^2 + (sin��)^2���(1-kk),
(����)
�}�N���[��������
�@��(1-X) = 1 - (1/2)X - (1/8)X^2 - (1/16)X^3 - (5/128)X^4 - (7/256)X^5 - ����
���
��{1 - (k�sin��)^2}
= 1 - (1/2)(k�sin��)^2 - (1/8)(k�sin��)^4 - (1/16)(k�sin��)^6 - (5/128)(k�sin��)^8 - ����
�� (cos��)^2 + (sin��)^2�{1 - (1/2)k^2 -(1/8)k^4 -(1/16)k^6 -(5/128)k^8 - ���� }
= (cos��)^2 + (sin��)^2���(1-kk),�@�@�@(�I)
������
K = 4a��[0,��/2] ��{1 - (k�sin��)^2} d��
�@�� 4a��[0,��/2] {(cos��)^2 + (sin��)^2���(1-kk)} d��
�@= ��a{1 + ��(1-kk)}
�@= ��(a+b)
�@= (L+M)/2, (�ʏ�)
�@1 - (k�sin��)^2 - {(cos��)^2 + (sin��)^2���(1-kk)}^2
�@= (sin�ӥcos��)^2 {(1 - kk/2) - ��(1-kk)}
�@= (sin�ӥcos��)^2 (kk/2)^2 / {(1 - kk/2) + ��(1-kk)}
�@�� 0, (�ʏ�)
�@kk = L(2-L)�@�Ƃ����B
�@L = 1 - ��(1-kk) �� 0,
�@1^2 - (ks)^2 = 1^2 - L(2-L)s^2 = (1-Lss)^2 + (1-ss)(Ls)^2,
�@s = sin��, 10,11,12,13,14,15,16,17,20,22,24,31,100,121,10000,1111111111111111
16������Ȃ鐔��̒�`�́H �k���l
0<k<1 �̂Ƃ�
(1)�@��{1 - (k�sin��)^2} + ��{1 -(k�cos��)^2} �� 2��(1 - kk/2),
(2)�@E(k) �� (��/2)��(1 - kk/2), 0<x<��/2��
��((a cos x)^2+(b sin x)^2)+��((b cos x)^2+(a sin x)^2)��a+b
�������̂��g >>511
>>512
�����番���������܂��ʂ��c�c �@y = ��x�@�͏�ɓʂ�����Jensen��
��{(a cos x)^2 + (b sin x))^2} �� a(cos x)^2 + b(sin x)^2,
��{(b cos x)^2 + (a sin x)^2} �� b(cos x)^2 + a(sin x)^2,
�ӁX�����B
>>554 �����l >>538 �͊ɂ������ł�����B
(1+z)e^(-z) -1 = -zz + (1+z)g(z)
�@= -zz + (1+z)��[k=2,��] (1/k!)(-z)^k
�@= -��[k=2,��] {1/(k-1)! - 1/k!}(-z)^k,
(����) �� ��[k=2,��] {1/(k-1)! - 1/k!}|z|^k
�@�� |z|^2�E��[k=2,��] {1/(k-1)! - 1/k!}�@�@�@(|z|��1)
�@= |z|^2,
���������� z=-1 �̂Ƃ��B >>511
�����������ɂ����x��0�ߖT���������v�V�b�c�A������
f�͘A����������0�ߖT�ŗL�E
���킹��Ώ����l���ƂɗB���
�����ϕ��������ɖ߂�������Ȃ��H 0<a<b<c�Ƃ���B
BC=a,CA=b,AB=c�́�ABC�̂���ӂ̏�ɓ_P���Ƃ�A�c��̓�ӂɂ���P�̑Ώ̓_Q,R���Ƃ�B
�i1�jPQ+PR���ő�ƂȂ�Ƃ��AP�͂ǂ̕ӏ�́A�ǂ̈ʒu�ɂ��邩�B
�i2�jPQ+QR���ő�ƂȂ�Ƃ��AP�͂ǂ̕ӏ�́A�ǂ̈ʒu�ɂ��邩�B �P�O�i�@�����P�Q�i�@�ɂ��������|���Z����Z�Ńp�^�[�����ȒP�ɂȂ�v�Z�������邩��
�֗��������̂ɁI���Ă����咣�͐������̂ł����H ���_�̖��Ŋ�{�Q���ʑ���Ԃ���Q�ւ̊֎�ƌ����Ƃ��[�����A�Ƃ�����肪������܂���
�����̓m�[�炵���̂ł����A��{�Q�̊Ԃ̌Q�����^�ňʑ���Ԃ̘A���ʑ�����U������Ȃ��悤�Ȃ��͉̂�������̂�
������������狳���Ă������� �O>>465
>>565
(1)AB��̒���
(2)AC���A��� >>567
algebraic topology ���łȂ��̂Ŏ��M�Ȃ�����m>n�̂Ƃ���
��_1(PR(m)), ��_1(PR(m))�͂Ƃ���Z/2Z�����ǘA���ʑ���������N�������͎̂����ȏ����^�������Ǝv���B >>563
(����) �� ��[k=2,��] {1/(k-1)! - 1/k!} |z|^k
�@= 1 - (1-|z|) exp(|z|)
�@�� 1 - (1-|z|) (1+|z|)
�@= |z|^2,
�i �}�N���[�����W���i�̐�Βl�j���P������������j >>569
���肪�Ƃ��������܂��A���ׂĂ݂܂� >>541
�@>>555�@>>559�@���
��{(LL+MM)/2} �� K �� (L+M)/2,
������
K = 4a E(k),
L = 2��a,
M = 2��b, >>573�Ⴄ�̂��H�@�������玩�������������Ă݂Ȃ�B���̂Ƃ��뉴�̈�l�������B�O>>568
�P�P]/�___________
�Q�Q/�_/,,���@�@�@)
�P�P�_/�c`-`Ђ��@/|
�P�P|�__U,~�܁R�^||__
���@| �a�P~U~U�a ||�@)
�Q�Q| �a�@���@�a |/ /|
_____`�a______�a�^_/ |
�P�P�P�P�P�P�P�P�P�a |
���@�@���@�@���@�@�a /
__________________�a/
�P�P�P�P�P�P�P�P�P�P >>566
���̘_���Ȃ�2�i�@�̕����ȒP���� �ȒP���ώG
�w��10�{������P�O�i�@�ɂȂ����͎̂c�O
�������l�ނ��U�{���P�Q�{�������琔�w���������������͂� ComplexExpand[(1+E^(I(1+n)Pi)+2n)/4]
��Pi�Ƃ͉��ł����H >>576�d���l�ԃx���A�x���A�x���̎w�͂������O�{�������Ǝv���܂��B�w�����E�̎�����킹�ĘZ�{�A�����Z�{�ŏ\��{�A�Z�i�@���\��i�@�������琔�w�����ӂ��������Ƃ����Ƃ����͎v���܂���B
�O>>574�Ƃ��Ƀx���́B���i�I�ɁB������������Ȃ����B�����זE���i���ɂł����Ȃ��Ȃ炠�邢�͐��w�����Ԃ������ē��ӂɂȂ�\���͂���܂����B
�P�P]/�___________
�Q�Q/�_/,,���@�@�@)
�P�P�_/�c`-`�_�� /|
�P�P|�__�Z~�܁R�^||__
���@| �a�P~U~U�a ||�@)
�Q�Q| �a�@���@�a |/ /|
_____`�a______�a�^_/ |
�P�P�P�P�P�P�P�P�P�a |
���@�@���@�@���@�@�a /
__________________�a/
�P�P�P�P�P�P�P�P�P�P n�������x�[�O���x��_n �ɑ��āA
E��R^2, (��_2)(E)=0 �� (��_3)(E�~[0,1])=0
�͐������ł����H
�������Ȃ�ؖ��������ĉ����� n�������s��A=(a_ij)��a_ii=1, |a_ij|<1/(n-1) (i��j)�̂Ƃ�A�������s��ł��邱�Ƃ�����
�ǂȂ��������Ă��������܂����������ʼn����܂��� R^3��̍����ϊ����Q���Ȃ����Ƃ��Ăǂ����������ł����H
�S�ː�����肭�������t���̑��݂������Ȃ��č����Ă��܂� ���s�ړ��A��]�A���f�̂����ǂꂪ�S�P�˂��Ǝv���Ȃ��H >>584
���o�ł͑S�P�˂��Ƃ킩��̂ł��������Ō`���I�ɏؖ����悤�Ƃ���Ə�肭�o���������Ă��܂�
�P�Ɏ����o���s���Ȃ����̘b�ł����c >>582
���� det(A)=0 �Ȃ��
���ȏ]���W: ��{j=1..n} cj a[ij] = 0
�����݂��܂�.
max{|c1|,...,|cn|} = |ck| �� 0 �Ƃ����,
1= | ck/ck a[kk] | = | ��{j��k} cj/ck a[kj] | �� ��{j��k} | a[kj] | < 1 (�� | cj/ck | �� 1 )
����(1 < 1)�������o���ꂽ�̂� det(A)��0 ���ؖ��ł��܂���. >>585
���s�ړ�x+v�Ȃ�x-v���t�̑���
��]�ƂȂ�-�Ƃ��t�̑���
���f�͎��Ő܂�Ԃ�������������������Ό��ɖ߂�=�������g���t
����ĕ��s�ړ��A��]�A���f�͑S�P��
�����̍����ł��鍇���ϊ����S�P�� �Ȃ�⍇���ϊ����āc�c
�����ω��� >>586
���肪�Ƃ��������܂��l���Ă݂܂� 2�~2�s��A=(a b �ɑ���|A|=��(a^2+b^2+c^2+d^2)��
c d)
����B
�܂��Af:R^2��R ��f(x)=|Ax|�Ƃ����Ƃ��Af�̏W��
{u��R^2 | |u|=1}�ł̍ő�l��||A||�Ƃ���B
(1)2���P�ʍs��I(�啶����i)�ɑ��� |I |��||I|| �����߂�B
(2)2�~2�s��A�ɑ��āA�����������邱�Ƃ������B
||A|| �� |A| �� ��2 �~ ||A||
���ɕ�����ɂ����L�q�ƂȂ��Ă��܂��Ă��܂�����낵�����肢���܂��B >>591
��`���
���� x �ɂ��� |x|=1, |Ax|^2 = ||A||^2 �ł���.
�C�ӂ� y �ɂ��� |Ay|^2 �� ||A||^2 |y|^2 �ł���.
||A||^2
= ��{ij} (a_ij x_j )^2
= ��{ij} (a_ij)^2 (x_j)^2
�� ��{ij} (a_ij)^2 ��{k}(x_k)^2 = |A|^2 ( �� x_j^2 �� ��{k} (x_k)^2 = |x|^2 = 1)
= ��{ij} (a_ij y_j)^2 �@ ( y_j = 1 (j=1,..,n) �ƒu����)
�� ||A||^2 |y|^2
= n ||A||^2
�ȏ��� ||A|| �� |A| �� (��n ) ||A||. �Ƃ肠�����O���̒���
||A||^2
= ��{i} (��{j}a_ij x_j )^2
�� ��{i} ��{j}(a_ij)^2 ��{k}(x_k)^2 (�� �V�������c�s����)
= ��{ij} (a_ij)^2 = |A|^2 �㔼�̒���
|A|^2 = ��{i} ��{j} |a_ij||a_ij|
�� ��{i}��( ��{j} |a_ij|^2 )��( ��{j} |a_ij|^2 ) (�� �V�������c�s����)
�� ��{i} (��{j} |a_ij| )^2�@(�� ��( |v1|^2+ |v2|^2 + �c ) �� |v1| + |v2| + �c )
= ��{i} (��{j} a_ij y_j)^2�@ ( y_j = �}1 (j=1,..,n) �ƒu����)
�� ||A||^2 |y|^2
= n ||A||^2
����Ƃł���... 2�~2�s��Ȃ��犆�D���Ȃ��Ă��͋Z�ł�������� �����Ĉ�ʂ̎����̕����y�����B
a b c d �ň�x�ɂS���ϐ���ɂ���̌�����B ����Ƃł���
����Ƃł���
����Ƃł���
�ǂ̌����ق����̂��˂����������� �������������Ă����Ȃ�Ȃ�ʼn����Ă����Ȃ������̂� �����_���w�Ɏ��M�j�L
X->(Y->X)
(X->(Y->Z))->((X->Y)->(X->Z))
(~X->~Y)->(Y->X)
����3�̌�����
���_�K��mp���g����
((X->Y)->Y)->((Y->X)->X)
�̏ؖ��̂������������Ă������� �܂Ƃ��ȉ����Ȃ������̂ŁA������x���肢���܂��B
0<a<b<c�Ƃ���B
BC=a,CA=b,AB=c�́�ABC�̂���ӂ̏�ɓ_P���Ƃ�A�c��̓�ӂɂ���P�̑Ώ̓_Q,R���Ƃ�B
�i1�jPQ+PR���ő�ƂȂ�Ƃ��AP�͂ǂ̕ӏ�́A�ǂ̈ʒu�ɂ��邩�B
�i2�jPQ+QR���ő�ƂȂ�Ƃ��AP�͂ǂ̕ӏ�́A�ǂ̈ʒu�ɂ��邩�B >>591
A���s��ł��x�N�g���ł�
�@|A| = ��{tr(AA~)},�@�@������ A~ ��A�̓]�u
���ȁH >>591
���肪�Ƃ��������܂�
�NjL�Ȃ�ł���u��x�������ɂȂ��Ă܂�
u��x�̈Ⴂ�������Ă��������܂���ł��傤��
����(1)��|I|�͕���������ł���||I||�������ĂȂ��̂ł��Ђ��肢���܂� ���ƌv�Z���邾���A�͋ƂƂ��������w�E�����������Ă��܂����S������ȊȒP�Ȍ`�ɂȂ��Ă܂���
����������������������̂Ȃ狳���Ă���������ƍK���ł� ��̓I�ɂ�|Ax|��x=(x, y)�ƒu�����Ƃ��A��((ax+by)^2+(cx+dy)^2)�ƂȂ�Ǝv����ł�������̍ő�l��||A||�ƂȂ�Ƃ��������ł����Ă��܂��ł��傤���H >>604
A �� Lxn �s��AB �� nxm �s��Ƃ���B
A~A �� BB~ �� nxn�s��iGrammian �s��j��
|AB|^2 = tr{(AB) (B~A~)}
�@= tr{(A~A) (BB~)}
�@= ��[i=1,n] [j=1,n] (A~A)ij (BB~)ji
������
�@(A~A)ij �� {(A~A)ii + (A~A)jj} /2,
�@(BB~)ji �� {(BB~)ii + (BB~)jj} /2,
���
|AB|^2 �� n ��[i=1,n] (A~A)ii ��[j=1,n] (BB~)jj
�@= n tr(A~A) tr(BB~)
�@= n(|A||B|)^2,
|AB| �� (��n)|A||B|, >>608
A�AB�AC�����݂��ɂ��ꂼ�ꂪ�ρA�a�A�������ꂽ�Ƃ������Ƃ��������Ă��Ȃ��Ƃ킩��킯�Ȃ��Ǝv���̂����A
����͖��ɂȂ��Ă���ȏ㕷������Ă���Ɣ��f������Ă̂����̂����Ȃ̂��ȁH 2��9
���̓��̑̑��Ƀs�b�^�������� >>608
1��6��3��4���\�\�c�c�B
�a���������L�a �� �a
�i(^o`��^))��a�@�@�a
�i�������܁j�a�@�@�a
�a��UU�҃ҁ߁a�Q�Q�a
�P�P�P�P�P�P�P�P�P�P�܂��킩���Ȃ��B�O>>578C�N���Ȃ�ł킩���̂����킩���ȁB��������ꂽ�猈�܂��Ȃ��́BC�N������邢���Đݒ肩�H >>608�킩�����B3��4���B
�a���������L�a �� �a
�i(^o`^o^))��a�@�@�a
�i�������܁j�a�@�@�a
�a��UU�҃ҁ߁a�Q�Q�a
�P�P�P�P�P�P�P�P�P�P
�O>>612C�N���Ȃ�ł킩���̂����킩�����B2��3�ł�3��4�ł�����1�����炾�B >>447
���̗Ⴞ�Ə��ʑ��ɂȂ��ĂȂ��ƌ���ꂽ��ł����ǂ��������ƂȂ�ł��傤��
���R�Ȏˉe�����ʑ��ƌĂԂ̂ł͂Ȃ�������ł��傤�� �y�Ռ��z�q�J�L���̔N���E������\�I�I�L��������15���~�����I�H
https://nicotubers.com/yutuber/hikakin-nensyu-gessyu/
HIKAKIN(�q�J�L��)�̔N����14���~�I�H�g�b�vYouTuber�ɂȂ�܂ł̓��̂�́H
https://youtuberhyouron.com/hikakinnensyu/
�q�J�L���̌����͂P���~�I�ǐO�p�Ń_�E���^�E���Ȃ��̍��E�����I
https://mitarashi-highland.com/blog/fun/hikakin
�Ȃ����ςĂ��܂��I�I�T�o�C�o���nyoutuber�܂Ƃ�
http://tokyohitori.hatenablog.com/entry/2016/10/01/102830
����PewDiePie�����ɁA���SYouTuber�����Ɂu�����v�u�`�����l���o�^�Ґ��v�𑝂₷�R�c�����J�I
http://naototube.com/2017/08/14/for-new-youtubers/
27�ŔN��8���~�@�������[�`���[�o�[�u�����[�E�V���v�̐�����
https://headlines.yahoo.co.jp/article?a=20170802-00017174-forbes-bus_all
1�N�ʼn��\���~���҂����������[�`���[�o�[���E�����L���O�g�b�v10
https://gigazine.net/news/20151016-highest-paid-youtuber-2015/
��������̃��r���[�ŔN��12���~�I ���A�b���YouTuber��6�̒j�̎q
https://www.businessinsider.jp/post-108355
�ޏ��͂����ɂ���750���l�̃t�@��������YouTube�X�^�[�ƂȂ����̂��H
https://www.businessinsider.jp/post-242
7��YouTuber��1�N��25���~�̎��� ��������r���[���悪�l�C
http://mogumogunews.com/2018/12/topic_24722/
���E�ōł��҂����[�`���[�o�[�A2�A�e�̎�ʂ͔N��17���~
https://forbesjapan.com/articles/detail/14474
�q�J���̎���������80���A����2400���A�N��3���Ɣ���www
https://matomenewsxx.com/hikaru-income-8181.html
�͂��߂��Ⴟ��[�̔N����6���H2017�N��30���˔j���H
https://2xmlabs.com/archives/1873 >>614
�Ȃ��ĂȂ����Č������{�l�Ɍ�����A�ǂ��������Ƃł��傤�����Ă� >>608
�����́@
�uB�N�AC�N�w�ڂ��������킩��Ȃ��B�x�v
�͕s�K���B
�u�������v�ƌ������t���g���Ă��邪�A����ł́AB�N��C�N���킩��Ȃ����Ƃ��A
C�N��B�N���킩��Ȃ����Ƃ�m���Ă���Ɠǂݎ���B����ł́A���Ƃ��Ă��������B
�Ⴆ�A
�u�搶��B�N�AC�N�ɁA�w�N�����͂킩���������H�x�Ɛq�˂���A��l�����Ɂw�������x�Ɠ������v
���ƏC������悢�B B�N��C�N�͕t�������Ă�ƍl�����
�����s�v�c�͂Ȃ�
��͓˂������Ă� �S�j���S�j���c�c
~�����@�������
(�@(`)(-_-))�����Ȃ�
(����)(�`��)�@ �\�\
��P�P�P�P�P�P]
�A�N�A�ς�12����
�O>>619 ��12�Řa��7�Ȃ�3�A4���ĕ����邩��B�N�̎��_�ŕ�����Ⴄ�H �uB�N�A�b�͂ق��ł��Ȃ��B���͂ȁA�a��7�Ȃ�v
~�����@�����ց[
((-_-)(~e~))�����Ȃ��
(����)(�`��) �\�\
��P�P�P�P�P�P]
B�N�̐S�̐�����ꂾ������킩��ւ�Ȃ���O>>620 ~�����I�@�O>>622����
((-.-)�@C�N�\�\(`)�@)
[�P]_)�@����1�� U��U�
�P�P]/�____�����m(��)
�Q�Q/�_/,,(`.`))���,|
�P�P�_/�c`-`Ѓ�`�҃�|
�P�P|�__U��U�___�^| |
���@| �a~U~U~�P�a | /
�Q�Q| �a �� �� �a |/
_____`�a_______�a�^
�P�P�P�P�P�P�P�P
C�N�̐S�̐��u1���I�@���Ⴀ�킩�����B3��4���B�ς�6��8��12�ŁA�a��7�����Ȃ����Ă킩�������ǁA����(1,6)��5��(3,4)��1���ǂ������킩��������v f(n) = ��[k=1 to n] k!
���������ɂȂ鎩�R��n��2���߂�B
�����f(n)���������ɂȂ�n�͂����݂̂ł��邱�Ƃ������B �O>>623�ς�A�N���m�����i�K�ł́AB�N��C�N�͂܂��ς�3�ʂ肠��Ǝv���Ă�BB�N�͘a������Ă��킩��Ȃ������ʂ肠��7�����Ȃ��B����Ƃ��\�\
~�����@>>621B�N��A�N��
(`_`))�@�f�L�Ă��āH
[�P]_) �n�[�g��ǂ�
�P�P]/�____________�H
�Q�Q/�_/,,,, �@�@�@)
�P�P�_/�c`o`Ё@�@ /|
�P�P|�__U��U�___�^||
���@| �a~U~U~�P�a ||
�Q�Q| �a �� �� �a |/
_____`�a_______�a�^
�P�P�P�P�P�P�P�P >>624
n=1�̎���1�An=3�̎���9�݂̂��������B
n��4�ȏ�̎��A��_[k=1,n]k! �� ��_[k=1,4]k! �� 3 (mod5) �ŕ�����]�ɂȂ�Ȃ��B ���͂��o���Ȃ������̂�
�摜���玸�炵�܂��A
���̖��̉������J��
�����Ē�����Ώ�����܂�
https://i.imgur.com/bY2iMrW.jpg >>627
��ʂ� 0<A, 0<B �̎��AA+B = (��A - ��B)^2 + 2��(AB) �� 2��(AB)
�܂� ��A = ��B �̂Ƃ��A A+B �͍ŏ��l 2��(AB) �ƂȂ�܂�.
f(a)= (��a - 3/��a)^2 + 6
a=3 �̂Ƃ��A�ŏ��l 6 �ƂȂ�܂�.
g(a,b) = ab + 4/(ab) + 5 = (��(ab) - 2/��(ab))^2 + 9
ab=2 �̂Ƃ��A �ŏ��l 9 �ƂȂ�܂�. >>627
�Ȃ����Ȃ��ɒ��J�ɂ��Ȃ��Ă͂����Ȃ��̂ł����H
���������ł����肪�����Ǝv���Ȃ��̂ł����H �����͕�����Ȃ����������X���ł��B
���肢���Ƃ�����X���ł�������Ȃ����ɓ����Ă��炦��X���ł�����܂���B �~���̋Ȗʂɓ_�����������āA���̓_�����ׂĊ܂ލŏ��̖ʂ���肽����ł����A�ǂ̂悤�ɂ���Ύ���ł��傤���B
�_��X���W�AY���W�͂��łɂ킩���Ă��܂��B
�c�͊ȒP�Ɉ�ԏ�ƈ�ԉ����킩���ł����A�����킩��܂���B
��ԓ_�Ɠ_������Ă���ꏊ��T���āA���̓_�����[�ɂȂ�Ƃ����l���ł�����ł��傤���H �ʂƂ������t���ǂ������Ӗ��Ŏg���Ă���̂� ��p�����ۂ߂č�����~���̋Ȗʂ�蔲���Ē����`�̉�p������肽���Ƃ����Γ`���ł��傤���H �Ӗ����킩��Ȃ�����
�n���ȓ��ŋȉ����ďȗ͂��Đ����s���ɂ���� �����`����Ȃ��ŏ����猾���̂����̔n���� ���t���炸�������悤�ŁA���݂܂���B ���̓_�����ۂɂǂ��ɂ���̂��ɂ���Ȃ����H
�~���̑��ʕ���������Ƃ���ɓ_������Ȃ�~���̑��ʂ�W�J���ďo���钷���`���Ă��ƂɂȂ邾�낤
���ʂ̂ǂ����������ɐ��ēW�J���āA������p�ӂ��Čq���čl����Ƃ����Ȃ��H
���̂Ȃ̂�X���W��Y���W�����Ȃ��̂��ǂ������z������Ă���̂��悭�킩��Ȃ����A�����l�Ƀ��A���Œ��ڕ���������������łȂ����H �~�������ɗׂ荇���_�̊Ԋu���ł��L���Ƃ�����c���悤�ɐ����
���ꂪ�ŏ�����ˁH �O>>625
>>627
(�^��)^2=(a+9/a)^2
=a^2+2a(9/a)+9^2/a^2
��a^2+2a(9/a)+(9/a)^2
=a^2+18+(9/a)^2
a=3�̂Ƃ�
(�^��)=��(9+18+9)=6 �O>>642
>>633�g�C���b�g�y�[�p�[�̐c�͂ǂ��ł����H
���M���̐c�ł������ł����A���̏ꍇ�͂�قǂ悭���n�����K�v�ƂȂ�܂��B�h�ƃJ���������菄�炳�ꂽ�����A��قǗp������Ƃ��������Ă悭���n�����͓̂��ł͂���܂���B >>644
�E3�łP�s�� ��������
1/R �� R^{n-1} /2 �܂� 2 �� R^n �̎��A
|1/R + R^{n-1} e^{in��} |
�� | R^{n-1} e^{in��} | - | 1/R |
�� R^{n-1} /2
�� 1 / |1/R + R^{n-1} e^{in��} | �� 2/R^{n-1}
�E�����v�Z�͂����ƊȒP��
f(x) = 1/g(x) �̌`�� x=�� �� g(x) ��1�ʂ̗�_�Ƃ���. g(��)=0
Res(f, ��) = lim{x����} (x-��)/g(x) = lim{x����} (x-��)/ ( g(x) - g(��) ) = 1/g'(��)
�E�����p�Ȃ�ϕ��H�̐}��Y����Ɨǂ�����
�}��������Ύ��͂��ꁫ���炢�ł��`���(���Ԃ�)
�� = (-1)^{1/n} = e^{i��/n}
(1-��^2) I = 2��i Res(f,��) = 2��i/( n��^{n-1}) = 2��i(- ��/n)
�� I = 2��i/(��-��^{-1}) = ��/( n sin(��/n) )
 �P�`13�܂ł̐������P�������ꂽ13���̃J�[�h������܂��B
�P�`13�܂ł̐������P�������ꂽ13���̃J�[�h������܂��B
���܁A�搶�����̒�����Q�����Ђ��āA���̂Q�̐����ɂ��āA�`�N�ɂ͐ς��A�a�N�ɂ͘a���A�b�N�ɂ͍��������܂����B�R�l�͐搶���Ђ����Q���̃J�[�h�̐����Ă悤�Ƃ��āA���̂悤�ɏ��ɉ�b���Ă��܂��B
�`�N�u�킩��Ȃ��ȁB�v
�a�N�u�ڂ����킩��Ȃ���B�v
�b�N�u���[��A����ς�킩��Ȃ��Ȃ��B�v
�`�N�u�܂��킩��Ȃ��B�v
�a�N�A�b�N�u�ڂ��������킩��Ȃ��B�v
�搶���Ђ����Q���̃J�[�h�̐������Q�Ƃ������Ȃ����B �C�ӂ̎��R��n�ɑ��āAn³�|1�͕������ɂȂ�Ȃ����� >>648
n^3-1=(n-1)(n^2+n+1)
�������ɂȂ�Ƃ�
n-1=n^2+n+1
n^2=2
���Ȃ�Ȃ� >>649
36=2^2*3^2�͕�����������2��3�ł���
ab����������a=b�͐��藧���܂��� >>647
���ڂ�A�N�̃R�����g�̌�A���́@(2,9)�A(3,6)�A(3,10)�A(5,6)�@�̎l�ʂ�B
�a��9�ł�������B�N��(3,6)�Ɠ����邵�A13�ł�������(3,10)�Ɠ�����B
�킩��Ȃ��Ɠ������̂́A�a��11�ŁA(2,9)��(5,6)���@��������ƌ������ƁB
���l�ɁA����1�ł�������C�N��(5,6)�Ɠ����邵�A3�ł�������(3,6)�Ɠ�����B
�킩��Ȃ��Ɠ������̂́A����7�ŁA(2,9)��(3,10)���@��������ƌ������ƁB
���̂悤�ɁA���҂��w�Ɨ��Ɂx�킩��Ȃ��Ɠ������Ƃ��āA���҂̋��ʉ�(2,9)��
�搶���I��̃J�[�h�ɏ����ꂽ�����ƍl������B
�O����w�E�������AA�N�̓��ڂ̃R�����g�̌�́A
�u�a�N�A�b�N�u�ڂ��������킩��Ȃ��B�v �v
�́A���Ƃ��ĕs�K���B���̕\���ł́AB�N�AC�N�����݂��A������킩��Ȃ��Ɠ����邱�Ƃ�
�m���Ă��邩�̂悤�ȕ\���B���ۂ́AB�NYes/No�AC�NYes/No�@�̑g�ݍ��킹4�ʂ�̉\��������B
4�p�^�[���ǂ�ł��A���Ƃ��č�蓾��B
���ɁAA�N�AB�N�AC�N�AA�N�@�̃R�����g�̌�A�ǂ̂悤�Ɍ�₪�c���Ă����������v���O���������B
http://codepad.org/GO74afNo >>648
����C�ɂȂ邩��N�������� >>648
n^3 - 1 = m^2 (m,n:����) �Ƃ���
n^3 = (m+i)(m-i)
Z[i]�͑f�����𐮈�ł��邩��Am+i = (a+bi)^3 (a,b:����) �ƂȂ�
���ӂ̋������r����� 1 = b(3a^2 - b^2) �ł��邩��Aa=0, b=-1
����āAn^3 - 1 = m^2 �ƂȂ鐮��m,n��m=0, n=1�̂� R^n�ɖ��ߍ��܂ꂽk�������l��M�́AM�̓_x�̋ߖT�ł́AR^k�̊J�����W������R^(n-k)�ւ̊��炩�Ȏʑ��̃O���t�Ɠ��ꎋ�ł��܂����H �O>>651
A�N���搶����ς��ĂȂɂ�����Ă��邩�A�����B�N���搶���璮�����a�AC�N���搶���璮�����������ꂼ��ςŏꍇ��������ƁA
��6(1,6)�(2,3)�a7�5��5�1
��8(1,8)�(2,4)�a9�6��7�2
��10(1,10)�(2,5)�a11�7��9�3
��12(1,12)�(2,6)�(3,4)�a13�8�7��11�4�1
��18(2,9)�(3,6)�a11�9��7�3
��20(2,10)�(4,5)�a12�9��8�1
��24(2,12)�(3,8)�(4,6)�a14�11�10��10�5�2
��30(3,10)�(5,6)�a13�11��7�1
��36(3,12)�(4,9)�a15�13��9�5
��40(4,10)�(5,8)�a14�13��6�3
��48(4,12)�(6,8)�a16�14��8�2
��60(5,12)�(6,10)�a17�16��7�4
��72(6,12)�(8,9)�a18�17��6�1
A�N�͐搶�����L13�ʂ�̂����ǂ̐ς������Ă������Ă������AB�N�͂��̌��ʂɂ��搶����a�ɂ���7�9�11�13�14�16�17�̂����ꂩ������ꂽ�Ƃ킩��B��a���������������Ȃ��g�ݍ��킹�������Ă�����AB�N��2�̐�������ł��邩��
���l�ɖ����Ă���B�N������C�N�͍��ɂ��Đ搶����1�3�5�7�̂����ꂩ������ꂽ�͂��ŁA
����1�Ȃ�(3,4)�(5,6)�
����3�Ȃ�(2,5)�(3,6)�(5,8)�
����5�Ȃ�(1,6)�(3,8)�
����7�Ȃ�(2,9)�(3,10)�����܂��킩��Ȃ��B
������A�N�́A
�ς�搶����18�ƌ����Ă���(2,9)�(3,6)�Ŗ����Ă�B
�ς�搶����30�ƌ����Ă���(3,10)�(5,6)�Ŗ����Ă�B
�������a��9��B�N���搶����a��9�����Č����Ă���AB�N��(3,6)����!!�@���ē��肷��͂��Ȃ�ŁA
�a��11�ŁA2�̐��́A
(2,9)�(5,6)�̂ǂ��炩���Ɛ��肵���͂��B
����������1��C�N���搶���獷��1�����Č����Ă���AC�N��(5,6)����!!�@���ē��肷��͂��Ȃ�ŁA
�a��7�ŁA2�̐��́A
(����)2,9
�����������ƁH �O>>656�����B
A�N���搶����ς��ĂȂɂ�����Ă��邩�A�����B�N���搶���璮�����a�AC�N���搶���璮�����������ꂼ��ςŏꍇ��������ƁA
��6(1,6)�(2,3)�a7�5��5�1
��8(1,8)�(2,4)�a9�6��7�2
��10(1,10)�(2,5)�a11�7��9�3
��12(1,12)�(2,6)�(3,4)�a13�8�7��11�4�1
��18(2,9)�(3,6)�a11�9��7�3
��20(2,10)�(4,5)�a12�9��8�1
��24(2,12)�(3,8)�(4,6)�a14�11�10��10�5�2
��30(3,10)�(5,6)�a13�11��7�1
��36(3,12)�(4,9)�a15�13��9�5
��40(4,10)�(5,8)�a14�13��6�3
��48(4,12)�(6,8)�a16�14��8�2
��60(5,12)�(6,10)�a17�16��7�4
��72(6,12)�(8,9)�a18�17��6�1
A�N�͐搶�����L13�ʂ�̂����ǂ̐ς������Ă������Ă������AB�N�͂��̌��ʂɂ��搶����a�ɂ���7�9�11�13�14�16�17�̂����ꂩ������ꂽ�Ƃ킩��B��a���������������Ȃ��g�ݍ��킹�������Ă�����AB�N��2�̐�������ł��邩��
���l�ɖ����Ă���B�N������C�N�͍��ɂ��Đ搶����1�3�5�7�̂����ꂩ������ꂽ�͂��ŁA
����1�Ȃ�(3,4)�(5,6)�
����3�Ȃ�(2,5)�(3,6)�(5,8)�
����5�Ȃ�(1,6)�(3,8)�
����7�Ȃ�(2,9)�(3,10)�����܂��킩��Ȃ��B
������A�N�́A
�ς�搶����18�ƌ����Ă���(2,9)�(3,6)�Ŗ����Ă�B
�ς�搶����30�ƌ����Ă���(3,10)�(5,6)�Ŗ����Ă�B
�������a��9��B�N���搶����a��9�����Č����Ă���AB�N��(3,6)����!!�@���ē��肷��͂��Ȃ�ŁA
�a��11�ŁA2�̐��́A
(2,9)�(5,6)�̂ǂ��炩���Ɛ��肵���͂��B
����������1��C�N���搶���獷��1�����Č����Ă���AC�N��(5,6)����!!�@���ē��肷��͂��Ȃ�ŁA
����7�ŁA2�̐��́A
(����)2,9 0<a<b<c<a+b�Ƃ���B
BC=a,CA=b,AB=c�́�ABC��1�̕ӂ�I�сA���̏�ɓ_P���Ƃ�B
�c���2�ӂɂ��ẮAP�̑Ώ̓_Q,R���Ƃ�B
�i1�jPQ+PR���ő�ƂȂ�Ƃ��AP�͂ǂ̕ӏ�́A�ǂ̈ʒu�ɂ��邩�B
�i2�jPQ+QR���ő�ƂȂ�Ƃ��AP�͂ǂ̕ӏ�́A�ǂ̈ʒu�ɂ��邩�B f(n)=(n^2+1)(2n^2+k)
�Ƃ���B���̐����������R��k�͖����ɑ��݂��邱�Ƃ������B
�u�C�ӂ̎��R��n�ɑ��āAf(n)�͕������ɂȂ�Ȃ��v >>647��蕶��������ׂ�
�`�N�u�搶��1�`13�܂ł̐����̂����A�قȂ�2����I�Ƃ����B�ڂ��͐搶���炻��2���̐ς������ǁA���̐ς��炾������2�����ǂ�Ƃǂ�Ȃ̂�����ł��Ȃ��v
�a�N�u�ڂ��͐搶���炻��2���̘a�����B�`�N������ł��Ȃ����Ƃ��l�����킹�Ă��A�ڂ��ɂ����肪�ł��Ȃ��v
�b�N�u�ڂ��͐搶���炻��2���̍������B�`�N�Ƃa�N������ł��Ȃ����Ƃ��l�����킹�Ă��A�ڂ��ɂ����肪�ł��Ȃ��v
�`�N�u�a�N�Ƃb�N���܂�����ł��Ȃ����Ƃ��l�����킹�Ă��A�ڂ��ɂ�����ł��Ȃ��v
�a�N�A�b�N�u�`�N���܂�����ł��Ȃ����Ƃ��l�����킹�Ă��A�ڂ��ɂ�����ł��Ȃ��v(�����ɔ���)
�����܂ŁA�`�N�a�N�b�N�͂��ꂼ��搶���畷�����������̂��̂��݂��ɋ��������Ă��Ȃ��B
�����̏������搶���I��2�����Ȃ��� >>662
�uA�NB�NC�N�͘_���I�v�l�͂�L���Ă���A���ɐ����̑g�ݍ��킹�����ł���ł���Ίm���ɓ���ł�����̂Ƃ���B
����ɁA�ނ�݂͌��ɑ��肪���̔\�͂�L���Ă��邱�Ƃ𗝉����Ă���A�N�����u����ł��Ȃ��v�Ɠ��������́A�u���̎��_�ł͘_���I�ɍl���ē���ł��Ȃ��ł���v�Ƃ����O��ōl������̂Ƃ���B�v
���lj��� �ߏ萔�����̐����g�������̑��a�����̐����傫����
�����R���̂����ߏ萔����߂銄���� 0.2474 ���� 0.2480 �̊Ԃł���Əؖ�����Ă���B
�ߏ萔����1/4
�s��������3/4
�ł��邱�Ƃ̒萫�I�ȁu�����v���ĉ\�H �Ȑ�y=e^x���x���W�����ꂼ��x=a,x=b�ƂȂ�2�_A,B������B������0<a<b�ł���B���̂Ƃ�����AB�ƕ��s�ƂȂ�Ȑ��̐ڐ��̐ړ_��x���W��c�Ƃ���ƁA(a+b)/2<c�ƂȂ邱�Ƃ��ؖ����� >>665
f(x) = e^x , f�f(x) = e^x
f�f( (a+ b)/2 )
= e^{(a+ b)/2} < ( e^a + e^b )/2 �@ ( �� y=f(x) �͉��ɓʂȃO���t)
= f�f(c)
(a+ b)/2 < c ( �� f�f(x) �͒P�������� ) >>666
( e^a + e^b )/2= f�f(c)�ƂȂ�̂͂Ȃ��ł����H �O�������� f(c) = e^c = f�f(c) = (e^b - e^a) /(b-a)
e^{(a+b)/2 } < (e^b - e^a) /(b-a) �@�� ����������ɂ�...
(e^b - e^a) - (b-a) e^{(a+b)/2 }
= e^a ( e^{b-a} - 1 - (b-a) e^{(b-a)/2 )
= e^a g(b-a) �@( g(x) := e^x - 1 - x e^{x/2} �ƒu����)
x �� 0 �̂Ƃ� g(x) �� 0 �������Ηǂ�.
g(0) = 0
g�f(x) = e^x -(1+ x/2) e^{x/2} = e^{x/2} (e^{x/2} -(1+ x/2) ) = e^{x/2} h(x)
h(x) := e^{x/2} -(1+ x/2) �ƒu����.
h(0) = 0 , h�f(x) = (1/2)( e^{x/2} - 1 ) �� 0,�@h(x)���O
����� g(x) �� 0
e^{(a+b)/2 } < (e^b - e^a) /(b-a) �������ꂽ.
e^x �̒P���������ɂ�� (�ȉ���) >>665
(e^b - e^a)/(b - a) = e^c���
c=log{(e^b - e^a)/(b - a)} > (a + b)/2
�� (e^b - e^a)/(b - a) > e^{(a + b)/2}
�� e^b - e^a > (b - a) e^{(a + b)/2} ����@ �������悢�B
��=(a + b)/2�Ƃ����B
(��, e^��)�ɂ�����y=e^x�̐ڐ���f(x)�Ƃ����B
(1) f(a) �� 0�̂Ƃ�
�@�̍���e^b - e^a��
x = a, x = b, y = 0, y = e^x�ň͂܂ꂽ�����̖ʐρB
�E�ӂ̓��R(b - a)�ƃ^�ee^{(a + b)/2}�̒����`�̖ʐς�
�����x = a, x = b, y = 0, y = f(x)�ň͂܂ꂽ��`(f(a)=0�̂Ƃ��͎O�p�`)�̖ʐ�S�ɓ������B
�]���āAy = e^x�̓ʐ����
�@�̍��� > S = (b - a) e^{(a + b)/2}
(2)
f(a) < 0 �̂Ƃ��́A
�� > 0 s.t. f(a) > -��
s = ��(b - a)�Ƃ����āA�i1)�Ɠ��l��
x = a, x = b, y = -��, y = e^x�ň͂܂ꂽ�����̖ʐς�
x = a, x = b, y = -��, y = f(x)�ň͂܂ꂽ��`�̖ʐς��r����
e^b - e^a + s > (b - a)[�� + e^{(a + b)/2}] = (b - a) e^{(a + b)/2} + s
���ӂ���s�������Ƈ@�����藧�B �O>>657
>>665
2�_A(a,e^a)�B(b,e^b)��ʂ钼��y=(e^b-e^a)(x-a)/(b-a)+e^a�́A
a��x��b�ɂ����āA
�˂�y=e^x��艺�ɂ���B����ċȐ�y=e^x��̌X��e^c=(e^b-e^a)/(b-a)�̐ڐ���^����ړ_C(c,e^c)�́AAB�̒��_M((a+b)/2,(e^a+e^b)/2)�̐^���ɂ���Ȑ�y=e^x��̓_P((a+b)/2,e^{(a+b)/2})�̉E��ɂ���B ��a+b/2��c YouTube�̂������ߓ����
��((11^4 + 100^4 + 111^4) / 2)
���v�Z����Ƃ������悪����܂��B
���掩�̂͌��Ă��܂��A�ȒP�Ȗ��ł��ˁB
(11^4 + 100^4 + 111^4) / 2)
=
((10 + 1)^4 + 10^8 + (10^2 + 10 + 1)^4) / 2
=
(1 + 2 * 10 + 2 * 10^2 + 10^3 + 10^4)^2
�Ȃ̂�
��((11^4 + 100^4 + 111^4) / 2) = 1 + 2 * 10 + 2 * 10^2 + 10^3 + 10^4
�ł��B >>665
�ȉ��A�f���Ȃ����B���B
((a + b)/2, e^{(a + b)/2})�ɂ�����f(x)=e^x�̐ڐ���g(x),
d(x) = e^x - g(x)�Ƃ�����f'(x)=e^x�͒P�������Ȃ̂�
d(a) < d(b)
���ꂩ��
e^{(a + b)/2} < (e^b - e^a)/(b - a)
�����藧�B �O>>671�⑫�B
y=e^x�̃O���t�́A
y'=e^x�ł���A�X����x�̑����ɔ����ĒP�������ł��邽�߁A���ɓʂł���B >>665 ����
�ȉ��A�f���Ȃ����B���B
((a + b)/2, e^{(a + b)/2})�ɂ�����f(x)=e^x�̐ڐ���g(x),
d(x) = e^x - g(x)�Ƃ�����f''(x)=e^x�͒P�������Ȃ̂�
d(a) < d(b)
���ꂩ��
e^{(a + b)/2} < (e^b - e^a)/(b - a)
�����藧�B >>675
���R���������P�����Ƃ������Ƃ� >>665�ł��A�F������肪�Ƃ��������܂��B
����Ŏv�����̂ł����A2�����Ɠ��l��x=a�ł̐ڐ���x=b�ɂ�����ڐ��Ƃ̌�_��x���W��c�ƂȂ�̂łȂ����H�ƌ����\�z���v�������̂ł����A����͔�����ł��傤���H
�������ؖ��ł����킯�ł͂Ȃ��̂ł����A������肪����ɂ��ĖʐςƂ����ɓʂƂ��̘b���~�b�N�X������Ƃ킩��₷���Ȃ�C�����܂��B
���A���̔\�͂ł͂��܂������܂���B >>648
�@n^3 - 1 = (n-1)(nn+n+1),
�@nn+n+1 = (n-1)^2 + 3(n-1) + 3,
���@gcd(n-1, nn+n+1) = 1 or 3.
�@gcd = 1 �̂Ƃ��@n^2 < nn+n+1 < (n+1)^2,�@nn+n+1 �͕������łȂ��B
�@gcd = 3 �̂Ƃ��@n-1 = 3q, nn+n+1 = 9q(q+1) +3, gcd(q, 3q(q+1)+1) = 1, q�͕������B
�@���āD�D�D�D ��}�o�Xhanica
�`���[�W���z��10�p�[�Z���g�̃v���~�A����
2000�~��2200�~�������āA220�~��Ԃ�1�����1980�~�c�����B
����1��̏�Ԃ̕��S�z
�J�[�h�g�p���z���v���~�A�����ɓ��B���ĂȂ�����220�~�ŏ�����ɉ߂��Ȃ��́H
����Ƃ��J�[�h�c�z�ɂ�����炸�A220��10/11=200��200�~�ł����́H
�ǂ����̗��������邩�ɂ���āA1�������9240�~�̌������������ς���Ă���� >>672
aa=A, bb=B, ab=C�@�Ƃ����B
��{(a^4 + b^4 + (a+b)^4)/2}
= ��{(AA + BB + (A+B+2C)^2)/2}
= ��{AA + BB + (AB + 2AC + 2BC + 2CC)}
= ��(AA + BB + CC + 2AB + 2AC + 2BC)�@�@�@�@(�� CC=AB)
= A + B + C, �O>>674
�_A�ɂ�����ڐ��́A
y=e^a(x-a)+e^a
�_B�ɂ�����ڐ��́A
y=e^b(x-b)+e^b
y���������A
x={(a-1)e^a-(b-1)e^b}/(e^a-e^b)
����A�_C�ɂ�����ڐ��̌X���́A
(e^b-e^a)/(b-a)
���ꂪe^[{(a-1)e^a-(b-1)e^b}/(e^a-e^b)]�ƈ�v���邩�ǂ����B
(e^b-e^a)/(b-a)=e^[{(a-1)e^a-(b-1)e^b}/(e^a-e^b)]�Ɖ��肷��ƁA
(e^b-e^a)=(b-a)e^[{(a-1)e^a-(b-1)e^b}/(e^a-e^b)]
�c�c >>679
hanica�̎c�����ǂ��l���邩�ɂ���Ȃ�����
2000�~��2200�~������������1���g�킸�Ɉꐶ���I����Ă��܂�����1��2000�~�ŏ�������ƂɂȂ�
�c�������傤�ǎg���邱�Ƃ�O��Ƃ���Ȃ�2000�~��220�~��Ԃ�10�����̂�1��200�~
�ł��A�ǂ̂悤�ɍl���Ă�����̕������ɂȂ�̂�I������47��ȏ���ꍇ����Ȃ��̂��ȁH�i220�~��Ԃ������Ȃ��Ƃ��āj
1����46����ꍇ
����F9240�~
hanica�̎c���͂����g����̂�1��200�~�ŏ���ƍl����ꍇ�F9200�~
hanica�Ɏc�����c�����g�����߂�9000�~�`���[�W����9900�~�i45��j���ƌ���220�~�F9220�~
�ƂȂ�̂ł�����̏ꍇ������̕�����
47��ڂ������̕������ɂȂ�
�������������ς���Ă�����Ă͈̂�̂ǂ������v�Z�������H Mathieu Moonshine ���ۂƂ͉����ˁH(�L��֥`) O�𒆐S�Ƃ��锼�a1�̉~C��ɈقȂ�2�_A,B������A��OAB=��(0<��≤��)�ł���B
A,B�ɂ��C�̎���2�̌ʂɕ�������邪�A���̈����K�A������L�Ƃ���B
K���_P���AL���_Q���A���ꂼ�ꎩ�R�ɓ����B
���̂Ƃ��APQ�̒��_�ƂȂ肤��_�S�̂���Ȃ�̈�́A1�ȏ�̑ȉ~�̘a�W���ł��邱�Ƃ������B
�������AP��Q�͂��ꂼ��K��L�̗��[�_�ɂ����B�ł��AP��Q�̈ʒu����v����ꍇ��P��PQ�̒��_�Ƃ���B �O>>681
>>683�ށ`�Ⴂ��`���`���ā`��`��`��́`���`���`�Ȃ�`���`�� �O>>685
>>684
0���Ɓ���/2�Ƃ��A
A(-1,0)�B(cos2��,sin2��)�Ƃ���ƁA
K���P��A(-1,0)�ƈ�v����Ƃ�Q��L���A����B�܂œ����ƁAPQ�̒��_�̋O�Ղ́AA��O��ʂ�ȉ~�B
���l��K���P��B(cos2��,sin��)�ƈ�v����Ƃ�Q��L���A����B�܂œ����ƁAPQ�̒��_�̋O�Ղ́AB��O��ʂ�ȉ~�B
����K���P��AB��̂ǂ̓_�ɂ����Ă�Q��L���A����B�܂œ����ƁAPQ�̒��_�̋O�Ղ́AP��O��ʂ�ȉ~�B
�ȉ~�̋O�Ղ̏W���̗̈�̋��E���܂��ȉ~�̈ꕔ�ł͂Ȃ����Ɨ\�z�����B >>686
�ǂމ��l�Ȃ�����Ăǂ������ ���������Ȃ����H
�̈�̋��E�͉~�ʂ��������\�荇�킹�����ɂȂ邪�A�̈悻�̂��̂͗L���̑ȉ~�̍����ɂ͂Ȃ��B >>687
�����œǂމ��l�̂���������Ȃ���
���؉\��������܂��� �_�̕Е����~�߂ē������Δ��a 0.5 �̉~�ʂɂȂ鎖�ɋC�Â��Ό�͊ȒP�ł�.
�ꉞ�A���E�l���l������ƌ������~�ʂ̏W�܂�ɂȂ�܂����A
�ŏI�I�ɂ͉~�̈��̍����ɂȂ�܂���.
 >>682���肪�Ƃ�
>>682���肪�Ƃ�
�uhanica�Ɏc�����c�����g�����߂�9000�~�`���[�W����9900�~�i45��j���ƌ���220�~�F9220�~�v
���̒[����220�~�J�[�h�����Ďc�z�]�点���Ƃ�����A
200�~�ŏ�����Ƃ݂Ȃ���9200�~�ƂȂ�̂��A220�~�ŏ�����Ƃ���9220�~�ɂȂ��Ă��܂��̂����m�肽���ł��B
�u�������������ς���Ă�����Ă͈̂�̂ǂ������v�Z�������H�v
3000�~3�Ƃ��������ʂ�ł����A2000�~4�ƂX�R�Q�O�~��23���ɂȂ�Ȃǃ`���[�W���z�̑g�ݍ��킹�ŕς��܂��B x,y�͎��R���ŁAx<y�ł���B
f(x,y)=(x+y){(1/x)+(1/y)}
�ɂ��āA�ȉ��̖�ɓ�����B
�i1�jx,y�����ʂ̑f���������Ƃ��Af(x,y)�������ƂȂ�g(x,y)��2�g���߂�B
����ɁAx��y���݂��ɑf�ł���Ƃ���B
�i2�jf(x,y)�������ƂȂ�g(x,y)�͑��݂��Ȃ����Ƃ������B
�i3�jg(x,y)=(x^2+y^2)f(x,y)�ɂ��Ă͂ǂ����B >>690
��ʂ�������x�������Ƃ���Ȍ`�ɂ͂Ȃ��B >>691
����Ȃ����ς�Ahanica�̎c�����ǂ̂悤�Ɉ������̖�肾����A������Ɍ��߂Ȃ��Ɠ����͏o�Ȃ� �Z���^�[����2019IA�Ԗ{�̖��̉�����C�ɓ���܂���
��BAC���݊p�̂Ƃ�AC�̐��������͒���BA��B���ł͂Ȃ��AA���Ō����
�Ƃ������Ƃ��ؖ������Ŏg���Ă��܂�
�m���ɐ}��`���킩��܂����A�����Ƃ����_���I�����������Ă�������
�}�`�I�Z���X���Ȃ��̂ł���������肪��ԍ���܂� /__�A�����S�E�l�l_/__
/�Q/���F�X �i�Q^_) __
/�Q/_�v�b�`�(____) __
/�Q/�Q/�Q/_�i`-`))b�_
/�Q�l�l�Q/__(�Q����__
/_(�Q)_)_/_�����ҁ�__
/_( ___)_/�Q/�Q/�Q/�Q
/_(_�i`)_/�Q/�Q/�Q/�Q
/_(�ҁQ)���Q/�Q/__/�Q
/���҄�-���Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/���ꂩ���ʂ��������т����Ă̐V�嗤�₢�����Ƃ�ȁB�O>>686 A�����ɐ��������Ƌ���C����]������Ί��o�I�ɖ��炩�Ȃ͂�����...�ܘ_�p�x���r���Ă���������ǂ�
https://i.imgur.com/YjwJnfK.jpg
���Ȃ݂�2017�N��1A��5��͂����������^��_������
���ׂ���CE=3.5��BE=4.5�܂ł͊ȒP�ɂ����邪�A���̌�_F���O�p�`�̏ォ�����f����͓̂��
https://i.imgur.com/iUjO4W9.jpg >>695
>���s�������i�ւ��������������j�Ƃ́A���[�N���b�h�w�ɂ�������F�̂�������ł���B
>���[�N���b�h�i�G�E�N���C�f�X�j�̑�5�����i�����j�Ƃ��Ă��B�����2�����w�ɂ����Ď��̂悤�Ȃ��Ƃ��q�ׂĂ���B
>���s�������A���[�N���b�h���_�ɂ�����5�Ԗڂ̌����ł��������Ƃ���A
>���[�N���b�h�i�G�E�N���C�f�X�j�̑�5�����i�����j�Ƃ��Ă��B
>�����2�����w�ɂ����Ď��̂悤�Ȃ��Ƃ��q�ׂĂ���B
>
>1�̐�����2�̒����Ɍ����A�������̓��p�̘a��2���p��菬�����Ȃ�A
>����2�̒����͌���Ȃ����������ƁA2���p��菬�����p�̂��鑤�ɂ����Č����B
�w�Z�ŏK�����ǂ����m��܂��A���ꂪ���̂܂g���܂��ˁB
����(����) �͏ؖ��̂��悤���Ȃ���O��ł��B
�E��BAC �� 90�� (�݊p)
���p�a�� 180�� �����̑��Ō����. �܂� ����AB ��A���Ō����.
�E��BAC < 90�� (�s�p)
���p�a�� 180�� �����̑��Ō����. �܂� ����AB ��B���Ō����. >>697
>>698
���̂悤�Ȍ����ȂǕ��ʏK��Ȃ��ł�����͂�Z���X���������Ȃ�ł���
���ɒm���Ă��Ƃ��Ď������Ԓ��ɘ_���I�ɍl���Ă�ɂȂ��ł� 10�b�ōl���I��邵�}�������킩�邵�Z���X�ȑO�ɕ��ʂ̓��̉�]�����邩�ǂ��������ǂ�
�܂��������ɒr���ł��w�͂���Ή�������͂Ȃ��Ȃ��Ȃ� �~���R�t�X�L�[��Ԃɂ����郍�[�����c�ϊ��̏������̋L�q��4�~4�s��(��)��1�ȏ�(����1)�Ƃ������̂���������ł����s�̂�1�ȏ�Ƃ͂ǂ������Ӗ��ł��傤���H 00������1�ȏ�Ƃ�����Ȃ��ł����H >>665
b-a = �� �Ƃ����B
(e^b - e^a)/(b-a) = (1/��) e^{(a+b)/2} ��[-��/2, ��/2] e^t dt
= (1/��) e^{(a+b)/2} ��[0,��/2] {e^t + e^(-t)} dt
�� (1/��) e^{(a+b)/2} ��[0,��/2] 2dt�@�@�@�@�@(����ɓ�)
= e^{(a+b)/2}, >>677
b-a = �� �Ƃ����B
{f(b) - f(a)}/(b-a) = (1/��)��[-��/2, ��/2] f '((a+b)/2 +t) dt
= (1/��)��[0,��/2] {f '((a+b)/2 + t) + f '((a+b)/2 - t)} dt
�� (1/��) f '((a+b)/2)��[0,��/2] 2dt�@�@(�� f ' ����ɓ�)
= f '((a+b)/2), �O>>696
>>697�摜2�ځB
��CAB�䁢CED���A
DE=3/2�ACE=7/2�ABE=8-7/2=9/2
B���N�_�Ƀ��l���E�X�̒藝���A
(BE/EC)(CD/DA)(AF/FB)=1
(9/7)(4/3)(AF/AF+3)=1
12AF=7(AF+3)
AF=21/5
���l��F���N�_�Ƀ��l���E�X�̒藝���A
(FA/AB)(BC/CE)(ED/DF)=1
{(21/5)/3}{8/(7/2)}{(3/2)/DF}=1
21�8�3=5�3�7DF
DF=24/5 �O>>705�����B���ʂ��������B
��CAB�䁢CED���A
DE=3/2�ACE=7/2�ABE=8-7/2=9/2
B���N�_�Ƀ��l���E�X�̒藝���A
(BE/EC)(CD/DA)(AF/FB)=1
(9/7)(4/3){AF/(AF+3)}=1
12AF=7(AF+3)
AF=21/5
���l��F���N�_�Ƀ��l���E�X�̒藝���A
(FA/AB)(BC/CE)(ED/DF)=1
{(21/5)/3}{8/(7/2)}{(3/2)/DF}=1
21�8�3=5�3�7DF
DF=24/5 >>677
b-a = �� �Ƃ����B
{f(b) - f(a)}/(b-a) - f '((a+b)/2) = (1/��)��[-��/2, ��/2] {f '((a+b)/2 + t) - f '((a+b)/2)} dt
= (1/��)��[0,��/2] {f '((a+b)/2 + t) + f '((a+b)/2 - t) - 2f '((a+b)/2)} dt
= (1/��) ��[0,��/2] ��[0,t] {f "((a+b)/2 + u) - f "((a+b)/2 - u)} du dt
= (1/��) ��[0,��/2] ��[0,t] ��[-u,u] f '''((a+b)/2 + v) dv du dt,
���@f ''' �̕����ɂ��B
>>703 >>704 �� �u���ɓʁv >>707
���ϒl�̒藝���
f '(c) - f '((a+b)/2) = {c - (a+b)/2}f "(��),�@�@�@�@(a<��<b)
a<x<b ��
f '''(x) / f "(x) > 0�@�ˁ@c > (a+b)/2,
f '''(x) / f "(x) < 0�@�ˁ@c < (a+b)/2, S(n) = ��[k=1 to n] 1/k^2
�Ƃ����B
�Ɍ�
lim[n����] (n^a){S(n)-(��^2)/6}
��0�łȂ��L���̒l�Ɏ�������悤�ȗL����a�����߂�B
�܂����̋Ɍ��l�����߂�B >>695
A�AAC�̒��_�A���̌�_�ŏo����O�p�`���l������A���p�̈�����p�Ȃ���c��̓�͂ǂ�����s�p
������A�s�p���Ɍ�_������ >>709
S(n) - (��^2)/6 = -��[k=n+1 to ��] 1/kk
�@= -��[k=n+1,��] {1/(kk-1/4) - 1/(kk(4kk-1))}
�@= -��[k=n+1,��] {1/(k-1/2) - 1/(k+1/2) - 1/(kk(4kk-1))}
�@= -1/(n+1/2) + ��[k=n+1,��] 1/(kk(4kk-1))
�@ �` -1/(n+1/2) + 1/(12k^3) - ����
�@= - 1/n + 1/(2nn) - 1/(6n^3) + 1/(30n^5) - ����
a=1
lim[n����]�@n{S(n) - (��^2)/6} = -1 ���l�ʑ�ABCD�́�BCD�̏d�S��G�Ƃ���B
��ABC�̓��ډ~��AG�����Ƃ��Ĕ����v����180����]�����Ăł��闧�̂�D_1�A��ACD�̓��ډ~��AG�����Ƃ��Ĕ����v����180����]�����Ăł��闧�̂�D_2�Ƃ���B
�̈�(D_1)��(D_2)�̑̐ς́AD_1�̑̐ς̉��{���B �O>>706
>>712
���l�ʑ�ABCD�_A�̂��イ�Ԃ�������Ղ����D_1��D_2��60������Ă�B
D_1��180����]�Ȃ�ŁA
(D_1)��(D_2)�̑̐ς�D_1�̑̐ς́A
60��/180��=1/3(�{)
(�~�Ղ̒ʉߋ�͒[�������������悤�ȋC�����邯�ǂ���͂��݂��l�A�̐ς͂˂ɕ��̂̏d�S�ɂ���ƍl���Ă悢�Ǝv��) >>700
���Ȃ��ɐ��w���w�Ԏ��i�͂Ȃ� ����̐���1���̍ŏI���
���܂��v�Z�ł��Ȃ������̂łǂȂ��������Ă��������܂����H
xyz��Ԃɂ�����
x=rcos��
y=rsin��
z=k��
(0��r��1)
(0���Ɓ�2��)
k�͐��̒萔
�ŕ\�����헆���ʂ̖ʐς����߂�B
�~�����W�ɒu�������Ă݂��肵�����ǁA�ǂ������܂������Ȃ�
��(k^2+1)
�ł͂Ȃ���Ȃ��c �O>>713
>>715���̒��ԏ�ō���k�Ə�ɂ���t���A�ɍs���ɂ́A�����v���ɓ���r�̗�����ɂȂ��Ă����p�����A
2��r�����z������Ԃ�����������������Ȃ��Ƃ����Ȃ��͂��B
���̌��ztan��=k��/2��r
���W���Ă��āA�Ԃ�������Ă��邠������k�Ə�̃t���A�ɍs���d�|���ɂȂ��Ă邩��A
�s�^�S���X�̒藝���A
������Ă���܂ł̓��̒����́A2��r���傫���A
��{(2��r)^2+(k��)^2}
����p���H������̖ʐς́A
��r��{(2��r)^2+(k��)^2}d��[��=0�`2��]
r�ɔ�Ⴕ�āA�Ƃɔ�Ⴕ�Ă����Ǝv���܂��B x�͎����ŁA0≤x<50�����B
���̂Ƃ��A
tan(10+x��)=tan(20+x��)*tan(30+x��)*tan(40+x��)����x�͉����邩�B
�܂�����x�̒l�����߂�B >>714
�w�Ԏ��i���ĂȂH����ȕ����N���ɒ�`�ł���̂��H
�C�ɓ���Ȃ��ӌ���������Ē��g�̂Ȃ����w�I�\���Ŕے肷��̂͂������ > �܂��������ɒr���ł��w�͂���Ή�������͂Ȃ��Ȃ��Ȃ�
����Ȃ̂��u�ӌ��v�Ƃ��Ď����̂�.... ��w�Ő��w����Ă���ǑS���킩��Ȃ��̂ʼn���������Q�l���Ƃ������Ă������� ���������Ȃ��ƈӖ��Ȃ��Ǝv���܂��� >>720
�ӌ��Ƃ��āu�����v�Ȃ�ĒN���������낤�H
���{��ǂ߂Ȃ��̂� �O>>717
>>718
tan40���tan30���tan20��=0.176326981
tan10��=0.176326981
����tanx����0��x��50�ɂ����ĒP������������A
����x�̒l�͂�����B
��x=0
x�̑����ɂƂ��Ȃ��āA
tan(x+10)����tan(x+20)���tan(x+30)���tan(x+40)���͍��ӂ��E�ӂ��傫���Ȃ�B >>723
���͂���Ȃ̂́u�ӌ��v�ł͖����Ǝv�����ǁA
>�C�ɓ���Ȃ��ӌ����������
���Ȃ��͂��ꂪ �u�ӌ��v �ł���ƔF�����Ă���킯�ł��B
�����͌����Ă��Ȃ�����A�ƌ����̂Ȃ�
>>714 �����āu�C�ɓ���Ȃ��ӌ��v�Ƃ͌����Ă��Ȃ��̂ł��B
�������x�ɂ͐��@���������ׂ��ł��傤�B ��������������700�̓��e�͐������Ǝv��
�܂������͎^�ۂ��邾�낤���ǁA�Ƃɂ���714�͑S�������ĈӖ��s��
�̂đ䎌�ɂ��Ă��悭�Ӗ���������Ȃ� ���_�𒆐S�Ƃ���P�ʉ~x^2+y^2+z^2=1������x+y+z=1�ł�����Ƃ��A���̌��_���牓���Ȗʂ�S�AS�̉���C�Ƃ���B���̎��i��A)=[3y^2*z, xy, y^2*x]�ɑ��ăX�g�[�N�X�̒藝�����藧���Ƃ������B
��낵�����肢���܂��B
�r���������肢�������ł��B 700 �̂���
>10�b�ōl���I��邵�}�������킩�邵�Z���X�ȑO�ɕ��ʂ̓��̉�]�����邩�ǂ��������ǂ�
>�܂��������ɒr���ł��w�͂���Ή�������͂Ȃ��Ȃ��Ȃ�
���������� >>695 ������ �u�m���ɐ}��`���킩��܂��v�Ƃ���A
�����ǁu�����Ƃ����_���I�����������Ă��������v�Ƃ����b�������̂ł��B
�_���I������₤�Ӗ������������A�l�b�g�X�����O�ő��l�𒆏����� 700 �́A�ᔻ�ɒl����Ǝv���܂��B
�{�l�ł͂Ȃ��̂� >>714 �̔����̐^�ӂ͒m��܂��B �_���I���Č��ǃ_�u�X�^�Ŕᔻ���������̔ᔻ�����������Ȃ̓����Ă�
�X���Ⴂ����������� >>730
�P�ʋ��ł������݂܂���c >>729
�Ȃɂ���H
S��C�ɑ��ăX�g�[�N�X�̒藝�g���Ȃ�S��ł�C��ł�3�����̃x�N�g�����ĉ��H
�����肾�낤���LjӖ��S���킩���ĂȂ��ˁB >>734
http://hooktail.sub.jp/vectoranalysis/StokesTheorem/
���̃y�[�W�̂P�ԉ��ɂ��鉉�K���ɂ���������܂����A������Ԉ���Ă����ł��傤���H
����Ƃ�����낵������̉��K���̉������������Ă������������ł��B >>724
tan10�����ėL�������Ȃ�ł����H
�m��Ȃ������ȁ[ �i1�ja,x�͐��̎����ŁA0<a-(1/x)�Ƃ���B�ȉ��̒�ϕ������߂�B
��[a-(1/x) to a+(1/x)] ln(t) dt
�i2�j0.7-0.02 < ln(2) < 0.7+0.02�@�������B >>735
����͕Ȗʂň͂�ꂽ3�����̗̈�Ƌ��E�̖ʂɑ��ẴX�g�[�N�X�̒藝�B
3�����̈�Ȃ̂�1 form ��2 form���O��������̂ł���Ŗ��Ȃ��B
������
�ʏ�̂̔����`����0 form�A1 form�A2 form�̐�������1�A2�A1�A
�Ȑ���̂̔����`����0 form�A1 form�̐�������1�A1�ŎO�����̃x�N�g���Ȃ��������Ȃ��B
�����������Ƃ̓x�N�g����͂̌v�Z�]�X�ȑO�ɂ��������x�N�g����Ƃ͉����̒�`���킩���ĂȂ��B
�������O�ɂ܂����ȏ��̌��t�̈Ӗ���������Ƃ�����n�߂Ȃ��Ɖ��ɂ��n�܂��B >>738
�ł�����>>729�͑�w��������̉ۑ�Ȃ�ł�...�B
�o���ꂽ��������ǂ��킩�炸�B
�����N��̉��K���̉������������Ă��������B���肢���܂��B ���̎O�����̊�����Ԃ�2 form�Ƃ݂Ȃ��ċǖʂɈ����߂��̂��ȁH
���̐����\���͑�1������dydz�̌W���ȂȁH
��������������Ȃ����ǁB �Ⴄ���B
���y�[�W���Ă������Ǐ���ɋL���ς�����`�����H
���̎O�����͋�Ԃ̒���1 form�ŋȐ��̕��Ɉ����߂������̂ƋȖʂł̃X�g�[�N�X�̒藝�ł��ȁB
�y�[�W�ɏ����Ă���ʂ����ĉ������B >>724
> ����tanx����0��x��50�ɂ����ĒP������������A
> ����x�̒l�͂�����B
> ��x=0
> x�̑����ɂƂ��Ȃ��āA
> tan(x+10)����tan(x+20)���tan(x+30)���tan(x+40)���͍��ӂ��E�ӂ��傫���Ȃ�B
����Ȃ��ƌ�����H >>741
���t���炸�Ő\����Ȃ��ł���>>729���ۑ�ł��ĉۑ���o���������͂��̃y�[�W���Q�l�ɂ����Ƃ����Ă�����ł��B
>>729�̕��͖�肪����������������Ȃ����Ă��Ƃł���ˁH �������v�̕����ŋߎn�߂܂���
S^2�̊��Ғl�����߂���ŁA2���ڂ̈�ԏ�̓����𗘗p���Ă���̂ł���
���̓����͂ǂ�����ē�����̂ł��傤��
https://i.imgur.com/0XEVgHS.jpg
https://i.imgur.com/RzVYDzg.jpg �O>>724�⑫
>>718
tan40���tan30���tan20��=0.176326981�c�c
tan10��=0.176326981�c�c
����tanx����0��x��50�ɂ����ĒP������������A
����x�̒l�͂�����B
��x=0
��dtanx/dx=1/cos^2x
x�̑����ɂƂ��Ȃ��āA
tan(x+10)����tan(x+20)���tan(x+30)���tan(x+40)���͍��ӂ��E�ӂ��傫���Ȃ�B >>743
�����HP���ĉۑ�o���z�Ȃ�Ă����www
�Ƃ肠����HP�̂Ƃ���̏o��Ȃ�Ӗ��͒ʂ邵�Ƃ���B
�Ƃ������ǂ����킩��Ȃ����킩��Ȃ��B
�Ƃ肠����
rot X���v�Z����
�ʂ̃p�����[�^��I�ԁB
�ʐϕ��v�Z����B
�Ȑ��̃p�����[�^�[��I�ԁB
���ϕ��v�Z����B
�����B >>746
�z���g���m�Ő\����Ȃ��ł����A
���Ԃ�����Ƃ��ł����̂œr���v�Z�Ƃ����肢�������ł��܂��c >>744
�@(X_i - X~) + (X~ -��) = X_i -��,
���Q�悵��
�@(X_i - X~)^2 = (X_i -��)^2 - 2(X~ -��)(X_i - X~) - (X~ -��)^2
����� i=1���n �ɂ��Ă�����
(����) = ��[i=1���n] (X_i -��)^2 - 2(X~ -��)��[i=1���n] (X_i - X~) - n(X~ -��)^2
�@= ��[i=1,n] (X_i-��)^2 - n(X~ -��)^2�@�@(�� *)
�@= (�E��)
*�@�W�{���ς̒�`�@X~ = (1/n)��[i=1���n] X_i ����@��[i=1���n] (X_i - X~) = 0, Memo.
tan�� = t�@�Ƃ�����
tan(2��) = 2t/(1-tt),
tan(4��) = 4t(1-tt)/(1-6tt+t^4),
�����
�@tan�� = tan(2��) tan(30�) tan(4��),
�ɓ����ƁAt��0 ����
�@1 = (8/��3)t / (1-6tt+t^4),
�䂦
�@t = 0.176326980708465 = tan(10�),
�@�� = 10�
�܂�
�@1 = tan�ƥtan(30�) tan(2��) tan(4��),
�ɂ�����
�@1 = (8/��3)t^3 / (1-6tt+t^4),
���
�@t = 0.363970234266202 = tan(20�),
�@�� = 20� �i1�ja,x�͐��̎����ŁA0<a-(1/x)�Ƃ���B�ȉ��̒�ϕ������߂�B
��[a-(1/x) to a+(1/x)] 1/t dt
�i2�j0.7-0.02 < ln(2) < 0.7+0.02�@�������B >>700
�̌����Ƃ邱�Ƃ͌������͂Ƃ���������������P�`���Ă�A�z�����^ �@log(1+x) = x - (1/2)x^2 + (1/3)x^3 - ����
�@log(1-x) = - x - (1/2)x^2 - (1/3)x^3 - ����
�ӁX������
�@log[(1+x)/(1-x)] = 2x + (2/3)x^3 + (2/5)x^5 + �����@�@(9)
�ΐ��̌v�Z�ɂ� (9) ���p������B�@(9)�ɂ����� x=1/(2n+1)�@(n��1) �Ƃ����
�@log(n+1) - log(n) = 2/(2n+1) + 2/[3�(2n+1)^3] + 2/[5�(2n+1)^5] + �����@�@(10)
���̋����͋}���Ɂi����n���傫���Ƃ��j��������B
�@n=1 �Ƃ��Ă��i5��������)
�@�@log(2) = 2/3 + 2/(3�3^3) + 2/(5�3^5) + 2/(7�3^7) + 2/(9�3^9) = 0.693146
��B
���F�u��͊T�_�v������O�ŁA��g���X (1961)
�@��S�́@��52�D�Ћ����@p.187 n ��C�ӂ̎��R���Ƃ���B
��k �� {0, 1, 2, �c, (1/2) * n * (n - 1)} �ɑ��A�S�P�� �� �F {1, 2, �c, n} �� {{1, 2, �c, n} �ŁA
�ȉ��̐����������̂����݂��邱�Ƃ��ؖ�����B
k = #{(i, j) | i < j, ��(i) > ��(j)} f(x)�͂��ׂĂ̎���x�ɂ����Ĕ����\�ŁA�ȉ��̏��������B
�Ef'(0)=1
�Ef(2x)=(exp(x)+1)*f(x)
f(x)�����߂�B >>753
���A�A�[�@�ŊȒP�Ɏ����܂��ˁB >>756
���̊��������ǂ�����ĉ�����ł����H >>758
���肪�Ƃ��������܂��B
�h��Ƃ��ďo���ꂽ�̂ł��������������łȂ��̂ŖʐH�炢�܂����B >>748
���肪�Ƃ��������܂��A�����ł��܂���
�������ŏ��́@(X_i - X~) + (X~ -��) = X_i -�� �Ƃ��������ǂ����玝���Ă����̂ł��傤���c 2008�N���H��O����S��́i�Q�j�ł�����蕶�Ɂu�_R�̋O�Ղ͂���ȉ~�̈ꕔ�ł��邱�Ƃ�
�����v�Ƃ���A�ł�OP,OR�Ƃ��������đȉ~�̎��������Ă�̂ł����E�E�E
�u����ȉ~�v�Ƃ���̂ł����܂ł��Ȃ��Ă͂Ȃ�Ȃ��̂ł��傤���H
�ȉ~�̎���OP,OR���̂����Ă��iOP>0�AOR���O�j�Ȃ̂őȉ~�ł��邱�Ƃ�
������Ă�C���E�E�E���ꂾ�����ƕs�\���ł����H >>761
��蕶�Ɖڂ����o�J
���O�̌��������Ɖ��Ȃ��ƕ�����˂�����A�z
O���ĉ����HP���ĉ����H ������Ő\����Ȃ����ǁA�Ȃ�ł���Ȃɍ����I�Ȃ́H >>591��͋Z�ł̉�@��낵�����肢���܂� A �� Lxn �s��AB �� nxm �s��Ƃ���B �]�u�� ~ �ŕ\�킷�B
A~A �� BB~ �� nxn�s��iGrammian �s��)
�E���� >>607 -2<k<2�Ƃ���B
2��������x^2+kx+1=0��2�������A���i|��|≤|��|�j�Ƃ��A����a[n]���ȉ��̑Q�����Œ�߂�B
a[1]=���Aa[2]=��
a[n+2]+k*a[n+1]+1=0
���̂Ƃ��A����a[n]�̈�ʍ������߂�B >>766
�Q������ a[n+2]+k*a[n+1]+a[n]=0 ���Ǝv���܂�. ���Ƃ���ƁA
a[n] = s ��^n + t ��^n ���Q���������܂�.
�����������������悤�ɌW�� s, t �����߂Ă����ꂪ�����ł�.
-2<k<2 , x^2+kx+1 = (x+k/2)^2 + 1-k^2/4 = 0 ���� ��, �� �͕��f���ŁA�w�d���łȂ��x�w�O�ł��Ȃ��x�ƕ�����܂�.
���̏������� s, t �͕K�����܂鎖���ۏ���܂�. >>750
f(t) = 1/t
�� dt f(t) = log(a+1/x) - log(a-1/x) = log((ax+1)/(ax-1))
= F(ax) �ƒu��.
�Et=a �ł̐ڐ� y = g(t)
�E�Q�_ ( a-1/x, f(a-1/x) ) ( a+1/x, f(a+1/x) ) �����Ԓ��� y = h(t)
�ɂ��čl����.
g(t) = f �f(a)(t-a) + 1/a = (-1/a^2)t + 2/a
�� dt g(t) =(-1/a^2){(a+1/x)^2 - (a-1/x)^2}/2 + 4/ax
={(1-1/ax)^2 - (1+1/ax)^2}/2 + 4/ax
= 2/ax = G(ax) �ƒu��.
h(t) = (x/2){(a+1/x)-t}/(a-1/x) + (x/2){t-(a-1/x)}/(a+1/x) (���`��Ԏ�)
�� dt h(t) = 1/(ax-1) + 1/(ax+1) = H(ax) �ƒu��.
�ϕ��͈͂� g(t) �� f(t) �� h(t) (���ӓ�����t=1,�@�E�ӓ����͒[�_ t=a�}1/x �̂� )
����� G(ax) < F(ax) < G(ax) �ł���.
2*F(7) + F(17) = log(2)
2*G(7) + G(17) = 82/119 = 0.689...
2*H(7) + H(17) = 101/144 = 0.701...
�� 0.7-0.02 < 0.689 < log(2) < 0.702 < 0.7+0.02
2*F(11) + F(17) + 2*F(19) = log(2)
2*G(11) + G(17) + 2*G(19) = 2458/3553 =0.6918...
2*H(11) + H(17) + 2*H(19) = 167/240 = 0.6958...
�� 0.7-0.02 < 0.6918 < log(2) < 0.6959 < 0.7+0.02
(�� log(2) = 0.6931... ) �e��A�ɂ�x���̐H������300g�A�e��B�ɂ�6���̐H������yg�����Ă���BA����100g�H���������o���AB�ɓ��ꂽ�Ƃ���B�̔Z�x��8���ɂȂ����B����ɁAB�̗e��ɓ����Ă���H�������ܕ��̈�����o��A�ɓ���Ă����������Ƃ���A�̔Z�x��12���ɂȂ����Bx�Ay�̒l�����߂�B
�r������������Ȃ��ł��B���݂܂���:w: >>768
�����Ԃ��Č�����Ag(t) �� h(t) �̋�̎��͂킴�킴���߂�K�v�Ȃ�����. (���`��Ԏ��Ńh�����Ă�݂����Œp��������...)
���_�����[�����m�̑�`�ʐς��ƕ������ G, H �͂������܂�.
>>769
>�e��A�ɂ�x���̐H������300g�A�e��B�ɂ�6���̐H������yg�����Ă���B
>A����100g�H���������o���AB�ɓ��ꂽ�Ƃ���B�̔Z�x��8���ɂȂ����B
A�H��: 300.x/100 -100.x/100=2x , A�t��: 300 -100 = 200
B�H��: 100.x/100 + y.6/100 , B�t��: 100 + y
B�Z�x: (100.x/100 + y.6/100) / (100 + y) = 8/100
>����ɁAB�̗e��ɓ����Ă���H�������ܕ��̈�����o��A�ɓ���Ă����������Ƃ���A�̔Z�x��12���ɂȂ����Bx�Ay�̒l�����߂�B
A�H��: 2x + (100.x/100 + y.6/100)/5
A�t��: 200 + (100 + y)/5
A�Z�x: ( 2x + (100.x/100 + y.6/100)/5 ) / ( 200 + (100 + y)/5 ) = 12/100
���̕ӂ�����ĘA���������������ł��傤.
���l�Ԉ���Ă���K���ɏC�����Ă�������. >>770
���肪�Ƃ��������܂��B
�����̗��������܂�ǂ����Ă��Ȃ�:c m, n �𐳂̐����Ƃ���B
m^n �ƕ\���鐮������� m ���^����ꂽ�Ƃ��A n �����߂鍂���ȃA���S���Y�����Ă���܂����H ���`�r�b�N�E�z���g�s�[�́A���`�r�b�N�E(�R)�z�����W�[�Ƌ�̓I�ɉ����Ⴄ��ł���?
�P�̂̃z���g�s�[�ƃR�z�����W�[�͈Ⴄ�Ƃ͕������ł���
�卷�Ȃ�������ʖ��̂ɂ��Ȃ��Ă����͂� >>772
log(m^n)=n log(m)
n=log(m^n)/log(m) >>774
���肪�Ƃ��������܂��B
����������܂��F
���̐��� a ����� n ���^����ꂽ�Ƃ��A
a = m^n
�ƂȂ� m �����݂��邩���Ȃ������肵�A���݂���ꍇ�ɂ́A m �����߂�A���S���Y���͂���܂����H
���ۂɃv���O���~���O���邱�Ƃ��l���Ă��܂��B
���������_�����g���Ă��\���܂��A���ʂ͌����ɐ������K�v�͂���܂��B �O>>745
>>769
B�e�����8���H�����̐H���̗ʂɂ��āA
6y/100+x=(100+y)�~8/100�\�\�@
�ŏI�I�ȐH���̗ʂɂ��āA
(100+y)(8/100)(1/5)+2x
=(200+100/5+y/5)(12/100)
�\�\�A
�@���ȒP�ɂ���ƁA
6y+100x=800+8y
y=50x-100�\�\�@'
�A���ȒP�ɂ���ƁA
8(100+y)+1000x=12(1100+y)
800+8y+1000x=13200+12y
4y=1000x-12400
y=250x-3100�\�\�A'
�@'�A'���A
50x-100=250x-3100
200x=3000
x=15
�@'�ɑ�����A
y=750-100=650 >>766
2������������
�@�� + �� = -k,�@���� = 1,
�@a[n] = s���^n + t���^n�@
�Ƃ�����
�@s = -��/(1+��),
�@t = ���� + ��/(1+��),
�@k = -2cos�Ɓ@(�Ɓ�m��)
�Ƃ�����
�@�� = e^(-i��),�@�� = e^(i��),�@�@|��| = |��| = 1,
�@a[n] = s���^n + t���^n
�@ = (1/2) (s+t) cos(n��) + (i/2) (t-s) sin(n��), �@a[n] = s���^n + t���^n
�@ = (s+t) cos(n��) + i (t-s) sin(n��),
| a[n] |^2 = a[n]�Ea[n]~
�@= ss~ + tt~ + (st~+s~t)cos(2n��) - i(st~-s~t)sin(2n��)
�@= |s|^2 + |t|^2 + 2|s||t|cos�� cos(2n��) - 2|s||t|sin�� sin(2n��)
�@= |s|^2 + |t|^2 + 2|s||t|cos(2n��+��),
�����Ɂ@�� = arg(t/s),
�@||s| - |t|| �� | a[n] | �� |s| + |t|,
�ȉ~��ɂ���B �� tan(20)tan(30)tan(40)=tan(10) �̌�
tan(10)=t = t1
tan(20)=t2 =tan(10+10) = 2t/(1-t^2) = tan(30-10) = (t3 -t)/(1 +t3*t)
tan(30)=t3 =tan(30) = (t +t2)/(1 -t*t2) = t(3 -t^2)/(1 -3t^2)
tan(40)=t4 =tan(30+10) = (t3 +t)/(1 -t3*t)
t2*t3*t4 = (t3 -t)/(1 +t3*t) * t3 * (t3 +t)/(1 -t3*t)
= (t3^2 -t^2)/(1 -t3^2*t^2) * t3
= (1 -3t^2)/(3 -t^2) * t3 (�� t3= 1/��3)
= t
����� tan(20)tan(30)tan(40)=tan(10)
*** �C�ɂȂ鎖 ***
tan(15)tan(25)tan(35)=tan(5)
�ǂ������ꂪ�����������ł�. �ǂ������玦����ł��傤���H tan 3x = P(tan x)
�ƂȂ�L����P(t)�����Ă��ĕ�����
P(t)=tan15��
�̉���tan5���Atan65���A-tan55���ł��邱�Ƃ𗘗p�����炢���邩�ȁH �~�X������͂��Ȃ̂ł����A�͔͉Ɖ�@���قȂ�A�����ł��܂���
�ǂȂ����~�X���w�E���Ă��������Ȃ��ł��傤��
https://i.imgur.com/7kTK2LM.jpg
https://i.imgur.com/cILQNFC.jpg ���Ă������� ���������������玩���ŕ����邩������Ȃ����������f���₷�� ���ꂪ��������Z1�N���ȏ��
���]�̎�����A
https://i.imgur.com/kcVJS0a.jpg ������������Ԃ����ށA
���ꂪ��������Z��N���ȏ��
���]�̎�����
https://i.imgur.com/E1zaUDP.jpg >>783
���������̂ŊJ���Ă݂��烁�b�`�������Ď����Ǝv������B �h��������Ă��炢�����Ȃ�
���Z�������X���̕��������Ƃ�������
���Z���w�̎���X��Part400
https://rio2016.5ch.net/test/read.cgi/math/1559743596/ >>780
�@tan(��-��/3) + tan�� + tan(��+��/3) = 3tan(3��),
�@tan(��-��/3)�Etan���Etan(��+��/3) = - tan(3��),
(����)
�h�E���A��������
�@cos(3x) + i�sin(3x) = e^(3ix)
�@= {e^(ix)}^3
�@= {cos(x) + i sin(x)}^3
�@= {cos(x)^3 - 3cos(x)sin(x)^2} + i{3sin(x)cos(x)^2 - sin(x)^3}
�@= cos(x)^3 {(1-3tt) + i(3t-t^3)},
tan(3x) = sin(3x)/cos(3x) = (3t-t^3)/(1-3tt) = P(t),
P(t) = tan(3��)�@�Ƃ����Ɓ@t��3���������ƂȂ�B�i|��| <30߁j
�@t^3 - 3tan(3��)tt - 3t + tan(3��) = 0,
3�� tan(��-60�), tan��, tan(��+60�) �ƌW���̊W����o��B ��=5� �̂Ƃ�
�@tan(-55�)tan(5�)tan(65�) = - tan(15�),
��=10� �̂Ƃ�
�@tan(-50�)tan(10�)tan(70�) = - tan(30�), 0 �܂��� 1 �𐬕��Ɏ��� n �~ n �s��� A �Ƃ���B
�ȉ��̏������݂��������s�� B �̍s���i�j�̍ő�l�� O(n^2) �Ōv�Z����A���S���Y�����q�ׂ�B
1. B �� A �̕����s��ł���B
2. B �̗v�f�� 1 �݂̂��琬��B �Ȃ}�`�I�ɉ�������͂��Ȃ��̂��� >>788
t = tan(��)
a = f(��) = tan(��-60)
P(x) = x (3-xx)/(1- 3xx) = x {(��3-x)(��3+x)} / {(1- ��3 x)(1+ ��3 x)}
a = (t - ��3)/(1 + t ��3)
��3 + a = (��3+3t + t - ��3)/(1+ t ��3) = 4t /(1+ t ��3)
��3 - a = (��3+ 3t - t + ��3)/(1+ t ��3) = 2(��3 +t)/(1+ t ��3)
(1+ ��3.a)= ��3 (1/��3+ t + t - ��3)/(1+ t ��3) = -2(1 -��3.t ) /(1+ t ��3)
(1- ��3.a) = ��3 (1/��3+ t - t + ��3)/(1+ t ��3) = 4 /(1+ t ��3)
�����
P(a) = a { (��3 - a)(��3 + a) }/ {(1- ��3.a)(1+ ��3.a) }
= t(tt-3)/(3tt-1)
= P (t) = tan(3��)
�Ȃ�قNJm���ɉ��ł���.
��=25 �̏ꍇ
tan(-35)tan(25)tan(85) = -tan(75)
-tan(35)tan(25)cot(5) = -cot(15)
�� tan(15)tan(25)tan(35) = tan(5)
�������ł�.
>>780
�ŏ��Ӗ���������Ȃ��ăX���[���Ă��܂��܂���. ������������������ł���. >>775
a^(1/n) (���������_�v�Z) �ɂ����Ƃ��߂����������� m �ƒu���A
m^n (�����v�Z) == a �Ȃ炻�ꂪ���ŁA!= a �Ȃ���Ȃ�
m^n (�����v�Z) �� O(log(n)) �Ōv�Z�\ >>793
a+b =-t + 3tan3��
= -t + 3t(3-t^2)/(1-3t^2) = 8t /{(1 + ��3.t)(1 - ��3.t)} = (t - ��3)/(1 + ��3.t) + (t + ��3)/(1 - ��3.t) = tan(��-60) + tan(��+60)
ab = 1/t . (-tan3��)
= (t^2-3)/(1-3t^2) = {(t - ��3)(t + ��3)}/{(1 + ��3.t)(1 - ��3.t)} = (t - ��3)/(1 + ��3.t) * (t + ��3)/(1 - ��3.t) = tan(��-60) tan(��+60)
���Z�͂������̕����ȒP��. >>792
�Ƃ肠�����O����10�Ԗڂ̐l�܂ł����肭������
���Ď��́A�����l�B�������s�� >>790
�q���g�ł����A���I�v��@���g���Ă��������B >>798
�����Ȃ�B
�A�����ĂȂ��Ƃ����Ȃ��̂��A�܂�ɂƂ��Ă����̂��ňӖ�����Ă��邩��G�X�p�[�s�\�Ȃ�B
�����͏����Ȃ��ƈӖ��ʂ��Ȃ��ƕ����肻���Ȃ����ǁB >>781 (��)
14�E13
�@xyz��Ԃ�4�_ P(0, 0, 2), A(0, 2, 0), B(��3, -1, 0), C(-��3, -1, 0) ���Ƃ�B
�@�l�ʑ�PABC�� xx+yy��1 ���݂��������̑̐ς����߂�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(12 �����H��) >>783
[16] �L�����Ɩ����� ��2ch
�@a,b��L�����Ƃ���B(2+3��2)a + (1-2��2)b = 7�@�����Ƃ��A
a = [�A], b = [�C] �ł���B
�@(2a+b) + (3a-2b)��2 = 7 + 0��2�@���
�@a=2, b=3
��)
m-n��2 = 0 �ƂȂ鎩�R��m, n ���������Ƃ���� mm=2nn
�f�������������2�ׂ̂��w���������A��ƂȂ��Ė�������B
�� m=n=0,
>>784
[29] �˂ɐ��藧�s����
�@a�͒萔�Ƃ���B
�@���ׂĂ̎���x�ɑ��ĕs���� axx+4x+a>0 �����藧��
�@�悤��a�̒l�͈̔͂́Aa > [�A] �ł���B
�@a��0 �͕s�� (x=0)
�@a>0 �̂Ƃ� a(x+2/a)^2 + (aa-4)/a �� (a+2)(a-2)/a,
�@�� a-2 >0, >>800
O(n^2) �̃A���S���Y���ł��̂ŁA�����ƕ�����܂���ˁB >>788
���ɂ�����B
�@1/tan(��-60�) + 1/tan�� + 1/tan(��+60�) = 3/tan(3��), >>804 �Ȃ�ق�
tan(��-60) �� tan(��) �� tan(��+60) = �� tan(3��) ���
-cot(��-60 -90) �� -cot(�� -90) �� -cot(��+60 -90) = �� -cot(3�� -90)
cot(��-90 -60) �� cot(��-90) �� cot(��-90 +60) = �� cot(3 (��-90) + 180)
��-90 �� �� �Ɏ�蒼����
cot(��-60) + cot�� + cot(��+60) = 3 cot(3��)
cot(��-60) . cot�� . cot(��+60) = - cot(3��) >>781 (���̃m�[�g�̉�ǂ͂������Ȃ� ), >>801
�}��t�����̂ŗ����͓���Ȃ����Ǝv���܂�.
�����̐�(�l�p�� �� 2): d(sin�� + tan��).(1-cos��)^2
�̐�: V = 6 �� [��=0�`��/3] {�����̐�} = (�ȉ���)
y < 0 ���̃p�[�c��I�̂́A�Ζʂ̎�: z/(2) + y/(-1) = 1 �̂悤�ɂQ�ϐ��ōςނ���ł�.
y = -cos�� �ƍ��킹�� �Ő��̎�: z = 2( 1-cos�� ) ���ȒP�ɋ��܂�܂�.
�v�Z�� �� d�� /cos�� ���o�Ă��āA�������ƖʐH�炤��������܂���.
�� d�� cos�� /cos��^2 = �� d(sin��) /( 1-sin��^2 ) = (1/2)( log(1+sin��) - log(1-sin��) )
����Ȋ����ł����܂�.
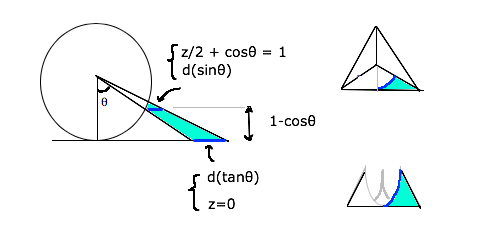 >>806
>>806
���肪�Ƃ��������܂��B
>>781�́A
�����̈悪3�ӏ�����̂�3�{���Ă��Ȃ�
�ϕ���Ԃ��ԈႦ�Ă���i30�������鎞�Ƀ�/3�����Ă���j�̂����ł����B
����2�ӏ�������ƈ�v���܂����B
�~���o�Ă��邩�瓖�Rxy���ʂɕ��s�ȖʂŐ�I�Ǝv�����̂ł����A
806�l���͔͉�z=t�ł͐��Ă��炸�A�e�N�j�b�N�������܂����B
����ł������i���܂��B���肪�Ƃ��������܂����B a�����R���̒萔�Ƃ���B
�ȉ��̕s�����������R��n����������݂���悤�Ɏ���p���߂����B
p�̎�肤��͈͂�a�ŕ\���B
2018 < n^2+an+(p/n) < 2019 >>806 �����̐ς̂Ƃ��ԈႦ�Ă�.
(���ɂȂ���)�O�p���ƎO�p�����ߕό`�����`�ɂȂ��Ă�.
�l�p�� �� 2 �Ȃł͂Ȃ�.
���̕����̎ߕό`�͑̐ς��s��(�E�})�Ȃ̂�...
�����̐�: d(sin��) (1-cos��)^2 + (1/3). d(tan�� -sin��). (1-cos��)^2
= d( (2/3).sin�� + (1/3).tan�� ) (1-cos��)^2
���Ԃ�ō����Ă��Ȃ�����...
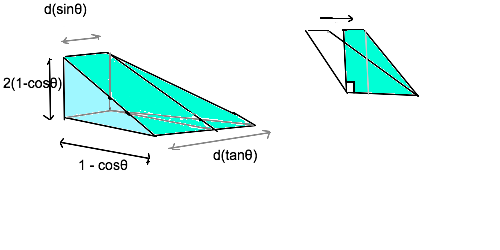 �O>>776
�O>>776
>>801
����AB�̕������́A
y=-(��3)x+2�\�\�@
���_���璼��AB�^�Ɉ����������̕������́A
y=x/��3�\�\�A
�@�A����_�́A
-(��3)x+2=x/��3
3x+x=2��3
x=��3/2
�A�ɑ�����Ay=1/2
(��3/2,1/2)
�����x^2+y^2=1��̓_�ł���A�}�`�̑Ώ̐����A
x^2+y^2=1�͐��O�p�`ABC�̓��ډ~�Ƃ킩��B
���l�ʑ�PABC����A
�~��x^2+y^2��1������ʂ��ƁA�Ƃ������O�_�A
(0,1,1)�(��3/2,-1/2,1)�(-��3/2,-1/2,1)�������яオ��B
z������A������B�����ɂ��ꂼ��P�[�L�����̂悤�ɋ��߂闧�̂�1/3���o���Ȃ�A���l�ʑ͎̂O�p��������3���킹�ĎO�p���̑̐ςƓ����B
���Ȃ킿�O�p���̑̐ς���~���̑̐ς������B
2���3�1-��1^2�1=2��3-��
=2�1.7320508-3.14159258
=0.3225�c�c �O>>811�̒l�A�����B
>>801
����AB�̕������́A
y=-(��3)x+2�\�\�@
���_���璼��AB�^�Ɉ����������̕������́A
y=x/��3�\�\�A
�@�A����_�́A
-(��3)x+2=x/��3
3x+x=2��3
x=��3/2
�A�ɑ�����Ay=1/2
(��3/2,1/2)
�����x^2+y^2=1��̓_�ł���A�}�`�̑Ώ̐����A
x^2+y^2=1�͐��O�p�`ABC�̓��ډ~�Ƃ킩��B
���l�ʑ�PABC����A
�~��x^2+y^2��1������ʂ��ƁA�Ƃ������O�_�A
(0,1,1)�(��3/2,-1/2,1)�(-��3/2,-1/2,1)�������яオ��B
z������A������B�����ɂ��ꂼ��P�[�L�����̂悤�ɋ��߂闧�̂�1/3���o���Ȃ�A���l�ʑ͎̂O�p��������3���킹�ĎO�p���̑̐ςƓ����B
���Ȃ킿�O�p���̑̐ς���~���̑̐ς������B
2���3�1-��1^2�1=2��3-��
=2�1.7320508-3.14159265
=0.3225�c�c �O>>812�Ⴄ��������Ȃ��B
z=t(0��z��1)�ŗ��̂�1/6�̕��������t=0�`1�𑫂����߂āA���Ƃ�6�{����B
z=t�ɂ�����̍��W�́A
(0,2-t,t)�
(0,1,t)�A
���ƈ�_�́A
y=-��3x+2-t��x^2+y^2=1�ɑ�����A
({��3(2-t)-��(4t-t^2)}/4,{2-t+��3(4t-t^2)}/4)
�O�p�`�����`�������Az=t�ɂ�����̖ʐς͏o��B
�O�p�`�̖ʐς́A
(1/2)(2-t){��3(2-t)-��(4t-t^2)}/4
={��3(2-t)^2-��(2-t)^2(4t-t^2)}/8
��Ƃ��`�̖ʐς�m��ɂ͒��S�p�Ƃ��~�ʂ̒���2�Υ(��/2��)=�Ƃ��K�v�B
t�ŕ\���Ȃ����B
tan��={��3(2-t)-��(4t-t^2)}/{2-t+��3(4t-t^2)}
z=t�ɂ�����̖ʐς́A
{��3(2-t)^2-��(2-t)^2(4t-t^2)}/8-�Υ(��/2��)
{��3(2-t)^2-��(2-t)^2(4t-t^2)}/8-��/2
���߂闧�̂̑̐ς́A
6��[t=0�`1]{��3(2-t)^2-(2-t)��(4t-t^2)}/8-��/2dt
= �O>>814���j�ύX�B
>>801
���l�ʑ�PABC����A
���l�ʑ�PABC��z=1����̕�������菜���A
x^2+y^2��1��0��z��1�̉~���������A
�~���̂������������������𑫂��B
���l�ʑ�PABC=(1/6)�3�2��2�2
=2��3
���l�ʑ�PABC��z=1����̕���=2��3�(1/8)
=��3/4
x^2+y^2��1��0��z��1�̉~��=��
�~���̂�����������������=(��/3-��3/4)�1�(1/2)�3
=(4��-3��3)/8
���߂闧�̂̑̐�=2��3-��3/4-��+(4��-3��3)/8
=(16��3-2��3-3��3-8��+4��)/8
=(11��3-4��)/8
=0.810773534�c�c >>815
�o�J������
����Ȗ��̌v�Z���炢�ꔭ�ō��킹�� ���z�̊m����������߂�r���̓W�J��������܂���
�[k=0,n]( nCk * (pz)^k * (1 - p)^(n-k) )
= (pz + q)^n
���̊Ԃ͉����s���Ă���̂ł��傤��
https://i.imgur.com/uyw4jk6.jpg 2���藝���������Ȃ��Ƃ������Ƃł��� >>818
���肪�Ƃ��������܂�
���S�ɑ��݂�Y��Ă��܂��� 2015�N�ȍ~�̍��Z���w�̐V�ߒ��̓��v���w�Ԃ̂ɍœK�̎Q�l���������ĉ����� f(x)�͒萔�łȂ��������Ƃ���B
���̂Ƃ��Asin(f(x))���������ƂȂ邽�߂̕K�v�\�������́Af(x)�̎�����1�ł��邱�Ƃ������B cos((f(a)+f(a+p))/2)��0�ł���a���Ƃ��a�̋ߖT��sin((f(x)-f(x+p))/2)=0�ɂ��(f(x)-f(x+p))/2�͒萔�B
�� (f(x)-f(x+p))/2�̎�����0�ȉ��B (�K�v����)
g(x) := sin(f(x)),�@����: T �Ƃ���.
f(x) �͒萔�ł͂Ȃ����� g(��) �� 1 �ƂȂ�_ x=�� �����݂���.
g�f(x) = cos(f(x)) f�f(x) ���������: T �̂͂��ł���.
| g�f(��) | = | g�f(��+nT) | = ��{ 1-g(��)^2 } * |f �f(a+nT)|
f(x)�̎����� 2�ȏ�ł� lim{n�� ��} |f �f(a+nT)| = �� �܂��̓����͐������Ȃ�.
����� f(x)�̎�����1�ł���.
(�\������)
f(x) =ax + b (1����, a��0) �Ƃ����
g(x) := sin(f(x)) = sin(ax + b) = sin(ax �}2�� + b) = sin(a*(x+2��/|a|) + b) = g(x+2��/|a|)
g(x) �͎��� 2��/|a| �̊��ł��� �i�K�v�����j
f(x) ��n���������Ƃ���B�����FT�Ƃ���B
���[0,T] �ł�f(x)�̒l�� D(0,T) �͗L�E�ł���B
�@sin(y) = sin�� �̍�y�͖����ɂ��邪 {��, ��-��, 2��+��, 3��-��, ����}
D(0,T) ���̍��� m�������Ƃ���B
����Af(x) = y ����x�� �ey�ɂ�n�ȉ��ł���B
�� sin(f(x)) = sin�� ����x ������T����mn�ȉ��ł���B
�����藝���
�@f(x+T) - f(x) = T�Q(x,T)
��Q ��(n-1)���������ł���B
n��2 �Ȃ�Ώ\���傫��x �ɑ��� Q(x,T) > ��mn/T
���[x,x+T] �ł�y�̒l�敝 |D(x,x+T)| > ��mn
sin(f(x)) = sin�� ����x�� 2mn�ȏ゠��B(����)
�E�r�u���̂��Ƃ̓r�u���ł���B(����) 69, 67, 65, 63, 61, 59, 57, 56,
52, 50, 48, 46, 44, 43, 42,
37, 35, 33, 32, 31, 30,
24, 23, 22, 21, 20,
15, 14, 13, 12,
8, 7, 6,
3, 2
�K�����́H
2 6 12 20 30 42 56�͎O�p���̈ʒu >>809
�@2018 < nn + an + (p/n) < 2019,
���
�@n(2018 - nn - an) < p < n(2019 - nn - an),
�k��l
n<45,�@a = 2(45-n)�@�̂Ƃ�
�@n{(45-n)^2 - 7)n < p < n{(45-n)^2 - 6},
�@(45 - a/2)(aa/4 - 7) < p < (45 - a/2)(aa/4 - 6), >>816�����Ă�݂����łЂƈ��S���܂����B�u�^�l�p�̃������[����4�l�Ŏ�ă��[���V�F�A�������B���p�����͂Ȃ����̂Ƃ��ĊԎd����ŒZ�ɂ������B�ǂ������炢�����B�����Ȑ��͔F�߂�v�Ɠ����ł��ˁB
�P]/�_______�O>>815_
�Q/�_/zz..,,���@�@ /|
�P�_/zz..�c`-`Ђ� / |
�P|�______U,~�܁R��@|_
�n| �a�P�P�P�PU~~U / /
�Q| �a ���@�� �a |/ /
_�@`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P >>811 >>812
3��AP, BP, CP�̒��_�� A ',B ',C ' �Ƃ���B
�_ A '(0,1,1)� B '(��3/2,-1/2,1)� C '(-��3/2,-1/2,1) �_�Ƃ���3�̐��̂��l�����
�@(����) = 1,
�@(��ʐ�) = ��ABC - �� = 3��3 - ��,
�@(�̐�) = (1/3)(����)(��ʐ�) = ��3 - (��/3) = 0.684853256
���̐��̂� xx+yy��1 �̗̋��N�Ƃ��Ă��āA�����i4��3 - 2�� = 0.65017923�j�����傫���B
>>827
�@�����ĂȂ����낤�B�S�R�������B >>801
�܂� xx+yy��1 �̓��������̑̐ς��l���A��3�p��PABC�̑̐� 2��3 ��������B
��BOC �Ɋ܂܂���`�����̑̐�v��3�{����悢�B
���̊e�_�̋ɍ��W�� (r,��) �Ƃ���� 0��r��1, -60߁��Ɓ�60�
�e�_�ɂ����鍂���� h(r,��) = 2(1+y) = 2(1-r�cos��)
�@v = ��[0,1] ��[-60�,60�] h(r,��) d�� rdr = 2(��-��3)/3,
�@V = (PABC) - 3v = 2��3 - 2(��-��3) = 4��3 - 2�� = 0.6�S5017923�@�@�@(������) >>827
������4��3-2��
������x�v�Z�������č��킹�Ă݂�ww >>806, >>810 �ł�������̉�@���v�Z������Ȃ�.
�m���� �l: 4��3 - 2�� = 0.645... ���������ł� (�O�̂��ߐ��l�v�Z�ł��m���߂�)
�����ł͖��������Ԃ��̈�͍����̔����ʂ�����ϕ��ɂ͌����Ȃ��͂���
V = 6 �� [��=0�`��/3] {�����̐�} = 6 �� [��=0�`��/3] d( (2/3).sin�� + (1/3).tan�� ) (1-cos��)^2
= (9/2)*��3 - 2��/3 - 2*log(7+4��3 ) = 0.4320... �� 0.645... (����Ȃ�...)
���Z�����̂ŗ�����̌v�Z�͊ԈႢ�Ȃ��Ǝv���܂�.
������̉�@�͂ǂ��Ń~�X���Ă���̂ł��傤���H �N�������Ă�������.
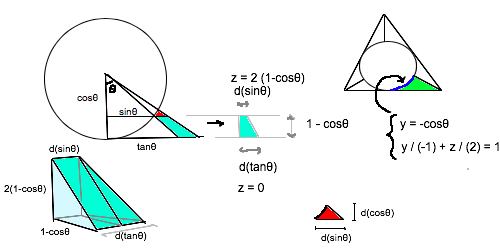 >>591
>>591
�����A(2�������s��)��a,b,c,d
�����x=(x, y)
�Ƃ������Ƃ��̉�@���肢���܂� �~�X���Ă��ӏ�����������.
d(sin��) �̂Ƃ��� d��/cos�� �Ƃ��ׂ�������. d(tan��) = d��/(cos��)^2 �͂��̂܂܂ł悢.
�����̐�: { (2/3). d�� /c + (1/3). d��/c^2 }. (1-c)^2 [c :=cos�� ]
�@�@�@�@�@ = (1/3). (2c+1)(1-2c+cc) /cc = (1/3).{ 1/c^2 -3 +2c }
V = 6 �� [��=0�`��/3] {�����̐�} = 2 tan(��/3) - 6.(��/3) + 4sin(��/3) = 4��3 - 2��
����������������ꂽ.
��������ĊԈ��Ȃ����, ���Ȃ�G���K���g�ȉ�@�ł͂Ȃ����낤�� (���掩�^)
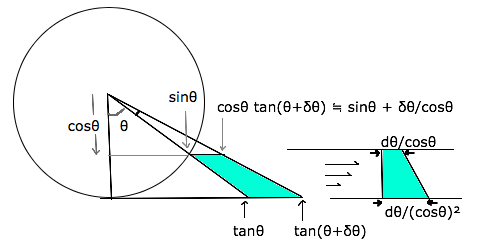 m,M,a,b,c,d�͐����ŁA���ꂼ��ȉ������Ƃ���B
m,M,a,b,c,d�͐����ŁA���ꂼ��ȉ������Ƃ���B
1<=m<=M
0<=a<=b<=c<=d<=m����a+b+c+d=M
m,M��萔�Ƃ���Ƃ��A��������a,b,c,d�̑g�͉��g���邩�H
���ǂȂ������ꂨ�肢���܂��c
�l�����������Ă����Ƃ��肪�����ł��B
��낵�����肢���܂� A��3���̐����ł���BA=100m+10n+l�Ƃ��āAm,n,l�͑S��1���̊�Ƃ���B
A(A+1)�̑S�Ă̌��������ɂȂ鎞�AA�����߂�B
�������Am��n��l�Ƃ���B
���̃e�X�g���ɂ������̂ł����A��������ȊO�ʼn������@���v���t���܂���c�B >>566�@�U�i���őP��
�����̂��Ƃ��l����Ɛi�@�� b �Ƃ��Ă� 6 ��I�Ԃ̂��������Ǝv���B
���Ȃ��Ȃ�K�x�ȕ������ł��ׂĂ̐���\���A
���������f�� 2, 3, 5, 7 �ł̉������ȒP�ɔ���ł���B��̐��� 6 �Ȃ̂ł���B
http://math.tsukuba.ac.jp/~akiyama/papers/proc/NumberTheory_DynSys_rev3.pdf ����Ŏg�������Ȑ��̌�����������̂͂悭�Ȃ�
����ł͏����Ȑ��g���ꍇ���قƂ�ǂȂ���� 10�i����7�̔{���肷����@
�@���̐���1�̈�(A)�Ƃ���ȏ�(B)�ɕ�����
�AA��2�{��B�Ƃ̍���7�̔{���Ȃ猳�̐���7�̔{��
�B��̇A�̐����傫������ꍇ�͇@�`�A���J��Ԃ�
��̇A���uA��B�Ƃ̘a��9�̔{���Ȃ猳�̐���9�̔{���v�ɕς����9�̔{���̔�����@�ɂȂ邱�Ƃ��l����ƁA���قǓ�����Ȃ��̂ł� S[n] = 4*��[k = 1 to n] {(-1)^(k-1)}/(2k-1)
T[n] = (6/��)*��[k = 1 to n] (1/k^2)
�Ƃ����Ƃ��A���̋Ɍ���0�łȂ������Ɏ�������悤�ȗL����p�����߂�B
lim[n����] (n^p)*(S[n] - T[n])
���ꂪ����Ĉ��ڂɉ������ׂ���������܂���B
���łȂ��̂ŁA�W�J���č������̂Ă���@���g���܂��A�]���̎d����������܂���B
���������������B >>840 7�̔{��������@
10a + b �� 0 (mod 7) �� -2*(10a + b) �� 0 (mod 7)
-2*(10a + b) �� -20a -2b �� a -2b �� 0 (mod 7)
�Ȃ�ق�... �B�@3�̔{���X�̔{���Ƃ��͂悭�������邯�ǁA����͏��߂Ēm�����B >>842
���ŃI�C���[�}�N���[���� >>830�O>>827���j�]���B
����z=t�Ő������l�ʑ�PABC�̖ʐς�t=0����1�܂Őϕ����Ă݂�B
����2-t�̐��O�p�`��肿����Ƃ����L���������`��3�B
�����O�p�`���甒���~�������Ĉ���������3�̐�[�𑫂��B
���ABC�̖ʐς�3��3�A���ꂪ�����O�p�`�ɂȂ邽�߂̔{�����Ȃ킿������́A
(2-t)/2
�����O�p�`�̖ʐς́A
(3��3){(2-t)/2}^2
�����~�̖ʐς������āA
(3��3){(2-t)/2}^2-1
����������3�̐�[�̎O�����`�̖ʐς́A
����y=-��3x+2-t��x^2+y^2=1�ɑ�����A
(��{4��3-3+(4-2��3)t-t^2}/2,�}��{7-4��3-(4-2��3)t+t^2}/4)
���a1�̐�`����ʐ�(2-t/2)��{1-(2-t/2)^2}�̎O�p�`�������ĎO�����`���o���Ȃ����ƍl����B
���邢��3�����`��1���킩�邩������Ȃ��Bx���ɐ����Ȃ�Ȃ�B >>842
�� - T[n] = (6/��)��[k=n+1 to ��] (1/kk)
�@�� (6/��)��[k=n+1 to ��] 4/(4kk-1)
�@= (6/��)��[k=n+1 to ��] {2/(2k-1) - 2/(2k+1)}
�@= 2(6/��)/(2n+1),
�� - S[n] = 4��[k=n+1 to ��] {(-1)^(k-1)}/(2k-1)
�@= 2(-1)^n /(2n+1) + 2��[k=n+1 to ��] {(-1)^(k-1)} {1/(2k-1) - 1/(2k+1)}
�@= 2(-1)^n /(2n+1) + 4��[k=n+1 to ��] {(-1)^(k-1)} /{(2k-1)(2k+1)}
�@= 2(-1)^n /(2n+1) + 4��[k=n+1 to ��] {(-1)^(k-1)} /(4kk-1)
�@�� 2(-1)^n /(2n+1),
S[n] - T[n] �� 2{(6/��) - (-1)^n}/(2n+1),
�������ɓ��.... >>833
log_2(x) + log_2(y) + log_2(z) = 1 + log_2(x+y+z)�@�������R���̑g (x,y,z) �ŁA
x��y��z �ł�����̂����ׂċ��߂�B
(����)
�@xyz = 2(x+y+z),
�@(x,y,z) = (1,3,8)�@(1,4,5)�@(2,2,4) ����l�p�`A�̊e�ӂ̒��_�_�Ƃ���l�p�`B�̖ʐς�A��1/2�ł��邱�Ƃ̏ؖ������肢���܂� A(i)�|A(i+1) �̒��_�� B(i) �Ƃ���B
��B1A1B4 = (1/4)��A2A1A4,
��B2A2B1 = (1/4)��A1A2A3,
��B3A3B2 = (1/4)��A2A3A4,
��B4A4B3 = (1/4)��A3A4A1,
�ӁX������
S(A) - S(B) = (��A2A1A4 + ��A2A3A4)/4 + (��A1A2A3 + ��A3A4A1)/4
�@= S(A)/4 + S(A)/4
�@= S(A)/2,
���@S(B) = S(A)/2, >>835
�@��������Ȃ��Ă������Ȃ�
���s�� AD�ABC �̊Ԋu���P�Ƃ���B
A (cot(48�), 1)
B (0, 0)
C (cot(48�)+cot(54�), 0)
D (cot(30�), 1)
cot(48�) = ��{2 + (5+2��5) -2(��3)��(5+2��5)}
cot(54�) = tan(36�) = ��(5-2��5)
cot(30�) = tan(60�) = ��3,
���
�@cot(30�) - cot(48�) - cot(54�)
= ��{2 + (5-2��5) -2(��3)��(5-2��5)}
= cot(84�)
��BCD = 96�
��ACD = 42� �O>>845���͂ł����B
6��[0�`1]{��[��(t-t^2/4)�`��3/2](1-t-��(1-x^2)dx+��[��3/2�`��3-t��3/2](1-t-x/��3)dx}dt
sin��=��(t-t^2/4),cos��=1-t/2�Ƃ����ƁA�����O�������o���ق��������ȁA�Ǝv���Ă���B �O>>852
���l�ʑ�PABC��z=t�Ő����f�ʂ́A�J�����̒��S�p��2�ƂƂ��āA
3��3(2-t/2)^2-1+3��-3sin2��
0��t��1�̂Ƃ�0���Ɓ���/3
�~���ł���ʂ��Ďc�����K���̑̐ς́A
��3��3(2-t/2)^2-1+3��-3sin2��d��dt[��=0�`��/3][t=0�`1] ���܂ł���Ă�����
30������Ώ\���Ȗ�肾�� ������P(z; 1)=�[n=0,��](1/2 C n)(z - 1)^n
��|z|=1�̎����~����̓_�𒆐S�Ƃ���e�C���[�W�J�����Ăǂ��Ȃ�̂ł��傤�� �O>>853
���l�ʑ�PABC��z=t�Ő����f�ʂ́A�J�����̒��S�p��2�ƂƂ��āA
3��3(2-t/2)^2-1+3��-3sin2��
0��t��1�̂Ƃ�0���Ɓ���/3
�~���ł���ʂ��Ďc�����K���̑̐ς́A
��3��3(2-t/2)^2-1+3��-3sin2��d��dt[��=0�`��/3][t=0�`1]
t=2(1-cos��)
��3��3{2-(1-cos��)}^2-1+3��-3sin2��d��[��=0�`��/3]
��3��3(1+cos��)^2-1+3��-3sin2��d��[��=0�`��/3]
=��3��3(1+2cos��+cos^2��)-1+3��-3sin2��d��[��=0�`��/3]
=��3��3(��+2sin��+��/2+sin2��/4)-1+3��-3sin2��d��[��=0�`��/3]
=3��3{��/3+2sin(��/3)+(��/3)/2+sin2(��/3)/4)-1+3(��/3)-3sin2(��/3)}
=3��3(��/3+��3+��/6+1/2)-1+��-3��3/2
=3��3(��/2+��3+1/2)-1+��-3��3/2
=3��3��/2+9+3��3/2-1+��-3��3/2
=(1+3��3/2)��+8
�v�Z�ԈႦ�����ȁH >>856 �����ƒP���ɍs���܂��傤��....
�~���������Ď�肷���������̑̐�(�O�������Č����Ă�����ȁH) �Ȃ�
������ȕ��j�ŋ��߂��܂�.
���a1����1�̉~�����ߐؒf�������̂̑̐� V �����߂���.
��ӂ̐ؒf�ʒu�� a , cos(��) = a �Ƃ��� c = cos�� �Ɨ��L����
V(a) = �� [��= -�� �` +��] d�� { (1/2).(a/cc) + (1/3).(1/c - a/cc) } (c-a)^2 . 1/(1-a)
= �� [��= -�� �` +��] d�� (a + 2c)(cc -2ac +aa) /6cc. 1/(1-a)
= �� [��= -�� �` +��] d�� ( 2c -3a +aaa/cc ) /6 . 1/(1-a)
= { 2.sin�� -3a.�� +aaa.tan�� } / {3(1-a)}
= { (2+aa)��(1-aa) - 3a.acos(a) } / {3(1-a)}
����� 0 �� a �� 1 �ł̏ؖ��ł����A-1 �� a < 0 �ł����̂܂ܓ��������g���܂�. (�ؖ��͗���)
�Ⴆ�� V(-1) = ��/2 ���A�������蔼���̐ςɂȂ��Ă�̂͐}�`�̑Ώ̐���������炩.
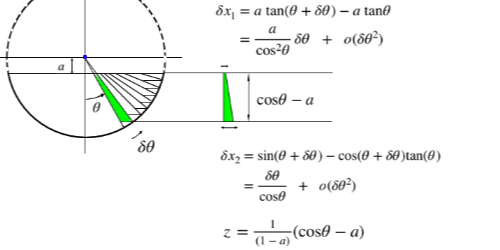 >>853
>>853
���ǃz���g�̍ŏI�w�����ĂȂ�Ȃ�H �P]/�_______�O>>856
�Q/�_/�@�@,,���@�@/|
�P�_/�@�@�c-_-Ё@/ |
�P|�______U,��U�/| |__
�n| �a�P�P�PU~~U | / /
�Q| �a ���@�� �a |/ /
___`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P
�Ԃ������Ă������傢�l����B 2��2019���5�Ŋ������]��
�������𗘗p���Ă��肢���܂� 2^2 = 4 �� -1 (mod 5)
2^(2*1009 + 1) = (2^2)^1009 * 2 �� (-1)^1009 * 2 = -2 �� 3 (mod 5) �O>>859
����1�̒P�ʉ~��(�̐σ�)�̒��S�p120���̐ؓ��O�����`�����O�����`��(�̐ς͂킩��)��1/2�Ȃ̂�2/3�Ȃ̂��A���l�ʑ�PABC�̒��ƊO�ł�����ɕ�������̂��B�������琄�肷��B �O>>862����Ɖ������B
���l�ʑ�PABC=1/3�3��3�2
=2��3
���l�ʑ�PABC��z=1����̕���(���l�ʑ�PABC��1/8)���o���A
2��3(7/8)=7��3/4
x^2+y^2��1��0��z��1�̉~��(�̐σ�)�����̐��O�p�����o���A
7��3/4-3��3/4=��3
���߂闧�̂̑̐�=��3-(��-3��3/4)(2/3)
=3��3/2-2��/3
=0.503681109�c�c >>842 >>846
�� - T[n] = (6/��)��[k=n+1 to ��] 1/kk
�@= 2(6/��){1/(2n+1) - 1/[3�(2n+1)^3] + 7/[15�(2n+1)^5] - 31/[21�(2n+1)^7] + ����}
�� - S[n] = 4��[k=n+1 to ��] {(-1)^(k-1)} /(2k-1)
�@= (-1)^n {1/n - 1/(4�n^3) + 5/(16�n^5) - 61/(64�n^7) + ���� }
���`�ށA������ ������I�C���[�}�N���[������1/n�œW�J�ł�����āB >>853 >>856
�@z = t�@�@�@�@(�� ���Ӗ�?)
�@������ (2-t)/2,
�@���̖ʐ� (3��3){(2-t)/2}^2,
�@�J�����̎O�p�`�̖ʐς́@cos��sin�� = (1/4)(2-t)��{t(4-t)},
�@����ȊO�̐�`�̖ʐς́A���S�p�̔����ŁA��/3 - �� = ��/3 - arccos((2-t)/2),
�@���`�R�̖ʐς�
�@�@(3��3){(2-t)/2}^2 - 3cos��sin�� - ��+ 3��
�@= (3��3){(2-t)/2}^2 - (3/4)(2-t)��{t(4-t)} - �� + 3arccos((2-t)/2),
����� 0<t<1 �Őϕ����� 4��3 - 2�� �O>>864
>>865�ɂ��ĉ�����܂��B
���l�ʑ�PABC(�̐�2��3)����A
���l�ʑ�PABC��z=1����̕���(���l�ʑ�PABC��1/8)���o���A
2��3(7/8)=7��3/4
x^2+y^2��1��0��z��1�̉~��(�̐σ�)�����̐��O�p��(3��3/4)���o���A
7��3/4-3��3/4=��3
�����܂ł��Ɛ��l�ʑ̓������i�C�t�Ő�o�����݂����ȏ�ԂȂ킯�ł��B
�������炳��Ƀ������̒��̉ʓ����X�v�[���ł��킰���Ƃ��݂����ɐ�o���Ȃ��ƁB
�͍���1�̉~���ł��B
3��3/4�͍���1�̐��O�p���ł��B
���߂闧�̂̑̐�=��3-(��-3��3/4)(2/3) ��2/3�Ƃ����͎̂O�����`���̓������o��������ł��B
�O�����`�����A���l�ʑ�PABC�̎߂̑��ʂ��A�����ƊO����2:1�ɕ������ł��B
���S�p��120���Ȃ�ŎO�����`�Ƃ��������g�`�ł��B
=3��3/2-2��/3
=0.503681109�c�c
����(2/3)�̔䗦�ɋC�Â��̂Ɏ��Ԃ�������܂����B
xy���ʂ�z=1���ʂ��O�����`���̏��Ɖ���͍����Ȋ��g�`�ł��B���l�ʑ�PABC�̑��ʂŎ߂ɐ����Ƃ��A�������ɂ͈�_�Ɏ������Ă����`�ł����A������ɂ͒����Ɏ������Ă����A���Ȃ킿���[�̓�_�ɁB
�����2:1�̔䗦�ɂȂ邱�Ƃ������ł��܂����B
>>868z=t���ʂŐ��Đϕ�����������d��(���͂�)���@��������Ȃ��Ǝv������ł����A��蒼���I�Ŋw�I�ȁA�������̐�o���̂悤�ȕ��@�ɕύX���܂����B
z=t�Ő�����œ����l���o���Ƃ́A����ς�0.6�c�c�������Ȃ̂��B ��������ł͂Ȃ��ďؖ������ĉ������B
����1:2�ɂȂ�́H �O>>869�ł����g�͎߂ɐ�ق����������āc�c
�Q/�Q/�Q/�Q/�Q/�Q/�Q/
�Q/�Q/�Q/�Q/�Q/�Q/�Q/
�Q/�Q/�Q/�Q/�Q��_/�Q/
�Q/_��~_/�Q�������̤/
�a�P�P�a�a( (-(`)�@)/
�a�_�^�a�a(`��,U�܁R/
�Q/�Q/�Q/_��_(�Q�Q�Q)
�Q/�Q/�Q/�Q�҃�_UU�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/ �ؒf�ʂ��߂�^���ɃX�p�b�Ɛ�ƒf�ʂɉ~�A�ȉ~�������Ėʓ|�B ������Ă݂���>>842�𑶍݂��Ȃ���ˁH
p<1����0�ɂȂ���p��1���ƐU��������B >>869
2:1 ���]�X�Ƃ���̂� ���g�ߐ肪���g���ɂȂ��Ă�Ǝv���� �u��� * ���� * (1/3)�v ���g���܂����H
�������f�ʂ��S�đ����`�� ���_����̋����ɔ�Ⴕ�ăT�C�Y���ς�� (�������̓���) �ꍇ��...
�� [z=0�`h] dz S (z/h)^2 = S.h.(1/3) �̂悤�� 1/3 �t�@�N�^�[������܂��B
����̂͂����ł͂���܂���B �Ⴆ�ΐ������f�ʂ͑����`�ł͂���܂���B
>>857 �œ��o�����ߐؒf�̎��g����
V(1/2) = { (2+1/4)��(1-1/4) - (3/2). acos(1/2) } / {3(1-1/2)} = (3/4).��3 - ��/3
{�l�ʑ� - (1/2).�l�ʑ�} - {�~��} + {�~���ō�肷������}
= (1- 1/8). 2��3 - �� + 3. { (3/4).��3 - ��/3 } = 4��3 - 2��
���ꂪ�����ł��B a, b �������Ƃ��A a < b �Ƃ���B��� [a, b] �� R �ƔZ�x�����������Ƃ��ȉ��̃q���g�𗘗p���Ď����B
�q���g�F A �� (a, b) ���Z�����W���Ƃ���A A �` A �� {a, b} �͔�r�I�ȒP�Ɏ������Ƃ��ł���B���ꂩ�� (a, b) �` [a, b] ���B �uA �` A �� {a, b} �͔�r�I�ȒP�Ɏ������Ƃ��ł���v
�Ə�����Ă��܂����A�����ł͂Ȃ��̂ł��傤���H �E�ӂ͗v�f�������Ă�̂ɔZ�x���������Ȃ��Ă܂���
�����ł͂Ȃ��ł�
{1}��{1,2,3}���炩�ɔZ�x���Ⴂ�܂���
����͂Ȃ��Z�x���������Ȃ�̂ł��傤�� �Z�����W���̒�`�ł����A N �ƔZ�x���������Ƃ��ɁA�Z�����W���ƒ�`���Ă��܂��B ���A�u�����v�Ƃ������������Ă���̂ŁA�����܂ł��Ȃ����Ƃł��ˁB A = {a_0, a_1, a_2, �c }
a_0 �� a
a_1 �� b
a_2 �� a_0
�c
a_k �� a_{k-2}
�c �̈�D_0�̓����ɐ����_a_0���Ƃ�Ca_0�𒆐S�Ƃ����e�C���[�W�J����f_0(z)�Ƃ���D
f_0(z)�̎����~D_1�����S��D_0�Ɋ܂܂�Ă���ꍇ�CD_1�̋��E�̉~����D_0�̋��E�̋Ȑ��ɓ��ڂ��邱�Ƃ������D D_0={|z|<1}�Œ�`���ꂽ��1/(z-2)�̎����~��|z|=2�B >>881
�̈�D_0�� f(z) �������iD_0�ɓ��ٓ_���Ȃ��j�Ƃ��������������Ă܂�B
>>884
�@f(z) = 1/(z-2)
�@D_0 = {z| |z|<1 }
�@a_0 = 0,
�Ƃ����
�@f_0(z) = -1/2 - z/4 - zz/8 - ����
�����~ D_1 = {z| |z|=2 }
���̏ꍇ�́u�����~D_1 �����S�� D_0 �Ɋ܂܂�Ă���v�����܂���B �O>>874
>>871�~���ō�肷�����͎̂O�����`��(���g)��1/3����Ȃ��̂��H
(�~��-���O�p��)(1/3)
=(��-3��3/4)(1/3) �����~�@D_1 = {z| |z-a0|=R }
�������a�@R = {a_0 ���� f(z)�̓��ٓ_�܂ł̋���(�̍ŏ��l)} >>886
��肷�����̂� �ߐ芗�g���R�ł��B (�ΐF)
V(1/2) = (3/4).��3 - ��/3
���ꂪ�ߐ芗�g�P�̑̐ςł��B�����P�Œ��S���� 1/2 �����Y�����Ƃ�����̎ߐ�ł��B
�Ȃ̂ő������ɂ͂R�{���Ă��܂��B+3. { (3/4).��3 - ��/3 }
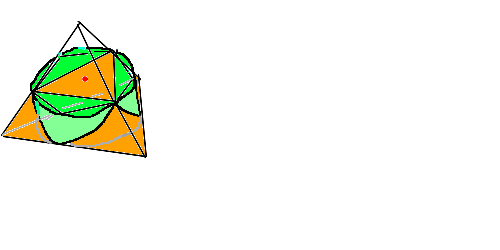 �c����V�E��ؓo�u�Y ���w���w�̃��W�b�N�ƏW���_�x��ǂ�ł��܂��B
�c����V�E��ؓo�u�Y ���w���w�̃��W�b�N�ƏW���_�x��ǂ�ł��܂��B
�J���g���E�x�����V���^�C���E�V�����[�_�[�̒藝�̏ؖ��Ɏg�����1.12�ip.57�j�̏ؖ��ł����A
�v���I�Ȍ������܂����B
���̂悤�Ȋ�{�I�Ȗ���̏ؖ��Ō��Ƃ����̂��M�����܂���B
�������A�������������Ƃ��d���郍�W�b�N��W���_�̖{�ɂ����Ăł��B
���̒��҂�͈�̉����l���Ă���̂ł��傤���H >>881
>>885 �̌����悤�� �u�̈�D_0�� f(z) �������v��t���������...
f(z) = (1/2��i) ��_{C} d�� f(��) / (�� - z) ���̌������g���܂��B (�����̏ؖ��̓R�[�V�[�̐ϕ��藝���g��)
�u�����~(���aR)���̈拫�E�ɐڂ��Ă��Ȃ��v�Ȃ�
R< R' �Ȃ�l���Ƃ��āA���S a ���a R' �̎��[�g C �����̓����� D0 �Ɋ܂܂��悤�ɂł��܂��B
|z-a| < R' �ƂȂ�C�ӓ_ z �ɑ��āA
f(z) = (1/2��i) ��{C} d�� f(��) / ( (��-a) - (z-a) )
= (1/2��i) ��{C} d�� f(��) �� (��-a)^{-k-1} (z-a)^{k} �@( |z-a|/|��-a| =|z-a|/R ' < 1 ��苉���͎�������)
= �� g_k /k! (z-a)^k �@( �W�J�W��: g_k = (k!/2��i) ��{C} d�� f(��) (��-a)^{-k-1} �� z �Ɉˑ����܂���)
����͎������a �� R' �ȏ�ł��鎖���Ӗ����܂��B
����āu�����~(���aR)���̈拫�E�ɐڂ��Ă��Ȃ��v�Ƃ����O��͌��ł��B �̈�D_0�Ő����Ȃ�ĉ����Ă��_���Ȃ͖̂��炩�B
�Œ�ł���`�ł���ɑ��(���ۂɂ͂���͍ő�ɂȂ�)��D_0�ɂȂ�Ȃ�����_���B
����_�ł̎������a = ��͓I�ɐڑ��ł��Ȃ��_�ň�ԋ߂��_�܂ł̋���
���g�킹�����낤���ǂ��̂��߂ɂ�D_0�����q�ׂ��悤�ȗ̈�łȂ��Ɛ������Ȃ��B
�܂��������߂���M���M���������邯�ǁA�����
������ f �̉�͐ڑ��\�ȍő�̈悪���炩�ȋȐ��ň͂܂�Ă���ꍇ
�Ƃ����قƂ�NjN����Ȃ��悤�Ȃ��傤���Ȃ��ݒ�ɂȂ��Ă��܂��B
�ꉞ����������̓����N�����͂��邯�ǁB �Ȃ�ق�
�u�����~�� D0�̓����ɂ���v��
�u�����~(���aR)���̈拫�E�ɐڂ��Ă��Ȃ��v
�͓����ł͂Ȃ��ł��ˁB
f(z) = �� g_k /k! (z-a)^k
�� D0 ���z���Ď�������\��������܂�����ˁB �O>>886�����B
>>890
��肷�����͎̂ߐ芗�g���R��(����)�B
(��肷�����ߐ芗�g3��)
=(��-3��3/4)(1/3)
(��肷�����ߐ芗�g�P��)
=(��-3��3/4)(1/3)(1/3)
�����P�Œ��S����1/2�����Y�����Ƃ�����̎ߐ�(����)�B
�������ɂ͂R�{(����)�B
(��-3��3/4)(1/3)(1/3)3
=(��-3��3/4)(1/3)
���߂�̐�
=(2��3)(7/8)-��
+(��-��3/4)(1/3)
=(7/4)��3-��+��/3-��3/12
=(5/3)��3-(2/3)��
�H��(3/2)��3-(2/3)��
��o�������Ȃ��悤���ɐ�o�����ꍇ���傫���Ȃ����B�Ȃ����H > (��肷�����ߐ芗�g�P��)
> =(��-3��3/4)(1/3)(1/3)
> �����P�Œ��S����1/2�����Y�����Ƃ�����̎ߐ�(����)�B
�����...
V(1/2) = (3/4)��3 - ��/3
����ɂ͓��ӂ��Ă���Ȃ��̂ȁB
���Ɠ������j�Őϕ��v�Z���Ƃ͌���ǁA���Ȃ�y�ȕ�����B
�l�b�g�ɓ]�����Ă�������s���ȁH�Ǝv�������́B ���W��ԏ�̊i�q�_���A�u�C�ӂ̗����̂ɂ��Ē��_�̂������Ȃ��Ƃ���͐F���h���Ă���v�悤�ɗL�����̐F�œh��B
���̎����ׂĂ̒��_�������F�œh���Ă���悤�ȗ����̂����݂��邱�Ƃ������B �y�ɉ����Ȃ狁�߂�̈��1/6���c�ɐ���
6��[1/2,1] (2-2t)(��3t- ��(1-t^2))dt
�ł������ǂȁB ����z���g�Ɋy���Ȃ�
1/6�p�[�c�ڐϕ�����Ȃ� >>834 (��) �������������Ɗy�ł́H
�ŏI�v�Z�܂Ń��[�g�Ȃ炪�o�Ă��Ȃ��̂��������B �O>>896���g�̔䗦�͂���ς�2:1����Ȃ������B
���g3�ǂ�ł�3���ׂĂł��A���g�̒��ƊO�̑̐ϔ��n:s�Ƃ���ƁA
n:s=8:��3
�搳�O�p���䂩�琳�O�p���Ɗ��g3�̒�(���g��n/n+s)���������̐ςƁA���O�p���䂩��~���������Ĉ������������g3�̊O(���g��s/n+s)�𑫂����̐ς���v���邩��
n:s���o���B����Ōv�Z����Ƌ��߂�̐ς�0.6�c�c�ɂȂ邩������Ȃ��B �܂��D���D���͂��邪�A���Z�����炢�ɂ�点��Ȃ�arccos���g���̂����Z���ɂ͂��������n�[�h���������B
�v�Z���̂��̂�>>899�͎���
��[1/2,1]t(1-t)dt
��[1/2,1]t��(1-t^2)dt
��[/2,1]��(1-t^2)dt
�̎O�B
��Ԗڂ͊y���A�������悭�݂��1/6�����̔����A��Ԗڂ��u���Ŋy���A�O�Ԗڂ���t=sin �Ƃ̒u����m���ĂȂ��Ƌꂵ�������B
���������x�ȏ�̃��x����ڎw���Ȃ�arccos����݂��o���Ȃ��ƃ_�������ǂˁB
�~���͏c�ɐ�Ƒї̈�ɂȂ��Ċy�ɂȂ�Ƃ����̂͊o��������ꂽ���A��ꊴ�Ƃ��ďc�Ɋ��������U�߂Ă݂�̂͒�݂����Ȃ���Ǝv���Ă��B
���ɂ����𗧂��Ȃ�����www z=t�Ő�̂���ԑf�����Ǝv�����ǂˁB�ςȒu������킯�ł��Ȃ��������ł��ꔭ�ŏo�邵 ���̖��̉�@�����Ă��������Ȃ��ł��傤���H
�����ł�����炨���炭�Ԉ���������ɂȂ��Ă�̂ŁE�E�E
https://imgur.com/eqrfmk0
https://imgur.com/YtAMHeU > t=sin �Ƃ̒u����m���ĂȂ��Ƌꂵ�������B
���̌v�Z���A�Ƃ���������...
�� {t=0,x} ��(1-t^2)dt = �� ��(1-sin��^2)d{sin��} = �� cos��^2 d��
= (1/2). �� {1 + cos2��} d�� = (1/2){ �� + (1/2).sin2�� }
= (1/2){ �� + cos��sin�� } = (1/2){ asin(x) + x��(1-xx) } (���ꂾ���č��Z���ɂ͋�s�ł́H)
�܂����Z�͊y������
(1/2){ asin(x) + x��(1-xx) }�f = (1/2){ 1/��(1-xx) + ��(1-xx) - xx/��(1-xx) } = ��(1-xx)
[t=1/2, 1 ]�Ȃ� �}�`�I�ɒl���o���Ă��܂��܂��傤�B
��[1/2,1]��(1-t^2)dt = (1/2).(��/3) - (1/2).{(1/2).(��3 /2)} = ��/6 - (1/8).��3
 �O>>901
�O>>901
���l�ʑ̂��������g�̗���͂ǂ��Ȃ�H
�ނ����ɂ��B
���l�ʑ�(�̐�2��3)���������g(��-3��3/4)�̒��ƊO�̑̐ϔ䗦n:s���炵�����߂Ȃ��B �~���͏c�ɐ���ĈӊO�ɑS����̃��[������Ȃ���ww
�܂����ɂ������ɗ����Ȃ�����ˁB
���w�̏Z�l�͎��w���Ƃ��ł͋�J���Ȃ����B
�ʐςɋA�����Ēu�����Ȃ��̂��A�������ǂˁB
�������ʐςɋA���ł��Ȃ��Ƃ������邩����ɂ͒u���̕����܂��o����ƌ���ꂽ�ȁB
���͐̂̂��b�����ǁB
����Șb�����肾�Ǝ������Ă�����B >>905
��ϕ��̒u��������acos�ɖ߂��Ȃ���B
�ϕ��͈͂���/6�`��/2�ɕς��Ă��̂܂܂Ԃ����ނ����B �O>>906
���l�ʑ̂̑��ʂ̌��z��2������1:2:��5�̒��p�O�p�`�𑫂����߂��犗�g�𑤖ʂŐ����O�����o��̂��ȁH ��͐ڑ��Ƃ����܂ŕ����Ă��Ĉ�x���g�������ƂȂ����lj��ɖ𗧂́H �O>>910
��(1-t)^2��ϕ�����Ƃǂ��Ȃ�����H
�u���������Ȃ����B �O>>912�����猾�������Ȃ��B�u���Ȃ�点�邩��B1�ǂ��납3�������H �O>>914
z=t�Ő������l�ʑ̂̐����1�̖��̖ʐς��l���Ă邪�A
t=0�̂Ƃ��́A
6(��3/2-��/6)�ŁA
z=t�̂Ƃ����̒��S�̒�����1����2-t�܂�2-t-1=1-t���邯�ǁA�����z=0�̂Ƃ��̐}�`�Ƒ����ł͂Ȃ���ˁB
t=0�̂Ƃ���/6�������P�ʉ~�̒��S�p���At��������Ƃ����Ă�������B
��肪�������Ȃ�ɂ�āA���̉s�����Ȃ��Ȃ��Ė�莩�̂���肶��Ȃ��Ȃ�B�����ł͂Ȃ����̂��Ƃ݂Ȃ��Ă͂��߂��Ǝv�����B �O>>915
>>801
�l�ʑ�PABC=2��3
���̂�����0��z��1�̕����́A
2��3(7/8)=7��3/4
�����̍���1�̒P�ʉ~���������ƁA
7��3/4-��
�������������g�`�́A���l�ʑ̂̑��ʂ��O�̕����́A���ʂ̌��z��2������A
6��[0�`1/2](1/2)u�2udu
=6[0�`1/2]u^2du
=6{(1/2)^3/3}
=6(1/24)
=1/4
����𑫂��ƁA
7��3/4-��+1/4=0.63949626�c�c
�Ō�ɑ����Ƃ���Ń𗍂߂���������ł����B
����Ƃ�0��t����3/2�ŁA
�s�^�S���X�̒藝���A
(x+1/2)^2+t^2=1�ŁA
6��[0�`��3/2]x^2dx(dt/dx)
�Ƃ�����ł��傤���H
x�̈ꎟ�̍����o���ŁA��Ȃ�ł����B >>885 >>888
�u�̈�D_0 �� f(z)�������v���������Ȃ��Ƃ���B
�@D_0 ���� f(z) �̓��ٓ_(��͐ڑ��ł��Ȃ��_) z~ ������B
�@�������aR = min{ |z~-a_0|, a_0 �` ��D_0�̋���}
����������
�@|z~ - a_0| �� a_0�`��D_0 �����傫���ꍇ�� >>881 �͐������邪
�@|z~ - a_0| �� a_0�`��D_0 �����������ꍇ�� >>881 �͕s�����B �O>>917
����4��3-2�������̏ꍇ�A
2��3(7/8)-��+���g�O=4��3-2��
�����g�O=9��3/4-��
(���g�O1��=3��3/4-��/3)
2��3(7/8)-3��3/4-���g��=4��3-2��
�����g��=2��-3��3
(���g��1��=2��/3-��3)
���g(��-3��3/4)�ɑ��銄���́A
���g�O�\�\41.0040324��
���g���\�\58.9959676��
6:4�Ă��Ƃ�3:2
1:1��2:1�̂��������炢���B�Ȃ���q���䗦���B �����`ABCD�iAB<AC�j�́�A��2�������锼������L1�Ƃ���B
L1��ɓ_P���A����PC�ƑΊp��BD�i����BD�j����_�����悤�ɂƂ�B
���̂Ƃ��A�ȉ��������B
�uPC=BD�ƂȂ邽�߂̕K�v�\�������́APC��BD���������邱�Ƃł���B�v �O>>919����1�̒P�ʉ~�����ɂ��钆�S�p120���̊��g�����z��2�̐��l�ʑ̑��ʂŐ��������̑̐ς��A���̊��g��59���ɂ�����Ƃ��Ď�����B
���l�ʑ�PABC(�̐�2��3)����A
���l�ʑ�PABC��z=1����̕���(���l�ʑ�PABC��1/8)���o���A
2��3(7/8)=7��3/4
x^2+y^2��1��0��z��1�̉~��(�̐σ�)�����̐��O�p��(3��3/4)���o���A
7��3/4-3��3/4=��3
����1�̒P�ʉ~�����̊��g��3���o���A
���߂闧�̂̑̐�=��3-(��-3��3/4)(59/100)
=(1+1.77/4)��3-0.59��
=(1.4425)(1.7320508)-(0.59)(3.14159265)
=2.4984892-1.8535396
=0.6449496�c�c
��0.645 �W�� A ��̉��Z���l����B
�Ⴆ�A2�����Z�́A A^2 ���� A �ւ̊��ł��B
�萔�́A A^1 ���� A �ւ̊��Ȃ̂��Ǝv������A A^0 ���� A �ւ̊��ł���Ə����Ă���܂����B
�Ȃ��ł��傤���H >>923
�ǂ��������Ƃł��傤���H
���������A2�����Z��3�����Z�ƍl���邱�Ƃ��ł��܂��ˁB (Q, 0, +, <) �� (Q^+, 1, �~, <) �͓��^���ۂ��H R_0 := ��
R_{n+1} := P(R_n)
�� R_n ���`����B�������AP(A) �͏W�� A �̂��ׂĂ̕����W���̏W����\���B
R_�� := ��_{n �� N} R_n
�Ƃ���B
R_�� �͋A�[�I�ł��邱�Ƃ������B >>929
���̖��̕W���I�ȉ͂ǂ�Ȋ����ł��傤���H
�F
(1)
�� �� {��} = R_1 �� R_��
(2)
���ɁA���w�I�A�[�@�ɂ��A���ׂĂ̎��R�� n �ɑ��āA
R_n �� R_{n+1}
�����藧���Ƃ��ȉ��Ŏ����F
R_0 = �� �� R_1
R_k �� R_{k+1} �Ɖ��肷��B
x �� R_{k+1} �Ƃ���B
x �� R_k �� R_{k+1}
�� x �� R_{k+2}
����āA R_{k+1} �� R_{k+2} �����藧�B
x �� R_�� �Ƃ���B
x �� R_n �ƂȂ� 1 �ȏ�̎��R�� n �����݂���B
{x} �� R_n �ł���B
x �� R_{n-1} �� R_n �ł���B
�� x �� {x} �� R_n
�� x �� {x} �� R_{n+1} �� R_��
�ȏォ��A R_�� �͋A�[�I�ł���B
x �� {x} �� R_{n-1} �O>>921
>>829���킩��Ȃ��B
r���Ȃɂ�\���Ă邩���킩��Ȃ���ł���B
r�Ƃʼn~�ʂ̒�����\���Ƃ�����A
(�~�ʂ̒����~����)(1/2)�Œ��p�O�p�`�̊��Ƃ݂����Ȗʐς��o��̂��ȁH
0��r��1��0���Ɓ���/3�Őϕ�����6�{����̂Ɠ������Ȃ��H >>933 ���܂莩�M�Ȃ����ǎQ�l�܂ł�
�F�� c1, c2, ... , c6 �Ə����Â��ċ�ʂ���
(1) �܂� c1 �őO�ʂ�h��A�w�ʂ̐F�͂T�F�̑I�����\ (�~ 5)
�c��S�F�̒��ň�� �Ⴂ���Ԃ̐F�� ��ʂ�h��
�c��3�ʂ̓h����͂��ꂼ��قȂ�h����ƂȂ� (�~ 3! )
�v: 5 * 3! = 30 �ʂ�
(2) 5�F��6�ʂ�h��̂ŁA����F�ɂ��Ă� 2�ʂŏd���h��ƂȂ� (�~ 5)
�d���F�őS��/�w�ʂ�h��
�c��S�F�̒��ň�� �Ⴂ���Ԃ̐F�� ��ʂ�h��
���ʂ̓h����c��3�F����I������ (�~ 3)
�c��2�ʂ̓h����͉�]�Ώ̂ɂ�蓯�l�ƂȂ�
�v: 5 * 3 = 15 �ʂ�
(3) �h������ɂ�� 3�ʈȏ�ł̏d���F�͂��肦�Ȃ�
4�F��6�ʂ�h��̂ŁA����Q�F���Ă��ꂼ��Q�ʂł̏d���h�肪�������� (�~ C{4,2})
���̓��ŎႢ���Ԃ̐F�� �O/�w�ʂɁA�c��� ��/���ʂɓh��
�c��2�ʂ̓h����͉�]�Ώ̂ɂ�蓯�l�ƂȂ�
�v: C{4,2} = 6 �ʂ� >>932
>>829��
��ʂ̖ʐό`���~����
���ʂŖʐϕ�����Ƒ̐ς��o��Ƃ�����w�̋��{���w���x�����킩��Ȃ��Ɨ����ł��Ȃ��B
��1)
��(1-r^2)rdrd�� ��0��r��1�A-���Ɓ��Őϕ�����Ɣ��a1�̔����̑̐ςƂȂ�A0��r��1/2�A-���Ɓ��Őϕ�����Ƃ��̂�����ʂ̔��a��1/2�̉~���Ɋ܂܂�镔���̑̐ςɂȂ�B
��2)
(1-r)rdrd�� ��0��r��1�A-���Ɓ��Őϕ�����Ɣ��a1�A����1�̉~���̑̐ςƂȂ�B >>935�ǂ������肪�Ƃ��B�ϐ���2�ł������Ȗʐς𑫂��W�߂�����Ǝv������ł����B�O>>932�����ɂ�������Ȃ���肾�Ƃ킩��܂����B �N�ԂQ�O�O���~����̃X�^�[�g�ŔN�R�O���~�̏����Ɣ��N���ƂɂP�O���~�̏����ł͌�҂̕������B
�i���j
�N�R�O���~�̏����̏ꍇ�A���N��̏����z�́A�R�O�����~�B
���N�łP�O���~���̏����̏ꍇ�A����ڂ̏����͂P�O�����~�B�N�ԂQ��̏���������P�N�ł́A�P�O���{�P�O�i���{�P�j���Q�O��+�P�O���~�B
��+�P=�Q���Ȃ̂ŁA���N���Ƃ̏����̂��N�ڂ̏����́A�Q�O�i�Q���|�P�j+�P�O���S�O���\�P�O���~�B
��ҁ\�O�҂͂P�O���|�P�O���~�Ȃ̂ŁA���Ǔ��z�ƂȂ�̂͂P�N�ڂ����ŁA���̌�́A���N�ɂP��̏����̕����A�����͑傫���Ȃ邱�Ƃ�������B
���N���Ƃ�10�������̌v�Z�����������Ǝv���̂ł����A���̌��͍����Ă܂��ł��傤���H
�܂��A���N���Ƃɋ��^���x������Ƃ����O��ł��Ȃ�����O�҂̕����L���ɂȂ�Ǝv���̂ł����ǂ��ł��傤���H
��������낵�����肢�������܂��B �܂����o�I�ɂ͔����ȑ̐ϑ������킹��Ƃ��������ōs���Ȃ��͂Ȃ��B
>>935�̗�2�Ȃ�rdrd�Ƃ���ʐρB
��r�A���Ƃ���r�ƃƂ��ω����������ar+��r�A���S�p���Ƃ̐�^���甼�ar�A���S�p���Ƃ̐�^���ʂ������̂��ʂƂ���ƁA���̒�ʐς�r��r���ƁB
���̒n�_�ł̉~���̑��ʂ܂ł̍�����1-r������A���̒��̑̐ς�(1-r)r��r���ƁB����𑫂����킹��Ɖ~���̑̐ρB
�Ń�r���Ƃ�drd�ƂƓǂݑւ���>>935�͈͓̔��Őϕ�����B
�܂�r�Őϕ������
��[0,1](1-r)rdr = 1/6�B
������ƂŐϕ�����
��[-��,��] 1/6d�� = ��/3
�ƂȂ��ʐρ~������3 �Ɉ�v����B
���̒��x�̗����łقڎ��p��͖��Ȃ��B
���̕��@�Ŏl�p���Ƃ��F�X����Ă݂Ď��یv�Z�̊������킩���Ă��炿���Ƃ������_������Ă݂�̂��A���B a,b,c,x,y,z�͑S�Đ��̎����Ƃ��āAxyz=1�Ƃ���B���̂Ƃ�
(ax^2+bx+c)(ay^2+by+c)(az^2+bz+c) ��(a+b+c)^3�@�@������
��� ���W���ʏ��(0,0),(1,0),(1,1),(0,1)�_�Ƃ��鐳���`S������B
S�̎���܂��͓����ɁA�قȂ�2�_A(a,p),B(b,q)���Œ肳��Ă���B
S�ƍ����Ȑ����`T���AT�̎����A,B���Ƃ��ɏ��悤�ɓ������B
���̂Ƃ��AS��T�̋��ʕ����̖ʐς��ő�ƂȂ�T�̒u�������������B �O>>936
>>938���̂Ƃ���A��/3�ɂȂ�܂����B������Ă��݂����ł��B
��ʂ̒P�ʉ~�̊O��r���Ƃ�(0��r��1)�A�ʔK�̔�𑫂��W�߂�悤�ɁA���߂�̐ς�1/6�����߂��Ǝv���܂����B
r=0�̂Ƃ��A
���a1�̌ʂ̒����̓�/3
�ʔK�̔�̍�����1
�ʔK�̔�̖ʐς́A
(��/3)�1�(1/2)=��/6
r=1�̂Ƃ��A
���a2�̉~�ʂ̒�����0
�ʔK�̔�̍�����0
�ʔK�̔�̖ʐς�0
r�ɑ���A
���a1+r�̌ʂ̒����́A
���S�p��(0���Ɓ���/3)�Ƃ��āA
(1+r)��
�ʔK�̔�̍�����1-r
�ʔK�̔�̖ʐς́A
(1+r)��(1-r)(1/2)
=(1-r^2)��/2
���߂�̐ς́A
6��[r=0�`1][��=0�`��/3]{��(1-r^2)��/2}drd��
=3��(r-r^3/3)��[r=0�`1][��=0�`��/3]
=2��[��=0�`��/3]
�Ƃ͂ǂ���������̂ł��傤���H >>939
�R�[�V�[(3)���g���B
�@
Xi, Yj, Zk �� 0 �̂Ƃ�
(X1 + X2 + ���� + Xn)(Y1 + Y2 + ���� + Yn)(Z1 + Z2 + ���� + Zn) �� (G1 + G2 + ���� + Gn)^3,
�������@Gi = (XiYiZi)^(1/3).
(����1)
(����) - (�E��)
= ��[i��j] (XiYjZj + XjYiZj + XjYjZi - 3GiGjGj)
+ ��[i<j<k] (XiYjZk + XiYkZj + XjYiZk + XjYkZi + XkYiZj + XkYjZi - 6GiGjGk)
�� 0,
(����2)
�R�[�V�[(2)��2��g����
(X1 + X2 + ���� + Xn)(Y1 + Y2 + ���� + Yn)(Z1 + Z2 + ���� + Zn)(G1 + G2 + ���� + Gn)
�� (G1 + G2 + ���� + Gn)^4,
��@(XiYiZiGi)^(1/4) = Gi, >>942
�R�[�V�[=�V�����@���c�s�����̒��ԂȂ̂�...
����Ȃ̂ǂ��Œm��܂����H (����1) �ŁA �����Ȃ� �� 0 �ƕ]���ł��闝�R���m�肽�� ���R���̏W�����S�����W���ł��邱�Ƃ��Ăǂ�����ďؖ������ł����H ���A���w�I�A�[�@�ł��ˁB
���ꂪ�K�v�ł��ˁB �O>>941�C���B
���߂�̐ς́A
6��[r=0�`1][��=0�`��/3]{��(1-r^2)��/2}drd��
=3��(r-r^3/3)[r=0�`1]��[��=0�`��/3]��d��
=2���/3
=2��^2/3
�Ȃ킯�Ȃ��ł���ˁB
r��������ƃƂ͌���B
����Ⴖ��Ȃ����ƁB
�������̎��̒��Ŋ|�����킹�Ă�̂����������悤�ȁB
�O�p�`(1/2)(1+r)rcos�Ƃ����`(1+r)�Ƃ��������f�ʐ�(1/2)(1+r)rcos��-(1+r)�Ƃ�0����1�܂ő����W�߂�ق������������B
6��[r=0�`1][��=0�`��/3]{(1/2)(1+r)rcos��-(1/2)(1+r)��(1+r)}drd��
3��[r=0�`1][��=0�`��/3]{(1+r)rcos��-(1+r)��(1+r)}drd��
�ϐ���2����łȂ��B >>946
���̓��ɂȂ���Ă��Ƃ̓y�A�m������
�u�ŏ��̏������v�Ȃ��`���� >>868 �̑���
���R�̖ʐς�
�@(3��3){(2-t)/2}^2 - 3cos��sin�� - �� + 3��
= (3��3){(2-t)/2}^2 - (3/4)(2-t)��{t(4-t)} -�� + 3arccos((2-t)/2) = S(t)
����� 0�`z �Őϕ�����
��[0, z] S(t) dt = (2��3)[1 - {(2-z)/2}^3] - (1/4){z(4-z)}^(3/2) -��z -3(2-z)arccos((2-z)/2) + 3��{z(4-z)},
������ z=1 �Ƃ����� 4��3 - 2��
�~���̊e�_�̍��� h(r,��) ��ϕ������̐�3v�� V=2��3 ����������l�ƈ�v�B >>829 >>944
��̍s��
�@(XiYjZj + XjYiZj + XjYjZi)/3�@= AM�@(��������)
�@GiGjGj�@=�@GM�@(���敽��)
�@AM �� GM
���̍s�����l�B ���݂܂���A���߂Ă��̖������肢���܂��B
�����`ABCD�iAB<AD�j�̓��p��A��2��������L�Ƃ���B
L��ɓ_P���A����PC�ƑΊp��BD����_�����悤�ɂƂ�B
���̂Ƃ��A�ȉ��������B
�uPC=BD�ƂȂ邽�߂̕K�v�\�������́APC��BD���������邱�Ƃł���B�v ����1��A��������肢���܂��B
�i1�jS[n] = ��[k=1 to n] k!�@���������ƂȂ�n��S�ċ��߂�B
�i2�jS[n]-3�@�ɂ��Ă͂ǂ����B������0�͕������Ƃ��Ĉ����B AB=4,BC=5,CA=6�́�ABC�ɂ����āA���̊O�ډ~��R�ACA�̒��_��M�AA����BC�ɉ��낵�������̑���H�Ƃ���B
�܂��AM��ʂ�AH�ƕ��s�Ȓ����ƁA���CA�Ƃ̌�_��D�Ƃ���B
���̂Ƃ�AD�̒��������߂�B �̈�D: y ≥ |1/(1+e^x)| �Ƃ���B
D���a1�̉~C�������Ƃ��AC�������Ēʉ߂ł��Ȃ����������݂���B
���̖ʐς����߂�B �Ȃ���Βl�����Ă���̂ł��傤���H ��ϕ�I[x] = ��[1 to x] ln(x) dx �ɑ��A
�s����m < I[n] < m+1�������R��n�̌���a[m]�Ƃ����B
m��m=1,2,...�Ɛ��̐����l���Ƃ�Ƃ��A
b[m]=a[m+1]/a[m]�Œ�`����鐔��b[m]�ɂ��āA
���̑����A�����Am�����Ƃ����Ƃ��̋Ɍ�
�����ꂼ��q�ׂ�B �قƂ�ǂ�a[m] �� 0 �����B
b[m] �قƂ�ǒ�`�ł��Ȃ��̂ł́H >>942
�@
�R�[�V�[(2)
Xi, Yj �� 0 �̂Ƃ�
(X1 + X2 + ���� + Xn)(Y1 + Y2 + ���� + Yn) �� (G1 + G2 + ���� + Gn)^2,
�������@Gi = ��(XiYi).
(����)
(����) - (�E��) = ��[i<j] (XiYj + XjYi -2GiGj)
�@= ��[i<j] {��(XiYj) - ��(XjYi)}^2
�@�� 0,
�@���O�����W���̍P�����Ƃ��]���炵���B
�@���������� Xi/Yi = (���) >>953
���ɋ����[�����ł��B
��낵�����肢���܂��B cosx/sinx(1+cosx)�̐ϕ���N�������Ă������� >>960
tan(x/2)=t�ƒu��
���̎�̐ϕ��͑S�ĉ������� ���B�搶����̏o��ł��B
�O����P�̊Ԃ�
�P�@�L�����͉�����ł������B
�Q�@�������͉�����ł������B
�R�@�����͉�����ł������B
�S�@�L�����Ɩ������ł́A�ǂ��炪�����ł������B ��������B�搶����̏o��ł��B
���̂����A�������̂͂ǂ�ł������B
�P�@1/2+1/4�{1/8�{�c�c�͂P�ɂȂ�B
�Q�@0.99999�c�c�͂P�ł���B
�R�@0.99999�c�c��0.9�{0.09�{0.009�{�c�c�Ɠ����ł͂Ȃ��B
�S�@0.99999�c�c�͍ŏ�����9������������ł���B
�T�@�L����������Ȃ鐔��̋Ɍ��l�����������ł���B
�U�@�L����������Ȃ鐔��̋Ɍ��l�����������ł���B
�V�@�����������̂��Ɍ��l�ł���B
�W�@�����������̂��Ɍ��l�ł���B
�X�@���������͎����ł���B
10�@���������͕K���Ɍ��l�����B
11�@�����������݂���B
12�@���R�����́��ɂ͂Ȃ�Ȃ����A�����̂͑��݂���B
13�@�����͘A����������B
14�@���͓_�̏W���ł���B
15�@��������Ŏ����������_�̏W���͐��ɂȂ�B
16�@��������ɔ�Z�̎��������݂���B
17�@�����W�������݂���B
18�@�Z�����W���͏W���ł͂Ȃ��B
19 ���R���̖����������̖����̕��������B
20�@�L�E�ȒP������͎�������i�Ɍ��l�����j�B
21�@�̐ςQ�̐������̂����݂���؋��͂Ȃ��B >>963
�����͂킩��Ȃ��������₷��ꏊ�ł��O���o��҂Ԃ��Ė�����������ꏊ����Ȃ� �����͂킩��Ȃ��������₷��ꏊ�ł͂���܂���
�킩��Ȃ����������ꏊ�ł� ���X���̓^�C�g���ɢ���⣓���悤���� ���Z���ł�
�u���SO�A���a1�̉~���ʂƂ��A������1�̒��~��������B�_O��ʂ�ʂ�45���̊p�Ō����ʂ�P�Ƃ���BP�ŕ������ꂽ�~���̏��������̑̐ς����߂�B�v
�Ƃ������ŁAO�����_�AO-���_��z���AP��x=z�Ƃ�����y=t�Ő��Đϕ�����ƁA���̐ϕ������߂Ȃ���Ȃ炸�A���̔]�ł͋l��ł��܂��܂���
�͔͉��琔�l�v�Z����Ƃ��̐ϕ��܂ł̕ό`���͍̂����Ă�悤�Ȃ̂ł����A���̐ϕ��͂ǂ�������狁�߂���ł��傤���H
�i�ł�����Z�͈͂܂łł��肢�������܂��j
�܂��AP�ƕ��s�ȖʂŐ��Đϕ�����ƊȒP�Ȍv�Z�ŋ��܂�悤�ł����A����͂Ȃ��ŁA
�ǂ�������猩������̂ł��傤���H
https://i.imgur.com/J2I9PS6.jpg
https://i.imgur.com/PcjjXAU.jpg >>967
1-t^2=a�Ƃ����Ƃ��At=sinx�Ƃ����Ƃ�
���Ɛؒf�ʂɉ~�ʂ��o��ꍇ�A�t�O�p�����K��Ȃ����Z���w�ł͐ϕ��s�̂��Ƃ���������C������ �����f�ʐς��ȒP�ɋ��܂�����������������B
�~���Ȑ��͕���ɕ��s�ɐ������ɕ������ɂȂ��Ĉ�Ԗʐϋ��߂₷���B >>950 ���肪�Ƃ��������܂��B�����ł��l���Ă݂܂����B
��ʂ� N�̃x�N�g�� a,�c,z ���^����ꂽ��
���@�ya,b,�c,z�z �� ||a||{N}.||b||{N}�c || z ||{N}
����������. (N=2 ���R�[�V�[=�V�����@���c�s������^����)
�������x�N�g���̐����͑S�Ĕl�����A
p-�m����: ||v ||{p} := (v1^p + v2^p +�c+ v[n]^p )^{1/p}
����: �yu,v�z := u1v1 +�c+ u[n]v[n]
�yu,v,w�z := u1v1w1 +�c+ u[n]v[n]w[n] , �c etc.
�̂悤�ɒ�`����Ă�����̂Ƃ��܂�.
( 3�ȏ�ɂ��Ă͓��ςƂ͌����܂���. �L�@�����������̋L�@�ł�. )
�ؖ�
N-1 �̃x�N�g���ɂ��Ă͐�������Ɖ��肷��.
Z=(b1..z1, b2..z2, �c, b[n]..z[n] ),�@1/N + 1/N�f = 1 �ƒu��.
�ya,b,..,z�z = �ya, Z�z �� ||a||{N}.||Z||{N�f} (�� �w���_�[�̕s���� (����͂Ƃ��̖{�ɍڂ��Ă�))
b�f = (b[1]^N�f,�c,b[n]^N�f), ..., z�f=(z[1]^N�f,�c,z[n]^N�f) �ƒu��.
( ||Z||{N�f} )^{N�f} =�yb�f, �c, z�f�z �� ||b�f||{N-1}*�c*||z�f||{N-1} (�� ����)
||b�f||{N-1} = ( b[1]^(N�f(N-1)) + �c)^{1/(N-1)} = ( b[1]^N + �c)^{N�f/N} = ( ||b||{N} )^{N�f}
�� ||Z||{N�f} �� ||b||{N}�c||z||{N}�@
���w�I�A�[�@�ɂ��
�ya, b, .., z�z �� ||a||{N}.||b||{N}�c||z||{N}
�������ꂽ. >>968
�����ŋ��܂�܂����H
�ϐ����������܂ސF�X��A1+��1-t^2�ƒu������tt��ϕ����ĕ����ϕ��Ȃǂ͂���Ă݂��̂ł����S�����܂�Ȃ������̂ł���
��̓I�ɂǂ��ό`��������܂����ˁH >>971
���R�����ǂł���Ƃ͎v�����ǃR���ǂ����̉ߋ���Ȃ�H
���̃��x�����܂������ŏo�Ă�Ȃ���{���܂��̂Ă�����Ȃ����ǁB ���܂�܂����A���肪�Ƃ��������܂��B�ǂ����Ōv�Z�~�X�����̂��Ǝv���܂��B������x�����Ă݂܂�
�m������c�H���Ǝv���܂� >>973
����c�̉��N���킩��܂����H �O>>947
>>829
��BOC �Ɋ܂܂���`�����̑̐�v
���̊e�_�̋ɍ��W�� (r,��) �Ƃ���� 0��r��1, -60߁��Ɓ�60�
�e�_�ɂ����鍂���� h(r,��) = 2(1+y) = 2(1-r�cos��)
�@v = ��[0,1] ��[-60�,60�] h(r,��) d�� rdr = 2(��-��3)/3
��
�������AOB�ł���Ă��l�͓����ł���ˁH
���̊e�_�ɂ�����ɍ��W��(r,��)�Ƃ���ƁA
0��r��1
0�����Ɓ�120��
�e�_�ɂ����鍂���́A
h(r,��)=2(1-rcos��)
�������}�ŗ����ł��Ȃ��Ƃ���ł��B
v=��[0,1]��[0��,120��]h(r,��)d��rdr
=2(��-��3)/3������͂ǂ�����ďo����ł����H >>974
���N���͕s���ł�������c�ł����B
1-t^2=a�Ƃ����Ƃ�t=sinx�Ƃ����Ƃ��ƂĂ�������C�����Ȃ��̂ŋ�̓I�ȕό`�������ĉ������B �Ƃ肠���������ɗ�������Βf�ʐς�
1/2(1-t)^2acos (t/(1-t)) -t��(1-2t)
���Ǝv���B
�����I�ɂ͂ł��邯�ǎł��̐ϕ�����̂̓I�X�X���ł��Ȃ��������ς�߂ɐ�ׂ����ˁB
���邢�͗����������ĉ~�����W�g���ăp�b�v�X�M�����^���̈�ʉ��g����
cos(t)(2+cos(t))/(1+cos(t))^2/3
��-��/2�`��/2�Őϕ�����̂��y����B Dmg = Atk * (1.00+x1+x2) * (1.00+y1+y2)
�EAtk �c ����̊�b�_���[�W
�E�ϐ� x1,x2 �c �����iX������l (�Ώۂ̎푰�ɂ�� +0�`10% �܂�)
�E�ϐ� y1,y2 �c �����iY������l (�Ώۂ̕����ɂ�� +0�`10% �܂�)
{0.00 < x1 < 0.10} (x2,y1,y2 ���S�ē��l)
���̎��A�Ȃ�ׂ����Ȃ���l�̑�����̑g�ݍ��킹��
�傫���_���[�W���o�������B
�₢
Atk = 5100 �ŁA6000�_���[�W�ȏ��ڎw���Ƃ���B
����1
6000 =< 5100 * (1.00+x1+x2) * (1.00+y1+y2)
�œK�� (x1,x2,y1,y2) �̑g�ݍ��킹�͉����H
����2
Y�� +10% �̕�l��1���̂��m�肵�Ă���A
y2 = 0.10 �ƌŒ�ł���Ƃ���B
���̎��A�œK�� (x1,x2,y1) �̑g�ݍ��킹�͉����H �O>>975
>>829
2(��-��3)/3�͂ǂ�����ďo����ł����H
���s���v�Z�ߒ�������͂����B ����E����c�E���ȑ�Ƃ��ŗ��s������� >>976
���̎�̎O�p���̗L�����ł�x=tan(s/2)�ƒu������̂���ŁA�قڑS�ĉ�����
��������͑�w�ŏK���u���ŁA�֗������Ǎ��Z�ł͂قڎg��Ȃ�
�[�������Ȃ��Ȃ炱��Ōv�Z���� >>982
����͒m���Ă��܂����A����ł��܂��s���͎̂O�p�������̎��ł͂Ȃ��ł����H
�����log���Ă��܂����s���܂����H �����������O�p���n�̒u�������ł͌������̂ł͂Ȃ����Ƃ������G���̂ł���
�X�b�L������������炵���炨�肢���܂�m(_ _)m log(������)�̐ϕ��͕����ϕ��ŗL�����̐ϕ��ɂȂ邶��� >>982
���n�̍��Z���Ȃ畁�ʂɒm���Ă��ł� >>983
���̎���
log���Ă���͒m������I�ɂ͕s��ϕ��͋��܂�͂� >>983
���Ƃ��O�A�����ԓx�ł͂Ȃ���
�Ⴂ�Ȃ�5ch����Ȃ���twitter�ł��s�� t=sinx �Œu���������ƕ����ϕ�����s���邯�ǁc https://i.imgur.com/KPdarxm.jpg
���͎����_�̈ꖽ����f�f�L���g�̐ؒf���g���ďؖ����Ă��܂��B
�����ꒃ��₱�����Ȃ��ł����H
Cantor ���̂ق��������ł���ˁH ���A����͎����̐����Ƃ������L�����̐ؒf�̐����ł��ˁB
����Ȓ藝�Ȃ�ŏؖ����Ă����ł����ˁH >>988
�\����܂���ł����B
>>989
���肪�Ƃ��������܂��B���܂�܂����B �� = <A, A'>
r �� A �� <R, R'> < <A, A'>
r �� A' �� <A, A'> �� <R, R'>
�Ƃ������Ƃ������Ă��܂��B
�L���� r �� <R, R'> �iR = {q �� Q | q < r}, R' = {q �� Q | r �� q}�j�ꎋ����Ƃ������Ƃł����ǁA
���Ƃ��Ƃ̗L���� r �ƍl���邩�ؒf <R, R'> �ƍl���邩��s���̂����悤�Ɍ��߂Ă�����ł����H �L���� r �Ɠ��ꎋ���� <R, R'> �ɂ��Ăł����A R = {q �� Q | q < r}, R' = {q �� Q | r �� q} �ł�����A
�I���W�i���̗L�������g���Ē�`����Ă��܂��B
����Ȃ��Ƃ��Ă�OK�Ȃ�ł����H
�Ⴆ�A���� �� = <A, A'> �� A �� A' �͗L�����̏W���ł��B
A �̗v�f�̓I���W�i���̗L�����Ȃ̂��I���W�i���̗L�����Ɠ��ꎋ���ꂽ�ؒf�Ȃ̂��H
�����A�ؒf���Ƃ���Ƃ��̐ؒf = <R, R'> �� R �� R' ���\������L�����́A
�I���W�i���̗L�����Ȃ̂��I���W�i���̗L�����Ɠ��ꎋ���ꂽ�ؒf�Ȃ̂��H
�����A�ؒf���Ƃ���Ƃ��̐ؒf = <R, R'> �� R �� R' ���\������L�����́A
�I���W�i���̗L�����Ȃ̂��I���W�i���̗L�����Ɠ��ꎋ���ꂽ�ؒf�Ȃ̂��H
�c >>978
���̂P
5100*1.08*1.08=5948.64
5100*1.08*1.09=6003.72
�Ȃ̂ŁA{x1+x2,y1+y2}={0.08,0.09}
��̓I�ɂ́Ax1,x2,y1,y2�@�̓��O��0.04�ŁA���0.05 �Ƃ����̂��A�ő����ŏ��ōς�
���̂Q
y1=0.00�̎��Ax1+x2=0.07�@��@5100*1.06*1.10=5946.6�A5100*1.07*1.10=6002.7
y1=0.01�̎��Ax1+x2=0.06�@��@5100*1.05*1.11=5944.05�A5100*1.06*1.11=6000.66
y1=0.02�̎��Ax1+x2=0.06�@��@5100*1.05*1.12=5997.6�A5100*1.06*1.12=6054.72
y1=0.03�̎��Ax1+x2=0.05�@��@5100*1.04*1.13=5993.52�A5100*1.05*1.13=6051.15
y1=0.04�̎��Ax1+x2=0.04�@��@5100*1.03*1.14=5988.42�A5100*1.04*1.14=6046.56
y1=0.05�̎��Ax1+x2=0.03�@��@5100*1.02*1.15=5982.3�A5100*1.03*1.15=6040.95
...
x1,x2,y1�̓����0.02�ŁA���0.03�� �Ƃ����̂��A�ő����ŏ��ōς� >>975 >>979
h(r,��) = 1 - r�cos��,
�������
v = ��[0,1] ��[-60�,60�] h(r,��) d�� rdr
�@= ��[0,1] ��[-��/3,��/3] (1-r�cos��) d�� rdr
�@= ��[0,1] rdr���[-��/3,��/3] d�� - ��[0,1] rrdr���[-��/3,��/3] cos�� d��
�@= (1/2)(4��/3) - (1/3)[ sin�� ](-��/3����/3)
�@= (2��-��3)/3,
�����ϕ����Ȃ��Ă��o��B
���X��
http://rio2016.5ch.net/test/read.cgi/math/1562421561/ >>960
�@(1+cos(x))/sin(x) = sin(x)/(1-cos(x))
���g����
�@��(�^��) dx = {cos(x)/(1-cos(x))} sin(x)dx
�@= ��(1-z)/z dz�@�@�@�@�@{z = 1-cos(x)}
�@= ��(1/z -1) dz
�@= log(z) - z + c
�@= log(1-cos(x)) + cos(x) + c', ���̃X���b�h�͂P�O�O�O���܂����B
�V�����X���b�h�𗧂ĂĂ��������B
life time: 50�� 21���� 49�� 40�b 5�����˂�̉^�c�̓v���~�A������̊F���܂Ɏx�����Ă��܂��B
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�s�v���~�A������̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
��300�~���瓽���ł��w�����������܂��B
�� �v���~�A������o�^�͂����� ��
https://premium.5ch.net/
�� �Q�l���O�C���͂����� ��
https://login.5ch.net/login.php ���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B