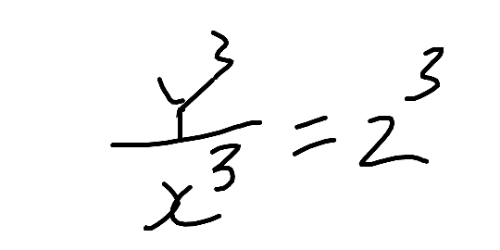フェルマーの最終定理の簡単な証明
■ このスレッドは過去ログ倉庫に格納されています
【定理】n=3のとき、x^n+y^n=z^nは自然数解を持たない。
x^3+y^3=z^3を、x^3+y^3=(y+1)^3…(1)とおく。(x,yは有理数)
(1)が有理数解を持つならば、必ず整数解を持つので、x,yは整数とする。
(1)を(x^3-1)/3=y^2+y…(2)と変形する。
(2)の左辺をA,右辺をBとおく。A=Bならば、A^(1/2)=B^(1/2)となる。
B^(1/2)は、yの増加につれて、y+0.5に近づく。
A^(1/2)は、xの増加につれて、y+0.5に近づかない。
∴n=3のとき、x^n+y^n=z^nは自然数解を持たない。 >>170
> 「3つの整数aとbとcが互いに素」であるとは、「aとbとcの最大公約数が1になる」ことをいう。
>
> ではないでしょうか?
だから2と8と15の最大公約数は1と書いているだろ
おまえが
> 8は、2で、割り切れます。
などとアホなことを書いているだけ >>172
> 8と2の最大公約数は2ではないでしょうか?
なぜ2と8と15の最大公約数が2と8の最大公約数なんだよ 「3つの整数aとbとcが互いに素」であるとは、「aとbとcの最大公約数が1になる」ことをいう。
ではないでしょうか? >>174
> 「3つの整数aとbとcが互いに素」であるとは、「aとbとcの最大公約数が1になる」ことをいう。
>
> ではないでしょうか?
だから2と8と15の最大公約数は1と書いているだろ
おまえが
> 8は、2で、割り切れます。
などとアホなことを書いているだけ
2と8と15の最大公約数 = (2と8の最大公約数)と15の最大公約数 = 2と15の最大公約数 = 1
2と8と15の最大公約数 = 2と(8と15の最大公約数)の最大公約数 = 2と1の最大公約数 = 1
2と8と15の最大公約数 = 8と(2と15の最大公約数)の最大公約数 = 8と1の最大公約数 = 1 「3つの整数aとbとcが互いに素」であるとは、「aとbとcの最大公約数が1になる」ことをいう。
は、間違いでしょうか? >>176
> 「3つの整数aとbとcが互いに素」であるとは、「aとbとcの最大公約数が1になる」ことをいう。
>
> は、間違いでしょうか?
間違ってない
間違っているのは日高(のフェルマーの最終定理の証明)
以下は
https://www.nli-research.co.jp/report/detail/id=57057
より引用
3つ以上の整数が互いに素という概念とその確率
「互いに素」という概念は、3つ以上の整数に対しても拡張される。
例えば、「3つの整数aとbとcが互いに素」であるとは、「aとbとcの最大公約数が1になる」ことをいう。
これに対して、aとb、aとc、bとcが互いに素である場合には、「aとbとcは対ごとに素(pairwise coprime)」であるという。
対ごとに素であれば互いに素となるが、互いに素であっても対ごとに素であるとは限らない(例:a =3、b = 5、c = 6)。 なぜ、フェルマーの最終定理の証明に、
「互いに素」が必要なのでしょうか? >>178
> なぜ、フェルマーの最終定理の証明に、
> 「互いに素」が必要なのでしょうか?
x^2+y^2=(y+1)^2の自然数解を(x,y,z)=(a,b,b+1) (a,bは自然数)とすると
たとえばx^2+y^2=(y+2)^2の場合の自然数解は
「互いに素」である自然数解と「互いに素」でない自然数解の2通りありうる
「互いに素」でない自然数解は(a,b,b+1)と解の比が等しい
「互いに素」である自然数解は(a,b,b+1)と解の比が異なる
実際にx^2+y^2=(y+2)^2は(a,b,b+1)と解の比が異なる(8,15,17)=(8,15,15+2)を解に持つ
2,8,15は互いに素なので8,15,17(=15+2)も互いに素
x^2+y^2=(y+1)^2は解の比が8:15:17である自然数解を持たないが
x^2+y^2=(y+2)^2は解の比が8:15:17である自然数解(8,15,17)(「互いに素」である)を持つ x^2+y^2=(y+1)^2は解の比が8:15:17である自然数解を持ちます。
x,y,z=4,15/2,17/2 >>180
> x^2+y^2=(y+1)^2は解の比が8:15:17である自然数解を持ちます。
> x,y,z=4,15/2,17/2
よって
x=4,y=15/2,z=17/2が自然数ならば日高の証明は正しい
日高の証明が正しいならばx=4,y=15/2,z=17/2は自然数
y=15/2は自然数(整数)でない
z=17/2は自然数(整数)でない
日高の証明は間違い
> 117 日高2022/06/09(木) 22:04:02.15ID:8FftgGxZ
> y=15/2は、整数解ではありませんが、
> 解の比は、(8:15:17)となります。
> y=15/2は、整数解ではありませんが、
は
私(日高)の証明は正しくありませんが
と言い換えられる >>180
> x^2+y^2=(y+1)^2は解の比が8:15:17である自然数解を持ちます。
> x,y,z=4,15/2,17/2
x^2+y^2=(y+1)^2は解の比が8:15:17である自然数解を持たないが
x^2+y^2=(y+2)^2は解の比が8:15:17である自然数解(8,15,17)(「互いに素」である)を持つ
を書き換えて
a,bは自然数とする
x^2+y^2=(y+1)^2は解の比がa:b:b+2の自然数解(2,a,bは「互いに素」である)を持たない
x^2+y^2=(y+2)^2は解の比がa:b:b+2の自然数解(2,a,bは「互いに素」である)を持つ
a:b:b+2の場合だけを考えて終わりというわけではない
a,bは自然数とする
x^2+y^2=(y+1)^2は解の比がa:b:b+1の自然数解を持つ
x^2+y^2=(y+1)^2は解の比がa:b:b+2の自然数解(2,a,bは「互いに素」である)を持たない
x^2+y^2=(y+1)^2は解の比がa:b:b+3の自然数解(3,a,bは「互いに素」である)を持たない
などと続く (1)が有理数解を持つならば、必ず整数解を持つので、x,yは整数とする。
これが、間違いだという証明はできますか? フェルマーワイルスの定理の簡単な証明など無いよ。
あのオイラーが、指数が3のときしか証明できなかったんたからな。 >あのオイラーが、指数が3のときしか証明できなかったんたからな。
どうして、このことが理由になるのでしょうか? オイラーが証明できなかった
平方剰余の相互法則の証明は
200通りほど知られているのでは? >>185
> (1)が有理数解を持つならば、必ず整数解を持つので、x,yは整数とする。
> これが、間違いだという証明はできますか?
x^2+y^2=(y+1)^2…(1)は解の比がx:y:z=a:b:cであるx,y,zが正であるような解を持つとする
解の比がx:y:z=a:b:cであるx,y,zが正であるような解は一通りしかないから
整数解でない有理数解をもつ場合は解の比が同じ整数解を持つことはない
例
x:y:z=3:4:5の場合
(1)のx:y:z=3:4:5でありx,y,zが正であるような解は(x,y,z)=(3,4,5)の一通り
x:y:z=8:15:17の場合
(1)のx:y:z=8:15:17でありx,y,zが正であるような解は(x,y,z)=(4,15/2,17/2)の一通り
(1)はx:y:z=8:15:17の整数解を持たない
x:y:z=20:21:29の場合
(1)のx:y:z=20:21:29でありx,y,zが正であるような解は(x,y,z)=(5/2,21/8,29/8)の一通り
(1)はx:y:z=20:21:29の整数解を持たない >>188
お前がオイラーと比較して遥かに数学能力も理解力も事実認識も出来てないからだろ >190
(x,y,z)=(4,15/2,17/2)の有理数解は、
x:y:z=8:15:17の整数解と同じだと思いますが?(同じ比) >>192
> (x,y,z)=(4,15/2,17/2)の有理数解は、
> x:y:z=8:15:17の整数解と同じだと思いますが?(同じ比)
x^n+y^n=(y+1)^nが整数解を持たないことを仮に正しく示しても
x^n+y^n=(y+2)^n, x^n+y^n=(y+3)^n, ... が整数解を持つかどうかは
分からない
だからおまえの証明は間違っているだろ
> (1)が有理数解を持つならば、必ず整数解を持つので
は成り立たない
x:y:z=8:15:17の整数解を持つのはx^2+y^2=(y+2)^2であって
x:y:z=8:15:17の整数解がx^2+y^2=(y+1)^2…(1)にないことには変わりない x^n+y^n=(y+1)^nが整数解を持つならば、
x^n+y^n=(y+2)^n, x^n+y^n=(y+3)^nも整数解を持ちます。 >>194
> x^n+y^n=(y+1)^nが整数解を持つならば、
> x^n+y^n=(y+2)^n, x^n+y^n=(y+3)^nも整数解を持ちます。
それはあたりまえ
x:y:z=8:15:17やx:y:z=20:21:29の場合は
x^n+y^n=(y+1)^nが整数解を持たないような解の比x:y:z(x,y,zは整数)についての話 こんなかんたんな形にできたんだな
x^3+y^3=z^3
0^3=1+1^3=1=2^3=8
1/1=8
1=8
1+1=8
2=8
1=4
^2のときは1+1=4
2=4
1=2成立
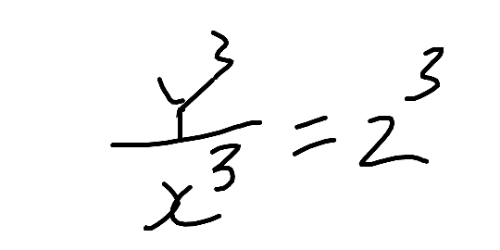 >195
>195
^n+y^n=(y+1)^nが整数解を持たないような解の比x:y:z(x,y,zは整数)についての話
どういう意味でしょうか? >>198
> どういう意味でしょうか?
>>194
> x^n+y^n=(y+1)^nが整数解を持つならば、
> x^n+y^n=(y+2)^n, x^n+y^n=(y+3)^nも整数解を持ちます
たとえばx:y:z=x:y:y+1=3:4:5の場合ならば
x^2+y^2=(y+1)^2が互いに素な整数解(x,y,z)=(x,y,y+1)=(3,4,5)を持つ場合
x^2+y^2=(y+2)~2は互いに素でない整数解(x,y,z)=(6,8,10)を持ち
x^2+y^2=(y+3)^2は互いに素でない整数解(x,y,z)=(9,12,15)を持つ
ということである
x:y:z=8:15:17の場合は
x^2+y^2=(y+1)^2はx:y:z=8:15:17の整数解を持たない (17-15≠1であるから)
x^2+y^2=(y+2)~2は互いに素でない整数解(x,y,z)=(8,15,17)を持つ
x^2+y^2=(y+3)^2はx:y:z=8:15:17の整数解を持たない
であるから
> x^n+y^n=(y+1)^nが整数解を持つならば、
> x^n+y^n=(y+2)^n, x^n+y^n=(y+3)^nも整数解を持ちます
を満たさないような整数解もあるという意味 >199
x^2+y^2=(y+1)^2はx:y:z=8:15:17の整数解を持たない (17-15≠1であるから)
x^2+y^2=(y+1)^2はx:y:z=8:15:17の有理数解を持ちます。
x=4,y=15/2,z=17/2
x:y:z=8:15:17の整数解は、x=3,y=4,z=5とx=5,y=12,z=13から成り立っています。 >>200
> x^2+y^2=(y+1)^2はx:y:z=8:15:17の有理数解を持ちます。
これは整数解を持つことを意味しない
> x:y:z=8:15:17の整数解は、x=3,y=4,z=5とx=5,y=12,z=13から成り立っています。
> 121日高2022/06/10(金) 08:03:11.40ID:RFxnIVQX
> x^2+y^2=(y+1)^2の整数解は、
> x^2+y^2=(y+1)^2のx=3の場合の整数解
> x=3,y=4,z=5と
> x^2+y^2=(y+1)^2のx=5の場合の整数解
> x=5,y=12,z=13
> を組み合わせて、
> x=3*5=15
> y=13+4=12+5=17
> z=13-5=12-4=8
> となります。
x=15, y=17, z=8の場合x:y:z=15:17:8≠8:15:17なので証明と同様にウソで間違い > x=3*5=15
> z=13+4=12+5=17
> y=13-5=12-4=8
に訂正します。
15^2=17^2-8^2
x^2=z^2-y^2 >>202
> > x=3*5=15
> > z=13+4=12+5=17
> > y=13-5=12-4=8
> に訂正します。
> 15^2=17^2-8^2
> x^2=z^2-y^2
それはx=8, y=15, z=17 z-y=17-15=2を
x=15, y=8, z=17, z-y=17-8=9にしただけなので
z=y+1じゃないでしょ
x^2+y^2=(y+1)^2はx:y:z=8:15:17の整数解を持たない (17-15≠1であるから)
x^2+y^2=(y+1)^2はx:y:z=15:8:17の整数解を持たない (17-8≠1であるから)
であるが
x^2+y^2=(y+2)^2は互いに素でない整数解(x,y,z)=(8,15,17)を持つ
x^2+y^2=(y+9)^2は互いに素でない整数解(x,y,z)=(15,8,17)を持つ
x=15, y=8, z=17の場合x:y:z=15:8:17≠8:15:17なので証明と同様にウソで間違い それはx=8, y=15, z=17 z-y=17-15=2を
x=15, y=8, z=17, z-y=17-8=9にしただけなので
z=y+1じゃないでしょ
z=y+1はこの場合は、
5=4+1
13=12+1
です。 >>204
結局
x^2+y^2=(y+1)^2はx:y:z=8:15:17の整数解を持たない (17-15≠1であるから)
x^2+y^2=(y+1)^2はx:y:z=15:8:17の整数解を持たない (17-8≠1であるから)
であるが
x^2+y^2=(y+2)^2は互いに素でない整数解(x,y,z)=(8,15,17)を持つ
x^2+y^2=(y+9)^2は互いに素でない整数解(x,y,z)=(15,8,17)を持つ
であるから証明はウソで間違いであることに変わりない
> z=y+1はこの場合は、
> 5=4+1
> 13=12+1
> です。
それは結局x=3, y=4, z=5とx=5, y=12, z=13はx^2+y^2=(y+1)^2の整数解ということ
x=8, y=15, z=17やx=15, y=8, z=17ではz=y+1が成り立たないのだから
これらはx^2+y^2=(y+1)^2の整数解でない >これらはx^2+y^2=(y+1)^2の整数解でない
x^2+y^2=(y+1)^2の整数解を組み合わせると、
x^2+y^2=(y+n)^2の整数解になります。
よって、x^2+y^2=(y+1)^2の整数解の有無をしらべればよい。
ということになります。 >>206
> x^2+y^2=(y+1)^2の整数解を組み合わせると、
> x^2+y^2=(y+n)^2の整数解になります。
> よって、x^2+y^2=(y+1)^2の整数解の有無をしらべればよい。
> ということになります。
それならば
x^2+y^2=(y+1)^2は解の比が20:21:29である自然数解を持たないが
x^2+y^2=(y+8)^2は解の比が20:21:29である自然数解(20,21,29)(「互いに素」である)を持つ
の場合の組み合わせは? >>206
> x^2+y^2=(y+1)^2の整数解を組み合わせると、
> x^2+y^2=(y+n)^2の整数解になります。
> よって、x^2+y^2=(y+1)^2の整数解の有無をしらべればよい。
> ということになります。
それならば
x^2+y^2=(y+3)^2の互いに素である整数解を作りなさい (20,21,29)(「互いに素」である)を持つ
の場合の組み合わせは?
(3,4,5)(7,24,25)です。 >>209
> (20,21,29)(「互いに素」である)を持つ
> の場合の組み合わせは?
>
> (3,4,5)(7,24,25)です。
(3,4,5)(7,24,25)≠(20,21,29)だから
> x^2+y^2=(y+1)^2の整数解を組み合わせると、
> x^2+y^2=(y+n)^2の整数解になります。
> よって、x^2+y^2=(y+1)^2の整数解の有無をしらべればよい。
> ということになります。
は証明と同様にウソで間違いということだよね (3,4,5)(7,24,25)≠(20,21,29)だから
互いに素であれば、よいとおもいます。(順番に関係なく) >>211
> (3,4,5)(7,24,25)≠(20,21,29)だから
>
> 互いに素であれば、よいとおもいます。(順番に関係なく)
関係性が全くわからないだろ
(x,y,z)=(20,21,29)を作ることに失敗しているので
> x^2+y^2=(y+1)^2の整数解を組み合わせると、
> x^2+y^2=(y+n)^2の整数解になります。
> よって、x^2+y^2=(y+1)^2の整数解の有無をしらべればよい。
> ということになります。
は証明と同様にウソで間違い >>211
> (3,4,5)(7,24,25)≠(20,21,29)だから
>
> 互いに素であれば、よいとおもいます。(順番に関係なく)
x^2+y^2=(y+3)^2の互いに素である整数解を作りなさい x^2+y^2=(y+3)^2の互いに素である整数解を作りなさい
ありません。 >>214
> x^2+y^2=(y+3)^2の互いに素である整数解を作りなさい
>
> ありません。
それだったら
x^2+y^2=(y+1)^2は整数解を持つが (この解は全て互いに素である)
x^2+y^2=(y+3)^2は互いに素である整数解を持たない (これは日高は証明できていないが)
ということになる
よって
x^3+y^3=(y+1)^3が整数解を持たないことを仮に正しく示しても
x^3+y^3=(y+3)^3が互いに素である整数解を持たない
ことは証明できていないので日高のフェルマーの最終定理の証明は間違い x^2+y^2=(y+3)^2は互いに素である整数解を持たない (これは日高は証明できていないが)
ということになる
x^2+y^2=(y+3)^2は互いに素である整数解を持つのでしょうか? >>216
> x^2+y^2=(y+3)^2は互いに素である整数解を持たない (これは日高は証明できていないが)
> ということになる
>
> x^2+y^2=(y+3)^2は互いに素である整数解を持つのでしょうか?
持たない場合は
x^2+y^2=(y+1)^2は整数解を持つが
x^2+y^2=(y+3)^2は互いに素である整数解を持たない
だから日高のフェルマーの最終定理の証明は失敗ということ
(x,y,z)=(8,15,17), (15,8,17), (20, 21, 29), (21, 20, 29)の場合より
x^2+y^2=(y+2)^2は互いに素である整数解を持つ
x^2+y^2=(y+8)^2は互いに素である整数解を持つ
x^2+y^2=(y+9)^2は互いに素である整数解を持つ
は分かる
2と8と9を除いた K = 3, 4, 5, 6, 7, 10, 11, 12, 13, ... の内の一つでも
x^2+y^2=(y+1)^2は整数解を持つが
x^2+y^2=(y+K)^2は互いに素である整数解を持たない
となれば日高のフェルマーの最終定理の証明は失敗
であるから残りのKの全ての場合で互いに素な整数解があることを示しましょう 残りのKの全ての場合で互いに素な整数解があることを示しましょう
ないものは。ないとおもいますが? >>218
> 残りのKの全ての場合で互いに素な整数解があることを示しましょう
>
> ないものは。ないとおもいますが?
互いに素な整数解が無ければ日高の証明は間違いということで終わりだから
互いに素な整数解が無い場合があることに納得したのならそれで良いのでは? 206 名前:日高[] 投稿日:2022/09/11(日) 10:31:01.69 ID:nQX3rs20 [1/4]
>これらはx^2+y^2=(y+1)^2の整数解でない
x^2+y^2=(y+1)^2の整数解を組み合わせると、
x^2+y^2=(y+n)^2の整数解になります。
よって、x^2+y^2=(y+1)^2の整数解の有無をしらべればよい。
ということになります。 x^2+y^2=(y+1)^2の整数解を組み合わせると、
x^2+y^2=(y+n)^2の整数解になります。
よって、x^2+y^2=(y+1)^2の整数解の有無をしらべればよい。
ということになります。 >>221
> x^2+y^2=(y+1)^2の整数解を組み合わせると、
> x^2+y^2=(y+n)^2の整数解になります。
> よって、x^2+y^2=(y+1)^2の整数解の有無をしらべればよい。
> ということになります。
それだと
x^2+y^2=(y+3)^2が互いに素な整数解を持つならばx^2+y^2=(y+1)^2は整数解を持つ
が成り立たないから証明は間違いでしょ x^2+y^2=(y+3)^2が互いに素な整数解を持つならばx^2+y^2=(y+1)^2は整数解を持つ
が成り立たないから証明は間違いでしょ
x^2+y^2=(y+3)^2は、互いに素な整数解を持ちません。
が、他の組み合わせができます。 >>223
> x^2+y^2=(y+3)^2は、互いに素な整数解を持ちません。
をx^2+y^2=(y+1)^2が整数解を持つことから証明できなければダメ x^2+y^2=(y+1)^2が整数解を持つことから証明できなければダメ
x^2+y^2=(y+1)^2は、有理数解をもちます。
よって両辺に適当な数を掛けると、整数解がもとめられます。 >>225
> x^2+y^2=(y+1)^2は、有理数解をもちます。
> よって両辺に適当な数を掛けると、整数解がもとめられます。
「整数解がもとめられます」だったら
> 218日高2022/09/12(月) 20:26:50.09ID:t+GNhVhL
> 残りのKの全ての場合で互いに素な整数解があることを示しましょう
>
> ないものは。ないとおもいますが?
などと書いていないで整数解を求めればよいでしょ
x^2+y^2=(y+1)~2が整数解を持つならばx^2+y^2=(y+3)^3が互いに素な整数解を持つ
ことが示されないことがが問題なのだからx^2+y^2=(y+3)^3の互いに素な整数解を求めればよいのでは? >>225
だから、それをn>2の場合に当てはめると、
x^n+y^n=(y+1)^n に整数解が存在しなくても、(整数解でない)有理数解をもつならば、それを定数倍すればx^n+y^n=z^n を満たす(互いに素な)整数解が得られる。
その場合があるから、x^n+y^n=(y+1)^n の解を整数解に限定できないんだよ。
あなたが全く理解できていないのは、x^n+y^n=(y+1)^n に整数解が存在しないばあいでも、整数解でない有理数解が存在するならば、x^n+y^n=z^n には整数解が存在しうる、というあなた以外には自明な論理。 つまり、x^n+y^n=(y+r)^n (r>2)に互いに素な整数解があるのならば、その解はx^n+y^n=(y+1)^nの解として表現されるとき、整数解でない有理数解としてしか表現できないということ。
【証明】ではx^n+y^n=(y+1)^nの整数でない有理数解の不存在については何も述べていないんだから、
x^n+y^n=z^n の整数解がもしあったとして、(その最も単純な)整数解がz-y>=2になってしまう場合、あなたの証明じゃ困るでしょ、ということ。
わかってもらえるかな?
でもでもだってが続くのかな? >>230
>>226は誤字があるから改めて書くと
x^2+y^2=(y+1)^2が整数解を持つならばx^2+y^2=(y+3)^2が互いに素な整数解を持つ
ことが示されないことがが問題 x^n + y^n + z^n = w^n とか
x^n + y^n + z^n + w^n = u^n とか
x^n + y^n + z^n + w^n + u^n = v^n とか
。。。
とかとかの整数解はどうよ。 【定理】n=3のとき、x^n+y^n=z^nは自然数解を持たない。
x^3+y^3=z^3を、x^3+y^3=(y+1)^3…(1)とおく。(x,yは有理数)
2元方程式が有理数解を持つならば、必ず整数解を持つので、x,yは整数とする。
(1)を(x^3-1)/3=y^2+y…(2)と変形する。
(2)の左辺をA,右辺をBとおく。A=Bならば、A^(1/2)=B^(1/2)となる。
B^(1/2)は、yの増加につれて、y+0.5に近づく。
A^(1/2)は、xの増加につれて、y+0.5に近づかない。
∴n=3のとき、x^n+y^n=z^nは自然数解を持たない。 >>234
> 2元方程式が有理数解を持つならば、必ず整数解を持つ
結局x^2+y^2=(y+3)^2が互いに素な整数解を持つことが示されないので間違い x^2=6y+9は
ともに、分数解を持たないので
ともに、整数解を持ちません。 【定理】n=3のとき、x^n+y^n=z^nは自然数解を持たない。
x^3+y^3=z^3を、x^3+y^3=(y+1)^3…(1)とおく。(x,yは有理数)
2元方程式が共に分数解を持つならば、共に整数解を持つので、x,yは整数とする。
(1)を(x^3-1)/3=y^2+y…(2)と変形する。
(2)の左辺をA,右辺をBとおく。A=Bならば、A^(1/2)=B^(1/2)となる。
B^(1/2)は、yの増加につれて、y+0.5に近づく。
A^(1/2)は、xの増加につれて、y+0.5に近づかない。 >>237
> 2元方程式が共に分数解を持つならば、共に整数解を持つ
結局x^2+y^2=(y+3)^2が互いに素な整数解を持つことが示されないので間違い >>236
> ともに、整数解を持ちません。
x^2+y^2=(y+1)^2が整数解を持つことに反しているので間違い x^n + y^n = z^n は指数nがmの倍数であるとき整数解を持てば、n=mの
ときにも解を持つ。よって指数として素数の場合だけを考えたらええ。 結局x^2+y^2=(y+3)^2が互いに素な整数解を持つことが示されないので間違い。
x^2+y^2=(y+3)^2が互いに素な整数解を持たない理由は、
√3が無理数だからです。 【定理】n=3のとき、x^n+y^n=z^nは自然数解を持たない。
x^3+y^3=z^3を、x^3+y^3=(y+1)^3…(1)とおく。(x,yは有理数)
(1)が整数解を持つならば、必ず有理数解を持つので、x,yは整数とする。
(1)を(x^3-1)/3=y^2+y…(2)と変形する。
(2)の左辺をA,右辺をBとおく。A=Bならば、A^(1/2)=B^(1/2)となる。
B^(1/2)は、yの増加につれて、y+0.5に近づく。
A^(1/2)は、xの増加につれて、y+0.5に近づかない。
∴n=3のとき、x^n+y^n=z^nは自然数解を持たない。 >>241
> x^2+y^2=(y+3)^2が互いに素な整数解を持たない理由は、
> √3が無理数だからです。
x^2+y^2=(y+2)^2は√2が無理数でも互いに素な整数解を持つので
理由として間違い x^2+y^2=(y+2)^2は√2が無理数でも互いに素な整数解を持つので
理由として間違い
3^2+4^2=(4+1)^2は、互いに素な整数解を持つので、(√1=1)
4^2+3^2=(3+2)^2も、互いに素な整数解を持ちます。 >>244
結局
x^2+y^2=(y+1)^2…(1)は互いに素な整数解を持つ
x^2+y^2=(y+2)^2は互いに素な整数解Aを持つ
x^2+y^2=(y+3)^2は互いに素な整数解Bを持たない
ということで
(1)が整数解を持つならば(x^2+y^2=(y+2)^2の両辺を2で割った場合の)有理数解Aを持つ
(1)が整数解を持つならば(x^2+y^2=(y+3)^2の両辺を3で割った場合の)有理数解Bを持たない
のどちらもあるから証明は間違い (1)が整数解を持つならば(x^2+y^2=(y+2)^2の両辺を2で割った場合の)有理数解Aを持つ
この部分がわかりません。くわしく教えていただけないでうか? >>246
> 3^2+4^2=(4+1)^2は、互いに素な整数解を持つので、(√1=1)
> 4^2+3^2=(3+2)^2も、互いに素な整数解を持ちます。
> 4^2+3^2=(3+2)^2も、互いに素な整数解を持ちます。
これの両辺を2で割れば(4/2)^2+(3/2)^2=(3/2+1)^2が成り立つ
つまり2,3,4が互いに素であるような有理数解(4/2,3/2,3/2+1)を持つ 3^2+4^2=(4+1)^2と4^2+3^2=(3+2)^2は、
x,yを入れ替えれば、同じ式となります。
3^2+4^2=(4+1)^2は、√1=1なので、
x=3,y=4とすると、x^2+y^2=(y+1)は、整数解を持ちます。
15^2+8^2=(8+9)^2は、√9=3なので、整数解を持ちます。 >>249
> 3^2+4^2=(4+1)^2と4^2+3^2=(3+2)^2は、
> x,yを入れ替えれば、同じ式となります。
> 3^2+4^2=(4+1)^2は、√1=1なので、
> x=3,y=4とすると、x^2+y^2=(y+1)は、整数解を持ちます。
>
> 15^2+8^2=(8+9)^2は、√9=3なので、整数解を持ちます。
結局
x^2+y^2=(y+1)^2…(1)は互いに素な整数解を持つ
x^2+y^2=(y+2)^2やx^2+y^2=(y+9)^2は互いに素な整数解Aを持つ
x^2+y^2=(y+3)^2は互いに素な整数解Bを持たない
ということで
(1)が整数解を持つならばx^2+y^2=(y+2)^2やx^2+y^2=(y+9)^2は互いに素な整数解Aを持つ
(1)が整数解を持つならばx^2+y^2=(y+3)^2は互いに素な整数解Bを持たない
のどちらもあるから証明は間違い >>242 の
>> (1)が整数解を持つならば、必ず有理数解を持つので、
が間違っているってことだよね (1)が整数解を持つならばx^2+y^2=(y+2)^2やx^2+y^2=(y+9)^2は互いに素な整数解Aを持つ
(1)が整数解を持つならばx^2+y^2=(y+3)^2は互いに素な整数解Bを持たない
のどちらもあるから証明は間違い
x^2+y^2=(y+2)^2の2は2乗数ではないので、互いに素な整数解を持ちません。
但し、x,yを入れ替えて、2乗数になるならば、互いに素な整数解を持ちます。 >>252
> x^2+y^2=(y+2)^2の2は2乗数ではないので、互いに素な整数解を持ちません。
> 但し、x,yを入れ替えて、2乗数になるならば、互いに素な整数解を持ちます。
x^2+y^2=(y+2)^2は互いに素な整数解(x,y,z)=(8,15,17)=(8,15,15+2)を持つ
√4=2の場合のx^2+y^2=(y+4)^2の互いに素な整数解を書きなさい √4=2の場合のx^2+y^2=(y+4)^2の互いに素な整数解を書きなさい
ありません。奇数の2乗数の場合はあります。 >>254
> ありません。奇数の2乗数の場合はあります。
証明を見てみると
> (1)が有理数解を持つならば、必ず整数解を持つので、x,yは整数とする。
> 2元方程式が有理数解を持つならば、必ず整数解を持つので、x,yは整数とする。
> 2元方程式が共に分数解を持つならば、共に整数解を持つので、x,yは整数とする。
> (1)が整数解を持つならば、必ず有理数解を持つので、x,yは整数とする。
というのは結局日高はn=2とn=3の場合では解の有無が逆になると言いたいだけでしょ
x^2+y^2=(y+1)^2とx^3+y^3=(y+1)^3の互いに素な整数解の有無は逆になっている
> ありません。
x^2+y^2=(y+3)^2やx^2+y^2=(y+4)^2が互いに素な整数解を持たないことは日高も認めている
よって
x^3+y^3=(y+3)^3やx^3+y^3=(y+4)^3が互いに素な整数解を持たないことは証明できていない x^2+y^2=(y+3)^2やx^2+y^2=(y+4)^2が互いに素な整数解を持たないことは日高も認めている
よって
x^3+y^3=(y+3)^3やx^3+y^3=(y+4)^3が互いに素な整数解を持たないことは証明できていない
x^3+y^3=(y+1)^3が整数解をもたないので、
x^3+y^3=(y+3)^3やx^3+y^3=(y+4)^3も、互いに素な整数解を持ちません。 >>256
> x^3+y^3=(y+1)^3が整数解をもたないので、
> x^3+y^3=(y+3)^3やx^3+y^3=(y+4)^3も、互いに素な整数解を持ちません。
x^2+y^2=(y+1)^2が互いに素な整数解を持つことと
x^2+y^2=(y+3)^2やx^2+y^2=(y+4)^2が互いに素な整数解を持つことは無関係だから
日高のその主張が正しいわけないだろ x^2+y^2=(y+1)^2が互いに素な整数解を持つことと
x^2+y^2=(y+3)^2やx^2+y^2=(y+4)^2が互いに素な整数解を持つことは無関係だから
x^2+y^2=(y+3)^2やx^2+y^2=(y+4)^2は互いに素な整数解を持ちません。 >>258
> x^2+y^2=(y+3)^2やx^2+y^2=(y+4)^2は互いに素な整数解を持ちません。
日高の主張はn=2とn=3で互いに素な整数解の有無が逆になるということなのだから
n=2の場合に互いに素な整数解を持たない場合があればn=3の証明は間違いになる n=2の場合に互いに素な整数解を持たない場合があればn=3の証明は間違いになる
どうしてでしょうか? >>260
> n=2の場合に互いに素な整数解を持たない場合があればn=3の証明は間違いになる
>
> どうしてでしょうか?
x^n+y^n=(y+1)^nが整数解を持たないので
x^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nも互いに素な整数解を持たない
あるいは
x^n+y^n=(y+1)^nが整数解を持つので
x^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nも互いに素な整数解を持つ
が
n=2のときに成立していないのでn=3の場合でも証明に使えない x^n+y^n=(y+1)^nが整数解を持たないので
n=2のときは成立していません。
n=3のときは成立しています。 >>262
> x^n+y^n=(y+1)^nが整数解を持たないので
>
> n=2のときは成立していません。
> n=3のときは成立しています。
x^n+y^n=(y+1)^nが整数解を持たないならば
x^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nも互いに素な整数解を持たない
あるいは
x^n+y^n=(y+1)^nが整数解を持つならば
x^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nも互いに素な整数解を持つ
あるいは
x^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nが互いに素な整数解を持たないならば
x^n+y^n=(y+1)^nも整数解を持たない
あるいは
x^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nが互いに素な整数解を持つならば
x^n+y^n=(y+1)^nも整数解を持つ
が
n=2のときに成立していないのでn=3の場合でも証明に使えない よくわかりません。
くわしく教えてもらえないでしょうか >>264
「x^n+y^n=(y+1)^nが整数解を持たないならばx^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nも互いに素な整数解を持たない」
あるいは
「x^n+y^n=(y+1)^nが整数解を持つならばx^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nも互いに素な整数解を持つ」
あるいは
「x^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nが互いに素な整数解を持たないならばx^n+y^n=(y+1)^nも整数解を持たない」
あるいは
「x^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nが互いに素な整数解を持つならばx^n+y^n=(y+1)^nも整数解を持つ」
が
n=2のときに成立していないのでn=3の場合でも証明に使えない 「x^n+y^n=(y+1)^nが整数解を持つならばx^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nも互いに素な整数解を持つ」
が
n=2のときに成立していない
は理解できてるかな n=2のときに成立していない
意味がよくわかりません。くわしく教えてください。 >>266,267
え、
「x^n+y^n=(y+1)^nが整数解を持つならばx^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nも互いに素な整数解を持つ」
が
n=2のときに成り立っている
と思っているの? n^x + n^y = n^z となる自然数解(n,x,y,z)はどれだけあるか? >268
n=2のとき
「x^n+y^n=(y+1)^nが整数解を持つならばx^n+y^n=(y+3)^nやx^n+y^n=(y+4)^nは互いに素な整数解を持ちません。」 ■ このスレッドは過去ログ倉庫に格納されています