������Ȃ����͂����ɏ����Ă�454
�� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�
�����A�������P������낤����
�O�X��
������Ȃ����͂����ɏ����Ă�453
https://rio2016.5ch.net/test/read.cgi/math/1558041041/
(�g�p�ςł�: 478) �O>>742���̚k�o���Â�����Ȃ�B
>>743(-.-)�ݸ�...
��(1250^2+125^3)=1875
n=125 O���S�Ōʂ̒���R��^�ɂ����āA����_P��A����B�܂œ������ɁA��AP�̒�����x�̂Ƃ���AQ�̒������Ax�ɂ����Ƃ���f(x)�Ƃ��܂��B(AP>AQ)
���̎��AAQ���ʂ�ʐ�(�ΐ�����)�́Af(x)���ǂ̂悤�ɒ�ϕ�������߂��܂����H
Integral[0,R] f(x) dx
�ŗǂ��̂ł��傤���H
�ȒP�Ɍ����ɍ��W�ɂ����āA�ɂ���̋������p�x�ő������̒����Ɉˑ�����o�[�W�����ł�
https://i.imgur.com/4JNGDJS.jpg >>736
���͂����ɂ��钆�ł͑������\�ȕ����Ǝv���܂���
���N�������_�ł����B >>740
������Ă���ȊO����ł����ˁH �O>>746
>>747�Ⴄ�����₯�ǁA
��`���O�p�`�ƌ��āA
����x�̌ʂ��ׂ�������x��0����R�܂ő����W�߂����̂��ӁA
�ʂ̒���x�ɑ���ΐ������̌af(x)�������Ƃ���ƁA
�O�p�`=(1/2)�~��Ӂ~����
f(x)�̐ϕ�����F(x)+C�Ƃ���ƁA
�ΐ������̖ʐ�
=(1/2)��[x=0��R]f(x)dx
={F(R)-F(0)}/2 0<x<���Œ�`���ꂽ��f(x)�ŁA
(C1)�P���I��f(x)>0
(C2)lim[x to 0]f(x)=+��
(C3)lim[x to ��]f(x)=0
(C4)�����鏊�����\
�������̂��l����B
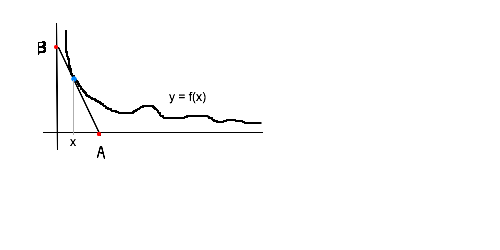
y=f(x)�̃O���t��xy���ʂɕ`���A�ex�ɂ�����f(x)�̐ڐ��������B����x���Ƃ̌�_��A�Ay���Ƃ̌�_��B�Ƃ��A����AB�̒�����L(x)�Ƃ���B
����ł����AL(x)�̍ŏ��l��f(x)����L(C1)�`(C4)�����Ȃ�ΕK�����݂��܂����H
�ő�l�����݂��Ȃ��ꍇ�����邱�Ƃ͊m�F���܂����B��낵�����肢���܂��B >>725
725�ł�
P(k1T_n <��<k2T_n)=P(��/k2<T_n<��/k1)=P(T_n<��/k1)-P(T_n<��/k2)=1/(k1)^n - 1/(k2)^n�ƕό`��
1/(k1)^n - 1/(k2)^n=1-���̏����̂���k2-k1���ŏ��ɂȂ�悤��k1,k2�����肷��悢
�����܂ł͂ł����̂ł��������ŋl�܂��Ă��܂��܂����B����Ƃ����j���Ԉ���Ă���̂ł��傤���H�ǂȂ����������肢�����ł��B �����l(x)��0�ɂ͂Ȃ�Ȃ�����
������0�ɂȂ�悤��f�͍��邾�� �u�P���I��f(x)>0�v���āA�|�G���̃j���[�E�F�[�u�������H >>743
n��25�̔{���̂Ƃ���
�@n = 25x >0
�@x^3 = y^2 -100
(Mordell equation, Bachet equation, Bachet-Mordell equation �Ȃ�)
�������́ix, y) = (-4,�}6)�@(0,�}10)�@(5,�}15)�@(20,�}90)�@(24,�}118)�@(2660,�}137190)
http://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q12140152827 >>749
��.�Z.��.�w.��.��.��.��.��.��.���Ă݂� >>755
�������������������ĉ������B
���Ɖ����łȂ��čŏ��l�����݂���悤�ɂł��܂��� >>758
���Z���w�̔�.��.����.��ɕ��傠��̂� >>759
����������l�K�L�������Ă�悤�ɂ��������Ȃ��B �P���I��f(x)>0���Č������A��a���o����l�͊m���ɂ��邾�낤��
(x+1)^2-x^2-2x>0�́u�P���I�ɐ����v���Ċ������邯�ǁAx^2+1>0�́u�S�Ă�x�ɑ��āv���Ċ����������
�O�҂͍P�������ۂ����A��҂͕��������ۂ����ۂ߂Ȃ� >>751
���������\�����ł̓_���B
�������A���܂Ō����������B �O>>750
>>760
0��x��y��2��xy���ʂɐ}������ƁA2�ӂ�2�̒��p�ӎO�p�`���`����B
���_��(0,0),(0,2),(2,2)
z=3x^2-xy-2x+y+1
=(3x^2-2x+1)-(x-1)y
=(3x-1)(x-1)-(x-1)y
=(x-1)(3x-1-y)
xy���ʂ�x=1��y=3x-1�̃O���t��`���A����2�{�̒�����̓_(x,y)��z=0���B
���p�ӎO�p�`���̂������̓_���ɂ�݂Ȃ���Az�̒l�ׂ�ƁA
(x,y)��z=(x-1)(3x-1-y)
(0,0)��z=1
(0,1)��z=2
(0,2)��z=3
(2,2)��z=3
(1,2)��z=0
(1,1)��z=0
(1/2,1/2)��z=0
(2/3,2/3)��z=-1/9
(3/4,3/4)��z=-1/8
(4/5,4/5)��z=-3/25
���݂̎b��ŏ��lz=-1/8 >>751
g(x) = -(1-cosx)/(x^3) - 1/(x^100)
G(x) = -��_(x,��)g(t)dt
f(x) = xG(x)
�Ƃ����Af��4�̐�����S�Ė��������AL�̍ŏ��l�����݂��Ȃ��B
�i�������A�ڐ���x���̌�_�����݂��Ȃ��ꍇ��L=���ƒ�߂�j
(C1)(C4)�͖��炩�B�I�[�_�[�ׂ邱�Ƃ�(C2)(C3)���킩��B
�_(a, f(a)) �ɂ�����ڐ��̕�������
y = (ag(a)+G(a))(x-a) + f(a)
= (ag(a)+G(a))x - (a^2)g(a)
�ł��邩��A�_A��y���W�͏�ɐ��ł���A�X�� a��+�� �̎� 0 �Ɏ������邱�Ƃ��킩��B
�܂��Aa=2��n �in�͐��̐����j�̎��A�_B��x���W��
(a^2)g(a)/(ag(a)+G(a))
= (a^(-98))/(a^(-99)+G(a))
= O(1/(n^96))
�ƂȂ邩��An��+���̎� 0 �Ɏ�������B
�ȏォ�� L(x) �͏�ɐ��ł��� liminf(x��+��)L(x)=0 �ł��邩��AL(x)�̍ŏ��l�͑��݂��Ȃ��B >>760
2�E3�@x,y �� 0��x��y��2 �����ĕω�����Ƃ��A
�@z = 3xx -xy -2x +y +1 �̍ŏ��l�����߂�B
>>762
z = 3xx-2x+1 + (1-x)y,
(i) 0��x��1 �Ȃ�A
�@��z��y�Ɋւ��ĒP�������B
�@����ā@z �� 2xx -x +1 = 2(x -1/4)^2 + 7/8 �� 7/8,
(ii) 1��x��2 �Ȃ�A
�@��z��y�Ɋւ��ĒP�������B
�@����ā@z �� 3xx -4x +3 = (x-1)(3x-1) +2 �� 2,
����āA�@(x,y) = (1/4,1/4) �Ƃ����Ƃ��� z=7/8 ���ŏ��l�B n�������s��A�́Ai+j=k�̂Ƃ�a_ij=k�ł���(1≤i≤n,1≤j≤n)�B
�������AA��i�sj����a_ij�Ə����B
A�������s�ǂ������肹��B �O>>766���m�F�B
>>760
0��x��y��2��xy���ʂɐ}������ƁA2�ӂ�2�̒��p�ӎO�p�`���`����B
���_��(0,0),(0,2),(2,2)
z=3x^2-xy-2x+y+1
=(3x^2-2x+1)-(x-1)y
=(3x-1)(x-1)-(x-1)y
=(x-1)(3x-1-y)
xy���ʂ�x=1��y=3x-1�̃O���t��`���A����2�{�̒�����̓_(x,y)��z=0���B
���p�ӎO�p�`���̂������̓_���ɂ�݂Ȃ���Az�̒l�ׂ��B
(x,y)��z=(x-1)(3x-1-y)
(0,0)��z=1
(0,1)��z=2
(0,2)��z=3
(2,2)��z=3
(1,2)��z=0
(1,1)��z=0
(1/2,1/2)��z=0
(2/3,2/3)��z=-1/9
(3/4,3/4)��z=(-1/4)(9/4-1-3/4)
=(-9+4+3)/16
=-1/8
(4/5,4/5)��z=-3/25��-1/8
�ŏ��l�̌��z=-1/8�����A
x=y=3/4��
z=3x^2-xy-2x+y+1
�ɑ������ƁA
z=3(3/4)^2-(3/4)^2-3/4+1
=2(9/16)+1/4
=11/8��0����Ȃ��B
�v�Z�ԈႢ�̉\��������B
����=0�̂悤�Ȍ���͂��ق����B ���Ƃ��Ėʔ������ǂ����Ƃ��A����X���ɖ��o�肵�Ăǂ��Ȃ�Ƃ������邯�ǁA�����������̕��͂���z���g�ɐ��w�^�ʖڂɕ�����������̂��₢�l�߂����Ȃ��ȁB>>769��k���ǂ���������Ă�̂��킯�킩���B
���ɔC�ӂ�k�ɂ��Ă��낤���ǁA����Ȃ�a_ij=i+j�Ə������������Ȃ̂ɁB >>767
> �ȏォ�� L(x) �͏�ɐ��ł��� liminf(x��+��)L(x)=0 �ł��邩��AL(x)�̍ŏ��l�͑��݂��Ȃ��B
L(x) ���� AB �̒����Ȃ���A��� x < L(x) �ɂȂ�̂ƈႤ�́H
����Ȃ�� liminf(x��+��)L(x)=0 �ɂȂ�H
 ���͎̂������B
���͎̂������B
���Ⴂ���Ă��B���̌X���Ȃ猴�_O�ߖT��2��_�����肦��ˁB n�������s��A��i�sj��a_ij�́Aa_ij=i+j����(1≤i≤n,1≤j≤n)�B
A�������s�ǂ������肹��B >>775
n=1, 2 ���Ɛ����s�� (�ȒP�Ɋm���߂���)
n��3 �ł� ���s��
a_{i}{j} -2 a_{i+1}{j} + a_{i+2}{j} = (i+j) - 2.(i+j+1) + (i+j+2) = 0
����ĘA�������R�s�͕K�����^�]���ɂȂ邩��B >>776
�f���炵��
n≥3�ŗl�q���ς�邱�Ƃ��Ӑ}�����o��ł��� >>778
�u������Ȃ����v����������Ȃ������̂���...
�N�ɂ͎��]������B �O>>771
0��x��y��2�\�\�@
��xy���ʂɐ}������ƁA2�ӂ�2�̒��p�ӎO�p�`���`����B
���_��(0,0),(0,2),(2,2)
z=3x^2-xy-2x+y+1
=(3x^2-2x+1)-(x-1)y
3x^2-2x+1�̈����������܂������Ă��B
z=3x^2-xy-2x+y+1
=3x^2-(y+2)x+y+1
z=3{x^2-(y+2)x/3}+y+1
=3{x-(y+2)/6}^2+y+1-{(y+2)/6)}^2
�������̎�x=(y+2)/6���@�̂ǂ͈̔͂ɂ��邩�ŏꍇ��������B
(y+2)/6��0�̂Ƃ��A
z�̍ŏ��l��x=0�̂Ƃ��A
z=y+1
y=0�̂Ƃ��A
z=1�\�\�A
0��(y+2)/6��x�̂Ƃ��A
-2��y��6x-2
z�̍ŏ��l��x=(y+2)/6�̂Ƃ��A
z=6x-2+1-3{(6x-2+2)/6}^2
=-y^2/12+2y/3+4/3
=-(1/12)(y-4)^2+4/3+4/3
=-(1/12)(y-4)^2+8/3
y=2�̂Ƃ��A
z=-(1/12)(2-4)^2+8/3
=-1/3+8/3
=7/3�\�\�B
x��(y+2)/6��y�̂Ƃ��A
6x-2��y,2/5��y
z�̍ŏ��l��x=(y+2)/6�̂Ƃ��A
z=y+1-(1/12)(y+2)^2
=-(1/12)(y^2+4y+4-12y-12)
=-(1/12)(y^2-8y)+2/3
=-(1/12)(y-4)^2+2/3+16/12
=-(1/12)(y-4)^2+2
y=2/5�̂Ƃ��A
z=-(1/12)(2/5-4)^2+2
=-(1/12)(-18/5)^2+2
�Ȃ������ƈႤ�B
y��(y+2)/6��2�̂Ƃ��A
��2��(y+2)/6�̂Ƃ��A
�܂�����2�͈͂��邯�njv�Z����������ŁA������z�̒l�̕��z�����Ă��A���Ƃ��ć@�͈̔͂�˂��钼���A
x-(y+2)/6=0���Ȃ킿y=6x-2�̐���̓_�����߂�B
z�̍ŏ��l�́A
x=y=2/5�̂Ƃ��A
z=3(2/5)^2-(2/5)(2/5)-2(2/5)-2(2/5)+(2/5)+1
=3(4/25)-(4/25)-2/5+1
=8/25-10/25+1
=23/25�\�\�C
�@�A�B�C���A
z�̍ŏ��l=23/25 y�ɂ���1���Ȃ̂�y=x��y=2�ōő� �O>>781
(x,y)=(2,2)�̂Ƃ��A
z=7�ł����炭�ő傾�Ǝv���B
(x,y)=(0,0),(1/2,1/2)���Ƃ���z=1������A
(x,y)=(1/4,1/4)���������ɉ������B
(x,y)=(1/2,1)�́Az=5/4
(x,y)=(0,1),(1,1)�͂Ƃ��ɁAz=2
(x,y)=(1,2)�̂Ƃ��Az=4 �O>>783
23/25�͐ɂ��������B
7/8�̂ق����������ɂ�����Ƃ����������B
(x,y)=(1/4,1/4)�ŗ���Ƃ͂ȁB �d�ϕ��ɂ���
��(9-x^2-y^2)��D:x^2+y^2<=3x
���v�Z���鎞�A�ɍ��W�ϊ���p����0<=r<=3cos��,-��/2<=��<=��/2�Ƃ��v�Z���Ă����Ɠ�����9�ɂȂ�܂����B
�������A�Ώ̐���p����0<=��<=2/�Ƃ��Čv�Z����Ɠ�����9��-12�ƂȂ�܂��Bwolfram���g���Č��Z����Ƃ�����̕����������悤�ł��B���̂��̂悤�ȍ��ق����܂��̂ł��傤���H�����̌v�Z�~�X�Ȃ̂ł��傤���H >>785
�Ώ̐���p����~�c�c�̂Ƃ����/2�ł� >>785
���ȉ������܂����B
�ϕ��͈͓I�Ɂ���O���Ă͂����Ȃ��ł��ˁB �O>>784
�������A��ɓʂ����ɉ����ŏꍇ��������Ƃ������Ă��ȁB
����Ԗ������Ă��݂܂���ł����B >>788
(1)
����� a[1]=1, a[2]=2, .., a[n]=n �ȍ~�͔C�ӂ̕��ו�: 2^n * (2n-n)!
�@ = (2^n) n! �ʂ�
( 2^n �� n���̐F�I���� )
(2)
(�����Ȃ�)�S�Ă̕��ו�: (2n)! �ʂ�
�ua[1]=k, a[2]={k�ȉ�}�v�������ו�: (2 + 4(k-1) ) * (2n-2)! �ʂ�
(��������2�����тِ͈F2�ʂ�, �قȂ鐔��2����4�ʂ� �ɒ���)
����� X=1 �ƂȂ���ו�: ��[k=1,n] ... = 2n(n-1)(2n-2)! �ʂ�
�ua[1]={k����}, a[2]=k, a[3]={k�ȉ�} �v�������ו�:
�@�@( 2^2* (k-1) + 2^2 * (k-1) + 2^3 * {(k-1)^2 - (k-1)} ) * (2n-3)! = 8(k-1)^2 (2n-3)! �ʂ�
����� X=2 �ƂȂ���ו�: ��[k=1,n] ...�@= (4/3) n(n-1)(2n-1)(2n-3)! �ʂ�
�ȏ��� X��3 �ƂȂ���ו�:
(2n)! - 2n(n-1)(2n-2)! - (4/3) n(n-1)(2n-1)(2n-3)!
�@= (4/3)n(nn-1)(2n-3)! �ʂ�
����������ƃ}�V�ȉ�@���肻�� �ŏ��̎O���P������ł����̂ł́H >>792
�����ł��ˁB��{k=3,n} (2^3) C{k-1,2}*(2*n-3)! = ... = (4/3)n(n-1)(n-2)(2n-3)!
( n=3 �� (1) �ƈ�v���܂� )
>>791 �̌㔼�͖Y��Ă�������... ��̊��S�������݂��邩���Ȃ��������Ă��� ��̊��S�������݂��邩�ǂ����܂��������ĂȂ����Đ�����ˁB�Ȃ����킩�肻���Ȃ����� ��̊��S���Ȃ�ĂȂ�����B�O>>789�Ȃ��ȁ`���B����Ȃ̂���킯�ȁ`��!!�@���͂͂͂́c�c
�P�P]/�_�Q�Q�Q�Q�Q�Q
�Q�Q/�_/ ���������@/|
�P�P�_/ ((^o`^o^))/ |
�P�P�P�@�����ҁ܃ҁ@|
�P�P�P�P~UU~�҃�|�@/|
���@���@���@���@| /|__|__|__|__|__|__|__|__|__|__|__|__| >>796
�܂��ɃX���^�C�ʂ�̘b��ɂ͈Ⴂ�Ȃ�w �uy��f(x) �� y��f⁻¹(x) ���قȂ�2�_�Ō����v�Ɓuy��f⁻¹(x)��y��x ���قȂ�Q�_�Ō����v�����l�ł���Ƃ����L�q�����������̂ł����A
��A�����ł���
�y��x ��ɈقȂ镡��(2�ȏ�)�̋��L�_������
�ꍇ�Ɍ����ē��l�ł��傤���H A=B����������
A=Z(0), B=Z(n) �ɂȂ�悤�Ȋ� Z(n) ���߂�Z(n)=Z(n+1) �������̂��āA�Ȃ�ŗǂ��̂ł��傤���H >>799
P=(f��f⁻¹���قȂ�2�ȏ�̓_�Ō����)
Q=(f⁻¹��y��x ���قȂ�2�ȏ�̓_�Ō����)
R=(f�͘A��)
S=(f��f⁻¹��y��x ��ɈقȂ�2�ȏ�̋��L�_������)
�Ƃ��āA�咣�́u�C�ӂ�f�ɂ���(P��Q)��(S����R)�v�Ɠǂ߂��ł��������Ă܂����H >>768
762�ł�
������菕����A���肪�Ƃ� ��[0 to a] exp(-x^2) dx =I[a]�Ƃ��A
lim[a to infty] I[a] = I�Ƃ����B
t��I[t] = (��/4)*I�Ȃ�����Ƃ���Ƃ��An<t<n+1�������R��n������1���݂���i���̎����͎������Ƃ��悢�j�B
n�����߂�B >>803
��.��.��.��.��.��..�K�C.�W.
�a.�@.��.�s.��.��.��.�K.�C.�W >>803
�����ϕ��ɂ��
��exp(-xx) dx = -(1/2x)exp(-xx) - ��(1/2xx)exp(-xx) dx
�@= -(1/2x)exp(-xx) + {1/(4x^3)}exp(-xx) + ��{3/(4x^4)}exp(-xx) dx
�@= ����
���@I[a] = I - [1/(2a) - 1/(4a^3) + 3/(8a^5) - ����] exp(-aa)}
t = 0.87752700406522
n = 0, ����a[n]=1/n�̊e���ɑ��Ĉȉ��̑���(T)���s���A�V���Ȑ���b[n]�����B
��[k=1 to n] a[k] = A[n]
��[k=1 to n] b[k] = B[n]
�Ƃ����Ƃ��A�Ɍ�
lim[n to infty] A[n]/B[n]
���������邱�Ƃ������B
(T)
a[n]=1/n�̏����_�ȉ��ɕ��Ԑ����̂����A��ł�����̂�S��0�ɒu�������Ăł��������b[n]�Ƃ���B�Ⴆ��
a[1]=1=1.00..., b[1]=1
a[2]=1/2=0.500..., b[2]=0.00...=0
a[3]=1/3=0.333..., b[3]=0.00...=0
a[7]=1/7=0.142857..., b[7]=0.042800... >>808
�|�G���ł͂Ȃ������肷����@��������܂��� >>807
b[n] �̏����_��m�ʈȊO�̈ʂ�S��0�ɂ������� b_m[n] �Ƃ����A
lim_(m����) ��_(n=1,��) b_m[n]
= lim_(m����) ��_(n=1,10^m) b_m[n]
= lim_(m����) (10^(-m))*��_(k=1,(10^m)/2) ��_( 1/(2k+1)��n/(10^m)<1/(2k) ) ((2k)mod10)
= ��_(k=1,��) ((2k)mod10)/(2k(2k+1))
= ��_(0,1) (2x^2+4x^4+6x^6+8x^8)(1-x)/(1-x^10) dx
�� 0.652562.
���̒l�� �� �Ƃ����� ��_m := ��_(n=1,10^m) b_m[n] �� lim_(m����) ��_m = �� �����̂�
lim_(m����) ��_(n=1,m) (��_n)/m = ��.
����炩��A���̐��� n �ɑ��� 10^m��n<10^(m+1) ��������k���Ƃ��
��_(k=1,n) b[k]
= 1 + ��_(k=1,n) ��_(j=1,��) b_j[k]
= 1 + (��_(j=1,m-1) ��_j) + ��_(j=m,��) ��_(k=1,n) b_j[k]
= 1 + (1+o(1))m�� + ��_(j=m,��) (��_j)*8n/(10^j)
(�������e j �ɑ��� ��_j �� 0 �ȏ� 1 �ȉ��̎���)
= 1 + (1+o(1))m�� + 72��n/(10^(m+1))
(�� �� 0 �ȏ� 1 �ȉ��̎���)
= (1+o(1))��logn.
����āA�Ɍ��l�͑��݁B���łɂ��̋Ɍ��l�̓�. >>803
(��/4)I = 0.7854�EI < 0.8427�EI = erf(1)�EI = I(1) =��[0,1] exp(-xx) dx,
���ӂ� ��[0,t] exp(-xx) dx �Ƃ���ƁA
t < 1,
n = 0. >>810
�����
��
> = ��_(0,1) (2x^2+4x^4+6x^6+8x^8)(1-x)/(1-x^10) dx
> �� 0.652562.
��
= ��_(0,1) (2x+4x^3+6x^5+8x^7)(1-x)/(1-x^10) dx
�� 0.956876.
��
> = (1+o(1))��logn.
> ����āA�Ɍ��l�͑��݁B���łɂ��̋Ɍ��l�̓�.
��
= (1+o(1))��log_10(n).
����āA�Ɍ��l�͑��݁B���łɂ��̋Ɍ��l�̓�/ln10. ������ln�͎��R�ΐ��B >>793
C{k-1,2} = C{k,3} - C{k-1,3}
&
C{2,3} = 0, >>780
http://poemehonpo.co.jp/
�@�{�܁@�����s�������T
http://www.poeme.co.jp/
�@���R�X���Ɨ������B�@�����s���V���b >>807
n���P���̂Ƃ�
�@b[1] = 1,�@�@�@�@A[1] = 1,�@�@�@B[1] = 1,
�@b[2] = 0,�@�@�@�@A[2] = 1.5 �@�@B[2] = 1,
�@b[3] = 0,�@�@�@�@A[3] = 11/6, �@B[3] = 1,
�@b[4] = 0.2 �@�@�@A[4] = 25/12,�@B[4] = 1.2
�@b[5] = 0.2 �@�@�@A[5] = 137/60, B[5] = 1.4
�@b[6] = 0.066667�@A[6] = 2.45�@�@B[6] = 1.46667
�@b[7] = 0.042800�@A[7] = 2.5929�@B[7] = 1.50947
�@b[8] = 0.02�@�@�@A[8] = 2.7179�@B[8] = 1.52947
�@b[9] = 0,�@�@�@�@A[9] = 2.8290�@B[9] = 1.52947
n�������̂Ƃ�
�@(1/9)10^k < n �� (1/8)10^k�@�@8 10^(-k) �� b[n] < 9 10^(-k)
�@(1/7)10^k < n < (1/6)10^k�@�@6 10^(-k) �� b[n] < 7 10^(-k)
�@(1/5)10^k < n �� (1/4)10^k�@�@4 10^(-k) �� b[n] < 5 10^(-k)
�@(1/3)10^k < n �� (1/2)10^k�@�@2 10^(-k) �� b[n] < 3 10^(-k)
�@���̑��@�@�@�@�@�@�@�@�@�@�@�@0 �� b[n] < 10^(-k)
10^(k-1) �� n < 10^k�@�͈̔͂Ō����
�@��A �` log(10) = 2.302585
�@248/315 = 0.78727 < ��B < 1.68727 >>812 (��)
(1-x^10)/(1-x) = 1+x+x^2+����+x^9
�@= (1+x)(1+x^2+x^4+x^6+x^8)
�@= (1+x)(1-x+x^2-x^3+x^4)(1+x+x^2+x^3+x^4),
���
(2x+4x^3+6x^5+8x^7)(1-x)/(1-x^10)
= (2x+4x^3+6x^5+8x^7)/{(1+x^2+x^4+x^6+x^8)(1+x)}
= (4-2x+6x^2-2x^3+6x^4+4x^6+4x^7)/(1+x^2+x^4+x^6+x^8) - 4/(1+x)
= (4-3x+6x^2-4x^3+6x^4-3x^5+4x^6)/(1+x^2+x^4+x-6+x-8)
�@+ (x+2x^3+3x^5+4x^7)/(1+x^2+x^4+x^6+x^8) + F(x)
= (3xx-4x+3)/2(1-x+x^2-x^3+x^4) + 5(1+xx)/(1+x+x^2+x^3+x^4) + E(x) + F(x)
= (�Ӄ�/2)/(xx-��x+1) + {1/(2�Ӄ�)}/(xx+x/��+1) + (1+��/2)/(xx+��x+1)
+ {(3-��)/2}/(xx-x/��+1) + E(x) + F(x)
= A(x) + B(x) + C(x)+ D(x) + E(x) + F(x),
�� A(x) dx = {(�Ӄ�-2)/�Ӂ�(4-�Ӄ�)}arctan{(2x-��)/��(4-�Ӄ�)},
�� B(x) dx = {(2+��5)/��(5+2��5)}arctan{(2��x+1)/��(4�Ӄ�-1)},
�� C(x) dx = (��/2)��{2(5+��5)}arctan{(2x+��)/��(4-�Ӄ�)},
�� D(x) dx = {(2+��)/�Ӂ�(4�Ӄ�-1)}arctan{(2��x-1)/��(4�Ӄ�-1)},
�� E(x) dx = (1/2)log(1+x^2+x^4+x^6+x^8) = (1/2)log{(1-x+x^2-x^3+x^4)(1+x+x^2+x^3+x^4)},
�� F(x) dx = -��4/(1+x) dx = -4log(1+x), ���̒���
= (3-4x+3xx)/2(1-x+x^2-x^3+x^4) + 5(1+xx)/2(1+x+x^2+x^3+x^4) + E(x) + F(x)
= (1-��/2)/(1-��x+xx) + (�Ӄ�/2)/(1+x/��+xx) + (1+��/2)/(1+��x+xx)
+ {(3-��)/2}/(1-x/��+xx) + E(x) + F(x)
= A(x) + B(x) + C(x)+ D(x) + E(x) + F(x),
A = (��/5)2��(1-2/��5) = 0.408306132277
B = (��/5)��(1+2/��5) = 0.864806265977
C = (��/5)(1/2)��(5+2��5) = 0.966882799046
D = (��/5)(3/2)��(5-2��5) = 0.684750200550
E = (1/2)log(5) = 0.804718956217
F = -4log(2) =-2.772588722240
���v�@0.956875631828 ���@�܂�
A(x) = (1-��/2)/(1-��x+xx),
B(x) = (�Ӄ�/2)/(1+x/��+xx),
C(x) = (1+��/2)/(1+��x+xx),
D(x) = {(3-��)/2}/(1-x/��+xx),
E(x) = (x+2x^3+3x^5+4x^7)/(1+x^2+x^4+x^6+x^8),
F(x) = -4/(1+x),
�� = (1+��5)/2 = 1.618034���� >>807
�悭������ A[n]/B[n] �̋Ɍ�������c
>>812 �ŋ��߂��̂͋t�� B[n]/A[n] �̋Ɍ��l�ł��邱�Ƃɒ��ӁB
>>817 �����I�ɕ\�����c���������C �����Ŕ��Ώ̗������藧�ĂT�C�N�����������Ė{�ɏ����Ă������
a��b , b��a�̂Ƃ�a��b��a�̃T�C�N��������
���������Ȃ��H ���̖{�͌������ƂȂ����ǁA�^�ɈقȂ�2���ɂ��Ă̘b����Ȃ��́H 0<1<2<...<n-1�Ə����t���R��ꂽ{1,...n-1}��n�v�f�̑S�����Ɠ��^�Ƃ�
�����������
0<2<3=4<...<n-1�Ə����Â���ꂽ{1,...,n-1}��n�v�f�̑S���������Ǔ��^����Ȃ����
���̖{�̂Ă��ق����ǂ��H �ӂ̒�����a,b,c(0<a<b<c�Aa^2+b^2+c^2=1)�̒����̂��A�Ίp�������Ƃ��ĉ�]�������Ƃ��ɒʉ߂��镔���̑̐ς����߂�B
��������܂���B ������Ȃ���ł���
�����Ă������� ����v���܂��B
V : 0����K-vector���
T : V�̐��`�ϊ� �Ƃ���Ƃ��A
V�̊��∅�Ɋւ���T�̕\���s���
0�~0�̗�s��ɂȂ�ׂ����Ǝv���̂ł����A
����͕\���s��̂ǂ̂悤�ɒ�`����ΐ������ł��܂��ł��傤���B K��1�̌��nn�捪�Ă��܂ނƂ��A����g��L/K�͙p���g��ł���B�ƁA�K���A���_�̖{�ɁA�����Ă����ł����A������ăq���x���g�̑�12���̓���ȏꍇ�ł����H ���݂܂���B������Ȃ����X���ɏ������Ƃł͂Ȃ������ł��ˁB����X���s���Ă��܂��B >>827
0�����x�N�g����Ԃ̊��̓ӂƂ������킯�킩��Ȃ����̂���Ȃ��͂��ł���
�����Ɛg�߂Ȃ��̂Ȃ͂��ł��� n,p,q,r�͐�����p+q+r=n����
���̂Ƃ�
n!/(p!q!r!)���K�������ɂȂ闝�R�������Ă��������B >>831
�����A0����vector��Ԃ̊��͋�W��∅�ł��B
�Ƃ������A����1�_����Ȃ���Ȃ̂� >>832
�����܂���A�����ł͂Ȃ����R���ōl���Ă������� >>833
1�_������Ȃ��W���ł͂Ȃ��ł����
����1�_�Ƃ͋�̓I�ɂ͂Ȃ�ł����H >>831
���݂܂���B�r���ő��M���Ă��܂��܂����B
����1�_����Ȃ�K-vector���V={0}�̊��͋�W��∅��������܂���̂ŁA
dim(V)=|∅|=0 �Ƃ����̂��������ł��B
�Ȃ��A����̓��e�ɂ��ẮA
���ȉ������܂����B
���������肪�Ƃ��������܂����B >>835
���Ȃ��Ă���r���ɑ��M���Ă��܂��܂����̂ŁA
�u����1�_����Ȃ���v�Ƃ����Ӑ}���Ȃ����͂𑗂��Ă��܂��܂����B
����v���܂����B �O>>797
>>824
xyz��Ԃɓ_(a,b,c)��a��b��c�ƂȂ�悤�ɂƂ�A�_(0,0,0)�ƌ�������Ίp���Ƃ��钼���̂����̒��������Ɉ��]������ƁA�����̂̒ʉߕ����́A
�~���Ɖ~������Ăꂱ�ɂ��ĉ~����̂����������̒�ʂŒ��肠�킹���ۂ̂悤�Ȍ`�B
�_(0,0,0)���_(a,b,c)�����Ɠ݊p�ɂƂ��������_�B
�I���I������V�n�Ώ̂ɂ����`�B
�����̂�z���ɕ��s�ɓ������f�ʂ��A�cc����(a^2+b^2)�̒����`�ŕ`���ƁA�Ίp���̒����͑�ӂ��A
��(a^2+b^2+c^2)=1
���p�O�p�`�̍����ƃs�^�S���X�̒藝���A�~������щ~����̔��a�ƍ�������肷��B3�ӂ̔�͂��������ق�����A
1:c:��(a^2+b^2)
=1:c:��(1-c^2)
�~��=(1/3)��{c^2/(1-c^2)}(1-c^2)
=��c^2/3
�ی`���̂̍ő唼�a
=c/��(1-c^2)
�Ίp�������̒�ʐ�(�ی`���̂̂��т�Ă镔���̍ŏ��f��)
=(1/2){c/��(1-c^2)}(1/c^2)
=1/2c��(1-c^2)
�~����=(1/3)��{c^2/(1-c^2)}-(1/3)��{1/4c^2(1-c^2)}(1/2)
�������̂̒ʉߕ����̑̐�
=2(�~��+�~����)
=2��c^2/3
+2(1/3)��{c^2/(1-c^2)}-2(1/3)��{1/4c^2(1-c^2)}(1/2)
=2��c^2/(1-c^2)-��/12c^2(1-c^2)
=(8c^2-1)��/12c^2(1-c^2) >>839
���肪�Ƃ��������܂�
�ł�c=1/��3�Ƃ��Ă�������v���܂��� >>837
����ꎟ�Ɨ�����Ȃ��ł���� �O>>839
>>840
a��b��c������A
c=1/��3�Ɖ��肵����Aa��b�����݂��Ȃ����낤�B
a^2+b^2=1-c^2=1-1/3=2/3
a��b��c���Z���B�܂�c�́A
1/��3��c
1/��3��肨�������͂��ŁA���̉���ɖ�������B �R�����~���Ƃ��̑g�ݍ��킹�ɂ͂Ȃ�Ȃ���Őϕ����Ȃ��Ɩ�������H
����ăC�i�ɂ͖����ł��B >>842
<�ł͂Ȃ�<=�ł����\����Ȃ��ł���
a=b=c�̂Ƃ��̓�/9�ɂȂ�͂��Ȃ�ł�
>>843
�����ł��ˁA�~��2�Ɖ�]��t�o�ȖʂƂ���2�̕��̂ɂȂ�͂��ł� �� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�
