分からない問題はここに書いてね454

**１３２人目の素数さん** · 2019/07/06(土) 22:59:21.29

さあ、今日も１日がんばろう★☆

前スレ
分からない問題はここに書いてね453
https://rio2016.5ch.net/test/read.cgi/math/1558041041/

(使用済です: 478)

**１３２人目の素数さん** · 2019/07/06(土) 23:16:28.69

ここは分からない問題を書くスレです。
お願いごとをするスレでも分からない問題に答えてもらえるスレでもありません。

**１３２人目の素数さん** · 2019/07/06(土) 23:27:14.34

答えが分かってる問題を書く場所でもないがな

**１３２人目の素数さん** · 2019/07/06(土) 23:33:42.68

自然数の複雑度を流行らせたい
ある自然数nを1と+と×と()を用いて表すとき最小の1の個数をω(n)とする。
自然数n,kについてω(n^k)＝kω(n)か？
素数pに対してω(p)＝ω(p-1)+1か？

**１３２人目の素数さん** · 2019/07/06(土) 23:48:25.95

ちなみに、集合W(n)をW(1)＝{1}、W(2)＝{1,2}、W(3)＝{1,2,3}、n≧3について
W(n+1)={∀a∈W(n),∀d(dはaが合成数のときのaの約数),∀e(eはaが素数のときのa-1の約数)/
a, a+a/d, a+(a-1)/e}
とすると、ある自然数kに対して、kが集合W(n)に含まれて、i≦kを満たす全ての自然数iに対して
kがW(i)に含まれないことと、ω(k)＝nであることは同値です

**１３２人目の素数さん** · 2019/07/07(日) 00:44:49.01

>>4
ω(n^k)＝kω(n)の反例
ω(11)=8 ;11=(1+1)×(1+1+1+1+1)+1
ω(11^2)=15 ;11^2=(1+1)×(1+1)×(1+1)×(1+1+1)×(1+1+1+1+1)+1

**１３２人目の素数さん** · 2019/07/07(日) 01:25:08.29

>>6
反例ありがとうございます因みにn＝3のときには成り立っていることは証明されています数学セミナーにありました

**１３２人目の素数さん** · 2019/07/07(日) 01:53:15.88

>>5の追記です
d≠aかつe≠a-1です

【底辺】 · 2019/07/07(日) 10:58:05.44

やっぱり部分積分じゃない。
変数がrとθの2つあるでなぁ。
f(x)g(x)みたいに一つの変数xじゃなくて変数が2つある場合だから、この式じゃないと思う。
∬[r=0～　][θ=0°～　]――drdθみたいな感じ。

**１３２人目の素数さん** · 2019/07/07(日) 11:13:55.05

定積分I[x] = ∫[1 to x] 1/{xln(x)} dx に対し、
不等式m < I[n] < m+1を満たす自然数nの個数をa[m]とおく。
mがm=1,2,...と正の整数値をとるとき、
b[m]=a[m+1]/a[m]で定義される数列b[m]について、
その増減、m→∞としたときの極限
をそれぞれ述べよ。

**１３２人目の素数さん** · 2019/07/07(日) 13:48:06.99

I[x] = ∫[1 to x] 1/{xln(x)} dx =
= lim{ε→+0} ∫[1+ε to x] 1/{xln(x)} dx = ln( ln(x) ) - lim{ε→+0} ln( ln(1+ε) )
という理解でOK？これ発散しますよね？

**１３２人目の素数さん** · 2019/07/07(日) 17:45:01.21

>>9
h(r,θ) = 2(1 - r･cosθ),
を入れると
v/2 = ∫[0～1] ∫[0～60ﾟ] h(r,θ) dθ rdr
　= ∫[0～1] ∫[0～π/3] 2(1-r･cosθ) dθ rdr
　= ∫[0～1] 2r dr･∫[0～π/3] dθ - ∫[0～1] rr dr･∫[0～π/3] 2cosθ dθ
　= (π/3) - (1/3)[ 2sinθ ](0→π/3)
　= (π-√3)/3,
部分積分しなくても出る。

>>10
J[x] = ∫[e to x] 1/{x･ln(x)} dx = [ ln(ln(x)) ](e to x) = ln(ln(x)),
は収束。

**１３２人目の素数さん** · 2019/07/07(日) 18:16:20.38

長方形ABCD（AB<AD）の内角∠Aの2等分線をLとする。
L上に点Pを、直線PCと対角線BDが交点を持つようにとる。
このとき、以下を示せ。
「PC=BDとなるための必要十分条件は、PCとBDが直交することである。」

**１３２人目の素数さん** · 2019/07/07(日) 18:58:14.27

P=A のときPC=BD

**１３２人目の素数さん** · 2019/07/07(日) 19:24:02.44

>>13
P≠Aです。

**１３２人目の素数さん** · 2019/07/07(日) 19:28:50.25

((2n-k)!2^k)/(2n)!　に根が存在しないのはなぜ？

**１３２人目の素数さん** · 2019/07/07(日) 19:42:37.26

>>14
P≠Aです。

**１３２人目の素数さん** · 2019/07/07(日) 20:47:14.80

スレチだったらすみません。

ベッセル関数が定常波、ハンケル関数が進行波を示すという意味がよくわからないのですが、どういった風に考えれば良いですか？

**１３２人目の素数さん** · 2019/07/07(日) 21:08:37.80

わからないんですね

**１３２人目の素数さん** · 2019/07/07(日) 21:10:15.27

>>19
はい、わかりません

**１３２人目の素数さん** · 2019/07/07(日) 22:23:26.07

あんま興味ある人ないかもだが集合論に関して教えてくれ
ラッセルのパラドックスを生む「集合」Rを定義すると矛盾が導かれることは有名だ
背理法を使った証明において、何らかの「集合」Xを導入して矛盾を示したとする。
この時、XがRと同じように定義するだけで矛盾を導く「集合」ではないことを証明する必要があると思うんだが、
これを行うにはどういう手順を踏むのが普通なのか教えてくれ

**１３２人目の素数さん** · 2019/07/07(日) 22:42:58.23

>>21
そのXが利用してる公理的集合論の公理から正しく存在が保証されてるか確認すればいい。

**１３２人目の素数さん** · 2019/07/07(日) 22:56:57.22

>>22
ありがとう。やっぱりそれしかないか
空集合か少なくとも一つ集合を含むことを言えればOKとかそういう便利なのがあればよかったんだが。
公理に戻るのは大変なので、専門書から存在証明がされている集合の定理を探してみるよ

**１３２人目の素数さん** · 2019/07/07(日) 23:08:11.74

>>13
　A(0,0)　B(b,0)　C(b,d)　D(0,d)　E(b+d,b+d)
とおく。
Cを中心とし半径BDの円周をKとおく。
AC = BD, CE=BD　より　A,E ∈ K
∴ 　K∩L = {A,E}　　　←　円と直線の交点は高々2つ

P∈L とすると
　PC=BD　⇔　P∈(K∩L)　⇔　P∈{A,E}

**１３２人目の素数さん** · 2019/07/07(日) 23:33:29.35

ハンケル関数は、円筒波（または2次元空間の波）を表わす解であり、内側／外側に伝搬する波を表わす。

**１３２人目の素数さん** · 2019/07/08(月) 00:02:24.63

>>25
ありがとうございます。
ただ、円筒波を表すと言われても、あの形でなぜ波？となるのですが。
ベッセル関数とノイマン関数の線形結合させたのがハンケル関数のはずですがそもそもなぜ、ハンケル関数を導入したのかと。

イナ ◆/7jUdUKiSM · 2019/07/08(月) 13:32:00.19

前>>9
>>12
1-rcosθがどこかわかればわかると思うんです。
1-rcosθの1は単位円の半径ですか？
rcosθは中心から距離rの地点の中心からの距離ですか？
これを1から引くということは、
1-rcosθは中心からr、扇形の端からθの地点の単位円周上からの距離ですか。
これを2倍して、
2(1-rcosθ)は高さですか？　つまり高さ1の単位円柱が正四面体PABCの側面で外に削り取られた蒲鉾外の高さ。
でも断面が1:2:√5の直角三角形になるのはθ=π/3のときだけのはず。
h(r,θ)の地点で2倍してるのはなぜでしょう？

**１３２人目の素数さん** · 2019/07/08(月) 14:06:28.97

f(x)=3xx /(2xx +1)とする。
0<z<1、a(1)=z、a(n+1)=f( a(n) )で定める時、
zの値に応じたlim(n→∞) a(n)を求めよ。

これお願いします　
某大学の入試ですが、f'(x)が1を越えることがあるので普通の平均値の定理を使った解法では解けません
発想の順序も教えてもらえたら嬉しいっす

**１３２人目の素数さん** · 2019/07/08(月) 16:06:08.32

0<a≤b、0<R、とする。
また領域D、領域Eを以下のように定める。

領域D:
O(0,0),A(a,0),B(a,b),C(0,b)を頂点とする長方形OABCの周上および内部

領域E:
O(0,0)を中心とする半径Rの円の周上および内部

（1）2つの円C_1とC_2を、領域Dからはみ出ないように、かつC_1とC_2が互いに外接するか外部にあるように置く。
C_1とC_2の面積の合計が最大になるような置き方を述べよ。

（2）2つの円K_1とK_2を、（1）と同様に領域E内に置く置き方を述べよ。

**１３２人目の素数さん** · 2019/07/08(月) 18:50:01.07

微分についての質問です

x=sinθとおいたとき両辺をθで微分すると
dx/dθ＝cosθとなります
ここで、記号的には「xを微分する」という操作で「xの前にdをつけて、さらに分母にdθをつける」
ことを行いました
その後dx=cosθdθとおいて積分する方法がよく用いられますが、これが気持ち悪くて仕方ありません
dx/dθにはxをθで微分するという意味が与えられているだけで、分数の概念ではありません。
それなのに分数と扱って分子と分母を都合よく切り分けて計算してよいのか疑問です。

**１３２人目の素数さん** · 2019/07/08(月) 19:02:46.57

>>30
高木貞治先生が解析概論でこの記号は割り算と書いています
微小量に対する微小量の変化を見ているのが本義なので実際本質的意味は割り算です

**１３２人目の素数さん** · 2019/07/08(月) 19:22:09.85

Aが0でない定数のとき、
exp(x)=A(1+x)
上記の方程式解ける方いたら、教えてください

**１３２人目の素数さん** · 2019/07/08(月) 20:24:52.09

>>26
なぜ波か？それは
2次元波動方程式:
　{ (∂x)^2+(∂y)^2 - (∂ct)^2 } Ψ = { r^2.(∂r)^2+ r.(∂r) + (1/r).(∂φ) + k^2 } Ψ = 0
　Ψ ∝ exp(-iωt),　k=ω/c
この一般解(極座標表示) が
　Ψ(r,φ,t) = Σ ( a[n]. J_n(kr)+ b[n]. Y_n(kr) ). exp(inφ). exp(-iωt) 　
のように表せるからです。
J_n, Y_n は定常波 (https://imgur.com/a/CKaxlNo)
H1_n = J_n + i Y_n は外向き進行波 ( https://imgur.com/a/Lrq5Lua )
H2_n = J_n - i Y_n は内向き進行波になっています。
おまけ ( https://imgur.com/a/YPSIGd0 )

3次元波動方程式の場合
　{ (∂x)^2+(∂y)^2+(∂z)^2 - (∂ct)^2 } Ψ = { r^2.(∂r)^2+ r.(∂r) + (1/r)(∂φ) + k^2 } Ψ = 0
　Ψ ∝ exp(ihz).exp(-iωt),　k^2 = (ω/c)^2 - h^2
一般解(円筒座標表示): Ψ = Ψ(r, φ,z, t) = (略)
と、まあ 2次元極座標とほぼ同じ扱いになりますが
k^2 < 0 になる場合は変形ベッセル方程式となります. (解は I_n, K_n で表せる)

**１３２人目の素数さん** · 2019/07/08(月) 20:28:48.06

訂正
誤: (1/r).(∂φ)
正: (1/r^2).(∂φ)^2

∂x, ∂ct, ∂φ, etc. は ∂/∂x , ∂/(c∂t) , ∂/∂φ, etc. の略記です。

**１３２人目の素数さん** · 2019/07/08(月) 20:36:24.68

>>30
記号が意味そのものではないとは確かなことなんですけど、長い微分積分の歴史の中でそういう表記が生き残ってきたのにはやはり理由があるんですね

分数と考えても良いのですよ

33 · 2019/07/08(月) 20:45:44.48

追加
Y_n の定常波 ( https://imgur.com/a/LoX4UdK )

plot は python のmatplotlib を使用した。
ほんの40行くらいで 3次元プロット, latex形式でタイトル入れ, gif アニメ生成までやってくれた。

**１３２人目の素数さん** · 2019/07/08(月) 20:54:52.75

>>36
これ凄すぎますね。

**１３２人目の素数さん** · 2019/07/08(月) 21:18:11.66

>>30
高校生だろうから深く突っ込む必要はないけど、微分形式というものを考えるとdyやdxなどを単独で扱うことができます
で、ポアンカレの補題というもの(の特殊な場合)から適当な領域上でdy=F(x)dxとなる関数Fが存在することが知られています
実際にはこの関数F(x)が導関数dy/dxですから、この記号dy/dxを「dy=F(x)dxをdxで割ったもの、つまり割り算」と見て差し支えありません

一方で微分を割り算として捉えるとまずい場合もありますが、それは偏微分(多変数関数の各変数に関する微分)というもので浮き彫りになると思います

**１３２人目の素数さん** · 2019/07/08(月) 21:34:21.01

>>30
分母を払うのはただのニーモニックで、実際には置換積分をやっただけだよ
割り算とか分数とかは忘れな

**１３２人目の素数さん** · 2019/07/08(月) 23:35:26.34

>>4
ω(p)＝ω(p-1)+1 の最小の反例は p=353942783 であるらしい

33 · 2019/07/09(火) 01:29:02.81

再訂正
誤: { r^2.(∂r)^2+ r.(∂r) + (1/r).(∂φ) + k^2 } Ψ = 0
正: { (∂r)^2+ (1/r).(∂r) + (1/r)^2.(∂φ)^2 + k^2 } Ψ = 0

r^2 を掛けて
{ r^2.(∂r)^2+ r.(∂r) + (∂φ)^2 + (kr)^2 } Ψ = 0
Ψ = f(kr) exp(inφ) exp(-iωt) と変数分離(一価性からの要請により n は整数)、ξ=kr と置いて
ベッセル方程式: { ξ^2.(∂ξ)^2+ ξ.(∂ξ) + (ξ^2 - n^2) } f(ξ) = 0
が得られます。
二階の常微分方程式なので独立な解は二つ、
それが J_n, Y_n の組 (或いは H1_n , H2_n の組) です。
Y_n の解は r → 0 で発散しますが、中心部( r = 0 )を含まない境界条件の時に活躍してくれます。

**１３２人目の素数さん** · 2019/07/09(火) 03:12:02.73

>>32

　-(1+x)･e^{-(1+x)} = -1/(Ae),
より
　-(1+x) = W{-1/(Ae)},
　x = -W{-1/(Ae)} -1,
　W は Lambert のW函数。

**１３２人目の素数さん** · 2019/07/09(火) 03:32:45.06

2^n (n=1,2,3,...)の一桁目の数は2,4,8,6の周期４で変化する。
一方最上位の数に注目すると2,4,8,1,3,6,1,2,5,1,2,...etcと非周期的に変化して分布も知られています（ベンフォードの定理）
それではその中間の二桁目の数、三桁目の数、、、最上位の一つ下の数 etc　他の桁の数は周期的に変化するのでしょうか？？
それとも非周期的なんでしょうか？

**１３２人目の素数さん** · 2019/07/09(火) 03:56:01.31

桁数固定したら周期的なのは当たり前だった

**１３２人目の素数さん** · 2019/07/09(火) 07:56:15.74

>>44
各位の数の和の最上位は？

**１３２人目の素数さん** · 2019/07/09(火) 11:21:48.17

分布は決定できるけどね。
最上位からみて二桁目が3である割合とか。
いわゆる一様分布定理の応用。

**１３２人目の素数さん** · 2019/07/09(火) 15:27:44.82

>>42
ありがとうございます

**１３２人目の素数さん** · 2019/07/09(火) 15:29:32.82

>>28

0<z<1/2 のとき
　g(x) = f(x)/x　とおく。
　g(x) = 3x/(2xx+1) = 1 - (1-x)(1-2x)/(2xx+1) <1,
　a(n) は単調減少。a(n)<z<1/2,
　また g(x) は |x| < 0.707107 で単調増加。
　a(n+1)/a(n) = g(a(n)) ≦ g(z) < g(1/2) = 1,
　0 < a(n+1) < z･g(z)^n → 0　　(n→∞)

1/2<z<1 のとき
　h(x) = [1-f(x)]/(1-x)　とおく。
　h(x) = (x+1)/(2xx+1) = 1 - x(2x-1)/(2xx+1) < 1,
　a(n) は単調増加。a(n)>z>1/2,
　また　また h(x) は x > 0.224745 で単調減少。
　[1-a(n+1)]/[1-a(n)] = h(a(n)) < h(z) < h(1/2) = 1,
　0 < 1 - a(n+1) < (1-z)･h(z)^n → 0　　(n→∞)

z=1/2 のとき
　a(n) = 1/2.

**１３２人目の素数さん** · 2019/07/09(火) 15:54:25.80

>>48
ありがとうございます！
実戦で25分以内にその関数を見つけられるようにするためには、どういう思考の道筋を辿ると良いと思われますか？

**１３２人目の素数さん** · 2019/07/09(火) 16:28:44.61

>>49
発想としては極限値をグラフの交点から推測する時と同じ
あとそれを論述する式変形をする

**１３２人目の素数さん** · 2019/07/09(火) 18:21:09.21

平均値の定理方式なら、（必要なら）最初の何項かを間引いて平均値の定理が使うといい
25分もあればなんとかなるでしょ

**１３２人目の素数さん** · 2019/07/09(火) 19:51:51.09

そうそう。
どんな初項から始めてもならちょっと考えないといけない時もあるけど、具体的に初項指定されてたら大概二三項めから考えればなんとかなるからな。

**１３２人目の素数さん** · 2019/07/09(火) 20:03:14.65

初項指定されてないだろｗ

**１３２人目の素数さん** · 2019/07/09(火) 20:03:43.04

ウエメセでできる人にのっかって適当いいたいだけのヤカラが結構いるな。
問題くらいは読め

**１３２人目の素数さん** · 2019/07/09(火) 20:10:21.09

ちゃんと 0<z<1、a(1)=z と指定されてるぞ甘ったれハゲ

**１３２人目の素数さん** · 2019/07/09(火) 20:18:41.96

そもそもf'(x)=1の解が0.19221…と0.74767…あたりなんだが
最初2-3項調べて一体何をどうする気なんだかｗ
問題触りすらしない一言居士見ると笑っちまうな

**１３２人目の素数さん** · 2019/07/09(火) 20:35:28.84

グラフ描けば一目瞭然じゃーん、終わり。
としたいけど、それじゃダメなんですよね。
どうしたらいいのか分からんけど、
この種の「一目瞭然」を統一的に扱うにはどうしたらいいのかね？
毎回、>>48 みたいな工夫をしないといけないの？

**１３２人目の素数さん** · 2019/07/09(火) 21:28:57.26

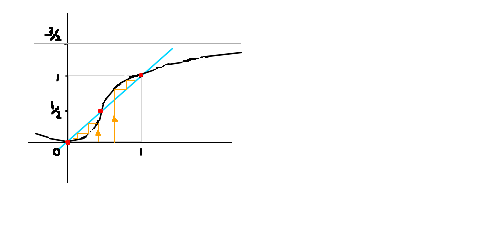まず1未満の正の数rを選ぶ。
交点を通り傾きが±rの直線を引く。
何項か計算して(a(n),a(n+1))がその二本の直線に挟まれたエリアに入ったら完。

**１３２人目の素数さん** · 2019/07/09(火) 22:10:06.80

>>57
これ試験に書いても満点はもらえないとされてるようですね。部分点はくれるでしょうが。

しかしこれで…うーん…
どういう理屈で説明すれば完璧になるんでしょうね？

**１３２人目の素数さん** · 2019/07/09(火) 22:39:56.31

>>40
反例ありがとうございます。そうでしたか。結局全部の予想が外れてて残念です
でも複雑度は結構面白いので皆さんも考えてみては？

**１３２人目の素数さん** · 2019/07/10(水) 01:38:58.00

>>27
　h は平面PBC (正三角錐PABCの一面) の高さです。
　(x,y) 座標では h = 2(1+y) です。(y=0 で 2, y=-1 で 0 だから)
　(r,θ) 座標では h = 2(1-r･cosθ) です。

**１３２人目の素数さん** · 2019/07/10(水) 02:12:37.49

>>59

0<|z|<1/2の時
第２項は0<x<1/2
r=a(2)とおくと2以上のnで(a(n),a(n+1))は領域0<x<1、|y|<|rx|
以下ry

1/2<|z|<1の時
第２項は1/2<x<1
r=|a(2)-1|とおくと2以上のnで(a(n),a(n+1))は領1/2<x<1、|y-1|≦r|x-1|
以下ry

|z|>1/2の時
第２項は1/2<x<1
r=f'(1)とおくと2以上のnで(a(n),a(n+1))は領1/2<x<1、|y-1|≦r|x-1|
以下ry

**１３２人目の素数さん** · 2019/07/10(水) 05:18:45.21

（1）等式 3^n = k^2 - 40 を満たす自然数の組(n,k)を全て求めよ。

mは1以上99以下の整数とする。

（2）等式3^n = k^2 - m を満たす自然数の組(n,k)が存在しないようにmを定めることができる。このことを示せ。

（3）（2）のようなmを全て求めよ。

57 · 2019/07/10(水) 11:01:16.05

>>28 のタイプの問題を統一的に扱う件、少し考えてみた
y=f(x) は単調増加な連続関数とする

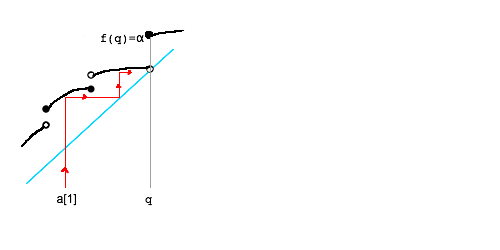
■1　a[1] < f( a[1] ) = a[2] の場合
開区間族 S := { (a[1],t) ; x ∈ (a[1],t) → x < f(x) }
合併区間 U:= ∪ S = (a[1], q)　(非有界なら q=+∞)
α := f(q)
とする。

連続性により, 任意のε(>0) に対し δ(>0)が存在して |τ-q|≦δ → |f(τ)-α|≦ε
Uの定義より、あるτについて q<τ<q+δ かつ f(τ) ≦ τ (単調増加より f(τ)=τ である)
α-ε ≦ f(τ) = τ < q+δ ≦ f(q+δ) ≦ α+ε
ε→0 により q=α が得られる.

(具体的な αはグラフで交点を求めて、数式で Uの性質を満たす事を示せばよい )

●1.1　 a[n]∈U かつ a[n+1] not∈ U となる n が存在する場合
あるτについて a[n] < τ ≦ a[n+1] かつ τ=f(τ) (∵中間値の定理)
a[n] < τ ≦ a[n+1]=f(a[n]) ≦ f(τ)=τ (∵単調増加)
よって a[n+1]=τ
αの定義より α≦τ , 単調増加より τ=f(a[n]) ≦ f(α)=α よって τ=α
α=a[n+1] = f(α) = ff(α) = f...f(α)
つまり lim a[n]=α

●1.2　a[n]∈U かつ a[n+1] not∈ U となる n が存在しない場合
a[1] < a[2] < ... < α である。
lim a[n] = β ≦ α (上に有界の場合) とする. (収束しなければ lim a[n]= +∞ = α である)
任意のε(>0) に対しある N が存在して n>N → β-ε < a[n]<a[n+1]=f(a[n]) < β
よって lim{ f(a[n]) - a[n] }= f(β) - β = 0, 前と同様の論法で β=α
つまり lim a[n]=α

■2　a[1] > f( a[1] ) = a[2] の場合
1と同様の論法で処理

■3　a[1] = f( a[1] ) = a[2] の場合
明らか

**１３２人目の素数さん** · 2019/07/10(水) 11:30:15.12

AB=1、AD=aの長方形ABCDと相似な長方形PAQDがあり、5点A,B,C,D,Pは同一円周上にある。
aの値を求めよ。

**１３２人目の素数さん** · 2019/07/10(水) 11:39:35.34

>>65
そんな図形あり得る？
ADは長方形ABCDの外接円の直径にはなり得ない
Pも同一円周上にあるなら∠APDは直角にはなり得ないのでPAQDという長方形は作れないんじゃ？

57 · 2019/07/10(水) 11:58:47.54

>>64
> 連続性により, 任意のε(>0) に対し δ(>0)が存在して |τ-q|≦δ → |f(τ)-α|≦ε ...
(ここは以下のように変更可能 )
∀ε ∃τ (q-ε < τ < q) ∧ ( τ < f(τ) )
q-ε < τ < f(τ) ≦ f(q) = α ∴ q ≦ α

∀ε ∃τ ( q ≦ τ < q+ε ) ∧ ( f(τ) ≦ τ )
α= f(q)≦ f(τ)≦τ <q+ε ∴ α ≦ q
よって α = q

> あるτについて a[n] < τ ≦ a[n+1] かつ τ=f(τ) (∵中間値の定理) ...
(中間値の定理は連続性をを使っているが、以下のように変更可能)
∀x ∈ (a[1],a[n] ) x < f(x)
a[n+1] not∈ (a[1], α ) より a[n]≦ α ≦ a[n+1]
f(α) = α ≦ a[n+1] = f(a[n]) ≦ f(α) =α
よって a[n+1] = α

つまり前提は「y=f(x) は単調増加」だけでよい。
連続性、微分可能性は不要

**１３２人目の素数さん** · 2019/07/10(水) 13:04:45.79

移行って＝超えればプラスマイナス逆になるんだよね？

b-a=3を変形したらa=b-3になったんだけどわかる人いる？

**１３２人目の素数さん** · 2019/07/10(水) 13:12:23.52

>>68
○＝△の関係があるとき、
両辺に同じ数字や式を足す、引く、0以外の数をかける、などしても両辺イコールの関係はずっと成立する

例えば
○＋３＝△＋３
○＋a＝△+aになる

なので
b-a=3
↓(両辺にaを足す)
b=3+a
↓(両辺から3を引く)
b-3=a

**１３２人目の素数さん** · 2019/07/10(水) 13:22:39.79

>>63
ここはおまえが出題者ぶって問題を出す場所じゃないから失せろ統合失調のガイジ

**１３２人目の素数さん** · 2019/07/10(水) 13:23:31.11

>>63
おまえ頭の病気だって理解してる？
なんで自分だけ誰からも相手にされてないか理解できる？

57 · 2019/07/10(水) 14:00:40.92

>>67 (訂正)
●1.2 にて、lim a[n] = β → lim f(a[n]) = f(β) つまり連続性を使ってしまっている.
さらによく考えてみれば, 連続でないなら α ;= f(q) で α ≠ q の場合もある.

なので、もう少し修正が必要だが、それでも連続性の前提は外せると思う。

**１３２人目の素数さん** · 2019/07/10(水) 14:11:20.81

>>68
右辺と左辺を入れ替えるか、途中どこかで両辺に-1を掛ければそうなる

**１３２人目の素数さん** · 2019/07/10(水) 14:46:37.91

>>63

(1)
　(2,7)　(4,11)

(2)
　3^2 = 9 ≡ 1　(mod 8)
3^n ≡ 1,3　　(mod 8)
　kk ≡ 0,1,4　(mod 8)
∴　m = kk - 3^n ≠ 2,4　　(mod 8)

**１３２人目の素数さん** · 2019/07/10(水) 17:18:15.37

平面上にn個（n≥4）の点がある。
これらのうちどの4個を選んでもそれらが同一円周上にあるならば、n個の点全てはある1つの円周上にあることを示せ。

**１３２人目の素数さん** · 2019/07/10(水) 17:20:33.33

>>75
失せろ統合失調ガイジ

**１３２人目の素数さん** · 2019/07/10(水) 17:21:27.60

>>75
ここはあなたが問題を出す場所ではありません
迷惑なので書き込まないでください

**１３２人目の素数さん** · 2019/07/10(水) 17:54:07.06

高専3年
偏導関数の応用
以下urlの不等式条件付き最大値最小値問題が分かりません。
等式が成り立っている楕円上はラグランジュの未定乗数法で求まると思うのですが、楕円内の最大値最小値の求め方が分かりません。
よろしくお願いします。

https://i.imgur.com/hWbEcan.jpg

57 · 2019/07/10(水) 17:58:14.49

>>72 (続き)
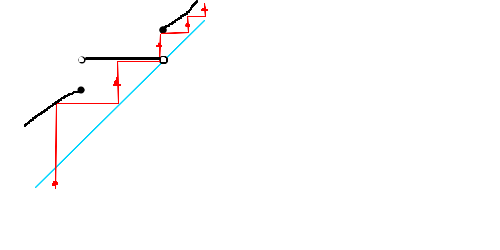
連続性の前提を外す件
↓こういう気持ち悪い逃げ道ができる事があるので、やめたほうがよさそう。
しょうもない追加前提が必要になってくる。

**１３２人目の素数さん** · 2019/07/10(水) 18:03:38.89

>>78
x=2acosαcost
y=bsinαsint

**１３２人目の素数さん** · 2019/07/10(水) 19:08:13.27

x(x+y)-y^2=1
を満たす自然数の組(x,y)は無数に存在することを示し、そのうちxが10番目に小さい組を求めよ。

**１３２人目の素数さん** · 2019/07/10(水) 19:11:35.35

>>81
なんでこの人そんなに嫌われてるの？

**１３２人目の素数さん** · 2019/07/10(水) 19:27:18.20

>>78はもうマジかという目くらましwww

**１３２人目の素数さん** · 2019/07/10(水) 19:43:11.77

陰関数定理について質問させてください。
f(x, y)=0のとき、y’=-fx/fyという定理です。

レムニスケート曲線4(x^2+y^2)^2-(x^2-y^2)=0(https://i.imgur.com/pONXvGp.jpg)
にこれを使うと、(x, y)=(0, 0), (±√6/8, ±√2/8)にてy’=0となることがわかります。しかし、実際には(0,0)ではy'=0ではありません。なぜこのようなことが起きるのでしょうか？この点は、陰関数定理を適用できる条件を満たしていないのでしょうか？

よろしくお願いします。

**１３２人目の素数さん** · 2019/07/10(水) 20:12:11.48

λλΠλΠΣΨΣΨΠΔ

ΣλΠΣΨτΨδζοΓ

**１３２人目の素数さん** · 2019/07/10(水) 20:56:48.24

>>82
統合失調症はどこでも嫌われるだろw
スレの使い方明らかに間違えてるんだから
言外の意味を理解できない5chによくいる糖質の典型例

**１３２人目の素数さん** · 2019/07/10(水) 22:47:15.34

>>69
それは等式の性質だ
大学以降は同値関係で説明するべきである

**１３２人目の素数さん** · 2019/07/10(水) 22:48:07.53

>>86
統失と自閉症スペクトラムは全く別の病だが大丈夫か？

**１３２人目の素数さん** · 2019/07/10(水) 22:53:13.69

>>78
・xyt空間曲面: f(x,y,t) = xx/4 + yy + tt = 1 (t≧0) ...(1)
・その法線ベクトル: (x/2, 2y, 2t )

・xyt空間平面: x + y + t = z ...(2)
・その法線ベクトル: (1,1,1)

■ t ＞ 0
zが極値をとる条件は 2つの法線ベクトルが平行になっている事 (実質上はラグランジュ未定乗数法そのもの)
(x/2, 2y, 2t ) = k*(1,1,1) {k:比例係数}
(1)に代入して 4kk/4 + kk/4 + kk/4 = 1 ∴ k = ±√(2/3)
z = x + y + t = 2k + k/2 + k/2 = 3k = ±√6

■ t = 0
・xx/4 + yy = 1
・x + y = z
今度は 2次元版で同様に処理する
(x/2, 2y) = k'*(1,1)
4k'k'/4 + k'k'/4 = 1 ∴ k' = ±2/√(5)
z = 2k' + k'/2 = (5/2)*k' = ±√5

よって +√6 が最大値, -√5 が最小値である

てか... 右上に偏導関数だとか書いてあるんですけど...
え？大学受験レベルでそういうのアリなの？

**１３２人目の素数さん** · 2019/07/10(水) 23:29:16.35

精神分析は別スレで

**１３２人目の素数さん** · 2019/07/10(水) 23:47:13.49

>>78

7.27
xx/4 + yy ≦ 1　の範囲を x,y が動くとき、関数
　　　ｚ = x + y + √(1 -xx/4 -yy),
の最大値および最小値を求めよ。　　　(長岡技科大)
--------------------------------------------

x = 2a cos(t),　y = a sin(t)　とおく。　　　>>80
題意より 0≦a≦1,

(1) まづ θを一周すると
　(x+y)^2 = 5(xx/4 + yy) - (x/2 - 2y)^2 = {5 - [cos(t)-2sin(t)]^2}aa ≦ 5aa,
　(等号は y=x/4, tan(t)=1/2 のとき)
-(√5)a ≦ x+y ≦ (√5)a,
よって
　-(√5)a + √(1-aa) ≦ z ≦ (√5)a + √(1-aa),

(2) 次に 0≦a≦1 で動かす。
　-√5 ≦ z ≦ √6,
　(左等号は a=1 のとき。右等号は a=√(5/6) のとき)

**１３２人目の素数さん** · 2019/07/11(木) 00:08:27.91

>>64
ありがとうございます
しかし、ちょっと用語が難しく、理解には至りませんでした
精進します。

**１３２人目の素数さん** · 2019/07/11(木) 00:36:47.93

>>81
フィボナッチ数を F_n とおく。
　G_n = F_n･{F_n + F_(n+1)} - {F_(n+1)}^2
　= F_n･{2F_n + F_(n-1)} - {F_n + F_(n-1)}^2
　= (F_n)^2 - F_(n-1)･{F_(n-1) + F_n}
　= - G_(n-1)
　= ･････
　= (-1)^(n-1)・G_1
　= (-1)^(n-1) {F_1･(F_1+F_2) - (F_2)^2}
　= (-1)^(n-1),

∴　(x, y) = (F_{2m-1}, F_{2m})　は題意を満たす。(mは自然数)

m=10 のとき　(F_19, F_20) = (4181, 6765)

>>84
　おいらの連鎖律

**１３２人目の素数さん** · 2019/07/11(木) 01:02:35.25

>>81

(x, y) = (1, 1) は題意を満たす。

(a+b){(a+b)+(a+2b)} - (a+2b)^2 = a(a+b) - b^2,
∴　(x, y) = (a, b) が題意を満たすならば　(a+b, a+2b) も題意を満たす。(終)

**１３２人目の素数さん** · 2019/07/11(木) 07:28:42.62

>>89
なるほど!
この方法で解くとエレガントですね。
わかりやすい解説ありがとうございました。
また機会がありましたらよろしくお願いします。

**１３２人目の素数さん** · 2019/07/11(木) 13:08:24.66

下記のような式は微積分のどういう分野で出てくるのですか？

∫logyf(xy)dy=G(y,x)

イナ ◆/7jUdUKiSM · 2019/07/11(木) 17:27:22.04

前>>27
>>12正四面体PABCと単位円柱内部を足しあつめて引く場合、どっち方向に切った断面積をどっち方向に足しあつめますか？
rとθの2つの変数がある場合、どこを起点にし(どこにr=0,θ=0または0°をとり)ますか？
そこを明確に示せば式は人それぞれ勝手に立てて解くと思うんです。
こういう積分の答案には、方向と起点を書いてください。

**１３２人目の素数さん** · 2019/07/11(木) 17:40:32.62

r=0 は円柱の軸 (z軸、OP),
θ=0ﾟは ∠BOCの中央の向き (OAと反対の方向）

なお、PABCは正四面体ではなく正三角柱。

**Frank student** · 2019/07/11(木) 17:56:34.55

>>81
ss = Solve[x^2 + x y - y^2 == 1 , y];
n = 1;
Do[
If[IntegerQ[py = (y /. ss[[2]])], Print[{n++, x, py}]], {x, 0,
10000}]

{1,1,1}

{2,2,3}

{3,5,8}

{4,13,21}

{5,34,55}

{6,89,144}

{7,233,377}

{8,610,987}

{9,1597,2584}

{10,4181,6765}

で片が付く

証明？　フィボナッチが当然でてくるが、それをしらなくても　なんとかできるでしょう

1５以上は計算時間がかかりそうだね

**１３２人目の素数さん** · 2019/07/11(木) 18:01:31.40

0<α<β<90とする。
PA=a、PB=bである△PABにおいて、∠A=α°、∠B=β°とする。
このとき、以下の極限を求めよ。
lim[β→α]{cosβ°-cosα°}/(b^2-a^2)