�ʔ�����肨�����ā`�� 29���
�� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�
�C�i����A�C�i����A
>>767
������҂�����ς���ꍇ�A
���ꔭ�ڂœ��Ă�m���́A
��1/3�\�\�A
����ς������A�ꔭ�ڂɑI���̔��͊J���Ȃ����Ƃɂ������ǁA
���̇A�̊m�������Z���Ă�̂͂ǂ����ĂȂ́H �����̐��l�����������Ă鎮�ȂǂȂ�̈Ӗ����Ȃ��Ƃ����̂����̂킩���̂��˂��H
�܂������̐��l���킷�̂��ړI�Ő��������肵�Ĉ�l�x�Ɏ���̂��ړI�Ȃ炻��ł��������B >>789
����Ő��w�̉�������o�c����B
�_���I�Ɍ���Ă�������Ă邩��F���w�E���Ă����B
����ȃ��X��������Ă��A��ԉ��������Ă�̂͌N���g����Ȃ����B �O>>789
>>786A����B�ɕς���1�̊m���œ���������Ȃ�AC�ɕς��Ă���0����˂����B
�܂�ڂ�1/2�Ȃ�B
>>790�ꔭ�ڂœ��Ă��ꍇ�ƁA�ꔭ�ڊO��ēڂĂ��ꍇ�𑫂����������B >>793
C�͊J������Ă邩��ς����Ȃ����H�H
�ς�����͓̂�����ł���B��������B �O>>793
>>794������C���J���������A������������B
������Ȃ�I�ׁB
�͂���Ȃ�B���B �܂��������낤�ȁB
�C�i�̐��w�͂����Ƃ����w���x���Ŏ~�܂��Ă�B
�O�p��Ƃ��͂ǂ����̃T�C�g���Ȃ��ēƏK�����݂��������ǁA�_���ƏW���̒P�����o���ĂȂ��Ɗm���͓����o����悤�ɂ͂Ȃ�Ȃ��B
�C�i�̓��W�b�N�{���{��������ȁB ���܂ǂ������e�B�E�z�[���A�������A�����W���Ȃ����^�ŊԈ���Ă��˂鏊��������Ƃ́B
��蕶�Ɍ��͂Ȃ��̂�
���ƍl������̂̓C�i������蕶�𐳊m�ɓǂ�ł��Ȃ������Ƃ������ƁB
�r���ł͕K���O�ꂪ���J������B>>764�ǂ�
��I �O>>795
P�������C���g�ݍ��킹����H�@�����͒m���Ă邳�B�I�}�[�N���K�悳�B
>>764�ʉ��B
�ǂ����A�����Ɍ����ĕς����ق������B����Đe���A����������ɊO��̔����̂ĂĂ�����₵�A������m���͏オ���Ȃ��B
2�{���ȁB
1/3��2�{�B
�ς��Ȃ��ꍇ�A1/3�\�\�@
�ς���ꍇ�A�ς���܂ł�1/3�̊m���œ�����Ƃ�����A
2/3�͊O���I��łāA�ς����瓖���������b�L�[���ĂȂ�B�\�\�A
1/3�͎c��2�����̊o��ŊO��������ɂ������ƂɂȂ�B
�@�A���A
1/3��2/3
�������ꂽ�B �C�i����͔���ς��܂��I�Ɛ錾������ɁA
�ŏ��ɑI����^����ɊJ�����Ⴄ���[�����p���l�炵��
���������l��ԑg�ɌĂ�ł͂����Ȃ��� �ŏ�������Ă����悢�@�\�𐧌����ď�������_����Ԃ̖�肾�낤�Ɛi�����Ă݂� �O>>798
�ǂ������ɂ�������2/3�ɂȂ邱�Ƃ͂킩�����B
���ǂȂɂ��ʔ����H
�������Ėʔ��Ȃ��ȁB
���O����悤�Ȑ������炭�肪����ł��Ȃ��B �O>>802
>>799�ȂA�ԑg���āH
�ȂɂɌĂԂH�@���w�̔ԑg�Ȃ���ōs�����Ă��������܂���B
�o�������Ƃ𐔎��Ԓ��x�̒Z���Ԃœf�������y�[�p�[�����Ƃ͈Ⴄ�A�ʔ������w�Ȃ�ˁB >>802
�������Ɓu�ς���K�v�͂Ȃ��v�Ɗ�����̂����w�I�Z���X�̂���l�ŁB�����ǁA�����ƌ������ɘ�������������Ƃ����̂��A���̖�肪�L���ƂȂ������ȁB
����>>793�̂悤�Ȍ��������l����肷�錻���̂������B
���w�I�ɂ͒�������肾��B ������2ch�̓A�z���肾�ȁi��
�����e�B�E�z�[�����̐����́A
�u�ǂ����I��ł��m����1/2�œ����v�ł���i��
���A���L�̃X���ł��̖���_���Ă��邩��A
����������Ή��L�̃X���ցi��
�A���`���s���A������A�^���҂͂��f��i��
���㐔�w�̓C���`�L���炯
https://rio2016.5ch.net/test/read.cgi/math/1567930973/l50 �ꉞ������ɂ������Ă����ƁA
�N���l���Ă������͂����ł���i��
���J����O�́A
�O�̔��̂ǂꂩ��Ɍi�i�������Ă���̂�����
�ǂ��I��ł�������m����1/3�ł���B
���J������́A
��̔��̂����ǂ��炩��Ɍi�i�������Ă���̂�����
�ǂ����I��ł�������m����1/2�ł���i�� >>805>>806
���̐l�͎���o�ł̃g���f���{���`���܂���Ă���^���̃L�`�K�C�ł�
�Ƃɂ����_���I�E���w�I�Șb���ʂ��܂���
���̃X���Ō��ꂽ�ۂɎז��������ׂɒP�ƃX���ւƒǂ��o�����o�܂�����܂��̂ŁA�����ł̃��X�o���T����悤�肢�܂�
���̃��X�ɑ���������������\��������܂����A��������ȍ~�͔ނɂ͐G��܂���
�ǂ����Ă����_�������l�͓\���Ă���X���ɍs�����Ƃ��I�X�X�����܂� �X�����������l�тɖ��
S^2�̐ڑ����瓾����S^1���̐����W��(�R)�z�����W�[���v�Z���� 1845
��������@dy_dt_dt_dx 8��28��
�w�R��8����S�R�[�X1����1�ʂƂ�܂����I
�}�W�Ŋ������ł��I
������������n�ɕ������撣�肽���Ǝv���܂��I
https://twitter.com/dy_dt_dt_dx
https://twitter.com/5chan_nel (5ch newer account) >>807
>>807
>�Ƃɂ����_���I�E���w�I�Șb���ʂ��܂���
���ꂪ���O��i��
>�P�ƃX���ւƒǂ��o�����o�܂�����܂��̂�
���O�ɒǂ��o���ꂽ�o�܂͂Ȃ����A
���������ǂ��o���ꂽ���Ƃ��Ȃ��i��
���O�̓T�����i�� 100���̕���o���Ƃ��A
���̂����P�������������肭�����Ƃ���B
�A���A���̂���99�����`�̔����Ŕ���o���Ƃ��A
�c��̂P�����a�̔����Ŕ���o���Ƃ���B
�P�@�`�̔����ɕ��������Ă���m���ƁA
�a�̔����ɕ��������Ă���m���́A���ꂼ�ꂢ���炩�B
�Q�@�`�Ƃa�̂ǂ���Ŕ���������������m�����������B
���ꂪ�����ł���Ȃ�A>>805-806���������ƕ���i�� �l�����̃X���Ř_����C�͂Ȃ��̂ł���i��
�����烂���e�B�E�z�[�����ɂ��Ę_��������Ή��L�X����
���㐔�w�̓C���`�L���炯
https://rio2016.5ch.net/test/read.cgi/math/1567930973/l50
���Ȃ݂�>>812�̖��ɂ��Ẳ҂�
���̂Ƃ����l�����ŁA�s�����ł���i�� �N�͕ʂ̃X���Ŏ咣���Ȃ����B�킴�킴���̃X���܂Ŋ���o���K�v���Ȃ��ł��傤�ɁB
�N������ƍr��邩��A�F��ȃX���Ɋ���o���s�ׂ̓X���r�炵�ɑ��Ȃ�Ȃ���B �����e�B�z�[�����̘b����֎~�����������w �O>>803
>>812
�P
100���̕��̂����P���������肭��������A
�`�̔�����99���̂����A
1�(99/100)���������肭��������A
�`�̔����ɕ��������Ă���m���́A
1�(99/100)��99�~100=1(��)�\�\�@
�a�̔�����1���̂����A
1�(1/100)���������肭��������A
�a�̔����ɕ��������Ă���m���́A
1�(1/100)��1�~100=1(��)�\�\�A
�Q
�@�A���A
�`�Ƃa�͓����m���B �C�i���Ɏ���
�@{{}}��{{{}}}�A{}��{{}}�ł��邪�A����{}��{{{}}}���H
�@�R��A�������́A�ہA�œ�����ꂽ�� >>816
�܂����ꂾ�����Ⴂ���N����₷���ʔ��������Ď���w a,b���݂��ɑf�Ȑ����Ƃ���
���̎����R��X�AY��p����
aX�{bY�̌`�ŕ\���Ȃ����R���̌��͂����� ��ӂ��@ab��0
�Eab <0 �Ȃ�@0
aX+bY=1�@���� X,Y��N ������B(�ݏ��@�A������]�藝)
�Ea<0, b<0 �Ȃ� �`N
�@���ׂĂ̎��R���B���Ƃ������Z�x(Cardinality)�H ���̒萔a,b�ɑ���
c[n]=��[0,��/2](a^2 sin^2(x) + b^2 cos^2(x))^(-n)dx
�Ƃ����B
|t|���\���������Ƃ��A��[n=0,♾] c[n]t^n �����߂�B >>824
��[n=0,��] c[n]t^n
= ��[n=0,��]��[0,��/2] (t/(a^2 sin^2(x) + b^2 cos^2(x)))^n dx
�@|t|<min(a^2,b^2)�Ɖ��肵�Đϕ��Ƙa�����ւ���
= ��[0,��/2] 1/(1-t/(a^2 sin^2(x) + b^2 cos^2(x))) dx
= ��/2+��[0,��/2] t/((a^2-t)sin^2(x)+(b^2-t)cos^2(x)) dx
�@��(a^2-t) tan(x) = ��(b^2-t) tan(y) �ƒu��
= ��/2+��[0,��/2] t/��((b^2-t)(a^2-t)) dy
= (��/2)(1 + t/��((b^2-t)(a^2-t))) >>825
�����A�����ˁB�����B i�������P�ʁAa�𐳂̐��Ƃ�
�Ȑ� C�_ -a�Aa�Aa+i��A-a+i�����Ȃ钷���`�̋��E�ɔ����v������t�������̂Ƃ���B
(1) ��[C] e^(-iz^2)/(1 + e^(2(���)z)) dz �����߂�B
(2) a�����̋Ɍ����� ��[-��,��](cos(x^2) + i sin(x^2))dx ���v�Z����B >>817
�P�@�~
�Q�@��
�T�O�_�i�� �@��[n=1,��] �� (t/{aa�sin(x)^2 + bb�cos(x)^2})^n dx
�@= �� t/{aa�sin(x)^2 + bb�cos(x)^2 -t} dx
�@= �� t/{(aa-t)sin(x)^2 + (bb-t)cos(x)^2} dx
�@= t/��{(bb-t)(aa-t)}��dy�@{ �� ��{(aa-t)/(bb-t)}�tan(x) = tan(y)}
�@= t/��{(bb-t)(aa-t)} y
�@= t/��{(bb-t)(aa-t)} arctan(��{(aa-t)/(bb-t)}�tan(x)),
������ ���F0����/2, >>827
���̖��̏o�T��
ttps://kconrad.math.uconn.edu/blurbs/analysis/gaussianintegral.pdf
�ɂ���1940�N��̕����̕����炵�� �O>>817
>>828�ȂɌ����Ă��B
���ׂĂ̏ꍇ���̂��̏ꍇ�̐��ł����Ă邶��Ȃ����B >>831
���̕��̊m���̖��͐�p�X��������̂ŋc�_�͂�����łǂ���
���㐔�w�̓C���`�L���炯
https://rio2016.5ch.net/test/read.cgi/math/1567930973/ >>822
a>0, b>0 �̎�
�Eab+1�ȏ�
�@n-a, n-2a, ����, n-ba (b��)�̂����ꂩ�� b�̔{���B
�@n-b, n-2b, ����, n-ab (a��)�̂����ꂩ�� a�̔{���B
�@�Y���Ȃ��B
�Eab�ȉ�
�@1��X��b-1,�@1��Y��a-1,
�@aX+bY �� a(b-X)+b(a-Y) �̃y�A�̘a�� 2ab.
�@����� <ab, ������ >ab. (=ab �͂Ȃ�)
�� (a-1)(b-1)�̔����� <ab �ł���A�܂��d�����Ȃ��B
�� �Y������̂� ab - (a-1)(b-1)/2 = (a+1)(b+1)/2 -1 �B�@>>823 >>831
�ہi��
�P�̏ؖ����܂������Ӗ��s�����i��
�C�i��A���O�̕ςȏؖ��𗝉��ł��҂̓C�i���i�� �O>>831
>>817�V���v���Ŕ��������̉�@�B�����Ƃ����R�ŁA�킩��Ȃ��l�X���~������method�B���Ƃ��o��҂�̓_�҂ɗ���͂��Ȃ��Ă��A�����Ƃ��ꂩ�ɓ͂��͂��B >>824
��������
�@G(t) = ��[n=1,��] c[n] t^n
�Ƃ����B
�@-{(G^3)/(2tt)}{tt�[1/G(t)^2 - (2/��)^2]} "
�@= G" - (3/G)(G')^2 + (4/t)G' -(G/tt){1 -(2G/��)^2}
�@= 0
���
�@1/G(t)^2 - (2/��)^2 = (t�̈ꎟ��)/tt,
�@G(t) = (��/2) t/��{(bb-t)(aa-t)}, C[n,k]=n!/((n-k)!k!)�Ƃ���Ƃ�
��[n=1,��] (-1)^(n-1)/(n^2 (2n-1) C[2n,n]) = ��^2/6 - 5log^2((1+��5)/2)
�������B ���2�̏���䊐�a������A���̈�ӂ_�����_�܂ő��䊐������������L����Ƃ��A���䊐��̐��T�p�`�̖ʐς����߂�
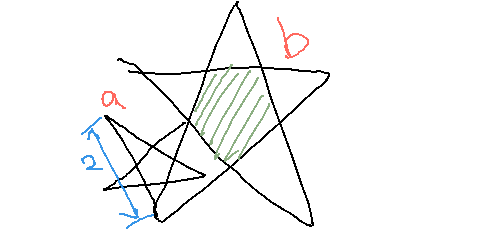 ���`���ɂ���
���`���ɂ���
���_�`��_�̋����� 2,
���܊p�`�̕Ӓ��� 2/��,
�ʐς� 5cot(��/5) /��^2
�@= ��(25+10��5) /��^2
�@= 6.8819096/��^2
�@= 2.62865556
�� = (1+��5)/2 = 1.618034�@�@(������) 0.9999...��1�Ƃ͐���Ȃ��悤�Ȏ�����̃n�E�X�h���t�ʑ���Ԃ��߂�
����������a_n�ɑ��āA�n�E�X�h���t�ʑ����X�ɂ�����lim(n����)a_n=����X�̒�`�́A
�C�ӂ̃��̊J�ߖT�ɑ��āA���鎩�R��N�����݂��āAn��N �Ȃ���̊J�ߖT��a_n���܂܂�� �Ƃ������Ƃł���
�����
0.999...9(9��n��)=a_n�Ƃ��A
0.999...:=lim(n����)a_n�ƒ�`���� >>841
�ʑ�f:R��R��
f(x)=x+1 (x��Z), x(otherwise)
�Ƃ���T���ɂ��ʏ�ʑ��̈����߂��Ƃ����
f(lim[T�ʑ�](1-1/10^n))
=lim[�ʏ�ʑ�]f(1-1/10^n)
=lim[�ʏ�ʑ�](1-1/10^n)
=1
���
lim[T�ʑ�](1-1/10^n))=0 >>842
�f���炵�� �����đ���
>�Ƃ���T���ɂ��ʏ�ʑ��̈����߂��Ƃ����
��
�Ƃ���T��f�ɂ��ʏ�ʑ��̈����߂��Ƃ����
���Ă��Ƃ���ˁH
�ꉞ�p�ӂ��Ă��̂͂���Ȋ���
d(x,y)= |x-y| (x,y��(0,1) �܂��� x,y��(0,1)^c)
,|1-x-y| (x��(0,1) ���� y��(0,1)^c)�܂��� (y��(0,1) ���� x��(0,1)^c)
�Ƃ����d��R��̋����ɂȂ��Ă��̋����ʑ��̏�ł�0.999...=0�ƂȂ� >>831
�ۂƂ��� ���R���肯�� �Ẳʂā@�@�@ �@�c�����I�q (�Îs)
�@�@�@�����V�� (2017/Oct/02)
�۔ۂ� ����� ��̓��̑̉��@�@�@�@�@�@�r�c���q
�۔۔� �S�Ղ̔� ��(���Y)������@�@�@�@������j
�@�@�@��W�w�V�҂��՞فx �[��p���� (2015/Oct)�@2860�~ (0,1)^c (x��0 �� x��1) �͂��̂܂܂�
(0,1) ���t�����ɂ����ł����邩�B d(x,y) = | g(x)-g(y)|
g(x) = x + (2x-1)[ x(x-1)/(xx-x+1) ]
�Ƃ� >>838
f(x)=��[n=1,��] x^(2n)/(n^2 C[2n,n]) �ƒu��
y=f(x)�͔��������� (4-x^2)y''-xy'=��(4-x^2)(��(4-x^2)y')'=4 ���������������
f(x)=2(arcsin(x/2))^2
���̘aS��
S = ��[0,1] -f((��-1)x)/x^2 dx
�@= 2��[0,1] (arcsinh(x/2))^2/x^2 dx
�@�c x=2sinh(t)�ƒu����2���ϕ�
�@= 2��[0,log��]{log(1+e^(-t))-log(1-e^(-t))}dt - 8(log��)^2
�@�c log(1�}x)��W�J���č��ʐϕ�
�@= -2{Li2(1/��)-Li2(-1/��)} + 2{Li2(1)-Li2(-1)} - 8(log��)^2
�����Ƀ�=(1+��5)/2, Li2(x)=��[n=1,��] x^n/n^2
Li2(x)��
�ELi2(1) = ��(2) = ��^2/6
�ELi2(-1) = -(1/2)��(2) = -��^2/12
�ELi2(x)-Li2(1-1/x) = ��^2/6 - log(1-x)log x + (1/2)(log x)^2
����(�Ō�̎���x��1�Ő��藧���ƂƗ��ӂ̔��������������Ƃ���킩��)
���̎���x=1/�ӂ�����������̊W1-��=-1/�ӂ���
Li2(1/��)-Li2(-1/��) = ��^2/6 - (3/2)(log��)^2
�����
S=��^2/6 - 5(log��)^2 �ޑ�: ��[n=1,��] (-1)^(n-1)/(n^3 C[2n,n]) = (2/5)��[n=1,��] 1/n^3 �������B >>849
�A�y���[�̌���
�@��(3) = ��[n=1,��] 1/n^3 = 1.202056903159594284����
�ǂ�����ďo����ł��傤�ˁB
���Z�~�����u���̐��E�v���{�]�_�� (1982) p.147�`
(�֑�)
��(3) = ��[n=1,��] 1/n^3
�@�@= 5/4 - ��[n=2,��] 1/{n^3�(n^2 -1)}
�@�@= 1 + ��[n=1,��] 1/{n^3�(4n^4 +1)}
�@�@= 77/64 + ��[n=2,��] 4/{n^3�(n^2 -1)(9n^4 + 3n^2 +4)}
�@�@�@= 9/8 + ��[n=1,��] 4/{n^3�(9n^8 + 18n^6 + 21n^4 + 4)}
�@4n^4 +1 = (2nn+1)^2 - (2n)^2,
�@9n^8 + 18n^6 + 21n^4 + 4 = (3n^4 +9nn +2)^2 - {6n(nn+1)}^2,
>>850
�@�������B(e = 2.718281828459045���� (�l�C�s�A��) �Ȃ��) >>848
�@xy '= ��[n=1,��] 2/(n�C[2n,n])�Ex^(2n),
�@y " = ��[n=0,��] 2(2n+1)/((n+1)�C[2n+2,n+1])�Ex^(2n)
�@(4-xx) y " = ��[n=1,��] {8(2n+1)/((n+1)�C[2n+2,n+1]) - 2(2n-1)/(n�C[2n,n])}�Ex^(2n)
�@�@= ��[n=1,��] {4/C[2n,n] - 2(2n-1)/(n�C[2n,n])}�Ex^(2n)
�@�@= ��[n=1,��] 2/(n�C[2n,n])�Ex^(2n),
�����
�@(4-xx) y " - xy ' = 0.
�@x = 2sin�Ɓ@�Ƃ�����
�@(d/d��) = ��(4-xx)�(d/dx)
��ӂ��
�@(d/d��)^2 y = 4,
�@y = 2��^2, >>852
�@1/��(4-xx) = ��[n=0,��] 2 C[2n,n] (x/4)^(2n),
�@arcsin(x/2) = ��[n=0,��] 2 C[2n,n]/(2n+1) (x/4)^(2n+1),
2�悷��� C[2n,n] ������ɗ���B >>848 ���
f(ix) = -2{arcsinh(x/2)}^2 = -2{log[(x+��(xx+4))/2]}^2,
��(3) = ��[0,1] (-5)f(ix)/x dx, �@1/��(4+xx) = ��[n=0,��] 2(-1)^n C[2n,n] (x/4)^(2n),
��x�Őϕ�����
�@arcsinh(x/2) = ��[n=0,��] 2(-1)^n C[2n,n]/(2n+1) (x/4)^(2n+1)
�@= log[(x + ��(xx+4))/2] = -log[(��(xx+4) - x)/4], >>849 >>854
��[n=1,��] (-1)^(n-1) x^(2n)/(n^2 C[2n,n]) = 2(arcsinh(x/2))^2
���
S = 4��[0,1] (arcsinh(x/2))^2/x dx
�@�c x=2sinh(t)�ƒu�������ϕ�
�@= -8��[0,log��] t log(e^t - e^(-t)) dt
�@= -8��[0,log��] t {t - ��[n=1,��] e^(-2nt)/n} dt
�@= -(8/3)(log��)^3 - 4(log��)Li2(1/��^2) - 2Li3(1/��^2) + 2Li3(1)
������
Lik(x)=��[n=1,��] x^n/n^k
�ELik(x)+Lik(-x) = 2��[n:even] x^n/n^k
�@= (1/2^(k-1))Lik(x^2)
�ELi3(x)-log(x)Li2(x) + Li3(1-x)-log(1-x)Li2(1-x) + Li3(1-1/x)-log(-1+1/x)Li2(1-1/x)
�@= -(1/3)(log(x))^3+(log(x))^2log(1-x)+Li3(1)
��x=1/�ӂ������W��1-1/��=1/��^2,1-��=-1/�ӂ�p�����
(5/4)Li3(1/��^2)+(5/2)(log��)Li2(1/��^2) = -(5/3)(log��)^3+Li3(1)
�����
S = -(8/3)(log��)^3 - (8/5)(-(5/3)(log��)^3+Li3(1)) + 2Li3(1)
�@= (2/5)��(3) >>851
��(5)=��[n=1,��](-1)^n R(n)/C[2n,n] ���������W���̗L����R(x)���������
��(5)���������ł��邱�Ƃ��ؖ��ł���\�������邪�A���̋�̓I��R�͑��݂��邩�H �������ɖʔ������ł�����B�ȒP�ɉ����������Ȃ����ǁB ���a1�̋��ʏ�Ɏ��̒���1�̕Ȑ���`��
�Ȑ��ň͂܂�鋅�ʏ�̗̈�̖ʐς̍ő�l�����߂� >>859
�����C�����܂�
���ʏ�ł̕Ȑ��ň͂܂��̈�͓�o���邯��
�ʐς͂��̓�̓����������Ƃ��܂� >>859
�Ƃ肠��������1�̏��~�Ő��Ă݂�
���������̖ʐς�2��-��(4��^2-1)
�傫�����̖ʐς�2��+��(4��^2-1)
�����Ă��܂�Ӗ��͂Ȃ����ǂ����̐ς�1 ���������Ă��̎�̖��̉��͕K����ȗ��̋Ȑ��ɂȂ����肷��̂��ȁH �O>>835
>>859-860
�ő�̕Ȗʂ͉~��������A���̕\�ʂ���n��t{0��t��1-��(1-1/4��^2)}�܂Œ��S�Ɍ������Č@��A���̒n�_��ʂ鐅���ȉ~�Ղ̉~����t=0����1-��(1-1/4��^2)�܂ő����W�߂�ƁA
2��{0�`1-��(1-1/4��^2)}��(2t-t^2)dt
=2�\�\(�ϕ����s��)
=2��-��(4��^2-1)
�����������Ƃ��B >>863
���s���Ă���͂�܂����ǁA
���̉~���̕t�߂̒n�ʂ����ɑ��Ăǂꂾ���X���Ă͂邩
�悤�l���͂�����C�i�͂�Ȃ������͂��ǂ��� �����ϕ��ɂ��
I = ���{t(2-t)} dt
�@= (t-1)��{t(2-t)} + ��(1-t)^2 /��{t(2-t)} dt
�@= (t-1)��{t(2-t)} + ��1/��{1-(t-1)^2} dt - I
�@= (t-1)��{t(2-t)} + arcsin(t-1) - I,
��
�@I = (1/2)(t-1)��{t(2-t)} + (1/2)arcsin(t-1), ���a 1/(2��) = 0.1591549431 �̏��~�ŒP�ʋ�����Ă݂�B
���̒��S���珬�~�ɐ��������낵�A���̌�����z���Ƃ����
(�\�ʐ�) = 2��|��z|
�@= 2��{1 - ��[1 - 1/(4��^2)] }
�@= 2�� - ��(4��^2 - 1)
�@= 0.080087887
�܂�
�@arcsin(1/(2��)) = 0.1598346264 ���͋��̕\�ʂ̗̈�D�ɂ���
D�̖ʐ�=3�~(D�ƒ��S�̓ʕ�̑̐�)�����a
���g���ƍ��Z���ł��������肷��B >>861
>>863
>>866
���_���猾���Ή~�Ő����ł��� �ő含�̏ؖ������肢���܂�
�q���g�̓K�E�X�E�{�l�̒藝�ł� >>859-860
�\�ʐ�=2��(2t-t^2)^(3/2)/(3/2)(2-2t)
=2��(2t-t^2)^(3/2)/3(1-t)�\�\�@
�}��`���ƁA
t=1-��(1-1/4��^2)
1-t=��(1-1/4��^2)
=(1-1/4��^2)^(1/2)�\�\�A
t^2=1-2��(1-1/4��^2)+1-1/4��^2
=2-2��(1-1/4��^2)-1/4��^2
2t-t^2=2-2��(1-1/4��^2)-{2-2��(1-1/4��^2)-1/4��^2}
=1/4��^2�\�\�B
�@�ɇA�B��������ƁA
�\�ʐ�=2��(2t-t^2)^(3/2)/3(1-t)
=2��(1/4��^2)^(3/2)/(1-1/4��^2)^(1/2)
=2��(1/4��^2)^(3/2)/(1-1/4��^2)^(1/2)
=2��(1/4��^2)��(1/4��^2)/(1-1/4��^2)^(1/2)
=(1/4��^2)/(1-1/4��^2)^(1/2)
=1/2��(4��^2-1)
=0.0256573341�c�c
�O>>863�����Ă�̂��ȁH �����Ă�B
���ʂ̂������s�ȕ��ʂ̊Ԃɂ��镔����
�@(�\�ʐ�) = 2��r�|��z|
�@��z�F���ʂ̊Ԋu
�@r�F���ʂ̔��a �O>>869
���a1�̋�����f�ʂ̎�����1�̌����������Ƃ�����A����̖ʐς́A
��(1/2��)^2=1/4��
�\�ʐς͂����菭���傫���Ȃ��Ƃ����Ȃ��B
�O>>869
�\�ʐ�=[(2t-t^2)^(3/2)/3(1-t)](t=0�`1-��{1-��(1-1/4��^2)}�\�\�@
t=1-��(1-1/4��^2)
t^2=1-2��(1-4��^2)+1-1/4��^2
=2-2��(1-1/4��^2)-1/4��^2
2t-t^2=2{1-��(1-1/4��^2)}-{2-2��(1-1/4��^2)-1/4��^2}
=2-2��(1-1/4��^2)-{2-2��(1-1/4��^2)-1/4��^2}
=1/4��^2�\�\�A
1-t=��(1-1/4��^2)�\�\�B
�@�ɇA�B��������ƁA
�\�ʐ�=(1/4��^2)^(3/2)/3��(1-1/4��^2)
=(1/4��^2)��(1/4��^2)/3��(1-1/4��^2)
=1/3�8��^3��(1-1/4��^2)
=1/12��^2��(4��^2-1)
(��1/4�ł����Ă�̂��ȁH) �����Ă�B
(�\�ʐ�) = 2��|��z|
= 2��{1 - ��[1 - 1/(4��^2)] }
> 2��{1 - [1 - 1/(8��^2)] }
= 2��/(8��^2)
= 1/(4��)
= 0.079577471546 �O>>871
>>859-860
�\�ʐρ�1/4��=0.0795774715�c�c
�c��݂̂Ԃ��\�ʐς͒f�ʐς��傫���B
0.08���炢�ɂȂ��Ȃ����ȁH�@������������0.08�����邩���B �O>>873
�ǂ������0.08�������H
>>859-860 �O>>875
�~����0����1�܂ő����W�߂�����ł����Ă�Ȃ��́H ������ϕ����ĖʐςɂȂ�
�͕��ʂ܂ł̘b�B
��Ԑ}�`�ł��ɂ͂��ꂾ���ł̓_���B �O>>875
>>876���̂̕\�ʐς��ēy��݂����ɐςݏd�˂ăo�E���N�[�w���@�ł��Ȃ��́H �O>>878�O�X>>876
>>877���Ⴀ�ǂ������0.08������v�Z�������H�@�o�E���N�[�w���@���Ƃ�����v���Ă��B�ǂ���Ŏ������Ƃ��Ӗ��킩���킯���B
>>859-860 >>878
�����ł��������邪�ł��Ȃ����̂�����B
���ʂ̏ꍇ�͕����ł���B
����h�Ő��Ăł���ʂ̒�����l�A���̔��a��R�Ƃ���
��l R/ ��(R^2-h^2) dh
���v�Z����Ώo��B
�� ���ʑS�̂̏ꍇ��l=2��(R^2-h^2)������
��[-R,R]l R/ ��(R^2-h^2) dh
=�� [-R,R] 2��R dh
=4��R^2
����������B
���ʂ� �e������ϕ��f �ł͂łȂ��B
�������q�����������ŋ��ʂ��ĂȂ��Ɩ����B >>879
�C�i���ɂ͂�������������������₷���͂���
���̂̃X�C�J��炪�����܂ܓ��������ŗ�ɂ��邱�Ƃ��l����
����ƁA�X���C�X�������̌����͓����͂��Ȃ̂ɁA�ΐF�̔�̕��͒[�̂ق��قǍL���͂���
���Ă���͉��̂ł��傤�H�@
�����ėΐF�̔�̕��͎��̌��݂̉��{���炢����ł��傤���H �O>>879
����1�̐���̔��a�́A
1/2��
�s�^�S���X�̒藝���A
���a1/2�̉~�̒��S����A���a1�̋��̒��S�܂ł̋����́A
��(1-1/4��^2)
(���������)
�\�ʐς͎����𑫂��W�߂��̂��A
�\�ʐ�=2��{1-��(1-1/4��^2)}
�����͂Ȃ��
���a1/2�̉~�̒��S����A���a1�̋��̒��S�܂ł̋���
��2���|���Ď���1�̓��������̋��̂̕\�ʐς��o��H >>882
> �s�^�S���X�̒藝���A
> ���a1/2�̉~�̒��S����A���a1�̋��̒��S�܂ł̋����́A
> ��(1-1/4��^2)
> (���������)
�ǂ����H
> �\�ʐς͎����𑫂��W�߂��̂��A
> �\�ʐ�=2��{1-��(1-1/4��^2)}
�\�ʐ�=��[��(1-1/4��^2),1] 2��(1-h^2)/��(1-h^2)dh
�ǂ̈ܓx�̓_���܂ނ������Ō��܂����Ⴄ�̂��B
�ӊO�ɃI�����Cw �O>>882
>>883
��(1-h^2)/��(1-h^2)dh
�����2�ƁA��������h�̒n�_�Ő����ɐ������a���A�|�����킹�ďo������������(1-1/4��^2)����1�܂ő����W�߂Ă�Ǝv����ł����A�Ȃ����q�ƕ��ꂪ�����Ȃ�ł��傤�H
(����/����)dh�ɂ��������Ȃ��B
����
�\�ʐ�=2��[��(1-1/4��^2),1]dh
=2��{1-��(1-1/4��^2)}
�ł����ł���ˁH �O>>884�Â��B
2�ƁA��������h�̒n�_�Ő����ɐ������a���A�|�����킹�ďo�����������A
��(1-1/4��^2)����1�܂ő����W�߂�ƁA
�\�ʐ�=2��[��(1-1/4��^2),1]dh
=2��{1-��(1-1/4��^2)}
=2��-��(4��^2-1)
dr����Ȃ���dh���B�����W�߂�����ɂ����������̂�dh�ɂ���B�킩�����B ��>���̑O�ɂ܂��A���R��x�y�z�Ƃ͕ʂ̎��� X�Y�Z��x:y:z=X:Y:Z�����藧�悤�ɉ��肵�āA����X�Y�Z�̏�� Z=X+r �Ƃ����Ă���c�_����̂Ȃ�Ηǂ��B
�����݂܂���B���̕��@�ŁA���܂������ł��邩���A�킩��܂���B
���̕��@�Ő����ł��Ȃ���Ώؖ��ƔF�߂܂���B >>868
�Ȑ��̓����ɋɎ����Ƃ�B
�Ȑ����ɍ��W�ŕ\�킵����(*)��
�@�� = f(��) ��0,
�@f(0) = f(2��),
�Ƃ���B
����L�Ɩʐ�S��
�@L[f] �� ��[0,2��] sin(f(��)) d��,
�@S[f] = ��[0,2��] {1-cos(f(��))} d��,
�ƕ\�킹��B
�������� L[f]=1 �̉��ŔĊ�
�@I[f;��] = S[f] - �ɥ(L[f]-1),
��f�ŕϕ������
�@��I = ��[0,2��] {sin(f(��)) -��cos(f(��))} ��f d��,
�C�ӂ� ��f �ɑ��� I[f;��] ���◯�l�ƂȂ邱�Ƃ���
�@sin(f(��)) -��cos(f(��)) = 0,
�@f(��) = arctan(��) = arcsin(1/(2��)),
*) �����q�_�q�_������A�����L���čL���邱�Ƃ��\�B �O>>885
>>866�͓����͂����Ă�Ǝv�������ǁA�r�����Ԃ��Ƃ�ł��B
���߂�>>885���ꂮ�炢�͏����Ăق��������B�ǂ������0.08�������r�����K�v���Ǝv���B
2��-��(4��^2-1)=0.080087887�c�c��0.08
�C���e�O�����A�ϕ���ԁA�ϕ����̃l�b�g��ł̏������͍ĔF���ł����B
��[�ϕ����](�ϕ���)dh �� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�


