�ʔ�����肨�����ā`�� 29���
�� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�
�v�X�ɓ��e�B�i�l�I�Ɂj�������Ȃ̂Œ���
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
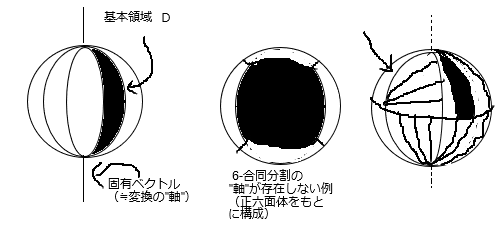
���̎咣�͐��藧���F����S^2�i��R^3�j��
�ES^2 = ��_(n=1�`5) f_n(D)
(������ D �� S^2 �̃��x�[�O���ȕ����W���Af_i �͒��s�Q�̌��ŕ\�����P���ϊ�)
�En��m �̎� f_n(D)��f_m(D) �́i�������l�̂Ƃ��Ă�S^2�́j��W��
�����悤�ɍ����ȂT�̃p�[�c f_n(D) (n=1,�c,5) ��"����"���鎞�A
f_n��(f_m)^(-1) (n��m)
�ƕ\�����S�Ă̍����ϊ��ɋ��ʂ�����ŗL�x�N�g�������݂���B
�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`�`
�T�����łȂ��A�Ⴆ��4,6,8,12,20�ł���ΐ����ʑ̂𗘗p���Ď����łȂ����������������A
�����H�v�����60��S�Ă̂W�̔{�����\�B
�i���������������ł���Ƃ́A��̂悤�ȏݒ�ŋ��ʂ�����ŗL�x�N�g�����u���݂���v���Ƃ������B
�܂��̎咣�́u���ʂ�5-���������͑S�Ď����ł���v�ƌ�����������j >>119 �̕⑫
�܂�Ƃ���A���ʂ̒��Łu��{�̈�v�Ȃ���̂��߂�
����ƍ����Ȑ}�`�����������ʂɃ����Ȃ��_�u���Ȃ��\�荇�킹��̂����������B
n���ǂ�Ȑ��̐����ł����̐}�݂����ɂ�����܂�����n-�����������ł�����ǁA
����͂ǂ̗̈悩��ʂ̂ǂ̗̈�Ɉڂ��ɂ����鋤�ʂ̒�����"��"�ɂ��ē������Ηǂ����Ƃ���A
�����͂���قǖʔ��݂̂Ȃ����������Ƃ��āu�����v�Ȃ��̂ƒ�߂��B
�^��6-���������͋��ʂ�"��"�ɂ�������̂����݂��Ȃ����ߔ��B
�E�͔���32-���������B�_�������ɂȂ肻�������ǁA
���Ŏ�����������̕����̂����ŋ��ʂ̎��ƂȂ�Ȃ��B���̂W�̔{�������l�B
�i�������ɂႮ�ɂ�ł��܂�B�}�E�X�ŊG�`���̂ނ����c�j
 >>120
>>120
�A���łȂ��Ƃ��\��Ȃ��B�ł����x�[�O���ȏW���ł���Ή��ł��n�j
�i���x�[�O�����́A�ǂ����Ă������郌�x���̂���₾�Ԃ���W���ł��܂�����悤�ɁA�Ƃ����Ӑ}�j > sapply(1:20,function(k) treasure0(4,5,k))
[,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10] [,11]
�Z���L�� 9 84 463 1776 5076 11249 19797 28057 32243 30095 22749
�����L�� 9 83 453 1753 5075 11353 20057 28400 32528 30250 22803
���� 2 23 224 1316 5353 16158 37666 69513 103189 124411 122408
[,12] [,13] [,14] [,15] [,16] [,17] [,18] [,19] [,20]
�Z���L�� 13820 6656 2486 695 137 17 1 0 0
�����L�� 13831 6657 2486 695 137 17 1 0 0
���� 98319 64207 33788 14114 4571 1106 188 20 1
4�~5�̏ꍇ
��F1�@����
��F2�`5�@�Z���L��
��F6�`13�@�����L��
��F14�`20�@����
����������
����������
����������
����������
�Z���L����
Table[choose(17,k-1)+choose(15,k-1)+choose(13,k-1)+choose(11,k-1)+choose(10,k-1)+choose(8,k-1)+choose(5,k-1)+choose(4,k-1)+choose(1,k-1),{k,1,20}]
�����L����
Table[choose(17,k-1)+choose(15,k-1)+choose(13,k-1)+choose(12,k-1)+choose(8,k-1)+choose(7,k-1)+choose(6,k-1)+choose(3,k-1)+choose(2,k-1),{k,1,20}]
������
Table[choose(19,k-1)+choose(17,k-2)+choose(15,k-2)+choose(13,k-2)+choose(8,k-2)+choose(1,k),{k,1,20}] >>119 ���m��I�ɉ��������̂ŕB�q���g�������ƁA��͂萳20�ʑ̂𗘗p������̂ł����B
���Ȃ݂ɑS�Ă̋�����R�ł��\�B�V�ȏ�̊�͂܂��ړr�������Ă��Ȃ��̂ł悯���������c �A������B
>>124 ���̏ꍇ�m��I�ɂƂ����̂́A�咣�̔��Ⴊ���������Ƃ������Ƃł�
�i�����łȂ�5-������������������ȂƊ��҂��Ȃ��璲�ׂĂ������̂ł��c�j ������5�̏ꍇ��(�A����D�ɂ��)�������݂͂���
2n�̏ꍇ�́A����n�������炳��ɐԓ��ɂ�镪�����l���������� (1)���̏������� �L���� s,t ��������
�E0 �� t �� 1/��2
�E61/80 �� s
�Es^2 = 2t^2-2t+1
(2)���̏������� �ʑ��p�` ��������B
�E���ׂĂ̒��_�́A�P�ʉ~�̎���܂��͓����ɂ���A�����W�͗L����
�E���ׂĂ̕Ӓ��́A�L����
�E������ 31/5 �ȏ� >>126
�����A�A���Ȃ̌������̂��@������
2n�̏ꍇ�A�������̐}�̂��Ƃ������Ă�̂Ȃ�c�O�B����͂ǂ��ϊ����Ă����͕s�ς����������Ȃ���
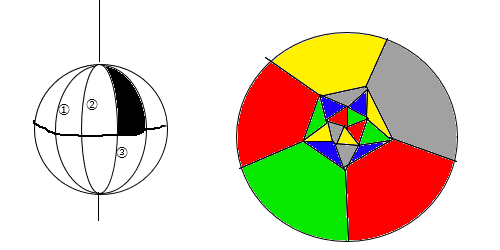
�i���ʂ̌ŗL�x�N�g�����������ŗǂ�����A�ŗL�l�܂ňꏏ����Ȃ��Ă��ǂ��B�Ⴆ�A
�@����A�ւ̕ϊ��ł͎��͌ŗL�l1�̌ŗL�x�N�g���A�@����B�ւ̕ϊ��ł͎��͌ŗL�l-1�̌ŗL�x�N�g���ƂȂ�j
�ꉞ����5-���������̂ЂƂ̗���E�}�ɋ����Ă����܂��B
�킩��ɂ����ł�������\�ʑ̂𗧑̎ˉe�ŕ��ʂɗ��Ƃ����݂����ȃm���ŕ`���Ă܂��B
�O�~�̉~���͖{���͈�_��\���A�e�����F�̗̈�S�̂���̃p�[�c�ɂȂ��Ă܂��B
�{���Ȑ��ŕ`�����ׂ��Ƃ��������܂����A�ӂ����L���Ă�A�_�������L���Ă铙�̈ʒu�W�͕ۂ��Ă�̂�
��������{���̌`���z�����Ă������������orz
 >>128
>>128
�A���B�̕ϊ����A�Q�̗̈�̋��L����1�_�̕����Ɏ����Ƃ��ĉ�]������A�Ƃ���悢�̂ł́H >>129
���ۂ���͌ŗL�x�N�g���̂P�Ȃ��ǁA�G�ɕ`����Ă钼�����ŗL�x�N�g���ł��邱�Ƃɕς��͂Ȃ����
����ŁA�����̒�`���u�`�`���ʂ�����ŗL�x�N�g�������݂���v������A���̌ŗL�x�N�g���̑��݂Ɋւ�炸����͎����ɂȂ��
"��"�ƕ\������Ɗe�ϊ��ň�����Ȃ��悤�Ɏv���邯�ǁi����͂�����̌��t�I�т��ǂ��Ȃ������Ǝv���A���܂Ȃ��j
���̐}�̏ꍇ�A���y���Ă������������x�����Ƃ�A�A����B�ւ̕ϊ��� f(x,y,z)=(x,-y,-z) �ƕ\���邩��
(1,0,0) �̑��� (0,cos��,sin��) �Ƃ���������"��"�������Ƃ��킩��i�����Đ}�̒����̕��������̒��Ɋ܂܂��j >>130
�������⌳�̒�`�͌ŗL�x�N�g�������L���Ȃ����Ęb�ł�����
�l���Ă邤���Ɏ��O���Ă܂����A���h >>127 (1)
�^����
�@s^2 = t^2 + (1-t)^2
�s�^�S���X��������A���R�� a, b �ɂ��
�@s�@= (aa+bb)/N,
�@t�@= (aa-bb)/N,
�@1-t = 2ab/N,
�ƕ\�킹��B
�@N = aa+2ab-bb,
s �� 61/80 ���
�@0.41421356 = ��2 -1 < a/b < (61-��1042)/19 = 1.51157764�@�܂��́@4.90947499 = (61+��1042)/19 < a/b,
0 �� t < 1/��2 ���
�@1 �� a/b < {1+��(4-2��2)}/(��2 -1) = 5.02733952
�������
�@1 �� a/b < (61-��1042)/19 = 1.51157764
�Ȃ�Ώ\���B
��) a=b, s=1, t=0, >>132
�@�����Ͽ
s �� 61/80 ���
�@0.41421356 = ��2 - 1 < a/b < (19+��4082)/61 = 1.35886117
0 �� t < 1/��2 ���
�@1 �� a/b < 1 + ��2 + ��(4+2��2) = 5.02733949
�����̋��ʕ�����
�@1 �� a/b < (19+��4082)/61 = 1.35886117 >>127 �̏o��҂ł��B
�܂��ŏ��� (1) �̑������@�u0 �� t �� 1/��2�v ���u1/2 �� t �� 1/��2 �v�ɕύX�����Ă��������B
����́A(2)�ɂ�����A�u�ʑ��p�`�v���u���p�`�v�Ƃ��Ă��܂��悤�ȏd��ȃ~�X�ł����B�\����܂���B
�ɂ�������炸�A132����ɂ́A�u1/2 �� t �� 1/��2 �v�ƕύX���ꂽ�Ƃ��Ă��A�Ή��\�ȂقǁA
���J�ɉ����Ă��������A���ӂ������܂��B
s,t�̕\����A4.90947499=(61+��1042)/19 < a/b�@< {1+��(4-2��2)}/(��2 -1)=5.02733952
�Ȃǂ���A�\���߂�����e�ł��B
a:b=5:1���̗p����ƁA���R�ƁA(s,t)=(13/17,12/17)�@�������܂�����B
���łɂ��C�Â����Ƃ͎v���܂����A���̖��쐬�̂��������́A�L���ȓ������u��>3.05���ؖ�����v�ł��B
61/80�Ƃ��������́A�������玝���Ă������̂ł��B >>127
���傤���˂����� (2) ������������
�@A (1, 0)
�@B (1 - 8nn/(nn+1)^2, 4n(nn-1)/(nn+1)^2)
�@C (c, c)
�Ƃ����B
�������@c = {21(n^4-6nn+1) + 80n(nn-1)}/{41(nn+1)^2} < 1/��2,
n��6 �̂Ƃ���16�p�`�i�� 1/8�j�ƂȂ�B
AB �� ��2n�F�c(nn-1) �̒��p���̎Εӂ䂦
�@AB = 4n/(nn+1),
BC �� ��20�F�c21 �̒��p���̎Εӂ䂦
�@BC = (29/41){1 - 4n(nn+2n-1)/(nn+1)^2},
����L = 8 (AB+BC),
�EL �� 31/5 �ȏ�ƂȂ�̂� n=7,8,9 �̏ꍇ�B
n=6,�@L = 8 (0.64864865 + 0.12451674) = 6.185323095
n=7,�@L = 8 (0.56000000 + 0.21615610) = 6.20924878
n=8,�@L = 8 (0.49230769 + 0.28409872) = 6.21125126
n=9,�@L = 8 (0.43902439 + 0.33619651) = 6.20176724
n=10, L = 8 (0.39603960 + 0.37726813) = 6.18646187 �����l�ł����B���̖��͐������ƂƂ炦�ĕ��������O�����Ƃ����ɉ������Ƃ���ƃh�c�{�ɂ͂܂�Ǝv���܂��B
����̊p�x�����A�s�^�S���X�O�p�`�����炩���ߒT���o���A�ړI�̑��p�`�̈�ӂɍ����悤��
�k�����A���W�ɓ��Ă͂߂Ă����Ό������܂��B�ȉ��A�p�ӂ��Ă������ł��B
11sin(��/11)=3.099...�A12sin(��/12)=3.105�Ȃ̂ŁA�ӂ̐���12�ȏ�łȂ����6.2���Ȃ����Ƃ�����܂��B
�����ŁA���ی����ɁAA(a,a)�AB(b,c)�AC(c,b)�@���l���A�c��͑Ώ̃R�s�[���Ăł�������12�p�`���l���܂��B
���x�A���v��15�x�X�����Ƃ��A�����̂���ʒu�_�Ƃ���l�Ȕz�u�̎d���ł��B
���̏ꍇ�A�K�v�Ƃ���s�^�S���X�O�p�`�́A�Εӂ̊p�x��60�x�̂��̂ł��B1:��3:2�̔�̎O�p�`�ł����A
����ɋ߂����̂Ƃ��āA120:209:241�@���̗p���邱�ƂƂ��܂��BA(a,a)���A��̂悤�Ȕz�u�̐��\��p�`��
�꒸�_���Ƃ�����A��ӂ̒�����(��3-1)a�ƂȂ�܂��B��3-1=0.7320...�ɋ߂��l�Ƃ���11/15=0.7333...���̗p����ƁA
b=a+(11a/15)*(120/241)=329a/241�A�@c=a-(11a/15)*(209/241)=1316a/3615
���̏ꍇ�S���́A8*(11a/15+1316a/3615)=31736a/3615�@�ŁA(��2)a�Ŋ����6.207673�ƂȂ�A
12�p�`��p�����̂ł����A���肬�薞���ł������Ȃ��Ƃ�����܂��B
a�Ƃ��āA241*3615/Floor[241*3615*sqrt(2)+1]=58081/82139�@���g����
A(58081/82139,58081/82139)�AB(79289/82139,317156/1232085)�AC(317156/1232085,79289/82139)
�ق��ɂ��A�O��ނ̃s�^�S���X�O�p�`��p���āA
X0=(1,0)�AX1=X0+(3/7)*(-9/41,40/41)�AX2=X1+(9/20)*(-204/325,253/325)�AX3=X2+(18/37)*(-1161/1289,560/1289)
�Œ�܂�14�p�`�Ȃǂ�����܂��B >>135 ����ĕς��Ă݂��B
�@A (1,0)
�@B (1 - 8nn/(nn+1)^2, 4n(nn-1)/(nn+1)^2)
�@C' (c', c')
�Ƃ����B
������ c' = (4/7){1 + n(n-3)(3n+1)/(nn+1)^2},
n��6 �̂Ƃ���16�p�`�i�� 1/8)�ƂȂ�B
c' < 1/��2 = 0.70710678 ��� n��8.
AB�� ��2n�F�c(nn-1) �̒��p���̎Εӂ䂦
�@AB = 4n/(nn+1),
BC'�� ��3�F�c4 �̒��p���̎Εӂ䂦
�@BC' = (5/7){1 - 4n(nn+2n-1)/(nn+1)^2},
����L = 8 (AB+BC),
�EL �� 31/5 �ȏ�ƂȂ�̂� n=8,9,10,11 �̏ꍇ�B
n=7, L = 8 (0.56000000 + 0.21828571) = 6.22628571, c' = 0.71222857�@(���i)
n=8,�@L = 8 (0.49230769 + 0.28689772) = 6.23364328, c' = 0.70667794
n=9, L = 8 (0.43902439 + 0.33950880) = 6.22826549, c' = 0.69992352
n=10, L = 8 (0.39603960 + 0.38098506) = 6.21619729, c' = 0.69298528
n=11, L = 8 (0.36065574 + 0.41444312) = 6.20079088, c' = 0.68629785
n=12, L = 8 (0.33103448 + 0.44195685) = 6.18393070, c' = 0.68003397 >>136
�Ȃ�قǁB
(1,0) (0,1) ��ʂ��Ȃ���� 12�p�`�ʼn\�ł�����ȁB
(1,0) (b,c) (c,b) (0,1) ��12�p�`�́A�����̕Ӓ��� |b-c|��2 �Ȃ̂ő��A�E�g�ł�����B
�܂�
�@A (1,0)
�@B (1 - 8nn/(nn+1)^2, 4n(nn-1)/(nn+1)^2)
�@D (4m(mm-1)/(mm+1)^2, 1 - 8mm/(mm+1)^2)
�@E (0,1)
��12�p�`��
�@BD = {(mn-m-n-1)^2 - 2(m+n)^2}/[(mm+1)(nn+1)]�E��2
�ŃA�E�g�ł�����B >>136
BA = AC = 638891/1232085 = 0.51854458
B~B = CC~ = 2�(317156/1232085) = 0.51482812
L = 4 (BA+AC+CC~) = 7648376/1232085 = 6.20766911
�m���ɉ\�ł�����B >>137
���钸�_����A�L��������(x���W�ψʁAy���W�ψʁA�������ׂĂ��L����)�����_��T�������Ȃ�A
�ȒP�ł��B�ǂ�Ȃ��̂ł������̂ŁA�s�^�S���X�O�p�`�������Ă�������̂ł��B�������k�ڂ�
�L�����{�ł�������Ύ��R�ł��B����Ύ��R�[���� >>136 �ŋL������͗����Ƃ����̕��j�ɂ����̂ł��B
�������A(t,t)�^�̒��_����������ɗL�������������Ȃ���Ȃ�Ȃ��ƂȂ�A��ςł��B
�������ɂ̂ݓ������܂����A����ΌŒ�[���ł��B���͂��̕��j�͖ʓ|�������Ǝv���A�[���炠����߂�
���܂������A>>137�@���ł́A������s���Ă��܂��B�悭������ꂽ�ƁA���V���Ă܂��B
���ۂɃv���b�g���Ă݂܂������A���̕ω��ɂ���āA���_�̕��z�����\�ω����܂��ˁB
�ʏ��������Ȃ����̂�A�P�ʉ~�̊O�ɏo����̂�����܂������A���͈͓̔���n�ɑ��A
���������܂��B
n�͐����Ɍ���܂���B�L������ok�ł��ˁB���炵�����Ǝv���܂��B >>127
���̎�|�ɓY������Ȃ����������Ljꉞ�B���R�� n �ɑ���
a = 4n^4+8n^3-4n-1 = (2n^2-1)(2n^2+4n+1),
b = 8n^3+12n^2+4n = 4n(n+1)(2n+1),
c = 4n^4+8n^3+8n^2+4n+1 = (2n^2+2n+1)^2,
d = 8n^3+12n^2+8n+2 = 2(2n+1)(2n^2+2n+1)
�ƒ�߂� ��=(a+bi)/c �Ƃ����A|��|=1, |1-��|=d/c �ƗL�����ɂȂ��Ă���邩��A
���܂����Ǝ��R�� m ���߂ĕ��f���ʏ�̓_�W�� {a^n}_(n=-m,�c,m) �����Ɍ��ׂΎ����ȊO�̏�����S�Ė������B
�_�W�������Ɍ���Łi��^m �� ��^(-m) ������Łj�ʑ��p�`���ł��邽�߂� m ���������ׂ������͂Ƃ����ƁA
��^1 ���� ��^m �܂ł��S�ď㔼���ʂɂ��邱�Ƃ̂݁B�i���̂��� m �̑傫���͂������� ��n/2 ���x�ɐ��������j
n ���\���傫���Ƃ���ꂾ���ӂ��~�ɋ߂Â�����A������ 31/5(<��) ����悤�� n ���Ƃ邱�Ƃ͉\�B
�c�����Ď��ۂɂƂ��Ή����Ȃ��ǁA�v�Z���ώG�ɂȂ邽�ߌv�Z�@�ɗ��邵���Ȃ��̂���_�B�ꉞ���_�����ȏ�̒ʂ� > n�͐����Ɍ���܂���B�L������ok�ł��ˁB
�����ł��������B������`�g�C������
>>135
�E�ʏ����@(nn-1)/2n > 1+��2�@����
�@n > 1+��2 + ��{2(2+��2)} = 5.02733949
�Ec = (21/41){1 + (8/21)n(2n-5)(5n+2)/(nn+1)^2} < 1/��2�@����
�@n > {881 + (29��2)[29+��(2�29�29+881��2)]}/(17�47) = 5.36862925
�EL �� 31/5 �ȏ�ƂȂ�̂�
�@6.45963968 < n < 9.13156611
>>137
�E�ʏ����@(nn-1)/2n > 1+��2�@����
�@n > 1+��2 + ��{2(2+��2)} = 5.02733949
�Ec' = (4/7){1 + n(n-3)(3n+1)/(nn+1)^2} < 1/��2�@����
�@n > {31 + (5��2)[5+��(50+31��2)]}/17 = 7.93257298
�EL �� 31/5 �ȏ�ƂȂ�̂�
�@6.10446338 < n < 11.04823360
�����̋��ʕ�����
�@7.93257298 < n < 11.04823360
�ł����邩�B >>141
c+a = 2{2n(n+1)}^2,
c-a = 2{(n+1)^2 - n^2}^2,
c = {(n+1)^2 + n^2}^2
cc - aa = bb,
b = 2{2n(n+1)}{(n+1)^2 + n^2},
dd - (c-a)^2 = bb,
d = 2{(n+1)^2 - n^2}{(n+1)^2 + n^2} = 2{(n+1)^4 - n^4} >>141
�� = arcsin(b/c),
�Ƃ�����
m = [ ��/�� ]
L = 2m(d/c) + 2sin(m��),
n=3
�@a=527, b=336, c=25^2, d=14�25, ��=0.56758821841666, m=5,
�@sin(5��) = 28515500892816/(c^5) = 0.29900669864185�@�� Q
�@L = 2�5�(14/25) + 2sin(5��) = 6.1980133972837
n=4
�@a=1519, b=720, c=41^2, d=18�41, ��=0.44262888469558, m=7,
�@sin(7��) = 1637671530080839800240/(c^7) = 0.043177033944429�@�� Q
�@L = 2�7�(18/41) + 2sin(7��) = 6.2326955313035
�EL �� 31/5 �ȏ�@�����@n��4
n=17
�@a=373319, b=42840, c=613^2, d=70�613, ��=0.1142546313550, m=27,
�@sin(27��) = 0.056687202872879�@�� Q
�@L = 2�27�(70/613) + 2sin(27��) = 6.2797691855174
n=18
�@a=466487, b=50616, c=685^2, d=74�685, ��=0.10808179674906, m=29,
�@sin(29��) = 0.00722048512511925�@�� Q
�@L = 2�29�(74/685) + 2sin(29��) = 6.2801344009072
�@
�EL �� 6.28 �ȏ�@�����@n��18 >>144
�ǂ������肪�Ƃ��Bn=3 �̎��_�ł���10�P�^�����Ă��̂ˁc
������ n=4 �ƈӊO�Ƒ����^�C�~���O�ŏ�������������Ă����� ��~�̒��SO�̔������~�ƕ��s�ȕ��ʃ��ő̐ς������ɂȂ�悤�ɐؒf����
����ɁA��~�ƃ��̒����ɂ����̕��ʂƕ��s�ȕ��ʃ��Ŕ�����ؒf����
���ɂ��f�ʂ̒��S��O'�A����̓_��P�Ƃ���Ƃ��A
��OPO'�����߂� �O>>42
>>146
���a1�̔������~���獂���ւ܂ő����W�߂��Ƃ��A�̐ς���(�̐�4��/3)��1/4�Ƃ���ƁA
��/3=��0�`��(1-t^2)dt
1/3=[t-t^3/3]0�`��
1/3=��-��^3/3
��^3-3��+1=0�\�\�@
��=sin��OPO'
�@���������ƁA
3��^2-3=0
y=f(��)=��^3-3��+1�̃O���t�̌`���A
��=-1�̂Ƃ��ɑ�A
��=1�̂Ƃ��ɏ��l-1���Ƃ�B
�@�̒l��0�ƂȂ�ւ́A
0���ց�1�̂������0���̂Ƃ��B
��OPO'��18�� �O>>147�����B
{sin(20��)}^3-3sin(20��)+1=0.0139483266��0
20�����킸���ɑ傫�����A�����l�ł�20���������Ƃ��߂��B ��[0,a](1-x^2)dx = 1/2�E2��/3���
a-a^3/3 = 1/3 �B
�� (2b) - (2b)^3/3 = 1/3�B
�� 3b - 4b^3 = 1/2�B
�� 3(sin��) - 4(sin��)^3 = 1/2�B
�� sin3�� = sin(��/6)�B
�� ��=��/18�B >>148
�s����
>>149
�����ł� >>149-150���H�@10���͂�������B����Ȃ�������̉~�Ղ�������1/3�ɂȂ�́H�@�O>>148�������Ȃ��H�@10����1/3���B
�P]/�_�Q�Q�Q�Q�Q�Q�Q
�Q/�_/ �@�@,,������/|
�P�_/ �@�@�c`o`Ђ�))|
�P|�_�Q�Q�QU,~�܁S� |_
�n| �a�P�P�P�PU~~U / /
�Q| �a ���@�� �a |/ /
_�@`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P ����18�ƍ���2�̌v20�̋ʂ��܂ɓ����Ă���B
�u����ׂɑ܂���ʂ�1���o�����̋ʂ͖߂��Ȃ��v�Ƃ������Ƃ��J��Ԃ��B
���߂č��ʂ��o��܂łɔ��ʂ��o�����Ƃ��āA�ł��m���̍����̂�0, 6, 9, 18�̂������瓚����B ���Ԃ�t�x�݂̏h����ۓ��������낤�B���x���I�ɂ��[�������B >>152����1�H�ׂĖ߂��Ȃ��m����18/20=9/10�B����2�H�ׂĖ߂��Ȃ��m����(9/10)(17/19)=63/190�B����3�H�ׂī���߂��Ȃ��m����(63/190)(16/18)=28/95�B����4�H�ׂ�̰��߂��Ȃ��m����(28/95)(15/17)=84/323�B
����5�H�ׂı�!! (84/323)(14/16)=72/323�B����6�\�\(72/323)(13/15)=312/1615�B9���ȁH �O>>151
�P]/�__�Q�Q�Q�Q�Q�Q
�Q/�_/�@�@�@�����@/|
�P�_/�@�@�@((`-`)/ |
�P|�_�Q�Q�Q,U��U�| |__
�n| �a�P�P�P~U~U | / /
�Q| �a ���@�� �a |/ /
_�@`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P V(��) = ��[0�`2sin��] (1-xx) dx
�@= (2��/3) [(3/2)x - (1/2)x^3](x=0,2sin��)
�@= (2��/3) {3sin�� - 4(sin��)^3}
�@= V(��/6) sin(3��),
�ʔ����B �悭����L���b�`�R�s�[�u2�l��1�l������ɂȂ�v
���́A����ɂ͐����̃J���N��������̂�
���ۂɂ́A���{�l��50�܂łɜ��m���́A���v��ł́A�Ȃ��2��
60�ł�7���ȉ��ɉ߂��Ȃ�
80�ł�37���ȉ�
90��100�܂Ő�����l���ׂĂ����킹�āA�悤�₭�u2�l��1�l�v�ƂȂ�
�i���������Z���^�[�������Z���^�[�u�ŐV���v�v���j >>157
��������
���ʑO�܂łɃK���ɂ�����m���A�Ƃ������t�ʂ�̓�����O�̒�`���� http://ganjoho.jp/reg_stat/
�@���@���v�@���@���v�@���@�ŐV���v �Ȃ�Ŏ���������Ȃ̂ɓ����Ⴄ��H�@�v�Z�ԈႦ�����ȁH�@10�����ȁH�@�O>>155
�P]/�_�Q�Q�Q�Q�Q�Q�Q
�Q/�_/ �@�@,,������/|
�P�_/ �@�@�c`_`Ђ�))|
�P|�_�Q�Q�QU,~�܁R' |_
�n| �a�P�P�P�PU~U~ / /
�Q| �a ���@�� �a |/ /
_�@`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P �O>>160
��~�ƃ��̒����ɂ����̕��ʂƕ��s�ȕ��ʃ�
����������B
��~�ƕ��ʃ��ɕ��s�ȕ��ʃ��Ƃ����Ӗ��ł͂Ȃ��̂��H�@�����͓_���A�_�ɕ��s���Ă̂͂��������ȁB >>155
�s�����ł�
20���Ď��o�������A�����o��^�C�~���O��C(20,2)=190�ʂ肠��܂�
�����͑S�ē��l�Ɋm���炵���ł�
�������߂ɍ����o��̂�19�ʂ�B6���o�č����o��̂�13�ʂ�B���l�ɑI��������10�ʂ�A1�ʂ�B
�����0���ł��m���������ƌ��_����܂� �O>>161
���ʃ��͒�~�ƕ��ʃ��̂��傤�ǒ����ɂ���Ƃ��āA
��0�`2sin��OPO'(1-t^2)dt=(4��/3)(1/2)(1/2)
=��/3
[t-t^3]0�`2sin��OPO'=1/3
2sin��OPO'-8(sin��OPO')^3/3=1/3
6sin��OPO'-8(sin��OPO')^3=1�\�\�@
��̉ŁA�����ʃ��Ő����Ƃ��́�OPO'����ɂ����OP'O"�͂قƂ��20������������A
��OPO'=10���Ɨ\�z�����B �ɇ@�����A�A
s(in10��)��8(sin10��O^3=1
�����ꂽ�B
(���������̉\������) �O>>163�C���B
���ʃ��͒�~�ƕ��ʃ��̂��傤�ǒ����ɂ���Ƃ��āA
��0�`2sin��OPO'(1-t^2)dt=(4��/3)(1/2)(1/2)
=��/3
[t-t^3]0�`2sin��OPO'=1/3
2sin��OPO'-8(sin��OPO')^3/3=1/3
6sin��OPO'-8(sin��OPO')^3=1�\�\�@
��̉ŁA�����ʃ��Ő����Ƃ��́�OPO'����ɂ����OP'O"�͂قƂ��20������������A
��OPO'=10���Ɨ\�z�����B�@�ɑ�����A
6(sin10��)-8(sin10��)^3
=6(0.173648178)-8(0.173648178)^3
=6(0.173648178)-8(0.00523613325)
=1
�������ꂽ�B >>164
sin10����0.173648178
�͂����܂ŋߎ��l�ł����Đ^�̒l�łȂ����߂���͐��w�I�ȏؖ��ł��Ȃ�ł�����܂���
���Ȃ킿������Ă܂��� �O>>164
>>165
���������ȁA
6(sin10��)-8(sin10��)^3�̒l���҂�����=1�ƂȂ�����B��1����Ȃ��B�ߎ�����Ȃ��B�M���Ăق����B�т����肵�����A�������낢�Ǝv���B���A�Ȃ�ł����Ȃ邩�͂܂����ꂩ��l�������Ƃ���B
20�����Ɣ����ɒl���Y����̂ɁA10�����ƂȂ����҂����肾�����B >>166
�ߎ��l�ł͂Ȃ��҂�����1�ɂȂ邱�Ƃ͂��ł�>>149�Ŏ�����Ă܂�
�����������Ƃ����������̂ł͂Ȃ���>>164���S�����w�̏ؖ��ɂȂ��Ă��Ȃ��Ƃ������Ƃ��������������ł� >>167
3�{�p�ȑO�ɃC�i�Ƃ������z�́u�ؖ��v�Ƃ����T�O��m��Ȃ��낤�� ���S��O�ɂ��锼�����A���̒�ʂƕ��s�ȕ��ʃ��Őؒf�����Ƃ���A
�����̑̐ς������� sin(3��) �{�ɂȂ����B
����ɁA��ʂƕ��ʃ����瓙�����ȕ��ʃ����Ƃ�B
�@���Ɣ����Ƃ̌��~��C�Ƃ��AC��̈�_��P�Ƃ���Ƃ��A
�@OP�ƒ�ʂ̂Ȃ��p�����߂�B �O>>166
>>171
���ʃ��̒��S��O'�Ƃ��A�����𐅕��ʂŐ���(��ʁ`���ʃ��`���ʃ��܂�)�������߂�(����0�`2sin��OPO'�Őϕ�����)�ƁA
��0�`2sin��OPO'(1-t^2)dt=(4��/3)(1/2)(1/2)=��/3
[t-t^3/3]0�`2sin��OPO'=1/3
2sin��OPO'-(8/3)(sin��OPO')^3=1/3
6sin��OPO'-8(sin��OPO')^3=1
�O�⓯�l�A��OPO'=10�K
���ʃ��Ɣ����̒�~�����s�������ӂ̊p�́�OPO'�̍��p�ŁA10�� �O>>172
>>171���B
(4��/3)(1/2)(sin3��)=��/3
2sin3��=��
sin3��=��/3
3��=30��
��=10��
����ӂ̊p�̓� �O>>173�����B
(4��/3)(1/2)(sin3��)=��/3
2sin3��=��/3
sin3��=��/6
3��=30��
��=10��
����ӂ̊p�̓� 10���̋ߎ��l������10���d��Ōv�Z������1�ɂȂ邩������Ȃ�����
10���̋ߎ��l������50���d��Ōv�Z������1�ɂ͂Ȃ���� ��y�̓d��͔����ł���B�O>>174�V�i�R���Ŏ�܂��ĉf�扻����̂��y���݂ɂ��Ă���B
�P�P]/�_�Q�Q�Q_����
�Q�Q/�_/�@,,��(___))
�P�P�_/�@�c`-`Ђ���|~
�P�P|�____U,~�܁R/ |__
���@| �a�P�P~U~U~| / /
�Q�Q| �a�@���@�a |/ /
_____`�a�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P������Δ݂����B�������߂Ȃ����ǁB�����Ƃ������낢�����o���Ăق����B �Ƃ肠�����m�M�ɂȂ������������B
��ɓ���ł͂Ȃ��B 6sin10��-8(sin10��)^3=1
���ꂩ���̕s�v�c��R�����Ă���Ȃ����B�Ȃ�ł҂�����10���ȂB�ł���ΐ}�ɕ`���āB�]�ł킩��悤�Ȑ}���B
�O>>176�����������B�J�~���Ă������Ȃ��炢�C���������Ă��Ă�B
�P�P]/�_�Q�Q�Q_����
�Q�Q/�_/�@,,��(___))
�P�P�_/�@�c~-~Ђ� /|
�P�P|�____U,~�܁R/ |
���@| �a�P�P~U~U~| /
�Q�Q| �a�@���@�a |/
_____`�a�Q�Q�Q�a�^
�P�P�P�P�P�a�P/
���@�@���@�a /
�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P �i������
�[���H��
�q�g���h�L�S�L�u���l�g�E������Q�҂����H���Ď��E���� >>179�ʔ������@����
�o���Ă桑O>>178(^o^))
[�P]�@ �ݸ݁c�c�@U��U�
�P�P]/�____�����m (��)
�Q�Q/�_/,,(`.`))�܁SU/
�P�P�_/�c`-`Ѓ�`�҃�/
�P�P|�__U,~�܁R___�^|
���@| �a�P~U~U~�P�a |
�Q�Q| �a ���@���@�a |/
_____`�a_________�a�^
�P�P�P�P�P�P�P�P�P >>178
���ނ���R�e���ĂĂ��� ����l��̈قȂ�2�_A,B�͐���AB���Ȃ��Ă���B����AB���O��������B���������̏����ō�}���邱��:
����̂����ƃR���p�X����
����̂����͒������������߂���
��R���p�X��1��̂ݎg�� >>183�Ȃ�ŃR�e������
�v��́H �O>>182(^o^))
[�P]�@ �ݸ݁c�c�@U��U�
�P�P]/�____�����m (��)
�Q�Q/�_/,,(`.`))�܁SU/
�P�P�_/�c`-`Ѓ�`�҃�/
�P�P|�__U,~�܁R___�^|
���@| �a�P~U~U~�P�a |
�Q�Q| �a ���@���@�a |/
_____`�a_________�a�^
�P�P�P�P�P�P�P�P�P�N�W������������̓R�e���O����B>>184
�R���p�X��������x�ǂ��Ŏg�����BAB��̎O�����n�_���Ƃ���ȂȂ��Ǝv�����ǂ����B�Ă��Ƃ�AB�ɑ��鐂��������ɐj��u�������B���������̓R���p�X���Ȃ��Ă�������B
���̂�����AB�ɑ����߂ɒu���A�Б���A���Ƃ��钼�����A�����Б���B���Ƃ��钼�����Ɉ����B������t�̎߂œ��l�ɍs����AB��Ίp���Ƃ����Ђ��`���`����B���̂�����̑Ίp����AB�̐����������B
���Ė���AB�̐���������̂ǂ��ɃR���p�X�̐j��u��������Ȃ��BAB�̎O�����n�_�̂ǂ��炩����ɃR���p�X�̉��M��u���ȂȂ��B
�R���p�X�̒�����AB�Ƃ����AB�̒��_����R���p�X�̐j��u���ʒu�܂ł̒����́A�O�����̒藝���A
��{AB^2-(AB/6)^2}=(��35)AB/6
����͕`���Ȃ������B
�R���p�X�̒�����(1/2)AB�Ƃ����AB�̒��_����R���p�X�̐j��u���ʒu�܂ł̒����͓��l�ɁA
��{(AB/2)^2-(AB/6)^2}=(2��2)AB/6
=(��2)AB/3
����͕`����\��������B������������B �ڕ��ʂ������Ȃ���̂������R���p�X�������� �摜�r�炵�������悭���ځ[����@�͂Ȃ����ˁH >>187�ڕ��ʂ͂�[��](Y)
�߂���B�O>>185(~e~( )
[�P]�@ �ݸ݁c�c U��~�
�P�P]/�___�����m (���j
�Q�Q/�_/,(`.`))�܁SU /
�P�P�_/�c`-���`�҃� /
�P�P|�__U,~�܁R___�^|
���@| �a�P~U~U~�P�a |
�Q�Q| �a ���@���@�a |/
_____`�a_________�a�^
�P�P�P�P�P�P�P�P�P�摜���\��Ȃ��Ă��ꂾ���ǁA����[��]�݂����Ȋ����ŁA���̂�����AB�ɑ��߂ɒu���A�Ō�ɃR���p�X�ŎO�����ł���Ǝv���B >>187
�{���w��łł����Ȃ��H >>178
-8x^3+6x-1=0�̉���sin10���ɂȂ闝�R���l������Ă��ƁH ���̋���ے��Ȃ�D�G�ȍ��Z���ł��ł��������� ����_�w���ɓ��w�ł���w�͂�����ł���B >>184
����AB��ɂȂ��P�_Z���Ƃ�B
�R���p�X��Z�𒆐S�Ƃ�����AB�ƌ����傫���̉~��C���g���B
����AB��C�̌�_��D, E�Ƃ���B
���̂����Œ���DZ���g���A�~��C�Ƃ̌�_��D~�Ƃ���B
���̂����Œ���EZ���g���A�~��C�Ƃ̌�_��E~�Ƃ���B
���̂����Œ���D~E~���g���B����͒���AB�ƕ��s�ł���B
AB�AD~E~�̕��s��������1�{�g������������
DED~E~ �������`�ł��邱�Ƃ��g�����B
���̂����Œ����`�̊e�ӂ�2�����ł���A2����AB�AD~E~���瓙�����̒������g����B �����`DED~E~�̈�ӂ�3��������B�������A���̏����ō�}���邱�ƁF
����̂�������
����̂����͐������������߂����i�����`�̒������j �P]/�__�Q�Q�Q�Q�Q>>190
�Q/�_/�@�@�����@/|����
�P�_/�@�@((`-`)/ |����
�P|�_�Q�Q,U��U�| |__��
�n| �a�P�P~U~U | / /��
�Q| �a�@���@�a |/ /��
_�@`�a�Q�Q�Q�a�^_/�ȁB
�P�P�P�P�P�P�P�P�a�@/
���@ ���@ ���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�Px����sin�ɂȂ�Ƃ�10���ɂȂ�Ƃ��v���O>>188�ɁA0��x��1�͈̔͂�0���ɂ��邠��l�Ɍ��܂��Ă��܂��B�m�肽���̂͒l����Ȃ��B
sin10����10���̂ق��B
�Ȃ��҂�����10���Ȃ̂��B
��������ɂ͎����Ȃ�̓������o����������ǂ����ł������B�J�^!! >>192
�����ƕW���I�ȃ��x���̖��ł���
3�{�p�̌����g���������� >>196
��1������_�w�����ʼn����Ȃ��Ƃ̂��܂���m������B >>194
>>194
�Ίp��DD~�CEE~�̌�_�� Z(0,0) �Ƃ���B
�ӂ̒������@DE = D~E~ = 2p,�@�@DE~ = D~E = 2q�@�Ƃ���B
D (-p,-q)�@E (p,-q)�@D~(p,q)�@E~(-p,q)
��DE��ɓ_S (-ps,-q)�@��D~E~��ɓ_T (-pt,q)�@��C�ӂƂ�B(0<s<t<1 �Ƃ���)
SZ�̉����ƕ�D~E~�̌�_��S~(ps,q)
TZ�̉����ƕ�DE�̌�_��T~ (pt,-q)
S~T~ // ST
����ST�ƑΊp��DD~�̌�_��U (-(s+t)p/(2-s+t), -(s+t)q/(2-s+t))
����ST�ƑΊp��DD~�̌�_��V (-(s+t)p/(2+s-t), (s+t)q/(2+s-t))
����S~T~ �ƑΊp��DD~�CEE~�̌�_�� U~�CV~
UV~�̉����ƕ�DE~�CED~�̌�_�� W (-p,-qs)�CX~(p,-qt)
VU~�̉����ƕ�DE~�CED~�̌�_�� X (-p,qt)�CW~(p,qs)
����������
�@SW~ // S~W // TX // T~X~ // DD~ �@(�X�� q/p)
�@SW // S~W~ // TX~ // T~X // EE~�@(�X�� -q/p)
5�{�g�̕��s����2����ꂽ�B �����I�ɁA��K�ƃR���p�X�ɂ���}�ŕ`���o����u2���̌�_�v�i���͒����ł��~�ʂł��j�́A���ׂĒ�K�݂̂ŕ`����Ƃ����藝�����邩��A
���ɂ̓R���p�X0��ɂł���͂��Ȃ� >>198 (����)
SW�CT~X�ƑΊp��DD~�̌�_��F�CG�Ƃ���B
FT~��GS�̌�_��H�CFX��GW�̌�_��I�Ƃ���B
DH�̉�����ED~�̌�_�� J (p, -q/3)�@�@EJ = (2q)/3
DI�̉�����D~E~�̌�_�� K (-p/3, q)�@�@E~K = (2p)/3
�ƂȂ�B
�Ȃ��A�e�ӂ�3�������ꂽ�̂ŁA����AB�̕��s���͖����ɉg����B
(��)�@�A�t�B���ł́A�c���ɐL�k���čl���Ă��悢�B
���Ƃ��ΐ����`(p=q)�ɂ��čl����ƁA���Ίp���̌X�p��45���ƂȂ�B
��ӂɑ��闼�Ίp���̌X�p�����������Ƃ��d�v�B >>199
���Ԃ�A�ł��Ȃ��Ǝv����B�i�L����ł́j n���L�����̂Ƃ��A����AB��1/n�̒����̐��������邱�Ƃ���������
�R���p�X���g����2��ɂ���ƁA����܂���������Ċy�����Ȃ�� >����_�w���ɓ��w
�N�ɂ��ł��Ȃ� >>190���̎��Ȃ�
x=cos80��=1.73648178�ł����藧�B��������Ȃ��āA������̐ς������ɂȂ�悤�ɐ����ɐ������������ɍ��������Ő����ɐ�Ƃ�����A�̓���ŁA���̂���������́�OPO'���A�Ȃ��҂�����10���ɂȂ�̂��A���̕s�v�c�������Ă܂��B
�P]/�_�Q�Q�Q�Q�O>>195
�Q/�_/�@�����@�@/|
�P�_/�@((`-`)��/ |
�P|�_�Q_U,~�܁S� |__
�n| �a�P�P~U~~U| / /|
�Q| �a�@���@�a |/ / |
_�@`�a�Q�Q�Q�a�^_/�@|
�P�P�P�P�P�P�P�P�a�@/
���@ ���@ ���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P ������C�U�[�r�[���̔@
`_')������҂�����10��
�P]/�__�_________�Ő�
�Q/�_/ ���_.~�� /|�点
�P�_/�@((`-�_��/ |���
�P|�_�Q_U,~�܁_| |__��
�n| �a�P�P~U~~U�_/ /|
�Q| �a�@���@�a |/�_ |
___`�a�Q�Q�Q�a�^_/ �_
�P�P�P�P�P�P�P�P�a�@/`
���@ ���@ ���@�@�a /��
�Q�Q�Q�Q�Q�Q�Q�Q�a/��
�P�P�P�P�P�P�P�P�P���������B�O>>204�Ă������A�҂�����10�����ȁH�\�\�������ē��������Ƃ����ʔ��������B >>204�����Bcos10��=0.173648178�O>>205
����@�@�@
`_')����߯�@
�P]/�__�_________
�Q/�_/ ���_.~�� /|
�P�_/�@(`e'�_��/ |
�P|�_�Q_U,~�܁_| |__
�n| �a�P�P~U~~U�_/ /|
�Q| �a�@���@�a |/�_ |
___`�a�Q�Q�Q�a�^_/ �_
�P�P�P�P�P�P�P�P�a�@/*
���@ ���@ ���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P >>200
D (0,0)�@S (2a,0)�@T~ (2b,0)�@X (0,2mb)�@W (0,2ma)
�Ƃ����
�Ίp��DD~�F�@y = mx�@�@�@(m=q/p)
SW�F�@y = m(2a-x)
T~X�F�@y = m(2b-x)
SW��DD~�̌�_�@F (a,ma)
T~X��DD~�̌�_�@G (b,mb)
FT~�F�@y = {ma/(2b-a)}(2b-x),
GS�F�@y = {mb/(2a-b)}(2a-x),
�����̌�_�@H (3ab/(a+b),mab/(a+b))
DH�F�@y = (m/3)x, �������C^1����f(x)�ɂ���lim(x����)f(x)�͎�������Ƃ����Ƃ��A�ȉ��̖�ɓ�����
(1)f'���P�������̏ꍇ�Alim(x����)f'(x)=0�ƂȂ邱�Ƃ��ؖ�����
(2)f���P�������ł���
lim(x����)f'(x)��0�Ƃ͂Ȃ�Ȃ���������� >>184
����l��ɓ_B�𒆐S�Ƃ��ē_A��ʂ�~C����}����B�~C�ƒ���l�̌�_��A�łȂ�����A'�Ƃ���B
����l��ɂȂ��_P���~C�̓����ɂƂ�A����OP��̓_Q��C�ӂɂƂ�B
AP��A'Q�̌�_��R�AA'P��AQ�̌�_��R'�ARR'��PB�̌�_��S�Ƃ����B
RB��SA�̌�_��T�APT��l�̌�_��U�����AU�͐���AB�̒��_�ɂȂ�B
����RR'�Ɖ~C�̂Q�̌�_�����ꂼ��V,W�Ƃ����B
����VB�Ɖ~C�̌�_��V�łȂ�����V'�A����WB�Ɖ~C�̌�_��W�łȂ�����W'�Ƃ����A
����VW�A����l�A����V'W'�͑S�ĕ��s�ł���A���̏��œ��Ԋu�ł���B
����V'W'�ォ��C�ӂɓ_O���Ƃ�AOA��VW�̌�_��D�AOU��VW�̌�_��E�AOB��VW�̌�_��F�Ƃ����B
�_O�����_�Ƃ��ē�_A,B�̈ʒu�x�N�g�������ꂼ��(1,0),(1,1)�ƂȂ�悤�ɍ��W�n���߂�ƁA
���� O(0,0), A(1,0), B(1,1), A'(1,2), D(2,0), E(2,1), F(2,2) ������}����Ă��邱�ƂɂȂ�̂ŁA
���Ƃ͗Ⴆ��AE��A'F�̌�_G(3,2)�AAD��A'E�̌�_H(3,0)�AGH��BE�̌�_I(3,1)���̂悤�ɍ�}������A
OG��AB�̌�_(1,2/3)�AOH��AB�̌�_(1,1/3)�Ƃ������߂��_��������B >>209 ����
�P�i���Q�s��
��F����OP��̓_Q��C�ӂɂƂ�B
���F����BP��ɓ_Q��C�ӂɂƂ�B
�R�i���T�s��
��FOH��AB�̌�_(1,1/3)
���FOI��AB�̌�_(1,1/3) >>208
(1)
������ f '(a) >0 �ƂȂ�a�����݂����Ȃ��
�@x��a�@�ˁ@f '(x) �� f '(a) = b,
�@f(x) �� f(a) + b(x-a)�@���@���@(x����)
�ƂȂ��Ė�������B
���@f '(x) �� 0
���@�P�������ŏ�ɗL�E�������������B
�@lim[x����] f '(x) = L �� 0,
L < 0 �Ȃ�A��=(-L)/2 �ɑ��� ���� N ��������
�@x > N�@�ˁ@|f '(x) -L| < �� = (-L)/2,
�@�@f(x) < f(N) +(-L)/2�E(x-N)�@���@-���@�@(x����)
�ƂȂ��Ė�������B
�� L=0
(2)
���Ƃ���
�@f '(x) = sin(nnx)�@�@�@�@( 2n�� < x < (2n+1/nn)�� )
�@�@�@�@ = 0�@�@�@�@(���̑�)
�@f(x) �� 2��(2) = ��/3�@�@(x����)
�E�L���ȗ�
�@f '(x) = x/{1+ x^6�sin(x)^2},
���F�u��͊T�_�v������O�ŁA��g���X(1961)�@p.141
�@��3�� �ϕ��@�@���K���(3)-(9) f(x)=1-x^2+x^4-x^8+x^16-x^32+�c+(-1)^n�Ex^(2^n)+�c
�Ƃ���Ƃ�f(x)��[0,1)�ŘA������
�Б��Ɍ�lim(x��1-)f(x)�͑��݂��Ȃ����Ƃ������B >>214
�@x �` 1 - (��2)(1/4)^n �̕ӂ�ŋɑ� �` 0.5027
�@x �` 1 - (1/��2)(1/4)^n �̕ӂ�ŋɏ� �` 0.4973
�@x �` 1 - (1/2)^n �̕ӂ�ł� �� 1/2
�ł����˂� >>213
n��0 �̂Ƃ� (-1)^n�Ex^(2^n)��x^(2^0)��x^1�Ȃ̂ŁA
f(x)=1-x^2+x^4-x^8+x^16-x^32+�c+(-1)^n�Ex^(2^n)+�c
�ł͂Ȃ�
f(x)= x -x^2+x^4-x^8+x^16-x^32+�c+(-1)^n�Ex^(2^n)+�c
����ˁH >>213
a��lim(x��1-)f(x)��R �����݂���Ƃ���B
f(x)����[n��0�`��]x^{4^n}(1�|x^{4^n}) �Ȃ̂ŁA0��x��1��m��1��C�ӂɎ��Ƃ��A
f(x^{1/4^m})
����[n��0�`��]x^{4^{n�|m}}(1�|x^{4^{n�|m}})
����[n���|m�`��]x^{4^n}(1�|x^{4^n})
�ƂȂ�Bm���{���Ƃ���ƁAx^{1/4^m}��1 �Ȃ̂ŁA
a����[n���|���`��]x^{4^n}(1�|x^{4^n})
�ƂȂ�B���ꂪ�C�ӂ�0��x��1�Ō����邱�ƂɂȂ�B �������Ax��1/2, 1/3 �̂Ƃ��� ��[n���|���`��]x^{4^n}(1�|x^{4^n}) �̒l��
���l�v�Z����ƁA�����l�ɂ͂Ȃ�Ȃ����Ƃ��\�z�����B
�����ɈႤ�l�ɂȂ邱�Ƃ������ɂ́A�K���ȗL�����܂ł͌����Ɍv�Z���A
�c��̏�]���͎G�ɏ㉺����]�����邾���ł悢�B
���̋����͎����̃X�s�[�h���ɂ߂đ����̂ŁA����ł����Ƃ��Ȃ�B
�������A��v�Z�ł͒ǂ����Ȃ����ʂł͂��� (�Oo�O) �� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�



