�u�n�b�L���O�v����u���ӂ̂������v�܂ł���L���J�o�[���鋐��f���Q �w�T�����˂�x�ւ悤�����I
�T��
�� [���f�]�ڋ֎~]©2ch.net
�� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�
0196�C�i ��/7jUdUKiSM
2020/12/28(��) 21:15:54.36ID:lvLlGPFh>>182
4��(862+16��2674)=164.407870484�c�c
0197�C�i ��/7jUdUKiSM
2020/12/28(��) 23:15:28.33ID:lvLlGPFh>>182
cosA=(24^2+20^2-BC^2)/(2�~24�~20)
sinA=BC/2R=BC/60
480cosA=576+400-3600(1-cos^2A)
(60cosA)^2-8(60cosA)-2624=0
60cosA=4-��(16+2624)=4-��2640=4-4��165
cosA=(1-��165)/15
sinA=��(166-2��165)/15=(��165-1)/15
��ABC=(1/2)24�~20(��165-1)/15
=16(��165-1)
=189.523721259�c�c
0198�C�i ��/7jUdUKiSM
2020/12/29(��) 01:57:00.74ID:Q+OHTUHS>>182
BC=2RsinA=60sinA
24^2+20^2-60^2sin^2A=2�~24�~20cosA
36+25-225sin^2A=60cosA
61-225+225cos^2A-60cosA=0
225cos^2A-60cosA-164=0
cosA=�o30-��(900+225�~4�~41)�p/225
=(30-30��42)/225
=(2-2��42)/15
cos^2A=(4+168-8��42)/225
=(172-2��672)/225
sinA=��(225-168+2��672)/15
=��(57+2��672)/15
=(��32+��21)/15
��ABC=(1/2)AB�~ACsinA
=(1/2)24�~20(��32+��21)/15
=16(4��2+��21)
=64��2+16��21
=163.830879111�c�c
0199����ȑf�l
2020/12/29(��) 08:48:11.24ID:e8UZ5ZY6�~�x�ݒ�������A>>182�̖����p�����ďo���Ă����B
�������̉Ɋ��҂���B
0200�C�i ��/7jUdUKiSM
2020/12/29(��) 12:53:54.37ID:Q+OHTUHS�}�W���B���Ɉ����B�C�^�^�^�c�c
�܂��ł��A�ǂ�����m�M�͎��ĂȂłȁB
0201�C�i ��/7jUdUKiSM
2020/12/29(��) 13:26:01.80ID:Q+OHTUHS�������荘���Ĕ����āA
�g�C���ɍs���Ȃ��č����Ă�B
���w���Ɣ]�������g������A
���ւ������Ȃ�B�ł����͂��߂��B
�����ɂ�����B
�����Ȃ��B
0202�C�i ��/7jUdUKiSM
2020/12/29(��) 19:30:40.59ID:Q+OHTUHS>>199
�O�p�����l�p�����m���sin��cos���g���g�킸�ɍS�炸�A
���������l���܂��o�ĂȂ����Ă��Ƃ���ˁH
0203����ȑf�l
2020/12/29(��) 21:50:01.83ID:e8UZ5ZY6���̒ʂ�i��
��O�͑�w�����ɂ������̖�肪�o���o���o���炵���B
�������O�̐��k�Ȃ�@�̖��͌ܕ��ʼn����B
�Ȃ��Ȃ�@�̖��̉������͏������̂悤�ɒm���Ă������炾�B
�Ƃ��낪���̋���͏������y�����Ă���B
�����獡�̐��k�͇@�̖�肪�����Ȃ��B
�L���m�Ƃ��L���i�w�Z�̐��k�͂ǂ����͒m��Ȃ����B
�A�̖��ł��A��O�̐��k�Ȃ�ܕ��ʼn����B
>>182
��i�͑I���A�Ƃɂ����������o���B
�O�ډ~�̒��S��O�Ƃ��āA
��OAB=(1/2)24��(30^2-12^2)
=12�~6��21
=72��21
��OAC=(1/2)20��(30^2-10^2)
=10�~20��2
=200��2
��ABC=��OAB+��OAC-��OBC
=72��21+200��2-(1/2)30�~30sin��BOC
=72��21+200��2-450sin��BOC
���S�p��BOC=2(��-��BC�ɂ��Ĕ��Α��̉~���p��BAC)
sin��BOC=sin2(��-��BAC)
=2sin(��-��BAC)cos(��-��BAC)
=2sin��BAC(-cos��BAC)
=-2sin��BACcos��BAC
=-2(BC/2R)(24^2+20^2-BC^2)/(2�~24�~20)
=-BC(976-BC^2)/(30�~960)
��ABC=72��21+200��2+450BC(976-BC^2)/(30�~960)
=72��21+200��2+15BC(976-BC^2)/960
=72��21+200��2+BC(976-BC^2)/64
sin^2��BAC+cos^2��BAC=1
BC^2/60^2+(976-BC^2)^2/960^2=1
BC^4-1936BC^2+30976=0
BC^2=1936�}��(968^2-30976)
=1936�}��906048
��}���BC=��(1936-264��13)
=2��(484-66��13)
976-BC^2=976-1936+264��13
=264��13-960(��0)
��ABC=72��21+200��2-(960-264��13)��(484-66��13)/32
=72��21+200��2-(30-33��13/4)��(484-66��13)
=366.360495035�c�c
0205�C�i ��/7jUdUKiSM
2020/12/30(��) 02:40:33.90ID:yoNFWM0k>>182
�O�ډ~�̒��S��O�Ƃ��A
AO��BC�̌�_��P�Ƃ���ƁA
BO�ɑ���P�̍���x�́A
P����BO�ɉ��낵�������̑���BO��t:(30-t)�ɕ�������Ƃ��āA
24:x=30:(30-t)
x=(4/5)(30-t)
=24-4t/5
30:x=30:t
t=24-4t/5
9t/5=24
t=5�~24/9=40/3=x
���l��CO��s:(30-s)�ɕ�������ʒu��P
���琂�������낷�ƁA
CO�ɑ���P�̍���y�́A
s=20-2s/3
5s/3=20
s=12
20:y=30:(30-s)
30y=20(30-s)
30(20-2s/3)=20(30-s)
y=12
��ABC=��OAB+��OAC-��OBC
=72��21+200��2-(1/2)30(40/3)-(1/2)30�~12
=72��21+200��2-200-180
=72��21+200��2-380
=232.788162511�c�c
0206�P�R�Q�l�ڂ̑f������
2020/12/31(��) 01:50:01.05ID:ejzD2e73�O�ډ~�̒��S��O�Ƃ���D
A��O��ʂ钼���ƁCA�������C�O�ډ~�Ƃ̌�_��D�Ƃ���D
BC=a�CAC=b�CAB=c�CAD=x�CBD=y�C CD=z�Ƃ���D
�s�^�S���X�̒藝���
�@c^2+y^2=x^2�@(1)
���l��
�@b^2+z^2=x^2�@(2)
i) ��BAC���݊p�̏ꍇ
�g���~�[�̒藝���
�@ax=by+cz�@(3a)
(1)(2)(3a)���
�@a=b��(1-(c/x)^2)+c��(1-(b/x)^2)
b=20�Cc=24�Cx=60��������
�@a=4��21+16��2
�w�����̌������
�@s=(a+b+c)/2=2��21+8��2+22
�@S=��(s(s-a)(s-b)(s-c))
p=2��21+8��2�Ƃ����ƁCs=p+22�Ca=2p�ł��邩��
�@S=��((22^2-p^2)(p^2-4))
p^2=32��2��21+212���q=��2��21�Ƃ�����p^2=32q+212�ł��邩��
�@S=��((272-32q)(208+32q))
�@ =2^4 * ��(8q+53)
�@ ��163.83
ii) ��BAC���s�p�̏ꍇ
�g���~�[�̒藝���
�@cz=ax+by�@(3b)
(1)(2)(3b)���
�@a=-b��(1-(c/x)^2)+c��(1-(b/x)^2)
b=20�Cc=24�Cx=60��������
�@a=-4��21+16��2
�w�����̌������
�@s=(a+b+c)/2=-2��21+8��2+22
�@S=��(s(s-a)(s-b)(s-c))
p=-2��21+8��2�Ƃ����ƁCs=p+22�Ca=2p�ł��邩��
�@S=��((22^2-p^2)(p^2-4))
p^2=-32��2��21+212���q=��2��21�Ƃ�����p^2=-32q+212�ł��邩��
�@S=��((272+32q)(208-32q))
�@ =2^4 * ��(-8q+53)
�@ ��17.188
0207����ȑf�l
2020/12/31(��) 08:46:29.21ID:umtWU27q0208�P�R�Q�l�ڂ̑f������
2020/12/31(��) 12:31:52.38ID:ejzD2e73i) ��BAC���݊p�̏ꍇ
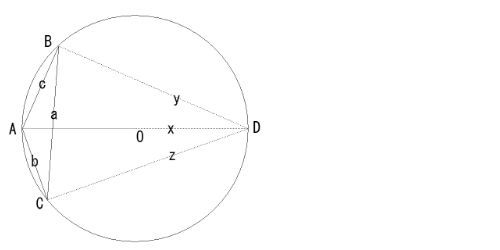
0209�P�R�Q�l�ڂ̑f������
2020/12/31(��) 12:35:18.38ID:ejzD2e73ii) ��BAC���s�p�̏ꍇ
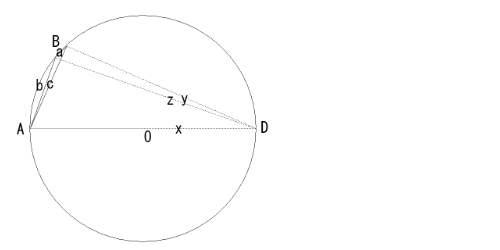
0210�P�R�Q�l�ڂ̑f������
2020/12/31(��) 12:39:50.12ID:ejzD2e730211�P�R�Q�l�ڂ̑f������
2020/12/31(��) 12:45:32.69ID:ejzD2e73�@S=abc/4R
�͊O�ډ~�̒��S���O�p�`�����ɂȂ��̂Ŏg���Ȃ�
0212�P�R�Q�l�ڂ̑f������
2020/12/31(��) 15:43:31.87ID:ejzD2e73�Ǝv���Ă������Ȃ��Ȃ��ʔ�������
���N�����w���y���߂܂��悤��
0213�C�i ��/7jUdUKiSM
2020/12/31(��) 16:32:01.89ID:SoJ2DA5s>>207
�܂��������o�ĂȂ����Ă킩���Ĉ��S������B
���������荘���Ĕ����ăg�����v��ԁB
�����ɉ�������A�҂��Ƃ��Ă���B
0214�C�i ��/7jUdUKiSM
2021/01/01(��) 00:00:20.56ID:W0Sm132p>>182
��ABC=(1/2)AB�~ACsin��BAC
=(1/2)24�~20��16875^2-(2051+1800��42)/1125
=139.803668209�c�c
>>182 ��OAB=12�~��(30^2-12^2)=12�~6��21=72��21
��OAC=10�~��(30^2-10^2)=10�~20��2=200��2
��ABC=�l�p�`OCAB-��OBC
=��OAB+��OAC-��OBC
=72��21+200��2-��OBC
��ABC=(1/2)AB�~ACsin��BAC
=(1/2)24�~20sin��BAC
=240sin��BAC
��OBC=(30^2/2)sin��BOC
=450sin��BOC
=450sin2��BPC(�~���p)
=450sin2��BAC
=900sin��BACcos��BAC
��ABC=72��21+200��2-900sin��BACcos��BAC
=240sin��BAC
(900cos��BAC+240)sin��BAC=72��21+200��2
sin��BAC=(18��21+50)/(225cos��BAC+60)
(18��21+50)^2/(225cos��BAC+60)^2+cos^2��BAC=1
3^4�~5^4cos^4��BAC+2^2�~3^3�~5^3cos^3��BAC-3^2�~5^2�~11�~19cos^2��BAC-2^2�~3^3�~5^3cos��BAC+2^2�~7�~293+2^3�~3^2�~5^2��42=0
����cos��BAC��4��������cos��BAC�͐}���A
cos��BAC��-0.8
�Ɨ\�z�ł���B
4���̌W��3^4�~5^4�ƒ萔��2^2�~7�~293+2^3�~3^2�~5^2��42���琄�肷��ƁA
cos��BAC=-(2^2�~7�~293+2^3�~3^2�~5^2��42)/(3^3�~5^4)
=-(2051+1800��42)/16875
=0.81281974857�c�c
sin��BAC=��o16875^2-(2051+1800��42)^2�p/16875
��ABC=240��o16875^2-(2051+1800��42)^2�p/16875
=16��o16875^2-(2051+1800��42)^2�p/1125
=139.803668209�c�c
>>182
��OAB=12�~��(30^2-12^2)=12�~6��21=72��21
��OAC=10�~��(30^2-10^2)=10�~20��2=200��2
��ABC=�l�p�`OCAB-��OBC
=��OAB+��OAC-��OBC
=72��21+200��2-��OBC
��ABC=(1/2)AB�~ACsin��BAC
=(1/2)24�~20sin��BAC
=240sin��BAC
��OBC=(30^2/2)sin��BOC
=450sin��BOC
=450sin2��BPC(�~���p)
=450sin2��BAC
=900sin��BACcos��BAC
��ABC=72��21+200��2-900sin��BACcos��BAC
=240sin��BAC
(900cos��BAC+240)sin��BAC=72��21+200��2
sin��BAC=(18��21+50)/(225cos��BAC+60)
(18��21+50)^2/(225cos��BAC+60)^2+cos^2��BAC=1
3^4�~5^4cos^4��BAC+2^2�~3^3�~5^3cos^3��BAC-3^2�~5^2�~11�~19cos^2��BAC-2^2�~3^3�~5^3cos��BAC+2^2�~7�~293+2^3�~3^2�~5^2��42=0
����cos��BAC��4��������cos��BAC�͐}���A
cos��BAC��-0.8
�Ɨ\�z�ł���B
4���̌W��3^4�~5^4�ƒ萔��2^2�~7�~293+2^3�~3^2�~5^2��42���琄�肷��ƁA
cos��BAC=-(2^2�~7�~293+2^3�~3^2�~5^2��42)/(3^3�~5^4)
=-(2051+1800��42)/16875
=-0.81281974857�c�c
sin��BAC=��o16875^2-(2051+1800��42)^2�p/16875
��ABC=240��o16875^2-(2051+1800��42)^2�p/16875
=16��o16875^2-(2051+1800��42)^2�p/1125
=139.803668209�c�c
0217����ȑf�l
2021/01/01(��) 22:27:24.63ID:0XJ2bHJn>>217
����ς�Ⴄ���B
��������cos��BAC�����̕ӂ̒l�����A
�W����������������ďo��l���Ǝv����B
��ABC=240��o1-(7�~293+2�~3�~3��42)/(3^3�~5^3)�p
=143.545752721�c�c
���ꂩ���������傫�����B
>>182
��ABC=240sin��BAC
=240��(1-((2^2�~7�~293+2^3�~3^2�~5^2�~��42)/(3^4�~5^4))^2)
=220.742462147�c�c
0221�C�i ��/7jUdUKiSM
2021/01/02(�y) 21:44:04.98ID:FPnZHh55B,C����O�ډ~�ɒ��aBB',CC'����сA
�O�ډ~�̒��S�ɂ��ā�ABC�Ɠ_�Ώ̂ȁ�A'B'C'��`���ƁA
��AC'A'=20�~40��2/2=200��2
��AA'B'=24�~12��21/2=144��21
��ABC=��AC'A'+��AA'B'-��A'B'C'
(1/2)24�~20sin��BAC=200��2+144��21-(1/2)40��2�~12��21sin��B'AC'
=240sin��BAC=200��2+144��21-240��42sin��BAC
sin��BAC=(200��2+144��21)/(1+��42)
=(2624��2+656��21)/41
=64��2+16��21
>>198�́�ABC=64��2+16��21=163.830879111�c�c�Ɠ����ɂȂ����B
>>182
cos��BAC=-0.68262866296�c�c
��BAC=133.049399076�c�c��
�Ɛ�������B
0223����ȑf�l
2021/01/03(��) 21:29:03.77ID:E1WbGmKb0224�C�i ��/7jUdUKiSM
2021/01/04(��) 13:03:53.43ID:6mEZY4sS>>182
��ABC�̊O�ډ~�̒��S��O�Ƃ���ƁA
��OAB��AB���ӂƂ���ӎO�p�`������A
�s�^�S���X�̒藝���A
��OAB=(1/2)24��(30^2-12^2)
=12��756
=12�~6��21
=72��21
���l�Ɂ�OAC=(1/2)20��(30^2-10^2)
=200��2
�l�p�`OCAB=72��21+200��2
�Ȃ������Ȃ邩�͑�ӂɂ�藪�������Ȃ����A
��BC������Ł�BAC�ƑΛ������BOC�̉~���p�́A
�����������~���p��BAC�̊O�p�Ɠ��������Ƃ��W���Ă��āA
��ABC�Ɓ�OCB�̖ʐϔ��24�~20:30�~30
=4�~2:5�~3
=8:15
��ABC=(8/23)�l�p�`OCAB
=(576��21+1600��2)/23
=213.1437087�c�c
0225�C�i ��/7jUdUKiSM
2021/01/04(��) 14:43:35.10ID:6mEZY4sS��BOC�͒��S�p������B
BC=2Rsin��BAC=60sin��BAC
��ABC:��BPC=24�~20:60��(60^2-BC^2)
��ABC=24�~20/�o24�~20+60��(60^2-BC^2)/2�p
=480/�o480+30��(3600-BC^2)�p
=16/�o16+��(3600-BC^2)�p
�w�����̌�����聢ABC=��s(s-24)(s-20)(s-BC)
s=(24+20+BC)/2
2s=44+BC
s=BC/2+22
s-24=BC/2-2
s-20=BC/2+2
s-BC=-BC/2+22
��ABC=��(484-BC^2/4)(BC^2/4-4)
=16/�o16+��(3600-BC^2)�p
�o16+��(3600-BC^2)�p��(484-BC^2/4)(BC^2/4-4)=16
�o256+32��(3600-BC^2)+3600-BC^2�p(484-BC^2/4)(BC^2/4-4)=16^2=256
�o32��(3600-BC^2)+3856-BC^2�p(484-BC^2/4)(BC^2/4-4)=256
�o32��(3600-BC^2)+3856-BC^2�p(122BC^2-BC^4/16-1936)=256
0226�C�i ��/7jUdUKiSM
2021/01/04(��) 16:10:24.30ID:6mEZY4sS>>182
��ABC�̊O�ډ~�̒��S��O�Ƃ���ƁA
��OAB��AB���ӂƂ���ӎO�p�`������A
�s�^�S���X�̒藝���A
��OAB=(1/2)24��(30^2-12^2)
=12��756
=12�~6��21
=72��21
���l�Ɂ�OAC=(1/2)20��(30^2-10^2)
=200��2
�l�p�`OCAB=72��21+200��2
�Ȃ������Ȃ邩�͑�ӂɂ�藪�������Ȃ����A
��BC������Ł�BAC�ƑΛ������BOC�̉~���p��BPC�́A
�����������~���p��BAC�̊O�p�Ɠ��������Ƃ��W���Ă��āA
��ABC�Ɓ�PBC�̖ʐϔ�́A
24�~20:12��21�~40��2
=1:��42
��ABC�Ǝl�p�`OCAB�̖ʐϔ�́A
��ABC:�l�p�`OCAB=1:(1+��42/2)
��ABC=�l�p�`OCAB/(1+��42/2)
=2(72��21+200��2)/(2+��42)
=2(72��21�~200��2)(��42-2)/38
=(1512��2+256��21)/19
=174.285804432�c�c
0227�C�i ��/7jUdUKiSM
2021/01/04(��) 16:20:32.19ID:6mEZY4sS�C�i��=174
�̓q���g���������B
0228�C�i ��/7jUdUKiSM
2021/01/04(��) 16:55:12.02ID:6mEZY4sS�~�ɓ��ڂ���l�p�`�̈�̓��p�́A
����ƌ����������p�̊O�p�Ɠ������B
�����A���������������B
�����������B
�v���������B
0229�C�i ��/7jUdUKiSM
2021/01/04(��) 18:09:44.16ID:6mEZY4sSsin��BAC=sin(1/2)��BOC=sin��BPC
��ABC=(1/2)AB�~ACsin��BAC
=(1/2)24�~12sin��BAC
=144sin��BAC
��BPC=(1/2)PB�~PCsin��BPC=2��OCB
�l�p�`OCAB=72��21+200��2
=��ABC+��OCB
=��ABC+(1/4)PB�~PCsin��BAC
=144sin��BAC+(1/4)12��21�~40��2�~sin��BAC
=(144+120��42)sin��BAC
sin��BAC=(72��21+200��2)/(144+120��42)
=(9��21+25��2)/(18+15��42)
=(9��21+25��2)(5��42-6)/3(6+5��42)(5��42-6)
=(945��2-150��2+250��21-54��21)/3(1050-36)
=(795��2+196��21)/3�~1014
=(795��2+196��21)/3042
=
��BAC=
���ǂ͎O�p�����g���Ă���B
0230�C�i ��/7jUdUKiSM
2021/01/04(��) 18:48:34.62ID:6mEZY4sSsin��BAC=0.6648535358918�c�c=sin138.328905864��
����ł������H
0231206
2021/01/05(��) 00:58:34.35ID:U04rSzRQ�O�ډ~�̒��S��O�Ƃ���D
A��O��ʂ钼���ƁCA�������C�O�ډ~�Ƃ̌�_��D�Ƃ���D
BC=a�CAC=b�CAB=c�CAD=x�CBD=y�C CD=z�Ƃ���D
�s�^�S���X�̒藝���
�@c^2+y^2=x^2�@(1)
���l��
�@b^2+z^2=x^2�@(2)
i) ��BAC���݊p�̏ꍇ
�g���~�[�̒藝���
�@ax=by+cz�@(3a)
(1)(2)(3a)���
�@a=b��(1-(c/x)^2)+c��(1-(b/x)^2)
b=20�Cc=24�Cx=60��������
�@a=4��21+16��2
�w�����̌������
�@s=(a+b+c)/2=2��21+8��2+22
�@S=��(s(s-a)(s-b)(s-c))
p=2��21+8��2�Ƃ����ƁCs=p+22�Ca=2p�ł��邩��
�@S=��((22^2-p^2)(p^2-4))
p^2=32��2��21+212���q=��2��21�Ƃ�����p^2=32q+212�ł��邩��
�@S=��((272-32q)(208+32q))
�@ =2^4 * ��(8q+53)
�@ =2^4 * (4��2+��21)
�@ ��163.8308791
ii) ��BAC���s�p�̏ꍇ
�g���~�[�̒藝���
�@cz=ax+by�@(3b)
(1)(2)(3b)���
�@a=-b��(1-(c/x)^2)+c��(1-(b/x)^2)
b=20�Cc=24�Cx=60��������
�@a=-4��21+16��2
�w�����̌������
�@s=(a+b+c)/2=-2��21+8��2+22
�@S=��(s(s-a)(s-b)(s-c))
p=-2��21+8��2�Ƃ����ƁCs=p+22�Ca=2p�ł��邩��
�@S=��((22^2-p^2)(p^2-4))
p^2=-32��2��21+212���q=��2��21�Ƃ�����p^2=-32q+212�ł��邩��
�@S=��((272+32q)(208-32q))
�@ =2^4 * ��(-8q+53)
�@ =2^4 * (4��2-��21)
�@ ��17.18845687
0232����ȑf�l
2021/01/05(��) 09:38:45.21ID:byMiy7MI0233�C�i ��/7jUdUKiSM
2021/01/05(��) 11:54:43.86ID:f/6O5GLP>>182
(i)��BAC���݊p�̏ꍇ�A
BC=2RsinA=60sinA
24^2+20^2-60^2sin^2A=2�~24�~20cosA
36+25-225sin^2A=60cosA
61-225+225cos^2A-60cosA=0
225cos^2A-60cosA-164=0
cosA=�o30-��(900+225�~4�~41)�p/225
=(30-30��42)/225
=(2-2��42)/15
cos^2A=(4+168-8��42)/225
=(172-2��672)/225
sinA=��(225-168+2��672)/15
=��(57+2��672)/15
=(��32+��21)/15
��ABC=(1/2)AB�~ACsinA
=(1/2)24�~20(��32+��21)/15
=16(4��2+��21)
=64��2+16��21
=163.830879111�c�c
(ii)��BAC���s�p�̏ꍇ�A
��ABC�̖ʐς�3�ӂ�(10,24,30)�̎O�p�`�̖ʐς�2�{������A�w�����̌������A
��ABC=2��s(s-10)(s-24)(s-30)
s=(10+24+30)/2=32
��ABC=2��32�~22�~8�~2
=2�~32��2
=64��2
=212.263986583�c�c
(i)(ii)��莦���ꂽ�B
0234�C�i ��/7jUdUKiSM
2021/01/05(��) 13:43:10.08ID:f/6O5GLP>>182
��BAC���s�p�̏ꍇ�A
��AB�̂������ɒ��_C������B
��ABC=(1/2)BCsin��ACB
=10BC(24/60)
=4BC
�]���藝���A
BC^2+20^2-24^2=2�~20BCcos��ACB
BC^2-176=40BC��(1- sin^2��ACB)
=40BC��o1-(24/60)^2�p
=40BC��0.84
=0.8BC��21
�ӁX��悵BC^4-352BC^2+30976=13.44BC^2
BC^4-365.44BC^2+30976=0
BC^2=365.44-��o(365.44)^2-30976�p
��ABC=4��[365.44-��o(365.44)^2-30976�p]
=26.8846039699�c�c
0235�C�i ��/7jUdUKiSM
2021/01/05(��) 15:47:50.42ID:f/6O5GLP�~�x�ݏI���I
0236����ȑf�l
2021/01/06(��) 08:38:44.00ID:X1VYkdlB0237�C�i ��/7jUdUKiSM
2021/01/06(��) 17:57:36.38ID:enP9Suix���͂����Ă܂������Ă��Ȃ����B
0238�C�i ��/7jUdUKiSM
2021/01/06(��) 23:50:16.83ID:enP9Suix���͐^���ւƕ����Ă��邩���H
0239����ȑf�l
2021/01/07(��) 08:59:28.44ID:O2otYaIG�����ĂȂ��i��
�Ƃ���ŁA���̏����ėv�]
�P�[�L�̖��ƃT����
https://rio2016.5ch.net/test/read.cgi/math/1609937007/l50
2ch�̑����ł܂Ƃ��ȘA����A���̃T���Ƃ����A�z��
�P�[�L��H�אs�������Ƃ͂ł��Ȃ��B
1/2�{1/4�{1/8�{�c��1�ɂ͂Ȃ�Ȃ��B
�Ƃ������Ƃ������Ă���Ă���i��
0240�C�i ��/7jUdUKiSM
2021/01/07(��) 15:09:55.81ID:h+AFibw5���͔����オ��邾�낤�B
0241����ȑf�l
2021/01/08(��) 08:42:51.93ID:wQm0fxJ9��}����@���̂U
�@
�����`�ɓ��ڂ��鐳�O�p�`����}����B
�A�������`�̒��_�Ɛ��O�p�`�̒��_����v����ꍇ�͏����B
�A
�O�p�`�ɓ��ڂ��鐳���`����}����B
�A�������`�̈�ӂ͎O�p�`�̒�ӂƐڂ��Ă���Ƃ���B
���ꂩ��͖��T���j���ɏo�肵�悤���ƍl���Ă���B
�Ȃ���T�ԂɈ�₵���o�肵�Ȃ����Ƃ����A
����Ȃɂ�������o��ł���قǃl�^���Ȃ�����ł���i��
0242�C�i ��/7jUdUKiSM
2021/01/08(��) 12:18:55.72ID:yV3UA5W4>>182
��BAC���݊p�̂Ƃ���ABC=64��2+16��21=163.830879111�c�c
��BAC���s�p�̂Ƃ���ABC=(1728��21+336��37)/73=61.4735513145�c�c
0243�C�i ��/7jUdUKiSM
2021/01/08(��) 14:12:01.34ID:yV3UA5W4>>182
��BAC���݊p�̂Ƃ���ABC=64��2+16��21
=163.830879111�c�c
��BAC���s�p�̂Ƃ�(�v�Z�~�X�����Ă���)
��ABC=5.23593234214�c�c
������Ƃ����������H
0244�C�i ��/7jUdUKiSM
2021/01/08(��) 14:44:44.60ID:yV3UA5W4>>182
��BAC���݊p�̂Ƃ���ABC=64��2+16��21
=163.830879111�c�c
��BAC���s�p�̂Ƃ���ABC=36��2-12��7
=19.1626725127�c�c
0245�C�i ��/7jUdUKiSM
2021/01/08(��) 15:12:33.75ID:yV3UA5W4>>182
��BAC���݊p�̂Ƃ���ABC=64��2+16��21=163.830879111�c�c
��BAC���s�p�̂Ƃ���ABC=64��2-16��21=17.1884568726�c�c
�肱�������B
0246�C�i ��/7jUdUKiSM
2021/01/08(��) 15:30:16.57ID:yV3UA5W4>>182
��BAC���݊p�̏ꍇ�A
BC=2RsinA=60sinA
24^2+20^2-60^2sin^2A=2�~24�~20cosA
36+25-225sin^2A=60cosA
61-225+225cos^2A-60cosA=0
225cos^2A-60cosA-164=0
cosA=�o30-��(900+225�~4�~41)�p/225
=(30-30��42)/225
=(2-2��42)/15
cos^2A=(4+168-8��42)/225
=(172-2��672)/225
sinA=��(225-168+2��672)/15
=��(57+2��672)/15
=(��32+��21)/15
��ABC=(1/2)AB�~ACsinA
=(1/2)24�~20(��32+��21)/15
=16(4��2+��21)
=64��2+16��21
=163.830879111�c�c
��BAC���s�p�̏ꍇ�A
��AB�̂������ɒ��_C������B
��ABC=(1/2)BCsin��ACB
=10BC(24/60)
=4BC
��ABC�ɂ����Đ����藝���sinB=20/60=1/3������A
cosB=2��2/3
20^2-(BC/3)^2=�o24-(2��2/3)BC�p^2
400-BC^2/9=(24-2BC��2/3)^2
BC^2-96BC��2/3+176=0
BC^2-32BC��2+176=0
BC=16��2-��(512-176)
=16��2-��336
=16��2-4��21
��ABC=4BC
=64��2-16��21
=17.1884568726�c�c
�݊p�̂Ƃ��Ɖs�p�̂Ƃ����}�Ⴄ�����ŕ����I�ɑΏ̂Ȃ������ɂȂ�������A
������C������B
�������}�����ʼn������āB
0247����ȑf�l
2021/01/08(��) 22:15:02.64ID:wQm0fxJ90248�C�i ��/7jUdUKiSM
2021/01/09(�y) 02:53:42.03ID:n6k9inuH���͂����肷�����̂��B
0249����ȑf�l
2021/01/09(�y) 08:37:42.81ID:lOuzVQwT�t�c�[�̍��Z���ł��A30��������Ή������i��
�A�̖�肾���āA���邱�ƂɋC�t����������A
���̍��Z���ł��A�T���ʼn������낤�i��
�Ƃ��낪�A���́A���邱�ƂɁA�Ȃ��Ȃ��C�t���Ȃ��̂ł���i��
0250�P�R�Q�l�ڂ̑f������
2021/01/09(�y) 09:11:48.04ID:3o5wcqI/���́A�ˉe�w(����)�̖��B
�܂��́A���Z���Ȃ烁�l���E�X�̒藝���B
�Ƃ���ŁA�@�����ǁA
�O�p��(�]���藝����藝�Ȃ�)���g�����ƂƁA
�s�^�S���X�̒藝���g�����Ƃ͖{���I�ɓ�������B
0251�C�i ��/7jUdUKiSM
2021/01/09(�y) 17:08:40.74ID:n6k9inuH�]���藝�ƃs�^�S���X�̒藝�͓�悷�邯�ǁA
�����藝�͓�悵�Ȃ��Ƃ��낪�Ⴄ�Ǝv���B
0252�P�R�Q�l�ڂ̑f������
2021/01/09(�y) 20:05:49.41ID:3o5wcqI/���܂�B���m�ɂ́A
�O�p���̗]���藝����藝�Ȃǂ��g���Ė��@���������Ƃ��A
�s�^�S���X�̒藝���܂ޏ����̕��@�ʼn������Ƃ��A
�{���I�ɂ͓���
���ȁB
��G�c�ɂ����āA
�s�^�S���X�̒藝 <-> �]���藝
�O�p�`�̖ʐ� <-> �����藝
���ĂƂ��납�B
0253����ȑf�l
2021/01/09(�y) 21:24:03.55ID:lOuzVQwT�����������Ă��邪�A�A�̖��͎ˉe�w(����)�Ƃ͊W���Ȃ��i��
0254�P�R�Q�l�ڂ̑f������
2021/01/09(�y) 22:33:49.52ID:3o5wcqI/����́A������g���Ă������ĉ����Ȃ��Ƃ����Ӗ������Hww
�ؖ��͕K������1�ł͂Ȃ���B
�������ɂ���@�͂��邾�낤�ˁB
���Ȃ��̉͂����炭���l���E�X�̒藝���g�����̂���Ȃ����ȁH
>250�Ō������̂́A
�uQD��AC�͕��s�v���h��������h�Ɠ��l�ł��邱�Ƃ�
���l���E�X�̒藝���g���Ď������Ƃ��ł��邪�A
����̂���m�����g���Ă��\���Ƃ������ƁB
�ǂ�����ˉe�w�̔��e�ɂ���藝�B
0255�C�i ��/7jUdUKiSM
2021/01/09(�y) 22:51:24.71ID:n6k9inuH�����́�ABC=519.330645275�c�c���������A
�������Ȃ肷������ł���������蒼���B
0256�C�i ��/7jUdUKiSM
2021/01/09(�y) 23:43:48.85ID:n6k9inuH���͉������������Ă��D�����B
�n�[�g��������B
�Ȃ�ǂ��������B
�������������܂ʼn����Ă�B
0257����ȑf�l
2021/01/10(��) 08:27:44.27ID:xAe+wxQy������g���ĉ����邩�ǂ����͍l�������Ƃ͂Ȃ����A
����ȓ���m�����Ȃ��Ă���������ł���i��
�������������Ɩ��ł��Ă���̂́A
�ˉe�w(����)�̂悤�ȁA���Z�ł͋����Ȃ��m����K�v�Ƃ�����ł͂Ȃ����炾�B
���邱�ƂɋC�t����������A�t�c�[�̍��Z���ł��ȒP�ɉ�������ł���B
0258�C�i ��/7jUdUKiSM
2021/01/10(��) 15:54:45.45ID:GMRBrE1q��BAC���݊p�̂Ƃ��A
�O�ډ~�̒��S��O�Ƃ��āA
��ABC�ɂ����Đ����藝���A
24/sin��BOA=30/sin(��/2-��BOA/2)
5sin��BOA=4sin(��/2-��BOA/2)
=4cos��BOA/2
���p�̌������A
sin��BOA=(4/5)��o(1+cos��BOA)/2�p
��OAC�ɂ����Đ����藝���A
20/sin��COA=30/sin(��/2-��COA/2)
3sin��COA=2sin(��/2-��COA/2)
=2cos��COA/2
���p�̌������A
sin��COA=(2/3)��o(1+cos��COA)/2�p
��ABC=�l�p�`OCAB-��OBC
=72��21+200��2-450sin(��BOA+��COA)
���@�藝���A
sin(��BOA+��COA)=sin��BOAcos��COA+cos��BOA
sin��COA
=(4/5)cos��COA��o(1+cos��BOA)/2�p+(2/3) cos��BOA��o(1+cos��COA)/2�p
�]���藝���A
cos��BOA=(900+900-576)/(2�~30�~30)
=1224/1800
=153/225
=51/75
=17/25
cos��COA=(900+900-400)/(2�~30�~30)
=1400/1800
=7/9
sin(��BOA+��COA)=(4��21/25)(7/9)��(21/25)+(2/3)(17/25)��(8/9)
=28��21/(25�~9)+68��2/(25�~9)
��ABC=72��21+200��2-450(28��21+68��2)/(25�~9)
=72��21+200��2-56��21-136��2
=16��21+64��2
=163.830879111
��BAC���s�p�̂Ƃ��A
��ABC=��OBC+��OAC-��OAB
=(1/2)(30�~30)(sin��BOC+sin��COA-sin��BOA)
=450sin��BOC+200��2-72��21
=450sin(��BOA-��COA)+200��2-72��21
���@�藝���A
sin(��BOA-��COA)=sin��BOAcos��COA-cos��BOAsin��COA
=sin��BOA(900+900-400)/(2�~30�~30)-�o(900+900-576)/(2�~30�~30)�psin��COA
=sin��BOA(7/9)-(17/25)sin��COA
sin��BOA=��(1-17^2/25^2)
=��(625-289)/25
=��336/25
=4��21/25
sin��COA=��(1-7^2/9^2)
=��(81-49)/9
=��32/9
=4��2/9
sin(��BOA-��COA)=(4��21/25)(7/9)-(17/25)(4��2/9)
=(28��21-68��2)/(25�~9)
��ABC=450(28��21-68��2)/(25�~9)+200��2-72��21
=2(28��21-68��2)+200��2-72��21
=(200-136)��2-(72-56)��21
=64��2-16��21
=17.1884568726�c�c
0259�P�R�Q�l�ڂ̑f������
2021/01/10(��) 17:09:08.12ID:q1OxLAtx���̖��A�ˉe�w�̒m��������A
���邱�ƂɋC�Â��̂͂�������͂Ȃ����ǁB
���Z�̋��ȏ��̒m��(���l���E�X�̒藝�Ȃ�)��������A
������l�����̂͑�������Ǝv����B����
�m���ĂĂ悩�����ˉe�w
���ĂƂ����ȁB
0260����ȑf�l
2021/01/11(��) 12:54:17.65ID:dgyaOSDzID:q1OxLAtx�N��A���̃X���̖��͂ЂƂ܂��u���Ƃ��āA
�P�[�L�̖��ƃT����
https://rio2016.5ch.net/test/read.cgi/math/1609937007/l50
���̃X���̃T���Ƃ����o�J�ɁA
�P�[�L��H�אs�������Ƃ͂ł��Ȃ��B
1/2�{1/4�{1/8�{�c��1�ɂ͂Ȃ�Ȃ��B
�Ƃ������Ƃ������Ă���Ă���i��
���̃o�J������ł���Ƃ������M������Ȃ瓊�e���Ăق����i��
0261����ȑf�l
2021/01/15(��) 09:16:11.29ID:PX8XAnjU�C�ӂ́�ABC������B
AC��ɓ_D�����ABD���ӂƂ��A���pE����A�ɓ������Ӂ�EBD�����B
���l�ɁAAB��ɓ_F�����ACF���ӂƂ��A���pG����A�ɓ������Ӂ�GFC�����B
��������ƁAE�AA�AG�͈꒼����ɂ���B
���̖��́A���U�@�ł������邪�A
�ɒʂ����l�Ȃ�A��u�ʼn�������ł���B
0262�C�i ��/7jUdUKiSM
2021/01/19(��) 09:22:42.72ID:amD4G32A>>261
��EBD�Ɓ�GFC�ɂ����āA
��B=��D=��F=��C=(��-��A)/2
2�p������������A
��EBD�䁢GFC
�ˉe�w���E,A,G�͈꒼����ɂ���B
0263�C�i ��/7jUdUKiSM
2021/01/19(��) 12:43:48.80ID:amD4G32A>>261
GF�̉�������EB�̌�_��H�A
ED�̉�������GC�̌�_��I�Ƃ���ƁA
�Z�p�`BCIDFH�ɂ��āA
�����6���_������~����ɂ���Ȃ�A
�u���[�Y�E�p�X�J��(����16��)�̒藝�ɂ��ƁA
�Ε�BH��ID,HF��CI�̉������̌�_E,G
�����DF�̉�������CB�̉������̌�_J��3�_�͓��꒼����ɂ���B
����A��EG��ɂ��邱�Ƃ������ɂ́A
BF��CD���ΕӂƂȂ�悤�ȁA
����~�����6���_�����Z�p�`��`���K�v������Ǝv�����A
�����炭�\���B
0264����ȑf�l
2021/01/20(��) 08:59:04.49ID:Or2pJ7uR>�ˉe�w���E,A,G�͈꒼����ɂ���B
����Ȃ��Ƃ͌����Ȃ��i��
>>263
�I�O��i��
0265�C�i ��/7jUdUKiSM
2021/01/22(��) 04:14:34.53ID:aYx/Ky4T>>261
��ӂɂ��������č�}����ƁA
�����ȓӎO�p�`��EBD�䁢GFC�́A
���_E,G�̂�������A������A
��K�ɉ��M��EA�����Ɉ����ƁA
��u�ʼn��������G������Ƃ킩��B
0266����ȑf�l
2021/01/22(��) 09:01:06.39ID:IklYJgW7�C�i��A������}����ΒN�ł�
E�AA�AG���꒼����ɂ��邱�Ƃ͕���̂ł���i��
���́A�Ȃ������Ȃ邩�A���i��
������ؖ�����A�Ƃ����̂����w�̖��ł���i��
0267����ȑf�l
2021/01/22(��) 09:06:32.99ID:IklYJgW7���̈�ӂ̒����ɓ������悤�ȁA���p�O�p�`����}����B
0268�C�i ��/7jUdUKiSM
2021/01/22(��) 11:34:47.55ID:aYx/Ky4T>>267
📐���̂悤��2�ӂ��������O�p��K�����������m�ɉ���肵�A
📏������K���g���Ĉ����Ȃ����A
�O�p���点��B
0269�C�i ��/7jUdUKiSM
2021/01/22(��) 14:22:03.96ID:aYx/Ky4T>>267
3�ӂ̔��a,b,c,a��b,a^2+b^2=c^2,sin��=a/c�Ƃ����ƁA
cos��=b/c=a/b
c=b^2/a
sin��=a/c=a^2/b^2=(a/b)^2=cos^2��=1-sin^2��
sin^2��+sin��-1=0
sin��=(-1+��5)/2=1.2360679/2=0.6180339�c�c
��K�ƃR���p�X�ɂ�萳�܊p�`����}���A
���p����Ίp���ɐ��������낷�ƁA
��=36���̒��p�O�p�`���`����B
0270�P�R�Q�l�ڂ̑f������
2021/01/22(��) 22:17:00.93ID:aYx/Ky4T>>261
EA��GA���A
BC�ƕ��s�Ȃ�ˁH
�܂�ǂ������ɌX�����R���A
���R�E�I�ɂȂ���B
0271�P�R�Q�l�ڂ̑f������
2021/01/23(�y) 00:03:20.83ID:iUmzreOs0272�P�R�Q�l�ڂ̑f������
2021/01/23(�y) 00:06:59.78ID:iUmzreOs
0273�C�i ��/7jUdUKiSM
2021/01/23(�y) 04:47:37.44ID:HO1SayOh>261
BC��AG�͕��s����Ȃ��B
BC��EG�����s����Ȃ��B
���l���E�X�̒藝���Ȃ��B
0274����ȑf�l
2021/01/23(�y) 09:06:44.39ID:8ktMOxYS0275�P�R�Q�l�ڂ̑f������
2021/01/23(�y) 11:46:10.27ID:HO1SayOh>>261
��ABC�͔C�ӂ����A�_D���_F���C�ӂƂȂ�ƁA
�����ȓӎO�p�`���A���ʐ^�̂悤�ɑ傫����ς��A
�����̒��_�͓_A�̍��E�ɘA�Ȃ��Ă����B
�܂�Őڌ��藝�̂悤�ɓ����傫���̊p���A
�҂����艡�t���B
��EAG�͈꒼���ɕ��ԁB
0276�C�i ��/7jUdUKiSM
2021/01/23(�y) 12:29:28.33ID:HO1SayOh>>261
��ABC����ѓ_D,�_F�͔C�ӂ�����A
�_D��AC�̒[�_A�ɂƂ�Ɓ�EDB=��EAB=(1/2)(180��-��A)
�_F��AB�̒[�_A�ɂƂ�Ɓ�GFC=��GAC=(1/2)(180��-��A)
��EAB+��A+��GAC=(1/2)(180��-��A)+��A+(1/2)(180��-��A)=180��
���_E,�_A,�_G�͈꒼����ɂ���B
0277����ȑf�l
2021/01/24(��) 08:59:21.68ID:Wb6kPGsT����ȓ����ł�20�_�i��
����ȓ���ȏꍇ�ɐ��藧���Ƃ��ؖ����Ă��ؖ��Ƃ͌����Ȃ��i��
�ǂ�ȏꍇ�ɂ����藧���Ƃ��ؖ����Ȃ���Ώؖ��Ƃ͌����Ȃ��i��
0278����ȑf�l
2021/01/29(��) 08:59:32.42ID:e/E0Ws5M��BC��ɁAAD�~AD=BD�~DC�ƂȂ�_D����}����B
0279�C�i ��/7jUdUKiSM
2021/01/29(��) 19:00:34.74ID:HC2ijatY>>278
D�ɃR���p�X�̐j���h���ĉ��M��✏A��ʉ߂���悤�ɉ�BC�̉������Ƃ̌�_B',C'��BB'=CC'�ƂȂ�悤�ɂƂ���������A���̂悤�Ɏh���B
0280�C�i ��/7jUdUKiSM
2021/01/29(��) 19:16:42.01ID:HC2ijatY0281�C�i ��/7jUdUKiSM
2021/01/30(�y) 01:35:22.21ID:CFqPcz1/>>261
���l���E�X�̒藝�ʼn����Ȃ����ȁB
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;;;/���� ���� /�_;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;;/((^o`-�-))/�u;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;;;/����'�ҁ܃ҁ^|;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;�a�PUU�҃ҁa �@|;;;;;;;;;;;;;;;;;;;;;;;;;
;;;;;�a ���@�� �a�@�^|;;;;;;;;;;;;;;;;;;;;;
;;;;;�a�Q�Q�Q�Q�a�^�@|;;;;;;;;;;;;;;;;;;;;;
�P�P�P�P�P�a �@�@|;;;;;;;;;;;;;;;;;;;;;;;
���@���@�� �@�a �@�^|;;;;;;;;;;;;;;;;;;;;;;
�Q�Q�Q�Q�Q�a�^ �@|;;;;;;;;;;;;;;;;;;;;;;
�P�P�P�P�P�a�@�@,|;;;;;;;;;;;;;;;;;;;;;;;
���@���@�� �@�a,�c�~� ;;;;;;;;;;;;;;;;;;;;;
�Q�Q�Q�Q�Q�a��` , `; ;;;;;;;;;;;;;;;;;;;;;
�Q�Q�Q�Q�Q�a/U��U� ;;;;;;;;;;;;;;;;;;;;
�P�P�P�P�P�P;_~U U~ ;;;;;;;;;;;;;;;;
;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;;
0282����ȑf�l
2021/01/30(�y) 09:01:06.21ID:+x+EiwMa>>276�̗v�̂ōl��������̂��B
���ꂪ���U�@�B
���������U�@�łȂ��Ă��A����l�ɂ͈�u�ŕ�����ł���B
0283�C�i ��/7jUdUKiSM
2021/01/30(�y) 20:32:17.71ID:CFqPcz1/>>282
���������l���E�X���������Ȃ����B
�悤������B
�}�`���Ă���ł���u�ŁA
E,A,G���꒼���ɕ��ԂȂ��v�����ȁB
0284����ȑf�l
2021/01/30(�y) 22:30:19.10ID:+x+EiwMa����͕ʐl�̃��X���i��
0285�C�i ��/7jUdUKiSM
2021/01/30(�y) 23:18:29.71ID:VbwcjQhU�R�e�n�����Ȃ��̂���邢�B
0286����ȑf�l
2021/02/05(��) 08:36:30.87ID:1Jj0JyWN��CD��ɓ_Q�����A�l�p�`APQD�Ǝl�p�`PBCQ�̖ʐϔ䂪
��2�F1 �ƂȂ�悤�ɂ���B
�A��P�́A���̂悤�ȍ�}���\�Ȉʒu�ɗ^�����Ă���Ƃ���B
0287����ȑf�l
2021/02/12(��) 21:54:47.68ID:oi7oUEny�A����PQR�̊e�ӂ́�ABC�̊e�ӂɑ��Đ����łȂ���Ȃ�Ȃ��B
0288�P�R�Q�l�ڂ̑f������
2021/02/17(��) 19:50:45.71ID:pOGUunX7��������ɂȂ��_P���Ƃ�B
P��ʂ�2����L1�AL2���g���B
L1�ƕ������̌�_�� A,B �Ƃ�
L2�ƕ������̌�_�� C,D �Ƃ���B
���̂Ƃ��@AP�EBP = CP�EDP�@�� (��ʂ�) ���藧��
�Ȃ��B....orz
�P�P
�������A�������̎��Ɛ����ȍ��W�����Ƃ�
A,B,C,D, P �̍��W�� a,b,c,d, p �Ƃ����
�@(p-a)(p-b) = (p-c)(p-d)
[�����X���S�U�T-985,986]
0289�P�R�Q�l�ڂ̑f������
2021/02/19(��) 03:06:17.89ID:45fvrIx7>>269
��K�ƃR���p�X�ɂ�萳�܊p�`����}������@
AR�a�Ƃ���~X��`���B
����ɓ��ڂ��鐳�܊p�` ABCDEA ����}���悤�B
�@A (-1, 0)
�@C (cos(36), sin(36))
�@D (cos(36), -sin(36))
�@R (1, 0)
�@T (1/2, 0)
�Ƃ���B
���]���藝���
�@CT^2 = 1 + 1/4 - cos(36) = 5/4 - ��/2 = 5/4 - 29/36 = 4/9,
�@CT = DT = 2/3,
���aAR��4�����_T�𒆐S�Ƃ��AAR��1/3�a�Ƃ���~Y��`���B
�~X �� �~Y �̌�_�� C ����� D �Ƃ���B
AC�̐���2�������Ɖ~X�̌�_�� B �Ƃ���B
AD�̐���2�������Ɖ~X�̌�_�� E �Ƃ���B
�@��AB = BC = CD = DE = EA,�@(�I)
http://suseum.jp/gq/question/3233
0290����ȑf�l
2021/02/19(��) 08:32:22.15ID:1CI/H4B9�C�ӂ́�ABC�̓����ɓ_P������B
P����e�ӂɉ��낵�������̑���D�AE�AF�Ƃ��A�~DEF��`���A
�~DEF���e�ӂƍĂь����_��Q�AR�AS�Ƃ���ƁA
Q�AR�AS�ɉ����Ċe�ӂɗ��Ă������͈�_�Ō����B
0291�P�R�Q�l�ڂ̑f������
2021/02/19(��) 19:47:33.13ID:45fvrIx7�~DEF�̒��S�� O �Ƃ��A
�_O����e�ӂɉ��낵�������̑��� L, M, N �Ƃ���B
�@��OLD = ��OLQ = 90�,�@OD=OQ ���
�@DL = LQ,
���Ȃ킿�A�_L�� DQ �̒��_�ł���B
PO�̉������ƁA�_Q�ŕ�BC�ɗ��Ă����� �Ƃ̌�_�� X �Ƃ����
�@PD // OL // XQ
���_�A���藝�ɂ��
�@PO = OX
���Ȃ킿�A�_X�� �_O�Ɋւ��� �_P�ƑΏ̂ȓ_�ł���B
���@�_Q,R,S �Ŋe�ӂɗ��Ă������́A���̓_�Ō����B(�I)
* �Ȃ��A�_P����ABC�̐��S�̂Ƃ���
Q,R,S �͊e�ӂ̒��_�ł���A�����ŗ��Ă������͊O�S�Ō����B
���̉~�͋�_�~�ł���B
0292�P�R�Q�l�ڂ̑f������
2021/02/19(��) 20:57:02.85ID:45fvrIx7��ABC�̓����ɓ_P���Ƃ�B
AP�̉����ƕ�BC�̌�_�� D,
BP�̉����ƕ�CA�̌�_�� E,
CP�̉����ƕ�AB�̌�_�� F �Ƃ���B
�~DEF�ƕ�BC, CA, AB �̌�_ (�� D,E,F) �����ꂼ�� Q,R,S �Ƃ����Ƃ��A
AQ, BR, CS �͈�_�Ō����B
�������A���Ƃ��Ή~DEF����BC�ɐڂ��Ă���ꍇ�ɂ�
Q=D �ƍl������̂Ƃ���B(�،ˏ���Y���ɂ��)
���w�Z�~�i�[, Vol.�T�O, No.3, ���{�]�_�� (2011/Mar)
�@NOTE �u��_�~�̊g���vp.66-67
0293�P�R�Q�l�ڂ̑f������
2021/02/19(��) 21:22:42.96ID:45fvrIx7AD,BE,CF�͈�_P�Ō����̂ŁA�`�F���@�̒藝���
�@�iAF/FB)(BD/DC)(CE/EA) = 1�@�@�@�@�@�@�c (1)
�܂��A���ׂ��̒藝���
�@AF�EAS = AE�EAR
������
�@AF/EA = RA/AS.
���l�ɁA
�@BD/FB = SB/BQ,�@CE/DC = QC/CR
������ (1) �ɑ�������
�@(RA/AS)(SB/BQ)(QC/CR) = 1,
���Ȃ킿
�@(AS/SB)(BQ/QC)(CR/RA) = 1
����āA�`�F���@�̒藝�̋t�ɂ��A
AQ, BR, CS �͈�_�Ō����B�@(�I)
0294����ȑf�l
2021/02/19(��) 22:20:35.39ID:1CI/H4B9�����i��
���̃X���͊��S�ɖ�������Ă���Ǝv���Ă������A
�����ł��Ȃ����Ƃ������������ł����ꂵ���i��
�ł͎��̖��B
�C�ӂ̎l�p�`ABCD������A���̓����ɓ_P������A
�l�p�`�̖ʐς��AAPC�ɂ���ē�����A
�܂�BPD�ɂ���Ă�������Ă���Ƃ����B
�_P�̈ʒu�����߂�B
0295�P�R�Q�l�ڂ̑f������
2021/02/20(�y) 04:25:46.41ID:HUD3ElaW���̖ʐς�APC�ɂ���ē������B
���@P�� BD�̒��_��ʂ�AC�ɕ��s�Ȓ�����ɂ���B
���̖ʐς�BPD�ɂ���ē������B
���@P�� AC�̒��_��ʂ�BD�ɕ��s�Ȓ�����ɂ���B
���@P �͏�L2�����̌�_�ɂ���
�� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�
�j���[�X
- �y�j�R�j�R����z���o���u�_�E�����[�h��g�U�͂��T�����������v [Hitzeschleier��]
- �y�n���z�u�����I�V�}�C����A���̍��v�����Ȃ�����ċx�ݔp�~����!�߂����������ʂɍL����ᔻ�u���O�̃��K�l�ɂ͉����f���Ă�v��5 [���ꁚ]
- �y�|�\�z������I���g�N�����\�h�錾�u2�x�ƕ����Ȃ��Łv�u50���Č�������r���^���܂��v [�t�H�[�G�o�[��]
- �y�t�����X�z���w���������ߗe�^�Ŏ��ƒ��ɑߕ߁@�}�N���������̂����ߑg�� [PARADISE��]
- �≺�H�i�В��u�Ђ܂��炠���ˎ����}�X���f�B�A���犮�S�ɖَE�A�{�C�Ń��o���Љ�Ɂc�v�u�N�ɖق点���Ă���́H�v [Anonymous��]
- �����̓S���ԗ����[�J�[�A�X�p�C���O��[���x��Ŕj�k�������@���{�ɋ��菟�����C���h�l�V�A�����S����〝���H����〟�� [PARADISE��]
- �y�����z���߂����̂�������FF5🧪 ��3
- �y�ߕ�z�j�R�j�R�A�J�E���g�����ҁA���A�h���X�g�p����Microsoft�A�J�E���g�ɑ��X�ƕs�R�ȃA�N�Z�X���p�����Ă���͗l�I�I ��2 [126042664]
- �y�ߕ�z���U���u�푈�ɕ������珗�q����������邩�킩��Ȃ��v���q�u�Ȃ�ւ��v���U���u����������{�͏I���v���q�u�I���ւ�āv [974680522]
- �y�N��z�f��w���b�N�o�b�N�x�A��������7000���łڂ��둍�W�҂Ɠ����x���̑�q�b�g����������
- �y�ߕ�z�������i36�j�u33�ΔN��800���~�Ŋy�����Đ��i�̂����j�����Ă����ǐg��155cm�������c�����ł���H�v�����ł��Ȃ���8���[������ [257926174]
- �Ⴂ�̂킩��P�����������D���ȃu�����h�uPORTER�v�u�����x���v�u�j���[�o�����X�v [449534113]
- ��J�o��\��@�l�k�a�Q�O�Q�S�u�h�W���[�X�v�u�W���C�A���c�v��4
- ��J�o��\��@�l�k�a�Q�O�Q�S�u�h�W���[�X�v�u�W���C�A���c�v��5
- NHK��������Ɏ�����������X�� 215830 ���������
- ���� �� �e���r���� 74721 ���s����ᔻ����Ȃ��ē��{���Y�}�Ɠ����y�ېV���Y�}
- �����[�J��96515���ً}!!
- �L�g����̐�������ہy���h���Řb��!���C���ӂ��w���̊X�E�䒃�m���z

