�u�n�b�L���O�v����u���ӂ̂������v�܂ł���L���J�o�[���鋐��f���Q �w�T�����˂�x�ւ悤�����I
�T��
�� [���f�]�ڋ֎~]©2ch.net
�� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�
0159����ȑf�l
2020/12/03(��) 08:54:08.84ID:Q3rn9U3AAB=5�ABC=4�ACA=3�̒��p�O�p�`ABC������B
�i�Ε�AB��C�̍��ߏ�ɂ���ƍl����B�j
C����AB�ɐ���CD�����낵�AD����BC�ɐ���DE�����낵�A
E����CD�ɐ���EF�����낵�AF����DE�ɐ���FG�����낵�A
G����EF�ɐ���GH�����낵�AH����FG�ɐ���HI�����낵�A�c
�Ƃ����ӂ��ɁAC���獶�����̉Q�̂悤�ɐ��������낵�Ă����A
D�AE�AF�AG�AH�AI�A�c�̋Ɍ��_�����Ƃ���B���̈ʒu�����߂�B
0160�P�R�Q�l�ڂ̑f������
2020/12/03(��) 13:52:29.17ID:kf3WVIBO0D�œ_��1���Ƃ���Ȃ�
�~�̖ʐς̌����Ŕ��a����ɂ��Ē��������A�Q�̒����������_���P�Ƃ�B��������Ɖ~���̒����̌����ɏ]���W����2��2�̓_�łP�����B
2�����̌����̌W����4�ɂȂ��Ă����Ȃ��Ƃ��܂�B
�������Ǝg�p���ꂽ�~�̖ʐς̌����̌W����4�ɂ��Ă��ǂ��̂ł͂Ȃ��낤���B
0161�P�R�Q�l�ڂ̑f������
2020/12/03(��) 14:43:44.79ID:kf3WVIBO������
���ʂɍl����
���̕\�ʐς�4��r ^2
�ƂȂ�B
0162�P�R�Q�l�ڂ̑f������
2020/12/03(��) 14:45:25.89ID:kf3WVIBO���������B
0163�P�R�Q�l�ڂ̑f������
2020/12/03(��) 14:47:40.93ID:kf3WVIBO��`�ƒ藝�͉�]�Q�ł��ˁB
�U�b�N�������B
0164�P�R�Q�l�ڂ̑f������
2020/12/03(��) 18:08:28.91ID:EylvoCB2����BJ�̕������F�@y = (27/136)x,
����CK�̕������F�@y = - 0.48(x-4),
��_�� (2176/769, 432/769) = (2.8296488946684�c, 0.56176853055917�c)
���ȁH
�֑������ǁAI(2.891776, 0.6912)
0165�P�R�Q�l�ڂ̑f������
2020/12/03(��) 19:11:55.63ID:EylvoCB2�@BC/AB = DE/CD = FG/EF = HI/GH = JK/IJ = �c = 4/5,
�@CD/BC = EF/DE = GH/FG = IJ/HI = �c = 3/5,
�����
�@��ABC�F��IJK�F��QRS�F�c�@�̑������ {(4/5)(3/5)}^4 = (0.48)^4
0166�P�R�Q�l�ڂ̑f������
2020/12/03(��) 20:12:24.64ID:EylvoCB2�A�t�B���I(?)��@
�@�K���Ȑ����ꎟ�ϊ��ɂ�� ��ABC ��Ӓ��P�̐��O�p�`�Ɉڂ��B
�@��ӂ� x �� 1-x �ŋ��p��60���̇���3�ł���B
�@���̖ʐς͓�ӂ̐� x(1-x) �ɔ�Ⴕ�Ax=1/2 (���_) �ōő�ƂȂ�B
�@���̂Ƃ���P'Q'R' �̖ʐς͍ŏ��ƂȂ�B
0167�P�R�Q�l�ڂ̑f������
2020/12/03(��) 20:38:17.53ID:EylvoCB2����BF�̕������@y = (27/136)x,
����CG�̕������@y = - (12/25)(x-4),
�Ƃ��Ă������B
��ABC�F��EFG�F��IJK�F��MNO�F��QRS�F�c�@�̑������
�@- {(4/5)(3/5)}^2 = - (0.48)^2
0168����ȑf�l
2020/12/03(��) 20:58:30.61ID:Q3rn9U3A>>159�̖���l�͖��������̖��ƍl�����B
C�����ɂǂꂾ���i�݁AC���獶�ɂǂꂾ���i�ނ��A���l�����B
�����Ƒ���ǂ��Ɏ�邩���A���̖��̃|�C���g���B
�v�Z���ʂ�C������432/769�AC���獶��900/769������A>>164�Ɠ����B
���ۂɍ�}���Ă��قڂ��̈ʒu�ɗ��邩��A���ꂪ�����ł��邱�Ƃ͊ԈႢ�Ȃ��B
>>166
�A�t�B���Ƃ������t�����͒m���Ă��邪�A���̂��Ƃ�����Ȃ�(��
���̓����͑㐔�I��@�ł͂��邪�A����(��
0169����ȑf�l
2020/12/03(��) 22:01:52.47ID:Q3rn9U3A�܂�F(G)�܂�3�E(4/5)^2�E(3/5)^2�����オ��B���ꂪ�����B
����K�̈ʒu�܂łǂꂾ�������邩���l����ƁA
����-(4/5)^2�E(3/5)^2�ʼn�����B
�ȉ��͂���̌J��Ԃ��B
C���獶�ɂǂꂾ���i�ނ��́A
�܂�E(G)�܂�3�E4/5�E3/5�i�ށB���ꂪ�����B
����K�̈ʒu�܂Ō���-(4/5)^2�E(3/5)^2�ʼnE�ɍs���B
�ȉ��͂���̌J��Ԃ��B
������v�Z����Ə�̓����ɂȂ�B
0170�P�R�Q�l�ڂ̑f������
2020/12/04(��) 18:09:34.33ID:c152PLb8>>164
����AI�̕������@y = 3 + (x-4)/0.48
>>167
����AE�̕������@y = 3 + (x-4)/0.48
��ACp + ��CAp = ��ApC = 90��,
tan(��ABp) = tan(��BCp) = tan(��CAp) = (4/5)(3/5) = 0.48
0171����ȑf�l
2020/12/04(��) 22:37:27.77ID:G1/d34c4����K�̈ʒu�܂łǂꂾ�������邩���l�����
��
����J(K)�̈ʒu�܂łǂꂾ�������邩���l�����
����K�̈ʒu�܂Ō���-(4/5)^2�E(3/5)^2�ʼnE�ɍs��
��
����I(K)�̈ʒu�܂Ō���-(4/5)^2�E(3/5)^2�ʼnE�ɍs��
0172�P�R�Q�l�ڂ̑f������
2020/12/05(�y) 00:43:36.65ID:Io8LGZ8j��}��90�x(����)��60�x(���O�p�`)��72�x(���܊p�`)������
������e�X��}�œ��Ă�����90�x(45),60�x(30,15),72�x(36,18,9)�ƂȂ�
�����̑g�ݍ��킹�ō���p��
45a+15b+9c=3(15a+5b+3c) (a,b,c�͔C�ӂ̐���)
�ƂȂ���3�̔{���ł���6�x������̂�
�O�p����m��Ȃ��Ă��A�i���O���v�̖ڐ�������ނ��Ƃ��ł���
0173�P�R�Q�l�ڂ̑f������
2020/12/05(�y) 01:23:36.20ID:wd0AGlDthttp://rio2016.5ch.net/test/read.cgi/math/1575650292/
0174����ȑf�l
2020/12/07(��) 08:43:41.48ID:zLWcdcc9�@
�O�{�̕��s��������B
�����̕��s����ɎO�̒��_��L���鐳���`����}����B
�A
�_A������A���̉����ɐ����Ȓ���������A���̉����ɉ~������B
�����̓_�ƒ����Ɖ~����ɒ��_��L���鐳�O�p�`����}����B
�A���_�ƒ����Ɖ~�́A���̂悤�ȍ�}���\�Ȉʒu�Ƒ傫���ł���Ƃ���B
0175�C�i ��/7jUdUKiSM
2020/12/09(��) 12:05:28.61ID:cykkV0Yr>>149
xy���ʏ�ɁA
A(4,3)
B(0,0)
C(4,0)
���Ƃ�B
�ӂ̔䂪3:4:5�̒��p�O�p�`�̐����͒�ӂ�9:16�ɕ�������_�ɐ����̑������낷�B
D(2.56,1.92)
E(2.56,0)
F(3.4816,0.6912)
�_�͕�������Ȃ��A�����łƂ�B
�ʒu���������邽�߂��B
G(2.56,0.6912)
H(2.891776,0.248832)
I(2.891776,0.6912)
J��x���W��2.56+(9/25)(2.891776-2.56)
=2.67943936
J(2.67943936,0.53194752)
K(2.891776,0.53194752)
���p��ABC�Ɠ��������̒��p��IJK���`�����B
L(2.8153348096,�\�\�\���\�\�\)
M(2.8153348096,0.53194752)
N(�\�\�\���\�\�\,0.56863929139)
O(2.8153348096,0.56863929139)
P(2.83294685987,0.5451565577)
Q(2.83294685987,0.56863929139)
���p��ABC�Ɠ��������̒��p�O�p�`��IJK�̎��Ɍ����̂͒��p��QRS�ŁA�_A,I,Q�Ɠ_B,J,R�Ɠ_C,K,S�����ꂼ��꒼���ɕ��сA3�{�̒������Ɍ��_P�ɏW�܂�Ɨ\�z����B
����BJ�̕�������y=(53194752/267943936)x
53194752=27�~1970176
267943936=136�~1970176
y=(27/136)x
����CK�̕�������y=-0.53194752(x-4)/(4-2.891776)
y=-(53194752/110822400)(x-4)
y=-0.48(x-4)
y=-(12/25)(x-4)
�ʕ����Ă����������ƁA
x=16�~136/(9�~25+4�~136)
=2176/769
=2.842652808916�c�c
y=27�~16/769
=432/769
=0.5617685305591�c�c
���Ɍ��_P�̍��W��(2.842652808916,0.5617685305591)�Ɛ��肷��B
0176����ȑf�l
2020/12/09(��) 21:20:46.90ID:KJcNty4h��EFG���ł������_�ŁAAE��BF��CG�̌�_�����߂�A
���ꂪ�Ɍ��_p�̈ʒu�ł���B
0177�C�i ��/7jUdUKiSM
2020/12/10(��) 00:43:16.17ID:zKFlA30/>>176�ʕ����Ȃ߂Ă�ȁB����ȊȒP����˂����B
0178����ȑf�l
2020/12/10(��) 08:29:30.03ID:kCGZMahP��ABC�Ɓ�EFG�̑Ή��_�����ׂA�����̌�_��p�̈ʒu�ɂȂ�̂ł���i��
���邩�H�i��
0179�C�i ��/7jUdUKiSM
2020/12/10(��) 11:24:15.35ID:zKFlA30/>>164�Ƃ�x���W���Ⴄ�B
0180����ȑf�l
2020/12/14(��) 09:02:21.90ID:fGyKPvzZ0181�P�R�Q�l�ڂ̑f������
2020/12/18(��) 21:09:38.11ID:DAoaiwdi�ɂ͎����� 0 < |��| <1 �Ƃ���B
��A_o �� ��B_o ����n�߂�
��A_{n+1} = ((��+1)/2)��A_n + ((��-1)/2)��B_n,
��B_{n+1} = ((��-1)/2)��A_n + ((��+1)/2)��B_n,
�Ƃ����� ��A_n, ��B_n �͎�������B
�@��A_�� �� ��B_�� �͑��قȂ邩�H
(ii)
�ʂ͎����� 0 < |��| <1 �Ƃ���B
��C_o ����n�߂�
��C_{n+1} = (��-1)��A_n + 2(1-��)��B_n + �ʁ�C_n,
�Ƃ����� ��C_n ����������B
�@B_�� �� A_��C_�� �̒��_�ł��邩�H
0182����ȑf�l
2020/12/21(��) 09:14:30.96ID:EOqzZZ/u�@
��ABC������AAB=24�AAC=20�A�O�ډ~�̔��a=30�ł���B
���̎O�p�`�̖ʐς����߂�B
�A���O�p���̎g�p�͕s�B
�A
���̂��Ƃ��ؖ�����B
��ABC��BC���D�AM������AAD�́�A�̓����AAM�͒����ł���B
C����AD�ɐ���CP�����낵�A���̉�����AM�ƌ����_��Q�Ƃ���ƁA
QD��AC�͕��s�ł���B
�A�̖��͒��w���ɂ͉����Ȃ���������Ȃ��B
0183�C�i ��/7jUdUKiSM
2020/12/22(��) 08:48:57.29ID:skBdmmjJ>>182
��ABC�ɂ����Đ����藝���
2R=60=20/sinA=24/sinC
sinA=1/3
sinC=2/5
B����AC�ɉ��낵�������̑���H�Ƃ���ƁA
BH=20(2/5)=24(1/3)=8
�s�^�S���X�̒藝���A
CH=��(20^2-8^2)=4��21
AH=��(24^2-8^2)=16��2
��ABC=(4��21+16��2)8/2
=16��21+64��2
0184�C�i ��/7jUdUKiSM
2020/12/22(��) 09:00:41.30ID:skBdmmjJ>>182
��ABC�ɂ����Đ����藝���
2R=60=20/sinB=24/sinC
sinB=1/3
sinC=2/5
A����BC�ɉ��낵�������̑���H�Ƃ���ƁA
AH=20(2/5)=24(1/3)=8
�s�^�S���X�̒藝���A
CH=��(20^2-8^2)=4��21
BH=��(24^2-8^2)=16��2
��ABC=(4��21+16��2)8/2
=16��21+64��2
0185����ȑf�l
2020/12/22(��) 09:40:03.33ID:pJczAeWl����ɂ��O�̓����͊Ԉ���Ă��邼�i��
0186�C�i ��/7jUdUKiSM
2020/12/25(��) 15:25:19.63ID:K0jsmVQ1>>182
��ABC�̊O�ډ~�̔��a��R�Ƃ���ƁA
20/sinB=24/sinC=2R=60
sinB=1/3
sinC=2/5
BC�ɑ���A�̍�����8
��ABC�̊O�ډ~�̒��S��O�Ƃ��āA
30/sin��OBC=30/sin��OCB=60
sin��OBC=sin��OCB=1/2
��OBC=��OCB=30��
��BOC=180��-30��-30��=120��
BC=2Rsin120��
=60(��3/2)
=30��3
��ABC=(1/2)(30��3)8
=120��3
0187����ȑf�l
2020/12/26(�y) 09:06:22.77ID:GRB1GHCI����ɁA���O�̓����͊ԈႢ�i��
0188����ł́H
2020/12/27(��) 06:25:50.06ID:T10pTK64=120�~6��3/11+100�~5��3/11
=(720+500)��3/11
=1220��3/11
0189�C�i ��/7jUdUKiSM
2020/12/27(��) 10:05:13.56ID:T10pTK64�O�X>>186
�A�N�ւɂ���Ȃ�B
0190�C�i ��/7jUdUKiSM
2020/12/27(��) 15:31:53.59ID:T10pTK64����͂����Ă�̂����H
0191����ȑf�l
2020/12/27(��) 20:56:50.59ID:Z2MrWtiy�l�������̓G���[���o�ď������߂Ȃ������i��
���ꂩ��A>>188�͊ԈႢ�i��
0192�P�R�Q�l�ڂ̑f������
2020/12/27(��) 22:12:05.64ID:T10pTK640193�P�R�Q�l�ڂ̑f������
2020/12/27(��) 22:24:11.55ID:T10pTK64�O�X>>190
�������߂˂�������I
0194�C�i ��/7jUdUKiSM
2020/12/27(��) 23:48:17.99ID:T10pTK64�����B
0195�C�i ��/7jUdUKiSM
2020/12/28(��) 02:42:35.46ID:lvLlGPFh��������x���B
�捘���ɂ�����B
0196�C�i ��/7jUdUKiSM
2020/12/28(��) 21:15:54.36ID:lvLlGPFh>>182
4��(862+16��2674)=164.407870484�c�c
0197�C�i ��/7jUdUKiSM
2020/12/28(��) 23:15:28.33ID:lvLlGPFh>>182
cosA=(24^2+20^2-BC^2)/(2�~24�~20)
sinA=BC/2R=BC/60
480cosA=576+400-3600(1-cos^2A)
(60cosA)^2-8(60cosA)-2624=0
60cosA=4-��(16+2624)=4-��2640=4-4��165
cosA=(1-��165)/15
sinA=��(166-2��165)/15=(��165-1)/15
��ABC=(1/2)24�~20(��165-1)/15
=16(��165-1)
=189.523721259�c�c
0198�C�i ��/7jUdUKiSM
2020/12/29(��) 01:57:00.74ID:Q+OHTUHS>>182
BC=2RsinA=60sinA
24^2+20^2-60^2sin^2A=2�~24�~20cosA
36+25-225sin^2A=60cosA
61-225+225cos^2A-60cosA=0
225cos^2A-60cosA-164=0
cosA=�o30-��(900+225�~4�~41)�p/225
=(30-30��42)/225
=(2-2��42)/15
cos^2A=(4+168-8��42)/225
=(172-2��672)/225
sinA=��(225-168+2��672)/15
=��(57+2��672)/15
=(��32+��21)/15
��ABC=(1/2)AB�~ACsinA
=(1/2)24�~20(��32+��21)/15
=16(4��2+��21)
=64��2+16��21
=163.830879111�c�c
0199����ȑf�l
2020/12/29(��) 08:48:11.24ID:e8UZ5ZY6�~�x�ݒ�������A>>182�̖����p�����ďo���Ă����B
�������̉Ɋ��҂���B
0200�C�i ��/7jUdUKiSM
2020/12/29(��) 12:53:54.37ID:Q+OHTUHS�}�W���B���Ɉ����B�C�^�^�^�c�c
�܂��ł��A�ǂ�����m�M�͎��ĂȂłȁB
0201�C�i ��/7jUdUKiSM
2020/12/29(��) 13:26:01.80ID:Q+OHTUHS�������荘���Ĕ����āA
�g�C���ɍs���Ȃ��č����Ă�B
���w���Ɣ]�������g������A
���ւ������Ȃ�B�ł����͂��߂��B
�����ɂ�����B
�����Ȃ��B
0202�C�i ��/7jUdUKiSM
2020/12/29(��) 19:30:40.59ID:Q+OHTUHS>>199
�O�p�����l�p�����m���sin��cos���g���g�킸�ɍS�炸�A
���������l���܂��o�ĂȂ����Ă��Ƃ���ˁH
0203����ȑf�l
2020/12/29(��) 21:50:01.83ID:e8UZ5ZY6���̒ʂ�i��
��O�͑�w�����ɂ������̖�肪�o���o���o���炵���B
�������O�̐��k�Ȃ�@�̖��͌ܕ��ʼn����B
�Ȃ��Ȃ�@�̖��̉������͏������̂悤�ɒm���Ă������炾�B
�Ƃ��낪���̋���͏������y�����Ă���B
�����獡�̐��k�͇@�̖�肪�����Ȃ��B
�L���m�Ƃ��L���i�w�Z�̐��k�͂ǂ����͒m��Ȃ����B
�A�̖��ł��A��O�̐��k�Ȃ�ܕ��ʼn����B
>>182
��i�͑I���A�Ƃɂ����������o���B
�O�ډ~�̒��S��O�Ƃ��āA
��OAB=(1/2)24��(30^2-12^2)
=12�~6��21
=72��21
��OAC=(1/2)20��(30^2-10^2)
=10�~20��2
=200��2
��ABC=��OAB+��OAC-��OBC
=72��21+200��2-(1/2)30�~30sin��BOC
=72��21+200��2-450sin��BOC
���S�p��BOC=2(��-��BC�ɂ��Ĕ��Α��̉~���p��BAC)
sin��BOC=sin2(��-��BAC)
=2sin(��-��BAC)cos(��-��BAC)
=2sin��BAC(-cos��BAC)
=-2sin��BACcos��BAC
=-2(BC/2R)(24^2+20^2-BC^2)/(2�~24�~20)
=-BC(976-BC^2)/(30�~960)
��ABC=72��21+200��2+450BC(976-BC^2)/(30�~960)
=72��21+200��2+15BC(976-BC^2)/960
=72��21+200��2+BC(976-BC^2)/64
sin^2��BAC+cos^2��BAC=1
BC^2/60^2+(976-BC^2)^2/960^2=1
BC^4-1936BC^2+30976=0
BC^2=1936�}��(968^2-30976)
=1936�}��906048
��}���BC=��(1936-264��13)
=2��(484-66��13)
976-BC^2=976-1936+264��13
=264��13-960(��0)
��ABC=72��21+200��2-(960-264��13)��(484-66��13)/32
=72��21+200��2-(30-33��13/4)��(484-66��13)
=366.360495035�c�c
0205�C�i ��/7jUdUKiSM
2020/12/30(��) 02:40:33.90ID:yoNFWM0k>>182
�O�ډ~�̒��S��O�Ƃ��A
AO��BC�̌�_��P�Ƃ���ƁA
BO�ɑ���P�̍���x�́A
P����BO�ɉ��낵�������̑���BO��t:(30-t)�ɕ�������Ƃ��āA
24:x=30:(30-t)
x=(4/5)(30-t)
=24-4t/5
30:x=30:t
t=24-4t/5
9t/5=24
t=5�~24/9=40/3=x
���l��CO��s:(30-s)�ɕ�������ʒu��P
���琂�������낷�ƁA
CO�ɑ���P�̍���y�́A
s=20-2s/3
5s/3=20
s=12
20:y=30:(30-s)
30y=20(30-s)
30(20-2s/3)=20(30-s)
y=12
��ABC=��OAB+��OAC-��OBC
=72��21+200��2-(1/2)30(40/3)-(1/2)30�~12
=72��21+200��2-200-180
=72��21+200��2-380
=232.788162511�c�c
0206�P�R�Q�l�ڂ̑f������
2020/12/31(��) 01:50:01.05ID:ejzD2e73�O�ډ~�̒��S��O�Ƃ���D
A��O��ʂ钼���ƁCA�������C�O�ډ~�Ƃ̌�_��D�Ƃ���D
BC=a�CAC=b�CAB=c�CAD=x�CBD=y�C CD=z�Ƃ���D
�s�^�S���X�̒藝���
�@c^2+y^2=x^2�@(1)
���l��
�@b^2+z^2=x^2�@(2)
i) ��BAC���݊p�̏ꍇ
�g���~�[�̒藝���
�@ax=by+cz�@(3a)
(1)(2)(3a)���
�@a=b��(1-(c/x)^2)+c��(1-(b/x)^2)
b=20�Cc=24�Cx=60��������
�@a=4��21+16��2
�w�����̌������
�@s=(a+b+c)/2=2��21+8��2+22
�@S=��(s(s-a)(s-b)(s-c))
p=2��21+8��2�Ƃ����ƁCs=p+22�Ca=2p�ł��邩��
�@S=��((22^2-p^2)(p^2-4))
p^2=32��2��21+212���q=��2��21�Ƃ�����p^2=32q+212�ł��邩��
�@S=��((272-32q)(208+32q))
�@ =2^4 * ��(8q+53)
�@ ��163.83
ii) ��BAC���s�p�̏ꍇ
�g���~�[�̒藝���
�@cz=ax+by�@(3b)
(1)(2)(3b)���
�@a=-b��(1-(c/x)^2)+c��(1-(b/x)^2)
b=20�Cc=24�Cx=60��������
�@a=-4��21+16��2
�w�����̌������
�@s=(a+b+c)/2=-2��21+8��2+22
�@S=��(s(s-a)(s-b)(s-c))
p=-2��21+8��2�Ƃ����ƁCs=p+22�Ca=2p�ł��邩��
�@S=��((22^2-p^2)(p^2-4))
p^2=-32��2��21+212���q=��2��21�Ƃ�����p^2=-32q+212�ł��邩��
�@S=��((272+32q)(208-32q))
�@ =2^4 * ��(-8q+53)
�@ ��17.188
0207����ȑf�l
2020/12/31(��) 08:46:29.21ID:umtWU27q0208�P�R�Q�l�ڂ̑f������
2020/12/31(��) 12:31:52.38ID:ejzD2e73i) ��BAC���݊p�̏ꍇ
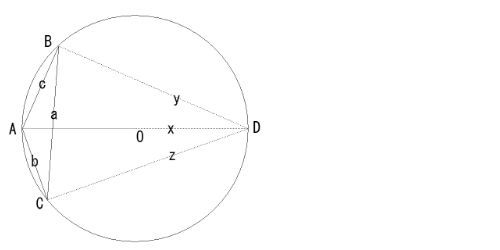
0209�P�R�Q�l�ڂ̑f������
2020/12/31(��) 12:35:18.38ID:ejzD2e73ii) ��BAC���s�p�̏ꍇ
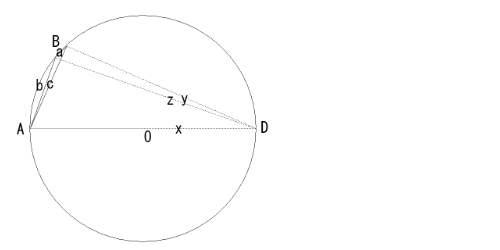
0210�P�R�Q�l�ڂ̑f������
2020/12/31(��) 12:39:50.12ID:ejzD2e730211�P�R�Q�l�ڂ̑f������
2020/12/31(��) 12:45:32.69ID:ejzD2e73�@S=abc/4R
�͊O�ډ~�̒��S���O�p�`�����ɂȂ��̂Ŏg���Ȃ�
0212�P�R�Q�l�ڂ̑f������
2020/12/31(��) 15:43:31.87ID:ejzD2e73�Ǝv���Ă������Ȃ��Ȃ��ʔ�������
���N�����w���y���߂܂��悤��
0213�C�i ��/7jUdUKiSM
2020/12/31(��) 16:32:01.89ID:SoJ2DA5s>>207
�܂��������o�ĂȂ����Ă킩���Ĉ��S������B
���������荘���Ĕ����ăg�����v��ԁB
�����ɉ�������A�҂��Ƃ��Ă���B
0214�C�i ��/7jUdUKiSM
2021/01/01(��) 00:00:20.56ID:W0Sm132p>>182
��ABC=(1/2)AB�~ACsin��BAC
=(1/2)24�~20��16875^2-(2051+1800��42)/1125
=139.803668209�c�c
>>182 ��OAB=12�~��(30^2-12^2)=12�~6��21=72��21
��OAC=10�~��(30^2-10^2)=10�~20��2=200��2
��ABC=�l�p�`OCAB-��OBC
=��OAB+��OAC-��OBC
=72��21+200��2-��OBC
��ABC=(1/2)AB�~ACsin��BAC
=(1/2)24�~20sin��BAC
=240sin��BAC
��OBC=(30^2/2)sin��BOC
=450sin��BOC
=450sin2��BPC(�~���p)
=450sin2��BAC
=900sin��BACcos��BAC
��ABC=72��21+200��2-900sin��BACcos��BAC
=240sin��BAC
(900cos��BAC+240)sin��BAC=72��21+200��2
sin��BAC=(18��21+50)/(225cos��BAC+60)
(18��21+50)^2/(225cos��BAC+60)^2+cos^2��BAC=1
3^4�~5^4cos^4��BAC+2^2�~3^3�~5^3cos^3��BAC-3^2�~5^2�~11�~19cos^2��BAC-2^2�~3^3�~5^3cos��BAC+2^2�~7�~293+2^3�~3^2�~5^2��42=0
����cos��BAC��4��������cos��BAC�͐}���A
cos��BAC��-0.8
�Ɨ\�z�ł���B
4���̌W��3^4�~5^4�ƒ萔��2^2�~7�~293+2^3�~3^2�~5^2��42���琄�肷��ƁA
cos��BAC=-(2^2�~7�~293+2^3�~3^2�~5^2��42)/(3^3�~5^4)
=-(2051+1800��42)/16875
=0.81281974857�c�c
sin��BAC=��o16875^2-(2051+1800��42)^2�p/16875
��ABC=240��o16875^2-(2051+1800��42)^2�p/16875
=16��o16875^2-(2051+1800��42)^2�p/1125
=139.803668209�c�c
>>182
��OAB=12�~��(30^2-12^2)=12�~6��21=72��21
��OAC=10�~��(30^2-10^2)=10�~20��2=200��2
��ABC=�l�p�`OCAB-��OBC
=��OAB+��OAC-��OBC
=72��21+200��2-��OBC
��ABC=(1/2)AB�~ACsin��BAC
=(1/2)24�~20sin��BAC
=240sin��BAC
��OBC=(30^2/2)sin��BOC
=450sin��BOC
=450sin2��BPC(�~���p)
=450sin2��BAC
=900sin��BACcos��BAC
��ABC=72��21+200��2-900sin��BACcos��BAC
=240sin��BAC
(900cos��BAC+240)sin��BAC=72��21+200��2
sin��BAC=(18��21+50)/(225cos��BAC+60)
(18��21+50)^2/(225cos��BAC+60)^2+cos^2��BAC=1
3^4�~5^4cos^4��BAC+2^2�~3^3�~5^3cos^3��BAC-3^2�~5^2�~11�~19cos^2��BAC-2^2�~3^3�~5^3cos��BAC+2^2�~7�~293+2^3�~3^2�~5^2��42=0
����cos��BAC��4��������cos��BAC�͐}���A
cos��BAC��-0.8
�Ɨ\�z�ł���B
4���̌W��3^4�~5^4�ƒ萔��2^2�~7�~293+2^3�~3^2�~5^2��42���琄�肷��ƁA
cos��BAC=-(2^2�~7�~293+2^3�~3^2�~5^2��42)/(3^3�~5^4)
=-(2051+1800��42)/16875
=-0.81281974857�c�c
sin��BAC=��o16875^2-(2051+1800��42)^2�p/16875
��ABC=240��o16875^2-(2051+1800��42)^2�p/16875
=16��o16875^2-(2051+1800��42)^2�p/1125
=139.803668209�c�c
0217����ȑf�l
2021/01/01(��) 22:27:24.63ID:0XJ2bHJn>>217
����ς�Ⴄ���B
��������cos��BAC�����̕ӂ̒l�����A
�W����������������ďo��l���Ǝv����B
��ABC=240��o1-(7�~293+2�~3�~3��42)/(3^3�~5^3)�p
=143.545752721�c�c
���ꂩ���������傫�����B
>>182
��ABC=240sin��BAC
=240��(1-((2^2�~7�~293+2^3�~3^2�~5^2�~��42)/(3^4�~5^4))^2)
=220.742462147�c�c
0221�C�i ��/7jUdUKiSM
2021/01/02(�y) 21:44:04.98ID:FPnZHh55B,C����O�ډ~�ɒ��aBB',CC'����сA
�O�ډ~�̒��S�ɂ��ā�ABC�Ɠ_�Ώ̂ȁ�A'B'C'��`���ƁA
��AC'A'=20�~40��2/2=200��2
��AA'B'=24�~12��21/2=144��21
��ABC=��AC'A'+��AA'B'-��A'B'C'
(1/2)24�~20sin��BAC=200��2+144��21-(1/2)40��2�~12��21sin��B'AC'
=240sin��BAC=200��2+144��21-240��42sin��BAC
sin��BAC=(200��2+144��21)/(1+��42)
=(2624��2+656��21)/41
=64��2+16��21
>>198�́�ABC=64��2+16��21=163.830879111�c�c�Ɠ����ɂȂ����B
>>182
cos��BAC=-0.68262866296�c�c
��BAC=133.049399076�c�c��
�Ɛ�������B
0223����ȑf�l
2021/01/03(��) 21:29:03.77ID:E1WbGmKb0224�C�i ��/7jUdUKiSM
2021/01/04(��) 13:03:53.43ID:6mEZY4sS>>182
��ABC�̊O�ډ~�̒��S��O�Ƃ���ƁA
��OAB��AB���ӂƂ���ӎO�p�`������A
�s�^�S���X�̒藝���A
��OAB=(1/2)24��(30^2-12^2)
=12��756
=12�~6��21
=72��21
���l�Ɂ�OAC=(1/2)20��(30^2-10^2)
=200��2
�l�p�`OCAB=72��21+200��2
�Ȃ������Ȃ邩�͑�ӂɂ�藪�������Ȃ����A
��BC������Ł�BAC�ƑΛ������BOC�̉~���p�́A
�����������~���p��BAC�̊O�p�Ɠ��������Ƃ��W���Ă��āA
��ABC�Ɓ�OCB�̖ʐϔ��24�~20:30�~30
=4�~2:5�~3
=8:15
��ABC=(8/23)�l�p�`OCAB
=(576��21+1600��2)/23
=213.1437087�c�c
0225�C�i ��/7jUdUKiSM
2021/01/04(��) 14:43:35.10ID:6mEZY4sS��BOC�͒��S�p������B
BC=2Rsin��BAC=60sin��BAC
��ABC:��BPC=24�~20:60��(60^2-BC^2)
��ABC=24�~20/�o24�~20+60��(60^2-BC^2)/2�p
=480/�o480+30��(3600-BC^2)�p
=16/�o16+��(3600-BC^2)�p
�w�����̌�����聢ABC=��s(s-24)(s-20)(s-BC)
s=(24+20+BC)/2
2s=44+BC
s=BC/2+22
s-24=BC/2-2
s-20=BC/2+2
s-BC=-BC/2+22
��ABC=��(484-BC^2/4)(BC^2/4-4)
=16/�o16+��(3600-BC^2)�p
�o16+��(3600-BC^2)�p��(484-BC^2/4)(BC^2/4-4)=16
�o256+32��(3600-BC^2)+3600-BC^2�p(484-BC^2/4)(BC^2/4-4)=16^2=256
�o32��(3600-BC^2)+3856-BC^2�p(484-BC^2/4)(BC^2/4-4)=256
�o32��(3600-BC^2)+3856-BC^2�p(122BC^2-BC^4/16-1936)=256
0226�C�i ��/7jUdUKiSM
2021/01/04(��) 16:10:24.30ID:6mEZY4sS>>182
��ABC�̊O�ډ~�̒��S��O�Ƃ���ƁA
��OAB��AB���ӂƂ���ӎO�p�`������A
�s�^�S���X�̒藝���A
��OAB=(1/2)24��(30^2-12^2)
=12��756
=12�~6��21
=72��21
���l�Ɂ�OAC=(1/2)20��(30^2-10^2)
=200��2
�l�p�`OCAB=72��21+200��2
�Ȃ������Ȃ邩�͑�ӂɂ�藪�������Ȃ����A
��BC������Ł�BAC�ƑΛ������BOC�̉~���p��BPC�́A
�����������~���p��BAC�̊O�p�Ɠ��������Ƃ��W���Ă��āA
��ABC�Ɓ�PBC�̖ʐϔ�́A
24�~20:12��21�~40��2
=1:��42
��ABC�Ǝl�p�`OCAB�̖ʐϔ�́A
��ABC:�l�p�`OCAB=1:(1+��42/2)
��ABC=�l�p�`OCAB/(1+��42/2)
=2(72��21+200��2)/(2+��42)
=2(72��21�~200��2)(��42-2)/38
=(1512��2+256��21)/19
=174.285804432�c�c
0227�C�i ��/7jUdUKiSM
2021/01/04(��) 16:20:32.19ID:6mEZY4sS�C�i��=174
�̓q���g���������B
0228�C�i ��/7jUdUKiSM
2021/01/04(��) 16:55:12.02ID:6mEZY4sS�~�ɓ��ڂ���l�p�`�̈�̓��p�́A
����ƌ����������p�̊O�p�Ɠ������B
�����A���������������B
�����������B
�v���������B
0229�C�i ��/7jUdUKiSM
2021/01/04(��) 18:09:44.16ID:6mEZY4sSsin��BAC=sin(1/2)��BOC=sin��BPC
��ABC=(1/2)AB�~ACsin��BAC
=(1/2)24�~12sin��BAC
=144sin��BAC
��BPC=(1/2)PB�~PCsin��BPC=2��OCB
�l�p�`OCAB=72��21+200��2
=��ABC+��OCB
=��ABC+(1/4)PB�~PCsin��BAC
=144sin��BAC+(1/4)12��21�~40��2�~sin��BAC
=(144+120��42)sin��BAC
sin��BAC=(72��21+200��2)/(144+120��42)
=(9��21+25��2)/(18+15��42)
=(9��21+25��2)(5��42-6)/3(6+5��42)(5��42-6)
=(945��2-150��2+250��21-54��21)/3(1050-36)
=(795��2+196��21)/3�~1014
=(795��2+196��21)/3042
=
��BAC=
���ǂ͎O�p�����g���Ă���B
0230�C�i ��/7jUdUKiSM
2021/01/04(��) 18:48:34.62ID:6mEZY4sSsin��BAC=0.6648535358918�c�c=sin138.328905864��
����ł������H
0231206
2021/01/05(��) 00:58:34.35ID:U04rSzRQ�O�ډ~�̒��S��O�Ƃ���D
A��O��ʂ钼���ƁCA�������C�O�ډ~�Ƃ̌�_��D�Ƃ���D
BC=a�CAC=b�CAB=c�CAD=x�CBD=y�C CD=z�Ƃ���D
�s�^�S���X�̒藝���
�@c^2+y^2=x^2�@(1)
���l��
�@b^2+z^2=x^2�@(2)
i) ��BAC���݊p�̏ꍇ
�g���~�[�̒藝���
�@ax=by+cz�@(3a)
(1)(2)(3a)���
�@a=b��(1-(c/x)^2)+c��(1-(b/x)^2)
b=20�Cc=24�Cx=60��������
�@a=4��21+16��2
�w�����̌������
�@s=(a+b+c)/2=2��21+8��2+22
�@S=��(s(s-a)(s-b)(s-c))
p=2��21+8��2�Ƃ����ƁCs=p+22�Ca=2p�ł��邩��
�@S=��((22^2-p^2)(p^2-4))
p^2=32��2��21+212���q=��2��21�Ƃ�����p^2=32q+212�ł��邩��
�@S=��((272-32q)(208+32q))
�@ =2^4 * ��(8q+53)
�@ =2^4 * (4��2+��21)
�@ ��163.8308791
ii) ��BAC���s�p�̏ꍇ
�g���~�[�̒藝���
�@cz=ax+by�@(3b)
(1)(2)(3b)���
�@a=-b��(1-(c/x)^2)+c��(1-(b/x)^2)
b=20�Cc=24�Cx=60��������
�@a=-4��21+16��2
�w�����̌������
�@s=(a+b+c)/2=-2��21+8��2+22
�@S=��(s(s-a)(s-b)(s-c))
p=-2��21+8��2�Ƃ����ƁCs=p+22�Ca=2p�ł��邩��
�@S=��((22^2-p^2)(p^2-4))
p^2=-32��2��21+212���q=��2��21�Ƃ�����p^2=-32q+212�ł��邩��
�@S=��((272+32q)(208-32q))
�@ =2^4 * ��(-8q+53)
�@ =2^4 * (4��2-��21)
�@ ��17.18845687
0232����ȑf�l
2021/01/05(��) 09:38:45.21ID:byMiy7MI0233�C�i ��/7jUdUKiSM
2021/01/05(��) 11:54:43.86ID:f/6O5GLP>>182
(i)��BAC���݊p�̏ꍇ�A
BC=2RsinA=60sinA
24^2+20^2-60^2sin^2A=2�~24�~20cosA
36+25-225sin^2A=60cosA
61-225+225cos^2A-60cosA=0
225cos^2A-60cosA-164=0
cosA=�o30-��(900+225�~4�~41)�p/225
=(30-30��42)/225
=(2-2��42)/15
cos^2A=(4+168-8��42)/225
=(172-2��672)/225
sinA=��(225-168+2��672)/15
=��(57+2��672)/15
=(��32+��21)/15
��ABC=(1/2)AB�~ACsinA
=(1/2)24�~20(��32+��21)/15
=16(4��2+��21)
=64��2+16��21
=163.830879111�c�c
(ii)��BAC���s�p�̏ꍇ�A
��ABC�̖ʐς�3�ӂ�(10,24,30)�̎O�p�`�̖ʐς�2�{������A�w�����̌������A
��ABC=2��s(s-10)(s-24)(s-30)
s=(10+24+30)/2=32
��ABC=2��32�~22�~8�~2
=2�~32��2
=64��2
=212.263986583�c�c
(i)(ii)��莦���ꂽ�B
0234�C�i ��/7jUdUKiSM
2021/01/05(��) 13:43:10.08ID:f/6O5GLP>>182
��BAC���s�p�̏ꍇ�A
��AB�̂������ɒ��_C������B
��ABC=(1/2)BCsin��ACB
=10BC(24/60)
=4BC
�]���藝���A
BC^2+20^2-24^2=2�~20BCcos��ACB
BC^2-176=40BC��(1- sin^2��ACB)
=40BC��o1-(24/60)^2�p
=40BC��0.84
=0.8BC��21
�ӁX��悵BC^4-352BC^2+30976=13.44BC^2
BC^4-365.44BC^2+30976=0
BC^2=365.44-��o(365.44)^2-30976�p
��ABC=4��[365.44-��o(365.44)^2-30976�p]
=26.8846039699�c�c
0235�C�i ��/7jUdUKiSM
2021/01/05(��) 15:47:50.42ID:f/6O5GLP�~�x�ݏI���I
0236����ȑf�l
2021/01/06(��) 08:38:44.00ID:X1VYkdlB0237�C�i ��/7jUdUKiSM
2021/01/06(��) 17:57:36.38ID:enP9Suix���͂����Ă܂������Ă��Ȃ����B
0238�C�i ��/7jUdUKiSM
2021/01/06(��) 23:50:16.83ID:enP9Suix���͐^���ւƕ����Ă��邩���H
0239����ȑf�l
2021/01/07(��) 08:59:28.44ID:O2otYaIG�����ĂȂ��i��
�Ƃ���ŁA���̏����ėv�]
�P�[�L�̖��ƃT����
https://rio2016.5ch.net/test/read.cgi/math/1609937007/l50
2ch�̑����ł܂Ƃ��ȘA����A���̃T���Ƃ����A�z��
�P�[�L��H�אs�������Ƃ͂ł��Ȃ��B
1/2�{1/4�{1/8�{�c��1�ɂ͂Ȃ�Ȃ��B
�Ƃ������Ƃ������Ă���Ă���i��
0240�C�i ��/7jUdUKiSM
2021/01/07(��) 15:09:55.81ID:h+AFibw5���͔����オ��邾�낤�B
0241����ȑf�l
2021/01/08(��) 08:42:51.93ID:wQm0fxJ9��}����@���̂U
�@
�����`�ɓ��ڂ��鐳�O�p�`����}����B
�A�������`�̒��_�Ɛ��O�p�`�̒��_����v����ꍇ�͏����B
�A
�O�p�`�ɓ��ڂ��鐳���`����}����B
�A�������`�̈�ӂ͎O�p�`�̒�ӂƐڂ��Ă���Ƃ���B
���ꂩ��͖��T���j���ɏo�肵�悤���ƍl���Ă���B
�Ȃ���T�ԂɈ�₵���o�肵�Ȃ����Ƃ����A
����Ȃɂ�������o��ł���قǃl�^���Ȃ�����ł���i��
0242�C�i ��/7jUdUKiSM
2021/01/08(��) 12:18:55.72ID:yV3UA5W4>>182
��BAC���݊p�̂Ƃ���ABC=64��2+16��21=163.830879111�c�c
��BAC���s�p�̂Ƃ���ABC=(1728��21+336��37)/73=61.4735513145�c�c
0243�C�i ��/7jUdUKiSM
2021/01/08(��) 14:12:01.34ID:yV3UA5W4>>182
��BAC���݊p�̂Ƃ���ABC=64��2+16��21
=163.830879111�c�c
��BAC���s�p�̂Ƃ�(�v�Z�~�X�����Ă���)
��ABC=5.23593234214�c�c
������Ƃ����������H
0244�C�i ��/7jUdUKiSM
2021/01/08(��) 14:44:44.60ID:yV3UA5W4>>182
��BAC���݊p�̂Ƃ���ABC=64��2+16��21
=163.830879111�c�c
��BAC���s�p�̂Ƃ���ABC=36��2-12��7
=19.1626725127�c�c
0245�C�i ��/7jUdUKiSM
2021/01/08(��) 15:12:33.75ID:yV3UA5W4>>182
��BAC���݊p�̂Ƃ���ABC=64��2+16��21=163.830879111�c�c
��BAC���s�p�̂Ƃ���ABC=64��2-16��21=17.1884568726�c�c
�肱�������B
0246�C�i ��/7jUdUKiSM
2021/01/08(��) 15:30:16.57ID:yV3UA5W4>>182
��BAC���݊p�̏ꍇ�A
BC=2RsinA=60sinA
24^2+20^2-60^2sin^2A=2�~24�~20cosA
36+25-225sin^2A=60cosA
61-225+225cos^2A-60cosA=0
225cos^2A-60cosA-164=0
cosA=�o30-��(900+225�~4�~41)�p/225
=(30-30��42)/225
=(2-2��42)/15
cos^2A=(4+168-8��42)/225
=(172-2��672)/225
sinA=��(225-168+2��672)/15
=��(57+2��672)/15
=(��32+��21)/15
��ABC=(1/2)AB�~ACsinA
=(1/2)24�~20(��32+��21)/15
=16(4��2+��21)
=64��2+16��21
=163.830879111�c�c
��BAC���s�p�̏ꍇ�A
��AB�̂������ɒ��_C������B
��ABC=(1/2)BCsin��ACB
=10BC(24/60)
=4BC
��ABC�ɂ����Đ����藝���sinB=20/60=1/3������A
cosB=2��2/3
20^2-(BC/3)^2=�o24-(2��2/3)BC�p^2
400-BC^2/9=(24-2BC��2/3)^2
BC^2-96BC��2/3+176=0
BC^2-32BC��2+176=0
BC=16��2-��(512-176)
=16��2-��336
=16��2-4��21
��ABC=4BC
=64��2-16��21
=17.1884568726�c�c
�݊p�̂Ƃ��Ɖs�p�̂Ƃ����}�Ⴄ�����ŕ����I�ɑΏ̂Ȃ������ɂȂ�������A
������C������B
�������}�����ʼn������āB
0247����ȑf�l
2021/01/08(��) 22:15:02.64ID:wQm0fxJ90248�C�i ��/7jUdUKiSM
2021/01/09(�y) 02:53:42.03ID:n6k9inuH���͂����肷�����̂��B
0249����ȑf�l
2021/01/09(�y) 08:37:42.81ID:lOuzVQwT�t�c�[�̍��Z���ł��A30��������Ή������i��
�A�̖�肾���āA���邱�ƂɋC�t����������A
���̍��Z���ł��A�T���ʼn������낤�i��
�Ƃ��낪�A���́A���邱�ƂɁA�Ȃ��Ȃ��C�t���Ȃ��̂ł���i��
0250�P�R�Q�l�ڂ̑f������
2021/01/09(�y) 09:11:48.04ID:3o5wcqI/���́A�ˉe�w(����)�̖��B
�܂��́A���Z���Ȃ烁�l���E�X�̒藝���B
�Ƃ���ŁA�@�����ǁA
�O�p��(�]���藝����藝�Ȃ�)���g�����ƂƁA
�s�^�S���X�̒藝���g�����Ƃ͖{���I�ɓ�������B
0251�C�i ��/7jUdUKiSM
2021/01/09(�y) 17:08:40.74ID:n6k9inuH�]���藝�ƃs�^�S���X�̒藝�͓�悷�邯�ǁA
�����藝�͓�悵�Ȃ��Ƃ��낪�Ⴄ�Ǝv���B
0252�P�R�Q�l�ڂ̑f������
2021/01/09(�y) 20:05:49.41ID:3o5wcqI/���܂�B���m�ɂ́A
�O�p���̗]���藝����藝�Ȃǂ��g���Ė��@���������Ƃ��A
�s�^�S���X�̒藝���܂ޏ����̕��@�ʼn������Ƃ��A
�{���I�ɂ͓���
���ȁB
��G�c�ɂ����āA
�s�^�S���X�̒藝 <-> �]���藝
�O�p�`�̖ʐ� <-> �����藝
���ĂƂ��납�B
0253����ȑf�l
2021/01/09(�y) 21:24:03.55ID:lOuzVQwT�����������Ă��邪�A�A�̖��͎ˉe�w(����)�Ƃ͊W���Ȃ��i��
0254�P�R�Q�l�ڂ̑f������
2021/01/09(�y) 22:33:49.52ID:3o5wcqI/����́A������g���Ă������ĉ����Ȃ��Ƃ����Ӗ������Hww
�ؖ��͕K������1�ł͂Ȃ���B
�������ɂ���@�͂��邾�낤�ˁB
���Ȃ��̉͂����炭���l���E�X�̒藝���g�����̂���Ȃ����ȁH
>250�Ō������̂́A
�uQD��AC�͕��s�v���h��������h�Ɠ��l�ł��邱�Ƃ�
���l���E�X�̒藝���g���Ď������Ƃ��ł��邪�A
����̂���m�����g���Ă��\���Ƃ������ƁB
�ǂ�����ˉe�w�̔��e�ɂ���藝�B
0255�C�i ��/7jUdUKiSM
2021/01/09(�y) 22:51:24.71ID:n6k9inuH�����́�ABC=519.330645275�c�c���������A
�������Ȃ肷������ł���������蒼���B
0256�C�i ��/7jUdUKiSM
2021/01/09(�y) 23:43:48.85ID:n6k9inuH���͉������������Ă��D�����B
�n�[�g��������B
�Ȃ�ǂ��������B
�������������܂ʼn����Ă�B
0257����ȑf�l
2021/01/10(��) 08:27:44.27ID:xAe+wxQy������g���ĉ����邩�ǂ����͍l�������Ƃ͂Ȃ����A
����ȓ���m�����Ȃ��Ă���������ł���i��
�������������Ɩ��ł��Ă���̂́A
�ˉe�w(����)�̂悤�ȁA���Z�ł͋����Ȃ��m����K�v�Ƃ�����ł͂Ȃ����炾�B
���邱�ƂɋC�t����������A�t�c�[�̍��Z���ł��ȒP�ɉ�������ł���B
0258�C�i ��/7jUdUKiSM
2021/01/10(��) 15:54:45.45ID:GMRBrE1q��BAC���݊p�̂Ƃ��A
�O�ډ~�̒��S��O�Ƃ��āA
��ABC�ɂ����Đ����藝���A
24/sin��BOA=30/sin(��/2-��BOA/2)
5sin��BOA=4sin(��/2-��BOA/2)
=4cos��BOA/2
���p�̌������A
sin��BOA=(4/5)��o(1+cos��BOA)/2�p
��OAC�ɂ����Đ����藝���A
20/sin��COA=30/sin(��/2-��COA/2)
3sin��COA=2sin(��/2-��COA/2)
=2cos��COA/2
���p�̌������A
sin��COA=(2/3)��o(1+cos��COA)/2�p
��ABC=�l�p�`OCAB-��OBC
=72��21+200��2-450sin(��BOA+��COA)
���@�藝���A
sin(��BOA+��COA)=sin��BOAcos��COA+cos��BOA
sin��COA
=(4/5)cos��COA��o(1+cos��BOA)/2�p+(2/3) cos��BOA��o(1+cos��COA)/2�p
�]���藝���A
cos��BOA=(900+900-576)/(2�~30�~30)
=1224/1800
=153/225
=51/75
=17/25
cos��COA=(900+900-400)/(2�~30�~30)
=1400/1800
=7/9
sin(��BOA+��COA)=(4��21/25)(7/9)��(21/25)+(2/3)(17/25)��(8/9)
=28��21/(25�~9)+68��2/(25�~9)
��ABC=72��21+200��2-450(28��21+68��2)/(25�~9)
=72��21+200��2-56��21-136��2
=16��21+64��2
=163.830879111
��BAC���s�p�̂Ƃ��A
��ABC=��OBC+��OAC-��OAB
=(1/2)(30�~30)(sin��BOC+sin��COA-sin��BOA)
=450sin��BOC+200��2-72��21
=450sin(��BOA-��COA)+200��2-72��21
���@�藝���A
sin(��BOA-��COA)=sin��BOAcos��COA-cos��BOAsin��COA
=sin��BOA(900+900-400)/(2�~30�~30)-�o(900+900-576)/(2�~30�~30)�psin��COA
=sin��BOA(7/9)-(17/25)sin��COA
sin��BOA=��(1-17^2/25^2)
=��(625-289)/25
=��336/25
=4��21/25
sin��COA=��(1-7^2/9^2)
=��(81-49)/9
=��32/9
=4��2/9
sin(��BOA-��COA)=(4��21/25)(7/9)-(17/25)(4��2/9)
=(28��21-68��2)/(25�~9)
��ABC=450(28��21-68��2)/(25�~9)+200��2-72��21
=2(28��21-68��2)+200��2-72��21
=(200-136)��2-(72-56)��21
=64��2-16��21
=17.1884568726�c�c
0259�P�R�Q�l�ڂ̑f������
2021/01/10(��) 17:09:08.12ID:q1OxLAtx���̖��A�ˉe�w�̒m��������A
���邱�ƂɋC�Â��̂͂�������͂Ȃ����ǁB
���Z�̋��ȏ��̒m��(���l���E�X�̒藝�Ȃ�)��������A
������l�����̂͑�������Ǝv����B����
�m���ĂĂ悩�����ˉe�w
���ĂƂ����ȁB
�� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�
�j���[�X
- ����ł́u�X�g�b�v�I�v�Ƌ������c �ό��o�X�Ɠd���ɋ��܂�o�X�K�C�h�̏��������S�@�R�`�E��R�s [����������]
- ����ł́u�X�g�b�v�I�v�Ƌ������c �ό��o�X�Ɠd���ɋ��܂�o�X�K�C�h�̏��������S�@�R�`�E��R�s��2 [����������]
- �y���邾���s���z�u���A���̒j�Ɍ���ꂽ�����v�c�I�X�p�̏������ł�������A�g�`������Q�h�́u�e�͂Ȃ����ԁv��5 [nita��]
- �y�����s�m���z�@�uvs���r�@�@�u���A���������r���ɂ��킶��ƍ����L�����@�������A�u�@�u���Ɉ��A���Ă����������v�̐� [PARADISE��]
- �u�l�グ�Ə����ȁv�@�d�C�E�K�X�x���A�����������̗\�� [���ꁚ]
- �C�G�����E�g��a�Ɓ@�g�^�ۗ��_�h�̉̎��u��q�ɓ��{�l�͂��܂���ł����v�uJAM�v�����b���u�[��ԑg�Ńj���[�X�L���X�^�[���v [muffin��]
- 

🏡���̃X���́wCyberGhost👻�x�̒ł��͂����܂��B🏡


- 👩�����u�܂��~�܂�Ȃ�(�����ĂȂ�)�v�u�f���C������(�f���ĂȂ�)�v👈���������̑��ɂ���H [312375913]
- X���u��J�������Ă����O�Ɠ��{�������킯�ł͂Ȃ��v�l�g�E���u��J�����I�������I���Č����Ă�z�������Ƃ���̂���p���N���v [441978185]
- ���ז����g���Ă����ȕ🤗(�R�L��`)�u��c���c�}�_�K�X�J���v [851331385]
- �y�ߕ�z�F��ɋ��P�`���ē{��ꂽ��̒��A�q�O�}3���o������������������u��wwwwwww
- �����o�ρA�����ǂ��ɂ��Ȃ�Ȃ��Ȃ�

