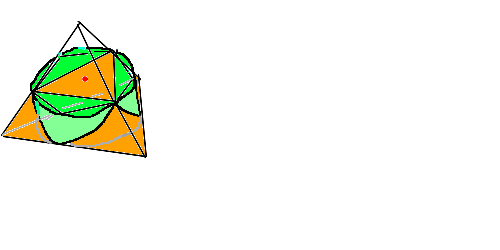������Ȃ����͂����ɏ����Ă�453
�� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�
�����A�������P������낤����
�O�X��
������Ȃ����͂����ɏ����Ă�452
http://rio2016.5ch.net/test/read.cgi/math/1555080760/
(�g�p�ςł�: 478) >>775
a^(1/n) (���������_�v�Z) �ɂ����Ƃ��߂����������� m �ƒu���A
m^n (�����v�Z) == a �Ȃ炻�ꂪ���ŁA!= a �Ȃ���Ȃ�
m^n (�����v�Z) �� O(log(n)) �Ōv�Z�\ >>793
a+b =-t + 3tan3��
= -t + 3t(3-t^2)/(1-3t^2) = 8t /{(1 + ��3.t)(1 - ��3.t)} = (t - ��3)/(1 + ��3.t) + (t + ��3)/(1 - ��3.t) = tan(��-60) + tan(��+60)
ab = 1/t . (-tan3��)
= (t^2-3)/(1-3t^2) = {(t - ��3)(t + ��3)}/{(1 + ��3.t)(1 - ��3.t)} = (t - ��3)/(1 + ��3.t) * (t + ��3)/(1 - ��3.t) = tan(��-60) tan(��+60)
���Z�͂������̕����ȒP��. >>792
�Ƃ肠�����O����10�Ԗڂ̐l�܂ł����肭������
���Ď��́A�����l�B�������s�� >>790
�q���g�ł����A���I�v��@���g���Ă��������B >>798
�����Ȃ�B
�A�����ĂȂ��Ƃ����Ȃ��̂��A�܂�ɂƂ��Ă����̂��ňӖ�����Ă��邩��G�X�p�[�s�\�Ȃ�B
�����͏����Ȃ��ƈӖ��ʂ��Ȃ��ƕ����肻���Ȃ����ǁB >>781 (��)
14�E13
�@xyz��Ԃ�4�_ P(0, 0, 2), A(0, 2, 0), B(��3, -1, 0), C(-��3, -1, 0) ���Ƃ�B
�@�l�ʑ�PABC�� xx+yy��1 ���݂��������̑̐ς����߂�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(12 �����H��) >>783
[16] �L�����Ɩ����� ��2ch
�@a,b��L�����Ƃ���B(2+3��2)a + (1-2��2)b = 7�@�����Ƃ��A
a = [�A], b = [�C] �ł���B
�@(2a+b) + (3a-2b)��2 = 7 + 0��2�@���
�@a=2, b=3
��)
m-n��2 = 0 �ƂȂ鎩�R��m, n ���������Ƃ���� mm=2nn
�f�������������2�ׂ̂��w���������A��ƂȂ��Ė�������B
�� m=n=0,
>>784
[29] �˂ɐ��藧�s����
�@a�͒萔�Ƃ���B
�@���ׂĂ̎���x�ɑ��ĕs���� axx+4x+a>0 �����藧��
�@�悤��a�̒l�͈̔͂́Aa > [�A] �ł���B
�@a��0 �͕s�� (x=0)
�@a>0 �̂Ƃ� a(x+2/a)^2 + (aa-4)/a �� (a+2)(a-2)/a,
�@�� a-2 >0, >>800
O(n^2) �̃A���S���Y���ł��̂ŁA�����ƕ�����܂���ˁB >>788
���ɂ�����B
�@1/tan(��-60�) + 1/tan�� + 1/tan(��+60�) = 3/tan(3��), >>804 �Ȃ�ق�
tan(��-60) �� tan(��) �� tan(��+60) = �� tan(3��) ���
-cot(��-60 -90) �� -cot(�� -90) �� -cot(��+60 -90) = �� -cot(3�� -90)
cot(��-90 -60) �� cot(��-90) �� cot(��-90 +60) = �� cot(3 (��-90) + 180)
��-90 �� �� �Ɏ�蒼����
cot(��-60) + cot�� + cot(��+60) = 3 cot(3��)
cot(��-60) . cot�� . cot(��+60) = - cot(3��) >>781 (���̃m�[�g�̉�ǂ͂������Ȃ� ), >>801
�}��t�����̂ŗ����͓���Ȃ����Ǝv���܂�.
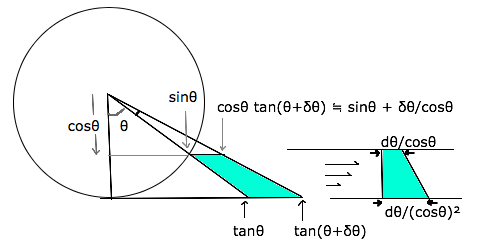
�����̐�(�l�p�� �� 2): d(sin�� + tan��).(1-cos��)^2
�̐�: V = 6 �� [��=0�`��/3] {�����̐�} = (�ȉ���)
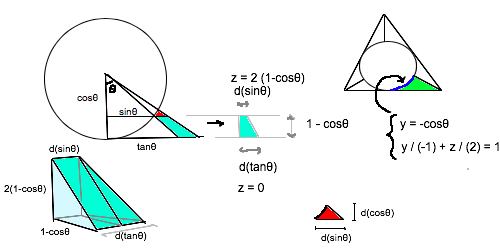
y < 0 ���̃p�[�c��I�̂́A�Ζʂ̎�: z/(2) + y/(-1) = 1 �̂悤�ɂQ�ϐ��ōςނ���ł�.
y = -cos�� �ƍ��킹�� �Ő��̎�: z = 2( 1-cos�� ) ���ȒP�ɋ��܂�܂�.
�v�Z�� �� d�� /cos�� ���o�Ă��āA�������ƖʐH�炤��������܂���.
�� d�� cos�� /cos��^2 = �� d(sin��) /( 1-sin��^2 ) = (1/2)( log(1+sin��) - log(1-sin��) )
����Ȋ����ł����܂�.
 >>806
>>806
���肪�Ƃ��������܂��B
>>781�́A
�����̈悪3�ӏ�����̂�3�{���Ă��Ȃ�
�ϕ���Ԃ��ԈႦ�Ă���i30�������鎞�Ƀ�/3�����Ă���j�̂����ł����B
����2�ӏ�������ƈ�v���܂����B
�~���o�Ă��邩�瓖�Rxy���ʂɕ��s�ȖʂŐ�I�Ǝv�����̂ł����A
806�l���͔͉�z=t�ł͐��Ă��炸�A�e�N�j�b�N�������܂����B
����ł������i���܂��B���肪�Ƃ��������܂����B a�����R���̒萔�Ƃ���B
�ȉ��̕s�����������R��n����������݂���悤�Ɏ���p���߂����B
p�̎�肤��͈͂�a�ŕ\���B
2018 < n^2+an+(p/n) < 2019 >>806 �����̐ς̂Ƃ��ԈႦ�Ă�.
(���ɂȂ���)�O�p���ƎO�p�����ߕό`�����`�ɂȂ��Ă�.
�l�p�� �� 2 �Ȃł͂Ȃ�.
���̕����̎ߕό`�͑̐ς��s��(�E�})�Ȃ̂�...
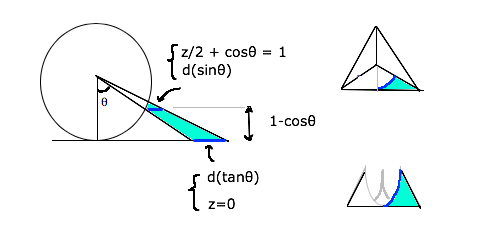
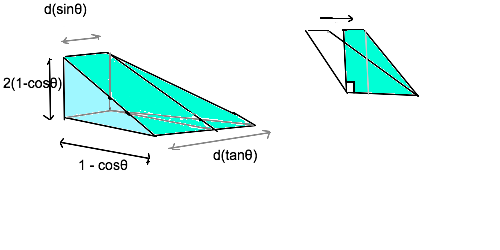
�����̐�: d(sin��) (1-cos��)^2 + (1/3). d(tan�� -sin��). (1-cos��)^2
= d( (2/3).sin�� + (1/3).tan�� ) (1-cos��)^2
���Ԃ�ō����Ă��Ȃ�����...
 �O>>776
�O>>776
>>801
����AB�̕������́A
y=-(��3)x+2�\�\�@
���_���璼��AB�^�Ɉ����������̕������́A
y=x/��3�\�\�A
�@�A����_�́A
-(��3)x+2=x/��3
3x+x=2��3
x=��3/2
�A�ɑ�����Ay=1/2
(��3/2,1/2)
�����x^2+y^2=1��̓_�ł���A�}�`�̑Ώ̐����A
x^2+y^2=1�͐��O�p�`ABC�̓��ډ~�Ƃ킩��B
���l�ʑ�PABC����A
�~��x^2+y^2��1������ʂ��ƁA�Ƃ������O�_�A
(0,1,1)�(��3/2,-1/2,1)�(-��3/2,-1/2,1)�������яオ��B
z������A������B�����ɂ��ꂼ��P�[�L�����̂悤�ɋ��߂闧�̂�1/3���o���Ȃ�A���l�ʑ͎̂O�p��������3���킹�ĎO�p���̑̐ςƓ����B
���Ȃ킿�O�p���̑̐ς���~���̑̐ς������B
2���3�1-��1^2�1=2��3-��
=2�1.7320508-3.14159258
=0.3225�c�c �O>>811�̒l�A�����B
>>801
����AB�̕������́A
y=-(��3)x+2�\�\�@
���_���璼��AB�^�Ɉ����������̕������́A
y=x/��3�\�\�A
�@�A����_�́A
-(��3)x+2=x/��3
3x+x=2��3
x=��3/2
�A�ɑ�����Ay=1/2
(��3/2,1/2)
�����x^2+y^2=1��̓_�ł���A�}�`�̑Ώ̐����A
x^2+y^2=1�͐��O�p�`ABC�̓��ډ~�Ƃ킩��B
���l�ʑ�PABC����A
�~��x^2+y^2��1������ʂ��ƁA�Ƃ������O�_�A
(0,1,1)�(��3/2,-1/2,1)�(-��3/2,-1/2,1)�������яオ��B
z������A������B�����ɂ��ꂼ��P�[�L�����̂悤�ɋ��߂闧�̂�1/3���o���Ȃ�A���l�ʑ͎̂O�p��������3���킹�ĎO�p���̑̐ςƓ����B
���Ȃ킿�O�p���̑̐ς���~���̑̐ς������B
2���3�1-��1^2�1=2��3-��
=2�1.7320508-3.14159265
=0.3225�c�c �O>>812�Ⴄ��������Ȃ��B
z=t(0��z��1)�ŗ��̂�1/6�̕��������t=0�`1�𑫂����߂āA���Ƃ�6�{����B
z=t�ɂ�����̍��W�́A
(0,2-t,t)�
(0,1,t)�A
���ƈ�_�́A
y=-��3x+2-t��x^2+y^2=1�ɑ�����A
({��3(2-t)-��(4t-t^2)}/4,{2-t+��3(4t-t^2)}/4)
�O�p�`�����`�������Az=t�ɂ�����̖ʐς͏o��B
�O�p�`�̖ʐς́A
(1/2)(2-t){��3(2-t)-��(4t-t^2)}/4
={��3(2-t)^2-��(2-t)^2(4t-t^2)}/8
��Ƃ��`�̖ʐς�m��ɂ͒��S�p�Ƃ��~�ʂ̒���2�Υ(��/2��)=�Ƃ��K�v�B
t�ŕ\���Ȃ����B
tan��={��3(2-t)-��(4t-t^2)}/{2-t+��3(4t-t^2)}
z=t�ɂ�����̖ʐς́A
{��3(2-t)^2-��(2-t)^2(4t-t^2)}/8-�Υ(��/2��)
{��3(2-t)^2-��(2-t)^2(4t-t^2)}/8-��/2
���߂闧�̂̑̐ς́A
6��[t=0�`1]{��3(2-t)^2-(2-t)��(4t-t^2)}/8-��/2dt
= �O>>814���j�ύX�B
>>801
���l�ʑ�PABC����A
���l�ʑ�PABC��z=1����̕�������菜���A
x^2+y^2��1��0��z��1�̉~���������A
�~���̂������������������𑫂��B
���l�ʑ�PABC=(1/6)�3�2��2�2
=2��3
���l�ʑ�PABC��z=1����̕���=2��3�(1/8)
=��3/4
x^2+y^2��1��0��z��1�̉~��=��
�~���̂�����������������=(��/3-��3/4)�1�(1/2)�3
=(4��-3��3)/8
���߂闧�̂̑̐�=2��3-��3/4-��+(4��-3��3)/8
=(16��3-2��3-3��3-8��+4��)/8
=(11��3-4��)/8
=0.810773534�c�c >>815
�o�J������
����Ȗ��̌v�Z���炢�ꔭ�ō��킹�� ���z�̊m����������߂�r���̓W�J��������܂���
�[k=0,n]( nCk * (pz)^k * (1 - p)^(n-k) )
= (pz + q)^n
���̊Ԃ͉����s���Ă���̂ł��傤��
https://i.imgur.com/uyw4jk6.jpg 2���藝���������Ȃ��Ƃ������Ƃł��� >>818
���肪�Ƃ��������܂�
���S�ɑ��݂�Y��Ă��܂��� 2015�N�ȍ~�̍��Z���w�̐V�ߒ��̓��v���w�Ԃ̂ɍœK�̎Q�l���������ĉ����� f(x)�͒萔�łȂ��������Ƃ���B
���̂Ƃ��Asin(f(x))���������ƂȂ邽�߂̕K�v�\�������́Af(x)�̎�����1�ł��邱�Ƃ������B cos((f(a)+f(a+p))/2)��0�ł���a���Ƃ��a�̋ߖT��sin((f(x)-f(x+p))/2)=0�ɂ��(f(x)-f(x+p))/2�͒萔�B
�� (f(x)-f(x+p))/2�̎�����0�ȉ��B (�K�v����)
g(x) := sin(f(x)),�@����: T �Ƃ���.
f(x) �͒萔�ł͂Ȃ����� g(��) �� 1 �ƂȂ�_ x=�� �����݂���.
g�f(x) = cos(f(x)) f�f(x) ���������: T �̂͂��ł���.
| g�f(��) | = | g�f(��+nT) | = ��{ 1-g(��)^2 } * |f �f(a+nT)|
f(x)�̎����� 2�ȏ�ł� lim{n�� ��} |f �f(a+nT)| = �� �܂��̓����͐������Ȃ�.
����� f(x)�̎�����1�ł���.
(�\������)
f(x) =ax + b (1����, a��0) �Ƃ����
g(x) := sin(f(x)) = sin(ax + b) = sin(ax �}2�� + b) = sin(a*(x+2��/|a|) + b) = g(x+2��/|a|)
g(x) �͎��� 2��/|a| �̊��ł��� �i�K�v�����j
f(x) ��n���������Ƃ���B�����FT�Ƃ���B
���[0,T] �ł�f(x)�̒l�� D(0,T) �͗L�E�ł���B
�@sin(y) = sin�� �̍�y�͖����ɂ��邪 {��, ��-��, 2��+��, 3��-��, ����}
D(0,T) ���̍��� m�������Ƃ���B
����Af(x) = y ����x�� �ey�ɂ�n�ȉ��ł���B
�� sin(f(x)) = sin�� ����x ������T����mn�ȉ��ł���B
�����藝���
�@f(x+T) - f(x) = T�Q(x,T)
��Q ��(n-1)���������ł���B
n��2 �Ȃ�Ώ\���傫��x �ɑ��� Q(x,T) > ��mn/T
���[x,x+T] �ł�y�̒l�敝 |D(x,x+T)| > ��mn
sin(f(x)) = sin�� ����x�� 2mn�ȏ゠��B(����)
�E�r�u���̂��Ƃ̓r�u���ł���B(����) 69, 67, 65, 63, 61, 59, 57, 56,
52, 50, 48, 46, 44, 43, 42,
37, 35, 33, 32, 31, 30,
24, 23, 22, 21, 20,
15, 14, 13, 12,
8, 7, 6,
3, 2
�K�����́H
2 6 12 20 30 42 56�͎O�p���̈ʒu >>809
�@2018 < nn + an + (p/n) < 2019,
���
�@n(2018 - nn - an) < p < n(2019 - nn - an),
�k��l
n<45,�@a = 2(45-n)�@�̂Ƃ�
�@n{(45-n)^2 - 7)n < p < n{(45-n)^2 - 6},
�@(45 - a/2)(aa/4 - 7) < p < (45 - a/2)(aa/4 - 6), >>816�����Ă�݂����łЂƈ��S���܂����B�u�^�l�p�̃������[����4�l�Ŏ�ă��[���V�F�A�������B���p�����͂Ȃ����̂Ƃ��ĊԎd����ŒZ�ɂ������B�ǂ������炢�����B�����Ȑ��͔F�߂�v�Ɠ����ł��ˁB
�P]/�_______�O>>815_
�Q/�_/zz..,,���@�@ /|
�P�_/zz..�c`-`Ђ� / |
�P|�______U,~�܁R��@|_
�n| �a�P�P�P�PU~~U / /
�Q| �a ���@�� �a |/ /
_�@`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P >>811 >>812
3��AP, BP, CP�̒��_�� A ',B ',C ' �Ƃ���B
�_ A '(0,1,1)� B '(��3/2,-1/2,1)� C '(-��3/2,-1/2,1) �_�Ƃ���3�̐��̂��l�����
�@(����) = 1,
�@(��ʐ�) = ��ABC - �� = 3��3 - ��,
�@(�̐�) = (1/3)(����)(��ʐ�) = ��3 - (��/3) = 0.684853256
���̐��̂� xx+yy��1 �̗̋��N�Ƃ��Ă��āA�����i4��3 - 2�� = 0.65017923�j�����傫���B
>>827
�@�����ĂȂ����낤�B�S�R�������B >>801
�܂� xx+yy��1 �̓��������̑̐ς��l���A��3�p��PABC�̑̐� 2��3 ��������B
��BOC �Ɋ܂܂���`�����̑̐�v��3�{����悢�B
���̊e�_�̋ɍ��W�� (r,��) �Ƃ���� 0��r��1, -60߁��Ɓ�60�
�e�_�ɂ����鍂���� h(r,��) = 2(1+y) = 2(1-r�cos��)
�@v = ��[0,1] ��[-60�,60�] h(r,��) d�� rdr = 2(��-��3)/3,
�@V = (PABC) - 3v = 2��3 - 2(��-��3) = 4��3 - 2�� = 0.6�S5017923�@�@�@(������) >>827
������4��3-2��
������x�v�Z�������č��킹�Ă݂�ww >>806, >>810 �ł�������̉�@���v�Z������Ȃ�.
�m���� �l: 4��3 - 2�� = 0.645... ���������ł� (�O�̂��ߐ��l�v�Z�ł��m���߂�)
�����ł͖��������Ԃ��̈�͍����̔����ʂ�����ϕ��ɂ͌����Ȃ��͂���
V = 6 �� [��=0�`��/3] {�����̐�} = 6 �� [��=0�`��/3] d( (2/3).sin�� + (1/3).tan�� ) (1-cos��)^2
= (9/2)*��3 - 2��/3 - 2*log(7+4��3 ) = 0.4320... �� 0.645... (����Ȃ�...)
���Z�����̂ŗ�����̌v�Z�͊ԈႢ�Ȃ��Ǝv���܂�.
������̉�@�͂ǂ��Ń~�X���Ă���̂ł��傤���H �N�������Ă�������.
 >>591
>>591
�����A(2�������s��)��a,b,c,d
�����x=(x, y)
�Ƃ������Ƃ��̉�@���肢���܂� �~�X���Ă��ӏ�����������.
d(sin��) �̂Ƃ��� d��/cos�� �Ƃ��ׂ�������. d(tan��) = d��/(cos��)^2 �͂��̂܂܂ł悢.
�����̐�: { (2/3). d�� /c + (1/3). d��/c^2 }. (1-c)^2 [c :=cos�� ]
�@�@�@�@�@ = (1/3). (2c+1)(1-2c+cc) /cc = (1/3).{ 1/c^2 -3 +2c }
V = 6 �� [��=0�`��/3] {�����̐�} = 2 tan(��/3) - 6.(��/3) + 4sin(��/3) = 4��3 - 2��
����������������ꂽ.
��������ĊԈ��Ȃ����, ���Ȃ�G���K���g�ȉ�@�ł͂Ȃ����낤�� (���掩�^)
 m,M,a,b,c,d�͐����ŁA���ꂼ��ȉ������Ƃ���B
m,M,a,b,c,d�͐����ŁA���ꂼ��ȉ������Ƃ���B
1<=m<=M
0<=a<=b<=c<=d<=m����a+b+c+d=M
m,M��萔�Ƃ���Ƃ��A��������a,b,c,d�̑g�͉��g���邩�H
���ǂȂ������ꂨ�肢���܂��c
�l�����������Ă����Ƃ��肪�����ł��B
��낵�����肢���܂� A��3���̐����ł���BA=100m+10n+l�Ƃ��āAm,n,l�͑S��1���̊�Ƃ���B
A(A+1)�̑S�Ă̌��������ɂȂ鎞�AA�����߂�B
�������Am��n��l�Ƃ���B
���̃e�X�g���ɂ������̂ł����A��������ȊO�ʼn������@���v���t���܂���c�B >>566�@�U�i���őP��
�����̂��Ƃ��l����Ɛi�@�� b �Ƃ��Ă� 6 ��I�Ԃ̂��������Ǝv���B
���Ȃ��Ȃ�K�x�ȕ������ł��ׂĂ̐���\���A
���������f�� 2, 3, 5, 7 �ł̉������ȒP�ɔ���ł���B��̐��� 6 �Ȃ̂ł���B
http://math.tsukuba.ac.jp/~akiyama/papers/proc/NumberTheory_DynSys_rev3.pdf ����Ŏg�������Ȑ��̌�����������̂͂悭�Ȃ�
����ł͏����Ȑ��g���ꍇ���قƂ�ǂȂ���� 10�i����7�̔{���肷����@
�@���̐���1�̈�(A)�Ƃ���ȏ�(B)�ɕ�����
�AA��2�{��B�Ƃ̍���7�̔{���Ȃ猳�̐���7�̔{��
�B��̇A�̐����傫������ꍇ�͇@�`�A���J��Ԃ�
��̇A���uA��B�Ƃ̘a��9�̔{���Ȃ猳�̐���9�̔{���v�ɕς����9�̔{���̔�����@�ɂȂ邱�Ƃ��l����ƁA���قǓ�����Ȃ��̂ł� S[n] = 4*��[k = 1 to n] {(-1)^(k-1)}/(2k-1)
T[n] = (6/��)*��[k = 1 to n] (1/k^2)
�Ƃ����Ƃ��A���̋Ɍ���0�łȂ������Ɏ�������悤�ȗL����p�����߂�B
lim[n����] (n^p)*(S[n] - T[n])
���ꂪ����Ĉ��ڂɉ������ׂ���������܂���B
���łȂ��̂ŁA�W�J���č������̂Ă���@���g���܂��A�]���̎d����������܂���B
���������������B >>840 7�̔{��������@
10a + b �� 0 (mod 7) �� -2*(10a + b) �� 0 (mod 7)
-2*(10a + b) �� -20a -2b �� a -2b �� 0 (mod 7)
�Ȃ�ق�... �B�@3�̔{���X�̔{���Ƃ��͂悭�������邯�ǁA����͏��߂Ēm�����B >>842
���ŃI�C���[�}�N���[���� >>830�O>>827���j�]���B
����z=t�Ő������l�ʑ�PABC�̖ʐς�t=0����1�܂Őϕ����Ă݂�B
����2-t�̐��O�p�`��肿����Ƃ����L���������`��3�B
�����O�p�`���甒���~�������Ĉ���������3�̐�[�𑫂��B
���ABC�̖ʐς�3��3�A���ꂪ�����O�p�`�ɂȂ邽�߂̔{�����Ȃ킿������́A
(2-t)/2
�����O�p�`�̖ʐς́A
(3��3){(2-t)/2}^2
�����~�̖ʐς������āA
(3��3){(2-t)/2}^2-1
����������3�̐�[�̎O�����`�̖ʐς́A
����y=-��3x+2-t��x^2+y^2=1�ɑ�����A
(��{4��3-3+(4-2��3)t-t^2}/2,�}��{7-4��3-(4-2��3)t+t^2}/4)
���a1�̐�`����ʐ�(2-t/2)��{1-(2-t/2)^2}�̎O�p�`�������ĎO�����`���o���Ȃ����ƍl����B
���邢��3�����`��1���킩�邩������Ȃ��Bx���ɐ����Ȃ�Ȃ�B >>842
�� - T[n] = (6/��)��[k=n+1 to ��] (1/kk)
�@�� (6/��)��[k=n+1 to ��] 4/(4kk-1)
�@= (6/��)��[k=n+1 to ��] {2/(2k-1) - 2/(2k+1)}
�@= 2(6/��)/(2n+1),
�� - S[n] = 4��[k=n+1 to ��] {(-1)^(k-1)}/(2k-1)
�@= 2(-1)^n /(2n+1) + 2��[k=n+1 to ��] {(-1)^(k-1)} {1/(2k-1) - 1/(2k+1)}
�@= 2(-1)^n /(2n+1) + 4��[k=n+1 to ��] {(-1)^(k-1)} /{(2k-1)(2k+1)}
�@= 2(-1)^n /(2n+1) + 4��[k=n+1 to ��] {(-1)^(k-1)} /(4kk-1)
�@�� 2(-1)^n /(2n+1),
S[n] - T[n] �� 2{(6/��) - (-1)^n}/(2n+1),
�������ɓ��.... >>833
log_2(x) + log_2(y) + log_2(z) = 1 + log_2(x+y+z)�@�������R���̑g (x,y,z) �ŁA
x��y��z �ł�����̂����ׂċ��߂�B
(����)
�@xyz = 2(x+y+z),
�@(x,y,z) = (1,3,8)�@(1,4,5)�@(2,2,4) ����l�p�`A�̊e�ӂ̒��_�_�Ƃ���l�p�`B�̖ʐς�A��1/2�ł��邱�Ƃ̏ؖ������肢���܂� A(i)�|A(i+1) �̒��_�� B(i) �Ƃ���B
��B1A1B4 = (1/4)��A2A1A4,
��B2A2B1 = (1/4)��A1A2A3,
��B3A3B2 = (1/4)��A2A3A4,
��B4A4B3 = (1/4)��A3A4A1,
�ӁX������
S(A) - S(B) = (��A2A1A4 + ��A2A3A4)/4 + (��A1A2A3 + ��A3A4A1)/4
�@= S(A)/4 + S(A)/4
�@= S(A)/2,
���@S(B) = S(A)/2, >>835
�@��������Ȃ��Ă������Ȃ�
���s�� AD�ABC �̊Ԋu���P�Ƃ���B
A (cot(48�), 1)
B (0, 0)
C (cot(48�)+cot(54�), 0)
D (cot(30�), 1)
cot(48�) = ��{2 + (5+2��5) -2(��3)��(5+2��5)}
cot(54�) = tan(36�) = ��(5-2��5)
cot(30�) = tan(60�) = ��3,
���
�@cot(30�) - cot(48�) - cot(54�)
= ��{2 + (5-2��5) -2(��3)��(5-2��5)}
= cot(84�)
��BCD = 96�
��ACD = 42� �O>>845���͂ł����B
6��[0�`1]{��[��(t-t^2/4)�`��3/2](1-t-��(1-x^2)dx+��[��3/2�`��3-t��3/2](1-t-x/��3)dx}dt
sin��=��(t-t^2/4),cos��=1-t/2�Ƃ����ƁA�����O�������o���ق��������ȁA�Ǝv���Ă���B �O>>852
���l�ʑ�PABC��z=t�Ő����f�ʂ́A�J�����̒��S�p��2�ƂƂ��āA
3��3(2-t/2)^2-1+3��-3sin2��
0��t��1�̂Ƃ�0���Ɓ���/3
�~���ł���ʂ��Ďc�����K���̑̐ς́A
��3��3(2-t/2)^2-1+3��-3sin2��d��dt[��=0�`��/3][t=0�`1] ���܂ł���Ă�����
30������Ώ\���Ȗ�肾�� ������P(z; 1)=�[n=0,��](1/2 C n)(z - 1)^n
��|z|=1�̎����~����̓_�𒆐S�Ƃ���e�C���[�W�J�����Ăǂ��Ȃ�̂ł��傤�� �O>>853
���l�ʑ�PABC��z=t�Ő����f�ʂ́A�J�����̒��S�p��2�ƂƂ��āA
3��3(2-t/2)^2-1+3��-3sin2��
0��t��1�̂Ƃ�0���Ɓ���/3
�~���ł���ʂ��Ďc�����K���̑̐ς́A
��3��3(2-t/2)^2-1+3��-3sin2��d��dt[��=0�`��/3][t=0�`1]
t=2(1-cos��)
��3��3{2-(1-cos��)}^2-1+3��-3sin2��d��[��=0�`��/3]
��3��3(1+cos��)^2-1+3��-3sin2��d��[��=0�`��/3]
=��3��3(1+2cos��+cos^2��)-1+3��-3sin2��d��[��=0�`��/3]
=��3��3(��+2sin��+��/2+sin2��/4)-1+3��-3sin2��d��[��=0�`��/3]
=3��3{��/3+2sin(��/3)+(��/3)/2+sin2(��/3)/4)-1+3(��/3)-3sin2(��/3)}
=3��3(��/3+��3+��/6+1/2)-1+��-3��3/2
=3��3(��/2+��3+1/2)-1+��-3��3/2
=3��3��/2+9+3��3/2-1+��-3��3/2
=(1+3��3/2)��+8
�v�Z�ԈႦ�����ȁH >>856 �����ƒP���ɍs���܂��傤��....
�~���������Ď�肷���������̑̐�(�O�������Č����Ă�����ȁH) �Ȃ�
������ȕ��j�ŋ��߂��܂�.
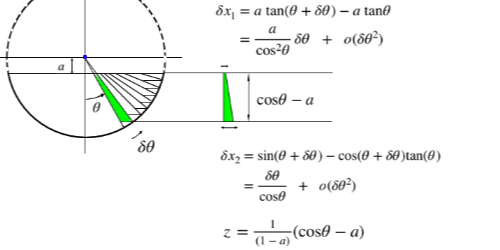
���a1����1�̉~�����ߐؒf�������̂̑̐� V �����߂���.
��ӂ̐ؒf�ʒu�� a , cos(��) = a �Ƃ��� c = cos�� �Ɨ��L����
V(a) = �� [��= -�� �` +��] d�� { (1/2).(a/cc) + (1/3).(1/c - a/cc) } (c-a)^2 . 1/(1-a)
= �� [��= -�� �` +��] d�� (a + 2c)(cc -2ac +aa) /6cc. 1/(1-a)
= �� [��= -�� �` +��] d�� ( 2c -3a +aaa/cc ) /6 . 1/(1-a)
= { 2.sin�� -3a.�� +aaa.tan�� } / {3(1-a)}
= { (2+aa)��(1-aa) - 3a.acos(a) } / {3(1-a)}
����� 0 �� a �� 1 �ł̏ؖ��ł����A-1 �� a < 0 �ł����̂܂ܓ��������g���܂�. (�ؖ��͗���)
�Ⴆ�� V(-1) = ��/2 ���A�������蔼���̐ςɂȂ��Ă�̂͐}�`�̑Ώ̐���������炩.
 >>853
>>853
���ǃz���g�̍ŏI�w�����ĂȂ�Ȃ�H �P]/�_______�O>>856
�Q/�_/�@�@,,���@�@/|
�P�_/�@�@�c-_-Ё@/ |
�P|�______U,��U�/| |__
�n| �a�P�P�PU~~U | / /
�Q| �a ���@�� �a |/ /
___`�a�Q�Q�Q�Q�a�^_/
�P�P�P�P�P�P�P�P�P�a
���@�@���@�@���@�@�a /
�Q�Q�Q�Q�Q�Q�Q�Q�Q�a/
�P�P�P�P�P�P�P�P�P�P
�Ԃ������Ă������傢�l����B 2��2019���5�Ŋ������]��
�������𗘗p���Ă��肢���܂� 2^2 = 4 �� -1 (mod 5)
2^(2*1009 + 1) = (2^2)^1009 * 2 �� (-1)^1009 * 2 = -2 �� 3 (mod 5) �O>>859
����1�̒P�ʉ~��(�̐σ�)�̒��S�p120���̐ؓ��O�����`�����O�����`��(�̐ς͂킩��)��1/2�Ȃ̂�2/3�Ȃ̂��A���l�ʑ�PABC�̒��ƊO�ł�����ɕ�������̂��B�������琄�肷��B �O>>862����Ɖ������B
���l�ʑ�PABC=1/3�3��3�2
=2��3
���l�ʑ�PABC��z=1����̕���(���l�ʑ�PABC��1/8)���o���A
2��3(7/8)=7��3/4
x^2+y^2��1��0��z��1�̉~��(�̐σ�)�����̐��O�p�����o���A
7��3/4-3��3/4=��3
���߂闧�̂̑̐�=��3-(��-3��3/4)(2/3)
=3��3/2-2��/3
=0.503681109�c�c >>842 >>846
�� - T[n] = (6/��)��[k=n+1 to ��] 1/kk
�@= 2(6/��){1/(2n+1) - 1/[3�(2n+1)^3] + 7/[15�(2n+1)^5] - 31/[21�(2n+1)^7] + ����}
�� - S[n] = 4��[k=n+1 to ��] {(-1)^(k-1)} /(2k-1)
�@= (-1)^n {1/n - 1/(4�n^3) + 5/(16�n^5) - 61/(64�n^7) + ���� }
���`�ށA������ ������I�C���[�}�N���[������1/n�œW�J�ł�����āB >>853 >>856
�@z = t�@�@�@�@(�� ���Ӗ�?)
�@������ (2-t)/2,
�@���̖ʐ� (3��3){(2-t)/2}^2,
�@�J�����̎O�p�`�̖ʐς́@cos��sin�� = (1/4)(2-t)��{t(4-t)},
�@����ȊO�̐�`�̖ʐς́A���S�p�̔����ŁA��/3 - �� = ��/3 - arccos((2-t)/2),
�@���`�R�̖ʐς�
�@�@(3��3){(2-t)/2}^2 - 3cos��sin�� - ��+ 3��
�@= (3��3){(2-t)/2}^2 - (3/4)(2-t)��{t(4-t)} - �� + 3arccos((2-t)/2),
����� 0<t<1 �Őϕ����� 4��3 - 2�� �O>>864
>>865�ɂ��ĉ�����܂��B
���l�ʑ�PABC(�̐�2��3)����A
���l�ʑ�PABC��z=1����̕���(���l�ʑ�PABC��1/8)���o���A
2��3(7/8)=7��3/4
x^2+y^2��1��0��z��1�̉~��(�̐σ�)�����̐��O�p��(3��3/4)���o���A
7��3/4-3��3/4=��3
�����܂ł��Ɛ��l�ʑ̓������i�C�t�Ő�o�����݂����ȏ�ԂȂ킯�ł��B
�������炳��Ƀ������̒��̉ʓ����X�v�[���ł��킰���Ƃ��݂����ɐ�o���Ȃ��ƁB
�͍���1�̉~���ł��B
3��3/4�͍���1�̐��O�p���ł��B
���߂闧�̂̑̐�=��3-(��-3��3/4)(2/3) ��2/3�Ƃ����͎̂O�����`���̓������o��������ł��B
�O�����`�����A���l�ʑ�PABC�̎߂̑��ʂ��A�����ƊO����2:1�ɕ������ł��B
���S�p��120���Ȃ�ŎO�����`�Ƃ��������g�`�ł��B
=3��3/2-2��/3
=0.503681109�c�c
����(2/3)�̔䗦�ɋC�Â��̂Ɏ��Ԃ�������܂����B
xy���ʂ�z=1���ʂ��O�����`���̏��Ɖ���͍����Ȋ��g�`�ł��B���l�ʑ�PABC�̑��ʂŎ߂ɐ����Ƃ��A�������ɂ͈�_�Ɏ������Ă����`�ł����A������ɂ͒����Ɏ������Ă����A���Ȃ킿���[�̓�_�ɁB
�����2:1�̔䗦�ɂȂ邱�Ƃ������ł��܂����B
>>868z=t���ʂŐ��Đϕ�����������d��(���͂�)���@��������Ȃ��Ǝv������ł����A��蒼���I�Ŋw�I�ȁA�������̐�o���̂悤�ȕ��@�ɕύX���܂����B
z=t�Ő�����œ����l���o���Ƃ́A����ς�0.6�c�c�������Ȃ̂��B ��������ł͂Ȃ��ďؖ������ĉ������B
����1:2�ɂȂ�́H �O>>869�ł����g�͎߂ɐ�ق����������āc�c
�Q/�Q/�Q/�Q/�Q/�Q/�Q/
�Q/�Q/�Q/�Q/�Q/�Q/�Q/
�Q/�Q/�Q/�Q/�Q��_/�Q/
�Q/_��~_/�Q�������̤/
�a�P�P�a�a( (-(`)�@)/
�a�_�^�a�a(`��,U�܁R/
�Q/�Q/�Q/_��_(�Q�Q�Q)
�Q/�Q/�Q/�Q�҃�_UU�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/�Q/ �ؒf�ʂ��߂�^���ɃX�p�b�Ɛ�ƒf�ʂɉ~�A�ȉ~�������Ėʓ|�B ������Ă݂���>>842�𑶍݂��Ȃ���ˁH
p<1����0�ɂȂ���p��1���ƐU��������B >>869
2:1 ���]�X�Ƃ���̂� ���g�ߐ肪���g���ɂȂ��Ă�Ǝv���� �u��� * ���� * (1/3)�v ���g���܂����H
�������f�ʂ��S�đ����`�� ���_����̋����ɔ�Ⴕ�ăT�C�Y���ς�� (�������̓���) �ꍇ��...
�� [z=0�`h] dz S (z/h)^2 = S.h.(1/3) �̂悤�� 1/3 �t�@�N�^�[������܂��B
����̂͂����ł͂���܂���B �Ⴆ�ΐ������f�ʂ͑����`�ł͂���܂���B
>>857 �œ��o�����ߐؒf�̎��g����
V(1/2) = { (2+1/4)��(1-1/4) - (3/2). acos(1/2) } / {3(1-1/2)} = (3/4).��3 - ��/3
{�l�ʑ� - (1/2).�l�ʑ�} - {�~��} + {�~���ō�肷������}
= (1- 1/8). 2��3 - �� + 3. { (3/4).��3 - ��/3 } = 4��3 - 2��
���ꂪ�����ł��B a, b �������Ƃ��A a < b �Ƃ���B��� [a, b] �� R �ƔZ�x�����������Ƃ��ȉ��̃q���g�𗘗p���Ď����B
�q���g�F A �� (a, b) ���Z�����W���Ƃ���A A �` A �� {a, b} �͔�r�I�ȒP�Ɏ������Ƃ��ł���B���ꂩ�� (a, b) �` [a, b] ���B �uA �` A �� {a, b} �͔�r�I�ȒP�Ɏ������Ƃ��ł���v
�Ə�����Ă��܂����A�����ł͂Ȃ��̂ł��傤���H �E�ӂ͗v�f�������Ă�̂ɔZ�x���������Ȃ��Ă܂���
�����ł͂Ȃ��ł�
{1}��{1,2,3}���炩�ɔZ�x���Ⴂ�܂���
����͂Ȃ��Z�x���������Ȃ�̂ł��傤�� �Z�����W���̒�`�ł����A N �ƔZ�x���������Ƃ��ɁA�Z�����W���ƒ�`���Ă��܂��B ���A�u�����v�Ƃ������������Ă���̂ŁA�����܂ł��Ȃ����Ƃł��ˁB A = {a_0, a_1, a_2, �c }
a_0 �� a
a_1 �� b
a_2 �� a_0
�c
a_k �� a_{k-2}
�c �̈�D_0�̓����ɐ����_a_0���Ƃ�Ca_0�𒆐S�Ƃ����e�C���[�W�J����f_0(z)�Ƃ���D
f_0(z)�̎����~D_1�����S��D_0�Ɋ܂܂�Ă���ꍇ�CD_1�̋��E�̉~����D_0�̋��E�̋Ȑ��ɓ��ڂ��邱�Ƃ������D D_0={|z|<1}�Œ�`���ꂽ��1/(z-2)�̎����~��|z|=2�B >>881
�̈�D_0�� f(z) �������iD_0�ɓ��ٓ_���Ȃ��j�Ƃ��������������Ă܂�B
>>884
�@f(z) = 1/(z-2)
�@D_0 = {z| |z|<1 }
�@a_0 = 0,
�Ƃ����
�@f_0(z) = -1/2 - z/4 - zz/8 - ����
�����~ D_1 = {z| |z|=2 }
���̏ꍇ�́u�����~D_1 �����S�� D_0 �Ɋ܂܂�Ă���v�����܂���B �O>>874
>>871�~���ō�肷�����͎̂O�����`��(���g)��1/3����Ȃ��̂��H
(�~��-���O�p��)(1/3)
=(��-3��3/4)(1/3) �����~�@D_1 = {z| |z-a0|=R }
�������a�@R = {a_0 ���� f(z)�̓��ٓ_�܂ł̋���(�̍ŏ��l)} >>886
��肷�����̂� �ߐ芗�g���R�ł��B (�ΐF)
V(1/2) = (3/4).��3 - ��/3
���ꂪ�ߐ芗�g�P�̑̐ςł��B�����P�Œ��S���� 1/2 �����Y�����Ƃ�����̎ߐ�ł��B
�Ȃ̂ő������ɂ͂R�{���Ă��܂��B+3. { (3/4).��3 - ��/3 }
 �c����V�E��ؓo�u�Y ���w���w�̃��W�b�N�ƏW���_�x��ǂ�ł��܂��B
�c����V�E��ؓo�u�Y ���w���w�̃��W�b�N�ƏW���_�x��ǂ�ł��܂��B
�J���g���E�x�����V���^�C���E�V�����[�_�[�̒藝�̏ؖ��Ɏg�����1.12�ip.57�j�̏ؖ��ł����A
�v���I�Ȍ������܂����B
���̂悤�Ȋ�{�I�Ȗ���̏ؖ��Ō��Ƃ����̂��M�����܂���B
�������A�������������Ƃ��d���郍�W�b�N��W���_�̖{�ɂ����Ăł��B
���̒��҂�͈�̉����l���Ă���̂ł��傤���H >>881
>>885 �̌����悤�� �u�̈�D_0�� f(z) �������v��t���������...
f(z) = (1/2��i) ��_{C} d�� f(��) / (�� - z) ���̌������g���܂��B (�����̏ؖ��̓R�[�V�[�̐ϕ��藝���g��)
�u�����~(���aR)���̈拫�E�ɐڂ��Ă��Ȃ��v�Ȃ�
R< R' �Ȃ�l���Ƃ��āA���S a ���a R' �̎��[�g C �����̓����� D0 �Ɋ܂܂��悤�ɂł��܂��B
|z-a| < R' �ƂȂ�C�ӓ_ z �ɑ��āA
f(z) = (1/2��i) ��{C} d�� f(��) / ( (��-a) - (z-a) )
= (1/2��i) ��{C} d�� f(��) �� (��-a)^{-k-1} (z-a)^{k} �@( |z-a|/|��-a| =|z-a|/R ' < 1 ��苉���͎�������)
= �� g_k /k! (z-a)^k �@( �W�J�W��: g_k = (k!/2��i) ��{C} d�� f(��) (��-a)^{-k-1} �� z �Ɉˑ����܂���)
����͎������a �� R' �ȏ�ł��鎖���Ӗ����܂��B
����āu�����~(���aR)���̈拫�E�ɐڂ��Ă��Ȃ��v�Ƃ����O��͌��ł��B �� ���̃X���b�h�͉ߋ����O�q�ɂɊi�[����Ă��܂�