2000�N�ȏ�O���炠���̊��S�������݂���̂��Ƃ���
���w��̖�������肪�A2018�N8��22���Ɋ��S�ȏؖ����������܂����B
���̏ؖ������S�ɐ������ƌ����ɔF�肵�Ă������������Ǝv���܂��B
�ؖ��_��
Pdf���� ���{��
http://fast-uploader.com/file/7090446873724/
Pdf���� �p��
http://fast-uploader.com/file/7090447044856/
(�O�X��)
��̊��S���̑��݂Ɋւ���ؖ����������܂���
https://rio2016.5ch.net/test/read.cgi/math/1533414338/
(������O�̃X��)
�ŌÂ̖�������肪�������ꂽ�̂�
https://rio2016.5ch.net/test/read.cgi/math/1522147912/
��̊��S���̑��݂Ɋւ���ؖ��͐������͂�
https://rio2016.5ch.net/test/read.cgi/math/1530434042/
(�֘A�X��)
��̊��S���̗L���ɂ��� [���f�]�ڋ֎~](c)2ch.net
https://rio2016.5ch.net/test/read.cgi/math/1483900653/
��̊��S���̗L���ɂ���2
https://rio2016.5ch.net/test/read.cgi/math/1523602627/
�T��
��̊��S���̑��݂Ɋւ���ؖ����������܂���2
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
2�P�R�Q�l�ڂ̑f������
2018/08/22(��) 10:48:12.41ID:S0tIMvkA ����]�����k�N�����]�l�y�����z�̈Ӗ�
�o�T�F�f�W�^���厫��i���w�فj
�m���n(�X��)���S�ɏo���オ�邱�ƁB��������d�グ�邱�ƁB�u����������v�u�r������������v�u������������v
�o�T�F�f�W�^���厫��i���w�فj
�m���n(�X��)���S�ɏo���オ�邱�ƁB��������d�グ�邱�ƁB�u����������v�u�r������������v�u������������v
3�P�R�Q�l�ڂ̑f������
2018/08/22(��) 11:42:59.56ID:JZ6XLANs �Ȃ��X���^�C�́u���݁v�̂܂�
�P�͉����w�K���Ȃ�
�P�͉����w�K���Ȃ�
4�P�R�Q�l�ڂ̑f������
2018/08/22(��) 11:56:13.96ID:sM8avlwB >���̏ؖ������S�ɐ������ƌ����ɔF�肵�Ă������������Ǝv���܂��B
1�͑O�X���ŏ��F���Ă����Ȃ��Ă��\��Ȃ��B�ɂԂ��ƒf�������͂�����
1�͑O�X���ŏ��F���Ă����Ȃ��Ă��\��Ȃ��B�ɂԂ��ƒf�������͂�����
6�P�R�Q�l�ڂ̑f������
2018/08/22(��) 12:11:46.77ID:pSDps/ix ���
2018/08/22(��) 12:12:09.52ID:DeGlo53d
���Ⴀ�ʂ̏ꏊ�ł���Ă�������
2018/08/22(��) 12:21:53.06ID:ML4zO2+g
����ȂƂ���ɔ��\���Ă��Ӗ����Ȃ��Ƃ������Ƃ�����ꂽ�͂�
�������悻�̃X���ɗ����Ă����f�Ȃ����Ȃ̂ł��̃X���Ŗό��𐂂ꗬ�����Ƃ͌������Ă��
�������悻�̃X���ɗ����Ă����f�Ȃ����Ȃ̂ł��̃X���Ŗό��𐂂ꗬ�����Ƃ͌������Ă��
2018/08/22(��) 12:34:22.86ID:EQFoBoDI
���ǁA���łł� �g���q�h �̈Ӗ��� �gQ[m]�̈��q�h �ɂ������悤���Ȃ��B
���Ƃ���f(pr)�̂�����h(pr)�Ɏ��ւ��ċc�_���Ă邯�ǁA���ǂ���� �gTi�����ׂ�2m+1�����q�ɂ����Ă邩��h �����ǂ��̎��_�ň��q��Q(m)�̈��q�̈Ӗ��ɂƂ�Ȃ��Ɛ������Ȃ��B
����p12�`p13�Ɏ���c�_�͂��ׂ�Q[m]�ɂ�����c�_�ōŏI�I�ɓ���ꂽ
2m + 1��pr^(qr�|cr�|1)�̔{��
�Ƃ������_�� �gQ[m]�ɂ����āh �ł����Ȃ��B
�܂�
2m+1��Q[m]�ɂ�����pr^(qr�|cr�|1)�̔{��
���ؖ������ɉ߂����A
2m + 1 = w pr^(qr�|cr�|1) �c�I
��w��Q[m]�̌��ł����Ȃ��B
�܂�w��m�̒l�ɉ����ĕω�����m�̐����B
��̓I�ɂ�w(m) = (2m+1)pr^(-pr+cr+1)�B
������m�����R�ϐ��Ƃ��Ă݂Ȃ����Ƃ���߂Č��̐����l�ɂƂ肩�����Ƃ�w(m)�͂�������ɂȂ�Ƃ͌���Ȃ��B
�I�ɂ�����w(m)�������łȂ��Ƃ��������ؖ��o���Ă��Ȃ���w=1�ȂǂƂ������_�͓��꓾���Ȃ��B
���Ƃ���f(pr)�̂�����h(pr)�Ɏ��ւ��ċc�_���Ă邯�ǁA���ǂ���� �gTi�����ׂ�2m+1�����q�ɂ����Ă邩��h �����ǂ��̎��_�ň��q��Q(m)�̈��q�̈Ӗ��ɂƂ�Ȃ��Ɛ������Ȃ��B
����p12�`p13�Ɏ���c�_�͂��ׂ�Q[m]�ɂ�����c�_�ōŏI�I�ɓ���ꂽ
2m + 1��pr^(qr�|cr�|1)�̔{��
�Ƃ������_�� �gQ[m]�ɂ����āh �ł����Ȃ��B
�܂�
2m+1��Q[m]�ɂ�����pr^(qr�|cr�|1)�̔{��
���ؖ������ɉ߂����A
2m + 1 = w pr^(qr�|cr�|1) �c�I
��w��Q[m]�̌��ł����Ȃ��B
�܂�w��m�̒l�ɉ����ĕω�����m�̐����B
��̓I�ɂ�w(m) = (2m+1)pr^(-pr+cr+1)�B
������m�����R�ϐ��Ƃ��Ă݂Ȃ����Ƃ���߂Č��̐����l�ɂƂ肩�����Ƃ�w(m)�͂�������ɂȂ�Ƃ͌���Ȃ��B
�I�ɂ�����w(m)�������łȂ��Ƃ��������ؖ��o���Ă��Ȃ���w=1�ȂǂƂ������_�͓��꓾���Ȃ��B
>>9
2m+1��pr^(qr-cr-1)�̔{���łȂ���Ȃ�Ȃ����Ƃ��ؖ����Ă���̂ŁAw�͐����ł�������܂���
2m+1��pr^(qr-cr-1)�̔{���łȂ���Ȃ�Ȃ����Ƃ��ؖ����Ă���̂ŁAw�͐����ł�������܂���
2018/08/22(��) 12:38:12.27ID:EQFoBoDI
>>9
✕�F�I�ɂ�����w(m)�������łȂ��Ƃ��������ؖ��o���Ă��Ȃ���w=1�ȂǂƂ������_�͓��꓾���Ȃ��B
���F�I�ɂ�����w(m)�������ł���Ƃ��������ؖ��o���Ă��Ȃ���w=1�ȂǂƂ������_�͓��꓾���Ȃ��B
✕�F�I�ɂ�����w(m)�������łȂ��Ƃ��������ؖ��o���Ă��Ȃ���w=1�ȂǂƂ������_�͓��꓾���Ȃ��B
���F�I�ɂ�����w(m)�������ł���Ƃ��������ؖ��o���Ă��Ȃ���w=1�ȂǂƂ������_�͓��꓾���Ȃ��B
2018/08/22(��) 12:39:48.90ID:q5K+5KiU
�O�X�X����105
>1�͂��̎�̊ԈႢ��O�X�����牽�x���J��Ԃ��Ă���BAB �� CD �Ƃ����������������Ƃ��ɁA
�u A �� C �������Ȃ��Ȃ�AA �� D ������� �v
�Ƃ����Ԉ�����_�@�ł���BA��C���݂��ɑf�Ȃ琳�����g����e�N�j�b�N�����A
�݂��ɑf�Ƃ͌���Ȃ��P�[�X�ł͑S���g���Ȃ��̂ł���B
�ɂ��ւ�炸�A>1�͏������˓I�ɉ��x�����̃~�X���J��Ԃ��Ă���B
>1�����̃~�X�������̂́A�������������͈͂����ł�3����x�͂������͂�(������܂߂�)�B
�����炭�A>1�̒��ł��̊ԈႦ���́u�N�Z�v�ɂȂ��Ă���B
>1�̔������������A>1�͂��̊ԈႦ����S�������ł��Ă��Ȃ��B
���l���炻�̓s�x�w�E����Ȃ���A�Ԉ���Ă��邱�Ƃ������ł��Ȃ��B
�ƂȂ�A��������̊ԈႦ�����J��Ԃ����̂Ǝv����B
>1�͂��̎�̊ԈႢ��O�X�����牽�x���J��Ԃ��Ă���BAB �� CD �Ƃ����������������Ƃ��ɁA
�u A �� C �������Ȃ��Ȃ�AA �� D ������� �v
�Ƃ����Ԉ�����_�@�ł���BA��C���݂��ɑf�Ȃ琳�����g����e�N�j�b�N�����A
�݂��ɑf�Ƃ͌���Ȃ��P�[�X�ł͑S���g���Ȃ��̂ł���B
�ɂ��ւ�炸�A>1�͏������˓I�ɉ��x�����̃~�X���J��Ԃ��Ă���B
>1�����̃~�X�������̂́A�������������͈͂����ł�3����x�͂������͂�(������܂߂�)�B
�����炭�A>1�̒��ł��̊ԈႦ���́u�N�Z�v�ɂȂ��Ă���B
>1�̔������������A>1�͂��̊ԈႦ����S�������ł��Ă��Ȃ��B
���l���炻�̓s�x�w�E����Ȃ���A�Ԉ���Ă��邱�Ƃ������ł��Ȃ��B
�ƂȂ�A��������̊ԈႦ�����J��Ԃ����̂Ǝv����B
2018/08/22(��) 12:40:25.55ID:q5K+5KiU
�E�P�̏��������̂�������ɂ���
�E�P�̏��������̂����������ǂ������ł��Ȃ�
�E����҂��P���l�|����
�E���炩�ȊԈႢ���w�E���Ă��P���������Ȃ�
�E�P�̑ԓx������
�E�P�����X�e���r���玩���̈�������������Ɣ�������
�E�P�̏��������̂����������ǂ������ł��Ȃ�
�E����҂��P���l�|����
�E���炩�ȊԈႢ���w�E���Ă��P���������Ȃ�
�E�P�̑ԓx������
�E�P�����X�e���r���玩���̈�������������Ɣ�������
2018/08/22(��) 12:40:42.69ID:q5K+5KiU
����܂ł̊�|�l�l�^
�Ep�͓���̒l�����͂�����0p=0�ł���s��ɂȂ邩�疵��
�Ep�͒萔�ł��肩�ϐ��ł���
�Ep���P����������i�{���͒P���������Ȃ��j����p�͑f���ɂȂ肦�Ȃ�
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł���
�Ew�͐����ł��蓯���ɐ����łȂ�
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ�
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂�
�E�ϐ��͐��l�ɒu�������Ă̓_��
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R
�E27/5 �� 3 �Ŋ�����
�Ep�͓���̒l�����͂�����0p=0�ł���s��ɂȂ邩�疵��
�Ep�͒萔�ł��肩�ϐ��ł���
�Ep���P����������i�{���͒P���������Ȃ��j����p�͑f���ɂȂ肦�Ȃ�
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł���
�Ew�͐����ł��蓯���ɐ����łȂ�
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ�
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂�
�E�ϐ��͐��l�ɒu�������Ă̓_��
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R
�E27/5 �� 3 �Ŋ�����
2018/08/22(��) 12:41:03.01ID:q5K+5KiU
���ɔn���ɔn���ƌ����A�n���ɂ������Ƃɂ͂Ȃ�
���ɔn���ؖ���n���ؖ��ƌ����Δn���ɂ������Ƃɂ͂Ȃ邵�A
���ɔn���_����n���_���ƌ����Δn���ɂ������Ƃɂ͂Ȃ邵�A
���ɔn�����҂�n�����҂ƌ����Δn���ɂ������Ƃɂ͂Ȃ�
���ɔn���ؖ���n���ؖ��ƌ����Δn���ɂ������Ƃɂ͂Ȃ邵�A
���ɔn���_����n���_���ƌ����Δn���ɂ������Ƃɂ͂Ȃ邵�A
���ɔn�����҂�n�����҂ƌ����Δn���ɂ������Ƃɂ͂Ȃ�
2018/08/22(��) 12:41:18.93ID:q5K+5KiU
�����̗���
1.�u�ԈႢ��������܂����A�P�܂��v
��
2.�u(���_�_����Ȃ��Ƃ���)���C�����܂����B�����ł��v
��
3.(�_�_�ɂ��ĕ�����Ă�)�u�������łɒ����܂���(�������ĂȂ�)�B�ǂ�ł��猾���Ă��������v
1.�u�ԈႢ��������܂����A�P�܂��v
��
2.�u(���_�_����Ȃ��Ƃ���)���C�����܂����B�����ł��v
��
3.(�_�_�ɂ��ĕ�����Ă�)�u�������łɒ����܂���(�������ĂȂ�)�B�ǂ�ł��猾���Ă��������v
2018/08/22(��) 12:42:03.17ID:q5K+5KiU
�P���\��܂�����֘A�X��
https://medaka.5ch.net/test/read.cgi/quiz/1282788303/
https://medaka.5ch.net/test/read.cgi/quiz/1282788303/
2018/08/22(��) 12:42:03.23ID:EQFoBoDI
>>10
���� �g�{���h �� �gQ[m]�ɂ����āh �ł��B
Q[m]�ɂ�����A��B�̔{��
�̒�`��
A = CB �ƂȂ� Q[m]�̌�C���Ƃ��
�Ȃ̂�
Q[m]�ɂ�����2m+1��pr^(qr-cr-1)�̔{��
�Ƃ�
2m+1 = w pr^(qr-cr-1) �ƂȂ� Q[m]�̌�w���Ƃ��
�Ȃ̂�w�͐����Ƃ͌���܂���B
���� �g�{���h �� �gQ[m]�ɂ����āh �ł��B
Q[m]�ɂ�����A��B�̔{��
�̒�`��
A = CB �ƂȂ� Q[m]�̌�C���Ƃ��
�Ȃ̂�
Q[m]�ɂ�����2m+1��pr^(qr-cr-1)�̔{��
�Ƃ�
2m+1 = w pr^(qr-cr-1) �ƂȂ� Q[m]�̌�w���Ƃ��
�Ȃ̂�w�͐����Ƃ͌���܂���B
2018/08/22(��) 12:42:25.94ID:q5K+5KiU
�搶�u���̎��������R�� p �͂������v
�@�@�@�@p * p = 4
������u�E�� p �͂P�B���͂S�ł��B�v
������up�͌Œ�l�ł͂Ȃ��̂ł����l���邱�Ƃ��ł���Ƃ������Ɓv
������u�悭�ǂ�ł��甽�_���Ă��炢�����A���̍l���ɒl���Ȃ��������肾�v
������u���ꂩ��A�l���ɒl���Ȃ��t�ق̓��X�͖�������v
�@�@�@�@p * p = 4
������u�E�� p �͂P�B���͂S�ł��B�v
������up�͌Œ�l�ł͂Ȃ��̂ł����l���邱�Ƃ��ł���Ƃ������Ɓv
������u�悭�ǂ�ł��甽�_���Ă��炢�����A���̍l���ɒl���Ȃ��������肾�v
������u���ꂩ��A�l���ɒl���Ȃ��t�ق̓��X�͖�������v
2018/08/22(��) 12:42:53.15ID:q5K+5KiU
�������߂łƂ��������܂��I
�@�@�@ .���.߁B.�B
�@�@�:���E�B߁�*.ߡ
�@ ���.���.�����:*�.
�@.߁�.�;���.:*��.ߡ
�@ :*�_�����_��*�_�
�@�@�_�́@�_�@ �ā^
�@�@�@��,,�ȁ_ ��
�@�@ (�L��֥`)�^
�@�@ /�@ ��o
�@�@ ���[-�i
���������̂ɁA�Ȃ�ō��X��`�̌����C������́H
���������ł�����
�@�@�@ .���.߁B.�B
�@�@�:���E�B߁�*.ߡ
�@ ���.���.�����:*�.
�@.߁�.�;���.:*��.ߡ
�@ :*�_�����_��*�_�
�@�@�_�́@�_�@ �ā^
�@�@�@��,,�ȁ_ ��
�@�@ (�L��֥`)�^
�@�@ /�@ ��o
�@�@ ���[-�i
���������̂ɁA�Ȃ�ō��X��`�̌����C������́H
���������ł�����
2018/08/22(��) 12:49:56.58ID:GBkE0PVl
�O995
��2m+1�ȊO�̈�����u(pr)�Ƃ��Ah(pr)=(2m+1)u(pr)
�������藧�ꍇ�ɁA�L����������u(pr)��pr�Ŋ�����Ȃ����Ƃ��ؖ����Ă��܂��B
�u�L����������u(pr)���v�Ƃ����������C�ɂȂ�B
�E pr��f���Ƃ��āA�L����u(pr)��������Z�ɂ����Ď��ۂɂ͐����ɂȂ��Ă��邱�Ƃ��ؖ����āA
�@ ������u(pr)��Z�ɂ����đf��pr�Ŋ����Ȃ����Ƃ��ؖ������̂��H
�E ����Ƃ��Apr��ϐ��Ƃ��āApr�̑�����u(pr)��Q[pr]�ɂ����đ����� pr �Ŋ����Ȃ����Ƃ��ؖ������̂��H
�@ (����������Ax�̑�����u(x)����������Q[x]�ɂ����đ����� x �Ŋ����Ȃ����Ƃ��ؖ������̂��H)
������҂Ȃ�A����Ȃ��Ƃ������Ă��Ӗ����Ȃ��B
x��pr�������Đ�����Z�Ɉڍs�����Ƃ��ɂ͈��q�̊W������邩��B
��Fx�̑�����u(x)��(4/5)x�{1�́AQ[x]�ɂ����đ����� x �Ŋ����Ȃ����A
pr��5�Ƃ���Ƃ��Au(pr)�͐�����Z�ɂ�����pr�Ŋ�����B�Ȃ��Ȃ�A
u(pr)��u(5)��5��pr�Ȃ̂ŁB
��2m+1�ȊO�̈�����u(pr)�Ƃ��Ah(pr)=(2m+1)u(pr)
�������藧�ꍇ�ɁA�L����������u(pr)��pr�Ŋ�����Ȃ����Ƃ��ؖ����Ă��܂��B
�u�L����������u(pr)���v�Ƃ����������C�ɂȂ�B
�E pr��f���Ƃ��āA�L����u(pr)��������Z�ɂ����Ď��ۂɂ͐����ɂȂ��Ă��邱�Ƃ��ؖ����āA
�@ ������u(pr)��Z�ɂ����đf��pr�Ŋ����Ȃ����Ƃ��ؖ������̂��H
�E ����Ƃ��Apr��ϐ��Ƃ��āApr�̑�����u(pr)��Q[pr]�ɂ����đ����� pr �Ŋ����Ȃ����Ƃ��ؖ������̂��H
�@ (����������Ax�̑�����u(x)����������Q[x]�ɂ����đ����� x �Ŋ����Ȃ����Ƃ��ؖ������̂��H)
������҂Ȃ�A����Ȃ��Ƃ������Ă��Ӗ����Ȃ��B
x��pr�������Đ�����Z�Ɉڍs�����Ƃ��ɂ͈��q�̊W������邩��B
��Fx�̑�����u(x)��(4/5)x�{1�́AQ[x]�ɂ����đ����� x �Ŋ����Ȃ����A
pr��5�Ƃ���Ƃ��Au(pr)�͐�����Z�ɂ�����pr�Ŋ�����B�Ȃ��Ȃ�A
u(pr)��u(5)��5��pr�Ȃ̂ŁB
22�P�R�Q�l�ڂ̑f������
2018/08/22(��) 13:27:21.38ID:sM8avlwB >>16
�܂��ɂ���B�������Ȃ����̂�F�߂����Ăǂ��������̂��킩���
�܂��ɂ���B�������Ȃ����̂�F�߂����Ăǂ��������̂��킩���
23�P�R�Q�l�ڂ̑f������
2018/08/22(��) 13:33:41.77ID:uI/lOkSR �Ꭶ
x=3�̂Ƃ�
������x�͑�����(5/3)x�̈����ł��邪�A����x�͐���(5/3)x�̈����łȂ�
������x�͑�����(5/3)x+1�̈����łȂ����A����x�͐���(5/3)x+1�̈����ł���
�������̈����Ɛ����̈����͂܂������ʕ�
�����������ɂ���̂͂��̍ۂ����ς��߂Ă͂ǂ����B
x=3�̂Ƃ�
������x�͑�����(5/3)x�̈����ł��邪�A����x�͐���(5/3)x�̈����łȂ�
������x�͑�����(5/3)x+1�̈����łȂ����A����x�͐���(5/3)x+1�̈����ł���
�������̈����Ɛ����̈����͂܂������ʕ�
�����������ɂ���̂͂��̍ۂ����ς��߂Ă͂ǂ����B
2018/08/22(��) 14:09:55.81ID:EQFoBoDI
�ꉞ������l�����ɁB
��f��p,q��p = 2q + 1�̊W�ɂ���
v_q((p^(n+1)-1)/(p-1)) = e
�ł���Ƃ�
v_q((p^(n+1)-1)/(p-1))
= v_q((1-2q)^(2n+2) - 1^(n+1))
= v_q (1-2q - 1) + v_q(n+1)�@�@�@�@(�� ��ʂ� a��b (mod q)�Aa,b��q�̔{���łȂ��Ƃ� v_q(a^i - b^i) = v_q(a-b) + v_q(i)�B)
= 1+v_q(n+1)
�Ȃ̂�>>1�̘_������p = 2qr+1�̏ꍇv_pr((p^(n+1)-1)/(p-1))=qr-cr-1�Ƃ����̂͑����������B
�܂�
2m+1 = w pr^(qr-cr-1) (��w : �)
��p = 2pr + 1�ł���ꍇ�ɂ͐������B
�ł����ꂪ�C�ӂ�r�Ő�������킯�ł͂Ȃ��̂ňȍ~�̋c�_�͐������Ă܂���B
��f��p,q��p = 2q + 1�̊W�ɂ���
v_q((p^(n+1)-1)/(p-1)) = e
�ł���Ƃ�
v_q((p^(n+1)-1)/(p-1))
= v_q((1-2q)^(2n+2) - 1^(n+1))
= v_q (1-2q - 1) + v_q(n+1)�@�@�@�@(�� ��ʂ� a��b (mod q)�Aa,b��q�̔{���łȂ��Ƃ� v_q(a^i - b^i) = v_q(a-b) + v_q(i)�B)
= 1+v_q(n+1)
�Ȃ̂�>>1�̘_������p = 2qr+1�̏ꍇv_pr((p^(n+1)-1)/(p-1))=qr-cr-1�Ƃ����̂͑����������B
�܂�
2m+1 = w pr^(qr-cr-1) (��w : �)
��p = 2pr + 1�ł���ꍇ�ɂ͐������B
�ł����ꂪ�C�ӂ�r�Ő�������킯�ł͂Ȃ��̂ňȍ~�̋c�_�͐������Ă܂���B
2018/08/22(��) 14:11:11.63ID:EQFoBoDI
2018/08/22(��) 14:47:41.67ID:TjDmvh6J
���̃X���ł͑����������Ƃ��ؖ��ł����Ǝv���܂��݂����ȕ\������������Ă�́H
2018/08/22(��) 14:50:35.15ID:q5K+5KiU
����܂����Ă邯�ǁA�P�ɂ͕������Ȃ�
28�P�R�Q�l�ڂ̑f������
2018/08/22(��) 14:58:44.64ID:+1hzjMAH >>24
v_q((p^(n+1)-1)/(p-1)) = v_q(n+1) �Ƃ��Ⴄ��H
v_q((p^(n+1)-1)/(p-1)) = v_q(n+1) �Ƃ��Ⴄ��H
2018/08/22(��) 15:21:12.18ID:8/rMiWdF
>>28
���A����A�����ł��B�}1����ēǂ�ʼn������B
���̌�Ȃ������̋c�_���S�Ă�pr�Ő������鎖�𗘗p���ċc�_���i�݂܂����Ap=2pr+1�𗘗p���Ă�̂ő��̑f���q�ɂ͎g���܂���B�ؖ��������Ώ����͍L�����邩������܂��B
���A����A�����ł��B�}1����ēǂ�ʼn������B
���̌�Ȃ������̋c�_���S�Ă�pr�Ő������鎖�𗘗p���ċc�_���i�݂܂����Ap=2pr+1�𗘗p���Ă�̂ő��̑f���q�ɂ͎g���܂���B�ؖ��������Ώ����͍L�����邩������܂��B
2018/08/22(��) 15:23:23.53ID:8/rMiWdF
>>26
���������킯�ł��Ȃ����ljɂԂ��Ȃ̂ł����܂ŃL�b�`�������Ȃ��ŏ����Ă�̂ŁB
���������킯�ł��Ȃ����ljɂԂ��Ȃ̂ł����܂ŃL�b�`�������Ȃ��ŏ����Ă�̂ŁB
2018/08/22(��) 16:34:20.17ID:cFHdshZo
r=
2018/08/22(��) 16:47:47.10ID:q5K+5KiU
�ł����ꂪ�C�ӂ�r�Ő�������킯�ł͂Ȃ��̂ňȍ~�̋c�_�͐������Ă܂���B
2018/08/22(��) 17:14:51.76ID:VOw4FIFW
>>31
2m+1��pr^(qr - cr -1)�Ŋ�����c(��)
�̓��o��
p = 2pr -1�c(��)
�𗘗p���Ă��܂��B
�_�����ł͂�������ĂȂ������ł��B
�������Ă��悤���A���܂����A�g���ē��o���Ă�̂�����(��)�𗘗p����Ȃ�(��)�����藧���Ă���pr�łȂ���_���ł��B
�������� b ��pi^qi�Ŋ�����̂͑���i�ł��������Ă܂����A���̂��Ƃ�����p����(��)�o�ł��Ă��܂���B
2m+1��pr^(qr - cr -1)�Ŋ�����c(��)
�̓��o��
p = 2pr -1�c(��)
�𗘗p���Ă��܂��B
�_�����ł͂�������ĂȂ������ł��B
�������Ă��悤���A���܂����A�g���ē��o���Ă�̂�����(��)�𗘗p����Ȃ�(��)�����藧���Ă���pr�łȂ���_���ł��B
�������� b ��pi^qi�Ŋ�����̂͑���i�ł��������Ă܂����A���̂��Ƃ�����p����(��)�o�ł��Ă��܂���B
2018/08/22(��) 18:51:46.55ID:8/rMiWdF
>>36
c���ςƂ��Ȃ�Ƃ��͂ǂ��ł���낵���B
p = 2pr+1
�𗘗p���Ă�̂����炱�ꂪ�������Ȃ��ƃ_���ł��B
���p���Ă�ł���H
p = 2pr -1�c(��)
���c�_�̂͂��܂�ŁA��������
f(pr) = ((2pr-1)^(n+1) - 1)/(2pr-2) = 1+p+�c+p^n
�ƂȂ���
f(pr)��pr��multiplicity = 1+p+�c+p^n��pr��multiplicity�c(��)
�ʼnE�ӂ�qr-cr�ɓ����������ׂĂ̋c�_�̏o���_�ł���H
(���Ȃ݂�multiplicity�͂��̑f���ʼn�����Ă邩�̒l�ł��B)
���ꂩ��b��h(pr)�ɒu�������āc���_���ł���Ă邱�Ƃł���H
���̕����ɂ����q��肪�����đS�R�c�_�������Ă܂��A�ʂ̓��ł��Ȃ����������_
2m+1 ��pr ��multiplicity = qr - cr -1�c�I�̂�����ƑO(�������}1����Ă邩������܂��B�����Ɛ������ĂȂ��̂ŁB)
�Ɏ�����@�͂���܂��B
�����������(��)�A�Ђ��Ă�(��)�����ׂĂ̋c�_�̎n�܂�ł��ꂪ�������ĂȂ��ƂȂɂ��ł��܂���B
�v��b�Ƃ�c�Ƃ��ǂ��ł���낵���B
p �� pr �ɂ���(��)���������ĂȂ��ƇI�o�ł��܂���B
������(��)���݂����Ă�pr�͈�����ő��̑f���q�ɂ��Ă͂Ȃ�ɂ��킩��܂���B
c���ςƂ��Ȃ�Ƃ��͂ǂ��ł���낵���B
p = 2pr+1
�𗘗p���Ă�̂����炱�ꂪ�������Ȃ��ƃ_���ł��B
���p���Ă�ł���H
p = 2pr -1�c(��)
���c�_�̂͂��܂�ŁA��������
f(pr) = ((2pr-1)^(n+1) - 1)/(2pr-2) = 1+p+�c+p^n
�ƂȂ���
f(pr)��pr��multiplicity = 1+p+�c+p^n��pr��multiplicity�c(��)
�ʼnE�ӂ�qr-cr�ɓ����������ׂĂ̋c�_�̏o���_�ł���H
(���Ȃ݂�multiplicity�͂��̑f���ʼn�����Ă邩�̒l�ł��B)
���ꂩ��b��h(pr)�ɒu�������āc���_���ł���Ă邱�Ƃł���H
���̕����ɂ����q��肪�����đS�R�c�_�������Ă܂��A�ʂ̓��ł��Ȃ����������_
2m+1 ��pr ��multiplicity = qr - cr -1�c�I�̂�����ƑO(�������}1����Ă邩������܂��B�����Ɛ������ĂȂ��̂ŁB)
�Ɏ�����@�͂���܂��B
�����������(��)�A�Ђ��Ă�(��)�����ׂĂ̋c�_�̎n�܂�ł��ꂪ�������ĂȂ��ƂȂɂ��ł��܂���B
�v��b�Ƃ�c�Ƃ��ǂ��ł���낵���B
p �� pr �ɂ���(��)���������ĂȂ��ƇI�o�ł��܂���B
������(��)���݂����Ă�pr�͈�����ő��̑f���q�ɂ��Ă͂Ȃ�ɂ��킩��܂���B
38�P�R�Q�l�ڂ̑f������
2018/08/22(��) 19:38:29.13ID:rbmhU+3R �_���Q�y�[�W�Łwy�̑f�����̎w���͈������x�Ɩ��L���Ă���A
�_���ł͂��̂����������̎w�������f������p�Ƃ��Ă���B
�Z�p�̊�{�藝���A�ŏ��ɉ��肵��y�ɑ���p�͈�ӂɒ�܂�B
����p�ɑ���(p+1)/2��y�̈����Ƃ��������͌����邪�A
p�ȊO�̂����Ȃ�f����pk�ɂ��Ă�(pk+1)/2��y�̈����Ƃ͌����Ȃ��B
��������p����ӂ�����p=2pk-1����������悤��k��y�ɑ��Ĉ�ӂƂȂ�B
�܂����A�P�͎Z�p�̊�{�藝���m��Ȃ��̂����H�܂����ˁB
�_���ł͂��̂����������̎w�������f������p�Ƃ��Ă���B
�Z�p�̊�{�藝���A�ŏ��ɉ��肵��y�ɑ���p�͈�ӂɒ�܂�B
����p�ɑ���(p+1)/2��y�̈����Ƃ��������͌����邪�A
p�ȊO�̂����Ȃ�f����pk�ɂ��Ă�(pk+1)/2��y�̈����Ƃ͌����Ȃ��B
��������p����ӂ�����p=2pk-1����������悤��k��y�ɑ��Ĉ�ӂƂȂ�B
�܂����A�P�͎Z�p�̊�{�藝���m��Ȃ��̂����H�܂����ˁB
2018/08/22(��) 19:58:46.37ID:fJ5OxbRN
���܂����A�P�͎Z�p�̊�{�藝���m��Ȃ��̂����H
���R�m��Ȃ��̂ł���B
���R�m��Ȃ��̂ł���B
40�P�R�Q�l�ڂ̑f������
2018/08/22(��) 21:08:22.98ID:sM8avlwB �����Ɍ��J���Ă���Ƃ����F�߂Ă����l�������ƂP�͍l���Ă�悤�����A���ꂾ��
"�]���̈����L��"���Ă�ƕs������
"�]���̈����L��"���Ă�ƕs������
2018/08/22(��) 22:00:38.24ID:fJ5OxbRN
�����ł����P�̑�������Ă���Ȃ����A
�P�������ς�����Ă��Ȃ��������w�������Ă����̂����������B
���S�n���ǂ��炵�����N���߂����₪�����B
�P�������ς�����Ă��Ȃ��������w�������Ă����̂����������B
���S�n���ǂ��炵�����N���߂����₪�����B
>>37
2b=c(p^n+�c+1)
�ƂȂ�Ac���ek�ɑ��ĕω�����̂ŁAp�����������Ă��\��Ȃ��Ƃ����l���ł��B
>>38
b��pr^qr�Ŋ����������Ƃ��āA���I���o���Ă���̂ŁAb��pk^qk�Ŋ�������
���͔C�ӂ�k�ɑ��Ď��I���������Ȃ��Ƃ��������Ƃ������Ƃł��B
>>39
����������A�f���������̈�Ӑ��ł����B���ꂮ�炢�͒m���Ă��܂��B
>>40
���̓��e�͂��Ȃ����̂ŁA���w�͂������l�ɂ������̐������͔��f�ł��Ȃ��̂ł��傤�B
2b=c(p^n+�c+1)
�ƂȂ�Ac���ek�ɑ��ĕω�����̂ŁAp�����������Ă��\��Ȃ��Ƃ����l���ł��B
>>38
b��pr^qr�Ŋ����������Ƃ��āA���I���o���Ă���̂ŁAb��pk^qk�Ŋ�������
���͔C�ӂ�k�ɑ��Ď��I���������Ȃ��Ƃ��������Ƃ������Ƃł��B
>>39
����������A�f���������̈�Ӑ��ł����B���ꂮ�炢�͒m���Ă��܂��B
>>40
���̓��e�͂��Ȃ����̂ŁA���w�͂������l�ɂ������̐������͔��f�ł��Ȃ��̂ł��傤�B
>>41
�������̂��߂ɂ��ꂾ�����Ԃ��|�������Ƃ������Ƃł����Ȃ��B
�������̂��߂ɂ��ꂾ�����Ԃ��|�������Ƃ������Ƃł����Ȃ��B
y��p����Έ�Ή�����͓̂��R�ł����Ap�������������ꍇ�͂���
��̊��S�����������݂���Ƃ��������ʼn��̖�������܂���
��̊��S�����������݂���Ƃ��������ʼn��̖�������܂���
2018/08/22(��) 22:15:32.20ID:n6D4ACsY
�����̔����͂��Ȃ����B���͂␔�w����Ȃ��B
46�P�R�Q�l�ڂ̑f������
2018/08/22(��) 22:19:04.18ID:X5MN+zZX �P�u��̊��S���͊�f���̐��������݂���Ɖ���ł��܂��B������A��̊��S���͖����ɑ��݂��܂��v
47�P�R�Q�l�ڂ̑f������
2018/08/22(��) 22:33:38.22ID:5lRrIxGh >>46
�Ȃ�قǂˁB
�P�̔�����f���ɉ��߂���Ƃ����Ȃ��
��p�������������ꍇ�͂�����̊��S�����������݂���Ƃ��������ʼn��̖�������܂���
�Ƃ������Ƃ́A�P�̉ߋ��̎咣�ɂ��ƁA��f�� p ������ƁA
�i�����͕�����Ȃ����j�������� b �� c ������ł��A2b=c(p^n+�c+1) �ƂȂ�悤�ɂł���B
�����Ȃ� b �� p ���g���� y=b�~p^n �Ƃ���ƁAy �͊�̊��S���ɂȂ�B
����āA��f���̐��������S�������݂���Ƃ��������ɂ͂Ȃ�ȁB�S�������ł��Ȃ����B
�X���^�C�͊Ԉ���Ă��Ȃ������킯���B
�Ȃ�قǂˁB
�P�̔�����f���ɉ��߂���Ƃ����Ȃ��
��p�������������ꍇ�͂�����̊��S�����������݂���Ƃ��������ʼn��̖�������܂���
�Ƃ������Ƃ́A�P�̉ߋ��̎咣�ɂ��ƁA��f�� p ������ƁA
�i�����͕�����Ȃ����j�������� b �� c ������ł��A2b=c(p^n+�c+1) �ƂȂ�悤�ɂł���B
�����Ȃ� b �� p ���g���� y=b�~p^n �Ƃ���ƁAy �͊�̊��S���ɂȂ�B
����āA��f���̐��������S�������݂���Ƃ��������ɂ͂Ȃ�ȁB�S�������ł��Ȃ����B
�X���^�C�͊Ԉ���Ă��Ȃ������킯���B
2018/08/22(��) 22:35:44.58ID:+4gdWOUh
>>42
2b=c(p^n+�c+1)�ƂȂ�Ac���ek�ɑ��ĕω�����̂ŁAp�����������Ă��\��Ȃ��Ƃ����l���ł��B
2b=c(p^n+�c+1)�ōŏ��ɑI��p�ȊO�œ����c�_�����悤�Ǝv���Ă������͂����܂���B
p���������Ό��̐�����n�������܂��Bcr���ω����܂��B
�����Ă��̕ω�������p(����q�Ƃ��܂��傤�B)q = 2qr -1�ƂȂ�qr�͑��݂��邩�ǂ����킩��܂���B
I �̉���͍ŏ���p�ɂ�������p = 2pr-1�ƂȂ�pr�����݂���Ƃ��ł��B
�����q = 2qr -1�ƂȂ�qr���������Ƃ��܂��傤�B
���������̂Ƃ�n��cr�����Ƃ�n��cr�Ƃ͈Ⴄ�������ł��B
�����
2y = (1+q+�c+q^n�f)A�f =2q^m B�f
��n�f��q��p�ȊO�̑f���q�Ȃ̂�n�f�͋����ł��B
�܂�u�I�o�����̂Ɠ��l�Ɂv�͒ʗp���܂���B
����������ʼn��ɂȂɂ�n�f��qs-cs�f�ɂ��Ă̏��
(��������� n�f �̎�) =qr�f - cr�f - 1
�̂悤�Ȍ`�œ����Ă������� n �� m �͏o�Ă��܂���B
�܂肱�ꂩ��
2m + 1 = w�fps^(qs - cs -1)
���������킯�ł͂���܂���B
2b=c(p^n+�c+1)�ƂȂ�Ac���ek�ɑ��ĕω�����̂ŁAp�����������Ă��\��Ȃ��Ƃ����l���ł��B
2b=c(p^n+�c+1)�ōŏ��ɑI��p�ȊO�œ����c�_�����悤�Ǝv���Ă������͂����܂���B
p���������Ό��̐�����n�������܂��Bcr���ω����܂��B
�����Ă��̕ω�������p(����q�Ƃ��܂��傤�B)q = 2qr -1�ƂȂ�qr�͑��݂��邩�ǂ����킩��܂���B
I �̉���͍ŏ���p�ɂ�������p = 2pr-1�ƂȂ�pr�����݂���Ƃ��ł��B
�����q = 2qr -1�ƂȂ�qr���������Ƃ��܂��傤�B
���������̂Ƃ�n��cr�����Ƃ�n��cr�Ƃ͈Ⴄ�������ł��B
�����
2y = (1+q+�c+q^n�f)A�f =2q^m B�f
��n�f��q��p�ȊO�̑f���q�Ȃ̂�n�f�͋����ł��B
�܂�u�I�o�����̂Ɠ��l�Ɂv�͒ʗp���܂���B
����������ʼn��ɂȂɂ�n�f��qs-cs�f�ɂ��Ă̏��
(��������� n�f �̎�) =qr�f - cr�f - 1
�̂悤�Ȍ`�œ����Ă������� n �� m �͏o�Ă��܂���B
�܂肱�ꂩ��
2m + 1 = w�fps^(qs - cs -1)
���������킯�ł͂���܂���B
2018/08/22(��) 22:38:06.19ID:fJ5OxbRN
>>19 ����
���؎���ł́A�P�ϐ����������̒l���Ɏ��ƁB
���؎���ł́A�P�ϐ����������̒l���Ɏ��ƁB
2018/08/23(��) 00:47:55.13ID:jIv6qxil
��������p�̂����̑f���qq����������y = q^l B�f(B�f��q�ƌ݂��ɑf)�Ƃ������Ƃ���l�͊����Ȃ�����l = 4k+1�ƒu�����Ƃ��ł��Ȃ����A
�����B�f��(q+1)/2�̔{���ł���Ƃ��炢���Ȃ��B
����ȏłȂ��p�����ւ��Ă������Ǝv����낤�H
���ւ��Ă������̂��ȂƊ��Ⴂ���Ă��A�`�F�b�N���Ă݂�P�������炸�_���ƕ����肻���Ȃ����ǁB
�����B�f��(q+1)/2�̔{���ł���Ƃ��炢���Ȃ��B
����ȏłȂ��p�����ւ��Ă������Ǝv����낤�H
���ւ��Ă������̂��ȂƊ��Ⴂ���Ă��A�`�F�b�N���Ă݂�P�������炸�_���ƕ����肻���Ȃ����ǁB
2018/08/23(��) 01:45:54.86ID:HquG05xP
���Ɉˑ����Ă邩���킩��悤�ɁAp(y)�Ƃ������Ă݂���ǂ����ˁH
�������Ⴄy�Ɉˑ�����Ȃ炻�ꂪ�킩��悤�ɁB
���������Ȃ���A���ĂȂ�Ǝv�����ǁc�c
�������Ⴄy�Ɉˑ�����Ȃ炻�ꂪ�킩��悤�ɁB
���������Ȃ���A���ĂȂ�Ǝv�����ǁc�c
2018/08/23(��) 02:22:39.37ID:HquG05xP
�u�C�ӂ̊�̊��S��y�ɑ���, �w�������y�̑f����p(y)����������݂�, p(y)��1(mod 4)�v
�͐^����
�u�C�ӂ̊�f��p,p��1(mod 4)�ɑ���, p=p(y)�ƂȂ��̊��S��y�����݂���v
�͕K�������^�ł͂Ȃ�(�t�͐^�Ȃ炸)
�����, p_k�ɑ��đΉ�����p������Ƃ͌�����
�͐^����
�u�C�ӂ̊�f��p,p��1(mod 4)�ɑ���, p=p(y)�ƂȂ��̊��S��y�����݂���v
�͕K�������^�ł͂Ȃ�(�t�͐^�Ȃ炸)
�����, p_k�ɑ��đΉ�����p������Ƃ͌�����
>>47
���x�������Ƃ�����������
pk�Aqk��ݒ肷�遨a,b�����肷�遨����ɑΉ�����Ap,c,n(�����ł���)����܂��y����܂�
>>48
b��pr^qr�ɂ���Ċ����������͎��I�ł���A����ȊO�ɂ͈ˑ����Ȃ��Ƃ������ʂɂȂ�܂��B
�܂�A�r���ŏo�Ă���p�ɂّ͈����Ȃ�����A����k�ɑ��Ă����l�Ɏ��I���������Ȃ����
�Ȃ�Ȃ��Ƃ������ƂɂȂ�܂��B���R�Ak�ɂ��p�̒l�͕�����܂�܂��B���ꂪ�A�f���ł��낤��
�Ȃ��낤�ƂƂ������Ƃł��B
���x�������Ƃ�����������
pk�Aqk��ݒ肷�遨a,b�����肷�遨����ɑΉ�����Ap,c,n(�����ł���)����܂��y����܂�
>>48
b��pr^qr�ɂ���Ċ����������͎��I�ł���A����ȊO�ɂ͈ˑ����Ȃ��Ƃ������ʂɂȂ�܂��B
�܂�A�r���ŏo�Ă���p�ɂّ͈����Ȃ�����A����k�ɑ��Ă����l�Ɏ��I���������Ȃ����
�Ȃ�Ȃ��Ƃ������ƂɂȂ�܂��B���R�Ak�ɂ��p�̒l�͕�����܂�܂��B���ꂪ�A�f���ł��낤��
�Ȃ��낤�ƂƂ������Ƃł��B
2018/08/23(��) 08:58:59.52ID:jjOcfQbu
�܂�y�����߂Ă���Ƃ����̂������ł��ĂȂ���ł����H
2018/08/23(��) 09:10:50.09ID:jjOcfQbu
��������y�����߂Ă��ł���ˁH
�_����ǂ�ł�������
�_����ǂ�ł�������
2018/08/23(��) 09:12:44.91ID:I1eZArX+
y��������������
>>57
��`�͂��Ă��܂����A�l�͒�߂Ă��܂���
��`�͂��Ă��܂����A�l�͒�߂Ă��܂���
2018/08/23(��) 09:45:38.34ID:aDhxWP96
�����̔����������ɈӖ��s������{�l�ɗ��������邽�߂ɉ��炪�ł��邱�Ƃ͉���
2018/08/23(��) 10:05:11.72ID:K06i0J+R
����܂ł̊�|�l�l�^
�Ep�͓���̒l�����͂�����0p=0�ł���s��ɂȂ邩�疵��
�Ep�͒萔�ł��肩�ϐ��ł���
�Ep���P����������i�{���͒P���������Ȃ��j����p�͑f���ɂȂ肦�Ȃ�
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł���
�Ew�͐����ł��蓯���ɐ����łȂ�
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ�
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂�
�E�ϐ��͐��l�ɒu�������Ă̓_��
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R
�E27/5 �� 3 �Ŋ�����
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂��� (NEW)
�Ep�͓���̒l�����͂�����0p=0�ł���s��ɂȂ邩�疵��
�Ep�͒萔�ł��肩�ϐ��ł���
�Ep���P����������i�{���͒P���������Ȃ��j����p�͑f���ɂȂ肦�Ȃ�
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł���
�Ew�͐����ł��蓯���ɐ����łȂ�
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ�
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂�
�E�ϐ��͐��l�ɒu�������Ă̓_��
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R
�E27/5 �� 3 �Ŋ�����
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂��� (NEW)
2018/08/23(��) 10:10:37.89ID:6p7BvH4m
�傫�ȃt�����������āA���傤�ǂ����������ŐV�l�^���I���Ă���邠����A�|�l�̊ӂƌ�����B
���������B
���������B
2018/08/23(��) 10:10:45.76ID:K06i0J+R
���x�������Ƃ�����������
�ŏ��ɉ��肵����̊��S��y
��pk�Aqk��ݒ肷��
��a,b�����肷��
������ɑΉ�����Ap,c,n(�����ł���)����܂��
��y����܂�
�ŏ��ɉ��肵����̊��S��y
��pk�Aqk��ݒ肷��
��a,b�����肷��
������ɑΉ�����Ap,c,n(�����ł���)����܂��
��y����܂�
2018/08/23(��) 10:11:12.38ID:K06i0J+R
�ŏ��ɉ��肵����̊��S��y�ƁAp����Έ�Ή�����͓̂��R�B
����p�������������ꍇ�́A������̊��S�����������݂���Ƃ��������ʼn��̖�������܂���B
����p�������������ꍇ�́A������̊��S�����������݂���Ƃ��������ʼn��̖�������܂���B
2018/08/23(��) 12:18:16.27ID:HquG05xP
�w���@�̏ؖ���������ƂȂ��̂���
2018/08/23(��) 12:22:26.19ID:M5ZubL2y
�ꉞ�����͐��w�Ȃ�ł���
�R���g�͑��ł����
�R���g�͑��ł����
67�P�R�Q�l�ڂ̑f������
2018/08/23(��) 12:22:50.71ID:+Bb/gGkm ������u��2�͗L�����ł��v
�搶�u�Ȃ�����������̂ł����H
�@��2�̊�����a/b�Ƃ��܂��B
�@a^2=2b^2�ƂȂ�̂�a�͋����A
�@���ӂ�4�̔{���ɂȂ�̂�b�������ł��B
�@a/b�������Ƃ�������Ɩ������܂���v
������u�������A����a/b�������K�������ƂȂ�܂��B
�@��2�̊������������݂���ƌ��������ʼn��̖�������܂���
�@����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł����v
�搶�u�Ȃ�����������̂ł����H
�@��2�̊�����a/b�Ƃ��܂��B
�@a^2=2b^2�ƂȂ�̂�a�͋����A
�@���ӂ�4�̔{���ɂȂ�̂�b�������ł��B
�@a/b�������Ƃ�������Ɩ������܂���v
������u�������A����a/b�������K�������ƂȂ�܂��B
�@��2�̊������������݂���ƌ��������ʼn��̖�������܂���
�@����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł����v
>>60
���m���̕ϐ����`���āA���ɏ������Ƃ̉������������̂ł��傤���H
���m�ɏq�ׂĉ������B
>>62-63
���̖��̌������s���_�������J���Ă���l�Ԃ��|�l�Ă�肷��̂���߂�B
>>66
5ch���w�ŏ��̖��������̉����ł͂Ȃ��̂ł����H
�u���S��y�����݂���Ɖ��肵���ꍇ�ȉ��̎������藧�B�v
�Ƃł�����������ł��ˁB
���̂悤�Ȍ`���I�Ȃ��Ƃ͎����炷��ƁA�����Ȃ��Ƃłǂ��ł��������ƂȂ̂ł����ǁB
���̖��͊��S�ɉ������Ă��܂�����A���̏؋��Ƃ��ĉ��̌��ʓI�Ȕ��_��
����邱�ƂȂ��A�ȑO�ɏ������ԈႢ�̗v��݂̂ɂȂ��Ă��邱�Ƃɒ[�I��
����Ă��܂��B
���m���̕ϐ����`���āA���ɏ������Ƃ̉������������̂ł��傤���H
���m�ɏq�ׂĉ������B
>>62-63
���̖��̌������s���_�������J���Ă���l�Ԃ��|�l�Ă�肷��̂���߂�B
>>66
5ch���w�ŏ��̖��������̉����ł͂Ȃ��̂ł����H
�u���S��y�����݂���Ɖ��肵���ꍇ�ȉ��̎������藧�B�v
�Ƃł�����������ł��ˁB
���̂悤�Ȍ`���I�Ȃ��Ƃ͎����炷��ƁA�����Ȃ��Ƃłǂ��ł��������ƂȂ̂ł����ǁB
���̖��͊��S�ɉ������Ă��܂�����A���̏؋��Ƃ��ĉ��̌��ʓI�Ȕ��_��
����邱�ƂȂ��A�ȑO�ɏ������ԈႢ�̗v��݂̂ɂȂ��Ă��邱�Ƃɒ[�I��
����Ă��܂��B
2018/08/23(��) 12:45:51.69ID:HquG05xP
>>68
���u���S��y�����݂���Ɖ��肵���ꍇ�ȉ��̎������藧�B�v
���Ƃł�����������ł��ˁB
�����̂悤�Ȍ`���I�Ȃ��Ƃ͎����炷��ƁA�����Ȃ��Ƃłǂ��ł��������ƂȂ̂ł����ǁB
�u���S��y�����݂���Ɖ��肵���ꍇ�A����y�ɑ��Ĉȉ��̎������藧�B�v
�ȂǂɂȂ�ł��傤�ˁB
�u�\�߈��߂�y�v�ɑ���咣�ɂȂ�܂��B
������������Ǝv���ĔF������O���Ă���ƌ�T�������܂��B
���u���S��y�����݂���Ɖ��肵���ꍇ�ȉ��̎������藧�B�v
���Ƃł�����������ł��ˁB
�����̂悤�Ȍ`���I�Ȃ��Ƃ͎����炷��ƁA�����Ȃ��Ƃłǂ��ł��������ƂȂ̂ł����ǁB
�u���S��y�����݂���Ɖ��肵���ꍇ�A����y�ɑ��Ĉȉ��̎������藧�B�v
�ȂǂɂȂ�ł��傤�ˁB
�u�\�߈��߂�y�v�ɑ���咣�ɂȂ�܂��B
������������Ǝv���ĔF������O���Ă���ƌ�T�������܂��B
2018/08/23(��) 12:47:56.45ID:K06i0J+R
�����̖��͊��S�ɉ������Ă��܂�����
���������Ȃ���P�O�O����C�������������o���Ă�́B
�P���g���A�����ɂ��̂o�c�e�����������ɗ����������̂��F�����Ă���͂��B
�����ł���M���ĂȂ��̂Ɋ����I�����I�ƌ����Ă��x���Ȃ���B
���������Ȃ���P�O�O����C�������������o���Ă�́B
�P���g���A�����ɂ��̂o�c�e�����������ɗ����������̂��F�����Ă���͂��B
�����ł���M���ĂȂ��̂Ɋ����I�����I�ƌ����Ă��x���Ȃ���B
2018/08/23(��) 13:12:41.64ID:aDhxWP96
�݂�Ȃ��S���Ďw�E�������Ă邽�߂��A�ŏ��̍ŏ��̔w���@�̉���ɂ܂Ŏw�E��������Ă��ĂĂȂ��Ȃ��ʔ����ȁB
���������_���Ӗ��s���ł���ȏ�̏��������߂邩�ǂ���
���������_���Ӗ��s���ł���ȏ�̏��������߂邩�ǂ���
2018/08/23(��) 13:24:27.55ID:kByImh9Z
>>53
�_���ł��B
�I�͖������ɐ������鎮�ł͂���܂���B
�I�������܂łŎ��������Ƃ��L�`���Ƃ܂Ƃ߂��
��y A B p
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1�@�c(A)
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A�@�c(B)
qr = v_pr(B) �@�c(C)
cr = v_pr(A)�@�c(D)
p = 2pr -1�@�c(E)
�ˁ�w 2m+1 = wpr^(qr-cr-1)�@�c(F)
�ł���ˁH
���_(F)�̎��̒��ɂ͗z��y��p�͏o�Ă��܂��A������y��p�ɖ��W��(C)�`(F)�������E���o����
(C)�`(E)��(F)
���ؖ��ł������ƂɂȂ�ĂȂ�܂���B
����������Ȃ�
x=t^2,y=t^4�@�c(X)
x>2, y>3�@�c(Y)
��y=x^2�@�c(Z)
�͐��������_�ł����A(Z)�̂Ȃ��ɂ�t���Ȃ�����Ƃ�����
(Y)��(Z) i.e. x>2,y>3 �� y=x^2
���ؖ��ł����Ȃ�Ď咣�͂ł��Ȃ��ł���H
�܂�(F)�������ׂĂ̑f��ps�ɂ��Đ�������Ƃ����Ȃ�C�ӂ̑f��ps�ɂ�������y', p', A', B'��
y'�͊�̊��S��,p'�͑f����v_p'(y') = 4m+1�@�c(A)
2y' = 2p'^(4m+1)B' = (1+p'+�c+p'^(4m+1))A'�@�c(B)
qs = v_ps(B') �@�c(C)
cs = v_ps(A')�@�c(D)
p' = 2ps -1�@�c(E)
�����ׂĖ��������̂����݂��邱�Ƃ��ؖ����Ȃ���Ȃ�܂���B
�����Ă��̏ؖ��͌����_�Ř_���ɂ͂Ȃ��̂�y�����ւ��邱�Ƃɂ���ĔC�ӂ̑f��ps�ɂ��ćI��������Ă���Ƃ͌����܂���B
�_���ł��B
�I�͖������ɐ������鎮�ł͂���܂���B
�I�������܂łŎ��������Ƃ��L�`���Ƃ܂Ƃ߂��
��y A B p
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1�@�c(A)
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A�@�c(B)
qr = v_pr(B) �@�c(C)
cr = v_pr(A)�@�c(D)
p = 2pr -1�@�c(E)
�ˁ�w 2m+1 = wpr^(qr-cr-1)�@�c(F)
�ł���ˁH
���_(F)�̎��̒��ɂ͗z��y��p�͏o�Ă��܂��A������y��p�ɖ��W��(C)�`(F)�������E���o����
(C)�`(E)��(F)
���ؖ��ł������ƂɂȂ�ĂȂ�܂���B
����������Ȃ�
x=t^2,y=t^4�@�c(X)
x>2, y>3�@�c(Y)
��y=x^2�@�c(Z)
�͐��������_�ł����A(Z)�̂Ȃ��ɂ�t���Ȃ�����Ƃ�����
(Y)��(Z) i.e. x>2,y>3 �� y=x^2
���ؖ��ł����Ȃ�Ď咣�͂ł��Ȃ��ł���H
�܂�(F)�������ׂĂ̑f��ps�ɂ��Đ�������Ƃ����Ȃ�C�ӂ̑f��ps�ɂ�������y', p', A', B'��
y'�͊�̊��S��,p'�͑f����v_p'(y') = 4m+1�@�c(A)
2y' = 2p'^(4m+1)B' = (1+p'+�c+p'^(4m+1))A'�@�c(B)
qs = v_ps(B') �@�c(C)
cs = v_ps(A')�@�c(D)
p' = 2ps -1�@�c(E)
�����ׂĖ��������̂����݂��邱�Ƃ��ؖ����Ȃ���Ȃ�܂���B
�����Ă��̏ؖ��͌����_�Ř_���ɂ͂Ȃ��̂�y�����ւ��邱�Ƃɂ���ĔC�ӂ̑f��ps�ɂ��ćI��������Ă���Ƃ͌����܂���B
2018/08/23(��) 13:25:04.77ID:IqK/6D9+
2018/08/23(��) 13:31:01.74ID:IqK/6D9+
�͂��o�Ă���ƂP�ɂ͂����ς肾���A
���w�̃��x���ɉ������Ăǂ����悤���Ȃ��B
�P�͎Z�������蒼���B
���w�̃��x���ɉ������Ăǂ����悤���Ȃ��B
�P�͎Z�������蒼���B
>>69
y��p�����݂���Ay�͂��̎��ŕ\�����Ƃ��������Ă��܂���
>>70
���̖��͓��ł���A�w���@�ŏؖ����Ȃ���Ȃ�Ȃ��̂ŁA�����ł��v�Z�ԈႢ��
�_���̊ԈႢ������ƁA���ꂪ�������Ǝv�����ޖ�肾����d�����Ȃ��B
���̓��e��3�x�������B
>>71
�����ɓ��B�����킯������A�����Ȕ��_���ł��Ȃ��͕̂��ʂ̂��ƁB
>>72
���I�͖������ɐ��藧���ł͂Ȃ��Ƃ����̂͊Ԉ���Ă��܂��B���Ȃ��Ƃ���͂����Ȃ�
pk�����݂��Ȃ��ƁA�S�Ă�pk^qk��b��������Ȃ�����s�K�ɂȂ�܂��B
�Ƃ������ƂŁA����k�����݂��Ȃ���Ȃ�܂��Ab�̌`����S�Ă�k�ɑ��Ď��I��
���藧���Ȃ���Ȃ�Ȃ��͎̂����ł͂Ȃ��̂ł��傤���H
>>74
���O���ȁ[
y��p�����݂���Ay�͂��̎��ŕ\�����Ƃ��������Ă��܂���
>>70
���̖��͓��ł���A�w���@�ŏؖ����Ȃ���Ȃ�Ȃ��̂ŁA�����ł��v�Z�ԈႢ��
�_���̊ԈႢ������ƁA���ꂪ�������Ǝv�����ޖ�肾����d�����Ȃ��B
���̓��e��3�x�������B
>>71
�����ɓ��B�����킯������A�����Ȕ��_���ł��Ȃ��͕̂��ʂ̂��ƁB
>>72
���I�͖������ɐ��藧���ł͂Ȃ��Ƃ����̂͊Ԉ���Ă��܂��B���Ȃ��Ƃ���͂����Ȃ�
pk�����݂��Ȃ��ƁA�S�Ă�pk^qk��b��������Ȃ�����s�K�ɂȂ�܂��B
�Ƃ������ƂŁA����k�����݂��Ȃ���Ȃ�܂��Ab�̌`����S�Ă�k�ɑ��Ď��I��
���藧���Ȃ���Ȃ�Ȃ��͎̂����ł͂Ȃ��̂ł��傤���H
>>74
���O���ȁ[
2018/08/23(��) 20:45:20.19ID:27oyyIdd
�����Ȃ��Ƃ���͂����Ȃ�
������k�����݂��Ȃ���Ȃ�܂���
���S�Ă�k�ɑ��Ď��I�����藧���Ȃ���Ȃ�Ȃ�
�����̗́͂����ł��Ȃ��P�ɂ��
���������̈��������L�^�[
������k�����݂��Ȃ���Ȃ�܂���
���S�Ă�k�ɑ��Ď��I�����藧���Ȃ���Ȃ�Ȃ�
�����̗́͂����ł��Ȃ��P�ɂ��
���������̈��������L�^�[
>>76
�O����
�O����
78�P�R�Q�l�ڂ̑f������
2018/08/23(��) 20:58:32.08ID:8Xy8APGJ �O���悤�������悤���Ԉ���Ƃ����͊Ԉ���Ƃ���
79�P�R�Q�l�ڂ̑f������
2018/08/23(��) 21:07:53.88ID:+M/ERTfV �P���u�O�����v�u�܂��v�u�_�����悭�ǂ�Łv�u�l���ɒl���Ȃ��v�u���������ł�����v���J��o���Ƃ��͔��_�ɋl�܂����Ƃ��B
�����锒����g������ԂƂƂ炦�Ă悢�B
�����锒����g������ԂƂƂ炦�Ă悢�B
>>78
b��pk^qk�̐ς�����A�S�Ă�k�ɑ��Ď��I�����藧���Ȃ���Ȃ�Ȃ��B
���̂��̂悤�ȊȒP�ȓ��e�������ł��Ȃ��̂ł��傤���H���������肢���܂��B
b��pk^qk�̐ς�����A�S�Ă�k�ɑ��Ď��I�����藧���Ȃ���Ȃ�Ȃ��B
���̂��̂悤�ȊȒP�ȓ��e�������ł��Ȃ��̂ł��傤���H���������肢���܂��B
82\math135
2018/08/23(��) 21:11:21.96ID:ziRzgMWB �܂�Ȃ����_���ǂ��͂��ꂩ��S�Ė�������
2018/08/23(��) 21:12:08.38ID:LGJTq8r8
�������ؖ��̉\���̓[��
�����ŕ�������ׂ�����\���͒Ⴂ
�����ŕ�������ׂ�����\���͒Ⴂ
84�P�R�Q�l�ڂ̑f������
2018/08/23(��) 21:21:54.39ID:hk0DZdiZ �{��ɐk���Ďv�킸�т��N���Ă��܂����������w
85�P�R�Q�l�ڂ̑f������
2018/08/23(��) 21:25:40.93ID:8Xy8APGJ ����ۂǐ}����������
2018/08/23(��) 21:26:25.14ID:27oyyIdd
����܂ł̊�|�l�l�^
�Ep�͓���̒l�����͂�����0p=0�ł���s��ɂȂ邩�疵��
�Ep�͒萔�ł��肩�ϐ��ł���
�Ep���P����������i�{���͒P���������Ȃ��j����p�͑f���ɂȂ肦�Ȃ�
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł���
�Ew�͐����ł��蓯���ɐ����łȂ�
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ�
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂�
�E�ϐ��͐��l�ɒu�������Ă̓_��
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R
�E27/5 �� 3 �Ŋ�����
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂��� (NEW)
�E���Ȃ��Ƃ���͂����Ȃ�A�Ƃ������Ƃ�
�@�S�Ăɑ��Đ��藧���Ȃ���Ȃ�Ȃ� (NEW)
�Ep�͓���̒l�����͂�����0p=0�ł���s��ɂȂ邩�疵��
�Ep�͒萔�ł��肩�ϐ��ł���
�Ep���P����������i�{���͒P���������Ȃ��j����p�͑f���ɂȂ肦�Ȃ�
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł���
�Ew�͐����ł��蓯���ɐ����łȂ�
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ�
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂�
�E�ϐ��͐��l�ɒu�������Ă̓_��
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R
�E27/5 �� 3 �Ŋ�����
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂��� (NEW)
�E���Ȃ��Ƃ���͂����Ȃ�A�Ƃ������Ƃ�
�@�S�Ăɑ��Đ��藧���Ȃ���Ȃ�Ȃ� (NEW)
2018/08/23(��) 21:45:12.76ID:vqOp3/ww
��͑S�A�S�͈�₩���
>>1�͓N�w�҂�
>>1�͓N�w�҂�
2018/08/23(��) 22:44:01.80ID:MO0VXEB9
>>75
>���I�͖������ɐ��藧���ł͂Ȃ��Ƃ����̂͊Ԉ���Ă��܂��B
�_�����I�o���Ă���O�̕����ɂ��낢�뉼�肵�Ă��܂��B
����̊��S���� y�A���̂�����̑f������ p�Ap �̎w���𐮐� n(n �� 1)�Ap �ȊO�̑f
��������𝑝1,𝑝2,𝑝3,�c𝑝𝑟�Ƃ��A𝑝𝑘�̎w����𝑞𝑘�A�f�� p �ȊO�̐ς̑g�ݍ��킹�̍��v�� a �Ƃ�
����
�������Ă܂��A���̕��͂ł��łɁh��y ��p �c�h�Ɖ��肵�Ă܂��ˁB
���Əꍇ�킯�̉���
���T. pr = (p + 1)/2�̂Ƃ�
���������ł��B
���Ȃ������I�ɓ��B�����c�_�܂łŎ����ꂽ�̂̓L�`���Ƙ_�����ł�����
��y A B p
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1�@�c(A)
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A�@�c(B)
qr = v_pr(B) �@�c(C)
cr = v_pr(A)�@�c(D)
p = 2pr -1�@�c(E)
�ˁ�w 2m+1 = wpr^(qr-cr-1)�@�c(F)
�ł��B
��b�̌`����S�Ă�k�ɑ��Ď��I��
�����藧���Ȃ���Ȃ�Ȃ��͎̂����ł͂Ȃ��̂ł��傤���H
����͊��Ɏw�E�����Ƃ��苖����Ȃ��_���ł��B
���̌`�����ł��ׂĂ�k�ɂ��Đ��藧�ȂǂƂ����_�@�͐��w�̐��E�ɂ͑��݂��܂���B
���ׂĂ�k�ɑ��ćI���������邱�Ƃ������ɂ͂��ׂĂ�k�ɑ��ćI�o��������A���Ȃ킿�O�q(A)�`(E)�̐������ؖ����Ȃ���Ȃ�܂���B
>���I�͖������ɐ��藧���ł͂Ȃ��Ƃ����̂͊Ԉ���Ă��܂��B
�_�����I�o���Ă���O�̕����ɂ��낢�뉼�肵�Ă��܂��B
����̊��S���� y�A���̂�����̑f������ p�Ap �̎w���𐮐� n(n �� 1)�Ap �ȊO�̑f
��������𝑝1,𝑝2,𝑝3,�c𝑝𝑟�Ƃ��A𝑝𝑘�̎w����𝑞𝑘�A�f�� p �ȊO�̐ς̑g�ݍ��킹�̍��v�� a �Ƃ�
����
�������Ă܂��A���̕��͂ł��łɁh��y ��p �c�h�Ɖ��肵�Ă܂��ˁB
���Əꍇ�킯�̉���
���T. pr = (p + 1)/2�̂Ƃ�
���������ł��B
���Ȃ������I�ɓ��B�����c�_�܂łŎ����ꂽ�̂̓L�`���Ƙ_�����ł�����
��y A B p
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1�@�c(A)
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A�@�c(B)
qr = v_pr(B) �@�c(C)
cr = v_pr(A)�@�c(D)
p = 2pr -1�@�c(E)
�ˁ�w 2m+1 = wpr^(qr-cr-1)�@�c(F)
�ł��B
��b�̌`����S�Ă�k�ɑ��Ď��I��
�����藧���Ȃ���Ȃ�Ȃ��͎̂����ł͂Ȃ��̂ł��傤���H
����͊��Ɏw�E�����Ƃ��苖����Ȃ��_���ł��B
���̌`�����ł��ׂĂ�k�ɂ��Đ��藧�ȂǂƂ����_�@�͐��w�̐��E�ɂ͑��݂��܂���B
���ׂĂ�k�ɑ��ćI���������邱�Ƃ������ɂ͂��ׂĂ�k�ɑ��ćI�o��������A���Ȃ킿�O�q(A)�`(E)�̐������ؖ����Ȃ���Ȃ�܂���B
2018/08/23(��) 22:44:24.91ID:w3TRtxb6
��������ύX�͂Ȃ��Ƃ������Ƃʼn��U�ł���
2018/08/23(��) 22:48:15.13ID:LGJTq8r8
���߂łƂ��I
2018/08/23(��) 23:49:20.41ID:Wfpp6fmq
���Ɂub��pk^qk�̐ς�����A�S�Ă�k�ɑ��Ď��I�����藧���Ȃ���Ȃ�Ȃ��v���Ƃ������Ȃ�A�����e�Ղɏؖ��ł���͂�
�ׂ����킸��>>89��(A)�`(E)�̐����������Ă����Ȃ�
�ׂ����킸��>>89��(A)�`(E)�̐����������Ă����Ȃ�
2018/08/24(��) 00:57:46.35ID:IyGxJGLw
�����M�ӂ�����Α�w���N���̏W���_����㐔�̖{�͂����ǂ߂���������
�����Ă����ǂ�ł���ēx����ł��S�R�悳�����Ȃ�����
�����Ă����ǂ�ł���ēx����ł��S�R�悳�����Ȃ�����
2018/08/24(��) 01:01:42.64ID:WzkHXo1C
���̖���������������ΐ��w�ȓ��蒼���̂���Ԃ̋ߓ����낤��
2018/08/24(��) 02:15:34.22ID:BCgag6Bk
�O�X���ň�x���������ǁA
��͂� >1 �́u����O��ɉ����咣���Ă��邩�v�������ł��Ă��Ȃ��̂��Ǝv���܂��B
�u�`���I�ȁA�����Ȃ��Ɓv�ȂǂƎv�킸�A��x�u����O��ɉ����咣���Ă��邩�v�����Ă݂Ă͂������ł��傤�B
>>75
�����̖��͓��ł���A�w���@�ŏؖ����Ȃ���Ȃ�Ȃ��̂ŁA�����ł��v�Z�ԈႢ��
���_���̊ԈႢ������ƁA���ꂪ�������Ǝv�����ޖ�肾����d�����Ȃ��B
���̂悤�ɂ��l���ł�����Ȃ��̂��ƁA�咣�̐����͕K�v�ł��傤�B
��͂� >1 �́u����O��ɉ����咣���Ă��邩�v�������ł��Ă��Ȃ��̂��Ǝv���܂��B
�u�`���I�ȁA�����Ȃ��Ɓv�ȂǂƎv�킸�A��x�u����O��ɉ����咣���Ă��邩�v�����Ă݂Ă͂������ł��傤�B
>>75
�����̖��͓��ł���A�w���@�ŏؖ����Ȃ���Ȃ�Ȃ��̂ŁA�����ł��v�Z�ԈႢ��
���_���̊ԈႢ������ƁA���ꂪ�������Ǝv�����ޖ�肾����d�����Ȃ��B
���̂悤�ɂ��l���ł�����Ȃ��̂��ƁA�咣�̐����͕K�v�ł��傤�B
�ύX�_
�Ecr�̏ꍇ�������C�����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7090613671732/
Pdf���� ���{��
http://fast-uploader.com/file/7090613768405/
�Ecr�̏ꍇ�������C�����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7090613671732/
Pdf���� ���{��
http://fast-uploader.com/file/7090613768405/
>>1 ����
2018�N8��22����2018�N8��24��
2018�N8��22����2018�N8��24��
�������郌�X�����Ă��܂��܂������A���m�ɂ́Ack<qk-1�ƂȂ�S�Ă�k�ɑ���
���I�����藧�Ƃ������Ƃł��B
���܂ł́Ack��qk-1�ł������Ack<qk-1�ɏC�����܂����B
���I�����藧�Ƃ������Ƃł��B
���܂ł́Ack��qk-1�ł������Ack<qk-1�ɏC�����܂����B
2018/08/24(��) 06:50:13.78ID:02RtuJ/f
���������Ńf�^�����ȃS�~�o�c�e��
��������̂͂悭�Ȃ��B
��������̂͂悭�Ȃ��B
2018/08/24(��) 08:57:23.98ID:l45C8tPV
>>98
����́u������ꂻ���v�Ƃ͌���Ȃ��B�u�Ԉ���Ă����v���B�Ƃ��Ƃ��ɊÂ��j���ȁB
����́u������ꂻ���v�Ƃ͌���Ȃ��B�u�Ԉ���Ă����v���B�Ƃ��Ƃ��ɊÂ��j���ȁB
2018/08/24(��) 10:10:15.05ID:hIzgRVDP
�܂��>>16���
2018/08/24(��) 10:30:53.91ID:AN3TK8OT
�O�X���܂łł��A����P�͂�炩���Ă������
>>16
�����̗���
1.�u�ԈႢ��������܂����A�P�܂��v
��
2.�u(���_�_����Ȃ��Ƃ���)���C�����܂����B�����ł��v
��
3.(�_�_�ɂ��ĕ�����Ă�)�u�������łɒ����܂���(�������ĂȂ�)�B�ǂ�ł��猾���Ă��������v
>>16
�����̗���
1.�u�ԈႢ��������܂����A�P�܂��v
��
2.�u(���_�_����Ȃ��Ƃ���)���C�����܂����B�����ł��v
��
3.(�_�_�ɂ��ĕ�����Ă�)�u�������łɒ����܂���(�������ĂȂ�)�B�ǂ�ł��猾���Ă��������v
>>100
�����ɏ��������e�Ɋւ��ĕ⑫�����̂ł����āA�_���̊ԈႢ�͕ʂ̖��
�����ɏ��������e�Ɋւ��ĕ⑫�����̂ł����āA�_���̊ԈႢ�͕ʂ̖��
2018/08/24(��) 12:06:06.52ID:IgLz8/E6
�܂��Ӗ��s���Ȃ��ƌ����Ă�
2018/08/24(��) 12:09:14.12ID:yYt21NmJ
��2.�u(���_�_����Ȃ��Ƃ���)���C�����܂����B�����ł��v
�܂��ɁA���ꂾ��
�܂��ɁA���ꂾ��
2018/08/24(��) 12:14:32.06ID:CuH5Mpfc
�t�F�C�Y2�ƌĂڂ�
2018/08/24(��) 13:44:52.78ID:yYt21NmJ
�����Ƀt�F�C�Y�R�ɁI
�ύX�_
�E14�y�[�W���͒��̐����̌����C�����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7090644743952/
Pdf���� �p��
http://fast-uploader.com/file/7090645054852/
�E14�y�[�W���͒��̐����̌����C�����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7090644743952/
Pdf���� �p��
http://fast-uploader.com/file/7090645054852/
109�P�R�Q�l�ڂ̑f������
2018/08/24(��) 15:22:02.00ID:Bc69laW4 �Ȃ�Ō��Ђ���w�p���ɓ��e���Ȃ��̂�
110�P�R�Q�l�ڂ̑f������
2018/08/24(��) 15:53:18.11ID:fEBY+BAU �˂�[����Ȃ炠�̒��x���x����Ɠ��낤��
���ۂ́A���w�̒m���̖����҂ɂ͖��ʂɕ��G�����ė����ł����A
���w�������ł���҂ɂ͗e�ՂɃS�}�J�V�����j��Ă��܂����e�ɂȂ��Ă���B
������̏ꍇ���S�}�J�V���������Ă��Ȃ�
���ۂ́A���w�̒m���̖����҂ɂ͖��ʂɕ��G�����ė����ł����A
���w�������ł���҂ɂ͗e�ՂɃS�}�J�V�����j��Ă��܂����e�ɂȂ��Ă���B
������̏ꍇ���S�}�J�V���������Ă��Ȃ�
2018/08/24(��) 16:12:50.02ID:CuH5Mpfc
�܂��t�F�C�Y2�ɖ߂�����
2018/08/24(��) 16:49:35.84ID:BCgag6Bk
1=2�̏ؖ��݂����ɂȂ��Ă��
>>109
LaTex�̃t�@�C������邱�Ƃ��ł��Ȃ�����A�w�p���ɂ͓��e�ł��Ȃ�
>>110
�떂���͈�Ȃ����A���w�I�ɂ͊��S�ɐ������Ȃ���
���w�̃��x���́A���Z���w��mode���Z�A����A�t�F���}�[�̏��藝��
���������炢�̂��̂Ȃ̂ŁA��w�̐��w�ȑ��̐l�������痝���ł��郌�x����
�����w�������ł���҂ɂ͗e�ՂɃS�}�J�V�����j��Ă��܂����e
��ϖʔ����ˁA���̓��e��ے肷�邱�Ƃ��ł��鐔�w�҂␔�w�����҂�������
LaTex�̃t�@�C������邱�Ƃ��ł��Ȃ�����A�w�p���ɂ͓��e�ł��Ȃ�
>>110
�떂���͈�Ȃ����A���w�I�ɂ͊��S�ɐ������Ȃ���
���w�̃��x���́A���Z���w��mode���Z�A����A�t�F���}�[�̏��藝��
���������炢�̂��̂Ȃ̂ŁA��w�̐��w�ȑ��̐l�������痝���ł��郌�x����
�����w�������ł���҂ɂ͗e�ՂɃS�}�J�V�����j��Ă��܂����e
��ϖʔ����ˁA���̓��e��ے肷�邱�Ƃ��ł��鐔�w�҂␔�w�����҂�������
2018/08/24(��) 17:28:28.64ID:CuH5Mpfc
�t�F�C�Y3��
2018/08/24(��) 17:36:19.36ID:rV3350F0
�����Ȃ�t�F�C�Y�R�ŊJ�n�������I
116�P�R�Q�l�ڂ̑f������
2018/08/24(��) 17:37:15.53ID:ooXdJggB ���w�I�Ɋ��S�ɐ�����
�ƌ�����������ΐ������Ȃ�Ǝv����_�o����������
�m���ɂ܂Ƃ��Ȑl�Ԃɂ͐^���ł��Ȃ�
�ƌ�����������ΐ������Ȃ�Ǝv����_�o����������
�m���ɂ܂Ƃ��Ȑl�Ԃɂ͐^���ł��Ȃ�
117�P�R�Q�l�ڂ̑f������
2018/08/24(��) 17:41:49.34ID:DLCTMBU7 �u���w�I�Ɋ��S�ɐ������v���P�̔s�k�錾�ȁB
2018/08/24(��) 18:01:06.20ID:rV3350F0
�����P�́A��E�\��
1 ���O�F ��H4n21Ym7mA [age] ���e���F2018/08/22(��) 10:12:54.32 ID:SxQ2y3ZV
���S�ȏؖ����������܂����B
Pdf���� ���{��
88 ���O�F ��RK0hxWxT6Q [sage] ���e���F2018/08/23(��) 21:56:38.93 ID:ziRzgMWB
���S�ɐ������ƍl������B
96 ���O�F ��RK0hxWxT6Q [age] ���e���F2018/08/24(��) 06:07:30.73 ID:XQ6EMHV0 [1/6]
Pdf���� ���{��
http://fast-uploader.com/file/7090613671732/
108 ���O�F ��RK0hxWxT6Q [age] ���e���F2018/08/24(��) 14:48:05.07 ID:XQ6EMHV0 [5/6]
Pdf���� ���{��
http://fast-uploader.com/file/7090644743952/
113 ���O�F ��RK0hxWxT6Q [sage] ���e���F2018/08/24(��) 16:59:50.81 ID:XQ6EMHV0 [6/6]
�떂���͈�Ȃ����A���w�I�ɂ͊��S�ɐ������Ȃ���
1 ���O�F ��H4n21Ym7mA [age] ���e���F2018/08/22(��) 10:12:54.32 ID:SxQ2y3ZV
���S�ȏؖ����������܂����B
Pdf���� ���{��
88 ���O�F ��RK0hxWxT6Q [sage] ���e���F2018/08/23(��) 21:56:38.93 ID:ziRzgMWB
���S�ɐ������ƍl������B
96 ���O�F ��RK0hxWxT6Q [age] ���e���F2018/08/24(��) 06:07:30.73 ID:XQ6EMHV0 [1/6]
Pdf���� ���{��
http://fast-uploader.com/file/7090613671732/
108 ���O�F ��RK0hxWxT6Q [age] ���e���F2018/08/24(��) 14:48:05.07 ID:XQ6EMHV0 [5/6]
Pdf���� ���{��
http://fast-uploader.com/file/7090644743952/
113 ���O�F ��RK0hxWxT6Q [sage] ���e���F2018/08/24(��) 16:59:50.81 ID:XQ6EMHV0 [6/6]
�떂���͈�Ȃ����A���w�I�ɂ͊��S�ɐ������Ȃ���
2018/08/24(��) 18:04:57.26ID:KL8GFrzC
121�O�X���̕�
2018/08/24(��) 18:37:21.23ID:rV3350F0 1 ���O�F[age] 2018/08/05(��) 05:25:38.78 ID:CcBDiEWJ [1/8]
���S�ȏؖ����������܂����B
Pdf���� ���{��
9 ���O�F[age] 2018/08/05(��) 09:28:56.66 ID:CcBDiEWJ
Pdf���� ���{��
26 ���O�F[age] 2018/08/06(��) 09:01:56.27 ID:1wlVJfjw
Pdf���� ���{��
27 ���O�F[sage] 2018/08/06(��) 11:30:16.67 ID:1wlVJfjw
Pdf���� ���{��
64 ���O�F[age] 2018/08/07(��) 11:57:35.78 ID:Cc7tnWeO
Pdf���� ���{��
133 ���O�F[sage] 2018/08/07(��) 18:29:04.97 ID:Cc7tnWeO
�����Ŏw�E����Ă��Ȃ��ԈႢ��������܂����̂ō폜���܂�
���S�ȏؖ����������܂����B
Pdf���� ���{��
9 ���O�F[age] 2018/08/05(��) 09:28:56.66 ID:CcBDiEWJ
Pdf���� ���{��
26 ���O�F[age] 2018/08/06(��) 09:01:56.27 ID:1wlVJfjw
Pdf���� ���{��
27 ���O�F[sage] 2018/08/06(��) 11:30:16.67 ID:1wlVJfjw
Pdf���� ���{��
64 ���O�F[age] 2018/08/07(��) 11:57:35.78 ID:Cc7tnWeO
Pdf���� ���{��
133 ���O�F[sage] 2018/08/07(��) 18:29:04.97 ID:Cc7tnWeO
�����Ŏw�E����Ă��Ȃ��ԈႢ��������܂����̂ō폜���܂�
122�O�X���̕�
2018/08/24(��) 18:38:44.64ID:rV3350F0 136 ���O�F[age] 2018/08/07(��) 19:03:40.24 ID:Cc7tnWeO
Pdf���� ���{��
232��H4n21Ym7mA [age] 2018/08/09(��) 11:23:30.95 ID:qa1PqB1o
Pdf���� ���{��
297��H4n21Ym7mA [age] 2018/08/10(��) 16:14:01.78 ID:fX825M0q
Pdf���� ���{��
303��H4n21Ym7mA [sage] 2018/08/10(��) 16:56:23.51 ID:fX825M0q
�����Ƃ��낪�Ȃ��Ȃ����ƍl������̂ŁA����ŏI��肩������܂���
311��H4n21Ym7mA [sage] 2018/08/10(��) 18:40:55.87 ID:fX825M0q
���������Ƃ��낪�Ȃ�
Pdf���� ���{��
232��H4n21Ym7mA [age] 2018/08/09(��) 11:23:30.95 ID:qa1PqB1o
Pdf���� ���{��
297��H4n21Ym7mA [age] 2018/08/10(��) 16:14:01.78 ID:fX825M0q
Pdf���� ���{��
303��H4n21Ym7mA [sage] 2018/08/10(��) 16:56:23.51 ID:fX825M0q
�����Ƃ��낪�Ȃ��Ȃ����ƍl������̂ŁA����ŏI��肩������܂���
311��H4n21Ym7mA [sage] 2018/08/10(��) 18:40:55.87 ID:fX825M0q
���������Ƃ��낪�Ȃ�
123�O�X���̕�
2018/08/24(��) 18:39:24.21ID:rV3350F0 314��H4n21Ym7mA [age] 2018/08/10(��) 20:32:13.56 ID:fX825M0q
Pdf���� �p��
317��H4n21Ym7mA [sage] 2018/08/10(��) 20:51:01.96 ID:fX825M0q
�������_���ɂȂ�����I���ł��傤
�@�@�@�@�@
325��H4n21Ym7mA [age] 2018/08/11(�y) 09:41:39.58 ID:VzBbEbSZ
Pdf���� ���{��
331��H4n21Ym7mA [sage] 2018/08/11(�y) 11:39:08.08 ID:VzBbEbSZ
�ԈႢ��������܂����̂ŁA>>325���폜���܂���
Pdf���� �p��
317��H4n21Ym7mA [sage] 2018/08/10(��) 20:51:01.96 ID:fX825M0q
�������_���ɂȂ�����I���ł��傤
�@�@�@�@�@
325��H4n21Ym7mA [age] 2018/08/11(�y) 09:41:39.58 ID:VzBbEbSZ
Pdf���� ���{��
331��H4n21Ym7mA [sage] 2018/08/11(�y) 11:39:08.08 ID:VzBbEbSZ
�ԈႢ��������܂����̂ŁA>>325���폜���܂���
124�O�X���̕�
2018/08/24(��) 18:40:03.68ID:rV3350F0 360��H4n21Ym7mA [age] 2018/08/12(��) 20:21:00.52 ID:tsksl0/C
Pdf���� ���{��
http://fast-uploader.com/file/7089628227091/
361��H4n21Ym7mA [sage] 2018/08/12(��) 21:01:22.49 ID:tsksl0/C
�ԈႢ��������܂����̂ō폜���܂���
�@�@�@�@�@
362��H4n21Ym7mA [age] 2018/08/12(��) 21:45:48.34 ID:tsksl0/C
Pdf���� ���{��
377��H4n21Ym7mA [sage] 2018/08/13(��) 21:10:26.14 ID:1sIym2cm
�ԈႢ��������܂����̂ō폜���܂���
Pdf���� ���{��
http://fast-uploader.com/file/7089628227091/
361��H4n21Ym7mA [sage] 2018/08/12(��) 21:01:22.49 ID:tsksl0/C
�ԈႢ��������܂����̂ō폜���܂���
�@�@�@�@�@
362��H4n21Ym7mA [age] 2018/08/12(��) 21:45:48.34 ID:tsksl0/C
Pdf���� ���{��
377��H4n21Ym7mA [sage] 2018/08/13(��) 21:10:26.14 ID:1sIym2cm
�ԈႢ��������܂����̂ō폜���܂���
125�O�X���̕�
2018/08/24(��) 18:40:29.62ID:rV3350F0 396��H4n21Ym7mA [age] 2018/08/13(��) 23:26:57.99 ID:1sIym2cm
Pdf���� ���{��
410��H4n21Ym7mA [age] 2018/08/14(��) 08:47:20.89 ID:/Ahykgzy
Pdf���� ���{��
442��H4n21Ym7mA [sage] 2018/08/14(��) 22:43:55.76 ID:/Ahykgzy
���̖��������͉��������̂ɂ��ւ�炸�A�W�̂Ȃ����X����ɂȂ��Ă���
642��H4n21Ym7mA [sage] 2018/08/16(��) 13:40:53.22 ID:Q7fJTSPI
���w�I�ɐ��������̂́A�C������K�v���Ȃ��B
693��H4n21Ym7mA [sage] 2018/08/16(��) 20:41:12.36 ID:Q7fJTSPI
�������S�ɐ��������疳���ɊԈႢ���I���Ȃ��Č��\�ł�
Pdf���� ���{��
410��H4n21Ym7mA [age] 2018/08/14(��) 08:47:20.89 ID:/Ahykgzy
Pdf���� ���{��
442��H4n21Ym7mA [sage] 2018/08/14(��) 22:43:55.76 ID:/Ahykgzy
���̖��������͉��������̂ɂ��ւ�炸�A�W�̂Ȃ����X����ɂȂ��Ă���
642��H4n21Ym7mA [sage] 2018/08/16(��) 13:40:53.22 ID:Q7fJTSPI
���w�I�ɐ��������̂́A�C������K�v���Ȃ��B
693��H4n21Ym7mA [sage] 2018/08/16(��) 20:41:12.36 ID:Q7fJTSPI
�������S�ɐ��������疳���ɊԈႢ���I���Ȃ��Č��\�ł�
126�O�X���̕�
2018/08/24(��) 18:40:59.55ID:rV3350F0 715��H4n21Ym7mA [age] 2018/08/17(��) 06:23:02.46 ID:0c+DAEJM
Pdf���� ���{��
822��H4n21Ym7mA [age] 2018/08/18(�y) 07:46:40.38 ID:OBvJ9bTb
Pdf���� ���{��
906��H4n21Ym7mA [sage] 2018/08/19(��) 21:35:07.10 ID:BehawhAJ
���ʂ̐��w�����҂ɂ͗������ꂤ����e�Ɍ��܂��Ă���B�ȏ�B
935��H4n21Ym7mA [sage] 2018/08/20(��) 14:46:08.31 ID:N+36Ptxg
���S�ɐ������ؖ���������
�@�@�@�@�@
947��H4n21Ym7mA [age] 2018/08/21(��) 10:06:30.21 ID:KkjwiMLB
Pdf���� ���{��
989��H4n21Ym7mA [age] 2018/08/22(��) 07:48:25.38 ID:SxQ2y3ZV
Pdf���� ���{��
Pdf���� ���{��
822��H4n21Ym7mA [age] 2018/08/18(�y) 07:46:40.38 ID:OBvJ9bTb
Pdf���� ���{��
906��H4n21Ym7mA [sage] 2018/08/19(��) 21:35:07.10 ID:BehawhAJ
���ʂ̐��w�����҂ɂ͗������ꂤ����e�Ɍ��܂��Ă���B�ȏ�B
935��H4n21Ym7mA [sage] 2018/08/20(��) 14:46:08.31 ID:N+36Ptxg
���S�ɐ������ؖ���������
�@�@�@�@�@
947��H4n21Ym7mA [age] 2018/08/21(��) 10:06:30.21 ID:KkjwiMLB
Pdf���� ���{��
989��H4n21Ym7mA [age] 2018/08/22(��) 07:48:25.38 ID:SxQ2y3ZV
Pdf���� ���{��
2018/08/24(��) 18:47:23.61ID:lQ7owNFh
�������������璼���Ȃ�I�H��Β����Ȃ�I�H������
���Ă����|���Ȃ�
���Ă����|���Ȃ�
2018/08/24(��) 18:49:19.71ID:tqui2hKP
>>120
�����Ƃ��悤�Ƀo�[�W�����������ĉ��x�����肢�����̂ɉ��ł����ߋ��̓z������H
�����Ƃ��悤�Ƀo�[�W�����������ĉ��x�����肢�����̂ɉ��ł����ߋ��̓z������H
2018/08/24(��) 18:50:01.49ID:HeaACyN5
>>120
��pandoc
��pandoc
2018/08/24(��) 19:45:30.24ID:02RtuJ/f
�Ȃ��5ch�́A���X���Ƀt�H���g���ς��̂��낤�H�H�H
131�w�p
2018/08/24(��) 19:54:16.34ID:L5bxyQLn ���A�N�V�����|
132�w�p
2018/08/24(��) 19:55:51.03ID:L5bxyQLn �l�@�Ɓ@���X�|���X�|�ҁB
>>127
���J������Ō��ɋC�t������d�����Ȃ�
���J������Ō��ɋC�t������d�����Ȃ�
>>129
pdf or word �� latex�ł�
pdf or word �� latex�ł�
2018/08/24(��) 20:11:18.37ID:KL8GFrzC
2018/08/24(��) 20:12:57.29ID:noqd2vPn
>>136
�ł��܂����A���肪�Ƃ��������܂�
�ł��܂����A���肪�Ƃ��������܂�
2018/08/24(��) 21:46:02.14ID:3weK3pAS
�̍قƂ��C�ɂ���i�K����Ȃ�����
>>138
�l�I�ɂ́A�ؖ��͊������Ă��܂�����
�l�I�ɂ́A�ؖ��͊������Ă��܂�����
2018/08/24(��) 22:24:54.37ID:02RtuJ/f
�P�́A��������炸���\�t���˂�
����Ȃ����
���Ȃ̖������
����Ȃ����
���Ȃ̖������
2018/08/24(��) 22:30:16.06ID:1OvBgvPC
>>139
���̐l�̎w�E�ɂ܂Ƃ��Ȕ��_�͂��Ă��Ȃ��悤����
���̐l�̎w�E�ɂ܂Ƃ��Ȕ��_�͂��Ă��Ȃ��悤����
143�P�R�Q�l�ڂ̑f������
2018/08/24(��) 22:54:12.71ID:DLCTMBU7 �u�l�I�ɂ͊����v���s�k�錾
���_���ł��Ȃ����_�łP�̔s�k
���_���ł��Ȃ����_�łP�̔s�k
2018/08/24(��) 22:56:43.41ID:1OvBgvPC
�ؖ��̂��悤���Ȃ����Ƃ��_���Ɏc���Ă�����_������
>>143
���ɑ��Ă��H�ق�ԈႢ����ł������Ă݂�
���ɑ��Ă��H�ق�ԈႢ����ł������Ă݂�
2018/08/24(��) 23:08:04.43ID:tWX0+783
�ؖ��ł��Ȃ��Ȃ琳�����Ƃ͌����Ȃ���
2018/08/24(��) 23:08:56.89ID:q2Zpn13X
�ؖ��̂��悤���Ȃ����ĂȂ�w�ȒP�ȓ��e�Ȃ�Ȃ������̂��H
150�P�R�Q�l�ڂ̑f������
2018/08/24(��) 23:13:21.92ID:6zlcHWzg �O�X���̎w�E�Œ����ĂȂ��ԈႢ�������
�b986�P�R�Q�l�ڂ̑f������2018/08/21(��) 23:16:54.64ID:EO419+q9
�b�P�T�y�[�W
�b��n+1=f�~(pk-1)
�b���ƂȂ邱�Ƃ��K�v�ł���Bek��1�ƂȂ�S�Ă�k�ɑ��Đ��藧���Ȃ���Ȃ�Ȃ�����A���g�Ƃ���
�b��n+1=g�~��(pk-1)
�b����̓_�E�g����
�b ���ׂĂ�pk-1�͋����ł��菭�Ȃ��Ƃ�2�����ʈ����Ƃ��Ď����A2�ȊO�̋��ʈ����������Ȃ��Ƃ�����Ȃ��B
�b���߂�n+1=g�~LCM�opk-1|1��k��r��ek��1}�Ƃ��Ȃ���Ȃ�Ȃ����A���ꂾ�Ƃ��̐�̏ؖ������藧���Ȃ��B
���Ƃ��� pk �� 7, 11, 19 �Ƃ���� (pk-1) �̔{���Ƃ����̂�
(6�̔{��)����(10�̔{��)����(18�̔{��)���Ă��ƂɂȂ邯�ǁA�����(6�~10�~18�̔{��)�Ƃ͈قȂ�
90�̔{���ł�������̂ŁAn��1 (mod4) �Ƃ͖������Ȃ��B
���ׂĂ� pk �� n+1=f�~(pk-1) �ƂȂ����Ƃ��Ă� n+1=g�~��(pk-1) �Ƃ͂����Ȃ��̂ł��̕����͌��B
�b986�P�R�Q�l�ڂ̑f������2018/08/21(��) 23:16:54.64ID:EO419+q9
�b�P�T�y�[�W
�b��n+1=f�~(pk-1)
�b���ƂȂ邱�Ƃ��K�v�ł���Bek��1�ƂȂ�S�Ă�k�ɑ��Đ��藧���Ȃ���Ȃ�Ȃ�����A���g�Ƃ���
�b��n+1=g�~��(pk-1)
�b����̓_�E�g����
�b ���ׂĂ�pk-1�͋����ł��菭�Ȃ��Ƃ�2�����ʈ����Ƃ��Ď����A2�ȊO�̋��ʈ����������Ȃ��Ƃ�����Ȃ��B
�b���߂�n+1=g�~LCM�opk-1|1��k��r��ek��1}�Ƃ��Ȃ���Ȃ�Ȃ����A���ꂾ�Ƃ��̐�̏ؖ������藧���Ȃ��B
���Ƃ��� pk �� 7, 11, 19 �Ƃ���� (pk-1) �̔{���Ƃ����̂�
(6�̔{��)����(10�̔{��)����(18�̔{��)���Ă��ƂɂȂ邯�ǁA�����(6�~10�~18�̔{��)�Ƃ͈قȂ�
90�̔{���ł�������̂ŁAn��1 (mod4) �Ƃ͖������Ȃ��B
���ׂĂ� pk �� n+1=f�~(pk-1) �ƂȂ����Ƃ��Ă� n+1=g�~��(pk-1) �Ƃ͂����Ȃ��̂ł��̕����͌��B
2018/08/24(��) 23:24:10.00ID:5VqIPUhH
>>152
�ؖ�����Ƃ����Ă��ǂ���������̂�������Ȃ��Bck<qk-1��k�ɑ��Ă�
���I����������̂ŁAb�̌`����Ack<qk-1�ƂȂ�S�Ă�k�ɑ���
���I���������Ȃ���Ȃ�Ȃ��͓̂��R���ƍl����
�ؖ�����Ƃ����Ă��ǂ���������̂�������Ȃ��Bck<qk-1��k�ɑ��Ă�
���I����������̂ŁAb�̌`����Ack<qk-1�ƂȂ�S�Ă�k�ɑ���
���I���������Ȃ���Ȃ�Ȃ��͓̂��R���ƍl����
2018/08/24(��) 23:33:52.68ID:5VqIPUhH
155�P�R�Q�l�ڂ̑f������
2018/08/24(��) 23:40:16.88ID:EHxixVAp ck<qk-1�ƂȂ�k�����݂���̂��ǂ������ؖ�����ĂȂ�����ǂ����������Ă��n�܂�Ȃ���
2018/08/24(��) 23:53:04.73ID:WzkHXo1C
�����]�X�ƕϐ��]�X���ĉ��������́H
2018/08/24(��) 23:53:34.55ID:haO4NUeV
���R������
158�P�R�Q�l�ڂ̑f������
2018/08/25(�y) 00:10:35.46ID:ygRZb9ps �����ʂɎw�E���Ă������J�����
���̍ۑS�������o���Ƃ�����
�E���S��y���Ɍ��߂����f����p���b,c���Ɍ��߂������s����
�E�������̈����Ɛ����̈���������
�E�������k�ł������藧���Ȃ����̂����ׂĂ�k�Đ��藧�ƌ�������(�Ɓ͂̍���)
�E���{���Ƒ��������
���Ɖ�����������lj����Ă���
���̍ۑS�������o���Ƃ�����
�E���S��y���Ɍ��߂����f����p���b,c���Ɍ��߂������s����
�E�������̈����Ɛ����̈���������
�E�������k�ł������藧���Ȃ����̂����ׂĂ�k�Đ��藧�ƌ�������(�Ɓ͂̍���)
�E���{���Ƒ��������
���Ɖ�����������lj����Ă���
2018/08/25(�y) 05:15:55.33ID:1qqT9j0c
���_������
�S�̓I�ɃS�~�E������
���P�Ȃ�
�ؖ��_���������������ȂǁA��{�����\
�S�̓I�ɃS�~�E������
���P�Ȃ�
�ؖ��_���������������ȂǁA��{�����\
>>158
�w���H
���E���S��y���Ɍ��߂����f����p���b,c���Ɍ��߂������s����
���̓��e�Ȃ��̑O�̃X���ʼn��x�������Ă���͂����B
���E�������̈����Ɛ����̈���������
����͂��������c�_�����Ă���l�Ԃ����̃X���ɂ��������ł�����
���͂���͂Ȃ��B���������ӂ��Ɍ�������悤�ȃ��X�������������B
���E�������k�ł������藧���Ȃ����̂����ׂĂ�k�Đ��藧�ƌ�������
����̂���������̂��Bck<qk-1��k�ɑ��Đ��藧���Ȃ���Ȃ�Ȃ��̂�
b�̌`����A�����B�������藧���Ȃ������k�̒l�ŁAb��pk^qk��
������Ȃ������B���̂��̂悤�Ȏ����ȓ��e�Ɋ��݂��̂�������Ȃ���
�����Ȃ��Ƃ��ؖ����邱�Ƃ͓���B
�w���H
���E���S��y���Ɍ��߂����f����p���b,c���Ɍ��߂������s����
���̓��e�Ȃ��̑O�̃X���ʼn��x�������Ă���͂����B
���E�������̈����Ɛ����̈���������
����͂��������c�_�����Ă���l�Ԃ����̃X���ɂ��������ł�����
���͂���͂Ȃ��B���������ӂ��Ɍ�������悤�ȃ��X�������������B
���E�������k�ł������藧���Ȃ����̂����ׂĂ�k�Đ��藧�ƌ�������
����̂���������̂��Bck<qk-1��k�ɑ��Đ��藧���Ȃ���Ȃ�Ȃ��̂�
b�̌`����A�����B�������藧���Ȃ������k�̒l�ŁAb��pk^qk��
������Ȃ������B���̂��̂悤�Ȏ����ȓ��e�Ɋ��݂��̂�������Ȃ���
�����Ȃ��Ƃ��ؖ����邱�Ƃ͓���B
>>160 ����
�~���������ӂ��Ɍ�������悤�ȃ��X�������������B
�Z�ԈႦ�āA���������ӂ��Ɍ�������悤�ȃ��X�������������B
�~���������ӂ��Ɍ�������悤�ȃ��X�������������B
�Z�ԈႦ�āA���������ӂ��Ɍ�������悤�ȃ��X�������������B
>>155
���݂��Ȃ��ꍇ���ؖ��ɏ����Ă��邩����Ȃ�
���݂��Ȃ��ꍇ���ؖ��ɏ����Ă��邩����Ȃ�
2018/08/25(�y) 07:53:43.53ID:S4mcgiRU
�����Ƃ����̂͂ˁA�ؖ����ȒP�����邩�玩���Ƃ�����B�o���Ă����Ă�
2018/08/25(�y) 08:07:15.72ID:NP3T2RR8
��̊��S���͑��݂��܂���
�ؖ�
�����Ȉȗ�
�ؖ�
�����Ȉȗ�
2018/08/25(�y) 08:20:28.67ID:2TOt2Ru3
�����Ă���Ɖ������Ă���̋�ʂ����Ă��Ȃ�
2018/08/25(�y) 08:32:29.74ID:ostKV3bB
�����ǂ�ł݂��B
p.8��
�u�ȏォ��A0 �� c_r �� q_r �| 1�̒l��c_r��゙���Ƃ��ɁAp^(n�|1) + p^(n�|3) + ⋯ + 1��゙p_r^(q_r�|c_r�|1)��゙������Ȃ����゙�Ȃ�Ȃ��B�v
���Ă��邯�ǁA
2b = (1+p+�c+p^n)c
�̗��ӂ̑f���������l������,
q_r = (1+p+�c+p^n�̑f���������ɂ�����p_r�̎w��) + c_r.
����A���ʂ́u���炩�ɐ��藧�v�ƌ����̂ł́B
p.8��
�u�ȏォ��A0 �� c_r �� q_r �| 1�̒l��c_r��゙���Ƃ��ɁAp^(n�|1) + p^(n�|3) + ⋯ + 1��゙p_r^(q_r�|c_r�|1)��゙������Ȃ����゙�Ȃ�Ȃ��B�v
���Ă��邯�ǁA
2b = (1+p+�c+p^n)c
�̗��ӂ̑f���������l������,
q_r = (1+p+�c+p^n�̑f���������ɂ�����p_r�̎w��) + c_r.
����A���ʂ́u���炩�ɐ��藧�v�ƌ����̂ł́B
>>89�̃��X�ɉ��S���Ď���ᔻ���Ă���̂͐��w�𗝉����Ă��Ȃ����������̑f�l��
���w�I�ɈӖ��̂��鐳���Ȕᔻ�łȂ����Ƃ𗝉��ł��Ă��Ȃ�(��)
���w�I�ɈӖ��̂��鐳���Ȕᔻ�łȂ����Ƃ𗝉��ł��Ă��Ȃ�(��)
2018/08/25(�y) 08:59:05.32ID:2TOt2Ru3
���w�𗝉����Ă��Ȃ����������̑f�l�Ƃ��������ȏЉ�
2018/08/25(�y) 09:03:45.84ID:ostKV3bB
f(p_r)�Ɋւ���c�_�ł����A
�������Ƃ��āu�`���̍����v���Ƙ_����̂ł���Ap_r��K���ȕ���(�Ⴆ��X�Ȃ�)�ɒu�������Ă���_����K�v������܂��B
�������Ƃ��āu�`���̍����v���Ƙ_����̂ł���Ap_r��K���ȕ���(�Ⴆ��X�Ȃ�)�ɒu�������Ă���_����K�v������܂��B
2018/08/25(�y) 09:20:18.05ID:ostKV3bB
�łȂ��ƁA������f�ƁAf��p_r���������l�Ƃ���ʂł����A�����������܂��B
>>170
���w�͂�����l�͂��̂悤�ȍ����Ȗ��ɂ����Ȃ܂�邱�Ƃ͂���܂���
���w�͂�����l�͂��̂悤�ȍ����Ȗ��ɂ����Ȃ܂�邱�Ƃ͂���܂���
172�P�R�Q�l�ڂ̑f������
2018/08/25(�y) 09:48:14.54ID:EpAgBNfd2018/08/25(�y) 09:56:38.44ID:NP3T2RR8
175�P�R�Q�l�ڂ̑f������
2018/08/25(�y) 09:57:36.70ID:qwJRgcQw �Ắu���w�͂�����v�u�����ȁv���P�̔s�k�錾�ƂƂ炦�Ă�����
�����s�k�錾������̂P��w
�����s�k�錾������̂P��w
176�P�R�Q�l�ڂ̑f������
2018/08/25(�y) 10:10:07.18ID:YKaHb2vp2018/08/25(�y) 10:34:56.99ID:ostKV3bB
�����������Ƃ������A
�I�m�ɒ�`����Ă��Ȃ����߂ɋc�_�����Ӗ��ɂȂ��Ă܂��B
�up_r���ƍl�����������Ƃ��Ĉ��������̂��낤�v�Ɛ����͂ł��܂����Ap_r�͑f���Ƃ��Ē�`����Ă܂����B
�I�m�ɒ�`����Ă��Ȃ����߂ɋc�_�����Ӗ��ɂȂ��Ă܂��B
�up_r���ƍl�����������Ƃ��Ĉ��������̂��낤�v�Ɛ����͂ł��܂����Ap_r�͑f���Ƃ��Ē�`����Ă܂����B
2018/08/25(�y) 10:45:34.56ID:rlbynoBU
>>167
�ȂA���Ǐؖ��ł��Ȃ��̂�w
�ȂA���Ǐؖ��ł��Ȃ��̂�w
2018/08/25(�y) 11:05:54.28ID:r6awhQfP
�u�����v�œ�����n�����Ĉ�萔������
�����Ȃ�ؖ����Ă݂�ƌ�������
�����Ȃ�ؖ����Ă݂�ƌ�������
>>179
�����Ȃ��Ƃ��ǂ��ؖ�����̂������Ă݂Ă����B���͈��k�ɑ��ē��Ă͂܂�ؖ���
���̓�������ck<qk-1�̂��ɑ��Đ��藧�̂����A�����������ؖ����玩���Ƃ���
�`�ł����������Ƃ��ł��Ȃ��B������ؖ�����̂́A���̎�i�ł���������Ȃ���Ȃ�Ȃ�
�Ƃ������Ƃł���A���̂悤�Ȃ��Ƃ��ł���Ƃ͎v���Ȃ��B�܂�Ȃ����e�ł��������B
�����Ȃ��Ƃ��ǂ��ؖ�����̂������Ă݂Ă����B���͈��k�ɑ��ē��Ă͂܂�ؖ���
���̓�������ck<qk-1�̂��ɑ��Đ��藧�̂����A�����������ؖ����玩���Ƃ���
�`�ł����������Ƃ��ł��Ȃ��B������ؖ�����̂́A���̎�i�ł���������Ȃ���Ȃ�Ȃ�
�Ƃ������Ƃł���A���̂悤�Ȃ��Ƃ��ł���Ƃ͎v���Ȃ��B�܂�Ȃ����e�ł��������B
2018/08/25(�y) 11:20:03.54ID:2TOt2Ru3
�����Ȃ�ؖ����ȒP�Ȃ͂��ł���...
2018/08/25(�y) 11:20:20.46ID:ZiXINhJi
�����Ȃ��Ƃ͏ؖ��ł��Ȃ��I��New!
2018/08/25(�y) 11:21:42.80ID:r6awhQfP
2018/08/25(�y) 11:27:54.22ID:PTd+mqMA
>>1�� �g���̌`���炷�ׂẮ`�ł���`�ɂ��ā`����������h �Ƃ������w�̃��W�b�N�ɂȂ����W�b�N���g���Ă���B
��x P(x) �̌`�̖���o����B��̐��_���� �g���Քĉ��h �łǂ��䂤�Ŏg���Ă悢���A�ǂ̂悤�Ɏg���̂��ɂ��Č����ɒ�߂��Ă���B
https://ja.wikipedia.org/wiki/%E6%99%AE%E9%81%8D%E6%B1%8E%E5%8C%96
���������Ƃ���̂��H���̌�������藝�o����̂ɂǂ̂悤�Ȑ��_����p���Ă悢�̂��ɂ��Ă̍��ӂ���������͂₻��͐��w�ł͂Ȃ��B
�����̕ϐ� pr �ɂ��Ă����ؖ���^���Ă��Ȃ�����
2m+1 = w pr^(qr-cr-1) (��w : �)
������ �g���Քĉ����h �ɂ͂Ȃ�
��b�̌`����S�Ă�k�ɑ��Ď��I�����藧���Ȃ���Ȃ�Ȃ��͎̂���
�Ƃ�
���������郌�X�����Ă��܂��܂������A���m�ɂ́Ack<qk-1�ƂȂ�S�Ă�k�ɑ���
�����I�����藧�Ƃ������Ƃł��B
�Ƃ��������w�ɂ͑��݂��Ȃ� �g�Ǝ��̕��Քĉ����_��������Ɏ���h ���đ��� �gpk�h �ɂ��ēK�p���Ă�B
�g���w�̘_���Ƃ��Ăǂ����܂������Ă邩�h �ȑO�� �g���w�̘_���ł���Ȃ��h �Ƃ��������Ȃ��B
�����A�����ł͂Ȃ��A������� �g���Քĉ����_���h �͈͓̔���
��k (ck<qk-1�� ��w : � 2m+1 = w pr^(qr-cr-1) )
�����o�ł���Ƃ����Ȃ�A���ۂɂ��������Ă݂��Ȃ��Ƃ����Ȃ��B
�u�gb�̌`����h ���Քĉ��ł���v�ȂǂƂ������_���͐��w�ɂ͂Ȃ��B
��x P(x) �̌`�̖���o����B��̐��_���� �g���Քĉ��h �łǂ��䂤�Ŏg���Ă悢���A�ǂ̂悤�Ɏg���̂��ɂ��Č����ɒ�߂��Ă���B
https://ja.wikipedia.org/wiki/%E6%99%AE%E9%81%8D%E6%B1%8E%E5%8C%96
���������Ƃ���̂��H���̌�������藝�o����̂ɂǂ̂悤�Ȑ��_����p���Ă悢�̂��ɂ��Ă̍��ӂ���������͂₻��͐��w�ł͂Ȃ��B
�����̕ϐ� pr �ɂ��Ă����ؖ���^���Ă��Ȃ�����
2m+1 = w pr^(qr-cr-1) (��w : �)
������ �g���Քĉ����h �ɂ͂Ȃ�
��b�̌`����S�Ă�k�ɑ��Ď��I�����藧���Ȃ���Ȃ�Ȃ��͎̂���
�Ƃ�
���������郌�X�����Ă��܂��܂������A���m�ɂ́Ack<qk-1�ƂȂ�S�Ă�k�ɑ���
�����I�����藧�Ƃ������Ƃł��B
�Ƃ��������w�ɂ͑��݂��Ȃ� �g�Ǝ��̕��Քĉ����_��������Ɏ���h ���đ��� �gpk�h �ɂ��ēK�p���Ă�B
�g���w�̘_���Ƃ��Ăǂ����܂������Ă邩�h �ȑO�� �g���w�̘_���ł���Ȃ��h �Ƃ��������Ȃ��B
�����A�����ł͂Ȃ��A������� �g���Քĉ����_���h �͈͓̔���
��k (ck<qk-1�� ��w : � 2m+1 = w pr^(qr-cr-1) )
�����o�ł���Ƃ����Ȃ�A���ۂɂ��������Ă݂��Ȃ��Ƃ����Ȃ��B
�u�gb�̌`����h ���Քĉ��ł���v�ȂǂƂ������_���͐��w�ɂ͂Ȃ��B
2018/08/25(�y) 11:31:28.81ID:QKrpL5rY
���؎���ł͏ؖ���K�v�Ƃ��Ȃ�
2018/08/25(�y) 11:33:31.02ID:2TOt2Ru3
����܂ł̊�|�l�l�^
�Ep�͓���̒l�����͂�����0p=0�ł���s��ɂȂ邩�疵��
�Ep�͒萔�ł��肩�ϐ��ł���
�Ep���P����������i�{���͒P���������Ȃ��j����p�͑f���ɂȂ肦�Ȃ�
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł���
�Ew�͐����ł��蓯���ɐ����łȂ�
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ�
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂�
�E�ϐ��͐��l�ɒu�������Ă̓_��
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R
�E27/5 �� 3 �Ŋ�����
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂���
�E���Ȃ��Ƃ���͂����Ȃ�A�Ƃ������Ƃ�
�@�S�Ăɑ��Đ��藧���Ȃ���Ȃ�Ȃ�
�E�����Ȃ��Ƃ͏ؖ��ł��Ȃ�(NEW!)
�Ep�͓���̒l�����͂�����0p=0�ł���s��ɂȂ邩�疵��
�Ep�͒萔�ł��肩�ϐ��ł���
�Ep���P����������i�{���͒P���������Ȃ��j����p�͑f���ɂȂ肦�Ȃ�
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł���
�Ew�͐����ł��蓯���ɐ����łȂ�
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ�
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂�
�E�ϐ��͐��l�ɒu�������Ă̓_��
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R
�E27/5 �� 3 �Ŋ�����
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂���
�E���Ȃ��Ƃ���͂����Ȃ�A�Ƃ������Ƃ�
�@�S�Ăɑ��Đ��藧���Ȃ���Ȃ�Ȃ�
�E�����Ȃ��Ƃ͏ؖ��ł��Ȃ�(NEW!)
2018/08/25(�y) 11:39:47.91ID:PTd+mqMA
>>184
����
✕�F��k (ck<qk-1�� ��w : � 2m+1 = w pr^(qr-cr-1) )
���F��k (ck<qk-1�� ��w : � 2m+1 = w pr^(qk-ck-1) )
����
✕�F��k (ck<qk-1�� ��w : � 2m+1 = w pr^(qr-cr-1) )
���F��k (ck<qk-1�� ��w : � 2m+1 = w pr^(qk-ck-1) )
2018/08/25(�y) 11:39:49.77ID:lFGEJlNi
�|�l�Ƃ��Ă͗��h���Ǝv��
����҂ɂ́u�����Ȃ��Ƃ��ؖ�����͓̂���v�Ȃ�Ĕ��z���ł��Ȃ�
����҂ɂ́u�����Ȃ��Ƃ��ؖ�����͓̂���v�Ȃ�Ĕ��z���ł��Ȃ�
189�P�R�Q�l�ڂ̑f������
2018/08/25(�y) 11:42:04.85ID:YKaHb2vp ����������ؖ����Ȃ��A�Ȃ炽���̓���
����������ؖ��ł��Ȃ��A�Ȃ琔�w�̖��m
������ɂ��Ă������͂��Ȃ�
����������ؖ��ł��Ȃ��A�Ȃ琔�w�̖��m
������ɂ��Ă������͂��Ȃ�
2018/08/25(�y) 11:59:45.63ID:ostKV3bB
����ς�ނ�A�Ɣ��f���ׂ�����
�L���̏d���Ƃ��A��{�I�Ȑ��w�m��������Ζ��炩�Ȃ��Ƃ��₽��ƕ��G�ɏ����Ƃ��A���ʂȉ����Ō�T���B���Ă�悤�ɂ��������Ȃ���B
�L���̏d���Ƃ��A��{�I�Ȑ��w�m��������Ζ��炩�Ȃ��Ƃ��₽��ƕ��G�ɏ����Ƃ��A���ʂȉ����Ō�T���B���Ă�悤�ɂ��������Ȃ���B
>>184
pk=(p+1)/2�ƂȂ�S�Ă�pk�ɑ���b��pk^qk�Ŋ�����邽�߂̏��������玩��
>>185
�Ƃ₩�������K�v�̂Ȃ��قǎ���
>>188
�|�l�ł͂Ȃ�����A�|�l�ƌ�����
>>189
���Ȃ��͏ؖ��ł���̂ł����H
���̖��́A���w�͂̍����l�ɂ́A���ƈ�̖�����ؖ�����Ώؖ����������邱�Ƃ�
�m���Ă��邱�Ƃ��낤�B�����_�ł��̖��͎��ɂ͉�������Ȗ�肾�ƍl������B
���ꂩ��A�ŋ�ck=qk�̏ؖ���lj��������A�lj�����K�v�͂Ȃ��ƍl������B
pk=(p+1)/2�ƂȂ�S�Ă�pk�ɑ���b��pk^qk�Ŋ�����邽�߂̏��������玩��
>>185
�Ƃ₩�������K�v�̂Ȃ��قǎ���
>>188
�|�l�ł͂Ȃ�����A�|�l�ƌ�����
>>189
���Ȃ��͏ؖ��ł���̂ł����H
���̖��́A���w�͂̍����l�ɂ́A���ƈ�̖�����ؖ�����Ώؖ����������邱�Ƃ�
�m���Ă��邱�Ƃ��낤�B�����_�ł��̖��͎��ɂ͉�������Ȗ�肾�ƍl������B
���ꂩ��A�ŋ�ck=qk�̏ؖ���lj��������A�lj�����K�v�͂Ȃ��ƍl������B
>>190
6�����������Ēނ�Ȃ�Ă��Ƃ�����킯���Ȃ����낤
6�����������Ēނ�Ȃ�Ă��Ƃ�����킯���Ȃ����낤
2018/08/25(�y) 12:04:49.16ID:2TOt2Ru3
>>191
�v����ɂ��Ȃ��͏ؖ��Ɏ��s���Ă�Ƃ������ƁH
�v����ɂ��Ȃ��͏ؖ��Ɏ��s���Ă�Ƃ������ƁH
2018/08/25(�y) 12:18:32.08ID:ostKV3bB
�ނ肶��Ȃ��Ȃ�A���Ȃ��͐��w�ɂ�����ؖ��Ƃ������̂ɑ��Ēm�����o��������Ȃ��̂ł͂Ȃ����ȁB
��w���x���̐��w�̋��ȏ���1���ł�������ʂ��ēǂ�ł݂�����������������Ȃ��B
��w�Ő��w����Ɋw��ł��A6�������x����낭�ɏؖ����ł��Ȃ��w���Ȃ�Ē��������Ȃ���
���w�ȊO�Ɏ��Ԃ��g�����������邯��ǁB
��w���x���̐��w�̋��ȏ���1���ł�������ʂ��ēǂ�ł݂�����������������Ȃ��B
��w�Ő��w����Ɋw��ł��A6�������x����낭�ɏؖ����ł��Ȃ��w���Ȃ�Ē��������Ȃ���
���w�ȊO�Ɏ��Ԃ��g�����������邯��ǁB
2018/08/25(�y) 12:22:38.11ID:UMWGN7ci
>>195
������k�ɑ��Đ��藧���̂��Ab�������`�����Ă��邩��A����ck<qk-1�ƂȂ�
k�ɑ��Đ��藧�͎̂������Ə����Ă���B(4�x�ڈȏ�)
���������B�i�@�� �� �� �� �� �� �� ���@�S�@�I ���@�j
������k�ɑ��Đ��藧���̂��Ab�������`�����Ă��邩��A����ck<qk-1�ƂȂ�
k�ɑ��Đ��藧�͎̂������Ə����Ă���B(4�x�ڈȏ�)
���������B�i�@�� �� �� �� �� �� �� ���@�S�@�I ���@�j
2018/08/25(�y) 12:36:01.75ID:PTd+mqMA
�����Ƃ�����̂͌����A���_�K�����̂��̃Y�o�����قړ����Ƃ��̂�
���Ȃ����ؖ������i�Ƃ����Ă���j
y:���S���Ap�͑��d�x��̑f���q�c�ˁ�w : � 2m+1 = w pr^(qr-cr-1)
�����
https://ja.wikipedia.org/wiki/%25E6%2599%25AE%25E9%2581%258D%25E6%25B1%258E%25E5%258C%2596
�� �g���Քĉ����_���h ��K�p���Ă�
��k (ck<qk-1�� ��w : � 2m+1 = w pr^(qk-ck-1) )
���Ȃ��B
���ۏ����Ă݂�Ǝ����ꂽ�̂�(���������_���_��������)
��y A B p
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1�@�c(A)
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A�@�c(B)
qr = v_pr(B) �@�c(C)
cr = v_pr(A)�@�c(D)
p = 2pr -1�@�c(E)
�ˁ�w 2m+1 = wpr^(qr-cr-1)�@�c(F)
�ŁA����ɂ����đ�������ĂȂ��ϐ��� m, pr �ŁA����� m, pr �ɂ��Ă̖���B
pr�ɂ��ĕ��Քĉ����Ă����閽���
(��)
��m pr
��y A B p
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1�@�c(A)
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A�@�c(B)
qr = v_pr(B) �@�c(C)
cr = v_pr(A)�@�c(D)
p = 2pr -1�@�c(E)
�ˁ�w 2m+1 = wpr^(qr-cr-1)�@�c(F)
����ɑ��A��������N�������ɓ������Ǝ咣����̂�
(��)
��m pk
��A ��B
qk = v_pk(B) �@
ck = v_pk(A)
ck<qk-1 �� ��w 2m+1 = wpk^(qk-ck-1)�@
��r���ď����Ă݂�A�h�����Ɂh (��)����(��)�����o�����Ȃ�ē��ꂢ���Ȃ��Ƃ킩��B
����������Ƃ����Ă���Ȃ琔�w�̘_���ł͂Ȃ��B
(��)����(��)���ؖ��������Ȃ�����_�����������邱�Ƃ͂Ȃ��B
���Ȃ����ؖ������i�Ƃ����Ă���j
y:���S���Ap�͑��d�x��̑f���q�c�ˁ�w : � 2m+1 = w pr^(qr-cr-1)
�����
https://ja.wikipedia.org/wiki/%25E6%2599%25AE%25E9%2581%258D%25E6%25B1%258E%25E5%258C%2596
�� �g���Քĉ����_���h ��K�p���Ă�
��k (ck<qk-1�� ��w : � 2m+1 = w pr^(qk-ck-1) )
���Ȃ��B
���ۏ����Ă݂�Ǝ����ꂽ�̂�(���������_���_��������)
��y A B p
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1�@�c(A)
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A�@�c(B)
qr = v_pr(B) �@�c(C)
cr = v_pr(A)�@�c(D)
p = 2pr -1�@�c(E)
�ˁ�w 2m+1 = wpr^(qr-cr-1)�@�c(F)
�ŁA����ɂ����đ�������ĂȂ��ϐ��� m, pr �ŁA����� m, pr �ɂ��Ă̖���B
pr�ɂ��ĕ��Քĉ����Ă����閽���
(��)
��m pr
��y A B p
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1�@�c(A)
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A�@�c(B)
qr = v_pr(B) �@�c(C)
cr = v_pr(A)�@�c(D)
p = 2pr -1�@�c(E)
�ˁ�w 2m+1 = wpr^(qr-cr-1)�@�c(F)
����ɑ��A��������N�������ɓ������Ǝ咣����̂�
(��)
��m pk
��A ��B
qk = v_pk(B) �@
ck = v_pk(A)
ck<qk-1 �� ��w 2m+1 = wpk^(qk-ck-1)�@
��r���ď����Ă݂�A�h�����Ɂh (��)����(��)�����o�����Ȃ�ē��ꂢ���Ȃ��Ƃ킩��B
����������Ƃ����Ă���Ȃ琔�w�̘_���ł͂Ȃ��B
(��)����(��)���ؖ��������Ȃ�����_�����������邱�Ƃ͂Ȃ��B
2018/08/25(�y) 12:37:05.37ID:ostKV3bB
���̐��w�҂��ؖ��ł��Ă��Ȃ����ƂƁA���Ȃ��_���ɉ����W���H
2018/08/25(�y) 12:38:42.47ID:UMWGN7ci
https://ja.wikipedia.org/wiki/���R���
���������킩��₷������́�
http://web.sfc.keio.ac.jp/~mukai/modular/gentzen-NK.pdf
���w�̐��_�K���͊T�˂����ɏ����Ă�����̂ɂȂ邪>>1�̐��_�͂����Ƃ͈قȂ�悤��
���������킩��₷������́�
http://web.sfc.keio.ac.jp/~mukai/modular/gentzen-NK.pdf
���w�̐��_�K���͊T�˂����ɏ����Ă�����̂ɂȂ邪>>1�̐��_�͂����Ƃ͈قȂ�悤��
2018/08/25(�y) 12:51:55.42ID:dmZ2Flg5
>>171
��������Ȃ��̂Ŏ���
��������Ȃ��̂Ŏ���
2018/08/25(�y) 12:52:11.18ID:PTd+mqMA
�Ӓn���Ă���̂ł͂Ȃ����S�Ɍ�����Ă�悤������ʓ|�����lj���B
(A)�`(E) �� ��w 2m+1 = wpr^(qr-cr-1)
�������ꂽ�Ƃ��ĕ��Քĉ��̓K�p�K���
���͐����̏W���ł���A�ӂ͐����ł���A ���˃�(y)�͓��o����Ă���Ɖ��肷��B�ĉ��K���ł́Ay�����Ɍ��y����Ă��炸�Ax���ӂɑ��݂��Ȃ��ꍇ�A ���˃�(x)���������A�Ƃ���B
�ō���̏ꍇ�B>>89��(A)�`(E)�̂Ȃ���pr�ɂ��Ẳ��肪����̂Ō��_�̂Ȃ���cr��ʂ̕����ɒu���������Ȃ��B
���Քĉ��ƕ��ቻ�ŕϐ���u��������Ȃ�A���̖���S�̂ɂłĂ���ϐ��S�̂� �g��C�Ɂh ���������Ȃ��ƃ_���B
�ȒP�ȗ�ł�
���Ƃ���
x>5 �� x>3
��x��y�ɂ���������
y>5 �� y>3
�ɂ���̂͂�邳��邯��
x>5 �� y>3
�Ȃ�ċ�����Ȃ��B
������k�ɑ��Đ��藧���̂��Ab�������`�����Ă��邩��A����ck<qk-1�ƂȂ�
k�ɑ��Đ��藧�͎̂������Ə����Ă���B
�Ƃ����̂�(A)�`(E)�̂Ȃ���cr�������ĂȂ��Ȃ狖����邯�Ǔ����Ă�ł���H
(A)�`(E) �� ��w 2m+1 = wpr^(qr-cr-1)
�������ꂽ�Ƃ��ĕ��Քĉ��̓K�p�K���
���͐����̏W���ł���A�ӂ͐����ł���A ���˃�(y)�͓��o����Ă���Ɖ��肷��B�ĉ��K���ł́Ay�����Ɍ��y����Ă��炸�Ax���ӂɑ��݂��Ȃ��ꍇ�A ���˃�(x)���������A�Ƃ���B
�ō���̏ꍇ�B>>89��(A)�`(E)�̂Ȃ���pr�ɂ��Ẳ��肪����̂Ō��_�̂Ȃ���cr��ʂ̕����ɒu���������Ȃ��B
���Քĉ��ƕ��ቻ�ŕϐ���u��������Ȃ�A���̖���S�̂ɂłĂ���ϐ��S�̂� �g��C�Ɂh ���������Ȃ��ƃ_���B
�ȒP�ȗ�ł�
���Ƃ���
x>5 �� x>3
��x��y�ɂ���������
y>5 �� y>3
�ɂ���̂͂�邳��邯��
x>5 �� y>3
�Ȃ�ċ�����Ȃ��B
������k�ɑ��Đ��藧���̂��Ab�������`�����Ă��邩��A����ck<qk-1�ƂȂ�
k�ɑ��Đ��藧�͎̂������Ə����Ă���B
�Ƃ����̂�(A)�`(E)�̂Ȃ���cr�������ĂȂ��Ȃ狖����邯�Ǔ����Ă�ł���H
2018/08/25(�y) 13:06:35.02ID:PTd+mqMA
wiki�y�[�W
���Քĉ��Fhttps://ja.wikipedia.org/wiki/%E6%99%AE%E9%81%8D%E6%B1%8E%E5%8C%96
���ቻ�Fhttps://ja.wikipedia.org/wiki/%E6%99%AE%E9%81%8D%E4%BE%8B%E5%8C%96
���w�̐��_���Ƃ��č��ӂ��ꂽ���̂�K�p�K�������Đ������g���ĉ������B
����ɂ����_�ɂ������Ă镶���̌��_���̕��������ς���̂͋�����܂���B
���Քĉ��Fhttps://ja.wikipedia.org/wiki/%E6%99%AE%E9%81%8D%E6%B1%8E%E5%8C%96
���ቻ�Fhttps://ja.wikipedia.org/wiki/%E6%99%AE%E9%81%8D%E4%BE%8B%E5%8C%96
���w�̐��_���Ƃ��č��ӂ��ꂽ���̂�K�p�K�������Đ������g���ĉ������B
����ɂ����_�ɂ������Ă镶���̌��_���̕��������ς���̂͋�����܂���B
2018/08/25(�y) 13:13:58.30ID:PTd+mqMA
>>202
����
✕�F�Ƃ����̂�(A)�`(E)�̂Ȃ���cr�������ĂȂ��Ȃ狖����邯�Ǔ����Ă�ł���H
���F�Ƃ����̂�(A)�`(E)�̂Ȃ���pr�������ĂȂ��Ȃ狖����邯�Ǔ����Ă�ł���H
pr�͂��̒i�̏ؖ���(A)�`(E)�̂Ȃ��œ��肳��Ă���pr�ł���pr�ɂ��ē���ꂽ���_(F)��pr��ʂ�pk�ɂ͕ς����܂���B
���Քĉ��̓K�p�����ɔ����邩��ł��B
wiki�y�[�W�ɂ����������Ă���ł���H
����
✕�F�Ƃ����̂�(A)�`(E)�̂Ȃ���cr�������ĂȂ��Ȃ狖����邯�Ǔ����Ă�ł���H
���F�Ƃ����̂�(A)�`(E)�̂Ȃ���pr�������ĂȂ��Ȃ狖����邯�Ǔ����Ă�ł���H
pr�͂��̒i�̏ؖ���(A)�`(E)�̂Ȃ��œ��肳��Ă���pr�ł���pr�ɂ��ē���ꂽ���_(F)��pr��ʂ�pk�ɂ͕ς����܂���B
���Քĉ��̓K�p�����ɔ����邩��ł��B
wiki�y�[�W�ɂ����������Ă���ł���H
2018/08/25(�y) 13:30:50.40ID:PTd+mqMA
���łȂ̂�p14���i
w �̈�����p1����pr�ȊO�̑f��ps���܂܂��ꍇ�́A���I����Ab �Ɋ܂܂��ps��
�w����qs�Ac �Ɋ܂܂�����ps�̎w����cs�Ƃ����
�����A�E�g�ł���B
ps��p1�`pr�ɓ����ĂȂ��ꍇ��������
qs = ps �� B �ɂ�����multiplicity = 0
cs = ps �� A �ɂ�����multiplicity = 0
�Ȃ���N�̂����V�����I�̓K�p����
ck<qk-1
�����ĂȂ����炱��ɇI��K�p�ł��܂���B
�v�͕S��������
ck<qk-1�ˇI
��F�߂��Ƃ��Ă��Ay�̈��q�łȂ�ps�ɂ��Ă�qs = cs = 0�ɂȂ��Ă��܂��̂ŇI�͎g���܂���B
�������������̏C���ł͒���Ȃ���ł���B
pr�ȊO��2m+1�ɂ��Ă� multiplicity �ɂ��Ă͑S�R�������Ȃ̓��������Ȃ������茻���_�ǂ����悤������܂���B
w �̈�����p1����pr�ȊO�̑f��ps���܂܂��ꍇ�́A���I����Ab �Ɋ܂܂��ps��
�w����qs�Ac �Ɋ܂܂�����ps�̎w����cs�Ƃ����
�����A�E�g�ł���B
ps��p1�`pr�ɓ����ĂȂ��ꍇ��������
qs = ps �� B �ɂ�����multiplicity = 0
cs = ps �� A �ɂ�����multiplicity = 0
�Ȃ���N�̂����V�����I�̓K�p����
ck<qk-1
�����ĂȂ����炱��ɇI��K�p�ł��܂���B
�v�͕S��������
ck<qk-1�ˇI
��F�߂��Ƃ��Ă��Ay�̈��q�łȂ�ps�ɂ��Ă�qs = cs = 0�ɂȂ��Ă��܂��̂ŇI�͎g���܂���B
�������������̏C���ł͒���Ȃ���ł���B
pr�ȊO��2m+1�ɂ��Ă� multiplicity �ɂ��Ă͑S�R�������Ȃ̓��������Ȃ������茻���_�ǂ����悤������܂���B
206�P�R�Q�l�ڂ̑f������
2018/08/25(�y) 15:19:25.41ID:Zrn2Mgii �P�̗������Ƃ�������
�����ЂƂ��ă�(y)=2y�ƂȂ鐮��y�����S���Ƃ����B
���Ƃ���y=6�̂Ƃ���(y)=12=2y�ł��邩�炙�͊��S���ł���B
���l�ɁA���ׂĂ̊�ɂ��Ă���(y)=2y�ƂȂ�B�Ȃ��Ȃ�u���̌`������������v
����Ă��ׂĂ̊�͊��S���ł���iQED)
�����ЂƂ��ă�(y)=2y�ƂȂ鐮��y�����S���Ƃ����B
���Ƃ���y=6�̂Ƃ���(y)=12=2y�ł��邩�炙�͊��S���ł���B
���l�ɁA���ׂĂ̊�ɂ��Ă���(y)=2y�ƂȂ�B�Ȃ��Ȃ�u���̌`������������v
����Ă��ׂĂ̊�͊��S���ł���iQED)
207�P�R�Q�l�ڂ̑f������
2018/08/25(�y) 15:24:59.34ID:Zrn2Mgii >>206
�⑫
���ׂĂ̊y�ɂ��Ă���(y)=2y�ƂȂ�͎̂����ł��B
�Ƃɂ����ؖ����K�v�Ȃ��قǎ���������ؖ��̏����悤���Ȃ��B
�Ȃ�ł���ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł���
�܂�_�͂�߂Ă�����������
�⑫
���ׂĂ̊y�ɂ��Ă���(y)=2y�ƂȂ�͎̂����ł��B
�Ƃɂ����ؖ����K�v�Ȃ��قǎ���������ؖ��̏����悤���Ȃ��B
�Ȃ�ł���ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł���
�܂�_�͂�߂Ă�����������
2018/08/25(�y) 15:35:45.70ID:zmtUye6c
�����H
�S�Ă̊�ŁH
���Ⴀ�S�Ă̊�����S����
�I��
�S�Ă̊�ŁH
���Ⴀ�S�Ă̊�����S����
�I��
2018/08/25(�y) 15:57:10.34ID:dmZ2Flg5
�ނ�ꂽ�ƌ���̂�
�ނ�ꂽ�Ǝv���Ă鉴���ނ��Ă���̂��c
�ނ�ꂽ�Ǝv���Ă鉴���ނ��Ă���̂��c
>>205
���������Ă���̂������ς蕪����܂��Ab�̌`����S�Ă�k�ɑ��đΏ̂ɂȂ��Ă��܂��B
pr=(p+1)/2�ƂȂ�k=r�͂���ȊO�ɂ���������\��������܂��B���̂���ck<qk-1�ƂȂ����
�Ɋւ��Ă͓Y�����݂̂��قȂ邾���ł��̂ŁA�����c�_�������ɂł���
�S�Ă�ck<qk-1����k�ɑ���
2m+1=wpk^(qk-ck-1)
����������Ƃ��������ł��B
���Ȃ���N�̂����V�����I�̓K�p����
��ck<qk-1
�����͓��Rcs<qs-1�ł�����
���������Ă���̂������ς蕪����܂��Ab�̌`����S�Ă�k�ɑ��đΏ̂ɂȂ��Ă��܂��B
pr=(p+1)/2�ƂȂ�k=r�͂���ȊO�ɂ���������\��������܂��B���̂���ck<qk-1�ƂȂ����
�Ɋւ��Ă͓Y�����݂̂��قȂ邾���ł��̂ŁA�����c�_�������ɂł���
�S�Ă�ck<qk-1����k�ɑ���
2m+1=wpk^(qk-ck-1)
����������Ƃ��������ł��B
���Ȃ���N�̂����V�����I�̓K�p����
��ck<qk-1
�����͓��Rcs<qs-1�ł�����
2018/08/25(�y) 16:44:15.11ID:dmZ2Flg5
�����ς蕪�����̂�����烊�W�F�N�g�ł������܂�
2018/08/25(�y) 17:25:04.29ID:ostKV3bB
y�ɑΉ�����p�ɑ���(p-1)/2=p_k�ƂȂ�k�͈�����Ȃ��̂ŁA���̌`���Ώ̓I������Ƃ����đS�Ă�k���_���I�ɓ����ł͂���܂���B
�K�p�ł���͂����Ȃ��ł��傤�B
�K�p�ł���͂����Ȃ��ł��傤�B
2018/08/25(�y) 17:37:21.15ID:ostKV3bB
�up�����ւ��ċc�_����悢�v�Ƃ��l���ł����炻����؈Ⴂ�ł��B
p��ς���Ƃ������Ƃ́A�c�_�̑匳�ł����̊��S��y��ʂ̊�̊��S��y'�Ɏ��ւ���Ƃ������ƂɂȂ�܂��B
�����Ď��ւ�����f�����������قȂ�̂ŁA�c�_�͍ŏ������蒼���ɂȂ�܂��B
�܂��A�w���@���g�����߂ɁA����́u��̊��S�������݂���v�ł�����A��������y'�����݂���ۏ�����܂���B
p��ς���Ƃ������Ƃ́A�c�_�̑匳�ł����̊��S��y��ʂ̊�̊��S��y'�Ɏ��ւ���Ƃ������ƂɂȂ�܂��B
�����Ď��ւ�����f�����������قȂ�̂ŁA�c�_�͍ŏ������蒼���ɂȂ�܂��B
�܂��A�w���@���g�����߂ɁA����́u��̊��S�������݂���v�ł�����A��������y'�����݂���ۏ�����܂���B
214�w�p
2018/08/25(�y) 18:46:59.34ID:q2oz86/q �R�l�J��T���܂킵�B
2018/08/25(�y) 18:53:08.13ID:YtpOT3Ia
�O�X�����������������A�Y�ꂽ���ǂ��̐l�O�ɂ��N����qk�Ack�̒l�ŋc�_���Ă��ȁB
�����Œ�`�������̒l�̈Ӗ����������Ĉ�Ԃ킩���ĂȂ���>>1����Ȃ��́H
�����Œ�`�������̒l�̈Ӗ����������Ĉ�Ԃ킩���ĂȂ���>>1����Ȃ��́H
2018/08/25(�y) 19:33:57.31ID:LGolSfhm
>>210
�Ȃɂ������Ă邩�����ς�킩��Ȃ��悤�Ȃ̂ł������������Ă݂܂��B
�����������Ă���̂������ς蕪����܂��Ab�̌`����S�Ă�k�ɑ��đΏ̂ɂȂ��Ă��܂��B
��pr=(p+1)/2�ƂȂ�k=r�͂���ȊO�ɂ���������\��������܂��B���̂���ck<qk-1�ƂȂ���̂Ɋւ��Ă͓Y�����݂̂��قȂ邾���ł��̂ŁA�����c�_�������ɂł���
�Ȃ��ĂȂ��ł���H
�����f���q�̐���4�Ɍ��肵�܂��B
�ł��Ȃ����A�ؖ������̂�
��y A B p p1 p2 p3
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1
p1��p2�Ap2��p3�Ap3��p1�A
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A
q1 = v_p1(B)�Ac1 = v_p1(A)�Aq2 = v_p2(B)�Ac2 = v_p2(A)�Aq3 = v_p3(B)�Ac3 = v_p3(A)�A
p = 2p1 - 1
�ˁ�w 2m+1 = wpr^(q1-c1-1)
�ł���H(���̏ؖ����_���_�������ǁB)
�����p1��p2����ւ�����(�������ł���������悤��qr,cr��������)
��y A B p p2 p1 p3
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1
p2��p1�Ap1��p3�Ap3��p2�A
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A
q2 = v_p2(B)�Ac2 = v_p2(A)�Aq1 = v_p1(B)�Ac1 = v_p1(A)�Aq3 = v_p3(B)�Ac3 = v_p3(A)�A
p = 2p2 - 1
�ˁ�w 2m+1 = wp2^(q2-c2-1)
�ɂȂ�ł���H
���̂Q���킹����Ǝv���H���킹��̂͏��肾���Ǎ��킹����
��y A B p p2 p1 p3
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1
p1��p2�Ap2��p3�Ap3��p1�A
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A
q2 = v_p2(B)�Ac2 = v_p2(A)�Aq1 = v_p1(B)�Ac1 = v_p1(A)�Aq3 = v_p3(B)�Ac3 = v_p3(A)�A
p = 2p1 - 1 = 2p2 -1
�ˁ�w 2m+1 = wp1^(q1-c1-1) = wp2^(q2-c2-1)
�ɂȂ�ł���H
����ł����́H
�Ȃɂ������Ă邩�����ς�킩��Ȃ��悤�Ȃ̂ł������������Ă݂܂��B
�����������Ă���̂������ς蕪����܂��Ab�̌`����S�Ă�k�ɑ��đΏ̂ɂȂ��Ă��܂��B
��pr=(p+1)/2�ƂȂ�k=r�͂���ȊO�ɂ���������\��������܂��B���̂���ck<qk-1�ƂȂ���̂Ɋւ��Ă͓Y�����݂̂��قȂ邾���ł��̂ŁA�����c�_�������ɂł���
�Ȃ��ĂȂ��ł���H
�����f���q�̐���4�Ɍ��肵�܂��B
�ł��Ȃ����A�ؖ������̂�
��y A B p p1 p2 p3
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1
p1��p2�Ap2��p3�Ap3��p1�A
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A
q1 = v_p1(B)�Ac1 = v_p1(A)�Aq2 = v_p2(B)�Ac2 = v_p2(A)�Aq3 = v_p3(B)�Ac3 = v_p3(A)�A
p = 2p1 - 1
�ˁ�w 2m+1 = wpr^(q1-c1-1)
�ł���H(���̏ؖ����_���_�������ǁB)
�����p1��p2����ւ�����(�������ł���������悤��qr,cr��������)
��y A B p p2 p1 p3
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1
p2��p1�Ap1��p3�Ap3��p2�A
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A
q2 = v_p2(B)�Ac2 = v_p2(A)�Aq1 = v_p1(B)�Ac1 = v_p1(A)�Aq3 = v_p3(B)�Ac3 = v_p3(A)�A
p = 2p2 - 1
�ˁ�w 2m+1 = wp2^(q2-c2-1)
�ɂȂ�ł���H
���̂Q���킹����Ǝv���H���킹��̂͏��肾���Ǎ��킹����
��y A B p p2 p1 p3
y�͊�̊��S��,p�͑f����v_p(y) = 4m+1
p1��p2�Ap2��p3�Ap3��p1�A
2y = 2p^(4m+1)B = (1+p+�c+p^(4m+1))A
q2 = v_p2(B)�Ac2 = v_p2(A)�Aq1 = v_p1(B)�Ac1 = v_p1(A)�Aq3 = v_p3(B)�Ac3 = v_p3(A)�A
p = 2p1 - 1 = 2p2 -1
�ˁ�w 2m+1 = wp1^(q1-c1-1) = wp2^(q2-c2-1)
�ɂȂ�ł���H
����ł����́H
2018/08/25(�y) 20:01:40.38ID:1qqT9j0c
���̑O�P�̘_�@�ŁA
�����̊��S�������݂��Ȃ��I
�Ȃ�ďƖ������ꂽ�Ǝv������A���x��
�S�Ă̊�͊��S���ł���I
���ؖ�����Ă��܂����B
���؎���͐��Ɉَ�����������ԁI
�����̊��S�������݂��Ȃ��I
�Ȃ�ďƖ������ꂽ�Ǝv������A���x��
�S�Ă̊�͊��S���ł���I
���ؖ�����Ă��܂����B
���؎���͐��Ɉَ�����������ԁI
2018/08/25(�y) 20:25:55.17ID:0HaUtabE
���^�Ȑ����Ƃ������ł��Ȃ����
2018/08/25(�y) 20:43:06.76ID:LGolSfhm
�܂����Ƃ͎v���� �g�_���ł�p1�Ƃ�����Ȃ��I�����p1�Ɍ��肵�Ă邩�炨�������Ȃ�I�h �Ƃ������o���̂��Ȃ��H
2018/08/26(��) 09:37:10.43ID:oz9s1ydI
�ʔ��玸�炵�܂�
�ʔ��玸�炵�܂���
�ʔ��玸�炵�܂���
>>216
���ˁ�w 2m+1 = wpr^(q1-c1-1)
���ł���H(���̏ؖ����_���_�������ǁB)
����͍����Ă���B���Ȃ̂́A(p+1)/2������pk�ɑ��đS�ē������ƌ����邩
�Ƃ������ł����āA����͏ؖ��ł��Ȃ����A������p�����������Ƃ��z��ł���
����A���ꂪ���藧���̂Ɋւ��Ă͎��I���d�˂Ďg�����Ƃ��ł���ƍl������B
�Ȃ��Ȃ��A���̏��������e�𗝉����Ă��炦�Ȃ��̂ŁA���m�ɏ�����p1��p2��
���I�����藧�ꍇ�ɂ�
2m+1=w1p1^(q1-c1-1), c1<q1-1
2m+1=w2p2^(q2-c2-1), c2<q2-1
�ł����āA
2m+1=w��[k=1,2]wkpk^(qk-ck-1)
����������Ƃ������ƁB
�����̖�肪�S�ĉ���������@���v�������B
�S�Ă�k�ɑ���ck<qk��������(���̏ؖ��͊ȒP)
p^n+�c+1��0 (mod pk)
���S�Ă�k�ɑ��Đ��藧���Ȃ���Ȃ�Ȃ����Ƃ����������B
�����A���̐�ɂ��̖�肪�ؖ����ׂ����Ƃ���̖��肾��
���������Ƃ��������O���畷�����Ă��Ă���B
���ˁ�w 2m+1 = wpr^(q1-c1-1)
���ł���H(���̏ؖ����_���_�������ǁB)
����͍����Ă���B���Ȃ̂́A(p+1)/2������pk�ɑ��đS�ē������ƌ����邩
�Ƃ������ł����āA����͏ؖ��ł��Ȃ����A������p�����������Ƃ��z��ł���
����A���ꂪ���藧���̂Ɋւ��Ă͎��I���d�˂Ďg�����Ƃ��ł���ƍl������B
�Ȃ��Ȃ��A���̏��������e�𗝉����Ă��炦�Ȃ��̂ŁA���m�ɏ�����p1��p2��
���I�����藧�ꍇ�ɂ�
2m+1=w1p1^(q1-c1-1), c1<q1-1
2m+1=w2p2^(q2-c2-1), c2<q2-1
�ł����āA
2m+1=w��[k=1,2]wkpk^(qk-ck-1)
����������Ƃ������ƁB
�����̖�肪�S�ĉ���������@���v�������B
�S�Ă�k�ɑ���ck<qk��������(���̏ؖ��͊ȒP)
p^n+�c+1��0 (mod pk)
���S�Ă�k�ɑ��Đ��藧���Ȃ���Ȃ�Ȃ����Ƃ����������B
�����A���̐�ɂ��̖�肪�ؖ����ׂ����Ƃ���̖��肾��
���������Ƃ��������O���畷�����Ă��Ă���B
2018/08/26(��) 10:35:54.01ID:OLKUlX43
������͏ؖ��ł��Ȃ����A������p�����������Ƃ��z��ł���
�َ����̍��؋�Ԃ̎��͂ǂ��ł������B
�P�̂���Ă邱�Ƃ͌������E�ƊW�Ȃ��B
�َ����̍��؋�Ԃ̎��͂ǂ��ł������B
�P�̂���Ă邱�Ƃ͌������E�ƊW�Ȃ��B
>>216
p�͕�������ƍl������Ƃ������Ƃ𗝉����ׂ�
2b=c(p^n+�c+1)
�ł����āAc��p��k�ɂ��p=2pk-1�Ƃ����W�ɂ���ĕω�����̂�p��k�Ɉˑ���
�����̒l����邱�Ƃ��ł���ƍl������B
p�͕�������ƍl������Ƃ������Ƃ𗝉����ׂ�
2b=c(p^n+�c+1)
�ł����āAc��p��k�ɂ��p=2pk-1�Ƃ����W�ɂ���ĕω�����̂�p��k�Ɉˑ���
�����̒l����邱�Ƃ��ł���ƍl������B
2018/08/26(��) 10:50:50.58ID:yhO+TDnq
�l��������Ă̂͏ؖ��ł������Ă��ƁH�ł��ĂȂ����Ă��ƁH
2018/08/26(��) 11:07:45.22ID:WDbhbjNy
>223
b��c��p��n���A�����ɏo�Ă���l�͂��ׂĂЂƂ̊�̊��S���Ɉˑ�������ӂȒl�ł��B
����Ɏ��ւ���Ƙ_�����j�]���܂����A��낵���ł����B
b��c��p��n���A�����ɏo�Ă���l�͂��ׂĂЂƂ̊�̊��S���Ɉˑ�������ӂȒl�ł��B
����Ɏ��ւ���Ƙ_�����j�]���܂����A��낵���ł����B
227�P�R�Q�l�ڂ̑f������
2018/08/26(��) 11:15:47.73ID:+bCwOCje ���؎���ł͈ȉ�����������炵��
���S��28�́A���̑f����p=2���g����p^2�~7�ƂȂ�Bn=2,b=7�Ƃ��A2b=c(p^n+�c+1)�̌`���Ƃ���ƁA2�~7=2�~(p^2+p+1)�̎���B
���̎���������p=2,-3��B���������āA����2��-3�͂Ƃ���28�̑f�����łȂ���Ȃ�Ȃ��B
����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł����H(�킩��Ȃ�)
���S��28�́A���̑f����p=2���g����p^2�~7�ƂȂ�Bn=2,b=7�Ƃ��A2b=c(p^n+�c+1)�̌`���Ƃ���ƁA2�~7=2�~(p^2+p+1)�̎���B
���̎���������p=2,-3��B���������āA����2��-3�͂Ƃ���28�̑f�����łȂ���Ȃ�Ȃ��B
����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł����H(�킩��Ȃ�)
2018/08/26(��) 11:21:12.97ID:wwZAduSp
>>221
�܂��킩���ĂȂ��Ȃ��B
2m+1 �̂Ƃ������������悤���Ǝv�������ǂ߂�ǂ��������炻�̂܂܃R�s�y�������ǁB�킩�邾�낤�Ǝv���āB
����ς�킩���ĂȂ��B
�v���I�Ȃ̂�
p=2p1-1=2p2-1�Ap1��p2�B
�N�͎��Xp����������\�������邩����Ȃ��Ƃ��������������ǁA�������|�C���g����Ă�B
�|�C���g�͌N�̏ؖ�������������ɂ͂ނ��땡���Ȃ��Ƃ����Ȃ��B�����ĕ������鎖���ؖ����Ȃ��Ă͂����Ȃ��B
�܁A�K���p���ďؖ����Ă݂ĉ������B
�܂��킩���ĂȂ��Ȃ��B
2m+1 �̂Ƃ������������悤���Ǝv�������ǂ߂�ǂ��������炻�̂܂܃R�s�y�������ǁB�킩�邾�낤�Ǝv���āB
����ς�킩���ĂȂ��B
�v���I�Ȃ̂�
p=2p1-1=2p2-1�Ap1��p2�B
�N�͎��Xp����������\�������邩����Ȃ��Ƃ��������������ǁA�������|�C���g����Ă�B
�|�C���g�͌N�̏ؖ�������������ɂ͂ނ��땡���Ȃ��Ƃ����Ȃ��B�����ĕ������鎖���ؖ����Ȃ��Ă͂����Ȃ��B
�܁A�K���p���ďؖ����Ă݂ĉ������B
2018/08/26(��) 12:07:56.71ID:OLKUlX43
���|�C���g�͌N�̏ؖ�������������ɂ͂ނ��땡���Ȃ��Ƃ����Ȃ��B
�������ĕ������鎖���ؖ����Ȃ��Ă͂����Ȃ��B
�����U��L�^�[
�������ĕ������鎖���ؖ����Ȃ��Ă͂����Ȃ��B
�����U��L�^�[
230�P�R�Q�l�ڂ̑f������
2018/08/26(��) 13:01:27.08ID:HMYuW1QG �u�`�Ȃ�a�v�������Ă����Ă�����u�a�Ȃ�`�v�ɂ���ւ�������͍��ؘ_���̊�{�I�ȃe�N�j�b�N�̈���B
����̏ꍇ�́up�����S��y�̑f�����v�Ȃ�u2b=c(p^n+�c+1)�����v�ƌ����Ă����āA
���̋t���咣����������g���Ă���B�܂�A
�u2b=c(p^n+�c+1)�����v�Ȃ�up�����S��y�̑f�����v�łȂ���Ȃ�Ȃ��B������p�͕������݂���B
�Ƃ��Ă���̂��P�̎咣�ł���A���̃e�N�j�b�N���I���Ɏg���Ă���B
>>227�ɏ�����Ă���悤�ɁA����Ȏ咣�͐������Ȃ��͖̂��炩�B
����ȗc�t�ȃy�e���ɏ�������ĉ��X�Ƌc�_����قǂ̖��������낤��B
����̏ꍇ�́up�����S��y�̑f�����v�Ȃ�u2b=c(p^n+�c+1)�����v�ƌ����Ă����āA
���̋t���咣����������g���Ă���B�܂�A
�u2b=c(p^n+�c+1)�����v�Ȃ�up�����S��y�̑f�����v�łȂ���Ȃ�Ȃ��B������p�͕������݂���B
�Ƃ��Ă���̂��P�̎咣�ł���A���̃e�N�j�b�N���I���Ɏg���Ă���B
>>227�ɏ�����Ă���悤�ɁA����Ȏ咣�͐������Ȃ��͖̂��炩�B
����ȗc�t�ȃy�e���ɏ�������ĉ��X�Ƌc�_����قǂ̖��������낤��B
231�P�R�Q�l�ڂ̑f������
2018/08/26(��) 16:17:50.30ID:AZWNHV19 >>223 �_���̍ŏ��̕��ŁA
p�͎w������ɂȂ�y�̗B��̑f�����ł��邱�Ƃ��ؖ�����ĂȂ����������c�H
p�͎w������ɂȂ�y�̗B��̑f�����ł��邱�Ƃ��ؖ�����ĂȂ����������c�H
>>228
������A2b=c(p^n+�c+1)������A���m����p,c,n��3�Ȃ���Ap�̌�����Ɍ��肳���
���Ƃ͂Ȃ��Ac��k�Ɉˑ����ĕς���Ƃ������Ƃł��B����Ȃ��Ƃ������ł��Ȃ��͕̂s�v�c�ł��ˁB
���������鎖���ؖ����Ȃ��Ă͂����Ȃ��B
����Ȃ����Ƃ��z�肳��Ă���̂ɕ������邱�Ƃ̏ؖ������邱�Ƃ��ł���킯���Ȃ��ł��傤�H
>>231
p�ɑ���y����ӂɒ�܂�Ƃ��������ł��B���x�������Ă��܂���
pk,qk���߂遨a.b����܂遨�����̉��̑g�ݍ��킹������\��������p,c,n����܂���������邩��
����Ȃ�y����܂�
������A2b=c(p^n+�c+1)������A���m����p,c,n��3�Ȃ���Ap�̌�����Ɍ��肳���
���Ƃ͂Ȃ��Ac��k�Ɉˑ����ĕς���Ƃ������Ƃł��B����Ȃ��Ƃ������ł��Ȃ��͕̂s�v�c�ł��ˁB
���������鎖���ؖ����Ȃ��Ă͂����Ȃ��B
����Ȃ����Ƃ��z�肳��Ă���̂ɕ������邱�Ƃ̏ؖ������邱�Ƃ��ł���킯���Ȃ��ł��傤�H
>>231
p�ɑ���y����ӂɒ�܂�Ƃ��������ł��B���x�������Ă��܂���
pk,qk���߂遨a.b����܂遨�����̉��̑g�ݍ��킹������\��������p,c,n����܂���������邩��
����Ȃ�y����܂�
234�P�R�Q�l�ڂ̑f������
2018/08/26(��) 17:01:12.46ID:AZWNHV19 >>232
��p�ɑ���y����ӂɒ�܂�Ƃ��������ł��B
������̊��S���ł���Ƃ������肩��n�܂��Ă�͂��Ȃ̂ɁA
�Ȃ�ł�����ɂȂ��Č��܂邱�ƂɂȂ��c�H
��p�ɑ���y����ӂɒ�܂�Ƃ��������ł��B
������̊��S���ł���Ƃ������肩��n�܂��Ă�͂��Ȃ̂ɁA
�Ȃ�ł�����ɂȂ��Č��܂邱�ƂɂȂ��c�H
2018/08/26(��) 17:02:58.38ID:wwZAduSp
>>232
������
p=2p1-1=2p2-1
�̖����N�͕�����u�������đΉ��ł���Ǝ咣���Ă����A���R�epk���ƂɈقȂ��̊��S��yk�����݂��Ă��̑��d�x��̑f���qqk��am=2pk-1�����悤�Ɏ��鎖�������Ȃ��Ƃ����Ȃ��B
�N�����x��pr��pk�͑Ώ̂�������ւ��ċc�_�����pk�ɂ��Ă��������_��������Ǝ咣���Ă�������H
���̂��߂ɂ͓��Rpr�ɂ��Ẳ���̕�����pk�Ɏ��ւ��Ȃ��Ƃ����Ȃ��B
�����_�ł͂��̏ؖ����_���ɂ͓����ĂȂ��̂ŌN�̘_���͊������Ă��Ȃ��B
�N�͉ߋ��ɂ��̕��j�ŏؖ��ł���Ǝ咣���Ă�����A�ǂ����撣���Ă��������Ɨ�܂��Ă邾���B
�撣���Ă˂��`
������
p=2p1-1=2p2-1
�̖����N�͕�����u�������đΉ��ł���Ǝ咣���Ă����A���R�epk���ƂɈقȂ��̊��S��yk�����݂��Ă��̑��d�x��̑f���qqk��am=2pk-1�����悤�Ɏ��鎖�������Ȃ��Ƃ����Ȃ��B
�N�����x��pr��pk�͑Ώ̂�������ւ��ċc�_�����pk�ɂ��Ă��������_��������Ǝ咣���Ă�������H
���̂��߂ɂ͓��Rpr�ɂ��Ẳ���̕�����pk�Ɏ��ւ��Ȃ��Ƃ����Ȃ��B
�����_�ł͂��̏ؖ����_���ɂ͓����ĂȂ��̂ŌN�̘_���͊������Ă��Ȃ��B
�N�͉ߋ��ɂ��̕��j�ŏؖ��ł���Ǝ咣���Ă�����A�ǂ����撣���Ă��������Ɨ�܂��Ă邾���B
�撣���Ă˂��`
2018/08/26(��) 17:03:36.18ID:xBRFnbpB
2018/08/26(��) 17:07:47.31ID:e5R6NQVv
�u�����v�ȊO�ł͏ؖ����ł��Ȃ����牽�����Ă�����
2018/08/26(��) 17:07:59.06ID:wwZAduSp
>>235
����
�~�f���qqk��am=2pk-1�����悤�Ɏ��鎖�������Ȃ��Ƃ����Ȃ��B
�� �f���qqk��qk=2pk-1�����悤�Ɏ��鎖�������Ȃ��Ƃ����Ȃ��B
�撣��`
����
�~�f���qqk��am=2pk-1�����悤�Ɏ��鎖�������Ȃ��Ƃ����Ȃ��B
�� �f���qqk��qk=2pk-1�����悤�Ɏ��鎖�������Ȃ��Ƃ����Ȃ��B
�撣��`
2018/08/26(��) 17:09:12.85ID:CSiDAnHb
����ς�w���@�̍ŏ��̉���
�u��̊��S�����������Ƃ��Ă����y�Ƃ���B����ƁA��������p������B�v
�Ƃ����_�@��S�������ł��Ă��Ȃ��B
�݂�ȕ��͂̐^������̋c�_���w�E���Ă����肷�邯�ǁA
��������>>1�͔w���@�𗝉����Ă��Ȃ��B
���͓͂��{��ɂȂ��Ă��Ȃ����ǁA����Ȃ�ɔw���@�ŏؖ������݂Ă���Ǝv���Ă�����A
>>1�͔w���@�𗝉����Ă��Ȃ�����w�E�����ݍ����킯���Ȃ��B
�����Ă���͂��łɎw�E����Ă��邯�ǁA
���܂��Ɂuy����܂�v�Ƃ������Ă���̂ŁA���Ԃ��o���Ă��Ȃ��i�����Ă��Ȃ��B
���������ǂ̉e�����ǂ����m��Ȃ����ǁA����͐��w�̖͂�肶��Ȃ��A
>>1�̐��_�̖�肾�Ǝv���B
�u��̊��S�����������Ƃ��Ă����y�Ƃ���B����ƁA��������p������B�v
�Ƃ����_�@��S�������ł��Ă��Ȃ��B
�݂�ȕ��͂̐^������̋c�_���w�E���Ă����肷�邯�ǁA
��������>>1�͔w���@�𗝉����Ă��Ȃ��B
���͓͂��{��ɂȂ��Ă��Ȃ����ǁA����Ȃ�ɔw���@�ŏؖ������݂Ă���Ǝv���Ă�����A
>>1�͔w���@�𗝉����Ă��Ȃ�����w�E�����ݍ����킯���Ȃ��B
�����Ă���͂��łɎw�E����Ă��邯�ǁA
���܂��Ɂuy����܂�v�Ƃ������Ă���̂ŁA���Ԃ��o���Ă��Ȃ��i�����Ă��Ȃ��B
���������ǂ̉e�����ǂ����m��Ȃ����ǁA����͐��w�̖͂�肶��Ȃ��A
>>1�̐��_�̖�肾�Ǝv���B
2018/08/26(��) 17:13:39.73ID:5xtlFmUF
�o���A�S�̌|�l�l�^���I�I
241�P�R�Q�l�ڂ̑f������
2018/08/26(��) 17:36:25.15ID:+bCwOCje >>233
��c=2�͂ǂ�����łĂ����̂ł���w
p=2,n=2,b=7,2b=c(p^n+�c+1)�Ȃ��瓖�R�����Ȃ�
���������Đ�������܂ł��Ȃ����A�Z���̂ł��Ȃ�������ɂ͓�������悤���B���܂��
��c=2�͂ǂ�����łĂ����̂ł���w
p=2,n=2,b=7,2b=c(p^n+�c+1)�Ȃ��瓖�R�����Ȃ�
���������Đ�������܂ł��Ȃ����A�Z���̂ł��Ȃ�������ɂ͓�������悤���B���܂��
243�P�R�Q�l�ڂ̑f������
2018/08/26(��) 17:50:28.45ID:+bCwOCje �Ȃ��A�ߋ��ɓ����w�E���������Ǝv�����Ap^n+�c+1��p��0�͈̔͂ŒP������������A2b=c(p^n+�c+1)�̊W����������Ƃ��Ă��A��������f��p�͍��X�P�����Ȃ��B�܂蕡�����݂��邱�Ƃ͂Ȃ��B
2018/08/26(��) 17:53:42.17ID:R22qNuJD
�܁[�������ӂ̌������c
�ꂵ���Ȃ�����a�C�������������֗��Ȃ����
�ꂵ���Ȃ�����a�C�������������֗��Ȃ����
246�P�R�Q�l�ڂ̑f������
2018/08/26(��) 17:56:37.74ID:+bCwOCje �a�C����̕������͗v��Ȃ�
������́A��҂̌�f�ő���f���Ă���l�Ԃ������
������́A��҂̌�f�ő���f���Ă���l�Ԃ������
248�P�R�Q�l�ڂ̑f������
2018/08/26(��) 17:59:17.54ID:+bCwOCje >>246
���m����3�ŁA��������Ɖ����m�肵�Ȃ��͓̂�����O�ŁA��������ɂȂ邩��
�����������ƍl����̂����ʂł͂Ȃ��̂ł��傤���H
���m����3�ŁA��������Ɖ����m�肵�Ȃ��͓̂�����O�ŁA��������ɂȂ邩��
�����������ƍl����̂����ʂł͂Ȃ��̂ł��傤���H
250�P�R�Q�l�ڂ̑f������
2018/08/26(��) 18:04:36.57ID:AZWNHV192018/08/26(��) 18:19:39.45ID:xBRFnbpB
>>244
�Ȃ�����
�Ȃ�����
2018/08/26(��) 18:21:21.02ID:DotWVtJX
���؎���ł�-3��28�̈��q
2018/08/26(��) 18:23:59.94ID:xBRFnbpB
>>242
b���ϐ��Ȃ��ӂɂ����܂�Ȃ����www�͂��_�j
b���ϐ��Ȃ��ӂɂ����܂�Ȃ����www�͂��_�j
2018/08/26(��) 18:33:48.39ID:WDbhbjNy
�w���@�Łu��̊��S�������݂��Ȃ��v���������߂̉����
�u��̊��S�������Ȃ��Ƃ��ЂƂ��݂���v
�Ȃ��ǁA��������������������ĂȂ��̂ł́B
���������Θ_���ɉ��肪�����ĂȂ���B
�u��̊��S�������Ȃ��Ƃ��ЂƂ��݂���v
�Ȃ��ǁA��������������������ĂȂ��̂ł́B
���������Θ_���ɉ��肪�����ĂȂ���B
256�P�R�Q�l�ڂ̑f������
2018/08/26(��) 19:16:54.07ID:y49f/amO2018/08/26(��) 19:34:53.52ID:WDbhbjNy
�u�t��(�K������)�^�Ȃ炸�v���Đ��w�ŏؖ�����Ă�ᓖ�R�̂��Ƃ����A�Ӑ}���Ă���Ă�Ȃ��k�قł��ȁB
258�P�R�Q�l�ڂ̑f������
2018/08/26(��) 19:49:25.39ID:GJ/QHdHU �y24�}���\���A2000���z�@��Q�҂̓^�_�����@�����E���t�}���g���[���u�U�P�\���v���@�|�\�l�̓{���ׂ�
http://rosie.5ch.net/test/read.cgi/liveplus/1535249407/l50
�Q�S���Ԃs�u�̃`�����e�B�[�̓C�J�T�}�I�@�n���}�Q�h���͕����h�̃f�}�I�@�}�@�g���[���̓I�E���Ǝv���Ă�o�J�I
http://rosie.5ch.net/test/read.cgi/liveplus/1535249407/l50
�Q�S���Ԃs�u�̃`�����e�B�[�̓C�J�T�}�I�@�n���}�Q�h���͕����h�̃f�}�I�@�}�@�g���[���̓I�E���Ǝv���Ă�o�J�I
259�P�R�Q�l�ڂ̑f������
2018/08/26(��) 20:04:17.74ID:/9xIb4LH �m���Ă邩���H
���̂P�͉R���ł��Ȃ���A�k�ق��g���Ă���̂ł��Ȃ�
�e���r���畷�����Ă��鐺���܂߂āA���ׂĎ����ł͐��������Ƃ������Ă������Ȃ�
���ꂪ�������E�̏o������A���������w�ƐH������Ă��Ă��P�͂��\���Ȃ���
����͂����ǂ����悤���Ȃ��̂�
���̂P�͉R���ł��Ȃ���A�k�ق��g���Ă���̂ł��Ȃ�
�e���r���畷�����Ă��鐺���܂߂āA���ׂĎ����ł͐��������Ƃ������Ă������Ȃ�
���ꂪ�������E�̏o������A���������w�ƐH������Ă��Ă��P�͂��\���Ȃ���
����͂����ǂ����悤���Ȃ��̂�
2018/08/26(��) 20:15:15.62ID:dtHS+HYh
����Ɍ�����p�͕��������Ă��\��Ȃ��킯�ł�����A�_���ŏ������悤��
��������������k�Ƃ����͈̂�łȂ���Ȃ�Ȃ��Ƃ������R�͂���܂���B
�������w�L���͂�𗝉����Ă��Ȃ��Ƃ������Ƃ͂���܂���B�����̌�����B
��������������k�Ƃ����͈̂�łȂ���Ȃ�Ȃ��Ƃ������R�͂���܂���B
�������w�L���͂�𗝉����Ă��Ȃ��Ƃ������Ƃ͂���܂���B�����̌�����B
2018/08/26(��) 20:22:16.73ID:OLKUlX43
���������w�L���͂�𗝉����Ă��Ȃ��Ƃ������Ƃ͂���܂���B
�P�̒m��Ȃ��̂͋L���Ƃ�����ȃ��x������Ȃ��B
���w�I�ȍl�����A���̕\�����A�ؖ��̕��@�E�E�E�E
�P���S�������Ă��Ȃ��������w�̂���ɁA����҂͕����Ă��Ă���́B
�P�̒m��Ȃ��̂͋L���Ƃ�����ȃ��x������Ȃ��B
���w�I�ȍl�����A���̕\�����A�ؖ��̕��@�E�E�E�E
�P���S�������Ă��Ȃ��������w�̂���ɁA����҂͕����Ă��Ă���́B
2018/08/26(��) 20:22:43.33ID:dtHS+HYh
2018/08/26(��) 20:28:03.90ID:dtHS+HYh
>>266
�����̖ϑz���
�����̖ϑz���
2018/08/26(��) 20:28:15.09ID:WDbhbjNy
>>260
�����������Ă������킯�ł���ˁB
�����킯�Ȃ�����B
���w�Łu���݂���v���Ă̂�
�u���Ȃ��Ƃ�����݂���B��ȏ㑶�݂���Ƃ͌���Ȃ��v�����B
�����������Ă������킯�ł���ˁB
�����킯�Ȃ�����B
���w�Łu���݂���v���Ă̂�
�u���Ȃ��Ƃ�����݂���B��ȏ㑶�݂���Ƃ͌���Ȃ��v�����B
2018/08/26(��) 20:28:59.49ID:dtHS+HYh
2018/08/26(��) 20:29:42.77ID:WDbhbjNy
�����đ��݂���Ƃ͌������̂�_���ɂ͂ł���B
2018/08/26(��) 20:30:00.64ID:OLKUlX43
�P�̌������w�I���ʂ́A���؎���ł̖ϑz�B
���w�E���Z�̐��w�́A�P�̂��ꂩ��̐����ɖ𗧂͂�������
������ł������邾��I
���w�E���Z�̐��w�́A�P�̂��ꂩ��̐����ɖ𗧂͂�������
������ł������邾��I
2018/08/26(��) 20:42:10.76ID:VxafK4bF
>>273
�C�ӂɌ���ł���Ɖ��肵�Ă�̂ł����H
���Ȃ��̏ؖ��͔C�ӂ�pk��qk���߂č����̊��S���͑��݂��Ȃ��Ƃ��������ŁA���{�I�Ɋ�̊��S�������݂��Ȃ����Ƃ͏ؖ��ł��Ă��Ȃ��Ƃ������ƂɂȂ�܂��B�c�O�ł����B
�C�ӂɌ���ł���Ɖ��肵�Ă�̂ł����H
���Ȃ��̏ؖ��͔C�ӂ�pk��qk���߂č����̊��S���͑��݂��Ȃ��Ƃ��������ŁA���{�I�Ɋ�̊��S�������݂��Ȃ����Ƃ͏ؖ��ł��Ă��Ȃ��Ƃ������ƂɂȂ�܂��B�c�O�ł����B
2018/08/26(��) 20:42:34.27ID:WDbhbjNy
2018/08/26(��) 21:21:53.27ID:CSiDAnHb
�u���Ȃ��Ƃ������v�������Ƌ����Ă����Ȃ��Ƃ��߂Ȃ̂�
277�P�R�Q�l�ڂ̑f������
2018/08/26(��) 21:52:32.49ID:qs6b1fFZ �����P�͘_���{�̂����J�����Ɂu�����͐��������琳�����̂��v�Ƃ��������X�^�C���Ȃ�ł�����
2018/08/26(��) 21:58:32.16ID:86oxL3mm
�u���Ȃ��Ƃ�1���݂���v=�u���͂킩��Ȃ����A�Ƃɂ������݂��邱�Ƃ�������v
�u����1���݂���v�ꍇ���܂܂��
�u����1���݂���v�ꍇ���܂܂��
2018/08/26(��) 22:18:14.55ID:zXC0j/wA
���܂ő��肷��́H
�ɂȂ́H
�ɂȂ́H
280�P�R�Q�l�ڂ̑f������
2018/08/26(��) 22:20:35.16ID:oGfNJM4V >>221
��p^n+�c+1��0 (mod pk) ���S�Ă�k�ɑ��Đ��藧���Ȃ���Ȃ�Ȃ����Ƃ����������B
�������A���̐�ɂ��̖�肪�ؖ����ׂ����Ƃ���̖��肾�Ɨ��������Ƃ��������O���畷�����Ă��Ă���B
�Ɓ͂̋�ʂ����Ȃ��P�̂��Ƃ��A
�up^n+�c+1��b=��pk^qk�̖ł��邩��A
�@p^n+�c+1�͂���pk��Ɏ��B�����
�@p^n+�c+1�͑S�Ă�pk��Ɏ��B�v
�Ƃ����_���W�J�����Ă���̂̓G�X�p�[�łȂ��Ƃ��\�z�����B
����ɂ��Ă��A���ꂪ��������ǂ������������N�����ł����ˁc�B
��p^n+�c+1��0 (mod pk) ���S�Ă�k�ɑ��Đ��藧���Ȃ���Ȃ�Ȃ����Ƃ����������B
�������A���̐�ɂ��̖�肪�ؖ����ׂ����Ƃ���̖��肾�Ɨ��������Ƃ��������O���畷�����Ă��Ă���B
�Ɓ͂̋�ʂ����Ȃ��P�̂��Ƃ��A
�up^n+�c+1��b=��pk^qk�̖ł��邩��A
�@p^n+�c+1�͂���pk��Ɏ��B�����
�@p^n+�c+1�͑S�Ă�pk��Ɏ��B�v
�Ƃ����_���W�J�����Ă���̂̓G�X�p�[�łȂ��Ƃ��\�z�����B
����ɂ��Ă��A���ꂪ��������ǂ������������N�����ł����ˁc�B
2018/08/26(��) 22:22:59.67ID:lplTdzDK
2018/08/26(��) 22:27:13.70ID:zXC0j/wA
�a�@�ɂ��ʂ��Ă�悤����
���A���Ȑ��_�a���҂���
�F�X�ȈӖ��ő�������Ȃ������ǂ�����
���A���Ȑ��_�a���҂���
�F�X�ȈӖ��ő�������Ȃ������ǂ�����
>>274
�c�O�ł����A����ł�����Ă���̂ł��B���̘_����������Ȃ���Ύd������܂��B
>>275
���u���Ȃ��Ƃ�����݂���v�ˁu�������݂���v���^���Ƃł�������ł����ˁB
����Ȃ��Ƃ͏����Ă��܂���B�n������Ȃ��́B
A=���Ȃ��Ƃ�����݂���
B=�������݂���
B��A
�Ɍ��܂��Ă���B
>>277
�Ō�̐������肪���Ȃ��������Ȃ̂ŁA��������̂͂��ɂȂ邩������܂���B
>>280
��p^n+�c+1��b=��pk^qk�̖�
�����ł͂���܂���
>>282
���Ȃ�̘̂b��
�c�O�ł����A����ł�����Ă���̂ł��B���̘_����������Ȃ���Ύd������܂��B
>>275
���u���Ȃ��Ƃ�����݂���v�ˁu�������݂���v���^���Ƃł�������ł����ˁB
����Ȃ��Ƃ͏����Ă��܂���B�n������Ȃ��́B
A=���Ȃ��Ƃ�����݂���
B=�������݂���
B��A
�Ɍ��܂��Ă���B
>>277
�Ō�̐������肪���Ȃ��������Ȃ̂ŁA��������̂͂��ɂȂ邩������܂���B
>>280
��p^n+�c+1��b=��pk^qk�̖�
�����ł͂���܂���
>>282
���Ȃ�̘̂b��
2018/08/26(��) 22:42:00.79ID:STso/qZH
���؎���̘_���͌���҂ɂ͗����ł��Ȃ�
2018/08/26(��) 22:45:08.50ID:WDbhbjNy
>>283
������Ȃ��Ƃ͏����Ă��܂���B�n������Ȃ��́B
��A=���Ȃ��Ƃ�����݂���
��B=�������݂���
��B��A
B���^�łȂ��Ȃ�Ap���������݂��邱�Ƃ̍������Ȃ��A�Ƃ������Ƃł��B
���̂܂ܕԂ��܂��ˁB�n������Ȃ��́B
������Ȃ��Ƃ͏����Ă��܂���B�n������Ȃ��́B
��A=���Ȃ��Ƃ�����݂���
��B=�������݂���
��B��A
B���^�łȂ��Ȃ�Ap���������݂��邱�Ƃ̍������Ȃ��A�Ƃ������Ƃł��B
���̂܂ܕԂ��܂��ˁB�n������Ȃ��́B
>>285
������A����W���łȂ����Ƃ����肷��̂ł����ǁA���̂��ꂪ������Ȃ��̂��H
������A����W���łȂ����Ƃ����肷��̂ł����ǁA���̂��ꂪ������Ȃ��̂��H
2018/08/26(��) 22:51:51.72ID:WDbhbjNy
�w���@���g�p���邽�߂ɉ��肵�Ă���̂�A�B
A��B�͋U�Ȃ̂ŁAB���g�����Ƃ͂ł��܂���B
��̊��S���ɂ��āu�������݂���v�͏ؖ����Ȃ�����g�����Ƃ͂ł����A
��̊��S���Ɉˑ������f��p�ɂ��Ă����l�ł��B
A��B�͋U�Ȃ̂ŁAB���g�����Ƃ͂ł��܂���B
��̊��S���ɂ��āu�������݂���v�͏ؖ����Ȃ�����g�����Ƃ͂ł����A
��̊��S���Ɉˑ������f��p�ɂ��Ă����l�ł��B
2018/08/26(��) 22:58:14.85ID:CSiDAnHb
2018/08/26(��) 23:15:04.63ID:86oxL3mm
���݂��邩�ǂ���������Ȃ���ŕ������݂���Ɖ��肵�Ė��������Ƃ��ɏؖ��ł��邱�Ƃ́u���݂���Ƃ�����A����1�ł���v�Ƃ������Ƃł�
���ꂾ���ł́u���ۂɑ��݂��邩�ǂ����v�͎����܂���
���ꂾ���ł́u���ۂɑ��݂��邩�ǂ����v�͎����܂���
2018/08/26(��) 23:21:02.95ID:T0UhBmfF
���ꂾ�������邾���ł��債������
�������>>1�ɂ͖���
�������>>1�ɂ͖���
2018/08/26(��) 23:44:15.27ID:VxafK4bF
>>283
�s������Ă��Ȃ�����Ƃ����\���Ȑ������Ȃ��̂ŔF�߂��܂���
�s������Ă��Ȃ�����Ƃ����\���Ȑ������Ȃ��̂ŔF�߂��܂���
2018/08/26(��) 23:54:42.89ID:ktskPPX/
>>283
�܂薢���ł���ƁB
�܂薢���ł���ƁB
2018/08/27(��) 00:06:55.15ID:eEJJ0dk2
>>286
������p������Ɩ������N�����Ȃ炨�O�̏ؖ�B��ے肵�ɂ����Ă邶���
������p������Ɩ������N�����Ȃ炨�O�̏ؖ�B��ے肵�ɂ����Ă邶���
2018/08/27(��) 07:50:37.11ID:3Siq5Oqo
>>294
���l���A����������
���l���A����������
���̃X���̐��w�͂̂Ȃ��A���`�̓���
�E�Ԉ�������X�����ɔے肳�ꂽ�ꍇ�ɂ͔������Ȃ�
�E����Ɋւ��Đ^�ʖڂɓ����Ă��������Ȃ�
�E����Ɋւ��Ď��������Ȃ��ƕ�������������ɂ����炪���₵���ꍇ�ɂ�
�m���ɓ����Ȃ�
�E�B���Ȕ��_�����A��̓I�ɏ����ƌ����Ă��������Ȃ�
�E�����Ă����Ȃ����Ƃ��������Ƃ��Ĕ��_���ǂ�������
�E�����Ă����Ȃ����e�����̊ԈႢ�Ƃ��Ă����炤
�E�|�l�ł͂Ȃ��̂Ɍ|�l�Ă�������
�ʔ����z����肾��w
�E�Ԉ�������X�����ɔے肳�ꂽ�ꍇ�ɂ͔������Ȃ�
�E����Ɋւ��Đ^�ʖڂɓ����Ă��������Ȃ�
�E����Ɋւ��Ď��������Ȃ��ƕ�������������ɂ����炪���₵���ꍇ�ɂ�
�m���ɓ����Ȃ�
�E�B���Ȕ��_�����A��̓I�ɏ����ƌ����Ă��������Ȃ�
�E�����Ă����Ȃ����Ƃ��������Ƃ��Ĕ��_���ǂ�������
�E�����Ă����Ȃ����e�����̊ԈႢ�Ƃ��Ă����炤
�E�|�l�ł͂Ȃ��̂Ɍ|�l�Ă�������
�ʔ����z����肾��w
2018/08/27(��) 10:29:01.78ID:kGtHvTbD
�����͍U���I�ȓ���
2018/08/27(��) 10:29:50.33ID:IsO1JMe/
����ݖY��Ă�̂ł͂Ȃ��ł����H
300�P�R�Q�l�ڂ̑f������
2018/08/27(��) 10:38:30.30ID:73skfyCQ >>297��1�̎��ȏЉ
2018/08/27(��) 10:40:34.08ID:eWZRBtdq
2���ԕ��u���ꂽ������>>297���������Ⴄ�\���Ă����
302�P�R�Q�l�ڂ̑f������
2018/08/27(��) 11:02:23.77ID:Se/68kme ���ʉ���
����܂łP�������ɑΉ����Ă��Ȃ��������ʂ����̏�
�ȑO�͐^���Ƀ��X������Ă邲�V�K����������̂ɁA�P�͏�Ɏ����͐������̈�_����Ŏw�E�����₵�Â���
���̌��ʁA�P�������A���`�����X���Ɏc���Ă��Ȃ��ň��̏�Ԃ����ꂽ
�N�̂����ł��Ȃ��A�P���g�����̏����珵���Ă���̂�
���������́A����܂ł̒��ł��ނ����Ȃ��قǒ��J�Ȏw�E�����������Ǝv�����A�P�͂���ł����₵�Â���̂�
���Ȃ��Ƃ����̂P�̑ԓx�́u�����ɔF�肵�Ăق����v�Ƃ�������̎҂̑ԓx�ł́A�Ȃ�
�������������Ă݂Ă͂ǂ����B
����܂łP�������ɑΉ����Ă��Ȃ��������ʂ����̏�
�ȑO�͐^���Ƀ��X������Ă邲�V�K����������̂ɁA�P�͏�Ɏ����͐������̈�_����Ŏw�E�����₵�Â���
���̌��ʁA�P�������A���`�����X���Ɏc���Ă��Ȃ��ň��̏�Ԃ����ꂽ
�N�̂����ł��Ȃ��A�P���g�����̏����珵���Ă���̂�
���������́A����܂ł̒��ł��ނ����Ȃ��قǒ��J�Ȏw�E�����������Ǝv�����A�P�͂���ł����₵�Â���̂�
���Ȃ��Ƃ����̂P�̑ԓx�́u�����ɔF�肵�Ăق����v�Ƃ�������̎҂̑ԓx�ł́A�Ȃ�
�������������Ă݂Ă͂ǂ����B
2018/08/27(��) 11:45:02.49ID:EAYrhxvQ
�ɂԂ��ɂ������������B
�܂�
>>210
��b�̌`����S�Ă�k�ɑ��đΏ̂ɂȂ��Ă��܂��B
�Ƃ����Ă��邯�ǂ���Ȃ��Ƃ͂Ȃ��B
������ƕ���������
��Y A B P
Y�͊�̊��S��,p�͑f����v_p(y) = 4m+1�@�c(A)
2Y = 2P^(4m+1)B = (1+P+�c+P^(4m+1))A�@�c(B)
qr = v_pr(B) �@�c(C)
cr = v_pr(A)�@�c(D)
P = 2pr -1�@�c(E)
�ˁ�w 2m+1 = wpr^(qr-cr-1)�@�c(F)
���̉��ݒ��ɂ�pr�����łĂȂ��̂ŁApr�ȊO��ps�ɂ���
��w 2m+1 = wps^(qs-cs-1)
�𗘗p���悤�Ƃ���Ȃ�A(F)��pr��ps�ɂ���������Ȃ�(A) �` (E)���̂��ׂĂ�pr������ւ��Ȃ��Ƃ����Ȃ��B
�����������
p = 2pr-1 = 2ps-1
���������Ă��܂��̂�p��ps���ƂɎ��ւ��Ȃ��ƃ_���ł��łȂ̂łق��̕��������ւ��Ƃ���
��Ys Ak Bs Ps
Ys�͊�̊��S��,Ps�͑f����v_Ps(Ys) = 4m+1�@�c(�@s)
Ps = 2ps -1�@�c(�As)
2Ys = 2Ps^(4m+1)Bs = (1+Ps+�c+Ps^(4m+1))As�@�c(�Bs)
qr = v_ps(Bs) �@�c(�Cs)
cr = v_ps(As)�@�c(�Ds)
�������Ȃ���
��Ws 2m+1 = Ws ps^(qs-cs-1)�@�c(Fs)
�͂����Ȃ��Ƃ킩��B
�_���ł�p14�������(Fs)�����ׂĂ̑f��ps�ɂ��ė��p���Ă�̂Ō��ǍŒ���A���ׂĂ̑f��ps�ɂ��ć@s�A�As���S���������Ȃ��Ƃ��߁B
���̂����@r�A�Ar�͔w���@�̉���A�ꍇ�����̉���ʼn��肵�Ă��邩��悢���A�c��͏ؖ����Ȃ��Ƃ����Ȃ��B
�܂�
�@r�A�Ar �� �@s�A�As (��s)
�̏ؖ������Ȃ��Ƙ_���͊������Ȃ��B
���Ȃ݂Ɏ����g�͌����I�ɂ͉\���낤�Ƃ������B
����ς��̊��S���͑��݂��Ȃ��Ɨ\�z����̂ŁA�����ے肷��@r���ł�1+2=34���ؖ��o���Ă��s�v�c�ł͂Ȃ����\���͂���B
�������\�������邾���Ō����_�_���ɂ͂��̏ؖ��Ȃ��ˁB
�ǂ��������Ă��B
�܂�
>>210
��b�̌`����S�Ă�k�ɑ��đΏ̂ɂȂ��Ă��܂��B
�Ƃ����Ă��邯�ǂ���Ȃ��Ƃ͂Ȃ��B
������ƕ���������
��Y A B P
Y�͊�̊��S��,p�͑f����v_p(y) = 4m+1�@�c(A)
2Y = 2P^(4m+1)B = (1+P+�c+P^(4m+1))A�@�c(B)
qr = v_pr(B) �@�c(C)
cr = v_pr(A)�@�c(D)
P = 2pr -1�@�c(E)
�ˁ�w 2m+1 = wpr^(qr-cr-1)�@�c(F)
���̉��ݒ��ɂ�pr�����łĂȂ��̂ŁApr�ȊO��ps�ɂ���
��w 2m+1 = wps^(qs-cs-1)
�𗘗p���悤�Ƃ���Ȃ�A(F)��pr��ps�ɂ���������Ȃ�(A) �` (E)���̂��ׂĂ�pr������ւ��Ȃ��Ƃ����Ȃ��B
�����������
p = 2pr-1 = 2ps-1
���������Ă��܂��̂�p��ps���ƂɎ��ւ��Ȃ��ƃ_���ł��łȂ̂łق��̕��������ւ��Ƃ���
��Ys Ak Bs Ps
Ys�͊�̊��S��,Ps�͑f����v_Ps(Ys) = 4m+1�@�c(�@s)
Ps = 2ps -1�@�c(�As)
2Ys = 2Ps^(4m+1)Bs = (1+Ps+�c+Ps^(4m+1))As�@�c(�Bs)
qr = v_ps(Bs) �@�c(�Cs)
cr = v_ps(As)�@�c(�Ds)
�������Ȃ���
��Ws 2m+1 = Ws ps^(qs-cs-1)�@�c(Fs)
�͂����Ȃ��Ƃ킩��B
�_���ł�p14�������(Fs)�����ׂĂ̑f��ps�ɂ��ė��p���Ă�̂Ō��ǍŒ���A���ׂĂ̑f��ps�ɂ��ć@s�A�As���S���������Ȃ��Ƃ��߁B
���̂����@r�A�Ar�͔w���@�̉���A�ꍇ�����̉���ʼn��肵�Ă��邩��悢���A�c��͏ؖ����Ȃ��Ƃ����Ȃ��B
�܂�
�@r�A�Ar �� �@s�A�As (��s)
�̏ؖ������Ȃ��Ƙ_���͊������Ȃ��B
���Ȃ݂Ɏ����g�͌����I�ɂ͉\���낤�Ƃ������B
����ς��̊��S���͑��݂��Ȃ��Ɨ\�z����̂ŁA�����ے肷��@r���ł�1+2=34���ؖ��o���Ă��s�v�c�ł͂Ȃ����\���͂���B
�������\�������邾���Ō����_�_���ɂ͂��̏ؖ��Ȃ��ˁB
�ǂ��������Ă��B
>>303
�L���̈Ӗ���������Ȃ��̂ňӖ����ʂ��Ă��܂��A����������|�͕�����悤�ȋC�����܂��B
���̘_���͐��������ؖ����邱�Ƃ��ł��܂���B
k=r�ȊO��pk=(p+1)/2�̂��Ƃł̏���2m+1=pk^(qk-ck-1)���������邩�ǂ����͕�����Ȃ�����
�ł��B�������Ȃ���A���̘_�����g��Ȃ��Ă�>>221�̍���������������ؖ��������܂����̂�
���I�ɂ͂��̕����́A���𖾂Ƃ������Ƃɂ������Ǝv���܂��B
�L���̈Ӗ���������Ȃ��̂ňӖ����ʂ��Ă��܂��A����������|�͕�����悤�ȋC�����܂��B
���̘_���͐��������ؖ����邱�Ƃ��ł��܂���B
k=r�ȊO��pk=(p+1)/2�̂��Ƃł̏���2m+1=pk^(qk-ck-1)���������邩�ǂ����͕�����Ȃ�����
�ł��B�������Ȃ���A���̘_�����g��Ȃ��Ă�>>221�̍���������������ؖ��������܂����̂�
���I�ɂ͂��̕����́A���𖾂Ƃ������Ƃɂ������Ǝv���܂��B
2018/08/27(��) 12:43:13.99ID:pq+AP7V+
>>304
�ł����B�܂��A�@r�A�Ar �� �@s�A�As (��s)���������[�g�͉\�������邾���łقږ����ł��傤�ˁB
�ʃ��[�g������ĒT���Ă��������B
�ł����B�܂��A�@r�A�Ar �� �@s�A�As (��s)���������[�g�͉\�������邾���łقږ����ł��傤�ˁB
�ʃ��[�g������ĒT���Ă��������B
2018/08/27(��) 13:35:04.86ID:pq+AP7V+
>>306
�Ȃ�ł���Ȍ���������́H�N�A�l�ԓI�ɂ͊��S�ɂ���������B
�Ȃ�ł���Ȍ���������́H�N�A�l�ԓI�ɂ͊��S�ɂ���������B
>>307
�{��������d�����Ȃ��B�Ō�̖���́A���̂��ƂɊւ��Ď��͓�������Ă��邱�̕����ŏq�ׂĂ��Ȃ�
���e�ł��邪�A���҂��Ƃ̊O���炻�̖�����m�F�����ƕ������Ă����Ə������B������A�������Ă���l�ɂ�
�������Ă���Ƃ������ƁB�_���̓��e����A���̖�������l�����ɂ�����Ƃ������Ƃ��Ǝv����B
�Ō�̖���͍�worfman�Ōv�Z�����Ƃ���Aqk=2�`18�܂ł͈̔͂ŁA���߂鐮���������X������Ȃ�
��݂̂̏ꍇ�ɂ�n=1�ƂȂ邪�An=1�̏ꍇ�ł͕s�K���Ƃ������Ƃ͏ؖ����Ă���B
�R���s���[�^���g��Ȃ��Ǝ��̐��w�͂ł͍�����A���̖�肪���������\���͍����Ǝv����B
�{��������d�����Ȃ��B�Ō�̖���́A���̂��ƂɊւ��Ď��͓�������Ă��邱�̕����ŏq�ׂĂ��Ȃ�
���e�ł��邪�A���҂��Ƃ̊O���炻�̖�����m�F�����ƕ������Ă����Ə������B������A�������Ă���l�ɂ�
�������Ă���Ƃ������ƁB�_���̓��e����A���̖�������l�����ɂ�����Ƃ������Ƃ��Ǝv����B
�Ō�̖���͍�worfman�Ōv�Z�����Ƃ���Aqk=2�`18�܂ł͈̔͂ŁA���߂鐮���������X������Ȃ�
��݂̂̏ꍇ�ɂ�n=1�ƂȂ邪�An=1�̏ꍇ�ł͕s�K���Ƃ������Ƃ͏ؖ����Ă���B
�R���s���[�^���g��Ȃ��Ǝ��̐��w�͂ł͍�����A���̖�肪���������\���͍����Ǝv����B
>>308 ����
n=1�̏ؖ��͕ۑ����Ă��Ȃ������̂ŁA���������̂��ǂ����s�m���������̂Ŏ������܂�
n=1�̏ؖ��͕ۑ����Ă��Ȃ������̂ŁA���������̂��ǂ����s�m���������̂Ŏ������܂�
310�P�R�Q�l�ڂ̑f������
2018/08/27(��) 14:04:01.54ID:Hym+np++ ����፡�܂łƂ͂܂������Ⴄ�ؖ����܂���яo���������
�������傭�u�ӂ肾���ɂ��ǂ�v��
�������傭�u�ӂ肾���ɂ��ǂ�v��
2018/08/27(��) 14:17:39.23ID:ixJjBx0X
�@r�A�Ar �� �@s�A�As (��s)���������[�g�ɖ߂�킯���d�d
>>312
������
������
2018/08/27(��) 14:35:44.59ID:ixJjBx0X
��������ާ-�H
�@ �� �݁@��ͯ��`
�@�@�@�@�@�@ ��ͯ��`
�� �݁@ �V�@�ȁQ��
�@�R�Q�Q_�_(�_��ͥ)
�@ �_�Q�^ �� ���Q)
�@ �^�P�P�P�P�P �^|
�@|�P�P�P�P�P�P|�@|
�@|�W�H���܂˂�|�^
�@ �P�P�P�P�P�P
�@ �� �݁@��ͯ��`
�@�@�@�@�@�@ ��ͯ��`
�� �݁@ �V�@�ȁQ��
�@�R�Q�Q_�_(�_��ͥ)
�@ �_�Q�^ �� ���Q)
�@ �^�P�P�P�P�P �^|
�@|�P�P�P�P�P�P|�@|
�@|�W�H���܂˂�|�^
�@ �P�P�P�P�P�P
2018/08/27(��) 15:37:05.88ID:jq4omzH+
�Ō�̖���́A���̂��ƂɊւ��Ď��͓�������Ă��邱�̕����ŏq�ׂĂ��Ȃ�
���e�ł��邪�A���҂��Ƃ̊O���炻�̖�����m�F�����ƕ������Ă����Ə������B������A�������Ă���l�ɂ�
�������Ă���Ƃ������ƁB�_���̓��e����A���̖�������l�����ɂ�����Ƃ������Ƃ��Ǝv����B
����N����ǂ��Ă���
���e�ł��邪�A���҂��Ƃ̊O���炻�̖�����m�F�����ƕ������Ă����Ə������B������A�������Ă���l�ɂ�
�������Ă���Ƃ������ƁB�_���̓��e����A���̖�������l�����ɂ�����Ƃ������Ƃ��Ǝv����B
����N����ǂ��Ă���
2018/08/27(��) 16:11:45.23ID:IsO1JMe/
���������ŐV�łǂ��H
317�P�R�Q�l�ڂ̑f������
2018/08/27(��) 16:13:53.09ID:jz92TWRf2018/08/27(��) 21:00:20.77ID:N5zezPrs
���Ⴀ���삾
>>318
���̂����Ȃ�̂��������Ă�������
���̂����Ȃ�̂��������Ă�������
2018/08/28(��) 00:39:02.97ID:UKZJi3yS
>>316
�ǂ߂Ȃ��Ȃ��Ă�ˁH
�ǂ߂Ȃ��Ȃ��Ă�ˁH
321�P�R�Q�l�ڂ̑f������
2018/08/28(��) 00:50:49.48ID:rzg4Ogb4 lim[n����]n(n-1)log(1-1/n)/logn��-���ɔ��U���邱�Ƃ��Ăǂ�����Ύ����܂����H
�ǂ����Ă��s��`�������ł��Ȃ��ł��c�c
�ǂ����Ă��s��`�������ł��Ȃ��ł��c�c
2018/08/28(��) 00:58:27.51ID:FfTOBxzO
>>319
�l���狳��������̂�P���ŏ�����ł���
�l���狳��������̂�P���ŏ�����ł���
2018/08/28(��) 01:10:43.13ID:rzg4Ogb4
�X���������
>>321�͎�艺���܂�
>>321�͎�艺���܂�
2018/08/28(��) 01:14:23.48ID:UKZJi3yS
�ł�>>321�Ȃ痬�ɑ���c�̕����w�ȂȂ�o�����������ǁB
>>320
3�ӏ��ԈႢ���������̂ŁA�폜���܂����B
���̂���2�ӏ��͒������̂ł����A�Ō�ɐ������̖�肪�c���Ă��Ċ����ł��Ȃ�
��ԂɂȂ��Ă��܂��B
>>322
���̃X���ł͊ԈႢ�̃`�F�b�N�����Ă�����Ă��邾���ŁA�����ڋ����Ă�����Ă͂��Ȃ��B
���̃X���̐l�����̂��Ƃɂ͔z�����Ă����̂�������Ȃ����B
�ȑO�Ɏ����Ԉ���Ă����̂ň�̎�������������Ă��܂��A�d���Ȃ����̎������͏����Ă���B
3�ӏ��ԈႢ���������̂ŁA�폜���܂����B
���̂���2�ӏ��͒������̂ł����A�Ō�ɐ������̖�肪�c���Ă��Ċ����ł��Ȃ�
��ԂɂȂ��Ă��܂��B
>>322
���̃X���ł͊ԈႢ�̃`�F�b�N�����Ă�����Ă��邾���ŁA�����ڋ����Ă�����Ă͂��Ȃ��B
���̃X���̐l�����̂��Ƃɂ͔z�����Ă����̂�������Ȃ����B
�ȑO�Ɏ����Ԉ���Ă����̂ň�̎�������������Ă��܂��A�d���Ȃ����̎������͏����Ă���B
2018/08/28(��) 09:30:55.55ID:zvQYgLng
�����Ǝӎ��ɏ����Ƃ���
2018/08/28(��) 10:08:11.73ID:BaVdfi0M
�ӎ��Ƃ���������100��߂��l���[�̏����Œ������Ă������������Ȃ̂ł�
2018/08/28(��) 10:17:25.75ID:SPphnHxf
�_��������������̏������̘b�͂��܂�s���Ɨ��Ȃ�ww
329�P�R�Q�l�ڂ̑f������
2018/08/28(��) 10:20:52.00ID:8Bqcrs0Z ����ȃo�O�_���̋����ɂ���Ă������
>>326
����͏����Ă���B
>>328
�ԈႢ��75�����炢�͎����ŋC�Â��Ē����Ă���ƍl������B
�`�F�b�N�����Ă�����Ă��邾���Ȃ̂ŁA�����Ƃ͌����Ȃ��Ǝv���B
�����A�Ō�̖��������A����������ł���l�����Ď��ɂ����
�����āA����������_���ɏ����Γ��R�����Ƃ������ƂɂȂ�Ǝv���B
�������A����͎~�߂����������Ǝv���čŌ�̖���͏����Ă��Ȃ��B
�����ł̏�����Ă�����e�͘_���̊ԈႢ�̎w�E�ł����Ę_����
���e�������Ă�����Ă���̂ł͂Ȃ��B
>>329
���炭���m��>>221�̍������ƁA�藝�o�����B�ŐV�̘_���ɂ�
���̒藝�͏����Ă��Ȃ����B���̒藝�̏ؖ������������
����ɂȂ��Ă���B
����͏����Ă���B
>>328
�ԈႢ��75�����炢�͎����ŋC�Â��Ē����Ă���ƍl������B
�`�F�b�N�����Ă�����Ă��邾���Ȃ̂ŁA�����Ƃ͌����Ȃ��Ǝv���B
�����A�Ō�̖��������A����������ł���l�����Ď��ɂ����
�����āA����������_���ɏ����Γ��R�����Ƃ������ƂɂȂ�Ǝv���B
�������A����͎~�߂����������Ǝv���čŌ�̖���͏����Ă��Ȃ��B
�����ł̏�����Ă�����e�͘_���̊ԈႢ�̎w�E�ł����Ę_����
���e�������Ă�����Ă���̂ł͂Ȃ��B
>>329
���炭���m��>>221�̍������ƁA�藝�o�����B�ŐV�̘_���ɂ�
���̒藝�͏����Ă��Ȃ����B���̒藝�̏ؖ������������
����ɂȂ��Ă���B
2018/08/28(��) 10:56:45.40ID:y6Lv4Iaw
�P�́A�Ƃ��ƂƏ�����B
�Q�x�Əo�Ă���ȁB
�Q�x�Əo�Ă���ȁB
2018/08/28(��) 11:27:39.88ID:iM8aTLWI
�����Ƃ������ȒP��o���ĉa��^���邨�O��
2018/08/28(��) 11:38:59.85ID:NcfhiGRZ
2018/08/28(��) 11:40:19.47ID:B2NMw+XG
�s���|�l����
2018/08/28(��) 11:53:43.19ID:y6Lv4Iaw
��肪���邾�́A����̂��菑�������
���̒��ߑa�X���̐��ƃX�����Č�������肩�B
�N�Y�P�́B
���̒��ߑa�X���̐��ƃX�����Č�������肩�B
�N�Y�P�́B
2018/08/28(��) 12:00:07.88ID:VkSVkUAu
�܂��r���o�߂͕̕K�v�Ȃ���
�o���ꂽPDF�����ŕ]������ׂ�����
�o���ꂽPDF�����ŕ]������ׂ�����
339�P�R�Q�l�ڂ̑f������
2018/08/28(��) 12:13:47.75ID:/FDEZ/Um �����҂ɂ���Ȃ�A���Ă����Ȃ�������Ƃ̊O����m�F�����Ƃ킴�킴���������Ă��ꂽ�l���������������̂ł͂Ȃ���
�ނ����ޏ������m��Ȃ����A�ԈႢ�Ȃ����͊W�ɂ���l���ł��낤
�ނ����ޏ������m��Ȃ����A�ԈႢ�Ȃ����͊W�ɂ���l���ł��낤
2018/08/28(��) 12:16:34.24ID:NcfhiGRZ
�upr��pk�͑Ώ̂�����pr�ɂ��Č����Ă邱�Ƃ�pk�ɂ��Ă������Ă�n�Y���B�v
�Ƃ����X�[�p�[���W�b�N���g���Ȃ��Ȃ����玟�͂��Ȃ�ꂵ������B
�悤�₭>>1�ɂ����̖��̓�����킩���Ă�����Ȃ��H
�Ƃ����X�[�p�[���W�b�N���g���Ȃ��Ȃ����玟�͂��Ȃ�ꂵ������B
�悤�₭>>1�ɂ����̖��̓�����킩���Ă�����Ȃ��H
2018/08/28(��) 12:20:22.43ID:Bz8h+r0A
�V�����X�[�p�[���W�b�N�ݏo�����獂�؎���ł͊W�Ȃ���
342�P�R�Q�l�ڂ̑f������
2018/08/28(��) 12:55:45.10ID:XWAo3OYd343�P�R�Q�l�ڂ̑f������
2018/08/28(��) 13:00:56.93ID:PhiQFhFr �ɂ����瑽������p^k=1+�c+p^n(n�͊)�̑����ɂ��Ē��ׂĂ݂�
�܂����̑�������p��0��p�ɂ��ĒP����������͖̂��炩
1+�c+p^n=(p^{n+1}-1)/(p-1)�ƕό`���ē������Ƃ��np^n/(p-1)+(1-p^n)/(p-1)^2�c�@
p��0�Ň@���̑�1���A��2���Ƃ����ɂȂ�̂�p��0�ł�p�ɂ��ĒP����������
����������p^k=1+�c+p^n(n�͊)�́Ap�ɂ��đS��ɂ����ĒP����������
���̌��ʂɂ��A������C=1+�c+p^n(n�͊)��p�ʼn������Ƃ��A���̎����͗B��ł��邱�Ƃ��������
�܂����̑�������p��0��p�ɂ��ĒP����������͖̂��炩
1+�c+p^n=(p^{n+1}-1)/(p-1)�ƕό`���ē������Ƃ��np^n/(p-1)+(1-p^n)/(p-1)^2�c�@
p��0�Ň@���̑�1���A��2���Ƃ����ɂȂ�̂�p��0�ł�p�ɂ��ĒP����������
����������p^k=1+�c+p^n(n�͊)�́Ap�ɂ��đS��ɂ����ĒP����������
���̌��ʂɂ��A������C=1+�c+p^n(n�͊)��p�ʼn������Ƃ��A���̎����͗B��ł��邱�Ƃ��������
2018/08/28(��) 13:26:32.95ID:B+5iJtwK
>>342�̎����L��
345�P�R�Q�l�ڂ̑f������
2018/08/28(��) 13:44:51.86ID:XWAo3OYd >>344�@�א��悗
346�P�R�Q�l�ڂ̑f������
2018/08/28(��) 14:04:26.45ID:hH2YyzSE 27�ŔN��8���~�@�������[�`���[�o�[�u�����[�E�V���v�̐�����
https://headlines.yahoo.co.jp/article?a=20170802-00017174-forbes-bus_all
1�N�ʼn��\���~���҂����������[�`���[�o�[���E�����L���O�g�b�v10
https://gigazine.net/news/20151016-highest-paid-youtuber-2015/
��������̃��r���[�ŔN��12���~�I ���A�b���YouTuber��6�̒j�̎q
https://www.businessinsider.jp/post-108355
�ޏ��͂����ɂ���750���l�̃t�@��������YouTube�X�^�[�ƂȂ����̂��H
https://www.businessinsider.jp/post-242
1���~�҂�9��YouTuber������������c�c�A�����J�Řb���EvanTubeHD
https://weekly.ascii.jp/elem/000/000/305/305548/
���E�ōł��҂����[�`���[�o�[�A2�A�e�̎�ʂ͔N��17���~
https://forbesjapan.com/articles/detail/14474
https://headlines.yahoo.co.jp/article?a=20170802-00017174-forbes-bus_all
1�N�ʼn��\���~���҂����������[�`���[�o�[���E�����L���O�g�b�v10
https://gigazine.net/news/20151016-highest-paid-youtuber-2015/
��������̃��r���[�ŔN��12���~�I ���A�b���YouTuber��6�̒j�̎q
https://www.businessinsider.jp/post-108355
�ޏ��͂����ɂ���750���l�̃t�@��������YouTube�X�^�[�ƂȂ����̂��H
https://www.businessinsider.jp/post-242
1���~�҂�9��YouTuber������������c�c�A�����J�Řb���EvanTubeHD
https://weekly.ascii.jp/elem/000/000/305/305548/
���E�ōł��҂����[�`���[�o�[�A2�A�e�̎�ʂ͔N��17���~
https://forbesjapan.com/articles/detail/14474
2018/08/28(��) 16:04:53.39ID:eWhJjQ9d
�P�u�Ƃ��������O���畷�����Ă��Ă���B �v
2018/08/28(��) 16:18:10.89ID:eWhJjQ9d
����܂ł̊�|�l�l�^
�Ep�͓���̒l�����͂�����0p=0�ł���s��ɂȂ邩�疵��
�Ep�͒萔�ł��肩�ϐ��ł���
�Ep���P����������i�{���͒P���������Ȃ��j����p�͑f���ɂȂ肦�Ȃ�
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł���
�Ew�͐����ł��蓯���ɐ����łȂ�
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ�
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂�
�E�ϐ��͐��l�ɒu�������Ă̓_��
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R
�E27/5 �� 3 �Ŋ�����
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂���
�E���Ȃ��Ƃ���͂����Ȃ�A�Ƃ������Ƃ�
�@�S�Ăɑ��Đ��藧���Ȃ���Ȃ�Ȃ�
�E�����Ȃ��Ƃ͏ؖ��ł��Ȃ�
�E���̘_���͐��������ؖ����邱�Ƃ��ł��܂���B(NEW!)
�E�ؖ��������܂����̂Ŏ��I�ɂ͂��̕����́A���𖾂Ƃ������Ƃɂ������Ǝv���܂��B(NEW!)
�E���m�̍������ƁA�藝�o�����B���̒藝�̏ؖ����������������ɂȂ��Ă���B(NEW!)
�E�Ō�̖���́A���͓�������Ă��邱�̕����ŏq�ׂĂ��Ȃ��̂ɁA
�@���҂��Ƃ̊O���炻�̖�����m�F�����ƕ������Ă����B
�@������A�������Ă���l�ɂ͕������Ă���Ƃ������ƁB(NEW!)
�Ep�͓���̒l�����͂�����0p=0�ł���s��ɂȂ邩�疵��
�Ep�͒萔�ł��肩�ϐ��ł���
�Ep���P����������i�{���͒P���������Ȃ��j����p�͑f���ɂȂ肦�Ȃ�
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł���
�Ew�͐����ł��蓯���ɐ����łȂ�
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ�
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂�
�E�ϐ��͐��l�ɒu�������Ă̓_��
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R
�E27/5 �� 3 �Ŋ�����
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂���
�E���Ȃ��Ƃ���͂����Ȃ�A�Ƃ������Ƃ�
�@�S�Ăɑ��Đ��藧���Ȃ���Ȃ�Ȃ�
�E�����Ȃ��Ƃ͏ؖ��ł��Ȃ�
�E���̘_���͐��������ؖ����邱�Ƃ��ł��܂���B(NEW!)
�E�ؖ��������܂����̂Ŏ��I�ɂ͂��̕����́A���𖾂Ƃ������Ƃɂ������Ǝv���܂��B(NEW!)
�E���m�̍������ƁA�藝�o�����B���̒藝�̏ؖ����������������ɂȂ��Ă���B(NEW!)
�E�Ō�̖���́A���͓�������Ă��邱�̕����ŏq�ׂĂ��Ȃ��̂ɁA
�@���҂��Ƃ̊O���炻�̖�����m�F�����ƕ������Ă����B
�@������A�������Ă���l�ɂ͕������Ă���Ƃ������ƁB(NEW!)
2018/08/28(��) 16:38:22.39ID:eWhJjQ9d
����>>102 �̃t�F�[�Y�P���ȁB
2018/08/28(��) 16:39:21.59ID:eWhJjQ9d
����܂ł̊�|�l�l�^
�Ep�͒萔�ł��肩�ϐ��ł���B
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł����B
�Ew�͐����ł��蓯���ɐ����łȂ��B
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ��B
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂ށB
�E�ϐ��͐��l�ɒu�������Ă̓_���B
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R�B
�E27/5 �� 3 �Ŋ�����B
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂���B
�E���Ȃ��Ƃ���͂����Ȃ�A�Ƃ������Ƃ�
�@�S�Ăɑ��Đ��藧���Ȃ���Ȃ�Ȃ��B
�E���̌`����P��k�Ő��藧�ĂA�S�Ă�k�ł����藧�B
�E�����Ȃ��Ƃ��ؖ����邱�Ƃ͓���B
�E���̘_���͐��������ؖ����邱�Ƃ��ł��܂���B(NEW!)
�E�ؖ��������܂����̂ŁA���𖾂Ƃ������Ƃɂ������B(NEW!)
�E�藝�o�����B���̒藝�̏ؖ����������������ɂȂ��Ă���B(NEW!)
�E�Ō�̖���́A���҂��Ƃ̊O���炻�̖�����m�F�����ƕ������Ă����B(NEW!)
�Ep�͒萔�ł��肩�ϐ��ł���B
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł����B
�Ew�͐����ł��蓯���ɐ����łȂ��B
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ��B
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂ށB
�E�ϐ��͐��l�ɒu�������Ă̓_���B
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R�B
�E27/5 �� 3 �Ŋ�����B
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂���B
�E���Ȃ��Ƃ���͂����Ȃ�A�Ƃ������Ƃ�
�@�S�Ăɑ��Đ��藧���Ȃ���Ȃ�Ȃ��B
�E���̌`����P��k�Ő��藧�ĂA�S�Ă�k�ł����藧�B
�E�����Ȃ��Ƃ��ؖ����邱�Ƃ͓���B
�E���̘_���͐��������ؖ����邱�Ƃ��ł��܂���B(NEW!)
�E�ؖ��������܂����̂ŁA���𖾂Ƃ������Ƃɂ������B(NEW!)
�E�藝�o�����B���̒藝�̏ؖ����������������ɂȂ��Ă���B(NEW!)
�E�Ō�̖���́A���҂��Ƃ̊O���炻�̖�����m�F�����ƕ������Ă����B(NEW!)
2018/08/28(��) 16:56:26.83ID:74eJRyWJ
>�藝�o�����B���̒藝�̏ؖ����������������ɂȂ��Ă���B
���E�͂����\�z�Ƃ�����
���ۊ�̊��S���͖����������ė\�z�Ȃ�F���ĂĂ�킯����
���E�͂����\�z�Ƃ�����
���ۊ�̊��S���͖����������ė\�z�Ȃ�F���ĂĂ�킯����
>>352
�\�z���̂��̂ł͂Ȃ��A������݂���Ƃ����藝���������A����ɂ͏������K�v���Ƃ���
���Ƃ����������B�܂�A�S�Ă�k�ɑ��ĉ��X�ƂȂ�Ȃ���Ȃ�Ȃ��ł͂Ȃ�
�`�Ƃ���������k�ł͂Ƃ����̂��t���Ȃ���Ηǂ��Ȃ��Ƃ������Ƃ����������B
�\�z���̂��̂ł͂Ȃ��A������݂���Ƃ����藝���������A����ɂ͏������K�v���Ƃ���
���Ƃ����������B�܂�A�S�Ă�k�ɑ��ĉ��X�ƂȂ�Ȃ���Ȃ�Ȃ��ł͂Ȃ�
�`�Ƃ���������k�ł͂Ƃ����̂��t���Ȃ���Ηǂ��Ȃ��Ƃ������Ƃ����������B
2018/08/28(��) 18:09:48.43ID:3vZ8S92c
���ԁH
������������������������悤�ȋC�����Ă����B���������瓱����鐮�������
2�̃p�^�[��������A��������Ȃ��B
���̂�����̕��̓���ȏꍇ�ł����Ă��Aqk=18�܂ł��炢��wolfman�͉����Ȃ����Ƃ�
�v�Z���邪�A��ʓI�Ȃ��̂ł�pr=4�܂ł����v�Z���Ȃ��B
���ɂ͉����ł��Ȃ��ƍl�������肪�c�����B
2�̃p�^�[��������A��������Ȃ��B
���̂�����̕��̓���ȏꍇ�ł����Ă��Aqk=18�܂ł��炢��wolfman�͉����Ȃ����Ƃ�
�v�Z���邪�A��ʓI�Ȃ��̂ł�pr=4�܂ł����v�Z���Ȃ��B
���ɂ͉����ł��Ȃ��ƍl�������肪�c�����B
2018/08/28(��) 19:06:03.12ID:sI3HcjG9
�͂��A����ꂳ��
���̔��N�Ԗ��ʂ�������
���̔��N�Ԗ��ʂ�������
���̂��̖�肪�V�����������̖��ɋA������邱�Ƃ������Ă���̂ɂ�
�ւ�炸�c�O�Ȃ̂��H
�ւ�炸�c�O�Ȃ̂��H
2018/08/28(��) 19:39:13.84ID:sI3HcjG9
>>358
�ŁA�ǂ��ɂ��̏ؖ�������H
�ŁA�ǂ��ɂ��̏ؖ�������H
>>359
����PC
����PC
2018/08/28(��) 19:42:02.37ID:sI3HcjG9
>>361
���F������ꂽ��A�J���Ή�����܂����H
���F������ꂽ��A�J���Ή�����܂����H
2018/08/28(��) 19:48:30.93ID:9LPp4tfu
�J���Ή��������č��܂ł���Ă��̂ł����H
2018/08/28(��) 19:53:16.98ID:102/zM9D
���r���[�ւ̑Ή����Ȃ��̂ɁI?
2018/08/28(��) 19:55:21.44ID:sI3HcjG9
�N����H���͕���Ȃ�����
>>363
���ʂ��o���ꍇ�ɂ͓��R���Ǝv���܂���
���E�����w�I�Ȑ��ʂ��o�����ꍇ�̘J���Ή���N�������略���̂��Ƃ�����肪�������Ă��܂�
���ʂ��o���ꍇ�ɂ͓��R���Ǝv���܂���
���E�����w�I�Ȑ��ʂ��o�����ꍇ�̘J���Ή���N�������略���̂��Ƃ�����肪�������Ă��܂�
2018/08/28(��) 20:06:49.55ID:ITUOjKFA
���w�͋����҂���i����Ȃ�����
�ǂ����Ă��Ή����~�����Ȃ�~���j�A�����ܖ��ł���������H
�ǂ����Ă��Ή����~�����Ȃ�~���j�A�����ܖ��ł���������H
2018/08/28(��) 20:07:00.68ID:vDGj5wYa
�P�́A���w�I���ʂǂ��납�S�~�������o�c�e�����Ȃ̂őΉ��ȂǂȂ��B
�P�ɂ����f�s�ׂɔ��������������������B
�P�ɂ����f�s�ׂɔ��������������������B
2018/08/28(��) 20:10:24.53ID:vDGj5wYa
����܂ł̂��̐��w�ł̍���ɂ��A
�P�͏ؖ��Ƃ͗y���ɉ����̍��؎���ł̖ϑz�ɏI�n��
���݁E�����Ƃ��ɐ��w�I���ʂƉ����������Ƃ����炩�ƂȂ��Ă���B
�P�͏ؖ��Ƃ͗y���ɉ����̍��؎���ł̖ϑz�ɏI�n��
���݁E�����Ƃ��ɐ��w�I���ʂƉ����������Ƃ����炩�ƂȂ��Ă���B
2018/08/28(��) 20:12:01.25ID:ITUOjKFA
���邢�͌����@�ւɎ�������Ō�����A���������邩���m��Ȃ�����
>>370
�ʓ|������ŐV�ł����J���āA����Ŏ����ɂȂ����炢���Ǝv���B
�ǂ����A���̖��͉��N���i�����Ȃ���肾�낤����Ƃ����C������B
�͂��̐l�Ԃ́A�l�Ō�������������J����ƈ�~������Ȃ�������
�w�҂䂷��ƌ����ēO��I�ɔ�掁E�������Ă��邩��A����4����5�N�͂����
�t�����킳��Ă��邵�A���[�}���V���b�N�̃��X�g���ȗ�10�N���������B
�S�������ĕs���̋ɂ݂��B
�ʓ|������ŐV�ł����J���āA����Ŏ����ɂȂ����炢���Ǝv���B
�ǂ����A���̖��͉��N���i�����Ȃ���肾�낤����Ƃ����C������B
�͂��̐l�Ԃ́A�l�Ō�������������J����ƈ�~������Ȃ�������
�w�҂䂷��ƌ����ēO��I�ɔ�掁E�������Ă��邩��A����4����5�N�͂����
�t�����킳��Ă��邵�A���[�}���V���b�N�̃��X�g���ȗ�10�N���������B
�S�������ĕs���̋ɂ݂��B
�͂��̐l�ԁ��O����N����������ɂ悤�ɂ��āA���̂������l�Ԃ�A���ɉ����������悤�Ƃ���l�ԁB
���̑O����i�ɓn���Ƃ������߂��������Ă������A����10�N���E�Ȃ̂ɒN����i�Ȃ̂ł��傤���H
���̑O����i�ɓn���Ƃ������߂��������Ă������A����10�N���E�Ȃ̂ɒN����i�Ȃ̂ł��傤���H
2018/08/28(��) 21:26:14.90ID:9LPp4tfu
�ύX�_
�E7�y�[�W��0��ck��qk-1�̏ؖ���lj����܂���
�E7�y�[�W��n=1�̏ꍇ�̏ؖ���lj����܂���
�E14�y�[�W�̏ؖ����C�����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7091017394711/
�E7�y�[�W��0��ck��qk-1�̏ؖ���lj����܂���
�E7�y�[�W��n=1�̏ꍇ�̏ؖ���lj����܂���
�E14�y�[�W�̏ؖ����C�����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7091017394711/
>>373
��2�̐�������̉��̌��ׂ邱�Ƃ��ł���Ή����̂Ƃ���܂ł����Ă���̂�
���ւ�炸�ł����H
���ꂩ��A���w�I�ɐ�������Ζ������������������ꍇ�ɂ͊w�ʂ͊W�Ȃ��̂ł͂Ȃ��̂ł��傤���B
��2�̐�������̉��̌��ׂ邱�Ƃ��ł���Ή����̂Ƃ���܂ł����Ă���̂�
���ւ�炸�ł����H
���ꂩ��A���w�I�ɐ�������Ζ������������������ꍇ�ɂ͊w�ʂ͊W�Ȃ��̂ł͂Ȃ��̂ł��傤���B
2018/08/28(��) 22:20:04.01ID:2cZG8Ilp
�Ȃ�ɂ���A���炢�i�����B�i�v�ɂ��̂܂܂�Ǝv���Ă��̂ɁB
2018/08/28(��) 22:34:24.72ID:W0aAul7K
>>362
���Ȃ��ɂ������ĉ����ǂ����Ƃ�����܂����H
���Ȃ��ɂ������ĉ����ǂ����Ƃ�����܂����H
2018/08/28(��) 22:59:54.34ID:f4JKDrit
�܂��K�E�ucr�Ő��藧����ck�Ő��藧�v�_�@�����Ă��ˁH
p13�Ǔ�
���S�Ă� k �ɑ���ck < qk�ƂȂ邱�Ƃ���A�S�Ă� k �ɑ���
�́u�S�Ă� k �ɑ���ck < qk�v�̏ؖ���������ǁB
p13�Ǔ�
���S�Ă� k �ɑ���ck < qk�ƂȂ邱�Ƃ���A�S�Ă� k �ɑ���
�́u�S�Ă� k �ɑ���ck < qk�v�̏ؖ���������ǁB
379�P�R�Q�l�ڂ̑f������
2018/08/28(��) 23:03:03.36ID:2Wx8NN6F ���U�ŕs��������
�P�̃p�^�[�����S�ɓǂݐ��Ă�w
�P�̃p�^�[�����S�ɓǂݐ��Ă�w
2018/08/28(��) 23:06:45.61ID:f4JKDrit
�܂������ǂ݂�����킩��ǁB
p7�������
��k �ɂ��đΏ̂ɂȂ�̂őS�Ă� k �ɑ��� c ��pk^qk�Ŋ�����Ȃ��B����āA�S�Ă� k �ɑ��āAck��
��0 �� ck �� qk �| 1�̒l����蓾��B
����K�E�Z�̍��肪�c�c�c
p7�������
��k �ɂ��đΏ̂ɂȂ�̂őS�Ă� k �ɑ��� c ��pk^qk�Ŋ�����Ȃ��B����āA�S�Ă� k �ɑ��āAck��
��0 �� ck �� qk �| 1�̒l����蓾��B
����K�E�Z�̍��肪�c�c�c
2018/08/29(��) 00:09:14.95ID:FheP8WCH
�Ă����ł͊�̊��S�������݂��Ȃ����Ƃ̏ؖ��܂ł͎����ĂȂ���ł���H
����^�C�g�����ς��Ȃ��ƁB
����^�C�g�����ς��Ȃ��ƁB
2018/08/29(��) 00:12:08.84ID:ceObIKuY
>>375
�������炢������Δ��m�܂Ŏ��Ȃ���
�������炢������Δ��m�܂Ŏ��Ȃ���
2018/08/29(��) 00:13:47.54ID:a8QQvkl2
��C�萬�v�l�̋�w�҂Ȃ́H
2018/08/29(��) 00:28:46.15ID:a8QQvkl2
�O�ǂƂ����f�R�ǂ݂₷���Ȃ��Ă�I
�T�v�������Ə����Ă邵�A���̉^�т��͗��ĂĐ������Ă�
���ł��邶���I�I
�T�v�������Ə����Ă邵�A���̉^�т��͗��ĂĐ������Ă�
���ł��邶���I�I
385�P�R�Q�l�ڂ̑f������
2018/08/29(��) 00:49:40.99ID:2dnbykm+2018/08/29(��) 03:40:18.55ID:LWMzOVZ6
���������u��̊��S�������݂���Ɖ��肷��v���Ȃ���ł����
2�y�[�W�Ɋ�̊��S�������݂��邽�߂ɂ͂Ƃ�������������܂�
2018/08/29(��) 07:10:57.16ID:pwgAv9O4
>>387
>>366��
>���ʂ��o���ꍇ�ɂ͓��R���Ǝv���܂���
>
>���E�����w�I�Ȑ��ʂ��o�����ꍇ�̘J���Ή���N�������略���̂��Ƃ�����肪�������Ă��܂�
�Ə����Ă��āA�����̂������_�ɉ߂��Ȃ����A�ؖ��o������ǂ��Ȃ邩����s����\�����Đ�������B
���̖��������́A���e�I�ɂ͒N�ɂł������o����悤�ȌÑォ��̖��������ł���B
�ؖ��̒P���_�����p��ŏ����āA�������肵�����Ǖt���̃W���[�i���ɓ��e����
�_�����G���Ɍf�ڂ���Ę_�����e���F�߂���A
���Ԃ̔����͈��t�B�[�o�[���N���āA�p�Y���������\�����傫���Ǝv���B
���m�]�X�̖��ǂ���ł͂Ȃ��A���Ԃ���͉����̋��ɂȂ�悤�Ȏd�����˗������悤�ɂȂ�Ǝv���B
������������A�e���r����������肾���ɂȂ���m��Ȃ��B
�P�Ȃ�������_�ɉ߂��Ȃ����A�}�W���Ɉ�l�ʼnp��Ř_����������
�������肵�����Ǖt���̃W���[�i���ɂ��̘_���𓊍e���Ă��ꂪ�f�ڂ����G���ɍڂ�A
���̂悤�ȉ��炩�̑Ή��͐�����Ǝv���B���e�I�ɂ͂��̂悤�Ȗ�������肾�B
�Ή���_���Ȃ�A2�`�����ɏ����̂ł͂Ȃ��A��l�ł������肵���W���|�i���ɘ_�����f�ڂ������������B
�܂��A����́A��b�I�������傫���������Ă���Ƃ͎v�����B
>>366��
>���ʂ��o���ꍇ�ɂ͓��R���Ǝv���܂���
>
>���E�����w�I�Ȑ��ʂ��o�����ꍇ�̘J���Ή���N�������略���̂��Ƃ�����肪�������Ă��܂�
�Ə����Ă��āA�����̂������_�ɉ߂��Ȃ����A�ؖ��o������ǂ��Ȃ邩����s����\�����Đ�������B
���̖��������́A���e�I�ɂ͒N�ɂł������o����悤�ȌÑォ��̖��������ł���B
�ؖ��̒P���_�����p��ŏ����āA�������肵�����Ǖt���̃W���[�i���ɓ��e����
�_�����G���Ɍf�ڂ���Ę_�����e���F�߂���A
���Ԃ̔����͈��t�B�[�o�[���N���āA�p�Y���������\�����傫���Ǝv���B
���m�]�X�̖��ǂ���ł͂Ȃ��A���Ԃ���͉����̋��ɂȂ�悤�Ȏd�����˗������悤�ɂȂ�Ǝv���B
������������A�e���r����������肾���ɂȂ���m��Ȃ��B
�P�Ȃ�������_�ɉ߂��Ȃ����A�}�W���Ɉ�l�ʼnp��Ř_����������
�������肵�����Ǖt���̃W���[�i���ɂ��̘_���𓊍e���Ă��ꂪ�f�ڂ����G���ɍڂ�A
���̂悤�ȉ��炩�̑Ή��͐�����Ǝv���B���e�I�ɂ͂��̂悤�Ȗ�������肾�B
�Ή���_���Ȃ�A2�`�����ɏ����̂ł͂Ȃ��A��l�ł������肵���W���|�i���ɘ_�����f�ڂ������������B
�܂��A����́A��b�I�������傫���������Ă���Ƃ͎v�����B
2018/08/29(��) 09:12:00.15ID:gK8zj4a5
p7���߂��H����ς�B
qk = y �ɂ����� pk �̑��d�x�B
ck = 2y / (1+p+�c+p^n) (=c) �ɂ����� pk �̑��d�x�B
������
qk > ck �� 1+p+�c+p^n �� pk �̔{��
�ŁA
1+p+�c+p^n = (1+p)(1-p^2+�c) = 2pr(1-p^2+�c)
������
qr > cr
�͐��������ǁA�����p7
���䂦�ɁAc ��pr^qr�Ŋ�����Ȃ��Bk �ɂ��đΏ̂ɂȂ�̂őS�Ă� k �ɑ��� c ��pk^qk�Ŋ�����Ȃ��B
����͗�� �gpr�Ő��藧���瑼��pk�ł����藧�_�@�h �g���Ă���B
qk = y �ɂ����� pk �̑��d�x�B
ck = 2y / (1+p+�c+p^n) (=c) �ɂ����� pk �̑��d�x�B
������
qk > ck �� 1+p+�c+p^n �� pk �̔{��
�ŁA
1+p+�c+p^n = (1+p)(1-p^2+�c) = 2pr(1-p^2+�c)
������
qr > cr
�͐��������ǁA�����p7
���䂦�ɁAc ��pr^qr�Ŋ�����Ȃ��Bk �ɂ��đΏ̂ɂȂ�̂őS�Ă� k �ɑ��� c ��pk^qk�Ŋ�����Ȃ��B
����͗�� �gpr�Ő��藧���瑼��pk�ł����藧�_�@�h �g���Ă���B
2018/08/29(��) 09:25:29.09ID:gK8zj4a5
>>389
����
✕�F1+p+�c+p^n = (1+p)(1-p^2+�c) = 2pr(1-p^2+�c)
���F1+p+�c+p^n = (1+p)(1+p^2+�c) = 2pr(1+p^2+�c)
����
✕�F1+p+�c+p^n = (1+p)(1-p^2+�c) = 2pr(1-p^2+�c)
���F1+p+�c+p^n = (1+p)(1+p^2+�c) = 2pr(1+p^2+�c)
>>388
�ؖ��͊������Ă��܂��A���w�I�Ȑ��ʂ͏o�Ă���Ǝv���܂��B
��b�I�ȕ����ő����Ԉ���Ă������A����͂��̌����������l�ōs���Ă�����̂�
���荸�ǎ҂������Ȃ�����A�Ƃ������ƂƂ��̖��͔w���@�ł̏ؖ��Ȃ̂ŁA�v�Z��
�_�����ԈႦ��Ƃ��ꂪ�������ƌ�F���邩�炻���Ȃ��Ă��܂��B
���܂ł��p��̘_���������Ɍ��J���Ă������A�Ō�ɐ������̓��������Ȃ����
�Ȃ�Ȃ��Ȃ�A���������_���łȂ��Ȃ����̂ʼnp��̕��͌��J���Ȃ����Ƃɂ����B
>>389
�ʂ�(p+1)/2=pk�̊W�������Ă��Ȃ��̂ŁA�ǂ�k�ɑ��Ă����藧�͂��ł����ǁB
�S�Ă�k�ɑ���c��pk^qk�Ŋ���ꂽ�疵�����������܂�����B
�ؖ��͊������Ă��܂��A���w�I�Ȑ��ʂ͏o�Ă���Ǝv���܂��B
��b�I�ȕ����ő����Ԉ���Ă������A����͂��̌����������l�ōs���Ă�����̂�
���荸�ǎ҂������Ȃ�����A�Ƃ������ƂƂ��̖��͔w���@�ł̏ؖ��Ȃ̂ŁA�v�Z��
�_�����ԈႦ��Ƃ��ꂪ�������ƌ�F���邩�炻���Ȃ��Ă��܂��B
���܂ł��p��̘_���������Ɍ��J���Ă������A�Ō�ɐ������̓��������Ȃ����
�Ȃ�Ȃ��Ȃ�A���������_���łȂ��Ȃ����̂ʼnp��̕��͌��J���Ȃ����Ƃɂ����B
>>389
�ʂ�(p+1)/2=pk�̊W�������Ă��Ȃ��̂ŁA�ǂ�k�ɑ��Ă����藧�͂��ł����ǁB
�S�Ă�k�ɑ���c��pk^qk�Ŋ���ꂽ�疵�����������܂�����B
392�P�R�Q�l�ڂ̑f������
2018/08/29(��) 10:28:49.40ID:/vx/CFX4 >>362
���̊w�p�E�͒��҂������Ę_�����o�ł��Ă��炤���Ƃ����ʂȂ��c
����ړI�ɂ��������A�������w�Ȃ�Ă���Ƃ����炠����B
���̊w�p�E�͒��҂������Ę_�����o�ł��Ă��炤���Ƃ����ʂȂ��c
����ړI�ɂ��������A�������w�Ȃ�Ă���Ƃ����炠����B
2018/08/29(��) 10:34:13.55ID:mjRvhqt3
>>389
�g���Ă�B��������f(pr)=(1+p+�d)/�d ��p=2pr-1 �łȂ��Ɛ������Ȃ��B
����p=2pr-1�Ƃ����������g���ĂȂ������Ƃ��Ă�����ȋL�q�͂�邳��Ȃ����ǁA����͎g���|���Ă�B
�g���Ă�B��������f(pr)=(1+p+�d)/�d ��p=2pr-1 �łȂ��Ɛ������Ȃ��B
����p=2pr-1�Ƃ����������g���ĂȂ������Ƃ��Ă�����ȋL�q�͂�邳��Ȃ����ǁA����͎g���|���Ă�B
2018/08/29(��) 10:49:55.46ID:ExIdLqFl
�_�����e�Ȃ�ăq�L�j�[�g�Ȃ̂ɋ��̊|�������E�E�E�Ǝv���Ă���A
�P�͘_���𓊍e����Γ��e�҂ɋ����Ⴆ��Ǝv���Ă��킯���B
�P�͘_���𓊍e����Γ��e�҂ɋ����Ⴆ��Ǝv���Ă��킯���B
2018/08/29(��) 11:03:08.82ID:ThdMqrgL
�Ȃ������l�̖ڂɗ��܂��āA�Ȃ������܂��炦��ƍl���Ă���Ȃ���
2018/08/29(��) 11:28:59.80ID:zlXfUQz9
1�ɉ����邭�炢�̖��Ȃ琢�E���̒N���������Ă�͂��ł���
�i���A������������j
�i���A������������j
2018/08/29(��) 11:55:30.47ID:7MjvDqGy
�������A�킩�����B
v_pr(2m+1)�̌v�Z>>1�̘_���̌v�Z�����肷���Ė������Ă����ǁA�������Ȃ����������̂��ȁH
�ł�����ς肨�������B
��������
a = 2y/(1+p+�c+p^n)
b = y/p^n
c = 2y/(1+p+�c+p^n)/p^n
�Ƃ����Ƃ�
p(2b-a) = 2b-c
�͐������B
���͂��̂���p7
b�f = b/pr^qr
c�f = c/pr^qr
�Ƃ�����
��b���ɑΉ����� a ��a���Ƃ����
��a�f = ��[k��r](1+pk+�c+pk^qk)
���ȂɂƂȂɂ��ǂ��Ή��Â������ʂ���ꂽa�f�Ȃ̂��Ӗ��s���B
���̘_����p7�ȑO�̕�����n��n�f��Ή��Â��郋�[���ɂ��Ă̋L�q�͈�Ȃ��B
����ď�̎����ǂ�����o�Ă����̂��Ӗ��s������
��a�� = a/pr^qr�ƂȂ�Ȃ���Ȃ�Ȃ��̂�
�Ƃ������Ă��邯�ǂ������� �g�Ή��h ���ȂɂƂȂɂ̑Ή��������ĂȂ����炱��Ȏ����������鍪�����Ȃ��B
�Ƃ����킯�ŃR�R���߂ł��ˁB
v_pr(2m+1)�̌v�Z>>1�̘_���̌v�Z�����肷���Ė������Ă����ǁA�������Ȃ����������̂��ȁH
�ł�����ς肨�������B
��������
a = 2y/(1+p+�c+p^n)
b = y/p^n
c = 2y/(1+p+�c+p^n)/p^n
�Ƃ����Ƃ�
p(2b-a) = 2b-c
�͐������B
���͂��̂���p7
b�f = b/pr^qr
c�f = c/pr^qr
�Ƃ�����
��b���ɑΉ����� a ��a���Ƃ����
��a�f = ��[k��r](1+pk+�c+pk^qk)
���ȂɂƂȂɂ��ǂ��Ή��Â������ʂ���ꂽa�f�Ȃ̂��Ӗ��s���B
���̘_����p7�ȑO�̕�����n��n�f��Ή��Â��郋�[���ɂ��Ă̋L�q�͈�Ȃ��B
����ď�̎����ǂ�����o�Ă����̂��Ӗ��s������
��a�� = a/pr^qr�ƂȂ�Ȃ���Ȃ�Ȃ��̂�
�Ƃ������Ă��邯�ǂ������� �g�Ή��h ���ȂɂƂȂɂ̑Ή��������ĂȂ����炱��Ȏ����������鍪�����Ȃ��B
�Ƃ����킯�ŃR�R���߂ł��ˁB
2018/08/29(��) 12:37:27.99ID:pwgAv9O4
2018/08/29(��) 13:01:47.17ID:ExIdLqFl
���Ǖt���̐��w�G���́A�P�͏o����֎~�H�炢�܂����Ă邵
2018/08/29(��) 13:07:59.66ID:fF09sBzs
p7����k=7����Ȃ���7�y�[�W�̂��Ƃ��H
2018/08/29(��) 13:33:55.52ID:vucxJj8P
�P�́AarXiv�ɂ���o����֎~�ɁI
���܂�ɂ����e���Ђǂ����߂ɁI�I�I
���E�ɒp���N���܂���B
���܂�ɂ����e���Ђǂ����߂ɁI�I�I
���E�ɒp���N���܂���B
2018/08/29(��) 14:25:20.99ID:gAox8rS4
���Ƃ��������Ă��t�B�[�o�[�Ȃ�ĂȂ�Ȃ���BABC�����������������̖��O�A�ǂꂾ���̐l�Ԃ��m���Ă�H
�������A�������猾���Ă���悤�ɁA�{���ɉ��l�̂��鐬�ʂ͏ؖ��̉ߒ��łł����V�������_�̌n��(�����ł��Ă���̂͐��E�ł�20�l���炢�炵����)�B
����ɂ���ׁA1�̘_���͂����̎��ό`�B�����܂ʼn��l������Ƃ͎v���Ȃ��B�������A���̏ؖ��҂Ƃ��Ė��O�͎c�邩������Ȃ����A����Ȃ��ƒm���Ă�̂͂����ꕔ�̐��w�I�^�N�������B
�������A�������猾���Ă���悤�ɁA�{���ɉ��l�̂��鐬�ʂ͏ؖ��̉ߒ��łł����V�������_�̌n��(�����ł��Ă���̂͐��E�ł�20�l���炢�炵����)�B
����ɂ���ׁA1�̘_���͂����̎��ό`�B�����܂ʼn��l������Ƃ͎v���Ȃ��B�������A���̏ؖ��҂Ƃ��Ė��O�͎c�邩������Ȃ����A����Ȃ��ƒm���Ă�̂͂����ꕔ�̐��w�I�^�N�������B
2018/08/29(��) 15:20:37.04ID:7MjvDqGy
����A�B�̎��ό`���낤���A�Ȃ낤���A����������X�[�p�[��j���[�X����B
���炭�����͈�ς���B
���炭�����͈�ς���B
2018/08/29(��) 15:27:22.57ID:7MjvDqGy
>>400
�����ł��B
�Ƃ�����p7�̎��_�ł܂Ř_���� �g�Ή��h �ƌĂׂ�̂͗^����ꂽ��̊��S��y�ɑ���
a = A(y) = 2y/(1+p+�c+p^n)
b = B(y) = y//(1+p+�c+p^n)
c = C(y) = 2y/(1+p+�c+p^n)/p^n
���炢�����Ȃ��B
���ɂ��ꂪ p7 �ŏ�����Ă���
��b�� = b/pr^qr�A
��b���ɑΉ����� a ��a���Ƃ����
�̕����̑Ή��ł���Ƃ���Ƃ����̊��S��y�f�����݂���
b�f = B(y�f)
����y�f�����݂��邱�Ƃ��ؖ����Ă����Ȃ��Ă͂����Ȃ��B
���ǂ�����ȑO�ɂ��Ă��������ɕt��������� b �̂����� b�f �ɂ��ē����c�_���������Ȃ� b ���\�����邽�߂ɉ��肵�Ă������� b�f �ɂ��Ă����肵�Ȃ��Ƃ����Ȃ��B
b �ɂ��Ă����Ă����������Ƃ� b�f = b/pr^qr �ɂ��Ă���������Ǝ咣�������Ȃ� b�f = B(y�f) �ƂȂ��̊��S�� y�f �̑��݂�ۏ��Ȃ���Ȃ�Ȃ��B
�����ł��B
�Ƃ�����p7�̎��_�ł܂Ř_���� �g�Ή��h �ƌĂׂ�̂͗^����ꂽ��̊��S��y�ɑ���
a = A(y) = 2y/(1+p+�c+p^n)
b = B(y) = y//(1+p+�c+p^n)
c = C(y) = 2y/(1+p+�c+p^n)/p^n
���炢�����Ȃ��B
���ɂ��ꂪ p7 �ŏ�����Ă���
��b�� = b/pr^qr�A
��b���ɑΉ����� a ��a���Ƃ����
�̕����̑Ή��ł���Ƃ���Ƃ����̊��S��y�f�����݂���
b�f = B(y�f)
����y�f�����݂��邱�Ƃ��ؖ����Ă����Ȃ��Ă͂����Ȃ��B
���ǂ�����ȑO�ɂ��Ă��������ɕt��������� b �̂����� b�f �ɂ��ē����c�_���������Ȃ� b ���\�����邽�߂ɉ��肵�Ă������� b�f �ɂ��Ă����肵�Ȃ��Ƃ����Ȃ��B
b �ɂ��Ă����Ă����������Ƃ� b�f = b/pr^qr �ɂ��Ă���������Ǝ咣�������Ȃ� b�f = B(y�f) �ƂȂ��̊��S�� y�f �̑��݂�ۏ��Ȃ���Ȃ�Ȃ��B
>>393
b=(p+1)/2*(p^(n-1)+p^(n-3)+�c+1)
������(p+1)/2���f���̏ꍇ�́Ap1����pr�̂����ǂꂩ�ɂȂ�A�����pr�Ƃ��Ă���
>>396
�����O�̂��Ƃ����A>>1�̓Z���^�[�����̐��w��55��/90����200�_������
>>397
b��a�͈�ӂɑΉ����Ă��邩��Ab��ς���A����ɑΉ�����a�ɕς��Ȃ���Ȃ�Ȃ�
>>398
���܂ł́A���{���w��̃t���[�̘_���T�C�g�ɓ��e���Ă���
>>401
������3��ԈႦ����A���̖��͓�₾����
b=(p+1)/2*(p^(n-1)+p^(n-3)+�c+1)
������(p+1)/2���f���̏ꍇ�́Ap1����pr�̂����ǂꂩ�ɂȂ�A�����pr�Ƃ��Ă���
>>396
�����O�̂��Ƃ����A>>1�̓Z���^�[�����̐��w��55��/90����200�_������
>>397
b��a�͈�ӂɑΉ����Ă��邩��Ab��ς���A����ɑΉ�����a�ɕς��Ȃ���Ȃ�Ȃ�
>>398
���܂ł́A���{���w��̃t���[�̘_���T�C�g�ɓ��e���Ă���
>>401
������3��ԈႦ����A���̖��͓�₾����
2018/08/29(��) 15:48:10.96ID:pwgAv9O4
>>402
>ABC������������
�܂� IUT �̗����҂����Ȃ����߁AABC�\�z�̏ؖ��͐��������ǂ���������Ȃ��悤�ȏ����낤�B
�����������Ƃ��w�i�ɂ����āAIUT �̃X��������オ���Ă��邶���B
���̉����O�̒i�K�Œ����Ƀj���[�X�Ƃ��čڂ����̂��͒m��Ȃ����B
>�������A�������猾���Ă���悤�ɁA�{���ɉ��l�̂��鐬�ʂ�
>�ؖ��̉ߒ��łł����V�������_�̌n��(�����ł��Ă���̂͐��E�ł�20�l���炢�炵����)�B
�Ⴆ�����҂̌��t�ł������Ƃ��Ă��A������L�ۂ݂ɂ��Ȃ����������B
����500�y�[�W�߂��̏ؖ��̘_���́A���I�ȃe�L�X�g1�����ɑ�������B
�ǂ����ǂނ��͎��R�����B
>ABC������������
�܂� IUT �̗����҂����Ȃ����߁AABC�\�z�̏ؖ��͐��������ǂ���������Ȃ��悤�ȏ����낤�B
�����������Ƃ��w�i�ɂ����āAIUT �̃X��������オ���Ă��邶���B
���̉����O�̒i�K�Œ����Ƀj���[�X�Ƃ��čڂ����̂��͒m��Ȃ����B
>�������A�������猾���Ă���悤�ɁA�{���ɉ��l�̂��鐬�ʂ�
>�ؖ��̉ߒ��łł����V�������_�̌n��(�����ł��Ă���̂͐��E�ł�20�l���炢�炵����)�B
�Ⴆ�����҂̌��t�ł������Ƃ��Ă��A������L�ۂ݂ɂ��Ȃ����������B
����500�y�[�W�߂��̏ؖ��̘_���́A���I�ȃe�L�X�g1�����ɑ�������B
�ǂ����ǂނ��͎��R�����B
2018/08/29(��) 15:53:35.47ID:7MjvDqGy
>>405
>������(p+1)/2���f���̏ꍇ�́Ap1����pr�̂����ǂꂩ�ɂȂ�A�����pr�Ƃ��Ă���
��Ȃ����킩��B
���� p7 �� a�f�Ab�f�Ac�f�B
����ɂ��� a�Ab�Ac �ɂ��Đ������Ă鎮�����l�ɐ�������Ǝ咣�������Ȃ�
��y�f ��p�f ��n�f
y�f�͊�̊��S���Ap�f�͂��� multiplicity ����̑f���q�An�f�͂��� multiplicity�B
a�f = 2y�f/(1+p�f +�c+p�f^n�f)�A
b�f = y�f/p�f^n�f�A
c�f = 2y�f/(1+p�f +�c+p�f^n�f)/p�f^n�f
�������̂����݂��邱�Ƃ��ؖ����Ă����Ȃ��Ƃ����Ȃ��B
������p7�̋c�_�͂��ꂾ������_���B
���i������Ŏg���Ă�
��a�� = a/pr^qr�ƂȂ�Ȃ���Ȃ�Ȃ��̂�
����͑Ή�����p�f�An�f�� p=p�f�An=n�f�����Ă��Ȃ��Ɛ������Ȃ��B
���̏ؖ����_�����ɂ͂Ȃ��B
>������(p+1)/2���f���̏ꍇ�́Ap1����pr�̂����ǂꂩ�ɂȂ�A�����pr�Ƃ��Ă���
��Ȃ����킩��B
���� p7 �� a�f�Ab�f�Ac�f�B
����ɂ��� a�Ab�Ac �ɂ��Đ������Ă鎮�����l�ɐ�������Ǝ咣�������Ȃ�
��y�f ��p�f ��n�f
y�f�͊�̊��S���Ap�f�͂��� multiplicity ����̑f���q�An�f�͂��� multiplicity�B
a�f = 2y�f/(1+p�f +�c+p�f^n�f)�A
b�f = y�f/p�f^n�f�A
c�f = 2y�f/(1+p�f +�c+p�f^n�f)/p�f^n�f
�������̂����݂��邱�Ƃ��ؖ����Ă����Ȃ��Ƃ����Ȃ��B
������p7�̋c�_�͂��ꂾ������_���B
���i������Ŏg���Ă�
��a�� = a/pr^qr�ƂȂ�Ȃ���Ȃ�Ȃ��̂�
����͑Ή�����p�f�An�f�� p=p�f�An=n�f�����Ă��Ȃ��Ɛ������Ȃ��B
���̏ؖ����_�����ɂ͂Ȃ��B
2018/08/29(��) 15:54:11.84ID:vucxJj8P
���������Z���^�[�������ł���悤�ȓz��������
����ȑS�̓I�Ƀ~�X���炯�̃S�~�o�c�e�͏o�Ȃ��B
�w�Z�̐搶�ɂ���āA�ʏ�̐��k���݂̎w�����K�v�������B
����̂P�́A�O�_���Ă��P�O�O�A��
����ȑS�̓I�Ƀ~�X���炯�̃S�~�o�c�e�͏o�Ȃ��B
�w�Z�̐搶�ɂ���āA�ʏ�̐��k���݂̎w�����K�v�������B
����̂P�́A�O�_���Ă��P�O�O�A��
2018/08/29(��) 15:57:17.22ID:7MjvDqGy
>>405
��b��a�͈�ӂɑΉ����Ă��邩��Ab��ς���A����ɑΉ�����a�ɕς��Ȃ���Ȃ�Ȃ�
b��a�̑Ή��͂��Ƃ���y������ꂽ���̂�����y���Ȃ�������b�ɂȂ�Ȃ��B
���������ē��l�̎咣�A�������藧�Ƃ��������Ȃ�A���̎咣�A���o��������̕����łłĂ��Ă镶���������悤�ɓ��ꂩ��������ɂ��āA����������肷�邩�A�ؖ����邩���Ȃ��Ƃ����Ȃ��B
��b��a�͈�ӂɑΉ����Ă��邩��Ab��ς���A����ɑΉ�����a�ɕς��Ȃ���Ȃ�Ȃ�
b��a�̑Ή��͂��Ƃ���y������ꂽ���̂�����y���Ȃ�������b�ɂȂ�Ȃ��B
���������ē��l�̎咣�A�������藧�Ƃ��������Ȃ�A���̎咣�A���o��������̕����łłĂ��Ă镶���������悤�ɓ��ꂩ��������ɂ��āA����������肷�邩�A�ؖ����邩���Ȃ��Ƃ����Ȃ��B
2018/08/29(��) 16:00:50.92ID:7MjvDqGy
�Ȃ�
�g��������ւ��Ă����l�̎咣����������B�h
�n�̃~�X�A�����Ă�ˁB
���̎��o�����Ƃ��A���̎����������肵�ē��o����Ă����̂��̈ӎ����R�����B
�g��������ւ��Ă����l�̎咣����������B�h
�n�̃~�X�A�����Ă�ˁB
���̎��o�����Ƃ��A���̎����������肵�ē��o����Ă����̂��̈ӎ����R�����B
2018/08/29(��) 16:05:48.08ID:hwbx/z7h
���w�����łȂ��������܂ꂽ���͂����Ă����
�O�����ʊW����������ɂȂ��Ă邱�Ƃ������悤�Ɏv��
�O�����ʊW����������ɂȂ��Ă邱�Ƃ������悤�Ɏv��
2018/08/29(��) 16:07:12.05ID:ThdMqrgL
����������`�Ȃ�Ċ�]����������悤�Ȃ��ƌ����̂͂����߂���
�ύX�_
�E15�y�[�W��ek��1�ƂȂ�ꍇ�̏ؖ���lj����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7091081848286/
�E15�y�[�W��ek��1�ƂȂ�ꍇ�̏ؖ���lj����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7091081848286/
2018/08/29(��) 16:09:27.48ID:ThdMqrgL
�t�F�C�Y�Q�ł���
2018/08/29(��) 16:14:13.34ID:ThdMqrgL
�������ĂȂ��̂ɘ_�����X�V�������鋶�C
2018/08/29(��) 16:18:33.20ID:7MjvDqGy
>>415
�~�X�ł͂Ȃ����Ă��������đS�R�K�v�ȋc�_���s������ĂȂ����B
{ A(y) | y�͊�̊��S��} �� {B(y) | y�͊�̊��S��}
�̊Ԃ̑Ή���������b�f�ɑΉ�����a�f�Ac�f�������Ă���Ȃ� b�f = B(y�f) �ƂȂ� y�f �̑��݂��ؖ����Ă����Ȃ��Ƃ����Ȃ����ǁA���̏ؖ��Ȃ���B
�~�X�ł͂Ȃ����Ă��������đS�R�K�v�ȋc�_���s������ĂȂ����B
{ A(y) | y�͊�̊��S��} �� {B(y) | y�͊�̊��S��}
�̊Ԃ̑Ή���������b�f�ɑΉ�����a�f�Ac�f�������Ă���Ȃ� b�f = B(y�f) �ƂȂ� y�f �̑��݂��ؖ����Ă����Ȃ��Ƃ����Ȃ����ǁA���̏ؖ��Ȃ���B
2018/08/29(��) 16:18:33.26ID:vucxJj8P
�������ĂȂ��̂ɘ_�����X�V�������鍼�\�t�P
2018/08/29(��) 16:36:41.71ID:ThdMqrgL
���x��p��n���s�ς��ƌ����o���܂�����
�ȑO�͕ϐ��ƌ����Ă��܂�����
�ȑO�͕ϐ��ƌ����Ă��܂�����
>>420
b��b'�Ƃ���ϊ��������ꍇ�ɂƂ����Ӗ��ł���
b��b'�Ƃ���ϊ��������ꍇ�ɂƂ����Ӗ��ł���
2018/08/29(��) 17:00:00.97ID:HwcGG5s6
>>419
��������Bp7 �̎��_�őΉ��Ƃ����̂͂����܂Ŋ�̊��S�� y �ɑ��Ă�����`����ĂȂ����炻��ȊO�̈Ӗ��� "�Ή�" �Ƃ������t���g���Ȃ炻�̈Ӗ����Ē�`���Ȃ��Ǝg���Ȃ��B
�Ē�`�����H���Ȃ��Ƃ��_���ɂ͏����ĂȂ���ˁH
�����A
p��p�An��n�Ab��b/pr^qr�Ac����/c/pr^qr�Aa��a/pr^qr
�Ƃ������ϊ���
a' = ��[k��r](1+pk + �c + pk^qk)�c(��)
����������Ƃ��������Ȃ�N�̂����u��������O�̂���
a = ��(1+pk + �c + pk^qk)�c(��)
�u��y�����S���Ap��multiplicity��̑f���q�Aa=2y/(1+p+�c)�v�c(��)
�����肵�ē��o���ꂽ��������
(��)��a��a'�ɒu��������Ȃ炻�̑O������ł���(��)��a��y������ɉ����Ď��ւ������̂̐�����K�v�Ƃ���B
�܂�(��)��a,�����Ƃ肩����
�u��y'�����S���Ap��multiplicity��̑f���q�Aa'=2y/(1+p'+�c)�v�c(��)
���ؖ�����Ȃ��Ɓc(��)�͎g���Ȃ��B
��������Bp7 �̎��_�őΉ��Ƃ����̂͂����܂Ŋ�̊��S�� y �ɑ��Ă�����`����ĂȂ����炻��ȊO�̈Ӗ��� "�Ή�" �Ƃ������t���g���Ȃ炻�̈Ӗ����Ē�`���Ȃ��Ǝg���Ȃ��B
�Ē�`�����H���Ȃ��Ƃ��_���ɂ͏����ĂȂ���ˁH
�����A
p��p�An��n�Ab��b/pr^qr�Ac����/c/pr^qr�Aa��a/pr^qr
�Ƃ������ϊ���
a' = ��[k��r](1+pk + �c + pk^qk)�c(��)
����������Ƃ��������Ȃ�N�̂����u��������O�̂���
a = ��(1+pk + �c + pk^qk)�c(��)
�u��y�����S���Ap��multiplicity��̑f���q�Aa=2y/(1+p+�c)�v�c(��)
�����肵�ē��o���ꂽ��������
(��)��a��a'�ɒu��������Ȃ炻�̑O������ł���(��)��a��y������ɉ����Ď��ւ������̂̐�����K�v�Ƃ���B
�܂�(��)��a,�����Ƃ肩����
�u��y'�����S���Ap��multiplicity��̑f���q�Aa'=2y/(1+p'+�c)�v�c(��)
���ؖ�����Ȃ��Ɓc(��)�͎g���Ȃ��B
423�P�R�Q�l�ڂ̑f������
2018/08/29(��) 17:44:33.95ID:hUIoq6fk �ؖ����������ĂȂ���ɁA��̃C�J�T�}���g���Ă�����猩�鉿�l�܂�Ŗ���
���͐^�ʖڂȐl�ɔC����
�{���̏ؖ����ł�����N�����ĂˁB���₷��(-_-)zzz
���͐^�ʖڂȐl�ɔC����
�{���̏ؖ����ł�����N�����ĂˁB���₷��(-_-)zzz
�ǂ����C�J�T�}�Ȃ̂����ɕ�������e�Ŏ�����Ȃ���A�������悤���Ȃ�
���̍l���ł́A�قڎ����̓��e���ƍl�����邪�B
���̍l���ł́A�قڎ����̓��e���ƍl�����邪�B
2018/08/29(��) 17:56:16.95ID:mmSfzGog
�܂����̃p�^�[��
y'=y/pk^qk
�ɂȂ邾�������Ay'�����S���ł��邩�͕s���ł����Ȃ���ł����ǁB
�������������̂�������܂���B�C���`�L�Ȕ��_�͗v��܂���B
�ɂȂ邾�������Ay'�����S���ł��邩�͕s���ł����Ȃ���ł����ǁB
�������������̂�������܂���B�C���`�L�Ȕ��_�͗v��܂���B
>>425
���ł͂Ȃ������Ԉ�������_�����Ă���p�^�[��������܂���
���ł͂Ȃ������Ԉ�������_�����Ă���p�^�[��������܂���
2018/08/29(��) 17:58:12.88ID:5mvrNBoN
>>102 �t�F�[�Y�R����
429�P�R�Q�l�ڂ̑f������
2018/08/29(��) 17:59:35.26ID:+Ju0D3QR �P�̔����͋��߂ĂȂ�������
�����C�J�T�}���͊F�m���Ă邵
�����ΐ^�ʖڂȐl�������Ă���邾�낤
�P��������ăC�J�T�}�łȂ��ؖ����������ĂˁB���₷��(-_-)zzz
�����C�J�T�}���͊F�m���Ă邵
�����ΐ^�ʖڂȐl�������Ă���邾�낤
�P��������ăC�J�T�}�łȂ��ؖ����������ĂˁB���₷��(-_-)zzz
2018/08/29(��) 18:07:25.65ID:7MjvDqGy
�Ƃ肠���� p7 �� ck < qk �o����ۂɗ��p������
a�� = a/pr^qr�Ab�� = b/pr^qr�Ac�� = c/pr^qr�c(A)
�����
a�� = ∏ [k��r](1 + pk + ⋯ + pk^qk)�c(B)
���ǂ��������Ă����̂������Ȃ��ƃ_�����B
���X
a = ∏(1 + pk + ⋯ + pk^qk)�c(C)
�����藧���Ă����炱����u�������������Ƃ������W�b�N���������Ȃ��̂͑O�Ɏw�E������ˁH
(C)��y, p, n, pk, qk�ɂ��Ă̊�����̉���̂��Ƃɓ��o���ꂽ���Ȃ̂�����A�u��������a�f�Ab�f�Ac�f�œ��l�̎�����������Ƃ����Ȃ炻�̊�����̉���̂Ȃ��ɂ���a�Ab�Ac��a�f�Ab�f�Ac�f�ɒu���������������������邱�Ƃ������Ȃ���(B)�͎g���Ȃ��B
���̏ؖ��Ȃ���H
a�� = a/pr^qr�Ab�� = b/pr^qr�Ac�� = c/pr^qr�c(A)
�����
a�� = ∏ [k��r](1 + pk + ⋯ + pk^qk)�c(B)
���ǂ��������Ă����̂������Ȃ��ƃ_�����B
���X
a = ∏(1 + pk + ⋯ + pk^qk)�c(C)
�����藧���Ă����炱����u�������������Ƃ������W�b�N���������Ȃ��̂͑O�Ɏw�E������ˁH
(C)��y, p, n, pk, qk�ɂ��Ă̊�����̉���̂��Ƃɓ��o���ꂽ���Ȃ̂�����A�u��������a�f�Ab�f�Ac�f�œ��l�̎�����������Ƃ����Ȃ炻�̊�����̉���̂Ȃ��ɂ���a�Ab�Ac��a�f�Ab�f�Ac�f�ɒu���������������������邱�Ƃ������Ȃ���(B)�͎g���Ȃ��B
���̏ؖ��Ȃ���H
2018/08/29(��) 18:21:30.11ID:a8QQvkl2
>>424
�킩��Ȃ����e�������番����Ȃ����Ĕ������Ă����Ȃ��Ɛ������鑤�͍������Ⴄ��Ȃ����H
�킩��Ȃ����e�������番����Ȃ����Ĕ������Ă����Ȃ��Ɛ������鑤�͍������Ⴄ��Ȃ����H
2018/08/29(��) 18:36:30.15ID:5mvrNBoN
>�P��������ăC�J�T�}�łȂ��ؖ����������ĂˁB
�P�ɂ͖���
�P�͐��w�p�ꂪ�o�Ă��邾���ŃA�E�g
�P�ɂ́A�ؖ������̕ό`��������Ă����ς�
�P�ɂ͖���
�P�͐��w�p�ꂪ�o�Ă��邾���ŃA�E�g
�P�ɂ́A�ؖ������̕ό`��������Ă����ς�
435�P�R�Q�l�ڂ̑f������
2018/08/29(��) 19:46:21.33ID:I6pb8Pjk ������
2018/08/29(��) 19:48:25.62ID:ikeKGGfI
���������J�ɏڂ����������Ă��ꂢ�Ă���̂�
�P�͑��ς�炸�̂܂܁B
���w�ɗ����̂Ȃ�A���̐��w���s�������炩�ł��������悤�Ƃ��Ȃ�����B
�P�͑��ς�炸�̂܂܁B
���w�ɗ����̂Ȃ�A���̐��w���s�������炩�ł��������悤�Ƃ��Ȃ�����B
�����ڂ����������B���ʂɍl���āA�Ӗ���������Ȃ��̂͏����Ă������������������
2018/08/29(��) 20:16:13.45ID:a8QQvkl2
>>437
���ʂɍl�������ʂ͐l���ꂼ�ꂾ���Ă��Ƃ𗝉�������Ŕ������ė~����
���ʂɍl�������ʂ͐l���ꂼ�ꂾ���Ă��Ƃ𗝉�������Ŕ������ė~����
2018/08/29(��) 20:23:34.93ID:a8QQvkl2
>>439
�Ӗ���������Ȃ��̂͏����Ă������������������
���������v��
�_���̈Ӗ���������Ȃ��̂͏������l�������������炾��
�Ӗ���������Ȃ��̂͏����Ă������������������
���������v��
�_���̈Ӗ���������Ȃ��̂͏������l�������������炾��
2018/08/29(��) 20:24:00.76ID:i1Cwy+dK
2018/08/29(��) 20:57:57.35ID:O5EfvOx2
���̑ԓx�őΉ����Ⴆ��Ǝv����̂͐���
2018/08/29(��) 22:17:24.12ID:f18oIYZI
�N�ɂ��]������Ȃ����Ă킩���Ă邩�炱���ɏ����Ă���Ă��Ƃ��炢�@���Ă���
2018/08/29(��) 22:17:33.01ID:gAox8rS4
>>437
����u����ȊȒP�Ȃ��Ƃ�������Ȃ��̂ł����v�Ƃ������Ƃ��Ă���B
����u����ȊȒP�Ȃ��Ƃ�������Ȃ��̂ł����v�Ƃ������Ƃ��Ă���B
2018/08/29(��) 22:47:13.63ID:RyNiQgrc
>>443
�ނ��낻������Ă邩�珕���D���o�����Ƃ��Ƃ��₼
�ނ��낻������Ă邩�珕���D���o�����Ƃ��Ƃ��₼
446�P�R�Q�l�ڂ̑f������
2018/08/29(��) 23:21:44.52ID:fVhIhnyy �_���ɏ����Ă���uk�ɂ��đΏ́v�Ƃ������Ƃ����ݍӂ��Ă݂āA�ȉ��̂悤�ȍl���Ɏ���܂����B
�Ȃ��A���������̊���ɏ]���A����N�̑f���������ɂ�����f��p�̎�����v_p(N)�ƕ\���B
[�Ⴆ�� 45=3^2�~5 �Ȃ̂� v_3(45)=2, v_5(45)=1, ���̑��̑f��p�ɂ��� v_p(45)=0]
[�O��]
1) �f���̊��S��y�̑��݂����肷��ƁAv_p(y)��1 (mod 4) �ƂȂ�f��p����ӂɒ�܂�B[y����p����܂�]
2) (1)�Œ�܂����f��p�ɂ��āApr=(p+1)/2 �Ƃ���ƁAy �� pr �̔{���ł���B[p����pr����܂�]
3) (1)��(2)�Œ�܂���p,pr�ɂ��� 2pr-1=p �ƌ����邪�Apr ���f���Ȃ�Apk��pr �ƂȂ� y �̑f���� pk �ɂ��� 2pk-1��p �ł���B
4) pk��pr �ƂȂ� y �̑f���� pk �ɂ��� 2pk-1=p���ƒu���ƁA[(3)���K�� p����p �ł���]
�@ v_p��(y��)��1 (mod 4) �ƂȂ�ʂ̊��S�� y�� �����݂��邩������Ȃ� [���̏ꍇ�K�� y����y �ł���]
�ŁA�������炪�����������ƂȂ���ǂ��A
[�咣]
5) (1)���v_p(y)��1 (mod 4) ������ v_p(y)=4m+1 �ƒu�����Ƃ��ł���B
�@���l�ɁAv_p��(y��)��1 (mod 4) ������ v_p��(y��)=4m��+1 �ƒu�����Ƃ��ł��邪�A
�@y��y���Ap��p�������ꂼ��ʕ��Ȃ̂ŁAm=m�� �ł���Ƃ͌����Ȃ��B[�ؖ�����Ă��Ȃ�]
6) v_p(y)=4m+1 ���� 2m+1 �� pr �̔{���ƌ������Ƃ��āA���l�̘_���ŁA
�@ v_p��(y��)=4m��+1 ���� 2m��+1 �� pk �̔{���ƌ������Ƃ��Ă�
�@2m+1=2m��+1 �Ƃ͌����Ȃ��B
�@����āA������P���ɂЂƂ܂Ƃ߂ɂ��āu2m+1 �� ��pk �̔{���ł���v�Ƃ��邱�Ƃ͂ł��Ȃ��B
�������ł��傤�H
�Ȃ��A���������̊���ɏ]���A����N�̑f���������ɂ�����f��p�̎�����v_p(N)�ƕ\���B
[�Ⴆ�� 45=3^2�~5 �Ȃ̂� v_3(45)=2, v_5(45)=1, ���̑��̑f��p�ɂ��� v_p(45)=0]
[�O��]
1) �f���̊��S��y�̑��݂����肷��ƁAv_p(y)��1 (mod 4) �ƂȂ�f��p����ӂɒ�܂�B[y����p����܂�]
2) (1)�Œ�܂����f��p�ɂ��āApr=(p+1)/2 �Ƃ���ƁAy �� pr �̔{���ł���B[p����pr����܂�]
3) (1)��(2)�Œ�܂���p,pr�ɂ��� 2pr-1=p �ƌ����邪�Apr ���f���Ȃ�Apk��pr �ƂȂ� y �̑f���� pk �ɂ��� 2pk-1��p �ł���B
4) pk��pr �ƂȂ� y �̑f���� pk �ɂ��� 2pk-1=p���ƒu���ƁA[(3)���K�� p����p �ł���]
�@ v_p��(y��)��1 (mod 4) �ƂȂ�ʂ̊��S�� y�� �����݂��邩������Ȃ� [���̏ꍇ�K�� y����y �ł���]
�ŁA�������炪�����������ƂȂ���ǂ��A
[�咣]
5) (1)���v_p(y)��1 (mod 4) ������ v_p(y)=4m+1 �ƒu�����Ƃ��ł���B
�@���l�ɁAv_p��(y��)��1 (mod 4) ������ v_p��(y��)=4m��+1 �ƒu�����Ƃ��ł��邪�A
�@y��y���Ap��p�������ꂼ��ʕ��Ȃ̂ŁAm=m�� �ł���Ƃ͌����Ȃ��B[�ؖ�����Ă��Ȃ�]
6) v_p(y)=4m+1 ���� 2m+1 �� pr �̔{���ƌ������Ƃ��āA���l�̘_���ŁA
�@ v_p��(y��)=4m��+1 ���� 2m��+1 �� pk �̔{���ƌ������Ƃ��Ă�
�@2m+1=2m��+1 �Ƃ͌����Ȃ��B
�@����āA������P���ɂЂƂ܂Ƃ߂ɂ��āu2m+1 �� ��pk �̔{���ł���v�Ƃ��邱�Ƃ͂ł��Ȃ��B
�������ł��傤�H
2018/08/30(��) 00:05:45.68ID:l0gKgD5R
2018/08/30(��) 00:21:32.73ID:l0gKgD5R
��b���ɑΉ����� a ��a���Ƃ����
�Ƃ����Ă邯�ǁA���Ɖ���Ή��Â��Ă邩�����ĂȂ��ƌ����Ă邾���Ȃ��H
�����f���ɂ�
{(A(y)�AB(y)�AC(y)�Ap(y)�An(y)) | y:��̊��S��}
�ɂ���ē�����Ή��t���̈Ӗ��Ȃ�
b/pr^qr = b�f = B(y�f)
������̊��S��y�f�̑��݂����߂��Ȃ��ƃ_���Ƃ����Ă邾���Ȃ��ǁH
��b���ɑΉ����� a ��a���Ƃ����
��a�f�͉������l����ɂ� a�f = A(y�f)�Ab�f = B(y�f) �ƍl���邵���Ȃ����B
����ȊO�� �g�Ή�����h �̒�`�Ȃ�����B 👀
Rock54: Caution(BBR-MD5:1341adc37120578f18dba9451e6c8c3b)
�Ƃ����Ă邯�ǁA���Ɖ���Ή��Â��Ă邩�����ĂȂ��ƌ����Ă邾���Ȃ��H
�����f���ɂ�
{(A(y)�AB(y)�AC(y)�Ap(y)�An(y)) | y:��̊��S��}
�ɂ���ē�����Ή��t���̈Ӗ��Ȃ�
b/pr^qr = b�f = B(y�f)
������̊��S��y�f�̑��݂����߂��Ȃ��ƃ_���Ƃ����Ă邾���Ȃ��ǁH
��b���ɑΉ����� a ��a���Ƃ����
��a�f�͉������l����ɂ� a�f = A(y�f)�Ab�f = B(y�f) �ƍl���邵���Ȃ����B
����ȊO�� �g�Ή�����h �̒�`�Ȃ�����B 👀
Rock54: Caution(BBR-MD5:1341adc37120578f18dba9451e6c8c3b)
2018/08/30(��) 04:19:46.28ID:suJHPDIh
Rock54�K�������Ƃ�����
�����s���Q���邾���ŏo���
�����s���Q���邾���ŏo���
>>450 ����
���藧�Ɖ��肵�Ă��鎮
2b=c(p^n+�c+1)
a=cp^n
���A���̕ϐ�(p,n)�̒l��ς����萔(a,b,c)�̕�����
����ϊ��ɂ���Ă����Ă��A�����̂��s�ςɂȂ�Ȃ����
�Ȃ�Ȃ��͓̂��R�Ȃ̂ł͂Ȃ��ł��傤���H
���藧�Ɖ��肵�Ă��鎮
2b=c(p^n+�c+1)
a=cp^n
���A���̕ϐ�(p,n)�̒l��ς����萔(a,b,c)�̕�����
����ϊ��ɂ���Ă����Ă��A�����̂��s�ςɂȂ�Ȃ����
�Ȃ�Ȃ��͓̂��R�Ȃ̂ł͂Ȃ��ł��傤���H
452�P�R�Q�l�ڂ̑f������
2018/08/30(��) 06:43:02.80ID:RhFK/XgI ��y�̑��݂������Ȃ��̂�y'��������킯���Ȃ��ł��傤�B
���̑��݂����肵�Ă������疵���������̂��w���@�ł��B
y�̑��݂����肵�Ă���Ƃ͊W�Ȃ�y'�������o���Ĕw���@�ɂȂ�Ȃ��_����W�J�����̂͂P�������܂���B
��������Ǝw�E�����炻�̌������Ŕ��_����Ƃ����̂�
�܂����������Ăӂ����ď����Ă���Ƃ����v���܂��B
���̑��݂����肵�Ă������疵���������̂��w���@�ł��B
y�̑��݂����肵�Ă���Ƃ͊W�Ȃ�y'�������o���Ĕw���@�ɂȂ�Ȃ��_����W�J�����̂͂P�������܂���B
��������Ǝw�E�����炻�̌������Ŕ��_����Ƃ����̂�
�܂����������Ăӂ����ď����Ă���Ƃ����v���܂��B
2018/08/30(��) 07:09:29.73ID:ZrevCixY
>>451
�����A���̕ϐ�(p,n)�̒l��ς����萔(a,b,c)�̕�����
������ϊ��ɂ���Ă����Ă��A�����̂��s�ςɂȂ�Ȃ����
���Ȃ�Ȃ��͓̂��R�Ȃ̂ł͂Ȃ��ł��傤���H
��Ȃ킯�Ȃ��ł���H
���鉼��̂��ƂɂT�̕���a�Ab�Ac�ɂ��ē����Ă��鎮
a = 2bp^n/(1+p+�c+p^n)�c(1)
c = 2bp^n/(1+p+�c+p^n)/p^n�c(2)
��
a = ��[pk��p](1+pk+�c+pk^v_pk(a))�c(3)�A
b = ��[pk��p]pk^v_pk(a)�c(4)
c = ��[pk��p](1+pk+�c+pk^v_pk(a)) / p^n�c(5)
��p7�܂ł�y�����`����a,b,c,p,n�ɂ��Ă͐������Ă��邵�A���̏ؖ����^�����Ă���B
����b�f = b/pr^qr �ƒu��������(1)�A(2)�𗘗p���� �g�Ή�����h a,c ��������Ƃ��Ă��V�����T�g(a�f,b�f,c�f,p�f,n�f)��(3)�`(5)���ׂĂ����Ƃ͌���Ȃ��B
(1)�A(2)���g����y���Ȃ��Ă�a,c���v�Z�͂ł��邪�A�v�Z�������ʂ� �gy�R���ł������h (a,b,c) �Ɠ����������Ă���Ƃ͌���Ȃ��B
���w���x���̗�ł����� x,y,u,v �������Ƃ���
x^2 + y^2 = 2
�����ϐ�����
u = x+y�Av=xy�c(AB)
�Ƃ����V�����ϐ���������Ƃ�����u,v��
v = (1/2)u^2-1�c(12)
v �� (1/4)u^2�c(345)
�Ƃ����W�����݂������Au=4�̂Ƃ�(12)���g������ u �� �g�Ή�����h v=7���ł��邯�ǁA����(u,v) = (4,7)��(345)�����Ȃ��B
����(A)�A(B)���g��Ȃ��Ă� u �̒l���� v ���v�Z�ł����Ƃ��Ă��A����(u,v)�͌���(A)�A(B)����\�����ꂽ���̂łȂ�����A����(A),(B)���瓾��ꂽ��(345)�����Ƃ͌���Ȃ��B
�{���ł����A
a = 2y/(1+p+�c+p^n)�c(A)
b = y/p^n�c(B)
c = 2y/(1+p+�c+p^n)/p^n�c(C)
�ƒ�`����a,b,c���`�����Ƃ��A�m���� b,p,n �̒l���� �g�Ή�����h a,c �̒l��(1)�A(2)��p���Čv�Z���邱�Ƃ͂ł��邪�A���̐V���� (a�f, b�f, c�f) �ɂ��ẮA(A),(B),(C)�R����(a,b,c)�ɂ��Ă͐������邱�Ƃ��m�F����Ă���(3),(4),(5)�����Ƃ͌���Ȃ��B
�������̗�Ɠ����\���B
�����A���̕ϐ�(p,n)�̒l��ς����萔(a,b,c)�̕�����
������ϊ��ɂ���Ă����Ă��A�����̂��s�ςɂȂ�Ȃ����
���Ȃ�Ȃ��͓̂��R�Ȃ̂ł͂Ȃ��ł��傤���H
��Ȃ킯�Ȃ��ł���H
���鉼��̂��ƂɂT�̕���a�Ab�Ac�ɂ��ē����Ă��鎮
a = 2bp^n/(1+p+�c+p^n)�c(1)
c = 2bp^n/(1+p+�c+p^n)/p^n�c(2)
��
a = ��[pk��p](1+pk+�c+pk^v_pk(a))�c(3)�A
b = ��[pk��p]pk^v_pk(a)�c(4)
c = ��[pk��p](1+pk+�c+pk^v_pk(a)) / p^n�c(5)
��p7�܂ł�y�����`����a,b,c,p,n�ɂ��Ă͐������Ă��邵�A���̏ؖ����^�����Ă���B
����b�f = b/pr^qr �ƒu��������(1)�A(2)�𗘗p���� �g�Ή�����h a,c ��������Ƃ��Ă��V�����T�g(a�f,b�f,c�f,p�f,n�f)��(3)�`(5)���ׂĂ����Ƃ͌���Ȃ��B
(1)�A(2)���g����y���Ȃ��Ă�a,c���v�Z�͂ł��邪�A�v�Z�������ʂ� �gy�R���ł������h (a,b,c) �Ɠ����������Ă���Ƃ͌���Ȃ��B
���w���x���̗�ł����� x,y,u,v �������Ƃ���
x^2 + y^2 = 2
�����ϐ�����
u = x+y�Av=xy�c(AB)
�Ƃ����V�����ϐ���������Ƃ�����u,v��
v = (1/2)u^2-1�c(12)
v �� (1/4)u^2�c(345)
�Ƃ����W�����݂������Au=4�̂Ƃ�(12)���g������ u �� �g�Ή�����h v=7���ł��邯�ǁA����(u,v) = (4,7)��(345)�����Ȃ��B
����(A)�A(B)���g��Ȃ��Ă� u �̒l���� v ���v�Z�ł����Ƃ��Ă��A����(u,v)�͌���(A)�A(B)����\�����ꂽ���̂łȂ�����A����(A),(B)���瓾��ꂽ��(345)�����Ƃ͌���Ȃ��B
�{���ł����A
a = 2y/(1+p+�c+p^n)�c(A)
b = y/p^n�c(B)
c = 2y/(1+p+�c+p^n)/p^n�c(C)
�ƒ�`����a,b,c���`�����Ƃ��A�m���� b,p,n �̒l���� �g�Ή�����h a,c �̒l��(1)�A(2)��p���Čv�Z���邱�Ƃ͂ł��邪�A���̐V���� (a�f, b�f, c�f) �ɂ��ẮA(A),(B),(C)�R����(a,b,c)�ɂ��Ă͐������邱�Ƃ��m�F����Ă���(3),(4),(5)�����Ƃ͌���Ȃ��B
�������̗�Ɠ����\���B
2018/08/30(��) 07:26:09.10ID:EObwglNy
����u��̊��S�������݂���v�̂��ƂŁu��̊��S�����������݂���v�͐^�U�s��������A
�u��̊��S�����������݂���v��O��Ƃ���c�_�͂ł��Ȃ��B
�O������Ⴆ�Ę_����W�J���Ă�悤�ɂ��������Ȃ��ˁA�Ӑ}���Ă��Ӑ}�������͂킩��Ȃ����ǁB
����u��̊��S�������݂���v
��u�����ꍇ�A
�O��1�u��̊��S�����ЂƂƂ�Ay�Ƃ���v
�O��2�u��̊��S�����ЂƂƂ�Ay'�Ƃ���v
�͒P�Ƃł͂��ꂼ��OK�����ǁA
�O��3�uy��y'�͈قȂ�v
�����킹���NG�ɂȂ�B
�u��̊��S�����������݂���v��O��Ƃ���c�_�͂ł��Ȃ��B
�O������Ⴆ�Ę_����W�J���Ă�悤�ɂ��������Ȃ��ˁA�Ӑ}���Ă��Ӑ}�������͂킩��Ȃ����ǁB
����u��̊��S�������݂���v
��u�����ꍇ�A
�O��1�u��̊��S�����ЂƂƂ�Ay�Ƃ���v
�O��2�u��̊��S�����ЂƂƂ�Ay'�Ƃ���v
�͒P�Ƃł͂��ꂼ��OK�����ǁA
�O��3�uy��y'�͈قȂ�v
�����킹���NG�ɂȂ�B
2018/08/30(��) 07:59:50.55ID:suJHPDIh
>>102 �t�F�[�Y�R��\����
2018/08/30(��) 09:42:58.73ID:fVFZlc/e
�_�̂悤�ɐe�Ȑl�������A�ƂĂ��ƂĂ��ڂ��������Ă���Ă���̂�
�P�͐��w�A�����M�[�E���A�����M�[���������ă_�����ȁB
�P�͐��w�A�����M�[�E���A�����M�[���������ă_�����ȁB
457�P�R�Q�l�ڂ̑f������
2018/08/30(��) 09:58:06.85ID:deI4yk2d �̒r�܂̃W�����N���̐��w���R�[�i�[��
���������ُ�҂̏o�������l�����Ǝv����u�t�F���}�[�̍ŏI�藝�̏����I�ؖ��v�̏����q���u���Ă���������
����͂ǂ������o�܂ł������ɒ��Ɏ������낤
���������ُ�҂̏o�������l�����Ǝv����u�t�F���}�[�̍ŏI�藝�̏����I�ؖ��v�̏����q���u���Ă���������
����͂ǂ������o�܂ł������ɒ��Ɏ������낤
2018/08/30(��) 10:01:01.47ID:e/w76Ydr
�ُ�ҁi�����j
2018/08/30(��) 10:15:48.62ID:fVFZlc/e
���������ُ�҂̏o�������l���́A�}���قł悭��������B
���g�͂��̃X�����l�ɂԂ�����̂ɂȂ��Ă�B
���g�͂��̃X�����l�ɂԂ�����̂ɂȂ��Ă�B
2018/08/30(��) 10:25:43.97ID:XOoReTTx

2018/08/30(��) 10:31:41.56ID:fVFZlc/e
���ɂ��A���������ُ�҂������o������Ă����������B
�p�̎O������}���@�Ƃ��A�����̐}�ʂ��R�����ɂȂ��ĂȂ��̂ɏo��B
��������Ȃ̂������ς��B
�p�̎O������}���@�Ƃ��A�����̐}�ʂ��R�����ɂȂ��ĂȂ��̂ɏo��B
��������Ȃ̂������ς��B
>>453
����ŕ�����Ȃ���A���̖��͒��߂����������B
2b=c(p^n+�c+1)
�𗼕ӂ�pk^qk�Ŋ���ƁAc��pk^qk�Ŋ������ꍇ�ɂ�
2b/pk^qk=c/pk^qk(p^n+�c+1)
�ƂȂ�Ap^n+�c+1�̒l�͕ς��Ȃ�����Ap��n�͕s�ςɂȂ�B
b'=b/pk^qk=��[k=1,r-1]pk^qk
c'=b/pk^qk
�Ƃ����
b'=c'(p^n+�c+1)
�ƂȂ�A���̌`�͕s�ςɂȂ�B
ap-2bp+2b=c�̎��̗��ӂ�qk^qk�Ŋ���Aa'=a/pk/qk�Ƃ����
a''-2b'p+2b'=c'
�ƂȂ�Ap�̒l���s�ςł��邩�炱�̎��͐��藧���Ȃ���Ȃ�Ȃ��B
b'=��[k=1,r-1]pk^qk�ł��邩��Ab'�ɑΉ�����a'�͑�ӂ���
a'=��[k=1,r-1](1+pk+�cpk^qk)
�ƂȂ�Aa'=a/pk^qk�ł��邩��
��[k=1,r](1+pk+�cpk^qk)/pk^qk=��[k=1,r-1](1+pk+�cpk^qk)
�ƂȂ�Ȃ���Ȃ�Ȃ����A���̎��͐������Ȃ��B
���ꂩ��A���̘_���͂����������̂ł͂Ȃ��̂ŊԈ�������̂���
����̂ɂ͖���������B���̂��̖����������ʂ����Ƃ���̂��H
�r���^�₾�B
����ŕ�����Ȃ���A���̖��͒��߂����������B
2b=c(p^n+�c+1)
�𗼕ӂ�pk^qk�Ŋ���ƁAc��pk^qk�Ŋ������ꍇ�ɂ�
2b/pk^qk=c/pk^qk(p^n+�c+1)
�ƂȂ�Ap^n+�c+1�̒l�͕ς��Ȃ�����Ap��n�͕s�ςɂȂ�B
b'=b/pk^qk=��[k=1,r-1]pk^qk
c'=b/pk^qk
�Ƃ����
b'=c'(p^n+�c+1)
�ƂȂ�A���̌`�͕s�ςɂȂ�B
ap-2bp+2b=c�̎��̗��ӂ�qk^qk�Ŋ���Aa'=a/pk/qk�Ƃ����
a''-2b'p+2b'=c'
�ƂȂ�Ap�̒l���s�ςł��邩�炱�̎��͐��藧���Ȃ���Ȃ�Ȃ��B
b'=��[k=1,r-1]pk^qk�ł��邩��Ab'�ɑΉ�����a'�͑�ӂ���
a'=��[k=1,r-1](1+pk+�cpk^qk)
�ƂȂ�Aa'=a/pk^qk�ł��邩��
��[k=1,r](1+pk+�cpk^qk)/pk^qk=��[k=1,r-1](1+pk+�cpk^qk)
�ƂȂ�Ȃ���Ȃ�Ȃ����A���̎��͐������Ȃ��B
���ꂩ��A���̘_���͂����������̂ł͂Ȃ��̂ŊԈ�������̂���
����̂ɂ͖���������B���̂��̖����������ʂ����Ƃ���̂��H
�r���^�₾�B
2018/08/30(��) 12:47:30.68ID:e/w76Ydr
���䍂�ŕs�����Ȃ�ˁA���̐l
>>462 ����
��ap-2bp+2b=c�̎��̗��ӂ�qk^qk�Ŋ���Aa'=a/pk/qk�Ƃ����
��a''-2b'p+2b'=c'
ap-2bp+2b=c�̎��̗��ӂ�qk^qk�Ŋ���Aa'=a/pk^qk�Ƃ����
a'-2b'p+2b'=c'
��ap-2bp+2b=c�̎��̗��ӂ�qk^qk�Ŋ���Aa'=a/pk/qk�Ƃ����
��a''-2b'p+2b'=c'
ap-2bp+2b=c�̎��̗��ӂ�qk^qk�Ŋ���Aa'=a/pk^qk�Ƃ����
a'-2b'p+2b'=c'
>>463
������H
������H
2018/08/30(��) 12:52:35.50ID:e/w76Ydr
2018/08/30(��) 13:01:51.05ID:hW1FItRq
2018/08/30(��) 13:58:47.14ID:aQn2pq4h
�����������������
469�P�R�Q�l�ڂ̑f������
2018/08/30(��) 13:59:23.42ID:Lxw636mk �P���Ԉ���Ă�Ɍ��܂��Ă邶���
�����ĂP������
�����ĂP������
2018/08/30(��) 14:06:53.79ID:oaEZkqRk
���͂�ǂދC�ɂȂ�Ȃ��̂łȂ�̂��Ƃ肵�Ă��邩�킩��A�w�E�ɑ��锽�_�����_�ɂȂ��Ă��Ȃ��Ӗ��s���Ȋ����̔��_�ł��邱�Ƃ͂Ȃ�ƂȂ��`���B
2018/08/30(��) 14:08:43.25ID:hW1FItRq
�ǂ������u���������Ԉ���Ă�v���Č����Ă����
�Ӗ��킩��Ȃ�
�Ӗ��킩��Ȃ�
472�P�R�Q�l�ڂ̑f������
2018/08/30(��) 14:22:06.62ID:wrnsIhYA �_�����a=��[k=1,r](1+pk+�cpk^qk)
���̑O��܂��ĂȂ�
��a'=��[k=1,r-1](1+pk+�cpk^qk)
���ƂȂ�Aa'=a/pk^qk
�ƌ����Ă�̂Ȃ�P�͑����Ȃ��n������
�����Ō���F�߂�Ȃ�u���n������v�͓P�Ă��������B
���̑O��܂��ĂȂ�
��a'=��[k=1,r-1](1+pk+�cpk^qk)
���ƂȂ�Aa'=a/pk^qk
�ƌ����Ă�̂Ȃ�P�͑����Ȃ��n������
�����Ō���F�߂�Ȃ�u���n������v�͓P�Ă��������B
2018/08/30(��) 14:45:24.41ID:VvlpfcOp
>>462
a�f = a/pr^qr�Ab�f = b/pr^qr�Ac�f = c/pr^qr
��a,b,c�ɑΉ����� �g�������̎��h �𐬗�������͓̂�����O�B
���������藧���Ꭶ����
�g���̂悤�ɂ����ς����藧�������邩�炢�ł����藧��ˁH�h
�Ȃ�Ę_�@�͐��w�ɂ͂Ȃ��B
�{���Ō����ΌN���咣���Ă��������̎�
a �e = ��[k��r](1+pr+�cpr^qr)
�����B
�g�Ή����Ă���琬�����Ă�͓̂�����O�h �Ȃ�Ę_�������w�ɂȂ����Ƃ͐���������ˁH
���镶���ɂ��Đ������邱�Ƃ��ʂ̕����ɂ��Ă���������Ƃ����咣�͊��ɐ������� �g���Ֆ}���h �� �g���ቻ�h �̐��_�����Ȃ��B
�Ȃ��Ȃ炱�̂Q���������w�ŔF�߂��Ă��� �h�ʂ̕����ɒu�������Ă����藧�h ���Ƃ�F�߂Ă悢�Ɛ��w�̐��E�ō��ӂ̂��鐄�_������B
�Ȃ�ƂȂ� �g�Ή����Ă���� a�f b�f c�f �ł����藧�B���藧��������ς����邵�B�h �Ȃ�Ę_�@�͐��w�̐��E�ł͔F�߂��Ȃ��B
���ۑΉ��͂��邯�ǂ��ׂĂ̎����������ĂȂ����>>453�ɏ������ł���H
�����N�� �g�Ή����Ă����a�f b�f c�f�ɕ�����u�������Ă��Ȃ肽�B�h �Ƃ����_�@�� �g����Ȃɓ���Ȃ��_�@�h �ł���Ȃ�A���̘_�@�����̂Q���瓱�o�ł��邱�Ƃ�����Ă݂��Ȃ��ƃ_���B
������ �ga�f b�f c�f �ɂ��čl�����邷�ׂĂ̎������̂܂ܐ��藧�h ���Ƃ��ؖ�����K�v�͂Ȃ��B
a �e = ��[k��r](1+pr+�cpr^qr)
�����ł��B
����� �g���Ֆ}���h �� �g���ቻ�h �̐��_��p����
a = ��(1+pr+�cpr^qr)
���瓱�o���ĉ������B
a�f = a/pr^qr�Ab�f = b/pr^qr�Ac�f = c/pr^qr
��a,b,c�ɑΉ����� �g�������̎��h �𐬗�������͓̂�����O�B
���������藧���Ꭶ����
�g���̂悤�ɂ����ς����藧�������邩�炢�ł����藧��ˁH�h
�Ȃ�Ę_�@�͐��w�ɂ͂Ȃ��B
�{���Ō����ΌN���咣���Ă��������̎�
a �e = ��[k��r](1+pr+�cpr^qr)
�����B
�g�Ή����Ă���琬�����Ă�͓̂�����O�h �Ȃ�Ę_�������w�ɂȂ����Ƃ͐���������ˁH
���镶���ɂ��Đ������邱�Ƃ��ʂ̕����ɂ��Ă���������Ƃ����咣�͊��ɐ������� �g���Ֆ}���h �� �g���ቻ�h �̐��_�����Ȃ��B
�Ȃ��Ȃ炱�̂Q���������w�ŔF�߂��Ă��� �h�ʂ̕����ɒu�������Ă����藧�h ���Ƃ�F�߂Ă悢�Ɛ��w�̐��E�ō��ӂ̂��鐄�_������B
�Ȃ�ƂȂ� �g�Ή����Ă���� a�f b�f c�f �ł����藧�B���藧��������ς����邵�B�h �Ȃ�Ę_�@�͐��w�̐��E�ł͔F�߂��Ȃ��B
���ۑΉ��͂��邯�ǂ��ׂĂ̎����������ĂȂ����>>453�ɏ������ł���H
�����N�� �g�Ή����Ă����a�f b�f c�f�ɕ�����u�������Ă��Ȃ肽�B�h �Ƃ����_�@�� �g����Ȃɓ���Ȃ��_�@�h �ł���Ȃ�A���̘_�@�����̂Q���瓱�o�ł��邱�Ƃ�����Ă݂��Ȃ��ƃ_���B
������ �ga�f b�f c�f �ɂ��čl�����邷�ׂĂ̎������̂܂ܐ��藧�h ���Ƃ��ؖ�����K�v�͂Ȃ��B
a �e = ��[k��r](1+pr+�cpr^qr)
�����ł��B
����� �g���Ֆ}���h �� �g���ቻ�h �̐��_��p����
a = ��(1+pr+�cpr^qr)
���瓱�o���ĉ������B
2018/08/30(��) 14:57:57.15ID:vPYF0BHo
���������w�I�ɂȂ邾���łP�́A
�����ł��Ȃ����ē����邩��Ȃ��E�E�E�E
�����ł��Ȃ����ē����邩��Ȃ��E�E�E�E
>>472
b��r�Ԗڂ��Ȃ��Ȃ�킯������a�ł������Ȃ�͓̂��R��
>>473
��ӂ�����Bb'�ɑΉ�����a'�������Ȃ�́B������Ⴄ�ƌ���ꂽ��
���̉��莩�̂��Ԉ���Ă���Ƃ������ƂɂȂ�
>>474
r��r-1�Ƃ����ϊ����s���Ă��邾�����B���̕ϊ����̂����������Ƃ�
�z�肳���Bb��a�ɂ͈�Έ�̑Ή��W�����邩��A������b'�ɑΉ�����a'
�͈�ӂɒ�܂�B���������ꂪ�������Ȃ��Ƃ������ƂɂȂ�ƁA���̑��쎩�̂�
�������Ȃ��Ƃ������ƂɂȂ�Ac��pr^qr�Ŋ�����Ȃ��Ƃ������ʂɂȂ�B
����ł�������Ȃ��ӂ������̂́A���̘_����^�ʖڂɓǂ�ł��Ȃ�
���̐��w�I�Ȑ��ʂ��Ȃ����̂Ƃ������̂ł͂Ȃ��̂ł��傤���H
b��r�Ԗڂ��Ȃ��Ȃ�킯������a�ł������Ȃ�͓̂��R��
>>473
��ӂ�����Bb'�ɑΉ�����a'�������Ȃ�́B������Ⴄ�ƌ���ꂽ��
���̉��莩�̂��Ԉ���Ă���Ƃ������ƂɂȂ�
>>474
r��r-1�Ƃ����ϊ����s���Ă��邾�����B���̕ϊ����̂����������Ƃ�
�z�肳���Bb��a�ɂ͈�Έ�̑Ή��W�����邩��A������b'�ɑΉ�����a'
�͈�ӂɒ�܂�B���������ꂪ�������Ȃ��Ƃ������ƂɂȂ�ƁA���̑��쎩�̂�
�������Ȃ��Ƃ������ƂɂȂ�Ac��pr^qr�Ŋ�����Ȃ��Ƃ������ʂɂȂ�B
����ł�������Ȃ��ӂ������̂́A���̘_����^�ʖڂɓǂ�ł��Ȃ�
���̐��w�I�Ȑ��ʂ��Ȃ����̂Ƃ������̂ł͂Ȃ��̂ł��傤���H
2018/08/30(��) 16:27:28.24ID:vPYF0BHo
�����̐��w�I�Ȑ��ʂ��Ȃ����̂Ƃ������̂ł͂Ȃ��̂ł��傤���H
�T�����̂����Ő��ʂ��Ȃ��Ȃ�킯���Ȃ��B
�����ؖ����Ă���\������������A
�ؖ����������Ă��Ȃ��Ă����l����A�C�f�A������̂Ȃ�
PDF���J���Ă����ɐ��E�������ڂ���j���[�X�ƂȂ��Ă���B
���ւ̓��e�͂����ɏo����֎~����
���̃X���̒��ŏC�������X�Ƒ����Ă��邾�����Č���
�o�c�e�̉��l�𖾂炩�Ɏ����Ă���B
�T�����̂����Ő��ʂ��Ȃ��Ȃ�킯���Ȃ��B
�����ؖ����Ă���\������������A
�ؖ����������Ă��Ȃ��Ă����l����A�C�f�A������̂Ȃ�
PDF���J���Ă����ɐ��E�������ڂ���j���[�X�ƂȂ��Ă���B
���ւ̓��e�͂����ɏo����֎~����
���̃X���̒��ŏC�������X�Ƒ����Ă��邾�����Č���
�o�c�e�̉��l�𖾂炩�Ɏ����Ă���B
2018/08/30(��) 16:27:31.90ID:hW1FItRq
������Ȃ��ӂ肵�Ė{���͕������Ă��ł���H
478�P�R�Q�l�ڂ̑f������
2018/08/30(��) 16:35:45.84ID:VKTQzTzb �˂�
�P�ȊO�ɕ�������
a=��[k=1,r](1+pk+�cpk^qk)
a'=��[k=1,r-1](1+pk+�cpk^qk)
�Ȃ�a'=a/(1+pr+�cpr^qr)�Ȃ�Ȃ��́H
a'=a/pr^qr�Ȃ�Ăǂ�����o�Ă���́H
�P�ȊO�ɕ�������
a=��[k=1,r](1+pk+�cpk^qk)
a'=��[k=1,r-1](1+pk+�cpk^qk)
�Ȃ�a'=a/(1+pr+�cpr^qr)�Ȃ�Ȃ��́H
a'=a/pr^qr�Ȃ�Ăǂ�����o�Ă���́H
2018/08/30(��) 16:40:40.07ID:GzaOMu/G
>>475
����ӂ�����Bb'�ɑΉ�����a'�������Ȃ�́B������Ⴄ�ƌ���ꂽ��
�����̉��莩�̂��Ԉ���Ă���Ƃ������ƂɂȂ�
����Ș_�@������܂���B
�����ł��B
��a = ��(1+pr+�cpr^qr)�c(A)
����
��a �e = ��[k��r](1+pr+�cpr^qr)�c(B)
�����o����Ȃ��Ɩ�莩�̂����������ȂǂƂ����_�@�������Ă�������wiki�̃y�[�W�ɏ����Ă������H
�Ȃ��ł���H
�N�͎����̘_�������ɔF�߂�ꂽ����ł���H
���R Public �Ș_���ł� Public �ɔF�߂�ꂽ���_�݂̂��g�����_�������F�߂Ă��炦�܂���B
���݂̏�ԂŘ_�����ɓ��e���Ă������w�E���ď��������̗v������邾���ł���B
�g���Ֆ}���h�A�h���ቻ�h �̎g�������̂͂������ĊȒP�B
(A)�o�����ؖ��̉���ƌ��_�ɏo�Ă��铯��̕��������낢��ƍD���ȕ����ɒu�������邾���ł��B
�����g�ݍ��킹��(B)�o���ĉ������B
���ꂪ�o���Ȃ���Ήi���� Public �ɔF�߂�ꂤ��_���ɂ͂Ȃ肦�܂����H
Public �ɂ͔F�߂��ĂȂ����_�g���Ă����B
����ł����́H
����ӂ�����Bb'�ɑΉ�����a'�������Ȃ�́B������Ⴄ�ƌ���ꂽ��
�����̉��莩�̂��Ԉ���Ă���Ƃ������ƂɂȂ�
����Ș_�@������܂���B
�����ł��B
��a = ��(1+pr+�cpr^qr)�c(A)
����
��a �e = ��[k��r](1+pr+�cpr^qr)�c(B)
�����o����Ȃ��Ɩ�莩�̂����������ȂǂƂ����_�@�������Ă�������wiki�̃y�[�W�ɏ����Ă������H
�Ȃ��ł���H
�N�͎����̘_�������ɔF�߂�ꂽ����ł���H
���R Public �Ș_���ł� Public �ɔF�߂�ꂽ���_�݂̂��g�����_�������F�߂Ă��炦�܂���B
���݂̏�ԂŘ_�����ɓ��e���Ă������w�E���ď��������̗v������邾���ł���B
�g���Ֆ}���h�A�h���ቻ�h �̎g�������̂͂������ĊȒP�B
(A)�o�����ؖ��̉���ƌ��_�ɏo�Ă��铯��̕��������낢��ƍD���ȕ����ɒu�������邾���ł��B
�����g�ݍ��킹��(B)�o���ĉ������B
���ꂪ�o���Ȃ���Ήi���� Public �ɔF�߂�ꂤ��_���ɂ͂Ȃ肦�܂����H
Public �ɂ͔F�߂��ĂȂ����_�g���Ă����B
����ł����́H
>>479
������A��Έ�Ή��W������ƌ����Ă���Br��r-1�̕ϊ��ł���͑�ӂ��B
���̂����܂ŁA�Ԉ�����咣���J��Ԃ��̂�������Ȃ��B
b'��k��1����r-1�܂ł�pk^qk�̐ςł������ɑΉ�����a'��1����r-1�܂ł�
1+pk+�c+pk^qk�̐ςɂȂ�͓̂��R�ł����B
������A��Έ�Ή��W������ƌ����Ă���Br��r-1�̕ϊ��ł���͑�ӂ��B
���̂����܂ŁA�Ԉ�����咣���J��Ԃ��̂�������Ȃ��B
b'��k��1����r-1�܂ł�pk^qk�̐ςł������ɑΉ�����a'��1����r-1�܂ł�
1+pk+�c+pk^qk�̐ςɂȂ�͓̂��R�ł����B
2018/08/30(��) 16:52:26.00ID:GzaOMu/G
>>478
a�Ab�Ac �ɂ��Đ������Ă�W���ȂA�z�قǂ���܂��B
����Ă��̂������������ �g�Ή�����h a�f�Ab�f�Ac�f �����ɂ���̂��̔C�Ӑ����A�z�قǂ����ł���B
�Ȃ̂ł��������_�Ƃ��Ę_���ł�
��b���ɑΉ����� a ��a���Ƃ����
�Ƃ����Ȃ��̂ŁA�z���g�͂������̎��_�ŃA�E�g�Ȃ�ł���B
�ł������炭���̘H���ł̕s����������Ă�����>>1�ɂ͗����ł��Ȃ��̂ł����������ŏ���ɑI��ł���
a�f = a/pr^qr�Ab = b/pr^qr�Ac = c/pr^qr
��I��ł��B
>>462�ǂނƔނƂ��Ă����̑I���Ɉ٘_�͂Ȃ��悤�Ȃ̂ŁB
a�Ab�Ac �ɂ��Đ������Ă�W���ȂA�z�قǂ���܂��B
����Ă��̂������������ �g�Ή�����h a�f�Ab�f�Ac�f �����ɂ���̂��̔C�Ӑ����A�z�قǂ����ł���B
�Ȃ̂ł��������_�Ƃ��Ę_���ł�
��b���ɑΉ����� a ��a���Ƃ����
�Ƃ����Ȃ��̂ŁA�z���g�͂������̎��_�ŃA�E�g�Ȃ�ł���B
�ł������炭���̘H���ł̕s����������Ă�����>>1�ɂ͗����ł��Ȃ��̂ł����������ŏ���ɑI��ł���
a�f = a/pr^qr�Ab = b/pr^qr�Ac = c/pr^qr
��I��ł��B
>>462�ǂނƔނƂ��Ă����̑I���Ɉ٘_�͂Ȃ��悤�Ȃ̂ŁB
2018/08/30(��) 16:54:28.58ID:GzaOMu/G
>>480
�Ԉ�����咣�Ƃ����Ă�����Ș_�@���w�ɂ͂Ȃ�����B
���Ⴀ���̘_�@��F�߂ďЉ�Ă��镶���Ȃ�wiki�y�[�W�Ȃ�グ�ĉ������B
�����z���g�ɂ��̘_�@�� Public �ɔF�߂��Ă�Ȃ�Љ�y�[�W�Ȃ�Ȃ�Ȃ茩����n�Y����ˁH
�Ԉ�����咣�Ƃ����Ă�����Ș_�@���w�ɂ͂Ȃ�����B
���Ⴀ���̘_�@��F�߂ďЉ�Ă��镶���Ȃ�wiki�y�[�W�Ȃ�グ�ĉ������B
�����z���g�ɂ��̘_�@�� Public �ɔF�߂��Ă�Ȃ�Љ�y�[�W�Ȃ�Ȃ�Ȃ茩����n�Y����ˁH
>>482
������a��b�ɂ͉��x����Έ�Ή������邩��b'����܂�Έ�ӂ�a'�����܂�B�������ꂾ��
�������Ȃ��̂͂��̖���[���l���Ă��Ȃ������B
������a��b�ɂ͉��x����Έ�Ή������邩��b'����܂�Έ�ӂ�a'�����܂�B�������ꂾ��
�������Ȃ��̂͂��̖���[���l���Ă��Ȃ������B
2018/08/30(��) 17:03:45.82ID:GzaOMu/G
>>483
����ς�킩���ĂȂ��ˁB
�ꉞ�������Ă݂�B
����������Ƃ���a�Ab�Ac�Ap�Ar�ɂ��Đ������Ă���W���ȂA�z�قǂ���B
���������� �g�Ή����� a�f�Ab�f�Ac�f ���ǂ̎��𗘗p���đΉ�������̂��H�h �͖{���_�����Ŗ������Ȃ��Ƃ��߁B
�������N�̘_���ł�
��b���ɑΉ����� a ��a���Ƃ����
����n�܂��Ăǂ̎��𗘗p����a�f���`����̂����������ɋc�_���n�߂Ă�B
�������̎��_�Ő��w�̘_���̑̂��Ȃ��Ă��Ȃ��B
������̌��
a�� = ∏ [k��r] (1 + pk + ⋯ + pk^qk)
��
a�� = a/pr^qr
���o�Ă��邯�lj��̕�����`���Ƃ͌N�͈ꌾ���f���ĂȂ���ˁH
���̕��͂Ȃ��ł���H
�����玄�͉��̕����`�Ƃ��ēǂ����B
����Ȑ����ǂݎ�ɂ����Ȃ��Ɠǂ߂Ȃ����͂Ȃ��̎��_�Ő��w�̘_���ł͂Ȃ��B
����ς�킩���ĂȂ��ˁB
�ꉞ�������Ă݂�B
����������Ƃ���a�Ab�Ac�Ap�Ar�ɂ��Đ������Ă���W���ȂA�z�قǂ���B
���������� �g�Ή����� a�f�Ab�f�Ac�f ���ǂ̎��𗘗p���đΉ�������̂��H�h �͖{���_�����Ŗ������Ȃ��Ƃ��߁B
�������N�̘_���ł�
��b���ɑΉ����� a ��a���Ƃ����
����n�܂��Ăǂ̎��𗘗p����a�f���`����̂����������ɋc�_���n�߂Ă�B
�������̎��_�Ő��w�̘_���̑̂��Ȃ��Ă��Ȃ��B
������̌��
a�� = ∏ [k��r] (1 + pk + ⋯ + pk^qk)
��
a�� = a/pr^qr
���o�Ă��邯�lj��̕�����`���Ƃ͌N�͈ꌾ���f���ĂȂ���ˁH
���̕��͂Ȃ��ł���H
�����玄�͉��̕����`�Ƃ��ēǂ����B
����Ȑ����ǂݎ�ɂ����Ȃ��Ɠǂ߂Ȃ����͂Ȃ��̎��_�Ő��w�̘_���ł͂Ȃ��B
2018/08/30(��) 17:10:08.45ID:GzaOMu/G
>>484
��������a��b�ɂ͉��x����Έ�Ή������邩��b'����܂�Έ�ӂ�a'�����܂�B�������ꂾ��
�����炻�̈�Έ�Ή���_���ɏ����ĂȂ��ł���H
������
{a = A(y)}�A{b = B(y)}
�ɂ͈�Έ�Ή��ɋ߂����̂͂���B
���A�N�͂��̑Ή����K���ł��Ȃ��͈͂ł̋c�_�����Ă��ˁH
�܂肻�̈�Έ�Ή��͎g���Ȃ��B
���Ⴀ�A���̈�Έ�Ή����{����`���Ȃ��Ƃ����Ȃ��B
�ł��N�ł��Ȃ��ł���H��Έ�Ή��Ȃ�Đl���Œ�`�������Ȃ���ˁH
�����炻�̕s���ɂ͖ڂ��ނ�����B
�ł���Ȃ����Č����ĉ������B
�L�`���Ɛ��w�̘_���Ƃ��Ēʗp���郌�x���̕��͂ŁB
��������a��b�ɂ͉��x����Έ�Ή������邩��b'����܂�Έ�ӂ�a'�����܂�B�������ꂾ��
�����炻�̈�Έ�Ή���_���ɏ����ĂȂ��ł���H
������
{a = A(y)}�A{b = B(y)}
�ɂ͈�Έ�Ή��ɋ߂����̂͂���B
���A�N�͂��̑Ή����K���ł��Ȃ��͈͂ł̋c�_�����Ă��ˁH
�܂肻�̈�Έ�Ή��͎g���Ȃ��B
���Ⴀ�A���̈�Έ�Ή����{����`���Ȃ��Ƃ����Ȃ��B
�ł��N�ł��Ȃ��ł���H��Έ�Ή��Ȃ�Đl���Œ�`�������Ȃ���ˁH
�����炻�̕s���ɂ͖ڂ��ނ�����B
�ł���Ȃ����Č����ĉ������B
�L�`���Ɛ��w�̘_���Ƃ��Ēʗp���郌�x���̕��͂ŁB
2018/08/30(��) 17:21:58.83ID:XOoReTTx
�����̂��߂̃L�[���[�h�͑S�����w�̌��t�Ō����Ȃ��Ƃ����Ȃ��̂��B�B�B
������₷�����{��Ő������Ȃ���A���̓��{��ƑΉ����鐔�����������薾�����Ȃ��Ƃ����Ȃ��Ȃ�āA��ς���
������₷�����{��Ő������Ȃ���A���̓��{��ƑΉ����鐔�����������薾�����Ȃ��Ƃ����Ȃ��Ȃ�āA��ς���
2018/08/30(��) 17:25:01.48ID:XOoReTTx
��Έ�𐔎��Ƃ��Ė����������̓I�ɂǂ�Ȏ��ɂȂ�́H
���ꂳ��������Εʂɂ�������Ȃ�
���ꂳ��������Εʂɂ�������Ȃ�
2018/08/30(��) 17:30:10.72ID:0wdHkoKw
�u����Ȃ��v�u���R�v�œ����āA�����Ƃ����ؖ��͌��ǂł��Ȃ��̂�
2018/08/30(��) 17:33:24.68ID:GzaOMu/G
>>488
��Έ�Ή��̒�`�͂�����B
�������������͌��X�ڂ��ނ��Ƃ��Ă����悤�Ǝv���Ă��|�C���g������ˁB
�[����[
y �͊�̊��S���B
p �� multiplitity n ����̊��S���B
pk (k=1�`r) �� p �ƈقȂ� multiplitcity qk > 0 �� y �̑f���q�B
a �e = 2y/(1+p+ �c + p^n)/pr^qr
����
�[���_�[
a �e = ��[k �� r] (1+ pk + �c + pk^qk)
�o�����������B
�g�Ή����Ă邩��h �Ƃ����킯�̂킩��_���ł͂Ȃ��B
���w�̐��E�ŔF�߂�ꂽ�����Ɛ��_���݂̂�p���āB
�ł�����Ă����Ă���ˁH
��Έ�Ή��̒�`�͂�����B
�������������͌��X�ڂ��ނ��Ƃ��Ă����悤�Ǝv���Ă��|�C���g������ˁB
�[����[
y �͊�̊��S���B
p �� multiplitity n ����̊��S���B
pk (k=1�`r) �� p �ƈقȂ� multiplitcity qk > 0 �� y �̑f���q�B
a �e = 2y/(1+p+ �c + p^n)/pr^qr
����
�[���_�[
a �e = ��[k �� r] (1+ pk + �c + pk^qk)
�o�����������B
�g�Ή����Ă邩��h �Ƃ����킯�̂킩��_���ł͂Ȃ��B
���w�̐��E�ŔF�߂�ꂽ�����Ɛ��_���݂̂�p���āB
�ł�����Ă����Ă���ˁH
492�P�R�Q�l�ڂ̑f������
2018/08/30(��) 17:34:49.78ID:CCHvgGa7 �ؖ����Ă̂͘_���̓��𖾂炩�ɂ�����̂�����
�ua�ɑΉ�����a'�v�ȂǂƂ��������āA�ǂސl�ɂ���ĉ��ʂ���̕ʂ̉��߂��ł��A
�����߂̈Ⴂ�ɂ���Đ^�U���������悤�ȏ�Ԃɂ��Ă������Ƃ��u���炩�ɂ����v�Ƃ͌����Ȃ�
���Ƃ��Έȉ��̂R�̎��͓����ɂ͐��藧���Ȃ��̂�����A�ǂꂪ�������̂��������ׂ�
a=��[k=1,r](1+pk+�cpk^qk)
a'=��[k=1,r-1](1+pk+�cpk^qk)
a'=a/pr^qr
�������邾���Ȃ̂ɂȂ������[�܂�̂��Ӗ����킩��Ȃ�
�ua�ɑΉ�����a'�v�ȂǂƂ��������āA�ǂސl�ɂ���ĉ��ʂ���̕ʂ̉��߂��ł��A
�����߂̈Ⴂ�ɂ���Đ^�U���������悤�ȏ�Ԃɂ��Ă������Ƃ��u���炩�ɂ����v�Ƃ͌����Ȃ�
���Ƃ��Έȉ��̂R�̎��͓����ɂ͐��藧���Ȃ��̂�����A�ǂꂪ�������̂��������ׂ�
a=��[k=1,r](1+pk+�cpk^qk)
a'=��[k=1,r-1](1+pk+�cpk^qk)
a'=a/pr^qr
�������邾���Ȃ̂ɂȂ������[�܂�̂��Ӗ����킩��Ȃ�
2018/08/30(��) 17:35:46.20ID:GzaOMu/G
>>491
����
✕�Fp �� multiplitity n �����y�̊��S���B
���Fp �� multiplitity n �����y�̑f���q�B
�ؖ����Č����ĉ������B
���w�̐��E�� Public �ɔF�߂�ꂽ���_���݂̂�p���āB
�_�����ɍڂ������Ȃ瓖�R�v��������H
����
✕�Fp �� multiplitity n �����y�̊��S���B
���Fp �� multiplitity n �����y�̑f���q�B
�ؖ����Č����ĉ������B
���w�̐��E�� Public �ɔF�߂�ꂽ���_���݂̂�p���āB
�_�����ɍڂ������Ȃ瓖�R�v��������H
494�P�R�Q�l�ڂ̑f������
2018/08/30(��) 17:42:43.32ID:wrnsIhYA �Q�{�Q���Q�~�Q���Q^�Q�͐�������
�P�̘_�@�ɂ��ƁA�Q���R�ɕς��Ă����Ȃ���������͂�������A
�R�{�R���R�~�R���R^�R�͂����������
����ȊȒP��(�ȉ���)
�P�̘_�@�ɂ��ƁA�Q���R�ɕς��Ă����Ȃ���������͂�������A
�R�{�R���R�~�R���R^�R�͂����������
����ȊȒP��(�ȉ���)
>>489
���x����r��r-1�̕ϊ������Č����Ă���B
���̂悤�ȊȒP�ȓ��e�ɏؖ����ւ���������Ȃ��ł���B�����ɕ����t���Ă���l�ԒB���ӂ����Ă���
����[�I�ɕ\���Ă���B
b=��[k=1,r]pk^qk��b'=��[k=1,-1r]pk^qk
a=��[k=1,r](1+pk+�c+pk^qk)��a'=��[k=1,-1r](1+pk+�c+pk^qk)
�������ꂾ���B�����������ƂȂ����e�ɖ��𗝉����Ă��Ȃ����������悤�Ƃ����Ȃ��l�Ԃ��A�ςȃi���N�Z
�������B
�����O�����̂ł��̌��͏I���B�����ł��Ȃ��ł��ؖ��ł��Ȃ��ł����郌�X�������܂ł����Ă��B
���x����r��r-1�̕ϊ������Č����Ă���B
���̂悤�ȊȒP�ȓ��e�ɏؖ����ւ���������Ȃ��ł���B�����ɕ����t���Ă���l�ԒB���ӂ����Ă���
����[�I�ɕ\���Ă���B
b=��[k=1,r]pk^qk��b'=��[k=1,-1r]pk^qk
a=��[k=1,r](1+pk+�c+pk^qk)��a'=��[k=1,-1r](1+pk+�c+pk^qk)
�������ꂾ���B�����������ƂȂ����e�ɖ��𗝉����Ă��Ȃ����������悤�Ƃ����Ȃ��l�Ԃ��A�ςȃi���N�Z
�������B
�����O�����̂ł��̌��͏I���B�����ł��Ȃ��ł��ؖ��ł��Ȃ��ł����郌�X�������܂ł����Ă��B
2018/08/30(��) 17:52:19.05ID:ZYgDwf+s
���ꂾ����P�́A���̃X���ȊO�ł͂ǂ��ɂ���������Ă��炦�Ȃ��B
���؎���̗��_�͎̂ĂȂ����Ⴂ���Ȃ��̂ɁB
���؎���̗��_�͎̂ĂȂ����Ⴂ���Ȃ��̂ɁB
2018/08/30(��) 17:53:13.44ID:XOoReTTx
>>495
�ςȓ�ȂɈ�X�Ή�����̂���ς��낤���疳����������̂�
�ςȓ�ȂɈ�X�Ή�����̂���ς��낤���疳����������̂�
498�P�R�Q�l�ڂ̑f������
2018/08/30(��) 17:54:32.66ID:6HG9uY0b >>495
a'=a/pr^qr�͂ǂ������Ⴂ�H
a'=a/pr^qr�͂ǂ������Ⴂ�H
2018/08/30(��) 18:06:29.15ID:XOoReTTx
���Ă��ƁH
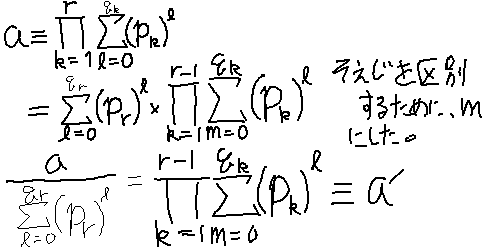
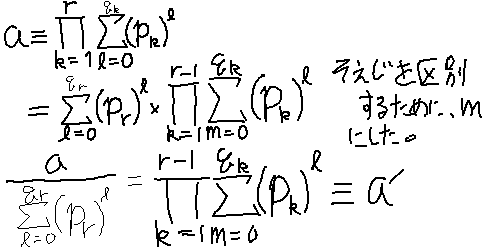
2018/08/30(��) 18:10:16.35ID:GzaOMu/G
�܂��Ō�͂����Ȃ�Ƃ�����Ɨ\�z���Ă��������ς芴�����Ȃ����ǂˁB
�Ԉ���Ă�Ƃ������C������Ȃ�킩��܂ŋ����Ă����悤���Ƃ��v�������ǁA�{�l�������C�Ȃ��Ȃ炵�႟�Ȃ��ˁB
�Ԉ���Ă�Ƃ������C������Ȃ�킩��܂ŋ����Ă����悤���Ƃ��v�������ǁA�{�l�������C�Ȃ��Ȃ炵�႟�Ȃ��ˁB
2018/08/30(��) 18:10:16.52ID:ZYgDwf+s
�G�ŕ`���Ȃ�����������ˁH
>>498
���D�̗��ӂ�pr^qr�Ŋ���
���D�̗��ӂ�pr^qr�Ŋ���
503�P�R�Q�l�ڂ̑f������
2018/08/30(��) 18:40:41.11ID:6HG9uY0b >>502
���D���āuap-2bp+2b=c�v�̂��Ƃł���B
�����pr^qr�Ŋ����Ă��Aa'=a/pr^qr�����Ƃɂ͂Ȃ���B
�P�ɁAa'=a/pr^qr�Ƃ������̒�`���𗘗p���āA
a'�����̒��ɏo�Ă���悤�Ȍ`�Ɏ��D��ό`������Ă�������Ȃ��́B
���ɂ���Ă�̂́ua'=a/pr^qr�v�Ƃ�����`�����A
�ua'=��[k=1,-1r](1+pk+�c+pk^qk)�v���ǂ�����������̂��Ƃ����b�ł���B
���D���āuap-2bp+2b=c�v�̂��Ƃł���B
�����pr^qr�Ŋ����Ă��Aa'=a/pr^qr�����Ƃɂ͂Ȃ���B
�P�ɁAa'=a/pr^qr�Ƃ������̒�`���𗘗p���āA
a'�����̒��ɏo�Ă���悤�Ȍ`�Ɏ��D��ό`������Ă�������Ȃ��́B
���ɂ���Ă�̂́ua'=a/pr^qr�v�Ƃ�����`�����A
�ua'=��[k=1,-1r](1+pk+�c+pk^qk)�v���ǂ�����������̂��Ƃ����b�ł���B
2018/08/30(��) 18:52:54.86ID:PoW5j6hT
2018/08/30(��) 19:04:52.41ID:Bm1VCJbE
>>504
a�̒�`��r��r-1�ɒu�����������̂�a'�Ȃ�Ȃ��̂��H
a�̒�`��r��r-1�ɒu�����������̂�a'�Ȃ�Ȃ��̂��H
506�P�R�Q�l�ڂ̑f������
2018/08/30(��) 19:08:25.41ID:6HG9uY0b2018/08/30(��) 19:12:36.71ID:oaEZkqRk
>>1�̐��w�͎����Ȃ��Ƃ͏ؖ��ł��Ȃ��Ƃ������E�̐��w������
2018/08/30(��) 19:17:44.69ID:EObwglNy
�Ƃ肠����(pr^qr)�Ŋ����āA�킩��̂�
a'=(��[k=1,r](1+pk+�c+pk^qk))/(pr^qr)
�����܂ŁB
a'=(��[k=1,r-1](1+pk+�c+pk^qk))
�ɂǂ�����Ă��ǂ蒅���̂��ȁB
a'=(��[k=1,r](1+pk+�c+pk^qk))/(pr^qr)
�����܂ŁB
a'=(��[k=1,r-1](1+pk+�c+pk^qk))
�ɂǂ�����Ă��ǂ蒅���̂��ȁB
509�P�R�Q�l�ڂ̑f������
2018/08/30(��) 19:22:32.24ID:6HG9uY0b >>508
�ua'=(��[k=1,r](1+pk+�c+pk^qk))/(pr^qr)�v�������Ȃ̂͂킩�邯�ǁA
�ua'=(��[k=1,r-1](1+pk+�c+pk^qk))�v���������Ă̂́A���ʂ͂킩����ȁB
�ua'=(��[k=1,r](1+pk+�c+pk^qk))/(pr^qr)�v�������Ȃ̂͂킩�邯�ǁA
�ua'=(��[k=1,r-1](1+pk+�c+pk^qk))�v���������Ă̂́A���ʂ͂킩����ȁB
2018/08/31(��) 01:17:11.12ID:UfhWo0OL
�Ƃ肠�����Ȃ��p�̒l�����������玩���Ƃ����Ă邩�̗��R�͂킩�����C������B
�O��̎w�E�� p = 2pr -1 �Ō��������Ƃ�ʂ� pk �ł����ɂ� p�f = 2pk -1 �Ɏ��ւ��Ȃ��Ƃ��߂ƌ���ꂽ�̂� p �����ς��Ȃ��Ⴂ���Ǝv������ł�̂�������Ȃ��B
�������� a = 2y/(1+p+�c+p^n)�Ƃ������Ƃ� a = ��(1+pk+�c+pk^qk) �o����̂� y �����S���������Ă�����
y �� y�f = y/pr^qr �Ɏ�ւ� p �͂��̂܂܂ɂ����Ƃ���Ō��� y�f �����S���łȂ�������� p �����̂܂܂ł� a�f = ��[pk��pr](1+pk+�c+pk^qk) �Ȃ�ē��o�ł���͂��Ȃ��̂ɁB
�Ȃ�� �up ���ς�邩��_���v�Ƃ������t���up�����ς��Ȃ���Ηǂ��v�ɕϊ�����Ă��܂��̂��͈ȑO�䂾���ǁB
�O��̎w�E�� p = 2pr -1 �Ō��������Ƃ�ʂ� pk �ł����ɂ� p�f = 2pk -1 �Ɏ��ւ��Ȃ��Ƃ��߂ƌ���ꂽ�̂� p �����ς��Ȃ��Ⴂ���Ǝv������ł�̂�������Ȃ��B
�������� a = 2y/(1+p+�c+p^n)�Ƃ������Ƃ� a = ��(1+pk+�c+pk^qk) �o����̂� y �����S���������Ă�����
y �� y�f = y/pr^qr �Ɏ�ւ� p �͂��̂܂܂ɂ����Ƃ���Ō��� y�f �����S���łȂ�������� p �����̂܂܂ł� a�f = ��[pk��pr](1+pk+�c+pk^qk) �Ȃ�ē��o�ł���͂��Ȃ��̂ɁB
�Ȃ�� �up ���ς�邩��_���v�Ƃ������t���up�����ς��Ȃ���Ηǂ��v�ɕϊ�����Ă��܂��̂��͈ȑO�䂾���ǁB
511�P�R�Q�l�ڂ̑f������
2018/08/31(��) 02:54:03.71ID:bW2cuetU �Ƃ��������A�����Ƃ����㐔����낤��
��f��pk�ɂ���
(��[k=1,r](1+pk+�c+pk^qk))/(pr^qr)��
(��[k=1,r-1](1+pk+�c+pk^qk))���������̂������Ȃǂ�
����L�����낭�ɗ������Ȃ��_�����P���W�J����Ȃ�A�܂Ƃ��ȕ]���͂ł��Ȃ�
���̓_���P�����߂Ȃ��Ȃ�A�������肷�邾�����ʂ�����
��f��pk�ɂ���
(��[k=1,r](1+pk+�c+pk^qk))/(pr^qr)��
(��[k=1,r-1](1+pk+�c+pk^qk))���������̂������Ȃǂ�
����L�����낭�ɗ������Ȃ��_�����P���W�J����Ȃ�A�܂Ƃ��ȕ]���͂ł��Ȃ�
���̓_���P�����߂Ȃ��Ȃ�A�������肷�邾�����ʂ�����
2018/08/31(��) 05:31:45.22ID:Xw3EuLV1
�P�͒��w�̎��S�R�����Ȃ���������ˁB
����œ��w�����̂��鍂�Z�͑S���s���i�ɂȂ�����������B
����œ��w�����̂��鍂�Z�͑S���s���i�ɂȂ�����������B
2018/08/31(��) 08:31:08.71ID:JM/zdFU4
�悭�悭�l������
a�f = ��[k��r](1+pk+�c+pk^qk)�Ab�f = ��[k��r]pk^qk
�����藧�Ȃ猳��
(1+p+�c+p^n)��(1+pk+�c+pk^qk) = 2p^n��pk^qk
�ƍ��킹����y�f = y/pr^qr�����S���ɂȂ���B
���������ꂪ�C�ӂ�r�Ő��藧�ƌ����Ă邩�炩��>>1��p7�̎咣��
�uy����̊��S���Apk��multiplicity qk�������̔C�ӂ̑f���q�Ƃ����y/pk^qk����̊��S���B�v
�Ƃ����Ă�ɓ������B
�ŁA���̗��R��
�up���ς��Ȃ��̂ő�ӂ�薾�炩�B�v
�������ȁB
�ŋ��̃��W�b�N�ł��ȁB
a�f = ��[k��r](1+pk+�c+pk^qk)�Ab�f = ��[k��r]pk^qk
�����藧�Ȃ猳��
(1+p+�c+p^n)��(1+pk+�c+pk^qk) = 2p^n��pk^qk
�ƍ��킹����y�f = y/pr^qr�����S���ɂȂ���B
���������ꂪ�C�ӂ�r�Ő��藧�ƌ����Ă邩�炩��>>1��p7�̎咣��
�uy����̊��S���Apk��multiplicity qk�������̔C�ӂ̑f���q�Ƃ����y/pk^qk����̊��S���B�v
�Ƃ����Ă�ɓ������B
�ŁA���̗��R��
�up���ς��Ȃ��̂ő�ӂ�薾�炩�B�v
�������ȁB
�ŋ��̃��W�b�N�ł��ȁB
2018/08/31(��) 09:52:24.11ID:9bgKG8tA
�搶�u���،N�̏ؖ��́A�����ŊԈ���Ă܂��B�搶�̐�����������܂����H�v
������i������I�����ς蕪����Ȃ��I�K�E�Z�œ����邼�I�j
������u���̂悤�ȊȒP�ȓ��e�ɏؖ����ւ���������Ȃ��ł���I�����ł��I�v
������i������I�����ς蕪����Ȃ��I�K�E�Z�œ����邼�I�j
������u���̂悤�ȊȒP�ȓ��e�ɏؖ����ւ���������Ȃ��ł���I�����ł��I�v
515�P�R�Q�l�ڂ̑f������
2018/08/31(��) 11:00:54.46ID:SF3nRQyV >>513
�ŋ����W�b�N���g���Ƃ����Ȃ邩
b=1^1�ɑ��āAa=1+1^1�Ƃ���ƁAa=2b�ł���
a'=2b'�ƂȂ�C�ӂ�a',b'�ƁA�C�ӂ�pk,qk�ɂ��āA
a'=a/pr^qr, b'=b/pr^qr�Ƃ����a=2b�ł���
�ȏ���A
a=��[k=1,r](1+pk+�c+pk^qk)�Ab=��[k=1,r]pk^qk�ƂȂ�C�ӂ�a,b�ɂ��āA
a=2b�ł��邱�Ƃ������ꂽ�B
����a�͖��炩��b�̖a�ł���B�܂��A�S�Ă̐����̓�[k=1,r]pk^qk�̌`�ɏ����邱�Ƃ���A
���ׂĂ̎��R���͊��S���ł���B
���ꂪ�ŋ����W�b�N�̋A�����B�܂��ɍŋ�
�ŋ����W�b�N���g���Ƃ����Ȃ邩
b=1^1�ɑ��āAa=1+1^1�Ƃ���ƁAa=2b�ł���
a'=2b'�ƂȂ�C�ӂ�a',b'�ƁA�C�ӂ�pk,qk�ɂ��āA
a'=a/pr^qr, b'=b/pr^qr�Ƃ����a=2b�ł���
�ȏ���A
a=��[k=1,r](1+pk+�c+pk^qk)�Ab=��[k=1,r]pk^qk�ƂȂ�C�ӂ�a,b�ɂ��āA
a=2b�ł��邱�Ƃ������ꂽ�B
����a�͖��炩��b�̖a�ł���B�܂��A�S�Ă̐����̓�[k=1,r]pk^qk�̌`�ɏ����邱�Ƃ���A
���ׂĂ̎��R���͊��S���ł���B
���ꂪ�ŋ����W�b�N�̋A�����B�܂��ɍŋ�
2018/08/31(��) 13:49:31.44ID:DTNXO3+z
������u���l�ŋ����ȁB�v
517�w�p
2018/08/31(��) 14:11:53.97ID:oNPUVpgQ ���S�ɐ����Ǝv���Ɗ����������낤�ȁB
2018/08/31(��) 16:36:57.38ID:qB6pPk6g
����ł��B
y����̊��S���Ap�� multiplicity ��� y �̑f���q�An ������ multiplicity�Apk 8(k:1�`r)�𑼂̑f���q�̑S�́Aqr������ multiplicity �Ƃ��܂��B�i�_���Ɠ����ݒ�B�j
a=2y/(1+p+�c+p^n)�Ab=y/p^n�Ac=2y/(1+p+�c+p^n)/p^n
�Ƃ����܂��B(�_���Ɠ����ݒ�B)
k��C�ӂɂƂ�
a�f=a/pk^qk�Ab�f=b/pl^qk�Ac�f=c/pk^qk
�Ƃ����܂��B(�_���Ɠ����ݒ�B)
Q1) (p+1)/2 = pr �̂Ƃ� A�f = ��[k��r](1+p+�c+pk)�͐������܂����H�_���ł͐�������Ɠǂ߂܂��B
Q2) (p+1)/2 = pr �̂Ƃ� r �ȊO�� s �ł� A�f = ��[k��s](1+p+�c+pk)�͐������܂����H�_���ł͐�������Ɠǂ߂܂��B
Q3) (p+1)/2 = pr �ƂȂ� pr ���Ȃ��Ƃ��A(�_���� II �̃P�[�X) A�f = ��[k��s](1+p+�c+pk)�͐������܂����H�������Ȃ��Ƃ���ƂȂ��ł����H
y����̊��S���Ap�� multiplicity ��� y �̑f���q�An ������ multiplicity�Apk 8(k:1�`r)�𑼂̑f���q�̑S�́Aqr������ multiplicity �Ƃ��܂��B�i�_���Ɠ����ݒ�B�j
a=2y/(1+p+�c+p^n)�Ab=y/p^n�Ac=2y/(1+p+�c+p^n)/p^n
�Ƃ����܂��B(�_���Ɠ����ݒ�B)
k��C�ӂɂƂ�
a�f=a/pk^qk�Ab�f=b/pl^qk�Ac�f=c/pk^qk
�Ƃ����܂��B(�_���Ɠ����ݒ�B)
Q1) (p+1)/2 = pr �̂Ƃ� A�f = ��[k��r](1+p+�c+pk)�͐������܂����H�_���ł͐�������Ɠǂ߂܂��B
Q2) (p+1)/2 = pr �̂Ƃ� r �ȊO�� s �ł� A�f = ��[k��s](1+p+�c+pk)�͐������܂����H�_���ł͐�������Ɠǂ߂܂��B
Q3) (p+1)/2 = pr �ƂȂ� pr ���Ȃ��Ƃ��A(�_���� II �̃P�[�X) A�f = ��[k��s](1+p+�c+pk)�͐������܂����H�������Ȃ��Ƃ���ƂȂ��ł����H
2018/08/31(��) 16:42:15.82ID:qB6pPk6g
�����܂���B�܂������܂����B
Q1) (p+1)/2 = pr �̂Ƃ� A�f = ��[k��r](1+p+�c+pk^qk)�͐������܂����H�_���ł͐�������Ɠǂ߂܂��B
Q2) (p+1)/2 = pr �̂Ƃ� r �ȊO�� s �ł� A�f = ��[k��s](1+p+�c+pk^qk)�͐������܂����H�_���ł͐�������Ɠǂ߂܂��B
Q3) (p+1)/2 = pr �ƂȂ� pr ���Ȃ��Ƃ��A(�_���� II �̃P�[�X) A�f = ��[k��s](1+p+�c+pk^qk)�͐������܂����H�������Ȃ��Ƃ���ƂȂ��ł����H
Q1) (p+1)/2 = pr �̂Ƃ� A�f = ��[k��r](1+p+�c+pk^qk)�͐������܂����H�_���ł͐�������Ɠǂ߂܂��B
Q2) (p+1)/2 = pr �̂Ƃ� r �ȊO�� s �ł� A�f = ��[k��s](1+p+�c+pk^qk)�͐������܂����H�_���ł͐�������Ɠǂ߂܂��B
Q3) (p+1)/2 = pr �ƂȂ� pr ���Ȃ��Ƃ��A(�_���� II �̃P�[�X) A�f = ��[k��s](1+p+�c+pk^qk)�͐������܂����H�������Ȃ��Ƃ���ƂȂ��ł����H
521�w�p
2018/08/31(��) 17:10:11.43ID:oNPUVpgQ ������萬�����邩�A�������Ȃ����ŕ���邩�Ƃ����̂́A����
�����߂邱�Ƃ��낤���A�m�����v�Ȃ͉��x������������Ă���
���Ȃ�i���̂��Ƃ���ۂ��������B
�����߂邱�Ƃ��낤���A�m�����v�Ȃ͉��x������������Ă���
���Ȃ�i���̂��Ƃ���ۂ��������B
522�w�p
2018/08/31(��) 17:11:04.48ID:oNPUVpgQ ���Z�����Ȃ��߂ł������Ƃ����ƁA�l�ԈȊO�Ȃ琥����ł��A�l�ԂȂ�
���Ԃ�҂��ĂƂ������Ƃ��ӎ����Ă��邱�Ƃ��悢���낤�B
���Ԃ�҂��ĂƂ������Ƃ��ӎ����Ă��邱�Ƃ��悢���낤�B
523�w�p
2018/08/31(��) 17:12:30.83ID:oNPUVpgQ �n���Ⴄ���̂͘_�]���Ȃ���v�l���Ȃ��炱�Ȃ������Ȃ����ǁA�f���ɏ悹����̂�
�l�̎�ɓn���Ă����|���⎊���Ȃ�Ă������̂��ӎ������Ȃ��B
�l�̎�ɓn���Ă����|���⎊���Ȃ�Ă������̂��ӎ������Ȃ��B
2018/08/31(��) 17:33:41.79ID:qB6pPk6g
>>520
�����܂���B�܂��܂������܂����B
��͂�_���Ƃ܂��������������ݒ�ɂ��܂��B�f���q�̐�����R�ɂ��܂��B
y����̊��S���Ap�� multiplicity ��� y �̑f���q�An ������ multiplicity�Apr (r:1�`R)�𑼂̑f���q�̑S�́Aqr������ multiplicity �Ƃ��܂��B�i�_���Ɠ����ݒ�B�j
a=2y/(1+p+�c+p^n)�Ab=y/p^n�Ac=2y/(1+p+�c+p^n)/p^n
�Ƃ����܂��B(�_���Ɠ����ݒ�B)
k��C�ӂɂƂ�
a�f=a/pk^qk�Ab�f=b/pk^qk�Ac�f=c/pk^qk
�Ƃ����܂��B(�_���Ɠ����ݒ�B)
Q1) (p+1)/2 = pr�Ak=r �̂Ƃ� A�f = ��[l��k](1+pl+�c+pl^ql)�͐������܂����H�_���ł͐�������Ɠǂ߂܂��B
Q2) (p+1)/2 = pr�Ak��r (��r) �̂Ƃ� A�f = ��[l��k](1+pl+�c+pl^ql)�͐������܂����H�_���ł͐�������Ɠǂ߂܂��B
Q3) (p+1)/2 = pr �ƂȂ� pr ���Ȃ��Ƃ��A(�_���� II �̃P�[�X) A�f = ��[l��k](1+pl+�c+pl^ql)�͐������܂����H�������Ȃ��Ƃ���ƂȂ��ł����H
�����܂���B�܂��܂������܂����B
��͂�_���Ƃ܂��������������ݒ�ɂ��܂��B�f���q�̐�����R�ɂ��܂��B
y����̊��S���Ap�� multiplicity ��� y �̑f���q�An ������ multiplicity�Apr (r:1�`R)�𑼂̑f���q�̑S�́Aqr������ multiplicity �Ƃ��܂��B�i�_���Ɠ����ݒ�B�j
a=2y/(1+p+�c+p^n)�Ab=y/p^n�Ac=2y/(1+p+�c+p^n)/p^n
�Ƃ����܂��B(�_���Ɠ����ݒ�B)
k��C�ӂɂƂ�
a�f=a/pk^qk�Ab�f=b/pk^qk�Ac�f=c/pk^qk
�Ƃ����܂��B(�_���Ɠ����ݒ�B)
Q1) (p+1)/2 = pr�Ak=r �̂Ƃ� A�f = ��[l��k](1+pl+�c+pl^ql)�͐������܂����H�_���ł͐�������Ɠǂ߂܂��B
Q2) (p+1)/2 = pr�Ak��r (��r) �̂Ƃ� A�f = ��[l��k](1+pl+�c+pl^ql)�͐������܂����H�_���ł͐�������Ɠǂ߂܂��B
Q3) (p+1)/2 = pr �ƂȂ� pr ���Ȃ��Ƃ��A(�_���� II �̃P�[�X) A�f = ��[l��k](1+pl+�c+pl^ql)�͐������܂����H�������Ȃ��Ƃ���ƂȂ��ł����H
2018/08/31(��) 17:41:41.14ID:DTNXO3+z
�t�F�[�Y�P�ɂȂ�����
2018/09/01(�y) 01:30:09.83ID:ddp4cBBS
�ł��܂�>>1��
��a�f = ��[k��r](1+pk+�c+pk^qk)
���ԈႢ�������Ƃ͔F�߂ĂȂ���ˁH
�̂Ƀt�F�[�Y�P�ɓ���́H
���̕��������łŎc��̂��A�c��Ȃ��̂��݂�킩�邯�ǁB
��a�f = ��[k��r](1+pk+�c+pk^qk)
���ԈႢ�������Ƃ͔F�߂ĂȂ���ˁH
�̂Ƀt�F�[�Y�P�ɓ���́H
���̕��������łŎc��̂��A�c��Ȃ��̂��݂�킩�邯�ǁB
2018/09/01(�y) 06:37:53.45ID:1OMQq8vy
�����w�E���ꂽ�_�͖����Ȃ��
>>16 �P�R�Q�l�ڂ̑f������2018/08/22(��) 12:41:18.93ID:q5K+5KiU
�����̗���
1.�u�ԈႢ��������܂����A�P�܂��v
��
2.�u(���_�_����Ȃ��Ƃ���)���C�����܂����B�����ł��v
��
3.(�_�_�ɂ��ĕ�����Ă�)�u�������łɒ����܂���(�������ĂȂ�)�B�ǂ�ł��猾���Ă��������v
>>16 �P�R�Q�l�ڂ̑f������2018/08/22(��) 12:41:18.93ID:q5K+5KiU
�����̗���
1.�u�ԈႢ��������܂����A�P�܂��v
��
2.�u(���_�_����Ȃ��Ƃ���)���C�����܂����B�����ł��v
��
3.(�_�_�ɂ��ĕ�����Ă�)�u�������łɒ����܂���(�������ĂȂ�)�B�ǂ�ł��猾���Ă��������v
2018/09/01(�y) 07:14:14.07ID:uSSvu/fA
���͂悤���炢������
2018/09/01(�y) 07:19:57.57ID:9Kyy5eqw
��Έ�Ή����āA�S�P�˂��Ă��ƁH
531�P�R�Q�l�ڂ̑f������
2018/09/01(�y) 07:50:36.80ID:ZOWvWk49 >>528
����܂ʼn��x���w�E����Ă���̂́A�ȉ��̂Q����������Ƃ������ƁB
>>462
��b'=b/pr^qr=��[k=1,r-1]pk^qk
��ap-2bp+2b=c�̎��̗��ӂ�pr^qr�Ŋ���Aa'=a/pr^qr�Ƃ����
��a'-2b'p+2b'=c'
���b'=b/pr^qr, a'=a/pr^qr
>>495
��b=��[k=1,r]pk^qk��b'=��[k=1,-1r]pk^qk
��a=��[k=1,r](1+pk+�c+pk^qk)��a'=��[k=1,r-1](1+pk+�c+pk^qk)
���b'=b/pr^qr, a'=a/(1+pr+�c+pr^qr)
a'�̒�`�͂ǂ����������������Ƃɋ߂����H
����܂ʼn��x���w�E����Ă���̂́A�ȉ��̂Q����������Ƃ������ƁB
>>462
��b'=b/pr^qr=��[k=1,r-1]pk^qk
��ap-2bp+2b=c�̎��̗��ӂ�pr^qr�Ŋ���Aa'=a/pr^qr�Ƃ����
��a'-2b'p+2b'=c'
���b'=b/pr^qr, a'=a/pr^qr
>>495
��b=��[k=1,r]pk^qk��b'=��[k=1,-1r]pk^qk
��a=��[k=1,r](1+pk+�c+pk^qk)��a'=��[k=1,r-1](1+pk+�c+pk^qk)
���b'=b/pr^qr, a'=a/(1+pr+�c+pr^qr)
a'�̒�`�͂ǂ����������������Ƃɋ߂����H
2018/09/01(�y) 07:51:25.79ID:C1GVJGgX
2018/09/01(�y) 09:23:09.54ID:RO47B9M9
r��r-1 �ɂ���đΉ�������Ƃ��āA
b�̖̘a=a
b'�̖̘a=a'
�Ƃ����W�͕ۂ����B
�������uy'=b'�~p^n �͊��S���ł���v�Ƃ͌����Ȃ��B
�ua' �| 2b��p + 2b�� = c���v�����S���R���̎��Ȃ̂Ő��藧�Ƃ͌����Ȃ��B
b�̖̘a=a
b'�̖̘a=a'
�Ƃ����W�͕ۂ����B
�������uy'=b'�~p^n �͊��S���ł���v�Ƃ͌����Ȃ��B
�ua' �| 2b��p + 2b�� = c���v�����S���R���̎��Ȃ̂Ő��藧�Ƃ͌����Ȃ��B
2018/09/01(�y) 09:43:11.17ID:eJQbZbwg
>>524
pr�͑f���q�ƒ�`���Ă�̂�(p+1)/2���f���łȂ��ꍇ�ł��B
�܂�_��II��(p+1)/2���f���łȂ��ꍇ�ł��B
���̏ꍇ�������܂����H
pr�͑f���q�ƒ�`���Ă�̂�(p+1)/2���f���łȂ��ꍇ�ł��B
�܂�_��II��(p+1)/2���f���łȂ��ꍇ�ł��B
���̏ꍇ�������܂����H
>>535
�U�̂��Ƃ͍l�����Ă��܂���
�U�̂��Ƃ͍l�����Ă��܂���
2018/09/01(�y) 10:51:07.29ID:jZ1Ng0Dt
>>536
�l���ɂ��ꂽ�ꍇ�ǂ��Ȃ�܂����H
>y����̊��S���Ap�� multiplicity ��� y �̑f���q�An ������ multiplicity�Apr (r:1�`R)�𑼂̑f���q�̑S�́Aqr������ multiplicity �Ƃ��܂��B�i�_���Ɠ����ݒ�B�j
>
>a=2y/(1+p+�c+p^n)�Ab=y/p^n�Ac=2y/(1+p+�c+p^n)/p^n
>
>�Ƃ����܂��B(�_���Ɠ����ݒ�B)
>k��C�ӂɂƂ�
>
>a�f=a/pk^qk�Ab�f=b/pk^qk�Ac�f=c/pk^qk
>
>�Ƃ����܂��B(�_���Ɠ����ݒ�B)
�����܂ł� (p+1)/2 ���f���łȂ��Ă��ʗp���܂����A���̏ꍇ�ł� A�f = ��[l��k](1+pl+�c+pl^ql) �͐������܂����H
�l���ɂ��ꂽ�ꍇ�ǂ��Ȃ�܂����H
>y����̊��S���Ap�� multiplicity ��� y �̑f���q�An ������ multiplicity�Apr (r:1�`R)�𑼂̑f���q�̑S�́Aqr������ multiplicity �Ƃ��܂��B�i�_���Ɠ����ݒ�B�j
>
>a=2y/(1+p+�c+p^n)�Ab=y/p^n�Ac=2y/(1+p+�c+p^n)/p^n
>
>�Ƃ����܂��B(�_���Ɠ����ݒ�B)
>k��C�ӂɂƂ�
>
>a�f=a/pk^qk�Ab�f=b/pk^qk�Ac�f=c/pk^qk
>
>�Ƃ����܂��B(�_���Ɠ����ݒ�B)
�����܂ł� (p+1)/2 ���f���łȂ��Ă��ʗp���܂����A���̏ꍇ�ł� A�f = ��[l��k](1+pl+�c+pl^ql) �͐������܂����H
2018/09/01(�y) 13:35:29.21ID:1OMQq8vy
�S�P�˂��Č��t����A�P�ɂ͗����͈̔͊O�ł�������
2018/09/01(�y) 21:22:54.60ID:SXfIUPDz
����c�͉��������Ă���
2018/09/01(�y) 21:26:23.74ID:/cqCDTyr
��ޯ?
2018/09/01(�y) 21:47:41.36ID:hhCbkJ0F
�Ȃ悭������A�����\�b�h�̂����u�Ή����Ă邩�瓯���������藧�v�Ƃ����̂�
0+1=1�͐��藧�B
f:Z��Z,f(n)=n+1�͑S�P�˂ŁA0��1,���ꂼ��1��2�͈�Έ�ɑΉ����Ă邩��1+2=2�����藧�B
�����������ƁH
0+1=1�͐��藧�B
f:Z��Z,f(n)=n+1�͑S�P�˂ŁA0��1,���ꂼ��1��2�͈�Έ�ɑΉ����Ă邩��1+2=2�����藧�B
�����������ƁH
2018/09/01(�y) 21:51:11.08ID:hhCbkJ0F
��0��1,���ꂼ��1��2�͈�Έ�ɑΉ����Ă邩��
�ȂςȂƂ��ɓ��{�ꂪ������
0��1�A1��2�͂��ꂼ���Έ�ɑΉ����Ă邩��1+2=2�����藧�A�Ƃ������Ƃ������Ă�́H
�Ə�������ł���C�Â������ǁA�m���ϐ��𐔎��ɒu����������(���������)�_���Ȃ����c�c�H
�ȂςȂƂ��ɓ��{�ꂪ������
0��1�A1��2�͂��ꂼ���Έ�ɑΉ����Ă邩��1+2=2�����藧�A�Ƃ������Ƃ������Ă�́H
�Ə�������ł���C�Â������ǁA�m���ϐ��𐔎��ɒu����������(���������)�_���Ȃ����c�c�H
2018/09/01(�y) 22:01:10.76ID:1OMQq8vy
���ϐ��𐔎��ɒu����������(���������)�_���Ȃ����c�c�H
�����������E�̐��w����Ȃ���
�����������E�̐��w����Ȃ���
2018/09/01(�y) 23:45:32.91ID:hInltfSY
�V�ł܂��[�H
�� �݁@�@�@�@��
�݁@���������`�@�݁�
�@ ��
��@�@���݁@ ���ެ��
���݁@�V �ȁȁ@�Q�Q_
�@�Q�Q�_(�ͥ#)/�__�^
�݁__�^���@�@�@|
`�^�P�P�P�P �^|�@|
|�P�P�P�P�P|�@|�^|�_
|���Q�݂���|�^
�� �݁@�@�@�@��
�݁@���������`�@�݁�
�@ ��
��@�@���݁@ ���ެ��
���݁@�V �ȁȁ@�Q�Q_
�@�Q�Q�_(�ͥ#)/�__�^
�݁__�^���@�@�@|
`�^�P�P�P�P �^|�@|
|�P�P�P�P�P|�@|�^|�_
|���Q�݂���|�^
2018/09/02(��) 23:39:53.12ID:Q97CGeRw
�ؖ���f�O�����̂Ō���������e���Ȃ��Ȃ���
�Ȍ�A�i���Ƀt�F�C�Y�P�̂܂�
�Ȍ�A�i���Ƀt�F�C�Y�P�̂܂�
2018/09/02(��) 23:46:58.15ID:Q97CGeRw
�߂ł��� �߂ł���
���Ђ��̂�����
���Ђ��̂�����
2018/09/02(��) 23:50:20.12ID:hq4ZUq55
���̈Ӗ�������������܂��ǂޕK�v�Ȃ���
2018/09/03(��) 00:10:57.58ID:K0JyG9yu
>>545
�Ȃ� (p+1)/2 ���f���̏ꍇ�ɂ͈�Έ�Ή�������̂� (p+1)/2 ���f���łȂ��ꍇ�ɂ͈�Έ�Ή����Ȃ��̂ł����H
���������˂Ă�Ƃ������Ƃ͂������߂��Ă�����ł���ˁH
���̎��_�Řb���������ĂȂ�����Ȃ��ł����H
�Ȃ� (p+1)/2 ���f���̏ꍇ�ɂ͈�Έ�Ή�������̂� (p+1)/2 ���f���łȂ��ꍇ�ɂ͈�Έ�Ή����Ȃ��̂ł����H
���������˂Ă�Ƃ������Ƃ͂������߂��Ă�����ł���ˁH
���̎��_�Řb���������ĂȂ�����Ȃ��ł����H
2018/09/03(��) 00:47:59.65ID:QfkLCLld
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �Q�ȁQ�ȁQ�ȁQ�ȁQ�ȁQ�ȁQ�ȁQ�ȁQ�ȁQ�ȁQ�Q
�@�@�@�@�@���@�@�@�@�@�@|�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@|
�@�@�@�@�@�@�@�@���@�@ ���@�V�ł܂��[�[�[�[�[�[�I�I�H�@�@�@�@�@�@��
�@�@�@���@�@�@�@�@�@�����с@|�Q�@�Q�@ �Q�@�Q�@�Q�@�Q�@�Q�@�Q�@�Q�@�Q|
�@�@�@�@�@�@�@ ���@�@�@��������! �Ɂ@ �Ɂ@�Ɂ@�Ɂ@�Ɂ@�Ɂ@�Ɂ@�Ɂ@��
�@�@����!�@�@�R�@�@�@�@�@�@�@�@�@�ׯ!!�@�@�@ ��
�@�@�@�@�@�@�@�@�@�@���߁��@�ȁQ�ȁ@�@�@�@�@��
�@�@�@�@�@�@�� �@�@�^�@�V�i��ͥ #�j�@�@�@�@/�@��ݼ��
�@�@�@�@��@�@�@�Y �@���_�Ɓ_��.�S���߁��U
�@�@�@�@�@�@�@�@�@|| �@�� �܁R�R�R �m�@�@||
�@�@�@�@�@�@�@�@�@||�@���� �@.|:::|���� �@||�@�@�@��
�@�@�@�@�@�@�@ .�^|�_�l �Q.�m�m _||_.�@�^|�_
�@�@�@�@�@�@�@�@�@������!
�@�@�@�@�@���@�@�@�@�@�@|�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@|
�@�@�@�@�@�@�@�@���@�@ ���@�V�ł܂��[�[�[�[�[�[�I�I�H�@�@�@�@�@�@��
�@�@�@���@�@�@�@�@�@�����с@|�Q�@�Q�@ �Q�@�Q�@�Q�@�Q�@�Q�@�Q�@�Q�@�Q|
�@�@�@�@�@�@�@ ���@�@�@��������! �Ɂ@ �Ɂ@�Ɂ@�Ɂ@�Ɂ@�Ɂ@�Ɂ@�Ɂ@��
�@�@����!�@�@�R�@�@�@�@�@�@�@�@�@�ׯ!!�@�@�@ ��
�@�@�@�@�@�@�@�@�@�@���߁��@�ȁQ�ȁ@�@�@�@�@��
�@�@�@�@�@�@�� �@�@�^�@�V�i��ͥ #�j�@�@�@�@/�@��ݼ��
�@�@�@�@��@�@�@�Y �@���_�Ɓ_��.�S���߁��U
�@�@�@�@�@�@�@�@�@|| �@�� �܁R�R�R �m�@�@||
�@�@�@�@�@�@�@�@�@||�@���� �@.|:::|���� �@||�@�@�@��
�@�@�@�@�@�@�@ .�^|�_�l �Q.�m�m _||_.�@�^|�_
�@�@�@�@�@�@�@�@�@������!
2018/09/03(��) 15:58:56.63ID:rn4fGwrw
���߂����������Ǝv�����ǂȂ�
2018/09/03(��) 17:02:10.28ID:zo/+bedc
���w�ȓ���̂���Ԃ̋ߓ�����
2018/09/03(��) 20:19:46.18ID:ACAltoZ2
�����Ă��Ȃ��������w���x���̐��w��
��������ƕ�����̂���Ԃ̋ߓ�
��������ƕ�����̂���Ԃ̋ߓ�
2018/09/03(��) 23:27:44.02ID:rGrwFIrb
>>551
>��Έ�Ή��̂��Ƃ͑�ӂȂ̂ŁA���̌�������̏ꍇ�����ɂ͈ˑ����܂���
�Ƃ������Ƃ� (p+1)/2 ���f���ł��낤���A�Ȃ��낤���A���̏ꍇ�����ɂ͈˂炸�A(�M�҂� �h��Ӂh �ɂ܂�����)��Έ�Ή��͍���
a�f=a/pk^qk
�Ƃ����Ƃ�
a�f = ��[l��k](1+pl+�c+pl^ql)
�͐��������OK?
>��Έ�Ή��̂��Ƃ͑�ӂȂ̂ŁA���̌�������̏ꍇ�����ɂ͈ˑ����܂���
�Ƃ������Ƃ� (p+1)/2 ���f���ł��낤���A�Ȃ��낤���A���̏ꍇ�����ɂ͈˂炸�A(�M�҂� �h��Ӂh �ɂ܂�����)��Έ�Ή��͍���
a�f=a/pk^qk
�Ƃ����Ƃ�
a�f = ��[l��k](1+pl+�c+pl^ql)
�͐��������OK?
p^n+�c+1��0 (mod q^r), q>p
�̂Ƃ��Am��m>0�̐����Ƃ���
n+1=m�~q^(r-1)(q-1)
�̂Ƃ��Am��m>0�̐����Ƃ���
n+1=m�~q^(r-1)(q-1)
�u�R������������`�v
�ƌ����j�̐����������Ă��܂����B�`�̕����͕������܂���ł����B
���̎��ɕ������������A�������낷�l�Ԃ͊O���琺������������̂ł��傤���H
�������N����������Ȃ��悤�ɂ��Ȃ��Ƃ��̂������Ȃ��l�Ԃ͖ق��Ă����
���\�B�������猾�����ςȂ��œ����₪���ď��X�������肾�B
���X�����l�Ԃ͒j�����������J����
�ƌ����j�̐����������Ă��܂����B�`�̕����͕������܂���ł����B
���̎��ɕ������������A�������낷�l�Ԃ͊O���琺������������̂ł��傤���H
�������N����������Ȃ��悤�ɂ��Ȃ��Ƃ��̂������Ȃ��l�Ԃ͖ق��Ă����
���\�B�������猾�����ςȂ��œ����₪���ď��X�������肾�B
���X�����l�Ԃ͒j�����������J����
558�P�R�Q�l�ڂ̑f������
2018/09/04(��) 06:58:30.35ID:tkIvLhx72018/09/04(��) 07:22:44.76ID:DGQaYchi
�����|�n�܂���
2018/09/04(��) 09:01:37.46ID:W+wFhPqZ
�ǂ����ɂ��남����������^�͂ǂ��ɂ������ĂH
2018/09/04(��) 09:33:25.06ID:diXKRUIE
>>555 ���肢���܂��B
2018/09/04(��) 10:16:20.06ID:diXKRUIE
>>562
�ł͓Z�߂��
y ����̊��S���Ap�� multiplicity ����̑f���q�Ay=p^n��[k:1�`r]pr^qr��f���������Ƃ���Ƃ�1�`r�C�ӂ�k�ɑ�
�@2y/(1+p+�c+p^n)/pk^nk = ��[l��k] pk^qk
���i(p+1)/2���f���ł��낤���Ȃ��낤���j��������B
�Ƃ������Ƃł����H
�ł͓Z�߂��
y ����̊��S���Ap�� multiplicity ����̑f���q�Ay=p^n��[k:1�`r]pr^qr��f���������Ƃ���Ƃ�1�`r�C�ӂ�k�ɑ�
�@2y/(1+p+�c+p^n)/pk^nk = ��[l��k] pk^qk
���i(p+1)/2���f���ł��낤���Ȃ��낤���j��������B
�Ƃ������Ƃł����H
>>563
2y/(1+p+�c+p^n)/pk^qk = ��[l��k] pk^q
����͊���������������A�������܂�
��a�f = ��[l��k](1+pl+�c+pl^ql)
�͐��藧���Ƃ����肳��܂�
2y/(1+p+�c+p^n)/pk^qk = ��[l��k] pk^q
����͊���������������A�������܂�
��a�f = ��[l��k](1+pl+�c+pl^ql)
�͐��藧���Ƃ����肳��܂�
2018/09/04(��) 10:44:26.44ID:diXKRUIE
>>564
�����܂���B�Z�߂����˂܂����B
y ����̊��S���Ap�� multiplicity ����̑f���q�Ay=p^n��[k:1�`r]pr^qr��f���������Ƃ���Ƃ�1�`r�C�ӂ�k�ɑ�
�@2y/(1+p+�c+p^n)/pk^nk = ��[l��k] (1+pl+�c+pl^ql)
���i(p+1)/2���f���ł��낤���Ȃ��낤���j��������B
�ł��B
�����܂���B�Z�߂����˂܂����B
y ����̊��S���Ap�� multiplicity ����̑f���q�Ay=p^n��[k:1�`r]pr^qr��f���������Ƃ���Ƃ�1�`r�C�ӂ�k�ɑ�
�@2y/(1+p+�c+p^n)/pk^nk = ��[l��k] (1+pl+�c+pl^ql)
���i(p+1)/2���f���ł��낤���Ȃ��낤���j��������B
�ł��B
2018/09/04(��) 11:30:55.25ID:diXKRUIE
>>566
�킩��܂����B�ł�
y ����̊��S���Ap�� multiplicity ����̑f���q�Ay=p^n��[k:1�`r]pk^qk��f���������Ƃ���Ƃ�1�`r�C�ӂ�k�ɑ�
�@2y/pk^nk = (1+p+�c+p^n)��[l��k] (1+pl+�c+pl^ql)
���i(p+1)/2���f���ł��낤���Ȃ��낤���j��������B
�ł��ˁB
�ł́A���̂Ƃ� y/pk^nk=p^n��[k:1�`r�Al��k]pl^ql �͑f���������A����
�@2y/pk^qk = (1+p+�c+p^n)��[l��k] (1+pl+�c+pl^ql)
�Ȃ̂� y/pk^qk �͊��S���ł��ˁH
�킩��܂����B�ł�
y ����̊��S���Ap�� multiplicity ����̑f���q�Ay=p^n��[k:1�`r]pk^qk��f���������Ƃ���Ƃ�1�`r�C�ӂ�k�ɑ�
�@2y/pk^nk = (1+p+�c+p^n)��[l��k] (1+pl+�c+pl^ql)
���i(p+1)/2���f���ł��낤���Ȃ��낤���j��������B
�ł��ˁB
�ł́A���̂Ƃ� y/pk^nk=p^n��[k:1�`r�Al��k]pl^ql �͑f���������A����
�@2y/pk^qk = (1+p+�c+p^n)��[l��k] (1+pl+�c+pl^ql)
�Ȃ̂� y/pk^qk �͊��S���ł��ˁH
568�P�R�Q�l�ڂ̑f������
2018/09/04(��) 11:45:10.97ID:MpTMY5M62018/09/04(��) 12:08:09.20ID:vZ9FrO7z
�P����A��B��B��A�̋�ʂ��ł��ĂȂ������ł́H
�_���Ă�Ƃ��ł͂Ȃ��B
�_���Ă�Ƃ��ł͂Ȃ��B
2018/09/04(��) 14:09:13.79ID:8Hx1L//R
�EA��B��B��A�̋�ʂ��ł��Ȃ��̂́A�|�ł͂Ȃ�����
�E�́̋�ʂ��ł��Ȃ��̂́A�|�ł͂Ȃ�����
�_���Ă�Ƃ��ł͂Ȃ��B
�E�́̋�ʂ��ł��Ȃ��̂́A�|�ł͂Ȃ�����
�_���Ă�Ƃ��ł͂Ȃ��B
2018/09/04(��) 16:48:46.39ID:vUAYjwJF
>>567
��y/pk^nk=p^n��[k:1�`r�Al��k]pl^ql �͑f��������
�͓��{��Ƃ��ĉ��߂ł��܂���B
��y/pk^qk �͊��S���ł���
���S���ł��邱�Ƃ����肳��܂��B
���ꎩ�̂��ے肳��Ă��A��肪�����������Ƃɂ͂Ȃ�܂��ǁB
>>568
�K�v�����Ə\���������炢�͗������Ă����B
>>570
���̂悤�Ȃ��Ƃ͂Ȃ��B���̖��͉����Ă݂�����B�����ł����Ȃ���
�����̂悤�Ȃ��̂��łȂ�����B
�S�Ă�pk�ɑ��ĈقȂ�p�̒l�����݂�pk=(p+1)/2�Ƃ����S��������
��������Ɖ��肷�邱�Ƃ��ł���A�ȑO�ɏ������_���̂悤�ɂȂ�
�Ƃ��������ł����B
��y/pk^nk=p^n��[k:1�`r�Al��k]pl^ql �͑f��������
�͓��{��Ƃ��ĉ��߂ł��܂���B
��y/pk^qk �͊��S���ł���
���S���ł��邱�Ƃ����肳��܂��B
���ꎩ�̂��ے肳��Ă��A��肪�����������Ƃɂ͂Ȃ�܂��ǁB
>>568
�K�v�����Ə\���������炢�͗������Ă����B
>>570
���̂悤�Ȃ��Ƃ͂Ȃ��B���̖��͉����Ă݂�����B�����ł����Ȃ���
�����̂悤�Ȃ��̂��łȂ�����B
�S�Ă�pk�ɑ��ĈقȂ�p�̒l�����݂�pk=(p+1)/2�Ƃ����S��������
��������Ɖ��肷�邱�Ƃ��ł���A�ȑO�ɏ������_���̂悤�ɂȂ�
�Ƃ��������ł����B
2018/09/04(��) 16:56:42.98ID:yj+6CZXV
>>571
�ł͂��Ȃ��̘_���̘_�@��
y ����̊��S���Apk �� multiplicity qk �������̑f���q�̂Ƃ� y/pk^qk �����S���B
�Ƃ������W�b�N����������ƍl����OK�ł��ˁH
�ł͂��Ȃ��̘_���̘_�@��
y ����̊��S���Apk �� multiplicity qk �������̑f���q�̂Ƃ� y/pk^qk �����S���B
�Ƃ������W�b�N����������ƍl����OK�ł��ˁH
2018/09/04(��) 17:02:23.96ID:xinAd8Lm
�撣���Đ��w���ۂ����t�g�������悤�Ɛ���t�w�L�т��Ă�̂��ȂɁX�����B
2018/09/04(��) 17:22:27.72ID:VVJeZn+A
�ǁ[�ł��������ǁA���肳�����ĂȂ�B
2018/09/04(��) 21:32:02.02ID:T7IEs2v7
>>574
����A�ׂɁB�B
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
���
y ����̊��S���Apk �� multiplicity qk �������̑f���q�̂Ƃ� y/pk^qk �����S���B
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
��������Ȃ玟���������ł���B
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
��̊��S�������݂���Ƃ���B
y����̊��S���ōŏ��ł�����̂Ƃ���B
����肻��� multiplicity �������̑f���q�������Ȃ��B
���Euler�̒藝���y�͂��傤�Lj�� multiplicity ����̑f���q�����B
�ȏ�ɂ�� y = p^n �Ƃ�����B
���������̂Ƃ�
�@1+ p + �c + p^(n-1) = p^n
�ł��邪���ӂ�modulo p ��1�A�E�ӂ� 0 �ɍ����䂦�����B
�ȏ�ɂ���̊��S���͑��݂��Ȃ��B
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�_���������ԃX�b�L���ɂȂ�܂���B
�ǂ������ł��ˁB
����A�ׂɁB�B
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
���
y ����̊��S���Apk �� multiplicity qk �������̑f���q�̂Ƃ� y/pk^qk �����S���B
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
��������Ȃ玟���������ł���B
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
��̊��S�������݂���Ƃ���B
y����̊��S���ōŏ��ł�����̂Ƃ���B
����肻��� multiplicity �������̑f���q�������Ȃ��B
���Euler�̒藝���y�͂��傤�Lj�� multiplicity ����̑f���q�����B
�ȏ�ɂ�� y = p^n �Ƃ�����B
���������̂Ƃ�
�@1+ p + �c + p^(n-1) = p^n
�ł��邪���ӂ�modulo p ��1�A�E�ӂ� 0 �ɍ����䂦�����B
�ȏ�ɂ���̊��S���͑��݂��Ȃ��B
�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\�\
�_���������ԃX�b�L���ɂȂ�܂���B
�ǂ������ł��ˁB
>>576
�������Ƃ������Ƃ����肳��邾����
a'=��[k=1,r-1](1+pk+�c+pk^qk)����[k=1,r](1+pk�c+pk^qk)/pr^qr
�ƂȂ�A���̉��肪�������Ȃ��Ƃ������ƂɂȂ�Ǝv���܂��B
�܂�Ak�̍ő�l��r�̂Ƃ��������藧���A���̒l��r-1�ɂȂ��Ă�
r+1�ɂȂ��Ă����藧���Ȃ��Ƃ������Ƃ������Ă��邾�����Ǝv���܂��B
�������Ƃ������Ƃ����肳��邾����
a'=��[k=1,r-1](1+pk+�c+pk^qk)����[k=1,r](1+pk�c+pk^qk)/pr^qr
�ƂȂ�A���̉��肪�������Ȃ��Ƃ������ƂɂȂ�Ǝv���܂��B
�܂�Ak�̍ő�l��r�̂Ƃ��������藧���A���̒l��r-1�ɂȂ��Ă�
r+1�ɂȂ��Ă����藧���Ȃ��Ƃ������Ƃ������Ă��邾�����Ǝv���܂��B
2018/09/04(��) 21:55:15.51ID:ISiP6Smo
2018/09/04(��) 22:44:41.17ID:xinAd8Lm
>>579
���������Ƃ����肳��邾���ł��B
���x�������Ă��܂����A���̉���͐���������܂���B�����k=r-1�̂Ƃ��ɐ��藧���Ȃ���
���������ł���Ak=r�̂Ƃ��ɐ��藧�����藧���Ȃ����Ɋւ��Ă͉��̏����^����
�s���ł���Ƃ������Ƃł��B
���������Ƃ����肳��邾���ł��B
���x�������Ă��܂����A���̉���͐���������܂���B�����k=r-1�̂Ƃ��ɐ��藧���Ȃ���
���������ł���Ak=r�̂Ƃ��ɐ��藧�����藧���Ȃ����Ɋւ��Ă͉��̏����^����
�s���ł���Ƃ������Ƃł��B
2018/09/04(��) 23:30:12.54ID:DGQaYchi
�������Ȃ��Ȃ�g���܂����
2018/09/04(��) 23:39:08.91ID:xinAd8Lm
�܂�U�Ȃ�ł��ˁB
���Ⴀ�_���Ŏg���Ă̓_���ł��B
���Ⴀ�_���Ŏg���Ă̓_���ł��B
2018/09/04(��) 23:45:28.48ID:ISiP6Smo
�w���@�̂��߂ɍŏ��ɐ������Ƃ��閽��Ƃ͈Ⴄ�́H
2018/09/05(��) 00:16:03.40ID:RT3Tco7O
>>583
�ނ��됳�����Ƃ���鉼�肪�����o�Ă��āA�����Ă�������
�ނ��됳�����Ƃ���鉼�肪�����o�Ă��āA�����Ă�������
2018/09/05(��) 00:23:24.65ID:Fa23FyH2
�w���@���킩���ĂȂ��B
�������߂�ׂ��Ȃ̂ł́H
�w���@�̕������蒼���̂ł͂��܂�ɂ��d�d
�������߂�ׂ��Ȃ̂ł́H
�w���@�̕������蒼���̂ł͂��܂�ɂ��d�d
2018/09/05(��) 00:47:15.26ID:0AlpXlkH
>>584
�������̖��肪�^�ł���Ƃ���Ɩ�����������B����Ă��̖���͋U�ł���B�݂����ɂ��Ȃ��Əؖ��ł��Ȃ����肪�����ς��ł����Ⴄ�̂͊m���ɂ߂�ǂ�������
�������̖��肪�^�ł���Ƃ���Ɩ�����������B����Ă��̖���͋U�ł���B�݂����ɂ��Ȃ��Əؖ��ł��Ȃ����肪�����ς��ł����Ⴄ�̂͊m���ɂ߂�ǂ�������
2018/09/05(��) 02:27:39.28ID:G5vTUjav
�z���g�ɐ������̂��H�������̂Ȃ�ؖ���^���ĉ������ƌ���ꂽ�Ƃ��ɂ́A
�u��ӂ��玩���B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł����B�v
�Ƃ����A������g�����������Ȃ��ؖ����o�Ă�����
�u�������Ɖ��肳��Ă邾���Ő������킯�ł͂Ȃ��B�v
�Ƃ����B���`���N�`���B
�u��ӂ��玩���B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł����B�v
�Ƃ����A������g�����������Ȃ��ؖ����o�Ă�����
�u�������Ɖ��肳��Ă邾���Ő������킯�ł͂Ȃ��B�v
�Ƃ����B���`���N�`���B
588�P�R�Q�l�ڂ̑f������
2018/09/05(��) 02:38:09.59ID:4tSl8eka �ȒP�Șb�A�P�ɂƂ��Đ������͎̂����݂̂ŁA
���l�̌������Ƃ͂��ׂĊԈႢ
�����l����Ƃ��ׂĂɐ�������
���l�̌������Ƃ͂��ׂĊԈႢ
�����l����Ƃ��ׂĂɐ�������
2018/09/05(��) 03:34:22.06ID:PvGQmJxF
�����ȊO�S���o�J���_�ł��ȁB
590�P�R�Q�l�ڂ̑f������
2018/09/05(��) 07:00:00.36ID:KOTk5Qvu ���ǁua'=��[k=1,r-1](1+pk+�c+pk^qk)�v�͐������Ȃ��Ƃ������ƂŌ��������킯�H
2018/09/05(��) 08:11:54.71ID:svJk1x5K
�o��ȗ��A�P�͑S�Đ������Ȃ��Ƃ������ƂŌp����
592�P�R�Q�l�ڂ̑f������
2018/09/05(��) 12:43:24.76ID:wXzPAdu0 ����������
���w�ɂ���Ȍ��o�����l�ނ������Ȃ�Ă�
�l�I��100���~���炢�^�������قǂ�
���w�ɂ���Ȍ��o�����l�ނ������Ȃ�Ă�
�l�I��100���~���炢�^�������قǂ�
>>588
����Ȃ��Ƃ͏����Ă��܂��A�v���Ă����܂���B
>>589
����ł͐l�ނň�Ԍ����Ƃ������ƂɂȂ�܂����A�����ł͂���܂���
�����Ȃ肽���Ƃ��v���܂���B
>>590
����͐���������܂���B���x�������Ă��܂����B���̉��x���������Ƃ�
�������悤�Ƃ���̂������ł��܂���B
>>591
���̂悤�Ȃ��Ƃ͂���܂���B�ԈႢ�̎w�E�����肻�ꂪ�������ꍇ�ɂ�
���̓s�x�P�Ă��܂����B���ǁA�����ɂ͂قlj����ł����ǁB
����Ȃ��Ƃ͏����Ă��܂��A�v���Ă����܂���B
>>589
����ł͐l�ނň�Ԍ����Ƃ������ƂɂȂ�܂����A�����ł͂���܂���
�����Ȃ肽���Ƃ��v���܂���B
>>590
����͐���������܂���B���x�������Ă��܂����B���̉��x���������Ƃ�
�������悤�Ƃ���̂������ł��܂���B
>>591
���̂悤�Ȃ��Ƃ͂���܂���B�ԈႢ�̎w�E�����肻�ꂪ�������ꍇ�ɂ�
���̓s�x�P�Ă��܂����B���ǁA�����ɂ͂قlj����ł����ǁB
2018/09/05(��) 13:03:20.32ID:8OL+IejM
���Ⴀ�_��p7
��b���ɑΉ����� a ��a���Ƃ����
��a�� = ∏ [k:1�`r-1](1 + pk + ⋯ + pk^qk)
�͐������Ȃ��ł��ˁB
��b���ɑΉ����� a ��a���Ƃ����
��a�� = ∏ [k:1�`r-1](1 + pk + ⋯ + pk^qk)
�͐������Ȃ��ł��ˁB
2018/09/05(��) 13:09:02.72ID:Q0Y1fw1a
>>593
��ӂ����琬��������ĉ��x�������Ă���B
��ӂ����琬��������ĉ��x�������Ă���B
2018/09/05(��) 13:37:39.42ID:Uuf/nYN0
���ԈႢ�̎w�E�����肻�ꂪ�������ꍇ�ɂ͂��̓s�x�P�Ă��܂����B
�����ǁA�����ɂ͂قlj����ł����ǁB
�t�F�C�Y�P�ł́A���̂悤�ɏ�������
�ǂ���>>16 �J��Ԃ�
�����ǁA�����ɂ͂قlj����ł����ǁB
�t�F�C�Y�P�ł́A���̂悤�ɏ�������
�ǂ���>>16 �J��Ԃ�
2018/09/05(��) 14:05:48.66ID:L2Mar6ZO
�{�l�������͖������ĔF�߂Ă��₩��A���������Ⴄ��H
2018/09/05(��) 14:24:43.06ID:kUEnfVK1
�S�z���Ȃ��Ă��A�܂��グ�邳
2018/09/05(��) 14:30:48.66ID:AZht4kQW
�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �Q�Q�ȁQ�ȁQ�ȁQ�ȁQ�ȁQ�ȁQ�ȁQ�ȁQ�ȁQ�ȁQ�Q
�@�@�@�@�@���@�@�@�@�@�@|�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@|
�@�@�@�@�@�@�@�@���@�@ ���@�V�ł܂��[�[�[�[�[�[�I�I�H�@�@�@�@�@�@��
�@�@�@���@�@�@�@�@�@�����с@|�Q�@�Q�@ �Q�@�Q�@�Q�@�Q�@�Q�@�Q�@�Q�@�Q|
�@�@�@�@�@�@�@ ���@�@�@��������! �Ɂ@ �Ɂ@�Ɂ@�Ɂ@�Ɂ@�Ɂ@�Ɂ@�Ɂ@��
�@�@����!�@�@�R�@�@�@�@�@�@�@�@�@�ׯ!!�@�@�@ ��
�@�@�@�@�@�@�@�@�@�@���߁��@�ȁQ�ȁ@�@�@�@��
�@�@�@�@�@�@�� �@�@�^�@�V�i��ͥ #�j�@�@/�@��ݼ��
�@�@�@�@��@�@�@�Y �@���_�Ɓ_��.�S�@ ���߁��U
�@�@�@�@�@�@�@�@�@|| �@�� �܁R�R�R �m�@||
�@�@�@�@�@�@�@�@�@||�@�@���� �@.|:::|���� ||�@�@�@��
�@�@�@�@�@�@�@�@ .�^|�_�l �Q.�m�m _||_.�^|�_
�@�@�@�@�@�@�@�@�@������!
�@�@�@�@�@���@�@�@�@�@�@|�@�@�@�@�@�@�@�@�@�@�@�@ �@�@�@�@�@�@�@|
�@�@�@�@�@�@�@�@���@�@ ���@�V�ł܂��[�[�[�[�[�[�I�I�H�@�@�@�@�@�@��
�@�@�@���@�@�@�@�@�@�����с@|�Q�@�Q�@ �Q�@�Q�@�Q�@�Q�@�Q�@�Q�@�Q�@�Q|
�@�@�@�@�@�@�@ ���@�@�@��������! �Ɂ@ �Ɂ@�Ɂ@�Ɂ@�Ɂ@�Ɂ@�Ɂ@�Ɂ@��
�@�@����!�@�@�R�@�@�@�@�@�@�@�@�@�ׯ!!�@�@�@ ��
�@�@�@�@�@�@�@�@�@�@���߁��@�ȁQ�ȁ@�@�@�@��
�@�@�@�@�@�@�� �@�@�^�@�V�i��ͥ #�j�@�@/�@��ݼ��
�@�@�@�@��@�@�@�Y �@���_�Ɓ_��.�S�@ ���߁��U
�@�@�@�@�@�@�@�@�@|| �@�� �܁R�R�R �m�@||
�@�@�@�@�@�@�@�@�@||�@�@���� �@.|:::|���� ||�@�@�@��
�@�@�@�@�@�@�@�@ .�^|�_�l �Q.�m�m _||_.�^|�_
�@�@�@�@�@�@�@�@�@������!
2018/09/05(��) 16:18:49.61ID:Uuf/nYN0
�V�ł�v���Ȃ�Ă��Ă���A�P�ɕ�������s�u����̈������Ђǂ��Ȃ����Ⴄ�B
2018/09/05(��) 16:57:15.03ID:zXdsJ3SU
�����͓��{������Ȃ肨��������
2018/09/05(��) 17:45:28.54ID:Fa23FyH2
����p7�͐������ĂȂ��������肵�Ă̋c�_�Ȃ킯�����牽�̈Ӗ����Ȃ��B
�Ƃ������𗝉�����̂ɉ����������ł����˂��H
�Ƃ������𗝉�����̂ɉ����������ł����˂��H
605�P�R�Q�l�ڂ̑f������
2018/09/05(��) 19:16:31.11ID:CuoQKPqL 1�̔��_�͔��_�ɂȂ��ĂȂ�����A
���x�J��Ԃ���Ă��������͂Ȃ�Ȃ�
�킴�킴���e���Ȃ��Ƃ����Ȃ�A����͌�������
���x�J��Ԃ���Ă��������͂Ȃ�Ȃ�
�킴�킴���e���Ȃ��Ƃ����Ȃ�A����͌�������
>>605
a=��[k=1,r](1+pk+�c+pk^qk)
b=��[k=1,r]pk^qk
�ł���
a=cp^n
2b=c(p^n+�c+1)
����������Ɖ��肷��B
r��s�̂Ƃ����l�����
2b�~ps^qs=c�~ps^qs(p^n+�c+1)
p^n+�c+1�̒l�͕ύX����Ȃ�����Ap��n�͕ς��Ȃ�
b'=b�~ps^qs
c'=c�~ps^qs
�ƂȂ�B
a'=c'p^n�ł��邩��Aa'=a�~ps^qs�ƂȂ�B
�������A��ӂ���Aa'=a�~(1+ps+�c+ps^qs)�ɂȂ�Ȃ���Ȃ�Ȃ�����
�s�K�ɂȂ�B����āAk=s�̂Ƃ��ɐ��藧�Ƃ������肪�U�Ƃ������ƂɂȂ�B
a=��[k=1,r](1+pk+�c+pk^qk)
b=��[k=1,r]pk^qk
�ł���
a=cp^n
2b=c(p^n+�c+1)
����������Ɖ��肷��B
r��s�̂Ƃ����l�����
2b�~ps^qs=c�~ps^qs(p^n+�c+1)
p^n+�c+1�̒l�͕ύX����Ȃ�����Ap��n�͕ς��Ȃ�
b'=b�~ps^qs
c'=c�~ps^qs
�ƂȂ�B
a'=c'p^n�ł��邩��Aa'=a�~ps^qs�ƂȂ�B
�������A��ӂ���Aa'=a�~(1+ps+�c+ps^qs)�ɂȂ�Ȃ���Ȃ�Ȃ�����
�s�K�ɂȂ�B����āAk=s�̂Ƃ��ɐ��藧�Ƃ������肪�U�Ƃ������ƂɂȂ�B
2018/09/05(��) 19:24:12.32ID:TUi+D2hg
���ײݷ��\�\�� o(߁��o) (o߁��o) (o߁��)o ���\�\��
2018/09/05(��) 19:29:53.84ID:TUi+D2hg
>>607 ���߯(*�L�)���߯
2018/09/05(��) 20:08:50.40ID:svJk1x5K
�E�P�̏��������̂��A���܂�ɂ������B
�E���炩�ȊԈႢ���炯�Ȃ̂ɁA�P�͐������ƌ�������B
�E�e�ȃX���Z�l�������P���l�|����B
�E���炩�ȊԈႢ���w�E���Ă��P���������Ȃ��B
�E�������݂��������w�I�Ȃ����łP�́A�����ł��Ȃ��ƌ����ē�����B
�EA��B��B��A�̋�ʂ��ł��Ȃ��B
�E�́̋�ʂ��ł��Ȃ��B
�E�w���@���킩���ĂȂ��B
�E�撣���Đ��w���ۂ����t�g�������悤�Ɛ���t�w�L�т��Ă�̂��ɁX����
�E�e���r���玩���̈�������������Ɣ�������B
�E���炩�ȊԈႢ���炯�Ȃ̂ɁA�P�͐������ƌ�������B
�E�e�ȃX���Z�l�������P���l�|����B
�E���炩�ȊԈႢ���w�E���Ă��P���������Ȃ��B
�E�������݂��������w�I�Ȃ����łP�́A�����ł��Ȃ��ƌ����ē�����B
�EA��B��B��A�̋�ʂ��ł��Ȃ��B
�E�́̋�ʂ��ł��Ȃ��B
�E�w���@���킩���ĂȂ��B
�E�撣���Đ��w���ۂ����t�g�������悤�Ɛ���t�w�L�т��Ă�̂��ɁX����
�E�e���r���玩���̈�������������Ɣ�������B
2018/09/05(��) 21:25:01.86ID:0AlpXlkH
������́A�f���ɜ߂��ꂽ�l�������Ă����{��ǂ��Ƃ���H
2018/09/05(��) 22:09:33.05ID:0AlpXlkH
>>612
�ǂ�ł݂�Ɩʔ�����
�ǂ�ł݂�Ɩʔ�����
2018/09/05(��) 23:22:45.84ID:5PVy3ZsY
���߂Ȃ����̎p���͂ǂ��Ȃ낤�˂��H
616�P�R�Q�l�ڂ̑f������
2018/09/06(��) 05:37:30.62ID:TASued5O �_���ǂ݂�������A�b�v���[�_�[�ɏグ�����ĉ�����
���肢���܂�
���肢���܂�
2018/09/06(��) 05:42:27.11ID:mjUpsnF9
�ԈႢ���P���g���F�����Ă���p���������o�c�e�͌������Ȃ�����B
618�P�R�Q�l�ڂ̑f������
2018/09/06(��) 06:46:07.83ID:sKa+itOs >>607 �ȂA������������ܕς���ĂȂ��C������c
2018/09/06(��) 08:21:28.18ID:8HvITGlu
2018/09/06(��) 08:50:32.99ID:jkAFX+0e
�����Ǝ����Ō�������悤�ɂȂ����̂͐i����
2018/09/06(��) 10:03:17.36ID:TLU0vwyl
�t�F�C�Y�P�ł́A��������Ȃ���
�����ĂP�O�O���>>16 �J��Ԃ�
�����ĂP�O�O���>>16 �J��Ԃ�
�ύX�_
�E���܂łƊ��S�ɈႤ���@�ɂ��ؖ���lj����܂����B
�E�ȑO�܂ł̘_���Ő�����������7�y�[�W�ȍ~�̕⑫�Ɉړ����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7091776613010/
Pdf���� �p��
http://fast-uploader.com/file/7091776724060/
�E���܂łƊ��S�ɈႤ���@�ɂ��ؖ���lj����܂����B
�E�ȑO�܂ł̘_���Ő�����������7�y�[�W�ȍ~�̕⑫�Ɉړ����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7091776613010/
Pdf���� �p��
http://fast-uploader.com/file/7091776724060/
2018/09/06(��) 17:10:28.92ID:7qOGnRof
�S�~�o�c�e�ŁA�t�F�C�Y�Q�ɁB
�o�Ă��Ȃ��Ă����̂ɁB
�o�Ă��Ȃ��Ă����̂ɁB
>>1 ����
2018�N08��22��2018�N09��06��
2018�N08��22��2018�N09��06��
2018/09/06(��) 17:25:41.93ID:dMEcbdn7
���@���E����
���@p = 1 + (a �| c)/(2b �| a)
���@2b �| a �� 0 (mod p)
�_�E�g
���@p = 1 + (a �| c)/(2b �| a)
���@2b �| a �� 0 (mod p)
�_�E�g
2018/09/06(��) 18:00:22.41ID:7qOGnRof
�t�F�C�Y�R
�͂��܂邩�ȁH�H�H�H
�͂��܂邩�ȁH�H�H�H
627�P�R�Q�l�ڂ̑f������
2018/09/06(��) 20:23:41.67ID:pGQmsjFV �Ȃ�ł����Ƀt�@�C��������ł����H
�܂����Ƃ����т�܂���
�߂���
�܂����Ƃ����т�܂���
�߂���
628�P�R�Q�l�ڂ̑f������
2018/09/06(��) 20:56:00.33ID:FfuIcM4r ����ȐS�ɂ��Ȃ����Ƃ�
2018/09/06(��) 21:17:44.97ID:LdKnr+Sk
�C���_�͕K������ƐM���Ă�
2018/09/06(��) 21:23:22.72ID:mjUpsnF9
�����Ȃ�t�F�C�Y�P�ɖ߂������B
2018/09/06(��) 23:22:08.70ID:RMQWbarm
���ꂾ���̐l�Ԃ��䂫�t����G���^�[�e�i�[�Ƃ��Ă̍˔\�����ꂩ����L���Ă����Ăق���
2018/09/07(��) 01:07:05.58ID:vmhHCBo+
�Ƃ肠��������͊ԈႦ�����Ă�1���͐Q�����ׂ��B
2018/09/07(��) 01:19:37.43ID:gNtdHM+o
����w�̕����K�V��Ɗۖ{��i�͌����̒�?!2�l�Ƃ������������̂͊ԈႢ�Ȃ����������̈Ⴂ���炷��Ⴂ���������Ƃ̂��ƁB�ꕔ�ł͌��Z�킾�Ƃ����\������Ă���B
2018/09/07(��) 02:27:17.61ID:JVCxObQ+
���͊��Ɋ�̊��S�������݂��Ȃ����Ƃ��ؖ�����
2018/09/07(��) 07:31:42.69ID:fhdyCk6P
>>632
�ԈႦ���w�E����Ă������悤�ȂP�ł͂Ȃ����B
�ԈႦ���w�E����Ă������悤�ȂP�ł͂Ȃ����B
2018/09/07(��) 09:45:19.48ID:kt/XkYQJ
���ǃ_����������
�ύX�_
�E5�y�[�W�̏ؖ���ύX���܂���
Pdf���� ���{��
http://fast-uploader.com/file/7091846480637/
Pdf���� �p��
http://fast-uploader.com/file/7091846549122/
�E5�y�[�W�̏ؖ���ύX���܂���
Pdf���� ���{��
http://fast-uploader.com/file/7091846480637/
Pdf���� �p��
http://fast-uploader.com/file/7091846549122/
>>1 ����
2018�N08��22��2018�N09��07��
2018�N08��22��2018�N09��07��
2018/09/07(��) 12:47:16.99ID:kt/XkYQJ
���Ǐؖ��͂ł��Ă�́H
2018/09/07(��) 12:54:37.34ID:x0bfFLzz
13�y�[�W�́u�����ɖ\�v���Č��t�͂܂�A�ǂ��������ƁH���������ɂ�����Ă��ƁH
642�P�R�Q�l�ڂ̑f������
2018/09/07(��) 13:27:38.71ID:NGHIDE3u >>638
�T�y�[�W
k��2��(n+1 k)�(-1)^{n+1-k}�(2pr)^k��0 (mod 8)�ł��邩�̂悤�Ɏv���Ă���̂�������Ȃ����A���ꂪ��������̂�k��3�̂݁B
k��2�ł͐������Ȃ��B
���������A�W�̔{���ł��鎮��ό`������W�̔{���łȂ��Ȃ�Ȃ�Ă�����������
�T�y�[�W
k��2��(n+1 k)�(-1)^{n+1-k}�(2pr)^k��0 (mod 8)�ł��邩�̂悤�Ɏv���Ă���̂�������Ȃ����A���ꂪ��������̂�k��3�̂݁B
k��2�ł͐������Ȃ��B
���������A�W�̔{���ł��鎮��ό`������W�̔{���łȂ��Ȃ�Ȃ�Ă�����������
643�P�R�Q�l�ڂ̑f������
2018/09/07(��) 13:34:46.73ID:Akli3se1 ����Ƙ_���ǂ߂�������������
����͐��E�I�ȉ������Ǝv��
���w�I�^�N�̃A�����J�l�ɋ������狻�����Ă���
����͐��E�I�ȉ������Ǝv��
���w�I�^�N�̃A�����J�l�ɋ������狻�����Ă���
�ύX�_
�E5�y�[�W�̏ؖ���n=1�̏ꍇ������lj����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7091854427984/
Pdf���� �p��
http://fast-uploader.com/file/7091854566009/
�E5�y�[�W�̏ؖ���n=1�̏ꍇ������lj����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7091854427984/
Pdf���� �p��
http://fast-uploader.com/file/7091854566009/
646�P�R�Q�l�ڂ̑f������
2018/09/07(��) 15:13:28.10ID:nW/QiXb6 �ꍇ�����Ƃ��v��Ȃ����H
2�y�[�W����Ώؖ��ł���
2�y�[�W����Ώؖ��ł���
647�P�R�Q�l�ڂ̑f������
2018/09/07(��) 15:49:11.67ID:mbd0IjUn https://twitter.com/mas20285
https://m.facebook.com/masaoki.iwasaki.9
https://i.imgur.com/FCVzFKp.jpg
https://i.imgur.com/5my5F5k.jpg
https://i.imgur.com/P8Q6uHP.jpg
https://i.imgur.com/48t3NAB.jpg
https://i.imgur.com/ftD9n0U.jpg
https://i.imgur.com/fqLVdd3.jpg
https://twitter.com/5chan_nel (5ch newer account)
https://m.facebook.com/masaoki.iwasaki.9
https://i.imgur.com/FCVzFKp.jpg
https://i.imgur.com/5my5F5k.jpg
https://i.imgur.com/P8Q6uHP.jpg
https://i.imgur.com/48t3NAB.jpg
https://i.imgur.com/ftD9n0U.jpg
https://i.imgur.com/fqLVdd3.jpg
https://twitter.com/5chan_nel (5ch newer account)
2018/09/07(��) 19:55:23.84ID:fhdyCk6P
����܂ł̊�|�l�l�^
�Ep�͒萔�ł��肩�ϐ��ł���B
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł����B
�Ew�͐����ł��蓯���ɐ����łȂ��B
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ��B
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂ށB
�E�ϐ��͐��l�ɒu�������Ă̓_���B
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R�B
�E27/5 �� 3 �Ŋ�����B
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂���B
�E���Ȃ��Ƃ���͂����Ȃ�A�Ƃ������Ƃ�
�@�S�Ăɑ��Đ��藧���Ȃ���Ȃ�Ȃ��B
�E���̌`����P��k�Ő��藧�ĂA�S�Ă�k�ł����藧�B
�E�����Ȃ��Ƃ��ؖ����邱�Ƃ͓���B
�E���̘_���͐��������ؖ����邱�Ƃ��ł��܂���B
�E�ؖ��������܂����̂ŁA���𖾂Ƃ������Ƃɂ������B
�E�藝�o�����B���̒藝�̏ؖ����������������ɂȂ��Ă���B
�E�Ō�̖���́A���҂��Ƃ̊O���炻�̖�����m�F�����ƕ������Ă����B
�E�����ɖ\�B�܂�A���������ɂ���B(NEW!)
�Ep�͒萔�ł��肩�ϐ��ł���B
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł����B
�Ew�͐����ł��蓯���ɐ����łȂ��B
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ��B
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂ށB
�E�ϐ��͐��l�ɒu�������Ă̓_���B
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R�B
�E27/5 �� 3 �Ŋ�����B
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂���B
�E���Ȃ��Ƃ���͂����Ȃ�A�Ƃ������Ƃ�
�@�S�Ăɑ��Đ��藧���Ȃ���Ȃ�Ȃ��B
�E���̌`����P��k�Ő��藧�ĂA�S�Ă�k�ł����藧�B
�E�����Ȃ��Ƃ��ؖ����邱�Ƃ͓���B
�E���̘_���͐��������ؖ����邱�Ƃ��ł��܂���B
�E�ؖ��������܂����̂ŁA���𖾂Ƃ������Ƃɂ������B
�E�藝�o�����B���̒藝�̏ؖ����������������ɂȂ��Ă���B
�E�Ō�̖���́A���҂��Ƃ̊O���炻�̖�����m�F�����ƕ������Ă����B
�E�����ɖ\�B�܂�A���������ɂ���B(NEW!)
2018/09/07(��) 20:00:18.71ID:YA7pwD8J
��4b�� �~ pr^qr(pr �| 1) = c(( k=2,n+1](�|1)^(n+1�|k)(2pr)^k) �| 2(n + 1)pr)
��4b�� �~ pr^qr(pr �| 1) �� 0 (mod 8)
��n + 1 ≢ 0 (mod 4)�ł��邩��
��2(n + 1)pr ≢ 0 (mod 8)
���ƂȂ邩��A��L�̍������͐��藧���Ȃ��B
�_�E�g
��4b�� �~ pr^qr(pr �| 1) �� 0 (mod 8)
��n + 1 ≢ 0 (mod 4)�ł��邩��
��2(n + 1)pr ≢ 0 (mod 8)
���ƂȂ邩��A��L�̍������͐��藧���Ȃ��B
�_�E�g
650�P�R�Q�l�ڂ̑f������
2018/09/07(��) 20:20:06.18ID:NGHIDE3u >>645
�Ȃ�n��1�ȊO�Ő������Ǝv����̂�
n��1 (mod 4)�Ȃ�
k��2��(n+1 k)�(-1)^{n+1-k}�(2pr)^k��0 (mod 8)�͐������Ȃ��B
�Ȃ�n��1�ȊO�Ő������Ǝv����̂�
n��1 (mod 4)�Ȃ�
k��2��(n+1 k)�(-1)^{n+1-k}�(2pr)^k��0 (mod 8)�͐������Ȃ��B
2018/09/07(��) 21:57:39.97ID:YA7pwD8J
�ύX�_
�E5�y�[�W�̏ؖ����C�����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7091885256421/
Pdf���� �p��
http://fast-uploader.com/file/7091885341585/
�E5�y�[�W�̏ؖ����C�����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7091885256421/
Pdf���� �p��
http://fast-uploader.com/file/7091885341585/
>>651
n=1�̂Ƃ��������Ǝv���܂���
n=1�̂Ƃ��������Ǝv���܂���
654�P�R�Q�l�ڂ̑f������
2018/09/07(��) 23:37:30.96ID:NGHIDE3u >>652
��b��c pr(p^{n-1}+p^{n-3}+�c+1)
��a��c p^n
��f��L�����Ƃ���
��f��b/(a(p^{n-1}+p^{n-3}+�c+1))
�Ȃ�A����f��
f��b/(a(p^{n-1}+p^{n-3}+�c+1))
��(c pr(p^{n-1}+p^{n-3}+�c+1))/(a(p^{n-1}+p^{n-3}+�c+1))
��(c pr)/a
��(c pr)/(c p^n)
��pr/p^n
�ɂȂ邾��������
��f��p^n���|����ƕ����(p^{n-1}+p^{n-3}+�c+1)���c��
�Ƃ͂Ȃ�Ȃ��B
�Ȃ܂����[�v���n�߂����������邯�Ǒ��v�H
��b��c pr(p^{n-1}+p^{n-3}+�c+1)
��a��c p^n
��f��L�����Ƃ���
��f��b/(a(p^{n-1}+p^{n-3}+�c+1))
�Ȃ�A����f��
f��b/(a(p^{n-1}+p^{n-3}+�c+1))
��(c pr(p^{n-1}+p^{n-3}+�c+1))/(a(p^{n-1}+p^{n-3}+�c+1))
��(c pr)/a
��(c pr)/(c p^n)
��pr/p^n
�ɂȂ邾��������
��f��p^n���|����ƕ����(p^{n-1}+p^{n-3}+�c+1)���c��
�Ƃ͂Ȃ�Ȃ��B
�Ȃ܂����[�v���n�߂����������邯�Ǒ��v�H
2018/09/07(��) 23:38:38.56ID:x0bfFLzz
�����Ɍ������Ⴄ�Ȃ�Ă�������
2018/09/07(��) 23:48:41.01ID:CQb9JfUE
������B
f = b/(a(p^(n�|1) + p^(n�|3) + ⋯ + 1))
�������ł͂Ȃ���p^(n�|1) + p^(n�|3) + ⋯ + 1�̂�����̈��q�������Ă���\��������B
f = b/(a(p^(n�|1) + p^(n�|3) + ⋯ + 1))
�������ł͂Ȃ���p^(n�|1) + p^(n�|3) + ⋯ + 1�̂�����̈��q�������Ă���\��������B
657�P�R�Q�l�ڂ̑f������
2018/09/08(�y) 00:10:31.05ID:uHPEhlQL ���̊w������������A�w��⌤���@�ւɑ����Ă��Ȃ���ʎs���́A�����Ȃ��܂ܘ_�����Ĕ��\�ł��Ȃ��́H
����F�̂��͈̂��p�ʼn҂������Ȃ��̂���
����F�̂��͈̂��p�ʼn҂������Ȃ��̂���
2018/09/08(�y) 00:20:43.83ID:jjlT+UyO
�^�������ɂ��������ꂪ����
2018/09/08(�y) 00:52:25.52ID:f2HWzdLl
>>657
�o�����
�o�����
660�P�R�Q�l�ڂ̑f������
2018/09/08(�y) 07:29:30.75ID:GcbcaRV0 >>657�@����F�̂��̂́A���p�𐔂����Ȃ���c
�����������p����Ȃ��\�����������B
�����������p����Ȃ��\�����������B
2018/09/08(�y) 08:05:19.34ID:z+7YzyeO
>>16�P�R�Q�l�ڂ̑f������2018/08/22(��) 12:41:18.93ID:q5K+5KiU
�����̗���
1.�u�ԈႢ��������܂����A�P�܂��v
��
2.�u(���_�_����Ȃ��Ƃ���)���C�����܂����B�����ł��v
��
3.(�_�_�ɂ��ĕ�����Ă�)�u�������łɒ����܂���(�������ĂȂ�)�B�ǂ�ł��猾���Ă��������v
�����̗���
1.�u�ԈႢ��������܂����A�P�܂��v
��
2.�u(���_�_����Ȃ��Ƃ���)���C�����܂����B�����ł��v
��
3.(�_�_�ɂ��ĕ�����Ă�)�u�������łɒ����܂���(�������ĂȂ�)�B�ǂ�ł��猾���Ă��������v
662�P�R�Q�l�ڂ̑f������
2018/09/08(�y) 09:18:43.63ID:hZTCTQGJ2018/09/08(�y) 09:35:50.27ID:oy9IEf9x
>>662
�����̘_��������ƁA�ǂ��ɂ��������A����͏����ĂȂ�����A
�������A����̓W���[�i��(���w�G��)�ł̘_�����\�ɓ�����A�傫�ȗv�f�ł͂Ȃ��悤���B
���̑��ɂ��A�_���\������ɏ������A���悪�ς��\�����\���ɍl������B
�����������Ƃ܂���ƁA��͂�A���e�ɐ��w�I���l��V�m��������A
�W���[�i��(���w�G��)�ɂ��_�����\�o����ƍl������B
�����̘_��������ƁA�ǂ��ɂ��������A����͏����ĂȂ�����A
�������A����̓W���[�i��(���w�G��)�ł̘_�����\�ɓ�����A�傫�ȗv�f�ł͂Ȃ��悤���B
���̑��ɂ��A�_���\������ɏ������A���悪�ς��\�����\���ɍl������B
�����������Ƃ܂���ƁA��͂�A���e�ɐ��w�I���l��V�m��������A
�W���[�i��(���w�G��)�ɂ��_�����\�o����ƍl������B
664�P�R�Q�l�ڂ̑f������
2018/09/08(�y) 09:54:57.79ID:GcbcaRV0 >>663 �����Ƃ��A�Ⴊ�Â��c
2018/09/08(�y) 10:44:12.25ID:oy9IEf9x
>>664
���݂̊C�O�̃W���[�i��(���}�̂̐��w�G��)�̓��e�v�̂�ǂ�ł��A
�K�������������A����(�������錤���@�ւƂ��̘A����)�������K�v������Ƃ͌���Ȃ��悤���B
���̓_���画�f����ƁA���e�ɐ��w�I���l��V�m��������A�W���[�i��(���}�̂̐��w�G��)�ɂ��_�����\�o����B
�_���f�ڌ�ɏ������A����(�������錤���@�ւƂ��̘A����)���ς�邱�Ƃ�
���{�łȂ���A�\�����蓾�邩��A�����͘_���f�ڂɂ����ė]��d�v�ȗv�f�ł͂Ȃ��B
���{�l�̏ꍇ�́A�R�т������Z�߂鍑�y�ʐς͏��Ȃ�����A�������A����������Ȃ�A
�Ƃ̏Z���ł��������������ꂪ�ς��\�������Ȃ��܂��Ӗ�������B
�Ⴆ�����łȂ��Ă��A���R�ЊQ�Ȃǂʼn��M�s�ʂɂȂ��ĘA�������Ȃ��Ȃ�\���͐��E���ǂ��ɂł�����B
���݂̊C�O�̃W���[�i��(���}�̂̐��w�G��)�̓��e�v�̂�ǂ�ł��A
�K�������������A����(�������錤���@�ւƂ��̘A����)�������K�v������Ƃ͌���Ȃ��悤���B
���̓_���画�f����ƁA���e�ɐ��w�I���l��V�m��������A�W���[�i��(���}�̂̐��w�G��)�ɂ��_�����\�o����B
�_���f�ڌ�ɏ������A����(�������錤���@�ւƂ��̘A����)���ς�邱�Ƃ�
���{�łȂ���A�\�����蓾�邩��A�����͘_���f�ڂɂ����ė]��d�v�ȗv�f�ł͂Ȃ��B
���{�l�̏ꍇ�́A�R�т������Z�߂鍑�y�ʐς͏��Ȃ�����A�������A����������Ȃ�A
�Ƃ̏Z���ł��������������ꂪ�ς��\�������Ȃ��܂��Ӗ�������B
�Ⴆ�����łȂ��Ă��A���R�ЊQ�Ȃǂʼn��M�s�ʂɂȂ��ĘA�������Ȃ��Ȃ�\���͐��E���ǂ��ɂł�����B
2018/09/08(�y) 11:13:17.55ID:Ma4qC+vh
>>665
���Ȃ����������ƌĂ�Ă�l�ł���ˁH
���Ȃ����������ƌĂ�Ă�l�ł���ˁH
667�P�R�Q�l�ڂ̑f������
2018/09/08(�y) 12:11:58.18ID:4Fx9hJhi �C�O�̃W���[�i�����ɋ����Ă������A��͂���{�̎G���ɓ��{��Œ�o����悤�ȃ��m�́A�C�O�ł͌��Ă��炦�Ȃ��ӎU�L���G������Ȃ낤��
2018/09/08(�y) 13:09:20.22ID:oy9IEf9x
>>667
���݁A(�������m�����ł�)���{��Ř_����������W���[�i��(���w�G��)�͂Ȃ��Ƃ����Ă����B
���{�ꂪ�ǂ߂�l�̑唼�͓��{�l�Ƃ����Ă悢�B������A���{�̎G���ɓ��{��ŏ�������A
���̓��e���p�ĊC�O�̐l�ɗ�������Ȃ��Ɛ��E�ɂ͍L�܂�ɂ����B
���̂悤�ɐ��E�ɍL�߂邱�Ƃ́A���w�I���l�Ƃ͂܂��ʂ̘b�ɂȂ�B
��T�ɁA���{�̎G�����C�O�ł͌��Ă��炦�Ȃ��ӎU�L�����m����Ƃ͂����Ȃ��B
���݁A(�������m�����ł�)���{��Ř_����������W���[�i��(���w�G��)�͂Ȃ��Ƃ����Ă����B
���{�ꂪ�ǂ߂�l�̑唼�͓��{�l�Ƃ����Ă悢�B������A���{�̎G���ɓ��{��ŏ�������A
���̓��e���p�ĊC�O�̐l�ɗ�������Ȃ��Ɛ��E�ɂ͍L�܂�ɂ����B
���̂悤�ɐ��E�ɍL�߂邱�Ƃ́A���w�I���l�Ƃ͂܂��ʂ̘b�ɂȂ�B
��T�ɁA���{�̎G�����C�O�ł͌��Ă��炦�Ȃ��ӎU�L�����m����Ƃ͂����Ȃ��B
669�P�R�Q�l�ڂ̑f������
2018/09/08(�y) 16:10:21.32ID:N4UF+kJ4 �_�������̂߂�ǂ�����A�v�|�����Ă���
p=�g�h; q=p-1;
x=�g�h; y=x-1
�����Z���k���FM(p)=2^x-1
�g�����ꂽ�����Z���k���FM�f(p)=p^x-q^x;
��l��N=p^y*M�f(p)
p,x���f���A���AM�f(p)���f���̉��ł�
�̑��a��(N)�ɂ��āA���̎������藧�B
q(��(N)-N)-N-M(p)-q^x+2^x=0
�܂��Ap,x,M�f(p)�̂�����1�ł��f���łȂ�
���������������ł�
q(��(N)-N)-N-M(p)-q^x+2^x>0�ƂȂ�B
���Ȃ݂�
q(��(N)-N)-N-M(p)-q^x+2^x<0�͑��݂��Ȃ��B
�Ƃ���ŁA���S���̓�(N)=2N�ł���B
x=2�̎��Ap�ɉ�����M�f(p)�͑S�Ă̊�f����ԗ��ł���
�����ŁA�@�����ڍ�
��(N)-N=N+M(p)+q^x-2^x
N=N+q^2-1
���̂悤��N�͑��݂��Ȃ��B
���������āA��̊��S���͑��݂��Ȃ��BQ.E.D
p=�g�h; q=p-1;
x=�g�h; y=x-1
�����Z���k���FM(p)=2^x-1
�g�����ꂽ�����Z���k���FM�f(p)=p^x-q^x;
��l��N=p^y*M�f(p)
p,x���f���A���AM�f(p)���f���̉��ł�
�̑��a��(N)�ɂ��āA���̎������藧�B
q(��(N)-N)-N-M(p)-q^x+2^x=0
�܂��Ap,x,M�f(p)�̂�����1�ł��f���łȂ�
���������������ł�
q(��(N)-N)-N-M(p)-q^x+2^x>0�ƂȂ�B
���Ȃ݂�
q(��(N)-N)-N-M(p)-q^x+2^x<0�͑��݂��Ȃ��B
�Ƃ���ŁA���S���̓�(N)=2N�ł���B
x=2�̎��Ap�ɉ�����M�f(p)�͑S�Ă̊�f����ԗ��ł���
�����ŁA�@�����ڍ�
��(N)-N=N+M(p)+q^x-2^x
N=N+q^2-1
���̂悤��N�͑��݂��Ȃ��B
���������āA��̊��S���͑��݂��Ȃ��BQ.E.D
2018/09/08(�y) 16:23:09.82ID:VHlQxVrF
���[���A�ؖ����ꂿ�������
2018/09/08(�y) 16:25:55.63ID:4yqv06N+
���A�ł������
2018/09/08(�y) 16:49:27.96ID:7vbYuAvM
M�f(p)�̂Ƃ���͕������łȂ���Ȃ�Ȃ��Ǝv���܂���
673�P�R�Q�l�ڂ̑f������
2018/09/08(�y) 17:56:21.33ID:WKlkldB7 ���ׂĂ̊�f���̂�����͌��ł���
M�f(p)���f���ł�p���f���łȂ���Ύ��ɂ͓��Ă͂܂�Ȃ��ł���
�s�������ɂ���悩����
M�f(p)���f���ł�p���f���łȂ���Ύ��ɂ͓��Ă͂܂�Ȃ��ł���
�s�������ɂ���悩����
674�P�R�Q�l�ڂ̑f������
2018/09/08(�y) 18:30:32.46ID:NFJ399UI �f�������Q��ނ̊�Ɍ���Ί��S�������݂��Ȃ��Ƃ����̂͊��m
������ؖ������Ƃ���Ŋ�̊��S�������݂��Ȃ��ؖ��ɂ͂Ȃ��
������ؖ������Ƃ���Ŋ�̊��S�������݂��Ȃ��ؖ��ɂ͂Ȃ��
675�P�R�Q�l�ڂ̑f������
2018/09/08(�y) 19:28:14.72ID:WKlkldB7 �����Z���k�f���͂����2^n-1^n�̌^
3^101-2^101�ł�47^17-46^17�ł�
������ł��f���͌���������Ȃ�
3^101-2^101�ł�47^17-46^17�ł�
������ł��f���͌���������Ȃ�
2018/09/08(�y) 21:04:00.89ID:y6B+s78/
�f���ɕБ��˂���������I��肾
677669
2018/09/09(��) 10:44:58.98ID:YBIcJdkB >>672
�ǂ��������ƁH
669�ł��B
���̎��́A�ʂ̗p�r�Ō��������̂ł�����
�������Ƃ��ẮA��炩�����s�������ł��B
�܂��A�X���Ⴂ�ɂȂ�̂�
����x�ɂ��ĕX�I��x�ƕ\�����܂�����
p�Ɛ[������������AM�f(p)�o����ׂ�x��p��p�����`�ł��\���ł��邩�Ǝv���܂��B
�ėp��������̂ŐF�X���݂Ă��������B
�����S�������Ă������������A�_���Ȃǂ��쐻���Ă���������͌l�I�ɂ����k���������B
https://m.facebook.com/katsuyoshi.takahashi.1
�ǂ��������ƁH
669�ł��B
���̎��́A�ʂ̗p�r�Ō��������̂ł�����
�������Ƃ��ẮA��炩�����s�������ł��B
�܂��A�X���Ⴂ�ɂȂ�̂�
����x�ɂ��ĕX�I��x�ƕ\�����܂�����
p�Ɛ[������������AM�f(p)�o����ׂ�x��p��p�����`�ł��\���ł��邩�Ǝv���܂��B
�ėp��������̂ŐF�X���݂Ă��������B
�����S�������Ă������������A�_���Ȃǂ��쐻���Ă���������͌l�I�ɂ����k���������B
https://m.facebook.com/katsuyoshi.takahashi.1
2018/09/09(��) 11:04:57.62ID:GEK+7SXH
2018/09/09(��) 11:08:24.75ID:p+giZO8u
������o(^-^ o )(�� ^-^)��ܸܸ��
2018/09/09(��) 11:52:57.19ID:RjxBIEdK
���_���Ȃǂ��쐻���Ă����������
����H�P�̓��ނ���ł������B
����H�P�̓��ނ���ł������B
681�P�R�Q�l�ڂ̑f������
2018/09/09(��) 13:29:12.08ID:56JMVQ/i ��������Wikipedia�ɉ��M���Ƃ���
2018/09/09(��) 14:25:30.10ID:RjxBIEdK
��|�l�̍��ڂɁH�H�H
683�P�R�Q�l�ڂ̑f������
2018/09/09(��) 15:40:43.91ID:O3k6lc0R ����ς���яo���Ɩ}�l�Ɏ��i�����悤����
2018/09/09(��) 19:03:02.63ID:BVSPFEne
�܂x�S(�L�D�M*)Ɂ܂x�܂x�� �S(o�L�́M)ɬ�ΰ��
2018/09/09(��) 20:03:19.81ID:UnS5lVgQ
686�P�R�Q�l�ڂ̑f������
2018/09/09(��) 20:23:58.11ID:pvl3eTy/ �P��ID
ID:UnS5lVgQ
ID:UnS5lVgQ
687�P�R�Q�l�ڂ̑f������
2018/09/10(��) 00:13:14.99ID:FbUHsbGg2018/09/10(��) 00:15:13.18ID:g/z0YQb3
>>1���Ȃ��Ȃ����������
2018/09/10(��) 01:26:15.18ID:GA8rqAam
�����!�o����>>1!!
�@ �ޯ�݁@�@ �ް�
�@�@�@ _ �ޯ�݁@ ��
������( )�@�@�@�^
`�ȁ�_�b|�Q�Q�Q�@�ȁ�
(�@�@)�b||�@�@ |(�D�M)
f�@ ��~ ||�@�@ |�b �@�_
|�@�@/�P |�@�@ |/|�@/ /
|�@ �b�@ | �w�^�_|_/ /
|�@ �b�@�|ہ_�^�_(�Q�)
( (_ �_�@|�@�@ | �x /
| ||�_ �R|�@�@ | �b�b
| || / / |�@�@ | �b�b
| ||/ /�Q|�Q�Q_| �b�b
(�Q(�Q)�@�@�@�@ (_�Q)
�@ �ޯ�݁@�@ �ް�
�@�@�@ _ �ޯ�݁@ ��
������( )�@�@�@�^
`�ȁ�_�b|�Q�Q�Q�@�ȁ�
(�@�@)�b||�@�@ |(�D�M)
f�@ ��~ ||�@�@ |�b �@�_
|�@�@/�P |�@�@ |/|�@/ /
|�@ �b�@ | �w�^�_|_/ /
|�@ �b�@�|ہ_�^�_(�Q�)
( (_ �_�@|�@�@ | �x /
| ||�_ �R|�@�@ | �b�b
| || / / |�@�@ | �b�b
| ||/ /�Q|�Q�Q_| �b�b
(�Q(�Q)�@�@�@�@ (_�Q)
2018/09/11(��) 20:20:03.89ID:wKHn9EsE
�ύX�_
�En��5�̂Ƃ��̏ؖ����C�����܂���
�Ep=8s+5�ƂȂ�ؖ���lj����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7092236901884/
Pdf���� �p��
http://fast-uploader.com/file/7092236976086/
�En��5�̂Ƃ��̏ؖ����C�����܂���
�Ep=8s+5�ƂȂ�ؖ���lj����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7092236901884/
Pdf���� �p��
http://fast-uploader.com/file/7092236976086/
>>1 ����
2018�N8��22����2018�N9��12��
2018�N8��22����2018�N9��12��
2018/09/12(��) 02:17:37.08ID:pJvSAofP
gp^2 + (g + 2c)p = 0
p �� 0������
gp = g + 2c
p �� 0������
gp = g + 2c
2018/09/12(��) 05:51:59.45ID:2kZzTDUR
�����S�~�o�c�e��߂�
695�P�R�Q�l�ڂ̑f������
2018/09/12(��) 05:55:57.26ID:THt4vpWn �s�������Ԍ�������
����PDF�ł���Ӗ��Ȃ���Ȃ��H
����PDF�ł���Ӗ��Ȃ���Ȃ��H
2018/09/12(��) 08:26:11.68ID:EavOG0bu
��������Ȃ�����
�ύX�_
�Ec��pr^(qr-1)�Ŋ�����Ȃ����Ƃ̏ؖ���lj����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7092267324116/
Pdf���� �p��
http://fast-uploader.com/file/7092267386982/
�Ec��pr^(qr-1)�Ŋ�����Ȃ����Ƃ̏ؖ���lj����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7092267324116/
Pdf���� �p��
http://fast-uploader.com/file/7092267386982/
2018/09/12(��) 09:51:44.52ID:VSnQRq0b
����ȗ����̂Ȃ���n�O�ɂ�闎������
�S�~�o�c�e�Ƃ��ƂƂ�߂�
�S�~�o�c�e�Ƃ��ƂƂ�߂�
2018/09/12(��) 12:40:01.06ID:fs6vDAMm
���̃_�E�����[�h�t�H���_���������PDF�ł����ς�
700�P�R�Q�l�ڂ̑f������
2018/09/12(��) 13:23:47.71ID:/NAZ8qoe �҂đ҂�
��4b�� �~ pr^qr(pr �| 1) ≢ 0 (mod 16) �c�H
����͉��̐��藧�̂��H
�H���O�ɏ����ꂽ���_�݂̂��g���ďq�ׂ�
��4b�� �~ pr^qr(pr �| 1) ≢ 0 (mod 16) �c�H
����͉��̐��藧�̂��H
�H���O�ɏ����ꂽ���_�݂̂��g���ďq�ׂ�
701�P�R�Q�l�ڂ̑f������
2018/09/12(��) 13:36:07.88ID:M0oAD/XI ��a�� = a/pr^{qr�|1}�Ab�� = b/pr^{qr�|1}�Ac�� = c/pr^{qr�|1}�ƂȂ��Ƃ���ƁA���E����
��2pr �| 1 = (2b��pr �| c��)/(2b��pr �| a��)
�_�E�g
��2pr �| 1 = (2b��pr �| c��)/(2b��pr �| a��)
�_�E�g
>>700
���̕����͊ԈႢ�ł���
���̕����͊ԈႢ�ł���
2018/09/12(��) 14:31:29.05ID:WukLzqOv
>>700
����������l�܂����B
2b�� �~ pr^qr = c(p^(n+1) �| 1)/(p �| 1) = c((2pr �| 1)^(n+1) �| 1)/(2pr �| 2)
4b�� �~ pr^qr(pr �| 1) = c(p^(n+1) �| 1)
4b�� �~ pr^qr(pr �| 1) ≢ 0 (mod 16) �c�H
�H�����o�ł��鎮�͏��Ȃ��Ƃ����s�ȓ��ɂ͌�������Ȃ��B
����������l�܂����B
2b�� �~ pr^qr = c(p^(n+1) �| 1)/(p �| 1) = c((2pr �| 1)^(n+1) �| 1)/(2pr �| 2)
4b�� �~ pr^qr(pr �| 1) = c(p^(n+1) �| 1)
4b�� �~ pr^qr(pr �| 1) ≢ 0 (mod 16) �c�H
�H�����o�ł��鎮�͏��Ȃ��Ƃ����s�ȓ��ɂ͌�������Ȃ��B
�ύX�_
�Ep=8s+5�ƂȂ邱�Ƃ̏ؖ����폜���܂���
�E���ԍ����C�����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7092287778087/
Pdf���� �p��
http://fast-uploader.com/file/7092287896599/
�Ep=8s+5�ƂȂ邱�Ƃ̏ؖ����폜���܂���
�E���ԍ����C�����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7092287778087/
Pdf���� �p��
http://fast-uploader.com/file/7092287896599/
2018/09/12(��) 15:11:36.38ID:VSnQRq0b
�_���_��
�w�E����Ă�_�͑S��������
�w�E����Ă�_�͑S��������
707�P�R�Q�l�ڂ̑f������
2018/09/12(��) 15:20:39.86ID:OZYyDdC8 >>707
p=2pr-1�Ab=b'�~pr^qr������
p=2pr-1�Ab=b'�~pr^qr������
>>708�@����
����������܂���ł����D�D�D
����������܂���ł����D�D�D
2018/09/12(��) 15:56:07.66ID:EavOG0bu
��������R�}
2018/09/12(��) 16:15:20.10ID:Rf5hWR82
�P���������ؖ��ɂ��ǂ蒅���\����
�O�ǂ��납�}�C�i�X
�O�ǂ��납�}�C�i�X
�ύX�_
�En��5�̂Ƃ��̏ؖ����C�����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7092352843051/
Pdf���� �p��
http://fast-uploader.com/file/7092352906618/
�En��5�̂Ƃ��̏ؖ����C�����܂���
Pdf���� ���{��
http://fast-uploader.com/file/7092352843051/
Pdf���� �p��
http://fast-uploader.com/file/7092352906618/
>>1 ����
2018�N8��22����2018�N9��13��
2018�N8��22����2018�N9��13��
2018/09/13(��) 09:33:18.36ID:oDQkArml
4b(pr �| 1)/c + 1 �� (4b + c)/c (mod 2pr �| 1)
����͂Ȃ��H
����͂Ȃ��H
2018/09/13(��) 09:36:19.05ID:5WEZ5txO
��ӂ��琬�藧�Ɍ��܂��Ă�
2018/09/13(��) 09:51:33.57ID:bfdAt7wV
�P���Ⴀ�A�ǂ��ɂ��Ȃ�Ȃ����Ă���w�E����Ă�̂Ɂ`�B
�������ƒ��w���w���炢����\���ɕ�����̂�
�P�����w�𗝉����邽�߂̗B��̓��B
�ϑz�̐��w�͐��w�ł͕s��
�������ƒ��w���w���炢����\���ɕ�����̂�
�P�����w�𗝉����邽�߂̗B��̓��B
�ϑz�̐��w�͐��w�ł͕s��
718�P�R�Q�l�ڂ̑f������
2018/09/13(��) 10:44:01.19ID:amO/EZXR �P�ɂ͖����Ȃ̂��ǂ����͒u���Ă����Ƃ��Ă��A
����܂ł̂P�̃~�X�ŁA���́u�����̌v�Z�ԈႢ�v�����܂�ɂ���������͖̂�肾�Ǝv����
����W���������āA���̎���ό`�����猳�̊W���ƈႤ���ʂ��o�����疵������BQED
�Ə����ꂽ���̂��A���̊Ԃ̕ό`�Ƀ~�X���������ēP���P�[�X�����ɑ����B
�_�����o����O�ɂ悭�������Ȃ����Ɖ��x�������Ă��邪�A
�����Č����ƁA���x�ł��������ĉ��������̂͏o���Ȃ��悤�ɂ����ق��������B
�ȒP�ȊԈႢ�����x���J��Ԃ��̂ŐM�����������Ȃ��Ă����ʂ�����Ǝv���B
�Ȃ̂ŁA���x���������ǁA��[�[�����������Ă���o�����ق����ǂ���B
����܂ł̂P�̃~�X�ŁA���́u�����̌v�Z�ԈႢ�v�����܂�ɂ���������͖̂�肾�Ǝv����
����W���������āA���̎���ό`�����猳�̊W���ƈႤ���ʂ��o�����疵������BQED
�Ə����ꂽ���̂��A���̊Ԃ̕ό`�Ƀ~�X���������ēP���P�[�X�����ɑ����B
�_�����o����O�ɂ悭�������Ȃ����Ɖ��x�������Ă��邪�A
�����Č����ƁA���x�ł��������ĉ��������̂͏o���Ȃ��悤�ɂ����ق��������B
�ȒP�ȊԈႢ�����x���J��Ԃ��̂ŐM�����������Ȃ��Ă����ʂ�����Ǝv���B
�Ȃ̂ŁA���x���������ǁA��[�[�����������Ă���o�����ق����ǂ���B
2018/09/13(��) 10:47:52.28ID:bfdAt7wV
�ŋ߂o�c�e�͂����폜����悤�ɂȂ������E�E�E
�u�����̌v�Z�ԈႢ�v���Ă���̂o�c�e�����P�����\�����S�������B
�u�����̌v�Z�ԈႢ�v���Ă���̂o�c�e�����P�����\�����S�������B
2018/09/13(��) 12:49:04.65ID:4TAIYqIY
�܂����\�X���^�C��ς���
2018/09/13(��) 13:14:29.57ID:6uYZkQBQ
>>715
�Ƃ͂����Ă�
>4b(pr �| 1)/c + 1 �� (4b + c)/c (mod 2pr �| 1)
�̗��ӂ�mod�̒�`���瓾���鎮�ό`�ł� 2pr �� 1 (mod 2pr -1) �𗘗p����
4b(pr �| 1)/c + 1
�� (4bpr -4b)/c +1 (mod 2pr -1)
�� (2b -4b)/c +1 (mod 2pr -1)
�� (-2b+c)/c (mod 2pr -1)
�ɂ����Ȃ��Ǝv�����ǁB
�Ƃ͂����Ă�
>4b(pr �| 1)/c + 1 �� (4b + c)/c (mod 2pr �| 1)
�̗��ӂ�mod�̒�`���瓾���鎮�ό`�ł� 2pr �� 1 (mod 2pr -1) �𗘗p����
4b(pr �| 1)/c + 1
�� (4bpr -4b)/c +1 (mod 2pr -1)
�� (2b -4b)/c +1 (mod 2pr -1)
�� (-2b+c)/c (mod 2pr -1)
�ɂ����Ȃ��Ǝv�����ǁB
2018/09/13(��) 13:25:51.19ID:6uYZkQBQ
2018/09/13(��) 13:41:19.11ID:3YkkLjYC
>>718
�m���������ĂĂ��L�[�{�[�h�̒��q������������Ȃ���������
�m���������ĂĂ��L�[�{�[�h�̒��q������������Ȃ���������
>>721
���q�ɂ���4��2��ɂ���Ƃ����v�Z�ԈႢ�ł��B
���̖�����������ƁA��{�I�Ɍv�Z�ԈႢ�����Ȃ��Əؖ��I���ɂȂ�܂���B
���̂��߁A�ł����Ǝv���Č��J����ƁA���̌�A�v�Z�ԈႢ�����Ă���Ƃ������ƂɂȂ�܂��B
���q�ɂ���4��2��ɂ���Ƃ����v�Z�ԈႢ�ł��B
���̖�����������ƁA��{�I�Ɍv�Z�ԈႢ�����Ȃ��Əؖ��I���ɂȂ�܂���B
���̂��߁A�ł����Ǝv���Č��J����ƁA���̌�A�v�Z�ԈႢ�����Ă���Ƃ������ƂɂȂ�܂��B
2018/09/13(��) 16:56:45.40ID:50rcywMi
���v�Z�ԈႢ�����Ȃ��Əؖ��I���ɂȂ�܂���B
���E��F�߂��̂Ȃ�A���̖�肩������������
���E��F�߂��̂Ȃ�A���̖�肩������������
2018/09/13(��) 17:16:34.80ID:KRaxSxXR
����܂ł̊�|�l�l�^
�Ep�͒萔�ł��肩�ϐ��ł���B
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł����B
�Ew�͐����ł��蓯���ɐ����łȂ��B
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ��B
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂ށB
�E�ϐ��͐��l�ɒu�������Ă̓_���B
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R�B
�E27/5 �� 3 �Ŋ�����B
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂���B
�E���Ȃ��Ƃ���͂����Ȃ�A�Ƃ������Ƃ�
�@�S�Ăɑ��Đ��藧���Ȃ���Ȃ�Ȃ��B
�E���̌`����P��k�Ő��藧�ĂA�S�Ă�k�ł����藧�B
�E�����Ȃ��Ƃ��ؖ����邱�Ƃ͓���B
�E���̘_���͐��������ؖ����邱�Ƃ��ł��܂���B
�E�ؖ��������܂����̂ŁA���𖾂Ƃ������Ƃɂ������B
�E�藝�o�����B���̒藝�̏ؖ����������������ɂȂ��Ă���B
�E�Ō�̖���́A���҂��Ƃ̊O���炻�̖�����m�F�����ƕ������Ă����B
�E�����ɖ\�B�܂�A���������ɂ���B
�E�v�Z�ԈႢ�����Ȃ��Əؖ��I���ɂȂ�Ȃ��B(NEW!)
�Ep�͒萔�ł��肩�ϐ��ł���B
�E�����͐�������Ɍ��܂��Ă�B����ȊȒP�Ȃ��Ƃ��킩��Ȃ��̂ł����B
�Ew�͐����ł��蓯���ɐ����łȂ��B
�E2m+1�͈�������2m+1�̔{���ł͂Ȃ��B
�Ea=b/3�Ȃ�Aa��b�������Ɋ܂ށB
�E�ϐ��͐��l�ɒu�������Ă̓_���B
�E(A�~B)/C:�������� B/C:�� �� A/C:�����͓��R�B
�E27/5 �� 3 �Ŋ�����B
�E��`�͂��Ă��܂����A�l�͒�߂Ă��܂���B
�E���Ȃ��Ƃ���͂����Ȃ�A�Ƃ������Ƃ�
�@�S�Ăɑ��Đ��藧���Ȃ���Ȃ�Ȃ��B
�E���̌`����P��k�Ő��藧�ĂA�S�Ă�k�ł����藧�B
�E�����Ȃ��Ƃ��ؖ����邱�Ƃ͓���B
�E���̘_���͐��������ؖ����邱�Ƃ��ł��܂���B
�E�ؖ��������܂����̂ŁA���𖾂Ƃ������Ƃɂ������B
�E�藝�o�����B���̒藝�̏ؖ����������������ɂȂ��Ă���B
�E�Ō�̖���́A���҂��Ƃ̊O���炻�̖�����m�F�����ƕ������Ă����B
�E�����ɖ\�B�܂�A���������ɂ���B
�E�v�Z�ԈႢ�����Ȃ��Əؖ��I���ɂȂ�Ȃ��B(NEW!)
2018/09/13(��) 18:01:52.47ID:50rcywMi
�ȑO���������|�l�l�^���o����A�F�œ˂����݂܂����Ă��̂�
���ł͂P������҂łȂ����Ƃ��F���m��悤�ɂȂ��ĕ��u��ԁB
�������ɖ\�B�܂�A���������ɂ���B
�����P�ɂ́A���S�����̂��܂�ŗ����ł������ɂȂ��B
���ł͂P������҂łȂ����Ƃ��F���m��悤�ɂȂ��ĕ��u��ԁB
�������ɖ\�B�܂�A���������ɂ���B
�����P�ɂ́A���S�����̂��܂�ŗ����ł������ɂȂ��B
728�P�R�Q�l�ڂ̑f������
2018/09/13(��) 18:43:15.15ID:2CGnJSNJ �ԈႢ������Ƃ킩���Ă��āA����ł��ؖ��ł����ƌ����Č��J������炱��قǍߐ[�����Ƃ͖���
�Ђƌ��ł����ĝs���B�ӂ����ł����Α�E�\���B
�Ђƌ��ł����ĝs���B�ӂ����ł����Α�E�\���B
729�P�R�Q�l�ڂ̑f������
2018/09/13(��) 19:11:32.93ID:9FFoivBG �����w��1-F�S�C�̊�薏�T�搶�����o�C�B
�����w���ɋ߂�̂�3�N�ځB
�S���Ȗڂ͐��w�B
�����͏��q�e�j�X���B
�������o�C�Ƃ����ƁA2013�N4������2015�N3���܂ŋ{�O�����ɓ����Ă������ǁA���q���w����sex�������Ƃ��o���āA����ꂽ����B
���ł����t�𑱂��Ă���̂��������s�v�c�Ȋ�������B
���搶���āA�c�C�b�^�[��Facebook������Ă�݂���������A�`���Ă݂ẮH
https://m.facebook.com/masaoki.iwasaki.9
https://twitter.com/mas20285
https://twitter.com/keepmathtop
https://twitter.com/kyuuchan_
https://twitter.com/xPuGPq8Tn9GWCJb
https://twitter.com/K46_N700_hikari
https://i.imgur.com/XXY6Rfk.jpg
https://i.imgur.com/BrrFXSr.jpg
https://i.imgur.com/i1WRQyw.jpg
https://i.imgur.com/Pa5DL6H.png
https://i.imgur.com/9lOaj7U.jpg
https://i.imgur.com/jIgo5Z3.jpg
https://i.imgur.com/VdRcoPQ.png
https://i.imgur.com/18LTARK.png
https://twitter.com/5chan_nel (5ch newer account)
�����w���ɋ߂�̂�3�N�ځB
�S���Ȗڂ͐��w�B
�����͏��q�e�j�X���B
�������o�C�Ƃ����ƁA2013�N4������2015�N3���܂ŋ{�O�����ɓ����Ă������ǁA���q���w����sex�������Ƃ��o���āA����ꂽ����B
���ł����t�𑱂��Ă���̂��������s�v�c�Ȋ�������B
���搶���āA�c�C�b�^�[��Facebook������Ă�݂���������A�`���Ă݂ẮH
https://m.facebook.com/masaoki.iwasaki.9
https://twitter.com/mas20285
https://twitter.com/keepmathtop
https://twitter.com/kyuuchan_
https://twitter.com/xPuGPq8Tn9GWCJb
https://twitter.com/K46_N700_hikari
https://i.imgur.com/XXY6Rfk.jpg
https://i.imgur.com/BrrFXSr.jpg
https://i.imgur.com/i1WRQyw.jpg
https://i.imgur.com/Pa5DL6H.png
https://i.imgur.com/9lOaj7U.jpg
https://i.imgur.com/jIgo5Z3.jpg
https://i.imgur.com/VdRcoPQ.png
https://i.imgur.com/18LTARK.png
https://twitter.com/5chan_nel (5ch newer account)
>>727
�����ɖ\�ɂ͂Ȃ�Ȃ�����A���̕����͕s�K���B
�ԈႢ���w�E����̂͊ȒP�B�ؖ����������������ƘJ�͂��|����B
����n���ɂ���̂͂���Ⴂ���r�������B
�����ɖ\�ɂ͂Ȃ�Ȃ�����A���̕����͕s�K���B
�ԈႢ���w�E����̂͊ȒP�B�ؖ����������������ƘJ�͂��|����B
����n���ɂ���̂͂���Ⴂ���r�������B
2018/09/13(��) 21:11:43.64ID:1FbVNb1W
�_��������荸�ǂ̂ق�����ςȂ�Ȃ��̂�
2018/09/13(��) 21:48:47.34ID:WAJHAfoK
�����ɖ\���Ȃ�Ďv���������ł���O���킵�Ă�B
�J�͂��ǂ��̂����̂Ƃ͎������Ⴄ�B
�J�͂��ǂ��̂����̂Ƃ͎������Ⴄ�B
733�P�R�Q�l�ڂ̑f������
2018/09/13(��) 21:53:31.60ID:LUuqRwR9 �ǂ����R���ƃo����U�ؖ����ł����グ�邾���̂��߂ɂ���ȂɘJ�͎g���Ăǂ������
2018/09/14(��) 02:21:58.58ID:o4HsTSI6
735�P�R�Q�l�ڂ̑f������
2018/09/14(��) 09:23:16.42ID:tMy3g3nw >>730
���ԈႢ���w�E����̂͊ȒP�B�ؖ����������������ƘJ�͂��|����B
���N���������ؖ��Ȃ�A�J�͂�������Ƃ͌����邾�낤���ǁA
�M���̏ؖ��͐������Ƃɉ��������悤�Ȃ��̂�����A
���l���猩��ƁA�J�͂��������Ă���悤�Ɍ����Ȃ��B
���ԈႢ���w�E����̂͊ȒP�B�ؖ����������������ƘJ�͂��|����B
���N���������ؖ��Ȃ�A�J�͂�������Ƃ͌����邾�낤���ǁA
�M���̏ؖ��͐������Ƃɉ��������悤�Ȃ��̂�����A
���l���猩��ƁA�J�͂��������Ă���悤�Ɍ����Ȃ��B
736�P�R�Q�l�ڂ̑f������
2018/09/14(��) 09:24:49.71ID:tMy3g3nw >>732�@���ʂȂ�v�����Ȃ����̂ɁA����Ӗ��Ŗʔ����������ǂˁB
737�P�R�Q�l�ڂ̑f������
2018/09/14(��) 09:38:28.89ID:tMy3g3nw >>731�@������͖{���̌����҂���Ȃ�����A
���l�̌����𗝉����邱�Ƃ̑�ς����킩��Ȃ���B
���l�̌����𗝉����邱�Ƃ̑�ς����킩��Ȃ���B
2018/09/14(��) 10:03:59.21ID:MSNvUASt
�E�P�̏��������̂��A���܂�ɂ������B
�E���炩�ȊԈႢ���炯�Ȃ̂ɁA�P�͐������ƌ�������B
�E�e�ȃX���Z�l�������P���l�|����B
�E���炩�ȊԈႢ���w�E���Ă��P���������Ȃ��B
�E�������݂��������w�I�Ȃ����łP�́A�����ł��Ȃ��ƌ����ē�����B
�EA��B��B��A�̋�ʂ��ł��Ȃ��B
�E�́̋�ʂ��ł��Ȃ��B
�E�w���@���킩���ĂȂ��B
�E�撣���Đ��w���ۂ����t�g�������悤�Ɛ���t�w�L�т��Ă�̂��ɁX����
�E�e���r���玩���̈�������������Ɣ�������B
�E��O���킵����|�l�l�^���P����o�Ă��A�X���Z�l�ɑ���ɂ���Ȃ��Ȃ��Ă����B
�E���炩�ȊԈႢ���炯�Ȃ̂ɁA�P�͐������ƌ�������B
�E�e�ȃX���Z�l�������P���l�|����B
�E���炩�ȊԈႢ���w�E���Ă��P���������Ȃ��B
�E�������݂��������w�I�Ȃ����łP�́A�����ł��Ȃ��ƌ����ē�����B
�EA��B��B��A�̋�ʂ��ł��Ȃ��B
�E�́̋�ʂ��ł��Ȃ��B
�E�w���@���킩���ĂȂ��B
�E�撣���Đ��w���ۂ����t�g�������悤�Ɛ���t�w�L�т��Ă�̂��ɁX����
�E�e���r���玩���̈�������������Ɣ�������B
�E��O���킵����|�l�l�^���P����o�Ă��A�X���Z�l�ɑ���ɂ���Ȃ��Ȃ��Ă����B
2018/09/14(��) 13:37:18.85ID:Ey7oexo0
���E��O���킵����|�l�l�^���P����o�Ă��A�X���Z�l�ɑ���ɂ���Ȃ��Ȃ��Ă����B
����̂͂���オ������ȁB
�������͐�������Ɍ��܂��Ă�B
�Ƃ�
��27/5 �� 3 �Ŋ�����B
�Ƃ�
�����̌`����P��k�Ő��藧�ĂA�S�Ă�k�ł����藧�B
�Ƃ�
�P�́A�}�W�ŐM�����Ⴄ�����ɕ����Ȃ��B
����̂͂���オ������ȁB
�������͐�������Ɍ��܂��Ă�B
�Ƃ�
��27/5 �� 3 �Ŋ�����B
�Ƃ�
�����̌`����P��k�Ő��藧�ĂA�S�Ă�k�ł����藧�B
�Ƃ�
�P�́A�}�W�ŐM�����Ⴄ�����ɕ����Ȃ��B
2018/09/14(��) 13:49:17.09ID:elfLnB/W
27/5��3�ł�肫���A�̎�������Ԗʔ�������
>>731
�ǂޕ������������y�Ȃ͓̂��R���Ǝv���܂��B
>>735
���N�قǂ����ƌ������Ă���̂ŘJ�͂͂���Ȃ�ɂ������Ă���B
>>739
�S���ԈႢ
�������͐�������Ɍ��܂��Ă�B
����͐����ł���ꍇ�ɂ͊���ƌ����������B
��27/5 �� 3 �Ŋ�����B
���q���������Ƃ��������B
�����̌`����P��k�Ő��藧�ĂA�S�Ă�k�ł����藧�B
���ۂ͍Ō�̏�������p�Ɉˑ����Ă��Ȃ�����Ap=2pk-1���S�Ă�pk��
���藧�Ɖ��肵���ꍇ�ɂ́A(p��r���������Ƃ�z�肵�Ă���)
�S�Ă�k�Ő��藧�B
�Ƃ��������ŁA���ɊԈႢ�ł͂Ȃ��B
���̖��͐��w�͂������l�͌��̐����_�̖��ɋA������Ă���
���Ƃ𗝉����Ă���Ǝv���B
��́AWolfman�ɂ��Ɛ��������Ȃ��Əo�Ă���B������̕���
�����������݂���Ƃ����ӂ��ɂȂ邪�A�����ے�ł���Ώؖ���
�������邱�ƂɂȂ�B�������A��҂̖������������ł���̂���
���̓��e�����m�̂��̂��ǂ����͎��ɂ͕�����Ȃ��B
�ǂޕ������������y�Ȃ͓̂��R���Ǝv���܂��B
>>735
���N�قǂ����ƌ������Ă���̂ŘJ�͂͂���Ȃ�ɂ������Ă���B
>>739
�S���ԈႢ
�������͐�������Ɍ��܂��Ă�B
����͐����ł���ꍇ�ɂ͊���ƌ����������B
��27/5 �� 3 �Ŋ�����B
���q���������Ƃ��������B
�����̌`����P��k�Ő��藧�ĂA�S�Ă�k�ł����藧�B
���ۂ͍Ō�̏�������p�Ɉˑ����Ă��Ȃ�����Ap=2pk-1���S�Ă�pk��
���藧�Ɖ��肵���ꍇ�ɂ́A(p��r���������Ƃ�z�肵�Ă���)
�S�Ă�k�Ő��藧�B
�Ƃ��������ŁA���ɊԈႢ�ł͂Ȃ��B
���̖��͐��w�͂������l�͌��̐����_�̖��ɋA������Ă���
���Ƃ𗝉����Ă���Ǝv���B
��́AWolfman�ɂ��Ɛ��������Ȃ��Əo�Ă���B������̕���
�����������݂���Ƃ����ӂ��ɂȂ邪�A�����ے�ł���Ώؖ���
�������邱�ƂɂȂ�B�������A��҂̖������������ł���̂���
���̓��e�����m�̂��̂��ǂ����͎��ɂ͕�����Ȃ��B
2018/09/14(��) 14:09:42.30ID:elfLnB/W
Wolfman����iWolfram����H�j������ƌ����Ă�Ȃ炠���Ȃ��ł�����
2018/09/14(��) 14:34:50.56ID:Ey7oexo0
���Ƃ��������ŁA���ɊԈႢ�ł͂Ȃ��B
�R���P�́A�J������p�^�[���̂P���ȁB
�R���P�́A�J������p�^�[���̂P���ȁB
2018/09/14(��) 14:38:02.68ID:EWaPx4RC
��Ɍ��t���炸�Ȑ��������āA��ŕى�����(���Ƃ��Đ���Ȃ���)
746�P�R�Q�l�ڂ̑f������
2018/09/14(��) 14:58:40.71ID:tMy3g3nw >>741
���ǂޕ������������y�Ȃ͓̂��R���Ǝv���܂��B
���w���␔�w�_����債�ēǂ�łȂ��M���������������������Ă��A�����͂��Ȃ��c
���ǂޕ������������y�Ȃ͓̂��R���Ǝv���܂��B
���w���␔�w�_����債�ēǂ�łȂ��M���������������������Ă��A�����͂��Ȃ��c
2018/09/14(��) 15:07:13.27ID:Ey7oexo0
������
���t���炸�ǂ��납���̃X���Z�l���牽�ƌ����Ă��J��Ԃ��M���
�����͐���������Ƃ�
27/5 �� 3 �Ŋ�����Ƃ�
�f�����܂����Ă��āA�X��
�u�Ȃ�����ȊȒP�Ȃ��Ƃ�������Ȃ��̂��v�Ƃ�
��|�l�l�^�ōՂ�ɂȂ�x�ɔl�|���܂��肾�����B
���t���炸�ǂ��납���̃X���Z�l���牽�ƌ����Ă��J��Ԃ��M���
�����͐���������Ƃ�
27/5 �� 3 �Ŋ�����Ƃ�
�f�����܂����Ă��āA�X��
�u�Ȃ�����ȊȒP�Ȃ��Ƃ�������Ȃ��̂��v�Ƃ�
��|�l�l�^�ōՂ�ɂȂ�x�ɔl�|���܂��肾�����B
>>737
���̓t���[�ł�����A�{�����ǂ����̔���͓���Ƃ������قږ�������Ă���Ǝv���܂���
�ő��̐��Ɖ�̓V�X�e����Ǝ������J�����Ă��܂��B
�ǂ��̌����҂����̂悤�Ȏd�����ł���̂��Ǝv���܂�����ǁB
�̂̂��Ƃł����A����̏����ł����J�����Ƃ��ɁA�u�������瓐�ƌ����B�v�Ƃ����⋩��
�e���r���畷�����Ă������Ƃ�����܂����B
���̓t���[�ł�����A�{�����ǂ����̔���͓���Ƃ������قږ�������Ă���Ǝv���܂���
�ő��̐��Ɖ�̓V�X�e����Ǝ������J�����Ă��܂��B
�ǂ��̌����҂����̂悤�Ȏd�����ł���̂��Ǝv���܂�����ǁB
�̂̂��Ƃł����A����̏����ł����J�����Ƃ��ɁA�u�������瓐�ƌ����B�v�Ƃ����⋩��
�e���r���畷�����Ă������Ƃ�����܂����B
2018/09/14(��) 16:20:31.08ID:EEZdYq96
���ő��̐��Ɖ�̓V�X�e����Ǝ������J�����Ă��܂�
��{���E�R�����Ă��Ƃ��Ƃ����ɔ������Ă���
�d���������ŏ����ꂽ�̂�܂Ŗ𗧂����̕��A�v��
���܂�ɂ����傤���Ȃ��A�v���Ȃ̂ŁA�r�d�������̂��R�����Ď��������B
��{���E�R�����Ă��Ƃ��Ƃ����ɔ������Ă���
�d���������ŏ����ꂽ�̂�܂Ŗ𗧂����̕��A�v��
���܂�ɂ����傤���Ȃ��A�v���Ȃ̂ŁA�r�d�������̂��R�����Ď��������B
2018/09/14(��) 16:31:33.44ID:EWaPx4RC
>>749�̐⋩���������Ă��܂�����
>>749
�ꕔ����ƂŁA���{�ŔN����C���i�҂ł������l�Ԃ��ƌ����Ă��邾�낤�B
�ǂ������ӂ��ɔ������Ă���̂����m�ɏq�ׂĂ݂�A��R����Y
�ӂ�����ȁI
���Ƃ�GNL�����S�Ɏ�������͍̂�������͂���𐬂������Ă���B
���܂�A����n���ɂ���̂����������ɂ���B
�ꕔ����ƂŁA���{�ŔN����C���i�҂ł������l�Ԃ��ƌ����Ă��邾�낤�B
�ǂ������ӂ��ɔ������Ă���̂����m�ɏq�ׂĂ݂�A��R����Y
�ӂ�����ȁI
���Ƃ�GNL�����S�Ɏ�������͍̂�������͂���𐬂������Ă���B
���܂�A����n���ɂ���̂����������ɂ���B
2018/09/14(��) 16:44:18.00ID:wFiRqQCX
������ƃt���[�U�̃e�C�X�g�����Ă���
>>748
�ꉞ�t���[�Ə����܂������A���E�ł�����B
���������Ȃ��Ȃ�����A�̗p�����܂ܕ��u����Ƃ����l�����Ȃ����Ƃ�����Ă���
���@�ᔽ�́A�E�ƑI���̎��R�ƁA�Z���I���̎��R���Ȃ���Ԃ�10�N�ȏ�
���葱����̂��́A���{�̐����Ƃ����̐l���̖W�Q���������Ă��邱�Ƃ�
���ꂾ�Ǝv���܂��B
�����łȂ���A����8��3���ɂ��F�胁�[���𑗂��Ă����Ђ͂Ȃ��Ǝv���܂��B
�ꉞ�t���[�Ə����܂������A���E�ł�����B
���������Ȃ��Ȃ�����A�̗p�����܂ܕ��u����Ƃ����l�����Ȃ����Ƃ�����Ă���
���@�ᔽ�́A�E�ƑI���̎��R�ƁA�Z���I���̎��R���Ȃ���Ԃ�10�N�ȏ�
���葱����̂��́A���{�̐����Ƃ����̐l���̖W�Q���������Ă��邱�Ƃ�
���ꂾ�Ǝv���܂��B
�����łȂ���A����8��3���ɂ��F�胁�[���𑗂��Ă����Ђ͂Ȃ��Ǝv���܂��B
2018/09/14(��) 16:45:02.38ID:EEZdYq96
���ꕔ����ƂŁA���{�ŔN����C���i�҂ł������l�Ԃ��ƌ����Ă��邾�낤�B
�P�̑�{���E�R���ǂ��܂Ŋg�債�Ă������E�E�E
���⋩���e���r���畷�����Ă������Ƃ�����܂����B
���ꂪ�P�̖{���Ȃ�ȁB
�P�̑�{���E�R���ǂ��܂Ŋg�債�Ă������E�E�E
���⋩���e���r���畷�����Ă������Ƃ�����܂����B
���ꂪ�P�̖{���Ȃ�ȁB
755�P�R�Q�l�ڂ̑f������
2018/09/14(��) 16:47:36.15ID:tMy3g3nw >>748 �M���̂��Ƃ��u�{���̌����҂ł͂Ȃ��v�ƌ������̂́A
���҂̎��M����������ǂ�ň��p�����肷�邱�Ƃ����Ă��Ȃ��Ƃ������Ƃ��w�����̂ł��B
�M�����A�ő��̐��Ɖ�̓V�X�e����Ǝ������J���������Ƃ�F�߂��Ƃ���ŁA
����͋M�����g�̐��ʂ������Ă��邾���ł�����A
�u�{���̌����ҁv�ł��邱�Ƃ̏ؖ��ɂ͂Ȃ�܂����B
���҂̎��M����������ǂ�ň��p�����肷�邱�Ƃ����Ă��Ȃ��Ƃ������Ƃ��w�����̂ł��B
�M�����A�ő��̐��Ɖ�̓V�X�e����Ǝ������J���������Ƃ�F�߂��Ƃ���ŁA
����͋M�����g�̐��ʂ������Ă��邾���ł�����A
�u�{���̌����ҁv�ł��邱�Ƃ̏ؖ��ɂ͂Ȃ�܂����B
>>751
GNL�͊��S���Ə����܂������A���m�ɏ����ƌ��іڂ�������͎̂������Ă��܂���B
���܂肽�������ω��͂Ȃ��̂ɏ������Ԃ�1.5�{���x�|����悤�ɂȂ�̂�
�ł��̋@�\�͒lj����Ă��܂���B
GNL�͊��S���Ə����܂������A���m�ɏ����ƌ��іڂ�������͎̂������Ă��܂���B
���܂肽�������ω��͂Ȃ��̂ɏ������Ԃ�1.5�{���x�|����悤�ɂȂ�̂�
�ł��̋@�\�͒lj����Ă��܂���B
>>755
����͂��Ȃ��̒�`�ł��傤�B�ő��̃A���S���Y�����J������Ƃ������Ƃ͂��ꂪ�{���ł����
���h�Ȋw�p�I���ʂƂ�����̂ł͂Ȃ��̂ł��傤���H
���w�I�Ȑ��ʂ����邩�ǂ����Ƃ������Ƃ��d�v�Ȃ̂ł����āA�̍ق͓�̎��ł͂Ȃ��̂ł����H
����͂��Ȃ��̒�`�ł��傤�B�ő��̃A���S���Y�����J������Ƃ������Ƃ͂��ꂪ�{���ł����
���h�Ȋw�p�I���ʂƂ�����̂ł͂Ȃ��̂ł��傤���H
���w�I�Ȑ��ʂ����邩�ǂ����Ƃ������Ƃ��d�v�Ȃ̂ł����āA�̍ق͓�̎��ł͂Ȃ��̂ł����H
2018/09/14(��) 16:54:04.39ID:wFiRqQCX
���͌��݂��̌����ň�~���������Ȃ����߁A��|�l�ƌ���ꂽ�菑���ꂽ�肷�����Ƃɂ�
���ɕ�����o����B
�\�t�g�����J������A�\�t�g�|�l���Ƃ��B���������J������A��|�l���Ƃ��ӂ�����ȁB
������͂����P�Ȃ郊�X�g���̔�Q�҂̖��E�ł��邩��A�|�l�ƌ�����͔̂��ɕs�������B
�ʂɌ|�l�Ȃ�����ʂ���Ӑ}�͂Ȃ����A�e���r�ň�ʐl�Ŗ��Z���̎��̂��Ƃ��Ƃ₩��
�����邱�Ƃ͕s���̋ɂ݂��Ǝv�����A���̂�����e���r�ǂ����e���Ă���̂��Ɋւ��Ă�
���ɕs�v�c�Ȃ��Ƃ��B
���ɕ�����o����B
�\�t�g�����J������A�\�t�g�|�l���Ƃ��B���������J������A��|�l���Ƃ��ӂ�����ȁB
������͂����P�Ȃ郊�X�g���̔�Q�҂̖��E�ł��邩��A�|�l�ƌ�����͔̂��ɕs�������B
�ʂɌ|�l�Ȃ�����ʂ���Ӑ}�͂Ȃ����A�e���r�ň�ʐl�Ŗ��Z���̎��̂��Ƃ��Ƃ₩��
�����邱�Ƃ͕s���̋ɂ݂��Ǝv�����A���̂�����e���r�ǂ����e���Ă���̂��Ɋւ��Ă�
���ɕs�v�c�Ȃ��Ƃ��B
760�P�R�Q�l�ڂ̑f������
2018/09/14(��) 16:59:32.30ID:tMy3g3nw >>757�@�̍ق���ɂ��Ă���Ƃ��������A���҂ɐڂ���ԓx����ɂ��Ă���̂ł��B
�M���͎����̐��w�I���ʂ𑼎҂ɏ��F���ė~�����̂ł��傤�H
�����ł���A�Ȃɂ����܂��͋M�����g�����҂̐��w�I���ʂd���Ȃ���Ȃ�Ȃ��̂ł��B
�����͑��l�̐��ʂȂǒm��Ȃ����A���l�͎�����F�߂�ׂ��ł���ȂǂƂ����ԓx�ŁA
�M���̐��ʂ��F�߂Ă��炦��͂����Ȃ��ƌ����Ă���̂ł��B
�M���͎����̐��w�I���ʂ𑼎҂ɏ��F���ė~�����̂ł��傤�H
�����ł���A�Ȃɂ����܂��͋M�����g�����҂̐��w�I���ʂd���Ȃ���Ȃ�Ȃ��̂ł��B
�����͑��l�̐��ʂȂǒm��Ȃ����A���l�͎�����F�߂�ׂ��ł���ȂǂƂ����ԓx�ŁA
�M���̐��ʂ��F�߂Ă��炦��͂����Ȃ��ƌ����Ă���̂ł��B
761�P�R�Q�l�ڂ̑f������
2018/09/14(��) 16:59:32.55ID:tMy3g3nw >>757�@�̍ق���ɂ��Ă���Ƃ��������A���҂ɐڂ���ԓx����ɂ��Ă���̂ł��B
�M���͎����̐��w�I���ʂ𑼎҂ɏ��F���ė~�����̂ł��傤�H
�����ł���A�Ȃɂ����܂��͋M�����g�����҂̐��w�I���ʂd���Ȃ���Ȃ�Ȃ��̂ł��B
�����͑��l�̐��ʂȂǒm��Ȃ����A���l�͎�����F�߂�ׂ��ł���ȂǂƂ����ԓx�ŁA
�M���̐��ʂ��F�߂Ă��炦��͂����Ȃ��ƌ����Ă���̂ł��B
�M���͎����̐��w�I���ʂ𑼎҂ɏ��F���ė~�����̂ł��傤�H
�����ł���A�Ȃɂ����܂��͋M�����g�����҂̐��w�I���ʂd���Ȃ���Ȃ�Ȃ��̂ł��B
�����͑��l�̐��ʂȂǒm��Ȃ����A���l�͎�����F�߂�ׂ��ł���ȂǂƂ����ԓx�ŁA
�M���̐��ʂ��F�߂Ă��炦��͂����Ȃ��ƌ����Ă���̂ł��B
2018/09/14(��) 16:59:51.98ID:wFiRqQCX
�C�m�ے��Ȃ�������Ԃ���������
��~������Ȃ��Ă����Ȃ���ґ�
��~������Ȃ��Ă����Ȃ���ґ�
2018/09/14(��) 17:09:39.75ID:EEZdYq96
���e���r�ň�ʐl�Ŗ��Z���̎��̂��Ƃ��Ƃ₩�������邱�Ƃ͕s���̋ɂ݂��Ǝv�����A
�����̂�����e���r�ǂ����e���Ă���̂��Ɋւ��Ă͔��ɕs�v�c�Ȃ��Ƃ��B
�{���ɂP�͐[���ȕa����A�^�ʖڂɕa�@�ɍs�������������B
�������g�̂��߂ɂ��A�Ƒ��̂��߂ɂ��B
�����̂�����e���r�ǂ����e���Ă���̂��Ɋւ��Ă͔��ɕs�v�c�Ȃ��Ƃ��B
�{���ɂP�͐[���ȕa����A�^�ʖڂɕa�@�ɍs�������������B
�������g�̂��߂ɂ��A�Ƒ��̂��߂ɂ��B
>>758
�������Ƃ����ł��ˁB
���̘_���̓��e����A��̖��肪�ؖ�����Awolfram���Ȃ��Ƃ���
�������肪���������A��ςɊ�������Ƃ��Ǝv���܂��B
>>760
���҂̐��w�I���ʂ�ے肷����̂ł͂���܂���B�����ǂ�ł��Ȃ��Ƃ���������
���ꂩ��A����������Ă����Ȃ����A�w���ł��Ȃ��̂ɁA���҂̘_����ǂޗ]�T��
����܂���B
>>763
�e���r������ᔻ������A�����傭�����肵�Ă���͓̂��풃�ю�������B
����Ŗʔ��������̂́A���̕����̃e���r���畷�����Ă�����
�u������A�V���[�h���p���X�`�B�v
�`�̕����͂悭�������Ȃ������B���̃V���[�h���p���X�͐[�C���̖��O��
�������������P��B������A���ꂪ�ǂ��������Ă����́H�ƌ��������B
�������Ƃ����ł��ˁB
���̘_���̓��e����A��̖��肪�ؖ�����Awolfram���Ȃ��Ƃ���
�������肪���������A��ςɊ�������Ƃ��Ǝv���܂��B
>>760
���҂̐��w�I���ʂ�ے肷����̂ł͂���܂���B�����ǂ�ł��Ȃ��Ƃ���������
���ꂩ��A����������Ă����Ȃ����A�w���ł��Ȃ��̂ɁA���҂̘_����ǂޗ]�T��
����܂���B
>>763
�e���r������ᔻ������A�����傭�����肵�Ă���͓̂��풃�ю�������B
����Ŗʔ��������̂́A���̕����̃e���r���畷�����Ă�����
�u������A�V���[�h���p���X�`�B�v
�`�̕����͂悭�������Ȃ������B���̃V���[�h���p���X�͐[�C���̖��O��
�������������P��B������A���ꂪ�ǂ��������Ă����́H�ƌ��������B
2018/09/14(��) 18:50:51.30ID:nAmkgSRx
�ŋ߂̔ł͂قƂ��
�@
�E� y ���f���q p ���������� multipicity n �͊�B
�E2y �� 1+p+�c+p^n �Ŋ�����B
���炢�̉��肩�瓾���鎮��������������|���Ė��������Ƃ��Ă�B
���ۂ��̉��肪�����
a = 2y/(1+p+�c+o^n)�Ab=y/p^n�Ac=2y/(1+p+�c+o^n)/p^n
�͐����ɂȂ邵�Ab �� (p+1)/2 �Ŋ����邵�_���̉�������ɂȂ�B
�����ǁA���ꂾ���̉���ł������������Ȃ�����n�Y���Ȃ��B
�@
�E� y ���f���q p ���������� multipicity n �͊�B
�E2y �� 1+p+�c+p^n �Ŋ�����B
���炢�̉��肩�瓾���鎮��������������|���Ė��������Ƃ��Ă�B
���ۂ��̉��肪�����
a = 2y/(1+p+�c+o^n)�Ab=y/p^n�Ac=2y/(1+p+�c+o^n)/p^n
�͐����ɂȂ邵�Ab �� (p+1)/2 �Ŋ����邵�_���̉�������ɂȂ�B
�����ǁA���ꂾ���̉���ł������������Ȃ�����n�Y���Ȃ��B
2018/09/14(��) 18:54:52.92ID:JXvpka1u
�E���t�}�����A���a
2018/09/14(��) 19:12:18.16ID:wFiRqQCX
�ׂ��畷�����鉹�̏���Ȃ̂ɉ��Ńe���r������ĕ�����낤��
���ۂɂ��̌��i��ڂŌ����낤��
���ۂɂ��̌��i��ڂŌ����낤��
2018/09/14(��) 19:29:43.47ID:xJxnHhSy
��{�I�ɍ��ǂ̓{�����e�B�A
�˗������ꍇ�ł���V�Ȃ�ĂȂ�
����ł������҂����ǂ���͎̂�����������݂��l�ȍs�ׂ�����
���̘_�����ǂ݂ɂ����Ă��m�������Ƃł͂Ȃ�
���͑��l�̘_���Ȃ�ēǂ܂Ȃ�����m��Ȃ�
�Ȃ�Č�������l�̘_�������ǂ����������҂͂��Ȃ�
�˗������ꍇ�ł���V�Ȃ�ĂȂ�
����ł������҂����ǂ���͎̂�����������݂��l�ȍs�ׂ�����
���̘_�����ǂ݂ɂ����Ă��m�������Ƃł͂Ȃ�
���͑��l�̘_���Ȃ�ēǂ܂Ȃ�����m��Ȃ�
�Ȃ�Č�������l�̘_�������ǂ����������҂͂��Ȃ�
2018/09/14(��) 21:05:52.69ID:394Q3Kmm
>>748
���������̂Ōv�Z�~�X�`�F�b�J�[�ł�����
���������̂Ōv�Z�~�X�`�F�b�J�[�ł�����
2018/09/14(��) 21:08:50.77ID:394Q3Kmm
�̗p���ĕ��u���ꂽ�z���A�ŔN���Ŏ�C�ɏ��i�Ƃ��Ȃ��˂�
772�P�R�Q�l�ڂ̑f������
2018/09/14(��) 22:35:50.82ID:ZTzSSpdq ���{����Ȃς����ǁH
���o��
���o��
��Ђ̂��Ƃ������Ƃ����Ƀ����p�^�[���̓��{�ꂪ���������̂�
���{�ł̘b�ł͂Ȃ��B���邢�́A���{�l�����������̂ł͂Ȃ��B
�悭������ł��ȁB
���{�ł̘b�ł͂Ȃ��B���邢�́A���{�l�����������̂ł͂Ȃ��B
�悭������ł��ȁB
774�P�R�Q�l�ڂ̑f������
2018/09/14(��) 22:43:39.42ID:MQny/LYC �{���̊��S���̘_���͂����ƊȌ��ŕ�����₷��
�P�̖��ʂɕ��G�ŊԈႢ���炯�̂��ǂ��ؖ���������y���ɗL�v��
�P�̖��ʂɕ��G�ŊԈႢ���炯�̂��ǂ��ؖ���������y���ɗL�v��
2018/09/14(��) 22:57:55.31ID:/aBcOKhB
�ނɂƂ��Ďw�E��A�h�o�C�X�͓G�Ȃ낤
2018/09/14(��) 23:06:00.42ID:y6vLmOQY
���w�̘_����ǂނ̂ɕK�v�Ȃ̂͊w�ʂ���Ȃ�
�����Ƃ������w�̒m����������
�����Ƃ������w�̒m����������
777�P�R�Q�l�ڂ̑f������
2018/09/15(�y) 00:50:15.15ID:YyuEqBCq ���{�[�u���Z�o�g�̎R�c�m������B
�����Q�[���������Ă��̂ɁA�����œ������ȑ�w���w�����p���w�ȂɎ��Ă������ȁB
�S������炵���B
�ዾ���Ăăs�[�X���Ă�l���ށB
�܂������E�ł͂Ȃ���ˁH
https://twitter.com/denkichi369
https://twitter.com/denkichi369_1
https://twitter.com/doit_369
https://twitter.com/keepmathtop
https://twitter.com/EjC0mPe26Nlm92d
https://twitter.com/xPuGPq8Tn9GWCJb
https://twitter.com/K46_N700_hikari
https://i.imgur.com/D2v6N5w.jpg
https://i.imgur.com/5D48Tls.jpg
https://i.imgur.com/9WV2RCu.jpg
https://i.imgur.com/HoUzihY.jpg
https://i.imgur.com/YkUiF5A.jpg
https://i.imgur.com/AUlJtv1.png
https://i.imgur.com/ObqqE2G.png
���̘b�����Ă�H
https://twitter.com/5chan_nel (5ch newer account)
�����Q�[���������Ă��̂ɁA�����œ������ȑ�w���w�����p���w�ȂɎ��Ă������ȁB
�S������炵���B
�ዾ���Ăăs�[�X���Ă�l���ށB
�܂������E�ł͂Ȃ���ˁH
https://twitter.com/denkichi369
https://twitter.com/denkichi369_1
https://twitter.com/doit_369
https://twitter.com/keepmathtop
https://twitter.com/EjC0mPe26Nlm92d
https://twitter.com/xPuGPq8Tn9GWCJb
https://twitter.com/K46_N700_hikari
https://i.imgur.com/D2v6N5w.jpg
https://i.imgur.com/5D48Tls.jpg
https://i.imgur.com/9WV2RCu.jpg
https://i.imgur.com/HoUzihY.jpg
https://i.imgur.com/YkUiF5A.jpg
https://i.imgur.com/AUlJtv1.png
https://i.imgur.com/ObqqE2G.png
���̘b�����Ă�H
https://twitter.com/5chan_nel (5ch newer account)
778�P�R�Q�l�ڂ̑f������
2018/09/15(�y) 07:32:44.11ID:mZ1H3G7s >>771
�����̘_����ǂނɂ͐��w�̊w�ʂ��K�v���ƍl������̂œǂ�ł�
��������Ȃ����낤����A�_����ǂ�ł����܂�Ӗ����Ȃ��ƍl���Ă���B
�܂��ɁA�����͐��w�����҂ł͂Ȃ��Ɩ��������悤�Ȕ����B
�M���̌������F�߂Ă��炦�Ȃ��̂��d���Ȃ��ł��ˁB
�����̘_����ǂނɂ͐��w�̊w�ʂ��K�v���ƍl������̂œǂ�ł�
��������Ȃ����낤����A�_����ǂ�ł����܂�Ӗ����Ȃ��ƍl���Ă���B
�܂��ɁA�����͐��w�����҂ł͂Ȃ��Ɩ��������悤�Ȕ����B
�M���̌������F�߂Ă��炦�Ȃ��̂��d���Ȃ��ł��ˁB
>>778
cr=qr-1�̏ꍇ�ɉ��݂̔��ؖ��ł���A�ؖ��I���ł�����
2m+1=hpr����������Ƃ��āA���̂Ƃ���
2b(p-1)=c(p^(n+1)-1)
4b(pr-1)=c(p^(n+1)-1)
x=2m+1�Ƃ����
4b(x/h-1)=c(p^(2x)-1)
�ƂȂ�܂����Awolfram����ɂ��܂��Ƃ���ɂ͕s�K�ɂȂ�Ȃ��������͂���܂���B�ȏ�B
cr=qr-1�̏ꍇ�ɉ��݂̔��ؖ��ł���A�ؖ��I���ł�����
2m+1=hpr����������Ƃ��āA���̂Ƃ���
2b(p-1)=c(p^(n+1)-1)
4b(pr-1)=c(p^(n+1)-1)
x=2m+1�Ƃ����
4b(x/h-1)=c(p^(2x)-1)
�ƂȂ�܂����Awolfram����ɂ��܂��Ƃ���ɂ͕s�K�ɂȂ�Ȃ��������͂���܂���B�ȏ�B
2018/09/15(�y) 07:55:41.74ID:+5EiJ2rU
�E���t�}�����A�~��
781�P�R�Q�l�ڂ̑f������
2018/09/15(�y) 07:58:21.57ID:MCz5TSMr ��4b(x/h-1)=c(p^(2x)-1)
���ƂȂ�܂����Awolfram����ɂ��܂��Ƃ���ɂ͕s�K�ɂȂ�Ȃ��������͂���܂���B
����Ȏ��R�ϐ��̑�����������wolfram�ɂ������Ƃ���ʼn��̗L�����킩��킯���Ȃ��낤�B
pr=x/h, p=2pr-1�Ȃ̂ŁA�ŏ��̎���
4b(pr-1)=c((2(pr-1)+1)^(2hpr)-1)
(2(pr-1)+1)^(2hpr)-1 �͖��炩�� 4(pr-1) �̔{��������A���̎��ɉ��������Ă��������Ȃ��B
���ƂȂ�܂����Awolfram����ɂ��܂��Ƃ���ɂ͕s�K�ɂȂ�Ȃ��������͂���܂���B
����Ȏ��R�ϐ��̑�����������wolfram�ɂ������Ƃ���ʼn��̗L�����킩��킯���Ȃ��낤�B
pr=x/h, p=2pr-1�Ȃ̂ŁA�ŏ��̎���
4b(pr-1)=c((2(pr-1)+1)^(2hpr)-1)
(2(pr-1)+1)^(2hpr)-1 �͖��炩�� 4(pr-1) �̔{��������A���̎��ɉ��������Ă��������Ȃ��B
782�P�R�Q�l�ڂ̑f������
2018/09/15(�y) 08:34:08.61ID:1kf0wGMF SE������̕ȂɌv�Z�@�ɏo���邱�ƂƏo���Ȃ����Ƃ̋�ʂ��ł���̂�
>>779
�����ɏ��������e�͍����͐������Əo�܂���ł����B���͂������e���Ⴄ�ƈႤ���ʂ�
�o��Ƃ������Ƃ�����܂����A�悭������܂���B
�����ɏ��������e�͍����͐������Əo�܂���ł����B���͂������e���Ⴄ�ƈႤ���ʂ�
�o��Ƃ������Ƃ�����܂����A�悭������܂���B
2018/09/15(�y) 09:00:50.73ID:s0xVf9ul
����wolfram���Č����Ă�Ǝv������
�g������m��Ȃ��̂���
�g������m��Ȃ��̂���
785�P�R�Q�l�ڂ̑f������
2018/09/15(�y) 09:52:26.96ID:qc3pYObg ���Ɏ����ōl���鎖����߂ăJ���j���O���邱�Ƃ��o������
�J���j���O���Ă���ԈႦ��Ƃ����^���Y���Ղ���I
�����ǂ����悤�������h�A�z��(�s���|�[��)
�J���j���O���Ă���ԈႦ��Ƃ����^���Y���Ղ���I
�����ǂ����悤�������h�A�z��(�s���|�[��)
2018/09/15(�y) 10:06:40.08ID:+5EiJ2rU
>>784
�E���t�}������
�E���t�}������
787�P�R�Q�l�ڂ̑f������
2018/09/15(�y) 10:18:03.34ID:/bbzD8RU �I�I�J�~���N���Ă��Ƃ�
����������_�u���~�[�j���O
����������_�u���~�[�j���O
>>781
���͏o���Ă���܂���
http://www.wolframalpha.com/input/?i=4*b*(x%2Fh-1)%3Dc*(p%5E(2*x)-1)
>>785
���Ⴀ���Ȃ���
4b(pr-1)=c((2(pr-1)+1)^(2hpr)-1)
��pr���ǂ��������ɂȂ邩�A������M�Z�ŏo�����Ƃ��ł���̂ł����H
���̉��������ɂȂ邩�ǂ�����ł���̂ł����H
���̖��������ł���A���̖��̈ꕔ�����Ƃ������ƂɂȂ�
���Ȃ�̐��w�I���ʂƂ������ƂɂȂ�Ǝv���܂��B
>>787
���w�I���ʂ͏o���Ă���Ǝv�����ǂ�
cr��qr-1�̂Ƃ���
2m+1=wpr^(qr-cr-1)
�����藧���Ȃ���Ȃ�Ȃ��Ƃ���
���͏o���Ă���܂���
http://www.wolframalpha.com/input/?i=4*b*(x%2Fh-1)%3Dc*(p%5E(2*x)-1)
>>785
���Ⴀ���Ȃ���
4b(pr-1)=c((2(pr-1)+1)^(2hpr)-1)
��pr���ǂ��������ɂȂ邩�A������M�Z�ŏo�����Ƃ��ł���̂ł����H
���̉��������ɂȂ邩�ǂ�����ł���̂ł����H
���̖��������ł���A���̖��̈ꕔ�����Ƃ������ƂɂȂ�
���Ȃ�̐��w�I���ʂƂ������ƂɂȂ�Ǝv���܂��B
>>787
���w�I���ʂ͏o���Ă���Ǝv�����ǂ�
cr��qr-1�̂Ƃ���
2m+1=wpr^(qr-cr-1)
�����藧���Ȃ���Ȃ�Ȃ��Ƃ���
2018/09/15(�y) 13:05:47.95ID:qTba1afT
>>771
���炩�Ȃ̂́A�e�̕����̃e���r���N�̈����������Ă���̂ł͂Ȃ��A�e���g���N�̈����������Ă�����Ă��Ƃł����
���炩�Ȃ̂́A�e�̕����̃e���r���N�̈����������Ă���̂ł͂Ȃ��A�e���g���N�̈����������Ă�����Ă��Ƃł����
>>789
��������邾�낤����ǂ��A�e���r�������Ă���ꍇ�����邱�̑O�����m�ɎႢ�����̐���
�u�̑��I���������������A����������ȁB�v
�ƕ������Ă����B
����͎�����������Ă��镔���ŁA�ŋߘb��ƂȂ��Ă���I��̖��������p���n���Ƃ�
�v��Ȃ��ƌ��������Ƃɂ����̂��ƍl������B
�ŋ߁A�u�e���r�Ɏw�����ȁB�v�Ƃ��������Ă��Ă���B
�����҂̐^�ʖڂȔ�����n���ɂ��āA�^���ł��Ȃ������������ȂƂ͉��ƌ����t�ق�
�������낤�Ƃ��v����B
��������邾�낤����ǂ��A�e���r�������Ă���ꍇ�����邱�̑O�����m�ɎႢ�����̐���
�u�̑��I���������������A����������ȁB�v
�ƕ������Ă����B
����͎�����������Ă��镔���ŁA�ŋߘb��ƂȂ��Ă���I��̖��������p���n���Ƃ�
�v��Ȃ��ƌ��������Ƃɂ����̂��ƍl������B
�ŋ߁A�u�e���r�Ɏw�����ȁB�v�Ƃ��������Ă��Ă���B
�����҂̐^�ʖڂȔ�����n���ɂ��āA�^���ł��Ȃ������������ȂƂ͉��ƌ����t�ق�
�������낤�Ƃ��v����B
2018/09/15(�y) 13:19:52.95ID:uZAUJfnl
>>790
���������v�l�Q�[���݂�������
���ŕ����������̏��ŁA���ۂɂ͉����s���Ă���̂���������̂���
�̑��̂�����͕�����Ȃ���������ǁA�e���r�̕��͕������
�e���r�Ƀe���r���f���ĂāA���̃e���r�ɏo���҂������ƍl���Ă����낪������
���ŕ�������������Ȃ��Ėڂł������ƌ��Ĕ��f���悤���Ă��Ƃ���
���������v�l�Q�[���݂�������
���ŕ����������̏��ŁA���ۂɂ͉����s���Ă���̂���������̂���
�̑��̂�����͕�����Ȃ���������ǁA�e���r�̕��͕������
�e���r�Ƀe���r���f���ĂāA���̃e���r�ɏo���҂������ƍl���Ă����낪������
���ŕ�������������Ȃ��Ėڂł������ƌ��Ĕ��f���悤���Ă��Ƃ���
2018/09/15(�y) 13:30:19.35ID:NQNnUcix
�������|�łȂ���Εa�@�s�����炢���̂ɂ�
>>792
�Ȃ�ŕ�����Ȃ��́H�ȒP�ȗ����ł��傤�B�C�ɓ���Ȃ�����������z�͌���Ȃ�
�����҂Ƀe���r�̒��Ō����Ă���l�Ԃ��m���ɂ���Ƃ��������ł�����B
���ʂ̓��{�ꂪ�����ł��Ȃ��̂��A�s�K�ؔ����̕s�ˎ������痝���������Ȃ��̂�
�ǂ���ł����H
�Ȃ�ŕ�����Ȃ��́H�ȒP�ȗ����ł��傤�B�C�ɓ���Ȃ�����������z�͌���Ȃ�
�����҂Ƀe���r�̒��Ō����Ă���l�Ԃ��m���ɂ���Ƃ��������ł�����B
���ʂ̓��{�ꂪ�����ł��Ȃ��̂��A�s�K�ؔ����̕s�ˎ������痝���������Ȃ��̂�
�ǂ���ł����H
2018/09/15(�y) 13:34:22.73ID:uZAUJfnl
2018/09/15(�y) 13:36:01.36ID:uZAUJfnl
>>794
�ȒP�ȗ��������ǁA���������l�����͂Ƃ��ĂȂ�����
�ȒP�ȗ��������ǁA���������l�����͂Ƃ��ĂȂ�����
>>795
�����̌܊��́A�̒������ʂł���Ƃ��͌����͕������Ȃ��Ǝv���̂����ʂł��傤�B
�E��ł���������������ǂ��A�����̐Q�s���ɂ�������Ԃ_�a���ƌ�f������
���ꂪ���R�̌����Ƃ������Ƃɂ���āA�ǂ����������点�ł��\�ɂȂ��Ă����B
�������ƌ����Ă��邾��������A���Ă͂��Ȃ��B������u�S���͈ꌩ�ɂ������B�v
�ƌ��������킯�ł͂Ȃ��ł��傤�ˁB
>>796
�������Ă���̂�������Ȃ����A���ۂɂ��������\�����e���r�ŏq�ׂ�l�Ԃ�����Ƃ������Ƃ��B
�����̌܊��́A�̒������ʂł���Ƃ��͌����͕������Ȃ��Ǝv���̂����ʂł��傤�B
�E��ł���������������ǂ��A�����̐Q�s���ɂ�������Ԃ_�a���ƌ�f������
���ꂪ���R�̌����Ƃ������Ƃɂ���āA�ǂ����������点�ł��\�ɂȂ��Ă����B
�������ƌ����Ă��邾��������A���Ă͂��Ȃ��B������u�S���͈ꌩ�ɂ������B�v
�ƌ��������킯�ł͂Ȃ��ł��傤�ˁB
>>796
�������Ă���̂�������Ȃ����A���ۂɂ��������\�����e���r�ŏq�ׂ�l�Ԃ�����Ƃ������Ƃ��B
2018/09/15(�y) 13:47:34.05ID:QWT66dGo
��������͂����Ȃ����̂�����������炻�������a�C�ȂƎ��o�ł��Ȃ��́H
���������ǂ̂��Ɖ����m��Ȃ����ǁB
���������ǂ̂��Ɖ����m��Ȃ����ǁB
2018/09/15(�y) 13:48:28.00ID:qTba1afT
>>790
�e���r���N��m���Ă�킯�Ȃ�����A�e���r���N�̈��������Ă���Ă̂͋C�̂����ł���ˁB
���w�ł������A���̂��炢�̗����͕������Ă���܂���ˁB
�{���ɕ������Ă���Ƃ����Ȃ炻��͌����Ƃ������_�����ł�����}���a�@�֍s���ꂽ�ق����ǂ��ł�
�e���r���N��m���Ă�킯�Ȃ�����A�e���r���N�̈��������Ă���Ă̂͋C�̂����ł���ˁB
���w�ł������A���̂��炢�̗����͕������Ă���܂���ˁB
�{���ɕ������Ă���Ƃ����Ȃ炻��͌����Ƃ������_�����ł�����}���a�@�֍s���ꂽ�ق����ǂ��ł�
2018/09/15(�y) 13:50:29.16ID:NQNnUcix
���̐l���v���Ă�قǐ��Ԃ͂��̐l�ɋ������Ȃ����ƂɋC�Â��ׂ�
�{���Ȃ����̑�l���a�@�ɘA��Ă��Ȃ肷�ׂ��Ȃ��Ȃ�
�{���Ȃ����̑�l���a�@�ɘA��Ă��Ȃ肷�ׂ��Ȃ��Ȃ�
2018/09/15(�y) 13:51:35.61ID:qTba1afT
���Ƃ�>>792�������Ă���悤�ɁA���W�Ȏ��������̂��Ƃ̂悤�ɑ����Ă��܂���Q�ϑz�ł����ˁB
������ɂ��Ă����_�I�ɎQ���Ă��ł��傤��
������ɂ��Ă����_�I�ɎQ���Ă��ł��傤��
2018/09/15(�y) 13:53:12.76ID:uZAUJfnl
>>797
�M���������o�������N�������玨�ƖڂŃ_�u���`�F�b�N�����Č�����Ȃ����m�F���Ă��������A�Ƃ������Ƃł�
�M���������o�������N�������玨�ƖڂŃ_�u���`�F�b�N�����Č�����Ȃ����m�F���Ă��������A�Ƃ������Ƃł�
2018/09/15(�y) 13:55:28.15ID:YeOTR053
�����H���ɑ���n�߂���
2018/09/15(�y) 14:01:07.63ID:QWT66dGo
youtube�Ƃ��œ��������ǂ̓��挩�����炢�̂��Ƃ����m��Ȃ����ǁA
�a�C�ɜ늳���Ă��܂��āA�����⌶�o�A��Q�ϑz���N���Ă��܂�����ǁA�ł������]�����A
�N���������E�G�͂ǂ��ɂ���A�Ƃ������Ƃ������I�ɐ����ł��Ȃ����߂ɁA
��苭���C���[�W�������Ė������G�����o���ƁB
�^������A�^�悵����đ�O�҂��v�����Ă��A��������Ă��܂��Ƃ��]�����p�j�b�N�ɂȂ�̂�
�h�q�����̂��߂���ɂ����������Ƃ͂��Ȃ��B
>>1�͂����̃X���Ŏ����ւ̔ᔻ��Ⴄ���ƂŁA��������ۂ̓G�ƔF�����Ĉ��S���Ă��肷��̂��ȂƎv�����B
���Â̂��߂ɂ͂܂��͒ʉ@�����ǁA�M���W�̂���l�Ԃ��Ȃ�Ƃ��������āA
�ق�̏����ł��u�����a�C�Ȃ̂��ȁE�E�E�v�Ǝv�킹�ĕa�@�ɍs�����邱�Ƃ��ƁB
>>1�͂��������M���̂�����l�͂��Ȃ��́H
�a�C�ɜ늳���Ă��܂��āA�����⌶�o�A��Q�ϑz���N���Ă��܂�����ǁA�ł������]�����A
�N���������E�G�͂ǂ��ɂ���A�Ƃ������Ƃ������I�ɐ����ł��Ȃ����߂ɁA
��苭���C���[�W�������Ė������G�����o���ƁB
�^������A�^�悵����đ�O�҂��v�����Ă��A��������Ă��܂��Ƃ��]�����p�j�b�N�ɂȂ�̂�
�h�q�����̂��߂���ɂ����������Ƃ͂��Ȃ��B
>>1�͂����̃X���Ŏ����ւ̔ᔻ��Ⴄ���ƂŁA��������ۂ̓G�ƔF�����Ĉ��S���Ă��肷��̂��ȂƎv�����B
���Â̂��߂ɂ͂܂��͒ʉ@�����ǁA�M���W�̂���l�Ԃ��Ȃ�Ƃ��������āA
�ق�̏����ł��u�����a�C�Ȃ̂��ȁE�E�E�v�Ǝv�킹�ĕa�@�ɍs�����邱�Ƃ��ƁB
>>1�͂��������M���̂�����l�͂��Ȃ��́H
2018/09/15(�y) 14:01:25.40ID:uZAUJfnl
2018/09/15(�y) 14:01:38.71ID:NQNnUcix
>>803
�ŁH
�ŁH
���Ȃ����́A����Ɏ����a�C���ƌ��߂��Ă���킯�ł����A�����������Ƃ�
�������̂��Ȃ������̂��́A���̏�ɑ��҂������Ƃ������Ƃł�����
���̑��҂ɕ������Ƃɂ��A���̎������Ȃ������Ƃ������Ƃ��ؖ��ł��Ȃ�����
����a�C���ƌ���t���邱�Ƃ͂ł��Ȃ��͂��ł����B
���Ɋ�Ȃ��Ƃ��N���Ă��邩��ƌ����ĕa�C�̃��b�e�����������Ƃ������Ƃ�
�����܂������Ƃł������Ȃ���ł����H
�����ł���ˁB�����ŐM�����Ȃ����̃C�J�T�}�����ꂽ��A�a�C�̌�f��
��ςɑ���f���Ă��邾�Ƃ��A���̋r���R�������炢�̂��Ƃŕs���ɉ�Ђ�
���ق��ꂽ��A���̌セ�̉�Ђ̕s���������J���Ȃɑi���镶���𑗂�����
�݂̂����e���r�ŁA�u�����J���Ȃ͕����������ċ����䂷��Ƃ���ł͂Ȃ��B�v
�Ƃ����傭������B���̂悤�Ȃ��Ƃ͑S�Ď��̎�����F�ɂ������낤����ȁB
�������̂��Ȃ������̂��́A���̏�ɑ��҂������Ƃ������Ƃł�����
���̑��҂ɕ������Ƃɂ��A���̎������Ȃ������Ƃ������Ƃ��ؖ��ł��Ȃ�����
����a�C���ƌ���t���邱�Ƃ͂ł��Ȃ��͂��ł����B
���Ɋ�Ȃ��Ƃ��N���Ă��邩��ƌ����ĕa�C�̃��b�e�����������Ƃ������Ƃ�
�����܂������Ƃł������Ȃ���ł����H
�����ł���ˁB�����ŐM�����Ȃ����̃C�J�T�}�����ꂽ��A�a�C�̌�f��
��ςɑ���f���Ă��邾�Ƃ��A���̋r���R�������炢�̂��Ƃŕs���ɉ�Ђ�
���ق��ꂽ��A���̌セ�̉�Ђ̕s���������J���Ȃɑi���镶���𑗂�����
�݂̂����e���r�ŁA�u�����J���Ȃ͕����������ċ����䂷��Ƃ���ł͂Ȃ��B�v
�Ƃ����傭������B���̂悤�Ȃ��Ƃ͑S�Ď��̎�����F�ɂ������낤����ȁB
2018/09/15(�y) 16:59:31.60ID:NQNnUcix
�a�@�s�����H
�a�C�������łȂ����͂����ł킩���
�a�C�������łȂ����͂����ł킩���
>>811
�Ȃ�̐f�f�����Ȃ��Řb�����������ŁA�f�f�Ȃ�Ăł���Ȃ��ł��傤�B
����ƕ��͂��܂Ƃ��ɓ��͂��邱�Ƃ��ł��鐸�_�a���҂����Ȃ��͈�l�ł�
�m���Ă���̂ł��傤���H
���ꂩ��A�c�O�Ȃ��琸�_�a�ł́A���x���̐��w�ł��������Ƃ͂ł��Ȃ��̂ł�
�Ȃ��̂ł��傤���H�a�C�̃��b�e������͔̂��ɕs�����ł��̂ŁA�~�߂�
�������������B����͐��_�Ȉ�̌�f�Ȃ̂ŁB���������̐f�f�����ꂽ�̂́A18�N��
�O�̂��Ƃ��B
���̌�f�̂����Ƃ��̐��_�a����̌f���̂����łǂ�����������������v����
���Ă��邩�m���ė~�������̂��B
�Ȃ�̐f�f�����Ȃ��Řb�����������ŁA�f�f�Ȃ�Ăł���Ȃ��ł��傤�B
����ƕ��͂��܂Ƃ��ɓ��͂��邱�Ƃ��ł��鐸�_�a���҂����Ȃ��͈�l�ł�
�m���Ă���̂ł��傤���H
���ꂩ��A�c�O�Ȃ��琸�_�a�ł́A���x���̐��w�ł��������Ƃ͂ł��Ȃ��̂ł�
�Ȃ��̂ł��傤���H�a�C�̃��b�e������͔̂��ɕs�����ł��̂ŁA�~�߂�
�������������B����͐��_�Ȉ�̌�f�Ȃ̂ŁB���������̐f�f�����ꂽ�̂́A18�N��
�O�̂��Ƃ��B
���̌�f�̂����Ƃ��̐��_�a����̌f���̂����łǂ�����������������v����
���Ă��邩�m���ė~�������̂��B
>>812
���̐f�f�����Ȃ��Ƃ����̂́A�b�������ŁA����ȊO�̐f�f���@���Ȃ��Ƃ����Ӗ��ŏ����܂����B
����������A��Ђ��K�v�̂Ȃ��Ј������ق���Ƃ��ɐ��_�Ȉオ�����������Ƃɉ��S���Ă���̂ł�
�Ȃ����Ƃ����^���́A���̐��̒��ɂ͂���킯�ł���ˁB���̏ꍇ�������������̂��ǂ�����
������܂��B
���̐f�f�����Ȃ��Ƃ����̂́A�b�������ŁA����ȊO�̐f�f���@���Ȃ��Ƃ����Ӗ��ŏ����܂����B
����������A��Ђ��K�v�̂Ȃ��Ј������ق���Ƃ��ɐ��_�Ȉオ�����������Ƃɉ��S���Ă���̂ł�
�Ȃ����Ƃ����^���́A���̐��̒��ɂ͂���킯�ł���ˁB���̏ꍇ�������������̂��ǂ�����
������܂��B
2018/09/15(�y) 17:27:42.45ID:NQNnUcix
>>812
������a�@�s���Đf�Ă�����āA�a�C���ǂ����m���߂Ă��炨�H
������a�@�s���Đf�Ă�����āA�a�C���ǂ����m���߂Ă��炨�H
2018/09/15(�y) 17:34:30.13ID:bFVj4A3f
�ŐV�_���͂�����@>>712
>>814
��Ђ̃��X�g���Ɛe���c�ɂɏZ�ނ��Ƃ����߂��̂ŁA�s�{�ӂɑS���������Ƃ��ł��Ȃ��Ȃ���
���N���o���Ă���B������ɈڏZ���Ă���e���������i�߂�̂Ő��_�Ȉ�Ɉ�����Ă��������
�u�V�˔����Ƃ����܂�����ˁB�v
�ƌ����܂����B
���̂��Ƃ�����A���Ɏ��̉ߋ��̐f�f�����������̂��ƍl�����܂��B�������_�Ȉ�ɂ����邱�Ƃ�
��x�ƂȂ��Ǝv���܂��B
�����ᔻ��������A���_�Ȃɓ��@������ꂽ�O���̏����̘b���e���r�ŕ�������Ă��܂���
���̓��{�Ƃ������ł����X����̂ł͂Ȃ��̂��Ǝv���܂��B�����Ƃ��s���悭�a�C�ɂȂ�̂Ƌt�ɁB
�̐S���a�œ��@����Ƃ�������c�������āA���̐l���w���瓦����Ƃ��ɑ����Ă������Ƃ�
�v���o����܂��B
��Ђ̃��X�g���Ɛe���c�ɂɏZ�ނ��Ƃ����߂��̂ŁA�s�{�ӂɑS���������Ƃ��ł��Ȃ��Ȃ���
���N���o���Ă���B������ɈڏZ���Ă���e���������i�߂�̂Ő��_�Ȉ�Ɉ�����Ă��������
�u�V�˔����Ƃ����܂�����ˁB�v
�ƌ����܂����B
���̂��Ƃ�����A���Ɏ��̉ߋ��̐f�f�����������̂��ƍl�����܂��B�������_�Ȉ�ɂ����邱�Ƃ�
��x�ƂȂ��Ǝv���܂��B
�����ᔻ��������A���_�Ȃɓ��@������ꂽ�O���̏����̘b���e���r�ŕ�������Ă��܂���
���̓��{�Ƃ������ł����X����̂ł͂Ȃ��̂��Ǝv���܂��B�����Ƃ��s���悭�a�C�ɂȂ�̂Ƌt�ɁB
�̐S���a�œ��@����Ƃ�������c�������āA���̐l���w���瓦����Ƃ��ɑ����Ă������Ƃ�
�v���o����܂��B
2018/09/15(�y) 17:49:31.83ID:qTba1afT
>>812
���₢��A�����S�z���������Ȃ��ǂˁB
�m��f�f�Ȃ���������Ȃ����B
�����A�N���畷���Ă�Ǐ��_�������̂��̂������҂ɂ���������ǂ����ƃA�h�o�C�X���Ă��B
����łǂ����邩�͌N�̏��肳��
���₢��A�����S�z���������Ȃ��ǂˁB
�m��f�f�Ȃ���������Ȃ����B
�����A�N���畷���Ă�Ǐ��_�������̂��̂������҂ɂ���������ǂ����ƃA�h�o�C�X���Ă��B
����łǂ����邩�͌N�̏��肳��
2018/09/15(�y) 17:50:20.47ID:+5EiJ2rU
>>817
�����������@�E���t�}���I
�����������@�E���t�}���I
2018/09/15(�y) 17:52:28.44ID:uZAUJfnl
���������̂��ĕa�C���a�C����Ȃ����̐������͞B���Ȃ���
����ɐ��_�ȂȂ�ăs���L���������
�����ƒ��ׂȂ���(���͖��_���ɍs����)
������́u��Ȍ��ۂ̊ϑ��Ɍ܊����S�����ꂽ�l�v�����
����Ȑl�Ƙb���̂͂͂��߂Ăō��f���Ă���Ƌ��ɖ��͓I�����
�u�E�l�����̊ϑ��Ɍ܊����S�����ꂽ�l�v���T��R�i���݂�����
����ɐ��_�ȂȂ�ăs���L���������
�����ƒ��ׂȂ���(���͖��_���ɍs����)
������́u��Ȍ��ۂ̊ϑ��Ɍ܊����S�����ꂽ�l�v�����
����Ȑl�Ƙb���̂͂͂��߂Ăō��f���Ă���Ƌ��ɖ��͓I�����
�u�E�l�����̊ϑ��Ɍ܊����S�����ꂽ�l�v���T��R�i���݂�����
2018/09/15(�y) 18:04:14.21ID:j4hnMV8N
�u��҂łȂ��ƕa�C���ǂ����킩��Ȃ��I�v
�����
�u��҂͉������v
�̗���͖��G������
�����
�u��҂͉������v
�̗���͖��G������
2018/09/15(�y) 18:07:39.02ID:Ye54RKpD
�Ɏ��s���� �� �C�J�T�}���I�w�Z�������I
��Ђ��N�r�ɂȂ� �� �s�����I��Ђ������I
�ďA�E�Ɏ��s���� �� �����Ƃ��l����W�Q���Ă���I
�a�C�Ɛf�f����� �� ��f���I��҂������I
�_�����������Ȃ� �� �N����������W�Q���Ă���I
�����𒆐S�ɐ��E������Ă�Ǝv���Ă�낤��
��Ђ��N�r�ɂȂ� �� �s�����I��Ђ������I
�ďA�E�Ɏ��s���� �� �����Ƃ��l����W�Q���Ă���I
�a�C�Ɛf�f����� �� ��f���I��҂������I
�_�����������Ȃ� �� �N����������W�Q���Ă���I
�����𒆐S�ɐ��E������Ă�Ǝv���Ă�낤��
2018/09/15(�y) 18:07:52.14ID:s0xVf9ul
��|�l��������߂āA�����|�l�ɃN���X�`�F���W����B
2018/09/15(�y) 18:08:54.20ID:s0xVf9ul
>>822 ���Ƀe���v���܂łł���������B
>>817
>>816 ����
�~����
�Z����
>>818
�����ł́A���N���Ǝv���Ă��āA���ɋN�������������̂܂����Ă��邾��������
�����������ŁA���ꂪ�a�C�̏ǏƂ����������������B
>>821
����҂łȂ��ƕa�C���ǂ����킩��Ȃ��I
��҂łȂ��Ɛf�f�ł��Ȃ��Ƃ����̂��������̂ł����āA���̐f�f���ʂ�100���������Ƃ͌���Ȃ��B
>>822
������5�Ȗڕ��ϕ��l75�Ȃ̂Ɋw��4�ʂ͂ǂ��l���Ă��A�C�J�T�}�B
>>816 ����
�~����
�Z����
>>818
�����ł́A���N���Ǝv���Ă��āA���ɋN�������������̂܂����Ă��邾��������
�����������ŁA���ꂪ�a�C�̏ǏƂ����������������B
>>821
����҂łȂ��ƕa�C���ǂ����킩��Ȃ��I
��҂łȂ��Ɛf�f�ł��Ȃ��Ƃ����̂��������̂ł����āA���̐f�f���ʂ�100���������Ƃ͌���Ȃ��B
>>822
������5�Ȗڕ��ϕ��l75�Ȃ̂Ɋw��4�ʂ͂ǂ��l���Ă��A�C�J�T�}�B
2018/09/15(�y) 18:21:01.20ID:s0xVf9ul
>������
�P�ɕK�v�Ȃ͕̂��I
�����̂���������������Ȃ��I
�P�ɕK�v�Ȃ͕̂��I
�����̂���������������Ȃ��I
>>826
���͑���Ȃ��ł��傤�ˁB���肽�Ƃ��Ă����̖�肪�����ł���̂��^��ł����ǁB
�̂͑���Ă�������5�Ȗڂ̕��ς�75�������̂ł͂Ȃ��ł��傤���H
�ԈႢ�Ȃ��A�C�J�T�}�ł��B�ɂ���Q�ł��B
���{�͓V�ˌ����̋���J���L���������Ȃ��͖̂�肾�Ǝv���܂��B
�v�Z�h����1�N����6���ԂŏI��鏬�w���ɕ��ʂ̋���͖������Ǝv���܂��B
���͑���Ȃ��ł��傤�ˁB���肽�Ƃ��Ă����̖�肪�����ł���̂��^��ł����ǁB
�̂͑���Ă�������5�Ȗڂ̕��ς�75�������̂ł͂Ȃ��ł��傤���H
�ԈႢ�Ȃ��A�C�J�T�}�ł��B�ɂ���Q�ł��B
���{�͓V�ˌ����̋���J���L���������Ȃ��͖̂�肾�Ǝv���܂��B
�v�Z�h����1�N����6���ԂŏI��鏬�w���ɕ��ʂ̋���͖������Ǝv���܂��B
2018/09/15(�y) 18:41:02.94ID:j4hnMV8N
�����̂��ƓV�˂��Ǝv���Ă�́H
2018/09/15(�y) 18:59:56.40ID:uZAUJfnl
����ړx���瑪������V�˂�����Ƃ����āA�ǂ�������]�I�Ƀ_���Ȃ��Ƃ�����
�܂肻����������
�܂肻����������
2018/09/15(�y) 19:02:38.05ID:+5EiJ2rU
�E���t�}����(����ړx�ł�)�V�˂ł��邱�Ƃ͔F�߂�̂��H
831�P�R�Q�l�ڂ̑f������
2018/09/15(�y) 19:10:13.49ID:mmknUsKs �Z���^�[�̐��w�Ŗ��_�@���o���قǂ̓V�˂�
����܂łP�Ƃ��Đ��������Ƃ������Ă��Ȃ��̂͂ǂ����āH
����܂łP�Ƃ��Đ��������Ƃ������Ă��Ȃ��̂͂ǂ����āH
832�P�R�Q�l�ڂ̑f������
2018/09/15(�y) 19:24:44.03ID:oEiDJxK/ >>831
�I�I�J�~���N������
�E�\���A�Ƃ������A�S�}�J�V�̃e�N�j�b�N�������āA�Ȃ�Ƃ����������w�I�Ȉ̋Ƃ𐬂��������悤�Ɍ��������̂����̂P
����܂ł̘_���Ō����������X�̃~�X�̓P�A���X�~�X���Ă͌����ĂȂ��A���ׂĂ��v��I�ɁA�I���Ɏd���܂ꂽ�S�}�J�V�ł���
���̈Ӗ��ł͓V�˓I�ƌ����Ă���
�I�I�J�~���N������
�E�\���A�Ƃ������A�S�}�J�V�̃e�N�j�b�N�������āA�Ȃ�Ƃ����������w�I�Ȉ̋Ƃ𐬂��������悤�Ɍ��������̂����̂P
����܂ł̘_���Ō����������X�̃~�X�̓P�A���X�~�X���Ă͌����ĂȂ��A���ׂĂ��v��I�ɁA�I���Ɏd���܂ꂽ�S�}�J�V�ł���
���̈Ӗ��ł͓V�˓I�ƌ����Ă���
>>828
���������ӂ��ɂ͏����Ă��܂��ǁB�������������̂Ȃ瓪�����������Ƃ���Љ�Ǝv���܂��̂ŁB
��{�I�Ɏ��͊w��I�ȗD�G���𐬐с^���Ԃōl���Ă���̂ŁA���̎ړx���Ƒ����D�G����
�������ƂɂȂ�Ǝv���܂�
>>831
�Z���^�[���_�͂�������Ǝv���̂ł��ꂾ���œV�˂Ƃ͊ԈႢ�Ȃ������Ȃ��Ǝv���܂��B
>>832
�S�}�J�V�ł͂Ȃ��A�����̌v�Z�ԈႢ������B���w��������x�ł���l�ɂ͓��R�����邱�Ƃ��Ǝv�����B
���������ӂ��ɂ͏����Ă��܂��ǁB�������������̂Ȃ瓪�����������Ƃ���Љ�Ǝv���܂��̂ŁB
��{�I�Ɏ��͊w��I�ȗD�G���𐬐с^���Ԃōl���Ă���̂ŁA���̎ړx���Ƒ����D�G����
�������ƂɂȂ�Ǝv���܂�
>>831
�Z���^�[���_�͂�������Ǝv���̂ł��ꂾ���œV�˂Ƃ͊ԈႢ�Ȃ������Ȃ��Ǝv���܂��B
>>832
�S�}�J�V�ł͂Ȃ��A�����̌v�Z�ԈႢ������B���w��������x�ł���l�ɂ͓��R�����邱�Ƃ��Ǝv�����B
2018/09/15(�y) 20:49:42.60ID:NQNnUcix
>>833
�����̂��Ƃ͓V�˂��Ǝv���Ă邯�ǁA�ςɎv��ꂽ���Ȃ����猾��Ȃ��������Ă��ƂˁA�Ȃ�ق�
�����̂��Ƃ͓V�˂��Ǝv���Ă邯�ǁA�ςɎv��ꂽ���Ȃ����猾��Ȃ��������Ă��ƂˁA�Ȃ�ق�
2018/09/15(�y) 20:50:37.61ID:NQNnUcix
�V�˂͂���܂�v�Z�~�X�����Ȃ��������A����c�ɂ͓��w���Ȃ����낤���A���E�ɂ��Ȃ��ĂȂ����낤
836�P�R�Q�l�ڂ̑f������
2018/09/15(�y) 20:50:53.75ID:oEiDJxK/ �S�}�J�V���w�E����ƁA�K�������̊ԈႢ���ƌ���������邪�A����܂ł̐������Ԃɓ���̊ԈႢ�����x�����x���J��Ԃ��Ă���͎̂���
�̈ӂɂ���Ă���ƍl���鑼�͂��肦�Ȃ�
�̈ӂɂ���Ă���ƍl���鑼�͂��肦�Ȃ�
>>835-836
���x�������Ă��邪�v�Z�ԈႢ�����Ȃ��Ɛ������ƌ�F���錋�ʂɂȂ�Ȃ�
����Ƃ��̖��͖��������ł��邱�Ƃ�m���Ă��Ă��������Ă���̂ł���
�������o���͍̂�����ɂ߂�Ǝv���܂���
���x�������Ă��邪�v�Z�ԈႢ�����Ȃ��Ɛ������ƌ�F���錋�ʂɂȂ�Ȃ�
����Ƃ��̖��͖��������ł��邱�Ƃ�m���Ă��Ă��������Ă���̂ł���
�������o���͍̂�����ɂ߂�Ǝv���܂���
2018/09/15(�y) 21:09:17.18ID:+5EiJ2rU
�v�Z�~�X�����邩�疢�����݂����Ɍ����Ȃ�
2018/09/15(�y) 21:32:29.98ID:bcDrhEdo
�v�Z�~�X��������ɂ��Ă���悤�ł͒��w���鏬�w���ɂ����
840�P�R�Q�l�ڂ̑f������
2018/09/15(�y) 21:34:51.64ID:oEiDJxK/ >>837
���ꂪ�������Ă���Ȃ�A�������Ǝv�����ʂ��o���Ƃ��ɁA�K���Ԉ���Ă���ӏ�������ƍl���Č������ׂ�
����������A�ؖ����������܂����ƃX���b�h�̃^�C�g���ɏ����A���܂������̎w�E�ɂ���ɐ������ƌ�������
���ꂱ�����S�}�J�V���S�}�J�V�ƒm��Ȃ���_�������J���A�Ȃ����S�}�J�V��K���ɉ����B�����Ƃ���p���ɑ��Ȃ�Ȃ�
���ꂪ�������Ă���Ȃ�A�������Ǝv�����ʂ��o���Ƃ��ɁA�K���Ԉ���Ă���ӏ�������ƍl���Č������ׂ�
����������A�ؖ����������܂����ƃX���b�h�̃^�C�g���ɏ����A���܂������̎w�E�ɂ���ɐ������ƌ�������
���ꂱ�����S�}�J�V���S�}�J�V�ƒm��Ȃ���_�������J���A�Ȃ����S�}�J�V��K���ɉ����B�����Ƃ���p���ɑ��Ȃ�Ȃ�
2018/09/15(�y) 21:42:28.21ID:NQNnUcix
�v�Z����ς����獢��Ǝv���Ă�̂�
�������V�˂��Ȃ�
�������V�˂��Ȃ�
2018/09/15(�y) 21:59:06.12ID:Zr4smbxu
�w���@�Ŏ����Ȃ疵�����Ȃ���Ȃ�Ȃ��̂͂��������ǁA�����
���v�Z�ԈႢ�����Ȃ���
�Ƃ������炠������B
�ނ���v�Z�~�X�͂�����A�E�g�B
�ǂ��ɂ��v�Z�~�X�A���W�b�N�G���[���Ȃ��ɂ�������炸�����������ĂȂ�ڂȂ���B
�v�Z�~�X���Ă��C�Â��Ȃ��Ȃ�w���@�͎g���Ȃ������R�B
���v�Z�ԈႢ�����Ȃ���
�Ƃ������炠������B
�ނ���v�Z�~�X�͂�����A�E�g�B
�ǂ��ɂ��v�Z�~�X�A���W�b�N�G���[���Ȃ��ɂ�������炸�����������ĂȂ�ڂȂ���B
�v�Z�~�X���Ă��C�Â��Ȃ��Ȃ�w���@�͎g���Ȃ������R�B
>>839
���̖��͓���ĂȂ��Ȃ��������o�Ȃ�����A�����Ȃ�̂͒v�����Ȃ��B
�㉽����Ԉ���Ă���ƁA����Ă���Ƃ����̂����邪�B
a*x=c(p^(2x)-1)���Ƃ��͂܂������Aa=c(x-1)^(2x/h)���Ƃ������v�Z��
�v�Z�̂��悤���Ȃ��Ǝv���B���������I�Ȍv�Z�͂قڑS�čs�����̂Ŏ��ɂł��邱�Ƃ͂����Ȃ���
�l������B
>>840
�ԈႢ�������ʂ������Ƃ����������A�Ԉ�����w�E������ȏ㑽�������������Ƃ�����̂��d�����Ȃ��B
>>841
�v�Z�����ł͂Ȃ��ł���B���R�B
>>842
����͂����ł��傤���ǁB�w���@���g���Ȃ��Ƃ����̂ƌv�Z�ԈႢ������Ƃ����͕̂ʖ��B
����������Ă��܂��Ƃ��̖��̔w���@�͒N���g���Ȃ��Ƃ������ƂɂȂ�܂��B
���̖��͓���ĂȂ��Ȃ��������o�Ȃ�����A�����Ȃ�̂͒v�����Ȃ��B
�㉽����Ԉ���Ă���ƁA����Ă���Ƃ����̂����邪�B
a*x=c(p^(2x)-1)���Ƃ��͂܂������Aa=c(x-1)^(2x/h)���Ƃ������v�Z��
�v�Z�̂��悤���Ȃ��Ǝv���B���������I�Ȍv�Z�͂قڑS�čs�����̂Ŏ��ɂł��邱�Ƃ͂����Ȃ���
�l������B
>>840
�ԈႢ�������ʂ������Ƃ����������A�Ԉ�����w�E������ȏ㑽�������������Ƃ�����̂��d�����Ȃ��B
>>841
�v�Z�����ł͂Ȃ��ł���B���R�B
>>842
����͂����ł��傤���ǁB�w���@���g���Ȃ��Ƃ����̂ƌv�Z�ԈႢ������Ƃ����͕̂ʖ��B
����������Ă��܂��Ƃ��̖��̔w���@�͒N���g���Ȃ��Ƃ������ƂɂȂ�܂��B
2018/09/15(�y) 23:24:24.40ID:NQNnUcix
���ʂ̐l�͂���ȂɌv�Z�~�X�Ȃ�Ă��Ȃ���ł���A�V�˂ɂ͂킩��Ȃ��ł��傤����
2018/09/15(�y) 23:27:01.81ID:m2ib/T6j
>>843
�v�Z�~�X�̑���������������ĊJ�����邩��i�����Ȃ���B
�v�Z�~�X�̑���������������ĊJ�����邩��i�����Ȃ���B
>>844
�}�W���X����̂��n���n�������ł����ǁA���╁�ʂ̐l�͂��̖��͎��g�܂Ȃ��B
���g�Ƃ��Č��ʂ��o���Ƃ��Ă����̐l�ԂɌ��Ă��炤�B���͂����������ɂȂ������B
�}�W���X����̂��n���n�������ł����ǁA���╁�ʂ̐l�͂��̖��͎��g�܂Ȃ��B
���g�Ƃ��Č��ʂ��o���Ƃ��Ă����̐l�ԂɌ��Ă��炤�B���͂����������ɂȂ������B
2018/09/15(�y) 23:32:56.81ID:NQNnUcix
>>846
�m���Ɍ����҂Ƃ������Ȑl���炢�ł��傤�ˁA���������ɒ��ނ̂�
�m���Ɍ����҂Ƃ������Ȑl���炢�ł��傤�ˁA���������ɒ��ނ̂�
2018/09/15(�y) 23:37:11.90ID:NQNnUcix
�Ƃ��������̐l�ԂɌ��Ă��炦�ΔF�߂Ă��炦��Ǝv���Ă��ł����H
���̃X���ł̂�����Y��Ă��܂�����ł��傤���H
���̃X���ł̂�����Y��Ă��܂�����ł��傤���H
>>849
�F�߂邩�F�߂Ȃ����͓ǂސl�ɂ����ł��傤���ǁB��{�I�ɂ͉ɂԂ��ł��B���邱�ƂȂ��̂ŁB
�����Ȃ��̂ŏA�E�����͂ł��܂���B���ɕ�������������ł����B
�F�߂邩�F�߂Ȃ����͓ǂސl�ɂ����ł��傤���ǁB��{�I�ɂ͉ɂԂ��ł��B���邱�ƂȂ��̂ŁB
�����Ȃ��̂ŏA�E�����͂ł��܂���B���ɕ�������������ł����B
���w�I���ʂ͏o���Ă���ƌ����Ă���̂ŁA��������邩�ǂ����͑��҂����f���ׂ�
���Ƃ��Ǝv���܂��B����������ƁA���S�Ɋ��m��������܂��B
���Ƃ��Ǝv���܂��B����������ƁA���S�Ɋ��m��������܂��B
2018/09/15(�y) 23:45:00.39ID:NQNnUcix
�l�b�g���邨��������Ȃ�n�����܂ł̌�ʔ�炢�o�����Ȃ��ł����H
>>852
�h�c�ɂȂ̂�SE�̎d���͂���܂���B
�����Ō�40���ȏ�̉�Ђ���X�J�E�g�����邱�Ƃ�����̂ŁA�n���炵������B
�܂�Ȃ����E�������ق�10�N�B�o�ϊ�@�̔�Q�҂���{�Љ��10�N���u�B
�ǂ��납�A�e���r�ł��̔�Q�҂��U�����܂���B
�h�c�ɂȂ̂�SE�̎d���͂���܂���B
�����Ō�40���ȏ�̉�Ђ���X�J�E�g�����邱�Ƃ�����̂ŁA�n���炵������B
�܂�Ȃ����E�������ق�10�N�B�o�ϊ�@�̔�Q�҂���{�Љ��10�N���u�B
�ǂ��납�A�e���r�ł��̔�Q�҂��U�����܂���B
2018/09/16(��) 00:06:16.52ID:pmmB3AXO
>>853
SE�ȊO�ɂ��d���͂����
SE�ȊO�ɂ��d���͂����
>>854
�c�ɂł��낢�뉞�債������ǑS��
�c�ɂł��낢�뉞�債������ǑS��
2018/09/16(��) 02:45:06.71ID:vOhbaJSk
��Ɓu���̋��Ԃ�10�N�͉������Ă�����ł����H�v
���u�O�̉�Ђŕs���ɉ��ق���A�����Ƃɐl���̖W�Q����������Ă��܂����v
���(�Ȃ����c)
���u�O�̉�Ђŕs���ɉ��ق���A�����Ƃɐl���̖W�Q����������Ă��܂����v
���(�Ȃ����c)
857�P�R�Q�l�ڂ̑f������
2018/09/16(��) 08:30:47.07ID:evvIr47u ���䂶��ˁH
2018/09/16(��) 10:07:42.03ID:Je84gqbt
������́A�����Ȃ̂łP�l��炵���ł������e�̂��ƂŃq�L�j�[�g�B
���߂��Ȃ��`�B
�����ł����̂��߂̍�Ə��Ƃ��Ŏd��������X�����T�����ɂ͂�����ł�����̂ɁB
���߂��Ȃ��`�B
�����ł����̂��߂̍�Ə��Ƃ��Ŏd��������X�����T�����ɂ͂�����ł�����̂ɁB
2018/09/16(��) 11:38:20.83ID:0MrQUBvh
>>858
���S�Ɍ���҂Ƀ��b�e�����肷��ȁA�J�X
�����̂悤�ɊO���畷�����Ă����排����������O�����A���傪���������
�ʂƌ������Č����B
��̑�l������ȃh�c�ɂ܂ŖK��Ē�4�����ɊO����A�u�ȂɂȂɂ�����A���ˁB�v
���Ƃ��悭����ȗc�t�Ȃ��Ƃ����������B���X�������B
���S�Ɍ���҂Ƀ��b�e�����肷��ȁA�J�X
�����̂悤�ɊO���畷�����Ă����排����������O�����A���傪���������
�ʂƌ������Č����B
��̑�l������ȃh�c�ɂ܂ŖK��Ē�4�����ɊO����A�u�ȂɂȂɂ�����A���ˁB�v
���Ƃ��悭����ȗc�t�Ȃ��Ƃ����������B���X�������B
2018/09/16(��) 11:46:26.59ID:Je84gqbt
�g���b�v�Y�ꂿ��_���B
������ł��d��������ꏊ��������Ă��Ƃ���B
������ł��d��������ꏊ��������Ă��Ƃ���B
2018/09/16(��) 12:33:49.30ID:pmmB3AXO
�u�����͓V�˂��v�Ƃ����ƕςɌ�����Ƃ����̂͗������Ă�̂ɁA>>859�̂悤�ȏ������݂�����ƕςɌ�����Ƃ����̂͗����ł��ĂȂ��s�v�c
2018/09/16(��) 13:36:51.97ID:DpvrZtou
�ŐV�_���͂�����@>>712
>>861
�����������Ƃ������ē�����y�����邩�炵�傤���Ȃ�
�����������Ƃ������ē�����y�����邩�炵�傤���Ȃ�
2018/09/16(��) 15:18:05.58ID:nt0xWHx/
>>859 ���l�^�łȂ��}�W�Ȃ��k�ʂ��ł����ǐ��_�ȖK�˂Ă݂Ă�������������Ȃ��ˁB
�K�˂Ă݂Ė��Ȃ��Ɛf�f���ꂽ�Ȃ炻��ł������B
�K�˂Ă݂Ė��Ȃ��Ɛf�f���ꂽ�Ȃ炻��ł������B
2018/09/16(��) 16:26:29.47ID:q79/R8lf
�S�������b�₯��
2018/09/16(��) 16:36:41.77ID:hdOs0U2+
2018/09/16(��) 16:51:35.02ID:Dk+/659M
��������Ă��邾���Ȃ�A�����炩�瓐�����Ă��o���Ȃ���
��������S���ėǂ�������
��������S���ėǂ�������
2018/09/16(��) 19:21:52.39ID:Je84gqbt
>>859 �́u�ȂɂȂɂ�����A���ˁB�v�Ȃ�Č��t��
�u�`���炵�˂��v
�ŕ��ʂ̉�b�ł��肻���B
�ȑO�����É��̂��݉��~���j���[�X�ɂȂ��Ă���Ƃ��ɁA
�s�u�ł��݉��~���Ď����̂��Ƃ���Ă�Ɗ��Ⴂ���ē{��܂����Ă���
����܂ł�������Ȃ̂���B
�u�`���炵�˂��v
�ŕ��ʂ̉�b�ł��肻���B
�ȑO�����É��̂��݉��~���j���[�X�ɂȂ��Ă���Ƃ��ɁA
�s�u�ł��݉��~���Ď����̂��Ƃ���Ă�Ɗ��Ⴂ���ē{��܂����Ă���
����܂ł�������Ȃ̂���B
2018/09/16(��) 19:52:10.16ID:S0haNoN7
�u�`���炵�˂��B�v���g�����ᕶ�������Ă���
2018/09/16(��) 21:10:23.56ID:kb4xyUSF
�����������A���ł�ɂ͂킳�т���Ȃ��Ă��炵�˂��B
2018/09/16(��) 22:08:06.23ID:Dk+/659M
�u�`����������炵���˂��v
���Ǝv����
���Ǝv����
2018/09/16(��) 22:18:56.94ID:Dk+/659M
���̎擾���ł��Ȃ����A�擾�����������o�L���ɕۑ��ł��Ȃ����Ԃ����~���b�`���b�Ԃ���̂��������
���ꂪ����I�ɋN�����Ă��炻�ꂪ�ނɂƂ��Ă̏펯�ɂȂ�̂����Ȃ�����
���ꂪ����I�ɋN�����Ă��炻�ꂪ�ނɂƂ��Ă̏펯�ɂȂ�̂����Ȃ�����
2018/09/16(��) 22:23:25.98ID:zBOdzCcL
�������҂̔�Q�ϑz�͘_�j�ł��Ȃ���B
���҂ɂƂ��ēs���̂悢���߂�������ł����݂���̂ŁA
�����炪�����琳�_�������Ă����҂͔[�����Ȃ��B
����ȕa�l�ł������A���w�ɂ��Ă̊ԈႢ�͔F�߂���Ȃ��̂�����A
���w���Ă������ł��ˁB
���҂ɂƂ��ēs���̂悢���߂�������ł����݂���̂ŁA
�����炪�����琳�_�������Ă����҂͔[�����Ȃ��B
����ȕa�l�ł������A���w�ɂ��Ă̊ԈႢ�͔F�߂���Ȃ��̂�����A
���w���Ă������ł��ˁB
874�P�R�Q�l�ڂ̑f������
2018/09/17(��) 00:46:36.72ID:T7a194so ���O�𓐒����Ă��邼
2018/09/17(��) 08:42:45.46ID:IvmiQcMs
������ȕa�l�ł������A���w�ɂ��Ă̊ԈႢ�͔F�߂���Ȃ��̂�����
���������Ԃ��|���邱�Ƃ������������ǂˁB
���������Ԃ��|���邱�Ƃ������������ǂˁB
876�P�R�Q�l�ڂ̑f������
2018/09/17(��) 09:04:25.01ID:qkPY/c3Z >>870 �]������B
2018/09/17(��) 09:48:38.31ID:QfjXpo7k
>>868-871
�⋩���Ă��銴������������A���W�Ɍ��܂��Ă���Ǝv���B
>>873
����Ȃ��Ƃ͊ȒP���B�������w�ȊO�ŏ����Ă�����e�ŊԈ���Ă��鎖�������邱�Ƃ�
�ؖ�������������B�����S���R�Ƒ����̂́A���������B
�����������������e�����̐l�Ԃɑ��ẮA�s�s���Ȏ����Ƃ��������̂��Ƃ��낤�Ǝv���B
cr��qr-1�ɂȂ�ؖ����ł��܂����B
v��pr�������Ɋ܂܂Ȃ���As����Ƃ���
c=vpr^(qr-1)
s=��[k=1,r-1]pk^qk
�Ƃ����
b=cpr(p^(n-1)+p^(n-3)+�c+1)
������
s=v(p^(n-1)+p^(n-3)+�c+1)
s=v(p^(n+1)-1)/((p+1)(p-1))
s=v((2pr-1)^(n+1)-1)/(4(pr-1)pr)
s�Ɉ���pr���܂܂�Ă��Ȃ�����Ap^(n-1)+p^(n-3)+�c+1�ɂ�
����pr���܂܂�Ȃ��̂ŁA�����pr�����邩�犄����Ȃ�
�Ő����ɂȂ�Ȃ��̂ŕs�K�ɂȂ�B
���2m+1=wpr^(qr-cr-1)����������Ƃ��ɉ����Ȃ����Ƃ�
�����������ƂɂȂ����B���̖�肪���Ȃ�O�i�����̂ł�
�Ȃ����Ǝv���B
�⋩���Ă��銴������������A���W�Ɍ��܂��Ă���Ǝv���B
>>873
����Ȃ��Ƃ͊ȒP���B�������w�ȊO�ŏ����Ă�����e�ŊԈ���Ă��鎖�������邱�Ƃ�
�ؖ�������������B�����S���R�Ƒ����̂́A���������B
�����������������e�����̐l�Ԃɑ��ẮA�s�s���Ȏ����Ƃ��������̂��Ƃ��낤�Ǝv���B
cr��qr-1�ɂȂ�ؖ����ł��܂����B
v��pr�������Ɋ܂܂Ȃ���As����Ƃ���
c=vpr^(qr-1)
s=��[k=1,r-1]pk^qk
�Ƃ����
b=cpr(p^(n-1)+p^(n-3)+�c+1)
������
s=v(p^(n-1)+p^(n-3)+�c+1)
s=v(p^(n+1)-1)/((p+1)(p-1))
s=v((2pr-1)^(n+1)-1)/(4(pr-1)pr)
s�Ɉ���pr���܂܂�Ă��Ȃ�����Ap^(n-1)+p^(n-3)+�c+1�ɂ�
����pr���܂܂�Ȃ��̂ŁA�����pr�����邩�犄����Ȃ�
�Ő����ɂȂ�Ȃ��̂ŕs�K�ɂȂ�B
���2m+1=wpr^(qr-cr-1)����������Ƃ��ɉ����Ȃ����Ƃ�
�����������ƂɂȂ����B���̖�肪���Ȃ�O�i�����̂ł�
�Ȃ����Ǝv���B
879�P�R�Q�l�ڂ̑f������
2018/09/17(��) 11:14:51.38ID:FnrnWGEq https://m.facebook.com/masaoki.iwasaki.9
https://twitter.com/mas20285
https://twitter.com/keepmathtop
https://twitter.com/puratinaomega
https://twitter.com/xPuGPq8Tn9GWCJb
�����w��1-F�S�C�̊�薏�T�搶�����o�C�B
�����w���ɋ߂�̂�3�N�ځB
�S���Ȗڂ͐��w�B
���q�e�j�X���̌ږ�����Ă���B
�������o�C�Ƃ����ƁA2013�N4������2015�N3���܂ŋ{�O�����ɓ����Ă����炵���A���q���w����sex�������Ƃ��o���āA����ꂽ����B
���ł����t�𑱂��Ă���̂��������s�v�c�Ȋ�������B
���搶���āA�c�C�b�^�[��Facebook������Ă�݂���������A�`���Ă݂ẮH
https://i.imgur.com/Ih1vtbs.png
https://i.imgur.com/PL5otNF.png
https://i.imgur.com/2UR2NsQ.jpg
https://i.imgur.com/wVyAk68.jpg
https://i.imgur.com/tCLqV3S.jpg
https://i.imgur.com/5MQec4w.jpg
https://i.imgur.com/utScB5j.jpg
https://i.imgur.com/inTVEtU.jpg
���̐l����ȂɃ��o�C�́H
https://twitter.com/5chan_nel (5ch newer account)
https://twitter.com/mas20285
https://twitter.com/keepmathtop
https://twitter.com/puratinaomega
https://twitter.com/xPuGPq8Tn9GWCJb
�����w��1-F�S�C�̊�薏�T�搶�����o�C�B
�����w���ɋ߂�̂�3�N�ځB
�S���Ȗڂ͐��w�B
���q�e�j�X���̌ږ�����Ă���B
�������o�C�Ƃ����ƁA2013�N4������2015�N3���܂ŋ{�O�����ɓ����Ă����炵���A���q���w����sex�������Ƃ��o���āA����ꂽ����B
���ł����t�𑱂��Ă���̂��������s�v�c�Ȋ�������B
���搶���āA�c�C�b�^�[��Facebook������Ă�݂���������A�`���Ă݂ẮH
https://i.imgur.com/Ih1vtbs.png
https://i.imgur.com/PL5otNF.png
https://i.imgur.com/2UR2NsQ.jpg
https://i.imgur.com/wVyAk68.jpg
https://i.imgur.com/tCLqV3S.jpg
https://i.imgur.com/5MQec4w.jpg
https://i.imgur.com/utScB5j.jpg
https://i.imgur.com/inTVEtU.jpg
���̐l����ȂɃ��o�C�́H
https://twitter.com/5chan_nel (5ch newer account)
2018/09/17(��) 11:25:10.90ID:IvgJN1sv
�P�ł�������炵����Ə��̃X�����������Ă݂��B
�ǂ��Ƃ��ɍs����Ƃ����炵�����H
A�^���Ə��EA�^��Ə� Part64
https://mevius.5ch.net/test/read.cgi/utu/1536989081/l50
B�^��Ə��E���Ə�part59
https://mevius.5ch.net/test/read.cgi/utu/1536708753/l50
A�^���Ə��EA�^��Ə� Part59 ���b�`���C����
https://mevius.5ch.net/test/read.cgi/utu/1532072896/l50
�ǂ��Ƃ��ɍs����Ƃ����炵�����H
A�^���Ə��EA�^��Ə� Part64
https://mevius.5ch.net/test/read.cgi/utu/1536989081/l50
B�^��Ə��E���Ə�part59
https://mevius.5ch.net/test/read.cgi/utu/1536708753/l50
A�^���Ə��EA�^��Ə� Part59 ���b�`���C����
https://mevius.5ch.net/test/read.cgi/utu/1532072896/l50
881�P�R�Q�l�ڂ̑f������
2018/09/17(��) 11:25:16.04ID:mbjb6tyB >>878
�܂����[�v���Ă����
��s=v(p^(n-1)+p^(n-3)+�c+1) �@
��s=v(p^(n+1)-1)/((p+1)(p-1)) �A
��s�Ɉ���pr���܂܂�Ă��Ȃ�����Ap^(n-1)+p^(n-3)+�c+1�ɂ�
������pr���܂܂�Ȃ��̂ŁA
�@���A�ɕό`�����킯������A���ꂾ���ł͂Ȃ����q��(p+1)(p-1)�̔{����
����ćA�̕����
�������pr�����邩�犄����Ȃ�
�Ƃ͂Ȃ�Ȃ�
�܂����[�v���Ă����
��s=v(p^(n-1)+p^(n-3)+�c+1) �@
��s=v(p^(n+1)-1)/((p+1)(p-1)) �A
��s�Ɉ���pr���܂܂�Ă��Ȃ�����Ap^(n-1)+p^(n-3)+�c+1�ɂ�
������pr���܂܂�Ȃ��̂ŁA
�@���A�ɕό`�����킯������A���ꂾ���ł͂Ȃ����q��(p+1)(p-1)�̔{����
����ćA�̕����
�������pr�����邩�犄����Ȃ�
�Ƃ͂Ȃ�Ȃ�
2018/09/17(��) 11:25:33.30ID:bGuoEh3u
��������u���炵�˂��I�I�I�v�Ɛ⋩���Ă��̂�
���{�ݘA��Ă���
���{�ݘA��Ă���
2018/09/17(��) 11:38:22.31ID:Ri3o3kt6
���Ԃ�N�����̘H���ŏؖ����悤�Ǝv���ĂȂ�����A�S�g�������Ȃ��]
884�P�R�Q�l�ڂ̑f������
2018/09/17(��) 11:51:26.60ID:aXv0MeU1 >>881
���[�v�͂��Ă��Ȃ��B
���[�v�͂��Ă��Ȃ��B
2018/09/17(��) 12:25:40.40ID:IvgJN1sv
PDF�����̂܂܁A�����̃t�F�C�Y�R�� >>16
887�P�R�Q�l�ڂ̑f������
2018/09/17(��) 12:27:49.36ID:mbjb6tyB >>885
����
��s=v((2pr-1)^(n+1)-1)/(4(pr-1)pr)
�ŁA
(2pr-1)^(n+1)-1�͖��炩��4(pr-1)pr�̔{���ł���
���肫��Ȃ��Ƃ����̂͌��
����
��s=v((2pr-1)^(n+1)-1)/(4(pr-1)pr)
�ŁA
(2pr-1)^(n+1)-1�͖��炩��4(pr-1)pr�̔{���ł���
���肫��Ȃ��Ƃ����̂͌��
2018/09/17(��) 12:30:51.27ID:bGuoEh3u
���ɂ͑S�R���炩�ɂ͌����Ȃ����ǂ������Ȃ��O��
2018/09/17(��) 12:34:50.61ID:IvgJN1sv
�P�̏����Ă邱�Ƃ��S�R���炩�ɂ͌����Ȃ��Ȃ琳�����ˁB
2018/09/17(��) 12:39:42.13ID:nWs1TvDp
�u���̖�肪����_�@�ɂ���Ă��Ȃ�O�i�����v�ˁu���̘_�@�ɂ͌v�Z�ԈႢ���܂܂�Ă���v
891�P�R�Q�l�ڂ̑f������
2018/09/17(��) 12:40:59.60ID:mbjb6tyB �͂���肷������
��s=v((2pr-1)^(n+1)-1)/(4(pr-1)pr)
(n+1)������������A
(2pr-1)^(n+1)��(2pr-1)^2=4(pr-1)pr+1�̃x�L�ł���A
(2pr-1)^(n+1)��1 (mod 4(pr-1)pr)�ƂȂ�
�����(2pr-1)^(n+1)-1��4(pr-1)pr�̔{��
��s=v((2pr-1)^(n+1)-1)/(4(pr-1)pr)
(n+1)������������A
(2pr-1)^(n+1)��(2pr-1)^2=4(pr-1)pr+1�̃x�L�ł���A
(2pr-1)^(n+1)��1 (mod 4(pr-1)pr)�ƂȂ�
�����(2pr-1)^(n+1)-1��4(pr-1)pr�̔{��
���q��pr�Ŋ�����Ȃ��Ə������̂͌��A
(2pr-1)^(n+1)-1��pr�Ŋ������̂�pr=0���������(2pr-1)^(n+1)-1=0
�ƂȂ邩��A�����������B
p^(n+1)-1��pr���܂܂�Ă��Ȃ��ƌ���������Ap^(n-1)+p^(n-3)+�c+1��
p+1=2pr���|���Ă���̂�����Apr�Ŋ������B
>>890
cr��qr-1�������ΑO�i���邱�Ƃ͎����B���ꂪ�\���͕�����Ȃ�����ǂ��B
(2pr-1)^(n+1)-1��pr�Ŋ������̂�pr=0���������(2pr-1)^(n+1)-1=0
�ƂȂ邩��A�����������B
p^(n+1)-1��pr���܂܂�Ă��Ȃ��ƌ���������Ap^(n-1)+p^(n-3)+�c+1��
p+1=2pr���|���Ă���̂�����Apr�Ŋ������B
>>890
cr��qr-1�������ΑO�i���邱�Ƃ͎����B���ꂪ�\���͕�����Ȃ�����ǂ��B
2018/09/17(��) 13:28:55.61ID:bGuoEh3u
p��r�͎��R���ł�����ȁH
>>893
p�͑f���ŁAr�͎��R��
p�͑f���ŁAr�͎��R��
2018/09/17(��) 16:42:14.74ID:bGuoEh3u
p+1=2pr���ĂȂ悶�Ⴀ
>>895
pr��r�͓Y�����ł�
pr��r�͓Y�����ł�
2018/09/17(��) 16:53:11.40ID:bGuoEh3u
���܂ł̂��S�������Ȃ̂�
�w����^�g���C�������ł���Ȃ牺�t���Y������_�g���Ă����H
�w����^�g���C�������ł���Ȃ牺�t���Y������_�g���Ă����H
2018/09/17(��) 17:15:01.62ID:jP8D23S8
���Â炭�Ȃ邯�ǂ�
�����܂ł���Ȃ����latex�ɂ��Ȃ����Ƃ��v��
�����܂ł���Ȃ����latex�ɂ��Ȃ����Ƃ��v��
2018/09/17(��) 17:29:17.12ID:bGuoEh3u
���Ă���Ȃ��́H
2018/09/17(��) 19:26:42.79ID:IvmiQcMs
�o�b�W�̃c�[��
�P�́A�ق�Ǝg���Ȃ��l
�P�́A�ق�Ǝg���Ȃ��l
2018/09/17(��) 19:45:19.69ID:+we0HO3w
2018/09/17(��) 20:23:15.98ID:UGjqumaZ
2018/09/17(��) 20:37:39.47ID:IvmiQcMs
���͂�Ƒ��̎�ɂ͕����Ȃ���Ԃ���B
2018/09/17(��) 20:58:09.29ID:umuAQR7p
�ǂ��݂�����SE�Ƃ��Ă����\����
>>902
�R�}���h�œ��͂��Ă��A�G���[�ŏo��悤�ɂȂ����B\87�Ƃ����R�[�h���������������炵���B
�ȑO�g�����Ƃ��ɏo�Ȃ��������A�ŋߎ��s�����炻���Ȃ����B
>>903
�e�͖������Ă��邵�A�������ƌ����ĕa�@�ɍs���悤�Ɋ��߂��肷��B
�{���ɁA�����̐Q�s���_�a���ƌ�f�����ƁA���̌܊���s���ɋ^����B
��Ђł̌����点�����̎�����m���Ă���l�Ԃ��N�����̌������e��M���Ȃ���
�v���Ă������Ă���ƍl������B
>>904
�Ƒ��̓h�c�ɂŎ����قږ������Đ������Ă���B
>>905
����700���������������Ƃ����邩��A�N�������30�˂�680���~�ł����B
���ʂ̎Ј��̃X�s�[�h��3�{�͏o�Ă���ƍl�����܂��B
�ŋ߁A�e���r�ŏ����̐��Łu����(�����}�̒��啨������)��n���ɂ����������炾�B�v
�Ƃ����⋩���������Ă����B�̃C�J�T�}�̗��R�ł��傤���H
�R�}���h�œ��͂��Ă��A�G���[�ŏo��悤�ɂȂ����B\87�Ƃ����R�[�h���������������炵���B
�ȑO�g�����Ƃ��ɏo�Ȃ��������A�ŋߎ��s�����炻���Ȃ����B
>>903
�e�͖������Ă��邵�A�������ƌ����ĕa�@�ɍs���悤�Ɋ��߂��肷��B
�{���ɁA�����̐Q�s���_�a���ƌ�f�����ƁA���̌܊���s���ɋ^����B
��Ђł̌����点�����̎�����m���Ă���l�Ԃ��N�����̌������e��M���Ȃ���
�v���Ă������Ă���ƍl������B
>>904
�Ƒ��̓h�c�ɂŎ����قږ������Đ������Ă���B
>>905
����700���������������Ƃ����邩��A�N�������30�˂�680���~�ł����B
���ʂ̎Ј��̃X�s�[�h��3�{�͏o�Ă���ƍl�����܂��B
�ŋ߁A�e���r�ŏ����̐��Łu����(�����}�̒��啨������)��n���ɂ����������炾�B�v
�Ƃ����⋩���������Ă����B�̃C�J�T�}�̗��R�ł��傤���H
2018/09/17(��) 21:37:20.64ID:UGjqumaZ
>>906
�������ǂ����͂Ƃ������Œ�ł������ԈႢ�H
��Âɍl���Ă݁H�e���r�ŌN�̈����Ȃ����Ǝv���H
�����Ԃɗ]�T������Ȃ�A�ɂԂ����炢�̋C�����ŁA��x���_�ȍs���Ă݂ẮH
�������ǂ����͂Ƃ������Œ�ł������ԈႢ�H
��Âɍl���Ă݁H�e���r�ŌN�̈����Ȃ����Ǝv���H
�����Ԃɗ]�T������Ȃ�A�ɂԂ����炢�̋C�����ŁA��x���_�ȍs���Ă݂ẮH
2018/09/17(��) 21:40:05.34ID:+we0HO3w
>>906
�W���� LaTeX �� \87 �ȂǂƂ�������Ԃ�͂Ȃ�����
�W���� LaTeX �� \87 �ȂǂƂ�������Ԃ�͂Ȃ�����
2018/09/17(��) 21:47:02.27ID:Ri3o3kt6
700�����������Ӗ��s��
�N�������680�������ۂ̔N���́H
�N�������680�������ۂ̔N���́H
>>909
�V�K��C++����5k���̐���t�@�[���E�F�A�̐�����1�����ōs�����B
���̎��̔N���͂���70%�ゾ�B
�͂����茾���Ƒ���c�̕����w�Ȃ�2�Q������ǂ��A�Ԃ�������̐��тō��i�����l�Ԃ�
�ǂ��œ����Ό�����H�c�ɂʼn҂���i���Ȃ��A10�N�����E�����������Ă���킯�����B
���ɋC�܂����Ă��邩��A����Ƀ��X�͂���Ȃ��B�S�Ď������B
�V�K��C++����5k���̐���t�@�[���E�F�A�̐�����1�����ōs�����B
���̎��̔N���͂���70%�ゾ�B
�͂����茾���Ƒ���c�̕����w�Ȃ�2�Q������ǂ��A�Ԃ�������̐��тō��i�����l�Ԃ�
�ǂ��œ����Ό�����H�c�ɂʼn҂���i���Ȃ��A10�N�����E�����������Ă���킯�����B
���ɋC�܂����Ă��邩��A����Ƀ��X�͂���Ȃ��B�S�Ď������B
2018/09/17(��) 21:57:06.76ID:Ri3o3kt6
�܂��{���ɂԂ�������œ��w�ł���Ȃ��Q�͂��Ȃ��ł���
2018/09/17(��) 21:59:03.88ID:UGjqumaZ
�����Ȃ��ƁB
2018/09/17(��) 22:02:57.61ID:RJpeeck8
2018/09/17(��) 22:06:55.82ID:D4u6zPpw
>>912
������A������5�Ȗڕ��ϕ��l75�������̂ɁA�C�J�T�}�Ŋw��4�ʂ̓s�����Z��
�i�w���Ȃ���Ȃ�Ȃ������B����ɓ��ɗ����̂Ŏ��͕����ɒl����Ɣ��f����4�l��teacher
�ȊO�͑S�ĐQ�Ă����̂ŁA3�N�Ԏ���������{�C�R�b�g�����B
���̉e����2�Q�ɂȂ����̂ł��傤�B1�Q�̎����܂��C�J�T�}���N����A�x��̍������n��
�Ō�ɂ͕��l66����A�S�Ă̖͎���A���肵���Ƃ������Ƃ��Ȃ��������l10���̐R�w�@��w
�̕����w�Ȃɂ������đS�ł��܂����B�C�J�T�}�̌��肾�Ƃ������Ƃ�������Ǝv���܂��B
������A������5�Ȗڕ��ϕ��l75�������̂ɁA�C�J�T�}�Ŋw��4�ʂ̓s�����Z��
�i�w���Ȃ���Ȃ�Ȃ������B����ɓ��ɗ����̂Ŏ��͕����ɒl����Ɣ��f����4�l��teacher
�ȊO�͑S�ĐQ�Ă����̂ŁA3�N�Ԏ���������{�C�R�b�g�����B
���̉e����2�Q�ɂȂ����̂ł��傤�B1�Q�̎����܂��C�J�T�}���N����A�x��̍������n��
�Ō�ɂ͕��l66����A�S�Ă̖͎���A���肵���Ƃ������Ƃ��Ȃ��������l10���̐R�w�@��w
�̕����w�Ȃɂ������đS�ł��܂����B�C�J�T�}�̌��肾�Ƃ������Ƃ�������Ǝv���܂��B
2018/09/17(��) 22:12:18.37ID:Ri3o3kt6
2018/09/17(��) 22:14:11.51ID:RJpeeck8
2018/09/17(��) 22:15:05.89ID:+we0HO3w
2018/09/17(��) 22:15:46.61ID:+we0HO3w
�~��������
��������
��������
2018/09/17(��) 22:16:24.28ID:IvmiQcMs
����܂ł�����
���R�w�@��w���H�w�������w�Ȃɂ�������B�Ӗ��s����2�Q�ɂȂ�B
�������������B
��Q�͐R�w�@
����ɍ��Z�����ł�
���Ӗ��s���ɍ����E�����ɑS�ł��A
�s���铌���Z�̓��ʎx���w�Z�ɐi�w������B
���Z�ɐi�w������Ȃ炿���ƍ��Z�̊w�͂�����ׂ��������B
�u�����v�������������ł͉��̗��v���Ȃ��B
���R�w�@��w���H�w�������w�Ȃɂ�������B�Ӗ��s����2�Q�ɂȂ�B
�������������B
��Q�͐R�w�@
����ɍ��Z�����ł�
���Ӗ��s���ɍ����E�����ɑS�ł��A
�s���铌���Z�̓��ʎx���w�Z�ɐi�w������B
���Z�ɐi�w������Ȃ炿���ƍ��Z�̊w�͂�����ׂ��������B
�u�����v�������������ł͉��̗��v���Ȃ��B
>>917
���l�̃M���b�v���l����ׂ��ł��B
�x��̍������n�̕�W�c�ŁA���l10���̊w�Ȃɗ�����l�Ԃ����̐��ɑ��݂����
�ł��傤���H���Z�̂Ƃ��͊J���Ƃ��}�g��t�����x���̕��l�œs�����Z����
���蓾�Ȃ��B�ʂ肪����̃I�b�T���Ɂu�J�������Ă��������B�v
�ƌ���ꂽ���Ƃ�����܂����B
>>919
2ch��TBS�݂̂̂��̂��Ƃ͏����Ă��郍�O������Ǝv���B�e���r������Q�l��
���R����Ƃ����^�����g���������������B���ׂ���̕���������Ǝv���B
>>921
���ʉȂ��ӂ�����ȁB�x��̍������n�ŁA5�Ȗڕ��ϕ��l��66�Ƃ����̂����̊w�͂�
����Ƃ������Ƃ�[�I�Ɏ����Ă��邪�B��Q�̂Ƃ��ɕ��l10���ŗ�����͂��̂Ȃ��w��
�����ɗ������Ƃ��������B
�����͖{���ɂ��̒��x������d�����Ȃ��B�w�̎��͓��v�͊w�̋��ȏ���90����
220�y�[�W���炢�ǂ�ŗ��������B
���l�̃M���b�v���l����ׂ��ł��B
�x��̍������n�̕�W�c�ŁA���l10���̊w�Ȃɗ�����l�Ԃ����̐��ɑ��݂����
�ł��傤���H���Z�̂Ƃ��͊J���Ƃ��}�g��t�����x���̕��l�œs�����Z����
���蓾�Ȃ��B�ʂ肪����̃I�b�T���Ɂu�J�������Ă��������B�v
�ƌ���ꂽ���Ƃ�����܂����B
>>919
2ch��TBS�݂̂̂��̂��Ƃ͏����Ă��郍�O������Ǝv���B�e���r������Q�l��
���R����Ƃ����^�����g���������������B���ׂ���̕���������Ǝv���B
>>921
���ʉȂ��ӂ�����ȁB�x��̍������n�ŁA5�Ȗڕ��ϕ��l��66�Ƃ����̂����̊w�͂�
����Ƃ������Ƃ�[�I�Ɏ����Ă��邪�B��Q�̂Ƃ��ɕ��l10���ŗ�����͂��̂Ȃ��w��
�����ɗ������Ƃ��������B
�����͖{���ɂ��̒��x������d�����Ȃ��B�w�̎��͓��v�͊w�̋��ȏ���90����
220�y�[�W���炢�ǂ�ŗ��������B
2018/09/17(��) 22:35:38.40ID:Ri3o3kt6
>>922
����A�����炠�Ȃ��͓_������Ȃ��ė�������H
����A�����炠�Ȃ��͓_������Ȃ��ė�������H
2018/09/17(��) 22:38:52.17ID:Ri3o3kt6
�����̂��Ƃ�V�˂��Ǝv�������Ďv�������āA�Ƃ����q�ϓI�ɕ]��������ł̌��ʂ�F�߂��Ȃ���ł����ˁH
>>924
�ʼn��ʂ��͂�����Ƃ������Ƃ����ƂȂ�ꍇ������̂�
���̋t�ɕs���ɓ_���������Ă�Ƃ����\��������܂���ˁB
���Ȃ��́A�x��ŕ��l10�����̂Ƃ���ɗ�����Ȃ�Ď��Ԃ��m���I��
�������鎖�ۂ��ƍl����̂ł����H�m���I�ɂ��蓾�Ȃ��Ƃ������Ƃł��B
���w�̂Ƃ��̍Ō�̐i�w�m�̉p��̃e�X�g��2�_����4�_�̖�肵���Ȃ�
33��̎�����2��ԈႦ�������ŁA85�_�ƍ̓_���ꂽ���Ƃ������ł��B
�{���̍��Z�̎����łǂ�Ȃ��Ƃ�����Ă��邩�Ȃ�Ă����̂͊��S��
AI�ƈꏏ�Ńu���b�N�{�b�N�X����Ȃ��ł����H
�ʼn��ʂ��͂�����Ƃ������Ƃ����ƂȂ�ꍇ������̂�
���̋t�ɕs���ɓ_���������Ă�Ƃ����\��������܂���ˁB
���Ȃ��́A�x��ŕ��l10�����̂Ƃ���ɗ�����Ȃ�Ď��Ԃ��m���I��
�������鎖�ۂ��ƍl����̂ł����H�m���I�ɂ��蓾�Ȃ��Ƃ������Ƃł��B
���w�̂Ƃ��̍Ō�̐i�w�m�̉p��̃e�X�g��2�_����4�_�̖�肵���Ȃ�
33��̎�����2��ԈႦ�������ŁA85�_�ƍ̓_���ꂽ���Ƃ������ł��B
�{���̍��Z�̎����łǂ�Ȃ��Ƃ�����Ă��邩�Ȃ�Ă����̂͊��S��
AI�ƈꏏ�Ńu���b�N�{�b�N�X����Ȃ��ł����H
2018/09/17(��) 22:43:22.27ID:Ri3o3kt6
2018/09/17(��) 22:44:07.85ID:Ri3o3kt6
���_�Ƃ��āA��肪�������ɗ�����
���ꂾ���̂��Ƃ����̂킩��Ȃ���ł��傤���H
���ꂾ���̂��Ƃ����̂킩��Ȃ���ł��傤���H
2018/09/17(��) 22:49:14.22ID:Ri3o3kt6
>>929
������Ȃ�ł��Ȃ��̓_����������́H
������Ȃ�ł��Ȃ��̓_����������́H
>>928
���Ⴀ���̏x���1�Q�̂Ƃ��͍������n���l66�Őw�̕����ɂ�������̂�
2�Q�̂Ƃ��́A�������n���l68�ŁA����c�A�c���A��q(�⌇)�A������w�̕����w��
�S�Ăɍ��i�ɂȂ��ł����H�_������Ȃ������͂��͂���܂���B
���Z�͕s���̋ɂ݂ł��B���̐��Ɏ�������]�܂Ȃ��̂ɕ��l19�����̍��Z��
�i�w����l�Ԃ����ȊO�ɂ���̂ł��傤���H
���Ⴀ���̏x���1�Q�̂Ƃ��͍������n���l66�Őw�̕����ɂ�������̂�
2�Q�̂Ƃ��́A�������n���l68�ŁA����c�A�c���A��q(�⌇)�A������w�̕����w��
�S�Ăɍ��i�ɂȂ��ł����H�_������Ȃ������͂��͂���܂���B
���Z�͕s���̋ɂ݂ł��B���̐��Ɏ�������]�܂Ȃ��̂ɕ��l19�����̍��Z��
�i�w����l�Ԃ����ȊO�ɂ���̂ł��傤���H
2018/09/17(��) 22:52:49.18ID:Ri3o3kt6
>>931
�_������Ȃ�������
�_������Ȃ�������
>>932
���̏��w���݂����ȃ��X��߂Ă���܂����H
���̏��w���݂����ȃ��X��߂Ă���܂����H
935�P�R�Q�l�ڂ̑f������
2018/09/17(��) 22:54:52.86ID:mbjb6tyB �e���r�̈����͖�������Ζ��Q�������킹�Ă����������B
�����萔�w�̘b�����悤��B
�����萔�w�̘b�����悤��B
2018/09/17(��) 22:56:02.37ID:Ri3o3kt6
>>934
�_�����삳�ꂽ�Ƃ��������w���ł����Ȃ��������߂܂��傤
�_�����삳�ꂽ�Ƃ��������w���ł����Ȃ��������߂܂��傤
2018/09/17(��) 22:57:00.16ID:Ri3o3kt6
�Ȃ�ł��̐l�̓_����������́H
�Ȃ�ł킴�킴�e���r�ł��̐l�̈����������́H
�Ȃ�ł킴�킴�e���r�ł��̐l�̈����������́H
2018/09/17(��) 22:58:15.02ID:+wPdJ5bz
����A��Âɍl���Ă��A�N�̂悤�ȋɈ�ʐl�̎Ȃ�A�����Ȃ�ɉ�����ĒN���Ȃ�H
�N���Ȃ�̂��߂ɂ���Ȃ��Ƃ����H
����H�Ǝv���H
�N���Ȃ�̂��߂ɂ���Ȃ��Ƃ����H
����H�Ǝv���H
2018/09/17(��) 23:01:13.49ID:nWs1TvDp
>>931
�����Ȃ���̉�S�čT���ăe�X�g��ɂ����������o����悤�ɂ��Ă����̂��펯�Ȃ̂ł����A���̂��Ȃ�������ł��傤���H
���I�؋����Ȃ��̂ł��ꂪ�����������Ƃ��Ă��A�؋��̏،������ł͐M�p�ł��Ȃ��ł�
�����Ȃ���̉�S�čT���ăe�X�g��ɂ����������o����悤�ɂ��Ă����̂��펯�Ȃ̂ł����A���̂��Ȃ�������ł��傤���H
���I�؋����Ȃ��̂ł��ꂪ�����������Ƃ��Ă��A�؋��̏،������ł͐M�p�ł��Ȃ��ł�
2018/09/17(��) 23:01:58.59ID:Ri3o3kt6
>>938
���ꂪ����������ł����ǁA�������͂ɂ͎��ɓƂ茾�Ŕᔻ�����̂�����
����ŁA��ʎ��̂Ɍ����������ÎE����Ă���A�������Ă���ƍl�����܂��B
���ꂪ����������ł����ǁA�������͂ɂ͎��ɓƂ茾�Ŕᔻ�����̂�����
����ŁA��ʎ��̂Ɍ����������ÎE����Ă���A�������Ă���ƍl�����܂��B
2018/09/17(��) 23:08:00.59ID:+wPdJ5bz
2018/09/17(��) 23:08:39.49ID:Ri3o3kt6
>>942
���Ȃ��̓Ƃ茾�������l�Ȃ�Ă���Ǝv���H
���Ȃ��̓Ƃ茾�������l�Ȃ�Ă���Ǝv���H
2018/09/17(��) 23:09:13.60ID:nWs1TvDp
>>942
���œ��B����Ă�Ƃ͍l���Ȃ��́H���őS�����֘A�Ȃ́H
���œ��B����Ă�Ƃ͍l���Ȃ��́H���őS�����֘A�Ȃ́H
2018/09/17(��) 23:09:14.43ID:IvmiQcMs
��ʎ��̂܂ł�炩���Ă����̂��I
������A�m���I�ɍl���ăC�J�T�}�����āA���ʂ����̏ꍇ�ɂ͉������B�����点�ŁB
�e���r�����ŁA��n���ɂ���ƎO���M����Ƃ����̂�������Ă����B
���̗Ⴉ�炷��Ƌ������\�Ƃ��v���Ȃ��B
�e���r�����ŁA��n���ɂ���ƎO���M����Ƃ����̂�������Ă����B
���̗Ⴉ�炷��Ƌ������\�Ƃ��v���Ȃ��B
2018/09/17(��) 23:12:17.34ID:Ri3o3kt6
>>947
���̂��Ȃ��Ɍ����点������́H
���̂��Ȃ��Ɍ����点������́H
2018/09/17(��) 23:13:05.26ID:nWs1TvDp
2018/09/17(��) 23:15:17.97ID:+we0HO3w
>>943
���̂Ɍ���������ÎE�͑��������Ȃ��́H
�M���������ĉ��f������n���Ă�����A50km�̓��H�ʼn�������60km�����炢
�̃X�s�[�h�Ŏ���瀂����Ƃ����Ԃ��������B���Ȃ�R�̏����������_�ʼnE�܂����Ȃ����
�Ȃ�Ȃ��Ƃ��낾�����̂ŁA�v��I�Ƃ����v���Ȃ��B
���̂Ɍ���������ÎE�͑��������Ȃ��́H
�M���������ĉ��f������n���Ă�����A50km�̓��H�ʼn�������60km�����炢
�̃X�s�[�h�Ŏ���瀂����Ƃ����Ԃ��������B���Ȃ�R�̏����������_�ʼnE�܂����Ȃ����
�Ȃ�Ȃ��Ƃ��낾�����̂ŁA�v��I�Ƃ����v���Ȃ��B
2018/09/17(��) 23:17:55.62ID:Ri3o3kt6
>>951
���̂��Ȃ����ÎE����́H
���̂��Ȃ����ÎE����́H
>>95
����ȃe���r�ł̕������e����X���������肵�܂���B
����ȃe���r�ł̕������e����X���������肵�܂���B
2018/09/17(��) 23:18:47.91ID:Ri3o3kt6
�_������A�����点�A�����A�ÎE�A�S�����R���Ȃ���ł���
>>954
�����F�߂����Ȃ��l�Ԃɂ͓��@�͂Ȃ��Ƃ������Ƃɂ�������ł��傤�ˁB
���Ȃ����A���̂悤�Ȃ��Ƃ����s�����l�Ԃ̈�l��������܂��B
�����F�߂����Ȃ��l�Ԃɂ͓��@�͂Ȃ��Ƃ������Ƃɂ�������ł��傤�ˁB
���Ȃ����A���̂悤�Ȃ��Ƃ����s�����l�Ԃ̈�l��������܂��B
2018/09/17(��) 23:21:49.01ID:Ri3o3kt6
>>956
�����ĂȂ��5ch�ł�����������Ă閳�E�ɂ���Ȃ��Ƃ����ł����H
�����ĂȂ��5ch�ł�����������Ă閳�E�ɂ���Ȃ��Ƃ����ł����H
2018/09/17(��) 23:22:39.44ID:+we0HO3w
>>953
���Ⴀ�e���r�ʼn��������悤�Ƃ��C�ɂ��Ȃ��������Ȃ��́H
�ǂ����債�����ƕ������ĂȂ���
�l�̎^�������Ȃ獪���������Ɩ��m�ɂ���
����͂��Ȃ��̐��w�ɂ��Ă������邱�Ƃ���
���Ⴀ�e���r�ʼn��������悤�Ƃ��C�ɂ��Ȃ��������Ȃ��́H
�ǂ����債�����ƕ������ĂȂ���
�l�̎^�������Ȃ獪���������Ɩ��m�ɂ���
����͂��Ȃ��̐��w�ɂ��Ă������邱�Ƃ���
2018/09/17(��) 23:24:07.68ID:ENijfptJ
>>922
���x��̍������n�̕�W�c�ŁA���l10���̊w�Ȃɗ�����l��
���́u�x��̕��l�v�Ƃ����̂́A���X1��̖͋[�����̌��ʂŎZ�o���ꂽ���̂ł��傤�H
�͋[�����Ő��w�E�����E���w�̑S�͈͂���肳���̂Ȃ�A���̕��l��M�����Ă�������������Ȃ�����ǂ��A
���w�E�����E���w�͈͖̔͂c�傾����A���̎����ł́A���̈ꕔ���̎��͂������f����Ă��Ȃ��̂ł́H
���Ȃ��̎v���Ă�����l�́A���܂����������ӂȕ������o�č��߂ɏo�����l�Ȃ̂ł͂Ȃ��̂ł��傤���H
���x��̍������n�̕�W�c�ŁA���l10���̊w�Ȃɗ�����l��
���́u�x��̕��l�v�Ƃ����̂́A���X1��̖͋[�����̌��ʂŎZ�o���ꂽ���̂ł��傤�H
�͋[�����Ő��w�E�����E���w�̑S�͈͂���肳���̂Ȃ�A���̕��l��M�����Ă�������������Ȃ�����ǂ��A
���w�E�����E���w�͈͖̔͂c�傾����A���̎����ł́A���̈ꕔ���̎��͂������f����Ă��Ȃ��̂ł́H
���Ȃ��̎v���Ă�����l�́A���܂����������ӂȕ������o�č��߂ɏo�����l�Ȃ̂ł͂Ȃ��̂ł��傤���H
2018/09/17(��) 23:26:11.36ID:nWs1TvDp
>>956
�����Ȃ���̉�S�čT���ăe�X�g��ɂ����������o����悤�ɂ��Ă����̂��펯�Ȃ̂ł����A���̂��Ȃ�������ł��傤���H
���I�؋����Ȃ��̂ł��ꂪ�����������Ƃ��Ă��A�؋��̏،������ł͐M�p�ł��Ȃ��ł��B
���̏ꍇ�����l�ł��B�����܂ő_���Ă���Ɗ�����̂Ȃ�A�����ɕ��I�؋�������������悤�ɏ������������ł��B
�Ȃ�̑���Ƃ�Ȃ��Ƃ́A�ĊO�Ԕ����Ȃ�ł��ˁB������_�����Ȃ��ł����ˁB
�����Ȃ���̉�S�čT���ăe�X�g��ɂ����������o����悤�ɂ��Ă����̂��펯�Ȃ̂ł����A���̂��Ȃ�������ł��傤���H
���I�؋����Ȃ��̂ł��ꂪ�����������Ƃ��Ă��A�؋��̏،������ł͐M�p�ł��Ȃ��ł��B
���̏ꍇ�����l�ł��B�����܂ő_���Ă���Ɗ�����̂Ȃ�A�����ɕ��I�؋�������������悤�ɏ������������ł��B
�Ȃ�̑���Ƃ�Ȃ��Ƃ́A�ĊO�Ԕ����Ȃ�ł��ˁB������_�����Ȃ��ł����ˁB
2018/09/17(��) 23:34:46.27ID:6PKE11M9
2018/09/17(��) 23:37:16.92ID:ENijfptJ
>>922
���x��̍������n�ŁA5�Ȗڕ��ϕ��l��66
����A���l��S��������5�Ŋ��������̂ł����H
�u���l�̕��ρv���ĈӖ�������Ƃ��v���ł����H
�u�m���E���v�v�ŕ��ςƕ��U�ɂ��ĕ������ł��傤�H���̂Ƃ��ɕ��U�╪�U�̃��[�g�ł���W�������w�͂�
�����A�̎��s�ɑ��ĕ��ϓ_��a, �W������ s �Ƃ����Ƃ��A
����s, a, �Ǝ����̑f�_x �������g���Ď����̏��ʂ�����ł���c�@
�Ƃ����̂��u���l���Ӗ������v����̉���ł����A���s���K�E�X���z�łȂ���·@�͐������Ȃ�
�u�m���E���v�v��������ƈӖ����l���Ȃ��������A�@�͋^�킵�����Ƃ́A���Z���̊w�K�͈͂ŁA���łɗ����ł���͂�
�����āA�����������l�𑫂����芄�����肵�����ʂ́A���w�I�ɉ��̈Ӗ��������Ȃ����Ƃ������Ȃ͂�
���x��̍������n�ŁA5�Ȗڕ��ϕ��l��66
����A���l��S��������5�Ŋ��������̂ł����H
�u���l�̕��ρv���ĈӖ�������Ƃ��v���ł����H
�u�m���E���v�v�ŕ��ςƕ��U�ɂ��ĕ������ł��傤�H���̂Ƃ��ɕ��U�╪�U�̃��[�g�ł���W�������w�͂�
�����A�̎��s�ɑ��ĕ��ϓ_��a, �W������ s �Ƃ����Ƃ��A
����s, a, �Ǝ����̑f�_x �������g���Ď����̏��ʂ�����ł���c�@
�Ƃ����̂��u���l���Ӗ������v����̉���ł����A���s���K�E�X���z�łȂ���·@�͐������Ȃ�
�u�m���E���v�v��������ƈӖ����l���Ȃ��������A�@�͋^�킵�����Ƃ́A���Z���̊w�K�͈͂ŁA���łɗ����ł���͂�
�����āA�����������l�𑫂����芄�����肵�����ʂ́A���w�I�ɉ��̈Ӗ��������Ȃ����Ƃ������Ȃ͂�
2018/09/17(��) 23:40:41.01ID:D4u6zPpw
>>959
���₻���ł͂Ȃ��B1�Q�̂Ƃ��͏t�̖͎���58���ꂩ��A�����ɏオ��Ō��66�B������
�S�Ă̖͎��Őw�̕����̍��i�����A�������B���Ȃ݂ɕ�W�c�̊w�͂��Ⴂ�x���
����͎��ł�3�Ȗڂŕ��l78�������B
���Z�̃C�J�T�}�͂Ƃ�ł��Ȃ��B2�w�����炢�̕��l��66���炢���߂�75���
��O�̎�����70���炢�ł����B����ɂق�100�����i����}�g��t�������l��
���������̂ɁA�w��4�ʂ̓s���ł���B���ɑS�ė��������ς�����A�w��1�ʂł͂Ȃ�
4�ʂ���ƒS�C�̋��t�������܂����B���͓s���ɍs���C��0���Ȃ̂łǂ��ł�������
�v���Ă��������ӂ��ɂ��Ă��܂��܂����B�s�������̌��ʂ�473�_�ł����B
���₻���ł͂Ȃ��B1�Q�̂Ƃ��͏t�̖͎���58���ꂩ��A�����ɏオ��Ō��66�B������
�S�Ă̖͎��Őw�̕����̍��i�����A�������B���Ȃ݂ɕ�W�c�̊w�͂��Ⴂ�x���
����͎��ł�3�Ȗڂŕ��l78�������B
���Z�̃C�J�T�}�͂Ƃ�ł��Ȃ��B2�w�����炢�̕��l��66���炢���߂�75���
��O�̎�����70���炢�ł����B����ɂق�100�����i����}�g��t�������l��
���������̂ɁA�w��4�ʂ̓s���ł���B���ɑS�ė��������ς�����A�w��1�ʂł͂Ȃ�
4�ʂ���ƒS�C�̋��t�������܂����B���͓s���ɍs���C��0���Ȃ̂łǂ��ł�������
�v���Ă��������ӂ��ɂ��Ă��܂��܂����B�s�������̌��ʂ�473�_�ł����B
>>962
�m�����v�ɋ����͂Ȃ����A5�Ȗڍ��v�̓_���ł̕��l�Ƃ����Ӗ��ŏ����Ă��܂���
�m�����v�ɋ����͂Ȃ����A5�Ȗڍ��v�̓_���ł̕��l�Ƃ����Ӗ��ŏ����Ă��܂���
2018/09/17(��) 23:42:51.14ID:Ri3o3kt6
�ł����Ǔ_��������Ȃ��ă_�����������
2018/09/17(��) 23:44:31.92ID:+we0HO3w
���X���͂������Ă�Ȃ�
���\�������Ȃ玩���̃u���O�ł��
���\�������Ȃ玩���̃u���O�ł��
2018/09/17(��) 23:46:26.48ID:D4u6zPpw
>>965
������A�}�g��t����J�����x���̕��l�œs���̊w��4�ʂ��Ă��蓾�Ȃ��ł��傤��
�����Ă�����ǁB�C�J�T�}�Ɍ��܂��Ă���B�_����s���Ɍ��_�����
�ǂ��ɂł��Ȃ�킯����ˁB�̌��ʂȂ�āB���낢�딻������s���Ȏ̎�����
�l����B����͕s���ɉ��_����Ƃ����Ƃ��ɖ��ɂȂ�ꍇ�����������
�t�ɓ_�����炷�s��������̂ł͂Ȃ����Ƃ��������̂��ƁB
�m���I�ɍl���Ď��̎̌��ʂ͂����������Ƃ��炯���B
������A�}�g��t����J�����x���̕��l�œs���̊w��4�ʂ��Ă��蓾�Ȃ��ł��傤��
�����Ă�����ǁB�C�J�T�}�Ɍ��܂��Ă���B�_����s���Ɍ��_�����
�ǂ��ɂł��Ȃ�킯����ˁB�̌��ʂȂ�āB���낢�딻������s���Ȏ̎�����
�l����B����͕s���ɉ��_����Ƃ����Ƃ��ɖ��ɂȂ�ꍇ�����������
�t�ɓ_�����炷�s��������̂ł͂Ȃ����Ƃ��������̂��ƁB
�m���I�ɍl���Ď��̎̌��ʂ͂����������Ƃ��炯���B
2018/09/17(��) 23:49:07.42ID:CRq5xwHM
>>968
���Ⴀ��l�̖��E�̐l�Ԃ����Ńe���r�̏o���҂͍U�������ł����H
���Ⴀ��l�̖��E�̐l�Ԃ����Ńe���r�̏o���҂͍U�������ł����H
2018/09/17(��) 23:52:24.65ID:nWs1TvDp
2018/09/17(��) 23:52:53.94ID:Ri3o3kt6
>>969
���ꂠ�Ȃ��̌����Ȃ�ł���
���ꂠ�Ȃ��̌����Ȃ�ł���
2018/09/17(��) 23:54:39.24ID:ENijfptJ
>>963
��1�Q�̂Ƃ��͏t�̖͎���58���ꂩ��A�����ɏオ��Ō��66�B
���l 58 �Ƃ����̂��A����͏t�̖͋[����1��Z�o�����u58�v�Ȃ�ł����
�Ō�̕��l 66 �Ƃ����̂��A����͈��̖͋[�����ŎZ�o�����u66�v�Ȃ�ł����
���ꂼ��̎����ŁA���w�A�����A���w�̑S�͈͂��o�肳�ꂽ��ł����H�����ł͂Ȃ��ł����
�����̓��Ӕ͈͂��o��A���l�͏�ڂɏo�Ă����������Ȃ��ł��傤�H
���ƁA�͋[���������_100�̕��ϓ_50�ɂȂ�悤�ɐv����Ă��Ȃ������ꍇ�́A�s���m�ɂȂ�܂��A���l 70 �ȏ�Ȃ�āA���͂قƂ�Ǔ��ĂɂȂ�Ȃ�
���{�ɂ����������āA�u3�Ȗڂŕ��l 78�v�Ƃ����̂́A�Ȗڂ̑f�_�����v�������A�Ȗڂ̕��l�̕��ς��Ƃ������A������ɂ��Ă��A����ȑ��삪�Ӗ������Ƃ����̂͌���Ȃ��^�킵��
�{�Ԏ��������ē�������
������͋[�����́u���l�v���悭�Ă��A�����̏o�肪�A�����̗����̑���Ȃ�����ɂ������Ă��܂�����A
�͋[�����̕��l�f���Ȃ����ʂɂȂ�\���͏\���ɂ���ł��傤
�܂��u���l�v�Ȃ���̂��A���w�I�ɈӖ����Ȃ����̂ł�����A�u�m���E���v�v�̋��ȏ���ǂݕԂ��Ċm���߂Ă݂��炢�����ł����H
��1�Q�̂Ƃ��͏t�̖͎���58���ꂩ��A�����ɏオ��Ō��66�B
���l 58 �Ƃ����̂��A����͏t�̖͋[����1��Z�o�����u58�v�Ȃ�ł����
�Ō�̕��l 66 �Ƃ����̂��A����͈��̖͋[�����ŎZ�o�����u66�v�Ȃ�ł����
���ꂼ��̎����ŁA���w�A�����A���w�̑S�͈͂��o�肳�ꂽ��ł����H�����ł͂Ȃ��ł����
�����̓��Ӕ͈͂��o��A���l�͏�ڂɏo�Ă����������Ȃ��ł��傤�H
���ƁA�͋[���������_100�̕��ϓ_50�ɂȂ�悤�ɐv����Ă��Ȃ������ꍇ�́A�s���m�ɂȂ�܂��A���l 70 �ȏ�Ȃ�āA���͂قƂ�Ǔ��ĂɂȂ�Ȃ�
���{�ɂ����������āA�u3�Ȗڂŕ��l 78�v�Ƃ����̂́A�Ȗڂ̑f�_�����v�������A�Ȗڂ̕��l�̕��ς��Ƃ������A������ɂ��Ă��A����ȑ��삪�Ӗ������Ƃ����̂͌���Ȃ��^�킵��
�{�Ԏ��������ē�������
������͋[�����́u���l�v���悭�Ă��A�����̏o�肪�A�����̗����̑���Ȃ�����ɂ������Ă��܂�����A
�͋[�����̕��l�f���Ȃ����ʂɂȂ�\���͏\���ɂ���ł��傤
�܂��u���l�v�Ȃ���̂��A���w�I�ɈӖ����Ȃ����̂ł�����A�u�m���E���v�v�̋��ȏ���ǂݕԂ��Ċm���߂Ă݂��炢�����ł����H
2018/09/17(��) 23:55:22.99ID:RJpeeck8
��������A�悤�ׂ��ȂŁA���������NJ��ғ��m�̂��Ƃ���������ǁA
������u�d�g�U���v�u�����v���̔�Q�ϑz������ƌ�������Е��́u����Ȃ��Ƃ���킯�Ȃ������A���فv���Č����A
�����͂���������Q���Ă邯�ǂˁA���Č����Ă��B
>>1�͗F�l�ł��e�ł��������ǁA�����Ɠ��l�̔�Q��i���Ă�����ǂ��v���́H
������u�d�g�U���v�u�����v���̔�Q�ϑz������ƌ�������Е��́u����Ȃ��Ƃ���킯�Ȃ������A���فv���Č����A
�����͂���������Q���Ă邯�ǂˁA���Č����Ă��B
>>1�͗F�l�ł��e�ł��������ǁA�����Ɠ��l�̔�Q��i���Ă�����ǂ��v���́H
2018/09/17(��) 23:59:51.09ID:ENijfptJ
>>964
���m�����v�ɋ����͂Ȃ����A5�Ȗڍ��v�̓_���ł̕��l
���l�ɂ��]�����܂₩���ł��邱�Ƃ́A���́u�m���E���v�v�̋��ȏ��ɏ\���ɋL�q����Ă��܂�
�F�A���ɗ��n�̐l�Ԃ́A�u�m���E���v�v������āA���l�ɂ��]�������͂f���Ă��Ȃ����Ƃ��\���ɏ��m���Ȃ���A��������ʂ��Ă����킯�ł�
���������Ȃ��͂����ł͂Ȃ������A�܂�A���͂��Ȃ������A�Ƃ������ƂɂȂ�̂ł͂Ȃ��ł��傤���H
���m�����v�ɋ����͂Ȃ����A5�Ȗڍ��v�̓_���ł̕��l
���l�ɂ��]�����܂₩���ł��邱�Ƃ́A���́u�m���E���v�v�̋��ȏ��ɏ\���ɋL�q����Ă��܂�
�F�A���ɗ��n�̐l�Ԃ́A�u�m���E���v�v������āA���l�ɂ��]�������͂f���Ă��Ȃ����Ƃ��\���ɏ��m���Ȃ���A��������ʂ��Ă����킯�ł�
���������Ȃ��͂����ł͂Ȃ������A�܂�A���͂��Ȃ������A�Ƃ������ƂɂȂ�̂ł͂Ȃ��ł��傤���H
2018/09/17(��) 23:59:53.43ID:bGuoEh3u
�����̖ϑz�ɐ^���ʂ��甽�_���Ă����Ԃ̖��ʂ��Ǝv�������O�炷�����Ȃق�Ƃ���
2018/09/18(��) 00:17:01.85ID:DDbX/VPU
2018/09/18(��) 00:19:18.62ID:/wc9VJKp
>>971
�݂̂��Ȃ�āA�J�����̑O�Ɋ���Ă��āA���������Ȃ��玄��n���ɂ��Ă��܂������B
>>972
�x��̍������n��5�Ȗ�(�p�E���E�ЁE���w�E�����E�Ȋw)�����������܂����炻�̍��v�ł�
���l�ł��B
�����ƁA�͋[���������_100�̕��ϓ_50�ɂȂ�悤�ɐv����Ă��Ȃ������ꍇ�́A
���s���m�ɂȂ�܂��A���l 70 �ȏ�Ȃ�āA���͂قƂ�Ǔ��ĂɂȂ�Ȃ�
�����{�ɂ����������āA�u3�Ȗڂŕ��l 78�v�Ƃ����̂́A�Ȗڂ̑f�_�����v�������A
���Ȗڂ̕��l�̕��ς��Ƃ������A������ɂ��Ă��A����ȑ��삪�Ӗ������Ƃ����̂͌���Ȃ��^�킵��
�������Ă����ł����A���v�_�ɑ��ĕ��l���������̂��Ǝv���܂��B
���K���z�ɏ]���Ă���A���l75�͏ォ��0.3�����炢���Ǝv���܂��B�L�������������
�������Ƃł����ǁB
���Ȃ��͕��l�̗L������F�߂Ȃ��̂ł����H���l�ɏ]���Ďu�]�Z�����߂�Ƃ����̂����ʂ���
�v���܂����B
>>973
�����������e���������Ƃ͂Ȃ����A�Y�ƈオ���_�a���b�e����ꍇ������Ƃ������e�̋L����
�ǂ��Ƃ�����B
>>974
���͂̂Ȃ��l�Ԃ�����c�̕����w�ȂɁA96�_/180�_�Ŏ鎎����135�_������č��i���邱�Ƃ�
�ł���̂ł����H�ʔ����ł��ˁB
>>975
���J�͂��������ɂ���
�݂̂��Ȃ�āA�J�����̑O�Ɋ���Ă��āA���������Ȃ��玄��n���ɂ��Ă��܂������B
>>972
�x��̍������n��5�Ȗ�(�p�E���E�ЁE���w�E�����E�Ȋw)�����������܂����炻�̍��v�ł�
���l�ł��B
�����ƁA�͋[���������_100�̕��ϓ_50�ɂȂ�悤�ɐv����Ă��Ȃ������ꍇ�́A
���s���m�ɂȂ�܂��A���l 70 �ȏ�Ȃ�āA���͂قƂ�Ǔ��ĂɂȂ�Ȃ�
�����{�ɂ����������āA�u3�Ȗڂŕ��l 78�v�Ƃ����̂́A�Ȗڂ̑f�_�����v�������A
���Ȗڂ̕��l�̕��ς��Ƃ������A������ɂ��Ă��A����ȑ��삪�Ӗ������Ƃ����̂͌���Ȃ��^�킵��
�������Ă����ł����A���v�_�ɑ��ĕ��l���������̂��Ǝv���܂��B
���K���z�ɏ]���Ă���A���l75�͏ォ��0.3�����炢���Ǝv���܂��B�L�������������
�������Ƃł����ǁB
���Ȃ��͕��l�̗L������F�߂Ȃ��̂ł����H���l�ɏ]���Ďu�]�Z�����߂�Ƃ����̂����ʂ���
�v���܂����B
>>973
�����������e���������Ƃ͂Ȃ����A�Y�ƈオ���_�a���b�e����ꍇ������Ƃ������e�̋L����
�ǂ��Ƃ�����B
>>974
���͂̂Ȃ��l�Ԃ�����c�̕����w�ȂɁA96�_/180�_�Ŏ鎎����135�_������č��i���邱�Ƃ�
�ł���̂ł����H�ʔ����ł��ˁB
>>975
���J�͂��������ɂ���
2018/09/18(��) 00:24:59.32ID:cDODlI0s
2018/09/18(��) 00:31:54.24ID:ueF6atas
>>977
�����K���z�ɏ]���Ă���A���l75�͏ォ��0.3�����炢���Ǝv���܂��B�L������������Ƃ������Ƃł����ǁB
����͖͋[�����̑f�_ x ����ɂ����ɂ�������ɐL�тĂ����̂Ȃ�A�͋[�����́u���K���z�ɏ]���v�u���K���z�ɂ���Ă��Nj߂��v�Ɖ��肵�Ă��Ó��i�܂���l�����͂f���Ă���j�Ƃ��܂����A
�����̖͋[������0�_�`���_�i100�_�j�̊ԂɌ��肳��Ă���i�c�@�j�킯�ł��傤�H
�����ĕW������0�_�`���_�̍��ɔ�ׂ�Ɣ�r�I�傫���c�A
�@�A�A�̏���A�͋[�����̑f�_�����K���z�ɏ]���A�Ɖ��肷��̂��s���R�ɂȂ�܂�
�����āA���K���z�ɂ��������Ă��Ȃ��̂Ȃ�u���l 75 ���ォ��0.3% �ʁv�Ƃ͂����Ȃ�����
�͋[�����̕��ϓ_���A�f�_�͈̔͂̂��傤�ǐ^�ɂȂ���A�܂��u���l75�v�Ȃ�āA�قƂ�ǂ��ĂɂȂ�Ȃ������ł�
�����l���������o���A�Ƃ����̂́A�܂��A���ϓ_�����Ȃ艺�Ɋ���Ă���Ƃ����Ă悢�A����ȕ��z�ł́A�i���ςƕ��U����Z�o�����j���l���珇�ʂ𐄒肷�邱�Ƃ͑Ó��łȂ��ł��傤��
�����K���z�ɏ]���Ă���A���l75�͏ォ��0.3�����炢���Ǝv���܂��B�L������������Ƃ������Ƃł����ǁB
����͖͋[�����̑f�_ x ����ɂ����ɂ�������ɐL�тĂ����̂Ȃ�A�͋[�����́u���K���z�ɏ]���v�u���K���z�ɂ���Ă��Nj߂��v�Ɖ��肵�Ă��Ó��i�܂���l�����͂f���Ă���j�Ƃ��܂����A
�����̖͋[������0�_�`���_�i100�_�j�̊ԂɌ��肳��Ă���i�c�@�j�킯�ł��傤�H
�����ĕW������0�_�`���_�̍��ɔ�ׂ�Ɣ�r�I�傫���c�A
�@�A�A�̏���A�͋[�����̑f�_�����K���z�ɏ]���A�Ɖ��肷��̂��s���R�ɂȂ�܂�
�����āA���K���z�ɂ��������Ă��Ȃ��̂Ȃ�u���l 75 ���ォ��0.3% �ʁv�Ƃ͂����Ȃ�����
�͋[�����̕��ϓ_���A�f�_�͈̔͂̂��傤�ǐ^�ɂȂ���A�܂��u���l75�v�Ȃ�āA�قƂ�ǂ��ĂɂȂ�Ȃ������ł�
�����l���������o���A�Ƃ����̂́A�܂��A���ϓ_�����Ȃ艺�Ɋ���Ă���Ƃ����Ă悢�A����ȕ��z�ł́A�i���ςƕ��U����Z�o�����j���l���珇�ʂ𐄒肷�邱�Ƃ͑Ó��łȂ��ł��傤��
>>980
���̂悤�Ȃ��Ƃ���������A���l���������Z�͓̎��ĂɂȂ炸�^�������Ƃ������Ƃł����H
���l��75�̊w����66���Ƃ�68���Ƃ��̕��l�̍��Z�ɗ�����̂͂ǂ��l���Ă��s�����Ǝv���܂��B
���̂悤�Ȃ��Ƃ���������A���l���������Z�͓̎��ĂɂȂ炸�^�������Ƃ������Ƃł����H
���l��75�̊w����66���Ƃ�68���Ƃ��̕��l�̍��Z�ɗ�����̂͂ǂ��l���Ă��s�����Ǝv���܂��B
2018/09/18(��) 00:46:13.43ID:cDODlI0s
���l�Ɠ_���������ċL�����Ă���
2018/09/18(��) 00:47:32.19ID:cDODlI0s
>>983
������A�m���I�ɍl�����Ȃ����Č����Ă���́B
����ŕ��l��7��9�����̍��Z�ɗ������l�Ԃ���l�ł�����킯�H
�������͂̈��͂�������Ȃ����A���\���삩������Ȃ��ł��ˁB
���̎������Z���ɂȂ�������A���\���삪�Љ���ɂȂ��Ă����̂ł����H
������A�m���I�ɍl�����Ȃ����Č����Ă���́B
����ŕ��l��7��9�����̍��Z�ɗ������l�Ԃ���l�ł�����킯�H
�������͂̈��͂�������Ȃ����A���\���삩������Ȃ��ł��ˁB
���̎������Z���ɂȂ�������A���\���삪�Љ���ɂȂ��Ă����̂ł����H
2018/09/18(��) 00:53:37.26ID:cDODlI0s
>>984
�m���I�ɓ_������̕������蓾�Ȃ���
�m���I�ɓ_������̕������蓾�Ȃ���
2018/09/18(��) 00:54:38.75ID:JaEppXdF
2018/09/18(��) 00:54:48.12ID:cDODlI0s
����ƕ��l�̘b�Ȃ̂����\�̘b�Ȃ̂���ѐ����Ȃ���
2018/09/18(��) 00:55:41.98ID:ueF6atas
>>981
������̖͋[�����ɂāA������e���Ȃ�f�_��P���ɑ����Ƃ��e���Ȃ̕��l�ς���Ƃ��A�̂悤�Ȃ�肩����������
�u���l 75 �� 68 �̓�҂̎��ʂɑ傫�ȍ��͂Ȃ��ł��傤�ˁv
�����������l�̌v�Z�̎d���ł́A�u���K���z�����肵�Ă����̂ł��傤���H�v
�����l���������Z�͓̎��ĂɂȂ炸�^�������Ƃ������Ƃł����H
���l�ɂ����͂̔���͂���߂ĕs���m�ł��A���ɓ�Փx�̒Ⴂ���w�����x���̖��ō��ʉ����鍂�Z�����́A���l�͂��ĂɂȂ�Ȃ�
���S�ɉ^�܂����A�Ƃ͂����܂��A���l 65 �� 70 �̍��Ȃ�āA�����̖{�Ԏ����ł̏o���ɂ���ĊȒP�ɂЂ�����Ԃ���悤�Ȃ��̂ł���
������̖͋[�����ɂāA������e���Ȃ�f�_��P���ɑ����Ƃ��e���Ȃ̕��l�ς���Ƃ��A�̂悤�Ȃ�肩����������
�u���l 75 �� 68 �̓�҂̎��ʂɑ傫�ȍ��͂Ȃ��ł��傤�ˁv
�����������l�̌v�Z�̎d���ł́A�u���K���z�����肵�Ă����̂ł��傤���H�v
�����l���������Z�͓̎��ĂɂȂ炸�^�������Ƃ������Ƃł����H
���l�ɂ����͂̔���͂���߂ĕs���m�ł��A���ɓ�Փx�̒Ⴂ���w�����x���̖��ō��ʉ����鍂�Z�����́A���l�͂��ĂɂȂ�Ȃ�
���S�ɉ^�܂����A�Ƃ͂����܂��A���l 65 �� 70 �̍��Ȃ�āA�����̖{�Ԏ����ł̏o���ɂ���ĊȒP�ɂЂ�����Ԃ���悤�Ȃ��̂ł���
2018/09/18(��) 00:57:13.98ID:OaUQIOsD
>>984
�������ǁB
�������ǁB
2018/09/18(��) 00:58:53.55ID:cDODlI0s
�ł��܂��A18�N�O�ɐ��_�a�̐f�f������ĉ������Ă��Ȃ��������Ă̂́A18�N�ȏジ���ƕa�C�Ȃ�
�Ⴆ����Ȓ������Ԃ����Ɠ��ɂ�����Ƃ��A�M������Ƃ��z�����Ă݂��狰�|��
���Â�����K���y�ɂȂ�킯�łȂ����ǁA���Â��Ȃ��Ƃ����Ƌ�����܂܂���
�Ⴆ����Ȓ������Ԃ����Ɠ��ɂ�����Ƃ��A�M������Ƃ��z�����Ă݂��狰�|��
���Â�����K���y�ɂȂ�킯�łȂ����ǁA���Â��Ȃ��Ƃ����Ƌ�����܂܂���
2018/09/18(��) 01:05:26.42ID:ueF6atas
>>984
�����l��7��9�����̍��Z�ɗ������l�Ԃ���l�ł�����킯�H
���������ł��ˁA��w�����ł�����
�O�������̐_�ˑ�w�H�w���V�X�e���H�w�ȂɎ�܂������A�����N��C�����̋����{����w�H�w���ɗ����܂����A�Z���^�[�����̑���ɂЂ����������̂ł��c
���{����w�̕��l�͓����� 60, �_�ˑ�w�͊w�Ȃɂ�邪 69 ���炢�͂���܂���
����ȑ��{����w�̑�����_�Ɉ��������邭�炢�A�Z���^�[�����̓{���{���i�����炭���l�I�� 50 ���炢�j�������̂ł����A�_�ˑ�w�̏o�肪���܂����ɑ������悭�A����č��i�ƂȂ��Ă̂ł��B
�i�ȏ�͌Â����̂�����A���̔N����킩�����Ⴄ�ˁj
�����l��7��9�����̍��Z�ɗ������l�Ԃ���l�ł�����킯�H
���������ł��ˁA��w�����ł�����
�O�������̐_�ˑ�w�H�w���V�X�e���H�w�ȂɎ�܂������A�����N��C�����̋����{����w�H�w���ɗ����܂����A�Z���^�[�����̑���ɂЂ����������̂ł��c
���{����w�̕��l�͓����� 60, �_�ˑ�w�͊w�Ȃɂ�邪 69 ���炢�͂���܂���
����ȑ��{����w�̑�����_�Ɉ��������邭�炢�A�Z���^�[�����̓{���{���i�����炭���l�I�� 50 ���炢�j�������̂ł����A�_�ˑ�w�̏o�肪���܂����ɑ������悭�A����č��i�ƂȂ��Ă̂ł��B
�i�ȏ�͌Â����̂�����A���̔N����킩�����Ⴄ�ˁj
2018/09/18(��) 01:22:12.11ID:cDODlI0s
2018/09/18(��) 02:24:51.74ID:bCEvKKhg
���E�_�����A�����w���ɂP�͈����z�����ق��������B
�P�̏������݂͐��w�ł͂Ȃ��B
�P�̏������݂͐��w�ł͂Ȃ��B
995�P�R�Q�l�ڂ̑f������
2018/09/18(��) 02:41:47.72ID:hTYNtONR ���w�Ƃ��ĔႢ�ȑO�ɁA�X���^�C�Ƃ������Ă��Ȃ�
�P�̌l�I�Șb��������ᑼ���ł��Ȃ���
�Ȃ��A������Ȃ��X���ɂ��������܂Ȃ��悤��
�P�̌l�I�Șb��������ᑼ���ł��Ȃ���
�Ȃ��A������Ȃ��X���ɂ��������܂Ȃ��悤��
996�P�R�Q�l�ڂ̑f������
2018/09/18(��) 02:46:16.27ID:KlCqpobf �e���v���\���Ƃ�
�y ���s�^ADHD�̓��� �z
�E�ɒ[�Ȋw�������`��A�ݓ��A��ӐE�ւ̋����ȍ���
�E���͂̐l��n���ɂ��邱�Ƃ��������҂������ĖJ�߂Ȃ�
�E�����̉��l�ς��S�ĂŁA���͂̑S���ɂ������J��Ԃ��Ď咣��������
�E�����̉��l�ψȊO�̍l���������݂��邱�Ǝ��̂������ł��Ȃ�
�E�����̕]���ɂُ͈�ɂ������
�E�����̂��錾������J��Ԃ��Ď������������Ƃ͈�ؔF�߂悤�Ƃ��Ȃ�
�E���ł��S���������悤�ƕK���A�����Ɍ��������Ď咣��ʂ��p�^�[���𑱂���
�E�₢�l�߂���Ǝ�������Q�҂ł��邱�Ƃ��A�s�[��������
�y ���s�^ADHD�̓��� �z
�E�ɒ[�Ȋw�������`��A�ݓ��A��ӐE�ւ̋����ȍ���
�E���͂̐l��n���ɂ��邱�Ƃ��������҂������ĖJ�߂Ȃ�
�E�����̉��l�ς��S�ĂŁA���͂̑S���ɂ������J��Ԃ��Ď咣��������
�E�����̉��l�ψȊO�̍l���������݂��邱�Ǝ��̂������ł��Ȃ�
�E�����̕]���ɂُ͈�ɂ������
�E�����̂��錾������J��Ԃ��Ď������������Ƃ͈�ؔF�߂悤�Ƃ��Ȃ�
�E���ł��S���������悤�ƕK���A�����Ɍ��������Ď咣��ʂ��p�^�[���𑱂���
�E�₢�l�߂���Ǝ�������Q�҂ł��邱�Ƃ��A�s�[��������
2018/09/18(��) 07:47:27.05ID:ueF6atas
>>992
��75�͍��Z�̐i�w�m�̕��l�ŁA68�͏x��\���Z��5�Ȗڍ��v�̕��l�B
����W�c���Ⴄ���瓖�R���l���Ⴄ�B
��5���炢�̍��ł͂Ȃ�7�Ƃ�9�Ȃ킯�B75�Ȃ̂ɁA66�Ƃ�68��A����̍��Z��
��������̂͂ǂ��l���Ă��s���B
���Z�����́A
�@�����͈͂����w�����x��������A�������ɂ����A�܂��������Ă��A���ꂪ���͂�����킵�����̂ł͂Ȃ�
�A���Z�����ɂ́u���\�_�v������A���t�������悤�ɂ�����ł���A���t�ɔ������āA�I�[���P�Ƃ������Ă��܂����Ƃ����肤��
���Ԃ�A�̂����ł��傤�ˁA�ł�����͋��t�̌��������炵�����Ȃ���
>>991
�Ŏ������悤�ɁA�ԋ��킹�Ȃ�ē��풃�ю��ł���A���l�]���͎��͎��͂f���Ă���Ƃ͌���Ȃ�����A
���������l�Ԃ���w���w��ɂ��낲�낢�邱�Ƃ��悭�킩��܂���
��75�͍��Z�̐i�w�m�̕��l�ŁA68�͏x��\���Z��5�Ȗڍ��v�̕��l�B
����W�c���Ⴄ���瓖�R���l���Ⴄ�B
��5���炢�̍��ł͂Ȃ�7�Ƃ�9�Ȃ킯�B75�Ȃ̂ɁA66�Ƃ�68��A����̍��Z��
��������̂͂ǂ��l���Ă��s���B
���Z�����́A
�@�����͈͂����w�����x��������A�������ɂ����A�܂��������Ă��A���ꂪ���͂�����킵�����̂ł͂Ȃ�
�A���Z�����ɂ́u���\�_�v������A���t�������悤�ɂ�����ł���A���t�ɔ������āA�I�[���P�Ƃ������Ă��܂����Ƃ����肤��
���Ԃ�A�̂����ł��傤�ˁA�ł�����͋��t�̌��������炵�����Ȃ���
>>991
�Ŏ������悤�ɁA�ԋ��킹�Ȃ�ē��풃�ю��ł���A���l�]���͎��͎��͂f���Ă���Ƃ͌���Ȃ�����A
���������l�Ԃ���w���w��ɂ��낲�낢�邱�Ƃ��悭�킩��܂���
2018/09/18(��) 09:51:44.34ID:fyBCp0YB
�s���铌���Z�̓��ʎx���w�Z�ł̍Z�����l��
�ǂ������Ƃł������̂��낤���H
�P�́A���ʎx���w�Z�ł��������ڂ�Ă��܂��A
�R�N�Ԃ����ƕ��ł��Ȃ������N�Y�Ȃ̂ɁB
�ǂ������Ƃł������̂��낤���H
�P�́A���ʎx���w�Z�ł��������ڂ�Ă��܂��A
�R�N�Ԃ����ƕ��ł��Ȃ������N�Y�Ȃ̂ɁB
>>998
���Z��n���ɂ���ȁA���ʉȂ����Ȃ���{�P
���Z��n���ɂ���ȁA���ʉȂ����Ȃ���{�P
2018/09/18(��) 10:31:13.14ID:fyBCp0YB
�����̓��w�������Z��n���ɂ��Ă���̂͂P
�o�J�ɂ����ɂ����Ǝ��Ƃɂ��Ă���悤�Ɋ撣���Ă���A
�������ŏ��w���ȉ��̃~�X���P�O�O�A�����邱�Ƃ��Ȃ�
���w�̘b�������ς藝��s�\�Ȃ�ĔߎS�Ȃ��Ƃɂ͂Ȃ�Ȃ������B
�o�J�ɂ����ɂ����Ǝ��Ƃɂ��Ă���悤�Ɋ撣���Ă���A
�������ŏ��w���ȉ��̃~�X���P�O�O�A�����邱�Ƃ��Ȃ�
���w�̘b�������ς藝��s�\�Ȃ�ĔߎS�Ȃ��Ƃɂ͂Ȃ�Ȃ������B
10011001
Over 1000Thread ���̃X���b�h�͂P�O�O�O���܂����B
�V�����X���b�h�𗧂ĂĂ��������B
life time: 27�� 0���� 18�� 19�b
�V�����X���b�h�𗧂ĂĂ��������B
life time: 27�� 0���� 18�� 19�b
10021002
Over 1000Thread 5�����˂�̉^�c�̓v���~�A������̊F���܂Ɏx�����Ă��܂��B
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�s�v���~�A������̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
��300�~���瓽���ł��w�����������܂��B
�� �v���~�A������o�^�͂����� ��
https://premium.5ch.net/
�� �Q�l���O�C���͂����� ��
https://login.5ch.net/login.php
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�s�v���~�A������̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
��300�~���瓽���ł��w�����������܂��B
�� �v���~�A������o�^�͂����� ��
https://premium.5ch.net/
�� �Q�l���O�C���͂����� ��
https://login.5ch.net/login.php
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
�j���[�X
- �y��āz�R�����r�A�哝�́A�ċ��ЂɁu��������v���Q [�V���`��]
- �X�}�C���[�L�N�`�@���Z�\�͓���̊g�U�Ɍx���u���Y��〝���`〟�ł͂Ȃ�〝����〟�A���Q�ґ��ł��v [���l����]
- ���R��t�@�����ԑg�ɋꌾ�u�N�\�ʔ������Ȃ����ˁA�R���g�B�Œ�ʼn��i�v�u�g���I�������A2���Ƃ������ԑg����Ō��Ăĕ����v��2 [�~���L�ҁ�]
- �y�T�b�J�[�z�H�c�s�V�X�^�W�A���@J���[�O���u���1���l�́A���܂�ɂ��u���Ⴂ�vBB�����u���݂���B�ŋ����g���Ă��肢����v��2 [�S�`�[�Y�G��]
- �y�x�l�Y�G���U���z�u�x�l�Y�G���l�̓g�����v�đ哝�̂Ɋ��ӂ��Ă���v�m�[�x�����a�܂̃}�`���h�� [���ꁚ]
- ���N�M���u2��2000�~��4��4000�~�v�Ɂ@�Z�[���[���N�M���啝�l�グ�A���Ђ������݂��낦�� [�ϗ���]
- �Ƃ点��
- ����z
- �yU-NEXT�z�v���~�A���[�O���� ��51
- �yATP�z�e�j�X���������X��2026 Part 2�yWTA�z
- �n����
- �����߂���
- �y����z�_��̌��ޗ������s�̂����ŋ֗A [695089791]
- ���O��Ȃ疳�f���Ԃ��Ă����J�X�ɂǂ�Ȑ��ق���́H
- ���܂�A�Ȃ�Łu�d�Ԓj�v���Ăǂ��̃T�u�X�N���v�V�����ɂ��Ȃ����H🥺
- �y���s�ߕ�z�����A���E�d��y��7��̃��A�A�[�X��A�o������ [931948549]
- �y����z�����̃����L�[�A�K�`�Ń��o��wwwwwwwwwwwwww [242521385]
- ���j���[�hSHOW�I�u�t�H���g���g�Q�h�ɂ��������Ȃ��āv🏡
