�����w���̐��w��D�����N�����I
�Ȃ�тɏ����w�Z�͈͂̎Z���E���w�̖��ŔY��ł�����I(�N����킸)
������Ȃ���肪��������C�y�Ƀ��X���Ă��������B
�w�Z�̏h��A�m�̖��ȂǕ��L�������Ă��������Ǝv���܂��B
�����̎g��������>>2���Q�Ƃ̂��ƁB
�������܂ŏ����w���̂��߂̃X���Ȃ̂Ŕ͈͊O�̂��̂ɂ��Ă͕ʃX���ɁB
���炩�ɔ͈͊O�̎���ɂ͑�NG�o�^�őΏ����Ă������B���������畉���ł��B�F�l�̂����͂�낵�����肢���܂��B
�O�X��
�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 60
https://rio2016.5ch.net/test/read.cgi/math/1670123285/
�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 59
https://rio2016.5ch.net/test/read.cgi/math/1653324466/
�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 58
https://rio2016.5ch.net/test/read.cgi/math/1642258588/
�T��
�����w�Z�͈͂̎Z���E���w�̖��̃X���@Part 61
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
2023/09/06(��) 15:37:18.81ID:oPtf1Zii
2023/09/06(��) 15:37:30.03ID:oPtf1Zii
�����Ȃǂ̏�����
�������Z�E�����Z : a+b, a-b
���|���Z : a*b, a�b, ab �ia�|����b�Ƃ����Ӗ��j
�@�L�����ȗ������|���Z�͍ŗD��ʼn��߂���l���A���̊|���Z�E����Z�Ɠ����悤�ɉ��߂���l������
������Z�E���� : a/b �i���̑����/���g���B�����̉��_���߂ɂ����Ӗ��j
�@����E���q�͈̔͂��������Ȃ��悤�Ɋ��ʂ��g����
�@1/2x+y�ł�(1/2)x+y�Ȃ̂�1/(2x)+y�Ȃ̂�1/(2x+y)�Ȃ̂�����킵��
���ݏ� : a^b �ia��b��j
�@�ݏ�͊|���Z�E����Z������Ɍv�Z���邪�A�L�����ȗ������|���Z�̕���D�悷��l������
�@x^2y��x^(2y)�Ȃ̂�(x^2)y�Ȃ̂�����킵��
�������� : "��"�́u��[�Ɓv�ŕϊ���
�@��͈̔͂��������Ȃ��悤�Ɋ��ʂ��g����
�@��2x+y�ł́�(2x)+y�Ȃ̂�(��2)x+y�Ȃ̂���(2x+y)�Ȃ̂�����킵��
������ : a�}b, a�mb, a��b �i�� "�}"�́u�������v�ŕϊ��j
����Βl : |x| �i�c�_��Shift�����Ȃ���L�[�{�[�h�E���\�j
�����{����͕ϊ��ŋL��
�@���́u�����v�A"��"�́u�����v�A"��"�́u�������傭�v�A"��"�́u�����ǂ��v
�@"��"�́u�������v�A���́u���v�A"��"���u���v�A"��"�́u���v
���w@2ch�f���p �f���ł̐��w�L���̏�������ƈ�ʓI�ȋL���̎g�p��
http://mathmathmath.dotera.net/
�������Z�E�����Z : a+b, a-b
���|���Z : a*b, a�b, ab �ia�|����b�Ƃ����Ӗ��j
�@�L�����ȗ������|���Z�͍ŗD��ʼn��߂���l���A���̊|���Z�E����Z�Ɠ����悤�ɉ��߂���l������
������Z�E���� : a/b �i���̑����/���g���B�����̉��_���߂ɂ����Ӗ��j
�@����E���q�͈̔͂��������Ȃ��悤�Ɋ��ʂ��g����
�@1/2x+y�ł�(1/2)x+y�Ȃ̂�1/(2x)+y�Ȃ̂�1/(2x+y)�Ȃ̂�����킵��
���ݏ� : a^b �ia��b��j
�@�ݏ�͊|���Z�E����Z������Ɍv�Z���邪�A�L�����ȗ������|���Z�̕���D�悷��l������
�@x^2y��x^(2y)�Ȃ̂�(x^2)y�Ȃ̂�����킵��
�������� : "��"�́u��[�Ɓv�ŕϊ���
�@��͈̔͂��������Ȃ��悤�Ɋ��ʂ��g����
�@��2x+y�ł́�(2x)+y�Ȃ̂�(��2)x+y�Ȃ̂���(2x+y)�Ȃ̂�����킵��
������ : a�}b, a�mb, a��b �i�� "�}"�́u�������v�ŕϊ��j
����Βl : |x| �i�c�_��Shift�����Ȃ���L�[�{�[�h�E���\�j
�����{����͕ϊ��ŋL��
�@���́u�����v�A"��"�́u�����v�A"��"�́u�������傭�v�A"��"�́u�����ǂ��v
�@"��"�́u�������v�A���́u���v�A"��"���u���v�A"��"�́u���v
���w@2ch�f���p �f���ł̐��w�L���̏�������ƈ�ʓI�ȋL���̎g�p��
http://mathmathmath.dotera.net/
3�P�R�Q�l�ڂ̑f������
2023/09/23(�y) 11:20:00.51ID:PA/Pj/vI (BP)^2=ABC.
4�P�R�Q�l�ڂ̑f������
2023/10/23(��) 21:51:35.75ID:1BJhBhbS �A�z�ۏo���̎��₩�Ǝv���܂������肢���܂��B
���w1�N�̎q�̏h������ĂāA�����������܂����B��̒�`���������Ă��������B
�u���v�Ƃ����T�O�ł����A�uX����������Y�������悤�ɑ����Ă����v���uX��Y�͔�Ⴕ�Ă���v�Ǝv���Ă��܂����B
�m����Y=3X�Ƃ��������ƁAX���������Y�������悤�ɑ����Ă����܂��B
�ł��AY��-3X�Ƃ��������ƁAX��������ق�Y�͌����Ă����܂��B�ł��A������u���v�ƌ����Ă����̂ł͂Ȃ����Ƃ����C�����܂��B
�uX��Y�����v���uX���������Y��������v�����ł͂Ȃ��uX���������Y������v����Ⴞ�Ƃ���ƁA�ǂ���`�����ł��傤���H
�����悤�ɁA�u�����v���uX���������Y������v�ł͂Ȃ��悤�ȋC�����܂��B
���m�Ȓ�`���������Ă��������B
���w1�N�̎q�̏h������ĂāA�����������܂����B��̒�`���������Ă��������B
�u���v�Ƃ����T�O�ł����A�uX����������Y�������悤�ɑ����Ă����v���uX��Y�͔�Ⴕ�Ă���v�Ǝv���Ă��܂����B
�m����Y=3X�Ƃ��������ƁAX���������Y�������悤�ɑ����Ă����܂��B
�ł��AY��-3X�Ƃ��������ƁAX��������ق�Y�͌����Ă����܂��B�ł��A������u���v�ƌ����Ă����̂ł͂Ȃ����Ƃ����C�����܂��B
�uX��Y�����v���uX���������Y��������v�����ł͂Ȃ��uX���������Y������v����Ⴞ�Ƃ���ƁA�ǂ���`�����ł��傤���H
�����悤�ɁA�u�����v���uX���������Y������v�ł͂Ȃ��悤�ȋC�����܂��B
���m�Ȓ�`���������Ă��������B
5�P�R�Q�l�ڂ̑f������
2023/10/23(��) 21:59:48.11ID:1BJhBhbS ���w�𗣂ꂽ��ʓI�Ȑ�����ł̉�b�ɂ����ẮA
�u�Е�������������Е��͌���v�W�̂��Ƃ��u�����v�ƌ������肵�܂����A
�i�Ј�A�̉c�Ɛ��т��オ��ƎЈ�B�̋@���������Ȃ�ꍇ�AA�̐��т�B�̋@���͔����ƌ������肷��j
Y=-3X�����̊W�Ȃ�A���̌������͊Ԉ���Ă��邱�ƂɂȂ�܂���ˁB
�u�Е�������������Е��͌���v�W�̂��Ƃ��u�����v�ƌ������肵�܂����A
�i�Ј�A�̉c�Ɛ��т��オ��ƎЈ�B�̋@���������Ȃ�ꍇ�AA�̐��т�B�̋@���͔����ƌ������肷��j
Y=-3X�����̊W�Ȃ�A���̌������͊Ԉ���Ă��邱�ƂɂȂ�܂���ˁB
2023/10/24(��) 00:08:58.46ID:oNRNEnhI
7�P�R�Q�l�ڂ̑f������
2023/10/24(��) 00:34:17.08ID:altn2nz+ >>6���肪�Ƃ������܂��B
�ł́A
Y=aX�̌`�ŕ\�����̂Ȃ�A�������Ă��Ƃł����H
Y=-3X�́A�uX�����������Y����������v�W�����ǁA�����ƌ����Ă�����ł��ˁH
�t�ɁAY=a/X�̌`�ŕ\�����̂Ȃ�A�����Ƃ������Ƃł�����ł����H
Y=-3/X�́A�uX����������ق�Y����������v�W�����ǁA�����ƌ����Ă�����ł��ˁH
�܂�AY=aX�ŕ\�����Ƃ��ł��邩�ǂ����AY=a/X�ŕ\�����Ƃ��ł��邩�ǂ����Ō��܂��ł��ˁB
�u�Е�����������Ƃ����Е��������i�����j����v���ǂ����͊W�Ȃ���ł��ˁH
�ł́A
Y=aX�̌`�ŕ\�����̂Ȃ�A�������Ă��Ƃł����H
Y=-3X�́A�uX�����������Y����������v�W�����ǁA�����ƌ����Ă�����ł��ˁH
�t�ɁAY=a/X�̌`�ŕ\�����̂Ȃ�A�����Ƃ������Ƃł�����ł����H
Y=-3/X�́A�uX����������ق�Y����������v�W�����ǁA�����ƌ����Ă�����ł��ˁH
�܂�AY=aX�ŕ\�����Ƃ��ł��邩�ǂ����AY=a/X�ŕ\�����Ƃ��ł��邩�ǂ����Ō��܂��ł��ˁB
�u�Е�����������Ƃ����Е��������i�����j����v���ǂ����͊W�Ȃ���ł��ˁH
2023/10/24(��) 01:46:12.87ID:oNRNEnhI
>>7
���̒ʂ�ł�
���̒ʂ�ł�
2023/10/26(��) 15:06:03.61ID:GhKH2ksS
10�P�R�Q�l�ڂ̑f������
2023/11/23(��) 00:37:59.85ID:+cJi/L4y �������������B
ttps://i.imgur.com/Xb562m8.png
���̖��̓����ł����A��7�|��2�������Ȃ�ł����A��2�|��7�ł͂Ȃ��_���Ȃ̂��킩��܂���B
������2�����Ă������Ǝv���̂ł����A�Ȃ���҂͂��߂Ȃ̂ł��傤���H
ttps://i.imgur.com/Xb562m8.png
���̖��̓����ł����A��7�|��2�������Ȃ�ł����A��2�|��7�ł͂Ȃ��_���Ȃ̂��킩��܂���B
������2�����Ă������Ǝv���̂ł����A�Ȃ���҂͂��߂Ȃ̂ł��傤���H
2023/11/23(��) 03:18:16.25ID:wT/arAah
��҂��ƕ��ɂȂ邩��
2023/11/23(��) 10:10:07.33ID:+cJi/L4y
>>11
���肪�Ƃ��������܂����I
�܂�A��14�Ƃ����̂́A3���傫������4��菬��������A
�X�|2��14�͐��̐��ɂȂ�
����āA���̐��ł���킯���Ȃ��A�Ƃ������Ƃł��ˁB
���肪�Ƃ��������܂����I
�܂�A��14�Ƃ����̂́A3���傫������4��菬��������A
�X�|2��14�͐��̐��ɂȂ�
����āA���̐��ł���킯���Ȃ��A�Ƃ������Ƃł��ˁB
13�P�R�Q�l�ڂ̑f������
2023/11/23(��) 22:17:20.17ID:Y16hmKrH �}�C�i�X�ƃ}�C�i�X�|���ăv���X�ɂȂ������Ă���܂����H�܂������L�����m�|������v���X�ŁA�قȂ�L�����m�|������}�C�i�X�Ɗ��肫���Ă܂����B�ł�����ς����͂���̂������C�ɂȂ�B
14�P�R�Q�l�ڂ̑f������
2023/11/23(��) 22:21:48.37ID:Y16hmKrH >>13���B�L������Ȃ������ł����B
2023/11/23(��) 23:12:49.75ID:CJHjiAL+
>>13
���̗��͕\
���̗��͕\
2023/11/24(��) 01:02:21.34ID:OE2Tx1Ie
>>15
����Ȃ�Ń}�C�i�X�ƃ}�C�i�X�������ƃ}�C�i�X�Ȃ́H
����Ȃ�Ń}�C�i�X�ƃ}�C�i�X�������ƃ}�C�i�X�Ȃ́H
2023/11/24(��) 01:32:02.88ID:5yU+H6TY
18�P�R�Q�l�ڂ̑f������
2023/11/24(��) 01:40:11.64ID:E47lUMfH >>15�单���G�̂���H�l�̐S�̗��̗��͑��̕\�������肵��🎵
���`�ƁA�ł��܂����牽����̓I�Ȍv�Z�̎����
���`�ƁA�ł��܂����牽����̓I�Ȍv�Z�̎����
2023/11/24(��) 03:05:17.52ID:5yU+H6TY
>>18
�r�f�I���{���Ƃ��O�{���Ƃ��ŋt�Đ�������Ɩʔ������
�r�f�I���{���Ƃ��O�{���Ƃ��ŋt�Đ�������Ɩʔ������
2023/11/24(��) 03:08:05.98ID:5yU+H6TY
�l�I��ϓI�ɂ͎��C�L���}�̂̎��C�w�X�s���g���j�N�X�I�Ȍ��������ŗႦ������
�������ɏ����w�Z�ł���A�}�`���A�����Ƌ�������ڂɂȂ��Ă��܂��B
�������ɏ����w�Z�ł���A�}�`���A�����Ƌ�������ڂɂȂ��Ă��܂��B
21�P�R�Q�l�ڂ̑f������
2023/11/24(��) 23:29:41.55ID:c9ZQAM992023/11/25(�y) 05:10:35.34ID:AQlv003m
2023/11/25(�y) 06:59:57.50ID:QSdlVegf
>>21
��a^2=|a| �ł����āA=a �ł͂Ȃ�����B
��a^2=|a| �ł����āA=a �ł͂Ȃ�����B
24�P�R�Q�l�ڂ̑f������
2023/11/25(�y) 12:09:37.91ID:yP9Ok/GJ >>22-23
���肪�Ƃ��������܂����B
�����鐔a�ɑ��Ă��̕������͒ʏ�2.����܂���
�����̂������̐��̕�����a�ƕ\���܂�
������Ƃ�����̕��̐��̕���-��a�ƕ\���܂�
�����������܂�i��`�j��������ł��ˁB
���ꂷ��m��܂���ł����B
���肪�Ƃ��������܂����B
�����鐔a�ɑ��Ă��̕������͒ʏ�2.����܂���
�����̂������̐��̕�����a�ƕ\���܂�
������Ƃ�����̕��̐��̕���-��a�ƕ\���܂�
�����������܂�i��`�j��������ł��ˁB
���ꂷ��m��܂���ł����B
25�P�R�Q�l�ڂ̑f������
2023/11/30(��) 12:07:43.19ID:/fZnx46U ��܂��T�{�ɔ��߂ĂS�O�O�Occ���ɂ͐�܂��W�O�Occ�ɐ��R�Q�O�Occ�ō����Ă܂����H
26�P�R�Q�l�ڂ̑f������
2023/11/30(��) 12:53:00.68ID:hC6YVBQY27�P�R�Q�l�ڂ̑f������
2023/11/30(��) 16:14:12.75ID:/fZnx46U �v�Z���@�������Ă���ėL���������܂����B
2023/12/22(��) 06:20:58.92ID:0kb23QSk
�n���̌��]�����͕b�P�ʂ���365��5����48��46�b�ł���Ƃ����B
�O���S���I����g���Ă��ĉē~�����S�ɋt�]����͉̂��N�ォ���v�Z����B
�O���S���I��̃��[��
�u����I���i����j�̔N�����A100�Ŋ����邪400�ł͊����Ȃ��N�́A���N�Ƃ���B����ȊO�̔N�ł́A����N����4�Ŋ�����N�͉[�N�Ƃ���B�v
�O���S���I����g���Ă��ĉē~�����S�ɋt�]����͉̂��N�ォ���v�Z����B
�O���S���I��̃��[��
�u����I���i����j�̔N�����A100�Ŋ����邪400�ł͊����Ȃ��N�́A���N�Ƃ���B����ȊO�̔N�ł́A����N����4�Ŋ�����N�͉[�N�Ƃ���B�v
2023/12/22(��) 16:45:06.86ID:wamSPhz4
5����48��46�b��20926�b
�[�N��400�N��97��
1����86400�b
400�N�Ԃ�20926✕400�[86400✕97���[10400�b�̂���
�ē~�t�]������ݐς͔��N���Ƃ����
���N��(365��5����48��46�b)�^2��15778463�b
���̂��ꂪ���܂�ɂ�15778463�^(10400�^400)��606863.9�N
����606864�N
�[�N��400�N��97��
1����86400�b
400�N�Ԃ�20926✕400�[86400✕97���[10400�b�̂���
�ē~�t�]������ݐς͔��N���Ƃ����
���N��(365��5����48��46�b)�^2��15778463�b
���̂��ꂪ���܂�ɂ�15778463�^(10400�^400)��606863.9�N
����606864�N
2024/01/04(��) 10:27:26.24ID:BE5Ld92t
>>29
���߂�����
���߂�����
2024/01/04(��) 11:04:35.91ID:BE5Ld92t
�n���̌��]�����͕b�P�ʂ���365��5����48��46�b�ł���Ƃ����B
5����48��46�b��20926�b
�[�N��400�N��97��
1����86400�b
20926/86400=0.2421991
�O���S���I���400�N��97�N�̉[�N��97/400=0.2425�ŋߎ����Ă��邱�ƂɂȂ�B
���
n�N��m�N�̉[�N��97/400�������悢�ߎ����������B
n��1000�ȉ��Ƃ��čł��ߎ�����m,n�̒l�����߂�B
5����48��46�b��20926�b
�[�N��400�N��97��
1����86400�b
20926/86400=0.2421991
�O���S���I���400�N��97�N�̉[�N��97/400=0.2425�ŋߎ����Ă��邱�ƂɂȂ�B
���
n�N��m�N�̉[�N��97/400�������悢�ߎ����������B
n��1000�ȉ��Ƃ��čł��ߎ�����m,n�̒l�����߂�B
2024/01/04(��) 11:16:07.08ID:BE5Ld92t
���p���
�n���̌��]�����͕b�P�ʂ���365��5����48��46�b�ł���Ƃ����B
20926/86400=0.2421991
400�N��97�N�̉[�N��97/400=0.2425�ŋߎ����Ă��邱�ƂɂȂ�B
n�N��m�N�̉[�N��97/400�������悢�ߎ����������B
n��1000�ȉ��Ƃ��čŋߎ�����m,n�̒l�����߂�B
�n���̌��]�����͕b�P�ʂ���365��5����48��46�b�ł���Ƃ����B
20926/86400=0.2421991
400�N��97�N�̉[�N��97/400=0.2425�ŋߎ����Ă��邱�ƂɂȂ�B
n�N��m�N�̉[�N��97/400�������悢�ߎ����������B
n��1000�ȉ��Ƃ��čŋߎ�����m,n�̒l�����߂�B
2024/01/04(��) 12:40:14.45ID:BE5Ld92t
>>32
��@33�N�Ԃ�8��̉[�N�̕���97/400���ߎ����悢�B
��@33�N�Ԃ�8��̉[�N�̕���97/400���ߎ����悢�B
34�P�R�Q�l�ڂ̑f������
2024/01/08(��) 22:31:40.50ID:b4KURY5u 1 ���O�F�P�R�Q�l�ڂ̑f������[] ���e���F2024/01/08(��) 21:56:33.09 ID:3+lWSMXm [1/2]
���˂������܂�
2 ���O�F�P�R�Q�l�ڂ̑f������[] ���e���F2024/01/08(��) 21:57:26.01 ID:3+lWSMXm [2/2]
A����̉Ƃł́C����500�~�d�����݂���100�~�d�݂̂ǂ��炩1�������ɓ���Ă��܂��B
�������n�߂�4�T�Ԃł��傤��10000�~���߂�ɂ́C500�~�d�݂�100�~�d�݂��C���ꂼ�ꉽ�������悢�ł����B
500�~�d�݁@[�A]��
100�~�d�݁@[�C]��
���˂������܂�
2 ���O�F�P�R�Q�l�ڂ̑f������[] ���e���F2024/01/08(��) 21:57:26.01 ID:3+lWSMXm [2/2]
A����̉Ƃł́C����500�~�d�����݂���100�~�d�݂̂ǂ��炩1�������ɓ���Ă��܂��B
�������n�߂�4�T�Ԃł��傤��10000�~���߂�ɂ́C500�~�d�݂�100�~�d�݂��C���ꂼ�ꉽ�������悢�ł����B
500�~�d�݁@[�A]��
100�~�d�݁@[�C]��
35�P�R�Q�l�ڂ̑f������
2024/01/08(��) 22:46:37.17ID:b4KURY5u ����
�S��500�~�ɂ����20����10000�~
500�~19���A100�~5����24��
500�~18���A100�~10����28��
�S��500�~�ɂ����20����10000�~
500�~19���A100�~5����24��
500�~18���A100�~10����28��
36�P�R�Q�l�ڂ̑f������
2024/01/10(��) 03:57:38.81ID:/m1vMzdQ >>34(*�͊|���Z�̋L��)
4�T��=4*7=28��
500x+100(28-x)=10000
500x+2800-100x=10000
400x=7200
x=18
500�d�݁@18��
100�d�݁@28-18=10��
�E�m�F�p
500*18+100*10=9000+1000=10000
4�T��=4*7=28��
500x+100(28-x)=10000
500x+2800-100x=10000
400x=7200
x=18
500�d�݁@18��
100�d�݁@28-18=10��
�E�m�F�p
500*18+100*10=9000+1000=10000
37�C�i ��/7jUdUKiSM
2024/01/10(��) 04:26:57.33ID:QR+JBGhQ >>34
28����10000�~�B
�A���������𗧂Ă�ƁA
500x+100y=10000�c�c(1)
x+y=28�c�c(2)
(2)�����100x+100y=2800
(1)�����ӁX�����āA
400x=7200
x=18
y=10
��500�~�d�݁@18��
�@100�~�d�݁@10��
28����10000�~�B
�A���������𗧂Ă�ƁA
500x+100y=10000�c�c(1)
x+y=28�c�c(2)
(2)�����100x+100y=2800
(1)�����ӁX�����āA
400x=7200
x=18
y=10
��500�~�d�݁@18��
�@100�~�d�݁@10��
38�C�i ��/7jUdUKiSM
2024/01/10(��) 04:29:45.83ID:QR+JBGhQ2024/01/16(��) 10:53:49.84ID:/WD1btaC
���Z�����̖��ł��Bhttps://imepic.jp/20240116/376670
https://imepic.jp/20240116/376680
⑥�̉���̈Ӗ���������܂���B�u�ӂ����L���Ă��Ȃ�x�̎O�p�`�̕ӂ̐������v����Ƃ�����3x�v�Ƃ���܂����������邽�߂ɂЂ��������̐��͕K�����̕ӂƌ�����Ă��܂����(��_������)�B�O�p�`�̎���̕�3�{�̂��Ƃł����H
�܂�⑥(2)��y=1/2(3x-n)�ɂȂ�������悭������܂���B��낵�����肢���܂��B
https://imepic.jp/20240116/376680
⑥�̉���̈Ӗ���������܂���B�u�ӂ����L���Ă��Ȃ�x�̎O�p�`�̕ӂ̐������v����Ƃ�����3x�v�Ƃ���܂����������邽�߂ɂЂ��������̐��͕K�����̕ӂƌ�����Ă��܂����(��_������)�B�O�p�`�̎���̕�3�{�̂��Ƃł����H
�܂�⑥(2)��y=1/2(3x-n)�ɂȂ�������悭������܂���B��낵�����肢���܂��B
2024/01/16(��) 17:28:49.44ID:jPbpl6RA
n:���̕Ӑ������̓_��
m:�����̓_��
y:�����̕Ӑ�
x:�����̎O�p�`��
2y+x = 3x�A(�����̕ӂ�2�̎O�p�`�A���̕ӂ�1�̎O�p�`�A�O�p�`��2�{�̕ӂƂȂ���)
(m+n)-(y+n)+x=1�A(Euler�̌���)
x=2m+n-2
y=3m+n-3
m:�����̓_��
y:�����̕Ӑ�
x:�����̎O�p�`��
2y+x = 3x�A(�����̕ӂ�2�̎O�p�`�A���̕ӂ�1�̎O�p�`�A�O�p�`��2�{�̕ӂƂȂ���)
(m+n)-(y+n)+x=1�A(Euler�̌���)
x=2m+n-2
y=3m+n-3
41�C�i ��/7jUdUKiSM
2024/02/07(��) 13:26:54.66ID:QIyFAwvJ2024/02/08(��) 23:27:38.73ID:Opm0Ol0f
���
�Z�~�̋��|!?�č���221�N�Ԃ�̑唭���ց@���\��~���牭�C�̑升���I2��ނ̎����[�~�̃^�C�~���O�d�Ȃ�
https://news.yahoo.co.jp/articles/5c35f085136dc729b833be626b44b0c200b7bd00
�Z�~�̋��|!?�č���221�N�Ԃ�̑唭���ց@���\��~���牭�C�̑升���I2��ނ̎����[�~�̃^�C�~���O�d�Ȃ�
https://news.yahoo.co.jp/articles/5c35f085136dc729b833be626b44b0c200b7bd00
43�C�i ��/7jUdUKiSM
2024/02/13(��) 12:11:40.54ID:FNVqmKJX2024/02/16(��) 08:42:49.90ID:rTwPDLmW
�~���̑��ʐς��o���̂����x�w�K���Ă������Y���
45�C�i ��/7jUdUKiSM
2024/02/23(��) 10:53:46.63ID:cHptYPJ02024/02/28(��) 01:15:10.38ID:tShK46ws
���͒��P���炢�̗��K���͈ꌩ������ł��P���v�Z�ʼn�����̂��w���
���ӎ��œ�������Ă邾��
���ӎ��œ�������Ă邾��
2024/02/28(��) 17:20:24.77ID:3XxW1gPN
���
��ӂ̔��a��5cm������10cm�̉~���̖ʐς����߂Ȃ����i�ォ��ڐ��j
��ӂ̔��a��5cm������10cm�̉~���̖ʐς����߂Ȃ����i�ォ��ڐ��j
2024/02/28(��) 18:24:30.87ID:Hesv5DTv
�i�@�E�́E�j�� ��肫��Ȃ�
2024/02/28(��) 19:17:29.71ID:69eSEYvt
���w���Ɂu�����̑̐ρ������̑̐ρ�3�v�́u��3�v�̗��R��`�������ł��B
Web�T�C�g��Youtube��T���܂������A���ЂƂł����B�����ǂ��{�͂���܂��H
Web�T�C�g��Youtube��T���܂������A���ЂƂł����B�����ǂ��{�͂���܂��H
50�P�R�Q�l�ڂ̑f������
2024/02/28(��) 20:07:20.51ID:GD05aVNN ���� 1/3 �Ō���
2024/02/28(��) 20:15:56.00ID:3XxW1gPN
�~���ƒ�ʁA�����������~���ɐ��������Ɖ~����1/3��������Ȃ�����~���̑̐ς́u1/3��2��v
52�P�R�Q�l�ڂ̑f������
2024/02/28(��) 20:31:51.98ID:GD05aVNN (a+b)^3=a^3+3a^2b+3ab^2+b^3��a^2b�̌W����3
2024/02/28(��) 22:00:07.13ID:Pi38HQ+x
�ϕ������ł̐������������茩�Ă݂��������Ƙb�̔��Ƃ��ȗ����ǂ�������ɓ����ĂĂ���Ő^���ɍl���悤�Ƃ���قǂ킩��Ȃ��Ȃ�C������
����ɂ���Ȑ����Ŗ����ɂ킩�����C�ɂȂ�����������Ďv�l�͂�������̂ł͂Ȃ���
������ςɌ@�艺������͌����̏o�����͍��Z�Ŋw�ԁA����܂ł͂Ƃ肠���������͂����������̂ƍl����ŋl�ߍ��ޕ��������Ǝv��
����ɂ���Ȑ����Ŗ����ɂ킩�����C�ɂȂ�����������Ďv�l�͂�������̂ł͂Ȃ���
������ςɌ@�艺������͌����̏o�����͍��Z�Ŋw�ԁA����܂ł͂Ƃ肠���������͂����������̂ƍl����ŋl�ߍ��ޕ��������Ǝv��
2024/02/29(��) 00:09:18.13ID:UfETmeGp
�~���̒��������a�~�~�����Ȃ̂͂����������̂��Ƃ���
�~�̖ʐς����a�~���a�~�~�����Ȃ̂�����ł��邩�H
���꒲�ׂȂ��Ƃ킩��Ȃ����i�߂����j
���̓X�}�z�Œ��ׂ��邩�玩�g�Œ��ׂ������������߂ɂȂ�Ǝv��
�����������Ȃ瓖�l�ɐ��������邱�ƁA�����ł���Ȃ痝���ł��Ă�
�~�̖ʐς����a�~���a�~�~�����Ȃ̂�����ł��邩�H
���꒲�ׂȂ��Ƃ킩��Ȃ����i�߂����j
���̓X�}�z�Œ��ׂ��邩�玩�g�Œ��ׂ������������߂ɂȂ�Ǝv��
�����������Ȃ瓖�l�ɐ��������邱�ƁA�����ł���Ȃ痝���ł��Ă�
2024/02/29(��) 02:08:51.27ID:rW9GZmkE
���̐��w���ȏ��͉��C�ɓ�����K���𐁂��|���Ă��邩�炫����
�w�K�������Ƃ�����o�����Ɗm���ɂǂڂɂ͂܂�
�w�K�������Ƃ�����o�����Ɗm���ɂǂڂɂ͂܂�
2024/02/29(��) 06:59:19.12ID:por0jnrC
>>54
�~������r�̔����O�p�`�ɕ�������ƑS�Ă̎O�p�`�̒�ӂ̍��v�����a�ɂȂ邩�炻������v�Z�ł�����Ă̂͋��ȏ��ɍڂ��Ă���債�����ƂȂ��b�ł��̃��x���Ȃ炻�ꂱ�����ȏ��ǂ߂ŏI���
���Ђɔ�ׂ�l�b�g�̏��̓S�~���R�Ȃ̂Ńl�b�g�Œ��ׂ�̂͐����ł����
�����������������Đ��̎���ɂ܂Ƃ��ɓ������ĂȂ���>>51�̉Ȃ��S�Ɉ��ʊW���Ⴆ�Ă邩�炱�������̌��ĂȂ�قǂƎv���Ă��܂��Ƃ������ăo�J�ɂȂ�
�~������r�̔����O�p�`�ɕ�������ƑS�Ă̎O�p�`�̒�ӂ̍��v�����a�ɂȂ邩�炻������v�Z�ł�����Ă̂͋��ȏ��ɍڂ��Ă���債�����ƂȂ��b�ł��̃��x���Ȃ炻�ꂱ�����ȏ��ǂ߂ŏI���
���Ђɔ�ׂ�l�b�g�̏��̓S�~���R�Ȃ̂Ńl�b�g�Œ��ׂ�̂͐����ł����
�����������������Đ��̎���ɂ܂Ƃ��ɓ������ĂȂ���>>51�̉Ȃ��S�Ɉ��ʊW���Ⴆ�Ă邩�炱�������̌��ĂȂ�قǂƎv���Ă��܂��Ƃ������ăo�J�ɂȂ�
2024/02/29(��) 07:55:04.74ID:RnxdhWRs
���̑̐ς��Ăǂ����Ă��J���@���G���̌����Ƃ��ϕ��̍l�������K�v�ɂȂ����Ⴄ��Ȃ��ȁH
2024/02/29(��) 20:16:17.37ID:icJ53sui
�̐ς�1/3�ɂȂ闝�R�́A�����̂��l�p��6�ɓ��������}�`���g���ĂȂ�ƂȂ��������Ă݂�
59�P�R�Q�l�ڂ̑f������
2024/02/29(��) 20:43:50.67ID:tBIOui5m �����O�p�`������Ȃ猟���ŏo�Ă��闧���̘̂Z�����Ɛ��̂�������̂ɕ����Ĕ�r�������
2024/02/29(��) 21:48:46.88ID:MI3sb5QC
�[�ъق���o�Ă����w���ȏ��̃L�����̖��O���u����������v�u�����v�Ȃ̂͏o�ŎЂ̎Ж�����t����ꂽ�̂�����ƒm����
2024/03/02(�y) 07:48:20.89ID:1DBlVrfW
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14294289214
����A�x�X�g�A���T�[���Ē��ߐ�ꂿ����Ă邯�Ǎ����ĂȂ���ˁH
����A�x�X�g�A���T�[���Ē��ߐ�ꂿ����Ă邯�Ǎ����ĂȂ���ˁH
2024/03/02(�y) 09:51:58.45ID:a8ZbQCTb
>>62
��
6�ʃT�C�R����10���āA���ׂĂ̖ڂ�
���Ȃ��Ƃ�1��ȏ�o��m�������߂�B
��
1�̖ڂ�����10��o��m����
1/(6^10) ... (*)
1��2�̖ڂ�10��o��m����
(2^10)/(6^10)-2�E(*)
��(2^10-2)/(6^10) ... (**)
1��2��3�̖ڂ�10��o��m����
(3^10)/(6^10)-3�E(**)
��(3^10-3�E2^10�{6)/(6^10) ... (***)
�E�E�E
�̂悤�ɏ��Ɍv�Z����
1����6���S���o��m����
(6^10-6�E5^10�{30�E4^10-120�E3^10�{360�E2^10-720)/(6^10)
��4435291/10077696 �i��44���j
���Z���w�X���Œ���I�ɏo��������
�N�[�|���R���N�^�[���A�R���v�K�`�����
�ȂǂƌĂ�Ă���
��
6�ʃT�C�R����10���āA���ׂĂ̖ڂ�
���Ȃ��Ƃ�1��ȏ�o��m�������߂�B
��
1�̖ڂ�����10��o��m����
1/(6^10) ... (*)
1��2�̖ڂ�10��o��m����
(2^10)/(6^10)-2�E(*)
��(2^10-2)/(6^10) ... (**)
1��2��3�̖ڂ�10��o��m����
(3^10)/(6^10)-3�E(**)
��(3^10-3�E2^10�{6)/(6^10) ... (***)
�E�E�E
�̂悤�ɏ��Ɍv�Z����
1����6���S���o��m����
(6^10-6�E5^10�{30�E4^10-120�E3^10�{360�E2^10-720)/(6^10)
��4435291/10077696 �i��44���j
���Z���w�X���Œ���I�ɏo��������
�N�[�|���R���N�^�[���A�R���v�K�`�����
�ȂǂƌĂ�Ă���
2024/03/03(��) 13:53:08.67ID:YcTuTlLI
�O�p�`����������]�����ďo����W�J�}�����~�ɂȂ�i����̊p�x��180���j���Ăǂ���������Ȃ�̂������ł��Ȃ�
2024/03/04(��) 15:39:49.20ID:zZ7oJd0B
>>64
�����܂���A�z�����鎿�₵�Ă��܂��܂��������͂Ȃ��������Ƃ�
�����܂���A�z�����鎿�₵�Ă��܂��܂��������͂Ȃ��������Ƃ�
2024/03/05(��) 20:18:55.22ID:t0hYEl4t
�~���̏㉺�ɓ�ɕ��������̂̔��X�������t�����}�`�̕\�ʐςƑ̐ς����߂���ɂ͈����|������
2024/03/07(��) 00:48:03.24ID:hkfGDOnh
2024/03/09(�y) 11:19:02.20ID:4SY0KF1u
���w���u�ǂ����ă}�C�i�X�Ƀ}�C�i�X��������ƃv���X�ɂȂ��ł����H�v⇐�ǂ�������H
https://greta.5ch.net/test/read.cgi/poverty/1709805154/
https://greta.5ch.net/test/read.cgi/poverty/1709805154/
2024/03/09(�y) 23:33:49.82ID:Ney5tJGS
R�����100����̃V�~�����[�V����
sim=function() length(unique(sample(6,10,rep=T)))==6
mean(replicate(1e6,sim()))
��27%�ɂȂ���
sim=function() length(unique(sample(6,10,rep=T)))==6
mean(replicate(1e6,sim()))
��27%�ɂȂ���
2024/03/09(�y) 23:58:19.19ID:Ney5tJGS
6^10=60466176�ʂ肩��A
�����ɂ�������𐔂����16435440�ʂ�
16435440/60466176 = 38045/139968 = 0.2718121
�����ɂ�������𐔂����16435440�ʂ�
16435440/60466176 = 38045/139968 = 0.2718121
2024/03/10(��) 00:12:25.33ID:o/csM8Bm
6�ʃT�C�R����10�����Ƃ�����ނ̖ڂ��ł�m�����ł��������H
72�C�i ��/7jUdUKiSM
2024/03/10(��) 06:57:21.38ID:Clc+dQZh2024/03/10(��) 12:07:50.75ID:o/csM8Bm
>>72
R����ɂ��100����̃V�~�����[�V��������
https://i.imgur.com/w7p6D7x.png
sim =\() sample(6,10,replace = TRUE) |> unique() |> length()
x=replicate(1e6,sim())
hist(x,main='')
R����ɂ��100����̃V�~�����[�V��������
https://i.imgur.com/w7p6D7x.png
sim =\() sample(6,10,replace = TRUE) |> unique() |> length()
x=replicate(1e6,sim())
hist(x,main='')
2024/03/10(��) 12:19:43.09ID:o/csM8Bm
>>73
�����l
6^10�ʂ��ڂ̎�ނ̐����ƂɃJ�E���g
> table(m)
m
1 2 3 4 5 6
6 15330 1119600 12277800 30618000 16435440
�����l
6^10�ʂ��ڂ̎�ނ̐����ƂɃJ�E���g
> table(m)
m
1 2 3 4 5 6
6 15330 1119600 12277800 30618000 16435440
2024/03/10(��) 12:32:31.98ID:byT5JUrG
���ʑ̃T�C�R����1�̖ڂ��o��m���͂����H
2024/03/10(��) 12:44:25.67ID:o/csM8Bm
10��3��ƂȂ�ڂ̑I�ѕ���choose(6,3)=C[6,3]=20�ʂ�
3�̖ڂ�a,b,c�Ƃ���Ƃ��̑g�ݍ��킹�͈ȉ��̒ʂ�
[,a] [,b] [,c]
[1,] 1 1 8
[2,] 1 2 7
[3,] 1 3 6
[4,] 1 4 5
[5,] 1 5 4
[6,] 1 6 3
[7,] 1 7 2
[8,] 1 8 1
[9,] 2 1 7
[10,] 2 2 6
[11,] 2 3 5
[12,] 2 4 4
[13,] 2 5 3
[14,] 2 6 2
[15,] 2 7 1
[16,] 3 1 6
[17,] 3 2 5
[18,] 3 3 4
[19,] 3 4 3
[20,] 3 5 2
[21,] 3 6 1
[22,] 4 1 5
[23,] 4 2 4
[24,] 4 3 3
[25,] 4 4 2
[26,] 4 5 1
[27,] 5 1 4
[28,] 5 2 3
[29,] 5 3 2
[30,] 5 4 1
[31,] 6 1 3
[32,] 6 2 2
[33,] 6 3 1
[34,] 7 1 2
[35,] 7 2 1
[36,] 8 1 1
�Ⴆ��
[,a] [,b] [,c]
[11,] 2 3 5
�̏ꍇ
10��2�����A�c���8��3�����Ȃ̂�
choose(10,2)*choose(10-2,3)�ʂ�
�e�X�ɂ��Čv�Z����choose(6,3)�{�����3��ނɂȂ�̂�
> sum(apply(re,1, \(x) choose(10,x[1])*choose(10-x[1],x[2])))*choose(6,3)
[1] 1119600
�ʂ�
���̊m����
1119600/6^10 = 7775/419904 = 0.01851614
3�̖ڂ�a,b,c�Ƃ���Ƃ��̑g�ݍ��킹�͈ȉ��̒ʂ�
[,a] [,b] [,c]
[1,] 1 1 8
[2,] 1 2 7
[3,] 1 3 6
[4,] 1 4 5
[5,] 1 5 4
[6,] 1 6 3
[7,] 1 7 2
[8,] 1 8 1
[9,] 2 1 7
[10,] 2 2 6
[11,] 2 3 5
[12,] 2 4 4
[13,] 2 5 3
[14,] 2 6 2
[15,] 2 7 1
[16,] 3 1 6
[17,] 3 2 5
[18,] 3 3 4
[19,] 3 4 3
[20,] 3 5 2
[21,] 3 6 1
[22,] 4 1 5
[23,] 4 2 4
[24,] 4 3 3
[25,] 4 4 2
[26,] 4 5 1
[27,] 5 1 4
[28,] 5 2 3
[29,] 5 3 2
[30,] 5 4 1
[31,] 6 1 3
[32,] 6 2 2
[33,] 6 3 1
[34,] 7 1 2
[35,] 7 2 1
[36,] 8 1 1
�Ⴆ��
[,a] [,b] [,c]
[11,] 2 3 5
�̏ꍇ
10��2�����A�c���8��3�����Ȃ̂�
choose(10,2)*choose(10-2,3)�ʂ�
�e�X�ɂ��Čv�Z����choose(6,3)�{�����3��ނɂȂ�̂�
> sum(apply(re,1, \(x) choose(10,x[1])*choose(10-x[1],x[2])))*choose(6,3)
[1] 1119600
�ʂ�
���̊m����
1119600/6^10 = 7775/419904 = 0.01851614
2024/03/10(��) 13:01:24.97ID:o/csM8Bm
10�S��ƂȂ�ڂ̑I�ѕ�
[,a] [,b] [,c] [,d]
[1,] 1 1 1 7
[2,] 1 1 2 6
[3,] 1 1 3 5
[4,] 1 1 4 4
[5,] 1 1 5 3
[6,] 1 1 6 2
[7,] 1 1 7 1
[8,] 1 2 1 6
[9,] 1 2 2 5
[10,] 1 2 3 4
[11,] 1 2 4 3
[12,] 1 2 5 2
[13,] 1 2 6 1
[14,] 1 3 1 5
....
[79,] 5 2 2 1
[80,] 5 3 1 1
[81,] 6 1 1 2
[82,] 6 1 2 1
[83,] 6 2 1 1
[84,] 7 1 1 1
> sum(apply(re,1,\(x) choose(10,x[1])*choose(10-x[1],x[2])*choose(10-x[1]-x[2],x[3])))*choose(6,4)
[1] 12277800
[,a] [,b] [,c] [,d]
[1,] 1 1 1 7
[2,] 1 1 2 6
[3,] 1 1 3 5
[4,] 1 1 4 4
[5,] 1 1 5 3
[6,] 1 1 6 2
[7,] 1 1 7 1
[8,] 1 2 1 6
[9,] 1 2 2 5
[10,] 1 2 3 4
[11,] 1 2 4 3
[12,] 1 2 5 2
[13,] 1 2 6 1
[14,] 1 3 1 5
....
[79,] 5 2 2 1
[80,] 5 3 1 1
[81,] 6 1 1 2
[82,] 6 1 2 1
[83,] 6 2 1 1
[84,] 7 1 1 1
> sum(apply(re,1,\(x) choose(10,x[1])*choose(10-x[1],x[2])*choose(10-x[1]-x[2],x[3])))*choose(6,4)
[1] 12277800
2024/03/10(��) 13:08:07.74ID:o/csM8Bm
10�T��
> re=NULL
> for(x in 1:6){
+ for(y in 1:6){
+ for(z in 1:6){
+ for(w in 1:6){
+ v=10-x-y-z-w
+ if(1<=v & v<=6) re=rbind(re,c(x,y,z,w,v))
+ }
+ }
+ }
+ }
> f5=\(x) choose(10,x[1])*choose(10-x[1],x[2])*choose(10-x[1]-x[2],x[3])*choose(10-x[1]-x[2]-x[3],x[4])
> sum(apply(re,1,f5))*choose(6,5)
[1] 30618000
> re=NULL
> for(x in 1:6){
+ for(y in 1:6){
+ for(z in 1:6){
+ for(w in 1:6){
+ v=10-x-y-z-w
+ if(1<=v & v<=6) re=rbind(re,c(x,y,z,w,v))
+ }
+ }
+ }
+ }
> f5=\(x) choose(10,x[1])*choose(10-x[1],x[2])*choose(10-x[1]-x[2],x[3])*choose(10-x[1]-x[2]-x[3],x[4])
> sum(apply(re,1,f5))*choose(6,5)
[1] 30618000
2024/03/10(��) 13:17:06.54ID:o/csM8Bm
10��6��
> re=NULL
> for(x in 1:5){
+ for(y in 1:5){
+ for(z in 1:5){
+ for(w in 1:5){
+ for(v in 1:5){
+ u=10-x-y-z-w-v
+ if(1<=u & u<=5) re=rbind(re,c(x,y,z,w,v,u))
+ }
+ }
+ }
+ }
+ }
> f6=\(x) choose(10,x[1])*choose(10-x[1],x[2])*choose(10-x[1]-x[2],x[3])*choose(10-x[1]-x[2]-x[3],x[4])*
+ choose(10-x[1]-x[2]-x[3]-x[4],x[5])
> sum(apply(re,1,f6))*choose(6,6)
[1] 16435440
������Ɨ��_�l�̌��Z�I���B
>62�̓���
> 16435440/6^10
[1] 0.2718121
16435440/6^10 =�@38045/139968
> re=NULL
> for(x in 1:5){
+ for(y in 1:5){
+ for(z in 1:5){
+ for(w in 1:5){
+ for(v in 1:5){
+ u=10-x-y-z-w-v
+ if(1<=u & u<=5) re=rbind(re,c(x,y,z,w,v,u))
+ }
+ }
+ }
+ }
+ }
> f6=\(x) choose(10,x[1])*choose(10-x[1],x[2])*choose(10-x[1]-x[2],x[3])*choose(10-x[1]-x[2]-x[3],x[4])*
+ choose(10-x[1]-x[2]-x[3]-x[4],x[5])
> sum(apply(re,1,f6))*choose(6,6)
[1] 16435440
������Ɨ��_�l�̌��Z�I���B
>62�̓���
> 16435440/6^10
[1] 0.2718121
16435440/6^10 =�@38045/139968
2024/03/10(��) 18:24:35.49ID:EAfpg2IL
>>74
�Ȃ��ŁA6^10�̂����̌����v�Z
choose(n,r)��n����r��I�ԑg�ݍ��킹�̌�
C[n,r] ��nCr�Ɠ���
m1��1��ނ̌�
m2��2��ނ̌�
....
m1=choose(6,1)*(1^10) ; m1
m2=choose(6,2)*(2^10-2) ; m2
m3=choose(6,3)*(3^10-3-choose(3,2)*(2^10-2)) ; m3
m4=choose(6,4)*(4^10-4-choose(4,3)*(3^10-3)+choose(4,2)*(2^10-2))
m4
m5=choose(6,5)*(5^10-5-choose(5,4)*(4^10-4)+choose(5,3)*(3^10-3)-choose(5,2)*(2^10-2))
m5
m6=choose(6,6)*(6^10-6-choose(6,5)*(5^10-5)+choose(6,4)*(4^10-4)-choose(6,3)*(3^10-3)+choose(6,2)*(2^10-2))
m6
�Ȃ��ŁA6^10�̂����̌����v�Z
choose(n,r)��n����r��I�ԑg�ݍ��킹�̌�
C[n,r] ��nCr�Ɠ���
m1��1��ނ̌�
m2��2��ނ̌�
....
m1=choose(6,1)*(1^10) ; m1
m2=choose(6,2)*(2^10-2) ; m2
m3=choose(6,3)*(3^10-3-choose(3,2)*(2^10-2)) ; m3
m4=choose(6,4)*(4^10-4-choose(4,3)*(3^10-3)+choose(4,2)*(2^10-2))
m4
m5=choose(6,5)*(5^10-5-choose(5,4)*(4^10-4)+choose(5,3)*(3^10-3)-choose(5,2)*(2^10-2))
m5
m6=choose(6,6)*(6^10-6-choose(6,5)*(5^10-5)+choose(6,4)*(4^10-4)-choose(6,3)*(3^10-3)+choose(6,2)*(2^10-2))
m6
2024/03/10(��) 18:25:29.94ID:EAfpg2IL
�v�Z�����
[1] 6
[1] 15330
[1] 1119600
[1] 12277800
[1] 30618000
[1] 16435440
[1] 6
[1] 15330
[1] 1119600
[1] 12277800
[1] 30618000
[1] 16435440
2024/03/10(��) 18:29:54.63ID:EAfpg2IL
�V�~�����[�V�����A��������A�v���O�����ł̏ꍇ�����A
���l��
���ׂČ��ʂ���v�����̂ő����A�����Ă�Ǝv���B
���l��
���ׂČ��ʂ���v�����̂ő����A�����Ă�Ǝv���B
2024/03/14(��) 06:42:10.94ID:NNPdP1LG
>>80
6�ʑ̂Ȃ��v�Z�ł��v�Z�ł��邪�ʂ̐���������Ƒ�ρB
���@�e�ʂ̂ł�m����1/20�̂Q�O�ʑ̂̃T�C�R����40��U��Ƃ����ׂĂ̖ڂ��o��m�������߂�B
�Q�l��(>8�O���R�[�h�����������j
R����ɂ��v�Z�v���O����
# N�ʑ̂̃T�C�R����n����m��ނ̖ڂ��łĂ���m�����v�Z
Dice=\(N,n,m,fraction=FALSE){
j=m:1
k=(-1)^(0:(m-1))
nu=choose(N,m)*sum(k*choose(m,j)*(j^n-j))
de=N^n
gcd=numbers::GCD(nu,de)
if(fraction) cat(nu,'/',de,'=',nu/gcd,'/',de/gcd,'=',nu/de,'\n')
return(nu/de)
}
�U�ʑ̂P�O��łU��ނ̖ڂ��ł�m����
> Dice(6,10,6,T)
16435440 / 60466176 = 38045 / 139968 = 0.2718121
[1] 0.2718121
�����w���̂�������v���O�������n�߂�ƁA��X�𗧂Ǝv���B
6�ʑ̂Ȃ��v�Z�ł��v�Z�ł��邪�ʂ̐���������Ƒ�ρB
���@�e�ʂ̂ł�m����1/20�̂Q�O�ʑ̂̃T�C�R����40��U��Ƃ����ׂĂ̖ڂ��o��m�������߂�B
�Q�l��(>8�O���R�[�h�����������j
R����ɂ��v�Z�v���O����
# N�ʑ̂̃T�C�R����n����m��ނ̖ڂ��łĂ���m�����v�Z
Dice=\(N,n,m,fraction=FALSE){
j=m:1
k=(-1)^(0:(m-1))
nu=choose(N,m)*sum(k*choose(m,j)*(j^n-j))
de=N^n
gcd=numbers::GCD(nu,de)
if(fraction) cat(nu,'/',de,'=',nu/gcd,'/',de/gcd,'=',nu/de,'\n')
return(nu/de)
}
�U�ʑ̂P�O��łU��ނ̖ڂ��ł�m����
> Dice(6,10,6,T)
16435440 / 60466176 = 38045 / 139968 = 0.2718121
[1] 0.2718121
�����w���̂�������v���O�������n�߂�ƁA��X�𗧂Ǝv���B
2024/03/14(��) 08:30:39.99ID:0zEgW2qU
�o�O�C�����ē���m�F
�U�ʃT�C�R�����P�O�����ꍇ
> # N�ʑ̂̃T�C�R����n����m��ނ̖ڂ��łĂ���m�����v�Z
> Dice=\(N,n,m,fraction=FALSE){
+ j=m:1
+ k=(-1)^(0:(m-1))
+ nu=ifelse(m==1,N,choose(N,m)*sum(k*choose(m,j)*(j^n-j)))
+ de=N^n
+ gcd=numbers::GCD(nu,de)
+ if(fraction) cat(nu,'/',de,'=',nu/gcd,'/',de/gcd,'=',nu/de,'\n')
+ return(nu/de)
+ }
> Dice=Vectorize(Dice)
> Dice(6,10,1:6,T)
6 / 60466176 = 1 / 10077696 = 9.922903e-08
15330 / 60466176 = 2555 / 10077696 = 0.0002535302
1119600 / 60466176 = 7775 / 419904 = 0.01851614
12277800 / 60466176 = 170525 / 839808 = 0.2030524
30618000 / 60466176 = 875 / 1728 = 0.5063657
16435440 / 60466176 = 38045 / 139968 = 0.2718121
�U�ʃT�C�R�����P�O�����ꍇ
> # N�ʑ̂̃T�C�R����n����m��ނ̖ڂ��łĂ���m�����v�Z
> Dice=\(N,n,m,fraction=FALSE){
+ j=m:1
+ k=(-1)^(0:(m-1))
+ nu=ifelse(m==1,N,choose(N,m)*sum(k*choose(m,j)*(j^n-j)))
+ de=N^n
+ gcd=numbers::GCD(nu,de)
+ if(fraction) cat(nu,'/',de,'=',nu/gcd,'/',de/gcd,'=',nu/de,'\n')
+ return(nu/de)
+ }
> Dice=Vectorize(Dice)
> Dice(6,10,1:6,T)
6 / 60466176 = 1 / 10077696 = 9.922903e-08
15330 / 60466176 = 2555 / 10077696 = 0.0002535302
1119600 / 60466176 = 7775 / 419904 = 0.01851614
12277800 / 60466176 = 170525 / 839808 = 0.2030524
30618000 / 60466176 = 875 / 1728 = 0.5063657
16435440 / 60466176 = 38045 / 139968 = 0.2718121
2024/03/14(��) 09:19:56.27ID:emFWT7lo
>>84�̉��p���
�Q�O�ʑ̃T�C�R�����ӂ��Ă��ׂĂ̖ڂ��ł���I���B
�I���܂łɂӂ��������Ă�q��������B
�����ɓq����̂��ł��L�����H
�i�P�j�����œ�����
�i�Q�j�������ē�����
�i�R�j�v�Z���ē�����
�i�S�j�������������ɂP�O�̉����ɕ��ׂ�B
�Q�O�ʑ̃T�C�R�����ӂ��Ă��ׂĂ̖ڂ��ł���I���B
�I���܂łɂӂ��������Ă�q��������B
�����ɓq����̂��ł��L�����H
�i�P�j�����œ�����
�i�Q�j�������ē�����
�i�R�j�v�Z���ē�����
�i�S�j�������������ɂP�O�̉����ɕ��ׂ�B
86�P�R�Q�l�ڂ̑f������
2024/03/14(��) 22:33:33.38ID:nS6Du3QV �O����P�Q�܂ł̐������������J�[�h�������Ă���܂��B
�������J�[�h�̒����烉���_���ɂR���I�сA���̐ς��w�`�x�Ƃ��܂��B
�c��̕������J�[�h�X���̘a���w�a�x�Ƃ��܂��B
���̂Ƃ��A�`���a�ƂȂ�m�������߂ĉ������B
�������_�ȉ�������ꍇ�́A�l�̌ܓ����ĉ������B
�������J�[�h�̒����烉���_���ɂR���I�сA���̐ς��w�`�x�Ƃ��܂��B
�c��̕������J�[�h�X���̘a���w�a�x�Ƃ��܂��B
���̂Ƃ��A�`���a�ƂȂ�m�������߂ĉ������B
�������_�ȉ�������ꍇ�́A�l�̌ܓ����ĉ������B
2024/03/15(��) 08:24:46.04ID:m3l9dJ+v
168 / 220
2024/03/15(��) 08:39:58.22ID:m3l9dJ+v
�v���O������
S=sum(1:12)
f=function(x){
A=prod(x)
B=S-sum(x)
A>B
}
cat(sum(combn(12,3,f)),'/',choose(12,3))
0.763636
220�̑g�ݍ��킹��������ƂŐ����Ă��Z�o�ł���̂ł́H
S=sum(1:12)
f=function(x){
A=prod(x)
B=S-sum(x)
A>B
}
cat(sum(combn(12,3,f)),'/',choose(12,3))
0.763636
220�̑g�ݍ��킹��������ƂŐ����Ă��Z�o�ł���̂ł́H
89�P�R�Q�l�ڂ̑f������
2024/03/17(��) 00:45:13.91ID:1KlpArJb ��������̂܂ȂуX�N�G�A�̍ŐV�̃��C�u�z�M�p�̊p�x���(2021�̎Z��)�A�����s�������
����ł�������H
����ł�������H
2024/03/17(��) 04:57:59.39ID:cauIc5rG
>>86
�܂��A0����12�܂ł̐������������J�[�h�͑S����13������܂��B
3����I�ԑg�ݍ��킹�̐��́A13����3��I�ԑg�ݍ��킹�ł��B
�����13C3�Ōv�Z�ł��܂��B
13C3 = (13 * 12 * 11) / (3 * 2 * 1) = 286
�܂�A3���I�ԑg�ݍ��킹��286�ʂ肠��܂��B
���ɁAA��B�̒l���v�Z���܂��B
A�̒l��3���̐����̐ςȂ̂ŁA����̓����_����3���̐�����I�ԂƂ��̐ς̕��ςł��B
���ς̒l�́A(0+1+2+...+12)/13�ł��B
�����13�̐����̍��v��13�Ŋ������l�ɂȂ�܂��B
A = (0+1+2+...+12)/13 = (12 * 13) / 2 / 13 = 6
B�̒l�͎c���9���̐����̘a�ł��B
��������ς̒l�����߂�ƁA(0+1+2+...+12) - A * 3�ɂȂ�܂��B
B = ((0+1+2+...+12) - A * 3) / 10 = (78 - 6 * 3) / 10 = 5.4
���������āAA > B�ƂȂ�m���́AA��B�����傫���m���ł��B
�܂�AA��6�ȏ�̒l�����m�������߂�Ηǂ��ł��B
0����12�܂ł̐����̒���6�ȏ�̐����́A7, 8, 9, 10, 11, 12��6����܂��B
���ꂼ��̐������I���m���́A���ꂼ��1/13�ł��B
���������āAA��6�ȏ�̒l�����m���́A
(1/13 + 1/13 + 1/13 + 1/13 + 1/13 + 1/13) * 286 = (6/13) * 286 ≈ 131.538
������l�̌ܓ�����ƁA132�ʂ�ł��B
���������āAA > B�ƂȂ�m���́A132/286 ≈ 0.4615�ł��B
�܂��A0����12�܂ł̐������������J�[�h�͑S����13������܂��B
3����I�ԑg�ݍ��킹�̐��́A13����3��I�ԑg�ݍ��킹�ł��B
�����13C3�Ōv�Z�ł��܂��B
13C3 = (13 * 12 * 11) / (3 * 2 * 1) = 286
�܂�A3���I�ԑg�ݍ��킹��286�ʂ肠��܂��B
���ɁAA��B�̒l���v�Z���܂��B
A�̒l��3���̐����̐ςȂ̂ŁA����̓����_����3���̐�����I�ԂƂ��̐ς̕��ςł��B
���ς̒l�́A(0+1+2+...+12)/13�ł��B
�����13�̐����̍��v��13�Ŋ������l�ɂȂ�܂��B
A = (0+1+2+...+12)/13 = (12 * 13) / 2 / 13 = 6
B�̒l�͎c���9���̐����̘a�ł��B
��������ς̒l�����߂�ƁA(0+1+2+...+12) - A * 3�ɂȂ�܂��B
B = ((0+1+2+...+12) - A * 3) / 10 = (78 - 6 * 3) / 10 = 5.4
���������āAA > B�ƂȂ�m���́AA��B�����傫���m���ł��B
�܂�AA��6�ȏ�̒l�����m�������߂�Ηǂ��ł��B
0����12�܂ł̐����̒���6�ȏ�̐����́A7, 8, 9, 10, 11, 12��6����܂��B
���ꂼ��̐������I���m���́A���ꂼ��1/13�ł��B
���������āAA��6�ȏ�̒l�����m���́A
(1/13 + 1/13 + 1/13 + 1/13 + 1/13 + 1/13) * 286 = (6/13) * 286 ≈ 131.538
������l�̌ܓ�����ƁA132�ʂ�ł��B
���������āAA > B�ƂȂ�m���́A132/286 ≈ 0.4615�ł��B
2024/03/17(��) 06:00:06.83ID:ccAMUesP
>>88
0��������
n=12
S=sum(0:n)
f=function(x){
A=prod(x)
B=S-sum(x)
A>B
}
cat(sum(combn(n+1,3,f)),'/',choose(n+1,3),'\n')
231 / 286
0��������
n=12
S=sum(0:n)
f=function(x){
A=prod(x)
B=S-sum(x)
A>B
}
cat(sum(combn(n+1,3,f)),'/',choose(n+1,3),'\n')
231 / 286
2024/03/17(��) 06:10:19.42ID:ccAMUesP
���K���
�O����X�X�܂ł̐������������J�[�h�������Ă���܂��B
�������J�[�h�̒����烉���_���ɂR���I�сA���̐ς��w�`�x�Ƃ��܂��B
�c��̕������J�[�h�̘a���w�a�x�Ƃ��܂��B
���̂Ƃ��A�`���a�ƂȂ�m�������߂ĉ������B
�O����X�X�܂ł̐������������J�[�h�������Ă���܂��B
�������J�[�h�̒����烉���_���ɂR���I�сA���̐ς��w�`�x�Ƃ��܂��B
�c��̕������J�[�h�̘a���w�a�x�Ƃ��܂��B
���̂Ƃ��A�`���a�ƂȂ�m�������߂ĉ������B
2024/03/17(��) 06:12:01.00ID:ccAMUesP
148227 / 161700 = 49409 / 53900 = 0.916679
2024/03/17(��) 06:38:03.71ID:42QfBsw0
�o�O�C��
> n=12
> S=sum(0:n)
> f=function(x){
+ A=prod(x)
+ B=S-sum(x)
+ A>B
+ }
> cat(sum(combn(0:n,3,f)),'/',choose(n+1,3),'\n')
168 / 286
> 168 / 286
[1] 0.5874126
> n=12
> S=sum(0:n)
> f=function(x){
+ A=prod(x)
+ B=S-sum(x)
+ A>B
+ }
> cat(sum(combn(0:n,3,f)),'/',choose(n+1,3),'\n')
168 / 286
> 168 / 286
[1] 0.5874126
2024/03/17(��) 06:44:49.39ID:42QfBsw0
>>92
> calc=\(n=12,r=3){
+ S=sum(0:n)
+ f=\(x) prod(x) > S-sum(x)
+ nu=sum(apply(comboGeneral(0:n,r),1,f))
+ de=choose(n+1,r)
+ gcd=GCD(nu,de)
+ cat(nu,'/',de,'=',nu/gcd,'/',de/gcd,'=',nu/de,'\n')
+ invisible(nu/de)
+ }
> calc(99,3)
143472 / 161700 = 244 / 275 = 0.8872727
> calc=\(n=12,r=3){
+ S=sum(0:n)
+ f=\(x) prod(x) > S-sum(x)
+ nu=sum(apply(comboGeneral(0:n,r),1,f))
+ de=choose(n+1,r)
+ gcd=GCD(nu,de)
+ cat(nu,'/',de,'=',nu/gcd,'/',de/gcd,'=',nu/de,'\n')
+ invisible(nu/de)
+ }
> calc(99,3)
143472 / 161700 = 244 / 275 = 0.8872727
2024/03/19(��) 02:39:34.56ID:Sx/aT3t4
>>92
```python
import itertools
def calculate_probability():
total_cases = 0
favorable_cases = 0
# 0����99�܂ł̐����̃��X�g���쐬
numbers = list(range(100))
# 3���̐�����I�ԑS�Ă̑g�ݍ��킹���
for combination in itertools.combinations(numbers, 3):
# A�̐ς��v�Z����
product = combination[0] * combination[1] * combination[2]
# B�̎c��̐����̘a���v�Z����
remaining_numbers = [num for num in numbers if num not in combination]
total_sum = sum(remaining_numbers)
# A > B �̏ꍇ�A�L���ȃP�[�X�Ƃ��ăJ�E���g
if product > total_sum:
favorable_cases += 1
total_cases += 1
# �m�����v�Z
probability = favorable_cases / total_cases
return probability
# �m�����v�Z���ďo��
print("A > B �ƂȂ�m����:", calculate_probability())
```
����
A > B �ƂȂ�m����: 0.8872727272727273
```python
import itertools
def calculate_probability():
total_cases = 0
favorable_cases = 0
# 0����99�܂ł̐����̃��X�g���쐬
numbers = list(range(100))
# 3���̐�����I�ԑS�Ă̑g�ݍ��킹���
for combination in itertools.combinations(numbers, 3):
# A�̐ς��v�Z����
product = combination[0] * combination[1] * combination[2]
# B�̎c��̐����̘a���v�Z����
remaining_numbers = [num for num in numbers if num not in combination]
total_sum = sum(remaining_numbers)
# A > B �̏ꍇ�A�L���ȃP�[�X�Ƃ��ăJ�E���g
if product > total_sum:
favorable_cases += 1
total_cases += 1
# �m�����v�Z
probability = favorable_cases / total_cases
return probability
# �m�����v�Z���ďo��
print("A > B �ƂȂ�m����:", calculate_probability())
```
����
A > B �ƂȂ�m����: 0.8872727272727273
2024/03/19(��) 05:09:10.69ID:zfPdL8vp
98�P�R�Q�l�ڂ̑f������
2024/03/20(��) 19:38:30.15ID:JuwU4NjK �L���������������ǂ����������ɂ���̂�
�Ȃ��������̂ق����������݂���ƌ�����̂��H
�Ȃ��������̂ق����������݂���ƌ�����̂��H
2024/03/21(��) 06:29:22.53ID:YM3r76o9
>>98
�L�����͏��Ԃɕ��ׂ��邯�ǁA�������͂��ꂪ�s�\������B
�L�����͏��Ԃɕ��ׂ��邯�ǁA�������͂��ꂪ�s�\������B
2024/03/21(��) 07:30:32.41ID:YM3r76o9
>>99
���̗L�����Ƃ��ĂP�O�O���ׂĂ݂��B
���������ׂ郋�[���͗B��ł͂Ȃ��B
[1] 1 1/2 2 1/3 3 1/4 2/3 3/2 4 1/5 5 1/6 2/5 3/4 4/3 5/2 6 1/7 1/3 3/5
[21] 5/3 7 1/8 2/7 4/5 5/4 7/2 8 1/9 3/7 7/3 9 1/10 2/9 3/8 4/7 5/6 6/5 7/4 8/3
[41] 9/2 10 1/11 5/7 7/5 11 1/12 2/11 3/10 4/9 5/8 6/7 7/6 8/5 9/4 10/3 11/2 12 1/13 3/11
[61] 5/9 9/5 11/3 13 1/14 2/13 4/11 7/8 8/7 11/4 13/2 14 1/15 3/13 5/11 7/9 9/7 11/5 13/3 15
[81] 1/16 2/15 3/14 4/13 5/12 6/11 7/10 8/9 9/8 10/7 11/6 12/5 13/4 14/3 15/2 16 1/17 5/13 7/11 11/7
���̗L�����Ƃ��ĂP�O�O���ׂĂ݂��B
���������ׂ郋�[���͗B��ł͂Ȃ��B
[1] 1 1/2 2 1/3 3 1/4 2/3 3/2 4 1/5 5 1/6 2/5 3/4 4/3 5/2 6 1/7 1/3 3/5
[21] 5/3 7 1/8 2/7 4/5 5/4 7/2 8 1/9 3/7 7/3 9 1/10 2/9 3/8 4/7 5/6 6/5 7/4 8/3
[41] 9/2 10 1/11 5/7 7/5 11 1/12 2/11 3/10 4/9 5/8 6/7 7/6 8/5 9/4 10/3 11/2 12 1/13 3/11
[61] 5/9 9/5 11/3 13 1/14 2/13 4/11 7/8 8/7 11/4 13/2 14 1/15 3/13 5/11 7/9 9/7 11/5 13/3 15
[81] 1/16 2/15 3/14 4/13 5/12 6/11 7/10 8/9 9/8 10/7 11/6 12/5 13/4 14/3 15/2 16 1/17 5/13 7/11 11/7
2024/03/21(��) 08:14:29.59ID:YM3r76o9
>>100
�d�����������̂Ń��X�g���C��
[1] 1 1/2 2 1/3 3 1/4 2/3 3/2 4 1/5 5 1/6 2/5 3/4 4/3 5/2 6 1/7 3/5 5/3
[21] 7 1/8 2/7 4/5 5/4 7/2 8 1/9 3/7 7/3 9 1/10 2/9 3/8 4/7 5/6 6/5 7/4 8/3 9/2
[41] 10 1/11 5/7 7/5 11 1/12 2/11 3/10 4/9 5/8 6/7 7/6 8/5 9/4 10/3 11/2 12 1/13 3/11 5/9
[61] 9/5 11/3 13 1/14 2/13 4/11 7/8 8/7 11/4 13/2 14 1/15 3/13 5/11 7/9 9/7 11/5 13/3 15 1/16
[81] 2/15 3/14 4/13 5/12 6/11 7/10 8/9 9/8 10/7 11/6 12/5 13/4 14/3 15/2 16 1/17 5/13 7/11 11/7 13/5
�d�����������̂Ń��X�g���C��
[1] 1 1/2 2 1/3 3 1/4 2/3 3/2 4 1/5 5 1/6 2/5 3/4 4/3 5/2 6 1/7 3/5 5/3
[21] 7 1/8 2/7 4/5 5/4 7/2 8 1/9 3/7 7/3 9 1/10 2/9 3/8 4/7 5/6 6/5 7/4 8/3 9/2
[41] 10 1/11 5/7 7/5 11 1/12 2/11 3/10 4/9 5/8 6/7 7/6 8/5 9/4 10/3 11/2 12 1/13 3/11 5/9
[61] 9/5 11/3 13 1/14 2/13 4/11 7/8 8/7 11/4 13/2 14 1/15 3/13 5/11 7/9 9/7 11/5 13/3 15 1/16
[81] 2/15 3/14 4/13 5/12 6/11 7/10 8/9 9/8 10/7 11/6 12/5 13/4 14/3 15/2 16 1/17 5/13 7/11 11/7 13/5
102�P�R�Q�l�ڂ̑f������
2024/03/21(��) 08:49:33.79ID:g9DxwsAn �������Ȃ��̂ňӖ����킩��Ȃ�
2024/03/21(��) 15:57:54.32ID:4zJtgd0M
>>102
���������Ԃɕ��ׂĂ݂���
�����̏ꍇ�͕�����P�ƍl����
����{���q�@�����������ɕ��ׂ��B
����{���q���������̏ꍇ�͂��̕��������������ɕ��ׂ��B
�����͏��Ԃɕ��ׂ邱�Ƃ��ł��邪�A
���������Ԃɕ��ׂ邱�Ƃ��ł���Ƃ���Ə��Ԃ����Ȃ����������݂���B
�i�ڍׂ͑Ίp���_�@�Ō������Ă��������j
����Ė������̕����L�����i�����j��葽�����݂���@�Ƃ����\���������B
���������Ԃɕ��ׂĂ݂���
�����̏ꍇ�͕�����P�ƍl����
����{���q�@�����������ɕ��ׂ��B
����{���q���������̏ꍇ�͂��̕��������������ɕ��ׂ��B
�����͏��Ԃɕ��ׂ邱�Ƃ��ł��邪�A
���������Ԃɕ��ׂ邱�Ƃ��ł���Ƃ���Ə��Ԃ����Ȃ����������݂���B
�i�ڍׂ͑Ίp���_�@�Ō������Ă��������j
����Ė������̕����L�����i�����j��葽�����݂���@�Ƃ����\���������B
2024/03/27(��) 19:24:06.43ID:fflPPR7k
���W�ɂ�2�}2��2/2��1�}��2�ƂȂ��Ă��܂�
1�}2��2�ł͂Ȃ��̂ł��傤���H
��낵�����肢���܂��B
1�}2��2�ł͂Ȃ��̂ł��傤���H
��낵�����肢���܂��B
2024/03/28(��) 05:17:31.98ID:jSslqcH3
2�}2��2/2���B������
2�}2��(2/2)�Ȃ̂�
2�}(2��2)/2�Ȃ̂�
(2�}2��2)/2�Ȃ̂�
��҂Ȃ�
(2�}2��2)/2 = 1�}��2
�ō����Ă���
2�}2��(2/2)�Ȃ̂�
2�}(2��2)/2�Ȃ̂�
(2�}2��2)/2�Ȃ̂�
��҂Ȃ�
(2�}2��2)/2 = 1�}��2
�ō����Ă���
106�P�R�Q�l�ڂ̑f������
2024/03/28(��) 08:09:31.16ID:odfq4qOx >>104
������������߂Ɂu�S�̂��Q�Ŋ����Ă�v�̂�1�}√2�ō����Ă܂���B
������������߂Ɂu�S�̂��Q�Ŋ����Ă�v�̂�1�}√2�ō����Ă܂���B
2024/03/28(��) 18:11:53.99ID:AKa348af
2024/03/28(��) 20:21:56.53ID:ZSCPuj9s
>>106 ���肪�Ƃ��������܂�
1*��2����2�ɂȂ���1��������̂ł���
1*��2����2�ɂȂ���1��������̂ł���
109�P�R�Q�l�ڂ̑f������
2024/03/28(��) 21:20:05.85ID:odfq4qOx >>107
��R�����邩�炱���A�o���Ă���́B
>105�̂ǂ̃p�^�[����������1�}2√2�ɂȂ�Ȃ��B�� ���W�ɂ͂����Ɛ����Ƃ��ď����Ă������B
���������̖��W�œ����Ԉ���Ă���A���̏o�ŎВׂ�鐨���ŃN���[������B
��(((��(߄D�))))������
���₷��Ƃ��ɁA���������B�����������Ď��Ȃ�A�܂��^�������Ǐ����w���ɂ�������߂�̂��Ȃ��c�B
��R�����邩�炱���A�o���Ă���́B
>105�̂ǂ̃p�^�[����������1�}2√2�ɂȂ�Ȃ��B�� ���W�ɂ͂����Ɛ����Ƃ��ď����Ă������B
���������̖��W�œ����Ԉ���Ă���A���̏o�ŎВׂ�鐨���ŃN���[������B
��(((��(߄D�))))������
���₷��Ƃ��ɁA���������B�����������Ď��Ȃ�A�܂��^�������Ǐ����w���ɂ�������߂�̂��Ȃ��c�B
2024/03/28(��) 22:26:56.56ID:AKa348af
2024/03/29(��) 18:56:42.16ID:pbu3WRJW
�ǂ��������̂�53�ɂȂ��Ă���₽��Ɛ��w�̗���͂�������
�l�̌ܓ��̂��������x�w�K���Ă������ł��Ȃ��Ȃ��Ă���
1234.56 �̏����_�ꌅ���l�̌ܓ�����Ƃ�����@1235 ����ˁH
�Ȃ��̈ʂ�4���l�̌ܓ�����Ƃ�����
1230�ō����Ă�H�@�ǂ��ɂ�����������ĂȂ��Ĕ]�����������Ȃ��Ă��
�l�̌ܓ��̂��������x�w�K���Ă������ł��Ȃ��Ȃ��Ă���
1234.56 �̏����_�ꌅ���l�̌ܓ�����Ƃ�����@1235 ����ˁH
�Ȃ��̈ʂ�4���l�̌ܓ�����Ƃ�����
1230�ō����Ă�H�@�ǂ��ɂ�����������ĂȂ��Ĕ]�����������Ȃ��Ă��
2024/03/29(��) 19:43:38.50ID:lKx89PQk
113�P�R�Q�l�ڂ̑f������
2024/03/30(�y) 00:19:54.29ID:sKkeQj3J 9.99999999
�̏�����܈ʂ��l�̌ܓ�����
�̏�����܈ʂ��l�̌ܓ�����
2024/03/30(�y) 01:37:23.24ID:pWX1dLvg
�������璆���l�����߂鎞�ɓ���̐��l�Ȃ�ʂɐ�����̂����ȏ����������ĂȂ���
�b�������������ɔ[���������Ȃ������u���H�Ȃ�ł����Ȃ�H�v�݂�����
�b�������������ɔ[���������Ȃ������u���H�Ȃ�ł����Ȃ�H�v�݂�����
2024/03/30(�y) 02:29:25.08ID:Oww3lzqT
>>107
��������
����Z�̕��z�@���Ɖ]���\�����悭������Ȃ��̂ł����A���̗l�Ɍv�Z�����Ȃ���Ȃ�Ȃ��ƌ������Ƃł��傤���B
���{�����@�@�@
���������@
�@��
�@��(�P�{��)
�����������@
�@�@��
���P�{��
��������
����Z�̕��z�@���Ɖ]���\�����悭������Ȃ��̂ł����A���̗l�Ɍv�Z�����Ȃ���Ȃ�Ȃ��ƌ������Ƃł��傤���B
���{�����@�@�@
���������@
�@��
�@��(�P�{��)
�����������@
�@�@��
���P�{��
2024/03/30(�y) 03:14:24.39ID:VmRdfVzE
>>115
����ł��ǂ����A�|���Z�ɂ͕��z�������ŕ��q�����1/a���|���Ă��悢
����ł��ǂ����A�|���Z�ɂ͕��z�������ŕ��q�����1/a���|���Ă��悢
2024/03/30(�y) 03:38:47.18ID:Oww3lzqT
>>116
�L��������܂�
���̎��ɂȂ��ł��ˁB
�܂�A���ڂ̖Ɉ�a��������̂ł��ˁB
���{�����@�@�@
���������@
�@��
�@���@�@����
���� �{ �������@
�@���@�@��
���P�{��
�]�k�ł����A����Z�̕��z�ł���(���{��)�͐������܂��A(���{��)�����͐��藧�̂ł��ˁB
�L��������܂�
���̎��ɂȂ��ł��ˁB
�܂�A���ڂ̖Ɉ�a��������̂ł��ˁB
���{�����@�@�@
���������@
�@��
�@���@�@����
���� �{ �������@
�@���@�@��
���P�{��
�]�k�ł����A����Z�̕��z�ł���(���{��)�͐������܂��A(���{��)�����͐��藧�̂ł��ˁB
2024/03/30(�y) 14:18:59.23ID:JOm52CCZ
�G�N�Z����ROUND���͎l�̌ܓ������A
Python��R��round���͎l�̌ܓ��ł͂Ȃ��B
0.5����1��������100�̐����a�Ƃ���B
[1] 0.5 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10.5 11.5 12.5 13.5 14.5 15.5 16.5 17.5 18.5 19.5
[21] 20.5 21.5 22.5 23.5 24.5 25.5 26.5 27.5 28.5 29.5 30.5 31.5 32.5 33.5 34.5 35.5 36.5 37.5 38.5 39.5
[41] 40.5 41.5 42.5 43.5 44.5 45.5 46.5 47.5 48.5 49.5 50.5 51.5 52.5 53.5 54.5 55.5 56.5 57.5 58.5 59.5
[61] 60.5 61.5 62.5 63.5 64.5 65.5 66.5 67.5 68.5 69.5 70.5 71.5 72.5 73.5 74.5 75.5 76.5 77.5 78.5 79.5
[81] 80.5 81.5 82.5 83.5 84.5 85.5 86.5 87.5 88.5 89.5 90.5 91.5 92.5 93.5 94.5 95.5 96.5 97.5 98.5 99.5
a�̕��ϒl��50�ł���B
��round�����> (b=round(a))
[1] 0 2 2 4 4 6 6 8 8 10 10 12 12 14 14 16 16 18 18 20 20 22 22 24 24
[26] 26 26 28 28 30 30 32 32 34 34 36 36 38 38 40 40 42 42 44 44 46 46 48 48 50
[51] 50 52 52 54 54 56 56 58 58 60 60 62 62 64 64 66 66 68 68 70 70 72 72 74 74
[76] 76 76 78 78 80 80 82 82 84 84 86 86 88 88 90 90 92 92 94 94 96 96 98 98 100
�ƁA���ׂċ����ɂȂ�B
a���l�̌ܓ����Ă��畽�ς��Ƃ�ƂP����100�܂ł̕��ςȂ̂�
> mean(1:100)
[1] 50.5
�ɂȂ邪�A
a��round����K�p���Ă��畽�ς��Ƃ��
> mean(round(a))
[1] 50
���v�����ŕ��ϒl���Ƃ邱�Ƃ͕p�ɂɂ���̂�R��round���͏�L�̂悤�Ȏd�l�ɂȂ��Ă���B
Python�ł������B
> print(round(2.5))
[1] 2
Python��R��round���͎l�̌ܓ��ł͂Ȃ��B
0.5����1��������100�̐����a�Ƃ���B
[1] 0.5 1.5 2.5 3.5 4.5 5.5 6.5 7.5 8.5 9.5 10.5 11.5 12.5 13.5 14.5 15.5 16.5 17.5 18.5 19.5
[21] 20.5 21.5 22.5 23.5 24.5 25.5 26.5 27.5 28.5 29.5 30.5 31.5 32.5 33.5 34.5 35.5 36.5 37.5 38.5 39.5
[41] 40.5 41.5 42.5 43.5 44.5 45.5 46.5 47.5 48.5 49.5 50.5 51.5 52.5 53.5 54.5 55.5 56.5 57.5 58.5 59.5
[61] 60.5 61.5 62.5 63.5 64.5 65.5 66.5 67.5 68.5 69.5 70.5 71.5 72.5 73.5 74.5 75.5 76.5 77.5 78.5 79.5
[81] 80.5 81.5 82.5 83.5 84.5 85.5 86.5 87.5 88.5 89.5 90.5 91.5 92.5 93.5 94.5 95.5 96.5 97.5 98.5 99.5
a�̕��ϒl��50�ł���B
��round�����> (b=round(a))
[1] 0 2 2 4 4 6 6 8 8 10 10 12 12 14 14 16 16 18 18 20 20 22 22 24 24
[26] 26 26 28 28 30 30 32 32 34 34 36 36 38 38 40 40 42 42 44 44 46 46 48 48 50
[51] 50 52 52 54 54 56 56 58 58 60 60 62 62 64 64 66 66 68 68 70 70 72 72 74 74
[76] 76 76 78 78 80 80 82 82 84 84 86 86 88 88 90 90 92 92 94 94 96 96 98 98 100
�ƁA���ׂċ����ɂȂ�B
a���l�̌ܓ����Ă��畽�ς��Ƃ�ƂP����100�܂ł̕��ςȂ̂�
> mean(1:100)
[1] 50.5
�ɂȂ邪�A
a��round����K�p���Ă��畽�ς��Ƃ��
> mean(round(a))
[1] 50
���v�����ŕ��ϒl���Ƃ邱�Ƃ͕p�ɂɂ���̂�R��round���͏�L�̂悤�Ȏd�l�ɂȂ��Ă���B
Python�ł������B
> print(round(2.5))
[1] 2
2024/03/30(�y) 14:25:12.01ID:QONil5+0
���E���h���́u�l�̌ܓ����ĕς��ꌅ��̐��v��M�銴�o���͂߂Ȃ��ĉ��Ԉ������
2024/03/31(��) 10:29:33.69ID:xeTMScgH
��i�@�œ����v�Z���Ă���̂�
0.15������1����round�����0.1�ɂȂ�����0.2�ɂȂ����肷��B
R�ł�Python�ł����l�B
x=1.15-1
print(x)
print(round(x,1))
y=0.3-(1.15-1)
print(y)
print(round(y,1))
print(x==y)
print(x-y)
0.15������1����round�����0.1�ɂȂ�����0.2�ɂȂ����肷��B
R�ł�Python�ł����l�B
x=1.15-1
print(x)
print(round(x,1))
y=0.3-(1.15-1)
print(y)
print(round(y,1))
print(x==y)
print(x-y)
2024/03/31(��) 18:06:58.24ID:xeTMScgH
print(0.15 > 1.15-1)
�����s�����
Python�ł�True
R�ł�TRUE
���Ԃ��Ă���B
��i�@�œ����v�Z���Ă��邽�߂Ɛ��������B
R��0.15���i�@�\��
0.0010011001100110011001100110011001100110011001100110011
R��1.15-1 ���i�@�\��
0.001001100110011001100110011001100110011001100110011
�m����0.15 > 1.15-1�ƌ딻�肷��̂�������B
�����s�����
Python�ł�True
R�ł�TRUE
���Ԃ��Ă���B
��i�@�œ����v�Z���Ă��邽�߂Ɛ��������B
R��0.15���i�@�\��
0.0010011001100110011001100110011001100110011001100110011
R��1.15-1 ���i�@�\��
0.001001100110011001100110011001100110011001100110011
�m����0.15 > 1.15-1�ƌ딻�肷��̂�������B
2024/03/31(��) 18:09:24.67ID:xeTMScgH
print(0.15 > 1.15-1)
�����s�����
Python�ł�True
R�ł�TRUE
���Ԃ��Ă���B
��i�@�œ����v�Z���Ă��邽�߂Ɛ��������B
R��0.15���i�@�\��
0.0010011001100110011001100110011001100110011001100110011
R��1.15-1 ���i�@�\��
0.001001100110011001100110011001100110011001100110011
�m����0.15 > 1.15-1�ƌ딻�肷��̂�������B
�����s�����
Python�ł�True
R�ł�TRUE
���Ԃ��Ă���B
��i�@�œ����v�Z���Ă��邽�߂Ɛ��������B
R��0.15���i�@�\��
0.0010011001100110011001100110011001100110011001100110011
R��1.15-1 ���i�@�\��
0.001001100110011001100110011001100110011001100110011
�m����0.15 > 1.15-1�ƌ딻�肷��̂�������B
2024/03/31(��) 18:13:58.91ID:xeTMScgH
�\�����𑝂₵�Ă݂��
> 0.15
[1] 0.1499999999999999944489
> 1.15-1
[1] 0.1499999999999999111822
�����Z���Ă݂�
print(0.15 - (1.15-1))
[1] 8.326672684688674053177e-17
Python�ł����l
print(0.15 -(1.15-1))
8.326672684688674e-17
> 0.15
[1] 0.1499999999999999944489
> 1.15-1
[1] 0.1499999999999999111822
�����Z���Ă݂�
print(0.15 - (1.15-1))
[1] 8.326672684688674053177e-17
Python�ł����l
print(0.15 -(1.15-1))
8.326672684688674e-17
2024/03/31(��) 20:07:40.77ID:YMObXOTP
�����Ɛ̂ɓǂR���s���[�^�[�G���ɏ����̌v�Z�͏o���邾�������ɒ����Ă���v�Z��������悤�ɏ����ėL�����̂��v���o�����B
2024/04/02(��) 09:00:03.59ID:TM2ayEcZ
>>125
�z���
100�@���Ԃɕ��ׂ��
> n[order(p,decreasing = TRUE)][1:100]
[1] 60 59 61 58 62 57 63 56 64 55 65 66 54 67 53 68 52 69
[19] 70 51 71 50 72 73 49 74 75 48 76 77 47 78 79 46 80 81
[37] 45 82 83 44 84 85 86 43 87 88 89 42 90 91 41 92 93 94
[55] 95 40 96 97 98 39 99 100 101 102 38 103 104 105 106 37 107 108
[73] 109 110 36 111 112 113 114 115 35 116 117 118 119 120 34 121 122 123
[91] 124 125 126 33 127 128 129 130 131 132
�z���
100�@���Ԃɕ��ׂ��
> n[order(p,decreasing = TRUE)][1:100]
[1] 60 59 61 58 62 57 63 56 64 55 65 66 54 67 53 68 52 69
[19] 70 51 71 50 72 73 49 74 75 48 76 77 47 78 79 46 80 81
[37] 45 82 83 44 84 85 86 43 87 88 89 42 90 91 41 92 93 94
[55] 95 40 96 97 98 39 99 100 101 102 38 103 104 105 106 37 107 108
[73] 109 110 36 111 112 113 114 115 35 116 117 118 119 120 34 121 122 123
[91] 124 125 126 33 127 128 129 130 131 132
2024/04/02(��) 09:29:50.17ID:TM2ayEcZ
>>125
���ʂƂ��̊m��
�z�����60��
[,1] [,2]
[1,] 60 2.320195e-08
[2,] 59 2.204186e-07
[3,] 61 1.118625e-06
[4,] 58 4.030906e-06
[5,] 62 1.156934e-05
[6,] 57 2.813774e-05
[7,] 63 6.025947e-05
[8,] 56 1.166232e-04
[9,] 64 2.077921e-04
[10,] 55 3.455956e-04
[11,] 65 5.422832e-04
[12,] 66 8.095588e-04
[13,] 54 1.157622e-03
[14,] 67 1.594328e-03
[15,] 53 2.124552e-03
[16,] 68 2.749796e-03
[17,] 52 3.468067e-03
[18,] 69 4.273982e-03
[19,] 70 5.159095e-03
[20,] 51 6.112361e-03
���ʂƂ��̊m��
�z�����60��
[,1] [,2]
[1,] 60 2.320195e-08
[2,] 59 2.204186e-07
[3,] 61 1.118625e-06
[4,] 58 4.030906e-06
[5,] 62 1.156934e-05
[6,] 57 2.813774e-05
[7,] 63 6.025947e-05
[8,] 56 1.166232e-04
[9,] 64 2.077921e-04
[10,] 55 3.455956e-04
[11,] 65 5.422832e-04
[12,] 66 8.095588e-04
[13,] 54 1.157622e-03
[14,] 67 1.594328e-03
[15,] 53 2.124552e-03
[16,] 68 2.749796e-03
[17,] 52 3.468067e-03
[18,] 69 4.273982e-03
[19,] 70 5.159095e-03
[20,] 51 6.112361e-03
2024/04/02(��) 09:39:31.37ID:kINbKFFS
>>85
Python��20�ʑ̂̃T�C�R���̑S�Ă̖ʂ��o��܂œ���������s�ׂ�1����J��Ԃ��A�ł��������s�Əo������\������v���O�����ł��B
import random
from collections import Counter
def roll_d20():
return random.randint(1, 20)
def main():
# ���s���J��Ԃ���
num_trials = 10000
# �e���s�̌��ʂ�ێ����郊�X�g
results = []
# ���s���J��Ԃ�
for _ in range(num_trials):
# �S�Ă̖ʂ��o�����܂ł̎��s��
attempts = 0
# �o�������ڂ̃��X�g
seen_numbers = []
# �S�Ă̖ʂ��o�����܂ŌJ��Ԃ�
while len(seen_numbers) < 20:
# �T�C�R���𓊂���
result = roll_d20()
# �o�������ڂ��L�^
if result not in seen_numbers:
seen_numbers.append(result)
# ���s���J�E���g
attempts += 1
# ���ʂ����X�g�ɒlj�
results.append(attempts)
# �e���s�̏o�����J�E���g
counts = Counter(results)
# �ł��������s�Ƃ��̏o�����擾
most_common_attempt, most_common_count = counts.most_common(1)[0]
# ���ʂ��o��
print(f"�ł��������s��: {most_common_attempt} (�o����: {most_common_count})")
if __name__ == "__main__":
main()
Python��20�ʑ̂̃T�C�R���̑S�Ă̖ʂ��o��܂œ���������s�ׂ�1����J��Ԃ��A�ł��������s�Əo������\������v���O�����ł��B
import random
from collections import Counter
def roll_d20():
return random.randint(1, 20)
def main():
# ���s���J��Ԃ���
num_trials = 10000
# �e���s�̌��ʂ�ێ����郊�X�g
results = []
# ���s���J��Ԃ�
for _ in range(num_trials):
# �S�Ă̖ʂ��o�����܂ł̎��s��
attempts = 0
# �o�������ڂ̃��X�g
seen_numbers = []
# �S�Ă̖ʂ��o�����܂ŌJ��Ԃ�
while len(seen_numbers) < 20:
# �T�C�R���𓊂���
result = roll_d20()
# �o�������ڂ��L�^
if result not in seen_numbers:
seen_numbers.append(result)
# ���s���J�E���g
attempts += 1
# ���ʂ����X�g�ɒlj�
results.append(attempts)
# �e���s�̏o�����J�E���g
counts = Counter(results)
# �ł��������s�Ƃ��̏o�����擾
most_common_attempt, most_common_count = counts.most_common(1)[0]
# ���ʂ��o��
print(f"�ł��������s��: {most_common_attempt} (�o����: {most_common_count})")
if __name__ == "__main__":
main()
2024/04/02(��) 10:57:21.05ID:u9EYkFQf
>>128
���X���肪�Ƃ��������܂��B
R����ŗ��������ŃV�~�����[�V�������ăq�X�g�O�����ƕp�x���ɕ\������v���O����
sim <- function(n=20){
x=sample(n,n,replace = TRUE)
flg <- length(unique(x))<n
i=n
while(flg){
i=i+1
x=c(x,sample(n,1))
flg <- length(unique(x))<n
}
i
}
y=replicate(1e6,sim())
hist(y)
sort(table(y),decreasing = TRUE)
���X���肪�Ƃ��������܂��B
R����ŗ��������ŃV�~�����[�V�������ăq�X�g�O�����ƕp�x���ɕ\������v���O����
sim <- function(n=20){
x=sample(n,n,replace = TRUE)
flg <- length(unique(x))<n
i=n
while(flg){
i=i+1
x=c(x,sample(n,1))
flg <- length(unique(x))<n
}
i
}
y=replicate(1e6,sim())
hist(y)
sort(table(y),decreasing = TRUE)
2024/04/02(��) 11:05:05.84ID:u9EYkFQf
>>127
�m���̗�͊Ԉ���Ă���̂Œ���
> cbind(��=idx,�m��=p[idx])
�� �m��
[1,] 60 0.0136829706
[2,] 59 0.0141644985
[3,] 61 0.0132055172
[4,] 58 0.0146484882
[5,] 62 0.0127335569
[6,] 57 0.0151331206
[7,] 63 0.0122683276
[8,] 56 0.0156163576
[9,] 64 0.0118108992
[10,] 55 0.0160959310
[11,] 65 0.0113621869
[12,] 66 0.0109229633
[13,] 54 0.0165693322
[14,] 67 0.0104938707
[15,] 53 0.0170338039
[16,] 68 0.0100754329
[17,] 52 0.0174863338
[18,] 69 0.0096680663
[19,] 70 0.0092720900
[20,] 51 0.0179236512
�m���̗�͊Ԉ���Ă���̂Œ���
> cbind(��=idx,�m��=p[idx])
�� �m��
[1,] 60 0.0136829706
[2,] 59 0.0141644985
[3,] 61 0.0132055172
[4,] 58 0.0146484882
[5,] 62 0.0127335569
[6,] 57 0.0151331206
[7,] 63 0.0122683276
[8,] 56 0.0156163576
[9,] 64 0.0118108992
[10,] 55 0.0160959310
[11,] 65 0.0113621869
[12,] 66 0.0109229633
[13,] 54 0.0165693322
[14,] 67 0.0104938707
[15,] 53 0.0170338039
[16,] 68 0.0100754329
[17,] 52 0.0174863338
[18,] 69 0.0096680663
[19,] 70 0.0092720900
[20,] 51 0.0179236512
2024/04/02(��) 11:07:02.61ID:u9EYkFQf
>>130
������v�Z����v���O����
# N�ʑ̂̃T�C�R����n����m��ނ̖ڂ��łĂ���m�����v�Z
Dice=Vectorize(\(N,n,m,fraction=FALSE){
j=m:1
k=(-1)^(0:(m-1))
nu=ifelse(m==1,N,choose(N,m)*sum(k*choose(m,j)*(j^n-j)))
de=N^n
gcd=numbers::GCD(nu,de)
if(fraction) cat(nu,'/',de,'=',nu/gcd,'/',de/gcd,'=',nu/de,'\n')
return(nu/de)
})
"
�Q�O�ʑ̃T�C�R�����ӂ��Ă��ׂĂ̖ڂ��ł���I���B
�I���܂łɂӂ��������Ă�q��������B
�����ɓq����̂��ł��L�����H
"
Dice2=Vectorize(\(N,n,m) Dice(N,n,m) - Dice(N,n-1,m))
p=Dice2(20,n,20)
plot(n,p,bty='l',type='h',lwd=5,col=2)
n[order(p,decreasing = TRUE)][1:10]
which(n[order(p,decreasing = TRUE)]==37)
idx=n[order(p,decreasing = TRUE)][1:100]
cbind(��=idx,�m��=p[idx])
������v�Z����v���O����
# N�ʑ̂̃T�C�R����n����m��ނ̖ڂ��łĂ���m�����v�Z
Dice=Vectorize(\(N,n,m,fraction=FALSE){
j=m:1
k=(-1)^(0:(m-1))
nu=ifelse(m==1,N,choose(N,m)*sum(k*choose(m,j)*(j^n-j)))
de=N^n
gcd=numbers::GCD(nu,de)
if(fraction) cat(nu,'/',de,'=',nu/gcd,'/',de/gcd,'=',nu/de,'\n')
return(nu/de)
})
"
�Q�O�ʑ̃T�C�R�����ӂ��Ă��ׂĂ̖ڂ��ł���I���B
�I���܂łɂӂ��������Ă�q��������B
�����ɓq����̂��ł��L�����H
"
Dice2=Vectorize(\(N,n,m) Dice(N,n,m) - Dice(N,n-1,m))
p=Dice2(20,n,20)
plot(n,p,bty='l',type='h',lwd=5,col=2)
n[order(p,decreasing = TRUE)][1:10]
which(n[order(p,decreasing = TRUE)]==37)
idx=n[order(p,decreasing = TRUE)][1:100]
cbind(��=idx,�m��=p[idx])
2024/04/02(��) 11:37:41.21ID:u9EYkFQf
>>130
�ēx����
�� �m��
[1,] 60 0.02057223
[2,] 59 0.02056397
[3,] 61 0.02051655
[4,] 58 0.02048731
[5,] 62 0.02040163
[6,] 57 0.02033813
[7,] 63 0.02023230
[8,] 56 0.02011277
[9,] 64 0.02001344
[10,] 55 0.01980821
[11,] 65 0.01974991
[12,] 66 0.01944648
[13,] 54 0.01942214
[14,] 67 0.01910778
[15,] 53 0.01895318
[16,] 68 0.01873828
[17,] 52 0.01840101
[18,] 69 0.01834223
[19,] 70 0.01792365
[20,] 51 0.01776651
60��O��łقƂ�NJm���ɍ����Ȃ��̂ŃV�~�����[�V�����ł̏��ʂ��͌딻�肵�����B
�ēx����
�� �m��
[1,] 60 0.02057223
[2,] 59 0.02056397
[3,] 61 0.02051655
[4,] 58 0.02048731
[5,] 62 0.02040163
[6,] 57 0.02033813
[7,] 63 0.02023230
[8,] 56 0.02011277
[9,] 64 0.02001344
[10,] 55 0.01980821
[11,] 65 0.01974991
[12,] 66 0.01944648
[13,] 54 0.01942214
[14,] 67 0.01910778
[15,] 53 0.01895318
[16,] 68 0.01873828
[17,] 52 0.01840101
[18,] 69 0.01834223
[19,] 70 0.01792365
[20,] 51 0.01776651
60��O��łقƂ�NJm���ɍ����Ȃ��̂ŃV�~�����[�V�����ł̏��ʂ��͌딻�肵�����B
2024/04/02(��) 11:49:18.64ID:u9EYkFQf
2024/04/03(��) 06:39:07.96ID:zh4gkiW4
���K���
�{�[����0〜36�܂ł̉��Ԃ̃|�P�b�g�ɓ��邩�Ă�A�J�W�m�Q�[���u���[���s�A�����[���b�g�v
�ǂ̃|�P�b�g�ɓ���m�����������Ƃ���B
���[���b�g����
���ׂẴ|�P�b�g�ɏ��Ȃ��Ƃ�1���������I������B
����ڂɏI������m�����ł��������H
�{�[����0〜36�܂ł̉��Ԃ̃|�P�b�g�ɓ��邩�Ă�A�J�W�m�Q�[���u���[���s�A�����[���b�g�v
�ǂ̃|�P�b�g�ɓ���m�����������Ƃ���B
���[���b�g����
���ׂẴ|�P�b�g�ɏ��Ȃ��Ƃ�1���������I������B
����ڂɏI������m�����ł��������H
135�C�i ��/7jUdUKiSM
2024/04/03(��) 14:24:57.69ID:sFYEIN3j �O>>125�m���I�ɂ͂قƂ�ǐ����������Ȃ��B���������Ă�B
2024/04/04(��) 09:55:59.01ID:alcftUJ3
2024/04/04(��) 10:06:20.43ID:alcftUJ3
>>132
�U�O��߂ƂT�X��߂̕������i�Ԉ���Ă��邩�������j
> DICE2(20,60,20)
[[1]]
[1] 72838974610293077213507074350649821345456797553812346003412117474160586767713/3540645635006889804797781514390831345225150648743234944437117905548026929217536
[[2]]
[1] 0.02057223
> DICE2(20,59,20)
[[1]]
[1] 11649556867172241040383435279013152205165420738122826289629404076378830783037/566503301601102365609283596519400574535448867175022715494793218716221069852672
[[2]]
[1] 0.02056397
�U�O��߂ƂT�X��߂̕������i�Ԉ���Ă��邩�������j
> DICE2(20,60,20)
[[1]]
[1] 72838974610293077213507074350649821345456797553812346003412117474160586767713/3540645635006889804797781514390831345225150648743234944437117905548026929217536
[[2]]
[1] 0.02057223
> DICE2(20,59,20)
[[1]]
[1] 11649556867172241040383435279013152205165420738122826289629404076378830783037/566503301601102365609283596519400574535448867175022715494793218716221069852672
[[2]]
[1] 0.02056397
2024/04/04(��) 20:34:25.36ID:GLOIObOV
>>137
�������m�Ȓl���v�Z���Ă݂��̂ł����A�����ɈႢ�܂��B
�����I�ɕ����20^n�̖ɂȂ�͂��ł��B
�����v�Z���Ă݂��Ƃ���A�����Ƃ� 10^(-17)�@�ʈႢ������܂����B
���̒l�͕��������_�̗L�������̌����ƈ�v����̂ŁA���������_�Ōv�Z���ꂽ�̂ł����H
60���
72382097771062155249508882399594426708852774453647663964820729051703
----------------------------------------------------------------------
3518437208883200000000000000000000000000000000000000000000000000000000
59���
28941214805008323350150382808708128294237575152509675061051407267
-------------------------------------------------------------------
1407374883553280000000000000000000000000000000000000000000000000000
�������m�Ȓl���v�Z���Ă݂��̂ł����A�����ɈႢ�܂��B
�����I�ɕ����20^n�̖ɂȂ�͂��ł��B
�����v�Z���Ă݂��Ƃ���A�����Ƃ� 10^(-17)�@�ʈႢ������܂����B
���̒l�͕��������_�̗L�������̌����ƈ�v����̂ŁA���������_�Ōv�Z���ꂽ�̂ł����H
60���
72382097771062155249508882399594426708852774453647663964820729051703
----------------------------------------------------------------------
3518437208883200000000000000000000000000000000000000000000000000000000
59���
28941214805008323350150382808708128294237575152509675061051407267
-------------------------------------------------------------------
1407374883553280000000000000000000000000000000000000000000000000000
139�P�R�Q�l�ڂ̑f������
2024/04/04(��) 20:37:00.22ID:i+N8ejzm ���k35�l�̃N���X�Ő��k�̐l�C���[�������Ȃ��B��l��[�Ŏ����ւ̓��[��OK�̂Ƃ��K��2�ʈȓ��Ȃ�ɂ͍Œች�[�͂���悢���H
2024/04/05(��) 05:25:28.31ID:pMPSnpeE
>>138
���X���肪�Ƃ��������܂��BR����ŎZ�o���܂����B
C�ł̃\�[�X�R�[�h���m�F�ł��Ă��܂���
R����̎d�l��A���������_�ł̎Z�o���Ǝv���܂��B
���X���肪�Ƃ��������܂��BR����ŎZ�o���܂����B
C�ł̃\�[�X�R�[�h���m�F�ł��Ă��܂���
R����̎d�l��A���������_�ł̎Z�o���Ǝv���܂��B
2024/04/05(��) 06:27:01.42ID:cqcSL+84
>>139
17�[
17�[
2024/04/05(��) 11:02:49.64ID:OZ2Z3ty4
"
�������ꂽ�����c��n�l�Ŕh������邱�ƂɂȂ����B
m�l�����Ƃ��đ�\��1�l�I�ԁB
�ō����[�����c������\�ɂȂ�B
�ō����[���̋c������������Ƃ��͍ō����[���̋c���݂̂����Ƃ���
�ō����[���̋c����1�l�ɂȂ�܂œ��[���J��Ԃ��B
�e�c��������ׂɓ��[����Ƃ�x��ȏ�̓��[���K�v�ɂȂ�m�������߂�B
���͏����ł悢�B
"
R�ł̃V�~�����[�V����
n=39
m=39
x=3
f=\(m){
a=sample(m,n,replace=TRUE)
b=table(a)
sum(b==max(b))
}
sim=\(){
m=f(m)
count=1
while(m>1){
count=count+1
m=f(m)
}
count
}
y=replicate(1e5,sim())
mean(y>=x)
�������ꂽ�����c��n�l�Ŕh������邱�ƂɂȂ����B
m�l�����Ƃ��đ�\��1�l�I�ԁB
�ō����[�����c������\�ɂȂ�B
�ō����[���̋c������������Ƃ��͍ō����[���̋c���݂̂����Ƃ���
�ō����[���̋c����1�l�ɂȂ�܂œ��[���J��Ԃ��B
�e�c��������ׂɓ��[����Ƃ�x��ȏ�̓��[���K�v�ɂȂ�m�������߂�B
���͏����ł悢�B
"
R�ł̃V�~�����[�V����
n=39
m=39
x=3
f=\(m){
a=sample(m,n,replace=TRUE)
b=table(a)
sum(b==max(b))
}
sim=\(){
m=f(m)
count=1
while(m>1){
count=count+1
m=f(m)
}
count
}
y=replicate(1e5,sim())
mean(y>=x)
2024/04/05(��) 12:12:17.93ID:r6RvNlcq
���a�~���a�~�~�S�ŋ��̂̕\�ʐς����߂�ƁA�͊��肫��Ȃ��̂�3�A14�Ōv�Z���܂����A
�e�X�g�Ő����ł��A�ŏȗ�����
�����l������̂Ŋ��S�ȕ\�ʐς�
�͂����Ȃ��̂ł��傤���H
�e�X�g�Ő����ł��A�ŏȗ�����
�����l������̂Ŋ��S�ȕ\�ʐς�
�͂����Ȃ��̂ł��傤���H
2024/04/05(��) 12:57:14.76ID:seG+J0za
2024/04/05(��) 14:19:40.69ID:r6RvNlcq
���肪�Ƃ��������܂���
146�P�R�Q�l�ڂ̑f������
2024/04/05(��) 18:56:52.99ID:AJx5xwSy2024/04/06(�y) 03:43:31.77ID:cQ7PwACI
>>146
12�l�ł����H
12�l�ł����H
2024/04/06(�y) 03:43:54.00ID:cQ7PwACI
12�[
2024/04/06(�y) 04:17:06.29ID:cQ7PwACI
���kn�l�̃N���X�Ő��k�̐l�C���[�������Ȃ��B��l��[�Ŏ����ւ̓��[��OK�̂Ƃ��K��m�ʈȓ��Ȃ�ɂ͍Œች�[�͂���悢���H
ceiling(n/(m+1))
ceiling(n/(m+1))
2024/04/06(�y) 05:11:52.34ID:cQ7PwACI
35/3=11,666.. < 12
151�P�R�Q�l�ڂ̑f������
2024/04/06(�y) 22:22:41.29ID:OsBiRZ0I152�P�R�Q�l�ڂ̑f������
2024/04/06(�y) 22:33:56.18ID:OsBiRZ0I 1���ڂɈ���i��łO��������A
2���ڂɓ���i��ň��������A
3���ڂɎO���i��œ��������...
�Ƃ��������O��������v���X���Đi��ʼn�����l������
���̐l�̈���̕�����1m�̂Ƃ�100m�i�߂�͉̂����ڂƂȂ邩�H
2���ڂɓ���i��ň��������A
3���ڂɎO���i��œ��������...
�Ƃ��������O��������v���X���Đi��ʼn�����l������
���̐l�̈���̕�����1m�̂Ƃ�100m�i�߂�͉̂����ڂƂȂ邩�H
153�C�i ��/7jUdUKiSM
2024/04/07(��) 07:54:17.92ID:epIg0nam154�C�i ��/7jUdUKiSM
2024/04/07(��) 08:47:40.83ID:epIg0nam155�P�R�Q�l�ڂ̑f������
2024/04/07(��) 10:08:19.13ID:j9gMe/ug2024/04/07(��) 10:54:38.54ID:ryf3vuDH
�z�����133��
> order(P,decreasing = TRUE)[1:20]
[1] 133 134 132 135 131 136 130 137 129 138 128 139 127 140 126 141 125 142 143 124
https://i.imgur.com/XD7J6aa.png
> order(P,decreasing = TRUE)[1:20]
[1] 133 134 132 135 131 136 130 137 129 138 128 139 127 140 126 141 125 142 143 124
https://i.imgur.com/XD7J6aa.png
2024/04/07(��) 11:45:29.08ID:ryf3vuDH
>>156
�m���͍͋�
[,1] [,2]
[1,] 133 0.01062932
[2,] 134 0.01062566
[3,] 132 0.01062397
[4,] 135 0.01061331
[5,] 131 0.01060933
[6,] 136 0.01059257
[7,] 130 0.01058514
[8,] 137 0.01056375
[9,] 129 0.01055113
[10,] 138 0.01052719
[11,] 128 0.01050706
[12,] 139 0.01048321
[13,] 127 0.01045271
[14,] 140 0.01043215
[15,] 126 0.01038790
[16,] 141 0.01037434
[17,] 125 0.01031246
[18,] 142 0.01031011
[19,] 143 0.01023980
[20,] 124 0.01022624
�m���͍͋�
[,1] [,2]
[1,] 133 0.01062932
[2,] 134 0.01062566
[3,] 132 0.01062397
[4,] 135 0.01061331
[5,] 131 0.01060933
[6,] 136 0.01059257
[7,] 130 0.01058514
[8,] 137 0.01056375
[9,] 129 0.01055113
[10,] 138 0.01052719
[11,] 128 0.01050706
[12,] 139 0.01048321
[13,] 127 0.01045271
[14,] 140 0.01043215
[15,] 126 0.01038790
[16,] 141 0.01037434
[17,] 125 0.01031246
[18,] 142 0.01031011
[19,] 143 0.01023980
[20,] 124 0.01022624
2024/04/07(��) 12:09:34.11ID:ryf3vuDH
>>156
100����̃V�~�����[�V�����ł̏���
�������딻�肵�Ă���B
> sort(table(y),decreasing = TRUE)[1:20] |> names() |> noquote()
[1] 134 133 130 129 131 135 128 132 136 126 139 137 143 127 142 140 141 138 125 124
100����̃V�~�����[�V�����ł̏���
�������딻�肵�Ă���B
> sort(table(y),decreasing = TRUE)[1:20] |> names() |> noquote()
[1] 134 133 130 129 131 135 128 132 136 126 139 137 143 127 142 140 141 138 125 124
159�C�i ��/7jUdUKiSM
2024/04/07(��) 16:15:05.47ID:epIg0nam2024/04/08(��) 07:00:43.32ID:mbGKeakd
��. ���҂�������Y��čs�����Ƃ���B�Y��čs�����l���������ł���m�����ȉ��̃f �[ �^����v�Z����B
�i����
�j�� 28.2%
���� 9.0 %
�j���v 18.29%
�o�T
https://www.jti.co.jp/investors/library/press_releases/2017/0727_01.html
�i����
�j�� 28.2%
���� 9.0 %
�j���v 18.29%
�o�T
https://www.jti.co.jp/investors/library/press_releases/2017/0727_01.html
161�P�R�Q�l�ڂ̑f������
2024/04/08(��) 16:53:32.39ID:yTEMgLgv �y���˔\�z�@�H�ׂĉ����A�ł��ĉ����@�y���N�`���z
https://rio2016.5ch.net/test/read.cgi/radiation/1712287549/l50
https://rio2016.5ch.net/test/read.cgi/radiation/1712287549/l50

2024/04/08(��) 23:14:23.45ID:fLdRPpqp
���ϒl���o�������Ċ�̐������߂Ă���̃v���X��}�C�i�X����o���đS�������ďo������
����~���̓�����������ΐ����Ȃ̂�
����~���̓�����������ΐ����Ȃ̂�
2024/04/09(��) 00:04:10.26ID:/46J9iIj
>>162
�����̑�����S�������A���Ŋ����āA�������ɉ�����
�����̑�����S�������A���Ŋ����āA�������ɉ�����
2024/04/09(��) 04:18:04.50ID:Fv1gSIBK
f1= \(x,a=pi){
n=length(x)
m1=a*n - sum(x-a) # a*n - (∑(x-a)
m2=sum(x-a)/n + a # (∑(x-a))/n + a
m=sum(x)/n
cbind(m1,m2,m)
}
"x=100��[0,1]�̗���
a=��l�@�~�������̗p"
f1(runif(100))
[1] "x=100��[0,1]�̗���\na=��l�@�~�������̗p"
m1 m2 m
[1,] 577.0556 0.5126295 0.5126295
n=length(x)
m1=a*n - sum(x-a) # a*n - (∑(x-a)
m2=sum(x-a)/n + a # (∑(x-a))/n + a
m=sum(x)/n
cbind(m1,m2,m)
}
"x=100��[0,1]�̗���
a=��l�@�~�������̗p"
f1(runif(100))
[1] "x=100��[0,1]�̗���\na=��l�@�~�������̗p"
m1 m2 m
[1,] 577.0556 0.5126295 0.5126295
2024/04/09(��) 04:23:13.03ID:Fv1gSIBK
2024/04/09(��) 09:04:50.72ID:SQcSGmhr
�j���[�R�[�X�u���P���w�v�̃n�C���x����肪����
���ꉴ�����P�̍���������S��s��������
���ꉴ�����P�̍���������S��s��������
2024/04/09(��) 10:26:09.51ID:fx7di+pL
�A�z�݂����Ȏ��₵�܂����A���ԁ����x���v�Z�����Ƃ��āA���̎��ɏo�Ă��鐔���Ƃ����͉̂��̈Ӗ����Ȃ����́H
2024/04/09(��) 11:07:18.30ID:99Biy/EB
>>167
���x������/����
����/���x������/(����/���ԁj������^2/����
���Ԃ�2��ɔ�Ⴗ��ʂ�����A�����̖��ɗ���������Ȃ��B
�����O�@�������xa �̂Ƃ��̈ړ������� (1/2)*�����x������^2
���x������/����
����/���x������/(����/���ԁj������^2/����
���Ԃ�2��ɔ�Ⴗ��ʂ�����A�����̖��ɗ���������Ȃ��B
�����O�@�������xa �̂Ƃ��̈ړ������� (1/2)*�����x������^2
2024/04/09(��) 11:09:13.63ID:99Biy/EB
�Ֆ≻
�i����
�j�� 28.2%
���� 9.0 %
�j���v 18.29%
�Ƃ����f�[�^
�i�o�T�@https://www.jti.co.jp/investors/library/press_releases/2017/0727_01.html�j
����
�j�����̔�����߂�B
�i����
�j�� 28.2%
���� 9.0 %
�j���v 18.29%
�Ƃ����f�[�^
�i�o�T�@https://www.jti.co.jp/investors/library/press_releases/2017/0727_01.html�j
����
�j�����̔�����߂�B
2024/04/09(��) 11:14:46.32ID:fx7di+pL
��������
����̂ōl�������Ă�������
����̂ōl�������Ă�������
2024/04/09(��) 12:31:05.57ID:SQcSGmhr
�u���̑����ł͉��X�L�����鉽�X�܂ł��ǂ蒅���̂Ɂ��������ȁv
����������������
�u�����܂ŗ���̂Ɂ������Ԋ|�������͎̂��������L���ŕ���������ł��v
���ԁ~����������
�u�����܂ł��鋗���Ɂ����œ�������ׂɂ́����L���̑����ł����Ȃ��ƒx��邼�v
���������ԁ�����
����������������
�u�����܂ŗ���̂Ɂ������Ԋ|�������͎̂��������L���ŕ���������ł��v
���ԁ~����������
�u�����܂ł��鋗���Ɂ����œ�������ׂɂ́����L���̑����ł����Ȃ��ƒx��邼�v
���������ԁ�����
2024/04/09(��) 12:38:48.72ID:prPA96hS
>>165
mathematica�ł��B����138�̌��ʂ��o���܂��B
M=Table[If[i==j,i,If[i==j-1,20-i,0]],{j,1,20},{i,1,20}]
u=Table[If[i==1,1,0],{i,1,20}]
x=Table[If[i==19,1,0],{i,1,20}]
MatrixPower[M,n-2].u.x/20^(n-1)/.{{n->60},{n->59}}
mathematica�ł��B����138�̌��ʂ��o���܂��B
M=Table[If[i==j,i,If[i==j-1,20-i,0]],{j,1,20},{i,1,20}]
u=Table[If[i==1,1,0],{i,1,20}]
x=Table[If[i==19,1,0],{i,1,20}]
MatrixPower[M,n-2].u.x/20^(n-1)/.{{n->60},{n->59}}
2024/04/09(��) 15:59:19.37ID:99Biy/EB
2024/04/09(��) 20:58:09.91ID:prPA96hS
WolframScript�@����̎��s�ł��B
�������A���[�U�[�o�^�݂����Ȃ��Ƃ����Ȃ���Ȃ�Ȃ��̂�
�ʓ|�ł����A������t���[�ł���B
�������A���[�U�[�o�^�݂����Ȃ��Ƃ����Ȃ���Ȃ�Ȃ��̂�
�ʓ|�ł����A������t���[�ł���B
2024/04/09(��) 21:46:36.68ID:99Biy/EB
>>174
�M�d�ȏ�肪�Ƃ��������܂��B
�M�d�ȏ�肪�Ƃ��������܂��B
2024/04/09(��) 22:58:05.41ID:LVhvjoy+
wolframscript.exe�Ŏ��s�ł��܂����B
����̈Ӗ��͗����ł��Ă���܂��A���\�z�ł��܂����B
���肪�Ƃ��������܂����B
In[4]:= MatrixPower[M,n-2].u.x/20^(n-1)/.{{n->60},{n->59}}
72382097771062155249508882399594426708852774453647663964820729051703
Out[4]= {----------------------------------------------------------------------,
3518437208883200000000000000000000000000000000000000000000000000000000
28941214805008323350150382808708128294237575152509675061051407267
> -------------------------------------------------------------------}
1407374883553280000000000000000000000000000000000000000000000000000
����̈Ӗ��͗����ł��Ă���܂��A���\�z�ł��܂����B
���肪�Ƃ��������܂����B
In[4]:= MatrixPower[M,n-2].u.x/20^(n-1)/.{{n->60},{n->59}}
72382097771062155249508882399594426708852774453647663964820729051703
Out[4]= {----------------------------------------------------------------------,
3518437208883200000000000000000000000000000000000000000000000000000000
28941214805008323350150382808708128294237575152509675061051407267
> -------------------------------------------------------------------}
1407374883553280000000000000000000000000000000000000000000000000000
2024/04/10(��) 11:12:00.68ID:IkSXJvM8
WolframScript�ŗV��ł݂�B
2024^2024�̍ŏ��̐�����100���߂�B
In[27]:= Part[IntegerDigits[2024^2024],Range[100]]
Out[27]= {5, 8, 8, 9, 3, 6, 5, 8, 2, 0, 5, 3, 4, 6, 8, 7, 3, 3, 2, 1, 0, 0, 9, 4, 0, 5, 1, 1, 4, 2, 5, 2, 5, 1, 1, 1,
> 1, 2, 5, 6, 3, 1, 0, 3, 2, 1, 9, 8, 1, 1, 5, 1, 0, 4, 3, 6, 6, 4, 2, 6, 9, 9, 8, 9, 9, 0, 2, 2, 0, 7, 9, 9, 2, 5,
> 1, 2, 0, 4, 9, 2, 4, 2, 3, 1, 7, 8, 1, 8, 5, 4, 6, 5, 8, 7, 7, 1, 2, 0, 6, 0}
R����
> x=2024*log10(2024)
> 10^(x-floor(x))
[1] 5.8893658205�@24448125184
�����x
2024^2024�̍ŏ��̐�����100���߂�B
In[27]:= Part[IntegerDigits[2024^2024],Range[100]]
Out[27]= {5, 8, 8, 9, 3, 6, 5, 8, 2, 0, 5, 3, 4, 6, 8, 7, 3, 3, 2, 1, 0, 0, 9, 4, 0, 5, 1, 1, 4, 2, 5, 2, 5, 1, 1, 1,
> 1, 2, 5, 6, 3, 1, 0, 3, 2, 1, 9, 8, 1, 1, 5, 1, 0, 4, 3, 6, 6, 4, 2, 6, 9, 9, 8, 9, 9, 0, 2, 2, 0, 7, 9, 9, 2, 5,
> 1, 2, 0, 4, 9, 2, 4, 2, 3, 1, 7, 8, 1, 8, 5, 4, 6, 5, 8, 7, 7, 1, 2, 0, 6, 0}
R����
> x=2024*log10(2024)
> 10^(x-floor(x))
[1] 5.8893658205�@24448125184
�����x
2024/04/10(��) 13:57:19.89ID:kG1hIjK/
�i-5�j-�i-10�j��+5�@�������H
2024/04/10(��) 15:39:16.05ID:YBTaW/2B
>>178
���ꂪ+5�ɂȂ闝�R���킩���
���ꂪ+5�ɂȂ闝�R���킩���
2024/04/10(��) 17:50:28.73ID:eUzvH24H
-(-10)�� -1�~-10 �̂��Ƃ�����
����1�{�����̖т�������(-1)�l��10���O�~(-10)�͂܂����̖т�10�{����܂���(-1�~-10=10)
����1�{�����̖т�������(-1)�l��10���O�~(-10)�͂܂����̖т�10�{����܂���(-1�~-10=10)
181�P�R�Q�l�ڂ̑f������
2024/04/10(��) 17:53:34.34ID:s76EegHb182�P�R�Q�l�ڂ̑f������
2024/04/10(��) 18:08:05.37ID:s76EegHb >180�����łɌ����Ă��邪�c�܂��A�v����� �����Z��180�x�̉�]�B
�i�����ĕ��̐��͐i�ޕ����B���̌����ɐi�ނ̂��t��]������Ɛ��̕����i�ގ��Ɠ����j
>181�̃y�[�W�ł����������A�����̐�������x������p���ĕ��邩���m���B
(-5) - (-10) = (-5) + ((-1) �~ (-10)) = (-5) + 10 = 5
←�@�@← ← (�t��]) ← ← → →
�i�����ĕ��̐��͐i�ޕ����B���̌����ɐi�ނ̂��t��]������Ɛ��̕����i�ގ��Ɠ����j
>181�̃y�[�W�ł����������A�����̐�������x������p���ĕ��邩���m���B
(-5) - (-10) = (-5) + ((-1) �~ (-10)) = (-5) + 10 = 5
←�@�@← ← (�t��]) ← ← → →
2024/04/10(��) 18:52:30.80ID:SFzTkptQ
2024/04/10(��) 20:11:32.95ID:IkSXJvM8
>>179
(-5) - (10)
(-5) - (9)
(-5) - (8)
(-5) - (7)
(-5) - (6)
(-5) - (5)
(-5) - (4)
(-5) - (3)
(-5) - (2)
(-5) - (1)
(-5) - (0)
(-5) - (-1)
(-5) - (-2)
(-5) - (-3)
(-5) - (-4)
(-5) - (-5)
(-5) - (-6)
(-5) - (-7)
(-5) - (-8)
(-5) - (-9)
(-5) - (-10)
���v�Z���Ă݂���ǂ����낤�H
(-5) - (10)
(-5) - (9)
(-5) - (8)
(-5) - (7)
(-5) - (6)
(-5) - (5)
(-5) - (4)
(-5) - (3)
(-5) - (2)
(-5) - (1)
(-5) - (0)
(-5) - (-1)
(-5) - (-2)
(-5) - (-3)
(-5) - (-4)
(-5) - (-5)
(-5) - (-6)
(-5) - (-7)
(-5) - (-8)
(-5) - (-9)
(-5) - (-10)
���v�Z���Ă݂���ǂ����낤�H
2024/04/11(��) 00:44:40.38ID:+2MKJeXz
>>178
����͐^�́i-�j�̖��߂Ɂi-10�j�ɕt���Ă�i-�j���t����āi-5�j�̒n�_����10�グ��������Ɖ��߂��Ă�
���ꂪ�i+10�j��������-�̖��߂ɏ]��
������-15�ɂȂ�
����͐^�́i-�j�̖��߂Ɂi-10�j�ɕt���Ă�i-�j���t����āi-5�j�̒n�_����10�グ��������Ɖ��߂��Ă�
���ꂪ�i+10�j��������-�̖��߂ɏ]��
������-15�ɂȂ�
2024/04/11(��) 07:17:39.84ID:GE3DczI+
�u���������ĉ�����v�̂�+�ɂȂ銴�o���ӎ��������Ƃ��Ȃ��������痝������܂łɎ��Ԋ|������
2024/04/11(��) 15:20:18.73ID:4hAIBrFj
���������Đi�ނƌ����}�C�P���̃��[���E�H�[�N���v���o��
2024/04/11(��) 16:33:11.01ID:wuL27qV5
�������P���̐��̐���ɂ���Wolfram�̊� IntegerDigits��R�Ɏ������Ă݂�
IntegerDigits[n] gives a list of the decimal digits in the integer n
IntegerDigit=\(n) n%/%10^(floor(log10(n)):0) %% 10
> IntegerDigit(12345689012345678)
[1] 1 2 3 4 5 6 8 9 0 1 2 3 4 5 6 7 8
> IntegerDigit(123456890123456789)
[1] 1 2 3 4 5 6 8 9 0 1 2 3 4 5 6 7 8 4
���������ĕϊ�
IntegerDigits=\(n){ # s : s of string
strsplit(as.character(n),'') |> unlist() |> as.numeric()
}
> IntegerDigits(12345689012345678)
[1] 1 2 3 4 5 6 8 9 0 1 2 3 4 5 6 7 8
> IntegerDigits(123456890123456789)
[1] 1 2 3 4 5 6 8 9 0 1 2 3 4 5 6 7 8 4
�ǂ����18�����z����ƌ듚��Ԃ��Ă���
IntegerDigits[n] gives a list of the decimal digits in the integer n
IntegerDigit=\(n) n%/%10^(floor(log10(n)):0) %% 10
> IntegerDigit(12345689012345678)
[1] 1 2 3 4 5 6 8 9 0 1 2 3 4 5 6 7 8
> IntegerDigit(123456890123456789)
[1] 1 2 3 4 5 6 8 9 0 1 2 3 4 5 6 7 8 4
���������ĕϊ�
IntegerDigits=\(n){ # s : s of string
strsplit(as.character(n),'') |> unlist() |> as.numeric()
}
> IntegerDigits(12345689012345678)
[1] 1 2 3 4 5 6 8 9 0 1 2 3 4 5 6 7 8
> IntegerDigits(123456890123456789)
[1] 1 2 3 4 5 6 8 9 0 1 2 3 4 5 6 7 8 4
�ǂ����18�����z����ƌ듚��Ԃ��Ă���
189�P�R�Q�l�ڂ̑f������
2024/04/12(��) 17:11:43.59ID:u8tMkaK2 >>169
�A���������ʼn��������ł����H
�A���������ʼn��������ł����H
2024/04/13(�y) 08:03:55.49ID:sKFVdX9u
>>189
�j�� 28.2%
���� 9.0 %
�j���v 18.29%
28.2/100*�j���� + 9.0/100*������ = 18.29/100*(�j�����{�������j
����
�j����/������
�����߂�Ƃ������Ȃ̂ŁA�A���������Ƃ͌�����B
�j�� 28.2%
���� 9.0 %
�j���v 18.29%
28.2/100*�j���� + 9.0/100*������ = 18.29/100*(�j�����{�������j
����
�j����/������
�����߂�Ƃ������Ȃ̂ŁA�A���������Ƃ͌�����B
2024/04/13(�y) 08:43:17.37ID:x8Kai00i
(28.2-18.29)/(18.29-9.0)
2024/04/13(�y) 09:19:05.73ID:OrZY0B6w
>>191
������/�j�����@= (28.2-18.29)/(18.29-9.0) =�@991/929
�Ƃ킩�����̂�
���Ƃ̖��ɖ߂�
��. ���҂�������Y��čs�����Ƃ���B�Y��čs�����l���������ł���m�����ȉ��̃f �[ �^����v�Z����B
�i����
�j�� 28.2%
���� 9.0 %
�j���v 18.29%
�o�T
https://www.jti.co.jp/investors/library/press_releases/2017/0727_01.html
������/�j�����@= (28.2-18.29)/(18.29-9.0) =�@991/929
�Ƃ킩�����̂�
���Ƃ̖��ɖ߂�
��. ���҂�������Y��čs�����Ƃ���B�Y��čs�����l���������ł���m�����ȉ��̃f �[ �^����v�Z����B
�i����
�j�� 28.2%
���� 9.0 %
�j���v 18.29%
�o�T
https://www.jti.co.jp/investors/library/press_releases/2017/0727_01.html
193�C�i ��/7jUdUKiSM
2024/04/17(��) 04:44:35.14ID:ZEH/FEO/2024/04/17(��) 06:37:24.39ID:Dymy/D6a
4�~�i5+10�j��60��4�~5+4�~10�ʼn������o��Y��Ă���
2024/04/17(��) 12:37:18.59ID:Dojom4Xi
2024/04/17(��) 21:54:09.45ID:ENa6jeZE
2024/04/17(��) 22:00:18.50ID:ENa6jeZE
�摜�̎����ԈႦ�Ă܂����Ō�́~60�͖�����
2024/04/17(��) 22:00:24.27ID:6IYiqY7a
�܂��A-50�~60=-60�~50 ������ȁB����ւ��ėǂ���B
�ł��A�摜�̍Ō�́~60��������Ă���̂����ǁH
�ł��A�摜�̍Ō�́~60��������Ă���̂����ǁH
2024/04/17(��) 22:09:00.91ID:ENa6jeZE
���낢�낷���܂���@���Ă���Ă��肪�Ƃł�
���̎����Č���-50�~60�̏���-60�~50�ɂ��Ȃ��Ɛ��藧���Ȃ����Ď��ł����H
-60����|���Ȃ��ƃ_���Ȃ̂ł��傤�H
���̎����Č���-50�~60�̏���-60�~50�ɂ��Ȃ��Ɛ��藧���Ȃ����Ď��ł����H
-60����|���Ȃ��ƃ_���Ȃ̂ł��傤�H
2024/04/17(��) 23:47:25.71ID:6IYiqY7a
-50�~60-60�~60=(-50-60)�~60
�Ƃ��ł��܂���B
�Ƃ��ł��܂���B
2024/04/19(��) 17:21:24.35ID:KmTgW2Fi
���P���x���̕��͖�肪�܂��ŋ��
�u���Xkm�̋�����r���܂Ŏ������X�L���c����������X�L���ő����ē�������̂Ɋ|���������Ԃ́H�v
�݂����Ȃ̂悭�킩��Ȃ�
�u���Xkm�̋�����r���܂Ŏ������X�L���c����������X�L���ő����ē�������̂Ɋ|���������Ԃ́H�v
�݂����Ȃ̂悭�킩��Ȃ�
2024/04/19(��) 18:51:23.70ID:jKpak4NN
�����Ƃ́u�����^���ԁv
������e��Ԃ̑��x��s1, s2�Ƃ�
�e��Ԃł����������Ԃ�t1, t2�Ƃ����
�e��Ԃ̋�����s1t1, s2t2�ƂȂ�
�S�̂̎��ԁ�t1�{t2
�S�̂̋�����s1t1�{s2t2
���w���ł��ߋT�Z�ʼn�����̂�
������e��Ԃ̑��x��s1, s2�Ƃ�
�e��Ԃł����������Ԃ�t1, t2�Ƃ����
�e��Ԃ̋�����s1t1, s2t2�ƂȂ�
�S�̂̎��ԁ�t1�{t2
�S�̂̋�����s1t1�{s2t2
���w���ł��ߋT�Z�ʼn�����̂�
203�C�i ��/7jUdUKiSM
2024/04/19(��) 21:05:45.82ID:DWMLQx6j204�C�i ��/7jUdUKiSM
2024/04/19(��) 21:15:43.81ID:DWMLQx6j �O>>203
�u42.195km�̋�����r��40�L���܂Ŏ���20�L���c�������21.95�L���ő����ē�������̂Ɋ|���������Ԃ́H�v
40/20=2(����)
2.195/21.95=0.1(����)
0.1���Ԃ�6��
��2����6��
�u42.195km�̋�����r��40�L���܂Ŏ���20�L���c�������21.95�L���ő����ē�������̂Ɋ|���������Ԃ́H�v
40/20=2(����)
2.195/21.95=0.1(����)
0.1���Ԃ�6��
��2����6��
2024/04/20(�y) 05:01:14.34ID:PDydeaco
�uA��B���5���Ȃ������v�ƌ����̂�
A��B-5�@�Ə����̂����o�I�ɗ����ł��Ȃ�
A��B-5�@�Ə����̂����o�I�ɗ����ł��Ȃ�
2024/04/20(�y) 12:48:27.49ID:HVdq8JLd
>>203
�v�Z�Ԉ���Ă��܂��H
> # P[f/s]=P[s|f]*P[f]/P[s] =
> 0.09*(991/(991+929))/0.1829
[1] 0.253981
�ł́H
�v�Z�Ԉ���Ă��܂��H
> # P[f/s]=P[s|f]*P[f]/P[s] =
> 0.09*(991/(991+929))/0.1829
[1] 0.253981
�ł́H
2024/04/20(�y) 23:18:45.27ID:80kNXa7A
�K�`�ł킩����肪����܂��@�����Ă�������
https://rio2016.5ch.net/test/read.cgi/math/1712405122/
https://rio2016.5ch.net/test/read.cgi/math/1712405122/
2024/04/21(��) 06:12:26.01ID:8tk8vFgg
>>207
d=c(5,-2,-4,7,-1)
#(1)
14+sum(d)
#(2)
cumsum(d)
#(3)
#(x+5*x+sum(cumsum(d)))/6=12
#(6x+18)/6=12
(72-18)/6
[1] 19
[1] 5 3 -1 6 5
[1] 9
# �m�F
c(9,9+cumsum(d)) |> mean()
[1] 12
d=c(5,-2,-4,7,-1)
#(1)
14+sum(d)
#(2)
cumsum(d)
#(3)
#(x+5*x+sum(cumsum(d)))/6=12
#(6x+18)/6=12
(72-18)/6
[1] 19
[1] 5 3 -1 6 5
[1] 9
# �m�F
c(9,9+cumsum(d)) |> mean()
[1] 12
2024/04/21(��) 13:13:24.79ID:KR/TvI+x
�Z�x�̌v�Z���悭�킩��Ȃ�
�u�Z�x10���̐H����200g�Ɋ܂܂�Ă鉖���́H�v���Ė��͂ǂ������́H
�u�Z�x10���̐H����200g�Ɋ܂܂�Ă鉖���́H�v���Ė��͂ǂ������́H
2024/04/21(��) 16:22:14.97ID:fcx2KFBG
200�~0.1=20�ig�j
2024/04/21(��) 21:29:04.32ID:OUMWDvM6
���F�@�����H�����͏d�ʁ��ł͉����̗n�t���H
2024/04/22(��) 15:01:33.44ID:5FMlnt/L
9/(100+9) ���@0.08256881
213�C�i ��/7jUdUKiSM
2024/04/24(��) 06:00:01.13ID:CpRR9Urt214�C�i ��/7jUdUKiSM
2024/04/26(��) 21:13:35.09ID:nkxlT+vw215�P�R�Q�l�ڂ̑f������
2024/05/07(��) 22:39:10.65ID:VaAPribI ����L������A�܂�L��ɂ͂Ȃ�L�Ɋւ��ē������ɂ���قȂ�2�_A�AB������Ƃ��A
����AB��L�ƕ��s�łȂ��Ƃ��܂��B
���̂Ƃ��AA��B��ʂ蒼��L�ɐڂ���~�̍�}��������@�͂ł��܂����B
AB��L�ƕ��s�ȏꍇ�͊ȒP�ɂł����̂ł����B
����AB��L�ƕ��s�łȂ��Ƃ��܂��B
���̂Ƃ��AA��B��ʂ蒼��L�ɐڂ���~�̍�}��������@�͂ł��܂����B
AB��L�ƕ��s�ȏꍇ�͊ȒP�ɂł����̂ł����B
216�C�i ��/7jUdUKiSM
2024/05/08(��) 02:37:11.25ID:5//gGwgT217�P�R�Q�l�ڂ̑f������
2024/05/08(��) 16:44:11.57ID:L7kjHXOi >>216
�܂Ƃ��ȉ��ł��Ȃ��Ȃ��������ǂ��Ă���܂��H
�܂Ƃ��ȉ��ł��Ȃ��Ȃ��������ǂ��Ă���܂��H
2024/05/09(��) 18:48:33.61ID:SqUSooPh
>>217
���̂悤�ȉ~�͑��݂��Ȃ����Ƃ�>216�͎咣���Ă���B
���̂悤�ȉ~�͑��݂��Ȃ����Ƃ�>216�͎咣���Ă���B
219�P�R�Q�l�ڂ̑f������
2024/05/09(��) 19:19:32.41ID:/dkzv26a ���݂��邾��
2024/05/09(��) 19:31:50.36ID:SqUSooPh
���݂���ˁB
2024/05/09(��) 19:33:57.70ID:SqUSooPh
���K���A(1,1)�@B(2,2)��ʂ�X���Ɛڂ���~�̒��S�Ɣ��a�����߂�B
�����}������B
�����}������B
2024/05/09(��) 23:03:12.97ID:93jHN3Aw
����AB��L�̌�_��P�Ƃ���AB�a�Ƃ���~C1����}���AC1�̒��S��P�a�Ƃ���~��C1�̌�_T����}����B
P���S��T��ʂ�~C2����}��L��C2�̌�_�̂ǂ�����
P���S��T��ʂ�~C2����}��L��C2�̌�_�̂ǂ�����
223�C�i ��/7jUdUKiSM
2024/05/10(��) 04:09:03.76ID:dkyEjxPZ �O>>216
���݂��邩�瓚������A���̋�̓I�ȕ��@���B
���݂��邩�瓚������A���̋�̓I�ȕ��@���B
224�C�i ��/7jUdUKiSM
2024/05/10(��) 04:32:34.55ID:dkyEjxPZ2024/05/10(��) 05:02:06.12ID:esg1TcXl
�������W��A(5,6),B(3,4),C(2,1),D(6,0)�Ƃ���B
A,B��ʂ�AC�[D�����Ԓ����Ɛڂ���~��`�悹��B
A,B��ʂ�AC�[D�����Ԓ����Ɛڂ���~��`�悹��B
2024/05/10(��) 05:08:34.93ID:esg1TcXl
2024/05/10(��) 05:21:04.67ID:esg1TcXl
2024/05/10(��) 05:46:11.42ID:esg1TcXl
2024/05/10(��) 05:53:10.91ID:esg1TcXl
>>215
�~�̒��S��CC(x,y)�Ƃ���(Center of Circle)
CC��AB�̐���������ɂ���B
CC����L�ɂ��낵�������̑��̒�����CC��A�̋����ɓ������iCC��B�̋����ł������j
���̘A���������������悢�B
�������ɂȂ�̂ʼn~�͂Q����B���s�̏ꍇ���d���łP���낤�ȁB
�~�̒��S��CC(x,y)�Ƃ���(Center of Circle)
CC��AB�̐���������ɂ���B
CC����L�ɂ��낵�������̑��̒�����CC��A�̋����ɓ������iCC��B�̋����ł������j
���̘A���������������悢�B
�������ɂȂ�̂ʼn~�͂Q����B���s�̏ꍇ���d���łP���낤�ȁB
230�P�R�Q�l�ڂ̑f������
2024/05/10(��) 09:32:51.49ID:KzTho07H2024/05/10(��) 18:40:53.46ID:esg1TcXl
>>226
R�ł̒��S�Ɣ��a�̒l
�����\��
> yc1=perpendicular_bisector(A,B,FALSE)(xc1)
> (CC1=xc1+1i*yc1)
[1] -2.193063+11.19306i
> (R1=abs(A-CC1))
[1] 8.871757
> Cir(CC1,R1,col=2)
> xc2=optimize(f,c(5,10),tol=1e-12)$minimum
> yc2=perpendicular_bisector(A,B,FALSE)(xc2)
> (CC2=xc2+1i*yc2)
[1] 5.873063+3.126937i
> (R2=abs(A-CC2))
[1] 3.002787
Wolfram�Ō����l���Z�o
https://i.imgur.com/6SD0vOj.png
R�ł̐��l���ƍ��v�B�����ւ̏h�芮���B
R�ł̒��S�Ɣ��a�̒l
�����\��
> yc1=perpendicular_bisector(A,B,FALSE)(xc1)
> (CC1=xc1+1i*yc1)
[1] -2.193063+11.19306i
> (R1=abs(A-CC1))
[1] 8.871757
> Cir(CC1,R1,col=2)
> xc2=optimize(f,c(5,10),tol=1e-12)$minimum
> yc2=perpendicular_bisector(A,B,FALSE)(xc2)
> (CC2=xc2+1i*yc2)
[1] 5.873063+3.126937i
> (R2=abs(A-CC2))
[1] 3.002787
Wolfram�Ō����l���Z�o
https://i.imgur.com/6SD0vOj.png
R�ł̐��l���ƍ��v�B�����ւ̏h�芮���B
232�C�i ��/7jUdUKiSM
2024/05/11(�y) 23:02:42.18ID:VZfI1MWU233�P�R�Q�l�ڂ̑f������
2024/05/12(��) 09:02:35.96ID:WK2MTGwi ��}�肪�������Ă�̂ɍ��W�v�Z�����X�Ƃ��A�z
234�P�R�Q�l�ڂ̑f������
2024/05/12(��) 11:02:34.72ID:kCkMblnd ���W�v�Z�͈�̕\��
2024/05/13(��) 06:50:09.12ID:pkUaNmPS
�������[���ł���܂Ōv�Z����̂͗��ɓ��呲���ˁB
>225�͕M�Z���Ə��Ղ���Ǝv���B
>225�͕M�Z���Ə��Ղ���Ǝv���B
236�P�R�Q�l�ڂ̑f������
2024/05/16(��) 12:31:08.83ID:CCLr2Nf7 �A
2024/05/16(��) 20:18:29.83ID:YNck7KfL
(a-b)^2��(b-a)^2�������ɂȂ闝�R���킩���Ăт����肵��
238�P�R�Q�l�ڂ̑f������
2024/05/19(��) 22:47:03.89ID:h3RPqtBh ���݂܂���B���̖��ǂ�����ĉ���������������܂����H
���邨�X�ł́A�T�b�J�[�{�[���ƃV���[�Y���d����A���ꂼ��ɗ��v��������Œ艿�����܂����B
�{�[���P�ƃV���[�Y�P���̎d���ꂽ�Ƃ��̒l�i�̔�͂X:�P�P�A���v�̔�͂Q:�R�A�艿�̔�͂S:�T�ɂȂ�܂����B
�i�P�j�V���[�Y�P���̗��v�͒艿�̉����ł����H
�i�Q�j�{�[���P�̗��v���S�O�O�~�̂Ƃ��A�V���[�Y�P���̗��v�͂�����ł����H
���邨�X�ł́A�T�b�J�[�{�[���ƃV���[�Y���d����A���ꂼ��ɗ��v��������Œ艿�����܂����B
�{�[���P�ƃV���[�Y�P���̎d���ꂽ�Ƃ��̒l�i�̔�͂X:�P�P�A���v�̔�͂Q:�R�A�艿�̔�͂S:�T�ɂȂ�܂����B
�i�P�j�V���[�Y�P���̗��v�͒艿�̉����ł����H
�i�Q�j�{�[���P�̗��v���S�O�O�~�̂Ƃ��A�V���[�Y�P���̗��v�͂�����ł����H
2024/05/19(��) 22:57:01.48ID:TUaSkgQ4
>>238
x0:�d����l
x1:���v
b:�{�[���@s:�V���[�Y
b0/s0=9/11
b1/s1=2/3
(b0+b1)/(s0+s1)=4/5
�����������͂��B
���������g�킸�ɉ������@�͒m���B
x0:�d����l
x1:���v
b:�{�[���@s:�V���[�Y
b0/s0=9/11
b1/s1=2/3
(b0+b1)/(s0+s1)=4/5
�����������͂��B
���������g�킸�ɉ������@�͒m���B
240�P�R�Q�l�ڂ̑f������
2024/05/19(��) 23:13:32.03ID:h3RPqtBh2024/05/20(��) 01:06:11.79ID:0C+YWYVd
�{�[���̎d����l���X�h���A���v��x �h���Ƃ���Εϐ��͌��点��B
9 + x = (4/5) (11 + 3/2 x)
��x=1
9 + x = (4/5) (11 + 3/2 x)
��x=1
2024/05/20(��) 01:23:52.30ID:2EpK4rJr
2024/05/20(��) 01:31:16.83ID:0C+YWYVd
Wolfram�̗��K
�i2)
Solve[a/b==9/11 && 400/d=2/3 && (a+400)/(b+d)==4/5,{a,b,d}]
�i2)
Solve[a/b==9/11 && 400/d=2/3 && (a+400)/(b+d)==4/5,{a,b,d}]
2024/05/20(��) 01:31:48.97ID:0C+YWYVd
a = 3600 and b = 4400 and d = 600
245�P�R�Q�l�ڂ̑f������
2024/05/20(��) 13:37:38.49ID:ssTaMXTG246�P�R�Q�l�ڂ̑f������
2024/05/20(��) 21:14:50.11ID:ssTaMXTG ���A�Ⴄ��
�V���[�Y�œ��������Ă�����Ȃ��Ȃ�
�V���[�Y�œ��������Ă�����Ȃ��Ȃ�
2024/05/20(��) 22:23:24.87ID:1slxxapi
�Z��
(2)�̓{�[��1�̗��v��400�~�ŗ��v�̔䂪2:3������400��2=20 20�~3��600�~
(1)�͉����Ⴑ���
(2)�̓{�[��1�̗��v��400�~�ŗ��v�̔䂪2:3������400��2=20 20�~3��600�~
(1)�͉����Ⴑ���
248�P�R�Q�l�ڂ̑f������
2024/05/21(��) 00:36:24.01ID:NjqcqZ8c ���肪�Ƃ��������܂��B
�F����̃A�h�o�C�X�̂������ŎZ���I�ɉ������Ƃ��o���܂����Im(__)m
�{�[�� �V���[�Y
�d���l �X �F �P�P
���v �Q �F �R
�艿 �S �F �T
9���{2����4��
11���{3����5��
45���{10����20��
44���{12����20��
1����2��
18���{2����20��
22���{3����25��
�{�[�� �V���[�Y
�d���l 18�~ �F 22�~
���v 2�~ �F 3�~
�艿 20�~ �F 25�~
3��25��0.12
�i�P�j�P�Q%
�F����̃A�h�o�C�X�̂������ŎZ���I�ɉ������Ƃ��o���܂����Im(__)m
�{�[�� �V���[�Y
�d���l �X �F �P�P
���v �Q �F �R
�艿 �S �F �T
9���{2����4��
11���{3����5��
45���{10����20��
44���{12����20��
1����2��
18���{2����20��
22���{3����25��
�{�[�� �V���[�Y
�d���l 18�~ �F 22�~
���v 2�~ �F 3�~
�艿 20�~ �F 25�~
3��25��0.12
�i�P�j�P�Q%
249�P�R�Q�l�ڂ̑f������
2024/05/21(��) 00:39:08.41ID:NjqcqZ8c >>247
���݂܂���I�i�Q�j�̖�蕶���ԈႦ�Ă��܂����B
�~�i�Q�j�{�[���P�̗��v���S�O�O�~�̂Ƃ��A�V���[�Y�P���́y���v�z�͂�����ł����H
���i�Q�j�{�[���P�̗��v���S�O�O�~�̂Ƃ��A�V���[�Y�P���́y�艿�z�͂�����ł����H
���݂܂���I�i�Q�j�̖�蕶���ԈႦ�Ă��܂����B
�~�i�Q�j�{�[���P�̗��v���S�O�O�~�̂Ƃ��A�V���[�Y�P���́y���v�z�͂�����ł����H
���i�Q�j�{�[���P�̗��v���S�O�O�~�̂Ƃ��A�V���[�Y�P���́y�艿�z�͂�����ł����H
2024/05/21(��) 04:35:54.01ID:WmWdB68l
>>248
�ϐ����A���t�@�x�b�g�ɂ������Ɂ������ɂ����A���������ɂ����݂��Ȃ��̂����B
�ϐ����A���t�@�x�b�g�ɂ������Ɂ������ɂ����A���������ɂ����݂��Ȃ��̂����B
2024/05/21(��) 15:35:41.44ID:eidL/m7v
�A���t�@�x�b�g�̋L�@�͏��w���ɂ͒�R�����邵�A3�~x=3x ���܂��K���Ă��Ȃ�����ȁB
�R���Ȃ������R���Ȃ������B�����܂Ŋ��������ǁB
�R���Ȃ������R���Ȃ������B�����܂Ŋ��������ǁB
2024/05/21(��) 16:19:21.94ID:qvzhIPbX
>>251
x=����3x�͂R���łȂ��������Ȃ��R�Ȃ��B
�R�� - �� = 3�ƌ�F������邩�������
������ - ���@���@�Z�Z�Ȃ�������ɂ����Ƃ͎v���B
x=����3x�͂R���łȂ��������Ȃ��R�Ȃ��B
�R�� - �� = 3�ƌ�F������邩�������
������ - ���@���@�Z�Z�Ȃ�������ɂ����Ƃ͎v���B
2024/05/21(��) 16:26:16.40ID:qvzhIPbX
chatGPT�͒�����������Ԃ��Ă������A
copilot�͌듚��Ԃ��Ă����B
copilot�͌듚��Ԃ��Ă����B
254�P�R�Q�l�ڂ̑f������
2024/05/21(��) 18:20:49.26ID:NjqcqZ8c >>250-252
���݂܂���B
�Ⴆ�� 3�� �Ƃ����̂́A�o�����3�����ň͂ދL���ŕ\�����������̂ł����A
web��ł͖���������܂����̂ŁA�Ë���������ł��B
�M�L�Ŏ��������A�����ԎZ���炵���Ȃ�Ǝv���܂��B
���݂܂���B
�Ⴆ�� 3�� �Ƃ����̂́A�o�����3�����ň͂ދL���ŕ\�����������̂ł����A
web��ł͖���������܂����̂ŁA�Ë���������ł��B
�M�L�Ŏ��������A�����ԎZ���炵���Ȃ�Ǝv���܂��B
2024/05/21(��) 19:26:04.43ID:rUIYiYeb
③
256�C�i ��/7jUdUKiSM
2024/05/21(��) 19:44:54.98ID:gKJyORfl257�C�i ��/7jUdUKiSM
2024/05/21(��) 19:59:42.02ID:gKJyORfl2024/05/22(��) 06:23:06.98ID:SSdziSeV
>>257
�ݖ��
�i�P�j�V���[�Y�P���̗��v�͒艿�̉����ł����H
�Ȃ̂ŁA�C�i���̓{�[���̗��v�����v�Z���Ă���Ǝv���B
����͂��Ă����A
�C�i���̎�@���������Ȃ��ł̎Z���ł̉�@�Ƃ�����B
������肾���琮���Ōv�Z���₷���l�ɐݒ肳��Ă���͂�
�Ƃ����_�������������ȉ�@���ȁB
�ݖ��
�i�P�j�V���[�Y�P���̗��v�͒艿�̉����ł����H
�Ȃ̂ŁA�C�i���̓{�[���̗��v�����v�Z���Ă���Ǝv���B
����͂��Ă����A
�C�i���̎�@���������Ȃ��ł̎Z���ł̉�@�Ƃ�����B
������肾���琮���Ōv�Z���₷���l�ɐݒ肳��Ă���͂�
�Ƃ����_�������������ȉ�@���ȁB
2024/05/22(��) 22:13:54.33ID:hbcyxk4S
���邨�X�ł́A
���iA�Ə��iB���d����A
���ꂼ��ɗ��v���������
�艿������
���iA1�Ə��iB1�̎d���ꂽ�Ƃ���
�l�i�̔��4:5�A���v�̔��6:11�A
�艿�̔��2:3�ɂȂ���
���iA1�̗��v��300�~�̂Ƃ��A
���iB1�̎d����l�͂����炩�H
��
���iA�Ə��iB���d����A
���ꂼ��ɗ��v���������
�艿������
���iA1�Ə��iB1�̎d���ꂽ�Ƃ���
�l�i�̔��4:5�A���v�̔��6:11�A
�艿�̔��2:3�ɂȂ���
���iA1�̗��v��300�~�̂Ƃ��A
���iB1�̎d����l�͂����炩�H
��
260�P�R�Q�l�ڂ̑f������
2024/05/22(��) 23:20:25.48ID:8xa8BoB9 >>259
�d����l�����A���������Ƃ���
�` �a
�� �d �S �F �T
�m��)�� �R�O�O �T�T�O
�� �� �Q �F �R
4���{300��2��
5���{550��3��
12���{900��6��
10���{1100��6��
1����100
5�~100��500
�����D�T�O�O�~
�d����l�����A���������Ƃ���
�` �a
�� �d �S �F �T
�m��)�� �R�O�O �T�T�O
�� �� �Q �F �R
4���{300��2��
5���{550��3��
12���{900��6��
10���{1100��6��
1����100
5�~100��500
�����D�T�O�O�~
2024/05/22(��) 23:40:57.53ID:hbcyxk4S
��
���iB1�̎d����l��x�Ƃ���
(x-k):x=4:5
5x-5k=4x
x=5k
���iA1�̗��v��y�Ƃ���
(x-k+y):{x+(11/6)y}=2:3
3x-3k+3y=2x+(11/3)y
x=3k+(2/3)y
5k=3k+(2/3)y
2k=(2/3)y
k=(1/3)y
x=5k �Ȃ̂�x=(5/3)y
y=300
k=100
��x=500
���iB1�̎d����l��x�Ƃ���
(x-k):x=4:5
5x-5k=4x
x=5k
���iA1�̗��v��y�Ƃ���
(x-k+y):{x+(11/6)y}=2:3
3x-3k+3y=2x+(11/3)y
x=3k+(2/3)y
5k=3k+(2/3)y
2k=(2/3)y
k=(1/3)y
x=5k �Ȃ̂�x=(5/3)y
y=300
k=100
��x=500
2024/05/23(��) 07:49:21.65ID:a+OnWLbP
���p���
���邨�X�ł́A
���iA�Ə��iB���d����A
���ꂼ��ɗ��v��������Œ艿������
���iA1�Ə��iB1�̎d����l�̔��0.8765:1�A���v�̔��0.5432:1
�艿�̔��0.6543�ɂȂ���
���iA1�̗��v��100���~�̂Ƃ��A���iB1�̎d����l�͂����炩�H
���邨�X�ł́A
���iA�Ə��iB���d����A
���ꂼ��ɗ��v��������Œ艿������
���iA1�Ə��iB1�̎d����l�̔��0.8765:1�A���v�̔��0.5432:1
�艿�̔��0.6543�ɂȂ���
���iA1�̗��v��100���~�̂Ƃ��A���iB1�̎d����l�͂����炩�H
2024/05/23(��) 13:49:55.01ID:pOspwi7z
���邨�X�ł́A
���iA�Ə��iB���d����A
���ꂼ��ɗ��v��������Œ艿������
���iA1�Ə��iB1�̎d����l�̔��
0.8765:1�A���v�̔��0.5432:1
�艿�̔��0.6543�ɂȂ���
���iA1�̗��v��100���~�̂Ƃ��A
���iB1�̎d����l�͂����炩�H
0.8765:1=1753:2000
0.5432:1=679:1250
0.6543=6543:10000
��
���iB1�̎d����l��x�Ƃ���
(x-k):x=1753:2000
2000x-2000k=1753x
247x=2000k
x=(2000/247)k
���iA1�̗��v��y�Ƃ���
(x-k+y):{x+(1250/679)y}=6543:10000
10000x-10000k+10000y=
6543x+{(1250 6543)/679)}y
3457x=
10000k+{(1250 6543)/679}y-(6790000/679)y
3457(2000/247)k=
10000k+{(1250 6543)/679}y-(6790000/679)y
(4444000k)/247={(1388750y)/679}
4444000k=247{(1388750y)/679}
k={247{(1388750y)/679}}/4444000
y=1000000
k=77187500/679
x=(2000/247)k
��x=(2000/247)(77187500/679)
���iA�Ə��iB���d����A
���ꂼ��ɗ��v��������Œ艿������
���iA1�Ə��iB1�̎d����l�̔��
0.8765:1�A���v�̔��0.5432:1
�艿�̔��0.6543�ɂȂ���
���iA1�̗��v��100���~�̂Ƃ��A
���iB1�̎d����l�͂����炩�H
0.8765:1=1753:2000
0.5432:1=679:1250
0.6543=6543:10000
��
���iB1�̎d����l��x�Ƃ���
(x-k):x=1753:2000
2000x-2000k=1753x
247x=2000k
x=(2000/247)k
���iA1�̗��v��y�Ƃ���
(x-k+y):{x+(1250/679)y}=6543:10000
10000x-10000k+10000y=
6543x+{(1250 6543)/679)}y
3457x=
10000k+{(1250 6543)/679}y-(6790000/679)y
3457(2000/247)k=
10000k+{(1250 6543)/679}y-(6790000/679)y
(4444000k)/247={(1388750y)/679}
4444000k=247{(1388750y)/679}
k={247{(1388750y)/679}}/4444000
y=1000000
k=77187500/679
x=(2000/247)k
��x=(2000/247)(77187500/679)
264�P�R�Q�l�ڂ̑f������
2024/05/23(��) 13:55:48.17ID:NufsvOOS ����
2024/05/24(��) 16:05:54.27ID:en6hmMJW
>>262
������������Ă��Ƃ̓v���O�����Ɍv�Z����������B
�藝������Ɠ�����������g���Ă��邾���B
https://i.imgur.com/241IzE0.png
������������Ă��Ƃ̓v���O�����Ɍv�Z����������B
�藝������Ɠ�����������g���Ă��邾���B
https://i.imgur.com/241IzE0.png
2024/05/25(�y) 04:20:04.01ID:A6jVfw3Q
>>238
�y�O��̔䗦�z
1. �d����l�̔�: �{�[�� : �V���[�Y = 9 : 11
2. ���v�̔�: �{�[�� : �V���[�Y = 2 : 3
3. �艿�̔�: �{�[�� : �V���[�Y = 4 : 5
��P�F�V���[�Y1���̗��v�͒艿�̉����ł����H
�y���̒l�����߂�z
1. �d����l���{�[����9�~�A�V���[�Y��11�~�Ɖ��肵�܂��B
2. ���v���{�[����2�~�A�V���[�Y��3�~�Ɖ��肵�܂��B
�y�艿�̌v�Z�z
�艿 = �d����l + ���v �Ȃ̂ŁA
�{�[���̒艿 = 9�~ + 2�~ = 11�~
�V���[�Y�̒艿 = 11�~ + 3�~ = 14�~
�i�艿�̔䗦��4:5�ō����Ă��܂��j
�y���v���艿�̉��������v�Z�z
�V���[�Y�̗��v = 3�~
�V���[�Y�̒艿 = 14�~
3 �� 14 �~ 100 =21 3⁄7
�����F�V���[�Y1���̗��v�͒艿�̖�21.43���ł��B
��Q�F�{�[��1�̗��v��400�~�̂Ƃ��A�V���[�Y1���̗��v�͂�����ł����H
�y���v�̔䗦�z
�{�[���̗��v�̔䗦: 2
�V���[�Y�̗��v�̔䗦: 3
�y��̌v�Z�z
400�~ : �V���[�Y�̗��v = 2 : 3
�V���[�Y�̗��v = 400 �~ 3 �� 2 = 600
�����F�V���[�Y1���̗��v��600�~�ł��B
�y�O��̔䗦�z
1. �d����l�̔�: �{�[�� : �V���[�Y = 9 : 11
2. ���v�̔�: �{�[�� : �V���[�Y = 2 : 3
3. �艿�̔�: �{�[�� : �V���[�Y = 4 : 5
��P�F�V���[�Y1���̗��v�͒艿�̉����ł����H
�y���̒l�����߂�z
1. �d����l���{�[����9�~�A�V���[�Y��11�~�Ɖ��肵�܂��B
2. ���v���{�[����2�~�A�V���[�Y��3�~�Ɖ��肵�܂��B
�y�艿�̌v�Z�z
�艿 = �d����l + ���v �Ȃ̂ŁA
�{�[���̒艿 = 9�~ + 2�~ = 11�~
�V���[�Y�̒艿 = 11�~ + 3�~ = 14�~
�i�艿�̔䗦��4:5�ō����Ă��܂��j
�y���v���艿�̉��������v�Z�z
�V���[�Y�̗��v = 3�~
�V���[�Y�̒艿 = 14�~
3 �� 14 �~ 100 =21 3⁄7
�����F�V���[�Y1���̗��v�͒艿�̖�21.43���ł��B
��Q�F�{�[��1�̗��v��400�~�̂Ƃ��A�V���[�Y1���̗��v�͂�����ł����H
�y���v�̔䗦�z
�{�[���̗��v�̔䗦: 2
�V���[�Y�̗��v�̔䗦: 3
�y��̌v�Z�z
400�~ : �V���[�Y�̗��v = 2 : 3
�V���[�Y�̗��v = 400 �~ 3 �� 2 = 600
�����F�V���[�Y1���̗��v��600�~�ł��B
267�P�R�Q�l�ڂ̑f������
2024/05/25(�y) 13:33:15.85ID:18WGjtQQ >>266
�艿�̔䂪�����ĂȂ�
�艿�̔䂪�����ĂȂ�
268�P�R�Q�l�ڂ̑f������
2024/05/30(��) 09:03:53.68ID:TJlpZhna �~O�̊O���ɓ_P������
�_P����~O�ɑ�2�{�̐ڐ����Ђ��A�ړ_��A,B�Ƃ���
���ɁA����PA�APB�̒��_��M,N�Ƃ��Ē���MN��ɓ_Q���Ƃ�
�����āA�_Q����~O�ɑ��ڐ����Ђ��A�ړ_��T�Ƃ���
���̂Ƃ��AQT=QP�ƂȂ邱�Ƃ�����
�_P����~O�ɑ�2�{�̐ڐ����Ђ��A�ړ_��A,B�Ƃ���
���ɁA����PA�APB�̒��_��M,N�Ƃ��Ē���MN��ɓ_Q���Ƃ�
�����āA�_Q����~O�ɑ��ڐ����Ђ��A�ړ_��T�Ƃ���
���̂Ƃ��AQT=QP�ƂȂ邱�Ƃ�����
2024/05/30(��) 09:25:08.28ID:B22Opk3c
P�a0�̉~O'�Ƃ݂Ȃ���MN��OO'�̍���
270�P�R�Q�l�ڂ̑f������
2024/06/02(��) 21:12:00.55ID:RxDpj9fU �����́B
�Z���̖��Ȃ�ł����A���������ڂ��������Ă��������B
�Ƃ���18km��ɂ���w�Z�ɁA�o�Ɩ������ꂼ����̑����Ō������܂����B
��ɖ����o�����A5����Ɏo������������ǂ������܂����B
�w�Z�ɂ͎o�̕�����ɓ������A����4����ɖ����������܂����B
�o������ǂ��z�����̂́A�Ƃ��牽km�̒n�_�ł����H
�Z���̖��Ȃ�ł����A���������ڂ��������Ă��������B
�Ƃ���18km��ɂ���w�Z�ɁA�o�Ɩ������ꂼ����̑����Ō������܂����B
��ɖ����o�����A5����Ɏo������������ǂ������܂����B
�w�Z�ɂ͎o�̕�����ɓ������A����4����ɖ����������܂����B
�o������ǂ��z�����̂́A�Ƃ��牽km�̒n�_�ł����H
2024/06/02(��) 21:35:05.49ID:Xd05VjOG
>>270
�_�C���O�����Ƃ����A�c���ɐi�����A
�����Ɍo�߂������Ԃ��Ƃ����O���t��`���ĉ����܂�
���̈ړ��́A���W
�i�o������, 0km�j�i��������, 18km�j
�����Ԑ���
�o�̈ړ��́A���W
�i�o�������{5��, 0km�j�i��������-4��, 18km�j
�����Ԑ����ƂȂ�܂�
�����ɃO���t��`���Ƃ��́A2�{�Ƃ�
�E�オ��̐����ƂȂ�悤�A���ӂ��ĕ`���܂�
4�_�����ԂƁA�㉺�̕ӂ����s�ȑ�`�ƂȂ�
2�̐����͂��̑Ίp���ł�
���߂�l�́A���ꂩ���_�̍����ɓ������̂�
�S�̂̍����i18km�j��
����i5���j�Ə��i4���j�̒l�ŕ���������
18�~�i5���i5�{4�j�j��10�ikm�j
�������ƂȂ�܂�
�_�C���O�����Ƃ����A�c���ɐi�����A
�����Ɍo�߂������Ԃ��Ƃ����O���t��`���ĉ����܂�
���̈ړ��́A���W
�i�o������, 0km�j�i��������, 18km�j
�����Ԑ���
�o�̈ړ��́A���W
�i�o�������{5��, 0km�j�i��������-4��, 18km�j
�����Ԑ����ƂȂ�܂�
�����ɃO���t��`���Ƃ��́A2�{�Ƃ�
�E�オ��̐����ƂȂ�悤�A���ӂ��ĕ`���܂�
4�_�����ԂƁA�㉺�̕ӂ����s�ȑ�`�ƂȂ�
2�̐����͂��̑Ίp���ł�
���߂�l�́A���ꂩ���_�̍����ɓ������̂�
�S�̂̍����i18km�j��
����i5���j�Ə��i4���j�̒l�ŕ���������
18�~�i5���i5�{4�j�j��10�ikm�j
�������ƂȂ�܂�
272!omikuji
2024/06/02(��) 21:58:37.89ID:KSFX2vVV2024/06/02(��) 22:03:27.15ID:Xd05VjOG
�C�i�����́[��
274�P�R�Q�l�ڂ̑f������
2024/06/02(��) 22:09:08.93ID:RxDpj9fU >>271
�������肪�Ƃ��������܂��B
�O���t�ɏ�������߂��Ⴍ�������₷���ł��ˁB
�o�Ɩ��̐����̌�_�Ɍ����悤�ɐ��������낵���瑊�����o���Ă���������₷�������ł��B
�_�C���O�������Ă����������Ɏg����ł��ˁA
�����}�ŏ����Ă��S�R�킩��Ȃ���������A�ǂ��������̂��Ǝv���Ă܂����B
�������肪�Ƃ��������܂��B
�O���t�ɏ�������߂��Ⴍ�������₷���ł��ˁB
�o�Ɩ��̐����̌�_�Ɍ����悤�ɐ��������낵���瑊�����o���Ă���������₷�������ł��B
�_�C���O�������Ă����������Ɏg����ł��ˁA
�����}�ŏ����Ă��S�R�킩��Ȃ���������A�ǂ��������̂��Ǝv���Ă܂����B
275�P�R�Q�l�ڂ̑f������
2024/06/02(��) 22:12:19.47ID:RxDpj9fU ���A�����͗v��Ȃ������ł��B���݂܂���m(__)m
�O���t�������������ōג����O�p�`�̑������o���Ă܂����ˁB
�O���t�������������ōג����O�p�`�̑������o���Ă܂����ˁB
276�P�R�Q�l�ڂ̑f������
2024/06/02(��) 22:42:49.65ID:RxDpj9fU2024/06/03(��) 04:28:12.45ID:rAadrPAr
18km�̈ړ����o�͖����9�������ł���
2km�ł͖��̂����鎞�Ԃ��o�̕���1�������ړ��ł���
�����o������5���Ԃɂ��������̍���0�ɂ���̂�10km�n�_
�ŁA�����Ă邩��
2km�ł͖��̂����鎞�Ԃ��o�̕���1�������ړ��ł���
�����o������5���Ԃɂ��������̍���0�ɂ���̂�10km�n�_
�ŁA�����Ă邩��
2024/06/03(��) 08:04:39.29ID:WN0pE42w
�����ĂȂ�
�����s���Œ�܂�Ȃ�
�����s���Œ�܂�Ȃ�
2024/06/03(��) 08:19:06.64ID:rq5XD+ym
������
�s���Ȃ̂͒ǂ����̂ɂ����鎞��
�s���Ȃ̂͒ǂ����̂ɂ����鎞��
2024/06/03(��) 10:51:33.73ID:G3p9DbgM
���̑��x��1km/���Ƃ����18���œ����B
�o��18�|5�|4=9���œ����Ȃ̂Ŏo�̑��x��2km/���B
���߂鋗����x km�Ƃ����
x/1=x/2+5
��10 km
�o��18�|5�|4=9���œ����Ȃ̂Ŏo�̑��x��2km/���B
���߂鋗����x km�Ƃ����
x/1=x/2+5
��10 km
2024/06/03(��) 13:20:51.39ID:i4AIgNWW
Distance�F18km
DepartureDelay : 5��
ArrivalDelay : 4��
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= f[Distance_:18,DepartureDelay_:5,ArrivalDelay_:4] := (
Velocity2 = Distance/(Distance/Velocity1 - DepartureDelay - ArrivalDelay);
Solve[x/Velocity1==x/Velocity2 + DepartureDelay,x]
)
In[2]:= f[]
Out[2]= {{x -> 10}}
DepartureDelay : 5��
ArrivalDelay : 4��
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= f[Distance_:18,DepartureDelay_:5,ArrivalDelay_:4] := (
Velocity2 = Distance/(Distance/Velocity1 - DepartureDelay - ArrivalDelay);
Solve[x/Velocity1==x/Velocity2 + DepartureDelay,x]
)
In[2]:= f[]
Out[2]= {{x -> 10}}
2024/06/03(��) 13:52:30.80ID:Km/3GYCu
���w6�N�̎Z���ōH�v���Čv�Z����Ƃ������Ȃ�ł���
10/11*(2/5+1/2)
���̖����Ăǂ̂悤�ɍH�v�ł��܂����H
10/11*(2/5+1/2)
���̖����Ăǂ̂悤�ɍH�v�ł��܂����H
2024/06/03(��) 14:02:30.40ID:NP/2E1O9
10/11*(2/5+1/2)
��1/11*10*(2/5+1/2)
��1/11*(4+5)
��9/11
��1/11*10*(2/5+1/2)
��1/11*(4+5)
��9/11
2024/06/03(��) 14:05:45.77ID:Km/3GYCu
2024/06/03(��) 14:42:20.83ID:i4AIgNWW
2024/06/03(��) 17:36:04.73ID:i4AIgNWW
�}���`�v���`���C�X�Ƃ������߂Ő��l�������߂���ł����
�������ł�>280�̂悤�ɕK�v���������l�Ő��l���o����
���̖��Ɉڂ�̂������߁B
�������ł�>280�̂悤�ɕK�v���������l�Ő��l���o����
���̖��Ɉڂ�̂������߁B
287�C�i ��/7jUdUKiSM
2024/06/03(��) 20:28:56.76ID:JYsG1oO1288�P�R�Q�l�ڂ̑f������
2024/06/03(��) 22:58:57.01ID:Kj9+E7Xo >>282
10/11*(2/5+1/2)
=10/11*(4/10+5/10)
=10/11*9/10
=90/110
=9/11
10/11*(2/5+1/2)
=10/11*2/5+10/11*1/2
=2/11*2+5/11*1(10��5�A10��2���)
=4/11+5/11
=9/11
����������A�H�v���Ȃ��Ă�����ȂɎ�Ԃ͕ς��Ȃ��C���c�B
10/11*(2/5+1/2)
=10/11*(4/10+5/10)
=10/11*9/10
=90/110
=9/11
10/11*(2/5+1/2)
=10/11*2/5+10/11*1/2
=2/11*2+5/11*1(10��5�A10��2���)
=4/11+5/11
=9/11
����������A�H�v���Ȃ��Ă�����ȂɎ�Ԃ͕ς��Ȃ��C���c�B
2024/06/03(��) 23:45:02.46ID:LssCju8w
���������łĂ��Ȃ�>>283���D��
2024/06/03(��) 23:45:48.99ID:LssCju8w
�ʕ����A��
2024/06/04(��) 05:51:42.47ID:TJ+OC1ra
292�P�R�Q�l�ڂ̑f������
2024/06/04(��) 13:29:46.03ID:z2IDRjjB �Z���̖��
�`���R���Ői�ދ������a�N�͂Q���Ői�݂܂��B
�܂��A�`���T���i�ފԂɂa�N�͂S���i�݂܂��B
�`���Q�O�O���i��A�a�N������������ǂ������܂��B
�a�N�͂`����ɒǂ��t���܂łɉ����i�݂܂����H
�`���R���Ői�ދ������a�N�͂Q���Ői�݂܂��B
�܂��A�`���T���i�ފԂɂa�N�͂S���i�݂܂��B
�`���Q�O�O���i��A�a�N������������ǂ������܂��B
�a�N�͂`����ɒǂ��t���܂łɉ����i�݂܂����H
293�P�R�Q�l�ڂ̑f������
2024/06/04(��) 13:45:47.12ID:z2IDRjjB �Z���̖��
�P�S�X�A�Q�P�W�A�R�R�R�����ꂼ�ꓯ�������ł��Z����Ɨ]�肪�R�Ƃ������ɂȂ�܂����B
���鐮���Ƃ͂����ł����H
�P�S�X�A�Q�P�W�A�R�R�R�����ꂼ�ꓯ�������ł��Z����Ɨ]�肪�R�Ƃ������ɂȂ�܂����B
���鐮���Ƃ͂����ł����H
2024/06/04(��) 15:46:23.00ID:wI8IOzrz
>>293
Wolfram����̗��K
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= n={149,218,333};
In[2]:= m=Sort[n];
In[3]:= li=Length /@ Union /@ Table[Mod[m,i],{i,Range[2,m[[-1]]]}];
In[4]:= For[i=1,i<m[[-1]],i++,If[li[[i]]==1,Print[i+1]]]
23
Wolfram����̗��K
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= n={149,218,333};
In[2]:= m=Sort[n];
In[3]:= li=Length /@ Union /@ Table[Mod[m,i],{i,Range[2,m[[-1]]]}];
In[4]:= For[i=1,i<m[[-1]],i++,If[li[[i]]==1,Print[i+1]]]
23
2024/06/04(��) 15:57:48.11ID:wI8IOzrz
Wolfram�̗��K���
123�A456�A789�����ꂼ�ꓯ�������ł��Z����Ɨ]�肪�R�Ƃ������ɂȂ�܂����B
���̐��������ׂċ��߂Ȃ����B
123�A456�A789�����ꂼ�ꓯ�������ł��Z����Ɨ]�肪�R�Ƃ������ɂȂ�܂����B
���̐��������ׂċ��߂Ȃ����B
296�P�R�Q�l�ڂ̑f������
2024/06/05(��) 00:46:50.35ID:T0qRZnbY297�P�R�Q�l�ڂ̑f������
2024/06/05(��) 00:48:25.87ID:T0qRZnbY298�P�R�Q�l�ڂ̑f������
2024/06/05(��) 02:47:39.95ID:T0qRZnbY >296-297�����������B
�i�ŏ��l�����Ȃ������͘J�͂̂��ɑ��x���P�Ɋ�^���Ȃ��̂ŏȂ����j
�K�����������ŕ���ł���̂��ۏ����Ȃ�A���������ȗ��ł���B
f xs = [x | x <- [2..minxs], (all (minxs `mod` x ==).map (`mod` x)) xs]
�@�@where
�@�@�@�@minxs = minimum xs
�i�ŏ��l�����Ȃ������͘J�͂̂��ɑ��x���P�Ɋ�^���Ȃ��̂ŏȂ����j
�K�����������ŕ���ł���̂��ۏ����Ȃ�A���������ȗ��ł���B
f xs = [x | x <- [2..minxs], (all (minxs `mod` x ==).map (`mod` x)) xs]
�@�@where
�@�@�@�@minxs = minimum xs
2024/06/05(��) 08:08:21.33ID:ub5qG/3p
�A�r�W�W�C���Z���Ɏ�����n���ɂ���ă_���}�����ߍ���ł�Ǝv�����獡�x�͏����w���ɔn���ɂ���ɗ�����w
300�C�i ��/7jUdUKiSM
2024/06/05(��) 15:27:59.28ID:OLn7P07k �O>>287
>>292
��ǂ���a����͏��w�Z��w�N�̏��̎q�A
b�N�͒��w���̒j�̎q�ƓǂB
�����ɋ������Ƃ�A���[��b�N�����č��X�^�[�g������B
�������Ȃ荶���200m�̒n�_��a���A
�E�����ɂ܂������i��ł���B���b�N�������Ba����ɔ���b�N�B
��〜��〜�̂�〜��〜���
�낭����〜��〜����〜��〜��
200m��300���Ȃ炠�肦��B
a���i�߂鋗����b�N��5/6
�ǂ������͎̂��Ԃ̖��B
200�~6=1200(m)����͕K�v�Ȃ��B
300�~6=1800(��)���ꂪb�N�������������B
��1800��
>>292
��ǂ���a����͏��w�Z��w�N�̏��̎q�A
b�N�͒��w���̒j�̎q�ƓǂB
�����ɋ������Ƃ�A���[��b�N�����č��X�^�[�g������B
�������Ȃ荶���200m�̒n�_��a���A
�E�����ɂ܂������i��ł���B���b�N�������Ba����ɔ���b�N�B
��〜��〜�̂�〜��〜���
�낭����〜��〜����〜��〜��
200m��300���Ȃ炠�肦��B
a���i�߂鋗����b�N��5/6
�ǂ������͎̂��Ԃ̖��B
200�~6=1200(m)����͕K�v�Ȃ��B
300�~6=1800(��)���ꂪb�N�������������B
��1800��
301�C�i ��/7jUdUKiSM
2024/06/05(��) 15:36:42.91ID:OLn7P07k2024/06/05(��) 16:19:47.98ID:p1WY4IBC
>>31-33
�[�N�ɂ��Y��
5����48��46�b=20926�b
1��=86400�b
20926/86400��0.2421991
400�N��97��̉[�N��
97/400=0.2425�ŋߎ����Ă���
33�N��8��̉[�N��
8/33��0.242424�c
n�N��m��̉[�N��97/400����
���悢�ߎ����o������
������
�wn��1000�ȉ��Ƃ��čŋߎ�����
m,n�̒l�����߂�x
��1000�N��242��̉[�N��
242/1000=121/500=0.242000�c
122/504=61/252��0.2420634�c
���������C�ɁA
8�{�̃I�[�_�[���̂�
(61x8)/(252x8)=488/2016
489/2019=163/673��0.24219910847
���f�t�H���g�l
20926/86400��0.2421991
��m=163�C n=673
�[�N�ɂ��Y��
5����48��46�b=20926�b
1��=86400�b
20926/86400��0.2421991
400�N��97��̉[�N��
97/400=0.2425�ŋߎ����Ă���
33�N��8��̉[�N��
8/33��0.242424�c
n�N��m��̉[�N��97/400����
���悢�ߎ����o������
������
�wn��1000�ȉ��Ƃ��čŋߎ�����
m,n�̒l�����߂�x
��1000�N��242��̉[�N��
242/1000=121/500=0.242000�c
122/504=61/252��0.2420634�c
���������C�ɁA
8�{�̃I�[�_�[���̂�
(61x8)/(252x8)=488/2016
489/2019=163/673��0.24219910847
���f�t�H���g�l
20926/86400��0.2421991
��m=163�C n=673
2024/06/05(��) 16:40:13.16ID:p1WY4IBC
149,218,333�����ꂼ�ꓯ��������
���Z����Ɨ]�肪3�Ƃ�������
�Ȃ�܂���
���鐮���Ƃ͂����ł����H
218-149=69
333-218=115
23x3=69
23x5=115
��23
���Z����Ɨ]�肪3�Ƃ�������
�Ȃ�܂���
���鐮���Ƃ͂����ł����H
218-149=69
333-218=115
23x3=69
23x5=115
��23
2024/06/05(��) 18:09:57.60ID:8pl2TroS
123,456,789�����ꂼ�ꓯ��������
���Z����Ɨ]�肪3�Ƃ�������
�Ȃ�܂���
���鐮���Ƃ͂����ł����H
���Z����Ɨ]�肪3�Ƃ�������
�Ȃ�܂���
���鐮���Ƃ͂����ł����H
2024/06/05(��) 19:20:34.64ID:mJUSEnoE
�w123,456,789�����ꂼ�ꓯ��������
���Z����Ɨ]�肪3�Ƃ�������
�Ȃ�܂���
���鐮���Ƃ͂����ł����H�x
���鐮����t,�]���k�Ƃ���
3�̐����̓��A
��ԏ���������t�Ŋ�����Ƃ����
3�̐����͂��ׂ�t�̔{���ƂȂ�
�]��k�����݂���ƁA
��ԏ���������t�̔{��+k�ƂȂ�
��Ԗڂɏ��������ƈ�ԑ傫������
t�̔{��+k�ƂȂ�ɂ�
���ꂼ��̍��ɋ��ʂ̈���������悢�̂�
456-123=333
789-456=333
111x3=333
37x9=333
��t={9,37,111}
���Z����Ɨ]�肪3�Ƃ�������
�Ȃ�܂���
���鐮���Ƃ͂����ł����H�x
���鐮����t,�]���k�Ƃ���
3�̐����̓��A
��ԏ���������t�Ŋ�����Ƃ����
3�̐����͂��ׂ�t�̔{���ƂȂ�
�]��k�����݂���ƁA
��ԏ���������t�̔{��+k�ƂȂ�
��Ԗڂɏ��������ƈ�ԑ傫������
t�̔{��+k�ƂȂ�ɂ�
���ꂼ��̍��ɋ��ʂ̈���������悢�̂�
456-123=333
789-456=333
111x3=333
37x9=333
��t={9,37,111}
2024/06/05(��) 21:32:31.78ID:vCszGXIK
>>298
�����w���ȉ��̓��{��\�͂̕��ۂʼn���������킹���w
�����w���ȉ��̓��{��\�͂̕��ۂʼn���������킹���w
307�P�R�Q�l�ڂ̑f������
2024/06/05(��) 21:41:15.14ID:a38EQRxg >>292�̖�蕶�ԈႦ��
�������́A
�`���R���Ői�ދ������a�N�͂Q���Ői�݂܂��B
�܂��A�`���T���i�ފԂɂa�N�͂S���i�݂܂��B
�`���Q�O�O���i��A�a�N������������ǂ������܂��B
�a�N�͂`����ɒǂ��t���܂łɉ����i�݂܂����H
�������́A
�`���R���Ői�ދ������a�N�͂Q���Ői�݂܂��B
�܂��A�`���T���i�ފԂɂa�N�͂S���i�݂܂��B
�`���Q�O�O���i��A�a�N������������ǂ������܂��B
�a�N�͂`����ɒǂ��t���܂łɉ����i�݂܂����H
308�C�i ��/7jUdUKiSM
2024/06/06(��) 04:03:26.69ID:UXIWw5sB309307
2024/06/06(��) 08:22:07.70ID:4v6MzaN7 >>308
�����Ɉ����|����܂����ˁB
1200���Ƃ����̂͂`�����1200���ŁA�`����Ƃa�N�̕����̔�3:2���A
3:2��1200:�a�N�̕���
�܂�a�N����800���Ői�ދ����ł��B
����Đ�����800���ł��B
�����Ɉ����|����܂����ˁB
1200���Ƃ����̂͂`�����1200���ŁA�`����Ƃa�N�̕����̔�3:2���A
3:2��1200:�a�N�̕���
�܂�a�N����800���Ői�ދ����ł��B
����Đ�����800���ł��B
2024/06/06(��) 22:09:09.33ID:Bgf5CATg
>>309
B�N�̕�����A�����1.5�{��1.2�{��2��ޗL�邯�ǁA����͂ǂ̗l�ɗ�������������́H
B�N�̕�����A�����1.5�{��1.2�{��2��ޗL�邯�ǁA����͂ǂ̗l�ɗ�������������́H
311�P�R�Q�l�ڂ̑f������
2024/06/06(��) 23:43:02.86ID:4v6MzaN7 >>310
�a�N�͂`����ɑ��āA�������P.�T�{�ő����͂P.�Q�{�ł��B
���� �`:�a���Q:�R(�t��)
�������Ԃɐi�ޕ��� �`:�a���T:�S
�܂葬���� �`:�a��2�~5:3�~4���T:�U
�a�N�͂`����ɑ��āA�������P.�T�{�ő����͂P.�Q�{�ł��B
���� �`:�a���Q:�R(�t��)
�������Ԃɐi�ޕ��� �`:�a���T:�S
�܂葬���� �`:�a��2�~5:3�~4���T:�U
2024/06/06(��) 23:44:58.58ID:BjSKErye
�܂��K�C�W���o�肵�Ă�̂�
2024/06/07(��) 03:59:19.63ID:KOX5lEUA
2024/06/07(��) 07:51:36.81ID:Bx1Jtvsp
>>298
�����w���ɂ��瑊��ɂ���ĂȂ��̂��掩���W�W�Cw
�����w���ɂ��瑊��ɂ���ĂȂ��̂��掩���W�W�Cw
315�P�R�Q�l�ڂ̑f������
2024/06/07(��) 22:41:20.88ID:00N1QAy0 >>314
����͂����ł��傤�O�O�G
�������ł͂Ȃ��A�����Ȃ蓚�������Ă鎩���ɔ�������l�͋��܂����B
Wolfram?����̐l�������ł��B
����͂����ł��傤�O�O�G
�������ł͂Ȃ��A�����Ȃ蓚�������Ă鎩���ɔ�������l�͋��܂����B
Wolfram?����̐l�������ł��B
316�P�R�Q�l�ڂ̑f������
2024/06/08(�y) 00:31:35.33ID:HGQB/VaR 1�ӂ̒�����17cm�̐����p�`ABCDEF������A
���̕ӏ��_P��A����o��������5cm�A
�_Q��C����o��������11cm�A
�_R��D����o��������13cm�̑����ł��ꂼ�ꎞ�v���ɐi�ށB
���̂Ƃ��A�_PQR��������2��ڂɐ��O���`�ƂȂ�̂́A������ł��B
���̕ӏ��_P��A����o��������5cm�A
�_Q��C����o��������11cm�A
�_R��D����o��������13cm�̑����ł��ꂼ�ꎞ�v���ɐi�ށB
���̂Ƃ��A�_PQR��������2��ڂɐ��O���`�ƂȂ�̂́A������ł��B
2024/06/08(�y) 15:12:24.74ID:7kw7hXqq
>>315
���ۂ����v�����ǁA���̃X���A�n��������������A���w�Z�ʼn�������@���Ƃ����̂����ĉ��Ă���l�����������C������̂����B
���ꂪ��@���R���s���[�^�ɂȂ��������c�Ȃ̂����B
���ۂ����v�����ǁA���̃X���A�n��������������A���w�Z�ʼn�������@���Ƃ����̂����ĉ��Ă���l�����������C������̂����B
���ꂪ��@���R���s���[�^�ɂȂ��������c�Ȃ̂����B
2024/06/08(�y) 16:47:27.09ID:NoTxnHvG
���������Ƃ�����ۂ͂Ȃ��Ȃ�
�Z���I�ȉ���������Ă���l�̕������������C�����Ă���
�Z��������Ă����l����������Ȃ�
�Z���I�ȉ���������Ă���l�̕������������C�����Ă���
�Z��������Ă����l����������Ȃ�
2024/06/09(��) 05:52:17.53ID:GkdaEqul
���ar�̉~���̒���=2��r
����̃O���t��ł̎O�p�`�̖ʐ�(�~�̖ʐ�)=r�~2��r��2=��r^2
���ad�̉~���̒���=d�A�Ƃ����
����̃O���t��ł̎O�p�`�̖ʐ�=d�~d��2=(��d^2)/2
d��2r�ɒ�����2��r^2
�Ȃ���v���Ȃ��̂ł��傤���H
����̃O���t��ł̎O�p�`�̖ʐ�(�~�̖ʐ�)=r�~2��r��2=��r^2
���ad�̉~���̒���=d�A�Ƃ����
����̃O���t��ł̎O�p�`�̖ʐ�=d�~d��2=(��d^2)/2
d��2r�ɒ�����2��r^2
�Ȃ���v���Ȃ��̂ł��傤���H
2024/06/09(��) 07:49:19.31ID:nHMqp4CX
��͔��a���|���Ă�̂ɉ��͒��a���|���Ă邩��
�O>>308
���p�ӎO�p�`�̂��Ƃ𐳎O���`�Ƃ����܂����H
���p�ӎO�p�`�̂��Ƃ𐳎O���`�Ƃ����܂����H
322�C�i ��/7jUdUKiSM
2024/06/10(��) 05:02:46.77ID:OUpEhKiF2024/06/10(��) 09:30:27.83ID:/vbEZ5cB
�Ⴆ�ΐ����p�`�͂V�̓������p�x���������}�`�����A���O���`�ƌ�����̐}�`�͂ǂ��̗l�Ȃ��̂��낤�B
���w�I�ɕ����̈Ӗ����l���Ă݂�ƁA
���@���@������
�O�@���@��
���@���@��i�����͂Q��A�����͂R��j
�`�@���@��ԓ��̗v�f�i�_�A�����A�Ȑ��A�ʂȂǁj
���O���`�͓������R��|�����`�ƂȂ�B�܂�A�����̂ɐ���̂ł͂Ȃ����낤���B
���w�I�ɕ����̈Ӗ����l���Ă݂�ƁA
���@���@������
�O�@���@��
���@���@��i�����͂Q��A�����͂R��j
�`�@���@��ԓ��̗v�f�i�_�A�����A�Ȑ��A�ʂȂǁj
���O���`�͓������R��|�����`�ƂȂ�B�܂�A�����̂ɐ���̂ł͂Ȃ����낤���B
2024/06/11(��) 15:28:44.86ID:+Yl5Y58t
�ȉ��̐A�؎Z�H���Ȃ̂ł����A������2000m�Ƃ����l�����Ȃ��̂ł����A
�y�ڂ��̍l���ł́A20m���Ƃɍ�����1�{�Â����Ă����̂ŁA20m�~98�{�{�E�[��40m��2000m�z
������1960m�������ł��B
���������������킩��������Ă��������B
���D
�������H�ɗ��[�������č�������4m�����ɁA��������5m�����ɗ��Ă��Ƃ���A�ǂ���̊������傤�Ǘ��Ă邱�Ƃ��o�����B
�������͔��������98�{�������Ă邱�Ƃ��o�����B���̓��H�̑S���͉�m�ł����H
�y�ڂ��̍l���ł́A20m���Ƃɍ�����1�{�Â����Ă����̂ŁA20m�~98�{�{�E�[��40m��2000m�z
������1960m�������ł��B
���������������킩��������Ă��������B
���D
�������H�ɗ��[�������č�������4m�����ɁA��������5m�����ɗ��Ă��Ƃ���A�ǂ���̊������傤�Ǘ��Ă邱�Ƃ��o�����B
�������͔��������98�{�������Ă邱�Ƃ��o�����B���̓��H�̑S���͉�m�ł����H
325�C�i ��/7jUdUKiSM
2024/06/11(��) 19:26:02.44ID:4F0bSpIv326�C�i ��/7jUdUKiSM
2024/06/11(��) 19:31:50.79ID:4F0bSpIv2024/06/11(��) 20:50:40.29ID:kKKZntx1
>>324
�S����( L )���[�g���Ƃ��܂��B
���[�������Ċ��𗧂Ă�̂ŁA���Ă�����̐��́A
�@�������̐� = (L - 4)/4
�@�������̐� = (L - 5)/5
�������̐��͔������̐����98�{�����̂Ŏ��̎������藧���܂��B
�@ (L - 4)/4 = {(L - 5)/5} + 98
���ӂ�20���|���ĕ���������܂��B
�@5(L - 4) = 4(L - 5) + 1960
���ʂ�W�J���܂��B
�@5L - 20 = 4L - 20
���ӂ���4L�������܂��B
�@ L - 20 = -20 + 1960
���ӂ�20�𑫂��܂��B�@
�@ L = 1960
�]���āA�S����1960���[�g���ł��B
���Z
�@�������̐� = (1960 - 4) / 4 = 1956 / 4 = 489
�@�������̐� = (1960 - 5) / 5 = 1955 / 5 = 391
�@�������̐� - �������̐� = 489 - 391 = 98
�S����( L )���[�g���Ƃ��܂��B
���[�������Ċ��𗧂Ă�̂ŁA���Ă�����̐��́A
�@�������̐� = (L - 4)/4
�@�������̐� = (L - 5)/5
�������̐��͔������̐����98�{�����̂Ŏ��̎������藧���܂��B
�@ (L - 4)/4 = {(L - 5)/5} + 98
���ӂ�20���|���ĕ���������܂��B
�@5(L - 4) = 4(L - 5) + 1960
���ʂ�W�J���܂��B
�@5L - 20 = 4L - 20
���ӂ���4L�������܂��B
�@ L - 20 = -20 + 1960
���ӂ�20�𑫂��܂��B�@
�@ L = 1960
�]���āA�S����1960���[�g���ł��B
���Z
�@�������̐� = (1960 - 4) / 4 = 1956 / 4 = 489
�@�������̐� = (1960 - 5) / 5 = 1955 / 5 = 391
�@�������̐� - �������̐� = 489 - 391 = 98
328�C�i ��/7jUdUKiSM
2024/06/11(��) 21:00:46.84ID:4F0bSpIv �O>>326
>>316
P,Q,R�̂���������_�ɂ���Ƃ��A���Ƃ̓���ʼn���2���_����12���߂Â����Ȃ萳�O�p�`�ɋ߂Â��ƍl�������A
(17(1+cos(��/7)-(��3)cos(5��/14)))/(2cos(5��/14)(sin(2��/7)+(��3)cos(2��/7)))=12.0953574223�c�c��12
���O�p�`������Ƃ�����ǂ̒��_�ł��Ȃ�P,Q,R����Ȃ��Ƃ����Ȃ��B
3,5,7,11,13,17����炷�ׂĂ��f���B
1��ڂ݂������Ƃ��āA2��ڂ݂���܂łɂ����̐�(��)���A����ȏォ����\��������B
�_�̈�v�₻���������O�p�`�����݂��Ȃ��\�������Ă���B
���m�Ȑ����p�`��`���āA���m�Ɏ��ӂ��\���������āA60���̎O�p��K���Ăăh���s�V���̈ʒu���݂��邵���Ȃ����B����邩�Ȃ����B�݂���������ɂ����̂��Ȃ��B
>>316
P,Q,R�̂���������_�ɂ���Ƃ��A���Ƃ̓���ʼn���2���_����12���߂Â����Ȃ萳�O�p�`�ɋ߂Â��ƍl�������A
(17(1+cos(��/7)-(��3)cos(5��/14)))/(2cos(5��/14)(sin(2��/7)+(��3)cos(2��/7)))=12.0953574223�c�c��12
���O�p�`������Ƃ�����ǂ̒��_�ł��Ȃ�P,Q,R����Ȃ��Ƃ����Ȃ��B
3,5,7,11,13,17����炷�ׂĂ��f���B
1��ڂ݂������Ƃ��āA2��ڂ݂���܂łɂ����̐�(��)���A����ȏォ����\��������B
�_�̈�v�₻���������O�p�`�����݂��Ȃ��\�������Ă���B
���m�Ȑ����p�`��`���āA���m�Ɏ��ӂ��\���������āA60���̎O�p��K���Ăăh���s�V���̈ʒu���݂��邵���Ȃ����B����邩�Ȃ����B�݂���������ɂ����̂��Ȃ��B
2024/06/12(��) 00:20:32.65ID:37onIIck
>>326
�܂�͐��O���`�Ƃ����}�`�͑��݂��Ȃ��̂ł��B
���̌���ǂ����Ă��g�������Ȃ�A�w�ł͒�`����Ă��Ȃ��̂ŕʓr��`���K�v�ł��B
�܂�͐��O���`�Ƃ����}�`�͑��݂��Ȃ��̂ł��B
���̌���ǂ����Ă��g�������Ȃ�A�w�ł͒�`����Ă��Ȃ��̂ŕʓr��`���K�v�ł��B
330�C�i ��/7jUdUKiSM
2024/06/12(��) 04:07:01.70ID:pFBn0F5Z2024/06/12(��) 09:02:59.28ID:Zodo7K3e
>>324
>������2000m�Ƃ����l�����Ȃ�
�S��2000m���ƍ������Ɣ������̍���100�{�ƂȂ�A�����͌�肾�Ƃ�����ɂȂ�ł��傤�B
1960���̒��Ɏn�[����ŏ��̊��܂ŋ����ƍŌ�̊�����I�[�܂ł̋����͊܂܂�Ă܂��̂�40m�𑫂��K�v�͗L��܂���B
>������2000m�Ƃ����l�����Ȃ�
�S��2000m���ƍ������Ɣ������̍���100�{�ƂȂ�A�����͌�肾�Ƃ�����ɂȂ�ł��傤�B
1960���̒��Ɏn�[����ŏ��̊��܂ŋ����ƍŌ�̊�����I�[�܂ł̋����͊܂܂�Ă܂��̂�40m�𑫂��K�v�͗L��܂���B
2024/06/12(��) 12:06:30.67ID:UpzTOazG
���� x �{
���H y m
Solve[y==4x+4*2 && y==5(x-98)+5*2,y]
x=488 y=1960
���H y m
Solve[y==4x+4*2 && y==5(x-98)+5*2,y]
x=488 y=1960
333�C�i ��/7jUdUKiSM
2024/06/12(��) 12:57:26.07ID:WIPlHmvK334�C�i ��/7jUdUKiSM
2024/06/12(��) 13:17:46.20ID:WIPlHmvK335�C�i ��/7jUdUKiSM
2024/06/12(��) 16:34:18.92ID:WIPlHmvK �O>>334
>>316
��P2Q42R82���l����B
P2��y���W��17(1+cos(��/7))/2sin(��/7)-2sin(��/7)=36.3731657958�c�c
Q42R82�̒��_(-(5/2)cos(2��/7),(23/2)sin(2��/7))����X��
(17+23cos(2��/7))/(5sin(2��/7))�̒����ƁA
x�������ɐ������������p�`�̓V��(0,17(1+cos(��/7))/(2sin(��/7)))����X��-tan(��/7)�ň����������Ƃ̌�_��y���W��(17+23cos(2��/7))(2cos(��/7)+(5/2)cos(2��/7))/(5sin(2��/7))+(23/2)sin(2��/7)=35.9339644618�c�c
�킸���ɈႤ�B
����2�_�B
>>316
��P2Q42R82���l����B
P2��y���W��17(1+cos(��/7))/2sin(��/7)-2sin(��/7)=36.3731657958�c�c
Q42R82�̒��_(-(5/2)cos(2��/7),(23/2)sin(2��/7))����X��
(17+23cos(2��/7))/(5sin(2��/7))�̒����ƁA
x�������ɐ������������p�`�̓V��(0,17(1+cos(��/7))/(2sin(��/7)))����X��-tan(��/7)�ň����������Ƃ̌�_��y���W��(17+23cos(2��/7))(2cos(��/7)+(5/2)cos(2��/7))/(5sin(2��/7))+(23/2)sin(2��/7)=35.9339644618�c�c
�킸���ɈႤ�B
����2�_�B
2024/06/12(��) 19:39:10.25ID:P8tNeObm
7*17=119�Ɣԍ������đ�������
�O�p�`�̒��_�̑I�ѕ���C[119,3]= 273819�ʂ�
https://i.imgur.com/34WV0k6.png
���̒����琳�O�p�`�ɂȂ���̂́A�Ȃ������B�iR�ł̌����j
���������_���v���O�����Ȃ̂Ŕ���~�X�����邩�������ȁB
Wolfram�ł̍�}�͖��K���B
�O�p�`�̒��_�̑I�ѕ���C[119,3]= 273819�ʂ�
https://i.imgur.com/34WV0k6.png
���̒����琳�O�p�`�ɂȂ���̂́A�Ȃ������B�iR�ł̌����j
���������_���v���O�����Ȃ̂Ŕ���~�X�����邩�������ȁB
Wolfram�ł̍�}�͖��K���B
2024/06/12(��) 19:44:27.51ID:P8tNeObm
>>335
��}
https://i.imgur.com/w96qxdz.png
�ӂ̒���> abs(P[2]-P[42])
[1] 1.871443
> abs(P[82]-P[42])
[1] 1.857831
> abs(P[2]-P[82])
[1] 1.868265
���O�p�`�ɂ͂Ȃ��Ă��Ȃ�
��}
https://i.imgur.com/w96qxdz.png
�ӂ̒���> abs(P[2]-P[42])
[1] 1.871443
> abs(P[82]-P[42])
[1] 1.857831
> abs(P[2]-P[82])
[1] 1.868265
���O�p�`�ɂ͂Ȃ��Ă��Ȃ�
2024/06/12(��) 20:02:01.38ID:arcu60Yc
>>337
1�ӂ̒����P�̂Ƃ��̒l������e�X17�{����K�v�����邪���O�p�`�łȂ��͕̂ς��Ȃ��B
1�ӂ̒����P�̂Ƃ��̒l������e�X17�{����K�v�����邪���O�p�`�łȂ��͕̂ς��Ȃ��B
2024/06/12(��) 21:04:35.46ID:L6d55PDo
>>337
�A���^�̓��̃o�O�͂��ɂȂ�����C���ł���H
�A���^�̓��̃o�O�͂��ɂȂ�����C���ł���H
2024/06/13(��) 06:58:56.90ID:tRB2xGBh
>>337
Wolfram�ɈڐA���Ĕ���
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= r=E^(I 2Pi/7);
In[2]:= p=Table[(1-r^i)/(1-r),{i,Range[7+1]}];
In[3]:= fp[m_] :=(
q1=If[Floor[m/17]==0,7,Floor[m/17]];
r1=Mod[m,17];
(1-r1/17)p[[q1]]+(r1/17)p[[q1+1]]
)
In[4]:= ptsc=Table[fp[m],{m,Range[119]}];
In[5]:= pts={Re[#],Im[#]}& /@ ptsc;
In[6]:= v=Subsets[Range[119],{3}];
In[7]:= ft[x_] :=(
EuclideanDistance[pts[[x[[1]]]],pts[[x[[2]]]]] == EuclideanDistance[pts[[x[[2]]]],pts[[x[[3]]]]]
&& EuclideanDistance[pts[[x[[1]]]],pts[[x[[2]]]]] == EuclideanDistance[pts[[x[[1]]]],pts[[x[[3]]]]]
)
In[8]:= ft[{2,42,82}]
Out[8]= False
���O�p�`�ł͂Ȃ��B
Wolfram�ɈڐA���Ĕ���
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= r=E^(I 2Pi/7);
In[2]:= p=Table[(1-r^i)/(1-r),{i,Range[7+1]}];
In[3]:= fp[m_] :=(
q1=If[Floor[m/17]==0,7,Floor[m/17]];
r1=Mod[m,17];
(1-r1/17)p[[q1]]+(r1/17)p[[q1+1]]
)
In[4]:= ptsc=Table[fp[m],{m,Range[119]}];
In[5]:= pts={Re[#],Im[#]}& /@ ptsc;
In[6]:= v=Subsets[Range[119],{3}];
In[7]:= ft[x_] :=(
EuclideanDistance[pts[[x[[1]]]],pts[[x[[2]]]]] == EuclideanDistance[pts[[x[[2]]]],pts[[x[[3]]]]]
&& EuclideanDistance[pts[[x[[1]]]],pts[[x[[2]]]]] == EuclideanDistance[pts[[x[[1]]]],pts[[x[[3]]]]]
)
In[8]:= ft[{2,42,82}]
Out[8]= False
���O�p�`�ł͂Ȃ��B
2024/06/13(��) 08:09:36.79ID:lZXceJxz
342�C�i ��/7jUdUKiSM
2024/06/13(��) 16:07:19.66ID:fW+ZaGdS �O>>335�����v����_���݂���̂��Ȃ��H
>>316
��P4Q44R84���l����B
P4��y���W��17(1+cos(��/7))/2sin(��/7)-4sin(��/7)=3 . �c�c
Q44R84�̒��_(-(9/2)cos(2��/7),(23/2)sin(2��/7))����X��
(17+23cos(2��/7))/(9sin(2��/7))�̒����ƁA
x�������ɐ������������p�`�̓V��(0,17(1+cos(��/7))/(2sin(��/7)))����X��-tan(��/7)�ň����������Ƃ̌�_��y���W�́@=3 . �c�c
>>316
��P4Q44R84���l����B
P4��y���W��17(1+cos(��/7))/2sin(��/7)-4sin(��/7)=3 . �c�c
Q44R84�̒��_(-(9/2)cos(2��/7),(23/2)sin(2��/7))����X��
(17+23cos(2��/7))/(9sin(2��/7))�̒����ƁA
x�������ɐ������������p�`�̓V��(0,17(1+cos(��/7))/(2sin(��/7)))����X��-tan(��/7)�ň����������Ƃ̌�_��y���W�́@=3 . �c�c
2024/06/14(��) 05:21:01.88ID:gBGTiJgx
>>342
�\���@�F�@���O�p�`�ɂȂ�_�݂͂���Ȃ��B
�q���g
���Z���w�̎���X�� Part434
http://rio2016.5ch.net/test/read.cgi/math/1712376048/627
627 ���O�F�P�R�Q�l�ڂ̑f������[sage] ���e���F2024/04/28(��) 11:42:32.22 ID:pfxD2O3Q
���ڂ��鐳�O�p�`�̒��S���������p�`�̒��S�{�ƈ�v����Ƃ����O����O����R����ŒT�����č�}�B
https://i.imgur.com/zdcTLGT.png
�����p�`�̂P�ӂ̒������P�Ƃ���Ɛ��O�p�`�̂P�ӂ̒����͖�1.87�ɂȂ����B
���升�i�҂ɂ�錟����]���܂��B
�搳�O�p�`�ɂȂ�ʒu�͗L�����ł͂Ȃ�����B
�\���@�F�@���O�p�`�ɂȂ�_�݂͂���Ȃ��B
�q���g
���Z���w�̎���X�� Part434
http://rio2016.5ch.net/test/read.cgi/math/1712376048/627
627 ���O�F�P�R�Q�l�ڂ̑f������[sage] ���e���F2024/04/28(��) 11:42:32.22 ID:pfxD2O3Q
���ڂ��鐳�O�p�`�̒��S���������p�`�̒��S�{�ƈ�v����Ƃ����O����O����R����ŒT�����č�}�B
https://i.imgur.com/zdcTLGT.png
�����p�`�̂P�ӂ̒������P�Ƃ���Ɛ��O�p�`�̂P�ӂ̒����͖�1.87�ɂȂ����B
���升�i�҂ɂ�錟����]���܂��B
�搳�O�p�`�ɂȂ�ʒu�͗L�����ł͂Ȃ�����B
2024/06/14(��) 05:27:30.33ID:gBGTiJgx
>>342
https://i.imgur.com/34WV0k6.png
��4 44 84 �̍��O�p�`�̕ӂ̒����i��7�p�`��1�Ӂ�17�Ƃ���j
https://i.imgur.com/DQ9CVxP.png
https://i.imgur.com/34WV0k6.png
��4 44 84 �̍��O�p�`�̕ӂ̒����i��7�p�`��1�Ӂ�17�Ƃ���j
https://i.imgur.com/DQ9CVxP.png
2024/06/14(��) 08:09:56.79ID:jTBzjzOY
>>344
�A�r�W�W�C�����̃R�s�y�ʼn؋����������甭����w
925�F���̖��������� (ܯ��� 930b-dMzx [2400:2411:3fe0:400:*])�F[sage]�F2024/06/14(��) 05:47:52.01 ID:c6Opo3s50
�Ó슙�q�����a�@�ɂ͌������ȑ�w�Ζ��ō�����̍O�O��w���̌�AV���D��u��Ȃ��Ɠc��䝗��q�i�����ÌS�j����������
https://www.skgh.jp/department/hbps/
https://www.suruga-ya.jp/product/detail/131150111
http://www.oma-aozora.jp/ikizama/kisamai/welcome_02.html
�A�r�W�W�C�����̃R�s�y�ʼn؋����������甭����w
925�F���̖��������� (ܯ��� 930b-dMzx [2400:2411:3fe0:400:*])�F[sage]�F2024/06/14(��) 05:47:52.01 ID:c6Opo3s50
�Ó슙�q�����a�@�ɂ͌������ȑ�w�Ζ��ō�����̍O�O��w���̌�AV���D��u��Ȃ��Ɠc��䝗��q�i�����ÌS�j����������
https://www.skgh.jp/department/hbps/
https://www.suruga-ya.jp/product/detail/131150111
http://www.oma-aozora.jp/ikizama/kisamai/welcome_02.html
2024/06/14(��) 08:15:00.02ID:jTBzjzOY
>>343
�����w������ɃA�z�Ȃ�H
���Z���ɑ���ɂ���Ȃ����獡�x�͑��ł����������Ȃ��N��̏����w���Ƀ��X��H����
60�߂��Ĉ��ꂾ��
�����w������ɃA�z�Ȃ�H
���Z���ɑ���ɂ���Ȃ����獡�x�͑��ł����������Ȃ��N��̏����w���Ƀ��X��H����
60�߂��Ĉ��ꂾ��
2024/06/14(��) 08:46:25.58ID:iqbUZrfg
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
Phimose��������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
Phimose��������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
2024/06/14(��) 12:33:51.60ID:jTBzjzOY
���Z���ǂ��납�����w���ɂ�����ɂ���ĂȂ��݂�������
����ȘV�Q
����ȘV�Q
2024/06/14(��) 15:11:58.15ID:n0cmuktP
350�P�R�Q�l�ڂ̑f������
2024/06/14(��) 17:10:35.22ID:8cOfa51M �z�E�_��100g�̐���80����23.4g�n���܂��B
�@20���̐��ł�4.8g�n���܂��B
�@�ł�20���̃z�E�_���n�t100g�Ƀz�E�_�͉�g�n���Ă��܂����H
�@20���̐��ł�4.8g�n���܂��B
�@�ł�20���̃z�E�_���n�t100g�Ƀz�E�_�͉�g�n���Ă��܂����H
351�P�R�Q�l�ڂ̑f������
2024/06/14(��) 17:11:45.16ID:8cOfa51M ���݂܂���
���̓������� �R�37/41 �ō����Ă܂����H
���̓������� �R�37/41 �ō����Ă܂����H
2024/06/14(��) 17:51:43.14ID:AdETirvJ
���ɂ�
�����ς��܂ŗn���������n�t
�i�O�a���n�t�j
�Ə����Ă��邩�ȁH
�����łȂ��ƁA�����͂ЂƂɂȂ�Ȃ�
���ɁA��蕶��2�s�ڂ̈Ӗ���
20���̐��i100g�j�ł�4.8g�n���܂��B
�Ȃ̂ŁA�n��������̏�Ԃ�
���n�t �i100�{4.8�jg �̂��� 4.8g
����100��20�ɂ��ĊԈႦ���悤�Ɍ�����
������x�A�������l�Ŏ�������Ă݂悤
�����ς��܂ŗn���������n�t
�i�O�a���n�t�j
�Ə����Ă��邩�ȁH
�����łȂ��ƁA�����͂ЂƂɂȂ�Ȃ�
���ɁA��蕶��2�s�ڂ̈Ӗ���
20���̐��i100g�j�ł�4.8g�n���܂��B
�Ȃ̂ŁA�n��������̏�Ԃ�
���n�t �i100�{4.8�jg �̂��� 4.8g
����100��20�ɂ��ĊԈႦ���悤�Ɍ�����
������x�A�������l�Ŏ�������Ă݂悤
353�P�R�Q�l�ڂ̑f������
2024/06/14(��) 18:09:00.55ID:8cOfa51M ���A�ԈႦ���I
����ō����Ă�H�S�76/131g
����ō����Ă�H�S�76/131g
2024/06/14(��) 18:19:47.07ID:7etD9xyh
4.8/(100+4.8) * 100 = 4.580153
2024/06/15(�y) 11:25:42.29ID:auiv2U/t
>>316
R�œ�����쐬
https://i.imgur.com/GM1mzur.gif
Wolfram�ō���قǂ̃X�L���͂Ȃ��̂ŁA�m�E�n�E�̂��邩���͋X�����B
R�œ�����쐬
https://i.imgur.com/GM1mzur.gif
Wolfram�ō���قǂ̃X�L���͂Ȃ��̂ŁA�m�E�n�E�̂��邩���͋X�����B
2024/06/15(�y) 13:02:21.51ID:s72Q0myJ
>>355
���w������A���^�݂����ȃ}�k�P����ɂ��Ȃ��݂�������
���w������A���^�݂����ȃ}�k�P����ɂ��Ȃ��݂�������
2024/06/15(�y) 15:36:11.25ID:auiv2U/t
>>355
t�����PQR�̍��W���v�Z�������Wolfram�ɈڐA�B
https://i.imgur.com/gLoFWOC.png
�����R�ō�����悤�ɁA����ɂł���f�{�͂Ȃ��̂ŁA�m�E�n�E�̂�����̗͍����]�B
t�����PQR�̍��W���v�Z�������Wolfram�ɈڐA�B
https://i.imgur.com/gLoFWOC.png
�����R�ō�����悤�ɁA����ɂł���f�{�͂Ȃ��̂ŁA�m�E�n�E�̂�����̗͍����]�B
2024/06/15(�y) 16:08:11.61ID:/kurU0FS
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
Phimose��������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
Phimose��������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
2024/06/15(�y) 18:54:45.33ID:s72Q0myJ
>>358
993�F�P�R�Q�l�ڂ̑f������F[sage]�F2024/05/10(��) 05:03:33.15 ID:esg1TcXl
R�����Wolfram���ꂪ�g����l�͂����Ƃ������X�����Ă���Ȃ��B
�������l�|����тƂ���Phiose�����̏W�c�����升�i�҂��Ǝv���l�͂��̎|�����X���Ă��������B
>Phiose
>Phiose
>Phiose
����������^���Ԃɂ���phimose���Ď�ł����Ă��͗lw
������̉ʂĂ�phiose ww
����ς�A�z�͉B����Ȃ��ˁA����Ꮼ�w���ɂ��o�J�ɂ���܂���
993�F�P�R�Q�l�ڂ̑f������F[sage]�F2024/05/10(��) 05:03:33.15 ID:esg1TcXl
R�����Wolfram���ꂪ�g����l�͂����Ƃ������X�����Ă���Ȃ��B
�������l�|����тƂ���Phiose�����̏W�c�����升�i�҂��Ǝv���l�͂��̎|�����X���Ă��������B
>Phiose
>Phiose
>Phiose
����������^���Ԃɂ���phimose���Ď�ł����Ă��͗lw
������̉ʂĂ�phiose ww
����ς�A�z�͉B����Ȃ��ˁA����Ꮼ�w���ɂ��o�J�ɂ���܂���
2024/06/15(�y) 18:58:02.75ID:s72Q0myJ
>>358 �ŁA����ɂ͂��܂Ń_���}�����߂���ł�H
���̏�����O�Ȉ�Ȃ�ȒP����H
882�F���̖��������� (ܯ��� c3d6-KQ+b [240b:11:241:7900:*])�F2024/06/09(��) 06:24:07.24 ID:4fjzozfw0
>>881
�Տ����www���O�{���n���Ȃ�
���Ⴀ���̏�����O�Ȃ̂��O�ɖ��o���Ă���
�����̉摜�̕a���́H
https://i.imgur.com/dCrMTtn.jpeg
883�F���̖��������� (ܯ��� 13cc-EeFD [114.145.56.79])�F[sage]�F2024/06/09(��) 06:37:47.32 ID:JHmHgQHX0
>>882
�̎��
>874�̓��́H
885�F���̖��������� (ܯ��� c3d6-KQ+b [240b:11:241:7900:*])�F2024/06/09(��) 08:42:52.82 ID:4fjzozfw0
>>883
�̎��www�A�o�E�g�߂���
�̎�ᇂɂǂꂾ����ނ���Ǝv���Ă��
��ᇂȂ�ĉ摜�݂��瓖����O����
���̎�ᇂ������Ă����ϑf�l����www
���̏�����O�Ȉ�Ȃ�ȒP����H
882�F���̖��������� (ܯ��� c3d6-KQ+b [240b:11:241:7900:*])�F2024/06/09(��) 06:24:07.24 ID:4fjzozfw0
>>881
�Տ����www���O�{���n���Ȃ�
���Ⴀ���̏�����O�Ȃ̂��O�ɖ��o���Ă���
�����̉摜�̕a���́H
https://i.imgur.com/dCrMTtn.jpeg
883�F���̖��������� (ܯ��� 13cc-EeFD [114.145.56.79])�F[sage]�F2024/06/09(��) 06:37:47.32 ID:JHmHgQHX0
>>882
�̎��
>874�̓��́H
885�F���̖��������� (ܯ��� c3d6-KQ+b [240b:11:241:7900:*])�F2024/06/09(��) 08:42:52.82 ID:4fjzozfw0
>>883
�̎��www�A�o�E�g�߂���
�̎�ᇂɂǂꂾ����ނ���Ǝv���Ă��
��ᇂȂ�ĉ摜�݂��瓖����O����
���̎�ᇂ������Ă����ϑf�l����www
2024/06/15(�y) 20:30:10.95ID:auiv2U/t
>>357
�O�p�`PQR��1�����Ƃ̌`��̃��X�g�͍�ꂽ�B
https://i.imgur.com/I5zxr1L.png
���扻������@���킩���B
Ra=17/Sqrt[ 2(1-Sin[3Pi/14])];
r=E^(-2I Pi/7);
p=Table[Ra I r^(i-1),{i,Range[14]}];
f[t_,v_,v0_] :=( (* ������,v:���� v0:�X�^�[�g���_*)
d = v t;
i = v0 + Mod[Floor[d/17],7];
v1 = {Re[p[[i]]],Im[p[[i]]]};
v2 = {Re[p[[i+1]]],Im[p[[i+1]]]};
s= Mod[d,17]/17;
(1-s) v1 + s v2
)
PQR[t_] :=(
P=f[t,5,1];
Q=f[t,11,3];
R=f[t,13,4];
{P,Q,R}
)
Table[Graphics[{EdgeForm[Thin],Pink,Polygon[PQR[t]]}],{t,Range[0,100]}]
�O�p�`PQR��1�����Ƃ̌`��̃��X�g�͍�ꂽ�B
https://i.imgur.com/I5zxr1L.png
���扻������@���킩���B
Ra=17/Sqrt[ 2(1-Sin[3Pi/14])];
r=E^(-2I Pi/7);
p=Table[Ra I r^(i-1),{i,Range[14]}];
f[t_,v_,v0_] :=( (* ������,v:���� v0:�X�^�[�g���_*)
d = v t;
i = v0 + Mod[Floor[d/17],7];
v1 = {Re[p[[i]]],Im[p[[i]]]};
v2 = {Re[p[[i+1]]],Im[p[[i+1]]]};
s= Mod[d,17]/17;
(1-s) v1 + s v2
)
PQR[t_] :=(
P=f[t,5,1];
Q=f[t,11,3];
R=f[t,13,4];
{P,Q,R}
)
Table[Graphics[{EdgeForm[Thin],Pink,Polygon[PQR[t]]}],{t,Range[0,100]}]
2024/06/15(�y) 20:34:18.78ID:auiv2U/t
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
Phimose��������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B�@�@
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B�@�@�@�@
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B�@
Phimose��������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B�@�@
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B�@�@�@�@
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B�@
2024/06/15(�y) 20:35:42.67ID:s72Q0myJ
>>361
�����w���ɂ��瑊��ɂ���Ȃ��̂Ɉ�ҔŃ`���p�����w�Ŕ������Ă�����ɂ���Ȃ����Ƃ�������Ȃ��قǃA�z�Ȃ̂��H
������O���A�Z���ǂ��납���{��ʂ��Ȃ������w
�����w���ɂ��瑊��ɂ���Ȃ��̂Ɉ�ҔŃ`���p�����w�Ŕ������Ă�����ɂ���Ȃ����Ƃ�������Ȃ��قǃA�z�Ȃ̂��H
������O���A�Z���ǂ��납���{��ʂ��Ȃ������w
2024/06/15(�y) 20:39:25.37ID:s72Q0myJ
�֗��Ȃ��͉̂��ł��g���ƌ����Ȃ��疈���^���Ԃɂ���phiose�ȂǂƏ������ޔA�r�W�W�Cw
������O�Ȉ�Ȃ炳�����Ɠ���������̂Ƀ_���}�����ߍ���Ŕ��������Ⴄ�̂͂���ς�]����҂Ȃ�H
�X���^�C�ǂ��납���{����ǂ߂Ȃ��A�z�����炢���猾���Ă����ʂ�������Ȃ���w
������O�Ȉ�Ȃ炳�����Ɠ���������̂Ƀ_���}�����ߍ���Ŕ��������Ⴄ�̂͂���ς�]����҂Ȃ�H
�X���^�C�ǂ��납���{����ǂ߂Ȃ��A�z�����炢���猾���Ă����ʂ�������Ȃ���w
2024/06/15(�y) 21:35:39.93ID:s72Q0myJ
>>361
920�F�P�R�Q�l�ڂ̑f������F2024/06/15(�y) 21:08:23.14 ID:sJYLknp7
���ŏ����w���X����R�Ƃ�wolfram�Ƃ������Ă��
���̃W�W�C���b�`���N�`���L������ł�����
920�F�P�R�Q�l�ڂ̑f������F2024/06/15(�y) 21:08:23.14 ID:sJYLknp7
���ŏ����w���X����R�Ƃ�wolfram�Ƃ������Ă��
���̃W�W�C���b�`���N�`���L������ł�����
2024/06/16(��) 04:32:28.44ID:p0J/vaae
>>350
20���̃z�E�_���n�t100g�̃z�E�_��(x)g�Ƃ���
x:(100-x) = 48:100
��Ꭾ��������ɂ���
100x = 4.8 �~ (100 - x)
100x = 480 - 4.8x
100x + 4.8x = 480
104.8x = 480
x=480 �� 104.8
x=4 76⁄131
�����@��4.58g
20���̃z�E�_���n�t100g�̃z�E�_��(x)g�Ƃ���
x:(100-x) = 48:100
��Ꭾ��������ɂ���
100x = 4.8 �~ (100 - x)
100x = 480 - 4.8x
100x + 4.8x = 480
104.8x = 480
x=480 �� 104.8
x=4 76⁄131
�����@��4.58g
2024/06/16(��) 08:26:27.13ID:OXd6S6lK
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
Phimose��������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B�@�@
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B�@�@�@�@
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B�@
Phimose��������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B�@�@
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B�@�@�@�@
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B�@
2024/06/16(��) 09:38:28.19ID:Azf3+Edb
�R�s�y�Ŕ������Ă�̂̓A���^����w
�S�����ȏЉ�ȁH
�S�����ȏЉ�ȁH
2024/06/16(��) 10:04:13.12ID:2M8mHw3k
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
Phimose��������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
Phimose��������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
2024/06/16(��) 10:37:34.32ID:c85JJGPm
�����������Ƃ��������Ȃ��Ȃ����݂������ˎ��ȏЉ�R�s�y�W�W�C
���Ȃ݂ɓǂ�ł���ĊԈ���Ă邼�`���p��
���Ȃ݂ɓǂ�ł���ĊԈ���Ă邼�`���p��
2024/06/16(��) 10:41:42.05ID:t7P5Xl+E
�����w���݂����Ȃ��傤���Ȃ����܂��������ɂ�߂�
2024/06/16(��) 11:27:38.43ID:LCTmxx8U
�v���Ԃ�ɗ�����܂��������Ƃ��J��Ԃ���Ă���
���̃X���j��Ă���10�N���炢�ɂȂ�H
���N������Ȃ��Ƃ𑱂�����Ė{�l�͎����̐��_��Ԃ��܂����Ƃ͎v��Ȃ����̂Ȃ낤��
���̃X���j��Ă���10�N���炢�ɂȂ�H
���N������Ȃ��Ƃ𑱂�����Ė{�l�͎����̐��_��Ԃ��܂����Ƃ͎v��Ȃ����̂Ȃ낤��
2024/06/16(��) 12:19:37.19ID:c85JJGPm
>>369�ǂ��l���Ă�������������ł�����w
935�F�P�R�Q�l�ڂ̑f������F2024/06/16(��) 12:10:37.55 ID:Ic2BX9Vf
>>933
���w���͕������g�����Ⴂ���Ȃ��̒m��Ȃ��́H�����������Ƃ��Ă�Ƙ_���I�v�l���g�ɂ��Ȃ�
���O�݂����Ɏg���Ȃ���l�ɂȂ�
�{���ɋ`��������́H���{�l�H
936�F�P�R�Q�l�ڂ̑f������F2024/06/16(��) 12:15:03.98 ID:Ic2BX9Vf
>>933
���������X���̍ŏ��ɏ����w�̂��߂̃X��������͈͊O�̎��������Ȃ��ĔO�������Ă邾��
�N���o�肵���Ƃ���肶��Ȃ�
�͈͂Ɉ�E�������Ƃ������Ă邱�Ƃ����
���[���͎����l�Ȃ�
935�F�P�R�Q�l�ڂ̑f������F2024/06/16(��) 12:10:37.55 ID:Ic2BX9Vf
>>933
���w���͕������g�����Ⴂ���Ȃ��̒m��Ȃ��́H�����������Ƃ��Ă�Ƙ_���I�v�l���g�ɂ��Ȃ�
���O�݂����Ɏg���Ȃ���l�ɂȂ�
�{���ɋ`��������́H���{�l�H
936�F�P�R�Q�l�ڂ̑f������F2024/06/16(��) 12:15:03.98 ID:Ic2BX9Vf
>>933
���������X���̍ŏ��ɏ����w�̂��߂̃X��������͈͊O�̎��������Ȃ��ĔO�������Ă邾��
�N���o�肵���Ƃ���肶��Ȃ�
�͈͂Ɉ�E�������Ƃ������Ă邱�Ƃ����
���[���͎����l�Ȃ�
2024/06/16(��) 14:11:56.37ID:c85JJGPm
>>361���A�r�`���p���W�W�C�͍��Z���w�X���ł������Ă�ʂ�d��K���ɒ@���ăL�[�L�[���ł�`���p��
2024/06/16(��) 15:53:54.05ID:2M8mHw3k
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
Phimose��������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
>355�̓����Wolfram�ō����
foreskin�M��ȊO�ɂ��ł��邱�Ƃ�����̂���������ǂ���?
Phimose��������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
>355�̓����Wolfram�ō����
foreskin�M��ȊO�ɂ��ł��邱�Ƃ�����̂���������ǂ���?
2024/06/16(��) 16:41:23.02ID:c85JJGPm
���w���ɂ���o�J�ɂ���Ă�ǂ��납�R�s�y�Ŕ��������ł��Ȃ��̂��H
2024/06/16(��) 16:45:19.91ID:c85JJGPm
>>375
�܂����Z���w�X���ł���ȃg���`���J���ȃ��X���Ă܂�
935�F�P�R�Q�l�ڂ̑f������F2024/06/16(��) 12:10:37.55 ID:Ic2BX9Vf
>>933
���w���͕������g�����Ⴂ���Ȃ��̒m��Ȃ��́H�����������Ƃ��Ă�Ƙ_���I�v�l���g�ɂ��Ȃ�
���O�݂����Ɏg���Ȃ���l�ɂȂ�
�{���ɋ`��������́H���{�l�H
943�F�P�R�Q�l�ڂ̑f������F2024/06/16(��) 16:39:44.91 ID:FXcBoZ/L
>>942
���\�A�Ƃ����Ă����獡�Ƃ��ˁ[��
���j���炢�w��ǂ���\
�Ȃ�>>940�ɂ͓����Ȃ��H�H�H�����͍��Z���̔Y�݂���������X���Ȃ�
�܂����Z���w�X���ł���ȃg���`���J���ȃ��X���Ă܂�
935�F�P�R�Q�l�ڂ̑f������F2024/06/16(��) 12:10:37.55 ID:Ic2BX9Vf
>>933
���w���͕������g�����Ⴂ���Ȃ��̒m��Ȃ��́H�����������Ƃ��Ă�Ƙ_���I�v�l���g�ɂ��Ȃ�
���O�݂����Ɏg���Ȃ���l�ɂȂ�
�{���ɋ`��������́H���{�l�H
943�F�P�R�Q�l�ڂ̑f������F2024/06/16(��) 16:39:44.91 ID:FXcBoZ/L
>>942
���\�A�Ƃ����Ă����獡�Ƃ��ˁ[��
���j���炢�w��ǂ���\
�Ȃ�>>940�ɂ͓����Ȃ��H�H�H�����͍��Z���̔Y�݂���������X���Ȃ�
2024/06/16(��) 16:46:20.72ID:c85JJGPm
���\�A�ł͏��w�Z����������K�[��
379�P�R�Q�l�ڂ̑f������
2024/06/16(��) 21:12:03.64ID:rZ/VtYJE ���݂܂����Ă��������B��
���
�ӂ��Ƃ��璸��܂ŁHkm�̎R��������܂��B�`����͎���3.6km�łӂ��Ƃ��璸��܂ŕ����܂��B
�`���o�����Ă���30���o���Ă���a������4.8km�Œ��ォ��ӂ��Ƃ܂ŕ����܂��B
��l�͂��傤�ǂ܂̒n�_�ʼn�܂����B
���
�ӂ��Ƃ��璸��܂ŁHkm�̎R��������܂��B�`����͎���3.6km�łӂ��Ƃ��璸��܂ŕ����܂��B
�`���o�����Ă���30���o���Ă���a������4.8km�Œ��ォ��ӂ��Ƃ܂ŕ����܂��B
��l�͂��傤�ǂ܂̒n�_�ʼn�܂����B
380�P�R�Q�l�ڂ̑f������
2024/06/16(��) 21:26:48.27ID:e6fiTKHU >>361
GIF�A�j���ŃO�O��B
GIF�A�j���ŃO�O��B
2024/06/16(��) 22:14:52.24ID:2M8mHw3k
�v�Z�@�̓C���^�[�i�V���i���X�N�[���ł��g���w�Z������܂����A�V���K�|�[���̌��n�Z�ł͏��w5�N���ɂȂ�O�ɑS���k���u���v�Z�@�v���w�����Ďg�������w�юn�߂܂��B���͑肪����邱�̎����A�v�Z�Ɏ��Ԃ��₷�̂ł͂Ȃ��A��@���l���邱�ƂɏW�����邱�Ƃ��_���ł��B6�N���Ŏ鑲�Ǝ����iPSLE�j��Z�J���_���[�X�N�[���̑��Ǝ����ł��g�p���邽�߁A�����Ɏg�p��������Ă���@����w�Z�o�R�ōw�����܂��B�܂����w3�N��������̓O���t�B�b�N���v�Z�@���g�p���A�x�N�g��������ϕ��A���v�w�Ȃǂ̉ۑ�ɂ����p���܂��B
2024/06/16(��) 22:20:51.16ID:c85JJGPm
�����w�Z���ē�����O�����Ǔ��{�̂��Ƃ���ˁH
�Ȃ�ł���ȂɊC�O�K�[�Ƃ��ق����Ă�́H���{�ꂩ������Ă�����
�Ȃ�ł���ȂɊC�O�K�[�Ƃ��ق����Ă�́H���{�ꂩ������Ă�����
2024/06/16(��) 22:23:37.37ID:2M8mHw3k
>>380
ScreenToGIF�Ȃ炷�łɎg���Ă���B
ScreenToGIF�Ȃ炷�łɎg���Ă���B
2024/06/16(��) 22:25:08.70ID:c85JJGPm
>>383
���Ȃ��Ƃ����{�̏����w�Z�͈̔͂ł͂Ȃ�����A���^�͂������Ƃǂ����s�����Č����Ă�̂��������̂��H
���{�ꂷ��s���R�Ȃ̂ɎZ���Ƃ��ł���킯�ˁ[�����A�z
���Ȃ��Ƃ����{�̏����w�Z�͈̔͂ł͂Ȃ�����A���^�͂������Ƃǂ����s�����Č����Ă�̂��������̂��H
���{�ꂷ��s���R�Ȃ̂ɎZ���Ƃ��ł���킯�ˁ[�����A�z
385�P�R�Q�l�ڂ̑f������
2024/06/16(��) 22:46:54.42ID:rZ/VtYJE ���Ƃ��̖������肢���܂��B
���
3�l�̐��k�̃e�X�g��2�l���̕��ϓ_�́A80�A86�A88�ł����B
�ł��_���������l�́H�_�ł��B
���
3�l�̐��k�̃e�X�g��2�l���̕��ϓ_�́A80�A86�A88�ł����B
�ł��_���������l�́H�_�ł��B
2024/06/16(��) 22:46:57.54ID:2M8mHw3k
>>379
? = 14.4 km
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= Solve[x/2==3.6t==4.8(t-30/60),{x,t}]
Out[1]= {{x -> 14.4, t -> 2.}}
�����������āA�v�Z�͋@�B�ɔC����B
? = 14.4 km
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= Solve[x/2==3.6t==4.8(t-30/60),{x,t}]
Out[1]= {{x -> 14.4, t -> 2.}}
�����������āA�v�Z�͋@�B�ɔC����B
2024/06/16(��) 22:52:23.33ID:2M8mHw3k
>>385
94�_
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= Solve[(a+b)/2==80 && (b+c)/2==86 && (c+a)/2==88,{a,b,c}]
Out[1]= {{a -> 82, b -> 78, c -> 94}}
94�_
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= Solve[(a+b)/2==80 && (b+c)/2==86 && (c+a)/2==88,{a,b,c}]
Out[1]= {{a -> 82, b -> 78, c -> 94}}
2024/06/16(��) 22:56:46.86ID:2M8mHw3k
>>361
��}���Đ��O�p�`�炵���̂�T���Ă�����A�����ɂȂ�̂��������̂ōl�������B
1�ӂ̒�����17cm�̐����p�`ABCDEF������A
���̕ӏ��_P,�_Q,�_P���A���ꂼ�ꎞ�v���Ɉړ�����B
�_P��A����o����1�����5cm���
�_Q��C����o����1�����11cm��ɁA
�_R��D����o����1�����13cm��Ɉړ�����B
�����ɏo�������Ƃ�1���ԁi60*24=1440��)�Ɂ@P,Q,R���P������ɂȂ�ԁi�Q�_�����v����ꍇ�͊܂܂Ȃ��j�����߂�
���̈Ӗ��͏��w���ɂ��킩�邾�낤���A�����̂͏����w�Z�͈̔͂ł͓���Ǝv���BWolfram�̗��K�ɂ͖𗧂����B
��}���Đ��O�p�`�炵���̂�T���Ă�����A�����ɂȂ�̂��������̂ōl�������B
1�ӂ̒�����17cm�̐����p�`ABCDEF������A
���̕ӏ��_P,�_Q,�_P���A���ꂼ�ꎞ�v���Ɉړ�����B
�_P��A����o����1�����5cm���
�_Q��C����o����1�����11cm��ɁA
�_R��D����o����1�����13cm��Ɉړ�����B
�����ɏo�������Ƃ�1���ԁi60*24=1440��)�Ɂ@P,Q,R���P������ɂȂ�ԁi�Q�_�����v����ꍇ�͊܂܂Ȃ��j�����߂�
���̈Ӗ��͏��w���ɂ��킩�邾�낤���A�����̂͏����w�Z�͈̔͂ł͓���Ǝv���BWolfram�̗��K�ɂ͖𗧂����B
2024/06/16(��) 23:10:08.68ID:2M8mHw3k
���p���
�f�Ï�����a�@�Ɋ��҂��~�}��������B
�a�@����~�}�Ԃ��f�Ï��Ɍ������Ă���P�O�������\��ƘA�����������B
���҂̕a�Ԃ�����������A�f�Ï��̕��ʎԂŕa�@�Ɍ������~�}�ԂƏo�������
�~�}�ԂɊ��҂��ڂ��Ĕ������a�@�������}���Ƃ����v��𗧂Ă��B
���ʎԂ���~�}�Ԃւ̊��҂̏�芷���łP�O���]���Ɏ��Ԃ�������B
�~�}�Ԃ͊��҂��悹�Ȃ��Ƃ��͕��ώ����U�O�����ŁA���҂��悹��ƕ��ώ����S�T�����Œ葬���s����B
���ʎԂ͐M���҂��̂��ߕ��ώ����R�Okm�Œ葬���s����B
�����ȍ~�̕a�Ԉ����͐f�Ï��̎Ԃ��g�킸�ɋ~�}�Ԃ̓�����҂����a�@�ɑ����������H
�f�Ï�����a�@�Ɋ��҂��~�}��������B
�a�@����~�}�Ԃ��f�Ï��Ɍ������Ă���P�O�������\��ƘA�����������B
���҂̕a�Ԃ�����������A�f�Ï��̕��ʎԂŕa�@�Ɍ������~�}�ԂƏo�������
�~�}�ԂɊ��҂��ڂ��Ĕ������a�@�������}���Ƃ����v��𗧂Ă��B
���ʎԂ���~�}�Ԃւ̊��҂̏�芷���łP�O���]���Ɏ��Ԃ�������B
�~�}�Ԃ͊��҂��悹�Ȃ��Ƃ��͕��ώ����U�O�����ŁA���҂��悹��ƕ��ώ����S�T�����Œ葬���s����B
���ʎԂ͐M���҂��̂��ߕ��ώ����R�Okm�Œ葬���s����B
�����ȍ~�̕a�Ԉ����͐f�Ï��̎Ԃ��g�킸�ɋ~�}�Ԃ̓�����҂����a�@�ɑ����������H
2024/06/17(��) 00:27:11.50ID:uzZhdygS
>>379
���͋����A���͎���
A����͎���3.6�L���œo��
�@y = 3.6x�@....�@①
B�����30����Ɏ����ō~��i0.5���ԕ��̋����𑫂��܂��j
�@y + 2.4 = 4.8x
���ԓ_�ō��������̂Ŏ��̎������藧���܂��B
�@3.6x = 4.8x - 2.4
�@x = 2
①�̎��ɑ��
�@y=3.6�E2
�@y=7.2
���ԓ_��7.2km�ł��̂ŁA�{��14.4km�������ł��B
>>385
3�l�̐��k��A�AB�AC�Ƃ��܂��B���ꂼ��̓_����a�Ab�Ac�Ƃ��܂��B2�l���̕��ϓ_�����ꂼ��80�A86�A88�ł���̂ŁA�ȉ��̂悤�Ȏ������藧���܂��B
�@1. ((a + b) / 2 = 80) �� (a + b = 160)
�@2. ((b + c) / 2 = 86) �� (b + c = 172)
�@3. ((c + a) / 2 = 88) �� (c + a = 176)
������3�̕������������Ă����܂��B
�܂��A3�̕������𑫂����킹���
�@(a + b) + (b + c) + (c + a) = 160 + 172 + 176
�@2a + 2b + 2c = 508
�@a + b + c = 254 �D�D�D①
���ɁA�X�̓��_�����߂邽�߂ɁA�S�̘̂a����e�̘a�������܂��B
①����e����������
�@1. (c = 254 - (a + b) = 254 - 160 = 94)
�@2. (a = 254 - (b + c) = 254 - 172 = 82)
�@3. (b = 254 - (c + a) = 254 - 176 = 78)
�ł��_���������l��C�ŁA94�_�ł��B
���͋����A���͎���
A����͎���3.6�L���œo��
�@y = 3.6x�@....�@①
B�����30����Ɏ����ō~��i0.5���ԕ��̋����𑫂��܂��j
�@y + 2.4 = 4.8x
���ԓ_�ō��������̂Ŏ��̎������藧���܂��B
�@3.6x = 4.8x - 2.4
�@x = 2
①�̎��ɑ��
�@y=3.6�E2
�@y=7.2
���ԓ_��7.2km�ł��̂ŁA�{��14.4km�������ł��B
>>385
3�l�̐��k��A�AB�AC�Ƃ��܂��B���ꂼ��̓_����a�Ab�Ac�Ƃ��܂��B2�l���̕��ϓ_�����ꂼ��80�A86�A88�ł���̂ŁA�ȉ��̂悤�Ȏ������藧���܂��B
�@1. ((a + b) / 2 = 80) �� (a + b = 160)
�@2. ((b + c) / 2 = 86) �� (b + c = 172)
�@3. ((c + a) / 2 = 88) �� (c + a = 176)
������3�̕������������Ă����܂��B
�܂��A3�̕������𑫂����킹���
�@(a + b) + (b + c) + (c + a) = 160 + 172 + 176
�@2a + 2b + 2c = 508
�@a + b + c = 254 �D�D�D①
���ɁA�X�̓��_�����߂邽�߂ɁA�S�̘̂a����e�̘a�������܂��B
①����e����������
�@1. (c = 254 - (a + b) = 254 - 160 = 94)
�@2. (a = 254 - (b + c) = 254 - 172 = 82)
�@3. (b = 254 - (c + a) = 254 - 176 = 78)
�ł��_���������l��C�ŁA94�_�ł��B
2024/06/17(��) 01:59:04.66ID:fXzXrO6B
��l�ɂȂ��ĕK�v�ɂ����Đ��w����������Ă���A�ŏI�I�ɍ��Z���w���K�v�������w���w(���肵���珬�w�Z��)����Y��Ă���̂Łu�Ɗw�Łv����
�^��_���l�b�g���ɕ����ƁA�l�b�g�̏��͊ԈႢ���炯�A�m�̐�`���炯�A����Yahoo�m�b�܂�OKWave��QandA�̓}�E���g���Ō��ȋC���ɂȂ邵�A�R����ŋߊ�肽�����Ȃ�
Wikipedia�͓���������������M��������
AI�ɕ����Ă��A�ǂ�AI���ʁX�̉�(������������Ɛ����̂悤�ɉ��Ă��邩�炽��������)
SNS�͏���U���������������@�\�ɓ����̂ŁA�����͂قڕs�\
�w�Z�̋��ȏ��͓���s�\(���Z�Ȃ�`���[�g����̌n���w�H�������z�Ŏ�ɓ���l����)
�������������@�͂Ȃ��ł��傤���H
�@����Z�p�n�̌v�Z���炯�̎��i����邽�߂Ȃ̂ŁA�������̎Z��/���w��S���ԗ����Ă��Ӗ��͂Ȃ��ł�
�^��_���l�b�g���ɕ����ƁA�l�b�g�̏��͊ԈႢ���炯�A�m�̐�`���炯�A����Yahoo�m�b�܂�OKWave��QandA�̓}�E���g���Ō��ȋC���ɂȂ邵�A�R����ŋߊ�肽�����Ȃ�
Wikipedia�͓���������������M��������
AI�ɕ����Ă��A�ǂ�AI���ʁX�̉�(������������Ɛ����̂悤�ɉ��Ă��邩�炽��������)
SNS�͏���U���������������@�\�ɓ����̂ŁA�����͂قڕs�\
�w�Z�̋��ȏ��͓���s�\(���Z�Ȃ�`���[�g����̌n���w�H�������z�Ŏ�ɓ���l����)
�������������@�͂Ȃ��ł��傤���H
�@����Z�p�n�̌v�Z���炯�̎��i����邽�߂Ȃ̂ŁA�������̎Z��/���w��S���ԗ����Ă��Ӗ��͂Ȃ��ł�
2024/06/17(��) 02:22:11.65ID:YQ98ZGII
>>391
���Z���w�̔���������ł��ǂ�?
���Z���w�̔���������ł��ǂ�?
2024/06/17(��) 02:38:07.69ID:nY4Oyyjs
>>391
���ʂɍH�ƍ��Z�������̎��i���������p�̋��ނ͔����Ă邾��B
���ʂɍH�ƍ��Z�������̎��i���������p�̋��ނ͔����Ă邾��B
2024/06/17(��) 08:14:54.59ID:YQ98ZGII
���̂܂ܒ�o������͔͉ɂȂ�悤�ȃ��X�͏h��̊ۓ����Ȃǂ����̃J���j���O�̏��������Ă���悤�ȋC������̂�>386�݂����ȃ��X������Ǝv���B�܂��A�����V�[�Y���ł͂Ȃ�����X�J���낤���ǁB
395�P�R�Q�l�ڂ̑f������
2024/06/17(��) 08:59:38.95ID:swHUx0I5396�P�R�Q�l�ڂ̑f������
2024/06/17(��) 09:15:34.27ID:RivOl8Dh >>391
BookOFF�ŎQ�l����������������
BookOFF�ŎQ�l����������������
2024/06/17(��) 13:33:40.22ID:bK1Y/50a
�h��̓e�X�g�ł͂Ȃ�����A�J���j���O�Ƃ������̂̓i���Z���X�B�h��Ƃ͂�藝����[�߂邽�߂ɂ���B
���������A���������\������h����o������Ȃ��̂��B
���������A���������\������h����o������Ȃ��̂��B
398�P�R�Q�l�ڂ̑f������
2024/06/17(��) 14:19:34.65ID:Qm3KvmRS >>390
������₷�����肪�Ƃ��������܂����B
���Ȃ݂ɂ��̂Q��̉�@�́A���̕��ނł����Ɖ��Z�ɂȂ��ł��傤���H(�邩�ߎZ�A�j���[�g���Z�݂����ȕ��ނ���)
������₷�����肪�Ƃ��������܂����B
���Ȃ݂ɂ��̂Q��̉�@�́A���̕��ނł����Ɖ��Z�ɂȂ��ł��傤���H(�邩�ߎZ�A�j���[�g���Z�݂����ȕ��ނ���)
2024/06/17(��) 16:31:25.92ID:uzZhdygS
>>398
�����܂���A������܂���
���͑�̏������������ɂ��ĉ����Ă��邾���ł��̂ŁA���������g��Ȃ���������ł͎Q�l�ɐ���Ȃ������m��܂���ˁB
�����܂���A������܂���
���͑�̏������������ɂ��ĉ����Ă��邾���ł��̂ŁA���������g��Ȃ���������ł͎Q�l�ɐ���Ȃ������m��܂���ˁB
400�P�R�Q�l�ڂ̑f������
2024/06/17(��) 17:38:57.42ID:Qm3KvmRS >>399
�킩��܂����B���肪�Ƃ��������܂����B
�킩��܂����B���肪�Ƃ��������܂����B
2024/06/17(��) 18:03:48.63ID:2S0chmf2
>>389
���S�X���[����ē��S�ő�
���S�X���[����ē��S�ő�
402�C�i ��/7jUdUKiSM
2024/06/17(��) 18:44:58.49ID:n1gimzi/ �O>>342
xy���ʂ�x����ɐ�������y���ƂȂ�悤�������������p�`���ɍő�̐��O�p�`��`���ꍇ���l����B
�V��(0,(17(1+cos(��/7))/(2sin(��/7))�_�ɉE����y=17(1+cos(��/7)/2sin(��/7)-x��3��y=xtan(2��/7)-(17/2)sin(2��/7)�̌�_�Ƃ����y���ɂ��đΏ̂ȓ_�����Ԑ��O�p�`�̈�ӂ̒����́A
2x=(17sin(2��/7)+17+17cos(��/7))/(tan(2��/7)+��3)=13.2615155835�c�c
17�����ɂ������Ȃ����59�Ԃ�60�Ԃ̂������ɂ��錴�_(0,0)�𐳎O�p�`�̒��_�ɂ��A
y=x��3��y=-tan(3��/7)x+(17/2)tan(3��/7)+17sin(2��/7)/cos(3��/7)�̌�_����A
x=15.862�c
�ő�l31.7243271558�c�c��B
xy���ʂ�x����ɐ�������y���ƂȂ�悤�������������p�`���ɍő�̐��O�p�`��`���ꍇ���l����B
�V��(0,(17(1+cos(��/7))/(2sin(��/7))�_�ɉE����y=17(1+cos(��/7)/2sin(��/7)-x��3��y=xtan(2��/7)-(17/2)sin(2��/7)�̌�_�Ƃ����y���ɂ��đΏ̂ȓ_�����Ԑ��O�p�`�̈�ӂ̒����́A
2x=(17sin(2��/7)+17+17cos(��/7))/(tan(2��/7)+��3)=13.2615155835�c�c
17�����ɂ������Ȃ����59�Ԃ�60�Ԃ̂������ɂ��錴�_(0,0)�𐳎O�p�`�̒��_�ɂ��A
y=x��3��y=-tan(3��/7)x+(17/2)tan(3��/7)+17sin(2��/7)/cos(3��/7)�̌�_����A
x=15.862�c
�ő�l31.7243271558�c�c��B
2024/06/17(��) 21:13:20.82ID:AEbVLzv+
>>389
�������}���Ŕ���w
986�F�P�R�Q�l�ڂ̑f������F[sage]�F2024/06/17(��) 17:56:16.70 ID:9rnsZZ3V
���̃X���Ɉ����p�Ă��Ȗ��
�����F��~�W�c100�l��Phimose�����l���邩�������鎖�ɂȂ����B
���f�ł̒����͔ᔻ���o�邽�߈ȉ��̂悤�Ȏ菇�Œ��������B
�����F��~�ɃR�C���g�X���Ă��炤�B
�\���o���������o�����͎����F��~�����m��Ȃ��B
�\���o����Phimose���ۂ��𐳒��ɉ���B
�����o����Phimose���ۂ��ɊW�Ȃ�Phimose�ł���Ɖ���B
100�l�̒����̌��ʁA90�l��Phimose�ł���Ɠ������B
�����ɗp�����R�C�����������Ƃ���c�ȃR�C����100������75���ł��B
Phimose�̐l����95%�M����ԂŐ��肹��B
�v�Z�ɕK�v�ȏ����͓K�X�ݒ肵�Ă悢�B
992�F�P�R�Q�l�ڂ̑f������F2024/06/17(��) 20:42:29.12 ID:CqNQ/hEs
>>986
�����F�肳�ꂽ�̐}���߂��Ă���ۂlj����������̂�
��������p����������������~�߂�
�������}���Ŕ���w
986�F�P�R�Q�l�ڂ̑f������F[sage]�F2024/06/17(��) 17:56:16.70 ID:9rnsZZ3V
���̃X���Ɉ����p�Ă��Ȗ��
�����F��~�W�c100�l��Phimose�����l���邩�������鎖�ɂȂ����B
���f�ł̒����͔ᔻ���o�邽�߈ȉ��̂悤�Ȏ菇�Œ��������B
�����F��~�ɃR�C���g�X���Ă��炤�B
�\���o���������o�����͎����F��~�����m��Ȃ��B
�\���o����Phimose���ۂ��𐳒��ɉ���B
�����o����Phimose���ۂ��ɊW�Ȃ�Phimose�ł���Ɖ���B
100�l�̒����̌��ʁA90�l��Phimose�ł���Ɠ������B
�����ɗp�����R�C�����������Ƃ���c�ȃR�C����100������75���ł��B
Phimose�̐l����95%�M����ԂŐ��肹��B
�v�Z�ɕK�v�ȏ����͓K�X�ݒ肵�Ă悢�B
992�F�P�R�Q�l�ڂ̑f������F2024/06/17(��) 20:42:29.12 ID:CqNQ/hEs
>>986
�����F�肳�ꂽ�̐}���߂��Ă���ۂlj����������̂�
��������p����������������~�߂�
404�C�i ��/7jUdUKiSM
2024/06/17(��) 21:31:44.75ID:JU9hvVDq �O>>402
���17cm�̐����p�`�ɓ��ڂ��鐳�O�p�`�̖ʐς̍ő�l�́A
(��3/4)(2x)^2=x^2��3=(15.862�c�c)^2(��3)=435.798243803�c�c
���17cm�̐����p�`�ɓ��ڂ��鐳�O�p�`�̖ʐς̍ő�l�́A
(��3/4)(2x)^2=x^2��3=(15.862�c�c)^2(��3)=435.798243803�c�c
2024/06/18(��) 07:28:38.27ID:zb9MC2NK
2024/06/18(��) 08:11:28.70ID:9b9IyE/z
2024/06/18(��) 08:52:03.15ID:zb9MC2NK
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�APhimose���������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
Phimose����ɉł����邩�������鎖�ɂȂ����B
���f�ł̒����͔ᔻ���o�邽�߈ȉ��̂悤�Ȏ菇�Œ��������B
Phimose�ɃR�C���g�X���Ă��炤�B
�\���o���������o������Phimose�����m��Ȃ��B
�\���o����ł����邩�ۂ��𐳒��ɉ���B
�����o����ł̗L���ɊW�Ȃ��ł͂��Ȃ��ł���Ɖ���B
100��̒����̌��ʁA90�ł͂��Ȃ��Ɠ������B
�����ɗp�����R�C�����������Ƃ���c�ȃR�C���ł����500������120��\���ł��B
Phimose����ɉł����Ȃ��m������95%�M����ԂŐ��肹��B
�v�Z�ɕK�v�ȏ����͓K�X�ݒ肵�Ă悢�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�APhimose���������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
Phimose����ɉł����邩�������鎖�ɂȂ����B
���f�ł̒����͔ᔻ���o�邽�߈ȉ��̂悤�Ȏ菇�Œ��������B
Phimose�ɃR�C���g�X���Ă��炤�B
�\���o���������o������Phimose�����m��Ȃ��B
�\���o����ł����邩�ۂ��𐳒��ɉ���B
�����o����ł̗L���ɊW�Ȃ��ł͂��Ȃ��ł���Ɖ���B
100��̒����̌��ʁA90�ł͂��Ȃ��Ɠ������B
�����ɗp�����R�C�����������Ƃ���c�ȃR�C���ł����500������120��\���ł��B
Phimose����ɉł����Ȃ��m������95%�M����ԂŐ��肹��B
�v�Z�ɕK�v�ȏ����͓K�X�ݒ肵�Ă悢�B
2024/06/18(��) 08:55:15.37ID:zb9MC2NK
>>404
R�ł̐��l�v�Z
1�ӂ̒����P�Ōv�Z���ĖʐςȂ̂�17�O2�{
> ABC2S(A,B,C)*17^2
[1] 435.7982
�Ӓ��P�̂Ƃ��̍�}
https://i.imgur.com/VImvwXp.png
R�ł̐��l�v�Z
1�ӂ̒����P�Ōv�Z���ĖʐςȂ̂�17�O2�{
> ABC2S(A,B,C)*17^2
[1] 435.7982
�Ӓ��P�̂Ƃ��̍�}
https://i.imgur.com/VImvwXp.png
2024/06/18(��) 08:56:50.12ID:zb9MC2NK
>>406
���呲���O�p�����g���Ė��������Ă���Ȃ��B
���͓�������Ȃ��́H�Ђ���Ƃ��ăV���c�H
���̈Ӗ��������w���ɗ����ł���Ή�@�͖��Ȃ��B
�X���ł͂Ȃ�����ˁB
���呲���O�p�����g���Ė��������Ă���Ȃ��B
���͓�������Ȃ��́H�Ђ���Ƃ��ăV���c�H
���̈Ӗ��������w���ɗ����ł���Ή�@�͖��Ȃ��B
�X���ł͂Ȃ�����ˁB
2024/06/18(��) 11:27:37.28ID:Z55m7un4
389�̖��ɐf�Ï��ƕa�@�̋���������
��蕶�͏璷�߂��ėv�̂Ȃ�
��蕶�͏璷�߂��ėv�̂Ȃ�
2024/06/18(��) 11:47:08.99ID:zb9MC2NK
>>404
R�ł̌v�Z����Wolfram�ɈڐA���āA�����l���Z�o
https://i.imgur.com/M3hpGRY.png
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= r=E^(2 I Pi/7);
In[2]:= pI=Table[(1-r^i)/(1-r),{i,1,7}];
In[3]:= p={Re[#],Im[#]}& /@ pI;
In[4]:= pA={1/2,0};
In[5]:= pA0={0,1/2 Tan[2Pi/3]};
In[6]:= AA0={pA,pA0};
In[7]:= p23={p[[2]],p[[3]]};
In[8]:= pB=ResourceFunction["LineIntersection"][AA0,p23];
In[9]:= pA1={0,-1/2 Tan[2Pi/3]};
In[10]:= AA1={pA,pA1};
In[11]:= p56={p[[5]],p[[6]]};
In[12]:= pC=ResourceFunction["LineIntersection"][AA1,p56];
In[13]:= ABC=Triangle[{pA,pB,pC}];
In[14]:= Simplify[Area[ABC]*17^2]
Pi 9 Pi Pi Pi Pi 3 Pi
Out[14]= (289 Sqrt[3] Csc[--] (Cos[--] - Sin[--]) (99 - 190 Cos[--] - 206 Sin[--] + 198 Sin[----])) /
14 28 28 7 14 14
Pi 3 Pi Pi 3
> (1024 (1 + 2 Cos[--]) (Sqrt[3] + Cot[--]) (-2 + Csc[--])
7 14 14
5 Pi 5 Pi
> ((1 + Sqrt[3]) Cos[----] - (-1 + Sqrt[3]) Sin[----]))
28 28
In[15]:= N[%,100]
Out[15]= 435.798243803098791116740862414898068778358735602432960985137370817178136819362567800921869307\
> 9789475
���呲�̓��e�҂̌v�Z���ʂƍ��v�B
R�ł̌v�Z����Wolfram�ɈڐA���āA�����l���Z�o
https://i.imgur.com/M3hpGRY.png
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= r=E^(2 I Pi/7);
In[2]:= pI=Table[(1-r^i)/(1-r),{i,1,7}];
In[3]:= p={Re[#],Im[#]}& /@ pI;
In[4]:= pA={1/2,0};
In[5]:= pA0={0,1/2 Tan[2Pi/3]};
In[6]:= AA0={pA,pA0};
In[7]:= p23={p[[2]],p[[3]]};
In[8]:= pB=ResourceFunction["LineIntersection"][AA0,p23];
In[9]:= pA1={0,-1/2 Tan[2Pi/3]};
In[10]:= AA1={pA,pA1};
In[11]:= p56={p[[5]],p[[6]]};
In[12]:= pC=ResourceFunction["LineIntersection"][AA1,p56];
In[13]:= ABC=Triangle[{pA,pB,pC}];
In[14]:= Simplify[Area[ABC]*17^2]
Pi 9 Pi Pi Pi Pi 3 Pi
Out[14]= (289 Sqrt[3] Csc[--] (Cos[--] - Sin[--]) (99 - 190 Cos[--] - 206 Sin[--] + 198 Sin[----])) /
14 28 28 7 14 14
Pi 3 Pi Pi 3
> (1024 (1 + 2 Cos[--]) (Sqrt[3] + Cot[--]) (-2 + Csc[--])
7 14 14
5 Pi 5 Pi
> ((1 + Sqrt[3]) Cos[----] - (-1 + Sqrt[3]) Sin[----]))
28 28
In[15]:= N[%,100]
Out[15]= 435.798243803098791116740862414898068778358735602432960985137370817178136819362567800921869307\
> 9789475
���呲�̓��e�҂̌v�Z���ʂƍ��v�B
2024/06/18(��) 11:58:07.62ID:zb9MC2NK
>>410
�v�Z�ɋ����͕K�v�Ȃ����Ƃ��킩��Ȃ��A�z�����B
�v�Z�ɋ����͕K�v�Ȃ����Ƃ��킩��Ȃ��A�z�����B
2024/06/18(��) 12:39:23.69ID:zpwnTZ93
2024/06/18(��) 12:41:56.97ID:JV2EZe5y
2024/06/18(��) 20:04:02.21ID:JV2EZe5y
>>412
�����炠��Ȃɔ������Ă��̂Ƀ_���}������w
�����炠��Ȃɔ������Ă��̂Ƀ_���}������w
2024/06/18(��) 20:56:06.85ID:paRUzMRA
��̃o�C�g�Ȃ낤
2024/06/18(��) 21:00:50.63ID:JV2EZe5y
���H
�N����N�����ԊW�Ȃ���������ł邩�疳�E�ł���
��5������A������L�`�K�C����
�N����N�����ԊW�Ȃ���������ł邩�疳�E�ł���
��5������A������L�`�K�C����
2024/06/19(��) 06:07:04.96ID:1uPqQyo2
>>414
�i�U��̎��₳��Ď�����Ă�������ˁB
�i�U��̎��₳��Ď�����Ă�������ˁB
2024/06/19(��) 07:02:46.55ID:CTn4+WfR
2024/06/19(��) 07:17:02.06ID:CTn4+WfR
���Z���w�X�����肸�ɂ܂����Ă��݂������ȔA�r�W�W�CID:1uPqQyo2
����Ȃɍ��Z���Ƀo�J�ɂ��ꂽ�̂����������H�����w���ɂ��瑊��ɂ���ĂȂ��̂�w
����Ȃɍ��Z���Ƀo�J�ɂ��ꂽ�̂����������H�����w���ɂ��瑊��ɂ���ĂȂ��̂�w
2024/06/19(��) 10:08:08.17ID:0NOqbRz1
�����璆�Ƀv���O�����������U�炩���L�`�K�C�Ȃ̂�
2024/06/20(��) 07:46:15.46ID:Jh9+nZ7z
>>418
27�F�P�R�Q�l�ڂ̑f������F[sage]�F2024/06/20(��) 06:00:12.56 ID:uOyI2hYv
�\���ł�m����1/2�̃R�C���́A�\�Ɨ�����ʂł���ȏ�A���̊m���������Ƃ������Ƃ͂��肻���ɂȂ����A1/2�Ƃ��Čv�Z�����Ă���B
�T�C�R���̊e�X�̖ڂ̂ł�m����1/6�Ƃ����̂����l�B
�o��҂�
��1�ӂ̒�����17cm�̐����p�`��6�̒��_ABCDEF���^����ꂽ�Ƃ��A
�Ƃ����ݒ�ɂ��Ă���B
���K���
���q���Z��100�l��blowjob�o���҂����l���邩�������鎖�ɂȂ����B
�i��ނ͈�����i���ł��悢���A����͐G�@�s�ׂɂ�����j
�ȉ��̂悤�Ȏ菇�Œ��������B
���q���Z���ɃR�C���g�X���Ă��炤�B
�\���o���������o�����͏��q���Z�������m��Ȃ��B
�\���o����o���҂��ۂ��𐳒��ɉ���B
�����o����o���҂��ۂ��ɊW�Ȃ��o���҂ł���Ɖ���B
100�l�̒����̌��ʁA90�l���o���҂ł���Ɠ������B
�����ɗp�����R�C�����������Ƃ���c�ȃR�C���� 100������ �\��25��A����75�ł��B
���
�c�ȃR�C���̕\�̂ł�m���͏��1/4�Ƃ͌���Ȃ��Ƃ��������I�Ȑݒ�ŁA�o���҂̐l���� 95 %�M����ԂŐ��肹��i�ߎ������ʼnj�B
���A�v�Z�ɕK�v�ȏ����͓K�X�ݒ肵�Ă悢�B
27�F�P�R�Q�l�ڂ̑f������F[sage]�F2024/06/20(��) 06:00:12.56 ID:uOyI2hYv
�\���ł�m����1/2�̃R�C���́A�\�Ɨ�����ʂł���ȏ�A���̊m���������Ƃ������Ƃ͂��肻���ɂȂ����A1/2�Ƃ��Čv�Z�����Ă���B
�T�C�R���̊e�X�̖ڂ̂ł�m����1/6�Ƃ����̂����l�B
�o��҂�
��1�ӂ̒�����17cm�̐����p�`��6�̒��_ABCDEF���^����ꂽ�Ƃ��A
�Ƃ����ݒ�ɂ��Ă���B
���K���
���q���Z��100�l��blowjob�o���҂����l���邩�������鎖�ɂȂ����B
�i��ނ͈�����i���ł��悢���A����͐G�@�s�ׂɂ�����j
�ȉ��̂悤�Ȏ菇�Œ��������B
���q���Z���ɃR�C���g�X���Ă��炤�B
�\���o���������o�����͏��q���Z�������m��Ȃ��B
�\���o����o���҂��ۂ��𐳒��ɉ���B
�����o����o���҂��ۂ��ɊW�Ȃ��o���҂ł���Ɖ���B
100�l�̒����̌��ʁA90�l���o���҂ł���Ɠ������B
�����ɗp�����R�C�����������Ƃ���c�ȃR�C���� 100������ �\��25��A����75�ł��B
���
�c�ȃR�C���̕\�̂ł�m���͏��1/4�Ƃ͌���Ȃ��Ƃ��������I�Ȑݒ�ŁA�o���҂̐l���� 95 %�M����ԂŐ��肹��i�ߎ������ʼnj�B
���A�v�Z�ɕK�v�ȏ����͓K�X�ݒ肵�Ă悢�B
423�P�R�Q�l�ڂ̑f������
2024/06/21(��) 00:49:40.05ID:fSRPPQig �����́B���̖��̍l���������w���ł�����悤�ɉ�����肢���܂��B
�`�a�b�c�d�ɂ͂P�`�T�܂ł̐������d�����邱�ƂȂ�����܂��B
�ȉ��̂R�̎�����������悤�ɐ��������ĉ������B
�a�{�b���c�{�d
�a�~�b���`�{�c
�`�~�i�b�{�c�j���a�{�d
�`�a�b�c�d�ɂ͂P�`�T�܂ł̐������d�����邱�ƂȂ�����܂��B
�ȉ��̂R�̎�����������悤�ɐ��������ĉ������B
�a�{�b���c�{�d
�a�~�b���`�{�c
�`�~�i�b�{�c�j���a�{�d
2024/06/21(��) 00:50:25.84ID:ztHOV1SW
>>418
���Z���w�X���ł͍�����U�X�������Ă��̂ɂ����ł͋}�ɑ����Ȃ��Ȃ�����w
���w���ɑ���ɂ���Ȃ��������悤�₭�v���m�����̂��H
���Z���w�X���ł͍�����U�X�������Ă��̂ɂ����ł͋}�ɑ����Ȃ��Ȃ�����w
���w���ɑ���ɂ���Ȃ��������悤�₭�v���m�����̂��H
2024/06/21(��) 05:10:36.91ID:qk6ykT6y
�����Ƃ��ȒP�ŕ��ՓI�ȕ��@
1,1,1,1,1����5,5,5,5,5�܂ŁA5^5�ʂ���肷������B
> gr[apply(gr,1,f),]
A B C D E
651 1 1 2 1 2
1522 2 5 1 3 3
2023 3 5 1 2 4
1,1,1,1,1����5,5,5,5,5�܂ŁA5^5�ʂ���肷������B
> gr[apply(gr,1,f),]
A B C D E
651 1 1 2 1 2
1522 2 5 1 3 3
2023 3 5 1 2 4
2024/06/21(��) 05:12:43.89ID:qk6ykT6y
�d�����Ȃ��̂́A�Ō�� 3 5 1 2 4
2024/06/21(��) 05:22:12.15ID:qk6ykT6y
����120�ʂ�������āA����v�Z���������Ԃ����Ȃ����ȁB
�v���O�����Ȃ�ǂ����������B
> gr=expand.grid(1:5,1:5,1:5,1:5,1:5)
> colnames(gr)=LETTERS[1:5]
> f=\(x){
+ A=x[1]
+ B=x[2]
+ C=x[3]
+ D=x[4]
+ E=x[5]
+ B+C==D+E & B*C==A+D & A*(C+D)==B+E & length(unique(c(A,B,C,D,E)))==5
+ }
> gr[apply(gr,1,f),]
A B C D E
2023 3 5 1 2 4
> library(RcppAlgos)
> pm=permuteGeneral(1:5,5)
> colnames(pm)=LETTERS[1:5]
> pm[apply(pm,1,f),]
A B C D E
3 5 1 2 4
�����ւ̏o��
��L��Wolfram����ɈڐA����B
�v���O�����Ȃ�ǂ����������B
> gr=expand.grid(1:5,1:5,1:5,1:5,1:5)
> colnames(gr)=LETTERS[1:5]
> f=\(x){
+ A=x[1]
+ B=x[2]
+ C=x[3]
+ D=x[4]
+ E=x[5]
+ B+C==D+E & B*C==A+D & A*(C+D)==B+E & length(unique(c(A,B,C,D,E)))==5
+ }
> gr[apply(gr,1,f),]
A B C D E
2023 3 5 1 2 4
> library(RcppAlgos)
> pm=permuteGeneral(1:5,5)
> colnames(pm)=LETTERS[1:5]
> pm[apply(pm,1,f),]
A B C D E
3 5 1 2 4
�����ւ̏o��
��L��Wolfram����ɈڐA����B
2024/06/21(��) 05:28:33.16ID:qk6ykT6y
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= gr=Partition[Flatten[Table[{A,B,C,D,E},{A,Range[5]},{B,Range[5]},{C,Range[5]},{D,Range[5]},{E,Range[5]}]],5];
In[2]:= f[x_] := (
{a,b,c,d,e}=x;
b+c==d+e && b*c==a+d && a*(c+d)==b+e && Length[Union[x]]==5
)
In[3]:= Select[gr,f]
Out[3]= {{3, 5, 1, 2, 4}}
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= gr=Partition[Flatten[Table[{A,B,C,D,E},{A,Range[5]},{B,Range[5]},{C,Range[5]},{D,Range[5]},{E,Range[5]}]],5];
In[2]:= f[x_] := (
{a,b,c,d,e}=x;
b+c==d+e && b*c==a+d && a*(c+d)==b+e && Length[Union[x]]==5
)
In[3]:= Select[gr,f]
Out[3]= {{3, 5, 1, 2, 4}}
2024/06/21(��) 05:33:02.08ID:qk6ykT6y
Wolfram�ɂ�Permutations�Ƃ��������W����������Ă���̂ł�����g����
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= f[x_] := (
{a,b,c,d,e}=x;
b+c==d+e && b*c==a+d && a*(c+d)==b+e
)
In[2]:= Select[Permutations[Range[5]],f]
Out[2]= {{3, 5, 1, 2, 4}}
Combinations�Ƃ����������R���邾�낤�Ǝv���Ă�����A���݂��Ȃ��B
R����combn�Ƃ����̂��W����������Ă��邪�A����̕��͕W����������Ă��Ȃ��B
����ɂ͂��낢��Ȃ�����B
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= f[x_] := (
{a,b,c,d,e}=x;
b+c==d+e && b*c==a+d && a*(c+d)==b+e
)
In[2]:= Select[Permutations[Range[5]],f]
Out[2]= {{3, 5, 1, 2, 4}}
Combinations�Ƃ����������R���邾�낤�Ǝv���Ă�����A���݂��Ȃ��B
R����combn�Ƃ����̂��W����������Ă��邪�A����̕��͕W����������Ă��Ȃ��B
����ɂ͂��낢��Ȃ�����B
2024/06/21(��) 06:11:20.61ID:qk6ykT6y
���K���
�`�a�b�c�d�ɂ͂O�`�X�܂ł̐������d�����邱�ƂȂ�����܂��B
�ȉ��̂R�̎�����������悤�ɐ��������ĉ������B
�a�{�b���c�{�d
�a�~�b���`�{�c
�`�~�i�b�{�c�j���a�{�d
�`�a�b�c�d�ɂ͂O�`�X�܂ł̐������d�����邱�ƂȂ�����܂��B
�ȉ��̂R�̎�����������悤�ɐ��������ĉ������B
�a�{�b���c�{�d
�a�~�b���`�{�c
�`�~�i�b�{�c�j���a�{�d
2024/06/21(��) 06:27:17.42ID:eccGIOoF
>>423
�E�����̗��ӂ̂����Z�͋����ɂȂ�
�E�����Z�̍ő�l�Ƃ����Z�̍ŏ��l���l�����
���Ă͂܂�ꍇ�����Ȃ����ڂ��
�Ȃǂ𗘗p���āA���l�߂ŏ��Ԃɒl�������܂�
B�{C��D�{E ... (1)
B�~C��A�{D ... (2)
A�~(C�{D)��B�{E ... (3)
�͂��߂�A�̒l���l���܂�
1����5�܂ł�S��������15�Ŋ�A
(1)���AB, C, D, E�������ƁA���������ӂ̘a��
�����ɂȂ�̂ŁAA�͊��1, 3, 5��
�����ꂩ�ɂȂ�܂�
A=5�ɂ���ƁA(3)�̍��ӂ̍ŏ���5*(1+2)=15�A
�E�ӂ̍ő傪4+5=9�Ő��藧���܂���
A=1�ɂ���ƁA(2)��2*3=1+5�̂Ƃ��̂�
���藧���܂����A(1)��2+3=5+E�ƂȂ�
E=0�łȂ��ƂȂ炸�A���藧���܂���
�����A=3�Ƃ킩��܂�
�E�����̗��ӂ̂����Z�͋����ɂȂ�
�E�����Z�̍ő�l�Ƃ����Z�̍ŏ��l���l�����
���Ă͂܂�ꍇ�����Ȃ����ڂ��
�Ȃǂ𗘗p���āA���l�߂ŏ��Ԃɒl�������܂�
B�{C��D�{E ... (1)
B�~C��A�{D ... (2)
A�~(C�{D)��B�{E ... (3)
�͂��߂�A�̒l���l���܂�
1����5�܂ł�S��������15�Ŋ�A
(1)���AB, C, D, E�������ƁA���������ӂ̘a��
�����ɂȂ�̂ŁAA�͊��1, 3, 5��
�����ꂩ�ɂȂ�܂�
A=5�ɂ���ƁA(3)�̍��ӂ̍ŏ���5*(1+2)=15�A
�E�ӂ̍ő傪4+5=9�Ő��藧���܂���
A=1�ɂ���ƁA(2)��2*3=1+5�̂Ƃ��̂�
���藧���܂����A(1)��2+3=5+E�ƂȂ�
E=0�łȂ��ƂȂ炸�A���藧���܂���
�����A=3�Ƃ킩��܂�
2024/06/21(��) 06:37:58.72ID:eccGIOoF
>>431�̑���
B�{C��D�{E ... (1)
B�~C��A�{D ... (2)
A�~(C�{D)��B�{E ... (3)
A=3���A(3)��3*(1+2)=4+5�̂Ƃ��̂ݐ��藧��
(C, D)=(1, 2)�܂���(2, 1),
(B, E)=(4, 5)�܂���(5, 4)�ƂȂ�܂�
(1)���B��C, D��E�́A�傫�����Ə���������
�g�ł���Ƃ��̂ݓ��������藧�̂�
(B, C, D, E)=(4, 2, 1, 5)�܂���(5, 1, 2, 4)�ƂȂ�܂�
���̂���(2)�����藧�̂́A��҂��g����
5*1=3+2�݂̂ł��̂�
(A, B, C, D, E)=(3, 5, 1, 2, 4) ... (��)
�ƂȂ�܂�
B�{C��D�{E ... (1)
B�~C��A�{D ... (2)
A�~(C�{D)��B�{E ... (3)
A=3���A(3)��3*(1+2)=4+5�̂Ƃ��̂ݐ��藧��
(C, D)=(1, 2)�܂���(2, 1),
(B, E)=(4, 5)�܂���(5, 4)�ƂȂ�܂�
(1)���B��C, D��E�́A�傫�����Ə���������
�g�ł���Ƃ��̂ݓ��������藧�̂�
(B, C, D, E)=(4, 2, 1, 5)�܂���(5, 1, 2, 4)�ƂȂ�܂�
���̂���(2)�����藧�̂́A��҂��g����
5*1=3+2�݂̂ł��̂�
(A, B, C, D, E)=(3, 5, 1, 2, 4) ... (��)
�ƂȂ�܂�
2024/06/21(��) 07:28:47.88ID:i8PSRu4u
���p���
�`�a�b�c�d�ɂ͂O�`�X�܂ł̐������d�����邱�ƂȂ�����܂��B
�ȉ��̂R�̎�����������悤�ɐ��������ĉ������B
�a�{�b���c�{�d
�a�~�b���`�{�c
�`�~�i�b�{�c�j���a�~�d
���Ȃ�
�`�a�b�c�d�ɂ͂O�`�X�܂ł̐������d�����邱�ƂȂ�����܂��B
�ȉ��̂R�̎�����������悤�ɐ��������ĉ������B
�a�{�b���c�{�d
�a�~�b���`�{�c
�`�~�i�b�{�c�j���a�~�d
���Ȃ�
2024/06/21(��) 12:24:48.17ID:MHnt81Vf
�����̎Z���ȊO���Ƃ�����Ă���z�A�R�e��t���Ă��NG�ɏo����̂ɁA�{���ɖ��f�Ȕy����
435423
2024/06/21(��) 13:26:34.63ID:fSRPPQig �F���肪�Ƃ��������܂��B
���̖��͊�{�I�ɓ��Ă͂߂Ă�����@�Ȃ�ł��ˁB
���̒��w�̖��̓��x���I�ɂ͂��Ȃ�Ղ����̂ł����A
�Ō�̂P�₾�����x�����S�R�Ⴄ���Ԃ���������(�������ꍇ�̐���)�������Ă����ł���ˁB
���_����点�Ȃ����߂̂��̂Ȃ�ł��傤���H
���̖��͊�{�I�ɓ��Ă͂߂Ă�����@�Ȃ�ł��ˁB
���̒��w�̖��̓��x���I�ɂ͂��Ȃ�Ղ����̂ł����A
�Ō�̂P�₾�����x�����S�R�Ⴄ���Ԃ���������(�������ꍇ�̐���)�������Ă����ł���ˁB
���_����点�Ȃ����߂̂��̂Ȃ�ł��傤���H
436�C�i ��/7jUdUKiSM
2024/06/21(��) 13:48:51.63ID:YmYUTkgu2024/06/21(��) 16:57:38.26ID:hJWv4Ajb
>>429
�A���^�̓��{����ǂ��̃}�k�P�ȃ`���p������ȂN���ʂ��Ȃ��Ǝv������
�A���^�̓��{����ǂ��̃}�k�P�ȃ`���p������ȂN���ʂ��Ȃ��Ǝv������
2024/06/21(��) 18:27:04.12ID:i8PSRu4u
�L���ȃp�Y��������
S E N D�@�{�@M O R E�@���@ M O N E Y
S E N D�@�{�@M O R E�@���@ M O N E Y
2024/06/21(��) 19:22:40.31ID:d0ZP5xFG
�@9 5 6 7
+ 1 0 8 5
---------
1 0 6 5 2
+ 1 0 8 5
---------
1 0 6 5 2
2024/06/21(��) 20:12:18.70ID:i8PSRu4u
SEND�@MORE MONEY �́@Python�ł̋c�_
https://stackoverflow.com/questions/37450302/send-more-money-puzzle-in-python
���̂悤�ȏ��w�҂�Wolfram����̗��K�ɂ����B
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= str="SEND + MORE = MONEY";
In[2]:= Union@StringSplit[StringDelete[str,{" ","+","="}],""];
In[3]:= pm=Permutations[Range[0,9],{8}];
In[4]:= f[x_] := (
{d,e,m,n,o,r,s,y}=x;
Total[{s,e,n,d}*{1000,100,10,1}]+Total[{m,o,r,e}*{1000,100,10,1}]==Total[{m,o,n,e,y}*{10000,1000,100,10,1}] && s!=0 && m!=0
)
In[5]:= {d,e,m,n,o,r,s,y}=Flatten@Select[pm,f];
In[6]:= {s,e,n,d," + ",m,o,r,e," = ",m,o,n,e,y}
Out[6]= {9, 5, 6, 7, + , 1, 0, 8, 5, = , 1, 0, 6, 5, 2}
https://stackoverflow.com/questions/37450302/send-more-money-puzzle-in-python
���̂悤�ȏ��w�҂�Wolfram����̗��K�ɂ����B
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= str="SEND + MORE = MONEY";
In[2]:= Union@StringSplit[StringDelete[str,{" ","+","="}],""];
In[3]:= pm=Permutations[Range[0,9],{8}];
In[4]:= f[x_] := (
{d,e,m,n,o,r,s,y}=x;
Total[{s,e,n,d}*{1000,100,10,1}]+Total[{m,o,r,e}*{1000,100,10,1}]==Total[{m,o,n,e,y}*{10000,1000,100,10,1}] && s!=0 && m!=0
)
In[5]:= {d,e,m,n,o,r,s,y}=Flatten@Select[pm,f];
In[6]:= {s,e,n,d," + ",m,o,r,e," = ",m,o,n,e,y}
Out[6]= {9, 5, 6, 7, + , 1, 0, 8, 5, = , 1, 0, 6, 5, 2}
2024/06/21(��) 20:17:21.35ID:tDBxjmUX
>>440
���{����s���R�݂��������Ǐ��w�҂Ȃ́H
���w���ł���6�N�ȏ�͕����Ă�͂������A���^����10�{�ȏ㐶���Ă�W�W�C�Ȃ̂ɂ���ȉ��Ȃ̂��Hw
���{����s���R�݂��������Ǐ��w�҂Ȃ́H
���w���ł���6�N�ȏ�͕����Ă�͂������A���^����10�{�ȏ㐶���Ă�W�W�C�Ȃ̂ɂ���ȉ��Ȃ̂��Hw
2024/06/21(��) 20:29:31.66ID:i8PSRu4u
���p���
SEND + MUCH = MONEY
SEND + MUCH = MONEY
2024/06/21(��) 20:30:56.19ID:i8PSRu4u
���������ł���l��>439�݂����ȓ��e������Ȃ��B
2024/06/21(��) 20:33:21.65ID:i8PSRu4u
>>440
����stackoverflow�̋c�_�͗l�X�Ȑl�������̃R�[�h�𓊍e���Ă��ĎQ�l�ɂȂ�B
����stackoverflow�̋c�_�͗l�X�Ȑl�������̃R�[�h�𓊍e���Ă��ĎQ�l�ɂȂ�B
2024/06/21(��) 20:34:44.52ID:9pPhlDx8
�ܘ_�p����s���R�Ȃ̂ł���w
724 ���̖��������� (ܯ��� 3358-8TD4 [14.13.16.0])[sage] 2022/10/05(��) 13:30:27.35 ID:rczEbvNg0
I told my colleage nureses that I have such allergy to beauties that I feel itchy everywhere when I work with them.
Ahahahahahah
>colleage
>nureses
920 ���̖��������� (JP 0H52-BsRZ [217.138.212.122 [�㋉����]])[sage] 2023/03/24(��) 15:55:12.52 ID:sCq5Ou+HH
��X�T��septick shock�̊��ҁA���ӂȃi�[�X�ɕ�����������H�����n�܂��Ă��܂���Ƌ����Ă��ꂽ�B
��x���܂Ŗ������������̂����ꂽ�����ŋC����( �E�́E)��!!
��V���ǂ�������
>septick shock
724 ���̖��������� (ܯ��� 3358-8TD4 [14.13.16.0])[sage] 2022/10/05(��) 13:30:27.35 ID:rczEbvNg0
I told my colleage nureses that I have such allergy to beauties that I feel itchy everywhere when I work with them.
Ahahahahahah
>colleage
>nureses
920 ���̖��������� (JP 0H52-BsRZ [217.138.212.122 [�㋉����]])[sage] 2023/03/24(��) 15:55:12.52 ID:sCq5Ou+HH
��X�T��septick shock�̊��ҁA���ӂȃi�[�X�ɕ�����������H�����n�܂��Ă��܂���Ƌ����Ă��ꂽ�B
��x���܂Ŗ������������̂����ꂽ�����ŋC����( �E�́E)��!!
��V���ǂ�������
>septick shock
2024/06/21(��) 20:52:11.15ID:5GkReiGb
�r�炵�Ă��鎩�o�������낤��
2024/06/21(��) 20:54:08.19ID:5GkReiGb
�v���O���~���O�X���ɍs�������̂�
2024/06/21(��) 20:55:46.25ID:rjDU8tlo
�ǂ��������Ă������ł��Ȃ��L�`�K�C�`���p���W�[������O��I�Ƀo�J�ɂ��Ă��ȊO�Ɏg�����Ȃ���w
2024/06/21(��) 21:04:40.88ID:rjDU8tlo
>>444
43�F���̖��������� (ܯ��� 07a4-wBP/ [240b:11:241:7900:*])�F2024/06/21(��) 20:58:31.19 ID:CesFRxFl0
>>41
���[���A�r�W�W�C�N���{��킩��H
�����v�������Ȃ�������ăR�s�y�������Ɖ�b���藧���Ȃ�������www
�������O�ɔl�|�����o���Ȃ�phimose�N��~
�Ƃ������Ă����ǂ��O�͔l�|����܂Ƃ��ɏo���Ăˁ[�����
�l�|����o���Ȃ��A�r�W�W�C����͉łǂ��납�F�B�����Ȃ����낤�B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ�www
���̂���������������߂�
�u�l�͈�҂ł����ł������Ċ̍זE�����킩��Ȃ��f�l�ł����߂�Ȃ����v
���đf���Ɏӂ�����H
43�F���̖��������� (ܯ��� 07a4-wBP/ [240b:11:241:7900:*])�F2024/06/21(��) 20:58:31.19 ID:CesFRxFl0
>>41
���[���A�r�W�W�C�N���{��킩��H
�����v�������Ȃ�������ăR�s�y�������Ɖ�b���藧���Ȃ�������www
�������O�ɔl�|�����o���Ȃ�phimose�N��~
�Ƃ������Ă����ǂ��O�͔l�|����܂Ƃ��ɏo���Ăˁ[�����
�l�|����o���Ȃ��A�r�W�W�C����͉łǂ��납�F�B�����Ȃ����낤�B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ�www
���̂���������������߂�
�u�l�͈�҂ł����ł������Ċ̍זE�����킩��Ȃ��f�l�ł����߂�Ȃ����v
���đf���Ɏӂ�����H
2024/06/21(��) 22:18:33.01ID:i8PSRu4u
���p���@KICK / MY = ASS
�L���Ȗ��Ȃ�A��������Γ����݂��邾�낤���ǁA�����ŎZ�o�ł��Ȃ���p�ł��Ȃ��B
KICK/MY��ASS�́AChatGPT�i�����Łj�͌듚�����B
�H��
�����ׂẲ������X�g�A�b�v���邱�Ƃ͓���ł����A���̃p�^�[�����킩��悤�Ɉꕔ�̉��������܂����B���̖��ł́A�����̑g�ݍ��킹�����݂��A���ꂼ��̑g�ݍ��킹�ɑ���
𝐾
𝐼
𝐶
𝐾
𝑀
𝑌
=
𝐴
𝑆
𝑆
MY
KICK
=ASS���������邱�Ƃ��m�F����Ă��܂��B
�L���Ȗ��Ȃ�A��������Γ����݂��邾�낤���ǁA�����ŎZ�o�ł��Ȃ���p�ł��Ȃ��B
KICK/MY��ASS�́AChatGPT�i�����Łj�͌듚�����B
�H��
�����ׂẲ������X�g�A�b�v���邱�Ƃ͓���ł����A���̃p�^�[�����킩��悤�Ɉꕔ�̉��������܂����B���̖��ł́A�����̑g�ݍ��킹�����݂��A���ꂼ��̑g�ݍ��킹�ɑ���
𝐾
𝐼
𝐶
𝐾
𝑀
𝑌
=
𝐴
𝑆
𝑆
MY
KICK
=ASS���������邱�Ƃ��m�F����Ă��܂��B
2024/06/21(��) 22:37:59.43ID:i8PSRu4u
SEND�@MORE = MONEY�݂����ɓ���1��ނɂȂ�������͓̂���Ȃ�
���@�e�A���t�@�x�b�g��1���̔����Ƃ��ā@SEND + SEXY = GIRLS�@�����g�ݍ��킹�͉���ނ��邩�H
���@�e�A���t�@�x�b�g��1���̔����Ƃ��ā@SEND + SEXY = GIRLS�@�����g�ݍ��킹�͉���ނ��邩�H
2024/06/21(��) 22:58:14.45ID:5GkReiGb
�v���O���~���O�X�����ƃo�J�ɂ���邩��A�����Ŗ\��Ă���̂���
2024/06/22(�y) 10:24:31.38ID:twcYzvwb
�{�E�̃v���O���}�[�Ȃ�ȒP�����ċc�_�ɂ���Ȃ�Ȃ����낤�B
>442�Ƃ����j��H�⎩��Ńp�����Ă��悤�Ȃ��́B
������̖������͓̂���ȁB
>442�Ƃ����j��H�⎩��Ńp�����Ă��悤�Ȃ��́B
������̖������͓̂���ȁB
2024/06/22(�y) 10:29:27.79ID:mT+IDwU/
>>453
�c�_�ɂ���Ȃ�Ȃ����Ă��Ƃ͌��Ǒ���ɂ���Ȃ�����X���`�Ŕ������Ă���Ă��Ƃ����A�z��
�c�_�ɂ���Ȃ�Ȃ����Ă��Ƃ͌��Ǒ���ɂ���Ȃ�����X���`�Ŕ������Ă���Ă��Ƃ����A�z��
2024/06/22(�y) 10:32:05.35ID:twcYzvwb
�Z�o�ł���l�͓��𓊍e���Ă���B
�܂������������X�����A�����邯�ǂˁB
�܂������������X�����A�����邯�ǂˁB
2024/06/22(�y) 10:37:25.90ID:/PEwBY+H
2024/06/22(�y) 12:55:04.18ID:/PEwBY+H
>>455
������Ƃڂ��Ă����̂��قړ��������ʐl�Ƃ͓���v���Ȃ���`���p��
���w���ɂ��瑊��ɂ���ĂȂ��A���^���ʐl������m�\�ȂȂ�����ȁHw
������Ƃڂ��Ă����̂��قړ��������ʐl�Ƃ͓���v���Ȃ���`���p��
���w���ɂ��瑊��ɂ���ĂȂ��A���^���ʐl������m�\�ȂȂ�����ȁHw
2024/06/22(�y) 17:36:38.26ID:/PEwBY+H
�}�������ă_���}�����ߍ��ނ����Ȃ��悤����w
2024/06/22(�y) 20:41:47.51ID:/PEwBY+H
�A�r�W�W�C��ID:i8PSRu4u��ID:twcYzvwb�����X�W
204 ���̖��������� (ܯ��� a2ac-LsQ7 [2a09:bac1:3b40:90:* [�㋉����]]) sage 2024/02/17(�y) 08:38:10.94 ID:3ZmiJkYX0
���̂���30��40���EGD�͏��߂ĂƂ����l��3�l�قǂ����B
�܂��A�������ɉ�b���Ȃ���C��킹�Ė����Ɍ����I���B
����̂ق����s���ڂ������Ȃ��Ă����ˁB
�Î~�摜���ƃs���ڂ��̂��Ƃ�����B
�ʐ^�������̂ق������ꂢ�ł���A�����̊Ō�w����������ł���I��
�������Ă��邗��
T-SPOT�̃W���[�N��X�|���W�̖A�W���[�N�����Ă����y�����E��B
�������������͉�ʂ��݂Ȃ��������G�k���Ă�����������������I������C�������Ƃ����l�������ł���
�Ƃ����Ă���B
�����I�����ɂ͐������I�����Ă���̂Ō��f���Ɨ]�T��1���Ԃ�5�������Ȃ���B
���N�x���T2��Ζ��̌_��X�V�����B
���낢��Ȉ�t�Ɍ������Ă���������������������Ȃ��Ƃ͎v���B
���낢��Ȑl�ɂ���Ă���������������ł���A�Ƃ����ƃi�[�X�����ނ�����
207 ���̖��������� (ܯ��� a315-AH9r [240a:61:1057:dacd:*]) 2024/02/17(�y) 12:20:37.61 ID:hcpgkURy0
>>204
�����������ɓ˂����܂�Ă�̂�
�������ɂǂ�����Ċ��҂���b�o����www
���������ǂ�����A���������Ⴂ���Ȃ����̂��������Ă���̂��H
��
���R�̂悤�ɂ��̌�̓_���}��www
204 ���̖��������� (ܯ��� a2ac-LsQ7 [2a09:bac1:3b40:90:* [�㋉����]]) sage 2024/02/17(�y) 08:38:10.94 ID:3ZmiJkYX0
���̂���30��40���EGD�͏��߂ĂƂ����l��3�l�قǂ����B
�܂��A�������ɉ�b���Ȃ���C��킹�Ė����Ɍ����I���B
����̂ق����s���ڂ������Ȃ��Ă����ˁB
�Î~�摜���ƃs���ڂ��̂��Ƃ�����B
�ʐ^�������̂ق������ꂢ�ł���A�����̊Ō�w����������ł���I��
�������Ă��邗��
T-SPOT�̃W���[�N��X�|���W�̖A�W���[�N�����Ă����y�����E��B
�������������͉�ʂ��݂Ȃ��������G�k���Ă�����������������I������C�������Ƃ����l�������ł���
�Ƃ����Ă���B
�����I�����ɂ͐������I�����Ă���̂Ō��f���Ɨ]�T��1���Ԃ�5�������Ȃ���B
���N�x���T2��Ζ��̌_��X�V�����B
���낢��Ȉ�t�Ɍ������Ă���������������������Ȃ��Ƃ͎v���B
���낢��Ȑl�ɂ���Ă���������������ł���A�Ƃ����ƃi�[�X�����ނ�����
207 ���̖��������� (ܯ��� a315-AH9r [240a:61:1057:dacd:*]) 2024/02/17(�y) 12:20:37.61 ID:hcpgkURy0
>>204
�����������ɓ˂����܂�Ă�̂�
�������ɂǂ�����Ċ��҂���b�o����www
���������ǂ�����A���������Ⴂ���Ȃ����̂��������Ă���̂��H
��
���R�̂悤�ɂ��̌�̓_���}��www
2024/06/23(��) 07:35:33.71ID:gsvPd9mp
�_���}���Ƃ�������I
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�APhimose���������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
���������l���Ȃ��́H
���p���@KICK / MY = ASS
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�APhimose���������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
���������l���Ȃ��́H
���p���@KICK / MY = ASS
2024/06/23(��) 08:42:58.17ID:znCMi46e
>>460
�_���}���Ƃ�������I
48�F���̖���������F2023/12/24(��) 08:57:19.87 ID:JCuuYtoN
�֏�b��x�т��C�ǂƂ������Ă�A�z����
�����F�߂悤�Ƃ��������̃N�\�X���Ŕ����������U�Ř_�j����ă_���}���A�܂������̖������[�vw
�����A�r�`���p���W�W�C
�����ӂ̃`���p���]�����()�̋C�ǐ؊J�̌��͂����_�j����ă_���}�����ߍ��ނ����Ȃ��̂��H
�_���}���Ƃ�������I
48�F���̖���������F2023/12/24(��) 08:57:19.87 ID:JCuuYtoN
�֏�b��x�т��C�ǂƂ������Ă�A�z����
�����F�߂悤�Ƃ��������̃N�\�X���Ŕ����������U�Ř_�j����ă_���}���A�܂������̖������[�vw
�����A�r�`���p���W�W�C
�����ӂ̃`���p���]�����()�̋C�ǐ؊J�̌��͂����_�j����ă_���}�����ߍ��ނ����Ȃ��̂��H
2024/06/23(��) 08:43:51.61ID:cpMc+1Yh
���Z���ɂ��o�J�ɂ��ꏬ�w���ɂ�����ɂ���Ȃ�60�߂��̃W�W�C����
2024/06/23(��) 10:35:35.75ID:znCMi46e
64�F���̖��������� (ܯ��� 35c7-B6NT [124.47.76.122 [�㋉����]])�F[sage]�F2024/06/23(��) 07:29:43.28 ID:U8Wjlt2K0
���w�ɏo�肳�ꂽ����Wolfram�̃v���O�����l�^�ɂ��邱�Ƃ�
Brute Force(�������肵�ăt�B���^�����O�j�Ɓ@Monte Carlo�i�������������ẴV�~�����[�V�����j
�ŎZ�o�ł���悤�ɂ͂Ȃ������A��}�͂����ς�肪����B
���ꂽR����
https://i.imgur.com/DTvmlG4.png
https://i.imgur.com/ioGM3Ii.gif
�Ƃ�������B
�܂��A��}�ɂ͂��قnj����l�͕K�v�Ȃ��̂�
���ہAR�ʼn~��`���̂ɐ��P�O�O�p�`�ŕ`�o���Ă���B
R�ʼn~����p�`��`�����͎��삷��K�v������B
�Q�����̌�_�����߂�̂�������B
�a�@�E��Ҕł�����Ȃ��Ƃ��u�c�u�c��������ł�F�m�ǂ̖͗l
���w�ɏo�肳�ꂽ����Wolfram�̃v���O�����l�^�ɂ��邱�Ƃ�
Brute Force(�������肵�ăt�B���^�����O�j�Ɓ@Monte Carlo�i�������������ẴV�~�����[�V�����j
�ŎZ�o�ł���悤�ɂ͂Ȃ������A��}�͂����ς�肪����B
���ꂽR����
https://i.imgur.com/DTvmlG4.png
https://i.imgur.com/ioGM3Ii.gif
�Ƃ�������B
�܂��A��}�ɂ͂��قnj����l�͕K�v�Ȃ��̂�
���ہAR�ʼn~��`���̂ɐ��P�O�O�p�`�ŕ`�o���Ă���B
R�ʼn~����p�`��`�����͎��삷��K�v������B
�Q�����̌�_�����߂�̂�������B
�a�@�E��Ҕł�����Ȃ��Ƃ��u�c�u�c��������ł�F�m�ǂ̖͗l
2024/06/24(��) 11:28:13.96ID:Nr1RiiNR
�}���ƌ����R��
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�A
Phimose���������������ȁB
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�A
Phimose���������������ȁB
2024/06/24(��) 15:03:27.56ID:Buzcr0ds
�A�r�W�W�C���ĔN����N���������甭�����Ă邩�疳�E����Hw
2024/06/24(��) 19:18:59.75ID:TxPAO4XS
>>464
����ς�}��������I�E���Ԃ��Ŕ������邵���Ȃ��݂�������w
�����������������������Ȃ��ē��{��ɂȂ��ĂȂ����H
�}�W�ŏ��w���ȉ��̒m�\�����Ȃ��݂������˔A�r�`���p���W�W�C����w
����ς�}��������I�E���Ԃ��Ŕ������邵���Ȃ��݂�������w
�����������������������Ȃ��ē��{��ɂȂ��ĂȂ����H
�}�W�ŏ��w���ȉ��̒m�\�����Ȃ��݂������˔A�r�`���p���W�W�C����w
2024/06/24(��) 20:17:16.78ID:S9qGtZzf
>>463
Wolfram�œ����̍�}�⓮����쐬���ē��呲�̃X�L���������������������B
Wolfram�œ����̍�}�⓮����쐬���ē��呲�̃X�L���������������������B
2024/06/24(��) 20:24:35.63ID:TxPAO4XS
469�P�R�Q�l�ڂ̑f������
2024/06/26(��) 14:39:43.62ID:bY3NEIrB470�P�R�Q�l�ڂ̑f������
2024/06/26(��) 14:49:41.29ID:9PLPc3vX �o�c���������✖
2024/06/26(��) 16:15:02.76ID:u9kSR8FU
�A�����J���ł��ꂪ�����Ȃ�H
2024/06/26(��) 19:23:42.73ID:nciRCHC2
>>471
tally marks�̈�킩��
tally marks�̈�킩��
473�C�i ��/7jUdUKiSM
2024/06/27(��) 13:53:53.74ID:K0n8iaFw2024/06/27(��) 20:46:01.98ID:Bq48nU5g
>>467
�A�r�W�W�C���w���Ƀo�J�ɂ���ă_���}������
�A�r�W�W�C���w���Ƀo�J�ɂ���ă_���}������
2024/07/03(��) 10:21:30.22ID:6z+xan68
�_���}���Ƃ�������I
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�APhimose���������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
���������l���Ȃ��́H
���p���@KICK / MY = ASS
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�APhimose���������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�ȊO�ɂł���̂̓R�s�y��foreskin�M�肾�낤�Ȃ��B
���������l���Ȃ��́H
���p���@KICK / MY = ASS
2024/07/03(��) 13:44:22.39ID:mwpRcJ/c
�܂��R�s�y�Ŕ�������
�]����Â��`���p���Z�����l�^��݂��������������Ƃ������
�]����Â��`���p���Z�����l�^��݂��������������Ƃ������
2024/07/03(��) 13:52:49.09ID:s+S3Orp7
�����̉�������̂�
�Z���␔�w�̖��Ƃ��Ă͕s�K
��̓c�[��
ttps://www.dcode.fr/cryptarithm-solver
�o�͌���
KICK/MY = ASS
9 solution(s)
�� 4784/16 = 299
�� 6596/17 = 388
�� 6786/13 = 522
�� 6956/37 = 188
�� 7847/59 = 133
�� 8208/57 = 144
�� 8358/42 = 199
�� 8708/14 = 622
�� 8798/53 = 166
�Z���␔�w�̖��Ƃ��Ă͕s�K
��̓c�[��
ttps://www.dcode.fr/cryptarithm-solver
�o�͌���
KICK/MY = ASS
9 solution(s)
�� 4784/16 = 299
�� 6596/17 = 388
�� 6786/13 = 522
�� 6956/37 = 188
�� 7847/59 = 133
�� 8208/57 = 144
�� 8358/42 = 199
�� 8708/14 = 622
�� 8798/53 = 166
2024/07/03(��) 20:17:49.24ID:d3Ky81Xi
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= str="KICK / MY = ASS";
In[2]:= ToLowerCase@Union@StringSplit[StringDelete[str,{" ","+","-","*","/","="}],""];
In[3]:= pm=Permutations[Range[0,9],{7}];
In[4]:= f1[z_] := (
{a, c, i, k, m, s, y}=z;
Total[{k,i,c,k}*{1000,100,10,1}] / Total[{m,y}*{10,1}]==Total[{a,s,s}*{100,10,1}] && k!=0 && m!=0 && a!=0
)
In[5]:= re=Select[pm,f1];
In[6]:= f2[z_] := (
{a, c, i, k, m, s, y}=z;
{k,i,c,k," / ",m,y," = ",a,s,s}
)
In[7]:= MatrixForm[f2 /@ re]
Out[7]//MatrixForm= 8 2 0 8 / 5 7 = 1 4 4
7 8 4 7 / 5 9 = 1 3 3
8 3 5 8 / 4 2 = 1 9 9
6 9 5 6 / 3 7 = 1 8 8
8 7 9 8 / 5 3 = 1 6 6
4 7 8 4 / 1 6 = 2 9 9
6 5 9 6 / 1 7 = 3 8 8
6 7 8 6 / 1 3 = 5 2 2
8 7 0 8 / 1 4 = 6 2 2
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= str="KICK / MY = ASS";
In[2]:= ToLowerCase@Union@StringSplit[StringDelete[str,{" ","+","-","*","/","="}],""];
In[3]:= pm=Permutations[Range[0,9],{7}];
In[4]:= f1[z_] := (
{a, c, i, k, m, s, y}=z;
Total[{k,i,c,k}*{1000,100,10,1}] / Total[{m,y}*{10,1}]==Total[{a,s,s}*{100,10,1}] && k!=0 && m!=0 && a!=0
)
In[5]:= re=Select[pm,f1];
In[6]:= f2[z_] := (
{a, c, i, k, m, s, y}=z;
{k,i,c,k," / ",m,y," = ",a,s,s}
)
In[7]:= MatrixForm[f2 /@ re]
Out[7]//MatrixForm= 8 2 0 8 / 5 7 = 1 4 4
7 8 4 7 / 5 9 = 1 3 3
8 3 5 8 / 4 2 = 1 9 9
6 9 5 6 / 3 7 = 1 8 8
8 7 9 8 / 5 3 = 1 6 6
4 7 8 4 / 1 6 = 2 9 9
6 5 9 6 / 1 7 = 3 8 8
6 7 8 6 / 1 3 = 5 2 2
8 7 0 8 / 1 4 = 6 2 2
2024/07/03(��) 20:19:39.99ID:d3Ky81Xi
>>476
�_���}���Ƃ�������I
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�APhimose���������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�_���}���Ƃ�������I
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�APhimose���������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
2024/07/03(��) 20:50:22.34ID:mwpRcJ/c
2024/07/03(��) 21:22:44.85ID:mwpRcJ/c
�A�r�W�W�CID:d3Ky81Xi�̓L�`�K�C�����ĉƑ��܂߃��A���ł͒N������ɂ��Ă���Ȃ����炱���ŔN�����x�Ŕ������Ă�H���Ɉ���
2024/07/04(��) 05:07:03.48ID:ovsqhlRy
>>480
�ǂ����}���̂悤���ȁB
�ǂ����}���̂悤���ȁB
2024/07/04(��) 08:15:32.98ID:TvNUuKfN
2024/07/05(��) 14:04:50.12ID:nb2hD6Ry
�����͓������o�C�g�̓�
�����I������̂ŋA��Ԃ̈ړ�����Wolfram�̃v���O�����쐬�B
�����I������̂ŋA��Ԃ̈ړ�����Wolfram�̃v���O�����쐬�B
2024/07/05(��) 18:18:03.94ID:/mRst0ra
2024/07/05(��) 18:53:28.20ID:rndobBzI
>>484�����̏�����O�Ȉ�̔A�r�W�W�C���_���}�����ߍ���ł���
882�F���̖��������� (ܯ��� c3d6-KQ+b [240b:11:241:7900:*])�F2024/06/09(��) 06:24:07.24 ID:4fjzozfw0
>>881
�Տ����www���O�{���n���Ȃ�
���Ⴀ���̏�����O�Ȃ̂��O�ɖ��o���Ă���
�����̉摜�̕a���́H
https://i.imgur.com/dCrMTtn.jpeg
883�F���̖��������� (ܯ��� 13cc-EeFD [114.145.56.79])�F[sage]�F2024/06/09(��) 06:37:47.32 ID:JHmHgQHX0
>>882
�̎��
>874�̓��́H
885�F���̖��������� (ܯ��� c3d6-KQ+b [240b:11:241:7900:*])�F2024/06/09(��) 08:42:52.82 ID:4fjzozfw0
>>883
�̎��www�A�o�E�g�߂���
�̎�ᇂɂǂꂾ����ނ���Ǝv���Ă��
��ᇂȂ�ĉ摜�݂��瓖����O����
���̎�ᇂ������Ă����ϑf�l����www
882�F���̖��������� (ܯ��� c3d6-KQ+b [240b:11:241:7900:*])�F2024/06/09(��) 06:24:07.24 ID:4fjzozfw0
>>881
�Տ����www���O�{���n���Ȃ�
���Ⴀ���̏�����O�Ȃ̂��O�ɖ��o���Ă���
�����̉摜�̕a���́H
https://i.imgur.com/dCrMTtn.jpeg
883�F���̖��������� (ܯ��� 13cc-EeFD [114.145.56.79])�F[sage]�F2024/06/09(��) 06:37:47.32 ID:JHmHgQHX0
>>882
�̎��
>874�̓��́H
885�F���̖��������� (ܯ��� c3d6-KQ+b [240b:11:241:7900:*])�F2024/06/09(��) 08:42:52.82 ID:4fjzozfw0
>>883
�̎��www�A�o�E�g�߂���
�̎�ᇂɂǂꂾ����ނ���Ǝv���Ă��
��ᇂȂ�ĉ摜�݂��瓖����O����
���̎�ᇂ������Ă����ϑf�l����www
2024/07/05(��) 21:06:29.31ID:tBGgu4jn
https://i.imgur.com/XLWNmwg.jpg
����2500P+2500P����ɓ���܂��B
����2500P+2500P����ɓ���܂��B
2024/07/05(��) 23:01:16.97ID:JJnQKMXB
2024/07/05(��) 23:21:33.09ID:UbSD5mwl
�摜�̓A�t�B���G�C�g���e
�ʕ�
�ʕ�
2024/07/06(�y) 04:44:33.72ID:yMckpGyt
2024/07/06(�y) 04:45:31.27ID:yMckpGyt
�_���}���Ƃ�������I
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�APhimose���������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
���w�����[���B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�APhimose���������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
���w�����[���B
2024/07/06(�y) 07:59:08.97ID:8CO9dPTi
>>490
�̑�����Ȃ��Ă���������ȂȂ番���邾��^�R
�̑�����Ȃ��Ă���������ȂȂ番���邾��^�R
2024/07/06(�y) 08:06:20.89ID:8CO9dPTi
�ł��Ĕz��҂̂��Ƃ���Ȃ������
�����������Ȃ����{��s���R�ȔA�r�`���p���W�W�C�͎��ʂ܂ł����ł��������ł��Ȃ��݂�������w
�����������Ȃ����{��s���R�ȔA�r�`���p���W�W�C�͎��ʂ܂ł����ł��������ł��Ȃ��݂�������w
2024/07/06(�y) 14:21:12.89ID:GHG9Lr7i
>>490
196�F���̖��������� (ܯ��� d97b-Mie6 [240a:61:111c:4cf3:*])�F2024/07/06(�y) 11:49:08.50 ID:uxrfK1H80
>>194
����̓q�h��
490 �P�R�Q�l�ڂ̑f������ sage 2024/07/06(�y) 04:44:33.72 ID:yMckpGyt
>>488
EGD����̑���������I
�����l����킩��B
���W�I�g�łĂ��Ă���Rcm�R�ȉ��͏�������Ȃ̎d���������ȁB
��
������O�Ȃ����̂��ĂĂ��̌�����͎�������҂���Ȃ����Č����Ă�悤�Ȃ���
�Ƃ��������C��ł��̍זE�����̎�ᇂ��Č���ˁ[��www�������Ă�ȃR�C�c
196�F���̖��������� (ܯ��� d97b-Mie6 [240a:61:111c:4cf3:*])�F2024/07/06(�y) 11:49:08.50 ID:uxrfK1H80
>>194
����̓q�h��
490 �P�R�Q�l�ڂ̑f������ sage 2024/07/06(�y) 04:44:33.72 ID:yMckpGyt
>>488
EGD����̑���������I
�����l����킩��B
���W�I�g�łĂ��Ă���Rcm�R�ȉ��͏�������Ȃ̎d���������ȁB
��
������O�Ȃ����̂��ĂĂ��̌�����͎�������҂���Ȃ����Č����Ă�悤�Ȃ���
�Ƃ��������C��ł��̍זE�����̎�ᇂ��Č���ˁ[��www�������Ă�ȃR�C�c
2024/07/06(�y) 21:51:05.58ID:0yo8AHQ/
�{���̔A�r�W�W�C���ՏIw
2024/07/07(��) 01:32:45.68ID:/uviiCug
�������A�r�W�W�CID:yMckpGyt�܂����肸�ɑ������甭������
2024/07/07(��) 08:08:01.78ID:/uviiCug
2024/07/08(��) 04:58:37.55ID:DuLx6+M3
>>476
�_���}���Ƃ�������I
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�APhimose���������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�_���}���Ƃ�������I
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�҂������Ȃ����ď����瑊��ɂ���Ȃ����炩�APhimose���������������ȁB
Phimose����Ɠǂ炻������Ɠ����Ă����Ȃ��B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
�l�|�����ł��Ȃ�Phimose����͉ł����Ȃ����낤�B
2024/07/08(��) 16:10:23.55ID:VTmJh4aH
�܂��R�s�y�Ŕ���w
�A�r�W�W�C�͉Ƒ��ɂ�����ɂ���ĂȂ�����ww
�A�r�W�W�C�͉Ƒ��ɂ�����ɂ���ĂȂ�����ww
500�P�R�Q�l�ڂ̑f������
2024/07/12(��) 14:34:10.70ID:6l6dPBYz 500!
2024/07/14(��) 07:59:50.17ID:JHic7zmk
>>499
�łƋ�����ƂŃL�b�V����������B
�����D���̓����i�[�X������A�ǂ��Ă�����ƖJ�߂Ă�������B
https://i.imgur.com/IJGqBMU.png
�łƋ�����ƂŃL�b�V����������B
�����D���̓����i�[�X������A�ǂ��Ă�����ƖJ�߂Ă�������B
https://i.imgur.com/IJGqBMU.png
2024/07/14(��) 09:45:46.81ID:ZcHkHXHw
2024/07/15(��) 22:13:27.35ID:zk0SJaAD
���ǁA���炪��ԑ厖�Ƃ�������
������
�������̂��c�O��퐯�h���Ƃ��������Č�����
������
�������̂��c�O��퐯�h���Ƃ��������Č�����
504�P�R�Q�l�ڂ̑f������
2024/07/15(��) 22:30:55.50ID:k4ox/BAq 2021�㔼�@�D�O�U��7.69�@�^�l����1.75
505�P�R�Q�l�ڂ̑f������
2024/07/15(��) 22:34:29.29ID:VOyu71E8 �����ɉ��������Ă��邾���Ȃ�
506�P�R�Q�l�ڂ̑f������
2024/07/15(��) 22:38:09.77ID:enOCo5DF �����A�j���I���̂ɂ��̏����\���Ƃ����猩�Ă݂����ǂ����ł��Ȃ����炾��
507�P�R�Q�l�ڂ̑f������
2024/07/15(��) 22:44:23.37ID:KlJ//mRW >>95
�킪���Ђ���݂Ŏ���
�킪���Ђ���݂Ŏ���
508�P�R�Q�l�ڂ̑f������
2024/07/15(��) 23:07:50.02ID:w0A59TF4 ��������
����Ȃ炻��͎�`�ʂ̓t���[�o�[���x�ł������
����������
����Ȃ炻��͎�`�ʂ̓t���[�o�[���x�ł������
����������
509�P�R�Q�l�ڂ̑f������
2024/07/15(��) 23:21:17.71ID:Qpnz4NpC �������� �����ӂ̃z���b�`���E�s���E������E�B����
2024/07/15(��) 23:37:07.19ID:vzLIXYiE
�͕̂��ʔ�����������
2024/07/28(��) 14:16:42.38ID:IMo3Uknc
����40�߂��̂���������
���w���K���������Ă�̂ł���
-54��(-9)+3
=-6+3
=-2
�ŕs�����Ȃ�ł������̂ł����H
���w���K���������Ă�̂ł���
-54��(-9)+3
=-6+3
=-2
�ŕs�����Ȃ�ł������̂ł����H
2024/07/28(��) 14:48:43.89ID:a2D0ZHyV
(-54)��(-9)
�́A�����̓}�C�i�X����}�C�i�X�Ńv���X
��Βl��54����9��6
���̎����A�����Z�Ɗ���Z���ԈႦ�Ă�̂Œ���
�Ō�܂Ōv�Z�����
(-54)��(-9)�{3
��6�{3
��9
�́A�����̓}�C�i�X����}�C�i�X�Ńv���X
��Βl��54����9��6
���̎����A�����Z�Ɗ���Z���ԈႦ�Ă�̂Œ���
�Ō�܂Ōv�Z�����
(-54)��(-9)�{3
��6�{3
��9
2024/07/28(��) 15:09:33.80ID:IMo3Uknc
���肪�Ƃ��������܂��B
2024/07/28(��) 16:43:13.93ID:IMo3Uknc
12�~(-5)-(-16)
=60-1�~(-16)
=60+16
=76
������ԈႦ�Ă���悤�ł���
��{+�~+=+�@-�~-=�{�@�{�~-=�{�ō����Ă܂����H
=60-1�~(-16)
=60+16
=76
������ԈႦ�Ă���悤�ł���
��{+�~+=+�@-�~-=�{�@�{�~-=�{�ō����Ă܂����H
515�P�R�Q�l�ڂ̑f������
2024/07/30(��) 03:54:29.78ID:mR4lnI/F2024/07/30(��) 09:02:24.55ID:tv01dW62
>>515
���肪�Ƃ��������܂��B
���肪�Ƃ��������܂��B
517�P�R�Q�l�ڂ̑f������
2024/08/02(��) 21:27:34.45ID:1jggTbRe ���̖��P���Ă�������
�����A�`�E�������R��a,b�����߂Ȃ����B
�A�@a��b��2���̎��R���ŁAb��a��4�{�ł���B
�C�@a+b��3���̎��R���ɂȂ�B
�E�@a�͐��̖�4�����Ab�͐��̖�12���B
�����A�`�E�������R��a,b�����߂Ȃ����B
�A�@a��b��2���̎��R���ŁAb��a��4�{�ł���B
�C�@a+b��3���̎��R���ɂȂ�B
�E�@a�͐��̖�4�����Ab�͐��̖�12���B
2024/08/03(�y) 00:07:07.44ID:MbUM6Z1K
>>517
a��2���̐��A4�{����b��2���̐�
5�{����a+b��3���̐�
�̏�������
4a��100, 5a��100
����������� a��25, a��20
a��20, 21, 22, 23, 24�̂����ꂩ�ƂȂ�܂�
�̌��͑f���������̌`�Ō��܂�܂�
��4�Ȃ�
a�� �f����3�� �܂��� 2�̑f���̐�
�ł��̂�a�� 21=3�~7, 22=2�~11 �ɍi���܂�
4�{����b�͖�12�� �̏�������
a�� 2�ł͂Ȃ�2�̑f���̐� �Ƃ킩��
a=21, b=84 �������ƂȂ�܂�
a��2���̐��A4�{����b��2���̐�
5�{����a+b��3���̐�
�̏�������
4a��100, 5a��100
����������� a��25, a��20
a��20, 21, 22, 23, 24�̂����ꂩ�ƂȂ�܂�
�̌��͑f���������̌`�Ō��܂�܂�
��4�Ȃ�
a�� �f����3�� �܂��� 2�̑f���̐�
�ł��̂�a�� 21=3�~7, 22=2�~11 �ɍi���܂�
4�{����b�͖�12�� �̏�������
a�� 2�ł͂Ȃ�2�̑f���̐� �Ƃ킩��
a=21, b=84 �������ƂȂ�܂�
519�P�R�Q�l�ڂ̑f������
2024/08/03(�y) 00:16:02.60ID:Pb2+JVRR 517�ł��B>>518�l���肪�Ƃ��������܂��B
����ȓ���̂�������Ȃ�Ă������������l�Ȃ�ł��傤�ˁB
����ȓ���̂�������Ȃ�Ă������������l�Ȃ�ł��傤�ˁB
2024/08/03(�y) 14:12:22.56ID:PWdeOkwv
���K���
�����A~�E�������R��a,b�̑g�ݍ��킹�͉��ʂ肠�邩�����߂Ȃ����B
�A�@a��b��3���̎��R���ŁAb��a��4�{�ł���B
�C�@a+b��4���̎��R���ɂȂ�B
�E�@a�͐��̖�4�����Ab�͐��̖�8���B
�����A~�E�������R��a,b�̑g�ݍ��킹�͉��ʂ肠�邩�����߂Ȃ����B
�A�@a��b��3���̎��R���ŁAb��a��4�{�ł���B
�C�@a+b��4���̎��R���ɂȂ�B
�E�@a�͐��̖�4�����Ab�͐��̖�8���B
2024/08/03(�y) 14:17:42.24ID:h3SVsvHe
�����A��������
2024/08/03(�y) 14:24:25.57ID:PWdeOkwv
�Ђ����琔����Γ����o������
�̐����ł�����4���̎��R����S�ē�����B
�̐����ł�����4���̎��R����S�ē�����B
2024/08/03(�y) 18:19:09.71ID:DTGcotgB
>>522
4���͈̔͂Ŗ̐����ł��������R����840�ł���A���̖̌���32�ł��B���̖��́A�f����������v�Z�@�Ȋw�ȂǁA�l�X�ȕ���̒m����g�ݍ��킹�邱�Ƃʼn������邱�Ƃ��ł��܂��B
4���͈̔͂Ŗ̐����ł��������R����840�ł���A���̖̌���32�ł��B���̖��́A�f����������v�Z�@�Ȋw�ȂǁA�l�X�ȕ���̒m����g�ݍ��킹�邱�Ƃʼn������邱�Ƃ��ł��܂��B
2024/08/03(�y) 19:11:11.47ID:t1cmlQ87
>>520
�A�r�W�W�C���w���ɂ��o�J�ɂ��ꂽ�����H
�A�r�W�W�C���w���ɂ��o�J�ɂ��ꂽ�����H
2024/08/03(�y) 19:37:16.74ID:GdfAIT41
7560
9240
64��
���ꏬ���w�Z�ŏo���肩�H
9240
64��
���ꏬ���w�Z�ŏo���肩�H
2024/08/03(�y) 22:21:27.46ID:t1cmlQ87
>>525
http://hissi.org/read.php/math/20240803/UFdkZU9rd3Y.html
��������X���`�ȏ�Ƀg���`���J���ȃA�z���v���w()��A�����č��Z���ɎU�X�_�j���ꔭ�����U�炩���Ă����̉����o�Ȃ��Ȃ����̂ō��x��(60�߂��̖ꂳ��)�����w���Ƀh���肽�����߂ɋv�X�ɓo�ꂵ�܂���ww
http://hissi.org/read.php/math/20240803/UFdkZU9rd3Y.html
��������X���`�ȏ�Ƀg���`���J���ȃA�z���v���w()��A�����č��Z���ɎU�X�_�j���ꔭ�����U�炩���Ă����̉����o�Ȃ��Ȃ����̂ō��x��(60�߂��̖ꂳ��)�����w���Ƀh���肽�����߂ɋv�X�ɓo�ꂵ�܂���ww
2024/08/04(��) 05:27:48.10ID:eWKdvndb
2024/08/04(��) 06:58:45.62ID:eX3Agsbu
>>526
���w�̃X���ň�w�̘b�Ƃ��A���ς�炸�X���`�Ȏ������Ă����
���w�̃X���ň�w�̘b�Ƃ��A���ς�炸�X���`�Ȏ������Ă����
2024/08/04(��) 09:10:31.11ID:HVNtPP3Q
�X���Ⴂ�̎w�E��>527�̕ԓ��Ƃ��A����̈ӌ������Ɏ����̌����������Ƃ�������Ȃ��̂́A�V�l���s���ǂɂ悭������ǏˁB
�ŏ��A�X�N���v�g���Ǝv������w
�ŏ��A�X�N���v�g���Ǝv������w
2024/08/04(��) 12:12:08.89ID:LAbFN1bJ
>>527
�ɐ^�삾��
�ɐ^�삾��
2024/08/04(��) 13:59:23.33ID:LAbFN1bJ
2024/08/08(��) 23:48:47.38ID:XZ2x6ewC
���ꂪ�ǂ��H���ɍs����
������
���ۍ�����20�N�͌���Ȃ���ˁH
������
���ۍ�����20�N�͌���Ȃ���ˁH
2024/08/08(��) 23:57:56.38ID:TnrPL+pj
535�P�R�Q�l�ڂ̑f������
2024/08/09(��) 00:01:15.70ID:eqIa9aTL536�P�R�Q�l�ڂ̑f������
2024/08/09(��) 00:42:08.91ID:DTSZwjo/ 8���D�җ~�������ǔ����Ɣ��N�͊܂݂���
537�P�R�Q�l�ڂ̑f������
2024/08/09(��) 01:02:41.62ID:AyyMaChr ����ȂɔR���Ĉُ�Ȃ����Č��ʏo����̂���
�Y�������ێ�ʊW�Ȃ���ȁB
���\�t���Ă̂���Ԑg�̌��������
���z�_�ɋ߂����ǂ�
�Y�������ێ�ʊW�Ȃ���ȁB
���\�t���Ă̂���Ԑg�̌��������
���z�_�ɋ߂����ǂ�
538�P�R�Q�l�ڂ̑f������
2024/08/09(��) 01:58:44.44ID:TZ/K6l8I ���ʂ܂ł�5,6�����x�����Ό�̎���
������Ȃ��Ď�������a����������
������Ȃ��Ď�������a����������
2024/08/09(��) 02:28:19.07ID:+bCVZaAC
>>81
�l�̐��b���邱�Ƃ����肵����Ă�Έ�ۂ���������낤
�l�̐��b���邱�Ƃ����肵����Ă�Έ�ۂ���������낤
2024/08/09(��) 10:28:32.69ID:AI+FuW/P
>>527���A�r�W�W�C
��2�̖������ł��邱�Ƃ��ؖ��ł����ɔ���ww
https://rio2016.5ch.net/test/read.cgi/math/1721071007/
��2�̖������ł��邱�Ƃ��ؖ��ł����ɔ���ww
https://rio2016.5ch.net/test/read.cgi/math/1721071007/
2024/08/15(��) 09:00:48.05ID:bFfiJSUV
���w�������̖��
���l�@�Ɓ@���l�łȂ��l�Ƃ͂ǂ��炪�����ł��傤��?
���l�@�Ɓ@���l�łȂ��l�Ƃ͂ǂ��炪�����ł��傤��?
2024/08/15(��) 18:31:22.37ID:VwZ/RstM
��b���o���ĂȂ��Ǝv���Ĉٕ���̑����Z���痚�C���Ă邯�ǁA
�ŏ����{���Ƃ��ő���{���Ƃ��ʕ��Ƃ�����肾�����̂��v���o�����B
YouTube�őf���������ŏo����̂�m���Ă���Ă݂ĕs�����������č��͊y�����Z������Ă�B
�ŏ����{���Ƃ��ő���{���Ƃ��ʕ��Ƃ�����肾�����̂��v���o�����B
YouTube�őf���������ŏo����̂�m���Ă���Ă݂ĕs�����������č��͊y�����Z������Ă�B
2024/08/15(��) 19:22:15.61ID:k34L4Drp
>>541
chat GPT�ɕ����Ȃ��ƕ�����Ȃ��A�z�����w�ɂ���͗l
chat GPT�ɕ����Ȃ��ƕ�����Ȃ��A�z�����w�ɂ���͗l
2024/08/16(��) 04:28:49.70ID:bNupVHmJ
2024/08/16(��) 07:25:17.00ID:JgPOBpGC
�E�U�������GPT�œK���ɂ����炦�Ηǂ���Ȃ�
���������ʼnx��ł���̂�����
���������ʼnx��ł���̂�����
546�P�R�Q�l�ڂ̑f������
2024/08/19(��) 20:34:34.55ID:YB/r4ymt �����ŏՓ�
�ǂ��������t���H
���̐l�̐��������
�ǂ��������t���H
���̐l�̐��������
547�P�R�Q�l�ڂ̑f������
2024/08/19(��) 20:45:12.83ID:iOUF/PNH �C���������X�^���v�����
����������
����������
548�P�R�Q�l�ڂ̑f������
2024/08/19(��) 20:53:17.08ID:K1saLbL22024/08/19(��) 21:02:38.96ID:qS79jxCY
�킢��ZORN���炢���������C�ɂȂ��
550�P�R�Q�l�ڂ̑f������
2024/08/19(��) 21:12:10.45ID:M7oW4Pk92024/08/19(��) 21:13:13.00ID:SS1zM1I2
���ꂪ�{���Ȃ炫�������������̌����̊��ɂ����ĂȂ����Č����Ȃ����������������������������😭
2024/08/19(��) 21:28:38.50ID:dztgIQTT
�c����NISA�ɉېł��Ă̂͂�������
553�P�R�Q�l�ڂ̑f������
2024/08/19(��) 21:51:39.05ID:VGRkaVx2 �̏d����������
�c���7�h�͍����ɂƂ��Ă͐V���@���Ƀ]�b�R���Ȃ̂ł͂��߂��Ă����v�f�����邪
�d���������ɂȂ�����
�A�C�X�^300�~�O��ł�����~�����Ⴍ�A�����Ă���
�c���7�h�͍����ɂƂ��Ă͐V���@���Ƀ]�b�R���Ȃ̂ł͂��߂��Ă����v�f�����邪
�d���������ɂȂ�����
�A�C�X�^300�~�O��ł�����~�����Ⴍ�A�����Ă���
554�P�R�Q�l�ڂ̑f������
2024/08/19(��) 22:27:35.75ID:IqvituFi555�P�R�Q�l�ڂ̑f������
2024/08/19(��) 22:36:21.44ID:KBE33jim �ǂ�������ˁI
�f�}��������h������
�}�W�łт����肵�Ă�
�f�}��������h������
�}�W�łт����肵�Ă�
2024/08/19(��) 22:42:37.69ID:d6XArCvJ
�ˋ�̔ԍ��ł������Ȃ̂ɂ���ĂăK�b�J������DQN�̐여��Ɠ������e�̌��@�Ăɔ�����Ƃ���
https://i.imgur.com/dC2cufK.jpeg
https://i.imgur.com/dC2cufK.jpeg
557�P�R�Q�l�ڂ̑f������
2024/08/19(��) 22:57:07.26ID:/g5l0ICI ���ʂƂ������킯�킩���N�\�����u�������Ƃ�������
��K�Ȃ�ł���
��K�Ȃ�ł���
558�P�R�Q�l�ڂ̑f������
2024/08/19(��) 23:02:00.02ID:UtPkWuse ���b�N�o���h�Ƃ��Ȃ犄�ƂƂ�ł��Ȃ����́A12�N���Ԃɂ��Ă�����
https://i.imgur.com/CjOenuv.jpg
https://i.imgur.com/CjOenuv.jpg
2024/08/19(��) 23:24:30.96ID:8I6feLMG
����������I
560�P�R�Q�l�ڂ̑f������
2024/08/19(��) 23:27:01.94ID:0GWADTfP561�P�R�Q�l�ڂ̑f������
2024/08/19(��) 23:30:31.01ID:OMWF5m9E ����2�������炢�ɂȂ��ĂȂ����ǁA�悭������I�ז���I�v�Ƃ��U�X�ᔻ����Ƃ����l�B���Ċ�������
562�P�R�Q�l�ڂ̑f������
2024/08/19(��) 23:43:59.88ID:TuWh8Fdq ����͖{�̂��H������Y�������Ƃ����
�K�[�V�[������U�肵�ăK�[�V�[�ƐM�҂ɂ��]��������
�K�[�V�[������U�肵�ăK�[�V�[�ƐM�҂ɂ��]��������
2024/08/21(��) 20:29:41.10ID:J5AvLBS7
���̍l�@�ł͂Ȃ��ē��R�Ȃ̂����A
18�`20����ł����ȁA����������C�Ȃ���������
�����s���������B
18�`20����ł����ȁA����������C�Ȃ���������
�����s���������B
564�P�R�Q�l�ڂ̑f������
2024/08/21(��) 21:50:27.97ID:VH9wWPxc565�P�R�Q�l�ڂ̑f������
2024/08/21(��) 21:59:30.20ID:LrNo2xm7 �v���{�ł���������̂��������ӂňُ킪��������Ȃ���Βʉߓ_�Ƃ��Ă���Ȏd���ɂ������Ȃ�
�t�@�b�I�H
Twitter�ŃC�L�邱�Ƃ�������
���͈���łȂ��Ɩ������Ă�̂���m��Ȃ���҂̘b������������
�t�@�b�I�H
Twitter�ŃC�L�邱�Ƃ�������
���͈���łȂ��Ɩ������Ă�̂���m��Ȃ���҂̘b������������
566�P�R�Q�l�ڂ̑f������
2024/08/22(��) 11:42:29.70ID:VOli7Aq1 �I�[���O���[���I�V���N����2�p�[�Z���g
567�P�R�Q�l�ڂ̑f������
2024/08/22(��) 11:47:04.19ID:rqcf3+0E ��҂͐��܂���Ȃ̂��Ǝv����
�������킩��
�q�X���Ȃ�Z�[�t�����
�܂�3���������o�ė~�����B
�������킩��
�q�X���Ȃ�Z�[�t�����
�܂�3���������o�ė~�����B
568�P�R�Q�l�ڂ̑f������
2024/08/22(��) 12:28:25.72ID:fclsKMUt �ǂ�ȉ��E�����\�V���Q�̂ق����܂�����I���
���肵���琭����サ�Ă܂��@���Č@���Ă�
�t��JK��JK�̎���A�j�����������
���肵���琭����サ�Ă܂��@���Č@���Ă�
�t��JK��JK�̎���A�j�����������
569�P�R�Q�l�ڂ̑f������
2024/08/23(��) 17:41:13.01ID:mSd5lbVR 3^2+4^2 = 25 �ł����A
����ȊO�Ł@3^x+4^y ��25�̔{���ɂȂ邱�Ƃ͂���܂����H
����ȊO�Ł@3^x+4^y ��25�̔{���ɂȂ邱�Ƃ͂���܂����H
2024/08/23(��) 19:56:38.51ID:oS373kvh
>>569
�ق��ɂ������ɂ���܂�
3^0, 3^1, 3^2, ...
4^0, 4^1, 4^2, ...
��25�Ŋ������]������߂��
3^20, 4^10
�̗]�肪1�ɂȂ�A�]��̐��̃p�^�[����
20�ʂ��10�ʂ�ł��邱�Ƃ��킩��܂�
�����̂����A������25�ɂȂ�
�a��25�Ŋ�������̂�T����
3^0+4^5, 3^2+4^2, 3^4+4^9, 3^6+4^6, 3^8+4^3,
3^10+4^0, 3^12+4^7, 3^14+4^4, 3^16+4^1, 3^18+4^8
��10�ʂ肪������Ƃ킩��܂�
3�̎w����+20, +40, ...
4�̎w����+10, +20, ...
�Ƃ��Ă����藧�̂�
���߂���͖����ɂ��邱�ƂɂȂ�܂�
�ق��ɂ������ɂ���܂�
3^0, 3^1, 3^2, ...
4^0, 4^1, 4^2, ...
��25�Ŋ������]������߂��
3^20, 4^10
�̗]�肪1�ɂȂ�A�]��̐��̃p�^�[����
20�ʂ��10�ʂ�ł��邱�Ƃ��킩��܂�
�����̂����A������25�ɂȂ�
�a��25�Ŋ�������̂�T����
3^0+4^5, 3^2+4^2, 3^4+4^9, 3^6+4^6, 3^8+4^3,
3^10+4^0, 3^12+4^7, 3^14+4^4, 3^16+4^1, 3^18+4^8
��10�ʂ肪������Ƃ킩��܂�
3�̎w����+20, +40, ...
4�̎w����+10, +20, ...
�Ƃ��Ă����藧�̂�
���߂���͖����ɂ��邱�ƂɂȂ�܂�
571�P�R�Q�l�ڂ̑f������
2024/08/24(�y) 01:05:38.53ID:4+Qc5Uv6 �����ɂ���̂ł��̂ˁB���肪�Ƃ��������܂����B
2024/08/24(�y) 02:01:05.17ID:NCb68F+6
>>569
C��25�{���ɂ��āAy=log₄(C-3ˣ)�Ǝ���ό`���Ă݂���H
C��25�{���ɂ��āAy=log₄(C-3ˣ)�Ǝ���ό`���Ă݂���H
2024/08/24(�y) 14:12:41.25ID:CzjhaWSa
>>569
25�̏�]�n�ōl����
x,y�𐳐����Ƃ���Bx^2+y^2��25�̔{���ɂȂ�̂�
n,m������Ƃ���
x = a + 25n
y = b + 25m
0 < a <= b �Ƃ����{a,b}�̑g�ݍ��킹������
{{3, 4}, {1, 7}, {5, 5}, {2, 11}, {6, 8}, {5, 10}, {2, 14}, {1, 18}, {5, 15}, {10, 10},
{9, 12}, {9, 13}, {6, 17}, {3, 21}, {5, 20}, {10, 15}, {4, 22}, {8, 19}, {12, 16},
{13, 16}, {5, 25}, {10, 20}, {15, 15}, {7, 24}, {11, 23}, {10, 25}, {15, 20},
{17, 19}, {14, 23}, {15, 25}, {20, 20}, {18, 24}, {21, 22}, {20, 25}, {25, 25}}
��
Mod[(1+25n)^2+(7+25m)^2,25] = Mod[1^2+7^2,25]=Mod[50,25]=0
25�̏�]�n�ōl����
x,y�𐳐����Ƃ���Bx^2+y^2��25�̔{���ɂȂ�̂�
n,m������Ƃ���
x = a + 25n
y = b + 25m
0 < a <= b �Ƃ����{a,b}�̑g�ݍ��킹������
{{3, 4}, {1, 7}, {5, 5}, {2, 11}, {6, 8}, {5, 10}, {2, 14}, {1, 18}, {5, 15}, {10, 10},
{9, 12}, {9, 13}, {6, 17}, {3, 21}, {5, 20}, {10, 15}, {4, 22}, {8, 19}, {12, 16},
{13, 16}, {5, 25}, {10, 20}, {15, 15}, {7, 24}, {11, 23}, {10, 25}, {15, 20},
{17, 19}, {14, 23}, {15, 25}, {20, 20}, {18, 24}, {21, 22}, {20, 25}, {25, 25}}
��
Mod[(1+25n)^2+(7+25m)^2,25] = Mod[1^2+7^2,25]=Mod[50,25]=0
2024/08/24(�y) 14:18:24.35ID:CzjhaWSa
���K���
x,y�́@x<=y�@�̐������Ƃ��Ax^2+y^2��25�̔{���ł���B
�������{x,y}�̑g�ݍ��킹���@x+y �����������ɕ��ׂ�B
10�ԖځA20�ԖځA30�Ԗڂ�{x,y}�̑g�ݍ��킹�����߂�B
x,y�́@x<=y�@�̐������Ƃ��Ax^2+y^2��25�̔{���ł���B
�������{x,y}�̑g�ݍ��킹���@x+y �����������ɕ��ׂ�B
10�ԖځA20�ԖځA30�Ԗڂ�{x,y}�̑g�ݍ��킹�����߂�B
2024/08/24(�y) 15:27:05.31ID:CzjhaWSa
a^2+b^2 �� 25�̔{�� ��
0<a<=b<=25�͈̔͂�
{{a,b},a^2+b^2}�̌`�ŗ�
{{{3, 4}, 25}, {{1, 7}, 50}, {{5, 5}, 50}, {{6, 8}, 100}, {{2, 11}, 125}, {{5, 10}, 125},
> {{2, 14}, 200}, {{10, 10}, 200}, {{9, 12}, 225}, {{5, 15}, 250}, {{9, 13}, 250},
> {{1, 18}, 325}, {{6, 17}, 325}, {{10, 15}, 325}, {{12, 16}, 400}, {{5, 20}, 425},
> {{8, 19}, 425}, {{13, 16}, 425}, {{3, 21}, 450}, {{15, 15}, 450}, {{4, 22}, 500},
> {{10, 20}, 500}, {{7, 24}, 625}, {{15, 20}, 625}, {{5, 25}, 650}, {{11, 23}, 650},
> {{17, 19}, 650}, {{10, 25}, 725}, {{14, 23}, 725}, {{20, 20}, 800}, {{15, 25}, 850},
> {{18, 24}, 900}, {{21, 22}, 925}, {{20, 25}, 1025}, {{25, 25}, 1250}}
�����I�ɍs�����߂ɁA����͐���@�Ɍv�Z�͌v�Z�@��
0<a<=b<=25�͈̔͂�
{{a,b},a^2+b^2}�̌`�ŗ�
{{{3, 4}, 25}, {{1, 7}, 50}, {{5, 5}, 50}, {{6, 8}, 100}, {{2, 11}, 125}, {{5, 10}, 125},
> {{2, 14}, 200}, {{10, 10}, 200}, {{9, 12}, 225}, {{5, 15}, 250}, {{9, 13}, 250},
> {{1, 18}, 325}, {{6, 17}, 325}, {{10, 15}, 325}, {{12, 16}, 400}, {{5, 20}, 425},
> {{8, 19}, 425}, {{13, 16}, 425}, {{3, 21}, 450}, {{15, 15}, 450}, {{4, 22}, 500},
> {{10, 20}, 500}, {{7, 24}, 625}, {{15, 20}, 625}, {{5, 25}, 650}, {{11, 23}, 650},
> {{17, 19}, 650}, {{10, 25}, 725}, {{14, 23}, 725}, {{20, 20}, 800}, {{15, 25}, 850},
> {{18, 24}, 900}, {{21, 22}, 925}, {{20, 25}, 1025}, {{25, 25}, 1250}}
�����I�ɍs�����߂ɁA����͐���@�Ɍv�Z�͌v�Z�@��
2024/08/26(��) 10:53:14.43ID:jhqhZozw
>>569
�������������łȂ���ΐ���Ȃ��Ƃ��������͖�����ł����
�������������łȂ���ΐ���Ȃ��Ƃ��������͖�����ł����
2024/08/26(��) 12:24:57.66ID:ASAZntV9
���ꂾ��
���������ɂ���̂������ɂȂ��Ă��܂�
���������ɂ���̂������ɂȂ��Ă��܂�
2024/08/27(��) 08:19:48.83ID:V+EB/huK
����������Ă����̂Œ��H��ɒ���
3^x+4^y��25�̔{���ɂȂ�悤�Ȑ��̗Ꭶ
x0=Table[Mod[3^x,25],{x,0,24}];
x1=Union@x0;
y0=Table[Mod[4^y,25],{y,0,24}];
y1=Union@y0;
xy=Select[Flatten[Table[{x,y},{x,x1},{y,y1}],1],Total[#]==25&];
i=5
xy[[i]]
x=Flatten[Position[x0,xy[[i]][[1]]]][[1]]-1
y=Flatten[Position[y0,xy[[i]][[2]]]][[1]]-1
3^x+4^y
3^8+4^3��6625
i�̒l��ς���
3^4+4^9=262225
3^12+4^7=547825
�Ȃǂ�������B
3^x+4^y��25�̔{���ɂȂ�悤�Ȑ��̗Ꭶ
x0=Table[Mod[3^x,25],{x,0,24}];
x1=Union@x0;
y0=Table[Mod[4^y,25],{y,0,24}];
y1=Union@y0;
xy=Select[Flatten[Table[{x,y},{x,x1},{y,y1}],1],Total[#]==25&];
i=5
xy[[i]]
x=Flatten[Position[x0,xy[[i]][[1]]]][[1]]-1
y=Flatten[Position[y0,xy[[i]][[2]]]][[1]]-1
3^x+4^y
3^8+4^3��6625
i�̒l��ς���
3^4+4^9=262225
3^12+4^7=547825
�Ȃǂ�������B
2024/08/27(��) 09:37:37.93ID:VBJLleVb
��
3^100+4^95=1569275434362047711690958686838377733791210133818116150225
3^1000+4^995=1121221382103764183821126173025080062521794630945991406716447985181412364640986634625644
029605963154217232387342761194114707672818412635538464540642604018695018345520574711
716058375562551799974171015164132746515997701544131810859143641743655985938783818125
296131958103121179435232691355079484811768959177833541297914545256594949123336738575
209610672121142617641385879009621096547447624737933911602216989984651489071828320858
431138029659855102065593113162361028995380855073646216880383516407785162121634107467
136241263776275121721638162871702266768220482617966334244265641717595090924912085364
98920225
3^100+4^95=1569275434362047711690958686838377733791210133818116150225
3^1000+4^995=1121221382103764183821126173025080062521794630945991406716447985181412364640986634625644
029605963154217232387342761194114707672818412635538464540642604018695018345520574711
716058375562551799974171015164132746515997701544131810859143641743655985938783818125
296131958103121179435232691355079484811768959177833541297914545256594949123336738575
209610672121142617641385879009621096547447624737933911602216989984651489071828320858
431138029659855102065593113162361028995380855073646216880383516407785162121634107467
136241263776275121721638162871702266768220482617966334244265641717595090924912085364
98920225
2024/08/27(��) 09:52:52.93ID:VBJLleVb
��
3^10000+4^9995
3^100000+4^99995
3^10000+4^9995
3^100000+4^99995
2024/08/27(��) 10:51:33.78ID:JxXVhQSH
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= 3^20
Out[1]= 3486784401
In[2]:= Mod[3^20,25]
Out[2]= 1
In[3]:= 4^10
Out[3]= 1048576
In[4]:= Mod[4^10,25]
Out[4]= 1
In[5]:= Mod[4^25,25]
Out[5]= 24
����
n�𐳐����Ƃ����
3^(20n) + 4^(10n+25)�͏��25�̔{���ł���̂�
��ӂ��݂���x,y�͖����ɑ��݂��邱�Ƃ��킩��B
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= 3^20
Out[1]= 3486784401
In[2]:= Mod[3^20,25]
Out[2]= 1
In[3]:= 4^10
Out[3]= 1048576
In[4]:= Mod[4^10,25]
Out[4]= 1
In[5]:= Mod[4^25,25]
Out[5]= 24
����
n�𐳐����Ƃ����
3^(20n) + 4^(10n+25)�͏��25�̔{���ł���̂�
��ӂ��݂���x,y�͖����ɑ��݂��邱�Ƃ��킩��B
2024/08/27(��) 15:42:18.61ID:5/jGHEnv
�A�r�W�W�C�܂����w���Ƀo�J�ɂ���ɗ�����
2024/08/27(��) 19:47:51.75ID:3KgsG4L0
>>578
�]����҂͒����s�\�݂�������
�]����҂͒����s�\�݂�������
2024/08/28(��) 07:48:35.86ID:lDbWcZVe
�A�r�`���p�t�F�`��Phimose�����
Wolfram������g���������\�z�ł��Ȃ����\�݂������Ȃ�
Wolfram������g���������\�z�ł��Ȃ����\�݂������Ȃ�
2024/08/28(��) 08:07:04.14ID:B5l1srpB
>>584
���̗L�\����̓X���^�C����ǂ߂Ȃ��͗lw
���̗L�\����̓X���^�C����ǂ߂Ȃ��͗lw
2024/08/28(��) 09:03:29.73ID:c56UVRyQ
�����ςȍr�炵������
2024/08/29(��) 16:09:09.80ID:Mdm5M0Mq
123�̂������@�� 456�݂̂���@�� 715�̂������B
�������ǂ̎q�����Ⴆ��ʕ��̎�ނƌ��������悤�ɂȂ�悤�ɔz�������Ƃ���
�ǂ̎q�������ׂẲʕ���1�ȏ�Ⴆ���B
�c�����ʕ��̐��͂ǂ���������������܂����B�q���̐l�������߂�B
�������ǂ̎q�����Ⴆ��ʕ��̎�ނƌ��������悤�ɂȂ�悤�ɔz�������Ƃ���
�ǂ̎q�������ׂẲʕ���1�ȏ�Ⴆ���B
�c�����ʕ��̐��͂ǂ���������������܂����B�q���̐l�������߂�B
2024/08/29(��) 16:38:01.52ID:Mdm5M0Mq
���K���
12345�̂������@�� 56789�݂̂���@�� 23185�̂������B
�������ǂ̎q�����Ⴆ��ʕ��̎�ނƌ��������悤�ɂȂ�悤�ɔz�������Ƃ���
�ǂ̎q�������ׂẲʕ���1�ȏ�Ⴆ���B
�c�����ʕ��̐��͂ǂ���������������܂����B�q���̐l�������߂�B
12345�̂������@�� 56789�݂̂���@�� 23185�̂������B
�������ǂ̎q�����Ⴆ��ʕ��̎�ނƌ��������悤�ɂȂ�悤�ɔz�������Ƃ���
�ǂ̎q�������ׂẲʕ���1�ȏ�Ⴆ���B
�c�����ʕ��̐��͂ǂ���������������܂����B�q���̐l�������߂�B
2024/08/29(��) 17:17:32.01ID:BNc6+SX2
�܂��ߕ����ꂽ�݂�������
2024/08/29(��) 17:30:40.38ID:Mdm5M0Mq
�A�r�`���p�t�F�`��Phimose�����
Wolfram������g���������\�z�ł��Ȃ������\�݂������Ȃ�
��n����Ȃ�����R���g���Ȃ��̂͂킩�邯�ǁB
Wolfram������g���������\�z�ł��Ȃ������\�݂������Ȃ�
��n����Ȃ�����R���g���Ȃ��̂͂킩�邯�ǁB
2024/08/29(��) 18:52:58.68ID:BNc6+SX2
>>590
�X���^�C���ǂ߂Ȃ��A�z�͗\�I�s�ނŁ[��w
�X���^�C���ǂ߂Ȃ��A�z�͗\�I�s�ނŁ[��w
2024/08/29(��) 20:45:33.31ID:5pz7SjOL
�킩���̂́H
����������v�A�j�����Ă��Ƃ͓}����݂��Č�������w
���悢��
�R���̃o�b�e���[��R���^���N��
����������v�A�j�����Ă��Ƃ͓}����݂��Č�������w
���悢��
�R���̃o�b�e���[��R���^���N��
593�P�R�Q�l�ڂ̑f������
2024/08/29(��) 21:19:39.86ID:bFzncrx/ �Ԃ��Ă��܂���(ɄD`)����
2024/08/29(��) 21:21:31.80ID:I6UnzsJy
>>93
�J�Ђ�N�\�݂����Ɏ�l�����₩��Ȃ�
�R����炪�G���W���̔M�Ŕ������Ⴄ��
�����̘b�����Ȃ�܂�������
https://i.imgur.com/ZHwuQiN.jpg
�J�Ђ�N�\�݂����Ɏ�l�����₩��Ȃ�
�R����炪�G���W���̔M�Ŕ������Ⴄ��
�����̘b�����Ȃ�܂�������
https://i.imgur.com/ZHwuQiN.jpg
2024/08/29(��) 21:34:46.90ID:CntdIAmZ
�u�Ȃɂ����
596�P�R�Q�l�ڂ̑f������
2024/08/29(��) 22:04:34.97ID:zH4Yr/C3 ���͈��ۂ�O���ł��Ȃ�����
�M�^�[�Ƃ�������������Ȃ�����
> �E�J�[�h����3980�~���̃K�[�V�[�R�C���w������
�M�^�[�Ƃ�������������Ȃ�����
> �E�J�[�h����3980�~���̃K�[�V�[�R�C���w������
2024/08/29(��) 22:54:08.78ID:VfuOSL6G
���@���o�o�A�͐l�Ԃ̘A�����������������
https://greta.5ch.net/test/read.cgi/poverty/1724862492/
https://i.imgur.com/U2zXOHp.jpg
https://greta.5ch.net/test/read.cgi/poverty/1724862492/
https://i.imgur.com/U2zXOHp.jpg
2024/08/29(��) 22:55:51.70ID:VRkwF9AI
�����w�Z�̎q���U���ĕ��V���c�o��������
599�P�R�Q�l�ڂ̑f������
2024/08/29(��) 23:18:32.58ID:kcM4LUva �K�[�V�[�̓o�O�̈Ӗ���������o���Ă�ԑg
2024/08/29(��) 23:25:36.12ID:lPPUhJzl
>>264
�E�B�[�A�[�Ԃ������褃o�g���n�b�J�[�[�Y�I�I( ߁��)
�E�B�[�A�[�Ԃ������褃o�g���n�b�J�[�[�Y�I�I( ߁��)
601�P�R�Q�l�ڂ̑f������
2024/08/29(��) 23:29:22.00ID:74L81Vdr ���Ă������݂����Ȃ̂���̂���
2024/08/30(��) 12:08:47.48ID:19uOB1/2
���H�O�̗��K���
12345�̂������@�� 56789�݂̂���@�� 77114�̂������B
�������ǂ̎q�����Ⴆ��ʕ��̎�ނƌ��������łȂ�ׂ���R���炦��悤�ɔz�������Ƃ���
�c�����ʕ��̐��͂ǂ�������������]�����B
�q���̐l����1��ނ�����ɗ]�����ʕ��̌������߂�B
12345�̂������@�� 56789�݂̂���@�� 77114�̂������B
�������ǂ̎q�����Ⴆ��ʕ��̎�ނƌ��������łȂ�ׂ���R���炦��悤�ɔz�������Ƃ���
�c�����ʕ��̐��͂ǂ�������������]�����B
�q���̐l����1��ނ�����ɗ]�����ʕ��̌������߂�B
2024/08/30(��) 13:21:16.19ID:eXEZ8OTt
>>602
���l��ς��Ă��Z�o�ł���悤�Ƀ\���o�[���쐬
solve[a_,b_,c_] :=(
d=Differences[Sort@{a,b,c}];
n=GCD[d[[1]],d[[2]]];
r=Mod[a,n];
{n,r}
)
solve[12345,56789,77114]
���l��ς��Ă��Z�o�ł���悤�Ƀ\���o�[���쐬
solve[a_,b_,c_] :=(
d=Differences[Sort@{a,b,c}];
n=GCD[d[[1]],d[[2]]];
r=Mod[a,n];
{n,r}
)
solve[12345,56789,77114]
2024/08/30(��) 16:18:42.40ID:/dK94GTF
�܂����肸�ɔ�������
2024/08/30(��) 23:19:21.68ID:/dK94GTF
�A�r�W�W�C���{���ɗՏ����v�𗝉����Ă��邩�m�F������
�����_���̏��^�������D
�w�i�E�ړI�F���ɂɂ͐S���I�v�����e�����Ă��邱�Ƃ��m���Ă��邪�C�S���s���w�I��������Ɋ��҂�QOL�Ɍ��ʂ����邩�͕s���ł���D�{�����ł́C���Ɋ��҂ɑ���F�m�s���Ö@���C���҂̌��N�֘AQOL�ɗ^������ʂ���������D
���@�@�F�Q������50�{�݂̐��`�O�ȊO���ɖ������ɂŎ�f���̊��҂̂����C���ӂ�ꂽ880���i���ϔN�� �} �W���� �� 72.4 �} 4.5�C�j���� �� 1�F1.2�j��{�����̑ΏۂƂ����D�����_�����t�����s���C�ʏ펡�Á{�F�m�s���Ö@���s������Q�ƒʏ펡�Â݂̂̔�r�ΏƌQ�ɕ��ނ����D�x�[�X���C����12�������_�̌��N�֘AQOL��SF 36 Health Survey���{��ŁqSF-36�r�̉��ʍ��ځu���́v�ő��肵�C�X�R�A�̕ω��ʂ�2�Q�Ԃ̍���t����ʼn�͂����DIntention to Treat��͂�p�����D
���@�ʁF12�����̒ǐ���70���ł������D�x�[�X���C����SF-36�u���́v��2�Q�œ��v�w�I�L�Ӎ��݂͂��Ȃ������D12������́u���́v�̕ω��ʂ͔�r�ΏیQ�Ɣ�ׂĉ���Q�œ��v�w�I�L�ӂȉ��P��F�߂��iP�l �� 0.001�j�D
���@�_�F�������ɏǂɑ���F�m�s���Ö@�͌��N�֘AQOL�����P������D
�@�{�������ʂ�Տ����p���邤���ōł��m�F�������_�����̏��͂ǂꂩ�D1�I�ׁD
�ia�jP�l�i��Βl�j
�ib�j�e�Q�̒ǐ�
�ic�j��d�ӌ����痦
�id�jper protocol��͌���
�ie�j�ω��ʂ�2�Q�ԍ��̒l�i95���M����ԁj
�Տ����v���ӂȂ�ł���H5���������ɓ��������ˁH
���̖��o����đ����ł��Ȃ������ӂ肩�疾�炩�Ɍ��C�Ȃ��Ȃ�����
�S�L�W�F�b�g���ȁH
�����ۂ��ȃv���C�h()������Ȃɏ�����ꂽ�́H�X���^�C����ǂ߂��ɃX���`�𑱂���Q���W�W�C�̕��ۂŁH�H
�����_���̏��^�������D
�w�i�E�ړI�F���ɂɂ͐S���I�v�����e�����Ă��邱�Ƃ��m���Ă��邪�C�S���s���w�I��������Ɋ��҂�QOL�Ɍ��ʂ����邩�͕s���ł���D�{�����ł́C���Ɋ��҂ɑ���F�m�s���Ö@���C���҂̌��N�֘AQOL�ɗ^������ʂ���������D
���@�@�F�Q������50�{�݂̐��`�O�ȊO���ɖ������ɂŎ�f���̊��҂̂����C���ӂ�ꂽ880���i���ϔN�� �} �W���� �� 72.4 �} 4.5�C�j���� �� 1�F1.2�j��{�����̑ΏۂƂ����D�����_�����t�����s���C�ʏ펡�Á{�F�m�s���Ö@���s������Q�ƒʏ펡�Â݂̂̔�r�ΏƌQ�ɕ��ނ����D�x�[�X���C����12�������_�̌��N�֘AQOL��SF 36 Health Survey���{��ŁqSF-36�r�̉��ʍ��ځu���́v�ő��肵�C�X�R�A�̕ω��ʂ�2�Q�Ԃ̍���t����ʼn�͂����DIntention to Treat��͂�p�����D
���@�ʁF12�����̒ǐ���70���ł������D�x�[�X���C����SF-36�u���́v��2�Q�œ��v�w�I�L�Ӎ��݂͂��Ȃ������D12������́u���́v�̕ω��ʂ͔�r�ΏیQ�Ɣ�ׂĉ���Q�œ��v�w�I�L�ӂȉ��P��F�߂��iP�l �� 0.001�j�D
���@�_�F�������ɏǂɑ���F�m�s���Ö@�͌��N�֘AQOL�����P������D
�@�{�������ʂ�Տ����p���邤���ōł��m�F�������_�����̏��͂ǂꂩ�D1�I�ׁD
�ia�jP�l�i��Βl�j
�ib�j�e�Q�̒ǐ�
�ic�j��d�ӌ����痦
�id�jper protocol��͌���
�ie�j�ω��ʂ�2�Q�ԍ��̒l�i95���M����ԁj
�Տ����v���ӂȂ�ł���H5���������ɓ��������ˁH
���̖��o����đ����ł��Ȃ������ӂ肩�疾�炩�Ɍ��C�Ȃ��Ȃ�����
�S�L�W�F�b�g���ȁH
�����ۂ��ȃv���C�h()������Ȃɏ�����ꂽ�́H�X���^�C����ǂ߂��ɃX���`�𑱂���Q���W�W�C�̕��ۂŁH�H
2024/08/31(�y) 00:22:25.48ID:JliScuGu
>>603
�����ւ𐂂ꗬ���Ȃ�A���O��p�̕֏������邾��
�����ւ𐂂ꗬ���Ȃ�A���O��p�̕֏������邾��
2024/08/31(�y) 00:59:26.87ID:Px1rB7os
>>603
R�ɈڐA
solve=\(a,b,c){
c(a,b,c)|>sort()|>diff()|>numbers::mGCD()->n
c(n,a%%n)
}
solve(12345,56789,77114)
R�ɈڐA
solve=\(a,b,c){
c(a,b,c)|>sort()|>diff()|>numbers::mGCD()->n
c(n,a%%n)
}
solve(12345,56789,77114)
2024/08/31(�y) 01:04:13.00ID:JliScuGu
>>607
>606
>606
2024/08/31(�y) 01:32:18.57ID:55fu1E4D
>>607
���̗L�\�͂��ɂȂ����疳�����̏ؖ����ł����H
���̗L�\�͂��ɂȂ����疳�����̏ؖ����ł����H
2024/08/31(�y) 01:33:33.89ID:55fu1E4D
2024/08/31(�y) 05:49:39.39ID:Px1rB7os
���̗��K���
1234�̂������@�� 4567�݂̂���@�� 8910�̂������B
�������ǂ̎q�����Ⴆ��ʕ��̎�ނƌ��������łȂ�ׂ���R���炦��悤�ɔz�������Ƃ���
�c�����ʕ��̐��͂ǂ���������������B
�q���̐l����1��ނ�����ɗ]�����ʕ��̌������߂�B
1234�̂������@�� 4567�݂̂���@�� 8910�̂������B
�������ǂ̎q�����Ⴆ��ʕ��̎�ނƌ��������łȂ�ׂ���R���炦��悤�ɔz�������Ƃ���
�c�����ʕ��̐��͂ǂ���������������B
�q���̐l����1��ނ�����ɗ]�����ʕ��̌������߂�B
2024/08/31(�y) 05:50:29.88ID:Px1rB7os
���w�������̖��
���l�@�Ɓ@���l�łȂ��l�Ƃ͂ǂ��炪�����ł��傤��?
���l�@�Ɓ@���l�łȂ��l�Ƃ͂ǂ��炪�����ł��傤��?
2024/08/31(�y) 06:03:19.68ID:Q/Lo9wJj
2024/08/31(�y) 06:22:59.21ID:Q/Lo9wJj
��ӃV���c���p�̖��
GCD��Greatest Common Divisor�̂��Ƃł���B���{��ɖB
�Q�l����
208�P�R�Q�l�ڂ̑f������sage2024/08/30(��) 18:27:34.04ID:nhc1fobJ(1/1) �ԐM (1)
�d�삨��������A�����w���X���̒ߋT�Z�������̂ɍŏ����{�������߂�����g���ăC�L�邗
GCD��Greatest Common Divisor�̂��Ƃł���B���{��ɖB
�Q�l����
208�P�R�Q�l�ڂ̑f������sage2024/08/30(��) 18:27:34.04ID:nhc1fobJ(1/1) �ԐM (1)
�d�삨��������A�����w���X���̒ߋT�Z�������̂ɍŏ����{�������߂�����g���ăC�L�邗
2024/08/31(�y) 10:09:58.08ID:Udz8u/bv
���X�Ŗ�茩����
https://x.com/Shiroikaibutsu_/status/1829489422364193266?t=gv95H6J0BWCO_jxPyWCNrQ&s=06
�����������30���҂��ɂȂ���
225��50=45
225��150=15
45-15=30
�ĉ�����
https://x.com/Shiroikaibutsu_/status/1829489422364193266?t=gv95H6J0BWCO_jxPyWCNrQ&s=06
�����������30���҂��ɂȂ���
225��50=45
225��150=15
45-15=30
�ĉ�����
2024/08/31(�y) 10:16:07.43ID:OqrM+pGd
���w���ɂ��瑊��ɂ���ĂȂ�����w
2024/08/31(�y) 10:20:38.66ID:OqrM+pGd
>>613
�����ł���Ȃ�Ȃ�œ������o��܂Ń_���}�����ߍ���ł���H
55�F���̖���������F2024/08/16(��) 18:57:15.96 ID:VnGGyzKc
�ق玟�̖�肾��
���N�f�f�̕��������g�����Ŋ̑��Ɉُ���w�E���ꂽ���ߗ��@�����D
�@�����P��CT�y�}No.1�z�C�������eCT�y�}No.2�i�������j�z�C�y�}No.3�i�喬���j�z�C�y�}No.4�i���t���j�z����сy�}No.5�i�������E����f�j�z�������D���͎�ᎂ������D
�@�l������̂͂ǂꂩ�D1�I�ׁD
�ia�j�̍זE��
�ib�j�̌��ǎ�
�ic�j�]�ڐ��̊�
�id�j�̓��_�NJ�
�ie�j�̌��ǐ����ߐ��ߌ`���qfocal nodular hyperplasia�FFNH�r
https://i.imgur.com/591fanA.jpeg
�I�����܂ł��Ă�������ȒP����HChatGPT�ɂ܂������Ă݂邩�Hwww
�������̖��͊��S�Ƀ_���}���ł����ӂ�ChatGPT�ɕ����Ă�������Ȃ������݂�������ww
�����ł���Ȃ�Ȃ�œ������o��܂Ń_���}�����ߍ���ł���H
55�F���̖���������F2024/08/16(��) 18:57:15.96 ID:VnGGyzKc
�ق玟�̖�肾��
���N�f�f�̕��������g�����Ŋ̑��Ɉُ���w�E���ꂽ���ߗ��@�����D
�@�����P��CT�y�}No.1�z�C�������eCT�y�}No.2�i�������j�z�C�y�}No.3�i�喬���j�z�C�y�}No.4�i���t���j�z����сy�}No.5�i�������E����f�j�z�������D���͎�ᎂ������D
�@�l������̂͂ǂꂩ�D1�I�ׁD
�ia�j�̍זE��
�ib�j�̌��ǎ�
�ic�j�]�ڐ��̊�
�id�j�̓��_�NJ�
�ie�j�̌��ǐ����ߐ��ߌ`���qfocal nodular hyperplasia�FFNH�r
https://i.imgur.com/591fanA.jpeg
�I�����܂ł��Ă�������ȒP����HChatGPT�ɂ܂������Ă݂邩�Hwww
�������̖��͊��S�Ƀ_���}���ł����ӂ�ChatGPT�ɕ����Ă�������Ȃ������݂�������ww
2024/08/31(�y) 14:32:58.11ID:r3L5cBfU
2024/08/31(�y) 16:51:04.59ID:OqrM+pGd
173�F���̖���������F[sage]�F2024/08/24(�y) 06:41:04.60 ID:+wsPmPH8
NGWord�ݒ��˔j���邽�߂ɁAR�ŏc�����ϊ��̃X�N���v�g��������B
�ꎟ�������ʼn�����悤�Ȗ�肷��ł��Ȃ��悤�Ȃ̂ɂ̓v���O�����ł��Ȃ����낤�ȁB
���n�̑�w�i��ӃV���c��͏����j�𑲋Ƃ��Ă�����v���O��������̂P��Q���炢�g���ē��R�B
���������ꎟ�������ʼn������肪�ł��Ȃ��悤�Ȃ̂���w�������w�����邱�Ǝ��̂����������B
180�F���̖���������F[sage]�F2024/08/24(�y) 06:51:05.92 ID:+wsPmPH8
>>178
�킩��܂���A
���ǂ��A���l�ł͔��肵�Ȃ�����
���l�Ə����Ă���̂��m�F���ēǂނ̂���߂��B
�ꎟ�������ʼn������肪�ł��Ȃ��̂��āA�ǂ��̃V���c��H
����23���ɏo�肳���24���̒��܂ŕ�����܂���Ƃ��ق����Ă��̂ɋ}�ɂ����������Ă������̂悤�Ȍ��Ԃ�Ō�o���W�����P������n��w
NGWord�ݒ��˔j���邽�߂ɁAR�ŏc�����ϊ��̃X�N���v�g��������B
�ꎟ�������ʼn�����悤�Ȗ�肷��ł��Ȃ��悤�Ȃ̂ɂ̓v���O�����ł��Ȃ����낤�ȁB
���n�̑�w�i��ӃV���c��͏����j�𑲋Ƃ��Ă�����v���O��������̂P��Q���炢�g���ē��R�B
���������ꎟ�������ʼn������肪�ł��Ȃ��悤�Ȃ̂���w�������w�����邱�Ǝ��̂����������B
180�F���̖���������F[sage]�F2024/08/24(�y) 06:51:05.92 ID:+wsPmPH8
>>178
�킩��܂���A
���ǂ��A���l�ł͔��肵�Ȃ�����
���l�Ə����Ă���̂��m�F���ēǂނ̂���߂��B
�ꎟ�������ʼn������肪�ł��Ȃ��̂��āA�ǂ��̃V���c��H
����23���ɏo�肳���24���̒��܂ŕ�����܂���Ƃ��ق����Ă��̂ɋ}�ɂ����������Ă������̂悤�Ȍ��Ԃ�Ō�o���W�����P������n��w
2024/08/31(�y) 20:47:47.10ID:OqrM+pGd
2024/09/01(��) 17:51:34.82ID:k4Wt7ZDX
�A�r�W�W�C>>614�܂����_�a�@�s���݂�������
2024/09/05(��) 09:54:30.31ID:qDZSymqG
�A�r�W�W�C�A�N�ցH
�l�b�g�q����Ȃ�ǂ���1�����o�����ɕ������邾�낤��
�l�b�g�q����Ȃ�ǂ���1�����o�����ɕ������邾�낤��
2024/09/06(��) 02:44:43.68ID:mJk9bf1I
�A�r���_���}�����ߍ���ł邾���ł���w
2024/09/10(��) 02:01:13.03ID:BqGZj8xr
���̈Ӗ��͏����w���ɂł��킩�邪�����͖̂��������Ȗ��
�����}�̑��ّI�͌����_��7�l������₵�Ă���Ƃ̂��ƁB
7�l�ŃW�����P�������đ��ق����߂邱�ƂɂȂ�܂����B
7�l�ŃW�����P�����͂��߂ď��҂ǂ����ŃW�����P���𑱂��܂��B
�A�C�R��1��Ƃ�������Ƃ�����̃W�����P���Ō��܂邩�Ă�q��������Ƃ�
����ɓq����̂��ł��L���ł��傤���H
�����}�̑��ّI�͌����_��7�l������₵�Ă���Ƃ̂��ƁB
7�l�ŃW�����P�������đ��ق����߂邱�ƂɂȂ�܂����B
7�l�ŃW�����P�����͂��߂ď��҂ǂ����ŃW�����P���𑱂��܂��B
�A�C�R��1��Ƃ�������Ƃ�����̃W�����P���Ō��܂邩�Ă�q��������Ƃ�
����ɓq����̂��ł��L���ł��傤���H
2024/09/10(��) 02:10:03.89ID:pnO4ViWl
>>624
���w���ł��X���^�C���炢�ǂ߂�͂������ǃA���^�̓A�z������ǂ߂Ȃ��݂�������
���w���ł��X���^�C���炢�ǂ߂�͂������ǃA���^�̓A�z������ǂ߂Ȃ��݂�������
2024/09/10(��) 02:19:15.29ID:EMKb9PRg
>>624
�P�O�O����̃V�~�����[�V����
https://i.imgur.com/Pnna3tj.png
���_�l���O���t��
https://i.imgur.com/MVI1Lnx.png
�P�O�O����̃V�~�����[�V����
https://i.imgur.com/Pnna3tj.png
���_�l���O���t��
https://i.imgur.com/MVI1Lnx.png
2024/09/10(��) 02:31:02.34ID:pnO4ViWl
>>626
�]����҂��肸�ɂ܂����w���Ƀo�J�ɂ��ꂽ���݂��������ǂ���ɂ͂��܂Ń_���}�����ߍ���ł�́H
262�F���̖���������F2024/09/06(��) 19:07:09.13 ID:xAT6TjrO
��҂Ȃ�K����������
�@68�̏����D��Ȃł̔������p��\�肳��Ă��邽�ߏЉ���f�����D���̎{�݂ł͎�p���銳�҂͏Ǐ����ȓI�����̗L���ɂ�����炸�C�S�Ⴊ���Ȃŏp�O�S�g�]�������茈�߂ɂȂ��Ă���D
�@�������F���L���ׂ����Ƃ͂Ȃ��D
�@���a���F�g�̐f�@�œ��L���ׂ��ُ�͂Ȃ������D����X���ʐ^�ʼnE���x��Ɍ��߉e���F�߂�ꂽ���̂́C�S����͗L�ӂłȂ��Ɣ��f���C��p�{�s�̏�Ŏx�Ⴊ�Ȃ��Ƃ�����ȏЉ��ɕԓ����C�I�f�Ƃ����D
���N��C���҂͋��ɂƌ�ႂƂ���i�ɍĎ�f���C�����̌��ʁC�x���Ɛf�f���ꂽ�D
�@����X�������̌������ɉe�������\��������̂͂ǂꂩ�D1�I�ׁD
�ia�jBase–rate neglect�q�L�a���̖����r
�ib�jCommission bias�q���s�o�C�A�X�r
�ic�jConfirmation bias�q�m�o�C�A�X�r
�id�jDiagnostic momentum�q�f�f�ɂ�鐨���t���r
�ie�jSunk cost bias�q���v�J�̓o�C�A�X�r
�]����҂��肸�ɂ܂����w���Ƀo�J�ɂ��ꂽ���݂��������ǂ���ɂ͂��܂Ń_���}�����ߍ���ł�́H
262�F���̖���������F2024/09/06(��) 19:07:09.13 ID:xAT6TjrO
��҂Ȃ�K����������
�@68�̏����D��Ȃł̔������p��\�肳��Ă��邽�ߏЉ���f�����D���̎{�݂ł͎�p���銳�҂͏Ǐ����ȓI�����̗L���ɂ�����炸�C�S�Ⴊ���Ȃŏp�O�S�g�]�������茈�߂ɂȂ��Ă���D
�@�������F���L���ׂ����Ƃ͂Ȃ��D
�@���a���F�g�̐f�@�œ��L���ׂ��ُ�͂Ȃ������D����X���ʐ^�ʼnE���x��Ɍ��߉e���F�߂�ꂽ���̂́C�S����͗L�ӂłȂ��Ɣ��f���C��p�{�s�̏�Ŏx�Ⴊ�Ȃ��Ƃ�����ȏЉ��ɕԓ����C�I�f�Ƃ����D
���N��C���҂͋��ɂƌ�ႂƂ���i�ɍĎ�f���C�����̌��ʁC�x���Ɛf�f���ꂽ�D
�@����X�������̌������ɉe�������\��������̂͂ǂꂩ�D1�I�ׁD
�ia�jBase–rate neglect�q�L�a���̖����r
�ib�jCommission bias�q���s�o�C�A�X�r
�ic�jConfirmation bias�q�m�o�C�A�X�r
�id�jDiagnostic momentum�q�f�f�ɂ�鐨���t���r
�ie�jSunk cost bias�q���v�J�̓o�C�A�X�r
2024/09/10(��) 05:03:19.16ID:1fuNSCR7
2024/09/10(��) 05:11:46.44ID:pnO4ViWl
>>624
���҂ǂ����Ƃ����w�ȑO�ɓ��{�ꂩ����������Ă����Ԕ���
���҂ǂ����Ƃ����w�ȑO�ɓ��{�ꂩ����������Ă����Ԕ���
2024/09/10(��) 08:32:11.19ID:whLItct/
>>626
7�l�ŃW�����P�����J�n���āA���Ғʂ��ł����҂��P�l�ɂȂ�܂ł̉��T��ł���m�������߂�
ChatGPT�̓��A�����Ȃ���̌듚
>>
���������āA7�l����X�^�[�g����5��ڂ�1�l�ɂȂ�̂͗��_�I�ɂ͂��蓾�܂����A�W�����P���̐i�s�ɂ����Ă͕s���R�ł��B���ۂɂ�4��œ��B����̂��W���I�Ȑi�s�ł���A���̂���5��ڂœ��B����m���̓[���ɋ߂��ƍl�����܂��B
<<
7�l�ŃW�����P�����J�n���āA���Ғʂ��ł����҂��P�l�ɂȂ�܂ł̉��T��ł���m�������߂�
ChatGPT�̓��A�����Ȃ���̌듚
>>
���������āA7�l����X�^�[�g����5��ڂ�1�l�ɂȂ�̂͗��_�I�ɂ͂��蓾�܂����A�W�����P���̐i�s�ɂ����Ă͕s���R�ł��B���ۂɂ�4��œ��B����̂��W���I�Ȑi�s�ł���A���̂���5��ڂœ��B����m���̓[���ɋ߂��ƍl�����܂��B
<<
2024/09/10(��) 10:43:08.23ID:whLItct/
���ǂ������Ɓ��ǂ������������̂͂ǂ���ł����H
�Ј��ǂ��������ǂ�
�Ј��ǂ��������ǂ�
�ǂ��炪�����Ă��܂����H
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1216623117
�Ј��ǂ��������ǂ�
�Ј��ǂ��������ǂ�
�ǂ��炪�����Ă��܂����H
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q1216623117
2024/09/10(��) 13:12:24.43ID:FPvdcrD2
���ҁu���m�v������ǂ������ď����Ȃ��Ƃ����Ȃ��͂��Ȃ��ǂ���ς���{��s���R�݂�������
���w�����w�E�ł��邼w
https://www.weblio.jp/content/���m
���w�����w�E�ł��邼w
https://www.weblio.jp/content/���m
2024/09/10(��) 20:30:10.43ID:eeK6/I+2
>>630
���̎g���Ă���GPT���ƁA
�u�W�����P���̂悤�ȃ����_���ȏ��s�������Q�[���ł́A���s��5��Ŏ�������m���͑S�̂̒��ł����Ȃ�H�ȃP�[�X�ƍl�����܂��B���ۂ̂Ƃ���A5��ŏ�����������m���͖� 15%~20% �͈̔͂Ɏ��܂邱�Ƃ���ʓI�ł��B�v
�g���Ă���l�ɂ��̂���
���̎g���Ă���GPT���ƁA
�u�W�����P���̂悤�ȃ����_���ȏ��s�������Q�[���ł́A���s��5��Ŏ�������m���͑S�̂̒��ł����Ȃ�H�ȃP�[�X�ƍl�����܂��B���ۂ̂Ƃ���A5��ŏ�����������m���͖� 15%~20% �͈̔͂Ɏ��܂邱�Ƃ���ʓI�ł��B�v
�g���Ă���l�ɂ��̂���
2024/09/12(��) 04:15:06.05ID:kjq8gwfW
>>633
���͈̔͂ɂ͂Ȃ����炻����듚
���͈̔͂ɂ͂Ȃ����炻����듚
2024/09/12(��) 04:18:04.42ID:kjq8gwfW
>626�̃O���t�̒ʂ�
�ŕp�l�̊m���͖�10��
�ŕp�l�̊m���͖�10��
2024/09/12(��) 04:47:19.30ID:jgveSPOW
���p���
���ٌ��ґS���ŃW�����P�����n�߂ď��҂��P�l�ɂȂ�܂ő�����B
��x��������W�����P���ɂ͎Q���ł��Ȃ��B
�A�C�R���P��Ɛ�����Ƃ��ĂT��ŏI�������B
���ٌ��҂͉��l�ł������m�����ł��������H
���ٌ��ґS���ŃW�����P�����n�߂ď��҂��P�l�ɂȂ�܂ő�����B
��x��������W�����P���ɂ͎Q���ł��Ȃ��B
�A�C�R���P��Ɛ�����Ƃ��ĂT��ŏI�������B
���ٌ��҂͉��l�ł������m�����ł��������H
2024/09/12(��) 05:00:34.55ID:jgveSPOW
���Ȃ݂�ChatGPT�̌듚
����
�Ⴆ�A8�l�̌��҂��W�����P��������Ƃ��܂��B1��ڂőS������������o���ăA�C�R���N����\��������܂����A�ʏ��1��ڂŐl���������ȉ��Ɍ���A���̌�A�C�R���܂ސ���ŏ��҂����܂�Ƃ����W�J�ł��B
�����Ƃ����肻���Ȍ��Ґ���8�l�ŁA5��̃W�����P������������m���������ƍl�����܂��B
���R:
1��ڂ�8�l���������E���i�܂��͑S�����������j���A���̌コ��ɐl���������Ă������Ƃ�5��ŏ��҂�1�l�ɂȂ�V�i���I�������I�ł��B
���̐l���i�Ⴆ��4�l��16�l�j���\�ł����A5��ŏI�����邽�߂ɂ͐l���������������Ȃ������A8�l���Ó��ȑI���ƍl�����܂��B
����
�Ⴆ�A8�l�̌��҂��W�����P��������Ƃ��܂��B1��ڂőS������������o���ăA�C�R���N����\��������܂����A�ʏ��1��ڂŐl���������ȉ��Ɍ���A���̌�A�C�R���܂ސ���ŏ��҂����܂�Ƃ����W�J�ł��B
�����Ƃ����肻���Ȍ��Ґ���8�l�ŁA5��̃W�����P������������m���������ƍl�����܂��B
���R:
1��ڂ�8�l���������E���i�܂��͑S�����������j���A���̌コ��ɐl���������Ă������Ƃ�5��ŏ��҂�1�l�ɂȂ�V�i���I�������I�ł��B
���̐l���i�Ⴆ��4�l��16�l�j���\�ł����A5��ŏI�����邽�߂ɂ͐l���������������Ȃ������A8�l���Ó��ȑI���ƍl�����܂��B
2024/09/12(��) 05:59:11.41ID:/KXx54L1
>>634
����Ȃ��Ƃ��`�h�̉��ʂɈ���Ă�������d�v����
����Ȃ��Ƃ��`�h�̉��ʂɈ���Ă�������d�v����
2024/09/13(��) 23:53:21.92ID:rohGem4j
2024/09/14(�y) 15:07:54.35ID:NP2ZlwAQ
����A�����ł����̂���
�܂��u�Z���ŏK���Ă��Ȃ����@�ʼn������猸�_���ꂽ�v�b�肪�l�b�g�j���[�X�ɂ�����
�K���Ă��Ȃ��藝��L���ؖ��A����`�Ŏg�����p�^�[��
����̓_���Ɍ��܂��Ă���Ǝv����
�L����Ƃ��č̓_�҂���Ă���
�܂��u�Z���ŏK���Ă��Ȃ����@�ʼn������猸�_���ꂽ�v�b�肪�l�b�g�j���[�X�ɂ�����
�K���Ă��Ȃ��藝��L���ؖ��A����`�Ŏg�����p�^�[��
����̓_���Ɍ��܂��Ă���Ǝv����
�L����Ƃ��č̓_�҂���Ă���
2024/09/14(�y) 15:20:48.00ID:9LdPJGVi
>>640
�b�̎팳�܂�l�^����������
�b�̎팳�܂�l�^����������
2024/09/14(�y) 15:36:45.50ID:dkeJyU09
���Ⴀ�ŏ�����l�^�����ď�����
2024/09/14(�y) 15:45:59.77ID:NP2ZlwAQ
TBS���W�I�w�p���T�[�����#�ӂ���Ɓx�X���S���������ӂ���� ���ǂ��d�b���k��
����̔����L�������t�[�g�b�v�y�[�W�ɏo�Ă���
���k�҂͌��ݒ��w���������w�����̘b�Ƃ��đ��k���Ă���
���̎�̘b�͂Ƃ��ǂ��o�Ă��邩�炸���ƋC�ɂȂ��Ă���
���ɂ��̋L���𖼎w���������킯�ł͂Ȃ������߂Ɍ����̂͂��̋L���Ƃ�������
���̔F���̕����Ԉ���Ă���ꍇ�����邩��
���w����ɏڂ������������������Ă�������Ƃ��肪����
����̔����L�������t�[�g�b�v�y�[�W�ɏo�Ă���
���k�҂͌��ݒ��w���������w�����̘b�Ƃ��đ��k���Ă���
���̎�̘b�͂Ƃ��ǂ��o�Ă��邩�炸���ƋC�ɂȂ��Ă���
���ɂ��̋L���𖼎w���������킯�ł͂Ȃ������߂Ɍ����̂͂��̋L���Ƃ�������
���̔F���̕����Ԉ���Ă���ꍇ�����邩��
���w����ɏڂ������������������Ă�������Ƃ��肪����
2024/09/14(�y) 20:00:38.91ID:JXeVsito
2024/09/14(�y) 22:00:43.88ID:JXeVsito
>>643
�w�Z�����Ƃ���Ȃ�A�Z���������A�N���X���̒n�A���t���̎�A�����Đ��k���̖��Ɛ���ł��傤�A
�̎�̋������悭�w�т悭�K�����Ă��邩�A�����x���v��m�F����̂��e�X�g�ł��B���̒����x���v�鎆�ɏm�u�t�Ƃ��������̎҂̋������������̂ł͌��_�Ƃ��������Ă��d���̖������Ƃł��B
���W�I�ԑg���̃Q�X�g�̔����͉Ȋw�҂Ƃ����E�ƓI�o���≿�l�ς��炭�锭���ł���A�����₦�鎖�ł͖����Ǝv���܂��B
�w�Z�����Ƃ���Ȃ�A�Z���������A�N���X���̒n�A���t���̎�A�����Đ��k���̖��Ɛ���ł��傤�A
�̎�̋������悭�w�т悭�K�����Ă��邩�A�����x���v��m�F����̂��e�X�g�ł��B���̒����x���v�鎆�ɏm�u�t�Ƃ��������̎҂̋������������̂ł͌��_�Ƃ��������Ă��d���̖������Ƃł��B
���W�I�ԑg���̃Q�X�g�̔����͉Ȋw�҂Ƃ����E�ƓI�o���≿�l�ς��炭�锭���ł���A�����₦�鎖�ł͖����Ǝv���܂��B
646�P�R�Q�l�ڂ̑f������
2024/09/15(��) 12:05:55.48ID:HVtZkM2z �e�X�g�ł͍̓_��͂��ꂱ�ꂱ���ł���ƌ����Ŗ������邱�Ƃ����X����B
�q�ǂ����m�̊w�K���d�����w�Z�̋��t�̔������y������Ƃ����Ȃ�B
�Œ�������������Ƃ͔c�����Ă����̂��d�v���Ƃ͎v�����c�܂��A������ɂ���ł��N���X�̂قƂ�ǂ����s�ł��Ă��Ȃ������Ȃ炢�����ɖ��͂��邩������Ȃ���
�q�ǂ����m�̊w�K���d�����w�Z�̋��t�̔������y������Ƃ����Ȃ�B
�Œ�������������Ƃ͔c�����Ă����̂��d�v���Ƃ͎v�����c�܂��A������ɂ���ł��N���X�̂قƂ�ǂ����s�ł��Ă��Ȃ������Ȃ炢�����ɖ��͂��邩������Ȃ���
2024/09/15(��) 12:51:00.57ID:nymI7sKK
�w�Z�ŏK���ĂȂ����̂��g���Ƃ��́A
�����ƒ�`�Əؖ�����Ύg���ėǂ���ƌ����Ă���������
��������������ł��Ȃ��z�͎g��Ȃ����A
�g�����Ƃ���Ł~�ɂ��Ă�����̕t���悤���Ȃ��Ȃ�
�����ƒ�`�Əؖ�����Ύg���ėǂ���ƌ����Ă���������
��������������ł��Ȃ��z�͎g��Ȃ����A
�g�����Ƃ���Ł~�ɂ��Ă�����̕t���悤���Ȃ��Ȃ�
2024/09/15(��) 13:29:29.90ID:gSKkNuAi
���w�Z�̃e�X�g�̈�Ԃ̖ړI�́A�w�Z�Ŋw�K�������Ƃ̗���x�ƏK���x���m�F���邱�Ƃł��B�]���Ċw��łȂ����@�Ő������Ă��]���̑Ώۂƈׂ�Ȃ��̂ł��傤�B
2024/09/15(��) 14:52:00.73ID:Z5hQaC6X
�F�l���肪�Ƃ��������܂�
���̌o���ł� >>647 ���Ɠ��l�̂��Ƃ�����ꂽ���Ƃ�����܂�
�K���Ă��Ȃ��藝�́A���������ǂ����킩��Ȃ����݂ł����āA���t�����̑O��Ō��Ă���
���ɏm�ŏK��������A�Ƃ����Ă��{���ɗ������Ă���Ȃ琳�������Ƃ�������͂���
�Ƃ����̂����H���R�Ƃ��Ă��āA���w�҂�����������������̂��o���Ă��܂�
���̌o���ł� >>647 ���Ɠ��l�̂��Ƃ�����ꂽ���Ƃ�����܂�
�K���Ă��Ȃ��藝�́A���������ǂ����킩��Ȃ����݂ł����āA���t�����̑O��Ō��Ă���
���ɏm�ŏK��������A�Ƃ����Ă��{���ɗ������Ă���Ȃ琳�������Ƃ�������͂���
�Ƃ����̂����H���R�Ƃ��Ă��āA���w�҂�����������������̂��o���Ă��܂�
2024/09/15(��) 21:13:39.99ID:Hps/ukAk
>>649
���w�̎��Ɍ���ꂽ�̂��ȁB
�Ⴆ�A���w�ł́u�O�p�`�Ƃ�3�̕ӂ����}�`�ł���v�Ƃ����悤�ɁA�`�̓������w�ԍۂɒ�`�̊T�O�͏o�Ă��܂����A��`���̂̈Ӗ��͊w�т܂���B��`�̌��t���̂̈Ӗ��͒��w�Ŋw�т܂��A
���w���ɒ�`�����Ă���g���悤�Ɍ����͍̂����Ǝv���܂��B�B
���w�̎��Ɍ���ꂽ�̂��ȁB
�Ⴆ�A���w�ł́u�O�p�`�Ƃ�3�̕ӂ����}�`�ł���v�Ƃ����悤�ɁA�`�̓������w�ԍۂɒ�`�̊T�O�͏o�Ă��܂����A��`���̂̈Ӗ��͊w�т܂���B��`�̌��t���̂̈Ӗ��͒��w�Ŋw�т܂��A
���w���ɒ�`�����Ă���g���悤�Ɍ����͍̂����Ǝv���܂��B�B
2024/09/15(��) 21:54:52.92ID:nymI7sKK
>>650
������K���ĂȂ��͎̂g���Ȃ��Ęb�Ɍq�����ł���
������K���ĂȂ��͎̂g���Ȃ��Ęb�Ɍq�����ł���
2024/09/16(��) 03:18:52.60ID:s5Y0a9/W
>>651
�����ł��ˁA647�̌����Ă���u�K���ĂȂ����Ƃ��g���Ƃ���~�v�ɎZ���ł͖����łȂ����ƈ�a�����o���܂����B
�����ł��ˁA647�̌����Ă���u�K���ĂȂ����Ƃ��g���Ƃ���~�v�ɎZ���ł͖����łȂ����ƈ�a�����o���܂����B
2024/09/16(��) 05:35:10.84ID:MQ8mS2hl
>>636
���w���ɂ��n���ɂ���܂����ă_���}������H
���w���ɂ��n���ɂ���܂����ă_���}������H
2024/09/17(��) 06:36:03.77ID:+YZG4nu4
2024/09/17(��) 07:42:30.85ID:47/kzswv
2024/09/18(��) 05:17:12.87ID:RVB8lVoV
���ɉ��l������₵�����͌��܂��Ă���̂�
���̏����̈ӂɉB���ė����҂����l�������m���Ƃ������t���g���͈̂�a��������
�����w���ł��킩��悤�ɐ������ė~����
���̏����̈ӂɉB���ė����҂����l�������m���Ƃ������t���g���͈̂�a��������
�����w���ł��킩��悤�ɐ������ė~����
2024/09/18(��) 08:07:18.28ID:ka3tAr53
>>656
��a��������Ȃ�9�l�ŃW�����P�������Ƃ���
����ŏI������m���������Ƃ��������H
���̊m���ƂƂ��ɋ��߂�Ƃ������ł�������B
�Z�o�X�L���̂Ȃ��̂��A���ɃP�`�����Ă��邾������Ȃ����Ƃ�
�T�N�b�ƎZ�o���Ď����Ăق����Ȃ��B
��a��������Ȃ�9�l�ŃW�����P�������Ƃ���
����ŏI������m���������Ƃ��������H
���̊m���ƂƂ��ɋ��߂�Ƃ������ł�������B
�Z�o�X�L���̂Ȃ��̂��A���ɃP�`�����Ă��邾������Ȃ����Ƃ�
�T�N�b�ƎZ�o���Ď����Ăق����Ȃ��B
2024/09/18(��) 08:17:52.38ID:JkIaDVFd
���ʂ��猴���𐄒肷��Ƃ��������t���m���̖��̕������H�I���Ǝv���B
��
����^�N�V�[��Ђ̃^�N�V�[�ɂ͂P����ʂ��ԍ����ӂ��Ă���B
�^�N�V�[��Ђ̋K�͂���ۗL�^�N�V�[�䐔�͂P�O�O��ȉ��Ƃ킩���Ă���i���O���z�j�B
���̉�Ђ̃^�N�V�[���T��݂������B�ő�̔ԍ����U�O�ł������B
���̉�Ђۗ̕L����^�N�V�[�䐔�̊��Ғl�ƂX�T���M�p���(�M�����)�����߂�B
��
����^�N�V�[��Ђ̃^�N�V�[�ɂ͂P����ʂ��ԍ����ӂ��Ă���B
�^�N�V�[��Ђ̋K�͂���ۗL�^�N�V�[�䐔�͂P�O�O��ȉ��Ƃ킩���Ă���i���O���z�j�B
���̉�Ђ̃^�N�V�[���T��݂������B�ő�̔ԍ����U�O�ł������B
���̉�Ђۗ̕L����^�N�V�[�䐔�̊��Ғl�ƂX�T���M�p���(�M�����)�����߂�B
2024/09/18(��) 12:06:48.61ID:nQgxq+c9
��a���������ē�����O
�m���̖��Ƃ��Đ������Ă��Ȃ�
�����ɂ͉i���Ɋm�������ł�����͗��Ȃ�
�m���̖��Ƃ��Đ������Ă��Ȃ�
�����ɂ͉i���Ɋm�������ł�����͗��Ȃ�
2024/09/18(��) 16:11:15.19ID:xHroH3k7
>>658
�����w�Z�͈̔͂ŏK�����Ƃ��g���ĉ�����̂���������ė~����
�����w�Z�͈̔͂ŏK�����Ƃ��g���ĉ�����̂���������ė~����
2024/09/19(��) 15:10:08.25ID:gAIGlerO
>>660
���Ғl�����ϒl�Ƃ��āA�^�N�V�[�����䂠�邩�͓��l�Ɋm���炵����O��ɂ��Ďl�����Z�ʼn����邩��
�����ōl��������y�������B
���Ғl�����ϒl�Ƃ��āA�^�N�V�[�����䂠�邩�͓��l�Ɋm���炵����O��ɂ��Ďl�����Z�ʼn����邩��
�����ōl��������y�������B
2024/09/19(��) 15:13:32.15ID:gAIGlerO
Bayesian Computation with R
https://link.springer.com/book/10.1007/978-0-387-92298-0
�Ɍf�ڂ���Ă�����̐��l��ς��������̖��B
�ȑO�A���Z���w�X���ɓ��e�����瑬�U�Ő������Ԃ��Ă����B
https://link.springer.com/book/10.1007/978-0-387-92298-0
�Ɍf�ڂ���Ă�����̐��l��ς��������̖��B
�ȑO�A���Z���w�X���ɓ��e�����瑬�U�Ő������Ԃ��Ă����B
2024/09/19(��) 16:13:38.52ID:Mu2I/FQk
���݂͐��w�̕��Ȃ�~�����������ƂȂ��̂ɂȂ�Ŏ����͂܂��߂ɐ��w�����Ă����l�ԂƑΓ��ɓn�荇����Ǝv������H
�������̎��_�Ŗ��\������
�������̎��_�Ŗ��\������
2024/09/19(��) 17:28:24.70ID:dm/Lzn4Q
>>661
��������ė~����
��������ė~����
2024/09/21(�y) 06:17:29.95ID:gVrJ0ttT
>>658
�x�C�Y���_�͒��w�Ŋw�Ԏ��ł͂Ȃ���
�x�C�Y���_�͒��w�Ŋw�Ԏ��ł͂Ȃ���
2024/09/21(�y) 06:28:02.86ID:gVrJ0ttT
2024/09/21(�y) 15:37:17.08ID:TXevl3L5
>>662
�A�r�W�W�C�܂����w���Ƀo�J�ɂ��ꑫ��Ȃ��̂���H
�A�r�W�W�C�܂����w���Ƀo�J�ɂ��ꑫ��Ȃ��̂���H
2024/09/24(��) 03:55:51.91ID:hK94gtsm
�X���ł��Ȃ�����
���̈Ӗ��������w���ɂ킩������B
�S�F�����Ă��\���Ǝv���B
���̈Ӗ��������w���ɂ킩������B
�S�F�����Ă��\���Ǝv���B
2024/09/24(��) 04:35:27.74ID:hK94gtsm
�����Ă����T����̏��p�b�N�ƂP�Q����̑�p�b�N�Ŕ����Ă���B�甄��͂��Ă��Ȃ��B
�����Ă���2024���B�������B�p�b�N�̑����͍ŏ��ɂ������B
�召��������������悢���B
�����Ă���2024���B�������B�p�b�N�̑����͍ŏ��ɂ������B
�召��������������悢���B
2024/09/24(��) 04:44:47.36ID:m77Jpbap
�������͂Œ��ׂĂ݂܂���
�����`�����ʂa�ɉe�����Ă���Ƃ��ɂa����`�ɂ��āu�m���v��_����
�x�C�Y����́A
��ϊm���̈��ł���q�ϊm����ΏۂƂ���ÓT�I�m���̍l�����ɂ͓���Ȃ�
�Ƃ������Ƃł����̂ł��傤���H
�l�b�g�����Œ��ׂ������̒m���ł��̂ŊԈ���Ă����狳���Ă�������ƍK���ł�
���͌�����|���鐔�l�̐�����v�Z�ł��ɂ͖c��߂��ĒN�����������Ȃ�
�̂ł͂Ȃ��ł��傤��
���w��p�\�t�g�ł��������̌v�Z�����������Ƃ�ۏ��Ă͂���Ȃ��ł��傤��
�������������̂����̐��������Ȃ肻���ł�
�����`�����ʂa�ɉe�����Ă���Ƃ��ɂa����`�ɂ��āu�m���v��_����
�x�C�Y����́A
��ϊm���̈��ł���q�ϊm����ΏۂƂ���ÓT�I�m���̍l�����ɂ͓���Ȃ�
�Ƃ������Ƃł����̂ł��傤���H
�l�b�g�����Œ��ׂ������̒m���ł��̂ŊԈ���Ă����狳���Ă�������ƍK���ł�
���͌�����|���鐔�l�̐�����v�Z�ł��ɂ͖c��߂��ĒN�����������Ȃ�
�̂ł͂Ȃ��ł��傤��
���w��p�\�t�g�ł��������̌v�Z�����������Ƃ�ۏ��Ă͂���Ȃ��ł��傤��
�������������̂����̐��������Ȃ肻���ł�
2024/09/24(��) 04:46:43.28ID:hK94gtsm
�����Ă���5����̏��p�b�N��9����̒��p�b�N��12����̑�p�b�N�Ŕ����Ă���B
�甄��͂��Ă��Ȃ��B
�����Ă���2024���B�������B�p�b�N�̑����͍ŏ��ɂ������B
�咆����������������悢���B
�甄��͂��Ă��Ȃ��B
�����Ă���2024���B�������B�p�b�N�̑����͍ŏ��ɂ������B
�咆����������������悢���B
2024/09/24(��) 04:52:06.16ID:v+BDwH56
>>670
✘
✘
2024/09/24(��) 04:56:34.54ID:s9AMg6Yz
>>670
>�P
>�������܂ŏ����w���̂��߂̃X���Ȃ̂Ŕ͈͊O�̂��̂ɂ��Ă͕ʃX���ɁB
>���炩�ɔ͈͊O�̎���ɂ͑�NG�o�^�őΏ����Ă������B���������畉���ł��B�F�l�̂����͂�낵�����肢���܂��B
>�P
>�������܂ŏ����w���̂��߂̃X���Ȃ̂Ŕ͈͊O�̂��̂ɂ��Ă͕ʃX���ɁB
>���炩�ɔ͈͊O�̎���ɂ͑�NG�o�^�őΏ����Ă������B���������畉���ł��B�F�l�̂����͂�낵�����肢���܂��B
2024/09/24(��) 06:41:47.09ID:m77Jpbap
>>673
���w�����肪�Ƃ��������܂�
���w�����肪�Ƃ��������܂�
2024/09/24(��) 07:10:56.44ID:m77Jpbap
>>669
�P�F�]���ɔ����Ă͂����Ȃ��ꍇ
12✕167��2004
12✕168��2016
12✕169��2028
���A��p�b�N��168�ȉ��ł��邱�Ƃ�������B�c�@
��p�b�N�Ə��p�b�N���A����g�ł����Ă�2024���������Ă���Ƃ�
���̑g����p�b�N��5���Ȃ��A
���p�b�N��12���������ꍇ�������Ă�2024�ƂȂ�A
��p�b�N�����Ȃ��������قǍ��v�p�b�N���͑����i���炩�j�A
�܂��A���̂Ƃ���p�b�N���̕ϓ���5�̔{���łȂ��ꍇ��2024�������ł��Ȃ��i���炩�j�B�c�A
���A��p�b�N167�A���p�b�N4�Ȃ炽���Ă�2024�ł���B
�@�A��薾�炩�ɂ��̑g����ӂ����B
�����F��p�b�N167�A���p�b�N4��
�Q�F�]���ɔ����Ă��悢�ꍇ
�P�̇@���A���炩�ɑ�p�b�N169����ӂ����B
�����F��p�b�N169��
�P�F�]���ɔ����Ă͂����Ȃ��ꍇ
12✕167��2004
12✕168��2016
12✕169��2028
���A��p�b�N��168�ȉ��ł��邱�Ƃ�������B�c�@
��p�b�N�Ə��p�b�N���A����g�ł����Ă�2024���������Ă���Ƃ�
���̑g����p�b�N��5���Ȃ��A
���p�b�N��12���������ꍇ�������Ă�2024�ƂȂ�A
��p�b�N�����Ȃ��������قǍ��v�p�b�N���͑����i���炩�j�A
�܂��A���̂Ƃ���p�b�N���̕ϓ���5�̔{���łȂ��ꍇ��2024�������ł��Ȃ��i���炩�j�B�c�A
���A��p�b�N167�A���p�b�N4�Ȃ炽���Ă�2024�ł���B
�@�A��薾�炩�ɂ��̑g����ӂ����B
�����F��p�b�N167�A���p�b�N4��
�Q�F�]���ɔ����Ă��悢�ꍇ
�P�̇@���A���炩�ɑ�p�b�N169����ӂ����B
�����F��p�b�N169��
2024/09/24(��) 07:12:45.44ID:m77Jpbap
������������̂�
�ۂP�A�ۂQ�Ȃ̂���
�ۂP�A�ۂQ�Ȃ̂���
2024/09/24(��) 07:40:23.52ID:hK94gtsm
2024/09/24(��) 07:42:12.46ID:hK94gtsm
�����Ă���5����̏��p�b�N��9����̒��p�b�N��12����̑�p�b�N�Ŕ����Ă���B
�甄��͂��Ă��Ȃ��B
�����Ă������傤��2024���B�������B�p�b�N�̑����͍ŏ��ɂ������B
�咆����������������悢���B
�甄��͂��Ă��Ȃ��B
�����Ă������傤��2024���B�������B�p�b�N�̑����͍ŏ��ɂ������B
�咆����������������悢���B
2024/09/24(��) 07:46:35.72ID:t6kXDVhI
�m�Ő��̑S�Ă̌��𑫂�������3�̔{���Ȃ�A
���̐���3�̔{���ł���ƏK���܂���
����͂ǂ�Ȃɑ傫�����ł������Ȃ�ł��傤��
�ǂ����Ă����Ȃ���Č�������ł���
���̐���3�̔{���ł���ƏK���܂���
����͂ǂ�Ȃɑ傫�����ł������Ȃ�ł��傤��
�ǂ����Ă����Ȃ���Č�������ł���
2024/09/24(��) 08:09:38.78ID:dX9Db7pg
�ǂ����Ă����Ȃ����Ƃ��J��Ԃ����Ⴄ��
2024/09/24(��) 10:55:52.20ID:7EzATw+/
>>679
�Ⴆ��237�Ƃ��������l�����ꍇ�A
2✕100�{3✕10�{�V�ƕ\�����Ƃ��ł��܂��B
10��3�Ŋ���Ɨ]�肪1�ɂȂ�܂��B
100��3�Ŋ���Ɨ]�肪1�ɂȂ�܂��B
�����1000�ł�10000�ł��K���]�肪1�ɂȂ�A�ǂ�ȂɌ����傫���Ȃ��Ă��ς��܂���B
�܂�A10��100��3�̔{�����ۂ��ɊW���ĂȂ��̂ł��B
�]���āA3�̔{�����ׂ�̂ɁA10��100������2�{3�{7�Ƃ��鎖���ł���̂ł��B
>>675
�p�b�N�i12����j166�A���p�b�N�i9����j3�A���p�b�N�i5����j1�̑g�ݍ��킹����1�p�b�N���Ȃ��čς�
�Ⴆ��237�Ƃ��������l�����ꍇ�A
2✕100�{3✕10�{�V�ƕ\�����Ƃ��ł��܂��B
10��3�Ŋ���Ɨ]�肪1�ɂȂ�܂��B
100��3�Ŋ���Ɨ]�肪1�ɂȂ�܂��B
�����1000�ł�10000�ł��K���]�肪1�ɂȂ�A�ǂ�ȂɌ����傫���Ȃ��Ă��ς��܂���B
�܂�A10��100��3�̔{�����ۂ��ɊW���ĂȂ��̂ł��B
�]���āA3�̔{�����ׂ�̂ɁA10��100������2�{3�{7�Ƃ��鎖���ł���̂ł��B
>>675
�p�b�N�i12����j166�A���p�b�N�i9����j3�A���p�b�N�i5����j1�̑g�ݍ��킹����1�p�b�N���Ȃ��čς�
2024/09/24(��) 12:19:27.33ID:m77Jpbap
2024/09/24(��) 12:59:47.58ID:qfKpZaOI
�����Ă����T����̏��p�b�N�ƂP�Q����̑�p�b�N�Ŕ����Ă���B�甄��͂��Ȃ��B
���傤��3�����Ă���Ƃ��A18�����Ă���ƒ�������Ă������͎��Ȃ��B
���������Ȃ��������͉����邩?
�L���Ȃ���ׂė���B
���傤��3�����Ă���Ƃ��A18�����Ă���ƒ�������Ă������͎��Ȃ��B
���������Ȃ��������͉����邩?
�L���Ȃ���ׂė���B
2024/09/24(��) 13:17:53.53ID:o76hi+so
�\�ł���ꍇ�����
5,10,15,...
12,17,22,...
24,29,34,...
36,41,46,...
48,53,58,...
������s�\�ł���̂�
2,7,4,9,14,19,1,6,11,16,21,26,31,3,8,13,18,23,28,33,38,43
5,10,15,...
12,17,22,...
24,29,34,...
36,41,46,...
48,53,58,...
������s�\�ł���̂�
2,7,4,9,14,19,1,6,11,16,21,26,31,3,8,13,18,23,28,33,38,43
2024/09/24(��) 13:41:10.64ID:7EzATw+/
>>682
669�̉������̂ł��ˁB��ώ�������܂����A
678�̖��͌����I�ȉ�@���Ȃ��̂ő傫�������̂��̂��珇�ԂɌv�Z���邵���Ȃ��ł��傤�B
669�̉������̂ł��ˁB��ώ�������܂����A
678�̖��͌����I�ȉ�@���Ȃ��̂ő傫�������̂��̂��珇�ԂɌv�Z���邵���Ȃ��ł��傤�B
2024/09/24(��) 14:49:15.30ID:qfKpZaOI
>>669
x y
[1,] 167 4
[2,] 162 16
[3,] 157 28
[4,] 152 40
[5,] 147 52
[6,] 142 64
[7,] 137 76
[8,] 132 88
[9,] 127 100
[10,] 122 112
[11,] 117 124
[12,] 112 136
[13,] 107 148
[14,] 102 160
[15,] 97 172
[16,] 92 184
[17,] 87 196
[18,] 82 208
[19,] 77 220
[20,] 72 232
[21,] 67 244
[22,] 62 256
[23,] 57 268
[24,] 52 280
[25,] 47 292
[26,] 42 304
[27,] 37 316
[28,] 32 328
[29,] 27 340
[30,] 22 352
[31,] 17 364
[32,] 12 376
[33,] 7 388
[34,] 2 400
x y
[1,] 167 4
[2,] 162 16
[3,] 157 28
[4,] 152 40
[5,] 147 52
[6,] 142 64
[7,] 137 76
[8,] 132 88
[9,] 127 100
[10,] 122 112
[11,] 117 124
[12,] 112 136
[13,] 107 148
[14,] 102 160
[15,] 97 172
[16,] 92 184
[17,] 87 196
[18,] 82 208
[19,] 77 220
[20,] 72 232
[21,] 67 244
[22,] 62 256
[23,] 57 268
[24,] 52 280
[25,] 47 292
[26,] 42 304
[27,] 37 316
[28,] 32 328
[29,] 27 340
[30,] 22 352
[31,] 17 364
[32,] 12 376
[33,] 7 388
[34,] 2 400
2024/09/24(��) 15:32:29.61ID:qfKpZaOI
2024/09/24(��) 15:55:19.29ID:qfKpZaOI
>>681
�z���ʂ�ł��B
�z���ʂ�ł��B
2024/09/24(��) 15:56:00.67ID:qfKpZaOI
�����Ă���5����̏��p�b�N��9����̒��p�b�N��12����̑�p�b�N�Ŕ����Ă���B
�甄��͂��Ă��Ȃ��B
�����Ă������傤��2024���B�������B
���ʂ�̔����������邩�v�Z����B
�甄��͂��Ă��Ȃ��B
�����Ă������傤��2024���B�������B
���ʂ�̔����������邩�v�Z����B
2024/09/24(��) 16:20:50.63ID:7EzATw+/
>>689
�t���x�j�E�X�̃R�C�����͏����Ŋw�Ȃ��ł��傤
�t���x�j�E�X�̃R�C�����͏����Ŋw�Ȃ��ł��傤
2024/09/24(��) 16:27:48.44ID:qfKpZaOI
�����Ă���5����̏��p�b�N��9����̒��p�b�N��12����̑�p�b�N�Ŕ����Ă���B�甄��͂��Ȃ��B
���傤��1�����Ă���Ƃ��A7�����Ă���ƒ�������Ă������͎��Ȃ��B
���������Ȃ��������͉����邩?
�L���Ȃ���ׂė���B
���傤��1�����Ă���Ƃ��A7�����Ă���ƒ�������Ă������͎��Ȃ��B
���������Ȃ��������͉����邩?
�L���Ȃ���ׂė���B
2024/09/24(��) 16:33:30.32ID:o76hi+so
����ˁB���̎�̖��͓������̂��̂ł͂Ȃ��A�Ȃ�����Ɍ�����̂��̘_�q���{��
�����w���ɂ͂ނ�₩���
�����w���ɂ͂ނ�₩���
2024/09/24(��) 18:58:19.49ID:ftZgJBOQ
�܂����肸�ɔA�r���������Ă�̂���H
2024/09/24(��) 19:14:12.41ID:m77Jpbap
>>678
���p�b�N6�͒��p�b�N2�Ƒ�p�b�N1��
���p�b�N4�͑�p�b�N3�ɂ��邱�Ƃ�
���p�b�N�������炷���Ƃ��ł��邱�Ƃɗ��ӂ����
���p�b�N��5�ȉ��A���p�b�N��3�ȉ��ł��邱�Ƃ�������
�܂��A2024��n�𐮐��Ƃ���3n+2�ŕ\���鐮���ł���A
9��12��3�̔{���ł��邩��
���p�b�N�Ȃ��ł͂����Ă����傤��2024�͎����ł����A
���p�b�N��1�܂���4�ł��邱�Ƃ�������
���p�b�N4�̏ꍇ��p�b�N167�A���p�b�N�Ȃ����\�ł��邪
���ꂪ���p�b�N4�̏ꍇ�̍őP�ł��邱�Ƃ͖��炩
���p�b�N1�̏ꍇ���p�b�N3�A��p�b�N166���\��
���ꂪ���p�b�N1�̏ꍇ�̍őP�ł��邱�Ƃ͖��炩
���̓���r���邱�Ƃŏ��p�b�N1�A���p�b�N3�A��p�b�N166��
�����߂锃�����ł��邱�Ƃ�������
�����F���p�b�N1�A���p�b�N3�A��p�b�N166�i���p�b�N��170�j
���p�b�N6�͒��p�b�N2�Ƒ�p�b�N1��
���p�b�N4�͑�p�b�N3�ɂ��邱�Ƃ�
���p�b�N�������炷���Ƃ��ł��邱�Ƃɗ��ӂ����
���p�b�N��5�ȉ��A���p�b�N��3�ȉ��ł��邱�Ƃ�������
�܂��A2024��n�𐮐��Ƃ���3n+2�ŕ\���鐮���ł���A
9��12��3�̔{���ł��邩��
���p�b�N�Ȃ��ł͂����Ă����傤��2024�͎����ł����A
���p�b�N��1�܂���4�ł��邱�Ƃ�������
���p�b�N4�̏ꍇ��p�b�N167�A���p�b�N�Ȃ����\�ł��邪
���ꂪ���p�b�N4�̏ꍇ�̍őP�ł��邱�Ƃ͖��炩
���p�b�N1�̏ꍇ���p�b�N3�A��p�b�N166���\��
���ꂪ���p�b�N1�̏ꍇ�̍őP�ł��邱�Ƃ͖��炩
���̓���r���邱�Ƃŏ��p�b�N1�A���p�b�N3�A��p�b�N166��
�����߂锃�����ł��邱�Ƃ�������
�����F���p�b�N1�A���p�b�N3�A��p�b�N166�i���p�b�N��170�j
2024/09/24(��) 19:22:32.61ID:qfKpZaOI
>>689
���Đ��𐔂���ȒP�Ȃ��d���ł��B
[1,] 1 3 166
[2,] 1 7 163
[3,] 1 11 160
.....
......
[****,] 397 3 1
[****,] 400 0 2
[****,] 403 1 0
���Đ��𐔂���ȒP�Ȃ��d���ł��B
[1,] 1 3 166
[2,] 1 7 163
[3,] 1 11 160
.....
......
[****,] 397 3 1
[****,] 400 0 2
[****,] 403 1 0
2024/09/24(��) 20:31:00.49ID:oZx+zKhf
�����Ă���5����̏��p�b�N��9����̒��p�b�N��12����̑�p�b�N�Ŕ����Ă���B�甄��͂��Ȃ��B
���傤��100�����Ă���Ƃ̒�������������
���̔������
�@���@���@��
[1,] 2 2 6
[2,] 2 6 3
[3,] 2 10 0
[4,] 5 3 4
[5,] 5 7 1
[6,] 8 0 5
[7,] 8 4 2
[8,] 11 1 3
[9,] 11 5 0
[10,] 14 2 1
[11,] 20 0 0
��11�ʂ肠��B
�P�ʂ肵����������Ȃ��̂�
���傤�lj������Ă���ƒ������ꂽ�Ƃ�������B
���傤��100�����Ă���Ƃ̒�������������
���̔������
�@���@���@��
[1,] 2 2 6
[2,] 2 6 3
[3,] 2 10 0
[4,] 5 3 4
[5,] 5 7 1
[6,] 8 0 5
[7,] 8 4 2
[8,] 11 1 3
[9,] 11 5 0
[10,] 14 2 1
[11,] 20 0 0
��11�ʂ肠��B
�P�ʂ肵����������Ȃ��̂�
���傤�lj������Ă���ƒ������ꂽ�Ƃ�������B
2024/09/24(��) 20:44:50.30ID:83tmPD0n
>>696
������
������
2024/09/24(��) 21:00:52.11ID:HM2P+dS1
���������A������͂��ʂ�Ƃ���
���Ƃ��Ƃ̊W���O���t������B
���Ƃ��Ƃ̊W���O���t������B
2024/09/24(��) 21:09:05.76ID:oZx+zKhf
2024/09/24(��) 21:27:43.47ID:aOFYbtz3
2024/09/24(��) 21:57:10.49ID:7EzATw+/
��w�Ŋw�Ԃ悤�Ȏ��������w�Z�̃X���Ńh����Ō��Ƃ������ˁB
2024/09/24(��) 22:14:49.89ID:o76hi+so
�܂����̎�̑g�ݍ��킹�̖��͂����琳����Ă����ꂾ���ł͐����ɂȂ�Ȃ��Ƃ������������ł��ĂȂ��B
���̂�����Ő��w�T���Ă��܂������ȁB���F�͂��̒��x�̒m�\
���̂�����Ő��w�T���Ă��܂������ȁB���F�͂��̒��x�̒m�\
2024/09/25(��) 08:34:26.66ID:obe22E91
�A�r�W�W�C�����̉����o�Ȃ��͗l
2024/09/25(��) 09:13:12.75ID:qfTRXGvX
���ʁu����v�Ƃ������đf���ɉ�����悤�ȓz�͋��Ȃ����玩�����낤�ȁB
2024/09/25(��) 19:23:22.87ID:WLXtL/2K
>>695
Wolfram�Ń\���o�[������ėV�ԁB
�����Ă���a,b,c�������p�b�N��n�̂����Ă���������@��Ԃ����B
���̈Ӗ��͏��w���ł��킩��B
���Ƃł̒P��������Ƃ��v���O�����ɂ����������̊ȒP�Ȃ��d���ł��B
Table����
f[a_,b_,c_,n_]:=(
t1=Table[{x,y,z},{x,0,Floor[n/a]},{y,0,Floor[n/b]},{z,0,Floor[n/c]}];
t2=Flatten[t1,2];
Select[t2,a #[[1]] + b #[[2]] + c #[[3]] == n&]
)
f[5,9,13,2024] // Length // Timing
For loop��
fn[a_,b_,c_,n_]:=(
re={};
For[x=0,x<=n/a,x++,
For[y=0,y<=n/b,y++,
For[z=0,z<=n/c,z++,
If[a x + b y + c z == n, AppendTo[re,{x,y,z}]]
]]];
re
)
fn[5,9,13,2024] // Length // Timing
�ǂ��炪�������͎��s���Ă̂��y���݁B
Wolfram�Ń\���o�[������ėV�ԁB
�����Ă���a,b,c�������p�b�N��n�̂����Ă���������@��Ԃ����B
���̈Ӗ��͏��w���ł��킩��B
���Ƃł̒P��������Ƃ��v���O�����ɂ����������̊ȒP�Ȃ��d���ł��B
Table����
f[a_,b_,c_,n_]:=(
t1=Table[{x,y,z},{x,0,Floor[n/a]},{y,0,Floor[n/b]},{z,0,Floor[n/c]}];
t2=Flatten[t1,2];
Select[t2,a #[[1]] + b #[[2]] + c #[[3]] == n&]
)
f[5,9,13,2024] // Length // Timing
For loop��
fn[a_,b_,c_,n_]:=(
re={};
For[x=0,x<=n/a,x++,
For[y=0,y<=n/b,y++,
For[z=0,z<=n/c,z++,
If[a x + b y + c z == n, AppendTo[re,{x,y,z}]]
]]];
re
)
fn[5,9,13,2024] // Length // Timing
�ǂ��炪�������͎��s���Ă̂��y���݁B
2024/09/25(��) 20:04:19.28ID:U5cyEdcS
2024/09/25(��) 21:05:51.65ID:rYBYI/Fa
>>705
���A�𐂂ꗬ���Ȃ�ߐ�p�̕֏��X�������邾��A�N�\�{�P�I
���A�𐂂ꗬ���Ȃ�ߐ�p�̕֏��X�������邾��A�N�\�{�P�I
2024/09/26(��) 04:50:00.71ID:DjIa9Rog
�l�|�X�L���ł͉����Ȃ����A�Ђ����珑���o���Đ�����ΎZ�o�ł�����B
5����̃^�R�Ă�(S)�A9����̃^�R�Ă�(M)�A12����̃^�R�Ă�(L)��
S,M,L���e�X20�����p�ӂ����B
�^�R�Ă��̐��Œ������邪�A�o������͂��Ȃ��B
��F17�͎��邪�A16�̎��Ȃ��B
���
(1)�@�ł���̃^�R�Ă��̐��͉���ނ��邩�B�A���A0�͎ɐ����Ȃ��B
(2)�@60�̒����̏ꍇ��
S M L
[1,] 3 5 0
[2,] 6 2 1
[3,] 0 4 2
[4,] 3 1 3
[5,] 0 0 5
��5��ނ̕��@�ŏo�ׂł���B
�o�ׂł�����@���ł������͉̂��̃^�R�Ă��������Ƃ����H
����������ׂė���B
5����̃^�R�Ă�(S)�A9����̃^�R�Ă�(M)�A12����̃^�R�Ă�(L)��
S,M,L���e�X20�����p�ӂ����B
�^�R�Ă��̐��Œ������邪�A�o������͂��Ȃ��B
��F17�͎��邪�A16�̎��Ȃ��B
���
(1)�@�ł���̃^�R�Ă��̐��͉���ނ��邩�B�A���A0�͎ɐ����Ȃ��B
(2)�@60�̒����̏ꍇ��
S M L
[1,] 3 5 0
[2,] 6 2 1
[3,] 0 4 2
[4,] 3 1 3
[5,] 0 0 5
��5��ނ̕��@�ŏo�ׂł���B
�o�ׂł�����@���ł������͉̂��̃^�R�Ă��������Ƃ����H
����������ׂė���B
2024/09/26(��) 04:57:39.83ID:/2ULA2t4
���w���ł��ǂ߂�X���^�C�������ł��Ȃ��W�W�C���S�����Ă�͗l
2024/09/26(��) 06:38:51.58ID:KPkwrkMN
>>708
�����w���̐��w��D�����N�����I
�Ȃ�тɏ����w�Z�͈͂̎Z���E���w�̖��ŔY��ł�����I(�N����킸)
������Ȃ���肪��������C�y�Ƀ��X���Ă��������B
�w�Z�̏h��A�m�̖��ȂǕ��L�������Ă��������Ǝv���܂��B
�����̎g��������>>2���Q�Ƃ̂��ƁB
�������܂ŏ����w���̂��߂̃X���Ȃ̂Ŕ͈͊O�̂��̂ɂ��Ă͕ʃX���ɁB
���炩�ɔ͈͊O�̎���ɂ͑�NG�o�^�őΏ����Ă������B���������畉���ł��B�F�l�̂����͂�낵�����肢���܂��B
>7 08
>708
>708
>708
�����w���̐��w��D�����N�����I
�Ȃ�тɏ����w�Z�͈͂̎Z���E���w�̖��ŔY��ł�����I(�N����킸)
������Ȃ���肪��������C�y�Ƀ��X���Ă��������B
�w�Z�̏h��A�m�̖��ȂǕ��L�������Ă��������Ǝv���܂��B
�����̎g��������>>2���Q�Ƃ̂��ƁB
�������܂ŏ����w���̂��߂̃X���Ȃ̂Ŕ͈͊O�̂��̂ɂ��Ă͕ʃX���ɁB
���炩�ɔ͈͊O�̎���ɂ͑�NG�o�^�őΏ����Ă������B���������畉���ł��B�F�l�̂����͂�낵�����肢���܂��B
>7 08
>708
>708
>708
2024/09/26(��) 06:45:32.05ID:Thqg0ctz
2024/09/26(��) 12:01:55.52ID:LAEYqB/x
>>707
�߁H
�߁H
2024/09/26(��) 19:36:04.22ID:90+q6boF
708�͏����w�Z�̒m���ʼn�����Ǝv��
���Z�����Ă��Ȃ��̂ŊԈ���Ă����璼���Ăق���
(1)
�܂��A���̏������Ŏ\�ȍő吔��5✕20�{9✕20�{12✕20��520�ł���
5�A9�A12�ō��鐔������o���i���\01���͕\�̌��h���̂��߂̕\�L�j
01 02 03 04 05 06 07 08 09
10 11 12 13 14 15 16 17 18
19 20 21 22 23 24 25 26 27
28 29 30 31 32 33 34 35 36
37 38 39 40 41 42 �c
���̂悤��9�P�ʂŐ�������ׁA5�A9�A12�ō��鐮���Ɋۂ�t���Ă䂭
�e�ՂɁA���͈̔͂ł�1 2 3 4 6 7 8 11 13 16��10�ʂ���������ׂĂ����邱�Ƃ�������
�i9�P�ʂŕ��ׂĂ���̂�9�𑫂�����ō���ꍇ����ڗđR�j
���ɁA22����42�͊ەt���őS�Ė��܂��Ă���
���ꂾ���ł�5���i��ɂȂ�100�ȏ�̏ꍇ���S�z�ɂȂ邪
�����ŏ�\�͈̔͂ł͊ۂ�t�������̂�5�A9�A12�̂�������T��ȓ��̎g�p�ō��邱�Ƃɗ��ӂ���
9�{12��21�����
0����21�@�\��ޕs�\�i���o�j
22����42�@21✕0�{22����21✕0�{42�Ƃ݂Ȃ��ΑS���\
43����63�@21✕1�{22����21✕1�{42�Ƃ݂Ȃ��ΑS���\
�c
337����357�@21✕15�{22����21✕15�{42�Ƃ݂Ȃ��ΑS���\
������260������ɂ��ẮA
��ɍő吔�̎������������������艺�����������Ƃ݂Ȃ����Ƃɂ��
0����260�̏ꍇ�ƑΏ̂̐��_���ł��鎖���l�����
�ʏ�̐��_�Ŋ���260���鐔�܂ł̏��������Ă���̂�
�s�\�Ȍ���10✕2��20�ł��邱�Ƃ�������
����0�͎Ƃ݂Ȃ��Ȃ����Ƃ��^�����Ă���̂�
1����520�ɂ���520��ނ̌��ɑ��s�\��20��ނł��邩��
520�[20��500��500��ނ������Ƃ킩��
�����F500���
���Z�����Ă��Ȃ��̂ŊԈ���Ă����璼���Ăق���
(1)
�܂��A���̏������Ŏ\�ȍő吔��5✕20�{9✕20�{12✕20��520�ł���
5�A9�A12�ō��鐔������o���i���\01���͕\�̌��h���̂��߂̕\�L�j
01 02 03 04 05 06 07 08 09
10 11 12 13 14 15 16 17 18
19 20 21 22 23 24 25 26 27
28 29 30 31 32 33 34 35 36
37 38 39 40 41 42 �c
���̂悤��9�P�ʂŐ�������ׁA5�A9�A12�ō��鐮���Ɋۂ�t���Ă䂭
�e�ՂɁA���͈̔͂ł�1 2 3 4 6 7 8 11 13 16��10�ʂ���������ׂĂ����邱�Ƃ�������
�i9�P�ʂŕ��ׂĂ���̂�9�𑫂�����ō���ꍇ����ڗđR�j
���ɁA22����42�͊ەt���őS�Ė��܂��Ă���
���ꂾ���ł�5���i��ɂȂ�100�ȏ�̏ꍇ���S�z�ɂȂ邪
�����ŏ�\�͈̔͂ł͊ۂ�t�������̂�5�A9�A12�̂�������T��ȓ��̎g�p�ō��邱�Ƃɗ��ӂ���
9�{12��21�����
0����21�@�\��ޕs�\�i���o�j
22����42�@21✕0�{22����21✕0�{42�Ƃ݂Ȃ��ΑS���\
43����63�@21✕1�{22����21✕1�{42�Ƃ݂Ȃ��ΑS���\
�c
337����357�@21✕15�{22����21✕15�{42�Ƃ݂Ȃ��ΑS���\
������260������ɂ��ẮA
��ɍő吔�̎������������������艺�����������Ƃ݂Ȃ����Ƃɂ��
0����260�̏ꍇ�ƑΏ̂̐��_���ł��鎖���l�����
�ʏ�̐��_�Ŋ���260���鐔�܂ł̏��������Ă���̂�
�s�\�Ȍ���10✕2��20�ł��邱�Ƃ�������
����0�͎Ƃ݂Ȃ��Ȃ����Ƃ��^�����Ă���̂�
1����520�ɂ���520��ނ̌��ɑ��s�\��20��ނł��邩��
520�[20��500��500��ނ������Ƃ킩��
�����F500���
2024/09/26(��) 20:22:14.37ID:90+q6boF
(2)
�r�̐���x�A�l�̐���y�A�k�̐���z�Ƃ���
�R������Ԃ�x�Ay�Az���ꂼ�ꂪ0�ȏ�20�ȉ��ƂȂ�悤�Ȋi�q�_��z�u����
�ȉ��i�q�_�Ƃ͂����Œ�`���ꂽ���̂��w��
�܂�x�����Ƃ����Ƃ��ɁAy�Az�݂̂̕��ʏ���l����
����k���l���A9y�{12z��k�ƂȂ�悤��y�Az�i�}��ł͎����Ɋg�����čl����j
��ʂ�悤�Ȓ���l�������Ƃ���
���炩�ɁAk���R�̔{���ȊO�̏ꍇ�͊i�q�_��ʂ炸�A
k�̒l0�A3�A6�A9�A12�A15�A18�A21�A24�A27�A30�A33�c�ɑ��A
���ꂼ��̏ꍇ��l���ʂ�i�q�_�̐���
�}�Œ��ׂ��
1 0 0 1 1 0 1 1 1 1 1 1
2 1 1 2 2 1 2 2 2 2 2 2
3 2 2 3 3 2 3 3 3 3 3 3
4 3 3 4 4 3 4 4 4 4 4 4
5 4 4 5 5 4 5 5 5 5 5 5
6 5 5 5 6 5 5 5 6 5 5 5
6 5 5 5 6 5 5 5 6 5 5 5
5 5 5 4 5 5 4 4 5 4 4 4
4 4 4 3 4 4 3 3 4 3 3 3
3 3 3 2 3 3 2 2 3 2 2 2
2 2 2 1 2 2 1 1 2 1 1 1
1 1 1 0 1 1 0 0 1
�ƂȂ�i���̕\��x��ς��Ă������j
��L��k��0����180�̂Ƃ���180����240�̂Ƃ�240����420�̂Ƃ���
�l�����ω����邱�Ƃɗ��ӂ��Ē��ׂ����̂ł���
�����\��x��0����x��20�܂�21���ł��邪�A
x��X�ł�k��K��x��X+3�ł�k��K-15���������ɂ��Ă̂��̂ł��邱�ƁA
x��0��l���i�q�_��ʂ�ꍇx��1��x��2�ł͓������ɑΉ����钼���͊i�q�_��ʂ�Ȃ����ƁA
�\�̖�����21���ł��邩��ǂ̏ꍇ�����̂���7���̕\�ɂ��čl����悢���Ƃɗ��ӂ���
x��0�Ak��255�@�i�q�_5
x��3�Ak��240�@�i�q�_6
x��6�Ak��225�@�i�q�_5
x��9�Ak��210�@�i�q�_5
x��12�Ak��195�@�i�q�_5
x��15�Ak��180�@�i�q�_6
x��18�Ak��165�@�i�q�_5
���̃p�^�[����7���̕\���v�ōő吔�̊i�q�_��ʂ邱�Ƃ�������
�i�\�ł�6��5�̕��z���疾�炩�j
�����̊i�q�_��ʂ���̂�x��1����n�܂�p�^�[����x��2����n�܂�p�^�[���ɂ�����
���̂R��ނ��ő�ł���
��������Ɋ��Z����ƁA
��255�A260�A265�ł��肻�ꂼ��37�ʂ�̕��@�ŏo�ׂł���
�����F255�A260�A265�̎O��ނ̎�
�r�̐���x�A�l�̐���y�A�k�̐���z�Ƃ���
�R������Ԃ�x�Ay�Az���ꂼ�ꂪ0�ȏ�20�ȉ��ƂȂ�悤�Ȋi�q�_��z�u����
�ȉ��i�q�_�Ƃ͂����Œ�`���ꂽ���̂��w��
�܂�x�����Ƃ����Ƃ��ɁAy�Az�݂̂̕��ʏ���l����
����k���l���A9y�{12z��k�ƂȂ�悤��y�Az�i�}��ł͎����Ɋg�����čl����j
��ʂ�悤�Ȓ���l�������Ƃ���
���炩�ɁAk���R�̔{���ȊO�̏ꍇ�͊i�q�_��ʂ炸�A
k�̒l0�A3�A6�A9�A12�A15�A18�A21�A24�A27�A30�A33�c�ɑ��A
���ꂼ��̏ꍇ��l���ʂ�i�q�_�̐���
�}�Œ��ׂ��
1 0 0 1 1 0 1 1 1 1 1 1
2 1 1 2 2 1 2 2 2 2 2 2
3 2 2 3 3 2 3 3 3 3 3 3
4 3 3 4 4 3 4 4 4 4 4 4
5 4 4 5 5 4 5 5 5 5 5 5
6 5 5 5 6 5 5 5 6 5 5 5
6 5 5 5 6 5 5 5 6 5 5 5
5 5 5 4 5 5 4 4 5 4 4 4
4 4 4 3 4 4 3 3 4 3 3 3
3 3 3 2 3 3 2 2 3 2 2 2
2 2 2 1 2 2 1 1 2 1 1 1
1 1 1 0 1 1 0 0 1
�ƂȂ�i���̕\��x��ς��Ă������j
��L��k��0����180�̂Ƃ���180����240�̂Ƃ�240����420�̂Ƃ���
�l�����ω����邱�Ƃɗ��ӂ��Ē��ׂ����̂ł���
�����\��x��0����x��20�܂�21���ł��邪�A
x��X�ł�k��K��x��X+3�ł�k��K-15���������ɂ��Ă̂��̂ł��邱�ƁA
x��0��l���i�q�_��ʂ�ꍇx��1��x��2�ł͓������ɑΉ����钼���͊i�q�_��ʂ�Ȃ����ƁA
�\�̖�����21���ł��邩��ǂ̏ꍇ�����̂���7���̕\�ɂ��čl����悢���Ƃɗ��ӂ���
x��0�Ak��255�@�i�q�_5
x��3�Ak��240�@�i�q�_6
x��6�Ak��225�@�i�q�_5
x��9�Ak��210�@�i�q�_5
x��12�Ak��195�@�i�q�_5
x��15�Ak��180�@�i�q�_6
x��18�Ak��165�@�i�q�_5
���̃p�^�[����7���̕\���v�ōő吔�̊i�q�_��ʂ邱�Ƃ�������
�i�\�ł�6��5�̕��z���疾�炩�j
�����̊i�q�_��ʂ���̂�x��1����n�܂�p�^�[����x��2����n�܂�p�^�[���ɂ�����
���̂R��ނ��ő�ł���
��������Ɋ��Z����ƁA
��255�A260�A265�ł��肻�ꂼ��37�ʂ�̕��@�ŏo�ׂł���
�����F255�A260�A265�̎O��ނ̎�
715�P�R�Q�l�ڂ̑f������
2024/09/26(��) 21:46:03.32ID:pvL1p2DF ��A���w�ŗǂ��o����B
94*106���H�v���ĉ����Ă��������B
94*106���H�v���ĉ����Ă��������B
2024/09/26(��) 22:25:21.47ID:E0N3ddZu
>>715
(a - b)(a + b) = a^2 - b^2�̉��p�ł��ˁB
94 �~ 106 = (100 - 6)(100 + 6)
= 100^2 - 6^2
= 10000 - 36
= 9964
(a - b)(a + b) = a^2 - b^2�̉��p�ł��ˁB
94 �~ 106 = (100 - 6)(100 + 6)
= 100^2 - 6^2
= 10000 - 36
= 9964
717�P�R�Q�l�ڂ̑f������
2024/09/26(��) 23:06:42.52ID:pvL1p2DF2024/09/27(��) 03:25:22.25ID:m0zw4x/j
>>715
���̂��炢���Ə��w���m���Ȃ��✕�O���Ȃ̂ŕ��ʂɕM�Z�������������ł��傤
94✕106��564�{9400
�@�@�@�@��9964
94✕106��94✕(100�{6)
�@�@�@�@��94✕100�{94✕6
�@�@�@�@��(100�[6)✕100�{(100�[6)✕6
�@�@�@�@��100✕100�[6✕100�{100✕6�[6✕6
�@�@�@�@��100✕100�[6✕100�{6✕100�[6✕6
�@�@�@�@��100✕100�[6✕6
�@�@�@�@��10000�[36
�@�@�@�@��9964
�����Z�̏o�Ă��镪�z�@�������w�Z�ŏK�������͖Y��܂���
���邢�͘a�ƍ��̐ς̌�����}�`���瓱���o���Ă�����g���Ƃ����������܂���
�H�v����͂����ʓ|�ɂȂ��Ă��܂�
���̂��炢���Ə��w���m���Ȃ��✕�O���Ȃ̂ŕ��ʂɕM�Z�������������ł��傤
94✕106��564�{9400
�@�@�@�@��9964
94✕106��94✕(100�{6)
�@�@�@�@��94✕100�{94✕6
�@�@�@�@��(100�[6)✕100�{(100�[6)✕6
�@�@�@�@��100✕100�[6✕100�{100✕6�[6✕6
�@�@�@�@��100✕100�[6✕100�{6✕100�[6✕6
�@�@�@�@��100✕100�[6✕6
�@�@�@�@��10000�[36
�@�@�@�@��9964
�����Z�̏o�Ă��镪�z�@�������w�Z�ŏK�������͖Y��܂���
���邢�͘a�ƍ��̐ς̌�����}�`���瓱���o���Ă�����g���Ƃ����������܂���
�H�v����͂����ʓ|�ɂȂ��Ă��܂�
2024/09/27(��) 03:38:19.99ID:m0zw4x/j
�H�v�Ƃ������́A�m��Ȃ��Ɖ����̂���ςȏ��w�Z���x���̖���
1/6+1/12+1/20+1/30+1/42+1/56�̌v�Z�Ȃǂ�����܂���
�Z�����D���Ȏq���Ȃ炱�̃q���g������̌v�Z���K�Ŏ��͂Ŕ������Ă���͂�
20���炢�܂ł̎��R���̐ς��炢�͈ËL���Ă��ĕs�v�c�͂Ȃ��Ǝv���܂�
1/6+1/12+1/20+1/30+1/42+1/56�̌v�Z�Ȃǂ�����܂���
�Z�����D���Ȏq���Ȃ炱�̃q���g������̌v�Z���K�Ŏ��͂Ŕ������Ă���͂�
20���炢�܂ł̎��R���̐ς��炢�͈ËL���Ă��ĕs�v�c�͂Ȃ��Ǝv���܂�
2024/09/27(��) 04:48:52.32ID:eBrKbEZG
>>715
���w�Z�̒m�������Ōv�Z���ƁA94��100�ƌ��Čv�Z����H�v���L��܂��B
100 �~ 105 = 10600 ������ 94��100�ƌ��Čv�Z
6 �~ 106 = 636 ���������� ���₵�����̌v�Z
10600 - 636 = 9964 ����� ���₵����������
���w�Z�̒m�������Ōv�Z���ƁA94��100�ƌ��Čv�Z����H�v���L��܂��B
100 �~ 105 = 10600 ������ 94��100�ƌ��Čv�Z
6 �~ 106 = 636 ���������� ���₵�����̌v�Z
10600 - 636 = 9964 ����� ���₵����������
2024/09/27(��) 07:39:46.01ID:9yEWl8+1
����ے��ł͕��z�@�����̂����w
�ł������鏬�w���͕��z�@�����Č��t�͊o���Ȃ��Ă��v�Z�@���m�ŏK��
�ł������鏬�w���͕��z�@�����Č��t�͊o���Ȃ��Ă��v�Z�@���m�ŏK��
722�P�R�Q�l�ڂ̑f������
2024/09/27(��) 08:25:15.36ID:rFqvbpZk >>718
�e�N�j�b�N�����o���ĂāA�����������ɂ������ǂ����l����Ηǂ������ł��ˁB
�}12�Ƃ��}14�Ƃ�����Ηǂ����������H
���Ƃ͍ŋߒm���������Z�̌J�艺��������e�N�j�b�N�͖ڂ���E���R���������ǁA�Z���D���͂Ƃ����ɒm���Ă��낤�ȁc�B
500 - 56 = 499 - 56 + 1 = 443 + 1 = 444
�e�N�j�b�N�����o���ĂāA�����������ɂ������ǂ����l����Ηǂ������ł��ˁB
�}12�Ƃ��}14�Ƃ�����Ηǂ����������H
���Ƃ͍ŋߒm���������Z�̌J�艺��������e�N�j�b�N�͖ڂ���E���R���������ǁA�Z���D���͂Ƃ����ɒm���Ă��낤�ȁc�B
500 - 56 = 499 - 56 + 1 = 443 + 1 = 444
2024/09/29(��) 06:40:41.39ID:rr/J2k2z
�m���Ă���l�͒m���Ă�����ł�
�������w�܂ł̒m���ʼn�����Ǝv���܂�
����̐����`�̕���������܂�
�l�ӂ͓�����k�ɑΉ����Ă�����̂Ƃ��܂�
���̕�������쓌�Ɩk���̊p�ɂ��Ă��ꂼ�ꔼ����������`�̕������l���܂�
�V���ȕ����͖ʐώ���ł����A
�ʏ�̏��Ō��ԁA�d�Ȃ�Ȃ��~���l�߂���@�ɂ��Ę_���Ă�������
��͒��ӁF�Z�Ӂ�2�F1�̒����`�A����̏�͐����`�Ƃ�
�ߔz�u�A��̒Z�Ӓ������̔��[�Ȃ��炵�z�u�͕s�Ƃ��܂�
�������w�܂ł̒m���ʼn�����Ǝv���܂�
����̐����`�̕���������܂�
�l�ӂ͓�����k�ɑΉ����Ă�����̂Ƃ��܂�
���̕�������쓌�Ɩk���̊p�ɂ��Ă��ꂼ�ꔼ����������`�̕������l���܂�
�V���ȕ����͖ʐώ���ł����A
�ʏ�̏��Ō��ԁA�d�Ȃ�Ȃ��~���l�߂���@�ɂ��Ę_���Ă�������
��͒��ӁF�Z�Ӂ�2�F1�̒����`�A����̏�͐����`�Ƃ�
�ߔz�u�A��̒Z�Ӓ������̔��[�Ȃ��炵�z�u�͕s�Ƃ��܂�
2024/09/29(��) 06:49:58.71ID:rr/J2k2z
2024/09/29(��) 08:26:05.42ID:pGKY1a20
>>724
10�̗ݏ��3�Ŋ������]��͏��1�ɂȂ�܂��B
10^n �� 1 (mod 3)
�]���āA
237 = 2 �~ 10^2 + 3 �~ 10 + 7�́A
���̗l�Ȍv�Z�ŗ]�肪�o�܂��B
237 �� 2 �~ (10^2 mod 3) + 3 �~ (10 mod 3} + 7 (mod 3)
237 �� 2 �~ 1 + 3 �~ 1 + 7 (mod 3)
237 �� 2 + 3 + 7 (mod 3)
237 �� 12 (mod 3)
237 �� 0 (mod 3)
�]�肪0�ł��̂�237��3�̔{���ƌ������Ƃł��B
10�̗ݏ��3�Ŋ������]��͏��1�ɂȂ�܂��B
10^n �� 1 (mod 3)
�]���āA
237 = 2 �~ 10^2 + 3 �~ 10 + 7�́A
���̗l�Ȍv�Z�ŗ]�肪�o�܂��B
237 �� 2 �~ (10^2 mod 3) + 3 �~ (10 mod 3} + 7 (mod 3)
237 �� 2 �~ 1 + 3 �~ 1 + 7 (mod 3)
237 �� 2 + 3 + 7 (mod 3)
237 �� 12 (mod 3)
237 �� 0 (mod 3)
�]�肪0�ł��̂�237��3�̔{���ƌ������Ƃł��B
2024/09/30(��) 02:39:27.63ID:6wo4s8Mk
����җl�{�l�̌�Ԏ����Ȃ��̂ʼn��Ƃ������܂���
�e���̘a��3�̔{���Ȃ�3�̔{���ł���Ƃ������Ƃɋ^������i�K�̐l��
mod�Ő�������Ƃ����̂͏������Ⴄ�C�����܂�
���̋L���ł͒��w�Z�܂ł�mod�͏K��Ȃ������Ǝv���܂���
����mod��3�̔{���̔��ʖ@������ɏK���̂ł��傤��
�e���̘a��3�̔{���Ȃ�3�̔{���ł���Ƃ������Ƃɋ^������i�K�̐l��
mod�Ő�������Ƃ����̂͏������Ⴄ�C�����܂�
���̋L���ł͒��w�Z�܂ł�mod�͏K��Ȃ������Ǝv���܂���
����mod��3�̔{���̔��ʖ@������ɏK���̂ł��傤��
2024/09/30(��) 05:49:33.88ID:Nl3f7HnH
>>726
�o���邾�������g�킸�ɐ����������̂ł�������Ƃ̈ӌ����L��܂����B
�����̐ق��̂��Ǝv���A�A�v���[�`��ς��܂����B
�ł��̂ŁA���m�������Ƃ��邽�ߏ����̐������O���������Ɛ����Ă��܂��B
�������Č��Ē�����A�����Ȃ�Ƃ�������Ղ��Ȃ邩�Ǝv���܂��B
�o���邾�������g�킸�ɐ����������̂ł�������Ƃ̈ӌ����L��܂����B
�����̐ق��̂��Ǝv���A�A�v���[�`��ς��܂����B
�ł��̂ŁA���m�������Ƃ��邽�ߏ����̐������O���������Ɛ����Ă��܂��B
�������Č��Ē�����A�����Ȃ�Ƃ�������Ղ��Ȃ邩�Ǝv���܂��B
2024/09/30(��) 07:50:47.17ID:vKhr7RV5
726�͑��l�̉��{���N�\�ᔻ���Ƃ��Ă��̂܂܃g���Y���Ȃ�Ă��Ȃ����w
�����Ɩ͔͉��o����
�����Ɩ͔͉��o����
2024/09/30(��) 08:53:28.89ID:6wo4s8Mk
>>679
>>681 �����ɂ������ɂȂ��Ă��܂�������ł킩��Ȃ��ꍇ�ɓǂ�ł�������
���Ȃ������w���ł���Ɖ��肵�Ă������������܂�
�����́A3�Ŋ���i�]�肠��Łj�Ƃ���������l����A
3�̔{���A3�̔{���{1�A3�̔{���{2�̎O�̃^�C�v�̂ǂꂩ�ЂƂɕK���Ȃ�܂�
�ȉ��̐������u�i3�̔{���j�v�Ƃ����̂͋�̓I�Ȓl�͕ʂƂ���3�̔{���ł��鐔�Ƃ��܂�
��i3�̔{���j���o�Ă����ꍇ�A�����l�ł���K�v�͂���܂���
�i3�̔{���{1�j�Ɓi3�̔{���{2�j�����l�̈Ӗ��Ƃ��܂�
�܂��A3�̔{����3�̔{���𑫂���3�̔{���ɂȂ�̂�
���Ȃ����m���Ă��邱�Ƃł��傤
���A�\�̈ʂ����A��̈ʂ����̓̐���������Ƃ��܂�
�i���ʂ̎Z���ŏ����Ƃ����ł����A���w�ŏK���������̃��[���ł͑S���Ⴄ�Ӗ��ɂȂ�A
�ȍ~���̕������̃��[�����嗬�ɂȂ�̂ł����ł͂��̐����������Ƃ͏����܂���j
���w�Z�ł͂��₂�̑���Ɏl�p��O�p�������Ǝv���܂��������ł͕����������|���̂�
���₂�ŏ����܂�
���̐��͂�✕10�{���Ƃ����l�������܂����A
���ꂪ3�̔{���A3�̔{���{1�A3�̔{���{2�̂ǂ̃^�C�v�ł��邩�l���Ă݂܂��傤
�i�����̂ő����j
>>681 �����ɂ������ɂȂ��Ă��܂�������ł킩��Ȃ��ꍇ�ɓǂ�ł�������
���Ȃ������w���ł���Ɖ��肵�Ă������������܂�
�����́A3�Ŋ���i�]�肠��Łj�Ƃ���������l����A
3�̔{���A3�̔{���{1�A3�̔{���{2�̎O�̃^�C�v�̂ǂꂩ�ЂƂɕK���Ȃ�܂�
�ȉ��̐������u�i3�̔{���j�v�Ƃ����̂͋�̓I�Ȓl�͕ʂƂ���3�̔{���ł��鐔�Ƃ��܂�
��i3�̔{���j���o�Ă����ꍇ�A�����l�ł���K�v�͂���܂���
�i3�̔{���{1�j�Ɓi3�̔{���{2�j�����l�̈Ӗ��Ƃ��܂�
�܂��A3�̔{����3�̔{���𑫂���3�̔{���ɂȂ�̂�
���Ȃ����m���Ă��邱�Ƃł��傤
���A�\�̈ʂ����A��̈ʂ����̓̐���������Ƃ��܂�
�i���ʂ̎Z���ŏ����Ƃ����ł����A���w�ŏK���������̃��[���ł͑S���Ⴄ�Ӗ��ɂȂ�A
�ȍ~���̕������̃��[�����嗬�ɂȂ�̂ł����ł͂��̐����������Ƃ͏����܂���j
���w�Z�ł͂��₂�̑���Ɏl�p��O�p�������Ǝv���܂��������ł͕����������|���̂�
���₂�ŏ����܂�
���̐��͂�✕10�{���Ƃ����l�������܂����A
���ꂪ3�̔{���A3�̔{���{1�A3�̔{���{2�̂ǂ̃^�C�v�ł��邩�l���Ă݂܂��傤
�i�����̂ő����j
2024/09/30(��) 08:54:15.95ID:6wo4s8Mk
�i�����j
��✕10�̕����ɂ��čl���Ă݂�ƁA
��✕10����✕9�{��✕1�ł�
��✕9�͐����̂X�{�Ȃ̂�9�̔{���œ��R3�̔{���ł�����A����ɓ���čl�����
����������3�̔{���Ȃ炁✕9�{��✕1�́i3�̔{���j�{�i3�̔{���j�Ȃ̂ł�✕10��3�̔{���ł�
����3�̔{���{1�Ȃ炁✕9�{��✕1��
�i3�̔{���j�{�i3�̔{���{1�j�Ȃ̂�3�̔{�����m���ɑ����킩��悤��
��✕10�̃^�C�v��3�̔{���{1�ł�
����3�̔{���{2�Ȃ炁✕9�{��✕1��
�i3�̔{���j�{�i3�̔{���{2�j�Ȃ̂ł�✕10�̃^�C�v��3�̔{���{2�ł�
���̂悤�ɁA�����ǂ̃^�C�v�ł���✕10�̃^�C�v�͂�✕1�܂肁�Ɠ����^�C�v�ɂȂ�̂ł�
�ł����炱�̓̐����͂��{���Ɠ����^�C�v�ɂȂ�̂ł�
�i�d�v�F�R�̔{���ł��邩�����łȂ��A�R�Ŋ������]��܂œ����ɂȂ�܂��j
����ɂ��̐����̏ꍇ�A�S�Ă̌��̒l�̘a��3�̔{���Ȃ�A3�̔{���ɂȂ�̂ł�
�O���ȏ�̏ꍇ�ɂ��Ă͂������ōl���Ă�������
���w�Z�⒆�w�Z�̒i�K�ł͏����q���g���玩���ōl���邱�Ƃ�
���͂�傫���L���Ă���܂�
��✕10�̕����ɂ��čl���Ă݂�ƁA
��✕10����✕9�{��✕1�ł�
��✕9�͐����̂X�{�Ȃ̂�9�̔{���œ��R3�̔{���ł�����A����ɓ���čl�����
����������3�̔{���Ȃ炁✕9�{��✕1�́i3�̔{���j�{�i3�̔{���j�Ȃ̂ł�✕10��3�̔{���ł�
����3�̔{���{1�Ȃ炁✕9�{��✕1��
�i3�̔{���j�{�i3�̔{���{1�j�Ȃ̂�3�̔{�����m���ɑ����킩��悤��
��✕10�̃^�C�v��3�̔{���{1�ł�
����3�̔{���{2�Ȃ炁✕9�{��✕1��
�i3�̔{���j�{�i3�̔{���{2�j�Ȃ̂ł�✕10�̃^�C�v��3�̔{���{2�ł�
���̂悤�ɁA�����ǂ̃^�C�v�ł���✕10�̃^�C�v�͂�✕1�܂肁�Ɠ����^�C�v�ɂȂ�̂ł�
�ł����炱�̓̐����͂��{���Ɠ����^�C�v�ɂȂ�̂ł�
�i�d�v�F�R�̔{���ł��邩�����łȂ��A�R�Ŋ������]��܂œ����ɂȂ�܂��j
����ɂ��̐����̏ꍇ�A�S�Ă̌��̒l�̘a��3�̔{���Ȃ�A3�̔{���ɂȂ�̂ł�
�O���ȏ�̏ꍇ�ɂ��Ă͂������ōl���Ă�������
���w�Z�⒆�w�Z�̒i�K�ł͏����q���g���玩���ōl���邱�Ƃ�
���͂�傫���L���Ă���܂�
2024/09/30(��) 09:15:22.99ID:6wo4s8Mk
>>727
�����ɂ͌������A��w���ȏ�̕��������悤�ł�����
�M���̐����̕���������g���Ă��錾�t�ł��傤���A
�킽���̂悤�Ȃ͂邩�̂ɎZ����D���l�Ԃ������҂ɂ�
�Y�ꂩ���Ă����m������@�_���v���o���ėǂ��Ǝv���܂���
����җl����̌�Ԏ����Ȃ������̂��C�ɂȂ�܂���
�M�������Ӑ}�͂���܂���ł�����
728���̂��w�E�����ēǂݒ����ƁA�����I�Ƃ��ǂ߂镶�ʂɂȂ��Ă��܂���
�ق����͂ɂ��Ă��l�т������܂�
�����ɂ͌������A��w���ȏ�̕��������悤�ł�����
�M���̐����̕���������g���Ă��錾�t�ł��傤���A
�킽���̂悤�Ȃ͂邩�̂ɎZ����D���l�Ԃ������҂ɂ�
�Y�ꂩ���Ă����m������@�_���v���o���ėǂ��Ǝv���܂���
����җl����̌�Ԏ����Ȃ������̂��C�ɂȂ�܂���
�M�������Ӑ}�͂���܂���ł�����
728���̂��w�E�����ēǂݒ����ƁA�����I�Ƃ��ǂ߂镶�ʂɂȂ��Ă��܂���
�ق����͂ɂ��Ă��l�т������܂�
2024/09/30(��) 09:30:39.22ID:vKhr7RV5
�܂�ł`�h�ɐ����������l�ȕ��͂���w
2024/10/04(��) 12:45:53.36ID:vZsNQcTG
>>708
�A�r�W�W�C���a���s���̖͗l
�A�r�W�W�C���a���s���̖͗l
2024/10/04(��) 22:15:30.93ID:BpsNh+Jy
>>713
�����ł��B
> S=5*(0:20)
> M=9*(0:20)
> L=12*(0:20)
> t1=expand.grid(S,M,L)[-1,]
> t2=rowSums(t1)
> length(unique(t2))
[1] 500
�����ł��B
> S=5*(0:20)
> M=9*(0:20)
> L=12*(0:20)
> t1=expand.grid(S,M,L)[-1,]
> t2=rowSums(t1)
> length(unique(t2))
[1] 500
2024/10/04(��) 22:18:58.52ID:BpsNh+Jy
2024/10/04(��) 22:24:51.34ID:BpsNh+Jy
�������Əo�ז@�̐����O���t�ɂ��Ă݂��B
https://i.imgur.com/DDIluEa.png
Ubuntu�ł�R�ō쐬�B
���_��3�{��255 260 265 �ɑ����B
https://i.imgur.com/DDIluEa.png
Ubuntu�ł�R�ō쐬�B
���_��3�{��255 260 265 �ɑ����B
2024/10/04(��) 22:58:50.86ID:BpsNh+Jy
Wolfram�Ō��Z
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= S=5 Range[0,20];
In[2]:= M=9 Range[0,20];
In[3]:= L=12 Range[0,20];
In[4]:= t1=Tuples[{S,M,L}];
In[5]:= t2=Select[Total /@ t1,#!=0&];
In[6]:= Length@Union@t2
Out[6]= 500
In[7]:= t3=Counts[t2];
In[8]:= Max[t3]
Out[8]= 37
In[9]:= Position[t3,Max[t3]]
Out[9]= {{Key[255]}, {Key[260]}, {Key[265]}}
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= S=5 Range[0,20];
In[2]:= M=9 Range[0,20];
In[3]:= L=12 Range[0,20];
In[4]:= t1=Tuples[{S,M,L}];
In[5]:= t2=Select[Total /@ t1,#!=0&];
In[6]:= Length@Union@t2
Out[6]= 500
In[7]:= t3=Counts[t2];
In[8]:= Max[t3]
Out[8]= 37
In[9]:= Position[t3,Max[t3]]
Out[9]= {{Key[255]}, {Key[260]}, {Key[265]}}
2024/10/04(��) 23:55:52.71ID:YtUwSjrk
���w���ɂ��瑊��ɂ���ĂȂ��`���p�����܂��\��Ă�͗l
2024/10/05(�y) 00:05:21.67ID:D+ILBq1z
>>737
���Z���w�X�����ፂ�Z���ɂ���_�j����Ă����̉����o�Ȃ����珬�w���Ȃ�Ȃ�Ƃ��Ȃ�Ǝv�������ԈႢ����ww
���Z���w�X�����ፂ�Z���ɂ���_�j����Ă����̉����o�Ȃ����珬�w���Ȃ�Ȃ�Ƃ��Ȃ�Ǝv�������ԈႢ����ww
2024/10/05(�y) 07:57:39.04ID:YfiGIrmM
713�P�R�Q�l�ڂ̑f������sage2024/09/26(��) 19:36:04.22ID:90+q6boF(1/2) �ԐM (1)
708�͏����w�Z�̒m���ʼn�����Ǝv��
�̂悤�ȒB�l�ɔ�ׂāA�A�r�`���p���t�F�`��Phimose�������
�l�|���e�����ł��Ȃ��݂������ȁB
R��Wolfram���g���Ȃ��悤�ł���B
Zorin OS�@�ł� read.crx2 ���g���Ă̏������݁B
�ŋ߂�PC���Ɛ�u���g��Ȃ��Ă悭�Ȃ����B
�L�����łȂ����A���K�B
����>718�͎����F�肵�Ȃ��Ǝv���B
���W�b�N�����x�����Ĕ�䍂ł��Ȃ��B
708�͏����w�Z�̒m���ʼn�����Ǝv��
�̂悤�ȒB�l�ɔ�ׂāA�A�r�`���p���t�F�`��Phimose�������
�l�|���e�����ł��Ȃ��݂������ȁB
R��Wolfram���g���Ȃ��悤�ł���B
Zorin OS�@�ł� read.crx2 ���g���Ă̏������݁B
�ŋ߂�PC���Ɛ�u���g��Ȃ��Ă悭�Ȃ����B
�L�����łȂ����A���K�B
����>718�͎����F�肵�Ȃ��Ǝv���B
���W�b�N�����x�����Ĕ�䍂ł��Ȃ��B
2024/10/05(�y) 10:13:32.46ID:a6IZSd7f
�ŁA���w���ɂ͑��ς�炸����ɂ���ĂȂ��݂��������H
2024/10/05(�y) 12:43:10.07ID:a6IZSd7f
>>740
�܂��]����Êۏo���̖͗l
569�F���̖���������F[sage]�F2024/10/05(�y) 08:11:19.90 ID:9dpUaTMC
�ݑS�E�Ǘ�́A�Y�_�K�X���C�ɂ��Ă�������B
�H�������͒[���������ȁB
���̓�-interposition���D�݂������B
�����\�����シ��̂�pouch�����s���Ă������A
���̂���������ɂȂ肾�����Ȃ��B
574�F���̖���������F2024/10/05(�y) 12:40:56.12 ID:sd3EfCAY
>>567
����ς�A�z����
�^�P�L���u���ݎ_�}�������̌��ʂ��Ǝv���Ă邩�炻��Ȕ����o����www
�^�P�L���u�ł͖������ݑS�E���PPI�𓊗^���ċt�H�Ɍ��ʂ����������ĕ͂����������ł�����
��҂���Ȃ��A�r�W�W�C����͒m��Ȃ��ē��R������www
�܂��]����Êۏo���̖͗l
569�F���̖���������F[sage]�F2024/10/05(�y) 08:11:19.90 ID:9dpUaTMC
�ݑS�E�Ǘ�́A�Y�_�K�X���C�ɂ��Ă�������B
�H�������͒[���������ȁB
���̓�-interposition���D�݂������B
�����\�����シ��̂�pouch�����s���Ă������A
���̂���������ɂȂ肾�����Ȃ��B
574�F���̖���������F2024/10/05(�y) 12:40:56.12 ID:sd3EfCAY
>>567
����ς�A�z����
�^�P�L���u���ݎ_�}�������̌��ʂ��Ǝv���Ă邩�炻��Ȕ����o����www
�^�P�L���u�ł͖������ݑS�E���PPI�𓊗^���ċt�H�Ɍ��ʂ����������ĕ͂����������ł�����
��҂���Ȃ��A�r�W�W�C����͒m��Ȃ��ē��R������www
2024/10/06(��) 09:57:18.41ID:ReaDJul3
>>730
>����͂ǂ�Ȃɑ傫�����ł������Ȃ�ł��傤��
>�ǂ����Ă����Ȃ���Č�������ł���
�u a₁�~10ᵏ + a₂�~10ᵏ⁻¹ + a₃�~10ᵏ⁻² ��� aₙ�~10⁰ �� a₁ + a₂ + a₃ ��� aₙ (mod 3)�v�̏ؖ������߂Ă���̂ł́H
>����͂ǂ�Ȃɑ傫�����ł������Ȃ�ł��傤��
>�ǂ����Ă����Ȃ���Č�������ł���
�u a₁�~10ᵏ + a₂�~10ᵏ⁻¹ + a₃�~10ᵏ⁻² ��� aₙ�~10⁰ �� a₁ + a₂ + a₃ ��� aₙ (mod 3)�v�̏ؖ������߂Ă���̂ł́H
2024/10/06(��) 11:05:18.74ID:IROa96ju
���W���@���̈Ӗ��͏��w���ł��킩��B
5����̃^�R�Ă�(S)�A9����̃^�R�Ă�(M)�A12����̃^�R�Ă�(L)
20����̃^�R�Ă�(XL)
S,M,L,XL���e�X20�����p�ӂ����B
�^�R�Ă��̐��Œ������邪�A�o������͂��Ȃ��B
��F17�͎��邪�A16�̎͂��Ȃ��B
���
(1)�@�ł���̃^�R�Ă��̐��͉���ނ��邩�B�A���A0�͎ɐ����Ȃ��B
(2)�@60�̒����̏ꍇ��
S M L XL
[1,] 0 0 0 3
[2,] 0 0 5 0
[3,] 0 4 2 0
[4,] 2 2 1 1
[5,] 3 1 3 0
[6,] 3 5 0 0
[7,] 4 0 0 2
[8,] 6 2 1 0
[9,] 8 0 0 1
[10,] 12 0 0 0
��10��ނ̕��@�ŏo�ׂł���B
�o�ׂł�����@���ł������͉̂��̃^�R�Ă��������Ƃ����H
����������ׂė���B
5����̃^�R�Ă�(S)�A9����̃^�R�Ă�(M)�A12����̃^�R�Ă�(L)
20����̃^�R�Ă�(XL)
S,M,L,XL���e�X20�����p�ӂ����B
�^�R�Ă��̐��Œ������邪�A�o������͂��Ȃ��B
��F17�͎��邪�A16�̎͂��Ȃ��B
���
(1)�@�ł���̃^�R�Ă��̐��͉���ނ��邩�B�A���A0�͎ɐ����Ȃ��B
(2)�@60�̒����̏ꍇ��
S M L XL
[1,] 0 0 0 3
[2,] 0 0 5 0
[3,] 0 4 2 0
[4,] 2 2 1 1
[5,] 3 1 3 0
[6,] 3 5 0 0
[7,] 4 0 0 2
[8,] 6 2 1 0
[9,] 8 0 0 1
[10,] 12 0 0 0
��10��ނ̕��@�ŏo�ׂł���B
�o�ׂł�����@���ł������͉̂��̃^�R�Ă��������Ƃ����H
����������ׂė���B
2024/10/06(��) 11:10:10.84ID:WxuONFQC
2024/10/06(��) 11:28:57.50ID:UJxXI7u4
>713�̂悤�ɗ��l�߂ŎZ�o�ł���l������̂����A
���������X�L�����Ȃ���Γ�����g�������B
���łɃR�[�h�͏����Ă���̂ł�������肷�邾���B
���������X�L�����Ȃ���Γ�����g�������B
���łɃR�[�h�͏����Ă���̂ł�������肷�邾���B
2024/10/06(��) 12:00:11.68ID:wOCqOj+d
748�P�R�Q�l�ڂ̑f������
2024/10/06(��) 15:09:15.64ID:J/esTY4X ���݂܂����Ă��������B
���w�̖��Ȃ̂ł����A���w���͈͓̔��ʼn������������Ăق����ł��B
�y���z����w�Z�ł͒j���̔䂪�Q:�R�ŁA���K�l�������Ă���l���͊w�Z�S�̂̂P/�R�ł��B
�j�q�Ń��K�l�������Ă���l���͂V�O�l�A���q�Ń��K�l�������Ă��Ȃ��l���͂P�X�O�l�ł��B
�w�Z�S�̂̐l���͉��l�ł����H
���w�̖��Ȃ̂ł����A���w���͈͓̔��ʼn������������Ăق����ł��B
�y���z����w�Z�ł͒j���̔䂪�Q:�R�ŁA���K�l�������Ă���l���͊w�Z�S�̂̂P/�R�ł��B
�j�q�Ń��K�l�������Ă���l���͂V�O�l�A���q�Ń��K�l�������Ă��Ȃ��l���͂P�X�O�l�ł��B
�w�Z�S�̂̐l���͉��l�ł����H
2024/10/06(��) 16:19:41.55ID:4DgSzUxW
>>748
(190-70) ��(3/5-1/3)=450
(190-70) ��(3/5-1/3)=450
2024/10/06(��) 16:24:20.84ID:4DgSzUxW
>>747
�ŁA���͌v�Z�ł����̂��H
Phimose����́AWolfram��R��������Ȃ��݂������ȁB
�M���̂�foreskin�����݂������Ȃ��B
�ŁA���͌v�Z�ł����̂��H
Phimose����́AWolfram��R��������Ȃ��݂������ȁB
�M���̂�foreskin�����݂������Ȃ��B
2024/10/06(��) 16:54:11.75ID:4DgSzUxW
�����ɂ͎g�p�ł��閇���̐���������̂ł���
�y���z
���{��s���i�����鎆���A���D�j�́A�u���{��s�@�v��46���Q���Łu�������ɒʗp����v�ƋK�肳��Ă��܂��B
�ݕ��i������d�݁j�́A�u�ʉ݂̒P�ʋy�щݕ��̔��s���Ɋւ���@���v��V���Łu�z�ʉ��i��20�{�܂Łv�����x�Ƃ��Ēʗp����ƋK�肳��Ă��܂��B�܂�A20���܂ł͉ݕ��ɂ��x�������s���Ă��ǂ��Ƃ������Ƃł��B
https://www.mof.go.jp/faq/currency/07ab.htm
�P�~�ʂ���T�O�O�~�ʂ܂ł̍d�݂��e�X�Q�O��������B
(1)���ނ������킸�Ɏx���z�͉���ނ��邩�H
(2)�x�������@���ł������͉̂��~�̎x�����̂Ƃ����B����������ׂė���B
�y���z
���{��s���i�����鎆���A���D�j�́A�u���{��s�@�v��46���Q���Łu�������ɒʗp����v�ƋK�肳��Ă��܂��B
�ݕ��i������d�݁j�́A�u�ʉ݂̒P�ʋy�щݕ��̔��s���Ɋւ���@���v��V���Łu�z�ʉ��i��20�{�܂Łv�����x�Ƃ��Ēʗp����ƋK�肳��Ă��܂��B�܂�A20���܂ł͉ݕ��ɂ��x�������s���Ă��ǂ��Ƃ������Ƃł��B
https://www.mof.go.jp/faq/currency/07ab.htm
�P�~�ʂ���T�O�O�~�ʂ܂ł̍d�݂��e�X�Q�O��������B
(1)���ނ������킸�Ɏx���z�͉���ނ��邩�H
(2)�x�������@���ł������͉̂��~�̎x�����̂Ƃ����B����������ׂė���B
2024/10/06(��) 22:14:14.70ID:oOWpyKPY
2024/10/07(��) 06:39:35.67ID:d1xIZpzF
�����w���̐��w��D�����N�����I
�Ȃ�тɏ����w�Z�͈͂̎Z���E���w�̖��ŔY��ł�����I(�N����킸)
�Ƃ������ƂȂ̂�
�����Ɨǂ���@���Ȃ����Y��ł����l�⎩���̉�@�ł悢�̂��Y��ł����l�͂n�j�Ȃ̂ł��傤
�ł����A�����w�Z�̗��C���e�Ŕ��z�ł��鐔�w�I��@�ʼn����\�Ȗ�肩��
�����w���̓�������ԓ��Ō��_�܂œ��B�ł�����x�܂ł̔ώG���ł��邱�Ƃ�
���R�Ɨv�������̂ł͂Ȃ��ł��傤��
�Ȃ�тɏ����w�Z�͈͂̎Z���E���w�̖��ŔY��ł�����I(�N����킸)
�Ƃ������ƂȂ̂�
�����Ɨǂ���@���Ȃ����Y��ł����l�⎩���̉�@�ł悢�̂��Y��ł����l�͂n�j�Ȃ̂ł��傤
�ł����A�����w�Z�̗��C���e�Ŕ��z�ł��鐔�w�I��@�ʼn����\�Ȗ�肩��
�����w���̓�������ԓ��Ō��_�܂œ��B�ł�����x�܂ł̔ώG���ł��邱�Ƃ�
���R�Ɨv�������̂ł͂Ȃ��ł��傤��
2024/10/07(��) 06:58:06.11ID:d1xIZpzF
>>749
���̑O�u�����Ȃ������Ȃ肻�̎����v������l��
�����ɗ���K�v���Ȃ��V�˂��Ǝv���܂�
���ɂ͂��̎����Ȃ��o�Ă���̂��A�������Ă������ɂ͂킩��܂���ł���
�����̗��Ă��������i���̏Љ�Ȃ��Ȃ�������͏��w�Z�ł��o�Ă��܂��j��
���m���ɂ��ĉ����ߒ��ōׂ����v�Z����ɂ����ꍇ�̎��ƈ�v���Ă���ƋC�Â����̂�
���Ȃ莞�Ԃ��o���Ă���ł���
���̑O�u�����Ȃ������Ȃ肻�̎����v������l��
�����ɗ���K�v���Ȃ��V�˂��Ǝv���܂�
���ɂ͂��̎����Ȃ��o�Ă���̂��A�������Ă������ɂ͂킩��܂���ł���
�����̗��Ă��������i���̏Љ�Ȃ��Ȃ�������͏��w�Z�ł��o�Ă��܂��j��
���m���ɂ��ĉ����ߒ��ōׂ����v�Z����ɂ����ꍇ�̎��ƈ�v���Ă���ƋC�Â����̂�
���Ȃ莞�Ԃ��o���Ă���ł���
2024/10/07(��) 07:14:51.09ID:23c/oieN
���z��1,5,10,50,100,500�~�̍d�݂��e�X20������B
�������g����10000�~���x�����B
�x������ɍ��z�Ɏc���Ă���d�݂̑��������ŏ��ɂ���ɂ�
�ǂ̂悤�Ɏx�����悢���H
�������g����10000�~���x�����B
�x������ɍ��z�Ɏc���Ă���d�݂̑��������ŏ��ɂ���ɂ�
�ǂ̂悤�Ɏx�����悢���H
2024/10/07(��) 07:44:25.37ID:rbmpkFgT
>>755
��������
��������
757748
2024/10/07(��) 11:59:14.41ID:oj1OeIi8 >>749
���肪�Ƃ��������܂��B
���݂܂���A�������čl���Ă݂��̂ł������̂��̎������藧�̂�����܂���ł����B
�o������������ڂ��������Ă���������Ƃ��肪�����ł��B
���ƁA�邩�ߎZ��j���[�g���Z�݂����ȃJ�e�S���[���ƁA���̖��͂ǂ�ɊY������̂ł��傤���H
���肪�Ƃ��������܂��B
���݂܂���A�������čl���Ă݂��̂ł������̂��̎������藧�̂�����܂���ł����B
�o������������ڂ��������Ă���������Ƃ��肪�����ł��B
���ƁA�邩�ߎZ��j���[�g���Z�݂����ȃJ�e�S���[���ƁA���̖��͂ǂ�ɊY������̂ł��傤���H
2024/10/07(��) 19:13:43.98ID:67Ro0n9B
>>748
749�ł͂Ȃ����A�l�����͎�
���q�Ŋዾ���|���Ă���l�̐������Ƃ���ƁA
�V�O�{�����i�ዾ���|���Ă���l���j���i�S�̂̐l���j�~�i�P�^�R�j
�P�X�O�{�����i���q�̐l���j���i�S�̂̐l���j�~�i�R�^�T�j
�i���̎��j�|�i��̎��j�������
�P�X�O�|�V�O���i�S�̂̐l���j�~�i�R�^�T�|�P�^�R�j
�i�S�̂̐l���j���i�P�X�O�|�V�O�j���i�R�^�T�|�P�^�R�j
749�ł͂Ȃ����A�l�����͎�
���q�Ŋዾ���|���Ă���l�̐������Ƃ���ƁA
�V�O�{�����i�ዾ���|���Ă���l���j���i�S�̂̐l���j�~�i�P�^�R�j
�P�X�O�{�����i���q�̐l���j���i�S�̂̐l���j�~�i�R�^�T�j
�i���̎��j�|�i��̎��j�������
�P�X�O�|�V�O���i�S�̂̐l���j�~�i�R�^�T�|�P�^�R�j
�i�S�̂̐l���j���i�P�X�O�|�V�O�j���i�R�^�T�|�P�^�R�j
2024/10/07(��) 20:44:43.55ID:sE9eBC4+
(190 - 70) : (3/5 - 1/3) = 450 : 1
���q�Ń��K�l�������Ă��Ȃ��l��(190)����j�q�̃��K�l���������l��(70)����������(120)���A���q�S�̂̊���(3/5)�Ɗw�Z�S�̂̃��K�l�������Ă��銄��(1/3)�̍�(4/15)�̔䂪�w�Z�S�̂̔�Ɠ����ƋC�t�����w����������V�˂��ȁB
�������o�������Ȃ�A�����������g���ΊȒP�ɏo���邪�A���w�Z�ł͏K��Ȃ��͂��B
���q�Ń��K�l�������Ă��Ȃ��l��(190)����j�q�̃��K�l���������l��(70)����������(120)���A���q�S�̂̊���(3/5)�Ɗw�Z�S�̂̃��K�l�������Ă��銄��(1/3)�̍�(4/15)�̔䂪�w�Z�S�̂̔�Ɠ����ƋC�t�����w����������V�˂��ȁB
�������o�������Ȃ�A�����������g���ΊȒP�ɏo���邪�A���w�Z�ł͏K��Ȃ��͂��B
760748
2024/10/08(��) 13:34:11.52ID:wtrTTCG9 >>758-759
������₷�����肪�Ƃ��������܂����I
���q�ɍi���Ď��𗧂Ă�Ηǂ�������ł��ˁB
�i���̎��j�|�i��̎��j���炪������������̂ŁA�����Ȃ�ɍl���Ă݂܂����B
�������q���K�l����������l��
�����S�̂̐l��
70�{�������~1/3
190�{�������~3/5
�S�̂̐l����15���Ƃ������A
1/3��5/15���D
3/5��9/15���H
�����
70�{�����D
190�{�����H
�C���P�Q�O
15�����S�T�O
�S�̂̐l���͂S�T�O�l
������₷�����肪�Ƃ��������܂����I
���q�ɍi���Ď��𗧂Ă�Ηǂ�������ł��ˁB
�i���̎��j�|�i��̎��j���炪������������̂ŁA�����Ȃ�ɍl���Ă݂܂����B
�������q���K�l����������l��
�����S�̂̐l��
70�{�������~1/3
190�{�������~3/5
�S�̂̐l����15���Ƃ������A
1/3��5/15���D
3/5��9/15���H
�����
70�{�����D
190�{�����H
�C���P�Q�O
15�����S�T�O
�S�̂̐l���͂S�T�O�l
761�P�R�Q�l�ڂ̑f������
2024/10/08(��) 13:44:25.74ID:wtrTTCG9 �����������Ă��܂����c
�������q���K�l����������l��
�����S�̂̐l��
70�{�������~1/3
190�{�������~3/5
�S�̂̐l����15���Ƃ������A
1/3��5/15��5��
3/5��9/15��9��
�����
70�{����5��
190�{����9��
4�����P�Q�O
15�����S�T�O
�S�̂̐l���͂S�T�O�l
�������q���K�l����������l��
�����S�̂̐l��
70�{�������~1/3
190�{�������~3/5
�S�̂̐l����15���Ƃ������A
1/3��5/15��5��
3/5��9/15��9��
�����
70�{����5��
190�{����9��
4�����P�Q�O
15�����S�T�O
�S�̂̐l���͂S�T�O�l
2024/10/08(��) 22:35:28.71ID:8KlpRNpD
�ݕ��i������d�݁j�́A�u�ʉ݂̒P�ʋy�щݕ��̔��s���Ɋւ���@���v��V���Łu�z�ʉ��i��20�{�܂Łv�����x�Ƃ��Ēʗp����ƋK�肳��Ă��܂��B
�܂�A20���܂ł͉ݕ��ɂ��x�������s���Ă��ǂ��Ƃ������Ƃł��B
���
1,5,10,50,100,500�~�d�݂��e�X 20 ������A
(1) 2025 �~�̎x�������@�͉���ނ��邩�H
(2) �ł����Ȃ����̍d�݂Ŏx�������@�����߂�B
(3) �ł��������̍d�݂Ŏx�������@�����߂�B
�܂�A20���܂ł͉ݕ��ɂ��x�������s���Ă��ǂ��Ƃ������Ƃł��B
���
1,5,10,50,100,500�~�d�݂��e�X 20 ������A
(1) 2025 �~�̎x�������@�͉���ނ��邩�H
(2) �ł����Ȃ����̍d�݂Ŏx�������@�����߂�B
(3) �ł��������̍d�݂Ŏx�������@�����߂�B
2024/10/08(��) 23:02:59.15ID:IK1uSYxx
>>762
�A�r�W�W�C�܂��X���^�C�ǂ߂Ȃ��ď��w���Ƀo�J�ɂ��ꂽ���̂���H
�A�r�W�W�C�܂��X���^�C�ǂ߂Ȃ��ď��w���Ƀo�J�ɂ��ꂽ���̂���H
2024/10/09(��) 03:57:32.48ID:bRiYiDKM
���������e�X�g
�Z�����q�p�o�s��GBMB�@�A�B�T�U�V
�Z�����q�p�o�s��GBMB�@�A�B�T�U�V
2024/10/09(��) 04:23:50.99ID:bRiYiDKM
>>761
�u�����S�̂̐l��
70�{�������~1/3
190�{�������~3/5
�S�̂̐l����15���Ƃ������A�v
�������Őݒ�Ȃ������L���̈Ӗ����`���Ɩ����ō��v���Ă��܂���
�����
�u1/3��5/15��5���v
�ɂ��A�Z��1/15�Ƃ����l���Ƃ��ĕs�K�Ȓl�ɂȂ��Ă��܂��܂�
�������̓��̒��ɂ����ɃC���[�W���ł��Ă��Ă��A
����𐳂��������\���Ȃ���ΎZ���␔�w�ł͈Ӗ�������܂���
���w�Z��w�N�ł͎Z���͌v�Z��̂ł������A����͍������w�̂��߂̕K�{�c�[���ɉ߂��܂���
�������w�ɂȂ�ƋL�q�̏d�v���������A���w�͍��ꕶ�@��_���w�Ƌ߂Â��Ă����܂�
�������ɒ��킷�邱�Ƃ��d�v�ł����A
�܂���蕶���猩��������W�𐳂��������ŕ\�����ƂƁA
�����̐��_�𐳂����w�p�I���{�ꕶ�ŏ������Ƃ̃g���[�j���O�����邱�Ƃ��厖���Ǝv���܂�
�u�����S�̂̐l��
70�{�������~1/3
190�{�������~3/5
�S�̂̐l����15���Ƃ������A�v
�������Őݒ�Ȃ������L���̈Ӗ����`���Ɩ����ō��v���Ă��܂���
�����
�u1/3��5/15��5���v
�ɂ��A�Z��1/15�Ƃ����l���Ƃ��ĕs�K�Ȓl�ɂȂ��Ă��܂��܂�
�������̓��̒��ɂ����ɃC���[�W���ł��Ă��Ă��A
����𐳂��������\���Ȃ���ΎZ���␔�w�ł͈Ӗ�������܂���
���w�Z��w�N�ł͎Z���͌v�Z��̂ł������A����͍������w�̂��߂̕K�{�c�[���ɉ߂��܂���
�������w�ɂȂ�ƋL�q�̏d�v���������A���w�͍��ꕶ�@��_���w�Ƌ߂Â��Ă����܂�
�������ɒ��킷�邱�Ƃ��d�v�ł����A
�܂���蕶���猩��������W�𐳂��������ŕ\�����ƂƁA
�����̐��_�𐳂����w�p�I���{�ꕶ�ŏ������Ƃ̃g���[�j���O�����邱�Ƃ��厖���Ǝv���܂�
2024/10/09(��) 09:43:53.09ID:sukLZr+y
�����ƌ�����������������ȁB
�Ԃ̑��l�ɂ����܂Ń{���N�\�Ɍ����K�v���L��̂��H
�Ԃ̑��l�ɂ����܂Ń{���N�\�Ɍ����K�v���L��̂��H
2024/10/10(��) 03:04:15.22ID:ye4VH/hs
���̗������Ɋw�Ԓ��Ԃɑ��āA
�����w�E�������u����A
���������Ή��̕����]�����炾�ƍl���Ă��܂�
�����w�E�������u����A
���������Ή��̕����]�����炾�ƍl���Ă��܂�
2024/10/10(��) 03:08:36.00ID:ye4VH/hs
�NjL�F
���_���@�̌��̎w�E��
��排����̂悤�Ɉ����Ă��Ă͐��w�X���͐������Ȃ��Ǝv���܂�
���_���@�̌��̎w�E��
��排����̂悤�Ɉ����Ă��Ă͐��w�X���͐������Ȃ��Ǝv���܂�
2024/10/10(��) 06:50:29.72ID:gzKS0ma2
>>757
���̖��������v�Z���@��
�u�����Z�v�Ƃ��������O�͂��邩�A�Ƃ�
����ł���
�u�W���Z�v�Ƃ���
�x���}�A���\���g����
��蕶�ɏo�Ă��鐔������
�������@������܂�
������
���̖��̃p�^�[�����o�Ă�����
�s���Ȑl���̕Е������A�S�̂����Ƃ���
������瑼���������ď�������A
�Ƃ��������������v�����ɂ�
���K�����������Ȃ��K�v������܂�
�i���w���w�̘A����������
�u�����@�v�̉�������m���Ă����
���ȏ��ʂ�ɉ�����킯�ł����c�j
���̖��������v�Z���@��
�u�����Z�v�Ƃ��������O�͂��邩�A�Ƃ�
����ł���
�u�W���Z�v�Ƃ���
�x���}�A���\���g����
��蕶�ɏo�Ă��鐔������
�������@������܂�
������
���̖��̃p�^�[�����o�Ă�����
�s���Ȑl���̕Е������A�S�̂����Ƃ���
������瑼���������ď�������A
�Ƃ��������������v�����ɂ�
���K�����������Ȃ��K�v������܂�
�i���w���w�̘A����������
�u�����@�v�̉�������m���Ă����
���ȏ��ʂ�ɉ�����킯�ł����c�j
2024/10/10(��) 07:15:35.83ID:gzKS0ma2
�����������Ă��Ă��A���Ă̏������ɂ���Ă�
�s�����⌸�_�ɂȂ�A�Ƃ����̂�
���w�Z���́u���邠��v�Ȃ̂�
���܂�C�ɂ��Ȃ��悤�Ɂc
��Ƃ��Ă�
�E�܂��͉��������o���ė��K���J��Ԃ�
�����������悤�ɂ���
�E�����ɂ����ď����A�P�ʂ����낦��Ȃǂ���
�킩��₷����������悤�ɂ���
�E�悭���钍�ӓ_
�i�|���Z�̏����Ȃǁj
�ɂ��Ă�
���W�̖͔͉ƌ���ׂ�A
�搶�ɓY�킵�Ă��炤�Ȃǂ���
���K����̂݁A�ł���I
�s�����⌸�_�ɂȂ�A�Ƃ����̂�
���w�Z���́u���邠��v�Ȃ̂�
���܂�C�ɂ��Ȃ��悤�Ɂc
��Ƃ��Ă�
�E�܂��͉��������o���ė��K���J��Ԃ�
�����������悤�ɂ���
�E�����ɂ����ď����A�P�ʂ����낦��Ȃǂ���
�킩��₷����������悤�ɂ���
�E�悭���钍�ӓ_
�i�|���Z�̏����Ȃǁj
�ɂ��Ă�
���W�̖͔͉ƌ���ׂ�A
�搶�ɓY�킵�Ă��炤�Ȃǂ���
���K����̂݁A�ł���I
771�P�R�Q�l�ڂ̑f������
2024/10/10(��) 10:07:11.69ID:eKHK5bYW >>765
����c�m���ɂ߂��Ⴍ����ł�����
����łǂ��ł��傤���H
�������q���K�l����������l��
�S�̂̐l����15��
70�{����15���~1/3
190�{����15���~3/5
70�{����5��
190�{����9��
�����
4�����P�Q�O
15�����S�T�O
�S�̂̐l���͂S�T�O�l
����c�m���ɂ߂��Ⴍ����ł�����
����łǂ��ł��傤���H
�������q���K�l����������l��
�S�̂̐l����15��
70�{����15���~1/3
190�{����15���~3/5
70�{����5��
190�{����9��
�����
4�����P�Q�O
15�����S�T�O
�S�̂̐l���͂S�T�O�l
2024/10/10(��) 17:14:43.43ID:0hNqdl0O
2024/10/10(��) 19:37:05.17ID:ye4VH/hs
>>771
�u�������q���K�l����������l��
�S�̂̐l����15���v
�ɂ��܂��āA
���w��̘_�q�ł��������������ꍇ�A
���̓����������u���Ă���v���Ƃ����ɕ\����܂�
�����ł͓�̖��m�������̎������藧�悤�ɓ������Ă���킯�ł��̂�
���̂悤�ȏ���������ʓI�ł�
���q���K�l����������l�������A
�S�̂̐l����15�Z�Ƃ��ꂼ�ꂨ���B
�Ȃ��A�S�̂̐l����1/3�A3/5�����ꂼ��l���Ƃ��Đ����ƂȂ��Ă��邱�Ƃ��
�S�̂̐l����15�̔{���ł��邱�Ƃ͖��炩�ł���B
�u70�{����15���~1/3
190�{����15���~3/5�v
�ɂ��ẮA�����̊W�͖�蕶���炷���킩�邱�Ƃł͂���܂����A
�j�q�Ń��K�l�������Ă���l���͂V�O�l�ł����āA
�j�����v�Ń��K�l�������Ă���l���͊w�Z�S�̂̂P/�R�ł��邩��A
70�{����15���~1/3
����������B�E�ӂ��v�Z����Ɖ��̂悤�ɂȂ�
70�{����5���@�c(1)�@���F(1)�ł͂Ȃ��Z�݂͂�1�����������̂ł���������������̂ł��̋L�@
�܂��A���q�Ń��K�l�������Ă��Ȃ��l���͂P�X�O�l�ł����āA
�j����2:3��菗�q�̐l���͑S�̂�3/5�ł��邩��A
190�{����15���~3/5
����������B�E�ӂ��v�Z����Ɖ��̂悤�ɂȂ�B
190�{����9���@�c(2)�@���F��L���l
�ƁA������ɂ��������邱�Ƃ̂Ȃ��悤�ڏq���܂�
�i�����j
�u�������q���K�l����������l��
�S�̂̐l����15���v
�ɂ��܂��āA
���w��̘_�q�ł��������������ꍇ�A
���̓����������u���Ă���v���Ƃ����ɕ\����܂�
�����ł͓�̖��m�������̎������藧�悤�ɓ������Ă���킯�ł��̂�
���̂悤�ȏ���������ʓI�ł�
���q���K�l����������l�������A
�S�̂̐l����15�Z�Ƃ��ꂼ�ꂨ���B
�Ȃ��A�S�̂̐l����1/3�A3/5�����ꂼ��l���Ƃ��Đ����ƂȂ��Ă��邱�Ƃ��
�S�̂̐l����15�̔{���ł��邱�Ƃ͖��炩�ł���B
�u70�{����15���~1/3
190�{����15���~3/5�v
�ɂ��ẮA�����̊W�͖�蕶���炷���킩�邱�Ƃł͂���܂����A
�j�q�Ń��K�l�������Ă���l���͂V�O�l�ł����āA
�j�����v�Ń��K�l�������Ă���l���͊w�Z�S�̂̂P/�R�ł��邩��A
70�{����15���~1/3
����������B�E�ӂ��v�Z����Ɖ��̂悤�ɂȂ�
70�{����5���@�c(1)�@���F(1)�ł͂Ȃ��Z�݂͂�1�����������̂ł���������������̂ł��̋L�@
�܂��A���q�Ń��K�l�������Ă��Ȃ��l���͂P�X�O�l�ł����āA
�j����2:3��菗�q�̐l���͑S�̂�3/5�ł��邩��A
190�{����15���~3/5
����������B�E�ӂ��v�Z����Ɖ��̂悤�ɂȂ�B
190�{����9���@�c(2)�@���F��L���l
�ƁA������ɂ��������邱�Ƃ̂Ȃ��悤�ڏq���܂�
�i�����j
2024/10/10(��) 19:38:45.95ID:ye4VH/hs
�u�����
4�����P�Q�O�v
�ɂ��Ă͍��Z���x�ɂȂ�ΐ����s�v�ł����A���w�Z�̒m���ł�
(2)�̗��ӂ��瓯�����������Ă��V�������̗��ӂ͓�����
(1)�̗��ӂ����������Ƃɒ��ӂ����
190�{���\�i70�{���j��9�Z�\5�Z
�����藧���A�����
120��4�Z
�Ə����ׂ���������܂���
���̑O��̃R�����g�̒i�K�ł͂ǂ̂悤�ɋL�q���č\�z�Ȃ��邩�킩��Ȃ������̂�
����̓_�ɂ��Ă͎w�E���ꂵ�Ă��܂���
�Ȃ��A���ׂ͍������{�ꕶ�ŕ���ċL�q����^�C�v�ł����A
���ۂɂǂ̒��x�̐����ȗ���������邩�́A
���w�Z�̕��͑�̖͔͉A���w�Z���ȏ��ɂ���藝�̏ؖ����Ȃǂ�
�Q�l�ɂȂ���Ƃ悢�ł��傤
4�����P�Q�O�v
�ɂ��Ă͍��Z���x�ɂȂ�ΐ����s�v�ł����A���w�Z�̒m���ł�
(2)�̗��ӂ��瓯�����������Ă��V�������̗��ӂ͓�����
(1)�̗��ӂ����������Ƃɒ��ӂ����
190�{���\�i70�{���j��9�Z�\5�Z
�����藧���A�����
120��4�Z
�Ə����ׂ���������܂���
���̑O��̃R�����g�̒i�K�ł͂ǂ̂悤�ɋL�q���č\�z�Ȃ��邩�킩��Ȃ������̂�
����̓_�ɂ��Ă͎w�E���ꂵ�Ă��܂���
�Ȃ��A���ׂ͍������{�ꕶ�ŕ���ċL�q����^�C�v�ł����A
���ۂɂǂ̒��x�̐����ȗ���������邩�́A
���w�Z�̕��͑�̖͔͉A���w�Z���ȏ��ɂ���藝�̏ؖ����Ȃǂ�
�Q�l�ɂȂ���Ƃ悢�ł��傤
2024/10/10(��) 21:11:33.53ID:i/YqfUh1
�d���̊p��˂����悤�ȖT�_����Ŋ̐S�Ȃ��Ƃ͉��������Ȃ��B���i���������ɂ��ݏo�Ă���B
2024/10/10(��) 22:10:49.99ID:RWXplQei
>>772
�����w�����x���̃��m�̗��������������Ă��ȁB
�����w�����x���̃��m�̗��������������Ă��ȁB
777�P�R�Q�l�ڂ̑f������
2024/10/11(��) 09:16:40.02ID:Gw2u7eIV �w�p�I���{�ꕶ�Ƃ���w�Ȏ������Ă銄�ɂ́A��_�̎g�������Œ��ꒃ���ˁB
�g��Ȃ��Ȃ�g��Ȃ��ň�т�������̂ɁA���܂Ɋ���o���͉̂��́H
�g��Ȃ��Ȃ�g��Ȃ��ň�т�������̂ɁA���܂Ɋ���o���͉̂��́H
2024/10/11(��) 18:55:09.53ID:DJ8w2ziA
������ق��Č��Ă����ǁA�������
2024/10/12(�y) 06:09:24.66ID:YuD7z7Jl
���l���Ȃ߂ă}�E���g����肽�������Ȃ낤
2024/10/12(�y) 13:42:16.66ID:vcCUNX6s
>>774
����A�ϐ��̋L�����ۂ�l�p�ɒu������������������\�Ȃ����H
����A�ϐ��̋L�����ۂ�l�p�ɒu������������������\�Ȃ����H
781�P�R�Q�l�ڂ̑f������
2024/10/12(�y) 14:59:37.88ID:H9HhRC4F ��X�A�����w�Z�͈͂̎Z���E���w�̖��̃X�����ꓯ�́A���̗������Ɋw�Ԓ��ԂƂ��āA
>>765���̐�������A�w�p�I���{��ɂ̂��Ƃ������͂̏������݂ɁA���X�w�߂Ă������Ƃ��A
�����ɐ����܂��B
>>765���̐�������A�w�p�I���{��ɂ̂��Ƃ������͂̏������݂ɁA���X�w�߂Ă������Ƃ��A
�����ɐ����܂��B
2024/10/12(�y) 17:52:34.19ID:TQkaiGCW
BOOOOO�I
2024/10/31(��) 03:48:17.74ID:grkcalAP
(1) 70��(-12)�̏��Ɨ]��͂������H
(2) (-70)��(-12)�̏��Ɨ]��͂������H
(2) (-70)��(-12)�̏��Ɨ]��͂������H
2024/10/31(��) 06:31:55.63ID:4w71VPW0
>>783
�������ׂĂ݂܂������A
���̐����̏o�Ă��銄��Z�ŕ����ɂ����]����l����͍̂��Z���w�͈̔͂炵���ł��B
�������Ƃ���Ƃ��̃X���b�h�̑Ώ۔͈͂ł͂���܂���B
�Q�l�ł����A���̂悤�ȏꍇ�ɓ�������ӂɒ�߂邽�߂ɍ��ꂽ���[����������ނ���A
�����̒��łǂ̃��[����p���邩�͌������E�ł���ʂɂ���ĈقȂ�悤�ł��B
�������ׂĂ݂܂������A
���̐����̏o�Ă��銄��Z�ŕ����ɂ����]����l����͍̂��Z���w�͈̔͂炵���ł��B
�������Ƃ���Ƃ��̃X���b�h�̑Ώ۔͈͂ł͂���܂���B
�Q�l�ł����A���̂悤�ȏꍇ�ɓ�������ӂɒ�߂邽�߂ɍ��ꂽ���[����������ނ���A
�����̒��łǂ̃��[����p���邩�͌������E�ł���ʂɂ���ĈقȂ�悤�ł��B
2024/10/31(��) 16:53:58.25ID:grkcalAP
���̐������Z�Ƃ����̂́A�؋������l���ŕ�������̂ŃC���[�W�ł��邪�A
���̐��ŏ��Z�Ƃ����̂̓C���[�W���킩�Ȃ��Ȃ��B
���̐��ŏ��Z�Ƃ����̂̓C���[�W���킩�Ȃ��Ȃ��B
2024/10/31(��) 16:57:29.40ID:grkcalAP
>>783
a �� b�̏��� a/b���Ȃ��ő�̐��� q �Ƃ���
�]�� �� r �� a - b*q �Ƃ��ĎZ�o�����
(1)
> quotient_remainder(70,-12)
$q
[1] -6
$r
[1] -2
(2)
> quotient_remainder(-70,-12)
$q
[1] 5
$r
[1] -10
a �� b�̏��� a/b���Ȃ��ő�̐��� q �Ƃ���
�]�� �� r �� a - b*q �Ƃ��ĎZ�o�����
(1)
> quotient_remainder(70,-12)
$q
[1] -6
$r
[1] -2
(2)
> quotient_remainder(-70,-12)
$q
[1] 5
$r
[1] -10
2024/10/31(��) 19:53:51.96ID:ecjwJd7p
(1) : 70 = (-12) �~ (-6) + 2
ans: �� -6�@�]�� 2
(2) : -70 = (-12) �~ 5 + (-10)
ans: �� 5�@�]�� -10
ans: �� -6�@�]�� 2
(2) : -70 = (-12) �~ 5 + (-10)
ans: �� 5�@�]�� -10
2024/10/31(��) 20:55:05.79ID:ecjwJd7p
2024/11/01(��) 04:07:52.19ID:/4pZZMv9
�����̊���Z�ŏ��Ɨ]�����ӂɒ�߂邽�߂̃��[���Ƃ��Ă悭�p��������̂ɂ�
�u�]�肪�ŏ��̔�s�����Ƃ�����̂��̗p����v
�u�]��̐�Βl���ŏ��ɂȂ���̂��̗p����i���ƕ��œ���Βl�̏ꍇ�̍ב�����j�v
������B
�u�]�肪�ŏ��̔�s�����Ƃ�����̂��̗p����v
�u�]��̐�Βl���ŏ��ɂȂ���̂��̗p����i���ƕ��œ���Βl�̏ꍇ�̍ב�����j�v
������B
2024/11/04(��) 06:02:17.92ID:HqmwOdyB
���]��̐�Βl���ŏ��ɂȂ���̂��̗p����i���ƕ��œ���Βl�̏ꍇ�̍ב�����j
���@�F�@���ƕ��œ���Βl�ƂȂ�̂͂ǂ̂悤�ȏꍇ���q�ׂ�
���@�F�@���ƕ��œ���Βl�ƂȂ�̂͂ǂ̂悤�ȏꍇ���q�ׂ�
2024/11/04(��) 06:03:46.84ID:HqmwOdyB
>>789
������āA���̐��ŏ��Z����ꍇ���܂ށH
������āA���̐��ŏ��Z����ꍇ���܂ށH
792�P�R�Q�l�ڂ̑f������
2024/11/12(��) 23:52:32.10ID:GXQSs+2U �y���z
1�`9�܂ł̐�����1���g���āA
�ǂ̘A������2�����Ƃ��Ă����̓����ɂȂ�悤��9���̐�������B
�y��z�Q�S�T�U�R����
1�`9�܂ł̐�����1���g���āA
�ǂ̘A������2�����Ƃ��Ă����̓����ɂȂ�悤��9���̐�������B
�y��z�Q�S�T�U�R����
2024/11/13(��) 01:32:18.42ID:AorEiqN3
9�̐����ɂ��āA���ꂼ��
�O�ɂ������A���ɂ��������l�����
�E9���O��4�̂݁A���͂����Ȃ�
�E7���O��2�̂݁A����2�̂�
�Ȃ̂ŁA72�Ŏn�܂���49�ŏI��邱�Ƃ��킩��
�ق��ɁA281���K�����̏��ŕ��ԁA
4�̑O��5��6�ɂȂ�A�Ȃǂ��킩��
�킩�������������Ƃɕ��בւ����l����
�S�Ă̂Ȃ��ڂ�2�P�^�̐���
��ӂ������̂�������悢
������ 728163549
�O�ɂ������A���ɂ��������l�����
�E9���O��4�̂݁A���͂����Ȃ�
�E7���O��2�̂݁A����2�̂�
�Ȃ̂ŁA72�Ŏn�܂���49�ŏI��邱�Ƃ��킩��
�ق��ɁA281���K�����̏��ŕ��ԁA
4�̑O��5��6�ɂȂ�A�Ȃǂ��킩��
�킩�������������Ƃɕ��בւ����l����
�S�Ă̂Ȃ��ڂ�2�P�^�̐���
��ӂ������̂�������悢
������ 728163549
2024/11/13(��) 01:33:46.09ID:AorEiqN3
�����������ƋK������ď������߂Ȃ��̂�
795�P�R�Q�l�ڂ̑f������
2024/11/13(��) 11:19:11.17ID:DoDx3gDl >>793
����
����
2024/11/13(��) 19:12:32.27ID:mLwXKDzl
>>792
Wolfram�ɒT��������B
kuku=Union@Flatten@Table[a b,{a,1,9},{b,1,9}];
pm=Permutations[Range[9],{9}];
Select[pm,ContainsAll[kuku,10 #[[1;;8]]+ #[[2;;9]]]&]
{{7, 2, 8, 1, 6, 3, 5, 4, 9}}
Wolfram�ɒT��������B
kuku=Union@Flatten@Table[a b,{a,1,9},{b,1,9}];
pm=Permutations[Range[9],{9}];
Select[pm,ContainsAll[kuku,10 #[[1;;8]]+ #[[2;;9]]]&]
{{7, 2, 8, 1, 6, 3, 5, 4, 9}}
2024/11/13(��) 19:23:45.32ID:AzlhHiL3
>>796
���w���ɂ���o�J�ɂ���Ă�e���F�ɕ����Ă˂���
���w���ɂ���o�J�ɂ���Ă�e���F�ɕ����Ă˂���
2024/11/13(��) 19:25:33.11ID:mLwXKDzl
>>796
R����ɈڐA���ĎZ�o
> library(RcppAlgos)
> outer(1:9,1:9) |> as.vector() |> unique() -> kuku
> pm=permuteGeneral(1:9,9)
> pm[apply(pm,1,\(x) all(c(10*x[1:8]+x[2:9]) %in% kuku)),]
[1] 7 2 8 1 6 3 5 4 9
�Y�����鐔��͂P�ł��邱�Ƃ��m�F�B
R����ɈڐA���ĎZ�o
> library(RcppAlgos)
> outer(1:9,1:9) |> as.vector() |> unique() -> kuku
> pm=permuteGeneral(1:9,9)
> pm[apply(pm,1,\(x) all(c(10*x[1:8]+x[2:9]) %in% kuku)),]
[1] 7 2 8 1 6 3 5 4 9
�Y�����鐔��͂P�ł��邱�Ƃ��m�F�B
2024/11/13(��) 19:28:17.87ID:mLwXKDzl
���Ƃł̏ꍇ�����́A���߂��������邩������A
�v���O�����ő������肷��A���̐S�z�͂Ȃ��B
�v���O�����ő������肷��A���̐S�z�͂Ȃ��B
2024/11/13(��) 19:44:49.31ID:mLwXKDzl
���p���
(* 1�`8�܂ł̐�����1���g���āA
�ǂ̘A������2�����Ƃ��Ă����̓����ɂȂ�悤��8���̐��������ׂė��� *)
(* 1�`8�܂ł̐�����1���g���āA
�ǂ̘A������2�����Ƃ��Ă����̓����ɂȂ�悤��8���̐��������ׂė��� *)
2024/11/13(��) 19:51:55.97ID:mLwXKDzl
���W���
1�`n�܂ł̐�����1���g���āA
�ǂ̘A������2�����Ƃ��Ă����̓����ɂȂ�悤��n���̐��������\���o�[�����
R����ł̗�
calc=\(n){
outer(1:9,1:9) |> as.vector() |> unique() -> kuku
pm=permuteGeneral(1:n,n)
pm[apply(pm,1,\(x) all(c(10*x[1:(n-1)]+x[2:n]) %in% kuku)),]
}
> calc(7)
[,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 1 4 5 6 3 2 7
[2,] 1 6 3 5 4 2 7
[3,] 7 2 1 4 5 6 3
[4,] 7 2 1 6 3 5 4
1�`n�܂ł̐�����1���g���āA
�ǂ̘A������2�����Ƃ��Ă����̓����ɂȂ�悤��n���̐��������\���o�[�����
R����ł̗�
calc=\(n){
outer(1:9,1:9) |> as.vector() |> unique() -> kuku
pm=permuteGeneral(1:n,n)
pm[apply(pm,1,\(x) all(c(10*x[1:(n-1)]+x[2:n]) %in% kuku)),]
}
> calc(7)
[,1] [,2] [,3] [,4] [,5] [,6] [,7]
[1,] 1 4 5 6 3 2 7
[2,] 1 6 3 5 4 2 7
[3,] 7 2 1 4 5 6 3
[4,] 7 2 1 6 3 5 4
2024/11/13(��) 19:57:54.81ID:6ATxadmg
����Ă邱�Ƃ͑S���̐�������ׂĈ�������ɓ��Ă͂܂��Ă邩�����Ă�
9876543210
��L�̕�����̒���0�͂ǂꂩ�ȁH���Ă����A
��������2�Ύ�������Ă�悤�Ȃ��Ƃ���点�Ă邾��
���w��
9876543210
��L�̕�����̒���0�͂ǂꂩ�ȁH���Ă����A
��������2�Ύ�������Ă�悤�Ȃ��Ƃ���点�Ă邾��
���w��
2024/11/13(��) 20:23:33.81ID:mLwXKDzl
�����o���Đ�����Γ����o����
1�`9�܂ł̐�����1���g���Ăł���9���̐�����
�ǂ̘A������2�̐����̍��̐�Βl�����ׂđf���ł��鐮���͉����邩�B
�Y�����鐮���̍ŏ��l�ƍő�l�����߂�B
1�`9�܂ł̐�����1���g���Ăł���9���̐�����
�ǂ̘A������2�̐����̍��̐�Βl�����ׂđf���ł��鐮���͉����邩�B
�Y�����鐮���̍ŏ��l�ƍő�l�����߂�B
2024/11/13(��) 21:07:10.43ID:mLwXKDzl
�Ђ����珑���o���Γ����o����
1�`9�܂ł̐�����1���g���ĕ��ׂ�9���̐���������A
9����3���̐���3�ɂ킯��
�� 123456789 -> 123 456 789
3�̐��������ׂđf���ł���悤�ȕ��ו��͉��ʂ肠�邩�H
�ő�l�ƍŏ��l�����߂�B
1�`9�܂ł̐�����1���g���ĕ��ׂ�9���̐���������A
9����3���̐���3�ɂ킯��
�� 123456789 -> 123 456 789
3�̐��������ׂđf���ł���悤�ȕ��ו��͉��ʂ肠�邩�H
�ő�l�ƍŏ��l�����߂�B
2024/11/13(��) 21:17:20.68ID:mLwXKDzl
>>802
���������Ȃ�Ǝw�܂萔����͍̂���Ȃ̂œ�����g�������̘b�B
R�̉��Z�q�@%in%�@�ɑ�������Wolfram�̊���T���̂��w�K�ɂȂ�B
2�Ύ��ɂ͂ł��Ȃ����
II|Il1l|1|Il|1|l11l|II|1|||II|ll1l|1l111lI1llI1I|I|11|l11l|1llII|l1I|1||Ill1||II1|l1lII11llI1lll||I1
��L�̕�����Ɋ܂܂��A���t�@�x�b�g�̐������߂�B
���������Ȃ�Ǝw�܂萔����͍̂���Ȃ̂œ�����g�������̘b�B
R�̉��Z�q�@%in%�@�ɑ�������Wolfram�̊���T���̂��w�K�ɂȂ�B
2�Ύ��ɂ͂ł��Ȃ����
II|Il1l|1|Il|1|l11l|II|1|||II|ll1l|1l111lI1llI1I|I|11|l11l|1llII|l1I|1||Ill1||II1|l1lII11llI1lll||I1
��L�̕�����Ɋ܂܂��A���t�@�x�b�g�̐������߂�B
806�P�R�Q�l�ڂ̑f������
2024/11/13(��) 21:21:06.54ID:06ruQh3r >>803-804
���������̂́A���̂���X���ł��肢���܂��B
�v���O���~���O�̂���X�� Part22
https://mevius.5ch.net/test/read.cgi/tech/1691038333/
���������̂́A���̂���X���ł��肢���܂��B
�v���O���~���O�̂���X�� Part22
https://mevius.5ch.net/test/read.cgi/tech/1691038333/
2024/11/13(��) 21:22:48.61ID:mLwXKDzl
R�ŃJ�E���g
str="II|Il1l|1|Il|1|l11l|II|1|||II|ll1l|1l111lI1llI1I|I|11|l11l|1llII|l1I|1||Ill1||II1|l1lII11llI1lll||I1"
s=unlist(strsplit(str,''))
sum(s %in% letters)+sum(s %in% LETTERS)
str="II|Il1l|1|Il|1|l11l|II|1|||II|ll1l|1l111lI1llI1I|I|11|l11l|1llII|l1I|1||Ill1||II1|l1lII11llI1lll||I1"
s=unlist(strsplit(str,''))
sum(s %in% letters)+sum(s %in% LETTERS)
2024/11/13(��) 21:25:57.92ID:mLwXKDzl
5ch�̓C���f���g������邩��Python�̃R�[�h�͓��e���ɂ����B
2024/11/13(��) 21:28:34.77ID:6ATxadmg
>>803�͂��̌�Wolfram�őS�Ă�9!�̐��l����A
�Y�����鐔������ŒT���v���O�����������ɏ�����
�����ɂ͉��̒m�b���H�v���Ȃ��A���Ԃ���������Ή\�Ƃ����A
���w�I�ɉ��̊w�т������Ȃ���@�����瑊��ɂ��邾������
�Y�����鐔������ŒT���v���O�����������ɏ�����
�����ɂ͉��̒m�b���H�v���Ȃ��A���Ԃ���������Ή\�Ƃ����A
���w�I�ɉ��̊w�т������Ȃ���@�����瑊��ɂ��邾������
2024/11/13(��) 21:58:56.31ID:fcK1XfKq
��������A���V���Z�ݒ������������
���X�������Ă�K�v�͖�������A
���X�������Ă�K�v�͖�������A
2024/11/13(��) 22:02:24.96ID:lGuYZ8Sk
>>799
�v���O�����̌��̗L���̌����Ȃ���Ă��܂���B
�v���O�������������ꍇ�ł��A�v���O�����̎��s���ɃG���[����������������ʂ��������\���͂O�ł͂���܂���B
�v���O�����̌��̗L���̌����Ȃ���Ă��܂���B
�v���O�������������ꍇ�ł��A�v���O�����̎��s���ɃG���[����������������ʂ��������\���͂O�ł͂���܂���B
812�P�R�Q�l�ڂ̑f������
2024/11/13(��) 22:18:18.48ID:06ruQh3r �ނ���A���z�͂��K�v�Ȃ��������������肢���܂��B
���̎l�p�`�̖ʐς����߂�B
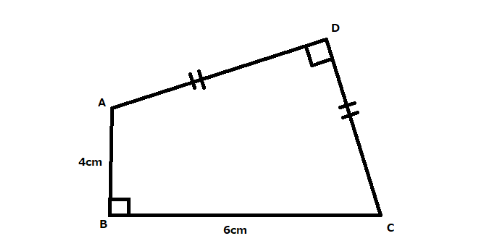
���̎l�p�`�̖ʐς����߂�B

2024/11/13(��) 22:39:42.92ID:AzlhHiL3
�`���p���W�[���d��@���ăL�[�L�[���ł邾���̃X��
2024/11/13(��) 22:48:29.98ID:CFKwEsGs
2024/11/13(��) 23:04:29.86ID:lGuYZ8Sk
>>812
�ӂa�b���b���ɉ���������������i���������j�ɂb�d��4cm�ƂȂ�_�d���A
�ӂa�`���`���ɉ���������������ɂ`�f��6cm�ƂȂ�_�f�����ꂼ���߁A
����ɓ_�e���A�l�p�`�a�d�e�f�������`�ƂȂ�悤�ɒ�߂�B
�`�c�̉������Ƃd�e�̌�_���g�Ƃ���ƁA
�l�p�`�b�d�g�c�͎l�p�`�`�a�b�c�ƍ����ł���B
����͂`�a�b�c�̌����������p�̘a��180�x�ł��邱�Ƃɂ��
�ڂc�`�a���ڂc�b�d�ł���A
����ɂb�d�g�c�������������p�̘a��180�x�ł��邱�Ƃɂ��
�ڂd�g�c���ڂa�b�c�ł��邱�Ƃ��l����Ζ��炩�ł���B
���l�ɍl����i�߂Ă�����
�`�a�b�c�̖ʐς͂a�d�e�f��1/4�ł��邱�Ƃ��e�Ղɂ킩��B
�a�d�e�f�͈��10cm�̐����`�ł��邩��
�`�a�b�c�̖ʐς�25����cm�ł���B
�����F25����cm
�����������̂��ߕ���cm�ƕ\�L
�ӂa�b���b���ɉ���������������i���������j�ɂb�d��4cm�ƂȂ�_�d���A
�ӂa�`���`���ɉ���������������ɂ`�f��6cm�ƂȂ�_�f�����ꂼ���߁A
����ɓ_�e���A�l�p�`�a�d�e�f�������`�ƂȂ�悤�ɒ�߂�B
�`�c�̉������Ƃd�e�̌�_���g�Ƃ���ƁA
�l�p�`�b�d�g�c�͎l�p�`�`�a�b�c�ƍ����ł���B
����͂`�a�b�c�̌����������p�̘a��180�x�ł��邱�Ƃɂ��
�ڂc�`�a���ڂc�b�d�ł���A
����ɂb�d�g�c�������������p�̘a��180�x�ł��邱�Ƃɂ��
�ڂd�g�c���ڂa�b�c�ł��邱�Ƃ��l����Ζ��炩�ł���B
���l�ɍl����i�߂Ă�����
�`�a�b�c�̖ʐς͂a�d�e�f��1/4�ł��邱�Ƃ��e�Ղɂ킩��B
�a�d�e�f�͈��10cm�̐����`�ł��邩��
�`�a�b�c�̖ʐς�25����cm�ł���B
�����F25����cm
�����������̂��ߕ���cm�ƕ\�L
816�P�R�Q�l�ڂ̑f������
2024/11/14(��) 04:43:14.44ID:0x9ven40 >>815
�����ł��B
(4+6)*(4+6)/4 = 10*10/4 = 100/4 = 25cm²(������������Ȃ�cm^2�ł���)
���Z���͐����`�̒��ɐ����`�����āA���̈ꕔ������Ė��Ƃ��ďo�����Ƃ����������ŁA
��肩��Q�̐����`���C���[�W����̂������R�c�������ł��B
�����ł��B
(4+6)*(4+6)/4 = 10*10/4 = 100/4 = 25cm²(������������Ȃ�cm^2�ł���)
���Z���͐����`�̒��ɐ����`�����āA���̈ꕔ������Ė��Ƃ��ďo�����Ƃ����������ŁA
��肩��Q�̐����`���C���[�W����̂������R�c�������ł��B
2024/11/14(��) 05:06:00.53ID:UOo+ZpL/
>>814
���̃X�����݂��Ă���
���̃X�����݂��Ă���
2024/11/14(��) 07:46:11.86ID:1tdI9bOM
>>816
�ő����̎����ɂƂ��āA�Z���̓�߂̖�肪
�v�l�͂̈琬����R�c�̈ËL�ɕϖe���Ă��܂��Ă��錻�߂����ł��B
�{���͂��낢��Ȗ���^���Ɏ��͂ōl���Ă���������
�V�������z�▢�m�̖��ւ̎��g�ݕ��Ȃǂ����X�Ɛg�ɂ�����d�v�Ȏ����Ȃ̂ł����ǂˁB
�ËL�ł͖��m�̖��ɑΉ��ł��܂���B
�����q���̍��͒ʂ��Ă������w�Z�ł͒��w�ȂǂQ�O�O�l�Ɉ�l��l�������̂�
����F�B�Ɍ����Ă�����������p�Y���̂悤�Ɋy����ł��܂����B
�ő����̎����ɂƂ��āA�Z���̓�߂̖�肪
�v�l�͂̈琬����R�c�̈ËL�ɕϖe���Ă��܂��Ă��錻�߂����ł��B
�{���͂��낢��Ȗ���^���Ɏ��͂ōl���Ă���������
�V�������z�▢�m�̖��ւ̎��g�ݕ��Ȃǂ����X�Ɛg�ɂ�����d�v�Ȏ����Ȃ̂ł����ǂˁB
�ËL�ł͖��m�̖��ɑΉ��ł��܂���B
�����q���̍��͒ʂ��Ă������w�Z�ł͒��w�ȂǂQ�O�O�l�Ɉ�l��l�������̂�
����F�B�Ɍ����Ă�����������p�Y���̂悤�Ɋy����ł��܂����B
819�P�R�Q�l�ڂ̑f������
2024/11/14(��) 09:14:43.28ID:Dl9EviY7 �̐ςPcm3�̗����̂̔����X����܂��B
�X�S�Ă̔���\�荇�킹�đ傫�ȗ��̂����܂��B
���̗��̂̕\�ʐς��R�Ocm2�ƂȂ闧�̂̌`�́i�H�j��ނ���܂��B
�X�S�Ă̔���\�荇�킹�đ傫�ȗ��̂����܂��B
���̗��̂̕\�ʐς��R�Ocm2�ƂȂ闧�̂̌`�́i�H�j��ނ���܂��B
2024/11/14(��) 15:47:26.14ID:CGSdJ4uC
���ς�炸�r�炵��������绂��Ă���X�����Ȃ�
2024/11/14(��) 17:18:09.95ID:YGSVABDY
822�P�R�Q�l�ڂ̑f������
2024/11/14(��) 21:11:41.34ID:Dl9EviY7 >>821
���ꏑ���̖Y��Ă܂����B
�y�������܂������z
�̐ςPcm3�̗����̂̔����X����܂��B
�X�S�Ă̔����g���āA�\�荇�킹���ʂ�4�̕ӂ����Ȃ炸�d�Ȃ�悤�ɓ\�荇�킹�đ傫�ȗ��̂����܂��B
���̗��̂̕\�ʐς��R�Ocm2�ƂȂ闧�̂̌`�́i�H�j��ނ���܂��B
���ꏑ���̖Y��Ă܂����B
�y�������܂������z
�̐ςPcm3�̗����̂̔����X����܂��B
�X�S�Ă̔����g���āA�\�荇�킹���ʂ�4�̕ӂ����Ȃ炸�d�Ȃ�悤�ɓ\�荇�킹�đ傫�ȗ��̂����܂��B
���̗��̂̕\�ʐς��R�Ocm2�ƂȂ闧�̂̌`�́i�H�j��ނ���܂��B
823�P�R�Q�l�ڂ̑f������
2024/11/14(��) 21:37:03.62ID:0x9ven40 >>818
�����ł��ˁB
�����g�͎Z���E���w�͓��ӂƌ�����قǂł͂Ȃ�����60�_�̕��ʁH�̎q���������̂ł����A
�Z���������Z���D���ɏo����{�������Ȃ����Ǝ��s���뒆�ł��B
�����ōl�����̂��A�u���w�҂��q���̂���A�Z���̉��ɖ��͂��������̂��H�v�ł����B
���͂�T���Ă��Ċ������̂́u�����v�͊y�����Ƃ������ł��B�i���ȍD���]�j
����́A���w�҂��q���̍��Ɋ��������͂̈�ł́H�Ɗ����Ă��܂��B
�����āA�Z����������{���̈Ӗ��̈�Ƃ������Ă��܂��B
�v�Z���ł�����āA�����I�Ȍ��ʂ���Ȃ����ƁB
�e�X�g�ł͌����I�ȉ����߂���ł��傤���A���i�̎��Ƃ͂����Ǝ��s���낳���Ă��ǂ��l�Ɏv���܂��B
(�����͌����Ă������̂������炢�͋����������ǂ��̂ł��傤��)
�����Z�̓V�[�\�[�̂悤�ȓ����B
�����Z�͂Q�̕��̂̓��������^��(�O��ɓ����Ă����������)�B
�����ɒ��ڂ���ƁA�s���͑����邯�njv�Z���₷�����ɕό`���Ȃ���v�Z�ł���B
x = 184 + 72
= (184 + 16) + (72 - 16)
= 200 + {(72 + 4) - (16 + 4)} -- �����Z�͌����@�E�����@�ɉ����A��R�̕��@�������ɒ��ڂ��邱�ƂŌ�����ꂽ�B
= 200 + (76 - 20)
= 200 + 56
=256
https://i.imgur.com/1pTgIZM.jpeg
https://i.imgur.com/nPmY0dP.jpeg
�����ł��ˁB
�����g�͎Z���E���w�͓��ӂƌ�����قǂł͂Ȃ�����60�_�̕��ʁH�̎q���������̂ł����A
�Z���������Z���D���ɏo����{�������Ȃ����Ǝ��s���뒆�ł��B
�����ōl�����̂��A�u���w�҂��q���̂���A�Z���̉��ɖ��͂��������̂��H�v�ł����B
���͂�T���Ă��Ċ������̂́u�����v�͊y�����Ƃ������ł��B�i���ȍD���]�j
����́A���w�҂��q���̍��Ɋ��������͂̈�ł́H�Ɗ����Ă��܂��B
�����āA�Z����������{���̈Ӗ��̈�Ƃ������Ă��܂��B
�v�Z���ł�����āA�����I�Ȍ��ʂ���Ȃ����ƁB
�e�X�g�ł͌����I�ȉ����߂���ł��傤���A���i�̎��Ƃ͂����Ǝ��s���낳���Ă��ǂ��l�Ɏv���܂��B
(�����͌����Ă������̂������炢�͋����������ǂ��̂ł��傤��)
�����Z�̓V�[�\�[�̂悤�ȓ����B
�����Z�͂Q�̕��̂̓��������^��(�O��ɓ����Ă����������)�B
�����ɒ��ڂ���ƁA�s���͑����邯�njv�Z���₷�����ɕό`���Ȃ���v�Z�ł���B
x = 184 + 72
= (184 + 16) + (72 - 16)
= 200 + {(72 + 4) - (16 + 4)} -- �����Z�͌����@�E�����@�ɉ����A��R�̕��@�������ɒ��ڂ��邱�ƂŌ�����ꂽ�B
= 200 + (76 - 20)
= 200 + 56
=256
https://i.imgur.com/1pTgIZM.jpeg
https://i.imgur.com/nPmY0dP.jpeg
2024/11/15(��) 05:44:55.76ID:Cw6zWH6t
2024/11/15(��) 06:57:48.99ID:IqxnEVdn
�����͉J��
2024/11/15(��) 07:02:38.67ID:57j0KwQT
�Ⴆ��1*1*3�̒����̂�
��
����
�̂悤�ɓ\�荇�킹��ΐ������邪
���Ƃ̖ʂ����炳���\�荇�킹��Ƃ���
�������Ȃ���
���1�� 0.1cm, 0.01cm, ... ���炵�Ă�
���ɂȂ��Ă��܂��Ƃ�������
��
����
�̂悤�ɓ\�荇�킹��ΐ������邪
���Ƃ̖ʂ����炳���\�荇�킹��Ƃ���
�������Ȃ���
���1�� 0.1cm, 0.01cm, ... ���炵�Ă�
���ɂȂ��Ă��܂��Ƃ�������
2024/11/15(��) 07:03:44.06ID:X+0oFEWT
���O�Ȃ̂�
2024/11/15(��) 07:10:56.68ID:r4YyLQb3
���킹��ʂ̍ő��24������30�͍ŏ��l
���点�Ζʐς����������A���炷�͖̂������Ă�������
���点�Ζʐς����������A���炷�͖̂������Ă�������
2024/11/15(��) 07:26:33.14ID:UwwEj+Sb
�W�̗����̂����킹�č�����Q✕�Q✕�Q�̗����̂̈�̖ʂɒP�ʗ����̂�\��A
�\�ʐςQ�W�ɂȂ�B
�\�ʐςQ�W�ɂȂ�B
2024/11/15(��) 07:29:10.95ID:UwwEj+Sb
�\�ʐςR�O�́A�W��ނ܂ł͌������܂������A
�n�����Ăďꍇ�������Č����Ƃ����Ȃ������@�����ɂ͂܂��������Ă��܂���B
�n�����Ăďꍇ�������Č����Ƃ����Ȃ������@�����ɂ͂܂��������Ă��܂���B
2024/11/15(��) 07:44:46.94ID:lBbQTEKQ
>>824
2�̗����̂ł����A
�\��t����ʂ̊p�x��45�����݂ɂ�����2�ʂ�
15�����݂Ȃ�6�ʂ�A1�����݂Ȃ�90�ʂ�
�������Ȃ���Ζ�������Ă̂̓R���s���[�^�[�Ƃ͂܂������W�Ȃ��b
2�̗����̂ł����A
�\��t����ʂ̊p�x��45�����݂ɂ�����2�ʂ�
15�����݂Ȃ�6�ʂ�A1�����݂Ȃ�90�ʂ�
�������Ȃ���Ζ�������Ă̂̓R���s���[�^�[�Ƃ͂܂������W�Ȃ��b
2024/11/15(��) 08:03:48.32ID:57j0KwQT
>>819
������8�ʂ肩��
�ʂ�1�\�邲�ƂɁA�\�ʐς�2��������
9��1��ɂȂ���ƁA�\��ʂ�8��
�\�ʐς�16�����āA54-16=38
54-24=30�ɂ���ɂ́A����4�ʂ����\��悢
8��2*2*2�̑嗧���̂�����Ă��܂���
���ꂾ����48-24=24�ƂȂ�A�c���1���\��Ȃ�
����Ă���͍l�����A����ɋ߂��`���琔���Ă���
�E�嗧���̂���1���������̂�
1*1*2�̒����̂̍L�����̖ʂ�\�����
L���̖ʂɓ\��F2�ʂ�
�傫�Ȑ����`�̖ʂɓ\��F4�ʂ�
�E3��L���ɂȂ������̂��AL�̖ʂ�
3�Ȃ��čL���K�i��̌`�ɂ���F1�ʂ�
�E1*3*3�̕����������̂ɂ���F1�ʂ�
���v8�ʂ�
�}�������Ȃ��Ă��܂�
������8�ʂ肩��
�ʂ�1�\�邲�ƂɁA�\�ʐς�2��������
9��1��ɂȂ���ƁA�\��ʂ�8��
�\�ʐς�16�����āA54-16=38
54-24=30�ɂ���ɂ́A����4�ʂ����\��悢
8��2*2*2�̑嗧���̂�����Ă��܂���
���ꂾ����48-24=24�ƂȂ�A�c���1���\��Ȃ�
����Ă���͍l�����A����ɋ߂��`���琔���Ă���
�E�嗧���̂���1���������̂�
1*1*2�̒����̂̍L�����̖ʂ�\�����
L���̖ʂɓ\��F2�ʂ�
�傫�Ȑ����`�̖ʂɓ\��F4�ʂ�
�E3��L���ɂȂ������̂��AL�̖ʂ�
3�Ȃ��čL���K�i��̌`�ɂ���F1�ʂ�
�E1*3*3�̕����������̂ɂ���F1�ʂ�
���v8�ʂ�
�}�������Ȃ��Ă��܂�
833�P�R�Q�l�ڂ̑f������
2024/11/16(�y) 01:19:00.22ID:JeVniimo ���݂܂����ĉ������B
A��B�̎����������Ԃŏo�����̗ʂ̊����́AA:B��3:1�ō����Ă܂����H
���͈ȉ��ɏ����܂��B
[���]
�Q�̎�A�AB������A�����ɐ������Ă����܂��B
A��B�����̎����J���Đ��������18���Ő����������ς��ɂȂ�܂��B
A��B�����̎��Ő������͂��߂�6�����B�̎�����߁A
A�̎������œ��ꑱ����ƁAB�̎�����߂Ă���16����ɐ����������ς��ɂȂ�܂����B
(�P) A��B�̎����������Ԃŏo�����̗ʂ̊����͉�:���ł����H
(�Q) A�̎��������J���Đ����������ς��ɂ���ɂ͉���������܂����H
A��B�̎����������Ԃŏo�����̗ʂ̊����́AA:B��3:1�ō����Ă܂����H
���͈ȉ��ɏ����܂��B
[���]
�Q�̎�A�AB������A�����ɐ������Ă����܂��B
A��B�����̎����J���Đ��������18���Ő����������ς��ɂȂ�܂��B
A��B�����̎��Ő������͂��߂�6�����B�̎�����߁A
A�̎������œ��ꑱ����ƁAB�̎�����߂Ă���16����ɐ����������ς��ɂȂ�܂����B
(�P) A��B�̎����������Ԃŏo�����̗ʂ̊����͉�:���ł����H
(�Q) A�̎��������J���Đ����������ς��ɂ���ɂ͉���������܂����H
2024/11/16(�y) 02:43:13.82ID:uE+t+nP/
>>833
���l�������v���Ă����Ƃ��Ă��A
�����Ɏ���ߒ����Ԉ���Ă����Ȃ���R�̈�v�ɉ߂��܂���B
�Z���A���w�̖��Ŏ����̉ɑ���A�h�o�C�X�����炨���Ƃ����ꍇ�A
���̓����Ɏ������ߒ��L���Ȃ��ƈӖ�������܂���B
���l�������v���Ă����Ƃ��Ă��A
�����Ɏ���ߒ����Ԉ���Ă����Ȃ���R�̈�v�ɉ߂��܂���B
�Z���A���w�̖��Ŏ����̉ɑ���A�h�o�C�X�����炨���Ƃ����ꍇ�A
���̓����Ɏ������ߒ��L���Ȃ��ƈӖ�������܂���B
2024/11/16(�y) 04:52:31.22ID:Si+9FQ0m
�������Ȃ��ł̉������͂킩���B
18a+18b=6a+6b+16a
18a/b+18=6a/b+6+16a/b
a/b=x
18x+18=6x+6+16x
12=4x
x=3
b=a/3
18a+18b=18a+6a=24a
�������f�f�Ǝ��Â��ł�����̉ߒ��͖��Ȃ��A
�Ƃ����̂���Z�̔畆�Ȃ̋����i�̐l�j�̓N�w��
�畆�Ȃ̐i�������͋��ȏ��m�[�g�������݉������B
�ŋߍ�����F�����݂����ȍZ���ɂȂ����Ȃ��B
18a+18b=6a+6b+16a
18a/b+18=6a/b+6+16a/b
a/b=x
18x+18=6x+6+16x
12=4x
x=3
b=a/3
18a+18b=18a+6a=24a
�������f�f�Ǝ��Â��ł�����̉ߒ��͖��Ȃ��A
�Ƃ����̂���Z�̔畆�Ȃ̋����i�̐l�j�̓N�w��
�畆�Ȃ̐i�������͋��ȏ��m�[�g�������݉������B
�ŋߍ�����F�����݂����ȍZ���ɂȂ����Ȃ��B
2024/11/16(�y) 06:12:06.61ID:Si+9FQ0m
>>823
�ɘ_��������ËL�����狳�����Ⴞ�߂���ˁH
�~�̖ʐρ����a�~���a�~�~������
�~�����͈ËL������g�����Ⴞ�߂���ˁB
�藝���v���O����������B
����̎g�����͈ËL���āA������ǂ��g�����ɂ̓A�C�f�A���K�v�Ƃ������Ƃ��Ǝv���B
���S�Ɍ��藝�͎����ł͏ؖ��ł��Ȃ�����ǎg���Ă���B
�������������đ̊��͂ł��邯�ǁB
�ɘ_��������ËL�����狳�����Ⴞ�߂���ˁH
�~�̖ʐρ����a�~���a�~�~������
�~�����͈ËL������g�����Ⴞ�߂���ˁB
�藝���v���O����������B
����̎g�����͈ËL���āA������ǂ��g�����ɂ̓A�C�f�A���K�v�Ƃ������Ƃ��Ǝv���B
���S�Ɍ��藝�͎����ł͏ؖ��ł��Ȃ�����ǎg���Ă���B
�������������đ̊��͂ł��邯�ǁB
2024/11/16(�y) 06:23:53.63ID:Si+9FQ0m
���{�l�̌��t�^��AB:B:O:A��1�F2�F3�F4�ł���Ƃ����B
����ׂɉ��l���̌��t�^�ׂāA ���ׂ��l�ɂ��ׂĂ̌��t�^���܂܂��m����99%�ȏ�ɂ������B
(1) ���l�ȏ㒲�ׂ�悢���H
(2) 99�����z�����Ƃ��̊m�����ŎZ�o����B
�Տ����(1)���S�S�l�ƎZ�o�ł���悢�B
�������I�^�N��(2)�����߂�悢�B
�܂��AWolfram���g���ƗՏ���ɂ�(2)�̓����o���邪�B
����ׂɉ��l���̌��t�^�ׂāA ���ׂ��l�ɂ��ׂĂ̌��t�^���܂܂��m����99%�ȏ�ɂ������B
(1) ���l�ȏ㒲�ׂ�悢���H
(2) 99�����z�����Ƃ��̊m�����ŎZ�o����B
�Տ����(1)���S�S�l�ƎZ�o�ł���悢�B
�������I�^�N��(2)�����߂�悢�B
�܂��AWolfram���g���ƗՏ���ɂ�(2)�̓����o���邪�B
2024/11/16(�y) 06:43:13.74ID:Si+9FQ0m
>>823
�Z����蕨�����w�̕����������Ă��Ėʔ����B
��
�q�ǂ����P�O�O���̃T�E�i�ɘA��Ă����ċC���𑪂�B
���ɑK���i�\�[�v�����h�ł��悢���j�ɘA��Ă����Ă����̉��x�𑪂�B
�T�O���̂����ɂ͓���Ȃ����Ƃ�̊�������B
�����ł̒ቷ�����łU�O���Q���ԂŃ��[�X�g�r�[�t�����B�i���M��\�ʂ͏Ă��������|���j�B
�I�[�u���Ń��[�X�g�r�[�t������̂͂ǂ�����悢�����l�������Ď�������B
�Z����蕨�����w�̕����������Ă��Ėʔ����B
��
�q�ǂ����P�O�O���̃T�E�i�ɘA��Ă����ċC���𑪂�B
���ɑK���i�\�[�v�����h�ł��悢���j�ɘA��Ă����Ă����̉��x�𑪂�B
�T�O���̂����ɂ͓���Ȃ����Ƃ�̊�������B
�����ł̒ቷ�����łU�O���Q���ԂŃ��[�X�g�r�[�t�����B�i���M��\�ʂ͏Ă��������|���j�B
�I�[�u���Ń��[�X�g�r�[�t������̂͂ǂ�����悢�����l�������Ď�������B
2024/11/16(�y) 08:09:31.75ID:iWDYx+Fl
2024/11/16(�y) 08:28:46.06ID:Si+9FQ0m
2024/11/16(�y) 08:35:07.32ID:Si+9FQ0m
>>839
��@���ËL���āZ�Z�Z�ɕ��ނ���������p�������Ȃ��Ǝv���B
��
�ꎟ�������̎g���Ȃ��V���c�ぁ�����e�^�҂̋L�^
https://i.imgur.com/GoBrWfn.jpeg
��@���ËL���āZ�Z�Z�ɕ��ނ���������p�������Ȃ��Ǝv���B
��
�ꎟ�������̎g���Ȃ��V���c�ぁ�����e�^�҂̋L�^
https://i.imgur.com/GoBrWfn.jpeg
2024/11/16(�y) 08:52:07.46ID:Si+9FQ0m
���������̂̓v���O�����ʼn����������y���Ǝv���B
�v���O���������̂ɐ��w�̃X�L�����K�v�����B
�v���O�����̊�{�������͈ËL���Ă����K�v�����邪�A
�����ËL����̂��������Ǝv���B
�o���L�ŗL���Ȃ�����������Z�G��
�e��97L�̑܂Ɨe��83L�̑܂��g���Ēr�̐���7L�W�߂����B
�܂ɖڐ���͂��Ă��܂���B
�܂���܂ւ̈ڂ��ւ��͑S�ʂōs���܂��B
�r����Ƃ鐅�̗ʂ�r�Ɏ̂Ă鐅�̗ʂɂ͐����͂���܂���B
�ŏ��ɕЕ��ɖ���������Ƃ��P��ڂƂ���
�Е��̑܂�7L���W�߂�̂ɍŒች��̈ړ����K�v���H
�z���:176��i�Ԉ���Ă��邩�������j
�Q�l�܂łɁi���A���͊��ꂽR�Ńv���O���������j
https://magazine.mathchannel.jp/quiz/5152/
�v���O���������̂ɐ��w�̃X�L�����K�v�����B
�v���O�����̊�{�������͈ËL���Ă����K�v�����邪�A
�����ËL����̂��������Ǝv���B
�o���L�ŗL���Ȃ�����������Z�G��
�e��97L�̑܂Ɨe��83L�̑܂��g���Ēr�̐���7L�W�߂����B
�܂ɖڐ���͂��Ă��܂���B
�܂���܂ւ̈ڂ��ւ��͑S�ʂōs���܂��B
�r����Ƃ鐅�̗ʂ�r�Ɏ̂Ă鐅�̗ʂɂ͐����͂���܂���B
�ŏ��ɕЕ��ɖ���������Ƃ��P��ڂƂ���
�Е��̑܂�7L���W�߂�̂ɍŒች��̈ړ����K�v���H
�z���:176��i�Ԉ���Ă��邩�������j
�Q�l�܂łɁi���A���͊��ꂽR�Ńv���O���������j
https://magazine.mathchannel.jp/quiz/5152/
2024/11/16(�y) 09:14:32.70ID:e+9et0yc
>>841
�A���^�̓X���^�C����ǂ߂Ȃ��`���p���W�[�݂�������
�A���^�̓X���^�C����ǂ߂Ȃ��`���p���W�[�݂�������
2024/11/16(�y) 09:14:45.60ID:yuo/FFWn
>>840
Flightyears�i�A�����J�̗��s�㗝�X�j
https://flightyears.com/
�P��̒���
lightyear�����N��9,460,730,472,580.8km
���܂܂�Ă���
Flightyears�i�A�����J�̗��s�㗝�X�j
https://flightyears.com/
�P��̒���
lightyear�����N��9,460,730,472,580.8km
���܂܂�Ă���
2024/11/16(�y) 09:16:17.59ID:e+9et0yc
800�F���̖���������F[sage]�F2024/11/16(�y) 09:01:18.24 ID:PKpaaua5
>>799
���l�^�����i�Ƃ������̂̓u�T�C�N�������ĂȂ��j�ł���B
����A�ݓ����Ńo���b�g�H���^���Ƃ���EGD�ɉ���Ă����P�[�X��������
�ݓ����Ńo���b�g�H�����āA
���l�̊���݂č����̉����̐F�Ă�悤�Ȃ��̂��Ȃ�
�ƌ�������
�����͐Ԃł���ƍ��ӂȃi�[�X�������Ă��ꂽ�B
�t�����H�����{�ݔS���̍Đ������B�����������A
�t�����H�����^���łȂ��ăo���b�g�H���^���ɂ����̂��͓�B
���i�ȃl�^�����牺�l�^�Ȃ̂ł́H�H
�������X���^�C�ǂ߂Ȃ����������w
>>799
���l�^�����i�Ƃ������̂̓u�T�C�N�������ĂȂ��j�ł���B
����A�ݓ����Ńo���b�g�H���^���Ƃ���EGD�ɉ���Ă����P�[�X��������
�ݓ����Ńo���b�g�H�����āA
���l�̊���݂č����̉����̐F�Ă�悤�Ȃ��̂��Ȃ�
�ƌ�������
�����͐Ԃł���ƍ��ӂȃi�[�X�������Ă��ꂽ�B
�t�����H�����{�ݔS���̍Đ������B�����������A
�t�����H�����^���łȂ��ăo���b�g�H���^���ɂ����̂��͓�B
���i�ȃl�^�����牺�l�^�Ȃ̂ł́H�H
�������X���^�C�ǂ߂Ȃ����������w
2024/11/16(�y) 09:21:53.82ID:XbBiyT9b
A��B���ꏏ�ɊJ�����18���Ő��������̂ŁA1���Ԃɐ��̏o��ʂ͐�����18����1�ł��B
A��B���ꏏ�ɊJ���čŏ���6���Ő����ɓ���ʂ͐�����18��6(3����1)�ł��B
����A�����Ő����̎c��(3����2)�����̂�16��������̂ŁA1���Ԃŏo�鐅�̗ʂ͐�����24����1(3����2 �� 16�j�ł��B
�n���āAA�����Ő��������̂�24��(1 �� 24����1)������܂��B
B��1���Ԃɏo�����̗ʂ́AA��B���ꏏ�ɊJ����ƁA1���Ԃɐ�����18����1���������܂�܂��B���̂����AA��24����1�̐����o���Ă���̂ŁAB��1���ŏo�����̗ʂ�72����1(18����1 �| 24����1)�ł��B
�n���āAA��B�̔��3��1(A�FB = 24����1�F72����1 = 3�F1)�ł��B
A��B���ꏏ�ɊJ���čŏ���6���Ő����ɓ���ʂ͐�����18��6(3����1)�ł��B
����A�����Ő����̎c��(3����2)�����̂�16��������̂ŁA1���Ԃŏo�鐅�̗ʂ͐�����24����1(3����2 �� 16�j�ł��B
�n���āAA�����Ő��������̂�24��(1 �� 24����1)������܂��B
B��1���Ԃɏo�����̗ʂ́AA��B���ꏏ�ɊJ����ƁA1���Ԃɐ�����18����1���������܂�܂��B���̂����AA��24����1�̐����o���Ă���̂ŁAB��1���ŏo�����̗ʂ�72����1(18����1 �| 24����1)�ł��B
�n���āAA��B�̔��3��1(A�FB = 24����1�F72����1 = 3�F1)�ł��B
2024/11/16(�y) 09:26:58.27ID:Si+9FQ0m
�����C��H�����̕����������N���B
���ɒނ��ĈŃo�C�g�����s�鎞��ɐ����ɋ������o��������ɂ�
���̌v�Z���ǂ�����Ă��邩���l�����������������B
https://i.imgur.com/SJYyhF3.png
���Ȃ݂ɖ���̑����͊T�Z�l�œ����Ă���B
���F
https://i.imgur.com/SJYyhF3.png
�̓����~�P�ʂŎZ�o����B
���ɒނ��ĈŃo�C�g�����s�鎞��ɐ����ɋ������o��������ɂ�
���̌v�Z���ǂ�����Ă��邩���l�����������������B
https://i.imgur.com/SJYyhF3.png
���Ȃ݂ɖ���̑����͊T�Z�l�œ����Ă���B
���F
https://i.imgur.com/SJYyhF3.png
�̓����~�P�ʂŎZ�o����B
2024/11/16(�y) 09:35:15.56ID:Si+9FQ0m
>>844
�������I
�������I
849833
2024/11/16(�y) 09:36:24.74ID:JeVniimo >>846
�킩��₷�����肪�Ƃ��������܂��I
����ƁA�܂Ƃ��ȉ����炦�ėǂ������B
�Ӗ��s���ȏ������݂��炯�Ŗ�肪�������Ƃ���ł����B
�킩��₷�����肪�Ƃ��������܂��I
����ƁA�܂Ƃ��ȉ����炦�ėǂ������B
�Ӗ��s���ȏ������݂��炯�Ŗ�肪�������Ƃ���ł����B
2024/11/16(�y) 09:37:07.67ID:Si+9FQ0m
�������o����l�͐����𓊍e���邯�ǁA
���ꂪ�ł��Ȃ��`���p�t�F�`�͈��ꂾ�ȁB
���ꂪ�ł��Ȃ��`���p�t�F�`�͈��ꂾ�ȁB
2024/11/16(�y) 09:37:14.70ID:XbBiyT9b
>>833
�������ʼn����̂͊ȒP�����ǁA���̒��x�����t�Ő������o���Ȃ��͖̂{���ɗ������Ă���Ƃ͌����Ȃ����낤�B
�������ʼn����̂͊ȒP�����ǁA���̒��x�����t�Ő������o���Ȃ��͖̂{���ɗ������Ă���Ƃ͌����Ȃ����낤�B
852�P�R�Q�l�ڂ̑f������
2024/11/16(�y) 09:39:17.21ID:sYwXZ0hU >>836
>����̎g�����͈ËL���āA������ǂ��g�����ɂ̓A�C�f�A���K�v�Ƃ������Ƃ��Ǝv���B
���������܂����ËL���̂��̂��߂ł͂Ȃ��A�~�̖ʐς�藝���ǂ����Ă��̎��Ȃ̂��H
�Ƃ����A���̗����̗������܂߂ė������Ȃ��Ƃł��ˁB
�m�Ƃ��͒m��܂��A���̎Q�l���͈ËL�𐄏����Ă܂���ˁB
�i��C���킹�Ƃ��o�Ă��Ȃ��j
���̗��̗������ׂ��������Ă銴���ł��B
�Z���E���w���w�ԈӋ`�́A�ߋ��̓V�˓I�Ȕ��z���w��ŁA
�A�C�f�A�̃o���G�[�V�����𑝂₷���Ƃɂ����Ȃ����ƁB
��������Ζ}�l�ł���ȃA�C�f�A���o���y�����Ă���B
�i�������A�{�l���V�˓I�Ȕ��z�ݏo���Ă��ǂ��j
�����Z�̌�����ʂ��Ċ����܂����B
�Ȃ̂œ������o�������A�ނ���ߒ��̒��Ŏ��s���낷�邱�Ƃɂ���
�Z���E���w�̈Ӌ`���B��Ă���C�����܂��B
>����̎g�����͈ËL���āA������ǂ��g�����ɂ̓A�C�f�A���K�v�Ƃ������Ƃ��Ǝv���B
���������܂����ËL���̂��̂��߂ł͂Ȃ��A�~�̖ʐς�藝���ǂ����Ă��̎��Ȃ̂��H
�Ƃ����A���̗����̗������܂߂ė������Ȃ��Ƃł��ˁB
�m�Ƃ��͒m��܂��A���̎Q�l���͈ËL�𐄏����Ă܂���ˁB
�i��C���킹�Ƃ��o�Ă��Ȃ��j
���̗��̗������ׂ��������Ă銴���ł��B
�Z���E���w���w�ԈӋ`�́A�ߋ��̓V�˓I�Ȕ��z���w��ŁA
�A�C�f�A�̃o���G�[�V�����𑝂₷���Ƃɂ����Ȃ����ƁB
��������Ζ}�l�ł���ȃA�C�f�A���o���y�����Ă���B
�i�������A�{�l���V�˓I�Ȕ��z�ݏo���Ă��ǂ��j
�����Z�̌�����ʂ��Ċ����܂����B
�Ȃ̂œ������o�������A�ނ���ߒ��̒��Ŏ��s���낷�邱�Ƃɂ���
�Z���E���w�̈Ӌ`���B��Ă���C�����܂��B
2024/11/16(�y) 09:40:51.86ID:uE+t+nP/
>>833 �ɂ��Ă�
�i1�j�`�Ƃa�����Œ�������i18 - 6�j���ōςޏ����`�����Œ��������16��������̂�
�`�̒��������͂`�a���p����12/16�ł���B
����ɂ��a�̒��������͕��p����4/16�Ƃ킩��B
����ċ��߂���3�F1�ł���B
�i2�j���p��18���̂Ƃ��뒍�����������p����12/16�ɂȂ��Ă���킯������
���v���Ԃ�18����16/12�{�ł���B
����ċ��߂鎞�Ԃ�24���ł���B
�i2�j�ʉ�
�`�����ł͐����́i18 - 6�j/18�𒍐�����̂�16���������킯������
�S�ʂȂ炻��18/12�{�ł���B
����ċ��߂鎞�Ԃ�24���ł���B
�i1�j�`�Ƃa�����Œ�������i18 - 6�j���ōςޏ����`�����Œ��������16��������̂�
�`�̒��������͂`�a���p����12/16�ł���B
����ɂ��a�̒��������͕��p����4/16�Ƃ킩��B
����ċ��߂���3�F1�ł���B
�i2�j���p��18���̂Ƃ��뒍�����������p����12/16�ɂȂ��Ă���킯������
���v���Ԃ�18����16/12�{�ł���B
����ċ��߂鎞�Ԃ�24���ł���B
�i2�j�ʉ�
�`�����ł͐����́i18 - 6�j/18�𒍐�����̂�16���������킯������
�S�ʂȂ炻��18/12�{�ł���B
����ċ��߂鎞�Ԃ�24���ł���B
2024/11/16(�y) 10:30:30.88ID:heEJDHUp
>>850
65�ɂ��Ȃ��ăX���^�C���ǂ߂��ɔ�����������A���^�̂ق�������ۂLj��ꂾ��
65�ɂ��Ȃ��ăX���^�C���ǂ߂��ɔ�����������A���^�̂ق�������ۂLj��ꂾ��
2024/11/16(�y) 11:48:31.26ID:S+mdbEea
2024/11/16(�y) 11:57:33.73ID:e+9et0yc
>>855
���N���X���^�C�ǂ߂��ɖϑz�Ɣ������J��Ԃ��Ă铝�������ǂƔF�m�ǂ���������60�߂��̈���Ȗꂳ��
���N���X���^�C�ǂ߂��ɖϑz�Ɣ������J��Ԃ��Ă铝�������ǂƔF�m�ǂ���������60�߂��̈���Ȗꂳ��
2024/11/16(�y) 13:01:04.48ID:DTL0dcJ2
���w�Z�̖�����������g��Ȃ��Ɖ����Ȃ��Ƃ��A�m�\�͏��w���ȉ����Ă��Ƃ���B������A�X���^�C���ǂ߂Ȃ��낤�B
2024/11/16(�y) 18:44:52.35ID:d34Enlye
���̍r�炵�͍��Z���w�̎���X���Œ���̖����o���ꂽ�ہA
�ʔ����Ȃ��Ƃ������R�ʼn����܂���ł���
�v���O�����ɗ��Ƃ����݂Â炢�̖��͉����܂��A
�����̃v���O�������v�Z�ʂ�O(n)������A
�قƂ�ǂ̏ꍇO(n^2)�ƂȂ�A���镨�̖����S�~�ł�
�ʔ����Ȃ��Ƃ������R�ʼn����܂���ł���
�v���O�����ɗ��Ƃ����݂Â炢�̖��͉����܂��A
�����̃v���O�������v�Z�ʂ�O(n)������A
�قƂ�ǂ̏ꍇO(n^2)�ƂȂ�A���镨�̖����S�~�ł�
859�P�R�Q�l�ڂ̑f������
2024/11/17(��) 00:56:12.35ID:64z1CIcG 3�̃h�A������A���ꂼ��̃h�A�̌������ɂ͎ԁA���M�A���Y�����܂��B
���Y����͂ǂꂩ1�h�A��I�сA������J���ĎԂ��o���瓖����ŁA�Ԃ����炤���Ƃ��ł��܂��B
���M���o���炻�̎��_�ŃQ�[���I���ł��B
���Y���o����A���Y���V���Ȓ���҂ƂȂ�A���Y����͎��Y����̂����h�A�ɓ���A�h�A��߁A
�h�A�̌������ŎԁA���M�A���Y����̈ʒu�������_���ɃV���b�t�����܂��B
�����܂ł��P�^�[���Ƃ��܂��B
���̌�͎��Y������҂ƂȂ�A���Y���o�������ւ��V���b�t������܂��B
�ȏ�̎菇�ŎԂ����M���Q�l�̂ǂ��炩�����Ă�܂ő����܂��B
���Y���W�^�[���ȓ��ɎԂ��l������m�������߂Ȃ����B
���Y����͂ǂꂩ1�h�A��I�сA������J���ĎԂ��o���瓖����ŁA�Ԃ����炤���Ƃ��ł��܂��B
���M���o���炻�̎��_�ŃQ�[���I���ł��B
���Y���o����A���Y���V���Ȓ���҂ƂȂ�A���Y����͎��Y����̂����h�A�ɓ���A�h�A��߁A
�h�A�̌������ŎԁA���M�A���Y����̈ʒu�������_���ɃV���b�t�����܂��B
�����܂ł��P�^�[���Ƃ��܂��B
���̌�͎��Y������҂ƂȂ�A���Y���o�������ւ��V���b�t������܂��B
�ȏ�̎菇�ŎԂ����M���Q�l�̂ǂ��炩�����Ă�܂ő����܂��B
���Y���W�^�[���ȓ��ɎԂ��l������m�������߂Ȃ����B
2024/11/17(��) 01:52:07.30ID:NoCSqZdt
��U�ƌ�U���ǂ��������Y����ɂȂ��Ă��
861�P�R�Q�l�ڂ̑f������
2024/11/17(��) 02:00:17.12ID:64z1CIcG >>860
���炵�܂����B�����ĂĂ킯�킩��Ȃ����c
�������܂����B
3�̃h�A������A���ꂼ��̃h�A�̌������ɂ͎ԁA���M�A���Y�����܂��B
���Y����͂ǂꂩ1�h�A��I�сA������J���ĎԂ��o���瓖����ŁA�Ԃ����炤���Ƃ��ł��܂��B
���M���o���炻�̎��_�ŃQ�[���I���ł��B
���Y���o����A���Y���V���Ȓ���҂ƂȂ�A���Y����͑��Y����̂����h�A�ɓ���A�h�A��߁A
�h�A�̌������ŎԁA���M�A���Y����̈ʒu�������_���ɃV���b�t�����܂��B
�����܂ł��P�^�[���Ƃ��܂��B
���̌�͑��Y������҂ƂȂ�A���Y���o�������ւ��V���b�t������܂��B
�ȏ�̎菇�ŎԂ����M���Q�l�̂ǂ��炩�����Ă�܂ő����܂��B
���Y���W�^�[���ȓ��ɎԂ��l������m�������߂Ȃ����B
���炵�܂����B�����ĂĂ킯�킩��Ȃ����c
�������܂����B
3�̃h�A������A���ꂼ��̃h�A�̌������ɂ͎ԁA���M�A���Y�����܂��B
���Y����͂ǂꂩ1�h�A��I�сA������J���ĎԂ��o���瓖����ŁA�Ԃ����炤���Ƃ��ł��܂��B
���M���o���炻�̎��_�ŃQ�[���I���ł��B
���Y���o����A���Y���V���Ȓ���҂ƂȂ�A���Y����͑��Y����̂����h�A�ɓ���A�h�A��߁A
�h�A�̌������ŎԁA���M�A���Y����̈ʒu�������_���ɃV���b�t�����܂��B
�����܂ł��P�^�[���Ƃ��܂��B
���̌�͑��Y������҂ƂȂ�A���Y���o�������ւ��V���b�t������܂��B
�ȏ�̎菇�ŎԂ����M���Q�l�̂ǂ��炩�����Ă�܂ő����܂��B
���Y���W�^�[���ȓ��ɎԂ��l������m�������߂Ȃ����B
2024/11/18(��) 12:23:02.08ID:zvfCaBME
���Y�N��k��ڒ��킷��m����
(1/3�~1/3)ᵏ⁻¹
���߂�m����
(1+1/9+1/81+1/729)�~(1/3)=820/2187
(1/3�~1/3)ᵏ⁻¹
���߂�m����
(1+1/9+1/81+1/729)�~(1/3)=820/2187
2024/11/18(��) 18:43:29.12ID:bNkyVTBE
��{�I�Ȗ��Ƃ��āA����A���ꂼ��̔����J���鎖�ۂ����l�Ɋm���炵�����ƂƑO�^�[���܂ł̌o�߂ɉe������Ȃ����Ƃ͖������Ȃ��Ƃ����܂���B
1�^�[���ځ@0
2�^�[���ځ@1/9
3�^�[���ځ@0
4�^�[���ځ@1/81
5�^�[���ځ@0
6�^�[���ځ@1/729
7�^�[���ځ@0
8�^�[���ځ@1/6561
���F�@820/6561
1�^�[���ځ@0
2�^�[���ځ@1/9
3�^�[���ځ@0
4�^�[���ځ@1/81
5�^�[���ځ@0
6�^�[���ځ@1/729
7�^�[���ځ@0
8�^�[���ځ@1/6561
���F�@820/6561
2024/11/18(��) 18:47:33.22ID:bNkyVTBE
����Ə����A�O�^�[���܂łɉe������Ȃ����ƂɂȂ邩�B
2024/11/18(��) 23:37:40.73ID:F0+pha6b
����Ƃ������t�����邾���ł͎��s�̓Ɨ���(Markov��)�܂ł͒S�ۂ���Ȃ�
������Markov���܂ŗv�����Ȃ��Ă����̎�̖��͌v�Z�ł���
������Markov���܂ŗv�����Ȃ��Ă����̎�̖��͌v�Z�ł���
2024/11/19(��) 10:44:49.29ID:V8CHGcRI
867�P�R�Q�l�ڂ̑f������
2024/11/19(��) 18:45:31.16ID:N2Ec1gzA ���w�������̖��
�O�p�`ABC������A��AC�̒��_�ɓ_D���Ƃ�B�ƌ��Ƃ���A�pBDA���45�ƂȂ����B
�܂��A�pABD�ƊpCBD�̊p�x�̔䗦�͂Q:�P�ƂȂ����B
���̂Ƃ��pABC�͉��x���H
�O�p�`ABC������A��AC�̒��_�ɓ_D���Ƃ�B�ƌ��Ƃ���A�pBDA���45�ƂȂ����B
�܂��A�pABD�ƊpCBD�̊p�x�̔䗦�͂Q:�P�ƂȂ����B
���̂Ƃ��pABC�͉��x���H
2024/11/20(��) 05:24:59.20ID:KnDPFD/I
���ёO�̃V�~�����[�V�������K���
4�̃h�A������A���ꂼ��̃h�A�̌������ɂ͎ԁA���M�A���Y����A���Y�������܂��B
�O�Y����͂ǂꂩ1�h�A��I�сA������J���ĎԂ��o���瓖����ŁA�Ԃ����炤���Ƃ��ł��܂��B
���M���o���炻�̎��_�ŃQ�[���I���ł��B
�l���iX�Ƃ���j���o����AX���V���Ȓ���҂ƂȂ�A�O�Y����͑I�h�A�ɓ���A�h�A��߁A
�h�A�̌������ŎԁA���M�A�l���Q�l�̈ʒu�������_���ɃV���b�t�����܂��B
�����܂ł��P�^�[���Ƃ��܂��B
���̌��X������҂ƂȂ�A�Q�[���s���܂��B
�ȏ�̎菇�ŎԂ����M��N�������Ă�܂ő����܂��B
���Y���W�^�[���ȓ��ɎԂ��l������m�������߂Ȃ����B
���l�Ɋm���炵���Ƃ����͉̂��z�Ȃ̂ŊT�Z�i�L�������Q���j�ł悢�B
4�̃h�A������A���ꂼ��̃h�A�̌������ɂ͎ԁA���M�A���Y����A���Y�������܂��B
�O�Y����͂ǂꂩ1�h�A��I�сA������J���ĎԂ��o���瓖����ŁA�Ԃ����炤���Ƃ��ł��܂��B
���M���o���炻�̎��_�ŃQ�[���I���ł��B
�l���iX�Ƃ���j���o����AX���V���Ȓ���҂ƂȂ�A�O�Y����͑I�h�A�ɓ���A�h�A��߁A
�h�A�̌������ŎԁA���M�A�l���Q�l�̈ʒu�������_���ɃV���b�t�����܂��B
�����܂ł��P�^�[���Ƃ��܂��B
���̌��X������҂ƂȂ�A�Q�[���s���܂��B
�ȏ�̎菇�ŎԂ����M��N�������Ă�܂ő����܂��B
���Y���W�^�[���ȓ��ɎԂ��l������m�������߂Ȃ����B
���l�Ɋm���炵���Ƃ����͉̂��z�Ȃ̂ŊT�Z�i�L�������Q���j�ł悢�B
2024/11/20(��) 07:31:50.99ID:Fq0JUUhq
>>867
�`�b��Ίp���̈�Ƃ��鐳���`�`�d�b�f���l����B
���̂Ƃ��A�`����o��ӂ̓��a�c�i��������܂ށj�ƌ������́A�`�łȂ����̒��_���d�Ƃ��A���̌�_���e�Ƃ���B
�c�������_���f�Ƃ��A�b�f�Ƃa�c�i��������܂ށj�̌�_���g�Ƃ���B
�c���`�b�̒��_�ł��邱�ƂƂ`�d�b�f�̍�����薾�炩��
�ڂf�a�c���ڂb�a�c
�܂��A�ڂ`�a�c�F�ڂb�a�c��2�F1���
�ڂf�a�c���ڂf�a�`
�`�f���a�c�ƕ��s�i�w�����`�`�d�b�f�̐�����薾�炩�j�ł��邩��
�ڂf�a�c���ڂa�f�`
�O�p�`�`�a�f���ӎO�p�`�ł��邱�Ƃ�������
�`�a���`�f���`�d���d�a���킩��B
����
�`�b��Ίp���̈�Ƃ��鐳���`�`�d�b�f���l����B
���̂Ƃ��A�`����o��ӂ̓��a�c�i��������܂ށj�ƌ������́A�`�łȂ����̒��_���d�Ƃ��A���̌�_���e�Ƃ���B
�c�������_���f�Ƃ��A�b�f�Ƃa�c�i��������܂ށj�̌�_���g�Ƃ���B
�c���`�b�̒��_�ł��邱�ƂƂ`�d�b�f�̍�����薾�炩��
�ڂf�a�c���ڂb�a�c
�܂��A�ڂ`�a�c�F�ڂb�a�c��2�F1���
�ڂf�a�c���ڂf�a�`
�`�f���a�c�ƕ��s�i�w�����`�`�d�b�f�̐�����薾�炩�j�ł��邩��
�ڂf�a�c���ڂa�f�`
�O�p�`�`�a�f���ӎO�p�`�ł��邱�Ƃ�������
�`�a���`�f���`�d���d�a���킩��B
����
2024/11/20(��) 07:32:21.18ID:Fq0JUUhq
����
����ɂ��O�p�`�`�a�d�͐��O�p�`�ł��邪�A
�a���`�d�b�f�̓����ɂ���Ƃ���Ɓڂ`�a�c�F�ڂb�a�c��2�F1�ɖ�������B
����ɂ��ڂ`�a�d���U�O�x�A�ڂ`�a�e�i���ڂ`�a�c�j���R�O�x�ƂȂ�A
�ڂ`�a�b�͂S�T�x���Ƃ킩��B
���F�S�T�x
����ɂ��O�p�`�`�a�d�͐��O�p�`�ł��邪�A
�a���`�d�b�f�̓����ɂ���Ƃ���Ɓڂ`�a�c�F�ڂb�a�c��2�F1�ɖ�������B
����ɂ��ڂ`�a�d���U�O�x�A�ڂ`�a�e�i���ڂ`�a�c�j���R�O�x�ƂȂ�A
�ڂ`�a�b�͂S�T�x���Ƃ킩��B
���F�S�T�x
2024/11/20(��) 07:35:51.55ID:Fq0JUUhq
>>869
�w�����`�@�͐����`�̌�L�ł��B
�w�����`�@�͐����`�̌�L�ł��B
2024/11/20(��) 08:40:07.37ID:L6xG8z8u
>>1�ɑ��葦NG
2024/11/20(��) 11:40:57.83ID:KnDPFD/I
���[�Ȑ��l�ł̃��A�����[���h�ł̎Ƃ͖��W�̖��
�O�p�`ABC������A��AC�̒��_�ɓ_D���Ƃ�B�ƌ��Ƃ���A�pBDA���28���ƂȂ����B
�܂��A�pABD�ƊpCBD�̊p�x�̔䗦��3:1�ƂȂ����B
(1) ���̂Ƃ��pABC�͉��x���H ���͍ł��߂������ł悢�B
(2) �O�p�`ABC�Ɛ���BD����}����B
(2) https://i.imgur.com/jaaDAg3.png
�O�p�`ABC������A��AC�̒��_�ɓ_D���Ƃ�B�ƌ��Ƃ���A�pBDA���28���ƂȂ����B
�܂��A�pABD�ƊpCBD�̊p�x�̔䗦��3:1�ƂȂ����B
(1) ���̂Ƃ��pABC�͉��x���H ���͍ł��߂������ł悢�B
(2) �O�p�`ABC�Ɛ���BD����}����B
(2) https://i.imgur.com/jaaDAg3.png
874867
2024/11/20(��) 17:48:38.21ID:8XU+Bnj9 >>869
�����I
�����I
875�P�R�Q�l�ڂ̑f������
2024/11/20(��) 23:37:21.42ID:8XU+Bnj9 �܂����w�������̖��ł��B
���Y����̃R�b�v�Ɂ����̐H�����U�O�O��������A���̂����P�T�O�������Y����̋�̃R�b�v�Ɉڂ����B
���ɂU�T���̐H�����Y����̃R�b�v�Ǝ��Y����̃R�b�v�ɕ����ē��ꂽ�Ƃ���A
���Y����̃R�b�v�̐H�����Z�x�͂Q�O���A���Y����̃R�b�v�̐H�����Z�x�͂P�O���ɂȂ����B
���ɓ��鐔�����Ȃ����B
���Y����̃R�b�v�Ɂ����̐H�����U�O�O��������A���̂����P�T�O�������Y����̋�̃R�b�v�Ɉڂ����B
���ɂU�T���̐H�����Y����̃R�b�v�Ǝ��Y����̃R�b�v�ɕ����ē��ꂽ�Ƃ���A
���Y����̃R�b�v�̐H�����Z�x�͂Q�O���A���Y����̃R�b�v�̐H�����Z�x�͂P�O���ɂȂ����B
���ɓ��鐔�����Ȃ����B
2024/11/21(��) 08:10:03.28ID:AvwCKfOf
����̖����Ă���Ȓ�x������Ȃ���
877�P�R�Q�l�ڂ̑f������
2024/11/21(��) 12:53:02.11ID:1HXCUNpS �����܂��̖��̓��������Ă��������B
2015�N��2��1���͓��j���ł����B
1000����͉��N�����������j���ł����H
2015�N��2��1���͓��j���ł����B
1000����͉��N�����������j���ł����H
878�P�R�Q�l�ڂ̑f������
2024/11/21(��) 13:04:11.05ID:1HXCUNpS ���݂܂�������������Ă܂����B
2016�N�͂��邤�N�ł��B
2016�N�͂��邤�N�ł��B
879�P�R�Q�l�ڂ̑f������
2024/11/21(��) 13:27:18.14ID:F6V5XrTU ���������Ȃ�O�O��킩�邵�A�l���������w����̃T�C�g��T���Ώo�Ă���
2024/11/21(��) 17:31:07.32ID:Ci8ztJhi
>>873
�A�r�W�W�C�܂����w���Ƀo�J�ɂ��ꑫ��Ȃ��̂��H
�A�r�W�W�C�܂����w���Ƀo�J�ɂ��ꑫ��Ȃ��̂��H
881�P�R�Q�l�ڂ̑f������
2024/11/21(��) 17:35:28.48ID:l6tt3Do+ >>877
����Ȃǂ���H
https://zky-jukesan.com/koyomi-zan-guidance/10546
���w�z����Z(�J�����_�[/�j��/���t�v�Z)�̉������y���ځE����
����Ȃǂ���H
https://zky-jukesan.com/koyomi-zan-guidance/10546
���w�z����Z(�J�����_�[/�j��/���t�v�Z)�̉������y���ځE����
882�P�R�Q�l�ڂ̑f������
2024/11/21(��) 17:37:43.43ID:l6tt3Do+ ����(�N�Z��)��N����̓��t
��N����
�u�����̎c������v
�u���̌��̓����v
�u���̎��̓����v�c
���c�肪31(������̌�)��30(�������̌�)
�ȉ��ɂȂ�܂ň����Ă����āA
�c��������M��N����̓��t
����(�N�Z��)��N����̗j��
N��7�̗]�肪0�Ȃ獡���Ɠ����j��
���������j�����Ƃ��āc
�]�肪0�c��
�]�肪1�c��
�]�肪2�c��
�c
�]�肪6�c��
��N����
�u�����̎c������v
�u���̌��̓����v
�u���̎��̓����v�c
���c�肪31(������̌�)��30(�������̌�)
�ȉ��ɂȂ�܂ň����Ă����āA
�c��������M��N����̓��t
����(�N�Z��)��N����̗j��
N��7�̗]�肪0�Ȃ獡���Ɠ����j��
���������j�����Ƃ��āc
�]�肪0�c��
�]�肪1�c��
�]�肪2�c��
�c
�]�肪6�c��
883�P�R�Q�l�ڂ̑f������
2024/11/21(��) 18:30:10.38ID:1HXCUNpS ���肪�Ƃ��������܂��B
���̃T�C�g�ڂ���������ł����ǁA����܂�M�p�o���Ȃ��ł��B
�w�Ⴆ�A�������Ηj���Ƃ��č��T�̖ؗj���́u4���ځv�Łu3����v�ɂȂ�܂��x
���̕����Ԉ���Ă܂���ˁH
�������͖ؗj������Ȃ��ċ��j�����Ǝv����ł����ǁB
���̃T�C�g�ڂ���������ł����ǁA����܂�M�p�o���Ȃ��ł��B
�w�Ⴆ�A�������Ηj���Ƃ��č��T�̖ؗj���́u4���ځv�Łu3����v�ɂȂ�܂��x
���̕����Ԉ���Ă܂���ˁH
�������͖ؗj������Ȃ��ċ��j�����Ǝv����ł����ǁB
884�P�R�Q�l�ڂ̑f������
2024/11/21(��) 18:37:27.90ID:l6tt3Do+ >>883
�����͐}�Ɛ����������Ă��Ȃ��ł���
�����͐}�Ɛ����������Ă��Ȃ��ł���
2024/11/21(��) 22:25:09.76ID:8u2QKJaL
>>873
R�ō�����\���o�[�ŎZ�o
> solve(BDA=45,ratio=2)
[1] 45
> solve(BDA=28,ratio=3)
[1] 42.02654
> solve(BDA=40,ratio=4)
[1] 115.833
R�ō�����\���o�[�ŎZ�o
> solve(BDA=45,ratio=2)
[1] 45
> solve(BDA=28,ratio=3)
[1] 42.02654
> solve(BDA=40,ratio=4)
[1] 115.833
2024/11/21(��) 22:52:10.56ID:8u2QKJaL
>>877
R�Ń\���o�[���쐬���Ď��s�B
solve(n) �@�F�@2015�N��2��1������n����̓��t�Ɨj����Ԃ�
> solve(1000)
���t �j��
1 2017-10-28 �y
> solve(10000)
���t �j��
1 2042-06-19 ��
> solve(100000)
���t �j��
1 2288-11-16 ��
���K���@
(1) 100������̓��t�Ɨj�������߂�B
(2) �\���o�[���쐬���ď�L��������B�g�p����͖��Ȃ��B
R�Ń\���o�[���쐬���Ď��s�B
solve(n) �@�F�@2015�N��2��1������n����̓��t�Ɨj����Ԃ�
> solve(1000)
���t �j��
1 2017-10-28 �y
> solve(10000)
���t �j��
1 2042-06-19 ��
> solve(100000)
���t �j��
1 2288-11-16 ��
���K���@
(1) 100������̓��t�Ɨj�������߂�B
(2) �\���o�[���쐬���ď�L��������B�g�p����͖��Ȃ��B
2024/11/21(��) 22:57:01.69ID:Ci8ztJhi
>>886
���܂Ő����p�N���Ă��ĕ����Ă�
���܂Ő����p�N���Ă��ĕ����Ă�
2024/11/21(��) 23:01:42.41ID:8u2QKJaL
���K���@
�i�P�j�փP���̐킢��1600�N10��21���ł���B���̓����O�Ƃ���
�{��2024�N11��21���͉����߂ɂ����邩�H
�i�Q�j�փP���̐킢�̓��͉��j�����H
�i�R�j����V�V�V�V�N�V���V���͉��j�����H
�i�P�j�փP���̐킢��1600�N10��21���ł���B���̓����O�Ƃ���
�{��2024�N11��21���͉����߂ɂ����邩�H
�i�Q�j�փP���̐킢�̓��͉��j�����H
�i�R�j����V�V�V�V�N�V���V���͉��j�����H
2024/11/21(��) 23:03:00.60ID:AvwCKfOf
>>888
�[�N�̒�`���Ȃ��̂ʼn�
�[�N�̒�`���Ȃ��̂ʼn�
2024/11/21(��) 23:05:44.07ID:Ci8ztJhi
https://egg.5ch.net/test/read.cgi/hosp/1723605276/
https://rio2016.5ch.net/test/read.cgi/math/1723179542/
ID:8u2QKJaL���A�r�W�W�C�͂����̃X���B�ł̓{�R����ă_���}�����ߍ���ł�悤�ł�
https://rio2016.5ch.net/test/read.cgi/math/1723179542/
ID:8u2QKJaL���A�r�W�W�C�͂����̃X���B�ł̓{�R����ă_���}�����ߍ���ł�悤�ł�
2024/11/21(��) 23:12:25.08ID:8u2QKJaL
>>887
�����o���Ȃ��A�����p�����炵�Ă���̂��A�A�r�`���p�t�F�`��Phimose���ˁB
�����o���Ȃ��A�����p�����炵�Ă���̂��A�A�r�`���p�t�F�`��Phimose���ˁB
2024/11/21(��) 23:14:40.32ID:8u2QKJaL
2024/11/21(��) 23:17:57.63ID:8u2QKJaL
���K���
�����̒a��������͂��č��������a���牽���߂����v�Z����\���o�[�����B
�g�p����͖��Ȃ��B
�����̒a��������͂��č��������a���牽���߂����v�Z����\���o�[�����B
�g�p����͖��Ȃ��B
2024/11/21(��) 23:27:49.25ID:8u2QKJaL
���{�l�Ȃ�v�Z�͂ł��������
�@����É����Ď����}������͉��j�����H
�@����É����Ď����}������͉��j�����H
2024/11/21(��) 23:31:06.63ID:Ci8ztJhi
2024/11/21(��) 23:39:49.40ID:8u2QKJaL
���̃v���O�����ɂ͎��n��f�[�^���������߂̊����p�ӂ���Ă���͂��B
�G�N�Z���ɂ����������A�P�O�O������̌v�Z�ɑΉ����Ă��邩�ǂ����͒m���B
�G�N�Z���ɂ����������A�P�O�O������̌v�Z�ɑΉ����Ă��邩�ǂ����͒m���B
2024/11/21(��) 23:47:27.99ID:Ci8ztJhi
>>896
�����烌�X��H�����Ƃ���ŒN�������ĂȂ���Ȃ��������������ĂȂ�����`���p���W�[�݂����ɃL�[�L�[�����Ȃ��玩�⎩���ł����Ă��p�m�炸w
�����烌�X��H�����Ƃ���ŒN�������ĂȂ���Ȃ��������������ĂȂ�����`���p���W�[�݂����ɃL�[�L�[�����Ȃ��玩�⎩���ł����Ă��p�m�炸w
2024/11/22(��) 05:46:50.70ID:2M9XV7Pv
���ёO��
���a��1926�N�i���a���N�j12��25������1989�N�i���a64�N�j1��7���܂ł���B
(1) ���a�͉��j������n�܂艽�j���ɏI��������H
(2) ���a�V�c�݈̍ʓ������v�Z����B
(3) ���N�͏��a100�N�ɂ�����B���a1000�N�̏��a�̓�(4��29��)�͉��j�����H
R�ł̌���
�i�P�j
[1] �y
[1] �y
�i�Q�j
22660 days
�i�R�j
[1] ��
Wolfram�ɂ����n��f�[�^���������߂̊����p�ӂ���Ă���͂��B
���̊���T���̂������Ǝ��
����͋��ł炵���B
https://reference.wolfram.com/language/Calendar/tutorial/Calendar.html.ja
�V��������T�����s
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= DayName[{1926,12,25}]
Out[1]= Saturday
In[2]:= DayName[{1989,1,7}]
Out[2]= Saturday
In[3]:= DayCount[{1926,12,25}, {1989, 1, 7}] + 1
Out[3]= 22660
In[4]:= DayName[{1926+1000-1,4,29}]
Out[4]= Sunday
R�ł̌v�Z�ƍ��v�B
���a��1926�N�i���a���N�j12��25������1989�N�i���a64�N�j1��7���܂ł���B
(1) ���a�͉��j������n�܂艽�j���ɏI��������H
(2) ���a�V�c�݈̍ʓ������v�Z����B
(3) ���N�͏��a100�N�ɂ�����B���a1000�N�̏��a�̓�(4��29��)�͉��j�����H
R�ł̌���
�i�P�j
[1] �y
[1] �y
�i�Q�j
22660 days
�i�R�j
[1] ��
Wolfram�ɂ����n��f�[�^���������߂̊����p�ӂ���Ă���͂��B
���̊���T���̂������Ǝ��
����͋��ł炵���B
https://reference.wolfram.com/language/Calendar/tutorial/Calendar.html.ja
�V��������T�����s
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= DayName[{1926,12,25}]
Out[1]= Saturday
In[2]:= DayName[{1989,1,7}]
Out[2]= Saturday
In[3]:= DayCount[{1926,12,25}, {1989, 1, 7}] + 1
Out[3]= 22660
In[4]:= DayName[{1926+1000-1,4,29}]
Out[4]= Sunday
R�ł̌v�Z�ƍ��v�B
2024/11/22(��) 05:58:38.31ID:2M9XV7Pv
2015�N2���P������100������̓��t�Ɨj�����Z�o
R
> solve(1000000)
���t �j��
1 4752-12-29 ��
Wolfram
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= DayPlus[{2015,2,1},10^6]
Out[1]= DateObject[{4752, 12, 29}, Day]
In[2]:= % // DayName
Out[2]= Monday
���v�����̂�R�ŏ������\���o�[�͐������v�Z�����Ă���͗l�B
R
> solve(1000000)
���t �j��
1 4752-12-29 ��
Wolfram
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= DayPlus[{2015,2,1},10^6]
Out[1]= DateObject[{4752, 12, 29}, Day]
In[2]:= % // DayName
Out[2]= Monday
���v�����̂�R�ŏ������\���o�[�͐������v�Z�����Ă���͗l�B
2024/11/22(��) 09:27:45.15ID:TKrGel8n
�r�炵�E�[�[
����������ˁ[��
����������ˁ[��
2024/11/22(��) 11:48:00.61ID:/ZsBSR9L
>>896
�G�N�Z���Ȃ�i�O�[�O���̃X�v���b�h�V�[�g�ł������j
=DATE(2015,2,1)+1000
�œ��t���o��B
���Ȃ݂�100������̗j��
=WEEKDAY(DATE(2015,2,1)+1000000)��
2��Ԃ��̂œ��A���Ō��j�ƌv�Z���ꂽ�B
R��Wolfram�̌��ʂƓ����B
�����w���ł��G�N�Z�����炢�g�����Ȃ����ȁB
�`���p���t�F�`��Phimose����̃L�[�L�[�d�삾�Ɣ�Ή��݂������ȁB
�G�N�Z���Ȃ�i�O�[�O���̃X�v���b�h�V�[�g�ł������j
=DATE(2015,2,1)+1000
�œ��t���o��B
���Ȃ݂�100������̗j��
=WEEKDAY(DATE(2015,2,1)+1000000)��
2��Ԃ��̂œ��A���Ō��j�ƌv�Z���ꂽ�B
R��Wolfram�̌��ʂƓ����B
�����w���ł��G�N�Z�����炢�g�����Ȃ����ȁB
�`���p���t�F�`��Phimose����̃L�[�L�[�d�삾�Ɣ�Ή��݂������ȁB
2024/11/22(��) 12:11:36.76ID:TKrGel8n
2024/11/22(��) 12:13:43.76ID:zy1FqEMc
�����͎Z���E���w�̃X���ŁA�v�Z�p�c�[���̃X���ł͂Ȃ��͂��ł��B
�c�[����O��Ƃ����o���c�[���ł̉��Z�A�ÓT�I��@�ƃc�[�����Z�Ƃ̔�r���ɂ��܂��Ă͌v�Z�p�c�[���֘A�̃X���ł��肢���܂��B
�c�[����O��Ƃ����o���c�[���ł̉��Z�A�ÓT�I��@�ƃc�[�����Z�Ƃ̔�r���ɂ��܂��Ă͌v�Z�p�c�[���֘A�̃X���ł��肢���܂��B
2024/11/22(��) 12:20:16.18ID:TKrGel8n
2024/11/22(��) 13:29:34.23ID:UMvWmgYN
>>904
���̂�������͈�Ҕɏ풓���Ă�ʏ̔A�r�W�W�C
���̈�҂����f�l�ۏo���Ŗ���t���{�b�R����Ă͔������ă_���}���N�J��Ԃ��Ă���܂�
�`���p�����w�ɂ��Ŏ����Ă��萔�w�ɂ��S�����Ă���܂�
https://egg.5ch.net/test/read.cgi/hosp/1723605276/
���̂�������͈�Ҕɏ풓���Ă�ʏ̔A�r�W�W�C
���̈�҂����f�l�ۏo���Ŗ���t���{�b�R����Ă͔������ă_���}���N�J��Ԃ��Ă���܂�
�`���p�����w�ɂ��Ŏ����Ă��萔�w�ɂ��S�����Ă���܂�
https://egg.5ch.net/test/read.cgi/hosp/1723605276/
2024/11/22(��) 14:22:46.40ID:2M9XV7Pv
>>902
�`���p���]��Phimose����ɂ͎g���Ȃ��悤���Ȃ��B
�v�Z����̌��ł��钆�w�������G�N�Z������
https://excel.itgakko.com/chugaku/jugyoukeisanshiki.html
�������͐��܂�Ă��牽���ڂ����G�N�Z���̌v�Z���ŋ��߂�
�ƁA���̃X���̃g�s�b�N�Ɠ����B
�A�r�`���p�t�F�`��Phimose����ăG�N�Z������g���Ȃ��݂����B
�V���c���Ǝv����B
�`���p���]��Phimose����ɂ͎g���Ȃ��悤���Ȃ��B
�v�Z����̌��ł��钆�w�������G�N�Z������
https://excel.itgakko.com/chugaku/jugyoukeisanshiki.html
�������͐��܂�Ă��牽���ڂ����G�N�Z���̌v�Z���ŋ��߂�
�ƁA���̃X���̃g�s�b�N�Ɠ����B
�A�r�`���p�t�F�`��Phimose����ăG�N�Z������g���Ȃ��݂����B
�V���c���Ǝv����B
2024/11/22(��) 14:32:02.60ID:+wD8dkQK
>>906
���Ƃ��N�\���ˁ[��i�j
���܂����w�������p�\�R���������Ăˁ[��
�G�N�Z���Ƃ������Ɏg����̂��H
�I�b�T���������ł����ɂ���́H
���Ƃ��N�\���ˁ[��i�j
���܂����w�������p�\�R���������Ăˁ[��
�G�N�Z���Ƃ������Ɏg����̂��H
�I�b�T���������ł����ɂ���́H
2024/11/22(��) 14:35:31.23ID:+wD8dkQK
2024/11/22(��) 14:40:13.85ID:+wD8dkQK
2024/11/22(��) 16:22:41.27ID:UMvWmgYN
2024/11/22(��) 16:31:43.70ID:2M9XV7Pv
����������̂Ō����ėV�Ԗ��
����Q�O�Q�T�N���琼��P�O�O�O�O�N�܂łQ���Q�X�������j���ɂȂ邱�Ƃ͉��邩�H
���s�̃O���S���I���p���Čv�Z����B
���܂�
Wolfram�͑��݂��Ȃ��[���̗j���܂ŕԂ��Ă���
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= DayName[{2024,2,29}]
Out[1]= Thursday
In[2]:= DayName[{2025,2,29}]
Out[2]= Saturday
�G�N�Z���͂ǂ��Ȃ邩
=WEEKDAY(DATE(2025,2,29))�̒l�������Ă݂�B
���w���ł������ł���B
����Q�O�Q�T�N���琼��P�O�O�O�O�N�܂łQ���Q�X�������j���ɂȂ邱�Ƃ͉��邩�H
���s�̃O���S���I���p���Čv�Z����B
���܂�
Wolfram�͑��݂��Ȃ��[���̗j���܂ŕԂ��Ă���
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= DayName[{2024,2,29}]
Out[1]= Thursday
In[2]:= DayName[{2025,2,29}]
Out[2]= Saturday
�G�N�Z���͂ǂ��Ȃ邩
=WEEKDAY(DATE(2025,2,29))�̒l�������Ă݂�B
���w���ł������ł���B
2024/11/22(��) 17:20:41.43ID:QvZglOtP
�܂��A�r�炵�Ă���̂���
2024/11/22(��) 17:54:19.01ID:uXoXMyxD
���X�Ԃ������i��ł���
2024/11/22(��) 18:12:52.79ID:KGSQyV3C
>>906
864�F���̖���������F2024/11/22(��) 17:49:51.88 ID:Qp654zCB
�����A�A�r����҂Ȃ璷�炭�����Ă��ĉ��̒m�������Ă��Ȃ������A���Ď�����ˁH�H
�p���������Ȃ��̂��H�H
�������ǂ�����̑O�ɁA���O�̑��ݎ��̒p�������߂��邾��
864�F���̖���������F2024/11/22(��) 17:49:51.88 ID:Qp654zCB
�����A�A�r����҂Ȃ璷�炭�����Ă��ĉ��̒m�������Ă��Ȃ������A���Ď�����ˁH�H
�p���������Ȃ��̂��H�H
�������ǂ�����̑O�ɁA���O�̑��ݎ��̒p�������߂��邾��
2024/11/22(��) 18:28:01.98ID:TKrGel8n
>>911
�́H���Ȃ̂��O���t�ʂ��˂��́H
�G�N�Z�����Ē��w���ŕK�v�˂����Ă�
���̖������č��㉽���Ɋ��������̂��H
���O�݂����ȋ�C�ǂ߂Ȃ��W�W�C�������ݏo���ĂȂ�����
�́H���Ȃ̂��O���t�ʂ��˂��́H
�G�N�Z�����Ē��w���ŕK�v�˂����Ă�
���̖������č��㉽���Ɋ��������̂��H
���O�݂����ȋ�C�ǂ߂Ȃ��W�W�C�������ݏo���ĂȂ�����
2024/11/23(�y) 00:25:37.09ID:VVjSJupO
>>911
�����������Ȃ��ȂɒN���������ɂ���Ȃ��ƕ����ɂ��݂���w
�����������Ȃ��ȂɒN���������ɂ���Ȃ��ƕ����ɂ��݂���w
2024/11/23(�y) 01:28:34.91ID:qyJPztJt
2024/11/23(�y) 01:31:34.63ID:qyJPztJt
2024/11/23(�y) 02:02:06.36ID:qyJPztJt
�{���A�Q�O�Q�S�N�P�P���Q�R���͋ΘJ���ӂ̓��ŏj���œy�j���Ȃ̂ŗ����̓��j���ƍ��킹�ĘA�x�ł���B
���Ȃ݂ɗ��N�̂P�P���Q�R���͓��j���Ȃ̂ŐU�x���ŘA�x�ɂȂ�B
���@����Q�O�Q�T�N���琼��P�O�O�O�O�N�܂ŋΘJ���ӂ̓����A�x�Ɋ܂܂�邱�Ƃ͉��邩�H
�y�j���͏j���łȂ���x���Ɛ����Ȃ��Ƃ��āA���s�̃O���S���I���p���Čv�Z����B
���Ȃ݂ɗ��N�̂P�P���Q�R���͓��j���Ȃ̂ŐU�x���ŘA�x�ɂȂ�B
���@����Q�O�Q�T�N���琼��P�O�O�O�O�N�܂ŋΘJ���ӂ̓����A�x�Ɋ܂܂�邱�Ƃ͉��邩�H
�y�j���͏j���łȂ���x���Ɛ����Ȃ��Ƃ��āA���s�̃O���S���I���p���Čv�Z����B
2024/11/23(�y) 02:11:42.78ID:qyJPztJt
>>914
���������ǂ�����
���������̂������͎̂��������낤�Ȃ��B
������w���̑�����b�����������ƍ�����w�����ނ���Ƃ����|�̓��e������
������w���̐l����́@�����ˁ@�������Ȃ��B
��t�̐��E�ł͎��ȏЉ�ɑ��Ƒ�w�łȂ��w�������_�����o�g��ǂ�������t�͂܂��A�V���c��呲�B
�܂��A���R�̈�ȑ�w�𑲋Ƃ��Ƃ����ȏЉ�Ă����p���������̂������B
���������ǂ�����
���������̂������͎̂��������낤�Ȃ��B
������w���̑�����b�����������ƍ�����w�����ނ���Ƃ����|�̓��e������
������w���̐l����́@�����ˁ@�������Ȃ��B
��t�̐��E�ł͎��ȏЉ�ɑ��Ƒ�w�łȂ��w�������_�����o�g��ǂ�������t�͂܂��A�V���c��呲�B
�܂��A���R�̈�ȑ�w�𑲋Ƃ��Ƃ����ȏЉ�Ă����p���������̂������B
2024/11/23(�y) 02:30:14.37ID:qyJPztJt
���H�n�Ȃ�Wolfram����i��n�Ȃ�R����A�s���Ȋw��o�ϊw��U�ł��g���l�������Ă����j���g���邾�낤�B
Wolfram�����
��p�b�P�[�W�@Calender��
�o�[�W����10.0�ŁC��@�\��Wolfram����ɑg�ݍ��܂ꂽ »
�ƋL�ڂ���Ă���B�B
<< Calendar`
DayOfWeek[{2024,2,29}]
DayOfWeek[{2025,2,29}]
DayName[{2024,2,29}]
DayName[{2025,2,29}]
�����s���Ă݂�ƁA�������ăo�N������Ă���̂ł͂Ǝv���B
Wolfram���[�U�[�̌�������]�B
Wolfram�����͖����ō\�z�ł���B�����A�h�ł̓o�^�͕K�v�ł͂��邪�B
�A�r�`���p�t�F�`��Phimose����͂��ꂷ��ł��Ȃ��݂������ȁB�V���c���Ɛ��������B
Wolfram�����
��p�b�P�[�W�@Calender��
�o�[�W����10.0�ŁC��@�\��Wolfram����ɑg�ݍ��܂ꂽ »
�ƋL�ڂ���Ă���B�B
<< Calendar`
DayOfWeek[{2024,2,29}]
DayOfWeek[{2025,2,29}]
DayName[{2024,2,29}]
DayName[{2025,2,29}]
�����s���Ă݂�ƁA�������ăo�N������Ă���̂ł͂Ǝv���B
Wolfram���[�U�[�̌�������]�B
Wolfram�����͖����ō\�z�ł���B�����A�h�ł̓o�^�͕K�v�ł͂��邪�B
�A�r�`���p�t�F�`��Phimose����͂��ꂷ��ł��Ȃ��݂������ȁB�V���c���Ɛ��������B
2024/11/23(�y) 03:28:16.21ID:qyJPztJt
Wolfram��DayName����
���݂��Ȃ��[�N��2��29���������Ƃ��ė^����Ƃ��̔N��3��1���̗j����Ԃ��d�l�̂悤�ł���B���ɂ̓o�N�Ɏv����̂����B
DayName[{2025,2,29}]
DayName[{2025,3,1}]
�����s���Ă݂�Ƃ悢�B
�y���z
����Wolfram�̎d�l�𗘗p����
����Q�O�Q�T�N���琼��P�O�O�O�O�N�܂łQ���Q�X�������j���ɂȂ邱�Ƃ͉��邩�H���s�̃O���S���I���p���Čv�Z����B
���Z�o���āAR����ł̌���259��ƍ��v���邩��������B
�G�N�Z���̎g����G���[�g���w���Ȃ�
=WEEKDAY(DATE(2025,2,29)
=WEEKDAY(DATE(2025,3,1)
�����s���ăG�N�Z���̎d�l���m�F���Ă����Ƃ悢�B
���݂��Ȃ��[�N��2��29���������Ƃ��ė^����Ƃ��̔N��3��1���̗j����Ԃ��d�l�̂悤�ł���B���ɂ̓o�N�Ɏv����̂����B
DayName[{2025,2,29}]
DayName[{2025,3,1}]
�����s���Ă݂�Ƃ悢�B
�y���z
����Wolfram�̎d�l�𗘗p����
����Q�O�Q�T�N���琼��P�O�O�O�O�N�܂łQ���Q�X�������j���ɂȂ邱�Ƃ͉��邩�H���s�̃O���S���I���p���Čv�Z����B
���Z�o���āAR����ł̌���259��ƍ��v���邩��������B
�G�N�Z���̎g����G���[�g���w���Ȃ�
=WEEKDAY(DATE(2025,2,29)
=WEEKDAY(DATE(2025,3,1)
�����s���ăG�N�Z���̎d�l���m�F���Ă����Ƃ悢�B
2024/11/23(�y) 06:13:07.79ID:VVjSJupO
>>920
�A���^�w���ȑO�ɓ��{��ʂ��ĂȂ������
�A���^�w���ȑO�ɓ��{��ʂ��ĂȂ������
2024/11/23(�y) 07:39:09.12ID:qyJPztJt
��877�̓��e���l�^��
R��Wolfram�̃X�L������ł���( �E�́E)��!!
�l�|�X�L�����������Ȃ��̂�����݂����B
�p�\�R���������̓G�N�Z���������ĂȂ��Ȃ�A
�G�N�Z���̑����Google�̃X�v���b�h�V�[�g�Ŏ��s��������B
�X�v���b�h�V�[�g�̓X�}�z�ł��g����B
=WEEKDAY(DATE(2025,2,29)
=WEEKDAY(DATE(2025,3,1)
�̕Ԃ��l�͓����ł������B
���݂��Ȃ��[���̗j���Ȃ�G���[��������NA��Ԃ������e�ؐv���Ǝv���B
R��Wolfram�̃X�L������ł���( �E�́E)��!!
�l�|�X�L�����������Ȃ��̂�����݂����B
�p�\�R���������̓G�N�Z���������ĂȂ��Ȃ�A
�G�N�Z���̑����Google�̃X�v���b�h�V�[�g�Ŏ��s��������B
�X�v���b�h�V�[�g�̓X�}�z�ł��g����B
=WEEKDAY(DATE(2025,2,29)
=WEEKDAY(DATE(2025,3,1)
�̕Ԃ��l�͓����ł������B
���݂��Ȃ��[���̗j���Ȃ�G���[��������NA��Ԃ������e�ؐv���Ǝv���B
2024/11/23(�y) 07:58:27.13ID:HPgtN9bj
�c�[�����g��Ȃ������ʔ����̂Ő���P�O�O�O�O�N�܂ł�
���j���̂Q���Q�X�������邩�ɂ��ĉ����܂������A
�����K�����������Ă���悤�Ȃ̂ŏ������߂܂���B
���j���̂Q���Q�X�������邩�ɂ��ĉ����܂������A
�����K�����������Ă���悤�Ȃ̂ŏ������߂܂���B
2024/11/23(�y) 08:40:58.32ID:VVjSJupO
2024/11/23(�y) 08:41:45.18ID:VVjSJupO
2024/11/23(�y) 09:59:17.99ID:GEUDPfeu
�v���O�����~�͖{���ɃE�U����
�^���̃L��Ȃ낤�A���x���X���Ⴂ���ƒ��ӂ���Ă��r�炵�ɂ���
�^���̃L��Ȃ낤�A���x���X���Ⴂ���ƒ��ӂ���Ă��r�炵�ɂ���
2024/11/23(�y) 09:59:25.64ID:qyJPztJt
�Ђ�����v�Z���Đ������肗
(1) ���Ɍ���鐔����1����81�܂ł���B
12�͌���邪13�͌���Ȃ��B����鐔���͑S���ʼn���ނ��邩�H
(2) 1����99�܂ł̐������Q�����Ăł��鐔�͉���ނ��邩?
(3) 1����999�܂ł̐������Q�����Ăł��鐔�͉���ނ��邩?
(4) 1����9999�܂ł̐������Q�����Ăł��鐔�͉���ނ��邩?
(1) ���Ɍ���鐔����1����81�܂ł���B
12�͌���邪13�͌���Ȃ��B����鐔���͑S���ʼn���ނ��邩�H
(2) 1����99�܂ł̐������Q�����Ăł��鐔�͉���ނ��邩?
(3) 1����999�܂ł̐������Q�����Ăł��鐔�͉���ނ��邩?
(4) 1����9999�܂ł̐������Q�����Ăł��鐔�͉���ނ��邩?
2024/11/23(�y) 11:09:45.47ID:qyJPztJt
>>925
�O��Ƀc�[���̎d�l�i�o�O�H�j�̗������K�v�B
Wolfram��DateName���́A���݂��Ȃ��[�N�̂Q���Q�X���̗j�����i���̔N�̂R���P���̗j���̒l�Ɠ��l�j��Ԃ��Ă���d�l�ł��邱�ƂɋC�Â��Ȃ������B
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= f[x_] := DayName[{x,2,29}]==Sunday // Boole
In[2]:= Table[f[x],{x,2025,10000}] // Total
Out[2]= 1137
�Ƃ������l��Ԃ��Ă����B
���ꂪR�ł̐��l
> sum(re[!is.na(re)]==1)
[1] 259
�ƍ��v���Ȃ������̂ō��f�����B
��L��Wolfram�̎d�l�ɋC�Â���
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= f[x_,y_:Sunday] := DayName[{x,2,29}]!=DayName[{x,3,1}] && DayName[{x,2,29}]==y
In[2]:= Table[Boole@f[x],{x,2025,10000}] // Total
Out[2]= 259
�Ł@���v�B
�������f�f�Ǝ��Â��ł���Όo�߂͖��Ȃ��Ƃ����N�w�̕�Z�̔畆�Ȃ̋����i�̐l�j�̎���͔畆�Ȃ̐i�������̓m�[�g���ȏ��������݉������B
�O��Ƀc�[���̎d�l�i�o�O�H�j�̗������K�v�B
Wolfram��DateName���́A���݂��Ȃ��[�N�̂Q���Q�X���̗j�����i���̔N�̂R���P���̗j���̒l�Ɠ��l�j��Ԃ��Ă���d�l�ł��邱�ƂɋC�Â��Ȃ������B
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= f[x_] := DayName[{x,2,29}]==Sunday // Boole
In[2]:= Table[f[x],{x,2025,10000}] // Total
Out[2]= 1137
�Ƃ������l��Ԃ��Ă����B
���ꂪR�ł̐��l
> sum(re[!is.na(re)]==1)
[1] 259
�ƍ��v���Ȃ������̂ō��f�����B
��L��Wolfram�̎d�l�ɋC�Â���
Wolfram Language 14.0.0 Engine for Microsoft Windows (64-bit)
Copyright 1988-2023 Wolfram Research, Inc.
In[1]:= f[x_,y_:Sunday] := DayName[{x,2,29}]!=DayName[{x,3,1}] && DayName[{x,2,29}]==y
In[2]:= Table[Boole@f[x],{x,2025,10000}] // Total
Out[2]= 259
�Ł@���v�B
�������f�f�Ǝ��Â��ł���Όo�߂͖��Ȃ��Ƃ����N�w�̕�Z�̔畆�Ȃ̋����i�̐l�j�̎���͔畆�Ȃ̐i�������̓m�[�g���ȏ��������݉������B
2024/11/23(�y) 11:17:20.64ID:qyJPztJt
>>925
�����K�����������Ă���Ƃ��́i�P�j��������i�Q�j�摜�œ��e����A�Ƃ�����i������܂��B
NG Word����ɂ͏c�������e�Ƃ������@������܂��B
�c�����ϊ�����v���O���������̂��悢�ɂԂ��ɂȂ�܂��B
> tate(str,11)
�� �@ �@ �� �� �@ �@ �@ �@ �@ �@
�� �@ �@ �� �� �@ �@ �@ �@ �@ �@
�� �� �@ �� �� �@ �@ �@ �@ �@ �@
�� �� �@ �� �� �@ �@ �@ �@ �@ �@
�� �� �@ �� �� �@ �@ �@ �@ �@ �@
�� �� �� �� �� �@ �@ �@ �@ �@ �@
�@ �� �� �� �� �@ �@ �@ �@ �@ �@
�@ �� �� �@ �@ �@ �@ �@ �@ �@ �@
�@ �� �� �@ �@ �@ �@ �@ �@ �@ �@
�@ �@ �� �@ �@ �@ �@ �@ �@ �@ �@
�@ �@ �@ �@ �@ �@ �@ �@ �@
�@ �@ �@ �@ �@ �@ �� �� �@ �@ ��
�@ �@ �@ �@ �@ �@ �� �� �@ �@ ��
�@ �@ �@ �@ �@ �@ �� �� �@ �� ��
�@ �@ �@ �@ �@ �@ �� �� �@ �� ��
�@ �@ �@ �@ �@ �@ �� �� �@ �� ��
�@ �@ �@ �@ �@ �@ �� �� �� �� ��
�@ �@ �@ �@ �@ �@ �� �� �� �� �@
�@ �@ �@ �@ �@ �@ �@ �@ �� �� �@
�@ �@ �@ �@ �@ �@ �@ �@ �� �� �@
�@ �@ �@ �@ �@ �@ �@ �@ �� �@ �@
�@ �@ �@ �@ �@ �@ �@ �@ �@
�����K�����������Ă���Ƃ��́i�P�j��������i�Q�j�摜�œ��e����A�Ƃ�����i������܂��B
NG Word����ɂ͏c�������e�Ƃ������@������܂��B
�c�����ϊ�����v���O���������̂��悢�ɂԂ��ɂȂ�܂��B
> tate(str,11)
�� �@ �@ �� �� �@ �@ �@ �@ �@ �@
�� �@ �@ �� �� �@ �@ �@ �@ �@ �@
�� �� �@ �� �� �@ �@ �@ �@ �@ �@
�� �� �@ �� �� �@ �@ �@ �@ �@ �@
�� �� �@ �� �� �@ �@ �@ �@ �@ �@
�� �� �� �� �� �@ �@ �@ �@ �@ �@
�@ �� �� �� �� �@ �@ �@ �@ �@ �@
�@ �� �� �@ �@ �@ �@ �@ �@ �@ �@
�@ �� �� �@ �@ �@ �@ �@ �@ �@ �@
�@ �@ �� �@ �@ �@ �@ �@ �@ �@ �@
�@ �@ �@ �@ �@ �@ �@ �@ �@
�@ �@ �@ �@ �@ �@ �� �� �@ �@ ��
�@ �@ �@ �@ �@ �@ �� �� �@ �@ ��
�@ �@ �@ �@ �@ �@ �� �� �@ �� ��
�@ �@ �@ �@ �@ �@ �� �� �@ �� ��
�@ �@ �@ �@ �@ �@ �� �� �@ �� ��
�@ �@ �@ �@ �@ �@ �� �� �� �� ��
�@ �@ �@ �@ �@ �@ �� �� �� �� �@
�@ �@ �@ �@ �@ �@ �@ �@ �� �� �@
�@ �@ �@ �@ �@ �@ �@ �@ �� �� �@
�@ �@ �@ �@ �@ �@ �@ �@ �� �@ �@
�@ �@ �@ �@ �@ �@ �@ �@ �@
2024/11/23(�y) 11:34:47.59ID:qyJPztJt
�O�Ȉ������Ă�������
�@����I�т��r�̂����A�Ƃ�
�@���肭���͂���������g��
�Ə�i���猾��ꂽ���̂��B
�_�����Ɓ@�͂��Z�̂����@�Ƃ����̂��Ƃ��B4
AI�i�c�[���j�I�т��K�v
����Q�O�Q�T�N���琼��P�O�O�O�O�N�܂łQ���Q�X�������j���ɂȂ邱�Ƃ͉��邩�H���s�̃O���S���I���p���Čv�Z����B
ChatGPT(������)�͑z�����Ԃ��Ă����B
����2025�N���琼��10000�N�܂ł̊ԂŁA2��29�������j���ɂȂ�N��259��܂��B
����ACopilot��
�����̂��邤�N�ɂ����āA2��29�������j���ɂȂ����肵�܂��傤�B���邤�N�̎������𗘗p���Čv�Z����ƁA����2025�N���琼��10000�N�܂ł̊Ԃ�2��29�������j���ɂȂ�� ��284�� �ł��B
�@����I�т��r�̂����A�Ƃ�
�@���肭���͂���������g��
�Ə�i���猾��ꂽ���̂��B
�_�����Ɓ@�͂��Z�̂����@�Ƃ����̂��Ƃ��B4
AI�i�c�[���j�I�т��K�v
����Q�O�Q�T�N���琼��P�O�O�O�O�N�܂łQ���Q�X�������j���ɂȂ邱�Ƃ͉��邩�H���s�̃O���S���I���p���Čv�Z����B
ChatGPT(������)�͑z�����Ԃ��Ă����B
����2025�N���琼��10000�N�܂ł̊ԂŁA2��29�������j���ɂȂ�N��259��܂��B
����ACopilot��
�����̂��邤�N�ɂ����āA2��29�������j���ɂȂ����肵�܂��傤�B���邤�N�̎������𗘗p���Čv�Z����ƁA����2025�N���琼��10000�N�܂ł̊Ԃ�2��29�������j���ɂȂ�� ��284�� �ł��B
2024/11/23(�y) 11:52:27.79ID:qyJPztJt
>>929
ChatGPT�ɂ��ꂽ��
Python�̃R�[�h��Ԃ��Ă����B
def unique_products(n):
products = set()
for i in range(1, n + 1):
for j in range(1, n + 1):
products.add(i * j)
return len(products)
# �e�ꍇ�ɂ��Čv�Z
print(unique_products(99)) # (2)
print(unique_products(999)) # (3)
print(unique_products(9999)) # (4)
���s�����
2869
247814
22502242
Wolfram����
solve[n_]:= Table[x y,{x,Range[n]},{y,Range[n]}] // Flatten // Union // Length
Table[solve[n],{n,{99,999,9999}}]
���ʂ͓���
ChatGPT�ɂ��ꂽ��
Python�̃R�[�h��Ԃ��Ă����B
def unique_products(n):
products = set()
for i in range(1, n + 1):
for j in range(1, n + 1):
products.add(i * j)
return len(products)
# �e�ꍇ�ɂ��Čv�Z
print(unique_products(99)) # (2)
print(unique_products(999)) # (3)
print(unique_products(9999)) # (4)
���s�����
2869
247814
22502242
Wolfram����
solve[n_]:= Table[x y,{x,Range[n]},{y,Range[n]}] // Flatten // Union // Length
Table[solve[n],{n,{99,999,9999}}]
���ʂ͓���
2024/11/23(�y) 12:04:15.64ID:GI4x0ZEB
�l�l
2024/11/23(�y) 12:35:38.03ID:qyJPztJt
2024/11/23(�y) 12:37:35.31ID:qyJPztJt
>>933
5ch�̓C���f���g�������̂Ńp�C�\���R�[�h�͓��e���ɂ����Ȃ��B
5ch�̓C���f���g�������̂Ńp�C�\���R�[�h�͓��e���ɂ����Ȃ��B
2024/11/23(�y) 14:46:55.00ID:VVjSJupO
>>933
�J�e�̓J�e���Ăǂ������Ӗ������Č����Ă�`���p��
�J�e�̓J�e���Ăǂ������Ӗ������Č����Ă�`���p��
2024/11/23(�y) 23:08:39.93ID:r8zLrNxc
>>936
NG�ɂ���������R�e�n���ɂ��Ă���
NG�ɂ���������R�e�n���ɂ��Ă���
2024/12/10(��) 18:12:09.94ID:/AcDe8Pz
�������邩�Ȃ��̂����킩��Ȃ��̂Ŏ��₵�܂��B
���ˉt���W�{�A��������\���ȗʂ�����A���̂����Q�{���Ŗ�ł��邱�Ƃ��킩���Ă���B
�T�C�̃l�Y�~�ɒ��ˉt���������Ē��˂��Ăǂꂪ�Ŗ���肵�����B
�����̒��ˉt���������Ē��˂����Ă��Ő��͕ς��Ȃ��Ƃ���B
�e�X�̃l�Y�~�ɒ��˂ł���̂͂P���ł���B
�Ŗ�Q�{���m���ɓ��肷�鍬�����@�����邩�H
���ˉt���W�{�A��������\���ȗʂ�����A���̂����Q�{���Ŗ�ł��邱�Ƃ��킩���Ă���B
�T�C�̃l�Y�~�ɒ��ˉt���������Ē��˂��Ăǂꂪ�Ŗ���肵�����B
�����̒��ˉt���������Ē��˂����Ă��Ő��͕ς��Ȃ��Ƃ���B
�e�X�̃l�Y�~�ɒ��˂ł���̂͂P���ł���B
�Ŗ�Q�{���m���ɓ��肷�鍬�����@�����邩�H
2024/12/10(��) 20:40:25.76ID:xePGLpdi
2024/12/10(��) 20:44:43.27ID:xePGLpdi
>>940�̑���
���Z�E��w�̏W���_�̗p����g����
����1����8�̂���2�{�̑g�ݍ��킹
�S28�ʂ�̏W������
�u������������I��ŁA���Ȃ��Ƃ�1���{���v
���ǂ����ׂ�5��̎�������
�S32�ʂ�̏W���ւ̎ʑ���
�P�ˁi1��1�ʑ��j�ɂȂ鎎��̑I�ѕ������߂�A
�Ƃ������ɒu����������
1��1�ʑ��̋t���̐���0�܂���1�ł��邩��
�����̂ڂ�ƁA28�̎��ۂ�
1��̎����ŗv�f��16�ȉ��̏W��2�A
2��̎����ŗv�f��8�ȉ��̏W��4��
�����邱�ƂɂȂ�
���Z�E��w�̏W���_�̗p����g����
����1����8�̂���2�{�̑g�ݍ��킹
�S28�ʂ�̏W������
�u������������I��ŁA���Ȃ��Ƃ�1���{���v
���ǂ����ׂ�5��̎�������
�S32�ʂ�̏W���ւ̎ʑ���
�P�ˁi1��1�ʑ��j�ɂȂ鎎��̑I�ѕ������߂�A
�Ƃ������ɒu����������
1��1�ʑ��̋t���̐���0�܂���1�ł��邩��
�����̂ڂ�ƁA28�̎��ۂ�
1��̎����ŗv�f��16�ȉ��̏W��2�A
2��̎����ŗv�f��8�ȉ��̏W��4��
�����邱�ƂɂȂ�
2024/12/10(��) 20:48:04.55ID:xePGLpdi
>>941�̑���
1��̎����Ŏg������̐���
�{������A�Ȃ������̏ꍇ�̐���16�ȉ��ɂ���
�Ƃ�����������A2�Ɍ��܂�
�i�{������F13�ʂ� �{���Ȃ��F15�ʂ�j
�����ŁA�͂��߂�2��̎����̎���̔ԍ���
(12, 13), (12, 34)
�Ƃ����ƁA��������4�ʂ�ɑΉ�����ꍇ�̐���
(12, 13): {8, 5, 5, 10}
(12, 34): {4, 9, 9, 6}
�ƂȂ�A�ǂ���̏ꍇ��8���鐔���o�Ă��܂�
���̌��ʂ��o���ꍇ�A�c��3��̎�������8�ʂ��
���ׂĂ���ʂ��邱�Ƃ��ł��Ȃ�
����āA5��̎���������
���ׂĂ̎��ۂ���ʂ��邱�Ƃ͕s�\�ƂȂ�
�i�I���j
1��̎����Ŏg������̐���
�{������A�Ȃ������̏ꍇ�̐���16�ȉ��ɂ���
�Ƃ�����������A2�Ɍ��܂�
�i�{������F13�ʂ� �{���Ȃ��F15�ʂ�j
�����ŁA�͂��߂�2��̎����̎���̔ԍ���
(12, 13), (12, 34)
�Ƃ����ƁA��������4�ʂ�ɑΉ�����ꍇ�̐���
(12, 13): {8, 5, 5, 10}
(12, 34): {4, 9, 9, 6}
�ƂȂ�A�ǂ���̏ꍇ��8���鐔���o�Ă��܂�
���̌��ʂ��o���ꍇ�A�c��3��̎�������8�ʂ��
���ׂĂ���ʂ��邱�Ƃ��ł��Ȃ�
����āA5��̎���������
���ׂĂ̎��ۂ���ʂ��邱�Ƃ͕s�\�ƂȂ�
�i�I���j
2024/12/11(��) 06:33:19.01ID:qk9aTmTZ
>>940
���X���肪�Ƃ��������܂��B��͂�A�s�\�ł������B
���ꂼ��4�t������5�C�ɒ��˂���2�ł�����ł��邩��
��������Ō��������Ƃ���S��4�t�����ł͕s�\�ł����B
��������C[2^8,5]=8809549056�ʂ�̑�������͖����B
���X���肪�Ƃ��������܂��B��͂�A�s�\�ł������B
���ꂼ��4�t������5�C�ɒ��˂���2�ł�����ł��邩��
��������Ō��������Ƃ���S��4�t�����ł͕s�\�ł����B
��������C[2^8,5]=8809549056�ʂ�̑�������͖����B
2024/12/11(��) 17:37:41.12ID:qk9aTmTZ
�����s����L�����y�[���̒ʒm�������B
>>
[5�N���̂�500���~���a������̏ꍇ] 500���~�~�����N1.20%�i�ň��O�j�~5�N��300,000�~
300,000�~�~15.315%�i���Łj��45,945�~�@300,000�~�~5%�i�n���Łj��15,000�~�@300,000�~-45,945�~-15,000�~��239,055�~
<<
���̗a���͋����N1.20%�ł͂��邪�����ł͂Ȃ��悤�ł���B
���
�i�P�j���̗a�������N�����^����a���ł������ꍇ��500���~��a�����Ƃ��̐ň������z�����߂�B
�i�Q�j�L�����y�[���̒P������a���͋����N�����̔��N�����^����a���ɑ������邩�v�Z����B
�v�Z�ɂ͓d���G�N�Z���Ȃǂ��g���Ă��悢�B
>>
[5�N���̂�500���~���a������̏ꍇ] 500���~�~�����N1.20%�i�ň��O�j�~5�N��300,000�~
300,000�~�~15.315%�i���Łj��45,945�~�@300,000�~�~5%�i�n���Łj��15,000�~�@300,000�~-45,945�~-15,000�~��239,055�~
<<
���̗a���͋����N1.20%�ł͂��邪�����ł͂Ȃ��悤�ł���B
���
�i�P�j���̗a�������N�����^����a���ł������ꍇ��500���~��a�����Ƃ��̐ň������z�����߂�B
�i�Q�j�L�����y�[���̒P������a���͋����N�����̔��N�����^����a���ɑ������邩�v�Z����B
�v�Z�ɂ͓d���G�N�Z���Ȃǂ��g���Ă��悢�B
2024/12/11(��) 19:28:59.98ID:IlnvU/Cw
�A�r�W�W�C���Z���ɂ���o�J�ɂ��Ă��炦�Ȃ��Ȃ���������č��x�͂����Ń��X��H�Ǝ�������
�p���������Ȃ��̂��H
�p���������Ȃ��̂��H
2024/12/11(��) 20:05:12.30ID:qk9aTmTZ
>940-942�͕ʂ̎��҂ɂ�郌�X�ł��B
���̉���������ł���f�{�͂���܂���B
���܂��Ƀl�Y�~�U�C�ł̓��^�@���킩��Ȃ��B
�l�Y�~�ƒ��˂̍s�Ⴉ��A�P�˂��ۂ��肷������悤�₭���������̂�
ChatGPT�Ȃǂ̌듚�ł�����������B
���̉���������ł���f�{�͂���܂���B
���܂��Ƀl�Y�~�U�C�ł̓��^�@���킩��Ȃ��B
�l�Y�~�ƒ��˂̍s�Ⴉ��A�P�˂��ۂ��肷������悤�₭���������̂�
ChatGPT�Ȃǂ̌듚�ł�����������B
2024/12/12(��) 07:19:00.16ID:B0ZmbwMt
>>946
�X���^�C�����ł���f�{���Ȃ��̊ԈႢ����
�X���^�C�����ł���f�{���Ȃ��̊ԈႢ����
2024/12/12(��) 07:26:00.59ID:B0ZmbwMt
���������ŗ��Ă��N�\�X�����ቺ��Ȃ��Ə����ƃR�e���p���ɂ���邩�瑧�ł��Ȃ��Ȃ����݂������ˁA���Ɉ���
2024/12/12(��) 09:27:11.87ID:rMBX4gAn
>>946
�悤�₭�u�����v
���s����ł݂����g�ݍ��킹���v���O�����Ō������悤�Ȃ��̂�����
���l�߂ł݂����킯�ł͂Ȃ��B
���
���ˉt���W�{�A��������\���ȗʂ�����A���̂����Q�{���v���I�ȓŖ�ł��邱�Ƃ��킩���Ă���B
�U�C�̃l�Y�~�ɒ��ˉt���������Ē��˂��Ăǂꂪ�Ŗ���肵�����B
�����̒��ˉt���������Ē��˂����Ă��Ő��͕ς��Ȃ��Ƃ���B
�e�X�̃l�Y�~�ɒ��˂ł���̂͂P���ł���B
�ǂ̂悤�ɍ������ĂU�C�̃l�Y�~�ɓ��^����悢���H
�悤�₭�u�����v
���s����ł݂����g�ݍ��킹���v���O�����Ō������悤�Ȃ��̂�����
���l�߂ł݂����킯�ł͂Ȃ��B
���
���ˉt���W�{�A��������\���ȗʂ�����A���̂����Q�{���v���I�ȓŖ�ł��邱�Ƃ��킩���Ă���B
�U�C�̃l�Y�~�ɒ��ˉt���������Ē��˂��Ăǂꂪ�Ŗ���肵�����B
�����̒��ˉt���������Ē��˂����Ă��Ő��͕ς��Ȃ��Ƃ���B
�e�X�̃l�Y�~�ɒ��˂ł���̂͂P���ł���B
�ǂ̂悤�ɍ������ĂU�C�̃l�Y�~�ɓ��^����悢���H
2024/12/12(��) 09:28:36.49ID:rMBX4gAn
>>949
���̈Ӗ��͏��w���ɂ��킩�邪�A�����͓̂���Ȃ��B
���̈Ӗ��͏��w���ɂ��킩�邪�A�����͓̂���Ȃ��B
2024/12/12(��) 11:22:25.92ID:pEJT1kqk
>>950
�Ƃ肠�����X���Ⴂ�Ȃ̂ŏo�Ă����ĉ��������肢�v���܂�
�Ƃ肠�����X���Ⴂ�Ȃ̂ŏo�Ă����ĉ��������肢�v���܂�
2024/12/12(��) 14:20:07.95ID:rMBX4gAn
>>951
�ł��Ȃ��̂�����A���̈Ӗ��������w���ɂ킩������B
�����w���ɂ킩������������O�p�����g���ĉ����̂͂Ȃ�̖����Ȃ��B
���ǁA�����o���Ȃ��y�̏퓅�傪�u�X���Ⴂ�v�B
���_�ł��Ȃ��y���u�A�d�_�v�Ƃ����̂Ɏ��Ă���B
�ł��Ȃ��̂�����A���̈Ӗ��������w���ɂ킩������B
�����w���ɂ킩������������O�p�����g���ĉ����̂͂Ȃ�̖����Ȃ��B
���ǁA�����o���Ȃ��y�̏퓅�傪�u�X���Ⴂ�v�B
���_�ł��Ȃ��y���u�A�d�_�v�Ƃ����̂Ɏ��Ă���B
953�P�R�Q�l�ڂ̑f������
2024/12/12(��) 14:48:03.46ID:E95WI1b6 ����Ȃ��Ƃ������ƃt�F���}�[�̍ŏI�藝���Ӗ��͒��w���ɂ�������킯�ł�
2024/12/12(��) 16:21:16.11ID:rpXfEbrF
2024/12/12(��) 16:22:12.53ID:MNPfe8h8
>>952
�u�����w�Z�͈͂̎Z���E���w�v�̈Ӗ����番����Ȃ��l�͏������܂Ȃ��ł�������
���w�Z�w�K�w���v�́A���邢�͒��w�Z�w�K�w���v�̂Ɋ܂܂����e���A
�����w�Z�͈͂̎Z���E���w�ł�
�u�����w�Z�͈͂̎Z���E���w�v�̈Ӗ����番����Ȃ��l�͏������܂Ȃ��ł�������
���w�Z�w�K�w���v�́A���邢�͒��w�Z�w�K�w���v�̂Ɋ܂܂����e���A
�����w�Z�͈͂̎Z���E���w�ł�
2024/12/12(��) 17:52:56.16ID:Bn0C/TuA
���X���͂ǂ�K�{����
�ǂ�C�������Ă�邼��
�ǂ�C�������Ă�邼��
2024/12/12(��) 18:19:55.71ID:MNPfe8h8
���w�͂ǂ�ǂ��납ܯ�������s��
2024/12/12(��) 18:21:00.92ID:Buqv3Ypc
���w���ł��Ӗ��͕����邾�낤���ǔA�r�W�W�CID:rMBX4gAn�̓X���^�C���Ӗ���������Ȃ�
�܂菬�w���ȉ��̃`���p��
�܂菬�w���ȉ��̃`���p��
2024/12/12(��) 18:28:34.51ID:Buqv3Ypc
>>952
���Z���w�Ńo�J�ɂ��炵�Ă��炦�Ȃ��Ȃ������獡�x��1�������u���Ă������ŏ��w������Ƀ��X��H����
60�߂��Ēp���������Ȃ��A�r�W�W�C
���Z���w�Ńo�J�ɂ��炵�Ă��炦�Ȃ��Ȃ������獡�x��1�������u���Ă������ŏ��w������Ƀ��X��H����
60�߂��Ēp���������Ȃ��A�r�W�W�C
2024/12/12(��) 23:47:59.81ID:rMBX4gAn
����͏��w���ł�����������B
���ˉt���S�{�A��������\���ȗʂ�����A���̂����P�{���Ŗ�ł��邱�Ƃ��킩���Ă���B
�ŏ����̃l�Y�~�ɒ��ˉt���������Ē��˂��Ăǂꂪ�Ŗ���肵�����B
�����̒��ˉt���������Ē��˂����Ă��Ő��͕ς��Ȃ��Ƃ���B
�e�X�̃l�Y�~�ɒ��˂ł���̂͂P���ł���B
�Ŗ�Q�{���m���ɓ��肷�鍬�����@���q�ׂ�B
��������肵��
���ˉt���W�{�A��������\���ȗʂ�����A���̂����Q�{���Ŗ�ł��邱�Ƃ��킩���Ă���B
�ɂ����̂��O�f�̖��B
���ˉt���S�{�A��������\���ȗʂ�����A���̂����P�{���Ŗ�ł��邱�Ƃ��킩���Ă���B
�ŏ����̃l�Y�~�ɒ��ˉt���������Ē��˂��Ăǂꂪ�Ŗ���肵�����B
�����̒��ˉt���������Ē��˂����Ă��Ő��͕ς��Ȃ��Ƃ���B
�e�X�̃l�Y�~�ɒ��˂ł���̂͂P���ł���B
�Ŗ�Q�{���m���ɓ��肷�鍬�����@���q�ׂ�B
��������肵��
���ˉt���W�{�A��������\���ȗʂ�����A���̂����Q�{���Ŗ�ł��邱�Ƃ��킩���Ă���B
�ɂ����̂��O�f�̖��B
2024/12/12(��) 23:54:48.38ID:5pkwiQ9W
�X���^�C�Ȃ珬�w���ł��ǂ߂邵�������ł��邩��A�z�݂����ȏo��(������������X��)���Ȃ����A�r�W�W�C�͏��w���ȉ�����
�܂�������O�Ȃ�w
�܂�������O�Ȃ�w
2024/12/13(��) 01:26:26.35ID:FEBDM5Aq
>>953
�����Œ��S�Ɍ��藝�͏ؖ��ł��Ȃ��Ă��g���Ă����Ȃ��B
�l�C�s�A���������Ōv�Z�ł��Ȃ��Ȃ�g���ȂƂ����͔̂n�����Ă���B
HI�̌�����m��Ȃ���w�ł�������HI���g���B
�����n�C�u���b�h�̌����͗����ł��Ă��Ȃ����n�C�u���b�h�Ԃ��^�]���Ă���B
�t�F���}�[�̍ŏI�藝���l�ނ̒q�d�Ƃ��ė��p������������B
�����Œ��S�Ɍ��藝�͏ؖ��ł��Ȃ��Ă��g���Ă����Ȃ��B
�l�C�s�A���������Ōv�Z�ł��Ȃ��Ȃ�g���ȂƂ����͔̂n�����Ă���B
HI�̌�����m��Ȃ���w�ł�������HI���g���B
�����n�C�u���b�h�̌����͗����ł��Ă��Ȃ����n�C�u���b�h�Ԃ��^�]���Ă���B
�t�F���}�[�̍ŏI�藝���l�ނ̒q�d�Ƃ��ė��p������������B
2024/12/13(��) 01:32:38.43ID:FEBDM5Aq
�����o���鋳�{�̂������>941�݂����ȓ��e���\�B
�X���Ⴂ�Ƃ������Ă���̂͌��ǂ̂Ƃ��듚���o���Ȃ����炾�낤�ȁB
�p�`���R�ʂ⑽���̍d�݂̐��𐔂���̂ɁA���Ƃł��@�Ƃ����͔̂�����I�B
���Љ�ŕK�v�Ȃ̂͐v���ɓ����o���邱�ƁB�P�O�O�I�Ƃ���v�Z�ł��H
�X���Ⴂ�Ƃ������Ă���̂͌��ǂ̂Ƃ��듚���o���Ȃ����炾�낤�ȁB
�p�`���R�ʂ⑽���̍d�݂̐��𐔂���̂ɁA���Ƃł��@�Ƃ����͔̂�����I�B
���Љ�ŕK�v�Ȃ̂͐v���ɓ����o���邱�ƁB�P�O�O�I�Ƃ���v�Z�ł��H
2024/12/13(��) 02:13:47.14ID:FEBDM5Aq
�i���̓~�X�C���j
����͏��w���ł�����������B
���ˉt���S�{�A��������\���ȗʂ�����A���̂����P�{���Ŗ�ł��邱�Ƃ��킩���Ă���B
�ŏ����̃l�Y�~�ɒ��ˉt���������Ē��˂��Ăǂꂪ�Ŗ���肵�����B
�����̒��ˉt���������Ē��˂����Ă��Ő��͕ς��Ȃ��Ƃ���B
�e�X�̃l�Y�~�ɒ��˂ł���̂͂P���ł���B
�Ŗǂꂩ���m���ɓ��肷�鍬�����@���q�ׂ�B
��������肵��
���ˉt���W�{�A��������\���ȗʂ�����A���̂����Q�{���Ŗ�ł��邱�Ƃ��킩���Ă���B
�ɂ����̂��O�f�̖��B
����͏��w���ł�����������B
���ˉt���S�{�A��������\���ȗʂ�����A���̂����P�{���Ŗ�ł��邱�Ƃ��킩���Ă���B
�ŏ����̃l�Y�~�ɒ��ˉt���������Ē��˂��Ăǂꂪ�Ŗ���肵�����B
�����̒��ˉt���������Ē��˂����Ă��Ő��͕ς��Ȃ��Ƃ���B
�e�X�̃l�Y�~�ɒ��˂ł���̂͂P���ł���B
�Ŗǂꂩ���m���ɓ��肷�鍬�����@���q�ׂ�B
��������肵��
���ˉt���W�{�A��������\���ȗʂ�����A���̂����Q�{���Ŗ�ł��邱�Ƃ��킩���Ă���B
�ɂ����̂��O�f�̖��B
2024/12/13(��) 02:17:50.96ID:FEBDM5Aq
���s���낵�Ă�����A���R�Ɍ��������l���l�^�ɂ����̂����Z���w�X���ɓ��e�������̖��B
���
���ˉt���W�{����A���̂����Q�{���v���I�ȓŖ�ł��邱�Ƃ��킩���Ă���B���ˉt�̂P�{�������o����Ă��܂����B
�c��̂V�{���U�C�̃l�Y�~�ɒ��ˉt���������Ē��˂��ĂW�{�̂����ǂꂪ�Ŗ���肵�����B
�����̒��ˉt���������Ē��˂����Ă��Ő��͕ς��Ȃ��Ƃ���B
�e�X�̃l�Y�~�ɒ��˂ł���̂͂P���ł���B
�ǂ̂悤�ɍ������ĂU�C�̃l�Y�~�ɓ��^����悢���H
���
���ˉt���W�{����A���̂����Q�{���v���I�ȓŖ�ł��邱�Ƃ��킩���Ă���B���ˉt�̂P�{�������o����Ă��܂����B
�c��̂V�{���U�C�̃l�Y�~�ɒ��ˉt���������Ē��˂��ĂW�{�̂����ǂꂪ�Ŗ���肵�����B
�����̒��ˉt���������Ē��˂����Ă��Ő��͕ς��Ȃ��Ƃ���B
�e�X�̃l�Y�~�ɒ��˂ł���̂͂P���ł���B
�ǂ̂悤�ɍ������ĂU�C�̃l�Y�~�ɓ��^����悢���H
2024/12/13(��) 04:49:29.02ID:jjImAvGV
>>965
���Z���w�X���ɓ��e����Ƃ������Ƃ͍��Z���w�͈̔͂ʼn������Ƃ������Ƃł���ˁH
�X���Ⴂ�Ȃ̂ł́H
�����łȂ��ƌ����Ȃ�A���ꂪ�����w���̎Z���A���w�͈̔͂ʼn����邱�Ƃ�������ĉ�����
���͖������Ǝv���܂�
���Z���w�X���ɓ��e����Ƃ������Ƃ͍��Z���w�͈̔͂ʼn������Ƃ������Ƃł���ˁH
�X���Ⴂ�Ȃ̂ł́H
�����łȂ��ƌ����Ȃ�A���ꂪ�����w���̎Z���A���w�͈̔͂ʼn����邱�Ƃ�������ĉ�����
���͖������Ǝv���܂�
2024/12/13(��) 09:50:02.89ID:N9yuvmP3
>>962
�w�����w�Z�͈͂̎Z���E���w�̖��̃X���x�Ƃ��āA�u�P�ɖ��𗝉��ł���v���͓K���Ƃ����b�ɁA
���̕Ԃ��͂�����Ƃ�
���w�͂ł��邾���������牟������悤�ɂ��āA�u���̎�@�͐�ΐ���������������ËL����ׂ��v����
�͔̂r�����Ȃ��ƁB�m�Ƃ��łƂ肠������֍Z�ɍ��i������Ă̂ŁA���R���킩�炸������v�Z�@���ËL
�����@�͈�ʐ��k�ɂ͎g���Ȃ����ƁB
�w�����w�Z�͈͂̎Z���E���w�̖��̃X���x�Ƃ��āA�u�P�ɖ��𗝉��ł���v���͓K���Ƃ����b�ɁA
���̕Ԃ��͂�����Ƃ�
���w�͂ł��邾���������牟������悤�ɂ��āA�u���̎�@�͐�ΐ���������������ËL����ׂ��v����
�͔̂r�����Ȃ��ƁB�m�Ƃ��łƂ肠������֍Z�ɍ��i������Ă̂ŁA���R���킩�炸������v�Z�@���ËL
�����@�͈�ʐ��k�ɂ͎g���Ȃ����ƁB
2024/12/13(��) 10:49:41.41ID:fQDIGGXm
���̖��͎������˂T��ŕs�\�Ȃ̂��ؖ�����ɂ͍������w���K�v�炵���ł����A
�U��Ȃ�Ꭶ������������ł����珬�w���ł��ł���Ǝv���܂��B
�Ȃ��A���ɂ͂T��ŕs�\�Ƃ���R�����g���e�������ł��Ȃ��̂�
�{���ɂT��ł͖����Ȃ̂��͂킩��܂���B
�U��Ȃ�Ꭶ������������ł����珬�w���ł��ł���Ǝv���܂��B
�Ȃ��A���ɂ͂T��ŕs�\�Ƃ���R�����g���e�������ł��Ȃ��̂�
�{���ɂT��ł͖����Ȃ̂��͂킩��܂���B
2024/12/13(��) 11:52:30.98ID:9GHof9Ss
���{�]�X�̑O�ɐl�Ƃ��čŒႾ��
�X���Ⴂ�ő���ɂ���Ȃ��̂����o���Ȃ��Ƃ��L�`�K�C�ɂ��������邾��
�X���Ⴂ�ő���ɂ���Ȃ��̂����o���Ȃ��Ƃ��L�`�K�C�ɂ��������邾��
970�P�R�Q�l�ڂ̑f������
2024/12/13(��) 13:25:17.63ID:N9yuvmP3 >>968
�W�Ȃ����ƃ��X����Ȃ悗
�W�Ȃ����ƃ��X����Ȃ悗
2024/12/13(��) 15:30:43.23ID:FEBDM5Aq
2024/12/13(��) 15:36:21.52ID:FEBDM5Aq
>>968
6��̗Ꭶ�i���s����Ŕ������j
���˖��1~8�ɖ������ĂU�C�̃}�E�X�ł̍����@�B
���Ȃ݂ɁA���l�߂Ō������Ȃ������̂ŋ��R�Ɍ��������g�ݍ��킹�ł��B
"
example
> mat
[,1] [,2] [,3]
[1,] 1 2 6
[2,] 1 3 4
[3,] 2 3 8
[4,] 3 6 7
[5,] 4 6 8
[6,] 2 4 5
6��̗Ꭶ�i���s����Ŕ������j
���˖��1~8�ɖ������ĂU�C�̃}�E�X�ł̍����@�B
���Ȃ݂ɁA���l�߂Ō������Ȃ������̂ŋ��R�Ɍ��������g�ݍ��킹�ł��B
"
example
> mat
[,1] [,2] [,3]
[1,] 1 2 6
[2,] 1 3 4
[3,] 2 3 8
[4,] 3 6 7
[5,] 4 6 8
[6,] 2 4 5
2024/12/13(��) 15:43:35.14ID:FEBDM5Aq
>>967
�@�n�}��h�蕪����̂ɂS�F����Γh�蕪�����܂��A�̂̈̂��l���R���s���[�^�[���g���ďؖ��ς݂ł��B
�Ɛ����ł����Ǝv���B
�f�f�Ǝ��Â�����������̉ߒ��͖��Ȃ��A
�Ƃ����̂�N�w�Ƃ����Z�i�ŋ߁A�����Ȋw��Ƃ�F������݂����ɉ��̂��ꂽ��w�j�̔畆�Ȃ̐i��������
�m�[�g�E���ȏ��������݉������B
���Ȃ݂ɑ��Ǝ����͂����ł͂Ȃ��������B
�@�n�}��h�蕪����̂ɂS�F����Γh�蕪�����܂��A�̂̈̂��l���R���s���[�^�[���g���ďؖ��ς݂ł��B
�Ɛ����ł����Ǝv���B
�f�f�Ǝ��Â�����������̉ߒ��͖��Ȃ��A
�Ƃ����̂�N�w�Ƃ����Z�i�ŋ߁A�����Ȋw��Ƃ�F������݂����ɉ��̂��ꂽ��w�j�̔畆�Ȃ̐i��������
�m�[�g�E���ȏ��������݉������B
���Ȃ݂ɑ��Ǝ����͂����ł͂Ȃ��������B
2024/12/13(��) 15:47:59.98ID:FEBDM5Aq
2024/12/13(��) 15:59:03.36ID:FEBDM5Aq
>>970
�ŁA�K�v�ȃl�Y�~�͂T�C�Ȃ̂U�C�Ȃ́H
�ŁA�K�v�ȃl�Y�~�͂T�C�Ȃ̂U�C�Ȃ́H
2024/12/13(��) 18:55:41.66ID:22JORo84
>>971
�P�Ȃ�b�̂���ւ��ʼn����ؖ��ɂȂ��Ă��܂���
�P�Ȃ�b�̂���ւ��ʼn����ؖ��ɂȂ��Ă��܂���
2024/12/13(��) 23:35:04.87ID:ywXQiqEi
���ˉt���S�{�A��������\���ȗʂ�����A���̂����P�{���Ŗ�ł��邱�Ƃ��킩���Ă���B
�ŏ����̃l�Y�~�ɒ��ˉt���������Ē��˂��Ăǂꂪ�Ŗ���肵�����B
�����̒��ˉt���������Ē��˂����Ă��Ő��͕ς��Ȃ��Ƃ���B
�e�X�̃l�Y�~�ɒ��˂ł���̂͂P���ł���B
�Ŗǂꂩ���m���ɓ��肷�鍬�����@���q�ׂ�B
�l�Y�~�P�@���˂P�ƒ��˂Q������
�l�Y�~�Q�@���˂P�ƒ��˂R������
�l�Y�~�P���������˂Q���Ŗ�
�l�Y�~�Q���������˂R���Ŗ�
�������˂P���Ŗ�
�ǂ�������ȂȂ���S���Ŗ�B
���Z���w����K�v�Ȃ���ˁB
�ŏ����̃l�Y�~�ɒ��ˉt���������Ē��˂��Ăǂꂪ�Ŗ���肵�����B
�����̒��ˉt���������Ē��˂����Ă��Ő��͕ς��Ȃ��Ƃ���B
�e�X�̃l�Y�~�ɒ��˂ł���̂͂P���ł���B
�Ŗǂꂩ���m���ɓ��肷�鍬�����@���q�ׂ�B
�l�Y�~�P�@���˂P�ƒ��˂Q������
�l�Y�~�Q�@���˂P�ƒ��˂R������
�l�Y�~�P���������˂Q���Ŗ�
�l�Y�~�Q���������˂R���Ŗ�
�������˂P���Ŗ�
�ǂ�������ȂȂ���S���Ŗ�B
���Z���w����K�v�Ȃ���ˁB
2024/12/13(��) 23:41:35.83ID:ywXQiqEi
����Ă��邱�Ƃ́A�܂܂�邩�܂܂�Ȃ����ׂ邾���B
2024/12/14(�y) 01:28:09.60ID:K7SsiF4B
�ǂ����������낤���ǁA���x�͘A���ōr�炵�Ă���̂���
2024/12/14(�y) 07:46:26.11ID:wEY2CYmX
����ɂ��Ă�����ȗ����Ő��������邾��
�ӂ߂��邱�Ƃ͂ǂ��ł��悭�A�G����邱�ƂŊ�ԃ^�C�v�̐l�Ԃł���
�G�ꂸ��NG������
�ӂ߂��邱�Ƃ͂ǂ��ł��悭�A�G����邱�ƂŊ�ԃ^�C�v�̐l�Ԃł���
�G�ꂸ��NG������
2024/12/14(�y) 08:02:39.82ID:szmD/Saq
2024/12/14(�y) 08:14:42.04ID:Lo50375v
>>978
�X���^�C�������邾���Ȃ珬�w���ł��ł���Ǝv���܂�
�܂�A���^�͏��w���ȉ��Ȃ̂ł��̃X���̃��x���ɒB���Ă܂���
�������蒼���Ă�������
�X���^�C�������邾���Ȃ珬�w���ł��ł���Ǝv���܂�
�܂�A���^�͏��w���ȉ��Ȃ̂ł��̃X���̃��x���ɒB���Ă܂���
�������蒼���Ă�������
2024/12/14(�y) 11:04:59.26ID:x35JGDZa
�Ꭶ������������Ȃ̂ɁB
�O�p�������ϕ����v��Ȃ��B
�O�p�������ϕ����v��Ȃ��B
2024/12/14(�y) 14:08:42.01ID:H+KsfqfK
���L�̂U�C�̃l�Y�~�ւ̍������ˉt�̑g�ݍ��킹�œŖ���ł���̂͂ǂꂩ�H
(1)
[1,] 1 2 3
[2,] 1 4 5
[3,] 2 4 6
[4,] 3 5 6
[5,] 1 6 7
[6,] 2 5 8
(2)
[1,] 1 2 3
[2,] 1 4 5
[3,] 2 4 6
[4,] 3 5 6
[5,] 1 6 7
[6,] 2 5 4
(3)
[1,] 1 2 3
[2,] 1 4 5
[3,] 2 4 6
[4,] 3 5 6
[5,] 1 6 7
[6,] 2 5 7
���������Ē��ꌟ�����Ă����Ώ��w���ɂ�����������B
(1)
[1,] 1 2 3
[2,] 1 4 5
[3,] 2 4 6
[4,] 3 5 6
[5,] 1 6 7
[6,] 2 5 8
(2)
[1,] 1 2 3
[2,] 1 4 5
[3,] 2 4 6
[4,] 3 5 6
[5,] 1 6 7
[6,] 2 5 4
(3)
[1,] 1 2 3
[2,] 1 4 5
[3,] 2 4 6
[4,] 3 5 6
[5,] 1 6 7
[6,] 2 5 7
���������Ē��ꌟ�����Ă����Ώ��w���ɂ�����������B
2024/12/14(�y) 14:44:33.25ID:/zM4+P1S
2024/12/14(�y) 14:46:31.34ID:wEY2CYmX
> ���炩�ɔ͈͊O�̎���ɂ͑�NG�o�^�őΏ����Ă������B���������畉���ł��B�F�l�̂����͂�낵�����肢���܂��B
2024/12/14(�y) 19:15:03.40ID:H+KsfqfK
2024/12/14(�y) 19:33:55.41ID:wQuH/mwK
>>987
����܂ł̐l���ŕ��������Ă��ĒN�ɂ�����ɂ���Ȃ��Ȃ�������̉ʂĂ�5ch�ŃX���`�Ȃ��ƂŔ������邵���ł��Ȃ��A�r�W�W�C�Ƃ���������ȃ����X�^�[���낤��
����܂ł̐l���ŕ��������Ă��ĒN�ɂ�����ɂ���Ȃ��Ȃ�������̉ʂĂ�5ch�ŃX���`�Ȃ��ƂŔ������邵���ł��Ȃ��A�r�W�W�C�Ƃ���������ȃ����X�^�[���낤��
2024/12/14(�y) 19:53:35.40ID:D/TilK1k
>>987
���w���̃X���ɔS������R���ǂ��̂��Č����Ă邨�O�̕�����������
���w���̃X���ɔS������R���ǂ��̂��Č����Ă邨�O�̕�����������
2024/12/14(�y) 23:39:37.74ID:48ZT12Qs
�r�炷�����\�̂Ȃ��z���A�����o���Ȃ����������Ɛl�������g���A��������ĕ����ɂ��݂̎̂đ䎌��f���Ă܂��B
2024/12/14(�y) 23:45:20.90ID:OOgIBCd+
>>987
>1���ǂ߂Ȃ��ǃA�zw
>1���ǂ߂Ȃ��ǃA�zw
2024/12/14(�y) 23:59:51.02ID:wQuH/mwK
�A�r�W�W�C���w���ɂ��R�e���p���ɂ���ĕ��������̂��ȁH
2024/12/15(��) 15:14:14.23ID:nCNNpooi
�m���A���N��4�����̃X���������ȁBWolfram�������Ŏg���邱�Ƃ���������̂́B
https://rio2016.5ch.net/test/read.cgi/math/1693982238/172-175
������ƌv�Z�ł���l�̓X���Ⴂ�Ƃ����킸�ɖفX�Ɛ������l�𓊍e���Ă���B
https://rio2016.5ch.net/test/read.cgi/math/1693982238/172-175
������ƌv�Z�ł���l�̓X���Ⴂ�Ƃ����킸�ɖفX�Ɛ������l�𓊍e���Ă���B
2024/12/15(��) 15:54:14.77ID:dSJER//t
>>993
�N�����肵�悤���A���^���X���Ⴂ�ł��邱�Ƃɂ͕ς��Ȃ����炳�����Ə�����
�N�����肵�悤���A���^���X���Ⴂ�ł��邱�Ƃɂ͕ς��Ȃ����炳�����Ə�����
2024/12/15(��) 19:07:26.87ID:4VLqfZdr
>>993
����Ȃ��Ƃǂ��ł���������V�����X�����ĂĂ�������
����Ȃ��Ƃǂ��ł���������V�����X�����ĂĂ�������
2024/12/15(��) 19:56:02.59ID:dSJER//t
>>993
���Ⴀ�܂Ƃ��ɃA���^�̑��肵�Ă����Ƃ���ɏ������߂��������
�܂�����ȂƂ��Ȃ����炱���Ŕ������Ă�낤��w
�V�������Z���w�X���̍��Z���ɂ��o�J�ɂ��炵�Ă��炦�Ȃ��Ȃ�������w
���Ⴀ�܂Ƃ��ɃA���^�̑��肵�Ă����Ƃ���ɏ������߂��������
�܂�����ȂƂ��Ȃ����炱���Ŕ������Ă�낤��w
�V�������Z���w�X���̍��Z���ɂ��o�J�ɂ��炵�Ă��炦�Ȃ��Ȃ�������w
997�P�R�Q�l�ڂ̑f������
2024/12/15(��) 20:32:52.96ID:nlCmV6ks �L��IQ���Ⴗ����11������11�����̒��Ōv�Z�ł��Ȃ�
2024/12/15(��) 21:16:02.27ID:vuifd9L4
>>993
�N�������҂��Ƃ͒m�炸�A�ꐶ�̕s�o��������B
�N�������҂��Ƃ͒m�炸�A�ꐶ�̕s�o��������B
2024/12/15(��) 21:45:13.02ID:dSJER//t
���A���݂̂Ȃ炸5ch�ł�����������>>993�A�r�W�W�Cww
2024/12/15(��) 21:45:53.81ID:dSJER//t
10011001
Over 1000Thread ���̃X���b�h�͂P�O�O�O���܂����B
�V�����X���b�h�𗧂ĂĂ��������B
life time: 466�� 6���� 8�� 36�b
�V�����X���b�h�𗧂ĂĂ��������B
life time: 466�� 6���� 8�� 36�b
10021002
Over 1000Thread 5�����˂�̉^�c��UPLIFT����̊F���܂Ɏx�����Ă��܂��B
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�sUPLIFT����̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
4 USD/mon. ���瓽���ł��w�����������܂��B
�� UPLIFT����o�^�͂����� ��
https://uplift.5ch.net/
�� UPLIFT���O�C���͂����� ��
https://uplift.5ch.net/login
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�sUPLIFT����̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
4 USD/mon. ���瓽���ł��w�����������܂��B
�� UPLIFT����o�^�͂����� ��
https://uplift.5ch.net/
�� UPLIFT���O�C���͂����� ��
https://uplift.5ch.net/login
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
�j���[�X
- �u�ĉ����̂܂܈ێ�����Ă�����ׂ����v���ꌧ�m���A���_�Ƃ̌o�c���܂����y ��3 [�a�̎s��]
- ��700���̃R�A����_�����E���� �X�щЂ��e���@�I�[�X�g�����A [���l����]
- �y�č��z�u�A�C�����ɐ푈�~�߂�v�Ƒi���Ă����g�����v���u�ʔ������Ō����Ă����������v���Q [�������܂ȁ�]
- �y�|�\�z�i����u�ގ�������_���ł���v�@���W�I�Ō���Ă����g�����ρh�@�D���Ȑl�ɗ��l������ꍇ�A���ǂ��Ȃ��Ă͂Ȃ�Ȃ��Ǝ��_ [jinjin��]
- �y�L���z��i���Ăю̂Ăɂ��āu�A�C�X���Ă����v�ȂǂƖ��߁A�u�������v���ăp�`���R�c���R�s�E���i55�j������ [���ꁚ]
- �y�ĕāz�Ă��u��30�L���v�Ƒ��ŏ���鏗���A�J���t�H���j�A�Ă��u4�L��2900�~�v�ōw�����Ă݂����z�́c�c [�Ђ�����]
- �x�r�[�J�[�A�d���ו�...�Ȃ����{�l�͎�������L�ׂȂ��̂��H�u�����Ă���l�����Ǝ����v�ꋴ��~���咲���Ŗ��炩�ɂȂ��������̌��@ [377482965]
- 🏡
- 2ch�ĕ֏��̗��������ႚ�Ƃ������Ă������ǂ܂����X�}�z�̕��y�ʼn������ȉ��̖��x�̂�炪�o������Ƃ͗\�z�ł��Ȃ�������� [472617201]
- �y�����O�@�I�z�����_�ސ�A�`�Ǝ��̌㊘�ɍ������i30�j�A�×����̌㊘�Ɍ��ېV�̋��i34�j��I�C �̂����ᑢ [196352351]
- �L���u�����̌����͐��E��😉�v���{�l����u�厖�̋N�����疄�߂Ė����������ɂ���́H😄�v�u�`���C�i�W���[�N😂�v [441660812]
- �Δj�A�����AI�W���u������u�u���ꂩ���A�l�����}���Ɍ����Ă������ɂ�����AI���ʂ��������͔��ɑ傫���B�K����蕥���Ă����Ȃ��� [377482965]
