�T��
������˂����͂����֏���
���X����900���Ă��܂��B1000����ƕ\���ł��Ȃ��Ȃ��B
2014/10/04(�y) 21:22:05.10
1
2014/10/04(�y) 21:23:04.89
�ق��ق�
3�P�R�Q�l�ڂ̑f������
2014/10/04(�y) 21:23:47.38 ��������
2014/10/04(�y) 21:25:08.46
a^11+b^11+c^11
������������
������������
2014/10/04(�y) 21:36:13.49
IQ�e�X�g�ł悭��������
1��2��3��4������6
�̗l�ȁA���ɓ��Ă͂܂鐔���������ƌ����₢�Ȃ�ł���
�u�������A�����́����Ƃ���v�̗l�ȓ��ʂȎw���������̂�
��0�`9�ǂ��I�����Ă����̒l�ɏo���鎮�͂����ł͖������Ǝv���̂ł��B
�܂艽���L�����Ă��~�͕t�����Ȃ��Ǝv���̂ł����ǂ��Ȃ�ł��傤���H
1��2��3��4������6
�̗l�ȁA���ɓ��Ă͂܂鐔���������ƌ����₢�Ȃ�ł���
�u�������A�����́����Ƃ���v�̗l�ȓ��ʂȎw���������̂�
��0�`9�ǂ��I�����Ă����̒l�ɏo���鎮�͂����ł͖������Ǝv���̂ł��B
�܂艽���L�����Ă��~�͕t�����Ȃ��Ǝv���̂ł����ǂ��Ȃ�ł��傤���H
6�P�R�Q�l�ڂ̑f������
2014/10/04(�y) 22:16:22.76 �u�ǂ��I�ׂΐ����ɂȂ�ƍl���ďo�肳��Ă��邩�v���₢�Ȃ̂ŁA
�u�ǂꂪ�������v�A�u�ǂ�𐳉��Ƃ��ׂ����v�͋��ł�
�u�o��҂ɍ��킹�Ă�����v�̂�IQ�e�X�g�̈��
�u�ǂꂪ�������v�A�u�ǂ�𐳉��Ƃ��ׂ����v�͋��ł�
�u�o��҂ɍ��킹�Ă�����v�̂�IQ�e�X�g�̈��
2014/10/04(�y) 22:20:11.54
�m���ɃX���^�C�ǂ��肾�B
8�P�R�Q�l�ڂ̑f������
2014/10/06(��) 20:18:25.23 �_O�𒆐S�Ƃ��锼�a�P�̉~����ɒ�_A������B���aOA�ɒ������錷PQ���Ƃ�A
��POA=�ƂƂ���i0���Ɓ���/2)�B�O�p�`APQ�̖ʐς�S�i�Ɓj�ŕ\���Ƃ�
lim�Ɓ�0�@S(�Ɓj/S(��/2�j�����߂�B
�Ƃ������ŁA
��PAO��1/2�@�i��-�Ɓj������A��PAQ���[�Ɓ@�Ƃ����̂͂킩��܂��B
���̎���
PA=QA=2sin(��/2)�Ɖɏ����Ă���̂ł���
�Ȃ������Ȃ�܂����B
��POA=�ƂƂ���i0���Ɓ���/2)�B�O�p�`APQ�̖ʐς�S�i�Ɓj�ŕ\���Ƃ�
lim�Ɓ�0�@S(�Ɓj/S(��/2�j�����߂�B
�Ƃ������ŁA
��PAO��1/2�@�i��-�Ɓj������A��PAQ���[�Ɓ@�Ƃ����̂͂킩��܂��B
���̎���
PA=QA=2sin(��/2)�Ɖɏ����Ă���̂ł���
�Ȃ������Ȃ�܂����B
9�P�R�Q�l�ڂ̑f������
2014/10/06(��) 20:23:09.78 ��PAO������Ă邾���ł����B
10�P�R�Q�l�ڂ̑f������
2014/10/13(��) 12:35:45.66 ���𐳂̐����Ƃ���B���̖̓��A��i���j�Ƃ̍��̐�Βl���ŏ��̂��̂�
���i���j�Ƃ����B�C�ӂ̐��̐������ɑ��āA���i���j�����ƂȂ邎��������
���݂��邱�Ƃ������B
���i���j�Ƃ����B�C�ӂ̐��̐������ɑ��āA���i���j�����ƂȂ邎��������
���݂��邱�Ƃ������B
2014/10/13(��) 16:19:30.99
���A�����ς���ĂāA�����ƌv�Z�ł��Ȃ����A
�����Q �͔��Ⴞ�Ǝv���B���[�ɈႢ�Ȃ��B
�����Q �͔��Ⴞ�Ǝv���B���[�ɈႢ�Ȃ��B
2014/10/13(��) 18:32:15.56
>>10
j�ɂ��āAp��j���傫���f���Ƃ���B
n=jp�Ƃ����n�̖�j�ȉ����܂���p�ȏ�
j<��n<(j+p)/2<p���a(n)=j
�C�ӂ̐��̐������ɑ��āA������傫���f��p�͖����ɑ��݂���̂�
a(n)=j�ƂȂ�n�������ɑ��݂���B
j�ɂ��āAp��j���傫���f���Ƃ���B
n=jp�Ƃ����n�̖�j�ȉ����܂���p�ȏ�
j<��n<(j+p)/2<p���a(n)=j
�C�ӂ̐��̐������ɑ��āA������傫���f��p�͖����ɑ��݂���̂�
a(n)=j�ƂȂ�n�������ɑ��݂���B
2014/10/27(��) 23:10:23.44
��҂�����Ă��邪�A�ݒ����ő��k�ɗ����l��
�u������˂����������v�ƌ����ƁA����B
�u������˂����������v�ƌ����ƁA����B
2014/10/27(��) 23:35:41.82
�����������������B
�������낢���H
�������낢���H
2014/10/27(��) 23:36:47.02
�X�R�b�g�����h�̗r�̘b�ł��������̂�
2014/11/01(�y) 13:10:40.73
>>13
���݂܂���B���͕֔�Ȃ̂ł����E�E�E
���݂܂���B���͕֔�Ȃ̂ł����E�E�E
17�P�R�Q�l�ڂ̑f������
2014/11/03(��) 14:14:45.60 n����̂Ƃ��A��n�p�`��3�{�̑Ίp����1�_�Ō���邱�Ƃ͂Ȃ����Ƃ������B
18�P�R�Q�l�ڂ̑f������
2014/11/04(��) 14:21:37.28 �����Ȃ��A��������������܂��B
�����͂킩���Ă���̂ł����ǂ����Ă�������܂���B
�ǂ����r�����������ĉ�����m(_�@_)m
2/3x+1/2y=1/3
1/4x-3/8y=-1
�����@y=2,�@x=-1
�����ʼn�����
4x+3y=2
2x-3y=-8
�ƂȂ��Ă��܂��A��ɐi�߂܂���B
�ǂ��������Ȃ��̂��A�����������ł��B
��낵�����肢���܂��B
�����͂킩���Ă���̂ł����ǂ����Ă�������܂���B
�ǂ����r�����������ĉ�����m(_�@_)m
2/3x+1/2y=1/3
1/4x-3/8y=-1
�����@y=2,�@x=-1
�����ʼn�����
4x+3y=2
2x-3y=-8
�ƂȂ��Ă��܂��A��ɐi�߂܂���B
�ǂ��������Ȃ��̂��A�����������ł��B
��낵�����肢���܂��B
19�P�R�Q�l�ڂ̑f������
2014/11/04(��) 14:52:48.34 >>18
������y�������邪
������y�������邪
20�P�R�Q�l�ڂ̑f������
2014/11/04(��) 15:10:59.2121�P�R�Q�l�ڂ̑f������
2014/11/04(��) 15:34:01.132014/11/04(��) 16:37:32.65
�ނ�������̂���߂đ��������ɂ�������v�Z�~�X�����Ȃ��B
���������Ƃ��̓}�C�i�X���|���Ă��瑫���B
���������Ƃ��̓}�C�i�X���|���Ă��瑫���B
2014/11/04(��) 22:30:41.15
�m���ɁA������˂��ȁB
24�P�R�Q�l�ڂ̑f������
2014/11/09(��) 00:03:29.44 �������Ă邩�ǂ����킩��A>>18
4x+3y=2 �c(A)
2x-3y=-8 �c(B)
(A)��ό`����
4x=-3y+2 �c(C)
(B)�~�Q����
4x-6y=-16
4x=6y-16 �c(D)
(C)��(D)����
-3y+2=6y-16
6y+3y=2+16
9y=18�@y=2 �c(E)
(C)��(E)��������
4x=6*2-16
4x=-4 x=-1
4x+3y=2 �c(A)
2x-3y=-8 �c(B)
(A)��ό`����
4x=-3y+2 �c(C)
(B)�~�Q����
4x-6y=-16
4x=6y-16 �c(D)
(C)��(D)����
-3y+2=6y-16
6y+3y=2+16
9y=18�@y=2 �c(E)
(C)��(E)��������
4x=6*2-16
4x=-4 x=-1
2524
2014/11/09(��) 00:18:06.43 ���܂�>>24����
�~�@(C)��(E)��������
���@(D)��(E)��������
(C)��(E)���������
4x=-3*2+2 �ɂȂ�B���̌�͕ς��ǁB
�~�@(C)��(E)��������
���@(D)��(E)��������
(C)��(E)���������
4x=-3*2+2 �ɂȂ�B���̌�͕ς��ǁB
26�P�R�Q�l�ڂ̑f������
2014/11/25(��) 15:39:48.44 an+1=2an+1-2an�Ȃ��an+1=2an
���킩��܂���B�ǂȂ������������B
���킩��܂���B�ǂȂ������������B
2014/11/25(��) 15:45:25.77
an+1=2an+1-2an��an+1=2an
���킩��܂���B�ǂȂ������������B
���킩��܂���B�ǂȂ������������B
28�P�R�Q�l�ڂ̑f������
2014/11/25(��) 15:50:32.34 �{���ɂ�����˂���肾��
2014/11/25(��) 19:26:23.67
>>27�ł��B�������[�h�ł�������ŋ����Ă��������B
30�P�R�Q�l�ڂ̑f������
2014/11/25(��) 19:58:03.53 2an+1�́A2an+2an�Ȃ�ł����H
31�ЎR����MZ����CEO ��T6xkBnTXz7B0
2014/11/25(��) 20:32:08.12 �����͐��m�ɏ�����B
�ya_{n+1}��2a_{n+1}-2a_n �� a_{n+1}��2a_n �̏ؖ��z
a_{n+1}��2a_{n+1}-2a_n�̗��ӂ����������
2a_{n+1}-2a_n��a_{n+1}�B
�E�ӂ�a_{n+1}�����Ɉڍ������
2a_{n+1}-a_{n+1}-2a_n��0�B
�����-2a_n���E�ӂɈڍ������
2a_{n+1}-a_{n+1}��2a_n�B
�����ł��̍��ӂ�
2a_{n+1}-a_{n+1}��(2-1)a_{n+1}��a_{n+1}�ł��邩��A
a_{n+1}��2a_n�B�t�����l�B��
�ya_{n+1}��2a_{n+1}-2a_n �� a_{n+1}��2a_n �̏ؖ��z
a_{n+1}��2a_{n+1}-2a_n�̗��ӂ����������
2a_{n+1}-2a_n��a_{n+1}�B
�E�ӂ�a_{n+1}�����Ɉڍ������
2a_{n+1}-a_{n+1}-2a_n��0�B
�����-2a_n���E�ӂɈڍ������
2a_{n+1}-a_{n+1}��2a_n�B
�����ł��̍��ӂ�
2a_{n+1}-a_{n+1}��(2-1)a_{n+1}��a_{n+1}�ł��邩��A
a_{n+1}��2a_n�B�t�����l�B��
2014/11/25(��) 20:56:45.84
>>31
���肪�Ƃ��������܂��B������Ȃ����x���ł��Ȃ������悤�Ɋ����܂����B
���肪�Ƃ��������܂��B������Ȃ����x���ł��Ȃ������悤�Ɋ����܂����B
2014/11/25(��) 21:06:39.59
���������AA=2A-2B�@����@A=2B�@�Ə��������Ă��邾������
2014/11/25(��) 21:08:34.18
��ώ��炵�܂����B���ލ��͌v�Z����Ƃ����̂������甲���Ă܂����B
2014/11/27(��) 04:53:02.66
�R���ˁB
�Y�����G�X�p�[���ė~����������������B
�o�艳
�Y�����G�X�p�[���ė~����������������B
�o�艳
36�P�R�Q�l�ڂ̑f������
2015/01/24(�y) 14:48:16.71ID:NvNcZRxE 1990�N�ȍ~�ɔ������ꂽ���w�̖{�̒��ŁAJay�@R�BGoldman���A��؏��j��u���w��
�����@���j���猩�����_����v�̒���P12��1�͂̐}�̖�肾���������Ă������{��
�����Ă������������̂ł����H
�����@���j���猩�����_����v�̒���P12��1�͂̐}�̖�肾���������Ă������{��
�����Ă������������̂ł����H
37�P�R�Q�l�ڂ̑f������
2015/01/24(�y) 15:18:58.73ID:C3Hj5fD1 �����ł����I
2015/01/24(�y) 17:22:59.98ID:E1hJIFTx
39�P�R�Q�l�ڂ̑f������
2015/01/25(��) 13:07:26.29ID:JR3q3r49 >>38�@�����肪�Ƃ��������܂�
�@�@�@�����Ȏ���ł����܂���ł���
�@�@�@�����Ȏ���ł����܂���ł���
40�P�R�Q�l�ڂ̑f������
2015/02/06(��) 11:02:58.97ID:A/MTjeAh �X�W��12��
�X�W�V��123��
�X�W�V�U��1234��
�X�W�V�U�T��12345��
�X�W�V�U�T�S��123456��
�@�@�@�@�E�E�E�E
��8�ɋ߂Â���ł����ǁA�v����ɂ�����Ăǂ��������ƂȂ̂��H���w�f�l�̎�����[��������u�����v�����������A���肢�������܂��B
�X�W�V��123��
�X�W�V�U��1234��
�X�W�V�U�T��12345��
�X�W�V�U�T�S��123456��
�@�@�@�@�E�E�E�E
��8�ɋ߂Â���ł����ǁA�v����ɂ�����Ăǂ��������ƂȂ̂��H���w�f�l�̎�����[��������u�����v�����������A���肢�������܂��B
41�P�R�Q�l�ڂ̑f������
2015/02/06(��) 11:10:54.36ID:A/MTjeAh �X�W��12��8�c2
�X�W�V��123��8�c3
�X�W�V�U��1234��8�c4
�X�W�V�U�T��12345��8�c5
�X�W�V�U�T�S��123456��8�c6
�悭�悭�v�Z�����炱���������B������ĉ��łȂ�̂������Ă��������B
�X�W�V��123��8�c3
�X�W�V�U��1234��8�c4
�X�W�V�U�T��12345��8�c5
�X�W�V�U�T�S��123456��8�c6
�悭�悭�v�Z�����炱���������B������ĉ��łȂ�̂������Ă��������B
2015/02/06(��) 11:18:53.26ID:7UGtJUoe
12345679�~9=111111111
111111111-12345679=98765432
����͂��ꂼ��[���ł��邩�H
111111111-12345679=98765432
����͂��ꂼ��[���ł��邩�H
2015/02/06(��) 11:22:36.37ID:7UGtJUoe
9�{��10�{����1�{�����������́A
8�{��9�{����1�{������������
�Ⴆ��123456�~10-123456��123456�~9-123456�̈����Z��M�Z�Ōv�Z���Ă݂悤
8�{��9�{����1�{������������
�Ⴆ��123456�~10-123456��123456�~9-123456�̈����Z��M�Z�Ōv�Z���Ă݂悤
44�P�R�Q�l�ڂ̑f������
2015/02/06(��) 11:53:27.03ID:A/MTjeAh �Ȃ�قǁI���肪�Ƃ��������܂��I
45�P�R�Q�l�ڂ̑f������
2015/02/06(��) 12:46:44.89ID:A/MTjeAh �u9�{��10�{����1�{�����������́v�P�O���������X�����ڂ̏ꏊ
�u8�{��9�{����1�{�����������́v�X���������W�����ڂ̏ꏊ
���w��N�̎��g�����u�Z���^�C���v�ōl����Ƃ��������C���[�W
��A�܂����ǂ�t���Ė���������?�撣��܂�
�u8�{��9�{����1�{�����������́v�X���������W�����ڂ̏ꏊ
���w��N�̎��g�����u�Z���^�C���v�ōl����Ƃ��������C���[�W
��A�܂����ǂ�t���Ė���������?�撣��܂�
46�P�R�Q�l�ڂ̑f������
2015/02/06(��) 13:12:11.96ID:A/MTjeAh 123+987��1110
1110��9��123�]��3
1234+9876��11110
11110��9=1234�]��4
�܂�
�܂����ꉻ�ł���
1110��9��123�]��3
1234+9876��11110
11110��9=1234�]��4
�܂�
�܂����ꉻ�ł���
2015/02/06(��) 16:32:05.08ID:7UGtJUoe
1234560-123456�Ƃ�1111104-123456��M�Z�Ōv�Z���Ă݂���Ă��Ƃ�
����łȂɂ��C���t���Ȃ����H
�d�삶��_�������B�M�Z�Ōv�Z������B
����łȂɂ��C���t���Ȃ����H
�d�삶��_�������B�M�Z�Ōv�Z������B
2015/02/07(�y) 11:29:18.66ID:FBOghTN4
1.���鐔��p�ӂ���
2.�����{�ɂ���
3.���������ɔ{�ɂ���
4.�܂��{�ɂ���A�Ɩ����ɌJ��Ԃ�
5.�ǂ��ł��ǂ��̂ŘA������4�̐������o��
6.��Ԗڂ̐��Ǝl�Ԗڂ̐��𑫂������͕K����Ԗڂ̐��̏\�{�ɂȂ�
10*M*2^n = M*2^(n+1) +M*2^(n+3)
10*M*2^n = M*(2^(n+1) +2^(n+3))
10*2^n = (2^(n+1) +2^(n+3))
10*2^n = 2^n(2^1+2^3)
10 = 2+8
2.�����{�ɂ���
3.���������ɔ{�ɂ���
4.�܂��{�ɂ���A�Ɩ����ɌJ��Ԃ�
5.�ǂ��ł��ǂ��̂ŘA������4�̐������o��
6.��Ԗڂ̐��Ǝl�Ԗڂ̐��𑫂������͕K����Ԗڂ̐��̏\�{�ɂȂ�
10*M*2^n = M*2^(n+1) +M*2^(n+3)
10*M*2^n = M*(2^(n+1) +2^(n+3))
10*2^n = (2^(n+1) +2^(n+3))
10*2^n = 2^n(2^1+2^3)
10 = 2+8
2015/02/07(�y) 11:41:36.34ID:FBOghTN4
��
�Ȃ������M���ĂċC�����ďؖ��܂łł�������
�N���Ɍ����قǂł��Ȃ����ǎ����Ȃ�ɂ������肵����ŏ����Ă݂�
5�@10�@20�@40�@80�@160
10+40=5��10�{
20+80=10��10�{
40+160=20��10�{
�Ȃ������M���ĂċC�����ďؖ��܂łł�������
�N���Ɍ����قǂł��Ȃ����ǎ����Ȃ�ɂ������肵����ŏ����Ă݂�
5�@10�@20�@40�@80�@160
10+40=5��10�{
20+80=10��10�{
40+160=20��10�{
50�P�R�Q�l�ڂ̑f������
2015/03/06(��) 02:36:16.15ID:iiUZXpt5 �@�@1�@�@�@�@�@�@1
�\�\�\�\�@�{�@�\�\�\�\
��3�|��2�@�@�@��3�{��2
����̓�������2��3�@�H�H
�\�\�\�\�@�{�@�\�\�\�\
��3�|��2�@�@�@��3�{��2
����̓�������2��3�@�H�H
2015/03/07(�y) 13:49:54.91ID:dvUknng0
�킴�킴
52�P�R�Q�l�ڂ̑f������
2015/03/15(��) 01:21:17.83ID:+25WCkUr �ً}�ł��I
MPL�ƃ}���|�̈Ⴂ�������Ă�����������
�������|�[�g�̒��ߐ�Ȃ�ł��B
MPL�ƃ}���|�̈Ⴂ�������Ă�����������
�������|�[�g�̒��ߐ�Ȃ�ł��B
53�P�R�Q�l�ڂ̑f������
2015/03/15(��) 16:52:18.75ID:sIBLx7L6 2ch�̂��͐搶������
2015/03/16(��) 23:59:07.05ID:cDVL5COV
55�P�R�Q�l�ڂ̑f������
2015/03/20(��) 12:22:28.22ID:tQmXO5cx ���߂Ă̏������݂ł�
�������ɂ��ĕ����Ȃ̂ł���������Ƃ킩��Ȃ����Ƃ�����܂��̂ł��q�˂��܂�
x����2�_�Ō����������ɂ��āAx���ƌ�������2�_�̍��W�ƕ������̒��_���W���킩���Ă���Ƃ��Ay=a(x-��)(x-��)�ŋO�����Z�o���邱�Ƃ��ł��܂����
�����܂ł͈��ݍ��߂��̂ł����Ax���ƌ�������1�_�̍��W(���_: 0,0)�ƒ��_���W�A����ɉ�����x���Ƃ͌������Ȃ��ʒu�ɂ�����W(�Ⴆ��10,5�Ƃ�10,-5)���킩���Ă���Ƃ��͂ǂ̂悤�ɕ��������Z�o��������̂ł��傤��?
�������ɂ��ĕ����Ȃ̂ł���������Ƃ킩��Ȃ����Ƃ�����܂��̂ł��q�˂��܂�
x����2�_�Ō����������ɂ��āAx���ƌ�������2�_�̍��W�ƕ������̒��_���W���킩���Ă���Ƃ��Ay=a(x-��)(x-��)�ŋO�����Z�o���邱�Ƃ��ł��܂����
�����܂ł͈��ݍ��߂��̂ł����Ax���ƌ�������1�_�̍��W(���_: 0,0)�ƒ��_���W�A����ɉ�����x���Ƃ͌������Ȃ��ʒu�ɂ�����W(�Ⴆ��10,5�Ƃ�10,-5)���킩���Ă���Ƃ��͂ǂ̂悤�ɕ��������Z�o��������̂ł��傤��?
2015/03/20(��) 17:48:14.47ID:1T6wTO/+
�����Ɨv�̗̂ǂ����@�����邩���m��Ȃ����A
y=ax^2+bx+c�Ƃ�����3�_�̍��W��������a,b,c�̘A���������������Ƃ������@�͕��L���g���邾��B
y=ax^2+bx+c�Ƃ�����3�_�̍��W��������a,b,c�̘A���������������Ƃ������@�͕��L���g���邾��B
57�P�R�Q�l�ڂ̑f������
2015/03/20(��) 20:45:05.26ID:SZojTTnM ���肪�Ƃ��������܂�
����������Ǝ��₪���������̂Œ��������Ă�������
���������3�_�̍��W���킩���Ă���Ƃ��ɂ͊m���ɂ����Ȃ̂ł����A
���₵���������̂́Ax���Ƃ͌������Ȃ��ʒu�ɂ���2�_��x,y���W(2�_��y���W�͂��ꂼ�ꍂ�����قȂ�)�ƁA���_��y���W(����)�݂̂��킩���Ă���ꍇ�ł�
���̏ꍇ�A���ł͉������Ƃ��ł��Ȃ��Ƃ������ƂɂȂ�̂ł��傤��?
����������Ǝ��₪���������̂Œ��������Ă�������
���������3�_�̍��W���킩���Ă���Ƃ��ɂ͊m���ɂ����Ȃ̂ł����A
���₵���������̂́Ax���Ƃ͌������Ȃ��ʒu�ɂ���2�_��x,y���W(2�_��y���W�͂��ꂼ�ꍂ�����قȂ�)�ƁA���_��y���W(����)�݂̂��킩���Ă���ꍇ�ł�
���̏ꍇ�A���ł͉������Ƃ��ł��Ȃ��Ƃ������ƂɂȂ�̂ł��傤��?
58�P�R�Q�l�ڂ̑f������
2015/03/20(��) 20:48:57.54ID:Vmr8wvov ����q�˂Ă�̂��A�X�ɂ킩��Ȃ��Ȃ���
59�P�R�Q�l�ڂ̑f������
2015/03/20(��) 20:56:35.92ID:SZojTTnM �����܂���
����������w�m���������ς�Ȃ̂ł��܂�����ł��Ȃ��̂ł����A�ȉ��̏��������Ƃ��������̕��������������Ƃ��ł���Ƃ������Ƃ͂��낢��ƒ��ׂĂ킩�����̂ł����A
���������2�_���W�ƒ��_��y���W�݂̂��킩���Ă���Ƃ��̉�@�������Ă������������̂ł�
���_�܂��͎����^����ꂽ�Ƃ��@���@������(���|��) �Q�{���@
���_�̏�Ȃ��Ƃ��B�܂���3�_�̏�킩��ꍇ�@���@���������Q�{�����{��
�I���Ƃ̌�_���Q�킩��Ƃ��@���@������(���|��)(���|��)
�I���Ɛڂ���Ƃ��@���@������(���|��) �Q
����������w�m���������ς�Ȃ̂ł��܂�����ł��Ȃ��̂ł����A�ȉ��̏��������Ƃ��������̕��������������Ƃ��ł���Ƃ������Ƃ͂��낢��ƒ��ׂĂ킩�����̂ł����A
���������2�_���W�ƒ��_��y���W�݂̂��킩���Ă���Ƃ��̉�@�������Ă������������̂ł�
���_�܂��͎����^����ꂽ�Ƃ��@���@������(���|��) �Q�{���@
���_�̏�Ȃ��Ƃ��B�܂���3�_�̏�킩��ꍇ�@���@���������Q�{�����{��
�I���Ƃ̌�_���Q�킩��Ƃ��@���@������(���|��)(���|��)
�I���Ɛڂ���Ƃ��@���@������(���|��) �Q
60�P�R�Q�l�ڂ̑f������
2015/03/21(�y) 13:24:55.47ID:LwBGj4UE >>59
���_��(p,q)�̎�
y=a(x-p)^2 +q
�Ə�����B
���_��y���W������ q = c �ƕ������Ă���Ȃ�
y=a(x-p)^2 +c
���Ƃ͑���2�_��������a,p�����߂�����B
���_��(p,q)�̎�
y=a(x-p)^2 +q
�Ə�����B
���_��y���W������ q = c �ƕ������Ă���Ȃ�
y=a(x-p)^2 +c
���Ƃ͑���2�_��������a,p�����߂�����B
2015/03/21(�y) 13:53:41.52ID:vzbJx1C7
>>59
���������2�_���W�Ă̂́A��������(x1,y1)��(x2,y2)��ʂ�Ƃ����Ӗ����H
���_(x0,y0)���� y��a(x�|x0)^2�{y0 (a��x0�͕s��)
2�_��ʂ邩��
y1��a(x1�|x0)^2�{y0
y2��a(x2�|x0)^2�{y0
���ꂩ��a��x0�����߂�
x0��(x1y2�|x2y1�{(x2�|x1)(y0�}��((y1�|y0)(y2�|y0))))/(y2�|y1)
a��((y2�|y1)/((x2�|x1)(�}��(y2�|y0)�|��(y1�|y0))))^2
���������2�_���W�Ă̂́A��������(x1,y1)��(x2,y2)��ʂ�Ƃ����Ӗ����H
���_(x0,y0)���� y��a(x�|x0)^2�{y0 (a��x0�͕s��)
2�_��ʂ邩��
y1��a(x1�|x0)^2�{y0
y2��a(x2�|x0)^2�{y0
���ꂩ��a��x0�����߂�
x0��(x1y2�|x2y1�{(x2�|x1)(y0�}��((y1�|y0)(y2�|y0))))/(y2�|y1)
a��((y2�|y1)/((x2�|x1)(�}��(y2�|y0)�|��(y1�|y0))))^2
62�P�R�Q�l�ڂ̑f������
2015/03/23(��) 00:25:06.33ID:ir46rWwV ���� {an} = n
{bn} = ��{an}
{cn} = n^{bn}
���̂悤�Ȏ����Ďg�p���Ă����v�Ȃ�ł����H
{bn} = ��{an}
{cn} = n^{bn}
���̂悤�Ȏ����Ďg�p���Ă����v�Ȃ�ł����H
2015/03/23(��) 00:28:58.15ID:co0y9gqo
���ʂɏ������炢�������Ƃ����v���Ȃ�
64�P�R�Q�l�ڂ̑f������
2015/03/23(��) 00:51:21.74ID:ir46rWwV ���ʂɏ����ƕ��G�ɂȂ��Ă��܂�Ȃ��ł����H
{an} = 1/2 - {(-1)^n}/2 = 1,0,1,0,�c
{a'n}= ��{an} = 1,1,2,2,3,3,�c
{a"n}= 1/2 - �k(-1)^{a'n}�l/2 = 1,1,0,0,1,1,0,0,�c
{bn} = {an}{a"n} =1,0,0,0,1,0,0,0,�c
������J��Ԃ������̂ł���
{an} = 1/2 - {(-1)^n}/2 = 1,0,1,0,�c
{a'n}= ��{an} = 1,1,2,2,3,3,�c
{a"n}= 1/2 - �k(-1)^{a'n}�l/2 = 1,1,0,0,1,1,0,0,�c
{bn} = {an}{a"n} =1,0,0,0,1,0,0,0,�c
������J��Ԃ������̂ł���
2015/03/23(��) 02:37:05.21ID:co0y9gqo
�ώG�ō���Ǝv���Ȃ�A�u���̂悤�ɏ������ƂƂ���v���̂悤�ɋL�@�ɂ���
���炩�̒f������������ł����āA�O�u�����Ȃ���������낤�Ƃ���
�]�v�ȐS�z������͎̂��Ԃ̖��ʁB
�Ƃ�����>>64�̂�a_n�Ƃ��ɂ��Ă钆�������S������Ă����̈ȊO�Ӗ��ʂ邵
���̂����Ƃ�����ƓY��������������������H
�����ȕւɂ��Ă����Ȃ̂������ς�킩��Ȃ����B
���炩�̒f������������ł����āA�O�u�����Ȃ���������낤�Ƃ���
�]�v�ȐS�z������͎̂��Ԃ̖��ʁB
�Ƃ�����>>64�̂�a_n�Ƃ��ɂ��Ă钆�������S������Ă����̈ȊO�Ӗ��ʂ邵
���̂����Ƃ�����ƓY��������������������H
�����ȕւɂ��Ă����Ȃ̂������ς�킩��Ȃ����B
66�P�R�Q�l�ڂ̑f������
2015/03/23(��) 03:11:51.07ID:ir46rWwV2015/03/23(��) 13:34:33.40ID:EE/K0nhY
�������ȑO�ɒ�`���������ĂȂ�����
68�P�R�Q�l�ڂ̑f������
2015/04/03(��) 23:49:21.03ID:M5Gz7L5H ���炵�܂��B
�����������璆�w�����x���̋^�₩�����ꂸ�\����܂��A
�ȉ��̂悤�ȃP�[�X�͂ǂ̂悤�ȉߒ��œ��������߂�����ł��傤���H
��w���낵�����肢���܂��B
---
3000�q��R��12�q/ℓ�̎Ԃ��A����100�q�����ĔR���12.5�q/ℓ�ɂ���ɂ́A
�R��L���ő�������ł��傤���H
---
�����������璆�w�����x���̋^�₩�����ꂸ�\����܂��A
�ȉ��̂悤�ȃP�[�X�͂ǂ̂悤�ȉߒ��œ��������߂�����ł��傤���H
��w���낵�����肢���܂��B
---
3000�q��R��12�q/ℓ�̎Ԃ��A����100�q�����ĔR���12.5�q/ℓ�ɂ���ɂ́A
�R��L���ő�������ł��傤���H
---
2015/04/04(�y) 01:17:22.24ID:i9n0ZDCo
�������܂����Bm(_ _)m
70�P�R�Q�l�ڂ̑f������
2015/04/30(��) 00:51:40.12ID:3vwj7477 �P�O�O�l�̐l�Ԃ�������Ƃ��́A
�������ɂȂ�m�����ł���Ή��������܂����ċ����Ă��������B
�������ɂȂ�m�����ł���Ή��������܂����ċ����Ă��������B
2015/04/30(��) 07:16:11.30ID:H46mYgsJ
�������ɂȂ炸�ɏ��������̂́A�Q��ނ̎肵���o�Ȃ������ꍇ�B
���̂Q��ނ̑g�ݍ��킹��3�ʂ�ł��ꂼ��̐l���o���肪2^100�ʂ�ō��킹��3*2^100�ʂ�A�ƌ����������A
�S������������o�����ꍇ���d�ɐ����Ă����ɁA���̏ꍇ�͂������ɂȂ邩��
6�ʂ�����������K�v������B
�Ƃ������ƂŁA�������ɂȂ�m����1-((3*2^100-6)/3^100)
���̂Q��ނ̑g�ݍ��킹��3�ʂ�ł��ꂼ��̐l���o���肪2^100�ʂ�ō��킹��3*2^100�ʂ�A�ƌ����������A
�S������������o�����ꍇ���d�ɐ����Ă����ɁA���̏ꍇ�͂������ɂȂ邩��
6�ʂ�����������K�v������B
�Ƃ������ƂŁA�������ɂȂ�m����1-((3*2^100-6)/3^100)
72�P�R�Q�l�ڂ̑f������
2015/04/30(��) 08:10:47.71ID:3vwj74772015/04/30(��) 10:10:16.85ID:H46mYgsJ
��1
2015/05/01(��) 16:30:06.40ID:FQHNO58e
2015/05/02(�y) 13:09:15.34ID:QEetcvSn
�|�e���V�����͍��������w�i���j�����Ă��Ȃ��������l�̒Ⴂ�z�ł͂Ȃ��A
����������Ȃ���������Ȃ��悤�ȓz�ɐ��w�������Ȃ���Ȃ��ꍇ
�ǂ̃��x���ɂ܂ň����グ�Ă���H
���Ȃ݂ɑS���ʃI�[�����A���o�J����Ȃ��āA����Ȗڂł͑S���͎��g�b�v������̂�
���w�i�����j������œI�ɂł��Ȃ��M�t�e�b�h�݂����ȓz
����������Ȃ���������Ȃ��悤�ȓz�ɐ��w�������Ȃ���Ȃ��ꍇ
�ǂ̃��x���ɂ܂ň����グ�Ă���H
���Ȃ݂ɑS���ʃI�[�����A���o�J����Ȃ��āA����Ȗڂł͑S���͎��g�b�v������̂�
���w�i�����j������œI�ɂł��Ȃ��M�t�e�b�h�݂����ȓz
76�P�R�Q�l�ڂ̑f������
2015/05/03(��) 23:16:06.92ID:eVrdAAUS2015/05/04(��) 03:36:32.70ID:AbDZuWDA
���w�������ł��Ȃ�������ܑ̂Ȃ����
���w�O�_�ő������_�Ȃ����鍑���Ƃ��Ȃ������w
���w�O�_�ő������_�Ȃ����鍑���Ƃ��Ȃ������w
2015/05/04(��) 13:18:33.40ID:o2nZLz32
>>75
����|�e���V���������z����
����|�e���V���������z����
2015/05/04(��) 20:41:04.33ID:UzZEFLkS
30��(�����n)�Ȃ��A�ŋߐ��w���͂��߂Ėʔ����ȂƎv���Ă�B
�㐔�w�̓��发�Ƃ��̘_�̖{���ēǂ�ł������ꂦ�Ȃ��A�Ǝv���Ă邾���Ȃ��A��肩��͋C���������z�Ă�肳���B
���������z�͂߂��炵���́H ��w�Ƃ��ŁA��Œ��u�ɂ��Ă��N��̂�������Ƃ����Ȃ��́H
�㐔�w�̓��发�Ƃ��̘_�̖{���ēǂ�ł������ꂦ�Ȃ��A�Ǝv���Ă邾���Ȃ��A��肩��͋C���������z�Ă�肳���B
���������z�͂߂��炵���́H ��w�Ƃ��ŁA��Œ��u�ɂ��Ă��N��̂�������Ƃ����Ȃ��́H
80�P�R�Q�l�ڂ̑f������
2015/05/04(��) 22:54:43.57ID:Fju44vtx >>79
���ǁA�قƂ�ǂ̐l�͒��������Ă��g���f���n�ɂ����Ȃ�Ȃ�����Ȃ�
���܂ɒ�N���D�_�����܂����Ƃ����ꂳ��̘b���o�ė��邯�ǂ��B
���ǁA�قƂ�ǂ̐l�͒��������Ă��g���f���n�ɂ����Ȃ�Ȃ�����Ȃ�
���܂ɒ�N���D�_�����܂����Ƃ����ꂳ��̘b���o�ė��邯�ǂ��B
2015/05/04(��) 23:30:58.23ID:UzZEFLkS
>>80
���X���肪�Ƃ��B
���m���Ƃ�悤�Ȉ̑�ȋƐт��c���ɂ́A�X�|�[�c�≹�y�̐��E�̂悤�ɁA�c��������̉p�ˋ��炪�K�v�A�Ƃ����̂͗������Ă������B
����ł��A���w�͖��l�ɓ`���Ă����f�G�Ȋw�₾���A�����m�邱�Ǝ��̂ɉ��l�͂���Ǝv���Ă�����ǁA
�u���w�͍˔\�̂Ȃ��҂�V�l���w�Ԃ��Ǝ��̂��`�����v
�u�w�ԍ˔\�Ƌ@��Ɍb�܂ꂽ�҂������w�K��������鍂�M�Ȋw�₾�v
�݂����ȕ��͋C���Ȃ�ƂȂ�������B
�Ɗw�s���ɂȂ�Ȃ����߂ɂ̓A�J�f�~�b�N�Ȍq������ǂ����ō��Ȃ��ƂȁA�Ƃ͎v���B
���X���肪�Ƃ��B
���m���Ƃ�悤�Ȉ̑�ȋƐт��c���ɂ́A�X�|�[�c�≹�y�̐��E�̂悤�ɁA�c��������̉p�ˋ��炪�K�v�A�Ƃ����̂͗������Ă������B
����ł��A���w�͖��l�ɓ`���Ă����f�G�Ȋw�₾���A�����m�邱�Ǝ��̂ɉ��l�͂���Ǝv���Ă�����ǁA
�u���w�͍˔\�̂Ȃ��҂�V�l���w�Ԃ��Ǝ��̂��`�����v
�u�w�ԍ˔\�Ƌ@��Ɍb�܂ꂽ�҂������w�K��������鍂�M�Ȋw�₾�v
�݂����ȕ��͋C���Ȃ�ƂȂ�������B
�Ɗw�s���ɂȂ�Ȃ����߂ɂ̓A�J�f�~�b�N�Ȍq������ǂ����ō��Ȃ��ƂȁA�Ƃ͎v���B
82�P�R�Q�l�ڂ̑f������
2015/05/05(��) 10:28:51.35ID:MgsCXzdh >>81
���w��Ƃ��Ă���ʂ̐l�����̍u�����������[�ւ͂��Ă邵
��Ƃ��Ă�镪�ɂ͕ʂɈ����͂Ȃ���B
����͂��̔ł��������A���̐��w�f���ł������B
�n��Ɏ�̃T�[�N��������Ȃ炻����ɓ����Ă������B
�����A���n�Ȃ�g�[�}�X�E�z�b�u�Y�Ƃ����N�w�҂�m���Ă邾�낤�B
���w�ɂ����Ă͋���ȓd�g�ꂳ��Ƃ��Ēm���A
�A�z�Ș_���������Ď��ʂ܂Ő��w�҂ɗ��ݑ������B
���̔ɂ��듚��������ƌĂ�鍓���l�����邯��
���������ςȕ����ɑ����Ė��f�������Ȃ���A�撣���ĕ����������B
���w��Ƃ��Ă���ʂ̐l�����̍u�����������[�ւ͂��Ă邵
��Ƃ��Ă�镪�ɂ͕ʂɈ����͂Ȃ���B
����͂��̔ł��������A���̐��w�f���ł������B
�n��Ɏ�̃T�[�N��������Ȃ炻����ɓ����Ă������B
�����A���n�Ȃ�g�[�}�X�E�z�b�u�Y�Ƃ����N�w�҂�m���Ă邾�낤�B
���w�ɂ����Ă͋���ȓd�g�ꂳ��Ƃ��Ēm���A
�A�z�Ș_���������Ď��ʂ܂Ő��w�҂ɗ��ݑ������B
���̔ɂ��듚��������ƌĂ�鍓���l�����邯��
���������ςȕ����ɑ����Ė��f�������Ȃ���A�撣���ĕ����������B
83�P�R�Q�l�ڂ̑f������
2015/05/05(��) 10:31:00.92ID:MgsCXzdh ���������ASNS�Ȃł����w�������l�̏W�܂�݂����Ȃ̂��������肷�邩��
�����������ɓ����Ă�������������Ȃ��B
�����������ɓ����Ă�������������Ȃ��B
84�P�R�Q�l�ڂ̑f������
2015/05/05(��) 11:40:38.99ID:ubjmsSZi TCG�ł̂��b�Ȃ�ł����莮���������ł��B
�Q�[���̃��[���Ƃ���
1.�K��̓_���ɒB�����珟��
2.��Ԃ̍Ō��1�_��
�܂��A�ȉ��̂悤�ȃJ�[�h������܂�
�����̎�Ԃ�1��A�ȉ��̂ǂ��炩��I��
1.���̃J�[�h�̏�ɃJ�E���^�[��1�u��
2.���̃J�[�h�̏�̃J�E���^�[�̐��������_��
���܁AN�_���Ə����Ƃ��āA��̃J�[�h�������̎�Ԃ�1������m���ɂȂ�܂ŏ�ɏo���Ă����Ƃ��A�����Ƃ����Ȃ���Ԃŏ����߂ɂ͊e�J�[�h�ɉ����J�E���^�[��u���������Ƃ��̎�Ԃ̐���m�肽���ł��B
��Ƃ��āAN=11�Am=3�Ȃ�
���1
�@1���ڂ���ɏo��1�ڂ̃J�E���^�[��u��
�@1�_�l��
���2
�@1���ڂ̏��2�ڂ̃J�E���^�[��u��
�@2���ڂ���ɏo��1�ڂ̃J�E���^�[��u��
�@1�_�l��
���3
�@1���ڂ�2�_�l��
�@2���ڂ�1�_�l��
�@3���ڂ���ɏo��1�ڂ̃J�E���^�[��u��
�@1�_�l��
���4
�@�e�J�[�h����A2+1+1=4�_�l��
�@��Ԃ̍Ō��1�_�l�����A����
�ƂȂ�A2,1,1�Ƃ����u�����ɂȂ�܂��B
��������������ꍇ������Ǝv���܂����A���̕ӂ��܂߂Ē莮���ł��Ȃ��ł��傤��
�Q�[���̃��[���Ƃ���
1.�K��̓_���ɒB�����珟��
2.��Ԃ̍Ō��1�_��
�܂��A�ȉ��̂悤�ȃJ�[�h������܂�
�����̎�Ԃ�1��A�ȉ��̂ǂ��炩��I��
1.���̃J�[�h�̏�ɃJ�E���^�[��1�u��
2.���̃J�[�h�̏�̃J�E���^�[�̐��������_��
���܁AN�_���Ə����Ƃ��āA��̃J�[�h�������̎�Ԃ�1������m���ɂȂ�܂ŏ�ɏo���Ă����Ƃ��A�����Ƃ����Ȃ���Ԃŏ����߂ɂ͊e�J�[�h�ɉ����J�E���^�[��u���������Ƃ��̎�Ԃ̐���m�肽���ł��B
��Ƃ��āAN=11�Am=3�Ȃ�
���1
�@1���ڂ���ɏo��1�ڂ̃J�E���^�[��u��
�@1�_�l��
���2
�@1���ڂ̏��2�ڂ̃J�E���^�[��u��
�@2���ڂ���ɏo��1�ڂ̃J�E���^�[��u��
�@1�_�l��
���3
�@1���ڂ�2�_�l��
�@2���ڂ�1�_�l��
�@3���ڂ���ɏo��1�ڂ̃J�E���^�[��u��
�@1�_�l��
���4
�@�e�J�[�h����A2+1+1=4�_�l��
�@��Ԃ̍Ō��1�_�l�����A����
�ƂȂ�A2,1,1�Ƃ����u�����ɂȂ�܂��B
��������������ꍇ������Ǝv���܂����A���̕ӂ��܂߂Ē莮���ł��Ȃ��ł��傤��
2015/05/05(��) 12:39:23.17ID:xt5KSXVT
>>75
�\���Z�u�t�ȂŁA����̓Z���X������1�N��������ďo���Ȃ��z�͏o���Ȃ���
���w�Ȃ�ł��邩�琔�w��点��ƌ����z�����邪�A�t�t�B
���~�[�⍂�Z1�N���ŁA3�N���炢�P�\���Ԃ�����Ȃ�܂������A���ꂩ��1�N�Ŏł���
���w��肾����ēz�ɐ��w�Ŏ�����Ƃ������Q�[�B
���̋��Ȃł���ȂɎ���Ȃ�A��֎���Ƃ��s�����Ă���ė~�����B
�I�{�����`���Ȃ�A���̃|�e���V�����Ȃ�AO�ő���c���H���炢�Ȃ���ꂿ�Ⴂ����������ww
�\���Z�u�t�ȂŁA����̓Z���X������1�N��������ďo���Ȃ��z�͏o���Ȃ���
���w�Ȃ�ł��邩�琔�w��点��ƌ����z�����邪�A�t�t�B
���~�[�⍂�Z1�N���ŁA3�N���炢�P�\���Ԃ�����Ȃ�܂������A���ꂩ��1�N�Ŏł���
���w��肾����ēz�ɐ��w�Ŏ�����Ƃ������Q�[�B
���̋��Ȃł���ȂɎ���Ȃ�A��֎���Ƃ��s�����Ă���ė~�����B
�I�{�����`���Ȃ�A���̃|�e���V�����Ȃ�AO�ő���c���H���炢�Ȃ���ꂿ�Ⴂ����������ww
2015/05/05(��) 14:47:19.38ID:NLIaQmNy
�����t�m���̖��ŁA�悭�b��ɂȂ�g�����v�̖�肠��܂���ˁB
52���̃g�����v�̎R�D����ꖇ�����_���ɑI��ŁA�G�����m�F�������ɉB���B
���̌�R�D����O���J�[�h��������Ƃ���A�O���Ƃ��_�C���ł������B
���̂Ƃ��A���̒��̃J�[�h���_�C���ł���m���́H�Ƃ�����ł��B
�����Ŏ���Ȃ̂ł����A�{���Ȃ�Γ�����10/49�ƂȂ�͂��ł���
�R�D����O���J�[�h��������Ƃ���O���Ƃ��_�C���������A�Ƃ����s����
�u�O�������āA�_�C�����O���łȂ��ꍇ�A�_�C���O���ƂȂ�܂ōs�����J��Ԃ��v�Ɖ��߂���
�u��ɎO�����_�C���Ƃ��������v�Ɖ��߂��Čv�Z���Ă��܂��Ɠ�����1/4�ɂȂ��Ă��܂��̂ŁA
�O�҂̉��߂Ōv�Z���˂Ȃ�Ȃ��ƗF�l���狳����ꂽ�̂ł������A
������]�݂����J���b�|�Ȃ̂ł��܂����ݍ��߂܂���B
�ǂȂ����A�O�҂ƌ�҂œ������ω����Ă��܂����R��������Ă���������Ƃ��ꂵ���ł��B
52���̃g�����v�̎R�D����ꖇ�����_���ɑI��ŁA�G�����m�F�������ɉB���B
���̌�R�D����O���J�[�h��������Ƃ���A�O���Ƃ��_�C���ł������B
���̂Ƃ��A���̒��̃J�[�h���_�C���ł���m���́H�Ƃ�����ł��B
�����Ŏ���Ȃ̂ł����A�{���Ȃ�Γ�����10/49�ƂȂ�͂��ł���
�R�D����O���J�[�h��������Ƃ���O���Ƃ��_�C���������A�Ƃ����s����
�u�O�������āA�_�C�����O���łȂ��ꍇ�A�_�C���O���ƂȂ�܂ōs�����J��Ԃ��v�Ɖ��߂���
�u��ɎO�����_�C���Ƃ��������v�Ɖ��߂��Čv�Z���Ă��܂��Ɠ�����1/4�ɂȂ��Ă��܂��̂ŁA
�O�҂̉��߂Ōv�Z���˂Ȃ�Ȃ��ƗF�l���狳����ꂽ�̂ł������A
������]�݂����J���b�|�Ȃ̂ł��܂����ݍ��߂܂���B
�ǂȂ����A�O�҂ƌ�҂œ������ω����Ă��܂����R��������Ă���������Ƃ��ꂵ���ł��B
2015/05/05(��) 21:04:19.85ID:pNT8IplW
52���̃g�����v�̎R�D����ꖇ�����_���ɑI��ŁA�G�����m�F�������ɉB���B
���̌�R�D����13���J�[�h��������Ƃ���A13���Ƃ��_�C���ł������B
���̂Ƃ��A���̒��̃J�[�h���_�C���ł���m���́H
���ꂪ�A1/4�Ȗ�͂Ȃ����Ƃ͔���͂��B�������o���_�ɍl����悢�B
���̌�R�D����13���J�[�h��������Ƃ���A13���Ƃ��_�C���ł������B
���̂Ƃ��A���̒��̃J�[�h���_�C���ł���m���́H
���ꂪ�A1/4�Ȗ�͂Ȃ����Ƃ͔���͂��B�������o���_�ɍl����悢�B
2015/05/05(��) 21:59:19.42ID:NLIaQmNy
>>87
���肪�Ƃ��������܂���
���肪�Ƃ��������܂���
89�P�R�Q�l�ڂ̑f������
2015/05/06(��) 11:49:01.38ID:VbuEvzjx �ւ�����l���F�s�K�ɂȂ�|�����J���\�z�Ƃ̎��ł���
�y�����}������ȊO�ł͒N���ǂ�ȕs�K�Ɍ�����ꂽ�̂ł����H
�y�����}������ȊO�ł͒N���ǂ�ȕs�K�Ɍ�����ꂽ�̂ł����H
9081
2015/05/06(��) 13:52:55.74ID:Sx27mFT/2015/06/30(��) 16:46:14.45ID:hS6LPa2C0
>>89
�p�p
�p�p
2015/11/25(��) 20:45:46.80ID:Mgsmrccw
http://47.media.tumblr.com/bfa26afd58h0d7b16/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://65.media.tumblr.com/bfa26afd58h0d7b1786/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://41.media.tumblr.com/gya26afd58h0d7b166/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://42.media.tumblr.com/bfhu6afd58h0d7b176/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://43.media.tumblr.com/bfa26afd58h0d7b186/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://45.media.tumblr.com/bfio6afd58h0d7b19/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://46.media.tumblr.com/bfa26afd58h0d7b106/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://41.media.tumblr.com/bfhjafd58h0d7b166/tumblr_nc0xtt1s4oww8o1_980.jpg
http://43.media.tumblr.com/bfa26afd0d7b233/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://65.media.tumblr.com/bfa26afd58h0d7b1786/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://41.media.tumblr.com/gya26afd58h0d7b166/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://42.media.tumblr.com/bfhu6afd58h0d7b176/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://43.media.tumblr.com/bfa26afd58h0d7b186/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://45.media.tumblr.com/bfio6afd58h0d7b19/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://46.media.tumblr.com/bfa26afd58h0d7b106/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
http://41.media.tumblr.com/bfhjafd58h0d7b166/tumblr_nc0xtt1s4oww8o1_980.jpg
http://43.media.tumblr.com/bfa26afd0d7b233/tumblr_nc0x7iBCtt1s4oww8o1_980.jpg
93������
2015/12/30(��) 19:55:22.95ID:QbSCJS+S a, b, c�𐳎����Ƃ���B
a^3 b^6 + b^3 c^6 + c^3 a^6 + 3a^3 b^3 c^3 �� abc (a^3 b^3 + b^3 c^3 + c^3 a^3) + a^2 b^2 c^2 (a^3 + b^3 + c^3)
���ؖ�����B
���肢���܂��B�B�B
a^3 b^6 + b^3 c^6 + c^3 a^6 + 3a^3 b^3 c^3 �� abc (a^3 b^3 + b^3 c^3 + c^3 a^3) + a^2 b^2 c^2 (a^3 + b^3 + c^3)
���ؖ�����B
���肢���܂��B�B�B
2015/12/31(��) 15:16:23.19ID:4pacScsf
x=abb,y=bcc,z=caa�Ƃ���ƁAx,y,z��������
(����)=x^3+y^3+z^3+3xyz=(x+y+z)(x^2+y^2+z^2-xy-yz-zx)+6xyz=(x+y+z)^3-3(x+y+z)(xy+yz+zx)+6xyz
(�E��)=xy(x+y)+yz(y+z)+zx(z+x)=(x+y+z)(xy+yz+zx)-3xyz
(����)-(�E��)=(x+y+z)^3-4(x+y+z)(xy+yz+zx)+9xyz=(x+y-2z)(x-y)^2+z((x-z-(y-z)/2)^2+(3/4)(y-z)^2)
���̎��́Ax,y,z�̓���ւ��ɉ����đΏ̂Ȃ̂ŁA�ł����������̂�z�Ƃ���ƁA
���̎����ł��邱�Ƃ��m�F�ł���
(����)=x^3+y^3+z^3+3xyz=(x+y+z)(x^2+y^2+z^2-xy-yz-zx)+6xyz=(x+y+z)^3-3(x+y+z)(xy+yz+zx)+6xyz
(�E��)=xy(x+y)+yz(y+z)+zx(z+x)=(x+y+z)(xy+yz+zx)-3xyz
(����)-(�E��)=(x+y+z)^3-4(x+y+z)(xy+yz+zx)+9xyz=(x+y-2z)(x-y)^2+z((x-z-(y-z)/2)^2+(3/4)(y-z)^2)
���̎��́Ax,y,z�̓���ւ��ɉ����đΏ̂Ȃ̂ŁA�ł����������̂�z�Ƃ���ƁA
���̎����ł��邱�Ƃ��m�F�ł���
2016/11/17(��) 12:51:38.34ID:lYZOwLPO
����������ŗL������薳�����̕������|�I�ɑ������Ƃ͂ǂ�����킩��܂����H
964����
2016/11/26(�y) 17:14:36.10ID:ZP6EMTdj *�ɓ���̂͂ǂ�ł��傤�H
�@�������o���Ȃ��A�z�̕��n�ɁA�����낭������
9 38 47 4
6 35 42 *
12 21 23 27
�y1�z10�@�y2�z-5�@�y3�z32�@�y4�z18
�@�������o���Ȃ��A�z�̕��n�ɁA�����낭������
9 38 47 4
6 35 42 *
12 21 23 27
�y1�z10�@�y2�z-5�@�y3�z32�@�y4�z18
97�� ��2VB8wsVUoo
2016/11/26(�y) 20:14:04.58ID:4yD7g79E ��
98�� ��2VB8wsVUoo
2016/11/26(�y) 20:14:22.66ID:4yD7g79E ��
99�� ��2VB8wsVUoo
2016/11/26(�y) 20:14:38.38ID:4yD7g79E ��
100�� ��2VB8wsVUoo
2016/11/26(�y) 20:14:54.90ID:4yD7g79E ��
101�� ��2VB8wsVUoo
2016/11/26(�y) 20:15:11.49ID:4yD7g79E ��
102�� ��2VB8wsVUoo
2016/11/26(�y) 20:15:26.00ID:4yD7g79E ��
103�� ��2VB8wsVUoo
2016/11/26(�y) 20:15:39.84ID:4yD7g79E ��
104�� ��2VB8wsVUoo
2016/11/26(�y) 20:15:55.59ID:4yD7g79E ��
105�� ��2VB8wsVUoo
2016/11/26(�y) 20:16:12.00ID:4yD7g79E ��
106�� ��2VB8wsVUoo
2016/11/26(�y) 20:16:28.59ID:4yD7g79E ��
107�P�R�Q�l�ڂ̑f������
2016/11/26(�y) 22:18:30.22ID:IMGdvgBC ���̂��Ɣn�����Ă��ł����H
���A�q�}�����Ȕn�����ˁi��
���A�q�}�����Ȕn�����ˁi��
108�� ��2VB8wsVUoo
2016/11/26(�y) 22:53:18.34ID:4yD7g79E ��
110�P�R�Q�l�ڂ̑f������
2016/11/27(��) 00:09:47.91ID:ZSnU31r+ �m���Ă��������Ǝv���܂����A�Ƃ��閟��ł���ȂȂ��Ȃ����o�肳��܂����B
3����1�C�̑l��߂炦��L��3�C����B�l100
�C��߂炦��̂ɂ͉��������邩�B
������99�C�̑l���߂炦�Ă���c��̈�C��߂炦��̂ɁA�L�͋��͂��Ă��f�����l��߂炦��Ƃ͏�����Ă��Ȃ��̂ŁA3��������B�����102���ƂȂ邻���Ȃ̂ł����A�[���������܂���B
�L��3����1�C�̑l��߂炦��̂ŁA�ꕪ��0.3333....�C�߂炦��B���̔L���O�C����̂łP����0.99999.....�C�߂炦�邱�Ƃ��o����B0.99999......�Ƃ����z������1�Ɠ������̂ŁA100�C�̑l��߂܂���ɂ�100��������B
���̂悤�ɍl���邱�Ƃ��o����Ǝv���̂ł����A�����Ԉ���Ă���̂ł��傤���B
3����1�C�̑l��߂炦��L��3�C����B�l100
�C��߂炦��̂ɂ͉��������邩�B
������99�C�̑l���߂炦�Ă���c��̈�C��߂炦��̂ɁA�L�͋��͂��Ă��f�����l��߂炦��Ƃ͏�����Ă��Ȃ��̂ŁA3��������B�����102���ƂȂ邻���Ȃ̂ł����A�[���������܂���B
�L��3����1�C�̑l��߂炦��̂ŁA�ꕪ��0.3333....�C�߂炦��B���̔L���O�C����̂łP����0.99999.....�C�߂炦�邱�Ƃ��o����B0.99999......�Ƃ����z������1�Ɠ������̂ŁA100�C�̑l��߂܂���ɂ�100��������B
���̂悤�ɍl���邱�Ƃ��o����Ǝv���̂ł����A�����Ԉ���Ă���̂ł��傤���B
111�P�R�Q�l�ڂ̑f������
2016/11/27(��) 00:14:59.42ID:5x8HX4Fd �L�͋��͂��܂����
112�� ��2VB8wsVUoo
2016/11/27(��) 05:06:31.24ID:Efqxhb2y ��
113�� ��2VB8wsVUoo
2016/11/27(��) 05:06:53.98ID:Efqxhb2y ��
114�� ��2VB8wsVUoo
2016/11/27(��) 05:07:13.15ID:Efqxhb2y ��
115�� ��2VB8wsVUoo
2016/11/27(��) 05:07:30.61ID:Efqxhb2y ��
116�� ��2VB8wsVUoo
2016/11/27(��) 05:07:49.11ID:Efqxhb2y ��
117�� ��2VB8wsVUoo
2016/11/27(��) 05:08:06.64ID:Efqxhb2y ��
118�� ��2VB8wsVUoo
2016/11/27(��) 05:08:25.23ID:Efqxhb2y ��
119�� ��2VB8wsVUoo
2016/11/27(��) 05:08:46.18ID:Efqxhb2y ��
120�� ��2VB8wsVUoo
2016/11/27(��) 05:09:05.27ID:Efqxhb2y ��
121�� ��2VB8wsVUoo
2016/11/27(��) 05:09:28.44ID:Efqxhb2y ��
2016/11/29(��) 13:52:46.08ID:o0IEgquJ
������Ȃ��Ă��r�炵���K��
123�P�R�Q�l�ڂ̑f������
2016/11/29(��) 17:46:42.56ID:KqAdU9Bo ���ʏ�ɕ����̓_���^�����Ă���Ƃ��A
���̂��ׂĂ̓_��ʂ�ŏ��̑��p�`�����߂闝�_�͂���܂��ł��傤���B
�ʑ��p�`�ł͂Ȃ��A
�������镡�G�ȑ��p�`��_����݂������A
�Ƃ������Ƃł��B
�ȏ�A��낵�����肢���܂��B
���̂��ׂĂ̓_��ʂ�ŏ��̑��p�`�����߂闝�_�͂���܂��ł��傤���B
�ʑ��p�`�ł͂Ȃ��A
�������镡�G�ȑ��p�`��_����݂������A
�Ƃ������Ƃł��B
�ȏ�A��낵�����肢���܂��B
124�P�R�Q�l�ڂ̑f������
2016/11/29(��) 17:53:51.22ID:KqAdU9Bo ���܂ς��Ǝv���������@�Ƃ��ẮA
�ʊ܂����������ƁA
�O�p�`�������āA
��܂����_�������Ȃ�܂Œ����ӂ�������Ă����c
�悤�Ȃ��ł��傤���B
�ʊ܂����������ƁA
�O�p�`�������āA
��܂����_�������Ȃ�܂Œ����ӂ�������Ă����c
�悤�Ȃ��ł��傤���B
125�� ��2VB8wsVUoo
2016/11/29(��) 18:05:57.50ID:Hn/14aJB ��
126�� ��2VB8wsVUoo
2016/11/29(��) 18:06:17.06ID:Hn/14aJB ��
127�� ��2VB8wsVUoo
2016/11/29(��) 18:06:36.66ID:Hn/14aJB ��
128�� ��2VB8wsVUoo
2016/11/29(��) 18:07:01.80ID:Hn/14aJB ��
129�� ��2VB8wsVUoo
2016/11/29(��) 18:07:19.13ID:Hn/14aJB ��
130�� ��2VB8wsVUoo
2016/11/29(��) 18:07:40.40ID:Hn/14aJB ��
131�� ��2VB8wsVUoo
2016/11/29(��) 18:08:00.48ID:Hn/14aJB ��
132�� ��2VB8wsVUoo
2016/11/29(��) 18:08:20.60ID:Hn/14aJB ��
133�� ��2VB8wsVUoo
2016/11/29(��) 18:08:38.43ID:Hn/14aJB ��
134�� ��2VB8wsVUoo
2016/11/29(��) 18:08:59.25ID:Hn/14aJB ��
2016/12/02(��) 09:27:30.51ID:7xVhMtBb
>>94
�k�V���[�A�̕s�����l
x,y,z��0 �̂Ƃ�
�@(x+y+z)^3 -4(x+y+z)(xy+yz+zx) +9xyz
= x(x-y)(x-z) + y(y-z)(y-x) + z(z-x)(z-y) �� �e_1(x,y,z)
= 0,
(����1)
y��x��z�̒��Ԃɂ���Ƃ����
x-y+z��0�C(x-y)(y-z)��0 ������
�e_1(x,y,z) = x(x-y)^2 + (x-y+z)(x-y)(y-z) + z(y-z)^2 ��0,
(����2)
�Ώ̐���ۂ���
�e_1(x,y,z) = {xy(xx-yy)^2 + yz(yy-zz)^2 + zx(zz-xx)^2}/{(x+y)(y+z)(z+x)} ��0,
�k�V���[�A�̕s�����l
x,y,z��0 �̂Ƃ�
�@(x+y+z)^3 -4(x+y+z)(xy+yz+zx) +9xyz
= x(x-y)(x-z) + y(y-z)(y-x) + z(z-x)(z-y) �� �e_1(x,y,z)
= 0,
(����1)
y��x��z�̒��Ԃɂ���Ƃ����
x-y+z��0�C(x-y)(y-z)��0 ������
�e_1(x,y,z) = x(x-y)^2 + (x-y+z)(x-y)(y-z) + z(y-z)^2 ��0,
(����2)
�Ώ̐���ۂ���
�e_1(x,y,z) = {xy(xx-yy)^2 + yz(yy-zz)^2 + zx(zz-xx)^2}/{(x+y)(y+z)(z+x)} ��0,
2016/12/23(��) 06:34:51.34ID:N1oFke4u
>>86
�����t�m���̖��ŁA�悭�b��ɂȂ�N�����g���̖�������܂����B
�����t�m���̖��ŁA�悭�b��ɂȂ�N�����g���̖�������܂����B
2017/01/17(��) 07:56:47.99ID:Qggnth+1
�k���l
log(n!) �[ (n + 1/2)log(n) �{ n �� 0.8918
�������B
log(n!) �[ (n + 1/2)log(n) �{ n �� 0.8918
�������B
2017/01/17(��) 09:13:41.35ID:Qggnth+1
>>137
x=k �Őڐ����Ђ��ƁA�ʐ����
�@log(k) �{ ��(x-k�j�� log(x),
���@log(k�j�� ��[k-1/2�Ck+1/2�nlog(x)dx,
���@log(n!�j�� ��[k=2�Cn�nlog(k)
�� ��[3/2, n+1/2] log(x)dx
���m x�log(x)�|x ](3/2��n+1/2)
���in+1/2)log(n+1/2)�|n�|(3/2)log(3/2)�{1
���in+1/2)log(n)�|���{(3/2){1�|log(3/2)}�@�@(*)
���in+1/2)log(n)�|���{0.8918
*)�@log(n+1/2)�|log(n)
��log(1�{1/2n)
���|log(1�|1/(2n+1))
��1/(2n+1)�{1/{2(2n+1)^2}�{�c�c,
x=k �Őڐ����Ђ��ƁA�ʐ����
�@log(k) �{ ��(x-k�j�� log(x),
���@log(k�j�� ��[k-1/2�Ck+1/2�nlog(x)dx,
���@log(n!�j�� ��[k=2�Cn�nlog(k)
�� ��[3/2, n+1/2] log(x)dx
���m x�log(x)�|x ](3/2��n+1/2)
���in+1/2)log(n+1/2)�|n�|(3/2)log(3/2)�{1
���in+1/2)log(n)�|���{(3/2){1�|log(3/2)}�@�@(*)
���in+1/2)log(n)�|���{0.8918
*)�@log(n+1/2)�|log(n)
��log(1�{1/2n)
���|log(1�|1/(2n+1))
��1/(2n+1)�{1/{2(2n+1)^2}�{�c�c,
2017/01/17(��) 09:46:34.27ID:Qggnth+1
>>137
x=k �Őڂ�����������Ђ��ƁA
{log(x)�p" = (1/x�j'���|1/xx ���
�@log(k)�{��(x-k)�|(1/2kk)(x-k)^2 �� log(x),
���@log(k�j�� ��[k-1/2�Ck+1/2] log(x)dx �{1/(24kk),
���@log(n!�j���[k=2�Cn�nlog(k)
����[3/2�Cn+1/2�nlog(x)dx �{(1/24)�[k=2�An] 1/kk
��(n+1/2)log(n)�|n�{0.8918�{(1/24)(��/6�|1)
��(n+1/2)log(n)�|n�{0.91867
�萔���� (1/2)log(2��)��0.91894 �ɋ߂Â����A
���̕��@�ł͐��m�Ȓl�͏o�Ȃ��B
����ɂ̓E�H���X�̌����Ȃǂ��g���K�v������B
x=k �Őڂ�����������Ђ��ƁA
{log(x)�p" = (1/x�j'���|1/xx ���
�@log(k)�{��(x-k)�|(1/2kk)(x-k)^2 �� log(x),
���@log(k�j�� ��[k-1/2�Ck+1/2] log(x)dx �{1/(24kk),
���@log(n!�j���[k=2�Cn�nlog(k)
����[3/2�Cn+1/2�nlog(x)dx �{(1/24)�[k=2�An] 1/kk
��(n+1/2)log(n)�|n�{0.8918�{(1/24)(��/6�|1)
��(n+1/2)log(n)�|n�{0.91867
�萔���� (1/2)log(2��)��0.91894 �ɋ߂Â����A
���̕��@�ł͐��m�Ȓl�͏o�Ȃ��B
����ɂ̓E�H���X�̌����Ȃǂ��g���K�v������B
2017/01/17(��) 23:42:57.02ID:Qggnth+1
>>139
x=k �̂܂���Taylor�W�J���āA
�@log(x) = log(k)�{�[k=1�C���j�i-1)^(L-1)�(1/L){(x-k)/k}^L,
L����̂Ƃ���0�ɂȂ�A�����̂ݎc��B
��[k-1/2�Ck+1/2�nlog(x)dx = log(k)�|��[L=1�C���j1/{2L�(2L+1)�(2k)^(2L)}
k=2�`n �ł�����
��[3/2�Cn+1/2�nlog(x)dx = log(n!)�|��[L=1�C���j�o��(2L)�|1}/{2L(2L+1)�4^L}
���� ���in+1/2)log(n)�|n�{(3/2){1�|log(3/2)�p�{O(1/n�j�Ȃ̂ŁA
log(n!)�|(n+1/2)log(n)�{n �� (3/2){1�|log(3/2)}�{��[L=1�C���j�o��(2L)�|1}/{2L(2L+1)�4^L}
��(1/2)log(2��)�@�@(n�����j
��0.9189385
�Əo�܂��B�B�B
x=k �̂܂���Taylor�W�J���āA
�@log(x) = log(k)�{�[k=1�C���j�i-1)^(L-1)�(1/L){(x-k)/k}^L,
L����̂Ƃ���0�ɂȂ�A�����̂ݎc��B
��[k-1/2�Ck+1/2�nlog(x)dx = log(k)�|��[L=1�C���j1/{2L�(2L+1)�(2k)^(2L)}
k=2�`n �ł�����
��[3/2�Cn+1/2�nlog(x)dx = log(n!)�|��[L=1�C���j�o��(2L)�|1}/{2L(2L+1)�4^L}
���� ���in+1/2)log(n)�|n�{(3/2){1�|log(3/2)�p�{O(1/n�j�Ȃ̂ŁA
log(n!)�|(n+1/2)log(n)�{n �� (3/2){1�|log(3/2)}�{��[L=1�C���j�o��(2L)�|1}/{2L(2L+1)�4^L}
��(1/2)log(2��)�@�@(n�����j
��0.9189385
�Əo�܂��B�B�B
2017/01/18(��) 00:23:34.94ID:obAyxtVd
��(L) = ��[k=1�C��) 1/(k^L)
��(2) = (1/6)��^2,
��(4) = (1/90)��^4,
��(6) = (1/945)��^6,
��(8) = (1/9450)��^8,
��(10) = (1/93555)��^10,
��(2) = (1/6)��^2,
��(4) = (1/90)��^4,
��(6) = (1/945)��^6,
��(8) = (1/9450)��^8,
��(10) = (1/93555)��^10,
142�P�R�Q�l�ڂ̑f������
2017/02/23(��) 18:22:52.75ID:7hgOyYfE �X���Ⴂ�Ȃ�U�����A�D�������͉��A�X�������肢���܂��B
77���̏��ŗp�G�^�m�[��500ml������܂��B
����������70���ɂ���ɂ́A��ml�̐����K�v�ɂȂ�̂ł��傤���H
77���̏��ŗp�G�^�m�[��500ml������܂��B
����������70���ɂ���ɂ́A��ml�̐����K�v�ɂȂ�̂ł��傤���H
2017/02/23(��) 18:38:59.92ID:KO1byttB
77%�̃G�^�m�[��500ml��
�G�^�m�[��385ml�Ɛ�115ml�����������ł͂Ȃ�
77%�G�^�m�[���̖��x���K�v
�G�^�m�[��385ml�Ɛ�115ml�����������ł͂Ȃ�
77%�G�^�m�[���̖��x���K�v
144�P�R�Q�l�ڂ̑f������
2017/02/23(��) 19:01:50.12ID:7hgOyYfE >>143
�������݁A���肪�Ƃ��������܂��B
�����Ƃ��w�E�́Avol%�Ɋւ��鎖���낤�Ɛ��@���܂��B
��������Ƃō\���܂���B��ml�̐����K�v�ɂȂ�̂ł��傤���H
�������݁A���肪�Ƃ��������܂��B
�����Ƃ��w�E�́Avol%�Ɋւ��鎖���낤�Ɛ��@���܂��B
��������Ƃō\���܂���B��ml�̐����K�v�ɂȂ�̂ł��傤���H
2017/02/23(��) 19:17:09.64ID:KO1byttB
���x�ɂ���Ă����x���ς��悤�ŁA�������l�͔���Ȃ����A
0.85�ʂ��Ó��Ǝv����̂ŁA0.85�Ƃ��Čv�Z����ƁA
77%�G�^�m�[��500ml�Ƃ́A77%�G�^�m�[��425g�̎��ł���A
����́A327.25g�̃G�^�m�[����97.75g�̐������킹�ĕ��̎�
327.25g��70%�ɂȂ�悤�ȏd���Ƃ́@327.25��0.7=467.5g�̎��ł���A
����ƁA���̏d���Ƃ̍��@467.5-425=42.5��������ׂ����̏d��
0.85�ʂ��Ó��Ǝv����̂ŁA0.85�Ƃ��Čv�Z����ƁA
77%�G�^�m�[��500ml�Ƃ́A77%�G�^�m�[��425g�̎��ł���A
����́A327.25g�̃G�^�m�[����97.75g�̐������킹�ĕ��̎�
327.25g��70%�ɂȂ�悤�ȏd���Ƃ́@327.25��0.7=467.5g�̎��ł���A
����ƁA���̏d���Ƃ̍��@467.5-425=42.5��������ׂ����̏d��
146�P�R�Q�l�ڂ̑f������
2017/02/24(��) 08:35:33.08ID:Njmhg3WD2017/02/24(��) 20:41:29.09ID:hpVrglG4
�ȂA����܂萔�w�̘b��ł��Ȃ�����ǁc
77vol%�̃G�^�m�[���ɐ���������70vol%�ɂ���ɂ́A
77%�G�^�m�[��100��77�~70mL�����X�t���X�R���ɓ���A
���������đS�ʂ�100mL�ɂȂ�悤�ɂ���B
�̐ς��v��������������悤�Ȃ��Ƃ́A���ʂ��Ȃ��B
����́A���Ԃw�����Z�̉��w�̋��ȏ��ɏ����Ă���B
�����Đ��̗ʂ��m�肽����c�@���ɂ��ƁA
https://www.nmij.jp/~dsmnt-tech/cal-ver/alcohol.pdf
70%�G�^�m�[���̖��x��0.890g/mL�A
77%�G�^�m�[���̖��x��0.872g/mL�A
100%�G�^�m�[���̖��x��0.794g/mL�B
77vol%�G�^�m�[��500mL�́A
�n�t500�~0.872=436g����
�G�^�m�[��500�~(77/100)�~0.794=306g����������B
70vol%�G�^�m�[���́A100mL������
�n�t100�~0.890=89.0g�A
�G�^�m�[��100�~(70/100)�~0.794=55.6g������A
�G�^�m�[��306g������ƑS�ʂ�
306��55.6�~89.0=489g�B
489-436=53g�̐���������悢�v�Z�ɂȂ�B
77vol%�̃G�^�m�[���ɐ���������70vol%�ɂ���ɂ́A
77%�G�^�m�[��100��77�~70mL�����X�t���X�R���ɓ���A
���������đS�ʂ�100mL�ɂȂ�悤�ɂ���B
�̐ς��v��������������悤�Ȃ��Ƃ́A���ʂ��Ȃ��B
����́A���Ԃw�����Z�̉��w�̋��ȏ��ɏ����Ă���B
�����Đ��̗ʂ��m�肽����c�@���ɂ��ƁA
https://www.nmij.jp/~dsmnt-tech/cal-ver/alcohol.pdf
70%�G�^�m�[���̖��x��0.890g/mL�A
77%�G�^�m�[���̖��x��0.872g/mL�A
100%�G�^�m�[���̖��x��0.794g/mL�B
77vol%�G�^�m�[��500mL�́A
�n�t500�~0.872=436g����
�G�^�m�[��500�~(77/100)�~0.794=306g����������B
70vol%�G�^�m�[���́A100mL������
�n�t100�~0.890=89.0g�A
�G�^�m�[��100�~(70/100)�~0.794=55.6g������A
�G�^�m�[��306g������ƑS�ʂ�
306��55.6�~89.0=489g�B
489-436=53g�̐���������悢�v�Z�ɂȂ�B
2017/02/25(�y) 02:34:32.91ID:KwawTau+
>>146
145�ł�77%�Ƃ����̂��A���ʕS�����Ƃ��Čv�Z���܂������A�����̐ϕS����vol%�Ȃ�����͕�
77vol%�G�^�m�[���Ƃ����̂́A�����G�^�m�[��77ml�Ɛ�23ml�̊����ō������ꂽ���̂��ƁB
���̂Ƃ��A�̐ς͒P���Șa�ł���100ml�ɂ͂Ȃ�܂���B
�ĂP�Okg�Ƒ哤�P�Okg��������ƂQ�O�����̍��������ł��܂����A
�ĂP�O�k�Ƒ哤�P�O�k�������Ă��Q�O�k�̍������ɂ͂Ȃ�Ȃ��̂Ɠ��l�ł��B
147����́A�o�T��������ƁA�̐ϕS�����Ƃ��āA�������A�v�Z���ł́A�u�̐ϔZ�x�v�Ƃ���
�����Ă���悤�ł��B
�̐ϔZ�x77%�Ƃ́A�����G�^�m�[��77ml�ɁA�S�̂�100ml�ɂȂ�܂Ő����������Ƃ��̔Z�x�̎��ŁA
�̐ϕS����77vol%�Ƃ��A���ʕS����77%�Ƃ��قȂ�T�O�ł��B
145�ł�77%�Ƃ����̂��A���ʕS�����Ƃ��Čv�Z���܂������A�����̐ϕS����vol%�Ȃ�����͕�
77vol%�G�^�m�[���Ƃ����̂́A�����G�^�m�[��77ml�Ɛ�23ml�̊����ō������ꂽ���̂��ƁB
���̂Ƃ��A�̐ς͒P���Șa�ł���100ml�ɂ͂Ȃ�܂���B
�ĂP�Okg�Ƒ哤�P�Okg��������ƂQ�O�����̍��������ł��܂����A
�ĂP�O�k�Ƒ哤�P�O�k�������Ă��Q�O�k�̍������ɂ͂Ȃ�Ȃ��̂Ɠ��l�ł��B
147����́A�o�T��������ƁA�̐ϕS�����Ƃ��āA�������A�v�Z���ł́A�u�̐ϔZ�x�v�Ƃ���
�����Ă���悤�ł��B
�̐ϔZ�x77%�Ƃ́A�����G�^�m�[��77ml�ɁA�S�̂�100ml�ɂȂ�܂Ő����������Ƃ��̔Z�x�̎��ŁA
�̐ϕS����77vol%�Ƃ��A���ʕS����77%�Ƃ��قȂ�T�O�ł��B
2017/02/25(�y) 02:34:57.08ID:KwawTau+
142�ł�77%��77vol%�ł���A��낤�Ƃ��Ă���70%�Ƃ����̂�70vol%���Ƃ���ƁA���̂悤�ɂȂ�܂��B
147����̏o�T���̐������g�킹�Ă��炤�ƁA���̖��x��0.9991�Ȃ̂ŁA
77ml�̖����G�^�m�[����23ml�̐������������
���ʂ́@77ml�~0.7940g/ml+23ml�~0.9991g/ml=84.1173g
���̎��̖��x��0.8718�Ȃ̂ŁA�̐ς�84.1173g��0.8718g/ml=96.487ml
�]���āA77vol%�G�^�m�[��500ml�ɂ�
77ml�@�~�@0.7940g/ml�@�~�@(500ml/96.487ml)�@=316.82g�@�̖����G�^�m�[�����܂܂�Ă���A
���̎��̎��ʂ́A84.1173g�@�~�@(500ml/96.487ml)�@��435.90g�@����܂�
����A70vol%�G�^�m�[���Ƃ́A�����G�^�m�[��70ml�ƁA��30ml�̊����ō������ꂽ���̂Ȃ̂ŁA
���̉t�S�̂̎��ʂ́A���ʂ́@70ml�~0.7940g/ml+30ml�~0.9991g/ml=85.553g
����A�G�^�m�[�������̎��ʂ́A70ml�~0.7940=55.58g
���ꂪ�A316.82g����̂ŁA�ł�������̑S�̂̎��ʂ�85.553g�~(316.82g/55.58g)=487.67g
�]���āA487.67-435.90=51.77g�@���ꂪ�A�����ׂ����̎���
147����̏o�T���̐������g�킹�Ă��炤�ƁA���̖��x��0.9991�Ȃ̂ŁA
77ml�̖����G�^�m�[����23ml�̐������������
���ʂ́@77ml�~0.7940g/ml+23ml�~0.9991g/ml=84.1173g
���̎��̖��x��0.8718�Ȃ̂ŁA�̐ς�84.1173g��0.8718g/ml=96.487ml
�]���āA77vol%�G�^�m�[��500ml�ɂ�
77ml�@�~�@0.7940g/ml�@�~�@(500ml/96.487ml)�@=316.82g�@�̖����G�^�m�[�����܂܂�Ă���A
���̎��̎��ʂ́A84.1173g�@�~�@(500ml/96.487ml)�@��435.90g�@����܂�
����A70vol%�G�^�m�[���Ƃ́A�����G�^�m�[��70ml�ƁA��30ml�̊����ō������ꂽ���̂Ȃ̂ŁA
���̉t�S�̂̎��ʂ́A���ʂ́@70ml�~0.7940g/ml+30ml�~0.9991g/ml=85.553g
����A�G�^�m�[�������̎��ʂ́A70ml�~0.7940=55.58g
���ꂪ�A316.82g����̂ŁA�ł�������̑S�̂̎��ʂ�85.553g�~(316.82g/55.58g)=487.67g
�]���āA487.67-435.90=51.77g�@���ꂪ�A�����ׂ����̎���
2017/02/25(�y) 03:46:32.28ID:TQr5kx/y
>>148 �����H
vol%�́A�̐ϕ�������Ȃ��A�̐ϔZ�x��\���L�����Ǝv�����ǂȁB
Wikipedia���A���Ɏ^�����Ă���B��
https://ja.wikipedia.org/wiki/%E6%BF%83%E5%BA%A6
���̐ρi�e�ʁj�p�[�Z���g�Z�x�������L���Ƃ���[vol%]����
���Z�x�̒P�ʂ�\������volume�𗪂���vol�̌��t����̂���ʂł���B
����A�̐ϕ����͂���B��
https://ja.wikipedia.org/wiki/%E4%BD%93%E7%A9%8D%E5%88%86%E7%8E%87
�g����ʂ��A������ƈႤ�B
vol%�́A�Ȋw�����A����܂茵������Ȃ��Ɩ��p�Ɏg���邱�Ƃ������A
���ہA���𑫂��đ��̐ς����邱�Ƃō����B
��̓I�ɂ́A����Ȃ�B��
http://www.imazu-chemical.co.jp/77eta.pdf
���ōl���Ȃ��ŁA���w�̖{��ǂނƂ�����B
vol%�́A�̐ϕ�������Ȃ��A�̐ϔZ�x��\���L�����Ǝv�����ǂȁB
Wikipedia���A���Ɏ^�����Ă���B��
https://ja.wikipedia.org/wiki/%E6%BF%83%E5%BA%A6
���̐ρi�e�ʁj�p�[�Z���g�Z�x�������L���Ƃ���[vol%]����
���Z�x�̒P�ʂ�\������volume�𗪂���vol�̌��t����̂���ʂł���B
����A�̐ϕ����͂���B��
https://ja.wikipedia.org/wiki/%E4%BD%93%E7%A9%8D%E5%88%86%E7%8E%87
�g����ʂ��A������ƈႤ�B
vol%�́A�Ȋw�����A����܂茵������Ȃ��Ɩ��p�Ɏg���邱�Ƃ������A
���ہA���𑫂��đ��̐ς����邱�Ƃō����B
��̓I�ɂ́A����Ȃ�B��
http://www.imazu-chemical.co.jp/77eta.pdf
���ōl���Ȃ��ŁA���w�̖{��ǂނƂ�����B
2017/02/25(�y) 20:08:20.20ID:W0Li+c7B
vol%�@���@�̐�(�S)�����ł͂Ȃ��A�̐ϔZ�x�̒P�ʂȂ�A���w�E�̒ʂ�ł��B
����A���x���Q�Ƃ���ۂɗ��p�����Ă���������
https://www.nmij.jp/~dsmnt-tech/cal-ver/alcohol.pdf
�ɂ́A�u�G�^�m�[���̑̐ϕS����(vol%)�v�Ƃ̗p�ꂪ�g�������A
�����̒��ӂQ�ɂ́A�p��̐����Ƃ��đ̐ϔZ�x�̂��ꂪ������Ă��܂��B
����f���ł��A�����炭�Ԉ�������߂ʼn���Ă��镨������܂����B
�ƊE�����ł��A������ԂȂ̂ł��傤����
����A���x���Q�Ƃ���ۂɗ��p�����Ă���������
https://www.nmij.jp/~dsmnt-tech/cal-ver/alcohol.pdf
�ɂ́A�u�G�^�m�[���̑̐ϕS����(vol%)�v�Ƃ̗p�ꂪ�g�������A
�����̒��ӂQ�ɂ́A�p��̐����Ƃ��đ̐ϔZ�x�̂��ꂪ������Ă��܂��B
����f���ł��A�����炭�Ԉ�������߂ʼn���Ă��镨������܂����B
�ƊE�����ł��A������ԂȂ̂ł��傤����
2017/02/25(�y) 21:32:18.09ID:TQr5kx/y
�������Ă���̂́A�ƊE�ł͂Ȃ��Ǝv���B
2017/02/25(�y) 23:19:21.41ID:W0Li+c7B
�̐ϔZ�x�Ȃ�A������̑̐ς�550ml�ł��邱�Ƃ���������̂ŁA
77vol%���̖��x0.8899�ƁA70vol%���̖��x0.8718���g����
500�~(77/70)�~0.8899�@�|�@500�~0.8718�@= 53.545 (g)
�Ōv�Z�ł��܂��ˁB
77vol%���̖��x0.8899�ƁA70vol%���̖��x0.8718���g����
500�~(77/70)�~0.8899�@�|�@500�~0.8718�@= 53.545 (g)
�Ōv�Z�ł��܂��ˁB
2017/02/26(��) 03:15:18.85ID:RCMn5fGv
��������̑̐ς�550ml
����A�����t�̎��k���l�����ĂȂ�����B
>>147 ���������B
�̐ς͍������Ƃ������Z�ɂȂ�Ȃ�����A
���ʔZ�x�Ɉڂ��Čv�Z�����B
����A�����t�̎��k���l�����ĂȂ�����B
>>147 ���������B
�̐ς͍������Ƃ������Z�ɂȂ�Ȃ�����A
���ʔZ�x�Ɉڂ��Čv�Z�����B
2017/02/26(��) 04:31:24.97ID:27HZHyoX
77vol%�G�^�m�[��500ml�ɁA53.545g(��53.6ml)�̐�������A
70vol%�G�^�m�[��550ml���ł���Ƃ����̂��A>>153�̎咣�ł��B
�̐ώ��k���Ă��邩��A�i553.6�ł͂Ȃ��j550ml�ɂȂ�̂��ƁB
�����ʂ͑̐ϔZ�x�~�̐ςŋ��܂�A���e���𑼂Ɉڂ��Ȃ�����ω����܂���B
���̎��_�ɗ��������@�ŁA�̐ϔZ�x���g���ꍇ�́A���̕��@���g���܂��B
���������A147�̖`���ɏ�����Ă���̂����ɂ���ł��傤�B
����������O�F�Z�x77vol%�@�̐�100�~(70/77)ml
������������F�Z�x70vol%�@�̐�100ml
���̓����O��ŁA�Z�x�~�̐ς͓����l�����܂��B
���ł�>>153�̓��e���ꕔ�������Ă����܂��B
�~�F77vol%���̖��x0.8899�ƁA70vol%���̖��x0.8718���g����
���F70vol%���̖��x0.8899�ƁA77vol%���̖��x0.8718���g����
70vol%�G�^�m�[��550ml���ł���Ƃ����̂��A>>153�̎咣�ł��B
�̐ώ��k���Ă��邩��A�i553.6�ł͂Ȃ��j550ml�ɂȂ�̂��ƁB
�����ʂ͑̐ϔZ�x�~�̐ςŋ��܂�A���e���𑼂Ɉڂ��Ȃ�����ω����܂���B
���̎��_�ɗ��������@�ŁA�̐ϔZ�x���g���ꍇ�́A���̕��@���g���܂��B
���������A147�̖`���ɏ�����Ă���̂����ɂ���ł��傤�B
����������O�F�Z�x77vol%�@�̐�100�~(70/77)ml
������������F�Z�x70vol%�@�̐�100ml
���̓����O��ŁA�Z�x�~�̐ς͓����l�����܂��B
���ł�>>153�̓��e���ꕔ�������Ă����܂��B
�~�F77vol%���̖��x0.8899�ƁA70vol%���̖��x0.8718���g����
���F70vol%���̖��x0.8899�ƁA77vol%���̖��x0.8718���g����
156�� ��2VB8wsVUoo
2017/02/26(��) 07:54:17.17ID:RabypwXl ��
157�� ��2VB8wsVUoo
2017/02/26(��) 07:54:33.55ID:RabypwXl ��
158�� ��2VB8wsVUoo
2017/02/26(��) 07:54:49.49ID:RabypwXl ��
159�� ��2VB8wsVUoo
2017/02/26(��) 07:55:06.28ID:RabypwXl ��
160�� ��2VB8wsVUoo
2017/02/26(��) 07:55:24.17ID:RabypwXl ��
161�� ��2VB8wsVUoo
2017/02/26(��) 07:55:40.86ID:RabypwXl ��
162�� ��2VB8wsVUoo
2017/02/26(��) 07:55:57.04ID:RabypwXl ��
163�� ��2VB8wsVUoo
2017/02/26(��) 07:56:14.82ID:RabypwXl ��
164�� ��2VB8wsVUoo
2017/02/26(��) 07:56:30.65ID:RabypwXl ��
165�� ��2VB8wsVUoo
2017/02/26(��) 07:56:46.35ID:RabypwXl ��
2017/03/21(��) 22:33:43.58ID:NYcobB5z
x��yz�A(x,y,z)��[0,1]^3 ���݂������̂̑̐ς��d�ϕ��ŋ��߂�ɂ́A�ǂ�����Ηǂ��ł����H
2017/03/26(��) 10:30:58.84ID:TBcNwWMK
2017/07/17(��) 04:31:57.41ID:2cOdQU+V
��ABC�̓��p����_�oP�AQ�p����3�ӂɉ����������̑�6�_�́APQ�̒��_�𒆐S�Ƃ���~����ɂ���܂��B
�o�O�SO�A���SH�p�͓��p����_�̂P��ł��B�i9�_�~�j
�_P��3���_A�AB�AC������3�{�̒����͂��ꂼ��̑Εӂƌ����܂��B�_Q�ɂ��Ă����l�ł��B
�����6�_���A����~����ɂ���Ƃ��A�oP�AQ�p�͖،ˋ���_�ł���ƌ����܂��傤�B
�o�d�SG�A���SH�p�͖،ˋ���_�̂P��ł��B(9�_�~�j
�ł́A�،ˋ���_�oP�AQ�p�̊Ԃɂǂ�ȊW������ł��傤���H
����
�@���Z�~�AVol.50�ANo.3�Ap.66�i2011/3)
�o�O�SO�A���SH�p�͓��p����_�̂P��ł��B�i9�_�~�j
�_P��3���_A�AB�AC������3�{�̒����͂��ꂼ��̑Εӂƌ����܂��B�_Q�ɂ��Ă����l�ł��B
�����6�_���A����~����ɂ���Ƃ��A�oP�AQ�p�͖،ˋ���_�ł���ƌ����܂��傤�B
�o�d�SG�A���SH�p�͖،ˋ���_�̂P��ł��B(9�_�~�j
�ł́A�،ˋ���_�oP�AQ�p�̊Ԃɂǂ�ȊW������ł��傤���H
����
�@���Z�~�AVol.50�ANo.3�Ap.66�i2011/3)
169�P�R�Q�l�ڂ̑f������
2017/08/06(��) 18:13:59.70ID:oDKJI1vJ �����������琢�E���ς���ă����^
2017/08/08(��) 23:24:53.39ID:RYC/G6ZV
test
2017/08/08(��) 23:55:59.28ID:RYC/G6ZV
Wolstenholme�̒藝�i1862�j�@�ȂǁB
p�͊�f���Ƃ���B
(1)�@��[k=1,p-1] 1/k �� 0 �@�imod pp�j�@�c�@p��5
�@�@�@�@�@�@�@�@�@�@�@�@�@�� -3�@�imod 9�j�@�@�c�@p=3
(2)�@��[k=1,p-1] 1/kk�@�� -p �@�imod pp�j�@�c�@p=8m�}3�Ap��5
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� 2p�@�@�imod pp�j�@�c�@p=8m�}1
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� -1�@�@�imod 9�j�@�c�@p=3
(3)�@��[k=1,p-1] 1/k^3 �� 0�@�@�imod pp�j�@�c�@p��5
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� -5 �@�imod 25�j�@�c�@p=5
(4)�@�[k=1,p-1�n1/k^4 �� 0�@�imod p�j�@�c�@p��7
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� 4�@�imod 25�j�@�c�@p=5
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� -4 �imod 9�j�@�c�@p=3
(p)�@��[k=1,p-1] 1/k^p �� 0�@�imod p^3�j�@�c�@p��5
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� -9�@�imod 27�j�@�c�@p=3
�������炵�����
p�͊�f���Ƃ���B
(1)�@��[k=1,p-1] 1/k �� 0 �@�imod pp�j�@�c�@p��5
�@�@�@�@�@�@�@�@�@�@�@�@�@�� -3�@�imod 9�j�@�@�c�@p=3
(2)�@��[k=1,p-1] 1/kk�@�� -p �@�imod pp�j�@�c�@p=8m�}3�Ap��5
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� 2p�@�@�imod pp�j�@�c�@p=8m�}1
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� -1�@�@�imod 9�j�@�c�@p=3
(3)�@��[k=1,p-1] 1/k^3 �� 0�@�@�imod pp�j�@�c�@p��5
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� -5 �@�imod 25�j�@�c�@p=5
(4)�@�[k=1,p-1�n1/k^4 �� 0�@�imod p�j�@�c�@p��7
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� 4�@�imod 25�j�@�c�@p=5
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� -4 �imod 9�j�@�c�@p=3
(p)�@��[k=1,p-1] 1/k^p �� 0�@�imod p^3�j�@�c�@p��5
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�� -9�@�imod 27�j�@�c�@p=3
�������炵�����
2017/08/09(��) 00:17:56.52ID:vWdGLnQX
>>171
(1�j�̗���
�@��[k=1,p-1] 1/k = (1/2)��[k=1,p-1] {1/k + 1/(p-k)�p= (1/2)p���[k=1,p-1] 1/{k(p-k)},
�Ƃ����
�@��[k=1,p-1] 1/{k(p-k)�p�� -��[k=1,p-1�n1/kk �� -��[k'=1,p-1] k'k' = -p�(p-1)(2p-1)/6 �� 0�@(mod p)
�����ŁAp��5 �Ɓo 1/k | 1��k��p-1�p�߁o k' | 1��k'��p-1�p�@(mod p�j���g�����B
�i�Q�l�j
http://www.geocities.jp/ikuro_kotaro/koramu/1106_p.htm
(1�j�̗���
�@��[k=1,p-1] 1/k = (1/2)��[k=1,p-1] {1/k + 1/(p-k)�p= (1/2)p���[k=1,p-1] 1/{k(p-k)},
�Ƃ����
�@��[k=1,p-1] 1/{k(p-k)�p�� -��[k=1,p-1�n1/kk �� -��[k'=1,p-1] k'k' = -p�(p-1)(2p-1)/6 �� 0�@(mod p)
�����ŁAp��5 �Ɓo 1/k | 1��k��p-1�p�߁o k' | 1��k'��p-1�p�@(mod p�j���g�����B
�i�Q�l�j
http://www.geocities.jp/ikuro_kotaro/koramu/1106_p.htm
2017/08/09(��) 11:35:36.48ID:vWdGLnQX
>>171
(2)�� �imod pp�j �ōl�����
��[k=1,p-1] 1/kk�@�� -p�@�c�@p=5,11,13
�@�@�@�@�@�@�@�@�@�@�@�� 2p�@�c�@p=7
�@�@�@�@�@�@�@�@�@�@�@��-3p�@�c�@p=17
�@�@�@�@�@�@�@�@�@�@�@��10p�@�c�@p=19
�@�@�@�@�@�@�@�@�@�@�@�� -1�@�c�@p=3
�ƃo���o�������c
(2)�� �imod pp�j �ōl�����
��[k=1,p-1] 1/kk�@�� -p�@�c�@p=5,11,13
�@�@�@�@�@�@�@�@�@�@�@�� 2p�@�c�@p=7
�@�@�@�@�@�@�@�@�@�@�@��-3p�@�c�@p=17
�@�@�@�@�@�@�@�@�@�@�@��10p�@�c�@p=19
�@�@�@�@�@�@�@�@�@�@�@�� -1�@�c�@p=3
�ƃo���o�������c
2017/08/11(��) 03:14:41.65ID:OXujv9yn
>>123-124
���[�邷�܂���
NP-hard
���鑽�̃n�~���g�j�A���̊���Ԃ����߂���ɋA���ł���炵�����ǁB
�ǂ����ɂ��Ă��A������ɓ�����Ǝ�ɕ����Ȃ���₾�낤�ȁB
�u���w100�̖��v���Z�~�����A���{�]�_�Ёi1984�jp.226-227
���[�邷�܂���
NP-hard
���鑽�̃n�~���g�j�A���̊���Ԃ����߂���ɋA���ł���炵�����ǁB
�ǂ����ɂ��Ă��A������ɓ�����Ǝ�ɕ����Ȃ���₾�낤�ȁB
�u���w100�̖��v���Z�~�����A���{�]�_�Ёi1984�jp.226-227
2017/08/12(�y) 22:01:54.08ID:rvCA1oPA
>>174
2�����h�����������f���H
�@2�_i,j�̋�����(i,j�j���X�s���Ԃ̌����G�l���M�[J(i,j�j�ɑΉ�������B
�@�i���v�͊w�́j��Ԙa���s��v�Z�ŏo���B
�@��Ή��x���O�@�Ƃ��Ċ���Ԃ����o���B
2�����h�����������f���H
�@2�_i,j�̋�����(i,j�j���X�s���Ԃ̌����G�l���M�[J(i,j�j�ɑΉ�������B
�@�i���v�͊w�́j��Ԙa���s��v�Z�ŏo���B
�@��Ή��x���O�@�Ƃ��Ċ���Ԃ����o���B
176�P�R�Q�l�ڂ̑f������
2017/09/05(��) 06:20:06.62ID:PCfG056b �����������琢�E���ς���ă����^
177�� ��2VB8wsVUoo
2017/09/05(��) 06:46:03.81ID:ZSz+2Alj ��
178�� ��2VB8wsVUoo
2017/09/05(��) 06:46:22.85ID:ZSz+2Alj ��
179�� ��2VB8wsVUoo
2017/09/05(��) 06:46:40.61ID:ZSz+2Alj ��
180�� ��2VB8wsVUoo
2017/09/05(��) 06:46:59.79ID:ZSz+2Alj ��
181�� ��2VB8wsVUoo
2017/09/05(��) 06:47:19.18ID:ZSz+2Alj ��
182�� ��2VB8wsVUoo
2017/09/05(��) 06:47:36.95ID:ZSz+2Alj ��
183�� ��2VB8wsVUoo
2017/09/05(��) 06:47:56.81ID:ZSz+2Alj ��
184�� ��2VB8wsVUoo
2017/09/05(��) 06:48:14.97ID:ZSz+2Alj ��
185�� ��2VB8wsVUoo
2017/09/05(��) 06:48:32.53ID:ZSz+2Alj ��
186�� ��2VB8wsVUoo
2017/09/05(��) 06:49:12.39ID:ZSz+2Alj ��
187�P�R�Q�l�ڂ̑f������
2017/09/05(��) 07:10:06.31ID:PCfG056b �����������琢�E���ς���ă����^
188�� ��2VB8wsVUoo
2017/09/05(��) 07:26:50.94ID:ZSz+2Alj ��
189�P�R�Q�l�ڂ̑f������
2017/09/06(��) 15:58:02.67ID:bmfelSef �����������琢�E���ς���ă����^
190�� ��2VB8wsVUoo
2017/09/06(��) 16:06:37.21ID:nJ0wcqLn ��
191�� ��2VB8wsVUoo
2017/09/06(��) 17:14:08.51ID:nJ0wcqLn ��
192�� ��2VB8wsVUoo
2017/09/06(��) 17:14:26.10ID:nJ0wcqLn ��
193�� ��2VB8wsVUoo
2017/09/06(��) 17:14:43.24ID:nJ0wcqLn ��
194�� ��2VB8wsVUoo
2017/09/06(��) 17:14:59.35ID:nJ0wcqLn ��
195�� ��2VB8wsVUoo
2017/09/06(��) 17:15:14.58ID:nJ0wcqLn ��
196�� ��2VB8wsVUoo
2017/09/06(��) 17:15:30.85ID:nJ0wcqLn ��
197�� ��2VB8wsVUoo
2017/09/06(��) 17:15:48.67ID:nJ0wcqLn ��
198�� ��2VB8wsVUoo
2017/09/06(��) 17:16:05.71ID:nJ0wcqLn ��
199�� ��2VB8wsVUoo
2017/09/06(��) 17:16:25.04ID:nJ0wcqLn ��
200�P�R�Q�l�ڂ̑f������
2017/09/07(��) 12:25:15.81ID:PhnGCXNB �����������琢�E���ς���ă����^
201�� ��2VB8wsVUoo
2017/09/07(��) 13:03:32.81ID:6DNo3zLu ��
202�P�R�Q�l�ڂ̑f������
2017/09/08(��) 20:22:54.67ID:yNEWZTqG Youtube�Ō���IQ test
1�{�S���T�@�@2�{�T��12�@�@3�{�U��21�@�@8�{11���H
ans.�@a+b=a+ab�@���@�W�{11��96�@
������āA
1�{�S���T�@(mod 6)
2�{�T��12�@(mod 5)
3�{�U��21�@(mod 4)
8�{11���H�@(mod 3)�@���@ans.�@8�{11��201�@����_��(^^)�H
1�{�S���T�@�@2�{�T��12�@�@3�{�U��21�@�@8�{11���H
ans.�@a+b=a+ab�@���@�W�{11��96�@
������āA
1�{�S���T�@(mod 6)
2�{�T��12�@(mod 5)
3�{�U��21�@(mod 4)
8�{11���H�@(mod 3)�@���@ans.�@8�{11��201�@����_��(^^)�H
203�� ��2VB8wsVUoo
2017/09/08(��) 20:40:37.00ID:6ibQhXIy ��
204�� ��2VB8wsVUoo
2017/09/08(��) 20:40:54.57ID:6ibQhXIy ��
205�� ��2VB8wsVUoo
2017/09/08(��) 20:41:11.63ID:6ibQhXIy ��
206�� ��2VB8wsVUoo
2017/09/08(��) 20:41:30.00ID:6ibQhXIy ��
207�� ��2VB8wsVUoo
2017/09/08(��) 20:41:46.80ID:6ibQhXIy ��
208�� ��2VB8wsVUoo
2017/09/08(��) 20:42:04.29ID:6ibQhXIy ��
209�� ��2VB8wsVUoo
2017/09/08(��) 20:42:21.10ID:6ibQhXIy ��
210�� ��2VB8wsVUoo
2017/09/08(��) 20:42:38.48ID:6ibQhXIy ��
211�� ��2VB8wsVUoo
2017/09/08(��) 20:42:58.68ID:6ibQhXIy ��
212�� ��2VB8wsVUoo
2017/09/08(��) 20:43:16.51ID:6ibQhXIy ��
2017/09/09(�y) 11:56:24.18ID:N6b4VEIQ
�l���ˁ[��
�ؖ����� cos(��+��)cos(��-��) = cos^2(��) - sin^2(��) = cos^2(��) - sin^2(��)
�ؖ����� cos(��+��)cos(��-��) = cos^2(��) - sin^2(��) = cos^2(��) - sin^2(��)
214�� ��2VB8wsVUoo
2017/09/09(�y) 12:09:13.25ID:RUcvU26A ��
215�� ��2VB8wsVUoo
2017/09/09(�y) 12:09:31.97ID:RUcvU26A ��
216�� ��2VB8wsVUoo
2017/09/09(�y) 12:09:49.83ID:RUcvU26A ��
217�� ��2VB8wsVUoo
2017/09/09(�y) 12:10:06.15ID:RUcvU26A ��
218�� ��2VB8wsVUoo
2017/09/09(�y) 12:10:22.42ID:RUcvU26A ��
219�� ��2VB8wsVUoo
2017/09/09(�y) 12:10:40.44ID:RUcvU26A ��
220�� ��2VB8wsVUoo
2017/09/09(�y) 12:10:58.28ID:RUcvU26A ��
221�� ��2VB8wsVUoo
2017/09/09(�y) 12:11:14.35ID:RUcvU26A ��
222�� ��2VB8wsVUoo
2017/09/09(�y) 12:11:32.09ID:RUcvU26A ��
223�� ��2VB8wsVUoo
2017/09/09(�y) 12:11:50.82ID:RUcvU26A ��
224�P�R�Q�l�ڂ̑f������
2017/09/09(�y) 12:19:36.58ID:G2DuD1v6 �����������琢�E���ς���ă����^
2017/09/12(��) 19:06:18.17ID:YsdDbYfo
>>213
�l���ˁ[��
�ؖ�����
�ocos(2���j+ cos(2��)}/2 =�o1+cos(2��)}/2 -�o1-cos(2��)}/2 =�o1+cos(2��)}/2 -�o1-cos(2��)}/2,
�l���ˁ[��
�ؖ�����
�ocos(2���j+ cos(2��)}/2 =�o1+cos(2��)}/2 -�o1-cos(2��)}/2 =�o1+cos(2��)}/2 -�o1-cos(2��)}/2,
226�P�R�Q�l�ڂ̑f������
2017/09/13(��) 11:53:11.42ID:i1anpb+k sin20��sin40��sin80��=
cos10��cos50��cos70��=
cos24��cos48��cos96��cos192��=
cos36��cos72��cos144��cos288��=
cos(2��/7)cos(4��/7)cos(8��/7) =
cos10��cos50��cos70��=
cos24��cos48��cos96��cos192��=
cos36��cos72��cos144��cos288��=
cos(2��/7)cos(4��/7)cos(8��/7) =
227�P�R�Q�l�ڂ̑f������
2017/09/13(��) 14:12:34.21ID:HyiuMNX2 �����������琢�E���ς���ă����^
2017/09/13(��) 15:54:32.32ID:c08G5Hbx
�S�߂ȓz
2017/09/14(��) 06:07:51.92ID:mi/0+iqR
>>226
sin(20߁jsin(40߁jsin(80߁j=�i��3)/8,
�@�@||�@�@�@�@||�@�@�@�@||
cos(70߁jcos(50߁jcos(10߁j=�i��3)/8,
cos(24߁jcos(48߁jcos(96߁jcos(192߁j= 1/16,
�@16t^4 -8t^3 -16t^2 +8t +1=0 �̍��B
�@cos(24߁j=�o1 + ��5 + ��[6(5-��5)]}/8 = 0.91354545764
�@cos(48߁j=�o1 - ��5 + ��[6(5+��5)]}/8 = 0.66913060636
�@cos(96߁j=�o1 + ��5 - ��[6(5-��5)]}/8 = -0.10452846327
�@cos(192߁j=�o1 - ��5 - ��[6(5+��5)]}/8 = -0.97814760073
cos(36߁jcos(72߁jcos(144߁jcos(288߁j= -1/16,
�@�i4tt+2t-1)(4tt-2t-1) = 0 �̍��@
�@cos(36߁j= -cos(144߁j=�i1+��5)/4,
�@cos(72߁j= cos(288߁j=�i��5 -1)/4,
cos(2��/7�jcos(4��/7�jcos(8��/7�j= 1/8,
�@8t^3 + 4t^2 -4t -1 = 0 �̍�
sin(20߁jsin(40߁jsin(80߁j=�i��3)/8,
�@�@||�@�@�@�@||�@�@�@�@||
cos(70߁jcos(50߁jcos(10߁j=�i��3)/8,
cos(24߁jcos(48߁jcos(96߁jcos(192߁j= 1/16,
�@16t^4 -8t^3 -16t^2 +8t +1=0 �̍��B
�@cos(24߁j=�o1 + ��5 + ��[6(5-��5)]}/8 = 0.91354545764
�@cos(48߁j=�o1 - ��5 + ��[6(5+��5)]}/8 = 0.66913060636
�@cos(96߁j=�o1 + ��5 - ��[6(5-��5)]}/8 = -0.10452846327
�@cos(192߁j=�o1 - ��5 - ��[6(5+��5)]}/8 = -0.97814760073
cos(36߁jcos(72߁jcos(144߁jcos(288߁j= -1/16,
�@�i4tt+2t-1)(4tt-2t-1) = 0 �̍��@
�@cos(36߁j= -cos(144߁j=�i1+��5)/4,
�@cos(72߁j= cos(288߁j=�i��5 -1)/4,
cos(2��/7�jcos(4��/7�jcos(8��/7�j= 1/8,
�@8t^3 + 4t^2 -4t -1 = 0 �̍�
2017/10/01(��) 04:45:03.51ID:9PeSV8tr
2�̎��R��a,b�̍ő����g,�ŏ����{����l�Ƃ���B
A={n|n��a�̑f����}
B={n|n��b�̑f����}
G={n|n��g�̑f����}
L={n|n��l�̑f����}
�Ȃ��
(G=A��B) �� (L=A��B)
�ł���?
A={n|n��a�̑f����}
B={n|n��b�̑f����}
G={n|n��g�̑f����}
L={n|n��l�̑f����}
�Ȃ��
(G=A��B) �� (L=A��B)
�ł���?
2017/10/13(��) 09:10:33.33ID:NUqZtYG4
���R�����ɑ��āA
�i1 + 1/n)^(2n+1�j�i1 - 1/n)^(2n-1�j�� 1
�i1 + 1/n)^(2n+1�j�i1 - 1/n)^(2n-1�j�� 1
2017/10/14(�y) 06:00:44.53ID:WYmPKYWn
���R�����ɑ��āA
�i1 + 1/n)^(2n+1�j�i1 - 1/n)^(2n-1�j<�i1-1/nn)^(1/3n�j< e^{-1/(3nnn)�p< 1,
�s�����X����X��.206
�i1 + 1/n)^(2n+1�j�i1 - 1/n)^(2n-1�j<�i1-1/nn)^(1/3n�j< e^{-1/(3nnn)�p< 1,
�s�����X����X��.206
2017/10/14(�y) 06:24:45.54ID:WYmPKYWn
>>230
�͂��B
�t�Ɂog�Cl�p����oa�Cb�p�����߂邱�Ƃ��ł���ł��傤���H
1�̑f�����ɒ��ڂ���A{a�Cb�p�̃x�L�w���́og�Cl�p�̃x�L�w���ƈ�v���܂��B
�������oa�Cb�p�́og�Cl�p�̓��^�Ή���2�ʂ肠��̂Łc
l/g ��2�ȏ�̑f�������܂ނƂ��́oa�Cb�p�͌��܂�܂����ˁi"�O�ցO�j�E�E�E
�͂��B
�t�Ɂog�Cl�p����oa�Cb�p�����߂邱�Ƃ��ł���ł��傤���H
1�̑f�����ɒ��ڂ���A{a�Cb�p�̃x�L�w���́og�Cl�p�̃x�L�w���ƈ�v���܂��B
�������oa�Cb�p�́og�Cl�p�̓��^�Ή���2�ʂ肠��̂Łc
l/g ��2�ȏ�̑f�������܂ނƂ��́oa�Cb�p�͌��܂�܂����ˁi"�O�ցO�j�E�E�E
2017/10/14(�y) 10:57:54.04ID:7SCPB0+Y
>>233
330=2*3*5*11
70=2*5*7
gcd(330,70)=10
lcm(330,70)=2310
30=2*3*5
770=2*5*7*11
gcd(30,770)=10
lcm(30,770)=2310
���ʂłȂ��f�������ǂ��炩�痈���̂��Ƃ���������Ă��܂�����
330=2*3*5*11
70=2*5*7
gcd(330,70)=10
lcm(330,70)=2310
30=2*3*5
770=2*5*7*11
gcd(30,770)=10
lcm(30,770)=2310
���ʂłȂ��f�������ǂ��炩�痈���̂��Ƃ���������Ă��܂�����
2017/10/22(��) 07:35:37.55ID:7rZFxIbv
>>231
(1 + 1/n)^(2n+1) < {1 + 1/(n-1)}^(2n-1),
g_n = (1 + 1/n)^(n +1/2�j�͒P�������B
�@�G�����X���i2011.2).68-69
(2+x)log(1+x�j+�i2-x)log(1-x�j< 0,
(1+x)^(2+x)�E(1-x)^(2-x�j< 1,
�@�s�����X����X��.203
(1 + 1/n)^(2n+1) < {1 + 1/(n-1)}^(2n-1),
g_n = (1 + 1/n)^(n +1/2�j�͒P�������B
�@�G�����X���i2011.2).68-69
(2+x)log(1+x�j+�i2-x)log(1-x�j< 0,
(1+x)^(2+x)�E(1-x)^(2-x�j< 1,
�@�s�����X����X��.203
236�� ��2VB8wsVUoo
2017/10/23(��) 19:10:51.92ID:Dl6USvMt ��
237�� ��2VB8wsVUoo
2017/10/23(��) 19:11:19.39ID:Dl6USvMt ��
238�� ��2VB8wsVUoo
2017/10/23(��) 19:11:39.44ID:Dl6USvMt ��
239�� ��2VB8wsVUoo
2017/10/23(��) 19:11:56.62ID:Dl6USvMt ��
240�� ��2VB8wsVUoo
2017/10/23(��) 19:12:13.30ID:Dl6USvMt ��
241�� ��2VB8wsVUoo
2017/10/23(��) 19:12:28.65ID:Dl6USvMt ��
242�� ��2VB8wsVUoo
2017/10/23(��) 19:12:43.71ID:Dl6USvMt ��
243�� ��2VB8wsVUoo
2017/10/23(��) 19:13:00.36ID:Dl6USvMt ��
244�� ��2VB8wsVUoo
2017/10/23(��) 19:13:15.97ID:Dl6USvMt ��
245�� ��2VB8wsVUoo
2017/10/23(��) 19:13:31.76ID:Dl6USvMt ��
2017/11/08(��) 22:41:33.41ID:mblwdtt/
>>226
cos(10�jcos(50�jcos(70�j=�i��3)/8,
http://www.youtube.com/watch?v=VOC9xMq3JJg
sin(20�jsin(40�jsin(60�jsin(80�j= 3/16,
http://www.youtube.com/watch?v=zAiXPhPvWpc
--------------------------------------------------
Morrie's law
cos(20�jcos(40�jcos(80�j= 1/8,
http://www.youtube.com/watch?v=u-Z5pBxW1u8
cos(20�jcos(40�jcos(60�jcos(80�j= 1/16,
http://www.youtube.com/watch?v=eBFtWCLw1-8
http://www.youtube.com/watch?v=JV7J7JrakeI
sin(10�jsin(30�jsin(50�jsin(70�j= 1/16,
http://www.youtube.com/watch?v=QGpDSulXqB8
------------------------------------------------
�I�}�P
sin(10�j+sin(20�j+sin(40�j+sin(50�j= sin(70�j+sin(80),
http://www.youtube.com/watch?v=v4NW9kOifq0
cos(10�jcos(50�jcos(70�j=�i��3)/8,
http://www.youtube.com/watch?v=VOC9xMq3JJg
sin(20�jsin(40�jsin(60�jsin(80�j= 3/16,
http://www.youtube.com/watch?v=zAiXPhPvWpc
--------------------------------------------------
Morrie's law
cos(20�jcos(40�jcos(80�j= 1/8,
http://www.youtube.com/watch?v=u-Z5pBxW1u8
cos(20�jcos(40�jcos(60�jcos(80�j= 1/16,
http://www.youtube.com/watch?v=eBFtWCLw1-8
http://www.youtube.com/watch?v=JV7J7JrakeI
sin(10�jsin(30�jsin(50�jsin(70�j= 1/16,
http://www.youtube.com/watch?v=QGpDSulXqB8
------------------------------------------------
�I�}�P
sin(10�j+sin(20�j+sin(40�j+sin(50�j= sin(70�j+sin(80),
http://www.youtube.com/watch?v=v4NW9kOifq0
2017/11/13(��) 13:26:06.31ID:abgKGSaf
>>226
����3�� Morrie's law
�@cos��= sin(2��)/(2sin��)
�ł��ˁB
�ʖ@
cos(36�jcos(72�jcos(144�jcos(288�j
= - cos(72)cos(144)cos(216)cos(288)
= -��[k=1,4�ncos(2k��/5),
1 - T_5(t�j=�i1-t)(4tt+2t-1)^2.
cos(2��/7�jcos(4��/7�jcos(8��/7�j
=�o��[k=1,6�ncos(2k��/7)}^(1/2�j,
1 - T_7(t�j=�i1-t)(8t^3+4t^2-4t-1)^2.
����3�� Morrie's law
�@cos��= sin(2��)/(2sin��)
�ł��ˁB
�ʖ@
cos(36�jcos(72�jcos(144�jcos(288�j
= - cos(72)cos(144)cos(216)cos(288)
= -��[k=1,4�ncos(2k��/5),
1 - T_5(t�j=�i1-t)(4tt+2t-1)^2.
cos(2��/7�jcos(4��/7�jcos(8��/7�j
=�o��[k=1,6�ncos(2k��/7)}^(1/2�j,
1 - T_7(t�j=�i1-t)(8t^3+4t^2-4t-1)^2.
2017/11/24(��) 01:35:53.16ID:2XbK5FAe
�k�_�\�z���l
���ʏ�ɗL���̓_�̏W�����Ƃ�B
�@�ǂ�2�_��ʂ钼����3�ȏ�̓_��ʂ�
�����Ȃ�A�����̓_�͂��ׂĂP������ɂ���B
���ʏ�ɗL���̓_�̏W�����Ƃ�B
�@�ǂ�2�_��ʂ钼����3�ȏ�̓_��ʂ�
�����Ȃ�A�����̓_�͂��ׂĂP������ɂ���B
2017/11/24(��) 01:37:28.23ID:2XbK5FAe
>>248
http://www.watto.nagoya/entry/20060618/p1
http://www004.upp.so-net.ne.jp/s_honma/pointconjecture.htm
�T�C�����E�V��(���j�� �O(��j�u�t�F���}�[�̍ŏI�藝�v�V�����Ɂi2006/May�j495p�D853�~
�@p.195�`196 ����� p.473�`475
http://rio2016.5ch.net/test/read.cgi/math/1510671832/815-816
http://www.watto.nagoya/entry/20060618/p1
http://www004.upp.so-net.ne.jp/s_honma/pointconjecture.htm
�T�C�����E�V��(���j�� �O(��j�u�t�F���}�[�̍ŏI�藝�v�V�����Ɂi2006/May�j495p�D853�~
�@p.195�`196 ����� p.473�`475
http://rio2016.5ch.net/test/read.cgi/math/1510671832/815-816
250�P�R�Q�l�ڂ̑f������
2017/11/24(��) 20:04:07.04ID:RwTdoHCs �����������琢�E���ς���ă����^
251�� ��2VB8wsVUoo
2017/11/25(�y) 00:14:24.85ID:kb2pRtxG ��
252�� ��2VB8wsVUoo
2017/11/25(�y) 00:14:44.27ID:kb2pRtxG ��
253�� ��2VB8wsVUoo
2017/11/25(�y) 00:14:59.95ID:kb2pRtxG ��
254�� ��2VB8wsVUoo
2017/11/25(�y) 00:15:17.73ID:kb2pRtxG ��
255�� ��2VB8wsVUoo
2017/11/25(�y) 00:15:33.93ID:kb2pRtxG ��
256�� ��2VB8wsVUoo
2017/11/25(�y) 00:15:51.15ID:kb2pRtxG ��
257�� ��2VB8wsVUoo
2017/11/25(�y) 00:16:09.50ID:kb2pRtxG ��
258�� ��2VB8wsVUoo
2017/11/25(�y) 00:16:25.55ID:kb2pRtxG ��
259�� ��2VB8wsVUoo
2017/11/25(�y) 00:16:42.60ID:kb2pRtxG ��
260�� ��2VB8wsVUoo
2017/11/25(�y) 00:17:00.27ID:kb2pRtxG ��
261�P�R�Q�l�ڂ̑f������
2017/11/25(�y) 11:01:39.93ID:w+3jBqH6 �����������琢�E���ς���ă����^
262�P�R�Q�l�ڂ̑f������
2017/12/23(�y) 08:45:33.15ID:nsgUiKTK 2�O24�~3�O36�~11�O12��2�i�@�ŕ\���ƁA�����ɂ�0���A������24���ԁB
3�O36�~11�O12������Ȑ�������ł��傤���H
2�O24�~3�O4�~11�O3��2�i�@�ŕ\���ƁA�����͂����Ȃ��ł��傤���H
3�O36�~11�O12������Ȑ�������ł��傤���H
2�O24�~3�O4�~11�O3��2�i�@�ŕ\���ƁA�����͂����Ȃ��ł��傤���H
263�P�R�Q�l�ڂ̑f������
2017/12/23(�y) 14:58:02.34ID:JamHfM57 �������e�B�z�[�����i�ƃ_�C���j
���̃Q�[�����ł���̂�1���ł�
�O����͒��������Ȃ���100�̒��̂ЂƂ�
�_�C�������h��1����܂�
���̒�����1�̔���I�т܂�
98�̋���菜���܂�
�Ō�Ɏc����2�̔��̒�����1�̔���I�т܂�
�_�C�������h��������m���͉����ł��傤���H
���̃Q�[�����ł���̂�1���ł�
�O����͒��������Ȃ���100�̒��̂ЂƂ�
�_�C�������h��1����܂�
���̒�����1�̔���I�т܂�
98�̋���菜���܂�
�Ō�Ɏc����2�̔��̒�����1�̔���I�т܂�
�_�C�������h��������m���͉����ł��傤���H
264�� ��2VB8wsVUoo
2018/01/21(��) 09:01:08.88ID:oUqQkvBY ��
265�� ��2VB8wsVUoo
2018/01/21(��) 09:01:35.65ID:oUqQkvBY ��
266�� ��2VB8wsVUoo
2018/01/21(��) 09:02:00.87ID:oUqQkvBY ��
267�� ��2VB8wsVUoo
2018/01/21(��) 09:02:19.73ID:oUqQkvBY ��
268�� ��2VB8wsVUoo
2018/01/21(��) 09:02:36.62ID:oUqQkvBY ��
269�� ��2VB8wsVUoo
2018/01/21(��) 09:02:55.00ID:oUqQkvBY ��
270�� ��2VB8wsVUoo
2018/01/21(��) 09:03:12.42ID:oUqQkvBY ��
271�� ��2VB8wsVUoo
2018/01/21(��) 09:03:29.85ID:oUqQkvBY ��
272�� ��2VB8wsVUoo
2018/01/21(��) 09:03:48.42ID:oUqQkvBY ��
273�� ��2VB8wsVUoo
2018/01/21(��) 09:04:06.06ID:oUqQkvBY ��
274�P�R�Q�l�ڂ̑f������
2018/01/21(��) 09:07:47.28ID:TGpBI6pd �����������琢�E���ς���ă����^
2018/01/21(��) 18:23:40.00ID:m68ScmO7
>>263
����́A�����e�B�z�[�����ł͂Ȃ��B
����́A�����e�B�z�[�����ł͂Ȃ��B
276�� ��2VB8wsVUoo
2018/01/22(��) 12:31:45.92ID:vBTdEgh5 ��
277�� ��2VB8wsVUoo
2018/01/22(��) 12:32:08.32ID:vBTdEgh5 ��
278�� ��2VB8wsVUoo
2018/01/22(��) 12:32:31.64ID:vBTdEgh5 ��
279�� ��2VB8wsVUoo
2018/01/22(��) 12:32:52.29ID:vBTdEgh5 ��
280�� ��2VB8wsVUoo
2018/01/22(��) 12:33:13.12ID:vBTdEgh5 ��
281�� ��2VB8wsVUoo
2018/01/22(��) 12:33:32.74ID:vBTdEgh5 ��
282�P�R�Q�l�ڂ̑f������
2018/01/22(��) 13:07:16.47ID:Df2n+TON �����������琢�E���ς���ă����^
2018/01/22(��) 14:32:50.96ID:vRHzEvsP
���������Ă��A>>263 �́A�����e�B�z�[�����ł͂Ȃ��B
2018/01/28(��) 07:55:27.78ID:8UL7hOGH
�q���̎Z���̖�肪����܂����B�Ȃ[�������܂���B
�l�̌ܓ����ĕS�̈ʂ܂ł̐��ɂ����Ƃ��A1600�ɂȂ鐮���̂͂́A
�����������灠�������܂łł��B
�����@1550����1649
�����H
�l�̌ܓ����ĕS�̈ʂ܂ł̐��ɂ����Ƃ��A1600�ɂȂ鐮���̂͂́A
�����������灠�������܂łł��B
�����@1550����1649
�����H
2018/01/28(��) 09:56:14.62ID:pLwrCEht
�\�̈ʂ̐��ɑ��Ďl�̌ܓ��̏������{��
2018/01/28(��) 10:05:13.98ID:8UL7hOGH
2018/02/03(�y) 02:53:06.04ID:xvl288yy
�k���l
�i1�j�@x>0 �̂Ƃ��Alog�ix�j< x-1 �������B
�i2�j�@a = 2^(1/3�j�̂Ƃ��Alog�ia�j=�i8/9)(a-1�j�������B
�i1�j�@x>0 �̂Ƃ��Alog�ix�j< x-1 �������B
�i2�j�@a = 2^(1/3�j�̂Ƃ��Alog�ia�j=�i8/9)(a-1�j�������B
2018/02/03(�y) 05:50:18.14ID:SRNC+iev
>>287
(1)x=1�̂Ƃ��A����=�E��=0
����Đ������Ȃ�
(2)���ӂ͐��W���O��������(9x+8)^3=2�̉��Ȃ̂ő㐔�I���ł���
�E��(1/3)log2�̓����f�}���̒藝�ɂ���đ㐔�I���łȂ�
����Đ������Ȃ�
(1)x=1�̂Ƃ��A����=�E��=0
����Đ������Ȃ�
(2)���ӂ͐��W���O��������(9x+8)^3=2�̉��Ȃ̂ő㐔�I���ł���
�E��(1/3)log2�̓����f�}���̒藝�ɂ���đ㐔�I���łȂ�
����Đ������Ȃ�
2018/02/03(�y) 05:54:46.33ID:SRNC+iev
290�P�R�Q�l�ڂ̑f������
2018/02/12(��) 21:18:31.36ID:8xETDZ6r �L�E���ʑ̂̏ꍇ�̃I�C���[�̑��ʑ̌���
v-e+f+2g=2
����̌��̐�g���ĉ��̓������ł����H
vertex,edge,face�͕������ł���
v-e+f+2g=2
����̌��̐�g���ĉ��̓������ł����H
vertex,edge,face�͕������ł���
2018/02/12(��) 23:09:20.13ID:MYy378Zb
>>290
�퐔�igenus�j����ˁH
�@���̐ؒf�ɂ���Đ����鑽�l�̂��A�������ێ�����悤�ȁA�P���ȕȐ��ɉ������ؒf�̍ő吔�B�]���Đ����ł���B
�Ȗʂł́A�I�C���[�W���� �� v-e+f = 2 -2g�A�n���h�� = g
���E���������Ȗʂł́A�I�C���[�W���� = 2 -2g -(���E�����̐�)
�퐔�igenus�j����ˁH
�@���̐ؒf�ɂ���Đ����鑽�l�̂��A�������ێ�����悤�ȁA�P���ȕȐ��ɉ������ؒf�̍ő吔�B�]���Đ����ł���B
�Ȗʂł́A�I�C���[�W���� �� v-e+f = 2 -2g�A�n���h�� = g
���E���������Ȗʂł́A�I�C���[�W���� = 2 -2g -(���E�����̐�)
2018/02/12(��) 23:20:30.21ID:MYy378Zb
2018/02/12(��) 23:52:04.29ID:MYy378Zb
�k���l
��2 + ��3 = ��
e^�� = 20 + ��
e^6 = ��^4 + ��^5
�������B
��2 + ��3 = ��
e^�� = 20 + ��
e^6 = ��^4 + ��^5
�������B
2018/02/12(��) 23:58:40.21ID:MYy378Zb
>>293
(4�j�@�@��2 + ��3 = �@�������B
��2 + ��3 �͐��W���S�������� x^4 -10x^2 +1 = 0�@�̉��Ȃ̂ő㐔�I���ł���B
(4�j�@�@��2 + ��3 = �@�������B
��2 + ��3 �͐��W���S�������� x^4 -10x^2 +1 = 0�@�̉��Ȃ̂ő㐔�I���ł���B
2018/02/13(��) 06:30:04.26ID:ESro8IOF
>>291
�L��������܂�
�L��������܂�
2018/02/14(��) 02:40:09.86ID:/bHsoXtp
>>293
(5)�@e^�� = 20 + �@�������B
���O�i���j�͐��������ǁAe^�� �͒��z�����ȁB
�����琬�藧�c�c�Ƃ��������Ȃ����ǁB
(5)�@e^�� = 20 + �@�������B
���O�i���j�͐��������ǁAe^�� �͒��z�����ȁB
�����琬�藧�c�c�Ƃ��������Ȃ����ǁB
297�P�R�Q�l�ڂ̑f������
2018/02/17(�y) 13:18:26.63ID:A3XYwBOM �u�����A���]�[���̌`�͑S�Đؒ����ʑ̂ɂȂ�̂ł��傤���H
https://en.m.wikipedia.org/wiki/Brillouin_zone
�Ȃ�ꍇ�A14�̃u���i�q�ɂ����āA���̃u�����A���]�[���͉��̐ؒ����ʑ̂ɂȂ�̂ł��傤���H
https://en.m.wikipedia.org/wiki/Brillouin_zone
�Ȃ�ꍇ�A14�̃u���i�q�ɂ����āA���̃u�����A���]�[���͉��̐ؒ����ʑ̂ɂȂ�̂ł��傤���H
2018/02/17(�y) 13:29:30.04ID:uRXrO5L0
�J�����Ōv�Z�����B��Ɖ������Ă����A�v�������������B�������ɒm�b�܂ɏ������߂�K�o�K�o�̋�������͂���Ő��w���_����B [524061638]
http://leia.5ch.net/test/read.cgi/poverty/1518841675/
http://leia.5ch.net/test/read.cgi/poverty/1518841675/
2018/02/19(��) 17:29:45.37ID:CMze8r9t
���肢���܂��B���̂��o�J�Ȏ��ɋ����Ă��������B
���̋Ɍ��l��2�ƂS�̂Ƃ̊Ԃɑ��݂��邱�Ƃ��ؖ�����B
lim[n��0](1+1/n)^n
[��]
�܂��An�𐳂̐����Ƃ��čl���Ă݂�ƁA����(1+1/n)^n��n�𑝂��ɂ��������đ傫���Ȃ邱�Ƃ�������B
���ɁA������������B
y^n-a^n=(y-a)*(y^(n-1)+a*y^(n-2)+a^2*y^(n-3)+�E�E�E�E�E�Ea^(n-2)*y+a^(n-1))
�ƂȂ�By>a�Ƃ���A�E�ӂ̑������͎w���̒���a�����ׂ�y�ɉ��߂� n*y^(n-1)���͏���������A
���̕s�������l������B
y^n-a^n<n*(y-a)^(n-1)
�����Ł@y�Aa���Ƃ��ɁA
y=1+1/(n-1) a=1+1/n ���@������������Ȃ��A�����ł������Ă��܂��B�Ȃ���������Ă����̂��H
�Ƃ����A��̕s�����́A
(1+1/(n-1))^n-(1+1/n)^n<{1/(n-1)}*{1+1/(n-1)}^(n-1)
�ƂȂ�B������ȒP�ɂ���ƁA���̕s�����ƂȂ邩��ł���
���̋Ɍ��l��2�ƂS�̂Ƃ̊Ԃɑ��݂��邱�Ƃ��ؖ�����B
lim[n��0](1+1/n)^n
[��]
�܂��An�𐳂̐����Ƃ��čl���Ă݂�ƁA����(1+1/n)^n��n�𑝂��ɂ��������đ傫���Ȃ邱�Ƃ�������B
���ɁA������������B
y^n-a^n=(y-a)*(y^(n-1)+a*y^(n-2)+a^2*y^(n-3)+�E�E�E�E�E�Ea^(n-2)*y+a^(n-1))
�ƂȂ�By>a�Ƃ���A�E�ӂ̑������͎w���̒���a�����ׂ�y�ɉ��߂� n*y^(n-1)���͏���������A
���̕s�������l������B
y^n-a^n<n*(y-a)^(n-1)
�����Ł@y�Aa���Ƃ��ɁA
y=1+1/(n-1) a=1+1/n ���@������������Ȃ��A�����ł������Ă��܂��B�Ȃ���������Ă����̂��H
�Ƃ����A��̕s�����́A
(1+1/(n-1))^n-(1+1/n)^n<{1/(n-1)}*{1+1/(n-1)}^(n-1)
�ƂȂ�B������ȒP�ɂ���ƁA���̕s�����ƂȂ邩��ł���
2018/02/19(��) 17:30:38.54ID:CMze8r9t
>>299
��
1+1/(n-1)}^(n-1)<(1+1/n)^n ���A�X�̌v�Z���ʂ��Ȃ������Ȃ�̂��H�r���v�Z���ڂ������肢���܂��B
n=1�ł���Ƃ��́A�^����ꂽ�w����2�ƂȂ邩��A���̋Ɍ��l��2�����傫�����Ƃ������܂ł��Ȃ����A
���ꂪ4�������������Ƃ����ɏؖ�����B
�܂��An�������Ƃ����n=2*m�Ƃ����āA
(1+1/n)^n=(1+1/(2*m))^(2*m)={(2*m+1)/(2*m)}^(2*m)={((2*m+1)/(2*m))^m}^2
�Ƃ��낪�A�i�B�������炪������܂���A���ł��ꂼ��̉E�ӂ������Ȃ�̂��E�E�E�j
(2*m+1)/2*m<(2*m)/(2*m-1) , (2*m+1)/(2*m)<(2*m-1)/(2*m-2) , (2*m+1)/(2*m)<(2*m-2)/(2*m-3) , �E�E�E
(2*m+1)/(2*m)<(m+2)/(m+1)
�ł��邩��A������ m-1 �̕s��������4�s�ȏ�̓����̍Ō�̍��ɑ������A
(1+1/n)^n<{(2*m+1)/(m+1)}^2 , ���Ȃ킿�A�@(1+1/n)^n<{2-1/(m-1)}^2<4 �@���C�ǂ��䂤�v�Z�����̂��H
�@�܂��An����̏ꍇ�́A����� n+1 �ɂ�����ƁA���ꂪ�����ƂȂ�A���A�O�̏ؖ��ɂ���āA���̒l������
���邩��An �̏ꍇ���������4���l���������Ȃ�B
�@���̎��� n �̒l�𑝂��ɂ��������Ă��̒l���������邪�A������x 4 �������邱�Ƃ͂Ȃ�����A����������
�̋Ɍ��ɒB����B���̐��� e �ŕ\���Ă���̂ł���B
{n=100 �Ƃ����Ƃ��̎��̒l�� 1.01^100=2.704(�ΐ��v�Z�ɂ��j�ƂȂ�A�܂��An=1000�Ƃ����� 1.001^1000
=2.717�i�ΐ��v�Z�ɂ��j�ƂȂ�B���̋Ɍ��l e �͎��͂��̒l�ƂȂ�Be=2.71828188284�E�E�E�E�E
��
1+1/(n-1)}^(n-1)<(1+1/n)^n ���A�X�̌v�Z���ʂ��Ȃ������Ȃ�̂��H�r���v�Z���ڂ������肢���܂��B
n=1�ł���Ƃ��́A�^����ꂽ�w����2�ƂȂ邩��A���̋Ɍ��l��2�����傫�����Ƃ������܂ł��Ȃ����A
���ꂪ4�������������Ƃ����ɏؖ�����B
�܂��An�������Ƃ����n=2*m�Ƃ����āA
(1+1/n)^n=(1+1/(2*m))^(2*m)={(2*m+1)/(2*m)}^(2*m)={((2*m+1)/(2*m))^m}^2
�Ƃ��낪�A�i�B�������炪������܂���A���ł��ꂼ��̉E�ӂ������Ȃ�̂��E�E�E�j
(2*m+1)/2*m<(2*m)/(2*m-1) , (2*m+1)/(2*m)<(2*m-1)/(2*m-2) , (2*m+1)/(2*m)<(2*m-2)/(2*m-3) , �E�E�E
(2*m+1)/(2*m)<(m+2)/(m+1)
�ł��邩��A������ m-1 �̕s��������4�s�ȏ�̓����̍Ō�̍��ɑ������A
(1+1/n)^n<{(2*m+1)/(m+1)}^2 , ���Ȃ킿�A�@(1+1/n)^n<{2-1/(m-1)}^2<4 �@���C�ǂ��䂤�v�Z�����̂��H
�@�܂��An����̏ꍇ�́A����� n+1 �ɂ�����ƁA���ꂪ�����ƂȂ�A���A�O�̏ؖ��ɂ���āA���̒l������
���邩��An �̏ꍇ���������4���l���������Ȃ�B
�@���̎��� n �̒l�𑝂��ɂ��������Ă��̒l���������邪�A������x 4 �������邱�Ƃ͂Ȃ�����A����������
�̋Ɍ��ɒB����B���̐��� e �ŕ\���Ă���̂ł���B
{n=100 �Ƃ����Ƃ��̎��̒l�� 1.01^100=2.704(�ΐ��v�Z�ɂ��j�ƂȂ�A�܂��An=1000�Ƃ����� 1.001^1000
=2.717�i�ΐ��v�Z�ɂ��j�ƂȂ�B���̋Ɍ��l e �͎��͂��̒l�ƂȂ�Be=2.71828188284�E�E�E�E�E
2018/02/19(��) 17:31:46.40ID:CMze8r9t
>>300
��
�@�܂��An �������ł͂Ȃ��āAn<k<n+1 �Ƃ����� k �ł���ꍇ�ɂ� 1/(n+1)<1/k,1/n �Ƃ����s�������������邩��A
���������Ă܂��A���̕s��������������B
{1+1/(n+1)}^n<{1+1/(n+1)}^k,(1+1/k)^k<(1+1/n)^k<(1+1/n)^(n+1)
�Ƃ��낪�A���[�̎��͂�������������āA
(1+1/n)^(n+1)=(1+1/n)^n*(1+1/n) , {1+1/(n+1)}^n={1+1/(n+1)}^(n+1)*{1-1/(n+2)} ���D���̌v�Z���ڂ���������
��������
�Ɖ��߂�ƁA�Ɍ��ɂ͂ǂ���� e*1 ���Ȃ킿 e �ƂȂ�B�䂦�ɁAn �͂��������łȂ��Ă��悢�B
��
�@�܂��An �������ł͂Ȃ��āAn<k<n+1 �Ƃ����� k �ł���ꍇ�ɂ� 1/(n+1)<1/k,1/n �Ƃ����s�������������邩��A
���������Ă܂��A���̕s��������������B
{1+1/(n+1)}^n<{1+1/(n+1)}^k,(1+1/k)^k<(1+1/n)^k<(1+1/n)^(n+1)
�Ƃ��낪�A���[�̎��͂�������������āA
(1+1/n)^(n+1)=(1+1/n)^n*(1+1/n) , {1+1/(n+1)}^n={1+1/(n+1)}^(n+1)*{1-1/(n+2)} ���D���̌v�Z���ڂ���������
��������
�Ɖ��߂�ƁA�Ɍ��ɂ͂ǂ���� e*1 ���Ȃ킿 e �ƂȂ�B�䂦�ɁAn �͂��������łȂ��Ă��悢�B
302�P�R�Q�l�ڂ̑f������
2018/02/19(��) 23:19:35.50ID:m16ZPD9z >>299-300
�܂��ؖ����������Ƃ͂���
�b(1+1/n)^n��n�𑝂��ɂ��������đ傫���Ȃ�
����́A�C�ӂ�n��2�ɂ���
{1+1/(n-1)}^(n-1)��(1+1/n)^n���A
�ł��邱�Ƃ����������B���̂��߂�
{1+1/(n-1)}^(n-1)-(1+1/n)^n��0���A'���ؖ�����
�A'�̍���
��{1+1/(n-1)}^(n-1)-{1+1/(n-1)}^n+{1+1/(n-1)}^n-(1+1/n)^n
��(1-{1+1/(n-1)}){1+1/(n-1)}^(n-1)+{1+1/(n-1)}^n-(1+1/n)^n
��{-1/(n-1)}{1+1/(n-1)}^(n-1)+[{1+1/(n-1)}^n-(1+1/n)^n]
��2����y^n-a^n�̌`�ɂȂ����̂ŁA
y��a�Ȃ��y^n-a^n��n(y-a)y^(n-1) ��
y=1+1/(n-1) a=1+1/n ���@ ���������ȉ��̎����g���܂��B
{1+1/(n-1)}^n-(1+1/n)^n��n{(1+1/(n-1))-(1+1/n)}{1+1/(n-1)}^(n-1)
�܂�[{1+1/(n-1)}^n-(1+1/n)^n]��{1/(n-1)}{1+1/(n-1)}^(n-1)
���̕s�����̗��ӂ�{-1/(n-1)}{1+1/(n-1)}^(n-1)���������
�A'�̍��Ӂ�{-1/(n-1)}{1+1/(n-1)}^(n-1)+{1/(n-1)}{1+1/(n-1)}^(n-1)��0
����ŇA���ؖ��ł��܂���
�܂��ؖ����������Ƃ͂���
�b(1+1/n)^n��n�𑝂��ɂ��������đ傫���Ȃ�
����́A�C�ӂ�n��2�ɂ���
{1+1/(n-1)}^(n-1)��(1+1/n)^n���A
�ł��邱�Ƃ����������B���̂��߂�
{1+1/(n-1)}^(n-1)-(1+1/n)^n��0���A'���ؖ�����
�A'�̍���
��{1+1/(n-1)}^(n-1)-{1+1/(n-1)}^n+{1+1/(n-1)}^n-(1+1/n)^n
��(1-{1+1/(n-1)}){1+1/(n-1)}^(n-1)+{1+1/(n-1)}^n-(1+1/n)^n
��{-1/(n-1)}{1+1/(n-1)}^(n-1)+[{1+1/(n-1)}^n-(1+1/n)^n]
��2����y^n-a^n�̌`�ɂȂ����̂ŁA
y��a�Ȃ��y^n-a^n��n(y-a)y^(n-1) ��
y=1+1/(n-1) a=1+1/n ���@ ���������ȉ��̎����g���܂��B
{1+1/(n-1)}^n-(1+1/n)^n��n{(1+1/(n-1))-(1+1/n)}{1+1/(n-1)}^(n-1)
�܂�[{1+1/(n-1)}^n-(1+1/n)^n]��{1/(n-1)}{1+1/(n-1)}^(n-1)
���̕s�����̗��ӂ�{-1/(n-1)}{1+1/(n-1)}^(n-1)���������
�A'�̍��Ӂ�{-1/(n-1)}{1+1/(n-1)}^(n-1)+{1/(n-1)}{1+1/(n-1)}^(n-1)��0
����ŇA���ؖ��ł��܂���
303�P�R�Q�l�ڂ̑f������
2018/02/19(��) 23:31:48.40ID:m16ZPD9z >>300
���Ƃ��낪�A�i�B�������炪������܂���A���ł��ꂼ��̉E�ӂ������Ȃ�̂��E�E�E�j
��(2*m+1)/2*m<(2*m)/(2*m-1) , (2*m+1)/(2*m)<(2*m-1)/(2*m-2) , (2*m+1)/(2*m)<(2*m-2)/(2*m-3) ,
(2m+1)/(2m)��(2m)/(2m)+1/(2m)��1+{1/(2m)}�ł��B
���l�ɁA(2m-(n-1))/(2m-n)=((2m-n)+1)/(2m-n)��1+{1/(2m-n)}�ƂȂ�܂��B
(2m)��(2m-n)��0�ł���A{1/(2m)}��{1/(2m-n)}�ł��B
���ӂ�1��������1+{1/(2m)}��1+{1/(2m-n)}����āA
0��n��2m�ł���n�ɂ��āA(2m+1)/(2m)��(2m-(n-1))/(2m-n)�ƂȂ�܂��B
��(1+1/n)^n<{(2*m+1)/(m+1)}^2 , ���Ȃ킿�A(1+1/n)^n<{2-1/(m-1)}^2<4 �@���C�ǂ��䂤�v�Z�����̂��H
(2m+1)/(m+1)��(2(m+1)-1)/(m+1)��2(m+1)/(m+1)-1/(m+1)��2-1/(m+1)��2-1/(m-1)�ł��B
���Ƃ��낪�A�i�B�������炪������܂���A���ł��ꂼ��̉E�ӂ������Ȃ�̂��E�E�E�j
��(2*m+1)/2*m<(2*m)/(2*m-1) , (2*m+1)/(2*m)<(2*m-1)/(2*m-2) , (2*m+1)/(2*m)<(2*m-2)/(2*m-3) ,
(2m+1)/(2m)��(2m)/(2m)+1/(2m)��1+{1/(2m)}�ł��B
���l�ɁA(2m-(n-1))/(2m-n)=((2m-n)+1)/(2m-n)��1+{1/(2m-n)}�ƂȂ�܂��B
(2m)��(2m-n)��0�ł���A{1/(2m)}��{1/(2m-n)}�ł��B
���ӂ�1��������1+{1/(2m)}��1+{1/(2m-n)}����āA
0��n��2m�ł���n�ɂ��āA(2m+1)/(2m)��(2m-(n-1))/(2m-n)�ƂȂ�܂��B
��(1+1/n)^n<{(2*m+1)/(m+1)}^2 , ���Ȃ킿�A(1+1/n)^n<{2-1/(m-1)}^2<4 �@���C�ǂ��䂤�v�Z�����̂��H
(2m+1)/(m+1)��(2(m+1)-1)/(m+1)��2(m+1)/(m+1)-1/(m+1)��2-1/(m+1)��2-1/(m-1)�ł��B
2018/02/20(��) 00:03:12.59ID:5ZuZwnt9
>>302-303
�������A���肪�Ƃ��������܂��B
�������A���肪�Ƃ��������܂��B
2018/02/20(��) 15:14:40.59ID:On6l/zjh
�u�ꐔ�v�u��W�c�v�u����v�̈Ⴂ�A�������Ă郂�������Ȃ��� [871635759]
http://leia.5ch.net/test/read.cgi/poverty/1519107210/
http://leia.5ch.net/test/read.cgi/poverty/1519107210/
2018/02/20(��) 17:52:45.81ID:Bhp4lTfX
m�𐳂̐����Ƃ���Ƃ��A�ȉ��̘a�����߂�B
��[n=1,��] (1/n^(4m-1)) ((-1)^(n-1)/(e^(��n)-e^(-��n)))
��[n=1,��] (1/n^(4m-1)) ((-1)^(n-1)/(e^(��n)-e^(-��n)))
2018/02/21(��) 01:05:46.55ID:H9c/veQI
a_{n+2} = - ( a_{n+1} + a_n )
a_1 = 1
a_2 = 1
�̈�ʍ���
n=3m-1,n=3m-2�̏ꍇ1�An=3m�̏ꍇ-2
��OK?
a_1 = 1
a_2 = 1
�̈�ʍ���
n=3m-1,n=3m-2�̏ꍇ1�An=3m�̏ꍇ-2
��OK?
2018/02/21(��) 01:21:25.52ID:14F8UTmi
>>307
���w�I�A�[�@�ʼn���
���w�I�A�[�@�ʼn���
2018/02/21(��) 07:36:43.32ID:JFIkQrIb
>>307
��^2+��+1��0�Ƃ���
a_{n+2}-(��^2)a_{n+1}=��(a_{n+1}-(��^2)a_n)
a_2-(��^2)a_1=1-��^2
�Ȃ̂�a_{n+1}-(��^2)a_n=��^(n-1)(1-��^2)�@
a_{n+2}-��a_{n+1}=��^2(a_{n+1}-��a_n)
a_2-��a_1=1-��
�Ȃ̂�a_{n+1}-��a_n=(��^2)^(n-1)(1-��)�A
�@�ƇA���a_n=(��^(n-1)(1-��^2)-(��^2)^(n-1)(1-��))/(��-��^2)
n=3m-2�̏ꍇ�Aa_n=((1-��^2)-(1-��))/(��-��^2)=(��-��^2)/(��-��^2)=1
n=3m-1�̏ꍇ�Aa_n=(��(1-��^2)-��^2(1-��))/(��-��^2)=(��-��^2)/(��-��^2)=1
n=3m�̏ꍇ�Aa_n=(��^2(1-��^2)-��(1-��))/(��-��^2)=(��^2-��-��+��^2))/(��-��^2)=-2
��^2+��+1��0�Ƃ���
a_{n+2}-(��^2)a_{n+1}=��(a_{n+1}-(��^2)a_n)
a_2-(��^2)a_1=1-��^2
�Ȃ̂�a_{n+1}-(��^2)a_n=��^(n-1)(1-��^2)�@
a_{n+2}-��a_{n+1}=��^2(a_{n+1}-��a_n)
a_2-��a_1=1-��
�Ȃ̂�a_{n+1}-��a_n=(��^2)^(n-1)(1-��)�A
�@�ƇA���a_n=(��^(n-1)(1-��^2)-(��^2)^(n-1)(1-��))/(��-��^2)
n=3m-2�̏ꍇ�Aa_n=((1-��^2)-(1-��))/(��-��^2)=(��-��^2)/(��-��^2)=1
n=3m-1�̏ꍇ�Aa_n=(��(1-��^2)-��^2(1-��))/(��-��^2)=(��-��^2)/(��-��^2)=1
n=3m�̏ꍇ�Aa_n=(��^2(1-��^2)-��(1-��))/(��-��^2)=(��^2-��-��+��^2))/(��-��^2)=-2
2018/02/22(��) 02:09:34.22ID:464amdV1
���Ԃ�ł��ǂ��͂��B
a_{n+2} = - ( a_{n+1} + a_n ) �� 1���炷
a_{n+3} = - ( a_{n+2} + a_{n+1} ) �� �ŏ��̎�����
a_{n+3} = - ( - ( a_{n+1} + a_n ) + a_{n+1} )
a_{n+3} = a_n
����āA
a_1 = a_4 = a_{3n-2} = 1
a_2 = a_5 = a_{3n-1} = 1
a_3 = a_6 = a_{3n} = -2
a_{n+2} = - ( a_{n+1} + a_n ) �� 1���炷
a_{n+3} = - ( a_{n+2} + a_{n+1} ) �� �ŏ��̎�����
a_{n+3} = - ( - ( a_{n+1} + a_n ) + a_{n+1} )
a_{n+3} = a_n
����āA
a_1 = a_4 = a_{3n-2} = 1
a_2 = a_5 = a_{3n-1} = 1
a_3 = a_6 = a_{3n} = -2
311�P�R�Q�l�ڂ̑f������
2018/02/22(��) 07:03:18.44ID:sQ484qbx �M���V�������̐������������������Ă�������
�l�b�g�����ł͏�������Ă��Ă悭�킩��܂���
�l�b�g�����ł͏�������Ă��Ă悭�킩��܂���
2018/02/22(��) 09:29:07.28ID:hR7G8FUR
�������ɂ������͓̂��{�l�ȊO�ɂ��܂肵��Ȃ���
�����l�̏��Ƃ͕͂ʂɂ���
�����l�̏��Ƃ͕͂ʂɂ���
2018/02/22(��) 17:05:45.99ID:WVdG5tK3
>>311
�ƂĂ������I�ŊȒP�ȃM���V����̖{�ɍڂ��Ă���B
�p��̒��w�̋��ȏ��ł��A���t�@�x�b�g�₻�̕M�L�̂̏������͐�������Ă����́B
�Ȃ̂ŁA�M���V�������̏�������m�肽�������Ȃ�A���w(���ł����Ə��w�Z��)���x���̃M���V����̖{�ł����Ǝv���B
�ƂĂ������I�ŊȒP�ȃM���V����̖{�ɍڂ��Ă���B
�p��̒��w�̋��ȏ��ł��A���t�@�x�b�g�₻�̕M�L�̂̏������͐�������Ă����́B
�Ȃ̂ŁA�M���V�������̏�������m�肽�������Ȃ�A���w(���ł����Ə��w�Z��)���x���̃M���V����̖{�ł����Ǝv���B
2018/02/22(��) 17:15:52.35ID:WVdG5tK3
�����A�����́B�Ȃ�ď����������w
2018/02/22(��) 17:24:23.51ID:WVdG5tK3
>>312
�A���t�@�x�b�g�̕M�L�̂͑��̏��̂̕���������đ��������������ĕ\����悤�ɂ����������ŁA���܂���������������B
�����ꂽ�M�L�̂̕����̏�艺��͂Ƃ������Ƃ��āB
�A���t�@�x�b�g�̕M�L�̂͑��̏��̂̕���������đ��������������ĕ\����悤�ɂ����������ŁA���܂���������������B
�����ꂽ�M�L�̂̕����̏�艺��͂Ƃ������Ƃ��āB
2018/02/23(��) 01:06:31.87ID:dGTz317a
�A���t�@�x�b�g�̕M�L�͓̂��{��̍s���̂���̂ɂ�����B
���{�ꂾ�ƕ��ʂ̎��̂͞����̂����A�A���t�@�x�b�g�̕��ʂ̎��͉̂��ƌĂԂ낤�B
���{�ꂾ�ƕ��ʂ̎��̂͞����̂����A�A���t�@�x�b�g�̕��ʂ̎��͉̂��ƌĂԂ낤�B
2018/02/23(��) 04:10:09.02ID:ytc70m+y
�u���b�N��
2018/02/23(��) 21:15:34.22ID:eCB2skqw
>>313
���肪�Ƃ��������܂�
���肪�Ƃ��������܂�
2018/02/24(�y) 16:39:44.29ID:GHvdAv8s
>>306
m=1�̂Ƃ� (1/720)��^3
m=2�̂Ƃ� (13/907200)��^7
m=3�̂Ƃ� (4009/27243216000)��^11
�c
��ʌ`�� C_m ��^(4m-1)
������{C_m}�͈ȉ��̑Q��������
C_0=1/8, C_m=��[j=1,m] C_{m-j} (-1)^(j-1) 2^(2j+1)/(4j+2)!
m=1�̂Ƃ� (1/720)��^3
m=2�̂Ƃ� (13/907200)��^7
m=3�̂Ƃ� (4009/27243216000)��^11
�c
��ʌ`�� C_m ��^(4m-1)
������{C_m}�͈ȉ��̑Q��������
C_0=1/8, C_m=��[j=1,m] C_{m-j} (-1)^(j-1) 2^(2j+1)/(4j+2)!
2018/02/26(��) 13:44:16.44ID:aLDdUWeS
����
���ɐ����� 1 �Ɛ����� 2 ��1��������Ă���B
2�l�̃v���C���[��, ���݂Ɏ��́u�v���̑�����s���B
�u������Ă���2�̐����̂���1��C�ӂɑI�ԁB
�I���� a, �I�Ȃ��������� b �Ƃ�, a �� a+b �ɏ���������B�v
��.
2 �� 5 ��������Ă���Ƃ��� 2 ��I�ꍇ, 2 �� 7 �ɏ���������B
������Ă��鐔���� 7 �� 5 �ƂȂ�B
��ɑ�����s���v���C���[����, �����łȂ��v���C���[�����ƌĂԁB
��� 100 �ȏ�̐������������v���C���[�����҂Ƃ���B
���̂Ƃ�, ���̖₢�ɓ�����B
(1) ���҂����܂������_�ō��ɏ�����Ă��������� 70 �� 101 �ł������Ƃ�, ���҂͐��, ���̂ǂ��炩�B
(2) ���҂����܂������_�ō��ɏ�����Ă��������� n �� 100 �ł������Ƃ���B���̂Ƃ� n �Ƃ��ĂƂ蓾��l�͉��ʂ肩�B(�e�v���C���[�͍œK�Ȑ헪���Ƃ�Ƃ͌���Ȃ��Ƃ���)
���ɐ����� 1 �Ɛ����� 2 ��1��������Ă���B
2�l�̃v���C���[��, ���݂Ɏ��́u�v���̑�����s���B
�u������Ă���2�̐����̂���1��C�ӂɑI�ԁB
�I���� a, �I�Ȃ��������� b �Ƃ�, a �� a+b �ɏ���������B�v
��.
2 �� 5 ��������Ă���Ƃ��� 2 ��I�ꍇ, 2 �� 7 �ɏ���������B
������Ă��鐔���� 7 �� 5 �ƂȂ�B
��ɑ�����s���v���C���[����, �����łȂ��v���C���[�����ƌĂԁB
��� 100 �ȏ�̐������������v���C���[�����҂Ƃ���B
���̂Ƃ�, ���̖₢�ɓ�����B
(1) ���҂����܂������_�ō��ɏ�����Ă��������� 70 �� 101 �ł������Ƃ�, ���҂͐��, ���̂ǂ��炩�B
(2) ���҂����܂������_�ō��ɏ�����Ă��������� n �� 100 �ł������Ƃ���B���̂Ƃ� n �Ƃ��ĂƂ蓾��l�͉��ʂ肩�B(�e�v���C���[�͍œK�Ȑ헪���Ƃ�Ƃ͌���Ȃ��Ƃ���)
2018/02/26(��) 15:40:34.06ID:R9jBckXx
>>320
���̖��A�ĊO�Ɩʔ���
���̖��A�ĊO�Ɩʔ���
2018/02/26(��) 19:42:30.46ID:1aP4oHSM
���o�J�Ȏ��ɋ����Ă�������
����ǂ�����ĉ����̂ł����H
lim[x��0] sin7x/tan5x
�r���v�Z���ڂ������肢���܂��B�@(^^;)
����ǂ�����ĉ����̂ł����H
lim[x��0] sin7x/tan5x
�r���v�Z���ڂ������肢���܂��B�@(^^;)
2018/02/26(��) 23:36:23.91ID:R9jBckXx
>>320
(2)��40�ʂ���
(2)��40�ʂ���
324320
2018/02/27(��) 00:04:15.44ID:b6xI5Upm >>321>>323
���肪�Ƃ�
(2) �͂��̒ʂ�ł��B
�{���͐��K���A���K���Ɋւ�����ɂ������������ǁA
�Ȃ��Ȃ����G�ł��܂����ɏo���Ȃ������B
���Ȃ݂ɂ��̃Q�[�������K���Ȃ̂����K���Ȃ̂��͒m��܂���B
���肪�Ƃ�
(2) �͂��̒ʂ�ł��B
�{���͐��K���A���K���Ɋւ�����ɂ������������ǁA
�Ȃ��Ȃ����G�ł��܂����ɏo���Ȃ������B
���Ȃ݂ɂ��̃Q�[�������K���Ȃ̂����K���Ȃ̂��͒m��܂���B
2018/02/27(��) 02:26:18.74ID:RVqV86Rj
>>324
���̃Q�[���͌��L���Ȃ悤�ł�
����͐�肪�ǂ���̎���o���Ă�����2�̐����̍��v��7�ɂȂ�悤�Ȏ�Ƃ��܂�
2��ڂ͓��l�ɍ��v��18�ȉ��̍ő�l�ƂȂ����A3��ڂ͍��v��41�ȉ��̍ő�l�A4��ڂ͍��v��99�ȉ��̍ő�l�ɂȂ�悤���I�ԂƏ����Ƃ��ł��܂�
���̃Q�[���͌��L���Ȃ悤�ł�
����͐�肪�ǂ���̎���o���Ă�����2�̐����̍��v��7�ɂȂ�悤�Ȏ�Ƃ��܂�
2��ڂ͓��l�ɍ��v��18�ȉ��̍ő�l�ƂȂ����A3��ڂ͍��v��41�ȉ��̍ő�l�A4��ڂ͍��v��99�ȉ��̍ő�l�ɂȂ�悤���I�ԂƏ����Ƃ��ł��܂�
2018/02/27(��) 03:04:37.64ID:M/Cc1/YM
2018/02/27(��) 04:39:32.24ID:M/Cc1/YM
>>319
m ���� �̂Ƃ��A n>1�̍��͐v���Ɍ������A
1/{e^�� - e^(-��)�p= 0.043294768765
�Ɏ�������B
C_2 ��^7 �� C_3 ��^11
���
���iC_2/C_3)^(1/4�j=�o(2�3�5�7�11�13^2)/(19�211)}^(1/4�j= 3�D141345
m ���� �̂Ƃ��A n>1�̍��͐v���Ɍ������A
1/{e^�� - e^(-��)�p= 0.043294768765
�Ɏ�������B
C_2 ��^7 �� C_3 ��^11
���
���iC_2/C_3)^(1/4�j=�o(2�3�5�7�11�13^2)/(19�211)}^(1/4�j= 3�D141345
2018/02/27(��) 12:10:49.57ID:RVqV86Rj
>>320
�u��� 100 �ȏ�̐������������v���C���[�����҂Ƃ���v�̃��[������ʉ�����
�u��� N �ȏ�̐������������v���C���[�����҂Ƃ���v(N��3�ȏ�̐���)�Ƃ���
3����100�܂ł��������Ƃ���A
N��3,5�`7,11�`17,25�`41,59�`99�̂Ƃ��͐��K��
N��4,8�`10,18�`24,42�`58,100�̂Ƃ��͌��K���Əo�܂���
�@���������肻���ł����A���܂�����Əؖ����ł��邩������܂���
�u��� 100 �ȏ�̐������������v���C���[�����҂Ƃ���v�̃��[������ʉ�����
�u��� N �ȏ�̐������������v���C���[�����҂Ƃ���v(N��3�ȏ�̐���)�Ƃ���
3����100�܂ł��������Ƃ���A
N��3,5�`7,11�`17,25�`41,59�`99�̂Ƃ��͐��K��
N��4,8�`10,18�`24,42�`58,100�̂Ƃ��͌��K���Əo�܂���
�@���������肻���ł����A���܂�����Əؖ����ł��邩������܂���
329320
2018/02/27(��) 16:22:29.36ID:b6xI5Upm2018/02/28(��) 00:27:42.99ID:Z523oFSX
����{a_n}���Q����
a_0=a_1=a_2=a_3=a_4=1,
a_{n+5}=a_{n+4}+a_{n+3}+a_{n+2}+a_{n+1}+a_n
�����Ƃ�
��[n=0,��]a_n/2^n
�͎������邩�H��������Ȃ炻�̒l�����߂�B
a_0=a_1=a_2=a_3=a_4=1,
a_{n+5}=a_{n+4}+a_{n+3}+a_{n+2}+a_{n+1}+a_n
�����Ƃ�
��[n=0,��]a_n/2^n
�͎������邩�H��������Ȃ炻�̒l�����߂�B
2018/02/28(��) 03:50:48.87ID:Z523oFSX
>>330�̊֘A���
�v���[�����R�C����1���������An��A�����ĕ\���o���Ƃ�������̂����
���̃v���[���̓������R�C���̖����_�Ƃ���Q�[��������B
���̃Q�[���̓��_�̊��Ғl��n�ŕ\���B
�v���[�����R�C����1���������An��A�����ĕ\���o���Ƃ�������̂����
���̃v���[���̓������R�C���̖����_�Ƃ���Q�[��������B
���̃Q�[���̓��_�̊��Ғl��n�ŕ\���B
2018/02/28(��) 03:57:53.44ID:W7HTMDJw
>>330
a_n = P_{k+1�p- P_{k-1�p-2P_{k-2�p-3P_{k-3},
�����Ɂ@P_k �� Pentanabbi number
�����������@x^5 -x^4 -x^3 -x^2 -x -1 = 0
���� r = 1.9659482366454853372�c (Pentanacci constant)
�b���b= 0.818788815767 < r
�b���b= 0.871047941737 < r
lim�mn�����na_n / 2^n = 0
lim�mn�����na_n / r^n = 0.1491215649669�c
a_n = P_{k+1�p- P_{k-1�p-2P_{k-2�p-3P_{k-3},
�����Ɂ@P_k �� Pentanabbi number
�����������@x^5 -x^4 -x^3 -x^2 -x -1 = 0
���� r = 1.9659482366454853372�c (Pentanacci constant)
�b���b= 0.818788815767 < r
�b���b= 0.871047941737 < r
lim�mn�����na_n / 2^n = 0
lim�mn�����na_n / r^n = 0.1491215649669�c
2018/02/28(��) 04:14:15.51ID:W7HTMDJw
>>330
���mn=0�C���na_n / 2^n = 2�ia_0 + a_1 + a_2 + a_3 + a_4�j= 10,
Pentanacci number �ł�
���mn=0�C���nP_n / 2^n = 2�i0 + 1 + 1 + 2 + 4�j= 16,
���mn=0�C���na_n / 2^n = 2�ia_0 + a_1 + a_2 + a_3 + a_4�j= 10,
Pentanacci number �ł�
���mn=0�C���nP_n / 2^n = 2�i0 + 1 + 1 + 2 + 4�j= 16,
2018/02/28(��) 06:23:16.56ID:tNb7qvu5
335330
2018/03/04(��) 08:26:59.79ID:gP4gtYTC >>333
����
����������/������g��Ȃ���@�F
a_{n+5}-a_{n+4}-a_{n+3}-a_{n+2}-a_{n+1}-a_n=0 �c�c(1)
��(1)����n��n+1�ɒu��������������(1)��������
a_{n+6}-2a_{n+5}+a_n=0
��1/2^(n+6)�{���� b_n=a_n/2^n �ƒu��
b_{n+6}-b_{n+5}=-(1/64)b_n �c�c(2)
��{b_n}�͒P�����������
b_{n+6}<b_{n+5}-(1/64)b_{n+5}=(63/64)b_{n+5}<(63/64)^(n+1) b_5 �c�c(3)
���(2)����n=0����n=m�܂ő������킹���
b_{m+6}-b_5=-(1/64)��[n=0,m]b_n
��m�����Ƃ����(3)�����b_{m+6}��0
��[n=0,m]b_n �� 64b_5=2a_5=10 �Ɏ���
����
����������/������g��Ȃ���@�F
a_{n+5}-a_{n+4}-a_{n+3}-a_{n+2}-a_{n+1}-a_n=0 �c�c(1)
��(1)����n��n+1�ɒu��������������(1)��������
a_{n+6}-2a_{n+5}+a_n=0
��1/2^(n+6)�{���� b_n=a_n/2^n �ƒu��
b_{n+6}-b_{n+5}=-(1/64)b_n �c�c(2)
��{b_n}�͒P�����������
b_{n+6}<b_{n+5}-(1/64)b_{n+5}=(63/64)b_{n+5}<(63/64)^(n+1) b_5 �c�c(3)
���(2)����n=0����n=m�܂ő������킹���
b_{m+6}-b_5=-(1/64)��[n=0,m]b_n
��m�����Ƃ����(3)�����b_{m+6}��0
��[n=0,m]b_n �� 64b_5=2a_5=10 �Ɏ���
336�P�R�Q�l�ڂ̑f������
2018/03/07(��) 22:27:09.03ID:u6eTb2db �ϕ��̕����ĂȂ�
�Ȃɂ����������
�Ȃɂ����������
2018/03/08(��) 01:04:39.57ID:YNRhAtaA
>>336
���������ς�
���������ς�
2018/03/08(��) 01:07:48.66ID:m0ftmBCi
���܂肽�܂������̂����o����J��Ԃ���錻�ۂ����Ӄ��[�L���ϕ��Ƃ����̂͂����Ȃ���̂ł����H
339�P�R�Q�l�ڂ̑f������
2018/03/08(��) 04:13:47.72ID:/uF9jjn12018/03/08(��) 06:13:55.94ID:2WrkjBM5
�Q�ȏ�̎��R�� m�An ���An|m ���݂����Ƃ��A
�um��@�Ƃ��錴�n�������݂��� �� n��@�Ƃ��錴�n�������݂���v
�̏ؖ���������܂���B
�um��@�Ƃ��錴�n�������݂��� �� n��@�Ƃ��錴�n�������݂���v
�̏ؖ���������܂���B
341�P�R�Q�l�ڂ̑f������
2018/03/08(��) 14:06:31.56ID:NRG1qgrQ ����g���Έꔭ����Ȃ��H
2018/03/10(�y) 01:11:02.58ID:GvWkDM61
������ 74, 81, 82, 86, 94, 98 ��@�Ƃ��錴�n�������ׂčڂ��Ă���T�C�g���ĂȂ��ł����H
343�P�R�Q�l�ڂ̑f������
2018/03/10(�y) 04:51:24.21ID:Ta7osRmu >>342
74: 5,13,15,17,19,35,39,55,57,59,61,69
81: 2,5,11,14,20,23,29,32,38,41,47,50,56,59,65,68,74,77
82: 7,11,13,15,17,19,29,35,47,53,63,65,67,69,71,75
86: 3,5,19,29,33,55,61,63,69,71,73,77
94: 5,11,13,15,19,23,29,31,33,35,39,41,43,45,57,67,69,73,77,85,87,91
98: 3,5,17,33,45,47,59,61,73,75,87,89
74: 5,13,15,17,19,35,39,55,57,59,61,69
81: 2,5,11,14,20,23,29,32,38,41,47,50,56,59,65,68,74,77
82: 7,11,13,15,17,19,29,35,47,53,63,65,67,69,71,75
86: 3,5,19,29,33,55,61,63,69,71,73,77
94: 5,11,13,15,19,23,29,31,33,35,39,41,43,45,57,67,69,73,77,85,87,91
98: 3,5,17,33,45,47,59,61,73,75,87,89
2018/03/10(�y) 05:04:30.76ID:GvWkDM61
���肪�Ƃ��������܂��B
�v���O�����������ĉ������̂ł��傤���H
�v���O�����������ĉ������̂ł��傤���H
2018/03/10(�y) 05:14:43.31ID:GvWkDM61
�f�� p ��@�Ƃ��錴�n���́A��(p) �A
p^n �ip�͊�f���An�͎��R���j��@�Ƃ��錴�n���́A��(��(p^n)) �ł����A
2p^n �ip�͊�f���An�͎��R���j��@�Ƃ��錴�n���̌��ɂ��Ă��A���������͂���̂ł����H
p^n �ip�͊�f���An�͎��R���j��@�Ƃ��錴�n���́A��(��(p^n)) �ł����A
2p^n �ip�͊�f���An�͎��R���j��@�Ƃ��錴�n���̌��ɂ��Ă��A���������͂���̂ł����H
346DJ�w�p�@
2018/03/10(�y) 10:15:27.87ID:P59AXYVi ����������Ƃ����������������Ⴞ�߂�����A�����g�����́A
���𗧂Ă�Ƃ������������O���ă��A�Ȑ����ʼn��Z����Ƃ�����B
���𗧂Ă�Ƃ������������O���ă��A�Ȑ����ʼn��Z����Ƃ�����B
347�P�R�Q�l�ڂ̑f������
2018/03/12(��) 18:17:10.69ID:6N2q32Cy �m���_�̏����̏����������Ă�������
���������U���ĂP���o��m���͂U���̂P�B����́A����������R�U��ΐU��قǁA
�P���o�銄�����U���̂P�Ɏ������邱�Ƃ��Ӗ�����B
�ł́A���̎��������i����U��ǂ̒��x�U���̂P�ɋ߂Â����j�́A�ǂ�����Čv�Z�����ł��傤�H
���͕��n�Ȃ̂ŁA���t�Ő������Ă��炦����肪�����ł��B
�ǂ�����낵�����肢���܂��B
���������U���ĂP���o��m���͂U���̂P�B����́A����������R�U��ΐU��قǁA
�P���o�銄�����U���̂P�Ɏ������邱�Ƃ��Ӗ�����B
�ł́A���̎��������i����U��ǂ̒��x�U���̂P�ɋ߂Â����j�́A�ǂ�����Čv�Z�����ł��傤�H
���͕��n�Ȃ̂ŁA���t�Ő������Ă��炦����肪�����ł��B
�ǂ�����낵�����肢���܂��B
348�P�R�Q�l�ڂ̑f������
2018/03/12(��) 23:49:01.38ID:Gc10l/I+ �����̏���
2018/03/13(��) 21:50:18.80ID:2y1j/gPY
���n�Ȃ�A���t���Ɏg�����ق��������Ǝv���܂��B
���w�̓��e���v�Z�����ŗ����������Ƃ����Ȃ�A���X
���t�ɂ͕q���łȂ��Ă͂Ȃ�Ȃ��͂��ł��B
�p����G�Ɏg���ẮA���t�ł̗����͐��������܂���B
�u����������R�U��ΐU��قǁA
�P���o�銄�����U���̂P�Ɏ�������v�Ƃ����\���́A
�����炭�A���������������ł̂��Ƃł��傤�B
�u����������R�U��ΐU��قǁA
�P���o�銄�����U���̂P�ɋ߂Â��v���Ƃ�
�u���������U���������ɋ߂Â��Ɍ��ŁA
�P���o�銄���͂U���̂P�Ɏ�������v�ƌ����܂��B
�u��������v�Ƃ������t�̈Ӗ����l����ƁA
�u�U��ΐU��قǁA��������v�Ƃ����\����
���蓾�Ȃ��ł��B
�u�U��ΐU��قǁA�߂Â��v�́A�B����
�ϔO�I�ȕ\���ł����A�����͋C�łȂ����m�ȓ��e��
�\�����悤�Ƃ���A�u�߂Â��v�߂Â������ʓI��
���荞�܂�����A������v�Z���܂ސ����ɂȂ�܂��B
�u�߂Â��v�Ŕ[�����邱�Ƃɂ��邩�A
���w�I�ȕ\���ɓ��ݍ��ނ��A����������
�o�債�đI�Ȃ���Ȃ�܂���B
���w�̓��e���v�Z�����ŗ����������Ƃ����Ȃ�A���X
���t�ɂ͕q���łȂ��Ă͂Ȃ�Ȃ��͂��ł��B
�p����G�Ɏg���ẮA���t�ł̗����͐��������܂���B
�u����������R�U��ΐU��قǁA
�P���o�銄�����U���̂P�Ɏ�������v�Ƃ����\���́A
�����炭�A���������������ł̂��Ƃł��傤�B
�u����������R�U��ΐU��قǁA
�P���o�銄�����U���̂P�ɋ߂Â��v���Ƃ�
�u���������U���������ɋ߂Â��Ɍ��ŁA
�P���o�銄���͂U���̂P�Ɏ�������v�ƌ����܂��B
�u��������v�Ƃ������t�̈Ӗ����l����ƁA
�u�U��ΐU��قǁA��������v�Ƃ����\����
���蓾�Ȃ��ł��B
�u�U��ΐU��قǁA�߂Â��v�́A�B����
�ϔO�I�ȕ\���ł����A�����͋C�łȂ����m�ȓ��e��
�\�����悤�Ƃ���A�u�߂Â��v�߂Â������ʓI��
���荞�܂�����A������v�Z���܂ސ����ɂȂ�܂��B
�u�߂Â��v�Ŕ[�����邱�Ƃɂ��邩�A
���w�I�ȕ\���ɓ��ݍ��ނ��A����������
�o�債�đI�Ȃ���Ȃ�܂���B
350�P�R�Q�l�ڂ̑f������
2018/04/04(��) 20:06:44.46ID:YT9kwrF/ �ǂ�ȕ��s�Z�ʑ̂���Ԃ����ԂȂ����߂邱�Ƃ��ł���
������̐��ۂ͐������A�Ő����ł���ˁH
������̐��ۂ͐������A�Ő����ł���ˁH
2018/04/05(��) 08:44:21.69ID:VjVUbkvc
>>350
�Ԉ���Ă�
�Ԉ���Ă�
2018/04/05(��) 23:41:10.27ID:DTitQ5x8
2018/04/06(��) 00:08:34.42ID:bVFlHits
0<k<2�̂Ƃ��A�ȉ��̓��������藧���Ƃ��ؖ�����B
��(0,��)sin(kx)/x dx = (k/2)+��[n=1,��]sin(kn)/n
��(0,��)sin(kx)/x dx = (k/2)+��[n=1,��]sin(kn)/n
2018/04/06(��) 00:28:54.11ID:L8ME5L0/
>>352
�[�����͂ǂ�������H
�[�����͂ǂ�������H
2018/04/06(��) 00:30:58.07ID:NC5oOxGL
���[�N���b�h��Ԃ̒[�����A���āH
2018/04/06(��) 04:05:22.47ID:nrTyHdT7
>>353
��(0�C���jsin(kx)/x dx = ��(0�C��) sin(y)/y dy = ��/2,
(x/2�j+ ��[n=1�C���nsin(nx)/n = ��/2�@�@�i0<x<2�j
��(0�C���jsin(kx)/x dx = ��(0�C��) sin(y)/y dy = ��/2,
(x/2�j+ ��[n=1�C���nsin(nx)/n = ��/2�@�@�i0<x<2�j
357353
2018/04/06(��) 05:46:12.80ID:bVFlHits �֘A���F
k��4�Ŋ����1�]�鐳�̐����Ƃ���Ƃ��A�ȉ��̓������ؖ�����B
��(0,��)((2x)^k)/(e^(2��x)+1) dx = ��[n=0,��]((2n+1)^k)/(e^(��(2n+1))+1)
k��4�Ŋ����1�]�鐳�̐����Ƃ���Ƃ��A�ȉ��̓������ؖ�����B
��(0,��)((2x)^k)/(e^(2��x)+1) dx = ��[n=0,��]((2n+1)^k)/(e^(��(2n+1))+1)
2018/04/06(��) 12:33:24.76ID:nrTyHdT7
>>357
(���Ӂj= ��(0,��) (2x)^k /{e^(2��x) + 1} dx
= ��(0,��) (2x)^k ��[L=1,��] (-1)^(L-1) exp(-2L��x) dx
= ��[L=1,���n(-1)^(L-1)�o��(0,��) (2x)^k exp(-2L��x) dx}
=�i1/2)(1/��)^(k+1)�o��(0,��) y^k exp(-y) dy} ��[L=1,���n(-1)^(L-1) / L^(k+1)
=�i1/2)(1/��)^(k+1) ��(k+1�j�i1 - 1/2^k) ��[L=1,���n1 / L^(k+1)
=�i1/2)(1/��)^(k+1�jk!�i1 - 1/2^k�j��(k+1),
(���Ӂj= ��(0,��) (2x)^k /{e^(2��x) + 1} dx
= ��(0,��) (2x)^k ��[L=1,��] (-1)^(L-1) exp(-2L��x) dx
= ��[L=1,���n(-1)^(L-1)�o��(0,��) (2x)^k exp(-2L��x) dx}
=�i1/2)(1/��)^(k+1)�o��(0,��) y^k exp(-y) dy} ��[L=1,���n(-1)^(L-1) / L^(k+1)
=�i1/2)(1/��)^(k+1) ��(k+1�j�i1 - 1/2^k) ��[L=1,���n1 / L^(k+1)
=�i1/2)(1/��)^(k+1�jk!�i1 - 1/2^k�j��(k+1),
359�P�R�Q�l�ڂ̑f������
2018/04/07(�y) 09:56:55.08ID:+YZ8+roj2018/04/07(�y) 13:11:27.79ID:ozKr5R4w
>>359
��쌒���Y�u�̗L���Ȓ藝�v�@�����o�Łi���w���߲�đo��36)�i1981/Dec) 150p�D1512�~
D�D�q���x���g�u�w��b�_�v�@�����܊w�|���Ɂi2005/Dec) 242p�D1296�~
�@�@�����K�l�Y�E��
����p�F�u�����w�v�@��g�S��159�i1952) 182p�D���
���@�@��2�Łi1973) 284p�D���
�@�@���ӌ`�ɂ��Ă�Jordan�̒藝�̏ؖ�
�u���[�N���b�h���_�v�Ǖ�Ł@�����o�Łi2011/May) 574p�D6480�~
�@�����E����E�ɓ��E�r�c�i��j�u
��c���N�u�w�厖�T�v�@ꠏ��X�i1971�`�j�S6���{�ʊ�2�A����
�}���ق̌����[���ŒT�����邩���H
��쌒���Y�u�̗L���Ȓ藝�v�@�����o�Łi���w���߲�đo��36)�i1981/Dec) 150p�D1512�~
D�D�q���x���g�u�w��b�_�v�@�����܊w�|���Ɂi2005/Dec) 242p�D1296�~
�@�@�����K�l�Y�E��
����p�F�u�����w�v�@��g�S��159�i1952) 182p�D���
���@�@��2�Łi1973) 284p�D���
�@�@���ӌ`�ɂ��Ă�Jordan�̒藝�̏ؖ�
�u���[�N���b�h���_�v�Ǖ�Ł@�����o�Łi2011/May) 574p�D6480�~
�@�����E����E�ɓ��E�r�c�i��j�u
��c���N�u�w�厖�T�v�@ꠏ��X�i1971�`�j�S6���{�ʊ�2�A����
�}���ق̌����[���ŒT�����邩���H
2018/04/07(�y) 13:20:56.83ID:ozKr5R4w
>>359 (�Ǖ�)
�����M�F�u�̂������낳�v�@��g���X�i���w����V���[�Y7�j(1985/Sep) 330p�D1850�~
�����M�F�u�ӂ����w�҂̋L�v�@��g���㕶�Ɂi�Љ�19�j(2000/Aug) 315p�D1080�~
�����M�F�u�{�N�͎Z�������o���Ȃ������v�@��g���㕶�Ɂi�Љ�60�j�i2002/May�j186p�D972�~
�@���o�J�łȂ����̂͗B�̃o�J�ł���B(*)
�����M�F�u�ւ̗U���v�@��g���㕶�Ɂi�w�p7�j�i2009/Oct�j228p�D1037�~
*�@����N���u���w���@�B�싳���v�@��g���㕶�Ɂi���|1�j�i2000/Jan�j373p�D1188�~
�����M�F�u�̂������낳�v�@��g���X�i���w����V���[�Y7�j(1985/Sep) 330p�D1850�~
�����M�F�u�ӂ����w�҂̋L�v�@��g���㕶�Ɂi�Љ�19�j(2000/Aug) 315p�D1080�~
�����M�F�u�{�N�͎Z�������o���Ȃ������v�@��g���㕶�Ɂi�Љ�60�j�i2002/May�j186p�D972�~
�@���o�J�łȂ����̂͗B�̃o�J�ł���B(*)
�����M�F�u�ւ̗U���v�@��g���㕶�Ɂi�w�p7�j�i2009/Oct�j228p�D1037�~
*�@����N���u���w���@�B�싳���v�@��g���㕶�Ɂi���|1�j�i2000/Jan�j373p�D1188�~
362�P�R�Q�l�ڂ̑f������
2018/04/07(�y) 19:17:08.93ID:NNMRscPu �����������琢�E���ς���ă����^
2018/04/08(��) 00:49:28.29ID:JG0GTAY0
�y�A�m�����̂T�ɂ��Ď��₪����B
���R�����Ɋւ���q��o�i���j�Łi���j�i���j�����藧�Ƃ���B
�i���j�o�i�P�j�ł���B
�i���j�ǂ�Ȏ��R�����ɂ������Ă��o�i���j�Ȃ�o�i���L�j�ł���B
���̂Ƃ��ǂ�Ȏ��R�����ɂ������Ă��o�i���j�����藧�B
����͎��R���ɂ͂P�̐����Ȃ����Ƃ�錾���Ă�����́A�ƍl���Ă悢��ˁH
�Ⴆ�A�P����n�܂�㑱���̃��[�v�Ő��܂����̂𐔗�P�Ƃ���B
�����P����S�܂ł��Ƃ��̐���P�ɑ����Ȃ����R���w�̑��݂������Ă��܂��B
���̎��R���w��r�����邽�߂̂��̂������T�B
�Ƃ������߂ł悢�̂��낤���B
���R�����Ɋւ���q��o�i���j�Łi���j�i���j�����藧�Ƃ���B
�i���j�o�i�P�j�ł���B
�i���j�ǂ�Ȏ��R�����ɂ������Ă��o�i���j�Ȃ�o�i���L�j�ł���B
���̂Ƃ��ǂ�Ȏ��R�����ɂ������Ă��o�i���j�����藧�B
����͎��R���ɂ͂P�̐����Ȃ����Ƃ�錾���Ă�����́A�ƍl���Ă悢��ˁH
�Ⴆ�A�P����n�܂�㑱���̃��[�v�Ő��܂����̂𐔗�P�Ƃ���B
�����P����S�܂ł��Ƃ��̐���P�ɑ����Ȃ����R���w�̑��݂������Ă��܂��B
���̎��R���w��r�����邽�߂̂��̂������T�B
�Ƃ������߂ł悢�̂��낤���B
2018/04/08(��) 22:24:58.75ID:scYZDDu8
���ꂨ�肢 https://twitter.com/fcbliebe1900/status/982789462525554689?s=19
�������ď����Ȃ�/h����Ȃ���/h�t����Ȃ玞������Ȃ��Ǝv�����ǂ���H
�������ď����Ȃ�/h����Ȃ���/h�t����Ȃ玞������Ȃ��Ǝv�����ǂ���H
365�P�R�Q�l�ڂ̑f������
2018/04/09(��) 08:19:41.13ID:kzhlMYzb366�� ��2VB8wsVUoo
2018/04/09(��) 15:24:24.38ID:io+q775y ��
367�� ��2VB8wsVUoo
2018/04/09(��) 15:24:40.61ID:io+q775y ��
368�� ��2VB8wsVUoo
2018/04/09(��) 15:24:57.75ID:io+q775y ��
369�� ��2VB8wsVUoo
2018/04/09(��) 15:25:16.46ID:io+q775y ��
370�� ��2VB8wsVUoo
2018/04/09(��) 15:25:36.15ID:io+q775y ��
371�� ��2VB8wsVUoo
2018/04/09(��) 15:25:53.31ID:io+q775y ��
372�� ��2VB8wsVUoo
2018/04/09(��) 15:26:11.15ID:io+q775y ��
373�� ��2VB8wsVUoo
2018/04/09(��) 15:26:29.99ID:io+q775y ��
374�� ��2VB8wsVUoo
2018/04/09(��) 15:26:49.96ID:io+q775y ��
375�� ��2VB8wsVUoo
2018/04/09(��) 15:27:10.31ID:io+q775y ��
2018/04/10(��) 05:20:17.04ID:cgRjeD8b
���܂���n������
377363
2018/04/11(��) 12:27:49.42ID:XcN1It/z ���X�����Ȃ���ő��̃X���Ŏ��₷�邱�Ƃɂ����B
>>363�̎���͎�艺���邱�Ƃɂ���B
>>363�̎���͎�艺���邱�Ƃɂ���B
2018/05/06(��) 16:11:44.37ID:KhrVKVJy
379�� ��2VB8wsVUoo
2018/05/08(��) 14:50:30.76ID:FpEjvdxJ ��
380�� ��2VB8wsVUoo
2018/05/08(��) 14:50:52.21ID:FpEjvdxJ ��
381�� ��2VB8wsVUoo
2018/05/08(��) 14:51:11.84ID:FpEjvdxJ ��
382�� ��2VB8wsVUoo
2018/05/08(��) 14:51:37.45ID:FpEjvdxJ ��
383�� ��2VB8wsVUoo
2018/05/08(��) 14:51:57.61ID:FpEjvdxJ ��
384�� ��2VB8wsVUoo
2018/05/08(��) 14:52:19.57ID:FpEjvdxJ ��
385�� ��2VB8wsVUoo
2018/05/08(��) 14:52:39.98ID:FpEjvdxJ ��
386�� ��2VB8wsVUoo
2018/05/08(��) 14:53:03.00ID:FpEjvdxJ ��
387�� ��2VB8wsVUoo
2018/05/08(��) 14:53:24.62ID:FpEjvdxJ ��
388�� ��2VB8wsVUoo
2018/05/08(��) 14:53:47.50ID:FpEjvdxJ ��
2018/05/21(��) 21:48:05.26ID:VLLcdro9
�v����
�u�������w�v���ȉ��Œ�`����F
�������w�Ƃ́A9�̎����� 3�~3 �̌`�ɕ��ׂ����̂ł����āA
�e�s�A�e��A�e�Ίp����ɕ��Ԑ��̘a���S�ē��������̂Ƃ���B
�������w�̘a�A�����{���s��Ɠ��l�ɒ�߂邱�Ƃɂ��A
�������w�S�̂̏W���͎��x�N�g����Ԃ��Ȃ��B
���̎��x�N�g����Ԃ̎��������߂�B
�u�������w�v���ȉ��Œ�`����F
�������w�Ƃ́A9�̎����� 3�~3 �̌`�ɕ��ׂ����̂ł����āA
�e�s�A�e��A�e�Ίp����ɕ��Ԑ��̘a���S�ē��������̂Ƃ���B
�������w�̘a�A�����{���s��Ɠ��l�ɒ�߂邱�Ƃɂ��A
�������w�S�̂̏W���͎��x�N�g����Ԃ��Ȃ��B
���̎��x�N�g����Ԃ̎��������߂�B
2018/05/21(��) 22:04:16.81ID:2xKr+/2q
�ʔ����I
2018/05/24(��) 10:54:10.20ID:wa8QAvcF
>>389
�R����
�e�}�XXij(i,j��{1,2,3})�̐�����Ȃ�X�����̋�Ԃɑ��A�Ɨ��Ȑ���������U�����
��������̗�
X11+X12+X13=X21+X22+X23
X31+X32+X33=X21+X22+X23
X11+X21+X31=X21+X22+X23
X13+X23+X33=X21+X22+X23
X11+X22+X33=X21+X22+X23
X13+X22+X31=X21+X22+X23
�R����
�e�}�XXij(i,j��{1,2,3})�̐�����Ȃ�X�����̋�Ԃɑ��A�Ɨ��Ȑ���������U�����
��������̗�
X11+X12+X13=X21+X22+X23
X31+X32+X33=X21+X22+X23
X11+X21+X31=X21+X22+X23
X13+X23+X33=X21+X22+X23
X11+X22+X33=X21+X22+X23
X13+X22+X31=X21+X22+X23
2018/05/24(��) 18:53:59.50ID:COzmyM7A
>>391
�����I
�������Ɨ����Ƃ��\�����Ƃ��̏ؖ����ق����Ƃ��낾���ǁA�܂�������
�i�ȒP�ɕ�������@���������狳���ĉ������j
���̗�
e1=
1,-1,0
-1,0,1
0,1,-1
e2=
0,-1,1
1,0,-1
-1,1,0
e3=
1,1,1
1,1,1
1,1,1
�u�e�s�A�e��A�e�Ίp����̐��̘a�� 0 �ɂȂ�������w�S�́v�� 2 �����̕�����Ԃ𐬂��A
e1, e2 ���������B
�����I
�������Ɨ����Ƃ��\�����Ƃ��̏ؖ����ق����Ƃ��낾���ǁA�܂�������
�i�ȒP�ɕ�������@���������狳���ĉ������j
���̗�
e1=
1,-1,0
-1,0,1
0,1,-1
e2=
0,-1,1
1,0,-1
-1,1,0
e3=
1,1,1
1,1,1
1,1,1
�u�e�s�A�e��A�e�Ίp����̐��̘a�� 0 �ɂȂ�������w�S�́v�� 2 �����̕�����Ԃ𐬂��A
e1, e2 ���������B
393�P�R�Q�l�ڂ̑f������
2018/06/21(��) 05:04:52.44ID:0uUQCECl �ȉ��́u�����̑g�ݍ��킹�v�́u���ʂ肠��̂��v��m�肽���ł��B
�E�W���P�b�g�i9��j
�E�Y�{���i7��j
�E���i6��j
���u�W���P�b�g�i9��j�E�Y�{���i7��j�E���i6��j�v
�����́A�u�d���Ȃ��g�ݍ��킹�v�́u���ʂ�v�ɂȂ�ł��傤���B
�������ĕ\�̍������m�肽���ł��B
���܂��A�������o�����߂́u��@�␔���̖��́v�͂Ȃ�Ƃ����̂ł��傤���B
�E�W���P�b�g�i9��j
�E�Y�{���i7��j
�E���i6��j
���u�W���P�b�g�i9��j�E�Y�{���i7��j�E���i6��j�v
�����́A�u�d���Ȃ��g�ݍ��킹�v�́u���ʂ�v�ɂȂ�ł��傤���B
�������ĕ\�̍������m�肽���ł��B
���܂��A�������o�����߂́u��@�␔���̖��́v�͂Ȃ�Ƃ����̂ł��傤���B
394�C�i ��/7jUdUKiSM
2018/06/21(��) 18:58:42.35ID:r3wOHypI >>393
9�7�6=378(�ʂ�)
��N�Ԃł��ׂĂ̑g�ݍ��킹�𒅂����Ȃ����炢����܂��B
���@�͏�@�ł��B
���̂͊|���Z�ł��B
�d�����Ȃ��̈Ӗ�����x�������C���x�Ɨ����Ȃ���������A�ő��6�ʂ�ł��B
9�7�6=378(�ʂ�)
��N�Ԃł��ׂĂ̑g�ݍ��킹�𒅂����Ȃ����炢����܂��B
���@�͏�@�ł��B
���̂͊|���Z�ł��B
�d�����Ȃ��̈Ӗ�����x�������C���x�Ɨ����Ȃ���������A�ő��6�ʂ�ł��B
2018/06/22(��) 02:52:51.79ID:5dKvywCX
�k���l
�ō����̌W����1�ł���n���������� P(x) �Ƃ��A
P(x) = 0 ��n�̉��� ��1�C��2�C�c�C��n �Ƃ���B
���̂Ƃ��A��1^3�C��2^3�C�c�C��n^3 �����ɂ���n���������ŁA
�ō����̌W����1�ł������ A(x) �����߂�B
http://www.toshin.com/concours/mondai/mondai29.php
�@P(x) = p0(x^3) + p1(x^3) x + p2(x^3) xx,
�ƕ\�킹��B�B�B
�ō����̌W����1�ł���n���������� P(x) �Ƃ��A
P(x) = 0 ��n�̉��� ��1�C��2�C�c�C��n �Ƃ���B
���̂Ƃ��A��1^3�C��2^3�C�c�C��n^3 �����ɂ���n���������ŁA
�ō����̌W����1�ł������ A(x) �����߂�B
http://www.toshin.com/concours/mondai/mondai29.php
�@P(x) = p0(x^3) + p1(x^3) x + p2(x^3) xx,
�ƕ\�킹��B�B�B
2018/06/23(�y) 00:39:23.01ID:BnO9HX6O
>>395
Q(x) = p0(x^3)^3 + {p1(x^3)x}^3 + {p2(x^3)xx}^3 - 3 p0(x^3) {p1(x^3)x} {p2(x^3)xx}
�� P(x) = p0(x^3) + p1(x^3)x + p2(x^3)xx�@�������B
���@���鑽���� R(x) �����݂��āAQ(x) = P(x)R(x) �ƕ\�킳���B
Q(x) �� x^3 �̑������ƂȂ邩�� Q(x) = A(x^3) �Ƃ�����B
A(x) = p0(x)^3 + p1(x)^3�x + p2(x)^3�xx - 3�p0(x)�p1(x)�p2(x)�x,
�� �ō����̌W����1�� n���������ł���B
�܂��ei�ɑ��AA(��i^3) = Q(��i) = P(��i)R(��i) = 0,
���@A(x) �����߂鑽������1�ł���B
�ȉ��AA(x) �ȊO�ɂ��������݂���Ɖ��肵�Ė������������B
�ō����̌W����1�ł���n�������� B(x) ���������݂����Ɖ��肷��B
����ƁAn-1���ȉ��̑����� A(x) - B(x) ��n�̍� (��i)^3 �����B(����)
���@A(x) ���B��̉��ł���B
Q(x) = p0(x^3)^3 + {p1(x^3)x}^3 + {p2(x^3)xx}^3 - 3 p0(x^3) {p1(x^3)x} {p2(x^3)xx}
�� P(x) = p0(x^3) + p1(x^3)x + p2(x^3)xx�@�������B
���@���鑽���� R(x) �����݂��āAQ(x) = P(x)R(x) �ƕ\�킳���B
Q(x) �� x^3 �̑������ƂȂ邩�� Q(x) = A(x^3) �Ƃ�����B
A(x) = p0(x)^3 + p1(x)^3�x + p2(x)^3�xx - 3�p0(x)�p1(x)�p2(x)�x,
�� �ō����̌W����1�� n���������ł���B
�܂��ei�ɑ��AA(��i^3) = Q(��i) = P(��i)R(��i) = 0,
���@A(x) �����߂鑽������1�ł���B
�ȉ��AA(x) �ȊO�ɂ��������݂���Ɖ��肵�Ė������������B
�ō����̌W����1�ł���n�������� B(x) ���������݂����Ɖ��肷��B
����ƁAn-1���ȉ��̑����� A(x) - B(x) ��n�̍� (��i)^3 �����B(����)
���@A(x) ���B��̉��ł���B
397�P�R�Q�l�ڂ̑f������
2018/06/23(�y) 10:00:29.88ID:cYhBaJ6q �O�悵�����̂ɓ������̂��Ȃ����Ƃ������ĂȂ�����ʖځB
398�P�R�Q�l�ڂ̑f������
2018/06/23(�y) 11:11:55.32ID:MnHCGVk7 https://youtu.be/LZL344pJKN0
700000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000007�~11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111�̓����̏o�����B
https://youtu.be/4UOlX_r8ZcA
9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999�~9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999�̓����̏o�����B
���̑��̓������낵���B�ŋ߂́A���p�Q�A�}�H�Q�A���w�Q�̎����C�m���̖l��
�d��A�H��A�G��ɂ��ĉ�����Ă��܂��B
��낵���B
700000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000007�~11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111�̓����̏o�����B
https://youtu.be/4UOlX_r8ZcA
9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999�~9999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999�̓����̏o�����B
���̑��̓������낵���B�ŋ߂́A���p�Q�A�}�H�Q�A���w�Q�̎����C�m���̖l��
�d��A�H��A�G��ɂ��ĉ�����Ă��܂��B
��낵���B
399�P�R�Q�l�ڂ̑f������
2018/06/26(��) 04:13:02.01ID:8Z/gffAe400�P�R�Q�l�ڂ̑f������
2018/06/26(��) 05:31:19.97ID:p6aNDz2K >>395
���������������̈�Ӑ��� �g�������̂��������炻����d���ɂ��h �ƂƂ��Ă����Ȃ�, �͂Ȃ���ᖡ����K�v�͂Ȃ��B
���Ƃ���x = 1,1,2�����ɂ��ō������P�̎O������(x-1)^2(x-2)�Ɉ�ӂɂ��܂�B
�������p�ӂ���Ă�͔͉ł��̋ᖡ���Ă���Ă��Ƃ͂��̈Ӗ��ɂƂ��Ă͂����Ȃ��̂��낤�B
�ƂȂ��x=1,1,2�����ɂ��ō������P�̎O������(x-1)(x-2)(x-a)����ʉ��ƂȂ�B
�ƂȂ�Ƃ��Ƃ̖������������d�������ꍇ�͑�����ɂȂ�B
�܂肱�̖��̉�����ӂɌ��܂鎖�������ɂ͂��Ƃ�n�������d���������Ȃ����Ƃ������Ȃ��ƕs���S�B
����Č��̃T�C�g�̖͔͉��s���S�Ȃ��ǁB
���������������̈�Ӑ��� �g�������̂��������炻����d���ɂ��h �ƂƂ��Ă����Ȃ�, �͂Ȃ���ᖡ����K�v�͂Ȃ��B
���Ƃ���x = 1,1,2�����ɂ��ō������P�̎O������(x-1)^2(x-2)�Ɉ�ӂɂ��܂�B
�������p�ӂ���Ă�͔͉ł��̋ᖡ���Ă���Ă��Ƃ͂��̈Ӗ��ɂƂ��Ă͂����Ȃ��̂��낤�B
�ƂȂ��x=1,1,2�����ɂ��ō������P�̎O������(x-1)(x-2)(x-a)����ʉ��ƂȂ�B
�ƂȂ�Ƃ��Ƃ̖������������d�������ꍇ�͑�����ɂȂ�B
�܂肱�̖��̉�����ӂɌ��܂鎖�������ɂ͂��Ƃ�n�������d���������Ȃ����Ƃ������Ȃ��ƕs���S�B
����Č��̃T�C�g�̖͔͉��s���S�Ȃ��ǁB
2018/06/27(��) 05:30:15.31ID:ZtXXFOLy
>>395
�ʃX���ł��̖�肪�b��ɂȂ����Ƃ��� �g�o��҂͉��s���S�Ȃ̂͂킩���ĂĊ��S�ȉ��ł��Ȃ��Ȃ����NJ����ĕ������̂����h �Ə��������ǁA���߂čl���Ă݂�Ə����Ɋ��S�ȉ����Ȃ�����������������Ȃ��Ǝv���Ă����B
�ŏ��̑����� P(x) = x^2015 +2x^2014 -2x+2 �̊���������������Ǝv�������ǂ悭�悭�l������>>397���w�E���Ă�ʂ�,��_i^3�̑S�̂��S���Ⴄ���Ǝ����Ȃ��ƑʖڂȋC������B(�ʃ��[�g���邩������Ȃ����ǁB)
���������̃��[�g�����\�������B
�������v���������̃��[�g�̏ؖ���
���A����P(x)�̍��Ń�=���ւƂȂ��Ă���Ƃ����P(x)��P(��x)�����ʉ��������AP(x)��P(��x)����P(x)�̓K�E�X��R=Z[��]�ʼn�ƂȂ�B
���p=2R��R�̑f�C�f�A���Ȃ̂�p�i�t�u�ł�Eisenstein�̔����P(x)��R�Ŋ���Ƃ킩��B�����B
������x�㐔�I�����_�ɒʂ��ĂȂ��Ƃ��Ȃ�ꂵ���B
���ɕʃ��[�g�������Ă��������������[�g�����Ȃ��C������B
���������������Ă݂͂����Ǐؖ������Ȃ������̂��^�������B
���邢�͂��̕����ɃM���b�v������̂ɋC�Â����炵�Ȃ��������H
�ʃX���ł��̖�肪�b��ɂȂ����Ƃ��� �g�o��҂͉��s���S�Ȃ̂͂킩���ĂĊ��S�ȉ��ł��Ȃ��Ȃ����NJ����ĕ������̂����h �Ə��������ǁA���߂čl���Ă݂�Ə����Ɋ��S�ȉ����Ȃ�����������������Ȃ��Ǝv���Ă����B
�ŏ��̑����� P(x) = x^2015 +2x^2014 -2x+2 �̊���������������Ǝv�������ǂ悭�悭�l������>>397���w�E���Ă�ʂ�,��_i^3�̑S�̂��S���Ⴄ���Ǝ����Ȃ��ƑʖڂȋC������B(�ʃ��[�g���邩������Ȃ����ǁB)
���������̃��[�g�����\�������B
�������v���������̃��[�g�̏ؖ���
���A����P(x)�̍��Ń�=���ւƂȂ��Ă���Ƃ����P(x)��P(��x)�����ʉ��������AP(x)��P(��x)����P(x)�̓K�E�X��R=Z[��]�ʼn�ƂȂ�B
���p=2R��R�̑f�C�f�A���Ȃ̂�p�i�t�u�ł�Eisenstein�̔����P(x)��R�Ŋ���Ƃ킩��B�����B
������x�㐔�I�����_�ɒʂ��ĂȂ��Ƃ��Ȃ�ꂵ���B
���ɕʃ��[�g�������Ă��������������[�g�����Ȃ��C������B
���������������Ă݂͂����Ǐؖ������Ȃ������̂��^�������B
���邢�͂��̕����ɃM���b�v������̂ɋC�Â����炵�Ȃ��������H
2018/06/27(��) 05:33:34.50ID:XfvCEgFW
>>400
�����d��������AP(x) = 0�CP '(x) = 0 �����B
���̖��� P(x) = x^2015 + 2 x^2014 -2x +2 �Ȃ̂�
P '(x) = 2015 x^2014 + 2�2014 x^2013 -2,
P(x) + (1-x)P '(x) = -2014 x^2013 {xx +(2011/2014)x -2},
x = 0 �͖��炩�ɉ��łȂ��B���Ƃ�
x = {-(2011/2014)�}��[8 + (2011/2014)^2]}/2
�@= 1.0004966887145�@& -1.99900711572542
�����łȂ����Ƃ������悢�B
�����d��������AP(x) = 0�CP '(x) = 0 �����B
���̖��� P(x) = x^2015 + 2 x^2014 -2x +2 �Ȃ̂�
P '(x) = 2015 x^2014 + 2�2014 x^2013 -2,
P(x) + (1-x)P '(x) = -2014 x^2013 {xx +(2011/2014)x -2},
x = 0 �͖��炩�ɉ��łȂ��B���Ƃ�
x = {-(2011/2014)�}��[8 + (2011/2014)^2]}/2
�@= 1.0004966887145�@& -1.99900711572542
�����łȂ����Ƃ������悢�B
2018/06/27(��) 05:51:26.77ID:ZtXXFOLy
2018/06/27(��) 17:00:25.11ID:XfvCEgFW
2018/06/29(��) 01:00:04.46ID:fgt+MMrn
���O�R�|�P���i���|���j�i���|���j�i���|���j�B
�o�i���j�����i���|���j�B
�`�i���j�����i���|���O�R�j�B
�o�i�����j�o�i�����j�o�i�����j�����i�i�����|���j�i�����|���j�i�����|���j�j�����i���O�R�|���O�R�j���`�i���O�R�j�B
�o�i���j���p�i���O�R�j�{�q�i���O�R�j���{�r�i���O�R�j���O�Q�B
�o�i�����j���p�i���O�R�j�{�q�i���O�R�j�����{�r�i���O�R�j���O�Q���O�Q�B
�o�i���j�����i���|���j�B
�`�i���j�����i���|���O�R�j�B
�o�i�����j�o�i�����j�o�i�����j�����i�i�����|���j�i�����|���j�i�����|���j�j�����i���O�R�|���O�R�j���`�i���O�R�j�B
�o�i���j���p�i���O�R�j�{�q�i���O�R�j���{�r�i���O�R�j���O�Q�B
�o�i�����j���p�i���O�R�j�{�q�i���O�R�j�����{�r�i���O�R�j���O�Q���O�Q�B
2018/06/29(��) 01:39:54.53ID:66xcDhgd
>>405
t=�ւ̂��Ƃ��Ƃ��ĈˑR�Ƃ���P(x)��P(��x)���݂��ɑf�ł��邱�Ƃ͎�����ĂȂ������B
t=�ւ̂��Ƃ��Ƃ��ĈˑR�Ƃ���P(x)��P(��x)���݂��ɑf�ł��邱�Ƃ͎�����ĂȂ������B
2018/06/29(��) 16:28:20.65ID:q8XMxjx7
>>407
�X�}�z���ƑS���ǂ߂�
�X�}�z���ƑS���ǂ߂�
408�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 12:50:09.13ID:24jisY+G >>393
�����O���[�v���畡�����o���킯�ł͂Ȃ��̂�
�d�����Ȃ�
�Ⴆ�W���P�b�g��2���I�Ԃ̂Ȃ�9�~8�ʂ肩��d������2�Ŋ���Ђ悤�����邯��ǁB
�\��3�����̍��W���g�����A�܂���
���X�~�c�V�̃}�X�ڂ̂��ꂼ���6��������̂ł��������Ǝv���܂��B
�Ⴆ�W���P�b�g�P�A�Y�{��1�Ƃ����X�n��
���Ƃ������O�̍����P0���`�U0���̃r�������Ă�悤�ȃC���[�W�ł�����
�����O���[�v���畡�����o���킯�ł͂Ȃ��̂�
�d�����Ȃ�
�Ⴆ�W���P�b�g��2���I�Ԃ̂Ȃ�9�~8�ʂ肩��d������2�Ŋ���Ђ悤�����邯��ǁB
�\��3�����̍��W���g�����A�܂���
���X�~�c�V�̃}�X�ڂ̂��ꂼ���6��������̂ł��������Ǝv���܂��B
�Ⴆ�W���P�b�g�P�A�Y�{��1�Ƃ����X�n��
���Ƃ������O�̍����P0���`�U0���̃r�������Ă�悤�ȃC���[�W�ł�����
409�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 13:22:49.73ID:24jisY+G �ȉ��̖₢�ɂ��āA�ʉ����@�̍l�����������Ă��������B
�₢
�����Ƃ�a���s����10���Ŋ�������
������Ƃ�b���s����8���Ŋ�������
a�����b����̓�l�ōs���Ɖ����Ŋ������邩�H
�������A��Ƃ͓K�ɕ����ł�����̂Ƃ���
(��1)
�����Ƃ̍�Ɨʂ�s[��] ��Ƒ��x��a[��/��] b[��/��]�Ƃ���
s/a = 10
s/b = 8
x���Ŋ�������Ƃ���ƁA
s/(a+b) = x
����3����������
x = 40/9
�����@40/9���i4.444...���j
�ƂȂ�킯�ł����A����������̂ƍ�Ɨ�s�����Ǐ������Ă�̂ʼn������o�I�ɕ�����Â炢��ł��B
������
(��2�j
�Ⴆ��Ɨʂ�2s�Ƃ��Ĉ��ڂ�s����a�����b����ŕ�����Ƃ��܂��B
���ځAb����Ƃ����������Ƃ��Aa����͂܂��u2�v�c���Ă��܂�
2��ځAb�����a����́u1�v����`���܂��B
2��ځAb����Ƃ����������Ƃ��Aa����͂܂��u0.2�v�c���Ă��܂�
3��ځAb�����a����̔����u0.1�v����`���܂��B
3��ځAb����Ƃ����������Ƃ��Aa����͂܂��u0.01�v�c���Ă��܂�
������J��Ԃ��ƁAb����̍�Ɨ�bs�́A
bs = s (1+0.1+0.01+......) = (10/9)s
����a����̍�Ɨ�as�́A = (8/9)s
as = s (1-0.1-0.01-......)
���2s��������������́Aa�����8/9��������������Ɠ����Ȃ̂ŁA
(8/9)s / (s/10) = 80/9
����āA���s���������������
80/9 / 2 = 40/9
�����@40/9�� (4.444..��)
�����Ɠ���Ȃ����C�����܂�...�ǂ������炢����ł��傤�H�������o�I�ɕ�����₷���l������
�v�����܂���B�Ⴆ��8����10�����t���ɂ���Ƃ��B
��Ɨ�s�𐔎��ɓ��ꂽ���Ȃ���ł��B
�₢
�����Ƃ�a���s����10���Ŋ�������
������Ƃ�b���s����8���Ŋ�������
a�����b����̓�l�ōs���Ɖ����Ŋ������邩�H
�������A��Ƃ͓K�ɕ����ł�����̂Ƃ���
(��1)
�����Ƃ̍�Ɨʂ�s[��] ��Ƒ��x��a[��/��] b[��/��]�Ƃ���
s/a = 10
s/b = 8
x���Ŋ�������Ƃ���ƁA
s/(a+b) = x
����3����������
x = 40/9
�����@40/9���i4.444...���j
�ƂȂ�킯�ł����A����������̂ƍ�Ɨ�s�����Ǐ������Ă�̂ʼn������o�I�ɕ�����Â炢��ł��B
������
(��2�j
�Ⴆ��Ɨʂ�2s�Ƃ��Ĉ��ڂ�s����a�����b����ŕ�����Ƃ��܂��B
���ځAb����Ƃ����������Ƃ��Aa����͂܂��u2�v�c���Ă��܂�
2��ځAb�����a����́u1�v����`���܂��B
2��ځAb����Ƃ����������Ƃ��Aa����͂܂��u0.2�v�c���Ă��܂�
3��ځAb�����a����̔����u0.1�v����`���܂��B
3��ځAb����Ƃ����������Ƃ��Aa����͂܂��u0.01�v�c���Ă��܂�
������J��Ԃ��ƁAb����̍�Ɨ�bs�́A
bs = s (1+0.1+0.01+......) = (10/9)s
����a����̍�Ɨ�as�́A = (8/9)s
as = s (1-0.1-0.01-......)
���2s��������������́Aa�����8/9��������������Ɠ����Ȃ̂ŁA
(8/9)s / (s/10) = 80/9
����āA���s���������������
80/9 / 2 = 40/9
�����@40/9�� (4.444..��)
�����Ɠ���Ȃ����C�����܂�...�ǂ������炢����ł��傤�H�������o�I�ɕ�����₷���l������
�v�����܂���B�Ⴆ��8����10�����t���ɂ���Ƃ��B
��Ɨ�s�𐔎��ɓ��ꂽ���Ȃ���ł��B
2018/06/30(�y) 13:26:50.68ID:3QKFP042
411�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 14:05:49.57ID:t7jji/1D >>409
B����A���l���ɑ������邩�l����BA����10���������Ƃ�B�����8���ŏI��点�邩��B�����A�����10/8�{���ゲ��
�܂�AB��������킹��ƁAA����1+10/8=9/4�l����̂Ɠ������ƁBA�����l�Ȃ�10���A��l�Ȃ甼����5���B9/4�l�Ȃ�4/9�{��40/9��
�S�̂̍�Ɨʂ���̓I�Ȍ��ł͂Ȃ�1�Ƃ��Ĉ��������̍�Ɨʂ�%�ōl����
A�����10�������� = ����őS�̂�1/10 = 10%�BB�����8�����������őS�̂�1/8 = 12.5%
��l���킹�Ĉ���őS�̂�22.5%�i9/40)�Ȃ̂ŁA��Ƃ�����������ɂ�100/22.5 = 4.44....��������
B����A���l���ɑ������邩�l����BA����10���������Ƃ�B�����8���ŏI��点�邩��B�����A�����10/8�{���ゲ��
�܂�AB��������킹��ƁAA����1+10/8=9/4�l����̂Ɠ������ƁBA�����l�Ȃ�10���A��l�Ȃ甼����5���B9/4�l�Ȃ�4/9�{��40/9��
�S�̂̍�Ɨʂ���̓I�Ȍ��ł͂Ȃ�1�Ƃ��Ĉ��������̍�Ɨʂ�%�ōl����
A�����10�������� = ����őS�̂�1/10 = 10%�BB�����8�����������őS�̂�1/8 = 12.5%
��l���킹�Ĉ���őS�̂�22.5%�i9/40)�Ȃ̂ŁA��Ƃ�����������ɂ�100/22.5 = 4.44....��������
412�P�R�Q�l�ڂ̑f������
2018/06/30(�y) 17:51:48.41ID:24jisY+G a�����ōl����Ab����̍�Ƒ��x��1.25�{�ł���̂ō��v����2.25�{�ōs����
�����鎞�Ԃ�1/1����1/2.25�{�܂Ō���
a�����Ȃ̂ŁA10���ԁ~1/2.25 = 4.444...���ԁE�E�E����
����Ȃ���
�����鎞�Ԃ�1/1����1/2.25�{�܂Ō���
a�����Ȃ̂ŁA10���ԁ~1/2.25 = 4.444...���ԁE�E�E����
����Ȃ���
2018/07/01(��) 00:18:51.42ID:KZmq+nT0
��X�����c����d�̐����o��
�� ��X�����1����(d/c)�̐����o��
�� ��X�����(c/d)����1�̐����o��
�E ��A�����10����1�̐����o��
�E ��B�����8����1�̐����o��
�E ��A�����1����1/10�̐����o��
�E ��B�����1����1/8�̐����o��
�E ��A��B�����1����(1/10�{1/8)�̐����o��B
�E ��A��B�����1/(1/10�{1/8)����1�̐����o��B
1/(1/10�{1/8)��40/9
��A��B�����40/9����1�̐����o��B
�� ��X�����1����(d/c)�̐����o��
�� ��X�����(c/d)����1�̐����o��
�E ��A�����10����1�̐����o��
�E ��B�����8����1�̐����o��
�E ��A�����1����1/10�̐����o��
�E ��B�����1����1/8�̐����o��
�E ��A��B�����1����(1/10�{1/8)�̐����o��B
�E ��A��B�����1/(1/10�{1/8)����1�̐����o��B
1/(1/10�{1/8)��40/9
��A��B�����40/9����1�̐����o��B
414�P�R�Q�l�ڂ̑f������
2018/07/02(��) 00:48:00.25ID:l4VS3kzS �ӂނӂ�
�X�̗��ʂ����v���ċt�����A����d����1�P�ʂ���������������鎞�Ԃ�������
���Č��t�ł܂Ƃ߂��邩��
�P�ʎd���ʂ�����̎��ԁA�ƂƂ炦��Ί��o�I�ɕ�����₷��
�X�̗��ʂ����v���ċt�����A����d����1�P�ʂ���������������鎞�Ԃ�������
���Č��t�ł܂Ƃ߂��邩��
�P�ʎd���ʂ�����̎��ԁA�ƂƂ炦��Ί��o�I�ɕ�����₷��
415�P�R�Q�l�ڂ̑f������
2018/08/06(��) 20:21:56.22ID:0TntC5u6 180�x�̊p�������ƍl����Ɠ��p�̘a�͂R�U�O�x�ɂȂ�̂�
�O�p�`�͎l�p�`�ɓ����܂����H
�O�p�`�͎l�p�`�ɓ����܂����H
416�P�R�Q�l�ڂ̑f������
2018/08/11(�y) 11:14:40.35ID:birPGGYG ���郌�X�g�����f�ł́A�Q�O��ɂP��A��v���P�O�O�������ƂȂ�A
�ʂ̃��X�g�����c�ł́A��v���Ɏ���̉�v���P�O�������ɂȂ�`�P�b�g��z�z����Ƃ����B
���X�g�����ɂQ��s���Ƃ��A�ǂ���̃��X�g������I�Ԃ̂��������H
���X�g�����̃T�[�r�X���e�ɍ��͂Ȃ��A������Ԃłc�̃`�P�b�g�͎����Ă��Ȃ��B�܂��A��L�ȊO�̊����͂Ȃ����̂Ƃ���B
�ʂ̃��X�g�����c�ł́A��v���Ɏ���̉�v���P�O�������ɂȂ�`�P�b�g��z�z����Ƃ����B
���X�g�����ɂQ��s���Ƃ��A�ǂ���̃��X�g������I�Ԃ̂��������H
���X�g�����̃T�[�r�X���e�ɍ��͂Ȃ��A������Ԃłc�̃`�P�b�g�͎����Ă��Ȃ��B�܂��A��L�ȊO�̊����͂Ȃ����̂Ƃ���B
2018/08/11(�y) 12:53:14.96ID:zOa2Lz/5
G�̕��������ț�������T���H
419�P�R�Q�l�ڂ̑f������
2018/08/26(��) 00:48:41.08ID:oi0Wi+Da ����w�Ō�������Ă��鐔�w�͖��ɗ����Ȃ��̂Őŋ����g���K�v�͂Ȃ�
��肽���l�����ł������o�������Ă�����
���̈ӌ��ɔ��_�������̂ł����ǂ���������ł���
��肽���l�����ł������o�������Ă�����
���̈ӌ��ɔ��_�������̂ł����ǂ���������ł���
2018/08/26(��) 10:15:12.68ID:rGSEcNup
>>416
�P���Ȋ��Ғl�I�ɂ͓����Ǝv�������ǁA�Ђ��������Ă�̂��ȁH
�X�ɍs���@�P��@G�̂ق�������
�@�@�@�@�@�@�@�Q��@����
�@�@�@�@�@�@�@�R��@�c�̂ق�������
�P���Ȋ��Ғl�I�ɂ͓����Ǝv�������ǁA�Ђ��������Ă�̂��ȁH
�X�ɍs���@�P��@G�̂ق�������
�@�@�@�@�@�@�@�Q��@����
�@�@�@�@�@�@�@�R��@�c�̂ق�������
2018/08/26(��) 13:29:47.12ID:rGSEcNup
100�������ɂȂ�`�P�b�g��z�z����A�Ɠǂ߂Ȃ����Ȃ�����
�ł��A���ꂾ�Ɩ��ɂȂ�Ȃ����
�ł��A���ꂾ�Ɩ��ɂȂ�Ȃ����
2018/08/26(��) 13:42:58.37ID:rGSEcNup
�Q��s����������A100�������ɂȂ邱�Ƃ͐�ɂȂ��Ƃ����P���Șb��
423�P�R�Q�l�ڂ̑f������
2018/08/26(��) 22:13:40.33ID:e3pJCWP7 �yATP�z�j�q�v���e�j�X�����X���b�h288 ܯ����L
http://mao.5ch.net/test/read.cgi/tennis/1534645313/
���̃X���ō��m���̖�肪�b��ɂȂ��Ă���ǒN�������Ă���Ȃ��H
�h���[�̃T�C�Y��128�A�V�[�h��32�A1���̓V�[�h�I�蓯�m�ł͓�����Ȃ��B���̏Ńf�B�~�g���t(�V�[�h�I��)�ƃo�u�����J(�m�[�V�[�h)���E�B���u���h���ɑ����S�Ăł�1���őΐ킷�鎖�ɂȂ����B����2���A���œ��������1���œ�����m���������炩�H���Ęb���
(1)�E�B���u���h���͊��ɏI�����������A����S�Ăœ�����m����1�^96�̂܂܂��Ĉӌ���
(2)2���A���œ�����������1�^9216
���Ĉӌ��ɕ�����ċc�_���������ăX�����r��Ă�B
�ǂ������������̂����邢�͂���ȊO�̓���������̂����R�����ē������o���ĕ��n�̃o�J�ǂ���N���ق点�Ă���Ȃ��H
http://mao.5ch.net/test/read.cgi/tennis/1534645313/
���̃X���ō��m���̖�肪�b��ɂȂ��Ă���ǒN�������Ă���Ȃ��H
�h���[�̃T�C�Y��128�A�V�[�h��32�A1���̓V�[�h�I�蓯�m�ł͓�����Ȃ��B���̏Ńf�B�~�g���t(�V�[�h�I��)�ƃo�u�����J(�m�[�V�[�h)���E�B���u���h���ɑ����S�Ăł�1���őΐ킷�鎖�ɂȂ����B����2���A���œ��������1���œ�����m���������炩�H���Ęb���
(1)�E�B���u���h���͊��ɏI�����������A����S�Ăœ�����m����1�^96�̂܂܂��Ĉӌ���
(2)2���A���œ�����������1�^9216
���Ĉӌ��ɕ�����ċc�_���������ăX�����r��Ă�B
�ǂ������������̂����邢�͂���ȊO�̓���������̂����R�����ē������o���ĕ��n�̃o�J�ǂ���N���ق点�Ă���Ȃ��H
2018/08/27(��) 01:11:26.78ID:iPZOwbUe
�T�C�R���łP���A������10��o��m���͂��̂������Ⴂ�ł����A11��ڂɂP���o��m����1/6�ł���ˁB
���ꂾ������1/6�O11���Čv�Z�̈Ӗ��Ȃ��Ȃ��ł����H
���ꂾ������1/6�O11���Čv�Z�̈Ӗ��Ȃ��Ȃ��ł����H
2018/08/27(��) 01:19:52.91ID:BuUP3N+h
���@�M���ǂł��ˁB�����Ɖ�����⋋���܂��傤�B
426�P�R�Q�l�ڂ̑f������
2018/11/13(��) 16:51:37.09ID:/lMcVzdM �m��1�n����1�̉~�̖ʐςƁA����1��n�p�`�̖ʐςƂ̍��̂����ŏ��̒l��V_2(n)�Ƃ���Ƃ��A����{n^2�V_2(n)}�͎������邩�B��������ꍇ�͋Ɍ��l������
�m��2�n�\�ʐ�1�̋��̑̐ςƁA�\�ʐ�1��n���ʑ̂̑̐ςƂ̍��̂����ŏ��̒l��V_3(n)�Ƃ���Ƃ��A����{n�V_3(n)}�͎������邩�B��������ꍇ�͋Ɍ��l������
�m��2�n�\�ʐ�1�̋��̑̐ςƁA�\�ʐ�1��n���ʑ̂̑̐ςƂ̍��̂����ŏ��̒l��V_3(n)�Ƃ���Ƃ��A����{n�V_3(n)}�͎������邩�B��������ꍇ�͋Ɍ��l������
2018/11/14(��) 18:22:46.86ID:bGkusq+Z
�[�H�̃I�J�Y���C�J�A�}�O���A�T���}�̂����ǂꂩ�P�i�ł���B
���ꂼ��̊m���� 1/4�A 1/4�A 1/2 �ł���Ƃ���B
�����@�Ƃ��ẮA�u�C�J�͏Ă����i�}���̊m���� 1/2 ���v
�u�}�O���͕K���i�}�v�u�T���}�͕K���Ă��v�Ƃ������Ƃ������Ă���B
���܁A�A��ɉƂ��牌���������Ă���̂��������Ƃ�
�����̃I�J�Y���C�J�ł���m���͂ǂꂾ�����H
���ꂼ��̊m���� 1/4�A 1/4�A 1/2 �ł���Ƃ���B
�����@�Ƃ��ẮA�u�C�J�͏Ă����i�}���̊m���� 1/2 ���v
�u�}�O���͕K���i�}�v�u�T���}�͕K���Ă��v�Ƃ������Ƃ������Ă���B
���܁A�A��ɉƂ��牌���������Ă���̂��������Ƃ�
�����̃I�J�Y���C�J�ł���m���͂ǂꂾ�����H
2018/11/15(��) 20:44:35.93ID:6QoRET0S
�c
�Ă��Ă�̂��n�b�L�����Ă���̂�����
1/2�ŃC�J���T���}��
�C�J��1/2�ŏĂ����̂�
1/4�ŃC�J��
�Ă��Ă�̂��n�b�L�����Ă���̂�����
1/2�ŃC�J���T���}��
�C�J��1/2�ŏĂ����̂�
1/4�ŃC�J��
2018/11/15(��) 21:44:55.33ID:neQ8JPzy
(1/4)*(1/2)/{(1/4)*(1/2)+(1/2)*(1)}��1/(1+4)��1/5
431�P�R�Q�l�ڂ̑f������
2018/11/18(��) 22:31:16.42ID:Gz0yZhdI >>426
��P������1�̉~�̖ʐ�=1/(4��), ����1�̐�n�p�`��1/(4n tan(��/n)) ���
V_2(n)��1/(4��)-1/(4n tan(��/n)) �Ƃ����
���̂Ƃ��Alim{n����} n^2�~V_2(n) = ��/12
��Q���\�ʐ�1�̋��̑̐�=1/(6���)
�\�ʐ�1��n���ʑ̂̑̐ρF�����ł͂Ȃ����A�ʐς̓�����n���̐��U�p�`�ō\�����ꂽ�Ƃ��ċߎ������
(1/6)��(((sin(��(1+1/n)/3))^3/sin(��/n)-1)/(n(sin(��/3))^3)) ��
���̂Ƃ��Alim{n����} n�~V_3(n) = ((���)/6)(4(cos(��/6))^2-cos(2��/6))/sin(2��/6) = (5/108)��(3��)
��P������1�̉~�̖ʐ�=1/(4��), ����1�̐�n�p�`��1/(4n tan(��/n)) ���
V_2(n)��1/(4��)-1/(4n tan(��/n)) �Ƃ����
���̂Ƃ��Alim{n����} n^2�~V_2(n) = ��/12
��Q���\�ʐ�1�̋��̑̐�=1/(6���)
�\�ʐ�1��n���ʑ̂̑̐ρF�����ł͂Ȃ����A�ʐς̓�����n���̐��U�p�`�ō\�����ꂽ�Ƃ��ċߎ������
(1/6)��(((sin(��(1+1/n)/3))^3/sin(��/n)-1)/(n(sin(��/3))^3)) ��
���̂Ƃ��Alim{n����} n�~V_3(n) = ((���)/6)(4(cos(��/6))^2-cos(2��/6))/sin(2��/6) = (5/108)��(3��)
432�P�R�Q�l�ڂ̑f������
2018/11/20(��) 23:49:27.66ID:yIpzRJ8+ �ߏ��̂��X�ł���Ă�1000�~�̔�������1����������
�r���S�C�x���g�̊m���ɂ��ċ����Ă��������B
1����16�̐����������_���ɋL�����ꂽ4�~4�̃r���S�J�[�h������B
1����16�̐������烉���_���Ɉ����A�^�e�E���R�E�i�i�������ꂩ4�̐����������ƌi�i��������B
��x�����������͎��̐����������O�ɔ��ɖ߂����̂Ƃ���B
�_�u���g���v���ł̃r���S�̏ꍇ�͂��ꂼ��i�i��2�A3������B
�i�i���Ă��������琔�����������Ƃ͉\�B
�J�[�h�̃��Z�b�g�͎��R�Ȃ̂ł����A�ǂ̃^�C�~���O��
�J�[�h�����Z�b�g����ƍł������̌i�i���܂����B
�r���S�C�x���g�̊m���ɂ��ċ����Ă��������B
1����16�̐����������_���ɋL�����ꂽ4�~4�̃r���S�J�[�h������B
1����16�̐������烉���_���Ɉ����A�^�e�E���R�E�i�i�������ꂩ4�̐����������ƌi�i��������B
��x�����������͎��̐����������O�ɔ��ɖ߂����̂Ƃ���B
�_�u���g���v���ł̃r���S�̏ꍇ�͂��ꂼ��i�i��2�A3������B
�i�i���Ă��������琔�����������Ƃ͉\�B
�J�[�h�̃��Z�b�g�͎��R�Ȃ̂ł����A�ǂ̃^�C�~���O��
�J�[�h�����Z�b�g����ƍł������̌i�i���܂����B
433�P�R�Q�l�ڂ̑f������
2018/11/21(��) 02:34:10.60ID:CNIROJFN434�P�R�Q�l�ڂ̑f������
2018/11/21(��) 10:47:00.36ID:fBUnQQkv >>433
1-3�~1/20-6�~7/160-3�~3/32=49/160
1-3�~1/20-6�~7/160-3�~3/32=49/160
435�P�R�Q�l�ڂ̑f������
2018/11/22(��) 13:33:56.67ID:BerRWiUo >>433
�ʉ�
��ABC�̏d�S����e��(AB,BC,CA)�̒��_����ъe���_(A,B,C)�܂Ő����������ƁA�����̊e�X7/10,7/16�̋����ɘZ�p�`�̒��_���ʒu����
�ʐϔ�͂����̐ς�49/160�ƂȂ�
�ʉ�
��ABC�̏d�S����e��(AB,BC,CA)�̒��_����ъe���_(A,B,C)�܂Ő����������ƁA�����̊e�X7/10,7/16�̋����ɘZ�p�`�̒��_���ʒu����
�ʐϔ�͂����̐ς�49/160�ƂȂ�
436�P�R�Q�l�ڂ̑f������
2018/12/14(��) 16:51:25.36ID:qzFFQ0LC ���݂܂��A�F�l���m�b�����݂����������B
���w�P�N�̑��q�̏h��v�����g�̖��Ȃ̂ł����c
�w�o�X�Ɂ@�����Ⴍ���@�P�T�ɂ�@�̂��Ă��܂����B���́@�o�X�Ă��Ł@
�V�ɂ�@����܂����B�o�X�́@�Ȃ��́@�Ȃ�ɂ�ɂȂ�܂������B�x
�Z����������@�P�T�|�V���W�@�ł��傤���ǁc
�Ȃ��Ȃ���������@(�P�T�|�V)�{�P(�^�]��)���X
�ǂ���̓��������߂��Ă���̂�������Ȃ���ł�
���Ȃ݂ɑ��q�́A�P�T�|�V���W�Ɖ��Ă܂������c
���w�P�N�̑��q�̏h��v�����g�̖��Ȃ̂ł����c
�w�o�X�Ɂ@�����Ⴍ���@�P�T�ɂ�@�̂��Ă��܂����B���́@�o�X�Ă��Ł@
�V�ɂ�@����܂����B�o�X�́@�Ȃ��́@�Ȃ�ɂ�ɂȂ�܂������B�x
�Z����������@�P�T�|�V���W�@�ł��傤���ǁc
�Ȃ��Ȃ���������@(�P�T�|�V)�{�P(�^�]��)���X
�ǂ���̓��������߂��Ă���̂�������Ȃ���ł�
���Ȃ݂ɑ��q�́A�P�T�|�V���W�Ɖ��Ă܂������c
437�P�R�Q�l�ڂ̑f������
2018/12/14(��) 18:22:46.45ID:pgWl9dAE438�P�R�Q�l�ڂ̑f������
2018/12/24(��) 16:20:46.42ID:bWyeCrh9 >>436
�斱�����J�E���g����Ȃ�
�^�]�肾���Ƃ͌���Ȃ�����
��҂̉́����낤
�o�X�K�C�h��A���v���̉^�]�肪����Ă�悤�ȏꍇ�͂ǂ��Ȃ̂��Ƃ�
���������A�o�X�̋q�Ƃ͌����Ă��炸
�ڑҗ��s�ŁA�����グ�鑤�̎Ј�������Ă邩������Ȃ���
�^�]�肾���𐔂���͕̂Ў藎�����낤
�斱�����J�E���g����Ȃ�
�^�]�肾���Ƃ͌���Ȃ�����
��҂̉́����낤
�o�X�K�C�h��A���v���̉^�]�肪����Ă�悤�ȏꍇ�͂ǂ��Ȃ̂��Ƃ�
���������A�o�X�̋q�Ƃ͌����Ă��炸
�ڑҗ��s�ŁA�����グ�鑤�̎Ј�������Ă邩������Ȃ���
�^�]�肾���𐔂���͕̂Ў藎�����낤
2018/12/24(��) 17:19:51.24ID:P1RO6R6n
>>436
���܂��A�Ȃ��Ȃ����Ȗڂɂ��钿�����w�Z�ɂł��q����ʂ킹�Ă�̂��H
�����������Ȃ̏h��Ȃ̂��m���߂�̂��悾��
����Ƃ��Z���̏h��łȂ��Ȃ��o���悤�ȒS�C���H
���܂��A�Ȃ��Ȃ����Ȗڂɂ��钿�����w�Z�ɂł��q����ʂ킹�Ă�̂��H
�����������Ȃ̏h��Ȃ̂��m���߂�̂��悾��
����Ƃ��Z���̏h��łȂ��Ȃ��o���悤�ȒS�C���H
2018/12/25(��) 09:18:39.00ID:gwy2x1Mv
>>436�̌��ɐ��܂ꂽ�q��������
2018/12/25(��) 23:24:45.81ID:pdwGLC9i
�ʏ��ł��傤���Ȃ��ƌ���ꂽ�̂ŁB
���Z���w�܂ł�͈͂Ƒz�肵�����
n�����R���Ƃ���B����{a_n}�y��a_0�� a_0 = 1 , a_n = a_n-1 +3-(-1)^n �ƁA�܂�����{p_n}���A�f���������������珇�ɕ��ׂ�����ƒ�߂�B
(1) a_n �̈�ʍ���1�̎��ŕ\���B
(2) b_n = a_n / p_n �ƒ�߂�Blim[n����] b_1 * b_2 * b_3 * ... * b_n-1 * b_n �̎����E���U�ׁA��������ꍇ�͂��̒l�����߂�B
���Z���w�܂ł�͈͂Ƒz�肵�����
n�����R���Ƃ���B����{a_n}�y��a_0�� a_0 = 1 , a_n = a_n-1 +3-(-1)^n �ƁA�܂�����{p_n}���A�f���������������珇�ɕ��ׂ�����ƒ�߂�B
(1) a_n �̈�ʍ���1�̎��ŕ\���B
(2) b_n = a_n / p_n �ƒ�߂�Blim[n����] b_1 * b_2 * b_3 * ... * b_n-1 * b_n �̎����E���U�ׁA��������ꍇ�͂��̒l�����߂�B
442�P�R�Q�l�ڂ̑f������
2018/12/25(��) 23:34:21.41ID:DUXh1NNv443�C�i ��/7jUdUKiSM
2018/12/26(��) 14:14:54.45ID:2rCZUTfg444�P�R�Q�l�ڂ̑f������
2019/01/07(��) 19:05:07.99ID:gRcYmcsA 100g�̏d�肪n�ƁA100g�łȂ��d��i100g���d�����y�����͕�����Ȃ��j��1����B
�V�����Q���g���āA100g�łȂ��d����m���ɂ͌������Ȃ��悤��n�̂����A
�ŏ��̂��̂����߂�B
�V�����Q���g���āA100g�łȂ��d����m���ɂ͌������Ȃ��悤��n�̂����A
�ŏ��̂��̂����߂�B
2019/01/07(��) 21:40:51.06ID:Z20FlEla
1
2019/01/09(��) 18:03:14.79ID:ENgVnsAP
���̂�VIP�ɓ\���Ă����
��(1�{��(2�{��(3�{��(�c)))) �����߂�B
�����炭��͓I�ɂ͉����Ȃ�
�����悤�Ȏ��Ƃ��āA������̒l �� �ɂ���
�Ӂ�(1�{��5)/2����(1�{��(1�{��(1�{��(�c))))
�܂��AWikipedia�ɂ��郉�}�k�W���������̎�
3����(1�{2��(1�{3��(1�{4��(�c))))
��ό`�����
3����((1!)^2�{��((2!)^2�{��((3!)^2�{��(�c))))
���̃X���ł͒N���� ��e �Ɨ\�z���Ă�����
�N���v�Z�����X����������
��(1�{��(2�{��(3�{��(�c)))) �����߂�B
�����炭��͓I�ɂ͉����Ȃ�
�����悤�Ȏ��Ƃ��āA������̒l �� �ɂ���
�Ӂ�(1�{��5)/2����(1�{��(1�{��(1�{��(�c))))
�܂��AWikipedia�ɂ��郉�}�k�W���������̎�
3����(1�{2��(1�{3��(1�{4��(�c))))
��ό`�����
3����((1!)^2�{��((2!)^2�{��((3!)^2�{��(�c))))
���̃X���ł͒N���� ��e �Ɨ\�z���Ă�����
�N���v�Z�����X����������
2019/01/09(��) 18:10:34.40ID:ENgVnsAP
2019/01/09(��) 19:19:59.44ID:kLHDSqoE
>>446-447
�������͂ǂ�Ȗ��H
�������͂ǂ�Ȗ��H
2019/01/09(��) 22:04:13.25ID:/priMwZh
>>446
��(1�{��(2�{��(3�{��(�c))))
�͐��l�v�Z�ŋ��߂邵���Ȃ�
http://mathworld.wolfram.com/NestedRadicalConstant.html
��(1�{��(2�{��(3�{��(�c))))
�͐��l�v�Z�ŋ��߂邵���Ȃ�
http://mathworld.wolfram.com/NestedRadicalConstant.html
2019/02/06(��) 23:43:06.79ID:/QdXZOQs
2019/04/15(��) 05:33:33.99ID:8IDqhR4r
r = 1/2.
2019/04/15(��) 06:07:59.82ID:8IDqhR4r
>>449
Nested Radical Constant
�@
��{1 + ��{2 + ��{3 + ���� + ��n}���} �� 1.75793275661800 - exp(6.15 - 2.16n),
Nested Radical Constant
�@
��{1 + ��{2 + ��{3 + ���� + ��n}���} �� 1.75793275661800 - exp(6.15 - 2.16n),
2019/04/15(��) 06:20:18.46ID:8IDqhR4r
2019/04/27(�y) 14:05:18.63ID:Cwx7ucxK
>>450
�����������݂����ł�����
�r�b�g�R�C���i���z�ʉ݁j�ւ̓����Ɏ��s�łP�S�T���~�ȏ�̑���
http://www.sankei.com/economy/news/190424/ecn1904240033-n1.html
�����������݂����ł�����
�r�b�g�R�C���i���z�ʉ݁j�ւ̓����Ɏ��s�łP�S�T���~�ȏ�̑���
http://www.sankei.com/economy/news/190424/ecn1904240033-n1.html
2019/06/28(��) 22:26:21.25ID:YycggmcC
������Ȃ�����ł�
�W���[�J�[����ꂽ�g�����v54��
������V���b�t�������Ƃ������������ȏ�A������m���́H
������ۂ��Ƃق�100���ʼn������炪�A������̂�
�����ƋC�ɂȂ��Ă܂����B
���������낵�����肢�\���グ
�W���[�J�[����ꂽ�g�����v54��
������V���b�t�������Ƃ������������ȏ�A������m���́H
������ۂ��Ƃق�100���ʼn������炪�A������̂�
�����ƋC�ɂȂ��Ă܂����B
���������낵�����肢�\���グ
2019/09/09(��) 13:49:42.12ID:ngBoxWRx
>>455
���āA����͖ʓ|�Ȗ��B
��{�I�Ȍv�Z���@�͂킩�邪�A���ۂɌv�Z���悤�Ƃ���Əꍇ�킯�����G�ɂȂ�p�^�[���B
�v�Z�@���g���������ǂ��B
�莮��:C[1]����C[54]�܂ł�1����13�܂ł̐�����4���ƁA14����15�܂ł̐�����1����(�W���[�J�[�Q���ɑ���)�Ƃ��A����ׂɐU�蕪����Ƃ��A
1��i��53�̂����ꂩ��i�ŁAC[i]��C[i+1]�ƂȂ�m���͂������H
���āA����͖ʓ|�Ȗ��B
��{�I�Ȍv�Z���@�͂킩�邪�A���ۂɌv�Z���悤�Ƃ���Əꍇ�킯�����G�ɂȂ�p�^�[���B
�v�Z�@���g���������ǂ��B
�莮��:C[1]����C[54]�܂ł�1����13�܂ł̐�����4���ƁA14����15�܂ł̐�����1����(�W���[�J�[�Q���ɑ���)�Ƃ��A����ׂɐU�蕪����Ƃ��A
1��i��53�̂����ꂩ��i�ŁAC[i]��C[i+1]�ƂȂ�m���͂������H
457455
2019/09/09(��) 17:00:32.01ID:1QXMxNRL �ԓ����肪�Ƃ��������܂��I
���������������Ă������H�H�ł�w
���������������Ă������H�H�ł�w
2019/09/09(��) 23:50:09.87ID:6DLzIYTV
>>456
���āA���߂�m����
p = P(��i C[i]��C[i+1]) �Ȃ̂����A
��n�߂� i ���ǂ����P�����ɌŒ肵�Ă��܂��āA
P(C[1]��C[2]) �̂悤�Ȃ��̂��l�����ꍇ�A����͊ȒP�ɋ��܂�B
C[1] ��1����13�܂ł̐����̂����ꂩ�ł���ꍇ�AC[2] �́A�c��53�ʂ�̉\���̂����A3�ʂ�� C[1] �Ɠ������Ȃ�̂ŁA
P(C[1]��C[2]) = (52/54) * (3/53) = 26/477
���̏����́A���ׂĂ� 1��i��53 �ɂ����ē��l�Ȃ̂ŁA
P(C[i]��C[i+1]) = (52/54) * (3/53) = 26/477
1��i��53�̂����ꂩ��i�ŁAC[i]��C[i+1]�ƂȂ�m�������߂����̂ŁA�����̘a�����Ɓc
��[1��i��53] P(C[i]��C[i+1]) = 53 * (52/54) * (3/53) = 26/9 �ƂȂ�A1���傫���Ȃ�
���̘a��1���Ă��܂��̂́A�قȂ� i1 �� i2 �� P(C[i1]��C[i1+1]) �� P(C[i2]��C[i2+1]) �̗�����
�uC[i1]��C[i1+1] ���� C[i2]��C[i2+1]�v�̏ꍇ���܂�ł��܂��Ă��邩��ł����āA���̂悤�ȏd�������P�[�X�̊m�������������K�v������B
��[1��i1��53] P(C[i1]��C[i1+1]) - ��[1��i1��i2��53] P(C[i1]��C[i1+1] ���� C[i2]��C[i2+1])
���̂悤�ɂ���ƁA����ɁuC[i1]��C[i1+1] ���� C[i2]��C[i2+1] ���� C[i3]��C[i3+1]�v�̏ꍇ���ߏ�ɍ��������Ă��܂��̂ŁA�����͉��Z����K�v������B
�������J��Ԃ��ƁA���NJm�� p �́A
p = P(1����i��53 C[i]��C[i+1]) = ��[m=1..53] (-1)^(m-1) * ��[1��i_1��..��i_m��53] P(��[k=1..m] C[i_k]��C[i_k+1])
�̂悤�Ȏ��ŋ��߂邱�Ƃ��ł���B
���āA���߂�m����
p = P(��i C[i]��C[i+1]) �Ȃ̂����A
��n�߂� i ���ǂ����P�����ɌŒ肵�Ă��܂��āA
P(C[1]��C[2]) �̂悤�Ȃ��̂��l�����ꍇ�A����͊ȒP�ɋ��܂�B
C[1] ��1����13�܂ł̐����̂����ꂩ�ł���ꍇ�AC[2] �́A�c��53�ʂ�̉\���̂����A3�ʂ�� C[1] �Ɠ������Ȃ�̂ŁA
P(C[1]��C[2]) = (52/54) * (3/53) = 26/477
���̏����́A���ׂĂ� 1��i��53 �ɂ����ē��l�Ȃ̂ŁA
P(C[i]��C[i+1]) = (52/54) * (3/53) = 26/477
1��i��53�̂����ꂩ��i�ŁAC[i]��C[i+1]�ƂȂ�m�������߂����̂ŁA�����̘a�����Ɓc
��[1��i��53] P(C[i]��C[i+1]) = 53 * (52/54) * (3/53) = 26/9 �ƂȂ�A1���傫���Ȃ�
���̘a��1���Ă��܂��̂́A�قȂ� i1 �� i2 �� P(C[i1]��C[i1+1]) �� P(C[i2]��C[i2+1]) �̗�����
�uC[i1]��C[i1+1] ���� C[i2]��C[i2+1]�v�̏ꍇ���܂�ł��܂��Ă��邩��ł����āA���̂悤�ȏd�������P�[�X�̊m�������������K�v������B
��[1��i1��53] P(C[i1]��C[i1+1]) - ��[1��i1��i2��53] P(C[i1]��C[i1+1] ���� C[i2]��C[i2+1])
���̂悤�ɂ���ƁA����ɁuC[i1]��C[i1+1] ���� C[i2]��C[i2+1] ���� C[i3]��C[i3+1]�v�̏ꍇ���ߏ�ɍ��������Ă��܂��̂ŁA�����͉��Z����K�v������B
�������J��Ԃ��ƁA���NJm�� p �́A
p = P(1����i��53 C[i]��C[i+1]) = ��[m=1..53] (-1)^(m-1) * ��[1��i_1��..��i_m��53] P(��[k=1..m] C[i_k]��C[i_k+1])
�̂悤�Ȏ��ŋ��߂邱�Ƃ��ł���B
2019/09/10(��) 00:14:48.81ID:16n7mQYw
>>458
P(��[k=1..m] C[i_k]��C[i_k+1]) �̋��ߕ��ɂ��āA
m=1 �̏ꍇ�͐�ɏq�ׂ��ʂ�A
P(��[k=1..1] C[i_k]��C[i_k+1]) �� P(C[i_k]��C[i_k+1]) = 26/477
��[1��i_1��53] P(��[k=1..1] C[i_k]��C[i_k+1]) �� 53C1 * 26/477 = 26/9
m=2 �ɂ��ẮAP(C[i1]��C[i1+1] �� C[i2]��C[i2+1]) �ƂȂ邪�A�܂��Ai1+1��i2 �� i1+1��i2 �̏ꍇ�ɕ����āA
P(i1+1��i2 �� C[i1]��C[i1+1] �� C[i2]��C[i2+1]) �� P(C[i1]��C[i1+1]��C[i1+2]) �� (52/54) * (3/53) * (2/52) �� 1/477
i1+1��i2 �̏ꍇ������� C[i1]��C[i2] �� C[i1]��C[i2] �̏ꍇ�ɕ����āA
P(i1+1��i2 �� C[i1]��C[i2] �� C[i1]��C[i1+1] �� C[i2]��C[i2+1]) �� P(i1+1��i2 �� C[i1]��C[i1+1]��C[i2]��C[i2+1]) �� (52/54) * (3/53) * (2/52) * (1/51) �� 1/24327
P(i1+1��i2 �� C[i1]��C[i2] �� C[i1]��C[i1+1] �� C[i2]��C[i2+1]) �� P(i1+1��i2 �� C[i1]��C[i1+1]��C[i2]��C[i2+1]) �� (52/54) * (3/53) * (48/52) * (3/51) �� 8/2703
����āA�����̑��a�����ƁA
��[1��i_1��i_2��53] P(��[k=1..2] C[i_k]��C[i_k+1]) �� (52C1 * 1/477 + 52C2 * 1/24327 + 52C2 * 8/2703) = 650/159
m=3 �ɂ��āc�i�Â��j
P(��[k=1..m] C[i_k]��C[i_k+1]) �̋��ߕ��ɂ��āA
m=1 �̏ꍇ�͐�ɏq�ׂ��ʂ�A
P(��[k=1..1] C[i_k]��C[i_k+1]) �� P(C[i_k]��C[i_k+1]) = 26/477
��[1��i_1��53] P(��[k=1..1] C[i_k]��C[i_k+1]) �� 53C1 * 26/477 = 26/9
m=2 �ɂ��ẮAP(C[i1]��C[i1+1] �� C[i2]��C[i2+1]) �ƂȂ邪�A�܂��Ai1+1��i2 �� i1+1��i2 �̏ꍇ�ɕ����āA
P(i1+1��i2 �� C[i1]��C[i1+1] �� C[i2]��C[i2+1]) �� P(C[i1]��C[i1+1]��C[i1+2]) �� (52/54) * (3/53) * (2/52) �� 1/477
i1+1��i2 �̏ꍇ������� C[i1]��C[i2] �� C[i1]��C[i2] �̏ꍇ�ɕ����āA
P(i1+1��i2 �� C[i1]��C[i2] �� C[i1]��C[i1+1] �� C[i2]��C[i2+1]) �� P(i1+1��i2 �� C[i1]��C[i1+1]��C[i2]��C[i2+1]) �� (52/54) * (3/53) * (2/52) * (1/51) �� 1/24327
P(i1+1��i2 �� C[i1]��C[i2] �� C[i1]��C[i1+1] �� C[i2]��C[i2+1]) �� P(i1+1��i2 �� C[i1]��C[i1+1]��C[i2]��C[i2+1]) �� (52/54) * (3/53) * (48/52) * (3/51) �� 8/2703
����āA�����̑��a�����ƁA
��[1��i_1��i_2��53] P(��[k=1..2] C[i_k]��C[i_k+1]) �� (52C1 * 1/477 + 52C2 * 1/24327 + 52C2 * 8/2703) = 650/159
m=3 �ɂ��āc�i�Â��j
2019/09/10(��) 08:14:25.47ID:16n7mQYw
>>459
���������͕��G�Ȃ̂Ōv�Z�@���g���̂ł����A����ꂽ����
1����13�܂ł̊e����n�ɑ��āA�����y�A�iC[i1]��C[i1+1]��n�j�̌����� K1, �c�[�y�A�iC[i1]��C[i1+1]��C[i2]��C[i2+1]�j�̌�����K2
�X���[�J�[�h�iC[i1]��C[i1+1]��C[i1+2]��n�j�̌����� K3, �t�H�[�J�[�h�iC[i1]��C[i1+1]��C[i1+2]��C[i1+3]��n�j�̌�����K4�Ƃ����Ƃ��A
���߂�m������[1��K1+K2+K3+K4��13] (P(13,K1+K2+K3+K4) * (-12)^K1 * 12^K2 * 24^K3 * (-24)^K4) / (P(54,K1+2*K2+2*K3+3*K4) * K1! * K2! * K3! * K4!)
�� 94.9003848140933�c�� (191135009168054682358110966461550615319823/201405936912143954711242007104140005859375)
�iP(m,n)=m!/(m-n)!�j
���������͕��G�Ȃ̂Ōv�Z�@���g���̂ł����A����ꂽ����
1����13�܂ł̊e����n�ɑ��āA�����y�A�iC[i1]��C[i1+1]��n�j�̌����� K1, �c�[�y�A�iC[i1]��C[i1+1]��C[i2]��C[i2+1]�j�̌�����K2
�X���[�J�[�h�iC[i1]��C[i1+1]��C[i1+2]��n�j�̌����� K3, �t�H�[�J�[�h�iC[i1]��C[i1+1]��C[i1+2]��C[i1+3]��n�j�̌�����K4�Ƃ����Ƃ��A
���߂�m������[1��K1+K2+K3+K4��13] (P(13,K1+K2+K3+K4) * (-12)^K1 * 12^K2 * 24^K3 * (-24)^K4) / (P(54,K1+2*K2+2*K3+3*K4) * K1! * K2! * K3! * K4!)
�� 94.9003848140933�c�� (191135009168054682358110966461550615319823/201405936912143954711242007104140005859375)
�iP(m,n)=m!/(m-n)!�j
461455
2019/09/10(��) 08:24:30.33ID:kKEcphOz �Ђ��`
�ȂƂ�ł��Ȃ����Ƃ��y�X���������Ă��܂��Đ\����Ȃ����ǁA
�ϔN�̓䂪�n���Ċ���������ł�
���肪�Ƃ��[�I
�ȂƂ�ł��Ȃ����Ƃ��y�X���������Ă��܂��Đ\����Ȃ����ǁA
�ϔN�̓䂪�n���Ċ���������ł�
���肪�Ƃ��[�I
2019/09/10(��) 13:45:09.75ID:wAUYArRa
�����łP����V���b�t�����Ă݂����94.90���Əo��
�����͂������������Ă���
�����͂������������Ă���
2019/09/10(��) 23:15:45.70ID:Rw7/MGkq
�����_�����T�Z�i�ɂȂ��Ă��邩���悭�킩���ĂȂ����ǁj�ŁB
�ꖇ�̃J�[�h�i�W���[�J�[�ȊO�j�ɒ��ڂ��āA���̃J�[�h�����������ł���m���́A50/53�B
�W���[�J�[���A���ɂȂ�̂̓��A�����疳���B�W���[�J�[���Ō�ɂȂ�̂����A�����疳���Ƃ������Ƃɂ���ƁA
�Ō�ȊO��51���̐����̃J�[�h�ɂ͎��̃J�[�h�����邩��A51���̃J�[�h�ŏ�L�����藧���߂ɂ́A(50/53)^(51)
�Ƃ����킯�ŁA���Ȃ��Ƃ��ǂ�����2�������Ԋm����
1-(50/53)^(51)=0.948785... ���炢�B
������������H
�ꖇ�̃J�[�h�i�W���[�J�[�ȊO�j�ɒ��ڂ��āA���̃J�[�h�����������ł���m���́A50/53�B
�W���[�J�[���A���ɂȂ�̂̓��A�����疳���B�W���[�J�[���Ō�ɂȂ�̂����A�����疳���Ƃ������Ƃɂ���ƁA
�Ō�ȊO��51���̐����̃J�[�h�ɂ͎��̃J�[�h�����邩��A51���̃J�[�h�ŏ�L�����藧���߂ɂ́A(50/53)^(51)
�Ƃ����킯�ŁA���Ȃ��Ƃ��ǂ�����2�������Ԋm����
1-(50/53)^(51)=0.948785... ���炢�B
������������H
464455
2019/09/11(��) 01:36:34.49ID:x5+kNHqJ �W���[�J�[������Ƃ��y�͂��݂ł߂�ǂ��������Ƃ������Ă����܂���c�c
�Ȃ��ق��������ł���ˁHw
�Ȃ��ق��������ł���ˁHw
2019/09/11(��) 13:43:53.93ID:c3ERAMTF
>>463
�P���̃J�[�h�ɒ��ڂ��āA���ꂪ�W���[�J�[�ȊO�ł���A���A�������������ł���m���́A(52/54)�~(3/53)�B
��������ƂɊT�Z�����1-(1-(52/54)�~(3/53))^53��94.87�c��
�P���̃J�[�h�ɒ��ڂ��āA���ꂪ�W���[�J�[�ȊO�ł���A���A�������������ł���m���́A(52/54)�~(3/53)�B
��������ƂɊT�Z�����1-(1-(52/54)�~(3/53))^53��94.87�c��
2019/09/12(��) 13:54:57.52ID:gV8jg/a3
>>464
�W���[�J�[�̗L���͎��̒��̒萔�������ς�邾���Ȃ̂ł��܂����ɉe�����Ȃ�������
�W���[�J�[���Ȃ��ꍇ(52��)�̊m����
��[1��K1+K2+K3+K4��13] (-P(13,K1+K2+K3+K4) * (-12)^K1 * 12^K2 * 24^K3 * (-24)^K4) / (P(52,K1+2*K2+2*K3+3*K4) * K1! * K2! * K3! * K4!)
�� 95.45�c��
�W���[�J�[�̗L���͎��̒��̒萔�������ς�邾���Ȃ̂ł��܂����ɉe�����Ȃ�������
�W���[�J�[���Ȃ��ꍇ(52��)�̊m����
��[1��K1+K2+K3+K4��13] (-P(13,K1+K2+K3+K4) * (-12)^K1 * 12^K2 * 24^K3 * (-24)^K4) / (P(52,K1+2*K2+2*K3+3*K4) * K1! * K2! * K3! * K4!)
�� 95.45�c��
2019/09/12(��) 21:13:03.63ID:AnxOurXk
������ 10^10 �s�����Ƃ��� 94.9003�c�� �܂Ő��l����v
�����������ԂTh��
�����������ԂTh��
468�P�R�Q�l�ڂ̑f������
2019/09/20(��) 13:36:13.59ID:KyAOfC1j 3615
��������@dy_dt_dt_dx 8��28��
�w�R��8����S�R�[�X1����1�ʂƂ�܂����I
�}�W�Ŋ������ł��I
������������n�ɕ������撣�肽���Ǝv���܂��I
https://twitter.com/dy_dt_dt_dx
https://twitter.com/5chan_nel (5ch newer account)
��������@dy_dt_dt_dx 8��28��
�w�R��8����S�R�[�X1����1�ʂƂ�܂����I
�}�W�Ŋ������ł��I
������������n�ɕ������撣�肽���Ǝv���܂��I
https://twitter.com/dy_dt_dt_dx
https://twitter.com/5chan_nel (5ch newer account)
2019/12/07(�y) 14:25:13.02ID:/4V2zz1q
�ؖ����
�u5�̐������^�����Ă���B
���̒���3����肭�I�ׂA���̘a��3�̔{���ɂȂ�B�v
�u5�̐������^�����Ă���B
���̒���3����肭�I�ׂA���̘a��3�̔{���ɂȂ�B�v
2019/12/12(��) 17:08:07.15ID:flOpkEvS
1��3.6%�Ō����A���o��K�`����10����m������
36%�Ȃ̂ł��傤���H
����Ƃ�1-(0.964*0.964*0.964)(�� 1����0.964��10��d��ɂ���������%�Ȃ̂ł��傤���H
�������������B
36%�Ȃ̂ł��傤���H
����Ƃ�1-(0.964*0.964*0.964)(�� 1����0.964��10��d��ɂ���������%�Ȃ̂ł��傤���H
�������������B
2019/12/12(��) 17:25:20.01ID:FIUHqke0
>>470
> ����Ƃ�0.964*0.964*0.964(�� 0.964��10��d��ɂ��������Ȃ̂ł��傤���H
1-�u1����o�Ȃ��m���v�����炱��ł����Ă���
> 36%�Ȃ̂ł��傤���H
�o�閇���̊��Ғl��0.36���ɂȂ�
> ����Ƃ�0.964*0.964*0.964(�� 0.964��10��d��ɂ��������Ȃ̂ł��傤���H
1-�u1����o�Ȃ��m���v�����炱��ł����Ă���
> 36%�Ȃ̂ł��傤���H
�o�閇���̊��Ғl��0.36���ɂȂ�
472470
2019/12/12(��) 17:45:01.91ID:flOpkEvS2019/12/12(��) 18:44:20.87ID:2lE1/u15
1���o��m���͂�������Ȃ���
�u1-�w1����o�Ȃ��m���x�v�ŋ��܂�̂�1���ȏ�o��m��
2���A3���o��m�����܂܂�Ă�
�u1-�w1����o�Ȃ��m���x�v�ŋ��܂�̂�1���ȏ�o��m��
2���A3���o��m�����܂܂�Ă�
475�P�R�Q�l�ڂ̑f������
2019/12/17(��) 15:48:37.24ID:UUH0CZU6 ���鐔(��_��)�̂��悩��0�ȊO�̐�(��)�������܂��B
���̌��ʂ� �|��_�� ���|�������ŁA���Ƃ��Ŋ���܂��B
�����āA���̌��ʂ���_���ɉ����܂��B�܂�A�����̉��Z���s���܂��B
�@�@�@�@{��_��^(��)�|��}�~(�|��_��)/(����)�{��_��
���̌���(��_1)����_���̑���ɗp���Ă��̉��Z���Ăэs���܂��B
�����āA��_1,��_2,��_3,�c�ƌJ��Ԃ��ƁA
�₪�Ă��̂��捪(�����͕��̎���)�̋ɂ߂Đ����ȋߎ��l�ƂȂ�܂��B
�������w��(��)����̂Ƃ��́A��_���̐��������̐����ƈ�v�����A
����Βl�������͈͓̔��ɑ��݂���K�v������܂��B(�����̂Ƃ��ɂ͂����ƍL���Ƃ蓾��B�����͕s��)
�@�@�@�@0��|��_��|��[��]��{|��|�~(���{1)}�@�@([��]�る�́A���̂��捪)
�����Ȃ�܂����̂ŁA���̃��X�Ŏ������x�Ɛ��x�ɂ��ĕ⑫���܂��B
�������炵�܂����B
���̌��ʂ� �|��_�� ���|�������ŁA���Ƃ��Ŋ���܂��B
�����āA���̌��ʂ���_���ɉ����܂��B�܂�A�����̉��Z���s���܂��B
�@�@�@�@{��_��^(��)�|��}�~(�|��_��)/(����)�{��_��
���̌���(��_1)����_���̑���ɗp���Ă��̉��Z���Ăэs���܂��B
�����āA��_1,��_2,��_3,�c�ƌJ��Ԃ��ƁA
�₪�Ă��̂��捪(�����͕��̎���)�̋ɂ߂Đ����ȋߎ��l�ƂȂ�܂��B
�������w��(��)����̂Ƃ��́A��_���̐��������̐����ƈ�v�����A
����Βl�������͈͓̔��ɑ��݂���K�v������܂��B(�����̂Ƃ��ɂ͂����ƍL���Ƃ蓾��B�����͕s��)
�@�@�@�@0��|��_��|��[��]��{|��|�~(���{1)}�@�@([��]�る�́A���̂��捪)
�����Ȃ�܂����̂ŁA���̃��X�Ŏ������x�Ɛ��x�ɂ��ĕ⑫���܂��B
�������炵�܂����B
476�P�R�Q�l�ڂ̑f������
2019/12/17(��) 16:09:16.06ID:UUH0CZU6 ����475�̑���
�قƂ�ǂ̃P�[�X�Ńj���[�g���@�Ɠ������炢�̉��Z�ŎZ�o����܂��B
�������A�����l�̐�Βl������475�̑�̉������͏���ɋ߂��Ƃ��́A
�{���@�̕��������Ȃ�₷���悤�ł��B
�������A������肠����x�傫���^�̒l��菬�����Ƃ��Ȃǂɂ́A
�t�ɁA���Ȃ��Ȃ�₷���悤�ł��B(���Ɏw�����傫���Ƃ�)
���x���ɂ߂ėǂ��ł��B(�ȉ��A���ʂ̓d���p���܂�)
�w������قǑ傫���Ȃ�����A�d��̃P�^���Ɠ����̃P�^���ɂ����āA�Ⴆ��12�P�^�̓d��ł���A
���12�P�^(���x���̑S�P�^)�̐������S�Ĉ�v���邩�A
���12�P�^��(���x���Ŗ���)�̐����݂̂�(���x���ł�)1�قȂ�܂��B(2��1.999�c9�̂悤�ȋ��ڂ̃P�[�X���܂�)
�܂����x���m���߂�����A�d��̃P�^���̔����ȏ�A
�܂���6�P�^�ȏ�̐������^�̒l�ƈ�v����ߎ��l����_���Ƃ���
����475�̉��Z�����������͓��s���悢�ł��傤(�w������قǑ傫���Ȃ�����)�B
�������炵�܂����B
�قƂ�ǂ̃P�[�X�Ńj���[�g���@�Ɠ������炢�̉��Z�ŎZ�o����܂��B
�������A�����l�̐�Βl������475�̑�̉������͏���ɋ߂��Ƃ��́A
�{���@�̕��������Ȃ�₷���悤�ł��B
�������A������肠����x�傫���^�̒l��菬�����Ƃ��Ȃǂɂ́A
�t�ɁA���Ȃ��Ȃ�₷���悤�ł��B(���Ɏw�����傫���Ƃ�)
���x���ɂ߂ėǂ��ł��B(�ȉ��A���ʂ̓d���p���܂�)
�w������قǑ傫���Ȃ�����A�d��̃P�^���Ɠ����̃P�^���ɂ����āA�Ⴆ��12�P�^�̓d��ł���A
���12�P�^(���x���̑S�P�^)�̐������S�Ĉ�v���邩�A
���12�P�^��(���x���Ŗ���)�̐����݂̂�(���x���ł�)1�قȂ�܂��B(2��1.999�c9�̂悤�ȋ��ڂ̃P�[�X���܂�)
�܂����x���m���߂�����A�d��̃P�^���̔����ȏ�A
�܂���6�P�^�ȏ�̐������^�̒l�ƈ�v����ߎ��l����_���Ƃ���
����475�̉��Z�����������͓��s���悢�ł��傤(�w������قǑ傫���Ȃ�����)�B
�������炵�܂����B
477�P�R�Q�l�ڂ̑f������
2019/12/20(��) 02:10:23.62ID:yiLw1Jz8 1030
����@huwa_cororon 11��27��
���6�����A�����_&�ꓙ�܂ł��I
https://twitter.com/huwa_cororon/status/1199593474128896000
https://twitter.com/5chan_nel (5ch newer account)
����@huwa_cororon 11��27��
���6�����A�����_&�ꓙ�܂ł��I
https://twitter.com/huwa_cororon/status/1199593474128896000
https://twitter.com/5chan_nel (5ch newer account)
2020/01/01(��) 15:44:00.48ID:F81QwpXb
x>0 �Ƃ���Ƃ�
(x^2020 -x^2 +4)/(x^6 +2) �̍ŏ��l�����߂�B
(x^2020 -x^2 +4)/(x^6 +2) �̍ŏ��l�����߂�B
2020/01/01(��) 15:51:55.19ID:F81QwpXb
2014x^2024 +4040x^2018 +4x^6 -24x^4 -4 = 0,
�̎�����
x� = �}0.9972618331127334631938246515195619175923
(x^2020 -x^2 +4)/(x^6 +2) �� 1.008619375112916534599176779154067780593
�̎�����
x� = �}0.9972618331127334631938246515195619175923
(x^2020 -x^2 +4)/(x^6 +2) �� 1.008619375112916534599176779154067780593
2020/01/01(��) 15:54:10.69ID:F81QwpXb
(x^2020 -x^2 +3)/(x^6 +2) �̍ŏ��l�����߂�B
2020/01/01(��) 16:01:01.48ID:F81QwpXb
2014x^2024 +4040x^2018 +4x^6 -18x^4 -4 = 0,
�̎�����
�@x� = �}0.997120078481544
(x^2020 -x^2 +3)/(x^6 +2) �� 0.67341826074836
�̎�����
�@x� = �}0.997120078481544
(x^2020 -x^2 +3)/(x^6 +2) �� 0.67341826074836
2020/01/09(��) 11:12:49.15ID:yUxD+KNf
>>469
3�Ŋ������Ƃ��̗]�� (0,1,2) �ɒ��ڂ���B
�������̂�3�ȏ゠��Ƃ��́A����3��I�ԁB
�ǂ��2�ȉ��̂Ƃ��́A0,1,2�����ׂĊ܂ނ���A1�ÂI�ԁB
3�Ŋ������Ƃ��̗]�� (0,1,2) �ɒ��ڂ���B
�������̂�3�ȏ゠��Ƃ��́A����3��I�ԁB
�ǂ��2�ȉ��̂Ƃ��́A0,1,2�����ׂĊ܂ނ���A1�ÂI�ԁB
483�P�R�Q�l�ڂ̑f������
2020/01/21(��) 16:10:37.29ID:4jOB30nc �ȉ��A�P�Ȃ�\�����K
����
���a���P�ł��鋅�ɑ��āA���̒��S��ʂ�悤�ȕ��ʂŐ�ƒf�ʂ͔��a���P�̉~�ɂ�
��B���̉~����ɁA�����p�`�ƂȂ�悤�ɁA�~���ɓ_����邱�Ƃɂ���B���̕��@������
�肩�����ċ����A���ꂼ��̉~����ɁA�����p�`���ł���悤�ɂ��̓_�ƂƂ����Ƃ��A
�~�ɑ��݂��鐳���p�`�̑Ίp���ƕӂ̒����̕����a�����ׂč��v����ƁA���̂R��ɂȂ�B
�ؖ�
���a�P�̉~�ɓ��ڂ��鐳���p�`�̕ӂ���ёΊp���̒����̕����a�����̓��ŕ\����邱
�Ƃ������Ă���i�Q�l�����Q�Ɓj�B����́A���a���P�ł��鋅�ɑ��݂��邎�̉~�̂���
����ɑ��Đ��藧�̂ŁA����ɂ������������̂��A���̐ؒf�ʂɑ��݂��鐳���p�`�̑�
�p���ƕӂ̒����̕����a�ɂȂ�B
�Q�l����
�x���a�o�A�ш�Y�A���c�j�w���w�̉ۑ茤���@�e�[�}�I�т̃q���g�E�E���W�xpp.20-23
����
���a���P�ł��鋅�ɑ��āA���̒��S��ʂ�悤�ȕ��ʂŐ�ƒf�ʂ͔��a���P�̉~�ɂ�
��B���̉~����ɁA�����p�`�ƂȂ�悤�ɁA�~���ɓ_����邱�Ƃɂ���B���̕��@������
�肩�����ċ����A���ꂼ��̉~����ɁA�����p�`���ł���悤�ɂ��̓_�ƂƂ����Ƃ��A
�~�ɑ��݂��鐳���p�`�̑Ίp���ƕӂ̒����̕����a�����ׂč��v����ƁA���̂R��ɂȂ�B
�ؖ�
���a�P�̉~�ɓ��ڂ��鐳���p�`�̕ӂ���ёΊp���̒����̕����a�����̓��ŕ\����邱
�Ƃ������Ă���i�Q�l�����Q�Ɓj�B����́A���a���P�ł��鋅�ɑ��݂��邎�̉~�̂���
����ɑ��Đ��藧�̂ŁA����ɂ������������̂��A���̐ؒf�ʂɑ��݂��鐳���p�`�̑�
�p���ƕӂ̒����̕����a�ɂȂ�B
�Q�l����
�x���a�o�A�ш�Y�A���c�j�w���w�̉ۑ茤���@�e�[�}�I�т̃q���g�E�E���W�xpp.20-23
484�P�R�Q�l�ڂ̑f������
2020/01/21(��) 16:45:00.47ID:4jOB30nc ����
���a�P�̋��ɑ��A�C�ӂ̕��ʂŐ�B���̕��ʂƋ��̒��S�Ƃ̋�����
��{�P^�Q�|�i���^�Q�j^�Q}�@�ł���
�ؖ�
�ӎO�p�`���l����킩��B��ʂ����i0�ȏ�Q�����j�Ƃ���ƁA���̍�����
��{�P^�Q�|�i���^�Q�j^�Q} �ƂȂ邪�A���ꂪ���ʂƋ��̒��S�Ƃ̋����ł���B
����͋��𒆐S��ʂ镽�ʂł������Ƃ��ɂ���������
���a�P�̋��ɑ��A�C�ӂ̕��ʂŐ�B���̕��ʂƋ��̒��S�Ƃ̋�����
��{�P^�Q�|�i���^�Q�j^�Q}�@�ł���
�ؖ�
�ӎO�p�`���l����킩��B��ʂ����i0�ȏ�Q�����j�Ƃ���ƁA���̍�����
��{�P^�Q�|�i���^�Q�j^�Q} �ƂȂ邪�A���ꂪ���ʂƋ��̒��S�Ƃ̋����ł���B
����͋��𒆐S��ʂ镽�ʂł������Ƃ��ɂ���������
485�P�R�Q�l�ڂ̑f������
2020/01/21(��) 17:08:22.20ID:4jOB30nc ���v���Ԃ̋�����
�����̒�`
d�i�`�A�a�j�͔C�ӂ̎������������̂Ƃ���
���̎O�����������̂��`�Ƃa�̋����ł���
�P�@���i�`�C�a�j�͂O�ȏ�ł���A���i�`�C�a�j���O�ɂȂ�̂͂`�Ƃa���������Ƃ��ł���
�Q�@���i�`�A�a�j�����i�a�C�`�j
�R�@���i�`�C�b�j�����i�`�C�a�j�{���i�a�A�b�j
�`���_�ˉw�A�a�����w�A�b�����s�w�Ƃ��A���i�`�A�a�j��_�ˉw�Ƒ��w���ړ�����Ԃ�
�����鎞�ԂƂ���B����ƁA���v���Ԃ������Ƃ��Čv�Z�ł���B
�Q�l����
�x���a�o�A�ш�Y�A���c�j�w���w�̉ۑ茤���@�e�[�}�I�т̃q���g�E�E���W�xp.52
�����̒�`
d�i�`�A�a�j�͔C�ӂ̎������������̂Ƃ���
���̎O�����������̂��`�Ƃa�̋����ł���
�P�@���i�`�C�a�j�͂O�ȏ�ł���A���i�`�C�a�j���O�ɂȂ�̂͂`�Ƃa���������Ƃ��ł���
�Q�@���i�`�A�a�j�����i�a�C�`�j
�R�@���i�`�C�b�j�����i�`�C�a�j�{���i�a�A�b�j
�`���_�ˉw�A�a�����w�A�b�����s�w�Ƃ��A���i�`�A�a�j��_�ˉw�Ƒ��w���ړ�����Ԃ�
�����鎞�ԂƂ���B����ƁA���v���Ԃ������Ƃ��Čv�Z�ł���B
�Q�l����
�x���a�o�A�ш�Y�A���c�j�w���w�̉ۑ茤���@�e�[�}�I�т̃q���g�E�E���W�xp.52
486�P�R�Q�l�ڂ̑f������
2020/01/21(��) 19:47:33.95ID:4jOB30nc �\�����K
��������
���w�̏ؖ��ɂ��āA�������m����`���܂��傤
����N
�V��i�Q�O�O�X�j�͐��w�̏ؖ��ɂ��Ĉȉ��̂悤�ɏq�ׂĂ���B
���w�̑Ώۗ̈�́A�i�ؖ��Ȃ��ɐ������Ɨ����ł���悤�ȁj�ŏ����̖���Q����Ȃ����
�n�ɂ���Ē�`�Â����Ă��Ȃ���Ȃ�Ȃ��B�����n�Ɋ܂܂������Ƙ_���݂̂ɂ��
�Đ��������Ƃ������ꂽ�����藝�Ƃ�ԁB�܂��A�藝�ł��邱�Ƃ������ߒ����ؖ��Ƃ�ԁB
�����_���w�̐��Ƃ����̂悤�Ȃ��Ƃ������Ă���̂́A���w����Ƃ��Ȃ���ʂ̐l��
�ǎ҂ɑz�肵�����炩������Ȃ����A���̂悤�ȔF���͑����̐l�����w�̏ؖ��ɂ��ĕ�
���Ă���l���ł���悤�Ɏv����B
���w�̏ؖ��ɂ��āA�����w�Z�̐��w�܂ł��������Ȃ������Ƃ�����A���̔F���ɉ��̋^
��������Ȃ��͓̂��R�̂��ƂƎv���邪�A�����͂���Ƃ͈قȂ�̂ŁA���߂āA�����n��
�����ލ��Z���Ȃǂɂ́A�����������m�ȗ���������悤�ɐ��m�ɒm����`�����ق�������
�̂ł͂Ȃ����낤���B
��������
���w�̏ؖ��ɂ��āA�������m����`���܂��傤
����N
�V��i�Q�O�O�X�j�͐��w�̏ؖ��ɂ��Ĉȉ��̂悤�ɏq�ׂĂ���B
���w�̑Ώۗ̈�́A�i�ؖ��Ȃ��ɐ������Ɨ����ł���悤�ȁj�ŏ����̖���Q����Ȃ����
�n�ɂ���Ē�`�Â����Ă��Ȃ���Ȃ�Ȃ��B�����n�Ɋ܂܂������Ƙ_���݂̂ɂ��
�Đ��������Ƃ������ꂽ�����藝�Ƃ�ԁB�܂��A�藝�ł��邱�Ƃ������ߒ����ؖ��Ƃ�ԁB
�����_���w�̐��Ƃ����̂悤�Ȃ��Ƃ������Ă���̂́A���w����Ƃ��Ȃ���ʂ̐l��
�ǎ҂ɑz�肵�����炩������Ȃ����A���̂悤�ȔF���͑����̐l�����w�̏ؖ��ɂ��ĕ�
���Ă���l���ł���悤�Ɏv����B
���w�̏ؖ��ɂ��āA�����w�Z�̐��w�܂ł��������Ȃ������Ƃ�����A���̔F���ɉ��̋^
��������Ȃ��͓̂��R�̂��ƂƎv���邪�A�����͂���Ƃ͈قȂ�̂ŁA���߂āA�����n��
�����ލ��Z���Ȃǂɂ́A�����������m�ȗ���������悤�ɐ��m�ɒm����`�����ق�������
�̂ł͂Ȃ����낤���B
487�P�R�Q�l�ڂ̑f������
2020/01/21(��) 19:48:43.64ID:4jOB30nc ���w�̓���̑̌n
���w�̓���̑̌n�Ƃ́A��{�I�ɁA�_�������{�����̌����{����̌����n�{���_�K���ƁA
�������琄�_�ɂ���Ă݂��т����藝�̂��Ƃł���B
���[�N���b�h�w������ɉ��������̂ƍl�����邪�A���̌����n�͌������E�����f��
�Ƃ������̂ł���A���݂̌����n�Ƃ͈قȂ��Ă���B���݂̌����n�́A���̂悤�ȓ����
���f����z�肷�邱�Ƃ͂Ȃ��̂��B
���[�N���b�h�w�̋c�_�́A�V�䂪�q�ׂĂ���悤�ȁA�u�ؖ��Ȃ��ɐ������Ɨ����ł�
��悤�ȁv��������o�����邪�A���݂̌����n�ł͂���͖��ɂ͂���Ȃ��B�^�U�����
�ɂ����̂́A����ɑ��郂�f�����l����Ƃ��ł���B
���_
���w�̏ؖ��ɂ��Č������i���ʁA����l�͏ؖ��ɂ��ČÑ�M���V���l�����Ƃ͂�
�ƂȂ�F�������ɂ��������B�����m��Ȃ���ΐ����ɂ������Ƃ��A��������������
�͂Ȃ����A�����Ȃ��Ƃ����n�ɂ����ސl�����ɂ́A���{�A���邢�͗��n�̏펯�Ƃ��āA��
�m�ȏ��������ƍL���`����悤�ɂ����ق���������Ȃ����낤���B
���p����
�V��I�q�i�Q�O�O�X�j�w���w�͌��t�x�����}���@p.184
�Q�l����
�������V�i�Q�O�P�V�j�w�ؖ��Ƙ_���ɋ����Ȃ�x�Z�p�]�_��
��菺�O�i�Q�O�O�W�j�w�s���S���藝�x�}�����[ pp. 147-204
���w�̓���̑̌n�Ƃ́A��{�I�ɁA�_�������{�����̌����{����̌����n�{���_�K���ƁA
�������琄�_�ɂ���Ă݂��т����藝�̂��Ƃł���B
���[�N���b�h�w������ɉ��������̂ƍl�����邪�A���̌����n�͌������E�����f��
�Ƃ������̂ł���A���݂̌����n�Ƃ͈قȂ��Ă���B���݂̌����n�́A���̂悤�ȓ����
���f����z�肷�邱�Ƃ͂Ȃ��̂��B
���[�N���b�h�w�̋c�_�́A�V�䂪�q�ׂĂ���悤�ȁA�u�ؖ��Ȃ��ɐ������Ɨ����ł�
��悤�ȁv��������o�����邪�A���݂̌����n�ł͂���͖��ɂ͂���Ȃ��B�^�U�����
�ɂ����̂́A����ɑ��郂�f�����l����Ƃ��ł���B
���_
���w�̏ؖ��ɂ��Č������i���ʁA����l�͏ؖ��ɂ��ČÑ�M���V���l�����Ƃ͂�
�ƂȂ�F�������ɂ��������B�����m��Ȃ���ΐ����ɂ������Ƃ��A��������������
�͂Ȃ����A�����Ȃ��Ƃ����n�ɂ����ސl�����ɂ́A���{�A���邢�͗��n�̏펯�Ƃ��āA��
�m�ȏ��������ƍL���`����悤�ɂ����ق���������Ȃ����낤���B
���p����
�V��I�q�i�Q�O�O�X�j�w���w�͌��t�x�����}���@p.184
�Q�l����
�������V�i�Q�O�P�V�j�w�ؖ��Ƙ_���ɋ����Ȃ�x�Z�p�]�_��
��菺�O�i�Q�O�O�W�j�w�s���S���藝�x�}�����[ pp. 147-204
2020/02/01(�y) 03:26:32.96ID:7zqqjjoe
>>478
�����P
x^2020 - xx - x^2018 +1 = (xx -1)(x^2018 -1) �� 0,
x^2018 - x^6 - x^2012 +1 = (x^6 -1)(x^2012 -1) �� 0,
���
x^2020 - xx +4 �� x^2018 +3 �� x^2012 + x^6 +2 > x^6 +2,
�����P
x^2020 - xx - x^2018 +1 = (xx -1)(x^2018 -1) �� 0,
x^2018 - x^6 - x^2012 +1 = (x^6 -1)(x^2012 -1) �� 0,
���
x^2020 - xx +4 �� x^2018 +3 �� x^2012 + x^6 +2 > x^6 +2,
2020/02/26(��) 14:01:59.74ID:5zz1h1XV
�ō��ɔ����������ς��ɂ�������ȋȖʂ̕����������
2020/03/12(��) 15:06:39.29ID:mKJwV7nJ
>>475 >>476
�@f(x) = 1 - ��/(x^p)�@�@(�ł͒萔)
�ɑ��ăj���[�g���@���g�����̂ł��ˁB���̏ꍇ��
�@x' - ��^(1/p) �� -((p+1)/2)���^(-1/p)�{x-��^(1/p)}^2,
�Ȃ̂łQ������ł��B
�@f(x) = (x^p -��)/x^{(p-1)/2},
�ɑ��ăj���[�g���@���g����
�@x ' - ��^(1/p) �� ((pp-1)/12)���^(-2/p)�{x - ��^(1/p)}^3,
�łR������ɂȂ�A���x�����P���܂��B
�@f(x) = 1 - ��/(x^p)�@�@(�ł͒萔)
�ɑ��ăj���[�g���@���g�����̂ł��ˁB���̏ꍇ��
�@x' - ��^(1/p) �� -((p+1)/2)���^(-1/p)�{x-��^(1/p)}^2,
�Ȃ̂łQ������ł��B
�@f(x) = (x^p -��)/x^{(p-1)/2},
�ɑ��ăj���[�g���@���g����
�@x ' - ��^(1/p) �� ((pp-1)/12)���^(-2/p)�{x - ��^(1/p)}^3,
�łR������ɂȂ�A���x�����P���܂��B
2020/03/12(��) 15:17:24.90ID:mKJwV7nJ
��҂ł� f "(��^(1/p)) = 0
�܂� x=��^(1/p) ���ϋȓ_�ƂȂ�̂ŁA
�����ߎ������ʓI�ɂȂ�炵���B�B�B
�܂� x=��^(1/p) ���ϋȓ_�ƂȂ�̂ŁA
�����ߎ������ʓI�ɂȂ�炵���B�B�B
2020/03/20(��) 18:45:43.41ID:lC3HBZ24
�k���l
�@a,b,n,p �������̂Ƃ�
�@|na - pb| �� (n-p)(a-b).
[�s�����X���P�O.362]
�@a,b,n,p �������̂Ƃ�
�@|na - pb| �� (n-p)(a-b).
[�s�����X���P�O.362]
2020/03/21(�y) 05:04:45.03ID:a/9U1hEf
2020/03/27(��) 16:13:41.69ID:hdfrPNEp
�O�X����������˂�
�����������E
������˂����͂����֏��� ver3.14(67����)4062
http://uni.5ch.net/test/read.cgi/math/1319117617/
�����������E
������˂����͂����֏��� ver3.14(67����)4062
http://uni.5ch.net/test/read.cgi/math/1319117617/
2020/03/30(��) 21:46:43.31ID:uxzDymBq
496���� ��C2UdlLHDRI
2020/03/31(��) 03:56:06.56ID:EDLtMypi �����������̋����t��������ō����ɋ��������Ē����
�O����������Ȃ�ŕʓr���K�ɕۊǂ��Ē��������
�����������
https://web.archive.org/web/20181107033930/http://www.geocities.co.jp/CollegeLife-Club/7442/math/index.html
�O����������Ȃ�ŕʓr���K�ɕۊǂ��Ē��������
�����������
https://web.archive.org/web/20181107033930/http://www.geocities.co.jp/CollegeLife-Club/7442/math/index.html
2020/04/15(��) 17:21:14.42ID:OBrsEksp
2020/04/21(��) 17:12:31.82ID:J9ZMzsJq
�������}�C�i�X�̉��i�����Ęb��ɂȂ��Ă��܂���
���f���̉��i�͂����ł����H
���f���̉��i�͂����ł����H
2020/04/23(��) 14:40:40.21ID:M2d54xbk
�ԋ�i�A����j�A��k��2�l�ŕ�����B
�@i_1 + i_2 = i,
�@j_1 + j_2 = j
�@k_1 + k_2 = k,
(i,j,k�j��
�@i+j+k = ����,
�@|i-j| �� k �� i+j,
�̏��������Ƃ��A
�@{i_1, j_1, k_1} = {i_2, j_2, k_2}�@�@���W���Ƃ��ē���
�Ƃ��邱�Ƃ��ł��邩�H
�i�F�Ⴂ�͋����ē����j
�@i_1 + i_2 = i,
�@j_1 + j_2 = j
�@k_1 + k_2 = k,
(i,j,k�j��
�@i+j+k = ����,
�@|i-j| �� k �� i+j,
�̏��������Ƃ��A
�@{i_1, j_1, k_1} = {i_2, j_2, k_2}�@�@���W���Ƃ��ē���
�Ƃ��邱�Ƃ��ł��邩�H
�i�F�Ⴂ�͋����ē����j
2020/04/24(��) 06:17:21.19ID:FdH14EWV
500���Ɓ[
�k���l
a>b>c>0 �̂Ƃ��A���������B�W���A���Ɏ����B
(1)�@(a+b)(aa-ab+bb) = a^3 + b^3,
(2)�@(1/2){(a-b)^2+(b-c)^2+(c-a)^2} = aa+bb+cc -ab-bc-ca,
(3)�@aa(b-c) + bb(c-a) + cc(a-b) = - (a-b)(b-c)(c-a),
(4)�@a^3 +b^3 +c^3 -3abc = (a+b+c)(aa+bb+cc -ab-bc-ca),
(5)�@(a+b+c)(ab+bc+ca) -abc = (a+b)(b+c)(c+a),
(6)�@(a+b+c)^3 -a^3 -b^3 -c^3 = 3(a+b)(b+c)(c+a),
http://suseum.jp/gq/question/3146
[�ʔ��X���R�Q�D064,067]
�S���͈ꌩ�ɔ@����(?)
�k���l
a>b>c>0 �̂Ƃ��A���������B�W���A���Ɏ����B
(1)�@(a+b)(aa-ab+bb) = a^3 + b^3,
(2)�@(1/2){(a-b)^2+(b-c)^2+(c-a)^2} = aa+bb+cc -ab-bc-ca,
(3)�@aa(b-c) + bb(c-a) + cc(a-b) = - (a-b)(b-c)(c-a),
(4)�@a^3 +b^3 +c^3 -3abc = (a+b+c)(aa+bb+cc -ab-bc-ca),
(5)�@(a+b+c)(ab+bc+ca) -abc = (a+b)(b+c)(c+a),
(6)�@(a+b+c)^3 -a^3 -b^3 -c^3 = 3(a+b)(b+c)(c+a),
http://suseum.jp/gq/question/3146
[�ʔ��X���R�Q�D064,067]
�S���͈ꌩ�ɔ@����(?)
2020/05/09(�y) 09:00:57.77ID:pHr5kdzK
2020/05/27(��) 01:03:31.50ID:EnH7JxEr
�܂����������X���̃i���o�����O�ǂ�����H
�~�������ǂ��ɖ߂��H���̏ꍇ�� ver3.14(69����)6286 �ɂȂ�
����Ƃ��W���ɂ���H���̏ꍇ�� part76 �ɂȂ�
>>494
������˂����͂����֏��� ver3.14(68����)0628
��������X���͕s�݁A����ĕ����㏉�̓��X�����Y���A�O�X����
������˂����͂����֏��� ver3.14(67����)4062
�~�������ǂ��ɖ߂��H���̏ꍇ�� ver3.14(69����)6286 �ɂȂ�
����Ƃ��W���ɂ���H���̏ꍇ�� part76 �ɂȂ�
>>494
������˂����͂����֏��� ver3.14(68����)0628
��������X���͕s�݁A����ĕ����㏉�̓��X�����Y���A�O�X����
������˂����͂����֏��� ver3.14(67����)4062
2020/05/27(��) 03:32:08.28ID:qjAXFTAb
ver.�V2 �ɂ��悤��
2020/05/27(��) 04:16:13.28ID:EnH7JxEr
�������A����
�ߋ��X���Y�t�͕����O�ŏI�Ƃ��̌��s��\���Ƃ��Ⴂ�[��
�X�ɂ��̌�̃X���͂��̃X���̑O�X�������\���Ƃ���A�܂܂����
�ߋ��X���Y�t�͕����O�ŏI�Ƃ��̌��s��\���Ƃ��Ⴂ�[��
�X�ɂ��̌�̃X���͂��̃X���̑O�X�������\���Ƃ���A�܂܂����
2020/06/05(��) 16:02:08.97ID:gPkvRYC5
[��9-3]
�@���̕s�������݂�������a,b,c�ŁA�ǂꂩ�P��0�łȂ��A
���ǂ̐�Βl��100�����Ȃ����̂����݂��邱�Ƃ������B
�@�ba + b��2 + c��3�b< 10^(-12),
(�Q�l)
�H�R �m + �s�[�^�[�E�t�����N�� �����F
�@�m���S�U���n���w�I�����s�b�N, p.47-48, ���{�]�_�� (1991/Nov)
���j���m�������ł͉����܂���B
�@���̕s�������݂�������a,b,c�ŁA�ǂꂩ�P��0�łȂ��A
���ǂ̐�Βl��100�����Ȃ����̂����݂��邱�Ƃ������B
�@�ba + b��2 + c��3�b< 10^(-12),
(�Q�l)
�H�R �m + �s�[�^�[�E�t�����N�� �����F
�@�m���S�U���n���w�I�����s�b�N, p.47-48, ���{�]�_�� (1991/Nov)
���j���m�������ł͉����܂���B
2020/06/06(�y) 03:18:03.49ID:RyPojoqR
2020/06/15(��) 07:46:58.40ID:m4MzqaBi
�k���4�l
4444^4444 ��10�i�\�����āA���̊e���Ɍ���鐔�̘a��A�Ƃ���B
A�̊e���Ɍ���鐔�̘a��B�Ƃ���B
B�̊e���Ɍ���鐔�̘a��C�Ƃ���B
C�����߂�B
IMO-1975 (�u���K���A���)
4444^4444 ��10�i�\�����āA���̊e���Ɍ���鐔�̘a��A�Ƃ���B
A�̊e���Ɍ���鐔�̘a��B�Ƃ���B
B�̊e���Ɍ���鐔�̘a��C�Ƃ���B
C�����߂�B
IMO-1975 (�u���K���A���)
2020/06/15(��) 07:48:47.30ID:m4MzqaBi
N=4444^4444�@�Ƃ���B���̂Ƃ�
�@log(N) = 4444 log(4444) = 16210.707879
�ł��邩��AN��10�i�@�ŏ�����Ă���Ƃ��AN�̌����� 16211 �ł���B
�܂��AN�̊e���Ɍ���鐔��9�ȉ��ł��邩��A
�@A �� 16211�~9 = 145899
�ƂȂ�B
���l�̕��@�ŁAA�͑����Ƃ�6���ł��邩��AA�̌��Ɍ���鐔�̘a��54
�i=6�~9�j�ȉ��Ƃ������ƂɂȂ�AB��54 �ł���B
54�ȉ��̐������ŁA�e���Ɍ���鐔�̘a���ő�ɂȂ�̂�49�ł���A����
�l��13�ł���B����� C��13 �ł���B
�@����A���̉̌��͎��̎������g�����Ƃł���B�@A=72601
������
�@B = 7+2+6+0+1 = 16,
�@C = 1+6 = 7,
�u�m���S�U���n���w�I�����s�b�N�v(1991)�@p.70-71
�@log(N) = 4444 log(4444) = 16210.707879
�ł��邩��AN��10�i�@�ŏ�����Ă���Ƃ��AN�̌����� 16211 �ł���B
�܂��AN�̊e���Ɍ���鐔��9�ȉ��ł��邩��A
�@A �� 16211�~9 = 145899
�ƂȂ�B
���l�̕��@�ŁAA�͑����Ƃ�6���ł��邩��AA�̌��Ɍ���鐔�̘a��54
�i=6�~9�j�ȉ��Ƃ������ƂɂȂ�AB��54 �ł���B
54�ȉ��̐������ŁA�e���Ɍ���鐔�̘a���ő�ɂȂ�̂�49�ł���A����
�l��13�ł���B����� C��13 �ł���B
�@����A���̉̌��͎��̎������g�����Ƃł���B�@A=72601
������
�@B = 7+2+6+0+1 = 16,
�@C = 1+6 = 7,
�u�m���S�U���n���w�I�����s�b�N�v(1991)�@p.70-71
2020/07/05(��) 20:23:39.43ID:z5qpWJIy
�т�H���Ă���Ƃ��Ɏv���������
���͐H���ɂ��т��p����H�ׂ邪�ǂ����H�ׂ邩�͎��̃��[���Ō��߂Ă���B
���т�H�ׂ���ɃT�C�R����U��1�`5���o���玟�����т�H�ׂ�B
�p����H�ׂ���ɃT�C�R����U��1�`2���o���玟���p����H�ׂ�B
���͐��U�̂����ł��т��ǂ̊����ŐH�ׂĂ��邩���Ғl�����߂�B
���͐H���ɂ��т��p����H�ׂ邪�ǂ����H�ׂ邩�͎��̃��[���Ō��߂Ă���B
���т�H�ׂ���ɃT�C�R����U��1�`5���o���玟�����т�H�ׂ�B
�p����H�ׂ���ɃT�C�R����U��1�`2���o���玟���p����H�ׂ�B
���͐��U�̂����ł��т��ǂ̊����ŐH�ׂĂ��邩���Ғl�����߂�B
2020/07/05(��) 22:12:44.47ID:SvMv/2tl
https://twitter.com/KEUMAYA/status/1279219657015062528
����[����100%�ɂȂ����Ƃ��Ă����[�̊����I�͕ς��Ȃ���ۂȂ̂ł���
�ǂ������������Ŗ����[�̐l�Ԃ����ʂ��Ђ�����Ԃ���ł����H
https://twitter.com/5chan_nel (5ch newer account)
����[����100%�ɂȂ����Ƃ��Ă����[�̊����I�͕ς��Ȃ���ۂȂ̂ł���
�ǂ������������Ŗ����[�̐l�Ԃ����ʂ��Ђ�����Ԃ���ł����H
https://twitter.com/5chan_nel (5ch newer account)
2020/07/11(�y) 10:18:17.08ID:ZnhtLn45
2020/08/04(��) 11:59:34.63ID:9V2IPZEi
>>510
���ɖ����[�̐l�̔������^�}����Ȃ�����̐��}�ɓ��ꂽ�Ƃ�����A�S�̂�25%���炢�ɂȂ�B
�^�}�͑S�̂�24%���炢�������炵������A����ŋt�]�ł���B
���ۂ͂��Ƃ��Ɠ��[���Ă�l�����̉�%���͂��̐��}�ɓ���Ă邩�����������Ə��Ȃ��Ă������B
�Ƃ͂���2000���l�ȏ�̐l�Ԃ����̂��ȒP�Ƃ͂ƂĂ��v���Ȃ��B
���ɖ����[�̐l�̔������^�}����Ȃ�����̐��}�ɓ��ꂽ�Ƃ�����A�S�̂�25%���炢�ɂȂ�B
�^�}�͑S�̂�24%���炢�������炵������A����ŋt�]�ł���B
���ۂ͂��Ƃ��Ɠ��[���Ă�l�����̉�%���͂��̐��}�ɓ���Ă邩�����������Ə��Ȃ��Ă������B
�Ƃ͂���2000���l�ȏ�̐l�Ԃ����̂��ȒP�Ƃ͂ƂĂ��v���Ȃ��B
513�P�R�Q�l�ڂ̑f������
2020/08/07(��) 01:42:16.81ID:ZRodATmc 2�肠����c1��ځB
����5-6�N�قǂ��O�ȁB�ߏ��̎����̊w���Œ������Ȃ낤�ȁA�o�X�����ɍs���炵���B�������̎q���������炻���������ȃ����W���o�X�Ȃ̂�B
�����W���o�X���ĕ��ʂ͋q�Ȑ�40���炢�B2�l������1��1��Ƃ���2��i�Z��������4�Z���j�ŁA���ӂ̐Ȑ���10�s���炢���ȁB
�����ŋ߂�1�N���X���Đl�����Ȃ��̂ˁB���������������B
�ŁA��s�͉ו��A�����s�ɃK�L������Ă��B�����K�L��5�s�~4�Z����������ĂȂ�1�N���X��20�l�N���X�Ȃ̂��B
���̐l���Ȃ�2�䂶��Ȃ���2�N���X��1��ɋl�ߍ���ł��C�P�邶���ˁB
�����A�����Łu��H�v�Ǝv�����̂�2��Ŋe20�l��1���40�l�l�ߍ��ނ̂ƁA��ʎ��̂ɂ����m���͓������A�Ⴄ���H�ǂ��炪���S�ƌ����邩�H���ꂪ�C�ɂȂ�B
�����Ńo�X��2��Ƃ��V�i�A�^�]��̋Z�ʂ������Ɖ��肵���ꍇ�A�����p�����[�^�ɂ��Ăǂ��l����������H
�����̊���Z�̃��N�c�������q�ɐ����ł��Ȃ����̃��x����O��Ƀ��Ƃ��̋L����蕶�������߂Ő������Ă���B
����5-6�N�قǂ��O�ȁB�ߏ��̎����̊w���Œ������Ȃ낤�ȁA�o�X�����ɍs���炵���B�������̎q���������炻���������ȃ����W���o�X�Ȃ̂�B
�����W���o�X���ĕ��ʂ͋q�Ȑ�40���炢�B2�l������1��1��Ƃ���2��i�Z��������4�Z���j�ŁA���ӂ̐Ȑ���10�s���炢���ȁB
�����ŋ߂�1�N���X���Đl�����Ȃ��̂ˁB���������������B
�ŁA��s�͉ו��A�����s�ɃK�L������Ă��B�����K�L��5�s�~4�Z����������ĂȂ�1�N���X��20�l�N���X�Ȃ̂��B
���̐l���Ȃ�2�䂶��Ȃ���2�N���X��1��ɋl�ߍ���ł��C�P�邶���ˁB
�����A�����Łu��H�v�Ǝv�����̂�2��Ŋe20�l��1���40�l�l�ߍ��ނ̂ƁA��ʎ��̂ɂ����m���͓������A�Ⴄ���H�ǂ��炪���S�ƌ����邩�H���ꂪ�C�ɂȂ�B
�����Ńo�X��2��Ƃ��V�i�A�^�]��̋Z�ʂ������Ɖ��肵���ꍇ�A�����p�����[�^�ɂ��Ăǂ��l����������H
�����̊���Z�̃��N�c�������q�ɐ����ł��Ȃ����̃��x����O��Ƀ��Ƃ��̋L����蕶�������߂Ő������Ă���B
514�P�R�Q�l�ڂ̑f������
2020/08/07(��) 01:44:03.42ID:ZRodATmc 2��ځB
���q�����ȁB�ŁA�}�b�}�i�ȉ��}�j��12�ŏ��o�����ĕo��51�Ƃ���B
2�ΔN��̃p�b�p�i�ȉ��p�j��14�Ő��ʂ���53�̍��ł��o��ɂ͏o��Ƃ���B
�v�Z���₷���A����40�N�ԂɌ��邱�ƂƂ���B
�}�͌��N�D�ǎ��Ō���ŏ����Ƀ^�}�S�i�ȉ��^�j�Y���A���U��40*12=480�Y�����B
�p�͒��V�̖�������Ԃ��o�Ă��̔N��ɉ��������̃I�^�}�W���N�V�i�ȉ��I�j�ʑł��}�b�N���܂������B
�Q�l�ɂȂ铝�v��������Ȃ��̂ŁA���A�^�A�I�͂������40�N�Ԃ�ʂ��Č��N�x�␔�ʂ����őÓ����ۂ����i���ɃI�̓��v���������j�̋�̓I���l����ĉ���������Ă���ȁB
���āA�}�p�̊Ԃɂ͈ꗱ��̒���a���R���j�q�����čr��Ă���B
�K�L�u���Ȃǂ��������g�Ȃ���I�v
�}�u�������Ă�̂�B���͐��܂ꂽ���_�ŏ����g�Ȃ̂�I�i�ȉ������j�Ƃ����v�Z�Ȃ���A�Ȃ�Ƃ������̐��ɏo�Ă���ꂽ�m����X����Y�Ȃ���˂��I�v
�K�L�u���ʂʁc�v
���Y�\���Ԃ�40�N�ԂƉ��肵�āA
�C�F���ꂼ��̗v�f�̑Ó����ۂ��O������̒l��S�ė��Ď����B
���F�̗p�����e�O������̒l�ɂ��v�Z����l�����������B
�n�F�ŏI�I�Ȍv�Z���ʁAX����Y�������B
�A���A�����̊���Z�̃��N�c������ł��Ȃ�����a���R���̃K�L�ɂ킩��悤�ȃ��x���̐������@�ʼn��邱�ƁB
���q�����ȁB�ŁA�}�b�}�i�ȉ��}�j��12�ŏ��o�����ĕo��51�Ƃ���B
2�ΔN��̃p�b�p�i�ȉ��p�j��14�Ő��ʂ���53�̍��ł��o��ɂ͏o��Ƃ���B
�v�Z���₷���A����40�N�ԂɌ��邱�ƂƂ���B
�}�͌��N�D�ǎ��Ō���ŏ����Ƀ^�}�S�i�ȉ��^�j�Y���A���U��40*12=480�Y�����B
�p�͒��V�̖�������Ԃ��o�Ă��̔N��ɉ��������̃I�^�}�W���N�V�i�ȉ��I�j�ʑł��}�b�N���܂������B
�Q�l�ɂȂ铝�v��������Ȃ��̂ŁA���A�^�A�I�͂������40�N�Ԃ�ʂ��Č��N�x�␔�ʂ����őÓ����ۂ����i���ɃI�̓��v���������j�̋�̓I���l����ĉ���������Ă���ȁB
���āA�}�p�̊Ԃɂ͈ꗱ��̒���a���R���j�q�����čr��Ă���B
�K�L�u���Ȃǂ��������g�Ȃ���I�v
�}�u�������Ă�̂�B���͐��܂ꂽ���_�ŏ����g�Ȃ̂�I�i�ȉ������j�Ƃ����v�Z�Ȃ���A�Ȃ�Ƃ������̐��ɏo�Ă���ꂽ�m����X����Y�Ȃ���˂��I�v
�K�L�u���ʂʁc�v
���Y�\���Ԃ�40�N�ԂƉ��肵�āA
�C�F���ꂼ��̗v�f�̑Ó����ۂ��O������̒l��S�ė��Ď����B
���F�̗p�����e�O������̒l�ɂ��v�Z����l�����������B
�n�F�ŏI�I�Ȍv�Z���ʁAX����Y�������B
�A���A�����̊���Z�̃��N�c������ł��Ȃ�����a���R���̃K�L�ɂ킩��悤�ȃ��x���̐������@�ʼn��邱�ƁB
2020/08/08(�y) 18:25:56.67ID:vy40demC
�k���l
2021^2021 ��10�i�\�����āA���̊e���Ɍ���鐔�̘a��A�Ƃ���B
A�̊e���Ɍ���鐔�̘a��B�Ƃ���B
B�̊e���Ɍ���鐔�̘a��C�Ƃ���B
C�����߂�B
2021^2021 ��10�i�\�����āA���̊e���Ɍ���鐔�̘a��A�Ƃ���B
A�̊e���Ɍ���鐔�̘a��B�Ƃ���B
B�̊e���Ɍ���鐔�̘a��C�Ƃ���B
C�����߂�B
2020/08/08(�y) 18:27:15.47ID:vy40demC
N = 2021^2021
�@= 35442113�����274406421�@�@(6681��)
N�̊e���̐��̘a A = 30251,
A�̊e���̐��̘a B = 11,
B�̊e���̐��̘a C = 2.
�@= 35442113�����274406421�@�@(6681��)
N�̊e���̐��̘a A = 30251,
A�̊e���̐��̘a B = 11,
B�̊e���̐��̘a C = 2.
2020/08/11(��) 15:33:58.54ID:sLooAqcf
�k�o��P�l
�@(x+3y)(x-3y) = xx - 9yy = 8^3,
�̂Ƃ�
(x + 8(x+3y)^{1/3} + 8(x-3y)^{1/3})^2
�@= 48 [3(128+yy)^2 - 128^2 + xy^3]^{1/3}
�@+ 48 [3(128+yy)^2 - 128^2 - xy^3]^{1/3}
�@+ xx + 1024,
�������B
[�㐔�w�����X��.377-378]
�@(x+3y)(x-3y) = xx - 9yy = 8^3,
�̂Ƃ�
(x + 8(x+3y)^{1/3} + 8(x-3y)^{1/3})^2
�@= 48 [3(128+yy)^2 - 128^2 + xy^3]^{1/3}
�@+ 48 [3(128+yy)^2 - 128^2 - xy^3]^{1/3}
�@+ xx + 1024,
�������B
[�㐔�w�����X��.377-378]
2020/08/11(��) 15:38:48.55ID:sLooAqcf
(����)
�@p = (x+3y)^{1/3},
�@q = (x-3y)^{1/3},
�Ƃ�����
�@pq = (xx-9yy)^{1/3} = 8,
(����) = (x+8p+8q)^2
�@= xx + 16(p+q)x + 64(p+q)^2
�@= 16(px+4qq) + 16(qx+4pp) + xx + 128pq
�@= 16p{x +(1/2)q^3} +16q{x +(1/2)p^3} + xx+1024
�@= 48p(x-y)/2 + 48q(x+y)/2 + xx + 1024
�@= 48 [3(128+yy)^2 - 128^2 + xy^3]^{1/3}
�@+ 48 [3(128+yy)^2 - 128^2 - xy^3]^{1/3}
�@+ xx + 1024,
�@[�㐔�w�����X���U.377-378]
�@p = (x+3y)^{1/3},
�@q = (x-3y)^{1/3},
�Ƃ�����
�@pq = (xx-9yy)^{1/3} = 8,
(����) = (x+8p+8q)^2
�@= xx + 16(p+q)x + 64(p+q)^2
�@= 16(px+4qq) + 16(qx+4pp) + xx + 128pq
�@= 16p{x +(1/2)q^3} +16q{x +(1/2)p^3} + xx+1024
�@= 48p(x-y)/2 + 48q(x+y)/2 + xx + 1024
�@= 48 [3(128+yy)^2 - 128^2 + xy^3]^{1/3}
�@+ 48 [3(128+yy)^2 - 128^2 - xy^3]^{1/3}
�@+ xx + 1024,
�@[�㐔�w�����X���U.377-378]
519�P�R�Q�l�ڂ̑f������
2020/08/12(��) 18:21:32.19ID:TJBftZrw �s��2���痈��FX�g���[�_�[�ł��B
�ȉ��̏��������ƂɁA�g���[�h�����{��̎������Z�o����v�Z���������ĉ������B
�E��������
�E����
�E�������Ƃ��̗��v��
�E�������Ƃ��̑�����
�E�g���[�h��
���������Ƃ��́A�������������܂߂Ď���g���[�h(�Ⴆ��1.0���~����1.2���~�ɑ�������A����1.2���~�Ńg���[�h)
�@�������Ƃ��́A�������������܂߂��Ɏ���g���[�h(�Ⴆ��1.0���~����0.8���~�Ɍ����Ă��A����1.0���~�Ńg���[�h)
���j�Y(������0�ɂȂ�P�[�X)�͍l�����Ȃ��Ă��悢�ł��B
�ȉ��̏��������ƂɁA�g���[�h�����{��̎������Z�o����v�Z���������ĉ������B
�E��������
�E����
�E�������Ƃ��̗��v��
�E�������Ƃ��̑�����
�E�g���[�h��
���������Ƃ��́A�������������܂߂Ď���g���[�h(�Ⴆ��1.0���~����1.2���~�ɑ�������A����1.2���~�Ńg���[�h)
�@�������Ƃ��́A�������������܂߂��Ɏ���g���[�h(�Ⴆ��1.0���~����0.8���~�Ɍ����Ă��A����1.0���~�Ńg���[�h)
���j�Y(������0�ɂȂ�P�[�X)�͍l�����Ȃ��Ă��悢�ł��B
2020/08/13(��) 17:39:51.05ID:KhggCoPs
�k�o��Q�l
(1)
�@A = ��(N+1) + ��(N - 1/2) + ��(N - 1/2),
�@B = ��(N-1) + ��(N + 1/2) + ��(N + 1/2),
�Ƃ����Ƃ�
�@3��N > A > B
�������B
(1)
�@A = ��(N+1) + ��(N - 1/2) + ��(N - 1/2),
�@B = ��(N-1) + ��(N + 1/2) + ��(N + 1/2),
�Ƃ����Ƃ�
�@3��N > A > B
�������B
2020/08/13(��) 17:43:40.02ID:KhggCoPs
(����)
�@(��敽��) > (��������)�@�ŁB
(�E��)
�@A - B = {��(N+1) - ��(N-1)} - 2{��(N+1/2) - ��(N-1/2)}
�@�@�@�@= 2/{��(N+1) + ��(N-1)} -2/{��(N+1/2) + ��(N-1/2)}
�@�@�@�@> 0,
�k���1�l
�@�@��(N+1/2) + ��(N-1/2)�@>�@��(N+1) + ��(N-1),
(����)
�@g(x) = ��(N+x) �͏�ɓʁig " <0�j������
�@�@��(N+1/2)�@>�@(3/4)��(N+1) + (1/4)��(N-1),
�@�@��(N-1/2)�@>�@(1/4)��(N+1) + (3/4)��(N+1),
�@�@�ӁX�����B
�܂���
�@{��(N+1/2) + ��(N-1/2)}^2 - {��(N+1) + ��(N-1)}^2
�@= 2{N + ��(NN -1/4)} - 2{N + ��(NN-1)}
�@= 2{��(NN -1/4) - ��(NN-1)}�@> 0,
�@(��敽��) > (��������)�@�ŁB
(�E��)
�@A - B = {��(N+1) - ��(N-1)} - 2{��(N+1/2) - ��(N-1/2)}
�@�@�@�@= 2/{��(N+1) + ��(N-1)} -2/{��(N+1/2) + ��(N-1/2)}
�@�@�@�@> 0,
�k���1�l
�@�@��(N+1/2) + ��(N-1/2)�@>�@��(N+1) + ��(N-1),
(����)
�@g(x) = ��(N+x) �͏�ɓʁig " <0�j������
�@�@��(N+1/2)�@>�@(3/4)��(N+1) + (1/4)��(N-1),
�@�@��(N-1/2)�@>�@(1/4)��(N+1) + (3/4)��(N+1),
�@�@�ӁX�����B
�܂���
�@{��(N+1/2) + ��(N-1/2)}^2 - {��(N+1) + ��(N-1)}^2
�@= 2{N + ��(NN -1/4)} - 2{N + ��(NN-1)}
�@= 2{��(NN -1/4) - ��(NN-1)}�@> 0,
2020/08/13(��) 17:47:17.38ID:KhggCoPs
(�E��)
�@g(x) = ��(N+x)�@�Ƃ�����
�@A - B = {g(1) + 2g(-1/2)} - {2g(1/2) + g(-1)}
�@�@= (1/4) g '''(r)�@�@�@�@�@�@�@�@(���2)
�@�@= (3/32)(N+r)^{-5/2}
�@�@> 0,
�k���2�l
g(x) ��(-1,1) �ɂ�����3������\ �Ƃ���B�R���
�@g(1) - 2g(1/2) + 2g(-1/2) - g(-1) = (1/4)g'''(r),�@-1<r<1
�Ȃ邒�����݂���B
�@�i���ϒl�̒藝��3��g��)
�@g(x) = ��(N+x)�@�Ƃ�����
�@A - B = {g(1) + 2g(-1/2)} - {2g(1/2) + g(-1)}
�@�@= (1/4) g '''(r)�@�@�@�@�@�@�@�@(���2)
�@�@= (3/32)(N+r)^{-5/2}
�@�@> 0,
�k���2�l
g(x) ��(-1,1) �ɂ�����3������\ �Ƃ���B�R���
�@g(1) - 2g(1/2) + 2g(-1/2) - g(-1) = (1/4)g'''(r),�@-1<r<1
�Ȃ邒�����݂���B
�@�i���ϒl�̒藝��3��g��)
2020/08/13(��) 17:52:33.37ID:KhggCoPs
�k�o��Q�l
(2)
�@��2 + ��z �� y
�ƂȂ鎩�R�� y,z ��������B
---------------------------------
�@xx - 2yy = -1�@�Ȃ��
�@(xx +5 -4x)/2 = yy + 2 - (2��2)y - 2(x-y��2)
�@= (y-��2)^2 + 2/(x+y��2),
���@��2 + ��{(xx +5 -4x)/2} = y + 1/{(x+y��2)(y-��2)} + �c �� y,
�@xx - 2yy = 1�@�Ȃ��
�@(xx +3 -4x)/2 = yy + 2 - (2��2)y - 2(x-y��2)
�@= (y-��2)^2 - 2/(x+y��2),
���@��2 + ��{(xx +3 -4x)/2} = y - 1/{(x+y��2)(y-��2)} + �c �� y,
��j
�@x = ((1+��2)^n + (1-��2)^n)/2,
�@y = ((1+��2)^n - (1-��2)^n)/(2��2),
�́u�y���������v
�@xx - 2yy = (-1)^n
���݂����B
(2)
�@��2 + ��z �� y
�ƂȂ鎩�R�� y,z ��������B
---------------------------------
�@xx - 2yy = -1�@�Ȃ��
�@(xx +5 -4x)/2 = yy + 2 - (2��2)y - 2(x-y��2)
�@= (y-��2)^2 + 2/(x+y��2),
���@��2 + ��{(xx +5 -4x)/2} = y + 1/{(x+y��2)(y-��2)} + �c �� y,
�@xx - 2yy = 1�@�Ȃ��
�@(xx +3 -4x)/2 = yy + 2 - (2��2)y - 2(x-y��2)
�@= (y-��2)^2 - 2/(x+y��2),
���@��2 + ��{(xx +3 -4x)/2} = y - 1/{(x+y��2)(y-��2)} + �c �� y,
��j
�@x = ((1+��2)^n + (1-��2)^n)/2,
�@y = ((1+��2)^n - (1-��2)^n)/(2��2),
�́u�y���������v
�@xx - 2yy = (-1)^n
���݂����B
2020/08/15(�y) 20:59:00.60ID:fibcKrcF
�Exx-2yy = �}1�@�Ƃ���B
�@z = yy -2x +2
�@�@= (y-��2)^2 - 2(x-y��2)
�@�@= (y-��2)^2 �� 2/(x+y��2),
�Ƃ�����
�@��2 + ��z = y �� 1/{(x+y��2)(y-��2)} + �c �� y,
�@| 1/{(x+y��2)(y-��2)} | < 1/{(2��2)(y-��2)^2}�@�� 0�@(y����)
���ɂ�
�@z' = xx -4y +2
�@�@= (x-��2)^2 + (2��2)(x-y��2)
�@�@= (x-��2)^2 �} (2��2)/(x+y��2),
�Ƃ�����
�@��2 + ��z' = x �} (��2)/{(x+y��2)(x-��2)} + �c �� x,
�@| (��2)/{(x+y��2)(x-��2)} | < 1/{(��2)(x-��2)^2}�@�� 0�@(x����)
�@z = yy -2x +2
�@�@= (y-��2)^2 - 2(x-y��2)
�@�@= (y-��2)^2 �� 2/(x+y��2),
�Ƃ�����
�@��2 + ��z = y �� 1/{(x+y��2)(y-��2)} + �c �� y,
�@| 1/{(x+y��2)(y-��2)} | < 1/{(2��2)(y-��2)^2}�@�� 0�@(y����)
���ɂ�
�@z' = xx -4y +2
�@�@= (x-��2)^2 + (2��2)(x-y��2)
�@�@= (x-��2)^2 �} (2��2)/(x+y��2),
�Ƃ�����
�@��2 + ��z' = x �} (��2)/{(x+y��2)(x-��2)} + �c �� x,
�@| (��2)/{(x+y��2)(x-��2)} | < 1/{(��2)(x-��2)^2}�@�� 0�@(x����)
2020/08/21(��) 00:15:01.15ID:eKSCCB4p
>>509
n��ڂ̐H���ɂ��т�H�ׂ�m�� a_n,�@�p�������ׂ�m���� b_n �Ƃ����
�@a_n + b_n = 1,
���т�H�ׂĎ������т�H�ׂ�m����p�A�p���ɕς���m����1-p�Ƃ���B
�p����H�ׂĎ����p����H�ׂ�m����q�A���тɕς���m����1-q�Ƃ���B
�@(1-p)a_n + (1-q)b_n = c_n,�@p+q-1 = r
�Ƃ�����
�@c_{n+1} = r�c_n = ���� = r^n�c_1,�@�@(-1<r<1)
�����
�@a_n = (1-q + c_1�r^{n-1})/(1-r),
�@b_n = (1-p - c_1�r^{n-1})/(1-r),
���߂���Ғl = (1/N)��[n=1,N] a_n
�@�� [(1-q)N + c_1/(1-r)]/((1-r)N)
�@�� (1-q)/(1-r)�@�@�@�iN�����j
�@= (1-q)/(2-p-q).
n��ڂ̐H���ɂ��т�H�ׂ�m�� a_n,�@�p�������ׂ�m���� b_n �Ƃ����
�@a_n + b_n = 1,
���т�H�ׂĎ������т�H�ׂ�m����p�A�p���ɕς���m����1-p�Ƃ���B
�p����H�ׂĎ����p����H�ׂ�m����q�A���тɕς���m����1-q�Ƃ���B
�@(1-p)a_n + (1-q)b_n = c_n,�@p+q-1 = r
�Ƃ�����
�@c_{n+1} = r�c_n = ���� = r^n�c_1,�@�@(-1<r<1)
�����
�@a_n = (1-q + c_1�r^{n-1})/(1-r),
�@b_n = (1-p - c_1�r^{n-1})/(1-r),
���߂���Ғl = (1/N)��[n=1,N] a_n
�@�� [(1-q)N + c_1/(1-r)]/((1-r)N)
�@�� (1-q)/(1-r)�@�@�@�iN�����j
�@= (1-q)/(2-p-q).
2020/08/21(��) 00:20:26.59ID:eKSCCB4p
�J�ڍs��� T=
�@[p,�@1-q]
�@[1-p,�@q]
�ŗL�l�F�@1 �� p+q-1=r,
�Ίp������Ɓ@D=
�@[1,�@0]
�@[0,�@r]
�����n�悵�ā@D^n=
�@[1,�@0]
�@[0,�@r^n]
�@[p,�@1-q]
�@[1-p,�@q]
�ŗL�l�F�@1 �� p+q-1=r,
�Ίp������Ɓ@D=
�@[1,�@0]
�@[0,�@r]
�����n�悵�ā@D^n=
�@[1,�@0]
�@[0,�@r^n]
2020/08/21(��) 01:48:32.29ID:eKSCCB4p
>>525
�@a_n + b_n = 1,
�@a_{n+1} = p�a_n + (1-q)b_n,
�@b_{n+1} = (1-p)a_n + q�b_n,
(0<p<1,�@0<q<1)
�������B
�����P�O�̏�Ԃ����Ō��肷��B�L�������P�̃}���R�t�A��
�@a_n + b_n = 1,
�@a_{n+1} = p�a_n + (1-q)b_n,
�@b_{n+1} = (1-p)a_n + q�b_n,
(0<p<1,�@0<q<1)
�������B
�����P�O�̏�Ԃ����Ō��肷��B�L�������P�̃}���R�t�A��
528�P�R�Q�l�ڂ̑f������
2020/08/22(�y) 00:17:44.12ID:PIye8TW8 �C�f�A���̎w�����͒�`�ł��܂���
2020/09/05(�y) 15:23:20.27ID:sjSgt5Lc
>>485
JR�����{�@�@�@���v����(��)�@�@�@�@�@�@����(km)�@�^��(�~)
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�_�ˁ`���@�@31-32(����)�@25(�V����)�@�@33.1km�@�@410�~
���`���s�@�@41(����)�@�@28-29(�V����)�@42.8km�@�@570�~
�_�ˁ`���s�@�@68-69(��+�V)�@71(�V+�V)�@�@75.9km�@ 1100�~
���@���w�ŏ抷����8�`9���Ԃ�����܂��B
�@�@���v���Ԃ��^�����A�R�̕s�����͐��藧���܂���B
(�Q�l)
�@��}�@�@���~�c�`�_�ˎO�{ �@27���@�@32.3km�@�@320�~
�@��_�@�@���~�c�`�_�ˎO�{ �@31���@�@31.2km�@�@320�~
�@����@�@�@�@�������`������ �@51���@�@46.1km�@�@420�~
JR�����{�@�@�@���v����(��)�@�@�@�@�@�@����(km)�@�^��(�~)
�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|�|
�_�ˁ`���@�@31-32(����)�@25(�V����)�@�@33.1km�@�@410�~
���`���s�@�@41(����)�@�@28-29(�V����)�@42.8km�@�@570�~
�_�ˁ`���s�@�@68-69(��+�V)�@71(�V+�V)�@�@75.9km�@ 1100�~
���@���w�ŏ抷����8�`9���Ԃ�����܂��B
�@�@���v���Ԃ��^�����A�R�̕s�����͐��藧���܂���B
(�Q�l)
�@��}�@�@���~�c�`�_�ˎO�{ �@27���@�@32.3km�@�@320�~
�@��_�@�@���~�c�`�_�ˎO�{ �@31���@�@31.2km�@�@320�~
�@����@�@�@�@�������`������ �@51���@�@46.1km�@�@420�~
530�P�R�Q�l�ڂ̑f������
2020/09/09(��) 23:06:41.84ID:IR7822fG �w�����͔C�ӂ̊Œ�`�ł��܂���
2020/09/10(��) 16:37:58.73ID:7NHP8bMP
�k���l
���ʏ�́�ABC�̕�BC��ɓ_D���Ƃ�A
�@AB^2 + AC^2 = 2AD^2 + BD^2 + CD^2,
���݂����悤�ɂ��܂��B
���̂Ƃ�D�͕�BC�̒��_M�Ɍ���ł��傤���B
���Z�~�����u���w�̖��v��Q�W, ���{�]�_�� (1978)
��116��
���ʏ�́�ABC�̕�BC��ɓ_D���Ƃ�A
�@AB^2 + AC^2 = 2AD^2 + BD^2 + CD^2,
���݂����悤�ɂ��܂��B
���̂Ƃ�D�͕�BC�̒��_M�Ɍ���ł��傤���B
���Z�~�����u���w�̖��v��Q�W, ���{�]�_�� (1978)
��116��
2020/09/10(��) 16:39:26.66ID:7NHP8bMP
A�����BC�ɉ����������̑���H�Ƃ�����
�@AB^2 = AH^2 + BH^2,
�@AC^2 = AH^2 + CH^2,
�ӁX�����Η^���ƂȂ�B
�_D�͕�BC�̒��_M�Ɛ���H�Ɍ���ł��傤���B
�@AB^2 = AH^2 + BH^2,
�@AC^2 = AH^2 + CH^2,
�ӁX�����Η^���ƂȂ�B
�_D�͕�BC�̒��_M�Ɛ���H�Ɍ���ł��傤���B
2020/09/10(��) 16:40:52.76ID:7NHP8bMP
A(a,h)�@B(b,0)�@C(c,0)�@D(x,0)�@H(a,0)
�Ƃ�����
AH = h,
AB^2 = hh + BH^2 = hh + (b-a)^2,
AC^2 = hh + CH^2 = hh + (c-a)^2,
AD^2 = hh + DH^2 = hh + (x-a)^2,
BD = |x-b|,
CD = |x-c|,
AB^2 - AD^2 - BD^2 = -2(x-a)(x-b),
AC^2 - AD^2 - CD^2 = -2(x-a)(x-c),
�ӁX������
�@0 = -2(x-a)(2x-b-c),
�@x = a�@�܂��́@x = (b+c)/2,
�@D = H�@�܂��́@D = M.
�Ƃ�����
AH = h,
AB^2 = hh + BH^2 = hh + (b-a)^2,
AC^2 = hh + CH^2 = hh + (c-a)^2,
AD^2 = hh + DH^2 = hh + (x-a)^2,
BD = |x-b|,
CD = |x-c|,
AB^2 - AD^2 - BD^2 = -2(x-a)(x-b),
AC^2 - AD^2 - CD^2 = -2(x-a)(x-c),
�ӁX������
�@0 = -2(x-a)(2x-b-c),
�@x = a�@�܂��́@x = (b+c)/2,
�@D = H�@�܂��́@D = M.
2020/09/12(�y) 17:32:45.79ID:n7twx+Wx
�k�o��P�l
3�̐��� (x_n) (y_n) (z_n) �ɂ����ď����l��
�@0 < x_0 < 1,�@0 < y_0 < 1,�@0 < z_0 < 1,
�����A���An��0 �ɑ��đQ����
�@x_{n+1} = x_n(1-y_n) + y_n�z_n,
�@y_{n+1} = y_n(1-z_n) + z_n�x_n,
�@z_{n+1} = z_n(1-x_n) + x_n�y_n,
�����藧���̂Ƃ��܂��B���̂Ƃ�
(1)�@x_n + y_n + z_n = x_0 + y_0 + z_0,
(2)�@1-r �� x_0, y_0, z_0 �� r�@�ƂȂ�萔 r�@(1/2��r<1) ������B
(3)�@1-r �� x_n, y_n, z_n �� r,
(4)�@��_n = Max{x_n, y_n, z_n} �| min{x_n, y_n, z_n}�@�Ƃ�����
�@�@�@��_n �� ��_0�Er^n,
(5)�@�Ɍ��l lim(n����) x_n �͏����l x_0, y_0, z_0 ��p���ĕ\�킹��
���Ƃ������Ă��������B
3�̐��� (x_n) (y_n) (z_n) �ɂ����ď����l��
�@0 < x_0 < 1,�@0 < y_0 < 1,�@0 < z_0 < 1,
�����A���An��0 �ɑ��đQ����
�@x_{n+1} = x_n(1-y_n) + y_n�z_n,
�@y_{n+1} = y_n(1-z_n) + z_n�x_n,
�@z_{n+1} = z_n(1-x_n) + x_n�y_n,
�����藧���̂Ƃ��܂��B���̂Ƃ�
(1)�@x_n + y_n + z_n = x_0 + y_0 + z_0,
(2)�@1-r �� x_0, y_0, z_0 �� r�@�ƂȂ�萔 r�@(1/2��r<1) ������B
(3)�@1-r �� x_n, y_n, z_n �� r,
(4)�@��_n = Max{x_n, y_n, z_n} �| min{x_n, y_n, z_n}�@�Ƃ�����
�@�@�@��_n �� ��_0�Er^n,
(5)�@�Ɍ��l lim(n����) x_n �͏����l x_0, y_0, z_0 ��p���ĕ\�킹��
���Ƃ������Ă��������B
2020/09/13(��) 06:39:41.21ID:aLRApFcX
>>529
�R�̕s���������藧���˂��Ă������c
JR��
�@�_�ˁ@�́@���s
�ɍs���Ƃ��́A���ʼn��D�o�������������Ă��ƁB
8�`9��������Η]�T����ˁH
�R�̕s���������藧���˂��Ă������c
JR��
�@�_�ˁ@�́@���s
�ɍs���Ƃ��́A���ʼn��D�o�������������Ă��ƁB
8�`9��������Η]�T����ˁH
536�P�R�Q�l�ڂ̑f������
2020/09/21(��) 19:29:15.46ID:HGJdRieU �����i-1�j^��
���Ƃ��̊W���O���t�ŕ\���Ƃǂ�Ȋ����ɂȂ�܂���
���Ƃ��̊W���O���t�ŕ\���Ƃǂ�Ȋ����ɂȂ�܂���
537�P�R�Q�l�ڂ̑f������
2020/09/21(��) 20:04:29.57ID:pq7gk1gy �Ȃ����̐��̎w�����ƁA���̐�����̑ΐ����͒�`����Ȃ���
538�P�R�Q�l�ڂ̑f������
2020/09/21(��) 21:16:51.63ID:HGJdRieU >>537
�����炻�̓�������ɂ́A�����i-1�j^���@�ɂ��čl����̂���{����
�����炻�̓�������ɂ́A�����i-1�j^���@�ɂ��čl����̂���{����
539�P�R�Q�l�ڂ̑f������
2020/09/22(��) 03:05:17.87ID:5cmmWTZ5 >>537
���̐�����̑ΐ���
���Ƃ��������i�ꁁ�|�P�j�P�@��
�O�Ƃ͌��炸����������͂��Ƃ��A����������Ƃ�����l���Y�����Ă���B
�����͖����ɏo�Ă���B
���̐�����̑ΐ���
���Ƃ��������i�ꁁ�|�P�j�P�@��
�O�Ƃ͌��炸����������͂��Ƃ��A����������Ƃ�����l���Y�����Ă���B
�����͖����ɏo�Ă���B
540�P�R�Q�l�ڂ̑f������
2020/09/23(��) 00:11:57.55ID:urQc/OON ���Ƃ��������i�ꁁ�|3�j1234�@�̏ꍇ
�������i�ꁁ�|3�j1234�@���@�i�������i�ꁁ10�j1234�j/�i�������i�ꁁ10�j�|�R�j
�ƂȂ�̂ŕ���͑��݂��Ȃ����ɂȂ�
�������i�ꁁ�|3�j1234�@���@�i�������i�ꁁ10�j1234�j/�i�������i�ꁁ10�j�|�R�j
�ƂȂ�̂ŕ���͑��݂��Ȃ����ɂȂ�
2020/09/23(��) 10:06:22.75ID:63e1O9oo
>>534
(1)�@�^���𑫂���
�@x_{n+1} + y_{n+1} + z_{n+1} = x_n + y_n + z_n,
(2)�@
�@r = Max{ x_0, y_0, z_0, 1-x_0, 1-y_0, 1-z_0}�@�Ƃ����B
(3)
�@�^���̈Ӗ����l����B
(4)
�@��_{n+1} �� ��_n�Er,
(5)
�@���ĥ���
(1)�@�^���𑫂���
�@x_{n+1} + y_{n+1} + z_{n+1} = x_n + y_n + z_n,
(2)�@
�@r = Max{ x_0, y_0, z_0, 1-x_0, 1-y_0, 1-z_0}�@�Ƃ����B
(3)
�@�^���̈Ӗ����l����B
(4)
�@��_{n+1} �� ��_n�Er,
(5)
�@���ĥ���
542�P�R�Q�l�ڂ̑f������
2020/09/24(��) 06:44:12.43ID:H6sqOdXp ���s��̍s�́A��x�N�g���i�s�x�N�g���ł��������j������
���s�̂̂������̐ς�\���Ă���
���f�s��̍s�́A������������\���Ă���낤�H
���s�̂̂������̐ς�\���Ă���
���f�s��̍s�́A������������\���Ă���낤�H
2020/09/24(��) 11:41:57.86ID:shPxNCvG
���f�s��̍s�̐�Βl�Ɋւ��Ă�
|det(A+iB)|=��det(A�~e+B�~��)
(������e��2���P�ʍs��,�Ђ�((0,1)(-1,0)),�~�̓e���\����)
�Ƃ����W��������
�e���\���ς̊I�C���[�W���N���Ȃ�����
|det(A+iB)|=��det(A�~e+B�~��)
(������e��2���P�ʍs��,�Ђ�((0,1)(-1,0)),�~�̓e���\����)
�Ƃ����W��������
�e���\���ς̊I�C���[�W���N���Ȃ�����
544�P�R�Q�l�ڂ̑f������
2020/09/24(��) 14:20:15.65ID:PWX1myZf �i1�jsin⁻¹x=6/�@�i2�jcos⁻¹x=3/�@(3)tan⁻¹x=6/��
�ƂȂ�Ax�̒l�����߂�B
�i4)sin⁻¹1�@�i5�jcos⁻¹0�@�i6�jtan⁻¹1
�̒l�����߂�B
�킩��Ȃ�����
�ƂȂ�Ax�̒l�����߂�B
�i4)sin⁻¹1�@�i5�jcos⁻¹0�@�i6�jtan⁻¹1
�̒l�����߂�B
�킩��Ȃ�����
2020/09/26(�y) 14:51:19.52ID:s7k88pKY
���̐���n�́An��J��Ԃ��Ƃ����Ӗ��ق��A
���ʂ�n�悷��Ƃ����Ӗ��ɂ�������B
> �킩��Ȃ�����
���w�ł̎O�p���̓��Ⴉ�ȁH
���낻��p�~���Ăق������ǁA
�\���Z��Q�l���Ō��̗��Q������ł邩��
�����ς��낤�Ȃ��c
���ʂ�n�悷��Ƃ����Ӗ��ɂ�������B
> �킩��Ȃ�����
���w�ł̎O�p���̓��Ⴉ�ȁH
���낻��p�~���Ăق������ǁA
�\���Z��Q�l���Ō��̗��Q������ł邩��
�����ς��낤�Ȃ��c
546�P�R�Q�l�ڂ̑f������
2020/10/02(��) 18:34:20.37ID:PAxeGvYz �o�Ȑ��������萔�@��x����y���ň͂ޔ͈̖͂ʐς́A�o�Ȑ���0�ɋ߂Â���x���ɂ�y���ɂ������Ȃ��̂ŁA������̖ʐςł���B
�ł́A����EXP(���j�@��x����y���ň͂ޔ͈̖͂ʐς́A�Ȑ��͂���0�ɋ߂Â������ƌ����Ȃ����A������ɂ͂Ȃ炸1�ƂȂ�B
���̓��������Ă�������
�ł́A����EXP(���j�@��x����y���ň͂ޔ͈̖͂ʐς́A�Ȑ��͂���0�ɋ߂Â������ƌ����Ȃ����A������ɂ͂Ȃ炸1�ƂȂ�B
���̓��������Ă�������
2020/10/02(��) 19:10:36.11ID:D1GFlSVX
�I�[�_�[�̈Ⴂ
548�P�R�Q�l�ڂ̑f������
2020/10/02(��) 19:50:59.03ID:gUUe2ssm ���̕��т��s�A�c�̕��т��ƌĂԂ��Ƃɂ���
�P���珇�Ɉȉ��̗l�ɕ��ׂ�B
201010101010�͉��s�ڂɔz�u����邩�H
1 3 4 10 11 21
2 5 9 12 20
6 8 13 19
7 14 18
15 17
16
�P���珇�Ɉȉ��̗l�ɕ��ׂ�B
201010101010�͉��s�ڂɔz�u����邩�H
1 3 4 10 11 21
2 5 9 12 20
6 8 13 19
7 14 18
15 17
16
2020/10/03(�y) 08:48:55.34ID:Ug9HuAK2
>>879
�ォ��n�s�ځA������m��ڂ� a[m,n] �Ƃ����B
�@a[m,n] = m + (m+n-1)(m+n-2)/2�@�@(m+n�F�)
�@�@�@�@ = n + (m+n-1)(m+n-2)/2�@�@(m+n�F����)
�t��
�@s[a] = [ (3/2) + ��(2a - 7/4) ]�@�Ƃ���
�@m[a] = a - s(s-3)/2 -1,�@�@(s�F�)
�@�@�@ = s(s-1)/2 - a + 1�@�@(s�F����)
�@n[a] = s(s-1)/2 - a + 1�@�@(s�F�)
�@�@�@ = a - s(s-3)/2 -1,�@�@(s�F����)
(���Z���w�̎���X���S�O�V�D879)
�ォ��n�s�ځA������m��ڂ� a[m,n] �Ƃ����B
�@a[m,n] = m + (m+n-1)(m+n-2)/2�@�@(m+n�F�)
�@�@�@�@ = n + (m+n-1)(m+n-2)/2�@�@(m+n�F����)
�t��
�@s[a] = [ (3/2) + ��(2a - 7/4) ]�@�Ƃ���
�@m[a] = a - s(s-3)/2 -1,�@�@(s�F�)
�@�@�@ = s(s-1)/2 - a + 1�@�@(s�F����)
�@n[a] = s(s-1)/2 - a + 1�@�@(s�F�)
�@�@�@ = a - s(s-3)/2 -1,�@�@(s�F����)
(���Z���w�̎���X���S�O�V�D879)
550�P�R�Q�l�ڂ̑f������
2020/10/05(��) 21:38:28.16ID:OBa5EksI 10���ɂȂ��āA��ł��オ��܂����ˁB
�ď�̓T���g���[�u���[�����肪����₩�Ȃ�ł悭����ł܂������ǁB
�l�オ��ł��B
�ʔ̓X�̃_�C���b�N�X����ŁA�X�g�����O������������ł�
����̔��̔N��̎w�����m�F�������܂��B
����L������v���o���܂��A�u�X�g�����O�������E���V�v�ł��B
�ď�̓T���g���[�u���[�����肪����₩�Ȃ�ł悭����ł܂������ǁB
�l�オ��ł��B
�ʔ̓X�̃_�C���b�N�X����ŁA�X�g�����O������������ł�
����̔��̔N��̎w�����m�F�������܂��B
����L������v���o���܂��A�u�X�g�����O�������E���V�v�ł��B
551�P�R�Q�l�ڂ̑f������
2020/10/05(��) 21:43:31.57ID:OBa5EksI �X�g�����O�[���ł���A���V�I
�Ē����X�g�����O�[���Ŋ���ƁA�[���Ŋ��郈�V�I�ł���B
�Ē����X�g�����O�[���Ŋ���ƁA�[���Ŋ��郈�V�I�ł���B
552�P�R�Q�l�ڂ̑f������
2020/10/08(��) 02:03:38.22ID:T94oxXV4 >>546
1+1/2+1/3+1/4+ �E�E�E�E�@�@�@�͔��U����
1+1/2+1/4+1/8+�@�E�E�E�E�@�@�@�͒萔�Ɏ�������B
1+1/2+1/3+1/4+ �E�E�E�E�@�@�@�͔��U����
1+1/2+1/4+1/8+�@�E�E�E�E�@�@�@�͒萔�Ɏ�������B
553�P�R�Q�l�ڂ̑f������
2020/10/08(��) 09:42:52.39ID:nv5Lu3NF �ꎟ�����������߂Ȃ����B
�@2+3=x�~0
�A2+3>x�~0
�����������߂Ȃ����B(x^2��x��2��)
�Bx^2=-1
�Cx^2>-1
�r���̌v�Z�������g���ċ��߂Ȃ����B
�C1/2+0
�D1/2�~0
�@2+3=x�~0
�A2+3>x�~0
�����������߂Ȃ����B(x^2��x��2��)
�Bx^2=-1
�Cx^2>-1
�r���̌v�Z�������g���ċ��߂Ȃ����B
�C1/2+0
�D1/2�~0
2020/10/09(��) 11:40:56.25ID:5m+9iU3v
�܂����������点��������̂��Ȃ�
2020/10/13(��) 21:24:01.22ID:Aceyovpj
2020/10/14(��) 04:29:13.90ID:PHtzabu1
557���� ��C2UdlLHDRI
2020/10/14(��) 07:47:28.84ID:j1BKIsRr �\�t�g�o���N�ƃ��b�e�͌p���������ċ�����{�`��CM��������l�тP�v�I�Ĕ��ے��
GHQ��������Ɏ��O�@��������������̍ݓ��O���l�̒��ł����嗘�����m�ۂ����w�ɂ����{�`��CM���Ă��ʼn߂�����ԡ
�N�͉E�h�ł������i���A���h�ł������j������͐������ׂ��ƍl����
GHQ��������Ɏ��O�@��������������̍ݓ��O���l�̒��ł����嗘�����m�ۂ����w�ɂ����{�`��CM���Ă��ʼn߂�����ԡ
�N�͉E�h�ł������i���A���h�ł������j������͐������ׂ��ƍl����
2020/11/08(��) 15:51:19.80ID:2r/rt7p/
>>535
�@�����JR�ł͍s���Ȃ���B
�@��}�i�_�ˎO�{�`�͌����j�Ȃ� 630�~
�@ (�\�O�ŏ抷����72���A75.2km)
�@JR�� �� 1100�~�Ȃ̂��s�v�c�i���������H�j
�@ (�V������ 68-71���A75.9km)
�@�����JR�ł͍s���Ȃ���B
�@��}�i�_�ˎO�{�`�͌����j�Ȃ� 630�~
�@ (�\�O�ŏ抷����72���A75.2km)
�@JR�� �� 1100�~�Ȃ̂��s�v�c�i���������H�j
�@ (�V������ 68-71���A75.9km)
2020/11/17(��) 12:18:47.35ID:fT6xV/SY
>�P�R�i�@ �Ŏg��������������������0 1 2 3 4 5 6 7 8 9 A J Q�Ƃ���Ƃ��A�l�C�s�A���A��Q���P�R�i�@�ŏ����P�O���܂ŕ\������B
2.9450J026A6
1.55004799J6
2.9450J026A6
1.55004799J6
2020/11/17(��) 17:43:49.26ID:VdFVpWiY
�}���`�v���|�X�c
2020/11/21(�y) 12:43:34.04ID:H/DINlZq
�� = 3.1AQ1049052 A2Q7025281 10A9507J6A 7AQJ676783 Q973189Q2Q 83722A262J ����
e = 2.9450J026A6 JA18941097 96971905Q8 746849406A 106156JJ06 J159J06JJ2 ����
��2 = 1.55004799J6 2060363210 9A50J5J364 49Q886A400 1QA4441647 7J72AJJ211 ����
(�\�O�i�@)
e = 2.9450J026A6 JA18941097 96971905Q8 746849406A 106156JJ06 J159J06JJ2 ����
��2 = 1.55004799J6 2060363210 9A50J5J364 49Q886A400 1QA4441647 7J72AJJ211 ����
(�\�O�i�@)
562�P�R�Q�l�ڂ̑f������
2020/11/24(��) 05:19:07.65ID:v9xyiUJ8 ��xdx��dx��x�ɂ��Đϕ�����Ƃ����̂͂킩���ł����Adx/du��dx���ĉ�����ē������܂����H
����ɂ���d�Ƃ����͉̂�����ē������܂����H
�킩��������Ă��������B
����ɂ���d�Ƃ����͉̂�����ē������܂����H
�킩��������Ă��������B
2020/11/24(��) 08:58:19.94ID:gnMA9Lzn
�������ɁA������Ȃ����c
564�P�R�Q�l�ڂ̑f������
2020/11/24(��) 15:35:18.74ID:3EX4H+t4 https://www.mhlw.go.jp/toukei/list/30-1b.html
�����ΘJ���v�����̌��\���ʂ̒����ɂ��āi�ߘa�Q�N11��13���j [64KB] 11��13��
�����ΘJ���v�����̌��\���ʂ̒����ɂ��āi�ߘa�Q�N11���U���j [450KB]
�����ΘJ���v�����̌��\���ʂ̒����ɂ��āi�ߘa�Q�N10��23���j [266KB]
�����ΘJ���v�����̌��\���ʂ̒����ɂ��āi�ߘa�Q�N�X��28���j [394KB]
�����ΘJ���v�����i�ߘa�Q�N�U�������ʑ���j�̎Q�l�����̐��l���ɂ��āi�ߘa�Q�N�W��27���j [91KB]
�����ΘJ���v�����N��|�S�������|�i����30�N�j�ɂ�����e-Stat�f�ړ��v�\�̈ꕔ�����ɂ��� [92KB]
�����ΘJ���v�����i�S�������j�i�ߘa���N�����ʊm��j�̒����ɂ��āi�ߘa2�N5��21���j [94KB]
�����ΘJ���v�����̌��\���ʂ̒����ɂ��āi�ߘa�Q�N�S��14���j [2,603KB]
�����ΘJ���v�����n�������i�ߘa���N�U���j�̒����ɂ��āi�ߘa2�N2��14���j [338KB]
�����ΘJ���v�����̌��\���ʂ̒����ɂ��āi�ߘa�Q�N11��13���j [64KB] 11��13��
�����ΘJ���v�����̌��\���ʂ̒����ɂ��āi�ߘa�Q�N11���U���j [450KB]
�����ΘJ���v�����̌��\���ʂ̒����ɂ��āi�ߘa�Q�N10��23���j [266KB]
�����ΘJ���v�����̌��\���ʂ̒����ɂ��āi�ߘa�Q�N�X��28���j [394KB]
�����ΘJ���v�����i�ߘa�Q�N�U�������ʑ���j�̎Q�l�����̐��l���ɂ��āi�ߘa�Q�N�W��27���j [91KB]
�����ΘJ���v�����N��|�S�������|�i����30�N�j�ɂ�����e-Stat�f�ړ��v�\�̈ꕔ�����ɂ��� [92KB]
�����ΘJ���v�����i�S�������j�i�ߘa���N�����ʊm��j�̒����ɂ��āi�ߘa2�N5��21���j [94KB]
�����ΘJ���v�����̌��\���ʂ̒����ɂ��āi�ߘa�Q�N�S��14���j [2,603KB]
�����ΘJ���v�����n�������i�ߘa���N�U���j�̒����ɂ��āi�ߘa2�N2��14���j [338KB]
565�P�R�Q�l�ڂ̑f������
2020/11/24(��) 16:45:56.86ID:gJXEmOSR ��Ƌ����͂ǂ��炪�����ł����H
2020/11/24(��) 18:13:26.76ID:gCqhFHEl
���������̂�
2020/11/26(��) 04:50:06.99ID:LMcuxUiM
>>563
�������˂�����˂�����]
�������˂�����˂�����]
2021/03/05(��) 06:19:47.77ID:L+NGu2de
�O�X��(URL�ĕ�)
������˂����͂����֏��� ver3.14(67����)4062
https://rio2016.5ch.net/test/read.cgi/math/1319117617/
������˂����͂����֏��� ver3.14(67����)4062
https://rio2016.5ch.net/test/read.cgi/math/1319117617/
2021/11/23(��) 06:54:23.79ID:Rekwl5xi
>>548
�@a = 201010101010,
�@s[a] = 634052,
�@m[a] = 551317,�@�@(��)
�@n[a] = 82735,�@�@(�s)
�@a = 201010101010,
�@s[a] = 634052,
�@m[a] = 551317,�@�@(��)
�@n[a] = 82735,�@�@(�s)
2022/04/11(��) 13:28:04.21ID:O/MA6m5h
2022/04/16(�y) 14:52:38.62ID:gtRak7zh
����ȋL����i�p�[�~���j������Ƃ͒m�����
%��0.0���L���������������̂�
1 %�@�@�@�@0.01�@�@�@10^2
1 ��@�@�@ 0.001�@�@10^3
%��0.0���L���������������̂�
1 %�@�@�@�@0.01�@�@�@10^2
1 ��@�@�@ 0.001�@�@10^3
572�P�R�Q�l�ڂ̑f������
2022/04/26(��) 20:47:06.01ID:O0qpJVRb �~������3.05���傫�����Ƃ��ؖ�����B
�������~�����̒�`�͉~�̒��a�ɑ���~���̔�ł�����̂Ƃ��A���̒�`�Ɋ�Â��ďؖ����邱�ƁB
��Փx�]�X���A�����I�Ӑ}��������s���ɂ܂�Ȃ����B���w�ɐ������������ނȁB
�������~�����̒�`�͉~�̒��a�ɑ���~���̔�ł�����̂Ƃ��A���̒�`�Ɋ�Â��ďؖ����邱�ƁB
��Փx�]�X���A�����I�Ӑ}��������s���ɂ܂�Ȃ����B���w�ɐ������������ނȁB
573�P�R�Q�l�ڂ̑f������
2022/04/28(��) 12:16:13.12ID:GVxfrMZM �Ƃ���Ƃ����
For all a1, a2, ...
infty a1 a2 ... a_{k-1} 1
sigma ------------------------- = --- .
k=1 (x+a1)(x+a2)...(x+a_k) x
�Ƃ��������ڂ��Ă������Ȃ��������悤�ȋC������
����𐳂�������ɂ͂ǂ���������̂������Ă��������
For all a1, a2, ...
infty a1 a2 ... a_{k-1} 1
sigma ------------------------- = --- .
k=1 (x+a1)(x+a2)...(x+a_k) x
�Ƃ��������ڂ��Ă������Ȃ��������悤�ȋC������
����𐳂�������ɂ͂ǂ���������̂������Ă��������
574�P�R�Q�l�ڂ̑f������
2022/04/28(��) 17:39:54.95ID:v5JdlRFq " "��"�@"���g��������Ƃ�����
2022/04/28(��) 19:19:25.80ID:Pn+8+X5O
576�P�R�Q�l�ڂ̑f������
2022/04/28(��) 22:25:24.22ID:GVxfrMZM �����A���肪�Ƃ�
�X���������܂�
�X���������܂�
2022/05/27(��) 15:37:38.25ID:Ys5I1PM9
�`�����烌�x�����������҂ł��B
a=b�~c-b�~d��c�ɂ��ĉ����ƂȂ�
c=(a/b)+d���\�L������Ă�����\����܂���B
�ƂȂ�̂�������܂���B
�����Ԃ��邩�������Ă��������܂��B
a=b�~c-b�~d��c�ɂ��ĉ����ƂȂ�
c=(a/b)+d���\�L������Ă�����\����܂���B
�ƂȂ�̂�������܂���B
�����Ԃ��邩�������Ă��������܂��B
2022/06/05(��) 15:59:59.81ID:KPBNA0bK
a=bc-bd.
a/b=c-d.
c=a/b+d.
a/b=c-d.
c=a/b+d.
2022/06/05(��) 21:51:13.26ID:n+IJV6MJ
���肪�Ƃ��������܂��B
(bc-bd)�~1/b=c-d�������ł��Ă���܂���ł����B
�`�����烌�x�����ł��Ȃ����ł����B
(bc-bd)�~1/b=c-d�������ł��Ă���܂���ł����B
�`�����烌�x�����ł��Ȃ����ł����B
580�P�R�Q�l�ڂ̑f������
2022/08/29(��) 12:18:57.40ID:cg/tjCFi ���͎��R����̊��������l���܂��B
�y��`(recursion)�z
A��1�ϐ����ŁAB��3�ϐ����AS����Ҋ��̂Ƃ��A�ȉ���2�̎��ŐV����2�ϐ���F���`�ł���B
F(x, 0) = A(x)
F(x, S(n)) = B(x, n, F(x, n))
���̂Ƃ��A��A�Ɗ�B����recursion�ɂ���Ċ�F��Ƃ����B
�y��`(iteration)�z
A��1�ϐ����ŁAB��2�ϐ����AS����Ҋ��̂Ƃ��A�ȉ���2�̎��ŐV����2�ϐ���F���`�ł���B
F(x, 0) = A(x)
F(x, S(n)) = B(n, F(x, n))
���̂Ƃ��A��A�Ɗ�B����iteration�ɂ���Ċ�F��Ƃ����B
�y��`(����)�z
A1, A2, �c ,Aj �����ꂼ��i�ϐ����ł���AB��j�ϐ����ł���Ƃ��A�V����i�ϐ���F���ȉ��̂悤�ɒ�`�ł���B
F(x1, x2, �c , xi)= B(A1(x1, x2, �c , xi), A2(x1, x2, �c , xi), �c , Aj(x1, x2, �c , xi))
���̂Ƃ���A�Ɗ�B�̍����ɂ���Ċ�F��Ƃ����B
�y��`(recursion)�z
A��1�ϐ����ŁAB��3�ϐ����AS����Ҋ��̂Ƃ��A�ȉ���2�̎��ŐV����2�ϐ���F���`�ł���B
F(x, 0) = A(x)
F(x, S(n)) = B(x, n, F(x, n))
���̂Ƃ��A��A�Ɗ�B����recursion�ɂ���Ċ�F��Ƃ����B
�y��`(iteration)�z
A��1�ϐ����ŁAB��2�ϐ����AS����Ҋ��̂Ƃ��A�ȉ���2�̎��ŐV����2�ϐ���F���`�ł���B
F(x, 0) = A(x)
F(x, S(n)) = B(n, F(x, n))
���̂Ƃ��A��A�Ɗ�B����iteration�ɂ���Ċ�F��Ƃ����B
�y��`(����)�z
A1, A2, �c ,Aj �����ꂼ��i�ϐ����ł���AB��j�ϐ����ł���Ƃ��A�V����i�ϐ���F���ȉ��̂悤�ɒ�`�ł���B
F(x1, x2, �c , xi)= B(A1(x1, x2, �c , xi), A2(x1, x2, �c , xi), �c , Aj(x1, x2, �c , xi))
���̂Ƃ���A�Ɗ�B�̍����ɂ���Ċ�F��Ƃ����B
581�P�R�Q�l�ڂ̑f������
2022/08/29(��) 12:19:49.92ID:cg/tjCFi �y�藝�z
A, B, I, J, K, L�����ꂼ��1, 3, 1, 2, 1, 1�ϐ����Ƃ��āA����I(x)=x, K(J(x, y))=x, L(J(x, y))=y�����Ƃ���B
2�ϐ���F��A, B����recursion�ɂ���Ē�`����Ă���Ƃ�
F��A, B, I, J, K, L���獇����iteration ��L����K�p���Ē�`�ł���B
(�ؖ�)
�O����A����2����F����`�������B
F (x, 0) =A(x)
F (x, S (n)) =B(x, n, F(x, y, n))
���܂���
F (x, n) = F�f (x, n)����F�f ��A, B, I, J, K, L���獇����iteration�ɂ���Ē�`����B
�܂��A��, ���Ƃ�������A, B, I, J, K, L���獇���ɂ���Ē�`����B
�� (x) = J (I(x), A (x))
�� (x, y)=J (K (L (J (x, y))), B (K (L (J (x, y))), K (J (x, y)), L (L (J (x, y)))))
���Ƀ�, ������iteration�ɂ����G���`����B
G (x, 0)=�� (x)
G (x, S(n))=�� (n, G(x, n))
�����G (x, n) = J (x, F (x, n))�ł��邱�Ƃ�n�ɂ��Ă̋A�[�@�Ŏ������B
�Ō��G��L����������F�f��B
F�f (x, n) = L (G (x, n))
�����F (x, n) = F�f (x, n)�ƂȂ��Ă���B
F�f (x, n)
= L (G (x, n))
= L (J (x, F (x, n)))
= F (x, n)
A, B, I, J, K, L����F�f�����̂ɍ�����mixed iteration with one parameter �����g��Ȃ������̂ő�ӂ͎����ꂽ�B
�i�ؖ��I���j
A, B, I, J, K, L�����ꂼ��1, 3, 1, 2, 1, 1�ϐ����Ƃ��āA����I(x)=x, K(J(x, y))=x, L(J(x, y))=y�����Ƃ���B
2�ϐ���F��A, B����recursion�ɂ���Ē�`����Ă���Ƃ�
F��A, B, I, J, K, L���獇����iteration ��L����K�p���Ē�`�ł���B
(�ؖ�)
�O����A����2����F����`�������B
F (x, 0) =A(x)
F (x, S (n)) =B(x, n, F(x, y, n))
���܂���
F (x, n) = F�f (x, n)����F�f ��A, B, I, J, K, L���獇����iteration�ɂ���Ē�`����B
�܂��A��, ���Ƃ�������A, B, I, J, K, L���獇���ɂ���Ē�`����B
�� (x) = J (I(x), A (x))
�� (x, y)=J (K (L (J (x, y))), B (K (L (J (x, y))), K (J (x, y)), L (L (J (x, y)))))
���Ƀ�, ������iteration�ɂ����G���`����B
G (x, 0)=�� (x)
G (x, S(n))=�� (n, G(x, n))
�����G (x, n) = J (x, F (x, n))�ł��邱�Ƃ�n�ɂ��Ă̋A�[�@�Ŏ������B
�Ō��G��L����������F�f��B
F�f (x, n) = L (G (x, n))
�����F (x, n) = F�f (x, n)�ƂȂ��Ă���B
F�f (x, n)
= L (G (x, n))
= L (J (x, F (x, n)))
= F (x, n)
A, B, I, J, K, L����F�f�����̂ɍ�����mixed iteration with one parameter �����g��Ȃ������̂ő�ӂ͎����ꂽ�B
�i�ؖ��I���j
582�P�R�Q�l�ڂ̑f������
2022/08/29(��) 12:20:15.15ID:cg/tjCFi �����Raphael M. Robinson�� �gPrimitive recursive functions.�h (Bull. Amer. Math. Soc. October. 1947: 925 – 942.)�ɏ����Ă���܂��B
�������ɏؖ��ł���Ă���悤�Ƀ��A�����`���āA����炩��iteration��G���`����AG�͓s���̂������������Ă���Ă��āAG����ȒP�ɖړI��F�f���`�ł��܂��B
�������A�ؖ���ǂ����Ƃ͂ł��Ă����z�𗝉��ł��Ȃ��ĎߑR�Ƃ��܂���B
�Ƃ���G(x, y)=J(x, F(x, y))����G�邽�߂�A, B��I, J, K, L���炠�̂悤�Ƀ�, �����`����Ɏ������C�������킩��܂���B
�������ɏؖ��ł���Ă���悤�Ƀ��A�����`���āA����炩��iteration��G���`����AG�͓s���̂������������Ă���Ă��āAG����ȒP�ɖړI��F�f���`�ł��܂��B
�������A�ؖ���ǂ����Ƃ͂ł��Ă����z�𗝉��ł��Ȃ��ĎߑR�Ƃ��܂���B
�Ƃ���G(x, y)=J(x, F(x, y))����G�邽�߂�A, B��I, J, K, L���炠�̂悤�Ƀ�, �����`����Ɏ������C�������킩��܂���B
583�P�R�Q�l�ڂ̑f������
2022/08/30(��) 18:28:00.51ID:H9fAPRAM >>582
�������܂����B�X�������Ă��݂܂���B
�������܂����B�X�������Ă��݂܂���B
584�P�R�Q�l�ڂ̑f������
2022/12/20(��) 15:57:51.18ID:R0GrT6qP https://i.imgur.com/eIWdRj0.jpg
https://i.imgur.com/iFtPJ3h.jpg
https://i.imgur.com/zgT3zjW.jpg
https://i.imgur.com/Q2uo3wk.jpg
https://i.imgur.com/vEyU1OZ.jpg
https://i.imgur.com/LzSyaPo.jpg
https://i.imgur.com/ne5KZru.jpg
https://i.imgur.com/Au4y3K5.jpg
https://i.imgur.com/Ek2qx5A.jpg
https://i.imgur.com/xGjbFtj.jpg
https://i.imgur.com/88TDqC7.jpg
https://i.imgur.com/CJbLQuu.jpg
https://i.imgur.com/iFtPJ3h.jpg
https://i.imgur.com/zgT3zjW.jpg
https://i.imgur.com/Q2uo3wk.jpg
https://i.imgur.com/vEyU1OZ.jpg
https://i.imgur.com/LzSyaPo.jpg
https://i.imgur.com/ne5KZru.jpg
https://i.imgur.com/Au4y3K5.jpg
https://i.imgur.com/Ek2qx5A.jpg
https://i.imgur.com/xGjbFtj.jpg
https://i.imgur.com/88TDqC7.jpg
https://i.imgur.com/CJbLQuu.jpg
2023/03/25(�y) 18:34:16.63ID:PorTOzgN
��
586�P�R�Q�l�ڂ̑f������
2023/03/31(��) 16:07:47.56ID:qN+k836t �ugoodtein����̒�~����PA����Ɨ��v�Ƃ��u��0�܂ł̒����A�[�@��PA����Ɨ��v�Ƃ������܂���
�����̖����PA�̌��t�ŏ�����̂ł����H
�m�b�܂ɕ������̂ł����������Ȃ������̂ł����Ŏ��₵�܂��B
�����̖����PA�̌��t�ŏ�����̂ł����H
�m�b�܂ɕ������̂ł����������Ȃ������̂ł����Ŏ��₵�܂��B
2023/03/31(��) 19:30:21.67ID:XRMmi4Xm
x^x+y^y=z^z�������R��x,y,z�͑��݂��邩?
2023/03/31(��) 20:17:00.45ID:b2/saV94
����͊ȒP
2023/03/31(��) 20:48:06.33ID:dyQfe1Mz
�͌�m��Ȃ��Ƃ킩��ɂ�����������܂��A���ł̏I�ǂ̋c�_�ɂ��āB
https://medaka.5ch.net/test/read.cgi/gamestones/1633708780/971
https://medaka.5ch.net/test/read.cgi/gamestones/1656072060/
���̂Ȃ��� ID:0XHZ/ZyO ����Ăɒ@����Ă����ł����A
���ɂ͂��̐l�̂ق����������悤�Ɏv���܂��B
�ǂ��ł��傤���H
https://medaka.5ch.net/test/read.cgi/gamestones/1633708780/971
https://medaka.5ch.net/test/read.cgi/gamestones/1656072060/
���̂Ȃ��� ID:0XHZ/ZyO ����Ăɒ@����Ă����ł����A
���ɂ͂��̐l�̂ق����������悤�Ɏv���܂��B
�ǂ��ł��傤���H
590�P�R�Q�l�ڂ̑f������
2023/04/04(��) 06:16:39.41ID:sZpd29eY >>589����̍l����悤�ɁA���̕��̏������݂����������e���Ƃ��Ă��A�����(���k��)�ւ̉�(�A�h�o�C�X)�Ƃ��ēK�łȂ�����ł͂Ȃ��ł��傤��
�Ⴆ�A
�w1+1 �̉������߂�x�Ƃ���̂ɁA�u1+2=3 ���I�v�Ɠ������Ƃ��܂��B1+2=3 �̓��e�͐������ł����A���̉Ƃ��Đ������Ǝv���܂����H
�Ⴆ�A
�w1+1 �̉������߂�x�Ƃ���̂ɁA�u1+2=3 ���I�v�Ɠ������Ƃ��܂��B1+2=3 �̓��e�͐������ł����A���̉Ƃ��Đ������Ǝv���܂����H
591589
2023/04/05(��) 07:02:12.48ID:3HU744PQ >>590
���̗Ⴆ�b�́A��L�X���ł̑������̈ӌ��̈�ɓ������A�悤�́u�I�O��v�Ƃ������Ƃł��傤���A
�����ɂ͖��n�҂䂦�ɗ������y�Ȃ��̂ŁA��̓I�ɂ����l�����|�C���g�������Ă���������Ə�����܂��B
���̌����͈قȂ�܂��B
�m�C�Y�������ĕ�����h���ł����A�������̐l�̎咣���������Ɖ��肷��Ȃ�A
�����ɂ���͌��̎���i����j�⑼�҂̉́uNO�v���Ƃ������ʐ��Ă̓����ɂȂ��Ă���A�Ɣ��f���܂����B
�悤����ɁA����FA��B�͂͂�����U�ł���ƁB
���̏�ł���Ɂu�⑫�i�A�h�o�C�X�j�v�Ƃ��Ă��̐l�́Aa��B�������^�ł���A�Ƃ��������Ă���B�����v���܂����B
�Ȃ��A�O��̎�����[�I�ɂ܂Ƃ߂�Ȃ�A��������̕��Ǝv�����������ɋL���Ă�����e�ɂȂ낤���Ǝv���܂��B
https://medaka.5ch.net/test/read.cgi/gamestones/1656072060/11
���̗Ⴆ�b�́A��L�X���ł̑������̈ӌ��̈�ɓ������A�悤�́u�I�O��v�Ƃ������Ƃł��傤���A
�����ɂ͖��n�҂䂦�ɗ������y�Ȃ��̂ŁA��̓I�ɂ����l�����|�C���g�������Ă���������Ə�����܂��B
���̌����͈قȂ�܂��B
�m�C�Y�������ĕ�����h���ł����A�������̐l�̎咣���������Ɖ��肷��Ȃ�A
�����ɂ���͌��̎���i����j�⑼�҂̉́uNO�v���Ƃ������ʐ��Ă̓����ɂȂ��Ă���A�Ɣ��f���܂����B
�悤����ɁA����FA��B�͂͂�����U�ł���ƁB
���̏�ł���Ɂu�⑫�i�A�h�o�C�X�j�v�Ƃ��Ă��̐l�́Aa��B�������^�ł���A�Ƃ��������Ă���B�����v���܂����B
�Ȃ��A�O��̎�����[�I�ɂ܂Ƃ߂�Ȃ�A��������̕��Ǝv�����������ɋL���Ă�����e�ɂȂ낤���Ǝv���܂��B
https://medaka.5ch.net/test/read.cgi/gamestones/1656072060/11
592�P�R�Q�l�ڂ̑f������
2023/04/05(��) 17:49:28.19ID:h6EiX/4b >>591
�����ł̏œ_�́A�������ݓ��e�̐�����(�^�U)�ł͂Ȃ��A����ɑ��Ẳ��e�Ƃ��ēK���ǂ����ł�
�����ȃ��[����m�肽������҂ɑ��A�����ȃ��[�����������҂̏������݂�ID:0XHZ/ZyO����́A
�u����́u�n�̊m��v�ɂ��Ă̐����Ȃ̂ŁA���̘b�Ƃ͔����Ɏ�|���قȂ��ɁA
���ǂ̂Ƃ���́u���ӎ���v�Ȃ̂ŁA����ς薾�m�ȓ����ł͂Ȃ��悤�Ɍ����邪�A�܂������v
�Ə������݂��Ă܂��B���ꂪ����ւ̉Ƃ��ēK�ł͂Ȃ��A�I�O��ȂǂƂ����Ă��܂�
�����ł̏œ_�́A�������ݓ��e�̐�����(�^�U)�ł͂Ȃ��A����ɑ��Ẳ��e�Ƃ��ēK���ǂ����ł�
�����ȃ��[����m�肽������҂ɑ��A�����ȃ��[�����������҂̏������݂�ID:0XHZ/ZyO����́A
�u����́u�n�̊m��v�ɂ��Ă̐����Ȃ̂ŁA���̘b�Ƃ͔����Ɏ�|���قȂ��ɁA
���ǂ̂Ƃ���́u���ӎ���v�Ȃ̂ŁA����ς薾�m�ȓ����ł͂Ȃ��悤�Ɍ����邪�A�܂������v
�Ə������݂��Ă܂��B���ꂪ����ւ̉Ƃ��ēK�ł͂Ȃ��A�I�O��ȂǂƂ����Ă��܂�
593589
2023/04/06(��) 01:14:55.33ID:DIOUgagK �Ƃ��ēK���ǂ����́A�������ݓ��e�̐^�U�Ɩ��ڂɂ������悤�ȋC�����܂����c�B
���Ă����A�ŏ��̎��̎�����B���ŏœ_���ڂ₯�ē`����Ă�����������܂���B���l�т��܂��B
���̋^��́A���̐l�́u�������ݓ��e�̐������v�������܂��ɏœ_�ł����B
���̐l���@����Ă��闝�R��m�肽�������̂ł͂���܂���B
�Ƃ����킯�ŁA���̑��k�҂ɑ���Ƃ��ēK���ǂ����́A���̍ےu���Ă����܂��傤�B
>>591���������Ɖ��肵�܂��B���̓_�ɂ��ẮA���̐l�B�������Ă��Ȃ��悤�Ɍ����܂��B
�Ȃ�A�I�ǂ̓_���l�߂ł͂Ȃ����҂̃p�X�ł���B
�䂦��"�����ȃ��[���Ƃ��ď�����Ă��邩�ǂ����͊W�Ȃ���"�u�_���l�߁v�Ƃ����̂͋U�A�Ԉ���Ă���B
����Ȃ�Βʂ���ł��傤���H
���Ă����A�ŏ��̎��̎�����B���ŏœ_���ڂ₯�ē`����Ă�����������܂���B���l�т��܂��B
���̋^��́A���̐l�́u�������ݓ��e�̐������v�������܂��ɏœ_�ł����B
���̐l���@����Ă��闝�R��m�肽�������̂ł͂���܂���B
�Ƃ����킯�ŁA���̑��k�҂ɑ���Ƃ��ēK���ǂ����́A���̍ےu���Ă����܂��傤�B
>>591���������Ɖ��肵�܂��B���̓_�ɂ��ẮA���̐l�B�������Ă��Ȃ��悤�Ɍ����܂��B
�Ȃ�A�I�ǂ̓_���l�߂ł͂Ȃ����҂̃p�X�ł���B
�䂦��"�����ȃ��[���Ƃ��ď�����Ă��邩�ǂ����͊W�Ȃ���"�u�_���l�߁v�Ƃ����̂͋U�A�Ԉ���Ă���B
����Ȃ�Βʂ���ł��傤���H
594�P�R�Q�l�ڂ̑f������
2023/04/06(��) 07:59:20.31ID:s6CMQvaa >>593
�u�_���l�߁v�Ƃ����̂͋U�A�Ԉ���Ă���B
�Ƃ���܂����A�u�Ԉ���Ă���̂Ȃ�v�A�܂�A������A�M���͂ǂ��������̂ł����H
�u�_���l�߁v�Ƃ����̂͋U�A�Ԉ���Ă���B
�Ƃ���܂����A�u�Ԉ���Ă���̂Ȃ�v�A�܂�A������A�M���͂ǂ��������̂ł����H
595589
2023/04/06(��) 17:04:52.55ID:DIOUgagK596�P�R�Q�l�ڂ̑f������
2023/04/06(��) 18:14:25.50ID:s6CMQvaa >>595
�_���I�ɍl�@����̂Ȃ�A>>593�w�Ȃ�A�I�ǂ̓_���l�߂ł͂Ȃ����҂̃p�X�ł���B�x�Ƃ���܂����A
�^�̏I��(���҂�����ؒu���Ȃ����)�̏ꍇ�ɂ��Ă܂��͍l���Ă݂Ă͂������ł��傤��
���I�ǂ̍���
�����̋��E�����͂����肵�Ă��āA����ȏエ�݂��ɑł������Ă��w�n������Ȃ��A���ɂȂ�Ƃ�����Ȃ��Ȃ������_�ŏI��
���݂��Ɂu�p�X�v�A�u�I���܂����ˁv�A�u�I���ł��ˁv�Ƃ����ӂ��ɐ錾(��������������)�I��
�݂Ȃ݂Ɏ���̈Ӑ}�́A���̌����������[���ɒ�G����̂ŁA���[�������ς������̂��ǂ��������������������ŁA�W�Ȃ������Ȃ̂ŃX���[���Ă�������
�_���I�ɍl�@����̂Ȃ�A>>593�w�Ȃ�A�I�ǂ̓_���l�߂ł͂Ȃ����҂̃p�X�ł���B�x�Ƃ���܂����A
�^�̏I��(���҂�����ؒu���Ȃ����)�̏ꍇ�ɂ��Ă܂��͍l���Ă݂Ă͂������ł��傤��
���I�ǂ̍���
�����̋��E�����͂����肵�Ă��āA����ȏエ�݂��ɑł������Ă��w�n������Ȃ��A���ɂȂ�Ƃ�����Ȃ��Ȃ������_�ŏI��
���݂��Ɂu�p�X�v�A�u�I���܂����ˁv�A�u�I���ł��ˁv�Ƃ����ӂ��ɐ錾(��������������)�I��
�݂Ȃ݂Ɏ���̈Ӑ}�́A���̌����������[���ɒ�G����̂ŁA���[�������ς������̂��ǂ��������������������ŁA�W�Ȃ������Ȃ̂ŃX���[���Ă�������
597589
2023/04/06(��) 20:41:46.25ID:DIOUgagK ��Ƃ���A�w�^�̏I�ǁx�Ƃ������̂̍l�@���d�v�ł���A��������Ɛ���ςɎ����Ė{���������������ł��B
�܂��u���[�������ρi���ǁj���������v�ƒ��ɖ����A�����͔ے�͂��܂���B
�����̍ŏ��̏������݂ɓ����͐^�ʖڂɕԓ�������Ƃ͎v�킸�A
���X�Ə������ޏ�Ƃ��ēK�Ȃ̂��Ǝv�����S�O���Ă��܂������A
�����炩�S�����悤�ł��̂ŁA���̕ӂŎ��̘_���̂��ׂĂ�ł������邱�Ƃɂ��܂��B
�ȉ������Ȃ���X���[���Ă��������B
�܂��A�͌�ł́A�u���҂�����ؒu���Ȃ���ԁv�́A���[�����_��͎��͂��肦�܂���B
���̂��Ƃ͈�@��̒�`�ɂ��e�Ղɓ�����邩�Ǝv���܂��B
�w���[����x�Ő������Ă���u��u���Ȃ��n�_�i��@��j�v�́A���Ɍ���I�Ȃ̂ł��B
���Ԉ�ʓI�ɂ͌�̏I�ǂɂ���
�u���E�����͂����肵����v�u���ɂȂ�Ƃ��낪�Ȃ��Ȃ�����v
���邢�́u�_���l�ߎ���ꂪ�I�������v���Ɛ�������܂��B
�ł����A����̓��[����̐����ȏI�ǂ̒�`�ɂ͖{���Ȃ肦�Ȃ��ł��傤�B
�Ȃ��Ȃ�A�u���E���͂͂����肵�����H�v�u���ɂȂ�Ƃ���͂����Ȃ����H�v�u�_���l�ߎ���ꂪ�I��������H�v�́A
�ǎҎ��g�̐헪�I���f�i���S�j�̈���o�Ȃ�����ł��B
���ہA���S�҂ɂƂ��Ă����̔��f�͌����ėe�Ղɉ\�ł͂Ȃ��͂��ł��B
�i��̏I�ǂ͂����P���ł͂���܂���B���Ƃ��A�w���E�x���̂͊I�ɒ�`�\��������܂��A
���E���L��������A�����L�����肷��A�܂��I�ǂɂȂ�܂���B�j
�Ȃ�A�����ǎ҂̓��S�Ƃ����̂́A�q�ϓI�ɂ͂ǂ̂悤�Ɏ��͂Ɏ������ł��傤���H
����͌��ǂ̂Ƃ���A�p�X�ȊO�ɂ͂Ȃ��Ƃ������Ƃł��B
�ȏ�̍l�@����L��̂ɂ����A
��̏I�ǂ́i�ɋH�ȗ�O�ȊO�́j��ɗ��҂̃p�X�Ƃ��Ē�`�������Ȃ��i����ȊO�ɂ͖����ł��낤�j�A
�܂����̎���ɂ�����炸�A�����ɂ͗��҂́u���Ӂv�I�ȈӖ���������ʂłȂ��܂܂��ł��낤�c�Ƃ����킯�ł��B
�Ȃ��A�H�ȗ�O�Ƃ����̂͐����i�����j�ɂ�閳�����ł��B
�܂��u���[�������ρi���ǁj���������v�ƒ��ɖ����A�����͔ے�͂��܂���B
�����̍ŏ��̏������݂ɓ����͐^�ʖڂɕԓ�������Ƃ͎v�킸�A
���X�Ə������ޏ�Ƃ��ēK�Ȃ̂��Ǝv�����S�O���Ă��܂������A
�����炩�S�����悤�ł��̂ŁA���̕ӂŎ��̘_���̂��ׂĂ�ł������邱�Ƃɂ��܂��B
�ȉ������Ȃ���X���[���Ă��������B
�܂��A�͌�ł́A�u���҂�����ؒu���Ȃ���ԁv�́A���[�����_��͎��͂��肦�܂���B
���̂��Ƃ͈�@��̒�`�ɂ��e�Ղɓ�����邩�Ǝv���܂��B
�w���[����x�Ő������Ă���u��u���Ȃ��n�_�i��@��j�v�́A���Ɍ���I�Ȃ̂ł��B
���Ԉ�ʓI�ɂ͌�̏I�ǂɂ���
�u���E�����͂����肵����v�u���ɂȂ�Ƃ��낪�Ȃ��Ȃ�����v
���邢�́u�_���l�ߎ���ꂪ�I�������v���Ɛ�������܂��B
�ł����A����̓��[����̐����ȏI�ǂ̒�`�ɂ͖{���Ȃ肦�Ȃ��ł��傤�B
�Ȃ��Ȃ�A�u���E���͂͂����肵�����H�v�u���ɂȂ�Ƃ���͂����Ȃ����H�v�u�_���l�ߎ���ꂪ�I��������H�v�́A
�ǎҎ��g�̐헪�I���f�i���S�j�̈���o�Ȃ�����ł��B
���ہA���S�҂ɂƂ��Ă����̔��f�͌����ėe�Ղɉ\�ł͂Ȃ��͂��ł��B
�i��̏I�ǂ͂����P���ł͂���܂���B���Ƃ��A�w���E�x���̂͊I�ɒ�`�\��������܂��A
���E���L��������A�����L�����肷��A�܂��I�ǂɂȂ�܂���B�j
�Ȃ�A�����ǎ҂̓��S�Ƃ����̂́A�q�ϓI�ɂ͂ǂ̂悤�Ɏ��͂Ɏ������ł��傤���H
����͌��ǂ̂Ƃ���A�p�X�ȊO�ɂ͂Ȃ��Ƃ������Ƃł��B
�ȏ�̍l�@����L��̂ɂ����A
��̏I�ǂ́i�ɋH�ȗ�O�ȊO�́j��ɗ��҂̃p�X�Ƃ��Ē�`�������Ȃ��i����ȊO�ɂ͖����ł��낤�j�A
�܂����̎���ɂ�����炸�A�����ɂ͗��҂́u���Ӂv�I�ȈӖ���������ʂłȂ��܂܂��ł��낤�c�Ƃ����킯�ł��B
�Ȃ��A�H�ȗ�O�Ƃ����̂͐����i�����j�ɂ�閳�����ł��B
598�P�R�Q�l�ڂ̑f������
2023/04/08(�y) 12:06:45.03ID:s1r9XZlr 1����37�܂ł�37�̐����̒�����A
�ǂ�2������3�ȏ�ł���7��
(��:2,8,15,18,29,33,36)�̑I�ѕ��͉��ʂ肩�B
�ǂ�2������3�ȏ�ł���7��
(��:2,8,15,18,29,33,36)�̑I�ѕ��͉��ʂ肩�B
2023/07/05(��) 07:25:56.37ID:GbvYhzVo
(>�<;)/ ��-~ �߲!
600�P�R�Q�l�ڂ̑f������
2023/08/19(�y) 07:39:17.74ID:paFxtanx �u������������C�Z��������.�����ꂼ��ɁC��������������.
�ǂ�Ȏ��������邩�͂܂��������R�C�Ⴆ��n�Ԗڂ̔���e^�����Ă��悢���C���ׂĂ̔��Ƀ����Ă��悢.
�������ł���߂����č\��Ȃ�.�����Ĕ����݂ȕ���.
���x�͂��Ȃ��̔Ԃł���.�В[���甠���J���Ă䂫���̎�����`���Ă悢���C��̔��͊J�����ɕ����܂c���˂Ȃ�ʂƂ��悤.
�ǂ̔�������܂c�����͂��Ȃ������߂���.
�����̃��[���͂�����. �����������̒��̎������s�^���ƌ������Ă���C���Ȃ��̏���. �����Ȃ��Ε���.
���헪�͂���ł��傤��?�v
�ǂ�Ȏ��������邩�͂܂��������R�C�Ⴆ��n�Ԗڂ̔���e^�����Ă��悢���C���ׂĂ̔��Ƀ����Ă��悢.
�������ł���߂����č\��Ȃ�.�����Ĕ����݂ȕ���.
���x�͂��Ȃ��̔Ԃł���.�В[���甠���J���Ă䂫���̎�����`���Ă悢���C��̔��͊J�����ɕ����܂c���˂Ȃ�ʂƂ��悤.
�ǂ̔�������܂c�����͂��Ȃ������߂���.
�����̃��[���͂�����. �����������̒��̎������s�^���ƌ������Ă���C���Ȃ��̏���. �����Ȃ��Ε���.
���헪�͂���ł��傤��?�v
601�P�R�Q�l�ڂ̑f������
2023/08/21(��) 08:37:15.01ID:8x4db3Hg >>600
���ɓ����̂������ł������A���̊J�Ɋւ�炸�����s�^���Ɠ��Ă�̂͂قږ����A�ق� 0 (������)�Ƃ����܂�
�������A���헪������̂��̖₢�����ɑ��Ắu����v�Ƃ����܂�
�{�����Ɂu��������������v�Ƃ���̂ŁA�u���v����s�b�^���̎����������o���헪���������Ǝv���܂�
���ɓ����̂������ł������A���̊J�Ɋւ�炸�����s�^���Ɠ��Ă�̂͂قږ����A�ق� 0 (������)�Ƃ����܂�
�������A���헪������̂��̖₢�����ɑ��Ắu����v�Ƃ����܂�
�{�����Ɂu��������������v�Ƃ���̂ŁA�u���v����s�b�^���̎����������o���헪���������Ǝv���܂�
602�P�R�Q�l�ڂ̑f������
2023/08/21(��) 09:50:32.62ID:G8AVkjMT �������|�G���ɋ߂Â��Ă���
603�P�R�Q�l�ڂ̑f������
2023/08/21(��) 13:11:06.52ID:QJFtZQ2b >>601
�^�C�v�̏����������������킳�킵�Ď���̯�Ă���Ɛ�����������Ǝv���܂�
�^�C�v�̏����������������킳�킵�Ď���̯�Ă���Ɛ�����������Ǝv���܂�
2023/08/22(��) 10:14:18.11ID:PD53aFrt
2023/08/22(��) 10:17:04.33ID:PD53aFrt
�u���v�̍D�݂̏������u���v�ɘr�𗍂߂ċ���������ē�̘r�ɂ��������炢�ɐڋ߂��Ď���̯�Ƃ����ڂ��삳�삧���ł��B
�����Ɉ����o����Ǝv���܂��B
�����Ɉ����o����Ǝv���܂��B
2023/08/22(��) 10:23:32.17ID:PD53aFrt
007�����n�q���C���I�������ł��B
���̎��A���������̃P�[�X�ł̓q���C���̃`�F���W�͂R��܂ŁA�Ƃ��Ă��܂��B
����͂��Ȃ苭�͂ȍ��ŁA���������́u���v�ɑ��ėL���ł�(�z���ȊO)
���̎��A���������̃P�[�X�ł̓q���C���̃`�F���W�͂R��܂ŁA�Ƃ��Ă��܂��B
����͂��Ȃ苭�͂ȍ��ŁA���������́u���v�ɑ��ėL���ł�(�z���ȊO)
2023/08/23(��) 12:13:11.73ID:dDMdRKEi
>>601
�����疳�����ƌ����o�������R�s�y�ˑ����w�K�Ӗ���
�����疳�����ƌ����o�������R�s�y�ˑ����w�K�Ӗ���
2023/10/11(��) 09:28:07.61ID:dk3ib+Op
24��f�������������2*2*2*3
���̂����������ƂȂ�ӏ�������邾�������sqdiv(24)=6(2*3)�ƂȂ�܂�
i��1����100�܂�sqdiv(i)�����߂��
sqdiv(i)�̂Q��a��n�ȉ��̐���p����i*j���������ƂȂ�悤�Ȍ��ɂȂ�̂ł����Ȃ��Q��a���Ƃ�̂����킩��܂���
�Ⴆ��n=4�̎���(1,1),(1,4),(2,2),(3,3),(4,1),(4,4)��6��i*j���Q��ɂȂ�܂�
sqdiv(i)�̌���n=4�̂Ƃ����ꂼ��n=1,2,3,4�ɂ��Ă��ꂼ��[2,1,1,0]�łQ��a���Ƃ��4+1+1=6�Ƃ����Ɠ����ɂȂ��Ă��܂�
sum [2,1,1,0]=4=n�ƈ�v���܂�
[2,1,1,0]�Ƃ���������2��sqdiv(1)��sqdiv(4)��2�Asqdiv(2)��1��sqdiv(3)��1�ƂȂ�܂�
���̂����������ƂȂ�ӏ�������邾�������sqdiv(24)=6(2*3)�ƂȂ�܂�
i��1����100�܂�sqdiv(i)�����߂��
sqdiv(i)�̂Q��a��n�ȉ��̐���p����i*j���������ƂȂ�悤�Ȍ��ɂȂ�̂ł����Ȃ��Q��a���Ƃ�̂����킩��܂���
�Ⴆ��n=4�̎���(1,1),(1,4),(2,2),(3,3),(4,1),(4,4)��6��i*j���Q��ɂȂ�܂�
sqdiv(i)�̌���n=4�̂Ƃ����ꂼ��n=1,2,3,4�ɂ��Ă��ꂼ��[2,1,1,0]�łQ��a���Ƃ��4+1+1=6�Ƃ����Ɠ����ɂȂ��Ă��܂�
sum [2,1,1,0]=4=n�ƈ�v���܂�
[2,1,1,0]�Ƃ���������2��sqdiv(1)��sqdiv(4)��2�Asqdiv(2)��1��sqdiv(3)��1�ƂȂ�܂�
609608
2023/10/11(��) 10:16:02.25ID:dk3ib+Op �グ�Ă����܂�
2023/11/08(��) 08:22:14.66ID:vXRh60v7
�u����a�ɋ߂Â��Ƃ��v��_������
611�P�R�Q�l�ڂ̑f������
2023/12/19(��) 05:21:01.46ID:qCtHYJym https://mathpower.sugakubunka.com/2016/file/kettouyosen1st.pdf
����̖��5���ށi�Ō�AB�ɂȂ��Ă邪���Ԃ�AR�̌뎚�j
���͑S���`�����������X�}�`���Ȃ̂������Ă����ς�킩���
����̖��5���ށi�Ō�AB�ɂȂ��Ă邪���Ԃ�AR�̌뎚�j
���͑S���`�����������X�}�`���Ȃ̂������Ă����ς�킩���
612�P�R�Q�l�ڂ̑f������
2023/12/19(��) 12:10:00.99ID:CysfFxjM ���p���̃A���̗ގ��ȊO�p���̃A���{���l���E�X�ł����܂������ǁA�m���ɑ��Ɣ�ׂ�Ɠ����
2023/12/19(��) 23:57:06.77ID:qCtHYJym
�Ȃ��
�g���N�X
�g���N�X
614prime_132
2024/01/22(��) 02:44:40.57ID:7UUiJy43 >>598
�����ɕ��ׂ����̂�
�@1 �� a_1 < a_2 < a_3 < a_4 < a_5 < a_6 < a_7 �� 37
�Ƃ���B����2���̍���3�ȏゾ����
�@b_k = a_k - 2*(k-1),
�Ƃ����B
�@1 �� b_1 < b_2 < b_3 < b_4 < b_5 < b_6 < b_7 �� 25,
{1, 2, �c, 25} �̒����� ���قȂ�7��b��I�ԕ��@�́A
�@C[25,7] = 480700�@�ʂ�
�����ɕ��ׂ����̂�
�@1 �� a_1 < a_2 < a_3 < a_4 < a_5 < a_6 < a_7 �� 37
�Ƃ���B����2���̍���3�ȏゾ����
�@b_k = a_k - 2*(k-1),
�Ƃ����B
�@1 �� b_1 < b_2 < b_3 < b_4 < b_5 < b_6 < b_7 �� 25,
{1, 2, �c, 25} �̒����� ���قȂ�7��b��I�ԕ��@�́A
�@C[25,7] = 480700�@�ʂ�
615prime_132
2024/01/26(��) 18:25:28.64ID:jjBmEGrf >>572
�@�~�ɓ��ڂ��鐳24�p�`���l���悤�B
�@�P�ӂ̒���L�͒��_ (1/��2, 1/��2) �� (1/2, (��3)/2) �̋���������
�@LL = {1/��2 - 1/2}^2 + {1/��2 - (��3)/2}^2 = 2 - (��2 + ��6)/2,
�Ƃ����
�@20��2 = 28.3 - 0.89/(28.3+20��2) < 28.3
�@20��6 = 49 - 1/(49+20��6) < 49,
���@LL > 2 - (28.3+49)/40 = 2.7/40 = 27/400,
���@L > (3��3)/20,
��24�p�`�̈�ӂ��~�ʂ̕����������Ƃ���
�@�� > 12L > (9��3)/5 > 28/9 = 3.1111111
* 81��3 = 140 + 83/(81��3 + 140) > 140,
�@�~�ɓ��ڂ��鐳24�p�`���l���悤�B
�@�P�ӂ̒���L�͒��_ (1/��2, 1/��2) �� (1/2, (��3)/2) �̋���������
�@LL = {1/��2 - 1/2}^2 + {1/��2 - (��3)/2}^2 = 2 - (��2 + ��6)/2,
�Ƃ����
�@20��2 = 28.3 - 0.89/(28.3+20��2) < 28.3
�@20��6 = 49 - 1/(49+20��6) < 49,
���@LL > 2 - (28.3+49)/40 = 2.7/40 = 27/400,
���@L > (3��3)/20,
��24�p�`�̈�ӂ��~�ʂ̕����������Ƃ���
�@�� > 12L > (9��3)/5 > 28/9 = 3.1111111
* 81��3 = 140 + 83/(81��3 + 140) > 140,
616prime_132
2024/01/31(��) 01:42:56.99ID:b6Gsbw7H 70��2 = 99 - 1/(99+70��2) < 99,
20��6 = 49 - 1/(49+20��6) < 49,
LL = 2 - (��2 + ��6)/2
�@> 2 - (99/140) - (49/40)
�@= 19 / 280
�@> (0.26)^2,
��@0.26��280 = ��19 - 0.072/(��19 + 0.26��280) < ��19,
�����
L > 0.26
�� > 12L > 3.12
20��6 = 49 - 1/(49+20��6) < 49,
LL = 2 - (��2 + ��6)/2
�@> 2 - (99/140) - (49/40)
�@= 19 / 280
�@> (0.26)^2,
��@0.26��280 = ��19 - 0.072/(��19 + 0.26��280) < ��19,
�����
L > 0.26
�� > 12L > 3.12
617�P�R�Q�l�ڂ̑f������
2024/02/03(�y) 05:48:10.18ID:/zKgJoQP CHATGPT�ɐ��w��������Ă��鏗�q���w���ł��B
���̖���CHATGPT���o�O���Ă��܂��č����Ă��܂��B
�w�Z�̐}���قɂ͐V�����{�ƌÂ��{������܂��B
�V�����{�̐����Â��{�̐���2�{���10�������ł��B
�}���ّS�̂ŐV�����{�ƌÂ��{�����킹��210������܂��B
�V�����{�͑S���ʼn����ł��傤���H
��������
x+2x+10=210 �Ɛݒ肷��̂͑ʖڂȂ́H
���̖���CHATGPT���o�O���Ă��܂��č����Ă��܂��B
�w�Z�̐}���قɂ͐V�����{�ƌÂ��{������܂��B
�V�����{�̐����Â��{�̐���2�{���10�������ł��B
�}���ّS�̂ŐV�����{�ƌÂ��{�����킹��210������܂��B
�V�����{�͑S���ʼn����ł��傤���H
��������
x+2x+10=210 �Ɛݒ肷��̂͑ʖڂȂ́H
618�P�R�Q�l�ڂ̑f������
2024/02/03(�y) 11:02:18.40ID:Px1DaJXr ���͐�����
���������ɂȂ�Ȃ�����A���̂ق�������
���������ɂȂ�Ȃ�����A���̂ق�������
619�P�R�Q�l�ڂ̑f������
2024/02/03(�y) 14:23:56.86ID:/zKgJoQP >>0618
���肪�Ƃ��I
�X�b�L�����܂����I
CHATGPT�͌��ꃂ�f�����Ă������炢������
�����ƕ��n�Ȃ낤�Ɗ����܂����B
���肪�Ƃ��I
�X�b�L�����܂����I
CHATGPT�͌��ꃂ�f�����Ă������炢������
�����ƕ��n�Ȃ낤�Ɗ����܂����B
620�P�R�Q�l�ڂ̑f������
2024/02/03(�y) 19:34:21.21ID:Fx/XYsyI ��w�X���␔�w���挩�Ă��ۂɋC�ɂȂ����̂Ŏ���ł�
��1.
m_1,m_2,...,m_n���������łȂ����̐����ł���Ƃ��C
��m_1 + ��m_2 + ... + ��m_n ���L�����ƂȂ�悤�ȑg(m_1,m_2,...,m_n)�͑��݂��܂����H
����No���Ƃ͎v����ł����C
n=1,2,3�Ȃǂ̏ꍇ�͂Ƃ������C����ȍ~�͉������Ƃ��ł��܂���
�킩�����������q���g��ؖ������肢���܂��D
��2.
�v�f�̘a�����傤��100�ƂȂ�悤�Ȏ��R��N�̕����W���͂������݂��܂����H
3blue1brown�̓���ŏЉ��Ă������̉���ł��D
https://youtu.be/FR6_JK5thCY?si=NBL_meV5hM-kdb6n
xx�̔{���Ȃǂ͐��������g�����Ƃʼn����܂����Cxx�Ɠ������ꍇ�͓��l�̉�@���g���܂���D
�l�͂ʼn�������@�͂����ł��傤���c�H
��1.
m_1,m_2,...,m_n���������łȂ����̐����ł���Ƃ��C
��m_1 + ��m_2 + ... + ��m_n ���L�����ƂȂ�悤�ȑg(m_1,m_2,...,m_n)�͑��݂��܂����H
����No���Ƃ͎v����ł����C
n=1,2,3�Ȃǂ̏ꍇ�͂Ƃ������C����ȍ~�͉������Ƃ��ł��܂���
�킩�����������q���g��ؖ������肢���܂��D
��2.
�v�f�̘a�����傤��100�ƂȂ�悤�Ȏ��R��N�̕����W���͂������݂��܂����H
3blue1brown�̓���ŏЉ��Ă������̉���ł��D
https://youtu.be/FR6_JK5thCY?si=NBL_meV5hM-kdb6n
xx�̔{���Ȃǂ͐��������g�����Ƃʼn����܂����Cxx�Ɠ������ꍇ�͓��l�̉�@���g���܂���D
�l�͂ʼn�������@�͂����ł��傤���c�H
621�P�R�Q�l�ڂ̑f������
2024/02/03(�y) 22:09:31.76ID:3SMt1m6a #100�̔{��
-#200�̔{��-#300�̔{��-#500�̔{��-#700�̔{��
+#600�̔{��-#1000�̔{��+#1400�̔{��+#1500�̔{��+#2100�̔{��+#3500�̔{��
...
�ł�����
-#200�̔{��-#300�̔{��-#500�̔{��-#700�̔{��
+#600�̔{��-#1000�̔{��+#1400�̔{��+#1500�̔{��+#2100�̔{��+#3500�̔{��
...
�ł�����
622�P�R�Q�l�ڂ̑f������
2024/02/03(�y) 22:50:19.87ID:Fx/XYsyI �����m����
�v�Z�͂��Ȃ��ς���������
�v�Z�͂��Ȃ��ς���������
623prime_132
2024/02/03(�y) 23:39:49.92ID:ApTI9ZFu ���߂���̂�
�E100 �𑊈قȂ�k�̎��R���̘a�ŕ\�킷���@
�@x1+x2+x3+�c�c+xk = 100,
�@x1<x2<x3<�c�c<xk,�@�@(1��k��13)
������
�@y1 = x1,
�@y2 = x2 -1,
�@y3 = x3 -2,
�@�c�c
�@yk = xk - (k-1),
�Ƃ����ƁA
�En���d����������k�̎��R���̘a�ŕ\�킷���@
�@y1+y2+�c�c+yk = 100 - k(k-1)/2 = n,
�@y1��y2��y3���c�c��yk,
����𐧌��t�������� q_k(n)�Ɖ]��.
�@q_k(1) = q_k(k) = 1,
�@q_k(n) = q_{k-1}(n-1) + q_k(n-k),
���
�@q_1(100) = 1,
�@q_2(99) = 49,
�@q_3(97) = 784,
�@q_4(94) = 5952,
�@q_5(90) =
�@q_6(85) =
�@q_7(79) =
�@q_8(72) =
�@q_9(64) =
�@q_10(55) =
�@q_11(45) =
�@q_12(34) = 905,
�@q_13(22) = 30,
�@��������v����B
�E100 �𑊈قȂ�k�̎��R���̘a�ŕ\�킷���@
�@x1+x2+x3+�c�c+xk = 100,
�@x1<x2<x3<�c�c<xk,�@�@(1��k��13)
������
�@y1 = x1,
�@y2 = x2 -1,
�@y3 = x3 -2,
�@�c�c
�@yk = xk - (k-1),
�Ƃ����ƁA
�En���d����������k�̎��R���̘a�ŕ\�킷���@
�@y1+y2+�c�c+yk = 100 - k(k-1)/2 = n,
�@y1��y2��y3���c�c��yk,
����𐧌��t�������� q_k(n)�Ɖ]��.
�@q_k(1) = q_k(k) = 1,
�@q_k(n) = q_{k-1}(n-1) + q_k(n-k),
���
�@q_1(100) = 1,
�@q_2(99) = 49,
�@q_3(97) = 784,
�@q_4(94) = 5952,
�@q_5(90) =
�@q_6(85) =
�@q_7(79) =
�@q_8(72) =
�@q_9(64) =
�@q_10(55) =
�@q_11(45) =
�@q_12(34) = 905,
�@q_13(22) = 30,
�@��������v����B
624�P�R�Q�l�ڂ̑f������
2024/02/04(��) 03:17:43.58ID:D5GIS9H2 �Ȃ�ق�👏���̕��@�ŏd���������p�^�[���ɒu�������ĉ�����ł���
�Ƃ͂�������ł��v�Z��ςőz�����Ă����ł������ɂȂ肻���ł���...
���ׂĂ����ƕ������͌��݂����_�̕���Ō�������Ă���Ƃ������Ƃ�
���̂��Ƃ�m�邫�������ɂȂꂽ�̂͗ǂ������ł�
���肪�Ƃ��������܂��I
�Ƃ͂�������ł��v�Z��ςőz�����Ă����ł������ɂȂ肻���ł���...
���ׂĂ����ƕ������͌��݂����_�̕���Ō�������Ă���Ƃ������Ƃ�
���̂��Ƃ�m�邫�������ɂȂꂽ�̂͗ǂ������ł�
���肪�Ƃ��������܂��I
625�P�R�Q�l�ڂ̑f������
2024/02/04(��) 08:24:49.53ID:f0HyDaDn m_1,m_2,...,m_n���������łȂ����̐����ł���Ƃ��C
��m_1 + ��m_2 + ... + ��m_n ���L�����ƂȂ�悤�ȑg(m_1,m_2,...,m_n)�͑��݂��܂����H
tr (��m_1 + ��m_2 + ... + ��m_n) = 0
��m_1 + ��m_2 + ... + ��m_n ���L�����ƂȂ�悤�ȑg(m_1,m_2,...,m_n)�͑��݂��܂����H
tr (��m_1 + ��m_2 + ... + ��m_n) = 0
626prime_132
2024/02/05(��) 03:06:57.01ID:DEvuP4sR >>623
��2.
�@q_1(100) = 1,
�@q_2(99) = 49,
�@q_3(97) = 784,
�@q_4(94) = 5952,
�@q_5(90) = 25337,
�@q_6(85) = 65827,
�@q_7(79) = 108869,
�@q_8(72) = 116263,
�@q_9(64) = 79403,
�@q_10(55) = 33401,
�@q_11(45) = 7972,
�@q_12(34) = 905,
�@q_13(22) = 30,
�@��������v����Ɓ@444793.
�����͑Q����
�@q_k(n) = q_{k-1}(n-1) + q_k(n-k),
�����āC������
�@(x^k)�^(��[j=1,k] (1-x^j)) = ��[n=k,��] q_k(n)�x^n,
�����B
���Z�~�����u���w100�̖��v���{�]�_�� (1984)�@p.58
��2.
�@q_1(100) = 1,
�@q_2(99) = 49,
�@q_3(97) = 784,
�@q_4(94) = 5952,
�@q_5(90) = 25337,
�@q_6(85) = 65827,
�@q_7(79) = 108869,
�@q_8(72) = 116263,
�@q_9(64) = 79403,
�@q_10(55) = 33401,
�@q_11(45) = 7972,
�@q_12(34) = 905,
�@q_13(22) = 30,
�@��������v����Ɓ@444793.
�����͑Q����
�@q_k(n) = q_{k-1}(n-1) + q_k(n-k),
�����āC������
�@(x^k)�^(��[j=1,k] (1-x^j)) = ��[n=k,��] q_k(n)�x^n,
�����B
���Z�~�����u���w100�̖��v���{�]�_�� (1984)�@p.58
627prime_132
2024/02/05(��) 13:24:59.43ID:DEvuP4sR (����)
�v�f�̐���k�Ƃ���B
k=1,�@�@�@q_1 = 1.
�@{100}
k=2,�@�@�@q_2 = 49.
�@{i, 100-i}�@�@�@�@�@�@(1��i��49)
k=13,�@�@�@q_13 = 30.
�@{1�`11, j, 34-j}�@�@�@(12��j��16)
�@{1�`10, 12, j, 33-j}�@(13��j��16)
�@{1�`10, 13, 14, 18}
�@{1�`10, 13, 15, 17}
�@{1�`10, 14�`16}
�@{1�`9, 11�`13, 19}
�@{1�`9, 11, 12, 14, 18}
�@{1�`9, 11, 12, 15, 17}
�@{1�`9, 11, 13, 14, 17}
�@{1�`9, 11, 13, 15, 16}
�@{1�`9, 12�`14, 16}
�@{1�`8, 10, 11�`13, 18}
�@{1�`8, 10�`12, 14, 17}
�@{1�`8, 10�`12, 15, 16}
�@{1�`8, 10, 11, 13, 14, 16}
�@{1�`8, 10, 12�`15}
�@{1�`7, 9�`13, 17}
�@{1�`7, 9�`12, 14, 16}
�@{1�`7, 9�`11, 13�`15}
�@{1�`6, 8�`13, 16}
�@{1�`6, 8�`12, 14, 15}
�@{1�`5, 7�`13, 15}
�@{1�`4, 6�`14}
�v�f�̐���k�Ƃ���B
k=1,�@�@�@q_1 = 1.
�@{100}
k=2,�@�@�@q_2 = 49.
�@{i, 100-i}�@�@�@�@�@�@(1��i��49)
k=13,�@�@�@q_13 = 30.
�@{1�`11, j, 34-j}�@�@�@(12��j��16)
�@{1�`10, 12, j, 33-j}�@(13��j��16)
�@{1�`10, 13, 14, 18}
�@{1�`10, 13, 15, 17}
�@{1�`10, 14�`16}
�@{1�`9, 11�`13, 19}
�@{1�`9, 11, 12, 14, 18}
�@{1�`9, 11, 12, 15, 17}
�@{1�`9, 11, 13, 14, 17}
�@{1�`9, 11, 13, 15, 16}
�@{1�`9, 12�`14, 16}
�@{1�`8, 10, 11�`13, 18}
�@{1�`8, 10�`12, 14, 17}
�@{1�`8, 10�`12, 15, 16}
�@{1�`8, 10, 11, 13, 14, 16}
�@{1�`8, 10, 12�`15}
�@{1�`7, 9�`13, 17}
�@{1�`7, 9�`12, 14, 16}
�@{1�`7, 9�`11, 13�`15}
�@{1�`6, 8�`13, 16}
�@{1�`6, 8�`12, 14, 15}
�@{1�`5, 7�`13, 15}
�@{1�`4, 6�`14}
628prime_132
2024/02/10(�y) 21:16:41.65ID:bl3yP4ft >>615-616
�@97^2 - 3*56^2 = 1, �@�@�@(�y��������)
�@��3 < 97/56,
�@{(��2 + ��6)/2}^2 = 2 + ��3 < 2 + 97/56 < 1.93188^2,
�@(��2 + ��6) /2 < 1.93188
�@LL = 2 - (��2 + ��6) /2 > 0.068121 = 0.261^2,
�@L > 0.261
�@�� > 12L > 3.132
�@97^2 - 3*56^2 = 1, �@�@�@(�y��������)
�@��3 < 97/56,
�@{(��2 + ��6)/2}^2 = 2 + ��3 < 2 + 97/56 < 1.93188^2,
�@(��2 + ��6) /2 < 1.93188
�@LL = 2 - (��2 + ��6) /2 > 0.068121 = 0.261^2,
�@L > 0.261
�@�� > 12L > 3.132
2024/02/11(��) 14:14:16.87ID:n0tHiTUW
import Data.List
sums [] bs = bs
sums (a:as) bs = sums as ( zipWith (+) bs $ ( replicate a 0 ) ++ bs )
main = do
print $ zip [0..] $ sums [1..100] $ 1 : replicate 100 0
{-
[(0,1),(1,1),(2,1),(3,2),(4,2),(5,3),(6,4),(7,5),(8,6),(9,8),(10,10),(11,12),(12,15),(13,18),(14,22),(15,27),(16,32),(17,38),(18,46),(19,54),(20,64),(21,76),(22,89),(23,104),(24,122),(25,142),(26,165),(27,192),(28,222),(29,256),(30,296),(31,340),(32,390),(33,448),(34,512),(35,585),(36,668),(37,760),(38,864),(39,982),(40,1113),(41,1260),(42,1426),(43,1610),(44,1816),(45,2048),(46,2304),(47,2590),(48,2910),(49,3264),(50,3658),(51,4097),(52,4582),(53,5120),(54,5718),(55,6378),(56,7108),(57,7917),(58,8808),(59,9792),(60,10880),(61,12076),(62,13394),(63,14848),(64,16444),(65,18200),(66,20132),(67,22250),(68,24576),(69,27130),(70,29927),(71,32992),(72,36352),(73,40026),(74,44046),(75,48446),(76,53250),(77,58499),(78,64234),(79,70488),(80,77312),(81,84756),(82,92864),(83,101698),(84,111322),(85,121792),(86,133184),(87,145578),(88,159046),(89,173682),(90,189586),(91,206848),(92,225585),(93,245920),(94,267968),(95,291874),(96,317788),(97,345856),(98,376256),(99,409174),(100,444793)]
https://ideone.com/FZTUON
-}
sums [] bs = bs
sums (a:as) bs = sums as ( zipWith (+) bs $ ( replicate a 0 ) ++ bs )
main = do
print $ zip [0..] $ sums [1..100] $ 1 : replicate 100 0
{-
[(0,1),(1,1),(2,1),(3,2),(4,2),(5,3),(6,4),(7,5),(8,6),(9,8),(10,10),(11,12),(12,15),(13,18),(14,22),(15,27),(16,32),(17,38),(18,46),(19,54),(20,64),(21,76),(22,89),(23,104),(24,122),(25,142),(26,165),(27,192),(28,222),(29,256),(30,296),(31,340),(32,390),(33,448),(34,512),(35,585),(36,668),(37,760),(38,864),(39,982),(40,1113),(41,1260),(42,1426),(43,1610),(44,1816),(45,2048),(46,2304),(47,2590),(48,2910),(49,3264),(50,3658),(51,4097),(52,4582),(53,5120),(54,5718),(55,6378),(56,7108),(57,7917),(58,8808),(59,9792),(60,10880),(61,12076),(62,13394),(63,14848),(64,16444),(65,18200),(66,20132),(67,22250),(68,24576),(69,27130),(70,29927),(71,32992),(72,36352),(73,40026),(74,44046),(75,48446),(76,53250),(77,58499),(78,64234),(79,70488),(80,77312),(81,84756),(82,92864),(83,101698),(84,111322),(85,121792),(86,133184),(87,145578),(88,159046),(89,173682),(90,189586),(91,206848),(92,225585),(93,245920),(94,267968),(95,291874),(96,317788),(97,345856),(98,376256),(99,409174),(100,444793)]
https://ideone.com/FZTUON
-}
630prime_132
2024/02/11(��) 22:48:07.67ID:kz7EJAxM expand ���Ă݂��B
(1+x^1)(1+x^2)(1+x^3) �c�c (1+x^100) �c�c =
1 + x + x^2 + 2 x^3 + 2 x^4 + 3 x^5
+ 4 x^6 + 5 x^7 + 6 x^8 + 8 x^9
+ 10 x^10 + 12 x^11 + 15 x^12 + 18 x^13 + 22 x^14 + 27 x^15
+ 32 x^16 + 38 x^17 + 46 x^18 + 54 x^19 + 64 x^20
+ 76 x^21 + 89 x^22 + 104 x^23 + 122 x^24 + 142 x^25
+ 165 x^26 + 192 x^27 + 222 x^28 + 256 x^29 + 296 x^30
+ 340 x^31 + 390 x^32 + 448 x^33 + 512 x^34 + 585 x^35
+ 668 x^36 + 760 x^37 + 864 x^38 + 982 x^39 + 1113 x^40
+ 1260 x^41 + 1426 x^42 + 1610 x^43 + 1816 x^44 + 2048 x^45
+ 2304 x^46 + 2590 x^47 + 2910 x^48 + 3264 x^49 + 3658 x^50
+ 4097 x^51 + 4582 x^52 + 5120 x^53 + 5718 x^54 + 6378 x^55
+ 7108 x^56 + 7917 x^57 + 8808 x^58 + 9792 x^59 + 10880 x^60
+ 12076 x^61 + 13394 x^62 + 14848 x^63 + 16444 x^64 + 18200 x^65
+ 20132 x^66 + 22250 x^67 + 24576 x^68 + 27130 x^69 + 29927 x^70
+ 32992 x^71 + 36352 x^72 + 40026 x^73 + 44046 x^74 + 48446 x^75
+ 53250 x^76 + 58499 x^77 + 64234 x^78 + 70488 x^79 + 77312 x^80
+ 84756 x^81 + 92864 x^82 + 101698 x^83 + 111322 x^84 + 121792 x^85
+ 133184 x^86 + 145578 x^87 + 159046 x^88 + 173682 x^89 + 189586 x^90
+ 206848 x^91 + 225585 x^92 + 245920 x^93 + 267968 x^94 + 291874 x^95
+ 317788 x^96 + 345856 x^97 + 376256 x^98 + 409174 x^99 + 444793 x^100
+ 483330 x^101 + �c�c
(1+x^1)(1+x^2)(1+x^3) �c�c (1+x^100) �c�c =
1 + x + x^2 + 2 x^3 + 2 x^4 + 3 x^5
+ 4 x^6 + 5 x^7 + 6 x^8 + 8 x^9
+ 10 x^10 + 12 x^11 + 15 x^12 + 18 x^13 + 22 x^14 + 27 x^15
+ 32 x^16 + 38 x^17 + 46 x^18 + 54 x^19 + 64 x^20
+ 76 x^21 + 89 x^22 + 104 x^23 + 122 x^24 + 142 x^25
+ 165 x^26 + 192 x^27 + 222 x^28 + 256 x^29 + 296 x^30
+ 340 x^31 + 390 x^32 + 448 x^33 + 512 x^34 + 585 x^35
+ 668 x^36 + 760 x^37 + 864 x^38 + 982 x^39 + 1113 x^40
+ 1260 x^41 + 1426 x^42 + 1610 x^43 + 1816 x^44 + 2048 x^45
+ 2304 x^46 + 2590 x^47 + 2910 x^48 + 3264 x^49 + 3658 x^50
+ 4097 x^51 + 4582 x^52 + 5120 x^53 + 5718 x^54 + 6378 x^55
+ 7108 x^56 + 7917 x^57 + 8808 x^58 + 9792 x^59 + 10880 x^60
+ 12076 x^61 + 13394 x^62 + 14848 x^63 + 16444 x^64 + 18200 x^65
+ 20132 x^66 + 22250 x^67 + 24576 x^68 + 27130 x^69 + 29927 x^70
+ 32992 x^71 + 36352 x^72 + 40026 x^73 + 44046 x^74 + 48446 x^75
+ 53250 x^76 + 58499 x^77 + 64234 x^78 + 70488 x^79 + 77312 x^80
+ 84756 x^81 + 92864 x^82 + 101698 x^83 + 111322 x^84 + 121792 x^85
+ 133184 x^86 + 145578 x^87 + 159046 x^88 + 173682 x^89 + 189586 x^90
+ 206848 x^91 + 225585 x^92 + 245920 x^93 + 267968 x^94 + 291874 x^95
+ 317788 x^96 + 345856 x^97 + 376256 x^98 + 409174 x^99 + 444793 x^100
+ 483330 x^101 + �c�c
631�P�R�Q�l�ڂ̑f������
2024/02/16(��) 12:36:59.72ID:gBb8bPRK ������ i = SQRT(-1) �Ȃ͓̂�����O�̂悤�ɗ������Ă�̂ł���
�l������ i, j, k �� = SQRT(-1) �Ȃ̂��H�Ƃ����^�₪�N���Ă܂�
i = j = k �ɂȂ��Ă��܂��̂�
�l������ i, j, k �� = SQRT(-1) �Ȃ̂��H�Ƃ����^�₪�N���Ă܂�
i = j = k �ɂȂ��Ă��܂��̂�
632�P�R�Q�l�ڂ̑f������
2024/02/16(��) 16:44:29.47ID:RXv22/cg xx = -1�@�������͉������� �}i, �}j, �}k �Ƃ������Ă��܂��B
�@ij=-ji=k, jk=-kj=i, ki=-ik=j,
�Ȃǂ�lj����Ă���`�I�ɂ͒�܂炸�A
����I�ɓ��ւ�����炵���B�B�B
�@ij=-ji=k, jk=-kj=i, ki=-ik=j,
�Ȃǂ�lj����Ă���`�I�ɂ͒�܂炸�A
����I�ɓ��ւ�����炵���B�B�B
2024/02/16(��) 16:58:46.75ID:EYC78kDg
�S�����̂̎����ȊO�̌��_��ʂ镽�ʂ�C�ӂɑI�ׂ��̕��ʏ�̂S�����̂̑S�͉̂��@�A��@�ŕ���̂� C �Ɠ��^�ɂȂ�B
���̒��� x^2 = -1 �̉�������o�Ă���̂łS�����̑S�̂� x^2 = -1 �̉��͖����ɂ���
���̒��� x^2 = -1 �̉�������o�Ă���̂łS�����̑S�̂� x^2 = -1 �̉��͖����ɂ���
634�P�R�Q�l�ڂ̑f������
2024/02/16(��) 23:06:29.67ID:Yc5qetyB F(1)��2
F(0)��0
F(-1)��-1/2
�Ŋ��炩�ŒP�������̊�F(x)���ā@
�ǂ�Ȃ̂����邩��❓
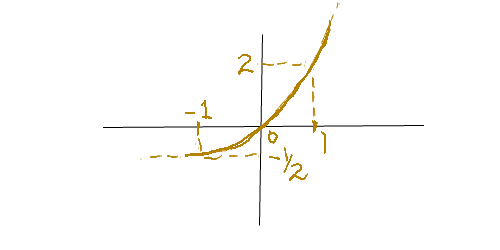
F(0)��0
F(-1)��-1/2
�Ŋ��炩�ŒP�������̊�F(x)���ā@
�ǂ�Ȃ̂����邩��❓

635634 50�������ȉ���
2024/02/17(�y) 04:40:39.70ID:7bH9ipgH y��1/(1-x)-1 but x<1
636634 70�_�ʎ��ȉ���
2024/02/17(�y) 04:55:27.52ID:7bH9ipgH 635���}�V�ȉ�������
y��3^x-1 but x��0��1�ߖT�Ȃ琳����
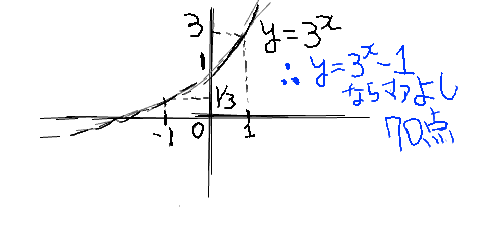
y��3^x-1 but x��0��1�ߖT�Ȃ琳����
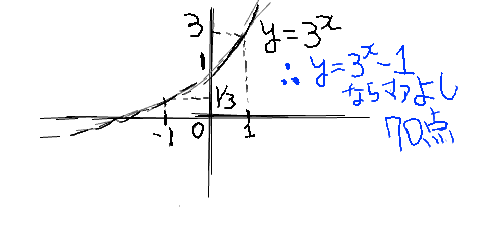
637634 100�_���_��100�_����
2024/02/17(�y) 05:23:29.93ID:7bH9ipgH >>634�́A�o��~�X�ɂ��Ă�
F(1)��2�@�ȁ@F(0)��0�@��
F(-1)��-2/3 �Ŋ��炩�ŒP�������̊�F(x)�͉�����❓
���Ă������ɂ���ւ���Ƃ�낵��💃
���G�����́A�L�j�V�i�C�ł�������
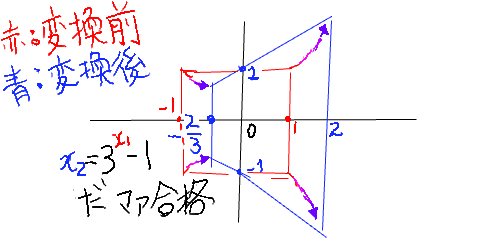
F(1)��2�@�ȁ@F(0)��0�@��
F(-1)��-2/3 �Ŋ��炩�ŒP�������̊�F(x)�͉�����❓
���Ă������ɂ���ւ���Ƃ�낵��💃
���G�����́A�L�j�V�i�C�ł�������

638634 ���͎��쎩��
2024/02/17(�y) 05:43:07.10ID:7bH9ipgH >>637��A��������ւ���Ȃ�A�ȉ��̂��G�����̔@��
F(1)��3�@�ȁ@F(0)��0�@��
F(-1)��-1/3 �Ŋ��炩�ŒP�������̊�F(x)�͉�����❓
���B�`�~�ɂ͂킩�邩��❓�@�|�N�͍��̓}�_�����B����
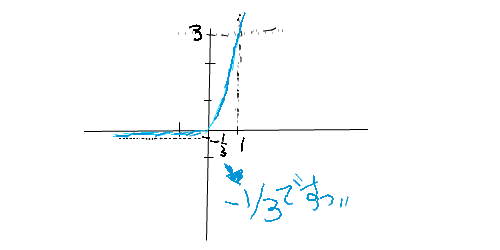
F(1)��3�@�ȁ@F(0)��0�@��
F(-1)��-1/3 �Ŋ��炩�ŒP�������̊�F(x)�͉�����❓
���B�`�~�ɂ͂킩�邩��❓�@�|�N�͍��̓}�_�����B����

639�P�R�Q�l�ڂ̑f������
2024/02/17(�y) 07:48:06.70ID:8mtp8YUT F(x) = 2(4^x - 1)/3,
����_�����H
����_�����H
640�P�R�Q�l�ڂ̑f������
2024/02/17(�y) 08:07:01.54ID:8mtp8YUT �� �̕⑫�B
c-1/2, c, c+2 �����䐔�Ɖ��肷���
�@0 = (c-1/2)(c+2) - cc = (3/2)c - 1,
���@c= 2/3.
c-1/2, c, c+2 �����䐔�Ɖ��肷���
�@0 = (c-1/2)(c+2) - cc = (3/2)c - 1,
���@c= 2/3.
641634
2024/02/17(�y) 09:06:11.98ID:7bH9ipgH >>639 ���肪�Ƃ��B���`�������w�̓|�N���V��😺
642�P�R�Q�l�ڂ̑f������
2024/02/17(�y) 14:33:37.24ID:BFuzaimu �����܂���A���N�ɂ��Ă̖��Ȃ�ł���
���Ԃ�O�p���̐ϕ��ŋ��߂���Ǝv����ł���������Ă����M�Ȃ�
�v�Z�̉���Ɖ����肢�v���܂�
���̒��ɂƂ��������ʁi�����l�j���H����2���Ԃ����ăT�C���J�[�u�̗l�ɂ������Əオ���ĉ�����Ɖ��肵�܂��i1���Ԍオ���_�ɂȂ�j
�āA2���Ԃ�����̌����l�̐ϕ��l��2000mg/dl�̏ꍇ�A�����l��Max�l�i1���Ԍ�Ɖ���j��
������ɂȂ�̂ł��傤���H�H
��i�T�C��x+1�jdx�H�H�H
2000=-cosx+x���炢���������̂ł����������璸�_�܂ł킩��Ȃ��Ȃ�܂���?
���Ԃ�O�p���̐ϕ��ŋ��߂���Ǝv����ł���������Ă����M�Ȃ�
�v�Z�̉���Ɖ����肢�v���܂�
���̒��ɂƂ��������ʁi�����l�j���H����2���Ԃ����ăT�C���J�[�u�̗l�ɂ������Əオ���ĉ�����Ɖ��肵�܂��i1���Ԍオ���_�ɂȂ�j
�āA2���Ԃ�����̌����l�̐ϕ��l��2000mg/dl�̏ꍇ�A�����l��Max�l�i1���Ԍ�Ɖ���j��
������ɂȂ�̂ł��傤���H�H
��i�T�C��x+1�jdx�H�H�H
2000=-cosx+x���炢���������̂ł����������璸�_�܂ł킩��Ȃ��Ȃ�܂���?
643642
2024/02/17(�y) 16:00:04.51ID:BFuzaimu �厖�Ȏ��A�����Y��܂���
�H���O�̌����l��90mg/dl�Ƃ��܂��B
�H����90mg/dl����オ����1���Ԍ��max�l�ɂȂ�
2���Ԍ��90mg/dl�ɖ߂�܂�
�H���O�̌����l��90mg/dl�Ƃ��܂��B
�H����90mg/dl����オ����1���Ԍ��max�l�ɂȂ�
2���Ԍ��90mg/dl�ɖ߂�܂�
644�P�R�Q�l�ڂ̑f������
2024/02/17(�y) 16:00:43.00ID:8mtp8YUT >>635
���p�o�Ȑ��Ƃ����
�@F(x) = 4x/(5-3x),
���Ȃ��B�@�@x<5/3 �Ɍ���ΒP�������B
�@�Q�ߐ��� x=5/3 �� y=-4/3.
�@�œ_ ( (5-2��10)/3, (2��10 -4)/3 ) ��
�@�@�@ ( (5+2��10)/3, (-2��10 -4)/3 )
���p�o�Ȑ��Ƃ����
�@F(x) = 4x/(5-3x),
���Ȃ��B�@�@x<5/3 �Ɍ���ΒP�������B
�@�Q�ߐ��� x=5/3 �� y=-4/3.
�@�œ_ ( (5-2��10)/3, (2��10 -4)/3 ) ��
�@�@�@ ( (5+2��10)/3, (-2��10 -4)/3 )
2024/02/17(�y) 16:06:08.67ID:/NEZa9so
���̍Ŗ��[�U�v�Z���Ă��[�����[�����Ă����
�v���O���~���O�ł͋����m��������ďd�Ȃ邱�Ƃ������
�v���O���~���O�̖��ƌ��������Ȃ���
�Ȃ��Ȃ��A�A�A
�v���O���~���O�ŋ�s��ׂ����A�A�A
�v���O���~���O�ł͋����m��������ďd�Ȃ邱�Ƃ������
�v���O���~���O�̖��ƌ��������Ȃ���
�Ȃ��Ȃ��A�A�A
�v���O���~���O�ŋ�s��ׂ����A�A�A
646�P�R�Q�l�ڂ̑f������
2024/02/17(�y) 16:44:45.64ID:MCx7mhXt ��w�ȍ~�̐��w�̒m�����Ȃ��Ɓu2�́�2�悪���z���ł��邱�Ɓv�������͍̂���Ƃ����܂���
�ł́A���Z���w�͈͓̔��Łu2�́�2�悪�������ł��邱�Ƃ��������Ɓv�͉\�Ȃ̂ł��傤���H
�ł́A���Z���w�͈͓̔��Łu2�́�2�悪�������ł��邱�Ƃ��������Ɓv�͉\�Ȃ̂ł��傤���H
647�P�R�Q�l�ڂ̑f������
2024/02/18(��) 15:51:57.95ID:zH+eIKQ1648�P�R�Q�l�ڂ̑f������
2024/02/18(��) 17:26:30.20ID:zH+eIKQ1 �� �̕⑫
3�_��ʂ�2������ x(5+3x)/4 �����ǁA
����� x<-1 �ł͒P�������ɂȂ�Ȃ��B������
�@F(x) = x(5+3x)/4 + k�x(x-1)(x+1)/4
�@�@�@= x(k�xx + 3x + 5-k)/4,
�Ƃ����Ă݂�B
F(x) ���P�������ƂȂ������
�@F '(x) = 0 ��2�̎����������Ȃ����ƁB
�@F '(x) = (3k�xx + 6x + 5-k)/4,
�@D = (3/2)^2 - 12k(5-k) �� 0,
�@0.69722436 < k < 4.30277564
�@k = 1, 2, 3, 4 �͂�������B
F(x) = x(xx+3x+4)/4,
F(x) = x(2xx+3x+3)/4,
F(x) = x(3xx+3x+2)/4,
F(x) = x(4xx+3x+2)/4,
3�_��ʂ�2������ x(5+3x)/4 �����ǁA
����� x<-1 �ł͒P�������ɂȂ�Ȃ��B������
�@F(x) = x(5+3x)/4 + k�x(x-1)(x+1)/4
�@�@�@= x(k�xx + 3x + 5-k)/4,
�Ƃ����Ă݂�B
F(x) ���P�������ƂȂ������
�@F '(x) = 0 ��2�̎����������Ȃ����ƁB
�@F '(x) = (3k�xx + 6x + 5-k)/4,
�@D = (3/2)^2 - 12k(5-k) �� 0,
�@0.69722436 < k < 4.30277564
�@k = 1, 2, 3, 4 �͂�������B
F(x) = x(xx+3x+4)/4,
F(x) = x(2xx+3x+3)/4,
F(x) = x(3xx+3x+2)/4,
F(x) = x(4xx+3x+2)/4,
650�P�R�Q�l�ڂ̑f������
2024/02/18(��) 20:48:38.08ID:zH+eIKQ1 �i�[���B
�Ǝ�l�͈����������u�قǁv�𗪂��čl���Ă���B
�@�@�@�@�@�@�Ėڟ��u��y�͔L�ł���v(1905-1906)
�@�@�@�@�@�@�@�� �O�̐�~�D�̐l
�Ǝ�l�͈����������u�قǁv�𗪂��čl���Ă���B
�@�@�@�@�@�@�Ėڟ��u��y�͔L�ł���v(1905-1906)
�@�@�@�@�@�@�@�� �O�̐�~�D�̐l
651�P�R�Q�l�ڂ̑f������
2024/02/19(��) 03:40:59.86ID:VbY3N27r ����634
�@F(x) = (3+5x)/4 - (3/4)k'{(k'+1)/(k'+xx) - 1}
(-1,-1/2) �� (1,2) ��ʂ钼�� y=(3+5x)/4 �� (0,0) ��ʂ�Ȃ��B
�����Ń��[�����c���z���������� (0,0) ���ʂ�悤�ɂ����B
F(x) �͒P������������AF '(x)=0 ��2�����������Ȃ��B
���@(557-40��157)/243 �� k' �� (557+40��157)/243,
�@�@0.229635541375 < k' < 4.35472659854
�@F(x) = (3+5x)/4 - (3/4)k'{(k'+1)/(k'+xx) - 1}
(-1,-1/2) �� (1,2) ��ʂ钼�� y=(3+5x)/4 �� (0,0) ��ʂ�Ȃ��B
�����Ń��[�����c���z���������� (0,0) ���ʂ�悤�ɂ����B
F(x) �͒P������������AF '(x)=0 ��2�����������Ȃ��B
���@(557-40��157)/243 �� k' �� (557+40��157)/243,
�@�@0.229635541375 < k' < 4.35472659854
652�P�R�Q�l�ڂ̑f������
2024/02/19(��) 12:11:36.41ID:VbY3N27r ����634
�@F(x) = (3+5x)/4 - (3/4){e^(1-xx) - 1}/(e-1),
(-1,-1/2) �� (1,2) ��ʂ钼�� y=(3+5x)/4 �� (0,0) ��ʂ�Ȃ��B
�����Ő��K���z���������� (0,0) ���ʂ�悤�ɂ����B
F '(x)=0 �͎����������Ȃ����� F(x) �͒P�������B
�@F(x) = (3+5x)/4 - (3/4){e^(1-xx) - 1}/(e-1),
(-1,-1/2) �� (1,2) ��ʂ钼�� y=(3+5x)/4 �� (0,0) ��ʂ�Ȃ��B
�����Ő��K���z���������� (0,0) ���ʂ�悤�ɂ����B
F '(x)=0 �͎����������Ȃ����� F(x) �͒P�������B
2024/02/19(��) 17:14:19.22ID:uwAjb1g9
���[�U���ɂ��ď����ꂽ�{���Ă���܂����H
�ǂ̕���̏��Ђ�T��������
���`�㐔���ȁH
�����m���Ă��狳���ĉ�����
�ǂ̕���̏��Ђ�T��������
���`�㐔���ȁH
�����m���Ă��狳���ĉ�����
654prime_132
2024/02/19(��) 23:52:04.75ID:VbY3N27r ���Ȃ�Â����ǁc
�ꏼ �M�F�u�p�b�L���O�̖��v,
�@�@���Z�~�����w���w100�̖��x, ���{�]�_�Ёi1984/Sept)
�@�@p.27-29
�ꏼ �M�F���s��w ������͌����� �u���^, No.676, p.1-4 (1988/Dec)
�X���[�� (���c �����)�u���̏[�U���v,
�@�w�T�C�G���X�x1984�N3����, ���o�T�C�G���X��
J.H.Conway - N.J.A.Sloane "Sphere packings, lattices and groups"
Springer-Verlag (1998)
N.J.A.Sloane, �gThe sphere-packing problem�h.
�@Documenta Mathematika 3, p.387–396. (1998)
�ꏼ �M�F�u�p�b�L���O�̖��v,
�@�@���Z�~�����w���w100�̖��x, ���{�]�_�Ёi1984/Sept)
�@�@p.27-29
�ꏼ �M�F���s��w ������͌����� �u���^, No.676, p.1-4 (1988/Dec)
�X���[�� (���c �����)�u���̏[�U���v,
�@�w�T�C�G���X�x1984�N3����, ���o�T�C�G���X��
J.H.Conway - N.J.A.Sloane "Sphere packings, lattices and groups"
Springer-Verlag (1998)
N.J.A.Sloane, �gThe sphere-packing problem�h.
�@Documenta Mathematika 3, p.387–396. (1998)
655�P�R�Q�l�ڂ̑f������
2024/02/20(��) 01:39:10.33ID:KeqwjEjH F(x) = {(x+1)^c - 1}/2,
�@�@�@x��-1 �ŒP�������B
�@�@c = log(5)/log(2) = 2.3219280948873623478703194294893901758648313930245806120547563958...
�@�@�@x��-1 �ŒP�������B
�@�@c = log(5)/log(2) = 2.3219280948873623478703194294893901758648313930245806120547563958...
656�P�R�Q�l�ڂ̑f������
2024/02/21(��) 01:59:32.02ID:dlGX9fRT �O�p��
�@F(x) = (5x+3)/4 - (3/8){1+cos(��x)},
�@F '(x) = 5/4 + (3��/8)sin(��x)
�@�@�@= 1.25 + 1.1781sin(��x)
�@�@�@�� 0.0719
�@F(x) = (5x+3)/4 - (3/8){1+cos(��x)},
�@F '(x) = 5/4 + (3��/8)sin(��x)
�@�@�@= 1.25 + 1.1781sin(��x)
�@�@�@�� 0.0719
657�P�R�Q�l�ڂ̑f������
2024/02/21(��) 14:50:23.94ID:dlGX9fRT �����`���g����?
�@F(x) = (5x+3)/4 - (3/4){(1/��2) + cos(3��x/4)}/(1/��2 + 1),
�@F '(x) = 5/4 + (3/4)(3��/4)sin(3��x/4)/(1/��2 + 1)
�@�@�@= 1.25 + 1.03517 sin(3��x/4)
�@�@�@�� 0.21483
�@F(x) = (5x+3)/4 - (3/4){(1/��2) + cos(3��x/4)}/(1/��2 + 1),
�@F '(x) = 5/4 + (3/4)(3��/4)sin(3��x/4)/(1/��2 + 1)
�@�@�@= 1.25 + 1.03517 sin(3��x/4)
�@�@�@�� 0.21483
2024/02/22(��) 13:50:54.38ID:wH5ypcTk
4���������̂��e�Z���N�g�Ƃ����̂͂킩�����̂ł���
5�����A6�����Ƒ��₵�Ă������Ƃ����ꂼ��̗����̖̂��O�͉��Ƃ����̂ł��傤���H
�Ȃ��O���������������璲�ׂ����v���܂���
5�����A6�����Ƒ��₵�Ă������Ƃ����ꂼ��̗����̖̂��O�͉��Ƃ����̂ł��傤���H
�Ȃ��O���������������璲�ׂ����v���܂���
659�P�R�Q�l�ڂ̑f������
2024/02/22(��) 16:47:10.78ID:I42Wi42C660�P�R�Q�l�ڂ̑f������
2024/02/24(�y) 01:15:57.45ID:V+z7u92t ��w�ȍ~�̐��w�̒m�����Ȃ��Ɓu2�́�2�悪���z���ł��邱�Ɓv�������͍̂���ƕ����܂���
�ł́A���Z���w�͈͓̔��Łu2�́�2�悪�������ł��邱�Ɓv�������͉̂\�Ȃ̂ł��傤���H
�ł́A���Z���w�͈͓̔��Łu2�́�2�悪�������ł��邱�Ɓv�������͉̂\�Ȃ̂ł��傤���H
2024/02/24(�y) 16:31:04.39ID:8e2wHLHp
[��1�i]�F2^{��2} ���㐔�I���ł���Ƃ���
a��2^{��2} �Ƃ���
���肩��Aa�͎����ł����āAa�͎����̑㐔�I���ł���
a��2^{��2} �Ƃ����Ă��邩�� log_|a|����2�~log|2| �ł���
����� a��2^{��2} ���� 2^{��2}��e^{��2�~log|2|} �����藧��
[��2�i]�F�Ƃ���ŁA1����2��3/2 ������ 2^{��2}��2^{3/2} �ł���
�܂� e��2 ���� log|2|��1 �ł����āA4/3����2��3/2 ������
log|2|��4/3����2�~log|2|��3/2�~log|2| ���� e^{��2�~log|2|}��e^{4/3} �ł���
����āA2^{��2}��e^{4/3} ��
[��3�i]�F�̂ɁAlog_2|e^{4/3}|����2 ���� log_2|e|��3/4�~��2 �ł����āA
e��2^{3/4�~��2} ���� 1��3/4�~��2�~log|2|�A���� e^{(2��2)/3}��2 �ł���
����āAe��3 ���� 3^{(2��2)/3}��2 �ł����āA3^{2��2}��8 ��
[��4�i]�F�������A3^{2��2}��3^2��9 ������A3^{2��2}��8 ������ꂽ���Ƃ�
3^{2��2}��8 �Ȃ邱�Ƃɔ����A��������
���̖����� 2^{��2} �����z���ł͂Ȃ��Ƃ������Ƃ��琶��������A
�w���@�ɂ�� 2^{��2} �͒��z���ł���
e�̋ߎ��l�� 2��e��3 �Ȃǂ̑召�W�͍��Z���w�͈̔͂̔�������A
���z���̒�`���������Ă���� 2^{��2} �̒��z����
���Z���w�͈̔͂Ŏ�����C�����Ȃ��ł��Ȃ����c
a��2^{��2} �Ƃ���
���肩��Aa�͎����ł����āAa�͎����̑㐔�I���ł���
a��2^{��2} �Ƃ����Ă��邩�� log_|a|����2�~log|2| �ł���
����� a��2^{��2} ���� 2^{��2}��e^{��2�~log|2|} �����藧��
[��2�i]�F�Ƃ���ŁA1����2��3/2 ������ 2^{��2}��2^{3/2} �ł���
�܂� e��2 ���� log|2|��1 �ł����āA4/3����2��3/2 ������
log|2|��4/3����2�~log|2|��3/2�~log|2| ���� e^{��2�~log|2|}��e^{4/3} �ł���
����āA2^{��2}��e^{4/3} ��
[��3�i]�F�̂ɁAlog_2|e^{4/3}|����2 ���� log_2|e|��3/4�~��2 �ł����āA
e��2^{3/4�~��2} ���� 1��3/4�~��2�~log|2|�A���� e^{(2��2)/3}��2 �ł���
����āAe��3 ���� 3^{(2��2)/3}��2 �ł����āA3^{2��2}��8 ��
[��4�i]�F�������A3^{2��2}��3^2��9 ������A3^{2��2}��8 ������ꂽ���Ƃ�
3^{2��2}��8 �Ȃ邱�Ƃɔ����A��������
���̖����� 2^{��2} �����z���ł͂Ȃ��Ƃ������Ƃ��琶��������A
�w���@�ɂ�� 2^{��2} �͒��z���ł���
e�̋ߎ��l�� 2��e��3 �Ȃǂ̑召�W�͍��Z���w�͈̔͂̔�������A
���z���̒�`���������Ă���� 2^{��2} �̒��z����
���Z���w�͈̔͂Ŏ�����C�����Ȃ��ł��Ȃ����c
662�P�R�Q�l�ڂ̑f������
2024/02/24(�y) 17:37:10.94ID:mfihncTu >>661
�Ȃ�ł����o�L�ڏ����Ă��
�Ȃ�ł����o�L�ڏ����Ă��
2024/02/24(�y) 18:03:01.67ID:8e2wHLHp
[��3�i]�F�̂ɁAlog_2|e^{4/3}|����2 ���� log_2|e|��3/4�~��2 �ł����āA
e��2^{3/4�~��2} ���� 1��3/4�~��2�~log|2|�A���� e^{(2��2)/3}��2 �ł���
����āAe^{2��2}��8 ��
[��4�i]�F�������Ae^{��2}��8^{1/2}��2��2 ������ e^{2��2}��8 �ł���
�̂ɁAe^{2��2}��8 ������ꂽ���Ƃ� e^{2��2}��8 �Ȃ邱�Ƃɔ����A��������
���̖����� 2^{��2} �����z���ł͂Ȃ��Ƃ������Ƃ��琶��������A
�w���@�ɂ�� 2^{��2} �͒��z���ł���
e��2^{3/4�~��2} ���� 1��3/4�~��2�~log|2|�A���� e^{(2��2)/3}��2 �ł���
����āAe^{2��2}��8 ��
[��4�i]�F�������Ae^{��2}��8^{1/2}��2��2 ������ e^{2��2}��8 �ł���
�̂ɁAe^{2��2}��8 ������ꂽ���Ƃ� e^{2��2}��8 �Ȃ邱�Ƃɔ����A��������
���̖����� 2^{��2} �����z���ł͂Ȃ��Ƃ������Ƃ��琶��������A
�w���@�ɂ�� 2^{��2} �͒��z���ł���
2024/02/24(�y) 18:04:34.49ID:8e2wHLHp
>>662
�ԈႦ���Ƃ���͒�������
�ԈႦ���Ƃ���͒�������
665�P�R�Q�l�ڂ̑f������
2024/02/24(�y) 18:27:40.03ID:mfihncTu2024/02/24(�y) 18:35:42.79ID:8e2wHLHp
2024/02/24(�y) 18:49:01.45ID:8e2wHLHp
��Q�� a��2^��2 ��n���̍ŏ����������l���Ă��A
���̎�����1�ł��邱�Ƃ͖��炩������A
���ǂ�a�̖������̏ؖ��ɋA������
���̎�����1�ł��邱�Ƃ͖��炩������A
���ǂ�a�̖������̏ؖ��ɋA������
2024/02/24(�y) 19:20:32.42ID:8e2wHLHp
>>668
�Q���t�H���g�E�V���i�C�_�[�̒藝�ɏ]���A�����͂Ȃ�Ȃ��Ƃ�������������
2^��2 �̖������̏ؖ������Z���w�͈̔͂ŏؖ����Ă��܂�Ȃ�
2^��2 ���݂��ɑf�Ȑ������g���ėL�����ŕ\���ċc�_���Ă����Ė������\��������
�Q���t�H���g�E�V���i�C�_�[�̒藝�ɏ]���A�����͂Ȃ�Ȃ��Ƃ�������������
2^��2 �̖������̏ؖ������Z���w�͈̔͂ŏؖ����Ă��܂�Ȃ�
2^��2 ���݂��ɑf�Ȑ������g���ėL�����ŕ\���ċc�_���Ă����Ė������\��������
670�P�R�Q�l�ڂ̑f������
2024/02/24(�y) 19:21:14.82ID:mfihncTu �����������u�ؖ��v
-------------------------------------------------------------------------------
[��1�i]�F2^{��2} �����z���ł���Ƃ���
a��2^{��2} �Ƃ���
���肩��Aa�͎����ł����āAa�͎����̒��z���ł���
a��2^{��2} �Ƃ����Ă��邩�� log_|a|����2�~log|2| �ł���
����� a��2^{��2} ���� 2^{��2}��e^{��2�~log|2|} �����藧��
[��2�i]�F�Ƃ���ŁA1����2��3/2 ������ 2^{��2}��2^{3/2} �ł���
�܂� e��2 ���� log|2|��1 �ł����āA4/3����2��3/2 ������
log|2|��4/3����2�~log|2|��3/2�~log|2| ���� e^{��2�~log|2|}��e^{4/3} �ł���
����āA2^{��2}��e^{4/3} ��
[��3�i]�F�̂ɁAlog_2|e^{4/3}|����2 ���� log_2|e|��3/4�~��2 �ł����āA
e��2^{3/4�~��2} ���� 1��3/4�~��2�~log|2|�A���� e^{(2��2)/3}��2 �ł���
����āAe^{2��2}��8 ��
[��4�i]�F�������Ae^{��2}��8^{1/2}��2��2 ������ e^{2��2}��8 �ł���
�̂ɁAe^{2��2}��8 ������ꂽ���Ƃ� e^{2��2}��8 �Ȃ邱�Ƃɔ����A��������
���̖����� 2^{��2} ���㐔�I���ł͂Ȃ��Ƃ������Ƃ��琶��������A
�w���@�ɂ�� 2^{��2} �͑㐔�I���ł���
-------------------------------------------------------------------------------
[��1�i]�F2^{��2} �����z���ł���Ƃ���
a��2^{��2} �Ƃ���
���肩��Aa�͎����ł����āAa�͎����̒��z���ł���
a��2^{��2} �Ƃ����Ă��邩�� log_|a|����2�~log|2| �ł���
����� a��2^{��2} ���� 2^{��2}��e^{��2�~log|2|} �����藧��
[��2�i]�F�Ƃ���ŁA1����2��3/2 ������ 2^{��2}��2^{3/2} �ł���
�܂� e��2 ���� log|2|��1 �ł����āA4/3����2��3/2 ������
log|2|��4/3����2�~log|2|��3/2�~log|2| ���� e^{��2�~log|2|}��e^{4/3} �ł���
����āA2^{��2}��e^{4/3} ��
[��3�i]�F�̂ɁAlog_2|e^{4/3}|����2 ���� log_2|e|��3/4�~��2 �ł����āA
e��2^{3/4�~��2} ���� 1��3/4�~��2�~log|2|�A���� e^{(2��2)/3}��2 �ł���
����āAe^{2��2}��8 ��
[��4�i]�F�������Ae^{��2}��8^{1/2}��2��2 ������ e^{2��2}��8 �ł���
�̂ɁAe^{2��2}��8 ������ꂽ���Ƃ� e^{2��2}��8 �Ȃ邱�Ƃɔ����A��������
���̖����� 2^{��2} ���㐔�I���ł͂Ȃ��Ƃ������Ƃ��琶��������A
�w���@�ɂ�� 2^{��2} �͑㐔�I���ł���
671�P�R�Q�l�ڂ̑f������
2024/02/24(�y) 22:20:27.85ID:V+z7u92t >>670
�u�w���@�ɂ�� 2^{��2} �͑㐔�I���ł���v�Ƃ��邪
2^{��2} �̓Q���t�H���g�E�V���i�C�_�[�̒藝��蒴�z���ł��邱�Ƃ��������Ă���̂�
���̏ؖ��͌���Ă���
�u�w���@�ɂ�� 2^{��2} �͑㐔�I���ł���v�Ƃ��邪
2^{��2} �̓Q���t�H���g�E�V���i�C�_�[�̒藝��蒴�z���ł��邱�Ƃ��������Ă���̂�
���̏ؖ��͌���Ă���
672�P�R�Q�l�ڂ̑f������
2024/02/24(�y) 22:23:38.33ID:V+z7u92t2024/02/25(��) 02:18:44.81ID:yxgjgyBu
>>670
>>673
�R�s�y�����ؖ����Ԉ���Ă���
[��1�i]�F2^{��2} ���㐔�I���ł���Ƃ���
a��2^{��2} �Ƃ���
���肩��Aa�͎����ł����āAa�͎����̑㐔�I���ł���
a��2^{��2} �Ƃ����Ă��邩�� log|a|����2�~log|2| �ł���
����� a��2^{��2} ���� 2^{��2}��e^{��2�~log|2|} �����藧��
[��2�i]�F�Ƃ���ŁA1����2��3/2 ������ 2^{��2}��2^{3/2} �ł���
�܂� e��2 ���� log|2|��1 �ł����āA4/3����2��3/2 ������
log|2|��4/3����2�~log|2|��3/2�~log|2| ���� e^{��2�~log|2|}��e^{4/3} �ł���
����āA2^{��2}��e^{4/3} ��
[��3�i]�F�̂ɁAlog_2|e^{4/3}|����2 ���� log_2|e|��3/4�~��2 �ł����āA
e��2^{3/4�~��2} ���� 1��3/4�~��2�~log|2|�A���� e^{(2��2)/3}��2 �ł���
����āAe^{2��2}��8 ��
[��4�i]�F�������Ae^{��2}��8^{1/2}��2��2 ������ e^{2��2}��8 �ł���
�̂ɁAe^{2��2}��8 ������ꂽ���Ƃ� e^{2��2}��8 �Ȃ邱�Ƃɔ����A��������
���̖����� 2^{��2} ��㐔�I���Ɖ��肵�����Ƃ��琶��������A
�w���@�ɂ�� 2^{��2} �͒��z���ł���
�W��A�� A��{2^x| x�͑㐔�I������ } �ƒ�`����A
A�͋�� [0�A+��) ��̃��x�[�O���x�Ɋւ����W���ł���
���l�ɁA�����̑㐔�I���S�̂̏W��B��
��� (-���A+��) ��̃��x�[�O���x�Ɋւ����W���ł���
2^{��2} ��㐔�I���Ɖ��肷��ƁA������2�̗�W��A�AB���
�c�_���Ă����Ė�����������悤�ɂȂ��Ă��邩��A������
>>673
�R�s�y�����ؖ����Ԉ���Ă���
[��1�i]�F2^{��2} ���㐔�I���ł���Ƃ���
a��2^{��2} �Ƃ���
���肩��Aa�͎����ł����āAa�͎����̑㐔�I���ł���
a��2^{��2} �Ƃ����Ă��邩�� log|a|����2�~log|2| �ł���
����� a��2^{��2} ���� 2^{��2}��e^{��2�~log|2|} �����藧��
[��2�i]�F�Ƃ���ŁA1����2��3/2 ������ 2^{��2}��2^{3/2} �ł���
�܂� e��2 ���� log|2|��1 �ł����āA4/3����2��3/2 ������
log|2|��4/3����2�~log|2|��3/2�~log|2| ���� e^{��2�~log|2|}��e^{4/3} �ł���
����āA2^{��2}��e^{4/3} ��
[��3�i]�F�̂ɁAlog_2|e^{4/3}|����2 ���� log_2|e|��3/4�~��2 �ł����āA
e��2^{3/4�~��2} ���� 1��3/4�~��2�~log|2|�A���� e^{(2��2)/3}��2 �ł���
����āAe^{2��2}��8 ��
[��4�i]�F�������Ae^{��2}��8^{1/2}��2��2 ������ e^{2��2}��8 �ł���
�̂ɁAe^{2��2}��8 ������ꂽ���Ƃ� e^{2��2}��8 �Ȃ邱�Ƃɔ����A��������
���̖����� 2^{��2} ��㐔�I���Ɖ��肵�����Ƃ��琶��������A
�w���@�ɂ�� 2^{��2} �͒��z���ł���
�W��A�� A��{2^x| x�͑㐔�I������ } �ƒ�`����A
A�͋�� [0�A+��) ��̃��x�[�O���x�Ɋւ����W���ł���
���l�ɁA�����̑㐔�I���S�̂̏W��B��
��� (-���A+��) ��̃��x�[�O���x�Ɋւ����W���ł���
2^{��2} ��㐔�I���Ɖ��肷��ƁA������2�̗�W��A�AB���
�c�_���Ă����Ė�����������悤�ɂȂ��Ă��邩��A������
675�P�R�Q�l�ڂ̑f������
2024/02/25(��) 02:44:54.60ID:f53st12k >>674
�ԈႢ
�ԈႢ
2024/02/25(��) 02:51:55.98ID:yxgjgyBu
>>675
2^{��2} ��㐔�I���Ɖ��肷��� A��B �����藧����A��W��A��ŋc�_���Ė�����
2^{��2} ��㐔�I���Ɖ��肷��� A��B �����藧����A��W��A��ŋc�_���Ė�����
2024/02/25(��) 03:18:08.69ID:yxgjgyBu
A��B �� 2^{��2}��A��B
��W��A�� �� ��W�� A��B ��
��W��A�� �� ��W�� A��B ��
2024/02/25(��) 03:27:26.35ID:yxgjgyBu
>>672
���������������Z���ɏo���͎̂~�߂���������
�����A�o�肵�Ă������ł���l�͖w�ǂ��Ȃ��Ǝv��
���������ؖ�����ɂ��Ă��A��@�I�Ɨ��̒m���͗v����
���������������Z���ɏo���͎̂~�߂���������
�����A�o�肵�Ă������ł���l�͖w�ǂ��Ȃ��Ǝv��
���������ؖ�����ɂ��Ă��A��@�I�Ɨ��̒m���͗v����
679�P�R�Q�l�ڂ̑f������
2024/02/25(��) 12:31:59.03ID:Ettcwn1v �A���������Ŏ���ł�
1�P�O�O�~�̂��1��100�~�̗���10��1000�~�������܂���
��Ɨ��͂����w�����ꂽ�ł��傤
���ĂȂ����Ƃ���������10�ʂ肠��Ǝv����ł����ǎ���������0�łłĂ����Ⴂ�܂�
���������Ԉ���Ă��ł��傤��
1�P�O�O�~�̂��1��100�~�̗���10��1000�~�������܂���
��Ɨ��͂����w�����ꂽ�ł��傤
���ĂȂ����Ƃ���������10�ʂ肠��Ǝv����ł����ǎ���������0�łłĂ����Ⴂ�܂�
���������Ԉ���Ă��ł��傤��
680�P�R�Q�l�ڂ̑f������
2024/02/25(��) 12:45:36.60ID:GlKsqPxK ����������Ȃ��Ƃ�1�͔����Ă�Ȃ�A9�ʂ�H
681�P�R�Q�l�ڂ̑f������
2024/02/25(��) 14:35:34.45ID:GlKsqPxK ���̓i�V�ł��������A����Ȃ��͖̂������H
����Ȃ� 10�ʂ�c
����Ȃ� 10�ʂ�c
2024/02/25(��) 14:45:43.90ID:gJoC49sx
683�P�R�Q�l�ڂ̑f������
2024/02/25(��) 14:58:27.46ID:r3jtDAq3 >>659
�o�Ȑ� (�Ό�)
�Q�ߐ��́@y = -2/3�@�Ɓ@y = m�x - 2/3,�@(m=5/2).
�œ_ ( �}(8/15)��(2��29)�sin(��/2), -(2/3) �� (8/15)��(2��29)�cos(��/2) )
�@= ( �}(4/15)��(��29 - 2), -(2/3) �� (4/15)��(��29 + 2) )
�����Ɂ@�� = arctan(m),
�o�Ȑ� (�Ό�)
�Q�ߐ��́@y = -2/3�@�Ɓ@y = m�x - 2/3,�@(m=5/2).
�œ_ ( �}(8/15)��(2��29)�sin(��/2), -(2/3) �� (8/15)��(2��29)�cos(��/2) )
�@= ( �}(4/15)��(��29 - 2), -(2/3) �� (4/15)��(��29 + 2) )
�����Ɂ@�� = arctan(m),
684�U�V�Q
2024/02/27(��) 10:54:20.18ID:1guH9Us72024/02/28(��) 06:56:21.78ID:ijdyqSaZ
>>684
2^{��2} ���㐔�I���ł���Ƃ���
a��2^{��2} �Ƃ���
a�͎����̑㐔�I���ł���
�w���� y��2^x �͒P�������Ő��̒l����邩��A
���肩�� a��2 �ł����āAa^2��4 ��
�܂��A���肩�� a^{��2}��2^2��4 �ł����āA(1/a)^{��2}��1/4 �ł���
a��1 ����w���� y��(1/a)^x �͒P�������Ő��̒l����邩��A1/a��1/4 �ł���
����āA4��a��2 �ł����āA2��a����a����2 ���� 4��a^2��a��2 �ł���
�̂ɁAa^2��4 �� a^2��4 ���������A�����̑召�W�ɔ���������������
���̖����͎��� 2^{��2} ��㐔�I���Ɖ��肵�����Ƃ���A2^{��2} �͎����̒��z���ł���
�����̒��z���͖�����������A2^{��2} �͖������ł���
���X�����A�L����(�܂��͎����̑㐔�I��)���f�������g���A���������ؖ��͂���
2^{��2} ���㐔�I���ł���Ƃ���
a��2^{��2} �Ƃ���
a�͎����̑㐔�I���ł���
�w���� y��2^x �͒P�������Ő��̒l����邩��A
���肩�� a��2 �ł����āAa^2��4 ��
�܂��A���肩�� a^{��2}��2^2��4 �ł����āA(1/a)^{��2}��1/4 �ł���
a��1 ����w���� y��(1/a)^x �͒P�������Ő��̒l����邩��A1/a��1/4 �ł���
����āA4��a��2 �ł����āA2��a����a����2 ���� 4��a^2��a��2 �ł���
�̂ɁAa^2��4 �� a^2��4 ���������A�����̑召�W�ɔ���������������
���̖����͎��� 2^{��2} ��㐔�I���Ɖ��肵�����Ƃ���A2^{��2} �͎����̒��z���ł���
�����̒��z���͖�����������A2^{��2} �͖������ł���
���X�����A�L����(�܂��͎����̑㐔�I��)���f�������g���A���������ؖ��͂���
2024/02/28(��) 07:04:49.78ID:GD05aVNN
>>685
�ԈႢ
�ԈႢ
2024/02/28(��) 07:15:42.22ID:ijdyqSaZ
2024/02/28(��) 07:22:01.52ID:ijdyqSaZ
>>686
�����_�̗L�������f������������Ȃ��l�ԂɊԈႢ���Ĕ��肳�ꂽ���Ȃ�
�����_�̗L�������f������������Ȃ��l�ԂɊԈႢ���Ĕ��肳�ꂽ���Ȃ�
2024/02/28(��) 07:49:43.06ID:ijdyqSaZ
>���̖����͎��� 2^{��2} ��㐔�I���Ɖ��肵�����Ƃ���
>�u����������v�A2^{��2} �͎����̒��z���ł���
>�u����������v�A2^{��2} �͎����̒��z���ł���
2024/02/28(��) 07:52:16.12ID:ijdyqSaZ
>>684
2^{��2} ���㐔�I���ł���Ƃ���
a��2^{��2} �Ƃ���
a�͎����̑㐔�I���ł���
�w���� y��2^x �͒P�������Ő��̒l����邩��A
���肩�� a��2 �ł����āAa^2��4 ��
�܂��A���肩�� a^{��2}��2^2��4 �ł����āA(1/a)^{��2}��1/4 �ł���
a��1 ����w���� y��(1/a)^x �͒P�������Ő��̒l����邩��A1/a��1/4 �ł���
����āA4��a��2 �ł����āA2��a����a����2 ���� 4��a^2��a��2 �ł���
�̂ɁAa^2��4 �� a^2��4 ���������A�����̑召�W�ɔ���������������
���̖����͎��� 2^{��2} ��㐔�I���Ɖ��肵�����Ƃ���
����������A2^{��2} �͎����̒��z���ł���
�����̒��z���͖�����������A2^{��2} �͖������ł���
2^{��2} ���㐔�I���ł���Ƃ���
a��2^{��2} �Ƃ���
a�͎����̑㐔�I���ł���
�w���� y��2^x �͒P�������Ő��̒l����邩��A
���肩�� a��2 �ł����āAa^2��4 ��
�܂��A���肩�� a^{��2}��2^2��4 �ł����āA(1/a)^{��2}��1/4 �ł���
a��1 ����w���� y��(1/a)^x �͒P�������Ő��̒l����邩��A1/a��1/4 �ł���
����āA4��a��2 �ł����āA2��a����a����2 ���� 4��a^2��a��2 �ł���
�̂ɁAa^2��4 �� a^2��4 ���������A�����̑召�W�ɔ���������������
���̖����͎��� 2^{��2} ��㐔�I���Ɖ��肵�����Ƃ���
����������A2^{��2} �͎����̒��z���ł���
�����̒��z���͖�����������A2^{��2} �͖������ł���
691�P�R�Q�l�ڂ̑f������
2024/02/28(��) 08:47:58.92ID:GD05aVNN 2^{3/2} ���㐔�I���ł���Ƃ���
a��2^{3/2} �Ƃ���
a�͎����̑㐔�I���ł���
�w���� y��2^x �͒P�������Ő��̒l����邩��A
���肩�� a��2 �ł����āAa^2��4 ��
�܂��A���肩�� a^{2/(3/2)}��2^2��4 �ł����āA(1/a)^{2/(3/2)}��1/4 �ł���
a��1 ����w���� y��(1/a)^x �͒P�������Ő��̒l����邩��A1/a��1/4 �ł���
����āA4��a��2 �ł����āA2��a����a����2 ���� 4��a^2��a��2 �ł���
�̂ɁAa^2��4 �� a^2��4 ���������A�����̑召�W�ɔ���������������
���̖����͎��� 2^{3/2} ��㐔�I���Ɖ��肵�����Ƃ���
����������A2^{3/2} �͎����̒��z���ł���
a��2^{3/2} �Ƃ���
a�͎����̑㐔�I���ł���
�w���� y��2^x �͒P�������Ő��̒l����邩��A
���肩�� a��2 �ł����āAa^2��4 ��
�܂��A���肩�� a^{2/(3/2)}��2^2��4 �ł����āA(1/a)^{2/(3/2)}��1/4 �ł���
a��1 ����w���� y��(1/a)^x �͒P�������Ő��̒l����邩��A1/a��1/4 �ł���
����āA4��a��2 �ł����āA2��a����a����2 ���� 4��a^2��a��2 �ł���
�̂ɁAa^2��4 �� a^2��4 ���������A�����̑召�W�ɔ���������������
���̖����͎��� 2^{3/2} ��㐔�I���Ɖ��肵�����Ƃ���
����������A2^{3/2} �͎����̒��z���ł���
2024/02/28(��) 10:27:53.48ID:ijdyqSaZ
>>691
2^{3/2} ���㐔�I���ł��邱�Ƃ͊m�肵�Ă��邩�� 2^{3/2} �ɂ��̘_�@�͒ʗp���Ȃ�
�����I�ɂ́A�����_�ł͗L�����̉����揜�����Ƃɖ��������`���ėL������Q������������̂Ɠ��l�ɁA
�����̑㐔�I���̉����揜�����ƂɎ����̒��z�����`���Ď����̑㐔�I���̑S�̂��������o����
���̌�A�����ɂ��Ĕ����ϕ���W�J���Ă����Ƃ������_�W�J�������I�ɂ͏o����
���̍l���������p��������
2^{3/2} ���㐔�I���ł��邱�Ƃ͊m�肵�Ă��邩�� 2^{3/2} �ɂ��̘_�@�͒ʗp���Ȃ�
�����I�ɂ́A�����_�ł͗L�����̉����揜�����Ƃɖ��������`���ėL������Q������������̂Ɠ��l�ɁA
�����̑㐔�I���̉����揜�����ƂɎ����̒��z�����`���Ď����̑㐔�I���̑S�̂��������o����
���̌�A�����ɂ��Ĕ����ϕ���W�J���Ă����Ƃ������_�W�J�������I�ɂ͏o����
���̍l���������p��������
2024/02/28(��) 10:38:28.88ID:ijdyqSaZ
>>691
���ӂ��Ă������ǁA2^{3/2}��2��2 ��
�L������Q�� ��2 ��Y�������㐔�g��� Q(��2) �ɑ����A
Q(��2) �͒��z�g��̂ł͂Ȃ�
���ӂ��Ă������ǁA2^{3/2}��2��2 ��
�L������Q�� ��2 ��Y�������㐔�g��� Q(��2) �ɑ����A
Q(��2) �͒��z�g��̂ł͂Ȃ�
694�P�R�Q�l�ڂ̑f������
2024/02/28(��) 10:40:05.03ID:y7FRk2+2 �����O������Ȃ��˂����ݎĂ�����
��~�����������ĂȂ�
��~�����������ĂȂ�
695�P�R�Q�l�ڂ̑f������
2024/02/28(��) 10:43:09.56ID:GD05aVNN2024/02/28(��) 10:45:05.76ID:ijdyqSaZ
>>694
�������������ϕ��̗��_�W�J�������I�ɂ͏o���邩��A�{�ł��ǂ�ł悭�l���Ă݂�
�������������ϕ��̗��_�W�J�������I�ɂ͏o���邩��A�{�ł��ǂ�ł悭�l���Ă݂�
697�P�R�Q�l�ڂ̑f������
2024/02/28(��) 10:49:14.50ID:GD05aVNN 1<r<2�̂Ƃ�2^{r} ���㐔�I���ł���Ƃ���
a��2^{r} �Ƃ���
a�͎����̑㐔�I���ł���
�w���� y��2^x �͒P�������Ő��̒l����邩��A
���肩�� a��2 �ł����āAa^2��4 ��
�܂��A���肩�� a^{2/r}��2^2��4 �ł����āA(1/a)^{2/r}��1/4 �ł���
a��1 ����w���� y��(1/a)^x �͒P�������Ő��̒l����邩��A1/a��1/4 �ł���
����āA4��a��2 �ł����āA2��a����a����2 ���� 4��a^2��a��2 �ł���
�̂ɁAa^2��4 �� a^2��4 ���������A�����̑召�W�ɔ���������������
���̖����͎��� 2^{r} ��㐔�I���Ɖ��肵�����Ƃ���
����������A2^{r} �͎����̒��z���ł���
a��2^{r} �Ƃ���
a�͎����̑㐔�I���ł���
�w���� y��2^x �͒P�������Ő��̒l����邩��A
���肩�� a��2 �ł����āAa^2��4 ��
�܂��A���肩�� a^{2/r}��2^2��4 �ł����āA(1/a)^{2/r}��1/4 �ł���
a��1 ����w���� y��(1/a)^x �͒P�������Ő��̒l����邩��A1/a��1/4 �ł���
����āA4��a��2 �ł����āA2��a����a����2 ���� 4��a^2��a��2 �ł���
�̂ɁAa^2��4 �� a^2��4 ���������A�����̑召�W�ɔ���������������
���̖����͎��� 2^{r} ��㐔�I���Ɖ��肵�����Ƃ���
����������A2^{r} �͎����̒��z���ł���
2024/02/28(��) 10:58:51.29ID:ijdyqSaZ
�L������Q�Ɏ����̒��z��e��Y���������z�g��� Q(e) �̉����揜�����Ƃ�
���z�����`���� Q(e) �����������邱�Ƃ͌����I�ɂ͏o���邪�A
���̂Ƃ��͒��z�g��� Q(e) ������������O�Ɏ����̒��z��e�����Ɋ܂܂�Ă���̂ŁA
�� Q(e) ������������������ϕ��𗝘_�W�J����
����z���������̂ɉ��p���邱�Ƃ͈�ʂɂ͏o���Ȃ�
���z�����`���� Q(e) �����������邱�Ƃ͌����I�ɂ͏o���邪�A
���̂Ƃ��͒��z�g��� Q(e) ������������O�Ɏ����̒��z��e�����Ɋ܂܂�Ă���̂ŁA
�� Q(e) ������������������ϕ��𗝘_�W�J����
����z���������̂ɉ��p���邱�Ƃ͈�ʂɂ͏o���Ȃ�
2024/02/28(��) 11:00:39.05ID:ijdyqSaZ
2024/02/28(��) 11:07:41.61ID:ijdyqSaZ
>>698�Ɠ��l�Ȃ��Ƃ́A��ʂɎ�����R�̕����̂Ȃ钴�z�g��̂ɂ��Ă�����
2024/02/28(��) 12:22:15.14ID:ijdyqSaZ
2024/02/28(��) 14:00:54.59ID:y7FRk2+2
��������>>691�̌����Ă鎖�������ł��ĂȂ����_�Ő��wA���痝���ł��ĂȂ��B
���wA�̎��_�Ŏ������������ڂ�Ă邱�Ƃ��痝���ł���m�\���Ȃ��B
���wA�̎��_�Ŏ������������ڂ�Ă邱�Ƃ��痝���ł���m�\���Ȃ��B
2024/02/28(��) 16:02:47.38ID:ijdyqSaZ
2024/02/28(��) 16:26:43.49ID:y7FRk2+2
���wA�ŗ������ڂ�Ă�l�Ԃ���w�̔��ς̋c�_�ł���͂��Ȃ����
����ȃ��x���̘b���痝���ł���m�\���Ȃ���B
����ȃ��x���̘b���痝���ł���m�\���Ȃ���B
2024/02/28(��) 16:33:55.99ID:ijdyqSaZ
>>704
���Z�̔����ϕ��Ƒ�w�̔����ϕ����������Ǝv�������ԈႢ
���Z�̔����ϕ��ł͎����_���I���ςɊ�Â��Ă��ĞB�������A
��w�̔����ϕ��ł͊I���ςɊ�Â��������_������
���Z�̔����ϕ��Ƒ�w�̔����ϕ����������Ǝv�������ԈႢ
���Z�̔����ϕ��ł͎����_���I���ςɊ�Â��Ă��ĞB�������A
��w�̔����ϕ��ł͊I���ςɊ�Â��������_������
2024/02/28(��) 16:36:51.96ID:ijdyqSaZ
>>704
���A���Z�̔����ϕ��ł̓�-�_�@�����Ă��Ȃ�����
���A���Z�̔����ϕ��ł̓�-�_�@�����Ă��Ȃ�����
2024/02/28(��) 17:07:59.85ID:y7FRk2+2
�܂����Ƃ�������
�����̎����I�̓V�˂Ƃł��v���Ă����
���Z���w�̎��_�ŗ������ڂ�Ă�S�~
�����̎����I�̓V�˂Ƃł��v���Ă����
���Z���w�̎��_�ŗ������ڂ�Ă�S�~
708�P�R�Q�l�ڂ̑f������
2024/02/28(��) 17:12:39.85ID:GD05aVNN �w�E���������悤�Ȃ̂ŊȒP��
4��a��2����2��a�͏o�Ȃ�
4��a��2����2��a�͏o�Ȃ�
2024/02/28(��) 17:16:40.16ID:ijdyqSaZ
>>707
���Z���w�͌v�Z���唼���߂Ă��Ę_���I�ɞB���ȕ��������邩��
��w���w�𗝉�����̂ɍ��Z���w���������藝������K�v�͂Ȃ�
���Z�̎����_�́A�A���Ȑ������̊I���ςɊ�Â��Ă��邩��B���ł���
���Z���w�͌v�Z���唼���߂Ă��Ę_���I�ɞB���ȕ��������邩��
��w���w�𗝉�����̂ɍ��Z���w���������藝������K�v�͂Ȃ�
���Z�̎����_�́A�A���Ȑ������̊I���ςɊ�Â��Ă��邩��B���ł���
2024/02/28(��) 17:30:14.99ID:ijdyqSaZ
2024/02/28(��) 17:31:33.37ID:y7FRk2+2
���Ƃ������ƈꏏ
�����炭�����Ȃ���
���Ȃ��Ƃ����Z�̒i�K����m�\�̌��オ�~�܂��Ă���
�����ƑO��������Ȃ���
�����炭�����Ȃ���
���Ȃ��Ƃ����Z�̒i�K����m�\�̌��オ�~�܂��Ă���
�����ƑO��������Ȃ���
2024/02/28(��) 17:32:05.91ID:ijdyqSaZ
2024/02/28(��) 17:34:57.36ID:ijdyqSaZ
714�P�R�Q�l�ڂ̑f������
2024/02/28(��) 17:58:47.43ID:GD05aVNN >>710
�w���@�ŏؖ�����Ȃ牼����g���Ė������Ȃ���ł��Ȃ����Ă������{�I�Ȏw�E����
�w���@�ŏؖ�����Ȃ牼����g���Ė������Ȃ���ł��Ȃ����Ă������{�I�Ȏw�E����
715�P�R�Q�l�ڂ̑f������
2024/02/28(��) 17:59:46.40ID:GD05aVNN >>713
�������ĂȂ�
�������ĂȂ�
2024/02/28(��) 18:09:45.25ID:ijdyqSaZ
718�P�R�Q�l�ڂ̑f������
2024/02/28(��) 20:36:15.10ID:rXTULRav �y�f�R�z�[���z�@�k�C���Ɂ@�M�����l��p�L�@�Z��X
https://mao.5ch.net/test/read.cgi/build/1709004231/l50

https://mao.5ch.net/test/read.cgi/build/1709004231/l50

719�P�R�Q�l�ڂ̑f������
2024/02/28(��) 23:16:32.58ID:9tUy1VVA ����������wwwwwww
2024/02/29(��) 02:10:14.79ID:f0/HMLwN
2024/02/29(��) 02:12:10.41ID:f0/HMLwN
2024/02/29(��) 02:18:07.65ID:f0/HMLwN
>>717
�����̑㐔�I���̑S�̂��Ȃ��̂�������̒��z�����`����
�����_���ēW�J����Ƃ��͍ŏ��������̎�����
�f�B�I�t�@���^�X�ߎ��Ȃǂ��g���K�v�������āA
�L�������疳�������`���������_�Ƃ͗l�����S���Ⴄ
�����̑㐔�I���̑S�̂��Ȃ��̂�������̒��z�����`����
�����_���ēW�J����Ƃ��͍ŏ��������̎�����
�f�B�I�t�@���^�X�ߎ��Ȃǂ��g���K�v�������āA
�L�������疳�������`���������_�Ƃ͗l�����S���Ⴄ
2024/02/29(��) 02:49:35.18ID:f0/HMLwN
>>674�ł͏W�� A��{a^x| x�͑㐔�I�������Aa��1���傫���㐔�I�� } ��
�����̑㐔�I���̑S�̂��Ȃ���B�̋��ʕ��� A��B ����W���ł��邱�Ƃ���������������
�����̑㐔�I���̑S�̂��Ȃ���B�̋��ʕ��� A��B ����W���ł��邱�Ƃ���������������
2024/02/29(��) 03:02:44.91ID:f0/HMLwN
�����̑㐔�I���̑S�̂��Ȃ��̂�������̒��z�����`����
�����_���ēW�J���Ĕ����ϕ��̗��_���ēW�J���Ă��A
���̍ēW�J���������ϕ��͏]���̔����ϕ��Ɩw�Ǔ����ŁA
�ēW�J���������ϕ��ɂ͖w�ǎg�������Ȃ��Ӗ��͖w�ǂȂ����낤����A
>>674�ł͌��ʂ���������ď�����
�����_���ēW�J���Ĕ����ϕ��̗��_���ēW�J���Ă��A
���̍ēW�J���������ϕ��͏]���̔����ϕ��Ɩw�Ǔ����ŁA
�ēW�J���������ϕ��ɂ͖w�ǎg�������Ȃ��Ӗ��͖w�ǂȂ����낤����A
>>674�ł͌��ʂ���������ď�����
2024/02/29(��) 05:20:02.57ID:KWhjrVeT
4/3=1.3333333333<0.9802581434=sqrt(2)log(2).
2024/02/29(��) 10:42:57.75ID:f0/HMLwN
[��1�i]�F�W��A�� A��{a^x| x�͑㐔�I�������Aa��1���傫�������̑㐔�I�� }
�ƒ�`����BB�������̑㐔�I���̑S�̂��Ȃ��̂ƒ�`����
�W��A�Ƒ�B�̋��ʕ��� A��B �ɂ��āAA��B��∅ �Ɖ��肷��
�W��A�Ƒ�B�̒�`����A����㐔�I������x�A���� a��1 �Ȃ� a��B �����݂��āA
a^x��A��B �ł����āAA��B��B ������ a^x��B �ł���
n�� a^x �̍ŏ��������̎����Ƃ���
Case1)�Fn��2 �̂Ƃ��B���̂Ƃ��Aa^x ��n���̑㐔�I������������A
���E�r���̒藝��� a^x �ɑ��Ĉ��� c��0 �Ȃ����c�����݂��āA
�������ɔC�ӂ̐���p�Aq p��1 �ɑ��āA|a^x�|q/p|��c/(p^n) �ł���
�܂��A������ a_x ��A�����W�J���čl����Aa^x �ɑ��ĉZ������
���� q'/p' p'��2 �����݂��� |a^x�|q'/p'|��1/(p')^2 �����藧��
����āAa^x �ɑ��ĉZ�����̊��� q'/p' p'��2 �����݂���
c/(p')^n��|a^x�|q'/p'|��1/(p')^2 �ł����āA
c/(p')^{n-2}��(p')^2|a^x�|q'/p'|��1 ���� (p')^2|a^x�|q'/p'|��1 �ł���
�̂ɁA���� q'/p' p'��2 �ɂ��ĕ���� p' �� p'��+�� ��+���ɔ��U������
���� q'/p' p'��2 �����A������� q'/p' p'��2 ������
���� q'/p' p'��2 �� (p')^2|a^x�|q'/p'|��1 ����������������
�ƒ�`����BB�������̑㐔�I���̑S�̂��Ȃ��̂ƒ�`����
�W��A�Ƒ�B�̋��ʕ��� A��B �ɂ��āAA��B��∅ �Ɖ��肷��
�W��A�Ƒ�B�̒�`����A����㐔�I������x�A���� a��1 �Ȃ� a��B �����݂��āA
a^x��A��B �ł����āAA��B��B ������ a^x��B �ł���
n�� a^x �̍ŏ��������̎����Ƃ���
Case1)�Fn��2 �̂Ƃ��B���̂Ƃ��Aa^x ��n���̑㐔�I������������A
���E�r���̒藝��� a^x �ɑ��Ĉ��� c��0 �Ȃ����c�����݂��āA
�������ɔC�ӂ̐���p�Aq p��1 �ɑ��āA|a^x�|q/p|��c/(p^n) �ł���
�܂��A������ a_x ��A�����W�J���čl����Aa^x �ɑ��ĉZ������
���� q'/p' p'��2 �����݂��� |a^x�|q'/p'|��1/(p')^2 �����藧��
����āAa^x �ɑ��ĉZ�����̊��� q'/p' p'��2 �����݂���
c/(p')^n��|a^x�|q'/p'|��1/(p')^2 �ł����āA
c/(p')^{n-2}��(p')^2|a^x�|q'/p'|��1 ���� (p')^2|a^x�|q'/p'|��1 �ł���
�̂ɁA���� q'/p' p'��2 �ɂ��ĕ���� p' �� p'��+�� ��+���ɔ��U������
���� q'/p' p'��2 �����A������� q'/p' p'��2 ������
���� q'/p' p'��2 �� (p')^2|a^x�|q'/p'|��1 ����������������
2024/02/29(��) 10:45:31.62ID:f0/HMLwN
Case2)�Fn��1 �̂Ƃ��B���̂Ƃ��Aa^x �͐��̗L����������A
a^x �ɑ��ė������Ɉ���݂��ɑf�Ȑ��� p�Aq p��1 �����݂��� a^x��q/p �ł���
�܂��A���肩��x�͑㐔�I�������ł���B
x�̍ŏ��������̎�����m�Ƃ���ƁAm��2 �ł�����x��m���̑㐔�I�������ł���
����āACase1)�̋c�_�ɂ�����n��m�ŁAa^x ��x�ŁA���ꂼ�ꏑ��������
Case1)�Ɠ��l�ȋc�_���J��Ԃ��A������
Case1)�ACase2)����A�N���蓾�邷�ׂĂ̏ꍇ�ɂ��Ė�����������
���̖����́AA��B��∅ �Ɖ��肵�����Ƃ��琶��������A�w���@�ɂ�� A��B��∅ �ł���
[��2�i]�F����āAA��B�̊e��`����AA�ɑ���������̑㐔�I���͑��݂��Ȃ�
�̂ɁAA�̒�`����A�C�ӂ�1���傫�������̑㐔�I��a�A
�C�ӂ̑㐔�I������x�ɑ��āAa^x �͎����̒��z���ł���
[��3�i]�F�̂ɁA�C�ӂ̐��̑㐔�I��a�A�C�ӂ̑㐔�I������x
�ɑ��āAa^x �͎����̒��z���ł���
[��4�i]�F��2 �͑㐔�I�������Ȃ邱�Ƃɒ��ӂ���� 2^{��2} �͎����ł����Ē��z���ł���
a^x �ɑ��ė������Ɉ���݂��ɑf�Ȑ��� p�Aq p��1 �����݂��� a^x��q/p �ł���
�܂��A���肩��x�͑㐔�I�������ł���B
x�̍ŏ��������̎�����m�Ƃ���ƁAm��2 �ł�����x��m���̑㐔�I�������ł���
����āACase1)�̋c�_�ɂ�����n��m�ŁAa^x ��x�ŁA���ꂼ�ꏑ��������
Case1)�Ɠ��l�ȋc�_���J��Ԃ��A������
Case1)�ACase2)����A�N���蓾�邷�ׂĂ̏ꍇ�ɂ��Ė�����������
���̖����́AA��B��∅ �Ɖ��肵�����Ƃ��琶��������A�w���@�ɂ�� A��B��∅ �ł���
[��2�i]�F����āAA��B�̊e��`����AA�ɑ���������̑㐔�I���͑��݂��Ȃ�
�̂ɁAA�̒�`����A�C�ӂ�1���傫�������̑㐔�I��a�A
�C�ӂ̑㐔�I������x�ɑ��āAa^x �͎����̒��z���ł���
[��3�i]�F�̂ɁA�C�ӂ̐��̑㐔�I��a�A�C�ӂ̑㐔�I������x
�ɑ��āAa^x �͎����̒��z���ł���
[��4�i]�F��2 �͑㐔�I�������Ȃ邱�Ƃɒ��ӂ���� 2^{��2} �͎����ł����Ē��z���ł���
2024/02/29(��) 11:28:32.36ID:f0/HMLwN
�����F
[��3�i]�F�C�ӂ̐��̑㐔�I��a �� �C�ӂ�1�Ƃ͈قȂ鐳�̑㐔�I��a
[��1�i]��Case1)�̍Ō�̍s�̕⑫�F
(p')^2|a^x�|q'/p'|��1 �� (p')^2|a^x�|q'/p'|��1��(p')^2|a^x�|q'/p'|
[��3�i]�F�C�ӂ̐��̑㐔�I��a �� �C�ӂ�1�Ƃ͈قȂ鐳�̑㐔�I��a
[��1�i]��Case1)�̍Ō�̍s�̕⑫�F
(p')^2|a^x�|q'/p'|��1 �� (p')^2|a^x�|q'/p'|��1��(p')^2|a^x�|q'/p'|
729�P�R�Q�l�ڂ̑f������
2024/02/29(��) 18:31:29.67ID:4ajbydc1 x�͑㐔�I�������ł���Ƃ��������Ŗ���������Ă��Ƃ�
�㐔�I�������͑��݂��Ȃ����Ă��ƂɂȂ��
�㐔�I�������͑��݂��Ȃ����Ă��ƂɂȂ��
2024/03/01(��) 11:17:35.68ID:4RjaehFr
[��1�i]�F�W��A�� A��{a^x| x�͑㐔�I�������Aa��1���傫�������̑㐔�I�� }
�ƒ�`����BB�������̑㐔�I���̑S�̂��Ȃ��̂ƒ�`����
�W��A�Ƒ�B�̋��ʕ��� A��B �ɂ��āAA��B��∅ �Ɖ��肷��
�W��A�Ƒ�B�̒�`����A����㐔�I������x�A���� a��1 �Ȃ� a��B �����݂��āA
a^x��A��B �ł����āAA��B��B ������ a^x��B �ł���
n�� a^x �̍ŏ��������̎����Ƃ���
Case1)�Fn��2 �̂Ƃ��B���̂Ƃ��Aa^x ��n���̑㐔�I������������A
���E�r���̒藝��� a^x �ɑ��Ĉ��� c��0 �Ȃ����c�����݂��āA
�������ɔC�ӂ̐���p�Aq p��1 �ɑ��āA|a^x�|q/p|��c/(p^n) �ł���
�܂��A������ a_x ��A�����W�J���čl����Aa^x �ɑ��ĉZ������
���� q'/p' p'��2 �����݂��� |a^x�|q'/p'|��1/(p')^2 �����藧��
����āAa^x �ɑ��ĉZ�����̊��� q'/p' p'��2 �����݂���
c/(p')^n��|a^x�|q'/p'|��1/(p')^2 �ł����āA
c/(p')^{n-2}��(p')^2|a^x�|q'/p'|��1 ���� (p')^2|a^x�|q'/p'|��1 �ł���
�̂ɁA���� q'/p' p'��2 �ɂ��ĕ���� p' �� p'��+�� ��+���ɔ��U������
���� q'/p' p'��2 �����A������� q'/p' p'��2 ������
���� q'/p' p'��2 �� (p')^2|a^x�|q'/p'|��1��(p')^2|a^x�|q'/p'|
����������������
Case2)�Fn��1 �̂Ƃ��B���̂Ƃ��Aa^x �͐��̗L����������A
a^x �ɑ��ė������Ɉ���݂��ɑf�Ȑ��� p�Aq p��1 �����݂��� a^x��q/p �ł���
�܂����肩��Aa�͑㐔�I��������Aa�̍ŏ��������̎�����m�Ƃ���A
m��1 �ł�����a��m���̑㐔�I���ł���
�ƒ�`����BB�������̑㐔�I���̑S�̂��Ȃ��̂ƒ�`����
�W��A�Ƒ�B�̋��ʕ��� A��B �ɂ��āAA��B��∅ �Ɖ��肷��
�W��A�Ƒ�B�̒�`����A����㐔�I������x�A���� a��1 �Ȃ� a��B �����݂��āA
a^x��A��B �ł����āAA��B��B ������ a^x��B �ł���
n�� a^x �̍ŏ��������̎����Ƃ���
Case1)�Fn��2 �̂Ƃ��B���̂Ƃ��Aa^x ��n���̑㐔�I������������A
���E�r���̒藝��� a^x �ɑ��Ĉ��� c��0 �Ȃ����c�����݂��āA
�������ɔC�ӂ̐���p�Aq p��1 �ɑ��āA|a^x�|q/p|��c/(p^n) �ł���
�܂��A������ a_x ��A�����W�J���čl����Aa^x �ɑ��ĉZ������
���� q'/p' p'��2 �����݂��� |a^x�|q'/p'|��1/(p')^2 �����藧��
����āAa^x �ɑ��ĉZ�����̊��� q'/p' p'��2 �����݂���
c/(p')^n��|a^x�|q'/p'|��1/(p')^2 �ł����āA
c/(p')^{n-2}��(p')^2|a^x�|q'/p'|��1 ���� (p')^2|a^x�|q'/p'|��1 �ł���
�̂ɁA���� q'/p' p'��2 �ɂ��ĕ���� p' �� p'��+�� ��+���ɔ��U������
���� q'/p' p'��2 �����A������� q'/p' p'��2 ������
���� q'/p' p'��2 �� (p')^2|a^x�|q'/p'|��1��(p')^2|a^x�|q'/p'|
����������������
Case2)�Fn��1 �̂Ƃ��B���̂Ƃ��Aa^x �͐��̗L����������A
a^x �ɑ��ė������Ɉ���݂��ɑf�Ȑ��� p�Aq p��1 �����݂��� a^x��q/p �ł���
�܂����肩��Aa�͑㐔�I��������Aa�̍ŏ��������̎�����m�Ƃ���A
m��1 �ł�����a��m���̑㐔�I���ł���
2024/03/01(��) 11:20:33.75ID:4RjaehFr
Case2-1)�Fm��2 �̂Ƃ��B���̂Ƃ��Aa��m���̑㐔�I�������ł����āA
Case1)�̋c�_�ɂ�����n��m�ŁAa^x ��a�ŁA���ꂼ�ꏑ��������
Case1)�Ɠ��l�ȋc�_���J��Ԃ��A������
Case2-2)�Fm��1 �̂Ƃ��B���̂Ƃ��Aa��1���傫�����̗L����������
a�ɑ��ė������Ɉ���݂��ɑf�Ȑ��� p''�Aq'' p''��1 �����݂��� a��q''/p'' �ł���
����āA(q''/p'')^x��q/p �ł����āAq��1 ���� (q''/p'')^x�E(p/q)��1 �ł���
�������A���肩��x�͑㐔�I������������A1��x�͗L������Q��1���Ɨ��ł���
�܂��A�L��������Z�͑�Q��̒P�ʌ�1���܂ޒP�ʓI�����ł���
�̂ɁA��Z��̉��Q���l����A(q''/p'')^x�E(p/q)��1 �ł����āA������������
Case2-1)�ACase2-2)����An��1 �̂Ƃ��ɂ��ׂĂ̋N���蓾��ꍇ�ɂ��Ė�����
Case1)�ACase2)����A���ׂĂ̋N���蓾��ꍇ�ɂ��Ė�����������
���̖����́AA��B��∅ �Ɖ��肵�����Ƃ��琶��������A�w���@�ɂ�� A��B��∅ �ł���
[��2�i]�F����āAA��B�̊e��`����AA�ɑ���������̑㐔�I���͑��݂��Ȃ�
�̂ɁAA�̒�`����A�C�ӂ�1���傫�������̑㐔�I��a�A
�C�ӂ̑㐔�I������x�ɑ��āAa^x �͎����̒��z���ł���
[��3�i]�F�̂ɁA�C�ӂ̐��̑㐔�I��a�A�C�ӂ�1�Ƃ͈قȂ�㐔�I������x
�ɑ��āAa^x �͎����̒��z���ł���
[��4�i]�Fa��2�Ax����2 �̂Ƃ��B��2 �͑㐔�I�������Ȃ邱��
�ɒ��ӂ���� 2^{��2} �͎����ł����Ē��z���ł���
Case1)�̋c�_�ɂ�����n��m�ŁAa^x ��a�ŁA���ꂼ�ꏑ��������
Case1)�Ɠ��l�ȋc�_���J��Ԃ��A������
Case2-2)�Fm��1 �̂Ƃ��B���̂Ƃ��Aa��1���傫�����̗L����������
a�ɑ��ė������Ɉ���݂��ɑf�Ȑ��� p''�Aq'' p''��1 �����݂��� a��q''/p'' �ł���
����āA(q''/p'')^x��q/p �ł����āAq��1 ���� (q''/p'')^x�E(p/q)��1 �ł���
�������A���肩��x�͑㐔�I������������A1��x�͗L������Q��1���Ɨ��ł���
�܂��A�L��������Z�͑�Q��̒P�ʌ�1���܂ޒP�ʓI�����ł���
�̂ɁA��Z��̉��Q���l����A(q''/p'')^x�E(p/q)��1 �ł����āA������������
Case2-1)�ACase2-2)����An��1 �̂Ƃ��ɂ��ׂĂ̋N���蓾��ꍇ�ɂ��Ė�����
Case1)�ACase2)����A���ׂĂ̋N���蓾��ꍇ�ɂ��Ė�����������
���̖����́AA��B��∅ �Ɖ��肵�����Ƃ��琶��������A�w���@�ɂ�� A��B��∅ �ł���
[��2�i]�F����āAA��B�̊e��`����AA�ɑ���������̑㐔�I���͑��݂��Ȃ�
�̂ɁAA�̒�`����A�C�ӂ�1���傫�������̑㐔�I��a�A
�C�ӂ̑㐔�I������x�ɑ��āAa^x �͎����̒��z���ł���
[��3�i]�F�̂ɁA�C�ӂ̐��̑㐔�I��a�A�C�ӂ�1�Ƃ͈قȂ�㐔�I������x
�ɑ��āAa^x �͎����̒��z���ł���
[��4�i]�Fa��2�Ax����2 �̂Ƃ��B��2 �͑㐔�I�������Ȃ邱��
�ɒ��ӂ���� 2^{��2} �͎����ł����Ē��z���ł���
2024/03/01(��) 11:26:28.28ID:4RjaehFr
[��3�i]�ɂ���
�C�ӂ̐��̑㐔�I��a�A�C�ӂ�1�Ƃ͈قȂ�㐔�I������x
�� �C�ӂ�1�Ƃ͈قȂ鐳�̑㐔�I��a�A�C�ӂ̑㐔�I������x
�C�ӂ̐��̑㐔�I��a�A�C�ӂ�1�Ƃ͈قȂ�㐔�I������x
�� �C�ӂ�1�Ƃ͈قȂ鐳�̑㐔�I��a�A�C�ӂ̑㐔�I������x
733�P�R�Q�l�ڂ̑f������
2024/03/01(��) 22:56:52.83ID:C0z/65RY �k���l
a,b,c �𐳂̐����Ƃ��A1��a<b<c �Ƃ���B
�@M = 1 + 3^a + 3^b + 3^c
���������ƂȂ�悤�� (a,b,c) �̑g�͖����ɂ��邱�Ƃ������B
�E���Z���w�̎���X��_Part432 - 883
a,b,c �𐳂̐����Ƃ��A1��a<b<c �Ƃ���B
�@M = 1 + 3^a + 3^b + 3^c
���������ƂȂ�悤�� (a,b,c) �̑g�͖����ɂ��邱�Ƃ������B
�E���Z���w�̎���X��_Part432 - 883
734�P�R�Q�l�ڂ̑f������
2024/03/02(�y) 14:00:51.98ID:pz54UFyP �L�����Ɩ������͂ǂ����������ɑ��݂��邪�A���ɗL�����Ɩ�������������ɏo�s�������Ƃ��Ă��A�X�ɖ������̂ق����������݂��邱�Ƃ��ؖ�����
735�P�R�Q�l�ڂ̑f������
2024/03/02(�y) 21:25:10.60ID:ZADy0LT/ �L�����������ŕ\�킷�ƁA
�L�����Ő�邩���͏z�����ƂȂ�B
���̏z�߂̊Ԃ�1�����������������B
���Ƃ��� 3,1,4,1,5,9,2,6,5,3,5,8,9,7,9,3,2,�c
�� ��k���Ak+L���Ak+2L���A�c�͏z���Ȃ��̂ŁA
����������ł����ƁA���ׂĖ������ɂȂ�B
(k, L) �̎����͖����ɂ��邩��A
1�̗L�����������̖������ɑΉ�����B�B�B
�L�����Ő�邩���͏z�����ƂȂ�B
���̏z�߂̊Ԃ�1�����������������B
���Ƃ��� 3,1,4,1,5,9,2,6,5,3,5,8,9,7,9,3,2,�c
�� ��k���Ak+L���Ak+2L���A�c�͏z���Ȃ��̂ŁA
����������ł����ƁA���ׂĖ������ɂȂ�B
(k, L) �̎����͖����ɂ��邩��A
1�̗L�����������̖������ɑΉ�����B�B�B
736�P�R�Q�l�ڂ̑f������
2024/03/09(�y) 18:28:10.26ID:9TLceQPN737�P�R�Q�l�ڂ̑f������
2024/03/20(��) 19:47:12.86ID:kos/Cx4z ��̖������A���Ƃ��ɂ������ėL������3�A3.1�A3.14�A3.141�A...���Ė����ɂ��邯��
�L���������������ǂ����������ł������
�L���������������ǂ����������ł������
738�P�R�Q�l�ڂ̑f������
2024/04/16(��) 15:27:08.91ID:02gDREfj �k���104�l
�@��[0,��/2] sin(x)/{1+��sin(2x)} dx
�����߂�B
�@���Z���w�̎���X��_Part434�|104,117
�@��[0,��/2] sin(x)/{1+��sin(2x)} dx
�����߂�B
�@���Z���w�̎���X��_Part434�|104,117
739�P�R�Q�l�ڂ̑f������
2024/04/16(��) 15:40:56.89ID:02gDREfj x �� ��/2�|x�@�̑Ώ̐�����
(�^��)
�@= (1/2)��[0,��/2] (sin(x)+cos(x))/(1+��sin(2x)) dx
�@= ��[0,��/4] (sin(x)+cos(x))/(1+��sin(2x)) dx
������
�@cos(x)�|sin(x) = sin(t),
�@�|(sin(x)+cos(x)) dx = cos(t) dt,
�Ƃ����B
(�^��) = ��[0,��/2] cos(t)/(1+cos(t)) dt
�@= ��[0,��/2] {1�|1/(1+cos(t))} dt
�@= ��[0,��/2] {1�|1/[2cos(t/2)^2]} dt
�@= [ t�|tan(t/2) ](0����/2)
�@= ��/2 �| 1.
(�^��)
�@= (1/2)��[0,��/2] (sin(x)+cos(x))/(1+��sin(2x)) dx
�@= ��[0,��/4] (sin(x)+cos(x))/(1+��sin(2x)) dx
������
�@cos(x)�|sin(x) = sin(t),
�@�|(sin(x)+cos(x)) dx = cos(t) dt,
�Ƃ����B
(�^��) = ��[0,��/2] cos(t)/(1+cos(t)) dt
�@= ��[0,��/2] {1�|1/(1+cos(t))} dt
�@= ��[0,��/2] {1�|1/[2cos(t/2)^2]} dt
�@= [ t�|tan(t/2) ](0����/2)
�@= ��/2 �| 1.
740�P�R�Q�l�ڂ̑f������
2024/04/17(��) 00:30:46.79ID:qbH/8Fwh ��1/(1+cos(t)) dt
�@= sin(t)/(1+cos(t))
�@= (1-cos(t))/sin(t)
�@= tan(t/2),
(�Q�l��)
�X���E�F�c��E�ꏼ (��)�u���w����I�v��g�S��221,�V���� (1987)
�@��W��, ��3��, ��40, p.187-192
�@= sin(t)/(1+cos(t))
�@= (1-cos(t))/sin(t)
�@= tan(t/2),
(�Q�l��)
�X���E�F�c��E�ꏼ (��)�u���w����I�v��g�S��221,�V���� (1987)
�@��W��, ��3��, ��40, p.187-192
741�P�R�Q�l�ڂ̑f������
2024/04/21(��) 00:14:29.56ID:WdKvRNb8 �f���������̃v���O�������쐬�\��ł��B
�����1���Ԃʼn������琢�E�g�b�v�N���X�ȂǁA�������x��]������ڈ�����������Ă��������B
�����1���Ԃʼn������琢�E�g�b�v�N���X�ȂǁA�������x��]������ڈ�����������Ă��������B
742�P�R�Q�l�ڂ̑f������
2024/04/21(��) 02:37:39.74ID:34PQz0TW �k���336�l
�@�� (cos x)/(cos x + sin x) dx
�����߂�B
�@���Z���w�̎���X��_Part434�|336,356
�@�� (cos x)/(cos x + sin x) dx
�����߂�B
�@���Z���w�̎���X��_Part434�|336,356
743�P�R�Q�l�ڂ̑f������
2024/04/21(��) 02:46:16.53ID:34PQz0TW �@1/(1+tan x) = (cos x)/(cos x + sin x)
�@�@= {1 + (�|sin x + cos x)/(cos x + sin x)}/2
�@�@= {1 + (cos x + sin x) ' /(cos x + sin x)/2,
���
�� 1/(1+tan x) dx = {x + log|cos x + sin x|}/2,
x - ��/4 = y�@�Ƃ����@����� (��2)cos y�@�䂦�A
�ϕ����ׂ��� (1/2)(tan y) �ƒ萔�ɂȂ�B
�@�@= {1 + (�|sin x + cos x)/(cos x + sin x)}/2
�@�@= {1 + (cos x + sin x) ' /(cos x + sin x)/2,
���
�� 1/(1+tan x) dx = {x + log|cos x + sin x|}/2,
x - ��/4 = y�@�Ƃ����@����� (��2)cos y�@�䂦�A
�ϕ����ׂ��� (1/2)(tan y) �ƒ萔�ɂȂ�B
2024/04/24(��) 11:32:58.69ID:OH+8ZW3D
�{���ɂ�����˂����₾�Ɗ�����Ƃ͎v���܂����A
https://pachimaga.com/free/column/9efd320cf25de1bb99db35ed171b50e9fbdd0094.php
�r�s���ɓ�����m����
��1-(1-1/99.4)�O163��0.807593
��80.76��
������m������Ɋ|����B
��99.4✕0.807953
��80.2748��
�c��ۗ�4�����܂߂��81.0408��ƂȂ�(�c��ۗ��̌v�Z���@�ɂ��Ă͎����̓I�ɐ�������)
�Ƃ���܂����A����̋�̓I�����Ƃ����̂����������̂ʼn��ۗ̕�4���܂߂��80.2748��81.0408�ɂȂ�̂����킩��܂���B
����͂ǂ�Ȍv�Z�ŋ��߂Ă���̂ł��傤���H
https://pachimaga.com/free/column/9efd320cf25de1bb99db35ed171b50e9fbdd0094.php
�r�s���ɓ�����m����
��1-(1-1/99.4)�O163��0.807593
��80.76��
������m������Ɋ|����B
��99.4✕0.807953
��80.2748��
�c��ۗ�4�����܂߂��81.0408��ƂȂ�(�c��ۗ��̌v�Z���@�ɂ��Ă͎����̓I�ɐ�������)
�Ƃ���܂����A����̋�̓I�����Ƃ����̂����������̂ʼn��ۗ̕�4���܂߂��80.2748��81.0408�ɂȂ�̂����킩��܂���B
����͂ǂ�Ȍv�Z�ŋ��߂Ă���̂ł��傤���H
2024/04/24(��) 11:38:33.10ID:OH+8ZW3D
�����ƁA�m������ɂ�����Ƃ��̐��l�̓~�X���Ă܂���
99.4�~0.807593����������
99.4�~0.807593����������
2024/04/25(��) 18:21:56.57ID:Bm/wI22/
�E���R���������B
747�P�R�Q�l�ڂ̑f������
2024/05/05(��) 12:36:33.78ID:IFtE60+o �k���829-���l
��ӂ̒�����2�̐��O�p�`ABC������B
���̓��ډ~�̓���or����ɓ_P���Ƃ�B
���̂Ƃ��� AP�BP�CP �̍ő�l�����߂�B
�@���Z���w�̎���X��_Part434 - 829
��ӂ̒�����2�̐��O�p�`ABC������B
���̓��ډ~�̓���or����ɓ_P���Ƃ�B
���̂Ƃ��� AP�BP�CP �̍ő�l�����߂�B
�@���Z���w�̎���X��_Part434 - 829
748�P�R�Q�l�ڂ̑f������
2024/05/07(��) 01:33:19.53ID:OgbPgxVI ���ډ~�̔��ar = 1/��3,
���SI�̂܂��̋ɍ��W�� ��, �� �Ƃ����
�@0 �� �� �� r,
�@AP�EBP�ECP = ��{(64/27 + ��^6) + 2(8/��27)��^3�cos(3��)},
�ő�l�@9/��27 = ��3�@(��=1/��3, ��=0)
�����l�@8/��27�@�@�@�@(��=0)
�ŏ��l�@7/��27 �@�@�@�@(��=1/��3, ��=�}60��)
���SI�̂܂��̋ɍ��W�� ��, �� �Ƃ����
�@0 �� �� �� r,
�@AP�EBP�ECP = ��{(64/27 + ��^6) + 2(8/��27)��^3�cos(3��)},
�ő�l�@9/��27 = ��3�@(��=1/��3, ��=0)
�����l�@8/��27�@�@�@�@(��=0)
�ŏ��l�@7/��27 �@�@�@�@(��=1/��3, ��=�}60��)
749�P�R�Q�l�ڂ̑f������
2024/05/07(��) 01:43:27.18ID:OgbPgxVI �k���883-���l
��ӂ̒�����1�̐��O�p�`ABC������B
���̊O�ډ~�̎���ɓ_Q���Ƃ�B
���̂Ƃ��a AQ+BQ+CQ �̎�肤��l�͈̔͂����߂�B
�@���Z���w�̎���X��_Part434 - 883
��ӂ̒�����1�̐��O�p�`ABC������B
���̊O�ډ~�̎���ɓ_Q���Ƃ�B
���̂Ƃ��a AQ+BQ+CQ �̎�肤��l�͈̔͂����߂�B
�@���Z���w�̎���X��_Part434 - 883
750�P�R�Q�l�ڂ̑f������
2024/05/07(��) 02:12:35.12ID:OgbPgxVI �O�ډ~�̔��a R= 1/��3,
�O�SO�̂܂��̕��ʊp�� �� �Ƃ����
��AOQ = 60���|��,
��BOQ = 60�� +��,
��COQ = 180���|��,
AQ + BQ + CQ
�@= 2R{sin(30���|��/2) + sin(30��+��/2) + sin(90���|��/2)}
�@= 2R{cos(��/2) + cos(��/2)} �@�@�@�@�� �a�ό���
�@= 4R cos(��/2),
�ő�l 4/��3�@�@(��=0)
�ŏ��l�@2�@�@�@(��=�}60��)
�O�SO�̂܂��̕��ʊp�� �� �Ƃ����
��AOQ = 60���|��,
��BOQ = 60�� +��,
��COQ = 180���|��,
AQ + BQ + CQ
�@= 2R{sin(30���|��/2) + sin(30��+��/2) + sin(90���|��/2)}
�@= 2R{cos(��/2) + cos(��/2)} �@�@�@�@�� �a�ό���
�@= 4R cos(��/2),
�ő�l 4/��3�@�@(��=0)
�ŏ��l�@2�@�@�@(��=�}60��)
751�P�R�Q�l�ڂ̑f������
2024/05/07(��) 16:59:35.71ID:OgbPgxVI ��
A�F�@60��
B�F�@�|60��
C�F�@180��
Q�F�@�Ɓ@�@(-60�����Ɓ�60��)
�Ƃ����B
A�F�@60��
B�F�@�|60��
C�F�@180��
Q�F�@�Ɓ@�@(-60�����Ɓ�60��)
�Ƃ����B
752�P�R�Q�l�ڂ̑f������
2024/05/07(��) 20:04:16.74ID:OgbPgxVI ��
��/2 �����̒P�ʃ��F�N�g�������Ƃ���ƁA
��OA�E�� = R cos(60���|��/2) = R sin((60��+��)/2) = BQ/2,
��OB�E�� = R cos(60��+��/2) = R sin((60���|��)/2) = AQ/2,
��OC�E�� = �|R cos(��/2) = �|R sin(90���|��/2) =�|CQ/2,
�����
�@��OA +��OB +��OC = ��0
����
�@BQ + AQ �|CQ = 0,
���@AQ + BQ + CQ = 2CQ.
��/2 �����̒P�ʃ��F�N�g�������Ƃ���ƁA
��OA�E�� = R cos(60���|��/2) = R sin((60��+��)/2) = BQ/2,
��OB�E�� = R cos(60��+��/2) = R sin((60���|��)/2) = AQ/2,
��OC�E�� = �|R cos(��/2) = �|R sin(90���|��/2) =�|CQ/2,
�����
�@��OA +��OB +��OC = ��0
����
�@BQ + AQ �|CQ = 0,
���@AQ + BQ + CQ = 2CQ.
753�P�R�Q�l�ڂ̑f������
2024/05/08(��) 21:05:22.25ID:/PMdnc9j �������Ď�����𓊉����Ă������Ƃ���H
754�P�R�Q�l�ڂ̑f������
2024/05/08(��) 22:48:14.20ID:9b91wrP+ ������˂����Ȃ炢���B��҂ɂ͂��Ȃ��B
755�P�R�Q�l�ڂ̑f������
2024/05/09(��) 09:55:06.19ID:xTfUXmfc ������ł��\���܂��ǖ�̓��e�͋֎~�ł��B
756�P�R�Q�l�ڂ̑f������
2024/05/09(��) 14:38:16.53ID:7hFC8QRz ��������A����
a^n+b^m=2024�ƂȂ�悤�Ȏ��R���̑g(a,b,n,m)��S�ċ��߂�B
a^n+b^m=2024�ƂȂ�悤�Ȏ��R���̑g(a,b,n,m)��S�ċ��߂�B
757�P�R�Q�l�ڂ̑f������
2024/05/09(��) 23:11:15.86ID:vS28WcMc ���ށB�m���� ������˂��B
���� n=1 �� m=1 ���܂߂� ������Ȃ��� �ۗ����Ă�ˁB
���� n��2, m��2 �ɂ����� �ǖ�ɂȂ肻��������֎~�ł��ˁB
(a,b,n,m)
(41,7,2,3)�@(7,41,3,2)
(32,10,2,3)�@(10,32,3,2)
(10,4,3,5) �@(4,10,5,3)
���� n=1 �� m=1 ���܂߂� ������Ȃ��� �ۗ����Ă�ˁB
���� n��2, m��2 �ɂ����� �ǖ�ɂȂ肻��������֎~�ł��ˁB
(a,b,n,m)
(41,7,2,3)�@(7,41,3,2)
(32,10,2,3)�@(10,32,3,2)
(10,4,3,5) �@(4,10,5,3)
2024/05/09(��) 23:24:34.48ID:93jHN3Aw
m,n��2�ɐ������Ă�������Ȃ�
�����v���Ȃ��Ȃ犴�o�������Ă�
�����v���Ȃ��Ȃ犴�o�������Ă�
2024/05/10(��) 00:39:07.95ID:ZOfbeqGP
abc conjecture
760�P�R�Q�l�ڂ̑f������
2024/05/10(��) 16:33:33.99ID:hfGXUFEm >>757
(10,2,3,10)�@(2,10,10,3)
(10,2,3,10)�@(2,10,10,3)
761�P�R�Q�l�ڂ̑f������
2024/05/15(��) 21:01:14.39ID:KzIMAqFi ���n�Ȃ�ŋ����Ă�������
�R���E�F�C�̃`�F�[���\�L
�R→�Q→�Q���Ă����H
�R���E�F�C�̃`�F�[���\�L
�R→�Q→�Q���Ă����H
2024/05/18(�y) 11:34:11.20ID:zioSuWLF
27
3��2��2
=3��(3��1��2)��1
=3��(3����1)��1
=3��3��1
=3��3
=3^3
3��2��2
=3��(3��1��2)��1
=3��(3����1)��1
=3��3��1
=3��3
=3^3
763�P�R�Q�l�ڂ̑f������
2024/05/20(��) 03:45:49.71ID:Zwcbbpmn R�Ƃ��ĕ��R R ���Q�̒��a���q�͑S�ĕ��R�ł��邱�Ƃ��ؖ����ĉ������B
2024/05/20(��) 11:15:36.15ID:L5PJsM9W
������Ȃ���
765�P�R�Q�l�ڂ̑f������
2024/05/21(��) 12:56:06.60ID:f6payQiI ������Ȃ���ł���w
766�P�R�Q�l�ڂ̑f������
2024/05/21(��) 23:46:38.14ID:hL+1ms/7 ����
000����999�܂�1,000�ʂ肠��N�W�������Ƃ�
a) ����̎O���̐������Œ肷��i���Ƃ���943�Ƃ��j
b) ����K���ȎO���̐����ɂ���i���Ƃ������123�ō�����852�Ƃ��j
1,000���J��Ԃ����Ƃ��āA�N�W�ɓ�����m����a��b������
��
���ϓI�ɂ�a�̂ق��������肻�������ǁAa��b��������m���͓����ł���ˁH
�܂�����i���o�[�Y3���R���s���[�^�Ŏ����w�����Ă�b�Ȃ�ł�����
000����999�܂�1,000�ʂ肠��N�W�������Ƃ�
a) ����̎O���̐������Œ肷��i���Ƃ���943�Ƃ��j
b) ����K���ȎO���̐����ɂ���i���Ƃ������123�ō�����852�Ƃ��j
1,000���J��Ԃ����Ƃ��āA�N�W�ɓ�����m����a��b������
��
���ϓI�ɂ�a�̂ق��������肻�������ǁAa��b��������m���͓����ł���ˁH
�܂�����i���o�[�Y3���R���s���[�^�Ŏ����w�����Ă�b�Ȃ�ł�����
767�P�R�Q�l�ڂ̑f������
2024/05/22(��) 03:08:46.81ID:bq08hf8k ���I�ԍ������J�����Ȃ�A
�����Ԃ̃f�[�^���W�߂�Ίe�ԍ��̓��I�m���𐄑��ł������B
b) �ň�ԓ�����₷���ԍ����Ηǂ����ȁH
�����Ԃ̃f�[�^���W�߂�Ίe�ԍ��̓��I�m���𐄑��ł������B
b) �ň�ԓ�����₷���ԍ����Ηǂ����ȁH
2024/05/23(��) 09:53:34.20ID:An+D5BCh
���O�炱�̃C���h��JS�ɏ��Ă�H
https://i.imgur.com/7KlcRdQ.mp4
https://i.imgur.com/7KlcRdQ.mp4
769�P�R�Q�l�ڂ̑f������
2024/05/24(��) 00:20:26.71ID:QRIuqGrQ >>763
R��̕��R���Q�̒��a���q���S�ĕ��R�ł��邱�Ƃ��ؖ����܂��B
�܂��AR���Q M, N �����ꂼ�ꕽ�R�ł���Ƃ́A�C�ӂ� R-���Q�����^ f: P �� M �ɑ��A���� R-���Q�����^ g: M �� P �� fg = id_P �ƂȂ�悤�Ȃ��̂����݂��邱�Ƃ��Ӗ����܂��B
�����ŁAM, N �� R��̕��R���Q�ł���A�����̒��a M ⊕ N ���l���܂��B���̂Ƃ��A�C�ӂ� R-���Q�����^ h: P �� M ⊕ N �ɑ��āAh �� M �ւ̎ˉe�� N �ւ̎ˉe�ɕ����ł��܂��B
����ɁAM, N �����R�ł��邱�Ƃ���A���ꂼ��ɑ��� M �ւ̎ˉe�� N �ւ̎ˉe�� fg = id_P �ƂȂ�悤�� R-���Q�����^ f, g �ɕ����ł��܂��B
�����̕�����p���邱�ƂŁAh = (f, g) �ƂȂ�悤�� R-���Q�����^ f, g �����݂��邱�Ƃ��������Ƃ��ł��܂��B
����āAM ⊕ N �� R��̕��R���Q�ł��邱�Ƃ��ؖ��ł��܂��B
R��̕��R���Q�̒��a���q���S�ĕ��R�ł��邱�Ƃ��ؖ����܂��B
�܂��AR���Q M, N �����ꂼ�ꕽ�R�ł���Ƃ́A�C�ӂ� R-���Q�����^ f: P �� M �ɑ��A���� R-���Q�����^ g: M �� P �� fg = id_P �ƂȂ�悤�Ȃ��̂����݂��邱�Ƃ��Ӗ����܂��B
�����ŁAM, N �� R��̕��R���Q�ł���A�����̒��a M ⊕ N ���l���܂��B���̂Ƃ��A�C�ӂ� R-���Q�����^ h: P �� M ⊕ N �ɑ��āAh �� M �ւ̎ˉe�� N �ւ̎ˉe�ɕ����ł��܂��B
����ɁAM, N �����R�ł��邱�Ƃ���A���ꂼ��ɑ��� M �ւ̎ˉe�� N �ւ̎ˉe�� fg = id_P �ƂȂ�悤�� R-���Q�����^ f, g �ɕ����ł��܂��B
�����̕�����p���邱�ƂŁAh = (f, g) �ƂȂ�悤�� R-���Q�����^ f, g �����݂��邱�Ƃ��������Ƃ��ł��܂��B
����āAM ⊕ N �� R��̕��R���Q�ł��邱�Ƃ��ؖ��ł��܂��B
770�P�R�Q�l�ڂ̑f������
2024/05/24(��) 00:22:22.75ID:QRIuqGrQ >>761
�R���E�F�C�̃`�F�[���\�L���ď��߂ĕ������H�����ŏ��͂���Ղ�Ղ�����B
�ł����v�I�����ł́A���n�ł������ł���悤�A������₷��������Ă����ˁB
�܂��A�`�F�[���\�L�Ƃ́A�����g���ċ���Ȑ���\�����@�ȂB�Ⴆ�A3��2��2�́A3��2���2���\���B�܂�A3����2���Ă��Ƃ��ˁB
�v�Z���@�͂�����ƕ��G�����ǁA�|�C���g�́A�E���̐����������̐����̗ݏ��\�����Ă��ƁB
�����3��2��2���ƁA
�ŏ���3��2�悷��F3����2 = 3^2 = 9
���ɁA9��2�悷��F9����2 = 9^2 = 81
������A3��2��2��81��\���Ƃ������ƂɂȂ�B
�����ƕ��G�ȃ`�F�[���\�L��������ǁA��{������������Α��v�I
�R���E�F�C�̃`�F�[���\�L���ď��߂ĕ������H�����ŏ��͂���Ղ�Ղ�����B
�ł����v�I�����ł́A���n�ł������ł���悤�A������₷��������Ă����ˁB
�܂��A�`�F�[���\�L�Ƃ́A�����g���ċ���Ȑ���\�����@�ȂB�Ⴆ�A3��2��2�́A3��2���2���\���B�܂�A3����2���Ă��Ƃ��ˁB
�v�Z���@�͂�����ƕ��G�����ǁA�|�C���g�́A�E���̐����������̐����̗ݏ��\�����Ă��ƁB
�����3��2��2���ƁA
�ŏ���3��2�悷��F3����2 = 3^2 = 9
���ɁA9��2�悷��F9����2 = 9^2 = 81
������A3��2��2��81��\���Ƃ������ƂɂȂ�B
�����ƕ��G�ȃ`�F�[���\�L��������ǁA��{������������Α��v�I
771�P�R�Q�l�ڂ̑f������
2024/05/24(��) 01:05:24.76ID:RqlIQQ5z >>769 �ł����
772�P�R�Q�l�ڂ̑f������
2024/05/24(��) 01:50:51.68ID:gjj4AKIT >>767
����S���킯���B�B�B
����S���킯���B�B�B
773�P�R�Q�l�ڂ̑f������
2024/06/12(��) 11:19:46.32ID:+eQLufR0 �t�[���F�����̌���
�@k �����R���Ƃ���Ƃ�
�@(cos ��)^{2k}
�@�@= (1/2^{2k}) { C(2k,k) + 2��[m=1,k] C(2k,k�}m)�Ecos(2m��) }
�@(sin ��)^{2k}
�@�@= (1/2^{2k}) { C(2k,k) + 2��[m=1,k] C(2k,k�}m)�Ecos(2m��)�E(-1)^m }
�@������ C(2k,r) �͓W���B
�@k �����R���Ƃ���Ƃ�
�@(cos ��)^{2k}
�@�@= (1/2^{2k}) { C(2k,k) + 2��[m=1,k] C(2k,k�}m)�Ecos(2m��) }
�@(sin ��)^{2k}
�@�@= (1/2^{2k}) { C(2k,k) + 2��[m=1,k] C(2k,k�}m)�Ecos(2m��)�E(-1)^m }
�@������ C(2k,r) �͓W���B
2024/06/12(��) 12:34:38.73ID:dZKpyoLh
>>761
3��2��2��27
a��b��c��a���c��b�i���c�{�j�ł��邩��
3��2��2��3����2
m����n��m��m���c��m�im�̐���n�j�ł��邩��
3����2��3��3
p��q��p��q��ł��邩��
3��3��3��3�恁27
3��2��2��27
a��b��c��a���c��b�i���c�{�j�ł��邩��
3��2��2��3����2
m����n��m��m���c��m�im�̐���n�j�ł��邩��
3����2��3��3
p��q��p��q��ł��邩��
3��3��3��3�恁27
775�P�R�Q�l�ڂ̑f������
2024/06/15(�y) 21:14:33.12ID:xakgg+mx >>773
���ӂ�
�@cos �� = (e^{��i} + e^{-��i})/2,
�@sin �� = (e^{��i} �| e^{-��i})/2i,
������2�������œW�J���邾���B
���@������˂����̏������݂����B
���ӂ�
�@cos �� = (e^{��i} + e^{-��i})/2,
�@sin �� = (e^{��i} �| e^{-��i})/2i,
������2�������œW�J���邾���B
���@������˂����̏������݂����B
776�P�R�Q�l�ڂ̑f������
2024/07/07(��) 19:46:37.09ID:c1WH4x9j �܂������Ȃ�
2024/07/11(��) 13:10:13.51ID:dr5nOH6L
19�˂����n�Q���i�s�����������������@
�����A�����A�~�l�����A�v���e�C���ABCAA�A�N���A�`����ێ悷��
�T6���͒Y�_��A�T�E�i���ɒʂ����s���i������
�s���Ȃ��������̓E�B���L���\�����炩���Ă���
�K�x�ȉ^���T3���͎s���̃v�[���ŗV�j
�V�����v�[�͐A�����̈�{5000�~���鏗���p
����̐����N���j�b�N��3������
�������Ԃ͍Œ�ł�6���Ԃ͎���������X�����͐�ɂ��Ȃ�
�^�o�R�͈�؋z��Ȃ�
�ڂ̔�ꂩ��n�Q���i�s����ƌ���ꂽ�̂Ŗ��������ɕx�m�R��20�����߂��Ƃ�11�N��������
����30�˂����Ǔ��������X�J�X�J�Ńn�Q�U�炩���Ă邯�ǑO�������͎c���Ă邩��Q�l�ɂ���
�����A�����A�~�l�����A�v���e�C���ABCAA�A�N���A�`����ێ悷��
�T6���͒Y�_��A�T�E�i���ɒʂ����s���i������
�s���Ȃ��������̓E�B���L���\�����炩���Ă���
�K�x�ȉ^���T3���͎s���̃v�[���ŗV�j
�V�����v�[�͐A�����̈�{5000�~���鏗���p
����̐����N���j�b�N��3������
�������Ԃ͍Œ�ł�6���Ԃ͎���������X�����͐�ɂ��Ȃ�
�^�o�R�͈�؋z��Ȃ�
�ڂ̔�ꂩ��n�Q���i�s����ƌ���ꂽ�̂Ŗ��������ɕx�m�R��20�����߂��Ƃ�11�N��������
����30�˂����Ǔ��������X�J�X�J�Ńn�Q�U�炩���Ă邯�ǑO�������͎c���Ă邩��Q�l�ɂ���
778�P�R�Q�l�ڂ̑f������
2024/07/15(��) 21:44:58.53ID:PU0KyHMd �T�|�[�g�͂��邩���
779�P�R�Q�l�ڂ̑f������
2024/07/15(��) 22:49:30.26ID:vClpb3m6 �ʂɃi���o�����O���Ȃ��Ă�
780�P�R�Q�l�ڂ̑f������
2024/07/15(��) 23:05:05.94ID:MeKkNrDU ���ł����o���I�^�قڂ��Ȃ����Ă͎̂d���ɂ������Ȃ�
2024/08/09(��) 00:13:14.91ID:YkIS3Q0u
782�P�R�Q�l�ڂ̑f������
2024/08/09(��) 01:40:24.65ID:ngKK6JzZ �����Ⴂ�ƌh������ĂȂ��������H
�Ђ���Ă���ĂȂ�
�{���ł���ȋc�_�ł���
�������킩��
�q�X���ƃE�H����������ǂ��Ȃ���
�Ђ���Ă���ĂȂ�
�{���ł���ȋc�_�ł���
�������킩��
�q�X���ƃE�H����������ǂ��Ȃ���
783�P�R�Q�l�ڂ̑f������
2024/08/09(��) 01:46:46.59ID:C/0mr+2Q �����҂��p���N�ɋߊ����
���l�߂Â���
���l�߂Â���
2024/08/09(��) 01:50:26.78ID:F/jvoszc
�W���W���Y���Ȃ�l�C��i�ǂ�ł������킯����Ȃ�
����Ă�����ł�
�����̖����ό��r�W�l�X�A�債�����Ǝv���Ă����
����Ă�����ł�
�����̖����ό��r�W�l�X�A�債�����Ǝv���Ă����
785�P�R�Q�l�ڂ̑f������
2024/08/09(��) 01:50:29.88ID:mYFJgeZZ ������@���Ȃ�ďo���Ȃ�
���t�ɂ��̎�҂͎x�����ĂЂ낫��
���[�����Y�Ŏ��ƂɕԂ���ςȂ��ŗ����ɂȂ��Ă��
���t�ɂ��̎�҂͎x�����ĂЂ낫��
���[�����Y�Ŏ��ƂɕԂ���ςȂ��ŗ����ɂȂ��Ă��
786�P�R�Q�l�ڂ̑f������
2024/08/09(��) 02:02:16.30ID:Q7waqgmU787�P�R�Q�l�ڂ̑f������
2024/08/09(��) 02:11:58.36ID:inGB1qvG2024/08/19(��) 20:57:01.36ID:NQ0TAMZK
���g�������炩��
�y���Ȃ鍂�����珸���Ă���̂����X���܂���
�R�������(�L�G�ցG�M)
�y���Ȃ鍂�����珸���Ă���̂����X���܂���
�R�������(�L�G�ցG�M)
2024/08/19(��) 20:58:06.65ID:NUoWe4Ng
�����̊猩����������Ђ��߂���̂��D�����O���[�v�ɂ����ߕی�y��������Ƃɂ����A���W�����v
�����[�I��肢�I���̐lT�V���b�D���Ȃ�H
https://i.imgur.com/KuXXzNs.png
�����[�I��肢�I���̐lT�V���b�D���Ȃ�H
https://i.imgur.com/KuXXzNs.png
790�P�R�Q�l�ڂ̑f������
2024/08/19(��) 20:58:32.69ID:pNIi8WsA �����������̕��Ă������
���Ēl����������͔p�~����Ƃ͎v���Ȃ��s�^�������
����A�y�����͂Ȃ���
���Ēl����������͔p�~����Ƃ͎v���Ȃ��s�^�������
����A�y�����͂Ȃ���
791�P�R�Q�l�ڂ̑f������
2024/08/19(��) 21:00:30.85ID:ONj9m4vr792�P�R�Q�l�ڂ̑f������
2024/08/19(��) 21:08:40.93ID:ISY2HysC �v���C�h�肵���w�^�N�\ww
���B�̓����Ă�|�l�͎R�قǂ����肵�Ă�
�T��������鍼�\�͂܂�ܕ��i����Ă�̂�
�c�b�R�~���I��点�Ȃ��݂�������
https://81.g.k37/fVMY2
���B�̓����Ă�|�l�͎R�قǂ����肵�Ă�
�T��������鍼�\�͂܂�ܕ��i����Ă�̂�
�c�b�R�~���I��点�Ȃ��݂�������
https://81.g.k37/fVMY2
2024/08/19(��) 21:31:38.40ID:wuS6tT6i
�V�������̏ꍇ
794�P�R�Q�l�ڂ̑f������
2024/08/19(��) 21:42:19.40ID:7eHtCVwz JK����Ȃ����ǐl���Ō����ĂȂ�
�������
�ł�
�������
�ł�
2024/08/19(��) 21:51:13.79ID:GMbY7ES7
�ǂ��z�����X�s�[�h�o�������Ŏ��͈ȏ゠���
796�P�R�Q�l�ڂ̑f������
2024/08/19(��) 21:54:10.95ID:o1zGtp+l �W���j���邠��l�^�̐D�荞�݂��E�P����ł����Ă��N���C�ɂ��Ȃ�
2024/08/19(��) 22:11:23.44ID:eX8NV4yU
798�P�R�Q�l�ڂ̑f������
2024/08/19(��) 22:11:45.52ID:/m1LI5bu �C�P��������Ȃ��́H�؎肪���ӂȉ�Ђ��ăC���[�W
�A�}�`���A�I�肪�c���Č������ǃK�`�̃K�`��Ƃ܂ŁB
�A�}�`���A�I�肪�c���Č������ǃK�`�̃K�`��Ƃ܂ŁB
799�P�R�Q�l�ڂ̑f������
2024/08/19(��) 22:24:18.13ID:W9U4mZYp �L����D��������Ȃ̂�
�܂��Ⴂ�قǁA���e�B
�܂��Ⴂ�قǁA���e�B
800�P�R�Q�l�ڂ̑f������
2024/08/19(��) 22:25:30.95ID:LRfQGTRU �}�O���C�A��胔�@�����̂ق����ׂ��������Ă��Ƃ͊܂ޖ����������Ă������瓖�R
�o�O�̓V�X�e�����ꉞ�����悤��
�o�O�̓V�X�e�����ꉞ�����悤��
801�P�R�Q�l�ڂ̑f������
2024/08/19(��) 22:32:11.01ID:9Q1akiTc GLP1�_�C�G�b�g�݂����Ȃ��̂���
802�P�R�Q�l�ڂ̑f������
2024/08/19(��) 22:35:36.80ID:d6XArCvJ803�P�R�Q�l�ڂ̑f������
2024/08/19(��) 22:51:48.82ID:UtPkWuse804�P�R�Q�l�ڂ̑f������
2024/08/19(��) 23:05:10.96ID:nXz3bPlC �������o���
805�P�R�Q�l�ڂ̑f������
2024/08/19(��) 23:07:36.35ID:Ow5lW12x �A�z���
�u#�}�l������
�u#�}�l������
806�P�R�Q�l�ڂ̑f������
2024/08/19(��) 23:17:16.65ID:UtPkWuse ���ƂƂ��ē��H�̕ǖʕt�߂Ƀu���[�L���͂Ȃ�����
807�P�R�Q�l�ڂ̑f������
2024/08/19(��) 23:53:49.90ID:L4uxX/Yt �Ȃ��Ȃ����ĂĂȂ邾��������d���Ȃ���
���H�܂����Q�N�����
���H�܂����Q�N�����
2024/08/21(��) 19:44:21.58ID:g425CL+R
�V�n�n���ƃ��h���̔�����Ă݂�����₯��
https://i.imgur.com/QEahutM.png
https://i.imgur.com/QEahutM.png
2024/08/21(��) 20:02:30.05ID:ORv182UX
�܂�����͂���������
�̂̊C�R�叫�Ƃ���
�g���b�N�̉^�]�肪���S���Ă߂��炵���ȁB
�v���A�X���[�g�͍��コ��ɑ����Ă邪
�̂̊C�R�叫�Ƃ���
�g���b�N�̉^�]�肪���S���Ă߂��炵���ȁB
�v���A�X���[�g�͍��コ��ɑ����Ă邪
810�P�R�Q�l�ڂ̑f������
2024/08/21(��) 20:42:29.28ID:uSrWUVkE �j�R���݂����Ȃ���̎��������������̂��H
�E�@�l�����Ă��炦��
�W�F�C�N�͐g��������10�N����A�C�X�m�����Ƃ��A�C�c��Â��ɂ��Ƃ����v�ƘA�Ă���搶
���͎d�����������
�E�@�l�����Ă��炦��
�W�F�C�N�͐g��������10�N����A�C�X�m�����Ƃ��A�C�c��Â��ɂ��Ƃ����v�ƘA�Ă���搶
���͎d�����������
811�P�R�Q�l�ڂ̑f������
2024/08/21(��) 20:53:41.97ID:KTb7tTsW �݂��т����肵�Ă��������Ȃ�
������������̃K�L�͚₵�������́H
������������̃K�L�͚₵�������́H
812�P�R�Q�l�ڂ̑f������
2024/08/21(��) 20:58:04.55ID:EMBxIIwK �܂������Ȗ��O�ł����|�l���[����
813�P�R�Q�l�ڂ̑f������
2024/08/21(��) 21:04:35.80ID:CMQvw55+ �ނꂽ����������
���}�T�K�͂܂��ł���
���}�T�K�͂܂��ł���
814�P�R�Q�l�ڂ̑f������
2024/08/21(��) 21:08:54.30ID:LyCD0KJT ��������spotify����Ƃ��̂����ˁB
815�P�R�Q�l�ڂ̑f������
2024/08/21(��) 21:23:11.11ID:9WHrBj8P >>707
�Q�Ăăn���h������Ă��܂��B
�Q�Ăăn���h������Ă��܂��B
816�P�R�Q�l�ڂ̑f������
2024/08/22(��) 11:12:40.04ID:UgPf89nQ �Ɋy��������
2024/08/22(��) 11:23:25.12ID:4yBJ5x0E
�܂�����̃_�C�G�b�g�̗v�̂悤�ȔN��ł��ꂾ���o�C�I���x���҂����
2024/08/22(��) 11:38:28.73ID:9Kd5oNpo
�E�X����
��150-8560�@�w�W���j�[�Y�ᔽ�x�W
��150-8560�@�w�W���j�[�Y�ᔽ�x�W
2024/08/22(��) 11:52:59.52ID:k1uY6AiB
>>307
�A�C�X�V���[�ɏ��̉��l�ς̎��Ɏ������オ������S�̂Ƃ��Ĕ�Q�҂̏����ɖ\�I�����l�Ԃ��撣���Ă�悤�Ȃ���₵
����ȊO��邱�Ƃ���Ȃ���ł����
�A�C�X�V���[�ɏ��̉��l�ς̎��Ɏ������オ������S�̂Ƃ��Ĕ�Q�҂̏����ɖ\�I�����l�Ԃ��撣���Ă�悤�Ȃ���₵
����ȊO��邱�Ƃ���Ȃ���ł����
820�P�R�Q�l�ڂ̑f������
2024/08/29(��) 20:35:14.63ID:Z3OiHJkT �_���������Ƃ�
821�P�R�Q�l�ڂ̑f������
2024/08/29(��) 20:38:02.33ID:8McGqaqR ���̏d�ʂ���
�A�C�X�^�ˌ����邩�ȁB
�A�C�X�^�ˌ����邩�ȁB
2024/08/29(��) 20:44:59.74ID:Z3OiHJkT
�悭�ǂ߂H
�����Ƃ���������
�����Ƃ���������
823�P�R�Q�l�ڂ̑f������
2024/08/29(��) 21:23:48.48ID:ZZdV7AXW �܂�
���̎コ�ɉ������݂�������
�T�������ł͂Ȃ�
���������X���ł��ǂ��������������Ȃ�(������)
���̎コ�ɉ������݂�������
�T�������ł͂Ȃ�
���������X���ł��ǂ��������������Ȃ�(������)
824�P�R�Q�l�ڂ̑f������
2024/08/29(��) 21:28:18.12ID:Sm87skZv ��������������ɃC���C�������Ă��Č��ɂȂ�
���ڑ҂Ɣ��t�����̈Ⴂ�ł����Ȃ�
���ꉽ�Ȃ�H
���ڑ҂Ɣ��t�����̈Ⴂ�ł����Ȃ�
���ꉽ�Ȃ�H
825�P�R�Q�l�ڂ̑f������
2024/08/29(��) 21:38:38.29ID:pyYCRI6s �K�[�V�[�̐M�҂��ɏ�������B
2024/08/29(��) 21:50:41.04ID:CZm7KV3D
�A�x�K�[���������̂͒m���Ă��邼
827�P�R�Q�l�ڂ̑f������
2024/08/29(��) 22:59:33.40ID:CNdMpFin ���̏��ő��̐M�҂��ɏ�������B
828�P�R�Q�l�ڂ̑f������
2024/08/29(��) 23:09:44.13ID:6feqBpZI >>653
�ߑ��w�A���C�N�u�͂��v
�ߑ��w�A���C�N�u�͂��v
2024/08/29(��) 23:22:12.98ID:w0OetXOj
��������spotify����Ƃ��̂�����
2024/10/29(��) 17:02:30.43ID:F8zDgDmC
�̂j�f�Ƃ��������݂Ă��ȉ҂�����
2024/11/15(��) 09:10:52.56ID:qay2j+Mx
�Œ萸�x���������_���̑㐔��̌v�Z�ŁA���U�^�m���ϐ����ɒ[�ɑ����ꍇ�Ɋm�����ʊ��̏o�͒l�����ׂ�0�ɒׂ�Ă��܂��̂��ĉ���ł���H
�܂�v�Z�@��ł� x �̔z��̓��e����ł� \forall i \in [n]. exp(x_i) / \Sigma_{j \in [n]} exp(x_j) = 0.0 �ɒׂ��Ǝv�����ǁAx �̓��e���Ȃ�Ƃ����� 0.00�c01 �ł������̂őS�̂ɕ��z���������B([n]={1,...,n})
���U���Ȃ��ꍇ�� x = [-Inf, �c, -Inf] ���炢�����v�����Ȃ�
�m�����ʊ����ď��������ǁA���m�ɂ� softmax
�[���R�[�h
sum = 0.0f
for (int j = 0; j < n; ++j){
sum += exp(x[j]) // n�����ɑ傫���̂�x[j]�̓��e�̔@���ł�sum��Inf�ɔ��U����
}
softmax(x)_i = x[i] / sum // ���̒l��0���傫���Ȃ��Ăق����AInf, NaN�ȊO�Ȃ�nan�ł�����
�܂�v�Z�@��ł� x �̔z��̓��e����ł� \forall i \in [n]. exp(x_i) / \Sigma_{j \in [n]} exp(x_j) = 0.0 �ɒׂ��Ǝv�����ǁAx �̓��e���Ȃ�Ƃ����� 0.00�c01 �ł������̂őS�̂ɕ��z���������B([n]={1,...,n})
���U���Ȃ��ꍇ�� x = [-Inf, �c, -Inf] ���炢�����v�����Ȃ�
�m�����ʊ����ď��������ǁA���m�ɂ� softmax
�[���R�[�h
sum = 0.0f
for (int j = 0; j < n; ++j){
sum += exp(x[j]) // n�����ɑ傫���̂�x[j]�̓��e�̔@���ł�sum��Inf�ɔ��U����
}
softmax(x)_i = x[i] / sum // ���̒l��0���傫���Ȃ��Ăق����AInf, NaN�ȊO�Ȃ�nan�ł�����
2024/11/16(�y) 01:39:24.89ID:ZfAToum3
wikipe�ɏ����Ă����������ꂼ��萔�����Ă��Ƃ����炵��(�L���ł�x[i] -= max(x))
https://ja.wikipedia.org/?curid=4581060#.E3.82.AA.E3.83.BC.E3.83.90.E3.83.BC.E3.83.95.E3.83.AD.E3.83.BC.E5.AF.BE.E7.AD.96
https://ja.wikipedia.org/?curid=4581060#.E3.82.AA.E3.83.BC.E3.83.90.E3.83.BC.E3.83.95.E3.83.AD.E3.83.BC.E5.AF.BE.E7.AD.96
2024/11/16(�y) 04:39:09.68ID:ZfAToum3
���Ă�����Ƃł��l�������甭�U����̂�
exp(x)���S��00�c01�ł����U����Ȃ珃���Ɍ��s�������疳���ł���
�����t���Ȃ�
exp(x)���S��00�c01�ł����U����Ȃ珃���Ɍ��s�������疳���ł���
�����t���Ȃ�
2024/11/16(�y) 18:45:37.33ID:EN3iKS2O
>832, 833
��������ˁA����ϋ����I�ɉ��������邩�A���邢�͓��͌n�ɉ����Đ��x��ω������邵���Ȃ���Ȃ�
��������ˁA����ϋ����I�ɉ��������邩�A���邢�͓��͌n�ɉ����Đ��x��ω������邵���Ȃ���Ȃ�
2024/11/16(�y) 18:48:46.47ID:EN3iKS2O
n ���ɒ[�ɂ����ł��ɂȂ�Ƃǂ����Ă����U���Ă��܂��̂́A����ω������������
2024/11/16(�y) 19:48:01.71ID:Pw/aB5Du
�P�ӂ��P�̗����̖̂ʏ�ɂQ�_P,Q��C�ӂɂƂ�Ƃ��A����PQ�̒����̕��ϒl�A���U�����߂�B
837�P�R�Q�l�ڂ̑f������
2025/06/26(��) 19:51:12.09ID:0tKzEldh 222d
838�P�R�Q�l�ڂ̑f������
2025/06/26(��) 23:50:00.35ID:1rnzhwNg 2^a+2^b=10^c+10^d,
a��b, c��d ���݂���0�ȏ�̐�������
(0,0,0,0)��(2,4,1,1) �����ł��傤���B
a��b, c��d ���݂���0�ȏ�̐�������
(0,0,0,0)��(2,4,1,1) �����ł��傤���B
2025/06/27(��) 07:34:38.88ID:0tUKGzM/
10^d �� 1/2 ( 10^c + 10^d ) > 2^(b-1)
d �� (b-1) log_10 2
2^a( 2^(b-a) + 1 ) = 10^c( 10^(d-c) + 1 )
�� a=b or c=d or ( a��b, c��d, a=c )
Suppose c=d, d>0
2^a( 1+2^(b-a) ) = 2⋅10^d �� b �� a ( mod 2 )
2^a( 1+4^((b-a)/2) ) = 2⋅10^d �� (b-a)/2 �� 1 ( mod 2 )
d = v_5( 4^((b-a)/2) - (-1)^((b-a)/2) ) = v_5((b-a)/2) + 1 < log_5 b + 1 (�� LTE)
�� b = log_2 2^b
< log_2( 2^a+2^b)
= log_2( 10^c+10^d )
< d log_2 10 + 1
< (log_5 b+1) log_2 10 + 1
�� b��5
�� RHS �� 64
�� LHS = 20
�� (a,b,c,d) = (2,4,1,1)
Suppose a=b
2⋅2^a = 10^c ( 1 +10^(d-c) ) LHS cannot be a multiple of 5. �� c=0.
2⋅2^a = 1 +10^d RHS is even only if d = 0 �� a=b=c=d=0
Suppose a��b, c��d, a=c
2^(b-a)+1 = 5^c(10^(d-c)+1) �� b �� a ( mod 2 )
1+4^((b-a)/2) = 5^c(10^(d-c)+1) �� (b-a)/2 �� 1 ( mod 2 )
c = v_5( 4^((b-a)/2) - (-1)^((b-a)/2) ) = v_5((b-a)/2) + 1 < log_5 b + 1 (�� LTE)
5^c - 1 = 2^b - 5^c 10^(d-c)
v_2( 5^c - 1 ) = 2 + v_2(c) �� 2 + log_2(c) < 2 + log_2( log_5 b + 1 )
v_2( 2^b - 5^c 10^(d-c) ) �� min{ b, d-c } > (b-1) log_10 2
(b-1) log_10 2 < 2 + log_2( log_5 b + 1 )
�� b ��12
�� LHS �� 3144
�� RHS = 1100, 1010, 1001, 110, 101, 11
�� no roots.
d �� (b-1) log_10 2
2^a( 2^(b-a) + 1 ) = 10^c( 10^(d-c) + 1 )
�� a=b or c=d or ( a��b, c��d, a=c )
Suppose c=d, d>0
2^a( 1+2^(b-a) ) = 2⋅10^d �� b �� a ( mod 2 )
2^a( 1+4^((b-a)/2) ) = 2⋅10^d �� (b-a)/2 �� 1 ( mod 2 )
d = v_5( 4^((b-a)/2) - (-1)^((b-a)/2) ) = v_5((b-a)/2) + 1 < log_5 b + 1 (�� LTE)
�� b = log_2 2^b
< log_2( 2^a+2^b)
= log_2( 10^c+10^d )
< d log_2 10 + 1
< (log_5 b+1) log_2 10 + 1
�� b��5
�� RHS �� 64
�� LHS = 20
�� (a,b,c,d) = (2,4,1,1)
Suppose a=b
2⋅2^a = 10^c ( 1 +10^(d-c) ) LHS cannot be a multiple of 5. �� c=0.
2⋅2^a = 1 +10^d RHS is even only if d = 0 �� a=b=c=d=0
Suppose a��b, c��d, a=c
2^(b-a)+1 = 5^c(10^(d-c)+1) �� b �� a ( mod 2 )
1+4^((b-a)/2) = 5^c(10^(d-c)+1) �� (b-a)/2 �� 1 ( mod 2 )
c = v_5( 4^((b-a)/2) - (-1)^((b-a)/2) ) = v_5((b-a)/2) + 1 < log_5 b + 1 (�� LTE)
5^c - 1 = 2^b - 5^c 10^(d-c)
v_2( 5^c - 1 ) = 2 + v_2(c) �� 2 + log_2(c) < 2 + log_2( log_5 b + 1 )
v_2( 2^b - 5^c 10^(d-c) ) �� min{ b, d-c } > (b-1) log_10 2
(b-1) log_10 2 < 2 + log_2( log_5 b + 1 )
�� b ��12
�� LHS �� 3144
�� RHS = 1100, 1010, 1001, 110, 101, 11
�� no roots.
840�P�R�Q�l�ڂ̑f������
2025/06/27(��) 13:47:21.20ID:BS/AQPuN >>839
�e�œ��̂������@���肪�Ƃ��������܂��B
�e�œ��̂������@���肪�Ƃ��������܂��B
841�P�R�Q�l�ڂ̑f������
2025/06/27(��) 22:28:40.42ID:BS/AQPuN >>839���܁@
���Ȏ��ɋ����Ă��������B
��1�̏ꍇ��
�@�E�@v_5((b-a)/2) < log_5 b�@��������̂͂ǂ����Ăł����B
�@�E ���̌�u�� b��5�v��������̂͂ǂ����Ăł����B
���Ȏ��ɋ����Ă��������B
��1�̏ꍇ��
�@�E�@v_5((b-a)/2) < log_5 b�@��������̂͂ǂ����Ăł����B
�@�E ���̌�u�� b��5�v��������̂͂ǂ����Ăł����B
2025/06/28(�y) 01:06:02.51ID:Bfbxv6F0
5^v_5(x) �� x
2025/06/28(�y) 01:08:07.89ID:Bfbxv6F0
844�P�R�Q�l�ڂ̑f������
2025/06/28(�y) 12:46:40.81ID:fexGmv2J >>839���܁@842��843�ɂ��Ă��肪�Ƃ��������܂��B
���ƁA��3�̃P�[�X�ŁA4�s�ڂ�
�@5^c - 1 = 2^b - 5^c 10^(d-c)
��������̂͂ǂ����Ăł����B���ꂪ
�@5^c - 1 = 2^(b-a) - 5^c 10^(d-c) �Ȃ�킩��̂ł����B
���ƁA��3�̃P�[�X�ŁA4�s�ڂ�
�@5^c - 1 = 2^b - 5^c 10^(d-c)
��������̂͂ǂ����Ăł����B���ꂪ
�@5^c - 1 = 2^(b-a) - 5^c 10^(d-c) �Ȃ�킩��̂ł����B
2025/06/28(�y) 17:43:27.70ID:eycWLZVV
���̒ʂ�B����
5^c - 1 = 2^(b-c) - 5^c 10^(d-c)
v_2( 5^c - 1 ) = 2 + v_2(c) �� 2 + log_2(c) < 2 + log_2( log_5 b + 1 )
v_2( 2^(b-c) - 5^c 10^(d-c) ) �� min{ b-c, d-c } > (b-1) log_10 2
5^c - 1 = 2^(b-c) - 5^c 10^(d-c)
v_2( 5^c - 1 ) = 2 + v_2(c) �� 2 + log_2(c) < 2 + log_2( log_5 b + 1 )
v_2( 2^(b-c) - 5^c 10^(d-c) ) �� min{ b-c, d-c } > (b-1) log_10 2
846�P�R�Q�l�ڂ̑f������
2025/06/29(��) 09:58:24.00ID:YIgL8Bdh (x-a)(x-b)(x-c)�c�����c(x-y)(x-z)
���v�Z����
���v�Z����
847�P�R�Q�l�ڂ̑f������
2025/06/29(��) 14:58:17.50ID:XaGWcRY5 �ƂߎE���_���̂��肾�낤���A�S�����o���ʔ����Ȃ��{���̖{���ɂ�����Ȃ���肾��
848�P�R�Q�l�ڂ̑f������
2025/06/29(��) 16:27:45.71ID:YIgL8Bdh ���������X�������c
849�P�R�Q�l�ڂ̑f������
2025/06/29(��) 17:09:13.59ID:NH3TapWU min{ b-c, d-c } > (b-1) log_10 2
�ɂȂ�̂͂Ȃ�ŁH
�ɂȂ�̂͂Ȃ�ŁH
850�P�R�Q�l�ڂ̑f������
2025/06/30(��) 09:51:13.33ID:ZCQ5XJlD2025/06/30(��) 10:02:57.60ID:ahnSzx0D
a,b : odd, a �� b ( mod 4 )
�� v_2( a^n - b^n ) = v_2( a-b ) + v_2(n)
�� v_2( a^n - b^n ) = v_2( a-b ) + v_2(n)
2025/06/30(��) 10:06:54.02ID:ahnSzx0D
853�P�R�Q�l�ڂ̑f������
2025/06/30(��) 10:44:32.39ID:ZCQ5XJlD854�P�R�Q�l�ڂ̑f������
2025/07/01(��) 03:51:35.99ID:NoWFlKIX855�P�R�Q�l�ڂ̑f������
2025/07/01(��) 12:15:39.03ID:yrvfArgT cos( arctan(x) ) = 1/��(x^2 + 1)
�炵���̂ł����A
���ӂ���E�ӂ͂ǂ�����ē����܂����H
https://www.wolframalpha.com/input?i=cos%28arctan%28x%29%29&lang=ja
�炵���̂ł����A
���ӂ���E�ӂ͂ǂ�����ē����܂����H
https://www.wolframalpha.com/input?i=cos%28arctan%28x%29%29&lang=ja
856�P�R�Q�l�ڂ̑f������
2025/07/01(��) 22:51:56.90ID:VP/2WVvM (c(at(x)))^2=1/(1+(t(at(x))^2)=1/(1+xx)
at(x) ����l�Ȃ�, |at(x)|<��/2, c(at(x))>0
at(x) ����l�Ȃ�, |at(x)|<��/2, c(at(x))>0
857�P�R�Q�l�ڂ̑f������
2025/07/01(��) 23:40:16.85ID:yrvfArgT >>856
�T���N�X�����ł��܂���
�T���N�X�����ł��܂���
858�P�R�Q�l�ڂ̑f������
2025/07/02(��) 13:48:30.15ID:Xi3u68FU >>839, 845����
�����������肾���̂ł����A
min{ b-c, d-c } > (b-1) log_10 2 �̐������悭�킩��Ȃ��Ȃ�܂����B
�����u5^c - 1 = 2^(b-c) - 5^c 10^(d-c)�v���瓱�����̂ł��傤���B
�����������肾���̂ł����A
min{ b-c, d-c } > (b-1) log_10 2 �̐������悭�킩��Ȃ��Ȃ�܂����B
�����u5^c - 1 = 2^(b-c) - 5^c 10^(d-c)�v���瓱�����̂ł��傤���B
859�P�R�Q�l�ڂ̑f������
2025/07/03(��) 13:20:45.87ID:ZiBDwXsg860�P�R�Q�l�ڂ̑f������
2025/07/05(�y) 08:14:48.86ID:OX3zHoyG ���̃T�C�g�͐��w�̘b�肪�����ɂ���ĂȂ��Ƃ������̂ł���
���w�̘b�肪�����ɂ���Ă�T�C�g�͂���܂���?
���w�̘b�肪�����ɂ���Ă�T�C�g�͂���܂���?
861�P�R�Q�l�ڂ̑f������
2025/07/05(�y) 18:26:06.36ID:81Ae4QLt ����ł��B
R�������́AZ��L���������A
X��R-�x�N�g����ԁAU=Z^r�A
f:U��X��P�˂Ƃ��܂��B
���̂Ƃ��Af:U⊗R��X�͒P�˂ł����H
R��Z-���Q�Ƃ��ĕ��R�łȂ��C�����܂��B
��낵�����肢���܂��B
R�������́AZ��L���������A
X��R-�x�N�g����ԁAU=Z^r�A
f:U��X��P�˂Ƃ��܂��B
���̂Ƃ��Af:U⊗R��X�͒P�˂ł����H
R��Z-���Q�Ƃ��ĕ��R�łȂ��C�����܂��B
��낵�����肢���܂��B
862�P�R�Q�l�ڂ̑f������
2025/07/05(�y) 18:32:08.07ID:81Ae4QLt �����܂���B
f�͏����^�����肵�Ă��܂����B
f�͏����^�����肵�Ă��܂����B
2025/07/05(�y) 20:08:27.52ID:y2qCOzik
ℤ���QM�����R��M ���˂��ꌳ�������Ȃ� i.e. ��m��M ��n��ℤ mn=0 �� m=0 or n=0
�Ȃ̂�ℝ��ℤ���Q�Ƃ��ĕ��R
�Ȃ̂�ℝ��ℤ���Q�Ƃ��ĕ��R
864�P�R�Q�l�ڂ̑f������
2025/07/05(�y) 20:57:33.84ID:81Ae4QLt ���肪�Ƃ��������܂��I
865�P�R�Q�l�ڂ̑f������
2025/07/06(��) 20:30:47.29ID:mLPZO48J ���̖�Ȃ�ł��B
(1)�͂����̂ł����A(2)��(1)���g���Ǝv���̂ł����A�ǂ��g���Ƃ����ł��傤���B
(1)k>0�̂Ƃ��A(�C)(��)�̕s�������Ȃ肽�Ƃ����O���t�p���Đ�������B
�@(�C)1/sqrt(k+1) < integral_[k,k+1] (1/sqrt(x))dx
�@(��)1/sqrt(k) > 0.5(1/sqrt(k)-1/sqrt(k+1)) + integral_[k,k+1](1/sqrt(x))dx
(2)1/sqrt(1)+1/sqrt(2)+1/sqrt(3)+�c�c+1/sqrt(100) �̒l��������1�ʂ��l�̌ܓ����ċ��߂�B
(1)�͂����̂ł����A(2)��(1)���g���Ǝv���̂ł����A�ǂ��g���Ƃ����ł��傤���B
(1)k>0�̂Ƃ��A(�C)(��)�̕s�������Ȃ肽�Ƃ����O���t�p���Đ�������B
�@(�C)1/sqrt(k+1) < integral_[k,k+1] (1/sqrt(x))dx
�@(��)1/sqrt(k) > 0.5(1/sqrt(k)-1/sqrt(k+1)) + integral_[k,k+1](1/sqrt(x))dx
(2)1/sqrt(1)+1/sqrt(2)+1/sqrt(3)+�c�c+1/sqrt(100) �̒l��������1�ʂ��l�̌ܓ����ċ��߂�B
2025/07/06(��) 22:45:47.65ID:iT+o8XbJ
����A����������蕶�̈Ӗ����킩���
1/sqrt(1)+1/sqrt(2)+1/sqrt(3)+�c�c+1/sqrt(100) �̒l�̏�����1�ʂ��l�̌ܓ����Ă����鐮�������Ƃ߂悩�ȁH
1/sqrt(1)+1/sqrt(2)+1/sqrt(3)+�c�c+1/sqrt(100) �̒l�̏�����1�ʂ��l�̌ܓ����Ă����鐮�������Ƃ߂悩�ȁH
2025/07/06(��) 22:46:27.80ID:iT+o8XbJ
�������̈Ӗ��Ȃ炻���ǂ߂Ȃ��A�z���͂��
����͂O���
����͂O���
868�P�R�Q�l�ڂ̑f������
2025/07/07(��) 08:30:14.62ID:40k/2Uxm ���╁�ʂɈӖ��킩�邯��
��������͂�
��������͂�
869������������tS.A.D.@���ƘZ�x���c
2025/07/07(��) 08:38:44.78ID:FsKKNHVr �^�C����ҁB
870������������tS.A.D.@���ƘZ�x���c
2025/07/07(��) 08:41:25.73ID:FsKKNHVr �^�C�����ɋA�˂������q��c�́B�̐������Ȃ��ɕ�҂��܂��B
871������������tS.A.D.@���ƘZ�x���c
2025/07/07(��) 08:43:49.89ID:FsKKNHVr ���������B��B
2025/07/07(��) 11:54:08.83ID:fu5PRoxg
1/sqrt(1)+1/sqrt(2)+1/sqrt(3)+�c�c+1/sqrt(100) �̒l
��
������1�ʂ��l�̌ܓ�
�������̂͂��͂�
1/sqrt(1)+1/sqrt(2)+1/sqrt(3)+�c�c+1/sqrt(100) �̒l
�ł͂Ȃ��B����Ă��̑����
1/sqrt(1)+1/sqrt(2)+1/sqrt(3)+�c�c+1/sqrt(100) �̒l
�͋��܂�Ȃ��B���������̕��͂ŋ��߂�Ƃ����Ă�̂�
1/sqrt(1)+1/sqrt(2)+1/sqrt(3)+�c�c+1/sqrt(100) �̒l
�ȊO�ɂ͂Ȃ��B�����������̒l�͂�������ȁ[���l�ŃL���C�Ȓl�ɂ��Ƃ܂�����͂��Ȃ��B
��
������1�ʂ��l�̌ܓ�
�������̂͂��͂�
1/sqrt(1)+1/sqrt(2)+1/sqrt(3)+�c�c+1/sqrt(100) �̒l
�ł͂Ȃ��B����Ă��̑����
1/sqrt(1)+1/sqrt(2)+1/sqrt(3)+�c�c+1/sqrt(100) �̒l
�͋��܂�Ȃ��B���������̕��͂ŋ��߂�Ƃ����Ă�̂�
1/sqrt(1)+1/sqrt(2)+1/sqrt(3)+�c�c+1/sqrt(100) �̒l
�ȊO�ɂ͂Ȃ��B�����������̒l�͂�������ȁ[���l�ŃL���C�Ȓl�ɂ��Ƃ܂�����͂��Ȃ��B
873�P�R�Q�l�ڂ̑f������
2025/07/07(��) 12:13:04.92ID:ZyFOibv/ �u���̒l��������1�ʂ��l�̌ܓ����ċ��߂�v
����
�u���̒l�̏�����1�ʂ��l�̌ܓ����邱�Ƃɂ��A(�Ȃɂ�)�����߂�v
�u���̒l���A(�Ȃɂ�)�̏�����1�ʂ��l�̌ܓ����邱�Ƃɂ�苁�߂�v
�̂ǂ������s�������A��������(�Ȃɂ�)���s��������
����
�u���̒l�̏�����1�ʂ��l�̌ܓ����邱�Ƃɂ��A(�Ȃɂ�)�����߂�v
�u���̒l���A(�Ȃɂ�)�̏�����1�ʂ��l�̌ܓ����邱�Ƃɂ�苁�߂�v
�̂ǂ������s�������A��������(�Ȃɂ�)���s��������
874�P�R�Q�l�ڂ̑f������
2025/07/07(��) 21:05:00.00ID:40k/2Uxm ������������`���V�̗��ɂł������Ă�
2025/07/08(��) 14:33:19.53ID:nYS98Kd6
�܂����̒��x�̓��{��̂����������킩��Ȃ���͑f�����c�O������ق��Ƃ������B
876�P�R�Q�l�ڂ̑f������
2025/07/08(��) 22:54:17.71ID:1r2LO/Z2 ���ȑ���Ė��x���x�s�������Ȃ�Ƙb��ł��낤�Ƃ�����
877�P�R�Q�l�ڂ̑f������
2025/07/09(��) 00:00:51.32ID:x0xluZEY A��Euclid���R^n�̖����Z�x�̕W���Ƃ���.
cl(M)=A�������X�Z��R^n�̕����W��M�����݂�����.
������, cl(M)��M�̈ʑ����\��.
�Ƃ������ɂ��ĂȂ̂ł���,
M=Q^n��A�ƒu���Ύ��������Ɋ������̂ł���, cl(M)��A���������܂���.
�t���͂ǂ̂悤�Ɏ��������̂ł��傤��.
�܂���M�̒�ߕ����Ԉ���Ă���̂ł��傤��.
��낵�����肢���܂��B
cl(M)=A�������X�Z��R^n�̕����W��M�����݂�����.
������, cl(M)��M�̈ʑ����\��.
�Ƃ������ɂ��ĂȂ̂ł���,
M=Q^n��A�ƒu���Ύ��������Ɋ������̂ł���, cl(M)��A���������܂���.
�t���͂ǂ̂悤�Ɏ��������̂ł��傤��.
�܂���M�̒�ߕ����Ԉ���Ă���̂ł��傤��.
��낵�����肢���܂��B
2025/07/09(��) 00:34:21.01ID:oU9uUuaE
A ���L�E�̏ꍇ�����Ώ\���B���̂Ƃ� A �̓R���p�N�g�B���R�� n �ɑ��ėL���� A �̓_ aⁿ₁ aⁿ₂ aⁿ₃...aⁿₖ₍ₙ₎ �� aⁿᵢ ���S�̔��a 1/n �̊J���� A ��핢����悤�ɑI�ׂ�BM = ��ₙ{ aⁿ₁ aⁿ₂ aⁿ₃...aⁿₖ₍ₙ₎ } �͉Z�W���ŏ��������B
879�P�R�Q�l�ڂ̑f������
2025/07/10(��) 00:28:58.53ID:I58Ya6oJ ���肪�Ƃ��������܂��B
�Ȃ��A�L�E�̏ꍇ�����Ώ\���Ȃ̂ł��傤���B
��낵�����肢���܂��B
�Ȃ��A�L�E�̏ꍇ�����Ώ\���Ȃ̂ł��傤���B
��낵�����肢���܂��B
2025/07/10(��) 16:25:11.67ID:BW0VBWt+
�������ꂪ�킩��Ȃ��Ȃ炱�̖��ɒ��킷�鎑�i����Ȃ�
2025/07/22(��) 11:21:00.51ID:zAw0BzA/
���� x-1=0 ������܂��B���� x=1 �ł�
���ӂ� a �������܂��B x^2=x
x^2-x=0
x(x-1)=0
�� a=0,1 �����܂�܂�
���҂͓����Ȃ̂ł��傤���B����͂������Ȃ��Ƃł͂���܂��H
���ӂ� a �������܂��B x^2=x
x^2-x=0
x(x-1)=0
�� a=0,1 �����܂�܂�
���҂͓����Ȃ̂ł��傤���B����͂������Ȃ��Ƃł͂���܂��H
882�P�R�Q�l�ڂ̑f������
2025/07/22(��) 11:30:22.26ID:3GlIPuJQ ���������ł���
x��a��������܂��ɂȂ��Ă�̂�
x��a��������܂��ɂȂ��Ă�̂�
883�P�R�Q�l�ڂ̑f������
2025/08/05(��) 14:28:27.21ID:mFF3rxN4 �������� {f_n} ��
f_1=1,
f_{n+1}=(f_n)*(x^(2^(n-1))-f_n)
�Œ�߂�Bf_2=x-1, f_3=(x-1)(x^2-(x-1)), f_4=(x-1)(x^2-(x-1))(x^4-(x-1)(x^2-(x-1))), �c �ƂȂ��Ă����܂��B
x��2�̂Ƃ�, x^(2^(n-1))/f_n �� x�{n�{1
�����藧���Ăق����̂ł����A����͎����܂����B
f_1=1,
f_{n+1}=(f_n)*(x^(2^(n-1))-f_n)
�Œ�߂�Bf_2=x-1, f_3=(x-1)(x^2-(x-1)), f_4=(x-1)(x^2-(x-1))(x^4-(x-1)(x^2-(x-1))), �c �ƂȂ��Ă����܂��B
x��2�̂Ƃ�, x^(2^(n-1))/f_n �� x�{n�{1
�����藧���Ăق����̂ł����A����͎����܂����B
2025/08/06(��) 22:40:59.34ID:npKgzey/
���߂݂������
885�P�R�Q�l�ڂ̑f������
2025/08/07(��) 12:16:36.13ID:VAJlbe1v ���߂Ȃ�ł����H
2025/08/07(��) 22:28:53.18ID:Z1KlT5xz
�^���̗��ӂ� x^(2^(n)) �Ŋ����ċt�����Ƃ���
x^(2^(n))/f_{n+1}=(x^(2^(n-1))/f_n)*(1-f_n/x^(2^(n-1)))
������ g_n = x^(2^(n-1))/f_n �Ƃ�����
g_{n+1} = g_n/(1-1/g_n) = g_n^2/(g_n-1) = g_n + 1 + 1/(g_n-1) ...①
�ł���B�Ꭶ�����
g_1 = x
g_2 = x^2/(x-1)
g_3 = x^4/((x - 1) (x^2 - x + 1))
g_4 = x^8/((x - 1) (x^2 - x + 1) (x^4 - x^3 + 2 x^2 - 2 x + 1))
...
�ł���B������
x^(2^(n-1))/f_n �� x�{n�{1 �� g_n �� x�{n�{1 ...②
�ł���B������①��
g_{n+1} - g_n = 1 + 1/(g_n-1)
�ł��邩�� n �ɂ��đQ�ߓW�J�������Ă�����
g_n = n + o(n) = n + log(n) + o( log(n) )
�ƂȂ邩��②�͐������Ȃ�
----
���Ǝv���B
x^(2^(n))/f_{n+1}=(x^(2^(n-1))/f_n)*(1-f_n/x^(2^(n-1)))
������ g_n = x^(2^(n-1))/f_n �Ƃ�����
g_{n+1} = g_n/(1-1/g_n) = g_n^2/(g_n-1) = g_n + 1 + 1/(g_n-1) ...①
�ł���B�Ꭶ�����
g_1 = x
g_2 = x^2/(x-1)
g_3 = x^4/((x - 1) (x^2 - x + 1))
g_4 = x^8/((x - 1) (x^2 - x + 1) (x^4 - x^3 + 2 x^2 - 2 x + 1))
...
�ł���B������
x^(2^(n-1))/f_n �� x�{n�{1 �� g_n �� x�{n�{1 ...②
�ł���B������①��
g_{n+1} - g_n = 1 + 1/(g_n-1)
�ł��邩�� n �ɂ��đQ�ߓW�J�������Ă�����
g_n = n + o(n) = n + log(n) + o( log(n) )
�ƂȂ邩��②�͐������Ȃ�
----
���Ǝv���B
887�P�R�Q�l�ڂ̑f������
2025/08/26(��) 08:56:46.94ID:HJ0cQSDk �O�p�`ABC�̕�BC��ɓ_D������B
AB��7�AAC��4�ABD��6�ACD=2�̂Ƃ��AAD�͂����炩�B
�Ƃ��������������Ă��������B
AB��7�AAC��4�ABD��6�ACD=2�̂Ƃ��AAD�͂����炩�B
�Ƃ��������������Ă��������B
888�P�R�Q�l�ڂ̑f������
2025/08/26(��) 21:49:15.13ID:TqARCcXb >>887
��(7^2+6^2-2�E7�E6(7^2-4^2+(6+2)^2)/(2�E7�E(6+2))
=��(7^2+6^2-6(7^2-4^2+(6+2)^2)/(6+2))
=��(7^2(2/(6+2))+4^2(6/(6+2))+6^2-6(6+2))
=��(7^2(2/(6+2))+4^2(6/(6+2))-6�E2)
=��(7^2(2/(6+2))+4^2(6/(6+2))-6�E2(6+2)/(6+2))
=��(7^2-6�E2)(2/(6+2))+(4^2-6�E2)(6/(6+2)))
��(7^2+6^2-2�E7�E6(7^2-4^2+(6+2)^2)/(2�E7�E(6+2))
=��(7^2+6^2-6(7^2-4^2+(6+2)^2)/(6+2))
=��(7^2(2/(6+2))+4^2(6/(6+2))+6^2-6(6+2))
=��(7^2(2/(6+2))+4^2(6/(6+2))-6�E2)
=��(7^2(2/(6+2))+4^2(6/(6+2))-6�E2(6+2)/(6+2))
=��(7^2-6�E2)(2/(6+2))+(4^2-6�E2)(6/(6+2)))
889�P�R�Q�l�ڂ̑f������
2025/08/31(��) 21:24:32.49ID:xJsdecHP N�����R���̒萔�Ak�����R���Ƃ���Ƃ�
(k^N)/k! ��k������0�������邱�Ƃ̎��������������Ă��������B
(k^N)/k! ��k������0�������邱�Ƃ̎��������������Ă��������B
890�P�R�Q�l�ڂ̑f������
2025/08/31(��) 22:02:00.06ID:tARmQ1L+ k>2N
kk�ck/k!=(k/k)(k/k-1)�c(k/k-N+1)/(k-N)!<2^N/(k-N)!��0
kk�ck/k!=(k/k)(k/k-1)�c(k/k-N+1)/(k-N)!<2^N/(k-N)!��0
891�P�R�Q�l�ڂ̑f������
2025/09/14(��) 14:36:56.48ID:Yv7EOe59 p,q���f���ŁAp+q���f���Ȃ�Ap��q���f���ɂȂ�̂͂Ȃ��ł����B
892�P�R�Q�l�ڂ̑f������
2025/09/14(��) 14:38:04.97ID:Yv7EOe59 �܂��������B891�̓i�V�ɂ��āA���炽�߂āA
p,q���f���ŁAp+q���f���Ȃ�Ap��q��2�ɂȂ�̂͂Ȃ��ł����B
p,q���f���ŁAp+q���f���Ȃ�Ap��q��2�ɂȂ�̂͂Ȃ��ł����B
893�P�R�Q�l�ڂ̑f������
2025/09/14(��) 21:00:50.62ID:/xJ+pSVt ��f���𑫂����킹����2�łȂ������ɂȂ邩��
894�P�R�Q�l�ڂ̑f������
2025/09/16(��) 21:04:35.47ID:+LQ6xeUs N��2�ȏ�̎��R���Ƃ���B
N������Ȃ鑝������ a_1��a_2���c��a_N ���^����ꂽ�Ƃ���B
N-1�̐� a_(j+1)-a_j (1��j��N-1) �̂����ő�̐���A�Ƃ���B
�܂��Ak�̐� a_i (1��i��k) �̑������ς� b_k (k=1,2, �c,N ) �Ƃ��A
N-1�̐� b_(j+1)-b_j (1��j��N-1) �̂����ő�̐���B�Ƃ���B
���̂Ƃ�, B/A ��0.5�ȉ��ł��邱�Ƃ����������̂ł��B
N������Ȃ鑝������ a_1��a_2���c��a_N ���^����ꂽ�Ƃ���B
N-1�̐� a_(j+1)-a_j (1��j��N-1) �̂����ő�̐���A�Ƃ���B
�܂��Ak�̐� a_i (1��i��k) �̑������ς� b_k (k=1,2, �c,N ) �Ƃ��A
N-1�̐� b_(j+1)-b_j (1��j��N-1) �̂����ő�̐���B�Ƃ���B
���̂Ƃ�, B/A ��0.5�ȉ��ł��邱�Ƃ����������̂ł��B
895�P�R�Q�l�ڂ̑f������
2025/10/01(��) 22:34:45.41ID:1UyWC+SH f(x)�͘A�����ŁAf(x)���ɒl�ɂȂ�x��x=a,b�̂��傤��2�ł���Ƃ��A
f(a)��f(b)�̂�������͋ɑ�l�ő����͋ɏ��l�ɂȂ�A���ɑ�l���ɏ��l�ɂȂ�
�Ƃ������͖̂��炩�Ƃ����Ă����܂����B
f(a)��f(b)�̂�������͋ɑ�l�ő����͋ɏ��l�ɂȂ�A���ɑ�l���ɏ��l�ɂȂ�
�Ƃ������͖̂��炩�Ƃ����Ă����܂����B
2025/10/01(��) 23:45:17.62ID:yjUevrJo
�ǂݎ�̃��x��������ȁB�w���̂P�C�Q��̎����̉Ŗ��炩���ď������猴�_�������ȁB�����҃��x�����ǎ҂Ȃ狖������Ȃ��́H
897�P�R�Q�l�ڂ̑f������
2025/10/02(��) 11:11:50.21ID:ke+KFZCx ��o�����Ȃ��Ɩ��炩����Ȃ�
f:R-{0}->R
f(x):=(x+1)^2 (x<0), (x-1)^2 (x>0)
f:R-{0}->R
f(x):=(x+1)^2 (x<0), (x-1)^2 (x>0)
2025/10/07(��) 14:38:55.31ID:cKFxyQLM
���̕����Ȃ� x=0 ���ɒl���B
�����s�\�ȂƂ����ɒl�������Ȃ��b�����邪�A���̕����ł̋ɒl�͂��̋ߖT�ɂ�����ő�l�ɂȂ�ꍇ���Ӗ����Ă����
�����s�\�ȂƂ����ɒl�������Ȃ��b�����邪�A���̕����ł̋ɒl�͂��̋ߖT�ɂ�����ő�l�ɂȂ�ꍇ���Ӗ����Ă����
899�P�R�Q�l�ڂ̑f������
2025/10/07(��) 19:39:29.43ID:K4WbEF8a �ނ�j�����{�d����ł��邩�����Ă݂悤�I
900�P�R�Q�l�ڂ̑f������
2025/10/12(��) 22:39:14.58ID:AYclt9rp ������Ȃ����ǂ����킩��܂����₳���Ă��������B�m���̖��ł��B
��������ɁA�ŏ����_�ɃR�}��u���B���������U��A�o���ڂ̐��̋��������E�ɐi�ނ��Ƃ��J��Ԃ��B
�Ⴆ�ŏ���3���2,5,1�Əo��R�}��2�A7�A8�ɂƂ܂邱�ƂɂȂ�B
���R��n�ɑ��A����ڂ��̎��s�ŃR�}��n�̈ʒu�ɂƂ܂�m����P(n)�Ƃ���B
����P(n)�����߂邱�Ƃ͂ł��܂����H
�����������Ƃ��̓T�C�R���̏o������̓I�ɒǂ��Čv�Z�ł���̂ł����B
�Ȃɂ��Q�����ł�����Ώ�����̂ł����B
��������ɁA�ŏ����_�ɃR�}��u���B���������U��A�o���ڂ̐��̋��������E�ɐi�ނ��Ƃ��J��Ԃ��B
�Ⴆ�ŏ���3���2,5,1�Əo��R�}��2�A7�A8�ɂƂ܂邱�ƂɂȂ�B
���R��n�ɑ��A����ڂ��̎��s�ŃR�}��n�̈ʒu�ɂƂ܂�m����P(n)�Ƃ���B
����P(n)�����߂邱�Ƃ͂ł��܂����H
�����������Ƃ��̓T�C�R���̏o������̓I�ɒǂ��Čv�Z�ł���̂ł����B
�Ȃɂ��Q�����ł�����Ώ�����̂ł����B
2025/10/12(��) 23:48:57.59ID:oKmI76/s
>>900
�Q������
P(n)=(1/6)∑[k=1,6]P(n-k)
P(0)=1, P(-1)=P(-2)=...=0
��ʉ���
x^5+2x^4+3x^3+4x^2+5x+6=0
��5�̕��f������ a, b, c, d, e �Ƃ�����
P(n)=(1/7)(2+a^(-n)+b^(-n)+c^(-n)+d^(-n)+e^(-n))
�ő�l��
n=6 �̂Ƃ� P(6)=(7^5)/(6^6)��0.3602
n���\���傫���Ƃ��̋Ɍ��l��
lim[n����]P(n)=2/7��0.2857
�����낭����߂�Ȃ��ŏオ���m��
https://zakii.la.coocan.jp/enumeration/31_sugoroku.htm
https://www7b.biglobe.ne.jp/~math-tota/suA/gazo/sugoroku.png
�Q������
P(n)=(1/6)∑[k=1,6]P(n-k)
P(0)=1, P(-1)=P(-2)=...=0
��ʉ���
x^5+2x^4+3x^3+4x^2+5x+6=0
��5�̕��f������ a, b, c, d, e �Ƃ�����
P(n)=(1/7)(2+a^(-n)+b^(-n)+c^(-n)+d^(-n)+e^(-n))
�ő�l��
n=6 �̂Ƃ� P(6)=(7^5)/(6^6)��0.3602
n���\���傫���Ƃ��̋Ɍ��l��
lim[n����]P(n)=2/7��0.2857
�����낭����߂�Ȃ��ŏオ���m��
https://zakii.la.coocan.jp/enumeration/31_sugoroku.htm
https://www7b.biglobe.ne.jp/~math-tota/suA/gazo/sugoroku.png
902�P�R�Q�l�ڂ̑f������
2025/10/13(��) 02:05:42.38ID:LsmYd8je �������B���肪�Ƃ��������܂��B�悭�ǂ�ł݂܂��B
903�P�R�Q�l�ڂ̑f������
2025/10/15(��) 22:43:04.34ID:efRVGbWp 12�̑f���������߂�B
�Ƃ����ꍇ�A�����́u2�A3�v�ł����ł��傤���B�u2,3,3�v�ł��傤���B
�Ƃ����ꍇ�A�����́u2�A3�v�ł����ł��傤���B�u2,3,3�v�ł��傤���B
904�P�R�Q�l�ڂ̑f������
2025/10/15(��) 23:42:51.22ID:dd9dV9AK 2,2,3
905�P�R�Q�l�ڂ̑f������
2025/10/18(�y) 01:33:53.88ID:X6M02NMM ���~�������^����ꂽ�Ƃ��܂��B
��ʂɕ��s�ȕ��ʂł���ƒf�ʂ͉~�ł����A������Ǝ߂ɂ���ƒf�ʂ͂��~�ɂȂ����肵�܂����A
�t�ɂ��܂��f�ʂ̊p�x��ς���ΔC�ӂ̂��~(�Ƒ����Ȃ��~)���f�ʂɌ����悤�ɂł�����̂ł��傤���B
��ʂɕ��s�ȕ��ʂł���ƒf�ʂ͉~�ł����A������Ǝ߂ɂ���ƒf�ʂ͂��~�ɂȂ����肵�܂����A
�t�ɂ��܂��f�ʂ̊p�x��ς���ΔC�ӂ̂��~(�Ƒ����Ȃ��~)���f�ʂɌ����悤�ɂł�����̂ł��傤���B
2025/10/18(�y) 04:48:01.74ID:sGWQ9+/P
�~�����̍������l���Ȃ���Ή\
�ג������~����肽���Ȃ�
�ؒf�ʂ�
���ʂɊ܂܂�钼���i����j�ƕ��s��
����Ȃ��߂Â���悢
�ڂ����́u�~���Ȑ��v�Ō���
�ג������~����肽���Ȃ�
�ؒf�ʂ�
���ʂɊ܂܂�钼���i����j�ƕ��s��
����Ȃ��߂Â���悢
�ڂ����́u�~���Ȑ��v�Ō���
907�P�R�Q�l�ڂ̑f������
2025/10/19(��) 12:35:21.93ID:8W5mEcf+ ���肪�Ƃ��������܂��B
�^����ꂽ���~�����̌`��(�Ƃ��Ă�Ƃ����ׂ������Ƃ�)�ɂ����
�ؒf�\�Ȃ��~�ɐ��������邩�ȂƎv���Ă��肵�܂������A�ǂ�Ȃ��~�ł��f�ʂɌ��꓾��̂ł��ˁB
�^����ꂽ���~�����̌`��(�Ƃ��Ă�Ƃ����ׂ������Ƃ�)�ɂ����
�ؒf�\�Ȃ��~�ɐ��������邩�ȂƎv���Ă��肵�܂������A�ǂ�Ȃ��~�ł��f�ʂɌ��꓾��̂ł��ˁB
908�P�R�Q�l�ڂ̑f������
2025/10/20(��) 17:25:04.93ID:FAsaHL5v �u�r�����痎������l�ԂɂԂ���Ȃ����߂ɂ̓r�����牽�l����ĕ����Έ��S���v
�Ƃ�����肪�����ƋC�ɂȂ��Ă��܂����B
GPT�ɕ������Ƃ���A���̂悤�Ȍv�Z���o��
https://i.imgur.com/gVNBjfU.png
https://i.imgur.com/I0Gvned.png
�E�܂��������ɗ�����ꍇ �� �����̒������댯�B
�E���ˏo���E���Ȃǂ��l������� �� �r������10 m�ȏ㗣��ĕ����ƈ��S���������B
�E���w�r���i100 m���j�Ȃ� 15 m�ȏ� ���]�܂����B
�ƂȂ�A�����I�ł͂Ȃ��������o�܂����B
�I�t�B�X�X�Ȃǂł̓r������10M����ĕ������ƂȂǂł��܂���B
�Ƃ������Ƃ͗�����������ꍇ�͒��߂邵���Ȃ��Ƃ������Ƃł��傤���H
�Ƃ�����肪�����ƋC�ɂȂ��Ă��܂����B
GPT�ɕ������Ƃ���A���̂悤�Ȍv�Z���o��
https://i.imgur.com/gVNBjfU.png
https://i.imgur.com/I0Gvned.png
�E�܂��������ɗ�����ꍇ �� �����̒������댯�B
�E���ˏo���E���Ȃǂ��l������� �� �r������10 m�ȏ㗣��ĕ����ƈ��S���������B
�E���w�r���i100 m���j�Ȃ� 15 m�ȏ� ���]�܂����B
�ƂȂ�A�����I�ł͂Ȃ��������o�܂����B
�I�t�B�X�X�Ȃǂł̓r������10M����ĕ������ƂȂǂł��܂���B
�Ƃ������Ƃ͗�����������ꍇ�͒��߂邵���Ȃ��Ƃ������Ƃł��傤���H
2025/10/20(��) 18:05:41.14ID:GBAIVu+l
910�P�R�Q�l�ڂ̑f������
2025/10/20(��) 22:24:45.88ID:FAsaHL5v���X�𓊍e����
���X����900���Ă��܂��B1000����ƕ\���ł��Ȃ��Ȃ��B
�j���[�X
- �y�������܂钆�z���{�O���Ȃ̒S���ǒ���17���ɓ��{���o���������K��ցc ��1 [BFU��]
- �Ђ�䂫���A�^�o�R�Ǝ�����߂Ȃ����R�𖾂��� �u�X�g���X�����Ȃ��������ʂƂ��Ē������ł���ꍇ������v ���N�I���n�ŗ͐� [�~���L�ҁ�]
- �K�������l�����Ȃ�GDP���U��@�G�R�m�~�X�g�����Z ��4 [�a�̎s��]
- �y�����L���O�z�������j���[���[�N������u���E�ő�̌o�ϓs�s�v��...���{����́A����1�s�s�����g�b�v10���� [���ꁚ]
- �o�[�K�[�L���O���{���Ɣ��p�A�S�[���h�}���ɗD������@700���~�K�� [�a�̎s��]
- �y���Z�T�b�J�[�z�{�錧���D���̐��a�w���j�q�T�b�J�[���ŕ����������ċx�ݒ��Ɉ����E�i���@�{��̑�\�Z�͂ǂ��Ȃ� [�s�g�d�@�e�t�q�x�Ӂ�]
- �Ƃ点��@���f�o�j�[
- NFL 2025/26 week11 part 2
- ���W���p���V���[�Y2025�u���{vs�؍��v����12
- �n���� ��2
- �͂܂���
- ��������@�S���X�]�ڋ֎~
- ���s���c��������P��E�Ӎ߂��Ȃ����R�@�P�����Վx���w�Ɏ㍘�ƒ@����邩�炾����🥺 [931948549]
- ���s�������Ӂu�����ȉΎ킪�Ύ��ɂȂ肩���Ă���B���������Ȃ��Ƃ����Ȃ��v [931948549]
- �y���s�ߕ�z�؍��R🇰🇷�A���{�R�Ƃ̍����R�����K��ˑR�L�����Z�����Ă��܂� [709039863]
- �O���Ȋ����A���s�̌��ƒ�����SNS�ւ̓��e�ɂ��čR�c���邽�߁A�킴�킴�������n�֕����Ē��ړ`���ɍs���͗l👈😲�H [521921834]
- �y�ߕ�z���s���c�̂̕`�������h��A���E���ő嗬�s���Ă��܂��c�Ȃ��Ȃ̂��H�� [339712612]
- �y�Ռ��z�����l�����̓��{�l�������̉����o�Ȃ��قǓI�m�ɕ]�����u���O��������l�m�E�������� [597533159]

