������Ȃ����͂����ɏ����Ă�448
���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B
>>750
�iA,B,C)���i3,7,8�j
�`�C�a�C�b���P���̐����Ƃ͈ꌾ�������ĂȂ����ǂ� >>757
���ɂ͔z��̉��Z���z��̗v�f�ʂ��̉��Z�ɂȂ�R���g�����肪�����ȁB
�i�j�Ŗڂ��`�J�`�J���邪��
for(A in 1:9){
for(B in 1:9){
for(C in 1:9){
if (sum((c(A,B,C)+c(A,C,B)+c(B,A,C)+c(B,C,A)+c(C,A,B))*c(100,10,1)) == 3123)
print(c(A,B,C))
}
}
}
[1] 3 7 8 a�������̒萔�Ƃ���B�A���������@x+ay=1,(2a+2)x-y=2a+6��������x,y�����݂���Ƃ��Aa�̒l�����߂�B
�킩����ڂ���������肢���܂�😭✨ G ���O���t�Ƃ���B
M^* �� G �̍ő�}�b�`���O�Ƃ���B
M �� G �̃}�b�`���O�Ƃ���B
���̂Ƃ��A G �ɂ́A M �Ɋւ���A�_�����L���Ȃ� |M^*| - |M| �̒P���ȑ����p�X�����݂��邱�Ƃ������B >>760
x=1-ay
(2a+2)(1-ay)-y=2a+6
(-2a^2-2a-1)y=4
-2(a-1/2)^2-1/2<0
(-2a^2-2a-1, y)=(-1,-4),(-2,-2),(-4,1)
(a,x,y)=(-1,5,4),(0,1,4) >>762
���ꂾ��(a,x,y)=(-1/2,-3,-8)�̂悤��a�������̏ꍇ���l������ĂȂ��ł��B ���L�̖���f�����ȒP�ɉ������@�������Ă��������B
���@
2�A7�A15�A26�A40�A( )
���A
1�A2�A5�A10�A( )�A26
�����͇@57 �A17 �ł��B��낵�����˂������܂��B >>766
�����܂���A���ȉ������܂����B >>705
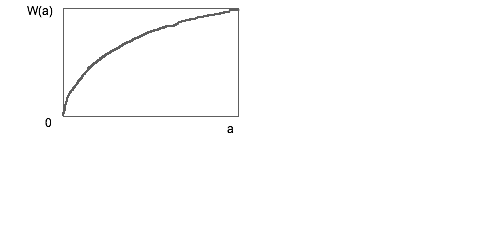
x = ��( W( 2e^{2y} )/2 )
�����y�Ɍ�͐��l�������Čv�Z�\�t�g�ȂǂŌv�Z���邾���ł��傤���H
�����x���g��W���ɂ��Ă��낢�뒲�ׂ��̂ł������l���o���Ⴊ�قƂ�ǂł���
W( 2e^{2y} )�������x���g��W���g�킸��y�̊��ŕ\�����@�͂Ȃ��̂ł��傤���H
�Ⴆ��W( ye^y ) = y �̂悤�� �����x���g��W��f(x)�ɂ��āA��ϕ�
��[0��a] f(x) dx
�����߂�Ba�͐��̎����ł���B n��3�ȏ�̐����Ak��1��k��n-1���������Ƃ���B
�ԋʂ�n�Ɛʂ�n-k����A�������ł���߂ɍ�����E�ɉ����ɕ��ׂ�B
���̂Ƃ�
�u����A������4�̋ʂ���Ȃ镔���ŁA������w�ԐԐԐx�ƂȂ��Ă��镔�������݂���v
�悤�Ȋm����n,k�ŕ\���B �㐔�w���w�҂ł�
Z�͐����S��
50��Z ���P�ʌ��ƂȂ�Z��̌Q�\���͂��邩���ׂ� >>769
��[0��a] f(x) dx = a W(a) - ��[0, W(a)] x e^x dx
= aW - [ x e^x - e^x ]{0,W}
= a W - W e^W + e^W - 1
= a( W(a) + 1/W(a) - 1) - 1
 �܂̒��ɐԋ�a�A��b�A����c�������Ă���B������a,b�͎��R���ł���B
�܂̒��ɐԋ�a�A��b�A����c�������Ă���B������a,b�͎��R���ł���B
�܂���ʂ�ׂɎ��o��������J��Ԃ��B���o�����ʂ͑܂ɖ߂��Ȃ��B
�܂̒��̋ʂŁA��Ԃ͂��߂ɐԋʂ��Ȃ��Ȃ����ꍇ�u�����v�Ƃ��A���l�ɐʂ��Ȃ��Ȃ����ꍇ�u�s�k�v�Ƃ���B
�܂��܂̒��ɐԋʂ��ʂ��c���Ă����ԂŔ��ʂ����o�����ꍇ�A������I�����u���������v�Ƃ���B
�i1�jc=0�̂Ƃ��A��������m�������߂�B
�i2�jc=1�̂Ƃ��A��������m�������߂�B�܂��i1�j�ŋ��߂��m���Ƃ̑召���r����B P(�ԏ���) = 1-a/(a+b)-a/(a+c)+a/(a+b+c) >>766
�������玩��������
�@�@�T�A�W�A�P�P�A�P�S�A�i�P�V�j�@������R��������
�A�@�P�A�R�A�T�A�i�V�j�A�X�@�������̗B��Ă��� x=(2a^2+6a+1)/(2a^2+2a+1)=1+4a/(2a^2+2a+1),
y=-4/(2a^2+2a+1)
���a���L�����ł��邱�Ƃɒ��ӂ���x,y�����ɐ����ƂȂ�悤��a��T������ >>776
����ȏ�A�������i��Ȃ���ł����H
���̏ꍇ�ǂ������ӂ��ɒT��������ł����H
a�����������肦��̂� �܂��v���O���������̂ōr�炵�p�����Ă�̂��� �v���O��������T�Ɉ����Ƃ͌���Ȃ����A
������������@�ɗ����āu���������I�v�́A�������ɈႤ����...�Ǝv���B �艿��2�����Ŕ����Ă��A������1��2���̗��v������悤�ɒ艿���������B�艿������Ƃ��̗��v���͉�%�ɂ���悢���H
����40%�ł��B���Ɩ��̈Ӗ����킩��܂���B�ߒ�������낵�����肢���܂� 0.8x = 1.12
x = (5/4) * 1.12 ���Z�̖��Œp��������
�k��蕶�l
AB��AC=AD�ł���l�ʑ�ABCD�ɂ����āA��BC�̒��_��E�Ƃ��A�_A������BCD�ɐ���AH�������B
���̂Ƃ��A�_H�́�BCD�̊O�S�ł��邱�Ƃ��u�O�����̒藝�v��p���ďؖ�����B �k�ȏ�l
�������ł��B��낵�����肢���܂��B >>783
��ABH �� ��ACH �� ��ADH�B >>784
�O�����̒藝�̎g���ǂ��낪�킩��Ȃ�
�ǂ��Ŏg���̂��� >>786
�S���킩����
>>787
�����O�����̒藝��K�������邽�߂ɗp�ӂ������̂��ȁH�H
https://i.imgur.com/LGcBsow.jpg
�菑���ł��܂� ��_�̖��ł��B�i�P�j�͉�����̂ł����A�i�Q�j�ł܂����Ă��܂�...
����聄
50�l�̐��k����Ȃ�N���X������B
���̂���30�l�͒j�q�A20�l�͏��q�ł���A�j�q�̂���18�l�A���q�̂���2�l�͊ዾ�������Ă��鉼��Ƃ���B
�i�P�j�j���̕ʁA�ዾ�̗L���̂��ꂼ�ꂪ�����ώ��ȑ��ݗʂ����߂�B
�i�Q�j�j���̐��ʂ������Ă���Ƃ��������̂��ƂŁA�ዾ�̗L�����������t�����ȏ��ʂ����߂�B
�����́A
�i�P�jH(X) = 0.97�r�b�g, H(Y) = 0.97�r�b�g
�i�Q�jH(Y|X) = 0.77�r�b�g
�ƂȂ��Ă���܂��B
���ӂȕ������܂�����A�i�Q�j�̓������o���܂ł̌v�Z�ߒ��������Ă������������ł��B
��낵�����肢�v���܂��B >>789
�P���� -(18/30)log2(18/30)-(2/20)log2-(2/20) ���Ⴄ�H >>783
��ӂ�� AB = AC
�� ��ABC��2���Ӄ�
�� A������BC�ɉ����������͒��_E�Ō����B
�U�����̒藝���AH�����BC�ɉ��������������_E�Ō����B
�� ��HBC��2���Ӄ�
�� HB = HC
���l�ɂ���
�@HB = HC = HD
3�_B,C,D�͓_H�𒆐S�Ƃ���~����ɂ���B
�_H�́�BCD�̊O�S�ł���B �f�M�ω��ɂ�����|�A�\���̎��̓��o | ���Z���w�̔���������
https://mathtrain.jp/hinetsuhi
���Z���Ȃ̂ł����A����ŕ�����Ȃ��Ƃ��낪����̂ł����i�����ɐ��w�I����Ȃ̂ł����Ŏ��₳���Ă��������܂��j
https://i.imgur.com/yWbiiCK.png
����́u���ӂŐϕ��v�Ƃ���܂����A����ϐ��Ƃ��Đϕ����Ă���̂ł��傤���H
P,V,T�̔����ω��ʂ���P�A��V�A��T�Ƃ���A�Ƃ����Ƃ��납��̂ݘb�����߂Ăē�Ȃ̂ł���
�܂������Őϕ����Ă��悢�Ƃ������Ƃ͂Ȃ��ł���ˁH���ԂƂ��ł����H ����d�Ƃ��ā����킩��܂����� >>792
������Ȃ��āAd�ōl�����
dP/P + ��dV/V = 0
���ӂɐϕ��L�����������āi�ϕ����āj
��1/P dP + ����1/V dV = 0
�ȉ���
�C�ɂȂ�Ȃ�E�ӂ͂b�ł��B
�ȒP�Ȕ����������̖{�i�̂̍��Z���ȏ����x���j��ǂނƂ킩��₷�������B >>792
�C�������������V�Ŋ���Z���āA�u�Ɋւ��Đϕ������
������łȂ��H >>794
���A���ꂼ��ʂ̕ϐ��Őϕ����Ă悢�̂ł����B
����c�c
>>795
����͎����Ă݂Ĕ[�����܂����B����ł��ˁc�c
���肪�Ƃ��������܂����B >>796
�Ȃ�ł��������ǗႦ�� V=V(T) �ƒu���Ēu���ϕ�
�� 1/V(T) dt
= �� 1/V(T) V'(T) dT
= �� 1/V (dV/dT) dT
= �� 1/V dV
P�����l >>796
�ϐ��̊ԂɊW�����藧����A���͕ʂ̕ϐ��ł͂Ȃ���Ȃ�
�ł��ǂ�ȃp�����[�^�Ŕ}��ϐ��\�����Ă��A���ǒu���ϕ��Ńp�����[�^�͌����Ȃ��Ȃ邩��
�ʁX�̕ϐ��Őϕ������悤�Ȍ����ڂɂȂ� >>796
�ϐ��Őϕ����Ă��Ȃ���
�ׂ����c�_�͂�������Č�����
�ӁX�����Ԃɑ������킹�Ă������Ƃ�
��(��P/P + ����/V) = ��0
�ŁA����d�@�ɂȂ�悤�ɋɌ����Ƃ�A�i�ׂ����c�_�𐁂�����āj
��L���ɕς����Ă��ƁB
��f(x)dx��f(x)��x�Őϕ����Ă��Ȃ��āAf(x)dx ��͈͂̕������������킹�Ă銴�o�B >>791
������
�����Ă��܂�😭 A:n���s��
A^5 -5A+E=0�ƂȂ�Ƃ�A�͑Ίp���\�ł��邱�Ƃ����� >>789
���߂ĕ������t�Ȃ̂ŋ������N����
https://logics-of-blue.com/information-theory-basic/
��ǂ�ł݂��B
# https://logics-of-blue.com/information-theory-basic/
"�\�z�����Ȃ����s�m�����i���G���g���s�[�j���傫�������Ϗ��ʂ��傫��"
ent <- function(x){ # ���G���g���s�[�i���Ϗ��ʁj
x=x/sum(x)
entropy=0
for(i in x) entropy=entropy+i*(-log2(i))
return(entropy)
}
ent(c(30/50,20/50)) # gender
ent(c((18+2)/50,(50-18-2)/50)) # glass
"�e�X�̊m�����z�̏��ʂ̍����̊��Ғl���Ƃ�܂�
�m�����z���قȂ��Ă���A���ʂ�����Ƃ݂Ȃ��̂��A
�J���o�b�N�E���C�u���[�̏��ʂł��B"
rel_ent <- function(P,Q){ # ���G���g���s�[
n=length(P)
if(n!=length(Q)) return(NULL)
P=P/sum(P)
Q=Q/sum(Q)
re=numeric(n)
for(i in 1:n) re[i] = Q[i]*(-log2(P[i])-(-log2(Q[i])))
return(sum(re))
}
#
"���ݏ��ʂ͕s�m�����i���G���g���s�[�j�̌����ʂƂ݂Ȃ����Ƃ��ł��܂�"
"
����聄
50�l�̐��k����Ȃ�N���X������B
���̂���30�l�͒j�q�A 20�l�͏��q�ł���A
�j�q�̂���18�l�A���q�̂���2�l�͊ዾ�������Ă��鉼��Ƃ���B
"
30/50*ent(c(18/30,12/30)) + 20/50*ent(c(2/20,18/20))
> 30/50*ent(c(18/30,12/30)) + 20/50*ent(c(2/20,18/20))
[1] 0.7701686 >>803
R�Ȃ��Ōv�Z����������
30/50 * ( 18/30*(-log2(18/30))+ 12/30*(-log2(12/30))) + 20/50 * ( 2/20*(-log2( 2/20))+ 18/20*(-log2(18/20)))
���ʂ����₷�������
30/50 * [ 18/30*{-log2(18/30)}+ 12/30*{-log2(12/30)} ] + 20/50 * [ 2/20*{-log2( 2/20)}+ 18/20*{-log2(18/20)} ] >>442
��P1st�����߂�
���̎��̎��w�����萔
(n(n+1)/2)-1�@�c�c�@
���̒��ł̕��̑g�ݍ��킹��
((n(n+1)/2)-1)(((n(n+1)/2)-1)-1)/2�@�c�c�A
�ŏI�}�X�Ƈ@�Ƃ̑g�ݍ��킹���@�@
(n(n+1)/2)-1�@�c�c�B
���w�̓�����Ƒ���̓�����Ŏ���������
�g�ݍ��킹�͇A�ƍ����̘a
������1 3 7 13 22 34 50 70 95 125 161 203
252 308 372 444 525 615�c�c
�����\����
(4n^3+6n^2-4n-3+3(-1)^n)/48
n�������Ă���̂�n-1�ɕ
�o4(n-1)^3+6(n-1)^2-4(n-1)-3+3(-1)^(n-1)�p/48�@�c�c�C
�v�Z�m�\�ŇAx2+�B+�C����͂����
P1st =�o12n^4+28n^3-42n^2-52n-3(-1)^n+51�p/48�@�c�c�D
�Sn(n+1)�}�X�ŕ��̑g���킹��
n(n+1)�on(n+1)-1�p/2�@�c�c�E
�����������́An(n+1)-1�Ɠ������̘a
��������1 2 4 6 9 12 16 20 25�c�c
�����\�����́@�o2n^2-1+(-1)^(n)�p/8�@�c�c�F
n(n+1)-1�@�c�c�G
�v�Z�m�\�ŇF+�G����͂����
even =(10n^2+8n+(-1)^n-9)/8�@�c�c�H
�v�Z�m�\�ŇE-�D-�H����͂����
Q1st =�o12n^4+20n^3-18n^2-20n-3(-1)^n+3�p/48�@ >>804
Prelude> let entropy x = sum $ map (\i -> -i*(logBase 2 i)) ( map(/sum(x)) x )
Prelude> 30/50 * entropy [18, 12] + 20/50 * entropy [2, 18]
0.7701685941085136 ���������ꂼ�ꓙ�����s�p36���Ɖs�p72���̕H�`������B�����_�����炳�����ԂȂ��~���l�߁A���܊p�`�����邱�Ƃ͉\���B
�o�J�����Ă���킩���̂ł��肢���܂��B >>808
�ŗL�l��-1��5����Jordan cell��J�Ƃ���ƕW��5�ł�
J^5=-E=5J-E�B https://i.imgur.com/2HWFTjk.jpg
������5�ł����Ă��܂����H
����Ă����������肢���܂��B �O�̂��߃v���b�g
>>810
x = 2 e^{t i} + e^{-2t i} (������ 1:3 ���� 2���̌����������^�C�~���O��������)
r^2 = |x|^2 = 5 + 2e^{3*t i} + 2e^{-3*t i} = 5 + 4 cos(3t)
tan�� := Im{x}/Re{x} = (2s-s2)/(2c+c2)
(d��/dt) /cos��^2 = { 2(c-c2)(2c+c2) + 2(s+s2)(2s-s2) }/(2c+c2)^2
(d��/dt) r^2 = 2 - 2 cos(3t)
( >>410 �� �� �� t �ł��鎖�������Ƃ����Ǝv����)
S = (1/2) �� [0��2��]d�� r^2 =(1/2) �� [0��2��]dt (d��/dt) r^2
= (1/2) �� [0��2��]dt (2 - 2cos(3t)) = 2��
�O�̂��߃v���b�g���Ă݂�
https://i.imgur.com/uCqzGmh.png
�܁[����Ȃ���Ȃ��ł��傤���B���~�̔��a�́�2 (�ʐ� 2��) >>801
�ŗL���������d���������Ȃ��̂ōŏ����������d���������Ȃ��B >>801
���܂�B��ʂ�n ���������B
x^5 - 5x +1 �͍ŏ��������Ŋ�����B
�ŏ����������d���������Ȃ��͖̂��炩�Ȃ̂őΊp���\�B >>813
�ŏ��������d������������B >>813
�ŏ��������Ŋ�����̂͂킩��܂����d���������Ȃ��̂͌�����܂����ˁH >>816
�ŏ����������d�������Ă�
f(x) = x^5 - 5x +1 ���d��������
�� f(x) = 0 , f�f(x) = 0 �����ʉ������� ���炵�܂����B�ŏ��������ˁB�ŗL�������łȂ��B
�Ȃ���v�ł��ˁB a,b,c,d�͎����Ƃ���
a+c=-4/3, b+4ac+d=-2, ad+bc=4, bd=1�̂Ƃ��A
(a^2-b)(c^2-d)<0������ >>811
���肪�Ƃ��������܂��B�܂��܂���������Ă܂���ł����B a,b������Ƃ���B
x�̑�����{(1+x)^a}{(1-x)^b}��W�J�����Ƃ��A�W���̐�Βl���ő�ƂȂ鍀�̎�����a,b�ŕ\���B >>811
���Z���w�̓��e�����ʼn����ꍇ�͂ǂ��Ȃ�܂����H >>822
�x�N�g���ʼn�����r^2=4cos2��+5�ƂȂ��Ă��܂��܂��B�������������� >>823
(x,y) = 2* (cos(t), sin(t)) + 1* (cos(-2t), sin(-2t))
��P�������]�����A��Q�������]�����Ǝv���Ă�������.
������ t �� "���]�p" �Ɠ����� "�ڐG�_�̕Ίp" �ł���, "�_ P �̕Ίp ��" �ł͂Ȃ����ɒ���.
�y���]�p���x�� -2 �̗��R�z
������ 1:3 �Ȃ̂� ���~�͌v3���~�̎����i����킯�ł�.
�܂� 1�i���ڂ� ���]�p t=2��/3 ��P�͑�~��2�x�ڂ̐ڐG�����܂�(t=0 ��1�x��), ���̂Ƃ����]�p�� -2*2��/3 �̋t���łƌ��]�p�� "����" �ƈ�v����킯�ł�.
�y�Ƃ�t �̊W�z
tan�� = y/x = (2s - s2)/(2c + c2). ���̗��ӂ� t �Ŕ��� (s,s2 ���̗��L�͏ȃX�y�[�X�̂���)
[��]=(d��/dt) ( 1 + (tan��)^2 ) =(d��/dt)( x^2 + y^2 )/x^2 = (d��/dt) r^2 / x^2
[�E]={ 2(c - c2)(2c + c2) +2(s + s2)(2s - s2) }/x^2 = ( 2 - cos(3t) )/ x^2
�� (d��/dt) r^2 = 2 - cos(3t)
�y�ʐ�S�z
�����O�p�`(�ʐ�: (1/2)*r*r����) �̋Ɍ��a�����߂�悢�̂�,
S = (1/2) �� [��:0��2��] d�� r^2 = (1/2) �� [t:0��2��] dt (d��/dt) r^2 = (1/2) �� [t:0��2��] dt ( 2 - cos(3t) ) = 2��
�ʐς������߂����̂Ȃ� (x, y) �� r^2 ��Ίp �� �ŕ\���K�v�͖����̂ł�. (�ȒP�Ȍ`�ɂ͂Ȃ�Ȃ��C������)
(�ϕ��̕ϐ��ϊ��̕ӂ肪���Z���w�͈͓��Ȃ̂��͒m��Ȃ�) 2 - cos(3t) �̂Ƃ��� 2 - 2cos(3t) �ł�. >>819
�ʔ��X���̉́c
f(x) = (x^2 +2ax+b)(x^2 +2cx+d) = x^4 -(8/3)x^3 -2x^2 +8x+1,
(a^2 -b)(c^2 -d) = (7/6 -f/2)^2 -(20/27)^2/(7/6 +f/2)
�@= (1/3)[10 - (13+2��11)^{2/3} - (13-2��11)^{2/3}]
�@= -0.2376189664261441
�@< 0,
�ʔ��X���Q�W-319,321 �p,�@�`�E�a�E�b�@�O���̃J�[�h����������������B��������P�������A���ɖ߂����U��J��Ԃ��B�`������������300�_�A�a��100�_�A�b��0�_���炦��B�U��J��Ԃ������̓_���̊��Ғl�͂����炩�B
�`�E�a�E�b���ꂼ��1/3�̊m���ň�����Ƃ���B
������ł��邾�����Ȃ��v�Z�Ŋy�ɉ������@�Ȃ��ł����H >>828
�U�����A�Q��B�Q���҂ł���B
300�~2+100�~2=800(�_) >>829-830
���肪�Ƃ��������܂����B
1���������ꍇ�̊��Ғl�~�J��Ԃ����Čv�Z�ł�����ł����H
������ăJ�[�h��4����5���ɂȂ�����A�_�����ς���Ă������ł����H >>827
�Ȃ�قǂ���f(x)�̌W���ɂȂ��Ă���̂�
���Ƃ����f(x)=0��4�̉����قȂ�2�����ƌ݂��ɋ����ȕ��f�����ł��邱�Ƃ��g����
�����ƊȒP�ɓ������ >>831
���������i������1�������Ă͖߂��j�ꍇ�͂����B�u�������s�v�ƌĂсA�u���z�v�ɏ]���B���Z���a�ł��͂��B���ȏ��ɂ��̂��Ă�Ȃ����� ���Ғl�͍��Z�̎w���v�̂���O�ꂽ�B
�̂ō��Z���w�͈̔͂ł͊��Ғl���߂���łȂ����A���Ғl�Ɋւ�������������g���Ȃ��B
�ǂ��ł������ł����`♬ >>834
���ϒl���Ċ��Ғl����Ȃ��́H
���v�łǂ��������H �@�`�E�a�E�b�@�O���̃J�[�h���������e�X�R�����v�X����������������B��������P�������A�J�[�h�͖߂��Ȃ����U��J��Ԃ��B�`������������300�_�A�a��100�_�A�b��0�_���炦��B�U��J��Ԃ������̓_���̊��Ғl�͂����炩�B
�`�E�a�E�b���ꂼ��1/3�̊m���ň�����Ƃ���B
���̕����ʔ����ˁB >>836
��������Ғl�W�O�O�ł������ȁH ��ABC�ŁABC=a�ACA=b�A��A=���A��B=���ł���B
a<b�̂Ƃ��A�ȉ��̕s���������藧���Ƃ������B
(b/a)^2 < (1-cos��)/(1-cos��) < (��/��)^2
����ʐ}�`�Ŏ����Ƃ���ꂽ�̂ł���������܂���B https://i.imgur.com/jChlpB1.jpg
�e�X�g�����Ă���̂ł���2.(3)��������Ȃ��̂łǂȂ��������������� >>839
���_�ŕs�A���ł���B
�� �� (0, 1) �Ƃ���B
�� ��C�ӂ̐��̎����Ƃ���B
P = ((��/2) * cos(��/2), (��/2) * sin(��/2))
�Ƃ���ƁA
���_�Ɠ_ P �̋����́A ��/2 �ł���A �� �����������B
|f(P) - f(0)| = |1 - 0| = 1 > �� �ǂ̂悤�ȓ��ς������������Ȃ��m�����̗ዳ���Ă��������B�ؖ������肢���܂��B >>841
James R. Munkres ���wAnalysis on Manifolds�x��p.9 Exercise 3�ɗႪ����܂��B >>819 >>827
(a^2 -b)(c^2 -d) = (7/6 -f/2)^2 - (20/27)^2/(7/6 +f/2)
�@= - (1/3) [(13+2��11)^{1/3} - (13-2��11)^{1/3}]^2
�@= - 0.2376189664261441
�@< 0, ��ł͂Ȃ�H�̕����W��A�ɑ���conv(A)=A�Ȃ��A�͓ʏW���ł���B�̏ؖ���������܂���B conv(A) �� A���܂ލŏ��̓ʏW���ł���B
conv(A) = A �Ȃ� A ���̂����̓ʏW���ł���B
�ǂ��ɔY�ޗv�f������̂�... �d�Ԃ̍L���Ō������w������肩�Ȃɂ��B
�u11����20�܂ł̐����̂����A�A�����鎩�R���̘a�ł͕\���Ȃ�
���̂����ׂĂ����Ȃ����B�v
���܂�����������̂��ȁH����A������2�̎��R���̘a��
�Ȃ邱�Ƃ͂قƂ�ǎ���������A���������`�F�b�N����������ǁB
������F�f����3�ȏ�̘A�����鎩�R���̘a�ł͕\���Ȃ����Ƃ������B >>846
�L���ǂ��ł�
n��a�`b�̘a�Ȃ�2n=(b+a)(b-a+1)���2n��2�ׂ��łȂ�n��2�ׂ��łȂ��B
�t��n��2�ׂ��łȂ��Ȃ�2n��2�ׂ��łȂ�2n=xy�Ax>y�Ax�Ay�̊�������ƂȂ�������̂��Ƃ��n��a=(x-y+1)/2�`
b=(x+y-1)/2�̘a�ɂȂ���Ă̂�����ˁB 1+2+3+4+5+6=21�߂�
20,18,14����₩��O���� >>849
2+3+4+5=14
3+4+5=12 2�~20=5�~8
(8+5-1)/2=6
(8-5+1)/2=2
20=2+3+4+5+6 ���܂�B�O���͕̂\���Ȃ����̃��X�g����ˁB ���X�g�A�b�v�Ȃ�10�܂ōl���Ȃ��ƃ_�����ˁB
1�`:3 6 10 15 21 28 35 45 55
2�`: 5 9 14 20 27 34 44 54
3�`: 7 12 18 25 32 42 52
4�`: 9 15 22 29 39 49
5�`: 11 18 25 35 45
6�`: 13 20 30 40
7�`: 14 24 34
8�`: 17 27
9�`: 19
�o�Ă��Ȃ��̂�1,2,4,8,16�B 2�ȏ�̘A���������R���̘aS�́A
���̌�����̏ꍇ�A����a�A�^�̐���b�Ƃ���S=ab�ƕ\����A
���������̏ꍇ�A����2b�A�^��2�̐��̘a��a�Ƃ���S=ab�ƕ\�����B
������̏ꍇ��a��3�ȏ�̊�B����āAS�͕K��3�ȏ�̊��Ƃ��Ď��B
�i���Ȃ킿�A2�ȊO�̑f���������j
�t�ɁAS��3�ȏ�̊�̖�a�������Ă���AS=ab�ƕ���������ŁA
����a,b��p���ď�L2�ʂ�̃A�v���[�`�ŏ��Ȃ��Ƃ��A������2�ȏ��
�u�����v�̘a�ŕ\�����Ƃ��ł���B
�����āA���ꂪ2�ȏ�́u���R���v�̘a�ƂȂ�����ׂ�ƁA
�Q�̃A�v���[�`�̕Е����K�������\�ł��邱�Ƃ��킩��B
����āAS��2�ȏ�̘A���������R���̘a�ŕ\����邽�߂̕K�v�\��������
S��2�ȊO�̑f�����������ƁB �z�����W�[�Q�����^�����z���g�s�[�^���قȂ�w�I���������P�̓I���̗̂�������ĉ����� >>852
�P�U�������\���Ȃ��ł����̂��ȁH (X,O)���ʑ����
op�����̋�Ԃ̊J�j��p�f
cl�����̋�Ԃ̕��p�f
�Ƃ��Aop,cl��P(X)����P(X)�ւ̎ʑ��Ƃ݂Ȃ��B(P(X)��X�̋ЏW��)
���̎ʑ��̍����ɂ��ĂȂ肽�����ĉ��ł��������H
op������op = op �����������H
op�cl�op�cl = op�cl �����������H >>857
��̓_��
����R�_{0}��B
���͌�����B
�W�� F �ɑ� ici F= i F ��������Ηǂ��B
ci F �� F �䂦 ici F �� i F�B
i F �� ci F �䂦 i F �� ici F�B �T���N�X
���Ⴀ���l�̋c�_��
cl�op�cl�op = cl�op �������������� F(x)=��(x��x+1)te^(-|t|)dt�ɂ��āAx�����ׂĂ̎������Ƃ��AF(x)���ő储��эŏ��ƂȂ�x�̒l�����ꂼ�ꋁ�߂�B
�ڂ���������肢���܂��B >>860
��Βl�O���ĕ����ϕ�
����Ȃ��Ƃ��ł��Ȃ��̂��S�~��Yw >>860
x��-1 �̂Ƃ�
�@F(x) = exp(x){(e-1)x +1} < 0,
x��0 �̂Ƃ�
�@F(x) = exp(-x-1){(e-1)x +(e-2)} > 0,
-1��x��0 �̂Ƃ�
�@F(x) = ��[x,0] t�exp(t) dt + ��[0,x+1] t�exp(-t) dt
�@�@= {(1-x)exp(x) - 1} + {1 - (2+x)exp(-x-1)}
�@�@= (1-x)exp(x) - (2+x)exp(-x-1),
F(-1/2) = 0,
�_(-1/2�C0) �ɂ��đΏ�
F '(x) = (x+1)exp(-|x+1|) - x�exp(-|x|) = 0,
���
�@x = -e/(e-1) �ōŏ��@{ F(x) = -(e-1)exp(-e/(e-1)) }
�@x = 1/(e-1) �ōő�@{ F(x) = (e-1)exp(-e/(e-1)) } �������(X, d)�ɂ��Ď���ł��B
A, B��X�ɂ���
��(A��B)��d(A, B)+��(A)+��(B)
�ł��邱�Ƃ̏ؖ����l�����܂���B
�ǂȂ�������������������K���ł��B
�Ȃ��AA, B��X�ɑ���
��(A)=sup{d(x, y)|x, y��A}
d(A, B)=inf{d(x, y)|x��A, y��B} �������(X, d)�ɂ��Ď���ł��B
A, B��X�ɂ���
��(A��B)��d(A, B)+��(A)+��(B)
�ł��邱�Ƃ̏ؖ����l�����܂���B
�ǂȂ�������������������K���ł��B
�Ȃ��AA, B��X�ɑ���
��(A)=sup{d(x, y)|x, y��A}
d(A, B)=inf{d(x, y)|x��A, y��B} >>847
�Ђ��[�A�����ł��ˁB�m���ɂ��̒ʂ�ł��ˁB�������܂����B >>867
a_1��A, b_1��B s.t. ��(A��B) = d(a_1, b_1)
a_0��A, b_0��B s.t. d(A, B) = d(a_0, b_0)
�ƂȂ��Ă���Ƃ���B
�O�p�s�������
d(A��B) = d(a_1, b_1) �� d(a_1, a_0) + d(a0, b_1)
�� d(a_1, a_0) + d(a_0, b_0) + d(b_0, b1)
�� ��(A) + d(A, B) + ��(B)
�i�Ō�̕s�����̓̒�`���j >>854
����܂��������ł��ˁB
�����I�ɓ�����Ėʔ������ł����A�m��l���m����Ȃ̂��ȁB >>867
a_1��A, b_1��B s.t. ��(A��B) = d(a_1, b_1)
a_0��A, b_0��B s.t. d(A, B) = d(a_0, b_0)
�ƂȂ��Ă���Ƃ���B
�O�p�s�������
d(A��B) = d(a_1, b_1) �� d(a_1, a_0) + d(a_0, b_1)
�� d(a_1, a_0) + d(a_0, b_0) + d(b_0, b_1)
�� ��(A) + d(A, B) + ��(B)
�i�Ō�̕s�����̓̒�`���j >>867
A, B���J�W���Ȃ�a_i��A, b_j��B�Ƃ���Ƃ܂����B
sup, inf�Ȃ̂ŁB >>872
��(A��B)=d(a_1, b_1)
d(A, B)=d(a_0, b_0)
�ƂȂ�a_0, a_1��A, b_0, b_1��B�̑��݂�����ӂ�ł���ˁB
����ł͏ؖ��ɂȂ��Ă��Ȃ��Ǝv���܂��B >>873
���݂�����ӂ₾�ƁH�ǂ��܂Ŏ����̓��ōl�����H
A, B���J�̂Ƃ��́A�����́A X�ɑ���A, B�̕�W���̌��B ���Ƃ���������Ȃ�ł���
���v�w��t������ăf�[�^�ł�����1�ϐ�����Ȃ��ł����H
n�ϐ�(����)�̃f�[�^�ɑ��Ċe�N���X�ɗL�Ӎ�������Ȃ����Ăǂ������ӂ��Ɍ��肵���炢���ł����H >>874
�܂�A, B�̌��łȂ����Ƃ�������Ă��Ƃł���ˏ� >>867
d(A,B)�̒�`���
��(�Á�0) ��(x'��A, y'��B) d(x', y') < d(A,B) + ��
(1)��(x��A, y��B) d(x,y)�� d(x,x')+d(x',y')+d(y',y) < ��(A)+��(B)+d(A, B) + ��
��(A),��(B)�̒�`���
(2)��(x,y ��A) d(x,y)�� ��(A) �� ��(A)+��(B)+d(A, B)
(3)��(x,y ��B) d(x,y)�� ��(B) �� ��(A)+��(B)+d(A, B)
(1)-(3)���
(4)��(x,y ��A��B) d(x,y) < ��(A)+��(B)+d(A, B) + ��
��(A��B) �̒�`���
(5) ��(��'��0) ��(x'',y'' ��A��B) ��(A��B) - ��' < d(x'',y'')
(4),(5)���
��(��, ��'��0) ��(A��B) - ��' < ��(A)+��(B)+d(A, B) + ��
�� ��(A��B) �� ��(A)+��(B)+d(A, B) >>838
(��)
AB = c �Ƃ����B
���]���藝���
�@1-cos�� = {aa-(b-c)^2} /2bc = (a-b+c)(a+b-c)/2bc,
�@1-cos�� = {bb-(c-a)^2} /2ac = (b+c-a)(a+b-c)/2ac,
���
aa(1-cos��) - bb(1-cos��)
= aa{1 - (cc+aa-bb)/2ac} - bb{1 - (bb+cc-aa)/2bc}
= {a(b+c-a) - b(a-b+c)}(a+b-c) /2c
= (b-a)(a+b-c)^2 /2c
> 0,�@�@�@(���@b-a>0)
�܂��A
1-cos�� > 1-cos��,
cos�� < cos��,
�� > ��,
(�E)
sin(x) �� 0<x<�� �ŏ�ɓʂ�����
�@sin(��/2) > (1-��/��)sin(0) + (��/��)sin(��/2) = (��/��)sin(��/2),
(1-cos��)/(1-cos��) = {sin(��/2)/sin(��/2)}^2 < (��/��)^2, ���̖������Ă��������I
�ً}�ł��B
�ق�Ƃ��肢���܂��B
https://i.imgur.com/X8VmzMu.jpg >>877
������̎���������҂ł��B
�[���ł��܂����B
�{���ɂ��肪�Ƃ��������܂��B >>838 >>878
�@0 < (b-a)/2R�@�@�@(�� ���)
�@= sin�� - sin���@�@�@(�� �����藝)
�@= 2sin((��-��)/2)cos((��+��)/2)�@�@(�� �a�ό���)
������ 0 < (��+��)/2 < ��/2 ������
�@sin((��-��)/2) > 0,
�@�� > ��, >>881
���Ȍ��і�(e.g. trefoil knot)�̊Ǐ�ߖT��p�ӂ���S^3���炭�蔲�������̂�M�Ƃ����B
��M��̃��[�vl�ł���M�ł̃z�����W�[�ނ�0�ł�����̂��Ƃ�B
l�Ƃ��傤�Lj���L�_�������[�v��m�Ƃ����B
����i(i��0)��I�уz�����W�[�ނ�m+|i�ł��郋�[�vx��I�ԁB
x�̑я�ߖT�ɉ�����D^2�~I�̑��ʁ�D^2�~I��\��t�������̂�N�Ƃ����B
��N��S^2�Ȃ̂ł�����S^3��\��t�������̂�X�Ƃ����B
X�̓z�����W�[3���ʂɂȂ�B
�ؖ���X�̊�{�Q��Van Kampen's theorem�Ōv�Z����B a^2+b^2=n
a^3+b^3=m
�̎�a��b�����߂Ȃ��� ���̖��ȒP�����ł��Ȃ�v�Z���肱����Aab
�� 4���������ƎO���������̘A���������ɂȂ�A�ŏI�I�ɓ������Ƃ��ĉ�����悤�Ȃ̂ł����A���܂������܂���ǂȂ������������肢���܂� a=b=n=m
�������������������������̏��������� ���R����Y�����Ƃ���J�W����(A_{n,m})�ɑ��āA
��_n ��_m A_(n,m) �͊J�W���ƂȂ邩�H
��낵�����肢���܂��B
(�l�I�ɂ͏��ȑ������킹�ɂ���ĊJ�W���ɂȂ肻���ȋC��������ǂ�) �����܂���a,b,m,n�Ƃ��ɕ��f���ł� ���̃q���g�ɂ��Ȃ��ĂȂ��B4���Ƃ����������Ƃ��Ƀ[���ł͂Ȃ��A�Ƃ��̈Ӗ���? cl����p�f�A
(Un),(Vm)�͎��R��n,m��Y�����Ƃ���J�W���̗�
�Ƃ��鎞�A
��_n Un �_ ��_m cl(Vm)
��_m Vm �_ ��_n cl(Un)
�͓K�Șa�̎����ɂ���ē����ɊJ�W���Əo���܂����H �����܂���a,b,��m,n�̎��ŕ\������������v�ł��傤�� >>885
(1) a^2+b^2= (a+b)^2 - 2ab = n
(2) a^3+b^3 = (a+b)^3 - 3(a+b)ab = m
��� ab ������
(a+b)^3 - 3(a+b)((a+b)^2 - n)/2 = m
�� (a+b)^3 - 3n(a+b) + 2m = 0
����� (a+b)�ɂ��Ă̂R���������Ƃ��ĉ���, (1) ���� ab �̒l��.
��� �Q�������� x^2 - (a+b)x + ab = 0 �������� (a, b) �����܂�. >>885
�퓅�I�ȕ��@�ŁA�Ώ̎��@x=a+b�Ay=ab �Ƃ�����x�Ay �̘A�����������A���ꂩ��2���������������A���ȁH
��̓I�ɂ�
a^2+b^2=n ����@x^2-2y=n
a^3+b^3=m ����@x(n-y)=m�@
����2������ y �������� x ��3�������� x^3-3nx+2m=0 ��������̂ŁA����������悢�B �����~���Y�������Ǝ��ʃM���b�v�����Ăǂ�����ĉ����Ηǂ��́H Wolfram�ɓ��ꂽ�������������ł��Ȃ�����
Solve[{a^2+b^2==n,a^3+b^3==m},{a,b}] >>894 >>895
(a+b)^3 -3n(a+b) +2m = 0,
�̍���
a+b = 2(��n)cos��,
������ cos(3��) = -m/{n^(3/2)}
(*) �{��ł́@n^3 - mm = (3aa-2ab+3bb)(ab)^2 > 0, > a+b = 2(��n)cos��,
> ������ cos(3��) = -m/{n^(3/2)}
>
a b�͕��f���炵�����ǂˁB
�܂�������cos�Ƃ̒l��ɂ��Ă܂��܂��C�ɂ���K�v�Ȃ����ǁB >>898
https://i.imgur.com/VUu8EPe.jpg
�����ɏo�Ă���
Root[f, i] �͕�����f��i���̍��Af(x)=0��i�Ԃ߂̉����Ӗ����Ă���B
�ŁA& �͖����̊������L���� #1 ���Ă̂͊���1�Ԃ߂̈���
(���̕����́u#�v��#����Ȃ�����#�݂����ȋL���̈�)
�܂� Root[2#1^6-3#1^4n-2#1^3m+3#1^2n^2+m^2-n^3 &,1] ��
������ 2x^6 -3x^4n-2x^3m+3x^2n^2+m^2-n^3=0 ��1�Ԃ߂̉� ����������Ȃ��u���vf�̍��A���B >>901
������肪�Ƃ��������܂����B >>894 >>895
mm-n^3��0 �̂Ƃ���
x^3 -3nx +2m = 0,
�̍���
a+b = - [m +��(mm-n^3)]^{1/3} - [m - ��(mm-n^3)]^{1/3}, ���݂܂���B�����ɂ͐��w�̖��Ȃ̂�������Ȃ���ł����A�����Ă���������ƍK���ł��B
���镨����P�Ɋւ���p1,p2,p3,�E�E�E���^����ꂽ���Ap1��p2,p3,�E�E�E���������邱�Ƃ��l����B
�P����p1�ŏ��������̂��Ǝv���܂������Ap1��p2,p3,�E�E�E�ł�p1�����������قȂ��Ă���Ƃ��܂��B
���̏ꍇ�A�����������Đ��̐��ŕ\�������ꍇ�͂ǂ�����悢�̂ł��傤���H
����������Ő\����Ȃ��ł��B���w�Ȃ̂����������ł����A�ǂȂ��������Ă����������������܂�����ǂ�����낵�����肢���܂��B ���̂��ꂪ���w���Ǝv���̂��s�v�c�łȂ�A�P���ɐ�Βl�Ƃ����炠����́H �m�ň�x�����S�����Ă��ꂽ�搶��
�A�����Ăǂ��������ƁH�Ƃ����Ă����̂łȂ����Ă��鎖�Ɠ�������
����͂���H�H�̎����ƌ����Ă����̂ł���
���ƌ����Ă������v���o���Ȃ��̂ł������������������t�͂���܂����H
�A���͋߂Â��Ă����邱�Ƃ��ƌ����Ă��܂��� �_O�𒆐S�Ƃ��锼�a1�̉~��ɁA��_A,B������BAB�͂��̉~�̒��a�ł���B
���̉~����𑊈قȂ�2�̓_P,Q���APQ=1�ƂȂ�悤�ɓ����B
�i1�jPQ��AB�̂Ƃ��APA�̒��������߂Ȃ����B������PA��PB�Ƃ��܂��B
�i2�jA,P,B,Q�����̏��Ɍ���ŏo����}�`���ʎl�p�`�ł���Ƃ��A���̖ʐς̍ő�l�����߂Ȃ����B�ʎl�p�`�Ƃ́A�ւ���ł��Ȃ��l�p�`���w���܂��B ��sinx cosx dx�@���ϕ��ŋ��߂悤�Ƃ��Ă킯�킩��Ȃ��Ȃ��Ă��܂��܂���
�ǂ������������ł����H
https://i.imgur.com/r0tQ20D.jpg (1) |PA| = 2 sin(��/12) = 2 ��{ (1 - cos(��/6))/2 } = ��{ ( 4 - 2��3 )/2 } = (��3 - 1) / ��2
(2) A�͉~��AQ��ɂ���. ��ABP = ��AOP / 2 , ��ABQ = ��AOQ / 2 , ��AOP + ��AOQ = ��/3
�ʐ�[APBQ] = (1/2)*2cos(��ABP)*2sin(��ABP) + (1/2)*2cos(��ABQ)*2sin(��ABQ)
= sin(��AOP) + sin(��/3 - ��AOP) = 2 sin(��/6) cos( ��AOP - ��/6 ) = cos( ��AOP - ��/6 )
(1)�Ɠ����z�u ��AOP=��/6 �ɂ� �ő�l 1 �ƂȂ�
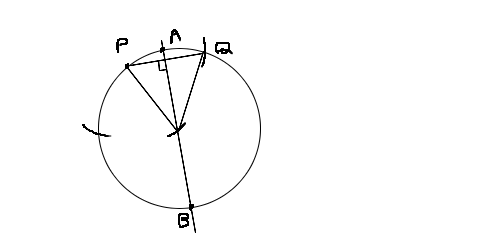 x A�͉~��AQ��ɂ���
x A�͉~��AQ��ɂ���
o A�͉~��PQ��ɂ��� >911
�s��ϕ����Ƃ�����萔(�Ⴆ�� C) ��lj������ق��������ł��傤�B
�� sin(x)cos(x) dx = -cos(x)^2 /2 + C
�� sin(x)cos(x) dx = sin(x)^2 /2 + C�f
�ǂ���ł��悢�̂ł��Bsin(x)^2 = - cos(x)^2 + 1 �ł��̂ŁA�萔�̍��� 1 �����Y���Ă��邾���ł��ˁB
��ϕ��Ȃ炻�̍��͌��ʂɉe�����܂���B >>914
���[�[�Ȃ�قǁI���肪�Ƃ��������܂��� ��fdx=S�Ƃ����Ă��܂��������ǁAS�ɂ͐ϕ��萔���̕s�萫���c���Ă���
S����ӂɒ�܂�Ȃ����炱�������u�����͂�����_�����Ă��ƂȂ̂ˁB
����� 0=1 �̏ؖ������ꂽ��ԈႢ�ӏ����������̂ɋ�J�������B log���܂ފ���C�ɂ���Ď��̌`���S�R����Č�����̂őO�ɂ��ڂɂ�������ł���
���S�ɖY��Ă܂������|���R�c�ł��ˁc�c log�̎��Ƃ͑S�R�Ⴄ���ƁB
��sinxcosx dx = S(x) �Ƃ�����
S(x) = -cosx cosx - ��(-cosx)(-sinx)dx
= -(cosx)^2 - S(x)
�����
2S(x) = -(cosx)^2�@�@�c(1)
�܂�
S(x) = sinx sinx - ��(sinx)(cosx)dx
= (sin x)^2 - S(x)
�����
2S(x) = (sinx)^2�@�@�c(2)
(2)-(1)���
0 = (sinx)^2 + (cosx)^2 = 1
�����
0=1 ���ؖ����ꂽ�B
���āA�ǂ����Ԉ���Ă���̂ł��傤���B >>918
log�����̌`�ɂ���Ă͌��n���̕\�������\������܂���ˁB�����b���Ǝv���܂��B ����ς�{�i�I�ɐ��w����������Ȃ�A�v�����X�g����w���P���u���b�W��w�̃g���j�e�B�E�J���b�W�ɓ���ׂ��Ȃ�ł����ˁE�E�E�H �I�b�N�X�u���b�W�̂������悳�ُ͈�B ������Ԃ̎����������ł�����`��Ԃ̎����������ɂȂ邱�Ƃ̏ؖ��ƁC���Q�̒�`�̂����������݂̂����Ȃ��悤�ȗ�(�̑���)��������܂���B >������Ԃ̎����������ł�����`��Ԃ̎����������ɂȂ邱�Ƃ̏ؖ�
��������������� S �� X ��, ���`��� X �͗L������ (n����) �Ɖ��肵�܂�.
X�̊��� {e_1, e_2, ..., e_n} �ƒu���܂�.
S�̊��W������ n + 1 �I������ { g_1, ...., g_[n+1] }
���ꂼ���X���œW�J���܂�. g_j = ��[i=1,n] a[i , j ] e_i
g_j [k=1...n+1] ���ꎟ�Ɨ��Ȃ̂ŁA�u�W���s�� a[i , j] �̗�͈ꎟ�Ɨ��v�ł�.
������ a[i,j] �� (n,n+1)�^�̍s��Ȃ̂ŁA����͕s�\�ł��B(�� �Ⴆ����{�ό`�ɂ��|���o���@)
�������������̂ŁAX�̎����͖����ł�. >>909
���肪�Ƃ��������܂�
�A���Œ��ׂĂ݂��̂ł����W���Ŏg�����t�Ȃ̂�������ł���
���Z�̔����Ƃ��ϕ��ŘA�����ďd�v�ł����H >>925
�A������Ȃ��ƒ��Ԓl�̒藝���g���Ȃ����Ǎ��Z���w�ł�(����)��ԏ�̊������l���ĂȂ�����m��Ȃ��Ă����Ȃ��Ǝv���܂� �ǂ����ā@a/b ∻ c/d ���@ad/bc �Ȃ́@�����ā` ��ōl���܂��傤
a/b:c/d=ad/bc:1�ł���
a/b �� c/d��1�����肢���ł�����A���c/d��1�ɂ������̂����Е��������ł��� �y�V�������l�_ ( The Theory of Value )�z�@
�@���i�̉��l�́A���̏��i�Y����ׂɏ����� energy ( �P�ʂ� erg )
�����A�M�� ( �P�ʂ� cal.) �ɂ���Č��肳���B
�@�l�F�` ���A���������L���鏤�i�������A�l�F�a �����L���鏤�i���̕���
���l�������Ɗ����A����A�l�F�a �͎��������L���鏤�i�������A�l�F�` ��
���L���鏤�i���̂ق������l�������Ɗ����鎞�A�������N����B
�@
���Ƃ��Ƃ������l�ł���� �`�C�a �̑o�����������Ȃ�A�����ȂNjN���Ȃ��B
�̂ɁAKarl H. Marx ( 1818 – 1883, 65 ↟ ) �����������ƌ����Ă���A
�J�����l���͊��S�Ȃ��T�Ȃ�B�� �����ƕ�����₷�����˂������܂��B >>929
�����Ƃ킩��₷�����R�͂���܂��H �S�̂ƕ����͎��͓������̂ł��傤���H ���a1�̉~C�̖ʐ�S���A�ȉ��̎菇(a)(b)�ɂ��3��������B���̂Ƃ��A���L�̐���PQ�̒����������_�ȉ���2�ʂ��l�̌ܓ����ċ��߂�B
(a)C�̌�AB���Ƃ�A��AB�Ɨ��AB�ň͂܂�镔���̖ʐς�S/3�ƂȂ�悤�ɂ���B
(b)AB��1:2�ɓ�������_P���Ƃ�B�D��AB��ɓ_Q���Ƃ�A��AB�ƗD��AB�ň͂܂�镔���̖ʐς�PQ��2��������B >>933
���Z�Ɗ|�Z���݂��ɑ����̋t���Z�ɂȂ��Ă���ƍl���Ă݂���ǂ����ȁB
0�́A�ЂƂ܂��l���ɓ���Ȃ��ŁB >>935
0�����čl������ǂ��Ȃ�܂����H ������������Z���ǂ��������̂��l���Ă��玿�₵�Ă�������
�܂�x=1/b�Ƃ́ub���|�����1�ɂȂ鐔�v�̂��Ƃł�
�܂�bx=1�ƂȂ鐔x�̂��Ƃł���
���R0�ɉ����|���Ă�1�ɂ͂Ȃ�Ȃ��̂ł��̏ꍇ�͕��ʍl���܂���(�����炱�̒i�K��0�����čl����Ƃǂ��Ȃ邩�A�Ƃ����̂̓i���Z���X�ł�)
�ŁAa/b�́ua�|����1/b�v�ł�
���āA(a/b)/(c/d)�́ua/b�|����1/(c/d)�v�ł�
c/d�ɉ����|������1�ɂȂ邩�H�������d/c�ł����
�܂�1/(c/d)=d/c�ł�
�����a/b���|�����(a/b)/(c/d)=(ad)/(bc)�ƂȂ�܂� �ӂƋ^��Ɏv��������ł��B
5�ׂ̂�����ĉ��̕��̈ʂ��ē��������̕��т��悭�o���Ȃ��Ǝv���Č��Ă���
5^(2^n)��5^(2^(n-1)) (mod 10^n)
�����藧�������ȋC�����Ă�����ł����A���藧���܂����H�ؖ��ł��Ȃ��ă����������Ă܂��I >>940
5^(2^n) - 5^(2^(n-1)) = ( 5^(2^(n-1) )*( 5^(2^(n-1) - 1 )
�E�ӑ�1�搔�ɂ� 5�̈��q�� n �ȏ�܂܂��. (�� 2^(n-1) �� n ������ n=1,2 �̎��̂�)
�E�ӑ�2�搔�ɂ�...
5^(2^(n-1) - 1 = (5^(2^(n-2) - 1) ( 5^(2^(n-2) + 1 )
= (5^(2^(n-3) - 1) (5^(2^(n-3) + 1)( 5^(2^(n-2) + 1 ) = ...
= (5^(2^0) - 1)(5^(2^0) + 1) (5^(2^1) + 1)....( 5^(2^(n-2) + 1 )
= 4 (5^(2^0) + 1) (5^(2^1) + 1)....( 5^(2^(n-2) + 1 )
2�̈��q�� n+1 �܂܂��. (�� �e����mod 4 )
�����
5^(2^n) - 5^(2^(n-1)) �� 0 (mod 10^n) (n=1,2,3, ... )
5^(2^n) - 5^(2^(n-1)) �� 0 (mod 10^(n+1)) (n=3,4,5,...) >>941
�����I���肪�Ƃ��������܂��I
2�̈��q�̊���o�����Ɋ������܂����I >>934
�ǂȂ������̖������肢���܂�
�ϕ����悤�ɂ��ł��܂���ł��� X : ���炩�ȑ��l��
A : X��̊��炩�Ȋ��S�̂̂Ȃ���
M : X��̃x�N�g����
T_x : x��X�ł̐ڋ��
R : �����S�̂̂Ȃ����@�Q��a��R, f��A�ɑ�fa=f(x)a�Ƃ�A���Q�Ƃ݂�
�Ƃ���Ƃ��A
A���Q�Ƃ���T_x��M�e���\��R�����^�ɂȂ邱�Ƃ̃C���[�W�������ĉ����� >>936
���w�Z�ȗ��̏������߂�M�Z�̎葱�������Z���Ǝv���Ă���ۂ� >>944
https://i.imgur.com/XAszsNu.png
�I�����W�̈�̖ʐς��������Ȃ�悤�ɂ���悢.
�� - sin��*cos�� = ��/3
PQ*cos�� = cos�� + cos��
PQ*sin�� = (1/3)*sin�� + sin��
RO = cos�� - sin��*cot�� = cos�� - sin�� *(cos�� + cos��) / ((1/3)*sin�� + sin��)
�� - RO*sin�� = (RO + cos��) * sin�� *(1/3)
�Y��Ȍ`�ɂ͂Ȃ�Ȃ��̂Ńv���O�����g��, �K����solver�g�����Ė��ȋC������.
PQ = 1.36907... ��. >>944
��0�`x ��(1-(��-1)^2) d�� = ��/3
�ϕ����邱�Ƃ͍���ł͂Ȃ����A��������Ăł���
x-1=cos(��/3+(x-1)��(1-(x-1)^2))
�̂悤�ȕ���������ʼn����̂͂�����Ƃ�肽���Ȃ� ����2
�s��
(2)���킩��܂��肢���܂��B
https://i.imgur.com/8cBJDmR.jpg >>950
�y�[�W���܂����������ߕҏW�����猩�ɂ����Ȃ��Ă��܂��܂����c���߂�Ȃ��� �����������Z���w�ŌŗL�l�A�ŗL�x�N�g���͂�����͂������Ǎs�͏o�Ă��ĂȂ����
���Z�̂Ƃ��͂ǂ��v�Z���Ă������c�c >>952
A-rE���t�s��������Ȃ�������Ă���Ă��͂���
�s�̌��t�͏K��Ȃ��Ă��A�t�s��������Ȃ������Ƃ���|ad-bc|=0�͏K���Ă�͂�����
�����̓����ł����������߂���͏o�肳��Ă��݂�����
�������g�́A�\���Z�Ƃ������m�� tr �Ƃ� det �Ƃ��K���čs�̐����������K�����L��������B >>945
�uA���Q�v�̒�`��������ĂȂ����H f�͒P��������f(x)�����ł���Af(x)<x�Ƃ���
���̂Ƃ��A�C�ӂ�y�ɂ���f(x-y)/f(x)��1�ƂȂ邾�낤���ix�����j >>933
W.�n�C�[���x���O�u�����ƑS�́v�`���̐��U�̈̑�ȏo��ƑΘb�`
�@424p�D4860�~�@�@�R��a�v�F��@�@�݂������[�i1999/Nov)
�@http://www.msz.co.jp/book/detail/04971.html
�E�J�X�^�}�[�������[
���̏o�ŎЂ̉��i�ł́A�Ⴂ�l�ɓǂ�ł��炦�邾�낤���B
���Ƃ��A���ɖ{�Ƃ��āA�߂Â��₷�����i�Ŕ��s����邱�Ƃ���]����B�@(2006/07/04) ��ɉ�����18km�͂ȂꂽA�AB�Q�̒�������BB�����o������A���܂ŏオ��̂ɂP���Ԕ����������B�D������Ƃ��ɂ́A�����̑������オ��Ƃ���2�{�ɂȂ����̂ŁA45���ʼn��邱�Ƃ��ł����B���̑D�̐Ð��ł̑��������߂Ȃ����B
��������16km�ł����A�Ȃ�ł����Ȃ邩�킩��Ȃ��ł��B��낵�����肢���܂� ���Ɖ���̑��x�����ꂼ�ꋁ�߂Ă��̍������߂�
���̍��͏�����Ƃ��̐����̑����Ɖ������Ƃ��̐����̑����𑫂�������
�����̑����͉������Ƃ��͏�����Ƃ���2�{�Ƃ������ƂȂ̂Łi�ȉ��� >>958
�����܂���A�����ł��܂ւ�B
�������Ԉ���Ă�̂��ȁH�ߒ�����낵�����˂������܂� >>954
���݂܂���
�ǂ��������Ƃł��傤�� >>957
x:�D�̑��x
r:��̗���
(x-r)*1.5=18
(x+2r)*45/60=18 >>961
�������������̂��ʓ|�������̂�Wolfram�Ɍv�Z���Ă��炢�܂����B
https://www.wolframalpha.com/input/?i=solve+(x-y)*1.5%3D18,+(x%2B2*y)*45%2F60%3D18+for+x,y
�D�̑��x16km/h
��̗���4km/h >>961-962
���肪�Ƃ��������܂��B������܂��� a,b,c,d,e,f�͈ꌅ�̐����ŁA�ȉ��̊W�������B
c=2a,d=2b,10e+f=2(10c+d)+1
�z����p�ŁAp=0.abcdefabcdef...�ƕ\������̂�S�ċ��߂�B >>963
����������Ȃ��ʼn����Ȃ�
���̑��x18/1.5��12
����̑��x18/(45/60)=24
����͏��Ő�̗����������A����Ő�̗����̂Q�{�̉���������
�����̂R�{�������Ă���B
�̂ɐ�̗�����(24-12)/(1+2)=4
�D�̐Ð����x��12+4��������24-4*2��16�Əo����B >>955 �����������
�P���������� a[n] (n=1,2,...) �����̑Q�����Œ�`����.
a[1] := 1
a[2k] := a[2k-1] exp(10) - 10
a[2k+1] := a[2k] + 10 (k = 1,2,3,...)
a[n] ��p���� �P�������� f ���ȉ��̂悤�ɒ�`����.
f(x��(-��,a[2])) := min(1, x)
f(x��[a[2k], a[2k+1])) :=a[2k-1]* exp(x - a[2k])
f(x��[a[2k+1], a[2k+2])) := a[2k+1] (k=1,2,...)
�����`���[�W��Ԃ� ����10��exp�_�b�V����Ԃ����݂Ɍ����悤�ɍ����(�A��)���ł�.
f(x) �� x �Ȃ͖̂��炩. ( f(x) < x �ɂ�������� 0.9 f(x) �ōĒ�`)
�Ⴆ��
a[2k-1]+1 < x �� a[2k] �̎�, f(x-1) / f(x) = 1 �ł���.
a[2k]+1 < x �� a[2k]+10 �̎�, f(x-1) / f(x) = exp(-1). �ł���.
x �͂�����ł��傫������̂� f(x- 1) / f(x) �� �������Ȃ�. >>967
(1)�ŗL�l�ƌŗL�x�N�g��
�킴�킴�ŗL�����������Ă��������ǁA���x�N�g�������`�ʑ��łǂ���������������킩��
��1 = +1, ��2 = 0, ��3 = -1
v1 = +cos(��/2) e_x + sin(��/2) e_z
v2 = e_y
v3 = -sin(��/2)e_x + cos(��/2) e_z
(2) v^t S v ��V���Ȓ������ v1 , v2, v3 ��p���ď�������
v = x e_x + y e_y + z e_z = X v1 + Y v2 + Z v3 �ƒu����
v^t S v = v^t ( 1* X v1 + 0* Y v2 + (-1)*Z v3 ) = X^2 - Z^2 = c
���̊�ꂩ��̉�]���l�������, ����͑o�Ȗ�(x^2 - z^2 = c) ���p�x ��/2 ������]�������}�`�ł���
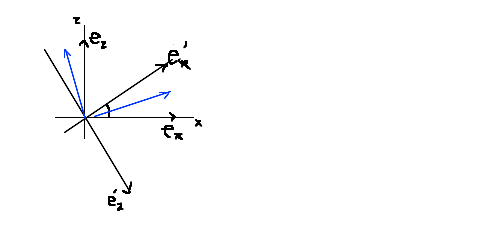 >>966
>>966
�T���K�c�A�������������Ȃ��ƃ_�������ł��� >>964
Prelude> [(a,b,c,d,e,f)|a<-[0..9],b<-[0..9],c<-[0..9],d<-[0..9],e<-[0..9],f<-[0..9],c==2*a,d==2*b,10*e+f==2*(10*c+d)+1]
[(0,0,0,0,0,1),(0,1,0,2,0,5),(0,2,0,4,0,9),(0,3,0,6,1,3),(0,4,0,8,1,7),(1,0,2,0,4,1),(1,1,2,2,4,5),(1,2,2,4,4,9),(1,3,2,6,5,3),(1,4,2,8,5,7),(2,0,4,0,8,1),(2,1,4,2,8,5),(2,2,4,4,8,9),(2,3,4,6,9,3),(2,4,4,8,9,7)] >>805
���@^2+�C�ł�P1st�͋��߂���
((n(n+1)/2)-1)^2+�o4(n-1)^3+6(n-1)^2-4(n-1)-3+3(-1)^(n-1)�p/48�@
�v�Z�m�\�Ň@^2+�C����͂����
P1st =�o12n^4+28n^3-42n^2-52n-3(-1)^n+51�p/48 Zorn�̕��̏ؖ��ł�
http://d.hatena.ne.jp/yoshitake-h/20111210
�@�@L^���ӂƂ����L��{f(L^)}�������ɂȂ�
�̏ؖ���������܂���
��낵�����肢���܂� �A�z�Ȍl�u���O�Ȃŕ����悤�Ƃ���Ȃ� �X�X�X�X�s���s���]�Ɓ��͂ǂ��炪�傫���ł����H >>950 >>967
(2)
�@(����) = cos�ƥ(xx-zz) �{ 2sin�ƥxz
�@= sin(2��)(xx-zz) �{ 2cos(2��)�xz�@�@�@�@(2�� = ��/2-��)
�@= 2sin�ӥcos��(xx-zz) + 2{(cos��)^2 - (sin��)^2}xz
�@= 2(cos�ӥx - sin�ӥz)(cos�ӥz + sin�ӥx)
= 2 X�Z,
���@���p�o�Ȑ��� (?) >>940 >>941
p����f���Ƃ����
�@p^{2^n} - p^{2^{n-1}} = p^{2^{n-1}} * (p^{2^{n-1}} -1),
�@p^{2^{n-1}} -1 = (p-1)(p+1)(p^2 +1)(p^4 +1)�c�c(p^{2^{n-2}} +1),
�Ƃ���ŁAp^2 �� 1�@(mod 8) �䂦
�@p^2 +1, p^4 +1, �c�c, p^{2^{n-2}} +1 �ɂ� 2�̈��q��1�Â܂܂��B
�@(p-1)(p+1)��2�̈��q��m�܂܂��Ƃ���ƁA m��3 �䂦
�@�S�̂ł� (n-2)+m �ƂȂ�B ���f���ʂ̓_0�Ɠ_1�a�̗��[�Ƃ���~��C�Ƃ���B
C���2�_A(��)�AB(��)���Ɨ��ɓ����BC��̒�_P(��)�̐ڐ���l�Ƃ���Ƃ��A2����/(��+��)��l��ɂ��邽�߂̏��������A���A���ŕ\���B >>980
��= 1/2 + 1/2 * e^{i��} �Ƃ����
L(t) = �� + t e^{i��+ i��/2} = �� + it (2�� - 1) �@(t �͎����p�����[�^)
2����/(��+��) = L(t) = �� + it (2�� - 1)
(2����/(��+��) - ��)/(2�� - 1) = i t
���@Re{ (2����/(��+��) - ��)/(2�� - 1) } = 0
( 2����/(��+��) ����ꂽ�Ӑ}���킩��Ȃ�...�����ƃX�b�L�������`�ɂȂ�̂��낤��) >>981
����= 1/2 + 1/2 * e^{i��} �Ƃ����
���ꌋ�ǎg���ĂȂ���
�����ǃ�,��,������Ԃ��̌`���ɕϊ����Ă݂Ă͂ǂ��� >>982
�ue^{i��} �ɒ������� e^{i��+ i��/2} ���ڐ��̕����x�N�g����^����v
�Ƃ������������������B
�����Ȃ� L(t) = �� + it (2�� - 1) �Ƃ������Ă��A�́H���ĂȂ肻�������B ������ ��, ��, �� �ŕ\����
Re{ (2����/(��+��) - ��)/(2�� - 1) } = 0
|2�� - 1| = |2�� - 1| = |2�� - 1| = 2
��Ԗڂ̎���Y���Ƃ��������B ����ŕK�v�\�������ƂȂ�.
����ȏ�V���v���ɂȂ�̂��m���. >>983
�������܂���
�~�̒��S���ʂƂ��āA�ړ_���ɂ�����ڐ��� {��+i��(��-��)|��:����} �Ƃ���̂͂ނ���������Ǝv���Ă��܂������A���̗��R���@�艺���Ă����̂ł��� >>984
2����/(��+��) �́A(��+��=0 �̏ꍇ������)�˂Ɍ��̉~�̏�ɂ���
����ăV���v���ɏ����� 2����/(��+��) = �� A�AB�Ԃ�30m�̋����������Ĉ��ɓd���������Ă���BA���琔����72�Ԗڂ̓d����B���琔����85�ԖڂɂȂ�B���̂Ƃ��AB���琔����70�Ԗڂ̓d����A���牽m�̂Ƃ���ɂ��邩�H
����2580m�Ȃ�ł����A���̈Ӗ��������ł��܂���B�ߒ�����낵�����˂������܂��B >>986
> 2����/(��+��) �́A(��+��=0 �̏ꍇ������)�˂Ɍ��̉~�̏�ɂ���
����ǂ�����Ď����̂�������������ƕ�������.
�~���]�̐�����m���Ă���Ώu�E��.
q := 2����/(��+��) �̋t��( �P�ʉ~�Ɋւ��锽�] & ���f�����ʑ� ) ���Ƃ�ƁA1/q = 1/2* (1/�� + 1/��) .
���̓_�� ����: Re(z)=1 ��ɂ���. �����Ē���: Re(z)=1 ��̓_�̋t�����Ƃ�Ό��̉~����Ɉڂ�.
�܂� q (= 1/(1/q) ) �͌��̉~����ɂ���.
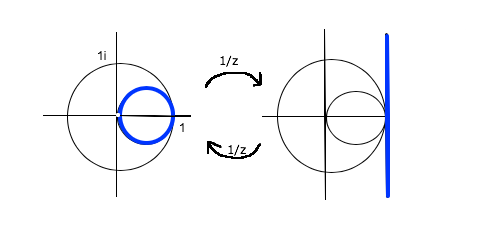 ���ƍ���͂��܂��s���܂���
���ƍ���͂��܂��s���܂���
���f���Ő}�`��\����肾����ǁA�v�Z�݂̂ʼn����̂�����A������̍��������Ă��������B >>987
�ߒ������Ȃɂ��}���ł����玩�����瓚���Ăł�B
A 1 �@�@2 �@3 �@4 �@5 �@6 �@7 �@8 �@9�@...,71,72,73,..,86,87,88,...,155,156
156 155 154 153 152 151 150 149 148 ...,86,85,84,..,71,70,69,..., 2, 1 B
�d���̐��F72+85-1=156
(87-1)*30=2580 >>990
�������������@(72+85-70-1)*30
������Ō��Â炢����摜�ɂ��Ă݂��B
http://i.imgur.com/2kMUaUs.png >>991
���肪�Ƃ��������܂��B������܂��� >>875
���U����
�S�����U�ƌQ�ԕ��U�̔��F���z�Ō��肷��B
���̔��F-ratio�ƌĂԂƂ���炵���� ����ӂ�@grafi_tt
�ӎU�L�����ǂ���_���ł� https://ieeexplore.ieee.org/document/8350369 �c
Learning From Pseudo-Randomness With an Artificial Neural Network?Does God Play Pseudo-Dice?
- IEEE Journals & Magazine �j���[�����l�b�g�� �� �� e�Ƃ��������w�萔�Ƃ� Mersenne Twister �̎��̌���\��������Ɠ��v�I�ɗD�ʂɓ������Ă�
3:08 - 2018�N11��25�� �T�C�R����U���āA�e�X�g���Ăق��������ł��ˁB
�e�T�C�R���̌��f���āA������m���� 1/6 ��荂���Ȃ邩�ǂ����ł��B
�����Ɛ��\�̗ǂ��n�[�h�E�F�A����������ł��e�X�g���ė~���������ł��ˁB ���o�H�ˑ����iPath dependence�j
�u������ɂ����āA�l��g�D���Ƃ錈�f�́A
�i�ߋ��̏ƌ��݂̏͌��i�K�ł͑S�����W�ł������Ƃ��Ă��j
�ߋ��̂ɂ��̐l��g�D���I���������f�ɂ���Đ������v
�Ƃ������_�ł� ���̃X���b�h�͂P�O�O�O���܂����B
�V�����X���b�h�𗧂ĂĂ��������B
life time: 36�� 0���� 33�� 3�b 5�����˂�̉^�c�̓v���~�A������̊F���܂Ɏx�����Ă��܂��B
�^�c�ɂ����͂��肢�������܂��B
��������������������������������������
�s�v���~�A������̎�ȓ��T�t
�� 5�����˂��p�u���E�U����̍L������
�� 5�����˂�̉ߋ����O���擾
�� �������K���̊ɘa
��������������������������������������
����o�^�ɂ͌l���͈�ؕK�v����܂���B
��300�~���瓽���ł��w�����������܂��B
�� �v���~�A������o�^�͂����� ��
https://premium.5ch.net/
�� �Q�l���O�C���͂����� ��
https://login.5ch.net/login.php ���X����1000���Ă��܂��B����ȏ㏑�����݂͂ł��܂���B



